Решение матричных уравнений. Подробные примеры решений
Предварительно рекомендуется изучить основные действия над матрицами.Даны матричные уравнения
A·X = B, (1)
Y·A = B, (2)
Нельзя ли определить деление матриц?
Вспомним, что в числовой области частное от деления b на a определяется как решение уравнения a∙x=b (или x∙a=b) и существует не всегда. Можно попытаться определить «деление» матриц, рассматривая уравнения (1) и (2), в которых, согласно правилу умножения, матрицы A, B, X, Y не могут иметь произвольную структуру. Так, в первом уравнении матрицы A и B должны иметь одинаковое число строк, а во втором – одинаковое число столбцов. Уже отсюда ясно, что если даже оба эти уравнения однозначно разрешимы (а это далеко не всегда так), то их решения вполне могут быть матрицами не только разными, но и разной структуры.

Матричные уравнения вида (1) и (2) решаются следующим образом. Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим слева обе части уравнения (1) на A-1: A-1·A·X = A-1·B, тогда получим E·X = A-1·B, или
X = A-1·B. (3)
Аналогично, умножая справа обе части равенства (2) на A-1, будем иметь: Y·A· A-1 = B· A-1, откуда находим, чтоY = B· A-1. (4)
Пример 1. Решить матричное уравнение .
Решение.
Пример 2. Решить матричное уравнение .

Решение. (в силу пропорциональности строк), т.е. матрица A – вырожденная, следовательно уравнение решения не имеет.
Пример 3. Решить уравнение .
Решение. Данное уравнение записываем в виде A∙X∙B = C. Умножаем обе части этого равенства слева на A
Находим обратные матрицы , , тогда
.
Проверка.
Перейти к онлайн решению своей задачи
Пример 6
Вариантов записей матричных уравнений может быть достаточно много, однако, все их можно свести к двум видам:- A·X = B
- Y·A = B
 Требуется найти матрицы X и Y.
Данные матричные уравнения решаются с помощью онлайн-калькулятора. Далее покажем на примерах, как можно свести все варианты записи матричных выражений к двум классическим.
Требуется найти матрицы X и Y.
Данные матричные уравнения решаются с помощью онлайн-калькулятора. Далее покажем на примерах, как можно свести все варианты записи матричных выражений к двум классическим.
Перед изучением материала необходимо иметь представление об операциях над матрицами:
- умножение матриц (
A*B): соответствующие элементы матриц умножаем и складываем: ; - сложение матриц (
C+B): складываются соответствующие элементы матриц - разница (вычитание) матриц (
A-B): из каждого элемента матрицы A вычитается соответствующий элемент матрицы B ; - умножение матрицы на число (
2*C): число умножается на каждый элемент матрицы ;
Пример 1. Решить матричные уравнения и сделать проверку.
Запишем данное матричное уравнение в матричной форме:A·X - B = 3C.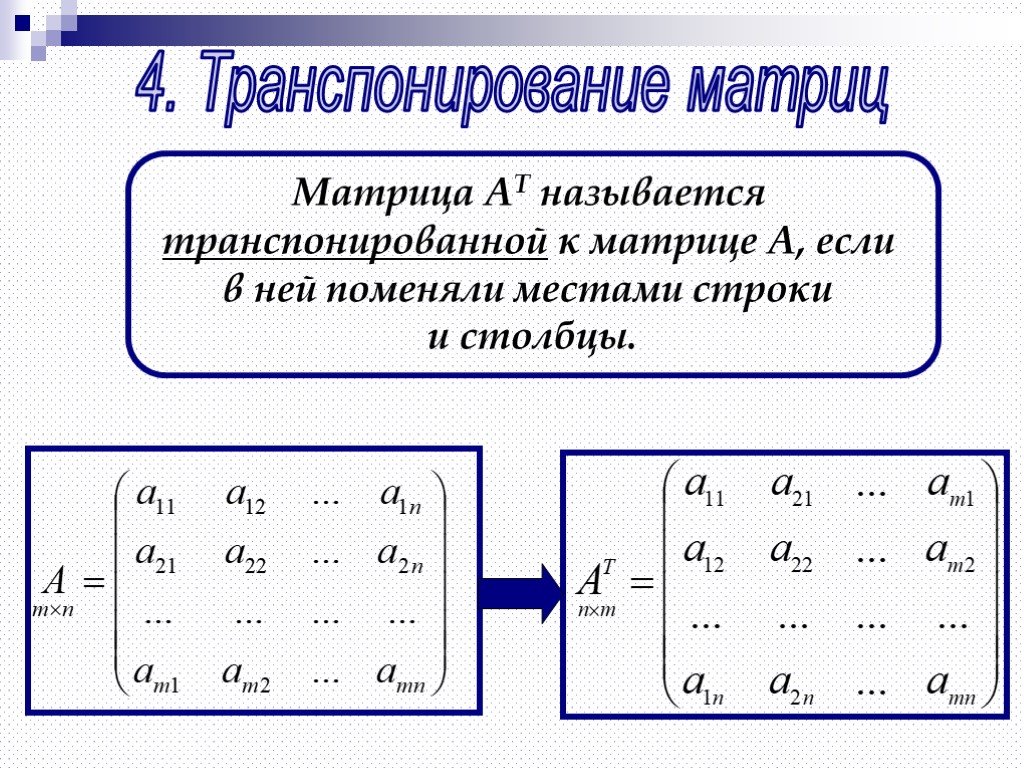 Его можно записать как
Его можно записать как A·X = 3C + B. Найдем сумму матриц:
| 3C + B = |
|
Обозначим:
| A = |
|
| B = |
|
Тогда матричное уравнение запишется в виде: A·X = B.
Вычислим определитель матрицы А:
∆ = 2*(4*4 – (-2)*(-2)) – 3*(1*4 – (-2)*1) + 3*(1*(-2) – 4*1) = -12
Определитель матрицы А равен detA=-12
 Умножим слева обе части уравнения на A-1: A-1·A·X = A-1·B, тогда получим E·X = A-1·B, или X = A-1·B.
Умножим слева обе части уравнения на A-1: A-1·A·X = A-1·B, тогда получим E·X = A-1·B, или X = A-1·B.Найдем обратную матрицу A-1.
Транспонированная матрица AT.
| AT = |
|
Алгебраические дополнения
| A1,1 = (-1)1+1 |
|
∆1,1 = (4*4 – (-2)*(-2)) = 12
| A1,2 = (-1)1+2 |
∆1,2 = -(1*4 – 1*(-2)) = -6
| A1,3 = (-1)1+3 |
∆1,3 = (1*(-2) – 1*4) = -6
| A2,1 = (-1)2+1 |
∆2,1 = -(3*4 – (-2)*3) = -18
| A2,2 = (-1) |
∆2,2 = (2*4 – 1*3) = 5
| A2,3 = (-1)2+3 |
∆2,3 = -(2*(-2) – 1*3) = 7
| A3,1 = (-1)3+1 |
| A3,2 = (-1)3+2 |
| A3,3 = (-1)3+3 |
Обратная матрица A-1.

| A-1 = 1/12 |
|
| X= 1/12 |
| · |
| = |
|
| X = |
|
Пример 2.
Данное выражение в матричной форме имеет вид:
X·A - B = 2C. Преобразуем к виду: X·A = 2C + B или X·A = D, где D = 2C + B
Пример 3.
Пример 4.
Здесь имеем следующий тип матричного уравнения:A - X·B = 2C. Сводим его к типу X·B = A + 2C или X·B = D, где D = A + 2C.
| A + 2C = |
Обозначим:
| A = |
|
Тогда матричное уравнение запишется в виде: Y·A = B.
Вычислим определитель матрицы А:
∆ = 3*(3*3 – 1*1) – 2*(2*3 – 1*2) + 1*(2*1 – 3*2) = 12
Определитель матрицы А равен detA=12
Так как A невырожденная матрица, то существует обратная матрица A-1.
 Умножим справа обе части уравнения на A-1: X·A·A-1 = B·A-1, откуда находим, что X = B·A-1
Умножим справа обе части уравнения на A-1: X·A·A-1 = B·A-1, откуда находим, что X = B·A-1Найдем обратную матрицу A-1.
Транспонированная матрица AT.
| AT = |
|
| A1,1 = (-1)1+1 |
| A1,2 = (-1)1+2 |
| A1,3 = (-1)1+3 |
| A2,1 = (-1)2+1 |
| A2,2 = (-1)2+2 |
| A2,3 = (-1)2+3 |
| A3,1 = (-1)3+1 |
| A3,2 = (-1)3+2 |
| A3,3 = (-1)3+3 |
Обратная матрица A-1.

| A-1 = 1/12 |
|
| X = | 1/12 |
| = |
|
| X = |
|
Пример 2.
Перейти к онлайн решению своей задачи
Пример №5. Решение матричных уравнений.
Обозначим:
| A = |
|
| C = |
|
Вычислим определитель матрицы А:
∆ = 3*(-2) – 5*(-1) = -1
Определитель матрицы А равен detA=-1
Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим слева обе части уравнения на A-1:Умножаем обе части этого равенства слева на A-1 и справа на B-1: A-1·A·X·B·B-1 = A-1·C·B-1. Так как A·A-1 = B·B-1 = E и E·X = X·E = X, то X = A-1·C·B-1
Найдем обратную матрицу A-1.

Транспонированная матрица AT.
| AT = |
|
A11 = (-1)1+1·-2 = -2; A12 = (-1)1+2·-1 = 1; A21 = (-1)2+1·5 = -5; A22 = (-1)2+2·3 = 3;
Обратная матрица A-1.
| A-1 = 1/-1 |
|
∆ = 5*8 – 7*6 = -2
Определитель матрицы B равен detB=-2
Найдем обратную матрицу B-1.
Транспонированная матрица BT.
Алгебраические дополнения:
A11 = (-1)1+1·8 = 8; A12 = (-1)1+2·6 = -6; A21 = (-1)2+1·7 = -7; A22 = (-1)2+2·5 = 5;
Обратная матрица B-1.

| B-1 = 1/-2 |
|
|
Матричные уравнения с примерами решения
Содержание:
- Примеры с решением
Обратной матрицей к квадратной матрице А называется такая матрица (обозначаетсячто ЛЗамечание. Если матрица существует, то она единственна.
Присоединенной матрицей к квадратной матрице называется матрица полученная транспонированием из матрицы, составленной из алгебраических дополнений к элементам Теорема 1. 3. Если квадратная матрица А — невырожденная (т. е. ), то (4.1)
3. Если квадратная матрица А — невырожденная (т. е. ), то (4.1)
Метод присоединенной матрицы вычисления обратной матрицы к невырожденной матрице А состоит в применении формулы (4.1). Метод элементарных преобразований (метод Гаусса) вычисления обратной матрицы к невырожденной матрице А состоит в следующем.
Приписывая справа к матрице А размера единичную матрицу размера получим прямоугольную матрицу размера С помощью элементарных преобразований над строками матрицы Г сначала приведем ее к ступенчатому виду где матрица — треугольная, а затем к виду Матричные уравнения простейшего вида с неизвестной матрицей записываются следующим образом (4.2) (4.3) (4,4)
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
В этих уравнениях — матрицы таких размеров, что все используемые операции умножения возможны, и с обеих сторон от знаков равенства находятся матрицы одинаковых размеров. Если в уравнениях (4.2), (4.3) матрица А невырожденная, то их решения записываются следующим образом: X Если в уравнении (4.4) матрицы А и С невырождены, то его решение записывается так:
Если в уравнениях (4.2), (4.3) матрица А невырожденная, то их решения записываются следующим образом: X Если в уравнении (4.4) матрицы А и С невырождены, то его решение записывается так:
В этих уравнениях А, В, С, X — матрицы таких размеров, что все используемые операции умножения возможны, и с обеих сторон от знаков равенства находятся матрицы одинаковых размеров. Если в уравнениях (4.2), (4.3) матрица А невырожденная, то их решения записываются следующим образом: Если в уравнении (4.4) матрицы А и С невырождены, то его решение записывается так:
Примеры с решением
Пример 1.
Найти (методом присоединенной матрицы) матрицу, обратную к данной:
Найдем det А:
Так как det , то матрица существует.
Возможно вам будут полезны данные страницы:
Объём тела вращения |
Разложение в ряд Тейлора |
Метод Гаусса: пример решения |
Метод Жордана Гаусса |
Найдем алгебраические дополнения ко всем элементам матрицы А:
Пример 2.

Запишем матрицу
Найдем матрицу
Сделаем проверку:
Пример 3.
Найти матрицу, обратную к матрице А
1) Найдем Матрица существует, только если
2) Найдем алгебраические дополнения к элементам матрицы А:
3) Запишем присоединенную матрицу:
Итак, для матрицы 2-го порядка присоединенная матрица находится очень просто — элементы главной диагонали меняются местами, а элементы побочной диагонали умножаются на (-1):
4) Найдем обратную матрицу 7.1. Типичные задачи Матричные уравнения естественно возникают в задачах, которые изначально выглядят, как «векторные».
Скажем, поиск собственных векторов объединяется одним уравнением (7.1) где — искомая матрица со столбцами в качестве собственных векторов. Другой характерный пример — линейное дифференциальное уравнение
Как известно, общее решение имеет вид где линейно независимые решения как вектор-столбцы, составляют матрицу фундаментальных решений удовлетворяющую матричному дифференциальному уравнению которое выгоднее рассматривать с самого начала вместо
Поиск преобразования X, обеспечивающего подобие матриц, порождает уравнение После умножения слева на X оно переходит в эквивалентное (7. 2) в предположении невырожденности X. Очевидно, (7.1) при заданной матрице Л представляет собой частный случай (7.2). Наконец, поиск функции Ляпуновадля линейной системы приводит к уравнению (7.3) относительно матрицы V.
2) в предположении невырожденности X. Очевидно, (7.1) при заданной матрице Л представляет собой частный случай (7.2). Наконец, поиск функции Ляпуновадля линейной системы приводит к уравнению (7.3) относительно матрицы V.
Обозначая неизвестную матрицу V через X и обобщая (7.3), приходим к уравнению (7.4) которое охватывает в качестве частных случаев все рассмотренные выше случаи, — разумеется, кроме дифференциального. Уравнение (7.4) линейно относительно элементов неизвестной матрицы X, и этим замечанием, казалось бы, можно закончить исследование, сославшись на предыдущее изучение линейных уравнений.
Но проблема заключается в том, что уравнение (7.4), как линейное, имеет нестандартную форму, опираясь на двухин-дексное описание переменных.
В принципе, нет никакой трудности в том, чтобы перенумеровать переменные вытянув их в строчку. Но при бесхитростной перенумерации содержательная информация о матрицах A, J9, С может разрушиться, что будет означать отсутствие смысловой связи между получаемыми линейными системами и исходными операторами действующими в Для решения таких задач имеется специальный инструмент — кронекерово произведение2) матриц, Если А и В — прямоугольные матрицы размера, соответственно, то
Размер
Свойства легко проверяются.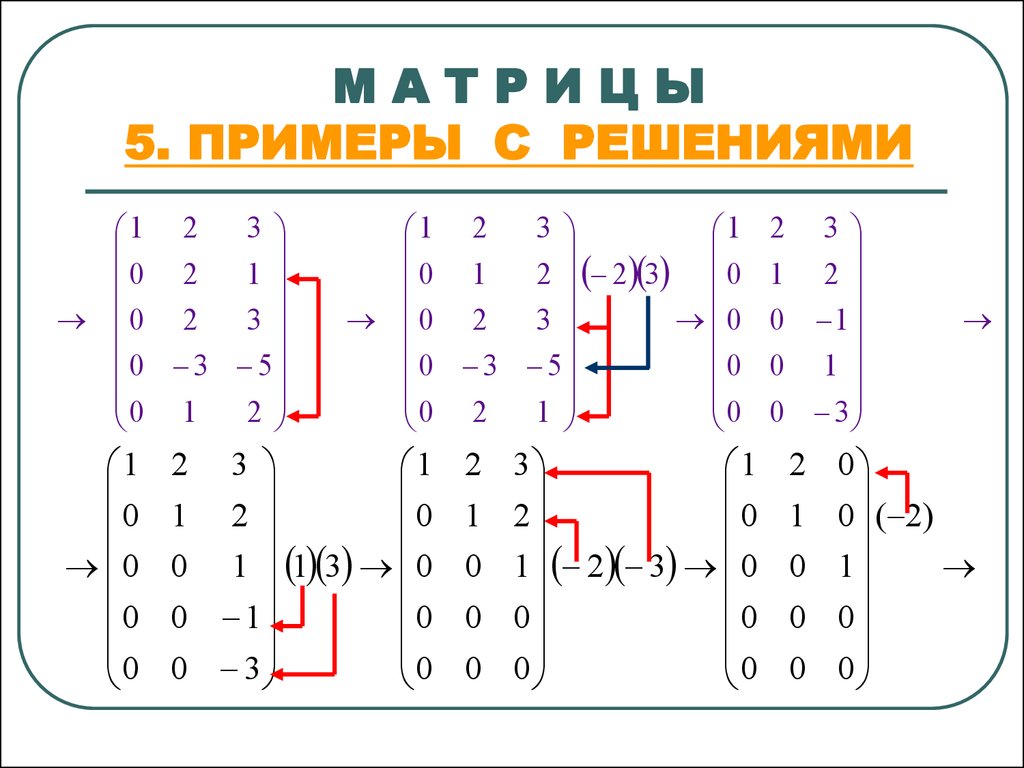
Важную роль играет формула (7.5) Легко проверяется Менее очевидно, что в случае невырожденности квадратных матриц А и В произведение тоже невырожденно) Если теперь допустить кратные собственные значения у А и В, то идея предельного перехода здесь работает без проблем. Собственные векторы в пределе могут становиться линейно зависимыми, но это в данном случае ничему не мешает.
Поэтому утверждение 7.2.1 справедливо без каких бы то ни было предположений о матрицах А и В. Сразу становится ясной отмечавшаяся выше невырожденность в случае невырожденности А и В.
Обычное соотношение может быть записано в виде где вектор это вытянутая в столбик матрица вектор из получен аналогично. Соотношение записывается иначе, Поэтому уравнение (7.4), с помощью кронекерова произведения можно переписать так { (7.7)
В этой перезаписи уравнения не было бы большого смысла, если бы она не позволяла делать выводы в терминах исходных матриц А и В.
Но специфика кронекерова произведения как раз такова, что она дает возможность судить о спектральных свойствах «®-матриц» во многих практических ситуациях. Причиной является следующий факт. Лемма. Если тo Результат сразу вытекает из (7.6),
Причиной является следующий факт. Лемма. Если тo Результат сразу вытекает из (7.6),
Лемма 7.3.1 означает, что матрицы А и В в могут быть приведены к желаемому виду (диагональному, треугольному, жордановому) независимо друг от друга.
Пусть, например. где — соответствующие жордановы формы. Тогда ясно, что спектры и что еше раз доказывает утверждение 7.2.1. Точно так же А и В могут быть приведены к своим жордановым формам) в (7.8) Отсюда ясно, что для невырожденности (7.8) необходимо и достаточно, чтобы не нашлось противоположных собственных значений, Это и является условием однозначной разрешимости уравнения (7.7), т.е. (7.4).
Как теоретический инструмент иногда полезна формула (7.9) дающая решение уравнения в случае, когда матрицы А и В гурвицевы, т.е. действительные части их собственных значений строго отрицательны. Устанавливается это совсем легко. Решением задачи Коши (7.10) является что проверяется подстановкой.
Из гурвицевости А и В следует экспоненциально быстрое убывание до нуля при Это позволяет проинтегрировать (7.
10) от 0 до оо, что сразу дает (7.9). В частности, решение уравнения в случае гурвицевой матрицы А приводит к положительно определенной функции Ляпунова Найти (методом элементарных преобразований) матрицу, обратную к данной:
Записывая матрицу размера (3 х 6), с помощью элементарных преобразований над строками приведем ее сначала к ступенчатому виду а затем к виду
Итак,
Сделаем проверку:
Матричное уравнение – объяснение и примеры У нас есть переменные в алгебраических уравнениях, а в матричных уравнениях мы имеем дело с матрицами, которые действуют как переменная.
Итак, что такое матричные уравнения?
Матричное уравнение — это уравнение, в котором целая матрица представляет собой переменную.
В этом уроке мы увидим матричное уравнение, как писать матричные уравнения и как решать матричные уравнения. Давайте начнем!
Что такое матричное уравнение?
Матричное уравнение — это уравнение, в котором матрица действует как переменная. Мы можем решать простые матричные уравнения, используя такие операции, как сложение матриц, вычитание матриц и скалярное умножение.
Мы можем решать простые матричные уравнения, используя такие операции, как сложение матриц, вычитание матриц и скалярное умножение.
Мы также рассмотрим очень простые матричные уравнения, в которых выполняется умножение матриц, и используется идея матрицы , обратной .
Как написать матричное уравнение
Давайте рассмотрим некоторые общие0003 алгебраическое уравнение примеры:
$ x + 5 = 10 $
$ x – 7 = { – 5 } $
$ 3x + 6 = 8 $
$ 2x = 18 $
- Для первого уравнения , чтобы найти $ x $, мы выполняем процесс вычитания .
- Для решения второго уравнения относительно $ x $ мы выполняем процесс сложения .
- Для решения третьего уравнения для $ x $ мы объединяем вычитание и деление .
- Для решения последнего уравнения относительно $ x $ мы используем отдел .
У нас могут быть похожие формы матричных уравнений , в которых мы должны выполнять те же операции, НО над матрицами! Давайте рассмотрим несколько примеров написания матричных уравнений:
$ \begin{bmatrix} { a } & { b } \\ { c } & { d } \end {bmatrix} + X = \begin{bmatrix} { e } & {f} \\ {g} & {h} \end {bmatrix} $
$ \begin{bmatrix} {a} & {b} \\ {c} & {d} \end {bmatrix} – X = \begin{bmatrix} { e } & { f } \\ { g } & { h } \ end {bmatrix} $
$ 3 \times \begin{bmatrix} { a } & { b } \\ { c } & { d } \ end {bmatrix} = \begin {bmatrix} { 6 } & { 12 } \\ { – 18 } & { 9 } \end {bmatrix} $
$ X \begin{bmatrix} {a } & {b} \\ {c} & {d} \end {bmatrix} = \begin{bmatrix} {e} & { f } \\ { g } & { h } \end {bmatrix} $
Эти $ 4 $ уравнения являются матричными уравнениями.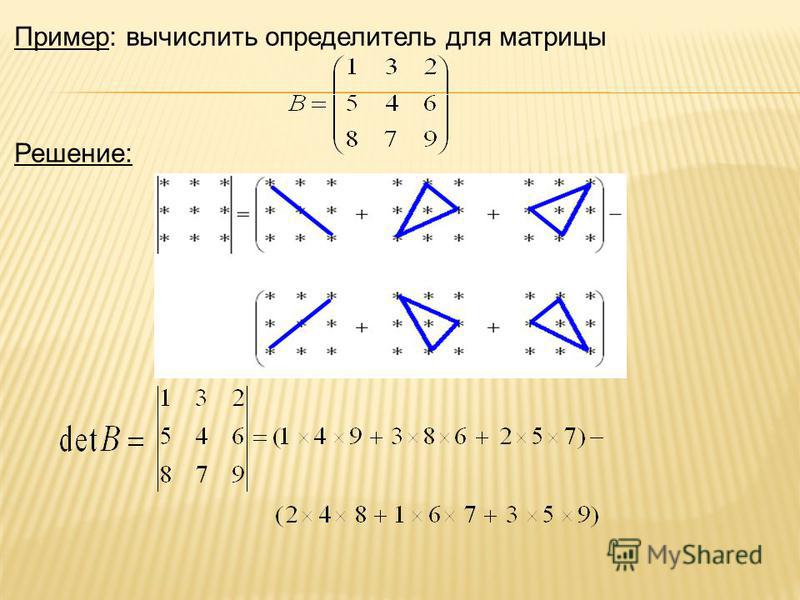 Нам нужно будет выполнить те же операции, но с матрицами, чтобы найти неизвестных матриц 9.0008 ! Далее мы рассмотрим, как решать эти типы матричных уравнений.
Нам нужно будет выполнить те же операции, но с матрицами, чтобы найти неизвестных матриц 9.0008 ! Далее мы рассмотрим, как решать эти типы матричных уравнений.
Как решать матричные уравнения
Как мы упоминали ранее, способ решения матричных уравнений заключается в простом выполнении основных арифметических операций, но с учетом правил сложения матриц, вычитания матриц, скалярного умножения и умножения матриц.
Проверим простую задачу сложения матриц:
$ A – \begin{bmatrix} { 3 } & { – 3 } \\ { 1 } & { 0 } \end {bmatrix} = \begin{bmatrix} { – 10 } & { 2 } \\ { – 1 } & { 1 } \ end {bmatrix} $
Обратите внимание, что $A$ — это матрица.
Подобно уравнениям, чтобы найти матрицу $A$, мы можем сложить первую матрицу со второй матрицей. Процесс показан ниже:
$ A = \begin{bmatrix} { – 10 } & { 2 } \\ { – 1 } & { 1 } \end {bmatrix} + \begin{bmatrix} { 3 } & { – 3 } \\ { 1 } & { 0 } \end {bmatrix} $
$ A = \begin{bmatrix} { – 10 + 3 } & { 2 + ( – 3 ) } \\ { -1 + 1 } & { 1 + 0 } \end {bmatrix} $
$ A = \begin{bmatrix} { – 7 } & { – 1 } \\ {0 } & { 1 } \end {bmatrix} $
Чтобы сложить две матрицы, первое условие должно состоять в том, что обе порядок матриц должен быть одинаковым! Обе матрицы здесь были $ 2 \times 2 $ матрицами. Чтобы выполнить сложение матриц, мы добавили каждую соответствующую запись друг к другу. Узнайте больше о добавлении матриц, прочитав эту статью!
Чтобы выполнить сложение матриц, мы добавили каждую соответствующую запись друг к другу. Узнайте больше о добавлении матриц, прочитав эту статью!
Давайте рассмотрим пару примеров!
Пример 1Решение для матрицы $ B $:
$ B + \begin{bmatrix} { 0 } & { – 1 } & 4 \\ { 11 } & { – 2 } & 0 \\ {3} & {6} & { – 2 } \end {bmatrix} = \begin{bmatrix} { 6 } & { 1 } & – 1 \\ { – 1 } & { 4 } & – 1 \\ { – 1 } & { – 2 } & { – 3 } \end {bmatrix} $
Решение
Как и уравнения, чтобы решить $ B $, мы должны вычесть первую матрицу из второй матрицы. Обе они являются матрицами $ 3 \times 3 $, и, таким образом, матрица $ B $ также будет матрицей $ 3 \ x 3 $. Процесс показан ниже:
$ B = \begin{bmatrix} { 6 } & { 1 } & – 1 \\ { – 1 } & { 4 } & – 1 \\ { – 1 } & { – 2 } & { – 3 } \ end {bmatrix} – \begin{bmatrix} { 0 } & { – 1 } & 4 \\ { 11 } & { – 2 } & 0 \\ {3} & {6} & { – 2 } \end {bmatrix } $
$ B = \begin{bmatrix} { 6 – 0 } & { 1 + 1 } & { -1 – 4} \\ { -1 – 11 } & { 4 + 2 } & -1 – 0 \ \ {-1 – 3} & {-2 – 6} & {-3 + 2} \end {bmatrix} $
$ B = \begin{bmatrix} { 6 } & { 2 } & {-5} \ \ {-12} & {6} & -1 \\ {-4} & {-8} & {-1} \end {bmatrix} $
Чтобы узнать больше о вычитании матриц, посмотрите этот урок!
Пример 2Решите следующее матричное уравнение для значений $ x $ и $ y $:
$ \begin{bmatrix} { 2 } & {2 } \\ { 3 } & { 4 } \end {bmatrix} \begin{bmatrix} { x } \\ y \end {bmatrix} = \begin{bmatrix} { 4 } \\ 8 \end {bmatrix} $
Решение
Обработка второй матрицы в качестве переменной мы знаем, что нам придется разделить матрицу с элементами $4$ и $8$ (третья матрица) на матрицу $2\times 2$ (первая матрица). 9{ – 1 } = \frac{1}{ad – bc} \begin{bmatrix} { d } & {-b } \\ {-c } & {a} \end {bmatrix}$.
9{ – 1 } = \frac{1}{ad – bc} \begin{bmatrix} { d } & {-b } \\ {-c } & {a} \end {bmatrix}$.
Найдем обратную матрицу $ \begin{bmatrix} { 2 } & {2 } \\ { 3 } & {4 } \end {bmatrix}$ :
$ = \frac{1} { (2)(4) – (2)(3) } \begin{bmatrix} { 4 } & {-2 } \\ { – 3 } & { 2 } \end {bmatrix} $
$ = \frac {1}{2} \begin{bmatrix} { 4 } & { -2 } \\ { – 3 } & { 2 } \end {bmatrix} $
$ = \begin{bmatrix} { 2 } & { – 1 } \\ { – \frac{3}{2} } & { 1 } \end {bmatrix} $
Теперь мы можем решить наше уравнение:
$ \begin{bmatrix} { 2 } & {2 } \\ { 3 } & {4 } \end {bmatrix} \begin{bmatrix} { x } \\ y \end {bmatrix} = \begin{bmatrix} { 4 } \\ 8 \end {bmatrix} $
$ \begin{bmatrix} { x } \\ y \end {bmatrix} = \begin{bmatrix} { 2 } & { -1 } \\ { – \frac{3}{2} } & { 1 } \end {bmatrix} \begin{bmatrix} { 4 } \\ 8 \end {bmatrix} $
$ \ begin{bmatrix} { x } \\ y \end {bmatrix} = \begin{bmatrix} {(2)(4) + (-1)(8)} \\ {(-\frac{3}{2} )(4) + (1)(8)}\end {bmatrix} $
$ \begin{bmatrix} { x } \\ y \end {bmatrix} = \begin{bmatrix} {8 – 8} \\ {-6 + 8}\end {bmatrix} $
$ \begin{ bmatrix} { x } \\ y \end {bmatrix} = \begin{bmatrix} {0} \\ 2\end {bmatrix} $
Таким образом,
$ x = 0 $ и $ y = 2 $.
Чтобы узнать больше о том, как мы делали это умножение, ознакомьтесь с нашим уроком по умножению матриц.
Практические вопросы- Решите для $a$, $b$, $c$ и $d$.
$ 3 \begin{bmatrix} { a } & { b } \\ { c } & { d } \end {bmatrix} = \begin{bmatrix} { – 6 } & { 12 } \\ { – 9 } & { – 3 } \end {bmatrix} $ - Учитывая матрицы:
$ A = \begin{bmatrix} 0 & 1 \\ 2 & 6 \end {bmatrix} $
$ B = \begin{bmatrix} 3 & – 1 \\ 2 & 3 \end {bmatrix} $
$ C = \begin{bmatrix} 4 & 3 \\ -2 & 5 \end {bmatrix} $Решить матричное уравнение $ X \cdot A + B = C $.
Ответы
Это скалярное матричное уравнение умножения .
$ 3 \begin{bmatrix} { a } & { b } \\ { c } & { d } \end {bmatrix} = \begin{bmatrix} { – 6 } & { 12 } \\ { – 9 } & { – 3 } \end {bmatrix} $
Нам нужно найти переменные $ a $, $ b $, $ c $ и $ d $. В левой части мы умножаем каждый элемент первой матрицы на скаляр «3».
 Сделаем так:
Сделаем так:$ \begin{bmatrix} { 3a } & {3 b } \\ { 3c } & {3 d } \end {bmatrix} = \begin{bmatrix} { – 6 } & { 12 } \ \ { – 9} & { – 3 } \end {bmatrix} $
Теперь у нас есть две матрицы $ 2 \times 2 $, равные друг другу. Это означает, что каждый соответствующий элемент равен друг другу. Приравниваем каждую и находим значения всех $4$ переменных.
$ 3a = – 6 $
$ a = – 2 $
Тогда
$ 3b = 12 $
$ b = 4 $
Далее,
c 5 $ 9 $ 3c = – 0 = – 3 $
Наконец,
$ 3d = – 3 $
$ d = – 1 $
Таким образом, у нас есть $ a = – 2 $, $ b = 4 $, $ c = – 3 $ и $ d = -1 $. Таким образом, неизвестная матрица может быть записана как:
$ \begin{bmatrix} { -2 } & { 4 } \\ { – 3 } & { – 1 } \end {bmatrix} $
- Лечение $X$ в качестве переменной имеем:
$ X \cdot A +B = C $
$ X \cdot A = C – B $
$ X = \frac{C-B}{A} $Вместо деления будем умножьте обратную матрицу $A$ на матрицу $C-B$.
 Найдем $C – B$:
Найдем $C – B$:$C – B = \begin{bmatrix} 4 & 3 \\ -2 & 5 \end {bmatrix} – \begin{bmatrix} 3 & -1 \\ 2 & 3 \ конец {bmatrix} $ 9{-1}(C – B) $
$ X = \begin{bmatrix} -3 & \frac{1}{2} \\ 1 & 0 \end {bmatrix} \begin{bmatrix} 1 & 4 \\ -4 & 2 \end {bmatrix} $
$ X = \begin{bmatrix} (-3)(1) + (\frac{1}{2})(-4) & (-3)(4) + (\frac{1}{2})(2) \\ (1)(1)+(0)(-4) & (1)(4)+(0)(2) \end {bmatrix} $
$ X = \begin{bmatrix} -5 & -11 \\ 1 & 4 \end {bmatrix} $
символьный — Примеры использования Mathematica для символьного решения матричных уравнений 9{-1} г. \end{align*}
Могу ли я заставить Mathematica сделать это? Я спрашиваю, потому что хотел бы закрытых форм более сложных блочно-матричных систем.
- матричный
- символический
- линейно-алгебраический
$\endgroup$
2
$\begingroup$
NCAlgebra была обновлена с тех пор, как я написал свой комментарий выше в 2015 году.

 10) от 0 до оо, что сразу дает (7.9). В частности, решение уравнения в случае гурвицевой матрицы А приводит к положительно определенной функции Ляпунова Найти (методом элементарных преобразований) матрицу, обратную к данной:
10) от 0 до оо, что сразу дает (7.9). В частности, решение уравнения в случае гурвицевой матрицы А приводит к положительно определенной функции Ляпунова Найти (методом элементарных преобразований) матрицу, обратную к данной: Сделаем так:
Сделаем так: Найдем $C – B$:
Найдем $C – B$: