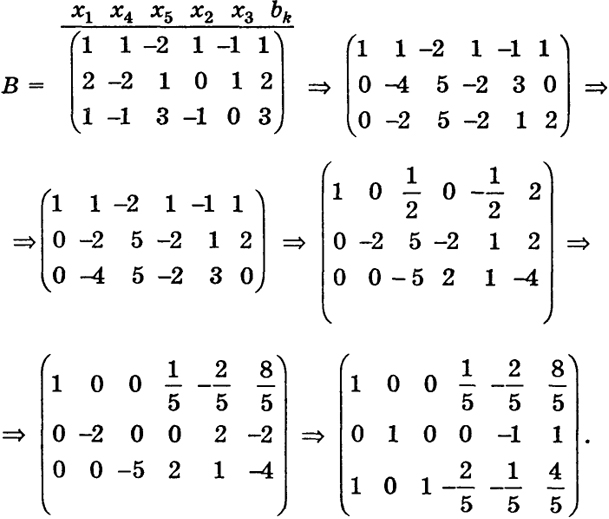Почему мы живем не в Матрице, а в матрице? / Хабр
Бог — это вечная и бесконечная истина, не имеющая ценности и смысла.Барух Бенедикт Спиноза
Сегодня я хочу рассказать вам о самой смелой и красивой гипотезе в современной теоретической физике. Многие ученые относятся к ней крайне скептически, некоторые называют ее откровенно шизофреническим бредом, а другие находят крайне интересной. Давайте же пустимся в путешествие, которое может навсегда изменить ваше представление о Вселенной.
В поисках «теории всего»
Начиная с середины 20-ого века самой сложной и перспективной задачей теоретической физики является поиск так называемой «теории всего», которая объединит в себе общую теорию относительности и квантовую механику, тем самым дав точное объяснение всем наблюдаемым физическим явлениям. На роль такой теории претендуют многочисленные теории струн, теория квантовой петлевой гравитации и многие другие. Но мы будем говорить не о них. Мы сделаем шаг еще дальше.
Но мы будем говорить не о них. Мы сделаем шаг еще дальше.
Профессор MIT Макс Тегмарк в своей книге «Наша математическая Вселенная» призывает нас задуматься о самом удивительном свойстве всех существующих физических теорий, которое обычно люди считают само собой разумеющимся — все наши физические теории описываются математикой.
С точки зрения эмпиризма (философия первичности материи по отношению к идее) в этом нет ничего удивительного, человек изобретал язык математики, наблюдая за реальным миром.Мы изобрели цифры и счет, чтобы считать предметы, мы изобрели геометрию, чтобы строить прочные здания. Со временем наши математические инструменты становились все более сложными и отдаленными от повседневных нужд — мы изобретали дифференциалы, интегралы, математический анализ, теорию групп, топологию. Но в конце концов мы всегда находили физические явления, которые поразительно хорошо описывались с помощью этих самых инструментов.
Но давайте взглянем на математичность физических законов с точки зрения идеализма (философия первичности идеи по отношению к материи). Все математические законы живут в пространстве идей и не зависят даже от существования нашей Вселенной. Если даже ничего не существовало бы, дважды два все также равнялось бы четырем. Рождение галактик и звезд, движение планет, химические реакции и генетические мутации строго следовали математическим формулам задолго до появления людей. Мы лишь открыли эти законы, но не изобрели их.
Все математические законы живут в пространстве идей и не зависят даже от существования нашей Вселенной. Если даже ничего не существовало бы, дважды два все также равнялось бы четырем. Рождение галактик и звезд, движение планет, химические реакции и генетические мутации строго следовали математическим формулам задолго до появления людей. Мы лишь открыли эти законы, но не изобрели их.
Так что же будет с теорией относительности, квантовой механикой или пресловутой теорией всего, если мы выкинем из них всю словесную шелуху, вроде слов «квант», «пространство», «свет». Там останутся только формулы, и ничего больше. И в этом месте рассуждений Макс Тегмарк задает интереснейший вопрос: что может полностью описываться чистой математикой? И он дает на него единственно разумный ответ. Чистой математикой может быть описана лишь сама чистая математика. Таким образом Тегмарк приходит к самой поразительной из возможных гипотез: вся наша Вселенная — это математическая структура.
Все из бита
Макс Тегмарк не был первым, кто пришел к такой идее. Задолго до него эту идею выдвигал знаменитый американский физик, научный руководитель Ричарда Фейнмана, Хью Эверетта и Кипа Торна, а также автор терминов «черная дыра» и «кротовая нора» Джон Уилер.
Задолго до него эту идею выдвигал знаменитый американский физик, научный руководитель Ричарда Фейнмана, Хью Эверетта и Кипа Торна, а также автор терминов «черная дыра» и «кротовая нора» Джон Уилер.
В своей статье «it from bit» Джон Уилер задумывался над тем фактом, что все свойства элементарных частиц вроде массы, заряда, спина, цвета, странности и красоты не имеют никакого собственного смысла, а лишь проявляются при взаимодействиях с другими частицами.
Таким образом, все эти свойства являются по сути битом информации в некоторой математической структуре. Уилер писал:
Все сущее — каждая частица, каждое силовое поле, даже сам пространственно-временной континуум — получают свою функцию, свой смысл и, в конечном счёте, самое своё существование — даже если в каких-то ситуациях не напрямую — из ответов, извлекаемых нами с помощью физических приборов, на вопросы, предполагающие ответ «да» или «нет», из бинарных альтернатив, из битов. «Всё из бита» символизирует идею, что всякий предмет и событие физического мира имеет в своей основе — в большинстве случаев в весьма глубокой основе — нематериальный источник и объяснение; то, что мы называем реальностью, вырастает в конечном счёте из постановки «да-нет»-вопросов и регистрации ответов на них при помощи аппаратуры
Чтобы вы лучше поняли, что имел в виду Джон Уилер, я приведу вам в пример картинку из книги Макса Тегмарка о том, как отношения между точками пространства (ребра куба) можно представить в виде матрицы битов:
Сами вершины этого куба, обозначенные индексом от 1 до 8, не несут никакого смысла, а вот матрица отношений между ними (ребер куба) уже обладает некоторыми уникальными свойствами: например, вращательной симметрией.
Инфляционная модель Вселенной и фракталы
Если мы все-таки живем в математической модели, то в какой?
Давайте посмотрим на нашу Вселенную: она состоит из множества скоплений миллиардов галактик, галактики состоят из миллиардов звезд, у многих звезд есть несколько планет, а у многих планет есть некоторое количество спутников. Более того, согласно гипотезе вечной инфляции, являющейся объяснением и расширением инфляционной модели развития вселенной, в отдаленном от нас пространстве ежесекундно происходят миллионы «больших взрывов», порождающих свои пузыри Вселенных.
Но вернемся к нашему миру: все скопления, галактики, звезды и планеты, в какой бы части Вселенной они не находились, очень похожи между собой, но все же уникальны. Какая математическая структура обладает такими свойствами? Это фрактал.
Фрактал порождается простейшей рекуррентной формулой, но развивается в красивейшую циклическую картину, каждый маленький кусочек которой одновременно и уникален, и похож на общую структуру.
Асимметрия времени и вычисление рекурсивной функции
И как раз фрактальная структура нашей Вселенной открывает нам глаза на самую главную загадку современной физики — время. Идет ли время только вперед? Линейно ли оно?
Современная физика говорит о существовании так называемой асимметрии времени или стрел времени. Первая стрела времени — психологическая: мы помним прошлое, но не будущее. Эта ассиметрия является частным случаем более общей второй стрелы времени — причинно-следственной. Причины порождают следствия, но не наоборот. С другой стороны это может быть лишь частью нашего восприятия и при обратном ходе времени мы бы приняли причины за следствия, а следствия за причины. Но существуют третья абсолютно объективная асимметрия времени, также называемая вторым законом термодинамики — энтропия в замкнутой системе со временем всегда растет.
Как это можно объяснить? Одним из первых объяснение, согласующееся с гипотезой математической Вселенной, дал немецкий пионер компьютеростроения и автор первого языка программирования высокого уровня Конрад Цузе. Он предположил, что наша Вселенная является не статичной математической моделью, а постоянно вычисляющийся чистой рекурсивной функцией. На вход такой функции поступает результат вычисления предыдущей итерации. Каждый тик такой функции является планковским временем, а проще говоря мгновением. Такая гипотеза очень хорошо объясняет все стрелы времени. Результат вычисления такой функции зависит от ее входа — будущее зависит от прошлого, но не наоборот. Со временем количество информации в такой системе будет расти, а значит будет расти и энтропия. И главное, эта гипотеза очень хорошо согласуется с фрактальностью нашей Вселенной, ведь фрактал — результат вычисления рекуррентной функции.
Таким образом, мы можем дать определение времени таким образом: время — это процесс вычисления чистой рекурсивной функции расчета развития нашей Вселенной.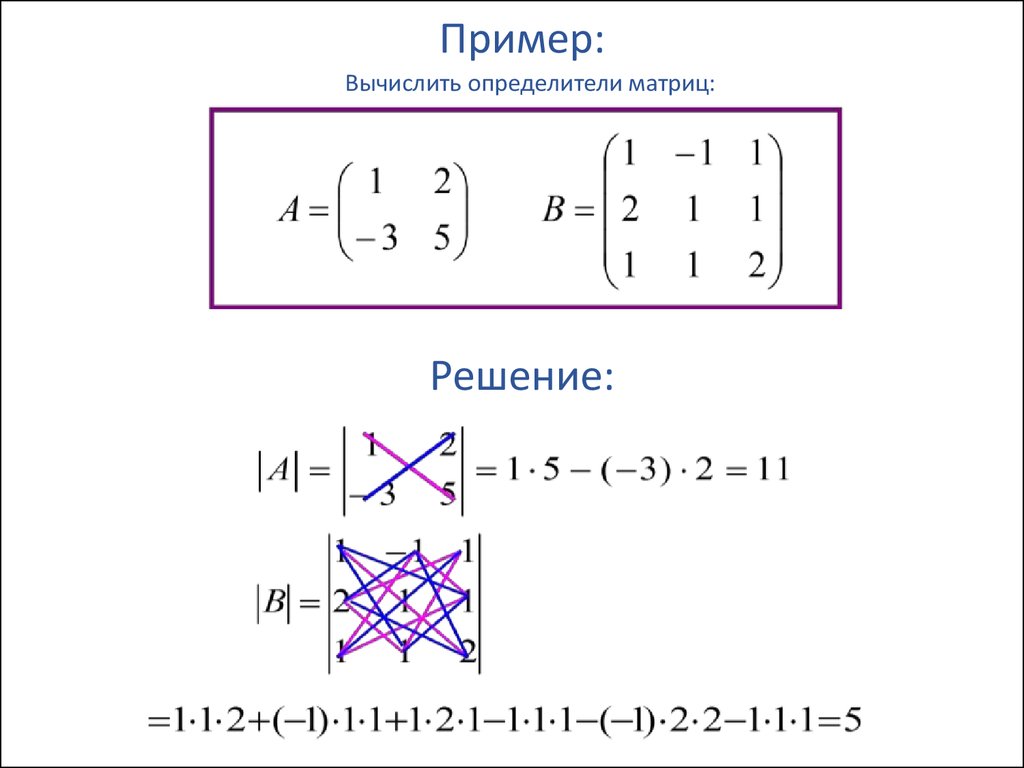
Вы можете возразить, что наша Вселенная недетерминирована и при коллапсе волновой функции Шредингера результат выхода кванта из суперпозиции непредсказуем. Но согласно многомировой интерпретации квантовой механики Эверетта в момент коллапса волновой функции наша Вселенная просто разделяется на две параллельных реальности, в одной из которых суперпозиция переходит в одно состояние, а в другой в противоположное.
Также стоит учесть, что это время — не то же самое, что описывается в общей теории относительности Эйнштейна. Это абсолютное время — тики процессора вычисляющего нашу Вселенную.
Матрица и антропный принцип
 Этот ряд можно продолжать до бесконечности и ни в одном уровне Матрицы не будет возможности доказать, существует или нет реальный мир более высокого уровня.
Этот ряд можно продолжать до бесконечности и ни в одном уровне Матрицы не будет возможности доказать, существует или нет реальный мир более высокого уровня.В любом случае, у Макса Тегмарка есть более красивое объяснение математичности нашей Вселенной. Для начала зададимся вопросом: почему мы живем именно в такой математической структуре, а не в какой-то другой? Тегмарк находит ответ на этот вопрос в антропном принципе: все непротиворечивые математические структуры существуют, но лишь в немногих из них может зародится такая тонко настроенная Вселенная, которая позволяет существовать нейронным сетям, способным осознать причинно-следственные связи.
Заключение
У гипотезы математической вычислимой Вселенной существуют интересные последствия: герои книг, фильмов, историй и даже ваш выдуманный друг столь же реальны, как и вы сами, так как точно так же являются математическими структурами, придуманными другой математической структурой внутри громадной математической структуры.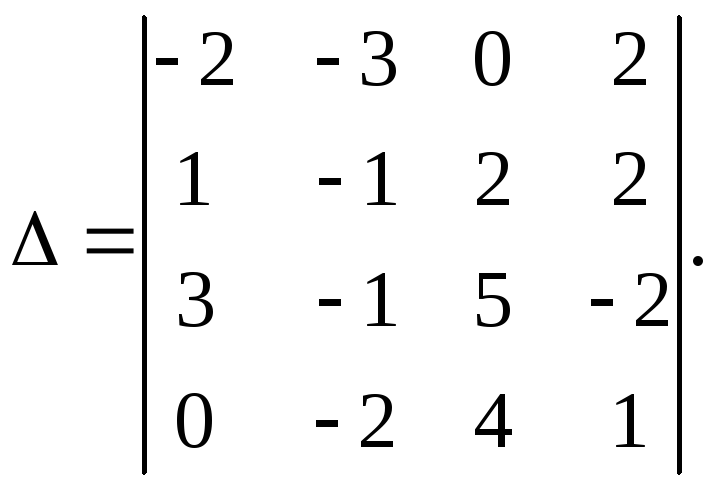 Это заставляет задуматься над самим значением слова «реальность».
Это заставляет задуматься над самим значением слова «реальность».
Для более глубокого ознакомления с данной темой я рекомендую книгу Макса Тегмарка “Наша математическая Вселенная” и статью в википедии про цифровую физику.
Краткое описание математических функций — Документация Qucs Help 0.0.19
В уравнениях Qucs могут применяться следующие операции и функции. Подробное описание смотрите в “Справочном руководстве по выражениям”. Параметры в квадратных скобках “[]” необязательны.
Операторы
Арифметические операторы
+x | Унарный плюс |
-x | Унарный минус |
x+y | Сложение |
x-y | Вычитание |
x*y | Умножение |
x/y | Деление |
x%y | Остаток от деления |
x^y | Возведение в степень |
Логические операторы
!x | Отрицание |
x&&y | И |
x||y | ИЛИ |
x^^y | Исключающее ИЛИ |
x?y:z | Сокращение для условного выражения – if x then y else z |
x==y | Равно |
x!=y | Не равно |
x<y | Меньше |
x<=y | Меньше или равно |
x>y | Больше |
x>=y | Больше или равно |
Математические функции
Векторы и матрицы: создание
eye(n) | Создает единичную матрицу n x n |
length(y) | Возвращает длину вектора y |
linspace(from,to,n) | Вещественный вектор с n линейно расставленными компонентами между from и to |
logspace(from,to,n) | Вещественный вектор с n логарифмически расставленными компонентами между from и to |
Векторы и матрицы: основные матричные функции
adjoint(x) | Сопряженная с x матрица (транспонированная и комплексно-сопряженная) |
det(x) | Детерминант матрицы x |
inverse(x) | Инверсия матрицы x |
transpose(x) | Транспонированная матрица для x (столбцы и строки меняются местами) |
Элементарные математические функции: основные вещественные и комплексные функции
abs(x) | Абсолютное значение, модуль комплексного числа |
angle(x) | Фазовый угол (в радианах) комплексного числа.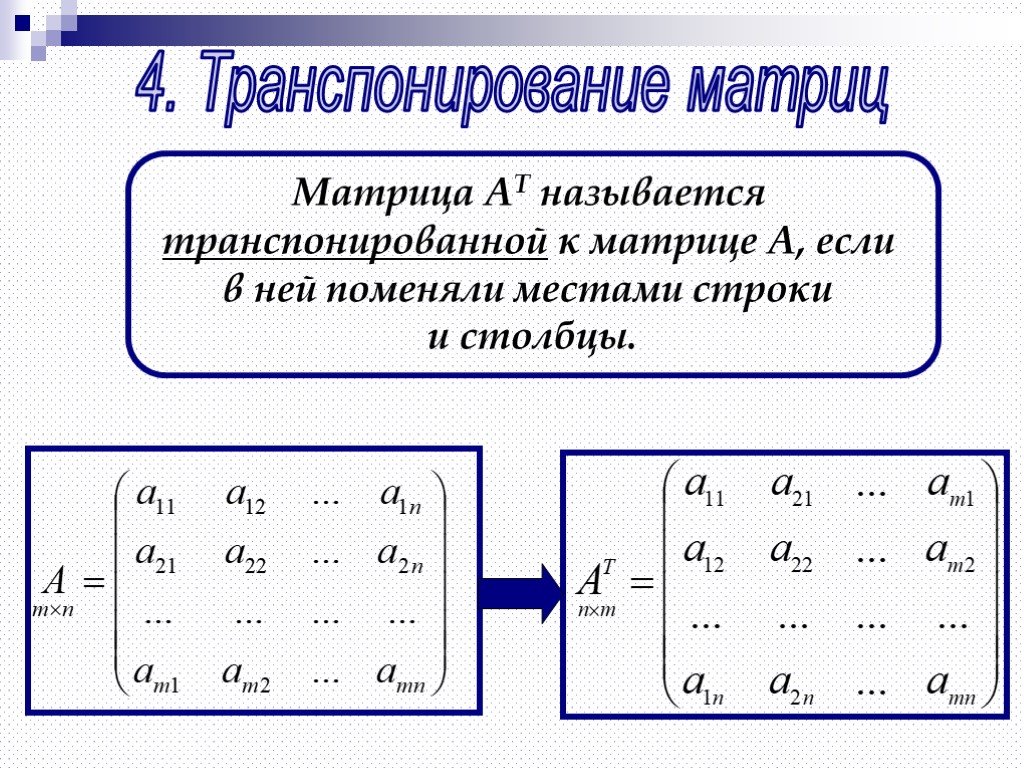 Синоним arg() Синоним arg() |
arg(x) | Фазовый угол (в радианах) комплексного числа |
conj(x) | Сопряжение комплексного числа |
deg2rad(x) | Преобразует фазу из градусов в радианы |
hypot(x,y) | Функция евклидового расстояния |
imag(x) | Мнимая часть комплексного числа |
mag(x) | Модуль комплексного числа |
norm(x) | Квадрат абсолютного значения вектора |
phase(x) | Фазовый угол (в градусах) комплексного числа |
polar(m,p) | Преобразование полярных координат m и p в комплексное число |
rad2deg(x) | Преобразует фазу из радианов в градусы |
real(x) | Вещественная часть комплексного числа |
sign(x) | Знаковая функция |
sqr(x) | Квадрат (вторая степень) числа |
sqrt(x) | Квадратный корень |
unwrap(p[,tol[,step]]) | Разворачивает угол p (радианы) – по умолчанию step = 2pi, tol = pi |
Элементарные математические функции: экспоненциальные и логарифмические функции
exp(x) | Экспоненциальная функция с основанием e |
limexp(x) | Ограниченная экспоненциальная функция |
log10(x) | Десятичный логарифм |
log2(x) | Двоичный логарифм |
ln(x) | Натуральный логарифм (основание e ) |
Элементарные математические функции: тригонометрия
cos(x) | Косинус |
cosec(x) | Косеканс |
cot(x) | Котангенс |
sec(x) | Секанс |
sin(x) | Синус |
tan(x) | Тангенс |
Элементарные математические функции: обратные тригонометрические функции
arccos(x) | Арккосинус (известный также как “обратный косинус”) |
arccosec(x) | Арккосеканс |
arccot(x) | Арккотангенс |
arcsec(x) | Арксеканс |
arcsin(x) | Арксинус (известный также как “обратный синус”) |
arctan(x[,y]) | Арктангенс (известный также как “обратный тангенс”) |
Элементарные математические функции: гиперболические функции
cosh(x) | Гиперболический косинус |
cosech(x) | Гиперболический косеканс |
coth(x) | Гиберболический котангенс |
sech(x) | Гиперболический секанс |
sinh(x) | Гиперболический синус |
tanh(x) | Гиперболический тангенс |
Элементарные математические функции: обратные гиперболические функции
arcosh(x) | Гиперболический ареакосинус |
arcosech(x) | Гиперболический ареакосеканс |
arcoth(x) | Гиперболический ареакотангенс |
arsech(x) | Гиперболический ареасеканс |
arsinh(x) | Гиперболический ареасинус |
artanh(x) | Гиперболический ареатангенс |
Элементарные математические функции: округление
ceil(x) | Округление до ближайшего большего целого |
fix(x) | Отбрасывание десятичных разрядов вещественного числа |
floor(x) | Округление до ближайшего меньшего целого |
round(x) | Округление до ближайшего целого |
Элементарные математические функции: специальные математические функции
besseli0(x) | Модифицированная функция Бесселя нулевого порядка |
besselj(n,x) | Функция Бесселя первого рода и n-го порядка |
bessely(n,x) | Функция Бесселя второго рода и n-го порядка |
erf(x) | Функция ошибки |
erfc(x) | Комплиментарная функция ошибки |
erfinv(x) | Обратная функция ошибки |
erfcinv(x) | Обратная комплиментарная функции ошибки |
sinc(x) | Sinc-функция (sin(x)/x или 1 при x = 0) |
step(x) | Шаговая функция |
Анализ данных: основные операции
cumprod(x) | Накопительное произведение элементов вектора |
cumsum(x) | Накопительная сумма элементов вектора |
interpolate(f,x[,n]) | Spline interpolation of vector f using n equidistant points of x |
prod(x) | Произведение элементов вектора |
sum(x) | Сумма элементов вектора |
xvalue(f,yval) | Returns x-value nearest to yval in single dependency vector f |
yvalue(f,xval) | Returns y-value nearest to xval in single dependency vector f |
Анализ данных: дифференцирование и интегрирование
ddx(expr,var) | Дифференцирует математическое выражение expr по переменной var |
diff(y,x[,n]) | Дифференцировать вектор y по вектору x n раз. По умолчанию По умолчанию n = 1 |
integrate(x,h) | Численно интегрировать вектор x, считая, что размер шага h постоянный |
Функции из электроники
Преобразование единиц измерения
dB(x) | Значение в дБ |
dbm(x) | Преобразовать напряжение в мощность в дБм |
dbm2w(x) | Преобразовать мощность в дБм в мощность в ваттах |
w2dbm(x) | Преобразовать мощность в ваттах в мощность в дБм |
vt(t) | Температурный потенциал для данной температуры t в градусах Кельвина |
Коэффициенты отражения и КСВН
rtoswr(x) | Преобразует коэффициент отражения в коэффициент стоячей волны по напряжению (КСВН) |
rtoy(x[,zref]) | Преобразует коэффициент отражения в полную проводимость; по умолчанию zref равно 50 Ом |
rtoz(x[,zref]) | Преобразует коэффициент отражения в полное сопротивление; по умолчанию zref равно 50 Ом |
ytor(x[,zref]) | Преобразует полную проводимость в коэффициент отражения; по умолчанию zref равно 50 Ом |
ztor(x[,zref]) | Преобразует полное сопротивление в коэффициент отражения; по умолчанию zref равно 50 Ом |
N-портовые матричные преобразования
stos(s,zref[,z0]) | Преобразует матрицу S-параметров в матрицу S-параметров с другим Z0 |
stoy(s[,zref]) | Преобразует матрицу S-параметров в матрицу Y-параметров |
stoz(s[,zref]) | Преобразует матрицу S-параметров в матрицу Z-параметров |
twoport(m,from,to) | Преобразует двух-портовую матрицу: from и to – это ‘Y’, ‘Z’, ‘H’, ‘G’, ‘A’, ‘S’ и ‘T’. |
ytos(y[,z0]) | Преобразует матрицу Y-параметров в матрицу S-параметров |
ytoz(y) | Преобразует матрицу Y-параметров в матрицу Z-параметров |
ztos(z[,z0]) | Преобразует матрицу Z-параметров в матрицу S-параметров |
ztoy(z) | Преобразует матрицу Z-параметров в матрицу Y-параметров |
Усилители
GaCircle(s,Ga[,arcs]) | Доступный коэффициент усиления мощности Ga окружностей (плоскость источника) |
GpCircle(s,Gp[,arcs]) | Операционный коэффициент усиления мощности Gp окружностей (плоскость нагрузки) |
Mu(s) | Mu – фактор устойчивости двухпортовой матрицы S-параметров |
Mu2(s) | Mu’ – фактор устойчивости двухпортовой матрицы S-параметров |
NoiseCircle(Sopt,Fmin,Rn,F[,Arcs]) | Окружности диаграммы шума(ов) F |
PlotVs(data,dep) | Возвращает данные, выбранные из data: зависимость dep |
Rollet(s) | Фактор устойчивости Роллета для двухпортовой матрицы S-параметров |
StabCircleL(s[,arcs]) | Окружность устойчивости в плоскости нагрузки |
StabCircleS(s[,arcs]) | Окружность устойчивости в плоскости источника |
StabFactor(s) | Фактор устойчивости двухпортовой матрицы S-параметров |
StabMeasure(s) | Мера устойчивости B1 двухпортовой матрицы S-параметров |
Номенклатура
Интервалы
LO:HI | Интервал от LO до HI |
:HI | Вплоть до HI |
LO: | От LO |
: | Нет ограничений интервала |
Матрицы и элементы матриц
M | Вся матрица M |
M[2,3] | Элемент, находящийся во 2-м ряду и 3-м столбце матрицы M |
M[:,3] | Вектор, состоящий из 3-го столбца матрицы M |
Непосредственно
2. | Вещественное число |
1.4+j5.1 | Комплексное число |
[1,3,5,7] | Вектор |
[11,12;21,22] | Матрица |
Приставки к единицам
E | экса, 1e+18 |
P | пета, 1e+15 |
T | тера, 1e+12 |
G | гига, 1e+9 |
M | мега, 1e+6 |
k | кило, 1e+3 |
m | милли, 1e-3 |
u | микро, 1e-6 |
n | нано, 1e-9 |
p | пико, 1e-12 |
f | фемто, 1e-15 |
a | атто, 1e-18 |
Названия величин
S[1,1] | Значение S-параметра |
nodename. V | Напряжение постоянного тока в узле nodename |
name.I | Постоянный ток через компонент name |
nodename.v | Переменное напряжение в узле nodename |
name.i | Переменный ток через компонент name |
nodename.vn | Шумовое напряжение переменного тока в узле nodename |
name.in | Шумовой переменный ток через компонент name |
nodename.Vt | Переходное напряжение в узле nodename |
name.It | Переходной ток через компонент name |
Примечание: Все напряжения и токи – пиковые значения.Примечание: Шумовые напряжения – СКЗ значения в полосе частот 1 Hz.
Константы
i, j | Мнимая единица (“квадратный корень из -1”) |
pi | 4*arctan(1) = 3. 14159… 14159… |
e | e = 2.71828… |
kB | Постоянная Больцмана = 1.38065e-23 Дж/K |
q | Элементарный заряд = 1.6021765e-19 Кл |
back to the top
Изучение матричной математики с помощью онлайн-курсов, занятий и уроков
Пройдите бесплатные онлайн-уроки матричной математики, чтобы улучшить свои навыки и повысить успеваемость в школе. Получите прочную основу для умножения матриц и линейной алгебры или освежите в памяти важные навыки решения задач.
Просмотреть все курсы edX
Похожие темы-Алгоритмы|Исчисление|Дифференциальные уравнения|Геометрия|Вывод статистики|Линейная алгебра|Предварительная алгебра|Вероятность
Learn Math Math
Что такое умножение матриц?
Умножение матриц — это функция линейной алгебры, позволяющая составить из двух матриц матрицу, представляющую собой композицию. Вычисление матричных произведений является центральной частью вычислительных приложений. Он позволяет упростить линейные уравнения, создавать ходы в таких приложениях, как теория игр, или улучшать визуализацию изображений, несмотря на небольшие сложности. Умножение матриц — дело непростое, но с помощью программ, которые сделают всю тяжелую работу за вас, вы сможете применить его к своим вычислениям без лишней работы. Изучив этот процесс, вы создадите свой набор инструментов для выполнения высокоуровневых команд программирования и откроете множество творческих программных решений.
Он позволяет упростить линейные уравнения, создавать ходы в таких приложениях, как теория игр, или улучшать визуализацию изображений, несмотря на небольшие сложности. Умножение матриц — дело непростое, но с помощью программ, которые сделают всю тяжелую работу за вас, вы сможете применить его к своим вычислениям без лишней работы. Изучив этот процесс, вы создадите свой набор инструментов для выполнения высокоуровневых команд программирования и откроете множество творческих программных решений.
Изучение умножения матриц в программировании
Умножение матриц — это всего лишь один из методов работы с алгоритмами. Это сложнее, чем скалярное умножение, основанное на скалярном произведении для умножения комбинаций различных столбцов и строк. В скалярных или векторных операциях вы применяете скаляр к каждому элементу в матрице. Для умножения матриц требуется больше ловкости. Эти операции являются неотъемлемой частью программирования нейронных сетей в рамках машинного обучения. Вы должны уметь строить операции, учитывающие различные решения в матрице, и каждая новая матрица — это возможность еще больше расширить алгоритм.
Вы должны уметь строить операции, учитывающие различные решения в матрице, и каждая новая матрица — это возможность еще больше расширить алгоритм.
Matrix Math Courses
Если вы не понимаете, как это применимо к программированию, вам может помочь edX. В партнерстве с ведущими учебными заведениями, включая Гарвард и IT Bombay, вы сможете изучить основы программирования алгоритмов и то, как умножение матриц вписывается в систему алгоритмов. Например, вы можете получить исчерпывающий обзор алгоритмов с помощью IT Bombay и узнать, как использовать умножение матриц в сети алгоритмов других типов для создания высокоуровневых приложений. Гарвардская серия программ по программированию также затрагивает умножение матриц. Вы получите представление об основных понятиях, начиная с самой первой матрицы и заканчивая фундаментальными свойствами матричной алгебры. Вы будете работать с реальными числами и создавать ноу-хау для различных операций.
Создайте свой набор инструментов для программирования с помощью матричной математики
Вам необходимо знать операции матричной математики и то, как она вписывается в экосистему алгоритмов программирования. Вы сможете анализировать количество столбцов и строк, разбираться в матричной алгебре, строить отчеты и работать со сложными матричными операциями. У матричной математики есть приложения для искусственного интеллекта, игр, рендеринга изображений и других областей, поэтому улучшите свои навыки программирования с четким пониманием. Ваше резюме по программированию будет вам благодарно.
Вы сможете анализировать количество столбцов и строк, разбираться в матричной алгебре, строить отчеты и работать со сложными матричными операциями. У матричной математики есть приложения для искусственного интеллекта, игр, рендеринга изображений и других областей, поэтому улучшите свои навыки программирования с четким пониманием. Ваше резюме по программированию будет вам благодарно.
Матричная математика | Высшее образование из Кембриджа
Microsoft прекращает выпуск Internet Explorer 11 в августе 2021 года. Если у вас возникли трудности с просмотром сайта в Internet Explorer 11, мы рекомендуем использовать другой браузер, например Microsoft Edge, Google Chrome, Apple Safari или Mozilla Firefox.
X
Главная
> Предметы
> Матричная математика
Скоро в продаже в мае 2023 г.- Учебник
- электронная коллекция
Авторы
Стефан Рамон Гарсия, Колледж Помона, Калифорния,
Роджер А. Хорн, Университет Юты
Хорн, Университет Юты
Описание
Используя современный матричный подход, этот строгий второй курс линейной алгебры помогает студентам старших курсов по математике, науке о данных и физическим наукам перейти от базовой теории к продвинутым темам и приложениям. Его ясность изложения вместе со множеством иллюстраций, более чем 900 упражнений и 350 концептуальных и числовых примеров помогают учащимся понять. Краткие главы способствуют целенаправленному продвижению основных идей. Темы выводятся и подробно обсуждаются, включая разложение по сингулярным числам, каноническую форму Жордана, спектральную теорему, QR-факторизацию,…
Добавить закладку
- Обзор
- Содержание
- Авторы
- Показатели
Основные характеристики
- Подчеркивает матричные факторизации, такие как унитарная триангуляризация, QR-факторизация, спектральная теорема и разложение по сингулярным числам.


 5
5