Матрица математика 1 курс: Конспект “матрицы 1 урок”

Высшая математика 1 курс – интернет энциклопедия для студентов

1. Линейная алгебра Матрицы
2. Метод Крамера
3. Метод Гаусса
4. Векторная алгебра Векторы и операции над ними

Несмотря на то, что зачастую этот предмет в вузах преподается разное количество времени (от 1 семестра для гуманитарных специальностей, и до 3 – для технических), список тем мало отличается. Чаще всего в дисциплине рассматриваются следующие разделы высшей математики: линейная и векторная алгебра, аналитическая геометрия, и линии второго порядка.

Линейная алгебра Матрицы

Изучаются матрицы размерностью n на m следующих видов: квадратные, диагональные, равные, единичные, трапецевидные, и треугольные.

Среди действий, которые возможно над ними выполнять рассматривают следующие:

• Сложение и вычитание матриц, сходных по размерности.
• Умножение их на число, вектор, и на другую матрицу.

Определитель

Изучают понятие определителя, его основные свойства, среди которых следующие:

• Для квадратных матриц А и В действует правило, что определитель произведения чисел А на В равняется определителю произведения В на А. И также равняется определителю А умноженному на определитель В. При этом произведение А на В не равняется произведению В на А.
• Определитель и его транспонируемая версия равны между собой.
• Если определитель содержит ряд из 0, или какие-либо 2 его ряда параллельны, то он равен нулю.
• Если матрица диагональная, то ее определитель есть числа, расположенные по диагонали, умноженные между собой. То же самое правило действует и для треугольных матриц.
• Если у чисел имеется общий множитель, то его можно вынести из определителя.

Изучаются основные правила теоремы Лапласа, связанной с разложением определителя.

Обратная матрица

Изучается понятие невырожденной матрицы. В связи с ним существует следующая схема, по которой вычисляется обратная матрица с положительным определителем:

• Элементы матрицы последовательно заменяются на соответствующие им алгебраические дополнения. В результате этого действия возникает союзная матрица.
• Происходит транспонирование.
• Элементы полученной матрицы нужно разделить на определитель матрицы.

Ранг матрицы

Понятие представляется как самое большое число линейно-зависимых строк матрицы и самый большой порядок, не равняющийся нулю, из миноров первоначальной матрицы.

Ранг матрицы имеет следующие два свойства:

• Он не подвержен изменению после транспонирования, после убирания нулевого ряда, и после совершения преобразований.
• Найти ранг можно по общему числу элементов на главной диагонали, отличающихся от нуля.

Метод Крамера

Используется для нахождения корней уравнений, в которых произведение А и Х равняется В. При этом важно, чтобы определитель А был отличным от нуля.

Если это условие совпадает, то можно воспользоваться следующим алгоритмом:

Находим ak, равное определителю Ак деленному на определитель А. Ак получают из А, подставив в него столбец свободного члена из В.

Метод Гаусса

Для его понятия изучают расширенную матрицу. А также несколько видов систем уравнений: совместные, определенные, равносильные, однородные.

Алгоритм для их решений таков:

• Первым делом находят ранги основной и расширенной.
• Если они отличаются друг от друга, то система является несовместной и на этом решение прекращают.
• Иначе сначала высчитывают базисный минор порядка, затем общее решение системы, и в итоге получают частные решения при подставлении произвольных значений в уравнения.

Векторная алгебра Векторы и операции над ними

Рассматривается основное определение вектора, его свойства, такие как длина и направления. Кроме этого изучают следующие различные векторы: противоположные, нулевые, коллинеарные и компланарные.

Существуют следующие действия над векторами:

• Суммирование;
• Скалярное, векторное и смешанное умножение на другой вектор, а также на другое число.

Аналитическая геометрия

Рассматривает определения плоскостей и трехмерного пространства.

Прямая на плоскости

Изучают несколько ее основных уравнений: нормальное уравнение, с угловым коэффициентом, через точку и направление, через 2 точки, в отрезках.

Плоскость и прямая в пространстве

Рассматривают уравнения, по которым плоскость задается в пространстве. Такие как: уравнения через точку перпендикулярно к вектору, через 3 точки, нормальное, и в отрезках.

При изучении прямой важно знать каноническое и по 2 точкам, общее, векторное, с направляющими коэффициентами.

Во всех трех случаях рассматривают формулы, по которым можно найти различные углы.

Взаимное расположение плоскостей и прямых

При рассмотрении данного вопроса изучают формулы углов, параллельность, перпендикулярность, принадлежность прямой к плоскости.

Линии второго порядка

В этом разделе рассматриваются определения и свойства нескольких фигур: эллипса, гиперболы и параболы.

В связи с эллипсом изучают его каноническое уравнение, а также определения эксцентриситета и директрис.

При рассмотрении гиперболы, изучают тоже самое, что и у эллипса. Но к этому добавляются понятия фокальных радиусов, а также уравнения асимптот.

При изучении параболы рассматривают, что представляет собой полуфокальный диаметр.

Чаще всего дисциплина высшей математики для первокурсников, заканчивается на изучении вышестоящей темы, но программа предмета может несущественно изменяться в зависимости от вуза.

Алгебра. Часть 1 | Открытые видеолекции учебных курсов МГУ

Курс “Алгебра. Часть 1” читается на механико-математическом факультете МГУ в 1 семестре. Это – первая часть курса алгебры, общая для отделения математики и механики (вторая часть курса алгебры, читающаяся в 3 семестре, предназначена только для отделения математики).

В содержание курса традиционно входят системы линейных уравнений, матрицы, определители, начальные сведения теории групп, колец, полей, основная теорема алгебры.

Страница курса: http://halgebra.math.msu.su/wi…

Список всех тем лекций

Лекция 1. Системы линейных уравнений.
Частные случаи линейных систем Определитель Матрица Общий вид системы линейных уравнений Решение системы линейных уравнений Однородные системы Метод Гаусса Улучшенный вид матрицы Теорема об эквивалентности системы после элементарных преобразований

Лекция 2. Метод Гаусса, векторные пространства.
Повтор предыдущей лекции Метод Гаусса Следствия метода Гаусса, строгоступенчатая матрица Арифметические векторные пространства

Лекция 3. Подпространства линейного пространства.
Лемма о выражении элемента через линейно независимый набор векторов Лемма о единственности выражения через линейно независимые элементы Подпространство Линейная оболочка Базис подпространства Размерность

Лекция 4. Фундаментальная система решений.
Лемма о множестве решений однородной системы Фундаментальная система решений Множество решений неоднородных систем Линейное подмногообразие Ранг матрицы

Лекция 5. Ранг матрицы.
Теорема о равенстве строчного и столбцового рангов матрицы Алгоритм нахождения базы системы векторов Теорема о размерности пространства решений однородной СЛУ Теорема о существовании для подпространства СЛУ, множеством решений которой является это подпространство Теорема Кронекера-Капелли (критерий совместности СЛУ)

Лекция 6. Операции над матрицами.

Критерий определённости СЛУ в терминах рангов Операции над матрицами Свойства умножения Транспонирование

Лекция 7. Обратная матрица.
Коммутативность Единичная матрица След матрицы Обратная матрица Теорема: ранг произведения матриц меньше или равен минимуму рангов матриц Основное правило комбинаторики

Лекция 8.

Подстановки.
Обратная подстановка Разложение подстановки в произведение независимых циклов Транспозиция Инверсия Знак подстановки Определители

Лекция 9.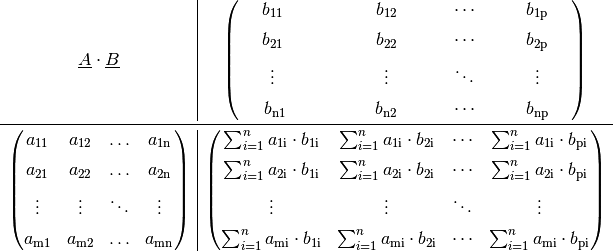 Определители.
Определители Свойства определителя Теорема о невырожденности определителя Теорема о функции, ставящей в соответствие набору векторов число

Лекция 10. Алгебраические дополнения.
Определитель с углом нулей Определитель Вандермонда Миноры Алгебраическое дополнение Разложение определителя Определитель произведения матриц Фальшивое разложение Присоединённая матрица Формула для присоединённой матрицы Формулы Крамера + теорема Крамера Теорема о ранге матрицы

Лекция 11. p, a,b – элементы поля Малая теорема Ферма

Лекция 13. Комплексные числа.
Комплексные числа Тригонометрическая форма записи Корень комплексного числа

Лекция 14. Многочлены от одной переменной.
Многочлены одной переменной Функциональное равенство Малая теорема Ферма Связь формальных и функциональных равенств Задача интерполяции Теорема о делении с остатком Корень многочлена Теорема Безу

Лекция 15. Производная многочлена, целое кольцо.
Число корней многочлена не превосходит его степени Производная многочлена Нахождение кратности корня Число корней многочлена с учётом их кратности не превосходит его степени Теория делимости, целостное кольцо

Лекция 16. Теория делимости.
Целостное кольцо Ассоциированность элементов Евклидовы кольца Лемма о норме произведения элементов Наибольший общий делитель Теорема о существовании НОД Лемма о линейном представлении НОД Взаимно простые элементы Простой и неприводимый элементы Лемма о делимости произведения элементов Теорема о разложении всякого ненулевого необратимого элемента Основная теорема алгебры Алгебраически замкнутое поле

Лекция 17. Основная теорема алгебры.
Существование корня многочлена, основная теорема алгебры Сходимость на комплексной плоскости Лемма о возрастании модуля Лемма Даламбера Доказательство основной теоремы алгебры Теорема Руффини – Абеля Отделение кратных корней

Лекция 18. Дополнения к О.Т.А., неприводимые многочлены.
Неприводимый многочлен Число, сопряжённое корню вещественного многочлена, является корнем Вещественный многочлен нечётной степени обладает вещественным корнем Неприводимый многочлен над полем рациональных чисел Алгоритм поиска корней многочлена с рациональными коэффициентами Теорема Декарта Теорема Штурма

Лекция 19. Рациональные дроби. Многочлены от нескольких переменных.
Рациональные числа Переход от целых чисел к рациональным Примеры Несократимая дробь Правильная дробь Простейшая дробь Теорема Лемма Многочлены от нескольких переменных Степень одночлена Лексикографический порядок Старший член многочлена Лемма о старшем члене произведения двух многочленов

Лекция 20. Симметрические многочлены.
Симметрические многочлены Элементарные симметрические многочлены Основная теорема о симметрических многочленах Теорема Виета Дискриминант

Лекция 21. Результант. Группа.
Дискриминант Результант Теорема о связи результанта и дискриминанта Выражение результанта через определитель Теория групп, определение группы Подгруппа Гомоморфизм

Лекция 22. Теория групп.
Гомоморфизм Изоморфизм Изоморфные группы Эндоморфизм и автоморфизм Ядро и образ Примеры групп Циклическая подгруппа Порядок элемента Циклическая группа

Лекция 23. Смежные классы и теорема Лагранжа.
Левый и правый смежные классы Индекс подгруппы Теорема Лагранжа Следствия теоремы Лагранжа Малая теорема Ферма Число левых смежных классов равно числу правых смежных классов

Матричная алгебра для инженеров | Coursera

Матричная алгебра для инженеров

Этот курс является частью специализации «Математика для инженеров»

Преподаватель: Джеффри Р. Часнов

Top Instructor

77,886 Курс уже зачислен

4 002 Получить представление о теме и узнать основы

---

4.9

(3 945 отзывов)

|

97%

Начальный уровень

Предыдущий опыт не требуется

19 часов (приблизительно)

Гибкий график

Учитесь в своем собственном темпе

Просмотр модулей курса

Чему вы научитесь

Подробности, которые нужно знать

90 3

Добавьте в свой профиль LinkedIn

Тесты и оценки

17 тестов, 4 оценки

Английский

Субтитры: арабский, французский,

Языки

Доступно на английском языке

Субтитры: арабский, французский, португальский (европейский), итальянский, вьетнамский, немецкий, русский, английский, испанский. |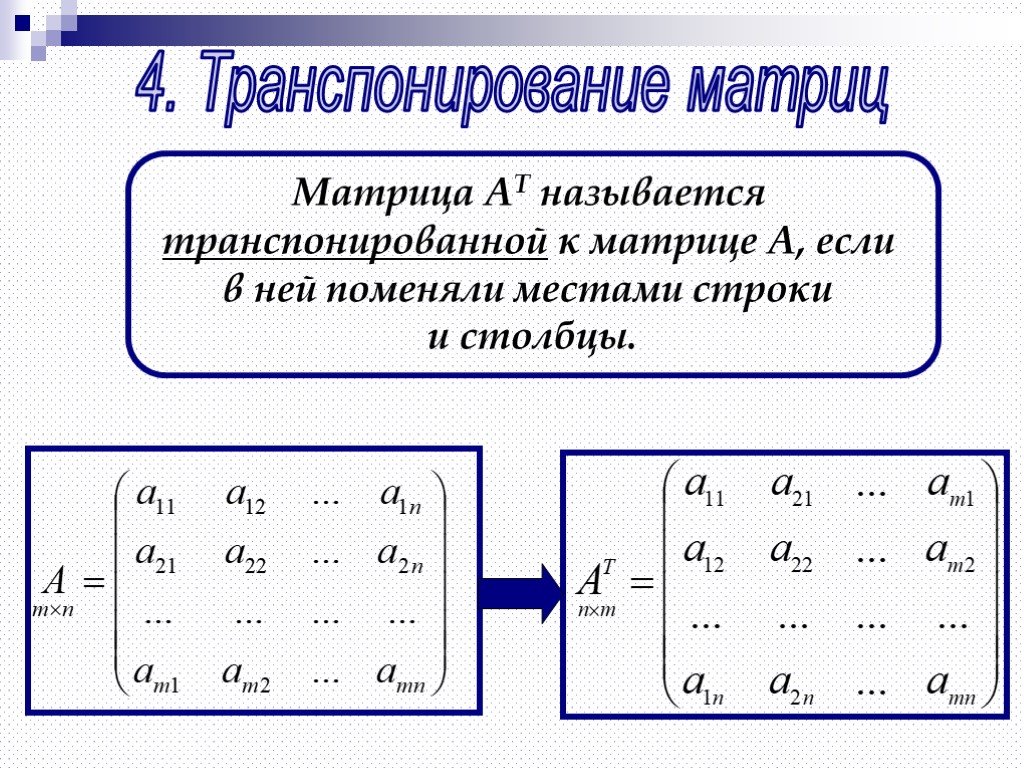

97%

Начальный уровень

Предыдущий опыт не требуется

19 часов (приблизительно)

Гибкий график

Учитесь в своем собственном темпе

Просмотр модулей курса

Узнайте больше о Coursera для бизнеса

Повысьте свои знания в предметной области

Этот курс является частью специализации «Математика для инженеров»

Когда вы зарегистрируетесь на этот курс, вы также будете зачислены на эту специализацию.

• Изучите новые концепции от отраслевых экспертов
• Получите базовое понимание предмета или инструмента
• Развивайте необходимые для работы навыки с помощью практических проектов
• Получите общий сертификат о карьере

В этом курсе 4 модуля

Этот курс полностью посвящен матрицам и кратко описывает линейную алгебру, которую должен знать инженер. Математика в этом курсе представлена ​​на уровне продвинутого старшеклассника, но рекомендуется, чтобы учащиеся проходили этот курс после прохождения университетского курса исчисления с одной переменной. Здесь не используются производные или интегралы, но ожидается, что учащиеся имеют базовый уровень математической зрелости. Несмотря на это, любой, кто заинтересован в изучении основ матричной алгебры, может присоединиться.

Курс состоит из 38 коротких лекций, за каждой из которых следует несколько задач для решения. После каждой основной темы проводится небольшая практическая викторина. Решения задач и практические тесты можно найти в конспектах лекций, предоставленных инструктором. Курс длится четыре недели, и в конце каждой недели проводится оцениваемый тест. Скачать конспект лекций по ссылке https://www.math.hkust.edu.hk/~machas/matrix-алгебра-для-инженеров.pdf И посмотрите рекламный ролик по ссылке https://youtu.be/IZcyZHomFQc

Матрицы — это прямоугольные массивы чисел, символов или выражений, расположенные в строках и столбцах. Мы определяем матрицы и показываем, как их складывать и умножать, определяем некоторые специальные матрицы, такие как единичная матрица и нулевая матрица, узнаем о транспонировании и инверсии матрицы, а также обсуждаем ортогональные матрицы и матрицы перестановок.

Что включено

10 видео27 чтений5 тестов

10 видео•Всего 79 минут

• Первая неделя Введение•0 минут•Модуль предварительного просмотра
• Определение матрицы | Лекция 1•7 минут
• Сложение и умножение матриц | Лекция 2•10 минут
• Специальные матрицы | Лекция 3•9 минут
• Транспонировать матрицу | Лекция 4•9 минут
• Внутренние и внешние изделия | Лекция 5•9 минут
• Обратная матрица | Лекция 6•12 минут
• Ортогональные матрицы | Лекция 7•4 минуты
• Матрицы вращения | Лекция 8•8 минут
• Матрицы перестановок | Лекция 9•6 минут

27 чтений•Всего 188 минут

• Приветствие и информация о курсе•1 минута
• Сертификат или аудит?•1 минута
• Как писать математические выражения в дискуссионных форумах с помощью MathJax•1 минута
• Construct Some Матрицы•5 минут
• Сложение и умножение матриц•5 минут
• AB=AC не влечет B=C•5 минут
• Умножение матриц не коммутирует•5 минут
• Ассоциативный закон для умножения матриц•10 минут
• AB=0, когда A и B отличны от нуля • 10 минут
• Произведение диагональных матриц • 5 минут
• Произведение треугольных матриц • 10 минут
• Транспонирование произведения матриц • 10 минут
• Любая квадратная матрица Записывается в виде суммы симметричной и кососимметричной матриц • 5 минут
• Построение квадратной симметричной матрицы • 5 минут
• Пример симметричной матрицы • 10 минут
• Сумма квадратов элементов матрицы • 10 минут
• Обратные матрицы два на два • 5 минут
• Обратные произведения матриц • 10 минут
• Обратные матрицы транспонирования • 10 минут
• Уникальность обратной • 10 минут
• Определитель как площадь • 10 минут
• Произведение ортогональных матриц • 5 минут
• Матрица идентичности ортогональна • 5 минут
• Матрица, обратная вращению • 5 минут
• Трехмерное вращение • 10 минут
• Матрицы перестановки три на три • 10 минут
• Инверсия матриц перестановок «три на три» • 10 минут

5 тестов • Всего 35 минут

• Диагностический тест • 5 минут
• Определения матриц • 10 минут гональные матрицы •10 минут
• Оценка первой недели (аудит)•0 минут

Систему линейных уравнений можно записать в матричной форме и решить методом исключения Гаусса. Мы узнаем, как привести матрицу к уменьшенной ступенчатой ​​форме строк, которую можно использовать для вычисления обратной матрицы. Мы также узнаем, как найти LU-разложение матрицы и как это разложение можно использовать для эффективного решения системы линейных уравнений с изменяющимися правыми частями.

Что включено

7 видео6 чтений3 теста

7 видео•Всего 70 минут

• Вторая неделя Введение•0 минут•Модуль предварительного просмотра
• Исключение по Гауссу | Лекция 10•14 минут
• Сокращенная форма эшелона строк | Лекция 11•8 минут
• Вычисление инверсий | Лекция 12•13 минут
• Элементарные матрицы | Лекция 13•11 минут
• LU Разложение | Лекция 14•10 минут
• Решение (LU)x = b | Лекция 15•11 минут

6 показаний•Всего 75 минут

• Исключение по Гауссу•15 минут
• Сокращенная форма эшелона строк•15 минут
• Вычисление инверсий•15 минут
• Элементарные матрицы•1 5 минут
  1
  • Решение (LU)x = b•10 минут

  3 теста•Всего 35 минут

  • Исключение Гаусса•20 минут
  • Разложение LU•15 минут
  • Вторая неделя Оценка (аудит)•0 минут

  Векторное пространство состоит из набора векторов и набора скаляров, которое замкнуто относительно сложения векторов и скалярного умножения и удовлетворяет обычным правилам арифметики. Мы изучим некоторые слова и фразы линейной алгебры, такие как линейная независимость, размах, базис и размерность. Мы узнаем о четырех фундаментальных подпространствах матрицы, процессе Грама-Шмидта, ортогональной проекции и матричной формулировке задачи наименьших квадратов о рисовании прямой линии, соответствующей зашумленным данным.

  Что включено

  13 видео14 чтений5 тестов

  13 видео•Всего 139 минут

  • Третья неделя Введение•0 минут•Модуль предварительного просмотра
  • Векторные пространства | Лекция 16•7 минут
  • Линейная независимость | Лекция 17•9 минут
  • Размах, основание и размер | Лекция 18•10 минут
  • Процесс Грама-Шмидта | Лекция 19•13 минут
  • Пример процесса Грама-Шмидта | Лекция 20•9 минут
  • Пустое пространство | Лекция 21•12 минут
  • Применение нулевого пространства | Лекция 22•14 минут
  • Пространство столбца | Лекция 23•9 минут
  • Пространство строки, левое пустое пространство и ранг | Лекция 24•14 минут
  • Ортогональные проекции | Лекция 25•11 минут
  • Задача о наименьших квадратах | Лекция 26•10 минут
  • Решение задачи наименьших квадратов | Лекция 27•15 минут

  14 чтений•Всего 90 минут

  • Нулевой вектор•5 минут
  • Примеры векторных пространств•5 минут
  • Линейная независимость • 5 минут
  • Ортонормированный базис • 5 минут
  • Процесс Грама-Шмидта • 5 минут
  • Грам-Шмидт на матрицах три на один • 5 минут
  • Грам-Шмидт на матрицах четыре на один •10 минут
  • Пустое пространство•10 минут
  • Недоопределенная система линейных уравнений•10 минут
  • Пространство столбцов•5 минут
  • Фундаментальные подпространства матрицы•10 минут
  • Ортогональные проекции•5 минут
  • Задача•5 минут
  • Линия наилучшего посадки • 5 минут

  5 Викторины • Всего 60 минут

  • Определения векторного пространства • 15 минут
  • Грамо-схмидт • 15 минут
  • .
  • Третья неделя Оценка (аудит)•0 минут

  Собственный вектор матрицы — это ненулевой вектор-столбец, который при умножении на матрицу умножается только на скаляр (называемый собственным значением). Мы узнаем о проблеме собственных значений и о том, как использовать определители для нахождения собственных значений матрицы. Мы узнаем, как вычислять определители, используя разложение Лапласа, формулу Лейбница и удаление строк или столбцов. Мы также узнаем, как диагонализовать матрицу, используя ее собственные значения и собственные векторы, и как это можно использовать для простого вычисления матрицы, возведенной в степень.

  Что включено

  13 видео20 чтений4 теста

  13 видео•Всего 118 минут

  • Четвертая неделя Введение•0 минут•Модуль предварительного просмотра
  • Два на три и три на три | Лекция 28•8 минут
  • Расширение Лапласа | Лекция 29•13 минут
  • Формула Лейбница | Лекция 30•11 минут
  • Свойства определителя | Лекция 31•15 минут
  • Проблема собственных значений | Лекция 32•12 минут
  • Нахождение собственных значений и собственных векторов (часть A) | Лекция 33•10 минут
  • Нахождение собственных значений и собственных векторов (Часть B) | Лекция 34•7 минут
  • Диагонализация матриц | Лекция 35•9 минут
  • Пример диагонализации матрицы | Лекция 36•15 минут
  • Степени матрицы | Лекция 37•5 минут
  • Степени матрицы Пример | Лекция 38•6 минут
  • Заключительные замечания•1 минута

  20 чтений•Всего 116 минут

  • Определитель единичной матрицы•5 минут
  • Перестановка строк•5 минут
  • Определитель матричного произведения•10 минут
  • Вычисление определителя с помощью разложения Лапласа•5 минут
  • Вычисление определителя с помощью формулы Лейбница•5 минут
  • Определитель матрицы с двумя равными строками•5 минут
  • Определитель является линейной функцией любой строки•5 минут
  • Определитель можно вычислить с помощью сокращения строк•5 минут
  • Вычисление определителя с использованием исключения Гаусса • 5 минут
  • Характеристическое уравнение для матрицы три на три • 10 минут
  • Собственные значения и собственные векторы матрицы два на два • 5 минут
  • Собственные значения и собственные векторы трехмерной матрицы Матрица на три • 10 минут
  • Комплексные собственные значения • 5 минут
  • Линейно независимые собственные векторы • 5 минут
  • Обратимость матрицы собственных векторов • 5 минут
  • Диагонализация матрицы «три на три» • 10 минут
  • Матричная экспонента•5 минут
  • Степени матрицы•10 минут
  • Пожалуйста, оцените этот курс•1 минута
  • Благодарности•0 минут

  4 теста•Всего 45 минут

  • Определители 01 Задача на собственные значения•15 минут
  • Диагонализация матрицы•15 минут
  • Оценка четвертой недели (аудит)•0 минут

  Преподаватель

  Рейтинги преподавателя

  Рейтинги преподавателя

  Мы попросили всех учащихся оставить отзыв о наших преподавателях, основываясь на качестве их стиля преподавания.

  4.8

  (1 260 оценок)

  Top Instructor

  Джеффри Р. Часнов

  Гонконгский университет науки и технологий

  16 курсов•173 655 учащихся

  4 9 04 003 9 51

  Гонконгский научный университет и технологии

  Предложено

  Гонконгским университетом науки и технологий

  HKUST — динамичный международный исследовательский университет, неустанно стремящийся к совершенству, ведущий вперед науку и технологии и обучающий новое поколение лидеров Азии и всего мира.

  Получите профессиональный сертификат

  Добавьте эти учетные данные в свой профиль LinkedIn, резюме или CV

  Поделитесь ими в социальных сетях и в своем обзоре эффективности

  Почему люди выбирают Coursera для своей карьеры

  Фелипе М.

  Учащийся с 2018 года

  “Возможность проходить курсы в своем собственном темпе и ритме была потрясающим опытом. Я могу учиться, когда это соответствует моему расписанию и настроению.”

  Дженнифер Дж.

  Учащийся с 2020 года

  «Я напрямую применила концепции и навыки, полученные на курсах, в новом увлекательном проекте на работе».

  Ларри В.

  Учащийся с 2021 года

  «Когда мне нужны курсы по темам, которых нет в моем университете, Coursera — одно из лучших мест».

  Чайтанья А.

  «Обучение — это не просто умение лучше выполнять свою работу: это гораздо больше. Coursera позволяет мне учиться без ограничений». Отзывов учащихся 2 10,29%

• 3 звезды

  0,96%

• 2 звезды

  0,17 %

• 1 звезда

  0,17%

J

JR

5

Отредактировано 5 августа 2021 г. остерегайтесь пролистывать детали: например. использование матричного формализма для решения задачи наименьших квадратов мало чем отличается от магии.

A

AM

5

Отзыв от 26 марта 2023 г.

Профессор Джефф – отличный лектор, способ его объяснения очень ясен и прост для понимания, поэтому курс интересен и дает отличное понимание матричной алгебры.

J

JP

5

Отзыв от 13 января 2021 г.

Он многому учит основам линейной алгебры. Я бы хотел, чтобы было больше примеров, но, возможно, это также зависит от ученика, если он хочет изучить больше задач.

Посмотреть другие обзоры

Откройте новые двери с Coursera Plus

Неограниченный доступ к более чем 7000 курсов мирового уровня, практическим проектам и программам сертификации готовых к работе — все это включено в вашу подписку

Узнать больше

Продвиньтесь по карьерной лестнице с онлайн-дипломом

Получите степень в университетах мирового класса — 100% онлайн в цифровой экономике

Узнать больше

Часто задаваемые вопросы

Доступ к лекциям и заданиям зависит от типа вашей регистрации. Если вы пройдете курс в режиме аудита, вы сможете увидеть большинство материалов курса бесплатно. Чтобы получить доступ к оцениваемым заданиям и получить сертификат, вам необходимо приобрести сертификат во время или после аудита. Если вы не видите вариант аудита:

• Курс может не предлагать вариант аудита. Вместо этого вы можете попробовать бесплатную пробную версию или подать заявку на финансовую помощь.

• Вместо этого курс может предлагать «Полный курс, без сертификата». Эта опция позволяет просмотреть все материалы курса, отправить необходимые оценки и получить итоговую оценку. Это также означает, что вы не сможете приобрести сертификат.

Записавшись на курс, вы получаете доступ ко всем курсам специализации, а по завершении работы получаете сертификат. Ваш электронный сертификат будет добавлен на вашу страницу достижений — оттуда вы можете распечатать свой сертификат или добавить его в свой профиль LinkedIn. Если вы хотите только читать и просматривать содержание курса, вы можете пройти бесплатный аудит курса.

Да. В некоторых учебных программах вы можете подать заявку на финансовую помощь или стипендию, если вы не можете позволить себе вступительный взнос. Если для выбора программы обучения доступна финансовая помощь или стипендия, вы найдете ссылку для подачи заявки на странице описания.

Дополнительные вопросы

Посетите справочный центр для учащихся

Изучайте матричную математику с помощью онлайн-курсов, занятий и уроков

Проходите бесплатные онлайн-уроки по матричной математике, чтобы улучшить свои навыки и повысить успеваемость в школе. Получите прочную основу для умножения матриц и линейной алгебры или освежите в памяти важные навыки решения задач.

Просмотреть все курсы edX

Курс

Курс

Курс

Курс

Курс

Курс

Курс

|Геометрические вычисления|Вычисления|Вычисления| Логическая статистика|Линейная алгебра|Предварительная алгебра |Вероятность

выучить матричную математику

Что такое умножение матриц?

Умножение матриц — это функция линейной алгебры, позволяющая составить из двух матриц матрицу, представляющую собой композицию. Вычисление матричных произведений является центральной частью вычислительных приложений. Он позволяет упростить линейные уравнения, создавать ходы в таких приложениях, как теория игр, или улучшать визуализацию изображений, несмотря на небольшие сложности. Умножение матриц — дело непростое, но с помощью программ, которые сделают всю тяжелую работу за вас, вы сможете применить его к своим вычислениям без лишней работы. Изучив этот процесс, вы создадите свой набор инструментов для выполнения высокоуровневых команд программирования и откроете множество творческих программных решений.

Изучение умножения матриц в программировании

Умножение матриц — это всего лишь один из методов работы с алгоритмами. Это сложнее, чем скалярное умножение, основанное на скалярном произведении для умножения комбинаций различных столбцов и строк. В скалярных или векторных операциях вы применяете скаляр к каждому элементу в матрице. Для умножения матриц требуется больше ловкости. Эти операции являются неотъемлемой частью программирования нейронных сетей в рамках машинного обучения. Вы должны уметь строить операции, учитывающие различные решения в матрице, и каждая новая матрица — это возможность еще больше расширить алгоритм.

Matrix Math Courses

Если вы не понимаете, как это применимо к программированию, edX может помочь. В партнерстве с ведущими учебными заведениями, включая Гарвард и IT Bombay, вы сможете изучить основы программирования алгоритмов и то, как умножение матриц вписывается в систему алгоритмов. Например, вы можете получить исчерпывающий обзор алгоритмов с помощью IT Bombay и узнать, как использовать умножение матриц в сети алгоритмов других типов для создания высокоуровневых приложений. Гарвардская серия программ по программированию также затрагивает умножение матриц. Вы получите представление об основных понятиях, начиная с самой первой матрицы и заканчивая фундаментальными свойствами матричной алгебры. Вы будете работать с реальными числами и создавать ноу-хау для различных операций.

Создайте свой набор инструментов для программирования с помощью матричной математики

Вам необходимо знать операции матричной математики и то, как она вписывается в экосистему алгоритмов программирования.