Матрица математика что такое: для чего нужны, применение, кто придумал, история возникновения - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Матрица (математика) – Wikiwand

ВведениеМатрица (математика)
История
ВведениеСистемы линейных уравненийЛинейные преобразования
ОпределенияПрямоугольная матрицаКвадратная матрицаВектор-строка и вектор-столбецЭлементарные преобразования матрицРанг матрицы
ОбозначенияТранспонированная матрицаДиагональная матрицаДругие диагонали матрицыЕдиничная матрицаНулевая матрица
Операции над матрицамиСложение матрицУмножение матрицы на числоУмножение матрицУмножение вектора на матрицуКомплексное сопряжениеТранспонирование и эрмитово сопряжениеМинорыСледОпределитель (детерминант)Перманент
Связанные понятияЛинейные комбинацииЛинейная зависимость
СвойстваМатричные операции
Примеры
Квадратная матрица и смежные определения
Кольцо матриц
Матрицы в теории групп
См. также
Примечания
Литература

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), который представляет собой совокупность строк и столбцов, на пересечении которых находятся его элементы. Количество строк и столбцов задает размер матрицы. Матрицу можно также представить в виде функции двух дискретных аргументов. Хотя исторически рассматривались, например, треугольные матрицы[1], в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.

Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.

Для матрицы определены следующие алгебраические операции:

сложение матриц, имеющих один и тот же размер^[⇨];
умножение матриц подходящего размера (матрицу, имеющую n{\displaystyle n} столбцов, можно умножить справа на матрицу, имеющую n{\displaystyle n} строк)^[⇨];
в том числе умножение матрицы на вектор-столбец и умножение вектор-строки на матрицу (по обычному правилу матричного умножения; вектор является в этом смысле частным случаем матрицы)^[⇨];
умножение матрицы на элемент основного кольца или поля (то есть скаляр)^[⇨].

Относительно сложения матрицы образуют абелеву группу; если же рассматривать ещё и умножение на скаляр, то матрицы образуют модуль над соответствующим кольцом (векторное пространство над полем). Множество квадратных матриц замкнуто относительно матричного умножения, поэтому квадратные матрицы одного размера образуют ассоциативное кольцо с единицей относительно матричного сложения и матричного умножения.

Доказано, что каждому линейному оператору, действующему в n{\displaystyle n}-мерном линейном пространстве, можно сопоставить единственную квадратную матрицу порядка n{\displaystyle n}; и обратно — каждой квадратной матрице порядка n{\displaystyle n} может быть сопоставлен единственный линейный оператор, действующий в этом пространстве.[2] Свойства матрицы соответствуют свойствам линейного оператора. В частности, собственные числа матрицы — это собственные числа оператора, отвечающие соответствующим собственным векторам.

То же можно сказать о представлении матрицами билинейных (квадратичных) форм.

В математике рассматривается множество различных типов и видов матриц. Таковы, например, единичная, симметричная, кососимметричная, верхнетреугольная (нижнетреугольная) и т. п. матрицы.

Особое значение в теории матриц занимают всевозможные нормальные формы, то есть канонический вид, к которому можно привести матрицу заменой координат. Наиболее важной (в теоретическом значении) и проработанной является теория жордановых нормальных форм. На практике, однако, используются такие нормальные формы, которые обладают дополнительными свойствами, например, устойчивостью.

МАТРИЦА • Большая российская энциклопедия

МА́ТРИЦА, таблица вида $$\begin{Vmatrix} a_{11} &a_{12} &… &a_{1n} \\ a_{21}& a_{22} & … & a_{2n}\\ …&… &… &… \\ a_{m1}&a_{m2} &… & a_{mn} \end{Vmatrix}$$

или $$\begin{pmatrix} a_{11} &a_{12} &… &a_{1n} \\ a_{21}& a_{22} & … & a_{2n}\\ …&… &.. *_{ij}$.

Действия над матрицами

(все М. рассматриваются над одним полем $K$). Важнейшими алгебраич. операциями над М. являются сложение М., умножение М. на число (элемент поля $K$), умножение матриц.

Суммой $A+B$ двух прямоугольных М. $A$ и $B$ одного размера $m×n$ называется М. $C$ размера $m×n$, для которой элемент $c_{ij}=a_{ij}+b_{ij}$, $i=1,…,m$, $j=1,…,n$, т. е. равен сумме соответствующих элементов слагаемых. Произведением М. $A$ на число $α$ называется М. $αA$, элементы которой получаются из элементов М. $A$ умножением на $α$ , т. е. $αA=||αa_{ij}||$, $i= 1,…,m$, $j=1,…,n$. Эти операции обладают свойствами

$$A+B=B+A,\\α(A+B)=αA+αB,\\A+(B+C)=(A+B)+C,\\(α+β)A=αA+βB,\\α(βA)=(αβ)A$$.

Умножение М. определяется только для таких пар М., у которых число столбцов в 1-м сомножителе равно числу строк во 2-м сомножителе, при этом произведение $AB$ М.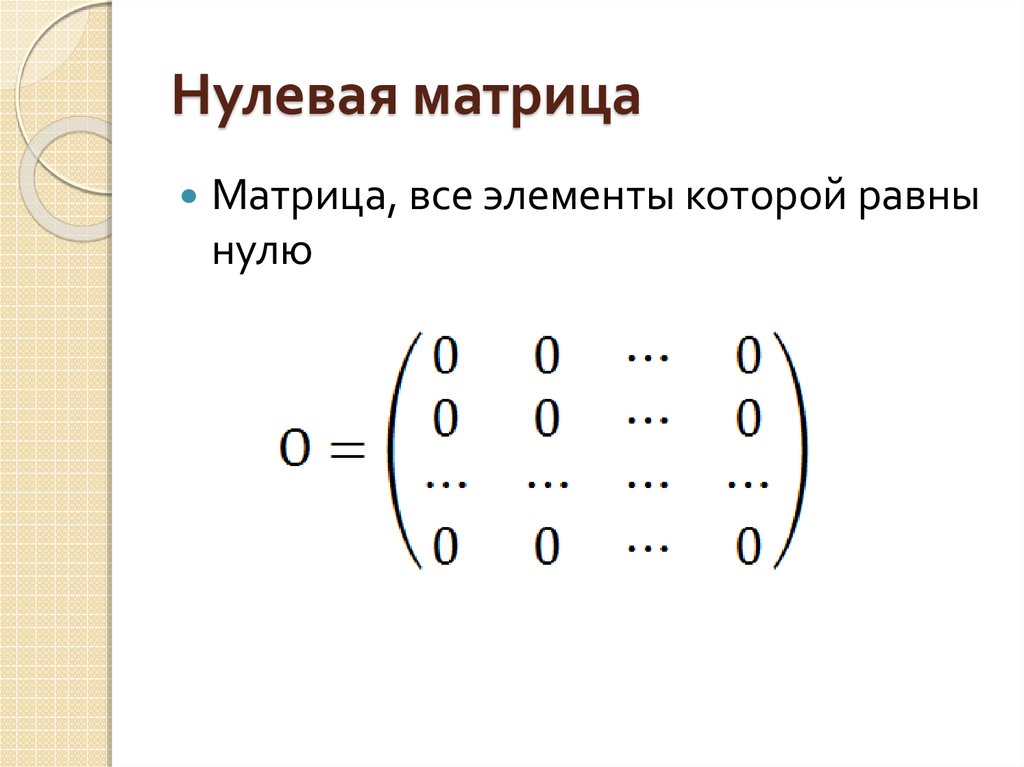 n$ называются диагональными; эти элементы расположены на т. н. главной диагонали М. Квадратная М., у которой все элементы, не лежащие на гл. диагонали, равны нулю, т. е. М. вида $$\begin{Vmatrix} d_1 &0 &… &0 \\ 0& d_2 & … & 0\\ …&… &… &… \\ 0&0 &… & d_n \end{Vmatrix}$$

называется диагональной и обычно обозначается $\textrm{diag} (d_1,…,d_n)$. Если в диагональной М. все элементы на гл. диагонали равны единице, то М. называется единичной и обозначается $E$ или $I$ (соответственно $E_n$ или $I_n$, если нужно указать её порядок): $$E=\begin{Vmatrix} 1 &0 &… &0 \\ 0& 1 & … & 0\\ …&… &… &… \\ 0&0 &… & 1 \end{Vmatrix}$$

Для любой М. $A$ размера $m×n$ справедливы равенства

$AE_n=A, \:E_mA=A.$

Каждой квадратной М. можно поставить в соответствие число (элемент поля $K$), называемое её определителем или детерминантом. {–1}AS$. Одной из задач теории М. является поиск М. $B$, подобной М. $A$ и имеющей более простой вид. Решение этой задачи связано с рассмотрением характеристич. многочлена М. $A$ и собственных векторов соответствующего линейного преобразования. В качестве канонич. вида М., подобной данной, принимается, напр., жорданова нормальная форма М., когда М. $B$ представляется в виде $$\begin{Vmatrix} B_1 &0 &… &0 \\ 0& B_2 & … & 0\\ …&… &… &… \\ 0&0 &… & B_p \end{Vmatrix} $$

где $B_1,…,B_p$ – т. н. жордановы клетки, т. е. квадратные матрицы вида $$\begin{Vmatrix} \lambda _i &1 & & & & &0 \\ &\lambda _i & 1 & & & & \\ & & . & & & & \\ & & & . & & & \\ & & & & . & & \\ & & & & & \lambda _i & 1\\ 0& & & & & &\lambda _i \end{Vmatrix},$$

где $λ_i$, $i=1,. k}{k!}.$$

Применения матриц

Матричный язык, обозначения и матричные вычисления используются в разл. областях совр. математики и её приложений. М. являются осн. математич. аппаратом линейной алгебры и применяются при исследовании линейных отображений векторных пространств, линейных и квадратичных форм, систем линейных уравнений. М. используются в математич. анализе, механике и теоретич. электротехнике, квантовой теории и др. (см. Матричные методы). Бесконечные М. используются в функциональном анализе (теория линейных операторов, теория представлений групп).

Историческая справка. Впервые М. как математич. понятие появилось в работах У. Гамильтона, А. Кэли и Дж. Сильвестра в сер. 19 в. Основы теории М. созданы К. Вейерштрассом и Ф. Г. Фробениусом во 2-й пол. 19 – нач. 20 вв. Совр. обозначение – две вертикальные черты – ввёл Кэли (1841).

2.1 Определения и матричная алгебра

Определение 2.1

An m ✕ n матрица представляет собой прямоугольную сетку чисел с 9 m строками и n столбцов.
Вектор-столбец представляет собой матрицу м ✕1.
Вектор-строка из представляет собой матрицу 1✕ n .
Квадратная матрица размером равна м ✕ м для некоторых м .

Набираем матрицы так: \[A= \begin{pmatrix} 1 & 2 & 3 \\ 0 & -1 & \pi \end{pmatrix}, B=\begin{pmatrix} 1\2\3 \end{pmatrix}, C=\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \конец{pmatrix}\] это матрица 2✕3, вектор-столбец 3✕1 и 3✕3 квадратная матрица соответственно.

Определение 2.2 Элемент матрицы i , j представляет собой число в строке i и столбец j .

Например, запись 1, 2 матрицы A выше равна 2, запись 2, 1 равна 0, а запись 2, 3 – это $\pi$. Очень часто мы пишем $A=(x_{ij})$, чтобы обозначить, что A является матрица, запись i , j которой равна $x_{ij}$.

Если две матрицы A и B имеют одинаковый размер (то есть обе м ✕ n для тех же м и n ) потом их складываем и вычитаем добавляя и вычитая каждую запись отдельно:

\[\begin{align*} \begin{pmatrix} 1 и 2 \\ 3 и 4 \end{pmatrix} + \begin{pmatrix} 0 и 1 \\-1 и -1 \end{pmatrix} &= \begin{pmatrix} 1 и 3 \\ 2 и 3 \end{pматрица} \\ \begin{pmatrix} 1&0 \end{pmatrix} – \begin{pmatrix} 9 и 9 \end{pmatrix} &= \begin{pmatrix} -8 и -9 \end{pматрица} \end{align*}\]

Мы также умножаем матрицы на числа по одной записи за раз («по входу»): \[2 \begin{pmatrix} 1&2&3 \\0 & 1 & 0 \end{pmatrix}= \begin{pmatrix} 2&4&6\\0&2&0 \end{pmatrix}\]

Это называется скалярным умножением на . Он удовлетворяет некоторые простые тождества: для любых матриц A и B одинакового размера и любой номер

л и м , \[\начать{выравнивать*} (l + m) A &= lA + m A \\ л(А+В) &= л А + л В \\ l(m A) &= (lm)A. \end{align*}\]
Определение 2.3 m ✕ n нулевая матрица , записанная $\mathbf{0}_{m\times n}$, равна ✕ 9Т = А\).
линейная алгебра – Какое самое строгое определение матрицы?
спросил 6 лет, 8 месяцев назад
Изменено 6 лет, 5 месяцев назад
Просмотрено 5к раз
$\begingroup$
Является ли матрица просто прямоугольным массивом символов и выражений, или ее можно определить более формально?
линейная алгебра
матрицы
определение
$\endgroup$
8
$\begingroup$
Пусть $I_n:=\{1,\cdots, n\}$.
$n \times m$-матрица с коэффициентами в кольце $\mathcal{R}$ есть функция $a: I_n \times I_m \to \mathcal{R}$. Определим $a_{i,j}:=a(i,j)$.
Другими словами, прямоугольный массив.
Примечание: с моей точки зрения, я думаю, что это особенно полезно рассматривать вышеприведенное определение как модель для концепции матрицы и подсознательно сохранить соответствующую идею прямоугольного массива в качестве основной концепции. Если вы действительно понимаете основную концепцию и имеете относительное удобство в математике, придумать приведенное выше определение несложно.
$\endgroup$
14
$\begingroup$
Стандартный способ определить таблицу значений в некотором множестве $S$ как математический объект состоит в том, чтобы закодировать позиции как набор индексов $S$ и представить таблицу как карту $I\to S$, которая связывает каждой позиции это значение в таблице.

Тогда матрицы с $n$ строками и $m$ столбцами и значениями в $R$ можно было бы представить (принимая обычное соглашение о размещении индекса строки перед индексом столбца) в виде карт $([n]\times[m])\ в R$, где $[n]$ — сокращение для $n$-элементного множества $\{1,\ldots,n\}$, а “$\times$” обозначает декартово произведение.
Однако у этого определения есть недостаток, заключающийся в том, что значения $n,m$ не всегда могут быть восстановлены из матрицы, даже если домен может быть восстановлен из карты. Проблема в том, что $[n]\times[m]=\emptyset$ всякий раз, когда $n=0$ или $m=0$, поэтому для матрицы, которая является уникальным отображением $\emptyset\в R$, нельзя восстановить значения $n,m$. Бурбаки даже прямо заявляет, что существует уникальная пустая матрица, упуская из виду тот факт, что это вызывает проблемы с определениями, которые сразу же следуют в их собственном изложении. При повседневном использовании матриц очень часто предполагается, что по матрице $n\times m$ известно, что такое $n$ и $m$, но с определением матрицы как карты это просто неверно.
в случае пустой матрицы. А пустые матрицы необходимы для кодирования линейных карт между конечномерными векторными пространствами, в случае, если векторное пространство размерности $~0$ является доменом или кодоменом линейной карты.
Одна из причин, по которой это реальная проблема, заключается в том, что умножение матриц определяется таким образом, что любое произведение матрицы $n\times k$ на матрицу $k\times m$ должно быть матрицей $n\times m$ , каждый элемент которого получается суммой $k$ слагаемых. Если $k=0$, то оба операнда умножения являются пустыми матрицами, поэтому каждый элемент произведения, являющийся суммой $0$ слагаемых, должен быть равен $0$, что дает нулевую матрицу размера $n\times m$. Однако для этого необходимо знать значения $n$ и $m$, а с определением матрицы как карты это невозможно. Просто нельзя определить произведение уникальной пустой матрицы на себя как нулевую матрицу другого размера в зависимости от обстоятельств.
Таким образом, вывод состоит в том, что для строгого определения матрицы необходимо записывать размеры как компоненты самой матрицы. Таким образом, правильное и строгое определение матрицы состоит в следующем.
Матрица с элементами в $R$ — это тройка $(n,m,f)$, где $n,m\in\Bbb N$ и $f$ — отображение $([n]\times[m]) \ до рупий.
$\endgroup$
7
$\begingroup$ 9{n\times m}$ определяется как $R$-модуль (векторное пространство, если $R$ — поле), свободно порожденный элементами $\{e_{i,j}\}$, где $1\leq i \leq n$ и $1 \leq j \leq m$. Элемент $e_{i,j}$ представляет собой матрицу, все элементы которой равны нулю, кроме элемента в $i$-й строке и $j$-м столбце, который равен единице.
Например, для $n=5, m=6$
$$e_{2,4}=\begin{pmatrix}0&0&0&0&0&0\\0&0&0&1&0&0\\0&0&0&0&0&0\\0&0&0&0&0&0\\0&0&0&0&0&0\end{pmatrix}$ $ 9н$.
$\endgroup$
11
$\begingroup$
Пусть $m$ и $n$ — натуральные числа, а $F$ — поле. Матрица $m$ на $n$ с элементами в $F$ — это функция из $S$ в $F$, где $S$ — множество всех упорядоченных пар целых чисел $(i,j)$, таких что $1 \leq i \leq m $ и $1\leq j \leq n $.
$\endgroup$
$\begingroup$
Другие ответы определяют матрицу как просто прямоугольный массив чисел. Это не только игнорирует красоту структур, но и делает доказательство многих основных фактов (например, что определитель является мультипликативным среди бесчисленного множества других) очень громоздким.
Конечно, матрицы могут иметь очень разные математические структуры в зависимости от того, как вы их интерпретируете. (например, линейные преобразования, билинейные формы и т. д.) Так как это наиболее распространено, вот как можно определить матрицу как линейное преобразование:
Пусть $V$ и $W$ — конечномерные векторные пространства над полем $F$ с базами $B$ и $C$ соответственно. Пусть $T:V\to W$ — линейное отображение. Тогда “матрица” для $T$ может быть определена как отображение $B\times C\to F$, которое отображает $(\beta,\gamma)$ в коэффициент при $T(\beta)$ в ( единственное) разложение $\gamma$ по образу $B$ при $T$, которое является базисом для $W$.
На самом деле теперь очевидно, как можно распространить это определение на «бесконечные матрицы».
$\endgroup$
3
$\begingroup$
В зависимости от того, насколько абстрактным/общим/формальным вы хотите стать, вы можете проверить (google) пространство Chu, например, https://en.wikipedia.org/wiki/Chu_space Ваша фраза “массив символов и выражений ” предполагает, что вы, возможно, захотите обсудить более абстрактные массивы, чем числа/поля/и т. д. Если страница в Википедии вызывает у вас аппетит, я бы сказал, что наиболее полное, но легкое для восприятия введение находится на странице http://boole.