как обозначается, определитель и свойства, отличие от обратной
Нам уже знакомо понятие матрицы. Этот математический объект имеет прикладное значение: он позволяет структурировать числа и информацию, проводить сложные расчёты. С ним можно проделывать различные операции, и одной из них является транспортирование.
Что такое транспонированная матрица, в чем отличие от обычной
Транспонирование – это алгоритм, при котором m-строки меняются местами с n-столбцами.
Транспонированная матрица, в отличие от обычной, помогает получить одинаковый результат при умножении на вектор-столбец и вектор-строку, что значительно упрощает дальнейшие математические вычисления.
Особенности, определитель и свойства целочисленных
- (AT )T = A;
- (k · A)T = k · AT;
- (A + B)T = AT + ВT;
- (A · B)T = ВT · AT
Если матрица А – квадратная (m=n), то определитель исходной и транспортированной матрицы равны: det AT = det A.
Напомним, что определитель – это некоторое число, с которым можно сравнить любую квадратную матрицу.
Формула, как обозначается транспонированная матрица
Если исходная матрица обозначается как А, то у транспортированной будет обозначение A
Тогда формула для транспортировки выглядит следующим образом:
A
T ij = A jiФормально, если А = m × n, то AT = n × m, но математически это записывается через индексы i и j.
Примеры задач на транспонирование матриц
Само транспортирование – довольно лёгкий процесс. Рассмотрим один пример.
Задача: даны А = (m × n) и В = (m × n).
Необходимо выполнить транспортирование.
Решение
Произведение и сумма транспонированных матриц
Теорема: транспонирование произведения матриц равно произведению транспонированных матриц, взятых в обратном порядке.
В математическом виде теорема выглядит так:
С
T = (A · B)T = ВT · АTПример:
Сумма вычисляется по аналогичной формуле:
C
T = (A + B)T = AT + ВTПериодически возникают сложности с учебой? ФениксХэлп может помочь!
Размер матрицы все, что нужно знать
Раньше было вполне логичным, что покупая компактную камеру, вы получали небольшую матрицу, а если выбирали крупногабаритную зеркалку со сменными объективами, матрица на ней была значительно больше. Это сказывалось на качестве фотографий, поскольку чем больше матрица, тем более детализированы были изображения.
Сейчас это в принципе, тоже в какой-то мере актуально, матрица — это самая дорогая часть камеры в плане производства, и чем больше матрица, тем и камера, соответственно, дороже. Потому на дорогие камеры обычно не устанавливаются матрицы 1/2. 3 дюймовые, а на дешевых, соответственно, не найти полнокадровую.
3 дюймовые, а на дешевых, соответственно, не найти полнокадровую.
Но надо сказать, что сейчас многие производители стали предлагать компактные камеры с относительно большими матрицами, точно так же как и камеры под сменные объективы с меньшими матрицами. Так что разобраться в ситуации, пожалуй, стало сложнее. Небольшие матрицы способны отлично срабатывать в различных условиях, и даже имеют некоторые преимущества перед большими.
За последние годы и сама технология создания матриц значительно продвинулась вперед, так что сегодня большое количество предлагаемых вариантов может смутить даже опытного пользователя, что уж говорить о тех, кто приобретает первую фотокамеру. А ведь размер матрицы еще и на фокусном расстоянии сказывается, так что учитывать при выборе камеры действительно нужно очень многое.
Итак, мы решили разобраться в различных типах матриц, чтобы расставить все по местам. Но для начала нужно уточнить, как именно размер матрицы влияет на эффективное фокусное расстояние.
Фокусное расстояние
Итак, мы уже выяснили, что размер матрицы связан с фокусным расстоянием, то есть с тем, какой именно объектив подойдет вашей камере. Если вы приобретаете компактный девайс с не съемным объективом, проблема сама собой отпадает, то есть с позиции покупателя это гораздо проще. Но не просто так профессионалы выбирают именно те камеры, где объективы можно менять. Любой объектив должен иметь поле (круг) изображения или диаметр света, который существует в объективе и который покрывает размер матрицы. Есть одно исключение, к которому мы вернемся позже.
Итак, встроенные или нет, объективы всегда помечены реальным фокусным расстоянием, а не эффективным фокусным расстоянием, которое вы получите при использовании на той или иной камере. Но проблема в том, что различные объективы с различной маркировкой могут в итоге обеспечить одно и то же фокусное расстояние для работы. Почему? Потому что они предназначены для разных матриц. Именно поэтому производители помимо маркировки указывают эквивалент, где основным расстоянием считается 35мм или полнокадровая матрица.
Вот — один из примеров: камера с матрицей меньше чем полнокадровая вполне может использоваться с 18-55мм объективом, но на деле фокусное расстояние, которое вы получите будет ближе к 27-82мм. Это все происходит потому, что матрица не достаточно велика, чтобы использовать объектив точно так же как смог бы полнокадровый. Из-за того, что периферическое пространство внутри объектива не принимается в расчет, получается тот же эффект как от использования объектива с большим фокусным расстоянием.
В компактных камерах может был установлен 19мм объектив, но из-за размера матрицы, который меньше фуллфрейма, вы получите в итоге большее фокусное расстояние, около 28мм. Точная длина определяется кроп-фактором, то есть числом, на которое нужно увеличить данное под фуллфрейм фокусное расстояние, чтобы выяснить какое расстояние получится на той или иной камере.
Размеры матриц
1/2.3 дюйма
Размер такой матрицы примерно 6.3 x 4.7 мм. Это — самая маленькая матрица, которую можно найти в современных камерах, и чаще всего — в бюджетных компактных моделях. Разрешение такой матрицы составляет, как правило, 16-20 Мп.
Разрешение такой матрицы составляет, как правило, 16-20 Мп.
По крайней мере такой расклад был самым популярным какое-то время назад. Сегодня многие производители стали делать больший упор на любительские фотоаппараты с большими матрицами, так что и размер такой не так распространен как ранее.
Однако, преимущество в том, что такой размер позволяет получить компактную камеру и использовать ее с длиннофокусными объективами, например компактными суперзумами. А большая матрица значит, что и объектив понадобится больший.
При хорошем освещении такие камеры могут предоставить неплохой результат, но для более придирчивых фотографов они точно не подойдут, поскольку при низкой освещенности будут зернить.
1/1.7 дюймов
Размер этих матриц 7.6 x 5.7мм. С такой матрицей гораздо проще выделить объект съемки из фона, и соответственно, производительность в плане деталей как в тени, так и на свету. Так что использовать их можно уже в более разнообразных условиях. Раньше такие камеры были самыми распространенными среди любителей, но сейчас их место стремительно занимают дюймовые матрицы, о которых речь и пойдет дальше.
Раньше такие камеры были самыми распространенными среди любителей, но сейчас их место стремительно занимают дюймовые матрицы, о которых речь и пойдет дальше.
А вот 1/1.7 дюймовые матрицы используются в некоторых относительно устаревших камерах Q-серии Pentax.
Дюймовые матрицы
Размер дюймовой матрицы 13.2мм x 8.8мм. Сегодня такие матрицы очень популярны на различных типах камер, размер позволяет им оставаться легкими и компактными. Логично, что самый популярный способ применения для дюймовой матрицы — это карманные любительские камеры, на которых объектив будет лимитирован 24-70мм или 24-100мм (если брать эквивалент 35мм). Однако, на некоторых суперзум камерах он тоже используется?, примеры — это Sony RX10 III и Panasonic FZ2000.
Гораздо лучше дюймовая матрица нам знакома по камерам Nikon серии 1, например Nikon 1 J5 — отличной и легкой камере, которая способна делать отличные фото и снимать 4К видео. Такую матрицу можно встретить даже среди смартфонов — Panasonic CM1.
Камеры с дюймовой матрицей способны показать результаты, значительно отличные от предыдущих вариантов. Качество их будет высоким, а даже компактные камеры, как правило, имеют широкую максимальную апертуру, так что на матрицу попадает достаточно света, потому и фотографии выходят четкими и резкими.
Частично, это результат технологии, а не только размера матрицы. Матрицы современного производства могут более эффективно захватывать свет.
Микро 4/3
Матрица микро 4/3 имеет физический размер 17.3 x 13мм. Этот формат используется в компактных зеркалках и беззеркалках Olympus и Panasonic. Они ненамного больше по размеру, чем дюймовые матрицы, но меньше чем APS-C, речь о которых пойдет ниже.
По сути, микро 4/3 — это четверть размера полнокадровой матрицы, так что считать для нее активное фокусное расстояние предельно просто: достаточно умножить фокусное расстояние на 2.
Иными словами, 17мм объектив на камере с матрицей микро 4/3 обеспечит фокусное расстояние такое же, как 34мм объектив на полнокадровой матрице. По аналогии, 12-35мм даст 24-70мм и так далее.
По аналогии, 12-35мм даст 24-70мм и так далее.
На камере Lumix DMC-LX100 используется матрица микро 4/3 разрешением 12.8 Мп. Это — одна из компактных цифровых камер, которые обладают большим количеством функций и небольшим размером. Камера оснащена объективом Leica с фокусным расстоянием 24-75мм.
APS-C
Средний физический размер такой матрицы 23.5 x 15.6мм. Такая матрица используется на зеркальных камерах для начинающих и любительских камерах, а сейчас и на многих беззеркалках. Матрица APS-C обеспечивает отличный баланс между качеством изображения, размером и вариативностью в плане совместимости с различными объективами.
Не все APS-C матрицы одинаковы по размеру, ведь это зависит от производителя тоже. Например, матрицы APS-C на камерах Canon физически немного меньше чем те, что установлены в Nikon и Sony, таким образом ее кроп-фактор равен 1.6x, а не 1.5x. В любом случае, APS-C — это всегда отличный вариант и профессиональные фотографы нередко предпочитают его для съемок природы и спортивных мероприятий, потому что благодаря кроп-фактору появляется возможность “приблизиться” к объекту съемки имеющимся объективом.
APS-C доступны на некоторых компактных камерах, например Fujifilm X100F, это обеспечивает высокое качество для фотографий на портативных камерах, особенно в комплекте с объективами с постоянным фокусным расстоянием. 23мм объектив на Fujifilm X100F, имеет широкую максимальную апертуру, потому с помощью этой камеры можно без труда добиться узкой глубины резкости.
APS-H
Размер матриц APS-H как правило равен 26.6 x 17.9мм. Сегодня этот формат практически не встречается, и ассоциируется только с устаревшими моделями Canon EOS-1D (EOS-1D Mark III и Mark IV). Сейчас, правда, в этой серии используются фуллфреймы.
Поскольку APS-H больше чем APS-C, но меньше полнокадровой матрицы, кроп-фактор, соответственно равен 1.3х, потому 24мм объектив обеспечит на такой камере фокусное расстояние приблизительно 31мм.
Одна из последних фотокамер, где можно встретить такую матрицу — это Sigma sd Quattro H. Однако и Canon решили не отказываться от APS-H совсем, и предпочли применить эту матрицу для камер наблюдения, а не для зеркальных фотоаппаратов.
Фуллфрейм
36 x 24мм она же фуллфрейм, она же полнокадровая матрица и она же примерно такая же по размеру как негатив пленочной фотографии. Используются полнокадровые матрицы на любительских и профессиональных камерах и считаются самым удобным вариантом для съемок. Размер такой матрицы позволяет ей принимать на себя больше света, вследствие чего и фото получаются выше по качеству чем с меньшими матрицами. Соответственно, и когда речь идет о количестве пикселей, выбор больше. А разрешение полнокадровых матриц варьируется от 12 до 50Мп.
Кроп-фактор, конечно, в случае с полнокадровой матрицей значения не имеет, так как маркировка объектива будет соответствовать активному фокусному расстоянию. Однако же, некоторые объективы, созданные под APS-C матрицы все равно можно использовать с фуллфреймами, но разрешение будет ограничено (камера обрежет углы, чтобы избежать виньетирования). Но проверять совместимость, разумеется, нужно всегда, иначе есть риск повредить зеркало.
Средняя (медиум) матрица
44мм x 33мм – размер такой матрицы. Это, очевидно, больше фуллфрейма и с момента появления такие матрицы вызвали оживленный интерес и дискуссии. Они использованы в камерах Fujifilm GFX 50S, Hasselblad X1D и Pentax 645Z, последняя немного старше остальных. Применяются они в основном, исключительно профессиональными фотографами в силу цены таких камер и их специфики.
Не факт, что на этом развитие матриц как таковых остановится, но пока что это — все доступные на рынке типы матриц, а какая подойдет для ваших фото интересов, решать только вам.
подключение, настройка и начало работы [Амперка / Вики]
Используйте светодиодную матрицу 8×8 Kitronik ZIP Tile из умных цветных светодиодов для отображения радужной анимации, бегущего текста и простых изображений. Матрицы объединяются в цепочки или гирлянды. Благодаря симметричному и равномерному размещению светодиодов по лицевой стороне из нескольких панелей легко собрать большой экран.
Светодиодная матрица Kitronik ZIP Tile сделана специально для контроллеров BBC micro:bit.
Подключение и настройка
Аппаратная часть
Подключите светодиодную матрицу к платформе mirco:bit, выберите один из двух способов:
- BBC micro:bit Hidden. Плата micro:bit расположена под светодиодной матрицей.
- BBC micro:bit Visible. Плата micro:bit расположена над светодиодной матрицей.
В обоих случаях платы скрепляются через 5 отверстий в краевом разъёме платы micro:bit и соответствующих резьбовых отверстий в Kitronik ZIP Tile. Для крепежа используйте металлические винты и пластиковые стойки, которые идут в комплекте.
Что понадобится
Источник питания для Kitronik ZIP Tile, например:
Крепёж из комплекта: винты и стойки
BBC micro:bit Hidden
- Установите micro:bit лицевой стороной сверху на обратную сторону платы Kitronik ZIP Tile.

- Подключите платформу micro:bit к компьютеру по USB.
- Подключите к полученному устройству питания через JST PH-2 разъём.
BBC micro:bit Visible
- Установите micro:bit обратной стороной сверху на обратную сторону платы Kitronik ZIP Tile.
- Подключите платформу micro:bit к компьютеру по USB.
- Подключите к полученному устройству питания через JST SH-2 разъём.
Программная часть
- Создайте новый проект.
- Установите дополнительное программное обеспечение для Kitronik ZIP Tile:
и вбейте в поиск строку . Далее жмите по иконке найденного расширения для установки модуля. После установки в окне компонентов вы увидите дополнительные блоки для светодиодной матрицы.
На этом этапе матрица настроена на работу с системой micro:bit и можно смело переходить к примерам работы.
Примеры работы
Рассмотрим несколько примеров по работе со светодиодной матрицей Kitronik ZIP Tile. Каждый пример сопровождается инструкцией по визуальному программированию, а затем кодом на JavaScript и Python.
Каждый пример сопровождается инструкцией по визуальному программированию, а затем кодом на JavaScript и Python.
Проверка матрицы
Для начала проведем тест матрицы, заставим светодиоды по очереди зажигаться красным, зелёным, синим и белым цветом.
Пример для визуального программирования
- Соберите схему из визуальных блоков.
- Нажмите на иконку со значком USB для загрузки программы в плату micro:bit.
- После прошивки micro:bit, светодиоды на Kitronik ZIP Tile будут мигать красным, зелёным, синим и белым цветом.
Пример для JavaScript
- Переключите визуальный режим MakeCode на текстовый редактор JavaScript.
- Прошейте платформу кодом приведённым ниже.
- microbit-kitronik-zip-tile-examples-blink-javascript.js
let tileDisplay = Kitronik_Zip_Tile.createZIPTileDisplay(1, 1, Kitronik_Zip_Tile.UBitLocations.Hidden) basic.forever(function () { tileDisplay.showColor(Kitronik_Zip_Tile. colors(ZipLedColors.Red))
basic.pause(1000)
tileDisplay.showColor(Kitronik_Zip_Tile.colors(ZipLedColors.Green))
basic.pause(1000)
tileDisplay.showColor(Kitronik_Zip_Tile.colors(ZipLedColors.Blue))
basic.pause(1000)
tileDisplay.showColor(Kitronik_Zip_Tile.colors(ZipLedColors.White))
})
colors(ZipLedColors.Red))
basic.pause(1000)
tileDisplay.showColor(Kitronik_Zip_Tile.colors(ZipLedColors.Green))
basic.pause(1000)
tileDisplay.showColor(Kitronik_Zip_Tile.colors(ZipLedColors.Blue))
basic.pause(1000)
tileDisplay.showColor(Kitronik_Zip_Tile.colors(ZipLedColors.White))
})
- После прошивки micro:bit, светодиоды на Kitronik ZIP Tile будут мигать красным, зелёным, синим и белым цветом.
Пример для Python
- Переключите визуальный режим MakeCode на текстовый редактор Python.
- Прошейте платформу кодом приведённым ниже.
- microbit-kitronik-zip-tile-examples-blink-python.py
tileDisplay = Kitronik_Zip_Tile.create_zip_tile_display(1, 1, Kitronik_Zip_Tile.UBitLocations.HIDDEN) def on_forever(): tileDisplay.show_color(Kitronik_Zip_Tile.colors(ZipLedColors.RED)) basic.pause(1000) tileDisplay.show_color(Kitronik_Zip_Tile.colors(ZipLedColors.GREEN)) basic.pause(1000) tileDisplay. show_color(Kitronik_Zip_Tile.colors(ZipLedColors.BLUE))
basic.pause(1000)
tileDisplay.show_color(Kitronik_Zip_Tile.colors(ZipLedColors.WHITE))
basic.forever(on_forever)
show_color(Kitronik_Zip_Tile.colors(ZipLedColors.BLUE))
basic.pause(1000)
tileDisplay.show_color(Kitronik_Zip_Tile.colors(ZipLedColors.WHITE))
basic.forever(on_forever)
- После прошивки micro:bit, светодиоды на Kitronik ZIP Tile будут мигать красным, зелёным, синим и белым цветом.
Радужное свечение
Каждый светодиод в матрице может светится отдельным индивидуальным цветом. Выведем на матрицу радужное свечение всех цветов.
Пример для визуального программирования
- Соберите схему из визуальных блоков.
- Нажмите на иконку со значком USB для загрузки программы в плату micro:bit.
- После прошивки micro:bit, светодиоды на Kitronik ZIP Tile зажгутся радужным свечением.
Пример для JavaScript
- Переключите визуальный режим MakeCode на текстовый редактор JavaScript.
- Прошейте платформу кодом приведённым ниже.
- microbit-kitronik-zip-tile-examples-rainbow-javascript.
 js
js let tileDisplay = Kitronik_Zip_Tile.createZIPTileDisplay(1, 1, Kitronik_Zip_Tile.UBitLocations.Hidden) tileDisplay.showRainbow(1, 360) basic.forever(function () { })
- microbit-kitronik-zip-tile-examples-rainbow-javascript.
- После прошивки micro:bit, светодиоды на Kitronik ZIP Tile зажгутся радужным свечением.
Пример для Python
- Переключите визуальный режим MakeCode на текстовый редактор Python.
- Прошейте платформу кодом приведённым ниже.
- microbit-kitronik-zip-tile-examples-rainbow-python.py
tileDisplay = Kitronik_Zip_Tile.create_zip_tile_display(1, 1, Kitronik_Zip_Tile.UBitLocations.HIDDEN) tileDisplay.show_rainbow(1, 360) def on_forever(): pass basic.forever(on_forever)
- После прошивки micro:bit, светодиоды на Kitronik ZIP Tile зажгутся радужным свечением.
Бегущая строка
А теперь выведем на матрицу бегущую строку с текстом .
Пример для визуального программирования
- Соберите схему из визуальных блоков.

- Нажмите на иконку со значком USB для загрузки программы в плату micro:bit.
- После прошивки micro:bit, вы увидите на матрице Kitronik ZIP Tile бегущую строку с текстом .
Пример для JavaScript
- Переключите визуальный режим MakeCode на текстовый редактор JavaScript.
- Прошейте платформу кодом приведённым ниже.
- microbit-kitronik-zip-tile-examples-amperka-javascript.js
let tileDisplay = Kitronik_Zip_Tile.createZIPTileDisplay(1, 1, Kitronik_Zip_Tile.UBitLocations.Hidden) basic.forever(function () { tileDisplay.scrollText( "Amperka", Kitronik_Zip_Tile.TextDirection.Left, 100, Kitronik_Zip_Tile.TextStyle.None, Kitronik_Zip_Tile.colors(ZipLedColors.Red), Kitronik_Zip_Tile.colors(ZipLedColors.Orange) ) })
- После прошивки micro:bit, вы увидите на матрице Kitronik ZIP Tile бегущую строку с текстом .
Пример для Python
- Переключите визуальный режим MakeCode на текстовый редактор Python.

- Прошейте платформу кодом приведённым ниже.
- microbit-kitronik-zip-tile-examples-amperka-python.py
tileDisplay = Kitronik_Zip_Tile.create_zip_tile_display(1, 1, Kitronik_Zip_Tile.UBitLocations.HIDDEN) def on_forever(): tileDisplay.scroll_text("Amperka", Kitronik_Zip_Tile.TextDirection.LEFT, 100, Kitronik_Zip_Tile.TextStyle.NONE, Kitronik_Zip_Tile.colors(ZipLedColors.RED), Kitronik_Zip_Tile.colors(ZipLedColors.ORANGE)) basic.forever(on_forever)
- После прошивки micro:bit, вы увидите на матрице Kitronik ZIP Tile бегущую строку с текстом .
Элементы платы
Светодиодная матрица
На лицевой стороне платы расположена матрица 8×8 адресных светодиодов WS2812B.
Каждый светодиод состоит из контроллера WS2812 и трёх кристаллов: R – красный, G – зелёный и B – синий. Изменяя ток одного, двух или трёх кристаллов одновременно, можно получить практически любой цвет излучения из видимого спектра. Электрически светодиодные модули WS2812B соединены между собой в цепочку от 1 до 64. Максимальный потребляемый ток каждого светодиода, когда все три кристалла горят на максимум — 41 мА.
Электрически светодиодные модули WS2812B соединены между собой в цепочку от 1 до 64. Максимальный потребляемый ток каждого светодиода, когда все три кристалла горят на максимум — 41 мА.
Для работы cо светодиодами используйте библиотеку Kitronik ZIP Tile для MakeCode и читайте в приведённых примерах работы.
Контакты ввода-вывода
При желании к Kitronik ZIP Tile можно подключать Troyka-модули для расширения возможностей девайса. Для этого необходимо напаять к плате парочку штырьков PLS-3, чтобы получить доступ к контактам micro:bit: и .
Разъём питания JST PH-2
Разъём служит для подключения внешнего источника напряжения для питания светодиодной матрицы. Воспользуйтесь одним из вариантов:
Регулятор напряжения
Входное напряжение от разъёма JST PH-2 поступает на понижающий регулятор напряжения, которое преобразуется до точных 3,3 вольт.
Контакты подключения BBC micro:bit
Светодиодная матрица Kitronik ZIP Tile содержит контакты подключения в виде 5 отверстий для коммуникации с платами BBC micro:bit. Возможно подключение двумя способами:
Возможно подключение двумя способами:
Видимое подключение — плата micro:bit прикручивается к винтовым площадкам ZIP Tile и выглядывает из-за светодиодной панели.
Потайное подключение — когда micro:bit прикручивается к ZIP Tile таким образом, что плата прячется за светодиодной панелью.
Разъёмы расширения матрицы
Габаритный чертёж
Характеристики
Модель: Kitronik ZIP Tile (SKU 5645)
Совместимость: микрокомпьютеры BBC micro:bit
Аппаратный интерфейс: контактные площадки под micro:bit
Светодиоды: цветные адресные LED WS2812B
Количество светодиодов: 64
Количество уровней яркости: 256
Разъём питания: JST PH-2
Напряжение питания: 3,3–5 В
Ток потребления: до 2,73 А (по 41 мА на светодиод)
Размеры: 71×58,4×9,7 мм
Ресурсы
Обращение матрицы
Пожалуйста, прочтите сначала наше Введение в матрицы.
Что такое обратная матрица?
Так же, как число имеет обратное …
Обратное число (примечание: 1 8 также можно записать 8 -1 )
Обратная матрица
Есть и другие сходства:
Когда мы умножаем число на его , обратное , получаем 1 :
8 × 1 8 = 1
Когда мы умножаем матрицу на ее , обратную , мы получаем Identity Matrix (которая похожа на «1» для матриц):
А × А -1 = I
То же самое с инверсией:
1 8 × 8 = 1
A -1 × A = I
Идентификационная матрица
Мы только что упомянули «Матрицу идентичности». Это матричный эквивалент числа “1”:
Это матричный эквивалент числа “1”:
I =
Матрица идентификации 3×3
- Это «квадрат» (в нем столько же строк, что и столбцов),
- Он имеет 1 с по диагонали и 0 с по всей остальной части.
- Его символ – заглавная буква I .
Матрица идентичности может иметь размер 2 × 2 или 3 × 3, 4 × 4 и т. Д.
Определение
Вот определение:
Аргумент A равен A -1 только тогда, когда:
AA -1 = A -1 A = I
Иногда обратного нет вообще.
(Примечание: написание AA -1 означает A, умноженное на A -1 )
Матрица 2×2
Хорошо, как рассчитать обратное?
Ну, для матрицы 2×2 обратное значение:
Другими словами: меняет местами позиций a и d, помещает негативов перед b и c, а делит всего на ad − bc .
Примечание: ad − bc называется определителем.
Давайте попробуем пример:
Как мы узнаем, что это правильный ответ?
Помните, что должно быть правдой следующее: AA -1 = I
Итак, давайте посмотрим, что произойдет, когда мы умножим матрицу на ее обратную:
=
4 × 0.6 + 7 × −0,24 × −0,7 + 7 × 0,4 2 × 0,6 + 6 × −0,22 × −0,7 + 6 × 0,4
=
2,4−1,4−2,8 + 2,8 1,2–1,2–1,4 + 2,4
И, привет !, мы получили Матрицу идентичности!
Так должно быть правильно.
Также должно быть , что: A -1 A = I
Почему бы вам не попробовать их умножить? Посмотрите, получите ли вы также Identity Matrix:
Зачем нужен инверс?
Потому что с матрицами мы не делим ! А если серьезно, то нет понятия деления матрицей.
Но мы можем умножить на обратное , что даст то же самое.
Представьте, что мы не можем делить на числа …
… и кто-то спрашивает “Как мне поделиться 10 яблоками с 2 людьми?”
Но мы можем взять , обратное из 2 (что составляет 0,5), поэтому мы ответим:
10 × 0,5 = 5
Получают по 5 яблок.
То же самое можно сделать и с матрицами:
Допустим, мы хотим найти матрицу X, и мы знаем матрицы A и B:
XA = B
Было бы неплохо разделить обе стороны на A (чтобы получить X = B / A), но помните, что мы не можем разделить .
Но что, если мы умножим обе стороны на A -1 ?
XAA -1 = BA -1
И мы знаем, что AA -1 = I, поэтому:
XI = BA -1
Мы можем удалить I (по той же причине мы можем удалить “1” из 1x = ab для чисел):
X = BA -1
И у нас есть ответ (при условии, что мы можем вычислить A -1 )
В этом примере мы очень внимательно следили за правильностью умножения, потому что в случае с матрицами порядок умножения имеет значение. AB почти никогда не совпадает с BA.
AB почти никогда не совпадает с BA.
Пример из реальной жизни: автобус и поезд
Группа поехала на автобусе по цене 3 доллара за ребенка и 3,20 доллара за взрослого на общую сумму 118,40 доллара.
Они вернулись на поезд по цене 3,50 доллара за ребенка и 3,60 доллара за взрослого, итого 135,20 доллара.
Сколько детей и сколько взрослых?
Во-первых, давайте настроим матрицы (будьте осторожны, чтобы строки и столбцы были правильными!):
Это как в примере выше:
XA = B
Итак, чтобы решить эту проблему, нам нужна обратная величина к “A”:
−1 = 1 3 × 3.6−3,5 × 3,2
Теперь у нас есть обратное, которое мы можем решить с помощью:
X = BA -1
=
118,4 × −9 + 135,2 × 8118,4 × 8,75 + 135,2 × −7,5
Было 16 детей и 22 взрослых!
Ответ кажется почти волшебным. Но он основан на хорошей математике.
Но он основан на хорошей математике.
Подобные вычисления (но с использованием гораздо больших матриц) помогают инженерам проектировать здания, используются в видеоиграх и компьютерной анимации, чтобы вещи выглядели трехмерными, и во многих других местах.
Это также способ решения систем линейных уравнений.
Расчеты производятся компьютером, но люди должны понимать формулы.
Порядок важен
Скажем, в данном случае мы пытаемся найти “X”:
AX = B
Это отличается от приведенного выше примера! X теперь после A.
Для матриц порядок умножения обычно меняет ответ. Не предполагайте, что AB = BA, это почти никогда не верно.
Так как же решить эту проблему? Используя тот же метод, но впереди поставьте A -1 :
.A -1 AX = A -1 B
И мы знаем, что A -1 A = I, поэтому:
IX = A -1 B
Мы можем удалить I:
X = A -1 B
И у нас есть ответ (при условии, что мы можем вычислить A -1 )
Почему бы нам не попробовать наш пример с автобусом и поездом, но с данными, настроенными таким образом.
Это можно сделать таким образом, но мы должны быть осторожны при настройке.
Вот как это выглядит как AX = B:
Выглядит так аккуратно! Я думаю, что предпочитаю это так.
Также обратите внимание, как строки и столбцы меняются местами в
(«транспонировано»)
по сравнению с предыдущим примером.
Для ее решения нам понадобится обратная величина к “A”:
−1 = 1 3 × 3,6−3,2 × 3,5
Он похож на обратный, который мы получили раньше, но
Transposed (строки и столбцы меняются местами).
Теперь мы можем решить, используя:
X = A -1 B
=
−9 × 118,4 + 8 × 135,2 8,75 × 118,4 – 7,5 × 135,2
Тот же ответ: 16 детей и 22 взрослых.
Итак, матрицы – это мощная вещь, но их нужно правильно настраивать!
Обратное может не существовать
Во-первых, для инверсии матрица должна быть «квадратной» (то же количество строк и столбцов).
Но также определитель не может быть нулем (или мы закончим делением на ноль).Как насчет этого:
24−24? Это равно 0, а 1/0 не определено .
Мы не можем идти дальше!
Эта матрица не имеет инверсии.
Такая матрица называется «сингулярной»,
что происходит только тогда, когда определитель равен нулю.
И это имеет смысл … посмотрите на числа: вторая строка просто удваивает первую строку, и не добавляет никакой новой информации .
И определитель 24−24 позволяет нам узнать об этом факте.
(Представьте, что в нашем примере с автобусом и поездом цены на поезд были ровно на 50% выше, чем на автобусе: так что теперь мы не можем найти никаких различий между взрослыми и детьми. Должно быть что-то, что их отличало бы. )
Большие матрицы
Обратное к 2×2 равно easy … по сравнению с более крупными матрицами (такими как 3×3, 4×4 и т. Д.).
Для этих больших матриц есть три основных метода вычисления обратного:
Заключение
- Обратное значение A – это A -1 , только если AA -1 = A -1 A = I
- Чтобы найти обратную матрицу 2×2: поменять местами позиций a и d, поставить негативов, перед b и c, и разделить всего на определитель (ad-bc).

- Иногда обратного нет вообще
Матричных преобразований
Цели
- Научитесь геометрически рассматривать матрицу как функцию.
- Изучите примеры матричных преобразований: отражение, растяжение, вращение, сдвиг, проекция.
- Понять словарь, окружающий преобразования: домен, кодомен, диапазон.
- Понимание домена, кодомена и диапазона матричного преобразования.
- изображений: преобразований общих матриц.
- Словарные слова: преобразование / функция , домен , домен , диапазон , преобразование идентичности , преобразование матрицы .
В этом разделе мы научимся понимать матрицы геометрически как функции или преобразования . Мы кратко обсудим преобразования в целом, а затем остановимся на матричных преобразованиях, которые являются преобразованиями, происходящими из матриц.
Неформально, функция – это правило, которое принимает входные данные и производит выходы. Например, f (x) = x2 – это функция, которая принимает на вход одно число x и выводит квадрат этого числа: f (2) = 4. В этом подразделе мы интерпретируем матрицы как функции.
Пусть A – матрица с m строками и n столбцами. Рассмотрим матричное уравнение b = Ax (мы пишем его так вместо Ax = b, чтобы напомнить читателю об обозначении y = f (x)). Если мы изменим x, то изменится и b; таким образом, мы думаем об A как о функции с независимой переменной x и зависимой переменной b.
- Независимая переменная (вход) – это x, который является вектором в Rn.
- Зависимая переменная (выход) – это b, который является вектором в Rm.
Набор всех возможных выходных векторов – это векторы b такие, что Ax = b имеет некоторое решение; это то же самое, что и пространство столбцов A в этом примечании в разделе 2.3.
Здесь удобно зафиксировать наши идеи и терминологию, касающуюся функций, которые в этой книге мы назовем преобразованиями . Это позволяет систематизировать обсуждение матриц как функций.
Это позволяет систематизировать обсуждение матриц как функций.
Определение
Преобразование из Rn в Rm – это правило T, которое присваивает каждому вектору x в Rn вектор T (x) в Rm.
- Rn называется доменом T.
- Rm называется кодоменом T.
- Для x в Rn вектор T (x) в Rm – это изображение x под T.
- Набор всех изображений {T (x) | xinRn} – это диапазон T.
Обозначение T: Rn− → Rm означает «T – преобразование из Rn в Rm».
Может быть полезно думать о T как о «машине», которая принимает x в качестве входных данных и дает вам T (x) в качестве выходных данных.
RnRmdomaincodomainTxT (x) rangeT Точки домена Rn – это входов T: это просто означает, что имеет смысл оценивать T на векторах с n записями, то есть списками из n чисел. Аналогично, точки кодомена Rm – это выходы T: это означает, что результатом вычисления T всегда является вектор с m элементами.
Диапазон T – это набор всех векторов в кодомене, которые фактически возникают как выходы функции T для некоторого входа. Другими словами, диапазон – это все векторы b в области, такие, что T (x) = b имеет решение x в области.
Определение
Преобразование идентичности IdRn: Rn → Rn – преобразование, определенное правилом
IdRn (x) = xforallxinRn.
Другими словами, тождественное преобразование не перемещает свой входной вектор: выход совпадает с входным.Его домен и домен равны Rn, а его диапазон также равен Rn, поскольку каждый вектор в Rn является выходом самого себя.
Теперь мы специализируем общие понятия и словарь из предыдущего раздела на функциях, определяемых матрицами, которые мы рассматривали в первом подразделе.
Определение
Пусть A – матрица размера m × n. Матричное преобразование , связанное с A, является преобразованием
T: Rn− → RmdeBnedbyT (x) = Ax.
Это преобразование, которое переводит вектор x в Rn в вектор Ax в Rm.
Если A имеет n столбцов, то имеет смысл умножать A только на векторы с n элементами. Вот почему область определения T (x) = Ax – это Rn. Если A имеет n строк, то Ax имеет m элементов для любого вектора x в Rn; вот почему область значений T (x) = Ax – это Rm.
Определение матричного преобразования T говорит нам, как вычислить T для любого заданного вектора: мы умножаем входной вектор на матрицу. Например, пусть
А = I123456J
, и пусть T (x) = Ax – соответствующее матричное преобразование.Тогда
TA − 1−2−3B = AA − 1−2−3B = I123456JA − 1−2−3B = I − 14−32J.
Предположим, что A имеет столбцы v1, v2, …, vn. Если мы умножим A на общий вектор x, мы получим
Ax = A ||| v1v2 ··· vn ||| BCGGEx1x2 … xnDHHF = x1v1 + x2v2 + ··· + xnvn.
Это просто общая линейная комбинация v1, v2, …, vn. Следовательно, выходы T (x) = Ax – это в точности линейные комбинации столбцов A: диапазон T – пространство столбцов A. См. Это примечание в разделе 2. 3.
3.
Пусть A – матрица размера m × n, и пусть T (x) = Ax – соответствующее преобразование матрицы.
- Домен T – это Rn, где n – количество столбцов A.
- Кодомен T – это Rm, где m – количество строк A.
- Диапазон T – это пространство столбцов A.
В случае квадратной матрицы размера n × n область и область значений T (x) = Ax равны Rn. В этой ситуации можно рассматривать T как , работающий на Rn: он перемещает векторы в том же пространстве.
примеров типов матриц для начинающих
Информация о типах матриц необходима для различных операций с матрицами. Как вы знаете, в матрице определены расстановки чисел в двух закрывающих скобках. Эти числа называются элементами матрицы.
Типы матриц
Матрица характеризуется строками и столбцами. Горизонтальные элементы в строках известны по строкам, а вертикальные – по столбцам.
Обычно, когда мы решаем матрицы, мы сосредотачиваемся только на операциях e. g., математическое умножение, сложение, вычитание и деление.
g., математическое умножение, сложение, вычитание и деление.
Нас не беспокоят элементы, откуда они взяты. Какова исходная проблема и для какой цели мы используем матричную формулировку, то есть математический подход?
Не менее важен и для новичков, чтобы они понимали причину его применения. Если вам интересно узнать об этом больше, дайте нам знать. Мы предоставим подробную информацию в следующих публикациях.
Хорошо, теперь мы увидим типы матриц для различных целей работы с матрицами.
№1. Скалярная матрица
Скалярная матрица – это квадратная матрица, и ее диагональные элементы равны одной и той же скалярной величине. В то время как недиагональные элементы равны нулю.
Для примера: матрицы A, B и C показаны ниже. Все диагональные элементы одинаковы по величине, а внедиагональные элементы равны нулю.
Это означает, что ij = постоянное значение; если i равно j порядка.Это значение будет равно нулю, если i не равно j-му порядку.
№2. Треугольная матрица
Матрица, элементы которой ниже или выше ненулевых диагональных элементов равны нулю. Чтобы понять эту строку, сначала вы увидите матрицу A на приведенном ниже рисунке.
ЧИТАЙТЕ ТАКЖЕ: Матрицы и введение
A и B – две треугольные матрицы, потому что все нулевые элементы находятся над диагональными элементами. Также диагональные элементы не равны нулю.Этот тип матриц (Часть-а) называется нижнетреугольными матрицами.
Матрицы C и D называются верхними треугольными матрицами (часть b). Треугольная матрица – это квадратная матрица.
№3. Нулевая или нулевая матрица
Все элементы нулевых матриц равны нулю. Это может быть квадратная, строчная или столбцовая матрица.
№4. Единица или идентификационная матрица
Квадратная матрица, все диагональные элементы которой равны единице (1), а остальные элементы равны нулю, называется единичной матрицей или единичной матрицей.
Матрицы A, B и C являются примером матрицы идентичности.
Вопрос к вам. Что вы думаете о матрице с одной строкой, у которой все элементы равны 1, будет ли это единичной матрицей? Аналогично матрице столбцов, все элементы которой равны 1.
Я начал типы матриц в обратном порядке, знаете, в чем причина? На самом деле, я подумал, что вы знаете о матрицах строк и столбцов. Но, если вы не знаете о матрицах строк и столбцов, я расскажу об этом в разделе ниже.
№5. Диагональная матрица
Диагональная матрица – это всегда квадратная матрица, недиагональные элементы которой всегда равны нулю. При этом диагональные элементы остаются ненулевыми.
Расскажите, пожалуйста, о природе диагональных элементов? Может ли какое-нибудь из этих чисел быть отрицательным или нулевым?
В предыдущем разделе мы видели скалярную матрицу. Не могли бы вы сообщить мне разницу между диагональной и скалярной матрицами?
№6.
 Квадратная матрица
Квадратная матрицаКвадратная матрица имеет такое же количество строк и столбцов, как вы можете видеть в приведенных ниже примерах. Квадратная матрица может иметь целые числа любого типа, такие как положительные, отрицательные и нулевые.
№ 7. Прямоугольная матрица
В прямоугольной матрице разное количество строк и столбцов. Если в строках четыре столбца, может быть 3 или 5 или любое число, отличное от числа 4.
Матрица содержит все типы целых чисел, как в квадратной матрице, которую вы видели.Но вы не можете определить диагональные элементы матрицы.
№8. Матрицы столбцов и строк
В приведенном ниже примере вы можете увидеть примеры матриц столбцов и строк. В матрице столбцов вы можете заметить, что есть только один столбец, а строк может быть много.
С другой стороны, в матрице строк строка одна, а столбцов может быть много.
Заключение
В этом посте вы получили общее представление о типах матриц.
Во-первых, это матрица, состоящая из строк и столбцов.
Число этих строк и столбцов определяет размер и порядок матрицы, т. Е. Называется размерностью матрицы.
Типы матриц, которые вы здесь проверили: скалярная матрица, единичная и единичная матрица, нулевая или нулевая матрица, треугольная матрица, с двумя вариантами: нижняя и верхняя треугольные матрицы. Затем диагональная матрица, прямоугольная матрица, матрицы строк и столбцов.
Просмотры сообщений: 2,033
Нравится:
Нравится Загрузка…
Матрица Python и введение в NumPy
Матрица – это двумерная структура данных, в которой числа расположены в строках и столбцах. Например:
Эта матрица представляет собой матрицу 3×4 (произносится как «три на четыре»), потому что она имеет 3 строки и 4 столбца.
Матрица Python
Python не имеет встроенного типа для матриц. Однако мы можем рассматривать список списка как матрицу. Например:
A = [[1, 4, 5],
[-5, 8, 9]]
Мы можем рассматривать этот список списка как матрицу, имеющую 2 строки и 3 столбца.
Обязательно изучите списки Python, прежде чем продолжить эту статью.
Давайте посмотрим, как работать с вложенным списком.
A = [[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]]
print ("A =", A)
print ("A [1] =", A [1]) # 2-я строка
print ("A [1] [2] =", A [1] [2]) # 3-й элемент 2-й строки
print ("A [0] [- 1] =", A [0] [- 1]) # Последний элемент 1-й строки
столбец = []; # пустой список
для строки в A:
column.append (строка [2])
print ("3-й столбец =", столбец)
Когда мы запустим программу, вывод будет:
A = [[1, 4, 5, 12], [-5, 8, 9, 0], [-6, 7, 11, 19]] A [1] = [-5, 8, 9, 0] A [1] [2] = 9 A [0] [- 1] = 12 3-й столбец = [5, 9, 11]
Вот еще несколько примеров, связанных с матрицами Python с использованием вложенных списков.
Использование вложенных списков в качестве матрицы работает для простых вычислительных задач, однако есть лучший способ работы с матрицами в Python с использованием пакета NumPy.
Массив NumPy
NumPy – это пакет для научных вычислений, который поддерживает мощный объект N-мерного массива. Прежде чем вы сможете использовать NumPy, вам необходимо установить его. Для доп. Информации:
После установки NumPy вы можете импортировать и использовать его.
NumPy предоставляет многомерный массив чисел (который на самом деле является объектом).Возьмем пример:
импортировать numpy как np
a = np.array ([1, 2, 3])
print (a) # Вывод: [1, 2, 3]
print (type (a)) # Вывод:
Как видите, класс массива NumPy называется ndarray .
Как создать массив NumPy?
Есть несколько способов создать массивы NumPy.
1. Массив целых чисел, чисел с плавающей запятой и комплексных чисел
импортировать numpy как np
А = np.массив ([[1, 2, 3], [3, 4, 5]])
печать (A)
A = np.array ([[1.1, 2, 3], [3, 4, 5]]) # Массив чисел с плавающей запятой
печать (A)
A = np. array ([[1, 2, 3], [3, 4, 5]], dtype = complex) # Массив комплексных чисел
печать (A)
array ([[1, 2, 3], [3, 4, 5]], dtype = complex) # Массив комплексных чисел
печать (A)
Когда вы запустите программу, вывод будет:
[[1 2 3] [3 4 5]] [[1.1 2. 3.] [3. 4. 5.]] [[1. + 0.j 2. + 0.j 3. + 0.j] [3. + 0.j 4. + 0.j 5. + 0.j]]
2. Массив нулей и единиц
импортировать numpy как np
zeors_array = np.нули ((2, 3))
печать (zeors_array)
'' '
Выход:
[[0. 0. 0.]
[0. 0. 0.]]
'' '
ones_array = np.ones ((1, 5), dtype = np.int32) // указываем dtype
print (ones_array) # Вывод: [[1 1 1 1 1]]
Здесь мы указали dtype на 32 бита (4 байта). Следовательно, этот массив может принимать значения от -2 -31 до 2 -31 -1 .
3. Использование arange () и shape ()
импортировать numpy как np
А = np.апельсин (4)
печать ('A =', A)
B = np.arange (12) .reshape (2, 6)
печать ('B =', B)
'' '
Выход:
A = [0 1 2 3]
B = [[0 1 2 3 4 5]
[6 7 8 9 10 11]]
'' '
Узнайте больше о других способах создания массива NumPy.
Матричные операции
Выше мы привели 3 примера: сложение двух матриц, умножение двух матриц и транспонирование матрицы. Раньше для написания этих программ мы использовали вложенные списки. Давайте посмотрим, как мы можем выполнить ту же задачу, используя массив NumPy.
Сложение двух матриц
Мы используем оператор + для добавления соответствующих элементов двух матриц NumPy.
импортировать numpy как np
A = np.array ([[2, 4], [5, -6]])
B = np.array ([[9, -3], [3, 6]])
C = A + B # поэлементное сложение
печать (C)
'' '
Выход:
[[11 1]
[8 0]]
'' Умножение двух матриц
Для умножения двух матриц мы используем метод dot () .Узнайте больше о том, как работает numpy.dot.
Примечание: * используется для умножения массивов (умножения соответствующих элементов двух массивов), а не для умножения матриц.
импортировать numpy как np
A = np. array ([[3, 6, 7], [5, -3, 0]])
B = np.array ([[1, 1], [2, 1], [3, -3]])
C = A. точка (B)
печать (C)
'' '
Выход:
[[36 -12]
[-1 2]]
'' '
array ([[3, 6, 7], [5, -3, 0]])
B = np.array ([[1, 1], [2, 1], [3, -3]])
C = A. точка (B)
печать (C)
'' '
Выход:
[[36 -12]
[-1 2]]
'' '
Транспонирование матрицы
Мы используем numpy.transpose для вычисления транспонирования матрицы.
импортировать numpy как np
A = np.array ([[1, 1], [2, 1], [3, -3]])
печать (A.transpose ())
'' '
Выход:
[[1 2 3]
[1 1-3]]
'' '
Как видите, NumPy значительно упростил нашу задачу.
Доступ к элементам матрицы, строкам и столбцам
Элементы матрицы доступа
Подобно спискам, мы можем получить доступ к элементам матрицы с помощью индекса. Начнем с одномерного массива NumPy.
импортировать numpy как np
А = np.массив ([2, 4, 6, 8, 10])
print ("A [0] =", A [0]) # Первый элемент
print ("A [2] =", A [2]) # Третий элемент
print ("A [-1] =", A [-1]) # Последний элемент
Когда вы запустите программу, вывод будет:
А [0] = 2 A [2] = 6 A [-1] = 10
Теперь давайте посмотрим, как мы можем получить доступ к элементам двумерного массива (который по сути является матрицей).
импортировать numpy как np
A = np.array ([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
# Первый элемент первой строки
print ("A [0] [0] =", A [0] [0])
# Третий элемент второй строки
print ("A [1] [2] =", A [1] [2])
# Последний элемент последней строки
print ("A [-1] [- 1] =", A [-1] [- 1])
Когда мы запустим программу, вывод будет:
А [0] [0] = 1 A [1] [2] = 9 A [-1] [- 1] = 19
Строки доступа к матрице
импортировать numpy как np
А = np.массив ([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print ("A [0] =", A [0]) # Первая строка
print ("A [2] =", A [2]) # Третья строка
print ("A [-1] =", A [-1]) # Последняя строка (в данном случае 3-я строка) Когда мы запустим программу, вывод будет:
A [0] = [1, 4, 5, 12] A [2] = [-6, 7, 11, 19] A [-1] = [-6, 7, 11, 19]
Доступ к столбцам матрицы
импортировать numpy как np
A = np. array ([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print ("A [:, 0] =", A [:, 0]) # Первый столбец
print ("A [:, 3] =", A [:, 3]) # Четвертый столбец
print ("A [:, - 1] =", A [:, - 1]) # Последний столбец (в данном случае 4-й столбец)
array ([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print ("A [:, 0] =", A [:, 0]) # Первый столбец
print ("A [:, 3] =", A [:, 3]) # Четвертый столбец
print ("A [:, - 1] =", A [:, - 1]) # Последний столбец (в данном случае 4-й столбец)
Когда мы запустим программу, вывод будет:
A [:, 0] = [1–5–6] A [:, 3] = [12 0 19] A [:, - 1] = [12 0 19]
Если вы не знаете, как работает приведенный выше код, прочтите раздел этой статьи о нарезке матрицы.
Нарезка матрицы
Нарезка одномерного массива NumPy похожа на список. Если вы не знаете, как работает нарезка списка, посетите раздел «Общие сведения о нотации фрагментов в Python».
Возьмем пример:
импортировать numpy как np
letter = np.array ([1, 3, 5, 7, 9, 7, 5])
Элементы с 3-го по 5-й
print (буквы [2: 5]) # Вывод: [5, 7, 9]
# С 1-го по 4-й элементы
print (буквы [: - 5]) # Вывод: [1, 3]
# 6-й до последнего элементы
print (letter [5:]) # Вывод: [7, 5]
# С 1-го по последний элементы
print (letter [:]) # Вывод: [1, 3, 5, 7, 9, 7, 5]
# переворачивание списка
print (буквы [:: - 1]) # Вывод: [5, 7, 9, 7, 5, 3, 1]
Теперь давайте посмотрим, как мы можем разрезать матрицу.
импортировать numpy как np
A = np.array ([[1, 4, 5, 12, 14],
[-5, 8, 9, 0, 17],
[-6, 7, 11, 19, 21]])
print (A [: 2,: 4]) # две строки, четыре столбца
''' Выход:
[[1 4 5 12]
[-5 8 9 0]]
'' '
print (A [: 1,]) # первая строка, все столбцы
''' Выход:
[[1 4 5 12 14]]
'' '
print (A [:, 2]) # все строки, второй столбец
''' Выход:
[5 9 11]
'' '
print (A [:, 2: 5]) # все строки, с третьего по пятый столбец
'''Выход:
[[5 12 14]
[9 0 17]
[11 19 21]]
'' '
Как видите, использование NumPy (вместо вложенных списков) значительно упрощает работу с матрицами, и мы даже не коснулись основ.Мы предлагаем вам подробно изучить пакет NumPy, особенно если вы пытаетесь использовать Python для науки о данных / аналитики.
Ресурсы NumPy, которые могут оказаться полезными:
Типы матриц – Матричные решаемые вопросы и часто задаваемые вопросы
Прежде чем обсуждать типы матриц, давайте обсудим, что такое матрица.
Матрица – это прямоугольный массив чисел или символов, которые обычно расположены в строках и столбцах.
Порядок матрицы определяется количеством строк и столбцов.{\ prime} $ матрица и записывается как $ m \ times n $, где $ n $ – количество строк, а $ m $ – количество столбцов.
Пример матрицы, у нас есть матрица $ 3 \ times 2 $, потому что количество строк здесь равно 3, а количество столбцов равно $ 2. $
$ \ begin {bmatrix} 2 & 5 & 6 \\ 5 & 2 & 7 \ end {bmatrix} $, известная как матрица $ 2 \ times 3 $.
Какие бывают типы матриц?
Существуют разные типы матриц.Вот они –
1) Матрица строк
2) Матрица столбцов
3) Нулевая матрица
4) Квадратная матрица
5) Диагональная матрица
6) Верхняя треугольная матрица
7) Нижняя треугольная матрица
8) Симметричная матрица
9) Кососимметричная матрица
10) Горизонтальная матрица
11) Вертикальная матрица
12) Идентификационная матрица
(Изображение будет скоро загружено)
Давайте обсудим различные типы матриц в математике , типы матриц подробно, определение и типы матриц.
1. Что такое нулевая матрица?
Если в матрице все элементы равны нулю, то она называется нулевой матрицей и обычно обозначается 0. Таким образом, $ A = \ left [a_ {ij} \ right] m \ times n $ является нулевой матрицей. матрица, если $ a_ {ij} = 0 $ для всех $ i $ и $ j $.
Первая матрица $ \ mathrm {O} $ представляет собой матрицу $ 2 \ times 2 $ со всеми элементами, равными нулю, а вторая матрица $ \ mathrm {O} $ представляет собой матрицу $ 3 \ times 3 $ со всеми элементами равно нулю.
$ O = \ begin {bmatrix} 0 & 0 \\ 0 & 0 \ end {bmatrix}, O = \ begin {bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \ end {bmatrix} $
2.Что такое треугольная матрица?
Квадратная матрица называется треугольной, если все ее элементы выше главной диагонали равны нулю, тогда треугольная матрица называется нижней треугольной матрицей или все ее элементы ниже главной диагонали равны нулю, тогда треугольная матрица называется верхнетреугольная матрица.
$ \ begin {bmatrix} 1 & 2 & 3 \\ 0 & 6 & 5 \\ 0 & 0 & 9 \ end {bmatrix} $
Приведенная выше матрица представляет собой верхнюю треугольную матрицу размером 3 \ times 3 $.
Приведенная ниже матрица является примером нижней треугольной матрицы размером $ 3 \ times 3 $.
$ \ begin {bmatrix} 1 & 0 & 0 \\ 2 & 4 & 0 \\ 3 & 5 & 6 \ end {bmatrix} $
3. Что такое вертикальная матрица?
Матрица порядка $ m \ times n $ известна как вертикальная матрица $ m> n $, где $ m $ равно количеству строк, а $ n $ равно количеству столбцов.
Пример матрицы
$ \ begin {bmatrix} 2 & 5 \\ 1 & 1 \\ 3 & 6 \\ 2 & 4 \ end {bmatrix} $
В приведенном ниже примере матрицы количество строк $ ( \ mathrm {m}) = 4 $, а количество столбцов $ (\ mathrm {n}) = 2.$ Следовательно, это делает матрицу вертикальной матрицей.
4. Что такое горизонтальная матрица?
Матрица порядка $ \ mathrm {m} \ times \ mathrm {n} $ называется горизонтальной матрицей, если $ \ mathrm {n}> \ mathrm {m} $, где $ \ mathrm {m} $ – равно количеству строк, а $ \ mathrm {n} $ равно количеству столбцов.
Пример матрицы
$ \ begin {bmatrix} 1 & 2 & 3 & 4 \\ 2 & 5 & 1 & 1 \ end {bmatrix} $
В приведенном ниже примере матрицы количество строк (m) = 2, а количество столбцов (n) = 4.Следовательно, можно сказать, что матрица является горизонтальной матрицей.
5. Что такое матрица строк?
Матрица, содержащая только одну строку, называется матрицей-строкой. Таким образом, A = \ [a_ {ij} m \ times n \] является матрицей-строкой, если m равно 1.
1. Это известно, потому что она имеет только одну строку, и поэтому порядок матрицы-строки всегда будет быть равным $ 1 \ times \ mathrm {n} $.
Пример матрицы строк,
$ A = \ begin {bmatrix} 4 & 6 & 9 \ end {bmatrix}, B = \ begin {bmatrix} 7 & 2 & 1 & 9 & 2 & 5 \ end { bmatrix} $
В приведенном выше примере матрицы матрица A имеет только одну строку, поэтому матрица B имеет одну строку, поэтому обе матрицы A и B являются матрицами-строками.
6. Что такое матрица столбцов?
Матрица с одним столбцом называется матрицей столбцов. Таким образом, A = \ [a_ {ij} m \ times n \] является матрицей столбцов, если n равно 1.
1. Это известно, потому что оно имеет только один столбец и, следовательно, порядок матрицы столбцов всегда будет быть равным $ \ mathrm {m} \ times 1 $.
Пример матрицы столбца,
$ A = \ begin {bmatrix} 3 \\ 4 \\ 8 \ end {bmatrix}, B = \ begin {bmatrix} 4 \\ 9 \\ 8 \\ 2 \ end {bmatrix} $
В приведенном выше примере матрицы матрица A имеет только один столбец, а матрица B – один столбец, поэтому обе матрицы A и B являются матрицами столбцов.
7. Что такое диагональная матрица?
Если все элементы матрицы, кроме главной диагонали в любой данной квадратной матрице, равны нулю, это называется диагональной матрицей. Таким образом, квадратная матрица A = \ [a_ {ij} \] является диагональной матрицей, если $ a_ {ij} = 0 $, когда $ i $ не равно $ j $
Например,
$ \ begin { bmatrix} 2 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 4 \ end {bmatrix} $
Пример, приведенный выше, представляет собой диагональную матрицу, поскольку она имеет элементы только по диагонали.
8. Что такое симметричная матрица?
Квадратная матрица $ A = \ left [a_ {i j} \ right] $ называется симметричной матрицей, если $ a_ {i j} = a_ {j i} $ для всех значений i, j.
Например,
$ A = \ begin {bmatrix} 1 & 2 & 3 \\ 2 & 4 & 5 \\ 3 & 5 & 2 \ end {bmatrix} $
9. Что такое Skew -Symmetric Матрица?
Квадратная матрица $ \ mathrm {A} = \ left [a_ {i j} \ right] $ является кососимметричной матрицей, если $ a_ {i j} = a_ {j i} $ для всех значений i, j. Таким образом, в кососимметричной матрице все диагональные элементы равны нулю.
Например,
$ \ begin {bmatrix} 0 & 2 & 1 \\ – 2 & 0 & -3 \\ – 1 & 3 & 0 \ end {bmatrix} $
10. Что такое матрица идентичности ?
Если все элементы главной диагонали в диагональной матрице равны 1, то она называется единичной матрицей. Единичную матрицу порядка $ \ mathrm {n} $ можно обозначить $ \ mathrm {In} $. Таким образом, квадратная матрица $ \ mathrm {A} $ $ \ left [a_ {ij} \ right] \ mathrm {m} \ times n $ является единичной матрицей, если все ее диагонали имеют значение 1.
Таким образом, квадратная матрица $ \ mathrm {A} $ $ \ left [a_ {ij} \ right] \ mathrm {m} \ times n $ является единичной матрицей, если все ее диагонали имеют значение 1.
$ \ text { Например,} A = \ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $
Вопросы, которые необходимо решить
Вопрос 1) Приведите пример единичной матрицы с числом строк и столбцов, равным двум.
Ответ) Мы знаем, что единичная матрица – это матрица, диагональные элементы которой равны 1, а все остальные элементы равны нулю.
Например, $ \ mathrm {A} = \ begin {bmatrix} 1 & 0 \\ 0 & 1 \ end {bmatrix} $
Базовые операции с матрицей – Пример MATLAB и Simulink
Этот пример показывает основные методы и функции для работы с матрицами на языке MATLAB®.
Во-первых, давайте создадим простой вектор из 9 элементов с именем a .
а = 1 × 9
1 2 3 4 6 4 3 4 5
Теперь давайте добавим 2 к каждому элементу нашего вектора, a , и сохраним результат в новом векторе.
Обратите внимание, что MATLAB не требует специальной обработки векторной или матричной математики.
b = 1 × 9
3 4 5 6 8 6 5 6 7
Создание графиков в MATLAB так же просто, как одна команда. Давайте нарисуем результат нашего векторного сложения линиями сетки.
MATLAB может также создавать другие типы графиков с метками осей.
бар (б)
xlabel ('Образец №')
ylabel ('Pounds') MATLAB также может использовать символы на графиках. Вот пример использования звездочек для обозначения точек.MATLAB предлагает множество других символов и типов линий.
участок (b, '*') ось ([0 10 0 10])
Одной из областей, в которой MATLAB выделяется, является матричное вычисление.
Создать матрицу так же просто, как создать вектор, используя точку с запятой (;) для разделения строк матрицы.
A = [1 2 0; 2 5 -1; 4 10 -1]
A = 3 × 3
1 2 0
2 5 -1
4 10 -1
Мы легко можем найти транспонирование матрицы A .
B = 3 × 3
1 2 4
2 5 10
0 -1 -1
Теперь перемножим эти две матрицы.
Еще раз обратите внимание, что MATLAB не требует, чтобы вы работали с матрицами как с набором чисел. MATLAB знает, когда вы имеете дело с матрицами, и соответствующим образом корректирует свои вычисления.
С = 3 × 3
5 12 24
12 30 59
24 59 117
Вместо умножения матриц мы можем умножить соответствующие элементы двух матриц или векторов с помощью оператора. *.
С = 3 × 3
1 4 0
4 25-10
0-10 1
Давайте воспользуемся матрицей A для решения уравнения A * x = b.Мы делаем это с помощью оператора \ (обратная косая черта).
Теперь мы можем показать, что A * x равно b.
MATLAB имеет функции почти для каждого типа вычисления общей матрицы.
Есть функции для получения собственных значений …
ans = 3 × 1
3,7321
0,2679
1,0000
.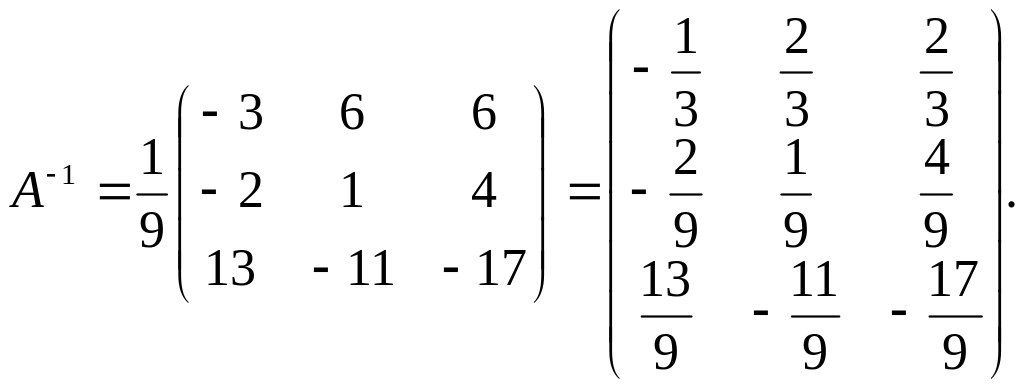 .. а также сингулярные числа.
.. а также сингулярные числа.
ans = 3 × 1
12,3171
0,5149
0,1577
Функция «poly» генерирует вектор, содержащий коэффициенты характеристического полинома.
Характеристический многочлен матрицы A равен
Мы можем легко найти корни многочлена, используя функцию корни .
Фактически это собственные значения исходной матрицы.
ans = 3 × 1
3,7321
1,0000
0,2679
MATLAB имеет множество приложений, помимо вычисления матриц.
Для свертки двух векторов …
q = 1 × 7
1-10 35-52 35-10 1
… или снова сверните и нанесите на график результат.
r = 1 × 10
1-15 90-278 480-480 278-90 15-1
В любое время мы можем получить список переменных, которые мы сохранили в памяти, с помощью команды who или whos .
Имя Размер Байт Атрибуты класса Двойной 3x3 72 B 3x3 72 двухместный C 3x3 72 двойной 1x9 72 двойной ans 3x1 24 двухместных b 3x1 24 двойной п 1х4 32 двойной q 1x7 56 двойной r 1x10 80 двойной x 3x1 24 двойных
Вы можете получить значение конкретной переменной, введя ее имя.
A = 3 × 3
1 2 0
2 5 -1
4 10 -1
Вы можете разместить несколько операторов в одной строке, разделив их запятыми или точками с запятой.
Если вы не назначаете переменную для хранения результата операции, результат сохраняется во временной переменной с именем и .
Как видите, MATLAB легко обрабатывает комплексные числа в своих вычислениях.
Связанные темы
10 лучших матричных операций в Numpy с примерами | Рукшан Прамодита
Около 30–40% математических знаний, необходимых для науки о данных и машинного обучения, поступает из линейной алгебры.Матричные операции играют важную роль в линейной алгебре. Сегодня мы обсудим 10 таких матричных операций с помощью мощной библиотеки numpy. Numpy обычно используется для выполнения численных расчетов в Python. Он также имеет специальные классы и подпакеты для матричных операций. Использование векторизации позволяет numpy более эффективно выполнять матричные операции, избегая многих циклов for.
Я буду включать значение, фоновое описание и примеры кода для каждой матричной операции, обсуждаемой в этой статье.Раздел «Основные выводы» в конце этой статьи предоставит вам некоторые более конкретные факты и краткое изложение матричных операций. Так что не забудьте прочитать и этот раздел.
Я расскажу о каждой матричной операции в следующем порядке. Вот список из 10 лучших матричных операций, которые я для вас тщательно отобрал.
- Внутренний продукт
- Точечный продукт
- Транспонирование
- Трассировка
- Рейтинг
- Детерминант
- Истинно инверсный
- Псевдо инверсный
- Собственные значения и собственные векторы
Предварительные требования
Чтобы получить все преимущества этой статьи, вы должны знать основы numpy и методы создания массивов. Если у вас нет этих знаний, прочтите следующую статью, написанную мной.
Если у вас нет этих знаний, прочтите следующую статью, написанную мной.
Давайте начнем с первого, внутреннего продукта .
Внутреннее произведение
Внутреннее произведение принимает два вектора равного размера и возвращает одно число (скаляр). Это вычисляется путем умножения соответствующих элементов в каждом векторе и сложения всех этих продуктов. В numpy векторы определяются как одномерные массивы numpy.
Чтобы получить внутренний продукт, мы можем использовать либо np.inner () , либо np.dot () . Оба дают одинаковые результаты. Входными данными для этих функций являются два вектора, и они должны быть одинакового размера.
Подождите, пока загрузится код Python! Внутреннее произведение двух векторов (Изображение автора)Точечное произведение
Точечное произведение определено для матриц. Это сумма произведений соответствующих элементов в двух матрицах. Чтобы получить скалярное произведение, количество столбцов в первой матрице должно быть равно количеству строк во второй матрице.
Чтобы получить скалярное произведение, количество столбцов в первой матрице должно быть равно количеству строк во второй матрице.
Есть два способа создать матрицы в numpy. Самый распространенный – использовать numpy ndarray class . Здесь мы создаем двумерные массивы numpy (объекты ndarray). Другой – использовать матричный класс numpy . Здесь мы создаем матричные объекты.
Скалярное произведение как объектов ndarray, так и объектов матрицы может быть получено с помощью np.dot () .
Подождите, пока загрузится код Python! Скалярное произведение двух матриц (Изображение автора) При умножении двух объектов ndarray с использованием оператора * результатом будет поэлементное умножение .С другой стороны, при умножении двух матричных объектов с использованием оператора * результатом является точечное (матричное) произведение , которое эквивалентно np. dot () , как и предыдущее.
dot () , как и предыдущее.
Транспонирование матрицы определяется переключением ее строк с ее столбцами. Мы можем использовать нп.Функция transpose () или метод NumPy ndarray.transpose () или ndarray.T (специальный метод, не требующий скобок), чтобы получить транспонирование. Все дают одинаковый результат.
Дождитесь загрузки кода Python! Получение транспонирования матрицы (Изображение автора)Транспонирование также можно применить к вектору. Однако технически одномерный массив numpy нельзя транспонировать.
импортировать numpy как npa = np.array ([1, 2, 3])Изображение автора
print ("a =")
print (a)
print ("\ na.T = ")
print (aT)
Если вы действительно хотите транспонировать вектор, он должен быть определен как двумерный массив numpy с двойными квадратными скобками.
import numpy as npa = np.array ( [[1, 2, 3]])Изображение автора Trace
print ("a =")
print (a)
print ("\ na.T =")
print (aT)
трасса – сумма диагональных элементов в квадратной матрице.Есть два метода вычисления трассы.Мы можем просто использовать метод trace () объекта ndarray или сначала получить диагональные элементы, а затем получить сумму.
импортировать numpy как npa = np.array ([[2, 2, 1],Изображение автора Рейтинг
[1, 3, 1],
[1, 2, 2]])
print ("a =")
print ( a)
print ("\ nTrace:", a.trace ())
print ("Trace:", sum (a.diagonal ()))
Рейтинг матрицы – это размеры векторного пространства, растянутого (сгенерированного) его столбцами или строками.Другими словами, его можно определить как максимальное количество линейно независимых векторов-столбцов или векторов-строк.
Ранг матрицы можно найти с помощью функции matrix_rank () , которая поступает из пакета numpy linalg .
импортировать numpy как npa = np.arange (1, 10)Изображение автора Определитель
a.shape = (3, 3)
print ("a =")
print (a)
rank = np.linalg.matrix_rank (a)
print ("\ nRank:", rank)
Определитель квадратной матрицы можно вычислить det () функция, которая также происходит от numpy linalg упаковка.Если определитель равен 0, эта матрица необратима. В терминах алгебры она известна как сингулярная матрица.
импортировать numpy как npa = np.array ([[2, 2, 1],Изображение автора Истинно инверсное
[1, 3, 1],
[1, 2, 2]]])
print ("a =")
print ( a)
det = np.linalg.det (a)
print ("\ nDeterminant:", np.round (det))
Истинное инверсное квадрата матрицу можно найти с помощью функции inv () пакета numpy linalg . Если определитель квадратной матрицы не равен 0, он имеет истинное обратное значение.
Если определитель квадратной матрицы не равен 0, он имеет истинное обратное значение.
импортировать numpy как npa = np.array ([[2, 2, 1],Изображение автора
[1, 3, 1],
[1, 2, 2]])
print ("a =")
print ( a)
det = np.linalg.det (a)
print ("\ nDeterminant:", np.round (det))
inv = np.linalg.inv (a)
print ("\ nInverse of a =" )
print (inv)
Если вы попытаетесь вычислить истинную инверсию сингулярной матрицы (квадратной матрицы, определитель которой равен 0), вы получите ошибку.
импортировать numpy как npa = np.array ([[2, 8],Изображение автора Псевдо обратная
[1, 4]])
print ("a =")
print (a)
det = np.linalg.det (a)
print ("\ nDeterminant:", np.round (det))
inv = np.linalg.inv (a)
print ("\ nInverse of a =")
print (inv)
Псевдо (не подлинная) обратная может быть вычислена даже для сингулярной матрицы (квадратная матрица, определитель которой равен 0) с помощью функции pinv () пакета numpy linalg .
импортировать numpy как npa = np.array ([[2, 8],Изображение автора
[1, 4]])
print ("a =")
print (a)
det = np.linalg.det (a)
print ("\ nDeterminant:", np.round (det))
pinv = np.linalg.pinv (a)
print ("\ nPseudo Inverse of a =")
print (pinv)
Там нет разницы между истинно обратной и псевдообратной, если квадратная матрица неособая (определитель , а не 0).
FlattenFlatten – это простой метод преобразования матрицы в одномерный массив numpy.Для этого мы можем использовать метод flatten () объекта ndarray.
импортировать numpy как npa = np.arange (1, 10)Изображение автора Собственные значения и собственные векторы
a.shape = (3, 3)
print ("a =")
print (a)
print ("\ nПосле выравнивания")
print ( "------------------")
print (a.flatten ())
Пусть A будет nxn матрица . Скаляр λ называется собственным значением из A , если существует ненулевой вектор x , удовлетворяющий следующему уравнению.
Скаляр λ называется собственным значением из A , если существует ненулевой вектор x , удовлетворяющий следующему уравнению.
Вектор x называется собственным вектором из A , что соответствует λ .
В numpy собственные значения и собственные векторы могут быть вычислены одновременно с помощью функции eig () .
импортировать numpy как npa = np.array ([[2, 2, 1],Изображение автора
[1, 3, 1],
[1, 2, 2]])
print ("a =")
print ( a)
w, v = np.linalg.eig (a)
print ("\ nEigenvalues:")
print (w)
print ("\ nEigenvectors:")
print (v)
Сумма собственных значений (1 + 5 + 1 = 7) равно следу (2 + 3 + 2 = 7) той же матрицы! Произведение собственных значений (1x5x1 = 5) равно определителю (5) той же матрицы!
Собственные значения и собственные векторы чрезвычайно полезны в анализе главных компонентов (PCA). В PCA собственные векторы корреляционной или ковариационной матрицы представляют главные компоненты (направления максимальной дисперсии), а соответствующие собственные значения представляют величину вариации, объясняемую каждым главным компонентом. Если вы хотите узнать о них больше, прочтите следующие статьи, написанные мной.
В PCA собственные векторы корреляционной или ковариационной матрицы представляют главные компоненты (направления максимальной дисперсии), а соответствующие собственные значения представляют величину вариации, объясняемую каждым главным компонентом. Если вы хотите узнать о них больше, прочтите следующие статьи, написанные мной.
Благодаря библиотеке numpy вы можете легко выполнять матричные операции с помощью одной или двух строк кода. Сегодня мы выполнили 10 матричных операций в numpy. Numpy имеет общие функции, а также специальные функции, предназначенные для линейной алгебры, например, пакет linalg имеет некоторые специальные функции, предназначенные для линейной алгебры.
В numpy матрицы и ndarrays – это разные вещи. Лучший способ познакомиться с ними – это поэкспериментировать с кодами самостоятельно. Всегда лучше проверять размеры матриц и ndarrays.
В библиотеках машинного обучения Scikit-learn большинство обсуждаемых сегодня матричных операций работают за кулисами, когда мы создаем и подбираем модель.


 colors(ZipLedColors.Red))
basic.pause(1000)
tileDisplay.showColor(Kitronik_Zip_Tile.colors(ZipLedColors.Green))
basic.pause(1000)
tileDisplay.showColor(Kitronik_Zip_Tile.colors(ZipLedColors.Blue))
basic.pause(1000)
tileDisplay.showColor(Kitronik_Zip_Tile.colors(ZipLedColors.White))
})
colors(ZipLedColors.Red))
basic.pause(1000)
tileDisplay.showColor(Kitronik_Zip_Tile.colors(ZipLedColors.Green))
basic.pause(1000)
tileDisplay.showColor(Kitronik_Zip_Tile.colors(ZipLedColors.Blue))
basic.pause(1000)
tileDisplay.showColor(Kitronik_Zip_Tile.colors(ZipLedColors.White))
}) show_color(Kitronik_Zip_Tile.colors(ZipLedColors.BLUE))
basic.pause(1000)
tileDisplay.show_color(Kitronik_Zip_Tile.colors(ZipLedColors.WHITE))
basic.forever(on_forever)
show_color(Kitronik_Zip_Tile.colors(ZipLedColors.BLUE))
basic.pause(1000)
tileDisplay.show_color(Kitronik_Zip_Tile.colors(ZipLedColors.WHITE))
basic.forever(on_forever) js
js


 array ([[1, 2, 3], [3, 4, 5]], dtype = complex) # Массив комплексных чисел
печать (A)
array ([[1, 2, 3], [3, 4, 5]], dtype = complex) # Массив комплексных чисел
печать (A)
 array ([[3, 6, 7], [5, -3, 0]])
B = np.array ([[1, 1], [2, 1], [3, -3]])
C = A. точка (B)
печать (C)
'' '
Выход:
[[36 -12]
[-1 2]]
'' '
array ([[3, 6, 7], [5, -3, 0]])
B = np.array ([[1, 1], [2, 1], [3, -3]])
C = A. точка (B)
печать (C)
'' '
Выход:
[[36 -12]
[-1 2]]
'' '
 array ([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print ("A [:, 0] =", A [:, 0]) # Первый столбец
print ("A [:, 3] =", A [:, 3]) # Четвертый столбец
print ("A [:, - 1] =", A [:, - 1]) # Последний столбец (в данном случае 4-й столбец)
array ([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print ("A [:, 0] =", A [:, 0]) # Первый столбец
print ("A [:, 3] =", A [:, 3]) # Четвертый столбец
print ("A [:, - 1] =", A [:, - 1]) # Последний столбец (в данном случае 4-й столбец)