Матрица примеры умножение: примеры, алгоритм умножения на вектор, число, свойства произведения

примеры, алгоритм умножения на вектор, число, свойства произведения

Произведение двух матриц

Определение 1

Произведение матриц (С= АВ) — операция только для согласованных матриц А и В, у которых число столбцов матрицы А равно числу строк матрицы В:

C⏟m×n=A⏟m×p×B⏟p×n

Пример 1

 Даны матрицы:

• A=a(ij) размеров m×n;
• B=b(ij) размеров p×n

Матрицу C, элементы cij которой вычисляются по следующей формуле:

cij=ai1×b1j+ai2×b2j+…+aip×bpj, i=1,…m, j=1,…m

Пример 2

Вычислим произведения АВ=ВА:

А=121012, В=100111

Решение, используя правило умножения матриц:

А⏟2×3×В⏟3×2=121012×100111=1×1+2×0+1×11×0+2×1+1×10×1+1×0+2×10×0+1×1+2×1==2323⏟2×2

В⏟3×2×А⏟2×3=100111×121012=1×1+0×01×2+0×11×1+0×20×1+1×00×2+1×10×1+1×21×1+1×01×2+1×11×1+1×2=121012133⏟3×3

Произведение АВ и ВА найдены, но являются матрицами разных размеров: АВ не равна ВА.

Свойства умножения матриц

Свойства умножения матриц:

• (АВ)С = А(ВС) — ассоциативность умножения матриц;
• А(В+С) = АВ + АС — дистрибутивность умножения;
• (А+В)С = АС + ВС — дистрибутивность умножения;
• λ(АВ)=(λА)В

Пример 1

Проверяем свойство №1: (АВ)С = А(ВС):

(А×В)×А=1234×5678×1002=19224350×1002=194443100,

А(В×С)=1234×56781002=1234×512716=194443100.

Пример 2

Проверяем свойство №2: А(В+С) = АВ + АС:

А×(В+С)=1234×5678+1002=1234×66710=20264658,

АВ+АС=1234×5678+1234×1002=19224350+1438=20264658.

Произведение трех матриц

Произведение трех матриц АВС вычисляют 2-мя способами:

• найти АВ и умножить на С: (АВ)С;
• либо найти сначала ВС, а затем умножить А(ВС).

​​​​​Пример 3

Перемножить матрицы 2-мя способами:

4375×-289338-126×7321

Алгоритм действий:

• найти произведение 2-х матриц;
• затем снова найти произведение 2-х матриц.

1). АВ=4375×-289338-126=4(-28)+3×384×93+3(-126)7(-28)+5×387×93+5(-126)=2-6-621

2). АВС=(АВ)С=2-6-6217321=2×7-6×22×3-6×1-6×7+21×2-6×3+21×1=2003.

Используем формулу АВС=(АВ)С:

1). ВС=-289338-1267321=-28×7+93×2-28×3+93×138×7-126×238×3-126×1=-10914-12

2). АВС=(АВ)С=7321-10914-12=4(-10)+3×144×9+3(-12)7(-10)+5×147×9+5(-12)=2003

Ответ: 4375-289338-1267321=2003

Умножение матрицы на число

Определение 2

Произведение матрицы А на число k — это матрица В=Аk того же размера, которая получена из исходной умножением на заданное число всех ее элементов:

bi,j=k×ai,j

Свойства умножения матрицы на число:

• 1×А=А
• 0×А=нулевая матрица
• k(A+B)=kA+kB
• (k+n)A=kA+nA
• (k×n)×A=k(n×A)

Пример 4

Найдем произведение матрицы А=4290   на 5.

Решение:

5А=542905×45×25×95×0=2010450

Умножение матрицы на вектор

Определение 3

Чтобы найти произведение матрицы и вектора, необходимо умножать по правилу «строка на столбец»:

• если умножить матрицу на вектор-столбец число столбцов в матрице должно совпадать с числом строк в векторе-столбце;
• результатом умножения вектора-столбца является только вектор-столбец:

АВ=а11а12⋯а1nа21а22⋯а2n⋯⋯⋯⋯аm1аm2⋯аmnb1b2⋯b1n=a11×b1+a12×b2+⋯+a1n×bna21×b1+a22×b2+⋯+a2n×bn⋯⋯⋯⋯am1×b1+am2×b2+⋯+amn×bn=c1c2⋯c1m

• если умножить матрицу на вектор-строку, то умножаемая матрица должна быть исключительно вектором-столбцом, причем количество столбцов должно совпадать с количеством столбцов в векторе-строке:

АВ=аа⋯аbb⋯b=a1×b1a1×b2⋯a1×bna2×b1a2×b2⋯a2×bn⋯⋯⋯⋯an×b1an×b2⋯an×bn=c11c12⋯c1nc21c22⋯c2n⋯⋯⋯⋯cn1cn2⋯cnn

Пример 5

Найдем произведение матрицы А и вектора-столбца В:

АВ=240-213-10112-1=2×1+4×2+0×(-1)-2×1+1×2+3×(-1)-1×1+0×2+1×(-1)=2+8+0-2+2-3-1+0-1=10-3-2

Пример 6

Найдем произведение матрицы А и вектора-строку В:

А=320-1, В=-1102

Решение:

АВ=3201×-1102=3×(-1)3×13×03×22×(-1)2×12×02×20×(-1)0×10×00×21×(-1)1×11×01×2=-3306-22040000-1102

Ответ: АВ=-3306-22040000-1102

Решение задач от 1 дня / от 150 р.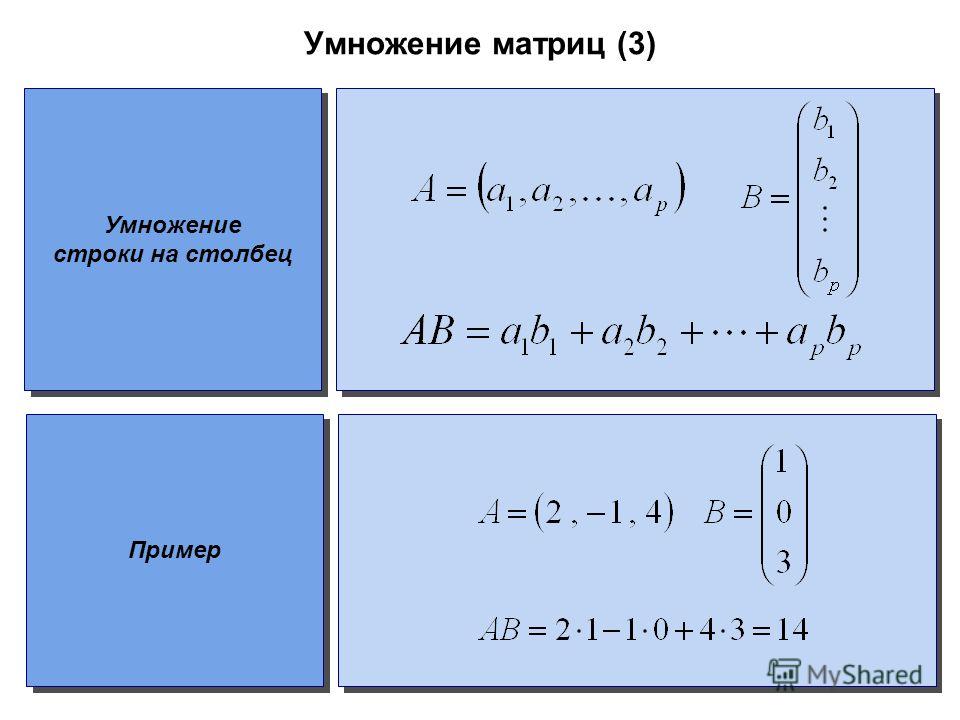 Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Примеры решения матриц с ответами

О чем статья

Алгоритм решения матриц

Теорема

Матрица – это математическая таблица с числовыми значениями. Обозначаются матрицы латинскими буквами.

Есть два отличия между матрицами:

1. Комплексные матрицы.  Это когда хотя бы одно число равно  комплексному.
2. Действительные матрицы. Это когда в матрице содержаться действительные числа.

С матрицей можно выполнять самые наипростейшие действия: умножение, деление, сложение, вычитание и трансформация.

Сложение и вычитание

Данные действия можно совершать тогда, когда матрицы равны между собой, чтобы в конце получилось выражение аналогичной размерности. Сложение и вычитание выполняются по аналогии друг друга.

Пример 1

Задание

Даны две матрицы, найдите их  сумму.

   

   

Решение

Элемент первой строки складывается с элементом второй. Абсолютно также совершается вычитание, только вместо плюса, нужно поставить минус.

   

Пример 2

Задание

Даны две матрицы, найдите их разность.

   

Решение

   

   

   

Пример 3

Задание

Найдите C=2A +3B, если :

   

   

Решение

   

   

Нужна помощь в написании работы?

Мы – биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Цена работы

Умножение

В математике умножать таблицу с числами можно абсолютно любую. В таком случае число умножается с показателем. Умножаем первое число на первой строке с числом второго столбца и так далее.

Пример

Задание

Даны две матрицы. Умножьте их друг на друга.

   

   

Решение

   

=

   

   

   

   

   

Матрицы можно перемножать друг на друга, только если количество столбцов в первой матрице, равно количеству строк второй. Элемент матрицы будет равняться сумме произведений (Aji), где i – строки в таблице; j – строки чисел второй таблицы.

Возведение матрицы в степень

Данную формулу используют лишь в случаях, если матрица стоит в квадратном выражении. Важно  знать, что степень должна быть у таких выражений натуральной!

   

Если число не будет натуральным, то это усложняет возведение матрицы в степень, так как степень n придётся умножить саму на себя n количество раз. Но если у Вас такой случай, то используется следующая формула.

   

Пример

Задание

Найдите

   

матрицы.

   

Решение

В первую очередь найдём, для этого нужно будет просто умножить её саму на себя.

   

   

   

После по формуле подставляем числовые значения.

   

Расчёт определителя

В математике линейной есть два понятия – определитель и детерминант. Определитель – это какое-либо число, которое ставится в соответствии с квадратной матрицей. Определитель используется при решении многих задач. Найти его можно с помощью формулы.

А детерминант находиться с помощью перемножения простых матриц, используются числа только с побочной и главной диагоналях.

Есть вероятность, что произведения матрицы будут значительно отличаться друг от друга. Если индекс чётный, то число будет со знаком плюс, если нечётный, то число будет со знаком минус. Обозначается определитель det А, а круглые скобки меняются на квадратные.

Пример 1

Дано

   

Решение

Пользуемся свойствам степеней – A^{3}=A^{2}*A

Возведём А в A^{2}

   

   

Далее используем свойство степеней

   

   

   

Ответ

   

Пример 2

Задание

Найдите определитель матрицы А.

   

Решение

   

   

   

Обратная матрица

Перед тем, как речь непосредственно пойдёт о самой обратной связи матрицы, давайте разберём алгоритм трансформирования матрицы. Во время трансформации столбцы и строки меняются местами.

Пример

Задание

Найти обратную матрицу А.

   

Решение

Приписываем к матрице А матрицу третьего ряда.

   

Переводим всё в единичную матрицу.

   

   

   

   

   

   

   

   

Ответ

   

   

Обратная матрица

Обратная матрица схожа с алгоритмом нахождения обратных чисел. К примеру, если умножить матричную таблицу на обратную матрицу, то в итоге мы получаем A*A(-1)=E. Но чтобы перейти уже к нахождению обратной матрицы, нам придётся найти её определитель.

Мы рассмотрим самый простой способ – алгебраических дополнений.

Пример 1

Задание

В пример возьмём квадратную матрицу, она находиться с помощью следующей формулы:

   

, где

   

-транспортированные матрицы;|А| – определитель.

Рассмотрим самый простейший пример, где размер таблицы  2*2.

Найти обратную матрицу

   

Решение

Для начала находим определитель матрицы.

   

Если ответ равен нулю, то обратной матрицы нет! Так как наш ответ равен -2, то всё в порядке. Следующим действием нам нужно будет рассчитать

матрицу миронов. Таблица элементов при этом не изменяется. Где прописан нужным нам элемент, нужно вычеркнуть строчку или столбец, оставшееся число и будет являться мироном.

   

Подставляем числа, возвращаясь к матрица, которая указана выше.

   

Всегда начинаем с левого верхнего угла и делаем следующее:

   

← линиями показано, что нужно и как зачеркнуть.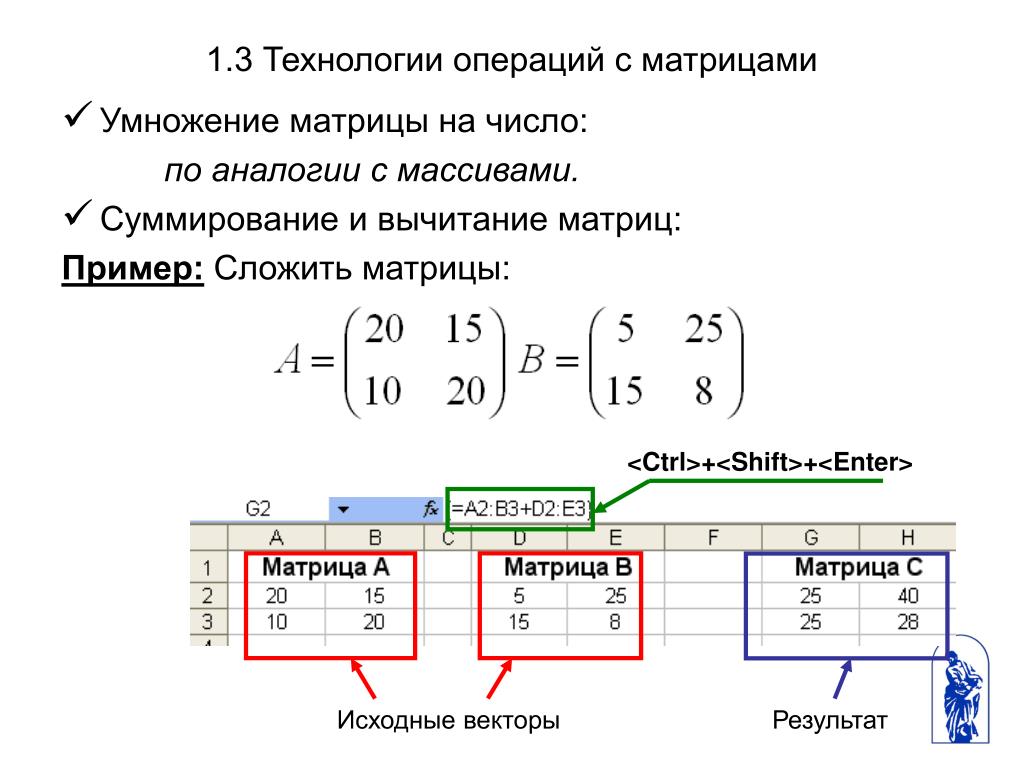

Как итог, у нас остаётся число 4

   

   

Теперь мы переходим к нахождению алгебраических дополнений.

Первым делом нужно поменять знаки у двух чисел в мироне.

   

  ← подчёркнуты те числа, у которых мы будем менять знаки.

   

, вот что у нас получилось.

И наконец-то мы переходим к завершающему этапу, к нахождению транспортированной матрице.

   

, вспоминаем формулу нахождения, и подставляем числовые значения

   

   

В завершении желательно проверить правильно ли мы нашли числовую таблицу. Это делать не обязательно, но рекомендуется, чтобы удостовериться в том, то ответ верный.

Пример 2

Задание

Найдите матрицу А.

   

Решение

Начинаем с определения матрицы.

   

   

Дело осталось за малым – осталось начти алгебраическое дополнение матрицы А:

   

   

   

   

   

   

   

   

   

Не забываем записать союзную матрицу:

   

И уже из неё находим обратную матрицу:

   

   

Получаем ответ

   

Средняя оценка 2 / 5. Количество оценок: 40

Поставьте вашу оценку

Сожалеем, что вы поставили низкую оценку!

Позвольте нам стать лучше!

Расскажите, как нам стать лучше?

65823

Закажите помощь с работой

Не отобразилась форма расчета стоимости? Переходи по ссылке

Не отобразилась форма расчета стоимости? Переходи по ссылке

описание, особенности, принципы работы с ней OTUS

В математике существует немалое количество важных элементов и значений для проведения расчетов. Некоторые из них изучаются в школах, а какие-то – в ВУЗах. Немаловажной составляющей является матрица.

Далее речь зайдет об этой математической единице – что она собой представляет, для чего необходима, какие действия с ней выполняются.

Что это

Матрица представляет собой прямоугольную таблицу элементов. Это – своеобразная таблица чисел.

Некий математический объект, который записывается в виде прямоугольной таблице элементов кольца или поля. Он представлен совокупностью строк и столбцов, на пересечении которых располагаются числа.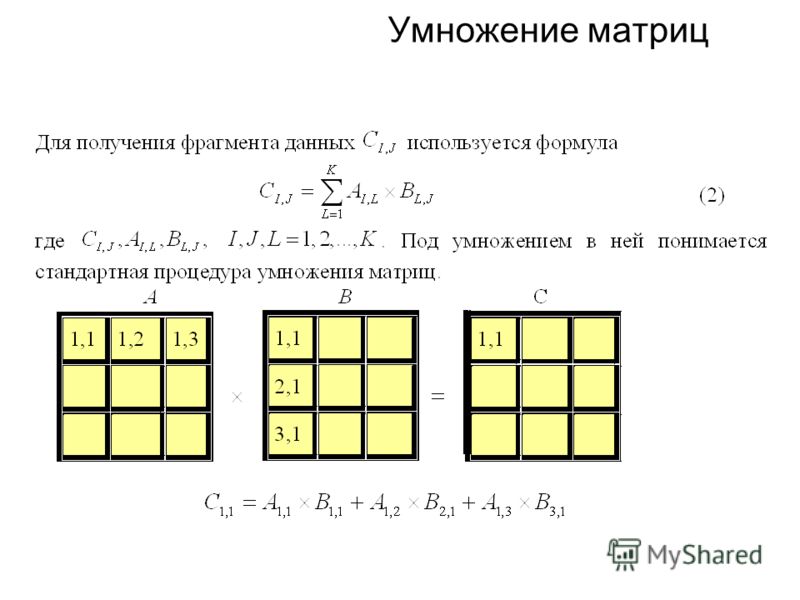 Последний – его компоненты.

Размер матрицы определяется количеством строк и столбцов. Исторически существуют разнообразные «предметы» данного типа. Пример — треугольные. Сейчас каждым математиком изучаются понятия квадратной матрицы и прямоугольной.

Возможные действия

С рассматриваемыми объектами можно выполнять различные действия:

• сложение;
• вычитание;
• умножение числа на заданную матрицу;
• нахождение определителя;
• комплексное сопряжение.

Далее поможем разобраться со всеми этими алгебраическими манипуляциями с наглядными примерами. Предложенная информация пригодится не только математикам, но и программистам.

Сложение

Складывать можно только матрицы, которые содержат в своем составе одинаковое количество чисел. Результатом будет служить объект такого же размера.

Чтобы провести операцию, требуется просто сложить их соответствующие компоненты. Пример приведен ниже.

Здесь манипуляции проделывались через матрицы a и b размером два на два. Сложение происходит и относительно положительных чисел, и относительно отрицательных.

Вычитание

При решении задач по математике, связанных с рассматриваемой темой, важно помнить об элементарных действиях. Вычитание производится по тем же принципам, что и сложение. На выходе получается матрица аналогичного размера.

Умножение на число

Любую матрицу допустимо умножить на произвольное число. Для этого предстоит:

• умножить каждый элемент оной на заданное число;
• произвести запись объекта с новыми данными.

Выше представлен пример умножения числа на заданную матрицу.

Между собой

Также в математике можно перемножать между собой рассматриваемые объекты. Но умножение матриц друг с другом представляется возможным не всегда.

Такая операция допускается, если число столбцов в объекте A равно числу строк объекта B. Каждый элемент, получившийся в i-ой строке и j-м столбце – это сумма произведений соответствующих компонентов в i-й строчке первого множителя и j-м столбце второго.

Все это – примеры того, как математик умножает рассматриваемые объекты между собой. Первый случай – теоретическая запись, второй – наглядное решение.

Транспонирование

Умножение числа на заданную матрицу – это не трудно. Но есть еще транспонирование. Так называют операцию, когда строки и столбцы меняются местами.

Выше – запись транспортированного объекта.

Определитель

Как осуществлять сложение двух матриц, а также их умножение, понятно. Достаточно помнить базовые алгебраические правила. Но рассматриваемый компонент может иметь определитель. Его также называют детерминантом. Встречается в линейной алгебре.

Определитель – численная характеристика квадратной матрицы. Она необходима для решения большого количества задач.

Для поиска определителя требуется вычислить разность произведений элементов главной и побочной диагоналей.

Определитель матрицы первого порядка (состоящей из одного компонента) – это то самое число, что в ней содержится. Если объект размером 3×3, справиться будет сложнее.

Для проведения расчетов необходимо запомнить, что:

1. Значение определителя будет равно сумме произведений главной диагонали и произведений элементов, лежащих на треугольниках с гранью параллельной главной диагонали.
2. От последней нужно вычесть произведение элементов побочной диагонали и произведение составляющих, лежащих на треугольниках с гранью параллельной побочной диагонали.
3. На практике определители крупных матриц необходимо в исключительных случаях.

Выше представлен пример нахождения детерминанта в квадратном объекте 2×2.

Обратные «модели»

Обратная матрица тоже встречается при решении задач. Вырожденная «модель» — это квадратный объект строк и столбцов n-го порядка, когда определитель равен нулю. Невырожденная – когда не равен ему соответственно.

Матрица A^-1 – обратная, если для нее актуально соотношение типа: A x A^-1=A^-1 x A = E.

Если A^-1 не вырождена, то существует всего одна обратная матрица A^-1. Она будет равна значению:

А вот несколько наглядных примеров:

Как найти

Для того, чтобы определить A^-1, необходимо:

• Найти детерминант A.
• Проверить, чтобы он не был равен нулю.
• Найти миноры матрицы – M_ij.
• Определить A_ij= (-1)^i+jM_ij.
• Построить матрицу алгебраических дополнений:

• Поделить каждое из слагаемых (каждый элемент матрицы) объекта на детерминант A.

Умножение числа на матрицу, как и другие операции – это не так трудно. Зная соответствующую базу, человек сможет производить вручную или через специальные калькуляторы необходимые подсчеты. А некоторые видео уроки объяснят теорию простым языком.

Как лучше разобраться в теме

Для того, чтобы лучше понимать рассматриваемую тему, можно отправиться на специализированные IT-курсы. Там помогут:

• получить практику;
• освоить разнообразные направления математики и информационных технологий;
• обзавестись новыми полезными знакомствами;
• заниматься максимально комфортно – в удобное время, через интернет.

В конце обучения выдается сертификат, подтверждающий знания в выбранном направлении. Предложения есть как для новичков, так и для продвинутых математиков/разработчиков/системных администраторов.

Хотите освоить современную IT-специальность? Огромный выбор курсов по востребованным IT-направлениям есть в Otus!

Также, возможно, вам будет интересен следующий курс:

Умножение матриц в Excel (5 примеров)

Матрица — важный инструмент, который ежедневно используется в статистике и научных исследованиях. Электронные таблицы Excel сами по себе представляют собой очень большие матрицы, содержащие 1 048 576 строк и 16 384 столбца. Неудивительно, что Excel предоставляет несколько полезных инструментов для матричных операций. В этой статье мы сосредоточимся на умножении матриц в Excel с различными примерами различных сценариев.

---

Скачать практическую рабочую тетрадь

Как выполнить умножение матриц?

5 подходящих примеров для умножения матриц в Excel

1. Матричное умножение двух массивов

2. Умножьте один столбец на один массив строк

3. Умножение массива одной строки и одного столбца в Excel

4. Вычислить квадрат матрицы из умножения матриц

5. Умножение матрицы на скаляр.

Ошибки при умножении матриц в Excel

Ограничение умножения матриц в Excel

Вывод

Статьи по Теме

Загрузить рабочую тетрадь

Вы можете загрузить книгу, содержащую все примеры, использованные в этой статье, из поля ниже.

---

Как выполнять умножение матриц?

Во-первых, давайте сосредоточимся на том, как на самом деле работает умножение матриц. Если есть две матрицы с размерами i x j и j x k , то каждый элемент первой строки будет умножен на элементы соответствующих им входных номеров из первого столбца второй матрицы. Затем все добавленные результаты будут указывать значение элемента первой строки и первого столбца результирующей матрицы, взяв номер строки из первой матрицы и номер столбца из второй. Это будет продолжаться i x k раза и в результате получим матрицу i x k .

Давайте возьмем пример, где мы добавляем две матрицы A и B.

Каждая запись из первой строки матрицы A будет умножаться на соответствующие записи из первого столбца матрицы B. Тогда результат даст нам значение 1×1 умноженной матрицы, скажем, C. В этом примере это будет 1 *4+2*6+3*8=40.

Тот же процесс повторяется для 1-й строки из A и 2-го столбца из B, 2-й строки из A и 1-го столбца из B, 2-й строки из A и 2-го столбца из B.

Наконец, результат будет выглядеть примерно так.

Это умножение матрицы А и В.

---

5 подходящих экземпляров для умножения матриц в Excel

Excel имеет встроенную функцию МУМНОЖ для умножения матриц. Эта функция принимает в качестве аргументов два массива. Мы можем использовать матрицы в качестве массивов аргументов в этой функции, чтобы получить желаемый результат.

---

1. Матричное умножение двух массивов

Возьмем две отдельные матрицы A и B. В Excel мы будем рассматривать их как массивы для умножения матриц.

Шаги:

• Сначала выберите ячейки, в которые вы хотите поместить свою матрицу.

• Затем запишите следующую формулу.

=МУМНОЖ(B5:D7,B10:D12)

• Теперь на клавиатуре нажмите Ctr+Shift+Enter . Вы получите результат матрицы AxB.

Вы можете сделать то же самое для матрицы BxA, введя матрицу B в качестве первого и матрицу A в качестве второго аргумента функции МУМНОЖ .

Подробнее: Как умножить 3 матрицы в Excel (2 простых метода)

---

2. Умножение одного столбца на массив одной строки

Возьмем следующий набор данных с матрицами, содержащими только один столбец и одну строку.

Перемноженная матрица AxB будет результатом умножения матриц с одним столбцом и одной строкой.

Шаги:

• Сначала выберите диапазон ячеек для перемножаемой матрицы.

• Затем запишите следующую формулу.

=МУМНОЖ(B5:B7,B10:D10)

• Наконец, нажмите Ctrl+Shift+Enter на клавиатуре. У вас получится результирующая матрица.

Подробнее: Как умножить несколько ячеек в Excel (4 метода)

---

Аналогичные показания

• Как умножать столбцы в Excel (9 простых и полезных способов)
• Умножение двух столбцов в Excel (5 самых простых способов)
• Как использовать функцию умножения в Excel (с 3 альтернативными методами)
• Если ячейка содержит значение, умножьте его с помощью формулы Excel (3 примера)

---

3.

Умножение массива одной строки и одного столбца в Excel

Для того же набора данных, который использовался в предыдущем методе, матричное умножение BxA будет означать умножение матриц из одной строки и одного столбца.

Шаги:

• Сначала выберите ячейку. Это умножение даст только одно значение, поэтому выберите здесь одну ячейку.

• Затем введите следующую формулу.

=МУМНОЖ(B10:D10,B5:B7)

• Теперь нажмите Ctrl+Shift+Enter на клавиатуре. Вы получите желаемый результат.

Подробнее: Формула умножения в Excel (6 быстрых подходов)

---

4. Вычисление площади матрицы путем умножения матриц

Вернемся к матрицам на примерах, использованных в первом примере. Здесь мы воспользуемся умножением матриц, чтобы определить квадраты матриц A и B.

Шаги:

• Выберите диапазон ячеек для вашей квадратной матрицы.

• Теперь запишите следующую формулу.

=МУМНОЖ(B5:D7,B5:D7)

• Теперь нажмите Ctrl+Shift+Enter на клавиатуре. У вас получится квадрат матрицы А.

Вы можете заменить диапазон матрицы A на диапазон матрицы B (B10:D12) и получить квадрат матрицы B тоже.

Подробнее: Что такое формула умножения в Excel для нескольких ячеек? (3 направления)

---

Аналогичные показания

• Как умножить столбец на число в Excel (4 простых метода)
• Умножение на проценты в Excel (4 простых способа)
• Как умножить столбец в Excel на константу (4 простых способа)
• Умножить два столбца, а затем суммировать в Excel

---

5. Умножение матрицы на скаляр

Когда матрица умножается только на число, все элементы матрицы умножаются на это число. Это также может быть достигнуто в Excel.

Для демонстрации я использую здесь матрицу A и умножаю ее на 7.

Шаги:

• Выберите диапазон ячеек для перемножаемой матрицы.

• Затем введите в поле следующую формулу.

=B5:D7*G7

• Нажмите Ctrl+Shift+Enter на клавиатуре.

Подробнее: Как умножать в Excel: столбцы, ячейки, строки и числа

---

Ошибки при умножении матриц в Excel

Существует несколько ошибок, с которыми вы можете столкнуться при выполнении умножения матриц в Excel.

из них #ЦЕННОСТЬ! Ошибка может возникнуть, если количество столбцов в первом массиве и количество строк во втором массиве не совпадают.

Вы получите ту же ошибку, если в ячейке массива есть хотя бы одно нечисловое значение.

Если вы выберете больше значений, чем выглядит ваша предполагаемая матрица умножения, вы получите ошибку #N/A , но только в дополнительных выбранных вами ячейках.

Подробнее: Как делить и умножать в одной формуле Excel (4 способа)

---

Ограничение умножения матриц в Excel

Если вы используете Excel 2003 или более раннюю версию, существует ограничение на умножение матриц размером 71×71. Но для более поздних версий вы можете выполнять операцию столько, сколько позволяет электронная таблица, ограничиваясь только оперативной памятью вашей системы.

---

Заключение

Это были разные ситуации, в которых вы можете выполнять умножение матриц в Excel. Надеюсь, вы нашли эту статью полезной и информативной. Если у вас есть какие-либо вопросы или предложения для нас, сообщите нам об этом ниже.

Для получения дополнительных руководств, подобных этим, посетите Exceldemy. com .

---

Связанные статьи

• Как составить таблицу умножения в Excel (4 метода)
• Умножение одной ячейки на несколько ячеек в Excel (4 способа)
• Как рассчитать ковариационную матрицу в Excel (с помощью простых шагов)
• Создание матрицы обучения в Excel (3 простых метода)
• Как создать матрицу прослеживаемости в Excel
• Создание корреляционной матрицы в Excel (2 удобных подхода)

Как перемножать матрицы? С Примерами

Умножение матриц является одной из фундаментальных, но продвинутых концепций матриц. Вы должны быть осторожны при умножении матриц. Это не так просто, как кажется. Вы должны хорошо знать все основные понятия, такие как, что такое матрица, строки и столбцы в матрице, как представлять матрицу и как умножать матрицы.

Снова в школу: Матрицы — это группы чисел, переменных, символов или выражений в прямоугольной таблице с различным количеством строк и столбцов. Это прямоугольные массивы с различными операциями, такими как сложение, умножение и транспонирование. Элементами матрицы являются числа или элементы, составляющие матрицу. Горизонтальные элементы матриц — это строки, а вертикальные — столбцы.

Количество строк и столбцов можно изобразить с помощью переменных. Например, пусть количество строк в матрице K равно «m», а количество столбцов — «n». Таким образом, мы можем представить матрицу K как [K] _{м х п} . Матрица представлена ​​в квадратных скобках «[]» с произведением ее строк и столбцов в нижнем индексе.

До 1812 года человечеству не было известно умножение матриц. Филипп Мари Бине, французский математик, изобрел умножение матриц в 1812 году для описания линейных карт с матрицами. Он обнаружил, что умножение матриц является бинарной операцией. Две матрицы перемножаются, образуя одну матрицу.

Далее в этой статье вы узнаете правила и основные принципы умножения матриц.

Что такое умножение матриц?

Во введении к этой статье вы прочитали, что умножение матриц — это бинарная операция. Это означает, что всякий раз, когда вы находите произведение двух или более матриц, ответом является единственная матрица, следующая за исходными матрицами. Для перемножения двух матриц проверяется их совместимость. Это означает, что две матрицы должны следовать набору правил для умножения.

Эти параметры совместимости описаны ниже:

• Значение количества столбцов в матрице один должно быть равно значению количества строк в матрице 2.
• Если вышеуказанное условие не выполняется, матрицы нельзя перемножать.
• Если матрицы являются квадратными матрицами одного порядка, их можно умножать друг на друга.
•  Квадратную матрицу 2 x 2 нельзя умножить на квадратную матрицу 3 x 3. Ее можно умножить на другую квадратную матрицу 2 x 2. 

Давайте рассмотрим пример, чтобы лучше понять это:

Пример 1: Предположим, у нас есть две матрицы, K и L. Порядок матриц задан как m x n и n x o соответственно. Выяснить, можно ли перемножать матрицы?

Решение: Дано

Матрица 1 = [ K ] _{m x n}  

Матрица 2 = [ L ] _{n x o}

Мы видим, что количество столбцов в матрице равно количеству строк K матрица L. Следовательно, две матрицы можно перемножить.

Результирующая матрица: Матрица, полученная путем умножения двух матриц, является результирующей матрицей. Эта матрица может быть представлена ​​как:

• Название матрицы в квадратных скобках
• Произведение количества строк матрицы 1 на количество столбцов матрицы два в порядке убывания.

Снова обратимся к приведенному выше примеру:

Мы знаем, что K и L совместимы с умножением. Таким образом, результирующая матрица, скажем, D, будет = [D] _{m x o} , где m = количество строк матрицы один и o = количество столбцов матрицы 2. 

Пример 2: Матрица [ K ] _{2 x 4} умножается на матрицу [ X ] _{4 х 2} . Если [ Y ] результирующая матрица, то каков порядок Y.

Решение: Нам дано

Матрица 1 = [ K ] _{2 x 4}

Матрица 2 = [ X ] _{4 x 2}

Поскольку количество столбцов матрицы K равно количеству строк матрицы X, K и X можно перемножить. Следовательно,

Матрица Y = [ Y ] _{2 x 2} 

Порядок матрицы Y равен 2 x 2. Y – квадратная матрица.

Ориентация двух матриц также является решающим фактором для определения произведения матриц. Если есть две матрицы, K и L, то чтобы найти произведение K и L, вы должны сначала написать матрицу K, а затем написать матрицу L. Если вы запишете матрицу L перед матрицей K, вы получите совершенно другую матрицу . Коммутативный закон не применяется при умножении матриц. Это означает, что KL ≠ LK.

Теперь, когда мы разобрались с правилами умножения двух матриц, давайте научимся умножать матрицы.

Как умножать матрицы?

Давайте изучим пошаговую процедуру умножения двух матриц. Поначалу это может показаться вам запутанным, но когда вы освоитесь, перемножать матрицы так же просто, как намазать маслом свой тост.

Шаг 1: Проверить совместимость предоставленных матриц. Если они несовместимы, оставьте умножение.

Шаг 2: Возьмите первую строку матрицы 1 и умножьте ее на первый столбец матрицы 2. Затем умножьте первую строку матрицы 1 на 2-й столбец матрицы 2. Теперь умножьте первую строку матрицы 1 на 3-й столбец матрицы 2 и так далее. Полученные из них значения заполнят первую строку матрицы продукта.

Шаг 3: Теперь возьмите вторую строку матрицы 1 и умножьте ее на первый столбец матрицы 2 и выполните те же шаги, что и для 2. Это заполнит вторую строку матрицы произведения.

Шаг 4: Продолжайте эти шаги, выполняя каждую строку, пока не будет получена матрица произведения.

Под умножением строк и столбцов мы подразумеваем, что элементы, присутствующие в этих строках и столбцах, будут умножены. Не забудьте умножить соответствующие элементы, а затем добавить продукты, чтобы найти элемент матрицы продукта.

Если вы не уверены в шагах, посмотрите на пример пошагового решения ниже:

Пример: Найдите произведение матриц, приведенных ниже:

K = и L =    

Решение:  

Шаг 1: Матрица K имеет порядок 1 x 4, а матрица L имеет порядок 4 x 2. Поскольку количество столбцов матрицы K соответствует количеству строк матрицы L, поэтому матрицы совместимы для умножения. Полученная матрица имеет порядок 1 x 2. 

Шаг 2: Поскольку K имеет только 1 строку, умножьте ее на первый столбец матрицы L следующим образом: (2 x 4) + (4 x 5) + (1 x 4) + (7 x 3) = 51. Обратите внимание, как 1-й элемент строки умножается на 1-й элемент столбца 1, аналогично 2-му, 3-му и 4-му. Затем они складываются вместе, чтобы получить результирующий матричный элемент.

Шаг 3: Теперь аналогичным образом умножьте 1-ю строку на второй столбец матрицы L. Результат будет (2 x 3) + (4 x 2) + (1 x 9) + (7 x 6) = 65 . 

Шаг 4: Разместите результат в матрице продуктов. Предположим, что [ X ] — результирующая матрица; следовательно, X = [51  65].

Мы только что научились перемножать две матрицы. В следующем разделе вы узнаете, как решить квадратную матрицу (2 x 2).

Мы только что научились перемножать две матрицы. В следующем разделе вы узнаете, как решить квадратную матрицу (2 x 2).

Как умножить матрицу 2 x 2

Для умножения матриц 2 x 2 вы должны хорошо знать шаги, описанные в предыдущем разделе. Поскольку мы перемножаем 2 квадратные матрицы одного порядка, нам не нужно проверять совместимость в этом случае. Помните, что матрица произведения также будет иметь тот же порядок, что и квадратная матрица. Давайте решим пример, чтобы понять, как умножить матрицу 2 x 2.

Пример: Умножить квадратную матрицу на

A = и B =

Шаг 1: Умножая первую строку матрицы A на первый столбец матрицы B. Получаем (2 x 1) + (9 x 3) = 29. Теперь умножаем первую строку матрицы A со вторым столбцом матрицы B. Получаем (2 x -4) + (9 x 7) = -8 + 63 = 55.

Шаг 2: Повторим шаг 1, но изменим строку матрица A. Первый и второй столбцы матрицы B будут умножены на строку 2 матрицы A. Результатом будет

(3 x 1) + (-7 x 3) = 3 – 21 = -18, и (3 x -4) + (-7 х 7) = -12 – 49= -61

Шаг 3: Разместите результаты правильно

.

Следовательно, результирующая матрица C =

Точно так же вы можете решать квадратные матрицы, такие как 3 x 3, 4 x 4 и так далее.

Определение, правила, свойства и примеры

Умножение матриц, которое также читается как умножение матриц, является одной из матричных бинарных операций, которые можно выполнять над матрицами. Умножение любой матрицы X на другую матрицу Y возможно, если обе предоставленные матрицы совместимы. Матрицы — это множественная форма матрицы, которая символизирует прямоугольный массив или таблицу, в которой числа/элементы организованы в строки и столбцы. Матрицы могут содержать любое количество столбцов и строк.

Над матрицами можно выполнять различные операции, такие как сложение матриц, вычитание матриц, скалярное умножение матриц, умножение матриц, транспонирование матрицы и т. д. Прокручивая вниз, мы узнаем об умножении матриц, умножении двух и трех матриц, правилах умножения матриц, о том, как умножать матрицы и многом другом с решенными примерами.

Умножение матриц

При работе с матрицами необходимо соблюдать определенные правила. Например, матрицы можно складывать или вычитать, если только они имеют одинаковое количество строк и столбцов. В то время как матрицы можно перемножать, если только столбцы в первой матрице и строки во второй идентичны. Умножение матриц — это бинарная операция, произведение которой также является матрицей при умножении двух матриц. Умножение матрицы X и Y, заданное как XY, которое не равно YX, т.е. мы можем сказать, что XY ≠ YX. Поскольку в этой статье мы сосредоточимся на умножении матриц, давайте проверим правила для того же самого.

Правила умножения матриц

Матрицы, о которых мы говорили выше, представляют собой организации чисел/символов/переменных в прямоугольной таблице, состоящей из нескольких строк и столбцов.

Числа или записи в строке и столбце матрицы признаются их элементами. Горизонтальные списки для матриц называются строками, а вертикальные записи известны как столбцы. Правила умножения матриц следующие:

• Для произведений матриц матрицы должны быть совместимы. Это утверждает, что две матрицы A и B совместимы, если количество столбцов в A равно количеству строк в B.
• Например, если A — матрица порядка n×m, а B — матрица порядка m×p, то можно считать, что матрицы A и B совместимы.
• Умножение матрицы порядка 4 × 3 на другую матрицу порядка 3 × 4 допустимо и дает матрицу порядка 4 × 4.
• Аналогично, если мы попытаемся умножить матрицу порядка 4 × 3 на другую матрица 2 × 3. Это умножение матрицы невозможно, поскольку две матрицы не подчиняются правилу совместимости.

Если вы читаете Умножение матриц, то вам также следует прочитать об определителях.

Как умножать матрицы?

Умножение матриц в математике включает умножение матрицы на константу или умножение матрицы на матрицу, также известное как умножение двух матриц. Для умножения двух совместимых матриц ниже приведены некоторые общие шаги, которые необходимо выполнить.

• Сначала проверьте, равно ли количество столбцов в первой матрице количеству строк во второй матрице.
• Если выполнено первое условие, то умножьте элементы отдельной строки первой матрицы на элементы всех столбцов второй матрицы.
• Затем добавьте товары и расположите добавленные товары в соответствующих столбцах.
• Мы поймем вышеуказанные шаги в следующем заголовке.

Давайте разберемся, как умножать матрицы с помощью скалярного/константного умножения, за которым следует умножение матриц 2×2 и 3×3 в приведенных ниже примерах.

Узнайте о диагональной матрице в статье по ссылке.

Умножение матриц на скалярную величину

Порядок умножения матриц по определению является необходимой вещью. Давайте теперь разберемся с умножением матрицы на скалярную величину. Если мы умножаем данную матрицу на скалярное значение, то это понимается как скалярное умножение матриц. Формула и обозначение для нее:

Если \(B=\left[b_{ij}\right]_{_{m\times n}}\) — матрица порядка m × n, скалярная величина, тогда \(pB=p\left[b_{ij}\right]_{_{m\times n}}=\left[p\left(b_{ij}\right)\right]_{_ {m\times n}}\) — результат скалярного умножения матриц. Это также известно как умножение матриц на константу. Например:

\(x.\ A=x\begin{bmatrix}a&b\\
c&d\end{bmatrix}=\begin{bmatrix}a.\ x&b.\ x\\
c.\ x&d.\ x\end {bmatrix}\)

Подробнее о правиле Крамера в этой связанной статье!

Умножение матриц 2×2

Всякий раз, когда мы умножаем матрицу на другую, мы должны получить «точечный продукт» строк 1-й матрицы и столбцов 2-й матрицы, чтобы получить результат. Ниже показано умножение двух матриц 2×2.

A. \(\ B=\begin{bmatrix}a&b\\c&d\end{bmatrix}.\begin{bmatrix}e&g\\f&h\end{bmatrix}=\begin{bmatrix}a.\ e+b .f&a.g+b.\ h\\c.\ e+d.f&c.g+d.\ h\end{bmatrix}\)

Узнайте о различных типах матриц здесь, в связанной статье.

Умножение матриц 3×3

Подобно умножению матриц 2×2, давайте поймем умножение двух матриц-матриц 3×3, как показано ниже:

\(X=\begin{bmatrix}x_{11} &\ \ x_{12}&x_{13}\\
x_{21}&\ \ x_{22}&x_{23}\\
x_{31}&x_{32}&x_{33}\end{bmatrix}
\)

\(Y=\begin{bmatrix} y_{11}&\ \ y_{12}&y_{13}\\
y_{21}&\ \ y_{22}&y_{23}\\
y_{31}&y_{32}&y_{33}\end {bmatrix}
\)
Произведение двух матриц равно:

\(X\times Y\)=

\(\begin{bmatrix}x_{11}y_{11}+x_{12} y_{21}+x_{13}y_{31}&\ \ x_{11}y_{12}+x_{12}y_{22}+x_{13}y_{32}&x_{11}y_{13} +x_{12}y_{23}+x_{13}y_{33}\\
x_{21}y_{11}+x_{22}y_{21}+x_{23}y_{31}&\ \ x_{21}y_{12}+x_{22}y_{22}+x_{ 23}y_{32}&\ \ x_{21}y_{13}+x_{22}y_{23}+x_{23}y_{33}\\
x_{31}y_{11}+x_{32 }y_{21}+x_{33}y_{31}&\ x_{31}y_{12}+x_{32}y_{22}+x_{33}y_{32}&\ x_{31}y_{ 13}+x_{32}y_{23}+x_{33}y_{33}\end{bmatrix}\)

Если мы умножаем матрицу на скалярное значение, то это распознается как скалярное умножение. T\), где T обозначает транспонирование матрицы. 9{*}\).

Если AB=0, это не означает, что A=0 или B=0.

Произведение двух ненулевых матриц может быть нулевой матрицей.

Некоторые дополнительные свойства скалярного умножения матриц: \(λ(µA)=(λµA)=µ(λA)\)

\((-λA)=-(λA)=λ(-A)\)

Мультипликативное свойство нуля

Всякий раз, когда мы умножаем число на ноль, произведение всегда равно нулю. Независимо от положения нуля, т.е. ноль может стоять до или после числа. Рассмотрим приведенный ниже пример, чтобы понять свойство.

Если \(A=\begin{bmatrix}1&2\\
3&4\end{bmatrix}\) умножается на нулевую матрицу \(B=\begin{bmatrix}0&0\\
0&0\end{bmatrix}\ ), тогда на выходе будет только нулевая матрица, как показано: {bmatrix}1.\ 0+2.\ 0&1.\ 0+2.\ 0\\
3.\ 0+4.\ 0&3.\ 0+4.\ 0\end{bmatrix}\)

Learn о Матрице трансформации в связанной статье здесь!

Решенные примеры умножения матриц

Давайте завершим тему некоторыми решенными примерами, относящимися к формуле, свойствам и правилам.

Решено Пример 1: Найдите скалярное произведение числа 2 с заданной матрицей \(A=\begin{bmatrix}-1&\ \ 2\\
\ 4&-3\end{bmatrix}\).

Решение: Скалярное произведение может быть получено как:
\(2.\begin{bmatrix}-1&\ \ 2\\
\ 4&-3\end{bmatrix}=\begin{bmatrix}-2&\ \ 4\\
\ \ 8&-6\end{bmatrix}\)

Решено Пример 2: Получить результат умножения A и B, где
\(A\ =\begin{bmatrix}1&0\\
2&4\end{bmatrix },\ B=\begin{bmatrix}2&1\\
0&2\end{bmatrix}\)

Решение:

\(A.\ B=\begin{bmatrix}1&0\\
2&4\end{ bmatrix}.\begin{bmatrix}2&1\\
0&2\end{bmatrix}\)

\(A.\ B=\begin{bmatrix}1.\ 2+0.0&1.1+0.\ 2\\
2.\ 2+4.0&2.1+4.\ 2\конец{bmatrix}\)

\(A.\ B=\begin{bmatrix}2&1\\
4&10\end{bmatrix}\)

Прочтите эту статью о применении матриц и определителей.

Решено Пример 3: Для приведенного ниже матричного условия:
\(A=\begin{bmatrix}2&3\\
1&2\end{bmatrix},\ B=\begin{bmatrix}x&4\\
y&- 2\end{bmatrix},\ A. B=\begin{bmatrix}3&2\\
1&0\end{bmatrix}\)
Каково значение x и y?

Решение:

\(A=\begin{bmatrix}2&3\\
1&2\end{bmatrix}\times\begin{bmatrix}x&4\\
y&-2\end{bmatrix}=\begin{bmatrix}3&2\\
1&0\end{bmatrix}\)

\(\Rightarrow \begin{bmatrix}2x+3y&8-6\\
x+2y&4-4\end{bmatrix}=\begin{bmatrix}3&2\\
1&0\end{bmatrix}\)

Итак, \(2x+3y =3\cdots\left(1\right)\)
\(x+2y=1\dots\left(2\right)\)
Решая уравнения 1 и 2, получаем:
x = 3 и y = – 1.

Решено Пример 4: Если \(A=\begin{bmatrix}2&-2\\ 92+6A=\begin{bmatrix}2&0\\
0&2\end{bmatrix}\)

Мы надеемся, что приведенная выше статья об умножении матриц поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.

Часто задаваемые вопросы об умножении матриц

В.1 Как умножить две матрицы?

Ответ 1 Вы можете умножать две матрицы только в том случае, если их размеры совместимы, что указывает на то, что количество столбцов в первой матрице идентично количеству строк во второй матрице.
Затем умножьте элементы отдельной строки первой матрицы на элементы всех столбцов второй матрицы, сложите продукты и расположите добавленные продукты в соответствующих столбцах.

В.2 Можно ли перемножить матрицу 2×2 и 3×3?

Ответ 2 Нет, мы не можем перемножать матрицы 2×2 и 3×3, так как эти матрицы несовместимы друг с другом.

Q.3 Какова формула умножения двух матриц?

Ответ 3 Формула умножения двух матриц:

\(A.\ B=\begin{bmatrix}a&b\\
c&d\end{bmatrix}.\begin{bmatrix}e&g\\
f&h\end{bmatrix}=\begin{bmatrix}a.