Матрица прямоугольная пример: (35)84.Что такое прямоугольные и квадратные матрицы? Примеры. - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Прямоугольная матрица – Энциклопедия по экономике

Прямоугольная матрица Р моделирует размещение производства или потребления различных видов нефтепродуктов в районах страны. Буквами от а до z обозначают виды нефтепродуктов. Цифровые индексы у букв означают № районов, например, Ь2 означает объем потребления второго вида нефтепродуктов во втором районе и т. д. Каждая строка характеризует объем и номенклатуру нефтепродуктов всех отраслей производства в одном из районов каждый столбец модели характеризует объем и размещение потребления одного из видов нефтепродуктов по всем районам. Число столбцов обычно не равно числу строк. [c.373]
Структура группирует по существенно важным признакам юридические и экономические отношения организации. Методология этой группировки носит статистический характер, и ее принципы позволяют сделать вывод о том, что бухгалтерский учет может рассматриваться как частный случай экономической статистики. При этом надо помнить, что модель структуры имеет форму прямоугольной матрицы, где по столбцам перечисляются дебетуемые счета, а по строкам — кредитуемые.

[c.166]

Отметим, что четвертая группа уравнений в модели Вальраса является своеобразным прообразом модели В. Леонтьева затраты — выпуск , однако она еще представляет собой прямоугольную матрицу (nxm) элементов, в то время как у В. Леонтьева — квадратную матрицу (пхп) элементов. Кроме того, в модели Леонтьева структурирован валовой выпуск (он подразделяется на промежуточный и конечный продукт), показаны источники производства добавленной стоимости, имеется, раздел баланса с характеристиками использования элементов конечного продукта и раздел перераспределения доходов. Но все же самая существенная идея модели затраты — выпуск уже содержалась в выводах Вальраса. [c.82]

Нечеткая прямоугольная матрица – это дважды индексированное [c.33]

Две прямоугольные матрицы С = (с у) и С”= ( “t) размером т п назовем эквивалентными (С С”), если с” у = с + а,- +Ру- / =1, 2,. .., т j — 1, 2,. .., п. Задачи выбора, определяемые эквивалентными матрицами, являются эквивалентными, так как можно доказать, что множества оптимальных назначений двух задач выбора с эквивалентными матрицами совпадают. [c.203]

Прямоугольная матрица 187 Прямоугольные игры 295 Прямые задачи управления 102 Прямые затраты 236, 295 Прямые инвестиции 121 Прямые налоги 210 Псевдослучайные величины 295 Псевдослучайные числа 295 Пуассоновский поток 270, 295 Пуассоновский случайный процесс 333 Пустое допустимое множество 237 Пустое множество 201 Путь 295 [c.485]

Для прямоугольных матриц определена операция транспонирования. Рассмотрим произвольную прямоугольную матрицу А. Матрица, получающаяся из матрицы А заменой строк столбцами, называется транспонированной по отношению к матрице А и обозначается А А [c.58]

Крупноформатный электронный бланк — это совокупность объектов, активных в данный момент и обычно представляемых в виде прямоугольной матрицы элементов, похожей на бумажную таблицу или ведомость, используемую в бухгалтерском учете. Каждой клетке этой таблицы на экране соответствует одна запись в памяти. Запись определяет правило нахождения значения, простейший вид которого предусматривает обработку элемента-клетки, например числа или фрагмента текста.

Более сложное правило может предусматривать нахождение значения по какой-либо математической формуле в зависимости от значений других элементов с учетом их относительных или абсолютных позиций либо (что гораздо лучше) присвоенных им имен. Правило нахождения значения может предусматривать также проверку некоторого условия и установление значения своего элемента в соответствии с результатом проверки. [c.101]

Как следует из определения, единичная матрица может быть только квадратной, прямоугольная матрица не может быть диагональной или единичной, так как у нее отсутствует ось симметрии, которой и является главная диагональ. [c.367]

При транспонировании прямоугольных матриц происходит изменение их размера с mxn на nxm, при транспонировании квадратных матриц размер их не изменяется. Ниже приводятся примеры транспонирования прямоугольной и квадратных матриц [c.374]

Значения / и J образуют две прямоугольных матрицы J+ и / . На пересечении г-й строки и /-го столбца первой матрицы стоит оценка обоснованности гипотезы сг=>+о/, а на том же месте во второй матрице — оценка обоснованности гипотезы с = о/.

[c.184]

Теорема о ранге матрицы. Нахождение ранга матрицы элементарными преобразованиями. Ранг произведения матриц. Представление прямоугольной матрицы в виде произведения двух матриц полного ранга. [c.11]

Если N > q, то естественно ожидать, что прямоугольная матрица Л имеет полный ранг по столбцам. Тогда условие d A = 0 возможно только если [c.17]

Нечеткие последовательности, нечеткие прямоугольные матрицы, нечеткие функции и операции над ними [c.35]

Нечеткая прямоугольная матрица – это дважды индексированное конечное множество нечетких чисел, причем первый индекс пробегает М строк, а второй – N столбцов. При этом, как и в случае матриц действительных чисел, операции над нечеткими прямоугольными матрицами сводятся к операциям над нечеткими компонентами этих матриц. Например, [c.35]

Введем в рассмотрение прямоугольные матрицы R T=[R I Rj )…. I Rn ], А = [I I A ,… I An ] и квадратные матрицы А вида [c.307]

Понятие матрица пришло из математики. Матричный орган, связанный взаимными отношениями, составленными в прямоугольную схему, называется матрицей. В матричной системе имеются главные и поперечные функции. [c.34]

Коэффициенты обычно располагаются в виде прямоугольной таблицы, которая состоит из определенного количества строк и столбцов в зависимости от разнообразия переменных. Схема такой таблицы, называемой в линейной алгебре матрицей, следующая [c.233]

Исходя из правил перемножения матриц, можно записать вектор потребностей как результат умножения прямоугольной нормативной матрицы [c.37]

Таким образом, при использовании электронно-вычислительных машин процесс расчета потребности в нефтепродуктах на выполнение всего объема работ по плану может быть сведен к перемножению прямоугольной нормативной матрицы на вектор объемов работ. [c.38]

Одним из факторов, влияющих на безотказность работы БИС ПЛМ является исключение возможности восстановления запрограммированной БИС, что обусловлено механизмом разрушения плавкой перемычки из нихрома в цепи запоминающего элемента (ЗЭ). Плавкая перемычка зажата в слоях из двуокиси кремния, сформированной на массивной кремниевой подложке и имеет форму, приведенную на рисунке. Для разрушения перемычки ЗЭ в матрице ПЛМ на нее воздействуют серией прямоугольных электрических импульсов, переводящих выбранный разряд в непроводящее состояние, что соответствует логическим О или 1 . Запрограммированная перемычка в процессе эксплуатации при воздействии на нее электрическими импульсами способна восстановиться. Одной, из причин восстановления перемычки является разброс геометрических параметров элементов ПЗУ при изготовлении. [c.31]

Первый квадрант МОБ — это прямоугольная таблица межотраслевых материальных связей. Показатели таблицы представляют собой величины прямых межотраслевых потоков продукции и обозначаются как ху, где / и j — соответственно номера производящих и потребляющих отраслей. Таким образом, этот квадрант имеет вид квадратной матрицы л, сумма всех элементов которой равна годовому фонду возмещения затрат средств производства в материальной сфере.

[c.508]

Матрица А размера га х п (т х п матрица) — это прямоугольный массив вещественных чисел 1 [c.23]

Подматрица матрицы Л есть прямоугольный массив, полученный из Л вычеркиванием некоторых строк и столбцов. Минором называется определитель квадратной подматрицы Л. Минором элемента а – называется определитель подматрицы Л, полученной вычеркиванием ее г-й строки и j-ro столбца. Алгебраическим дополнением а -, обозначаемым с -, называется произведение (— 1)г+-7 на минор aij. Матрица С = ( ij) называется матрицей алгебраических дополнений матрицы А. Транспонированная к С матрица называется присоединенной к Л и обозначается А . Имеем [c.30]

Замечание. Допущение 3° может быть ослаблено и заменено следующим Матрицы Ли( (й 4) прямоугольные, ранг Аи равен числу строк элементы мат- [c.245]

Это название объясняется следующей возможностью описания игр такого рода. Составим прямоугольную таблицу, в которой строки соответствуют стратегиям первого игрока, столбцы — стратегиям второго, а клетки таблицы, стоящие на пересечении строк и столбцов, соответствуют ситуациям игры. Если поставить в каждую клетку выигрыш первого игрока в соответствующей ситуации, то получим описание игры в виде некоторой матрицы. Эта матрица называется матрицей игры или матрицей выигрышей. П [c.25]

Сведение норм расхода (или удельных расходов) энергоресурсов, поступающих на предприятия со стороны, в прямоугольную матрицу, оличество строк соответствует количеству видов энергоресурсов, поступающих на предприятие со стороны, а количество и расположение столбцов то же, что и в матрице для энергоресурсов собственного производства (см. п. 2). [c.198]

В результате обследования рынков формируется прямоугольная матрица X = = ( ..), t=l,…, т j = 1,. .., п, где х . — значение /-и характеристики г -го рынка. Отметим, что здесь не рассматриваются вопросы планирования эксперимента, в частности, какие именно характеристики и как измерять. Можно считать, что в данной матрице отражены все доступные наблюдению характеристики рынков или же только те из них, которые мы считаем наиболее информативными. В этом случае выбор осуществляется на основе показателя информативности каждой из характеристик либо на основе результатов сравнения матриц близости между объектамиD. = (dkl ), k, I = 1,…, т, где, например, dkl = xkj -x , j = 1,…, п. [c.74]

Возможйые варианты (исходы) игры сводятся в прямоугольную таблицу — платежную матрицу, в которой строки соответствуют различным стратегиям игрока А, столбцы — стратегиям игрока В, qtj называется ценой игры (табл. 8.23). [c.150]

Как показывает практика, наиболее рациональна такая организация работ, при которой за каждой задачей закреп-ляется один ответственный. В предлагаемой модели принимается строгое разделение ответственности за выполнение каждой задачи за одной и той же задачей не должно быть назначено более одного ответственного ни одна задача не может не иметь ответственного. Условимся в матрице, учитывающей участие штатных категорий в выполнении задач, стоящих перед подразделением, ответственных за задачу обозначать знаком ++ . В общем случае функциональная схема многоцелевого подразделения (табл. 21) представляет собой прямоугольную таблицу размера N+n, где N — число задач, решаемых подразделением, п — число штатных категорий, принимающих участие в решении этих задач. Табл. 21 дает полную картину деятельности подразделения и взаимодействия отдельных штатных категорий в процессе ее. Так, например, рассматривая ыо строку таблицы, устанавливаем, что в решении [c.218]

МАТРИЦА [matrix] — система элементов (чисел, функций и других величин), расположенных в виде прямоугольной таблицы. Таблица имеет следующий вид [c.187]

ПРЯМОУГОЛЬНЫЕ ИГРЫ [re tangular games] — парные игры с нулевой суммой, имеющие седловую точку. Называются так, потому что их матрица игры прямоугольная. [c.295]

В частности, столбцы ортогональной матрицы являются ортонормированны-ми. Прямоугольная (не квадратная) матрица может обладать одним из свойств А А = I или А А = /, но не обоими одновременно. Такая матрица называется полу ортогональной. [c.26]

Матрицы Лiг( oi 1) прямоугольные, ранг Ац равен чрслу ее строк, элементы матрицы .((ш -1) и псевдообратной матрицы А (ш – >) неотрицательны и, кроме [c.247]

Сепдовыми точками являются здесь все четыре угловых ситуации. То, что прямоугольное множество (Г) выглядит здесь несвязным, не имеет значения порядок строк и столбцов матрицы может быть произвольно изменен (см. п. 1. 9). [c.35]

Матрицы. Основные понятия. Матрицей называется прямоугольная таблица чисел. Пример 13

Подборка по базе: Таблица основные теории происхождения государства.docx, Реабилитация после перелома шейки бедра — основные меры.pdf, 3. Основные методы педагогической психологии.pdf, Лекция 1. Основные положения теории автоматического управления.d, СР по теме Основы языка Паскаль и основные алгоримческие констру, Тема 1.3. Педагогика как наука, ее основные категории .pdf, Что такое современная филология. Основные особенности филологиче, Тема 1.1 Философия как наука, ее основные категории, понятия и ф, Тема 1 ТГП нац без основные термины.

docx, 1.Тема № 1 Россия в современном мире. основные направления социа

Матрицы.

Основные понятия.

Матрицей называется прямоугольная таблица чисел.

Пример 13. , , , .

В общем случае матрица может содержать строк и столбцов

Числа называются элементами матрицы, где – указывает номер строки, – указывает номер столбца.

Элементы образуют главную диагональ матрицы. Если число строк равно числу столбцов, то матрица называется квадратной. Квадратная матрица размеров называется матрицей – го порядка.

Матрицы называются равными, если у них равны элементы, стоящие на соответствующих местах, т. е. тогда и только тогда, когда , для всех , .

Квадратная матрица, у которой все элементы, кроме главной диагонали равны 0, называется диагональной.

Пример 14. .

Если все элементы матрицы равны нулю, то матрица называется нулевой.

Пример 15. .

Диагональная матрица, у которой каждый элемент диагонали равен 1, называется единичной.

Пример 16. , .

Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от диагонали, равны нулю.

Пример 17. , .

Матрица, содержащая одну строку (столбец), называется вектором(вектор-строкой, вектор-столбцом).

Пример 18. , .

Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется транспонированной .

Пример 19. ;

Очевидно, что .

Действия над матрицами.

Матрицы одинаковых размерностей можно складывать и вычитать. Если

, , то , причем

, для всех .

Пример 20. ,

Умножение матрицы на число.

Чтобы умножить матрицу на число, необходимо каждый ее элемент умножить на это число.

Пример 21. Пусть , тогда . Матрица называется противоположной к матрице .

Умножение матриц.

Умножение матриц можно только в том случае, когда число столбцов матрицы равно числу строк матрицы В этом случае справедливо соотношение , причем элементы матрицы равны , , . Другими словами строки матрицы умножаются на столбцы матрицы

Пример 22. Пусть , . Тогда

Видим, что в общем случае . Если же выполняется условие , то матрицы и называются перестановочными друг с другом.

Матрица называется ступенчатой, если для её элементов выполняются условия:

под первым не нулевым элементом каждой строки находится 0;
первый ненулевой элемент любой строки находится правее первого не нулевого элемента любой строки, расположенной выше.

Пример 23. Следующая матрица является ступенчатой.

Элементарные преобразования матриц.

Элементарными преобразованиями матриц являются:

Перестановка местами двух любых её строк (столбцов).
Умножение элементов какой-нибудь строки (столбца) на некоторое не нулевое число.
Прибавление ко всем элементам строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число.

Две матрицы называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований

Любую матрицу с помощью элементарных преобразований можно привести к ступенчатому виду.

Определители.

Определителемназывается квадратная числовая таблица, вычисляемая по определенным правилам.

Пример 24. Если , то . Так .

Если , то .

Так .

Если , то

. Так

При вычислении определителей 3-го порядка удобно пользоваться правилом треугольников. С плюсом берутся произведения элементов стоящих на главной диагонали и элементы, стоящие в вершинах следующих треугольников.

С минусом берутся произведения элементов, стоящих на второй диагонали и в вершинах следующих треугольников.

Второй метод заключается в том, что рядом с определителем справа записываются первый и второй столбцы и тогда с плюсом берутся произведения элементов, стоящих на главной диагонали и двух ей параллельных, с минусом – произведения элементов, стоящих на второй диагонали и двух ей параллельных.

Вычисление определителей более высоких порядков осуществляется путем использования их свойств.

Свойства определителей.

Пусть дана квадратная матрица

Из элементов этой матрицы можно составить определитель, который называется детерминантом матрицы и обозначается

Минором некоторого элемента определителя называют определитель, который получается вычеркиванием из него строки и столбца. Например

, .

Алгебраическим дополнениемэлемента определителя называют число . Например

, .

Свойства определителей.

1. Определитель не изменится, если его строки заменить столбцами и наоборот, т. е. .

2. Определитель меняет знак при перестановке любых двух его строк (столбцов).

3. Определитель, имеющий две равные строки (столбца), равен 0.

4. Общий множитель строки (столбца) можно выносить за знак определителя, например

5. Если элементы какой-нибудь строки (столбца) представимы в виде суммы двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, например

6. Определитель не изменится, если к какой-нибудь строке (столбцу) прибавить соответствующие элементы другой строки (столбца), умноженные на некоторое ненулевое число.

(I=I+II).

7. Определитель треугольной матрицы равен произведению её диагональных элементов.

8. Определитель равен сумме произведений элементов какой-нибудь его строки (столбца) на их алгебраические дополнения. Например

Для вычисления определителя мы использовали разложение по второй строке, так как она содержит большее число нулевых элементов.

9. Сумма произведений элементов какой-нибудь строки (столбца) на соответствующее алгебраическое дополнение другой строки (столбца) равна 0.

Описание основных видов матриц, определения и их примеры

Поможем решить контрольную, написать реферат, курсовую и диплом от 800р

Содержание:

Диагональные матрицы
Треугольные матрицы
Ступенчатая матрица

Определение

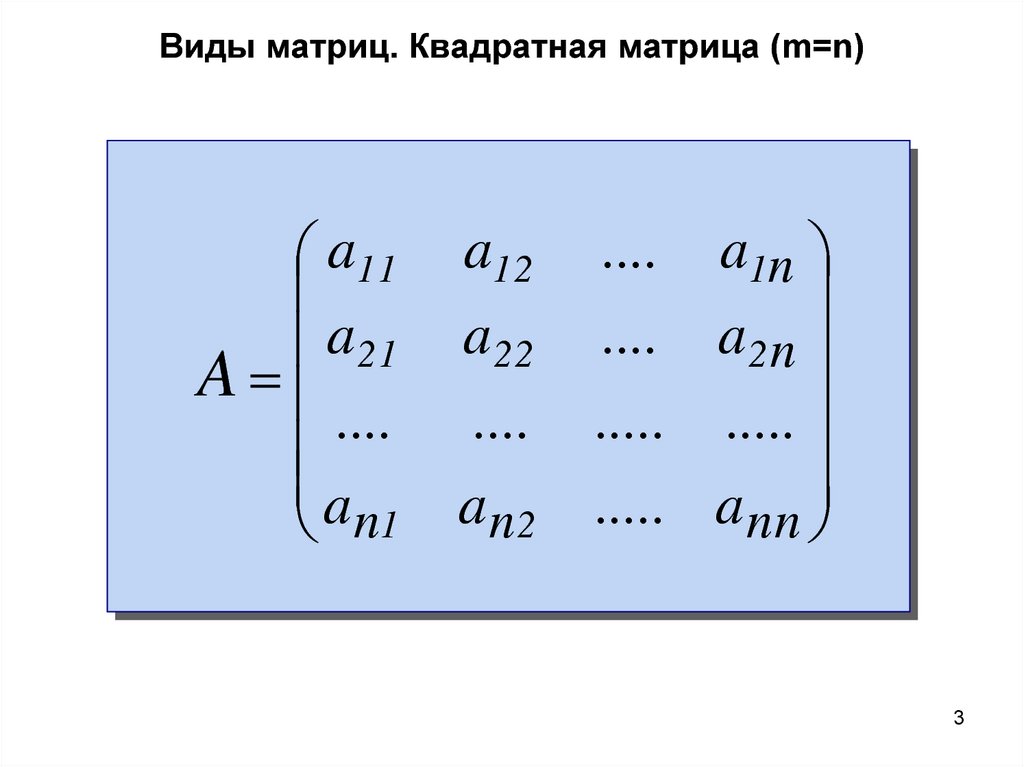
Матрица размера $n \times n$ называется квадратной, число $n$ называется порядком матрицы.

Пример

$A_{2 \times 2}=\left(\begin{array}{rr} 1 & -3 \\ 7 & 2 \end{array}\right)$ – квадратная матрица порядка 2 или матрица второго порядка.

Определение

Матрица $\Theta$ называется нулевой, если все её элементы равны нулю, т.е. $a_{i j}=0, \forall i, j$.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

$$\Theta=\left(\begin{array}{ll} 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{array}\right)$$

Определение

Матрица, состоящая из одной строки, называется вектор-строкой, а матрица, состоящая из одного столбца, – вектор-столбцом.

Пример

$B=(1 3 7)$ – вектор-строка; $B=\left(\begin{array}{l} 1 \\ 3 \\ 7 \end{array}\right)$ – вектор-столбец.

Диагональные матрицы

Определение

Квадратная матрица $D$ называется диагональной, если все ее элементы, стоящие вне главной диагонали, равны нулю.

Замечание. Диагональные элементы матрицы (т.е. элементы, стоящие на главной диагонали) могут также равняться нулю.

Пример

$$D=\left(\begin{array}{lll} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 3 \end{array}\right)=\operatorname{diag}(1 ; 0 ; 3)$$

Определение

Скалярной называется диагональная матрица $S$, у которой все диагональные элементы равны между собой.

Замечание. Если нулевая матрица является квадратной, то она также является и скалярной.

Пример

$$S=\left(\begin{array}{rr} -1 & 0 \\ 0 & -1 \end{array}\right)$$

Определение

Единичной матрицей $E_{n}$ называется скалярная матрица порядка $n$, диагональные элементы которой равны 1.

Замечание. Для сокращения записи порядок единичной матрицы можно не писать, тогда единичная матрица обозначается просто $E$.

Пример

$E_{2}=\left(\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right)$ – единичная матрица второго порядка.

Треугольные матрицы

Определение

Матрица называется верхней треугольной матрицей, если все элементы ниже главной диагонали равны нулю.

Матрица называется нижней треугольной матрицей, если все элементы выше главной диагонали равны нулю.

Замечание. Диагональная матрица – это пример матрицы, которая является одновременно верхне- и нижнетреугольной.

Пример

$C=\left(\begin{array}{lll} 2 & 5 & 0 \\ 0 & 4 & 1 \\ 0 & 0 & 3 \end{array}\right)$ – верхнетреугольная матрица.

Ступенчатая матрица

Определение

Ступенчатой называется матрица, удовлетворяющая следующим условиям:

если эта матрица содержит нулевую строку (т. е. строку, все элементы которой равны нулю), то все строки, расположенные под нею, также нулевые;
если первый ненулевой элемент некоторой строки расположен в столбце с номером $i$, то первый ненулевой элемент следующей строки должен находиться в столбце с номером большим, чем $i$.

Другое определение ступенчатой матрицы.

Определение

Ступенчатой называется матрица, которая содержит $m$ строк и у которой первые $r \leq m$ диагональных элементов ненулевые, а элементы, лежащие ниже главной диагонали и элементы последних $m-r$ строк равны нулю, то есть это матрица вида:

$$A=\left(\begin{array}{ccccccc} a_{11} & a_{12} & a_{13} & \ldots & a_{1 r} & \ldots & a_{1 n} \\ 0 & a_{22} & a_{23} & \ldots & a_{2 r} & \ldots & a_{2 n} \\ 0 & 0 & a_{33} & \ldots & a_{3 r} & \ldots & a_{3 n} \\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & 0 & \ldots & a_{r r} & \ldots & a_{r n} \\ 0 & 0 & 0 & \ldots & 0 & \ldots & 0 \\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & 0 & \ldots & 0 & \ldots & 0 \end{array}\right)$$

Определение

Главным элементом некоторой строки матрицы $A$ называется ее первый ненулевой элемент.

Пример

Задание. Найти главные элементы каждой строки матрицы $A=\left(\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 0 & 1 \end{array}\right)$

Решение. Главный элемент первой строки – это первый ненулевой элемент этой строки, а поэтому $a_{11}=1$ – главный элемент строки под номером 1; аналогично $a_{23}=1$ – главный элемент второй строки.

Другое определение ступенчатой матрицы.

Определение

Матрица $A$ называется ступенчатой, если:

все ее нулевые строки стоят после ненулевых;
в каждой ненулевой строке, начиная со второго, ее главный элемент стоит правее (в столбце с большим номером) главного элемента предыдущей строки.

По определению к ступенчатым матрицам будем относить нулевую матрицу $\Theta$, а также матрицу, которая содержит одну строку.

Пример

Примеры ступенчатых матриц:

$A=\left(\begin{array}{ll} 0 & 0 \\ 0 & 0 \end{array}\right)$, $B=(1 2 3 4)$, $C=\left(\begin{array}{lll} 1 & 2 & 3 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{array}\right)$, $D=\left(\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 1 & 2 \\ 0 & 0 & 8 \\ 0 & 0 & 0 \end{array}\right)$, $F=\left(\begin{array}{rrr} 1 & 2 & 3 \\ 0 & 1 & 1 \\ 0 & 0 & -7 \end{array}\right)$

Примеры матриц, которые не являются ступенчатыми:

$A=\left(\begin{array}{ll} 0 & 0 \\ 1 & 0 \end{array}\right)$, $B=\left(\begin{array}{lll} 1 & 2 & 3 \\ 0 & 0 & 1 \\ 0 & 0 & -3 \end{array}\right)$, $D=\left(\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 1 & 2 \\ 0 & 5 & 8 \\ 0 & 0 & 3 \end{array}\right)$

Пример

Задание. Выяснить, является ли матрица $A=\left(\begin{array}{llllll} 0 & 1 & 2 & 0 & 3 & 1 \\ 0 & 0 & 3 & 2 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right)$ ступенчатой.

Решение. Проверяем выполнение условий из определения:

все строки под первой нулевой строкой матрицы (четвертая строка) являются нулевыми;
первый ненулевой элемент строки № 1 находится во втором столбце, значит, первый ненулевой элемент второй строки должен находиться, по крайней мере, в третьем столбце – выполняется, т.к. первый ненулевой элемент второй строки $a_{23} = 3 \neq 0$ находится в третьем столбце; аналогично, первый ненулевой элемент третьей строки находится в шестом столбце, а первый ненулевой элемент предыдущей, второй, строки, находится в столбце с номером 3 и 3

Итак, заданная матрица $A$ является ступенчатой.

Читать дальше: операции над матрицами.

Сообщество Экспонента

Публикация
15.09.2022

Системы управления, Другое

Видел видос на канале экспоненты по созданию топливной системы. Вопрос заключается в наличии более полного описания готового примера или соответсвующее документации. Я новичок в симулинке и ещё многого не знаю. Адекватных и раскрытых пособий по созданию гидрав…

Моделирование гидравлических систем в simulink

Публикация
10.09.2022

Системы управления, Электропривод и силовая электроника, Другое

Планирую написать книгу про модельно-ориентированное программирование с автоматическим генерированием кода применительно к разработке разнообразных микропроцессорных систем управления электроприводов. В этой книге в научно-практическо-методической форме я план…

Публикация
24.08.2022

Цифровая обработка сигналов, Системы связи, Математика и статистика

&…

Здесь собрана литература по комбинированным методам множественного доступа, в которых используется разделение пользователей в нескольких ресурсных пространствах.

вопрос
23.08.2022

Математика и статистика, Радиолокация, Цифровая обработка сигналов

Есть записанный сигнал с датчика (синус с шумом). Как определить соотношение сигнал/шум?

4 Ответа

ЦОС
цифровая обработка сигналов

23.08.2022

Публикация
23.08.2022

Цифровая обработка сигналов, Системы связи, Математика и статистика

&. ..

Здесь соборана литература по методам множественного доступа с поляризационным разделением и разделением по орбитальном угловому моменту.

Публикация
16.08.2022

Цифровая обработка сигналов, Системы связи, Математика и статистика

Здесь собрана литература по методам множественного доступа с пространственным разделением.

вопрос
22.07.2022

Изображения и видео, Цифровая обработка сигналов, Математика и статистика, Биология, Встраиваемые системы, Глубокое и машинное обучение(ИИ), Автоматизация испытаний, ПЛИС и СнК, Системы управления, Другое

Здравствуйте. Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например: file_1_1.txt file_1_2.txt file_1_3.txt file_1_4.txt fil…

2 Ответа

чтение

22.07.2022

вопрос
17.07.2022

Математика и статистика, Цифровая обработка сигналов

Уважаемые коллеги, добрый вечер! В общем, возникла проблема следующего характера. Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…

MATLAB
Signal Processing

17.07.2022

вопрос
15.07.2022

Системы связи, Цифровая обработка сигналов

Здравствуйте! Сделала в симулинке модель сигнала с модуляцией QPSK. На входе сигнала подала последоватльномть с Генератора Бернули бинарного. Sample time: 1/8000. ПРи выводе сигнала на анализатор спек…

сигнал
модуляция
qpsk
скорость бита
битрейт
символьная скорость
скорость передачи информации
цифровая манипуляция

15.07.2022

Публикация
13.07.2022

Цифровая обработка сигналов, Системы связи, Математика и статистика

&…

Здесь собрана литература по методам множественного доступа с кодовым разделением

Результаты поиска

Нет результатов поиска, попробуйте задать другие параметры.

Решение матриц методы решений и примеров для чайников, формулы вычислений и действий с матрицами » Kupuk.net

В высшей математике существует понятие матрицы системы чисел. С комбинацией элементов, заключённых в таблице, выполняют различные операции. Прежде чем переходить к решению матриц сложными методами, следует ознакомиться с понятием этого выражения и простейшими логическими операциями над ним.

Понятие выражения

Определение гласит, что матрица — это прямоугольная таблица с заключёнными в ней числами. Её название обозначается латинскими прописными буквами (А, В). Таблицы бывают разной размерности — прямоугольной, квадратной, а также в виде строк и столбцов.

От количества строк и столбцов будет зависеть величина таблицы. Матрица размера m*n означает, что в таблице содержится m строк и n столбцов. Допустим, первая строка включает элементы а11, а12, а13, вторая — а21, а22, а23. Тогда элементы, где i = j (а11, а22) образовывают диагональ и называются диагональными.

Различают комплексные матрицы, у которых хотя бы один элемент равен комплексному числу, и действительные, когда все её элементы являются действительными числами. В математике комплексные числа представлены в виде a+b*i, где:

a — действительная часть числа;
b — мнимая часть;
i — мнимая единица (квадратный корень из -1).

На приведенном примере показаны варианты.

Простейшие действия с матрицами могут быть разными. К их числу относятся:

умножение;
вычитание;
умножение на число;
перемножение между собой;
транспортирование матриц.

Сложение и вычитание

Действия по сложению возможны только тогда, когда матрицы одинакового порядка равны между собой. В итоге получится новое матричное выражение такой же размерности. Сложение и вычитание выполняются по общей схеме — над соответствующими элементами таблиц проводят необходимые операции. Например, нужно сложить две матрицы А и В размерности 2*2.

Каждый элемент первой строки складывается по порядку с показателями верхней строчки второй матрицы. По аналогии производится вычитание, только вместо плюса ставится минус.

Умножение на число

Любую таблицу чисел можно умножить на число. Тогда каждый её элемент перемножается с этим показателем. К примеру, умножим матричное выражение на 2:

Операция перемножения

Матрицы подлежат перемножению одна на другую, когда количество столбцов первой таблицы равно числу строк второй. Каждый элемент Aij будет равняться сумме произведений элементов i-строки первой таблицы, перемноженных на числа в j-столбце второй. Способ произведения наглядно представлен на примере.

Возведение в степень

Формулу возведения в степень применяют только для квадратных матричных выражений. При этом степень должна быть натуральной. Формула возведения следующая:

Иначе, чтобы выполнить операцию возведения таблицы чисел в степень n, требуется умножить её на себя саму n раз. Для операции возведения в степень удобно применять свойство в соответствии с формулой:

Решение представлено на примере. 1 этап: необходимо возвести в степень, где n = 2.

2 этап: сначала возводят в степень n =2. Согласно формуле перемножают таблицу чисел саму на себя n = 2 раз.

3 этап: в итоге получаем:

Расчёт определителя

В линейной алгебре существует понятие определителя или детерминанта. Это число, которое ставят в соответствие каждой квадратной матрице, вычисленное из её элементов по специальной формуле. Определитель или модуль используется для решения большинства задач. Детерминант самой простой матрицы определяется с помощью вычитания перемноженных элементов из побочной диагонали и главной.

Определителем матрицы А n-энного порядка называется число, которое получают из алгебраической суммы n! слагаемых, попадающих под определённые критерии. Эти слагаемые являются произведением n-элементов, взятых единично из всех столбов и строк.

Произведения могут отличаться друг от друга составом элементов. Со знаком плюс будут включаться в сумму числа, если их индексы составляют чётную подстановку, в противоположном случае их значение меняется на минус. Определитель обозначается символом det A. Круглые скобки матричной таблицы, обрамляющие её элементы, заменяются на квадратные. Формула определителя:

Определитель первого порядка, состоящий из одного элемента, равен самому этому элементу. Детерминант матричной таблицы размером 2*2 второго порядка вычисляется путём перемножения её элементов, расположенных на главной диагонали, и вычитания из них произведения элементов, находящихся в побочной диагонали. Наглядный пример:

Для матрицы также можно найти дискриминант многочлена, отвечающий формуле:

Когда у многочлена имеются кратные корни, тогда дискриминант равен нулю.

Обратная матрица

Прежде чем переходить к понятию обратного выражения матрицы, следует рассмотреть алгоритм её транспонирования. Во время операции строки и столбцы переставляются местами. На рисунке представлен метод решения:

По аналогии обратная матрица сходна с обратными числами. Например, противоположной цифре 5 будет дробь 1/5 = 5 (-1) степени. Произведение этих чисел равно 1, выглядит оно так: 5*5 (-1) = 1. Умножение обычной матричной таблицы на обратную даст в итоге единичную: А* А (-1) = Е. Это аналог числовой единицы.

Но для начала нужно понять алгоритм вычисления обратной матрицы. Для этого находят её определитель. Разработано два метода решения: с помощью элементарных преобразований или алгебраических дополнений.

Более простой способ решения — путём алгебраических дополнений. Рассмотрим матричную таблицу А, обратная ей А (-1) степени находится по формуле:

Матрица обратного вида возможна только для квадратного размера таблиц 2*2, 3*3 и т. д. Обозначается она надстроенным индексом (-1). Задачу легче рассмотреть на более простом примере, когда размер таблицы равен 2*2. На первом этапе выполняют действия:

Обратного выражения матрицы не может быть, если определитель равен нулю. В рассматриваемом случае он равен -2, поэтому всё в порядке.

2 этап: рассчитывают матрицу миноров, которая имеет те же значения, что и первоначальная. Под минором k-того порядка понимается определитель квадратной матрицы порядка k*k, составленный из её элементов, которые располагаются в выбранных k- столбцах и k-строках.

При этом расположение элементов таблицы не меняется. Чтобы найти минор верхнего левого числа, вычёркивают строчку и столбец, в которых прописан этот элемент. Оставшееся число и будет являться минором. На выходе должна получиться таблица:

3 этап: находят алгебраические дополнения.

4 этап: определяют транспонированную матрицу.

Итогом будет:

Проверка решения: чтобы удостовериться, что обратная таблица чисел найдена верно, следует выполнить проверочную операцию.

В рассматриваемом примере получается единичная матрица, когда на главной диагонали находятся единицы, при этом другие элементы равняются нулю. Это говорит о том, что решение было найдено правильно.

Нахождение собственных векторов

Определение собственного вектора и значений матричного выражения легче понять на примере. Для этого задают матричную таблицу чисел и ненулевой вектор Х, называемый собственным для А. Пример выражения:

Согласно теореме собственными числами матричного выражения будут корни характеристического уравнения:

Из однородной системы уравнений можно определить координаты собственного вектора Х, который соответствует значению лямбда.

Метод Гаусса

Методом Гаусса называют способ преобразования системы уравнений линейного вида к упрощённой форме для дальнейшего облегчённого решения. Операции упрощения уравнений выполняют с помощью эквивалентных преобразований. К таким относят:

действия, когда в системе переставляются местами два уравнения;
произведение одного из уравнений в системе на действительное ненулевое число;
сложение первого уравнения со вторым, при этом последнее умножено на произвольное число.

Чтобы понять механизм решения, следует рассмотреть линейную систему уравнений.

Следует переписать эту систему в матричный вид:

А будет являться таблицей коэффициентов системы, b — это правая часть ограничений, а Х — вектор переменных координат, который требуется найти. Для решения используют ранг матрицы. Под ним понимают наивысший порядок минора, который отличается от 0.

В этом примере rang (A) = p. Способ эквивалентных преобразований не изменяет ранг таблицы коэффициентов.

Метод Гаусса предназначен для приведения матричной таблицы коэффициентов А к ступенчатому или диагональному виду. Расширенная система выглядит так:

Допустим, а11 не равен 0. В противном случае, если это не так, то меняют эту строку с другой, где в первом столбце находится элемент, отличный от нуля. Когда подобные строчки отсутствуют, переходят к другому столбцу. Все нижние элементы столбца после а11 обнуляют. Для этих целей выполняют операции сложения строк 2,3…m с первой строчкой, умноженной на а21/а11, -а31/а11….- аm1/a11. В результате система примет вид:

На втором шаге повторяют все действия с элементами столбца 2, которые расположены ниже а22. Если показатель равен нулю, строку также меняют местами со строчкой, лежащей ниже с ненулевым элементом во втором столбце. Затем обнулению подлежат все показатели ниже а22. Для этого складывают строки 2,3 ..m, как описано выше. Выполняя процедуру со всеми элементами, приходят к матричной таблице ступенчатого или диагонального вида. Полученная расширенная таблица будет выглядеть:

Обращают внимание на последние строки.

В этом случае система уравнений имеет решение, но когда хотя бы одно из этих чисел отличается от нуля, она несовместима. Таким образом, система совместима, если ранг таблицы А равен расширенному рангу В (А|b).

Если rang А=rang (A|b), то существует множество решений, где n-p — многообразие. Из этого следует n-p неизвестных Хр+1,…Xn выбираются произвольно. Неизвестные X1, X2,…Xp вычисляют следующим образом: из последнего уравнения выражают Хр через остальные переменные, вставляя в предыдущие выражения. Затем из предпоследнего уравнения получают Хр-1 через прочие переменные и подставляют их в предыдущие выражения. Процедуру повторяют.

Найти быстро ответ и проверить себя позволяет онлайн-калькулятор. Решение матрицы методом Гаусса с помощью такого расчёта показывает подробные этапы операций. Для нахождения достаточно указать количество переменных и уравнений, отметить в полях значения чисел и нажать кнопку «Вычислить».

Способ Крамера

Метод Крамера используют для решения квадратной системы уравнений, представленной в линейном виде, где определитель основной матрицы не равен нулю. Считается, что система обладает единственным решением. Например, задана система линейных уравнений:

Её необходимо заменить равноценным матричным уравнением.

Второй столбец вычисляют, а первый уже задан. Есть предположение, что определитель матрицы отличен от нуля. Из этого можно сделать выводы, что существует обратная матрица. Перемножив эквивалентное матричное уравнение на обратного формата матрицу, получим выражение:

В итоге получают выражения:

Из представленных уравнений выделяют формулы Крамера:

Метод Крамера не представляет сложности. Он может быть описан следующим алгоритмом:

Высчитывают определитель дельта базовой матрицы.

В матричной таблице А замещают первый столбец на вектор свободных элементов b.

Выполняют расчёт определителя дельта1 выявленной матрицы А1.

Определяют переменную Х1 = дельта1/дельта.

Повторяют шаги со 2 по 4 пункт в матрице А для столбов 2,3…n.

Проверить решение матрицы методом Крамера онлайн позволяет калькулятор автоматического расчёта. Для получения быстрого ответа в представленные поля подставляют переменные числа и их количество. Дополнительно может потребоваться указание вычислительного метода разложения по строке или столбу. Другой вариант заключается в приведении к треугольному виду.

Указывается также представление чисел в виде целого числа, обыкновенной или десятичной дроби. После введения всех предусмотренных параметров и нажатия кнопки «Вычислить» получают готовое решение.

Простое объяснение разложения по единственному значению с примерами

Просматривая записи моего курса Computation Techniques, я понял, что мне не совсем понятно, как получить разложение матрицы по сингулярным числам.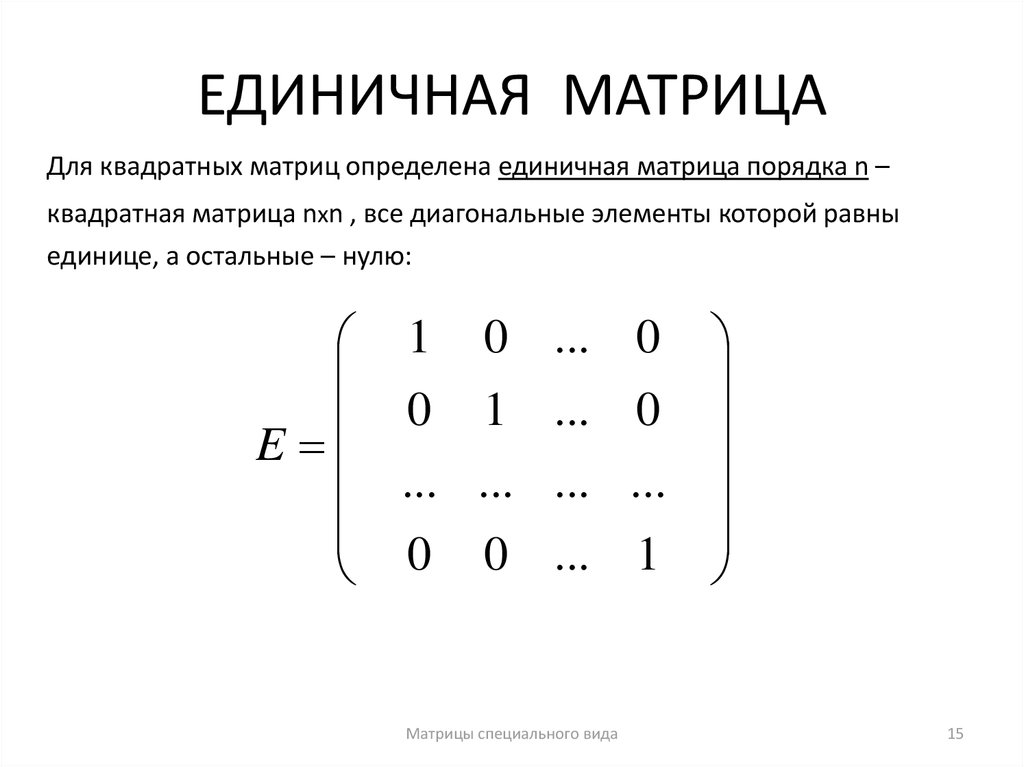 Математическое обоснование этого было не очень ясным или интуитивным. После быстрого поиска в Интернете я понял, что большинство доступных ресурсов одинаково бесполезны в обеспечении четкого понимания разложения по сингулярным значениям.

Если вы читаете это, есть большая вероятность, что вы тоже хотите правильно понять разложение по сингулярным числам. Я надеюсь, что после прочтения этой статьи математика разложения матрицы по сингулярным числам станет предельно ясной и позволит вам вспомнить, как получить разложение матрицы по сингулярным числам без необходимости что-либо запоминать.

Если вы лучше учитесь на примерах, не стесняйтесь сразу переходить к примерам. Я сделал это так, чтобы пример был достаточно подробным, чтобы вы могли понять математику, стоящую за всем, не читая ничего. теории. Но, очевидно, не стесняйтесь читать теорию, если что-то неясно, или даже комментировать ниже.

Теория

Пусть C будет матрицей, для которой мы хотим найти разложение по сингулярным числам.

В итоге мы хотим записать Cв виде произведения трех матриц — прямоугольной диагональной матрицы с неотрицательными действительными числами по диагонали, которая умножается на ортогональную матрицу с каждой стороны.

Что мы хотим

Проще говоря, мы хотим найти матрицы U, Σ и V такие, что

Где Σ — прямоугольная диагональная матрица тех же размеров, что и C, а U и V — ортогональные матрицы (это пригодится чуть позже).

Ключевые идеи

Ключевое понимание разложения по сингулярным числам исходит из двух уравнений.

Прежде чем мы приведем эти два уравнения, напомню, что U и V являются ортогональными матрицами, а это означает, что мы имеем UᵀU = UUᵀ = I и аналогично для V. Это означает, что Vᵀ является инверсией V, поэтому мы имеем V⁻ ¹=Vᵀ

Теперь давайте приведем два ключевых уравнения для разложения по сингулярным числам:

Из этих двух уравнений мы сможем вывести Σ, V и U.

Поиск

Σ и V

Если вы раньше немного занимались линейной алгеброй, то могли заметить, что первое уравнение по существу представляет собой задачу диагонализации матриц(A = SDS⁻¹), где A=CᵀC, S = V и D=ΣᵀΣ.

Возможно, вы также помните, что решение этой задачи включает в себя нахождение собственных значений и соответствующих собственных векторов матрицы CᵀC. Получив их, мы можем построить V как матрицу, состоящую из собственных векторов CᵀC, и ΣᵀΣ как диагональную матрицу, построенную из соответствующие собственные значения.

Итак, что мы хотим сделать, это найти собственные значения λ₁, λ₂, … λn для CᵀC и их соответствующие нормализованные собственные векторы, соответственно, v₁, v₂, … vn. Что позволяет нам получить V и ΣᵀΣ, как показано ниже. Важно, чтобы собственные векторы были нормализованы, поскольку V должна быть ортогональной матрицей.

Это все хорошо, но мы хотим Σ, а не ΣᵀΣ. Ничего страшного — мы можем вывести Σ из ΣᵀΣ. Мы знаем это, зная, что Σ является прямоугольной диагональной матрицей. Вы должны быть в состоянии убедиться, что, поскольку Σ представляет собой прямоугольную диагональную матрицу с диагональными элементами σ₁, σ₂, … σn,, мы имеем следующий:

Теперь мы ясно видим, что σ₁² = λ₁, σ₂² = λ₂, … σn² = λn. Это означает, что

где Σii представляет i-й элемент на диагонали Σ.

В поисках тебя

Теперь, когда у нас есть и Σ, и V, мы можем найти U, используя второе уравнение.

Поскольку Σ — прямоугольная диагональная матрица, вы должны быть в состоянии убедиться, что приведенное ниже уравнение следует из приведенного выше уравнения. Написание примера прямоугольной диагональной матрицы Σ и матрицы U и вычисление UΣ может помочь вам убедиться в том, что верно следующее.

Это означает, что j-й столбец U представляет собой просто j-й столбец CV, разделенный на j-й диагональный элемент Σ.

Итак, теперь мы можем построить полную конструкцию U, зная как C, так и V.

Собираем все вместе

И это все. Теперь, когда у нас есть U, V и Σ, мы можем просто сложить все это вместе, чтобы получить UΣVᵀ, который представляет собой разложение по сингулярным числам С.

Вот краткий обзор того, что нужно сделать, чтобы получить разложение по сингулярным числам матрицы C:

Найдите собственные значения CᵀC и их соответствующие нормализованные собственные векторы.
Пусть V = [ v₁, v₂, … vn] и Σ =[σ₁, σ₂, … σn ]где σ — квадратный корень из λ.
Пусть U = [ cv₁/σ₁, cv₂/σ₂, … cvn/σn], где cvn — это n-й столбец CV.
Дважды проверьте, что C = UΣVᵀ.

Надеюсь, теперь вы понимаете, почему эти шаги имеют смысл для нахождения разложения матрицы по сингулярным числам из приведенных выше объяснений. Не стесняйтесь оставлять любые комментарии ниже с любыми вопросами и попробовать приведенные ниже примеры.

Удобный трюк

Если матрица C, для которой вы хотите найти разложение по сингулярным числам, представляет собой матрицу m×n, где m‹n. Тогда CᵀCбудет матрицей n×n, тогда как CCᵀбудет матрицей m×m, которая меньше и с ней удобнее работать.

Если вы правильно поняли то, что было объяснено выше, вы сможете увидеть, что мы можем использовать аналогичные приемы для определения U, Σ иV используя CCᵀвместо CᵀC.

В частности, мы получаем следующие уравнения:

И снова первое уравнение — это просто проблема диагонализации матрицы, где ΣΣᵀ — диагональная матрица с нормализованными собственными значениями CCᵀ на диагонали и U — ортогональная матрица с соответствующими собственными векторами для ее столбцов.

Мы можем найти Σиз ΣΣᵀтак же, как и раньше. При этом Σявляется прямоугольной диагональной матрицей размером m×n с квадратными корнями ранее найденных собственных значений в качестве диагональных элементов.

Теперь мы можем также Vᵀиспользовать второе уравнение так же, как это делалось ранее.

И вот, теперь у вас есть сингулярное разложение C, которое вы получили с чуть меньшими усилиями.

Примеры

Простой подробный пример

Попробуем найти разложение по сингулярным числам

Чуть более сложный пример

Использование трюка

Давайте теперь попробуем найти разложение по сингулярным числам следующей матрицы:

Здесь C представляет собой m×n, где m ‹ n, поэтому было бы удобнее работать с CCᵀа не с CᵀC. Итак, давайте сделаем это!

Видео Рекомендация

Я рекомендую посмотреть это видео https://www. youtube.com/watch?v=cOUTpqlX-Xs от MIT OpenCourseWare на YouTube с еще одним хорошо объясненным примером линейной декомпозиции.

Прямоугольная матрица — определение, примеры, свойства, операции

Прямоугольная матрица — это матрица прямоугольной формы. Мы знаем, что элементы матрицы расположены в строках и столбцах. Если количество строк в матрице не равно количеству столбцов в ней, то матрица называется прямоугольной матрицей.

Давайте узнаем больше о прямоугольной матрице вместе с определением, примерами, свойствами и операциями над ней.

1.	Что такое прямоугольная матрица?
2.	Операции над прямоугольной матрицей
3.	Свойства прямоугольной матрицы
4.	Часто задаваемые вопросы о прямоугольной матрице

Что такое прямоугольная матрица?

Прямоугольная матрица — это матрица, в которой количество строк НЕ равно количеству столбцов. Это один из видов матриц. В геометрии прямоугольник — это четырехугольник, у которого длина отличается от ширины. Точно так же количество строк прямоугольной матрицы отличается от количества столбцов, отсюда и название «прямоугольная». Ниже приведена прямоугольная матрица порядка m x n (т. е. количество строк = m и количество столбцов = n).

Примеры прямоугольных матриц

Вот несколько прямоугольных матриц, и в каждой матрице количество строк НЕ равно количеству столбцов.

$\left[\begin{массив}{llll}
1 и 8 и 3 и 2 \\\
5 и 3 и 0 и -6
\end{array}\right]$ имеет 2 строки и 4 столбца — прямоугольная матрица порядка 2 x 4.
$\left[\begin{массив}{llll}
1 и 7\
2 и 4\\
6 и 3\
-5 и 0
\end{array}\right]$ имеет 4 строки и 2 столбца — прямоугольная матрица порядка 4 x 2.
$\left[\begin{массив}{llll}
1 и 7 и 8 и 2
\end{array}\right]$ имеет 1 строку и 4 столбца — прямоугольная матрица порядка 1 x 4.

Типы прямоугольных матриц

Прямоугольные матрицы могут быть двух типов: строк меньше, чем столбцов, и строк больше, чем столбцов. Вот примеры для каждого из этих типов:

Прямоугольная матрица, в которой строк меньше, чем столбцов: $\left[\begin{array}{llll}
1 и 8 и 3 и 2 \\\
5 и 3 и 0 и -6
\конец{массив}\справа]$
Прямоугольная матрица, в которой строк больше, чем столбцов: $\left[\begin{array}{llll}
1 и 7\
2 и 4\\
6 и 3\
-5 и 0
\конец{массив}\справа]$

Операции над прямоугольной матрицей

Все матричные операции не всегда возможны на прямоугольных матрицах. Вот несколько операций, которые возможны с прямоугольными матрицами с небольшими ограничениями.

Сложение и вычитание прямоугольных матриц

Сложение и вычитание двух или более прямоугольных матриц возможно, если все они одного порядка. Например:

$\left[\begin{array}{llll}
1 и 8 и 3 \\\
5 и 3 и 0
\end{массив}\right]_{2 \times 3}$ + $\left[\begin{array}{llll}
-2&3&5&2\\
1 и 0 и -2 и -6
\end{массив}\right]_{2 \times 4}$ НЕВОЗМОЖНО.
$\left[\begin{массив}{llll}
1 и 8 и 3 \\\
5 и 3 и 0
\end{массив}\right]_{2 \times 3}$ – $\left[\begin{array}{llll}
-2&3&5\\
1 и 0 и -2
\end{массив}\right]_{2 \times 3}$ возможно.

Умножение прямоугольных матриц

Умножение двух прямоугольных матриц A и B возможно только при выполнении следующего условия: количество столбцов матрицы A = количеству строк матрицы B. Другими словами, матрицы A и B должны быть порядков m x n и n x p. Произведение A и B в этом случае будет матрицей порядка m x p. Например:

$\left[\begin{array}{ll}
а&б&в\
в&г&е\
\end{массив}\right]_{2 \times 3}$ · $\left[\begin{array}{ll}
х и у
\end{массив}\right]_{2 \times 1}$ НЕВОЗМОЖНО.
$\left[\begin{массив}{ll}
а&б\
с&д\
э и ф
\end{массив}\right]_{3 \times 2}$ · $\left[\begin{array}{ll}
х и у
\end{массив}\right]_{2 \times 1}$ возможно.

Произведение двух прямоугольных матриц может быть или не быть прямоугольной матрицей. Например, $\left[\begin{array}{l}
1\
2\
6
\end{array}\right]_{3 \times 1}$ · [-1 2 3]$_{1 \times 3}$ — матрица порядка 3 x 3, которая является квадратной матрицей.

Транспонирование прямоугольной матрицы

Транспонирование матрицы достигается путем записи ее строк в виде столбцов (или записи ее столбцов в виде строк). Следовательно, если порядок прямоугольной матрицы m x n, то ее транспонированная матрица представляет собой прямоугольную матрицу порядка n x m. Например, транспонирование $\left[\begin{array}{ll}
а&б&в\
с&д&е\
\end{массив}\right]_{2 \times 3}$ равно $\left[\begin{array}{ll}
а и с \\
б&д\
с и е
\end{массив}\right]_{3 \times 2}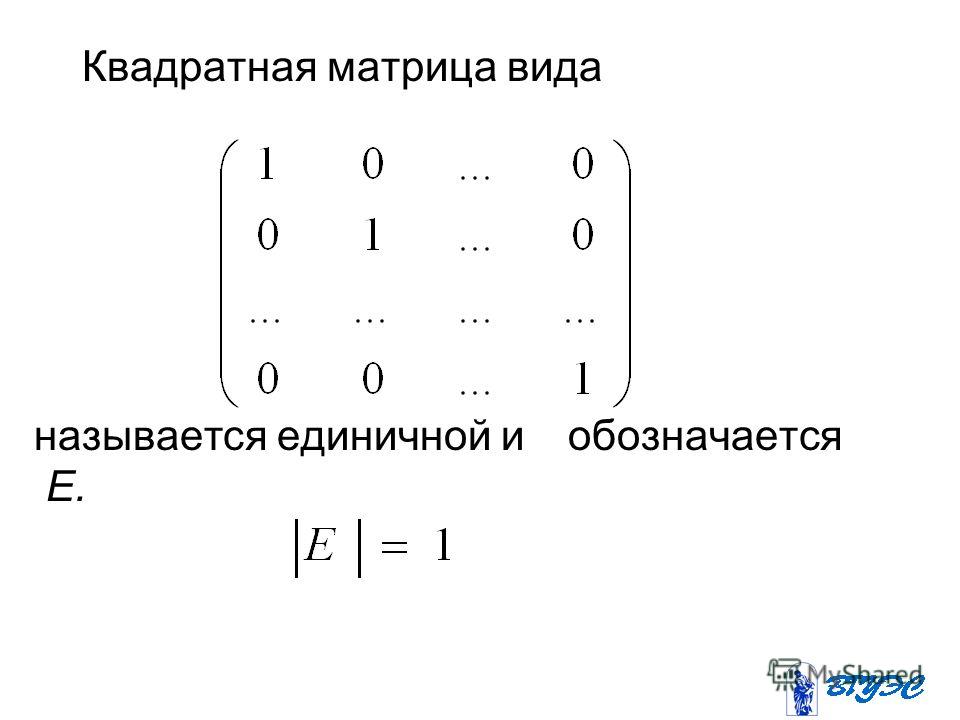$. Таким образом, прямоугольная матрица никогда не равна своей транспонированной и, следовательно, никогда не бывает симметричной.

Свойства прямоугольной матрицы

Вот свойства прямоугольной матрицы, основанные на ее определении.

В прямоугольной матрице количество строк и количество столбцов разное. Таким образом, порядок прямоугольной матрицы состоит из двух разных чисел.
Матрица строк или матрица столбцов с более чем одним элементом всегда является прямоугольной матрицей.
Например, [1 2 3] — матрица-строка порядка 1 x 3 и, следовательно, прямоугольная.
Определитель прямоугольной матрицы НЕ определен. Следовательно, понятия сингулярной матрицы и невырожденной матрицы НЕ применимы к прямоугольной матрице.
Прямоугольная матрица не может иметь сопряженной.
Прямоугольная матрица не может иметь обратной, так как ее сопряженная и определитель НЕ определены.
Прямоугольная матрица не может быть симметричной. Потому что, например, транспонированная прямоугольная матрица порядка 2 x 3 является матрицей порядка 3 x 2 и, следовательно, они не могут быть равны.
Сложение и вычитание двух прямоугольных матриц возможно только в том случае, если они одного порядка.
Умножение двух прямоугольных матриц A и B возможно только тогда, когда количество столбцов A равно количеству строк B.
Произведение двух прямоугольных матриц не обязательно должно быть прямоугольным.
Прямоугольная матрица не может иметь собственных значений (и, следовательно, не может иметь собственных векторов)
Тождественные матрицы, диагональные матрицы, скалярные матрицы, ортогональные матрицы, симметричные матрицы, сингулярные матрицы и т. д. никогда не бывают прямоугольными.

Связанные темы:

Матричный калькулятор
Калькулятор сложения матриц
Калькулятор умножения матриц
Калькулятор обратной матрицы

Примеры прямоугольных матриц

Пример 1: Какие из следующих матриц являются прямоугольными? (а) $\left[\begin{массив}{llll}
-1&5&8&0\\
2 и 3 и -1 и -6
\end{массив}\right]$ (b) $\left[\begin{массив}{llll}
1 и 2 и 3 \\ 4&5&6 \\
5 и 3 и 0
\end{array}\right]$
Решение:
Мы знаем, что в прямоугольной матрице количество строк не равно количеству столбцов.
(a) В данной матрице количество строк = 2 и количество столбцов = 4 и они не равны.
Следовательно, он прямоугольный.
(б) В данной матрице количество строк = количеству столбцов ( = 3).
Следовательно, он НЕ прямоугольный.
Ответ: (a) прямоугольное и (b) НЕ прямоугольное.
Пример 2: Найти транспонирование прямоугольной матрицы $\left[\begin{array}{llll}
-1&5&8\\
2 и 3 и -1
\end{array}\right]$ и определить, является ли он симметричным.
Решение:
Дана матрица A = $\left[\begin{array}{llll}
-1&5&8\\
2 и 3 и -1
\end{массив}\right]$.
Мы запишем столбцы данной матрицы в виде строк, чтобы найти ее транспонирование. Тогда
A ^T = $\left[\begin{array}{llll}
-1 и 2\
5&3\\
8&-1
\end{array}\right]$
A имеет порядок 2 x 3, а A ^T имеет порядок 3 x 2. Ясно, что они НЕ равны, и, следовательно, A НЕ симметричен.
Ответ: A ^T = $\left[\begin{array}{llll}
-1 и 2\
5&3\\
8&-1
\end{массив}\right]$ и A НЕ симметричен.
Пример 3: Какие из следующих операций над матрицами возможны?
(а) $\left[\begin{массив}{llll}
а&б&в\\\
д и е и ф
\end{массив}\right]_{2 \times 3}$ + $\left[\begin{array}{llll}
1&2&3\\\
-1 и 0 и -2
\end{массив}\right]_{2 \times 3}$
(б) $\left[\begin{массив}{ll}
1&3&-2\
0 и 1 и 4 \
\end{массив}\right]_{2 \times 3}$ · $\left[\begin{array}{ll}
5 и 6
\end{array}\right]_{2 \times 1}$
Решение:
(a) Мы можем сложить две прямоугольные матрицы, если они одного порядка.
Таким образом, данное сложение возможно, так как порядок каждой матрицы такой же, как 2 x 3.
(b) Чтобы перемножить две матрицы, количество столбцов первой матрицы должно совпадать с количеством строк второй матрицы. Но здесь они не совпадают, потому что
- количество столбцов первой матрицы = 3 и
- количество строк второй матрицы = 2
Таким образом, данная операция НЕвозможна.
Ответ: (a) Возможно (b) НЕ возможно.

перейти к слайдуперейти к слайдуперейти к слайду

Хотите построить прочную основу в математике?

Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.

Записаться на бесплатный пробный урок

Практические вопросы по прямоугольной матрице

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о прямоугольной матрице

Что такое определение прямоугольной матрицы?

Прямоугольная матрица — это тип матриц, в которых количество строк НЕ равно количеству столбцов. Это один из типов матриц. Например, $\left[\begin{array}{ll}
-2 и 6\
3 и 2 \
-8 и 4\
0 и 2
\end{array}\right]$ — прямоугольная матрица порядка 4 x 2.

Что такое свойства прямоугольной матрицы?

Кратко о свойствах прямоугольной матрицы: Прямоугольная матрица не может иметь определителя, сопряженной и, следовательно, обратной. Он также не может иметь собственных значений. Он не может быть сингулярным или симметричным. Дополнительные сведения о свойствах см. в разделе «Свойства прямоугольной матрицы» на этой странице.

Является ли квадратная матрица прямоугольной?

В геометрии мы говорим, что квадрат — это прямоугольник, но прямоугольник не обязательно должен быть квадратом. Точно так же мы можем сказать, что квадратная матрица является прямоугольной, но прямоугольная матрица не обязательно должна быть квадратной матрицей. Но в целом термин прямоугольная матрица используется только тогда, когда она имеет неравное количество строк и столбцов.

В чем разница между квадратной и прямоугольной матрицей?

Квадратная матрица и прямоугольная матрица — это два разных типа матриц.

В квадратной матрице количество строк равно количеству столбцов.
В прямоугольной матрице количество строк НЕ равно количеству столбцов.

Что такое собственные значения прямоугольной матрицы?

Собственные значения можно найти только для квадратных матриц. Таким образом, прямоугольная матрица не может иметь собственных значений. Следовательно, они не могут иметь собственных векторов.

Что такое транспонирование прямоугольной матрицы?

Транспонирование прямоугольной матрицы получается путем перестановки строк и столбцов. Транспонирование прямоугольной матрицы порядка p x q представляет собой прямоугольную матрицу порядка q x p.

Что такое порядок прямоугольной матрицы?

Порядок прямоугольной матрицы записывается как «количество строк x количество столбцов» и состоит из двух разных чисел. Например, порядок прямоугольных матриц может быть 2 x 3, 3 x 2, 4 x 5 и т. д.

Скачать БЕСПЛАТНО учебные материалы

ЛИСТКИ

Что такое код DataMatrix? | Основы 2D-кодов | Информация о штрих-коде и советы

Код
DataMatrix (ECC200) имеет две конфигурации, квадратную и прямоугольную, и всегда содержит четное количество модулей.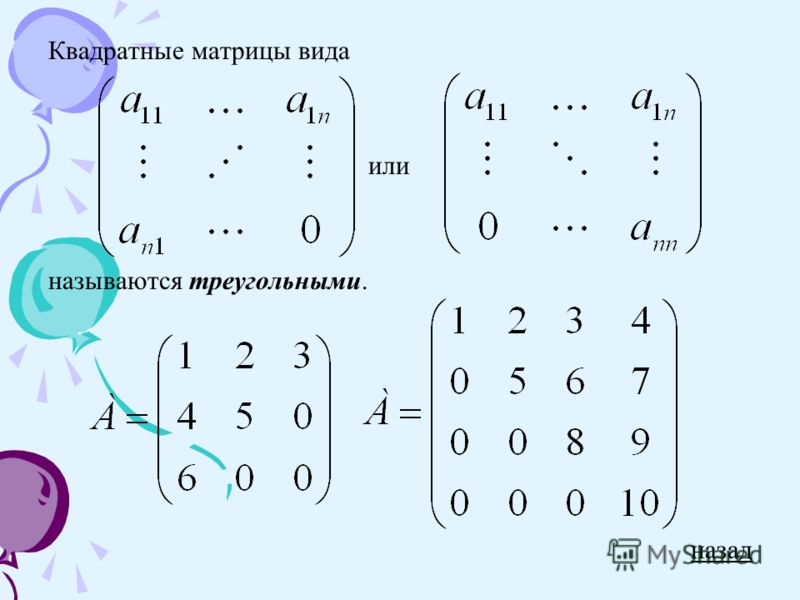
Структура кода DataMatrix
Структура кодов DataMatrix (ECC200)
Технические характеристики DataMatrix код
GS1 DataMatrix
Код
DataMatrix представляет собой матричный 2D-код, разработанный компанией ID Matrix в 1987 г. Он был зарегистрирован в стандарте ISS AIMI в 1996 г. и в стандарте ISO/IEC в 2000 г.
Технические характеристики
Минимальный размер 10 x 10 модулей
Максимальный размер 144 x 144 модуля
Максимальная емкость данных Цифровой 3116 символов
Буквенно-цифровой 2335 символов
Старые версии кода DataMatrix включают ECC000, ECC050, ECC080, ECC100 и ECC140.
ECC200 — это последняя версия кода DataMatrix, которая может иметь квадратную или прямоугольную конфигурацию.
Они состоят из модулей с нечетными номерами от 9 x 9 до 49 x 49 с использованием коррекции свертки.
Поскольку небольшое искажение мешает чтению при большом объеме данных, старые версии почти не используются.
Скачать
ECC200 модернизировал возможности исправления ошибок, чтобы устранить проблемы с искажениями.
Он использует Reed-Solomon для исправления ошибок, который восстанавливает данные, когда часть кода повреждена.
ECC200 соответствует международным стандартам. Обычно версия ECC200 используется, когда требуется код DataMatrix.
Разница между старыми версиями (ECC000, ECC050, ECC080, ECC100, ECC140) и новой версией (ECC200) заключается в количестве модулей на сторону. Старые версии имеют модули с нечетными номерами, а новая версия имеет модули с четными номерами.
ЕСС140 ЕСС200
Скачать
Область данных кодов DataMatrix окружена L-образной рамкой, называемой шаблоном выравнивания, и пунктирными линиями, называемыми шаблоном часов. Считыватели захватывают эти шаблоны, чтобы определить позицию кода при обработке изображений. Таким образом, коды DataMatrix можно считывать с любого направления.
А
Модель часов
Б
Шаблон выравнивания
При наличии более 24 x 24 модулей код разбивается на блоки, каждая сторона которых не превышает 24 модулей. Эта структура предотвращает искажение кода.
Скачать
Существует двадцать четыре размера кода, от 10 x 10 модулей до 144 x 144 модулей (включая шесть размеров для прямоугольного типа).
Когда код имеет более 26 x 26 модулей (более 24 x 24 модулей для данных), он делится на блоки, как показано ниже, которые не превышают 24 модулей на стороне. Эта структура предотвращает искажение кода.
Размер символа Блок Ячейка данных
от 10×10 до 26×26 1 от 8×8 до 24×24
от 28×28 до 52×52 4 от 14×14 до 24×24
От 64×64 до 104×104 16 от 14×14 до 24×24
От 120×120 до 144×144 36 от 18×18 до 22×22
Скачать
Поле вокруг кода DataMatrix должно быть больше модуля.
А
Маржа
Скачать
Код Рида-Соломона восстанавливает данные при повреждении части кода DataMatrix.
Скачать
Данные и коды исправления ошибок располагаются, как показано ниже.
Для преобразования «YSK» в код DataMatrix: YSK кодируются, а коды исправления ошибок рассчитываются, как показано ниже, и располагаются в квадрате.
А
Исходные данные
Б
Код (шестнадцатеричный)
С
Кодированные данные
Д
Код исправления ошибки
Скачать
Код
DataMatrix (ECC200) имеет две конфигурации, квадратную и прямоугольную, и всегда содержит четное количество ячеек.
Технические характеристики квадратного типа DataMatrix (ECC200)
Минимальный размер 10 x 10 модулей
Максимальный размер 144 x 144 модуля
Максимальная емкость данных 904:00 Цифровой 3116 символов
Буквенно-цифровой 2335 символов
Двоичный 1556 символов
Имеется двадцать четыре размера символов от 10 x 10 модулей до 144 x 144 модулей. При наличии более 24 x 24 модулей код разбивается на блоки, каждая сторона которых не превышает 24 модулей. Эта структура предотвращает искажение кода.
Технические характеристики прямоугольного типа DataMatrix (ECC200)
Минимальный размер 8 x 16 модулей
Максимальный размер 16 x 48 модулей
Максимальная емкость данных Цифровой 98 символов
Буквенно-цифровой 72 символа
Двоичный 47 символов
Существуют следующие шесть размеров прямоугольного типа.
8 x 18 модулей (1 блок)
12 x 26 модулей (1 блок)
16 x 36 модулей (1 блок)
8 x 32 модуля (2 блока)
12 x 36 модулей (2 блока)
16 x 48 модулей (2 блока)
В кодах DataMatrix скорость исправления ошибок автоматически определяется размером символа и емкостью данных. В отличие от QR-кода, его нельзя указать свободно.
Фактический размер кода DataMatrix определяется путем умножения размера символа на печатаемый размер модуля.
При размере модуля 0,25 мм,
Размер символа: 10 x 10 модулей = 2,5 x 2,5 мм
Размер символа: 32 x 32 модуля = 8,0 x 8,0 мм
Размер символа: 8 x 18 модулей = 2,0 x 4,5 мм
Скачать
Номера модулей Объем данных Скорость исправления ошибок
Цифровой Буквенно-цифровой Двоичный
10 х 10 6 3 1 25%
12 х 12 10 6 3 25%
14 х 14 16 10 6 от 28 до 39%
16 х 16 24 16 10 от 25 до 38%
18 х 18 36 25 16 от 22 до 34%
20 х 20 44 31 20 от 23 до 38%
22 х 22 60 43 28 от 20 до 34%
24 х 24 72 52 34 от 20 до 35%
26 х 26 88 64 42 от 19 до 35%
32 х 32 904:00 124 91 60 от 18 до 34%
36 х 36 172 127 84 от 16 до 30%
40 х 40 228 169 112 от 15 до 28%
44 х 44 288 214 142 от 14 до 27%
48 х 48 348 259 172 от 14 до 27%
52 х 52 408 304 202 от 15 до 27%
64 х 64 560 418 278 от 14 до 27%
72 х 72 736 550 366 от 14 до 26%
80 х 80 912 682 454 от 15 до 28%
88 х 88 1152 862 574 от 14 до 27%
96 х 96 1392 1042 694 от 14 до 27%
104 х 104 904:00 1632 1222 814 от 15 до 28%
120 х 120 2100 1573 1048 от 14 до 27%
132 х 132 2608 1954 1302 от 14 до 26%
144 х 144 3116 2335 1556 от 14 до 27%
Номера модулей Объем данных Скорость исправления ошибок
Цифровой Буквенно-цифровой Двоичный
8 х 18 10 6 3 25%
8 х 32 20 13 8 24%
12 х 26 32 22 14 от 23 до 37%
12 х 36 44 31 20 от 23 до 38%
16 х 36 64 46 30 от 21 до 38%
16 х 48 98 72 47 от 18 до 33%
Каждое количество символов в приведенной выше таблице является максимальным количеством символов, которые можно ввести.
Однако размер символа увеличивается в зависимости от компонента данных (например, комбинации цифр и символов или комбинации прописных и строчных букв), даже если данные содержат меньше символов, чем указано в таблице выше.
Скачать
GS1 DataMatrix — это двухмерный кодовый символ, который был стандартизирован GS1 для распространения. Он основан на стандарте ECC200 и определяет следующие правила, чтобы отличать его от обычного кода DataMatrix.
Используемый код DataMatrix ECC200
FNC1 [FNC1] помещается вверху данных, чтобы определить его как стандартную спецификацию GS1.
Идентификатор приложения (ИИ) Идентификационный код, который добавляется в начало полосы данных, чтобы определить, какая информация следует за этим идентификационным кодом. Идентификаторы приложений (AI) определяются ISO/IEC.
Данные переменной длины При вводе данных, в которых количество информации изменяется (данные переменной длины), например количества, вставьте [FNC1] в качестве разделителя после данных переменной длины. Этот [FNC1] предназначен для вывода [GS] (1Dh в коде ASCII) при чтении считывателем кодов.
* [GS]: Разделитель групп
Скачать
GS1 рекомендует следующие размеры модуля при печати кода GS1 DataMatrix.
Рекомендуемый размер модуля Максимальный размер модуля Минимальный размер модуля
Печать на этикетке 0,300 мм 0,615 мм 0,255 мм
ДПМ 0,380 мм 0,495 мм 0,380 мм
Скачать
Элемент АИ Данные
GTIN (14 фиксированных цифр) 01 045678904
Количество (переменная длина) 30 100
Срок реализации 17 120401
Скачать
Код GS1 DataMatrix имеет ту же структуру данных, что и код GS1-128. Таким образом, он, вероятно, будет использоваться, когда необходимо работать с большими объемами данных, несмотря на то, что область печати ограничена. Кроме того, код GS1 DataMatrix будет стандартизирован в медицинской отрасли. Поскольку коды должны быть напечатаны непосредственно на стальных медицинских инструментах, таких как хирургические ножи и ножницы, были установлены руководящие принципы.
Стальной медицинский инструмент: инструмент, изготовленный из таких материалов, как нержавеющая сталь, алюминий, медный сплав, титан или керамика, и повторно используемый в медицинских процедурах и операциях.
Скачать
Основы двумерных кодов Что такое двумерные коды?
Основы двумерных кодов Что такое QR-код?
ИНДЕКС
Что такое матрица?
Этот урок знакомит с матрицей — прямоугольным массивом, лежащим в основе матричная алгебра. Матричная алгебра довольно часто используется в расширенной статистике, в основном потому что это дает два преимущества.
Эффективные методы манипулирования наборами данных и решения наборов уравнения.
Определение матрицы
Матрица представляет собой прямоугольный массив чисел, расположенных в строки и столбцы. Массив чисел ниже является примером матрицы.
21 62 33 93
44 95 66 13
77 38 79 33
Число строк и столбцов матрицы называется ее размер или его порядок . Условно, строки перечислены первыми; и столбцы, во-вторых. Таким образом, мы бы сказали, что размер (или порядок) приведенной выше матрицы равен 3 x 4, что означает, что она имеет 3 строки и 4 столбца.
Числа, которые появляются в строках и столбцах матрицы, называются элементов матрицы. В приведенной выше матрице элемент в первом столбце первой строки — 21; элемент во втором столбец первой строки равен 62; и так далее.
Реклама
Матричное обозначение
Статистики используют символы для идентификации матричных элементов и матриц.
Элементы матрицы. Рассмотрим матрицу ниже, в котором матричные элементы полностью представлены символами.
A ₁ ₁ A ₁ ₂ A ₁ ₃ A ₁ ₄
A ₂ ₁ A ₂ ₂ A ₂ A ₂ A ₂ A ₂ A ₂ A ₂ A ₂ A1321 4
По соглашению первый нижний индекс относится к номер строки; и второй нижний индекс, к номеру столбца. Таким образом, первый элемент в первой строке представлен А ₁ ₁ . Второй элемент в первой строке равен в лице А ₁ ₂ . И так далее, пока не дойдем до четвертого элемента во второй строке, которая представлена А ₂ ₄ .
Матрицы. Существует несколько способов представления матрица символически. Простейший использовать жирный шрифт, например A , B , или С . Таким образом, A может представлять собой Матрица 2 x 4, как показано ниже.
A =
11 62 33 93
44 95 66 13
Еще один подход для представления матрицы A :
A = [ A _I9 _J2222222220 и J = 113229 _J] 2 и _I22221 J]. 2, 3, 4
Это обозначение указывает, что A представляет собой матрицу с 2 строками и 4 колонки. Фактические элементы массива не отображаются; они есть обозначается символом A _i _j .
Другие матричные обозначения будут вводиться по мере необходимости. Для описания всех матричных обозначений, используемых в этом руководстве, см. см. Приложение «Матричная нотация».
Равенство матриц
Чтобы понять алгебру матриц, нам нужно понять матрицу равенство. Две матрицы равны, если все три из следующих условий встречаются:
Каждая матрица имеет одинаковое количество строк.
Каждая матрица имеет одинаковое количество столбцов.
Соответствующие элементы в каждой матрице равны.
Рассмотрим три матрицы, показанные ниже.
А =
111 x
y 444

B =
111 222
333 444

C =
L
L 9009
L

0010 m n
o p q
If A = B , we know that x = 222 and у = 333; поскольку соответствующие элементы равных матриц также равны. И мы знаем, что матрица C не равно A или B , потому что C имеет больше столбцов, чем A или Б .
Проверьте свое понимание
Задача 1
Приведенные ниже обозначения описывают две матрицы – матрицу A и матрица B .
A = [ A _i _j ]
where i = 1, 2, 3 and j = 1, 2
B =
111 222 333 444
555 666 777 888
Какое из следующих утверждений о A и B верны?
I. Матрица A состоит из 5 элементов.
II. Размер матрицы B 4 х 2.
III. В матрице B элемент B ₂ ₁ есть равно 222.
(A) Только I
(B) Только II
(C) Только III
(D) Все вышеперечисленное
(E) Ничего из вышеперечисленного
Решение
Правильный ответ (Е).
Матрица имеет 3 строки и 2 столбца; то есть, 3 ряда по 2 элемента в каждом. Это составляет 6 элементов, всего – не 5.
Размер матрицы B 2 х 4, а не 4 х 2. То есть матрица B имеет 2 строки и 4 столбца – не 4 ряда и 2 столбца.
И, наконец, элемент B ₂ ₁ относится к первый элемент в вторая строка матрицы B , что равно 555, а не 222.
Последний урок Следующий урок
2.3 Типы матриц | Matrix Algebra Companion for Statistical Learning (matrix4sl)
Существуют различные виды матриц, которые обычно используются в методах статистического обучения. Кратко остановимся на некоторых из них.
2.3.1 Общая прямоугольная матрица
Самый распространенный тип матрицы — прямоугольная матрица. Это означает, что имеется произвольное количество $n$ строк и $p$ столбцов.
\[ \left[\begin{массив}{ccc} 1 и 2 и 3 \\ 4 и 5 и 6 \\ 7 и 8 и 9 \\ 10 и 11 и 12 \\ \конец{массив}\справа] \]
Если в матрице больше строк, чем столбцов $n > p$, иногда мы называем это вертикальной или высотой матрицей:
\[ \left[\begin{массив}{ccc} 1 и 2 и 3 \\ 4 и 5 и 6 \\ 7 и 8 и 9 \\ 10 и 11 и 12 \\ 13 и 14 и 15\ \конец{массив}\справа] \]
Напротив, если в матрице больше столбцов, чем строк, $p > n$, иногда мы называем это горизонталью, плоский или широкий матричный:
\[ \left[\begin{массив}{cccc} 1 и 2 и 3 и 4 и 5 \\ 6 и 7 и 8 и 9 и 10 \\ 11 и 12 и 13 и 14 и 15 \\ \конец{массив}\справа] \]
2.3.2 Квадратная матрица
Квадратная матрица – это матрица с одинаковым количеством строк и столбцов, $n = p$. \mathsf{T}}\).
\[ \left[\begin{массив}{ccc} 1 и 2 и 3 \\ 4 и 5 и 6 \\ 7 и 8 и 9 \\ \конец{массив}\справа] \]
2.3.3 Симметричная матрица
Симметричная матрица является частным случаем квадратной матрицы: соответствующие элементы соответствующих строк и столбцов равны. Другими словами, в симметричной матрице элемент $x_{ij}$ равен $x_{ji}$.
\[ \left[\begin{массив}{ccc} 1 и 2 и 3 \\ 2 и 4 и 5 \\ 3 и 5 и 6 \\ \конец{массив}\справа] \]
2.3.4 Диагональная матрица
Диагональная матрица является частным случаем симметричной матрицы, в которой все недиагональные элементы равны 0.
\[ \left[\begin{массив}{ccc} 1 и 0 и 0 \\ 0 и 2 и 0 \\ 0 и 0 и 3 \\ \конец{массив}\справа] \]
Другими словами, в симметричной матрице $x_{ij} = 0$ для $i \neq j$. Единственные элементы, которые не обязательно могут быть равны нулю, находятся на диагонали.
\[ \left[\begin{массив}{ccc} х_{11} & 0 & 0 \\ 0 и х_{22} и 0 \\ 0 и 0 и х_{33} \\ \конец{массив}\справа] \]
2.
3.5 Скалярная матрица
Скалярная матрица представляет собой особый тип диагональной матрицы, в которой все диагональные элементы являются равными скалярами.
\[ \left[\begin{массив}{ccc} 5 и 0 и 0 \\ 0 и 5 и 0 \\ 0 и 0 и 5 \\ \конец{массив}\справа] \]
2.3.6 Единичная матрица
Единичная матрица является частным случаем скалярной матрицы, в которой все диагональные элементы равны единице. Эта матрица обычно обозначается буквой $\mathbf{I}$. Чтобы указать размеры этой матрицы, мы обычно пишем ее с нижним индексом для количества строк (или столбцов). Например, $\mathbf{I}_{n}$ представляет единичную матрицу размерности $n \times n$.
\[ \mathbf{I}_{3} = \left[\begin{массив}{ccc} 1 и 0 и 0 \\ 0 и 1 и 0 \\ 0 и 0 и 1 \\ \конец{массив}\справа] \]
В матричной алгебре единичная матрица играет ту же роль, что и число 1 в обычной или скалярной алгебре.
2.3.7 Треугольная матрица
Квадратная матрица, имеющая только 0 над или под диагональю, называется треугольной матрицей . Существует два вида матрицы этого типа: верхняя треугольная и нижняя треугольная.
Верхняя треугольная матрица имеет нули ниже диагонали.
\[ \left[\begin{массив}{ccc} 1 и 2 и 3 \\ 0 и 5 и 6 \\ 0 и 0 и 9 \\ \конец{массив}\справа] \quad \textsf{или} \quad \left[\begin{массив}{ccc} 1 и 2 и 3 \\ & 5 & 6 \\ & & 9 \\ \конец{массив}\справа] \]
И наоборот, нижняя треугольная матрица имеет нули выше диагонали.
\[ \left[\begin{массив}{ccc} 1 и 0 и 0 \\ 4 и 5 и 0 \\ 7 и 8 и 9\\ \конец{массив}\справа] \quad \textsf{или} \quad \left[\begin{массив}{ccc} 1 & & \\ 4 и 5 и \\ 7 и 8 и 9 \\ \конец{массив}\справа] \]
2.3.8 Формы матриц
Чтобы обобщить различные типы матриц, описанные до сих пор, вот схема, изображающая их формы. Общий тип матрицы — это прямоугольная матрица, которую можно разделить на три типа: вертикальная или высокая ($n > p$), квадратная ($n = p$) и горизонтальная или широкая ($n < п$). Среди квадратных матриц понятие симметрии играет особую роль, а среди симметричных матриц можно сказать, что диагональные имеют наиболее базовую структуру.
Рисунок 2.2: Различные формы матриц
Сделать пожертвование
Если вы найдете этот ресурс полезным, рассмотрите возможность сделать разовое пожертвование в любой сумме. Ваша поддержка действительно имеет значение.
3.4 Прямоугольные структуры данных | Введение в науку о данных
Прямоугольные структуры данных обычно хранят данные в двумерном (2D) формате (т. е. в виде сетки, содержащей строки и столбцы). Когда все строки и все столбцы имеют одинаковую длину, результирующая структура равна 9.1745 прямоугольный .
Как уже было показано в таблице 3.1, мы различаем два основных типа двумерных структур данных в R: тип данных)
прямоугольных таблиц (называемых фреймами данных или tibbles в R) допускают разнородных данных: Они могут содержать разные типы данных в разных столбцах.
Путаница в отношении различных структур 2D-данных проясняется путем разграничения их формы и содержания: Матрицы и прямоугольные таблицы имеют прямоугольную форму (т. е. строки и столбцы). Однако матрицы и прямоугольные таблицы различаются по своему содержанию: В то время как матрица — это просто атомарный вектор (т. е. данные одного типа) с некоторыми дополнительными атрибутами формы, фрейм данных или табличка — это более сложная структура данных, которая объединяет несколько векторов (т. е. позволяет использовать разные типы данных).
Остерегайтесь «таблиц»
Мы используем неуклюжий термин «прямоугольная структура данных», поскольку более короткий термин «таблица» расплывчат и сбивает с толку. Всякий раз, когда речь идет о таблицах, нам нужно различать значения термина в общем языке и его конкретные воплощения в виде структуры данных в R.
и таблицы типа tibble. Но поскольку таблички на самом деле являются другим (более простым) типом фрейма данных, мы можем игнорировать это различие здесь (и пересмотрим его при введении 9пакет 0039 tibble в главе 5).
Сбивает с толку тот факт, что термин таблица иногда неофициально используется как надкатегория для любой прямоугольной структуры данных (т. е. включая фреймы данных и матрицы, например, в заголовке этого раздела).
Поскольку таблицы могут расширяться более чем в двух измерениях, другим термином для многомерных таблиц является массив . Однако в R объекты типа «массив» по сути являются векторами (т. е. атомарными) с дополнительными атрибутами формы (т. е. размерами массива).
В R гибкость или расплывчатость термина таблица усугубляется еще больше, поскольку R использует тип данных “таблица” для обозначения определенного типа массива (т. Таблица сопряженности).
В целом, мы видим, что термин таблица используется по-разному и для разных видов объектов. Однако имеет смысл различать матрицы и фреймы данных, поэтому далее мы обсудим эти два типа таблиц.
3.4.1 Матрицы
Когда прямоугольник данных содержит данные одного типа во всех ячейках (т. е. во всех строках и столбцах), у нас есть матрица данных. В R матрица представляет собой атомарный вектор с дополнительными атрибутами, которые определяют его форму и имена его строк или столбцов.
Создание матриц
Способ создания матрицы из атомарного вектора предоставляется функцией matrix() . Он содержит аргументы для данных , для количества строк nrow , число столбцов ncol и логический аргумент byrow , который упорядочивает данные по строкам и по столбцам:
# Преобразование атомарного вектора в прямоугольную матрицу: (m1 <- матрица (данные = 1:20, nrow = 5, ncol = 4, byrow = TRUE)) #> [1] [2] [3] [4] #> [1,] 1 2 3 4 #> [2,] 5 6 7 8 #> [3,] 9 10 11 12 #> [4,] 13 14 15 16 #> [5,] 17 18 19 20 (m2 <- матрица (данные = 1:20, nrow = 5, ncol = 4, byrow = FALSE)) #> [1] [2] [3] [4] #> [1,] 1 6 11 16 #> [2,] 2 7 12 17 #> [3,] 3 8 13 18 #> [4,] 4 914 19 #> [5,] 5 10 15 20
Матрицы также можно создавать из нескольких атомарных векторов (одного и того же типа данных), связывая их вместе:
# Создание 3 векторов: х <- 1:3 у <- 4:6 г <- 7:9 # Объединение векторов (одинаковой длины): ---- (m3 <- rbind(x, y, z)) # объединить в строки #> [1] [2] [3] #> х 1 2 3 #> у 4 5 6 #> я 7 8 9 (m4 <- cbind(x, y, z)) # объединить как столбцы #> х у г #> [1,] 1 4 7 #> [2,] 2 5 8 #> [3,] 3 6 9
Когда данные, которые должны быть преобразованы в матрицу, не совпадают друг с другом или аргументами размера, R пытается повторно использовать векторы или усекает их до предоставленных размеров. Обратите внимание, что все следующие команды создают предупреждающие сообщения, так как количество аргументов не соответствует матрице (необходимого размера):
m <- 1:2 п <- 3:5 rbind(m, n) # переработка m #> [1] [2] [3] #> м 1 2 1 #> п 3 4 5 cbind(m, n) # переработка m #> м н #> [1,] 1 3 #> [2,] 2 4 #> [3,] 1 5 matrix(data = 1:10, nrow = 3, ncol = 4) # переработка данных #> [1] [2] [3] [4] #> [1,] 1 4 7 10 #> [2,] 2 5 8 1 #> [3,] 3 6 92 matrix(data = 1:10, nrow = 3, ncol = 3) # усечение данных #> [1] [2] [3] #> [1,] 1 4 7 #> [2,] 2 5 8 #> [3,] 3 6 9
Все матрицы от m1 до m4 содержали числовые данные. Однако данные типа «логический» или «символьный» также могут храниться в матричной форме:
# Матрица логических значений: (m5 <- матрица (данные = 1:18 %% 4 == 0, nrow = 3, ncol = 6, byrow = TRUE)) #> [1] [2] [3] [4] [5] [6] #> [1,] ЛОЖЬ ЛОЖЬ ЛОЖЬ ИСТИНА ЛОЖЬ ЛОЖЬ #> [2,] ЛОЖЬ ИСТИНА ЛОЖЬ ЛОЖЬ ЛОЖЬ ИСТИНА #> [3,] ЛОЖЬ ЛОЖЬ ЛОЖЬ ИСТИНА ЛОЖЬ ЛОЖЬ # Матрица значений символов: (m6 <- матрица (образец (буквы, размер = 16), nrow = 4, ncol = 4, byrow = FALSE)) #> [1] [2] [3] [4] #> [1,] "у" "д" "с" "а" #> [2,] "j" "c" "z" "f" #> [3,] "м" "б" "е" "ж" #> [4,] "н" "т" "ч" "у"
Индексирование матриц
Извлечение значений из матрицы m работает аналогично индексированию векторов. Сначала мы рассмотрим числовую индексацию . Из-за двумерного характера матрицы нам теперь нужно указать два индекса в квадратных скобках: номер нужной строки и номер нужного столбца, разделенные запятой. Таким образом, чтобы получить или изменить значение строки r и столбца c матрицы m , мы нужно оценить м[р, к] . Как и в случае с векторами, предоставление нескольких числовых индексов выбирает соответствующие строки или столбцы. Если значение r или c не указано, выбираются все строк или столбцов.
# Выбор ячеек, строк или столбцов матриц: ---- m1[2, 3] # в m1: выберите строку 2, столбец 3 #> [1] 7 m2[3, 1] # в m2: выберите строку 3, столбец 1 #> [1] 3 m1[2, ] # в m1: выберите строку 2, все столбцы #> [1] 5 6 7 8 m2[ , 1] # в m1: выбрать столбец 1, все строки #> [1] 1 2 3 4 5 м3 #> [1] [2] [3] #> х 1 2 3 #> у 4 5 6 #> я 7 8 9m3[2, 2:3] # в m3: выберите строку 2, столбцы со 2 по 3 #> [1] 5 6 m3[1:3, 2] # в m3: выберите строки с 1 по 3, столбец 2 #> х у г #> 2 5 8 m4[] # в r4: выбрать все строки и все столбцы (т. е. все m4) #> х у г #> [1,] 1 4 7 #> [2,] 2 5 8 #> [3,] 3 6 9
Аналогичным образом мы можем расширить понятие логической индексации на матрицы:
m4 > 10 # возвращает матрицу логических значений #> х у г #> [1,] ЛОЖЬ ЛОЖЬ ЛОЖЬ #> [2,] ЛОЖЬ ЛОЖЬ ЛОЖЬ #> [3,] ЛОЖЬ ЛОЖЬ ЛОЖЬ тип(m4 > 10) #> [1] "логический" m4[m4 > 10] # индексация матриц #> целое (0)
Как и в случае с векторами, мы можем применять функции к матрицам. Типичные примеры включают:
# Применение функций к матрицам: ---- is.matrix(m1) #> [1] ИСТИНА тип(м2) #> [1] "целое число" # Обратите внимание на разницу между: is.numeric(m3) # тип m3? (1 значение) #> [1] ИСТИНА is.na(m3) # Значения NA в м3? (много значений) #> [1] [2] [3] #> x ЛОЖЬ ЛОЖЬ ЛОЖЬ #> y ЛОЖЬ ЛОЖЬ ЛОЖЬ #> z ЛОЖЬ ЛОЖЬ ЛОЖЬ # Вычисления с матрицами: сумма(м1) #> [1] 210 макс(м2) #> [1] 20 среднее (м3) #> [1] 5 colSums(m3) # суммы столбцов r3 #> [1] 12 15 18 rowSums(m4) # сумма строк r4 #> [1] 12 15 18
Так же, как length() предоставляет важную информацию о векторе, некоторые функции специально разработаны для предоставления размеров прямоугольных структур данных:
ncol(m4) # количество столбцов #> [1] 3 nrow(m4) # количество рядов #> [1] 3 dim(m4) # размеры в виде вектора c(строки, столбцы) #> [1] 3 3
Типичная функция в контексте матриц t() для транспонирования (т. е. замены строк и столбцов) матрицы:
t(m4) #> [1] [2] [3] #> х 1 2 3 #> у 4 5 6 #> я 7 8 9т(м5) #> [1] [2] [3] #> [1,] ЛОЖЬ ЛОЖЬ ЛОЖЬ #> [2,] ЛОЖЬ ИСТИНА ЛОЖЬ #> [3,] ЛОЖЬ ЛОЖЬ ЛОЖЬ #> [4,] ИСТИНА ЛОЖЬ ИСТИНА #> [5,] ЛОЖЬ ЛОЖЬ ЛОЖЬ #> [6,] ЛОЖЬ ИСТИНА ЛОЖЬ
3.4.2 Фреймы данных
Таблица 2.1 была прямоугольной и содержала три строки (значения для переменных имя , пол и возраст ) и пять столбцов (по одному для каждого человека плюс начальный столбец, указывающий имя переменной в каждой строке). Это совершенно корректная таблица, но не та, которая обычно используется в R.
Типичные таблицы данных в R также объединяют несколько векторов в более крупную структуру данных, но используют отдельные векторы в виде столбцов, а не строк. Такое сочетание нескольких векторов (в виде столбцов) показано в Таблице 3.2:
Таблица 3.2: Те же факты о пяти людях (в виде таблицы с 5 строками и 3 столбцами).
1Д атомный вектор список
2Д матрица таблица (фрейм данных/таблица)
нД массив
Важно отметить, что в Таблице 3.2 представлена та же информация, что и в Таблице 2.1, а также в трех отдельных векторах ( имя , пол и возраст ) выше, но в форме таблицы, в которой используются наши предыдущие векторы как его столбцов , а не как его строки.
Поскольку (атомарные) векторы в R должны иметь один и тот же тип данных (например, имя содержит символьные данные, тогда как age содержит числовые данные), информацию о каждом человеке — из-за наличия нескольких типов данных — нельзя хранить в виде вектора. Вместо этого мы представляем каждого человека в виде строк (также известных как наблюдений ) таблицы.
Создание фреймов данных
Чтобы создать фрейм данных, нам сначала нужно, чтобы данные были фреймированы в другой форме. Наиболее типичный сценарий заключается в том, что у нас есть данные в виде набора векторов. Если эти векторы имеют одинаковую длину, создание кадра данных из векторов может быть достигнуто с помощью data.frame() функция. Например, мы можем определить фрейм данных df из наших векторов имя , пол и возраст (сверху), назначив его data.frame(имя, пол, возраст) :
(df <- data.frame(имя, пол, возраст)) #> имя пол возраст #> 1 Адам мужского пола 21 #> 2 Бен мужчина 19 лет #> 3 Сесили женщина 20 #> 4 Давид мужчина 48 лет #> 5 Evelyn misc 45
Замечательный факт о фрейме данных df заключается в том, что это объект, который объединяет несколько типов данных. Внутри R представляет фреймы данных в виде списка атомарных векторов. Векторы формируют столбцы фрейма данных df , а не его строки. Более тривиально мы могли бы назвать наш объект some_data или Five_people , но имя df часто используется как короткое и удобное имя для фрейма данных, которое можно проверить и проверить позже.
Функция data.frame() является довольно мощной и преобразует различные объекты во фреймы данных. Например, мы можем использовать его для преобразования отдельных векторов или матриц во фреймы данных:
# Создание фреймов данных из вектора или матрицы: v <- 1:9 m <- матрица (v, nrow = 3) data.frame(v) # из вектора #> в #> 1 1 #> 2 2 #> 3 3 #> 4 4 #> 5 5 #> 6 6 #> 7 7 #> 8 8 #> 9 9 data.frame(m) # из матрицы #> Х1 Х2 Х3 #> 1 1 4 7 #> 2 2 5 8 #> 3 3 6 9
Из-за прямоугольной формы фрейма данных все его столбцы должны иметь одинаковую длину. Если векторы, используемые для создания фрейма данных, имеют разную длину, то более короткие векторы перерабатываются до длины самого длинного:
# Из векторов разной длины: абв <- буквы [1:3] data. frame(v, abc) #> v абв #> 1 1 а #> 2 2 б #> 3 3 с #> 4 4 а #> 5 5 б #> 6 6 в #> 7 7 а #> 8 8 б #> 9 9 c
Как мы узнали в главе 2, каждый объект характеризуется своей формой, мы можем спросить: какова форма фрейма данных df ? Для линейных структур данных (таких как векторы или списки) основная информация о форме предоставляется их length() . Для прямоугольных структур данных (таких как матрицы или фреймы данных) мы все еще можем спросить об их length() , но более информативная функция предоставляет их размеры dim() :
length(df) # количество векторов/столбцов #> [1] 3 dim(df) # размеры #> [1] 5 3 nrow(df) # затемнение[1] #> [1] 5 ncol(df) # тусклый[2] #> [1] 3
Поскольку фреймы данных являются наиболее распространенным способом хранения данных в R, существует специальная форма индексации, которая позволяет получить доступ к переменным фрейма данных (т. е. к столбцам фрейма данных) в виде векторов. .
Индексация фреймов данных на основе имени
Когда в таблице tb есть имена столбцов (например, столбец с именем имя ), мы можем получить соответствующий вектор с помощью индексации на основе имен (также известной как индексация имен ). Это наиболее удобный и наиболее часто используемый способ доступа к переменным (т. е. столбцам) таблиц (например, фреймам данных). Чтобы использовать эту форму индексации, мы используем специальную нотацию со знаком доллара: добавление $ и имя нужной переменной имя к имени объекта таблицы tb дает его столбец имя в виде вектора. Звучит сложно, но на самом деле это очень просто:
tb$name
В случае нашего фрейма данных df мы можем получить доступ к его 1-му и 2-му столбцам по их соответствующим именам:
name(df) # печатает ( столбец) имена #> [1] "имя" "пол" "возраст" имя df$ #> [1] «Адам» «Бен» «Сесили» «Дэвид» «Эвелин» df$gender #> [1] "мужской" "мужской" "женский" "мужской" "разное"
Индексирование фреймов данных
Обратите внимание, что все, что мы узнали о числовой и логической индексации векторов и матриц (см. выше), также применимо к фреймам данных. Таким образом, мы также можем использовать числовую индексацию фрейма данных, как и в случае с матрицами (см. выше). Например, чтобы получить все строки первого столбца, мы можем указать имя фрейма данных, за которым следует [ , 1] :
df[ , 1] # получить (все строки и) 1-й столбец df #> [1] «Адам» «Бен» «Сесили» «Дэвид» «Эвелин» df[ , 2] # получить (все строки и) второй столбец df #> [1] "мужской" "мужской" "женский" "мужской" "разное"
Таким образом, эти два выражения извлекают 1-й и 2-й столбцы фрейма данных df_1 (в виде векторов) соответственно. Поскольку это очень распространенная задача в R, существует более простой способ доступа к переменным (столбцам) фрейма данных.
Логическая индексация фреймов данных особенно эффективна, поскольку позволяет нам выбирать определенные строки (на основе условий, указанных в столбцах того же фрейма данных):
df[df$gender == "мужской", ] #> имя пол возраст #> 1 Адам мужского пола 21 #> 2 Бен мужчина 19 лет#> 4 Давид мужчина 48 лет df[df$возраст < 21, ] #> имя пол возраст #> 2 Бен мужчина 19 лет #> 3 Сесили жен. 20
Обратите внимание, что различные типы индексации можно гибко комбинировать. Например, следующая команда использует логическое индексирование
(для выбора строк df со значением возраста менее 30 лет)
числовая индексация (для выбора только столбцов 1 и 2)
индексация имени (чтобы получить переменную имя в виде вектора) и
числовая индексация (для выбора 3-го элемента этого вектора):
df[df$age < 30, c(1, 2)]$name[3] #> [1] "Cecily"
На практике такие сложные комбинации редко необходимы или полезны. Например, следующие выражения возвращают точно такой же результат, как и сложное, но имеют гораздо более простую семантику:
df[3, 1] #> [1] "Сесили" дф$имя[3] #> [1] "Cecily"
Поскольку фреймы данных являются списками, мы можем обращаться к их элементам так же, как и к элементам списка:
Используете списки или фреймы данных?
Зная, что фреймы данных являются списками , можно предположить, что не имеет значения, используем ли мы фрейм данных или список для хранения данных. Это впечатление ложно. Хотя многие наборы данных можно хранить как в виде списка, так и в виде прямоугольной таблицы, обычно лучше выбрать более простой формат, который поддерживается большим количеством инструментов.
В принципе, фреймы данных и списки могут хранить одни и те же данные (и даже являются вариантами одной и той же структуры данных R, т. е. список ). Однако прагматические причины склоняют чашу весов в пользу фреймов данных в большинстве случаев использования: Всякий раз, когда набор объединяемых векторов имеет одинаковую длину, их комбинация создаст прямоугольную форму. Поскольку многие функции R предполагают или оптимизированы для прямоугольных структур данных, использование фреймов данных обычно является лучшим выбором.
Урок, который следует здесь усвоить, заключается в том, что мы должны стремиться к простейшей структуре данных, которая соответствует свойствам наших данных. Хотя списки более гибкие, чем фреймы данных, они редко нужны в прикладных контекстах. Как правило, более простым структурам следует отдавать предпочтение перед более сложными:
Для линейных последовательностей однородных данных векторы предпочтительнее списков.
Для прямоугольных форм разнородных данных фреймы данных предпочтительнее списков.
Таким образом, пока данные укладываются в простые и правильные формы векторов и фреймов данных, нет необходимости в использовании списков. Векторы и фреймы данных обычно легче создавать и использовать, чем соответствующие списки. Кроме того, многие функции R написаны и оптимизированы для векторов и фреймов данных, а не для списков. Как следствие, списки следует использовать только тогда, когда данные требуют смешивания данных разных типов и форм или когда объекты данных становятся настолько сложными, нерегулярными или непредсказуемыми, что не помещаются в прямоугольную таблицу.
Строки как факторы
Обратите внимание, что функция data.frame() имеет аргумент stringsAsFactors . Этот аргумент определяет, преобразуются ли так называемые строковые переменные (т. е. типа данных «character») в факторы (т. е. категориальные переменные, которые внутренне представлены как целочисленные значения с текстовыми метками) при создании фрейма данных. К огорчению нескольких поколений пользователей R, значение этого аргумента по умолчанию было равно 9.1890 TRUE в течение нескольких десятилетий — что, по сути, означало, что любая символьная переменная во фрейме данных была преобразована в фактор, если только пользователь не указал stringsAsFactors = FALSE . Поскольку это вызвало много путаницы, значение по умолчанию было изменено с выпуском версии R 4.0.0 (24 апреля 2020 г.) на stringsAsFactors = FALSE . Это показывает, что боги R на https://cran.r-project.org/ реагируют на отзывы пользователей. Однако, поскольку любые такие изменения вряд ли произойдут быстро, безопаснее явно задавать аргументы функции. Чтобы увидеть разницу между обоими настройками, рассмотрим следующий пример:
df_1 <- data. frame(имя, пол, возраст, stringsAsFactors = FALSE) # новое значение по умолчанию (начиная с R 4.0.0+) df_2 <- data.frame(имя, пол, возраст, stringsAsFactors = TRUE) # старое значение по умолчанию (до R 3.6.3) # Оба фрейма данных выглядят одинаково: df_1 #> имя пол возраст #> 1 Адам мужского пола 21 #> 2 Бен мужчина 19 лет #> 3 Сесили женщина 20 #> 4 Давид мужчина 48 лет #> 5 Эвелин разное 45 df_2 #> имя пол возраст #> 1 Адам мужского пола 21 #> 2 Бен мужчина 19 лет#> 3 Сесили женщина 20 #> 4 Давид мужчина 48 лет #> 5 Evelyn misc 45
Печать двух фреймов данных df_1 и df_2 не показывает никакой разницы между ними. Однако, поскольку первые две переменные (т. е. имя и пол ) были строковыми переменными (т. е. типа «персонаж»), они представлены как множители в df_1 по сравнению с оставшимися символьными переменными в df_2 .
Давайте получим первый столбец каждого фрейма данных (в виде вектора). Используя именованное индексирование, мы можем легко получить и распечатать первый столбец (т. е. с именем 9).1890 name ) любого фрейма данных:
df_1$name #> [1] «Адам» «Бен» «Сесили» «Дэвид» «Эвелин» df_2$имя #> [1] Адам Бен Сесили Дэвид Эвелин #> Уровни: Адам Бен Сесили Дэвид Эвелин
Обратите внимание на различия в распечатке. Результат df_1$name выглядит как любой другой вектор символов (с пятью элементами, каждый из которых состоит из имени). Напротив, вывод df_2$name также печатает те же имена, но без характерных двойных кавычек вокруг каждого имени и со второй строкой, начинающейся с «Levels:», прежде чем кажется, что повторяются имена первой строки. Прежде чем пояснить, что это значит, проверьте другую переменную в обоих df_1 и df_2 , которые раньше были вектором символов пол :
df_1$gender #> [1] "мужской" "мужской" "женский" "мужской" "разное" df_2$пол #> [1] мужской мужской женский мужской разное #> Уровни: female male misc
Опять же, df_1$gender выглядит как вектор символов, но df_2$gender был преобразован во что-то другое. На этот раз строка, начинающаяся с «Уровни:», содержит каждую из меток пола только один раз и в алфавитном порядке.
Если вы еще не запутались, сравните выходные данные следующих команд:
typeof(df_1$name) #> [1] "персонаж" typeof(df_2$имя) #> [1] "integer"
В то время как df_1$name должен был иметь тип character , должно было стать сюрпризом, что df_2$name имеет тип integer . Учитывая, что df_2$name содержит целых чисел , у нас может возникнуть соблазн попробовать арифметические функции, такие как:
макс(df_2$имя) сумма (df_2 $ имя) mean(df_2$name)
Если мы попытаемся оценить эти выражения, мы получим либо предупреждения, либо сообщения об ошибках. Как мы можем понять все это?
Волшебное слово здесь фактор . Как предполагает stringsAsFactors = TRUE , символьные строки векторов name и gender были преобразованы в факторов при определении df_2 . Факторы — это категориальные переменные, которые заботятся только о том, принадлежат ли два значения одной и той же или разным группам. На самом деле, R изначально кодирует их как числовые значения (целые числа) для каждого уровня фактора. Но поскольку мы никогда не хотим производить вычисления с этими числовыми значениями (поскольку они не имеют никакого значения, кроме того, что они одинаковы или различны), им также присваивается метка, которая отображается при печати значений фактора.
Быстрый способ проверить, что мы имеем дело с фактором, — это функция is.factor() :
is.factor(df_1$name) #> [1] ЛОЖЬ is.factor(df_2$имя) #> [1] ИСТИНА is.factor(df_1$пол) #> [1] ЛОЖЬ is.factor(df_2$пол) #> [1] TRUE
Факторные переменные часто бывают полезны (например, для различения групп в статистических планах). Но преждевременно предполагать, что любая символьная переменная должна быть фактором при включении переменной во фрейм данных. Таким образом, хорошо, что аргумент по умолчанию в 9Функция 1890 data. frame() была изменена на stringsAsFactors = FALSE` в R v4.0.0.
Кому нужны факторы, они по-прежнему могут их получать и использовать — но начинающим пользователям больше не нужно иметь с ними дело постоянно.
3.4.3 Практика
Следующие практические упражнения позволят вам проверить свое понимание этого раздела.
Доступ и оценка матриц
Предполагая определения матриц м5 и м6 сверху, т. е.
м5 #> [1] [2] [3] [4] [5] [6] #> [1,] ЛОЖЬ ЛОЖЬ ЛОЖЬ ИСТИНА ЛОЖЬ ЛОЖЬ #> [2,] ЛОЖЬ ИСТИНА ЛОЖЬ ЛОЖЬ ЛОЖЬ ИСТИНА #> [3,] ЛОЖЬ ЛОЖЬ ЛОЖЬ ИСТИНА ЛОЖЬ ЛОЖЬ м6 #> [1] [2] [3] [4] #> [1,] "у" "д" "с" "а" #> [2,] "j" "c" "z" "f" #> [3,] "м" "б" "е" "ж" #> [4,] "n" "t" "h" "y"
предсказать, оценить и объяснить результат следующих R выражений:
м5[2, 6] m5[2, ] m5 == ЛОЖЬ сумма(м5) т (т (м5)) м6[2, 3] m6[ , 4] m6[nrow(m6), (ncol(m6) - 1)] м6 == "е" топпер(m6[4, ])
Числовое индексирование фреймов данных
Предполагая фрейм данных df_2 (сверху),
df_2 #> имя пол возраст #> 1 Адам мужского пола 21 #> 2 Бен мужчина 19 лет #> 3 Сесили женщина 20 #> 4 Давид мужчина 48 лет #> 5 Evelyn misc 45
прогнозировать, оценивать и объяснять, что происходит в следующих командах (с точки зрения числовой индексации ):
df_2[] df_2[ , 1] df_2[1:nrow(df_2), c(1)] df_2[nrow(df_2):1, c(1)] df_2 [реп (1, 3), с (1, 2)] df_2$имя[3] # сравнивать: df_2[1:nrow(df_2), 1:ncol(df_2)] df_2[1:nrow(df_2), ncol(df_2):1] df_2[nrow(df_2):1, ncol(df_2):1]
Логическое индексирование фреймов данных
Предполагая фрейм данных df_1 (сверху),
df_1 #> имя пол возраст #> 1 Адам мужского пола 21 #> 2 Бен мужчина 19 лет #> 3 Сесили женщина 20 #> 4 Давид мужчина 48 лет #> 5 Evelyn misc 45
предсказать, оценить и объяснить, что происходит в следующих командах (с точки зрения логической индексации):
df_1[ , 3] > 30 df_1[df_1$возраст > 30, ] df_1[df_1$пол != "мужской", c(1, 3, 2)] df_1$name[df_1$gender == "мужской"] sum(df_1$age[df_1$gender == "мужской"])
Кадры данных с коэффициентами
Учитывая, что наше определение df_2 использовало строк AsFactors = TRUE (см. выше), предсказать, оценить и объяснить, что происходит в следующих командах:
nchar(as.character(df_2$имя[3])) как.numeric(df_2$имя[3]) + 1 mean(as.numeric(df_2$name))
Почему следующие команды (которые являются более простыми вариантами последних трех выражений) выдают ошибки или предупреждения?
nchar(df_2$имя[3]) df_2$имя[3] + 1 среднее (df_2$имя)
Что произойдет, если те же самые команды будут использованы на df_1 (сверху)?
nchar (df_1 $ имя [3]) df_1$имя[3] + 1 mean(df_1$name)
Дополнительные сведения:
фреймы данных: data.frame() против as.data.frame()
tibble: as_tibble() (из пакета tibble ) преобразует фрейм данных в tibble
Способы доступа и управления таблицами
Применение функций к таблицам:
Проверка значений NA (в векторах или таблицах) с помощью функции is. na() .
DMRE
Что такое DMRE?
Код матрицы данных с дополнительными прямоугольными форматами.
В приведенном ниже примере кода показана расширенная прямоугольная матрица данных с размером модуля 8×64, хорошо вписывающимся в доступное пространство на объекте:
Сообщение о DMRE от Денниса Придди, одного из первых разработчиков матрицы данных
«Мне это нравится! Ваша реализация расширения не может быть более совершенной по своей простоте, исполнению и эффективности. И да, я немного горжусь тем, что Data Matrix все еще может помочь решить реальные проблемы — когда в руках очень умных людей.
Спасибо!
С уважением и наилучшими пожеланиями,
Деннис Придди”
Сообщение Анри Бартеля, председателя ISO/IEC JTC 1/SC31
“Мы только что опубликовали новый прямоугольный DataMatrix штрих-код (ISO/IEC 21471), который можно выгравировать на очень маленьких медицинских инструментах и оборудовании для больничных операционных и использовать для их отслеживания Мы также работаем над аналогичным подходом для прямоугольного QR-кода (ISO/IEC 23941). ”
Source: IEC e-tech
Current Data Matrix Rectangular Formats (not DMRE)
Data Matrix following ISO16022 ECC200 already features the following rectangular formats:
Size Numeric Alphanum Байт Пример
8 x 18 10 6 3
8 х 32 20 13 8
12 х 26 32 22 14
12 х 36 44 34 22
16 х 36 64 46 30
16 х 48 98 72 47
Варианты использования расширенных прямоугольных форматов Data Matrix
Следующие варианты использования требуют дополнительных прямоугольных размеров, если необходимо кодировать больший объем данных: используется и должен быть расширен до большей ширины, если закодировано более 13 буквенно-цифровых символов. Верхний пример кодирует стандартный идентификатор продукта в соответствии с рекомендациями EDIFICE для электронных продуктов.
Изогнутая поверхность

Изогнутые поверхности, такие как трубы, должны иметь код минимальной высоты (обычно 8 модулей) и увеличенной ширины. В примере показан код PPN на препарате.
Высота кода ограничена технологией печати
Технология непрерывной струйной печати ограничена высотой печати, а ширина печати может быть увеличена.
Следовательно, максимальная высота модуля 26 модулей не должна увеличиваться. Тем не менее, требования к объему данных для фармацевтических продуктов превышают объем символа 26×26, и поэтому прямоугольные символы помогают решить эту проблему.
В частности, различные проекты сериализации с процессами встроенной печати, в основном с использованием струйных технологий, показали явную потребность в этих новых прямоугольных форматах.
Стандарт ISO/IEC опубликован 03 февраля 2020 г. , его можно приобрести здесь:
https://www.iso.org/standard/70947.html
DMRE был разработан в рамках рабочей группы ISO/IEC 1 / SC 31 / WG 1 как проект 70947
https://sd.iso.org/projects/project/70947/overview#
Я хочу поблагодарить очень активных членов этой группы, которые сделали это возможным.
Следующая презентация, представленная на ISO/IEC JTC1 SC31 WG1 13 апреля 2021 г., содержит некоторые типографские проблемы, которые будут исправлены в редакции 2 стандарта:
WG1_21471_DMRE_2021_Tokyo.pdf в DIN16587 был другой набор выбранных форматов. Столбец «Стандарты» ниже включает документ, описывающий формат.
Форматы 24×32, 24×32 и 26×32 присутствовали в DIN16587 и не приняты ISO/IEC21471 из-за недостаточного отношения ширины к высоте.
Добавлены новые форматы с высотой 8 и 12, так как рассматриваются варианты использования для маркировки круглых объектов, особенно в рамках UDI.
Добавлены новые форматы высотой 20 и 22 для поддержки контактной струйной печати с дополнительной текстовой строкой под кодом.
0 4 x 9 0
0 8 089 90
Размер Числовой Буквенный Байтовый Стандартный Пример
36 25 16 ДИН16587+ИСО/МЭК21471
8 х 64 48 34 22 ДИН16587+ИСО/МЭК21471
8 х 80 64 46 30 ИСО/МЭК21471
8 х 96 76 55 36 ИСО/МЭК21471
8 х 120 98 72 47 ИСО/МЭК21471
8 х 144 126 93 61 ИСО/МЭК21471
12 х 64 86 63 41 ДИН16587+ИСО/МЭК21471
12 х 88 128 94 62 ИСО/МЭК21471
16 х 64 124 91 60 ДИН16587+ИСО/МЭК21471
20 х 36 88 64 42 ИСО/МЭК21471
20 х 44 112 82 54 ИСО/МЭК21471
20 х 64 186 124 82 ИСО/МЭК21471
22 х 48 144 106 70 ИСО/МЭК21471
24 х 48 160 118 78 ДИН16587+ИСО/МЭК21471
24 х 64 216 160 106 ДИН16587+ИСО/МЭК21471
26 х 40 140 103 68 ДИН16587+ИСО/МЭК21471
26 х 48 180 133 88 ДИН16587+ИСО/МЭК21471
26 х 64 236 175 116 ДИН16587+ИСО/МЭК21471
Генерация кода DMRE
Генератор WEB
Этот веб-интерфейс можно использовать для генерации кодов DMRE, выбрав:
Базовый проект bwipp обеспечивает генерацию кода DMRE для многих приложений, включая интеграцию с SAP и т. д. Проект на SourceForge (внешняя ссылка)
Готовый бинарный файл для Windows можно найти здесь:
https://sourceforge.net/projects/zint/files/zint/2.6.5/zint_2.6.5_win32.zip/download
На следующем рисунке показан пример кода, который можно получить, выбрав символику “DataMatrix” и размер DMRE (все доступные помимо стандартных размеров).
Продукты dLSoft для создания штрих-кодов
Продукты dLsoft для создания штрих-кодов имеют функцию DMRE:
https://www.dlsoft.com/barcode_types/DMRE.htm
Расширения штрих-кода для отчетов Crystal: https://www. dlsoft.com/products/BarcodesForCrystalReports.htm
Штрих-коды и этикетки для офиса: https://www.dlsoft.com/products/blo_dmre.htm
NiceLabel 2017.3 Особенности DMRE поддержки
Отличное полнофункциональное программное обеспечение для маркировки Necelabel Perform .org
Сканирование кода DMRE
Существуют следующие текущие возможности сканирования кодов DMRE:
Ручной сканер от Code Corporation
Ручной сканер от Code Corporation декодирует коды DMRE, начиная с прошивки 1096.
Пример сканера

Код управления: включить DMRE
REA Verifier
REA 2D Matrix Code Verifier поддерживает DMRE.
Приложение Scandit
Приложения Scandit для iOS и Android поддерживают DMRE. Вы можете активировать режим «Tiny-Code» в правом нижнем углу приложения.
Приложение CortexScan
Code Corporation Приложение CortexScan для iOS и Android поддерживает DMRE, начиная с версии 1.5.
CortexDecoder
Code Corporation CortexDecoder поддерживает DMRE и может быть встроен в приложения в самых разных системах.
Tachyon IQ
Эмуляция клавиатуры Cortex Decoder и SDK поддерживают DMRE на различных платформах, включая iOS, Android, Linux, Xamarin и Windows.
Сканер штрих-кода с открытым исходным кодом zxing (Android, iPhone и др.)
Приложение декодера штрих-кода с открытым исходным кодом zxing поддерживает DMRE в режиме декодирования и кодирования.
zxing-cpp: библиотека сканирования штрих-кодов C++ с открытым исходным кодом и оболочками для других языков
Расширение DMRE было добавлено этим запросом на включение и включено с версии 1.2.0.
Сканер Datalogic
Все сканеры серии Matrix-N (210N, 300N, 410N) поддерживают DMRE, начиная с версии программного обеспечения 1.3.0.811.
DMRE на самом деле также доступен для QuickScan QD2430 через специальную прошивку SS5916 вып.1.00 (номер по каталогу 610119500). В случае заинтересованности обратитесь в службу технической поддержки Datalogic.
Сканер Zebra
Компания Zebra успешно протестировала форматы DMRE ISO на одном из своих сканеров.
Сканер Honeywell
Компания Honeywell внедрила форматы DMRE ISO в стандартный декодер, где следующие сканеры поддерживают DMRE (январь 2021 г.):
Voyager XP 1470g с уровнем прошивки EZ000227BAA или выше
Voyager XP 1472g с уровнем прошивки FK000179BAA / CU000069BAA или выше
Xenon XP 1950g с уровнем прошивки EV000359BAA или выше
Xenon XP 1952g с уровнем прошивки BK000547BAA/FF000152BAA или выше
Дополнительная информация о продукте доступна на веб-сайте https://sps. honeywell.com/
Прошивка доступна на веб-сайте https://hsmftp.honeywell.com/
Поддержка
DMRE для других 2D-камер будет доступна в следующем стандартном/обслуживающем выпуске.
Сканер Cognex
Все стационарные сканеры DataMan серий 370 и 470 оснащены DMRE с микропрограммой версии 6.1.7 или выше.
Все ручные сканеры серии DataMan 8700 поддерживают DMRE с прошивкой 6.2.0 или выше.
DMRE также доступен для стационарных считывателей DataMan серий 50, 60, 170, 150 и 260 в виде специальной версии прошивки (5.7.0 cr23).
Дополнительную информацию о продукте можно найти на сайте http://www.cognex.com/
.
Верификатор Axicon
Верификаторы серии Axicon 15000 поддерживают DMRE с программным обеспечением версии 2.0.
Дополнительная информация о продукте на сайте https://www. axicon.com/
Визиотикс
SDK профессионального сканера штрих-кода Viziotix для Windows и Linux можно встраивать в приложения и решения для сканирования и декодирования кодов DMRE. Больше информации о продукте на https://www.viziotix.com/
Сканер Оптикон
Компания Opticon реализовала форматы DMRE ISO в своих модулях 2D-сканирования серии MDI-4xxx, где следующие сканеры поддерживают DMRE:
Презентационный сканер M-11, 2D, https://opticon.com/product/m-11/
Ручной сканер L-46X, 2D, https://opticon.com/product/l-46/
Ручной сканер L-51X, 2D, https://opticon.com/product/l-51x/
Ручной сканер L-22X, 2D, https://opticon.com/product/l-22x/
Сопутствующий сканер OPN-3102i, 2D, https://opticon.com/product/opn-3102i/
Серия мобильных компьютеров H-31/33 Android, 2D, https://opticon.
Оставить комментарий Отменить ответ
Для отправки комментария вам необходимо авторизоваться.
Поиск:
Рубрики
Вакансии
Востребованные вакансии
Обучение в Европе
Обучение за границей
Работа
Работа для всех
Советы абитуриенту
Студенту
Студенческие будни
Разное
2019 © Все права защищены. Карта сайта
Меню
Поиск:
Советы абитуриенту
Работа для всех
Востребованные вакансии
Студенческие будни
Обучение за границей

Технические характеристики
Минимальный размер	10 x 10 модулей
Максимальный размер	144 x 144 модуля
Максимальная емкость данных	Цифровой	3116 символов
Максимальная емкость данных	Буквенно-цифровой	2335 символов

Размер символа	Блок	Ячейка данных
от 10×10 до 26×26	1	от 8×8 до 24×24
от 28×28 до 52×52	4	от 14×14 до 24×24
От 64×64 до 104×104	16	от 14×14 до 24×24
От 120×120 до 144×144	36	от 18×18 до 22×22

Технические характеристики прямоугольного типа DataMatrix (ECC200)
Минимальный размер	8 x 16 модулей
Максимальный размер	16 x 48 модулей
Максимальная емкость данных	Цифровой	98 символов
	Буквенно-цифровой	72 символа
	Двоичный	47 символов

Номера модулей	Объем данных			Скорость исправления ошибок
Номера модулей	Цифровой	Буквенно-цифровой	Двоичный	Скорость исправления ошибок
10 х 10	6	3	1	25%
12 х 12	10	6	3	25%
14 х 14	16	10	6	от 28 до 39%
16 х 16	24	16	10	от 25 до 38%
18 х 18	36	25	16	от 22 до 34%
20 х 20	44	31	20	от 23 до 38%
22 х 22	60	43	28	от 20 до 34%
24 х 24	72	52	34	от 20 до 35%
26 х 26	88	64	42	от 19 до 35%
32 х 32 904:00	124	91	60	от 18 до 34%
36 х 36	172	127	84	от 16 до 30%
40 х 40	228	169	112	от 15 до 28%
44 х 44	288	214	142	от 14 до 27%
48 х 48	348	259	172	от 14 до 27%
52 х 52	408	304	202	от 15 до 27%
64 х 64	560	418	278	от 14 до 27%
72 х 72	736	550	366	от 14 до 26%
80 х 80	912	682	454	от 15 до 28%
88 х 88	1152	862	574	от 14 до 27%
96 х 96	1392	1042	694	от 14 до 27%
104 х 104 904:00	1632	1222	814	от 15 до 28%
120 х 120	2100	1573	1048	от 14 до 27%
132 х 132	2608	1954	1302	от 14 до 26%
144 х 144	3116	2335	1556	от 14 до 27%

Используемый код	DataMatrix ECC200
FNC1	[FNC1] помещается вверху данных, чтобы определить его как стандартную спецификацию GS1.
Идентификатор приложения (ИИ)	Идентификационный код, который добавляется в начало полосы данных, чтобы определить, какая информация следует за этим идентификационным кодом. Идентификаторы приложений (AI) определяются ISO/IEC.
Данные переменной длины	При вводе данных, в которых количество информации изменяется (данные переменной длины), например количества, вставьте [FNC1] в качестве разделителя после данных переменной длины. Этот [FNC1] предназначен для вывода [GS] (1Dh в коде ASCII) при чтении считывателем кодов. * [GS]: Разделитель групп

	Рекомендуемый размер модуля	Максимальный размер модуля	Минимальный размер модуля
Печать на этикетке	0,300 мм	0,615 мм	0,255 мм
ДПМ	0,380 мм	0,495 мм	0,380 мм

Элемент	АИ	Данные
GTIN (14 фиксированных цифр)	01	045678904
Количество (переменная длина)	30	100
Срок реализации	17	120401

	A ₁ ₁	A ₁ ₂	A ₁ ₃	A ₁ ₄
	A ₂ ₁	A ₂ ₂	A ₂	A ₂		A ₂	A ₂	A ₂	A ₂	A ₂	A1321 4

Прямоугольная матрица – Энциклопедия по экономике

Матрицы. Основные понятия. Матрицей называется прямоугольная таблица чисел. Пример 13

Описание основных видов матриц, определения и их примеры

Диагональные матрицы

Треугольные матрицы

Ступенчатая матрица

Сообщество Экспонента

Результаты поиска

Решение матриц методы решений и примеров для чайников, формулы вычислений и действий с матрицами » Kupuk.net

Понятие выражения

Сложение и вычитание

Умножение на число

Операция перемножения

Возведение в степень

Расчёт определителя

Обратная матрица

Нахождение собственных векторов

Метод Гаусса

Способ Крамера

Простое объяснение разложения по единственному значению с примерами

Теория

Что мы хотим

Ключевые идеи

Поиск

В поисках тебя

Собираем все вместе

Удобный трюк

Примеры

Простой подробный пример

Чуть более сложный пример

Использование трюка

Видео Рекомендация

Рекомендация веб-сайта

Прямоугольная матрица — определение, примеры, свойства, операции

Что такое прямоугольная матрица?

Примеры прямоугольных матриц

Типы прямоугольных матриц

Операции над прямоугольной матрицей

Сложение и вычитание прямоугольных матриц

Умножение прямоугольных матриц

Транспонирование прямоугольной матрицы

Свойства прямоугольной матрицы

Примеры прямоугольных матриц

Практические вопросы по прямоугольной матрице

Часто задаваемые вопросы о прямоугольной матрице

Что такое определение прямоугольной матрицы?

Что такое свойства прямоугольной матрицы?

Является ли квадратная матрица прямоугольной?

В чем разница между квадратной и прямоугольной матрицей?

Что такое собственные значения прямоугольной матрицы?

Что такое транспонирование прямоугольной матрицы?

Что такое порядок прямоугольной матрицы?

Что такое код DataMatrix? | Основы 2D-кодов | Информация о штрих-коде и советы

Что такое матрица?

Определение матрицы

Матричное обозначение

Равенство матриц

Проверьте свое понимание

2.3 Типы матриц | Matrix Algebra Companion for Statistical Learning (matrix4sl)

2.3.1 Общая прямоугольная матрица

2.3.2 Квадратная матрица

2.3.3 Симметричная матрица

2.3.4 Диагональная матрица

2.

2.3.6 Единичная матрица

2.3.7 Треугольная матрица

2.3.8 Формы матриц

3.4 Прямоугольные структуры данных | Введение в науку о данных

Остерегайтесь «таблиц»

3.4.1 Матрицы

Создание матриц

Индексирование матриц

3.4.2 Фреймы данных

Создание фреймов данных

Индексация фреймов данных на основе имени

Индексирование фреймов данных

Используете списки или фреймы данных?

Строки как факторы

3.4.3 Практика

Доступ и оценка матриц