Матрица сложение: Онлайн калькулятор. Сложение и вычитание матриц

Матрица. Сложение и умножение матриц

1. Матрицы.

Сложение и умножение
матриц.
Матрица.
Прямоугольная таблица чисел называется
матрицей. Если в указанной таблице m
строк и n столбцов, то ее в общем виде
можно записать так:
a11
a21
A
…
a
m1
a12
a22
…
am 2
… a1n
… a2 n
… …
… amn
A aij mn .
или
Числа
aij i 1, m;
j 1, n
называются элементами матрицы
А.
Главная диагональ
Для квадратной матрицы
a
ij nn
совокупность чисел
a11, a22 ,….., ann
называется ее главной диагональю.
Равные матрицы.
Две матрицы считаются равными,
если они имеют одинаковые размеры и их
соответственные элементы равны между
собой:
A aij mn B bij kl m k; n 1;
aij bij , i 1, m;
j 1, n.
Сложение матриц.
Если две матрицы имеют одинаковые
размеры, то их можно сложить,
складывая соответственные элементы.
Так, если
a11
a21
A
. ..
a
m1
a12
a22
…
am 2
… a1n
… a2 n
… …
… amn
и
b11 b12
b21 b22
B
… ….
b
m1 bm 2
… b1n
… b2 n
,
… …
… bmn
a11 b11 a12 b12
a21 b21 a22 b22
A B
…
…
a b
m1 m1 am 2 bm 2
то
a1n b1n
… a2 n b2 n
,
…
…
… amn bmn
…
или
(aij ) mn (bij ) mn (aij bij ) mn .
Умножение матрицы на число
Всякую матрицу можно умножить на любое
число согласно следующему определению:
aij mn aij mn
Пример 1. Даны матрицы А и В
0 2 1
1 2 1
, B
A
3
7
5
3
0
1
Найти матрицу
2 A 3B
Решение
1 2 1
0 2 1
3
2
3 0 1
3 7 5
2 4 2 0 6 3
6 0 2 9 21 15
2 2 5
.
3 21 17
Свойства.
Легко видеть, что операции сложения и
умножения матрицы на число
удовлетворяют следующим свойствам:
1.свойство коммуникативности
A B B A
2. Свойство ассоциативности
A ( B C ) ( A B) C
3.
( A B) A B
4.
5.
( ) A A A
( A) ( ) A
Нулевая матрица
Матрица, все элементы которой равны нулю,
называется нулевой. Ее будем обозначать
буквой О.
0
0
O
…
0
0 … 0
0 … 0
… … …
0 … 0
Умножение матриц
Пусть у нас имеются две матрицы
A aij mk
B bij kn
Здесь число столбцов первой матрицы равно
числу строк второй. Тогда произведение
матрицы А на матрицу В определяется
следующим образом:
a11
a21
…
a
m1
a12
a22
…
am 2
… a1k
… a2 k
… …
… amk
b11 b12
b21 b22
… …
b
k1 bk 2
… b1n
… b2 n
… …
… bkn
c11 c12
c21 c22
… …
c
m1 cm 2
… c1n
… c2 n
… …
… cmn
где
cij ai1b1 j ai 2b2 j … aik bkj
Оператор суммирования
Если воспользоваться оператором
суммирования
n
a
i 1
i
a1 a2 . .. an ,
то
k
cij aisbsj
s 1
Произведение матриц
Произведение матриц А и В записывается так:
C AB
Пример 1
Умножить матрицу
1 1 2
A
3 0 1
на матрицу
1 4
B 2 3
0 1
Решение
1 4
1 1 2
2 3
A B
3 0 1 0 1
1 1 1 2 2 0 1 4 1 3 2 1
3 4 0 3 1 1
3 1 0 2 1 0
1 3
3 13
Транспонирование матриц
Пусть у нас имеется матрица
A aij m n
.
Если каждую строку этой матрицы
заменить ее столбцом с тем же номером,
то получим новую матрицу размера
, которая называется
n m
транспонированной к данной и
обозначается
T :
A
a11
a
12
T
A
….
a
1n
a21 …. am1
a22 …. am 2
…. …. ….
a2 n …. amn
Определители второго и третьего
порядков
По определенному правилу каждой
квадратной матрице А ставится
определенное число, которое называется
ее определителем и обозначается A
Рассмотрим определители порядков
1, 2, 3.
Если порядок матрицы А равен единице,
то
A a11
Для квадратной матрицы второго порядка
a11 a12
A
a
a
21
22
A
a11
a12
a21 a22
a11a22 a12a21
Опираясь на это определение определителя
второго порядка дадим определение
определителя третьего порядка.
Если
a11 a12
A a21 a22
a
31 a32
a13
a23
a33
, то
a11
a12
a13
A a21 a22
a31
a11
a32
a22 a23
a32 a33
a31
a23
a33
a21
a12
a13
a22
a23
a12
a13
a32 a33
a11
a12
a13
a21 a22
a23 a11a22a33 a21a32 a13
a31
a33
a32
a31a12a23 a11a32a23 a21a12a33
a31a22a13.
Для запоминания правила вычисления
определителя третьего порядка
используется правило треугольников или
правило Саррюса.
Оно состоит в изображении (явном или
мысленном) элементов матрицы точками.
Точки, соответствующие произведениям,
которые входят в определитель,
соединяются отрезками.
В результате получаются два отрезка
(соответствующие главной и побочной
диагоналям), а также четыре треугольника,
два из которых имеют стороны,
параллельные главной диагонали, и двапараллельные побочной диагонали.
Главной диагонали и тем двум
треугольникам, основания которых
параллельны главной диагонали,
соответствуют произведения со знаком
«+», а побочной диагонали соответствуют
произведения со знаком «-».
Пример 1. Вычислить определитель
2
1 3
1
5 2
1 4 2
Решение:
2 5 2 1 4 3
1 2 1 1 5 3
1 1 2 4 2 2 20 12 2
15 2 16 27
Обратная матрица
Пусть у нас имеется квадратная матрица
A aij n n.
Матрица
B bij n n
обратной к матрице
называется
А, если
BA AB E ij n n ,
где
1, при i j,
ij
0, при i j.
ij
называется символом Кронекера.
Квадратная матрица называется
невырожденной, если ее определитель
не равен нулю. В противном случае
матрица называется вырожденной.
Пример:
Найти матрицу, обратную к
матрице
1 0 1
A 2 3 2
1 1 2
Решение.
Сначала проверим, является ли
определитель матрицы А отличным от
нуля:
1
A 2
0 1
3
1 1
2 6 2 3 2 1 0.
2
Отсюда вытекает, что матрица А
невырожденная и у нее есть обратная:
A11
1
1
A A12
A13
A
A21
A22
A23
A31
A32
A33
В нашем случае:
A11 1
1 1
A12 1
1 2
3 2
1 2
2
2
1 2
4;
6
2
A13 1
1 3
A21 1
1 1
2 1
A22 1
1 3
3
0 1
1
2
1
1
1
2
5;
1;
1;
A23 1
1
2 3
0
1 1
1;
A31 1
0 1
A32 1
1 1
3 1
3 2
3
2
2
2
3;
4;
A33 1
3 3
1 0
2 3
3.
Отсюда
4 1 3
1
A 6 1 4 .
5 1 3
Ранг матрицы
Пусть у нас имеется матрица
содержащая
a11
a21
…
a
m1
A aij n n
m строк и n столбцов:
a12
a22
. ..
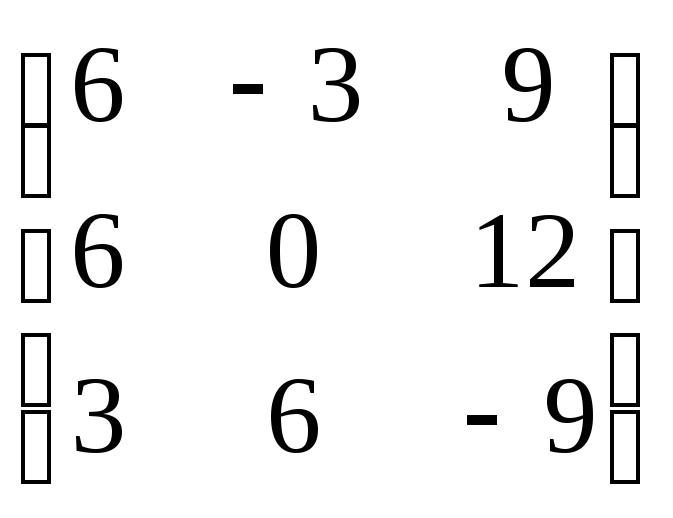am 2
… a1n
… a2 n
… …
… amn
Выделим в этой матрице k строк k столбцов
k m,
k n
элементов, стоящих на
пересечении выделенных строк и столбцов,
составим определитель k-го порядка. Все
такие определители называются минорами
нашей матрицы. Элементы матрицы- это
миноры первого порядка.
Определение: Рангом матрицы
называется наивысший порядок отличных
от нуля миноров этой матрицы.
Пример. Найти ранг матрицы
3 2 1 2
A 2 0 1 1
0 4 5 1
У этой матрицы 12 миноров первого
порядка, 18 миноров второго порядка:
3 2 3 1 3 2 2 1
,
,
,
,
2 0 2 1 2 1 0 1
2 2 1 2 3 2 3 1
,
,
,
,
0 1 1 2 0 4 0 5
3 2 2 1 2 2 1 2
,
,
,
,
0 1 4 5 4 1 5 1
2 0 2 1 2 1 0 1
,
,
,
,
0 4 0 5 0 1 4 5
0 1 1 1
,
,
4 1 5 1
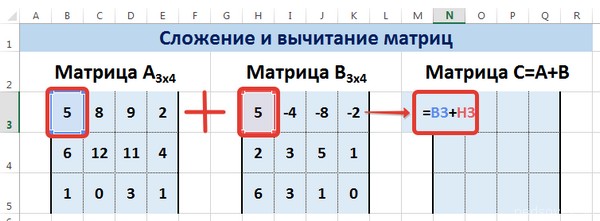
и наконец 4 минора третьего порядка:
3 2
1 3
1
2
2 0 1, 2 1 1 ,
0 4
5 0
5
1
3 2 2 2
1
2
2 0 1 , 0 1 1 .
0 4 1 4
5
1
Нетрудно проверить, что все миноры
третьего порядка матрицы А равны нулю,
а миноры второго порядка во всяком
случае не все равны нулю. Поэтому ранг
матрицы А равен 2
r A 2
При вычислении ранга матрицы
существенную роль играют элементарные
преобразования матрицы:
1) умножение элементов любой
строки (столбца) матрицы на число
0;
2) прибавление к строке (столбцу) другой
строки (столбца), умноженной на
некоторое число;
3) перестановка двух строк (столбцов)
матрицы.
При элементарных преобразованиях
ранг матрицы не изменяется. С помощью
элементарных преобразований любую
матрицу можно привести к виду
1 0 0 … 0 0 … 0
0 1 0 … 0 0 … 0
0 0 0 … 0 0 … 0
где на «главной диагонали» стоит r
единиц, а все остальные элементы матрицы
равны нулю. Ранг такой матрицы, а значит,
и исходной матрицы, равен r.
Если ранг матрицы А равен рангу
матрицы В, то матрицы А и В называются
эквивалентными. В этом случае пишут
A ~ B.
Системы линейных уравнений
Основные понятия и определения
Системой линейных алгебраических
уравнений с n переменными х1, х2, …, хn
называется система вида
a11 x1 a12 x2 … a1n xn b1
a x a x … a x b
21 1 22 2
2n n
2
……….
……….
……….
……….
….
am1 x1 am 2 x2 … amn xn bm .
Здесь числа
aij i 1, m;
j 1, n
называются коэффициентами системы,
а числа b1, b2, …,bm-ее свободными
членами.
Если b1= b2=…=bm=0, то система
называется однородной;
Если хотя бы одно из bi i 1, m
от нуля, то система называется
неоднородной
отлично
Решением системы называется всякая
упорядоченная совокупность n чисел
(с1, с2, …, сn), которая при подстановке
в каждое уравнение системы вместо
соответствующих переменных превращает
каждое уравнение в тождество.
Система называется совместной,
если у нее есть хотя бы одно решение, и
несовместной в противном случае.
Совместные системы делятся на
определенные и неопределенные.
Система, которая имеет только одно
решение, называется определенной.
Если система имеет больше одного
решения, то она называется
неопределенной.
Систему удобно записать в матричной
форме, для чего введем необходимые
понятия. Матрица
a11
a21
A
…
a
m1
a12
a22
…
am 2
… a1n
… a2 n
,
… …
… amn
элементы которой являются
коэффициентами системы, назовем
матрицей системы.
Введем еще две матрицы, каждая из
которых состоит из одного столбца
(матрицы-столбца):
x1
x2
X ,
…
x
n
b1
b2
B .
…
b
m
Это матрица-столбец переменных и
матрица-столбец свободных членов.
У матрицы А n столбцов, а у матрицы X n
строк, поэтому А можно умножить на X.
a11 x1 a12 x2 … a1n xn
a21 x1 a22 x2 … a2 n xn
AX
.
………… …………………….
a x a x … a x
mn n
m1 1 m 2 2
Как показывают равенства, каждый
элемент матрицы столбца АХ есть
соответствующий элемент матрицы В.
Отсюда в соответствии с определением
равенства матриц, получаем матричную
запись системы:
AX B.
Введем в рассмотрение матрицы-столбцы
a11
a12
a1n
a21
a22
a2 n
P1 , P2
,…,
P
,
n
…
…
…
a
a
a
m1
m2
mn
тогда система уравнений может быть
записана так:
x1P1 x2 P2 … xn Pn B
Две системы линейных алгебраических
уравнений называются эквивалентными
(равносильными), если всякое решение
одной из них является решением второй,
и наоборот.
Элементарными преобразованиями
системы линейных уравнений называют
следующие действия:
1) умножение на число, отличное от нуля
одного из уравнений системы;
2)
прибавление к одному уравнению
системы другого ее уравнения,
умноженного на произвольное число,
при этом сохраняются остальные
уравнения системы в том числе и то,
которое прибавлялось;
3) перестановка местами двух уравнений
системы.
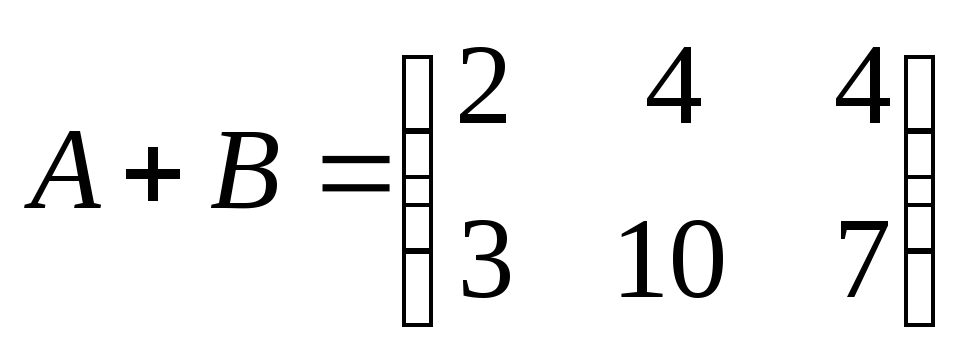
Формула Крамера
Пусть дана система n линейных
алгебраических уравнений с
n-переменными (неизвестными):
a11 x1 a12 x2 … aij x j … a1n xn b1
a x a x … a x … a x b
21 1 22 2
2j j
2n n
2
……….
……….
……….
……….
……….
……….
.
an1 x1 an 2 x2 … anj x j … ann xn bn .
Если определитель
системы
матрицы
A aij n n
отличен от нуля и система совместна,
то она и определенная.
Если система имеет решение, то оно
единственно и может быть найдено
по формулам, которые называются
формулами Крамера.
Пример. Решить систему линейных
уравнений
2 x1 x2 3 x3 x4 0
x2 2 x4 2
x
x
2
x
x
1
1
2
3
4
x1 2 x1 x3 3 x4 1
Решение. Вычислим определитель
системы следующим образом. Из первой
строки вычтем удвоенную третью строку,
из третьей-четвертую, тогда получим
2
1
3
1
0
1
0
2
1 1 2
1
1
3
2
1
2 2 1 2 3 4 1 2
0
1
0
2
1 1
1 2
2 1
1 3
1
2
1
3
0
3
1
1
0
1
0
2
0 3 3 2
1
2
1
3
a41 A41
3
1 1
5
1
1
0
2 1 0 2
3 3 2
3 6 18 2 7.
3 1
3 3
1
2
Определитель
0, следовательно,
правило Крамера применимо к системе.
Составим и вычислим определители
1 , 2 , 3 , 4 .
1
0
1
3
1
2
1
0
2
1 1 2
1
1
3
2
1
23,
2
3
2
0
3
1
0
2
0
2
1 1 2
1
1
1
1
3
2
1
0
1
0
1
2
2
1 1 1
1
1
3
2
1
2,
12,
4
2
1
3
0
0
1
0
2
1 1 2 1
1
2
1
8.
1
Отсюда искомое решение данной системы
1 23
x1
;
7
3 12
x3
;
7
2
2
x2
;
7
4
8
x4
.
7

Действия над матрицами. Сложение и вычитание

Определение 1

Если у матриц совпадает количество столбцов и строк, то, считается, что у таких матриц одинаковая размерность (одинаковый порядок).

Пример 1

А=1-204-21 и В=10-20-4-21

Данные матрицы одинакового порядка, т. к. у них одинаковое количество строк и столбцов (3 строки и 2 столбца).

Сложение матриц 

Замечание

Матрицы одинаковой размерности можно складывать и вычитать.

Определение 2

А=(αij)m×n и B=(bij)m×n – сумма матриц. Сумма этих матриц представлена выражением С=(сij) той же размерности, причем ее элементы вычисляются, как сумма соответствующих элементов исходных матриц:undefined. Сумма матриц имеет обозначение: А+B

Пример 2

Найти сумму матриц:

1). А=2-131, В= 12-1-35; 

2). А=2-131, В=-103-1253

Решение:

1). А+В=2-131+12-1-35=2+12-1+(-1)3+(-3)1+5=14-206

2). Сложить данные матрицы нельзя, потому что они разной размерности

Свойства сложения матриц 

Определение 3

Исходная матрица А=(aij)m×n. Противоположной матрицей считается выражение -А=(-аij)m×n,где все элементы противоположны исходным.

Свойства сложения матриц:

• А + В = В + А — коммуникативный закон сложения;
• (А + В) + С = А + (В + С) — ассоциативный закон сложения;
• А + 0 = 0 + А = А;
• А + (-А) = -А + А = 0.  

Вычитание матриц 

Определение 4

Разностью матриц А=(αij)m×n и B=(bij)m×n является матрица С=(сij), у которой такая же размерность. Ее элементы вычисляются как сумма соответствующих элементов матриц:

 А=(aij)m×n и -В=(-bij)m×n; cij=(aij)+(-bij)

Разность матриц обозначается как А — В.

Пример 3

Найти разность матриц:

1). А=2-131, В= 12-1-35; 

2). А=2-131, В=-103-1253

Решение:

1). А-В=2-131-12-1-35=2+(-12)-1+(-(-1))3+(-(-3))1+(-5)=2-12-1+13+31-5=-1006-4

2).Найти разность во втором варианте невозможно, потому что матрица разно размерные.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р.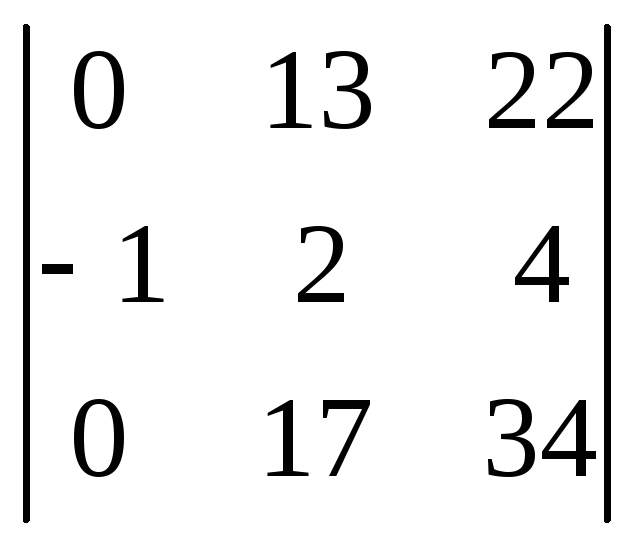

Реферат от 1 дня / от 700 р.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Навигация по статьям

Предыдущая статья

Арифметические корни натуральной степени

Следующая статья

Определитель матрицы

• Определитель матрицы
• Равенство матриц
• Ранг матрицы
• Умножение матриц
• Все темы по математике
• Курсовые работы
• Рефераты
• Контрольные работы
• Отчет по практике
• Эссе

Узнать подробнее

• Расчет состава строительной бригады и определение продолжительности строительных работ

  • Вид работы:

    Контрольная работа

  • Выполнена:

    10 июля 2022 г.

  • Стоимость:

    2 400 руб

  Заказать такую же работу

• РАЗРАБОТКА КОТЛОВАНА ВЫБОР ЭКСКАВАТОРА И АВТОСАМОСВАЛА

  • Вид работы:

    Контрольная работа

  • Выполнена:

    7 июля 2022 г.

  • Стоимость:

    1 300 руб

  Заказать такую же работу

• По домашней работе задание Задание таблица вариант таблица вариант схема Задание таблица вариант таблица вариант Задание вариант из таблицы П

  • Вид работы:

    Домашняя работа

  • Выполнена:

    24 мая 2022 г.

  • Стоимость:

    4 000 руб

  Заказать такую же работу

• Эксплуатация и тех обслуживание автортранспортных средств в особых условиях

  • Вид работы:

    Реферат

  • Выполнена:

    18 апреля 2022 г.

  • Стоимость:

    1 000 руб

  Заказать такую же работу

• Организация ремонта машиннотракторного парка в сельхозпредприятие с разработкой технологии ремонта заданной детали или сборочной еденицы

  • Вид работы:

    Курсовая работа

  • Выполнена:

    11 апреля 2022 г.

  • Стоимость:

    5 600 руб

  Заказать такую же работу

• задание в файлах

  • Вид работы:

    Чертёж

  • Выполнена:

    8 апреля 2022 г.

  • Стоимость:

    2 500 руб

  Заказать такую же работу

Смотреть все работы по строительству

Сложение матриц

1) Определение матрицы– Матрицей размера mxn называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Вектор-строкой называют матрицу, состоящую из одной строки. Вектор-столбцом – из одного столбца. Матрица, у которой количество столбцов равно количеству строк, называется квадратной матрицей n-ого порядка. Элементы матрицы, у которых номер строки и номер столбца совпадает, называются диагональными и образуют главную диагональ матрицы. Если все недиагональные элементы матрицы равны нулю, то матрицу называют диагональной. Если у диагональной матрицы n-ого порядка на главной диагонали все элементы равны 1, то матрица называется единичной и обозначается Е. Матрица любого размера, все элементы которой равны 0, называется нуль-матрицей.

Сложение и вычетание матриц– Сложение 2-х матриц: условие – складывать можно только матрицы одинакового размера. Суммой 2-х матриц А и В называется матрица С=А+В, каждый элемент которой находится по формуле С_ij=a_ij+b_ij. Для того, чтобы сложить 2 матрицы, необходимо складывать между собой элементы, стоящие на одинаковых местах.

Умножение матрицы на число- условий нет, умножить на число можно любую матрицу. Произведением матрицы А на число l называется матрица В, равная lА, каждый элемент которой находится по формуле: b_ij =l x a_ij. Для того, чтобы умножить матрицу на число необходимо умножить на это число каждый элемент матрицы.

Произведения матриц– умножение А на В возможно тогда и только тогда, когда число столбцов А равно числу строк В; произведением матрицы А размера mxk на матрицу В размера kxn называется матрица С размера mxn, каждый элемент которой равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В.

Определители 2-го и 3-го порядка– Определитель– число, характеризующее матрицу. Определителем матрицы 1-го порядка А=(а₁₁) является единственный элемент этой матрицы. Определителем 2-го порядка называется число, характеризующее матрицу 2-го порядка, которое находится по следующему правилу: из произведений элементов главной диагонали вычитается произведение элементов второй диагонали матрицы А.

Обратная матрица- Матрица А-1 называется обратной по отношению к квадратной матрице А, если при умножении её на заданную как справа так и слева получатся единичная матрица. Теорема (необходимое и достаточн.условие сущ-я обратн.матрицы): обратная матрица А-1 сущ-т и единственна тогда и только тогда, когда заданная матрица не вырожденная. Матрица называется вырожденной, если её определитель равен 0, в противном случае она – не вырожденная. Алгоритм: 1)Определитель заданной матрицы. 2)Транспонирование. 3)Алгебраические дополнения всех элементов транспонированной матрицы. 4) Присоед.матрица А@ (на месте каждого эл-та А^т его алгебраич.доп-я). 5) А^-1= 1/DА *A@. 6) Проверка=>А^-1 *А=Е.

Понятие о матрице

Матрица – множество чисел, образующих прямоугольную таблицу, которая содержит m-строк и n-столбцов. Для обозначения матрицы используется надпись:

a_ij, I – номер строки, j – номер столбца.

Элементы матрицы, стоящие на диагонали, идущие из верхнего левого угла называют главной диагональю, другую диагональ называют побочной.

пример 1.

Элементы главной диагонали: 1,6,5. Побочной диагонали: 3,6,3. (пример 1)

пример 2.

Если количество строк m матрицы не равно количеству столбцов n, то матрица называется прямоугольной (пример 2).

Если количество столбцов матрицы совпадают с количеством строк, то матрица называется квадратной (пример 1).

Количество строк или столбцов в квадратной матрице называются ее порядком.

Если все элементы квадратной матрицы, кроме элементов главной диагонали, равны нулю, то матрица называется диагональной (пример 3).

пример3

Если все числа главной диагонали равны единице, то матрица называется единичной (пример 4).

пример 4

Если в прямоугольной матрице m*n m=1, то получается матрица-строка (пример 5).

x^T = (2 3 5). пример 5.

Если n=1, то получается матрица-столбец (пример 6).

пример 6.

Матрицы-строки матрицы-столбцы называются векторами.

Свойства матриц:

Действия с матрицами

Матрицы одинакового размера можно складывать.

Суммой двух таких матриц А и В называется матрица С, элементы которой равны сумме соответствующих элементов матриц А и В. Символически будем записывать так: А+В=С.

Пример.

Легко видеть, что сложение матриц подчиняется переместительному и сочетательному законам:

А+В=В+А

(А+В)+С=А+(В+С).

Нулевая матрица при сложении матриц выполняет роль обычного нуля при сложении чисел: А+0=А.

2. Вычитание матриц.

Разностью двух матриц А и В одинакового размера называется матрица С, такая, что

С+В=А

Из этого определения следует, что элементы матрицы С равны разности соответствующих элементов матриц А и В.

Обозначается разность матриц А и В так: С=А – В.

Пример.

3. Умножение матриц

Рассмотрим правило умножения двух квадратных матриц второго порядка.

Произведением матрицы А на матрицу В называется матрица С=АВ.

Правила умножения прямоугольных матриц:

• Умножение матрицы А на матрицу В имеет смысл в том случае, когда число столбцов матрицы А совпадает с числом строк в матрице В.

• В результате умножения двух прямоугольных матриц получается матрица, содержащая столько строк, сколько строк было в первой матрице и столько столбцов, сколько столбцов было во второй матрице.

4. Умножение матрицы на число

При умножении матрицы A на число a все числа, составляющие матрицу A, умножаются на число a. Например, умножим матрицу на число 2. Получим , т.е. при умножении матрицы на число множитель «вносится» под знак матрицы.

5. Транспонирование матрицы

Транспонированная матрица – матрица A^Т, полученная из исходной матрицы A заменой строк на столбцы.

Формально, транспонированная матрица для матрицы A размеров m*n – матрица A^T размеров n*m, определённая как A^T[i, j] = A [j, i].

Например,

Свойства транспонированных матриц

1. (A^T)^T = A

2. (A + B)^T = A^T + B^T

3. (AB)^T = B^TA^T

4. detA = detA^T

Определители 2-го и 3-го порядков.

Будем рассматривать квадратные матрицы

Определители являются основными числовыми характеристиками квадратных матриц.

 Определителем (детерминантом) матрицы ,

 состоящей из одного числа  , называется само это число.

Определителем матрицы А=  второго порядка называется число, равное разности произведений элементов главной и побочной диагоналей:

Рассмотрим матрицу третьего порядка:

Определителем матрицы A третьего порядка называется число

Данная формула называется формулой разложения определителя 3 порядка по элементам первой строки. 

Пример 6. Вычислить определители заданных  матриц:

 1.

Решение :  

2.  

Решение:

3.

Решение.

В первой строке определителя уже есть два нулевых элемента. Преобразуем определитель так, чтобы еще два элемента этой строки обратились в ноль. Сделать это можно путем преобразований столбцов. Оставим без изменения 2-й и 5-й столбцы (там уже стоят нули). К 3-му столбцу прибавим 1-й, умноженный на -2, к 4-му ~ первый, умноженный на 1. При этом первый столбец в преобразованном определителе останется без изменения.

Теперь разложим определитель по элементам первой строки: 

В полученном определителе четвертого порядка преобразуем к нулю первые три элемента 1-й строки с помощью последнего 4-гo столбца: к 1-му прибавим 4-й, умноженный на 3, 2-ой  преобразовывать не нужно, к 3-му прибавим 4-ый, умноженный на -1. 

Разложим этот определитель по элементам первой строки:

Полученный определитель третьего порядка можно вычислить по правилу треугольников, однако проще и здесь, получив нули (легче всего в первом столбце), свести дело к определителю второго порядка.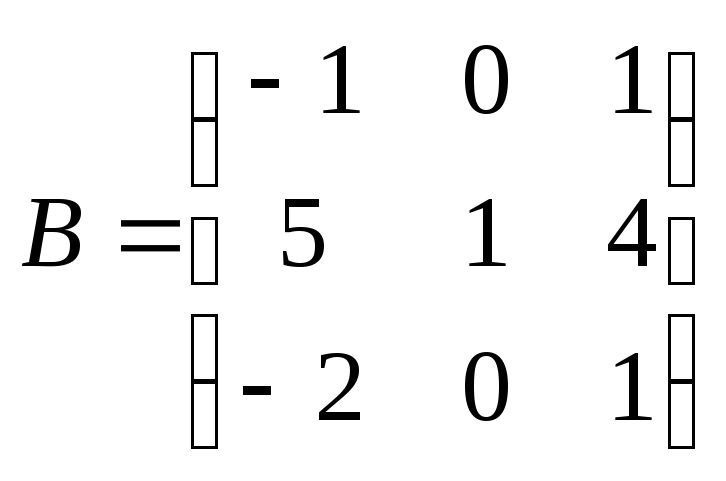 Ко 2-ой  строке прибавим 1-ю, умноженную на -4, 3-й – первую, умноженную на 3:

Разлагаем определитель по элементам первого столбца:

И здесь можно упростить вычисления: ко 2-ой строке прибавим 1-ую, затем ко 2-му столбцу прибавим 1-ый, умноженным на 2:

 Замечание 4.При использовании свойства 8, следует иметь в виду, что в преобразованном определителе меняется только та строка, к которой прибавляется другая (аналогично для столбцов). Так, если, например, к 3-ий строке прибавляется 1-ая, умноженная на 2, то в преобразованном определителе первая строка останется в неизменном виде, меняется только 3-я строка.

 

Программа на Python для добавления двух матриц

Цель: Программа для вычисления суммы двух матриц и последующего вывода ее на Python.

Примеры: 

  Ввод: 
 Х= [[1,2,3],
    [4 ,5,6],
    [7 ,8,9]]
 
Y = [[9,8,7],
    [6,5,4],
    [3,2,1]]
 
  Выход : 
 результат= [[10,10,10],
         [10,10,10],
         [10,10,10]] 

Рекомендуется: сначала попробуйте свой подход на {IDE} , прежде чем переходить к решению.

В Python мы можем выполнить сложение матриц следующими способами.   

Using for loop :  

Implementation:

Python

X = [[ 1 , 2 , 3 ],      [ 4 , 5 , 6 ],      [ 7 , 8 , 9 ]]   Y = [[ 9 , 8 , 7 ],      [ 6 , 5 , 4 ],      [ 3 , 2 , 1 ]]     result = [[ 0 , 0 , 0 ],          [ 0 , 0 , 0 ],          [ 0 , 0 , 0 ]]   for i in range ( len (X)):        for j in range ( len (X[ 0 ])):          result[i][j] = x [i] [j] + y [i] [j] для R в РЕЗУЛЬТАТ: 9003 .

Выход

 [10, 10, 10]
[10, 10, 10]
[10, 10, 10] 

Временная сложность: O(len(X) * len(X[0])) , так как мы используем вложенный цикл для обхода матрицы.
Вспомогательное пространство: O(len(X) * len(X[0])) , так как мы используем результирующую матрицу с дополнительным пространством.

Другой подход:

1. Объяснение :-  В этой программе мы использовали вложенные циклы for для перебора каждой строки и каждого столбца. В каждой точке мы добавляем соответствующие элементы в две матрицы и сохраняем результат.
2. Использование вложенного понимания списка : В Python мы можем реализовать матрицу как вложенный список (список внутри списка). Мы можем рассматривать каждый элемент как строку матрицы.

Implementation:

Python

X = [[ 1 , 2 , 3 ],      [ 4 , 5 , 6 ],      [ 7 , 8 , 9 ]]     Y = [[ 9 , 8 , 7 ],      [ 6 , 5 , 4 ],      [ 3 , 2 , 1 ]]   result = [[X[i][j] + Y[i][j]  for j in range ( LEN (x [ 0 ])] для I в Диапазон ( LEN (x ] 47474747474747474474747474747474747474747474747474747474747474747474747474747474747474747474748. 774748 ). для р в Результат: Печать (R)

Выход

 [10, 10, 10]
[10, 10, 10]
[10, 10, 10] 

Временная сложность: O(len(X) * len(X[0])) , так как мы используем вложенный цикл для обхода матрицы.
Вспомогательное пространство: O(len(X) * len(X[0])) , поскольку мы используем результирующую матрицу, которая является дополнительным пространством.

Другой подход:

1. Объяснение:- 
   Вывод этой программы такой же, как и выше. Мы использовали понимание вложенных списков для перебора каждого элемента в матрице. Понимание списков позволяет нам писать краткие коды, и мы должны стараться часто использовать их в Python. Они очень полезны.
2. Использование zip() и сумма  

Реализация:

Python

2     X = [[ 1 , 2 , 3 ],      [ 4 , 5 , 6 ],      [ 7 , 8 , 9 ]]     Y = [[ 9 , 8 , 7 ],      [ 6 , 5 , 4 ],      [ 3 , 2 , 1 ]]   result = [ map ( sum , zip ( * t)) for t in zip (X, Y)]     print (результат)

Выход

 [[10, 10, 10], [10, 10, 10], [10, 10, 10], [10, 10, 10, время 90: 10]] (len(X) * len(X[0]))  , так как мы используем функцию zip. 
  Вспомогательное пространство:   O(len(X) * len(X[0]))  , так как мы используем дополнительное пространство.
  Объяснение :-   Функция zip принимает итератор i каждого элемента (списка) матрицы, сопоставляет их, добавляет с помощью sum() и сохраняет в виде карты.
 Эта статья предоставлена ​​ ajay0007  . Если вам нравится GeeksforGeeks и вы хотите внести свой вклад, вы также можете написать статью с помощью write.geeksforgeeks.org или отправить ее по адресу [email protected]. Посмотрите, как ваша статья появится на главной странице GeeksforGeeks, и помогите другим гикам.
 
 M2 Сложение и вычитание матриц 
  
 14 июля 2021 г., 11:06 — AJ (e67821)
 Open image
 Матрица — это массив чисел. Существуют правила сложения и вычитания матриц, которые рассматриваются в этом модуле. Матрицы одинаковой формы (одинаковое количество строк и столбцов) можно складывать и вычитать.
 Сложение 
 Матрицы одинаковой формы (одинаковое количество строк и столбцов) могут быть добавлены путем добавления соответствующих элементов.
 Например, пусть \[\begin{align*}
A & =\left[\begin{массив}{ccc}
3 и 2 и -1\\
1 и 5 и -4
\end{массив}\right],\,B=\left[\begin{массив}{ccc}
1 и 0 и 2\\
3 и 1 и -2
\end{массив}\right]\;\textrm{and $C=\left[\begin{массив}{cc}
2 и -3\\
4 и 3
\end{массив}\right]$ }.
\end{align*}\] Обратите внимание, что \(A\) и \(B\) имеют одинаковую форму \(\left(2\times3\right)\), а \(C\) - это \(\left( 2\раз2\справа)\).
 Тогда \(A+B\) имеет смысл, потому что они оба \(\left(2\times3\right)\), и у нас есть \[\begin{align*}
A+B & =\left[\begin{массив}{ccc}
3 и 2 и -1\\
1 и 5 и -4
\end{массив}\right]+\left[\begin{массив}{ccc}
1 и 0 и 2\\
3 и 1 и -2
\конец{массив}\справа]\\
 & =\left[\begin{массив}{ccc}
3+1 и 2+0 и -1+2\\
1+3 и 5+1 и -4+(-2)
\конец{массив}\справа]\\
 & =\left[\begin{массив}{ccc}
4 и 2 и 1\\
4 и 6 и -6
\end{массив}\right]. \end{выравнивание*}\]
 Однако \(A+C\) не определено, поскольку \(A\) равно \(\left(2\times3\right)\) и \(C\) равно \(\left(2\times2\right) )\). Вы не можете добавлять матрицы, которые имеют различную форму.
 Обратите внимание, что порядок сложения такой же, как и для действительных чисел. То есть: \[\begin{align*}
А+В и =В+А
\end{align*}\]
 Вычитание 
 Матрицы одинаковой формы могут быть вычтены путем вычитания соответствующих элементов. Например, пусть \[\begin{align*}
A & =\left[\begin{массив}{ccc}
3 и 2 и -1\\
1 и 5 и -4
\end{массив}\right],\,B=\left[\begin{массив}{ccc}
1 и 0 и 2\\
3 и 1 и -2
\end{массив}\right]\;\textrm{and $C=\left[\begin{массив}{cc}
2 и -3\\
4 и 3
\end{массив}\right]$ }.
\end{align*}\] Тогда \(AB\) имеет смысл, потому что они оба \(\left(2\times3\right)\), и у нас есть \[\begin{align*}
AB & =\left[\begin{массив}{ccc}
3 и 2 и -1\\
1 и 5 и -4
\end{массив}\right]-\left[\begin{массив}{ccc}
1 и 0 и 2\\
3 и 1 и -2
\конец{массив}\справа]\\
 & =\left[\begin{массив}{ccc}
3-1 и 2-0 и -1-2\\
1-3 и 5-1 и -4-(-2)
\конец{массив}\справа]\\
 & =\left[\begin{массив}{ccc}
2 и 2 и -3\\
-2 и 4 и -2
\end{массив}\right]. \end{выравнивание*}\]
 Однако \(A-C\) не определяется, поскольку \(A\) равно \(\left(2\times3\right)\) и \(C\) равно \(\left(2\times2\right)\ ). Вы не можете вычесть матрицы, которые имеют различную форму. В качестве другого примера рассмотрим \(BA\), у нас есть \[\begin{alignat*}{1}
BA & =\left[\begin{массив}{ccc}
1 и 0 и 2\\
3 и 1 и -2
\end{массив}\right]-\left[\begin{массив}{ccc}
3 и 2 и -1\\
1 и 5 и -4
\конец{массив}\справа]\\
 & =\left[\begin{массив}{ccc}
1-3 и 0-2 и 2-(-1)\\
3-1 и 1-5 и -2-(-4)
\конец{массив}\справа]\\
 & =\left[\begin{массив}{ccc}
-2 и -2 и 3\\
2 и -4 и 2
\конец{массив}\справа]
\end{alignat*}\] Обратите внимание, что \(A-B\neq B-A\). Порядок вычитания матриц важен так же, как и при вычитании действительных чисел. На самом деле, \(B-A=-\left(A-B\right)\).
 Скалярное умножение 
 Матрицы можно умножать на число. Для этого каждый элемент матрицы умножается на число.
 Например, пусть \[\begin{align*}
A & =\left[\begin{массив}{cc}
1 и 2\\
5 и 4
\end{массив}\right]\textrm{ и $B=\left[\begin{массив}{cc}
2 и -3\\
0 и -1
\end{массив}\right]$ }
\end{align*}\], затем \[\begin{align*}
5A & =5\times\left[\begin{массив}{cc}
1 и 2\\
5 и 4
\конец{массив}\справа]\\
 & =\left[\begin{массив}{cc}
5\раз1 и 5\раз2\\
5\х5 и 5\х4
\конец{массив}\справа]\\
 & =\left[\begin{массив}{cc}
5 и 10\\
25 и 20
\end{массив}\right]. \end{выравнивание*}\]
 Другой пример: \[\begin{align*}
-2A & =-2\times\left[\begin{массив}{cc}
1 и 2\\
5 и 4
\конец{массив}\справа]\\
 & =\left[\begin{массив}{cc}
-2\раз1 и -2\раз2\\
-2\х5 и -2\х4
\конец{массив}\справа]\\
 & =\left[\begin{массив}{cc}
-2 и -4\\
-10 и -8
\end{массив}\right].
\end{align*}\]
 Вы также можете использовать скалярное умножение со сложением или вычитанием. Например: \[\begin{выравнивание*}
5A-2B & =5\times\left[\begin{массив}{cc}
1 и 2\\
5 и 4
\end{массив}\right]-2\times\left[\begin{массив}{cc}
2 и -3\\
0 и -1
\конец{массив}\справа]\\
 & =\left[\begin{массив}{cc}
5\раз1 и 5\раз2\\
5\х5 и 5\х4
\end{массив}\right]-\left[\begin{массив}{cc}
2\раз2 и 2\раз\влево(-3\вправо)\\
2\times0 и 2\times\влево(-1\вправо)
\конец{массив}\справа]\\
 & =\left[\begin{массив}{cc}
5 и 10\\
25 и 20
\end{массив}\right]-\left[\begin{массив}{cc}
4 и -6\\
0 и -2
\конец{массив}\справа]\\
 & =\left[\begin{массив}{cc}
5-4 и 10-\влево(-6\вправо)\\
25-0 и 20-\влево(-2\вправо)
\конец{массив}\справа]\\
 & =\left[\begin{массив}{cc}
1 и 16\\
25 и 22
\end{массив}\right]. \end{выравнивание*}\]
 Упражнения 
 Учитывая \[\begin{align*}
A & =\left[\begin{массив}{c}
2\\
3
\end{массив}\right],\;B=\left[\begin{массив}{cc}
1 и 2\\
4 и 3
\end{массив}\right],\;C=\left[\begin{массив}{cc}
5 и 3\\
-1 и 2
\end{массив}\right],\;D=\left[\begin{массив}{cc}
2 и 3\конец{массив}\справа],\;E=\влево[\начало{массив}{cc}
-1 и 0\\
2 и -1
\конец{массив}\справа],
\end{align*}\] найдите, если возможно: \[\begin{align*}
\begin{массив}{lllll}
a)\,A+B & b)\,B-C & c)\,A-D & d)\,B+E & e)\,E-D.\end{массив}
\end{выравнивание*}\]
 Учитывая \[\begin{align*}
A=\left[\begin{массив}{ccc}
2 и 3 и 1\\
0 и 1 и 2
\end{массив}\right],\;B=\left[\begin{массив}{c}
4\\
-1\\
2
\end{массив}\right],\;C=\left[\begin{массив}{ccc}
1 и -1 и 2\\
2 и 0 и 1
\end{массив}\right],\;D=\left[\begin{массив}{c}
1\\
0\\
-1
\end{массив}\right],\;E=\left[\begin{массив}{ccc}
0 и 1 и 3\\
1 и 0 и 2
\конец{массив}\справа],
\end{align*}\] найдите, если возможно: \[\begin{align*}
\begin{массив}{lllll}
a)\,2A+B & b)\,4D-B & c)\,3C-A & d)\,B+2D+E & e)\,3C-A+2E\end{массив}. \end{выравнивание*}\]
 Ответы 
 \[\begin{выравнивание*}
\начать{массив}{llllll}
1. & a)\,\textrm{Невозможно} & b)\,\left[\begin{array}{cc}
-4 и -1\\
5 и 1
\end{массив}\right] & c)\,\textrm{Невозможно} & d)\,\left[\begin{массив}{cc}
0 и 2\\
6 и 2
\end{массив}\right] & e)\,\textrm{Невозможно}.\end{массив}
\end{выравнивание*}\]
 \[\begin{выравнивание*}
\начать{массив}{llllll}
2. & a)\,\textrm{Невозможно} & b)\,\left[\begin{array}{c}
0\\
-1\\
-6
\end{массив}\right] & c)\,\left[\begin{массив}{ccc}
1 и -6 и 5\\
6 и -1 и 1
\end{массив}\right] & d)\,\textrm{Невозможно} & e)\,\left[\begin{array}{ccc}
1 и -4 и 11\\
8 и -1 и 5
\конец{массив}\справа].\конец{массив}
\end{выравнивание*}\]
 Скачать эту страницу, M2 Сложение и вычитание матриц
 (PDF 110 КБ)
 Что дальше... M3 Умножение матриц
 Ключевые слова: 
 Математика
 Матрицы
 матрицы - Сложение/умножение матриц с разными размерами 
 Вопрос задан  7 лет, 5 месяцев назад 
 Изменено
 1 год, 9 месяцев назад
 Просмотрено
 39 тысяч раз
 $\begingroup$
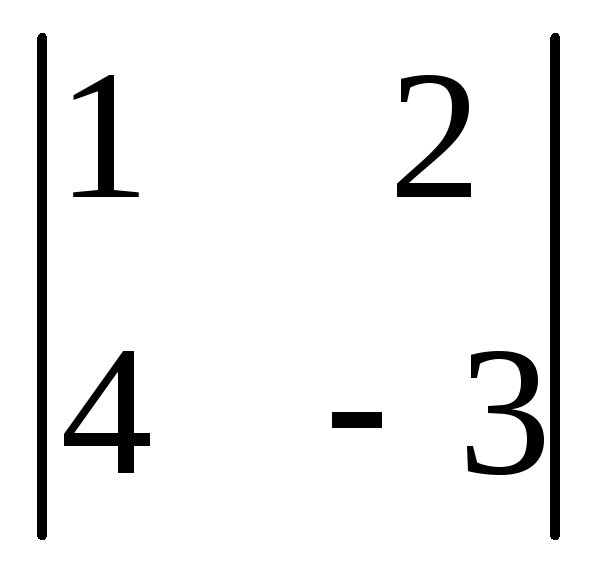
 У меня есть следующие две матрицы:
 $$A=\begin{pmatrix}1 & -2\\3 & 1\end{pmatrix}\text{ и }B=\begin{pmatrix}1 & 3 &
 2\\-1 & 0 & 2\end{pmatrix}$$
 Итак, у меня есть две матрицы разных размеров. Несколько источников говорят мне, что я не могу выполнять умножение или сложение с матрицами разных размеров. Так что я немного смущен. Могу ли я сделать это с этими? Как?
 матрицы
 $\endgroup$
 2
 $\begingroup$
 Предположим, у вас есть две матрицы $A$ и $B$ порядков $a_1\times a_2$ и $b_1\times b_2$ соответственно.
 Матричное сложение/вычитание двух матриц будет определено тогда и только тогда, когда $a_1=b_1$ и $a_2=b_2$
 Умножение матриц на них определено тогда и только тогда, когда $a_2=b_1$ для $AB$ должно быть определено и $b_2= a_1$ для определения $BA$. $AB$ будет иметь порядок $a_1\times b_2$, а $BA$ будет иметь порядок $b_1\times a_2$
 $\endgroup$
 2
 $\begingroup$
 Чтобы добавить две матрицы, они должны иметь одинаковые размеры, поэтому вы не можете добавлять свои матрицы.
 Для умножения на матрицы $M$ и $N$ количество столбцов матрицы $M$ должно быть равно количеству строк матрицы $N$. В вашем случае вы можете умножить $A\cdot B$, потому что количество столбцов $A$ равно $2$, а количество строк $B$ равно $2$.
 Вы не можете умножить $B\cdot A$, потому что количество столбцов $B$ равно $3$, а количество строк $A$ равно $2$.
 $\endgroup$
 $\begingroup$
 Сложение и умножение матриц не определялись ни с того ни с сего. Матрица $m\times n$ описывает линейное преобразование из векторного пространства размерности $n$ в векторное пространство размерности $m$.
 Сумма матриц соответствует преобразованию, которое представляет собой  сумму  двух заданных преобразований. Добавление линейных преобразований требует, чтобы домен и диапазон были идентичными.
 Произведение матриц соответствует преобразованию  состав  из двух заданных преобразований.