Матрица строка – Энциклопедия по экономике
Решение систем линейных уравнений с использованием матриц-строк. [c.191]На этот раз в четвертой ячейке столбца ответов мы получили отрицательный результат. Это означает, что нам следует инвестировать отрицательную сумму в размере 9,81% капитала в сберегательный счет. Чтобы решить проблему отрицательного X (т.е. когда значение на пересечении строки i и крайнего правого столбца меньшее или равно нулю), мы должны удалить из первоначальной расширенной матрицы строку i + 2 и столбец i и решить задачу для новой расширенной матрицы. Если значения последних двух строк крайнего правого столбца меньше или равны нулю, нам не о чем беспокоиться, поскольку они соответствуют множителям Лагранжа и могут принимать отрицательные значения. Так как отрицательное значение переменной соответствует отрицательному весу четвертого компонента, мы удалим из первоначальной расширенной матрицы четвертый столбец и шестую строку. Затем используем построчные операции для проведения элементарных преобразований, чтобы получить единичную матрицу [c.
Управляемая матрица. Матрица, строки которой опреде- [c.25]
Матрица помех. Матрица, строки которой определяют [c.26]
Пусть у > 0, тогда, очевидно, х > 0. Умножив равенство (2.8) слева на матрицу-строку рт а, получим с учетом (1.7) [c.266]
Умножая матрицы специального вида, сформируйте матрицу-столбец и матрицу-строку, соответственно равные j-му столбцу и i-й строке матрицы А. Вычислите суммы элементов j-ro столбца и i-й строки матрицы А. [c.55]
Здесь С — матрица-строка с компонентами [c.34]
Полагаем, что штраф за загрязнение пропорционален загрязнению, т.е. s(t, ) = SQ , гДе 50 — матрица-строка длины /. [c.48]
S > 0 — коэффициент дисконтирования), минимизация которого соответствует некоторому компромиссу между желаниями иметь поменьше загрязнений и побольше выпусков предприятий . При этом С1 — матрица-строка длины / с положительными компонентами, соответствующими вредности каждого типа загрязнений, С, — скалярные положительные величины, соответствующие ценности выпуска каждого предприятия. Эти коэффициенты находятся в ведении Центра и в данной постановке считаются заданными.
[c.49]
Эти коэффициенты находятся в ведении Центра и в данной постановке считаются заданными.
[c.49]
Матрица yl в формуле (6) — это матрица, строки которой образованы n-векторами (t) (0) таким образом, [c.67]
Стратегией в Т. и. наз. указание о способе действий соответствующего игрока в зависимости от всех возможных действий др. участников игры. Задачей Т. и. является нахождение наилучших (оптимальных) стратегий, поэтому ее часто паз. теорией стратегических игр. Если у каждого игрока имеется конечное число стратегий, игра наз. к о н е ч-н о и. Конечные игры двух лиц с нулевой суммой можно представить в виде матрицы, строки к-рой соответствуют стратегиям одного игрока, а столбцы — стратегиям его противника. Числа на пересечении строк и столбцов (элементы матрицы) указывают резуль- [c.153]
Второй квадрант представляет собой матрицу, строки которой являются продолжением строк первого квадранта, а столбцы отражают конечное использование продукции на удовлетворение личных и общественных потребностей, накопление основных и оборотных фондов, резервов. [c.45]
[c.45]
Преобразуем эту матрицу согласно алгоритму. Из каждой строки матрицы цен С вычитаем наименьший в этой строке элемент. Получим матрицу С”, изображенную на рис. 2.4, б. В образовавшейся матрице строк или столбцов, которые не содержали бы нулей, нет, и, следовательно, пока получить допустимое решение из нулевых элементов не получается. Поэтому вычеркиваем образовавшиеся нули минимальным числом прямых линий. Например, как это сделано на рис. 2.4, в. Находим среди невычеркнутых элементов последней матрицы наименьший. Это элемент с31 = 3. Вычитаем элемент с31 из всех невычеркнутых элементов матрицы С” и прибавляем его значение к значениям всех элементов, стоящих на пересечении прямых. В результате получаем матрицу С “, представленную на рис. 2.4, г. Допустимого решения по-прежнему еще нет. Поэтому продолжаем вычеркивание [c.164]
Данные, необходимые для принятия решения в условиях неопределенности, обычно задаются в форме матрицы, строки которой соответствуют возможным действиям (управленческим решения) RJ, а столбцы — возможным состояниям природы Sj.

Предложение. В ортогональной матрице строки также образуют ортонормированную систему векторов. [c.499]
Аналогично матрица-строка Рш = (Р (т), Р2(т),. .., Рп(т)) безусловных вероятностей после т этапов марковского процесса определяется соотношением [c.152]
Разбивка на фазы производится с учетом принадлежности изделия к определенному сектору гибкого планирования (СНГ) и его коэффициента обновления. СГП является элементом матрицы, строки которой характеризуют тип продукции (потребительские товары, продукция производственного назначения, оборонная продукция) с его разбивкой на группы по коэффициенту обновления, а столбцы характеризуют факторы, влияющие на длительность жизненного цикла (научно-технический прогресс, предпочтение потребителей, число конкурентов, мода, военная доктрина и международные соглашения, существование традиционных товаров) [8]. Алгоритм разбивки периода производства на фазы описан в [3]. [c.13]
Перемножение матриц осуществляется, как известно, по правилу строка на столбец [c. 186]
186]
Перемножая элементы первой строки матрицы А 1 на соответствующие элементы вектора-столбца V и суммируя произведения, получаем производственную программу по воде, т. е. задание для цеха № 1 [c.186]
Для выполнения расчета сетевого графика с помощью теории графов заполняется матрица связей между событиями. Матрица связей (рис. 4.И, о) представляет собой шахматную таблицу с числом столбцов и строк, равным количеству событий в сетевом графике. На пересечении /-и строки и t -ro столбца проставляется ожидаемое время выполнения. работы между f-м и /-М событиями. [c.73]
Для построения модели необходимо численно сформировать все входящие в нее условия, т. е. определить, какие конкретно числовые коэффициенты стоят перед каждым неизвестным. Таблица из коэффициентов перед неизвестными, записанная таким образом, что в каждой строке стоят коэффициенты одного и того же ограничения, в каждом столбце — коэффициенты перед одним и тем же неизвестным, называется матрицей. Поэтому для формирования модели необходимо сформировать ее матрицу.
Матрица заполняется или по строкам, или по столбцам согласно технологической схеме. [c.417]
Такой же наглядный смысл имеет и каждая строка матрицы. Например, свежий аммиак может расходоваться или на производство 1 т карбамида в количестве 0,586 т (столбец Рг), или на производство 1 т меламина в количестве 0,5 (столбец Рд), или, наконец, быть товарным продуктом (столбец Р4). Математически соответствующее ограничение на аммиак выглядит следующим образом 0,586 + 0,5л 3 -+- я4 = wlt где wl — ресурс аммиака. [c.417]
Итак, каждая строка матрицы отвечает некоторому равенству или неравенству. [c.417]
Можно подчеркнуть, что, заполняя матрицу, автоматически из каждой ее строки получаем соответствующее уравнение или неравенство, выписать которое с учетом заполненной строки матрицы не представляет никакого труда. Впрочем, выписывать уравнение [c.417]
После этого намечается несколько основных стратегий (способов использования средств и ресурсов) решения частных задач.
Основу матрицы составляет совокупность всех производственных подразделений. Каждое подразделение фигурирует дважды как производящее продукцию и как потребляющее ее. Каждому подразделению как производителю продукции соответствует определенная строка матриц, а как потребителю — определенный столбец. Если строки матрицы обозначить через i, а столбцы через /, то величины, находящиеся на пересечении 1-й строки и /-го столбца, определяют количество продукции, произведенное 1-м подразделением и потребленное /-м подразделением.
[c.157]
Если строки матрицы обозначить через i, а столбцы через /, то величины, находящиеся на пересечении 1-й строки и /-го столбца, определяют количество продукции, произведенное 1-м подразделением и потребленное /-м подразделением.
[c.157]
В каждом столбце нормативной матрицы показывают (в расчете на единицу продукции) затраты продукции и услуг вспомогательных цехов, покупных материалов, энергии, трудовые затраты, амортизацию. Строки нормативной матрицы показывают, где используется данная продукция (в какой цех поступает, на какую продукцию и в каком количестве тратится). [c.159]
Коэффициенты прямых затрат образуют квадрантную матрицу А (а/у), содержащую п строк и п столбцов. [c.159]
При взаимоувязке процессов по их началу элементы матрицы по данному процессу (строке) заполняются от первой захватки (ячейки) к последней — так называемый прямой счет. При увязке процессов по их завершению заполнение элементов матрицы идет наоборот — от последней захватки к первой по всей строке (обратный счет). [c.32]
[c.32]
Морфологический анализ разработан и применен впервые швейцарским астрономом Ф. Цвикки. Основная идея этого метода систематически находить все мыслимые варианты решения проблемы или реализации системы путем комбинирования выделенных элементов или их признаков. Цвикки предложил три метода морфологического исследования метод систематизированного покрытия поля, основанных на выделении так называемых опорных пунктов знания в любой исследуемой области и использовании для заполнения поля некоторых сформулированных принципов мышления метод отрицания и конструирования, заключающийся в том, что на пути конструктивного процесса стоят догмы и компромиссные ограничения, которые есть смысл отрицать, и следовательно, сформулировав некоторые предложения, полезно заменить их на противоположные и использовать при проведении анализа метод морфологического ящика, нашедший наиболее широкое применение. Идея здесь состоит в том, чтобы определить все мыслимые параметры, от которых может зависеть решение проблемы (например, технико-экономические показатели), представить их в виде матриц-строк, а затем определить в этом морфологическом матрице-ящике все возможные сочетания параметров по одному из каждой строки. Полученные таким образом варианты могут снова подвергаться оценке и анализу в целях выбора наилучшего. При использовании этого метода можно генерировать варианты так, как это показано в главе 6.
[c.347]
Полученные таким образом варианты могут снова подвергаться оценке и анализу в целях выбора наилучшего. При использовании этого метода можно генерировать варианты так, как это показано в главе 6.
[c.347]
Можно сказать, что структура современной западной экономической теории напоминает матрицу, строки которой образуют различные методологические подходы, а столбцы — различные экономические проблемы. Разумеется, многие элементы этой матрицы будут нулями — практически не существует методологических подходов, позволяющих объяснить все проблемы. Правда, неоклассический подход в принципе на это способен, но, как уже отмечалось, за счет понижения содержательности и утраты нетривиальности выводов. [c.761]
Выделяем матрицу-строку технологической трудоемкости Т”те1Я, необходимую для проведения последующих расчетов. [c.103]
В столбцах матричного техпромфинплана отражается структура материальных затрат каждого подразделения, а в одноименных строках содержатся данные о распределении объема продукции и услуг того же подразделения. На размерность матрицы влияет не только принцип классификации подразделений, но и принятая методика планирования. Так, в матрице выделяются подготовка и перекачка нефти, текущий ремонт подземного оборудования по каждому РИТСу, так как в НГДУ ведется планирование, учет и анализ видов работ.
[c.158]
На размерность матрицы влияет не только принцип классификации подразделений, но и принятая методика планирования. Так, в матрице выделяются подготовка и перекачка нефти, текущий ремонт подземного оборудования по каждому РИТСу, так как в НГДУ ведется планирование, учет и анализ видов работ.
[c.158]
В простейшем случае при п=1 (случай однономен-клатурного производства) матрицы Q и Т превращаются в векторы-строки, а матрица 5 = 0. [c.167]
При т=1 (однооперационный типовой или групповой процесс) и номенклатуре деталей матрица Q = 0, матрица Т превращается в вектор-строку im (t t2 . .. гн), а из совокупности матриц S используется полная матрица Sq, причем в диагонали 5ц—5 п содержатся нули. [c.167]
получение столбца и сложение — Нахождение максимального элемента
Матрица — это двумерный массив, состоящий из M строк и N столбцов. Матрицы часто используются в математических вычислениях. Программисты работают с матрицами в основном в научной области, однако их можно использовать и для других вещей, например, для быстрой генерации уровней в видео-игре.
Матрицы и библиотека NumPy
Программист может самостоятельно реализовать все функции для работы с матрицами: умножение, сложение, транспонирование и т. д. На Python это сделать гораздо проще, чем на более низкоуровневых языках, таких как C.
Но каждый раз писать одни и те же алгоритмы не имеет смысла, поэтому была разработана библиотека NumPy. Она используется для сложных научных вычислений и предоставляет программисту функции для работы с двумерными массивами.
Вместо того чтобы писать десятки строк кода для выполнения простых операций над матрицами, программист может использовать одну функцию из NumPy. Библиотека написана на Python, C и Фортране, поэтому функции работают даже быстрее, чем на чистом Python.
Подключение библиотеки NumPy
NumPy не встроена в интерпретатор Python, поэтому перед импортом её необходимо установить. Для этого в можно воспользоваться утилитой pip. Введите в консоле команду:
pip install numpy
Теперь, когда библиотека установлена, её можно подключить с помощью команды import. Для удобства переименуем
Для удобства переименуем numpy при импорте в np следующим образом:
import numpy as np
Ниже в примерах будет использован именно такой импорт, поэтому обращение к библиотеке будет через np, а не numpy!
Создание
Для создании матрицы используется функция array(). В функцию передаётся список. Вот пример создания, мы подаём в качестве аргумента функции двумерный список:
a = np.array([[3, 3, 3], [2, 5, 5]])
Вторым параметром можно задать тип элементов матрицы:
a = np.array([[3, 3, 3],[2, 5, 5]], int) print(a)
Тогда в консоль выведется:
[[3 3 3] [2 5 5]]
Обратите внимание, что если изменить int на str, то тип элементов изменился на строковый. Кроме того, при выводе в консоль NumPy автоматически отформатировал вывод, чтобы он выглядел как матрица, а элементы располагались друг под другом.
В качестве типов элементов можно использовать int, float, bool, complex, bytes, str, buffers. Также можно использовать и другие типы NumPy: логические, целочисленные, беззнаковые целочисленные, вещественные, комплексные. Вот несколько примеров:
Также можно использовать и другие типы NumPy: логические, целочисленные, беззнаковые целочисленные, вещественные, комплексные. Вот несколько примеров:
- np.bool8 — логическая переменная, которая занимает 1 байт памяти.
- np.int64 — целое число, занимающее 8 байт.
- np.uint16 — беззнаковое целое число, занимающее 2 байта в памяти.
- np.float32 — вещественное число, занимающее 4 байта в памяти.
- np.complex64 — комплексное число, состоящее из 4 байтового вещественного числа действительной части и 4 байтов мнимой.
Вы также можете узнать размер матрицы, для этого используйте атрибут shape:
size = a.shape print(size) # Выведет (2, 3)
Первое число (2) — количество строк, второе число (3) — количество столбцов.
Нулевая матрица
Если необходимо создать матрицу, состоящую только из нулей, используйте функцию zeros():
a_of_zeros = np.zeros((2,2)) print(a_of_zeros)
Результат этого кода будет следующий:
[[0.0.] [0. 0.]]
Получение строки, столбца и элемента
Чтобы получить строку двухмерной матрицы, нужно просто обратиться к ней по индексу следующим образом:
temp = a[0] print(temp) #Выведет [3 3 3]
Получить столбец уже не так просто. Используем срезы, в качестве первого элемента среза мы ничего не указываем, а второй элемент — это номер искомого столбца. Пример:
arr = np.array([[3,3,3],[2,5,5]], str) temp = arr[:,2] print(temp) # Выведет ['3' '5']
Чтобы получить элемент, нужно указать номер столбца и строки, в которых он находится. Например, элемент во 2 строке и 3 столбце — это 5, проверяем (помним, что нумерация начинается с 0):
arr = np.array([[3,3,3],[2,5,5]], str) temp = arr[1][2] print(temp) # Выведет 5
Умножение и сложение
Чтобы сложить матрицы, нужно сложить все их соответствующие элементы. В Python для их сложения используется обычный оператор «+».
Пример сложения:
arr1 = np.array([[3,3,3],[2,5,5]]) arr2 = np.array([[2,4,2],[1,3,8]]) temp = arr1 + arr2 print(temp)
Результирующая матрица будет равна:
[[ 5 7 5] [ 3 8 13]]
Важно помнить, что складывать можно только матрицы с одинаковым количеством строк и столбцов, иначе программа на Python завершится с исключением ValueError.
Умножение матриц сильно отличается от сложения. Не получится просто перемножить соответствующие элементы двух матриц. Во-первых, матрицы должны быть согласованными, то есть количество столбцов одной должно быть равно количеству строк другой и наоборот, иначе программа вызовет ошибку.
Умножение в NumPy выполняется с помощью метода dot().
Пример умножения:
arr1 = np.array([[3,3],[2,5]]) arr2 = np.array([[2,4],[1,3]]) temp = arr1.dot(arr2) print(temp)
Результат выполнения этого кода будет следующий:
[[ 9 21] [ 9 23]]
Как она получилась? Разберём число 21, его позиция это 1 строка и 2 столбец, тогда мы берем 1 строку первой матрицы и умножаем на 2 столбец второй. Причём элементы умножаются позиционно, то есть 1 на 1 и 2 на 2, а результаты складываются: [3,3] * [4,3] = 3 * 4 + 3 * 3 = 21.
Причём элементы умножаются позиционно, то есть 1 на 1 и 2 на 2, а результаты складываются: [3,3] * [4,3] = 3 * 4 + 3 * 3 = 21.
Транспонированная и обратная
Транспонированная матрица — это матрица, у которой строки и столбцы поменялись местами. В библиотеки NumPy для транспонирования двумерных матриц используется метод transpose(). Пример:
arr1 = np.array([[3,3],[2,5]]) temp = arr1.transpose() print(temp)
В результате получится матрица:
[[3 2] [3 5]]
Чтобы получить обратную матрицу, необходимо использовать модуль linalg (линейная алгебра). Используем функцию inv():
arr1 = np.array([[3,3],[2,5]]) temp = np.linalg.inv(arr1) print(temp)
Результирующая матрица будет равна:
[[ 0.55555556 -0.33333333] [-0.22222222 0.33333333]]
Получение максимального и минимального элемента
Чтобы получить максимальный или минимальный элемент, можно пройтись по всем элементам матрицы с помощью двух циклов for. Это стандартный алгоритм перебора, который известен почти каждому программисту:
Это стандартный алгоритм перебора, который известен почти каждому программисту:
arr = np.array([[3,3],[2,5]])
min = arr[0][0]
for i in range(arr.shape[0]):
for j in range(arr.shape[1]):
if min > arr[i][j]:
min = arr[i][j]
print("Минимальный элемент:", min) # Выведет "Минимальный элемент: 2"NumPy позволяет найти максимальный и минимальный элемент с помощью функций amax() и amin(). В качестве аргумента в функции нужно передать саму матрицу. Пример:
arr1 = np.array([[3,3],[2,5]])
min = np.amin(arr1)
max = np.amax(arr1)
print("Минимальный элемент:", min) # Выведет "Минимальный элемент: 2"
print("Максимальный элемент:", max) # Выведет "Максимальный элемент: 5"Как видим, результаты реализации на чистом Python и реализации с использованием библиотеки NumPy совпадают.
Заключение
На Python можно реализовать все необходимые функции для работы с матрицами. Чтобы упростить работу программистов, была создана библиотека NumPy. Она позволяет производить сложные математические вычисления легко и без ошибок, избавляя программиста от необходимости каждый раз писать один и тот же код.
Чтобы упростить работу программистов, была создана библиотека NumPy. Она позволяет производить сложные математические вычисления легко и без ошибок, избавляя программиста от необходимости каждый раз писать один и тот же код.
Таблицы, матрицы и списки в построителе отчетов Power BI – Power BI
- Статья
- Чтение занимает 5 мин
ОБЛАСТЬ ПРИМЕНЕНИЯ: ✔️ Power BI Report Builder служба Power BI ✔️ Power BI Desktop ❌
В построителе отчетов таблицы, матрицы и списки являются областями данных, отображающими данные отчетов с разбивкой на страницы в ячейках, которые упорядочены по строкам и столбцам. Ячейки, как правило, содержат текстовые данные, например текст, даты и числа, но могут также содержать датчики, диаграммы или элементы отчетов, такие как изображения. В совокупности таблицы, матрицы и списки часто называются областями данных табликса.
Ячейки, как правило, содержат текстовые данные, например текст, даты и числа, но могут также содержать датчики, диаграммы или элементы отчетов, такие как изображения. В совокупности таблицы, матрицы и списки часто называются областями данных табликса.
В основе шаблонов таблиц, матриц и списков лежит область данных табликса, которая представляет собой гибкую сетку, позволяющую отображать данные в ячейках. В шаблонах таблиц и матриц ячейки выстроены в виде строк и столбцов. Шаблоны — это разные варианты базовой универсальной области данных табликса, поэтому вы можете отображать данные в сочетании с форматами шаблонов и изменять таблицу, матрицу или список путем включения характеристик другой области данных по мере разработки отчета. Например, если после добавления таблицы обнаруживается, что она не соответствует конкретным требованиям, то можно добавить группы столбцов, чтобы преобразовать таблицу в матрицу.
Области данных таблиц и матриц могут отображать сложные связи между данными, включая вложенные таблицы, матрицы, списки, диаграммы и датчики. Таблицы и матрицы имеют табличный макет, а их данные поступают из одного набора данных, основанного на одном источнике данных. Основное различие между таблицами и матрицами заключает в том, что таблицы могут содержать только группы строк, тогда как матрицы содержат группы строк и столбцов.
Таблицы и матрицы имеют табличный макет, а их данные поступают из одного набора данных, основанного на одном источнике данных. Основное различие между таблицами и матрицами заключает в том, что таблицы могут содержать только группы строк, тогда как матрицы содержат группы строк и столбцов.
Списки имеют небольшое отличие. Они поддерживают свободный макет, который может содержать несколько одноранговых таблиц или матриц, каждая из которых использует данные из другого набора данных. Списки могут также использоваться для таких форм, как счета.
На приведенных ниже рисунках показаны простые отчеты с таблицей, матрицей или списком.
Таблицы
Таблица используется для отображения подробных данных, организации данных в группы строк либо для того и другого одновременно. Шаблон таблицы содержит три столбца со строкой заголовка таблицы и строкой подробных сведений для данных. На приведенном ниже рисунке показан исходный шаблон таблицы, выбранный в области конструктора.
Данные можно сгруппировать по одному полю, по нескольким полям или написать свое собственное выражение. Предусмотрена возможность создавать вложенные группы или независимые, смежные группы и отображать статистические значения для сгруппированных данных, а также добавлять итоги к группам. Например, если в таблице есть группа строк с именем Категория, можно добавить промежуточный итог для каждой группы, а также общий итог для отчета. Чтобы улучшить внешний вид таблицы и выделить данные, которые необходимо сделать более заметными, можно выполнить слияние ячеек и применить форматирование к заголовкам таблицы и данным.
Можно первоначально скрыть подробные или сгруппированные данные и включить в отчет переключатели углубленной детализации, позволяющие пользователям в интерактивном режиме выбирать, какие данные нужно показать.
Матрицы
Матрица используется для отображения статистических сводок по данным, сгруппированным в строки и столбцы, аналогично сводным или перекрестным таблицам. Число строк и столбцов для групп определяется числом уникальных значений для каждой группы строк и столбцов. На приведенном ниже рисунке показан исходный шаблон матрицы, выбранный в области конструктора.
Число строк и столбцов для групп определяется числом уникальных значений для каждой группы строк и столбцов. На приведенном ниже рисунке показан исходный шаблон матрицы, выбранный в области конструктора.
Данные можно группировать по нескольким полям либо выражениям в группах строк и столбцов. Во время выполнения, когда происходит объединение данных отчета и областей данных, матрица расширяется на странице по горизонтали и вертикали по мере добавления столбцов к группам столбцов и строк к группам строк. Значения в ячейках матрицы отображают статистические значения, областью действия которых являются пересечения групп строк и столбцов, к которым принадлежит ячейка. Например, если в матрице есть группа строк («Категория») и две группы столбцов («Территория» и «Год»), где отображается сумма продаж, то в отчете будут две ячейки с суммами продаж для каждого значения в группе «Категория». Областью действия ячеек являются два пересечения: “Категория” и “Территория”, а также “Категория” и “Год”. В матрице могут быть вложенные и смежные группы. Вложенные группы имеют связь «родители-потомки», а смежные группы — одноранговую связь. Предусмотрена возможность добавлять подытоги для всех уровней вложенных групп строк и столбцов в пределах матрицы.
В матрице могут быть вложенные и смежные группы. Вложенные группы имеют связь «родители-потомки», а смежные группы — одноранговую связь. Предусмотрена возможность добавлять подытоги для всех уровней вложенных групп строк и столбцов в пределах матрицы.
Чтобы сделать матричные данные более удобными для чтения и выделить данные, к которым необходимо привлечь внимание, можно выполнить слияние ячеек или провести разбиение по горизонтали и вертикали и применить форматирование к данным и заголовкам групп.
Можно также включить переключатели детализации, которые по умолчанию скрывают подробные данные, чтобы пользователи могли по желанию отобразить подробные сведения.
Списки
Список используется для создания макета свободной формы. Возможности не ограничены созданием макета сетки, поля можно располагать в списке произвольно. С помощью списка можно создавать формы для отображения большого количества полей набора данных или нескольких областей данных рядом для сгруппированных данных.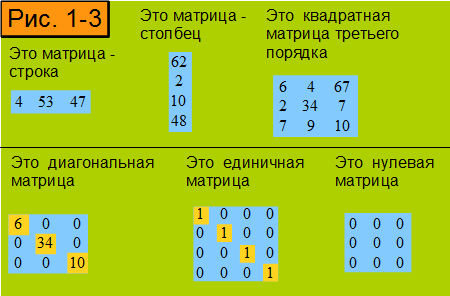 Например, можно определить для списка группу, добавить таблицу, диаграмму и изображение, затем отобразить каждое из значений в табличной или графической форме, как для записи о сотруднике или пациенте.
Например, можно определить для списка группу, добавить таблицу, диаграмму и изображение, затем отобразить каждое из значений в табличной или графической форме, как для записи о сотруднике или пациенте.
Подготовка данных
Такие области данных, как таблица, матрица и список, отображают данные из набора данных. Можно подготовить данные в запросе, который получает данные для набора данных, либо указать свойства в таблице, матрице или списке.
Языки запросов, например Transact-SQL, которые используются при получении данных для наборов данных отчета, позволяют подготавливать данные с помощью фильтров для включения только подмножества данных, с заменой значения NULL или пробелов константами, что делает отчет более удобным для чтения, а также обеспечивает сортировку и группирование данных.
Если решено подготавливать данные в области данных отчета (в таблице, матрице или списке), то свойства задаются применительно к области данных или к ячейкам в области данных. Если требуется фильтровать или сортировать данные, задавайте свойства применительно к области данных. Например, чтобы отсортировать данные, укажите столбцы, по которым выполняется сортировка, и направление сортировки. Если требуется предоставить альтернативное значение для поля, задайте значения текста ячейки, в которой отображается поле. Например, для отображения текста «Пусто» в пустом поле или поле со значением NULL можно использовать выражение, задающее такое значение.
Например, чтобы отсортировать данные, укажите столбцы, по которым выполняется сортировка, и направление сортировки. Если требуется предоставить альтернативное значение для поля, задайте значения текста ячейки, в которой отображается поле. Например, для отображения текста «Пусто» в пустом поле или поле со значением NULL можно использовать выражение, задающее такое значение.
Создание и настройка таблицы, матрицы или списка
При добавлении к отчету таблиц или матриц можно воспользоваться мастером таблиц и матриц или создать их вручную на основе шаблонов, предоставляемых построителем отчетов. Списки формируются вручную с помощью шаблона списка.
Мастер помогает быстро построить и настроить таблицу или матрицу. После завершения работы мастера или создания области данных табликса с нуля можно продолжить настройку и доработку этих объектов. Диалоговые окна, которые можно вызывать из контекстных меню в областях данных, упрощают ввод наиболее часто задаваемых свойств разрывов страницы, повторяемости и видимости верхних и нижних колонтитулов, параметров отображения, фильтров и сортировки. Однако множество дополнительных свойств, предусмотренных для области данных табликса, можно задавать только на панели «Свойства» построителя отчетов. Например, если набор данных для таблицы, матрицы или списка пуст, то для отображения соответствующего сообщения текст сообщения необходимо задать в свойстве табликса NoRowsMessage на панели “Свойства”.
Однако множество дополнительных свойств, предусмотренных для области данных табликса, можно задавать только на панели «Свойства» построителя отчетов. Например, если набор данных для таблицы, матрицы или списка пуст, то для отображения соответствующего сообщения текст сообщения необходимо задать в свойстве табликса NoRowsMessage на панели “Свойства”.
Изменение между шаблонами табликса
Выбор не ограничивается исходным шаблоном табликса. По мере добавления групп, итогов и меток может возникнуть необходимость изменить формат табликса. Например, можно начать с таблицы, затем удалить строку подробных сведений и добавить группы столбцов.
Далее можно создать таблицу, матрицу или список путем добавления любого элемента табликса. Среди возможностей табликса есть такие функции, как отображение подробных данных или статистики для сгруппированных данных в строках или столбцах. Можно создавать вложенные группы, независимые смежные или рекурсивные группы. Можно фильтровать и сортировать сгруппированные данные или без затруднений объединять группы путем включения нескольких выражений групп в определение группы
Кроме того, можно добавлять итоги по группам или общие итоги для области данных. Можно скрывать строки или столбцы, чтобы упростить внешний вид отчета и позволить пользователю включать и отключать отображение скрытых данных, как в отчете с углубленной детализацией.
Можно скрывать строки или столбцы, чтобы упростить внешний вид отчета и позволить пользователю включать и отключать отображение скрытых данных, как в отчете с углубленной детализацией.
Дальнейшие действия
- Сведения об отчетах с разбивкой на страницы в Power BI Premium
Row Matrix – определение, формула, свойства, примеры.
Матрица-строка — это матрица, все элементы которой расположены в одной строке. Элементы расположены горизонтально, а порядок матрицы строк равен 1 x n. Матрица-строка A = [a, b, c, d] имеет только одну строку и может иметь множество столбцов, количество которых равно количеству элементов в строке.
Давайте узнаем больше о свойствах матрицы-строки, матричных операциях над матрицей-строкой, на примерах, в часто задаваемых вопросах.
| 1. | Что такое матрица строк? |
| 2. | Свойства матрицы строк |
3. | Операции над матрицей строк |
| 4. | Примеры на матрице строк |
| 5. | Практические вопросы |
| 6. | Часто задаваемые вопросы о матрице строк |
Что такое матрица строк?
Матрица-строка — это матрица, в которой все элементы находятся в одной строке. Матрица-строка имеет только одну строку и несколько столбцов. Порядок матрицы-строки равен 1 × n, и она состоит из n элементов. Элементы расположены горизонтально, а количество элементов равно количеству столбцов в матрице-строке. Общая форма матрицы-строки выглядит следующим образом.
A = \(\begin{bmatrix}a_{11}&a_{12}&a_{13}&……&a_{1n}\end{bmatrix}_{1×n}\)
Примеры матрицы строк
Давайте рассмотрим три примера матрицы строк ниже.
B = \(\begin{bmatrix}3&2\end{bmatrix}_{1×2}\)
C = \(\begin{bmatrix}a&b&c\end{bmatrix}_{1×3}\)
D = \(\begin{bmatrix}5&7&9&11\end{bmatrix}_{1×4}\)
Свойства матрицы строк
Следующие свойства матрицы строк помогают глубже понять матрицу строк.
- Матрица строк имеет только одну строку.
- Матрица-строка имеет множество столбцов.
- Количество элементов в матрице строк равно количеству столбцов в матрице.
- Матрица-строка также является прямоугольной матрицей.
- Транспонирование матрицы строк является матрицей столбцов.
- Матрицу строк можно складывать или вычитать только из матрицы строк того же порядка.
- Матрица-строка может быть умножена только на матрицу-столбец
- Произведение матрицы строк на матрицу столбцов дает одноэлементную матрицу.
Операции над матрицей строк
Над матрицами-строками можно выполнять следующие алгебраические операции сложения, вычитания, умножения и деления. Операции сложения и вычитания над матрицами-строками можно выполнять так же, как и над любыми другими матрицами. Матрицу-строку можно добавлять или вычитать только из любой другой матрицы-строки. Здесь порядок двух матриц должен быть одинаковым.
A = \(\begin{bmatrix}3&-5&2&0\end{bmatrix}\), B = \(\begin{bmatrix}5&8&4&7\end{bmatrix}\)
A + B = \(\begin{bmatrix}3+5&(-5)+8&2+4&0+7\end{bmatrix}\) = \(\begin{bmatrix}8&3&6&7\end{bmatrix}\)
Умножение матрицы-строки возможно на матрицу-столбец. При выполнении условия умножения матриц количество столбцов в матрице-строке должно быть равно количеству строк в матрице-столбце. То есть количество столбцов в первой матрице для умножения должно быть равно количеству строк во втором столбце.
A = \(\begin{bmatrix}4&3&6&-15\end{bmatrix}\), B = \(\begin{bmatrix}6\\5\\4\\2\end{bmatrix}\)
A × B = \(\begin{bmatrix}4×6+3×5+6×4+(-15)×2\end{bmatrix}\) = \(\begin{bmatrix}24+15+24-30 \end{bmatrix}\) = \(\begin{bmatrix} 33 \end{bmatrix}\)
Умножение матрицы-строки на матрицу-столбец приводит к одноэлементной матрице. Кроме того, матрицу-строку нельзя использовать для деления, поскольку обратной матрицы-строки не существует.
Похожие темы
Следующие темы помогут лучше понять матрицу строк.
- Операции с матрицами
- Матрица трансформации
- Несингулярная матрица
- Эрмитова матрица
- Нильпотентная матрица
Примеры на матрице строк
Пример 1: Найдите транспонированную матрицу строк \(\begin{bmatrix}3&4&1\end{bmatrix}\).
Решение:
Дана матрица A = \(\begin{bmatrix}3&4&1\end{bmatrix}\).
Чтобы найти транспонирование этой матрицы строк, элементы строки записываются как элементы столбца.
A T = \(\begin{bmatrix}3\\4\\1\end{bmatrix}\).
Следовательно, транспонированная матрица-строка является матрицей-столбцом.
Пример 2: Найдите произведение матрицы строк \(\begin{bmatrix}1&2&-1\end{bmatrix}\) и матрицы \(\begin{bmatrix}3\\4\\1\end {bматрица}\).
Решение:
Даны матрицы A = \(\begin{bmatrix}1&2&-1\end{bmatrix}\) и B = \(\begin{bmatrix}3\\4\\1\ конец{bматрица}\).

A × B = \(\begin{bmatrix}1&2&-1\end{bmatrix}\) × \(\begin{bmatrix}3\\4\\1\end{bmatrix}\)
= \( \begin{bmatrix}1×3+2×4+(-1)×1\end{bmatrix}\)
= \(\begin{bmatrix}3+8-1\end{bmatrix}\)
= \(\begin{bmatrix}10\end{bmatrix}\)
Следовательно, произведение матрицы-строки и матрицы-столбца является одноэлементной матрицей.
перейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Забронировать бесплатный пробный урок
Практические вопросы по матрице строк
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о матрице строк
Что такое матрица-строка?
Матрица-строка — это матрица только с одной строкой, все элементы которой расположены один за другим на горизонтальной линии. В матрице строк A = \(\begin{bmatrix}a&b&c&d\end{bmatrix}\) четыре элемента размещены в одном столбце. Матрица строк имеет только одну строку и множество столбцов. Порядок матрицы-строки равен 1 × n.
В матрице строк A = \(\begin{bmatrix}a&b&c&d\end{bmatrix}\) четыре элемента размещены в одном столбце. Матрица строк имеет только одну строку и множество столбцов. Порядок матрицы-строки равен 1 × n.
Каков порядок матрицы строк?
Порядок матрицы строк равен 1 × n. Матрица-строка состоит из одной строки и n столбцов. Количество столбцов в матрице-строке равно количеству элементов.
Какой тип матрицы является матрицей-строкой?
Матрица строк представляет собой прямоугольную матрицу. Он имеет неравное количество строк и столбцов. Матрица строк равна одной строке и множеству столбцов в зависимости от количества элементов в матрице.
Что такое транспонирование матрицы строк?
Транспонирование матрицы строк дает матрицу столбцов. Матрица-строка порядка 1 × n имеет транспонированную матрицу, которая представляет собой матрицу-столбец порядка n × 1. Матрица-строка имеет элементы, расположенные горизонтально, а матрица-столбец имеет элементы, расположенные в вертикальном формате.
Какие операции выполняются над матрицей-строкой?
Матричные операции сложения, вычитания и умножения можно выполнять с помощью матрицы-строки. Обратная матрица-строка невозможна, так как это не квадратная матрица. Сложение или вычитание матриц возможно между двумя матрицами-строками одного порядка. Умножение матрицы-строки возможно на матрицу-столбец. При выполнении условия умножения матриц количество столбцов в матрице-строке должно быть равно количеству строк в матрице-столбце.
В чем разница между матрицей строк и матрицей столбцов?
В матрице строк элементы расположены горизонтально, а в матрице столбцов элементы расположены вертикально. Порядок матрицы-строки равен 1 × n, а порядок матрицы-столбца — n × 1. Матрица-строка или матрица-столбец имеют одинаковое количество элементов. А произведение матрицы строк и матрицы столбцов дает одноэлементную матрицу.
Пространство строки и пространство столбца матрицы
Пусть A будет матрицей m на n . Пространство, охватываемое строками A , называется пространством строк of A и обозначается RS(A) ; это подпространство R n . Пространство, занимаемое столбцами A , называется пространством столбцов of A и обозначается CS(A) ; это подпространство R m .
Пространство, охватываемое строками A , называется пространством строк of A и обозначается RS(A) ; это подпространство R n . Пространство, занимаемое столбцами A , называется пространством столбцов of A и обозначается CS(A) ; это подпространство R m .
The collection { r 1 , r 2 , …, r m } consisting of the rows of A may not form a basis for RS(A) , потому что набор не может быть линейно независимым. Однако максимальное линейно независимое подмножество { r 1 , r 2 , …, r m } дает базис для строки. Поскольку максимальное количество линейно независимых строк А равен рангу А ,
Аналогично, если C 1 , C 2 ,…, C N Обожпите колонны A , тогда максимальная линя , c 2 , …, c n } дает основу для пространства столбца A . Но максимальное количество линейно независимых столбцов также равно рангу матрицы, поэтому
Но максимальное количество линейно независимых столбцов также равно рангу матрицы, поэтому
Следовательно, хотя RS(A) является подпространством R n и CS(A) является подпространством R m 1 90, (** и 90, ) подразумевают, что
, даже если м ≠ n .
Пример 1 : Определить размерность и основу для пространства строк матрицы
Последовательность операций с элементарными строками сводит эту матрицу к ступенчатой матрице
Ранг B равен 3, поэтому dim RS(B) = 3. Базис для RS(B) состоит из ненулевых строк в сокращенной матрице:
Другим основанием для RS(B) , состоящим из некоторых исходных строк B , является
.
Обратите внимание, что поскольку пространство строк является трехмерным подпространством R 3 , оно должно состоять из R 3 .
Критерии принадлежности к пространству столбца . Если A является матрицей m x n , а x является вектором n , записанным в виде матрицы-столбца, то произведение A x равно линейной комбинации столбцов A :
По определению, вектор b в R m находится в пространстве столбцов A , если он может быть записан как линейная комбинация столбцов A . то есть b ∈ CS(A) именно тогда, когда существуют скаляры x 1 , x 2 , …, x 1 n 9 такие, что Объединение (*) и (**) приводит к следующему выводу: Пример 2 : Для какого значения b вектор b = (1, 2, 3, b ) T в пространстве столбцов следующей матрицы? Сформируйте расширенную матрицу [ A / b ] и уменьшите: Из-за нижнего ряда нулей в A ‘ (сокращенная форма A ) нижняя запись в последнем столбце также должна быть 0, что дает полный ряд нулей внизу [ A ‘ / b ′] — для того, чтобы система A x = b имела решение. Следовательно, b = (1, 2, 3, b ) T входит в CS(A) тогда и только тогда, когда b = 5. Поскольку элементарные операции со строками не изменяют ранг матрицы, ясно, что в приведенном выше расчете ранг A = ранг A ′ и ранг [ A / b ] = ранг [ A ′/ б ′]. (Поскольку нижний ряд из A ′ полностью состояла из нулей, ранг A ′ = 3, подразумевающий также ранг A = 3.) При b = 5 нижний ряд [ A ′/ b ′] также полностью состоит из нулей, что дает ранг [ A ′/ b ′] = 3. Однако, если бы b не было равно 5, то нижняя строка [ A ′/ b ′] была бы не состоять полностью из нулей, и ранг [ A ′/ b ′] был бы равен 4, а не 3. Пример 3 : Определить размерность и основу пространства столбца матрицы из примера 1 выше. Поскольку размерность пространства столбца матрицы всегда равна размерности ее пространства строки, CS(B) также должен иметь размерность 3: CS(B) является трехмерным подпространством R 4 . Поскольку B содержит только 3 столбца, эти столбцы должны быть линейно независимыми и, следовательно, составлять основу: Пример 4 : Найти основу для пространства столбца матрицы Поскольку пространство столбцов A состоит именно из тех векторов b , что A x = b является разрешимой системой, один из способов определить основу для CS(A) состоит в следующем. Поскольку в сокращенной форме A T осталось две ненулевых строки, ранг A T равен 2, поэтому Кроме того, поскольку { v 1 , v 2 } = {(1, 2, −3), (0, −4, 7)} является основой для РС(А Т ), сборник является основой для CS(A) , двумерного подпространства R 3 . ПРИМЕНЯЕТСЯ К: ✔️ Power BI Desktop ✔️ Служба Power BI Визуальное представление матрицы похоже на таблицу. Таблица поддерживает два измерения, а данные являются плоскими, то есть повторяющиеся значения отображаются, а не агрегируются. Матрица упрощает осмысленное отображение данных в нескольких измерениях — она поддерживает ступенчатый макет. Матрица автоматически агрегирует данные и позволяет выполнять детализацию. Вы можете создавать матричные визуальные элементы в отчетах Power BI и перекрестно выделять элементы в матрице с другими визуальными элементами на этой странице отчета. Например, вы можете выбирать строки, столбцы и даже отдельные ячейки и выделять их перекрестно. Кроме того, отдельные ячейки и выбор нескольких ячеек можно копировать и вставлять в другие приложения. С матрицей связано множество функций, и мы рассмотрим их в следующих разделах этой статьи. Примечание Чтобы поделиться своим отчетом с коллегой по Power BI, необходимо, чтобы у вас обоих были индивидуальные лицензии Power BI Pro или отчет был сохранен в емкости Premium. Прежде чем приступить к использованию визуального элемента матрицы, важно узнать, как Power BI вычисляет итоговые и промежуточные значения в таблицах и матрицах. Для итоговых и промежуточных строк Power BI оценивает меру по всем строкам в базовых данных — это не просто добавление значений в видимых или отображаемых строках. Это означает, что вы можете получить значения в итоговой строке, отличные от ожидаемых. Взгляните на следующие изображения матрицы. В этом примере каждая крайняя справа строка в визуальной матрице показывает Сумма для каждой комбинации продавец/дата. Однако, поскольку продавец появляется с несколькими датами, числа могут появляться более одного раза. Таким образом, точная сумма из базовых данных и простое добавление видимых значений не равны. Когда вы смотрите на итоги и промежуточные итоги, помните, что эти значения основаны на базовых данных. Они основаны не только на видимых значениях. Существует два способа расширения заголовков строк. Первый — через контекстное меню. Вы увидите параметры для расширения выбранного вами заголовка строки, всего уровня или всего, вплоть до самого последнего уровня иерархии. У вас также есть аналогичные параметры для свертывания заголовков строк. Вы также можете добавить кнопки +/- в заголовки строк через панель форматирования под Заголовки строк карт. По умолчанию значки будут соответствовать форматированию заголовка строки, но при желании вы можете настроить цвета и размеры значков отдельно. Когда значки включены, они работают так же, как значки сводных таблиц в Excel. Состояние раскрытия матрицы будет сохранено вместе с вашим отчетом. Примечание Если вы строите отчет на основе многомерной модели служб Analysis Services, необходимо учитывать некоторые особенности развертывания/свертывания, если в модели используется функция элемента по умолчанию. Дополнительные сведения см. в статье Работа с многомерными моделями в Power BI. С помощью визуального элемента матрицы можно выполнять всевозможные интересные действия по детализации, недоступные ранее. Это включает в себя возможность детализации по строкам, столбцам и даже по отдельным разделам и ячейкам. Давайте посмотрим, как работает каждый из них. На панели визуализаций, когда вы добавляете несколько полей в раздел Rows скважины Fields , вы включаете действия по детализации строк матричного визуального элемента. На следующем изображении раздел Rows содержит Этап продаж и Размер возможной сделки , создавая группировку (или иерархию) в строках, которые мы можем детализировать, чтобы увидеть подробности. Когда визуальный элемент имеет группу, созданную в разделе Rows , сам визуальный элемент отображает значки сверления и расширения в верхнем углу визуального элемента. Подобно детализации и развертыванию в других визуальных элементах, выбор этих кнопок позволяет нам детализировать (или создать резервную копию) иерархии. В этом случае мы можем перейти от Этап продаж к Размер возможной сделки , как показано на следующем рисунке, где Детализация на один уровень Значок (вилы) был выбран. Помимо использования этих значков, вы можете выбрать любой из этих заголовков строк и развернуть их, выбрав в появившемся меню. Обратите внимание, что в появившемся меню есть несколько параметров, которые дают разные результаты: Выбор Развертка расширяет матрицу для до уровня строки , исключая все остальные заголовки строк, кроме выбранного заголовка строки. . На следующем изображении Предложение > Было выбрано Развертка . Обратите внимание, что другие строки верхнего уровня больше не отображаются в матрице. Этот способ детализации является полезной функцией и становится особенно интересным, когда мы добираемся до раздела перекрестного выделения. Выберите значок Детализация , чтобы вернуться к предыдущему представлению верхнего уровня. Если затем выбрать Предложение > Показать следующий уровень , вы получите восходящий список всех элементов следующего уровня (в данном случае Размер возможной сделки ), без иерархической категоризации более высокого уровня. Выберите значок Детализация в верхнем углу, чтобы в матрице отображались все категории верхнего уровня, затем выберите Предложение > Расширить до следующего уровня , чтобы просмотреть все значения для обоих уровней иерархии — Этап продаж и Размер возможности . Вы также можете использовать пункт меню Expand для дальнейшего управления дисплеем. Например, выберите Сверлить значок . Затем выберите Proposal > Expand > Selection . Power BI отображает одну итоговую строку для каждого этапа продаж и всех параметров размера возможности для предложения . Аналогично возможности детализации строк, вы также можете детализировать столбцы. На следующем изображении в поле Columns есть два поля, что создает иерархию, подобную той, что мы использовали для строк ранее в этой статье. Чтобы развернуть столбцы, выберите Столбцы в меню Детализация , которое находится рядом со значками детализации и развертывания. Выберите регион East и выберите Drill Down 9.0110 . При выборе Детализация отображается следующий уровень иерархии столбцов для Регион > Восток , в данном случае это Количество возможностей . Другой регион скрыт. Остальные пункты меню работают со столбцами так же, как и со строками (см. предыдущий раздел, Детализация заголовков строк ). Вы можете Показать следующий уровень и Расширить до следующего уровня со столбцами так же, как со строками. Примечание Значки детализации и детализации применяются только к строкам. Чтобы развернуть столбцы, вы должны использовать контекстное меню. Матричный визуальный элемент автоматически устанавливает отступы для подкатегорий в иерархии под каждым родительским элементом, что называется ступенчатым макетом. В исходной версии матричного визуального элемента подкатегории отображались в совершенно другом столбце, занимая гораздо больше места в визуальном элементе. На следующем изображении показана таблица в исходном матричном визуальном представлении. обратите внимание на подкатегории в отдельном столбце. На следующем изображении вы видите матричный визуал со ступенчатой компоновкой в действии. Обратите внимание, что категория Qualify имеет подкатегории (маленький, средний и большой) с небольшим отступом, что обеспечивает более чистое и более сжатое изображение. Вы можете легко изменить настройки ступенчатого макета. Выбрав матричный визуальный элемент, в разделе Формат (значок кисти) панели Визуализации разверните раздел заголовков строк. У вас есть два варианта: Переключатель Stepped layout (включает или выключает его) и Stepped layout indentation (указывает величину отступа в пикселях). Если отключить ступенчатый макет, Power BI отображает подкатегории в другом столбце, а не с отступом под родительской категорией. Вы можете включить или выключить промежуточные итоги в матричных визуальных элементах как для строк, так и для столбцов. На следующем изображении вы можете видеть, что промежуточные итоги строк установлены на 9.0109 На и настроить отображение внизу. Когда вы включаете Промежуточные итоги строки и добавляете метку, Power BI также добавляет строку и ту же метку для общего итогового значения. Если вы хотите отключить промежуточные итоги и общий итог, в разделе форматирования панели визуализаций разверните карточку Промежуточные итоги строки . Поверните ползунок промежуточных итогов строки на Выкл. . При этом промежуточные итоги не отображаются. Тот же процесс применяется для промежуточных итогов столбца. Добавьте визуальные подсказки в таблицу или матрицу с помощью условных значков . В разделе формата панели Визуализации разверните карточку Элементы ячейки . Переместите ползунок Icons в положение On и выберите значок определений. Настройте условия, значки и цвета для вашей матрицы и выберите ОК . В этом примере мы использовали красный флажок для низких значений, фиолетовый кружок для высоких значений и желтый треугольник для всего, что между ними. С помощью матричного визуального представления можно выбрать любые элементы в матрице в качестве основы для перекрестного выделения. Выберите столбец в матрице, и Power BI выделит столбец, как и любые другие визуальные элементы на странице отчета. Этот тип перекрестного выделения был общей чертой других визуальных элементов и выбора точек данных, поэтому теперь матричный визуальный элемент предлагает ту же функцию. Кроме того, использование Ctrl+щелчок также работает для перекрестного выделения. Например, на следующем изображении коллекция подкатегорий была выбрана из матричного визуального элемента. Обратите внимание, что элементы, которые не были выбраны в визуальном элементе, отображаются серым цветом, а другие визуальные элементы на странице отражают выбор, сделанный в матричном визуальном элементе. Ваша матрица или таблица может иметь содержимое, которое вы хотели бы использовать в других приложениях: Dynamics CRM, Excel и другие отчеты Power BI. Чтобы скопировать значение одной ячейки, выберите ячейку, щелкните правой кнопкой мыши и выберите Копировать значение . Имея неформатированное значение ячейки в буфере обмена, теперь вы можете вставить его в другое приложение. Чтобы скопировать несколько ячеек, выберите диапазон ячеек или используйте клавишу CTRL, чтобы выбрать одну или несколько ячеек. Копировать выбор гарантирует, что показатели будут отформатированы в соответствии с правилами форматирования столбца, в отличие от неформатированного Команда копирования значения . Копия будет включать заголовки столбцов и строк. Чтобы создать копию самого визуального элемента, содержащего только выбранные ячейки, выберите одну или несколько ячеек с помощью клавиши CTRL, щелкните правой кнопкой мыши и выберите Копировать визуальный элемент . Если затем использовать Ctrl + V для вставки данных на холст, появится копия матричной визуализации, но она будет содержать только ваши скопированные данные. Если у вас есть столбец или мера, содержащие URL-адреса веб-сайтов, вы можете использовать условное форматирование, чтобы применить эти URL-адреса к полям в качестве активных ссылок. Вы найдете эту опцию под карточкой Cell elements на панели форматирования. Включите Web URL и выберите поле, которое будет использоваться в качестве URL-адреса для столбца. После применения значения в этом поле (столбце) становятся активными ссылками. Наведите указатель мыши, чтобы увидеть ссылку, и выберите для перехода на эту страницу. Дополнительные сведения см. в разделе Условное форматирование таблиц. С помощью визуального элемента матрицы можно применять условное форматирование (цвета, заливку и гистограммы) к фону ячеек в матрице, а также применять условное форматирование к тексту и самим значениям . Чтобы применить условное форматирование, выберите визуализацию матрицы и откройте панель Формат . Развернуть карту Cell elements и на Цвет фона , Цвет шрифта или Панели данных , переведите ползунок на Вкл. . Включение одного из этих параметров делает доступным значок его определений. Когда вы выбираете этот значок, вы можете настроить цвета и значения для цветового форматирования. Выберите значок определений, чтобы отобразить диалоговое окно, которое можно использовать для внесения изменений. В этом примере показано диалоговое окно для гистограмм . Неоднородная иерархия имеет уровни без данных. Хорошим примером является матрица сотрудников компании. В компании много уровней, от генерального директора и ниже. Генеральный директор является высшим уровнем в иерархии и не подчиняется другим сотрудникам. В настоящее время невозможно скрыть пустые строки или идентичные родительские и дочерние значения. И вы не можете контролировать, какие уровни иерархии можно и нельзя расширять. Тем не менее, есть несколько шагов, которые вы можете предпринять, чтобы сделать внешний вид более привлекательным. Выключить ступенчатую компоновку. На панели Формат разверните карточку Заголовки строк . Затем откройте раздел карты Options и установите переключатель Stepped layout на .Выкл . Все пустые значения для уровня иерархии теперь будут отображаться в одной строке. Отключить промежуточные итоги для строк и столбцов матрицы. На панели Формат установите ползунок Промежуточные итоги строк и ползунок Промежуточные итоги столбцов в положение Выкл . Если текстовые данные в ячейках или заголовках вашей матрицы содержат символы новой строки, эти символы будут игнорироваться, пока вы не включите параметр «Перенос слов» на соответствующей карточке панели форматирования элемента. Появятся полосы прокрутки, помогающие прокручивать ячейки тела, которые не все сразу помещаются на визуальном элементе, но столбцы заголовков строк фиксируются на матричном визуальном элементе и не будут прокручиваться. Если вы включите в матрицу слишком много заголовков строк, так что ячейки тела будут скрыты, прокрутка не покажет ячейки тела. Вместо этого уменьшите количество заголовков строк в визуальном элементе, отрегулируйте ширину столбца, уменьшите размер шрифта или иным образом обеспечьте видимость ячеек тела матрицы для доступа к вашим данным значения. Настройка (6 − 8 b ) − (17/27)(6 − 12 b ) равно 0, и решение для b дает
Настройка (6 − 8 b ) − (17/27)(6 − 12 b ) равно 0, и решение для b дает Этот пример иллюстрирует следующий общий факт: когда b находится в CS(A) , ранг [ A / b ] совпадает с рангом A ; и, наоборот, когда b не входит в CS(A) , ранг [ A / b ] не совпадает (строго больше) с рангом A . Следовательно, эквивалентный критерий принадлежности к пространству столбцов матрицы выглядит следующим образом:
Этот пример иллюстрирует следующий общий факт: когда b находится в CS(A) , ранг [ A / b ] совпадает с рангом A ; и, наоборот, когда b не входит в CS(A) , ранг [ A / b ] не совпадает (строго больше) с рангом A . Следовательно, эквивалентный критерий принадлежности к пространству столбцов матрицы выглядит следующим образом: сначала найдите пространство всех векторов b такое, что A x = b непротиворечиво, а затем постройте базис для этого пространства. Однако элементарное наблюдение подсказывает более простой подход: Поскольку столбцы A являются строками A T , нахождение основы для CS(A) эквивалентно нахождению основы для RS(A T ) . Сокращение ряда A T дает
сначала найдите пространство всех векторов b такое, что A x = b непротиворечиво, а затем постройте базис для этого пространства. Однако элементарное наблюдение подсказывает более простой подход: Поскольку столбцы A являются строками A T , нахождение основы для CS(A) эквивалентно нахождению основы для RS(A T ) . Сокращение ряда A T дает Создание визуального элемента матрицы в Power BI — Power BI

Понимание того, как Power BI вычисляет итоги
 Это распространенный шаблон, когда значение, которое вы суммируете, находится на стороне «один» отношения «один ко многим».
Это распространенный шаблон, когда значение, которое вы суммируете, находится на стороне «один» отношения «один ко многим». Матрицу можно прикрепить к развернутой или свернутой панели мониторинга. Когда эта плитка панели мониторинга выбрана и отчет открывается, состояние раскрытия по-прежнему можно изменить в отчете.
Матрицу можно прикрепить к развернутой или свернутой панели мониторинга. Когда эта плитка панели мониторинга выбрана и отчет открывается, состояние раскрытия по-прежнему можно изменить в отчете. Использование операций детализации с визуальным элементом матрицы
 Это похоже на создание иерархии, которая затем позволяет выполнять детализацию (а затем резервное копирование) этой иерархии и анализировать данные на каждом уровне.
Это похоже на создание иерархии, которая затем позволяет выполнять детализацию (а затем резервное копирование) этой иерархии и анализировать данные на каждом уровне.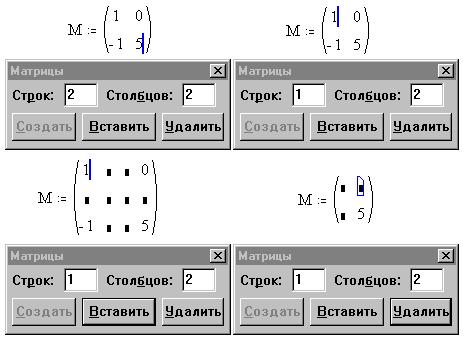

Детализация заголовков столбцов
 В Столбцы поле ну у нас Регион и Сегмент . Как только второе поле было добавлено в Columns , на визуальном элементе отображается новое раскрывающееся меню ( Drill on ), в настоящее время оно показывает Rows .
В Столбцы поле ну у нас Регион и Сегмент . Как только второе поле было добавлено в Columns , на визуальном элементе отображается новое раскрывающееся меню ( Drill on ), в настоящее время оно показывает Rows .
Ступенчатый макет с матричными визуальными элементами

Промежуточные итоги и общие итоги с матричными визуальными элементами
 Чтобы отформатировать общий итог, выберите параметр формата для Общий итог по строке .
Чтобы отформатировать общий итог, выберите параметр формата для Общий итог по строке . Добавление условных значков

Перекрестное выделение с помощью матричных визуальных элементов
Копирование значений из Power BI для использования в других приложениях
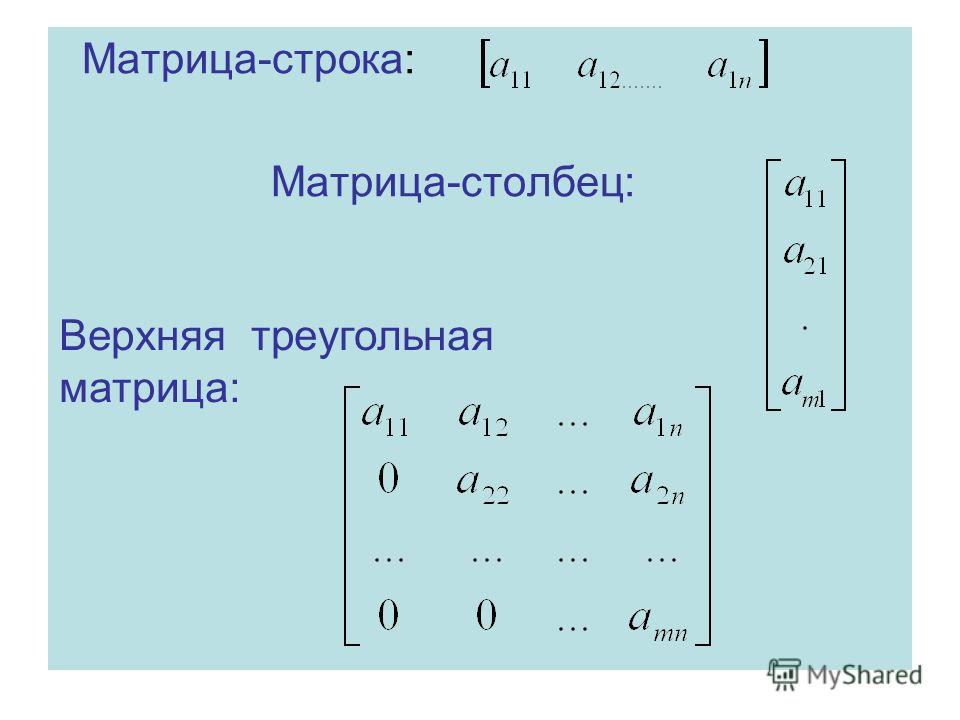 Щелкнув правой кнопкой мыши Power BI, вы можете скопировать одну ячейку или набор ячеек в буфер обмена. Затем вставьте их в другое приложение.
Щелкнув правой кнопкой мыши Power BI, вы можете скопировать одну ячейку или набор ячеек в буфер обмена. Затем вставьте их в другое приложение.
Установка значения матрицы в качестве пользовательского URL-адреса
Затенение и цвета шрифта с визуальными элементами матрицы

Рваная иерархия
 С другой стороны, любой другой сотрудник компании может подчиняться цепочке менеджеров, которые подчиняются вице-президенту, который подчиняется генеральному директору. В зависимости от их уровня в иерархии и того, как организован их отдел, сотрудники могут иметь данные для одного, двух, пяти или десяти уровней в иерархии. И для любого данного сотрудника может не быть данных для определенных уровней иерархии.
С другой стороны, любой другой сотрудник компании может подчиняться цепочке менеджеров, которые подчиняются вице-президенту, который подчиняется генеральному директору. В зависимости от их уровня в иерархии и того, как организован их отдел, сотрудники могут иметь данные для одного, двух, пяти или десяти уровней в иерархии. И для любого данного сотрудника может не быть данных для определенных уровней иерархии.
Соображения и устранение неполадок


 0.]
[0. 0.]]
0.]
[0. 0.]]