10 класс: Информатика от 9.04.2020
08.04.202018:278 апреля 2020 18:27:27
Здравствуйте!
Сегодня мы вернемся к изучению массивов. Одномерные массивы мы подробно рассмотрели, на очереди – матрицы.
С самим понятием матрицы мы знакомы из темы “Графы”.
[spoiler]Принцип работы с матрицами аналогичен работе с одномерными массивами: описание, заполнение, обработка, вывод.
Есть некоторые особенности объявления матриц – в квадратных скобках сначала указываем диапазон изменения строк, а затем столбцов.
Заполнение матрицы осуществляется как и у одномерных массивов: с клавиатуры, случайно, вычислением, из файла. На слайде ниже указан пример заполнения с использованием генератора псевдослучайных чисел. Обратите внимание, все действия с матрицей как правило происходят во вложенных циклах. В указанном примере заполнение проводится по строкам, так как внешний цикл отвечает за изменение номера строки.
Ну а теперь попробуем выполнить практическую часть…
Задания на урок:
«A»: Напишите
программу, которая заполняет квадратную матрицу случайными числами в интервале [10,99], и находит максимальный и минимальный элементы в матрице и их индексы.
Пример:
Матрица А: 12 14 67 45 32 87 45 63 69 45 14 11 40 12 35 15 Максимальный элемент A[2,2]=87 Минимальный элемент A[3,4]=11 |
«B»: Яркости пикселей рисунка закодированы числами от 0 до 255 в виде матрицы. Преобразовать рисунок в черно-белый по следующему алгоритму:
1) вычислить среднюю яркость пикселей по всему рисунку
2) все пиксели, яркость которых меньше средней, сделать черными (записать код 0), а остальные – белыми (код 255)
Пример:
Матрица А: 12 14 67 45 32 87 45 63 69 45 14 11 40 12 35 15 Средняя яркость 37.88 Результат: 0 0 255 255 0 255 255 255 255 255 0 0 255 0 0 0 |
«С»: Заполните матрицу, содержащую N строк и M столбцов, натуральными числами по спирали и змейкой, как на рисунках:
Текст программы вставляем в комментарий к этому сообщению, в теме указываем Фамилию и Имя.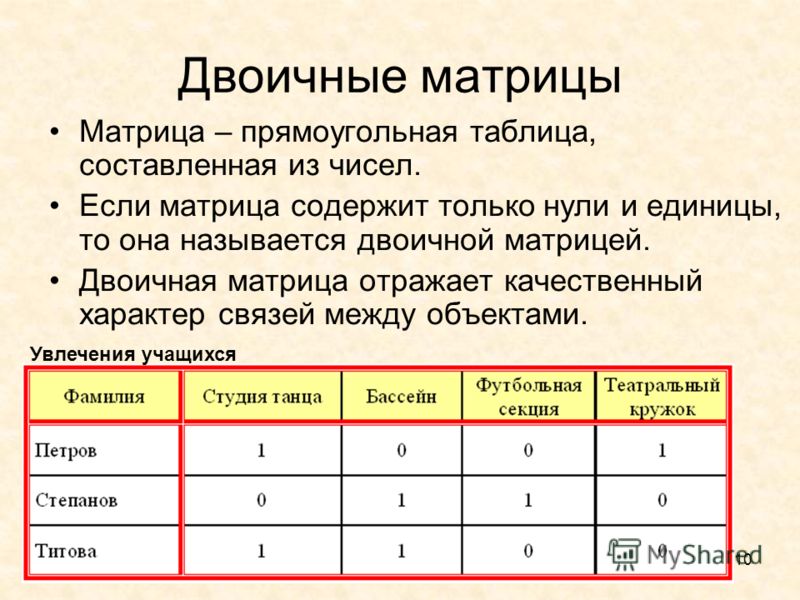
Удачи!
Внимание! Работы принимаю сегодня до 20.00!
Графы, деревья
Графы
Структурируем информацию о дорогах в населенных пунктах: Солнцево, Ясное и Грибное.
«От пос. Васюки идут три дороги в Солнцево, Ягодное и Грибное. Между Грибным и Солнцевым и между Грибным и Ягодным также есть дороги. Есть дорога, идущая из Грибного в лес и возвращается обратно в Грибное».
Нарисуем схему дорог:
Рисунок 1.
В информатике такие схемы называются графами.
Определение 1
Граф – это набор узлов (вершин) и связей между ними (рёбер).
Информацию об узлах и связях обычно записывают в таблицу (матрицу).
Рисунок 2.
Единица на пересечении строки и столбца означает наличие связи между узлами. Ноль говорит о том, что связи нет. Приведенная таблица называется матрицей смежности. Важно, что она симметрична относительно главной диагонали (серые клетки в таблице).
Пример 1
По условию есть дорога, идущая из Грибного в лес и возвращается обратно в Грибное, поэтому на пересечении строки $C$ и столбца $C$ поставлена единица и которая говорит о том, что в графе есть петля – ребро, которое начинается и заканчивается в одной и той же вершине.
Можно составить список смежности. Для каждого узла перечисляются все узлы, с которыми он связан. Для рассмотренного графа список смежности выглядит так:
Матрица смежности (и список смежности) не дают никакой информации о том, как именно расположены узлы друг относительно друга. Для таблицы, приведенной выше, возможны, например, такие варианты:
Рисунок 3.
В рассмотренном примере все узлы связаны, т.е. между любой парой узлов существует путь – последовательность ребер, по которым можно перейти из одного узла в другой, такой граф называется связным.
Пример 2
Теперь представим такую ситацию, что дороги Васюки – Солнцево, Васюки – Грибное и Грибное – Ягодное размыло дождем или завалило снегом так, что по ним не пройти. Тогда схема будет выглядеть следующим образом, как показано на схеме ниже.
Рисунок 4.
Эту схему тоже можно считать графом, но в таком графе есть две несвязанные части, и каждая часть является связным графом. Такие части называют компонентами связности.
Если в примере с дорогами нам нужно знать еще и расстояния между поселками, то каждой связи нужно сопоставить вес (число).
Рисунок 5.
Такой граф называется взвешенным, поскольку каждое ребро имеет свой вес. В реальных задачах это может быть не только расстояние, но и, например, стоимость проезда или другая величина.
Для взвешенного графа в таблице записывается не $1$ или $0$, а вес ребра-длина дороги. Если связи между двумя узлами нет, на бумаге можно оставить ячейку таблицы пустой, а при хранении в памяти компьютера записывать в нее условный код, например, $–1$. Такая таблица называется весовой матрицей, потому что содержит веса ребер. В данном случае она выглядит так:
Рисунок 6.
Также как и матрица смежности, весовая матрица симметрична относительно диагонали. Две пустые ячейки говорят о том, что между узлами $A$ и $D$ нет связи.
Если в графе немного узлов, весовая матрица позволяет легко определить наилучший маршрут из одного узла в другой простым перебором вариантов. Рассмотрим граф, заданный весовой матрицей (числа определяют стоимость поездки между соседними пунктами):
Рисунок 7.
Пример 3
Найдем наилучший путь из $A$ в $B$ – такой, при котором общая стоимость поездки минимальная. Сначала видим, что из пункта $A$ напрямую в $BB$ ехать нельзя, а можно ехать только в $C$ и $D$. Изобразим это на схеме:
Рисунок 8.
Числа около каждого ребер показывают стоимость поездки по этому участку, а индексы у названий узлов показывают общую стоимость проезда в данный узел из узла $A$.
Теперь разберем варианты дальнейшего движения из узла $C$ (узел $A$ уже не нужно рассматривать, так как мы из него пришли).
Рисунок 9.
Видим, что из $C$ сразу можно попасть в $B$, стоимость проезда в этом случае равна семи. Но, это может быть не самый лучший вариант, необходимо проверить еще путь через узел $E$. Действительно, оказывается, что стоимость можно сократить до шести:
Рисунок 10.
Исследовать дальше маршрут, содержащий цепочку $ACED$, нет смысла, потому что его стоимость явно будет больше шести. Аналогично строим вторую часть схемы.
Рисунок 11.
Таким образом, оптимальный (наилучший) маршрут – $ADEB$, его стоимость равна трем.
Если для каждого ребра ещё указывать направление движения, то граф называется ориентированным (или коротко орграфом). Примерами таких дорог может быть модель с односторонним движением. Тогда матрица смежности и весовая матрица для орграфа уже не будут симметричными.
Математика | Матрица Введение | Портал информатики для гиков
Матрица представляет собой набор чисел, расположенных в порядке строк и столбцов. Необходимо заключить элементы матрицы в скобки или скобки.
Матрица с 9 элементами показана ниже.
Эта матрица [M] имеет 3 строки и 3 столбца. Каждый элемент матрицы [M] может быть указан по номеру строки и столбца. Например, 23 = 6
Заказ Матрицы:
Порядок матрицы определяется по количеству строк и столбцов.
Порядок матрицы = Количество строк × Нет. колонн
Поэтому Matrix [M] является матрицей порядка 3 × 3.
Транспонировать Матрицу:
Транспонирование [M] T матрицы mxn [M] — это матрица nxm, полученная путем чередования строк и столбцов в [M].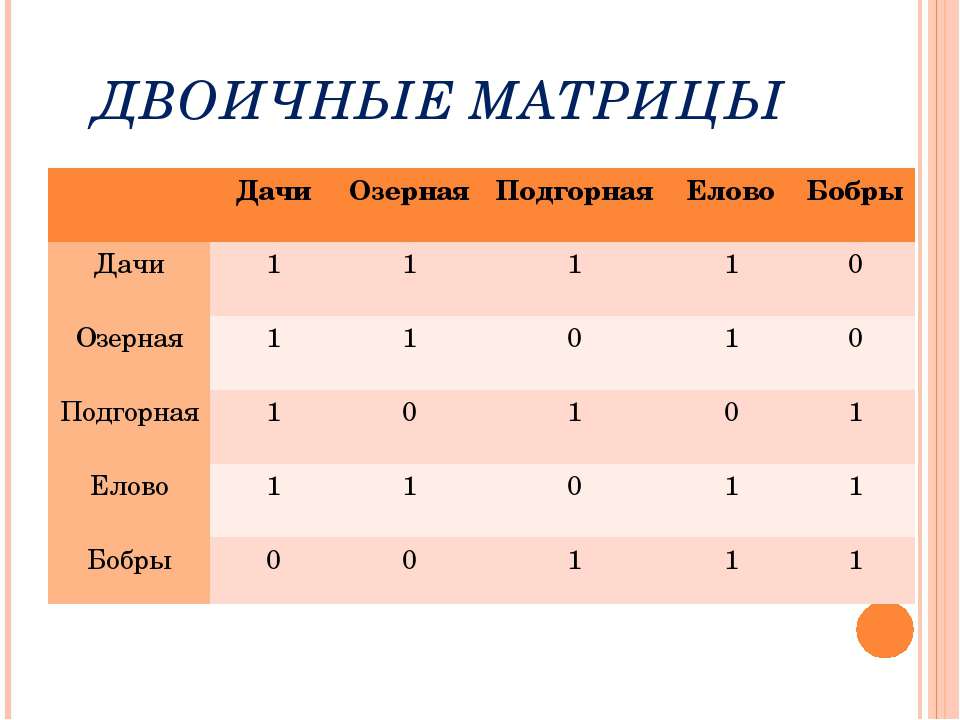
если A = [a ij ] mxn, то A T = [b ij ] nxm, где b ij = a ji
Свойства транспонирования матрицы:
- (A T ) T = A
- (A + B) T = A T + B T
- (AB) T = B T A T
Сингулярная и неособая матрица:
- Сингулярная матрица: квадратная матрица называется сингулярной матрицей, если ее определитель равен нулю, т. Е. | A | = 0
- Неособая матрица. Квадратная матрица называется неособой матрицей, если ее определитель не равен нулю.
Свойства сложения и умножения матриц:
- A + B = B + A (коммутативный)
- (A + B) + C = A + (B + C) (ассоциативный)
- AB ≠ BA (не коммутативный)
- (AB) C = A (BC) (ассоциативный)
- A (B + C) = AB + AC (распределительный)
Квадратная матрица: квадратная матрица имеет столько же строк, сколько столбцов. т.е. нет строк = нет столбцов.
Симметричная матрица: квадратная матрица называется симметричной, если транспонирование исходной матрицы равно ее исходной матрице. т.е. (A T ) = A.
Кососимметричная : Кососимметричная (или антисимметричная или антиметрическая [1]) матрица — это квадратная матрица, транспонирование которой равно ее отрицательному значению .ie (A T ) = -A.
Диагональная матрица. Диагональная матрица — это матрица, в которой все элементы вне главной диагонали равны нулю. Термин обычно относится к квадратным матрицам.
Матрица идентичности: квадратная матрица, в которой все элементы главной диагонали равны единице, а все остальные элементы равны нулю. Матрица идентичности обозначается как I.
Ортогональная матрица: матрица называется ортогональной, если AA T = A T A = I
Идемпонентная матрица.
Матрица называется идемпонентной, если A 2 = A
Инволюционная матрица. Матрица называется инволюционной, если A 2 = I.
Примечание. Каждая квадратная матрица может быть однозначно выражена как сумма симметричной матрицы и кососимметричной матрицы. A = 1/2 (AT + A) + 1/2 (A — AT).
Адъюнкт квадратной матрицы:
Свойства Adjoint:
- A (Adj A) = (Adj A) A = | A | Я н
- Adj (AB) = (Adj B). (Adj A)
- | Adj A | = | A | н-1
- Adj (kA) = k n-1 Adj (A)
Обратная квадратная матрица:
Здесь | A | не должно быть равно нулю, значит, матрица А должна быть неособой.
Свойства обратного:
1. (A -1 ) -1 = A
2. (AB) -1 = B -1 A -1
3. только неособая квадратная матрица может иметь обратную.
Где мы должны использовать обратную матрицу?
Если у вас есть набор одновременных уравнений:
7x + 2y + z = 21
3y — z = 5
-3x + 4y — 2x = -1
Как мы знаем, когда AX = B, то X = A -1 B, поэтому мы вычисляем инверсию A и, умножив ее на B, мы можем получить значения x, y и z.
Трассировка матрицы: трассировка матрицы обозначается как tr (A), которая используется только для квадратной матрицы и равна сумме диагональных элементов матрицы. Помните, что след матрицы также равен сумме собственного значения матрицы. Например:
Эта статья предоставлена Нитика Бансал . Если вы как GeeksforGeeks и хотели бы внести свой вклад, вы также можете написать статью с помощью contribute.geeksforgeeks.org или по почте статьи [email protected]. Смотрите свою статью, появляющуюся на главной странице GeeksforGeeks, и помогите другим вундеркиндам.
Пожалуйста, пишите комментарии, если вы обнаружите что-то неправильное или вы хотите поделиться дополнительной информацией по обсуждаемой выше теме.
Рекомендуемые посты:
Математика | Матрица Введение
0.00 (0%) 0 votes
Разъяснение: Матрицы | MIT News
Среди наиболее распространенных инструментов в электротехнике и информатике – прямоугольные сетки чисел, известные как матрицы. Числа в матрице могут представлять данные, а также математические уравнения. Во многих инженерных приложениях, чувствительных ко времени, умножение матриц может дать быстрые, но хорошие приближения для гораздо более сложных вычислений.Уравнение x – 2y = 0, например, имеет бесконечное количество решений как для x, так и для y, которые можно представить в виде прямой линии, проходящей через точки (0,0), (2,1), (4,2) и т. Д. Но если вы объедините его с уравнением x – y = 1, то будет только одно решение: x = 2 и y = 1. Точка (2,1) также является местом пересечения графиков двух уравнений.
Матрица, изображающая эти два уравнения, будет представлять собой сетку чисел два на два: верхняя строка будет [1-2], а нижняя строка будет [1-1], чтобы соответствовать коэффициентам переменные в двух уравнениях.
В различных приложениях, от обработки изображений до генетического анализа, компьютеры часто используются для решения систем линейных уравнений – обычно с большим числом переменных. Еще чаще их призывают перемножать матрицы.
Умножение матриц можно рассматривать как решение линейных уравнений для определенных переменных.Предположим, например, что выражения t + 2p + 3h; 4т + 5п + 6ч; и 7t + 8p + 9h описывают три различных математических операции, включая измерения температуры, давления и влажности. Их можно представить в виде матрицы с тремя строками: [1 2 3], [4 5 6] и [7 8 9].
Теперь предположим, что в два разных момента времени вы снимаете показания температуры, давления и влажности вне дома.
Эти показания также могут быть представлены в виде матрицы с первым набором показаний в одном столбце, а вторым – в другом.Умножение этих матриц вместе означает сопоставление строк из первой матрицы – той, которая описывает уравнения, – и столбцов из второй – той, которая представляет измерения – умножение соответствующих членов, их сложение и ввод результатов в новую матрицу. Числа в итоговой матрице могут, например, предсказать траекторию движения системы низкого давления.
Конечно, сведение сложной динамики моделей погодных систем к системе линейных уравнений само по себе является сложной задачей.Но это указывает на одну из причин того, что матрицы так распространены в информатике: они позволяют компьютерам, по сути, делать большую вычислительную тяжелую работу заранее. Создание матрицы, которая дает полезные результаты вычислений, может быть трудным, но выполнение матричного умножения, как правило, затруднительно.
Одной из областей информатики, в которой умножение матриц особенно полезно, является графика, поскольку цифровое изображение – это, по сути, матрица для начала: строки и столбцы матрицы соответствуют строкам и столбцам пикселей, а числовые записи соответствуют значениям цвета пикселей.Например, декодирование цифрового видео требует матричного умножения; Ранее в этом году исследователи Массачусетского технологического института смогли создать один из первых чипов, реализующий новый стандарт высокоэффективного кодирования видео для телевизоров сверхвысокой четкости, отчасти благодаря шаблонам, которые они обнаружили в используемых им матрицах.
Точно так же, как матричное умножение может помочь в обработке цифрового видео, оно может помочь в обработке цифрового звука. Цифровой аудиосигнал – это в основном последовательность чисел, представляющая изменение во времени давления воздуха акустического аудиосигнала.Многие методы фильтрации или сжатия цифровых аудиосигналов, такие как преобразование Фурье, основаны на матричном умножении.
Еще одна причина того, что матрицы так полезны в информатике, – это графики. В этом контексте граф – это математическая конструкция, состоящая из узлов, обычно изображаемых как круги, и ребер, обычно изображаемых как линии между ними. Сетевые диаграммы и родословные – это знакомые примеры графов, но в информатике они используются для представления всего, от операций, выполняемых во время выполнения компьютерной программы, до взаимосвязей, характерных для задач логистики.
Каждый граф может быть представлен в виде матрицы, где каждый столбец и каждая строка представляют узел, а значение на их пересечении представляет силу связи между ними (которая часто может быть равна нулю). Часто наиболее эффективным способом анализа графов является их сначала преобразование в матрицы, а решения проблем, связанных с графами, часто являются решениями систем линейных уравнений.
Кодирование матрицы
О курсе
Курс преподается в Университете Брауна с 2008 г.
и учат осенью
2017 г.Слайды из прошлых выпусков курса Университета Брауна доступны здесь.
Укороченная версия была обучена на Coursera. Цель этого курса – предоставить студентам, заинтересованным в
информатика – введение в векторы и матрицы, а также
их использование в приложениях CS.
Курс основан на заявках из областей, выбранных из среди: компьютерное зрение, криптография, теория игр, графика, поиск информации и веб-поиск, а также машинное обучение.
Ресурсы для курса
Данные и код поддержки, необходимые для выполнения здесь представлены задания.
Автоматическая оценка доступен для некоторых задач.
Вот
первая и вторая лаборатории из первого издания. У них ничего нет
делать с линейной алгеброй. Они предоставляются, чтобы принести
читатель быстро ознакомится с той частью Python, которую мы используем в книге.
Вот
документ, предназначенный для помощи людям в переходе
от петель к пониманию.
Слайды
Слайды из курса, прочитанного в Университете Брауна осенью 2013 года:
Вот примеры приложений, рассматриваемых в Кодирование Матрица .
кроссфейд
Отрезок между точками задается выпуклым
комбинации этих точек; если «точки» – изображения,
Линейный сегмент – это простой переход между изображениями.
Перспективное исправление
Учитывая фотографию доски, сделанную под углом, синтезируйте вид доски без перспективы.
Такое же преобразование можно использовать при использовании Wiimote для
недорогая интерактивная доска или световое перо (благодаря Джонни
Чанг Ли).
Коды с исправлением ошибок
Используются коды с исправлением ошибок, e.г., по мобильным телефонам на
сохранить данные, передаваемые по шумному каналу, в то время как
поддержание высокой пропускной способности.
Целочисленное разложение
522253825433285668885771662040104167 =
891428822186035241 ∙ 5858614983443
Факторизация целого числа – сложная вычислительная задача (и криптосистема RSA зависит от ее сложности). На ядро самых сложных алгоритмов целочисленного факторинга это простая задача линейной алгебры.
Размытие изображения
Размытие изображения – это простое линейное преобразование.
Поиск в аудиоклипе
Можно сформулировать поиск одного аудиоклипа в другом
как свертка.
Свертка может быть вычислена очень
быстро с помощью быстрого преобразования Фурье.
Поиск в изображении
Свертка также может выполняться в двух измерениях, что позволяет
для быстрого поиска части изображения в изображении.
Сжатие аудио и изображений
Сжатие аудио и изображений способствует эффективному хранению и
коробка передач. Методы сжатия с потерями, такие как
те, которые используются в MP3 (аудио) и JPEG (изображения), основаны на
часть по линейной алгебре,
например вейвлет-преобразование и преобразование Фурье.
100% оригинал размер
40% оригинал размер
10% оригинал размер
Распознавание лиц
«Классический» подход к распознаванию лиц – собственные лица,
техника, связанная с анализом главных компонент.
Преобразования 2D-графики
Простые преобразования, возникающие в графике, такие как
вращение, перемещение и масштабирование можно выразить с помощью
матрицы.
Погаснет
Lights Out – это головоломка, в которой вы должны выбрать
правильные кнопки нажимать, чтобы все огни погасли
вне.Поиск решения может быть выражен как проблема в
линейная алгебра.
Минимальный пролетный лес
Нахождение остовного дерева минимального веса графа может быть
интерпретируется как проблема поиска минимального веса
для векторного пространства
, полученного из графа.
Схема графика
Хороший рисунок графика может быть получен из собственных векторов
связанная матрица.
Когда большинство людей думают о слове «матрица , », они, вероятно, думают о фильме 1999 года с Киану Ривзом в главной роли. Фильм касается только математической концепции матриц, поскольку зловещие компьютеры в фильме используют матрицы для работы, как и многие реальные компьютеры.
Действительно, матрицы действительно используются в информатике , потому что они представляют собой удобный и компактный способ представления больших наборов чисел.Некоторые экономические теории также могут быть хорошо представлены с помощью матриц. В математике принципы матриц важны для теории графов и реального анализа.
Это руководство начинается с рассмотрения небольших матриц , а именно матриц с двумя столбцами и двумя строками.
Тема начинается с подробного описания их описания и выполнения операций с матрицами 2 × 2. Также объясняется, как эти концепции могут использоваться для представления информации.
Вторая тема в этом руководстве обобщает информацию из первой части на все матрицы.Он заканчивается введением стратегий сокращения строк для решения матриц и нескольких других более сложных тем, которые используются в других разделах математики.
Введение в матрицы 2 × 2
Матрица 2 × 2 имеет две строки и два столбца. У них есть некоторое сходство с таблицами, поскольку в них есть строки и столбцы, но есть существенные различия. Таблицы предназначены для графического отображения. Ими можно управлять, чтобы отображать информацию в определенном свете, но операции между таблицами не имеют смысла.
С другой стороны, матрицы – это массив набора чисел. Между числами нет жесткого деления, как в таблице, и есть способы выполнять операции с использованием матриц.
Операции с матрицами , однако, более сложны, чем основные математические операции, используемые для сложения, вычитания, умножения и деления отдельных членов или даже функций.
Частично это связано с тем, что матрица обычно содержит много элементов (также известных как элементы), и операции обычно выполняются с другими матрицами, за исключением случая скалярного умножения.Однако можно складывать, вычитать, умножать и брать степени матриц с некоторыми ограничениями. Также возможно найти инверсию некоторых матриц.
В этом разделе представлены эти концепции с матрицами 2 × 2 перед их обобщением для матриц любого размера в следующем разделе.
Он открывается описанием матриц, а затем вводит операции сложения, вычитания, скалярного умножения и умножения матриц. Затем обсуждается единичная матрица 2 × 2, показанная выше, и ее свойства.В следующем разделе рассматриваются детерминанты и то, как их можно использовать, чтобы определить, есть ли у матрицы инверсия, и если да, то что это такое.
Наконец, тема завершается способами математического использования матриц для представления информации.
Введение в другие матрицы
Концепции, представленные в первом разделе для матриц 2 × 2, могут быть распространены на другие матрицы. Технически матрица может иметь бесконечно много строк и столбцов, а матрица с m строками и n столбцами называется матрицей m x n (читается «m на n»).Представления общей матрицы обычно включают элементы с двумя нижними индексами.
Первый представляет строку элемента, а второй представляет столбец элемента.
Например, первый элемент в верхнем левом углу общей матрицы будет иметь индекс 11, а элемент в правом нижнем углу матрицы m x n будет иметь индекс mn, как показано на рисунке.
Матрицы, используемые для представления информации по таким предметам, как информатика, могут быть огромными, хотя на самом деле они представляют собой сжатое и удобное представление.
Хотя такие вещи, как умножение матриц, включают в себя множество шагов, существуют повторяющиеся алгоритмы, которые программы могут использовать для вычисления крупномасштабного умножения матриц.
Этот раздел начинается с общего введения в матрицы и матричные операции. Затем обсуждается, как найти определители 2×2 и 3×3, прежде чем обобщать процесс для любой квадратной матрицы.
Эта информация используется, чтобы объяснить, как упростить и найти инверсию таких матриц. В теме также рассказывается, как можно использовать обратное для решения систем уравнений, представленных с помощью матриц.Наконец, тема завершается объяснением методов сокращения строк и других применений матриц.
Введение в матрицы
Операции с матрицами
Применения матриц
Определитель матрицы
Инверсия матрицы
Решите 9194 с помощью системы уравнений детерминанты
Бесплатный онлайн-курс: Кодирование матрицы: линейная алгебра через приложения для компьютерных наук от Coursera
Проза Симиан закончил этот курс, проводя на нем 9 часов в неделю, и нашел его трудным.
Теперь закончено, я все еще разрываюсь с этим курсом. Но я поднял его до четырех звезд. Положительные: – используя Python – необходимость использовать доктесты (да, серьезно, я не совсем понял смешные комментарии, которым предшествует >>> перед этим: s) – строю свою редкую …
Читать далее Теперь, когда я закончил, я остаюсь в растерянности. Но я поднял его до четырех звезд. Положительные стороны:
– использование Python
– необходимость использования доктестов (да, серьезно, я действительно не понимал забавных комментариев, которым предшествует >>> перед этим: s)
– построение моей собственной разреженной простой матрицы и векторных классов
– GF2 (= “двоичная арифметика без цифры переноса”, когда этот сенокосец наконец понял это)
– тщательно подготовленный материал и лекции
– привязка линейных концепций к приложениям (мои фавориты: коррекция перспективы и разложение больших чисел)
– множественные интерпретации умножения матриц
– Профессор Кляйн и ТА чрезвычайно активны и полезны на форумах
Отрицательные:
– нет (в свободном доступе) текста для уточнения
– лекции немного быстро развиваются
– в лекциях несколько раз пропущены шаги, которые остались меня мучили часы, действительно ли я понимаю, что происходит.
– довольно много ошибок в лекциях
– резкие изменения громкости звука лекций
– проблемы с отправкой ответов (тесты для оценивания отличаются от предоставленных тестов, и – потому что некоторые из нас не знали, что тестовый пример для оценивателя был доступен запуск с флагом – прохождение доктестов, но провал грейдера приводит к ужасному ощущению опускания)
– ужасная схема выставления оценок (пороги сдачи / отличия применяются по разделам, с минимальным падением, а не до общего среднего. 20% штраф за позднюю подачу заявки получить различие, если опоздал более чем один раздел, было невозможно, даже со 100% нескорректированным.)
, возможно, только для меня
– трудности с поиском доказательств в форме лекций (возможно, мне просто нужно записать их и подумать о них больше)
– использование Python 3.x немного затруднительно.
В целом, несколько несовершенное исполнение отличной идеи. К сожалению, из-за недостатков, которые сделали и без того сложную тему немного сложнее – так что я надеюсь, что их можно сгладить в ходе повторных итераций.
Но что интересно, я горжусь тем, что завершил МООК. С нетерпением жду возможности переснять его – чтобы убедиться, что я действительно «понял» – и обещанных последующих действий профессора Кляйна.
(РЕДАКТИРОВАТЬ: но ненадолго; с форума: «Следующий курс еще не запланирован. Я еще не уверен, когда он будет запущен. Я объявлю в списке рассылки codingthematrix. Он будет скорее всего, не раньше, чем через год из-за предстоящего большого проекта с моей стороны. “)
Определение матрицы
Матрица – это сетка, используемая для хранения или отображения данных в структурированном формате. Он часто используется как синоним таблицы, которая содержит горизонтальные строки и вертикальные столбцы.
Хотя термины «матрица» и «таблица» могут использоваться как синонимы, матрицы (или матрицы) считаются более гибкими, чем таблицы. Например, таблицы обычно имеют фиксированное количество строк и столбцов, а размер матрицы может изменяться динамически.
Термин «матрица» также может использоваться для обозначения таблицы, которая имеет группы столбцов в одной строке.
При вычислениях матрица может использоваться для хранения группы связанных данных. Например, некоторые языки программирования поддерживают матрицы как тип данных, который обеспечивает большую гибкость, чем статический массив.Сохраняя значения в матрице, а не как отдельные переменные, программа может получать доступ к данным и выполнять операции с ними более эффективно.
В математике матрицы используются для отображения связанных чисел. Математические матрицы обычно представлены в виде списка чисел в квадратных скобках. Матрица, содержащая только одну строку, называется вектором-строкой, а матрица, содержащая один столбец, называется вектором-столбцом. Матрица, которая содержит такое же количество строк, что и столбцы (например, матрица 4×4), называется квадратной матрицей.
ПРИМЕЧАНИЕ: Хотя термин «матрица» имеет техническое значение как в вычислениях, так и в математике, он также используется в повседневной речи для описания структурированных данных. Например, сравнительную диаграмму можно также назвать сравнительной матрицей, потому что она содержит список значений в формате сетки.
Обновлено: 2 июля 2013 г.
TechTerms – Компьютерный словарь технических терминов
Эта страница содержит техническое определение Matrix. Он объясняет в компьютерной терминологии, что означает «Матрица», и является одним из многих технических терминов в словаре TechTerms.
Все определения на веб-сайте TechTerms составлены так, чтобы быть технически точными, но также простыми для понимания. Если вы сочтете это определение матрицы полезным, вы можете сослаться на него, используя приведенные выше ссылки для цитирования. Если вы считаете, что термин следует обновить или добавить в словарь TechTerms, отправьте электронное письмо в TechTerms!
Подпишитесь на рассылку TechTerms, чтобы получать избранные термины и тесты прямо в свой почтовый ящик.
Вы можете получать электронную почту ежедневно или еженедельно.
Подписаться
Матрица| математика | Britannica
Matrix , набор чисел, расположенных в строках и столбцах, чтобы сформировать прямоугольный массив.Числа называются элементами или элементами матрицы. Матрицы находят широкое применение в технике, физике, экономике и статистике, а также в различных областях математики. Исторически первым распознаванием была не матрица, а определенное число, связанное с квадратным массивом чисел, называемое определителем. Лишь постепенно возникла идея матрицы как алгебраической сущности. Термин матрица был введен английским математиком 19-го века Джеймсом Сильвестром, но именно его друг математик Артур Кэли развил алгебраический аспект матриц в двух статьях 1850-х годов.Кэли впервые применил их к изучению систем линейных уравнений, где они до сих пор очень полезны. Они также важны, потому что, как признал Кэли, определенные наборы матриц образуют алгебраические системы, в которых действуют многие обычные законы арифметики (например, ассоциативные и распределительные законы), но в которых действуют другие законы (например, закон коммутативности). недействительно. Матрицы также нашли важное применение в компьютерной графике, где они использовались для представления поворотов и других преобразований изображений.
Если имеется m строк и n столбцов, матрица называется матрицей « m на n », записанной « m × n ». Например,
– это матрица 2 × 3. Матрица с n строками и n столбцами называется квадратной матрицей порядка n . Обычное число можно рассматривать как матрицу 1 × 1; таким образом, 3 можно рассматривать как матрицу [3].
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.Подпишитесь сейчас В общепринятых обозначениях заглавная буква обозначает матрицу, а соответствующая строчная буква с двойным нижним индексом описывает элемент матрицы.
Таким образом, a ij – это элемент в i -й строке и j -м столбце матрицы A . Если A – это матрица 2 × 3, показанная выше, то a 11 = 1, a 12 = 3, a 13 = 8, a 21 = 2, a 22 = −4 и a 23 = 5.При определенных условиях матрицы можно складывать и умножать как отдельные объекты, в результате чего возникают важные математические системы, известные как матричные алгебры.
Матрицы естественным образом встречаются в системах одновременных уравнений. В следующей системе для неизвестных x и y ,
массив чисел
представляет собой матрицу, элементы которой являются коэффициентами неизвестных. Решение уравнений полностью зависит от этих чисел и от их конкретного расположения.Если бы 3 и 4 поменяли местами, решение было бы другим.
Две матрицы A и B равны друг другу, если они имеют одинаковое количество строк и одинаковое количество столбцов и если a ij = b ij для каждый i и каждый j . Если A и B – две матрицы m × n , их сумма S = A + B представляет собой матрицу m × n , элементы которой s ij = a ij + b ij .То есть каждый элемент S равен сумме элементов в соответствующих позициях A и B .
Матрица A может быть умножена на обычное число c , которое называется скаляром. Продукт обозначается как cA или Ac и представляет собой матрицу, элементы которой равны ca ij .
Умножение матрицы A на матрицу B для получения матрицы C определяется только тогда, когда количество столбцов первой матрицы A равно количеству строк второй матрицы B .
Чтобы определить элемент c ij , который находится в строке i и столбце j продукта, первый элемент в строке i строки A умножается на первый элемент в столбце j -й столбца B , второй элемент в строке – второй элемент в столбце и так далее, пока последний элемент в строке не умножится на последний элемент столбца; сумма всех этих произведений дает элемент c ij .В символах для случая, когда A имеет м столбцов, а B имеет м строк,
Матрица C имеет столько же строк, сколько A и столько же столбцов, сколько B .
В отличие от умножения обычных чисел a и b , в котором ab всегда равно ba , умножение матриц A и B не является коммутативным. Однако оно ассоциативно и распределительно по сравнению с сложением.То есть, когда операции возможны, всегда выполняются следующие уравнения: A ( BC ) = ( AB ) C , A ( B + C ) = AB + AC и ( B + C ) A = BA + CA . Если матрица 2 × 2 A , строки которой равны (2, 3) и (4, 5), умножается сама на себя, то произведение, обычно записываемое как A 2 , имеет строки (16, 21) и ( 28, 37).
Матрица O со всеми ее элементами 0 называется нулевой матрицей. Квадратная матрица A с единицами на главной диагонали (вверху слева направо вниз) и нулями во всех остальных местах называется единичной матрицей. Он обозначается I или I n , чтобы показать, что его порядок равен n . Если B – любая квадратная матрица, а I и O – единичная и нулевая матрицы одного порядка, всегда верно, что B + O = O + B = B и BI = IB = B .
Следовательно, O и I ведут себя как 0 и 1 в обычной арифметике. Фактически, обычная арифметика является частным случаем матричной арифметики, в которой все матрицы имеют размер 1 × 1.
Связано с каждой квадратной матрицей A – это число, известное как определитель A , обозначаемое det A . Например, для матрицы 2 × 2
det A = ad – bc . Квадратная матрица B называется невырожденной, если det B ≠ 0.Если B неособое, существует матрица, обратная B , обозначенная B -1 , так что BB -1 = B -1 B = Я . Уравнение AX = B , в котором A и B – известные матрицы, а X – неизвестная матрица, может быть решено однозначно, если A – невырожденная матрица, тогда A −1 существует, и обе части уравнения можно умножить слева на него: A −1 ( AX ) = A −1 B .Теперь A −1 ( AX ) = ( A −1 A ) X = IX = X ; следовательно, решение будет X = A -1 B . Система из m линейных уравнений в n неизвестных всегда может быть выражена как матричное уравнение AX = B , в котором A – это матрица коэффициентов неизвестных m × n , X – это матрица неизвестных размером n × 1, а B – это матрица n × 1, содержащая числа в правой части уравнения.
Проблема, имеющая большое значение во многих областях науки, заключается в следующем: по квадратной матрице A порядка n, найти матрицу n × 1 X, , называемую n -мерным вектором, таким образом, что AX = cX .
Здесь c – число, называемое собственным значением, а X – собственным вектором. Существование собственного вектора X с собственным значением c означает, что определенное преобразование пространства, связанное с матрицей A , растягивает пространство в направлении вектора X на коэффициент c .
5 приложений линейной алгебры в науке о данных | Сара А. Метвалли
Машинное обучение, без сомнения, является наиболее известным приложением искусственного интеллекта (ИИ). Основная идея машинного обучения – дать системам возможность автоматически учиться и совершенствоваться на основе опыта, не будучи явно запрограммированными на это. Машинное обучение функционирует через создание программ, которые имеют доступ к данным (постоянным или обновленным) для анализа, поиска закономерностей и обучения. Как только программа обнаруживает взаимосвязи в данных, она применяет эти знания к новым наборам данных.Вы можете узнать больше о том, как алгоритмы учатся, из этой статьи.
Линейная алгебра имеет несколько приложений в машинном обучении, таких как функции потерь, регуляризация, поддержка векторной классификации и многое другое. В этой статье, однако, мы рассмотрим только линейную алгебру в функциях потерь.
Функция потерь
Алгоритмы машинного обучения работают так: они собирают данные, анализируют их, а затем создают модель, используя один из многих подходов (линейная регрессия, логистическая регрессия, дерево решений, случайный лес и т. Д.). Затем, основываясь на результатах, они могут предсказать будущие запросы данных.
Но…
Как вы можете измерить точность вашей прогнозной модели?
Использование линейной алгебры, в частности, использование функций потерь. Функция потерь – это метод оценки точности ваших моделей прогнозирования . Будет ли он хорошо работать с новыми наборами данных? Если ваша модель полностью отключена, функция потерь выдаст большее число.
Если бы он был хорошим, функция потерь выдала бы меньшую сумму.
Регрессия моделирует взаимосвязь между зависимой переменной Y и несколькими независимыми переменными Xi. После того, как это соотношение построено, мы пытаемся уместить в пространстве линию этих переменных, а затем используем эту линию для прогнозирования будущих значений Xi. Существует много типов функций потерь, некоторые из которых сложнее других; однако наиболее часто используются два типа: средняя квадратичная ошибка и средняя абсолютная ошибка .
Среднеквадратичная ошибка (MSE), вероятно, является наиболее часто используемым подходом к ошибкам потерь, легким для понимания и реализации и обычно достаточно хорошо работает в большинстве задач регрессии.Большинство библиотек Python, используемых в науке о данных, Numpy, Scikit и TensorFlow, имеют собственную встроенную реализацию функциональности MSE. Несмотря на это, все они работают на основе одного и того же уравнения:
Где N – количество точек данных как в наблюдаемых, так и в прогнозируемых значениях.
Этапы вычисления MSE:
- Вычислите разницу между каждой парой наблюдаемых и прогнозируемых значений.
- Возьмите разницу в квадрате.
- Сложите квадраты разностей, чтобы найти кумулятивное значение.
- Вычислить среднюю ошибку накопленной суммы.
Вот код Python для расчета и построения графика MSE.
Большинство специалистов по обработке данных не любят использовать MSE, потому что он может не полностью отражать ошибку. Однако он обычно используется в качестве промежуточного шага к среднеквадратической ошибке (RMSE), которую можно легко получить, взяв квадратный корень из MSE.
Средняя абсолютная ошибка (MAE) очень похожа на MSE; разница в том, что мы вычисляем абсолютную разницу между наблюдаемыми и защищенными данными.
Стоимость MAE более высокая по сравнению с MSE. Однако недостатком MAE является то, что обрабатывать оператор абсолютного или модульного значения в математических уравнениях непросто.