Матрица в математике для чего нужна: для чего нужны, применение, кто придумал, история возникновения

Что такое матрица — Журнал «Код»

Разработчики нейросетей говорят, что все нейросети — это просто бесконечное перемножение матриц. Мы решили разобраться, что это за матрицы и как их перемножать, а для этого пришлось полезть в линейную алгебру. И это оказалось не так сложно, как мы думали:

Эксперимент: что нейронка думает о жизни, Вселенной и всём прочем

• Вектор — это просто группа из нескольких чисел, выстроенных в определённой последовательности. Например, рост и вес человека можно представить как вектор (172, 80). Ничего сложного. 
• У вектора может быть внутри сколько угодно чисел. Главное — чтобы мы договорились, что для нас значат эти числа, и не меняли их местами просто так, произвольно. 
• Векторы можно складывать, вычитать, умножать. Это чуть сложнее, чем с обычными числами. 
• У вектора есть понятие линейной зависимости. Грубо говоря — параллельны друг другу векторы или нет. От этого зависит, какие операции можно делать с этими векторами.  

Вектор — это «кирпичик» линейной алгебры. На его основе мы переходим к понятию матрицы. 

Что такое матрица

Если вектор — это строка с числами в определённом порядке, то матрица — это таблица с числами в определённом порядке. Как у любой таблицы, у матрицы есть столбцы и строки. В них сидят какие-то числа. Всё вместе — это математический объект, то есть в каких-то случаях всю эту таблицу можно рассматривать как единое целое и совершать с ним операции. 

Матрицы принято обозначать большими буквами латинского алфавита вроде А, В, С, D и так далее. 

Числа внутри матрицы называют элементами. Каждый элемент обозначается двумя цифрами: первая цифра указывает на строку, а вторая — на столбец. Это адрес числа внутри матрицы. Например, элемент А₂₃ означает, что нужное число находится во второй строке и третьем столбце. Нумерация элементов нужна для записи формул и устного объяснения того, где находится нужное число в матрице. 

В матрице может находиться неограниченное количество строк, столбцов и элементов. Из-за этого матрицы бывают разных видов и могут обладать разными особенностями. Например, если в матрице совпадает число строк и столбцов, то такая матрица называется квадратной. 

В этой статье и в следующих материалах мы будем рассматривать разные виды матрицы и постепенно изучим их особенности.

Общая схема матрицыПример квадратной матрицы с пятью строками и столбцами. Записывается как матрица размера 5×5. В числовой матрице мы не нумеруем элементы — они закрепляются за числами по умолчанию. Например, элементу А₂₃ соответствует число три

Простые операции с матрицами

Вынесение минуса за пределы матрицы. Если внутри матрицы у большинства элементов знак минус, то часто это мешает расчётам или приводит к ошибкам. Чтобы этого избежать, от минуса избавляются. Для этого нужно вынести минус за пределы матрицы и изменить знак всех элементов внутри самой матрицы. 

И наоборот: если внутри матрицы у большинства элементов знак минус и перед матрицей стоит минус, то минус можно внести в матрицу.

Выносим минус за пределы матрицы и получаем вместо двадцати одного отрицательного элемента — четыреПеред матрицей минус, и внутри у большинства элементов минус. Вносим минус в матрицу и делаем её удобной для дальнейших вычислений

Умножение матрицы на число. Для умножения матрицы на число достаточно каждый элемент матрицы умножить на это число.

Пример умножения матрицы на число

Транспонирование матрицы. Это операция, которая позже нам понадобится для решения матричных уравнений. Для транспонирования мы берём известную матрицу, меняем в ней местами строки со столбцами и получаем новую матрицу. Как бы поставили матрицу набок. 

⚠️ При этом в матрице запрещено в произвольном порядке менять элементы. Зато можно полностью менять местами строки или столбцы. Если мы поменяем местами первую и вторую строку, то это останется прежняя матрица.

Схема транспонирования матриц: первая строка переходит в первый столбец, вторая строка — во второй столбец и так далее в зависимости от количества элементов матрицыПример транспонирования. Транспонированная матрица обозначается буквой той же матрицы, из которой она получилась + надстрочечный индекс в виде печатной буквы «Т» Матрицу можно перетасовывать, но это нужно делать по правилам. Транспонирование — одно из таких правил

Сложение и вычитание матриц

Если в нескольких матрицах совпадает число строк и столбцов, то мы можем их складывать и вычитать. Для вычислений нам нужно поэлементно сложить или вычесть каждый элемент матриц: первый элемент первой матрицы складываем с первым элементом второй матрицы или вычитаем из него и так далее. В результате получаем новую матрицу.

Пример сложения двух прямоугольных матриц с тремя строками и двумя столбцами Пример вычитания двух матриц

Умножение матриц 

Матрицы умножаются по принципу строка на столбец. Мы умножаем первую строку первой матрицы, на первый столбец второй матрицы, складываем результаты и получаем первый элемент новой матрицы. По аналогичной схеме вычисляем все остальные элементы. Звучит запутанно, поэтому идём по шагам: 

1. У нас есть две матрицы A и B. Их нужно перемножить, чтобы получить новую матрицу C. 
2. Размер матрицы A два на два: есть две строки и два столбца. Первая строка состоит из элементов А₁₁ и А₁₂; вторая — А₂₁ и А₂₂. 
3. У матрицы B такая же размерность: есть две строки и два столбца. Первая строка состоит из элементов B₁₁ и B₁₂; вторая — B₂₁ и B₂₂. 
4. У нас две одинаковые по размеру матрицы с двумя строками и столбцами. Это значит, что и матрица C будет размером два на два. Первая строка будет состоять из элементов C₁₁ и C₁₂; вторая — C₂₁ и C₂₂. 
5. Считаем элемент C₁₁. Умножаем первый элемент первой строки матрицы А (А₁₁) на первый элемент первого столбика матрицы B (B₁₁). Это первая часть, после которой ставим знак плюс. Вторая часть: умножаем второй элемент первой строчки матрицы А (А₁₂) на второй элемент первого столбика матрицы B (B₂₁). Складываем обе части и получаем первый элемент первой строки матрицы С (C₁₁). 
6. Считаем элемент C₁₂. Умножаем первый элемент первой строки матрицы А (А₁₁) на первый элемент второго столбика матрицы B (B₁₂). Это первая часть. Вторая часть: умножаем второй элемент первой строчки матрицы А (А₁₂) на второй элемент второго столбика матрицы B (B₂₂). Складываем части и получаем второй элемент первой строки матрицы С (C₁₂). 
7. Считаем элемент C₂₁. Умножаем первый элемент второй строки матрицы А (А₂₁) на первый элемент первого столбика матрицы B (B₁₁). Это первая часть. Вторая часть: умножаем второй элемент второй строки матрицы А (А₂₂) на второй элемент первого столбика матрицы B (B₂₁). Складываем части и получаем первый элемент второй строки матрицы С (C₂₁). 
8. Считаем элемент C₂₂. Умножаем первый элемент второй строки матрицы А (А₂₁) на первый элемент второго столбика матрицы B (B₁₂). Это первая часть. Вторая часть: умножаем второй элемент второй строки матрицы А (А₂₂) на второй элемент второго столбика матрицы B (B₂₂). Складываем части и получаем второй элемент второй строки матрицы С (C₂₂). 

Если нам нужно найти матрицу в квадрате, то мы умножаем эту матрицу на саму себя. Если нужна матрица в кубе — умножаем её на саму себя три раза и так далее в зависимости от количества степеней. Если в одной из матриц все элементы нули, то она считается нулевой и после умножения на другую матрицу даёт нулевую матрицу — это как нуль умноженный на число всегда даёт нуль.

Формула умножения матрицПример умножения квадратных матриц размерностью 2×2

Что дальше 

В следующий раз продолжим знакомиться с базовыми понятиями, которые нам понадобятся для решения матричных уравнений. А на сегодня Нео свободен 👽

Текст:

Александр Бабаскин

Редактура:

Максим Ильяхов

Художник:

Даня Берковский

Корректор:

Ирина Михеева

Вёрстка:

Мария Дронова

Соцсети:

Олег Вешкурцев

Математика для ИИ: линейная алгебра

В мире IT сейчас часто можно услышать о машинном обучении, нейронных сетях и искусственном интеллекте. И не удивительно — эти отрасли быстро развиваются и используются для решения различного рода задач.

Большинство концепций были открыты ещё 50 лет назад, и множество из них основаны на математических принципах. Поэтому у людей, пытающихся войти в данную нишу, часто возникает вопрос: «На каком уровне нужно знать математику?». Эта статья даст представление о некоторых необходимых основах, в частности, о базовых концепциях линейной алгебры.

Базовые термины

По сути, вся линейная алгебра вертится вокруг нескольких понятий: векторы, скаляры, тензоры и матрицы, — всё это очень важно для машинного обучения, ведь благодаря им можно абстрагировать данные и модели. Например, каждая запись в каком-нибудь наборе данных может быть представлена в виде вектора в многомерном пространстве, а параметры нейронных сетей абстрагируются как матрицы. Каждое из понятий по своему специфично, так что рассмотрим их подробнее.

Скаляр

Скаляр — это просто число, в отличие от вектора или матрицы. Скаляры определены как элементы поля, предназначенные для описания пространства вектора. Несколько скаляров образуют вектор. Скаляры могут быть представлены разными типами чисел: вещественными, действительными или натуральными. Обозначаются скаляры строчными и прописными буквами латинского и греческого алфавита:

Вектор

Вектор — это упорядоченный массив скаляров. Скаляры выступают в роли координат точек в пространстве. Скопление векторов становится так называемым векторным пространством. Векторы можно складывать вместе, перемножать друг на друга и масштабировать. Они обозначаются жирным шрифтом. Каждый элемент вектора имеет индекс.

Матрица

Матрица — это двумерный массив скаляров. Обозначается жирным шрифтом в верхнем регистре. Например, если говорить о матрице из вещественных чисел, где m рядов и n столбцов, записывается такая матрица вот так:Поскольку матрица — двумерный массив, элементы матрицы имеют два индекса:Две матрицы могут быть сложены или вычтены одна из другой, только если у матриц одинаковое количество рядов и столбцов. Две матрицы могут быть перемножены только тогда, когда количество столбцов первой матрицы соответствует количеству рядов второй. Например, вы можете умножить матрицу A размера m, n на матрицу B размера n, p. В результате вы получите матрицу C размера m, p. Формула умножения выглядит вот так:

Важно заметить, что матричное произведение дистрибутивно и ассоциативно:

Однако, иногда может понадобиться перемножить элементы матриц между собой. Такую операцию называют произведением Адамара (обозначается  A ∘ B). Матрицы также можно умножать на векторы и на скаляры. Интересно, что произведением матрицы и вектора будет вектор:

Тензор

Тензор — это многомерный массив чисел. Обычно в нём больше двух измерений, так что он может быть изображён как многомерная сетка, состоящая из чисел. На самом деле, матрицы — те же тензоры, только они двухмерные, вот и все их отличия. Тензоры получили известность благодаря фреймворку для машинного обучения TensorFlow.

Операции

Есть несколько операций, которые можно производить с матрицами, и знание которых пригодится для понимания принципов работы ИИ.

Транспонирование матрицы

В результате выполнения этой операции появляется так называемая транспонированная матрица. По сути, это зеркальное отображение матрицы по главной диагональной линии, которая начинается в верхнем левом и идёт в правый нижний угол. Транспонированной матрицей от матрицы A будет матрица A^T (также A′, A^tr, ^tA или A^t). Кроме того, транспонированную матрицу можно получить, записав ряды матрицы A как столбцы матрицы A^T, а столбцы матрицы A — как ряды матрицы A^T.

Умножение единичной матрицы на вектор

Существует такое понятие как единичная матрица. Если умножить её на вектор, значения вектора не меняются. Элементы главной диагонали единичной матрицы имеют значение 1, а все остальные равны 0:

Перед тем, как вы продолжите, немного информации о диагональной матрице (она очень похожа на единичную). Все элементы матрицы, за исключением тех, что находятся на главной диагонали, равны нулю. Но, в отличие от единичной, на главной диагонали диагональной матрицы элементы имеют значение, не равное 1. Получается, единичная матрица — это вид диагональной матрицы. Они очень полезны для некоторых алгоритмов.

Умножение на обратную матрицу

Обратная матрица определяется следующим образом:

Если умножить матрицу A на обратную ей матрицу A^-1, получится единичная матрица. Обратная матрица похожа на обратное число. То есть для a обратным числом будет 1/a. Если обычное число умножить на обратное ему, получится единица: a * 1/a = 1. Здесь то же самое, только с матрицами. Но, увы, это работает только с квадратными матрицами.

Псевдоинверсия Мура-Пенроуза

Для неквадратных матриц нужно применять псевдоинверсию Мура-Пенроуза:Где U, D и V — сингулярное разложение матрицы A. Псевдоинверсия D⁺ матрицы D создаётся путём взятия элементов, обратных элементам матрицы, и её дальнейшим транспонированием. Но будьте осторожны с концепцией обратной матрицы A^-1, потому что пока что она больше используется в теории, чем на практике. Это обусловлено тем, что вычислительные способности современных компьютеров позволяют дать лишь приблизительный ответ.

Преобразование матрицы в скаляр

Бывает, что нужно преобразовать матрицу в скаляр, для этого нужно найти определитель, он обозначается det(A) или |A|. Так как преобразование возможно только с ними, вот пример с матрицей 2×2:Напоследок про линейную зависимость. Набор векторов будет линейно зависим, если хотя бы один вектор может быть представлен как комбинация других векторов из набора. Иначе набор будет линейно независим. Обычно векторы x и y будут линейно независимы, только если значения для скаляров a и b, удовлетворяющих ax + by = 0, будут равны a = b = 0.

Нормы

Иногда для работы с вектором нужно знать его размер. Для этого существуют специальные функции, которые называют нормами — Lⁿ. Маленькая буква n обозначает количество измерений, в которых находится вектор. В зависимости от того, сколько измерений в вашем векторном пространстве, нормы будут разными. Наиболее известная норма — норма двумерного пространства (Евклидова норма). Чаще всего она представляет собой Евклидово расстояние от начала вектора до точки в пространстве, находящейся на конце этого вектора. При обобщении пространства на несколько измерений используют глобальную норму:На самом деле, нормой может быть любая функция, удовлетворяющая следующим требованиям:

1. f(x + y) ≤ f(x) + f(yv) (удовлетворяет неравенству треугольника).
2. f(ax) = |a| f(x) (является абсолютно масштабируемой).
3. Если f(x) = 0, то x = 0 (определена положительно).

Часто, когда вы создаёте ИИ-приложение, очень важно различать элементы, равные 0, и элементы, имеющие значение, близкое к 0. Для этого используется норма L¹. Она проста и растёт с одинаковой скоростью во всех точках векторного пространства. Если любой элемент вектора x движется от 0 к a — эта функция вырастает на a:Как упоминалось выше, в глубоком обучении параметры нейронных сетей абстрагируются как матрицы. Следовательно, нужно знать размер матрицы, и с этим нам поможет норма Фробениуса:

Заключение

В этой статье мы затронули основы линейной алгебры, которые пригодятся, чтобы понять, что же происходит в мире нейронных сетей и искусственного интеллекта. Надеемся, эта статья поможет вам начать свой путь в этой сфере. Успехов!

Перевод статьи «Mathematics for Artificial Intelligence – Linear Algebra»

что это такое в математике, операции и действия, как составить, примеры

Способ Крамера

Метод Крамера используют для решения квадратной системы уравнений, представленной в линейном виде, где определитель основной матрицы не равен нулю. Считается, что система обладает единственным решением. Например, задана система линейных уравнений:

Её необходимо заменить равноценным матричным уравнением.

Второй столбец вычисляют, а первый уже задан. Есть предположение, что определитель матрицы отличен от нуля. Из этого можно сделать выводы, что существует обратная матрица. Перемножив эквивалентное матричное уравнение на обратного формата матрицу, получим выражение:

В итоге получают выражения:

Из представленных уравнений выделяют формулы Крамера:

Метод Крамера не представляет сложности. Он может быть описан следующим алгоритмом:

Высчитывают определитель дельта базовой матрицы.
В матричной таблице А замещают первый столбец на вектор свободных элементов b.
Выполняют расчёт определителя дельта1 выявленной матрицы А1.
Определяют переменную Х1 = дельта1/дельта.
Повторяют шаги со 2 по 4 пункт в матрице А для столбов 2,3…n.

Проверить решение матрицы методом Крамера онлайн позволяет калькулятор автоматического расчёта. Для получения быстрого ответа в представленные поля подставляют переменные числа и их количество. Дополнительно может потребоваться указание вычислительного метода разложения по строке или столбу. Другой вариант заключается в приведении к треугольному виду.

Указывается также представление чисел в виде целого числа, обыкновенной или десятичной дроби. После введения всех предусмотренных параметров и нажатия кнопки «Вычислить» получают готовое решение.

Предыдущая
АлгебраЧетность и нечетность функции как определить, примеры решения задач на исследование функции на определение четности и нечетности, условие
Следующая
АлгебраФункция y=k/х свойства и график, область определения функции, коэффициент в графике функции, примеры решения задач

Примечания

1. Катасонова Е.  Л. Японцы в реальном и виртуальном мирах: Очерки современной японской массовой культуры. — М.: Восточная литература РАН, 2012. — С. 107. — 357 с. — ISBN 978-5-02-036522-3.
2. Катасонова Е. Л. Мангамания // Восточная коллекция : журнал. — 2007. — № 2. — С. 70—81.
3. Chaim Gartenberg. . The Verge (20 августа 2019). Дата обращения: 20 августа 2019.
4. D’Alessandro, Anthony . Deadline.com (12 июня 2020). Дата обращения: 13 июня 2020.
5. . Box Office Mojo. Дата обращения: 5 декабря 2009.
6. . Box Office Mojo. Дата обращения: 5 декабря 2009.
7. . Box Office Mojo. Дата обращения: 5 декабря 2009.
8. Комментарии авторов на документальном сборнике The Matrix Revisited (англ.).

Лента

Деньги, как они есть. 1 серия Видео| позавчера 21:29

Что несёт Расе-Руси-России “Конец” христианского “Света”-3 (ОКОНЧАНИЕ) Аналитика| 2020-12-22 18:40

Материя Информация Мера Статья| 2020-12-21 22:52

Долгосрочная битва за шестой континент, вышиванки с пингвинами или зачем русские совершали великие географические открытия Статья| 2020-12-18 20:55

Смена вод (информации) в жизни общества Аналитика| 2020-12-18 10:56

Артефакты Тартарии #2. Валы, линии и крепости Видео| 2020-12-17 22:36

Сеанс разоблачения КОБ Видео| 2020-12-16 22:10

Куда ведет распятие Видео| 2020-12-16 22:01

Встреча с М.В.Величко 13.12.2020 Видео| 2020-12-15 14:31

Планы контролеров Статья| 2020-12-14 09:08

Новости сталинских репрессий. Про пересадку деревьев Видео| 2020-12-09 09:29

Каких событий ждёт Дональд Трамп до 20 января 2021 года? Статья| 2020-12-08 10:11

Запретная история России – 2. Русь изначальная Видео| 2020-12-07 18:56

“Чёрная знать” – заказчики и организаторы “перестройки”-развала СССР Аналитика| 2020-12-07 08:15

Песни про модную болезнь Видео| 2020-12-06 13:57

Горбачев. Зачем понадобился? Видео| 2020-12-01 20:29

Матрица (1999)

https://youtube.com/watch?v=ihTvN2iCnhA%3F

Томас Андерсон с виду обыкновенный парень. Днём от работает программистом, а в ночное время суток проводит жизнь в необычном формате. Он занимается хакерством. Однажды к нему нагрянули странные люди, они сказали ему, что герой находится в матрице. Объяснить толком, что собой представляет данное явление, гости не могли. Немного позже к Томасу прибыл мужчина, которого власти объявили террористом. Он предложил юноше пойти дальше в изучениях странного понятия. Если же герой боится предпринимать столь глобальные шаги, он должен принять синюю таблетку. В том случае, если любопытство подсказывает двигаться дальше, нужно выпить красную таблетку. Парень решил действовать до конца. С этого мгновения он увидел иное пространство, в которым привычные человеческие каноны бездействуют.

Факты о фильме:

• Режиссеры Вачовски применили странный метод подачи материала: кадры из мира Матрицы показаны в зеленоватом фильтре, тогда, как картины реальной жизни в синем.
• Перестрелка в холле длится три минуты, а вот в реальной жизни её снимали порядка девяти дней.
• Режиссёры, просчитав бюджет, выдвинули прайс на сумму 60 миллионов долларов, тогда как студия дала им только 9. В итоге на первую сцену были потрачены все финансы, и в дальнейшем многие сотрудники боялись, что картину вообще не получится снять до конца.
• Главные сцены были сняты в Австралии.
• Для съемки сцены с появлением главного героя в нескольких эпизодах одновременно, пришлось подбирать двойников.

Кто такой Нео?

Первый фильм «Матрица» заставляет нас вспомнить все древние пророчества, начиная с библейских; на каждом шагу нам твердят, что Нео – герой, Избранный, призванный спасти человечество от мира машин. Первая серия трилогии убеждает нас в этом, вторая «Матрица: Перезагрузка» – разочаровывает, третья «Матрица: Революция» – наполняет мессианскую роль Нео особым смыслом. Но кто же он, спаситель человечества эры машин?

Молодой человек по имени Томас Андерсон днём работает программистом в солидной компании, а ночью — взламывает компьютеры, орудуя под хакерским ником Нео.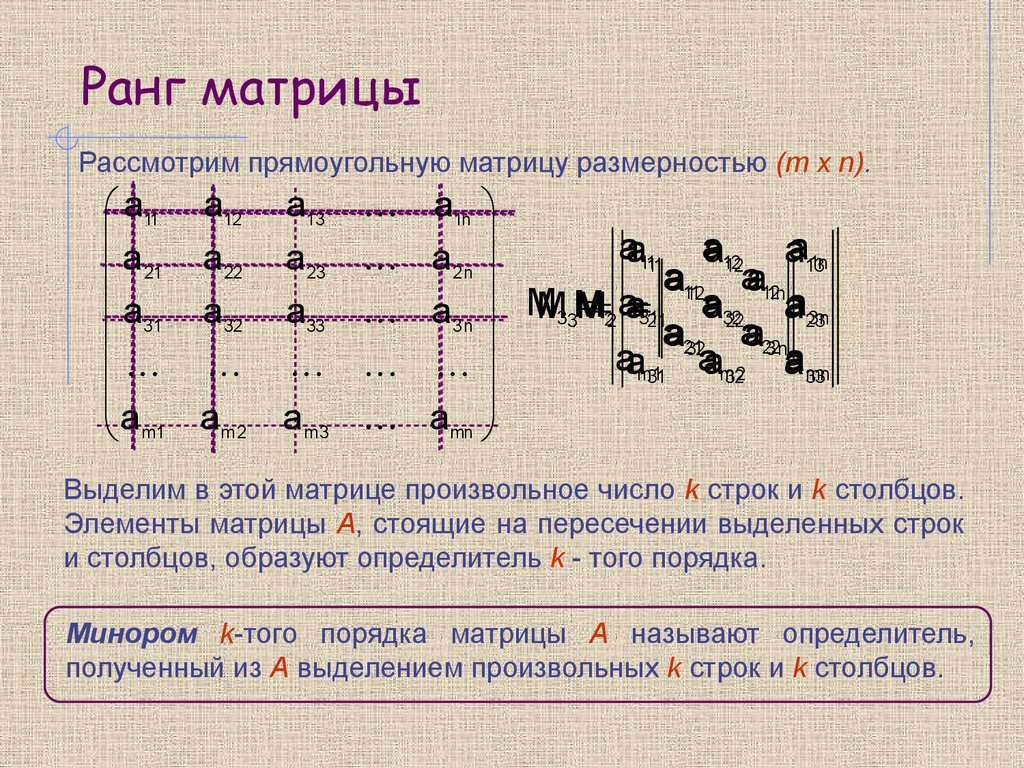 Это образ типичного борца с системой, подпольщика-одиночки, которому не хватает своей «партизанской ячейки». И вскоре она находится – в образе группы Морфеуса, бунтаря, который привык держать в руках оружие потяжелее компьютерной мышки.

Морфеус увлекает Нео за собой, уводит за пределы Матрицы в реальный мир. Символически это означает разрыв с системой, неповиновение властям, открытый переход на сторону террористов-повстанцев. Вот только имя Морфеуса слишком похоже на имя древнегреческого бога сна. Это символ обмана – Нео всё ещё во сне, он не освободился, хотя этого не знает.

Нео сначала сопротивляется навязываемой ему роли мессии; но потом принимает на себя ответственность за будущее человечества. Он готов бороться с системой, готов бороться с Матрицей, он верит в то, что спасёт мир. Но вторая и третья части трилогии «Матрица» обрушивают на голову Нео страшную правду: он – такой же винтик в огромной машине мироздания, как и все другие, его действия запрограммированы, предусмотрены, и ему приходится заключать договор с Главным Компьютером, который он хотел уничтожить, и даже действовать с ним заодно. {2}

Далее используем свойство степеней

Ответ

Пример 2

Задание

Найдите определитель матрицы А.

Решение

«Аниматрица»

Основная статья: Аниматрица

В 2003 году по мотивам вселенной «Матрицы» был выпущен сборник коротких аниме-OVA, связанных между собой общей тематикой и сеттингом. Название является комбинацией двух слов — «аниме» (англ. anime) и «матрица» (англ. matrix). По словам Вачовски, у них изначально были планы создать аниме по мотивам своего нашумевшего фильма, так как японские анимационные фильмы во многом послужили для них вдохновением. Вачовски являются авторами сценария только первого эпизода «Аниматрицы» («Последний полёт „Осириса“»). Для остальных эпизодов лично Вачовски были приглашены другие режиссёры (за исключением эпизода «Мировой рекорд»), которые сами написали сценарии своих работ.

Вычисление определителя матрицы при помощи теоремы Лапласа

Теорема Лапласа – это глубокое разложение определителя по элементам. При помощи данной теоремы можно решать матрицы не только третьего порядка, но и более высших порядков.

Напомним – минор – это определитель матрицы, который составлен методом вычёркивания – той строки и – того столбца. А алгебраическое дополнение – соответствующий минор, который берётся со знаком минус . Знаки же зависят от места элемента в определителе и определяются по схеме:

Приведём пример решения алгебраических дополнений по схеме:

Пример

Задача

Найти алгебраические дополнения элементов определителя:

Решение

Понятия алгебраического дополнения даёт возможность ещё одного способа определения определителя, который утверждается теоремой Лапласа (про распределение определителя):

Теорема

Определитель равняется сумме произведения элементов строк (столбца) на их алгебраические дополнения. Например,

. – это равенство проверяется непосредственно

Заметно, как последнее выражение совпадает с выражением из правила треугольника (правила Саррюса). Давайте по теореме Лапласа разберём несколько примеров:

Пример

Задача

Вычислить определитель матрицы, разложив его за элементами третьего порядка:

Решение

Ответ

.

Аниматрица (2003)

https://youtube.com/watch?v=94fPVqJqBGA%3F

Аниме сериал про Матрицу. Здесь представлено эпизодических девять частей, полностью открывающие истинность шаткого Мира Матрицы. Благодаря картине можно узнать историю создания иллюзорного пространства, откуда начался создаваться Мир Машин, прокатиться по последним городам человеческого существования, встретиться с последними представителями мира людей, увидеть воочию главные этапы битвы человечества и машин. Цивилизация людей канула в Лету, но вместе с ней появилась новая эпоха, неординарная и автоматизированная.

Список эпизодов аниме:

• Эпизод 1: Последний полёт «Осириса» (Final Flight of the Osiris. Авторы сценария: Лана и Лилли Вачовски. Режиссёр: Энди Джонс
• Эпизод 2: «Второе возрождение, часть 1» (The Second Renaissance. Part I). Автор сценария и режиссёр: Махиро Маэда
• Эпизод 3: «Второе возрождение, часть 2» (The Second Renaissance. Part II). Автор сценария и режиссёр: Махиро Маэда
• Эпизод 4: «История одного ребёнка» (Kid’s Story). Автор сценария и режиссёр Ватанабэ Синъитиро
• Эпизод 5: «Программа» (Program). Автор сценария и режиссёр: Кавадзири Ёсиаки
• Эпизод 6: «Мировой рекорд» (World Record). Автор сценария: Кавадзири Ёсиаки. Режиссёр: Койкэ Такэси
• Эпизод 7: «За гранью» (Beyond). Автор сценария и режиссёр: Моримото Кодзи
• Эпизод 8: «Детективная история» (A Detective Story). Автор сценария и режиссёр: Ватанабэ Синъитиро
• Эпизод 9: «Посвящённый» (Matriculated). Автор сценария и режиссёр: Питер Чеунг

Факты о мультфильме:

• Слоганом мультипликационной картины является фраза «Освободите свои разумы».
• Картину номинировали на «Golden Satellite Awards» в категории «лучшего аниме-сериала».
• Герой Майкла Карла Поппера присутствовал в «Матрице».
• Фрагмент, где робот B1-66-AR убивает агрессивного владельца, позаимствован из кинофильма «Блэйд Раннер».

Виды матриц в зависимости от значений их элементов.

Если все элементы матрицы $A_{m\times n}$ равны нулю, то такая матрица называется нулевой и обозначается обычно буквой $O$. Например, $\left( \begin{array} {cc} 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{array} \right)$, $\left( \begin{array} {ccc} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right)$ – нулевые матрицы.

Рассмотрим некоторую ненулевую строку матрицы $A$, т.е. такую строку, в которой есть хоть один элемент, отличный от нуля. Ведущим элементом ненулевой строки назовём её первый (считая слева направо) ненулевой элемент. Для примера рассмотрим такую матрицу:

Во второй строке ведущим будет четвёртый элемент, т.е. $w_{24}=12$, а в третьей строке ведущим будет второй элемент, т.е. $w_{32}=-9$.

Матрица $A_{m\times n}=\left(a_{ij}\right)$ называется ступенчатой, если она удовлетворяет двум условиям:

1. Нулевые строки, если они есть, расположены ниже всех ненулевых строк.
2. Номера ведущих элементов ненулевых строк образуют строго возрастающую последовательность, т.е. если $a_{1k_1}$, $a_{2k_2}$, …, $a_{rk_r}$ – ведущие элементы ненулевых строк матрицы $A$, то $k_1\lt{k_2}\lt\ldots\lt{k_r}$.

Примеры ступенчатых матриц:

Для сравнения: матрица $Q=\left(\begin{array}{ccccc} 2 & -2 & 0 & 1 & 9\\0 & 0 & 0 & 7 & 9\\0 & -5 & 0 & 10 & 6\end{array}\right)$ не является ступенчатой, так как нарушено второе условие в определении ступенчатой матрицы. Ведущие элементы во второй и третьей строках $q_{24}=7$ и $q_{32}=10$ имеют номера $k_2=4$ и $k_3=2$. Для ступенчатой матрицы должно быть выполнено условие $k_2\lt{k_3}$, которое в данном случае нарушено. Отмечу, что если поменять местами вторую и третью строки, то получим ступенчатую матрицу: $\left(\begin{array}{ccccc} 2 & -2 & 0 & 1 & 9\\0 & -5 & 0 & 10 & 6 \\0 & 0 & 0 & 7 & 9\end{array}\right)$.

Ступенчатую матрицу называют трапециевидной или трапецеидальной, если для ведущих элементов $a_{1k_1}$, $a_{2k_2}$, …, $a_{rk_r}$ выполнены условия $k_1=1$, $k_2=2$,…, $k_r=r$, т. е. ведущими являются диагональные элементы. В общем виде трапециевидную матрицу можно записать так:

Примеры трапециевидных матриц:

Дадим ещё несколько определений для квадратных матриц. Если все элементы квадратной матрицы, расположенные под главной диагональю, равны нулю, то такую матрицу называют верхней треугольной матрицей. Например, $\left( \begin{array} {cccc} 2 & -2 & 9 & 1 \\ 0 & 9 & 8 & 0 \\ 0 & 0 & 4 & -7 \\ 0 & 0 & 0 & 6 \end{array} \right)$ – верхняя треугольная матрица. Заметьте, что в определении верхней треугольной матрицы ничего не сказано про значения элементов, расположенных над главной диагональю или на главной диагонали. Они могут быть нулевыми или нет, – это несущественно. Например, $\left( \begin{array} {ccc} 0 & 0 & 9 \\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array} \right)$ – тоже верхняя треугольная матрица.

Если все элементы квадратной матрицы, расположенные над главной диагональю, равны нулю, то такую матрицу называют нижней треугольной матрицей. Например, $\left( \begin{array} {cccc} 3 & 0 & 0 & 0 \\ -5 & 1 & 0 & 0 \\ 8 & 2 & 1 & 0 \\ 5 & 4 & 0 & 6 \end{array} \right)$ – нижняя треугольная матрица. Заметьте, что в определении нижней треугольной матрицы ничего не сказано про значения элементов, расположенных под или на главной диагонали

Они могут быть нулевыми или нет, – это неважно. Например, $\left( \begin{array} {ccc} -5 & 0 & 0 \\ 0 & 0 & 0\\ 0 & 0 & 9 \end{array} \right)$ и $\left( \begin{array} {ccc} 0 & 0 & 0 \\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array} \right)$ – тоже нижние треугольные матрицы

Квадратная матрица называется диагональной, если все элементы этой матрицы, не лежащие на главной диагонали, равны нулю. Пример: $\left( \begin{array} {cccc} 3 & 0 & 0 & 0 \\ 0 & -2 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 6 \end{array} \right)$. Элементы на главной диагонали могут быть любыми (равными нулю или нет), – это несущественно.

Диагональная матрица называется единичной, если все элементы этой матрицы, расположенные на главной диагонали, равны 1. Например, $\left(\begin{array} {cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$ – единичная матрица четвёртого порядка; $\left(\begin{array} {cc} 1 & 0 \\ 0 & 1 \end{array}\right)$ – единичная матрица второго порядка.

Что такое матрицы в математике

Матрица в математике — это абстрактный объект, имеющий вид таблицы чисел или других математических величин. Чаще таблица прямоугольная, но встречаются и другие виды (квадратные, треугольные).

Обычно матрица называется заглавной буквой латинского алфавита: матрица A, матрица B. В таблице есть строки (их количество называется m) и столбцы (их количество называется n). Количество строк и столбцов определяет размер матрицы и может называться порядком. Матрицы такого типа называются матрицами строения m×n, или размера m×n, или порядка m×n.

Элементы матрицы, т.е. числа или остальные величины, называются строчной буквой. Они имеют 2 нижних индекса, необходимых для определения их положения в матрице. Например, элемент a13 располагается на пересечении 2 строки и 3 столбца. Значения элемента а13 читаются по-отдельности, не как целое число: «а один-три».

Откуда они взялись и чем полезны

Первые упоминания матрицы появились в Древнем Китае. Это была квадратная таблица, получившая название магического или волшебного квадрата. Самым древним и известным считается квадрат 3×3, датируемый около 2200 г до н.э. Он был высечен на панцире черепахи. В Китае его называют квадрат Ло Шу, а в Западной Европе — «Печать Сатурна».

Таким же древним является квадрат, найденный в Кхаджурахо, столице средневекового государства Чандела (IX–XIII вв. ) в Центральной Индии. Это первый из «дьявольских квадратов». Также он называется пандиагональным.

В древности матрицы были необходимы преимущественно для решения линейных уравнений. Когда матрицы появились в арабских странах, стали разрабатываться принципы работы с ними, в том числе, принцип сложения. В XVIII веке швейцарский математик, «отец линейной алгебры» Габриэль Крамер опубликовал правило Крамера. Это способ решения систем линейных уравнений с помощью матрицы.

Способ Крамера не подходит для решения тех систем линейных уравнений, в которых может быть бесконечное множество решений.

В следующем веке появляется метод немецкого математика Карла Фридриха Гаусса. Этот способ решения алгебраических уравнений не является открытием ученого. Впервые о методе Гаусса написали в китайском трактате «Математика в девяти книгах», а сам он только привел способ в удобную форму.

Для решения уравнений таким способом необходимо записать расширенную матрицу системы.

В отличие от метода Крамера, правило Гаусса можно использовать для решения любых систем линейных уравнений.

Детальная разработка теории матриц активно продолжилась с середины XIX века. Наиболее значимые ученые: Уильям Гамильтон, Артур Кэли, Карл Вейерштрасс, Мари Энмон Камиль Жордан, Фердинанд Георг Фробениус.

Сам термин «матрица» предложил английский математик Джеймс Сильвестр в 1850 г.

В наше время матрицы используются не только для записи и решения систем линейных уравнений. Списки, статистические данные, табеля с информацией — все это в какой-то степени матрица. Их применяют для упрощения подачи и работы с информацией в любой сфере. Например, таблица продаж, где указан год (первый столбец), вид продукции (первая строка), а остальные значения — количество проданных единиц.

Нео и Морфеус поменяются ролями

Сюжет «Матрицы 4» пока держится в строгом секрете. Между тем, некоторые слухи о содержании фильма все же просочились в Сеть. Они говорят нам о том, что на экранах мы вновь увидим персонажей предыдущих фильмов — Нео, Морфеуса, Тринити, Ниобе и некоторых других. Нео и Тринити должны сыграть роль своего рода моста, соединяющего все части франшизы.

Поговаривают, что это будет приквел, основанный на рассказе Морфеуса в первой части фильма. Напомним, после встречи с Нео он поведал парню о том, что когда-то давно был рожден человек, способный освободить человеческую расу от власти искусственного интеллекта. Этот человек, по его словам умер, но должен был родиться вновь и он родился: Нео — тот освободитель, которого они так ждали.

«Матрица» увидит продолжение в мае 2021 года. Кадр из фильма

Обладая этими знаниями, мы можем предположить, что теперь увидим прошлое, где герой Киану Ривза был уже взрослым, а Морфеус, напротив — молодым. В том прошлом именно первый Нео будет обучать Морфеуса, а не наоборот.

Кроме того, в картине может появиться новый персонаж — девушка, которая должна сыграть важную роль в истории человечества, как было с Нео в первом фильме. Если это приквел, то она вполне может оказаться будущей матерью Нео, если новый сиквел, тот, не сомневаемся, сценаристы придумали для нее не менее захватывающую судьбу.

Краткий сюжет трилогии «Матрица»

В чём смысл фильма «Матрица», невозможно понять, если пропустить основные вехи развития сюжета.

Начинается трилогия со знакомства с главным героем – Томасом Андерсеном (Киану Ривз). Жизнь Томаса протекает обычно, так живут миллионы жителей мегаполисов по всему миру: утром он уходит на работу, весь день кое-как выполняет свои обязанности в офисе. Зато вечером Андерсен увлечён любимым делом: хакерит в интернете под псевдонимом Нео.

Однажды на Нео выходит девушка-хакер Тринити. Он встречается с ней в ночном баре, затем разговаривает с её другом Морфеусом и получает подтверждение своим догадкам: есть где-то иная жизнь, не похожая на ту, которой он сейчас живёт.

Нео принимает красную капсулу в знак того, что согласен узнать правду. В ответ Морфеус показывает Андерсену истинную реальность. И она, к сожалению, ужасающа. Миром давно уже правят машины. Они поработили людей, заперли их в своеобразные капсулы и подключили к компьютерной матрице, чтобы получать энергию. Машины питаются этой энергией, они существуют за счет неё. А «нормальная» жизнь, которую Томас созерцал каждый день, – всего лишь иллюзия, часть программы.

Нео освободился из-под гнёта машин и присоединился к повстанцам, которые воюют против них и в реальном мире, и в матрице. Молодому человеку пришлось потерять многих друзей и отдать свою жизнь ради того, чтобы в финале Главный компьютер предоставил всем желающим людям возможность покинуть Матрицу.

Фильмы

«Матрица»

Основная статья: Матрица (фильм)

Программист одной американской компании Томас Андерсон, также известный в неофициальных кругах как хакер Нео, узнаёт, что наш мир, всё, что есть вокруг, это всего лишь порождение компьютерной программы — Матрицы. На самом же деле на Земле уже давно правят машины, которые выращивают людей на специальных плантациях и используют в качестве источников энергии. Но есть и люди, которые противостоят Машинам, они живут в единственном городе людей, до которого Машины ещё не смогли добраться, и периодически входят в Матрицу. Нео узнаёт, что он «избранный», и именно ему предстоит разрушить Матрицу, чтобы освободить людей от власти Машин.

«Матрица: Перезагрузка»

Основная статья: Матрица: Перезагрузка

Чтобы выполнить свою миссию избранного, Нео необходимо встретиться с Архитектором, с тем, кто создал Матрицу, но найти путь к Архитектору очень непросто. Тем временем Агент Смит нашёл возможность самопроизвольного копирования, и теперь Смит готов сразиться с Нео не в одиночку — Нео придётся сражаться с целой армией Агентов Смитов. Машины всё продолжают искать способы попасть в город людей — Зион, охотники рыщут повсюду. Нео остаётся последней надеждой человечества, если он не справится, мир людей перестанет существовать.

«Матрица: Революция»

Основная статья: Матрица: Революция

Машины начинают последний решающий штурм единственного города людей — Зиона. Сил защитников города не хватит на то, чтобы отразить этот натиск, им остаётся только умереть, защищая свой город. Нео решает отправиться в сердце города Машин, чтобы не допустить падения Зиона и выполнить предначертанное ему. Теперь уже не Матрица контролирует Смита, а Смит контролирует Матрицу, он вышел из-под контроля Машин. Если Нео сможет противостоять Смиту, то у людей и у Зиона появится шанс уцелеть, если же Нео не справится — всё будет кончено.

Затраты на фильмы и кассовые сборы

Фильм	Дата выходана экраны	Кассовые сборы (долл.)	Бюджет (долл.)	Примечание
США	Другие страны	Во всём мире
«Матрица»	31 марта 1999	171 479 930	292 037 453	463 517 383	63 000 000
«Матрица: Перезагрузка»	15 мая 2003	281 576 461	460 552 000	742 128 461	150 000 000
«Матрица: Революция»	5 ноября 2003	139 313 948	288 029 350	427 343 298	150 000 000
Итого	592 370 339	1 040 618 803	1 632 989 142	363 000 000

Актёры и персонажи

Персонаж	Фильм
«Матрица»	«Матрица: Перезагрузка»	«Матрица: Революция»
Нео / Избранный / Томас Андерсон	Киану Ривз
Морфеус	Лоуренс Фишборн
Тринити	Керри-Энн Мосс
Агент Смит / Смит	Хьюго Уивинг
Пифия	Глория Фостер	Мэри Элис
Сайфер	Джо Пантолиано
Агент Браун
Агент Джонс	Роберт Тейлор
Ниобе		Джада Пинкетт-Смит
Меровинген		Ламбер Вильсон
Персефона		Моника Беллуччи
Линк		Гарольд Перрино
Сераф
Зи		Нона Гэй
Бэйн (Смит)
Архитектор
Рама-Кандра
Близнецы		Эдриан и Нил Рэйменты
Мастер ключей		Рэндалл Дук Ким
Агент Джонсон		Даниэл Бернхардт
Агент Томпсон («Матрица: Перезагрузка») / вампир в клубе («Матрица: Революция»)		Мэтт Макколм
Агент Джексон
Проводник		Брюс Спенс
Главный компьютер		Генри Блейсингейм (образ)Кевин Майкл Ричардсон (голос)

См. также: Агенты

Съёмочная группа

Роль	Фильм
«Матрица»	«Матрица: Перезагрузка»	«Матрица: Революция»
Режиссёр	братья Вачовски
Продюсер	Джоэл Сильвер
Сценарист	братья Вачовски
Композитор	Дон Дэвис
Оператор	Билл Поуп

Гонорары

Гонорары режиссёров и основных актёров (в долларах США).

«Матрица» (1999)

• Киану Ривз (Нео) — 10 млн +10 % от сборов (17 млн), а также бонус в размере 8 млн[неавторитетный источник?]. Киану Ривз вложил собственные 38 млн в производство спецэффектов для двух сиквелов.
• Лоуренс Фишборн (Морфеус) — 500 тыс.
• Керри-Энн Мосс (Тринити) — 500 тыс.
• Хьюго Уивинг (агент Смит) — 500 тыс.

«Матрица

Перезагрузка» (2003)

• Эндрю и Ларри Вачовски (режиссёры) — 4 млн (+ % от сборов, составивший 6 млн) каждому
• Киану Ривз (Нео) — 15 млн (+15 % от сборов, составившие 42 млн). Киану Ривз отказался от причитающейся ему доли от продажи билетов, равной примерно 40 млн, после того как продюсеры засомневались, что картина окупит затраты на спецэффекты.
• Лоуренс Фишборн (Морфеус) — 1 млн
• Керри-Энн Мосс (Тринити) — 1 млн
• Хьюго Уивинг (агент Смит) — 1 млн
• Дэвид Килд (агент Джексон) — 500 тыс. (в неделю)

«Матрица

Революция» (2003)

• Эндрю и Ларри Вачовски (режиссёры) — 4 млн (+ % от сборов, составивший 6 млн) каждому
• Киану Ривз (Нео) — 15 млн (+15 % от сборов, составившие 21 млн)
• Лоуренс Фишборн (Морфеус) — 1 млн
• Керри-Энн Мосс (Тринити) — 1 млн
• Хьюго Уивинг (агент Смит) — 1 млн

Расчёт определителя

В линейной алгебре существует понятие определителя или детерминанта. Это число, которое ставят в соответствие каждой квадратной матрице, вычисленное из её элементов по специальной формуле. Определитель или модуль используется для решения большинства задач. Детерминант самой простой матрицы определяется с помощью вычитания перемноженных элементов из побочной диагонали и главной.

Произведения могут отличаться друг от друга составом элементов. Со знаком плюс будут включаться в сумму числа, если их индексы составляют чётную подстановку, в противоположном случае их значение меняется на минус. Определитель обозначается символом det A. Круглые скобки матричной таблицы, обрамляющие её элементы, заменяются на квадратные. Формула определителя:

Определитель первого порядка, состоящий из одного элемента, равен самому этому элементу. Детерминант матричной таблицы размером 2*2 второго порядка вычисляется путём перемножения её элементов, расположенных на главной диагонали, и вычитания из них произведения элементов, находящихся в побочной диагонали. Наглядный пример:

Для матрицы также можно найти дискриминант многочлена, отвечающий формуле:

Когда у многочлена имеются кратные корни, тогда дискриминант равен нулю.

Популярное

О масках и перчатках, если не слушать шоуменов и политиков 2002

Хочется “жечь напалмом” виновных в диверсии 1836

COVID-19: Правда врачей, а не чиновников 1642

Маски бесполезны: Учёные раскрыли “самую большую ложь” о COVID-19 1345

Каких событий ждёт Дональд Трамп до 20 января 2021 года? 1290

“Чёрная знать” – заказчики и организаторы “перестройки”-развала СССР 1260

Пландемия под диктовку или Как с потрохами продали Россию западным консалтинговым монстрам 1250

Как дышится в наморднике под лапой?! 1231

Горбачев. Зачем понадобился? 1192

Китай выдвинул предложения по мировому устройству после пандемии 1124

Контакт с “тонким миром” 1033

Ссученные патриоты и ментовское озверение 1017

Конституция или маскарад? 959

25 лет КОБ в Госдуме России 920

Планы контролеров 874

Поговорим о пирамиде власти 858

Что несёт Расе-Руси-России “Конец” христианского “Света”-2 843

Религиозность и её роль в жизни современного человека 819

Сеанс разоблачения КОБ 814

Артефакты Тартарии #2. Валы, линии и крепости 812

Новости сталинских репрессий. Про пересадку деревьев 781

Диалектика. Величко М.В. 761

Что такое Матрица?

Матрица — это замена реальности, виртуальный суррогат. Компьютер дарит людям фальшивую жизнь, доказывая, что очень хорошо узнал характер своих создателей и даже перенял их худшие черты.  Искусственный интеллект взял в руки бразды правления расхлябанной человеческой цивилизацией. В сущности, люди сами виноваты: они превратились из личностей в «пользователей», из самостоятельного биологического вида – в  батарейки, сырьевой придаток гаджетов, и можно только поражаться гениальному прозрению сценаристов, предвидевших развитие ситуации, которое мы наблюдаем сейчас.

Даже Пифия, пророчица, которой так искренне верит Морфеус – одна из программ. Она такая же часть Матрицы, как агенты, преследующие повстанцев, как грозный враг Нео – агент Смит, компьютерный вирус, взбунтовавшийся и против людей, и против машин. В этих сложных взаимоотношениях также прослеживается чёткий социальный и психологический смысл: любая система порождает антагонистов и внешних, и внутренних. На счастье Главного Компьютера, Нео и Смит не договорились друг с другом; Нео понял, что победа Смита приведёт ещё к худшим последствиям: тот действительно уничтожит Матрицу, но и человеческий род погубит тоже.

Архитектор, автор Матрицы, когда-то пытался создать идеальный мир для человечества, но в итоге вышел далеко не лучший вариант. Библейские оттенки образа Архитектора несомненны: это Бог искусственного интеллекта, действующий сразу в двух мирах: реальном и виртуальном. Именно  он объясняет Нео, что нет никакого пророчества, а его задача — перезагрузка Матрицы. Повстанческая группа Морфеуса —  это особый механизм саморегуляции Матрицы, который должен найти ошибки в её действующей версии. Уничтожение этого вспомогательного инструмента заранее запрограммировано. Никакого победного исхода не будет.

Эта мысль также отражает один из законов социальной и политической истории человечества: очень многие террористы негласно содержались самим государством, его правящими элитами, чтобы выявлять настроения народа и через такие подконтрольные группы находить и разоблачать реальных противников правящего строя.

В чём состоит психологическое новаторство трилогии?

В трилогии «Матрица» намеренно поставлена с ног на голову главная мечта человечества, ради которой совершалось столько подвигов и преступлений: чаяние светлого будущего. Конец света уже случился, и надо с этим жить.  Главный вопрос, который стоит перед героями – нужно ли покидать уютный, убаюкивающий, удобный мир Матрицы ради страшной реальности? Захочет ли человечество отказаться от комфорта ради самостоятельности?

Фактически, новый мессия компьютерной эры зовёт людей не вперёд, к вожделенному «светлому будущему», а назад, в прежние времена, когда они не были придатками к компьютерам. Сможет ли человек отвернуться от даров Матрицы, от всего, что создал силами своего интеллекта, попав к своему созданию в добровольное рабство?

Новый Морфеус и женский вариант Нео

Как мы уже отмечали выше, роль Нео в фильме продолжит играть Киану Ривз (кстати, ему уже 55 лет), роль его протеже Морфеуса, скорее всего, досталась актеру по имени Яхья Абдул Матин II («Рассказ служанки»), чье участие в проекте официально подтверждено.

Яхья может сыграть молодого Морфеуса Фото: Instagram / @yahya

Женского персонажа, подобного Нео, по некоторым данным, играет 27-летняя Джессика Хенвик («Фортитьюд», «Звездные войны: Пробуждение силы»). Актриса якобы так хорошо показала себя на пробах, что у Ланы Вачовски не было никаких сомнений относительно того, кому доверить столь важную роль.

Многих, конечно же, интересует, появится ли в фильме старый добрый агент Смит. Да, возможно, его мы увидим, вот только играть его будет уже не Хьюго Уивинг, также знакомый нам как Элронд из «Властелина колец».  Хьюго сам рассказал журналистам о том, что Вачовски звала его сниматься, но расхождения с рабочим графиком вынудили его отказаться и предпочесть четвертой «Матрице» другой проект — театральную постановку «Визит».

Роль Тринити, тем временем, продолжит играть Кэрри-Энн Мосс, роль Ниобе — Джада Пинкетт Смит. Кроме них в картине на экране могут появиться Приянка Чопра, Джонатан Грофф, Нил Патрик Харрис, Ламберт Уилсон, Эндрю Колдуэлл, Макс Римельт, Эрендира Ибарра, Тоби Онвумере, Уилльям Барбо.

Нахождение определителя матрицы

Определитель матрицы обозначается как $Δ$ или $\det$.

Замечание 2

Детерминант возможно найти только для квадратных разновидностей матриц.

В простейшем случае, когда матрица состоит из всего одного элемента, её определитель равен этому элементу:
$det A = |a_{11}|= a_{11}$

Вычислить определитель от матрицы порядка двух можно следуя такому правилу:

Определение 1

Определитель матрицы размера 2 равен разности произведений элементов, стоящих на главной диагонали с произведением элементов с побочной диагонали:

$\begin{array}{|cc|} a_{11}& a_{12} \\ a_{21} & a_{22} \\ \end{array} = a_{11} \cdot a_{22} – a_{12} \cdot a_{21}$

В случае если определитель матрицы задан размером $3 \times 3$, то найти его можно используя мнемонические правила: Саррюса или треугольников, также можно разложить матрицу по строчке или столбцу или воспользоваться преобразованиями Гаусса.

Для определителей большего размера можно использовать преобразования Гаусса и разложение по строчке.

Заключение

Итак, определитель квадратной матрицы – это число, полученное при помощи заданных чисел, расположенных в виде квадратной таблицы,которое вычисляется по рассмотренным выше формулам. Мы рассмотрели три основных способа вычисления определителя:

1. через сумму двух произведений сочетаний элементов квадратной матрицы;
2. по правилу разложения определителя по элементам строк (столбцов) квадратной матрицы;
3. по методу Гаусса, когда матрицу нужно привести к треугольному виду.

Также были рассмотрены формулы для решения матрицы второго, третьего и высших порядков.

Мы разобрали 10 свойств определителя матриц, благодаря которым можно быстрее и легче найти определитель матрицы.

Удобно решать матрицу третьего порядка методом Гаусса, где нужно выполнить элементарные преобразования матрицы и привести её к ступенчатому виду. Определитель матрицы равняется произведению элементов, которые стоят на главной диагонали.

Полезная литература

5.

1: Что такое матрица?

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

7672

• Роберт Ханнеман и Марк Риддл
• Калифорнийский университет, Риверсайд

Начнем с того, что матрица — это не что иное, как прямоугольное расположение набора элементов (на самом деле это немного сложнее, но мы вернемся к матрицам больше двух измерений чуть позже). Прямоугольники имеют размеры, которые описываются количеством строк элементов и столбцов элементов, которые они содержат. Матрица «3 на 6» имеет три строки и шесть столбцов; матрица «I на j» имеет I строк и j столбцов. Матрица, имеющая только одну строку, называется «вектор-строка».

Матрица, имеющая только один столбец, называется «вектор-столбец».0032

На рис. 5.1 показана матрица размером два на четыре. На рис. 5.2 показана матрица четыре на два. На данный момент игнорируйте содержимое ячеек (например, 1,1).

Рисунок 5.1. Пример матрицы «два на четыре»

1,1	1,2	1,3	1,4
2,1	2,2	2,3	2,4

Рисунок 5.2. Пример матрицы “четыре на два”

1,1	1,2
2,1	2,2
3,1	3,2
4,1	4,2

Элементы (ячейки) матрицы идентифицируются по их «адресам». Элемент 1,1 — это запись в первой строке и первом столбце; элемент 13,2 находится в 13-й строке и является вторым элементом этой строки.

Адреса ячеек были введены как матричные элементы в двух приведенных выше примерах.

Матрицы часто представляются в виде массивов элементов, окруженных вертикальными линиями слева и справа или квадратными скобками слева и справа. На веб-страницах проще использовать «таблицы» для представления матриц. Матрицам можно давать имена; эти имена обычно представляются заглавными жирными буквами. Социологи, использующие матрицы для представления социальных сетей, часто обходятся без математических соглашений и просто отображают свои данные в виде массива помеченных строк и столбцов. Метки на самом деле не являются частью матрицы, а просто для ясности представления. Например, матрица на рис. 5.3 представляет собой матрицу 4 на 4 с дополнительными метками.

Рисунок 5.3. Матрица четыре на четыре с дополнительными метками строк и столбцов

	А	Б	С	Д
А	—	1	0	0
Б	1	—	1	0
С	1	1	—	1
Д	0	0	1	—

Матрицы, используемые в анализе социальных сетей, часто являются «квадратными».

То есть они содержат одинаковое количество строк и столбцов. Но также используются «прямоугольные» матрицы, а также векторы-строки и столбцы. Ко всем этим вариациям применяются одни и те же соглашения.

Иногда аналитики социальных сетей используют «трехмерную» матрицу. Трехмерная матрица имеет строки, столбцы и «уровни» или «срезы». Каждый «срез» имеет те же строки и столбцы, что и каждый другой срез. UCINET рассматривает эти более сложные трехмерные массивы данных как набор двумерных матриц.

---

Эта страница под названием 5.1: Что такое матрица? распространяется по незаявленной лицензии, автором, ремиксом и/или куратором выступили Роберт Ханнеман и Марк Риддл.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Роберт Ханнеман и Марк Риддл

   Показать страницу TOC

   нет

2. Теги

   На этой странице нет тегов.

Определитель матрицы

Матрица представляет собой массив из множества чисел. Для квадратной матрицы , т. е. матрицы с одинаковым количеством строк и столбцов, можно зафиксировать важную информацию о матрице всего одним числом, называемым определителем . Определитель полезен для решения линейных уравнений, определения того, как линейное преобразование изменяет площадь или объем, а также для изменения переменных в интегралах.

Определитель можно рассматривать как функцию, входом которой является квадратная матрица, а выходом — число. Если $n$ — это количество строк и столбцов в матрице (помните, что мы имеем дело с квадратными матрицами), мы можем назвать нашу матрицу $n \times n$ матрицей. Самая простая квадратная матрица — это матрица $1 \times 1$, которая не очень интересна, поскольку содержит только одно число. Определитель матрицы $1 \times 1$ — это само это число.

При увеличении сложности следующая квадратная матрица представляет собой $2 \times 2$ матрица, которую мы можем записать как \начать{выравнивать*} \оставил[ \begin{массив}{cc} а и б\\ CD \конец{массив} \Правильно]. \конец{выравнивание*}

Вычислим определитель этой матрицы следующим образом. Мы продолжаем по первой строке, начиная с левого верхнего компонента $a$. Мы умножить компоненту $a$ на определитель «подматрицы» формируется путем игнорирования строки и столбца $a$. В этом случае эта подматрица матрица $1 \times 1$, состоящая из $d$, и ее определитель просто $д$. Таким образом, первый член определителя равен $ad$.

Далее переходим ко второму компоненту первой строки, т.е. правая верхняя компонента $b$. Умножаем $b$ на определитель подматрица, образованная игнорированием строки и столбца $b$, т.е. $c$. Итак, следующий член определителя равен $bc$. Общий определитель это просто первый член $ad$ минус второй член $bc$. Мы обозначать это как \начать{выравнивать*} \det\влево(\влево[ \begin{массив}{cc} а и б\\ CD \конец{массив} \верно-верно) = объявление-BC. \конец{выравнивание*}

Хорошо, это было много работы для простого факта. Большинство студентов не есть проблемы с запоминанием определителя матрицы $2 \times 2$ без такой чепухи. Причина прохождения этого процесса должен был упростить вычисление определителя $3 \times 3$ (и больше).

Вычислим определитель матрицы $3 \times 3$ \начать{выравнивать*} \оставил[ \begin{массив}{ccc} а и б и в \\ д и д и ж \\ г и ч и я \конец{массив} \Правильно] \конец{выравнивание*} точно таким же образом. Проходим по первой строке и умножаем каждой компоненты определителем подматрицы, образованной игнорированием строку и столбец этого компонента. С помощью этой процедуры мы вычисляем три термина, один для $a$, один для $b$ и один для $c$. Каждый из них члены складываются вместе, только с чередующимися знаками (т. е. первые срок минус второй срок плюс третий срок).

Теперь мы можем записать определитель матрицы $3 \times 3$. \начать{выравнивать*} \det\влево(\влево[ \begin{массив}{ccc} а и б и в \\ д и д и ж \\ г и ч и я \конец{массив} \верно-верно) &= a \det \left(\left[ \begin{массив}{cc} д и ж\\ Здравствуй \конец{массив} \верно-верно) -b \det\влево(\влево[ \begin{массив}{cc} д и ж\\ г и я \конец{массив} \верно-верно) +c \det \влево(\влево[ \begin{массив}{cc} д и е \\ г и ч \конец{массив} \верно-верно)\\ &=a(ei-fh) – b(di-fg) + c(dh-eg)\\ &=aei +bfg + cdh -afh -bdi -ceg \конец{выравнивание*}

Теперь, я думаю, вы могли бы запомнить окончательную формулу за 3 доллара. \times 3$ определитель. Но я предпочел бы использовать синаптическую связь моего мозга связи, чтобы сделать что-то более полезное. На самом деле, я боюсь, если я пытался запомнить это, я мог забыть что-то еще важное, например как сочетать одинаковые термины в алгебре.

Описанная выше процедура обобщается на более крупные определители. Например, чтобы вычислить определитель матрицы $4 \times 4$, у нас будет четыре члена, каждый из которых будет содержать определитель $3 x 3$. Если бы мы расширили все эти термины, используя приведенную выше формулу для определителя $3 \times 3$, вы можете себе представить, что у нас была бы довольно уродливая формула. Это слишком грязно, чтобы записывать. Но если надо, то можно. Однако обычно такие уродливые и скучные расчеты мы перекладывали на компьютер.

Ключевой факт, который следует помнить : определитель представляет собой одно число, вычисленное из матрицы.

Альтернативное обозначение

Мы часто записываем определитель $2 \times 2$ как $\left| \begin{массив}{cc} а и б\\ CD \end{array}\right|$ или определитель $3 \times 3$ как \начать{выравнивать*} \влево| \begin{массив}{ccc} а и б и в \\ д и д и ж \\ г и ч и я \конец{массив} \право|. \конец{выравнивание*} Это обозначение легче написать, чем исходное обозначение выше, поэтому мы будем часто использовать его.

Однако обратите внимание, что в этом случае вертикальные линии не среднее абсолютное значение. Определитель может быть отрицательным. В математике, нам нравится использовать одни и те же символы для обозначения разных вещей, это нормально, если это ясно из контекста. Поскольку абсолютный значение массива чисел бессмысленно, нотация однозначный.

Brilliant Math & Science Wiki

Содержание

• Формальное определение
• Основные операции
• Умножение матриц
• Транспонирование и детерминант
• Инвертирующие матрицы
• Решение систем линейных уравнений
• Смотрите также

Матрица представляет собой прямоугольный массив любых объектов, для которых определены сложение и умножение. Как правило, эти объекты являются числами, но в равной степени допустима и матрица символов, например

M=(♣∘■§✓★)M = \begin{pmatrix} \clubsuit & \circ & \blacksquare \\ \text{\S} & \checkmark & ​​\bigstar \end{pmatrix}M=(♣§​∘✓​■★​)

, если есть правильное понимание того, что такое (например) ✓×★\checkmark \times \bigstar✓×★ и ■+♣\blacksquare + \clubsuit■+♣. Говоря более формально, элементы матрицы можно извлечь из любого поля. Однако, как правило, лучше всего рассматривать матрицы как наборы действительных чисел.

Как правило, в матрице вертикальные элементы называются столбцами , а горизонтальные элементы называются строками . Размер матрицы измеряется числом 9\text{nd}2-й столбец. Точнее, M2,2=✓M_{2,2}=\checkmarkM2,2​=✓. Это обозначение особенно удобно, когда элементы связаны какой-либо формулой; например, матрица

M=(234345456)M = \begin{pmatrix}2&3&4\\3&4&5\\4&5&6\end{pmatrix}M=⎝⎛​234​345​456​⎠⎞​

может быть больше кратко записывается как Mi,j=i+jM_{i,j}=i+jMi,j​=i+j для 1≤i,j≤31 \leq i,j \leq 31≤i,j≤3, или еще более компактно, как M=(i+j)3,3M=(i+j)_{3,3}M=(i+j)3,3​ (((где 3,33,33,3 обозначает размер матрицы). \text{th}j-й столбец через M∗,j .M_{*,j}.M∗,j​.

В заданной матрице порядка m×n,m \times n,m×n присутствует m⋅nm\cdot nm⋅n элементов. Например, в матрице 3 на 3 число элементов равно 3×3=9,3 \times 3 = 9,3×3=9, а в случае матрицы 2 на 4 их 2×4=82 \ умножить на 4 = 82×4=8 присутствующих элементов.

Наконец, стоит определить матрицу ровно с одним столбцом как вектор-столбец , так как они особенно полезны для представления точек на nnn-мерной плоскости.

Есть несколько простых операций над матрицами и одна довольно сложная (умножение). Первый — сложение: сложение матриц определено только на двух матрицах одинакового размера и работает добавлением соответствующих элементов:

Что такое

(205168)+(357102)?\begin{pmatrix}2&0&5\\1&6&8\end{pmatrix} + \begin{pmatrix} 3 & 5 & 7 \\ 1 & 0 & 2\end{pmatrix}?(21​ 06​58​)+(31​50​72​)?

---

Матрицы складываются поэлементно, поэтому результат равен

(2+30+55+71+16+08+2)=(55122610). □\begin{pmatrix} 2+3 & 0+5 & 5+7 \\ 1+1 & 6+0 & 8+2 \end{pmatrix} = \begin{pmatrix} 5 & 5 & 12 \\ 2 & 6 и 10 \end{pmatrix}. \ _\квадрат(2+31+1​0+56+0​5+78+2​)=(52​56​1210​). □​

Если A=(2316−15)A = \begin{pmatrix} 2 & 3 & 1 \\ 6 & -1 & 5 \end{pmatrix}A=(26​3−1​15​) и B=(12 −10−13),B = \begin{pmatrix} 1 & 2 & -1 \\ 0 & -1 & 3 \end{pmatrix},B=(10​2−1​−13​), затем найдите матрица XXX такая, что A+B−2X=0A + B-2X = 0A+B−2X=0.

---

У нас есть

A+B−2X=0  ⟹  X=A+B2=12((2316−15)+(12−10−13))=12(3506−28)=(325203−14). □\begin{align} A + B – 2X = 0 \подразумевается X & = \dfrac{A + B}{2} \\ & = \dfrac12 \Bigg(\begin{pmatrix} 2 & 3 & 1 \\ 6 & -1 & 5 \end{pmatrix} + \begin{pmatrix} 1 & 2 & -1 \\ 0 & -1 & 3 \end{pmatrix}\Bigg) \\ & = \dfrac12 \begin{pmatrix} 3 & 5 & 0 \\ 6 & -2 & 8 \end{pmatrix} \\ & = \begin{pmatrix} \dfrac32 & \dfrac52 & 0 \\ 3 & -1 & 4 \end{pmatrix} .\ _\ квадрат \end{align}A+B−2X=0⟹X​=2A+B​=21​((26​3−1​15​)+(10​2−1​−13​))=21 ​(36​5−2​08​)=(23​3​25​−1​04​). □​​

Более формально можно сказать так:

Сумма SSS двух матриц A,BA,BA,B одинакового размера удовлетворяет соотношению

Si,j=Ai,j+Bi,jS_{i,j} = A_{i,j} + B_{i,j}Si,j​=Ai,j​+Bi,j​

для всех i, ji, ji, j в пределах размера матриц.

Также возможно умножение матриц на скаляров , т.е. одиночных чисел, путем поэлементного умножения:

Что такое

3,5(205168)?3,5\begin{pmatrix}2&0&5\\1&6&8\end{pmatrix}?3,5(21​06​58​)?

---

Каждый элемент умножается на 3,5, поэтому результат равен

.

(3,5⋅23,5⋅03,5⋅53,5⋅13,5⋅63,5⋅8)=(7017,53,52128). □\begin{pmatrix} 3.5 \cdot 2 и 3.5 \cdot 0 и 3.5 \cdot 5 \\ 3.5 \cdot 1 и 3.5 \cdot 6 и 3.5 \cdot 8 \end{pmatrix} = \begin{pmatrix} 7 & 0 & 17,5 \\ 3,5 & 21 & 28 \end{pmatrix}.\ _\square(3,5⋅23,5⋅1​3,5⋅03,5⋅6​3,5⋅53,5⋅8​)=(73,5​021​17,528​). □​

Более формально можно сказать так:

Произведение PPP константы ccc и матрицы AAA удовлетворяет соотношению

Pi,j=c⋅Ai,jP_{i,j} = c \cdot A_{i,j}Pi,j​=c⋅Ai,j​

для всех i, ji, ji, j в пределах размера матриц.

Если α=[1−648] \alpha =\begin{bmatrix} 1 & -6 \\ 4 & 8 \end{bmatrix}α=[14​−68​] и β=[2483],\beta =\begin{bmatrix} 2 & 4 \\ 8 & 3 \end{bmatrix},β=[28​43​], каково значение 3α−2β?{3\alpha}-{2\beta}? 3α−2β?

Выразите ответ в виде суммы всех элементов конечной матрицы.

Наконец, более сложная операция умножение матриц . Произведение двух матриц определяется только , когда количество столбцов первой матрицы равно количеству строк второй; другими словами, возможно только умножение матриц размера m×nm \times nm×n и n×pn \times pn×p. Причина этого становится понятной при определении продукта:

Произведение PPP матрицы AAA размера m×nm \times nm×n и матрицы BBB размера n×pn \times pn×p удовлетворяет

Pi,j=Ai,∗⋅B∗,jP_{i,j} = A_{i,*} \cdot B_{*,j}Pi,j​=Ai,∗​⋅B∗,j​ 9\text{th}j-й столбец BBB, который также является вектором. Таким образом, точка (⋅)(\cdot)(⋅) в этом смысле относится к умножению векторов, определяемых скалярным произведением. Обратите внимание, что iii и jjj определены на 1≤i≤m1 \leq i \leq m1≤i≤m и 1≤j≤p1 \leq j \leq p1≤j≤p, поэтому произведение PPP будет m×pm \times pm×p матрица.

Это правило кажется довольно условным, поэтому его лучше всего проиллюстрировать на примере:

Что такое

(123456)(123456)?\begin{pmatrix}1&2&3\\4&5&6\end{pmatrix}\begin{pmatrix}1&2\\3&4\\5&6\end{pmatrix}?(14​25​36​)⎝⎛ ​135​246​⎠⎞​?

---

Во-первых, обратите внимание, что первая матрица имеет размер 2×32 х 32 х 3, а вторая 3 х 23 х 23 х 2, поэтому их произведение действительно определено и будет матрицей 2 х 22 х 22 х 2. . Сначала рассмотрим элемент 1,11,11,1 произведения:

.

(P1,1P1,2P2,1P2,2)=(123456)(123456).\begin{pmatrix}\color{#20A900}{P_{1,1}} & P_{1,2}\\P_{ 2,1}&P_{2,2}\end{pmatrix} = \begin{pmatrix}1&2&3\\4&5&6\end{pmatrix}\begin{pmatrix}1&2\\3&4\\5&6\end{pmatrix}.(P1 ,1​P2,1​​P1,2​P2,2​)=(14​25​36​)⎝⎛​135​246​⎠⎞​. 9\text{st}1-й столбец второй матрицы, т.е.

(P1,1P1,2P2,1P2,2)=(123456)(123456)P1,1=(1,2,3)⋅(1,3,5)=1 ⋅ 1 + 2 ⋅ 3 + 3 ⋅ 5 =22. \begin{выровнено} \begin{pmatrix}\color{#20A900}{P_{1,1}} & P_{1,2}\\P_{2,1}&P_{2,2}\end{pmatrix} &= \begin{ pmatrix}\color{#D61F06}{1}&\color{#D61F06}{2}&\color{#D61F06}{3}\\4&5&6\end{pmatrix}\begin{pmatrix}\color{#3D99F6} {1}&2\\\color{#3D99F6}{3}&4\\\color{#3D99F6}{5}&6\end{pmatrix}\\\\ \color{#20A900}{P_{1,1}} &= (\color{#D61F06}{1, 2, 3}\color{#333333}{) \cdot (}\color{#3D99F6}{1, 3, 5}\color{#333333}{)} \\ &= \color{#D61F06}{1~}\color{#333333}{\cdot}\color{#3D99F6}{~1~}\color{#333333}{+}\color{#D61F06}{~ 2~}\color{#333333}{\cdot}\color{#3D99F6}{~3~}\color{#333333}{+}\color{#D61F06}{~3~}\color{#333333} {\cdot}\color{#3D99F6}{~5}\\ &=22. \end{выровнено}(P1,1​P2,1​​P1,2​P2,2​)P1,1​=(14​25​36​)⎝⎛​135​246​⎠⎞​= (1,2,3)⋅(1,3,5)=1 ⋅ 1 + 2 ⋅ 3 + 3 ⋅ 5=22.​

Таким образом, верхний левый элемент результата равен 22. Остальная часть матрицы может быть заполнена таким же образом; например,

(P1,1P1,2P2,1P2,2)=(123456)(123456).\begin{pmatrix}P_{1,1} & \color{#20A900}{P_{1,2}}\\P_{ 2,1}&P_{2,2}\end{pmatrix} = \begin{pmatrix}\color{#D61F06}{1}&\color{#D61F06}{2}&\color{#D61F06}{3} \\4&5&6\end{pmatrix}\begin{pmatrix}1&\color{#3D99F6}2\\3&\color{#3D99F6}{4}\\5&\color{#3D99F6}{6}\end{pmatrix} . (P1,1​P2,1​​P1,2​P2,2​​)=(14​25​36​)⎝⎛​135​246​⎠⎞​​.

Окончательный результат

Р=(22284964). □P = \begin{pmatrix}22&28\\49&64\end{pmatrix}.\ _\squareP=(22492864). □​

Если A=(1−2323−1−312)A = \begin{pmatrix} 1 & -2 & 3 \\ 2 & 3 & -1 \\ -3 & 1 & 2 \end{pmatrix} A=⎝⎛ ​12−3​−231​3−12​⎠⎞​ и B=(102012120),B = \begin{pmatrix} 1 & 0 & 2 \\ 0 & 1 & 2 \\ 1 & 2 & 0 \end {pmatrix},B=⎝⎛​101​012​220​⎠⎞​, затем найдите ABABAB и BABABA. Какой вывод можно сделать из последних двух матриц?

---

И ААА, и ВВВ являются квадратными матрицами порядка 3×33 х 33×3. Следовательно, и ABABAB, и BABABA корректно определены и являются матрицами одного порядка 3 × 33 \× 33 × 3.

AB=(1−2323−1−312)⋅(102012120)=(1⋅1+(−2)⋅0+3⋅11⋅0+(−2)⋅1+3⋅21⋅2+(− 2)⋅2+3⋅02⋅1+3⋅0+(−1)⋅12⋅0+3⋅1+(−1)⋅22⋅2+3⋅2+(−1)⋅0(−3 )⋅1+1⋅0+2⋅1−3⋅0+1⋅1+2⋅2−3⋅2+1⋅2+2⋅0)=(44−21110−15−4)BA=(102012120 )⋅(1−2323−1−312)=(−507−453541).\begin{aligned} AB & = \begin{pmatrix} 1 & -2 & 3 \\ 2 & 3 & -1 \\ -3 & 1 & 2 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 & 2 \\ 0 & 1 & 2 \\ 1 & 2 & 0 \end{pmatrix} \\ & = \begin{pmatrix} 1 \cdot 1 + (-2) \cdot 0 + 3 \cdot 1 и 1 \cdot 0 + (-2) \cdot 1 + 3 \cdot 2 и 1 \cdot 2 + (-2) \cdot 2 + 3 \ cdot 0 \\ 2 \cdot 1 + 3 \cdot 0 + (-1) \cdot 1 и 2 \cdot 0 + 3 \cdot 1 + (-1) \cdot 2 и 2 \cdot 2 + 3 \cdot 2 + (-1) \cdot 0 \\ (-3) \cdot 1 + 1 \cdot 0 + 2 \cdot 1 и -3 \cdot 0 + 1 \cdot 1 + 2 \cdot 2 & -3 \cdot 2 + 1 \cdot 2 + 2 \cdot 0 \end{pmatrix} \\ & = \begin{pmatrix} 4 & 4 & -2 \\ 1 & 1 & 10 \\ -1 & 5 & -4 \end{pmatrix} \ \\\ BA & = \begin{pmatrix} 1 & 0 & 2 \\ 0 & 1 & 2 \\ 1 & 2 & 0 \end{pmatrix} \cdot \begin{pmatrix} 1 & -2 & 3 \\ 2 & 3 & -1 \\ -3 & 1 & 2 \end{pmatrix} \ \ & = \begin{pmatrix} -5 & 0 & 7 \\ -4 & 5 & 3 \\ 5 & 4 & 1 \end{pmatrix}. \end{align}ABBA​=⎝⎛​12−3​−231​3−12​⎠⎞​⋅⎝⎛​101​012​220​⎠⎞​=⎝⎛​1⋅1+(−2) ⋅0+3⋅12⋅1+3⋅0+(−1)⋅1(−3)⋅1+1⋅0+2⋅1​1⋅0+(−2)⋅1+3⋅22⋅0 +3⋅1+(−1)⋅2−3⋅0+1⋅1+2⋅2​1⋅2+(−2)⋅2+3⋅02⋅2+3⋅2+(−1)⋅ 0−3⋅2+1⋅2+2⋅0​⎠⎞​=⎝⎛​41−1​415​−210−4​⎠⎞​=⎝⎛​101​012​220​⎠⎞​⋅⎝ ⎛​12−3​−231​3−12​⎠⎞​=⎝⎛​−5−45​054​731​⎠⎞​.​

Как видно, AB≠BAAB\neq BAAB​=BA. Таким образом, мы можем заключить, что умножение матриц не обязательно должно быть коммутативным . □_\квадрат□​

Предположим, что xxx и yyy удовлетворяют следующему равенству:

(xy21)(x0yx)=2(106−x30)+(52x4x).\left(\begin{array}{cc}x& y \\2&1 \ конец {массив}\справа)\влево(\начало{массив}{cc}x&0 \\y& x \end{массив}\справа)=2\влево(\begin{массив}{cc}10&6-x \\3&0 \end{массив}\right)+\left(\begin{array}{cc}5&2x \\4& x \end{массив}\right).(x2​y1​)(xy​0x​)=2(103 ​6−x0​)+(54​2xx​).

Оценка x+y.x+y.x+y.

До сих пор неясно, почему умножение матриц определяется таким образом. Одна из основных причин заключается в использовании систем линейных уравнений. Коэффициенты каждого уравнения могут быть собраны в матрицу коэффициентов , а переменные могут быть расположены в вектор-столбец. Произведение матрицы коэффициентов и вектора-столбца само по себе будет вектором-столбцом, значениями каждого уравнения. Например, система уравнений

{x+2y+3z=93x+y+4z=122x+4y-z=4\слева\lbrace \begin{выровнено} х + 2у + 3з &= 9 \\ 3х + у + 4з &= 12 \\ 2x + 4y – z &= 4 \end{выровнено} \Правильно. ⎩⎪⎨⎪⎧​x+2y+3z3x+y+4z2x+4y−z​=9=12=4​

можно более кратко записать в виде

(12331424−1)(xyz)=(9124 ).\begin{pmatrix}1&2&3\\3&1&4\\2&4&-1\end{pmatrix}\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}9\\12\\ 4\end{pmatrix}.⎝⎛​132​214​34−1​⎠⎞​⎝⎛​xyz​⎠⎞​= ⎝⎛​9124​⎠⎞​​.

Это очень полезная трансформация помимо экономии места; в частности, если бы можно было «разделить» матрицы, было бы легко узнать, что такое x, y, zx, y, zx, y, z, путем деления матрицы коэффициентов. К сожалению, определение деления требует дополнительных усилий, поэтому его дальнейшее объяснение оставлено в следующем разделе.

В качестве предупреждения об умножении матриц чрезвычайно важно понимать следующее:

Умножение матриц — это , а не , коммутативное. Другими словами, , а не вообще верно, что AB=BAAB=BAAB=BA.

Простейший способ убедиться в этом состоит в том, что умножение матриц определено только для матриц размера m×nm \times nm×n и n×pn \times pn×p; изменение их порядка дает произведение матрицы n×pn \times pn×p и матрицы m×nm \times nm×n, и ppp не обязательно равен mmm. Даже в таком случае (например, квадратные матрицы) умножение обычно не является коммутативным. Матрицы A, BA, BA, B, которые действительно удовлетворяют AB=BAAB = BAAB=BA, называются (соответственно) коммутирующие матрицы .

Сделайте две матрицы (1100)\begin{pmatrix}1&1\\0&0\end{pmatrix}(10​10​) и (2011)\begin{pmatrix}2&0\\1&1\end{pmatrix}(21​01​ ) ездить?

---

Нет, с

(1100)(2011)=(3100)\begin{pmatrix}1&1\\0&0\end{pmatrix}\begin{pmatrix}2&0\\1&1\end{pmatrix} = \begin{pmatrix}3&1\\0&0\ конец{pmatrix}(10​10​)(21​01​)=(30​10​)

но

(2011)(1100)=(2211). □\begin{pmatrix}2&0\\1&1\end{pmatrix}\begin{pmatrix}1&1\\0&0\end{pmatrix} = \begin{pmatrix}2&2\\1&1\end{pmatrix}.\ _\square( 21​01​)(10​10​)=(21​21​). □​

Наконец, стоит отметить специальную матрицу: единичная матрица

In=(100…0010…0001…0⋮⋮⋮⋱⋮000…1),I_n = \begin{pmatrix}1&0&0&\ldots&0 \\0&1&0&\ldots&0\\0&0&1&\ldots&0\\\vdots&\vdots&\vdots&\ddots&\vdots\\0&0&0&\ldots&1\end{pmatrix},In​=⎝⎜⎜⎜⎜⎜⎛​100⋮0​010⋮ 0​001⋮0​………⋱…​000⋮1​⎠⎟⎟⎟⎟⎟⎞​,

которое представляет собой матрицу n×nn \times nn×n, которая равна нулю везде, кроме главной диагонали, которая содержит все единицы. Например,

I2=(1001),I3=(100010001).I_2 = \begin{pmatrix}1&0\\0&1\end{pmatrix}, \qquad I_3 = \begin{pmatrix}1 & 0 & 0 \\0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix}.I2​=(10​01​),I3​= ⎝⎛​100​010​001​⎠⎞​​.

Удовлетворяет тому свойству, что

IA=AI=AIA = AI = AIA=AI=A

для любой матрицы n×nn \times nn×n AAA. Причина должна быть ясна из приведенных выше определений.

Две полезные функции для матриц — это транспонирование и 9Т = А.(АТ)Т=А.

Второй из них является наиболее полезным, так как он (примерно) означает, что свойства, истинные для левого умножения, справедливы и для правого умножения.

Более интересен определитель матрицы. Существует несколько равноправных определений определителя, хотя все они кажутся произвольными на данный момент без понимания того, что должен вычислять определитель.

Формально определитель представляет собой функцию det\text{det}det от множества квадратных матриц к множеству действительных чисел, которая удовлетворяет 3 важным свойствам:

• det(I)=1;\text{det}(I) = 1;det(I)=1;
• det\text{det}det линейно по строкам матрицы;
• , если две строки матрицы МММ равны, det⁡(M)=0.\det(M)=0.det(M)=0.

Второе условие является наиболее важным. Это означает, что любая из строк матрицы записывается как линейная комбинация двух других векторов, и определитель можно вычислить, «разбивая» эту строку. Например, в приведенном ниже примере вторая строка (0,2,3)(0,2,3)(0,2,3) может быть записана как 2⋅(0,1,0)+3⋅(0 ,0,1)2 \cdot (0,1,0) + 3 \cdot (0,0,1)2⋅(0,1,0)+3⋅(0,0,1), поэтому

det(100023001)=2⋅det(100010001)+3⋅det(100001001)=2.\text{det}\begin{pmatrix}1&0&0\\0&2&3\\0&0&1\end{pmatrix} = 2 \cdot \ text{det}\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}+3 \cdot \text{det}\begin{pmatrix}1&0&0\\0&0&1\\0&0&1\end{pmatrix}=2. det⎝⎛​100​020​031​⎠⎞​=2⋅det⎝⎛​100​010​001​⎠⎞​+3⋅det⎝⎛​100​000​011​⎠⎞​=2.

Ключевая теорема показывает это:

Существует ровно одна функция, удовлетворяющая трем указанным выше соотношениям.

К сожалению, с этим очень трудно работать для всех матриц, кроме самых простых, поэтому лучше использовать альтернативное определение. Основных два: определитель по младшим и определитель по перестановкам .

Первый из двух, определяемый минорами, использует рекурсию. Базовый случай прост: определитель матрицы 1 × 11 × 11 × 1 с элементом aaa равен просто aaa. Обратите внимание, что это согласуется с приведенными выше условиями, поскольку

det(a)=a⋅det(1)=a\text{det}\begin{pmatrix}a\end{pmatrix} = a \cdot \text{det} \begin{pmatrix}1\end{pmatrix}=adet(a​)=a⋅det(1​)=a 9{i+1}a_{1,i}\text{det}(A_{1i}) = a_{1,1}\text{det}A_{11}-a_{1,2}\text{det} A_{12}+\cdots.det(A)=i=1∑n​(−1)i+1a1,i​det(A1i​)=a1,1​detA11​−a1,2​detA12​+⋯ .

Например,

Какой определитель (abcd)?\begin{pmatrix}a&b\\c&d\end{pmatrix}?(ac​bd​)?

---

Пишем

det(abcd)=a det(d)−b det(c)=ad−bc. □\text{det}\begin{pmatrix}a&b\\c&d\end{pmatrix} = a ~\text{det}\begin{pmatrix}d\end{pmatrix} – b ~\text{det}\begin{ pmatrix}c\end{pmatrix} = ad-bc.\ _\squaredet(ac​bd​)=a det(d​)−b det(c​)=ad-bc. □​ 92?a2+b2?

К сожалению, эти вычисления могут оказаться довольно утомительными; уже для матриц 3 × 33 \× 33 × 3 формула слишком длинная, чтобы ее можно было запомнить на практике.

Альтернативное определение использует перестановки. {n}a_{i,\sigma(i)}\right).σ∈S∑​(sign(σ)i=1∏n​ai,σ(i)​).

Это может выглядеть более пугающе, чем предыдущая формула, но на самом деле она более интуитивно понятна. По сути, это говорит следующее:

Выберите nnn элементов ААА так, чтобы никакие два не находились в одной строке и не два в одном столбце, и умножьте их, возможно, также на -1-1-1, если перестановка имеет нечетный знак. Определитель — это сумма всех вариантов выбора этих nnn элементов.

Это определение особенно полезно, когда матрица содержит много нулей, так как тогда большинство произведений исчезает.

Найдите определитель матрицы

(10−19110−6−19110013−8013000970000−5).\left(\begin{array}{cc}1&0&-1&9&11\\0&-6&-1&9&11\\0&0&\frac {1}{3}&-80&\frac{1}{3}\\0&0&0&9&7\\0&0&0&0&-5 \end{массив}\right).⎝⎜⎜⎜⎜⎛​10000​0−6000​−1− 131​00​99−8090​111131​7−5​⎠⎟⎟⎟⎟⎞​.

Вот пример:

Какой определитель (abcd)?\begin{pmatrix}a&b\\c&d\end{pmatrix}?(ac​bd​)? 9{n}a_{i,\sigma(i)}\right) = 1 \cdot a_{1,1}a_{2,2} + (-1) \cdot a_{1,2}a_{2,1 } = ad-bc. det(A)=σ∈S∑​(sign(σ)i=1∏n​ai,σ(i)​)=1⋅a1,1​a2,2​+(−1 )⋅a1,2​a2,1​=ad−bc.

Неудивительно, что это тот же результат, что и выше. □_\квадрат□​

Вычислить det⁡(264−315937).\det\left(\begin{array}{cc}2&6&4\\-3&1&5\\9&3&7 \end{array}\right).det⎝⎛​2−39​ 613​457​⎠⎞​.

Определитель является очень важной функцией, поскольку он удовлетворяет ряду дополнительных свойств, которые могут быть получены из 3 условий, указанных выше. Они следующие: 9T).det(A)=det(AT).

Изменение знака при перестановке строк: если A’A’A’ представляет собой матрицу, образованную путем перестановки позиций двух строк, то det(A’)=-det(A).\text{det}(A’)=- \text{det}(A).det(A′)=-det(A).

Как показано в следующем разделе, свойство мультипликативности имеет особое значение.

В конце раздела, посвященного умножению матриц, было отмечено, что “деление” матриц было бы чрезвычайно полезной операцией. Чтобы попытаться создать его, важно понять определение деления чисел:

Деление на число ccc эквивалентно умножению на число 1c. \frac{1}{c}.c1​.

Другими словами, деление на ccc эквивалентно умножению на число ddd, такое что cd=1cd = 1cd=1. Это имеет смысл для того, что деление «должно» делать: деление на ccc с последующим умножением на ccc должно быть эквивалентно бездействию, то есть умножению на 1. Приведенное выше определение гарантирует это.

Матричное «деление», если оно существует, должно следовать тому же принципу: умножение на матрицу, а затем деление на нее должно быть эквивалентно бездействию. Однако при матричном умножении эквивалентом бездействия является умножение на III. 9{-1}\большой) &= \text{det}(I) \\ &= 1. \end{aligned}det(AA-1)det(A)det(A-1)​=det(I)=det(I)=1.​

Таким образом, это необходимо для det(A)\text{ det}(A)det(A) не равно нулю. Несколько сложнее, чтобы это было достаточным условием, но это действительно так:

Матрица имеет обратную тогда и только тогда, когда она имеет ненулевой определитель.

Стоит запомнить формулу в случае 2×22 \times 22×2:

Обратная матрица (abcd)\begin{pmatrix}a&b\\c&d\end{pmatrix}(ac​bd​), если она существует, равна 9\text{th}й столбец из AAA. Эта матрица удовлетворяет тому свойству, что

cof(A)A=A cof(A)=det(A)I.\text{cof}(A)A = A~\text{cof}(A) = \text{det}(A)I. cof(A)A=A cof(A)=det(A)I.

Это дает еще одну причину того, что ААА обратима тогда и только тогда, когда ее определитель не равен нулю. Также стоит отметить, что матрица кофакторов 2 × 22 \× 22 × 2 имеет вид (d−b−ca)\begin{pmatrix}d & -b\\-c & a \end{pmatrix}(d−c​ −ba​), что согласуется с приведенной выше формулой.

См. полную статью здесь: Решение линейных систем с использованием матриц. 9{-1}\mathbf{b}v=A−1b, что является простым умножением матриц.

x=5,y=7,z=-27 x=5, y=7, z=-27 x=5,y=7,z=-27 х=0,у=-33,г=14 х=0, у=-33, г=14 х=0,у=-33,г=14 х=-41,у=4,г=7 х=-41, у=4, г=7 х=-41,у=4,г=7 x=3,y=10,z=-21 x=3, y=10, z=-21 x=3,y=10,z=-21

Найдите решение следующей системы линейных уравнений:

x+3y+3z=-8x+3y+4z=-1x+4y+3z=-4. \begin{выровнено} х+3у+3г &=-8 \\ х+3у+4г &=-1 \\ х+4у+3г &=-4. \end{align}x+3y+3zx+3y+4zx+4y+3z​=−8=−1=−4.​

Есть одна потенциальная ловушка: обратного ААА не существует. Это означает, что определитель AAA равен 0, поэтому существуют две строки AAA, кратные друг другу; это означает, что исходная система уравнений состояла из двух уравнений, кратных друг другу. Это означает, что решений либо нет, либо они бесконечны.

ровно одно значение γ\gammaγ ровно два значения γ\gammaγ ровно три значения γ\gammaγ бесконечно много значений γ\gammaγ недостаточно информации

Система линейных уравнений

X+γY−Z=0γX−Y−Z=0X+Y−γZ=0\begin{aligned} X + \gamma Y – Z &=0 \\ \гамма X – Y – Z &=0 \\ X + Y – \гамма Z &=0 \end{align}X+γY−ZγX−Y−ZX+Y−γZ​=0=0=0​

имеет нетривиальное решение для __________.