1.1.4. Произведение матриц
Умножение матрицы А = ||Aij|| размера на матрицу В = ||Bij|| размера определено лишь для случая, когда число столбцов матрицы А совпадает с числом строк матрицы В, т. е. когда N=L. В этом случае произведение матриц определяется следующим образом:
Произведением матриц АВ называется матрица С = ||СIj|| размера , у которой , |
Иначе говоря, элемент Cij равен сумме произведений элементов I-ой строки матрицы А на соответствующий элемент J-ого столбца матрицы В. С помощью знака суммирования можно записать это так:
Пример 2.
Найти произведение матриц
и .
Имеем
.
Отметим, что произведение матриц некоммутативно, т. е. в общем случае АВ Не равно ВА. В приведённом выше примере матрицу
 Но, даже если А и В – квадратные матрицы одного порядка (тогда существуют произведения АВ и ВА), то, как показывает следующий пример, произведения АВ и ВА могут не совпадать.
Но, даже если А и В – квадратные матрицы одного порядка (тогда существуют произведения АВ и ВА), то, как показывает следующий пример, произведения АВ и ВА могут не совпадать.Пример 3.
Пусть , .
Тогда ,
.
Единичной матрицей называется квадратная матрица вида
.
Упражнение 5.
Доказать, что для любой квадратной матрицы А
АЕ=ЕА=А,
Где Е – единичная матрица того же порядка, что и А.
Доказательство.
Пусть А и Е – квадратные матрицы П-го порядка, В = АЕ.
Тогда Bij
Но Eij = 0 при I, не равном J, a Ejj = 1. Следовательно, Bij = Aij·1 = Aij. Таким образом, все элементы матрицы В равны соответствующим элементам матрицы А, то есть В = А.
Если матрица С = ЕА, то СIj = еI1А1J + еI2А2J + … + ЕIiАIj + … + ЕInАNj
(учитываем, что Eii = 1, Eij = 0 при I, не равном J). Значит, С = А. Утверждение доказано.
Приведём ряд свойств произведений матриц.
1. (АВ)С=А(ВС) |
Доказательство.
Пусть размер матрицы A = ||Aij|| матрицы B = ||Bij|| – а матрицы
C = ||Cij|| Имеем AB = ||AIj||, где
Тогда (AB)C = ||GIj||, где
Где – элемент матрицы ВС. Тем самым, если обозначить элемент матрицы
2. |
Доказательство.
Пусть матрица A = ||Aij|| имеет размер а матрицы B = ||Bij|| и C = ||Cij|| имеют размер Тогда для элементов матрицы А(В+С)= ||GIj|| имеем
Из определения произведения матриц вытекает, что
Упражнение 1.6.
Пусть А и В – квадратные матрицы одного порядка. Вывести формулу для (А+В)2 (при натуральном П Под СN Понимается произведение С·С·…·С).
Решение.
Используем свойства сложения и умножения матриц:
(А + В)2 = (А + В)(А + В) = (А + В)А + (А + В)В = А·А + В·А + А·В +В·В =
= А2 + В·А + А·В +В2.
Заметьте, что результат может совпасть с Формулой сокращенного умножения (А + В)2 = А2 + 2АВ + В2 Только в том случае, если АВ = ВА. В общем случае это неверно! |
Ответ: (А + В)2 = А2 + В·А + А·В +В2.
Упражнение7.
Пусть А и В – квадратные матрицы одного порядка. Разложить на множители выражение АВ+2В.
Решение.
Используем свойство единичной матрицы (см. упражнение 5):
Следовательно, В = ЕВ. Тогда АВ + 2В = АВ + (2Е)В = (А + 2Е)В
(использовано свойство 2 произведения матриц).
Ответ: АВ + 2В = (А + 2Е)В.
Упражнение 8.
Пусть А,В и С – квадратные матрицы одного порядка. Разложить на множители выражение А2С +АС 2.
Решение.
Поскольку А2 = А·А, С2 = С·С, запишем заданный матричный многочлен в виде: А2С +АС 2 = А·А·С +А·С·С
А·А·С +А·С·С = А(А·С +С·С) = А((А + С)С) = А(А + С)С.
Ответ: А2С +АС 2 = А(А + С)С.
Упражнение 9.
Найти АВ и ВА.
Решение.
Определим размеры матрицы А: и В: Следовательно, существуют оба произведения: и АВ, и ВА, причем размер матрицы С = АВ: а матрицы D = BA:
Вычислим элементы матрицы С:
Таким образом, матрица С имеет вид:
.
Матрица D состоит из единственного элемента:
Тогда .
Ответ: , .
| < Предыдущая | Следующая > |
|---|
Mathway | Популярные задачи
Популярные задачи
Элемент. математикаОсновы алгебрыАлгебраТригонометрияОсновы мат. анализаМатематический анализКонечная математикаЛинейная алгебраХимияPhysics
| Рейтинг | Тема | Задача | |
|---|---|---|---|
| 1 | Решить, используя обратную матрицу | x+2y=1 , 4x+5y=13 | , |
| 2 | Перемножить матрицы | [[1/( квадратный корень из 17),-4/( квадратный корень из 17)]][[1/( квадратный корень из 17)],[-4/( квадратный корень из 17)]] | |
| 3 | Найти область определения | x+y=3 | |
| 4 | Найти область определения | x-y=3 | |
| 5 | Найти область определения | y=-2x+3 | |
| 6 | Найти область определения | y=2x+1 | |
| 7 | Записать в виде векторного равенства | x=x^2+9x+3 , x=x+2 | , |
| 8 | Найти область определения | y=2x | |
| 9 | Найти область определения | y=-3x | |
| 10 | Найти область определения | y=3x-2 | |
| 11 | Найти область определения | y=4x | |
| 12 | Найти область определения | 3x+2y=6 | |
| 13 | Trovare la 5×5 Matrice Identità | 5 | |
| 14 | Trovare la 6×6 Matrice Identità | 6 | |
| 15 | Trovare la 4×4 Matrice Identità | 4 | |
| 16 | Решить, используя обратную матрицу | 2x+y=-2 , x+2y=2 | , |
| 17 | Решить, используя обратную матрицу | 4x+4=y , y=6x | , |
| 18 | Решить, используя обратную матрицу | 4x+2=5y-3 , y=3x-1 | , |
| 19 | Найти степенное множество | (3,4) | |
| 20 | Вычислить | кубический корень из 216 | |
| 21 | Найти степенное множество | (1,3) | |
| 22 | Найти область определения | 3x-2y=12 | |
| 23 | Найти область определения | y=5x+2 | |
| 24 | Найти область определения | y=2x-3 | |
| 25 | Найти область определения | y=2x-4 | |
| 26 | Найти область определения | y=2x+5 | |
| 27 | Найти область определения | y=1/2x | |
| 28 | Найти область определения | y=1/2x-3 | |
| 29 | Найти область определения | y=2/3x-2 | |
| 30 | Найти область определения | x=2y | |
| 31 | Найти область определения | x-2y=2 | |
| 32 | Найти область определения | x-2y=6 | |
| 33 | Найти область определения | 2y+x | |
| 34 | Найти область определения | 2x+y=0 | |
| 35 | Найти область определения | y=5x+6 | |
| 36 | Найти область определения | y=x+3 | |
| 37 | Solve Using a Matrix by Elimination | y=4x+3x-2 , y=6 | , |
| 38 | Проверить линейную зависимость | B={[[-10,2],[5,-2. 5]]} 5]]} | |
| 39 | Сложение | [[2,4],[6,-4]]+[[-3,-7],[20,10]] | |
| 40 | Проверить линейную зависимость | B={[[-1,2],[0,-2.5]]} | |
| 41 | Перемножить матрицы | [[0,0,1,1],[1,0,1,0],[0,0,0,1],[0,1,0,0]][[0,0,1,1],[1,0,1,0],[0,0,0,1],[0,1,0,0]] | |
| 42 | Найти область определения | y=5x | |
| 43 | Найти область определения | y=7x | |
| 44 | Найти область определения | y=-x-2 | |
| 45 | Найти область определения | y=x-2 | |
| 46 | Найти область определения | y=x-3 | |
| 47 | Привести матрицу к ступенчатому виду по строкам | [[4,-3,1,0],[1,0,-2,0],[-2,1,1,0]] | |
| 48 | Записать в виде векторного равенства | x+y+z=2 , 4x+5y+z=12 , 2x=-4 | , , |
| 49 | Найти определитель | [[0,-1,a],[3,-a,1],[1,-2,3]] | |
| 50 | Найти область определения | y=-x+2 | |
| 51 | Найти определитель | [[2,5,0],[1,0,-3],[2,-1,2]] | |
| 52 | Найти определитель | [[7,5,0],[4,5,8],[0,-1,5]] | |
| 53 | Найти обратный элемент | [[1,-3,0,-2],[3,-12,-2,-6],[-2,10,2,5],[-1,6,1,3]] | |
| 54 | Найти обратный элемент | [[1,2,3],[2,5,7],[3,7,9]] | |
| 55 | Привести матрицу к ступенчатому виду по строкам | [[0,1,5,-4],[1,4,3,-2],[2,7,1,-2]] | |
| 56 | Привести матрицу к ступенчатому виду по строкам | [[1,1,0],[1,0,1],[1,0,1],[2,1,0],[2,1,0]] | |
| 57 | Привести матрицу к ступенчатому виду по строкам | [[1,2,3],[4,5,6],[7,8,9]] | |
| 58 | Привести матрицу к ступенчатому виду по строкам | [[7,8]] | |
| 59 | Найти область определения | 2x+y=1 | |
| 60 | Записать в виде векторного равенства | 2x+y=-2 , x+2y=2 | , |
| 61 | Найти область определения | x-2y=4 | |
| 62 | Найти область определения | x-y=-1 | |
| 63 | Найти область определения | x+y=5 | |
| 64 | Найти область определения | x=-3y-8 | |
| 65 | Найти область определения | x=-2y-8 | |
| 66 | Найти область определения | x+y=6 | |
| 67 | Найти область определения | x+y=4 | |
| 68 | Найти область определения | x+2y=4 | |
| 69 | Найти область определения | x+y | |
| 70 | Найти область определения | y=7x+9 | |
| 71 | Найти область определения | y=1/2x-5 | |
| 72 | Найти область определения | y=1/2x+2 | |
| 73 | Найти область определения | y=1/2x+3 | |
| 74 | Найти область определения | x-y=-3 | |
| 75 | Найти область определения | x-y=4 | |
| 76 | Найти область определения | y=-2x | |
| 77 | Найти область определения | y=-2x+1 | |
| 78 | Найти область определения | y=2^(x+9) | |
| 79 | Найти область определения | y=10-x^2 | |
| 80 | Найти область определения | y=2x-6 | |
| 81 | Найти область определения | y=-2x-3 | |
| 82 | Найти область определения | y=3x-8 | |
| 83 | Найти область определения | y=3x | |
| 84 | Найти область определения | y=-3x+1 | |
| 85 | Найти область определения | y=4x+3 | |
| 86 | Найти область определения | y=3x-4 | |
| 87 | Найти область определения | y=4x-2 | |
| 88 | Найти область определения | y=-6x | |
| 89 | Найти область определения | y=x-4 | |
| 90 | Найти область определения | 7 корень четвертой степени из 567y^4 | |
| 91 | Найти область определения | c=5/9*(f-32) | |
| 92 | Найти область определения | f=9/5c+32 | |
| 93 | Вычислить | квадратный корень из 4 | |
| 94 | Привести матрицу к ступенчатому виду по строкам | [[-6,7],[2,6],[-4,1]] | |
| 95 | Найти собственные значения | [[2,1],[3,2]] | |
| 96 | Найти собственные значения | [[4,0,1],[2,3,2],[49,0,4]] | |
| 97 | Найти степенное множество | A=(2,3,4,5) | |
| 98 | Найти мощность | (2,1) | |
| 99 | Решить, используя обратную матрицу | -3x-4y=2 , 8y=-6x-4 | , |
| 100 | Решить, используя обратную матрицу | 2x-5y=4 , 3x-2y=-5 | , |
Линейная алгебра
Линейная алгебраЛинейная алгебра |
1. | назад | оглавление | вперёд |
Две матрицы A и B называются равными ,если они имеют
один и тот же порядок и если элементы стоящие на соответствующих местах равны.
К линейным операциям относятся :
Умножение матрицы на число
Для того чтобы умножить матрицу на число нужно каждый элемент
матрицы умножить на это число:
Сложение матриц.
Складывать можно только матрицы одинаковых размеров:
Свойства линейных операций
Если матрица в качестве элементов имеет нули , то такая матрица называется нулевой.
Произведение матриц .
Пример:
. ==
==
.=
.
Если для матриц А и В выполняется равенство А* В=В*А ,то
матрицы называются перестановочными.
Если для матриц А , В , С имеет смысл операция произведения,
то выполняются равенства
A(B*C)=(A*B)*C
A(B+C)=AB+AC
(B+C)A=BA+CA
Транспонирование матриц
Рассмотрим матрицы
AT называется транспонированной по отношению к A
Если AT получена из матрицы А заменой строк на столбцы то
назавают главной диагональю
Очевидно:
Если А является квадратной матрицей(n*n), то элементы матрицы
Если для квадратной матрицы выполняется условие
то матрица А называется симметричной и в этом случае достаточно указать элементы, стоящие на главной диагонали и элементы, стоящие над главной диагональю.
Понятие обратной матрицы.
Обратные матрицы существуют только для квадратных матриц. Квадратная матрица ,у которой на главной диагонали стоят
единицы, а вне главной диагонали – нули, называется единичной матрицей.
Например, единичная матрица второго порядка:
Теорема.
Если А и В – квадратные матрицы одного и того же порядка n, то определитель их произведения равен произведению определителей матриц-сомножителей:
Определение обратной матрицы:
Матрица В называется обратной для матрицы А , если А и В перестановочны и А*В=В*А=Е
Обозначение обратной матрицы:
Теорема.
Если матрица А имеет обратную ,то ее определитель отличен от
нуля.
Доказательство.
Так как А имеет обратную матрицу, то
Воспользуемся теоремой о том ,что определитель произведения
равен произведению определителей.
что и требовалось доказать.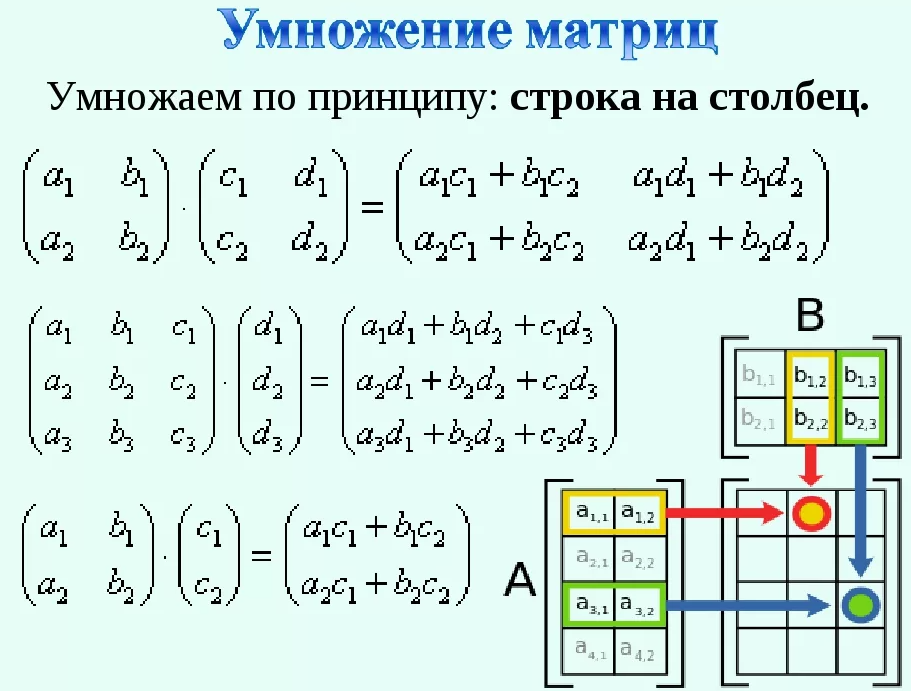
Нахождение обратной матрицы методом Крамера
Теорема.
Если квадратная матрица А имеет определитель отличный от нуля, то данная матрица имеет обратную.
Доказательство.
Пусть матрица А такова, что её определитель отличен от нуля.
Докажем, что существует матрица В, такая что:
*=
Отсюда, в частности, следует:
Система (3) –из трех уравнений с тремя неизвестными, и т.к. определитель системы (3) по условию отличен от нуля , то эту систему можно решить методом Крамера причем решение (3) – единственно.
Аналогично можно доказать существование и единственность всех остальных элементов матрицы В.
Алгоритм нахождения обратной матрицы методом Крамера.
Первоначально находим определитель матрицы А и если он
равен нулю , то обратной матрицы не существует.
Если определитель отличен от нуля , то находим союзную
матрицу
состоящую из алгебраических дополнений элементов матрицы А.
Элементарные преобразования матриц.
Эквивалентные матрицы.
К элементарным преобразованиям относятся:
- умножение любой строки матрицы на число , отличное от нуля;
- к любой строке можно добавить любую другую строку , умноженую на любое число;
- перестановка двух строк.
пример
=
Матрицы, полученные с помощью элементарных преобразований
называются эквивалентными
А~ В , В~ С , А~ С
Вычисление обратной матрицы с помощью элементарных преобразований.
Расмотрим квадратную матрицу А и предположим , что
тогда используя элементарные преобразования эту матрицу
можно привести к единичной матрице .Таким образом единичная
матрица эквивалентна любой невырожденой матрице того же
порядка.
Теорема
Если элементарные преобразования:
переводят невырожденую матрицу А в единичную , то
те же самые преобразования, взятые в том же порядке, переводят
единичную матрицу в обратную для A.
Доказательство:
отсюда
назад | оглавление | вперёд
обратная матрица
Обратная матрица
Определение и примеры
Напомним, что функции f и g обратны, если
f(g(x)) = г (f (х)) = х
Позже мы увидим, что матрицы можно рассматривать как функции из R n до R m и что матричное умножение равно состав этих функций. Обладая этим знанием, мы следующее:
Пусть А и B быть n x n матриц, то A и B являются обратными друг от друга, то
AB = BA = I n
Пример
Рассмотрим матрицы
Мы
можно проверить, что когда мы умножаем A и B
в любом порядке мы получаем единичную матрицу. (Проверьте это.)
(Проверьте это.)
Нет у всех квадратных матриц есть обратные. Если матрица имеет обратную, мы называем ее не единственное число или обратимый . Иначе он называется единственное число . В следующем разделе мы увидим, как определить, матрица вырожденная или невырожденная.
Свойства инверсий
Ниже приведены четыре свойства инверсий.
- Если А
неособый, то и A -1 и
(A -1 ) -1 = А - Если А
и Б
невырожденные матрицы, то
АБ
неособый и
(AB) -1 = B -1 A -1
-1
- Если А
неособо тогда
(А Т ) -1 = (А -1 ) Т
- Если А
и Б
матрицы с
АВ = I п
затем и Б являются инверсиями друг друга.
Обратите внимание, что четвертое свойство подразумевает, что если AB = I затем BA = I.
Доказательство первых трех свойств элементарно, а четвертого слишком продвинутый для этого обсуждения. Докажем второе.
Доказательство того, что (AB) -1 = B -1 А -1
По свойству 4 нам нужно только показать, что
(AB)(B -1 A -1 ) = I
У нас есть
(AB)(B -1 A -1 ) = A(BB -1 )A -1 ассоциативное свойство
= АИА -1 определение обратного
= АА -1 определение идентификационная матрица
= I определение обратного
Нахождение обратного
Теперь, когда мы поняли, что такое инверсия, мы хотели бы найти способ
вычисление и обращение невырожденной матрицы. Мы используем определения
обратное и матричное умножение. Пусть А
— невырожденная матрица, а B — обратная к ней.
Затем
Мы используем определения
обратное и матричное умножение. Пусть А
— невырожденная матрица, а B — обратная к ней.
Затем
АВ = Я
Напомним, что мы находим j -й столбец произведения путем умножения A на j th столбец B. Теперь некоторые обозначения. Позволять e j быть м x 1 матрица, то есть j th столбец единичной матрицы и x j быть й й столбец B. Затем 90 005
Топор j = е j
Мы можем записать это в расширенной форме
[A|e j ]
Вместо того, чтобы решать эти расширенные задачи по одной за раз, используя строку операций, мы можем решать их одновременно. Решаем
[А | я]
Найти обратную матрицу
Раствор
обратная матрица — это правая часть окончательной расширенной матрицы
.
Это Пример показывает, что если A эквивалентна по строкам единичной матрице, то A неособый.
Линейные системы и инверсии
Мы можем использовать обратную матрицу для решения линейных систем. Предполагать что
Топор = б
Тогда так же, как мы делим на коэффициент, чтобы изолировать x, мы можем применить A -1 с обеих сторон для изолировать х.
A -1 Топор = А -1 б
IX = A -1 b x = А -1 б
Пример
Решить
х + 4z = 2
х + у + 6z = 3
-3x – 10z = 4
Раствор
Мы представить эту систему в матричной форме
Топор = b
с
Решение
x = A -1 б
Мы уже вычислили обратное. Мы прибываем в
решение
х = -18 y = -9 z = 5
Уведомление что если b нулевой вектор, то
Топор = 0
может решить с помощью
х = А -1 0 = 0
Это демонстрирует теорему
Теорема неособых эквивалентностей
Следующие эквивалентны (TFAE)
- А неособый
- Топор = 0 имеет только тривиальное решение
- А является строковым эквивалентом I
- линейная система Ax = b имеет единственный решение для каждой матрицы n x 1 б
Назад на главную страницу матриц и приложений
Назад на домашнюю страницу линейной алгебры
Назад к математике Домашняя страница отдела
электронная почта Вопросы и предложения
Матрица Умножение Определено (стр. 2 из 3) Как и при сложении матриц, размеры матриц имеют значение, когда мы умножаем. Для умножения матриц для работы столбцы второй матрицы должны иметь одинаковые номера элементов, как и строки первой матрицы.
Если, используя вышеуказанные матрицы, Б имел бы только две строки, его столбцы были бы слишком короткими для умножения
против рядов А .
Затем “ АВ ”
не существовало бы; продукт был бы «неопределенным».
Аналогично, если Б имел, скажем, четыре ряда или, альтернативно, если A имел две или четыре колонки, затем AB не существовало бы, потому что A и В не было бы нужных размеров. Другими словами, для AB существовать (то есть, чтобы сам процесс умножения матриц был способный функционировать разумно), A должно иметь такое же количество столбцов, как Б имеет ряды; глядя на матрицы, строки A должны быть той же длины, что и столбцы B . Вы можете использовать этот факт для быстро проверить, определено ли данное умножение. Напишите продукт по размерам матрицы. В случае вышеуказанной проблемы A 23 года а Б 32, так АВ есть (23)(32). Средние значения совпадают: …так что умножение определено. Кстати, вы помните, что AB , матрица продукта, была 22. Вы также можете увидеть это на размерах: Используя это, вы можете видеть, что ВА должна быть отличная от 9 матрица0021 АБ , потому что: Продукт ВА определено (то есть мы можем сделать умножение), но произведение, когда
матрицы перемножаются в таком порядке, будет 33,
не 22.
Умножение работает так же, как и в предыдущей задаче, проходя по рядам и вниз столбцы. Я не буду пытаться снова рисовать свои руки, но вы можете видеть вычисления в следующих цветах: Авторское право Элизабет Стапель 2003-2011 Все права защищены Тогда ответ: Умножение матриц
Вероятно, впервые Коммутативный
Собственность когда-либо
была проблема. Помните, когда они сделали большое дело, еще в средней школе
или ранее о том, как “ ab
= ба “или” 56
= 65″? Это “правило”
вероятно, казался довольно глупым в то время, потому что вы уже знали, что
порядок не имеет значения в умножении. << Предыдущий Топ | 1 | 2 | 3 | Возвращаться к индексу Далее >>
|
|
|
Видео с вопросами: Определение условий равенства двух матриц
Стенограмма видео
Рассмотрите показанные матрицы. Матрица 𝐴 равна единице, двум, трем,
четыре. А матрица 𝐵 равна единице, двум,
три, 𝑘. Можно ли выбрать 𝑘 такой
что 𝐴𝐵 равно 𝐵𝐴? Если да, то чему должно быть равно 𝑘
к?
Матрица 𝐴 равна единице, двум, трем,
четыре. А матрица 𝐵 равна единице, двум,
три, 𝑘. Можно ли выбрать 𝑘 такой
что 𝐴𝐵 равно 𝐵𝐴? Если да, то чему должно быть равно 𝑘
к?
Итак, в этой задаче первым делом
мы собираемся посмотреть, как мы перемножаем матрицы вместе. Так что у нас есть два на два
матрицы. Итак, как бы мы умножили два
матрицы два на два? Что ж, давайте посмотрим на
это. У нас есть 𝑎, 𝑏, 𝑐, 𝑑 один
матрица, а 𝑒, 𝑓, 𝑔, ℎ — другая матрица. Теперь, если мы посмотрим на первый
элемент, у нас есть 𝑎𝑒 плюс 𝑏𝑔. Итак, что мы делаем, так это умножаем
первый элемент первой строки первой матрицы на первый элемент первой
столбец второй матрицы. А потом добавляем второй
элемент первой строки первой матрицы, умноженный на второй элемент
первый столбец второй матрицы. И тогда то, что мы делаем, завершено
этот образец для других элементов нашей матрицы.
И тогда то, что мы делаем, завершено
этот образец для других элементов нашей матрицы.
Хорошо, отлично. Итак, теперь нам нужно работать
выяснить, возможно ли, чтобы 𝐴𝐵 было равно 𝐵𝐴, если у нас есть значение 𝑘. Ну, при первом осмотре вы
может подумать, что 𝐴𝐵 будет таким же, как 𝐵𝐴, потому что если мы просто умножим
вещи, неважно, в каком они направлении. Тем не менее, это похоже на уже показанное
когда мы имеем дело с матрицами. Теперь есть два пути решения
Эта проблема. Прежде всего, просто взглянув
в наших двух матрицах мы, вероятно, могли видеть, каким должно быть значение 𝑘. Потому что, просто взглянув на
наши матрицы, мы видим, что 𝑘 будет равно четырем. И почему так? Ну, причина, по которой 𝑘 будет
равно четырем, потому что если 𝑘 равно четырем, то матрица 𝐴 и матрица 𝐵 равны
идентичный. Поэтому, если мы умножим их
вместе, либо 𝐴𝐵, либо 𝐵𝐴, это не повлияет на результат.
Но сейчас мы просто докажите это, заполнив 𝐴𝐵 и 𝐵𝐴. Ну, если у нас есть 𝐴𝐵, это 𝐴 умножить на 𝐵. Итак, у нас есть один, два, три, четыре умножить на один, два, три, 𝑘. Итак, если мы воспользуемся правило умножения, которое мы показали ранее, то для первого элемента мы получили бы единицу. умножить на один плюс два умножить на три, то второй элемент, один умножить на два плюс два 𝑘. Тогда у нас было бы три, умноженное на один плюс четыре умножить на три, а затем три умножить на два плюс четыре 𝑘. Таким образом, мы можем сказать, что 𝐴𝐵 будет равно матрице два на два семь, два плюс два 𝑘, 15, шесть плюс четыре 𝑘.
Итак, теперь мы можем перейти к
𝐵𝐴. Ну, 𝐵𝐴 будет матрицей
один, два, три, 𝑘 умножить на матрицу один, два, три, четыре. Тогда это будет равно единице
умножить на один плюс два умножить на три, затем один умножить на два плюс два
умножить на четыре, затем три умножить на один плюс три 𝑘 и, наконец, три
умножить на два плюс четыре 𝑘. Таким образом, результат будет
была матрицей два на два семь, 10, три плюс три 𝑘 и шесть плюс четыре 𝑘.
Таким образом, результат будет
была матрицей два на два семь, 10, три плюс три 𝑘 и шесть плюс четыре 𝑘.
Хорошо, отлично. Так что бы мы сделали сейчас? Ну, что мы можем сделать, так это найти 𝑘 по
приравнивая соответствующие элементы, а затем подставляя это обратно, чтобы увидеть, дает ли это
получим тот же результат для 𝐴𝐵 и 𝐵𝐴. Ну, если мы начнем с два плюс два
𝑘 равно 10, а затем вычтем два из каждой части уравнения, мы получим
два 𝑘 равно восьми. Делим на два, получаем 𝑘
равняется четырем. Ладно, верно. Так что теперь, если мы заменим 𝑘 равно
четыре в другие элементы, все мы получим то же самое для 𝐴𝐵 и 𝐵𝐴. Ну, а если мы посмотрим на
нижний левый элемент 𝐵𝐴, тогда у нас будет три плюс три 𝑘,
что то же самое, что три плюс три, умноженное на четыре, если 𝑘 равно четырем,
что будет равно 15. Отлично, вот что у нас получилось
𝐴𝐵.

 А(В+С)=АВ+АС, (В+С)А=ВА+СА
А(В+С)=АВ+АС, (В+С)А=ВА+СА 3. Матрицы. Операции над матрицами
3. Матрицы. Операции над матрицами 


 В частности, умножение матриц не является «коммутативным»;
вы не можете изменить порядок факторов и ожидать, что в конечном итоге
такой же результат. (Вы должны ожидать увидеть «концептуальный» вопрос
относящийся к этому факту в вашем следующем тесте.)
В частности, умножение матриц не является «коммутативным»;
вы не можете изменить порядок факторов и ожидать, что в конечном итоге
такой же результат. (Вы должны ожидать увидеть «концептуальный» вопрос
относящийся к этому факту в вашем следующем тесте.) Знакомство с этими правилами
тогда было, вероятно, бессмысленно, так как приказ не имело значения за все, что вы тогда умножали. Ну а теперь Закон Коммутативности
имеет значение, потому что порядок имеет значение для умножения матриц.
Всегда помните, что для матриц AB почти наверняка не равно BA .
Знакомство с этими правилами
тогда было, вероятно, бессмысленно, так как приказ не имело значения за все, что вы тогда умножали. Ну а теперь Закон Коммутативности
имеет значение, потому что порядок имеет значение для умножения матриц.
Всегда помните, что для матриц AB почти наверняка не равно BA .