Что такое матрицы и что с ними делать? *
Первым и, пожалуй, одним из простых понятий, встречающихся в математической науке, является матрица. В нашей статье речь пойдет не о знаменитом одноименном фильме, а о математической единице. Сегодня мы расскажем: что это такое и с чем это «есть», как применять на практике.
Что такое матрица?
Впервые с этим понятием сталкиваются студенты 1-2 курсов независимо от факультета и выбранной специальности. В общем виде матрица представляет собой прямоугольную таблицу с числами, притом каждое из них занимает определенное место и положение, имеет собственное обозначение.
Каждая матрица имеет свое имя. Оно обозначается заглавными буквами латинского алфавита: А, В, С и пр.
У каждой матрицы есть свой размер. Одежду подбирать ей не придется, но вот учитывать это параметр при действиях над матрицей нужно обязательно. Размер матрицы определяется, исходя из количества строк и столбцов, которые обозначают m и n соответственно.
Все числа, образующие таблицу (непосредственно матрицу), называют элементами матрицы. У каждого из них есть свое обозначение с учетом местоположения (строка+столбец). Например, элемент, находящийся в первой строке и первом столбце обозначают а11, а элемент в первой строке и втором столбце – а12.
Какие действия можно выполнять над матрицами?
Матрицы, как математическая единица, поддаются всем основным действиям: сложение, вычитание, умножение и даже деление. Каждая из операций будет иметь определенный порядок действий и потребует соблюдение конкретных условий.
Особенности сложения и вычитания матриц
Одним из важнейших требований в данном случае является соразмерность матриц. Оно означает, что размер матриц должен быть одинаковым. В противном случае сложить или вычесть один элемент из другого не удастся. При разном количестве элементов произвести необходимые действия не представляется возможным.
Сложение и вычитание соразмерных матриц производится следующим образом: все действия осуществляют над одними и теми же элементами из разных матриц.
Вычитание производится аналогично, поэлементно. Важно отметить, что количество слагаемых (суммируемых или вычитаемых матриц) может быть неограниченно.
Особенности умножения матриц
Умножение необходимо рассматривать в двух вариантах:
- Когда матрица умножается на число.
Это самый простой вариант развития событий. В данном случае необходимо умножит каждый элемент матрицы на число.
Пример умножения матрицы- Когда матрица умножается на матрицу.
Получить произведение матриц возможно не во всех случаях. Здесь также необходимо соблюдение определенных условий: число столбцов одной матрицы должно быть равнозначным числу строк другой матрицы.
Как умножаются матрицы?Специфика умножения матриц проявляется в следующем: умножение производится не просто поэлементно, но и с учетом строк и столбцов. Элементы новой матрицы получаются в ходе умножения элементов и суммирования двух произведений.
Рассмотрим порядок умножения матриц на примере:
Правила умножения матрицыДеление матриц
При делении матриц выделяют новое понятие – обратная матрица, которая обозначается А. Данный критерий действителен только в отношении квадратных матриц (когда число строк равно числу столбцов).
Раскрываем понятие деление матрицыПроизведение матрицы А и А даст единичную матрицу Е.
Транспонирование матрицы – это…
У матриц есть одно специфическое действие, когда можно поменять местами строки и столбцы. Такая операция называется транспонированием. Если обычная матрица обозначается А, то транспонированная — А.
Рассмотрим процесс транспонирования на конкретном примере:
Что такое транспортирование матрицы?Определитель матрицы – это…
Одним из важнейших элементов матрицы является ее определитель. Данный критерий представляет собой численную характеристику матрицы. Для ее получения нужно, чтобы матрица была квадратной. Расчет определителя производится на основе разности произведений диагоналей: главной и побочной.
Для ее получения нужно, чтобы матрица была квадратной. Расчет определителя производится на основе разности произведений диагоналей: главной и побочной.
Для чего нужны матрицы?
Матрицы успешно используются, как в математике, так и иных науках. В математическом направлении они позволяют просто и быстро решить систему уравнений.
В экономике использование матричных структур целесообразно при решении некоторых задач. При этом важно чтобы вычисление нужного параметра было можно представить в виде таблицы или системы уравнений.
Матрицы также уместны при вычислении в таких науках, как физика, механика, эконометрика и пр. Они упрощают процесс вычисления искомого параметра при грамотной интерпретации известных критериев.
Команда ОЦ DissHelp готова помочь в рении задач и выполнении контрольных, курсовых и дипломных работ для студентов всех направлений обучения с использованием матриц и без них. Наши специалисты грамотно и просто пояснят, как пользоваться ими в науке и жизни, решат любое задание независимо от уровня сложности.
Мы гарантируем высокое качество услуг, соблюдение сроков и индивидуальный подход, конфиденциальность данных.
Матрица Эйзенхауэра: что это, как пользоваться, примеры
Тренды
Телеканал
Газета
Pro
Инвестиции
РБК+
Новая экономика
Тренды
Недвижимость
Спорт
Стиль
Национальные проекты
Город
Крипто
Дискуссионный клуб
Исследования
Кредитные рейтинги
Франшизы
Конференции
Спецпроекты СПб
Конференции СПб
Спецпроекты
Проверка контрагентов
РБК Библиотека
Подкасты
ESG-индекс
Политика
Экономика
Бизнес
Технологии и медиа
Финансы
РБК КомпанииРБК Life
РБК Тренды
Фото: Shutterstock
Чтобы не отвлекаться на бесполезные дела и не откладывать важные, нужно верно расставлять приоритеты. В этом помогает Матрица Эйзенхауэра — метод тайм-менеджмента самого продуктивного президента США
В этом помогает Матрица Эйзенхауэра — метод тайм-менеджмента самого продуктивного президента США
1
Что такое матрица Эйзенхауэра
Матрица Эйзенхауэра — это метод тайм-менеджмента, помогающий расставлять приоритеты: делать важное и не тратить время на ненужное. Он подойдет всем, кто хочет разобраться с личным и рабочим временем, научиться планировать расписание, которое не съезжает. Матрица состоит из четырех квадратов: срочно и важно, несрочно и важно, срочно и неважно, несрочно и неважно. Идея такой матрицы отдаленно пересекается со знаменитым “правилом Парето”, согласно которому 20% усилий приводят к 80% результата и наоборот.
Матрица Эйзенхауэра
Идея распределять дела по такой методике появилась у 34-го президента США Дуайта Эйзенхауэра, руководившего страной с 1953-го по 1961 год. Эйзенхауэра считают одним из самых продуктивных президентов в истории Штатов.
Метод Эйзенхауэра оформил и популяризировал американский консультант Стивен Кови, описав его в книге «Семь навыков высокоэффективных людей».
Эффективность метода подтверждает исследование 2018 года [1]. Большинство людей выбирают срочные, а не важные дела. Ученые предложили участникам эксперимента выбрать, что делать в первую очередь. Срочные дела выбирали люди, которые описывали себя как «занятые». Зато когда их попросили обдумать последствия выбора той или иной задачи, они отдавали приоритет важным делам.
Читайте также: «Правила делегирования» — подборка РБК Pro
2
Как пользоваться матрицей Эйзенхауэра
Прежде чем заполнять матрицу, отследите в течение нескольких дней, какие задачи вы выполняете и сколько времени они отнимают. После наблюдения положите перед собой список дел и к каждому задайте три вопроса:
- Была ли задача для меня срочной?
- Была ли она для меня важной?
- Я единственный, кто мог это сделать?
Когда распределите задачи по блокам, посмотрите, в каком квадрате их больше всего. Последовательно разбирайтесь с каждым квадратом. В будущем старайтесь оставлять в одном квадрате не больше восьми задач, причем личные и рабочие задачи считаются вместе. А перед тем как добавлять новое дело, завершите одно из списка.
В будущем старайтесь оставлять в одном квадрате не больше восьми задач, причем личные и рабочие задачи считаются вместе. А перед тем как добавлять новое дело, завершите одно из списка.
3
Квадрат 1 — срочные и важные
Оперативно подхватить проект, пока коллега на больничном, закрыть задачу, прилетевшую за три часа до дедлайна, вылечить зуб с острой болью, — срочные и важные дела. Они требуют быстрого ответного действия. Обычно у таких задач есть осязаемые дедлайны и последствия, если не выполнить их вовремя. Сюда отнесем дела, возникшие из-за кризисов или форс-мажоров.
Если таких задач большинство. Возможно, у вас проблемы. Задачи в этом квадрате неизбежны, ведь ситуации и события, которыми нельзя управлять, будут происходить всегда. Но если фокусироваться только на срочных и важных делах, можно «заработать» хронический стресс, эмоциональное выгорание и ощущение потери контроля над жизнью. Это приведет к «внутренней миграции» — делам из четвертого квадрата.
Что делать. Старайтесь оставить здесь как можно меньше дел. Разработайте план по достижению актуальных целей. Поставьте дедлайны, составьте расписание. Проверьте в конце недели, что вы успели сделать, какие результаты получились и что будете делать на следующей неделе. Если срочные и важные задачи приходят извне, подумайте, как это предотвратить. Например, поговорите с начальством, коллегами или клиентом о перераспределении нагрузки или поменяйте рабочий план.
4
Квадрат 2 — несрочные и важные
Занятия в тренажерном зале, изучение языков, учеба на образовательных курсах — это задачи, связанные не с решением проблем, а с личным ростом. Эти дела помогают двигаться к долгосрочным целям с самыми ценными результатами. У них может не быть дедлайна или конечного срока, поэтому часто мы заменяем несрочные важные дела задачами из списка срочных.
Подкаст об образовании не поможет зарабатывать больше уже завтра, но поможет спланировать свою образовательную траекторию, чтобы зарабатывать больше в будущем. Это несрочно, но важно.
Это несрочно, но важно.
Если таких задач большинство. Вы расходуете свои ресурсы на то, что считаете важным. Уровень стресса снижается, вы почувствуете себя еще лучше, когда увидите первые результаты своих инвестиций.
Что делать. Это идеальная ситуация. Поддерживайте и сохраняйте ее как можно дольше.
5
Квадрат 3 — срочные и неважные
Сюда попадает проверка электронной почты и мессенджеров, рассылки документов, мытье посуды и другие бытовые дела. Это рутинные задачи, их результата ждут другие люди, но это почти не приближает вас к собственным целям. Автор книги «Сделай это завтра» Марк Форстер называет это занятостью. Занятость мешает делать «настоящую работу».
Если таких задач большинство. В этом квадрате можно увидеть эффект срочности: вы можете чувствовать драйв от поставленных галочек напротив списка дел. Как говорит знаменитый инвестор Уоррен Баффетт, каждым вечером следует задавать себе вопрос: «Стал ли я умнее сегодня, научился ли чему-то новому за день?» Другое дело, когда этот список состоит из мелких задач, которые почти ничего для вас не значат. Вместе с этим возникает ощущение, что вы занимаетесь не тем. Растет недовольство собой и своей жизнью.
Вместе с этим возникает ощущение, что вы занимаетесь не тем. Растет недовольство собой и своей жизнью.
Что делать. Стивен Кови советует делегировать такие задачи: службам доставки, личным ассистентам, клининговой службе, подрядчикам. Важно при этом грамотно делегировать задачи, чтобы не растерять уважение сотрудников, избегая при этом проявлений авторитаризма. Если делегирование невозможно — снизить их влияние на расписание. Например, выключать уведомления мессенджеров, ясно обозначать другим, сколько вам нужно времени на задачу, и говорить «нет», если таких дел становится слишком много. Еще один способ — заниматься задачами третьего квадрата, когда в первом и втором уже ничего нет.
6
Квадрат 4 — несрочные и неважные
Сюда попадают просмотры сериалов, пролистывание ленты в соцсетях и сортировка писем вместо ответа на них. Это «убийцы времени»: за этими занятиями мы проводим часы, но не получаем от них практической пользы в долгосрочной перспективе. Конечно, желание отвлечься, отдохнуть, полениться — это естественно. Самого Эйзенхауэра критиковали за игру в гольф в рабочее время. Но гольф и бридж создавали баланс между личным временем и стрессовой работой президента.
Конечно, желание отвлечься, отдохнуть, полениться — это естественно. Самого Эйзенхауэра критиковали за игру в гольф в рабочее время. Но гольф и бридж создавали баланс между личным временем и стрессовой работой президента.
В долгосрочной перспективе «убийцы времени» мешают достигать важных целей. Исследование 2019 года, опубликованное в Journal of Applied Psychology, это доказывает [2]. Ученые нашли взаимосвязь между досугом сотрудников и их продуктивностью на следующий день. Исследователи выяснили, что работники, которые накануне долго смотрели передачи, пришли на работу с хорошим настроем. Но к концу недели их настроение ухудшалось, а мотивация падала. При этом работники, которые занимались спортом, йогой, медитацией, слушали музыку и помогали другим, чувствовали себя более спокойными и мотивированными.
Если таких задач большинство. Вы можете застрять в рутине. Из-за этого появится стресс и ощущение эскапизма, бегства от проблем.
Что делать. Фиксируйте время. Это поможет определить главных «убийц времени». Когда их найдете, подумайте, чем их заменить или ограничить.
Это поможет определить главных «убийц времени». Когда их найдете, подумайте, чем их заменить или ограничить.
7
Где собирать матрицу Эйзенхауэра
Блокнот или тетрадь. Не имеет значения, будут ли это разлинованные листы или нет — главное, чтобы вы осознавали границы между квадратами. Чтобы сделать распределение нагляднее, используйте разные цвета и шрифты для каждого блока.
Матрица Эйзенхауэра на бумаге
Todoist. В приложении можно маркировать задачи с помощью четырех уровней приоритетности, которые можно отфильтровать.
Матрица Эйзенхауэра в Todoist
Notion.
Матрица Эйзенхауэра в Notion
Evernote. Это приложение для заметок. В нем есть шаблон матрицы, который можно настроить под себя: выбрать цвета, задачи. Можно заводить отдельную заметку с матрицей на каждый месяц, неделю или день.
Можно заводить отдельную заметку с матрицей на каждый месяц, неделю или день.
Матрица Эйзенхауэра в Evernote
Обновлено 08.06.2022
Текст
Наталья Шацкова
— APL Wiki Некоторые диалекты автоматически применяют его к подмассивам ранга 2 аргументов более высокого ранга. Он разделяет глиф
Quad Divide ⌹ (часто называемый Domino ) с монадической функцией Matrix Inverse.Содержимое
- 1 Пример
- 2 Применение
- 3 Внешние ссылки
- 3.1 Урок
- 3.2 Документация
Примеры
Результат X⌹Y равен (⌹Y)+.×X , что аналогично X÷Y равному (÷Y)×X . Как следствие, X≡Y+. верно для квадратных матриц.
⎕ ← X ← 2 2 ⍴ 1 2 3 4
1 2
3 4
⎕ ←Y ←2 2⍴5 6 7 8
5 6
7 8
X⌹Y
5 4
¯4 ¯3
(⌹Y)+.×X
5 4
¯4 ¯3
Х≡Y+.×X⌹Y
1
Applications
Благодаря свойствам обратного уравнения Мура-Пенроуза (которое использует Matrix Inverse), Matrix Divide можно использовать не только для решения системы линейных уравнений, но и для нахождения линейного решения методом наименьших квадратов для переопределенной системы.
В следующем примере решается система уравнений x+2y=5,2x−y=8{\displaystyle x+2y=5,2x-y=8}. Ответ: х = 4,2, у = 0,4 {\ displaystyle x = 4,2, y = 0,4}.
⎕ ←X ←2 2⍴1 2 2 ¯1
1 2
2 ¯1
Y ←5 8
Y⌹X
4,2 0,4
В следующем примере решается линейный метод наименьших квадратов по пяти точкам (1,5), (2,1), (3,4), (4,2), (5,8) {\ displaystyle (1,5 ),(2,1),(3,4),(4,2),(5,8)}. Ответ: y = 1,9 + 0,7x {\ displaystyle y = 1,9 + 0,7x}.
⎕ ← X ← 1, ⍪ ⍳ 5
1 1
1 2
1 3
1 4
1 5
Y ←5 1 4 2 8
Y⌹X
1,9 0,7
При использовании вещественных векторов в качестве обоих аргументов Y×X⌹Y дает проекцию X на базисный вектор Y. Оставшийся компонент X, а именно
Оставшийся компонент X, а именно R ←X-Y×X⌹Y , ортогонален Y ( R+.×Y равно нулю).
(X Y) ←(2 7)(3 1)
X⌹Y
1,3
Y×X⌹Y ⍝ Проекция X на Y
3,9 1,3
X-Y×X⌹Y ⍝ Оставшийся компонент в X
¯1,9 5,7
⎕CT>|Y+.×X-Y×X⌹Y ⍝ ∧ ортогонален Y (с незначительной ошибкой)
1
Внешние ссылки
Урок
- Выращивание АПЛ
Документация
- Диалог
- АПЛКС
- НАРС2000
- Словарь J, NuVoc (как
%.)
| Встроенные APL [править] | |||
|---|---|---|---|
| Примитивные функции | |||
| Скаляр | |||
| Монадический | Сопряженный ∙ Отрицать ∙ Сигнум ∙ Обратный ∙ Величина ∙ Экспоненциальный ∙ Натуральный логарифм ∙ Пол ∙ Потолок ∙ Факториал ∙ Не ∙ Число Пи ∙ Ролл ∙ Тип ∙ Мнимый ∙ Квадратный корень | ||
| Диадический | Сложение ∙ Вычитание ∙ Умножение ∙ Деление ∙ Остаток ∙ Степень ∙ Логарифм ∙ Минимум ∙ Максимум ∙ Двучлен ∙ Функции сравнения ∙ Булевы функции (И, ИЛИ, И, И) ∙ НОД ∙ НОД ∙ Циркуляр ∙ Комплекс ∙ Корень | ||
| Нескалярный | |||
| Структурный | Shape ∙ Reshape ∙ Tally ∙ Depth ∙ Ravel ∙ Enlist ∙ Table ∙ Catenate ∙ Reverse ∙ Rotate ∙ Transpose ∙ Raze ∙ Mix ∙ Split ∙ Enclose ∙ Nest ∙ Cut (K) ∙ Pair ∙ Link ∙ Partitioned Enclose | ||
| Выбор | Первый ∙ Выбрать ∙ Взять ∙ Выбросить ∙ Уникальный ∙ Идентификатор ∙ Выбрать ∙ Реплицировать ∙ Развернуть ∙ Установить функции (Пересечение ∙ Объединение ∙ Без) ∙ Индексация скобок ∙ Индекс | ||
| Селектор | Генератор индексов ∙ Оценка ∙ Индекс ∙ Интервальный индекс ∙ Индексы ∙ Сделка | ||
| Вычислительный | Совпадение ∙ Не совпадение ∙ Членство ∙ Найти ∙ Просеивание нубов ∙ Кодирование ∙ Декодирование ∙ Инверсия матрицы ∙ Разделение матрицы ∙ Форматирование ∙ Выполнение ∙ Материализация ∙ Диапазон | ||
| Примитивные операторы | Монадический | Каждый ∙ Коммутация ∙ Константа ∙ Репликация ∙ Расширение ∙ Уменьшение ∙ Оконное уменьшение ∙ Сканирование ∙ Внешний продукт ∙ Ключ ∙ I-Beam ∙ Порождение ∙ Функциональная ось | |
| Диадический | Bind ∙ Композиции (Compose, Reverse Compose, Beside, Withe, Atop, Over) ∙ Внутренний продукт ∙ Power ∙ At ∙ Under ∙ Rank ∙ Depth ∙ Variant ∙ Stencil ∙ Cut (J) | ||
| Квадратные имена | |||
| Массивы | Происхождение индекса ∙ Уровень миграции ∙ Атомарный вектор | ||
| Функции | Класс имени ∙ Преобразование регистра ∙ Преобразование Unicode | ||
| Операторы | Искать ∙ Заменить | ||
Разделение матриц \ для разреженных и сингулярных матриц – Общее использование
blob
#1
Кажется, что поведение матричного деления \ непоследовательно, если используются разреженные матрицы:
использование LinearAlgebra, SparseArrays А1=[1 1 ;0 0,0] В1=[4; 0,0] x1=A1\B1 #Ошибка: LAPACKException(2) x2=разреженный(A1)\разреженный(B1) #Ошибка: SingularException(2) x3=sparse(A1)\B1 #Ошибка: SingularException(2) x4=A1\разреженный(B1) #работает. Почему, если A\B нет? А2=[1 0 ;0 0,0] В2=[4; 0,0] x1=A2\B2 # дает 4 и NaN - почему, если A все еще треугольная и единственная? x2=sparse(A2)\sparse(B2) # дает 4 и NaN x3=sparse(A2)\B2 # дает 4 и NaN x4=A2\sparse(B2) # дает 4 и NaN А3=[1 1; 1 1] В3=[4; 4] x1=A3\B3 #Ошибка: SingularException(2) x2=sparse(A3)\sparse(B3) #Error: MethodError: нет метода, соответствующего lu! #почему другая ошибка? x3=sparse(A3)\B3 #Error: MethodError: нет метода, соответствующего lu! x4=A3\sparse(B3) #Ошибка: SingularException(2)
Не должен ли \ работать для разреженных матриц? Кроме того, почему нет решений методом наименьших квадратов для квадратной матрицы (как описано в «Линейной алгебре · Язык Джулии»)
zdenek_hurak
#2
Вы спросите, почему
блоб:
x4=A1\разреженный(B1)
работает, а все остальные комбинации разреженности — нет. Причина, возможно, связана со следующей проблемой: https://github.com/JuliaLang/julia/issues/33637. В нем говорится, что Джулия не поддерживает разреженность в правой части (поскольку базовый движок — SuitSparse) не поддерживает. Поэтому в этом случае правая часть остается плотной и A1\x1 решается. Проблема с 2019 года, и я не проверял, изменилось ли что-то, но я предполагаю, что она все еще актуальна.
капля
#3
Да, это идея, возможно, sparse(B1) преобразуется просто в B1 . Но если это должно работать для плотных матриц, я не понимаю, почему это не работает:
Но если это должно работать для плотных матриц, я не понимаю, почему это не работает:
x1=A1\B1
zdenek_hurak
#4
Похоже, что соглашение, принятое Джулией, заключается в том, что символ обратной косой черты, используемый в x = A\b с квадратной матрицей A, на самом деле означает исключительно обратную матрицу (возможно, вычисленную с использованием разложения LU). Если A является сингулярным (или обнаружено, что он близок к сингулярному), вызов x= A\b терпит неудачу. В таких ситуациях СВД вам в помощь: юлия> G = svd(A) СВД{Float64, Float64, Матрица{Float64}} U-фактор: Матрица 3×3{Float64}: -0,3322890,850246 0,408248 -0,549449 0,177311 -0,816497 -0,766609 -0,4…
Сравните с
julia> x1p = pinv(A1)*B1
2-элементный вектор{Float64}:
1. 9999999999999993
1.9999999999999993
9999999999999993
1.9999999999999993
капля
#5
Если x4=A1\sparse(B1) преобразует B1 в плотную матрицу, то A1\sparse(B1) должно быть эквивалентно А1\В1 . Но в моем случае A1\B1 терпит неудачу, тогда как A1\sparse(B1) дает решение. Вот и получается, что “конвертированный B1” как-то отличается – не знаю чем и почему.
Я знаю, что могу получить решение, используя другие методы, такие как pinv , дело в том, что я хотел бы избежать настройки моего решателя на каждую возможную матрицу, которую я мог бы получить.
Стивендж
#6
В таких ситуациях СВД твой друг
QR — это намного более дешевый способ получения решений методом наименьших квадратов сингулярных/неквадратичных систем: qr(A) \ b
Кроме того, QR работает и для разреженных матриц.
1 Нравится
zdenek_hurak
#7
Верно. На самом деле я упоминаю об этом в том посте.
zdenek_hurak
#8
Понятно.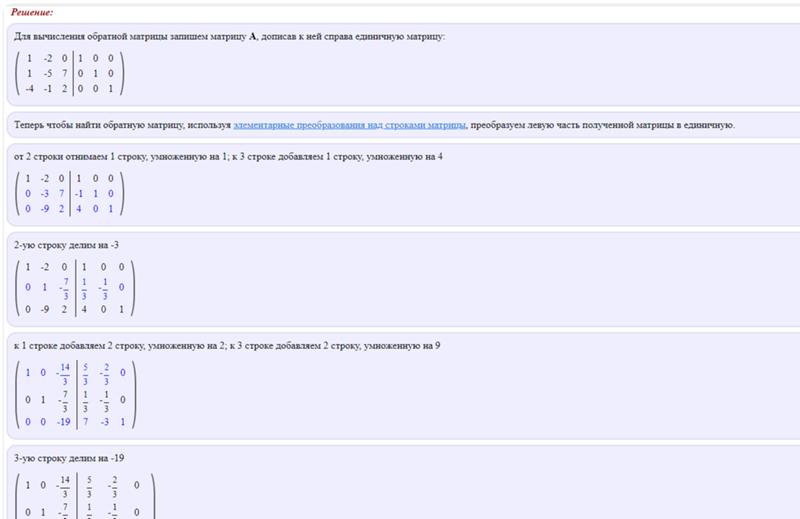 Ты прав. Несоответствие, о котором вы говорите, сначала ускользнуло от моего внимания. Действительно,
Ты прав. Несоответствие, о котором вы говорите, сначала ускользнуло от моего внимания. Действительно, A\b и A\sparse(b) ведут себя довольно противоречиво. Для удобства других читателей снова включаю код (ну, я немного изменил имена переменных):
julia> using LinearAlgebra, SparseArrays
Юлия> А=[1 1 ;0 0.0]
Матрица 2×2{Float64}:
1,0 1,0
0,0 0,0
юлия> b=[4; 0,0]
2-элементный вектор{Float64}:
4.0
0,0
юлия> x1=A\b
ОШИБКА: LAPACKException(2)
Трассировки стека:
[1] chklapackerror(ret::Int64)
@ LinearAlgebra.LAPACK /buildworker/worker/package_linux64/build/usr/share/julia/stdlib/v1.6/LinearAlgebra/src/lapack.jl:38
[2] trtrs!(uplo::Char, trans::Char, diag::Char, A::Matrix{Float64}, B::Vector{Float64})
@ LinearAlgebra.LAPACK /buildworker/worker/package_linux64/build/usr/share/julia/stdlib/v1.6/LinearAlgebra/src/lapack.jl:3426
[3] лдив!
@/buildworker/worker/package_linux64/build/usr/share/julia/stdlib/v1.6/LinearAlgebra/src/triangular.jl:739[встроенный]
[4] \
@ /buildworker/worker/package_linux64/build/usr/share/julia/stdlib/v1. 6/LinearAlgebra/src/triangular.jl:1673 [встроенный]
[5] \(A::Matrix{Float64}, B::Vector{Float64})
@ LinearAlgebra /buildworker/worker/package_linux64/build/usr/share/julia/stdlib/v1.6/LinearAlgebra/src/generic.jl:1134
[6] область верхнего уровня
@нет:1
Юлия> x2=разреженный(A)\разреженный(b)
ОШИБКА: SingularException(2)
Трассировки стека:
[1] _ldiv!(U::UpperTriangular{Float64, SparseMatrixCSC{Float64, Int64}}, B::Vector{Float64})
@ SparseArrays /buildworker/worker/package_linux64/build/usr/share/julia/stdlib/v1.6/SparseArrays/src/linalg.jl:706
[2] ldiv!(A::UpperTriangular{Float64, SparseMatrixCSC{Float64, Int64}}, B::Vector{Float64})
@ SparseArrays /buildworker/worker/package_linux64/build/usr/share/julia/stdlib/v1.6/SparseArrays/src/linalg.jl:632
[3] \(A::UpperTriangular{Float64, SparseMatrixCSC{Float64, Int64}}, b::SparseVector{Float64, Int64})
@ SparseArrays /buildworker/worker/package_linux64/build/usr/share/julia/stdlib/v1.6/SparseArrays/src/sparsevector.jl:1824
[4] \(A::SparseMatrixCSC{Float64, Int64}, B::SparseVector{Float64, Int64})
@ SparseArrays /buildworker/worker/package_linux64/build/usr/share/julia/stdlib/v1.
6/LinearAlgebra/src/triangular.jl:1673 [встроенный]
[5] \(A::Matrix{Float64}, B::Vector{Float64})
@ LinearAlgebra /buildworker/worker/package_linux64/build/usr/share/julia/stdlib/v1.6/LinearAlgebra/src/generic.jl:1134
[6] область верхнего уровня
@нет:1
Юлия> x2=разреженный(A)\разреженный(b)
ОШИБКА: SingularException(2)
Трассировки стека:
[1] _ldiv!(U::UpperTriangular{Float64, SparseMatrixCSC{Float64, Int64}}, B::Vector{Float64})
@ SparseArrays /buildworker/worker/package_linux64/build/usr/share/julia/stdlib/v1.6/SparseArrays/src/linalg.jl:706
[2] ldiv!(A::UpperTriangular{Float64, SparseMatrixCSC{Float64, Int64}}, B::Vector{Float64})
@ SparseArrays /buildworker/worker/package_linux64/build/usr/share/julia/stdlib/v1.6/SparseArrays/src/linalg.jl:632
[3] \(A::UpperTriangular{Float64, SparseMatrixCSC{Float64, Int64}}, b::SparseVector{Float64, Int64})
@ SparseArrays /buildworker/worker/package_linux64/build/usr/share/julia/stdlib/v1.6/SparseArrays/src/sparsevector.jl:1824
[4] \(A::SparseMatrixCSC{Float64, Int64}, B::SparseVector{Float64, Int64})
@ SparseArrays /buildworker/worker/package_linux64/build/usr/share/julia/stdlib/v1.

 Мы гарантируем высокое качество услуг, соблюдение сроков и индивидуальный подход, конфиденциальность данных.
Мы гарантируем высокое качество услуг, соблюдение сроков и индивидуальный подход, конфиденциальность данных. 9999999999999993
1.9999999999999993
9999999999999993
1.9999999999999993
 6/LinearAlgebra/src/triangular.jl:1673 [встроенный]
[5] \(A::Matrix{Float64}, B::Vector{Float64})
@ LinearAlgebra /buildworker/worker/package_linux64/build/usr/share/julia/stdlib/v1.6/LinearAlgebra/src/generic.jl:1134
[6] область верхнего уровня
@нет:1
Юлия> x2=разреженный(A)\разреженный(b)
ОШИБКА: SingularException(2)
Трассировки стека:
[1] _ldiv!(U::UpperTriangular{Float64, SparseMatrixCSC{Float64, Int64}}, B::Vector{Float64})
@ SparseArrays /buildworker/worker/package_linux64/build/usr/share/julia/stdlib/v1.6/SparseArrays/src/linalg.jl:706
[2] ldiv!(A::UpperTriangular{Float64, SparseMatrixCSC{Float64, Int64}}, B::Vector{Float64})
@ SparseArrays /buildworker/worker/package_linux64/build/usr/share/julia/stdlib/v1.6/SparseArrays/src/linalg.jl:632
[3] \(A::UpperTriangular{Float64, SparseMatrixCSC{Float64, Int64}}, b::SparseVector{Float64, Int64})
@ SparseArrays /buildworker/worker/package_linux64/build/usr/share/julia/stdlib/v1.6/SparseArrays/src/sparsevector.jl:1824
[4] \(A::SparseMatrixCSC{Float64, Int64}, B::SparseVector{Float64, Int64})
@ SparseArrays /buildworker/worker/package_linux64/build/usr/share/julia/stdlib/v1.
6/LinearAlgebra/src/triangular.jl:1673 [встроенный]
[5] \(A::Matrix{Float64}, B::Vector{Float64})
@ LinearAlgebra /buildworker/worker/package_linux64/build/usr/share/julia/stdlib/v1.6/LinearAlgebra/src/generic.jl:1134
[6] область верхнего уровня
@нет:1
Юлия> x2=разреженный(A)\разреженный(b)
ОШИБКА: SingularException(2)
Трассировки стека:
[1] _ldiv!(U::UpperTriangular{Float64, SparseMatrixCSC{Float64, Int64}}, B::Vector{Float64})
@ SparseArrays /buildworker/worker/package_linux64/build/usr/share/julia/stdlib/v1.6/SparseArrays/src/linalg.jl:706
[2] ldiv!(A::UpperTriangular{Float64, SparseMatrixCSC{Float64, Int64}}, B::Vector{Float64})
@ SparseArrays /buildworker/worker/package_linux64/build/usr/share/julia/stdlib/v1.6/SparseArrays/src/linalg.jl:632
[3] \(A::UpperTriangular{Float64, SparseMatrixCSC{Float64, Int64}}, b::SparseVector{Float64, Int64})
@ SparseArrays /buildworker/worker/package_linux64/build/usr/share/julia/stdlib/v1.6/SparseArrays/src/sparsevector.jl:1824
[4] \(A::SparseMatrixCSC{Float64, Int64}, B::SparseVector{Float64, Int64})
@ SparseArrays /buildworker/worker/package_linux64/build/usr/share/julia/stdlib/v1.