Матрицы элементы: Элемент матрицы

Создание визуального элемента “Матрица” в Power BI – Power BI

• Статья
• 09/23/2022
• Чтение занимает 10 мин

ОБЛАСТЬ ПРИМЕНЕНИЯ: ✔️ Power BI Desktop служба Power BI ✔️

Визуальный элемент “Матрица” похож на таблицу. Таблица поддерживает два измерения, а данные в ней неструктурированные, то есть повторяющиеся значения отображаются без суммирования. Матрица упрощает содержательное отображение данных по нескольким измерениям благодаря поддержке ступенчатого макета. Матрица автоматически агрегирует данные и позволяет детализировать их.

Вы можете создавать матричные визуальные элементы в отчетах Power BI и элементы перекрестного выделения в матрице с другими визуальными элементами на этой странице отчета.

Например, можно перекрестно выделять строки, столбцы и даже отдельные ячейки. Кроме того, отдельные ячейки и несколько выбранных ячеек можно копировать и вставлять в другие приложения.

Предусмотрено множество функций для матрицы, которые мы рассмотрим в следующих разделах этой статьи.

Примечание

Для предоставления общего доступа к отчету Power BI и вам, и коллеге необходимо иметь отдельные лицензии Power BI Pro или сохранить отчет в емкости Премиум.

Основные сведения о вычислении итогов в Power BI

Прежде чем использовать визуальный элемент “Матрица”, важно узнать, как в Power BI вычисляются промежуточные значения и итоговое в таблицах и матрицах. Для строк итогов и промежуточных итогов Power BI вычисляет меру на основе всех строк в базовых данных. Это не является простым сложением всех значений в видимых или отображаемых строках. Это значит, что в результате значения в строке итогов могут отличаться от ожидаемых.

Обратите внимание на следующие визуальные элементы “Матрица”.

В этом примере в каждой строке визуального элемента “Матрица” справа отображается сумма для каждого сочетания даты и имени менеджера по продажам. Но так как для одного менеджера проводится сопоставление с несколькими датами, число может отображаться несколько раз. Таким образом, точное итоговое значение на основе базовых данных и простое сложение отображаемых значений не эквивалентны. Это распространенный подход, когда при суммировании значение представляет сторону “один” в связи “один ко многим”.

Что касается итогов и промежуточных итогов, учитывайте, что эти значения основаны на базовых данных, а не только на отображаемых значениях.

Заголовки строк можно развернуть двумя способами. Первый — с помощью контекстного меню. Вы увидите команды, позволяющие развернуть заголовок выбранной строки, весь уровень или все содержимое до последнего уровня иерархии. Аналогичные команды также можно использовать для свертывания заголовков строк.

К заголовкам строк можно также добавить кнопки +/– в панели форматирования на карточке Заголовки строк. По умолчанию значки будут соответствовать форматированию заголовка строки, но при необходимости цвета и размеры значков можно настроить отдельно.

После включения значков они работают аналогично значкам сводной таблицы в Excel.

Состояние расширения матрицы будет сохранено вместе с отчетом. Матрицу можно закрепить на панели мониторинга развернутой или свернутой. Если выбран фрагмент панели мониторинга и отчет открывается, развернутое состояние по-прежнему можно изменять в отчете.

Примечание

Если отчет создается на основе многомерной модели Analysis Services, в которой используется функция “Элемент по умолчанию”, имеется ряд особенностей, касающихся развертывания и свертывания. Дополнительные сведения см. в статье “Работа с многомерными моделями” в Power BI.

Использование действий детализации с помощью визуального элемента “Матрица”

Визуальный элемент “Матрица” позволяет использовать подробные визуализации, недоступные ранее. Вы можете выполнить детализацию с использованием строк, столбцов и даже отдельных разделов и ячеек. Рассмотрим каждый из вариантов детализации.

В области “Визуализации” при добавлении нескольких полей в разделе Строки области Поля вы разрешаете выполнять действия детализации для строк визуального элемента “Матрица”. Это похоже на создание иерархии, которую затем можно детализировать (а потом обобщить), а также выполнить анализ данных на каждом уровне.

На следующем рисунке в разделе Строки содержатся элементы Этап продажи и Размер возможной сделки, формирующие группу (или иерархию) строк, которые можно детализировать.

Если визуальный элемент имеет группирование, созданное в разделе “Строки “, сам визуальный элемент отображает значки детализации и разворачивает их в верхнем углу визуального элемента.

Эти кнопки действуют так же, как и подобные кнопки для детализации и развертывания в других визуальных элементах: они позволяют перемещаться по уровням элементов иерархии вниз (или вверх). В этом случае мы можем перейти от элемента Этап продажи к элементу Размер возможной сделки, как показано на следующем рисунке, на котором выбран значок перехода на один уровень (в виде разветвления).

Помимо использования этих значков можно щелкнуть любой из заголовков строк и выбрать пункт детализации в появившемся меню.

Обратите внимание, что в этом меню есть несколько параметров, используя которые вы получите разные результаты.

Если выбрать пункт Детализация, будет развернута матрица для этого уровня строки, за исключением других заголовков строк, кроме выбранного заголовка строки. На следующем рисунке выбрано Предложение>Детализация. Обратите внимание, что другие строки верхнего уровня перестали отображаться в матрице. Этот способ детализации — полезная функция. Она очень пригодится, когда мы перейдем к разделу о перекрестном выделении.

Выберите значок Подняться, чтобы вернуться к предыдущему представлению верхнего уровня.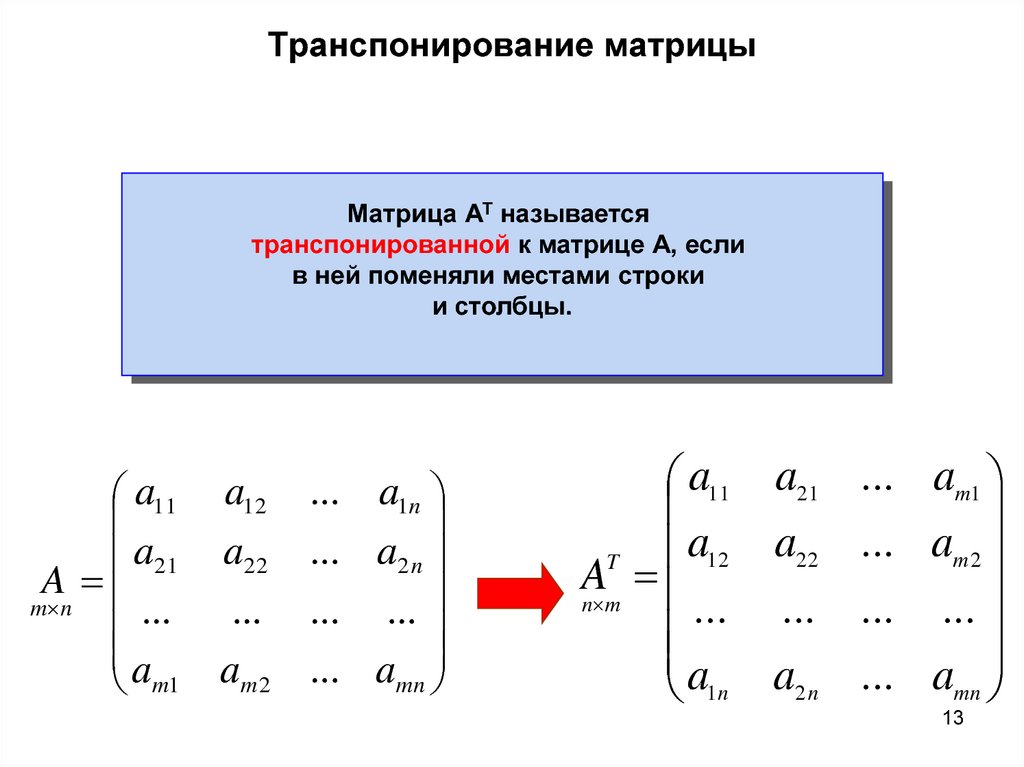 Если затем выбрать Предложение>Показать следующий уровень, появится список всех элементов следующего уровня (в данном случае поле Размер возможной сделки) с сортировкой по возрастанию без категоризации иерархии верхнего уровня.

Щелкните значок детализации в верхнем углу, чтобы матрица отображала все категории верхнего уровня, а затем выберите “Развернуть предложение>на следующий уровень“, чтобы просмотреть все значения для обоих уровней иерархии — этап продаж и размер возможностей.

Вы также можете использовать пункт меню Развернуть для дополнительного управления отображением. Например, щелкните значок детализации . Затем выберите>пункт “Развернуть>предложение”. Power BI отображает одну строку итогов для каждого параметра Этап продажи и все для Размер возможной сделки для поля Предложение.

Детализация по заголовкам столбцов

Аналогично детализации по строкам можно также выполнять детализацию по столбцам. На следующем рисунке видно, что в области полей Столбцы есть два поля, создающие иерархию, аналогичную той, которую мы использовали для строк ранее в этой статье. В области полей Столбцы есть поля Регион и Сегмент. Как только второе поле было добавлено в столбцы, в визуальном элементе отображается новое раскрывающееся меню (детализация), в котором отображаются строки.

Чтобы детализировать столбцы, выберите “Столбцы ” в меню “Детализация” , которое можно найти рядом с значками детализации и развернуть. Выберите восточный регион, а затем Детализация.

При выборе “Детализация” отображается следующий уровень иерархии столбцов для восточного региона>, который в данном случае — число возможных вариантов. Другой регион скрыт.

Остальные элементы меню действуют в столбцах так же, как в строках (см. предыдущий раздел о детализации по заголовкам строк). Вы можете показать следующий уровень для столбцов и раскрыть их до следующего уровня так же, как для строк.

Примечание

Значки детализации и детализации применяются только к строкам. Чтобы выполнить детализацию по столбцам, воспользуйтесь контекстным меню.

Ступенчатый макет с визуальными элементами с матрицей

Визуальный элемент “Матрица” позволяет автоматически сделать отступы для подкатегорий в иерархии под каждой родительской категорией. Вот что собой представляет ступенчатый макет.

В исходной версии визуального элемента “Матрица” подкатегории отображались в отдельном столбце, занимая больше места в визуальном элементе. На следующем рисунке показана таблица в исходном визуальном элементе матрицы; обратите внимание на подкатегории в отдельном столбце.

На следующем рисунке показан визуальный элемент “Матрица” со ступенчатым макетом. Обратите внимание, что категория “Квалифицировать ” имеет свои подкатегории (малый, средний и большой) слегка отступов, обеспечивая более чистый и гораздо более сжатый визуальный элемент.

Параметры ступенчатого макета можно легко настроить. Выбрав визуальный элемент матрицы, в разделе “Формат ” (значок кисти) области “Визуализации ” разверните раздел заголовков строк. У вас есть два варианта: переключатель макета с шагами (который включает или выключает) и отступ макета с шагами (который задает отступ в пикселях).

Если отключить ступенчатый макет, Power BI отобразит подкатегории в другом столбце, а не под родительской категорией.

Промежуточные и общие итоги с визуальными элементами матрицы

Промежуточные итоги можно включить или отключить в визуальных элементах матрицы для строк и столбцов. На приведенном ниже рисунке видно, что для строки промежуточных итогов задано значение Включено и настроено отображение внизу.

При включении промежуточных итогов строк и добавлении метки Power BI также добавляет строку и ту же метку для общего значения. Чтобы отформатировать общий итог, выберите параметр формата для общего числа строк.

Если вы хотите включить промежуточные итоги и общий итог в разделе формата области визуализаций, разверните карточку промежуточных итогов строк . Переведите ползунок строки промежуточных итогов в положение Выкл. После этого действия подытоги больше не будут отображаться.

Для столбцов применяется тот же процесс.

Добавление условных значков

Добавьте в таблицу или матрицу визуальные подсказки с помощью условных значков.

В разделе форматирования области “Визуализации” разверните карточку элементов ячейки . Включите ползунок значкови выберите значок определений.

Настройте условия, значки и цвета для матрицы и нажмите кнопку ОК. В этом примере мы использовали красный флажок для низких значений, сиреневый круг для высоких значений и желтый треугольник для всех значений между ними.

Перекрестное выделение с использованием визуальных элементов с матрицей

В визуальном элементе “Матрица” для перекрестного выделения вы можете выбрать все элементы в матрице. Выберите столбец в визуальном элементе “Матрица”, и Power BI выделит столбец, как и другие визуальные элементы на странице отчета. Этот способ перекрестного выделения был доступен для других визуальных элементов, а также при выборе точки данных. Теперь он реализован и для визуального элемента “Матрица”.

Кроме того, для перекрестного выделения можно также нажать клавишу CTRL и щелкнуть мышью. Например, на следующем рисунке коллекция подкатегорий была выбрана из визуального элемента матрицы. Обратите внимание, что элементы, которые не были выбраны в визуальном элементе, выделены серым цветом. Также оцените, как в других визуальных элементах на странице отражаются элементы, выбранные в визуальном элементе “Матрица”.

Копирование значений из Power BI для использования в других приложениях

Матрица или таблица могут иметь содержимое, которое вы можете использовать в других приложениях: Dynamics CRM, Excel или в других отчетах Power BI. Щелчком правой кнопки мыши в Power BI можно скопировать одну ячейку или набор ячеек в буфер обмена, а затем вставить их в другое приложение.

• Чтобы скопировать значение одной ячейки, выделите ее, щелкните правой кнопкой мыши и выберите ” Копировать значение“. Значение ячейки без формата помещается в буфер обмена, откуда его можно вставить в другое приложение.

• Чтобы скопировать несколько ячеек сразу, выберите нужный диапазон ячеек или выберите несколько ячеек по очереди, удерживая клавишу CTRL. Команда

  Копировать выделение гарантирует форматирование мер в соответствии с правилами форматирования столбца, в отличие от команды Копировать значение без форматирования.

• Такая копия будет содержать заголовки столбцов и строк.

• Чтобы создать копию самого визуального элемента, содержащего только выбранные ячейки, выделите одну или несколько ячеек с помощью клавиш CTRL, щелкните правой кнопкой мыши и выберите команду “Копировать визуальный элемент“.

• Если затем с помощью CTRL+V вставить данные на холст, появится копия визуализации матрицы, но она содержит только скопированные данные.

Задание значения матрицы в качестве настраиваемого URL-адреса

Если у вас есть столбец или мера, содержащие URL-адреса веб-сайтов, вы можете применить условное форматирование, чтобы отображать эти URL-адреса как активные ссылки. Этот параметр можно найти в карточке элементов ячейки в области форматирования.

Включите параметр URL-адрес и выберите поле, которое будет использоваться в качестве URL-адреса для столбца. После применения значения в этом поле (столбце) становятся активными ссылками. Наведите указатель мыши, чтобы увидеть ссылку, и щелкните ее, перейдя к этой странице.

Дополнительные сведения см. в разделе “Условное форматирование таблицы”.

Цвет заливки и шрифта с визуальными элементами матрицы

С помощью визуального элемента “Матрица” можно применить условное форматирование (цвет, заливка, гистограммы) фона для ячеек в матрице, а также условное форматирование текста и значений.

Чтобы применить условное форматирование, выберите визуальный элемент “Матрица” и откройте панель Форматирование. Разверните карточку элементов ячейки и цвет фона, цвет шрифта или гистограммы, включите ползунок в положение “Вкл. “. Включение одного из этих параметров делает его значком определений доступным. При выборе этого значка можно настроить цвета и значения для форматирования цвета.

Выберите значок определений, чтобы отобразить диалоговое окно, которое можно использовать для внесения изменений. Этот пример показывает диалоговое окно для параметра Гистограммы.

Неоднородная иерархия

Неоднородная иерархия имеет уровни без данных. Хороший пример — матрица сотрудников компании. У компании много уровней: от генерального директора и ниже. Генеральный директор представляет собой самый высокий уровень в иерархии и не отчитывается ни перед кем из сотрудников. С другой стороны, любой другой сотрудник компании может отчитываться перед цепочкой руководителей, которые отчитываются перед вице-президентом, отчитывающимся, в свою очередь, перед генеральным директором. В зависимости от уровня в иерархии и варианта организации отдела сотрудники могут иметь данные для одного, двух, пяти или десяти уровней иерархии.

И у любого конкретного сотрудника могут отсутствовать данные для определенных уровней иерархии.

В настоящее время невозможно скрыть пустые строки или одинаковые значения родительских и дочерних элементов. Вы также не можете контролировать, какие уровни иерархии можно расширить, а какие нет. Однако существует несколько действий, с помощью которых можно сделать визуальный элемент более привлекательным.

• Отключите ступенчатый макет. В области “Формат” разверните карточку заголовков строк . Затем откройте раздел “Параметры ” карточки и установите переключатель

  “Пошаговая разметка ” в значение “Выкл.”. Все пустые значения для уровня иерархии теперь будут отображаться в одной строке.

• Отключите подытоги для строк и столбцов матрицы. В области “Формат” установите ползунок промежуточных итогов строки и ползунок промежуточных итогов столбца в положение “Выкл. “.

Рекомендации и устранение неполадок

• Если текстовые данные в ячейках или заголовках матрицы содержат символы новой строки, эти символы будут игнорироваться, если не включить перенос по словам в карточке панели форматирования, связанной с элементом.

• Полосы прокрутки будут отображаться для прокрутки между ячейками текста, которые не все помещаются в визуальный элемент одновременно, но столбцы заголовков строк фиксируются в визуальном элементе матрицы и не будут прокручиваться. Если в матрицу слишком много заголовков строк, чтобы ячейки тела были скрыты, прокрутка не будет отображать ячейки тела. Вместо этого уменьшите количество заголовков строк в визуальном элементе, настройте ширину столбца, уменьшите размер шрифта или убедитесь, что ячейки текста матрицы видны для доступа к данным значений.

Дальнейшие действия

Визуализация Power Apps для Power BI

Типы визуализаций в Power BI

python – Сравнение элементов матрицы

Нужна помощь с поэлементным сравнением в матрице Для заданной матрицы размером 8 x 8 найти такие k, что элементы k-й строки матрицы совпадают с элементами k-ого столбца.

У меня ошибка в том что элементы сравнивает с учётом порядка,а надо без

from random import randint
n = 8
A = [[randint(1,2) for j in range(n)] for i in range(n)]
out_2 = [0] * n
out_1 = ["p"] * n
temp_row = [0] * n
temp_col = []
for i in range(n):
    temp_col.append([0] * n)
for Row in range(n):
    for Col in range(n):
        print("{0:02}".format(A[Row][Col]), end=" ")
    print()
for i in range(n):
    for j in range(n):
        temp_col[i][j] = A[j][i]
for i in range(n):
    temp_row[i] = A[i]
for i in range(n):
    for j in range(n):
        if temp_row[i] == temp_col[j]:
            out_1[i] = i
for i, (row, col) in enumerate(zip(A, zip(*A))):
    if sorted(row) == sorted(col):
        print(i+1,f"Ряд и колонка с индексом {i} полностью совпадают.")
    else:
        print(i+1,"Одинаковых строчек и столбцов в итерации ", i + 1, "не найдено")
for Row in range(n):
    for number in A[Row]:
        if number < 0:
            out_2[Row] = sum(A[Row])

выводит

02 02 02 02 01 02 01 01 
02 02 01 02 02 02 02 02 
02 01 01 01 02 02 01 01 
01 01 02 02 02 02 02 02 
01 01 01 02 01 01 01 01 
02 01 01 01 01 02 02 02 
01 01 01 02 02 02 02 02 
02 01 01 01 02 01 02 02 
1 Ряд и колонка с индексом 0 полностью совпадают.  
2 Одинаковых строчек и столбцов в итерации  2 не найдено
3 Одинаковых строчек и столбцов в итерации  3 не найдено
4 Одинаковых строчек и столбцов в итерации  4 не найдено
5 Одинаковых строчек и столбцов в итерации  5 не найдено
6 Одинаковых строчек и столбцов в итерации  6 не найдено
7 Ряд и колонка с индексом 6 полностью совпадают.
8 Одинаковых строчек и столбцов в итерации  8 не найдено

• python

3

Просто отсортируйте значения ряда и колонки прежде чем их сравнивать.

for i, (row, col) in enumerate(zip(A, zip(*A))):
    if sorted(row) == sorted(col):
        print(f"Ряд и колонка с индексами {i} полностью совпадают.")

Здесь zip(*A) транспонирует матрицу (т.е. её столбцы становятся рядами). Далее следующим zip берутся одновременно ряд из исходной матрицы и ряд из транспонированной (он же столбец из исходной). Ну и в enumerate обёрнуто, чтобы считать номер ряда/столбца).

9

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки

Элементы матрицы – положение, количество элементов, примеры

Элементы матрицы – это не что иное, как компоненты матрицы. Это могут быть числа, переменные, комбинация того и другого или любые специальные символы. Количество элементов матрицы равно произведению количества строк на количество столбцов в ней.

Давайте узнаем больше об элементах матрицы вместе с другими примерами.

1.	Что такое элементы матрицы?
2.	Количество элементов матрицы
3.	Позиции элементов матрицы
4.	Свойства элементов матрицы
5.	Часто задаваемые вопросы об элементах матрицы

Что такое элементы матрицы?

элементов матрицы — не что иное, как элементы матрицы. Это могут быть числа, переменные, любые математические выражения или любые другие символы внутри матрицы. Например, элементы матрицы A = \(\left[\begin{array}{rl}
5 и 2 \
х & у \\
-1 и 3
\end{array}\right]\) равны 5, 2, x, y, -1 и 3. Вот еще примеры:

• Элементы B = \(\left[\begin{array}{rl }
  а &1 \\\
  -1 и 5
  \end{array}\right]\) — это a, 1, -1 и 5.
• Элементы C = \(\left[\begin{array}{rl}
  1 и 2 и 5х + 3\
  3&-2&2\
  1 и 3 и х
  \end{array}\right]\) равны 1, 2, 5x+3, 3, -2, 2, 1, 3 и x.

При перечислении элементов матрицы, как показано в примерах, порядок не имеет значения.

Количество элементов матрицы

В приведенных выше примерах A имеет 2 строки, 3 столбца и 6 элементов; B имеет 2 строки и 2 столбца и 4 элемента; и C имеет 3 строки и 3 столбца и имеет 9элементы. Наблюдая за этими примерами, вы поняли, как посчитать количество элементов матрицы, не перечисляя и не считая элементы? Да, это не что иное, как произведение количества строк и количества столбцов. Количество элементов матрицы не зависит от типа присутствующих в ней элементов. Например, количество элементов матрицы с

• 5 строками и 2 столбцами равно 5 × 2 = 10.
• 5 строк и 2 столбца — это 2 × 5 = 10.
• 3 строки и 4 столбца — это 3 × 4 = 12.
• 4 строки и 3 столбца — это 4 × 3 = 12.

Если количество строк и количество столбцов матрицы A равно m и n соответственно, то ее порядок записывается как m × n, а количество элементов равно произведению m и n (т. е. mn).

Положения элементов матрицы

Каждый элемент матрицы имеет уникальное положение и определяется номером строки, за которым следует номер столбца (иногда через запятую) в нижнем индексе алфавита, представляющего матрицу. т. е. элемент матрицы A, присутствующий в i ^-я -я строка и j ^-й -й столбец представлены как A ᵢⱼ (или) Aᵢ,ⱼ (или) (i, j) ^-й элемент A. Например, если A = \(\left[\begin{array {rl}
5 и 2 \
х & у \\
-1 и 3
\end{array}\right]\) тогда:

• 5 — это элемент в строке 1 ^st и столбце 1 ^st . Записывается как A₁₁ (или) (или) A₁,₁ (или) (1, 1) ^-й -й элемент A .
• 2 — это элемент в 1 ^-й -й ряд и 2 ^-й -й столбец. Записывается как A₁₂ (или) A₁,₂ (или) (1, 2) ^-й -й элемент A.
• -1 — это элемент в строке 3 ^rd и столбце 1 ^st . Записывается как A₃₁ (или) A₃, ₁ (или) (3, 1) ^-й -й элемент A.

При записи позиции не забудьте сначала написать номер строки, а затем номер столбца (не в обратном порядке).

Свойства элементов матрицы

• Позиция элемента матрицы A представлена ​​буквой A с нижним индексом (номер строки, номер столбца).
• Если две матрицы A и B равны, то их соответствующие элементы равны. т. е. Aᵢ,ⱼ = Bᵢ,ⱼ для каждого i, j.
• Количество элементов матрицы порядка m x n равно mn.
• Число элементов квадратной матрицы всегда равно полному квадрату.
• Число элементов прямоугольной матрицы никогда не бывает полным квадратом.

☛ Похожие темы:

• Матричный калькулятор
• Свойства матриц
• Типы матриц
• Умножение матриц

 

Элементы матрицы Примеры

1. Пример 1: Список всех элементов матрицы A = \(\left[\begin{array}{cccc}
   1 и 8 и 3 и 2 \\
   & & & \\
   5 и 3 и 0 и -6
   \end{массив}\right]\).

   Решение:

   Элементами матрицы являются ее компоненты. Таким образом, элементами A являются 1, 8, 3, 2, 5, 3, 0 и -6.

   Ответ: 1, 8, 3, 2, 5, 3, 0 и -6.

2. Пример 2: В матрице, приведенной в Пример 1 , какой элемент присутствует в строке 2 ^nd и столбце 3 ^rd и как мы его представляем?

   Решение:

   Элемент, который присутствует в столбце 2 ^{N D} Строка и 3 ^RD . , ₃ = 0

3. Пример 3: Если матрицы A = \(\left(\begin{array}{ll}
   х+1 & -1 \\ \\
   2 и у -2
   \end{массив}\right)\) и B = \(\left(\begin{массив}{ll}
   3&-1\
   2 и 5
   \end{array}\right)\) равны, то найдите x и y.

   Решение:

   Дано, что A = B, т. е.

   \(\left(\begin{array}{ll}
   х+1 & -1 \\ \\
   2 и у -2
   \end{массив}\right)\) = \(\left(\begin{массив}{ll}
   3&-1\
   2 и 5
   \end{array}\right)\)

   По свойствам элементов матрицы соответствующие элементы вышеуказанных матриц равны. Так

   х + 1 = 3 ⇒ х = 2
   у – 2 = 5 ⇒ у = 7

   Ответ: х = 2 и у = 7.

перейти к слайдуперейти к слайдуперейти к слайду

Хотите создать прочную основу в математике?

Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.

Записаться на бесплатный пробный урок

Практические вопросы по элементам матрицы

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы об элементах матрицы

Как найти элементы матрицы?

элементов матрицы — это просто компоненты, присутствующие внутри матрицы и разделенные строками и столбцами. Например, элементы матрицы \(\left[\begin{array}{rrrr}
1 и 3 \\\
0 и 2
\end{array}\right]\) равны 1, 3, 0 и 2. Некоторые или все элементы матрицы могут быть одинаковыми.

Сколько элементов в матрице?

Количество элементов матрицы = количество строк, умноженное на количество столбцов. Например, если количество строк в матрице равно 3, а количество столбцов равно 4, то количество элементов в ней равно 3 x 4 = 12.

Как найти положение матрицы?

Положением матрицы является номер строки, за которым следует номер столбца, в котором присутствует этот элемент. Например, в матрице B = \(\left[\begin{array}{rrrr}
1&3&1&-1\
0 и 2 и 3 и 2
\end{array}\right]\), 1 присутствует в строке 1 ^st и столбце 3 ^rd , и, следовательно, мы можем написать B₁, ₃ = 1 (или) B₁₃ = 1.

Что такое Количество элементов квадратной матрицы?

Число элементов квадратной матрицы порядка n x n равно n ² . Таким образом, количество элементов квадратной матрицы всегда равно полному квадрату.

Как обозначаются элементы матрицы?

Мы представляем элементы матрицы по их позициям. Aₘ,ₙ представляет собой элемент матрицы A, лежащий в строке m и столбце n. Здесь сначала идет номер строки, а затем номер столбца.

Какая связь между элементами матрицы и ее порядком?

Если матрица состоит из m строк и n столбцов, то ее порядок записывается как m x n. Если мы просто умножим m и n, то произведение даст количество элементов матрицы.

Скачать БЕСПЛАТНЫЕ учебные материалы

ЛИСТКИ

Mathwords: Element of a Matrix

Mathwords: Element of a Matrix

индекс: нажмите на букву индекс: предметные области
	Элемент Матрицы Один из элементов матрицы. Оставить комментарий Отменить ответ Для отправки комментария вам необходимо авторизоваться. Меню Поиск: