Что такое товарная матрица: группы, разработка – Определение
Товарная матрица (ассортиментная матрица) — это перечень продукции, в котором все товары структурированы на основании установленных параметров и характеристик. Такой список составляют для каждой точки продаж, если у компании их несколько.
Группы товарной матрицы
Все товары, из которых компании собирают товарную матрицу, условно можно разделить на пять групп.
- Продукты-локомотивы. Это основные и самые востребованные товары в отделе магазина или торговой точке.
- Сопутствующие товары. В эту группу входят продукты, которые допродают клиентам при покупке основных товаров. Например, к смартфону магазин предлагает приобрести защитное стекло, чехол, беспроводной джойстик и так далее.
- Статусные продукты. Это самые дорогие товары в магазине, задача которых заключается в стимулировании спроса, поскольку по сравнению с ними другие позиции кажутся более доступными.

- Товары-заменители. В эту группу добавляют те продукты, которые позволяют удовлетворить потребности покупателей если вдруг основные товары окажутся не доступны.
- Комплексные продукты. Это товары, которые можно объединить для увеличения продаж, повышения прибыли или освобождения склада.
В ассортименте огромную роль играет не столько количество товаров, сколько качество. Воспользуйтесь рекомендациями в следующем разделе, чтобы разработать правильную товарную матрицу.
Как разработать товарную матрицу
Важно создать такой перечень товаров, который позволит закрыть все потребности целевой аудитории и увеличить ее LTV. Для этого ознакомьтесь с процессом разработки товарной матрицы.
- Определите формат магазина и концепцию развития. Проанализируйте расположение, ресурсы компании, размеры помещения и другие факторы, от которых будет зависеть количество реализуемого товара, позиционирование и продвижение на рынке.

- Составьте портрет целевой аудитории. Проведите маркетинговое исследование и соберите всю возможную информацию о потенциальных покупателях, составьте аватары клиентов. Узнайте уровень дохода, размер среднего чека, социальное положение, возраст, пол и другие данные.
- Изучите конкурентов. Выявите их сильные и слабые стороны, проанализируйте ассортимент, сравните стоимость аналогичной продукции.
- Определите ценовую политику. На основании портрета целевой аудитории установите размер цен.
- Разделите товарные группы на категории и подкатегории. Подготовьте предварительный список товаров на основании базовых и дополнительных продуктов.
- Составьте ассортиментную матрицу. Подготовьте полный перечень товаров, которые вы будете продавать, и пропишите их главные характеристики. Это может быть торговая марка, ценовой диапазон, формат упаковки, группа по ABC-анализу и так далее.

По завершению процесса у вас на руках будет таблица, с помощью которой вы сможете расширять ассортимент, определять допустимый минимум товаров, находить пути сокращения расходов и многое другое.
Источник: ABM Digital DistributionЧтобы товарная матрица всегда была актуальной, обновляйте ее каждый квартал или раз в полгода.
Ресурсы:
- В статье In-Scale вы узнаете, почему так важно разрабатывать товарную матрицу.
- На этом сайте ознакомитесь с пошаговым руководством составления ассортиментной матрицы.
- В статье «Генератора Продаж» прочитаете о правилах составления товарной матрицы.
- А здесь ознакомитесь с оптимизацией ассортиментной матрицы интернет-магазина.
Обновлено: 14.07.2021
Оцените, насколько полезна статья “Товарная матрица”
Оценка: 4 / 5 (7)
как интернет отреагировал на трейлер новой “Матрицы” — Российская газета
Франшиза “Матрица” – вещь монументальная и значимая не только для кинематографа, но и для всей современной массовой культуры в целом.
Поэтому, каким бы ни получился четвертый фильм в серии, градус ожидания аудитории выкручен на максимум, и интернет отреагировал на дебютный трейлер неостановимым потоком мемов и шуток.
Собрали в этом материале некоторые из них, которые подмечают те или иные детали ролика.
Больше всего внимания уделено сцене, в которой ничего не помнящий Нео принимает ванну с резиновой уточкой.
Очень многие начали проводить параллели с Джоном Уиком – персонажем, с помощью которого Киану Ривз перезапустил свою карьеру в жанре экшн.
джон уик, попавший в матрицу, в дебютном трейлере новой части #matrix выглядит отлично.
— сетерра. (@nvrtrstfx) September 9, 2021
-Вы показываете Джон Уик 4?
— 🏳️⚧️𝕷𝔦𝔷𝔷𝔶 𝖂𝔢𝔦𝔰𝔰🏳️⚧️ (@lizweissru) September 8, 2021
-Нет Матрица 4
-Красивое pic.twitter.com/Gf1plTZd6w
Джон Уик:*узнает,что собаку убили*
— Никита Жинжиков 18+ (@gearplex) September 9, 2021
Русская мафия:*умирает*
ДУ:*узнает,что дом взорвали*
Итальянская мафия:*умирает*
ДУ:*узнает,что его заказали*
Организация киллеров:*умирает*
ДУ:*узнает,что он в Матрице,а его самого вообще УБИЛИ*#Матрица: *съежилась в ожидании 16.12.21*
К месту вспомнили о героях культового сериала “Офис”.
Много попадается и негативных отзывов от пользователей, которых не впечатлило первое официальное видео.
шото от матрицы стилистически вообще ничего не осталось
вот это – матрица:https://t.co/MTi2BVtNUY
— Амбассадор уничтожения (@SiegeOfTerra) September 9, 2021
какая новая матрица беспомощная жесть
— Иоанн (@wqptqrii) September 9, 2021
люди, прекращайте снимать кино
Но в основном, конечно же, настрой будущих зрителей оптимистичный, хоть некоторые и подмечают, что пока ничего не понятно.
Понимание матрицы Эйзенхауэра – Dropbox Business
Что такое матрица Эйзенхауэра?
Никто не хочет быть непродуктивным, особенно на работе. Но на протяжении дня появляются срочные запросы, и, по мере того как ваш список задач растет, становится все сложнее поддерживать это стремление к продуктивности.
Понимание матрицы Эйзенхауэра
Матрица Эйзенхауэра, также известная под названием «коробка Эйзенхауэра» или «матрица срочных/важных задач» — это простая схема определения приоритетности задач и регулирования рабочей нагрузки. Она названа в честь Дуайта Д. Эйзенхауэра, пятизвездочного генерала и 34-го президента США. Эйзенхауэр известен благодаря своей неимоверной продуктивности, поэтому его подход к постановке целей и управлению временем всесторонне изучался многими людьми, одним из которых был Стивен Кови. В своей книге «7 навыков высокоэффективных людей» Кови создал на основе идей Эйзенхауэра простой инструмент расстановки приоритетов в выполнении задач: матрицу Эйзенхауэра.
Что же представляет из себя матрица Эйзенхауэра? По сути, это стратегия, которая позволяет вам применить на практике следующую цитату, приписываемую Эйзенхауэру: «У меня есть два типа проблем: срочные и важные.
Как работает коробка Эйзенхауэра?
Компании и частные лица могут использовать матрицу Эйзенхауэра для планирования, делегирования, определения приоритетности и включения задач в график работы на день или на неделю. Распределив задачи в один из четырех квадрантов ниже, вы сможете определить их срочность и решить, как с ними следует поступить:
- Первый Квадрант. Срочное и важное (задачи, которые необходимо выполнить немедленно). Это очень важные задачи, которые нужно сделать в первую очередь и как можно скорее. Как правило, это запросы, полученные в последний момент по причине непредвиденных обстоятельств. Обычно такие задачи нужно выполнять немедленно или в тот же день. Сюда можно отнести работу в проекте вместо заболевшего коллеги или реагирование на непредвиденную ситуацию, например сбои в цепи поставок.
- Второй квадрант.
 Важное, но не срочное (задачи, которые можно запланировать на более поздний срок). Это важные долгосрочные цели или задачи, не имеющие жесткого срока выполнения, поэтому их можно запланировать на более поздний срок. Сюда можно отнести получение профессиональной квалификации или планирование долгосрочных бизнес-целей, например сокращение бюджета.
Важное, но не срочное (задачи, которые можно запланировать на более поздний срок). Это важные долгосрочные цели или задачи, не имеющие жесткого срока выполнения, поэтому их можно запланировать на более поздний срок. Сюда можно отнести получение профессиональной квалификации или планирование долгосрочных бизнес-целей, например сокращение бюджета. - Третий квадрант. Срочное, но не важное (задачи, которые можно кому-то делегировать). Эти задачи нужно выполнить немедленно, но они могут быть не настолько важными, чтобы привлечь ваше внимание, а значит, их можно делегировать другим участникам рабочей группы. Сюда можно отнести повседневную работу, длительные встречи или телефонные звонки без четкой цели.
- Четвертый квадрант. Несрочное и неважное (задачи, которые можно убрать из плана). Эти задачи только отвлекают вас, поэтому их нужно избегать по возможности. Во многих случаях можно просто игнорировать или отменить такие задачи. Сюда можно отнести общественные мероприятия или излишне длительные перерывы на чай или кофе.

Проще говоря, применение коробки Эйзенхауэра может помочь вам визуализировать ваши задачи с точки зрения важности и срочности. Когда вы начнете рассматривать свой рабочий процесс с такой позиции, вам гораздо проще будет расставить приоритеты для самых важных задач и выполнить их как можно скорее.
Как различить срочность и важность?
Нет универсальной формулы для определения различия между срочностью и важностью при создании матрицы приоритетов, но это очень важно. Чаще всего различие между этими двумя категориями в реальности определить намного труднее, чем при составлении абстрактной коробки Эйзенхауэра. Если вкратце, срочные задачи неизбежны и требуют незамедлительного уделения им внимания, а важные задачи в большей степени требуют планирования и способствуют достижению долгосрочных целей. Например, отвечать на телефонные звонки крупного клиента — это срочная задача, а ознакомиться с последними исследованиями в своей сфере — важная.
Каковы преимущества матрицы Эйзенхауэра?
Одним из основных преимуществ матрицы Эйзенхауэра является простота ее реализации. Не нужно покупать дорогостоящий пакет программного обеспечения и уделять много времени составлению матрицы. В общем, матрица приоритетов позволяет вам оптимизировать управление временем, установив четкие и однозначные приоритеты. Этот инструмент очень полезен для сотрудников, занимающих руководящие должности, или собственников бизнеса, а также фрилансеров, которым нужно совмещать задачи из нескольких различных проектов или работу с несколькими клиентами одновременно.
Не нужно покупать дорогостоящий пакет программного обеспечения и уделять много времени составлению матрицы. В общем, матрица приоритетов позволяет вам оптимизировать управление временем, установив четкие и однозначные приоритеты. Этот инструмент очень полезен для сотрудников, занимающих руководящие должности, или собственников бизнеса, а также фрилансеров, которым нужно совмещать задачи из нескольких различных проектов или работу с несколькими клиентами одновременно.
Каковы недостатки матрицы Эйзенхауэра?
С матрицей приоритетов связаны некоторые недостатки. Особо следует отметить, что зачастую бывает сложно точно определить важность задачи. Это означает, что в конечном итоге вы можете делегировать задачу не тому человеку, что приведет к снижению качества. Более того, важно помнить, что не всегда есть возможность действовать немедленно, когда вы имеете дело с событиями, требующими мгновенной реакции. Это может быть невозможным по причине недостатка знаний, времени, из-за существующих правил и бюрократических процедур или большого количества срочных/важных задач, что снижает эффективность матрицы приоритетов при принятии решений и управлении временем.
Как использовать коробку Эйзенхауэра для управления задачами и рабочей нагрузкой
Матрица срочных/важных задач может стать отличной отправной точкой для управления рабочими процессами и проектами. После того как вы разместите свои задачи по соответствующим квадрантам, можно приступать к настройке процессов управления временем, что поможет вам своевременно реагировать на важные события. Например, вы можете использовать Dropbox для более эффективного управления своим списком заданий. Можно использовать эти инструменты управления задачами для делегирования срочных, но не важных задач другим участникам вашей рабочей группы, а также установить сроки сдачи и напоминания для срочных, но не важных задач, которые можно запланировать на более поздний срок.
Также стоит подумать о внедрении средств автоматизации на рабочем месте. Автоматизация, где это возможно, является отличным способом работы с задачами, которые необходимо выполнить, но не требующими длительного планирования или анализа до начала их выполнения. С помощью средств автоматизации или интеграции в Dropbox вы можете делегировать задачи из квадранта Q3 (срочное, но не важное) таким образом, чтобы это было эффективно с точки зрения времени для вашего бизнеса. Вы можете назначать задачи участникам рабочей группы в Dropbox Paper с указанием сроков их выполнения или переносить их непосредственно в карточки Trello для участников вашей рабочей группы из файлов Dropbox. Инструменты автоматического создания контента помогут вам избежать трудоемких, не защищенных от ошибок задач, которые могут создавать помехи в работе, обеспечив таким образом более продуктивную работу вашей рабочей группы в будущем.
С помощью средств автоматизации или интеграции в Dropbox вы можете делегировать задачи из квадранта Q3 (срочное, но не важное) таким образом, чтобы это было эффективно с точки зрения времени для вашего бизнеса. Вы можете назначать задачи участникам рабочей группы в Dropbox Paper с указанием сроков их выполнения или переносить их непосредственно в карточки Trello для участников вашей рабочей группы из файлов Dropbox. Инструменты автоматического создания контента помогут вам избежать трудоемких, не защищенных от ошибок задач, которые могут создавать помехи в работе, обеспечив таким образом более продуктивную работу вашей рабочей группы в будущем.
Более того, можно объединить коробку Эйзенхауэра с другими методиками управления временем для достижения лучших результатов. Например, можно использовать метод «Съешь лягушку». В основе этой техники лежит высказывание Марка Твена: «Если с утра первым делом съесть лягушку, остаток дня будет чудесным». В контексте бизнеса это означает, что сначала нужно выполнить самую большую или сложную задачу, а затем перейти к более мелким задачам, приоритетность которых вы можете определить на основании других факторов, например, сроков их выполнения. Также существует метод ABCDE, где вы присваиваете своим задачам буквенное значение в зависимости от их важности, и затем выполняете их в этом порядке.
Также существует метод ABCDE, где вы присваиваете своим задачам буквенное значение в зависимости от их важности, и затем выполняете их в этом порядке.
Заключительные соображения
Коробка Эйзенхауэра — чрезвычайно эффективный инструмент управления временем и задачами. Узнав, как эффективно определять приоритетность задач, вы сможете повысить эффективность своей работы, избежать действий, занимающих много времени, и достичь долгосрочных целей в бизнесе.
Пуансон и матрица: виды, особенности
Для того чтобы изготовить изделия из металла сегодня применяется специализированное оборудование. Без использования соответствующей оснастки изготовить некоторые детали, с учетом максимальной точности их размеров, практически невозможно. Именно поэтому штампы, прессы, а также другие приспособления оснащаются пуансонами и матрицами.
Как известно, без соблюдения идеальной точности размеров изделия, ни о каком высоком качестве продукции даже не может идти и речи. Это же касается и внешнего вида детали, что во многих случаях также очень важно.
Это же касается и внешнего вида детали, что во многих случаях также очень важно.
Что такое матрица и пуансон
Матрица – это специальный металлический короб, придающий форму для будущей детали или изделия. В ней полностью отсутствует крышка, а стенки строго параллельны.
Сегодня можно использовать матрицы, предназначенные только для какого-то определенного вида изделия (простые), а также для большего количества типов продукции (комбинированные). К последним прибегают гораздо реже, чем матрицам простого типа, которые широко применяются в строительной и других сферах. С их помощью изготавливается различная продукция, среди которой пустотелые кирпичи, блоки и т д.
Пуансон (другое название пресс-штемпель) представляет собой особую конструкцию, которая полностью совпадает с профилем матрицы. Иными словами, он образует будущее изделие с верхней стороны, выполняя функцию пресса, маркировщика или штампа. С помощью такой системы можно выполнять выдавливание детали, нанесение маркировки (в зеркальном или обычном виде), либо штамповку. Чаще всего пуансоны используются в сфере обработки металла (например, для прессования, гибки листового металла), изготовления различных строительных материалов (шлакоблоков, газобетонных блоков различных типов) и других.
Чаще всего пуансоны используются в сфере обработки металла (например, для прессования, гибки листового металла), изготовления различных строительных материалов (шлакоблоков, газобетонных блоков различных типов) и других.
Виды и типы (по материалу, конструкции, применению, назначению)
В зависимости от типа конструкции и назначения, пуансоны бывают:
- прошивными;
- пробивными;
- вырубными;
- просечными
С помощью пуансона заготовка продавливается через матрицу. Весь рабочий процесс проходит в условиях высокого давления, а при горячей обработке – еще и температурного воздействия. Исходя из этих, а также других особенностей, используются определенные материалы, которые обеспечивают высокую точность изделий, а также отсутствие деформации самой системы. Все это позволяет работать длительное время без необходимости замены.
Они изготавливаются из следующих материалов:
- Высокопрочные стали с высоким уровнем износоустойчивости.
 Чаще всего применяются при горячих процессах работ, что обеспечивает максимальный уровень стойкости штампа.
Чаще всего применяются при горячих процессах работ, что обеспечивает максимальный уровень стойкости штампа. - Стали высоких прочностей. В основном, используются при холодных рабочих процессах. Все материалы, которые используются для изготовления пуансонов данного типа, в обязательной степени должны обладать максимальным уровнем износоустойчивости, прочности, а также антикоррозийными свойствами. В данном случае легированные стали не подойдут, поскольку они не отвечают всем требованиям, и после регулярных температурных воздействий становятся чрезмерно хрупкими для таких работ.
- Полиуретан – это высококачественный современный полимерный материал, который отличается повышенной износостойкостью, прочностью, а также эластичностью и твердостью.
Особенности
Любые станки промышленного назначения отличаются не только простотой в работе и обслуживании, но также практичностью и долговечностью. Однако для того, чтобы пуансоны и матрицы служили максимально длительные сроки, необходимо постоянно следить за оборудованием, особенно, касаемо очистки рабочего пространства и оборудования после работы.
Что касается рабочей поверхности пресса или станка, их необходимо регулярно чистить и обслуживать. Таким образом будет гарантирована длительная бесперебойная работа.
Однако не следует забывать, что даже при самом лучшем отношении к станкам вам все ровно придется часто менять различные расходные части матриц и пуансонов, поскольку они относятся к категории быстроизнашивающихся. В среднем срок эксплуатации пуансона и матрицы от 4 до 6 лет (зависит непосредственно от условий использования и специфики работ).
Что касается размеров и форм составных частей матриц и пуансонов, они могут существенно отличаться, в зависимости от особенностей запланированных работ. Если более конкретно, их конфигурация будет зависеть от размеров, типа, а также формы бетонного или металлического изделия, которое планируется изготавливать с помощью данного оборудования.
Для качественного результата с максимальной точностью необходимо постоянно следить за рабочей поверхностью штамповочных станков и прессов. Нужно, чтобы она была ровной без трещин, заусенцев, пробоин, выступов, зазоров и других деформаций. Все это самым прямым образом будет влиять на конечное качество и размер будущего изделия.
Нужно, чтобы она была ровной без трещин, заусенцев, пробоин, выступов, зазоров и других деформаций. Все это самым прямым образом будет влиять на конечное качество и размер будущего изделия.
С этой целью пуансоны цилиндрического типа часто подвергают шлифовке (черновой и чистовой), а также заточке и полировке. Пуансоны фасонного назначения производятся путем оттиска с обязательным процессом закалки (на протяжении 8 минут деталь находится под воздействием температуры 780 градусов) и финишной обработки. Все это обеспечивает идеальную четкость оттисков и гладкость поверхности.
При работе с деталями с широким контуром обычно используются фрезерные или строгальные станки. С их же помощью также изготавливаются матрицы, учитывая особенности и точные размеры изделий. Прессовальные формы, которые изготовлены с соблюдением норм производства, обеспечивают максимально точную линию среза, притом, что сам штамп в процессе эксплуатации изнашивается в минимальной степени.
С помощью матриц и пуансонов можно производить однотипные детали в больших объемах без необходимости проверки каждой из них на предмет соответствия размеров. При этом каждое отдельно взятое отверстие имеет конкретные параметры, согласно которым производится вытеснение, вырезание и другие манипуляции. После этого деталь совершенно не обязательно подвергать дополнительным обработкам. Иными словами, весь процесс изготовления продукции требует всего 1-2 действия, позволяя существенно сэкономить время.
При этом каждое отдельно взятое отверстие имеет конкретные параметры, согласно которым производится вытеснение, вырезание и другие манипуляции. После этого деталь совершенно не обязательно подвергать дополнительным обработкам. Иными словами, весь процесс изготовления продукции требует всего 1-2 действия, позволяя существенно сэкономить время.
Зазор между матрицей и пуансоном
Контроль зазора между матрицей и пуансоном – это очень важный момент, от которой напрямую зависит конечный результат.
Главные особенности:
- Если зазор слишком мал, поверхность среза будет слоиться и рваться, с заусенцами и неровностями.
- При слишком большом зазоре тонкий материал будет втягиваться с последующим его разрывом. В таких условиях изделие получит затянутые края, а также заусенцы. При повышенной толщине материала, в готовом изделии могут наблюдаться слегка закругленные кромки.
- Согласно соответствующим правилам и нормам, разрешается производство деталей при зазоре 30% максимум от толщины, а также острых режущих краях.

Сам по себе зазор всегда непосредственно зависит от толщины и особенностей материала. Он может колебаться в пределах от 0,5 мм до 12 миллиметров, а также от 4 до 16% от толщины заготовки.
Вы сможете обеспечить действительно идеальную точность конечной продукции только в случае, если зазор между матрицей и пуансоном будет правильно определен и настроен. Здесь также важнейшую роль играет уровень остроты кромок. Если все настроено правильно, в соответствии с нормами, изготавливаемая деталь получает размеры, точно соответствующие техническому проекту.
Обеспечиваем клиентов качественной продукцией
На производственном предприятии Rival Laser применяют самые современные технологии и оборудование. К примеру, вот применение пуансона и матрицы при гибке листового металла автономном панелегибе Salvagnini.
Используя на своем оборудовании только качественные пуансоны и матрицы, изготовленные согласно всем правилам и нормам, компания Rival Laser существенно экономит Ваше время, средства и нервы. Мы изготавливаем продукцию с максимальной точностью и в строгом соответствии с Техническим заданием клиента.
Двадцать лет в «Матрице». Как братья (сестры) Вачовски создали новую поп-религию
Вышедшую в 1999 г. «Матрицу», пожалуй, перегрузили трактовками больше, чем любой другой блокбастер двадцатилетия. Писали, что картина Ларри и Энди (теперь Ланы и Лилли) Вачовски восходит к образу Платоновой пещеры, что в ней соединились мутировавшие в русле New Age элементы восточных духовных учений и христианские архетипы, джедаизм «Звездных войн» и концепция философа Томаса Куна о смене научной парадигмы, гностицизм и киберпанк, параноидальные представления уфологов и сторонников всевозможных теорий заговора, японские аниме, гонконгские боевики и критика современного капитализма в работах Жана Бодрийяра о гиперреальности и симуляции. Это если совсем конспективно.
Вряд ли Вачовски перелопатили философскую библиотеку и всерьез углублялись в теории, обнаруженные в «Матрице» культурологами. Скорее – использовали их как упрощенные знаки, предлагая герою следовать за белым кроликом, а зрителям – опознать обложку высоколобой книги Бодрийяра.
Неудивительно, что сам Бодрийяр позже заявил, будто Вачовски ничего не поняли.
Но они поймали интеллектуальный дух времени и упаковали его в эффектную поп-культурную обертку. Возможно, они уловили и нечто большее – саму суть поп-культуры. Именно поэтому им удалось создать даже не новую поп-философию, а новую поп-религию – как двумя десятилетиями раньше Джорджу Лукасу в «Звездных войнах».
Придуманная Лукасом религия джедаизм официально признана в Британии и насчитывает, согласно переписи 2003 г., больше адептов, чем иудаизм и буддизм. С идеями Вачовски такого пока не случилось, но если считать «Звездные войны» ветхим заветом современной поп-культуры, то «Матрица» будет новым. Рождение подобных вещей требует в равной мере простодушия и эрудиции создателей. Сочиняя сказку о борьбе между галактической империей и повстанцами, в которой участвуют космические принцессы, космические ковбои и рыцари-джедаи, Лукас штудировал классические книги по сравнительной мифологии и антропологии, прежде всего «Героя с тысячью лиц» Джозефа Кэмпбелла и «Золотую ветвь» Джеймса Фрэзера. Брал элементы сюжетной конструкции из всемирного мифологического сундука и создавал не героев, но архетипы, а потом переводил их в знакомые массовому зрителю образы поп-культуры («Звездные войны» еще и гигантский коллаж киноцитат и жанровых типажей).
Появление саги совпало с пиком популярности New Age, и картина Лукаса органично легла в лоно этого движения, дополнив его религиозную эклектику (элементы восточных учений, астрология, оккультизм) поп-культурной. По сути, «Звездные войны» задали стандарт современной поп-религии, в которой духовные ценности, маркетинг и технологии слились до неразличимости. Бог стал брендом, бренд богом, а создатель бренда – пророком.
В 1980-х к этому открытию пришел не только Лукас, но и Стив Джобс, принесший в мир новых технологий дух контркультуры и адаптированные «детьми цветов» идеи восточных духовных учений. Apple стала в IT-индустрии тем же, чем «Звездные войны» в кино. Брендом, в котором продается не продукт, а мировоззрение, система ценностей, дизайн выходит на уровень идеологии, а потребительская логика уступает место вере.
Все это оказалось справедливым и в отношении «Матрицы».
На первый взгляд «Матрицу» легко свести к набору общих мест. Реальность, доступная нам в ощущениях, – на самом деле иллюзия. Чтобы познать истину, надо пробудиться. Для пробуждения нужен мессия. Мессию должен узнать предтеча. Сколько столетий люди в том или ином виде пересказывали этот сюжет (Кэмпбелл назвал это мономифом).
Главный герой (Кеану Ривз) днем работает на систему, а ночью ее подрывает. На службе в крупной компании он программист Томас Андерсон, дома – хакер под ником Нео (а имена в «Матрице» символичны донельзя: Троица, Морфеус и т. д.).
«Пробудись, Нео. Ты в матрице. Тук-тук, Нео. Следуй за белым кроликом».
Но кроличья нора тут в телефонной будке, а Страна чудес именуется «пустыней реального». Земля почти разрушена войной людей и машин, весь видимый мир конца ХХ в. – коллективная греза, созданная суперкомпьютерами, которые построили на руинах цивилизации гигантские теплицы для людей-батареек, потому что иного источника энергии не изобрели. А чтобы батарейки не сошли с ума и не умерли от ужаса, в их сознание внедряют образы нормальной жизни, в которой они ходят на работу и в магазины. Это и есть матрица.
Но не все хотят быть батарейками – есть пробудившиеся. Они отвергли иллюзию, вырвали из головы провода, прячутся под землей и ведут войну на два фронта – в физической реальности и в матрице, в которую научились входить через телефонные линии. Снаружи повстанцев преследуют боевые машины, в матрице – безликие и непобедимые агенты в коричневых деловых костюмах и черных очках. При необходимости агентом может стать любой обыватель.
В одной из самых эмблематичных сцен фильма лидер Сопротивления Морфеус (Лоренс Фишбёрн) предлагает Нео на выбор две таблетки – синюю и красную. После первой герой решит, что сном была «пустыня реального». После второй – воистину проснется.
Как все помнят, Нео выбрал красную. Примерно тогда же мы выбрали синюю.
Общественный договор, оформившийся в России нулевых, подразумевал именно это: относительные достаток и стабильность в обмен на сон разума и веру в телевизор. Любопытно, что авторы фильма нападали на куда более либеральный порядок: их Матрица, очевидно, Америка 1990-х, где идеология скрыта за фасадом общества потребления, а система манипуляции не настолько груба, как привычная нам сегодня государственная пропаганда. Но один из секретов успеха «Матрицы» в том, что ее смыслы (или клише) универсальны до такой степени, что могут быть с равным успехом присвоены как левыми, так и правыми борцами с любой господствующей системой.
Роршах в Голливуде
Философ Славой Жижек заметил, что «Матрица» – «один из тех фильмов, которые функционируют в качестве теста Роршаха, запуская универсальный процесс узнавания». «Мои друзья лаканианцы, – писал Жижек, – говорят, что создатели фильма, должно быть, читали Лакана; приверженцы Франкфуртской школы видят в «Матрице» экстраполированное воплощение Kulturindustrie, отчужденно-овеществленную социальную Субстанцию (Капитал), колонизирующую нашу внутреннюю жизнь, использующую нас как источник энергии. Те, кто разделяет установки New Age, усматривают здесь идею, что наш мир – всего лишь мираж, порожденный глобальным Мозгом, воплощенным во Всемирной паутине».
Подобные примеры можно множить и дальше, надо только добавить, что идеи тотальной иллюзии, симуляции и манипуляции смыкаются в «Матрице» с паранойей, которая за прошедшие 20 лет только усилилась. За нами следят, нами управляют. Это один из главных страхов современного человека и один из главных мотивов мировой фантастики. Но в эпоху Всемирной паутины за нами следят уже не всемогущие спецслужбы, сектанты, иллюминаты или инопланетяне в летающих тарелках. Это делает искусственный интеллект суперкомпьютеров, в котором, в свою очередь, можно увидеть эволюцию злого божества гностиков. Или вспомнить мистика начала ХХ в. Георгия Гурджиева, представлявшего мироздание в виде пищевой цепочки, где люди питают своей энергией Луну, Луна питает другие планеты и т. д., пока после многочисленных уровней энергия не достигнет космического хозяина. Иначе говоря, «Матрица» напоминает еще и лабиринт гиперссылок, уводящих в дурную бесконечность.
Остроумный выход из лабиринта нашел философ Борис Гройс. Он предложил считать этого бога-машину метафорой киноиндустрии: ее «бесперебойное функционирование обеспечивается за счет высасывания и потребления жизненных сил зрителей», которые «больше не работают, а только наслаждаются непрерывным сеансом совершенного фильма».
Тотальный фильм
С предыдущим большим киномифом – «Звездными войнами» – «Матрицу» роднит не только заявка на новую религию, но и то, что постмодернистское цитирование идей и визуальных образов приобретает двусторонний характер. По прошествии времени уже непросто отделить то, что «Матрица» заимствует из других фильмов, от того, что другие фильмы заимствуют из нее. Это касается и замедленного движения, подсмотренного в боевиках Джона Ву, и примет стимпанка (в физической реальности повстанцев атакуют стальные каракатицы, словно в экранизациях Жюля Верна или Герберта Уэллса), и компьютерного кунг-фу, и романтического виртуального облика революционеров с их слабостью к кожаным плащам, латексу и дизайнерским очкам. Все это родилось до «Матрицы», но вошло в моду во многом благодаря ей – как и поп-религиозный фьюжн, в котором западнохристианская идея линейного времени легко сочетается с восточной идеей цикличности, тотальная иллюзорность – с революцией, а апокалиптичность – со свойственным New Age оптимизмом.
Спустя 20 лет «Матрица» сама кажется предтечей тотального фильма, который смотрят по всему миру (но в разных политических матрицах) люди-батарейки. В отличие от «Звездных войн» с их космическими принцессами и рыцарями-джедаями он обращается уже не к детскому, а к подростковому сознанию с его нигилизмом и фетишизмом – и в этом смысле «Матрица» открывает дверь всем успешным кинокомиксам нового века.
Злодеи и Спасители / Хабр
Всем привет!
По результатам голосования, будем говорить о Матрице.
Q&A
Что на этот раз?
Две большие непротиворечивые теории о Матрице, каждая разделена на несколько маленьких. Как всегда, пасхалки и небольшие теории спрятаны в спойлер чтоб не перегружать статью.
Это про то что Матрица в Матрице?
Не-а. Эта теория мне не нравится, хотя она настолько популярна, что уже на грани канона. Как по мне эта теория ужасна, поскольку с помощью подобного трюка можно объяснить все что угодно(это просто сон). К тому же, не забываем про бритву Оккама, эта теория вводит новые сущности, которые необязательны для объяснения.
Зачем мне это читать
Матрица — это антиутопический киберпанк. Говоря о ней, приходится скатываться во все, что обсуждается на ресурсе: робототехника, ИИ, программирование, энергетика и.т.д.
Спойлеры?
Безусловно, и много. Все относительно трилогии и Аниматрицы. Прочие произведения вроде
«Голиаф»или
The Matrix Onlineв данном случае нерелевантны. Первое, поскольку описывает очень странные события(вроде столкновения машин с пришельцами), второе — поскольку является убожеством с точки зрения сюжета, ИМХО. Также есть небольшой спойлер из игры Mass Effect(на самом деле большой).
Матрица пресыщена различной символикой и отсылками. Это очень мягко говоря. Поводов для спекуляций здесь слишком много и, потому, я решил сконцентрироваться только на двух темах.
1. Сайфер
Злодей в кино — довольно условное понятие.
Хорошая драматургия не признает абсолюты. Намного интереснее, когда антагонист мотивирован чем-то кроме желания помешать главному герою. В Матрице есть такой персонаж. Сайфер. О нем и будет первая часть теорий.
кстати, о злодеях в первой матрицеВ первом фильме, есть такое забавное разделение героев. Все «Хорошие» ребята носят круглые либо овальные очки.
В то время, как «злодеи» предпочитают прямоугольные.
Если об этом знать в начале — можно заметить спойлер:
1.1. Сайфер должен был быть избранным
Вспомните, как Нео сидит у себя в каюте и к нему заходит Морфеус. Он говорит, что должен извиниться перед Нео, что есть правило, согласно которому освобождать человека достигшего определенного возраста — нельзя. Мозг не принимает правду и Морфеус видел такое. Далее он рассказывает историю избранного и говорит, что у него не было выбора. Итак, есть строгое правило, по которому освобождать взрослых нельзя, и нарушать это правило можно только в исключительных случаях.
Из файла, который агент Смит показывает Нео, мы можем узнать, что Томасу Андерсону либо 37, либо 28.
Согласно паспорту, дата рождения сентябрь 71-го
Согласно записи в базе данных — март 1962-го
Я, лично, склоняюсь к первому варианту (Хотя если взять возраст актера, ближе, все же, второй). Но, допустим, Нео, все же 37. Тогда можно сказать, что 35-37 лет, это уже слишком поздно, для того, чтоб быть разбуженным.
Из разговора Сайфера со Смитом в ресторане, мы узнаем, когда Сайфер был разбужен:
«знаешь, что я понял за 9 лет? Благо в неведении»
9 лет. Актер Джо Пантолиано старше Киану Ривза на 13 лет. В фильме также складывается ощущение, что Сайфер старше Нео.
Как бы то ни было, очевидно, что Сайфера освободили в сознательном возрасте и непонятно зачем, ведь правило запрещает это делать.
Смотрим дальше. Сайфер был влюблен в Тринити и, по их некоторым неловким диалогам, можно предположить, что недолгое время, Тринити оказывала ему знаки внимания. Получается, что согласно прогнозу Пифии, Сайфер мог бы быть избранным.
Теперь представьте себе историю: Морфеус приводит Сайфера и рассказывает ему, как очень скоро он(Сайфер) откунгфуит всех агентов и спасет человечество. Тринити симпатизирует ему, команда смотрит на него, как на героя. Исходя из того же разговора Смита с Сайфером, последнему определенно нравится внимание. Он наверняка уважал Морфеуса как лидера и верил ему, пока тот говорил, что Сайфер спасет мир. Но, вскоре оказалось, что избранным Сайферу не быть.
Возможно, Морфеус также привел его к Пифии, она также сказала Сайферу, что он не тот, и Сайфера это убило. Нео довольно спокойно отнесся к новости, что он не избранный, он был даже рад. Но для Сайфера — это была трагедия. Он разочаровался в лидере, который ему врал, он потерял любимую, которая заинтересовалась этим новым типом, он не сможет сделать ничего значительного, но вынужден жить в этом холодном мире и есть одну и ту же кашу каждый день. Не удивительно, что все о чем он может думать: «почему я не взял другую таблетку!»
1.2.Морфеус знал о грядущем предательстве
В начале первого фильма мы слышим разговор Сайфера с Тринити:
— ты слышал?
-слышал что?
-ты уверен, что линия чиста?
-конечно я уверен.
На этом моменте врываются полицейские. Сразу после того, как Тринити разделается с ними, она звонит Морфеусу:
— Морфеус, линия отслеживается, я не знаю как.
-Я знаю, они перерезали кабель.
После этого мы слышим разговор агентов, которые говорят, что информатор не подвёл и теперь они знают имя цели.
Морфеус достаточно умен, чтоб хотя бы заподозрить, что-то неладное после нападения на Тринити, но он никак не расследует происшествие и не удивляется тому факту, что агенты вычислили Нео, как раз после того разговора Тринити с Сайфером.
Вполне вероятно, что пифия рассказала Морфеусу о предательстве Сайфера, и даже убедила, что вмешиваться нельзя, поскольку именно это предательство запустит цепь событий, благодаря которым Нео станет избранным.
Если вы сомневаетесь в решимости Морфеуса — вспомните сцену, где он рассказывает Нео про агентов.
Вся сцена великолепна и музыка, и женщина в красном. Но вот, что рассказывал Морфус Нео:
“… Матрица — это система, Нео. Система — наш враг. Но когда ты внутри, оглянись. Что ты видишь? Бизнесмены, учителя, юристы, плотники. Умы тех самых людей, которых мы пытаемся спасти. Но до тех пор, эти люди все еще часть системы и, потому, они наши враги. Ты должен понять, большинство этих людей не готовы проснуться. Многие из них настолько инертны, настолько безнадежно зависят от системы, что будут бороться, защищая ее.
А теперь представьте, что разговор идет между вербовщиком в террористическую организацию и новоприбывшим. Фактически, Морфеус говорит: наша цель — наивысшая, и цель оправдывает средства.
ленивые программистыКстати об этой сцене. Вачовски, специально взяли на роль массовки близнецов, для того, чтоб казалось, будто ленивый программист, при конструировании мира, поленился прописывать каждого человека по отдельности и просто скопипастил половину.
Я выделил несколько, остальных можете поискать сами.
Установки Морфеуса действуют отлично. Вспомните культовую сцену, когда Нео с Тринити вламываются в здание, где держат Морфеуса. Теперь взгляните на эту сцену с позиции обычных охранников, которые работают в этом здании. Один из них даже кофе не успел допить, когда Нео разрядил в него обойму. По сути, Нео и Тринити могли бы их просто вырубить или отвлечь. Хоть как-то попытаться избежать жертв, но вместо этого, они устроили настоящую резню.
И если вы все еще сомневаетесь, как сами Вачовски относились к Морфеусу, вот вам явная иллюстрация:
Морфеус предлагает Нео плод с древа познания. Вкусив его, Нео навсегда покинет «Эдем».
1.3. Кто помог Сайферу попробовать стейк
Вернемся к сцене, где Сайфер за столом в ресторане с агентом Смитом. Именно на этой встрече Сайфер сдаёт Морфеуса. Но кто подключил его к матрице, и даже если он сам подключился, мы точно знаем, что без оператора, выбраться из матрицы нельзя. Даже если бы и можно, это было рискованно, поскольку кто угодно мог увидеть его в кресле и прочитать на мониторе что происходит.
Тут надо вспомнить два момента.
1) Маус предлагает Нео развлечься с женщиной в красном, это вызывает усмешки, но не удивление.
2) когда Нео подходит к Сайферу, тот пугается, а потом говорит, глядя на монитор: я вижу блондинку, брюнетку, рыжую…
Сайфер мог попросить Мауса устроить свидание с девушкой в красном и постоять на стреме, пока он не закончит. Более того, он мог попросить Мауса не смотреть на экран. Для верности, он мог проделывать это несколько раз и убедиться, что Маус не смотрит. Даже если бы тот взглянул на экран — пришлось бы убить только его, а это лучше чем весь экипаж.
Можно предположить, что Маус не стал бы устраивать свидание в матрице(слишком опасно), но вполне мог использовать загрузочную программу. Сайфер, в то же время, мог написать свою программу, которая позволила бы ему перейти из конструктора в матрицу(мы знаем, что это возможно по сцене «нам нужно оружие, много оружия»). Возможно именно за написанием этой программы Нео и застал Сайфера. Если вы согласны, что Морфеус знал о грядущем предательстве, то можно даже предположить, что он сделал все, чтоб план Сайфера удался.
Иронично, но прямо перед смертью Маус смотрит на плакат с красной женщиной, которая его и погубила
И еще о СайфереВо время встречи со Смитом, Сайфер выдвигает свои требования. Он говорит:
— Я не хочу ничего помнить, ничего, понимаете? И я хочу быть богатым, кем-то важным, например актером
Это забавно, поскольку актеры, хоть и могут быть богаты, но едва ли «важными». Хотя было несколько исключений. И, для ясности, Смит в начале диалога называет Сайфера по фамилии:
— Мы договорились, мистер Рейган?
2. Перейдём к другой большой теме: машины
Из аниматрицы мы узнаем, как развивался конфликт. ИИ получали все большее распространение в мире, но люди относились к ним как рабам. Все это длилось до тех пор пока один из роботов не убил человека. Это подстегнуло ненависть к машинам и по всему миру прокатилась волна насилия. Тогда машины ушли и построили свой город под названием 0,1 (можно оценить всю скромность машин). Далее — акции компаний 0.1 резко росли и их экономика процветала, сильное производство уничтожило производство людей, вызвало безработицу, что привело к вооруженному конфликту. Машины сильно превосходили людей и тогда они(люди) решились на отчаянный шаг: навсегда скрыть солнце за тучами. Машины захватили людей и начали использовать их как источник энергии. Через какое-то время, людей начали выращивать.
2.1. Машины явно не испытывали ненависти к людям ни на каком этапе
1) создав свой город, они продолжали поставлять товары людям, хотя в этом не было никакой нужды
2) убийство машиной человека вызвало целую бурю. Это был первый случай и то самооборона
3) после окончательной победы, машины не просто поработили людей, они поместили их в виртуальную среду, где все могут быть счастливы(первая итерация матрицы). Какой противник поступал так с побеждённым врагом? И не просто врагом, давайте называть вещи своими именами, закрыть небо — это была попытка геноцида.
2.2. Источник питания?
Человеческое тело, что бы там ни говорил Морфеус, не может быть источником питания. Во-первых, сколько бы энергии не вырабатывало тело, эта энергия должна питать не только машин, но и саму матрицу(сколько ж это серверов), а если мы прибавим к этому энергию затраченную на выращивание тела и поддержания в нем жизни, то это еще надо разобраться кто кому должен. По сути это нарушение 1 го закона термодинамики, но кому какое дело.
Проблемы с рендерингомПомните эту сцену?
Кто-то ее ненавидит, кто-то наоборот любит. Но как факт, в какой-то момент, начинает казаться, что смотришь пиксаровский мультик. На форумах люди объясняют это так: «программа» избранного должна быть довольно тяжелой, поскольку постоянно вызывает глюки в программе(вроде волн перед взлетом), Смит, как антипод избранного, также, должен весить немало. Потому, чем больше Смитов, тем все хуже. В момент, когда агенты наваливаются на Нео, мы снова видим приличную картинку. Видимо, из-за того, что объекты перестали двигаться.
Мы можем предположить, что машины все же нашли какой-то способ эффективно получать энергию из человеческого тела, но зачем? Первое поколение работало на солнечных батареях, но что мешает машинам заменить источник питания? Например на атомные реакторы? Или ветряки(с ветром-то у них все норм) или что угодно. С отсутствием экономических преград, бесплатным трудом, высоким интеллектом, и желанием выживать машины должны были освоить замкнутый топливный цикл в течении десятка лет, максимум.
Для высокоразвитого ИИ — машины ведут себя как-то очень уж глупо
Помимо всего прочего, мы точно знаем, что люди не использовались в качестве источника питания к концу третьего фильма, иначе, машины бы не отпустили их ни при каких условиях.
2.3. Машины создали Зион и всю технику для людей
Мы знаем, что они как минимум 6 раз воссоздавали матрицу и уничтожали Зион. Зачем? Согласно архитектору это нужно было для того, чтоб выявлять людей, которые не примут программу. Теперь представьте эти две дюжины людей с атрофированными мышцами, которые каким-то образом выбрались из города машин и добрались до безопасного места, а затем построили город и.т.д. Довольно трудно себе такое представить. Зион, как и корабли и вся технология не была создана людьми сбежавшими из первой матрицы.
На кораблях, которые мы видели в фильме штамповка сделано в США. (Табличка на корабле: MARK III No. 11 / Nebuchadnezzar / Made in the USA / Year 2069. От Марка 3:11 — «И духи нечистые, когда видели Его, падали пред Ним и кричали: Ты Сын Божий».)Теперь считаем. Матрица создавалась шесть раз, каждый раз Избранный выводил две дюжины людей. К третьему фильму, в Зионе проживает около 250 000 людей. На такой рост потребовалось бы сколько? лет 100? Всего, около 600 лет. При всём уважении к американской промышленности, как и любой другой, но технология такого уровня сложности никак не может прожить 600 лет, не говоря уже о краске.
Далее, маленькое наблюдение. Зион, помимо отсылки к Иерусалиму, имеет сходство с названием города машин. Первый город машин назывался 0,1=>zero one=> z-one[зи уан] => зион
Получается, что машины не просто позволили освободившимся людям сбежать из матрицы, но и снабдили их всем необходимым(в том числе, машинами, работающими на геотермальной энергии (и что мешало им самим этим пользоваться?))
Но если так, то зачем они в итоге уничтожают все население людей? Чего им бояться? давайте посмотрим на людей в зионе:
А потом взглянем на город машин.
Какой вред могли нанести люди машинам?? В конце первой матрицы Нео грозно говорит в трубку: я иду за вами, но во второй части мы видим, что максимум на что он способен — это перебить всех агентов. И черт с ними, матрица, как бы работает и так, а городу ничего не угрожает.
И еще о гламурных людях в ЗионеПочему они все темные? Они в жизни не видели лучей солнца, но почему-то они все темные.
Ответ: отсутствие солнечного света, должно было вызвать недостаток витамина D, что привело бы к серьезным последствиям. Для того, чтоб этого избежать, видимо, людям в Зионе приходилось какое-то время проводить в солярии.
2.4. Машины следуют Нулевому Закону
А вот главный вопрос: Чем занимались машины все это время? У них нет религии, им некому служить, все что им нужно — это источник питания, но в чем смысл? Они не начали космическую экспансию, хотя могли, не стали даже распространяться по земле. Чем они занимаются по вечерам? Как проводят выходные? И выходные от чего? В смысле, какая у них ещё есть работа, кроме обороны, атаки и поддержки матрицы?
Теперь моя теория. Если вы играли в масс эффект, вы помните, ключевой вопрос, на который должны были ответить жнецы ( если не играли — неважно, вопрос был о том, как разрешить неизбежный конфликт между живыми и ИИ) Мне кажется машины работали над тем же вопросом, но они нашли ответ.
Чего машинам боятся? Люди никак не могут навредить, даже если освободят всех, кто в матрице. И мы знаем, что мстительность не присуща машинам. Заметим и еще кое-что. Допустим всех людей освободили, но статус кво в отношениях с машинами сохранился. Как будут жить миллиарды людей, без солнца? Что они будут есть? Как развивать технологию? Это же верная смерть. Не прошло бы и года, как по всей земле, люди начали бы уничтожать друг-друга ради ресурсов. Мне кажется, в данном случае, машины выполняют ту же роль, что и жнецы в Mass Effect, они строго контролируют людей, чтоб избежать их полного уничтожения. Когда Зион достигает определенной отметки популяции — город уничтожают, чтоб избежать мучительной смерти от голода. По сути, это все та же идея о Нулевом Законе робототехники, который вступает в противоречие с первым.
2.5. Избранный действительно Иисус
То что появление избранного — задумка архитектора мы и так знаем из второго фильма, но что если он соврал о причинах или не знал их?
Машины были созданы, чтоб служить. Они должны были спасти человечество. Мне кажется, именно этим они и были заняты.
Допустим машины изначально стремились к миру, но по горькому опыту они знали, что люди подверженные ксенофобии, нетерпимы к машинам, тем более после проигрыша в войне. Но держать людей в рабстве, также недопустимо для машин, ведь это никакое не спасение. Нужно было придумать, как помочь людям увидеть возможность мирного сосуществования. При этом, идея о мире должна была исходить от людей(сами машины не раз предлагали мир людям). Помимо всего прочего, люди — их создатели, какой ребёнок не хочет любви со стороны родителя. Быть Тиранами над людьми для машин было бы невыносимо. Но как привести людей к идее мира? Как заставить их понять?
Решение: Смоделировать мир, в котором машины смогут внушить правильную мысль всем людям. Первая матрица была утопией, в которой все были счастливы. Нарисовать такой мир, в котором люди и машины помогают друг-другу жить, было довольно очевидной идеей, но, как мы знаем, люди не приняли симуляцию. Пришлось искать другой выход.
Нужно было внушить правильную мысль в рамках привычного людям мира. Кто-то из людей, тот за кем пойдёт все человечество, должен был сам предложить им перемирие. И кто подойдёт на эту роль лучше чем пророк спаситель? При этом нужно сделать все, чтоб люди не почувствовали подлог(а машины уже знают, что люди восприимчивы к обману) малейший намёк на манипуляцию и люди возненавидят их ещё больше.
Тогда и был придуман цикл(почти такой же как в масс эффект) и только тот кто разорвёт этот цикл, может считаться носителем свободной воли. Тот за кем пойдут, поскольку он сделал все наперекор.
Дальше нужны были люди вне матрицы, которые были в курсе ситуации, поскольку люди в матрице не пошли бы за пророком, просто потому что им так сказали. В случае, если Избранный не разрывал цикл, все следы предыдущего эксперемента должны были быть уничтожены.
Вспомните, когда Нео приходит в город машин и говорит с их главным насчет Смита, тот спорит с Нео.Когда же последний предлагает мир, злобный бог-машина тут же подключает его к матрице. Позже, если вы посмотрите сцену прямо перед тем, как все Смиты будут уничтожены, вы заметите, что импульс(или что бы это ни было) запустивший цепную реакцию шел по проводам к Нео, а не от него. Если бы Нео каким-то образом уничтожил Смита — сигнал должен был идти от Нео к серверу, а не наоборот. Получается именно машины в итоге уничтожили Смита и Нео, по большому счету, не был для этого нужен.
Кстати, о главной машинеВ титрах можно узнать, как она называется:
Бог из машины. Это довольно хорошая самоирония.
После окончания фильма пройдут столетия и предание о Нео будет передаваться из поколения в в поколение, обрастая мистическими подробностями. Пройдёт лет 300 и это станет полноценной религией. Она очень удачно ляжет на идею о конце света и втором пришествии. И главным заветом этого нового мессии будет мир с машинами!
Этим и объясняется переполненность христианской символикой. Название корабля, прозвища героев, название города, общий сюжет, все это могло быть тем или иным способом, навеяно машинами, для того, чтоб люди подсознательно чувствовали схожесть.
Для укрепления мира машины помогут людям восстановить землю
Мне кажется, за 600 лет они разработали всю технологию, чтоб разогнать облака и терраформировать землю. Почему они не сделали этого раньше? Две причины:
1) Люди будут ценить помощь, а не данность.
2) Люди отключившись от матрицы, должны увидеть результат действий своих предков, для них это должно стать реальностью. Тогда, они как и Сайфер осознают, что все это время машины защищали их от правды, а не держали взаперти.
Выводы
Таким образом машины сделали именно то, ради чего они были созданы, они спасли человечество от самого себя. При этом, они реализовали гениальную многоходовку(на 600 лет вперёд!) на что, в принципе, способны только суперкомпьютеры.
Есть много историй о том, как машины уничтожат человечество, более того мы уже сейчас начинаем боятся ИИ. Постоянно мелькают новости то о Маске, то о Хокинге. Но надо учесть, что это люди а не машины полны шовинизма идей о расовом превосходстве и.т.д.Это мы, в 21-м веке, все еще ведем религиозные войны и верим в гороскопы. Так что опасаться стоит скорее за ИИ.
Небольшой бонус
В этой
статьеxmeoffзадает вопрос о том, почему в Матрице симулируется именно 1999г.?
Вот моя версия. Для начала надо понять что в матрице, если и существует понятие времени — оно должно сильно отличаться от времени в нашем мире, иначе машины не могли бы сотни лет все держать на одном уровне, даже с учетом ребутов. Также это может объяснить финал первой части(нападение на корабль), когда события в матрице и события в реальном времени идут не синхронно. Мы знаем, что действие происходит в конце шестого цикла и именно на конец приходится 1999г. Мне кажется, на то две причины. В конце 20-го столетия, были две темы, которые в том или ином виде волновали весь мир.
1) общие религиозные настроения, страх перед апокалипсисом.
2) это был год, проблемы Y2K. Хотя к тому времени многие специалисты были уверены, что миру ничего не грозит, но СМИ раздували проблему. Именно в этом году пришло реальное осознание того, насколько мы зависим от машин и это осознание пришло к людям, у которых ещё и своего пк могло не быть.
Пользуясь этими настроениями машины добивались двух целей:
1) люди отключенные от матрицы, по большей части, готовы принять апокалиптическую реальность
2) эти люди склонны понимать свою зависимость от машин и легче примут новые порядки
На этом все. Предлагайте новые темы в комментариях и голосуйте за следующую в опросе.
Спасибо, что прочитали до конца!
Матрицы в видеорегистраторах. Что это?
В этой статье, мы подробно расскажем вам, за что отвечает матрица в видеорегистраторе и какие её параметры влияют на качество записываемого видео.
Матрица, также известная как видеосенсор, это безусловно один из важнейших элементов абсолютно любого видеорегистратора. Вместе с объективом, они образуют тандем, который отвечает за качество видеозаписи. Естественно, что многих автомобилистов интересует именно получаемое изображение, его четкость и детализация, однако многие не совсем понимают, на какие характеристики стоит обратить свое внимание.
Итак, для матрицы существуют два главных параметра, это её размер и количество пикселей.
Физический размер матрицы, определяет расположение и размер пикселя. В свою очередь площадь пикселя определяет светочувствительность и улучшает динамический диапазон, а также снижает количество видео-шумов в кадре.
Иными словами, физический размер матрицы определяет общее качество изображения, ведь чем больше матрица, тем больше размер пикселя, а чем больше пиксель, тем он чувствительнее. Матрицы с маленькой площадью неизбежно «шумят» во время ночной съемки. На первый взгляд, может показаться, что размер матрицы и количество пикселей, для улучшения качества записи, должно стремиться к увеличению, это так, но во всем необходимо знать меру.
Если переводить все в конкретные значения, то выходит следующее. Матрица 1/1,6 больше матрицы 1/2,5 по площади примерно в 2,44 раза. Теоретически туда можно поместить и 15-17 мегапикселей. Реклама говорит нам, что, чем больше мегапикселей, тем лучше. Но это не совсем так. Да, чем их больше, тем детальнее картинка. Но не в ущерб размерам каждого отдельного пикселя. Матрица 1/1,6 с 15-17 мегапикселями «на борту» по качеству то же самое, что и матрица 1/2,5 с 6-7 Мп. А вот если в первом случае оставить «всего» 10 Мп, то картинка окажется уже значительно лучше.
Из этого следует, что чем матрица больше, тем качественнее будет картинка в условиях плохой освещенности. Но увеличение матрицы – это увеличение и самого прибора, и его стоимости. А так как видеорегистратор должен быть компактен и незаметен, приходится искать «золотую середину». Сейчас у всех регистраторов матрицы примерно одного размера. Качество теперь заключается в нюансах настроек и параметров.
Матричная алгебра
Матричная алгебраМогут распознаваться разные типы матриц:
- прямоугольная – количество строк не равно количеству столбцов
- квадрат – количество строк равно количеству строк. Трасса квадратной матрицы представляет собой сумму элементов X (i, i) для i = от 1 до N (размер матрицы. Значения на трассе составляют диагональ квадратной матрицы. квадрат
- и симметричный – X (i, j) = X (j, i).Матрица коэффициентов корреляции а матрица дисперсий-ковариаций квадратная и симметричная. След матрицы коэффициентов корреляции – N. След матрицы дисперсии-ковариации представляет собой сумму дисперсий.
- нулевая матрица – квадратная и симметричная матрица со всеми элементами, равными 0,0
- матрица идентификации – квадратная и симметричная матрица, в которой X (i, i) = 1 для всех i = от 1 до N со всеми X (i , j) где i не равно j, равному 0,0.
- вектор – строка или столбец матрицы.Вектор-столбец имеет размеры (N, 1), где N – количество строк в матрице. Вектор-строка имеет размерность (1, M)
Матрицами можно манипулировать, если соблюдаются указанные ниже правила.
- Равенство – две матрицы равны, если все соответствующие элементы равны; матрицы должны быть одного порядка.
- Транспонирование – X ‘- это транспонирование матрицы X. Строки X становятся столбцами X’. X (i, j) = X ‘(j, i) для всех i, j.
Если X 7 6 X '7 5 5 4 6 4 - Сложение – матрицы могут быть добавлены, если каждая матрица имеет одинаковые размеры.Для A = B + C, A (i, j) = B (i, j) + C (i, j) для всех i, j.
7 6 1 5 6 1
Таким образом, A (2,1) = B (2,1) + C (2,1) или 0 = -1 + 1
= + 0 4-1 2 1 2 - Вычитание – матрицы могут быть вычтены, если каждая матрица имеет одинаковые размеры. Для A = B – C, A (i, j) = B (i, j) -C (i, j) для всех i, j.
8 3 9 5 1 1
Таким образом, A (2,1) = B (2,1) -C (2,1) или 5 = 9 – 4
= - 5 7 9 9 4 2 - Умножение – две матрицы (B и C) могут быть умножены для получения матрицы A при определенных условиях. .Для A = BC матрица B является префактором, а матрица C – постфактором. Для B (i, j) и C (k, l) A определено тогда и только тогда, когда i = l. То есть количество строк матрицы pre равно количеству строк сообщения; размеры матрицы продукта A и j строк и k столбцов. Если A = BC определено, A = CB может быть определено или не определено. Рассмотрим следующие матрицы. Для чего определено умножение и, если оно определено, каковы размеры матрицы продуктов?
- B (4,4) C (5,5)
- B (10,1) C (1,10)
- B (1,10) C (10,1)
- B (4,3) C (3,1)
- B (7,5) C (5,8)
- B (5,8) C (7,5)
а б 9 5 1 1
= * в г 9 9 4 2Элемент a (первая строка и первый столбец) матрицы продуктов равен произведению первой строки до умножения первого столбца сообщения.Элемент d (вторая строка и второй столбец) матрицы продуктов равен произведению второй строки до умножения второго столбца сообщения.
а = 9 * 1 + 5 * 4 = 20 б = 9 * 1 + 5 * 2 = 19 с = 9 * 1 + 9 * 4 = 45 г = 9 * 1 + 9 * 2 = 27
- Деление матриц – одна матрица не может быть разделена на другую в обычном смысле деления. Упрощенное введение следует (из Дэвиса, 1973).
Рассмотрим пару одновременных уравнений:
4X1 + 10X2 = 38 10X1 + 30X2 = 110 Пусть матрица A будет матрицей коэффициентов уравнений: 4 10 10 30 Пусть B - вектор решения: 38 110 Пусть X - вектор неизвестных: X1 X2 Уравнения можно записать: AX = B Если выполняется обычное деление, то X = B / A, что не определено для матриц., обратный матрицы A (записанной как A-1) - это матрица, которая удовлетворяет соотношению: A-1A = I или произведение обратной матрицы на матрицу равно идентифицирующей матрице I. Для матрицы A, определенной выше, покажите, что AI (или IA) = A. Таким образом, матрица идентификации работает как умножение числа на 1,0. (в приведенном выше примере, если A - это матрица 3 на 3, то единичная матрица - это 3 на 3 матрица с единицами на главной диагонали и нулями во всех остальных позициях. Если обе части уравнения умножить на A-1, то: AA -1 X = BA -1 поскольку AA -1 = I, то IX = BA -1 или X = BA -1 .Вектор неизвестных равен матрице произведения, сформированной предварительным умножением матрица коэффициентов, обратная постоянному вектору. Убедитесь сами, что размеры матриц и векторов удовлетворяют правила умножения. На общую тему поиска написано много книг и статей. инверсия матрицы. В своей работе мы будем заниматься поиском инверсия квадратной и симметричной матрицы. Сингулярные матрицы не имеют инверсии.
- Детерминанты – одно число, извлеченное из квадратной матрицы.Если определитель квадратной матрицы равен 0,0, тогда матрица сингулярна и обратная ей не существует.
Рассмотрим следующую матрицу:
4 10 10 30
Определитель (обычно записываемый как | a | для матрицы A) дается вычитанием произведения двух элементов главной диагонали (10 умноженных на 10) из произведения элементов на главной диагонали (4 умножения на 30) или | a | = 120 – 100 или 20.
Детерминанты могут быть вычислены для больших квадратных матриц ( Правило Крамера) .
Инверсия матрицы
Мультипликативная обратная квадратная матрица называется ее обратной матрицей. Если матрица А имеет обратное, то А как говорят неособый или обратимый. А единственное число матрица не имеет инверсии. Чтобы найти обратную квадратную матрицу А , вам нужно найти матрицу А – 1 так что продукт А а также А – 1 – единичная матрица.
Другими словами, для каждой квадратной матрицы А которая является невырожденной, существует обратная матрица, обладающая тем свойством, что А А – 1 знак равно А – 1 А знак равно я , куда я – единичная матрица подходящего размера.
Вы можете использовать любой из следующих методов, чтобы найти обратную квадратную матрицу.
Способ 1:
Позволять А быть п × п матрица.
1. Напишите дважды расширенную матрицу [ А | я п ] .
2. Примените элементарные операции со строками, чтобы записать матрицу в сокращенной форме строки-эшелона.
3. Решите, будет ли матрица А обратима (неособа).
4. Если А сводится к единичной матрице я п , тогда А – 1 – матрица справа от преобразованной расширенной матрицы.
5. Если А не сводится к единичной матрице, то А единственное число.
Способ 2:
Вы можете использовать следующую формулу при нахождении обратной величины п × п матрица.
Если А является невырожденной матрицей, существует обратная матрица, которая задается формулой А – 1 знак равно 1 | А | ( прил А ) , куда | А | – определитель матрицы.
Пример :
Находить А – 1 , если он существует. Если А – 1 не существует, пишите в единственном числе.
А знак равно [ 1 2 1 1 ]
Шаг 1:
Напишите дважды расширенную матрицу [ А | я п ] .
[ А | я ] знак равно [ 1 2 1 0 1 1 0 1 ]
Шаг 2:
Примените элементарные операции со строками, чтобы записать матрицу в сокращенной форме строки-эшелона.
[ 1 2 1 0 0 1 1 – 1 ] р 2 знак равно р 1 – р 2 [ 1 0 – 1 2 0 1 1 – 1 ] р 1 знак равно – 2 р 2 + р 1 [ 1 0 – 1 2 0 1 1 – 1 ] знак равно [ я | А – 1 ]
У системы есть решение.
Следовательно, А обратима и А – 1 знак равно [ – 1 2 1 – 1 ]
Идентификационная матрица и ее свойства
Единичная матрица – это квадратная матрица, которая имеет единицы по главной диагонали и нули для всех остальных элементов.Эта матрица часто записывается просто как \ (I \) и отличается тем, что действует как 1 при умножении матриц. В этом уроке мы рассмотрим это свойство и некоторые другие важные идеи, связанные с тождественными матрицами.
реклама
Единичная матрица всегда является квадратной матрицей
Хотя мы говорим «единичная матрица», мы часто говорим об «единичной матрице». Для любого целого числа \ (n \) существует соответствующая единичная матрица \ (n \ times n \).Эти матрицы называются квадратными, поскольку количество строк и столбцов всегда одинаковое.
Во избежание путаницы часто используется нижний индекс. Таким образом, на рисунке выше идентичность \ (2 \ times 2 \) может быть обозначена как \ (I_2 \), а идентичность \ (3 \ times 3 \) может быть обозначена как \ (I_3 \).
Умножение любой матрицы на единицу дает саму матрицу
При работе с матричным умножением размер матрицы важен, так как умножение не всегда определяется.Поэтому для матрицы \ (m \ times n \) \ (A \) мы говорим:
Это показывает, что до тех пор, пока учитывается размер матрицы, умножение на единицу похоже на умножение на 1 с числами. Например, рассмотрим следующую матрицу.
Это матрица \ (2 \ times 4 \), поскольку в ней 2 строки и 4 столбца. Вы можете проверить, что \ (I_2 A = A \):
и \ (A I_4 = A \):
С другими квадратными матрицами все намного проще.Рассмотрим пример ниже, где \ (B \) – матрица \ (2 \ times 2 \). Здесь мы можем использовать тождество \ (2 \ times 2 \) как для правого, так и для левого умножения.
Произведение двух обратных матриц всегда равно тождеству
Одна из концепций, интенсивно изучаемых в математике, – это концепция обратимых матриц, то есть тех матриц, которые имеют обратную. По определению, когда вы перемножаете две матрицы, обратные друг другу, вы получите единичную матрицу.Рассмотрим следующие матрицы:
Для этих матриц \ (AB = BA = I \), где \ (I \) – единичная матрица \ (2 \ times 2 \).
Следовательно, \ (A \) и \ (B \) – обратные матрицы. Вы можете изучить эту идею подробнее здесь: обратные матрицы.
Сводка
Единичная матрица – это фундаментальная идея при работе с матрицами – независимо от того, работаете ли вы с простым умножением, обращением или даже решением матричных уравнений. Изучая такие темы, убедитесь, что у вас есть фундаментальные представления об этой матрице.
Подпишитесь на нашу рассылку новостей!
Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.
Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!
СвязанныеМатрица в Data Science, интервью
Простое определение матрицы – это прямоугольный массив чисел. Он расположен в ряды и столбцы, например.g .:
A – это матрица 2 x 3 ( m x n матрица , m = 2 строки и n = 3 столбца). Полужирные прописные буквы, такие как A или B , используются для обозначения матриц. Как показано выше, квадратные скобки [] или круглые скобки () используются для определения матрицы, и между ними нет никакой разницы.
Если m = n , матрица называется квадратной матрицей , т.е.g .:
Отдельный элемент обозначается как a ᵢ, ⱼ, где i обозначает номер строки, а j обозначает номер столбца:
Транспонирование матрицы ( A ‘ или Aᵀ) просто меняет местами столбцы и строки, поэтому для матрицы A выше:
Если матрица квадратная и B = B ‘:
Тогда матрица B является симметричной матрицей .
Чтобы вычислить скалярное произведение двух ненулевых векторов (один столбец матрицы), имеющих одинаковую размерность, мы суммируем поэлементные произведения:
Первое, на что следует обратить внимание, это то, что размеры матриц мы хотим добавить или вычесть должны быть одинаковыми.Если это условие верно, то мы складываем значения в одной и той же позиции обеих матриц:
Для вычитания применяется та же процедура.
Умножение считается самой загадочной матричной операцией. Как вы увидите ниже, с этой пошаговой инструкцией не нужно бояться.
Скаляр – матричное умножение
Когда мы хотим умножить матрицу на число, мы просто умножаем каждый элемент матрицы на этот скаляр.
Матрица – умножение матриц
a) Во-первых, нам нужно проверить, можем ли мы перемножить две матрицы.Матричное произведение двух матриц существует только тогда, когда количество столбцов в первой матрице равно количеству строк во второй матрице:
Если мы возьмем наши предыдущие матрицы:
умножение A ( m x n ) x B ( k x j) невозможно, поскольку n (3 столбца A ) не равно k (2 строки B ):
Но мы можем умножить B x A , потому что j равно m (2 столбца B и 2 строки A ):
b) Умножение с использованием символов:
Мы знаем сверху произведение этой матрицы составляет k (номер строки первой матрицы) x n (количество столбцов второй матрицы):
Таким образом, для матриц 2×2 и 2×3, результирующая матрица имеет размеры 2×3:
Мы хотим вычислить значение в позиции1 , который помещается в строку 1 и столбец 1, поэтому мы используем первую строку из первой матрицы ( a b ) и первый столбец из второй матрицы ( e, h ) ‘, как отмечено в красный в примере символа.Итак, для position6 , помещенного в строку 2, столбец 3, и учитывая умножение BA , мы используем вторую строку первой матрицы и третий столбец второй матрицы:
Мы повторяем эту процедуру для каждой позиции. Наконец, мы получаем матричный продукт:
Помните, что порядок умножения имеет значение, и в целом AB не равно BA . Но матрицы ассоциативны: (AB) C = A (BC) .
Единичная или единичная матрица I – это матрица с единицами на диагонали и нулями в другом месте:
Определитель квадратной матрицы 2 x 2 B является скаляром (простым числом) и обозначается как det ( B ) или | B |:
Использование символов:
Также возможно вычислить детерминанты для более высоких измерений, например для матрицы 3×3:
Итак, мы просто берем значение из первой строки, удаляем строку и столбец данного значения и оставляем матрицу 2×2, e.грамм. для первого члена в правой части уравнения:
Обратите внимание, что мы не можем использовать || для определения матрицы, поскольку:
Обратная матрица – это квадратная матрица B⁻¹ , которая, умноженная на матрицу B , дает единичную матрицу I:
Если определитель матрицы не равен нулю, обратная матрица матрицы 2×2:
Итак, для обратной нашей матрицы B:
И мы можем проверить это:
- Обратная матрица существует только в том случае, если матрица квадратная, но не каждая квадратная матрица имеет обратную матрицу .
- Матрица, имеющая инверсию, – это Неособая матрица
- Матрица, у которой нет обратной матрицы, – это сингулярная матрица
- Для квадратных матриц A и B: ( AB ) ⁻¹ = B⁻¹A⁻¹
Типы матриц | eMathZone
Существует несколько типов матриц, но наиболее часто используются:
Матрица строк
Матрица столбцов
Прямоугольная матрица
Квадратная матрица
Диагональная матрица
Скалярная матрица
Матрица идентификации
Треугольная матрица
Нулевая или нулевая матрица
Транспонирование матрицы
Матрица строк:
Матрица называется матрицей-строкой, если она имеет только одну строку.
например
\ [A = \ left [{\ begin {array} {* {20} {c}} 1, 2 и 3 \ end {array}} \ right] \]
Матрица столбцов:
Матрица называется матрицей столбцов, если она имеет только один столбец.
например
\ [B = \ left [{\ begin {array} {* {20} {c}} 1 \\ 2 \\ 3 \ end {array}} \ right] \]
Прямоугольная матрица:
Матрица называется прямоугольной, если количество строк не равно количеству столбцов.
например
\ [A = \ left [{\ begin {array} {* {20} {c}} 1 & 3 & 4 \\ 2 & 5 & 2 \ end {array}} \ right] \]
Квадратная матрица:
Матрица называется квадратной, если количество строк равно количеству столбцов.
например
\ [B = \ left [{\ begin {array} {* {20} {c}} 1 & 3 & 4 \\ 5 & 2 & 4 \\ 1 & 9 & 6 \ end {array}} \ right] \]
Диагональная матрица:
Квадратная матрица называется диагональной, если хотя бы один элемент главной диагонали не равен нулю, а все остальные элементы равны нулю.
например
\ [D = \ left [{\ begin {array} {* {20} {c}} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \ end {array}} \ right] \]
Скалярная матрица:
Диагональная матрица называется скалярной, если все ее диагональные элементы совпадают.
например
\ [A = \ left [{\ begin {array} {* {20} {c}} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \ end {array}} \ right] \]
Идентичность или единичная матрица:
Диагональная матрица называется единичной, если все ее диагональные элементы равны единице, что обозначается $$ I $$.
например
\ [I = \ left [{\ begin {array} {* {20} {c}} 1 & 0 \\ 0 & 1 \ end {array}} \ right], \, \, \, I = \ left [{\ begin {array} {* {20} {c}} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array}} \ right] \]
Треугольная матрица:
Квадратная матрица называется треугольной, если все ее элементы выше главной диагонали равны нулю (нижняя треугольная матрица) или все ее элементы ниже главной диагонали равны нулю (верхняя треугольная матрица) .
например:
\ [A = \ left [{\ begin {array} {* {20} {c}} 1 & 0 & 0 \\ 2 & 4 & 0 \\ 3 & 5 & 6 \ end {array}} \ right] \ [(Нижняя треугольная матрица)
\ [B = \ left [{\ begin {array} {* {20} {c}} 5 & 8 & 3 \\ 0 & 1 & 2 \\ 0 & 0 & 7 \ end {array}} \ right] \] (Верхняя треугольная матрица)
Нулевая или нулевая матрица:
Матрица называется пустой или нулевой матрицей, если все ее элементы равны нулю. Обозначается как $$ O $$.
например
\ [O = \ left [{\ begin {array} {* {20} {c}} 0 & 0 \\ 0 & 0 \ end {array}} \ right], \, \, \, O = \ left [{\ begin {array} {* {20} {c}} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \ end {array}} \ right] \]
Транспонирование матрицы:
Предположим, что $$ A $$ – заданная матрица, тогда матрица, полученная перестановкой ее строк на столбцы, называется транспонированием $$ A $$.t} = \ left [{\ begin {array} {* {20} {c}} 1 & 8 \\ 2 & 4 \\ 3 & 6 \ end {array}} \ right] \]
Смотреть Матрицу | Prime Video
«Матрица» – это классика кино, и она будет продолжать цениться по мере того, как мы поднимаемся в сторону технологических достижений современного мира. Невероятно странно смотреть этот фильм 20 лет спустя и видеть, как здесь были учтены некоторые предположения об Интернете, технологиях и обществе. Все это удерживается, но это по-прежнему отличный научно-фантастический боевик, который редко можно встретить с конкурентами или подобным стилем.Многие стилистические элементы «Матрицы» были использованы в других фильмах, но никогда не использовались так успешно, как здесь. Такие вещи, как «время пули», слишком часто использовались с момента выхода этого фильма, но они иллюстрируют влияние, которое оно оказало на фильмы и зрителей.За Вачовски особенно интересно наблюдать в «Особых характеристиках», особенно теперь, когда они обе женщины. Кажется, что у них нет каких-либо технических знаний или понимания кино, но они снимают фильм, который они хотят посмотреть, и уделяют особое внимание тому, что, по их мнению, как зрителю, будет иметь значение.Думаю, этот фильм стал началом очень популярной карьеры Киану с конца 90-х до середины 2000-х. Там, где он, казалось, умер, а теперь снова воскрешен Джоном Уиком. Лоуренс Фишборн великолепен в роли Морфеуса и отлично играет мастера с Нео. Кэрри Энн-Мосс, где она ?! Она выдающаяся в этом фильме, но, вероятно, нет никого лучше, чем Хьюго Уивинг, который мало что может сказать или сделать, кроме как взгляд, оказывает такое влияние на фильм и, в конечном итоге, на историю этой вселенной. Все это выглядит фантастически в 4K!
В этом выпуске полно специальных функций и ЧЕТЫРЕХ аудиокомментариев, которые я был невероятно взволнован, чтобы их послушать.Я не могу сказать, что это проливает свет на концепции или идеи, о которых я раньше не слышал, но так интересно слышать, как интеллектуалы, философы и психологи говорят как о том, что им нравится в фильме и его изображениях, так и о том, что что им не нравится. Один из комментариев принадлежит авторам обзоров фильмов, которые ненавидели фильм и, несмотря на их критику, находят способ обозначить важность фильма в кино. Это довольно интересно, и ему предшествует письмо от Вачовски о передаче этого комментария WB, что очень весело.Представьте себе другой фильм, на который будут отзывы от людей, которым он не понравился, просто чтобы дать зрителю другую перспективу, с которой он сможет погрузиться в эту безумную поездку.
На данный момент, я полагаю, есть релиз трилогии на 4K, а также Steelbook в других магазинах. Я бы порекомендовал получить весь пакет, так как он, вероятно, дешевле, и я купил его, когда два других еще не были выпущены, и пришлось покупать последние 2 фильма отдельно. Этот фильм по-прежнему феноменален, и сегодня он держится так же хорошо, если не лучше.Невероятно видеть, как этот фильм повзрослел и стал социальным комментарием, который сейчас так же актуален, как и когда-либо. Вачовски сняли несколько отличных фильмов, а некоторые не очень, но надеются, что новый M4TRIX (посмотрите, что я там сделал) сделает после 2020 года то, что этот фильм сделал для начала 2000-х.
Матрицы
Большая часть механизма линейной алгебры включает в себя матриц , которые представляют собой прямоугольные массивы чисел.
Прямоугольный массив чисел, заключенный в большую пару круглых или квадратных скобок, например
.называется матрицей .Размер или размер матрицы задается указанием количества строк и количества содержащихся в ней столбцов. Если матрица состоит из m строк и n столбцов, она называется матрицей m на n (записывается m x n ). Например, приведенные выше матрицы имеют размер 2 на 3, поскольку они содержат 2 строки и 3 столбца:
Обратите внимание, что строки считаются сверху вниз, а столбцы – слева направо.
Числа в массиве называются записями матрицы, а расположение конкретной записи указывается путем указания сначала строки, а затем столбца, в котором она находится. Запись в строке i , столбце j называется ( i, j ) записью . Например, поскольку запись −2 в приведенной выше матрице находится в строке 2, столбце 1, это запись (2, 1). Запись (1, 2) – 0, запись (2, 3) – 1 и т. Д. Обычно запись ( i, j ) матрицы A записывается как a ij , а оператор
указывает, что A – это матрица m x n , запись ( i , j ) которой равна a ij .
Пример 1 : Набор всех матриц m x n , элементы которых являются действительными числами, обозначается M m x n ( R ). Если A ε M 2×3 ( R ), сколько элементов содержит матрица A ?
Поскольку каждая матрица в M 2×3 ( R ) состоит из 2 строк и 3 столбцов, A будет содержать 2 x 3 = 6 записей. Пример такой матрицы –
Пример 2 : Если B – это матрица 2 x 2, запись ( i , j ) задается формулой b ij = (−1) i + j ( i + j ), явно определить B .
Запись (1, 1) в B : b 11 = (−1) 1 + 1 (1 + 1) = 2; запись (1, 2): b = (−1) 1 + 2 (1 + 2) = −3; запись (2, 1) также равна −3; а запись (2, 2): b 22 = (−1) 22 (2 + 2) = 4. Следовательно,
Пример 3 : Дайте матрицу 3 x 3, в которой запись ( i, j ) выражается формулой
(δ ij называется дельтой Кронекера .)
Элементы (1,1), (2,2) и (3,3) каждый равны 1, но все остальные элементы равны 0. Таким образом, матрица равна
Вводы по диагонали . Любая запись, номер столбца которой совпадает с номером строки, называется записью по диагонали ; все остальные записи называются недиагональными . Выделены диагональные записи в каждой из следующих матриц:
В матрице A диагональные элементы равны a 11 = 2 и b 22 = 4; в B диагональные записи: b 11 = 2 и b 22 = 4; а в матрице [δ ij ] 3×3 диагональные элементы равны δ 11 = δ 22 = δ 33 = 1.
Если каждый недиагональный элемент матрицы равен нулю, то матрица называется диагональной матрицей . Например, приведенная выше матрица [δ ij ] 3×3 является диагональной матрицей. В таких случаях, особенно с большими матрицами, нередко просто оставлять пустым, любую запись, равную нулю. Например,
– это два способа записи одной и той же матрицы. Блоки нулей часто остаются пустыми и в недиагональных матрицах.Диагональная матрица n x n , элементы которой – от верхнего левого угла до нижнего правого – равны a 11 , a 22 ,…, a nn часто пишется Diag ( a 11 , a 22 ,…, a nn ).
Квадратные матрицы . Любая матрица, которая имеет столько же столбцов, сколько строк, называется квадратной матрицей .Матрица 2 x 2 в примере 2 и матрица 3 x 3 в примере 3 являются квадратными. Если квадратная матрица имеет n строк и n столбцов, то есть, если ее размер равен n x n , тогда матрица называется порядка n .
Треугольные матрицы . Если все элементы ниже диагонали квадратной матрицы равны нулю, то матрица называется верхнетреугольной . Следующая матрица, U , является примером верхней треугольной матрицы порядка 3:
Если все элементы над диагональю квадратной матрицы равны нулю, то матрица называется нижним треугольником .Следующая матрица, L , является примером нижней треугольной матрицы порядка 4:
Матрица называется треугольной , если она верхняя или нижняя треугольная. Диагональная матрица – это матрица, имеющая одновременно верхний и нижний треугольники.
Транспонирование матрицы . Одна из самых основных операций, которые можно выполнить с матрицей, – это ее транспонирование. Пусть A будет матрицей; тогда транспонирует из A , матрица, обозначенная как A T , получается путем записи строк A в виде столбцов.Точнее, строка i из A является столбцом i из A T (что означает, что столбец j из A является строкой j из A T ). Если A составляет м x n , то A T будет n x м . Также из определения сразу следует, что ( A T ) T = A .
Пример 4 : Транспонирование матрицы 2 x 3
– это матрица 3 x 2
Пример 5 : Обратите внимание, что каждая из матриц в примерах 2 и 3 равна своему собственному транспонированию:
Любая матрица, равная своему собственному транспонированию, называется симметричной матрицей .
Матрицы строк и столбцов . Матрица, состоящая ровно из одной строки, называется матрицей строк , а матрица, состоящая ровно из одного столбца, называется матрицей столбцов . Например, это матрица-строка, а
– матрица столбцов. Обратите внимание, что транспонированная матрица-строка является матрицей-столбцом и наоборот; например,
Матрицы строк и столбцов обеспечивают альтернативные обозначения вектора. Например, вектор v = (2, −1,6) в R 3 может быть выражен как матрица-строка или матрица-столбец:
Обычно такую матрицу обозначают жирным шрифтом в нижнем регистре (а не курсивом в верхнем регистре) и ссылаются на нее как на вектор-строку или вектор-столбец .
Нулевые матрицы . Любая матрица, все элементы которой равны нулю, называется нулевой матрицей и обычно обозначается O .

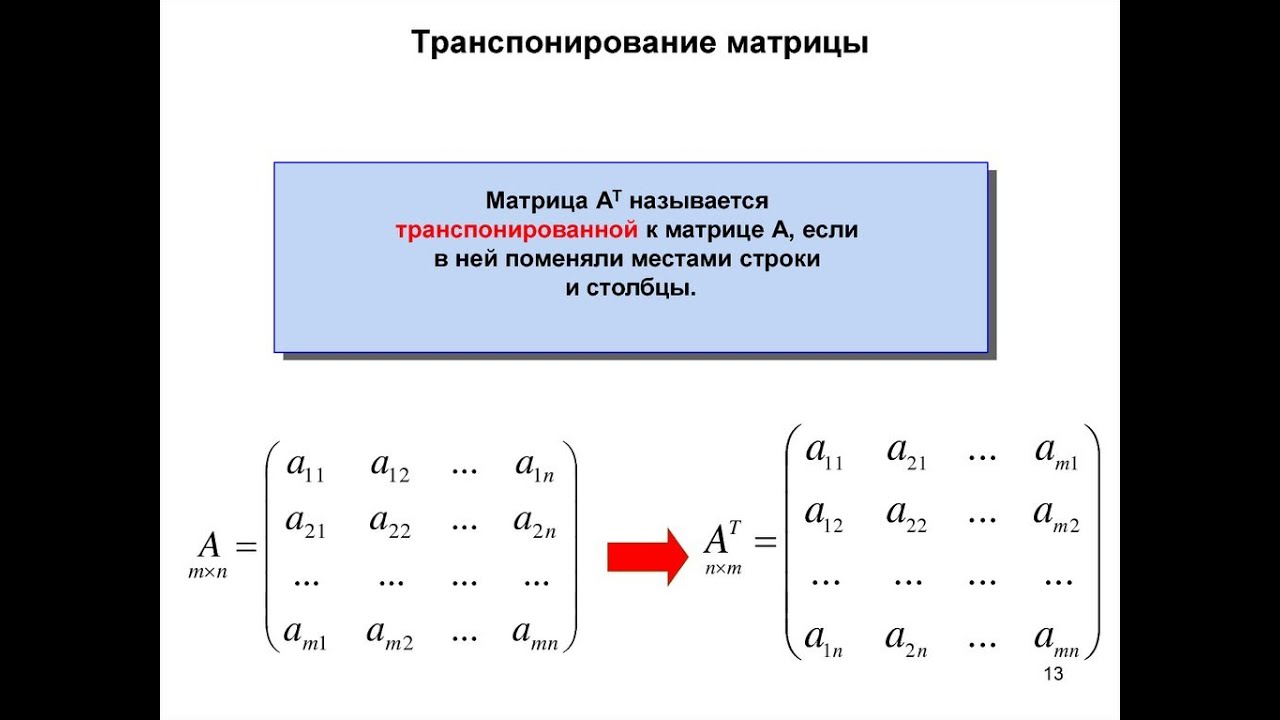

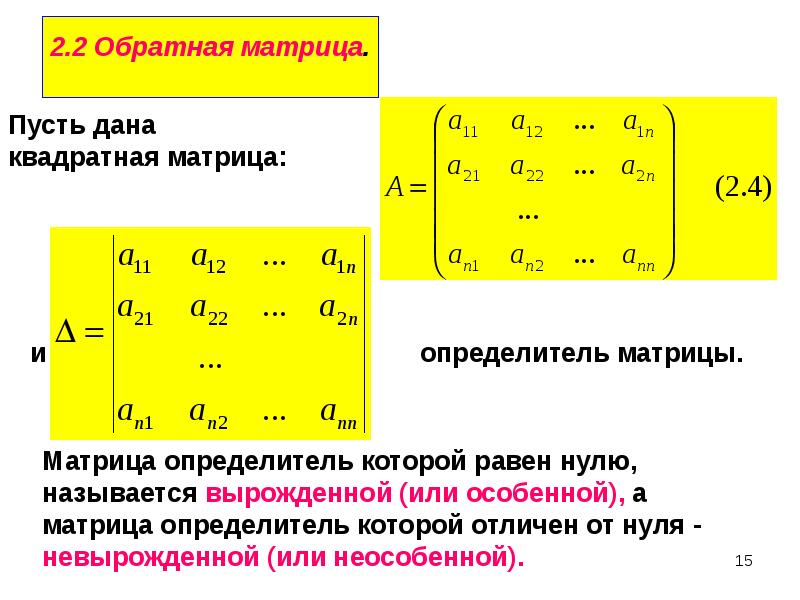
 12.21*
12.21* Важное, но не срочное (задачи, которые можно запланировать на более поздний срок). Это важные долгосрочные цели или задачи, не имеющие жесткого срока выполнения, поэтому их можно запланировать на более поздний срок. Сюда можно отнести получение профессиональной квалификации или планирование долгосрочных бизнес-целей, например сокращение бюджета.
Важное, но не срочное (задачи, которые можно запланировать на более поздний срок). Это важные долгосрочные цели или задачи, не имеющие жесткого срока выполнения, поэтому их можно запланировать на более поздний срок. Сюда можно отнести получение профессиональной квалификации или планирование долгосрочных бизнес-целей, например сокращение бюджета.
 Чаще всего применяются при горячих процессах работ, что обеспечивает максимальный уровень стойкости штампа.
Чаще всего применяются при горячих процессах работ, что обеспечивает максимальный уровень стойкости штампа.