Как найти обратную матрицу: формула, пример
В данной публикации мы рассмотрим, что такое обратная матрица, а также на практическом примере разберем, как ее можно найти с помощью специальной формулы и алгоритма последовательных действий.
- Определение обратной матрицы
- Алгоритм нахождения обратной матрицы
Определение обратной матрицы
Для начала вспомним, что из себя представляют обратные значения в математике. Допустим, у нас есть число 7. Тогда обратное ему будет равняться 7-1 или 1/7. Если умножить данные числа, в результате получится один, т.е. 7 · 7-1 = 1.
Почти то же самое и с матрицами. Обратной называется такая матрица, умножив которую на исходную, мы получим единичную. Обозначается она как A-1.
A · A-1 = E
Алгоритм нахождения обратной матрицы
Для нахождения обратной матрицы нужно уметь вычислять определитель матрицы, а также иметь навыки выполнения определенных действий с ними.
Сразу отметить, что найти обратную можно только для квадратной матрицы, а делается это по формуле ниже:
|A| – определитель матрицы;
ATM – транспонированная матрица алгебраических дополнений.
Примечание: если определитель равен нулю, то обратной матрицы не существует.
Пример
Давайте найдем для матрицы A ниже обратную ей.
Решение
1. Для начала найдем определитель заданной матрицы.
2. Теперь составим матрицу миноров, которая имеет те же самые размеры, что и исходная:
Нам нужно выяснить, какие числа должны стоять на месте звездочек. Начнем с верхнего левого элемента матрицы. Минор к нему находится путем зачеркивания строки и столбца, в котором он находится, т.е. в обоих случаях под номером один.
Число, которое останется после зачеркивания, и является требуемым минором, т.е. M11 = 8.
Аналогичным образом находим миноры для оставшихся элементов матрицы и получаем такой результат.
3. Определяем матрицу алгебраических дополнений. Как их посчитать для каждого элемента мы рассмотрели в отдельной публикации.
Например, для элемента a11 алгебраическое дополнение считается так:
A11 = (-1)1+1 · M11 = 1 · 8 = 8
4. Выполняем транспонирование полученной матрицы алгебраических дополнений (т. е. поменяем столбцы и строки местами).
5. Остается только воспользоваться формулой выше, чтобы найти обратную матрицу.
Ответ можем оставить в таком виде, не деля элементы матрицы на число 11, так как в этом случае получится некрасивые дробные числа.
Проверка результата
Чтобы убедиться в том, что мы получили обратную исходной матрицу, мы можем найти их произведение, которое должно равняться единичной матрице.
В результате мы получили единичную матрицу, значит все сделали верно.
Вычисление определителей. Миноры, алгебраические дополнения.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Квадратная таблица $$A=\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix}$$ составленная из четырех действительных или комплексных чисел называется квадратной матрицей 2-го порядка. Определителем 2-го порядка, соответствующим матрице $A$ (или просто определителем матрицы $A$) называется число $$\det A=\begin{vmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{vmatrix}=a_{11}a_{22}-a_{12}a_{21}.$$
Аналогично если $$A=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}$$
– квадратная матрица 3-го порядка, то соответсвующим ей определителем 3-го порядка называется число
$$\det A=\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}=$$ $$a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{23}a_{32}a_{11}. 2+5x+4=0:$
2+5x+4=0:$
$D=25-16=9$
$x_1=\frac{-5-3}{2}=-4;\qquad x_2=\frac{-5+3}{2}=-1.$
Ответ: $x_1=-4;\,\,\, x_2=-1.$
{jumi[*4]}
3.13. $\begin{vmatrix}3&4&-5\\8&7&-2\\2&-1&8\end{vmatrix}.$
Решение.
$\begin{vmatrix}3&4&-5\\8&7&-2\\2&-1&8\end{vmatrix}=3\cdot 7\cdot8+(-5)\cdot 8\cdot(-1)+4\cdot(-2)\cdot2-(-5)\cdot7\cdot2-$
$-4\cdot8\cdot8-3\cdot(-2)\cdot(-1)=168+40-16+70-256-6=0.$
Ответ: $0.$
3.16. $\begin{vmatrix}\sin\alpha&\cos\alpha&1\\\sin\beta&\cos\beta&1\\\sin\gamma&\cos\gamma&1\end{vmatrix}.$
Решение.
$\begin{vmatrix}\sin\alpha&\cos\alpha&1\\\sin\beta&\cos\beta&1\\\sin\gamma&\cos\gamma&1\end{vmatrix}=\sin\alpha\cos\beta+\sin\beta\cos\gamma+\cos\alpha\sin\gamma-$
$-\cos\beta\sin\gamma-\sin\alpha\cos\gamma-\cos\alpha\sin\beta=$
$=\sin(\alpha-\beta)+\sin(\beta-\gamma)+\sin(\gamma-\alpha). T=\det A.$
T=\det A.$
2) Если все элементы строки (столбца) умножить на одно и тоже число, то определитель умножится на это число.
3) Если поменять местами две строки (столбца), то определитель поменяет знак. В частности, если две строки (столбца) равны, то определитель равен нулю.
4) Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы), кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые, а во втором – вторые слагаемые.
5) Если одна строка (столбец) является линейной комбинацией других строк (столбцов), то определитель равен нулю.
6) Определитель не меняется если к одной из его строк (столбцов) добавить линейную комбинацию его других строк (столбцов).
Примеры:
3.24. Используя свойства определителя доказать следующее тождество: $\begin{vmatrix}a_1+b_1x&a_1-b_1x&c_1\\a_2+b_2x&a_2-b_2x&c_2\\a_3+b_3x&a_3-b_3x&c_3\end{vmatrix}=$ $-2x\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}. $
$
Доказательство.
$\begin{vmatrix}a_1+b_1x&a_1-b_1x&c_1\\a_2+b_2x&a_2-b_2x&c_2\\a_3+b_3x&a_3-b_3x&c_3\end{vmatrix}=$
$\begin{vmatrix}a_1&a_1-b_1x&c_1\\a_2&a_2-b_2x&c_2\\a_3&a_3-b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1-b_1x&c_1\\b_2x&a_2-b_2x&c_2\\b_3x&a_3-b_3x&c_3\end{vmatrix}=$
$=\begin{vmatrix}a_1&a_1&c_1\\a_2&a_2&c_2\\a_3&a_3&c_3\end{vmatrix}-$ $\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1&c_1\\b_2x&a_2&c_2\\b_3x&a_3&c_3\end{vmatrix}-$ $\begin{vmatrix}b_1x&b_1x&c_1\\b_2x&b_2x&c_2\\b_3x&b_3x&c_3\end{vmatrix}=$
$-\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1&c_1\\b_2x&a_2&c_2\\b_3x&a_3&c_3\end{vmatrix}=$ $-\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}-$ $\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}=$
$-2\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}=$ $-2x\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}. {3+4}\begin{vmatrix}2&-3&4\\4&-2&3\\3&-1&4\end{vmatrix}=$
{3+4}\begin{vmatrix}2&-3&4\\4&-2&3\\3&-1&4\end{vmatrix}=$
$=a(-27-8-8+3+24+24)-b(18+16+24-9-16-48)+$
$+c(-12-4-18+6+4+36)-d(-16-16-27+24+6+48)=$
$=8a+15b+12c-19d.$
Ответ: $8a+15b+12c-19d.$
{jumi[*4]}
3.61. Вычислить определитель: $\begin{vmatrix}2&1&1&1&1\\1&3&1&1&1\\1&1&4&1&1\\1&1&1&5&1\\1&1&1&1&6\end{vmatrix}.$
Решение.
Вычислим этот определитель с помощью приведения определителя к треугольному виду:
$\begin{vmatrix}2&1&1&1&1\\1&3&1&1&1\\1&1&4&1&1\\1&1&1&5&1\\1&1&1&1&6\end{vmatrix}=$ от каждой из первых четырех строк отнимем пятую $=\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\1&1&1&1&6\end{vmatrix}=$ от пятой строки отнимем первую, затем пятую строку умножим на два
$=\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&1&1&1&11\end{vmatrix}=$ $\frac{1}{2}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&2&2&2&22\end{vmatrix}=$ Далее от пятой строки отнимем вторую, после чего пятую строку умножим на $\frac{3}{2}:$ $=\frac{1}{2}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&2&2&27\end{vmatrix}=$ $\frac{1}{2}\frac{2}{3}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&3&3&40,5\end{vmatrix}=$ Теперь от пятой строки отнимем третью, после чего пятую строку умножим на $\frac{4}{3}:$ $=\frac{1}{3}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&3&45,5\end{vmatrix}=$ $\frac{1}{3}\frac{3}{4}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&4&\frac{182}{3}\end{vmatrix}=$ Отнимем от пятой строки четвертую и перемножив диагональные элементы получаем ответ: $=\frac{1}{4}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&0&\frac{197}{3}\end{vmatrix}=$ $=\frac{1}{4}\cdot2\cdot3\cdot4\cdot\frac{197}{3}=394.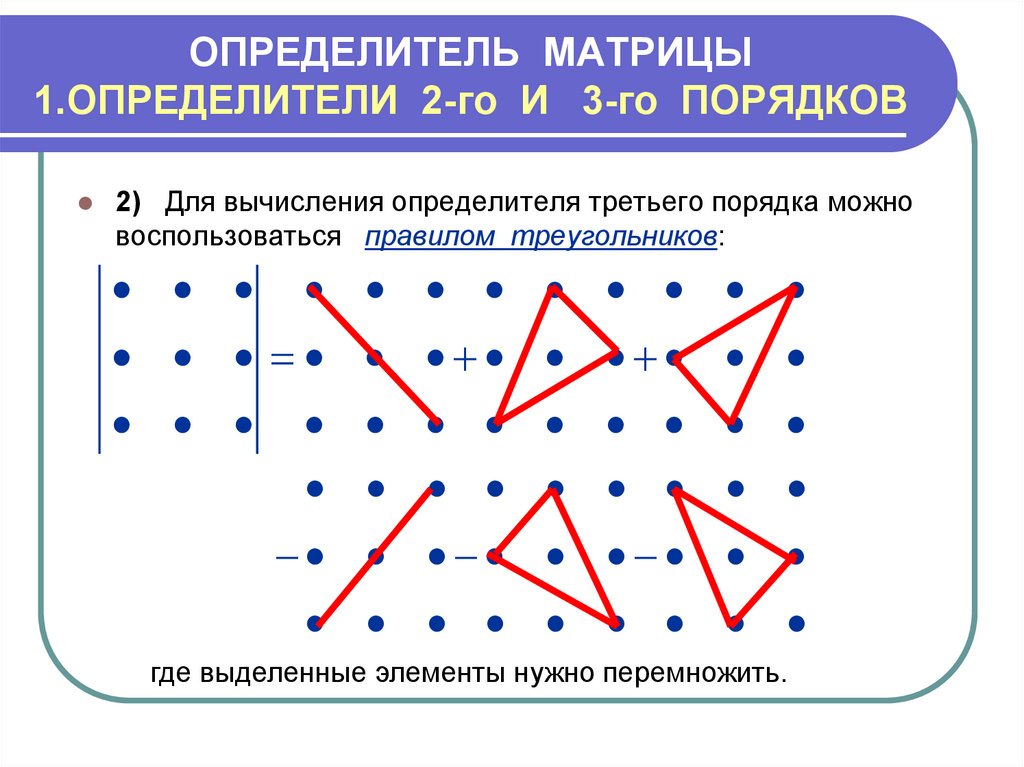 2.$
2.$
Вычислить определители, используя подходящее разложение по строке или столбцу.
3.51. $\begin{vmatrix}-1&5&2\\0&7&0\\1&2&0\end{vmatrix}.$
Ответ: $-14.$
3.52. $\begin{vmatrix}2&1&0\\1&2&1\\0&1&2\end{vmatrix}.$
Ответ: $4.$
3.54. (б) $\begin{vmatrix}5&a&2&-1\\4&b&4&-3\\2&c&3&-2\\4&d&5&-4\end{vmatrix}.$
Ответ: $2a-8b+c+5d.$
3.62. Вычислить определитель: $\begin{vmatrix}5&6&0&0&0\\1&5&6&0&0\\0&1&5&6&0\\0&0&1&5&6\\0&0&0&1&5\end{vmatrix}.$
Ответ: $665.$
{jumi[*4]}
Матричные уравнения
Цели
- Понимать эквивалентность между системой линейных уравнений, расширенной матрицей, векторным уравнением и матричным уравнением.

- Охарактеризовать векторы b так, что Ax=b непротиворечиво, с точки зрения диапазона столбцов A.
- Охарактеризуйте матрицы A таким образом, что Ax=b непротиворечиво для всех векторов b.
- Рецепт: умножить вектор на матрицу (два способа).
- Фото: множество всех векторов b, таких что Ax=b, непротиворечиво.
- Словарное слово: матричное уравнение .
В этом разделе мы представляем очень лаконичный способ записи системы линейных уравнений: Ax=b. Здесь A — матрица, а x,b — векторы (обычно разного размера), поэтому сначала мы должны объяснить, как умножать матрицу на вектор.
Когда мы говорим «A — матрица размера m×n», мы имеем в виду, что A имеет m строк и n столбцов.
Определение
Пусть A — матрица размера m×n со столбцами v1,v2,…,vn:
А=С|||v1v2···vn|||D
Произведение оператора A с вектором x в Rn является линейной комбинацией
Ax=C|||v1v2···vn|||DEIIGx1x2. ..xnFJJH=x1v1+x2v2+···+xnvn.
..xnFJJH=x1v1+x2v2+···+xnvn.
Это вектор в Rm.
Пример
Чтобы Ax имел смысл, количество элементов x должно совпадать с количеством столбцов A: мы используем элементы x как коэффициенты столбцов A в линейной комбинации. Результирующий вектор имеет то же количество элементов, что и число 9.0012 строк
Если A представляет собой матрицу размера m × n (m строк, n столбцов), то Ax имеет смысл, когда x имеет n элементов. Произведение Ax содержит m записей.
Свойства матрично-векторного произведения
Пусть A — матрица размера m × n, пусть u, v — векторы в Rn, а c — скаляр. Тогда:
- А(и+в)=Аи+Ав
- A(cu)=cAu
Определение
Матричное уравнение — это уравнение вида Ax=b, где A — матрица размера m×n, b — вектор в Rm, а x — вектор, коэффициенты которого x1,x2,…,xn неизвестны. .
В этой книге мы изучим два дополнительных вопроса о матричном уравнении Ax=b:
- При конкретном выборе b, каковы все решения Ax=b?
- Каковы все варианты b, чтобы Ax=b было непротиворечивым?
Первый вопрос больше похож на вопросы, к которым вы, возможно, уже привыкли на предыдущих курсах алгебры; у вас есть много практики решения уравнений типа x2−1=0 относительно x. Второй вопрос, возможно, является новой концепцией для вас. Теорема о рангах в разделе 2.9, который является кульминацией этой главы, говорит нам, что эти два вопроса тесно связаны.
Второй вопрос, возможно, является новой концепцией для вас. Теорема о рангах в разделе 2.9, который является кульминацией этой главы, говорит нам, что эти два вопроса тесно связаны.
Пример
В оставшейся части книги мы будем свободно перемещаться между четырьмя способами записи линейной системы снова и снова.
Другой способ вычислений Axe
Приведенное выше определение является полезным способом определения произведения матрицы на вектор, когда дело доходит до понимания взаимосвязи между матричными уравнениями и векторными уравнениями. Здесь мы даем определение, которое лучше подходит для ручных вычислений.
Определение
Вектор-строка представляет собой матрицу с одной строкой. Произведение вектора-строки длины n и вектора (столбца) длины n равно
.Aa1a2···anBEIIGx1x2…xnFJJH=a1x1+a2x2+···+anxn.
Это скаляр.
Рецепт: Правило строки-столбца для умножения матрицы на вектор
Если A — матрица размера m × n со строками r1,r2,.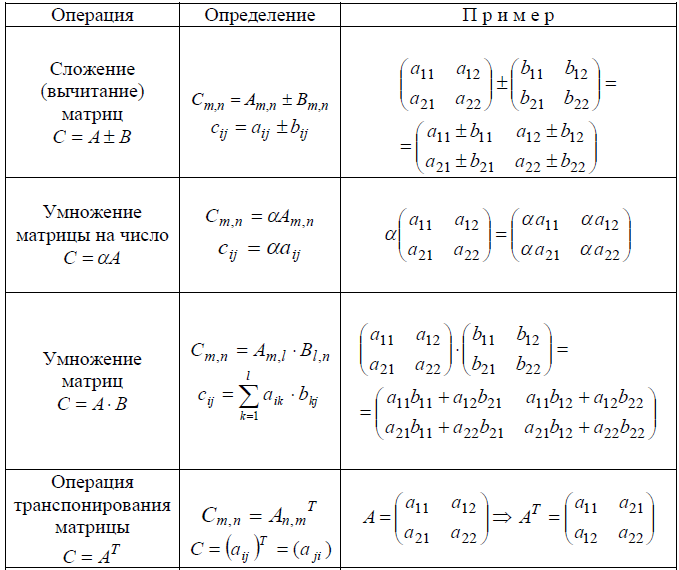
Ax=EIIG—r1——r2—…—rm—FJJHx=EIIGr1xr2x…rmxFJJH.
Пример
Пусть A — матрица со столбцами v1,v2,…,vn:
А=С|||v1v2···vn|||D.
Затем
Ax=bhas решение⇐⇒существуют x1,x2,…,xn такие, что AEIIGx1x2…xnFJJH=b⇐⇒существуют x1,x2,…,xn такие, что x1v1+x2v2+···+xnvn=b⇐⇒бисалинейная комбинация v1,v2,… ,vn⇐⇒bis находится в диапазоне столбцов матрицы A.
Диапазоны и согласованность
Матричное уравнение Ax=b имеет решение тогда и только тогда, когда b находится в интервале столбцов A.
Это дает эквивалентность между алгебраический оператор (Ax=b непротиворечив) и геометрический
Пример (несогласованная система)
Пример (согласованная система)
Когда решения всегда существуют
Опираясь на это примечание, у нас есть следующий критерий, когда Ax=b соответствует каждому выбору b.
Теорема
Пусть A — матрица размера m × n (нерасширенная). Следующие эквивалентны:
- Ax=b имеет решение для всех b в Rm.
- Длина столбцов A равна Rm.
- A имеет точку поворота в каждой строке.
Доказательство
Эквивалентность 1 и 2 устанавливается этим примечанием применительно к каждому b в Rm.
Теперь покажем, что 1 и 3 эквивалентны. (Поскольку мы знаем, что 1 и 2 эквивалентны, отсюда следует, что 2 и 3 также эквивалентны.) Если A имеет центральную точку в каждой строке, то его сокращенная ступенчатая форма строки выглядит следующим образом:
К10А0А01А0А0001АД,
и поэтому AAbB сводится к этому:
C10A0AA01A0AA0001AAD.Нет b, который делал бы его несовместимым, поэтому всегда есть решение. Наоборот, если A не имеет стержня в каждой строке, то его уменьшенная ступенчатая форма строки выглядит так:
К10А0А01А0А00000Д,
, что может привести к противоречивой системе после добавления b:
C10A0A001A0A00000016D.
Напомним, что эквивалентно означает, что для любой заданной матрицы A либо все условий приведенной выше теоремы верны или все они ложны.
Будьте внимательны при чтении утверждения приведенной выше теоремы. Первые два условия очень похожи на это примечание, но логически они совершенно разные из-за квантификатора « для всех b».
Интерактивный: критерии теоремы выполнены
Интерактив: Критерии теоремы не выполнены
Комментарии, исправления или предложения? (Требуется бесплатная учетная запись GitHub)
Матричная формула – Что такое матричная формула? Примеры
Матрица – это упорядоченное расположение чисел, выражений и даже символов в строках и столбцах. Если две матрицы имеют одинаковый размер (относительно их строк и столбцов), то их можно складывать, вычитать и умножать поэлементно. Давайте изучим матричные формулы вместе с несколькими решенными примерами.
Что такое формула матрицы?
Матрица – это массив чисел, разделенный на строки и столбцы и представленный в квадратных скобках. Если вы видите матрицу 2 × 2, это означает, что матрица имеет 2 строки и 2 столбца. Матричные формулы используются для вычисления коэффициента вариации, сопряженной матрицы, определителя матрицы и обратной матрицы. Матричная формула особенно полезна в тех случаях, когда нам нужно сравнить результаты двух разных опросов с разными значениями.
Если вы видите матрицу 2 × 2, это означает, что матрица имеет 2 строки и 2 столбца. Матричные формулы используются для вычисления коэффициента вариации, сопряженной матрицы, определителя матрицы и обратной матрицы. Матричная формула особенно полезна в тех случаях, когда нам нужно сравнить результаты двух разных опросов с разными значениями.
Матричные формулы
Формула 1: Формула коэффициента вариации может быть представлена как
\(M=\begin{bmatrix} m_{11} & m_{12}\\ m_{21} & m_ {22} \end{bmatrix}\)
Формула 2: Сопряженная формула матрицы 2 × 2 задается как
\( adj(M)=\begin{bmatrix} m_{22} & – m_{12}\\ -m_{21} & m_{11} \end{bmatrix}\)
Формула 3: Обратная формула матрицы 2×2 задается как
9T\) =A’= \(\begin{bmatrix}a&d\\b&e\\c&f\end{bmatrix}\)Формула 6: Матричная формула для сложения:
A= \(\begin{bmatrix }a&b&c\\d&e&f\\g&h&i\end{bmatrix}\)
B= \(\begin{bmatrix}j&k&l\\m&n&o\\p&q&r\end{bmatrix}\)
A+B= \(\begin{bmatrix}a+j&b+k&c+l\\d+m&e+n&f +o\\g+p&h+q&i+r\end{bmatrix}\)
Формула 7: Матричная формула для вычитания:
A = \(\begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix}\)
B= \(\begin{bmatrix}j&k&l\\m&n&o\\p&q&r\end{bmatrix}\)
A-B= \(\begin{bmatrix}a-j&b-k&c-l\\d-m&e-n&f-o \\g-p&h-q&i-r\end{bmatrix}\)
Формула 8: Матричная формула для умножения:
A= \(\begin{bmatrix}a&b&c\\d&e&f\end{bmatrix}\)
B = \(\begin{bmatrix}g&h\\i&j\\k&l\end{bmatrix}\)
AB = \(\begin{bmatrix}ag+bi+ck&ah+bj+cl\\dg+ei+fk&dh+ej+fl\end{bmatrix}\)
Формула 9: Для ортогональной матрицы произведение матрицы и ее транспонирования дает единичную матрицу.
M × M T = \(\begin{bmatrix}a&b\\c&d\end{bmatrix}\) × \(\begin{bmatrix}a&c\\b&d\end{ bmatrix}\) = \(\begin{bmatrix}1&0\\0&1\end{bmatrix}\)
Применение матричных формул
Матричные формулы обычно используются для нахождения решений линейных уравнений и исчисления, оптики, квантовой механики, и другие математические функции.
Давайте посмотрим, как использовать матричную формулу в следующем разделе примеров решения.
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами
Закажите бесплатный пробный урок
Примеры с использованием матричной формулы
Пример 1: Используя матричную формулу, определите определитель заданной матрицы.
\(\begin{bmatrix} 3 и 4 \\ 4 и 8 \end{bmatrix}\)
Решение:
Найти: Определитель матрицы.
\(m_{11}\) = 3, \(m_{12}\) = 4, \(m_{21}\) = 4 и, \(m_{22}\) = 8 (дано)
Используя матричную формулу для определителя,
|M| = \(m_{11}\)\(m_{22}\)–\(m_{12}\)\(m_{21}\)
= (3)(8) – (4)(4)
= 24 – 16
= 8
Ответ: определитель данной матрицы равен 8.
Пример 2 : Определите сопряженный элемент данной матрицы 2 x 2.
\(\begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix}\)
Решение:
Найти: примыкание к заданной матрице 2 x 2
Дано: \( m_{11}= 5, m_{12} = 6, m_{21} = 7 и, m_{22} = 8\)(дано)
Используя матричную формулу для сопряженной матрицы,
\ ( adj(M)=\begin{bmatrix} m_{22} & -m_{12}\\ -m_{21} & m_{11} \end{bmatrix}\)
Поместите все значения,
\ ( adj(M)=\begin{bmatrix} 8 & – 6\\ – 7 & 5 \end{bmatrix}\)
Ответ: Сопряженная матрица равна \(\begin{bmatrix} 8 & – 6\\ – 7 & 5 \end{bmatrix}\).
Пример 3: Используйте матричную формулу для определения определителя матрицы:
\(\begin{bmatrix} 2 & 4 \\ 6 & 5 \end{bmatrix}\)
Решение: 6
Найти: Определитель матрицы.
\(m_{11}\)= 2, \(m_{12}\) = 4, \(m_{21}\) = 6 и, \(m_{22}\) = 5 (дано)
Использование матричной формулы для определителя,
|M| = \(m_{11}\)\(m_{22}\)–\(m_{12}\)\(m_{21}\)
= (2)(5) – (4)(6)
= 10 – 24
= -14
Ответ: Определитель данной матрицы равен -14.
Часто задаваемые вопросы о матричной формуле
Что такое матричная формула в алгебре?
Матричные формулы используются для вычисления коэффициента вариации, сопряженного к матрице, определителя матрицы и обратной матрицы.
9{-1}=\frac{1}{|M|}\times adj(M)\)Что такое формула матрицы идентичности?
Единичная матрица — это квадратная матрица, состоящая из всех элементов главной диагонали, обозначенных единицами, и всех остальных элементов, обозначенных нулями.

