20.1.5. Умножение матрицы на число
Для умножения матрицы на число используются операции аналогичные сложению или вычитанию матриц. Для этого в ячейку, выделенную для первого элемента результирующей матрицы, записывается формула умножения первого элемента исходной матрицы на число. В этой формуле записывается адрес первого элемента, а в качестве числа записывается или его значение или его адрес (если число помещено в ячейку). Далее используется способ копирования формулы во все последующие ячейки результирующей матрицы.
20.1.6. Умножение матриц
Произведение двух матриц возможно в случае, когда количество столбцов первой матрицы равно количеству строк второй матрицы. Например: , где
,
Здесь четыре столбца матрицы А равны четырем строкам матрицы В.
Для умножения матриц необходимо выполнить следующие операции:
выделить область ячеек под результирующую матрицу.

Щелкнуть по кнопке Вставка функции,
в раскрывшемся окне Мастер функций в поле Категория выбрать строку Математические, а в поле Функция – имя функции МУМНОЖ,
щелкнуть по кнопке ОК,
нажать сочетание клавиш Ctrl+Shift+Enter.
В
результате этих действий в ячейках,
выделенных под результирующую матрицу,
появятся ее значения. Если этого не
произойдет, то следует щелкнуть указателем
мыши в строке формул и еще раз нажать
комбинацию клавиш Ctrl+Shift+Enter.
Если этого не
произойдет, то следует щелкнуть указателем
мыши в строке формул и еще раз нажать
комбинацию клавиш Ctrl+Shift+Enter.
20.2. Решение систем линейных уравнений
Большое количество прикладных задач в технике, и в электротехнике в частности, решаются с использованием систем линейных уравнений. Поэтому весьма важно владеть методикой их решения. Существует достаточное количество как ручных способов их решения, так и способов решения с помощью компьютера. Имеется ряд прикладных программ таких как Matlab, Matcad и других, позволяющих достаточно просто решать такую задачу. Но вместе с тем и программа MS Excel предлагает свои возможности для решения систем n линейных уравнений с n неизвестными.
Запись вида
где аij – произвольные числа, являющиеся коэффициентами при неизвестных,
xi – неизвестные, подлежащие вычислению,
bi – произвольные
числа, представляющие собой свободные
члены.
Такая форма записи системы линейных уравнений называется нормальной формой.
Если система уравнений имеет хотя бы одно решение, то она называется
Если система уравнений имеет только одно решение, то она называется определенной, если она имеет несколько решений, то ее называют неопределенной.
Приведенную систему уравнений можно представлять и в матричном виде:
где А – матрица коэффициентов или матрица системы:
X – матрица – столбец (вектор) неизвестных
В – матрица – столбец (вектор) свободных членов
В развернутом виде систему можно записать следующим образом:
Существует
ряд методов решения таких систем, в
частности, метод Крамера, Гаусса, обратной
матрицы и др. Наиболее удобным методом
решения такого вида систем уравнений
с помощью программы MS
Excel
является метод обратной матрицы. Решение
системы с помощью этого способа
представляется в виде:
Наиболее удобным методом
решения такого вида систем уравнений
с помощью программы MS
Excel
является метод обратной матрицы. Решение
системы с помощью этого способа
представляется в виде:
Программа MS Excel располагает необходимыми средствами для нахождения обратной матрицы и умножения матриц, что обеспечивает решения системы уравнений.
Порядок операций для решения системы линейных уравнений средствами MS Excel следующий:
ввести (разместить) матрицу коэффициентов А в определенной области электронной таблицы,
ввести матрицу – столбец свободных членов В,
выделить область ячеек под обратную матрицу (такого же размера, как и под матрицу коэффициентов А
щелкнуть по кнопке Вставки функции,
в раскрывшемся окне Мастер функций, в поле Категория, выбрать строку Математические, а в поле Функция – имя функции МОБР,
щелкнуть по кнопке ОК,
в раскрывшемся окне МОБР, в рабочем поле Массив, указать диапазон ячеек, занимаемый исходной матрицей А,
нажать сочетание клавиш Ctrl+Shift+Enter.

Если обратная матрица не появилась в указанном диапазоне, то следует щелкнуть мышью в строке формул и повторить нажатие клавиш Ctrl+Shift+Enter.
выделить диапазон ячеек под матрицу – столбец (из n ячеек) неизвестных Х,
щелкнуть по кнопке Вставки функции,
в раскрывшемся окне Мастер функций, в поле Категория, выбрать строку Математические
щелкнуть по кнопке ОК,
в раскрывшемся окне МУМНОЖ, в рабочем поле Массив1 ввести диапазон ячеек, занимаемой обратной матрицей А-1, а в рабочем поле Массив2 ввести диапазон ячеек, занимаемой обратной матрицей – столбцом свободных членов В,
нажать сочетание клавиш Ctrl+Shift+Enter.

После получения решения следует произвести проверку результата, выполнив операцию . Полученный результат должен быть равен вектору В.
Решение высшей математики онлайн
‹– Назад
Определение 14.4 Произведением матрицы размеров на матрицу размеров называется матрица размеров , элементы которой вычисляются по формуле
| (14.5) |
где , .
Во-первых, в этом определении нужно обратить внимание на то, что важен порядок сомножителей, нужно знать, какой сомножитель первый, а какой — второй.
Во-вторых, нужно отметить, что произведение определено только в том случае, если число столбцов первого сомножителя равно числу строк второго. Если это условие не выполняется, то произведение не определено.
В-третьих, размеры результата умножения определяются следующим образом: число строк результата равно числу строк первого сомножителя, а число столбцов результата равно числу столбцов второго сомножителя.
Правило вычисления элементов произведения можно сформулировать следующим образом.
Для того, чтобы вычислить элемент произведения, стоящий в -ой строке и -ом столбце, нужно взять -ую строку первого сомножителя и -ый столбец второго сомножителя, попарно перемножить их элементы, стоящие на одинаковых местах, и результаты сложить. (Точно так же мы поступаем, когда находим скалярное произведение двух векторов по их координатам, см. формулу (14.2).)
Пример 14.3 Даны матрицы , . Найдите произведения и .
Найдите произведения и .
Решение. Рассмотрим произведение . Число столбцов в первом сомножителе равно 3, число строк во втором сомножителе тоже равно 3. Числа совпали, следовательно, произведение определено.
Результатом умножения будет матрица , , у которой строк столько, сколько их в первом сомножителе, то есть 3, а столбцов столько, сколько их во втором сомножителе, то есть 2. Итак, матрица имеет размеры .
Находим элемент . В его вычислении участвует первая строка первого сомножителя и первый столбец второго сомножителя :
Находим элемент . В его вычислении участвует первая строка первого сомножителя и второй столбец второго сомножителя :
Все элементы первой строки матрицы вычислены. Находим элемент . В его вычислении участвует вторая строка первого сомножителя и первый столбец второго сомножителя :
Находим элемент .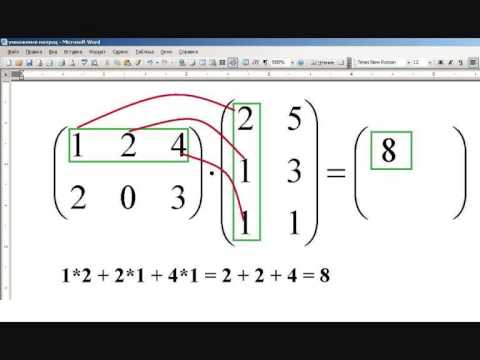 В его вычислении участвует вторая строка первого сомножителя и второй столбец второго сомножителя :
В его вычислении участвует вторая строка первого сомножителя и второй столбец второго сомножителя :
Вычислены все элементы второй строки матрицы . Аналогично находим элементы третьей строки:
Итак, .
Рассмотрим произведение . Число столбцов в первом сомножителе равно 2, число строк во втором сомножителе равно 3. Числа не совпали, следовательно, произведение не определено.
Ответ: , произведение не определено.
Замечание 14.3 Легко проверить, что произведение квадратных матриц одного порядка всегда существует (определено).
У читателя может возникнуть законный вопрос: “Зачем так сложно определять произведение матриц? Нельзя ли его определить попроще, например, как произведение элементов матриц-сомножителей, стоящих на одинаковых местах?” Ответ на этот вопрос мы увидим позже, когда будем рассматривать системы линейных уравнений, правило изменения координат векторов при изменении базиса и такие неизвестные пока читателю объекты как линейные преобразования и квадратичные формы. Тогда мы увидим, что введенное определение умножения матриц используется очень эффективно, что оно “похоже” на умножение чисел. Если же произведение матриц определить по-другому, то его не удается разумно использовать ни в математике, ни в прикладных науках.
Тогда мы увидим, что введенное определение умножения матриц используется очень эффективно, что оно “похоже” на умножение чисел. Если же произведение матриц определить по-другому, то его не удается разумно использовать ни в математике, ни в прикладных науках.
Рассмотрим, какими свойствами обладает операция умножения матриц.
Прежде всего отметим, что умножение матриц — некоммутативная операция. Это означает, что существуют такие матрицы и , что
Для прямоугольных матриц мы убедились в этом в примере 14.3. В нем произведение существует, а произведение — нет. Для квадратных матриц это видно из следующего примера. Пусть , . Тогда
то есть .
Предложение 14.4 Умножение матриц обладает следующими свойствами: — ассоциативность умножения; , где — число; , — дистрибутивность умножения; , , где — единичная матрица соответствующего порядка. Предполагается, что все указанные произведения имеют смысл.
Предполагается, что все указанные произведения имеют смысл.
Доказательство. На протяжении всего доказательства предполагается, что — матрица размеров .
Докажем свойство ассоциативности. Чтобы произведение было определено, матрица должна иметь размеры . Произведение обозначим буквой . Тогда матрица имеет размеры . Чтобы произведение было определено, матрица должна иметь размеры . Матрицу обозначим , матрицу обозначим , матрицу обозначим . Покажем, что элементы, стоящие в -ой строке и -ом столбце матриц и , равны друг другу, то есть что .
По определению
Подставив из второго равенства в первое, получим
В силу предложения 14.1
В силу предложения 14.3
(14. 6) 6) |
С другой стороны
откуда
Применим предложение 14.1
Сравнивая этот результат с (14.6), заключаем, что . Ассоциативность умножения доказана.
Свойство 2 предоставляем читателю доказать самостоятельно.
Докажем дистрибутивность умножения. Чтобы произведение было определено, матрицы и должны иметь размеры . Положим , , , , . Для доказательства равенства , нужно доказать, что , , .
Так как , то
По определению суммы матриц, . Следовательно,
| (14.7) |
С другой стороны,
Тогда
Сравнивая полученный результат с (14. 7), получаем . Первое равенство в свойстве дистрибутивности доказано. Второе равенство доказывается аналогично.
7), получаем . Первое равенство в свойстве дистрибутивности доказано. Второе равенство доказывается аналогично.
Докажем первое равенство в свойстве 4. Чтобы произведение было определено, матрица должна иметь порядок . Пусть . Тогда
где — символ Кронекера . Сумма справа имеет вид
Таким образом , первое равенство в свойстве 4 доказано. Второе равенство доказывается аналогично.
Замечание 14.4 Из ассоциативности умножения матриц следует, что если произведение содержит три и более сомножителей, то его можно записывать без использования скобок. Например, или . Эта кажущаяся очевидной запись произведения верна не для всяких математических объектов. Действительно, в силу предложения 10.23, для векторного произведения векторов запись неприемлема, так как результат вычисления этого произведения зависит от расстановки скобок.
Замечание 14.5 Свойство дистрибутивности позволяет раскрывать скобки в матричных выражениях. Но нужно обратить внимание, что, раскрывая скобки, нельзя менять порядок сомножителей.
Замечание 14.6 Свойство 4 объясняет происхождение названия “единичная” матрица. В умножении матриц единичная матрица ведет себя так же, как число 1 при умножении чисел.
Упражнение14.4.6. Докажите, что произведение двух верхних треугольных матриц одного порядка является верхней треугольной матрицей того же порядка. Докажите аналогичное утверждение для нижних треугольных матриц.
Упражнение14.4.7. По определению считается, что . Покажите, что для матриц формула не верна. Объясните почему.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
Как умножать матрицы? – GeeksforGeeks
Знание матриц необходимо для различных разделов математики. Матрицы — один из самых мощных инструментов в математике. В линейной алгебре умножение матриц — это одна из бинарных операций, которые можно выполнять над матрицами. Умножение любых двух матриц A и B возможно только в том случае, если обе матрицы совместимы. «Матрица» — это прямоугольный массив чисел, расположенных в строках и столбцах. Горизонтальные линии называются строками, а вертикальные — столбцами. Если матрица имеет «m» строк и «n» столбцов, то говорят, что это матрица «m на n» и записывается как матрица «m × n». Мы можем выполнять различные бинарные операции с матрицами, такие как сложение, вычитание, умножение и т. д. В этой статье мы подробно узнаем об умножении матриц.
Матрицы — один из самых мощных инструментов в математике. В линейной алгебре умножение матриц — это одна из бинарных операций, которые можно выполнять над матрицами. Умножение любых двух матриц A и B возможно только в том случае, если обе матрицы совместимы. «Матрица» — это прямоугольный массив чисел, расположенных в строках и столбцах. Горизонтальные линии называются строками, а вертикальные — столбцами. Если матрица имеет «m» строк и «n» столбцов, то говорят, что это матрица «m на n» и записывается как матрица «m × n». Мы можем выполнять различные бинарные операции с матрицами, такие как сложение, вычитание, умножение и т. д. В этой статье мы подробно узнаем об умножении матриц.
Умножение матриц
Умножение матриц — очень простая вещь в математике. Если умножать на число, то просто умножайте число на все элементы, присутствующие в матрице. Но если мы умножим матрицу на другую матрицу, то должны увидеть некоторые правила. Умножение любых двух матриц дает одну матрицу, а это возможно только в том случае, если количество столбцов в 1-й матрице равно количеству строк во 2-й матрице. Если «A = [a ij ] m×n » и «B = [b ij ] n×p » — две матрицы, то произведение A и B обозначается как AB, порядок которых равен «m × p». Обычно умножение матриц не является коммутативным, т. е. AB ≠ BA, или, проще говоря, произведение матриц A и B равно AB, но не BA.
Если «A = [a ij ] m×n » и «B = [b ij ] n×p » — две матрицы, то произведение A и B обозначается как AB, порядок которых равен «m × p». Обычно умножение матриц не является коммутативным, т. е. AB ≠ BA, или, проще говоря, произведение матриц A и B равно AB, но не BA.
Условия умножения матриц
Обратите внимание, что умножение любых двух матриц возможно только в том случае, если обе матрицы совместимы. Мы можем перемножить две матрицы, если количество столбцов в 1-й матрице равно количеству строк во 2-й матрице, иначе данные матрицы нельзя перемножить.
- Допустим, есть матрица размера 2×3 и другая матрица размера 3×2, тогда мы можем применить умножение между этими матрицами, потому что количество столбцов и строк одинаково в обеих матрицах. И результирующая матрица будет 2×2
- . Допустим, матрица размера 3×3 и другая матрица размера 4×2, тогда мы не можем применить умножение между этими матрицами, потому что количество столбцов и строк не то же самое в обе матрицы.
Умножение матриц на матрицы
Рассмотрим две матрицы 3 × 3, содержащие элементы [a ij ] и [b ij ] соответственно. Умножение будет таким, как показано на рисунке ниже:
Существует некоторое правило,
- Возьмите 1-ю строку первой матрицы и умножьте значения на 1-й столбец второй матрицы. Не умножайте строки на строки или столбцы на столбцы.
- В первой итерации умножьте значение строки на значение столбца и просуммируйте эти значения. Вот на этой картинке [a 00 ] умножается на [b 00 ], то 2-е значение 1-го столбца 1-й матрицы [a 10 ] умножается на 2-е значение 1-й строки 2-й матрицы [b 01 ]. Точно так же все значения умножаются.
- Затем после одной итерации все производственные значения суммируются и размещаются как элементы результирующей матрицы, как показано на рисунке.
Матрица Формула умножения для матриц «2 × 2»
Процесс умножения одинаков для матриц любого порядка. Мы должны умножить каждый элемент каждой строки первой матрицы на элементы каждого столбца второй матрицы и сложить все произведения, чтобы получить результирующую матрицу. Рассмотрим две матрицы «2 × 2» матрицы A и B.
Мы должны умножить каждый элемент каждой строки первой матрицы на элементы каждого столбца второй матрицы и сложить все произведения, чтобы получить результирующую матрицу. Рассмотрим две матрицы «2 × 2» матрицы A и B.
Матрица Формула умножения для матриц «3 × 3»
Рассмотрим две матрицы «3 × 3» матрицы P и Q. Теперь формула умножения матриц для матриц «3 × 3» показаны следующим образом:
Пример: Перемножьте приведенные ниже матрицы.
Решение:
Умножение матрицы на скалярное значение
Матрица может быть умножена на скалярное значение, что называется скалярным умножением, а также на матрицу, что называется умножением матриц. Скалярное умножение — это умножение матрицы на скалярное значение. Когда матрица «A = [a ij ]» умножается на скалярное значение «k», каждый элемент данной матрицы умножается на скалярное значение. Результирующая матрица выражается как kA, где kA = k[a ij ] = [ka ij ], для всех значений i и j.
Результирующая матрица выражается как kA, где kA = k[a ij ] = [ka ij ], для всех значений i и j.
Пример:
Свойства умножения матриц
Ниже приведены некоторые важные свойства мультипликации матриц:
- Коммуративное свойство: . Матиат. Если A и B — две матрицы, то AB ≠ BA.
- Ассоциативное свойство: Умножение матриц по своей природе ассоциативно. Если A, B и C — три матрицы, то A(BC) = (AB)C, если произведения A(BC) и (AB)C определены.
- Распределительное свойство: Если A, B и C — три матрицы, то, применяя распределительное свойство, мы получаем A (B + C) = AB + BC, если и только если A, B и C совместимы .
- Произведение со скаляром: Если A и B — две матрицы и AB определено, то k(AB) = (kA)B = A(Bk), где k — скалярное значение.
- Определитель: Если A и B — две матрицы и AB определено, то определитель матрицы «AB» равен произведению определителей матриц A и B, т.
 е. det (AB) = det A × дет Б.
е. det (AB) = det A × дет Б. - Транспонирование: Если A и B — две матрицы и AB определено, то (AB)T = BTAT, где T представляет собой транспонирование матрицы.
- Комплексное сопряжение: Если A и B две комплексные матрицы, то (AB)* = B*A*.
Произведение любых двух ненулевых матриц может дать нулевую матрицу, т. е. если AB = O, то это не означает, что A = O или B = O.
Решенные примеры
Пример 1. Пусть и найти A×B?
Решение:
Пример 2. Пусть и . Найти А×В?
Решение:
Пример 3. Пусть , и . Найти (AB + AC)?
Решение:
Теперь рассчитайте (AB + AC)
9003
Пример 4.
.0082 Пусть , и , тогда найдите значение p?
Solution:
First, calculate A 2 ,
Given
By placing the value of A 2 in the equation, we get
Теперь мы можем написать:
8 = 2p и -8 = -2p
Итак, p = 4
Значение p равно 4.
Пример 5. Найдите значение 3P, если .
Решение:
Часто задаваемые вопросы по умножению матриц
Вопрос 1: Что такое умножение матриц?
Ответ:
В линейной алгебре умножение матриц — это одна из бинарных операций, которые можно выполнять над матрицами.
Умножение любых двух матриц возможно только тогда, когда количество столбцов в первой матрице равно количеству строк во второй матрице.
Вопрос 2: Можно ли матрицу «3 × 2» умножить на матрицу «3 × 3»?
Ответ:
Умножение любых двух матриц возможно только тогда, когда количество столбцов в первой матрице равно количеству строк во второй матрице. Здесь первая матрица имеет 2 столбца, а вторая матрица имеет 3 строки. Таким образом, матрицу «3 × 2» нельзя умножить на матрицу «3 × 3», поскольку обе они несовместимы.
Вопрос 3: Как мы можем перемножить две матрицы?
Ответ:
Перед умножением данных матриц нам нужно проверить, равно ли количество столбцов в первой матрице количеству строк во второй матрице. Если матрицы удовлетворяют указанному выше требованию, то умножьте каждый элемент каждой строки первой матрицы на элементы каждого столбца второй матрицы и сложите все произведения.
MMULT Функция Excel для умножения матриц
Поскольку рабочий лист по сути представляет собой гигантскую матрицу, неудивительно, что умножение матриц в Excel очень просто — нам просто нужно использовать функцию МУМНОЖ Excel.
Умножение матриц с помощью функции МУМНОЖ Excel
Вы можете умножать матрицы в Excel благодаря функции МУМНОЖ. Эта функция массива возвращает произведение двух матриц, введенных на листе.
Синтаксис функции:
МУМНОЖ(массив1,массив2)
, где массив1 и массив2 — это массивы или матрицы, которые необходимо перемножить.
Результатом функции МУМНОЖ является массив с количеством строк, таким же, как у массива1, и количеством столбцов, таким же, как у массива2.
Если вы используете Excel 365, МУМНОЖ — это функция динамического массива. Это означает, что вы можете ввести формулу с помощью МУМНОЖ в одну ячейку, и Excel автоматически расширит диапазон, чтобы он соответствовал результату функции.
Если вы НЕ используете Excel 365, МУМНОЖ необходимо ввести как функцию массива, выбрав соответствующее количество ячеек для результирующего массива и нажав CTRL+SHIFT+ENTER.
Правила умножения матриц
Чтобы эффективно выполнять умножение матриц в Excel, в первую очередь полезно помнить, как работает умножение матриц. Итак, допустим, у нас есть две матрицы, A и B, как показано ниже:
Произведение этих двух матриц (назовем его C) находится путем умножения записей в первой строке столбца A на записи в первом столбце B и суммируя их вместе. Это также известно как скалярный продукт. Это единственное значение становится записью в первой строке и первом столбце матрицы C.
Продолжаем делать это до тех пор, пока не найдем скалярное произведение для каждой комбинации строки и столбца.
Поскольку мы умножаем строки матрицы A на столбцы матрицы B, результирующая матрица C будет иметь размер 2 x 2. Или, в более общем случае, матричное произведение имеет такое же количество строк, что и матрица A, и такое же количество столбцов, как у матрицы B .
Из-за того, как работает умножение матриц, также важно помнить, что мы можем умножать только две матрицы, если количество строк в B совпадает с количеством столбцов в A.
Понятно?
Если нет, ничего страшного. Надеюсь, несколько примеров прояснят ситуацию. 🙂
Примеры умножения матриц в Excel
Умножение матриц как функция массива (все версии Excel)
Давайте возьмем матрицы сверху и найдем произведение, используя умножение матриц в Excel с функцией МУМНОЖ:
Во-первых, давайте найти C, продукт AB.
Поскольку МУМНОЖ является функцией массива, она будет возвращать значения более чем в одну ячейку.
Мы знаем, что результатом будет матрица 2×2, потому что первая матрица, A, имеет две строки, а вторая матрица, B, имеет два столбца.
Итак, если мы работали в Excel 365 или любой предыдущей версии Excel, мы выбираем область на листе 2 ячейки в ширину и 2 ячейки в высоту:
Затем, когда область все еще выделена, введите формулу массива и выберите аргументы (я присвоил имена матрицам A и B):
Наконец, нажмите CTRL+SHIFT+ENTER (поскольку это формула массива), чтобы вернуть результирующее матричное произведение:
Умножение матриц как функция динамического массива (только Excel 365) необходимо выбрать правильное количество возвращаемых ячеек или нажать CTRL+SHIFT+ENTER.
 Просто введите формулу массива в самую верхнюю левую ячейку массива, и Excel динамически заполнит все полученные значения:
Просто введите формулу массива в самую верхнюю левую ячейку массива, и Excel динамически заполнит все полученные значения:Другие примеры MMULT в Excel
Что, если вместо вычисления матрицы C путем умножения матрицы A на B мы вычислим другую матрицу D, умножив матрицу B на A?
Поскольку первая матрица B имеет 3 строки, а вторая матрица A имеет 3 столбца, матрица D будет иметь 3 строки и 3 столбца. Итак, мы должны начать с выбора 3 ячейки в ширину и высоту :
Затем введите формулу для МУМНОЖ, выбрав B как массив1 и A как массив2…
… и нажмите CTRL+SHIFT+ENTER чтобы получить матрицу D:
Функция МУМНОЖ также работает для умножения матрицы (A) на массив (x). Конечно, остается в силе правило, что количество строк в x должно совпадать с количеством столбцов в A.
Результатом является массив F, который имеет 1 столбец и такое же количество строк, что и A:
МУМНОЖ Ошибки Excel (Почему МУМНОЖ не работает в Excel?)
Существует несколько способов получения ошибок в Excel с помощью функции МУМНОЖ:
МУМНОЖ #ЗНАЧ! Ошибка
А #ЗНАЧ! ошибка возникает, когда количество столбцов в массиве 1 (A ниже) не совпадает с количеством строк в array2 (x ниже).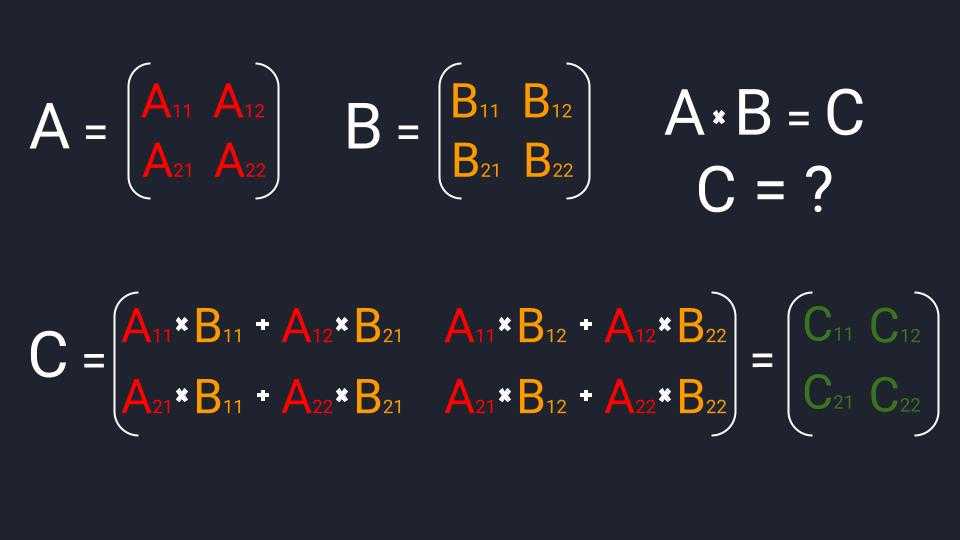
Чтобы исправить это, потребуется, чтобы массив x имел три строки, поэтому, вероятно, это означает, что одно из значений массива x отсутствует.
Если вы не используете Excel 365 и МУМНОЖ не вводится как формула массива путем нажатия CTRL+SHIFT+ВВОД, также будет возвращено #ЗНАЧ! ошибка в одной ячейке:
Наконец, #ЗНАЧ! Ошибка также возникает, если какой-либо из элементов массива1 или массива2 не содержит чисел.
МММУЛЬТ возвращает одно значение
Если вы не используете Excel 365 и МММУЛЬТ возвращает одно значение, это связано с тем, что для результирующего массива была выбрана только одна ячейка. В более ранних версиях Excel пользователь мог выбрать подходящее количество ячеек, в которые Excel возвращает результат. Если выбрана одна ячейка, МУМУЛЬТ выполнит умножение матриц и вернет первое значение в результирующем массиве в эту ячейку.
Такое поведение также возможно в Excel 365, если для результата выбрана одна ячейка, а функция МУМНОЖ введена как формула массива путем нажатия CTRL+SHIFT+ВВОД.
ММУЛЬТИ возвращает слишком много значений
Хотя это и не всегда является ошибкой, ММУЛЬТИ может возвращать неожиданные результаты, когда область вывода для функции больше требуемой.
Добавление дополнительных столбцов приводит к дублированию результатов:
МУЛЬТИ #Н/Д! Ошибка
Добавление дополнительных строк в массив MMULT приводит к ошибке #N/A! ошибка для отображения, хотя она отображается только в дополнительной ячейке:
Пределы умножения матриц в Excel
В текущих версиях Excel нет программных ограничений на размер матрицы, которую можно умножить. По сути, вы можете умножать матрицы любого размера, если на вашем компьютере достаточно оперативной памяти.
Однако, если вы все еще используете Excel 2003 или более раннюю версию, вы будете ограничены выводом 5046 ячеек при использовании функции МУМНОЖ (примерно матрица 71 × 71).






 е. det (AB) = det A × дет Б.
е. det (AB) = det A × дет Б.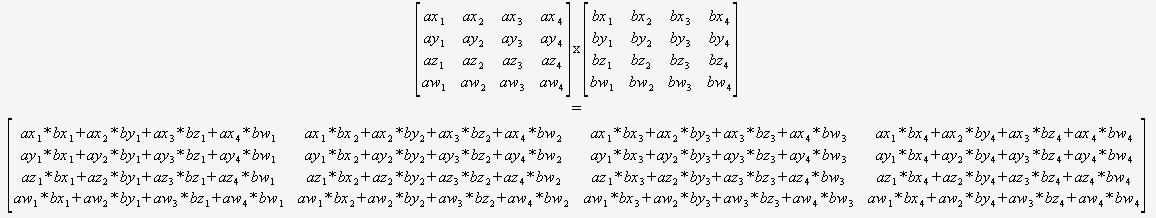 Умножение любых двух матриц возможно только тогда, когда количество столбцов в первой матрице равно количеству строк во второй матрице.
Умножение любых двух матриц возможно только тогда, когда количество столбцов в первой матрице равно количеству строк во второй матрице.