Матрицы гаусс: Как решить методом Гаусса СЛАУ (систему линейных уравнений). Правила, примеры

Error

Sorry, the requested file could not be found

More information about this error

Jump to… Jump to…Согласие на обработку персональных данных Учебно-тематический планАвторы и разработчики курсаИнформация для студентов и преподавателейВводная лекцияIntroductory lectureЛекция о системе обозначений Lecture on the notation systemВидеолекция (часть 1)Lecture (Part 1)Видеолекция 2. Операции над функциями. Свойства функции.Lecture 2. Operations on functions. The properties of the functionТеоретический материал Практическое занятие. Исследование свойств функций по определениюPractical lesson. Investigation of the properties of functions by definitionЗадачи для самостоятельной работыРешения задачТест 1.1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2.

The limit of a numeric sequence.Practical lesson 1. Study of properties of a numerical sequence by conventionПрактическое занятие 1 (часть 2)Теоретический материалЗадачи для самостоятельной работыРешения задачТест 1.1.2. Числовые последовательностиВидеолекция 1. Предел функции в точкеLecture 1. The limit of a function at a pointВидеолекция (часть 2)Практическое занятие 1. Вычисление пределов, неопределенности.Practical lesson 1. Calculation of limits. UncertaintiesПрактическое занятие 2. Вычисление пределов. Замечательные пределы.Practical lesson 2. Calculation of limits. Remarkable limits.Задачи для самостоятельной работыРешения задачТест 1.1.3. Предел функции в точкеВидеолекция. Непрерывность функции в точкеLecture 1. Сontinuity of a function at a pointПрактическое занятие. Исследование функций на непрерывность. Классификации точек разрываPractical lesson. The study of function continuity and classification of discontinuity pointsЗадачи для самостоятельной работыРешения задачТест 1.1.

4. Непрерывность функции в точкеВидеолекция (часть 1)Lecture 1. Differential calculus of functions of a single variableВидеолекция (часть 2)Lecture 2. Differentiation of a function given parametricallyПрактическое занятие 1. Правила дифференцированияПрактическое занятие 2. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрическиPractical lesson 1. Logarithmic differentiation. Differentiating a function defined parametricallyPractical lesson 2. Rules of differentiationЗадачи для самостоятельной работыРешения задачТаблица производныхТест 1.1.5 Производная функцииВидеолекция 1. Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1. 1.6. Геометрический и физический смысл производнойQuiz 1.1.6. Geometric and physical sense of the derivativeВидеолекция 1. Основные теоремы дифференциального исчисления.Lecture 1. Basic theorems of differential calculusВидеолекция 2. Исследование функций на монотонность и выпуклостьLecture 2. The study of the monotonicity of the functionПрактическое занятие 1. Исследование свойств функций с помощью производнойPractical lesson 1. Studying the properties of functions using a derivativeПрактическое занятие 2. Правило ЛопиталяPractical lesson 2. L’Hospital’s ruleЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.1.7 (часть 1). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 1)Тест 1.1.7 (Часть 2). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 2)Теоретический материал (Часть 1)Задачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Теоретический материал (Часть 2)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1. 1.8. Асимптоты графика функцииВидеолекция. Дифференциальное и интегральное исчислениеLecture. Differential and Integral CalculationЗадачи для самостоятельной работыРешения задачТаблица интеграловТест 1.2.1. Неопределенный интегралВидеолекция. Неопределенный интеграл: методы интегрирования.Lecture. Indefinite integral: methods of integration.Практическое занятие. Внесение функции под знак дифференциалаPractical lesson. Adding a function under the sign of the differentialЗадачи для самостоятельной работыРешения задачТест 1.2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2.

Integration of trigonometric functionsЗадачи для самостоятельного решенияРешения задачТест 1.2.3. Интегрирование рациональных дробей, тригонометрических и иррациональных функцийВидеолекция. Определенный интеграл: интеграл РиманаLecture. Definite integral: Riemann integral. Практическое занятие 1. Вычисление определенного интегралаPractical lesson 1. Calculating a certain integralЗадачи для самостоятельной работыРешения задачТест 1.2.4. Определенный интегралВидеолекция LectureЗадачи для самостоятельного решенияРешения задачТест 1.2.5 Приложения определенного интегралаВидеолекция. Несобственный интегралыLecture. Improper integralЗадачи для самостоятельного решенияРешения задачТест 1.2.6. Несобственные интегралыВидеолекция 1. Функции нескольких переменныхLecture 1. Functions of Multiple VariablesВидеолекция 2. Частные производныеLecture 2. Partial derivativesПрактическое занятие. Функция двух переменныхPractical lesson. Function of several variablesЗадачи для самостоятельной работыРешения задачТест 1. 3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1. Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3. Дифференцирование сложной функции и дифференцирование функции, заданной неявноPractical lesson 3. Differentiation of a composite function and differentiation of implicitly defined functionЗадачи для самостоятельного решенияРешения задачТест 1.3.3. Частные производныеQuiz 1.3.3Видеолекция 1. Экстремум функции двух переменныхВидеолекция 2. Экстремумы функции в замкнутой областиЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.3.4. Экстремум функции двух переменныхQuiz 1.3.4Видеолекция 1. Двойной интеграл Lecture 1. Double integral Видеолекция 2. Вычисление двойного интегралаLecture 2. Calculation of the double integralПрактическое занятие 1. Вычисление двойного интегралаPractical lesson 1. Calculating a certain integralПрактическое занятие 2. Вычисление двойного интегралаPractical lesson 2. Calculating a certain integralЗадачи для самостоятельного решения (Часть 1)Решения задач (Часть 1)Задачи для самостоятельного решения (Часть 2)Решения задач (Часть 2)Тест 1.

3.5. Двойной интегралQuiz 1.3.5Видеолекция. Криволинейные интегралыLecture. Curvilinear integralsПрактическое занятие. Вычисление криволинейные интегралов I и II родаPractical lesson. Calculating curvilinear integrals 1 and 2 kind Задачи для самостоятельного решенияРешения задачТест 1.3.6. Криволинейные интегралыАттестация по модулю 1Итоговое тестирование по курсу (2-1)Видеолекция 1. Система линейных уравнений: основные понятияПрактическое занятие 1. Системы линейных уравненийPractical lesson (part 1). Systems of linear equationsТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Видеолекция 2. Решение систем линейных уравнений методом ГауссаПрактическое занятие 2. Решение систем линейных уравнений методом гауссаPractical lesson (part 2). The system of linear equationsЗадачи для самостоятельной работы 2Решения задач 2Видеолекция 3. Исследование систем линейных уравненийLecture 3. A system of linear equationsPractical lesson (part 3). The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1. 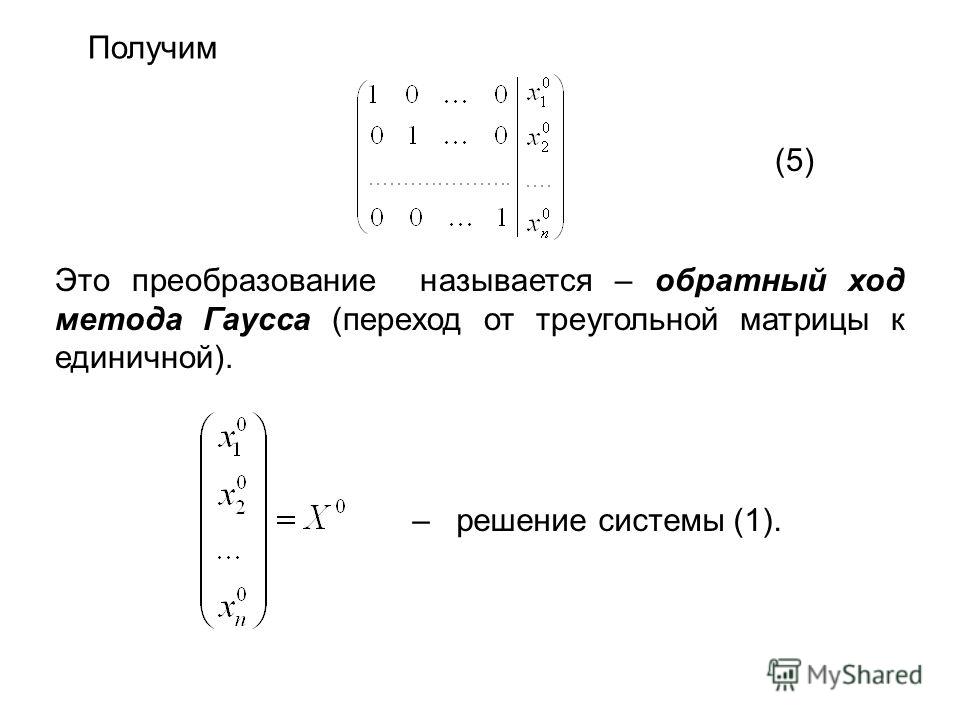Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2. Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2.1.3. Исследование систем линейных уравненийСправочникВидеолекция 1. Матрицы и определителиLecture 1. Matrix determinantВидеолекция 2. Операции над матрицамиLecture 2. Operations on matricesВидеолекция 3. Обратная матрицаLecture 3. Inverse matrixПрактическое занятие 1. Операции над матрицамиPractical lesson 1. The operations on matrices Практическое занятие 2. Вычисление определителейТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Теоретический материал (лекция 3)Тест 2. 1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson. Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1.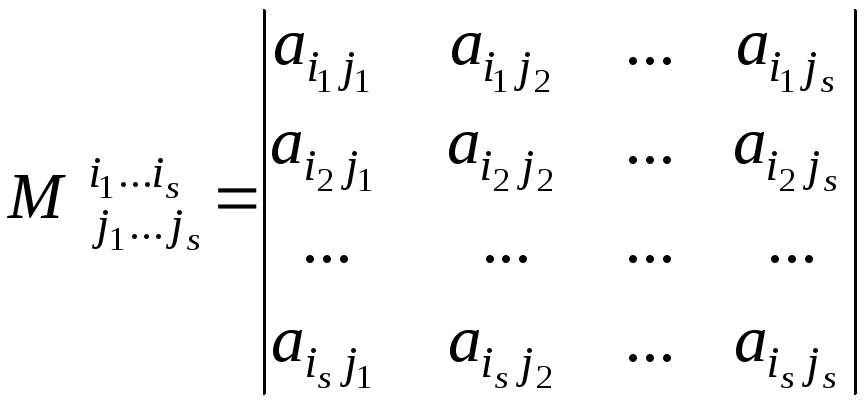 Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3. 1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3. 2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.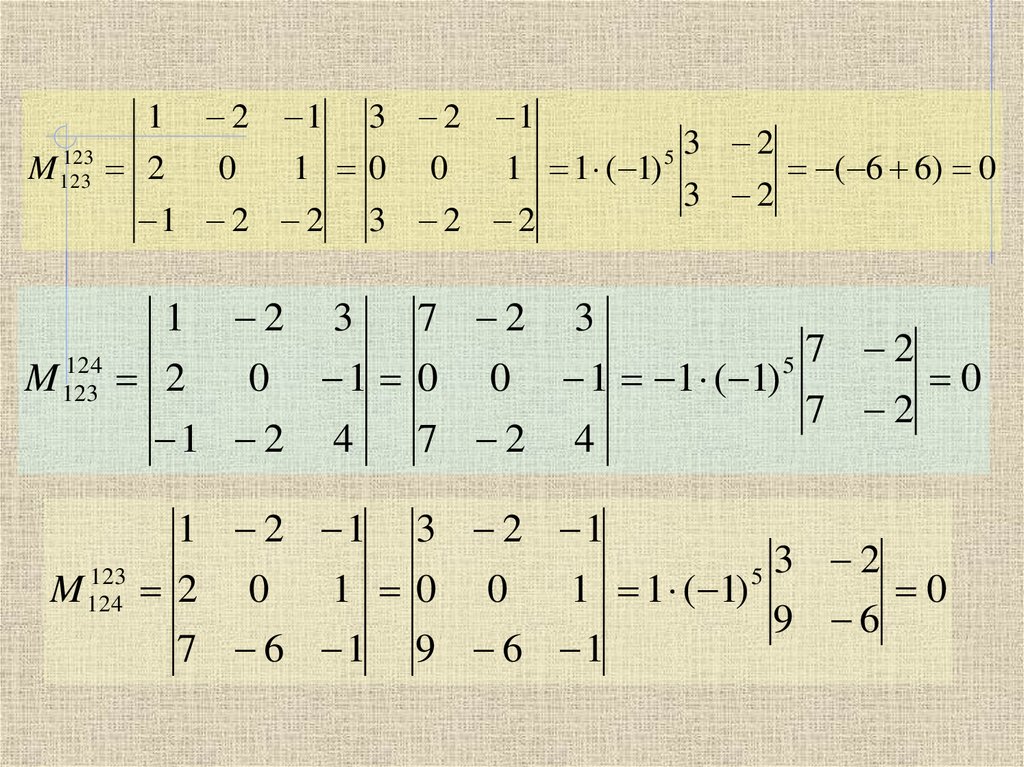 4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2. 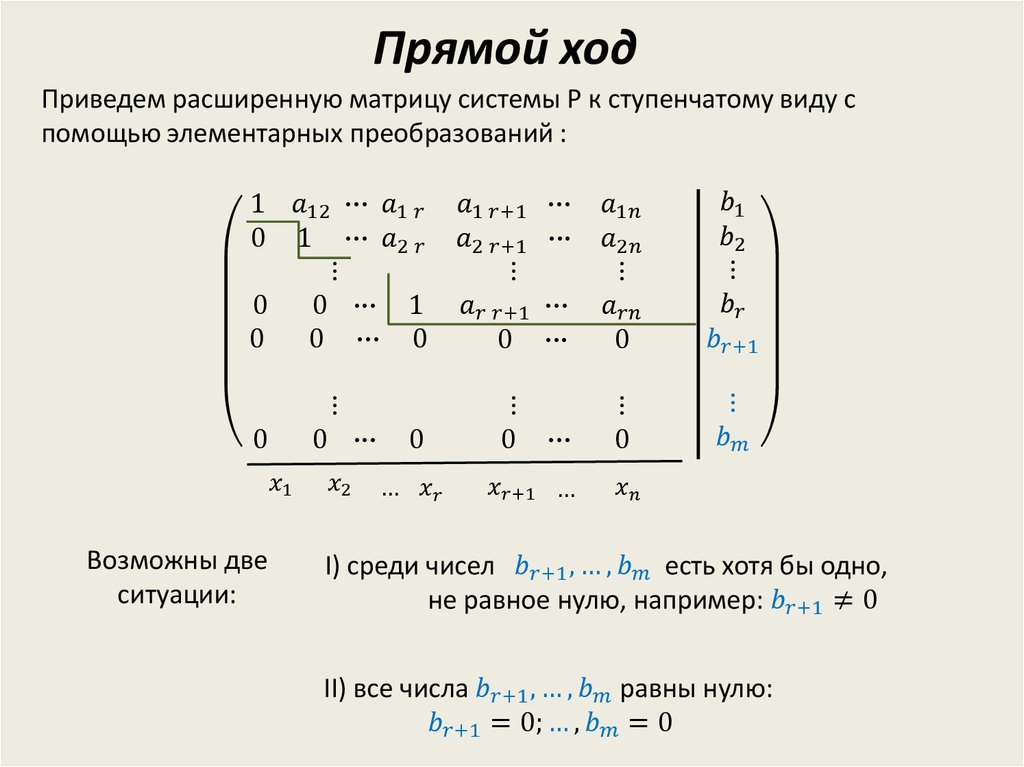Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2. Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2). Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)

Теория матриц

Теория матриц

Гантмахер Ф.Р. Теория матриц. – М.: Наука, 1968. – 576 с. Оглавление Предисловие автора к первому изданию Предисловие автора ко второму изданию ЧАСТЬ I. ОСНОВЫ ТЕОРИИ Глава I. Матрицы и действия над ними § 1. Матрицы. Основные обозначения § 2. Сложение и умножение прямоугольных матриц § 3. Квадратные матрицы § 4. Ассоциированные матрицы. Миноры обратной матрицы § 5. Обращение прямоугольных матриц. Псевдообратная матрица Глава II. Алгоритм Гаусса и некоторые его применения § 1. Метод исключения Гаусса § 2. Механическая интерпретация алгоритма Гаусса § 3. Детерминантное тождество Сильвестра § 4. Разложение квадратной матрицы на треугольные множители § 5. Разбиение матрицы на блоки. Техника оперирования с блочными матрицами. Обобщенный алгоритм Гаусса Глава III. Лииейиые операторы в n-мерном векторном пространстве § 1. Векторное пространство § 2. Линейный оператор, отображающий n-мерное пространство в m-мерное § 3. Сложение и умножение линейных операторов § 4. Преобразование координат § 5. Эквивалентные матрицы. Ранг оператора. Неравенства Сильвестра § 6. Линейные операторы, отображающие n-мерное пространство само в себя § 7. Характеристические числа и собственные векторы линейного оператора § 8. Линейные операторы простой структуры Глава IV. Характеристический и минимальный многочлены матрицы § 1. Сложение и умножение матричных многочленов § 2. Правое и левое деление матричных многочленов. Обобщенная теорема Безу § 3. Характеристический многочлен матрицы. Присоединенная матрица § 4. Метод Д. К. Фаддеева одновременного вычисления коэффициентов характеристического многочлена и присоединенной матрицы § 5. Минимальный многочлен матрицы Глава V. Функции от матрицы § 1. Определение функции от матрицы § 2. Интерполяционный многочлен Лагранжа–Сильвестра § 3. Другие формы определения f(A). Компоненты матрицы A § 4. Представление функций от матриц рядами § 5. Некоторые свойства функций от матриц § 6. Применение функций от матрицы к интегрированию системы линейных дифференциальных уравнений с постоянными коэффициентами § 7. Устойчивость движения в случае линейной системы Глава VI. Эквивалентные преобразования многочленных матриц. Аналитическая теория элементарных делителей § 1. Элементарные преобразования многочленной матрицы § 2. Канонический вид матрицы § 3. Инвариантные многочлены и элементарные делители многочленной матрицы § 4. Эквивалентность линейных двучленов § 5. Критерий подобия матриц § 6. Нормальные формы матрицы § 7. Элементарные делители матрицы f(A) § 8. Общий метод построения преобразующей матрицы § 9. Второй метод построения преобразующей матрицы Глава VII. Структура линейного оператора в n-мерном пространстве (геометрическая теория элементарных делителей) § 1. Минимальный многочлен вектора, пространства (относительно заданного линейного оператора) § 2. Расщепление на инвариантные подпространства с взаимно простыми минимальными многочленами § 3. Сравнения. Надпространство § 4. Расщепление пространства на циклические инвариантные подпространства § 5. Нормальная форма матрицы § 6. Инвариантные многочлены. Элементарные делители § 7. Нормальная жорданова форма матрицы § 8. Метод акад. А. Н. Крылова преобразования векового уравнения Глава VIII. Матричные уравнения § 1. Уравнение AX=XB § 2. Частный случай: A=B. Перестановочные матрицы § 3. Уравнение AX-XB=C § 4. Скалярное уравнение f(X)=0 § 5. Матричное многочленное уравнение § 6. Извлечение корня m-й степени из неособенной матрицы § 7. Извлечение корня m-й степени из особенной матрицы § 8. Логарифм матрицы Глава IX. Линейные операторы в унитарном пространстве § 1. Общие соображения § 2. Метризация пространства § 3. Критерий Грама линейной зависимости векторов § 4. Ортогональное проектирование § 5. Геометрический смысл определителя Грама и некоторые неравенства § 6. Ортогонализация ряда векторов § 7. Ортонормированный базис § 8. Сопряженный оператор § 9. Нормальные операторы в унитарном пространстве § 10. Спектр нормальных, эрмитовых, унитарных операторов § 11. Неотрицательные и положительно определенные эрмитовы операторы § 12. Полярное разложение линейного оператора в унитарном пространстве. Формулы Кэли § 13. Линейные операторы в евклидовом пространстве § 14. Полярное разложение оператора и формулы Кэли в евклидовом пространстве § 15. Коммутирующие нормальные операторы § 16. Псевдообратный оператор Глава X. Квадратичные и эрмитовы формы § 1. Преобразование переменных в квадратичной форме § 2. Приведение квадратичной формы к сумме квадратов. Закон инерции § 3. Метод Лагранжа приведения квадратичной формы к сумме квадратов. Формула Якоби § 4. Положительные квадратичные формы § 5. Приведение квадратичной формы к главным осям § 6. Пучок квадратичных форм § 7. Экстремальные свойства характеристических чисел регулярного пучка форм § 8. Малые колебания системы с n степенями свободы § 9. Эрмитовы формы § 10. Ганкелевы формы ЧАСТЬ II. СПЕЦИАЛЬНЫЕ ВОПРОСЫ И ПРИЛОЖЕНИЯ Глава XI. Комплексные симметричные, кососимметрические и ортогональные матрицы § 1. Некоторые формулы для комплексных ортогональных и унитарных матриц § 2. Полярное разложение комплексной матрицы § 3. Нормальная форма комплексной симметрической матрицы § 4. Нормальная форма комплексной кососимметрической матрицы § 5. Нормальная форма комплексной ортогональной матрицы ГЛАВА XII. СИНГУЛЯРНЫЕ ПУЧКИ МАТРИЦ § 1. Введение § 2. Регулярный пучок матриц § 3. Сингулярные пучки. Теорема о приведении § 4. Каноническая форма сингулярного пучка матриц § 5. Минимальные индексы пучка § 6. Сингулярные пучки квадратичных форм § 7. Приложения к дифференциальным уравнениям ГЛАВА XIII. МАТРИЦЫ С НЕОТРИЦАТЕЛЬНЫМИ ЭЛЕМЕНТАМИ § 1. Общие свойства § 2. Спектральные свойства неразложимых неотрицательных матриц § 3. Разложимые матрицы § 4. Нормальная форма разложимой матрицы § 5. Примитивные и импримитивные матрицы § 6. Стохастические матрицы § 7. Предельные вероятности для однородной цепи Маркова с конечным числом состояний § 8. Вполне неотрицательные матрицы § 9. Осцилляционные матрицы Глава XIV. Различные критерии регулярности и локализации собственных значений § 1. Критерий регулярности Адамара и его обобщения § 2. Норма матрицы § 3. Распространение критерия Адамара на блочные матрицы § 4. Критерий регулярности Фидлера § 5. Круги Гершгорина и другие области локализации Глава XV. Приложения теории матриц к исследованию систем линейных дифференциальных уравнений § 1. Системы линейных дифференциальных уравнений с переменными коэффициентами. Общие понятия § 2. Преобразование Ляпунова § 3. Приводимые системы § 4. Каноническая форма приводимой системы. Теорема Еругина § 5. Матрицант § 6. Мультипликативный интеграл. Инфинитезимальное исчисление Вольтерра § 7. Дифференциальные системы в комплексной области. Общие свойства § 8. Мультипликативный интеграл в комплексной области § 9. Изолированная особая точка § 10. Регулярная особая точка § 11. Приводимые аналитические системы § 12. Аналитические функции от многих матриц и их применение к исследованию дифференциальных систем. Работы И. A. Лaппo-Данилевского ГЛАВА XVI. ПРОБЛЕМА РАУСА-ГУРВИЦА И СМЕЖНЫЕ ВОПРОСЫ § 1. Введение § 2. Индексы Коши § 3. Алгоритм Рауса § 4. Особые случаи. Примеры § 5. Теорема Ляпунова § 6. Теорема Рауса-Гурвица § 7. Формула Орландо § 8. Особые случаи в теореме Рауса — Гурвица § 9. Метод квадратичных форм. Определение числа различных вещественных корней многочлена § 10. Бесконечные ганкелевы матрицы конечного ранга § 11. Определение индекса произвольной рациональной дроби через коэффициенты числителя и знаменателя § 12. Второе доказательство теоремы Рауса—Гурвица § 13. Некоторые дополнения к теореме Рауса—Гурвица. Критерий устойчивости Льенара и Шипара § 14. Некоторые свойства многочлена Гурвица. Теорема Стильтьеса. Представление многочленов Гурвица при помощи непрерывных дробей § 15. Область устойчивости. Параметры Маркова § 16. Связь с проблемой моментов § 17. Связь между определителями Гурвица и определителями Маркова § 18. Теоремы Маркова и Чебышева § 19. Обобщенная задача Рауса-Гурвица ДОБАВЛЕНИЕ. НЕРАВЕНСТВА ДЛЯ СОБСТВЕННЫХ И СИНГУЛЯРНЫХ ЧИСЕЛ § 1. Мажорирующие последовательности § 2. Неравенства Неймана-Хорна § 3. Неравенства Вейля § 4. Максимально-минимальные свойства сумм и произведений собственных чисел эрмитовых операторов § 5. Неравенства для собственных и сингулярных чисел сумм и произведений операторов § 6. Другая постановка задачи о спектре суммы и произведения эрмитовых операторов ЛИТЕРАТУРА

M$ в пределе большой размерности $M,N \to \infty$ с фиксированным $\alpha \equiv M/N$. Мы приводим строгий вывод явной формулы (впервые выведенной с использованием эвристического метода из статистической физики) для асимптотической среднеквадратической ошибки, полученной с помощью штрафных выпуклых оценок, таких как LASSO или эластичная сеть, для последовательности очень общей случайной матрицы $\mathbf {F}$, соответствующие вращательно-инвариантным матрицам данных произвольного спектра. Доказательство основано на анализе сходимости версии оракула векторной аппроксимированной передачи сообщений (oracle-VAMP) и на свойствах его уравнений эволюции состояния. Наш метод использует и подчеркивает связь между векторной приблизительной передачей сообщений, алгоритмами расщепления Дугласа-Рэчфорда и проксимального спуска, расширяя предыдущие результаты, полученные с помощью i.i.d. матрицы для большого класса задач. Мы иллюстрируем наши результаты на некоторых конкретных примерах и показываем, что, несмотря на то, что они асимптотичны, наши предсказания удивительно хорошо согласуются с числовыми значениями даже для очень умеренных размеров.

Процитировать эту статью

---

БибТекс

@InProceedings{pmlr-v125-gerbelot20a, title = {Асимптотические ошибки для многомерной выпуклой линейной регрессии со штрафом за пределами гауссовых матриц}, автор = {Gerbelot, C\'{e}dric и Abbara, Alia и Krzakala, Florent}, booktitle = {Материалы тридцать третьей конференции по теории обучения}, страницы = {1682--1713}, год = {2020}, редактор = {Абернети, Джейкоб и Агарвал, Шивани}, громкость = {125}, серия = {Материалы исследования машинного обучения}, месяц = ​​{09M$ в пределе большой размерности $M,N \to \infty$ с фиксированным $\alpha \equiv M/N$. Мы приводим строгий вывод явной формулы (впервые выведенной с использованием эвристического метода из статистической физики) для асимптотической среднеквадратической ошибки, полученной с помощью штрафных выпуклых оценок, таких как LASSO или эластичная сеть, для последовательности очень общей случайной матрицы $\mathbf {F}$, соответствующие вращательно-инвариантным матрицам данных произвольного спектра. Доказательство основано на анализе сходимости версии оракула векторной аппроксимированной передачи сообщений (oracle-VAMP) и на свойствах его уравнений эволюции состояния. Наш метод использует и подчеркивает связь между векторной приблизительной передачей сообщений, алгоритмами расщепления Дугласа-Рэчфорда и проксимального спуска, расширяя предыдущие результаты, полученные с помощью i.i.d. матрицы для большого класса задач. Мы иллюстрируем наши результаты на некоторых конкретных примерах и показываем, что, хотя они и являются асимптотическими, наши предсказания удивительно хорошо согласуются с числовыми значениями даже для очень умеренных размеров. M$ в пределе большой размерности $M,N \to \infty$ с фиксированным $\alpha \equiv M/N$. Мы приводим строгий вывод явной формулы (впервые выведенной с использованием эвристического метода из статистической физики) для асимптотической среднеквадратической ошибки, полученной с помощью штрафных выпуклых оценок, таких как LASSO или эластичная сеть, для последовательности очень общей случайной матрицы $\mathbf {F}$, соответствующие вращательно-инвариантным матрицам данных произвольного спектра. Доказательство основано на анализе сходимости версии оракула векторной аппроксимированной передачи сообщений (oracle-VAMP) и на свойствах его уравнений эволюции состояния. Наш метод использует и подчеркивает связь между векторной приблизительной передачей сообщений, алгоритмами расщепления Дугласа-Рэчфорда и проксимального спуска, расширяя предыдущие результаты, полученные с помощью i.i.d. матрицы для большого класса задач. Мы иллюстрируем наши результаты на некоторых конкретных примерах и показываем, что, несмотря на то, что они асимптотичны, наши предсказания удивительно хорошо согласуются с числовыми значениями даже для очень умеренных размеров.

АПА

Гербело, К., Аббара, А. и Крзакала, Ф.. (2020). Асимптотические ошибки для многомерной выпуклой линейной регрессии со штрафом за пределами гауссовых матриц. Труды тридцать третьей конференции по теории обучения , в Труды исследования машинного обучения 125:1682-1713 Доступно по адресу https://proceedings.mlr.press/v125/gerbelot20a.html.

---

Сопутствующий материал

Матрицы со случайными полосами Гаусса и свобода с объединением | Уведомления о международных математических исследованиях

Фильтр поиска панели навигации Уведомления о международных исследованиях в области математикиЭтот выпускPure MathematicsКнигиЖурналыOxford Academic Термин поиска мобильного микросайта

Закрыть

Фильтр поиска панели навигации Уведомления о международных исследованиях в области математикиЭтот выпускPure MathematicsКнигиЖурналыOxford Academic Термин поиска на микросайте

Расширенный поиск

Статья журнала

Получить доступ

Дмитрий Шляхтенко

Дмитрий Шляхтенко

Ищите другие работы этого автора на:

Оксфордский академический

Google ученый

Уведомления о международных математических исследованиях , том 1996 г. , выпуск 20, 1996 г., страницы 1013–1025, https://doi.org/10.1155/S1073792896000633

Опубликовано:

01 января 1996 г.

История статьи

Опубликовано:

1 января 1996 г.

Получено:

25 сентября 1996 г.

Фильтр поиска панели навигации Уведомления о международных исследованиях в области математикиЭтот выпускPure MathematicsКнигиЖурналыOxford Academic Термин поиска мобильного микросайта

Закрыть

Фильтр поиска панели навигации Уведомления о международных исследованиях в области математикиЭтот выпускPure MathematicsКнигиЖурналыOxford Academic Термин поиска на микросайте

Расширенный поиск

Предварительный просмотр первой страницы статьи PDF

Закрыть

Этот контент доступен только в формате PDF.

Copyright © 1996 Hindawi Publishing Corporation. Все права защищены.

Раздел выпуска:

Артикул

В настоящее время у вас нет доступа к этой статье.

Скачать все слайды

Войти

Получить помощь с доступом

Получить помощь с доступом

Доступ для учреждений

Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:

Доступ на основе IP

Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.

Войдите через свое учреждение

Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.

1. Нажмите Войти через свое учреждение.
2. Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
3. Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
4. После успешного входа вы вернетесь в Oxford Academic.

Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.

Войти с помощью читательского билета

Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.

Члены общества

Доступ члена общества к журналу достигается одним из следующих способов:

Войти через сайт сообщества

Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:

1. Щелкните Войти через сайт сообщества.
2. При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
3. После успешного входа вы вернетесь в Oxford Academic.

Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.

Вход через личный кабинет

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.

Личный кабинет

Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.

Просмотр ваших зарегистрированных учетных записей

Щелкните значок учетной записи в правом верхнем углу, чтобы:

• Просмотр вашей личной учетной записи, в которой выполнен вход, и доступ к функциям управления учетной записью.
• Просмотр институциональных учетных записей, предоставляющих доступ.

Выполнен вход, но нет доступа к содержимому

Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.

Ведение счетов организаций

Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.

Покупка

Стоимость подписки и заказ этого журнала

Варианты покупки книг и журналов в Oxford Academic

Кратковременный доступ

Чтобы приобрести краткосрочный доступ, пожалуйста, войдите в свой личный аккаунт выше.

У вас еще нет личного кабинета? регистр

Случайные матрицы гауссовых полос и свобода с объединением — доступ 24 часа

ЕВРО €15,00

13 фунтов стерлингов

16 долларов США.