| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Линейная алгебра. Вектора, матрицы, определители, миноры, детерминанты… / / Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц. Поделиться:
 Введите свой запрос: Введите свой запрос: | |||||||||
| Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | ||||||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||||||
Матрицы и действия над ними
Содержание:
Матрицы и действия над ними
- МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ /.
 | и £ = _j)> то !) ■ (-! -IMS?) ‘• 3. Обратная матрица Матрица должна быть квадратной. Матрица называется Матрица, обозначенная как я. A-A ~ l = Е. (90) Вы можете выполнить равенство (90). А ~ 1-А = Е. (91) Приведем теперь следующую основную теорему. Теорема. Для того чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы матрица А была невырожденной, т. Е.
| и £ = _j)> то !) ■ (-! -IMS?) ‘• 3. Обратная матрица Матрица должна быть квадратной. Матрица называется Матрица, обозначенная как я. A-A ~ l = Е. (90) Вы можете выполнить равенство (90). А ~ 1-А = Е. (91) Приведем теперь следующую основную теорему. Теорема. Для того чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы матрица А была невырожденной, т. Е.Чтобы ее определитель был отличен от нуля. … Доказательство Необходимость Предположим, что для матрицы А существует обратная матрица Л-1 Покажем, что в этом случае матрица А должна быть невырожденной, т е ее определитель | .. Л |. = £ 0 Действительно, если бы | Л | = 0, то определитель произведения \ A-A ~ 11 = | А |. | Л «11 = 0. Но это невозможно в силу равенства (91), из которого следует, что Л.Л-Ч = | £ | = 1- Достаточность. Пусть / ‘«11« 1з \ л = Я21 а% г а23 \ «3.« 32 «S3 /невырожденная матрица, т. е. ее определитель
Примеры решения и задачи с методическими указаниями
Решение задач Лекции Сборник и задачник Учебник - Покажем, что в этом случае существует обратная матрица.
 1» a2lxt + a% fK + а23х3 = с2, ф. (95) «31 * 1 Н ~« 32 * 2 «33 * 3 = С3 ‘ Рассмотрим матрицу системы / «11« 12 «13 Л =« 21 «22« 23 \ «31« 32 «33, и матрицы-столбцы неизвестных и свободных членов с, Х = .С = 1 с2 с3
1» a2lxt + a% fK + а23х3 = с2, ф. (95) «31 * 1 Н ~« 32 * 2 «33 * 3 = С3 ‘ Рассмотрим матрицу системы / «11« 12 «13 Л =« 21 «22« 23 \ «31« 32 «33, и матрицы-столбцы неизвестных и свободных членов с, Х = .С = 1 с2 с3«31« 32 «33 / \ * 3 / \« 81 * 1 + «32 * 2 +« 33 * 3у Данную систему (95) можно записать, используя определенное равенство матриц (стр. 2), следующим обра «11 * 1 +« 12 * 2 + «13 * 3 211» I «22Л2 23 3,« 31 * 1 + «32 * 2 +« 33 * 3 » или, короче, Л-Х = С. (96) Равенство (96) называется матричным уравнением. Если система (95) записана в форме матричного уравнения (96) и матрица Л системы невырожденная, то решается это уравнение следующим образом. Умножим обе части уравнения (96) на матрицу Л «1, обратную матрице Л : А’1- (Л.Х) = Л-1-С. Используя сочетательный закон умножения матриц, можно написать (Л-1-Л) .Х = Л-1.Х. И так, как Л-1-Л = Е и Е-Х = Х Х = А ~ 1-С. (97) Пример. х1 + 2хг = 10, 3xt + 2хг + х3 = 23, хг + 2х3 = 13. «11« 12 «1з \ / * Д /« Ц * 1 + «1Л +« 13 * з ‘ «21« 22 «23 • * 2 =« 41 * 1 + «22 * 2 +« 23 * 3
В этой системе запишется система видеонаблюдения.

Как мы видим, элемент матрицы-произведения, находящийся на пересечении I-й строки и к-го столбца, представляет собой сумму парных произведений элементов I-й строки первой матрицы на элементы к-го столбца второй матрицы. Например, элемент, стоящий во второй строке и первом столбце матрицы произведения Л-Б, равен сумме произведений элементов второй строки матрицы Л на элементы первого столбца матрицы в.
Матрица прямоугольника. Пример 1 / 2 1 0 \ (Х2 / 2-1 + Ь2 + 0-2 2-2 + 1,1 + 0,2 \ / 4 5 \ \ 3 1 1/1 2 2 / \ 3-1 + 1-2 + 1-2 3,2 + Ы + Ь2 J = \ 7 9 / Пример 2. / ап аи \ / * Л / 4i * i + «12 * 2 \ # \« 2, «22 / Ш \ 0, Л + в« Л / В результате перемножения двух матриц получается матрица, содержащая столько строк, сколько их имеет матрица-множимое, и столько столбцов, сколько их имеет матрица-множитель. Рассмотрим еще примеры умножения матриц. Пример 3. \ —1 2 / 1,3 1 / \ —Ь1 + 2-3 -1,1 + 2-1 У I / 1 1 \ / 3- / Ü3 + Ь (—1) 1 • (-1) 4- 1 -2 ‘ 3 1) \ — \ 2) —1) 3- (—1) 4-1-2.

Можно проверить, что умножение матриц подчиняется сочетательному закону А- (ВС) = (А-В) ‘С и распределительному закону (А + В) С = А-С + В.С. Матрица второго порядка имеет особое значение Легко проверить, что при умножении на квадратную матрицу А-Е = Е-А = А. (87) Матрица Е называется единичной матрицей. Единичная матрица третьего порядка имеет вид Очевидно, что определитель единичной матрицы | £ | = 1. (88)
Можно показать, что если А и В-две квадратные матрицы одного порядка с определителями \ А \ и \ В \, то определитель матрицы С -А-В будет равен произведению определителей перемножаемых матриц, т. Е. | С | = | Л |. | Я |. (89) Пример 5. Пусть Л = «» «2) ‘!)’ Мы видели в пример 3, Определители этих матриц таковы:3 —1-1 2 1 1 3 1 О 2 5 -1 Л | = = 5, | Б | = = -2, | С | = = —10. Итак, действительно, М |. | В | = | С Отметим следующий любопытный факт. Как известно, произведение двух отличных от нуля чисел не равно нулю.
 Для матриц подобное обстоятельство может и не иметь места, т. Е. Произведение двух ненулевых матриц может оказаться равным нуль-матрице.
Для матриц подобное обстоятельство может и не иметь места, т. Е. Произведение двух ненулевых матриц может оказаться равным нуль-матрице.Матрицы и действия над ними
МАТРИЦЫ И ДЕЙСТВИЯ НАД
НИМИ
12. Содержание
1. ПОНЯТИЕ И ВИДЫ МАТРИЦ
2. СТРОКИ, СТОЛБЦЫ, ЭЛЕМЕНТЫ
И РАЗМЕР МАТРИЦ
3. ОПЕРАЦИИ НАД МАТРИЦАМИ
2
ПОНЯТИЕ И ВИДЫ
МАТРИЦ
34. ОПРЕДЕЛЕНИЯ
МАТРИЦЕЙ НАЗЫВАЕТСЯ ПРЯМОУГОЛЬНАЯ ИЛИ КВАДРАТНАЯ
ТАБЛИЦА, ЗАПОЛНЕННАЯ
ЧИСЛАМИ.
ЧИСЛА, ЗАПОЛНЯЮЩИЕ
МАТРИЦУ, НАЗЫВАЮТСЯ
ЭЛЕМЕНТАМИ МАТРИЦЫ.
45. ВИДЫ МАТРИЦ
4
12
17 29 Прямоугольная
матрица
30 36
3 1 2
4 2 0 Квадратная
матрица
5 6 1
3
22
Матрица-столбец
0
5
1
3 2 0
Матрица-строка
5
СТРОКИ, СТОЛБЦЫ,
ЭЛЕМЕНТЫ И РАЗМЕР
МАТРИЦЫ
67. ПРИНЦИП НУМЕРАЦИИ СТРОК И СТОЛБЦОВ
СТРОКИ НУМЕРУЮТСЯ СВЕРХУ
ВНИЗ, НАЧИНАЯ С № 1.
СТОЛБЦЫ НУМЕРУЮТСЯ СЛЕВА
НАПРАВО, НАЧИНАЯ С № 1.
78. СТРОКА И СТОЛБЕЦ
12
17
30
4
29
36 3-я строка
12
4
17
29
30 36 2-й столбец
89. РАЗМЕР МАТРИЦЫ
МАТРИЦА, ИМЕЮЩАЯ m СТРОК И n
СТОЛБЦОВ, НАЗЫВАЕТСЯ МАТРИЦЕЙ
РАЗМЕРА
m НА n.
4
12
17 29 Матрица размера 3 на 2
(3строки, 2 столбца)
30 36
910. ОБЩИЙ ВИД МАТРИЦЫ РАЗМЕРА m НА n
a11 a12
a
a
21 22
A
…
…
a
a
m1 m2
… a1n
… a2n
… …
… amn
1011. ЭЛЕМЕНТ МАТРИЦЫ
Элемент
124
a31 три-один 30
÷
17
2
9
÷
30 36÷ (3-я строка,1-йстолбец)
1112. ДИАГОНАЛИ КВАДРАТНЫХ МАТРИЦ
3 1 2
÷
4
2
0
Главная
диагон
аль
÷
5 6 1
3 1 2
÷
Побочнаядиагон
4
2
0
аль
÷
5 6 1
1213.
 ТРЕУГОЛЬНЫЕ МАТРИЦЫ Верхняя треугольная матрица
ТРЕУГОЛЬНЫЕ МАТРИЦЫ Верхняя треугольная матрица
3 1 2
0 2 0 (под главной диагональю стоят нули)
0 0 1
Нижняя треугольная матрица
3 0 0
1 2 0 (над главной диагональю стоят нули)
2 0 1
13
ОПЕРАЦИИ НАД
МАТРИЦАМИ
1415. ЛЮБУЮ МАТРИЦУ МОЖНО УМНОЖИТЬ НА ЧИСЛО
3 1 2 15 5 10
5 4 2 0 20 10 0
5 6 1 25 30 5
1516. МАТРИЦЫ ОДИНАКОВОГО РАЗМЕРА МОЖНО СКЛАДЫВАТЬ И ВЫЧИТАТЬ
3 1 2 8 5 5
4 2 0 7 3 14
3 8 1 5 2 5
2 3
0 14
4 7
1617. ТРАНСПОНИРОВАНИЕ МАТРИЦЫ
4
12
Исходная
A 17 29
матрица (размер 3 на 2)
30 36
12 17 30 Транспонированная
A
матрица (размер 2 на 3)
4
29
36
T
1718. УМНОЖЕНИЕ СТРОКИ НА СТОЛБЕЦ (СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ)
7
÷
253253
× ×+×+×
07042
÷
÷4
1819. УМНОЖЕНИЕ МАТРИЦЫ НА СТОЛБЕЦ КАЖДАЯ СТРОКА МАТРИЦЫ СКАЛЯРНО УМНОЖАЕТСЯ НА СТОЛБЕЦ
3 1 2 8 3 8 + 1 7 + 2 2 21
4 2 0 7 4 8 + 2 7 + 0 2 46
5 6 1 2 5 8 + 6 7 + 1 2 4
1920.
 ВОЗМОЖНОСТЬ УМНОЖЕНИЯ МАТРИЦЫ НА МАТРИЦУ МАТРИЦУ A, ЗАПИСАННУЮ СЛЕВА,
ВОЗМОЖНОСТЬ УМНОЖЕНИЯ МАТРИЦЫ НА МАТРИЦУ МАТРИЦУ A, ЗАПИСАННУЮ СЛЕВА,
МОЖНО УМНОЖИТЬ НА
МАТРИЦУ B, ЗАПИСАННУЮ СПРАВА,
ТОГДА И ТОЛЬКО ТОГДА, КОГДА
ЧИСЛО СТОЛБЦОВ МАТРИЦЫ A
РАВНО ЧИСЛУ СТРОК МАТРИЦЫ B
2021. ПРАВИЛО УМНОЖЕНИЯ МАТРИЦЫ НА МАТРИЦУ КАЖДАЯ СТРОКА ЛЕВОЙ МАТРИЦЫ СКАЛЯРНО УМНОЖАЕТСЯ НА КАЖДЫЙ СТОЛБЕЦ ПРАВОЙ МАТРИЦЫ
С A B
A левая матрица, B правая матрица
2122. ПРИМЕР УМНОЖЕНИЯ МАТРИЦ
3 1 2 8 1
4 2 0 7 2
5 6 1 2 3
3 8+ 1 7+ 2 2 3 1+ 1 2+ 2 3 21 5
4 8+ 2 7+0 2 4 1+ 2 2+0 3 46 8
5 8+6 7+1 2 5 1+6 2+1 3 4 4
2223. УМНОЖЕНИЕ СТОЛБЦА НА СТРОКУ
7 5
7 2
7
0 2 5 3 0 2
0
5
4
4 2 4 5
14 35 21
0 0
0
8 20 12
7 3
0 3
4 3
2324. ВАЖНЫЕ ТИПЫ КВАДРАТНЫХ МАТРИЦ
1 0 0
Единичная матрица
E 0 1 0
(размер 3 на 3)
0 0 1
0 0 0
Нулевая матрица
0 0 0 0
(размер 3 на 3)
0 0 0
2425.
 СВОЙСТВО ЕДИНИЧНОЙ МАТРИЦЫ: A•E=E•A=A 5 7 4 1 0 0 5 7 4
СВОЙСТВО ЕДИНИЧНОЙ МАТРИЦЫ: A•E=E•A=A 5 7 4 1 0 0 5 7 4
3 6 8 0 1 0 3 6 8
11 4 0 0 0 1 11 4 0
1 0 0 5 7 4 5 7 4
0 1 0 3 6 8 3 6 8
0 0 1 11 4 0 11 4 0
2526. ВЫЧИСЛИТЬ A•E и E•A
A
5
7
4
3
6
8
11
4
0
Е
1
0
0
0
1
0
0
0
1
26Матрицы и действия над ними – определитель матрицы, умножение и сложение матриц, транспонирование матриц, обратная матрица
Что такое матрица
Таблица чисел вида
состоящая из строк и столбцов называется матрицей. Числа называются ее элементами.
Под решением матрицы обычно понимают проведение таких операций как нахождение обратной матрицы, нахождение определителя, умножение матрицы на число и другое. Кроме того действия могут проводиться сразу над несколькими матрицами. То есть матрицы могут между собой складываться, перемножаться.
 Все эти так называемые решения матриц проводятся по определенным схемам или алгоритмам.
Обратите внимание что действия над матрицами выполняются по определенным правилам и дело тут не в сложности этих правил, а в старательности и внимательности при вычислениях.
Все эти так называемые решения матриц проводятся по определенным схемам или алгоритмам.
Обратите внимание что действия над матрицами выполняются по определенным правилам и дело тут не в сложности этих правил, а в старательности и внимательности при вычислениях.
Определитель матрицы и его вычисление
Рассмотрим квадратную матрицу:
порядка . Из элементов этой матрицы составим всевозможные произведения так, чтобы они содержали по одному и только по одному элементу из каждой строки и каждого столбца. В каждом из этих произведений сомножители (которых будет ) расположим таким образом, чтобы первые индексы образовали перестановку . В результате полученные произведения будут иметь вид:
где – некоторая перестановка чисел 1,2,3…n. Очевидно, что число всевозможных произведений составленных из элементов матрицы по приведенному выше правилу будет равно числу всевозможных перестановок из множества вторых индексов сомножителей произведений, то есть из чисел , или то же самое, числу перестановок из чисел , а таких перестановок будет .
 Каждая перестановка будет иметь
некоторое число инверсий, образованных вторыми индексами сомножителей
произведений. Условимся перед
произведением ставить плюс если число инверсий четное (то есть перестановка
вторых индексов четная), и минус, если число инверсий нечетное (то есть
перестановка вторых индексов нечетная).
Каждая перестановка будет иметь
некоторое число инверсий, образованных вторыми индексами сомножителей
произведений. Условимся перед
произведением ставить плюс если число инверсий четное (то есть перестановка
вторых индексов четная), и минус, если число инверсий нечетное (то есть
перестановка вторых индексов нечетная).Просуммировав все произведения вида (*) составленные из матрицы и взятые с указанными знаками, получим число, называемое определителем.
Для определителя, как и для матрицы, используются такие понятия, как строка, столбец, главная и побочная диагонали и т. п. Квадратная матрица, определитель которой отличен от нуля, называется невырожденной, а матрица с определителем, равным нулю,— вырожденной.
Рассмотрим частные случаи определителей:
Определитель 2-го порядка:
Определитель третьего порядка:
Для его вычисления удобно пользоваться следующей схемой:
Для определителей порядка выше третьего неудобно запоминать какую-либо символическую схему, так как, например, определитель уже четвертого порядка есть алгебраическая сумма 24 слагаемых, каждое из которых является произведением четырех сомножителей.

Минором какого-либо элемента определителя называется определитель, полученный из данного вычерчиванием той строки и того столбца, которым принадлежит этот элемент.
Алгебраическим дополнением элемента определителя называется его минор, взятый со знаком .
В общем случае определителем порядка, соответствующим квадратной матрице порядка можно назвать число, равное сумме парных произведении элементов какой-либо строки (столбца) на их алгебраические дополнения.
Квадратная матрица называется невырожденной, если ее определитель отличен от нуля.
Обратная матрица
Пусть – квадратная невырожденная матрица n-го порядка. Обратной матрицей для матрицы называется матрица, для которой справедливо равенство:
где – единичная матрица
Обратная матрица определена только для квадратных невырожденных матриц и вычисляется по формуле:
где – определитель матрицы , а матрица (союзная матрица) получается из матрицы заменой всех ее элементов соответствующими им алгебраическими дополнениями.

Транспонирование матрицы
Замена каждой строки матрицы ее столбцов называется транспонированием. Транспонированная по отношению к матрице матрица обозначается .
Если задана матрица
то ее транспонированная матрица имеет вид:
Сумма матриц и произведение матрицы на число
Суммой матриц и называется матрица , элементы которой вычисляются по формуле:
Для суммы матриц используют обозначение
Произведением матрицы на число называется матрица , элементы которой вычисляются по формуле:
Для произведения матрицы на число используют обозначение .
Произведение матриц
Произведением матрицы на матрицу называется матрица , элементы которой вычисляются по формуле:
Из определения умножения матриц следует, что элемент в матрице является суммой произведений соответствующих элементов i-й строки матрицы и j-го столбца матрицы .
 На рисунке схематично показано получение элемент
в произведении
матриц
На рисунке схематично показано получение элемент
в произведении
матрицДля произведения матриц используют обозначение
Произведение матриц определено только в том случае, когда число столбцов первой матрицы равно числу строк второй матрицы. Произведение матриц содержит столько строк, сколько имеет первая матрица, и столько столбцов, сколько имеет вторая матрица.
Лекция 2 матрицы и действия над ними
Тема 1.
Лекция 2. Матрицы и действия над ними.
Основные вопросы
1. Матрицы и действия над ними.
1.1. Общие определения, связанные с понятием матрицы.
1.2. Действия над матрицами.
2. Обратная матрица.
1. Матрицы и действия над ними.
Матрицы, впервые появившиеся в середине 19-го века в работах англий-ских математиков У. Гамильтона (1805-1865) и А.
 Кэли (1821-1895), в настоя-щее время весьма
широко используются в прикладной
математике, они зна-чительно упрощают
рассмотрение сложных систем уравнений.
Кэли (1821-1895), в настоя-щее время весьма
широко используются в прикладной
математике, они зна-чительно упрощают
рассмотрение сложных систем уравнений.1.1. Общие определения, связанные с понятием матрицы.
Если при рассмотрении систем линейных уравнений из коэффициентов при неизвестных составить таблицы вида
или , то такие таблицы называются матрицами.
В общем случае матрицей называется прямоугольная таблица, состав-ленная из чисел или каких-либо других объектов. В дальнейшем будем рассматривать матрицы, составленные из вещественных чисел.
Матрицы обозначают одной буквой, например,
где круглые скобки, или двойные черточки – знак матрицы,
а числа а11 , а12 ,… – элементы матрицы.

Каждая матрица имеет определенные размеры (m×n) , т.е. количество строк m и количество столбцов n .
В общем, матрица имеет вид
, т.е. номер строки i меняется от 1 до m , номер столбца j – от 1 до n .
Разновидности матриц.
Если число строк равно числу столбцов, то матрица называется квадрат-ной , тогда говорят о её порядке. Квадратная матрица имеет определитель, составленный из элементов матрицы и обозначаемый (например, для матрицы А) .
Не следует смешивать понятия определителя и матрицы. Матрица есть только таблица, а определитель есть число, и он всегда квад-ратной формы.
Если определитель квадратной матрицы отличен от нуля, то матрица на-зывается невырожденной, если же он равен нулю, то матрица – вырожден-ная.

Квадратная матрица, у которой равны нулю все элементы, кроме стоя-щих на главной диагонали, называется диагональной .
Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной и обычно обозначается буквой Е.
Матрица, у которой все элементы равны нулю, называется нулевой (нуль-матрицей).
Матрица может содержать только один столбец, тогда она называется матрицей-столбцом, или только одну строку, тогда она называется матри-цей-строкой.
Матрицы, имеющие одинаковое число строк и число столбцов, а также равные соответствующие элементы, называются равными .
Так, если , то А = В при условии, что
Матрицы А и В называются соответственными, когда число столбцов матрицы А равно числу строк матрицы В.
 Наглядно
это можно показать так (рис.3.3):
Наглядно
это можно показать так (рис.3.3):к n
m A и
В к
Рис.3.3. Схематическое представление соответственных матриц.
В процессе дальнейшего изучения укажем ещё ряд матриц (симметри-ческая, транспонированная и др.).
1.2. Действия над матрицами.
Над матрицами можно производить следующие действия (операции): сложение, умножение матриц, а также обращение матриц.
1. Сложение матриц. Заметим, что складывать можно только матрицы одинаковых размеров.

Определение 3. Суммой двух матриц и называется матрица элементы которой определяются равенством .
Обозначается : С=А+В .
Пример 1. .
Сложение матриц подчиняется переместительному закону, т.е. А+В=В+А, и сочетательному закону, т.е. (А+В)+С=А+(В+С).
2. Умножение матриц на число.
Определение 4. Произведением матрицы А на число λ называется ма-трица
Матрица записывается как –А и называется матрицей, противоположной матрице А.
3. Умножение матриц. Отметим, что перемножать можно только соответственные матрицы .
Определение 5. Произведением имеющей m строк и k столбцов, на матрицу , имеющей k строк и n столбцов, называется матрица , имеющая m строк и n столбцов, у которой элемент Cij равен сумме произведений элементов i – той строки матрицы А и j -го столбца матрицы В, т.е.
.
Обозначается .
Пример 2.
Можно показать, что умножение матриц подчиняется сочетательному зако-ну и распределительному закону но не подчиняется переместительному закону, т.е. АВ ≠ ВА.
Замечание. Единичная матрица Е перестановочна с любой матрицей А того же порядка, что и матрица Е, т.е. АЕ = ЕА = А, т.е. только в этом случае умножение матриц подчиняется пере-местительному закону.
Убедимся в этом на примере матриц второго порядка
2. Обратная матрица. Рассмотрим так называемую обратную матрицу, понятие которой вводится только для квадратной матрицы.
Определение 6. Матрица А-1 называется обратной для квадратной мат-рицы А , если АА-1 = А-1А = Е.
Не любая матрица может иметь обратную.
Справедлива следующая теорема: Для существования обратной матрицы А-1 необходимо и достаточно, чтобы определитель матрицы А был не равен нулю () , т.е. чтобы матрица А была невырожденной . При составлении обратной матрицы осуществляется, так называемое, транспонирование матрицы.
Определение 7. Матрица АТ называется транспонированной по от-ношению к матрице А , если столбцы матрицы А явля-ются строками матрицы АТ . Таким образом, транспо-нирование – это переход от матрицы А к АТ, заклю-чающийся в замене соответствующих столбцов мат-рицы А строками .
Пример 3. Пусть
. Транспонированной матрицей АТ будет .
Алгоритмы составления обратной матрицы.
1. Вычислить определитель матрицы А , т.е. (если ∆ ≠ 0, то мат-рица А имеет обратную).
2. Вычислить алгебраические дополнения всех элементов определителя матрицы А, т.е. Аij .
3. Составить матрицу В путем замены в матрице А каждого элемента его алгебраическим дополнением, т.е. аij заменить на Аij .
4. Составить транспонированную матрицу ВТ по отношению к матрице В , поменяв местами в матрице В её строки и столбцы.
5. Разделив все элементы матрицы ВТ на определитель ∆ , составить обратную матрицу А-1, т.е.
.
6. Проверка. Найти произведение АА-1 , которое должно быть равно матрице Е .
Пример 4. Найти матрицу, обратную матрице
Решение.
1) , следовательно существует А-1 ;
2)
3)
4)
5)
6) Проверка.
Вывод: Обратная матрица А-1 составлена правильно.
Матричная запись, равные матрицы и математические операции с матрицами – видео и стенограмма урока
Нотация
Для начала рассмотрим правильную нотацию для матриц. Посмотрите на эту правильно написанную матрицу:
Правильные обозначения для матриц Наши номера расположены аккуратными рядами и столбцами. Нашу матрицу окружают квадратные скобки. Эти квадратные скобки говорят нам, что эта конкретная группа чисел принадлежит одной матрице.Мы также можем пометить нашу матрицу, назвав ее матрицей A. Если мы пометили нашу матрицу, мы можем либо записать матрицу со всеми числами в ней, либо мы можем записать ее, используя нашу метку, заключенную в квадратные скобки. Наши матрицы также описываются их размером. Эта конкретная матрица имеет три строки и три столбца, поэтому мы также можем назвать ее матрицей 3×3. Матрица с четырьмя строками и двумя столбцами представляет собой матрицу 4×2.
Равные матрицы
Хорошо, теперь, когда мы знаем, как выглядит правильная матричная запись, давайте поговорим о том, когда две матрицы равны друг другу.Вы знаете, что, когда два числа одинаковы, они являются одинаковыми числами, например, когда у вас есть 2 и 2. Ну, матрицы похожи, но это немного больше. Когда две матрицы одинаковы, все числа должны быть одинаковыми в одинаковых позициях, и обе матрицы должны быть одинакового размера. Например, эти две матрицы одинаковые:
Равные матрицы Они одинакового размера, и все номера одинаковые в одинаковых местах.Это обе матрицы 2×3.
Взгляните на эти матрицы. Это такие же?
Эти матрицы не равны. Это не одинаковые матрицы, потому что они разного размера. Тот факт, что две матрицы имеют одинаковые номера, не означает, что они равны. Их размеры тоже должны быть одинаковыми.
Сложение и вычитание матриц
Давайте рассмотрим виды математических операций, которые мы можем выполнять.Мы можем сделать сложение и вычитание . Сложение и вычитание матриц аналогично сложению и вычитанию чисел. Складываем или вычитаем число по числу. Поскольку мы должны сопоставить наше число с числом, наши две матрицы должны быть одинакового размера, например:
Матрицы должны быть одинакового размера для сложения или вычитания. Мы сопоставили числа вместе. Мы сопоставили число в первой строке и первом столбце первой матрицы с числом в первой строке и первом столбце второй матрицы и так далее.Мы не можем складывать или вычитать две матрицы разных размеров. Однако мы можем прибавлять или вычитать одно и то же число ко всем числам в матрице.
Добавление одного и того же числа ко всем числам матрицы Вычитание выполняется так же, как и сложение. Две матрицы должны быть одинакового размера, и мы вычитаем число из числа, сопоставляя расположение чисел вместе. Мы также можем вычесть одно и то же число из всех чисел в матрице.
Умножение матриц
Последняя математическая операция, которую мы можем сделать, это умножение матрицы . Нет такой вещи, как матричное деление. Умножение матриц сложнее умножения чисел. Вы можете легко умножить 3 и 5, чтобы получить 15. Но с матрицами, когда мы умножаем две матрицы вместе, мы должны использовать комбинацию умножения и сложения. Кроме того, количество столбцов в первой матрице должно соответствовать количеству строк во второй матрице. Итак, мы можем умножить матрицу 1×3 на матрицу 3×2, но мы не можем умножить матрицу 1×3 на матрицу 2×3.И в отличие от чисел, где порядок умножения не имеет значения, с матрицами имеет значение, какая матрица идет первой.
Давайте посмотрим, как мы умножаем две матрицы вместе:
Умножение с матрицами Чтобы умножить эти две матрицы, мы сопоставляем строки в первой матрице со столбцами во второй матрице. Затем мы берем каждую пару чисел по одному, умножая их по ходу дела, а затем складываем все продукты вместе в конце.Итак, для наших матриц мы берем первую строку первой матрицы и сопоставляем ее с первым столбцом второй матрицы. Это даст нам число в первой строке и первом столбце матрицы ответов. Мы сравниваем 1 с 0 и 2 с 2. Мы умножаем 1 на 0, 2 на 2, затем складываем все. У нас есть 1 (0) + 2 (2) = 0 + 4 = 4. Число в первой строке и первом столбце в матрице ответов равно 4.
У нас есть два столбца во второй матрице, поэтому нам нужно сопоставить первая строка ко второму столбцу.Нам нужно сопоставить каждую строку в первой матрице с каждым столбцом во второй матрице. Сопоставление первой строки в первом столбце со вторым столбцом во второй матрице дает нам число в первой строке и втором столбце в матрице ответов. Снова сопоставляя числа, мы получаем: 1 (1) + 2 (3) = 1 + 6 = 7.
Теперь, когда мы сопоставили первую строку в первой матрице с каждым столбцом во второй матрице, мы переходим к следующему этапу. во вторую строку первой матрицы. И мы делаем то же самое, сопоставляя его с каждым столбцом второй матрицы.Число во второй строке и первом столбце в матрице ответов: 3 (0) + 5 (2) = 0 + 10 = 10. Число во второй строке и втором столбце в матрице ответов: 3 (1) + 5 (3) = 3 + 15 = 18. Наш окончательный ответ – это матрица:
Окончательный ответ умножения Как видите, умножение матриц немного отличается от умножения чисел. Помните, что вы сопоставляете строки в первой матрице со столбцами во второй матрице.Мы умножаем пары чисел, а затем складываем их все.
Мы также можем просто умножить все числа в матрице на одно число. В этом случае каждое число в матрице умножается на одно и то же.
Резюме урока
Давайте рассмотрим то, что мы узнали. Матрицы – это математические объекты, в которых числа организованы в красивый прямоугольный массив строк и столбцов. Мы помечаем их буквой в квадратных скобках или их размером, например матрицей 3×2, которая сообщает нам, что есть три строки и два столбца.
Мы можем выполнять сложение, вычитание и умножение матриц. Для сложения и вычитания матрицы должны быть одинакового размера, и мы просто складываем и вычитаем числа, которые находятся в совпадающих местах в двух матрицах. Для умножения матриц мы сопоставляем каждую строку первой матрицы с каждым столбцом второй матрицы. Мы умножаем каждую пару чисел, а затем складываем их все.
Результаты обучения
Посмотрите и еще раз просмотрите этот урок о матрицах, чтобы убедиться, что вы можете:
- Дайте определение матриц
- Определите правильную матричную запись
- Определить равенство матриц
- Сложение, вычитание и умножение матриц
поддерживаемых операций для векторов и матриц – MATLAB и Simulink
Эта таблица суммирует интерпретацию операций присваивания для вектора и матричные операнды.
Присвойте значения всем элементам матрицы
В диаграммах, которые используют MATLAB в качестве языка действий, вы можете использовать одно действие, чтобы указать все элементов вектора или матрицы. Например, это действие присваивает каждому элемент матрицы 2 на 3
Aв другой значение:В диаграммах, которые используют C в качестве языка действий, вы можете использовать скаляр расширение , чтобы установить для всех элементов вектора или матрицы значение такое же значение.Скалярное расширение преобразует скалярные данные в соответствии с размерами векторные или матричные данные. Например, это действие устанавливает все элементы матрица
Aк10:Скалярное расширение применяется ко всем графическим функциям, функциям таблицы истинности, MATLAB и Simulink. Предположим, вы определяете формальные аргументы функция
fкак скаляры. В этой таблице описаны правила скалярное разложение для вызова функцииy = f (u).Выход yВход uРезультат Скалярный Скалярный Скалярное расширение не происходит. Скаляр Вектор или матрица Диаграмма генерирует ошибку несоответствия размера. Вектор или матрица Скаляр В диаграмме используется скалярное расширение для присвоения скалярное выходное значение
f (u)для каждого элементy:Вектор или матрица Вектор или матрица В диаграмме используется скалярное расширение для вычисления выходное значение для каждого элемента
Еслиuи присвоить его соответствующему элементуy:yиuне имеют одинаковый размер, диаграмма генерирует несоответствие размера ошибка.Для функций с несколькими выходами применяются те же правила, если только все выходы и входы – это векторы или матрицы. В этом случае диаграмма генерирует ошибку несоответствия размера, и скалярное расширение не происходит.
Диаграммы, которые используют MATLAB в качестве языка действий, не поддерживают скалярное расширение.
Матрица приоритетов действий – Инструменты управления временем от MindTools.com
Максимальное использование возможностей
Будь то яркие идеи для реализации, захватывающие возможности или интересные возможности, у большинства из нас в «списках желаний» гораздо больше занятий, чем у нас есть время, чтобы поработать над ними.
Разумно выбирая занятия, мы можем максимально использовать свое время и возможности. Однако, сделав неправильный выбор, мы можем увязнуть в отнимающих время и низкодоходных проектах, которые мешают нам двигаться вперед.
Вот где может пригодиться «Матрица приоритета действий». Эти простые диаграммы помогут вам выбрать виды деятельности, которые вам следует расставить по приоритетам, и те, которых следует избегать, если вы хотите максимально использовать свое время и возможности.
Как вы расставляете приоритеты задач в вашем списке дел?
Об инструменте
Матрицы приоритетов действий* (см. Рисунок 1 ниже) показывают, как расставлять приоритеты занятия, чтобы максимально использовать свое время, энергию и таланты.
Это полезно, потому что у нас редко бывает время выполнить все задачи и проекты из наших списков желаний. Когда мы используем матрицу для разумного выбора деятельности, мы можем тратить больше времени на важные дела, которые заставляют нас двигаться вперед.
Мы также можем отбрасывать задачи, которые мало помогают.
Рисунок 1. Матрица приоритетов действий
Чтобы использовать матрицу, вы оцениваете задачи, во-первых, по их влиянию, а во-вторых, по усилиям, необходимым для их выполнения.
Затем вы используете свои баллы для отображения этих действий в одном из четырех квадрантов:
Quick Wins (высокая отдача, минимум усилий)
быстрых побед являются наиболее привлекательными проектами, потому что они приносят хорошую прибыль при относительно небольших затратах. Сосредоточьтесь на них как можно больше.
Крупные проекты (высокая отдача, большие усилия)
Крупные проекты приносят хорошую прибыль, но требуют много времени. Это означает, что один крупный проект может «вытеснить» множество быстрых побед.
Заполнители (малое воздействие, малое усилие)
Не беспокойтесь об этих делах – если у вас есть свободное время, делайте их, но бросьте их или делегируйте их, если появится что-то получше.
неблагодарные задачи (малозатратные, большие усилия)
Старайтесь избегать этих действий. Мало того, что они дают небольшую отдачу, они также занимают время, которое вы должны использовать для быстрых побед.
Совет:
Как только вы поймете принципы, лежащие в основе матрицы приоритетов действий, вы, вероятно, обнаружите, что применяете ее быстро и интуитивно для новых задач и проектов.
Как использовать инструмент
Чтобы использовать матрицу приоритетов действий, загрузите нашу таблицу и выполните следующие действия:
Шаг 1
Перечислите основные действия, которые вы хотите или должны выполнить.
Шаг 2
Оцените их по удару (например, от 0 для отсутствия воздействия до 10 для максимального воздействия) и по приложенным усилиям (от, скажем, 0 при отсутствии реальных усилий до 10 при больших усилиях).
Шаг 3
Отобразите действия в матрице приоритетов действий на основе ваших оценок.
Шаг 4
Расставьте приоритеты и делегируйте или отказаться от занятий с низким уровнем воздействия.
Совет:
Используйте здравый смысл для интерпретации линий, разделяющих четыре квадранта. В конце концов, есть лишь небольшая разница между деятельностью с воздействием 4,9, определенной как «неблагодарная задача», и задачей с воздействием 5,1, определенной как «крупный проект».
Получите бесплатную рассылку новостей
Изучайте новые карьерные навыки каждую неделю, а также получайте бонус Рабочая тетрадь по управлению временем , бесплатно !
Прочтите нашу Политику конфиденциальностиВарианты инструмента
Подход, который мы описываем выше, объясняет, как вы можете использовать матрицу приоритетов действий в качестве неформального или личного способа определения приоритетов задач.Однако вы можете использовать этот подход в более крупном масштабе, используя, например, «финансовую отдачу» в качестве шкалы на вертикальной оси и «человеко-месяцы» на горизонтальной оси.
В качестве альтернативы, вы можете заменить «осуществимость» на «усилия» на горизонтальной оси, чтобы расставить приоритеты для проектов в зависимости от вашей способности их реализовать. (Этот вариант иногда называют «матрицей воздействия / осуществимости».)
Совет:
См. Также нашу статью о Принципе срочности / важности Эйзенхауэра. – это аналогичный инструмент, который вы можете использовать для управления своими приоритетами, и он особенно полезен для того, чтобы взять под контроль «пожаротушение».
Ключевые моменты
Матрица приоритетов действий – это простой инструмент, который поможет вам выбрать, какие действия установить в качестве приоритетных. , и какие действия делегировать или исключить. Это поможет вам наилучшим образом использовать имеющиеся у вас возможности.
Матрица имеет четыре квадранта:
- Быстрые победы.
- Крупных проектов.
- Заполн.
- Неблагодарные задания.
Чтобы использовать матрицу, составьте список ваших текущих действий и целей.Оцените каждую задачу по результативности и усилиям по шкале от 0 до 10. Затем нанесите на матрицу свои действия, а затем соответствующим образом расставьте приоритеты, делегируйте или отбрасывайте действия.
Скачать лист
* Источник неизвестен. Пожалуйста, свяжитесь с [email protected], если вы знаете, кто является автором.
Что такое матрица приоритетов действий?
Что такое матрица приоритетов действий?
Матрица приоритетов действий – это диаграмма, которая помогает людям определить, на каких задачах следует сосредоточиться и в каком порядке.
Эта матрица создается с использованием двух компонентов. Сначала нарисуйте график, на котором измеряется усилие по оси x и воздействие по оси y. Затем добавьте на график четыре прямоугольника, два наложенных друг на друга. С готовой диаграммой вы можете построить все свои инициативы, чтобы увидеть, являются ли они высокой отдачей и малыми усилиями, высокой отдачей и большими усилиями, малой отдачей и малыми усилиями или высокой отдачей и низкими усилиями.
Каковы четыре категории матрицы приоритетов действий?
Люди обычно классифицируют эти коробки следующим образом:
1.Быстрые победы (высокая отдача, низкие усилия)
2. Крупные проекты (высокая отдача, большие усилия)
3. Заполнения (низкая отдача, низкие усилия)
4. Неблагодарные задачи (низкая отдача, большие усилия)
Ваша матрица приоритетов действий будет похожа на показанную здесь.
Как менеджеры по продукту могут использовать матрицу приоритетов действий?
После того, как вы создали матрицу, вот как использовать ее с вашей командой разработчиков.
Первый шаг: составьте список своих инициатив
Вы можете использовать доску, слайд презентации или доску планирования в программе Product Roadmap на базе Интернета.Доска планирования выглядит следующим образом:
Посмотрите, как ProductPlan использует наш инструмент дорожной карты для определения приоритетов нашей собственной дорожной картыВторой шаг: оценка каждой инициативы
Вы можете создать любую шкалу оценки, если вы используете один и тот же метод для всех инициатив в вашей список. Один из распространенных подходов – это оценка от 0 до 10 для измерения как воздействия, так и усилий. Задачи, которые ваша команда оценивает от 1 до 5, вы оцениваете низко, а все, что от шести и выше, получает высокую оценку.
Третий шаг: нанесите на карту свои инициативы
Когда вы назначили и оценку воздействия, и оценку трудозатрат для каждой задачи или проекта, вы можете начать наносить их на свою матрицу.Вот пример нескольких элементов, нанесенных на матрицу приоритетов действий для группы разработки программного обеспечения:
Эта группа определила, что добавление опции экспорта в ее приложение будет представлять 6,5 по шкале воздействия (высокая) и 2,5 по шкале шкала усилий (низкая). Таким образом, инициатива была отнесена к категории быстрых побед.
Создание совершенно нового модуля для своего программного приложения, по мнению команды, окажет большое влияние (8.1), но также потребует больших усилий (6.8). С такими оценками данная инициатива заняла место в матрице категории крупных проектов.
Четвертый шаг: расставьте приоритеты для инициатив
Последний шаг с вашей матрицей – решить, как ваша команда хочет расставить приоритеты и распределить проекты, которые вы оценили и наметили. Не существует единственно правильного ответа на вопрос, как каждая продуктовая команда должна расставлять приоритеты в порядке своих задач.
Стоит ли начинать с быстрых побед или сразу же приступать к крупным проектам? Сколько ресурсов вы должны выделить для заполнения проектов? Стоит ли тратить время или ресурсы на неблагодарные дела?
Если завершение крупного проекта потребует от вас всех ресурсов разработки.Тем не менее, он представляет собой очень важный потенциал для вашего продукта или вашего бизнеса; возможно, вам придется отказаться даже от задач, которые приносят быстрый результат, и сосредоточить все внимание на завершении этого крупного проекта.
Но если ваша команда решит, что у вас много инициатив, приносящих быструю отдачу, и что эти быстрые победы могут в совокупности оказать сильное влияние на ваш бизнес, вы можете сосредоточить большую часть своих ресурсов на достижении этих быстрых побед. первый. Это поможет вашей команде набрать обороты и энтузиазм, что поможет им, когда придет время взяться за сложную работу над важным проектом.
Продолжайте изучать, как сбалансировать запланированную и внеплановую работу, на нашем веб-семинаре по установке приоритетов, приведенном ниже.
Хотите узнать больше о приоритезации?
Связанные термины:
приоритезация / матрица Эйзенхауэра / оценка возможностей / взвешенная оценка / сначала взвешенное кратчайшее задание (WSJF)
Поиск данных с помощью расчетных матриц Блок
Цели обучения
После завершения этого раздела вы сможете:
- Кратко опишите, что такое расчетные матрицы OmniStudio, а также почему и когда мы их используем.
- Объясните, как читать расчетную матрицу.
Ознакомьтесь с расчетными матрицами
Уровень управления услугамиOmniStudio включает службы данных, которые считывают, записывают, преобразовывают, вычисляют и отслеживают данные внутри и за пределами Salesforce. Этот уровень включает процессы и инструменты, позволяющие пользователям искать данные и настраивать сложные математические операции поверх платформы Salesforce: матрицы OmniStudio и процедуры расчета OmniStudio.
В этом модуле вы узнаете о матрицах OmniStudio и их использовании.
Но прежде чем переходить к матрицам вычислений, важно понимать, что такое процедуры вычислений OmniStudio. Процедуры вычислений позволяют настраивать сложные математические операции в OmniStudio. Иногда требуется нечто большее, чем простое математическое уравнение, и настройка процедур расчета позволяет выполнить именно такой комплексный и подробный набор шагов математической обработки.
Для обработки множества факторов, значений и вычислений процедура вычисления может вызывать одну или несколько матриц вычислений.Это просто таблицы поиска, которые принимают уникальный вход или набор входов и возвращают выход или набор выходов. Используйте расчетную матрицу всякий раз, когда вам нужно найти данные.
Вы подробнее остановитесь на процедурах расчета позже. А пока вот несколько примеров расчетных матриц.
- Матрица страховых премий , которая соответствует характеристикам застрахованного и страховым взносам
- Матрица предупреждений о погоде , которая устанавливает флаг предупреждения на основе погодных условий
- Демографическая матрица , которая выводит демографические данные на основе местоположения
- Матрица ценообразования , которая сопоставляет набор характеристик продукта с ценой или ценами
Матрица вычислений расширяет функциональность OmniScripts и процедур интеграции OmniStudio.Как вы знаете, если вы завершили работу с другими модулями OmniStudio, OmniScript – это инструмент для разработки и создания управляемых бизнес-процессов для пользователей, а OmniStudio Integration Rules – это инструмент, который извлекает, сохраняет и обрабатывает данные за кулисами. Матрицу расчета можно вызвать из любого инструмента с помощью действия «Матрица».
Существует три типа расчетных матриц, и их использование различается.
- Стандартная матрица вычисления: Используется, когда ваша матрица не обязательно должна быть частью группы или версией построчно.
- Матрица сгруппированных вычислений: Используется для группировки похожих матриц с одинаковыми заголовками ввода и вывода.
- Матрица вычисления с версиями по строкам: Используется, если у вас есть матрица с большим количеством строк и, возможно, потребуется изменять небольшие части данных за раз. Каждая строка имеет собственную дату и время начала
Как читать расчетную матрицу
Вот пример матрицы вычислений, которая выводит стоимость и уровень удержания на основе соглашения об уровне обслуживания (SLA).Давайте посмотрим, как он был создан и что вы обнаружите при его просмотре.
Эта матрица была создана путем загрузки CSV-файла teamSLAretention и последующего сопоставления данных, как показано в этой таблице.
Имя Тип заголовка Тип данных SLA
Ввод
Текст
Стоимость удержания
Выход
Валюта
Коэффициент удержания
Выход
процентов
Обратите внимание, что подробности в верхней части записи матрицы включают поля, которые указывают дату и время начала, приоритет, включена ли матрица, а также дату и время окончания.
Вот несколько вещей, о которых следует помнить о матрицах вычислений.
- Матрица будет запущена, только если текущая дата и время находятся между датой / временем начала и датой / временем окончания. Матрица с пустыми датой / временем окончания все еще работает; он просто настроен на неограниченное время работы.
- Если существует несколько версий матрицы, единовременно можно получить доступ только к одной версии, в зависимости от следующих факторов:
- Диапазон даты / времени в матрицах. (То есть они активны одновременно?)
- Если они оба активны, запускается активная матрица с наивысшим приоритетом.(1 – самый низкий приоритет.)
- Предыдущие версии матрицы всегда будут доступны, чтобы продукты со старыми ценами по-прежнему имели доступ к правильным таблицам цен.
- Если данных много, матрицы могут представлять диапазоны. Это делает их маленькими!
Теперь, когда вы знакомы с матрицами расчета, пришло время изучить процедуры расчета и то, как они работают вместе (подсказка: красиво!).
Хотите практиковаться?
У нас нет практических задач в этом модуле, но если вы хотите попробовать OmniStudio, вы найдете ссылку на руководство по выполнению упражнений в разделе “Ресурсы”.Для выполнения этих упражнений вам понадобится специальная организация Developer Edition, которая содержит OmniStudio и наши образцы данных. На обычной игровой площадке Trailhead нет OmniStudio или наших образцов данных. Руководство по выполнению упражнений включает инструкции о том, как зарегистрироваться в специальной организации (если вы еще этого не сделали), или перейдите по ссылке ниже в разделе «Ресурсы».
Ресурсы
Матричных игр
16.1 Матрица Игры
Цели обучения
- Как моделируются игры?
- Какая оптимальная игра?
Простейшая игра называется матрицей с двумя игроками.В матричной игре с выплатами Игра, в которой все действия выбираются одновременно., Все действия выбираются одновременно. Обычно игру с матричной выплатой описывают, как играемую игроком строки и игроком столбца. Игрок строки выбирает строку в матрице; игрок столбца одновременно выбирает столбец. Результатом игры является пара выплат, где первая запись – это выигрыш игрока строки, а вторая – выигрыша игрока столбца. На рис. 16.1 «Дилемма заключенного» представлен пример матричной игры с выплатами «2 × 2» – самой известной игры из всех – известной как «дилемма заключенного», в которой стратегии заключаются в том, чтобы признаться или не признаться; первый игрок, который признается, избегает тюрьмы.. Стратегия игры состоит в том, чтобы признаться или не признаться.
Рисунок 16.1 Дилемма заключенного
В дилемме заключенного двое преступников по имени Роу и Колонна были задержаны полицией и допрашиваются отдельно. Они вместе виновны в преступлении. Каждый игрок может выбрать, признаться ему или нет. Если Роу признается, мы находимся в верхней строке матрицы (соответствующей строке с надписью «Признание»). Точно так же, если Столбец признается, выплата будет в соответствующем столбце.В этом случае, если только один игрок признается, этот игрок выходит на свободу, а другой отбывает 20 лет тюрьмы. (Записи соответствуют количеству лет, потерянных в тюрьме. Первая запись – всегда выигрыш Строки; вторая запись – выплата Столбца.) Таким образом, например, если Столбец признается, а Строка – нет, соответствующая выплата – это первый столбец и второй ряд.
Рисунок 16.2 Решение дилеммы заключенного
Если Колонка признается, а Строка – нет, Строка теряет 20 лет, а Колонка не теряет лет; то есть идет бесплатно.Это выигрыш (–20, 0), обозначенный обратным цветом на рис. 16.2 «Решение дилеммы заключенного». Если оба признаются, их обоих признают виновным и ни один из них не выходит на свободу, но каждый из них отбывает срок 10 лет. Наконец, если ни один из них не признается, существует 10% -ная вероятность того, что они все равно будут осуждены (с использованием доказательств, отличных от признания), и в этом случае каждый из них в среднем проигрывает год.
Дилемма заключенного известна отчасти потому, что она легко разрешима. Во-первых, у Роу есть явное преимущество перед признанием, независимо от того, что Колонн собирается делать.Если Столбец признается, Строка получает –10 за признание, –20 за отказ от признания, и поэтому лучше признаться. Точно так же, если Столбец не признается, Строка получает 0 за признание (а именно, освобождается), –1 за отсутствие признания, и лучше, если он исповедуется. В любом случае, независимо от того, что делает Столбец, Строка должна выбрать признание. Это называется доминирующей стратегией – стратегией, оптимальной независимо от того, что делают другие игроки, стратегией, которая оптимальна независимо от того, что делают другие игроки.
Логика в точности аналогична для столбца: независимо от того, что делает строка, столбец должен выбрать признание.То есть Колонна также имеет доминирующую стратегию признания. Чтобы установить это, сначала подумайте, какое действие лучше всего сделать для Столбца, когда Столбец думает, что Строка признается. Затем подумайте о том, как лучше всего поступить с Колонкой, когда Колонна думает, что Строка не признается. В любом случае, Колонн получит более высокую награду (меньшее количество лет, потерянных в тюрьме), признавшись.
Наличие доминирующей стратегии делает дилемму заключенного особенно легкой для решения. Оба игрока должны признаться. Обратите внимание, что каждый из них получит по 10 лет тюрьмы, и, таким образом, с их точки зрения, это не очень хороший результат; но они ничего не могут с этим поделать в контексте игры, потому что для каждого альтернативой 10-летнему служению является 20-летний срок.Этот результат называется (Признаться, Признаться), где первая запись – это выбор игрока ряда, а вторая запись – выбор игрока столбца.
Рисунок 16.3 Начальная игра
Рассмотрим начальную игру, в которую играют Microsoft (игрок в ряд) и Piuny (игрок в столбец), небольшая начинающая компания. И Microsoft, и Piuny думают о выходе на новый рынок онлайн-услуг. На рис. 16.3 «Начальная игра» представлена структура выплат.
В этом случае, если обе компании войдут, Microsoft в конечном итоге выиграет рынок, заработав 2, а Piuny проиграет 2.Если у одной из фирм есть рынок, она получает 5, а другая – ноль. Если ни один из них не входит, они оба получают ноль. У Microsoft есть доминирующая стратегия для входа: она получает 2, когда Piuny входит, 5, когда Piuny не входит, и в обоих случаях он добивается большего успеха, чем когда он не входит. Напротив, у Piuny нет доминирующей стратегии: Piuny хочет войти, когда Microsoft этого не делает, и наоборот. То есть оптимальная стратегия Piuny зависит от действий Microsoft; или, точнее, оптимальная стратегия Piuny зависит от того, что, по мнению Piuny, сделает Microsoft.
Piuny может понять доминирующую стратегию Microsoft, если он знает выгоды Microsoft. Таким образом, Piuny может сделать вывод, что Microsoft собирается войти, а это означает, что Piuny не должен входить. Таким образом, равновесие в игре состоит в том, чтобы Microsoft входила, а Piuny не входила. Это равновесие достигается путем повторного исключения доминирующих стратегий Исключение стратегий путем последовательного удаления доминирующих для игрока стратегий, устранения стратегий путем последовательного удаления доминирующих для игрока стратегий.Во-первых, мы устранили доминирующую стратегию Microsoft в пользу ее доминирующей стратегии. У Microsoft была доминирующая стратегия входа, а это означает, что стратегия отказа от входа доминировала над стратегией входа, поэтому мы устранили доминирующую стратегию. Остается упрощенная игра, в которую входит Microsoft, как показано на рис. 16.4 «Устранение доминирующей стратегии».
Рисунок 16.4 Устранение доминирующей стратегии
В этой упрощенной игре, после устранения доминирующей стратегии Microsoft, у Piuny также есть доминирующая стратегия: не входить.Таким образом, мы повторяем и устраняем доминирующие стратегии снова – на этот раз устраняя доминирующие стратегии Piuny – и в итоге получаем один результат: Microsoft входит, а Piuny – нет. Повторное исключение доминирующих стратегий решает проблему.
Рисунок 16.5 «Игра 3 x 3» показывает другую игру с тремя стратегиями для каждого игрока.
Рисунок 16.5 Игра 3 x 3
Процесс повторного исключения доминирующих стратегий показан на Рисунке 16.6 «Устранение доминирующей стратегии» путем фактического удаления строк и столбцов следующим образом. Обратный цвет (белый текст на черном фоне) указывает на доминирующую стратегию.
Середина доминирует над нижней частью строки, давая:
Рисунок 16.6 Устранение доминирующей стратегии
Когда нижняя часть удалена, в левой колонке теперь преобладает либо центр, либо правый, что исключает левую колонку. Это показано на Рисунке 16.7 «Устранение другой доминирующей стратегии».
Рисунок 16.7 Устранение другой доминирующей стратегии
После исключения Left и Bottom, Top теперь доминирует над Middle for Row, как показано на Рисунке 16.8 «Устранение третьей доминирующей стратегии».
Рисунок 16.8 Устранение третьей доминирующей стратегии
Наконец, как показано на рис. 16.9 «Игра решена», в столбце выбирается значение «Справа» вместо «Центр», что дает уникальный результат после повторного исключения доминирующих стратегий, а именно (Вверху, справа).
Рисунок 16.9 Игра решена
Повторное исключение доминирующих стратегий – полезная концепция, и когда она применяется, прогнозируемый результат обычно бывает вполне разумным. Конечно, у него есть свойство, что ни у одного игрока нет стимула изменить свое поведение, учитывая поведение других. Однако есть игры, в которых это неприменимо, и для этих игр требуется механизм равновесия по Нэшу, названный в честь нобелевского лауреата Джона Нэша (1928–1928).
Основные выводы
- Стратегическое поведение возникает там, где участников рынка достаточно, чтобы их действия имели индивидуальное значение, и когда поведение одного участника влияет на выбор других участников.
- Теория игр – это исследование того, как люди играют в игры. Игра состоит из игроков, их информации, доступных действий и выплат.
- В матричной игре с выигрышем все действия выбираются одновременно. Игрок строки выбирает строку в матрице; игрок столбца одновременно выбирает столбец. Результатом игры является пара выплат, где первая запись – это выигрыш игрока строки, а вторая – выигрыша игрока столбца.
- В дилемме заключенного двое преступников по имени Роу и Колонна были задержаны полицией и допрашиваются отдельно.Они вместе виновны в преступлении. Каждый игрок может выбрать, признаться ему или нет. Признание выгодно каждому игроку по отдельности, но вместе они терпят ущерб.
- Доминирующая стратегия – это стратегия, которая лучше всего подходит для игрока, независимо от того, что выбирают другие.
- Повторяющееся исключение доминирующих стратегий сначала удаляет стратегии, в которых доминируют другие, затем проверяет, преобладают ли какие-либо новые стратегии, и удаляет их, и так далее. Во многих случаях повторное исключение доминирующих стратегий решает игру.
Обзор фильма «Матрица» и его краткое содержание (1999)
Жаль, потому что интригующая постановка. «Матрица» повторяет помещения «Темного города» и «Странные дни», усиливает жар и громкость и заимствует бросающую вызов гравитации хореографию гонконгских боевиков. Это весело, но могло быть и больше. Режиссеры – Ларри и Энди Вачовски, которые умеют снимать фильмы (их первый фильм, «Связанный», вошел в мой список 10 лучших в 1996 году). Здесь, с большим бюджетом и опытным продюсером боевиков Джоэлом Сильвером, они сыграли безопаснее; Нет ничего плохого в том, чтобы пойти на рынок акций в пятницу вечером, но вы можете стремиться выше и продолжать вести дела.
Предупреждение; впереди спойлеры. В сюжете участвует Нео (Киану Ривз), мягкий автор программного обеспечения днем и опасный хакер ночью. Он завербован группой кибер-повстанцев во главе с глубоким Морфеусом (Лоуренс Фишберн) и одетым в кожу воином Тринити (Кэрри-Энн Мосс). Они сделали фундаментальное открытие о мире: его не существует. На самом деле это форма виртуальной реальности, призванная убаюкивать нас жизнью слепого подчинения «системе». Мы послушно ходим на нашу грязную работу каждый день, мало осознавая, как Морфеус говорит Нео, что «Матрица – это шерсть, которую затянули тебе на глаза, – что ты раб.«Повстанцы хотят взломать структуру, удерживающую Матрицу на месте, и освободить человечество. Морфеус считает, что Нео – мессианский« Тот », который может возглавить это восстание, которое требует не только физической силы, но и силы разума. Против них выступают Агенты. , которые выглядят как братья Блюз. Сражения фильма происходят в виртуальной реальности, умы героев подключены к битве (хотя вас все равно могут убить: «Тело не может жить без разума»). как это было в «Странных днях», а также было предложено в романах Уильяма Гибсона («Идору») и других.Представление о том, что мир является искусственным сооружением, созданным посторонними для обмана и использования людей, исходит прямо из «Темного города». Однако оба этих фильма исследовали их значение, как часто делает лучшая научная фантастика. «Темный город» был очарован Незнакомцами, перед которыми стояла острая дилемма: они были умирающими пришельцами, которые надеялись научиться у людей методам адаптации и выживания.
В «Матрице», с другой стороны, за иллюзией не стоят существа из плоти и крови – только компьютерная программа, которая может думать и учиться.Агенты действуют в первую очередь как противники в компьютерной игре с высокими ставками. В фильме нет четкого объяснения того, почему программа создания Матрицы пошла на такие неприятности. Конечно, для программы выполнение – это награда сама по себе, но интеллектуальная программа может привнести ужасающую логику в свои решения.
И «Темный город», и «Странные дни» предлагали интригующие мотивы для подлости. «Матрица» больше похожа на супергеройский комикс, в котором судьба мира сводится к титанической драке между обозначенными представителями добра и зла.На самом деле жестоко – выкладывать на стол дразнящие идеи, а затем просить публику довольствоваться перестрелкой и поединком по боевым искусствам. Предположим, Нео победит. Что же тогда происходит с миллиардами, которые только что были «отключены» от Матрицы? У них еще есть работа? Дома? Личности? Все, что мы получаем, – это загадочный закадровый призыв в конце фильма. Парадокс в том, что мир Матрицы во всех отношениях похож на мир до Матрицы. (Мне вспоминается детский мультипликационный фильм «Первый фильм Дуга», в котором есть опыт виртуальной реальности, в котором все точно так же, как в реальной жизни, за исключением более дорогих.) Тем не менее, я не должен игнорировать достоинства фильма. Он великолепно выглядит как по своей конструкции, так и по кинетической энергии, которая питает его. Он использует безупречно интегрированные спецэффекты и анимацию для визуализации регионов киберпространства. Он создает устрашающих существ, в том числе механических осьминогов. Он трансформирует тела из «Терминатора II». Он использует f / x, чтобы позволить Нео и Тринити горизонтально бегать по стенам и зависать в воздухе достаточно долго, чтобы наносить удары ногами в карате.
- Покажем, что в этом случае существует обратная матрица.


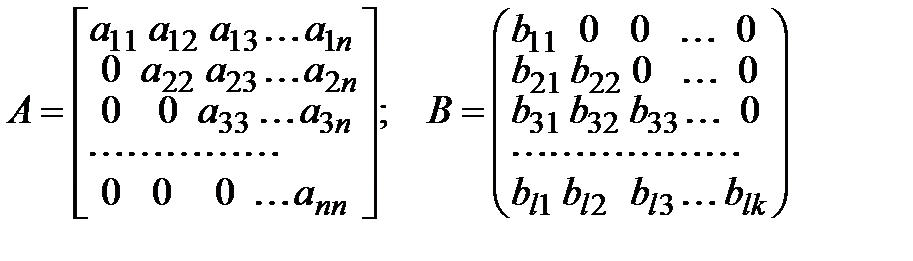 Матрица столбец: n=1. Например
Матрица столбец: n=1. Например
 Кососимметрическая матрица: m=n и aij=-aji (т.е. на симметричных относительно главной диагонали местах стоят противоположные элементы). Следовательно, на главной диагонали стоят нули (т.к. при i=j имеем aii=-aii)
Кососимметрическая матрица: m=n и aij=-aji (т.е. на симметричных относительно главной диагонали местах стоят противоположные элементы). Следовательно, на главной диагонали стоят нули (т.к. при i=j имеем aii=-aii)
 ..,m; j=1,2,…,n)
..,m; j=1,2,…,n)  | и £ = _j)> то !) ■ (-! -IMS?) ‘• 3. Обратная матрица Матрица должна быть квадратной. Матрица называется Матрица, обозначенная как я. A-A ~ l = Е. (90) Вы можете выполнить равенство (90). А ~ 1-А = Е. (91) Приведем теперь следующую основную теорему. Теорема. Для того чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы матрица А была невырожденной, т. Е.
| и £ = _j)> то !) ■ (-! -IMS?) ‘• 3. Обратная матрица Матрица должна быть квадратной. Матрица называется Матрица, обозначенная как я. A-A ~ l = Е. (90) Вы можете выполнить равенство (90). А ~ 1-А = Е. (91) Приведем теперь следующую основную теорему. Теорема. Для того чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы матрица А была невырожденной, т. Е. 1» a2lxt + a% fK + а23х3 = с2, ф. (95) «31 * 1 Н ~« 32 * 2 «33 * 3 = С3 ‘ Рассмотрим матрицу системы / «11« 12 «13 Л =« 21 «22« 23 \ «31« 32 «33, и матрицы-столбцы неизвестных и свободных членов с, Х = .С = 1 с2 с3
1» a2lxt + a% fK + а23х3 = с2, ф. (95) «31 * 1 Н ~« 32 * 2 «33 * 3 = С3 ‘ Рассмотрим матрицу системы / «11« 12 «13 Л =« 21 «22« 23 \ «31« 32 «33, и матрицы-столбцы неизвестных и свободных членов с, Х = .С = 1 с2 с3

 Для матриц подобное обстоятельство может и не иметь места, т. Е. Произведение двух ненулевых матриц может оказаться равным нуль-матрице.
Для матриц подобное обстоятельство может и не иметь места, т. Е. Произведение двух ненулевых матриц может оказаться равным нуль-матрице.
 ТРЕУГОЛЬНЫЕ МАТРИЦЫ Верхняя треугольная матрица
ТРЕУГОЛЬНЫЕ МАТРИЦЫ Верхняя треугольная матрица ВОЗМОЖНОСТЬ УМНОЖЕНИЯ МАТРИЦЫ НА МАТРИЦУ МАТРИЦУ A, ЗАПИСАННУЮ СЛЕВА,
ВОЗМОЖНОСТЬ УМНОЖЕНИЯ МАТРИЦЫ НА МАТРИЦУ МАТРИЦУ A, ЗАПИСАННУЮ СЛЕВА, СВОЙСТВО ЕДИНИЧНОЙ МАТРИЦЫ: A•E=E•A=A 5 7 4 1 0 0 5 7 4
СВОЙСТВО ЕДИНИЧНОЙ МАТРИЦЫ: A•E=E•A=A 5 7 4 1 0 0 5 7 4  Все эти так называемые решения матриц проводятся по определенным схемам или алгоритмам.
Обратите внимание что действия над матрицами выполняются по определенным правилам и дело тут не в сложности этих правил, а в старательности и внимательности при вычислениях.
Все эти так называемые решения матриц проводятся по определенным схемам или алгоритмам.
Обратите внимание что действия над матрицами выполняются по определенным правилам и дело тут не в сложности этих правил, а в старательности и внимательности при вычислениях.
 Каждая перестановка будет иметь
некоторое число инверсий, образованных вторыми индексами сомножителей
произведений. Условимся перед
произведением ставить плюс если число инверсий четное (то есть перестановка
вторых индексов четная), и минус, если число инверсий нечетное (то есть
перестановка вторых индексов нечетная).
Каждая перестановка будет иметь
некоторое число инверсий, образованных вторыми индексами сомножителей
произведений. Условимся перед
произведением ставить плюс если число инверсий четное (то есть перестановка
вторых индексов четная), и минус, если число инверсий нечетное (то есть
перестановка вторых индексов нечетная).

 На рисунке схематично показано получение элемент
в произведении
матриц
На рисунке схематично показано получение элемент
в произведении
матриц Кэли (1821-1895), в настоя-щее время весьма
широко используются в прикладной
математике, они зна-чительно упрощают
рассмотрение сложных систем уравнений.
Кэли (1821-1895), в настоя-щее время весьма
широко используются в прикладной
математике, они зна-чительно упрощают
рассмотрение сложных систем уравнений.

 Наглядно
это можно показать так (рис.3.3):
Наглядно
это можно показать так (рис.3.3):