Матрицы и действия над ними: § 2. Матрицы и действия над ними - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

§ 2. Матрицы и действия над ними

Литература: (1, с. 16-18; 2, с. 71-82; 3, с. 259-263)

Определение матрицы и основные понятия

Рассмотрим прямоугольную таблицу из m строк и n столбцов:

Такая таблица называется матрицей. Числа ,,,- элементы этой матрицы. Если(число строк матрицы равно числу ее столбцов), то матрица называется квадратной-го порядка. Каждая матрица имеет определённые размеры, т.е. количество строк и количество столбцов. Матрица, у которой всего один столбец, называется столбцевой или числовым вектором. Матрица у которой всего одна строка, называется строчной. Матрица, у которой все элементы равны нулю, называется нулевой. Квадратная матрица, у которой равны нулю все элементы, кроме стоящих на главной диагонали, называется диагональной. Диагональная матрица, у которой все диагональные элементы равны единице называется единичной.

Обозначим её

Если поменять местами строки и столбцы матрицы , то получим так называемую транспонированную матрицу

Квадратная матрица имеет определитель, который обозначим.

Две матрицы называются равными, если они одинакового размера и их соответствующие элементы равны . В этом случае -.

Суммой двух матриц одинакового размера называется матрица того же размера, каждый элемент которой равен сумме соответствующих элементов данных двух матриц . Символически это записывают.

Пример 1.

Аналогично определяется разность двух матриц.

Сложение матриц обладает переместительным и сочетательным свойствами, т.е. 1.) ;

2.) .

Умножение матрицы на число

Чтобы умножить матрицу на число , нужно каждый элемент этой матрицы умножить на это число:.

Пример 2.

При умножении матрицы на число справедливы следующие свойства: 1.) ; 2.); 3.).

Умножение матриц

Произведением матрицы изстрок истолбцов на матрицуизстрок истолбцов, элементкоторый равен сумме произведений элементов-й строки матрицына соответствующие элементы-го столбца матрицы, т.е.

Пример 3.

В результате перемножения двух матриц получается матрица, содержащая столько строк, сколько их имеет матрица-множимое, и столько столбцов, сколько их имеет матрица множитель, т.е.. Так, произведение двух матриц 3-го порядка можно символически представить:

При умножении матрицы справедливы свойства:

1.) – переместительный закон не верен;

2.) ;

3.) ;

4.) ;

5.) ;

6.) .

Обратная матрица

Определение: Матрица называется обратной для матрицы, если.

Теорема: Для того, чтобы квадратная матрица имела обратную матрицу, необходимо и достаточно, чтобы её определитель был отличен от нуля. Квадратная матрица, определитель которой отличен от нуля, называется невырожденной.

Нахождение матрицы, обратной данной:

Пусть дана невырожденная матрица

, .

Можно доказать, что обратная матрица определяется равенством: ,(6)

где есть алгебраическим дополнением элементаопределителя матрицы.

Замечание: Элементами обратной матрицы являются алгебраические дополнения элементов транспонированной матрицы, деление на определитель матрицы.

Пример 4. Найти матрицу обратную данной: .

Решение: Воспользуемся формулой (6). Найдем определитель матрицы .

Находим алгебраические дополнения:

; ;;

; ;.

Следовательно:

Ранг матрицы

Пусть дана матрица изстрок истолбцов. Выделим в ней произвольнострок истолбцов (,). Элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу-го порядка. Определитель этой матрицы называется минором-го порядка матрицы.

Наивысший из порядков миноров, отличных от нуля, называется рангом матрицы . Так, если ранг матрицы, то это означает, что среди миноров порядкаесть хотя бы один минор, не равный нулю, а все миноры высшего порядка (чем) равны нулю.

При определении ранга матрицы приходится вычислять большое количество определителей. Чтобы облегчить этот процесс, используют специальные приёмы. Вначале введем понятие элементарных преобразований матрицы:

умножение всех элементов какой-либо строки 9столбца) на число ;
прибавление к элементам какой-либо строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число;
перемена местами строк (столбцов) матрицы;
отбрасывание строк (столбцов) матрицы, все элементы которых равны нулю;

Матрицы, полученные одна из другой при элементарных преобразованиях, называются эквивалентными.

Эквивалентные матрицы имеют одинаковый ранг. .

Пример 5. Вычислить ранг матрицы

Решение: Используя элементарные преобразования получим:

. .

Так как минор второго порядка отличен от нуля, то .

Вопросы для самопроверки

Что называется матрицей? Как обозначается матрица и как определяется её размер?

Назовите виды матриц.

Как определяются линейные операции над матрицами и каковы их свойства?

Что называется произведением двух матриц? Каковы свойства произведений матриц?

Какая матрица называется обратной для данной матрицы? Всегда ли существует обратная матрица? Как можно найти обратную матрицу?

Что называется рангом матрицы и как его можно найти?

Примеры для самостоятельного решения

Выполнит действия:

; 2.;

3. ; 4.;

5. ; 6.

7. 8.;

9. ; 10..

11. Найти , где;

12. Найти , где;

13. Найти , где,-единичная матрица

14. Найти , при;

15. Найти , при;

Найти обратную матрицу , если

16. ; 17.;

18. ; 19.;

Определить ранг матрицы :

20. ; 21.;

22. ; 23..

Ответы к примерам

1. ; 2. ; 3.;

4. ; 5.; 6.;

7. ; 8.; 9.;

10. ; 11.; 12.;

13. ; 14.; 15.;

16. ; 17.; 18. ;

19. ; 20.;

21. ; 22.; 23..

определения, свойства и примеры решения задач, формулы и онлайн калькуляторы

Поможем решить контрольную, написать реферат, курсовую и диплом от 800р

Содержание:

Равные матрицы
Произведение матрицы на число
Сумма матриц
Произведение двух матриц
Транспонирование матриц
Свойства линейных операций:
Свойства произведения матриц:
Свойства транспонирования матриц:

Некоторые операции над матрицами, такие как сложение и вычитание, допускаются только для матриц одинакового размера.

Равные матрицы

Определение

Две матрицы называются равными, если они имеют одинаковые размеры и их соответствующие элементы равны:

$$A_{m \times n}=B_{m \times n} \Leftrightarrow a_{i j}=b_{i j}, i=\overline{1, m} ; j=\overline{1, n}$$

Пример

$A=\left( \begin{array}{cc}{2} & {3}\end{array}\right)$, $B=\left( \begin{array}{cc}{4-2} & {2+1}\end{array}\right)$.

Эти матрицы равны, т.к. равны их размеры: $A_{1 \times 2}$ и $B_{1 \times 2}$, а также соответствующие элементы: $a_{11}=2=b_{11}=4-2=2$; $a_{12}=3=b_{12}=2+1=3$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Пусть задана матрица $A=\left( \begin{array}{ll}{a} & {c} \\ {b} & {d}\end{array}\right)$ . Найти все элементы матрицы $A$, если известно, что она равна матрице $B=\left( \begin{array}{rr}{-1} & {3} \\ {0} & {0}\end{array}\right)$

Решение. Так как матрицы $A$ и $B$ равны, то равны и их соответствующие элементы, т.е. $a=-1, b=0, c=3, d=0$

Ответ. $a=-1, b=0, c=3, d=0$

Произведение матрицы на число

Определение

Произведением матрицы на число называется матрица, полученная из исходной умножением каждого ее элемента на заданное число.

Пример

Задание. Пусть $A=\left( \begin{array}{r}{3} \\ {-1}\end{array}\right)$. Найти матрицу $2A$.

Решение. $2 A=2 \cdot \left( \begin{array}{r}{3} \\ {-1}\end{array}\right)=\left( \begin{array}{c}{2 \cdot 3} \\ {2 \cdot(-1)}\end{array}\right)=\left( \begin{array}{r}{6} \\ {-2}\end{array}\right)$

Ответ. $2 A=\left( \begin{array}{r}{6} \\ {-2}\end{array}\right)$

Подробная теория про умножение марицы на число по ссылке.

Сумма матриц

Определение

Суммой матриц $A$ и $B$ одного размера называется матрица $C = A+B$ такого же размера, получаемая из исходных путем сложения соответствующих элементов.

Пример

Задание. Найти $A+B$, если $A=\left( \begin{array}{rrr}{1} & {-2} & {4} \\ {2} & {0} & {-1}\end{array}\right)$, $B=\left( \begin{array}{lll}{5} & {2} & {3} \\ {4} & {6} & {2}\end{array}\right)$

Решение. $C=A+B=\left( \begin{array}{rrr}{1} & {-2} & {4} \\ {2} & {0} & {-1}\end{array}\right)+\left( \begin{array}{lll}{5} & {2} & {3} \\ {4} & {6} & {2}\end{array}\right)=$

$=\left( \begin{array}{rrr}{1+5} & {-2+2} & {4+3} \\ {2+4} & {0+6} & {-1+2}\end{array}\right)=\left( \begin{array}{ccc}{6} & {0} & {7} \\ {6} & {6} & {1}\end{array}\right)$

Ответ. $C=\left( \begin{array}{lll}{6} & {0} & {7} \\ {6} & {6} & {1}\end{array}\right)$

Операции умножение матрицы на число и сумма матриц называются линейными.

Свойства линейных операций:

Везде далее матрицы $A$, $B$ и $C$ – матрицы одного размера.

Ассоциативность $(A+B)+C=A+(B+C)$
$A+\Theta=\Theta+A$, где $\Theta$ – нулевая матрица соответствующего размера.
$A-A=\Theta$
Коммутативность $A+B=B+A$
Дистрибутивность $\lambda(A+B)=\lambda A+\lambda B$
$(\lambda+\mu) A=\lambda A+\mu A$
$(\lambda \mu) A=\lambda(\mu A)$

Произведение двух матриц

Определение

Произведением матрицы $A_{m \times n}$ на матрицу $B_{n \times k}$ называется матрица $C_{m \times k}$ такая, что элемент матрицы $C$, стоящий в $i$-ой строке и $j$-ом столбце, т. е. элемент $C_{ij}$, равен сумме произведений элементов $i$-ой строки матрицы $A$ на соответствующие элементы $j$-ого столбца матрицы $B$.

Пример

Задание. Найти $AB$, если $A=\left( \begin{array}{rrr}{1} & {2} & {0} \\ {3} & {1} & {-1}\end{array}\right)$ , $B=\left( \begin{array}{l}{1} \\ {2} \\ {3}\end{array}\right)$

Решение. Так как $A=A_{2 \times 3}$, а $B=B_{3 \times 1}$, то в результате получим матрицу размера $C=C_{2 \times 1}$, т.е. матрицу вида $C=\left( \begin{array}{c}{c_{11}} \\ {c_{21}}\end{array}\right)$ . Найдем элементы данной матрицы:

$c_{11}=a_{11} \cdot b_{11}+a_{12} \cdot b_{21}+a_{13} \cdot b_{31}=1 \cdot 1+2 \cdot 2+0 \cdot 3=5 $ $c_{21}=a_{21} \cdot b_{11}+a_{22} \cdot b_{21}+a_{23} \cdot b_{31}=3 \cdot 1+1 \cdot 2+(-1) \cdot 3=2 $

Таким образом, получаем, что:

$C=A B=\left( \begin{array}{l}{5} \\ {2}\end{array}\right)$

Все вычисления можно было сделать в более компактном виде:

$A B=\left( \begin{array}{ccc}{1} & {2} & {0} \\ {3} & {1} & {-1}\end{array}\right)_{2 \times 3} \cdot \left( \begin{array}{l}{1} \\ {2} \\ {3}\end{array}\right)_{3 \times 1}=\left( \begin{array}{c}{1 \cdot 1+2 \cdot 2+0 \cdot 3} \\ {3 \cdot 1+1 \cdot 2+(-1) \cdot 3}\end{array}\right)$

Ответ. {T} $

Читать дальше: умножение матрицы на число.

Матрицы и операции над ними

Определение 1

Матрица – это множество чисел, оформленное в виде прямоугольной таблицы, состоящей из m строк и n столбцов.

Введение

Матрица является совокупностью ячеек, которые представляют собой прямоугольную таблицу, состоящую из m строк и n столбцов. Операции над матрицами осуществляются аналогично действиям с обычным набором ячеек памяти в определённом диапазоне. Каждая матрица имеет отдельный адрес, который пишется точно таким же образом, как и диапазон памяти. Вначале следует указать адрес начальной ячейки диапазона, а далее указывается адрес последней его ячейки.

Собственно, матрица представляет собой массив и для его обработки в разных языках программирования используются набор соответствующих инструментов. К примеру, для программного приложения Excel такими инструментами служат формулы. Основным их отличием от типовых формул является тот факт, что обычный стандартный набор формул способен сделать вывод лишь одного значения. Для использования в приложении Excel формул при обработке массивов, необходимо исполнить следующие действия:

Выделить участок с набором ячеек, куда необходимо задать значения.
Выбрать нужную для реализации вычислений формулу.
Одновременно нажать клавиши Ctrl + Shift +Enter.

После выполнения этих действий в поле для ввода появится формула массива. Её отличием от стандартных формул является присутствие фигурных скобок. Для редактирования или удаления формулы обработки массива, необходимо выделить требуемый диапазон и осуществить корректировку. При редактировании самой матрицы используются такие же сочетания кнопок, как и при её создании.

Операции над матрицами

Рассмотрим возможные операции над матрицами на примере использования программного приложения Excel, которое предназначено для работы с таблицами. Процесс обмена местами строчек и столбиков обозначается как транспонирование. Прежде чем начать такую процедуру, следует выделить отдельную зону, которая имеет количество строчек равное количеству столбиков матрицы, подлежащей преобразованию, и такую же операцию надо проделать для столбиков. Известно два метода осуществления операции транспонирования.

Первый метод состоит в выполнении следующих действий:

Сначала следует выделить диапазон ячеек, куда будет вставлен транспонируемый диапазон.
Далее нужно перейти в окно «Специальная вставка».
Сделать выбор клавиши «Транспонировать» и нажать ОК.

Суть другого метода состоит в следующем. Необходимо выделить ячейки, расположенные в левом верхнем углу диапазона, предназначенного для транспонируемой матрицы. Затем нужно войти в диалоговое окно, где есть набор функций, и сделать выбор функции ТРАНСП. Пример показан на рисунке ниже:

Рисунок 1. Окно программы. Автор24 — интернет-биржа студенческих работ.

Параметром функции является диапазон, который соответствует начальной матрице. Однако, если нажать кнопку ОК, то может появиться сообщение об ошибке, так как функция, которая подлежит вставке, не была определена как формула массива. Поэтому необходимо осуществить следующие действия:

Выделить набор ячеек, которые предназначены для транспонируемой матрицы.
Нажать клавишу F2.
Нажать комбинацию кнопок

Главным достоинством этого метода считается тот факт, что транспонируемая матрица может сразу выполнять коррекцию помещённых в неё информационных данных, одновременно с корректировкой исходной матрицы.

Очень популярной, также, является операция сложения матриц. Данная операция возможна лишь для тех диапазонов, которые обладают одинаковым количеством элементов. То есть, матрицы, которые пользователь желает сложить, должны обладать одинаковым размером. На рисунке ниже приведён пример сложения матриц:

Рисунок 2. Пример сложения матриц. Автор24 — интернет-биржа студенческих работ

В результирующей матрице нужно выделить первую ячейку и выполнить задание следующей формулы:

= Начальный элемент первой матрицы + Начальный элемент второй матрицы

Далее нужно сделать подтверждение формулы, нажатием кнопки Enter и использовать функцию автоматического заполнения (нижний правый угол, квадрат), чтобы скопировать все значения в новую матрицу. Результат операции изображён на рисунке ниже:

Рисунок 3. Результат операции. Автор24 — интернет-биржа студенческих работ

Приведём пример операции умножения. Предположим, есть некоторая матрица (таблица), и все её компоненты нужно перемножить на двенадцать, как показано на рисунке ниже:

Рисунок 4. Умножение на 12. Автор24 — интернет-биржа студенческих работ

Методика выполнения операции умножения, по сути, является аналогом сложения, но в данном случае необходимо весь набор ячеек матрицы умножить на двенадцать, а итоговый результат, как и при сложении, представить в другой матрице. Следует отметить, что надо указывать абсолютные ссылки на ячейки.

Формула имеет следующий вид:

=A1*$E$3

А результирующая матрица представлена на рисунке ниже:

Рисунок 5. Матрица. Автор24 — интернет-биржа студенческих работ

Далее приведём в качестве примера перемножение двух матриц. Эта операция допустима только при выполнении необходимого условия. А именно, количество строчек и столбиков у обеих матриц обязано быть одинаковым в зеркальном формате. То есть количество столбиков должно равняться количеству строчек, как показано на рисунке ниже:

Рисунок 6. Перемножение матриц. Автор24 — интернет-биржа студенческих работ

Чтобы было удобней, следует осуществить выделение диапазона результирующей матрицы. Нужно навести курсор на ячейку в левом верхнем углу и выполнить задание следующей формулы:

=МУМНОЖ(А9:С13;Е9:h21).

Затем нужно нажать одновременно следующие клавиши Ctrl + Shift + Enter, после чего появится результат:

Рисунок 7. Результат. Автор24 — интернет-биржа студенческих работ

Рассмотрим пример формирования обратной матрицы. Когда матрица, то есть её диапазон, имеет квадратную форму, что означает равенство количества ячеек по вертикали и по горизонтали, то это обстоятельство позволяет, если есть необходимость, осуществить определение обратной матрицы. Это можно сделать при помощи функции МОБР. Сначала нужно сделать выделение первой ячейки матрицы, куда будет вставлена обратная матрица. В неё нужно ввести формулу:

=МОБР(A1:A4).

В качестве аргумента нужно указать диапазон, для которого следует сформировать обратную матрицу. Далее нужно использовать комбинацию клавиш Ctrl + Shift + Enter.

Рисунок 8. Окно программы. Автор24 — интернет-биржа студенческих работ

Матрицы и действия над ними

	Дикие кошки	Грязевые коты
Цели	6	10
Шарики	30	24
Трикотажные изделия	14	20

	Лаборатория А	Лаборатория Б
Компьютеры	15	27
Компьютерные столы	16	34
Стулья	16	34

	Дикие кошки	Грязевые коты
Цели	6	10
Шарики	30	24
Трикотажные изделия	14	20

Вы можете изучить и скачать доклад-презентацию на тему Матрицы и действия над ними. Презентация на заданную тему содержит 27 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас – поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!
Презентации» Математика» Матрицы и действия над ними
Слайды и текст этой презентации
Слайд 1
Описание слайда:
МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
Слайд 2
Описание слайда:
Содержание 1. ПОНЯТИЕ И ВИДЫ МАТРИЦ 2. СТРОКИ, СТОЛБЦЫ, ЭЛЕМЕНТЫ И РАЗМЕР МАТРИЦ 3. ОПЕРАЦИИ НАД МАТРИЦАМИ
Слайд 3
Описание слайда:
Слайд 4
Описание слайда:
ОПРЕДЕЛЕНИЯ МАТРИЦЕЙ НАЗЫВАЕТСЯ ПРЯМО-УГОЛЬНАЯ ИЛИ КВАДРАТНАЯ ТАБЛИЦА, ЗАПОЛНЕННАЯ ЧИСЛАМИ. ЧИСЛА, ЗАПОЛНЯЮЩИЕ МАТРИЦУ, НАЗЫВАЮТСЯ ЭЛЕМЕНТАМИ МАТРИЦЫ.
Слайд 5
Описание слайда:
ВИДЫ МАТРИЦ
Слайд 6
Описание слайда:
Слайд 7
Описание слайда:
ПРИНЦИП НУМЕРАЦИИ СТРОК И СТОЛБЦОВ СТРОКИ НУМЕРУЮТСЯ СВЕРХУ ВНИЗ, НАЧИНАЯ С № 1. СТОЛБЦЫ НУМЕРУЮТСЯ СЛЕВА НАПРАВО, НАЧИНАЯ С № 1.
Слайд 8
Описание слайда:
СТРОКА И СТОЛБЕЦ
Слайд 9
Описание слайда:
РАЗМЕР МАТРИЦЫ МАТРИЦА, ИМЕЮЩАЯ m СТРОК И n СТОЛБЦОВ, НАЗЫВАЕТСЯ МАТРИЦЕЙ РАЗМЕРА m НА n.
Слайд 10
Описание слайда:
ОБЩИЙ ВИД МАТРИЦЫ РАЗМЕРА m НА n
Слайд 11
Описание слайда:
ЭЛЕМЕНТ МАТРИЦЫ
Слайд 12
Описание слайда:
ДИАГОНАЛИ КВАДРАТНЫХ МАТРИЦ
Слайд 13
Описание слайда:
ТРЕУГОЛЬНЫЕ МАТРИЦЫ
Слайд 14
Описание слайда:
Слайд 15
Описание слайда:
ЛЮБУЮ МАТРИЦУ МОЖНО УМНОЖИТЬ НА ЧИСЛО
Слайд 16
Описание слайда:
МАТРИЦЫ ОДИНАКОВОГО РАЗМЕРА МОЖНО СКЛАДЫВАТЬ И ВЫЧИТАТЬ
Слайд 17
Описание слайда:
ТРАНСПОНИРОВАНИЕ МАТРИЦЫ
Слайд 18
Описание слайда:
УМНОЖЕНИЕ СТРОКИ НА СТОЛБЕЦ (СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ)
Слайд 19
Описание слайда:
УМНОЖЕНИЕ МАТРИЦЫ НА СТОЛБЕЦ КАЖДАЯ СТРОКА МАТРИЦЫ СКАЛЯРНО УМНОЖАЕТСЯ НА СТОЛБЕЦ
Слайд 20
Описание слайда:
ВОЗМОЖНОСТЬ УМНОЖЕНИЯ МАТРИЦЫ НА МАТРИЦУ МАТРИЦУ A, ЗАПИСАННУЮ СЛЕВА, МОЖНО УМНОЖИТЬ НА МАТРИЦУ B, ЗАПИСАННУЮ СПРАВА, ТОГДА И ТОЛЬКО ТОГДА, КОГДА ЧИСЛО СТОЛБЦОВ МАТРИЦЫ A РАВНО ЧИСЛУ СТРОК МАТРИЦЫ B
Слайд 21
Описание слайда:
ПРАВИЛО УМНОЖЕНИЯ МАТРИЦЫ НА МАТРИЦУ КАЖДАЯ СТРОКА ЛЕВОЙ МАТРИЦЫ СКАЛЯРНО УМНОЖАЕТСЯ НА КАЖДЫЙ СТОЛБЕЦ ПРАВОЙ МАТРИЦЫ
Слайд 22
Описание слайда:
ПРИМЕР УМНОЖЕНИЯ МАТРИЦ
Слайд 23
Описание слайда:
УМНОЖЕНИЕ СТОЛБЦА НА СТРОКУ
Слайд 24
Описание слайда:
ВАЖНЫЕ ТИПЫ КВАДРАТНЫХ МАТРИЦ
Слайд 25
Описание слайда:
СВОЙСТВО ЕДИНИЧНОЙ МАТРИЦЫ: A•E=E•A=A
Слайд 26
Описание слайда:
ВЫЧИСЛИТЬ A•E и E•A
Слайд 27
Описание слайда:

Tags Матрицы и действия над ними
Похожие презентации
Презентация успешно отправлена!
Ошибка! Введите корректный Email!
Email
Операции с матрицами онлайн
Назначение сервиса. (-1)

Матрица – прямоугольная числовая таблица, имеющая m строк и n столбцов, поэтому схематически матрицу можно изображать в виде прямоугольника.
Нулевой матрицей (нуль-матрицей) называют матрицу, все элементы которой равны нулю и обозначают 0.
Единичной матрицей называется квадратная матрица вида

Две матрицы A и B равны, если они одинакового размера и их соответствующие элементы равны.
Вырожденной матрицей называется матрица, определитель которой равен нулю (Δ = 0).
Определим основные операции над матрицами.
Сложение матриц
Определение. Суммой двух матриц A=||aⁱ_k|| и B=||bⁱ_k|| одинакового размера называется матрица C=||cⁱ_k|| тех же размеров, элементы которой находятся по формуле cⁱ_k=aⁱ_k+bⁱ_k. Обозначается C=A+B.
Пример 6. .
Операция сложения матриц распространяется на случай любого числа слагаемых. Очевидно, что A+0=A.
Еще раз подчеркнем, что складывать можно только матрицы одинакового размера; для матриц разных размеров операция сложения не определена.
Вычитание матриц
Определение. Разностью B-A матриц B и A одинакового размера называется такая матрица C, что A+C=B.
Умножение матриц
Определение. Произведением матрицы A=||aⁱ_k|| на число α называется матрица C=||cⁱ_k||, получающаяся из A умножением всех ее элементов на α, cⁱ_k=α·aⁱ_k.
Определение. Пусть даны две матрицы A=||aⁱ_k|| (i=1,2,…,m; k=1,2,…,n) и B=||bⁱ_k|| (k=1,2,. ..,n; j=1,2,…,p), причем число столбцов A равно числу строк B. Произведением A на B называется матрица C=||cⁱ_k||, элементы которой находятся по формуле .
Обозначается C=A·B.
Схематически операцию умножения матриц можно изобразить так:

а правило вычисления элемента в произведении:

Подчеркнем еще раз, что произведение A·B имеет смысл тогда и только тогда, когда число столбцов первого сомножителя равно числу строк второго, при этом в произведении получается матрица, число строк которой равно числу строк первого сомножителя, а число столбцов равно числу столбцов второго. Проверить результат умножения можно через специальный онлайн-калькулятор.
Пример 7. Даны матрицы и . Найти матрицы C = A·B и D = B·A.
Решение. Прежде всего заметим, что произведение A·B существует, так как число столбцов A равно числу строк B.

Заметим, что в общем случае A·B≠B·A, т. е. произведение матриц антикоммутативно.
Найдем B·A (умножение возможно).
Пример 8. Дана матрица . Найти 3A² – 2A.
Решение.
.
Отметим следующий любопытный факт.
Как известно, произведение двух отличных от нуля чисел не равно нулю. Для матриц подобное обстоятельство может и не иметь места, то есть произведение ненулевых матриц может оказаться равным нуль-матрице.
Пример 9. Если и , то
.
Умножение матрицы на число
При умножении числа b матрицы A=(a_ij) получается матрица, элементы которой равны b·a_ij (каждый элемент матрицы умножается на число b).
Подробнее о том, почему нельзя делить матрицы.
Скачать.
Пример 9. Найти значение многочлена f(x) от матрицы A, если f(x)=2x²–3x+5.
2*A^2-3*A+5*B
где A – матрица из задания, B = E – единичная матрица.
Матрицы и действия над ними.ppt презентация, доклад, проект
Слайд 1Текст слайда:
СЛАЙД-ЛЕКЦИЯ № 1
ТЕМА ЛЕКЦИИ:
«МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ»
Слайд 2Текст слайда:
ПЛАН ЛЕКЦИИ

1. ПОНЯТИЕ И ВИДЫ МАТРИЦ
2. СТРОКИ, СТОЛБЦЫ, ЭЛЕМЕНТЫ
И РАЗМЕР МАТРИЦ
3. ОПЕРАЦИИ НАД МАТРИЦАМИ
Слайд 3Текст слайда:
ПОНЯТИЕ И ВИДЫ МАТРИЦ
Слайд 4Текст слайда:
ОПРЕДЕЛЕНИЯ
МАТРИЦЕЙ НАЗЫВАЕТСЯ ПРЯМО-УГОЛЬНАЯ ИЛИ КВАДРАТНАЯ ТАБЛИЦА, ЗАПОЛНЕННАЯ ЧИСЛАМИ.
ЧИСЛА, ЗАПОЛНЯЮЩИЕ МАТРИЦУ, НАЗЫВАЮТСЯ ЭЛЕМЕНТАМИ МАТРИЦЫ.
Слайд 5Текст слайда:
ВИДЫ МАТРИЦ
Слайд 6Текст слайда:
СТРОКИ, СТОЛБЦЫ, ЭЛЕМЕНТЫ И РАЗМЕР МАТРИЦЫ
Слайд 7Текст слайда:
ПРИНЦИП НУМЕРАЦИИ СТРОК И СТОЛБЦОВ
СТРОКИ НУМЕРУЮТСЯ СВЕРХУ
ВНИЗ, НАЧИНАЯ С № 1.
СТОЛБЦЫ НУМЕРУЮТСЯ СЛЕВА
НАПРАВО, НАЧИНАЯ С № 1.
Слайд 8Текст слайда:
СТРОКА И СТОЛБЕЦ
Слайд 9Текст слайда:
РАЗМЕР МАТРИЦЫ
МАТРИЦА, ИМЕЮЩАЯ m СТРОК И n
СТОЛБЦОВ, НАЗЫВАЕТСЯ МАТРИЦЕЙ
РАЗМЕРА m НА n.
Слайд 10Текст слайда:
ОБЩИЙ ВИД МАТРИЦЫ РАЗМЕРА m НА n
Слайд 11Текст слайда:
ЭЛЕМЕНТ МАТРИЦЫ
Слайд 12Текст слайда:
ДИАГОНАЛИ КВАДРАТНЫХ МАТРИЦ
Слайд 13Текст слайда:
ТРЕУГОЛЬНЫЕ МАТРИЦЫ
Слайд 14Текст слайда:
ОПЕРАЦИИ НАД МАТРИЦАМИ
Слайд 15Текст слайда:
ЛЮБУЮ МАТРИЦУ МОЖНО УМНОЖИТЬ НА ЧИСЛО
Слайд 16Текст слайда:
МАТРИЦЫ ОДИНАКОВОГО РАЗМЕРА МОЖНО СКЛАДЫВАТЬ И ВЫЧИТАТЬ
Слайд 17Текст слайда:
ТРАНСПОНИРОВАНИЕ МАТРИЦЫ
Слайд 18Текст слайда:
УМНОЖЕНИЕ СТРОКИ НА СТОЛБЕЦ (СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ)
Слайд 19Текст слайда:
УМНОЖЕНИЕ МАТРИЦЫ НА СТОЛБЕЦ КАЖДАЯ СТРОКА МАТРИЦЫ СКАЛЯРНО УМНОЖАЕТСЯ НА СТОЛБЕЦ
Слайд 20Текст слайда:
ВОЗМОЖНОСТЬ УМНОЖЕНИЯ МАТРИЦЫ НА МАТРИЦУ

МАТРИЦУ A, ЗАПИСАННУЮ СЛЕВА, МОЖНО УМНОЖИТЬ НА
МАТРИЦУ B, ЗАПИСАННУЮ СПРАВА, ТОГДА И ТОЛЬКО ТОГДА, КОГДА ЧИСЛО СТОЛБЦОВ МАТРИЦЫ A РАВНО ЧИСЛУ СТРОК МАТРИЦЫ B
Слайд 21Текст слайда:
ПРАВИЛО УМНОЖЕНИЯ МАТРИЦЫ НА МАТРИЦУ КАЖДАЯ СТРОКА ЛЕВОЙ МАТРИЦЫ СКАЛЯРНО УМНОЖАЕТСЯ НА КАЖДЫЙ СТОЛБЕЦ ПРАВОЙ МАТРИЦЫ
Слайд 22Текст слайда:
ПРИМЕР УМНОЖЕНИЯ МАТРИЦ
Слайд 23Текст слайда:
УМНОЖЕНИЕ СТОЛБЦА НА СТРОКУ
Слайд 24Текст слайда:
ВАЖНЫЕ ТИПЫ КВАДРАТНЫХ МАТРИЦ
Слайд 25Текст слайда:
СВОЙСТВО ЕДИНИЧНОЙ МАТРИЦЫ: A•E=E•A=A
Слайд 26Текст слайда:
§ 1. Матрицы и действия над ними
1. Определение и некоторые виды матриц
ОПРЕДЕЛЕНИЕ. Матрицей размера m×n называется таблица, образованная из элементов некоторого множества (например, чисел или функций) и имеющая m строк и n столбцов.
Если m ≠ n, то матрицу называют прямоугольной.
Если m = n, то матрицу называют квадратной, порядка n.
Элементы, из которых составлена матрица, называются элементами матрицы.
Например, a24 –
a13 –
Слайд 27Текст слайда:
Две матрицы A и B считаются равными, если они одинакового размера, и элементы, стоящие в A и B на одинаковых местах, равны между собой, т.е. aij = bij.
Слайд 28Текст слайда:
Некоторые частные случаи матриц
Слайд 29Текст слайда:
Элементы a11, a22, …, akk (где k = min{m,n}) будем называть элементами главной диагонали матрицы.
Квадратная матрица, у которой все элементы, стоящие вне главной диагонали, равны нулю, называется диагональной:
Диагональная матрица, у которой все элементы главной диагонали равны 1, называется единичной:
Обозначают: E или En.
Слайд 30Текст слайда:
5) Пусть A = (aij) – квадратная матрица порядка n. Элементы a1n, a2,n-1, a3,n-2, …, an1 будем называть элементами побочной диагонали матрицы.
Квадратные матрицы, у которых все элементы ниже (выше) главной или побочной диагонали равны нулю, называются треугольными :
Слайд 31Текст слайда:
6) Прямоугольную матрицу размера m × n будем называть трапециевидной, если все ее элементы ниже главной диагонали равны нулю, т.е. если она имеет вид:
Слайд 32Текст слайда:
2. Линейные операции над матрицами
1) Умножение матрицы на число;
2) Сложение матриц.
ОПРЕДЕЛЕНИЕ. Произведением матрицы A=(aij) на число α называется такая матрица B=(bij), элементы которой равны произведениям соответствующих элементов матрицы A на число α, т.е. bij= α·aij.
Обозначают: α·A, αA.
Частный случай: (-1)·A – противоположная матрице A,
Обозначают –A.
Слайд 33Текст слайда:
ОПРЕДЕЛЕНИЕ. Суммой двух матриц A=(aij) и B=(bij) одинакового размера, называется такая матрица C=(cij), элементы которой равны суммам соответствующих элементов матриц A и B, т.е. cij = aij + bij .
Обозначают: A+B
Частный случай: A+(–B) – разность матриц A и B.
Обозначают: A–B
Слайд 34Текст слайда:
Свойства линейных операции над матрицами
Слайд 35Текст слайда:
3. Нелинейные операции над матрицами
1) Умножение двух матриц;
2) Транспонирование матрицы.
ОПРЕДЕЛЕНИЕ. Пусть A=(a1i) и B=(bi1) – матрица-строка и матрица-столбец одинаковой длины n. Произведением матрицы-строки A на матрицу-столбец B называется число c, равное сумме произведений их соответствующих элементов, т.е.
c = a11 · b11 + a12 · b21 + a13 · b31 + … + a1n · bn1 .
Слайд 36Текст слайда:
ОПРЕДЕЛЕНИЕ. Пусть A=(aij) – матрица размера m × n, B=(bij) – матрица размера n × k (т.е. количество столбцов в матрице A совпадает с количеством строк матрицы B). Произведением матрицы A на матрицу B называется матрица C =(cij) размера m × k такая, что каждый ее элемент cij является произведением i-й строки матрицы A на j-й столбец матрицы B, т.е.
cij = ai1 · b1j + ai2 · b2j + ai3 · b3j + … + ain · bnj .
Обозначают: A ·B, AB.
Слайд 37Текст слайда:
Свойства операции умножения матриц
Слайд 38Текст слайда:
ОПРЕДЕЛЕНИЕ. Пусть A – матрица размера m × n. Матрица размера n × m, полученная из A заменой каждой ее строки столбцом с тем же номером, называется транспонированной к A и обозначается AТ.
Операция нахождения матрицы AТ называется транспонированием матрицы A.
Свойства операции транспонирования матриц
1) (AТ )T = A ;
2) (A + B)T = AT + BT ;
3) (αA)T = αAT ;
4) (A · B)T = BT · AT .
Слайд 39Текст слайда:
Пример
Ответ
назад
Слайд 40Текст слайда:
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной относительно данной.
Например:
Свойства
назад
Слайд 41Текст слайда:
В случае, когда АВ=ВА, матрицы А и В называют перестановочными или коммутативными.
Пример 1. Найти все перестановочные матрицы к матрице
Пример 2. Найти все перестановочные матрицы к матрице
назад
Слайд 42Текст слайда:
Ответ:
назад
Слайд 43Текст слайда:
Пример
Ответ
назад
Слайд 44Текст слайда:
Ответ:
назад
Слайд 45Текст слайда:
Пример
Ответ
назад
Слайд 46Текст слайда:
Ответ:
назад
Слайд 47Текст слайда:
Ответ:
или
или
назад
Матрицы и операции с матрицами | Колледж Алгебра
Результаты обучения
Определение размеров матрицы.
Сложите и вычтите две матрицы.
Умножить матрицу на скаляр, суммировать скаляры, кратные матрицам.
Перемножить две матрицы вместе.
Используйте калькулятор для выполнения операций с матрицами.
Две клубные футбольные команды, Wildcats и Mud Cats, надеются получить новую экипировку к предстоящему сезону. В таблице показаны потребности обеих команд.
Дикие кошки Грязевые коты
Цели 6 10
Шарики 30 24
Трикотажные изделия 14 20
Две команды соревнуются в футбольном матче. (кредит: «SD Dirk», Flickr)
Гол стоит 300 долларов; мяч стоит 10 долларов; а майка стоит 30 долларов. Как мы можем найти общую стоимость оборудования, необходимого для каждой команды? В этом разделе мы раскрываем метод, в котором данные в таблице футбольного оборудования могут отображаться и использоваться для расчета другой информации. После этого мы сможем рассчитать стоимость оборудования.
Сложение и вычитание матриц
Чтобы решить задачу, подобную описанной для футбольных команд, мы можем использовать матрицу , которая представляет собой прямоугольный массив чисел. Строка в матрице представляет собой набор чисел, выровненных по горизонтали. Столбец в матрице представляет собой набор чисел, выровненных по вертикали. Каждое число представляет собой элемент , иногда называемый элементом матрицы. Матрицы (во множественном числе) заключаются в [ ] или ( ) и обычно называются заглавными буквами. Например, ниже показаны три матрицы с именами [latex]A,B,\text{}[/latex] и [latex]C[/latex].
[латекс]A=\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right],B=\left[\begin{array}{ccc}1& 2& 7\ \ 0& -5& 6\\ 7& 8& 2\end{массив}\right],C=\left[\begin{массив}{c}-1\\ 0\\ 3\end{массив}\begin{массив} {c}3\\ 2\\ 1\end{массив}\right][/latex]
Описание матриц
Матрица часто упоминается по ее размеру или измерениям: [latex]\text{ }m\text { }\times \text{ }n\text{ }[/latex] с указанием [latex]m[/latex] строк и [latex]n[/latex] столбцов. Элементы матрицы определяются сначала по строке, а затем по столбцу. Например, чтобы найти запись в матрице [latex]A[/latex], идентифицированную как [latex]{a}_{ij},\text{}[/latex], мы ищем запись в строке [latex]i, \text{}[/latex] столбец [latex]j[/latex]. В матрице [latex]A[/latex], показанной ниже, записью в строке 2 столбца 3 является [latex]{a}_{23}[/latex].
[латекс]A=\left[\begin{array}{ccc}{a}_{11}& {a}_{12}& {a}_{13}\\ {a}_{21} & {a}_{22}& {a}_{23}\\ {a}_{31}& {a}_{32}& {a}_{33}\end{массив}\right][ /latex]
Квадратная матрица — это матрица с размерами [latex]\text{ }n\text{ }\times \text{ }n,\text{}[/latex], что означает, что она имеет тот же номер строк как столбцов. Матрица [latex]3\times 3[/latex] выше является примером квадратной матрицы.
Матрица из строк — это матрица, состоящая из одной строки с размерами [латекс]1\текст{ }\times \text{ }n[/латекс].
[латекс]\left[\begin{array}{ccc}{a}_{11}& {a}_{12}& {a}_{13}\end{array}\right][/latex ]
Матрица столбцов — это матрица, состоящая из одного столбца с размерами [latex]m\text{ }\times \text{ }1[/latex].
[латекс]\left[\begin{array}{c}{a}_{11}\\ {a}_{21}\\ {a}_{31}\end{array}\right][ /latex]
Матрица может использоваться для представления системы уравнений. В этих случаях числа представляют собой коэффициенты переменных в системе. Матрицы часто облегчают решение систем уравнений, потому что они не перегружены переменными. Мы исследуем эту идею подробнее в следующем разделе, но сначала мы рассмотрим основные матричные операции .
A Общее примечание: Матрицы
A Матрица представляет собой прямоугольный массив чисел, который обычно обозначается заглавной буквой: [latex]A,B,C,\text{}[/latex] и так далее. Каждая запись в матрице обозначается как [latex]{a}_{ij}[/latex], так что [latex]i[/latex] представляет строку, а [latex]j[/latex] представляет столбец. Матрицы часто упоминаются по их размерам: [латекс]m\times n[/латекс] указывает [латекс]m[/латекс] строк и [латекс]n[/латекс] столбцов.
Пример: нахождение размеров заданной матрицы и поиск элементов
заданная матрица [latex]A:[/latex]
Каковы размеры матрицы [latex]A?[/latex]
Что такое записи в [latex]{a}_{31}[/latex] и [latex]{a}_{22}?[/latex]
[латекс]A=\left[\begin{array}{rrrr}\hfill 2& \hfill & \hfill 1& \hfill 0\\ \hfill 2& \hfill & \hfill 4& \hfill 7\\ \hfill 3& \ hfill & \hfill 1& \hfill -2\end{массив}\right][/latex]
Показать раствор
Попробуйте
Сложение и вычитание матриц
Мы используем матрицы для перечисления данных или для представления систем. Поскольку записи являются числами, мы можем выполнять операции над матрицами. Мы добавляем или вычитаем матрицы, добавляя или вычитая соответствующие элементы.
Для этого записи должны совпадать. Поэтому сложение и вычитание матриц возможны только тогда, когда матрицы имеют одинаковые размеры . Мы можем добавить или вычесть матрицу [латекс]\текст{ }3\текст{ }\times \text{ }3\текст{ }[/латекс] и другую матрицу [латекс]\текст{ }3\текст{ }\times \text{ }3\text{ }[/latex] матрица, но мы не можем складывать или вычитать матрицу [latex]\text{ }2\text{ }\times \text{ }3\text{ }[/latex] и матрица [latex]\text{ }3\text{ }\times \text{ }3\text{ }[/latex], поскольку некоторым элементам в одной матрице не будет соответствующего элемента в другой матрице.
A Общее примечание: сложение и вычитание матриц
Даны матрицы [латекс]А[/латекс] и [латекс]В[/латекс] одинакового размера, сложение и вычитание [латекс]А[/латекс] и [латекс ]B[/latex] создаст матрицу [latex]C[/latex] или матрицу [latex]D[/latex] того же размера.
[латекс]A+B=C\text{ такой, что }{a}_{ij}+{b}_{ij}={c}_{ij}[/latex]
[латекс]A-B= D\text{ такое, что }{a}_{ij}-{b}_{ij}={d}_{ij}[/latex]
Сложение матриц коммутативно.
[латекс]А+В=В+А[/латекс]
Это тоже ассоциативно.
[латекс]\влево(А+В\вправо)+С=А+\влево(В+С\вправо)[/латекс]
Пример: нахождение суммы матриц
Нахождение суммы [латекс]А [/latex] и [latex]B \text{}[/latex] заданы
[latex]A=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right] \text{ and }B=\left[\begin{array}{cc}e& f\\ g& h\end{array}\right][/latex]
Показать решение
Пример: добавление матрицы
A и Matrix B
Найдите сумму [латекс]А[/латекс] и [латекс]В[/латекс].
[латекс]A=\left[\begin{array}{cc}4& 1\\ 3& 2\end{array}\right]\text{ и }B=\left[\begin{array}{cc} 5& 9\\ 0& 7\end{массив}\right][/latex]
Показать решение
Пример: нахождение разности двух матриц
Найдите разность [латекс]А[/латекс] и [латекс]В[/латекс].
[латекс]A=\left[\begin{array}{cc}-2& 3\\ 0& 1\end{array}\right]\text{ и }B=\left[\begin{array}{cc} 8& 1\\ 5& 4\end{массив}\right][/латекс]
Показать раствор
Пример: нахождение суммы и разности двух матриц 3 x 3
Даны [латекс]А[/латекс] и [латекс]В:[/латекс]
Найдите сумму.
Найдите разницу.
[латекс]A=\left[\begin{array}{rrr}\hfill 2& \hfill -10& \hfill -2\\ \hfill 14& \hfill 12& \hfill 10\\ \hfill 4& \hfill -2& \ hfill 2\end{массив}\right]\text{ и }B=\left[\begin{array}{rrr}\hfill 6& \hfill 10& \hfill -2\\ \hfill 0& \hfill -12& \hfill – 4\\ \hfill -5& \hfill 2& \hfill -2\end{массив}\right][/latex]
Показать раствор
Попробуйте
Добавьте матрицу [латекс]А[/латекс] и матрицу [латекс]В[/латекс].
[латекс]A=\left[\begin{array}{rr}\hfill 2& \hfill 6\\ \hfill 1& \hfill 0\\ \hfill 1& \hfill -3\end{массив}\right]\ text{и}B=\left[\begin{array}{rr}\hfill 3& \hfill -2\\ \hfill 1& \hfill 5\\ \hfill -4& \hfill 3\end{array}\right][ /латекс]
Показать решение
Произведения матриц
Помимо сложения и вычитания целых матриц, во многих ситуациях нам нужно умножить матрицу на константу, называемую скаляром. Напомним, что скаляр — это действительная числовая величина, которая имеет величину, но не направление. Например, время, температура и расстояние являются скалярными величинами. Процесс скалярного умножения включает умножение каждого элемента матрицы на скаляр. Скалярное число , кратное , — это любой элемент матрицы, полученный в результате скалярного умножения.
Рассмотрим реальный сценарий, в котором университету необходимо добавить к своему инвентарю компьютеры, компьютерные столы и стулья в двух лабораториях кампуса из-за увеличения числа учащихся. По их оценкам, в обеих лабораториях требуется на 15% больше оборудования. Текущий инвентарь школы отображается в таблице ниже.
Лаборатория А Лаборатория Б
Компьютеры 15 27
Компьютерные столы 16 34
Стулья 16 34
Преобразовав данные в матрицу, мы имеем
[латекс]{C}_{2013}=\left[\begin{array}{c}15\\ 16\\ 16\end{array}\ begin{array}{c}27\\ 34\\ 34\end{array}\right][/latex]
Чтобы рассчитать, сколько потребуется компьютерного оборудования, мы умножаем все элементы в матрице [latex]C[/latex] на 0,15.
[латекс]\влево(0,15\вправо){C}_{2013}=\влево[\begin{массив}{c}\влево(0,15\вправо)15\\ \влево(0,15\вправо)16\ \\left(0.15\right)16\end{массив}\begin{массив}{c}\left(0.15\right)27\\ \left(0.15\right)34\\ \left(0.15\right)34 \end{массив}\right]=\left[\begin{массив}{c}2.25\\ 2.4\\ 2.4\end{массив}\begin{массив}{c}4.05\\ 5.1\\ 5.1\end{ array}\right][/latex]
Мы должны округлить до следующего целого числа, поэтому количество необходимого нового оборудования равно
[латекс]\влево[\begin{array}{c}3\\ 3\\ 3\end{массив}\begin{массив}{c}5\\ 6\\ 6\end{массив}\right ][/latex]
Добавив две матрицы, как показано ниже, мы увидим новые суммы запасов.
[латекс]\влево[\begin{массив}{c}15\\ 16\\ 16\конец{массив}\begin{массив}{c}27\\ 34\\ 34\конец{массив}\вправо ]+\left[\begin{array}{c}3\\ 3\\ 3\end{array}\begin{array}{c}5\\ 6\\ 6\end{array}\right]=\ left[\begin{array}{c}18\\ 19\\ 19\end{array}\begin{array}{c}32\\ 40\\ 40\end{array}\right][/latex]
Это означает
[латекс]{C}_{2014}=\left[\begin{array}{c}18\\ 19\\ 19\end{array}\begin{array}{c}32\\ 40\\ 40\end{array}\right][/latex]
Таким образом, в лаборатории А будет 18 компьютеров, 19 компьютерных столов и 19 стульев; В лаборатории B будет 32 компьютера, 40 компьютерных столов и 40 стульев.
A Общее примечание: Скалярное умножение
Скалярное умножение включает в себя нахождение произведения константы по каждому элементу матрицы. Учитывая
[латекс]A=\left[\begin{array}{cccc}{a}_{11}& & & {a}_{12}\\ {a}_{21}& & & {a }_{22}\end{массив}\right][/latex]
скалярное кратное [латекс]cA[/латекс] равно
[латекс]\begin{array}{ll}cA & =c\left[\begin{array}{ccc}{a}_{11}& & {a}_{12}\\ {a}_{21}& & {a}_{22}\end{массив}\right]\hfill \\ & =\left[\begin{массив}{ccc }c{a}_{11}& & c{a}_{12}\\ c{a}_{21}& & c{a}_{22}\end{массив}\right]\hfill \ end{array}[/latex]
Скалярное умножение является дистрибутивным. Для матриц [latex]A,B[/latex] и [latex]C[/latex] со скалярами [latex]a[/latex] и [latex]b[/latex],
[латекс]\begin{array}{l}\\ \begin{array}{c}a\left(A+B\right)=aA+aB\\ \left(a+b\right)A= aA+bA\end{array}\end{array}[/latex]
Пример: умножение матрицы на скаляр
Умножение матрицы [latex]A[/latex] на скаляр 3.
[latex]A =\left[\begin{array}{cc}8& 1\\ 5& 4\end{array}\right][/latex]
Показать решение
Попробуйте
По заданной матрице [латекс]B,\текст{}[/латекс] найдите [латекс]-2В[/латекс], где
[латекс]В=\left[\begin{array}{cc} 4& 1\\ 3& 2\end{массив}\right][/latex]
Показать раствор
Пример: нахождение суммы скалярных множителей
Найдите сумму [латекс]3А+2В[/латекс].
[латекс]A=\left[\begin{array}{rrr}\hfill 1& \hfill -2& \hfill 0\\ \hfill 0& \hfill -1& \hfill 2\\ \hfill 4& \hfill 3& \hfill -6\end{массив}\right]\text{ и }B=\left[\begin{array}{rrr}\hfill -1& \hfill 2& \hfill 1\\ \hfill 0& \hfill -3& \hfill 2 \\ \hfill 0& \hfill 1& \hfill -4\end{массив}\right][/latex]
Показать решение
Попробуйте
Нахождение произведения двух матриц
Помимо умножения матрицы на скаляр, мы можем умножать две матрицы. Нахождение произведения двух матриц возможно только тогда, когда внутренние размерности совпадают, что означает, что количество столбцов первой матрицы равно количеству строк второй матрицы. Если [latex]A[/latex] является матрицей [latex]\text{ }m\text{ }\times \text{ }r\text{ }[/latex], а [latex]B[/latex] является [latex]\text{ }r\text{ }\times \text{ }n\text{ }[/latex] матрица, то матрица произведения [latex]AB[/latex] является [latex]\text{ } m\text{ }\times \text{ }n\text{ }[/latex] матрица. Например, продукт [latex]AB[/latex] возможен, потому что количество столбцов в [latex]A[/latex] совпадает с количеством строк в [latex]B[/latex]. Если внутренние размеры не совпадают, товар не определяется.
Мы умножаем записи [latex]A[/latex] на записи [latex]B[/latex] в соответствии с определенным шаблоном, как показано ниже. Процесс умножения матрицы на становится понятнее при решении задачи с вещественными числами.
Чтобы получить элементы в строке [latex]i[/latex] массива [latex]AB,\text{}[/latex], мы умножаем элементы в ряду [latex]i[/latex] массива [latex]A[ /latex] по столбцу [latex]j[/latex] в [latex]B[/latex] и добавить. Например, даны матрицы [латекс]А[/латекс] и [латекс]В,\текст{}[/латекс], где размеры [латекс]А[/латекс] равны [латекс]2\текст{ }\times \text{ }3[/latex] и размеры [latex]B[/latex] равны [latex]3\text{ }\times \text{ }3,\text{}[/latex] произведению [ latex]AB[/latex] будет матрицей [latex]2\text{ }\times \text{ }3[/latex].
[латекс]A=\left[\begin{array}{rrr}\hfill {a}_{11}& \hfill {a}_{12}& \hfill {a}_{13}\\ \ hfill {a}_{21}& \hfill {a}_{22}& \hfill {a}_{23}\end{массив}\right]\text{ и }B=\left[\begin{массив }{rrr}\hfill {b}_{11}& \hfill {b}_{12}& \hfill {b}_{13}\\ \hfill {b}_{21}& \hfill {b} _{22}& \hfill {b}_{23}\\ \hfill {b}_{31}& \hfill {b}_{32}& \hfill {b}_{33}\end{массив} \right][/latex]
Умножьте и сложите следующим образом, чтобы получить первую запись матрицы произведения [latex]AB[/latex].
Чтобы получить запись в строке 1, столбце 1 [latex]AB,\text{}[/latex] умножьте первую строку в [latex]A[/latex] на первый столбец в [latex]B[ /латекс] и добавить.
[латекс]\влево[\begin{array}{ccc}{a}_{11}& {a}_{12}& {a}_{13}\end{массив}\right]\cdot \left [\begin{массив}{c}{b}_{11}\\ {b}_{21}\\ {b}_{31}\end{массив}\right]={a}_{11} \cdot {b}_{11}+{a}_{12}\cdot {b}_{21}+{a}_{13}\cdot {b}_{31}[/latex]
Чтобы получить запись в строке 1, столбце 2 [latex]AB,\text{}[/latex] умножьте первую строку [latex]A[/latex] на вторую колонку в [latex]B[/latex]. ] и добавить.
[латекс]\влево[\begin{array}{ccc}{a}_{11}& {a}_{12}& {a}_{13}\end{массив}\right]\cdot \left [\begin{массив}{c}{b}_{12}\\ {b}_{22}\\ {b}_{32}\end{массив}\right]={a}_{11} \cdot {b}_{12}+{a}_{12}\cdot {b}_{22}+{a}_{13}\cdot {b}_{32}[/latex]
Чтобы получить запись в строке 1, столбце 3 в [latex]AB,\text{}[/latex] умножьте первую строку [latex]A[/latex] на третий столбец в [latex]B[/latex]. ] и добавить.
[латекс]\влево[\begin{array}{ccc}{a}_{11}& {a}_{12}& {a}_{13}\end{массив}\right]\cdot \left [\begin{массив}{c}{b}_{13}\\ {b}_{23}\\ {b}_{33}\end{массив}\right]={a}_{11} \cdot {b}_{13}+{a}_{12}\cdot {b}_{23}+{a}_{13}\cdot {b}_{33}[/latex]
Таким же образом получаем вторую строку [latex]AB[/latex]. Другими словами, строка 2 таблицы [latex]A[/latex] умножается на столбец 1 таблицы [latex]B[/latex]; 2-я строка [latex]A[/latex] умножается на 2-й столбец [latex]B[/latex]; строка 2 из [latex]A[/latex] умножается на столбец 3 из [latex]B[/latex]. По завершении матрица продуктов будет
[латекс]AB=\left[\begin{array}{c}\begin{array}{l}{a}_{11}\cdot {b}_{11} +{a}_{12}\cdot {b}_{21}+{a}_{13}\cdot {b}_{31}\\ \end{массив}\\ {a}_{21} \cdot {b}_{11}+{a}_{22}\cdot {b}_{21}+{a}_{23}\cdot {b}_{31}\end{массив}\begin {массив}{c}\begin{массив}{l}{a}_{11}\cdot {b}_{12}+{a}_{12}\cdot {b}_{22}+{a }_{13}\cdot {b}_{32}\\ \end{массив}\\ {a}_{21}\cdot {b}_{12}+{a}_{22}\cdot { b}_{22}+{a}_{23}\cdot {b}_{32}\end{массив}\begin{массив}{c}\begin{массив}{l}{a}_{11 }\cdot {b}_{13}+{a}_{12}\cdot {b}_{23}+{a}_{13}\cdot {b}_{33}\\ \end{массив }\\ {a}_{21}\cdot {b}_{13}+{a}_{22}\cdot {b}_{23}+{a}_{23}\cdot {b}_ {33}\end{массив}\right][/latex]
A Общее примечание: свойства умножения матриц
Для матриц [latex]A,B,\text{}[/latex] и [latex]C[/latex] выполняются следующие свойства.
Умножение матриц ассоциативно:
[латекс]\влево(AB\вправо)C=A\влево(BC\вправо)[/латекс]
Умножение матриц распределительное:
[латекс]\begin{массив}{l}\begin{массив}{l}\\ C\left(A+B\right)=CA+CB,\end{массив}\hfill \\ \left(A +B\right)C=AC+BC.\hfill \end{массив}[/latex]
Обратите внимание, что умножение матриц не является коммутативным.
Пример: перемножение двух матриц
Умножьте матрицу [латекс]А[/латекс] и матрицу [латекс]В[/латекс].
[латекс]A=\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]\text{ и }B=\left[\begin{array}{cc} 5& 6\\ 7& 8\end{массив}\right][/latex]
Показать решение
Пример. Умножение двух матриц
Даны [латекс]А[/латекс] и [латекс]В:[/латекс]
Найти [латекс]AB[/латекс].
Найти [латекс]БА[/латекс].
[латекс]A=\left[\begin{array}{l}\begin{array}{ccc}-1& 2& 3\end{array}\hfill \\ \begin{array}{ccc}4& 0& 5 \end{массив}\hfill \end{массив}\right]\text{ и }B=\left[\begin{массив}{c}5\\ -4\\ 2\end{массив}\begin{массив }{c}-1\\ 0\\ 3\end{массив}\right][/latex]
Показать решение
Вопросы и ответы
Можно ли определить AB, но не BA?
Да, рассмотрим матрицу A размерностью [латекс]3\умножить на 4[/латекс] и матрицу В размерностью [латекс]4\умножить на 2[/латекс]. Для продукта AB внутренние размеры равны 4, и продукт определен, но для продукта BA внутренние размеры равны 2 и 3, поэтому продукт не определен.
Пример: использование матриц в реальных задачах
Вернемся к задаче, представленной в начале этого раздела. У нас есть таблица ниже, представляющая потребности в оборудовании двух футбольных команд.
Дикие кошки Грязевые коты
Цели 6 10
Шарики 30 24
Трикотажные изделия 14 20
Нам также предоставлены цены на оборудование, как показано в таблице ниже.
Цель $300
Шар 10 долларов
Джерси $30
Преобразуем данные в матрицы. Таким образом, матрица потребности в оборудовании записывается как
[латекс]E=\left[\begin{array}{c}6\\ 30\\ 14\end{array}\begin{array}{c}10\\ 24\\ 20\end{array}\ right][/latex]
Матрица стоимости записывается как
[latex]C=\left[\begin{array}{ccc}300& 10& 30\end{array}\right][/latex]
Выполняем умножение матриц для получения стоимости оборудования.
[латекс]\begin{array}{l}\hfill \\ \hfill \\ CE & =\left[\begin{array}{rrr}\hfill 300& \hfill 10& \hfill 30\end{массив}\right ]\cdot \left[\begin{array}{rr}\hfill 6& \hfill 10\\ \hfill 30& \hfill 24\\ \hfill 14& \hfill 20\end{массив}\right]\hfill \\ & = \left[\begin{array}{rr}\hfill 300\left(6\right)+10\left(30\right)+30\left(14\right)& \hfill 300\left(10\right) +10\влево(24\вправо)+30\влево(20\вправо)\конец{массив}\вправо]\hfill \\ & =\влево[\begin{массив}{rr}\hfill 2520& \hfill 3840 \end{массив}\right]\hfill \end{массив}[/latex]
Общая стоимость оборудования для Wildcats составляет 2520 долларов США, а общая стоимость оборудования для Mudcats составляет 3840 долларов США.
Как выполнить операцию с матрицей, вычислить ее с помощью калькулятора

Сохранить каждую матрицу как матричную переменную
[латекс]\влево[A\вправо],\влево[B\вправо],\влево[C\вправо],..[/латекс]
Введите операцию в калькулятор, вызывая каждую переменную матрицы по мере необходимости.
Если операция определена, калькулятор представит матрицу решения; если операция не определена, будет отображаться сообщение об ошибке.
Пример: использование калькулятора для выполнения операций с матрицами \hfill 32\\ \hfill 41& \hfill -7& \hfill -28\\ \hfill 10& \hfill 34& \hfill -2\end{массив}\right],B=\left[\begin{array}{rrr} \hfill 45& \hfill 21& \hfill -37\\ \hfill -24& \hfill 52& \hfill 19\\ \hfill 6& \hfill -48& \hfill -31\end{массив}\right],\text{and}C =\left[\begin{массив}{rrr}\hfill -100& \hfill -89& \hfill -98\\ \hfill 25& \hfill -56& \hfill 74\\ \hfill -67& \hfill 42& \hfill -75\end{массив}\right][/latex].

Показать решение
Ключевые понятия
Матрица представляет собой прямоугольный массив чисел. Записи расположены в строках и столбцах.
Размеры матрицы относятся к количеству строк и количеству столбцов. Матрица [latex]3\times 2[/latex] имеет три строки и два столбца.
Мы складываем и вычитаем матрицы одинаковой размерности, добавляя и вычитая соответствующие элементы каждой матрицы.
Скалярное умножение включает умножение каждого элемента матрицы на константу.
Перед сложением или вычитанием часто требуется скалярное умножение.
Перемножение матриц возможно при одинаковых внутренних размерностях — количество столбцов в первой матрице должно совпадать с количеством строк во второй.
Произведение двух матриц, [латекс]А[/латекс] и [латекс]В[/латекс], получается путем умножения каждой записи в строке 1 матрицы [латекс]А[/латекс] на каждую запись в столбце 1 матрицы [латекс]В[/латекс]; затем умножьте каждую запись строки 1 [latex]A[/latex] на каждую запись в столбцах 2 [latex]B,\text{}[/latex] и так далее.
Многие реальные проблемы часто можно решить с помощью матриц.
Мы можем использовать калькулятор для выполнения матричных операций после сохранения каждой матрицы как матричной переменной.
Глоссарий
столбец
набор чисел, выровненных по вертикали в матрице
запись
элемент, коэффициент или константа в матрице
матрица
прямоугольный массив чисел
ряд
набор чисел, выровненных по горизонтали в матрице
скалярное кратное
запись матрицы, которая была умножена на скаляр
Операции с матрицами — сложение, вычитание, умножение, формулы, примеры
К матричным операциям относятся арифметические операции сложения, вычитания, умножения матриц. Кроме того, мы можем найти транспонирование и инверсию матрицы, которые также могут быть включены как операции над матрицами. Операции с матрицами помогают объединять две или более матриц в одну матрицу.
Давайте узнаем больше о различных матричных операциях с решенными примерами и практическими задачами.
1. Что такое матричные операции?
2. Дополнение – Матричные операции
3. Вычитание — матричные операции
4. Умножение — Операции с матрицами
5. Операция транспонирования матрицы
6. Обратная операция матрицы
7. Примеры матричных операций
8. Практические вопросы
9. Часто задаваемые вопросы о матричных операциях
Что такое матричные операции?
Операции с матрицами помогают нам объединить две или более матриц, чтобы сформировать одну матрицу. Над матрицами также можно выполнять арифметические операции сложения, вычитания, умножения. Кроме того, иногда матричные операции могут изменить саму матрицу. Операция транспонирования матрицы, обратная матрице, помогает преобразовать конкретную матрицу в саму себя.
Ниже перечислены некоторые важные матричные операции.
Дополнение — операции с матрицами
Вычитание — операции с матрицами
Умножение — операции с матрицами
Операция транспонирования матрицы
Обратная операция матрицы
Дополнение – Операции с матрицами
Сложение матриц — одна из основных операций, выполняемых над матрицами. Две или более матриц одного порядка могут быть добавлены путем добавления соответствующих элементов матриц. Если A = [$a_{ij}$] и B = [$b_{ij}$] — две матрицы с одинаковой размерностью, т. е. с одинаковым количеством строк и столбцов, то сложение матриц A и B: A+B = [$a_{ij}$] + [$b_{ij}$] = [$a_{ij}+b_{ij}$].
Матрицы для сложения могут быть как квадратными, так и прямоугольными, но матрицы должны быть одного порядка.
Сложение матриц подчиняется аналогичным свойствам сложения чисел: закону коммутации, ассоциативному закону, аддитивному обратному, аддитивному тождеству и т. д. Следующие свойства помогают в операциях сложения матриц.
Коммутативное свойство сложения матриц для матриц A = [$a_{ij}$] и B = [$b_{ij}$] одного порядка m × n равно A + B = B + А.
Ассоциативное свойство сложения матриц для матриц A = [$a_{ij}$], B = [$b_{ij}$] и C = [$c_{ij}$] одного порядка m × n равно (A+B)+C = A+(B+C).
Аддитивное тождество сложения матриц для матрицы A = [$a_{ij}$] порядка m × n — это нулевая матрица O порядка m × n такая, что A + O = O + A = A.
Аддитивное действие, обратное сложению матриц для матрицы A = [$a_{ij}$] порядка m × n, равно -A = [$-a_{ij}$] того же порядка m × n такое, что А + (-А) = О = А + (-А). .
Транспонировать Свойство сложения матриц для двух матриц A = [$a_{ij}$] и B = [$b_{ij}$] одного порядка: (A + B) ^T = A ^Т + Б ^Т
Определяющее свойство сложения матриц для двух матриц A = [$a_{ij}$] и B = [$b_{ij}$] одного порядка: |A + B| = |А| + |Б|
Вычитание — Операции с матрицами
Вычитание матриц — это матричная операция поэлементного вычитания матриц одного порядка, то есть матриц, имеющих одинаковое количество строк и столбцов. При вычитании двух матриц мы вычитаем элементы в каждой строке и столбце из соответствующих элементов в строке и столбце другой матрицы.
Рассмотрим две матрицы A и B одного и того же порядка m × n, где m — количество строк, а n — количество столбцов двух матриц, обозначаемых как A = [$a_{ij}\ )] и B = [\(b_{ij}$]. Теперь разность двух матриц A и B определяется как: A – B = [$a_{ij}$] – [$b_{ij}$] = [$a_{ij}-b_ {ij}$], где ij обозначает позицию каждого элемента в i ^-й-й строке и j ^-м-м столбце. Размерность разностной матрицы, то есть A – B, также равна m × n’.
Самая важная необходимость для вычитания матриц для сохранения всех этих свойств заключается в том, что вычитание матриц определяется только в том случае, если порядок матриц одинаков.
Количество строк и столбцов в соответствующих матрицах должно быть одинаковым для вычитания матриц.
Вычитание матриц некоммутативно, т. е. А – В ≠ В – А
Вычитание матриц не является ассоциативным, то есть (А – В) – С ≠ А – (В – С)
Вычитание матрицы из самой себя приводит к нулевой матрице, то есть A – A = O.
Вычитание матриц — это прибавление отрицательного значения одной матрицы к другой матрице, то есть A – B = A + (-B).
Умножение — операции с матрицами
Умножение матриц — это операция над двоичной матрицей, выполняемая над матрицей A и матрицей B, когда обе заданные матрицы совместимы. Основным условием умножения двух матриц является то, что количество столбцов в первой матрице должно быть равно количеству строк во второй матрице, и, следовательно, важен порядок матрицы. Умножение матриц не подчиняется коммутативному закону AB ≠ BA.
Две матрицы A и B называются совместимыми, если количество столбцов в A равно количеству строк в B. Результирующая матрица для умножения матрицы A порядка m × n на матрицу B порядка n × p — матрица C порядка m × p.
Для умножения двух матриц элементы строк матрицы умножаются на элементы столбцов следующей матрицы, и суммирование этого произведения дает элементы результирующей матрицы произведения. Это можно более ясно понять из приведенного ниже умножения двух матриц порядка 3 x 3.
Следующие свойства умножения матриц полезны для выполнения операции умножения матриц.
Некоммутативный для умножения матриц: Умножение матриц является некоммутативным, и произведение AB не равно произведению BA, AB ≠ BA.
Правильное распределение над сложением матриц для Матричное умножение матрицы A и матрицы B на другую матрицу C равно A(B + C) = AB + BC.
Умножение матриц на скаляр k для матриц A и B определяется как k(AB) = (kA)B = A(Bk).
Свойство транспонирования матричного умножения для двух матриц A и B может быть задано как (AB) ^T = B ^T A ^T
Комплексно-сопряженное свойство матричного умножения для двух матриц A и B равно (AB) ^* = B ^* A ^*
Ассоциативность для умножения матриц для трех матриц A, B и C, так что произведения (AB)C и A(BC) определяются как (AB)C = A(BC).
Скалярное умножение матрицы является произведением скалярного значения константы на каждый из элементов матрицы. Следующие свойства скалярного умножения матриц помогают легко выполнять скалярное умножение матриц. Здесь у нас есть две матрицы A, B и k, l — значения скалярных констант.
К(А + В) = КА + КБ
(К + 1)А = КА + 1А
(Кл)А = К(1А) = 1(КА)
Операция транспонирования матрицы
Матрица, полученная из данной матрицы после замены или обращения ее строк в столбцы и столбцов в строки, называется транспонированием матрицы. Прямоугольный массив чисел или функций, расположенных в виде строк и столбцов, называется матрицей. Этот массив чисел называется элементами или элементами матрицы. После нахождения транспонирования матрицы порядок матрицы изменяется с порядка m × n на порядок n × m.
Здесь для матрицы A элементы первой строки записаны в первый столбец новой матрицы, а элементы второй строки записаны во второй столбец новой матрицы. И эта новая матрица обозначается как A ^T , что является транспонированием данной матрицы A.
Порядок матрицы представляет количество строк и столбцов в данной матрице. Все горизонтальные линии элементов называются строками матрицы, обозначаемой буквой n, а вертикальные линии элементов называются столбцами матрицы, обозначаемой буквой m. Вместе они представляют порядок матрицы, который записывается как n × м. А порядок транспонирования данной матрицы записывается как m x n.
Давайте проверим приведенный ниже пример, чтобы лучше понять, как найти транспонирование матрицы.
A = $\left[\begin{массив}{ll}
-2&5&6\
5 и 2 и 7
\end{array}\right]$
В приведенном выше примере мы видим, что заданная матрица порядка 2 × 3. Элементы первой строки [-2, 5, 6] записаны в виде первый столбец, а элементы второй строки [5, 2, 7] записываются во второй столбец, чтобы получить транспонированную матрицу. Транспонирование матрицы A равно A ^T и имеет порядок 3 x 2.
A ^T = $\left[\begin{array}{ll}
-2 и 5\
5 и 2 \\6 и 7
\end{array}\right]$
Существуют различные свойства, связанные с операцией перестановки в матрицах, для матриц A и B, заданные как
(A ^T ) ^T = A
(A + B) ^T = A ^T + B ^T , A и B одного порядка.
(KA) ^T = KA ^T , K — любой скаляр (действительный или комплексный).
(AB) ^T = B ^T A ^T , A и B соответствуют продукту AB. (Этот закон также называют обратным законом.)
Обратная операция матрицы
Обратная матрица — это другая матричная операция, которая при умножении на данную матрицу дает мультипликативное тождество. Для матрицы A ее обратной является A ^-1 , а A.A ^-1 = I. Общая формула обратной матрицы порядка 2 × 2 равна сопряженной матрице, деленной на определитель матрицы. Обратная матрица существует только в том случае, если определитель матрицы имеет ненулевое значение. Матрица, определитель которой отличен от нуля и для которой можно вычислить обратную матрицу, называется обратимой матрицей.
A = $\left(\begin{matrix}a&b\\c&d\end{matrix}\right)$
A ^-1 = $\dfrac{1}{ad – bc}\left (\begin{matrix}d&-b\\-c&a\end{matrix}\right)$
A ^-1 = $\dfrac{1}{|A|}$ Adj A
Кроме того, для матриц более высокого порядка обратную матрицу можно вычислить, разделив сопряженную часть матрица на определитель матрицы. Обратную матрицу можно вычислить, выполнив следующие шаги:

Шаг 1: Вычислите минор для данной матрицы.
Шаг 2: Преобразование полученной матрицы в матрицу кофакторов
9{1 + 3} \left|\begin{matrix}a_{21}&a_{22}\\a_{31}&a_{32}\end{matrix}\right|\)
Adj A = Транспонирование матрицы кофакторов = Транспонирование $\begin{pmatrix} A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{32}&A_{33} \end{pmatrix}$ =$\begin{pmatrix} A_{11}&A_{21}&A_{31}\\A_{12}&A_{22}&A_{32}\\A_{13}&A_{23 }&A_{33}\end{pmatrix}$
A ^-1 = $\dfrac{1}{|A|}.\begin{pmatrix} A_{11}&A_{21}&A_{31} \\A_{12}&A_{22}&A_{32}\\A_{13}&A_{23}&A_{33}\end{pmatrix}$
Связанные темы
Следующие темы помогают лучше понять матричные операции.
Орден Матрицы
Ортогональная матрица
Симметричная матрица
Обратимая матрица
Сопряженная матрица
Транспонирование матрицы
Часто задаваемые вопросы о матричных операциях
Что такое матричные операции?
Операции с матрицами аналогичны арифметическим операциям, выполняемым над двумя или более числами. матричные операции включают сложение, вычитание, умножение матриц, транспонирование матрицы и обращение матрицы. Сложение, вычитание, умножение матриц включают две и более матриц, а транспонирование, обратные операции выполняются только над одной матрицей.
Какие три важные операции с матрицами?
Три важные матричные операции – операция сложения матриц, операция вычитания матриц и операция умножения матриц. Эти три важные операции помогают в объединении двух или более матриц. Здесь с помощью этих трех операций манипулируют отдельными элементами матриц для выполнения операций. Помимо сложения и вычитания матриц соответствующие элементы двух или более матриц добавляются или вычитаются для получения элементов результирующей матрицы.
Каковы условия для различных типов матричных операций?
Условие для матричных операций зависит от типа операции. Для сложения и вычитания матриц порядок обеих матриц должен быть одинаковым. Для умножения двух матриц порядок двух матриц таков, что количество столбцов в первой матрице равно количеству строк во второй матрице.
Какие существуют типы операций над матрицей умножения?
Операции с матрицами умножения бывают двух типов. Скалярное умножение матрицы и умножение двух или более матриц. Скалярное умножение включает в себя умножение скалярного значения на матрицу, которая включает в себя умножение каждого элемента матрицы на скалярное значение. А умножение матриц, включающих две матрицы, возможно, если количество столбцов в первой матрице равно количеству строк во второй матрице.
Для чего используются матричные операции?
Операции с матрицами полезны для объединения двух или более матриц в одну матрицу. Кроме того, матричные операции полезны для решения алгебраических уравнений с двумя или более переменными. Область искусственного интеллекта и машинного обучения в значительной степени зависит от операций с матрицами для одновременного представления множества переменных и работы с ними.
Операции со строками матрицы
Над строками используются 3 основные операции. матрица когда вы используете матрицу для решить систему линейных уравнений . Обычно цель состоит в том, чтобы левая часть матрицы выглядела как единичная матрица .
Три операции:
Переключение строк
Умножение строки на число
Добавление строк
Переключение строк
Вы можете поменять местами строки матрицы, чтобы получить новую матрицу.
[ 2 3 − 2 6 0 0 3 − 6 1 0 2 − 3 ] → [ 1 0 2 − 3 2 3 − 2 6 0 0 3 − 6 ]
В примере, показанном выше, мы перемещаем строку 1 грести 2 , Строка 2 грести 3 , и Строка 3 грести 1 . (Причина для этого состоит в том, чтобы получить 1 в левом верхнем углу.)
Умножение строки на число
Вы можете умножить любую строку на число. (Это означает умножение каждой записи в строке на одно и то же число.)
[ 1 0 2 − 3 2 3 − 2 6 0 0 3 − 6 ] → р 3 : 1 3 р 3 [ 1 0 2 − 3 2 3 − 2 6 0 0 1 − 2 ]
В этом примере мы умножили строку 3 матрицы на 1 3 . (Это дает нам 1 нам нужно в строке 3 , Столбец 3 .)
Добавление строк
Вы также можете добавить две строки вместе и заменить строку результатом.
Например, в матрицу, полученную в последнем примере, мы можем добавить строки 2 а также 3 вместе, запись за записью:
[ 2 3 − 2 6 ] + [ 0 0 1 − 2 ] _ [ 2 3 − 1 4 ]
Затем мы заменяем строку 2 с результатом.
[ 1 0 2 − 3 2 3 − 2 6 0 0 1 − 2 ] → р 2 : р 2 + р 3 [ 1 0 2 − 3 2 3 − 1 4 0 0 1 − 2 ]
Добавление нескольких строк
Мы сказали, что было всего три операции, и они есть. Но, используя последние две операции в сочетании, мы можем добавлять целые кратные строки к другим строкам, чтобы ускорить работу.
Шаг назад, поэтому у нас есть матрица:
[ 1 0 2 − 3 2 3 − 2 6 0 0 1 − 2 ]
Теперь вместо того, чтобы просто добавить строку 2 + Строка 3 , Добавить ряд 2 + ( 2 × Строка 3 ) :
[ 2 3 − 2 6 ] + [ 0 0 2 − 4 ] _ [ 2 3 0 2 ]
Затем замените строку 2 с результатом.
[ 1 0 2 − 3 2 3 − 2 6 0 0 1 − 2 ] → р 2 : р 2 + 2 р 3 [ 1 0 2 − 3 2 3 0 2 0 0 1 − 2 ]
Таким образом, мы получаем 0 в строке 2 , Столбец 3 .
Мы можем сделать это снова, чтобы получить 0 в строке 2 , Столбец 1 . Здесь мы умножаем ряд 1 по − 2 , добавьте строку 2 и замените строку 2 с результатом.
[ 1 0 2 − 3 2 3 0 2 0 0 1 − 2 ] → р 2 : − 2 р 1 + р 2 [ 1 0 2 − 3 0 3 − 4 8 0 0 1 − 2 ]
Мы покажем еще несколько шагов, чтобы получить 3 × 3 единичная матрица слева (и, таким образом, решить систему).
Следующим шагом является добавление Строка 2 + ( 4 × Строка 3 ) чтобы получить 0 в строке 2 , Столбец 3 .
[ 1 0 2 − 3 0 3 − 4 8 0 0 1 − 2 ] → р 2 : р 2 + 4 р 3 [ 1 0 2 − 3 0 3 0 0 0 0 1 − 2 ]
Далее нам нужен ноль в строке 1 , Столбец 3 .
[ 1 0 2 − 3 0 3 0 0 0 0 1 − 2 ] → р 1 : р 1 − 2 р 3 [ 1 0 0 1 0 3 0 0 0 0 1 − 2 ]
Последний шаг — это просто применение второй операции, умножение строки на число.
[ 1 0 0 1 0 3 0 0 0 0 1 − 2 ] → 1 3 р 3 [ 1 0 0 1 0 1 0 0 0 0 1 − 2 ]
Теперь у нас есть решение в виде заказанной тройки ( 1 , 0 , − 2 ) .
Важная заметка: Если уравнения, представленные вашей исходной матрицей, представляют собой одинаковые или параллельные линии, вы не сможете получить единичную матрицу, используя эти операции со строками. В этом случае решения либо не существует, либо существует бесконечно много решений системы.
7.5 Матрицы и операции с матрицами — College Algebra 2e
Цели обучения
В этом разделе вы:
Найдите сумму и разность двух матриц.
Найти скалярные кратные матрицы.
Найдите произведение двух матриц.
Рисунок 1 (Фото: «SD Dirk», Flickr)
Две клубные футбольные команды, Wildcats и Mud Cats, надеются приобрести новое оборудование к предстоящему сезону. В таблице 1 показаны потребности обеих команд.
Дикие кошки Грязевые коты
Цели 6 10
Шарики 30 24
Трикотажные изделия 14 20
Стол 1
Гол стоит 300 долларов; мяч стоит 10 долларов; а майка стоит 30 долларов. Как мы можем найти общую стоимость оборудования, необходимого для каждой команды? В этом разделе мы раскрываем метод, в котором данные в таблице футбольного оборудования могут отображаться и использоваться для расчета другой информации. После этого мы сможем рассчитать стоимость оборудования.
Нахождение суммы и разности двух матриц
Чтобы решить задачу, подобную описанной для футбольных команд, мы можем использовать матрицу, представляющую собой прямоугольный массив чисел. Строка в матрице — это набор чисел, выровненных по горизонтали. Столбец в матрице — это набор чисел, выровненных по вертикали. Каждое число является записью, иногда называемой элементом матрицы. Матрицы (во множественном числе) заключаются в [ ] или ( ) и обычно называются заглавными буквами. Например, ниже показаны три матрицы с именами A, B, A, B и CC.
A=[1234],B=[1270-56782],C=[-103321]A=[1234],B=[1270-56782],C=[-103321]
Описание матриц
Матрица часто упоминается по ее размеру или размерам: m×nm×n указывает мм строк и nn столбцов. Элементы матрицы определяются сначала по строке, а затем по столбцу. Например, чтобы найти запись в матрице AA, обозначенную как aij,aij, мы ищем запись в строке i,i, столбце j.j. В матрице A, A, , показанной ниже, запись в строке 2 столбца 3 имеет вид a23.a23.
А=[а11а12а13а21а22а23а31а32а33]А=[а11а12а13а21а22а23а31а32а33]
Квадратная матрица — это матрица размерами n×n,n×n, что означает, что в ней столько же строк, сколько столбцов. Приведенная выше матрица 3×33×3 является примером квадратной матрицы.
Матрица-строка — это матрица, состоящая из одной строки размерами 1×n.1×n.
[а11а12а13][а11а12а13]
Матрица-столбец — это матрица, состоящая из одного столбца с размерами m×1.m×1.
[а11а21а31][а11а21а31]
Матрица может использоваться для представления системы уравнений. В этих случаях числа представляют собой коэффициенты переменных в системе. Матрицы часто облегчают решение систем уравнений, потому что они не перегружены переменными.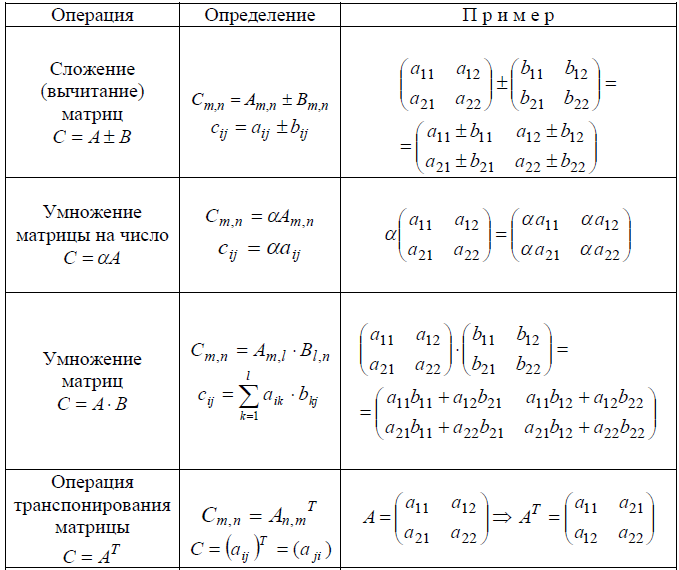 Мы рассмотрим эту идею подробнее в следующем разделе, но сначала мы рассмотрим основные матричные операции.
Матрицы
Матрица представляет собой прямоугольный массив чисел, который обычно обозначается заглавной буквой: A,B,C,A,B,C и так далее. Каждая запись в матрице обозначается как aij,aij, так что ii представляет строку, а jj представляет столбец. Матрицы часто обозначаются их размерами: m×nm×n указывает количество строк в миллиметрах и количество столбцов в nn.
Пример 1
Определение размеров данной матрицы и поиск элементов
Данная матрица A:A:
ⓐКаковы размеры матрицы A?A?
ⓑ Какие записи в a31a31 и a22?a22?
А=[21024731−2]А=[21024731−2]
Решение
ⓐРазмеры 3×33×3, потому что есть три строки и три столбца.
ⓑЗапись a31a31 — это число в строке 3 столбца 1, которое равно 3. Запись a22a22 — это число в строке 2 столбца 2, которое равно 4. Помните, сначала идет строка, затем столбец.
Сложение и вычитание матриц
Мы используем матрицы для перечисления данных или для представления систем. Поскольку записи являются числами, мы можем выполнять операции над матрицами. Мы добавляем или вычитаем матрицы, добавляя или вычитая соответствующие элементы.
Для этого записи должны совпадать. Следовательно, сложение и вычитание матриц возможно только тогда, когда матрицы имеют одинаковые размеры . Мы можем сложить или вычесть матрицу 3×33×3 и другую матрицу 3×33×3, но мы не можем сложить или вычесть матрицу 2×32×3 и матрицу 3×33×3, потому что некоторые элементы в одной матрице не будут иметь соответствующую запись в другой матрице.
Сложение и вычитание матриц
Имея матрицы AA и BB одинаковой размерности, сложение и вычитание AA и BB даст матрицу CC или
матрицу DD той же размерности.
A+B=C такой, что aij+bij=cijA+B=C такой, что aij+bij=cij
A−B=D такой, что aij-bij=dijA−B=D такой, что aij-bij=dij
Сложение матриц является коммутативным.
A+B=B+AA+B=B+A
Также является ассоциативным.
(А+В)+С=А+(В+С)(А+В)+С=А+(В+С)
Пример 2
Нахождение суммы матриц
Нахождение суммы AA и B,B по данным
A=[abcd]  и  B=[efgh]A=[abcd]  и  B=[efgh]
Решение
Добавить соответствующие записи.
A+B=[abcd]+[efgh]        =[a+eb+fc+gd+h]A+B=[abcd]+[efgh]        =[a+eb+fc+gd+h]
Пример 3
Сложение матрицы
A и матрицы B
Найдите сумму AA и B.B.
A=[4132] и  B=[5907]A=[4132] и  B=[5907]
Решение
Добавить соответствующие записи. Добавьте элемент в строке 1, столбце 1, a11,a11, матрицы AA к элементу в строке 1, столбце 1, b11,b11, матрицы BB. Продолжайте шаблон, пока не будут добавлены все элементы.
A+B=[4132]+[5907]        =[4+51+93+02+7]        =[
]A+B=[4132]+[5907]       =[4+51+93+02+ 7]        =[
]
Пример 4
Нахождение разности двух матриц
Нахождение разности AA и B.B.
A=[−2301] и B=[8154]A=[−2301] и B=[8154]
Решение
Вычитаем соответствующие элементы каждой матрицы.
A−B=[−2301]−[8154]        =[−2−83−10−51−4]        =[−102−5−3]A−B=[−2301]−[8154]        =[ −2−83−10−51−4]        =[−102−5−3]
Пример 5
Нахождение суммы и разности двух матриц 3 x 3
Учитывая АА и В:В:
ⓐНайти сумму.
ⓑНайди разницу.
A=[2−10−21412104−22]и B=[610−20−12−4−52−2]A=[2−10−21412104−22]и B=[610−20−12− 4−52−2]
Решение
ⓐДобавьте соответствующие записи.
A+B=[2−10−21412104−22]+[610−20−12−4−52−2]=[2+6−10+10−2−214+012−1210−44−5− 2+22−2]=[80−41406−100]A+B=[2−10−21412104−22]+[610−20−12−4−52−2]=[2+6−10+10 −2−214+012−1210−44−5−2+22−2]=[80−41406−100]
ⓑВычтите соответствующие записи.
A−B=[2−10−21412104−22]−[610−20−12−4−52−2]=[2−6−10−10−2+214−012+1210+44+5− 2−22+2]=[−4−2001424149−44]A−B=[2−10−21412104−22]−[610−20−12−4−52−2]=[2−6−10−10−2+214−012+1210+44+ 5−2−22+2]=[−4−2001424149−44]
Попытайся #1
Добавить матрицу AA и матрицу B.B.
A=[26101−3] и B=[3−215−43]A=[26101−3] и B=[3−215−43]
Нахождение скалярных множителей матрицы
Помимо сложения и вычитания целых матриц, во многих ситуациях нам нужно умножить матрицу на константу, называемую скаляром. Напомним, что скаляр — это действительная числовая величина, которая имеет величину, но не направление. Например, время, температура и расстояние являются скалярными величинами. Процесс скалярного умножения включает умножение каждого элемента матрицы на скаляр. Скалярное кратное — это любой элемент матрицы, полученный в результате скалярного умножения.
Рассмотрим реальный сценарий, в котором университет должен добавить к своему инвентарю компьютеры, компьютерные столы и стулья в двух лабораториях кампуса из-за увеличения числа учащихся. По их оценкам, в обеих лабораториях требуется на 15% больше оборудования. Текущий инвентарь школы показан в таблице 2.
Лаборатория А Лаборатория B
Компьютеры 15 27
Компьютерные столы 16 34
Стулья 16 34
Стол 2
Преобразовав данные в матрицу, мы имеем
C2013=[151616273434]C2013=[151616273434]
Чтобы рассчитать, сколько потребуется компьютерного оборудования, мы умножаем все записи в матрице CC на 0,15.
(0,15)C2013=[(0,15)15(0,15)16(0,15)16(0,15)27(0,15)34(0,15)34]=[2,252,42,44,055.15,1](0,15)C2013=[(0,15) )15(0,15)16(0,15)16(0,15)27(0,15)34(0,15)34]=[2,252,42,44,055,15,1]
Мы должны округлить до следующего целого числа, поэтому количество необходимого нового оборудования составляет
.
[333566][333566]
Складывая две матрицы, как показано ниже, мы видим новые суммы запасов.
[151616273434]+[333566]=[181

4040][151616273434]+[333566]=[181

4040]
Это означает
C2014=[181

4040]C2014=[181

4040]
Таким образом, в лаборатории А будет 18 компьютеров, 19 компьютерных столов и 19 стульев; В лаборатории B будет 32 компьютера, 40 компьютерных столов и 40 стульев.
Скалярное умножение
Скалярное умножение включает в себя нахождение произведения константы на каждый элемент матрицы. Учитывается
A = [A11A12A21A22] A = [A11A12A21A22]
Скалярное множественное CACA составляет
CA = C [A11A12A21A22] = [CA11CA12CA21CA22] CA = C [A11A12A21] = [CA11CA12CA21CA22] CA = C [A11A12A22] = [CA11CA12CA21CA22] CA = C [A11A12A22] = [CA11CA12CA21CA22]. 0017
Скалярное умножение является дистрибутивным. Для матриц A,B,A,B и CC со скалярами aa и b,b
a(A+B)=aA+aB(a+b)A=aA+bAa(A+B)=aA +аВ(а+б)А=аА+бА
Пример 6
Умножение матрицы на скаляр
Умножение матрицы AA на скаляр 3.
A=[8154]A=[8154]
Решение
Умножьте каждую запись в AA на скаляр 3.
3A=3[8154]= [3⋅83⋅13⋅53⋅4]= [2431512]3A=3[8154]= [3⋅83⋅13⋅53 ⋅4]= [2431512]
Попытайся #2
Для заданной матрицы B,B найдите −2B−2B, где
B=[4132]B=[4132]
Пример 7
Нахождение суммы скалярных кратных
Нахождение суммы 3A+2B.3A+2B.
A=[1−200−1243−6]и B=[−1210−3201−4]A=[1−200−1243−6]и B=[−1210−3201−4]
Решение
Сначала найдите 3A, 3A, затем 2B.2B.
3A=[3⋅13(−2)3⋅03⋅03(−1)3⋅23⋅43⋅33(−6)]=[3−600−36129−18]3A=[3⋅13 (−2)3⋅03⋅03(−1)3⋅23⋅43⋅33(−6)]=[3−600−36129−18]
2B=[2(−1)2⋅22⋅12⋅02(−3)2⋅22⋅02⋅12(−4)]=[−2420−6402−8]2B=[2( −1)2⋅22⋅12⋅02(−3)2⋅22⋅02⋅12(−4)]=[−2420−6402−8]
Теперь прибавьте 3A+2B. 3A+2B.
3A+2B=[3−600−36129−18]+[−2420−6402−8]            = [3−2−6+40+20+0−3−66+412+09+2−18− 8]            =[1−220−
11−26]3A+2B=[3−600−36129−18]+[−2420−6402−8]             = [3−2−6+40+20+0−3− 66+412+09+2−18−8]            =[1−220−
11−26]
Нахождение произведения двух матриц
Помимо умножения матрицы на скаляр, мы можем умножать две матрицы. Нахождение произведения двух матриц возможно только в том случае, если внутренние размерности одинаковы, а это означает, что количество столбцов первой матрицы равно количеству строк второй матрицы. Если AA представляет собой матрицу размера m × rm × r, а BB представляет собой матрицу размера r × nr × n, то матрица произведения ABAB представляет собой матрицу размера m × nm × n. Например, продукт ABAB возможен, потому что количество столбцов в AA совпадает с количеством строк в B.B. Если внутренние размеры не совпадают, продукт не определен.
Мы умножаем записи AA на записи BB в соответствии с определенным шаблоном, как показано ниже. Процесс умножения матриц становится более понятным при решении задачи с вещественными числами.
Чтобы получить записи в строке ii таблицы AB,AB, мы умножаем записи в строке ii таблицы AA на столбец jj таблицы BB и складываем. Например, для заданных матриц AA и B,B, где размеры AA равны 2×32×3, а размеры BB равны 3×3,3×3, произведение ABAB будет матрицей 2×32×3.
A=[a11a12a13a21a22a23]and B=[b11b12b13b21b22b23b31b32b33]A=[a11a12a13a21a22a23]and B=[b11b12b13b21b22b23b31b32b33]
следует за произведением, чтобы получить первый элемент матрицы AB, и получаем AB, чтобы получить первый элемент матрицы.
Чтобы получить запись в строке 1, столбце 1 AB,AB, умножьте первую строку в AA на первый столбец в B,B и сложите.
[a11a12a13][b11b21b31]=a11⋅b11+a12⋅b21+a13⋅b31[a11a12a13][b11b21b31]=a11⋅b11+a12⋅b21+a13⋅b31
Чтобы получить запись в строке 1 столбца 2 AB,AB, умножьте первую строку AA на второй столбец B,B и сложите.
[a11a12a13][b12b22b32]=a11⋅b12+a12⋅b22+a13⋅b32[a11a12a13][b12b22b32]=a11⋅b12+a12⋅b22+a13⋅b32
Чтобы получить запись в строке 1 столбца 3 AB,AB, умножьте первую строку AA на третий столбец B,B и сложите.
[a11a12a13][b13b23b33]=a11⋅b13+a12⋅b23+a13⋅b33[a11a12a13][b13b23b33]=a11⋅b13+a12⋅b23+a13⋅b33
Таким же образом получаем второй ряд AB.AB. Другими словами, 2-я строка AA умножается на 1-й столбец B;B; 2-й ряд AA умножить на 2-й столбец B;B; 2-я строка AA умножается на 3-й столбец BB. По завершении матрица произведения будет равна 9.0017
AB=[a11⋅b11+a12⋅b21+a13⋅b31a21⋅b11+a22⋅b21+a23⋅b31a11⋅b12+a12⋅b22+a13⋅b32a21⋅b12+a22⋅b22+a21⋅1b32a b23+a13⋅b33a21⋅b13+a22⋅b23+a23⋅b33]AB=[a11⋅b11+a12⋅b21+a13⋅b31a21⋅b11+a22⋅b21+a23⋅b31a11⋅b12+a12⋅b21+a13 ⋅b12+a22⋅b22+a23⋅b32a11⋅b13+a12⋅b23+a13⋅b33a21⋅b13+a22⋅b23+a23⋅b33]
Свойства матричного умножения
Для матриц A,B,A,B и CC выполняются следующие свойства.
Умножение матриц ассоциативно: (AB)C=A(BC).(AB)C=A(BC).
Матричное умножение является распределительным: C(A+B)=CA+CB,(A+B)C=AC+BC.C(A+B)=CA+CB,(A+B)C=AC+BC.
Обратите внимание, что умножение матриц не является коммутативным.
Пример 8
Умножение двух матриц
Умножение матрицы AA и матрицы B.B.
A=[1234] и B=[5678]A=[1234] и B=[5678]
Решение
Сначала проверяем размеры матриц. Матрица AA имеет размеры 2×22×2, а матрица BB имеет размеры 2×2,2×2. Внутренние размеры одинаковы, поэтому мы можем выполнить умножение. Изделие будет иметь размеры 2×2,2×2.
Выполняем операции, описанные ранее.
Пример 9
Умножение двух матриц
Учитывая AA и B:B:
ⓐ Найдите AB.AB.
ⓑ Найдите БА.БА.
A=[−123405]и B=[5−42−103]A=[−123405]и B=[5−42−103]
Решение
ⓐПоскольку размеры AA равны 2×32×3, а размеры BB равны 3×2,3×2, эти матрицы можно перемножить, поскольку количество столбцов в AA совпадает с количеством строк в B. B. В результате произведение будет матрицей 2×22×2, количество строк в AA на количество столбцов в B.B.
AB=[−123405]  [5−1−4023]=[−1(5)+2(−4)+3(2)−1(−1)+2(0)+3(3)4( 5)+0(−4)+5(2)4(−1)+0(0)+5(3)]=[−7103011]AB=[−123405]  [5−1−4023]=[− 1(5)+2(−4)+3(2)−1(−1)+2(0)+3(3)4(5)+0(−4)+5(2)4(−1 )+0(0)+5(3)]=[−7103011]
ⓑ Размеры BB равны 3 × 23 × 2, а размеры AA равны 2 × 3,2 × 3. Внутренние размеры совпадают, поэтому произведение определено и будет матрицей 3 × 33 × 3.
BA=[5−1−4023]  [−123405]=[5(−1)+−1(4)5(2)+−1(0)5(3)+−1(5)−4( −1)+0(4)−4(2)+0(0)−4(3)+0(5)2(−1)+3(4)2(2)+3(0)2(3 )+3(5)]=[−
4−8−1210421]BA=[5−1−4023]  [−123405]=[5(−1)+−1(4)5(2)+−1(0)5(3)+−1( 5)−4(−1)+0(4)−4(2)+0(0)−4(3)+0(5)2(−1)+3(4)2(2)+3( 0)2(3)+3(5)]=[−
4−8−1210421]
Анализ
Обратите внимание, что произведения ABAB и BABA не равны.
AB=[−7103011]≠[−
4−8−1210421]=BAAB=[−7103011]≠[−
4−8−1210421]=BA
Это иллюстрирует тот факт, что умножение матриц не является коммутативным.
вопросы и ответы
Можно ли за AB определить, но не BA ?
Да, рассмотрим матрицу A размером 3×43×4 и матрицу B размером 4×2,4×2. Для продукта AB внутренние размеры равны 4, и продукт определен, но для продукта BA внутренние размеры равны 2 и 3, поэтому продукт не определен.
Пример 10
Использование матриц в реальных задачах
Вернемся к задаче, представленной в начале этого раздела. У нас есть Таблица 3, представляющая потребности в оборудовании двух футбольных команд.
Дикие кошки Грязевые коты
Цели 6 10
Шарики 30 24
Трикотажные изделия 14 20
Стол 3
Цены на оборудование указаны в таблице 4.
Цель 300 долларов США
Шар 10 долларов
Джерси 30 $
Стол 4
Преобразуем данные в матрицы. Таким образом, матрица потребности в оборудовании записывается в виде
E=[63014102420]E=[63014102420]
Матрица затрат записывается в виде
C=[3001030]C=[3001030]
Выполняем умножение матриц для получения затрат для оборудования.
CE=[3001030][61030241420]=[300(6)+10(30)+30(14)300(10)+10(24)+30(20)]=[2,5203,840]CE =[3001030][61030241420]=[300(6)+10(30)+30(14)300(10)+10(24)+30(20)]=[2,5203,840]
Всего Стоимость оборудования для Wildcats составляет 2520 долларов, а общая стоимость оборудования для Mud Cats составляет 3840 долларов.
Как
Дана матричная операция, оцените с помощью калькулятора.
Сохранить каждую матрицу как матричную переменную [A],[B],[C],…[A],[B],[C],…
Введите операцию в калькулятор, вызывая каждую переменную матрицы по мере необходимости.
Если операция определена, калькулятор представит матрицу решения; если операция не определена, будет отображаться сообщение об ошибке.
Пример 11
Использование калькулятора для выполнения матричных операций
Найти AB-CAB-C учитывая
A=[−15253241−7−281034−2],B=[4521−37−2452196−48−31]и C=[−100−89−9825−5674−6742−75].A= [−15253241−7−281034−2],B=[4521−37−2452196-48-31], и C=[-100-89-9825-5674-6742-75].
Решение
На странице матрицы калькулятора мы вводим матрицу AA выше в качестве матричной переменной [A],[A], матрицу BB выше в качестве матричной переменной [B],[B] и матрицу CC выше в качестве матричной переменной [ С]. [С].
На главном экране калькулятора вводим задачу и вызываем каждую переменную матрицы по мере необходимости.
[A][B]−[C][A][B]−[C]
Калькулятор дает нам следующую матрицу.
[-983-4621361,8201,897-856-3112,032413][-983-4621361,8201,897-856-3112,032413]
7.5 Секционные упражнения
Устно
1.
Можем ли мы сложить вместе любые две матрицы? Если да, объясните почему; если нет, объясните почему и приведите пример двух матриц, которые нельзя сложить вместе.
2.
Можем ли мы умножить любую матрицу-столбец на любую матрицу-строку? Объясните, почему да или почему нет.
3.
Можно ли определить оба продукта ABAB и BABA? Если да, объясните как; если нет, объясните почему.
4.
Можно ли перемножить любые две матрицы одинакового размера? Если да, объясните, почему, а если нет, то объясните, почему, и приведите пример двух матриц одинакового размера, которые нельзя перемножать.
5.
Коммутирует ли умножение матриц? То есть AB=BA?AB=BA? Если да, то докажите, почему это так. Если нет, объясните, почему это не так.
Алгебраический
В следующих упражнениях используйте приведенные ниже матрицы и выполните сложение или вычитание матриц. Укажите, является ли операция неопределенной.
A=[1307],B=[214226],C=[158_{],D=[101472561],E=[612145],F=[097817154]A=[1307],B=[214226],C= [158_{],D=[101472561],E=[612145],F=[097817154]}}
6.
А+ВА+В
7.
К+ДК+Д
8.
А+КА+С
9.
B-EB-E
10.
C+FC+F
11.
Д-БД-Б
В следующих упражнениях используйте приведенные ниже матрицы для выполнения скалярного умножения.
A=[461312],B=[3
064],C=[163718
9],D=[18121381467421]A=[461312],B=[3

064],C=[1637189],D=[18121381467421] 7 7 12.

5А5А

13.

3B3B

14.

−2B−2B

15.

−4C−4C

16.

12C12C

17.

100Д100Д

В следующих упражнениях используйте приведенные ниже матрицы для выполнения матричного умножения.

А=[-1532],В=[364-8012],С=[410-2659],D=[2−31293108−10]A=[−1532],B=[364−8012],C=[410−2659],D=[2−31293108−10]

18.

АБАБ

19.

ВСВС

20.

ЦАЦА

21.

БДБД

22.

ДКДК

23.

CBCB

В следующих упражнениях используйте приведенные ниже матрицы для выполнения указанной операции, если это возможно. Если это невозможно, объясните, почему операция не может быть выполнена.

А=[2−567],В=[−96-42], C=[0971],D=[-87-5432092],E=[4537-6-5109]A=[2-567],B=[-96-42],C=[0971 ],D=[−87−5432092],E=[4537−6−5109]

24.

А+В-СА+В-С

25.

4А+5Д4А+5Д

26.

2С+В2С+В

27.

3D+4E3D+4E

28.

C-0,5DC-0,5D

29.

100D-10E100D-10E

A=[-1020525],B=[4010-2030],C=[-100-110]A=[-1020525],B=[4010-2030],C=[-100-110]

30.

АБАБ

31.

БАБА

32.

ЦАЦА

33.

ВСВС

34.

А2А2

35.

B2B2

36.

C2C2

37.

B2A2B2A2

38.

А2В2А2В2

39.

(АБ)2(АВ)2

40.

(БА)2(БА)2

A=[1023],B=[−234−11−5],C=[0,50.110,2−0,50,3],D=[10−1−675421]A=[1023],B=[−234 −11−5],C=[0,50.110,2−0,50,3],D=[10−1−675421]

41.

АБАБ

42.

БАБА

43.

БДБД

44.

ДКДК

45.

Д2Д2

46.

А2А2

47.

Д3Д3

48.

(АБ)К(АВ)К

49.

А(БК)А(БК)

Технология

А=[−20918-30,545], B=[0,530-416872],C=[101010101]A=[-20918-30,545],B=[0,530-416872],C=[101010101]

50.

АБАБ

51.

БАБА

52.

ЦАЦА

53.

ВСВС

54.

АБСАВС

Удлинители

В следующих упражнениях используйте приведенную ниже матрицу, чтобы выполнить указанную операцию над заданной матрицей.

В=[100001010]В=[100001010]

55.

B2B2

56.

B3B3

57.

B4B4

58.

B5B5

59.

Используя приведенные выше вопросы, найдите формулу для Bn.Bn. Проверьте формулу для B201B201 и B202,B202, используя калькулятор.

Свойства матричных операций

Свойства матричных операций

Свойства дополнения

Основные свойства сложения действительных чисел справедливы и для матрицы.

Пусть А, Б и С быть m x n матриц

А + В = В + А коммутативный
А + (В + С) = (А + В) + С ассоциативный
Есть уникальный м xn матрица O с
A + O = A добавка идентификатор
Для любого м xn матрица A существует матрица m x n Б (называемый -А) с
A + B = O добавка обратный

Все доказательства аналогичны. Докажем первое свойство.

Доказательство собственности 1

У нас есть

(А + В) _ij = A _ij + B _ij определение сложения матриц

= B _ij + A _ij коммутативный свойство сложения действительных чисел

= (B + A) _ij определение добавления матрицы

Обратите внимание, что нулевая матрица отличается для разных m и н. Например

Свойства умножения матриц

В отличие от сложения матриц, свойства умножения действительных чисел не не все обобщаются на матрицы. Матрицы редко коммутируют, даже если AB и бакалавр оба определены. Часто не существует мультипликативной обратной матрицы, даже если матрица квадратная. Есть несколько свойств умножение действительных чисел, которые обобщаются на матрицы. Мы излагаем их в настоящее время.

Пусть А, Б и С — матрицы размерностей такие, что следующие определения определены. Затем

А(ВС) = (АВ)С ассоциативный
А(В + С) = АВ + АС дистрибутив
(А + В)С = АС + ВС распределительный
Существуют уникальные матрицы I _m и I _n с
I _m А = А I _n = А мультипликативное тождество

Мы часто опускаем нижний индекс и пишем I вместо тождественная матрица. Единичная матрица представляет собой квадратную скалярную матрицу с единицами. по диагонали. Например

Мы докажем второе свойство, а остальное оставим вам.

Доказательство Имущества 2

Снова покажем, что общий элемент левой части такой же, как и правой сторона руки. У нас есть

(А(В + С)) _ij = S(A _ik (B + C) _kj ) определение умножения матриц

знак равно S(A _ik (B _kj + C _kj )) определение матричного сложения

знак равно S(A _ik B _kj + A _ik C _kj ) распределительное свойство действительных чисел

знак равно С А _ик б _кдж + С A _ik C _kj коммутативный свойство действительных чисел

= (AB) _ij + (AC) _ij определение умножения матриц

где сумма берется от 1 до k.

Пример

Мы продемонстрирует свойство 1 с

Мы есть

так что

Мы есть

так что

Свойства скалярного умножения

Поскольку мы можем умножить матрицу на скаляр, мы можем исследовать свойства что имеет это умножение. Все свойства умножения действительные числа обобщают. В частности, у нас есть

Пусть г и s — действительные числа и А и Б быть матрицами. Затем

r(sA) = (rs)A
(r + s)A = rA + sA
r(A + B) = rA + rB
А(rB) = r(AB) = (rA)B

Мы докажем свойство 3, а остальное оставим вам. У нас есть

(r(A + B)) _ij = (r)(A + B) _ij определение скалярного умножения

= (r)(A _ij + B _ij ) определение сложения матриц

= rA _ij + rB _ij распределительный свойство действительных чисел

= (rA) _ij + (rB) _ij определение скалярного умножения

= (rA + rB) _ij определение добавление матриц

Свойства транспонирования матрицы

Напомним, что транспонирование матрицы — это операция переключения строк и столбцы. Укажем следующие свойства. Мы доказали первое имущество в последнем разделе.

Пусть г быть действительным числом и A и В быть матрицы. Затем

(А ^Т ) ^Т = А
(А + В) ^Т = А ^Т + В ^Т
(AB) ^T = B ^T A ^T
(rA) ^T = rA ^T

Назад на главную страницу матриц и приложений

Назад на домашнюю страницу линейной алгебры

Назад к математике Домашняя страница отдела

электронная почта Вопросы и предложения

операций с массивами и матрицами – MATLAB и Simulink

Операции с массивами и матрицами

Введение

MATLAB ^® имеет два различных типа арифметических операций: операции с массивами и матричные операции. Вы можете использовать эти арифметические операции для выполнения числовых операций. вычисления, например, сложение двух чисел, возведение элементов массива в заданной мощности или умножение двух матриц.

Матричные операции следуют правилам линейной алгебры. Напротив, массив операции выполняют поэлементные операции и поддерживают многомерные массивы. Символ периода ( . ) отличает массив операции из матричных операций. Однако, поскольку матрица и массив операции сложения и вычитания одинаковы, пары символов .+ и .- не нужны.

Операции с массивами

Операции с массивами выполняют поэлементные операции над соответствующими элементами векторов, матриц и многомерных массивов. Если операнды одинаковы размер, то каждый элемент в первом операнде сопоставляется с элементом в то же самое место во втором операнде. Если операнды имеют совместимые размеры, то каждый вход неявно расширяется по мере необходимости, чтобы соответствовать размеру другого. Для большего информацию см. в разделе Совместимые размеры массивов для основных операций.

Если один операнд является скаляром, а другой нет, то MATLAB неявно расширяет скаляр до того же размера, что и другой операнд. Например, вы можете вычислить поэлементное произведение скаляра и матрица.

Неявное расширение также работает, если вы вычитаете вектор 1 на 3 из матрицы 3 на 3 потому что эти два размера совместимы. Когда вы выполняете вычитание, вектор неявно расширяется, чтобы стать матрицей 3 на 3.

Вектор-строка и вектор-столбец имеют совместимые размеры. Если вы добавите вектор 1 на 3 в вектор 2 на 1, то каждый вектор неявно расширяется в матрицу 2 на 3 перед MATLAB выполняет поэлементное сложение.

Если размеры двух операндов несовместимы, вы получите ошибку.

В следующей таблице приводится сводка арифметических операций с массивами в МАТЛАБ. Для получения информации о конкретной функции щелкните ссылку на функцию справочная страница в последнем столбце.

Operator	Purpose	Description	Reference Page
`+`	Addition	`A+B` добавляет `A` и `Б` .	`плюс`
`+`	Унарный плюс	`+A` возврат `А` .	`UPLUS`
`-`	Вычитание	`A -B` Подтекатели `B` от `A -B` . `А`	`минус`
`-`	Унарный минус	`-A` отрицает элементы `А` .	`UMINUS`
`.*`	Суммам элемента. `А` и `В` .	9B — матрица с элементами `A(i,j)` до `B(i,j)` сила.	`мощность`
`./`	Правое деление массива	`с элементами матрицы A2/B 92 А(i,j)/B(i,j) .`	`раздел`
`.\`	Левое деление массива	`A. \B` — матрица с элементами `B(i,j)/A(i,j)` .	`lразделить`
`.'`	Транспонирование массива	`A.'` - транспонированный массив `А` . Для комплексных матриц это не так. включают сопряжение.	`транспонирование`

Операции с матрицами

Операции с матрицами следуют правилам линейной алгебры и несовместимы с многомерные массивы. Требуемый размер и форма входов по отношению к друг друга зависит от операции. Для нескалярных входов матричные операторы обычно вычисляют разные ответы, чем их аналоги оператора массива.

Например, если вы используете оператор деления матрицы вправо, /, чтобы разделить две матрицы, матрицы должны иметь одинаковое количество столбцов. Но если вы используете оператор умножения матриц, * , чтобы умножить два матриц, то матрицы должны иметь общий внутренний размер . То есть количество столбцов в первом входе должно быть равно количеству строки во втором входе. Оператор умножения матриц вычисляет произведение двух матриц по формуле

C(i,j)=∑k=1nA(i,k)B(k,j).

В следующей таблице представлен обзор матричных арифметических операций в МАТЛАБ. Для получения информации о конкретной функции щелкните ссылку на функцию справочная страница в последнем столбце.

Operator	Purpose	Description	Reference Page
`*`	Умножение матриц	`C =` `A*B` — это линейное алгебраическое произведение матрицы `А` и `В` . количество столбцов `A` должно равняться числу рядов `B` .	`м раз`
`\`	Левое деление матрицы	`x = A\B` - решение уравнения Топор = В . Матрицы `A` и `B` должны иметь одинаковое количество рядов.	`млразделить`
`/`	Правое деление матрицы	`x = B/A` — решение уравнения х А = В . Матрицы `A` и `B` должны иметь одинаковое количество столбцов. Оставить комментарий Отменить ответ Для отправки комментария вам необходимо авторизоваться. Поиск: Рубрики Вакансии Востребованные вакансии Обучение в Европе Обучение за границей Работа Работа для всех Советы абитуриенту Студенту Студенческие будни Разное 2019 © Все права защищены. Карта сайта Меню Поиск: Советы абитуриенту Работа для всех Востребованные вакансии Студенческие будни Обучение за границей

Цель	$300
Шар	10 долларов
Джерси	$30

1.	Что такое матричные операции?
2.	Дополнение – Матричные операции
3.	Вычитание — матричные операции
4.	Умножение — Операции с матрицами
5.	Операция транспонирования матрицы
6.	Обратная операция матрицы
7.	Примеры матричных операций
8.	Практические вопросы
9.	Часто задаваемые вопросы о матричных операциях

Цель	300 долларов США
Шар	10 долларов
Джерси	30 $