Матрицы и определители примеры и решения: 404 - Страница не найдена - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Определители задачи с решением и примерами по высшей математике

Определители

Пусть дана квадратная матрица

Определителем (детерминантом) матрицы называют число, которое ставится в соответствие данной матрице и обозначается

Определитель матрицы второго порядка

Если в квадратной матрице вычеркнуть -ю строку и -ый столбец, то получим матрицу размера . Определитель этой матрицы называется минором элемента и обозначается .

Алгебраическим дополнением элемента называется минор этого элемента, умноженный на , т. е.

Теорема. Сумма произведений элементов какой-нибудь строки (столбца) на их алгебраические дополнения равна определителю матрицы. Сумма же произведений элементов какой-нибудь строки (столбца) на алгебраические дополнения другой строки (столбца) равна нулю.

Воспользовавшись этой теоремой, найдем определитель матрицы третьего порядка:

Вычисление определителей n-го порядка

Всякие чисел, расположенные в определенном порядке, образуют перестановку.

Меняя порядок расположения цифр в перестановке, получим другую перестановку. Всего перестановок из чисел —. Если в перестановке меньшее число следует за большим, то говорят, что имеется инверсия. Перестановка из -элементов называется четной, если число инверсий в ней четно и нечетной, если оно нечетно.

Пусть дана матрица

Определителем -го порядка квадратной матрицы называется алгебраическая сумма -слагаемых вида , состоящих из сомножителей, взятых по одному из каждой строки и из каждого столбца. При этом слагаемые, у которых вторые индексы сомножителей образуют четную перестановку, берутся со знаком «+», нечетную перестановку — со знаком «-». Таким образом, , где — число инверсий в перестановке ().

Свойства определителей n-го порядка

При замене строк столбцами определитель не меняется.
При перестановке двух строк определитель меняет знак.
Если все элементы какой-нибудь строки равны нулю, то определитель равен нулю.
Если элементы строки умножить (разделить) на число , то значение определителя увеличится (уменьшится) в -раз.
Если матрица имеет две одинаковые или пропорциональные строки, то ее определитель равен нулю.
Если элементы какой-либо строки матрицы представляют собой сумму слагаемых, то определитель этой матрицы равен сумме двух определителей соответствующих матриц.

Определитель -го порядка вычисляется путем приведения его к треугольному виду. Метод вычисления определителя путем приведения к треугольному виду заключается в том, что, используя свойства определителей, приводят его к виду

который называется треугольным. Очевидно, что

Задача №3.

Дана матрица

Найти алгебраические дополнения элементов второго столбца.

Решение:

Задача №4.

Вычислить определитель

преобразовав его так, чтобы два элемента некоторого ряда равнялись нулю, и разлагая полученный определитель по элементам этого ряда.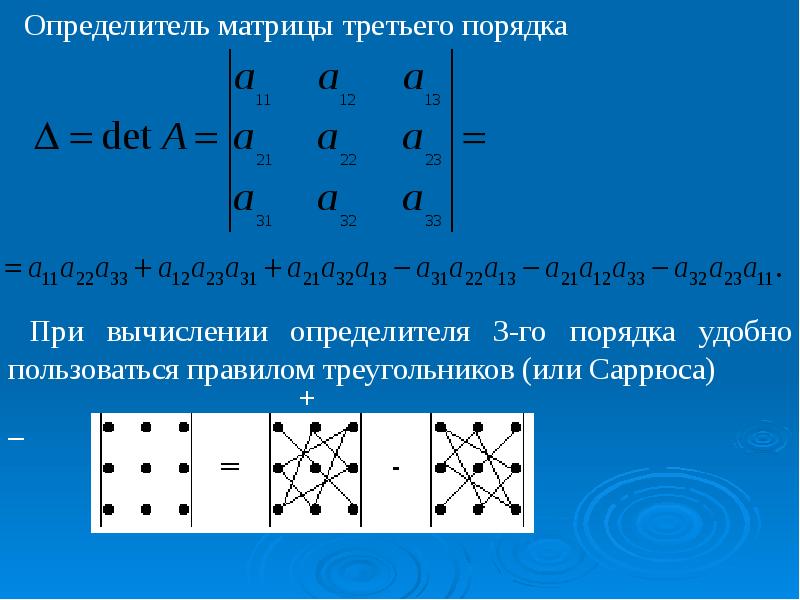

Решение:

Используя свойства определителей, преобразуем данный определитель следующим образом: к первой строке прибавим вторую, а к третьей — вторую, умноженную на 2. Получим

Этот материал взят со страницы кратких лекций с решением задач по высшей математике:

Решение задач по высшей математике

Возможно эти страницы вам будут полезны:

Определитель матрицы.

Навигация по странице:

Определитель матрицы или детерминант матрицы – это одна из основных численных характеристик квадратной матрицы, применяемая при решении многих задач.

Определение.

Определителем матрицы n×n будет число:

det(A) =	Σ	(-1)^{N(α₁,α₂,…,α_n)}·a_α₁1·a_α₂2·…·a_{α_nn}
	(α₁,α₂,. ..,α_n)

где (α₁,α₂,…,α_n) – перестановка чисел от 1 до n, N(α₁,α₂,…,α_n) – число инверсий в перестановке, суммирование идёт по всем возможным перестановкам порядка n.

Обозначение

Определитель матрици A обычно обозначается det(A), |A|, или ∆(A).

Свойства определителя матрицы

Определитель матрицы с двумя равными строками (столбцами) равен нулю.
Определитель матрицы с двумя пропорциональными строками (столбцами) равен нулю.
Определитель матрицы, содержащий нулевую строку (столбец), равен нулю.
Определитель матрицы равен нулю если две (или несколько) строк (столбцев) матрицы линейно зависимы.
При транспонировании значение определителя матрицы не меняется:
det(A) = det(A^T

)
Определитель обратной матрицы:
det(A^-1) = det(A)^-1
Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить другую строку (столбец), умноженную на некоторое число.
Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить линейную комбинации других строк (столбцов).
Если поменять местами две строки (столбца) матрицы, то определитель матрицы поменяет знак.
Общий множитель в строке (столбце) можно выносить за знак определителя:
a₁₁a₁₂…a_1na₂₁a₂₂…a_2n….k·a_i1k·a_i2…k·a_in….a_n1a_n2…a_nn = k·a₁₁a₁₂…a_1na₂₁a₂₂…a_2n….a_i1a_i2…a_in….a_n1a_n2…a_nn
Если квадратная матрица n-того порядка умножается на некоторое ненулевое число, то определитель полученной матрицы равен произведению определителя исходной матрицы на это число в n-той степени:
B = k·A => det(B) = kⁿ·det(A)
где A матрица n×n, k – число.
Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем:
a₁₁a₁₂…a_1na₂₁a₂₂…a_2n….b_i1 + c_i1b_i2 + c_i2…b_in + c_in….a_n1a_n2…a_nn = a₁₁a₁₂…a_1n
a₂₁a₂₂…a_2n….b_i1b_i2…b_in….a_n1a_n2…a_nn + a₁₁a₁₂…a_1na₂₁a₂₂…a_2n….c_i1c_i2…c_in….a_n1a_n2…a_nn
Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.
Определитель произведения матриц равен произведению определителей этих матриц:
det(A·B) = det(A)·det(B)

Методы вычисления определителя матрицы

Вычисление определителя матрицы 1×1

Правило:

Для матрицы первого порядка значение определителя равно значению элемента этой матрицы:

∆ = |a₁₁| = a₁₁

Вычисление определителя матрицы 2×2

Правило:

Для матрицы 2×2 значение определителя равно разности произведений элементов главной и побочной диагоналей:

∆ =

= a₁₁·a₂₂ – a₁₂·a₂₁

Пример 1.

Найти определитель матрицы A

A =

	5	7
	-4	1

Решение:

det(A) =

= 5·1 – 7·(-4) = 5 + 28 = 33

Вычисление определителя матрицы 3×3

Правило треугольника для вычисления определителя матрицы 3-тего порядка

Правило:

Для матрицы 3×3 значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.


+		–

∆ =

a₁₁	a₁₂	a₁₃
a₂₁	a₂₂	a₂₃
a₃₁	a₃₂	a₃₃

= a₁₁·a₂₂·a₃₃ + a₁₂·a₂₃·a₃₁ + a₁₃·a₂₁·a₃₂ – a₁₃·a₂₂·a₃₁ – a₁₁·a₂₃·a₃₂ – a₁₂·a₂₁·a₃₃

Правило Саррюса для вычисления определителя матрицы 3-тего порядка

Правило:

Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком “плюс”; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком “минус”:

∆ =

a₁₁	a₁₂	a₁₃	a₁₁	a₁₂
a₂₁	a₂₂	a₂₃	a₂₁	a₂₂
a₃₁	a₃₂	a₃₃	a₃₁	a₃₂

= a₁₁·a₂₂·a₃₃ + a₁₂·a₂₃·a₃₁ + a₁₃·a₂₁·a₃₂ – a₁₃·a₂₂·a₃₁ – a₁₁·a₂₃·a₃₂ - a₁₂·a₂₁·a₃₃

Пример 2.

Найти определитель матрицы A = 571-410203

Решение:

det(A) = 571-410203 = 5·1·3 + 7·0·2 + 1·(-4)·0 – 1·1·2 – 5·0·0 – 7·(-4)·3 = 15 + 0 + 0 – 2 – 0 + 84 = 97

Вычисление определителя матрицы произвольного размера

Разложение определителя по строке или столбцу

Правило:

Определитель матрицы равен сумме произведений элементов строки определителя на их алгебраические дополнения:

	n
det(A) =	Σ	a_ij·A_ij	– разложение по i-той строке
	j = 1

Правило:

Определитель матрицы равен сумме произведений элементов столбца определителя на их алгебраические дополнения:

	n
det(A) =	Σ	a_ij·A_ij	– разложение по j-тому столбцу
	i = 1

При разложение определителя матрицы обычно выбирают ту строку/столбец, в которой/ом максимальное количество нулевых элементов.

Пример 3.

Найти определитель матрицы A

A =

2	4	1
0	2	1
2	1	1

Решение: Вычислим определитель матрицы разложив его по первому столбцу:

= 2·(-1)¹⁺¹· 2111 + 0·(-1)²⁺¹· 4111 + 2·(-1)³⁺¹· 4121 =

= 2·(2·1 – 1·1) + 2·(4·1 – 2·1) = 2·(2 – 1) + 2·(4 – 2) = 2·1 + 2·2 = 2 + 4 = 6

Пример 4.

Найти определитель матрицы A

A = 2411020021134023

Решение: Вычислим определитель матрицы, разложив его по второй строке (в ней больше всего нулей):

det(A) = 2411020021134023 = – 0· 411113023 + 2· 211213423 – 0· 241213403 + 0· 241211402 =

= 2·(2·1·3 + 1·3·4 + 1·2·2 – 1·1·4 – 2·3·2 – 1·2·3) = 2·(6 +12 + 4 – 4 – 12 – 6) = 2·0 = 0

Приведение определителя к треугольному виду

Правило:

Используя свойства определителя для элементарных преобразований над строками и столбцами 8 – 11, определитель приводится к треугольному виду, и тогда его значение будет равно произведению элементов стоящих на главной диагонали.

Пример 5.

Найти определитель матрицы A приведением его к треугольному виду

A = 2411021021134023

Решение:

det(A) = 2411021021134023

Сначала получим нули в первом столбце под главной диагональю. Для этого отнимем от 3-тей строки 1-ую строку, а от 4-той строки 1-ую строку, умноженную на 2:

det(A) = 241102102 – 21 – 41 – 13 – 14 – 2·20 – 4·22 – 1·23 – 1·2 = 241102100-3020-801

Получим нули во втором столбце под главной диагональю. Для этого поменяем местами 2-ой и 3-тий столбцы (при этом детерминант сменит знак на противоположный):

det(A) = – 2141012000-3200-81

Получим нули в третьем столбце под главной диагональю. Для этого к 3-ему столбцу добавим 4-тий столбец, умноженный на 8:

det(A) = – 214 + 1·81012 + 0·8000-3 + 2·8200-8 + 1·81 = – 211210120001320001 = -2·1·13·1 = -26

Теорема Лапласа

Теорема:

Пусть ∆ – определитель n-ого порядка.

Выберем в нем произвольные k строк (столбцов), причем k < n. Тогда сумма произведений всех миноров k-ого порядка, которые содержатся в выбранных строках (столбцах), на их алгебраические дополнения равна определителю.

Присоединяйтесь

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне [email protected]

Определители квадратных матриц

К оглавлению

I. Определитель матрицы первого порядка

Определителем матрицы первого порядка, или определителем первого порядка, называется элемент, называется элемент а₁₁:

II. Определитель матрицы второго порядка

Определителем матрицы второго порядка, или определителем второго порядка, называется число, которое вычисляется по формуле:

Например, пусть

III. Определитель матрицы третьего порядка

Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:

Это число представляет алгебраическую сумму, состоящую из шести слагаемых. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Каждое слагаемое состоит из произведения трех сомножителей.

Знаки, с которыми члены определителя входят в формулу нахождения определителя третьего порядка можно определить, пользуясь приведенной схемой, которая называется правилом треугольников или правилом Сарруса. Первые три слагаемые берутся со знаком плюс и определяются из левого рисунка, а последующие три слагаемые берутся со знаком минус и определяются из правого рисунка.

Пример. Вычислить определитель третьего порядка:

Решение.

Замечание. Вычисление определителей четвертого и более высокого порядка приводит к большим вычислениям, так как

· для нахождения определителя первого порядка мы находим одно слагаемое, состоящее из одного сомножителя,

· для нахождения определителя второго порядка нужно вычислить алгебраическую сумму из двух слагаемых, где каждое слагаемое состоит из произведения двух сомножителей,

· для нахождения определителя третьего порядка нужно вычислить алгебраическую сумму из шести слагаемых, где каждое слагаемое состоит из произведения трех сомножителей,

· для нахождения определителя четвертого порядка нужно вычислить алгебраическую сумму из двадцати четырех слагаемых, где каждое слагаемое состоит из произведения четырех сомножителей и т. д.

Определить количество слагаемых в алгебраической сумме, можно вычислив факториал:

Вычисление определителя четвертого порядка приводит к большим вычислениям. Поэтому в этом случае используют искусственные методы, о которых мы остановимся позже.

IV. Примеры для самостоятельного решения

А. Вычислить определитель второго порядка:

Б. Вычислить определитель третьего порядка:

В. Решить уравнение:

К оглавлению

Дифференциальные уравнения – Обзор: матрицы и векторы

Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки

Похоже, вы используете устройство с “узкой” шириной экрана (, т. е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.

Раздел 5-2: Обзор: матрицы и векторы

Этот раздел призван стать уловкой для многих основных концепций, которые иногда используются при работе с системами дифференциальных уравнений.В этом разделе не будет много деталей, и мы не будем работать с большим количеством примеров. Кроме того, во многих случаях мы не будем рассматривать общий случай, поскольку нам не понадобятся общие случаи в нашей работе с дифференциальными уравнениями.

Начнем с основных обозначений матриц. {\ text {th}} \) столбец обозначается \ (a_ {ij} \).Краткий метод записи общей матрицы \ (n \ times m \) следующий.

\ [A = {\ left ({\ begin {array} {* {20} {r}} {{a_ {11}}} & {{a_ {12}}} & \ cdots & {{a_ {1m}) }} \\ {{a_ {21}}} & {{a_ {22}}} & \ cdots & {{a_ {2m}}} \\ \ vdots & \ vdots & {} & \ vdots \\ {{ a_ {n1}}} & {{a_ {n2}}} & \ cdots & {{a_ {nm}}} \ end {array}} \ right) _ {n \ times m}} = {\ left ({ {a_ {ij}}} \ right) _ {n \ times m}} \]

Размер или размер матрицы при необходимости указывается в нижнем индексе, как показано.Если это не требуется или не ясно из проблемы, индексированный размер часто опускается из матрицы.

Специальные матрицы

Есть несколько «специальных» матриц, которые мы можем иногда использовать. Первая специальная матрица – это квадратная матрица . Квадратная матрица – это любая матрица, размер (или размер) которой равен \ (n \ умножить на n \). Другими словами, в нем столько же строк, сколько и столбцов. В квадратной матрице диагональ, которая начинается в верхнем левом углу и заканчивается в правом нижнем углу, часто называется главной диагональю .

Следующие две специальные матрицы, которые мы хотим рассмотреть, – это нулевая матрица и единичная матрица. Нулевая матрица , обозначенная \ (0_ {n \ times m} \), является матрицей, все элементы которой являются нулями. Единичная матрица представляет собой квадратную матрицу \ (n \ умноженную на n \), обозначенную \ (I_ {n} \), все главные диагонали которой равны единицам, а все остальные элементы равны нулю. Вот общие нулевая и единичная матрицы.

\ [{0_ {n \ times m}} = {\ left ({\ begin {array} {* {20} {r}} 0 & 0 & \ cdots & 0 \\ \ vdots & \ vdots & {} & \ vdots \\ 0 & 0 & \ cdots & 0 \ end {array}} \ right) _ {n \ times m}} \ hspace {0.25 дюймов} \ hspace {0,25 дюйма} {I_n} = {\ left ({\ begin {array} {* {20} {r}} 1 & 0 & \ cdots & 0 \\ 0 & 1 & \ cdots & 0 \\ \ vdots & \ vdots & \ ddots & \ vdots \\ 0 & 0 & \ cdots & 1 \ end {array}} \ right) _ {n \ times n}} \]

В матричной арифметике эти две матрицы будут действовать в матричной работе как ноль, а единица – в действительной системе счисления.

Последние две специальные матрицы, которые мы здесь рассмотрим, – это матрица столбцов и матрица строк .Это матрицы, состоящие из одного столбца или одной строки. В целом их

\ [x = {\ left ({\ begin {array} {* {20} {r}} {{x_1}} \\ {{x_2}} \\ \ vdots \\ {{x_n}}} \ end {массив }} \ right) _ {n \ times 1}} \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} y = {\ left ({\ begin {array} {* {20} {r }} {{y_1}} & {{y_2}} & \ cdots & {{y_m}} \ end {array}} \ right) _ {1 \ times m}} \]

Мы часто будем называть их векторами .

Арифметика

Теперь нам нужно взглянуть на арифметику с матрицами.Начнем с , сложения и вычитания двух матриц. Итак, предположим, что у нас есть две матрицы \ (n \ times m \), \ (A \) и \ (B \). Сумма (или разность) этих двух матриц тогда равна

. \ [{A_ {n \ times m}} \ pm {B_ {n \ times m}} = {\ left ({{a_ {ij}}} \ right) _ {n \ times m}} \ pm {\ left ({{b_ {ij}}} \ right) _ {n \ times m}} = {\ left ({{a_ {ij}} \ pm {b_ {ij}}} \ right) _ {n \ times m}} \]

Сумма или разность двух матриц одинакового размера – это новая матрица одинакового размера, элементы которой представляют собой сумму или разность соответствующих элементов из двух исходных матриц. Обратите внимание, что мы не можем добавлять или вычитать записи разных размеров.

Теперь давайте посмотрим на скалярное умножение . При скалярном умножении мы собираемся умножить матрицу \ (A \) на константу (иногда называемую скаляром) \ (\ alpha \). В этом случае мы получаем новую матрицу, все элементы которой умножены на константу \ (\ alpha \).

\ [\ alpha {A_ {n \ times m}} = \ alpha {\ left ({{a_ {ij}}} \ right) _ {n \ times m}} = {\ left ({\ alpha \, { a_ {ij}}} \ right) _ {n \ times m}} \] Пример 1 Учитывая следующие две матрицы, \ [A = \ left ({\ begin {array} {* {20} {r}} 3 & {- 2} \\ {- 9} & 1 \ end {array}} \ right) \ hspace {0.25 дюймов} \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} B = \ left ({\ begin {array} {* {20} {r}} {- 4} & 1 \\ 0 & {- 5} \ end {array }} \Правильно)\]

вычислить \ (A-5B \).

Показать решение

Здесь особо нечем заняться, кроме работы.

\ [\ begin {align *} A – 5B & = \ left ({\ begin {array} {* {20} {r}} 3 & {- 2} \\ {- 9} & 1 \ end {array}} \ справа) – 5 \ left ({\ begin {array} {* {20} {r}} {- 4} & 1 \\ 0 & {- 5} \ end {array}} \ right) \\ & = \ left ( {\ begin {array} {* {20} {r}} 3 & {- 2} \\ {- 9} & 1 \ end {array}} \ right) – \ left ({\ begin {array} {* {20 } {r}} {- 20} & 5 \\ 0 & {- 25} \ end {array}} \ right) \\ & = \ left ({\ begin {array} {* {20} {r}} {23 } & {- 7} \\ {- 9} & {26} \ end {array}} \ right) \ end {align *} \]

Сначала мы умножили все элементы \ (B \) на 5, затем вычли соответствующие элементы, чтобы получить элементы в новой матрице.

Последняя матричная операция, которую мы рассмотрим, это умножение матрицы . Здесь мы начнем с двух матриц, \ (A_ {n \ times p} \) и \ (B_ {p \ times m} \). Обратите внимание, что \ (A \) должен иметь такое же количество столбцов, как \ (B \) имеет строки. {\ text {th}} \), \ (c_ {ij} \), находится путем умножения строки \ (i \) матрицы \ (A \) на столбец \ (j \) матрицы \ (B \).Это не всегда имеет смысл на словах, поэтому давайте рассмотрим пример.

Пример 2 Дан \ [A = {\ left ({\ begin {array} {* {20} {r}} 2 & {- 1} & 0 \\ {- 3} & 6 & 1 \ end {array}} \ right) _ {2 \ times 3}} \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} B = {\ left ({\ begin {array} {* {20} {r}} 1 & 0 & {- 1} & 2 \\ {- 4} & 3 & 1 & 0 \ \ 0 & 3 & 0 & {- 2} \ end {array}} \ right) _ {3 \ times 4}} \]

вычислить \ (AB \).

Показать решение

Новая матрица будет иметь размер \ (2 \ умножить на 4 \).Запись в строке 1 и столбце 1 новой матрицы будет найдена путем умножения строки 1 матрицы \ (A \) на столбец 1 матрицы \ (B \). Это означает, что мы умножаем соответствующие записи из строки \ (A \) и столбца \ (B \), а затем складываем результаты. Вот пара записей, рассчитанных полностью.

\ [\ begin {align *} {c_ {11}} & = \ left (2 \ right) \ left (1 \ right) + \ left ({- 1} \ right) \ left ({- 4} \ right » ) + \ left (0 \ right) \ left (0 \ right) = 6 \\ {c_ {13}} & = \ left (2 \ right) \ left ({- 1} \ right) + \ left ({ – 1} \ right) \ left (1 \ right) + \ left (0 \ right) \ left (0 \ right) = – 3 \\ {c_ {24}} & = \ left ({- 3} \ right ) \ left (2 \ right) + \ left (6 \ right) \ left (0 \ right) + \ left (1 \ right) \ left ({- 2} \ right) = – 8 \ end {align *} \]

Вот полное решение.

\ [C = \ left ({\ begin {array} {* {20} {r}} 6 & {- 3} & {- 3} & 4 \\ {- 27} & {21} & 9 & {- 8} \ end {array}} \ right) \]

В этом последнем примере обратите внимание, что мы не могли сделать продукт BA , поскольку количество столбцов в \ (B \) не соответствует количеству строк в \ (A \). Важно отметить, что то, что мы можем вычислить \ (AB \), не означает, что мы можем вычислить \ (BA \). Точно так же, даже если мы можем вычислить как \ (AB \), так и \ (BA \), они могут быть одной и той же матрицей, а могут и не быть.

Определитель

Следующая тема, которую нам нужно рассмотреть, – это определитель матрицы. Определитель на самом деле является функцией, которая преобразует квадратную матрицу в число. Фактическая формула функции несколько сложна и определенно выходит за рамки этого обзора.

Основной метод вычисления определителей любой квадратной матрицы называется методом сомножителей. Поскольку мы собираемся иметь дело почти исключительно с матрицами \ (2 \ times 2 \) и случайной матрицей \ (3 \ times 3 \), мы не будем вдаваться в этот метод.Мы можем дать простые формулы для каждого из этих случаев. Стандартным обозначением определителя матрицы \ (A \) является.

\ [\ det \ left (A \ right) = \ left | A \ right | \]

Вот формулы для определителя матриц \ (2 \ times 2 \) и \ (3 \ times 3 \).

\ [\ left | {\ begin {array} {* {20} {r}} a & c \\ b & d \ end {array}} \ right | = ad – cb \] \ [\ left | {\ begin {array} {* {20} {r}} {{a_ {11}}} & {{a_ {12}}} & {{a_ {13}}} \\ {{a_ {21}} } & {{a_ {22}}} & {{a_ {23}}} \\ {{a_ {31}}} & {{a_ {32}}} & {{a_ {33}}} \ end { массив}} \ right | = {a_ {11}} \ left | {\ begin {array} {* {20} {r}} {{a_ {22}}} & {{a_ {23}}} \\ {{a_ {32}}} и {{a_ {33}} } \ end {array}} \ right | – {a_ {12}} \ left | {\ begin {array} {* {20} {r}} {{a_ {21}}} & {{a_ {23}}} \\ {{a_ {31}}} и {{a_ {33}} } \ end {array}} \ right | + {a_ {13}} \ left | {\ begin {array} {* {20} {r}} {{a_ {21}}} & {{a_ {22}}} \\ {{a_ {31}}} и {{a_ {32}} } \ end {array}} \ right | \] Пример 3 Найдите определитель каждой из следующих матриц.\ [A = \ left ({\ begin {array} {* {20} {r}} {- 9} & {- 18} \\ 2 & 4 \ end {array}} \ right) \ hspace {0.25in} \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} B = \ left ({\ begin {array} {* {20} {r}} 2 & 3 & 1 \\ {- 1} & {- 6} & 7 \\ 4 & 5 & {- 1 } \ end {array}} \ right) \] Показать решение

Для \ (2 \ times 2 \) ничего не остается, кроме как вставить его в формулу.

\ [\ det \ left (A \ right) = \ left | {\ begin {array} {* {20} {r}} {- 9} & {- 18} \\ 2 & 4 \ end {array}} \ right | = \ left ({- 9} \ right) \ left (4 \ right) – \ left ({- 18} \ right) \ left (2 \ right) = 0 \]

Для \ (3 \ times 3 \) мы могли бы подставить его в формулу, однако, в отличие от случая \ (2 \ times 2 \), запомнить эту формулу непросто.Есть более простой способ получить тот же результат. Более быстрый способ получить тот же результат – сделать следующее. Сначала запишите матрицу и прикрепите к ее концу копии первых двух столбцов следующим образом.

\ [\ det \ left (B \ right) = \ left | {\ begin {array} {* {20} {r}} 2 & 3 & 1 \\ {- 1} & {- 6} & 7 \\ 4 & 5 & {- 1} \ end {array}} \ right | \, \, \, \, \ begin {array} {* {20} {r}} 2 & 3 \\ {- 1} & {- 6} \\ 4 & 5 \ end {array} \]

Теперь обратите внимание, что есть три диагонали, идущие слева направо, и три диагонали, идущие справа налево. Что мы делаем, так это умножаем записи на каждой диагонали вверх, и если диагональ идет слева направо, мы складываем их, а если диагональ идет справа налево, мы вычитаем их.

Вот работа для этой матрицы.

\ [\ begin {align *} \ det \ left (B \ right) & = \ left | {\ begin {array} {* {20} {r}} 2 & 3 & 1 \\ {- 1} & {- 6} & 7 \\ 4 & 5 & {- 1} \ end {array}} \ right | \, \, \, \, \ begin {array} {* {20} {r}} 2 & 3 \\ {- 1} & {- 6} \\ 4 & 5 \ end {array} \\ & = \ left (2 \ right) \ left ( {- 6} \ right) \ left ({- 1} \ right) + \ left (3 \ right) \ left (7 \ right) \ left (4 \ right) + \ left (1 \ right) \ left ( {- 1} \ right) \ left (5 \ right) – \\ & \ hspace {0.25 дюймов} \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ left (3 \ right) \ left ({- 1} \ right) \ left ({- 1} \ right) – \ left (2 \ right) \ left (7 \ right) \ left (5 \ right) – \ left (1 \ right) \ left ({- 6} \ right) \ left (4 \ right) \\ & = 42 \ end {align *} \ ]

Вы можете использовать формулу или сокращение, чтобы получить определитель \ (3 \ times 3 \).

Если определитель матрицы равен нулю, мы называем эту матрицу сингулярной , а если определитель матрицы не равен нулю, мы называем матрицу невырожденной .{-1} \).

Вычислить обратную матрицу \ (A \) довольно просто. Сначала формируем новую матрицу

\ [\ left ({A \, \, \, {I_n}} \ right) \]

, а затем используйте операции со строками из предыдущего раздела и попробуйте преобразовать эту матрицу в форму

\ [\ left ({{I_n} \, \, \, B} \ right) \]

Если мы можем, то \ (B \) обратен \ (A \). Если мы не можем, то не существует обратной матрицы \ (A \).

Пример 4 Найдите обратную матрицу, если она существует.\ [A = \ left ({\ begin {array} {* {20} {r}} 2 & 1 & 1 \\ {- 5} & {- 3} & 0 \\ 1 & 1 & {- 1} \ end {array}} \ right ) \] Показать решение

Сначала мы формируем новую матрицу, добавляя к ней единичную матрицу \ (3 \ times 3 \). Это

\ [\ left ({\ begin {array} {* {20} {r}} 2 & 1 & 1 \\ {- 5} & {- 3} & 0 \\ 1 & 1 & {- 1} \ end {array} \ quad \ begin { array} {* {20} {r}} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array}} \ right) \]

Теперь мы будем использовать операции со строками, чтобы попытаться преобразовать первые три столбца в идентичность \ (3 \ times 3 \).Другими словами, нам нужна 1 на диагонали, которая начинается в верхнем левом углу и равна нулю во всех остальных записях в первых трех столбцах.

Если задуматься, этот процесс очень похож на процесс, который мы использовали в предыдущем разделе для решения систем, но он идет немного дальше. Вот работа для этой проблемы.

\ [\ left ({\ begin {array} {* {20} {r}} 2 & 1 & 1 \\ {- 5} & {- 3} & 0 \\ 1 & 1 & {- 1} \ end {array} \ quad \ begin { array} {* {20} {r}} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array}} \ right) \ begin {array} {* {20} {c}} {{R_1} \ leftrightarrow {R_3} } \\ \ Rightarrow \ end {array} \ left ({\ begin {array} {* {20} {r}} 1 & 1 & {- 1} \\ {- 5} & {- 3} & 0 \\ 2 & 1 & 1 \ end {array} \ quad \ begin {array} {* {20} {r}} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \ end {array}} \ right) \ begin {array} {* {20} {c}} { {R_2} + 5 {R_1}} \\ {{R_3} – 2 {R_1}} \\ \ Rightarrow \ end {array} \] \ [\ left ({\ begin {array} {* {20} {r}} 1 & 1 & {- 1} \\ 0 & 2 & {- 5} \\ 0 & {- 1} & 3 \ end {array} \ quad \ begin { array} {* {20} {r}} 0 & 0 & 1 \\ 0 & 1 & 5 \\ 1 & 0 & {- 2} \ end {array}} \ right) \ begin {array} {* {20} {c}} {\ frac {1 } {2} {R_2}} \\ \ Rightarrow \ end {array} \ left ({\ begin {array} {* {20} {r}} 1 & 1 & {- 1} \\ 0 & 1 & {\ frac {- 5 }} {2}} \\ 0 & {- 1} & 3 \ end {array} \ quad \ begin {array} {* {20} {r}} 0 & 0 & 1 \\ 0 & {\ frac {1} {2}} & {\ frac {5} {2}} \\ 1 & 0 & {- 2} \ end {array}} \ right) \ begin {array} {* {20} {c}} {{R_3} + {R_2}} \ \ \ Rightarrow \ end {массив} \] \ [\ left ({\ begin {array} {* {20} {r}} 1 & 1 & {- 1} \\ 0 & 1 & {\ frac {{- 5}} {2}} \\ 0 & 0 & {\ frac {1}) {2}} \ end {array} \ quad \ begin {array} {* {20} {r}} 0 & 0 & 1 \\ 0 & {\ frac {1} {2}} & {\ frac {5} {2}} \\ 1 & {\ frac {1} {2}} & {\ frac {1} {2}} \ end {array}} \ right) \ begin {array} {* {20} {c}} {2 { R_3}} \\ \ Rightarrow \ end {array} \ left ({\ begin {array} {* {20} {r}} 1 & 1 & {- 1} \\ 0 & 1 & {\ frac {{- 5}} {2} } \\ 0 & 0 & 1 \ end {array} \ quad \ begin {array} {* {20} {r}} 0 & 0 & 1 \\ 0 & {\ frac {1} {2}} & {\ frac {5} {2}} \\ 2 & 1 & 1 \ end {array}} \ right) \ begin {array} {* {20} {c}} {{R_2} + \ frac {5} {2} {R_3}} \\ {{R_1} + {R_3}} \\ \ Rightarrow \ end {array} \] \ [\ left ({\ begin {array} {* {20} {r}} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array} \ quad \ begin {array} {* {20} {r}} 2 & 1 & 2 \ \ 5 & 3 & 5 \\ 2 & 1 & 1 \ end {array}} \ right) \ begin {array} {* {20} {c}} {{R_1} – {R_2}} \\ \ Rightarrow \ end {array} \ left ({ \ begin {array} {* {20} {r}} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array} \ quad \ begin {array} {* {20} {r}} {- 3} & {- 2 } & {- 3} \\ 5 & 3 & 5 \\ 2 & 1 & 1 \ end {array}} \ right) \]

Итак, мы смогли преобразовать первые три столбца в единичную матрицу \ (3 \ times 3 \), поэтому существует обратное, и оно есть,

\ [{A ^ {- 1}} = \ left ({\ begin {array} {* {20} {r}} {- 3} & {- 2} & {- 3} \\ 5 & 3 & 5 \\ 2 & 1 & 1 \ конец {массив}} \ right) \]

Итак, был пример, в котором существует обратное. Давайте посмотрим на пример, в котором обратного не существует.

Пример 5 Найдите обратную матрицу, если она существует. \ [B = \ left ({\ begin {array} {* {20} {r}} 1 & {- 3} \\ {- 2} & 6 \ end {array}} \ right) \] Показать решение

В этом случае мы используем тождество \ (2 \ times 2 \), чтобы получить новую матрицу, а затем попытаемся преобразовать первые два столбца в единичную матрицу \ (2 \ times 2 \).

\ [\ left ({\ begin {array} {* {20} {r}} 1 & {- 3} & 1 & 0 \\ {- 2} & 6 & 0 & 1 \ end {array}} \ right) \, \, \, \ begin {массив} {* {20} {c}} {2 {R_1} + {R_2}} \\ \ Rightarrow \ end {array} \, \, \ left ({\ begin {array} {* {20} { r}} 1 & {- 3} & 1 & 0 \\ 0 & 0 & 2 & 1 \ end {array}} \ right) \, \, \]

И дальше идти не надо.Чтобы идентификатор \ (2 \ times 2 \) находился в первых двух столбцах, мы должны иметь 1 во второй записи второго столбца и 0 во второй записи первого столбца. Однако нет способа получить 1 во второй записи второго столбца, которая сохранит 0 во второй записи в первом столбце. Следовательно, мы не можем получить тождество \ (2 \ times 2 \) в первых двух столбцах, и, следовательно, обратного к \ (B \) не существует.

Мы закончим обсуждение инверсий следующим фактом.{-1} \) НЕ будет существовать.

Я предоставлю вам проверить этот факт на двух предыдущих примерах.

Новый взгляд на системы уравнений

Нам нужно сделать быстрый пересмотр систем уравнений. Начнем с общей системы уравнений.

\ [\ begin {уравнение} \ begin {выровнено} {a_ {11}} {x_1} + {a_ {12}} {x_2} + \ cdots + {a_ {1n}} {x_n} & = {b_1} \ \ {a_ {21}} {x_1} + {a_ {22}} {x_2} + \ cdots + {a_ {2n}} {x_n} & = {b_2} \\ \ vdots \ hspace {0.8in} & \\ {a_ {n1}} {x_1} + {a_ {n2}} {x_2} + \ cdots + {a_ {nn}} {x_n} & = {b_n} \ end {align} \ label { уравнение: уравнение1} \ end {уравнение} \]

Теперь превратите каждую сторону в вектор, чтобы получить,

\ [\ left ({\ begin {array} {* {20} {r}} {{a_ {11}} {x_1} + {a_ {12}} {x_2} + \ cdots + {a_ {1n}}) {x_n}} \\ {{a_ {21}} {x_1} + {a_ {22}} {x_2} + \ cdots + {a_ {2n}} {x_n}} \\ \ vdots \\ {{a_ { n1}} {x_1} + {a_ {n2}} {x_2} + \ cdots + {a_ {nn}} {x_n}} \ end {array}} \ right) = \ left ({\ begin {array} { * {20} {r}} {{b_1}} \\ {{b_2}} \\ \ vdots \\ {{b_n}} \ end {array}} \ right) \]

Левую часть этого уравнения можно рассматривать как умножение матриц.

\ [\ left ({\ begin {array} {* {20} {r}} {{a_ {11}}} & {{a_ {12}}} & \ cdots & {{a_ {1n}}}} \ \ {{a_ {21}}} & {{a_ {22}}} & \ cdots & {{a_ {2n}}} \\ \ vdots & \ vdots & \ ddots & \ vdots \\ {{a_ {n1) }}} & {{a_ {n2}}} & \ cdots & {{a_ {nn}}} \ end {array}} \ right) \ left ({\ begin {array} {* {20} {r} } {{x_1}} \\ {{x_2}} \\ \ vdots \\ {{x_n}} \ end {array}} \ right) = \ left ({\ begin {array} {* {20} {r }} {{b_1}} \\ {{b_2}} \\ \ vdots \\ {{b_n}} \ end {array}} \ right) \]

Немного упрощая обозначения дает,

\ [\ begin {уравнение} A \ vec x = \ vec b \ label {eq: eq2} \ end {уравнение} \]

где, \ (\ vec x \) – вектор, компоненты которого являются неизвестными в исходной системе уравнений.Мы называем \ (\ eqref {eq: eq2} \) матричной формой системы уравнений \ (\ eqref {eq: eq1} \), а решение \ (\ eqref {eq: eq2} \) эквивалентно решению \ (\ eqref {eq: eq1} \). Процесс решения идентичен. Расширенная матрица для \ (\ eqref {eq: eq2} \) равна

\ [\ left ({A \, \, \, \ vec b} \ right) \]

Когда у нас есть расширенная матрица, мы действуем так же, как и с системой, которая не была записана в матричной форме.

У нас также есть следующий факт о решениях \ (\ eqref {eq: eq2} \).

Факт

Учитывая систему уравнений \ (\ eqref {eq: eq2} \), у нас есть одна из следующих трех возможностей решения.

Решений не будет.
Будет ровно одно решение.
Решений будет бесконечно много.

На самом деле, теперь мы можем пойти немного дальше. Поскольку мы предполагаем, что у нас столько же уравнений, сколько и неизвестных, матрица \ (A \) в \ (\ eqref {eq: eq2} \) является квадратной матрицей, и поэтому мы можем вычислить ее определитель.Это дает следующий факт.

Факт

Учитывая систему уравнений в \ (\ eqref {eq: eq2} \), мы имеем следующее.

Если \ (A \) неособо, то у системы будет ровно одно решение.
Если \ (A \) сингулярно, то у системы либо не будет решения, либо решений будет бесконечно много.

Матричная форма однородной системы

\ [\ begin {уравнение} A \ vec x = \ vec 0 \ label {eq: eq3} \ end {уравнение} \]

, где \ (\ vec 0 \) – вектор всех нулей.В однородной системе мы гарантированно имеем решение \ (\ vec x = \ vec 0 \). Тогда для однородных систем приведенный выше факт равен

Факт

Для однородной системы \ (\ eqref {eq: eq3} \) имеем следующее.

Если \ (A \) неособое, то единственным решением будет \ (\ vec x = \ vec 0 \).
Если \ (A \) сингулярно, то у системы будет бесконечно много ненулевых решений.

Линейная независимость / Линейная зависимость

Это не первый раз, когда мы встречаемся с этой темой.Мы также увидели линейную независимость и линейную зависимость, когда рассматривали дифференциальные уравнения второго порядка. В этом разделе мы имели дело с функциями, но здесь концепция по сути та же. Если мы начнем с \ (n \) векторов,

\ [{\ vec x_1}, \, \, {\ vec x_2}, \, \, \ ldots, \, \, {\ vec x_n} \]

Если мы сможем найти константы, \ (c_ {1} \), \ (c_ {2} \),…, \ (c_ {n} \) с как минимум двумя ненулевыми, такими, что

\ [\ begin {уравнение} {c_1} {\ vec x_1} + {c_2} {\ vec x_2} + \, \ ldots + {c_n} {\ vec x_n} = \ vec 0 \ label {eq: eq4} \ конец {уравнение} \]

, то мы называем векторы линейно зависимыми.Если в \ (\ eqref {eq: eq4} \) работают только константы \ (c_ {1} = 0 \), \ (c_ {2} \) = 0,…, \ (c_ {n} = 0 \), то векторы назовем линейно независимыми.

Если мы дополнительно сделаем предположение, что каждый из векторов \ (n \) имеет \ (n \) компоненты, , то есть , каждый из векторов будет выглядеть так:

\ [\ vec x = \ left ({\ begin {array} {* {20} {r}} {{x_1}} \\ {{x_2}} \\ \ vdots \\ {{x_n}} \ end { массив}} \ справа) \]

, мы можем получить очень простой тест на линейную независимость и линейную зависимость.Обратите внимание, что это не обязательно, но во всей нашей работе мы будем работать с \ (n \) векторами, каждый из которых имеет \ (n \) компоненты.

Факт

Учитывая \ (n \) векторов, каждый с компонентами \ (n \),

\ [{\ vec x_1}, \, \, {\ vec x_2}, \, \, \ ldots, \, \, {\ vec x_n} \]

образуют матрицу,

\ [X = \ left ({\ begin {array} {* {20} {r}} {{{\ vec x} _1}} & {{{\ vec x} _2}} & \ cdots & {{{ \ vec x} _n}} \ end {array}} \ right) \]

Итак, матрица \ (X \) – это матрица, столбец \ (i ^ {\ text {th}} \) которой является вектором \ (i ^ {\ text {th}} \), \ ({\ vec x_i} \).Затем

Если \ (X \) неособое число (, т.е. \ (\ det (X) \) не равно нулю), то векторы \ (n \) линейно независимы, и

, если \ (X \) сингулярно (, т.е. \ (\ det (X) = 0 \)), то векторы \ (n \) линейно зависимы, а константы, которые делают \ (\ eqref {eq: eq4} \) true можно найти, решив систему \ [X \, \ vec c = \ vec 0 \]

, где \ (\ vec c \) – вектор, содержащий константы из \ (\ eqref {eq: eq4} \).{(3)}} = \ left ({\ begin {array} {* {20} {r}} 6 \\ {- 2} \\ 1 \ end {array}} \ right) \] Показать решение

Итак, первое, что нужно сделать, это сформировать \ (X \) и вычислить его определитель.

\ [X = \ left ({\ begin {array} {* {20} {r}} 1 & {- 2} & 6 \\ {- 3} & 1 & {- 2} \\ 5 & 4 & 1 \ end {array}} \ right ) \ quad \ quad \ Rightarrow \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ det \ left (X \ right) = – 79 \]

Эта матрица неособая, поэтому векторы линейно независимы.{(3)}} = \ left ({\ begin {array} {* {20} {r}} 2 \\ {- 1} \\ 4 \ end {array}} \ right) \] Показать решение

Как и в предыдущем примере, сначала сформируйте \ (X \) и вычислите его определитель.

\ [X = \ left ({\ begin {array} {* {20} {r}} 1 & {- 4} & 2 \\ {- 1} & 1 & {- 1} \\ 3 & {- 6} & 4 \ end { array}} \ right) \ quad \ quad \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ det \ left (X \ right) = 0 \]

Итак, эти векторы линейно зависимы.Теперь нам нужно найти взаимосвязь между векторами. Это означает, что нам нужно найти константы, которые сделают \ (\ eqref {eq: eq4} \) истинным.

Итак, нам нужно решить систему

\ [X \, \ vec c = \ vec 0 \]

Вот расширенная матрица и решение для этой системы.

\ [\ left ({\ begin {array} {* {20} {r}} 1 & {- 4} & 2 \\ {- 1} & 1 & {- 1} \\ 3 & {- 6} & 4 \ end {array} \ quad \ begin {array} {* {20} {r}} 0 \\ 0 \\ 0 \ end {array}} \ right) \ begin {array} {* {20} {c}} {{R_2} + {R_1}} \\ {{R_3} – 3 {R_1}} \\ \ Rightarrow \ end {array} \ left ({\ begin {array} {* {20} {r}} 1 & {- 4} & 2 \\ 0 & {- 3} & 1 \\ 0 & 6 & {- 2} \ end {array} \ quad \ begin {array} {* {20} {r}} 0 \\ 0 \\ 0 \ end {array}} \ справа) \ begin {array} {* {20} {c}} {{R_3} + 2 {R_2}} \\ \ Rightarrow \ end {array} \ left ({\ begin {array} {* {20} { r}} 1 & {- 4} & 2 \\ 0 & {- 3} & 1 \\ 0 & 0 & 0 \ end {array} \ quad \ begin {array} {* {20} {r}} 0 \\ 0 \\ 0 \ end {array}} \ right) \ begin {array} {* {20} {c}} {- \ frac {1} {3} {R_2}} \\ \ Rightarrow \ end {array} \] \ [\ left ({\ begin {array} {* {20} {r}} 1 & {- 4} & 2 \\ 0 & 1 & {- \ frac {1} {3}} \\ 0 & 0 & 0 \ end {array} \ quad \ begin {array} {* {20} {r}} 0 \\ 0 \\ 0 \ end {array}} \ right) \ begin {array} {* {20} {c}} {{R_1} + 4 {R_2}} \\ \ Rightarrow \ end {array} \ left ({\ begin {array} {* {20} {r}} 1 & 0 & {\ frac {2} {3}} \\ 0 & 1 & {- \ frac { 1} {3}} \\ 0 & 0 & 0 \ end {array} \ quad \ begin {array} {* {20} {r}} 0 \\ 0 \\ 0 \ end {array}} \ right) \ quad \ Rightarrow \ quad \ begin {array} {* {20} {r}} {{c_1} + \ frac {2} {3} {c_3} = 0} \\ {{c_2} – \ frac {1} {3} {c_3} = 0} \\ {0 = 0} \ end {array} \ quad \ Rightarrow \ quad \ begin {array} {* {20} {l}} {{c_1} = – \ frac {2} { 3} {c_3}} \\ {{c_2} = \ frac {1} {3} {c_3}} \\ {} \ end {array} \]

Теперь нам нужны фактические значения для констант, поэтому, если использовать \ ({c_3} = 3 \), мы получим следующее решение \ ({c_1} = – 2 \), \ ({c_2} = 1 \), и \ ({c_3} = 3 \).{(3)}} = \ left ({\ begin {array} {* {20} {r}} 0 \\ 0 \\ 0 \ end {array}} \ right) \]

Исчисление с матрицами

В этом нет ничего особенного, кроме как просто убедиться, что мы можем иметь дело с исчислением с матрицами.

Во-первых, до этого момента мы рассматривали только матрицы с числами в качестве элементов, но элементы в матрице также могут быть функциями. Итак, мы можем посмотреть на матрицы в следующем виде:

\ [A \ left (t \ right) = \ left ({\ begin {array} {* {20} {r}} {{a_ {11}} \ left (t \ right)} & {{a_ {12 }} \ left (t \ right)} & \ cdots & {{a_ {1n}} \ left (t \ right)} \\ {{a_ {21}} \ left (t \ right)} & {{a_ {22}} \ left (t \ right)} & \ cdots & {{a_ {2n}} \ left (t \ right)} \\ \ vdots & \ vdots & {} & \ vdots \\ {{a_ { m1}} \ left (t \ right)} & {{a_ {m2}} \ left (t \ right)} & \ cdots & {{a_ {mn}} \ left (t \ right)} \ end {массив }} \Правильно)\]

Теперь мы можем поговорить о дифференцировании и интегрировании матрицы такого вида.Чтобы дифференцировать или интегрировать матрицу этой формы, все, что мы делаем, – это дифференцируем или интегрируем отдельные записи.

\ [A ‘\ left (t \ right) = \ left ({\ begin {array} {* {20} {r}} {{{a’} _ {11}} \ left (t \ right)} & {{{a ‘} _ {12}} \ left (t \ right)} & \ cdots & {{{a’} _ {1n}} \ left (t \ right)} \\ {{{a ‘} _ {21}} \ left (t \ right)} & {{{a ‘} _ {22}} \ left (t \ right)} & \ cdots & {{{a’} _ {2n}} \ left (t \ right)} \\ \ vdots & \ vdots & {} & \ vdots \\ {{{a ‘} _ {m1}} \ left (t \ right)} & {{{a’} _ {m2 }} \ left (t \ right)} & \ cdots & {{{a ‘} _ {mn}} \ left (t \ right)} \ end {array}} \ right) \] \ [\ int {{A \ left (t \ right) \, dt}} = \ left ({\ begin {array} {* {20} {r}} {\ int {{{a_ {11}}} \ left (t \ right) \, dt}}} & {\ int {{{a_ {12}} \ left (t \ right) \, dt}}} & \ cdots & {\ int {{{a_ {1n) }} \ left (t \ right) \, dt}}} \\ {\ int {{{a_ {21}} \ left (t \ right) \, dt}}} & {\ int {{{a_ { 22}} \ left (t \ right) \, dt}}} & \ cdots & {\ int {{{a_ {2n}} \ left (t \ right) \, dt}}} \\ \ vdots & \ vdots & {} & \ vdots \\ {\ int {{{a_ {m1}} \ left (t \ right) \, dt}}} & {\ int {{{a_ {m2}} \ left (t \ right) \, dt}}} & \ cdots & {\ int {{{a_ {mn}} \ left (t \ right) \, dt}}} \ end {array}} \ right) \]

Итак, когда мы сталкиваемся с подобными вещами, не волнуйтесь об этом.Просто дифференцируйте или интегрируйте, как обычно.

В этом разделе мы рассмотрели очень сжатый набор тем из линейной алгебры. Когда мы вернемся к дифференциальным уравнениям, многие из этих тем будут время от времени появляться, и вам, по крайней мере, нужно будет знать, что означают эти слова.

Основная тема линейной алгебры, которую вы должны знать, однако, если вы собираетесь уметь решать системы дифференциальных уравнений, является темой следующего раздела.

Как получить определитель матрицы – Видео и стенограмма урока

Квадратные матрицы

Когда количество строк и столбцов одинаково, мы получаем квадратную матрицу .Это означает, что у нас может быть квадратная матрица размером 1х1, 2х2 или 3х3. Поскольку у них одинаковое количество строк и столбцов, математический способ определения квадратной матрицы состоит в том, чтобы сказать, что это любая матрица, которая имеет размер N x N .

Квадратная матрица известна в математике как матрица NxN.

Причина, по которой нам нужно знать, что такое квадратная матрица, заключается в том, что определитель может быть вычислен только на квадратных матрицах.Пока это квадратная матрица, определитель любой матрицы – это просто число, поэтому определитель берет матрицу и сводит ее к одному значению. На самом деле вычисление определителя становится все труднее и труднее по мере того, как матрица становится все больше и больше, поэтому мы начнем с рассмотрения наименьшей квадратной матрицы (1×1) и попрактикуемся с большими и большими.

Определение определителя матрицы 1х1 математики называют «тривиальным». Это потому, что делать по сути нечего. Например, определитель матрицы (обозначен прямыми столбиками вместо скобок) | 4 | всего 4.Или определитель матрицы | -5 | просто -5. Обратите внимание, что матрица больше не в скобках, а только в виде прямых полос вверх и вниз, что-то вроде знаков абсолютного значения. Хотя | | символы выглядят так же, как и абсолютное значение, это просто совпадение и, вероятно, связано с тем, что математики ленивы и не хотят рисовать что-либо более сложное.

Матрица 2×2

Определение определителя матрицы 2×2 становится немного сложнее. Давайте посмотрим на пример | 5 4, 8 2 |.Опять же, потому что матрица окружена | | мы знаем, что нас просят вычислить числовое значение определителя. Теперь нам нужно начать с процесса, который включает в себя умножение диагоналей и вычитание произведений. Начнем с диагонали от верхнего левого угла к нижнему правому; в этом примере мы бы сделали (5) (2). Мы вычитаем диагональ от нижнего левого угла к верхнему правому, что составляет (8) (4). В итоге мы получаем 10-32 = -22, поэтому определитель этой матрицы просто -22.

Умножьте диагнозы и вычтите произведения, чтобы найти определитель.

Другой быстрый пример: | -1 5, -4 3 |.Здесь мы бы сделали (-1) (3) – (-4) (5). Будьте осторожны при вычитании отрицательного числа, так как оно меняет знак. Итак, (-1) (3) – (- 4) (5) = -3 + 20 = 17.

Рассмотрение общей матрицы с переменными в качестве записей вместо чисел (| ab, cd |) дает нам формулу для определителя матрицы 2×2 как ad – bc , которую мы снова получаем путем умножения диагонали вверху слева внизу справа и вычитая диагональ внизу слева вверху справа.

Общий вид определителя матрицы 2×2

Матрицы большего размера

Как только мы перейдем к матрицам больше 2×2, нам придется вычислить ряд меньших определителей в строке, чтобы вычислить главный определитель.Этот навык не является существенным для этого класса, поэтому мы просто быстро рассмотрим его, чтобы вы могли познакомиться с ним, но не беспокойтесь о запоминании процесса.

Например, если бы мы хотели вычислить определитель этой матрицы 3×3 прямо здесь, нам нужно было бы умножить 2 на детерминант матрицы 2X2, который вы получите, когда закроете строку и столбец, в которых находится 2. Теперь мы отнимет 1, умноженную на определитель матрицы 2X2, который вы получите, когда закроете строку и столбец, в которых находится 1.Наконец, -3-кратный детерминант, который вы получаете, когда закрываете строку и столбец, в которых находится -3. Теперь это превращается в процесс оценки детерминантов этих меньших детерминантов 2X2 с помощью формулы, которую мы только что узнали, а именно ad – до н.э. В этом случае мы бы получили определитель этой матрицы 3×3 равным 25. Если бы мы взяли определитель 4X4, или 5X5, или 10X10, или 50X50, он стал бы все более и более сложным, но, по сути, это один и тот же процесс во всем. опять таки. Вы продолжаете брать все меньшие и меньшие детерминанты, пока не дойдете до определителей 2X2, где вы действительно можете начать вычислять значения.

Покрытие строк и столбцов, чтобы получить меньший определитель

Нахождение определителя для матриц большего размера

Оценка детерминант меньших детерминант

Резюме урока

Матрицы помечаются # строками X # столбцами и часто обозначаются как MXN .
Матрица с одинаковым количеством строк и столбцов называется квадратной матрицей
Любая квадратная матрица имеет определитель, который представляет собой одно числовое значение, связанное с матрицей.
Определитель матрицы 1×1 – это просто единственное число в матрице.
Определитель матрицы 2×2 равен ad – bc .
Определители больших матриц можно вычислить, разбив их на группу матриц меньшего размера 2X2.
Как выглядят столбики абсолютных значений | | помещаются снаружи определителя, чтобы указать, что нас просят вычислить определитель.

Определители, линейное уравнение | Реальная статистика с использованием Excel

Определение 1 : Определитель , det A, также обозначается | A | , квадратной матрицы n × n определяется рекурсивно следующим образом:

Если A является матрицей 1 × 1 [ a ] (т.е.е. скаляр), затем det A = a . В противном случае

, где A _ij – это матрица A с удаленной строкой i и столбцом j .

Обратите внимание, что если A =, то мы используем обозначение для det A .

Функции Excel : Excel предоставляет следующую функцию для вычисления определителя квадратной матрицы:

MDETERM ( A ): если A – квадратный массив, тогда MDETERM ( A ) = det А .Это не функция массива.

Функция реальной статистики DET ( A ) обеспечивает эквивалентную функциональность.

Свойство 1 :

det A ^T = det A
Если A – диагональная матрица, то det A = произведение элементов на главной диагонали матрицы A

Доказательство: оба этих свойства являются простым следствием определения 1

Свойство 2: = ad – bc

Пример 1 : вычислить det A , где

из определения 1 и Свойство 2 следует, что

Конечно, мы можем получить тот же ответ, используя функцию Excel MDETERM ( A ).

Свойство 3 : Если A и B – квадратные матрицы одинакового размера, то det AB = det A ∙ det B

Свойство 4 : квадратная матрица A обратима тогда и только тогда, когда det A ≠ 0. Если A обратимо, то

Первое утверждение эквивалентно утверждению, что квадратная матрица A сингулярна тогда и только тогда, когда det A = 0 .

Свойство 5 : Правила оценки определителей:

Определитель треугольной матрицы – это произведение элементов на диагонали.
Если мы поменяем местами две строки, определитель новой матрицы будет отрицательным по сравнению со старой.
Если мы умножим одну строку на константу, определитель новой матрицы будет определителем старой, умноженной на константу.
Если мы добавим одну строку к другой, умноженную на константу, определитель новой матрицы будет таким же, как и у старой.

Наблюдение : Правил свойства 5 достаточно для вычисления определителя любой квадратной матрицы. Идея состоит в том, чтобы преобразовать исходную матрицу в треугольную, а затем использовать правило 1 для вычисления значения определителя.

Теперь мы представляем алгоритм, основанный на Свойстве 5 для вычисления det A , где A = [ a _ij ] – это матрица n × n . Начните с установки значения определителя на 1, а затем выполните шаги с 1 по n следующим образом.

Шаг k – часть 1 (a): Если a _kk ≠ 0, умножьте текущее значение определителя на a _kk , а затем разделите все записи в строке k на a _kk (правило 3 свойства 5).

Шаг k – часть 1 (b): Если a _kk = 0, заменить строку k на любую строку m под ней (т.е. k < m ≤ n ) для которого a _mk ≠ 0, умножьте текущее значение определителя на -1 (правило 2), а затем выполните шаг 1 (a) выше.Если такой строки не существует, завершите алгоритм и верните значение 0 для определителя.

Шаг k – часть 2: для каждого ряда м под рядом k , прибавить – a _mk раза ряд k к ряду m (правило 4). Это гарантирует, что a _ij = 0 для всех i > k и j ≤ k .

После завершения шага n у нас будет треугольная матрица, диагональ которой содержит все единицы, и поэтому по правилу 1 определитель равен текущему значению определителя.

Пример 2 : Используя свойство 5, найдите

Мы представляем шаги, смотрящие слева направо, а затем сверху вниз на рисунке 1. Для каждого шага указывается используемое правило, а также множитель определитель рассчитан до этого момента.

Рисунок 1. Вычисление определителя в примере 2

Это показывает, что определитель равен -5, тот же ответ, что и при использовании функции Excel MDETERM.

Наблюдение : На этапе k – часть 1 (b) вышеупомянутой процедуры мы меняем две строки, если a _kk = 0.Учитывая, что нам нужно иметь дело с ошибками округления, что произойдет, если _kk мало, но не совсем равно нулю? Чтобы уменьшить влияние ошибок округления, мы должны изменить шаг k – часть 1 следующим образом:

Шаг k – часть 1: найти m ≥ k так, чтобы абсолютное значение a _mk самый большой. Если это a _mk ≈ 0 (т.е. | a _mk | <ϵ, где ϵ - некоторая предопределенная небольшая величина), то завершите процедуру.Если m > k , поменяйте местами строки m и k .

Наблюдение : Определитель можно использовать для решения систем линейных уравнений, как описано в Системе линейных уравнений с помощью правила Крамера. Кроме того, метод исключения Гаусса, используемый для вычисления определителя, также может использоваться для решения систем линейных уравнений.

Определители (алгебра 2, матрицы) – Mathplanet

Определитель det (A) или | A | квадратной матрицы A – это число, кодирующее определенные свойства матрицы.Детерминанты названы по размеру матриц. В следующем примере мы покажем, как определить детерминанты второго порядка.

Пример

$$ A = \ begin {bmatrix} a & b \\ c & d \ end {bmatrix} $$

Определитель A (определитель второго порядка) равен

$$ det (A) = \ begin {vmatrix} a & b \\ c & d \ end {vmatrix} = ad-bc $$

Определители матриц 3 × 3 называются определителями третьего порядка. Один из методов оценки детерминант третьего порядка называется разложением по минорам.Младший элемент – это определитель, формируемый при удалении строки и столбца, содержащих этот элемент.

$$ \ begin {vmatrix} a & b & c \\ d & e & f \\ g & h & i \ end {vmatrix} = a \ begin {vmatrix} e & f \\ h & i \ end { vmatrix} -b \ begin {vmatrix} d & f \\ g & i \ end {vmatrix} + c \ begin {vmatrix} d & e \\ g & h \ end {vmatrix} $$

Определители могут использоваться для определения площади треугольника, если известны координаты вершин. Если вершинами треугольников являются (a, b), (c, d) и (e, f), площадь равна

$$ A = \ frac {1} {2} \ begin {vmatrix} a & b & 1 \\ c & d & 1 \ e & f & 1 \ end {vmatrix} $$

Если A оказывается отрицательным, мы должны использовать абсолютное значение для A, чтобы иметь неотрицательное значение для нашей области.

Пример

Найдите площадь треугольника с вершинами, расположенными в точках (-2,2), (1,3) и (3,0) (этот пример также показан в нашем видео-уроке).

Подставляем координаты вершин в формулу площади

$$ A = \ frac {1} {2} \ begin {vmatrix} -2 & 2 & 1 \\ 1 & 3 & 1 \\ 3 & 0 & 1 \ end {vmatrix} $$

и продолжается с

$$ = \ frac {1} {2} (- 2 \ begin {vmatrix} 3 & 1 \\ 0 & 1 \ end {vmatrix} -2 \ begin {vmatrix} 1 & 1 \\ 3 & 1 \ end {vmatrix} +1 \ begin {vmatrix} 1 & 3 \\ 3 & 0 \ end {vmatrix}) = \\ \\ = \ frac {1} {2} (- 2 (3 \ cdot1-1 \ cdot 0 ) -2 (1 \ cdot 1-1 \ cdot 3) +1 (1 \ cdot 0-3 \ cdot 3)) = \\ \\ = \ frac {1} {2} (- 6 + 4-9) = \ frac {-11} {2} = – 5.5 $$

Мы получили отрицательное значение для A, и площадь не может быть отрицательной, поэтому мы должны взять абсолютное значение для A:

$$ \ mid A \ mid = \ mid -5.5 \ mid = 5.5 \; $$

Итак, площадь треугольников составляет 5,5 квадратных единиц.

Видеоурок

Найдите область из приведенного выше примера.

Свойства детерминантов – объяснение, важные свойства, решаемые примеры и часто задаваемые вопросы

Детерминанты и их свойства

В линейной алгебре определитель – это уникальное число, которое можно определить из квадратной матрицы.Определители матрицы говорят, что K представляется как det (K) или | K | или det K. Детерминанты и их свойства полезны, поскольку они позволяют нам получать те же результаты с различными и более простыми конфигурациями элементов. Определитель считается важной функцией, поскольку он удовлетворяет некоторым дополнительным свойствам определителей, которые выводятся из следующих условий.

Мультипликативность; det (XY) = det (X) det (y)
Инвариантность при транспонировании det (X) = det (Xt).
Инвариантность при операциях со строками; если X ’представляет собой матрицу, образованную суммированием кратного числа любой строки с другой строкой, тогда det (X) = det (X’).
Под заменой строк изменился знак. Если X ’представляет собой матрицу, полученную путем перестановки позиций двух строк, тогда det (X’) = -det (x)

Что известно как детерминанты?

Определитель квадратной матрицы – это значение, определяемое элементами матрицы. В матрице 2 × 2.Детерминанты рассчитываются по формуле

Det \ [\ begin {pmatrix} a & b \\ c & d \ end {pmatrix} \] = ad – bc

У больших матриц есть более сложные формулы ..

Детерминанты имеют различные различные приложения по математике. Например, они используются в формулах шнурков для расчета площади, которая полезна в качестве условия коллинеарности, поскольку три коллинеарных точки определяют треугольник, равный 0. Определитель также используется в исчислении нескольких переменных (в основном в Якобине) и в вычислениях. перекрестное произведение векторов.

Основные свойства определителей

Некоторые основные свойства определителей приведены ниже:

Если In – единичная матрица порядка m × m, то det (I) равен 1
Если матрица XT является транспонированной матрицей X, тогда det (XT) = det (X)
Если матрица X-1 является обратной матрице X, то det (X-1) = 1 / det (x) = det ( X) -1
Если две квадратные матрицы x и y имеют одинаковый размер, то det (XY) = det (X) det (Y)
Если матрица X сохраняет размер a × a и C является константа, то det (CX) = Ca det (X)
Если A, B и C – три положительные полуопределенные матрицы равного размера, то следующее уравнение выполняется вместе со следствием det (A + B) ≥ det (A) + det (B) для A, B, C ≥ 0 det (A + B + C) + det C ≥ det (A + B) + det (B + C)
В треугольной матрице определитель равен произведению диагональных элементов.
Определитель матрицы равен нулю, если каждый элемент матрицы равен нулю.
Формула Лапласа и сопряженная матрица.

Важные свойства детерминантов

Есть 10 важных свойств детерминантов, которые широко используются. Описание каждого из 10 важных свойств детерминантов приводится ниже.

1. Свойство отражения

Свойство детерминантов отражения определяет, что детерминанты не изменяются, если строки преобразуются в столбцы, а столбцы – в строки.

2. Свойство «полностью ноль»

Определители будут эквивалентны нулю, если каждый член строк и столбцов равен нулю.

3. Пропорциональность (свойство повторения)

Если каждый член строк или столбцов аналогичен столбцу какой-либо другой строки (или столбца), то определитель эквивалентен нулю.

4. Свойство переключения

Перестановка любых двух строк (или столбцов) определителя меняет его знаки.

5. Свойство фактора

Если определитель Δ становится равным 0 при учете значения x = α, то (x -α) рассматривается как коэффициент Δ.

6. Скалярное свойство множественности

Если все элементы строки (или столбцов) определителя умножаются на ненулевую константу, то определитель умножается на аналогичную константу.

7. Свойство суммы

\ [\ begin {vmatrix} j_ {1} + k_ {1} & l_ {1} & m_ {1} \\ j_ {2} + k_ {2} & l_ {2} & m_ {2} \\ j_ {3} + k_ {3} & l_ {3} & m_ {3} \ end {vmatrix} \] = \ [\ begin {vmatrix} j_ {1} & l_ {1} & m_ {1} \\ j_ {2} & l_ {2} & m_ {2} \\ j_ {3} & l_ {3} & m_ {3} \ end {vmatrix} \] + \ [\ begin { vmatrix} + k_ {1} & l_ {1} & m_ {1} \\ + k_ {2} & l_ {2} & m_ {2} \\ + k_ {3} & l_ {3} & m_ {3 } \ end {vmatrix} \]

8. {2} \]

В указанных выше определителях матрицы кофакторов Cij обозначает кофактор элементов aij в Δ.

10. Свойство инвариантности

\ [\ begin {vmatrix} a_ {1} & b_ {1} & c_ {1} \\ a_ {2} & b_ {2} & c_ {2} \\ a_ { 3} & b_ {3} & c_ {3} \ end {vmatrix} \] = \ [\ begin {vmatrix} a_ {1} + \ alpha b_ {1} + \ beta c_ {1} & b_ {1} & c_ {1} \\ a_ {2} + \ alpha b_ {2} + \ beta c_ {2} & b_ {2} & c_ {2} \\ a_ {3} + \ alpha b_ {3} + \ beta c_ {3} & b_ {3} & c_ {3} \ end {vmatrix} \]

Это означает, что определитель остается неизменным при действии члена Ci ⟶ Ci + αCj + βCkj, где j и k не эквивалентно i, или математическая операция члена Ri ⟶ Ri + αRj + βRk, где j и k не эквивалентны i.

Примеры Задачи о свойствах определителей

Некоторые важные примеры свойств определителей приведены ниже:

1. Используя свойства определителя, докажите, что

\ [\ begin {vmatrix} x & y & z \\ y & z & x \\ z & x & y \ end {vmatrix} \] = (x + y + z) (xy + yz + zx – x² – y² – z²)

Решение: С помощью инвариантности и скаляра По множеству свойств определителя можно доказать указанный выше определитель.

Δ = \ [\ begin {vmatrix} x & y & z \\ y & z & x \\ z & x & y \ end {vmatrix} \] = \ [\ begin {vmatrix} x + y + z & y & z \\ y + z + x & z & x \\ z + x + y & z & y \ end {vmatrix} \] [Операционная C \ [_ {1} \] ⟶ C \ [_ { 1} \] + C \ [_ {2} \] + C \ [_ {3} \]]

= (x + y + z) \ [\ begin {vmatrix} 1 & y & 0 \\ 1 & z & x \\ 1 & x & y \ end {vmatrix} \]

= (x + y + z) \ [\ begin {vmatrix} 1 & y & z \\ 0 & zy & xz \\ 1 & xy & yz \ end {vmatrix} \] [Эксплуатация (R \ [_ {2} \] ⟶ R \ [_ {2} \] – R \ [_ {1} \] и (R \ [_ { 3} \] ⟶ R \ [_ {3} \] – R \ [_ {1} \])]

= (x + y + z) [(z – y) (y – z) – (x – y) (x – z)

= (x + y + z) (xy + yz + zx – x² – y² – Z²)

2.Используя свойства определителя, докажите, что

\ [\ begin {vmatrix} a & b & c \\ d & e & f \\ g & h & i \ end {vmatrix} \] = \ [\ begin {vmatrix} b & h & e \\ a & g & d \\ c & i & f \ end {vmatrix} \]

Решение: поменять местами строки и столбцы по диагоналям, используя свойство отражения, а затем свойство переключения решимости мы можем получить желаемый результат.

LHS = \ [\ begin {vmatrix} a & b & c \\ d & e & f \\ g & h & i \ end {vmatrix} \] = \ [\ begin {vmatrix} a & d & g \\ b & e & h \\ c & f & i \ end {vmatrix} \]

(Перестановка строк и столбцов по диагоналям)

= (-1) \ [\ begin {vmatrix} a & g & d \\ b & h & e \\ c & i & f \ end {vmatrix} \] = (1) ² = \ [\ begin {vmatrix} b & h & e \\ a & g & d \\ c & i & f \ end {vmatrix} \] = \ [\ begin {vmatrix} b & h & e \\ a & g & d \\ c & i & f \ end {vmatrix} \] = R.HS

Время проверки

1. Согласно свойствам определителя значение определителя равно нулю, если строка равна

Умножено на строку
Умножено на столбец
Разделено на строку

2. Детерминанты матрицы в матрицах представлены

Вертикальными линиями вокруг матрицы.
Горизонтальные линии вокруг матрицы
Кронштейн вокруг матрицы
Ни один из вышеперечисленных

Детерминанты – определение, свойства, решенные примеры

Детерминанты – это скалярная величина, полученная как сумма произведений элементов квадратной матрицы в соответствии с заданным правилом.Определители помогают найти сопряженную, обратную матрицу. Далее для решения линейных уравнений методом обращения матриц нам необходимо применить эту концепцию определителей. Перекрестное произведение двух векторов легко запоминается посредством вычисления определителей. Детерминанты представлены аналогично матрице, но со знаком модуля. В этой статье давайте узнаем больше о детерминантах, их свойствах, правилах поиска определителей разного порядка и их вычисления на решенных примерах.

Что такое детерминанты?

Детерминанты рассматриваются как коэффициент масштабирования матриц. Их можно рассматривать как функции растяжения и сжатия матриц. Детерминанты принимают квадратную матрицу на входе и возвращают одно число на выходе. Квадратная матрица может быть определена как матрица с равным количеством строк и столбцов.

Детерминанты Определение

Для каждой квадратной матрицы C = [\ (c_ {ij} \)] порядка n × n определитель может быть определен как вещественное скалярное значение или комплексное число, где \ (c_ {ij} \) – это (i, j) ^{-й элемент} матрицы C.Определитель может быть обозначен как det (C) или | C |, здесь определитель записывается путем взятия сетки чисел и их расположения внутри столбцов абсолютного значения вместо использования квадратных скобок.

Рассмотрим матрицу C = \ (\ left [\ begin {array} {ll} 1 & 2 \\ 3 & 4 \ end {array} \ right] \)

Тогда его определитель может быть представлен как:

| C | = \ (\ left | \ begin {array} {ll} 1 & 2 \\ 3 & 4 \ end {array} \ right | \)

Как рассчитать детерминанты?

Для простейшей квадратной матрицы порядка 1 × 1, имеющей только одно число, определитель становится самим числом.Давайте узнаем, как вычислить определители для матриц второго, третьего и четвертого порядков.

Расчет детерминантов в 2D

Для любой двумерной квадратной матрицы или квадратной матрицы порядка 2 × 2 мы можем использовать формулу определителя для вычисления ее определителя:

C = \ (\ left [\ begin {array} {ll} a & b \\ c & d \ end {array} \ right] \)

Его двумерный определитель можно рассчитать как:

| C | = \ (\ left | \ begin {array} {ll} a & b \\ c & d \ end {array} \ right | \)

| C | = (а × г) – (б × в)

Например: C = \ (\ left [\ begin {array} {ll} 8 & 6 \\ 3 & 4 \ end {array} \ right] \)

Его определитель можно рассчитать как:

| C | = \ (\ left | \ begin {array} {ll} 8 & 6 \\ 3 & 4 \ end {array} \ right | \)

| C | = (8 × 4) – (6 × 3) = 32 – 18 = 14

Расчет 3D детерминантов

Для любой трехмерной квадратной матрицы или квадратной матрицы порядка 3 × 3 это процедура вычисления ее определителя.

\ (C = \ left [\ begin {array} {ccc} a_ {1} & b_ {1} & c_ {1} \\ a_ {2} & b_ {2} & c_ {2} \\ a_ { 3} & b_ {3} & c_ {3} \ end {array} \ right] \)

Его определитель можно рассчитать как:

| C | = \ (\ left | \ begin {array} {ccc} a_ {1} & b_ {1} & c_ {1} \\ a_ {2} & b_ {2} & c_ {2} \\ a_ {3} & b_ {3} & c_ {3} \ end {array} \ right | \)

Шаги в вычислении детерминантов 3D

\ (a_ {1} \) фиксируется как номер привязки, и вычисляется двухмерный определитель его подматрицы, которая является квадратной матрицей.
Следующий номер привязки берется по порядку, теперь это \ (b_ {1} \), вычисляется малый определитель, и, наконец, \ (c_ {1} \) берется как номер привязки и его двухмерный определитель. рассчитывается.
Поочередно умножайте маленький определитель на номер привязки и на его знак.
| C | = \ (\ left | \ begin {array} {ccc} + & – & + \\ – & + & – \\ + & – & + \ end {array} \ right | \)
Наконец, подведем итоги.

| C | = \ (a_ {1} \ cdot \ left | \ begin {array} {ll} b_ {2} & c_ {2} \\ b_ {3} & c_ {3} \ end {array} \ right | -b_ {1} \ cdot \ left | \ begin {array} {cc} a_ {2} & c_ {2} \\ a_ {3} & c_ {3} \ end {array} \ right | + c_ {1} \ cdot \ left | \ begin {array} {ll} a_ {2} & b_ {2} \\ a_ {3} & b_ {3} \ end {array} \ right | \)

| C | = \ (a_ {1} \ left (b_ {2} c_ {3} -b_ {3} c_ {2} \ right) -b_ {1} \ left (a_ {2} c_ {3} -a_ {3 } c_ {2} \ right) + c_ {1} \ left (a_ {2} b_ {3} -a_ {3} b_ {2} \ right) \)

Рассмотрим этот пример:

\ (B = \ left [\ begin {array} {ccc} 3 & 1 & 1 \\ 4 & -2 & 5 \\ 2 & 8 & 7 \ end {array} \ right] \)

Его определитель рассчитывается как:

| B | = \ (\ left | \ begin {array} {ccc} 3 & 1 & 1 \\ 4 & -2 & 5 \\ 2 & 8 & 7 \ end {array} \ right | \)

\ (| C | = 3 \ cdot \ left | \ begin {array} {ll} -2 & 5 \\ 8 & 7 \ end {array} \ right | -1 \ cdot \ left | \ begin {array} {cc} 4 & 5 \\ 2 & 7 \ end {array} \ right | +1 \ cdot \ left | \ begin {array} {ll} 4 & -2 \\ 2 & 8 \ end {array} \ right | \)

| C | = 3 × ((-2) (7) – (5) (8)) -1 × ((4) (7) – (5) (2)) + 1 × ((4) (8) – (- 2) (2))

= 3 × ((-14) – (40)) -1 × ((28) – (10)) + 1 × ((32) – (-4))

= 3 × (-54) -1 × (18) + 1 × (36)

= – 162 – 18 + 36

= -144

Вычисление определителя матрицы 4 × 4

Рассмотрим нижеупомянутую четырехмерную квадратную матрицу или квадратную матрицу порядка 4 × 4, при нахождении определителя матрицы 4 × 4 следует учитывать следующие изменения:

B = \ (\ left [\ begin {array} {cccc} a_ {1} & b_ {1} & c_ {1} & d_ {1} \\ a_ {2} & b_ {2} & c_ {2 } & d_ {2} \\ a_ {3} & b_ {3} & c_ {3} & d_ {3} \\ a_ {4} & b_ {4} & c_ {4} & d_ {4} \ end {array} \ right] \)

плюс \ (a_ {1} \), умноженный на определитель матрицы, отсутствующей в строке или столбце \ (a_ {1} \)
минус \ (b_ {1} \), умноженное на определитель матрицы, отсутствующей в строке или столбце \ (b_ {1} \).
плюс \ (c_ {1} \), умноженный на определитель матрицы, которая не находится в строке или столбце \ (c_ {1} \).
минус \ (d_ {1} \), умноженное на определитель матрицы, которая не находится в строке или столбце \ (d_ {1} \).

| B | = \ (a_ {1} \ cdot \ left | \ begin {array} {lll} b_ {2} & c_ {2} & d_ {2} \\ b_ {3} & c_ {3} & d_ {3} \\ b_ {4} & c_ {4} & d_ {4} \ end {array} \ right | -b_ {1} \ cdot \ left | \ begin {array} {ccc} a_ {2} & c_ {2 } & d_ {2} \\ a_ {3} & c_ {3} & d_ {3} \\ a_ {4} & c_ {4} & d_ {4} \ end {array} \ right | + c_ {1 } \ cdot \ left | \ begin {array} {ccc} a_ {2} & b_ {2} & d_ {2} \\ a_ {3} & b_ {3} & d_ {3} \\ a_ {4} & b_ {4} & d_ {4} \ end {array} \ right | -d_ {1} \ cdot \ left | \ begin {array} {ccc} a_ {2} & b_ {2} & c_ {2} \\ a_ {3} & b_ {3} & c_ {3} \\ a_ {4} & b_ {4} & c_ {4} \ end {array} \ right | \)

Мы можем использовать метод, упомянутый в предыдущем разделе, чтобы найти определитель матриц 3 × 3.

Умножение определителей

Мы используем метод, называемый умножением массивов, для умножения двух определителей квадратных матриц. Давайте посмотрим на правило умножения по столбцам для умножения двух определителей квадратных матриц A и B:

Умножение детерминантов 2 × 2

Рассмотрим две квадратные матрицы A и B порядка 2 × 2, сначала обозначим их соответствующие определители как | A | и | B | как показано ниже:

| A | = \ (\ left | \ begin {array} {ll} \ mathrm {a} _ {1} & \ mathrm {~ b} _ {1} \\\ mathrm {a} _ {2} & \ mathrm {~ б} _ {2} \ end {array} \ right | \)

| B | = \ (\ left | \ begin {array} {ll} \ mathrm {p} _ {1} & \ mathrm {~ q} _ {1} \\\ mathrm {p} _ {2} & \ mathrm {~ q} _ {2} \ end {array} \ right | \)

| A | × | B | = \ (\ left | \ begin {array} {ll} \ mathrm {a} _ {1} & \ mathrm {~ b} _ {1} \\\ mathrm {a} _ {2} & \ mathrm {~ b} _ {2} \ end {array} \ right | \ times \ left | \ begin {array} {cc} p_ {1} & \ mathrm {~ q} _ {1} \\ p_ {2} & \ mathrm {~ q} _ {2} \ end {array} \ right | = \ left | \ begin {array} {ll} \ mathrm {a} _ {1} p_ {1} + \ mathrm {b} _ { 1} p_ {2} & \ mathrm {a} _ {1} \ mathrm {~ q} _ {1} + \ mathrm {b} _ {1} \ mathrm {~ q} _ {2} \\\ mathrm {a} _ {2} p_ {1} + \ mathrm {b} _ {2} p_ {2} & \ mathrm {a} _ {2} \ mathrm {~ q} _ {1} + \ mathrm {b } _ {2} \ mathrm {~ q} _ {2} \ end {array} \ right | \)

Умножение детерминантов 3 × 3

Рассмотрим две матрицы C и D порядка 3 × 3, сначала обозначим их соответствующие определители как | C | и | D | как показано ниже:

| C | = \ (\ left | \ begin {array} {lll} a_ {1} & b_ {1} & c_ {1} \\ a_ {2} & b_ {2} & c_ {2} \\ a_ {3} & b_ {3} & c_ {3} \ end {array} \ right | \)

| D | = \ (\ left | \ begin {array} {lll} p_ {1} & q_ {1} & r_ {1} \\ p_ {2} & q_ {2} & r_ {2} \\ p_ {3} & q_ {3} & r_ {3} \ end {array} \ right | \)

| C | × | D | = \ (\ left | \ begin {array} {lll}
a_ {1} p_ {1} + b_ {1} p_ {2} + c_ {1} p_ {3} и a_ {1} q_ {1} + b_ {1} q_ {2} + c_ {1} q_ {3} & a_ {1} r_ {1} + b_ {1} r_ {2} + c_ {1} r_ {3} \\ a_ {2} p_ {1} + b_ {2} p_ {2} + c_ {2} p_ {3} & a_ {2} q_ {1} + b_ {2} q_ {2} + c_ {2} q_ {3} & a_ {2} r_ {1} + b_ {2} r_ {2} + c_ {2} r_ {3} \\ a_ {3} p_ {1} + b_ {3} p_ {2} + c_ {3} p_ {3} & a_ {3} q_ {1} + b_ {3} q_ {2} + c_ {3} q_ {3} & a_ {3} r_ {1} + b_ {3} r_ {2} + c_ {3} r_ {3} \ end {array} \ справа | \)

Вот некоторые моменты, которые следует помнить при умножении двух определителей:

Чтобы перемножить два определителя, нам нужно убедиться, что оба определителя имеют один и тот же порядок
Значение определителя не изменяется, когда строки и столбцы меняются местами, поэтому мы также можем следовать правилам умножения столбец за строкой, строка за строкой или столбец за столбцом, чтобы умножить два определителя.

Свойства детерминантов

Для квадратных матриц разных типов при вычислении определителя они вычисляются на основе некоторых важных свойств определителей. Вот список некоторых важных свойств определителей:

Свойство 1: определитель единичной матрицы всегда 1

Рассмотрим определитель единичной матрицы B,

| B | = (1) (1) – (0) (0) = 1

Таким образом, определитель любой единичной матрицы всегда равен 1.

Свойство 2: Если любая квадратная матрица B порядка n × n имеет нулевую строку или нулевой столбец, то det (B) = 0.

Рассмотрим определитель единичной матрицы B,

| B | = \ (\ left | \ begin {array} {ll} 2 & 2 \\ 0 & 0 \ end {array} \ right | \)

| B | = (2) (0) – (2) (0) = 0

Здесь квадратная матрица B имеет одну нулевую строку, и, таким образом, определитель этой квадратной матрицы становится нулевым.

Свойство 3: Если C – верхнетреугольная или нижнетреугольная матрица, то det (C) – это произведение всех ее диагональных элементов.

Рассмотрим верхнетреугольную матрицу C с диагональными элементами 3, 2 и 4. Определитель | C | можно найти как:

| C | = \ (\ left | \ begin {array} {ccc} 3 & 1 & 1 \\ 0 & 2 & 5 \\ 0 & 0 & 4 \ end {array} \ right | \)

| C | = 3 × 2 × 4 = 24

Свойство 4: Если D – квадратная матрица, то если ее строка умножается на константу k, то константа может быть вычтена из определителя.

| D | = \ (\ left | \ begin {array} {ll} k × a & k × b \\ c & d \ end {array} \ right | \)

| D | = k × \ (\ left | \ begin {array} {ll} a & b \\ c & d \ end {array} \ right | \)

| D | = \ (\ left | \ begin {array} {ll} 2 & 4 \\ 1 & 5 \ end {array} \ right | \)

= (2) (5) – (4) (1) = 10-4 = 6

| D | = 2 × \ (\ left | \ begin {array} {ll} 1 & 2 \\ 1 & 5 \ end {array} \ right | \)

= 2 × ((1) (5) – (2) (1)) = 2 × (5-2) = 2 × 3 = 6

Таким образом, определитель остается одинаковым в обоих случаях.

Другими важными свойствами детерминантов являются:

Квадратная матрица C считается обратимой тогда и только тогда, когда det (C) ≠ 0.
Если B и C – две квадратные матрицы порядка n × n, то det (BC) = det (B) × det (C) = det (C) × det (B)
Связь между определителем матрицы D и присоединенным к ней adj (D) может быть представлена как D × adj (D) = adj (D) × D = | D | × I. Здесь D – квадратная матрица, I – единичная матрица.

Правила операций с детерминантами

Следующие правила полезны для выполнения операций со строками и столбцами над определителями.

Значение определителя остается неизменным, если строки и столбцы меняются местами.
Знак определителя меняется, если поменять местами любые две строки или (два столбца).
Если любые две строки или столбца матрицы равны, то значение определителя равно нулю.
Если каждый элемент определенной строки или столбца умножается на константу, то значение определителя также умножается на константу.
Если элементы строки или столбца выражены как сумма элементов, то определитель может быть выражен как сумма определителей.
Если элементы строки или столбца складываются или вычитаются с соответствующими кратными элементами другой строки или столбца, то значение определителя остается неизменным.

☛ Также проверьте:

Важные примечания по детерминантам

Вот список из нескольких моментов, которые следует помнить при изучении детерминантов

Детерминанты можно рассматривать как функции, которые принимают квадратную матрицу на входе и возвращают одно число на выходе.
Квадратная матрица может быть определена как матрица с равным количеством строк и столбцов.
Для простейшей квадратной матрицы порядка 1 × 1 матрица, которая имеет только одно число, определитель становится самим числом.

Часто задаваемые вопросы о детерминантах

Что такое детерминанты?

\ (C = \ left | \ begin {array} {ll} 4 & 2 \\ 5 & 3 \ end {array} \ right | \)

Для чего используются детерминанты?

Детерминанты играют важную роль в линейных уравнениях, где они используются для регистрации изменения переменных в целых числах и того, как линейные преобразования изменяют объем или площадь.Определители особенно полезны в приложениях, где используются обратные и сопряженные матрицы. Перекрестное произведение двух векторов легко запоминается посредством вычисления определителей.

Что такое формула детерминанта для матрицы 2 × 2?

Для любой квадратной 2-мерной матрицы или квадратной матрицы порядка 2 × 2 мы можем использовать эту формулу определителя для вычисления ее определителя:

\ (C = \ left | \ begin {array} {ll} a & b \\ c & d \ end {array} \ right | \). Формула для вычисления детерминанта 2D: | C | = (а × г) – (б × в)

Каковы примеры детерминант?

Рассмотрим на примере квадратной матрицы D,

D = \ (\ left [\ begin {array} {ll} 8 & 6 \\ 3 & 4 \ end {array} \ right] \)

Его определитель можно рассчитать как:

| D | = \ (\ left | \ begin {array} {ll} 8 & 6 \\ 3 & 4 \ end {array} \ right | \)

| D | = (8 × 4) – (6 × 3) = 32 – 18 = 14

Коммутативны ли детерминанты?

Да, умножение определителей коммутативно, и это можно хорошо понять с помощью этого свойства: если B и C – две квадратные матрицы с порядком n × n, то det (BC) = det (B) × det (C) = det ( C) × det (B).

Каковы свойства детерминант?

Вот список некоторых важных свойств определителей:

Определитель единичной матрицы всегда 1
Если любая квадратная матрица B порядка n × n имеет нулевую строку или нулевой столбец, то det (B) = 0.
Если C верхнетреугольная или нижнетреугольная матрица, то det (C) является произведением всех ее диагональных элементов.
Если D – квадратная матрица, то если ее строка умножена на константу k, то константа может быть вычтена из определителя.
Квадратная матрица C считается обратимой тогда и только тогда, когда det (C) ≠ 0.
Если B и C – две квадратные матрицы порядка n × n, то det (BC) = det (B) × det (C) = det (C) × det (B)
Связь между определителем матрицы D и присоединенным к ней adj (D) может быть представлена как D × adj (D) = adj (D) × D = | D | × I. Здесь D – квадратная матрица, I – единичная матрица.

Как вы оцениваете детерминанты матрицы 3×3?

Любой определитель 3 × 3 можно оценить следующим образом:

\ (C = \ left [\ begin {array} {ccc} a_ {1} & b_ {1} & c_ {1} \\ a_ {2} & b_ {2} & c_ {2} \\ a_ { 3} & b_ {3} & c_ {3} \ end {array} \ right] \)
Его определитель можно рассчитать как:

\ (a_ {1} \) фиксируется как номер привязки, и вычисляется двухмерный определитель его подматрицы, которая является квадратной матрицей.
Следующий номер привязки берется по порядку, теперь это \ (b_ {1} \), вычисляется малый определитель, и, наконец, \ (c_ {1} \) берется как номер привязки и его двухмерный определитель. рассчитывается.
Поочередно умножайте маленький определитель на номер привязки и на его знак.
| C | = \ (\ left | \ begin {array} {ccc} + & – & + \\ – & + & – \\ + & – & + \ end {array} \ right | \)
| C | = \ (\ left | \ begin {array} {ccc} a_ {1} & b_ {1} & c_ {1} \\ a_ {2} & b_ {2} & c_ {2} \\ a_ {3} & b_ {3} & c_ {3} \ end {array} \ right | \)
| C | = \ (a_ {1} \ cdot \ left | \ begin {array} {ll} b_ {2} & c_ {2} \\ b_ {3} & c_ {3} \ end {array} \ right | -b_ {1} \ cdot \ left | \ begin {array} {cc} a_ {2} & c_ {2} \\ a_ {3} & c_ {3} \ end {array} \ right | + c_ {1} \ cdot \ left | \ begin {array} {ll} a_ {2} & b_ {2} \\ a_ {3} & b_ {3} \ end {array} \ right | \)
Наконец, подведите итоги.| C | = \ (a_ {1} \ left (b_ {2} c_ {3} -b_ {3} c_ {2} \ right) -b_ {1} \ left (a_ {2} c_ {3} -a_ {3 } c_ {2} \ right) + c_ {1} \ left (a_ {2} b_ {3} -a_ {3} b_ {2} \ right) \)

Каковы правила выполнения операций со строками и столбцами над определителями?

Следующие правила полезны для выполнения операций со строками и столбцами над определителями.

Значение определителя остается неизменным, если строки и столбцы меняются местами.
Знак определителя меняется, если поменять местами любые две строки или (два столбца).
Если любые две строки или столбца матрицы равны, то значение определителя равно нулю.
Если каждый элемент определенной строки или столбца умножается на константу, то значение определителя также умножается на константу.
Если элементы строки или столбца выражены как сумма элементов, то определитель может быть выражен как сумма определителей.
Если элементы строки или столбца складываются или вычитаются с соответствующими кратными элементами другой строки или столбца, то значение определителя остается неизменным.

Что такое определитель треугольной матрицы?

Определитель треугольной матрицы можно найти, вычислив произведение всех ее диагональных элементов. Это применимо как к верхнетреугольным, так и к нижнетреугольным матрицам.

Могут ли детерминанты быть отрицательными?

Детерминанты представляют собой скалярную величину, которая является действительным числом. Таким образом, детерминанты могут быть отрицательными. Если детерминанты отрицательны, это означает, что матрица изменила ориентацию своего базового вектора.| -A | = (-1) ⁿ | A |. Возьмите любой положительный определитель, переключите любые две строки или столбцы матрицы и найдите его определитель, который даст отрицательный результат.

Определители 2 на 2

Детерминанты: 22 Детерминанты (стр. 1 из 2)

Разделы: 22 определителя, 33 детерминанты

Детерминанты подобны матрицам, но заключены в столбцы абсолютных значений вместо квадратных скобок.Там есть многое, что вы можете сделать с детерминантами (и поучиться на них), но вам понадобится дождаться продвинутого курса, чтобы узнать о них. На этом уроке я просто покажу вам, как вычислить 22 и 33 детерминанты. (Возможно для вычисления более крупных детерминант, но процесс намного сложнее.)

Если у вас квадратная матрица, его определитель записывается, взяв ту же самую сетку чисел и положив их внутри столбцов абсолютных значений вместо квадратных скобок:

Если это “матрица A ” (или « A »)…	… тогда это «определитель из A » (или “ дет. A “).

Как абсолютные значения можно оценить и упростить, чтобы получить одно число, как и определители.Процесс оценки детерминант довольно запутан, поэтому давайте начнем простой, с корпусом 22.

Для матрицы 22 определитель находится путем вычитания произведений его диагоналей, что является причудливым способ выразить словами то, что следующее говорит в картинках:

г. матрица A	г. определитель A (“дет. A “)

г. матрица A	г. определитель A (“дет. A “)

В другими словами, чтобы взять определитель матрицы 22, вы умножаете диагональ сверху-слева-вниз-вправо, и из нее вы вычитаете произведение диагонали снизу-слева-вверх-вправо.

“Но погоди!” я слышу, как ты плачешь; “Разве абсолютные ценности не всегда должны быть положительными? Вы показываете, что вторая матрица выше имеет отрицательный определитель. Что с этим? “Вы правильно подметили. Детерминанты похожи на абсолютные значения и используют те же обозначения, но они не идентичны, и одно из различий состоит в том, что детерминанты действительно могут быть отрицательными.

Оцените следующее определитель:

Найти определитель следующей матрицы:

конвертирую из матрицы до определителя, умножить по диагоналям, вычесть и упростить:

Верх | 1 | 2 | Возвращение к указателю Вперед >>

Цитируйте эту статью как:

Стапель, Елизавета.«Детерминанты: детерминанты 2×2». Purplemath . Доступный из
https://www.

Оставить комментарий Отменить ответ

Для отправки комментария вам необходимо авторизоваться.