Матрицы метод гаусса: Как решить методом Гаусса СЛАУ (систему линейных уравнений). Правила, примеры

Уничтожение матриц. Исключение матриц (или система решения… | Соломон Се | Основы линейной алгебры

Исключение матриц (или решение системы линейных уравнений ) является самым первым и фундаментальным навыком в линейной алгебре. Это, наверное, первый урок из всех курсов

Прежде чем изучать решение систем линейных уравнений , вам действительно нужно ознакомиться со всеми основными терминами, иначе перейти к следующему этапу может быть очень сложно.
И в этом случае лучший способ узнать об этом — через Википедию.

JFR, основные термины: Гауссовая ликвидация , Гаусс-Джордан Элиминация , Акматированная матрица , Элементарные ряды , Элементарная матрица , Row Echelon Form (ref) , Redued Row Echelon Форма (RREF) , Треугольная форма .

Это Алгоритм сокращения строк решить Систему линейных уравнений.

См. вики: Исключение Гаусса
См. простую вики: Исключение Гаусса
Пример: showme.com

для создания типа матрицы, называемой расширенной матрицей .
Затем элементарных операции над строками используются для упрощения матрицы.
Цель исключения Гаусса состоит в том, чтобы получить матрицу в ступенчато-строковой форме .
Если матрица имеет форму строк-ступеней , которая также называется Треугольная форма .
В некоторых определениях исключения Гаусса говорится, что результат матрицы должен быть в уменьшенной ступенчато-строковой форме .
Исключение Гаусса, которое создает уменьшенный результат матрицы строк-ступеней, иногда называют Исключение Гаусса-Жордана .

Для упрощения вот структура:

• Алгоритм: Исключение Гаусса
• Шаг 1: Перепишите систему в расширенную матрицу .
• Шаг 2: Упростите матрицу с помощью Элементарные операции со строками .
• Результат:
• Строка Эшелон Форма или
• Сокращенная Эшелон Форма

0016

• Алгоритм: Исключение Гаусса-Жордана
• Шаг 1: Перепишите систему в расширенную матрицу .
• Шаг 2: Упростите матрицу с помощью Элементарные операции со строками .
• Результат: Только в Сокращенная форма эшелона

Элементарные операции со строками используются для упрощения матрицы .

Используются три типа операций со строками:

• Тип 1: Переключение одной строки на другую ряд .
• Тип 2: Умножение строки на ненулевое число .
• Тип 3: Добавление строки из другой строки . (!Примечание: вы можете только ДОБАВИТЬ их, но не вычесть , но вы можете ДОБАВИТЬ отрицательное)

Запутанная операция: Посмотрите, где был поставлен отрицательный знак :

Предположим, цель состоит в том, чтобы найти решение для линейной системы ниже:

Сначала нам нужно превратить его в Augmented Matrix form:

Затем мы применяем Elementary Row Operations , и в результате получаем Row Echelon Form :

В конце, если мы хотим, мы можем дополнительно применить некоторые операции со строками, чтобы получить матрицу in Сокращенная форма строки Echelon :

Чтение этой матрицы говорит нам о том, что решения этой системы уравнений возникают, когда x = 2, y = 3 и z = -1.

Обратитесь к этому видео-лекции: REF & RREF.

Неважно, это Квадратная матрица или нет, может быть Диагональ или Основная диагональ , или вы вообще не можете провести диагональ.
Имеет значение только ЧТО ВЫШЕ 1 И ЧТО НИЖЕ 1.

• REF: Для каждого столбца все числа ниже 1 ДОЛЖНЫ БЫТЬ 0. Не имеет значения, какие числа больше 1.
• RREF : Для каждого столбца все числа выше и ниже 1 ДОЛЖНЫ БЫТЬ 0. Нас не волнует, если в столбце нет 1.

Значит, вносим в матрицу еще один столбец, представляющий Правую часть системы уравнений, числа справа от знака =

5.

Когда мы применяем исключение к линейным уравнениям , мы работаем с обеими сторонами одновременно. Но для компьютерных программ это часто относится к Левая сторона и помните операции, например. умножьте число или сложите уравнения вместе, когда левая сторона будет закончена, примените те же операции к правой стороне.

Если для данной Матрицы было сказано, что это Расширенная Матрица , мы должны предположить, что Последний Столбец — это Столбец Решения .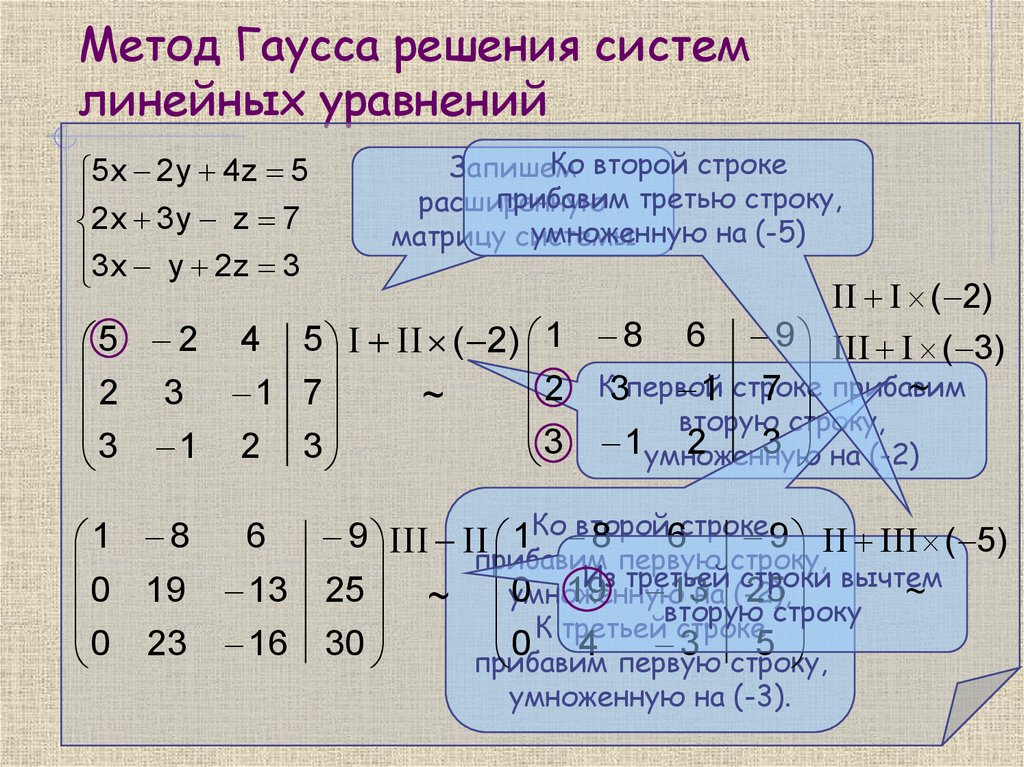

• Эквивалентные системы: Линейные системы с ТАКИМ НАБОРОМ РЕШЕНИЙ.

• Эквивалентные матрицы: две матрицы, где одна матрица может быть превращена в другую матрицу с помощью элементарных операций над строками .

Или называется Курсор или Базовая или Базовая переменная .

См. это видео от mathispower4u.

Это означает значение, которое представляет неизвестную переменную в каждом столбце. В столбце нет разворота , если вы не можете получить 1 в этом столбце.

Если в столбце нет сводной точки, это означает, что эта неизвестная переменная столбца может быть любым числом , поэтому мы называем это свободной переменной .

опорные точки находятся после сокращения строк , а затем возвращаются к Исходной матрице, столбцы С опорными точками называются опорными столбцами .

Все просто: когда вы решаете одну неизвестную переменную в линейной системе, вы подставляете значение обратно в другие уравнения. Мы называем этот процесс обратной заменой .

-

Гаэль | Устранение Гаусса

Образовательный инструмент для экспериментов с матрицами и методом Гаусса:
① Отредактируйте или создайте случайную матрицу. ② Работайте, щелкая ячейки. ③ Получайте удовольствие!

Гаэль версия 0.4 – Инструкции

Copyright © 2020 Майкл Эйзерманн, Институт геометрии и топологии (IGT), Университет Штутгарта. Вы можете использовать мою работу на условиях Лицензия Creative Commons Attribution-NonCommercial-ShareAlike (CC BY-NC-SA 4.0). Этот интерактивный инструмент расчета носит исключительно образовательный характер и не предназначен для каких-либо других целей. Он использует JavaScript с родным BigInt как это предусмотрено вашим браузером.

Что здесь происходит? Исключение Гаусса — это алгоритм решения систем линейных уравнений над полем. Происходит последовательность элементарных операций, выполняемых по строкам или столбцам соответствующей матрицы коэффициентов. Этот метод также может быть использован для нахождения ранга матрицы, вычислить определитель матрицы, и вычислить обратную обратимую квадратную матрицу. Метод назван в честь Карла Фридриха Гаусса (1777–1855). Веб-страница Gaël сделает за вас арифметику и учет коэффициентов, так что вы можете сосредоточиться на изучении матричных операций и легко экспериментировать с ними.

Что делают кнопки? Кнопки должны быть понятными. Редактировать/Возобновить [Ввод]: изменить размер и коэффициенты матрицы. Глобальный знаменатель в верхнем левом углу применяется ко всем элементам матрицы. Random [alt+r]: случайным образом установить ключ и сгенерировать матрицу на его основе.

Генерировать [alt+g]: Генерировать матрицу из заданного ключа для воспроизводимой случайности. Очистить [alt+c]: очистить матрицу, сохранив ее размер. Сброс : Сброс всех данных, включая размер и историю. История [alt+f/p/n/l]: Навигация по архиву; первый/предыдущий/следующий/последний. Консоль вашего браузера [ctrl+shift+i] показывает подробный журнал всех операций; нажмите [alt+c], чтобы очистить консоль. Нажмите [alt+w], чтобы переключить стиль отображения между стандартным и широким.

Как манипулировать матрицей? Щелчок правой кнопкой мыши по матрице редактирует ячейку в фокусе. Щелчок левой кнопкой мыши запускает определенное действие в зависимости от положения ячейки. Щелкните вверху слева. : Транспонируйте матрицу. Нажмите на коэффициент (внутренняя ячейка): пометьте эту ячейку как источник или цель следующим образом.

Как работают операции со строками и столбцами? Операции со строками: Отметьте позиции (i,0) и (j,0) , чтобы переставить строки i и j . Отметьте позиции (i,j) и (i,0) , чтобы нормализовать коэффициент (i,j) путем масштабирования строки

i . Отметить позиции (i,k) и (j,k) в той же колонке k добавить множитель строки i к строке j , чтобы убрать коэффициент (j,k) .

Операции со столбцами: Отметьте позиции (0,i) и (0,j) , чтобы переставить столбцы i и j . Отметьте позиции (i,j) и (0,j) , чтобы нормализовать коэффициент (i,j) по столбцу масштабирования j . Отметить позиции (k,i) и (k,j) в одном ряду k добавить множитель столбца

i к столбцу j , чтобы убить коэффициент (k,j) . Попробуйте сами! Это легче сделать, чем сказать.

Что такое аддитивный режим? Это все еще экспериментально. В аддитивном режиме вы работаете только с помощью отрицания и сложения, поэтому вы работаете с целыми числами, действуя \(\GL_m\Z\) слева с операциями строки и \(\GL_n\Z\) справа с операциями со столбцами. Это может быть полезно для создания упражнений с матрицами, обладающими определенными свойствами: Начните с желаемого результата, скажем, в форме уменьшенного эшелона строк, и зашифровать матрицу некоторыми аддитивными операциями.