Матрицы методом гаусса онлайн: Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса

Онлайн-регрессия разреженного гауссовского процесса и ее приложения

. 2011 февраля; 20 (2): 391-404.

doi: 10.1109/TIP.2010.2066984. Epub 2010 16 августа.

Анант Ранганатан ¹ , Мин-Сюань Ян, Джеффри Хо

принадлежность

• ¹ Научно-исследовательский институт Honda, Маунтин-Вью, Калифорния 94041, США. [email protected]

• PMID: 20716500
• DOI: 10.1109/ТИП.2010.2066984

Анант Ранганатан и др. Процесс преобразования изображений IEEE. 2011 Февраль

. 2011 Февраль;20(2):391-404.

doi: 10.1109/TIP.2010.2066984. Epub 2010 16 августа.

Авторы

Анант Ранганатан ¹ , Мин-Сюань Ян, Джеффри Хо

принадлежность

• ¹ Научно-исследовательский институт Honda, Маунтин-Вью, Калифорния 94041, США. [email protected]

• PMID: 20716500
• DOI: 10.1109/ТИП.2010.2066984

Абстрактный

Мы представляем новый алгоритм вывода гауссовского процесса (GP), называемый онлайн-разреженными матричными гауссовскими процессами (OSMGP), и демонстрируем его достоинства, применяя его к задачам оценки позы головы и визуального отслеживания.

OSMGP основан на наблюдении, что для ядер с локальной поддержкой матрица Грама обычно разрежена. Поддержание и обновление разреженного фактора Холецкого матрицы Грама можно эффективно выполнять с помощью поворотов Гивенса. Это приводит к точному онлайн-алгоритму, время обновления которого линейно зависит от размера матрицы Грама. Кроме того, мы предоставляем метод для работы OSMGP с постоянным временем с использованием матричных понижений. Давления поддерживают коэффициент Холецкого на постоянном уровне, удаляя определенные строки и столбцы, соответствующие отброшенным обучающим примерам. Мы демонстрируем, что, используя эти матричные понижения, онлайн-оценка гиперпараметров может быть включена по стоимости, линейной по отношению к общему количеству обучающих примеров. Мы описываем надежную систему оценки позы головы на основе внешнего вида, основанную на OSMGP. Многочисленные эксперименты и сравнения с существующими методами с использованием системы с большим набором данных демонстрируют эффективность и точность нашей системы. Кроме того, чтобы продемонстрировать применимость OSMGP к широкому спектру проблем, мы также опишем метод визуального отслеживания на основе регрессии. Эксперименты показывают, что наш алгоритм OSMGP хорошо обобщает использование онлайн-обучения.

Похожие статьи

• Передача визуального априора для онлайн-отслеживания объектов.

  Ван К., Чен Ф., Ян Дж., Сюй В., Ян М.Х. Ван Кью и др. Процесс преобразования изображений IEEE. 2012 июль; 21 (7): 3296-305. doi: 10.1109/TIP.2012.21

  . Epub 2012 5 апр. Процесс преобразования изображений IEEE. 2012. PMID: 22491081

• Дизайн разреженного гауссовского классификатора процессов на основе проверки.

  Шеваде С., Сундарараджан С. Шеваде С. и соавт. Нейронные вычисления.

  2009 г., июль; 21(7):2082-103. doi: 10.1162/neco.2009.03-08-724. Нейронные вычисления. 2009. PMID: 19292648

• Построение байесовских формулировок методов обучения с разреженным ядром.

  Cawley GC, Talbot NL. Cawley GC, et al. Нейронная сеть. 2005 июнь-июль;18(5-6):674-83. doi: 10.1016/j.neunet.2005.06.002. Нейронная сеть. 2005. PMID: 16085387

• Обучение модели в реальном времени с использованием инкрементной регрессии гауссовского процесса с разреженным спектром.

  Гийсбертс А., Метта Г. Гийсбертс А. и др. Нейронная сеть. 2013 Май; 41:59-69. doi: 10.1016/j.neunet.2012.08.011. Epub 2012 6 сентября. Нейронная сеть. 2013. PMID: 22985935

• Использование Интернета и информационных технологий в лечении сахарного диабета.

  Кауфман Н. Кауфман Н. Int J Clin Pract Suppl. 2010 февраль;(166):41-6. doi: 10.1111/j.1742-1241.2009.02277.x. Int J Clin Pract Suppl. 2010. PMID: 20377663 Обзор.

Посмотреть все похожие статьи

Цитируется

• Модель прогнозирования горячей пластичности литой стали с низкотемпературной трансформированной структурой при непрерывном литье заготовок.

  Хонг Д.Г., Квон С.Х., Йим Ч. Хонг Д.Г. и соавт. Материалы (Базель). 2022 13 мая; 15 (10): 3513. дои: 10.3390/ma15103513. Материалы (Базель). 2022. PMID: 35629539 Бесплатная статья ЧВК.

• Исследование и уточнение данных с помощью нескольких мобильных датчиков.

  Шекарамиз М. , Мун Т.К., Гюнтер Дж.Х. Шекарамиз М. и соавт. Энтропия (Базель). 2019 5 июня; 21 (6): 568. дои: 10.3390/e21060568. Энтропия (Базель). 2019. PMID: 33267282 Бесплатная статья ЧВК.

• ИССЛЕДОВАНИЕ И УТОЧНЕНИЕ ДАННЫХ С ПОМОЩЬЮ НЕСКОЛЬКИХ МОБИЛЬНЫХ ДАТЧИКОВ НА ОСНОВЕ ГАУССОВА ПРОЦЕССОВ.

  Шекарамиз М., Мун Т.К., Гюнтер Дж.Х. Шекарамиз М. и соавт. Conf Rec Asilomar Conf Signals Syst Comput. 2017;51:885-889. doi: 10.1109/ACSSC.2017.8335476. Epub 2017 29 октября. Conf Rec Asilomar Conf Signals Syst Comput. 2017. PMID: 29706751 Бесплатная статья ЧВК.

• Представление регрессии гауссовского процесса (GPR) на языке разметки прогнозирующих моделей (PMML).

  Парк Дж., Лешевалье Д., Ак Р., Фергюсон М., Лоу К.

  Х., Ли Ю.Т., Рачури С. Парк Дж. и др. Smart Sustain Manuf Syst. 2017;1(1):121-141. дои: 10.1520/SSMS20160008. Epub 2017 29 марта. Smart Sustain Manuf Syst. 2017. PMID: 29202125 Бесплатная статья ЧВК.

• Быстрая онлайн-оптимизация экспериментов с ультрахолодным атомом с помощью машинного обучения.

  Wigley PB, Everitt PJ, van den Hengel A, Bastian JW, Sooriyabandara MA, McDonald GD, Hardman KS, Quinlivan CD, Manju P, Kuhn CC, Petersen IR, Luiten AN, Hope JJ, Robins NP, Hush MR. Вигли П.Б. и др. Научный представитель 2016 г. 16 мая; 6: 25890. дои: 10.1038/srep25890. Научный представитель 2016. PMID: 27180805 Бесплатная статья ЧВК.

Онлайн-калькулятор для расчета определителя 5×5

Онлайн-калькулятор для расчета определителя 5×5

Онлайн-калькулятор вычисляет значение определителя матрицы 5×5 с разложением Лапласа по строке или столбцу и алгоритмом Гаусса.

Определитель 5×5

det A=|a11a12a13a14a15a21a22a23a24a25a31a32a33a34a35a41a42a43a44a45a51a52a53a54a55|

Введите коэффициенты

а ₁₁ =

а ₁₂ =

а ₁₃ =

₁₄ =

а ₁₅

=

а ₂₁ =

а ₂₂ =

а ₂₃ =

а ₂₄ =

а ₂₅ =

₃₁ =

а ₃₂ =

а ₃₃ =

а ₃₄ =

₃₅ =

а ₄₁ =

а ₄₂ =

а ₄₃ =

а ₄₄ =

а ₄₅ =

а ₅₁ =

а ₅₂ =

₅₃ =

₅₄ =

а ₅₅ =

Вычисление значения определителя с помощью расширения Лапласа

Вы можете выбрать строку или столбец, которые будут использоваться для расширения.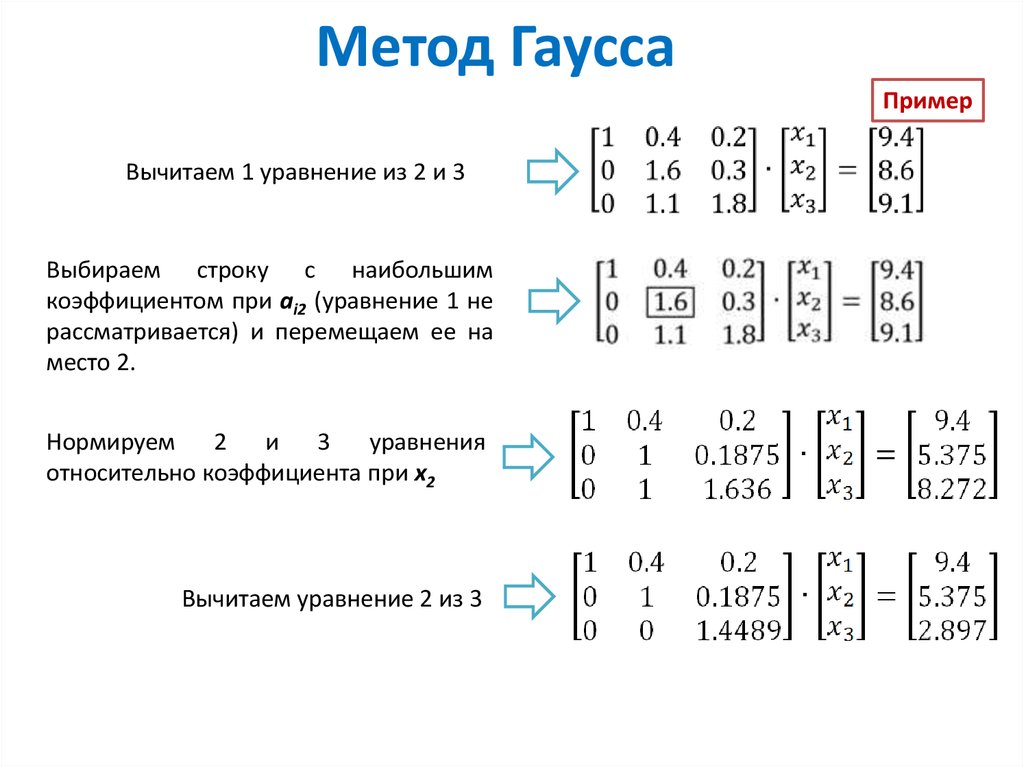

Расчет с помощью алгоритма Гаусса

Примечание:

Если ведущие коэффициенты равны нулю, то столбцы или строки меняются местами соответственно, чтобы было возможно деление на старший коэффициент. Значение определителя правильное, если после преобразований нижняя треугольная матрица равна нулю, а все элементы главной диагонали равны 1.

Объяснение методов

Теорема разложения Лапласа

Теорема развития Лапласа предлагает метод вычисления определителя, в котором определитель развивается после строки или столбца. Размерность уменьшается и может быть уменьшена далее шаг за шагом до скаляра.

det A=∑i=1n-1i+j⋅aijdetAij ( Расширение по j-му столбцу )

det A=∑j=1n-1i+j⋅aijdetAij ( Разложение по i-й строке )

где A _ij , подматрица матрицы A, возникающая при удалении i-й строки и j-го столбца.

Пример разложения Лапласа по первой строке матрицы 3×3.

det A=|a11a12a13a21a22a23a31a32a33|

Первый элемент задается коэффициентом a ₁₁ и субдетерминантом, состоящим из элементов с зеленым фоном.

|a11a12a13a21a22a23a31a32a33|=>a11|a22a23a32a33|

Второй элемент определяется коэффициентом a ₁₂ и субдетерминант, состоящий из элементов с зеленым фоном.

|a11a12a13a21a22a23a31a32a33|=>a12|a21a23a31a33|

Третий элемент задается коэффициентом a ₁₃ и субдетерминантом, состоящим из элементов с зеленым фоном.

|a11a12a13a21a22a23a31a32a33|=>a13|a21a22a31a32|

С тремя элементами определитель может быть записан как сумма определителей 2×2.

det A=|a11a12a13a21a22a23a31a32a33|=a11|a22a23a32a33|-a12|a21a23a31a33|+a13|a21a22a31a32|

Важно учитывать, что знаки элементов чередуются следующим образом.

|+-+-+-+-+|

Метод Гаусса

В методе Гаусса определитель преобразуется таким образом, что элементы нижней матрицы треугольника становятся равными нулю. Для этого вы используете правила коэффициента строки и добавление строк. Добавление строк не меняет значения определителя. Факторы ряда должны рассматриваться как множители перед определителем.