Матрицы примеры: определение, свойства и примеры решения задач

Сайт преподавателей информатики КМТТМП – Примеры и задачи для самостоятельного решения.

    I. Сложение матриц

Рассмотрим пример сложения двух матриц размером 2х3.

Пример 1. 

Даны две матрицы одинакового размера.

Найти сумму А+В двух матриц.

Решение.

Пример 2.

Пусть даны матрицы:

Решение.

II. Умножение матрицы на число

Пусть

Найти результат умножения матрицы  А  на число  4.

III. Вычитание матриц

Пример 3. 

Даны две матрицы одинакового размера  4х4

Найти разность двух матриц

Решение.

Примеры для самостоятельного решения

Пример 4. 

Найти сумму двух матриц  А  и  В  в каждом из следующих случаев:

Пример 5.

 

Найти матрицу: С=-5А+2В

IV. Транспонирование матриц

Транспонирование матриц – переход от матрицы  А  к матрице, в которой строки и столбцы поменялись местами с сохранением порядка.

 Пример 5. 

Составить транспонированную матрицу, полученную из А:

Решение: 

Поменяем местами строки и столбцы, сохраняя порядок:

Примеры для самостоятельного решения:

 Пример 6. 

Составить из исходной матрицы транспонированную матрицу:

II. Умножение матриц

Пример 7. 

Решение:

Пример 8. 

Найти произведение двух матриц:

Решение: 

В первом случае найдем произведение:

Во втором случае найдем произведение:

Пример 9.

Вычислить значение многочлена f(x)=2x²-5x+3  от матрицы:

Решение. 

В многочлен f(x) подставим вместо  

х  матрицу  А, вместо числа 3 используем матрицу  3Е, где  Е – единичная матрица 2-го порядка.

Теперь получим окончательный результат

Примеры для самостоятельного решения

I. Найти произведение матриц:

II. Найти значение многочлена  от матрицы А:

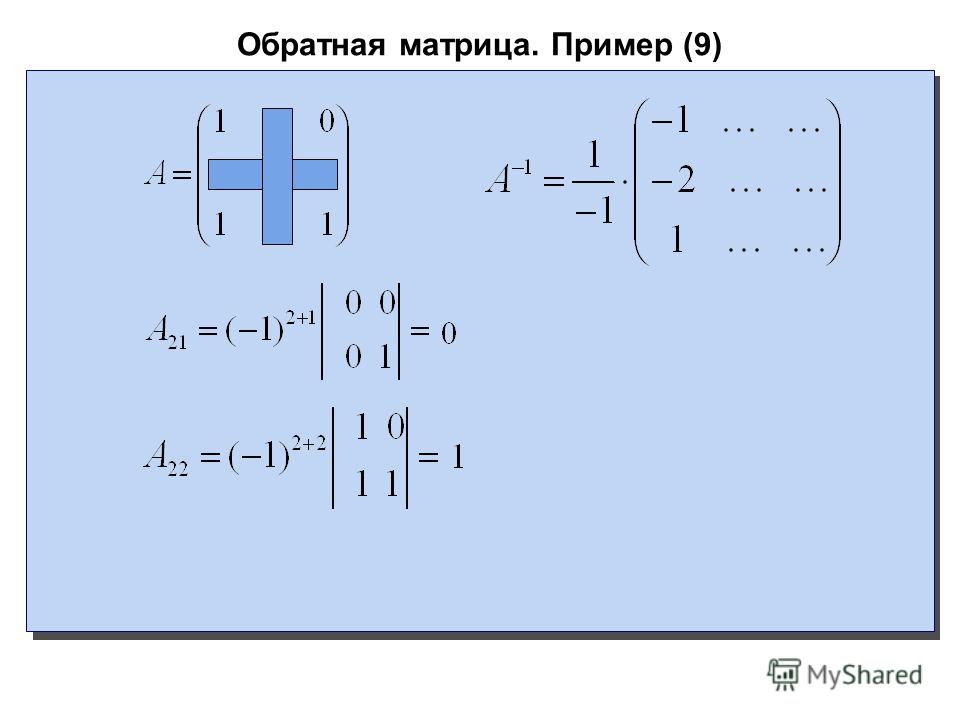
Обратная матрица. Примеры вычисления

Нахождение обратной матрицы является важной составляющей в разделе линейной алгебры. С помощью таких матриц, если они существуют, можно быстро найти решение системы линейных уравнений.

Матрицаназывается обратной к матрице,если выполняются следующие равенства.

.

Если определитель матрицыотличен от нуля, то матрицу называют не особо или невырожденной.

Для того, чтобы матрица имела обратную необходимо и достаточно, чтобы она была невырожденной

Алгоритм нахождения обратной матрицы

Пусть имеем квадратную матрицу

и нужно найти обратную к ней. Для этого нужно выполнить следующие действия:

1. Найти определитель матрицы. Если он не равен нулю то выполняем следующие действия. В противном случае данная матрица вырождена и для нее не существует обратной

2. Найти алгебраические дополнения элементов матрицы . Они равны минорам, умноженным на в степени суммы строки и столбца, для которого ищем.

3. Составить матрицу из алгебраических дополнений элементов матрицы матрицы и протранспонировать ее. Эта матрица называется присоединенной или союзной и обозначается .

4. Разделить присоединенную матрицу на детерминант . Полученная матрица будет обратной и иметь свойства, которые изложены в начале статьи.

——————————————–

Пример 1.

Найти матрицу, обратную к матрице (Дубовик В. П., Юрик И.И. “Высшая математика. Сборник задач”)

1) (1.127)

2) (1.130)

3) (1.133)

Решение.

1)Находим определитель матрицы

Так как детерминант не равен нулю (), то обратная матрица существует. Находим матрицу, составленную из алгебраических дополнений

Матрица дополнений примет вид

Транспонируем ее и получаем присоединенную

Разделим ее на определитель и получим обратную

Видим, что в случае, когда определитель равен единице присоединена и обратная матрицы совпадают.

2) Вычисляем определитель матрицы

Находим матрицу алгебраических дополнений

Конечный вид матрицы дополнений

Транспонируем ее и находим союзную матрицу

Находим обратную матрицу

3) Вычислим детерминант матрицы. Для этого разложим его на первую строчку. В результате получим два отличны от нуля слагаемые

Находим матрицу алгебраических дополнений. Расписание определителя проводим по строкам и столбцам, в которых больше нулевых элементов (обозначены черным цветом).

Конечный вид матрицы дополнений следующий

Транспонируем ее и находим присоединенную матрицу

Поскольку определитель матрицы равен единице то обратная матрица совпадает с присоединенной. Данный пример назад.

При вычислениях обратной матрицы типичными являются ошибки связанные с неправильными знаками при вычислении определителя и матрицы дополнений.

——————————————–

——————————

Виды матриц.

Навигация по странице:

Определение.

Квадратной матрицей называется матрица, у которой количество строк равно количеству столбцов (размера n×n), число n называется порядком матрицы.

Пример.

	4	1	-7		– квадратная матрица размера 3×3
	-1	0	2
	4	6	7

Определение.

Нулевой матрицей называется матрица, все элементы которой равны нулю, т.е. a_ij = 0, ∀i, j.

Пример.

	0	0	0		– нулевая матрица
	0	0	0

Определение.

Вектор-строкой называется матрица, состоящая из одной строки.

Пример.

1

4

-5

– вектор-строка

Определение.

Вектор-столбцом называется матрица, состоящая из одного столбца.

Пример.

	8		– вектор-столбец
	-7
	3

Определение.

Диагональной матрицей называется квадратная матрица, все элементы которой, стоящие вне главной диагонали, равны нулю.

Пример диагональной матрицы.

	4	0	0		– диагональные элементы произвольныене диагональные элементы равны нулю
	0	5	0
	0	0	0

Определение.

Единичной матрицей называется диагональная матрица, диагональные элементы которой равны 1.

Обозначение.

Единичную матрицу обычно обозначают символом E.

Пример единичной матрицы.

E =		1	0	0		– диагональные элементы равны 1не диагональные элементы равны нулю
		0	1	0
		0	0	1

Определение.

Верхней треугольной матрицей называется матрица, все элементы которой ниже главной диагонали равны нулю.

Пример верхней треугольной матрицы.

	7	-6	0
	0	1	6
	0	0	0

Определение.

Нижней треугольной матрицей называется матрица, все элементы которой выше главной диагонали равны нулю.

Пример нижней треугольной матрицы.

	7	0	0
	6	1	0
	-2	0	5

N.B. Диагональная матрица – матрица, которая одновременно является верхней треугольной и нижней треугольной.

Определение.

Ступенчатой матрицей называется матрица, удовлетворяющая следующим условиям:

• если матрица содержит нулевую строку, то все строки, расположенные под нею, также нулевые;
• если первый ненулевой элемент некоторой строки расположен в столбце с номером i, и следующая строка не нулевая, то первый ненулевой элемент следующей строки должен находиться в столбце с номером большим, чем i.

Примеры ступенчатых матриц.

7   0   8   0   0   4

7   0   8   8   8   0   0   1   3   5   0   0   0   -3   5   0   0   0   0   0   0   0   0   0   0

Функция МОБР

Функция МОБР возвращает обратную матрицу для матрицы, храняной в массиве.

Примечание: Если у вас установлена текущая версия Microsoft 365, можно просто ввести формулу в верхней левой ячейке диапазона вывода и нажать клавишу ВВОД, чтобы подтвердить использование формулы динамического массива.

Иначе формулу необходимо вводить с использованием прежней версии массива, выбрав диапазон вывода, введя формулу в левой верхней ячейке диапазона и нажав клавиши CTRL+SHIFT+ВВОД для подтверждения. Excel автоматически вставляет фигурные скобки в начале и конце формулы. Дополнительные сведения о формулах массива см. в статье Использование формул массива: рекомендации и примеры.

Синтаксис

МОБР(массив)

Аргументы функции МОБР описаны ниже.

Замечания

• Массив может быть задан как диапазон ячеек, например A1:C3 как массив констант, например {1;2;3: 4;5;6: 7;8;9} или как имя диапазона или массива.

• Если какие-либо ячейки в массиве пустые или содержат текст, функции МОБР возвращают #VALUE! ошибку “#ВЫЧИС!”.

• МоБР также возвращает #VALUE! если массив не имеет равного числа строк и столбцов.

• Обратные матрицы, такие как определители, обычно используются для решения систем математических уравнений с несколькими переменными. Произведением матрицы и обратной является матрица удостоверений — квадратный массив, в котором диагональные значения равны 1, а все остальные — 0.

• В качестве примера вычисления обратной матрицы, рассмотрим массив из двух строк и двух столбцов A1:B2, который содержит буквы a, b, c и d, представляющие любые четыре числа. В таблице приведена обратная матрица для массива A1:B2.

	Столбец A	Столбец B
Строка 1	d/(a*d-b*c)	b/(b*c-a*d)
Строка 2	c/(b*c-a*d)	a/(a*d-b*c)

• Функция МОБР производит вычисления с точностью до 16 значащих цифр, что может привести к незначительным ошибкам округления.

• Некоторые квадратные матрицы невозможно инвертировать и возвращают #NUM! в функции МОБР. Определител непревратимой матрицы 0.

Примеры

Чтобы указанные выше формулы вычислялись правильно, нужно вводить их в виде формул массивов. После ввода формулы нажмите ввод, если у вас есть текущая Microsoft 365 подписка. в противном случае нажмите CTRL+SHIFT+ВВОД. Если формула не будет введена как формула массива, возвращается единственный результат.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

основные понятия и примеры с решением

Невырожденные матрицы

Основные понятия

Пусть — квадратная матрица -го порядка

Квадратная матрица называется невырожденной, если определитель не равен нулю: . В противном случае () матрица называется вырожденной.

Матрицей, союзной к матрице , называется матрица

где — алгебраическое дополнение элемента данной матрицы (оно определятся так же, как и алгебраическое дополнение элемента , определителя).

Матрица называется обратной матрице , если выполняется условие

где — единичная матрица того же порядка, что и матрица . Матрица имеет те же размеры, что и матрица .

Обратная матрица

Теорема 3.1. Всякая невырожденная матрица имеет обратную.

Проведем доказательство для случая матрицы 3-го порядка. Пусть

, причем .

Составим союзную матрицу

и найдем произведение матриц и :

т. е.

Здесь мы использовали свойства 7 и 8 определителей (см. п. 2.2).

Аналогично убеждаемся, что

Равенства (3.2) и (3.3) перепишем в виде

Сравнивая полученные результаты с определением (3.1), получаем

т. е.

Отметим свойства обратной матрицы:

Пример №3.1.

Найти если .

Решение:

1) Находим : .

2) Находим : поэтому .

3) Находим : .

Проверка:

Дополнительные примеры:

Ранг матрицы

Рассмотрим матрицу размера .

Выделим в ней строк и столбцов . Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель -го порядка. Все такие определители называются минорами этой матрицы. В матрице пунктиром выделен минор 2-го порядка. (Заметим, что таких миноров можно составить штук, где — число сочетаний из элементов по .)

Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Обозначается или .

Очевидно, что , где — меньшее из чисел и .

Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров.

Пример №3.4.

Найти ранг матрицы:

Решение:

Вес миноры 3-го порядка равны нулю. Есть минор 2-го порядка, отличный от нуля . Значит, . Базисный минор стоит на пересечении 2 и 3 строки с 1 и 3 столбцами.

Отметим свойства ранга матрицы:

1. При транспонировании матрицы ее ранг не меняется.

2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится.

3. Ранг матрицы не изменяется при элементарных преобразованиях матрицы (см. с. 18).

Ранг канонической матрицы равен числу единиц на главной диагонали. На этом основан один из способов вычисления ранга матрицы.

Дополнительный пример №3.5.

На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

Другие темы по высшей математике возможно вам они будут полезны:

Математика онлайн

Решение математики онлайн

Math34. biz – это современный способ решения математики, в том числе для сравнения самостоятельных решений с машинными вычислениями.

Пользование сервисом удобно и понятно каждому человеку, попавшему на сайт впервые. Сразу выбираете нужный калькулятор, вводите необходимые данные по вашей задаче и нажимаете кнопку «Решение». За считанные секунды ответ готов.

Чтобы не возникало трудностей с вводом данных, мы подготовили специальную статью Как вводить данные? Помимо правил написания формул и чисел, в ней вы можете увидеть, как правильно вводятся различные константы и математические функции.

О калькуляторах

По мере возможности добавляются новые математические калькуляторы. На сегодняшний день их более 85.

Если не удалось найти нужный калькулятор, которым может быть решена ваша математическая задача, или есть предложение по улучшению имеющегося калькулятора, пожалуйста, сообщите об этом на почту [email protected]

Преимущества

1. Бесплатно
Решение математики онлайн не будет вам стоить ни копейки. Наш сервис абсолютно бесплатный и доступен любому пользователю интернета.

2. Без регистрации
Для пользования калькуляторами не требуется регистрации на сайте, отнимая время на заполнение почтовых ящиков и других личных данных.

3. Подробные решения
На многие задачи вы получите пошаговый развернутый ответ, что позволяет понять, каким образом было получено решение задачи.

4. Разные способы решения задач
Для популярных калькуляторов доступны разные методы решения задач, если они применимы, что позволяет, во-первых, лучше понять, как решается задача известным вам способом, а, во-вторых, научиться решать ту же самую задачу альтернативными методами.

5. Точность вычислений
В полученном ответе не приходится сомневаться, ведь мощная система расчета обеспечивает высокую точность при решении математических задач онлайн.

Однако, мы не исключаем возможность каких-либо ошибок, ведь известно, что алгоритмы пишутся хотя и очень умными, но всё же людьми. В случае обнаружения ошибки, пожалуйста, не поленитесь и сообщите нам о ней.

Определитель матрицы 2×2, 3×3, 4×4…

Определитель (детерминант) квадратной матрицы A – это число, обладающее определенными свойствами, которое может быть получено из элементов матрицы рядом методов.

Обозначения

Пусть $ A = \begin{pmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{pmatrix}$

$det(A) = \left|A\right| = \begin{vmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{vmatrix}$

Свойства определителя

1. Если матрица имеет строку или столбец, все элементы которого равны нулю, то ее определитель равен 0.

   Пример 12
   $\begin{vmatrix} 1 & 4 & 2\\ 0 & 0 & 0\\ 3 & 9 & 5 \end{vmatrix}= 0$ или $\begin{vmatrix} 1 & 4 & 0\\ 4 & 2 & 0\\ 3 & 9 & 0 \end{vmatrix}=0$

2. Если в матрице есть две одинаковых строки или два одинаковых столбца, то ее определитель равен 0.

   Пример 13
   $\begin{vmatrix} 1 & 4 & 2\\ 1 & 4 & 2\\ 3 & 9 & 5 \end{vmatrix}= 0$ или $\begin{vmatrix} 1 & 4 & 1\\ 4 & 2 & 4\\ 3 & 9 & 3 \end{vmatrix}=0$

3. Если в матрице есть две пропорциональных строки или два пропорциональных столбца, то ее определитель равен 0.

   Пример 14
   $\begin{vmatrix} 1 & 4 & 2\\ 2 & 8 & 4\\ 3 & 9 & 5 \end{vmatrix}= 0$ (две первые строки пропорциональны)
   или
   $\begin{vmatrix} 8 & 4 & 7\\ 4 & 2 & 3\\ 18 & 9 & 8 \end{vmatrix}=0$ (два первых столбца пропорциональны)

4. Если некоторая строка (столбец) является суммой или разностью других строк (столбцов), то определитель равен 0.

   Пример 15
   $\begin{vmatrix} 1 & 4 & 2\\ 7 & 2 & 3\\ 8 & 6 & 5 \end{vmatrix}= 0$     $R_{1} +R_{2} =R_{3}$ или

   $ \begin{vmatrix} 9 & 12 & 3\\ 1 & 8 & 7\\ 5 & 7 & 2 \end{vmatrix}=0$     $C_{1}+C_{3}=C_{2}$

5. При вычислении определителя можно выносить общие множители целых строк или столбцов.

   Пример 16
   В определителе
   $\begin{vmatrix} 3 & 9 & 12\\ 5 & 1 & 8 \\ 7 & 4 & 2 \end{vmatrix}$, можно вынести множитель 3 из первой строки $(R_{1})$, тогда получаем:
   $3 \cdot \begin{vmatrix} 1 & 3 & 4\\ 5 & 1 & 8\\ 7 & 4 & 2 \end{vmatrix}$, затем выносим 2 из третьего столбца $(C_{3})$:
   $6\cdot \begin{vmatrix} 1 & 3 & 2\\ 5 & 1 & 4\\ 7 & 4 & 1 \end{vmatrix}$

6. При вычислении определителя можно прибавлять (отнимать) строки к другим строкам и столбцы к другим столбцам; определитель матрицы при этом не меняется.

   Пример 17
   $\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{R_{1}+R_{2}} \begin{vmatrix} 4 & 13\\ 3 & 8 \end{vmatrix}$
   Пример 18
   $\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{C_{1}+C_{2}} \begin{vmatrix} 6 & 5\\ 11 & 8 \end{vmatrix}$

7. При вычислении определителя можно прибавлять или отнимать строки и столбцы, умноженные на произвольный коэффициент.

   Пример 19
   $\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{2R_{1}+3R_{2}} \begin{vmatrix} 11 & 34\\ 3 & 8 \end{vmatrix}$

   Пример 20
   $\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{5C_{1}-C_{2}} \begin{vmatrix} 0 & 5\\ 7 & 8 \end{vmatrix}$

8. Определитель матрицы равен определителю транспонированной матрицы.
9. Определитель произведения двух квадратных матриц равен произведению определителей данных матриц.

Минор матрицы

Определитель матрицы, полученной вычеркиванием некоторых строк и столбцов матрицы, называется минором этой матрицы.

Пример 21
$A=\begin{pmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{pmatrix}$

Один из миноров матрицы A есть $\begin{vmatrix} 1 & 4\\ 5 & 3 \end{vmatrix}$ (он получается вычеркиванием строки 3 и столбца 3 из матрицы A)

Другим минором является $\begin{vmatrix} 1 & 2 \\ 6 & 1 \end{vmatrix}$ (получается вычеркиванием строки 2 и столбца 2 из матрицы A)

Пример 22
$B=\begin{pmatrix} 2 & 5 & 1 & 3\\ 4 & 1 & 7 & 9\\ 6 & 8 & 3 & 2\\ 7 & 8 & 1 & 4 \end{pmatrix} $

Один из миноров матрицы B есть $ \begin{vmatrix} 1 & 7 & 9\\ 8 & 3 & 2\\ 8 & 1 & 4 \end{vmatrix}$ (получается вычеркиванием строки 1 и столбца 1 из матрицы B)

Другим минором является $\begin{vmatrix} 1 & 7 \\ 8 & 3 \end{vmatrix}$ (получается вычеркиванием строк 1 и 4 и столбцов 1 и 4 из матрицы B)

Пусть $A= \begin{pmatrix} a_{1,1} & a_{1,2} & a_{1,3} & . & . & a_{1,n}\\ a_{2,1} & a_{2,2} & a_{2,3} & . & . & a_{2,n}\\ a_{3,1} & a_{3,2} & a_{3,3} & . & . & a_{3,n}\\ . & . & . & . & .& .\\ a_{n,1} & a_{n,2} & a_{n,3} & . & . & a_{n,n} \end{pmatrix}$

Можно определить минор $\Delta_{i,j}$, полученный вычеркиванием строки i и столбца j, для любого элемента $a_{i,j}$ квадратной матрицы A. Такой минор называется дополнительным.

Пример 23
$ A = \begin{pmatrix} 4 & 7\\ 2 & 9 \end{pmatrix}$

Определить дополнительный минор элемента 2. Так как данный элемент находится в строке 2, столбце 1, видно, что это $a_{2,1}$.

Нужно вычеркнуть строку 2 и столбец 1 из матрицы A, после чего получаем

Минор, дополнительный к элементу 2, есть $\Delta_{2,1} = 7$.

Пример 24
$B=\begin{pmatrix} 1 & 4 & 2\\ 5 & 3 & 7\\ 6 & 2 & 1\\ \end{pmatrix}$

Нужно найти минор, дополнительный к элементу 7. Так как данный элемент находится в строке 2, столбце 3, видно, что это $a_{2,3}$.

Мы должны вычеркнуть строку 2 и столбец 3 из матрицы B, после чего мы получаем

Минор, дополнительный к элементу 7, – это $\Delta_{2,3}= \begin{vmatrix} 1 & 4\\ 6 & 2 \end{vmatrix}$

Пример 25
$C=\begin{pmatrix} 2 & 5 & 1 & 3\\ 4 & 1 & 7 & 9\\ 6 & 8 & 3 & 2\\ 7 & 8 & 1 & 4 \end{pmatrix}$

Нужно найти минор, дополнительный к элементу 5. Так как данный элемент находится в строке 1, столбце 2, видно, что это $a_{1,2}$.

Мы должны вычеркнуть строку 1 и столбец 2 из матрицы C, после чего мы получаем

Минор, дополнительный к элементу 5, – это $\Delta_{1,2}= \begin{vmatrix} 4 & 7 & 9\\ 6 & 3 & 2\\ 7 & 1 & 4\\ \end{vmatrix}$

Алгебраическое дополнение элемента матрицы

Пусть $A=\begin{pmatrix} a_{1,1} & a_{1,2} & a_{1,3} & . & . & a_{1,n}\\ a_{2,1} & a_{2,2} & a_{2,3} & . {7}\cdot\Delta_{2,5}= -\Delta_{2,5} $ соответствует элементу $a_{2,5}$.

Порядок определителя

Порядок определителя матрицы равен числу ее строк и столбцов.

Пример 26
$\begin{vmatrix} 1 & 4\\ 6 & 2\\ \end{vmatrix}$ (матрица имеет 2 строки и 2 столбца, так что порядок определителя равен 2)

Пример 27
$\begin{vmatrix} 4 & 7 & 9\\ 6 & 3 & 2\\ 7 & 1 & 4\\ \end{vmatrix}$ (матрица имеет 3 строки и 3 столбца, так что порядок определителя равен 3)

Вычисление определителя матрицы

Определитель матрицы равен сумме произведений элементов любой строки или любого столбца и их алгебраических дополнений.

$\left| A\right| = \begin{vmatrix} a_{1,1} & a_{1,2} & a_{1,3} & . & . & a_{1,n}\\ a_{2,1} & a_{2,2} & a_{2,3} & . & . & a_{2,n}\\ a_{3,1} & a_{3,2} & a_{3,3} & . & . & a_{3,n}\\ . & . & . & . & .& .\\ a_{n,1} & a_{n,2} & a_{n,3} & . {4}\cdot\Delta_{1,3}=$ $a_{1,1}\cdot\Delta_{1,1}-a_{1.2}\cdot\Delta_{1,2}+a_{1.3}\cdot\Delta_{1,3}$

$\Delta_{1,1}= \begin{vmatrix} a_{2,2} & a_{2,3}\\ a_{3,2} & a_{3,3} \end{vmatrix} = a_{2,2}\cdot a_{3,3}-a_{2,3}\cdot a_{3,2}$

$\Delta_{1,2}= \begin{vmatrix} a_{2,1} & a_{2,3}\\ a_{3,1} & a_{3,3} \end{vmatrix} = a_{2,1}\cdot a_{3,3}-a_{2,3}\cdot a_{3,1}$

$\Delta_{1,3}= \begin{vmatrix} a_{2,1} & a_{2,2}\\ a_{3,1} & a_{3,2} \end{vmatrix} = a_{2,1}\cdot a_{3,2}-a_{2,2}\cdot a_{3,1}$

$\left| A\right| =a_{1,1}\cdot( a_{2,2}\cdot a_{3,3}-a_{2,3}\cdot a_{3,2})-a_{1,2}\cdot(a_{2,1}\cdot a_{3,3}-a_{2,3}\cdot a_{3,1})+$ $a_{1,3}\cdot(a_{2,1}\cdot a_{3,2}-a_{2,2}\cdot a_{3,1})=$ $a_{1,1}\cdot a_{2,2}\cdot a_{3,3}-a_{1,1}\cdot a_{2,3}\cdot a_{3,2}-a_{1,2}\cdot a_{2.1}\cdot a_{3,3}+a_{1,2}\cdot a_{2,3}\cdot a_{3,1}+$ $a_{1,3}\cdot a_{2,1}\cdot a_{3,2}-a_{1,3}\cdot a_{2,2}\cdot a_{3,1}=$ $\color{red}{a_{1,1}\cdot a_{2,2}\cdot a_{3,3}+a_{1,2}\cdot a_{2,3}\cdot a_{3,1}+a_{1,3}\cdot a_{2,1}\cdot a_{3,2}-}$ $\color{red}{(a_{1,1}\cdot a_{2,3}\cdot a_{3,2}+a_{1,2}\cdot a_{2,1}\cdot a_{3,3}+a_{1,3}\cdot a_{2,2}\cdot a_{3,1})}$

Упростить получение последней формулы можно следующим образом.

Начнем с того, что перепишем первые две строки под определителем как показано ниже.

$\begin{vmatrix} \color{red}{a_{1,1}} & a_{1,2} & a_{1,3}\\ \color{red}{a_{2,1}} & \color{red}{a_{2,2}} & a_{2,3}\\ \color{red}{a_{3,1}} & \color{red}{a_{3,2}} & \color{red}{a_{3,3}} \end{vmatrix}$
$\hspace{2mm}\begin{array}{ccc} a_{1,1} & \color{red}{a_{1,2}} & \color{red}{a_{1,3}}\\ a_{2,1} & a_{2,2} & \color{red}{a_{2,3}}\\ \end{array}$

Умножаем элементы на каждой из трех красных диагоналей (на главной диагонали и на диагоналях под ней) и складываем результаты:
$\color{red}{a_{1,1}\cdot a_{2,2}\cdot a_{3,3}+ a_{2,1}\cdot a_{3,2}\cdot a_{1,3}+a_{3,1}\cdot a_{1,2}\cdot a_{2,3}}$

$\begin{vmatrix} \color{red}{a_{1,1}} & \color{red}{a_{1,2}} & \color{blue}{a_{1,3}}\\ \color{red}{a_{2,1}} & \color{blue}{a_{2,2}} & \color{blue}{a_{2,3}}\\ \color{blue}{a_{3,1}} & \color{blue}{a_{3,2}} & \color{blue}{a_{3,3}} \end{vmatrix}$
$\hspace{2mm} \begin{array}{ccc} \color{blue}{a_{1,1}} & \color{blue}{a_{1,2}} & \color{red}{a_{1,3}}\\ \color{blue}{a_{2,1}} & \color{red}{a_{2,2}} & \color{red}{a_{2,3}}\\ \end{array}$

Умножаем элементы на каждой из трех синих диагоналей (на побочной диагонали и на диагоналях под ней) и складываем результаты:

$\color{blue}{a_{1,3}\cdot a_{2,2}\cdot a_{3,1}+ a_{2,3}\cdot a_{3,2}\cdot a_{1,1}+a_{3,3}\cdot a_{1,2}\cdot a_{2,1}}$

Вычитая вторую сумму из первой, получаем формулу определителя:

$\color{red}{a_{1,1}\cdot a_{2,2}\cdot a_{3,3}+ a_{2,1}\cdot a_{3,2}\cdot a_{1,3}+a_{3,1}\cdot a_{1,2}\cdot a_{2,3}-}$ $\color{red}{(a_{1,3}\cdot a_{2,2}\cdot a_{3,1}+ a_{2,3}\cdot a_{3,2}\cdot a_{1,1}+a_{3,3}\cdot a_{1,2}\cdot a_{2,1})}$

Пример 30
$A=\begin{pmatrix} 1 & 4 & 3 \\ 2 & 1 & 5\\ 3 & 2 & 1\\ \end{pmatrix}$

$\begin{vmatrix} 1 & 4 & 3 \\ 2 & 1 & 5\\ 3 & 2 & 1\\ \end{vmatrix}$
$\hspace{2mm}\begin{array}{ccc} 1 & 4 & 3\\ 2 & 1 & 5\\ \end{array}$

$ = 1\cdot1\cdot1 + 2\cdot2\cdot3 + 3\cdot4\cdot5 -(3\cdot1\cdot3 + 5\cdot2\cdot1 + 1\cdot4\cdot2) =$ $ 1 + 12 + 60 -(9 + 10 + 8)=73-27=46$

Пример 31
$A=\begin{pmatrix} 3 & 5 & 1 \\ 1 & 4 & 2\\ 7 & 1 & 9\\ \end{pmatrix}$

$\begin{vmatrix} 3 & 5 & 1 \\ 1 & 4 & 2\\ 7 & 1 & 9\\ \end{vmatrix}$
$\hspace{2mm}\begin{array}{ccc} 3 & 5 & 1\\ 1 & 4 & 2\\ \end{array} $

$= 3\cdot4\cdot9 + 1\cdot1\cdot1 + 7\cdot5\cdot2 -(1\cdot4\cdot7 + 2\cdot1\cdot3 + 9\cdot5\cdot1) =$ $ 108 + 1 + 70 -(28 + 6 + 45)=79-79=100$

Элементы матрицы могут быть обозначены буквами. {2} \end{vmatrix}= $

$\begin{vmatrix} a-c & b-c \\ (a-c)(a+c) & (b-c)(b+c) \end{vmatrix}=$ $(a-c)(b-c)\begin{vmatrix} 1 & 1\\ a+c & b+c \end{vmatrix}=$

$=(a-c)(b-c)[(b+c)-(a+c)]=$ $(a-c)(b-c)(b+c-a-c)=(a-c)(b-c)(b-a)$

Вычисление определителя матрицы 4×4

Вычислить определитель матрицы 4×4 можно с использованием общей формулы для определителя матрицы 3×3.

Но сначала надо использовать свойства определителей:

1. Проверим, не выполняется ли одно из условий того, что определитель равен 0.
2. Проверим, нельзя ли вынести общий множитель из одной или нескольких строк или столбцов.
3. Проверим, не является ли данная матрица матрицей Вандермонде, возможно, такой, в которой некоторые строки или столбцы переставлены.

В любом из этих случаев нам пригодятся соответствующие методы вычисления определителей матриц 3×3. Модифицируем строку или столбец так, чтобы все его элементы, кроме одного, обратились в 0. Определитель будет равен произведению этого ненулевого элемента на его алгебраическое дополнение. В этом случае, алгебраическое дополнение – это определитель матрицы 3×3, который считается по уже известной формуле.

Пример 33
$\begin{vmatrix} 1 & 3 & 9 & 2\\ 5 & 8 & 4 & 3\\ 0 & 0 & 0 & 0\\ 2 & 3 & 1 & 8 \end{vmatrix}$

Замечаем, что все элементы в строке 3 равны нулю, а значит, определитель равен 0.

Пример 34
$\begin{vmatrix} 1 & 3 & 1 & 2\\ 5 & 8 & 5 & 3\\ 0 & 4 & 0 & 0\\ 2 & 3 & 2 & 8 \end{vmatrix}$
Замечаем, что $C_{1}$ равно $C_{3}$, следовательно, определитель равен 0.

Пример 35
$\begin{vmatrix} 1 & 3 & 9 & 2\\ 5 & 8 & 4 & 3\\ 10 & 16 & 18 & 4\\ 2 & 3 & 1 & 8 \end{vmatrix}$
Замечаем, что строки 2 и 3 пропорциональны друг другу, следовательно, определитель равен 0.

Пример 36
$\begin{vmatrix} \color{red}{4} & 3 & 2 & 2\\ 0 & 1 & -3 & 3\\ 0 & -1 & 3 & 3\\ 0 & 3 & 1 & 1 \end{vmatrix}$

Поскольку в столбце 1 только один элемент отличен от нуля, применяем общую формулу, используя этот столбец. Алгебраические дополнения нулевых элементов считать не надо, так как их произведения на эти элементы все равно будут равны нулю.

=
$=4(1\cdot3\cdot1 +(-1)\cdot1\cdot3+3\cdot(-3)\cdot3$ $-(3\cdot3\cdot3+3\cdot1\cdot1 +1\cdot(-3)\cdot(-1)))$ $=4(3-3-27-(27+3+3))=4\cdot(-60)=-240$

Пример 37
$\begin{vmatrix} 4 & 3 & 2 & 2\\ 0 & 1 & 0 & -2\\ 1 & -1 & 3 & 3\\ 2 & 3 & 1 & 1 \end{vmatrix}$

Чтобы изменить строку так, чтобы в ней стало больше нулей, нужно совершать операции со столбцами, и наоборот. Выбираем строку или столбец, содержащий элемент 1, поскольку из него можно получить любое число простым умножением. {2+2}\cdot \begin{vmatrix} 4 & 2 & 8\\ 1 & 3 & 1\\ 2 & 1 & 7 \end{vmatrix}=$
$=4\cdot3\cdot7 + 1\cdot1\cdot8 + 2\cdot2\cdot1$ $-(8\cdot3\cdot2 + 1\cdot1\cdot4 + 7\cdot2\cdot1) =$ $ 84 + 8 + 4- 48-4-14=30$

Пример 38
$\begin{vmatrix} 1 & -2 & 3 & 2\\ 2 & 3 & 1 & -1\\ 3 & 3 & 3 & 3\\ -1 & 4 & 2 & 1\\ \end{vmatrix}$

Можно вынести множитель 3 из строки 3:
$3\cdot \begin{vmatrix} 1 & -2 & 3 & 2\\ 2 & 3 & 1 & -1\\ 1 & 1 & 1 & 1\\ -1 & 4 & 2 & 1\\ \end{vmatrix}$

Поскольку в строке 3 все элементы равны 1, легко обратить получить нули.

$\begin{vmatrix} 1 & -2 & 3 & 2\\ 2 & 3 & 1 & -1\\ 1 & 1 & 1 & 1\\ -1 & 4 & 2 & 1 \end{vmatrix}$ $ \xlongequal{C_{1} – C_{4},C_{2}-C_{4},C_{3}-C_{4}} \begin{vmatrix} -1 & -4 & 1 & 2\\ 3 & 4 & 2 & -1\\ 0 & 0 & 0 & \color{red}{1}\\ -2 & 3 & 1 & 1 \end{vmatrix}$ $=1\cdot(-1)^{3+4}\cdot$ $=(-1)\cdot \begin{vmatrix} -1 & -4 & 1\\ 3 & 4 & 2 \\ -2 & 3 & 1\\ \end{vmatrix}$
$=-((-1)\cdot 4\cdot 1 +3 \cdot 3\cdot1 + (-2)\cdot (-4)\cdot 2$ $- (1\cdot 4\cdot (-2) + 2\cdot 3\cdot (-1) + 1\cdot (-4)\cdot3))$ $=-(-4 + 9 + 16 + 8 + 6 + 12) =-47$

Пример 39
$\begin{vmatrix} 2 & 5 & 1 & 4\\ 4 & 1 & 6 & 3\\ 5 & 3 & 7 & 2\\ 1 & 0 & 2 & 4 \end{vmatrix}$

Здесь мы можем использовать единицу из последней строки и обратить остальные элементы первого столбца в нули. {4+1}\cdot \begin{vmatrix} 5 & -3 & -4\\ 1 & -2 & -13\\ 3 & -3 & -18 \end{vmatrix}=$ $(-1)\cdot \begin{vmatrix} 5 & -3 & -4\\ 1 & -2 & -13\\ 3 & -3 & -18 \end{vmatrix}$

Выносим общий множитель -1 из столбца 2 и еще раз -1 из столбца 3.
$ (-1)\cdot(-1)\cdot(-1)\cdot \begin{vmatrix} 5 & 3 & 4\\ 1 & 2 & 13\\ 3 & 3 & 18 \end{vmatrix}=$ $(-1)\cdot \begin{vmatrix} 5 & 3 & 4\\ 1 & 2 & 13\\ 3 & 3 & 18 \end{vmatrix}=$ $-[5\cdot 2\cdot 18 + 1\cdot 3\cdot 4+ 3\cdot 3\cdot 13 – (4\cdot 2\cdot 3\cdot + 13\cdot 3\cdot 5 + 18\cdot 3\cdot 1)]=$ $-(180+12+117-24-195-54)=36$

Пример 40
$\begin{vmatrix} 4 & 7 & 2 & 3\\ 1 & 3 & 1 & 2\\ 2 & 5 & 3 & 4\\ 1 & 4 & 2 & 3 \end{vmatrix}$

Мы видим элемент 1 в столбце 3, так что мы можем обратить остальные элементы строки 2 в нули.

$\begin{vmatrix} 4 & 7 & 2 & 3\\ 1 & 3 & 1 & 2\\ 2 & 5 & 3 & 4\\ 1 & 4 & 2 & 3 \end{vmatrix}$ $\xlongequal{C_{1}-C_{3}, C_{2}-3C_{3},C_{4}-2C_{3}} \begin{vmatrix} 2 & 1 & 2 & -1\\ 0 & 0 & \color{red}{1} & 0 \\ -1 & -4 & 3 & -2\\ -1 & -2 & 2 & -1 \end{vmatrix}=$ $=1\cdot(-1)^{2+5}\cdot \begin{vmatrix} 2 & 1 & -1\\ -1 & -4 & -2\\ -1 & -2 & -1 \end{vmatrix}$

Выносим общий множитель -1 из строки 2 и еще раз -1 из строки 3.
$ (-1)\cdot(-1)\cdot(-1)\cdot \begin{vmatrix} 2 & 1 & -1\\ 1 & 4 & 2\\ 1 & 2 & 1 \end{vmatrix}=$ $(-1)\cdot \begin{vmatrix} 2 & 1 & -1\\ 1 & 4 & 2\\ 1 & 2 & 1 \end{vmatrix}=$ $-[2\cdot 4\cdot 1 + 1\cdot 2\cdot (-1)+ 1\cdot 1\cdot 2 – ((-1)\cdot 4\cdot 1 + 2\cdot 2\cdot 2 + 1\cdot 1\cdot 1)]=$ $-(8-2+2+4-8-1)=-3$

Пример 41
$\begin{vmatrix} 2 & 1 & 3 & 4\\ 1 & 3 & 4 & 2\\ 3 & 4 & 2 & 1\\ 4 & 2 & 1 & 3\\ \end{vmatrix}$

Заметим, что все строки и все столбцы состоят из одних и тех же элементов, но в разном порядке. В таком случае мы можем сложить все строки или все столбцы.

$\begin{vmatrix} 2 & 1 & 3 & 4\\ 1 & 3 & 4 & 2\\ 3 & 4 & 2 & 1\\ 4 & 2 & 1 & 3 \end{vmatrix}$ $\xlongequal{L_{1}+L_{2}+L_{3}+L_{4}} \begin{vmatrix} 10 & 10 & 10 & 10\\ 1 & 3 & 4 & 2\\ 3 & 4 & 2 & 1\\ 4 & 2 & 1 & 3 \end{vmatrix} =$ $10\cdot \begin{vmatrix} 1 & 1 & 1 & 1\\ 1 & 3 & 4 & 2\\ 3 & 4 & 2 & 1\\ 4 & 2 & 1 & 3 \end{vmatrix}$ $\xlongequal{C_{1} – C_{4},C_{2}-C_{4},C_{3}-C_{4}}10\cdot \begin{vmatrix} 0 & 0 & 0 & \color{red}{1}\\ -1 & 1 & 2 & 2\\ 2 & 3 & 1 & 1\\ 1 & -1 & -2 & 3 \end{vmatrix}=$

$=10\cdot1\cdot(-1)^{1+4}$

$ = (-10)\cdot \begin{vmatrix} -1 & 1 & 2\\ 2 & 3 & 1\\ 1 & -1 & -2 \end{vmatrix}=$ $(-10)\cdot((-1)\cdot 3\cdot (-2) +2 \cdot (-1)\cdot2 + 1\cdot 1\cdot 1$ $-(2\cdot 3\cdot 1 + 1\cdot (-1)\cdot (-1) + (-2)\cdot1\cdot2))$ $= -10\cdot(6 -4 +1 -6 – 1 + 4) =0$

Матрица строк – обзор

(1)

Определите, какой из следующих наборов является базисом для R2, ​​рассматриваемого как матрицы строк.

(а)

1011.

(б)

1011.

(в)

1112.

(г)

1213

(г)

1213

1224.

(ж)

102010-20.

(ж)

1020-10-20.

(h)

111221

(2)

Определите, какой из следующих наборов является базисом для R2, ​​рассматриваемого как векторы-столбцы.

(а)

232-3.

(б)

1200.

(в)

121-2.

(г)

12−1−2.

(д)

10202030.

(ж)

50100100150.

(g)

12.

(h)

121314.

(3)

Определите, какие из следующих наборов являются базами для R3, рассматриваемыми как векторы-строки.

(а)

100010001.

(б)

110011101.

(в)

100110111.

(г)

4

11001

110011131.

(f)

110011141.

(g)

123456000.

(h)

123456789.

(4)

Определить следующие наборы являются основаниями для R3, рассматриваемыми как векторы-столбцы.

(а)

121T120T.

(б)

120T121T122T.

(в)

120T121T241T.

(г)

120T240T241T.

(д)

12−3T120T10−3T.

(ж)

111T211T221T.

(г)

211T221T22−1T.

(h)

121T131T141T151T.

(5)

Определите, какой из следующих наборов является основанием для M2 × 2.

(а)

1000010000100001.

(б)

1100−11000011000−1.

(в)

1000110011101111.

(d)

1110110110110111.

(6)

Определите, какие из следующих наборов являются базовыми для P1.

(а)

{ т + 1, т }.

(b)

{ t + 1, 1}.

(c)

{ t + 1, t , 1}.

(d)

{ т + 1, т – 1}.

(7)

Определите, какие из следующих наборов являются базовыми для P2.

(а)

{ т ² + т + 1, т }.

(b)

{ т ² + т , т + 1, т ² + 1, 1}.

(c)

{ т ² + т + 1, т + 1, 1}.

(d)

{ т ² + т + 1, т + 1, т – 1}.

(д)

{ т ² + т , т + 1, т ² + 1}.

(ж)

{ т ² + т + 1, т + 1, т ² }.

(8)

Определите, какие из следующих наборов являются базовыми для P3.

(a)

{ т ³ + т ² + т , т ² + т + 1, т + 1}.

(b)

{ т ³ , т ² , т , 1}.

(c)

{ т ³ + т ² + т , т ² + т + 1, т + 1, 1}.

(d)

{ т ³ + т ² , т ² + т , т + 1, 1}.

(д)

{ т ³ + т ² + т , т ³ + т ² 3, т т , т , т + 1, 1}.

(ж)

{ т ³ + т ² , т ³ – т ² , т + 1, } т + 1, } т + 1, } т .

(г)

{ т ³ + т ² + 1, т ³ + т ² , т + 1, т 1}.

(в)

{ т ³ + т ² + т , т ³ + т ² 3 + т т , т ³ + т }.

(9)

Найдите представление кортежа n для координат [1 3] относительно множеств, приведенных в (a) Задаче 1 (a) и (b) Задаче 1 (d) ).

(10)

Найдите представление кортежа n для координат [2 2] относительно множеств, заданных в (a) Задаче 1 (a) и (b) Задаче 1 (d).

(11)

Найдите представление набора с числом n для координат [1 – 1] относительно множеств, приведенных в (a) Задаче 1 (a) и (b) Задаче 1 ( б).

(12)

Найдите представление набора n для координат [1 – 2] ^T по отношению к множествам, заданным в (a) Задача 2 (c) и (b) Проблема 2 (е).

(13)

Найдите представление набора n для координат [100 – 100] ^T по отношению к множествам, заданным в (a) Задача 2 (e) и (b) Проблема 2 (е).

(14)

Найдите представление кортежа n для координат [1 1 0] относительно множеств, заданных в (a) Задаче 3 (a), (b) Задаче 3 (b) , и (c) Проблема 3 (c).

(15)

Найдите представление набора n для координат t + 2 по отношению к множествам, заданным в (a) Задаче 6 (a) и (b) Задаче 6 (b) .

(16)

Найдите представление набора n для координат t ² по отношению к множествам, данным в (a) Задаче 8 (c) и (b) Задаче 8 (d) ).

(17)

Пусть S – остовное множество для векторного пространства V, и пусть v∈S.Докажите, что если v является линейной комбинацией других векторов в наборе, то набор, который остается после удаления v из S, также является охватывающим набором для V.

(18)

Покажите, что любой охват набор для векторного пространства V можно свести к основанию, удалив из S подходящее количество векторов.

(19)

Уменьшите набор, отображаемый в примере 3, до базиса для M2 × 2.

(20)

Покажите, что набор, показанный в Задаче 1 (h), является охватывающим набором для R2, ​​и сведите его к основанию.

(21)

Покажите, что набор, показанный в задаче 7 (b), является охватывающим набором для P2, и сведите его к основанию.

(22)

Докажите, что любой линейно независимый набор векторов в векторном пространстве V может быть расширен до базиса для V. Совет: добавьте к набору известный базис и затем используйте Задачу 18.

( 23)

Расширить набор, показанный в примере 2, на основу для P3.

(24)

Покажите, что набор, показанный в Задаче 4 (а), линейно независим, и расширьте его до основы для R3.

(25)

Покажите, что набор, показанный в Задаче 8 (a), линейно независим, и расширьте его до основы для P3.

(26)

Докажите, что остовное множество для векторного пространства V не может содержать меньше элементов, чем размерность V.

(27)

Докажите, что любой набор из двух векторов в R2 является базисом если один вектор не является скалярным кратным другому.

(28)

Пусть W – подпространство векторного пространства V, а S – базис для W. Докажите, что S можно расширить до базиса для V.

(29)

Пусть W – подпространство векторного пространства V. Докажите, что dimW≤dimV.

(30)

Пусть W – подпространство векторного пространства V. Докажите, что если dimW − dimV, то W = V.

(31)

Докажите, что в n -мерном векторном пространстве V ни один набор из n – 1 векторов не может охватывать V.

(32)

Докажите, что если { v ₁ , v ₂ } – это основа для векторного пространства, тогда также { u ₁ , u ₂ }, где u ₁ = v ₁ + v ₂ и u ₂ = v ₁ – v ₂ .

(33)

Докажите, что если { v ₁ , v ₂ , v ₃ } является основой для векторного пространства, то тоже будет { u ₁ , u ₂ , u ₃ }, где u ₁ = v ₁ + v ₂ + v _{3 2 = v 2 – v 3 и u 3 = v 3 .}

(34)

Докажите, что если { v ₁ , v ₂ ,…, v _n } является основой для векторного пространства, то тоже { k ₁ v ₁ , k ₂ v ₂ ,…, k _n v _n 908 } , u ₂ , u ₃ }, где k ₁ , k ₂ ,…, k _n – любой набор ненулевых скаляров.

Умножающие матрицы – MathBootCamps

Хотя сложение или вычитание матриц относительно несложно, умножение матриц сильно отличается от большинства математических операций, которые вы усвоили заранее. Здесь мы рассмотрим хороший способ умножения двух матриц и некоторые важные свойства, связанные с ним. Вы также узнаете, как определить, когда умножение не определено.

реклама

Содержание:

1. Умножение двух матриц: «строки попадают в столбцы» (анимация)
2. Умножение матриц не всегда определяется
3. Умножение матриц не коммутативно
4. Примеры умножения матриц
5. Обзор свойств

Умножение двух матриц: «строки попадают в столбцы»

Чтобы понять общую схему умножения двух матриц, представьте, что «строки попадают в столбцы и заполняются строками».Рассмотрим следующий пример.

Первая строка «попадает» в первый столбец, давая нам первую запись продукта. Обратите внимание, что, поскольку это произведение двух матриц 2 x 2 (количество строк и столбцов), результатом также будет матрица 2 x 2. Как на это влияет размер матрицы, мы рассмотрим позже в статье.

Теперь первая строка «попадает» во второй столбец, заполняя строку продукта.

Закончились столбцы для «попадания», теперь мы работаем со второй строкой.

Осталась одна последняя запись для расчета. Вторая строка теперь «попадает» во второй столбец.

Наконец, нам просто нужно выполнить арифметику, чтобы получить окончательный ответ.

Анимация этого процесса

Вы можете увидеть анимацию этого процесса здесь. Нет звука – не беспокойтесь о поиске наушников!

Вскоре мы увидим еще пару примеров, но сначала нам нужно обсудить, как размер матрицы влияет на результат при умножении.Фактически, бывают случаи, когда из-за размера матрицы умножение не определено.

Умножение матриц не всегда определяется

При умножении матриц размер двух задействованных матриц определяет, будет ли определен продукт. Вы также можете использовать размеры, чтобы определить результат умножения двух матриц. Напомним, что размер матрицы – это количество строк по количеству столбцов. Матрицы выше были 2 x 2, так как каждая из них имела 2 строки и 2 столбца.

Как видите, размеры матриц не обязательно должны быть одинаковыми, вам просто нужно, чтобы два средних числа совпадали, когда вы пишете размеры рядом. В противном случае продукт не определен.

Подумайте об этом: например, если матрица A имеет размер 3 x 4, то произведение A и самого себя не будет определено, поскольку внутренние числа не будут совпадать. Это всего лишь один пример того, как умножение матриц ведет себя не так, как вы могли бы ожидать.

Умножение матриц некоммутативное

Из начальной школы вы знаете, что произведение (2) (3) = (3) (2).Неважно, в каком порядке вы умножаете числа, результат тот же. В целом это не работает для матриц. Только в особых случаях можно сказать, что AB = BA. Итак, в общем, вы должны предполагать, что они не равны. Может даже случиться так, что AB определен, а BA не определен!

Даже если продукт определен, опять же, маловероятно, что результаты будут одинаковыми для AB и BA.

Примеры умножения матриц

Теперь, когда мы рассмотрели некоторые важные свойства умножения матриц, давайте рассмотрим пару примеров.

Пример

Найдите продукт AB, где:
\ (A = \ left [\ begin {array} {cc} -5 & 3 \\ -4 & -1 \\ \ end {array} \ right] \)
and
\ ( B = \ left [\ begin {array} {cc} 1 & -1 \\ 2 & 6 \\ \ end {array} \ right] \)

Решение

Помните, что строки попадают в столбцы и заполняют строки. Здесь каждая из матриц имеет размер 2 x 2, поэтому результатом будет матрица 2 x 2.

\ (\ begin {align} AB & = \ left [\ begin {array} {cc} -5 & 3 \\ -4 & -1 \\ \ end {array} \ right] \ left [\ begin {array} {cc} 1 & -1 \\ 2 & 6 \\ \ end {array} \ right] \\ & = \ left [\ begin {array} {cc} -5 (1) + 3 (2) & -5 (-1) + 3 (6) \\ -4 (1) + (- 1) (2) & (-4) (- 1) + (- 1) (6) \\ \ end {array} \ right ] \\ & = \ boxed {\ left [\ begin {array} {cc} 1 & 23 \\ -6 & -2 \\ \ end {array} \ right]} \ end {align} \)

Пример

Найдите продукт AB где:

\ (A = \ left [\ begin {array} {cccc} -2 & -1 & 0 & 0 \\ 1 & 2 & 1 & 1 \\ \ end {array} \ right] \)
и
\ (B = \ left [\ begin {array} {cccc} 3 & 1 & 1 & 2 \\ -1 & -1 & 0 & 1 \\ \ end {array} \ right] \)

Решение

Здесь матрица 2 x 4 умножена на матрицу 2 x 4. Внутренние числа этих размеров не совпадают, поэтому:

\ (\ boxed {AB \ text {не определено}} \)

Пример

Найдите продукт AB, где:
\ (A = \ left [\ begin {array} {cc} 1 & 2 \\ -2 & 0 \\ 3 & 1 \\\ end {array} \ right] \)

и
\ (B = \ left [\ begin {array} {cc} 4 & 0 \\ 0 & 1 \\ \ end {array} \ right] \)

Решение

Это произведение матрицы 3 x 2 и матрицы 2 x 2. Внутренние числа совпадают, поэтому продукт определен.Результатом будет матрица 3 x 2.

\ (\ begin {align} AB & = \ left [\ begin {array} {cc} 1 & 2 \\ -2 & 0 \\ 3 & 1 \\\ end {array} \ right] \ left [\ begin {массив} {cc} 4 & 0 \\ 0 & 1 \\ \ end {array} \ right] \\ & = \ left [\ begin {array} {cc} 1 (4) + 2 (0) & 1 (0) + 2 (1) \\ -2 (4) + 0 (0) & -2 (0) + 0 (1) \\ 3 (4) + 1 (0) & 3 (0) + 1 ( 1) \\\ end {array} \ right] \\ & = \ boxed {\ left [\ begin {array} {cc} 4 & 2 \\ -8 & 0 \\ 12 & 1 \\\ end {массив } \ right]} \ end {align} \)

реклама

Сводка

Помните следующее всякий раз, когда вы умножаете две или более матриц.

1. Строки попадают в столбцы и заполняют строки.
2. Умножение матриц не всегда определяется – сначала проверьте размеры матрицы!
3. Умножение матриц в общем случае не коммутативно.

Подпишитесь на нашу рассылку новостей!

Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.

Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!

Связанные

Матричная арифметика

Матричная арифметика

Большая часть линейной алгебры включает математические объекты, называемые матрицами .Матрица – это конечный прямоугольный массив чисел:

В этом случае числа являются элементами (или). Как правило, записи будут элементы некоторого коммутативного кольца или поля.

В этом разделе я объясню операции с матрицами на примере. Я рассмотрю и докажу некоторые свойства этих операций. позже.

Размеры матриц. Матрица – это матрица с m строками и n столбцами.Иногда это выражают, говоря, что габариты матрицы .

Матрица называется n-мерный вектор-строка . Например, вот трехмерный вектор-строка:

Точно так же матрица называется n-мерным вектором-столбцом . Вот Трехмерный вектор-столбец:

Матрица называется квадратом матрица . Например, вот квадратная матрица:

Обратите внимание, что по соглашению количество строк указывается первым, а количество столбцов в секунду.Это соглашение также применяется к указанию к конкретным элементам матриц. Рассмотрим следующая матрица:

Элемент – это элемент в строке 2 и столбец 4, который есть. (Обратите внимание, что первая строка строка 1, а не строка 0, и аналогично для столбцов. ) Элемент – это элемент в строке 3 и столбце 3, то есть 13.

Равенство матриц. Две матрицы равны , если они имеют одинаковые размеры и соответствующие записи равны.Например, предположим

Затем, если я сопоставляю соответствующие элементы, я вижу, что, и.

Определение. Если R коммутативное кольцо, то набор матриц с записи в R.

Примечание: некоторые люди используют обозначения.

Например, это набор матриц с действительными записями. – набор матриц с элементами в.

Сложение и вычитание матриц . Для этих примеры, я предполагаю, что матрицы имеют записи в формате.

Вы можете складывать (или вычитать) матрицы, добавляя (или вычитая) соответствующие записи.

Матрица сложения ассоциативная — символически,

Это означает, что если вы добавляете несколько матриц, вы можете сгруппировать их как хотите:

Вот пример вычитания:

Обратите внимание, что сложение матриц коммутативно :

Символически, если A и B – матрицы с одинаковыми размерами, то

Конечно, вычитание матриц не коммутативно.

Вы можете складывать или вычитать только матрицы с одинаковыми размерами. Эти две матрицы нельзя складывать или вычитать:

Сложение или вычитание матриц более . Вы складываете или вычитаете матрицы, добавляя или вычитая соответствующие записи, но вся арифметика выполняется в.

Например, вот сложение и вычитание:

Обратите внимание, что во втором примере в середина вычисления, но окончательный ответ был выражен полностью с точки зрения элементов.

Определение. А ноль матрица – это матрица, все элементы которой равны 0.

Для каждой пары положительные размеры m и n.

Если вы добавите нулевую матрицу к другой матрице A, вы получите A:

В символах, если – нулевая матрица, а А – матрица того же размера, то

Нулевая матрица называется тождеством элемент для сложения матрицы.

Примечание. В какой-то момент я могу просто написать «0» вместо “” (жирным шрифтом) для нуля матрица, и полагаться на контекст, чтобы отличить ее от числа 0.

Умножение матриц на числа. Ты можешь умножьте матрицу на число, умножив каждую запись на количество. Вот пример с действительными числами:

Все работает точно так же, но все арифметика выполняется в формате. Вот пример закончился:

Обратите внимание, что, как обычно, я упростил мой окончательный ответ, чтобы все записи матрицы были в наборе .

В отличие от операций, которые я обсуждал до сих пор, умножение матриц (умножение двух матриц) работает не так, как вы могли ожидать: Вы не просто умножаете соответствующие элементы матриц, способ добавления соответствующих элементов для добавления матриц.

Чтобы объяснить умножение матриц, я сначала напомню вам, как вы возьмите скалярное произведение двух векторов ; ты вероятно, видел это в курсе многомерного исчисления. (Если ты увидев это впервые, не волнуйтесь – это просто!) Вот пример скалярного произведения двух трехмерных векторов действительных числа:

Обратите внимание, что векторы должны быть одинакового размера, и что продукт номер .На самом деле это пример матрицы умножение, и мы увидим, что результат технически должен быть матрица. Но для скалярных произведений мы напишем

Если вы видели скалярные произведения в многомерном исчислении, возможно, вы видел это так написано:

Но для того, что я буду делать дальше, я хочу различать строку (первый) вектор и вектор-столбец (второй).

Умножающие матрицы. Чтобы вычислить произведение двух матриц, возьмите точку произведения строк матрицы A на столбцы матрицы B.В этом примере Предположим, что все матрицы имеют действительные элементы.

На этом схематическом изображении показано, как располагаются строки первой матрицы. “точечно-произведенный” со столбцами второй матрицы, чтобы производим 4 элемента продукта:

Вы можете видеть, что вы берете скалярные произведения строк первая матрица с столбцами второй матрицы.

Чтобы умножение работало, матрицы должны иметь совместимые размеры: количество столбцов в A должно равняться количество строк B. Таким образом, если A – матрица, а B – матрица, будет матрицей. Например, это не сработает:

Вы понимаете почему? Строки первой матрицы имеют 4 элемента, но столбцы второй матрицы имеют 3 записи. Вы не можете взять точку продукты, потому что записи не совпадают.

Вот еще два примера, опять же с использованием матриц с реальными записями:

Вот пример с матрицами в формате. Вся арифметика выполняется в формате.

Обратите внимание, что я упрощаю окончательный результат, так что все записи в .

Если вы умножите матрицу на нулевую матрицу, вы получите нулевую матрицу:

В символах, если – нулевая матрица, а А – матрица совместим с ним для умножения, тогда

Умножение матриц требует небольшой практики, но это несложно.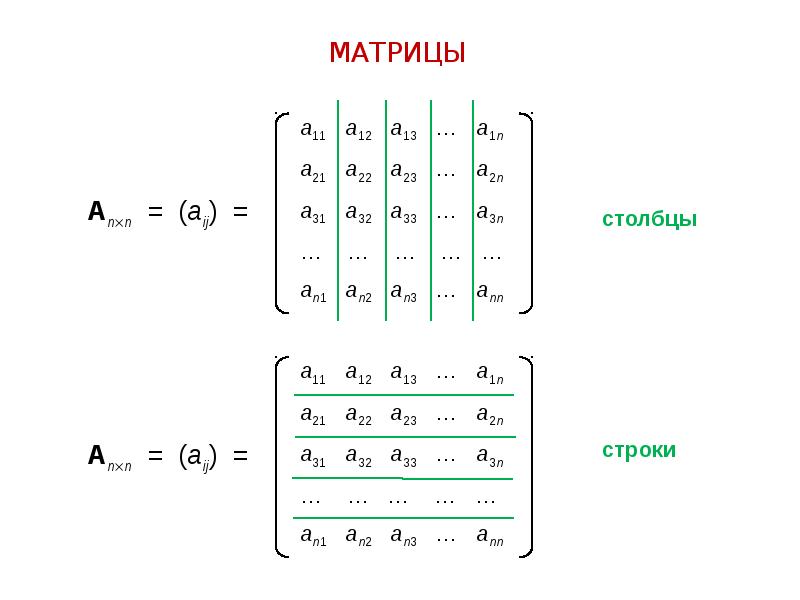 В Важный принцип, который следует убрать, заключается в том, что вы берете скалярные произведения строк первой матрицы с столбцами вторая матрица. Эта картина умножения матриц будет очень важно для нашей работы с матрицами.

Я должен сказать кое-что о том, что я упоминал ранее: почему бы и нет? умножать матрицы вот так?

Вы, , могли бы таким образом определить умножение матриц, но к сожалению, это бесполезно для приложений (таких как решение систем линейных уравнений).Или когда мы изучаем связь между матрицами и линейными преобразованиями, мы увидим что умножение матриц, которое мы определили с помощью скалярных произведений соответствует совокупности преобразований. Так что, хотя определение “соответствующие элементы” кажется более простым, оно не соответствует способу использования матриц.

Вот предварительный просмотр того, как матрицы связаны с системами линейных уравнения.

Пример. Напишите систему уравнений, которая соответствуют матричному уравнению

Две матрицы равны, если их соответствующие элементы равны, поэтому приравнять соответствующие записи:

Пример. Напишите следующую систему линейных уравнения как матричное уравнение умножения:

Возьмите 9 коэффициентов переменных x, y и z слева. и превратить их в матрицу. Положите переменные в трехмерный вектор-столбец. Сделайте 3 числа на правая часть в 3-мерные векторы-столбцы. Вот что мы получать:

Определите умножение в левой части этого уравнения и вы увидите, как это представляет исходную систему.

Это действительно важно! Это позволяет нам представить систему уравнения как матричное уравнение. В конце концов, мы выясним, как решить исходную систему, работая с матрицами.

Матрицы идентичности. Есть специальные матрицы которые служат тождествами для умножения: Единичная матрица – это квадратные матрицы с 1 по главной диагонали — диагональ бежит с северо-запада на юго-восток — и повсюду 0. Для Например, единичная матрица

Если I – единица, а A – матрица, совместима для умножения с A, то

Например,

Умножение матриц подчиняется некоторым алгебраическим законам, которые вы знаком с. Например, матричное умножение – ассоциативное : если A, B и C – матрицы и их размеры совместимы для умножения, тогда

Однако умножение матриц равно , а не . коммутативный в общем.То есть для всех матриц A, B.

Один тривиальный способ получить контрпример – позволить A быть и пусть B быть. Тогда это пока есть. Поскольку и имеют разные размеры, они не может быть равных.

Однако легко придумать контрпримеры, даже если они имеют одинаковые размеры. Для Например, рассмотрим следующие матрицы в:

Затем вы можете проверить, выполнив умножение, что

Многие свойства матричной арифметики вполне ожидаемы. — например, сложение матриц коммутативно или матрица умножение ассоциативно. Вы должны платить особенно внимание, когда что-то работает не так, как вы ожидали , и это вот такой случай. Очень важно, что умножение матриц не всегда коммутативен.

Транспонирует. Если A – матрица, транспонировать A получается поменять местами строки и столбцы A. Например,

Обратите внимание, что транспонированная матрица матрица.

Пример. Рассмотрим следующие матрицы с реальные записи:

(а) Вычислить.

(б) Вычислить.

а)

(б)

Обратная матрица. инверсия матрицы A – это матрица, которая удовлетворяет

В общем, нет такого понятия, как деление матриц, потому что некоторые матрицы не имеют инверсии .Но если у A есть обратное, вы можете смоделировать деление, умножив на. Это часто бывает полезно при решении матричных уравнений.

Матрица, не имеющая обратной, называется называется в единственном числе .

Позже мы подробно обсудим инверсии матриц и то, как их найти. А пока вот формула, которую мы будем часто использовать.

Предложение. Рассмотрим следующую матрицу с элементами коммутативного кольца с единицей R.

Предположим, что он обратим в R.Тогда инверсия A есть

Примечание. Число называется определителем матрицы . Мы обсудим детерминанты позже.

Помните, что не каждый элемент коммутативного кольца с единицей имеет обратное. Например, не определено в . Если мы имеем дело с действительными числами, то имеет мультипликативный обратный тогда и только тогда, когда это ненулевое значение.

Доказательство. Чтобы показать, что формула дает инверсия A, я должен это проверить и:

Это доказывает, что формула дает обратную матрицу.

Вот пример этой формулы для матрицы с действительными записями. Заметить, что . Так

(Если у меня есть дробь за пределами матрицы, я могу не умножать его в матрицу, чтобы результат выглядел лучше. Как правило, если есть является целым числом вне матрицы, я умножу его на.)

Напомним, что матрица, не имеющая обратной, называется сингулярной . Предположим, у нас есть вещественная матрица

Приведенная выше формула даст обратное if обратимое, что означает для действительных чисел.Итак, матрица сингулярна, если.

Пример. Для каких значений x следующие вещественная матрица сингулярная?

Матрица сингулярна — необратима — если

Решите для x:

Это дает или. Матрица единственное число для и для.

Будь осторожен! Следующая матрица сингулярна над:

Однако его определитель , которая не равна нулю. Дело в том, что 2 – это необратимый в , даже если он ненулевой.

Пример. (а) Найти в.

(b) Найдите матрицу, обратную следующей.

(Вы должны умножить любые числа вне матрицы на матрицу, и упростите все числа в окончательном ответе на.)

(а) Так как в, у меня есть.

(б) Во-первых, определитель . Я видел в (а) это.Так

Я уменьшил все цифры на последнем шаг; например, в. В качестве проверки

То есть, когда я умножаю обратную матрицу на исходную, я получаю единичная матрица. Убедитесь сами, что это тоже работает, если я перемножьте их в обратном порядке.

Мы обсудим решение систем линейных уравнений позже, но вот пример этого, который помещает многие идеи, которые мы обсуждали вместе.

Пример. ( Решение системы уравнений) Решите следующую систему для x и y, используя обратную матрицу.

Запишите уравнение в матричной форме:

Используя формулу, обратную матрице, я нахожу, что

Умножьте обе стороны на обратную матрицу:

Слева квадратная матрица и обратная к ней сокращаются, так как они умножаем на I.(Вы понимаете, что это похоже на “деление на матрица »?) Справа

Следовательно,

Решение -.

---

Контактная информация

Домашняя страница Брюса Икенаги

Авторские права 2020 Брюс Икенага

Что такое единичная матрица?

Идентификационная матрица

Узнав о нулевой матрице, пора изучить другой тип матрицы, содержащий постоянный определенный набор значений, каждый раз, пора нам изучить единичные матрицы.

Что такое единичная матрица?

Единичная матрица – это заданная квадратная матрица любого порядка, которая содержит на своей главной диагонали элементы со значением, равным единице, в то время как остальные элементы матрицы равны нулю.

Чтобы по частям объяснить это определение, давайте начнем с напоминания о том, что квадратная матрица относится к матрице, содержащей одинаковое количество строк и столбцов. Порядок матрицы определяется ее размерами, а ее главная диагональ относится к массиву элементов внутри матрицы, которые образуют наклонную линию от верхнего левого угла к нижнему правому углу.Учитывая характеристики единичной матрицы, мы также можем заключить, что этот тип матриц также является диагональными матрицами.

Диагональная матрица – это матрица, в которой все элементы ее элементов равны нулю, за исключением элементов, находящихся на ее главной диагонали. В этом случае все ненулевые элементы матрицы будут иметь значение, равное единице, и это является одной из причин, по которой единичную матрицу иногда также называют единичной матрицей.
В случае обозначения матричной линейной алгебры единичная матрица служит объектом, эквивалентным единице в числовой алгебре (другая причина, почему она называется единичной матрицей). Другими словами, единичная матрица эквивалентна единице, но в данном случае это алгебраический объект с размерами и организацией массива, который может использоваться в операциях с другими массивами упорядоченных чисел (другими матрицами).
В следующем разделе мы рассмотрим свойства единичной матрицы, и определение единичной матрицы будет иметь гораздо больший смысл, особенно в случае умножения матриц, включая единичную матрицу (см. Свойство номер 3).Математически единичная матрица представлена ​​как:
Уравнение 1: Общее выражение единичной матрицы Не путать с идентичностью матрицы, обратите внимание, что единичная матрица имеет столько же главных диагональных элементов, сколько ее порядок (обозначается субиндексом n в члене, находящемся в левой части уравнения). Примеры матриц идентичности разных размеров можно увидеть в следующем уравнении: Уравнение 2: Примеры матриц идентичности разных размеров Помните, что порядок матрицы относится к количеству содержащихся в ней строк и столбцов, которые также называются ее размерами mxn. Обратите внимание, что, поскольку единичная матрица является квадратной матрицей, она содержит такое же количество строк и столбцов, поэтому ее порядок можно обозначать просто как nxn или как однозначный субиндекс, как показано в уравнениях 1 и 2, которые мы называем ” n “(учитывая, что размеры m и n из типичной записи матриц равны для квадратных матриц, только одна из этих букв необходима в качестве субиндекса для описания порядка таких матриц).
Итак, в уравнении 2 мы можем легко увидеть, что I2 относится к единичной матрице с двумя строками и двумя столбцами, которая в то же время имеет только два элемента на своей главной диагонали; обозначение I3 соответствует единичной матрице порядка 3 или матрице, содержащей три строки и три столбца и 3 элемента на своей главной диагонали; и система обозначений продолжается таким же образом для любого субиндекса n.

Свойства матрицы идентичности

1. Единичная матрица всегда является квадратной матрицей:
   Как видно из уравнений 1 и 2, порядок единичной матрицы всегда равен n, что относится к размерам nxn (то есть всегда одинаковое количество строк и столбцов в матрица).
2. Единичная матрица способна перемножать любую матрицу любого порядка (размерности), если она соответствует следующим правилам:
   1. Если при умножении единичная матрица является первым множителем, то единичная матрица должна иметь размеры с таким количеством столбцов, какое количество строк в умножаемой матрице.Уравнение 3: Умножение единичной матрицы на неединичную матрицу
   2. Если единичная матрица является вторым множителем при умножении, единичная матрица должна иметь такое же количество строк, что и матрица, которая умножает ее, имеет столбец. Уравнение 4: Умножение неединичной матрицы на единичную матрицу Эти два правила исходят из условий умножения матриц.
   3. В результате первых двух правил, если единичная матрица умножает квадратную матрицу тех же размеров, результатом также будет квадратная матрица, которая будет такой же, как неединичная матрица умножения, независимо от порядок, в котором матрицы перемножаются друг на друга.
3. Следуя двум уравнениям из второго свойства, объясненного выше, из всех свойств единичной матрицы, главное из них можно четко наблюдать в уравнениях 3 и 4: всякий раз, когда единичная матрица умножает другую матрицу, умножение может быть решено (следуя правилам для умножения матриц) результат равен задействованной неединичной матрице. Математически говоря: Уравнение 5: Умножение единичной матрицы на другую матрицу Если задуматься, это эквивалент умножения обычного действительного числа на единицу (на единицу).Любое число, умноженное на единицу, дает такое же исходное число. То же самое касается матрицы, умноженной на единичную матрицу, результатом всегда является одна и та же исходная неединичная (неединичная) матрица, и, таким образом, как объяснялось ранее, единичная матрица получает псевдоним «единичная матрица».
4. Умножение матрицы на обратную приведет к единичной матрице того же порядка, что и умножаемые матрицы. Математически говоря: Уравнение 6: Умножение матрицы на обратную ей Матрицы, участвующие в таком умножении, называются мультипликативно инверсными друг другу.Мы оставим объяснение об обратных матрицах для последующих уроков, начиная с темы об обратных матрицах 2×2. На данный момент просто важно, чтобы вы знали, что это одно из свойств единичной матрицы, которое мы можем использовать для решения матричных уравнений.
5. Определитель единичной матрицы In всегда равен 1, а ее след равен n. Хотя мы до сих пор не видели, что такое определитель, на данный момент важно знать, что причина, по которой определитель любой единичной матрицы равен единице, заключается в том, что диагональ этих матриц содержит только единицы, а остальные элементы внутри них матрицы нули.Мы представим концепцию определителя в следующем уроке, который называется определителем матрицы 2×2, где определитель единичной матрицы будет объяснен более подробно.
   С другой стороны, след гораздо проще объяснить. К настоящему моменту вы должны знать, что след матрицы относится к сложению элементов, найденных на ее главной диагонали. Поскольку единичная матрица имеет диагональные элементы, все равные единице, при добавлении их всех для получения трассировки у вас всегда будет столько элементов, сколько соответствует порядку единичной матрицы, то есть n.В качестве примера возьмем следующую единичную матрицу: Уравнение 7: Пример единичной матрицы порядка 3×3 Уравнение 7 показывает единичную матрицу 3×3, таким образом, n = 3 для этой матрицы. Таким образом, след представляет собой сложение элементов его диагонали, то есть трех элементов значения 1, сложенных друг с другом, и, таким образом, след равен 3. Следовательно, след единичной матрицы равен n .
6. Последнее свойство мы начнем с вопроса: обратима ли единичная матрица? Ответ положительный.Мы объясним больше по этой теме в нашем уроке об обратимой матрице 2×2, а пока просто помните: инверсия единичной матрицы сама по себе. Уравнение 8: единичная матрица как обратная мультипликативная сама себе. Мы можем доказать, что матрица, обратная единице, – это сама матрица, умножив их вместе. Помните из нашего четвертого свойства, что умножение матрицы на ее инверсию дает единичную матрицу, и поэтому мы вычислили соответствующее умножение для этого случая (показанного в уравнении 8) и доказали, что инверсия единичной матрицы 2×2 есть сама.

Примеры проблем с идентификационной матрицей

Используя свойства, изученные в предыдущем разделе, и определение единичной матрицы, данное в начале этого урока, решите следующие примеры задач:

Пример 1

Учитывая матрицы ниже: Уравнение 9: матрицы A и B Выполните следующие операции с матрицами:

1. I3⋅AI_ {3} \ cdot AI3 ⋅A
   В этом случае у нас есть пример третьего свойства единичной матрицы: умножение с использованием единичной матрицы и любой другой матрицы, если определенная по правилам умножения матриц, результатом будет неединичная матрица (в данном случае матрица A).Итак, это умножение происходит следующим образом: Уравнение 10: Умножение матриц с использованием единичной матрицы
2. 2A + 4I32A + 4I_ {3} 2A + 4I3
   Для этой матричной операции мы вычисляем два случая скалярного умножения, второй из которых включает единичную матрицу 3×3. Решение такой операции идет как: Уравнение 11: сложение двух умножений скалярных матриц
3. −4B + 2I2-4B + 2I_ {2} −4B + 2I2
   Еще раз, эта операция состоит в использовании единичной матрицы для сложения двух скалярных умножений, где второе умножение включает единичную матрицу 2×2.Решаем их так, как показано ниже: Уравнение 12: сложение двух умножений скалярных матриц
4. I2⋅BI_ {2} \ cdot BI2 ⋅B
   По третьему свойству мы знаем, что результатом этого умножения является матрица B: Уравнение 13: Умножение единичной матрицы 2×2 на другую матрицу того же порядка
5. 0⋅I40 \ cdot I_ {4} 0⋅I4
   В этом случае у нас есть скалярное умножение единичной матрицы на ноль, таким образом, результатом должна быть нулевая матрица, как показано ниже: Уравнение 14: Скалярное умножение единичной матрицы, дающее нулевую матрицу

Пример 2

Покажите, являются ли следующие матрицы мультипликативно инверсными друг другу:

1. Имея матрицы X и Y, как показано ниже: Уравнение 15: матрицы X и Y Произведем матричное умножение X ⋅ \ cdot⋅ Y: Уравнение 16: Умножение матриц X и Y Учитывая, что результатом является единичная матрица, мы заключаем, что X и Y являются мультипликативными обратными друг другу.
2. Имея матрицы A и B, как показано ниже: Уравнение 17: матрицы A и B Произведем матричное умножение A ⋅ \ cdot⋅ B: Уравнение 18: Умножение матриц A и B Таким образом, A и B мультипликативно инвертируют друг друга.
3. Имея матрицы C и D, как показано ниже: Уравнение 19: матрицы C и D Произведем матричное умножение C ⋅ \ cdot⋅ D: Уравнение 20: Умножение матриц C и D Хотя матрица, полученная в результате вышеописанной операции, очень похожа, она не является единичной матрицей.Следовательно, эта операция показывает, что C и D НЕ являются мультипликативными обратными друг другу.
4. Имея матрицы E и F, как показано ниже: Уравнение 21: матрицы E и F Произведем матричное умножение E ⋅ \ cdot⋅ F: Уравнение 22: Умножение матриц E и F Следовательно, E и F мультипликативно инвертируют друг друга.

Итак, мы завершаем этот урок, когда узнали, что такое единичная матрица и ее свойства. В последующих уроках имейте в виду, что для простоты мы могли бы называть единичную матрицу единичной матрицей.
Прежде чем мы уйдем, позвольте нам порекомендовать вам следующую небольшую ссылку, кратко определяющую единичную матрицу, и эту статью, которая связывает темы умножения матриц и единичной матрицы, говоря о коммутативном свойстве умножения любой квадратной матрицы на матрицу. единичная матрица того же порядка (точно так же, как описано в третьем свойстве во втором разделе этого урока) и как это не применяется к другим умножениям матриц.
Итак, на сегодня все, до встречи на следующем уроке!

Матрицы

Матрица – это прямоугольный массив элементов (действительных или комплексных чисел), расположенных в строках и столбцах.Массив заключен в квадратные скобки или круглые скобки.

Матрица с m строками и n столбцами называется матрицей m x n или m x n.
Это также называется его порядком.

Если m = n, матрица называется квадратной матрицей.
Если m = 1, матрица называется матрицей-строкой или вектором-строкой.
Если n = 1, матрица называется матрицей-столбцом или вектором-столбцом.

Примеры

Элементы

Каждому элементу в матрице адресуется его
строка и столбец как двойные суффиксы.
a _ij обозначает элемент в строке i ^th и столбце j ^th .

Элементы матрицы m x n:

Пример

a ₁₃ = 3 a ₂₁ = 4 a ₃₄ не существует

Матричная запись

Матрица m x n часто обозначается заглавной буквой жирным шрифтом.
В письменной работе под заглавной буквой проводится волнистая линия.
Его также можно обозначить общим элементом, заключенным в скобки.

Может обозначаться как A “ (a _ij ) или (a)

Матрица строк или столбцов часто обозначается строчной буквой жирным шрифтом.

может обозначаться как y “ (y _j ) или (y)

Равенство

Две матрицы равны, только если они одного порядка и содержат соответствующие элементы.

Примеры

Сложение и вычитание матриц

Допускаются только матрицы одного порядка. добавлено или вычтено.
Каждый элемент добавляется или вычитается из соответствующего ему элемента.
Матричное сложение коммутативно

Пример

Пример

Пример

Умножение скалярных матриц

Чтобы умножить матрицу на скаляр, умножьте каждый элемент на скаляр.

Пример

Умножение матриц

Это можно сделать, только если количество столбцов в первой матрице равно количеству строк во второй.

, т.е. если A – это матрица m x n, а B – это матрица n x p
тогда продукт A.B возможен, но B.A невозможен.

Пусть B будет матрицей m x n, а A будет матрицей n x p.

B.A возможно, AB невозможно

Пусть произведение BA = C

C определяется

или

Умножение матриц можно описать как нахождение скалярного произведения каждой строки первой матрицы на каждый столбец второй.

Пример

Пусть

B – матрица 3×3 A – матрица 3×2
так Б.Возможен .

A.B невозможно, поэтому умножение здесь не коммутативно.

Примечание

Произведение матрицы размера m x n на матрицу n x p
матрица порядка m x p

В произведении B.A
A предварительно умножается на B
B умножается на A

Матричное умножение ассоциативное

и распределительный

при условии, что B и C имеют тот же порядок, что и
количество столбцов в A равно числу
строк в B и C.

Транспонировать

Транспонирование матрицы A записывается A ’ или A ^T
Его можно найти, меняя местами строки и столбцы, так что
a ’ _ij = a _ji

Пример

Обратите внимание, что ведущая диагональ остается прежней

, а остальные записи были перевернуты.

Примечание

Матрицы специальные

Квадратная матрица симметрична, если _ij = a _ij

Пример

Симметричная матрица имеет транспонирование A ^T = A

Квадратная матрица является кососимметричной, если A ^T = -A

Обратите внимание, что первая диагональ равна нулю

Диагональная матрица – это квадратная матрица,
не ведущие диагональные элементы – нули.

Матрица единиц или идентичности – это диагональная матрица,
ведущие диагональные элементы – все единицы.
Он называется I .

Нулевая или нулевая матрица – это матрица, состоящая исключительно из нулей.
Он называется 0 .

В отличие от обычной алгебры,
A.B = 0 не позволяет предположить, что
либо A , либо B равно нулю.

Пример

Матрицы преобразования

Линейные преобразования можно описать отображением
такой, что T отображает точки (x, y) в (x ’, y’)

или

где A (матрица mxn)
называется матрицей преобразования T.

T: x ’= ax + by, y’ = cx + dy можно записать

Пример

Найдите изображения точек A (1,2), B (3,4) и C (5,6)
после его перевода матрицей

Отражения

Отражение по оси x

Отражение по оси y

Отражение в линии y = x

Отражение в строке y = -x

Повороты

Поворот на 90 ^◦ против часовой стрелки относительно начала координат.

Поворот на 180 ^◦ относительно исходной точки.

Поворот на 90 ^◦ по часовой стрелке вокруг начала координат.

Поворот θ против часовой стрелки относительно начала координат.

x ’= xcosθ – ysinθ y’ = xsinθ + ycosθ

Увеличение с масштабным коэффициентом

Пример: масштабный коэффициент 2

Пример: масштабный коэффициент 1/2

Чтобы отменить эффекты преобразования,
предварительно умножьте вектор изображения на значение, обратное
матрица преобразования.

Если обратная матрица преобразования
равна его транспонированию, тогда матрица преобразования
ортогонален.

Если точка преобразуется в собственное изображение, она называется инвариантной.

© Александр Форрест Умножение матриц

– ChiliMath

Умножение матриц – это «беспорядочный тип», потому что вам нужно будет следовать определенному набору процедур, чтобы сделать это правильно.Это «беспорядочный тип», потому что процесс более сложен. Однако позже, пройдя процедуру и несколько примеров, вы поймете, что необходимые шаги можно выполнить. Не волнуйтесь, я помогу вам в этом!

Но сначала нам нужно убедиться, что две матрицы «разрешено» умножать вместе. В противном случае данные две матрицы «несовместимы» для умножения. В этом случае мы говорим, что решение не определено.

---

Умножение матрицы на матрицу a.k.a «Грязный тип»

Всегда помни об этом!

Чтобы умножение матриц работало, количество столбцов левой матрицы ДОЛЖНО РАВНО количеству строк правой матрицы.

Предположим, нам даны матрицы A и B, найдите AB (произведите умножение матриц, если применимо). Определите, какая из них левая и правая матрицы, в зависимости от их расположения. Это очень важный шаг.

Чтобы определить, могу ли я перемножить две заданные матрицы, мне нужно обратить внимание на количество столбцов матрицы A и количество строк матрицы B.Если они равны, я могу перейти к умножению матриц. В противном случае сделаю вывод, что ответ неопределенный!

Поскольку матрица A имеет количество столбцов 2 , а матрица B имеет количество строк 3 , и они не равны (2 ≠ 3), я заключаю, что AB = undefined . Это означает, что их продукт невозможно найти.

---

Примеры умножения матриц, также известные как «Беспорядочный тип»

Направления : Для следующих матриц выполните указанную операцию.

---

Пример 1 : Рассчитайте, если возможно, произведение B и E.

Чтобы матрицы B и E имели произведение, количество столбцов левой матрицы B должно равняться количеству строк правой матрицы E.

количество столбцов = 3

количество строк = 3

В этом случае их можно перемножить. Теперь это шаги:

Шаг 1: Поместите их рядом.

Шаг 2: Умножьте строки B на столбцы E, умножив соответствующие элементы каждой строки на каждый элемент столбца, а затем сложите их вместе.

Внимательно посмотрите анимированное решение.

Если у вас нет терпения смотреть приведенное выше анимированное решение о том, как выполнять матричное умножение, вы можете просмотреть обычное решение, которое я включил ниже.

---

Пример 2 : Рассчитайте, если возможно, произведение E и F.

Сначала проверьте, существует ли произведение двух матриц, убедившись, что количество столбцов левой матрицы E равно количеству строк правой матрицы F.

количество столбцов = 2

количество строк = 2

Это замечательно, поскольку количество столбцов матрицы E равняется количеству строк матрицы F. Это означает, что произведение EF определено, поэтому мы можем продолжить и выполнить умножение матриц.См. Ниже анимированное пошаговое решение умножения матриц.

---

Пример 3 : Вычислить, если возможно, произведение F и E.

В нашем предыдущем примере мы успешно получили продукт EF. На этот раз мы хотим выяснить, сможем ли мы найти произведение E [латекс] и [латекс] F в указанном порядке.

Напомню, что действительные числа коммутативны при операции умножения, что означает, что порядок умножения не влияет на конечный результат.Например …

Таким образом, возникает большой вопрос, работает ли это также при умножении матриц?

Проверим, равно ли количество столбцов матрицы F количеству строк матрицы E.

количество столбцов = 2

количество строк = 3

Очевидно, что количество столбцов в матрице F не равно количеству строк в матрице E. Подразумевается, что произведение FE не может быть вычислено, поэтому оно не определено!

В общем случае умножение матриц не коммутативно.

---

Пример 4 : Рассчитайте, если возможно, произведение AE.

Стандартный способ описать размер или размерность матрицы – это …

(указать количество строк) x (указать количество столбцов)

… читается как «количество строк по количеству столбцов».

3 x 3 (матрица три на три)

3 x 2 (матрица три на два)

Поскольку количество столбцов в матрице A , равное , равно количеству строк в матрице E , равному , мы заключаем, что произведение AE определено.

Давайте разберемся. См. Анимированное решение ниже.

---

Пример 5 : Рассчитайте, если возможно, произведение E и A.

3 x 2 (матрица три на два)

3 x 3 (матрица три на три)

Очевидно, что количество столбцов матрицы E не равно количеству столбцов матрицы A. Следовательно, произведение EA не может быть вычислено или не определено.

---

Пример 6 : Вычислить, если возможно, произведение D и F.2}. Другими словами, мы возводим в квадрат матрицу C.

Здесь нужно проявлять осторожность. Обратите внимание, что возвести в квадрат можно только квадратную матрицу. Напомним, квадратная матрица – это матрица, в которой номер строки равен номеру столбца.

Я предоставлю вам возможность проверить правильность приведенного ниже решения. Такие математические задачи, как эта, хотя и утомительны, я всегда рекомендую решать их вручную, используя карандаш и бумагу.

---

Практика с рабочими листами

---

Возможно, вас заинтересует:

Сложение и вычитание матриц

Скалярное умножение

типов матриц в линейной алгебре для машинного обучения

Последнее обновление 5 января 2021 г.

Многое из линейной алгебры связано с операциями над векторами и матрицами, и существует много различных типов матриц.

Есть несколько типов матриц, с которыми вы можете сталкиваться снова и снова, когда начинаете заниматься линейной алгеброй, в частности, части линейной алгебры, относящиеся к машинному обучению.

В этом руководстве вы откроете для себя набор различных типов матриц из области линейной алгебры, с которыми вы можете столкнуться в машинном обучении.

После прохождения этого руководства вы будете знать:

• Квадратные, симметричные, треугольные и диагональные матрицы, соответствующие их названиям.
• Матрицы идентичности, которые имеют нулевые значения, кроме вдоль главной диагонали, где значения равны 1.
• Ортогональные матрицы, обобщающие идею перпендикулярных векторов и обладающие полезными вычислительными свойствами.

Начните свой проект с моей новой книги «Линейная алгебра для машинного обучения», включающей пошаговых руководств и файлов исходного кода Python для всех примеров.

Приступим.

• Обновление от февраля 2018 г. : исправлена ​​небольшая опечатка в уравнении эквивалентности для ортогональной матрицы.

Нежное введение в типы матриц в линейной алгебре
Фотография Тони, некоторые права защищены.

Обзор учебного пособия

Это руководство разделено на 6 частей, чтобы охватить основные типы матриц; их:

1. Квадратная матрица
2. Симметричная матрица
3. Треугольная матрица
4. Диагональная матрица
5. Матрица идентичности
6. Ортогональная матрица

Нужна помощь с линейной алгеброй для машинного обучения?

Пройдите мой бесплатный 7-дневный ускоренный курс электронной почты (с образцом кода).

Нажмите, чтобы зарегистрироваться, а также получите бесплатную электронную версию курса в формате PDF.

Загрузите БЕСПЛАТНЫЙ мини-курс

Квадратная матрица

Квадратная матрица – это матрица, в которой количество строк (n) равно количеству столбцов (m).

Квадратная матрица контрастирует с прямоугольной матрицей, в которой количество строк и столбцов не равно.

При совпадении количества строк и столбцов размеры обычно обозначаются как n, e.грамм. п х п. Размер матрицы называется порядком, поэтому квадратная матрица четвертого порядка составляет 4 x 4.

Вектор значений по диагонали матрицы от верхнего левого угла до нижнего правого угла называется главной диагональю.

Ниже приведен пример квадратной матрицы третьего порядка.

1, 2, 3 М = (1, 2, 3) 1, 2, 3

1, 2, 3 M = (1, 2, 3) 1, 2, 3

Квадратные матрицы легко складываются и перемножаются и являются основой многих простых линейных преобразований, таких как вращения (как при поворотах изображений).

Симметричная матрица

Симметричная матрица – это тип квадратной матрицы, в которой правый верхний треугольник совпадает с левым нижним треугольником.

Без преувеличения можно сказать, что симметричные матрицы S – это самые важные матрицы, которые когда-либо видел мир – в теории линейной алгебры, а также в приложениях.

– стр. 338, Введение в линейную алгебру, пятое издание, 2016 г.

Чтобы быть симметричным, ось симметрии всегда является главной диагональю матрицы, от верхнего левого угла до нижнего правого.

Ниже приведен пример симметричной матрицы 5 × 5.

1, 2, 3, 4, 5 2, 1, 2, 3, 4 М = (3, 2, 1, 2, 3) 4, 3, 2, 1, 2 5, 4, 3, 2, 1

1, 2, 3, 4, 5 2, 1, 2, 3, 4 M = (3, 2, 1, 2, 3) 4, 3, 2, 1, 2 5, 4, 3, 2, 1

Симметричная матрица всегда квадратная и равна своему собственному транспонированию.

Треугольная матрица

Треугольная матрица – это тип квадратной матрицы, все значения которой находятся в верхнем правом или нижнем левом углу матрицы, а остальные элементы заполнены нулевыми значениями.

Треугольная матрица со значениями только выше главной диагонали называется верхней треугольной матрицей. В то время как треугольная матрица со значениями только ниже главной диагонали называется нижней треугольной матрицей.

Ниже приведен пример верхней треугольной матрицы 3 × 3.

1, 2, 3 М = (0, 2, 3) 0, 0, 3

1, 2, 3 M = (0, 2, 3) 0, 0, 3

Ниже приведен пример нижней треугольной матрицы 3 × 3.

1, 0, 0 М = (1, 2, 0) 1, 2, 3

1, 0, 0 M = (1, 2, 0) 1, 2, 3

Разложение LU разрешает заданную матрицу на верхнюю и нижнюю треугольные матрицы.

NumPy предоставляет функции для вычисления треугольной матрицы из существующей квадратной матрицы. Функция tril () для вычисления нижней треугольной матрицы из заданной матрицы и triu () для вычисления верхней треугольной матрицы из заданной матрицы

Пример ниже определяет квадратную матрицу 3 × 3 и вычисляет из нее нижнюю и верхнюю треугольные матрицы.

# треугольные матрицы из массива импорта numpy из numpy import tril от numpy import triu M = массив ([[1, 2, 3], [1, 2, 3], [1, 2, 3]]) печать (M) нижний = трил (М) печать (нижняя) верхний = триу (М) печать (верхняя)

# треугольные матрицы из numpy import array из numpy import tril из numpy import triu M = array ([[1, 2, 3], [1, 2, 3], [1, 2 , 3]]) печать (M) нижняя = трил (M) печать (нижняя) верхняя = триу (M) печать (верхняя)

При выполнении примера печатается заданная матрица, за которой следуют нижняя и верхняя треугольные матрицы.

[[1 2 3] [1 2 3] [1 2 3]] [[1 0 0] [1 2 0] [1 2 3]] [[1 2 3] [0 2 3] [0 0 3]]

[[1 2 3] [1 2 3] [1 2 3]] [[1 0 0] [1 2 0] [1 2 3]] [[1 2 3] [0 2 3] [0 0 3]]

Диагональная матрица

Диагональная матрица – это матрица, в которой значения за пределами главной диагонали имеют нулевое значение, а главная диагональ берется из верхнего левого угла матрицы в нижний правый.

Диагональная матрица часто обозначается переменной D и может быть представлена ​​как полная матрица или как вектор значений на главной диагонали.

Диагональные матрицы состоят в основном из нулей и имеют ненулевые элементы только вдоль главной диагонали.

– стр. 40, Глубокое обучение, 2016 г.

Ниже приведен пример квадратной диагональной матрицы 3 × 3.

1, 0, 0 D = (0, 2, 0) 0, 0, 3

1, 0, 0 D = (0, 2, 0) 0, 0, 3

В качестве вектора он будет представлен как:

Или с указанными скалярными значениями:

Диагональная матрица не обязательно должна быть квадратной.В случае прямоугольной матрицы диагональ будет охватывать самое короткое измерение; например:

1, 0, 0, 0 0, 2, 0, 0 D = (0, 0, 3, 0) 0, 0, 0, 4 0, 0, 0, 0

1, 0, 0, 0 0, 2, 0, 0 D = (0, 0, 3, 0) 0, 0, 0, 4 0, 0, 0, 0

NumPy предоставляет функцию diag (), которая может создавать диагональную матрицу из существующей матрицы или преобразовывать вектор в диагональную матрицу.

В приведенном ниже примере определяется квадратная матрица 3 × 3, основная диагональ извлекается как вектор, а затем создается диагональная матрица из извлеченного вектора.

# диагональная матрица из массива импорта numpy из numpy import diag M = массив ([[1, 2, 3], [1, 2, 3], [1, 2, 3]]) печать (M) # извлечь диагональный вектор d = диаг (М) печать (d) # создать диагональную матрицу из вектора D = диаг (d) печать (D)

# диагональная матрица из массива импорта numpy из массива импорта numpy diag M = array ([[1, 2, 3], [1, 2, 3], [1, 2, 3]]) print (M) # извлечь диагональный вектор d = diag (M) print (d) # создать диагональную матрицу из вектора D = diag (d) print (D)

При выполнении примера сначала печатается заданная матрица, затем вектор главной диагонали и диагональная матрица, построенная на основе вектора.

[[1 2 3] [1 2 3] [1 2 3]] [1 2 3] [[1 0 0] [0 2 0] [0 0 3]]

[[1 2 3] [1 2 3] [1 2 3]] [1 2 3] [[1 0 0] [0 2 0] [0 0 3]]

Матрица идентификации

Единичная матрица – это квадратная матрица, которая не меняет вектор при умножении.

Значения единичной матрицы известны. Все скалярные значения по главной диагонали (от верхнего левого угла до нижнего правого) имеют значение один, а все остальные значения равны нулю.

Единичная матрица – это матрица, которая не меняет какой-либо вектор, когда мы умножаем этот вектор на эту матрицу.

– стр. 36, Глубокое обучение, 2016 г.

Единичная матрица часто представляется с использованием обозначения «I» или размерности «In», где n – это нижний индекс, указывающий размерность квадратной единичной матрицы.В некоторых обозначениях идентичность может называться единичной матрицей или «U», чтобы учитывать одно значение, которое она содержит (это отличается от унитарной матрицы).

Например, единичная матрица размером 3 или I3 будет иметь следующий вид:

1, 0, 0 Я = (0, 1, 0) 0, 0, 1

1, 0, 0 I = (0, 1, 0) 0, 0, 1

В NumPy матрица идентичности может быть создана с определенным размером с помощью функции identity ().

В приведенном ниже примере создается единичная матрица I3.

# единичная матрица из идентификатора импорта numpy I = идентичность (3) печать (I)

# матрица идентичности из numpy import identity I = identity (3) print (I)

При выполнении примера распечатывается созданная матрица идентичности.

[[1.0. 0.] [0. 1. 0.] [0. 0. 1.]]

[[1. 0. 0.] [0. 1. 0.] [0. 0. 1.]]

Сама по себе единичная матрица не так интересна, хотя она является компонентом в других операциях с матрицей импорта, таких как инверсия матрицы.

Ортогональная матрица

Два вектора ортогональны, когда их скалярное произведение равно нулю, что называется ортонормированным.

или

Это интуитивно понятно, если учесть, что одна линия ортогональна другой, если она перпендикулярна ей.

Ортогональная матрица – это тип квадратной матрицы, столбцы и строки которой являются ортонормированными единичными векторами, например перпендикулярно и иметь длину или величину 1.

Ортогональная матрица – это квадратная матрица, строки которой взаимно ортонормированы, а столбцы взаимно ортонормированы

– стр. 41, Глубокое обучение, 2016.T указывает на транспонирование Q, а I – единичная матрица.

Матрица ортогональна, если ее транспонирование равно обратному.

Другой эквивалент ортогональной матрицы – это то, что скалярное произведение матрицы и самого себя равно единичной матрице.

Ортогональные матрицы часто используются для линейных преобразований, таких как отражения и перестановки.

Ниже приведена простая ортогональная матрица 2 × 2, которая является примером матрицы отражения или координатного отражения.

1, 0 Q = (0, -1)

1, 0 Q = (0, -1)

В приведенном ниже примере создается эта ортогональная матрица и проверяются приведенные выше эквивалентности.

# ортогональная матрица из массива импорта numpy из numpy.linalg import inv Q = массив ([[1, 0], [0, -1]]) печать (Q) # обратная эквивалентность V = inv (Q) печать (Q.Т) печать (V) # идентичность эквивалентности I = Q.dot (Q.T) печать (I)

# ортогональная матрица из массива импорта numpy из массива импорта numpy.linalg Q = array ([[1, 0], [0, -1]]) print (Q) # inverse эквивалентность V = inv (Q) print (QT) print (V) # идентичность эквивалентность I = Q.dot (QT) print (I)

При выполнении примера сначала печатается ортогональная матрица, затем печатается обратная ортогональная матрица, а затем печатается транспонированная ортогональная матрица, и показано, что они эквивалентны.Наконец, печатается единичная матрица, которая вычисляется из скалярного произведения ортогональной матрицы с ее транспонированием.

[[1 0] [0 -1]] [[1 0] [0 -1]] [[1. 0.] [-0. -1.]] [[1 0] [0 1]]

[[1 0] [0-1]] [[1 0] [0-1]] [[1. 0.] [-0.-1.]] [[1 0] [0 1]]

Ортогональные матрицы являются полезными инструментами, поскольку они дешевы в вычислительном отношении и стабильны, чтобы вычислить их инверсию как просто их транспонирование.

Расширения

В этом разделе перечислены некоторые идеи по расширению учебника, которые вы, возможно, захотите изучить.

• Измените каждый пример, используя собственные небольшие надуманные данные.
• Напишите свои собственные функции для реализации каждой операции.
• Изучите один пример, в котором каждая операция использовалась в машинном обучении.

Если вы изучите какое-либо из этих расширений, я хотел бы знать.

Дополнительная литература

В этом разделе представлены дополнительные ресурсы по теме, если вы хотите углубиться.

Книги

API

Статьи

Сводка

В этом руководстве вы обнаружили набор различных типов матриц из области линейной алгебры, с которыми вы можете столкнуться в машинном обучении.

В частности, вы выучили:

• Квадратные, симметричные, треугольные и диагональные матрицы, соответствующие их названию.
• Матрицы идентичности, которые имеют нулевые значения, кроме вдоль главной диагонали, где значения равны 1.