Решение высшей математики онлайн
‹– Назад
В этом разделе рассмотрим еще одну важную числовую характиристику матрицы, связанную с тем, насколько ее строки (столбцы) зависят друг от друга.
Определение 14.10 Пусть дана матрица размеров и число , не превосходящее наименьшего из чисел и : . Выберем произвольно строк матрицы и столбцов (номера строк могут отличаться от номеров столбцов). Определитель матрицы, составленной из элементов, стоящих на пересечении выбранных строк и столбцов, называется минором порядка матрицы .
Пример 14.9 Пусть .
Минором первого порядка является любой элемент матрицы. Так 2, , — миноры первого порядка.
Миноры второго порядка:
- возьмем строки 1, 2, столбцы 1, 2, получим минор ;
- возьмем строки 1, 3, столбцы 2, 4, получим минор ;
- возьмем строки 2, 3, столбцы 1, 4, получим минор
Миноры третьего порядка:
строки здесь можно выбрать только одним способом,
- возьмем столбцы 1, 3, 4, получим минор ;
- возьмем столбцы 1, 2, 3, получим минор .
Предложение 14.23 Если все миноры матрицы порядка равны нулю, то все миноры порядка , если такие существуют, тоже равны нулю.
Доказательство. Возьмем произвольный минор порядка . Это определитель матрицы порядка . Разложим его по первой строке. Тогда в каждом слагаемом разложения один из множителей будет являться минором порядка исходной матрицы. По условию миноры порядка равны нулю. Поэтому и минор порядка будет равен нулю.
Определение 14.11 Рангом матрицы называется наибольший из порядков миноров матрицы , отличных от нуля. Ранг нулевой матрицы считается равным нулю.
Единое, стандартное, обозначение ранга матрицы отсутствует. Следуя учебнику [1], мы будем обозначать его .
Пример 14.
10 Матрица примера 14.9 имеет ранг 3, так как есть минор третьего порядка, отличный от нуля, а миноров четвертого порядка нет.
Ранг матрицы равен 1, так как есть ненулевой минор первого порядка (элемент матрицы ), а все миноры второго порядка равны нулю.
Ранг невырожденной квадратной матрицы порядка равен , так как ее определитель является минором порядка и у невырожденной матрицы отличен от нуля.
Предложение 14.24 При транспонировании матрицы ее ранг не меняется, то есть .
Доказательство. Транспонированный минор исходной матрицы будет являться минором транспонированной матрицы , и наоборот, любой минор является транспонированным минором исходной матрицы . При транспонировании определитель (минор) не меняется ( предложение 14.6). Поэтому если все миноры порядка в исходной матрице равны нулю, то все миноры того же порядка в тоже равны нулю.
Если же минор порядка в исходной матрице отличен от нуля, то в есть минор того же порядка, отличный от нуля. Следовательно, .
Определение 14.12 Пусть ранг матрицы равен . Тогда любой минор порядка , отличный от нуля, называется базисным минором.
Пример 14.11 Пусть . Определитель матрицы равен нулю, так как третья строка равна сумме первых двух. Минор второго порядка, расположенный в первых двух строках и первых двух столбцах, равен . Следовательно, ранг матрицы равен двум, и рассмотренный минор является базисным.
Базисным минором является также минор, расположенный, скажем, в первой и третьей строках, первом и третьем столбцах: . Базисным будет минор во второй и третьей строках, первом и третьем столбцах: .
Минор в первой и второй строках, втором и третьем столбцах равен нулю и поэтому не будет базисным. Читатель может самостоятельно проверить, какие еще миноры второго порядка будут базисными, а какие нет.
Так как столбцы (строки) матрицы можно складывать, умножать на числа, образовывать линейные комбинации, то можно ввести определения линейной зависимости и линейной независимости системы столбцов (строк) матрицы. Эти определения аналогичны таким же определениям 10.14, 10.15 для векторов.
Определение 14.13 Система столбцов (строк) называется линейно зависимой, если существует такой набор коэффициентов, из которых хотя бы один отличен от нуля, что линейная комбинация столбцов (строк) с этими коэффициентами будет равна нулю.
Определение 14.14 Система столбцов (строк) является линейно независимой, если из равенства нулю линейной комбинации этих столбцов (строк) следует, что все коэффициенты этой линейной комбинации равны нулю.
Верно также следующеее предложение, аналогичное предложению 10.6.
Предложение 14.25 Система столбцов (строк) является линейно зависимой тогда и только тогда, когда один из столбцов (одна из строк) является линейной комбинацией других столбцов (строк) этой системы.
Сформулируем теорему, которая называется теорема о базисном миноре.
Теорема 14.2 Любой столбец матрицы является линейной комбинацией столбцов, проходящих через базисный минор.
Доказательство можно найти в учебниках по линейной алгебре, например, в [1], [3].
Предложение 14.26 Ранг матрицы равен максимальному числу ее столбцов, образующих линейно независимую систему.
Доказательство. Пусть ранг матрицы равен . Возьмем столбцы, проходящие через базисный минор. Предположим, что эти столбцы образуют линейно зависимую систему. Тогда один из столбцов является линейной комбинацией других.
Поэтому в базисном миноре один столбец будет линейной комбинацией других столбцов. По предложениям 14.15 и 14.18 этот базисный минор должен быть равен нулю, что противоречит определению базисного минора. Следовательно, предположение о том, что столбцы, проходящие через базисный минор, линейно зависимы, не верно. Итак, максимальное число столбцов, образующих линейно независимую систему, больше либо равно .
Предположим, что столбцов образуют линейно независимую систему. Составим из них матрицу . Все миноры матрицы являются минорами матрицы . Поэтому базисный минор матрицы имеет порядок не больше . По теореме о базисном миноре, столбец, не проходящий через базисный минор матрицы , является линейной комбинацией столбцов, проходящих через базисный минор, то есть столбцы матрицы образуют линейно зависимую систему. Это противоречит выбору столбцов, образующих матрицу . Следовательно, максимальное число столбцов, образующих линейно независимую систему, не может быть больше . Значит, оно равно , что и утверждалось.
Предложение 14.27 Ранг матрицы равен максимальному числу ее строк, образующих линейно независимую систему.
Доказательство. По предложению 14.24 ранг матрицы при транспонировании не меняется. Строки матрицы становятся ее столбцами. Максимальное число новых столбцов транспонированной матрицы, (бывших строк исходной) образующих линейно независимую систему, равно рангу матрицы.
Предложение 14.28 Если определитель матрицы равен нулю, то один из его столбцов (одна из строк) является линейной комбинацией остальных столбцов (строк).
Доказательство. Пусть порядок матрицы равен . Определитель является единственным минором квадратной матрицы, имеющим порядок . Так как он равен нулю, то . Следовательно, система из столбцов (строк) является линейно зависимой, то есть один из столбцов (одна из строк) является линейной комбинацией остальных.
Результаты предложений 14.15, 14.18 и 14.28 дают следующую теорему.
Теорема 14.3 Определитель матрицы равен нулю тогда и только тогда, когда один из ее столбцов (одна из строк) является линейной комбинацией остальных столбцов (строк).
Нахождение ранга матрицы с помощью вычисления всех ее миноров требует слишком большой вычислительной работы. (Читатель может проверить, что в квадратной матрице четвертого порядка 36 миноров второго порядка.) Поэтому для нахождения ранга применяется другой алгоритм. Для его описания потребуется ряд дополнительных сведений.
Определение 14.15 Назовем элементарными преобразованиями матриц следующие действия над ними:
1) перестановка строк или столбцов;
2) умножение строки или столбца на число отличное от нуля;
3) добавление к одной из строк другой строки, умноженной на число или добавление к одному из столбцов другого столбца, умноженного на число.
Предложение 14.29 При элементарных преобразованиях ранг матрицы не меняется.
Доказательство. Пусть ранг матрицы равен , — матрица, получившаяся в результате выполнения элементарного преобразования.
Рассмотрим перестановку строк. Пусть — минор матрицы , тогда в матрице есть минор , который или совпадает с , или отличается от него перестановкой строк. И наоборот, любому минору матрицы можно сопоставить минор матрицы или совпадающий с , или отличающийся от него порядком строк. Поэтому из того, что в матрице все миноры порядка равны нулю, следует, что в матрице тоже все миноры этого порядка равны нулю. И так как в матрице есть минор порядка , отличный от нуля, то и в матрице тоже есть минор порядка , отличный от нуля, то есть .
Рассмотрим умножение строки на число , отличное от нуля. Минору из матрицы соответствует минор из матрицы или совпадающий с , или отличающийся от него только одной строкой, которая получается из строки минора умножением на число, отличное от нуля.
В последнем случае . Во всех случаях или и одновременно равны нулю, или одновременно отличны от нуля. Следовательно, .
Пусть к -ой строке матрицы прибавлена ее -ая строка, умноженная на число . Рассмотрим миноры порядка в матрице . Если через минор не проходит -ая строка, то он совпадает с минором , расположенным в тех же строках и столбцах в матрице , и следовательно, равен нулю.
Если через минор проходят и -ая и -ая строки, то он получается из минора , расположенного в тех же строках и столбцах матрицы , прибавлением к -ой строке минора -ой строки, умноженной на . По свойству определителя . Следовательно, .
Пусть через минор проходит -ая строка и не проходит -ая. Тогда отличается от -ой строкой. Эта строка в является строкой , к которой добавлены элементы -ой строки, умноженные на . По свойствам определителей , где — минор порядка матрицы , стоящий в -ой строке и в тех же строках, что и минор , исключая -ую, а знак ” ” связан с возможным изменением порядка строк.
Так как все миноры порядка в матрице равны нулю, то .
Итак, в матрице все миноры порядка равны нулю. Следовательно, , то есть при выполнении элементарного преобразования третьего типа ранг не может повыситься. Предположим, что , и . Тогда в матрице к -ой строке прибавим -ую строку, умноженную на число . В результате получим исходную матрицу . По только что доказанному . Получили противоречие: . Предположение не верно, следовательно, .
Алгоритм вычисления ранга матрицы похож на алгоритм вычисления определителя и заключается в том, что с помощью элементарных преобразований матрица приводится к простому виду, для которого найти ранг не представляет труда. Так как при каждом преобразовании ранг не менялся, то, вычислив ранг преобразованной матрицы, мы тем самым находим ранг исходной матрицы.
Алгоритм нахождения ранга матрицы.
Пусть требуется вычислить ранг матрицы размеров .
Если матрица нулевая, то по определению . В противном случае с помощью перестановки строк и столбцов матрицы добиваемся того, чтобы в левом верхнем углу матрицы стоял ненулевой элемент. Итак, считаем, что .
Первую строку оставляем без изменений. Ко второй строке прибавляем первую, умноженную на число . В результате вторая строка принимает вид
Затем к третьей строке прибавляем первую строку, умноженную на число . В результате третья строка принимает вид
Процесс продолжаем до тех пор, пока не получим нуль на первом месте в последней строке.
Преобразованная матрица имеет вид
Если все строки, начиная со второй, в полученной матрице нулевые, то ее ранг равен 1, так как есть минор первого порядка, отличный от нуля . В противном случае перестановкой строк и столбцов матрицы с номерами, большими единицы, добиваемся, чтобы второй элемент второй строки был отличен от нуля.
Итак, считаем, что .
Первую и вторую строки оставляем без изменений. К третьей строке прибавляем вторую, умноженную на число . В результате получим, что второй элемент третьей строки равен нулю. Затем к четвертой строке прибавляем вторую, умноженную на число , и т.д. В результате получаем матрицу
Если все строки, начиная с третьей, нулевые, то , так как минор . В противном случае перестановкой строк и столбцов с номерами, большими двух, добиваемся, чтобы третий элемент третьей строки был отличен от нуля. Далее, добавлением третьей строки, умноженной на соответствующие числа, к строкам с большими номерами получаем нули в третьем столбце, начиная с четвертого элемента, и т.д.
На каком-то этапе мы придем к матрице, у которой все строки, начиная с -ой , равны нулю (или отсутствуют при ), а минор в первых строках и первых столбцах является определителем треугольной матрицы с ненулевыми элементами на диагонали.
Ранг такой матрицы равен . Следовательно, .
Замечание 14.15 В предложенном алгоритме нахождения ранга матрицы все вычисления должны производиться без округлений. Сколь угодно малое изменение хотя бы в одном из элементов промежуточных матриц может привести к тому, что полученный ответ будет отличаться от ранга исходной матрицы на несколько единиц.
Замечание 14.16 Если в исходной матрице элементы были целыми числами, то и вычисления удобно производить без использования дробей. Поэтому на каждом этапе целесообразно умножать строки на такие числа, чтобы при вычислениях дроби не возникали.
Пример 14.12 Найдите ранг матрицы .
Решение. Первую строку оставляем без изменений. Чтобы избежать появления дробей, умножим вторую, третью и четвертую строки на 2:
Первую строку умножим на и прибавим ко второй.
Получим строку . Первую строку умножим на и прибавим к третьей. Получим строку . Первую строку умножим на и прибавим к четвертой. Получим строку . В итоге имеем матрицу
Вторую строку оставляем без изменений. К третьей строке прибавляем вторую, умноженную на 2. Получим строку . К четвертой строке прибавляем вторую. Получим нулевую строку. Преобразованная матрица имеет вид
Поменяем местами третий и четвертый столбцы:
Базисный минор матрицы стоит в первых трех столбцах и первых трех строках, . Следовательно, .
Замечание 14.17 В приведенном примере вычисления были бы проще, если сначала четвертый столбец сделать первым и четвертую строку сделать первой. Но для того, чтобы догадаться об этом, нужно анализировать вопросы делимости чисел, что достаточно сложно описать в алгоритме, пригодном для всех случаев.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
4.1.3 Действия над матрицами
Ранее определили матрицу, как прямоугольную числовую таблицу, имеющую строк и столбцов, поэтому схематически матрицу можно изображать в виде прямоугольника (рис.
1).
Нулевой матрицей (нуль-матрицей) называют матрицу, все элементы которой равны нулю и обозначают 0.
Единичной матрицей называется квадратная матрица вида
.
Две матрицы и равны, если они одинакового размера и их соответствующие элементы равны.
Определим основные операции над матрицами.
Определение. Суммой двух матриц и одинакового размера называется матрица тех же размеров, элементы которой находятся по формуле . Обозначается .
Пример 6. .
Операция сложения матриц распространяется на случай любого числа слагаемых. Очевидно, что .
Еще раз подчеркнем, что складывать можно только матрицы одинакового размера; для матриц разных размеров операция сложения не определена.
Определение. Разностью матриц и одинакового размера называется такая матрица , что .
Определение. Произведением матрицы на число называется матрица , получающаяся из умножением всех ее элементов на , .
Определение. Пусть даны две матрицы и , причем число столбцов равно числу строк . Произведением на называется матрица , элементы которой находятся по формуле .
Обозначается .
Схематически операцию умножения матриц можно изобразить так:
а правило вычисления элемента в произведении:
Подчеркнем еще раз, что произведение имеет смысл тогда и только тогда, когда число столбцов первого сомножителя равно числу строк второго, при этом в произведении получается матрица, число строк которой равно числу строк первого сомножителя, а число столбцов равно числу столбцов второго.
Пример 7. Даны матрицы и . Найти матрицы и .
Решение. Прежде всего заметим, что произведение существует, так как число столбцов равно числу строк .
Заметим, что в общем случае , т. е. произведение матриц антикоммутативно.
Найдем (умножение возможно).
Пример 8. Дана матрица . Найти .
Решение.
.
; .
.
Отметим следующий любопытный факт.
Как известно, произведение двух отличных от нуля чисел не равно нулю. Для матриц подобное обстоятельство может и не иметь места, то есть произведение ненулевых матриц может оказаться равным нуль-матрице.
Пример 9. Если и , то
.
Определение. Если – квадратная матрица, то обратной для нее матрицей называется матрица, обозначаемая и удовлетворяющая условиям , где – единичная матрица.
Из этого определения следует, что если матрица является обратной для , то и будет обратной для . Обратную матрицу имеет только квадратная матрица, определитель которой отличен от нуля. Такие матрицы называются невырожденными.
Приведем схему нахождения обратной матрицы.
1. Находим определитель данной квадратной матрицы .
2. Находим алгебраические дополнения ко всем элементам мат-рицы .
3. Записываем алгебраические дополнения элементов строк в столбцы.
4. Делим каждый элемент полученной матрицы на определитель матрицы .
Пример 10. Найти матрицу, обратную матрице .
Решение.
1. Найдем .
2. Ищем алгебраические дополнения каждого элемента матрицы :
; ; .
Получили алгебраические дополнения элементов первой строки. Аналогично для элементов второй и третьей строк получаем:
; ; .
; ; .
Объединяя 3 и 4 пункты, получаем обратную матрицу
.
Для проверки убедимся, что .
.
| < Предыдущая | Следующая > |
|---|
2D Матрица(список) – Обсудить Scratch
- Создать
- Изучить
- Идеи
- О
#1авг. 9, 2016 17:02:59
- ггение Скретчер
100+ сообщений
2D-матрица (список)
Было бы очень полезно, если бы можно было составить список переменных, который содержит больше элементов, вместо этого было бы лучше иметь встроенную функцию
для 2D-списка:
установить элемент (0) ( 0) = 0
установить элемент (0) (1) = 0
установить элемент (1) (1) = 0
и т.
#2Aug. 9, 2016 18:56:22
- Зигги741 Скретчер
1000+ сообщений
2D Matrix(список)
Что бы он делал? Не могли бы вы дать больше информации? Спасибо!
#3авг. 10, 2016 01:09:44
- ггение Скретчер
100+ сообщений
2D Матрица (список)
вы можете получить доступ к таблице чисел, например:
| 1 | 2 | 3 | 4| 5 | 6 | 7 | 8 |
| 1 | 3 |-4| -2|12|23|-22|6 |15|
| 2 | 3 |-6| 26|32|12|-33|3 |12|
| 3 | 3 |22| 33|64|66|-44|4|32|
| 4 | 3 |33| -1|-5|-5|-55|9 |-23|
| 5 | 3 |-3| 26|-5|32|-66|1 |11|
| 6 |3 |12| -1|33|17|-77|4 |23|
| 7 | 3 |-4| 55|45|-3|-88|7 |45|
| 8 | 3 |43| 34|85|23|-12|8 |65|
поэтому, если я наберу переменную
= элемент (5) (7)
, тогда переменная будет состоять из 5 строк и 7 столбцов, так что это -3
элемент(1)(1)=3
элемент(3)(4)=-1
элемент(6)(4)=-55
#4авг.
10, 2016 01:16:39
- Зигги741 Скретчер
1000+ сообщений
2D Matrix(список)
ggenije написал:
вы можете получить доступ к таблице чисел, например:| 1 | 2 | 3 | 4| 5 | 6 | 7 | 8 |
| 1 | 3 |-4| -2|12|23|-22|6 |15|
| 2 | 3 |-6| 26|32|12|-33|3 |12|
| 3 | 3 |22| 33|64|66|-44|4|32|| 4 | 3 |33| -1|-5|-5|-55|9 |-23|
| 5 | 3 |-3| 26|-5|32|-66|1 |11|
| 6 |3 |12| -1|33|17|-77|4 |23|
| 7 | 3 |-4| 55|45|-3|-88|7 |45|
| 8 | 3 |43| 34|85|23|-12|8 |65|, поэтому, если я наберу переменную
= элемент (5) (7)
, тогда переменная будет состоять из 5 строк и 7 столбцов, поэтому это -3
элемент(1)(1)=3
элемент(3)(4)=-1
элемент(6)(4)=-55
и аналогично
Я не понимаю.
#5авг. 10, 2016 03:11:39
- pvz_pro
500+ сообщений
2D Matrix(список)
нет поддержки, слишком сложно для нуля
если вы это читаете, хорошо
#6авг. 10, 2016 13:47:57
- -усы- Скретчер
500+ сообщений
2D Matrix(список)
pvz_pro написал:
нет поддержки, слишком сложно для нуля
Почему вы так считаете?
3×3 pb: 13,240
3×3 в среднем: ~21-26
#7авг.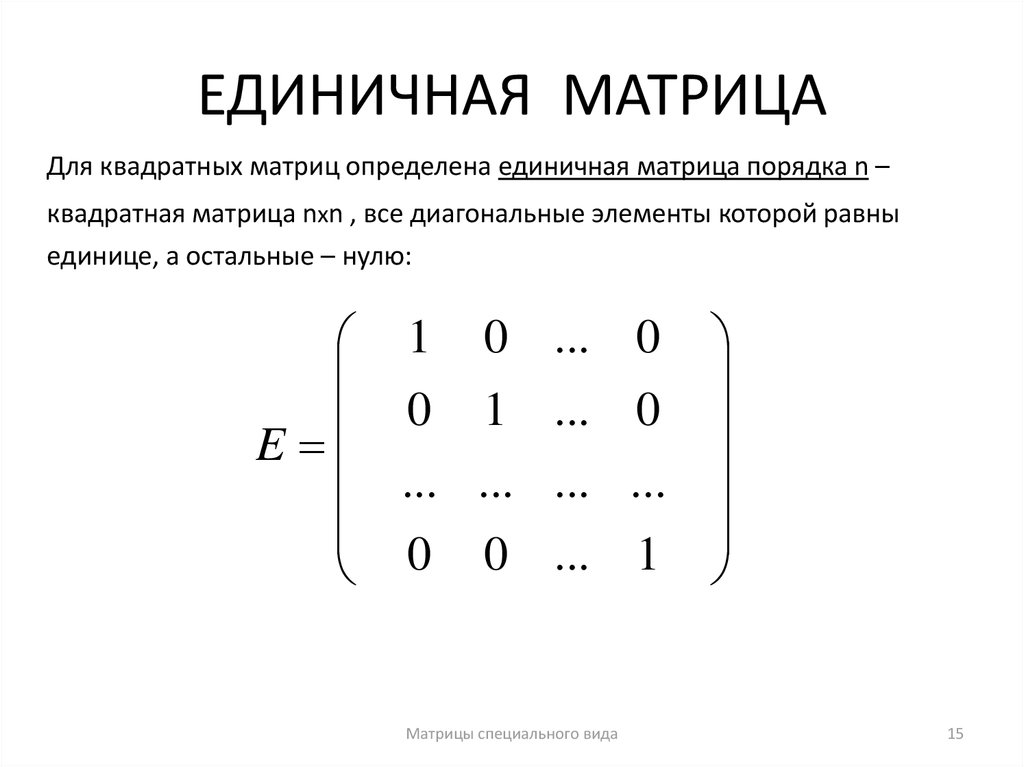
10, 2016 13:51:01
- 1MatsuLover Скретчер
500+ сообщений
2D Матрица(список)
Нет Поддержки, это сложно, а значит слишком сложно для понимания.
Я ушел с форумов. Извиняюсь.
(Оригинал удален ST.)
#8авг. 10, 2016 15:11:53
- -усы- Скретчер
500+ постов
2D Matrix(list)
Я несколько поддерживаю, но хотел бы, чтобы это было реализовано в виде списков первого класса.
3×3 pb: 13,240
3×3 в среднем: ~21-26
#9авг.
10, 2016 17:19:51
- Овчарка Скретчер
1000+ сообщений
2D Матрица(список)
pvz_pro написал:
нет поддержки, слишком сложно для нуля
Я думаю, вы слышали об этом блоке:
перейти к x: (0) y: (0)
Система позиционирования спрайтов находится на двумерной сетке, а это значит, что если кто-то может понять концепцию X и Y, то он может понять, что такое двумерный список.
– Sheep_maker Это подпись без кумквата. : Р
Это моя подпись. Он появляется под всеми моими сообщениями. Обсуждайте это в моем профиле, а не на форумах. Вот как сделать свой собственный.
.postsignature { переполнение: авто; } .
scratchblocks { переполнение-х: авто; переполнение-у: скрыто; }#10авг. 11, 2016 02:13:54
- ггение Скретчер
100+ сообщений
2D Матрица (список)
список в списке -> каждый элемент в списке является списком с переменными базовый список) 65 -124 13 -52 221 -3
…..
список.100(базовый список)15 -234 -13 -2 1 -42
так что вы просто говорите (помещаете)
переменная=список номер 21 в списке со списками элемент 4
, поэтому вам не нужно создавать 100 списков (это невозможно), но вы можете легко создавать списки списков (матрица двумерного массива и другие имена)
#11авг. 11, 2016 02:18:35
- ггение Скретчер
100+ сообщений
2D-матрица (список)
Очень хорошее объяснение 2D-массива -> arrays2D
Как сделать матрицы в нулях?
- Создать
- Исследуйте
- Идеи
- О
#1дек.
29, 2021 12:26:46
- ипдыба Скретчер
24 сообщения
Как сделать матрицы в нулях?
Я хочу сделать вращающийся квадрат в 3D, но я не знаю, как использовать матрицы в нулях (но я знаю, как в Python) кто-нибудь может мне помочь?
#2дек. 29, 2021 12:34:55
- The_Imaginarium Скретчер
1000+ сообщений
Как сделать матрицы в нулях?
К сожалению, вам придется создавать отдельные переменные для каждого элемента, или вы могли бы создать список, но это было бы утомительно, потому что вам пришлось бы назначать каждому элементу определенную строку или столбец.
#3дек. 30, 2021 12:07:15
- ипдыба Скретчер
24 сообщения
Как сделать матрицы в нулях?
но пришлите мне код, пожалуйста?
#4дек. 30, 2021 20:21:41
- The_Imaginarium Скретчер
1000+ сообщений
Как сделать матрицы в нулях?
Нет никакого кода для отправки, если только вы не имеете в виду умножение матриц, в котором вы взяли бы скалярное произведение n-й строки первой матрицы и n-го столбца второй.
#5дек. 30, 2021 20:36:21
- badatprogrammingibe Скретчер
500+ сообщений
Как сделать матрицы в нулях?
На самом деле вам не нужно реализовывать матрицы с нуля, чтобы реализовать трехмерный квадрат, вы можете сделать матричные преобразования частью пользовательского блока.
Вы можете хранить координаты вершин в четырех списках, список с координатами x,y,z и w. Затем вы должны создать пользовательский блок, который применяет определенную матрицу 4×4 к некоторым координатам, используя формулу X_new = TX, где X — матрица координат, а T — матрица преобразования 4×4. Используйте обычные правила умножения матриц.
#6дек. 30, 2021 22:13:30
- Скретч-миньон Скретчер
1000+ сообщений
Как сделать матрицы в нулях?
Предположим, мы хотим умножить точку (x,y,z) на матрицу 3×3, как показано ниже, чтобы вычислить (новый x, новый y, новый z)
(новый x) (m1 m2 m3) (x)
( новый y) = (m4 m5 m6) (y)
(новый z) (m7 m8 m9) (z)
Создайте переменные m1, m2 … m9 и установите их значения.