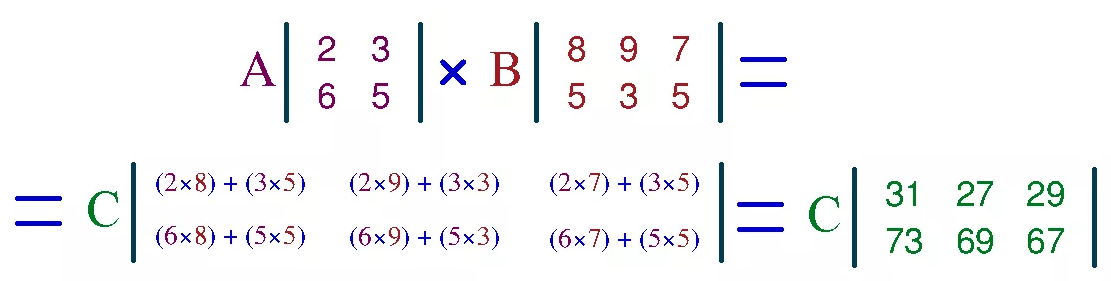Математика онлайн
Решение математики онлайн
Math34.biz – это современный способ решения математики, в том числе для сравнения самостоятельных решений с машинными вычислениями.
Пользование сервисом удобно и понятно каждому человеку, попавшему на сайт впервые. Сразу выбираете нужный калькулятор, вводите необходимые данные по вашей задаче и нажимаете кнопку «Решение». За считанные секунды ответ готов.
Чтобы не возникало трудностей с вводом данных, мы подготовили специальную статью Как вводить данные? Помимо правил написания формул и чисел, в ней вы можете увидеть, как правильно вводятся различные константы и математические функции.
О калькуляторах
По мере возможности добавляются новые математические калькуляторы. На сегодняшний день их более 85.
Если не удалось найти нужный калькулятор, которым может быть решена ваша математическая задача, или есть предложение по улучшению имеющегося калькулятора, пожалуйста, сообщите об этом на почту info@math34.
Преимущества
1. Бесплатно
Решение математики онлайн не будет вам стоить ни копейки. Наш сервис абсолютно бесплатный и доступен любому пользователю интернета.
2. Без регистрации
Для пользования калькуляторами не требуется регистрации на сайте, отнимая время на заполнение почтовых ящиков и других личных данных.
3. Подробные решения
На многие задачи вы получите пошаговый развернутый ответ, что позволяет понять, каким образом было получено решение задачи.
4. Разные способы решения задач
Для популярных калькуляторов доступны разные методы решения задач, если они применимы, что позволяет, во-первых, лучше понять, как решается задача известным вам способом, а, во-вторых, научиться решать ту же самую задачу альтернативными методами.
5. Точность вычислений
В полученном ответе не приходится сомневаться, ведь мощная система расчета обеспечивает высокую точность при решении математических задач онлайн.
Однако, мы не исключаем возможность каких-либо ошибок, ведь известно, что алгоритмы пишутся хотя и очень умными, но всё же людьми. В случае обнаружения ошибки, пожалуйста, не поленитесь и сообщите нам о ней.
Умножение двух матриц в Java
Умножение матриц (реализовано в Java)
, например, две матрицы *arr1[n][m]arr2[m][k]=arr3[n][k]。
Пока мы можем написать код:
import java.util.Scanner; public class test { public static void main(String[] args) { Scanner sc=new Scanner(System.in); int n=sc.nextInt(); int m=sc.nextInt(); int k=sc.nextInt(); int Maze[][]=new int[n][m]; int Maze1[][]=new int[m][k]; int Maze2[][]=new int[n][k]; for(int i=0;i<n;i++) { for(int j=0;j<m;j++) { Maze[i][j]=sc.nextInt(); } } for(int i=0;i<m;i++) { for(int j=0;j<k;j++) { Maze1[i][j]=sc.nextInt(); } } for(int i=0;i<n;i++) { for(int u=0;u<k;u++) { for(int j=0;j<m;j++) { Maze2[i][u]+=Maze[i][j]*Maze1[j][u]; } } } for(int i=0;i<n;i++) { for(int j=0;j<k;j++) { System.out.print(Maze2[i][j]+" "); } System.out.println(); } } }
Самый важный код:
for(int i=0;i<n;i++)
{
for(int u=0;u<k;u++)
{
for(int j=0;j<m;j++)
{
Maze2[i][u]+=Maze[i][j]*Maze1[j][u];
}
}
}
Как понять этот фрагмент кода? На самом деле, это очень легко понять. Прежде всего, новая матрица, которую вы создаете, – это то, что я сказал в начале
arr1[n][m]*arr2[m][k]=arr3[n][k]
Итак, поведение i новой созданной вами матрицы указано как u, так почему бы не поместить j во второй цикл, а в третий цикл? Поскольку если u становится номером столбца этого нового массива, скорость изменения (я не знаю, можно ли ее здесь описать как скорость) должна быть ниже, чем скорость j, поэтому j следует записать на самом внутреннем уровне, а u следует записать Это относительно снаружи.
Maze2[i][u]+=Maze[i][j]*Maze1[j][u];
Почему мы здесь складываем? Это связано с характером умножения матриц, например:
Хорошо, это все, что нужно для сегодняшнего обсуждения. Я все еще в пути. Надеюсь, каждый сможет указать мне на недостатки или обсудить более эффективные методы вместе!
Матриц произведение – Справочник химика 21
Отметим основные свойства произведения матриц 1) произведение двух матриц, вообще говоря, зависит от порядка множителей. Две матрицы, произведения которых не зависят от порядка множителей, называют коммутирующими матрицами-,Матрица произведения С = АВ будет также квадратной матрицей и той же размерности. Для того чтобы получить произвольный элемент матрицы произведения, например Сц, необходимо про- [c.233]
При соблюдении размерностей перемножаемых матриц операция умножения обладает следующими свойствами умножение матриц ассоциативно (АВ) С = Л (ВС)-, умножение матриц дистрибутивно А – – В) С = АС + ВС единичная матрица коммутативна (перестановочная) с любой квадратной матрицей того же порядка, т.

В качестве примера рассмотрим программу умножения двух матриц. Произведением матриц А ж В будет матрица С, элементы которой являются суммой произведений элементов строки матрицы А на элементы соответствующего столбца матрицы В [c.280]
Приравняем элементы -ой строки матрицы р/йг и матрицы-произведения [c.225]
Известно, что определитель матрицы произведения равен произведению определителей матриц сомножителей тогда для /с = + 1 из формулы (15) находим
Для матрицы А размера m X я и матрицы В размера р X Q при выполнении условия п = р можно определить матрицу произведения С, размер которой [c.565]
Транспонированная матрица произведения (АЯ)Т равна произведению транспонированных матриц Ат и Вт, взятому в обратном порядке [c. 566]
566]
Таким образом, в получаемой матрице-произведении С будет столько строк, сколько было в матрице А, и столько столбцов, сколько было в матрице В. (Примеры умножения матриц см. в разделах 2.4.2,.
При этом, если Ца есть тр-матрица, а 6Ц — /)и.-матрица, произведение а и II 6II будет ти.-матрицей. [c.247]
Мы получили, таким образом, правило (12) вычисления элементов с ,-матрицы-произведения С из элементов матриц-сомножителей А ц В. Законы умножения матриц отличаются от законов умножения обычных чисел тем, что произведение матриц в общем некоммутативно, т, е. зависит от порядка сомножителей. Это следует непосредственно из формулы (12), а также очевидно интуитивно результат двух преобразований может зависеть от порядка, в котором эти преобразования совершены. [c.444]
Итак, элементы матрицы произведения с==Ьа даются соотношением [c.232]
Матрица Е имеет размер пх X Щ, ее строки отвечают различным длинам волн, а столбцы — различным компонентам. Матрица С имеет размер щ X j ее строки отвечают различным компонентам, а столбцы — различным растворам. В теории матриц доказывается, что ранг матрицы-произведения не может превышать ранга ни одной из матриц-сомножителей, поэтому [c.50]
Матрица С имеет размер щ X j ее строки отвечают различным компонентам, а столбцы — различным растворам. В теории матриц доказывается, что ранг матрицы-произведения не может превышать ранга ни одной из матриц-сомножителей, поэтому [c.50]
Таким образом, в получаемой матрице — произведении С будет столько строк, сколько было в матрице А, и столько столбцов, сколько было в матрице В. Практически для вычисления произведения А В удобно записывать матрицы А ъ В таким образом, чтобы верхний правый угол матрицы А касался нижнего левого угла матрицы В. Тогда произведение А В будет такого размера, что оно заполнит прямоугольник, ограниченный продолжением последней строки матрицы А и последнего столбца матрицы В. Элемент произведения А В, стоящий на пересечении -й строки матрицы А и /с-го столбца матрицы В, будет равен сумме попарных произведений соответствующих элементов -й строки А и /с-го столбца В.
Физический смысл уравнения (39) таков произведение представляет собой боковое давление на единицу площади стенки матрицы, произведение является удельной силой трения, величина Ькт.

Здесь используется правило о том, что транспонированная матрица, представляющая собой произведение матриц, равна произведению всех транспонированных матриц произведения, взятых в обратном порядке [76], т. е. (РО) г = Стрт. [c.253]
Т. е. элементы матрицы произведения двух матриц равны суммам произведений элементов соответствующей строки множимого на элементы соответствующего столбца множителя. В связи с этим уместно подчеркнуть, что произведение матриц в общем случае не является коммутативным, т. е. [c.248]
Заметим, что в рассматриваемых случаях потоки реагирующих веществ как исходных, так и промежуточных и конечных, должны быть выражены в молях в единицу времени. Если по каким-либо причинам желательно иметь другую размерность указанных потоков, то вместо матрицы стехиометрических коэффициентов необходимо использовать следующую матрицу — произведение [c. 157]
157]
Для простой открытой последовательности полный импеданс получается перемножением первой строки матрицы [М] на матричный столбец Ki/ai . Поскольку при этом нет необходимости складывать строки, концентрация (Ь) не входит в величину Д. Наоборот, для простой замкнутой последовательности суммирование всех строк матрицы произведения приводит к появлению концентрации (Ь) в величине Д. [c.300]
Блочная форма матриц сохраняется в произве Д.ении двух блочных матриц, а в блоках матрицы-произведения нет произведений разных блоков. Если оказывается невозможным найти такое преобразование подобия, которое придавало бы всем матрицам 0( “)(/ ) [или В (или Г) блочную форму, то говорят, что совокупность матриц 0(/ ) является полностью приведенной. В этом случае представление Р ) (или Г( )) является неприводимым представлением группы 2). [c.346]
Процедура MULT предназначена для умножения квадратных матриц. Ее формальными параметрами являются А, В — матрица-множимое и матрица-множитель соответственно, С — матрица-произведение п — порядок. Процедура МА ТА предназначена для сложения матриц, умножения матрицы на константу, сложения с единичной матрицей, присваивания значений элементов одной матрицы элементам другой. Выполнение этих функций обеспечивается соответствующими значениями фактических параметров. Выходным параметром процедуры является массив А. Назначение [c.244]
Процедура МА ТА предназначена для сложения матриц, умножения матрицы на константу, сложения с единичной матрицей, присваивания значений элементов одной матрицы элементам другой. Выполнение этих функций обеспечивается соответствующими значениями фактических параметров. Выходным параметром процедуры является массив А. Назначение [c.244]
И В ней можно узнать детерминант произведения двух матриц Сц и yJ (х). Равенство (3) вытекает теперь из стандартной теоремы о равенстве детерминанта произведения матриц произведению детерминантов сомножителей. [c.62]
Таким образом, в матрице-произведении элемент П есть скалярное произведение первой строки матрицы а и первого столбца матрицы Ь элемент 12—первой строки матрицы а на второй столбец матрицы Ь и т. д. [c.230]
Для матр1щы Л размера тХ п и матрицы В размера рХ q при выполпении условия п == р можно определить матрицу произпедения С, размер которой тХ q. Элементы матрицы произведения С при этом вычисляются по формуле [c.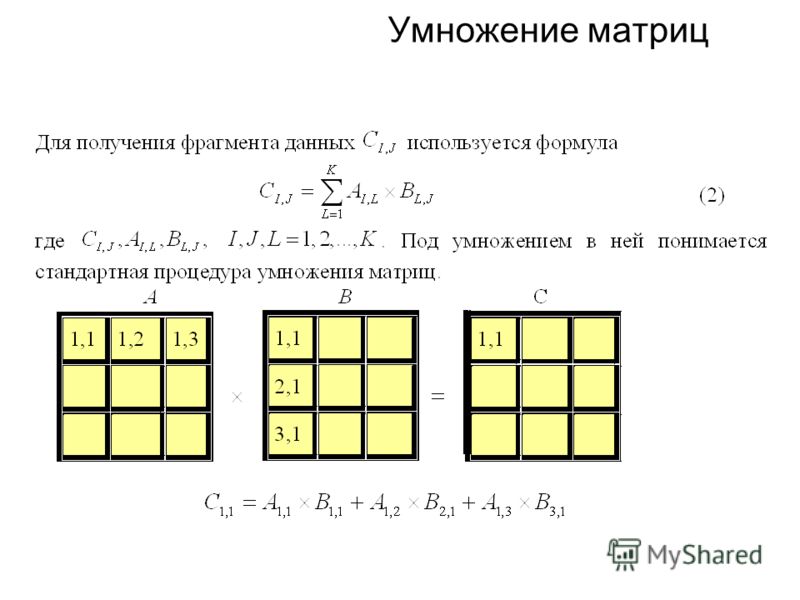 551]
551]
Траиспонировапная матрица произведения (ЛВ) равна произведению транс-ионированных матриц Л и В , взятому в обратном порядке [c.552]
НИЯ В конкретной ситуации. Выбираются группы материалов, наилучшим образом удовлетворяющие требованиям к крышке газонокосилки. Каждому материалу дается определенное число баллов (от О до 1,0) в зависимости от значимости свойств, перечисленных в верхней части матрицы, которое записывается в верхней части клеток матрицы. Произведение числа баллов на коэффициенты значимости записывается в нижней части клеток. Затем вычисляется сумма очков для каждого материала. В рассматриваемом случае по сумме очков наилучшим материалом является листовая сталь. Далее после тщатель-ргаго анализа свойств листовых сталей выбирается конкретная марка стали. [c.59]
Spur(GF), или след , — сумма диагональных элементов матрицы произведения GF. Второй коэффициент Сг дается формулой [c.372]
При этом, если а 1 есть тгр-матрица, а > — р/г-матрица, произведение а и 1 6 будет пгге-матрицей. [c.247]
[c.247]
Структурное умножение коммутативно вплоть до гомомеризмов. Оба произведения структуры АВ и ВА означают взаимную ориентацию Л и б, и поэтому различия между ними формальны. Матрицы произведений различаются только номерами А и В, а это и есть гомомерия. Матрицы ориентации Qab и Qba в Л5 (Qab) и в ВА (Qba) тоже имеют одни и те же элементы, относящиеся к одним и тем же диагональным элементам матриц А и В, но расположенные в разном порядке под разными нормами, отчего структура не меняется. Поэтому ЛВ(Qab) гомомерно BA(Qba). [c.439]
Первый диагональный элемент матрицы-произведения, обозначаемый обычно Си, является суммой aI 6ll-f012621 в приведенном примере Сц=26. Если нужно перемножить матрицы не 2×2, а пХт и тХ1, то произведением будет матрица пх1 и первый ее элемент будет Си = а11б11 + а12б21+ 1з з1+. .. -1- 1т т1 элемент [c.102]
При таких преобразованиях, как уже было сказано, матрица А последовательно умножается на ортогональные матрицы 8 , (слева). В результате выполненных умножений А переходит в SA, где S — произведение преобразующих матриц. Произведение ортогональных матриц есть вновь ортогональная матрица. Поэтому S — ортогональна. [c.105]
В результате выполненных умножений А переходит в SA, где S — произведение преобразующих матриц. Произведение ортогональных матриц есть вновь ортогональная матрица. Поэтому S — ортогональна. [c.105]
Произведение матриц обозначается следующим образом С = АВ. Умножать можно матрицы, у которых внутренний размер совпадает. Так, если имеем А тхпь -8(лх ). то внутренний размер этой пары есть п, и можно выполнить операцию умножения. Элементы матрицы произведения С при этом получаются посредством перемножения и суммирования элементов исходных матриц, а именно для получения элемента с номером ( , /) надо по очереди перемножить пары элементов 1-й строки матрицы А и /-Г0 столбца матрицы В (первый с первым, второй со вторым и т. д.), а затем просуммировать их. [c.127]
Умножение матриц – примеры
М. Борна
На этой странице вы можете увидеть множество примеров умножения матриц.
Вы можете повторно загружать эту страницу сколько угодно раз и каждый раз получать новый набор чисел и матриц. Вы также можете выбрать матрицы разного размера (внизу страницы).
(Если вам сначала нужна дополнительная информация о матрицах, вернитесь к разделу «Введение в матрицы» и «Умножение матриц»).
Пример
Умножение матриц A и B .
|
|
Ответ
Для экономии работы мы сначала проверяем, можно ли их умножить.
У нас есть (3 × 3) × (3 × 4), и поскольку количество столбцов в A совпадает с количеством строк в B (в данном случае средние два числа равны 3), мы можем перемножить эти матрицы. Нашим результатом будет матрица (3 × 4).
Первый шаг – записать две матрицы рядом, как показано ниже:
|
|
Мы умножаем отдельные элементы в первой строке матрицы A, на соответствующие элементы в первом столбце матрицы B и складываем результаты.Это дает нам число, которое нам нужно поместить в первую строку, первую позицию столбца в матрице ответов.
|
|
6 × 5 + -2 × 8 + 4 × 7 = 42
После этого мы умножаем элементы по первой строке матрицы A, на соответствующие элементы по второму столбцу матрицы B , затем складываем результаты.Это дает нам ответ, который нам нужно будет поместить в первую строку, второй столбец матрицы ответов.
|
|
6 × 6 + -2 × 3 + 4 × -1 = 26
Продолжаем по строкам и столбцам следующим образом:
|
|
| = | 6 × 5 + -2 × 8 + 4 × 7 | 6 × 6 + -2 × 3 + 4 × -1 | 6 × 4 + -2 × 0 + 4 × 9 | 6 × -4 + -2 × -2 + 4 × 10 | ||
| -1 × 5 + -3 × 8 + 0 × 7 | -1 × 6 + -3 × 3 + 0 × -1 | -1 × 4 + -3 × 0 + 0 × 9 | -1 × -4 + -3 × -2 + 0 × 10 | |||
| 7 × 5 + 1 × 8 + 2 × 7 | 7 × 6 + 1 × 3 + 2 × -1 | 7 × 4 + 1 × 0 + 2 × 9 | 7 × -4 + 1 × -2 + 2 × 10 |
| = | 42 | 26 | 60 | 20 | ||
| -29 | -15 | -4 | 10 | |||
| 57 | 43 | 46 | -10 |
Посмотреть другой пример?
Вы можете обновить эту страницу, чтобы увидеть другой пример с матрицами другого размера и другими числами; ИЛИ
Выберите нужные вам размеры матрицы и нажмите кнопку.
Объяснитель урока: Свойства умножения матриц
В этом пояснении мы узнаем, как определять свойства матрицы. умножение, включая транспонирование произведения двух матриц, и как они соотносятся со свойствами умножения чисел.
Чтобы начать обсуждение свойств умножения матриц, давайте начнем напоминая определение общей матрицы.
Определение: умножение матриц
Предположим, что 𝐴 – матрица с порядком 𝑚 × 𝑛 и что 𝐵 – матрица с порядок 𝑛 × 𝑝 такой, что 𝐴 = ⎛⎜⎜⎝𝑎𝑎… 𝑎𝑎𝑎… 𝑎 ⋮⋮ ⋱ ⋮ 𝑎𝑎… 𝑎⎞⎟⎟⎠, 𝐵 = ⎛⎜⎜⎜⎝𝑏𝑏… 𝑏𝑏𝑏… 𝑏 ⋮⋮ ⋱ ⋮ 𝑏𝑏… 𝑏⎞⎟⎟⎟⎠.
Тогда матричное произведение 𝐴𝐵 = 𝐶 представляет собой матрицу с порядок 𝑚 × 𝑝, имеющего вид 𝐴𝐵 = ⎛⎜⎜⎝𝑐𝑐… 𝑐𝑐𝑐… 𝑐 ⋮⋮ ⋱ ⋮ 𝑐𝑐… 𝑐⎞⎟⎟⎠, где каждый элемент 𝑐 является попарным суммированием записи из 𝐴 и 𝐵, заданные 𝑐 = 𝑎𝑏 = 𝑎𝑏 + ⋯ + 𝑎𝑏.
Уже должно быть очевидно, что умножение матриц – это операция, которая является гораздо более строгим, чем его аналог с действительным числом. Во-первых, мы знаем что матричное произведение 𝐴𝐵 может существовать, только если 𝐴 имеет порядок 𝑚 × 𝑛 и 𝐵 имеет порядок 𝑛 × 𝑝, что означает, что количество столбцов в 𝐴 должно быть таким же, как количество строк в 𝐵.
Еще одна вещь, которую следует учитывать, – это то, что многие свойства, относящиеся к умножение действительных чисел не применяется к матрицам. Например, для любого два действительных числа 𝑎 и 𝑏, мы имеем 𝑎𝑏 = 𝑏𝑎.
Это называется коммутативным свойством .
Если бы матричное умножение также было коммутативным, это означало бы, что 𝐴𝐵 = 𝐵𝐴 для любых двух матриц 𝐴 и 𝐵. Предполагая, что 𝐴 имеет порядок 𝑚 × 𝑛 и 𝐵 имеет порядок 𝑛 × 𝑝, то вычисление 𝐵𝐴 будет означает попытку объединить матрицу с порядком 𝑛 × 𝑝 и матрица порядка 𝑚 × 𝑛.Это означает, что Корректно определено, только если 𝑚 = 𝑝. Это сразу показывает нам, что умножение матриц не всегда может быть коммутативен по той простой причине, что изменение порядка не всегда может быть возможный.
Предположим, что у нас действительно была ситуация, когда 𝑚 = 𝑝. Рассмотрим две матрицы 𝐴 = 2310809, 𝐵 = − 6−45104.
Так как 𝐴 – матрица 2 × 3 и 𝐵 – матрица 3 × 2, произведение Существует и является матрицей 2 × 2. Продемонстрируем расчет первой записи, где мы вычислили 2⋅ (−6) + 3⋅5 + 10⋅0 = 3.Мы можем продолжить это процесс для других записей, чтобы получить следующую матрицу: 𝐴𝐵 = 2310809 − 6−45104 = 335−484.
Однако давайте теперь рассмотрим умножение в обратном направлении (т. Е. 𝐵𝐴). Поскольку 𝐵 – матрица 3 × 2 и 𝐴 – матрица 2 × 3, результатом будет Матрица 3 × 3. Для первой записи у нас есть где мы вычислили (−6) ⋅2 + (- 4) ⋅8 = −44. Повторяя этот процесс для остальных записей получаем 𝐵𝐴 = − 6−451042310809 = − 44−18−9618155932036.
Итак, даже если 𝐴𝐵 и 𝐵𝐴 в порядке определены, две матрицы имеют порядки 2 × 2 и 3 × 3 соответственно, что означает, что они не могут быть равны. В Фактически, единственная ситуация, в которой заказы 𝐴𝐵 и 𝐵𝐴 может быть равным, если 𝐴 и 𝐵 – квадратные матрицы одного порядка (т. Е. Когда 𝐴 и 𝐵 имеют порядок 𝑛 × 𝑛). Однако даже в этом случае нет гарантии, что 𝐴𝐵 и 𝐵𝐴 будет равно. Это общее свойство матрицы умножение, о котором мы говорим ниже.
Свойство: Некоммутативность умножения матриц
Если 𝐴 и 𝐵 – матрицы порядков 𝑚 × 𝑛 и 𝑛 × 𝑚 соответственно, тогда в общем случае 𝐴𝐵 ≠ 𝐵𝐴.
Другими словами, матричное умножение некоммутативно .
Отметим, что хотя возможно, что матрицы могут коммутировать при определенных условиях, как правило, это не так. Чтобы убедиться в этом, давайте рассмотрим несколько примеров для демонстрации некоммутативности матрицы умножение.В первом примере мы определим произведение двух квадратные матрицы в обоих направлениях и сравнить их результаты.
Пример 1: Вычисление умножения двух матриц в обоих направлениях
При условии, что 𝐴 = − 422−4, 𝐵 = − 3−3−11, найдите 𝐴𝐵 и 𝐵𝐴.
Ответ
В этом примере мы хотим определить матричное умножение двух 2 × 2 матрицы в обоих направлениях.
Так как 𝐴 и 𝐵 имеют порядок 2 × 2, их произведение в любом направлении будет иметь заказ 2 × 2.Рассмотрим расчет первый элемент матрицы 𝐴𝐵. У нас есть
, где мы вычислили (−4) ⋅ (−3) + 2⋅ (−1) = 10. Мы продолжайте делать это для каждой записи 𝐴𝐵, что дает нам следующая матрица: 𝐴𝐵 = − 422−4 − 3−3−11 = 1014−2−10.
Осталось посчитать 𝐵𝐴, что мы можем сделать, переставив матрицы вокруг, давая нам 𝐵𝐴 = − 3−3−11 − 422−4 = 666−6.
Отметим, что 𝐴𝐵 не равно 𝐵𝐴, это означает, что в этом случае умножение не коммутируется.
Рассмотрим другой пример, в котором мы проверяем, меняется ли порядок умножение матриц дает тот же результат.
Пример 2: Проверка коммутативности умножения двух матриц
Рассмотрим матрицы 2 × 2 𝐴 = 1100 и 𝐵 = 0101. = 𝐵𝐴?
Ответ
В этом примере мы хотим определить матричное умножение двух 2 × 2 матрицы в обоих направлениях для проверки коммутативность матричного умножения.
Вычисление умножения в одном направлении дает нам 𝐴𝐵 = 11000101 = 0200.
Между тем вычисление в обратном направлении дает нам 𝐵𝐴 = 01011100 = 0000.
Если мы исследуем запись (1,2) обоих матрицы, мы видим, что 2 ≠ 0, что означает, что две матрицы не равны. Следовательно, 𝐴𝐵 ≠ 𝐵𝐴.
Увидев два примера, в которых умножение матриц не коммутативно, мы могли бы задаться вопросом, есть ли какие-нибудь матрицы, которые коммутируют друг с другом.Напомним конкретный класс матриц, для которых это может быть так.
Определение: диагональная матрица
Предположим, что 𝐴 = 𝑎 – квадратная матрица (т.е. матрица порядка 𝑛 × 𝑛). Тогда 𝐴 – диагональная матрица если все записи вне главной диагонали равны нулю, или, другими словами, если 𝑎 = 0 для 𝑖 ≠ 𝑗. То есть матрицы такого типа имеют следующий вид: 𝐴 = ⎛⎜⎜⎝𝑎0 ⋯ 00𝑎 ⋯ 0 ⋮ ⋱ ⋮ 00 ⋯ 𝑎⎞⎟⎟⎠.
В случаях 2 × 2 и 3 × 3 (которые мы будем преимущественно рассматривать в этом пояснении) диагональные матрицы принимают формы 𝐴 = 𝑎00𝑎, 𝐴 = 𝑎000𝑎000𝑎.
Теперь в следующем примере мы покажем, что, хотя умножение матриц некоммутативен, вообще говоря, он фактически коммутативен для диагональных матриц. В В частности, мы будем рассматривать диагональные матрицы 2 × 2.
Пример 3: Проверка утверждения о матричной коммутативности
Верно или неверно: Если 𝐴 и 𝐵 оба являются 2 × 2 матрицы, то 𝐴𝐵 никогда не бывает одинаковым как 𝐵𝐴.
Ответ
В этом примере мы хотим определить, возможность коммутативности при умножении матриц истинна или ложна.
Чтобы доказать ложность утверждения, нам нужно найти только один пример, где это не выполняется. Для этого рассмотрим два произвольных диагональные матрицы 𝐴 и 𝐵 (т. е. матрицы, у которых все недиагональные элементы равны нулю): 𝐴 = 1002, 𝐵 = 300−1.
Вычисляя 𝐴𝐵, находим 𝐴𝐵 = 1002300−1 = 300−2.
Далее, если мы вычислим 𝐵𝐴, мы найдем 𝐵𝐴 = 300−11002 = 300−2.
Таким образом, поскольку обе матрицы имеют одинаковый порядок и все их записи равны, то 𝐴𝐵 = 𝐵𝐴.Это доказывает, что утверждение неверно: 𝐴𝐵 может быть таким же, как 𝐵𝐴.
Явление, продемонстрированное выше, характерно не только для матриц. 𝐴 и 𝐵 мы использовали в примере, и мы можем фактически обобщить этот результат, чтобы сделать утверждение обо всех диагональных матрицы.
Свойство: коммутативность диагональных матриц
Если 𝐴 и 𝐵 обе диагональные матрицы с порядка 𝑛 × 𝑛, то две матрицы коммутируют. В другими словами, 𝐴𝐵 = 𝐵𝐴.
Чтобы доказать это для случая 2 × 2, рассмотрим два диагональные матрицы 𝐴 и 𝐵: 𝐴 = 𝑎00𝑎, 𝐵 = 𝑏00𝑏.
Тогда их продукция в обоих направлениях 𝐴𝐵 = 𝑎00𝑎𝑏00𝑏𝐵𝐴 = 𝑏00𝑏𝑎00𝑎 = 𝑎𝑏00𝑎𝑏, = 𝑏𝑎00𝑏𝑎.
Таким образом, 𝐴𝐵 = 𝐵𝐴 для любых двух 2 × 2 диагональные матрицы. Обратите внимание, что произведение двух диагональных матриц всегда приводит к диагональной матрице, где каждый диагональный элемент является произведением два соответствующих диагональных элемента из исходных матриц. Таким образом, легко представить, как это можно расширить за пределы 2 × 2 кейс.
Важно отметить, что свойство сохраняется только тогда, когда обе матрицы диагональные. Например, рассмотрим две матрицы 𝐴 = 700−3, 𝐵 = − 10583, где 𝐴 – диагональная матрица, а – не диагональная матрица. В этом случае мы находим, что 𝐴𝐵 = − 7035−24−9, 𝐵𝐴 = − 70−1556−9.
Таким образом, даже если диагональные элементы совпадают, недиагональные записи нет, поэтому ≠ 𝐵𝐴.
Несмотря на то, что свойство коммутативности может выполняться не для всех диагональные матрицы в паре с недиагональными матрицами, на самом деле, есть определенные типы диагональных матриц, которые могут коммутировать с любой другой матрицей того же порядок.Давайте рассмотрим особый пример этого: единичную матрицу .
Определение: идентификационная матрица
Идентификационная матрица (также известная как единичная матрица) – это диагональная матрица, в которой все диагональных элементов равны 1. другими словами, единичные матрицы принимают вид 𝐼 = ⎛⎜⎜⎝10 ⋯ 001 ⋯ 0 ⋮ ⋱ ⋮ 00 ⋯ 1⎞⎟⎟⎠, где 𝐼 обозначает единичную матрицу порядка 𝑛 × 𝑛 (если размер указывать не нужно, Вместо этого часто используется 𝐼).
В большинстве случаев, которые мы будем рассматривать, единичные матрицы принимать формы 𝐼 = 1001, 𝐼 = 100010001, 𝐼 = ⎛⎜⎜⎝1000010000100001⎞⎟⎟⎠.
Ключевым свойством единичных матриц является то, что они коммутируют с каждой матрицей. 𝐴 того же порядка. Однако у них также есть более мощное свойство, которое мы продемонстрируем в следующем примере.
Пример 4: Вычисление матричных продуктов с использованием матрицы идентичности
При условии, что 𝐴 = − 14−111 и 𝐼 – это единичная матрица одного и того же заказать как 𝐴, найти 𝐴 × 𝐼 и 𝐼 × 𝐼.
Ответ
Напомним, что единичная матрица – это диагональная матрица, в которой все диагонали записи 1.Учитывая, что 𝐴 является 2 × 2 и что единичная матрица имеет вид того же порядка, что и 𝐴, поэтому 𝐼 является Матрица 2 × 2 вида 𝐼 = 1001.
Нас попросили найти × 𝐼 и 𝐼 × 𝐼, поэтому найдем их, используя матрицу умножение. Во-первых, у нас есть 𝐴 × 𝐼 = − 14−1111001 = − 14−111 = 𝐴.
Далее у нас есть 𝐼 × 𝐼 = 10011001 = 1001 = 𝐼.
Таким образом, мы показали, что 𝐴 × 𝐼 = 𝐴 и 𝐼 × 𝐼 = 𝐼.
Последний пример продемонстрировал, что произведение произвольной матрицы на единичная матрица привела к той же самой матрице, и что продукт единичная матрица сама с собой была также единичной матрицей.Фактически, если бы мы вычислил 𝐼𝐴, мы бы аналогичным образом обнаружили, что 𝐼 × 𝐴 = 1001 − 14−111 = − 14−111 = 𝐴.
Итак, 𝐴𝐼 = 𝐼𝐴 = 𝐴, что означает, что не только матрицы коммутируют, но произведение также равно 𝐴 в обоих случаях.
Можно заметить, что это свойство похоже на свойство числа 1 (иногда называется мультипликативным тождеством). Для действительных чисел, а именно для любого действительного числа имеем 𝑎⋅1 = 1⋅𝑎 = 𝑎.
Фактически, это свойство, которое работает почти так же для идентификации матрицы.
Свойство: Мультипликативная идентичность для матриц
Единичная матрица 𝐼 является мультипликативной идентичностью для матричное умножение. То есть для любой матрицы 𝐴 порядка 𝑚 × 𝑛, то 𝐴𝐼 = 𝐼𝐴 = 𝐴, где 𝐼 и 𝐼 – × 𝑛 и 𝑚 × 𝑚 единичные матрицы соответственно.
Отметим, что порядки использованных выше тождественных матриц выбраны исключительно так, чтобы что умножение матриц корректно определено. В случае, если 𝐴 – квадратная матрица, 𝑚 = 𝑛, поэтому 𝐼 = 𝐼.
Докажем это свойство для случая 2 × 2 с помощью рассматривая общую матрицу 2 × 2 𝐴 = 𝑎𝑎𝑎𝑎.
Если вычислить произведение этой матрицы на единичную матрицу 𝐼, мы находим, что 𝐴𝐼 = 𝑎𝑎𝑎𝑎1001 = 𝑎𝑎𝑎𝑎 = 𝐴.
Изменяя порядок, получаем 𝐼𝐴 = 1001𝑎𝑎𝑎𝑎 = 𝑎𝑎𝑎𝑎 = 𝐴.
Таким образом, действительно верно, что 𝐴𝐼 = 𝐼𝐴 = 𝐴 для любого 2 × 2 матрица 𝐴, и она в равной степени можно показать это для случаев более высокого порядка.
На данный момент мы обнаружили, что, несмотря на то, что коммутативность является свойством умножение действительных чисел, это свойство не переносится на матричное умножение. Однако, несмотря на то, что это конкретное свойство не Но существуют и другие свойства умножения действительных чисел. что мы можем применить к матрицам. Рассмотрим их сейчас.
Напомним, что для любых действительных чисел, 𝑏 и 𝑐 у нас есть (𝑎𝑏) 𝑐 = 𝑎 (𝑏𝑐).
Это называется ассоциативным свойством .Ассоциативное свойство означает, что в ситуациях, когда нам нужно выполнить умножение дважды, мы можем выбрать, в каком порядке это делать; мы можем либо найти 𝑎𝑏, то умножьте это на 𝑐, или мы можем найти 𝑏𝑐 и умножить на 𝑎, и оба ответа будут одинаковыми.
Чтобы выяснить, применимо ли это свойство также к умножению матриц, рассмотрим пример с умножением трех матриц.
Пример 5: Исследование ассоциативного свойства матричного умножения
Учитывая, что 𝐴 = 03−216−1, 𝐵 = − 5−614, 𝐶 = − 304−2, правда ли, что (𝐴𝐵) 𝐶 = 𝐴 (𝐵𝐶)?
Ответ
В этом примере нам поручено вычислить произведение трех матрицы в двух возможных порядках; либо мы можем вычислить 𝐴𝐵, а затем умножьте его справа на 𝐶, или мы можем вычислить 𝐵𝐶 и умножить это слева.
Начнем с поиска 𝐴𝐵. Поскольку 𝐴 является 3 × 2 и 𝐵 равно 2 × 2, 𝐴𝐵 будет Матрица 3 × 2. Для демонстрации процесса перенесем детали умножения для первой строки. У нас есть
, где мы вычислили 0⋅ (−5) + 3⋅1 = 3. Для следующей записи в В строке мы имеем
, так как 0⋅ (−6) + 3⋅4 = 12. Повторение этого процесса для каждой записи в 𝐴𝐵 получаем 𝐴𝐵 = 03−216−1 − 5−614 = 3121116−31−40.
Далее, чтобы найти (𝐴𝐵) 𝐶, мы умножаем эту матрицу справа от 𝐶.Это дает нам (𝐴𝐵) 𝐶 = 3121116−31−40 − 304−2 = 39−2431−32−6780.
Теперь нам нужно найти 𝐴 (𝐵𝐶), что означает, что мы сначала нужно вычислить 𝐵𝐶 (2 × 2 матрица). Это дает нам 𝐵𝐶 = − 5−614 − 304−2 = −
−8.Затем, чтобы найти 𝐴 (𝐵𝐶), мы умножаем это на слева на 𝐴. Это дает нам 𝐴 (𝐵𝐶) = 03−216−1 −
−8 = 39−2431−32−6780.В заключение видим, что рассчитанные нами матрицы для (𝐴𝐵) 𝐶 и 𝐴 (𝐵𝐶) эквивалентны.Таким образом, мы можем заключить, что ассоциативное свойство выполнено и данное утверждение верно.
Как мы видели в предыдущем примере, ассоциативность матрицы сохраняется для три произвольно выбранные матрицы. Собственно говоря, это общий свойство, которое выполняется для всех возможных матриц, для которых умножение действителен (хотя полное доказательство этого довольно громоздко и не особенно поучительно, поэтому мы не будем здесь его описывать).
Свойство: ассоциативность умножения матриц
Пусть 𝐴 – матрица порядка 𝑚 × 𝑛, 𝐵 – матрица порядка 𝑛 × 𝑝, а 𝐶 – матрица порядка 𝑝 × 𝑞. Тогда у нас есть (𝐴𝐵) 𝐶 = 𝐴 (𝐵𝐶).
То есть умножение матриц ассоциативно.
Пока мы занимаемся изучением свойств умножения матриц и эквивалентны ли они умножению действительных чисел, позвольте нам рассмотрим еще одно полезное свойство.
Напомним, что для любых действительных чисел 𝑎, 𝑏 и 𝑐 имеем 𝑎 (𝑏 + 𝑐) = 𝑎𝑏 + 𝑎𝑐.
Это известно как свойство дистрибутива , и оно дает нам простой способ раскрыть круглые скобки в выражениях. Собственно говоря, у нас есть уже было видно, что это свойство выполняется для скалярного умножения матрицы. Напомним, что скалярное умножение матриц можно определить как следует.
Определение: скалярное умножение
Для матрицы порядка 𝑚 × 𝑛, определяемой 𝐴 = ⎛⎜⎜⎝𝑎𝑎… 𝑎𝑎𝑎… 𝑎 ⋮⋮ ⋱ ⋮ 𝑎𝑎… 𝑎⎞⎟⎟⎠, скалярное кратное 𝐴 на константу находится путем умножения каждой записи 𝐴 на 𝑘, или, другими словами, 𝑘𝐴 = ⎛⎜⎜⎜⎝𝑘𝑎𝑘𝑎… 𝑘𝑎𝑘𝑎𝑘𝑎… 𝑘𝑎 ⋮⋮ ⋱ ⋮ 𝑘𝑎𝑘𝑎… 𝑘𝑎⎞⎟⎟⎟⎠.
Как мы видели, свойство дистрибутивности выполняется для скалярного умножения таким же образом, как и для действительных чисел: а именно, учитывая скаляр 𝑎 и две матрицы 𝐵 и 𝐶 того же порядка, мы имеем 𝑎 (𝐵 + 𝐶) = 𝑎𝐵 + 𝑎𝐶.
Что касается умножения полной матрицы, мы можем подтвердить, что это действительно так. что распределительное свойство все еще сохраняется, что приводит к следующему результату.
Свойство: Дистрибутивность умножения матриц
Пусть 𝐴 – матрица порядка 𝑚 × 𝑛 и 𝐵 и 𝐶 – матрицы порядка 𝑛 × 𝑝.Тогда у нас есть 𝐴 (𝐵 + 𝐶) = 𝐴𝐵 + 𝐴𝐶.
Другими словами, умножение матриц является дистрибутивным по отношению к матрице добавление.
Важно знать порядок матриц, приведенных выше. свойство, поскольку как сложение 𝐵 + 𝐶, так и умножения 𝐴𝐵, 𝐴𝐶 и 𝐴 (𝐵 + 𝐶) необходимо правильно определить.
Обратите внимание, что, как и свойство ассоциативности, конкретное доказательство этого более отнимает много времени, чем интересно, так как это всего лишь случай его доказательства запись за записью с использованием определений умножения и сложения матриц.
Давайте рассмотрим пример, где мы можем увидеть применение дистрибутивность матриц.
Пример 6: Исследование распределительных свойств матрицы Умножение на сложение
Предположим, что 𝐴 = 1−3−42, 𝐵 = 201−1 и 𝐶 = 01−30.
- Найдите 𝐴𝐵.
- Найдите 𝐴𝐶.
- Найдите 𝐴 (2𝐵 + 7𝐶).
- Экспресс 𝐴 (2𝐵 + 7𝐶) в пересчете на 𝐴𝐵 и 𝐴𝐶.
Ответ
Часть 1
Для начала нас попросили вычислить 𝐴𝐵, что мы можем сделать, используя умножение матриц.𝐴 и – матрицы 2 × 2, поэтому их продукт также будет матрицей 2 × 2. Демонстрировать при вычислении записи в нижнем левом углу имеем
, где мы вычислили (−4) 2 + 2⋅1 = −6. Повторяя это для оставшихся записи, мы получаем 𝐴𝐵 = 1−3−42201−1 = − 13−6−2.
Часть 2
Мы можем вычислить 𝐴𝐶 почти так же, как и мы 𝐴𝐵. 𝐴𝐶 также будет Матрица 2 × 2, поскольку 𝐴 и 𝐶 – обе матрицы 2 × 2.Произведя умножение матриц, получим 𝐴𝐶 = 1−3−4201−30 = 91−6−4.
Часть 3
Для следующей части нас попросили найти 𝐴 (2𝐵 + 7𝐶). Чтобы вычислить это напрямую, мы сначала нужно найти скалярные числа, кратные 𝐵 и 𝐶, а именно 2𝐵 и 7𝐶. Мы делаем это, умножая каждый элемент матриц на соответствующий скаляр. Таким образом, мы имеем 2𝐵 = 2201−17𝐶 = 701−30 = 402−2, = 07−210.
Следующим шагом является сложение матриц с помощью сложения матриц.Мы делаем это сложение записей в одинаковых позициях вместе. Это дает нам 2𝐵 + 7𝐶 = 402−2 + 07−210 = 47−19−2.
Наконец, чтобы найти 𝐴 (2𝐵 + 7𝐶), умножаем эту матрицу на 𝐴. Как и раньше, мы получим Матрица 2 × 2, поскольку мы берем произведение двух Матрицы 2 × 2. Мы получаем 𝐴 (2𝐵 + 7𝐶) = 1−3−4247−19−2 = 6113−54−32.
Часть 4
В заключительной части мы должны выразить 𝐴 (2𝐵 + 7𝐶) через 𝐴𝐵 и 𝐴𝐶.Самый простой способ сделать это – использовать дистрибутивное свойство матричного умножения. То есть для матриц 𝐴, 𝑋 и 𝑌 соответствующих порядок, у нас есть 𝐴 (𝑋 + 𝑌) = 𝐴𝑋 + 𝐴𝑌.
В этом случае, если подставить в 𝑋 = 2𝐵 и 𝑌 = 7𝐶, находим, что 𝐴 (2𝐵 + 7𝐶) = 𝐴 (2𝐵) + 𝐴 (7𝐶) = 2𝐴𝐵 + 7𝐴𝐶.
Таким образом, мы выразили 𝐴 (2𝐵 + 7𝐶) через из 𝐴𝐵 и 𝐴𝐶. Тем не менее, мы можем хотите убедиться, что наше решение правильное и что законы распределенность держится.Поскольку мы уже подсчитали 𝐴 (2𝐵 + 7𝐶), 𝐴𝐵 и 𝐴𝐶 в предыдущих частях это должно быть довольно легко сделать это. 2𝐴𝐵 и 7𝐴𝐶 можно найти с помощью скалярное умножение 𝐴𝐵 и 𝐴𝐶; то есть, 2𝐴𝐵 = 2 − 13−6−27𝐴𝐶 = 791−6−4 = − 26−12−4, = 637−42−28.
Наконец, мы можем сложить эти две матрицы вместе, используя сложение матриц, чтобы получить 2𝐴𝐵 + 7𝐴𝐶 = − 26−12−4 + 637−42−28 = 6113−54−32.
Так как это соответствует матрице 𝐴 (2𝐵 + 7𝐶), которое мы вычислили в предыдущем часть, мы можем подтвердить, что наше решение действительно правильное: 𝐴 (2𝐵 + 7𝐶) = 2𝐴𝐵 + 7𝐴𝐶.
В заключительной части этого объяснения мы рассмотрим, как матрица транспонирует взаимодействует с матричным умножением. Начнем с напоминания определения.
Определение: транспонирование матрицы
Предположим, что 𝐴 – матрица порядка 𝑚 × 𝑛. Транспонирование матрицы есть оператор, переворачивающий матрицу по диагонали. Другими словами, он переключает индексы строк и столбцов матрицы. Эта операция создает другую матрицу порядок 𝑛 × 𝑚 обозначается 𝐴.
Если 𝑎 – элементы матрицы 𝐴 с 𝑖 = 1,…, 𝑚 и 𝑗 = 1,…, 𝑛, то 𝑎 – записи 𝐴 и принимает вид 𝐴 = ⎛⎜⎜⎝𝑎𝑎 ⋯ 𝑎𝑎𝑎 ⋯ 𝑎 ⋮⋮ ⋱ ⋮ 𝑎𝑎 ⋯ 𝑎⎞⎟⎟⎠.
Например, рассмотрим 2 × 3 матрица 𝐴 = 5681−29.
Транспонирование этой матрицы 𝐴 выглядит следующим образом Матрица 3 × 2: 𝐴 = 516−289.
Как оказалось, умножение матриц и транспонирование матриц имеют интересное свойство в сочетании, которое мы рассмотрим в теореме ниже.
Свойство: умножение матриц и транспонирование
Предположим, что 𝐴 – матрица порядка 𝑚 × 𝑛 а 𝐵 – матрица порядка 𝑛 × 𝑝, гарантируя, что матричное произведение корректно определено. В транспонировать 𝐴 и – матрицы 𝐴 и 𝐵 заказов 𝑛 × 𝑚 и 𝑝 × 𝑛 соответственно, поэтому их произведение в противоположном направлении 𝐵𝐴 равно также хорошо определен.
Умножение матриц в сочетании с транспонированием удовлетворяет следующему свойству: (𝐴𝐵) = 𝐵𝐴.
Опять же, мы не будем включать полное доказательство этого, поскольку оно включает с использованием определений умножения и транспонирования по каждой записи основание.
В последнем примере мы продемонстрируем это свойство транспонирования матрицы умножение для данного продукта.
Пример 7: Свойства умножения и транспонирования матрицы
При условии, что 𝐵𝐴 = 8−4−7−5, что такое 𝐴𝐵?
Ответ
В этом примере мы хотим определить произведение транспонирования двух матрицы, учитывая информацию об их продукте.
Напомним, что транспонирование матрицы размера 𝑚 × переключает строки и столбцы, чтобы создать другую матрицу порядка 𝑛 × 𝑚. Умножение матриц в сочетании с транспонировать удовлетворяет свойству (𝐵𝐴) = 𝐴𝐵.
Следовательно, для расчета произведения 𝐴𝐵, нам просто нужно транспонировать 𝐵𝐴 используя это свойство.
Отсюда имеем 𝐴𝐵 = (𝐵𝐴) = 8−4−7−5 = 8−7−4−5.
В заключение напомним свойства умножения матриц, которые мы узнали в ходе этого объяснителя.
Ключевые моменты
- Умножение матриц, как правило, не коммутативно; то есть, 𝐴𝐵 ≠ 𝐵𝐴.
- Если 𝐴 и 𝐵 – диагональные матрицы того же порядка, то 𝐴𝐵 = 𝐵𝐴.
- Единичная матрица 𝐼 – это диагональная матрица с 1 для каждого диагонального входа. Матрицы идентичности (до 4-го порядка) принимают показанные формы ниже: 𝐼 = 1001, 𝐼 = 100010001, 𝐼 = ⎛⎜⎜⎝1000010000100001⎞⎟⎟⎠.
- Если 𝐼 – единичная матрица и квадратная матрица того же порядка, то 𝐴𝐼 = 𝐼𝐴 = 𝐴.
- Умножение матриц ассоциативно; то есть для действительных матриц 𝐴, 𝐵 и 𝐶 имеем (𝐴𝐵) 𝐶 = 𝐴 (𝐵𝐶).
- Умножение матриц является распределительным по сравнению с сложением, поэтому для допустимых матриц 𝐴, 𝐵 и 𝐶 имеем 𝐴 (𝐵 + 𝐶) = 𝐴𝐵 + 𝐴𝐶.
- Для любого действительного матричного произведения 𝐴𝐵 транспонирование матрицы удовлетворяет следующему свойству: (𝐴𝐵) = 𝐵𝐴.
Программа Python для умножения двух матриц
В Python мы можем реализовать матрицу как вложенный список (список внутри списка).
Мы можем рассматривать каждый элемент как строку матрицы.
Например, X = [[1, 2], [4, 5], [3, 6]] будет представлять матрицу 3x2 .
Первая строка может быть выбрана как X [0] . И элемент в первой строке, первом столбце может быть выбран как X [0] [0] .
Умножение двух матриц X и Y определяется, только если количество столбцов в X равно количеству строк Y .
Если X – это матрица n x m, а Y – это матрица m x l , тогда XY определен и имеет размерность n x l (но YX не определен). Вот несколько способов реализовать умножение матриц в Python.
: умножение матриц с использованием вложенного цикла
# Программа для умножения двух матриц с использованием вложенных циклов
# 3x3 матрица
X = [[12,7,3],
[4, 5,6],
[7, 8,9]]
# 3x4 матрица
Y = [[5,8,1,2],
[6,7,3,0],
[4,5,9,1]]
# результат 3x4
результат = [[0,0,0,0],
[0,0,0,0],
[0,0,0,0]]
# перебирать строки X
для i в диапазоне (len (X)):
# перебирать столбцы Y
для j в диапазоне (len (Y [0])):
# перебирать строки Y
для k в диапазоне (len (Y)):
результат [i] [j] + = X [i] [k] * Y [k] [j]
для r в результате:
печать (r)
Выход
[114, 160, 60, 27] [74, 97, 73, 14] [119, 157, 112, 23]
В этой программе мы использовали вложенные для циклов для перебора каждой строки и каждого столбца.Сумму произведений накапливаем в результате.
Этот метод прост, но требует больших вычислительных ресурсов, поскольку мы увеличиваем порядок матрицы.
Для операций с большими матрицами мы рекомендуем оптимизированные программные пакеты, такие как NumPy, который в несколько (порядка 1000) раз быстрее, чем приведенный выше код.
Исходный код: умножение матриц с использованием вложенного списка
# Программа для умножения двух матриц с использованием списка
# 3x3 матрица
X = [[12,7,3],
[4, 5,6],
[7, 8,9]]
# 3x4 матрица
Y = [[5,8,1,2],
[6,7,3,0],
[4,5,9,1]]
# результат 3x4
result = [[сумма (a * b для a, b в zip (X_row, Y_col)) для Y_col в zip (* Y)] для X_row в X]
для r в результате:
печать (r)
Вывод этой программы такой же, как и выше.Чтобы понять приведенный выше код, мы должны сначала узнать о встроенной функции zip () и распаковке списка аргументов с помощью оператора *.
Мы использовали понимание вложенного списка для перебора каждого элемента в матрице. Код сначала выглядит сложным и нечитабельным. Но как только вы освоите понимание списков, вы, вероятно, не вернетесь к вложенным циклам.
Умножение матриц 3×3 – Примеры
В этой статье будет про умножение матриц порядка 3х3, примеры и порядок получения продукта.
Быстрый доступ
! Нажмите на кнопки ниже, чтобы перейти прямо к нужному разделу статьи!
Перейти к примерам
Как умножить матрицы 3×3
В этой статье мы собираемся разработать различные примеры того, как умножить матрицу 3×3. Когда мы умножаем 2 матрицы, важно убедиться, что одна из матриц имеет такое же количество строк, что и столбцы другой матрицы, это означает, что если одна из матриц имеет 3 строки, другая матрица должна иметь 3 столбца, в противном случае , мы не можем умножить матрицы.
Основываясь на предыдущем объяснении, мы всегда можем умножить две матрицы 3×3, потому что всегда выполняется предыдущее правило. Результатом умножения двух матриц 3×3 будет другая матрица того же порядка.
| А 11 | А 12 | А 13 |
| А 21 | А 22 | А 23 |
| А 31 | А 32 | А 33 |
| В 11 | В 12 | В 13 |
| В 21 | В 22 | В 23 |
| B 31 | В 32 | В 33 |
Умножение матриц выполняется путем умножения каждой строки первой матрицы на каждый столбец второй матрицы и последующего сложения результатов, как в следующем примере.
- Ряд 1
- C 11 = (A 11 * B 11 ) + (A 12 * B 21 ) + (A 13 * B 31 )
- C 12 = (A 11 * B 12 ) + (A 12 * B 22 ) + (A 13 * B 32 )
- C 12 = (A 11 * B 13 ) + (A 12 * B 23 ) + (A 13 * B 33 )
- Ряд 2
- C 21 = (A 21 * B 11 ) + (A 22 * B 21 ) + (A 23 * B 31 )
- C 22 = (A 21 * B 12 ) + (A 22 * B 22 ) + (A 23 * B 32 )
- C 22 = (A 21 * B 13 ) + (A 22 * B 23 ) + (A 23 * B 33 )
- Ряд 3
- C 31 = (A 31 * B 11 ) + (A 32 * B 21 ) + (A 33 * B 31 )
- C 32 = (A 31 * B 12 ) + (A 32 * B 22 ) + (A 33 * B 32 )
- C 32 = (A 31 * B 13 ) + (A 32 * B 23 ) + (A 33 * B 33 )
Теперь, увидев это, мы собираемся сделать пример того, как умножить две матрицы 3×3
Примеры умножения матриц 3×3
Пример 1: Умножьте следующие матрицы 3×3.
Матрица A
Матрица B
Теперь с матрицей, которую мы собираемся умножить, мы собираемся умножить каждую строку первой матрицы на каждый столбец второй матрицы, и таким образом мы собираемся найти каждую позицию в результирующей матрице (C)
- Сначала решаем первую строку
- С 11 = (5 * 0) + (5 * -1) + (0 * 0)
- С 11 = 0-5 + 0
- С 11 = -5
- С 12 = (5 * -1) + (5 * 0) + (0 * 0)
- С 12 = -2 + 0 + 0
- С 12 = -2
- С 13 = (5 * -1) + (5 * -1) + (0 * -1)
- С 13 = -2-5 + 0
- С 13 = -7
- Теперь второй ряд
- С 21 = (2 * 0) + (2 * -1) + (1 * 0)
- С 21 = 0-2 0
- С 21 = -2
- С 22 = (2 * -1) + (2 * 0) + (1 * 0)
- С 22 = -2 + 0 + 0
- С 22 = -2
- С 23 = (2 * -1) + (2 * -1) + (1 * -1)
- С 23 = -2-2-1
- С 23 = -5
- А теперь третий ряд
- С 31 = (3 * 0) + (3 * -1) + (2 * 0)
- С 31 = 0-3 + 0
- С 31 = -3
- С 32 = (3 * -1) + (3 * 0) + (2 * 0)
- С 32 = -3 + 0 + 0
- С 32 = -3
- С 33 = (3 * -1) + (3 * -1) + (2 * -1)
- С 33 = -3 – 3-2
- С 33 = -8
Результирующая матрица (C)
| -5 | -2 | -7 |
| -2 | -2 | -5 |
| -3 | -3 | -8 |
Иисус – сын Божий, посланный на смерть, чтобы каждый, кто верит в него, имел жизнь вечную.
Узнать больше
Пример 2: ¿Какая матрица получается при умножении следующих двух матриц?
Матрица A
Матрица B
Теперь умножаем каждую строку и столбец
- Ряд 1
- С 11 = (2 * 8) + (1 * 4) + (5 * 2)
- С 11 = 16 + 4 + 10
- С 11 = 30
- С 12 = (2 * 7) + (1 * 2) + (5 * 3)
- С 12 = 14 + 2 + 15
- С 12 = 31
- С 13 = (2 * 1) + (1 * 7) + (5 * 5)
- С 13 = 2 + 7 + 25
- С 13 = 34
- Ряд 2
- С 21 = (2 * 8) + (10 * 4) + (5 * 2)
- С 21 = 16 + 40 + 10
- С 21 = 66
- С 22 = (2 * 7) + (10 * 2) + (5 * 3)
- С 22 = 14 + 20 + 15
- С 22 = 49
- С 23 = (2 * 1) + (10 * 7) + (5 * 5)
- С 23 = 2 + 70 + 25
- С 23 = 97
- Ряд 3
- С 31 = (3 * 8) + (1 * 4) + (4 * 2)
- С 31 = 24 + 4 + 8
- С 31 = 36
- С 32 = (3 * 7) + (1 * 2) + (4 * 3)
- С 32 = 21 + 2 + 12
- С 32 = 35
- С 33 = (3 * 1) + (1 * 7) + (4 * 5)
- С 33 = 3 + 7 + 20
- С 33 = 30
Результирующая матрица (C)
| 30 | 31 | 34 |
| 66 | 49 | 97 |
| 36 | 35 | 30 |
Пример 3: Умножьте A x B и найдите результат “C”
Матрица A
Матрица B
- Решить строку 1
- С 11 = (3 * 3) + (1 * 3) + (1 * 10)
- С 11 = 9 + 3 + 10
- С 11 = 22
- С 12 = (3 * 5) + (1 * 1) + (1 * 5)
- С 12 = 15 + 1 + 5
- С 12 = 21
- С 13 = (3 * 7) + (1 * 8) + (1 * 2)
- С 13 = 21 + 8 + 2
- С 13 = 31
- Решить строку 2
- С 21 = (8 * 3) + (9 * 3) + (4 * 10)
- С 21 = 24 + 27 + 40
- С 21 = 91
- С 22 = (8 * 5) + (9 * 1) + (4 * 5)
- С 22 = 40 + 9 + 20
- С 22 = 69
- С 23 = (8 * 7) + (9 * 8) + (4 * 2)
- С 23 = 56 + 72 + 8
- С 23 = 136
- Решить строку 3
- С 31 = (2 * 3) + (5 * 3) + (6 * 10)
- С 31 = 6 + 15 + 60
- С 31 = 81
- С 32 = (2 * 5) + (5 * 1) + (6 * 5)
- С 32 = 10 + 5 + 30
- С 32 = 45
- С 33 = (2 * 7) + (5 * 8) + (6 * 2)
- С 33 = 14 + 40 + 12
- С 33 = 66
Результирующая матрица (C)
| 22 | 21 | 31 |
| 91 | 69 | 136 |
| 81 | 45 | 66 |
– обзор
4.2 Умножение матриц
Умножение матрицы на матрицу, или, для краткости, умножение матриц между матрицей M размера i × j (i строк на j столбцов) и матрицей N j × k дает матрицу P размера i × k. стандарта базовых подпрограмм линейной алгебры (BLAS) (см. врезку «Функции линейной алгебры» в главе 3: Масштабируемое параллельное выполнение). Эта функция является основой многих решателей линейной алгебры, таких как LU-разложение. Как мы увидим, умножение матриц предоставляет возможности для сокращения обращений к глобальной памяти, которые могут быть зафиксированы относительно простыми методами.Скорость выполнения функций матричного умножения может варьироваться на порядки, в зависимости от уровня сокращения обращений к глобальной памяти. Следовательно, умножение матриц представляет собой отличный начальный пример для таких методов.
При выполнении матричного умножения каждый элемент выходной матрицы P является внутренним произведением строки M и столбца N . Мы продолжим использовать соглашение, где P Row, Col – это элемент в строке th позиции в вертикальном направлении и Col th позиции в горизонтальном направлении.Как показано на рис. 4.2, P Row, Col (маленький квадрат в P ) является внутренним произведением вектора, образованного из строки строки M (показано как горизонтальная полоса в M ) и вектор, образованный из столбца Col th N (показан вертикальной полосой в N ). Внутреннее произведение двух векторов, также называемое скалярным произведением, представляет собой сумму произведений отдельных элементов вектора, т. Е. PRow, Col = ∑MRow, k * Nk, Col, для k = 0,1,… Ширина − 1 .Например,
Рисунок 4.2. Умножение матриц с использованием нескольких блоков путем разбиения P.
P1,5 = undefinedM1,0 * N0,5 + undefinedM1,1 * N1,5 + undefinedM1,2 * N2,5 + ⋯ + undefinedM1, Width − 1 * NWidth − 1 , 5
В нашей начальной реализации умножения матриц мы сопоставляем потоки с элементами P с тем же подходом, который мы использовали для colorToGreyscaleConversion; т.е. каждый поток отвечает за вычисление одного элемента P. Индексы строки и столбца для элемента P, вычисляемые каждым потоком, следующие:
Row = blockIdx.y * blockDim.y + threadIdx.y
и
Col = blockIdx.x * blockDim.x + threadIdx.x.
При таком взаимно-однозначном сопоставлении индексы потоков Row и Col также являются индексами строк и столбцов для выходного массива. На рис. 4.3 показан исходный код ядра, основанный на отображении потока в данные. Читатель должен сразу увидеть знакомую схему вычисления Row, Col и проверку оператора if, если и Row, и Col находятся в пределах допустимого диапазона. Эти операторы почти идентичны своим аналогам в colorToGreyscaleConversion.Единственное существенное отличие состоит в том, что мы предполагаем квадратные матрицы для matrixMulKernel, таким образом заменяя ширину и высоту на Width.
Рисунок 4.3. Ядро простого матричного умножения, использующее один поток для вычисления одного элемента P.
Отображение потока в данные эффективно разделяет P на плитки, один из которых показан в виде большого квадрата на рис. 4.2. Каждый блок отвечает за вычисление одной из этих плиток.
Теперь обратим внимание на работу, выполняемую каждым потоком.Напомним, что P Row, Col – это внутреннее произведение строки -го -го строки M и столбца Col -го N. На рис. 4.3 мы используем цикл for для выполнения этой операции внутреннего продукта. Перед входом в цикл мы инициализируем локальную переменную Pvalue равной 0. Каждая итерация цикла получает доступ к элементу из строки -й строки строки M и одному элементу из столбца -й строки столбца N столбца N, умножает два элемента вместе и накапливает продукт в Pvalue.
Во-первых, мы сосредоточимся на доступе к элементу M внутри цикла for.Напомним, что M линеаризуется в эквивалентный одномерный массив, где строки M размещаются одна за другой в пространстве памяти, начиная с 0 -й строки . Следовательно, начальным элементом 1-й строки является M [1 * Ширина], потому что нам нужно учесть все элементы строки 0 -го . Как правило, начальным элементом строки -й строки является M [строка * ширина]. Поскольку все элементы строки размещаются в последовательных местах, k-й элемент строки -й строки находится в M [Row * Width + k].Этот метод был применен на рис. 4.3.
Теперь обратим наше внимание на N. Как показано на рис. 4.3, начальный элемент столбца -го столбца -й элемент строки 0 -й , то есть N [столбец]. Доступ к каждому дополнительному элементу в столбце -го столбца требует пропуска целых строк. Причина в том, что следующий элемент того же столбца на самом деле является тем же элементом в следующей строке. Следовательно, элемент k th столбца th столбца равен N [k * Width + Col].
После выхода из цикла for все потоки имеют свои значения P-элемента в переменных Pvalue. Затем каждый поток использует одномерное эквивалентное индексное выражение Row * Width + Col для записи своего P-элемента. Опять же, этот шаблон индекса аналогичен используемому в ядре colorToGreyscaleConversion.
Теперь мы используем небольшой пример, чтобы проиллюстрировать выполнение ядра матричного умножения. На рис. 4.4 показан P 4 × 4 с BLOCK_WIDTH = 2. Небольшие размеры позволяют уместить весь пример на одной картинке.Матрица P теперь разделена на четыре плитки, и каждый блок вычисляет одну плитку. Мы делаем это, создавая блоки, которые представляют собой массивы потоков 2 × 2, причем каждый поток вычисляет один элемент P. В этом примере поток (0,0) блока (0,0) вычисляет P 0,0 , тогда как поток (0,0) блока (1,0) вычисляет P 2,0 .
Рисунок 4.4. Небольшой пример выполнения matrixMulKernel.
Строка и столбец в matrixMulKernel идентифицируют элемент P, который должен быть вычислен потоком. Row также определяет строку M, тогда как Col определяет столбец N как входные значения для потока.Рис. 4.5 иллюстрирует операции умножения в каждом блоке потока. В примере умножения малых матриц потоки в блоке (0,0) производят четыре скалярных произведения. Переменные Row и Col потока (1,0) в блоке (0,0) равны 0 * 0 + 1 = 1 и 0 * 0 + 0 = 0. Он сопоставляется с P 1,0 и вычисляет скалярное произведение строки 1 M и столбца 0 N.
Рисунок 4.5. Матричные действия умножения одного блока потока.
Мы рассмотрим выполнение цикла for на рис. 4.3 для резьбы (0,0) в блоке (0,0). Во время 0-й итерации (k = 0), Row * Width + k = 0 * 4 + 0 = 0 и k * Width + Col = 0 * 4 + 0 = 0. Следовательно, мы получаем доступ к M [0] и N [0], которые являются одномерным эквивалентом M 0,0 и N 0,0 , согласно рис. 3.3. Обратите внимание, что это действительно 0 -е элементы строки 0 M и столбца 0 N. Во время 1-й итерации (k = 1) Row * Width + k = 0 * 4 + 1 = 1 и k * Width + Столбец = 1 * 4 + 0 = 4. Мы получаем доступ к M [1] и N [4], которые являются одномерным эквивалентом M 0,1 и N 1,0 , согласно рис.3.3. Это первые элементы строки 0 M и столбца 0 N.
Во время второй итерации ( k = 2), Row * Width + k = 0 * 4 + 2 = 2 и k * Width + Col = 8, что дает M [2] и N [8]. Следовательно, доступные элементы являются одномерными эквивалентами M 0,2 и d_N 2,0 . Наконец, во время 3-й итерации ( k = 3), Row * Width + k = 0 * 4 + 3 и k * Width + Col = 12, что приводит к M [3] и N [12], одномерному эквиваленту M 0,3 и N 3,0 . Теперь мы проверили, что цикл for выполняет внутреннее произведение между строкой 0 M и столбцом 0 N.После цикла поток записывает P [Row * Width + Col], что является P [0], одномерным эквивалентом P 0,0 . Таким образом, поток (0,0) в блоке (0,0) успешно вычислил внутреннее произведение между строкой 0 M и столбцом 0 N и поместил результат в P 0,0 .
Мы оставим читателю в качестве упражнения выполнить и проверить цикл for для других потоков в блоке (0,0) или в других блоках.
Обратите внимание, что matrixMulKernel может обрабатывать матрицы размером до 16 × 65 535 элементов в каждом измерении.В ситуации, когда матрицы, превышающие этот предел, должны быть умножены, можно разделить матрицу P на подматрицы с размерами, которые могут быть покрыты сеткой. Затем мы можем использовать код хоста для итеративного запуска ядер и заполнения матрицы P. В качестве альтернативы мы можем изменить код ядра, чтобы каждый поток вычислял больше P элементов.
Мы можем оценить влияние эффективности доступа к памяти, рассчитав ожидаемый уровень производительности кода ядра матричного умножения на рис.4.3. Доминирующей частью ядра с точки зрения времени выполнения является цикл for, который выполняет вычисление внутреннего продукта:
for (intk = 0; k На каждой итерации этого цикла выполняется два доступа к глобальной памяти для одного умножения с плавающей запятой и одного сложения с плавающей запятой. Один доступ к глобальной памяти выбирает элемент M, а другой – элемент N. Одна операция с плавающей запятой умножает выбранные элементы M и N, а другая накапливает произведение в Pvalue.Таким образом, отношение объема вычислений к доступу к глобальной памяти в цикле составляет 1,0. Из нашего обсуждения в главе 3, Масштабируемое параллельное выполнение, это соотношение, вероятно, приведет к использованию менее 2% пиковой скорости выполнения современных графических процессоров. Нам необходимо увеличить это соотношение по крайней мере на порядок, чтобы производительность вычислений современных устройств была хорошей. В следующем разделе мы покажем, что мы можем использовать специальные типы памяти в устройствах CUDA для достижения этой цели. Математическая операция умножения одной матрицы на другую матрицу называется умножением матриц. В матрицах записи (или элементы) расположены в строках и столбцах. Нас сбивает с толку, как математически умножать две или более матриц, когда матрицы участвуют в умножении. Однако существует систематическая процедура умножения матриц. Итак, давайте научимся умножать матрицы в математике. Умножение матриц возможно, если общее количество элементов в строке первой матрицы равно общему количеству элементов в столбце второй матрицы. $ A \, = \, \ big [a_ {ij} \ big] _ {m \ times r} $ и $ B \, = \, \ big [b_ {ij} \ big] _ {r \ times n } $ $ A $ и $ B $ – две матрицы. Матрица $ A $ – это матрица порядка $ m \ times r $, а матрица $ B $ – это матрица порядка $ r \ times n $. $ A_ {ij} $ и $ b_ {ij} $ представляют каждую запись в матрицах $ A $ и $ B $ соответственно. Здесь $ i $ и $ j $ представляют «номер строки» и «номер столбца» элемента. Умножение матриц записывается в математике следующим образом. $ \ подразумевает $ $ A \ times B $ $ \, = \, $ $ \ big [a_ {ij} \ big] _ {m \ times r} $ $ \ times $ $ \ big [b_ {ij} \ big] _ {r \ times n} Предположим, что C – матрица, представляющая произведение матриц $ A $ и $ B $. $ \, \, \, \ следовательно \, \, \, \, \, \, $ C $ $ \, = \, $ $ \ big [c_ {ij} \ big] _ {m \ times n } $ Количество строк в матрице $ C $ равно количеству строк в матрице $ A $. Аналогично, количество столбцов в матрице $ C $ равно количеству столбцов в матрице $ B $.Следовательно, произведение матриц $ A $ и $ B $ есть матрица $ C $ порядка $ m \ times n $. Этот алгебраический анализ можно очень ясно понять из приведенного ниже раздела с примерами. Есть два простых шага для умножения матриц в математике. Давайте узнаем, как умножать матрицы из следующих двух примеров. $ (1). \, \, \, $ {\ Begin {bmatrix} 1 & 2 \\ 3 & 4 \\ \ end {bmatrix}} $ $ \ times $ $ {\ begin {bmatrix} 5 & 6 \\ 7 & 8 \\ \ end {bmatrix}} $ \ подразумевает $ $ \ begin {bmatrix} 1 & 2 \\ 3 & 4 \\ \ end {bmatrix} $ $ \ times $ $ \ begin {bmatrix} 5 & 6 \\ 7 & 8 \\ \ end { bmatrix} $ $ \, = \, $ $ \ begin {bmatrix} 1 \ times 5 + 2 \ times 7 & 1 \ times 6 + 2 \ times 8 \\ 3 \ times 5 + 4 \ times 7 & 3 \ times 6 + 4 \ times 8 \\ \ end {bmatrix} $ $ \, = \, $ $ \ begin {bmatrix} 5 + 14 & 6 + 16 \\ 15 + 28 & 18 + 32 \\ \ end {bmatrix} $ $ \, \, \, \ следовательно \, \, \, \, \, \, $ $ \ begin {bmatrix} 1 & 2 \\ 3 & 4 \\ \ end {bmatrix} $ $ \ times $ $ \ begin {bmatrix} 5 & 6 \\ 7 & 8 \\ \ end {bmatrix} $ $ \, = \, $ $ \ begin {bmatrix} 19 & 22 \\ 43 & 50 \\ \ end {bmatrix} $ Порядок каждой матрицы умножения в этом примере составляет $ 2 $.Следовательно, порядок их матрицы продуктов также равен $ 2 \ times 2 $. $ (2). \, \, \, $ $ {\ Begin {bmatrix} 1 & 2 & 3 \\ \ end {bmatrix}} $ $ \ times $ {\ begin {bmatrix} 4 & 5 \\ 6 и 7 \\ 8 и 9 \\ \ end {bmatrix}} $ \ подразумевает $ $ {\ begin {bmatrix} 1 & 2 & 3 \\ \ end {bmatrix}} $ $ \ times $ $ {\ begin {bmatrix} 4 & 5 \\ 6 & 7 \\ 8 & 9 \\ \ end {bmatrix}} $ $ \, = \, $ $ {\ begin {bmatrix} 1 \ times 4 + 2 \ times 6 + 3 \ times 8 & 1 \ times 5 + 2 \ times 7 + 3 \ умножить на 9 \\ \ end {bmatrix}} $ \ подразумевает $ $ {\ begin {bmatrix} 1 & 2 & 3 \\ \ end {bmatrix}} $ $ \ times $ $ {\ begin {bmatrix} 4 & 5 \\ 6 & 7 \\ 8 & 9 \\ \ end {bmatrix}} $ $ \, = \, $ $ {\ begin {bmatrix} 4 + 12 + 24 & 5 + 14 + 27 \\ \ end {bmatrix}} $ $ \, \, \, \ следовательно \, \, \, \, \, \, $ $ {\ begin {bmatrix} 1 & 2 & 3 \\ \ end {bmatrix}} $ $ \ times $ $ { \ begin {bmatrix} 4 & 5 \\ 6 & 7 \\ 8 & 9 \\ \ end {bmatrix}} $ $ \, = \, $ $ {\ begin {bmatrix} 40 & 46 \\ \ end {bmatrix }} Порядок первой матрицы равен $ 1 \ times 3 $, а порядок второй матрицы равен $ 3 \ times 2 $.Следовательно, порядок их матрицы продуктов равен $ 1 \ times 2 $. Список практических вопросов по умножению матриц с решениями, чтобы научиться умножать матрицы одного или другого порядка в математике. В этом руководстве мы рассмотрим различные способы выполнения умножения матриц с использованием массивов NumPy. Мы научимся перемножать матрицы разного размера вместе. Кроме того, мы узнаем, как ускорить процесс умножения с помощью графического процессора и других актуальных тем, так что приступим! Прежде чем двигаться дальше, лучше рассмотреть некоторые основные термины матричной алгебры. Вектор: Алгебраически вектор – это совокупность координат точки в пространстве. Матрица: Матрица (множественные матрицы) – это двумерное расположение чисел или набор векторов. Точечное произведение: Скалярное произведение – это математическая операция между двумя векторами равной длины . С ясным пониманием этой терминологии, мы готовы к работе. Давайте начнем с простой формы умножения матриц – между матрицей и вектором. Прежде чем продолжить, давайте сначала разберемся, как создать матрицу с помощью NumPy. Метод NumPy array () используется для представления векторов, матриц и многомерных тензоров. Давайте определим 5-мерный вектор и матрицу 3 × 3 с помощью NumPy. Вывод: При умножении матрицы на вектор следует учитывать следующие моменты: Вывод: Теперь мы поняли умножение матрицы на вектор; было бы легко вычислить умножение двух матриц. Давайте рассмотрим умножение матрицы A размера m x n на матрицу B размера n x p: Вывод: Вы можете установить любое другое целое число в качестве начального числа, но я предлагаю установить его на 42 для этого руководства, чтобы ваш вывод соответствовал показанным на снимках экрана вывода. Теперь перемножим две матрицы с помощью метода np.matmul () . Полученная матрица должна иметь форму 3 х 4. Вывод: Умножение трех матриц будет состоять из двух операций умножения на 2 матрицы, и каждая из этих двух операций будет следовать тем же правилам, что обсуждались в предыдущем разделе. Допустим, мы перемножаем три матрицы A, B и C, и получаем произведение D = ABC. В результирующей матрице будут строки, равные количеству строк в A и столбцов равно количеству столбцов в C. Важным свойством операции умножения матриц является то, что является ассоциативным . Например, в нашем примере умножения трех матриц D = ABC не имеет значения, выполняем ли мы сначала AB или сначала BC. Вывод: Давайте произведем умножение в обоих порядках и проверим свойство ассоциативности. Вывод: 3D-матрица – это не что иное, как набор (или стек) множества 2D-матриц, точно так же, как 2D-матрица представляет собой набор / стек многих одномерных векторов. Итак, матричное умножение трехмерных матриц включает многократное умножение двумерных матриц, которое в конечном итоге сводится к скалярному произведению между их векторами строки / столбца. Рассмотрим пример матрицы A формы (3,3,2), умноженной на другую трехмерную матрицу B формы (3,2,4). Вывод: Умножение матриц между этими двумя будет включать три умножения между соответствующими двумерными матрицами A и B, имеющими формы (3,2) и (2,4) соответственно. В частности, первое умножение будет между A [0] и B [0], второе умножение будет между A [1] и B [1], и, наконец, третье умножение будет между A [2] и БИ 2]. Результат каждого отдельного умножения 2D-матриц будет иметь форму (3,4). Следовательно, конечный продукт двух 3D-матриц будет матрицей формы (3,3,4). Давайте реализуем это с помощью кода. Вывод: Помимо np.matmul (), есть два других способа умножения матриц – метод np.dot () и ‘ @ ‘оператор , каждый из которых предлагает некоторые различия / гибкость в операциях матричного умножения. Вы можете использовать этот метод для нахождения скалярного произведения векторов, но если мы передадим две двумерные матрицы, он будет вести себя аналогично методу «np.matmul () ’и вернет результат матричного умножения двух матриц. Давайте посмотрим на пример: Выход: разница между np.dot () и np.matmul () заключается в их работе с трехмерными матрицами. np.dot () для двух 3D-матриц A и B возвращает произведение суммы по последней оси A и предпоследней оси B. Итак, если A имеет форму (a, b, c), а B имеет форму (d, c, e), то результат np.dot (A, B) будет иметь форму (a, d, b, e), индивидуальный элемент которого в позиции (i, j, k, m) определяется выражением: Давайте проверим пример: Вывод: Вывод: Оператор @, представленный в Python 3.5, выполняет ту же операцию, что и «np.matmul ()». Давайте рассмотрим предыдущий пример ‘np.matmul ()’ с использованием оператора @ и увидим тот же результат, что и возвращенный ранее: Вывод: Раньше нам приходилось вызывать «np.matmul ()» несколько раз и передавать их результаты в качестве параметра следующему вызову. Вывод: До сих пор мы выполнили умножение матрицы на вектор или другую матрицу. Но что происходит, когда мы выполняем умножение матриц на скалярное или одно числовое значение? Результат такой операции получается умножением каждого элемента в матрице на скалярное значение.Таким образом, выходная матрица имеет тот же размер, что и входная матрица. Обратите внимание, что «np.matmul ()» не позволяет умножать матрицу на скаляр. Этого можно добиться, используя метод np.dot () или оператор ‘*’. Давайте посмотрим на это на примере кода. Вывод: Иногда мы хотим произвести умножение соответствующих элементов двух матриц одинаковой формы. Этого можно добиться, вызвав функцию multiply () NumPy или используя оператор ‘*’ . Вывод: Фактически, матричное умножение на скаляр также включает в себя широковещательную передачу скалярного значения в матрицу формы, равной операнду матрицы при умножении. Это означает, что когда мы умножаем матрицу формы (3,3) на скалярное значение 10, NumPy создаст другую матрицу формы (3,3) с постоянными значениями десять во всех позициях в матрице и выполнит поэлементно умножение между двумя матрицами. Давайте разберемся в этом на примере: Вывод: Точно так же, как мы можем возвести скалярное значение в степень, мы можем проделать ту же операцию с матрицами. Например, если мы возведем матрицу A в степень n, она будет равна умножению матриц n матриц, каждая из которых будет матрицей A. Эта операция предоставляется в Python с помощью метода NumPy linalg.matrix_power () , который принимает в качестве параметров базовую матрицу и целочисленную степень. Давайте посмотрим на пример на Python: Вывод: Вывод: Важный вопрос, который возникает в результате этой операции: Что происходит, когда мощность равна 0? Это единичная матрица. Итак, возведение матрицы n x n в степень 0 приводит к единичной матрице I формы n x n. Давайте быстро проверим это на Python, используя нашу предыдущую матрицу A. Вывод: Точно так же, как мы можем выполнять поэлементное умножение матриц, мы также можем выполнять поэлементное возведение в степень, то есть возводить каждый отдельный элемент матрицы в некоторую степень. Это может быть достигнуто в Python с помощью стандартного оператора экспоненты « ** » – примера перегрузки оператора на .мощности: \ n {}, shape = {} \ n “.format (C, C.shape)) Вывод: Предположим, у нас есть матрица A 5 x 6 и еще одна матрица 3 x 3 B. Очевидно, мы не можем умножить эти две вместе из-за несоответствия размеров. Но что, если бы мы захотели умножить подматрицу 3 × 3 в матрице A на матрицу B, оставив при этом другие элементы в A неизменными? Давайте посмотрим на это в действии. Вывод: Кроме того, нет необходимости перезаписывать исходную матрицу. Мы также можем записать результат в новую матрицу, сначала скопировав исходную матрицу в новую матрицу, а затем записав произведение в позиции подматрицы. Мы знаем, что NumPy ускоряет матричные операции за счет распараллеливания большого количества вычислений и использования возможностей параллельных вычислений нашего ЦП. Однако современным приложениям нужно нечто большее.ЦП предлагают ограниченные вычислительные возможности, и этого недостаточно для большого количества необходимых нам вычислений, обычно в таких приложениях, как глубокое обучение. Вот где на сцену выходят графические процессоры. Они предлагают большие вычислительные возможности и отличную инфраструктуру параллельных вычислений, которая помогает нам значительно экономить время, выполняя сотни тысяч операций за доли секунды. В этом разделе мы рассмотрим, как можно выполнять умножение матриц на графическом процессоре, а не на центральном процессоре, и при этом сэкономить много времени. NumPy не предлагает функции для умножения матриц на GPU. Поэтому мы должны установить некоторые дополнительные библиотеки, которые помогут нам достичь нашей цели. Сначала мы установим библиотеки « scikit-cuda » и « PyCUDA » с помощью pip install. Эти библиотеки помогают нам выполнять вычисления на графических процессорах на базе CUDA. Чтобы установить эти библиотеки с вашего терминала, если на вашем компьютере установлен графический процессор. Если у вас нет графического процессора на вашем компьютере, вы можете попробовать ноутбуки Google Colab и разрешить доступ к графическому процессору; это бесплатно для использования.Теперь мы напишем код для генерации двух матриц 1000 × 1000 и выполнения матричного умножения между ними двумя способами: Во втором методе мы будем генерировать матрицы на CPU; затем мы сохраним их на графическом процессоре (используя метод PyCUDA « gpuarray.to_gpu () ») перед выполнением умножения между ними.Мы будем использовать модуль « время » для вычисления времени вычисления в обоих случаях. Вывод: На некоторых старых аппаратных системах вы можете получить ошибку памяти, но если вам повезет, она будет работать долгое время (зависит от вашей системы). Теперь давайте выполним то же умножение на графическом процессоре и посмотрим, как время вычислений различается между ними. Вывод: В этом руководстве мы рассмотрели, как происходит умножение двух матриц, правила, управляющие им, и как их реализовать в Python. Мы также рассмотрели поэлементные вычисления в матрицах, такие как поэлементное умножение матриц или поэлементное возведение в степень. Наконец, мы рассмотрели, как можно ускорить процесс умножения матриц, выполняя его на графическом процессоре. Умножение матриц
Введение
Состояние
Процедура
Примеры
Проблемы
20+ примеров для умножения матриц NumPy
Основные термины
Таким образом, вектор с двумя значениями представляет точку в 2-мерном пространстве. В информатике вектор – это расположение чисел в одном измерении.Он также широко известен как массив, список или кортеж.
Напр. [1,2,3,4]
Пример: [[1,2,3],
[4,5,6],
[7,8,9]]
Он равен сумме произведений соответствующих элементов векторов. Умножение матриц на вектор
импортировать numpy как np
a = np.array ([1, 3, 5, 7, 9])
б = нп.массив ([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
print ("Вектор a: \ n", a)
Распечатать()
print ("Матрица b: \ n", b)
Давайте теперь посмотрим, как происходит умножение между матрицей и вектором.
Мы будем использовать метод NumPy matmul () для большинства операций умножения матриц.
Давайте определим матрицу 3 × 3 и умножим ее на вектор длины 3. импортировать numpy как np
a = np.array ([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
b = np.array ([10, 20, 30])
print ("A =", a)
print ("b =", b)
print ("Ab =", np.матмуль (а, б))
Обратите внимание, что результатом является вектор, длина которого равна строкам матрицы умножителя. Умножение на другую матрицу
Но перед этим давайте рассмотрим наиболее важные правила умножения матриц:
Произведение двух матриц C = AB будет иметь m строк и p столбцов.
Каждый элемент в матрице произведения C является результатом скалярного произведения между вектором-строкой в A и вектором-столбцом в B.
Давайте теперь выполним матричное умножение двух матриц в Python, используя NumPy.
Мы случайным образом сгенерируем две матрицы размеров 3 x 2 и 2 x 4.
Мы будем использовать метод np.random.randint () для генерации чисел. импортировать numpy как np
np.random.seed (42)
A = np.random.randint (0, 15, размер = (3,2))
B = np.random.randint (0, 15, размер = (2,4))
print ("Матрица A: \ n", A)
print ("shape of A =", A.shape)
Распечатать()
print ("Матрица B: \ n", B)
print ("shape of B =", B.shape)
Примечание: мы устанавливаем случайное начальное число, используя «np.random.seed () ’, чтобы сделать генератор случайных чисел детерминированным.
При каждом запуске этого фрагмента кода будут генерироваться одни и те же случайные числа. Этот шаг важен, если вы хотите воспроизвести результат позже. C = np.matmul (A, B)
print ("произведение A и B: \ n", C)
print ("shape of product =", C.shape) Умножение между 3 матрицами
Здесь количество столбцов в A должно быть равно количеству строк в B, а количество строк в C должно быть равно количеству столбцов в B.
При многоматричном умножении порядок отдельных операций умножения не имеет значения и, следовательно, не дает разных результатов.
Оба заказа дадут одинаковый результат. Давайте сделаем пример на Python. импортировать numpy как np
np.random.seed (42)
A = np.random.randint (0, 10, размер = (2,2))
B = np.random.randint (0, 10, размер = (2,3))
C = np.random.randint (0, 10, размер = (3,3))
print ("Матрица A: \ n {}, shape = {} \ n" .format (A, A.форма))
print ("Матрица B: \ n {}, shape = {} \ n" .format (B, B.shape))
print ("Матрица C: \ n {}, shape = {} \ n" .format (C, C.shape))
Основываясь на правилах, которые мы обсуждали выше, умножение этих трех матриц должно дать результирующую матрицу формы (2, 3).
Обратите внимание, что метод np.matmul () принимает только две матрицы в качестве входных данных для умножения, поэтому мы вызовем метод дважды в том порядке, в котором мы хотим умножить, и передадим результат первого вызова в качестве параметра в второй.
(Мы найдем лучший способ справиться с этой проблемой в следующем разделе, когда введем оператор «@») D = нп.матмул (нп.матмул (A, B), C)
print ("Результат умножения в порядке (AB) C: \ n \ n {}, shape = {} \ n" .format (D, D.shape))
D = np.matmul (A, np.matmul (B, C))
print ("Результат умножения в порядке A (BC): \ n \ n {}, shape = {}". format (D, D.shape))
Как мы видим, результат умножения трех матриц остается неизменным независимо от того, умножаем ли мы сначала A и B или сначала B и C.
Таким образом, свойство ассоциативности подтверждается.
Кроме того, форма результирующего массива (2, 3) находится на ожидаемых строках. NumPy 3D-матричное умножение
импортировать numpy как np
np.random.seed (42)
A = np.random.randint (0, 10, размер = (3,3,2))
B = np.random.randint (0, 10, размер = (3,2,4))
print ("A: \ n {}, shape = {} \ nB: \ n {}, shape = {}". format (A, A.shape, B, B.shape))
Первая матрица представляет собой стопку из трех 2D-матриц, каждая из которых имеет форму (3,2), а вторая матрица представляет собой стопку из 3 2D-матриц, каждая из которых имеет форму (2,4). C = np.matmul (A, B)
print ("Продукт C: \ n {}, shape = {}". format (C, C.shape)) Альтернативы np.matmul ()
Метод «np.dot ()»
импортировать numpy как np
# матрица 3x2
A = np.array ([[8, 2, 2],
[1, 0, 3]])
# матрица 2x3
B = np.array ([[1, 3],
[5, 0],
[9, 6]])
# точечный продукт должен возвращать продукт 2x2
C = np.dot (A, B)
print ("произведение A и B: \ n {} shape = {}". format (C, C.shape))
Здесь мы определили матрицу 3 × 2, а матрицу 2 × 3 и их скалярное произведение дает результат 2 × 2, который является матричным умножением двух матриц,
то же, что и what ‘np .matmul () ’вернулся бы.
В то время как ‘np.matmul ()’ работает с двумя 3D-матрицами, вычисляя матричное умножение соответствующих пар 2D-матриц (как обсуждалось в последнем разделе), np.dot (), с другой стороны, вычисляет скалярные произведения различных пар векторы-строки и векторы-столбцы из первой и второй матрицы соответственно.
Это не интуитивно понятно и трудно понять. точка (A, B) [i, j, k, m] = sum (A [i, j ,:] * B [k,:, m])
импортировать numpy как np
np.random.seed (42)
A = np.random.randint (0, 10, размер = (2,3,2))
B = np. random.рандинт (0, 10, размер = (3,2,4))
print ("A: \ n {}, shape = {} \ nB: \ n {}, shape = {}". format (A, A.shape, B, B.shape))
Если теперь передать эти матрицы методу np.dot (), он вернет матрицу формы (2,3,3,4), отдельные элементы которой вычисляются с использованием формулы, приведенной выше. . C = np.dot (A, B)
print ("np.dot (A, B) = \ n {}, shape = {}". format (C, C.shape))
Еще одно важное различие между ‘np.matmul () »и« np.dot () »заключаются в том, что« np.matmul () »не допускает умножение на скаляр (мы обсудим это в следующем разделе), в то время как« np.dot () »разрешает это. Оператор «@»
импортировать numpy как np
np.random.seed (42)
А = np.random.randint (0, 15, размер = (3,2))
B = np.random.randint (0, 15, размер = (2,4))
print ("Матрица A: \ n {}, shape = {}". format (A, A.shape))
print ("Матрица B: \ n {}, shape = {}". format (B, B.shape))
С = А @ В
print ("произведение A и B: \ n {}, shape = {}". format (C, C.shape))
Оператор ‘@’ становится удобным, когда мы выполняем матричное умножение более двух матриц.
Теперь мы можем выполнить ту же операцию более простым (и более интуитивно понятным) способом: импортировать numpy как np
np.random.seed (42)
A = np.random.randint (0, 10, размер = (2,2))
B = np.random.randint (0, 10, размер = (2,3))
C = np.random.randint (0, 10, размер = (3,3))
print ("Матрица A: \ n {}, shape = {} \ n" .format (A, A.shape))
print ("Матрица B: \ n {}, shape = {} \ n" .format (B, B.shape))
print ("Матрица C: \ n {}, shape = {} \ n" .format (C, C.shape))
D = A @ B @ C # ранее np.матмул (np.matmul (A, B), C)
print ("Продукт ABC: \ n \ n {}, shape = {} \ n" .format (D, D.shape)) Умножение на скаляр (одно значение)
импортировать numpy как np
A = np.array ([[1,2,3],
[4,5, 6],
[7, 8, 9]])
В = А * 10
print ("Матрица A: \ n {}, shape = {} \ n".формат (A, A.shape))
print ("Умножение A на 10: \ n {}, shape = {}". format (B, B.shape)) Поэлементное умножение матриц
Эта операция также называется произведением Адамара . Он принимает две матрицы одинаковых размеров и создает третью матрицу того же размера. импортировать numpy как np
np.random.seed (42)
A = np.random.randint (0, 10, размер = (3,3))
B = np.random.randint (0, 10, размер = (3,3))
print ("Матрица A: \ n {} \ n" .format (A))
print ("Матрица B: \ n {} \ n" .format (B))
C = np.multiply (A, B) # или A * B
print ("Поэлементное умножение A и B: \ n {}". format (C))
Единственное правило, которое вам нужно помнить для поэлементного умножения, состоит в том, что две матрицы должны иметь одинаковую форму .
Однако, если одно измерение матрицы отсутствует, NumPy будет транслировать его, чтобы соответствовать форме другой матрицы. импортировать numpy как np
np.random.seed (42)
A = np.random.randint (0, 10, размер = (3,4))
B = np.array ([[1,2,3,4]])
print ("Матрица A: \ n {}, shape = {} \ n" .format (A, A.shape))
print ("Матрица B: \ n {}, shape = {} \ n" .format (B, B.shape))
С = А * В
print ("Поэлементное умножение A и B: \ n {}". format (C))
Обратите внимание, как вторая матрица, имеющая форму (1,4), была преобразована в матрицу (3,4) посредством широковещательной рассылки, и произошло поэлементное умножение между двумя матрицами. Матрица, возведенная в степень (матрица возведения в степень)
Подобно тому, как увеличение скалярного значения (основания) до степени n равносильно многократному умножению n оснований, такая же закономерность наблюдается при возведении матрицы в степень, которое включает в себя многократные умножения матриц.
Обратите внимание, что для того, чтобы эта операция была возможна, базовая матрица должна быть квадратной .
Это необходимо для обеспечения того, чтобы количество столбцов в предыдущей матрице = количеству строк в следующей матрице. импортировать numpy как np
np.random.seed (10)
А = np.random.randint (0, 10, размер = (3,3))
A_to_power_3 = np.linalg.matrix_power (A, 3)
print ("Матрица A: \ n {}, shape = {} \ n" .format (A, A.shape))
print ("A в степени 3: \ n {}, shape = {}". format (A_to_power_3, A_to_power_3.shape))
Мы можем проверить этот результат, выполнив обычное матричное умножение с тремя операндами (все они A), используя оператор «@»: В = А @ А @ А
print ("B = A @ A @ A: \ n {}, shape = {}". format (B, B.форма))
Как видите, результаты обеих операций совпадают.
Чтобы ответить на этот вопрос, давайте рассмотрим, что происходит, когда мы возводим скалярное основание в степень 0.
Мы получаем значение 1, верно? Итак, что эквивалентно 1 в матричной алгебре? Вы угадали! C = np.linalg.matrix_power (A, 0)
print ("A в степени 0: \ n {}, shape = {}". format (C, C.shape)) Поэлементное возведение в степень
Умножение на конкретный индекс
Для лучшего понимания обратитесь к следующему изображению:
Вы можете выполнить эту операцию в Python, используя нарезку матрицы для извлечения подматрицы из A, выполняя умножение на B и затем записывая результат по соответствующему индексу в A . импортировать numpy как np
np.random.seed (42)
A = np.random.randint (0, 10, размер = (5,6))
B = np.random.randint (0, 10, размер = (3,3))
print ("Матрица A: \ n {}, shape = {} \ n" .format (A, A.shape))
print ("Матрица B: \ n {}, shape = {} \ n" .format (B, B.shape))
C = A [1: 4,2: 5] @ B
A [1: 4,2: 5] = C
print ("Матрица A после умножения подматрицы: \ n {}, shape = {} \ n" .format (A, A.shape))
Как видите, только элементы с индексами строк с 1 по 3 и с индексами столбцов со 2 по 4 были умножены на B, и то же самое было записано обратно в A, в то время как остальные элементы A остались. без изменений. Умножение матриц с использованием графического процессора
pip install pycuda
pip install scikit-cuda
Используя CPU
импортировать numpy как np
время импорта
# создание матриц размером 1000 x 1000
np.random.seed (42)
x = np.random.randint (0,256, размер = (1000,1000)). astype ("float64")
y = np.random.randint (0,256, размер = (1000,1000)). astype ("float64")
# вычисление времени умножения на CPU
tic = time.time ()
г = нп.матмул (х, у)
toc = время.время()
time_taken = toc - tic # время в с
print ("Время, затраченное на CPU (в мс) = {}". format (time_taken * 1000))
Использование графического процессора
# вычисление времени умножения на GPU
linalg.в этом()
# сохранение массивов на GPU
x_gpu = gpuarray.to_gpu (x)
y_gpu = gpuarray.to_gpu (у)
tic = time.time ()
# выполнение умножения
z_gpu = linalg.mdot (x_gpu, y_gpu)
toc = time.time ()
time_taken = toc - tic # время в с
print ("Время, затраченное на GPU (в мс) = {}". format (time_taken * 1000))
Как мы видим, выполнение той же операции на графическом процессоре дает нам ускорение в 70 раз по сравнению с процессором.
Это было еще небольшое вычисление. Для крупномасштабных вычислений графические процессоры дают нам ускорение на несколько порядков. Заключение
Мы также рассмотрели различные варианты стандартного умножения матриц (и их реализацию в NumPy), такие как умножение более двух матриц, умножение только по определенному индексу или степень матрицы.