Раздел 3. Линейная алгебра с элементами аналитической геометрии
Раздел 3. Линейная алгебра с элементами аналитической геометрии
6.
Матрицы, определители
6.1.
Основы линейной алгебры. Матрицы. Виды матриц. Операции над матрицами
Сегодня вы изучите вопросы
-
Основы линейной алгебры
-
Основные понятия линейной алгебры
-
Понятие матрицы
Изучив тему занятия, вы сможете
-
умножать матрицу на число;
-
производить линейные операции над матрицами;
-
умножать матрицы;
-
возводить матрицы в натуральную степень.
Элементы линейной алгебры широко используются при решении большого числа прикладных экономических и управленческих задач. Успешное усвоение основных понятий данного занятия является основой для ее применения.
Основные понятия
6.1.1.
Матрица. Основные понятия
Матрицей размера называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.
Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, A, B, C,…, X, Y, Z, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: , где
— номер строки;
— номер столбца.
Например, матрица размеров имеет вид:
или в сокращенной записи
Например, матрица размеров имеет вид:
.
Наряду с круглыми скобками для обозначения матриц используются
Две матрицы А и В одинаковой размерности называются равными, если при всех
Виды матриц
Матрица, состоящая из одного столбца, называется матрицей (вектором)-столбцом и обозначается , а состоящая из одной строки — матрицей (вектором)-строкой, соответственно обозначается .
Матрица называется квадратной n-го порядка, если число ее строк равно числу столбцов и равно n:
.
Элементы образуют главную диагональ квадратной матрицы порядка n, а элементы — побочную диагональ.
Например,
— квадратная матрица третьего порядка, элементами главной диагонали являются числа 1, 5, 9, а побочной — 7, 5 ,3.
Если все элементы, кроме элементов, образующих главную диагональ квадратной матрицы, равны нулю, то такая матрица называется диагональной.
Например, — диагональная матрица третьего порядка.
Если у диагональной матрицы n-го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей n-го порядка и обозначается буквой Е.
Например, — единичная матрица третьего порядка.
Матрица, все элементы которой равны нулю, называется нулевой и обозначается буквой О. Нулевая матрица имеет следующий вид:
.
В линейной алгебре матрицы Е и О играют такую же роль, какую играют числа 1 и 0 в арифметике.
Матрица, полученная из данной матрицы А заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной и обозначается .
Пример 1. Так, если , то .
Транспонированная матрица обладает следующим свойством: .
6.1.2.
Действия над матрицами
Умножение матрицы на число
Пусть — произвольная матрица, — произвольное действительное число.
Произведением матрицы А на число называется новая матрица, каждый элемент которой равен произведению соответствующего элемента матрицы А на число , т.е.
.
Например,
Таким образом, можно выделить следующее следствие.
Общий множитель всех элементов матрицы можно выносить за знак матрицы.
Сложение и вычитание матриц
Эта операция определяется только для матриц одинаковой размерности (формата).
Суммой двух матриц А и В одинаковой размерности называется новая матрица С того же размера, каждый элемент которой равен сумме соответствующих (стоящих на одинаковых местах) элементов данных матриц.
Например, пусть А и В — матрицы размерности . Тогда по определению под суммой понимается
или .
Вышеприведенные действия над матрицами называются линейными.
Линейные операции над матрицами обладают следующими свойствами.
-
Переместительность (коммутативность) умножения матрицы на число .
-
Сочетательность (ассоциативность) со скалярным множителем .
-
Переместительность (коммутативность) сложения матриц .
-
Сочетательность (ассоциативность) сложения матриц .
-
Распределительность (дистрибутивность) сложения матриц относительно умножения на число .
-
Распределительность (дистрибутивность) относительно сложения чисел .
Таким образом, линейные операции над матрицами можно выполнять по аналогии с привычными правилами алгебры чисел.
Вычитание для матриц (как и для чисел) определяется как действие, обратное сложению.
Разностью матриц А и В(А — В) одинаковой размерности называется такая матрица С, что
В + С = А.
Легко заметить, что матрица С, удовлетворяющая этому условию, всегда существует, и притом только одна. Ее элементы определяются равенствами
.
Таким образом, при вычитании матриц вычитаются соответствующие элементы этих матриц.
Например, .
Замечание. Знаки сравнения () для матриц любого формата лишены смысла.
Умножение матриц
Умножение матрицы А на матрицу В (рассматриваются именно в таком порядке) определено, если число столбцов первой матрицы равно числу строк второй матрицы. В этом случае матрица А называется согласованной с матрицей В.
Иначе говоря, если порядок матрицы А равен , то порядок согласованной с ней матрицы В должен быть , где — любые натуральные числа.
Произведением матрицы на матрицу называется такая матрица , что
, где
Таким образом, для вычисления элемента , стоящего в строке и в столбце матрицы С, следует каждый элемент строки матрицы А умножить на соответственный элемент столбца матрицы В и результат сложить.
Примеры:
1) .
2) .
Умножение матриц обладает следующими свойствами:
1) ;
2) ;
3) ;
4) .
Заметим, что умножение матриц некоммутативно: .
Выше было определено, что операция умножения имеет место только для согласованных матриц А и В, при этом матрицы, взятые в ином порядке (В и А), могут оказаться несогласованными, тогда их произведение не определено. Но даже в том случае, когда согласованность матриц не нарушается, произведения АВ и ВА могут оказаться разными.
Например, для матриц
и имеем:
, но
.
Если АВ = ВА, то матрицы А и В называются перестановочными (коммутирующими). Очевидно, это может иметь место только в том случае, когда А и В — квадратные матрицы одного и того же порядка.
Например, коммутирующими являются матрицы
и .
Действительно,
,
то есть для данных матриц АВ = ВА.
Еще одно замечание: произведение двух матриц может быть нуль-матрицей, даже если ни один из сомножителей не является нуль-матрицей.
Например, пусть даны матрицы и . Найдем произведение АВ и ВА:
;
.
Отсюда следует, что умножение матриц обладает рядом свойств, не характерных для умножения действительных чисел, поэтому при действиях с матрицами необходимо проявлять осмотрительность и аккуратность.
В заключение, отметим свойства, присущие операции транспонирования:
1) ;
2) ;
3) .
Возведение в степень
На основе определения произведения матриц умножать матрицу А на себя можно только в том случае, если это квадратная матрица.
Пусть k — целое неотрицательное число, тогда k-й степенью квадратной матрицы А называется матрица, которая вычисляется следующим образом:
Пример. Найти куб матрицы .
;
.
Контрольные вопросы
-
Что называется матрицей? Перечислите виды матриц.
-
Какую роль в линейной алгебре играют единичная и нулевая матрицы?
-
Какая матрица называется диагональной?
-
Дайте определение квадратной матрицы.
-
Какая матрица называется транспонированной по отношению к данной?
-
Для каких матриц определена операция сложения?
-
Перечислите основные свойства сложения матриц.
-
Какие матрицы называются коммутирующими между собой?
-
Для каких матриц определена операция умножения?
-
Перечислите основные свойства умножения матриц.
Задания для самостоятельной работы
Задание 1. Примеры для самоподготовки
(действия над матрицами)
-
Найти сумму матриц
+
Ответ.
-
Найти сумму матриц
+
Ответ.
-
Найти сумму матриц
+
Ответ.
-
Найти разность матриц
—
Ответ.
-
Найти разность матриц
—
Ответ.
-
Найти произведение действительного числа на матрицу
Ответ.
-
Найти произведение действительного числа на матрицу
Ответ.
-
Найти произведение матриц
∙
Ответ.
-
Найти произведение матриц
∙
Ответ.
-
Найти произведение матриц
∙
Ответ.
Задание 2. Примеры для самопроверки
(отметьте правильный вариант ответа)
-
Найти сумму матриц
+
1) ;
2) ;
3) ;
4) ;
5)
-
Найти сумму матриц
+
1) ;
2) ;
3) ;
4) ;
5) .
-
Найти сумму матриц
+
1) ;
2) ;
3) ;
4) ;
5)
-
Найти разность матриц
—
1) ;
2) ;
3)
4) ;
5)
-
Найти разность матриц
—
1) ;
2) ;
3) ;
4) ;
5) .
-
Найти разность матриц
—
1) ;
2) ;
3) ;
4) ;
5) .
-
Найти произведение действительного числа на матрицу
1) ;
2) ;
3) ;
4) ;
5) .
-
Найти произведение действительного числа на матрицу
1) ;
2) ;
3) ;
4) ;
5) .
-
Найти произведение действительного числа на матрицу
1) ;
2) ;
3) ;
4) ;
5) .
-
Найти произведение матриц
∙
1) ;
2) ;
3) ;
4) ;
5) .
-
Найти произведение матриц
∙
1) ;
2) ;
3) ;
4) ;
5) .
-
Найти произведение матриц
∙
1) ;
2) ;
3) ;
4) ;
5) .
-
Найти произведение матриц
∙
1) ;
2) ;
3) ;
4) ;
5) .
-
Найти произведение матриц
∙
1) ;
2) ;
3) ;
4) ;
5) .
-
Найти произведение матриц
∙
1) ;
2) ;
3) ;
4) ;
5) .
-
Найти произведение матриц
∙ :
1) ;
2) ;
3) ;
4) ;
5) .
Матрицы. Определение, виды и основные понятия | Математика
Определение матрицы
Матрицей называется прямоугольная таблица, составленная из чисел.
Для обозначения матрицы применяются круглые скобки и прописные буквы А, В, С и так далее.
Например,
| (1.1) |
есть общий вид записи матрицы из чисел.
Числа составляющие матрицу, называются ее элементами.
Помощь с решением задач
Горизонтальные ряды матрицы называются строками матрицы, вертикальные — столбцами.
Индексы у элемента , где
означают, что этот элемент расположен в i-й строке и j-м столбце.
Например, элемент расположен во второй строке и в третьем столбце.
Числа и , указывающие количество строк и столбцов матрицы, называются размерами матрицы.
Наряду с обозначением (1.1) матрица обозначается также в форме:
| (1.2) |
,где
Виды матриц
Матрица, у которой число строк равно числу ее столбцов называется квадратной матрицей.
При этом число ее строк (столбцов) называется порядком матрицы.
Например, матрица есть квадратная матрица третьего порядка.
Квадратная матрица n-го порядка записывается в виде
| (1.3) |
В квадратной матрице (1.3) числа образуют главную диагональ матрицы, а числа побочную диагональ.
Квадратная матрица, у которой все числа, не стоящие на главной диагонали, равны нулю, называется диагональной матрицей.
Например, матрица есть диагональная матрица второго порядка.
Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной матрицей. Единичную матрицу обозначают прописной буквой Е.
Например, матрица есть единичная матрица второго порядка.
Матрица, состоящая только из одной строки, называется матрицей-строкой, состоящая только из одного столбца матрицей — столбцом.
Например, матрица А=(2 О 5 4) есть матрица — строка.
Матрица называется транспонированной по отношению к матрице А, если столбцы (строки) матрицы являются соответствующими строчками (столбцами) матрицы .
Например, если матрица равна
, то
- Действия над матрицами
- Курс математики
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
Скачать рамки A4
Скачать миллиметровки
Скачать шрифты ГОСТ
Сохранить или поделиться с друзьями
Заказать решение
Поиск математических формул
Матрицы: что такое, понятия, типы, применение
- Ферровиал
- СТЕРЖЕНЬ
Матрицы представляют собой двумерный набор чисел или символов , распределенных в прямоугольной форме по вертикальным и горизонтальным линиям так, что их элементы расположены в строках и столбцах.
Они полезны для описания систем линейных или дифференциальных уравнений, , а также представляет собой линейное приложение.
Каждая матрица представлена заглавной буквой , , а ее элементы указаны строчными буквами в списке, заключенном в круглые или квадратные скобки. Каждый, в свою очередь, имеет двойной верхний индекс: первый относится к строке, а второй — к столбцу, которому он принадлежит.
Это математическое выражение можно складывать, умножать и разлагать, поэтому оно обычно используется в линейной алгебре .
Какие понятия связаны с матрицами?Некоторые понятия, необходимые для завершения определения и анализа матриц:
- Элементы: числа, составляющие матрицу.
- Измерение: результат умножения количества строк на количество столбцов. Буква м используется для обозначения числа рядов и n для числа столбцов.
- Кольца : этот алгебраический термин относится к системе, образованной набором внутренних операций, которые реагируют на набор свойств. Под матрицами понимаются элементы кольца.
- Функция: правило соответствия между двумя множествами, в котором элемент первого множества соответствует исключительно одному элементу второго множества.
Матрица может быть:
- Прямоугольной: имеет разное количество строк и столбцов.
- Ряд: прямоугольный массив с одной строкой.
- Столбец: прямоугольная матрица с одним столбцом.
- Null: массив, содержащий нулевые элементы.
- Квадрат порядка n : матрица, имеющая такое же количество строк, как и столбцов. В матрице такого типа размерность называется порядком , а ее значение совпадает с количеством строк и столбцов.
- Диагональ: разновидность квадратной матрицы, в которой элементы, не расположенные на главной диагонали, равны нулю.
- Скаляр: диагональная матрица, в которой все элементы на главной диагонали равны.
- Идентичность: это скалярная матрица, в которой элементы главной диагонали равны единице, а все остальные элементы равны нулю.
- Инверсия: противоположность другой матрицы, элементы которой имеют знаки, противоположные основной матрице. То есть матрица, обратная матрице А, называется -А, а все элементы множества противоположны элементам матрицы А.
- Транспонирование: матрица, полученная при преобразовании строк в столбцы. Верхний индекс t используется для его представления, а его размерность n x m .
- Верхняя треугольная: это квадратная матрица, в которой хотя бы одно из слагаемых выше главной диагонали не равно нулю, а все члены ниже главной диагонали равны нулю.
- Нижняя треугольная: В отличие от предыдущего типа, этот тип матрицы имеет хотя бы один элемент ниже главной диагонали, который отличен от нуля, а все те, что выше главной диагонали, равны нулю.
Матрицы имеют множество применений, особенно , представляющие коэффициенты в системах уравнений или линейных приложениях ; матрица может выполнять ту же функцию, что и векторные данные в линейной системе приложения. В зависимости от этого к некоторым приложениям относятся:
- В информатике: одна из областей, где матрицы наиболее часто используются, учитывая их эффективность при работе с информацией. Матрицы идеально подходит для графических представлений и , анимирующих фигуры .
- В робототехнике: матрицы используются для программирования роботов , которые могут выполнять различные задачи. Одним из примеров этого является бионическая рука , которая может использовать программируемые механические процессы для выполнения функций, аналогичных функциям человеческой руки. Все это программирование — результат вычислений с использованием матриц.
Одним из примеров этого является бионическая рука , которая может использовать программируемые механические процессы для выполнения функций, аналогичных функциям человеческой руки. Все это программирование — результат вычислений с использованием матриц.Загрузите здесь PDF-файл со всем содержанием математики.
Гугл игры Магазин приложений- Ресурсы
- Связаться с нами
- СТЕРЖЕНЬ
- Доступность
- Официальное уведомление
- Политика конфиденциальности
- Политика в отношении файлов cookie
- Твиттер
- Линкедин
- Фейсбук
- Инстаграм
- ТИК Так
- Пинтерест
- YouTube
Матрицы — SAT II Math I
Все ресурсы SAT II Math I
6 Диагностические тесты 113 практических тестов Вопрос дня Карточки Учитесь по концепции
← Предыдущая 1 2 Следующая →
SAT II Math I Help » Математические отношения » Матрицы
Определить .
Дать.
Возможные ответы:
не определено.
Правильный ответ:
не определено.
Объяснение:
Обратной матрицей 2 x 2, если она существует, является матрица
Во-первых, нам нужно установить, что обратное определено, что оно является тогда и только тогда, когда определитель .
Установить и проверить:
Определитель равен 0, поэтому не имеет обратного.
Сообщить об ошибке
Укажите определитель матрицы
Возможные ответы:
Правильный ответ:
Пояснение:
Определитель матрицы равен
.
Заместитель:
Отчет о ошибке
Упрощайте:
Возможные ответы:
Правильный ответ:
Объяснение:
Сложение матриц очень просто! Все, что вам нужно сделать, это добавить каждый корреляционный элемент друг к другу.
Подумайте об этом так:
Теперь просто упростите:
Вот ваш ответ!
Сообщить об ошибке
Упрощение:
Возможные ответы:
Правильный ответ:
Пояснение:
Сложение матриц очень просто — не переусердствуйте! Все, что вам нужно сделать, это объединить две матрицы по принципу один к одному для каждого индекса:
Затем просто упростите все эти простые сложения и вычитания:
Сообщить об ошибке
Оценить:
Возможные ответы:
Правильный ответ:
Объяснение:
В этой задаче используется скалярное умножение на матрицу. Просто распределите отрицательную тройку и умножьте это значение на каждое число в матрице 2 на 3.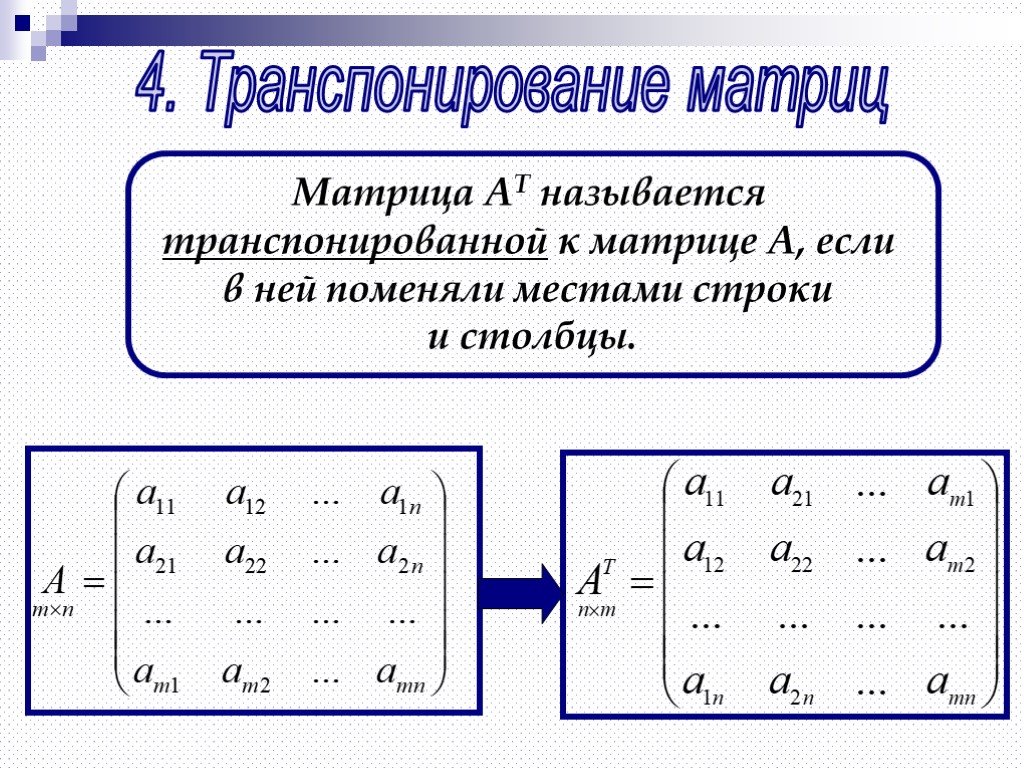
Строки и столбцы не изменятся.
Сообщить об ошибке
Упрощение:
Возможные ответы:
Правильный ответ:
Объяснение:
Скалярное умножение и сложение матриц очень просты. Как и в случае с обычными скалярными значениями, вы сначала выполняете умножение:
Сложение матриц очень просто. Вам просто нужно добавить их непосредственно вместе, напрямую соотнеся пробелы.
Сообщить об ошибке
Что такое ?
Возможные ответы:
Правильный ответ:
Объяснение:
Вы можете начать с обработки этого уравнения так, как оно было:
То есть вы можете разделить обе части на :
Теперь, для скалярного умножения матриц, вам просто нужно умножить скаляр на каждый компонент:
Тогда упростите:
Следовательно,
Сообщите об ошибке
Учитывая следующие матрицы, каково произведение и ?
Возможные ответы:
Правильный ответ:
Объяснение:
При вычитании матриц вы хотите вычесть каждую соответствующую ячейку.
Теперь решайте и
Отчет о ошибке
, если?
Возможные ответы:
Правильный ответ:
Объяснение:
С матрицами можно обращаться так же, как с другими членами уравнения. Следовательно, вы можете вычесть матрицу
из обеих частей уравнения. Это дает вам:
Теперь матричное вычитание очень просто. Вы просто вычитаете каждый элемент, сопоставляя соответствующие пробелы друг с другом:
Тогда вы упрощаете:
Следовательно,
Отчет о ошибке
Упрощение:
Возможные ответы:
Правильный ответ:
02 Объяснение:
Размеры матриц 2 на 2.