Механика физика кинематика: Механика. Раздел кинематика – движение тел

Физика механика кинематика

yurii Фев 25, 2023

Вид материала

Закон

Законы сохранения в механике. Механика жидкостей и газов. Молекулярная физика. термодинамика Основы термодинамики. Идеальный газ. Жидкости и твердые тела. Основы электродинамики Постоянный электрический ток Магнитное поле, электромагнитная индукция. Колебания и волны Звук Электромагнитные колебания и волны. Основы специальной теории относительности Квантовая физика

Подобный материал:

• Учебник Физика 10, С. В. Громов механика I полугодие Кинематика, 152.44kb.
• Рабочая программа по дисциплине «Теоретическая механика и основы механики сплошных, 254.51kb.
• Учебная программа дисциплины физика (название), 122.36kb.
• Рабочая программа утверждаю: по курсу общей физики (механика, молекулярная физика, 80. 5kb.
• Программа подраздела «История механики», 75.11kb.
• Программа-минимум кандидатского экзамена по специальности 01. 04. 02 «Теоретическая, 115.8kb.
• Тематическое планирование учебного материала по физике в 10 кл Учебник: Г. Я. Мякишев,, 155.64kb.
• Программа по физике для 10-11 классов общеобразовательных, 75.87kb.
• Рабочая программа учебной дисциплины «Физика конденсированного состояния, термодинамика,, 223.9kb.
• Программа для поступающих на направление подготовки магистратратуры 011200 «физика», 54.39kb.

ФИЗИКА

МЕХАНИКА

Кинематика. Механическое движение. Относительность движе­ния. Система отсчета. Материальная точка. Траектория. Путь и пере­мещение. Скорость. Ускорение.

Равномерное и равноускоренное прямолинейное движение. Сво­бодное падение тел. Ускорение свободного падения. Уравнение прямо­линейного равноускоренного движения.

Криволинейное движение точки на примере движения по окруж­ности с постоянной по модулю скоростью.

Центростремительное ускорение.

Основы динамики. Инерция. Первый закон Ньютона. Инерциальные системы отсчета.

Взаимодействие тел. Масса. Импульс. Сила. Второй закон Ньюто­на. Принцип суперпозиции сил. Принцип относительности Галилея.

Силы в природе. Сила тяготения. Закон всемирного тяготения. Вес тела. Невесомость. Первая космическая скорость. Сила упругости. За­кон Гука. Сила трения. Коэффициент трения. Закон трения скольжения.

Третий закон Ньютона.

Момент силы. Условие равновесия тел.

Законы сохранения в механике. Закон сохранения импульса. Ра­кеты.

Механическая работа. Мощность. Кинетическая энергия. Потенци­альная энергия. Закон сохранения энергии в механике. Простые меха­низмы. Коэффициент полезного действия механизма.

Механика жидкостей и газов. Давление.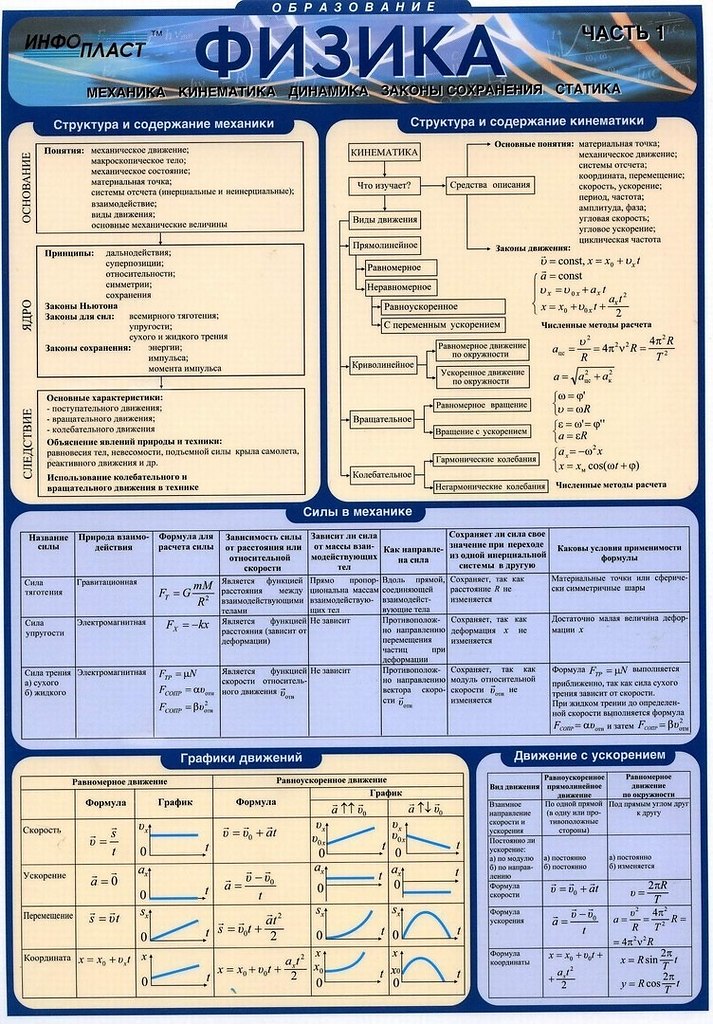 Атмосферное давление. Изменение атмосферного давления с высотой. Закон Паскаля для жид­костей и газов. Барометры и манометры. Сообщающиеся сосуды. Принцип устройства гидравлического пресса.

Архимедова сила для жидкостей и газов. Условия плавания тел на поверхности жидкости.

Движение жидкости по трубам. Зависимость давления жидкости от

скорости ее течения.

Измерение расстояний, промежутков времени, силы, объёма, мас­сы, атмосферного давления.

МОЛЕКУЛЯРНАЯ ФИЗИКА. ТЕРМОДИНАМИКА

Основы молекулярно-кинетической теории. Опытное обоснова­ние основных положений молекулярно-кинетической теории. Броунов­ское движение. Диффузия. Масса и размер молекул. Измерение скоро­сти молекул. Опыт Штерна. Количество вещества. Моль. Постоянная Авогадро. Взаимодействие молекул. Модели газа, жидкости и твёрдого тела.

Основы термодинамики. Тепловое равновесие. Температура и её измерение. Абсолютная температурная шкала. Внутренняя энергия. Количество теплоты.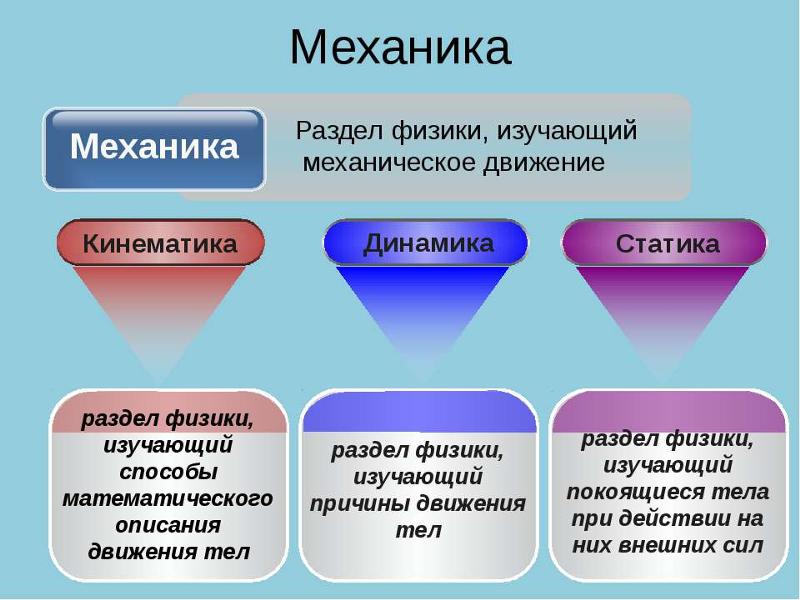 Теплоемкость вещества. Работа в термодинамике. Первый закон термодинамики. Изотермический, изохорный и изобар­ный процессы. Адиабатный процесс.

Необратимость тепловых процессов. Второй закон термоди­намики и его статистическое истолкование. Преобразование энергии в тепловых двигателях. КПД теплового двигателя.

Идеальный газ. Связь между давлением и средней кинетической энергией молекул идеального газа. Связь температуры со средней кине­тической энергией частиц газа.

Уравнение Клапейрона-Менделеева. Универсальная газовая посто­янная.

Жидкости и твердые тела. Испарение и конденсация. Насыщен­ные и ненасыщенные пары. Влажность воздуха. Кипение жидкости.

Кристаллические и аморфные тела. Преобразование энергии при изменениях агрегатного состояния вещества.

Измерение давления газа, влажности воздуха, температуры, плотности вещества.

ОСНОВЫ ЭЛЕКТРОДИНАМИКИ

Электростатика. Электризация тел. Электрический заряд. Взаи­модействие зарядов. Элементарный электрический заряд. Закон сохра­нения электрического заряда. Закон Кулона.

Электрическое поле. Напряженность электрического поля. Элек­трическое поле точечного заряда. Потенциальность электростати­ческого поля. Разность потенциалов. Принцип суперпозиции по­лей.

Проводники в электрическом поле. Электрическая ёмкость. Кон­денсатор. Емкость плоского конденсатора.

Диэлектрики в электрическом поле. Диэлектрическая прони­цаемость. Энергия электрического поля плоского конденсатора.

Постоянный электрический ток. Электрический ток. Сила тока. Напряжение. Носители свободных электрический зарядов в металлах, жидкостях и газах. Сопротивление проводников. Закон Ома для участка цепи. Последовательное и параллельное соединение проводников. Электродвижущая сила. Закон Ома для полной цепи. Работа и мощ­ность тока. Закон Джоуля-Ленца.

Полупроводники. Собственная и примесная проводимость полу­проводников, p-n-переход.

Магнитное поле, электромагнитная индукция.

Взаимодействие магнитов. Взаимодействие проводников с током. Магнитное поле. Действие магнитного поля на электрические заряды. Индукция магнит­ного поля. Сила Ампера. Сила Лоренца. Магнитный поток. Электро­двигатель.

Электромагнитная индукция. Закон электромагнитной индукции Фарадея. Правило Ленца. Вихревое электрическое поле. Самоиндукция. Индуктивность. Энергия магнитного поля.

Измерение силы тока, напряжения, сопротивления проводника.

КОЛЕБАНИЯ И ВОЛНЫ

Механические колебания и волны. Гармонические колебания. Амплитуда, период и частота колебаний. Свободные колебания. Мате­матический маятник. Период колебаний математического маятника.

Превращение энергии при гармонических колебаниях. Вы­нужденные колебания. Резонанс. Понятие об автоколебаниях.

Механические волны. Скорость распространения волны. Длина волны. Поперечные и продольные волны. Уравнение гармонической волны.

Звук

Электромагнитные колебания и волны. Колебательный контур. Свободные электромагнитные колебания в контуре. Превращение энер­гии в колебательном контуре. Собственная частота колебаний в кон­туре. Вынужденные электрические колебания. Переменный электриче­ский ток. Генератор переменного тока. Действующие значения силы тока и напряжения. Активное, емкостное и индуктивное сопротивле­ния. Резонанс в электрической цепи.

Трансформатор. Производство, передача и потребление электриче­ской энергии.

Идеи теории Максвелла. Электромагнитные волны. Скорость рас­пространения электромагнитных волн. Свойства электромагнитных волн. Принципы радиосвязи. Шкала электромагнитных волн.

ОПТИКА

Свет – электромагнитная волна. Прямолинейное распространение, отражение и преломление света. Луч. Законы отражения и преломления света. Показатель преломления. Полное отражение. Предельный угол полного отражения. Ход лучей в призме. Построение изображений в плоском зеркале.

Собирающая и рассеивающая линзы. Формула тонкой линзы.

Построение изображений в линзах. Фотоаппарат. Глаз. Очки. Ин­терференция света. Когерентность. Дифракция света. Дифракционная решетка. Поляризация света. Поперечность световых волн.

Дисперсия света. Измерение фокусного расстояния собирающей, линзы, показате­ля преломления вещества, длины волны света.

ОСНОВЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ

Инвариантность скорости света. Принцип относительности Эйн­штейна. Пространство и время в специальной теории относительности. Связь массы и энергии.

КВАНТОВАЯ ФИЗИКА

Тепловое излучение. Постоянная Планка. Фотоэффект. Опыты Столетова. Уравнение Эйнштейна для фотоэффекта.

Гипотеза Луи де Бройля. Дифракция электронов. Корпускулярно-волновой дуализм.

Радиоактивность. Альфа-, бета-, гамма-излучения. Методы наблю­дения и регистрации частиц в ядерной физике.

Опыт Резерфорда по рассеянию α-частиц. Планетарная модель атома. Боровская модель атома водорода. Спектры. Люминесценция.

Лазеры.

Закон радиоактивного распада. Нуклонная модель ядра. Заряд яд­ра. Массовое число ядра. Энергия связи частиц в ядре. Деление ядер. Синтез ядер. Ядерные реакции. Сохранение заряда и массового числа при ядерных реакциях. Выделение энергии при делении и синтезе ядер. Использование ядерной энергии. Дозиметрия.

Элементарные частицы. Фундаментальные взаимодействия.

МЕТОДЫ НАУЧНОГО ПОЗНАНИЯ

И ФИЗИЧЕСКАЯ КАРТИНА МИРА

Эксперимент и теория в процессе познания мира. Моделирование явлений и объектов природы. Научные гипотезы. Физические законы и границы их применимости. Роль математики в физике. Принцип соот­ветствия. Принцип причинности. Физическая картина мира.

2.1. Кинематика. Механика. Физика. Курс лекций

2.1.1. Механическое движение. Физические модели реальных тел, используемые в механике. Система отсчета. Траектория. Виды движений

2.1.2. Кинематические уравнения движения. Длина пути и вектор перемещения

2. 1.3. Кинематические характеристики. Скорость

2.1.4. Кинематические характеристики. Ускорение

2.1.5. Поступательное и вращательное движение твердого тела

2.1.6. Связь между кинематическими характеристиками при различных видах движений

2.1.1. Механическое движение. Физические модели реальных тел, используемые в механике. Система отсчета. Траектория. Виды движений

1. Механическое движение – изменение положения тела или отдельных его частей в пространстве с течением времени.

Внутреннее строение движущихся тел, их химический состав не влияет на механическое движение. Для описания движения реальных тел в зависимости от условий задачи пользуются различными моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело и т.д.

Материальной точкой называется тело, размерами и формой которого можно пренебречь в условиях данной задачи. В дальнейшем вместо термина “материальная точка” будем употреблять термин “точка”. Одно и то же тело можно свести к материальной точке в одной задаче, и необходимо учитывать его размеры в условиях другой задачи. Например, расчет движения самолета, летящего над Землей, можно производить, считая его материальной точкой. А при расчете обтекания воздухом крыла того же самолета надо учитывать форму и размеры крыла.

Любое протяженное тело можно рассматривать как систему материальных точек.

Абсолютно твердое тело (а.т.т.) – тело, деформацией которого можно пренебречь в условиях данной задачи. А.т.т. можно рассматривать как систему жестко связанных между собой материальных точек, т.к. расстояние между ними не изменяются при любых взаимодействиях.

Абсолютно упругое тело – тело, деформация которого подчиняется закону Гука (см. § 2.2.2.), и после прекращения силового воздействия оно полностью восстанавливает первоначальные размеры и форму.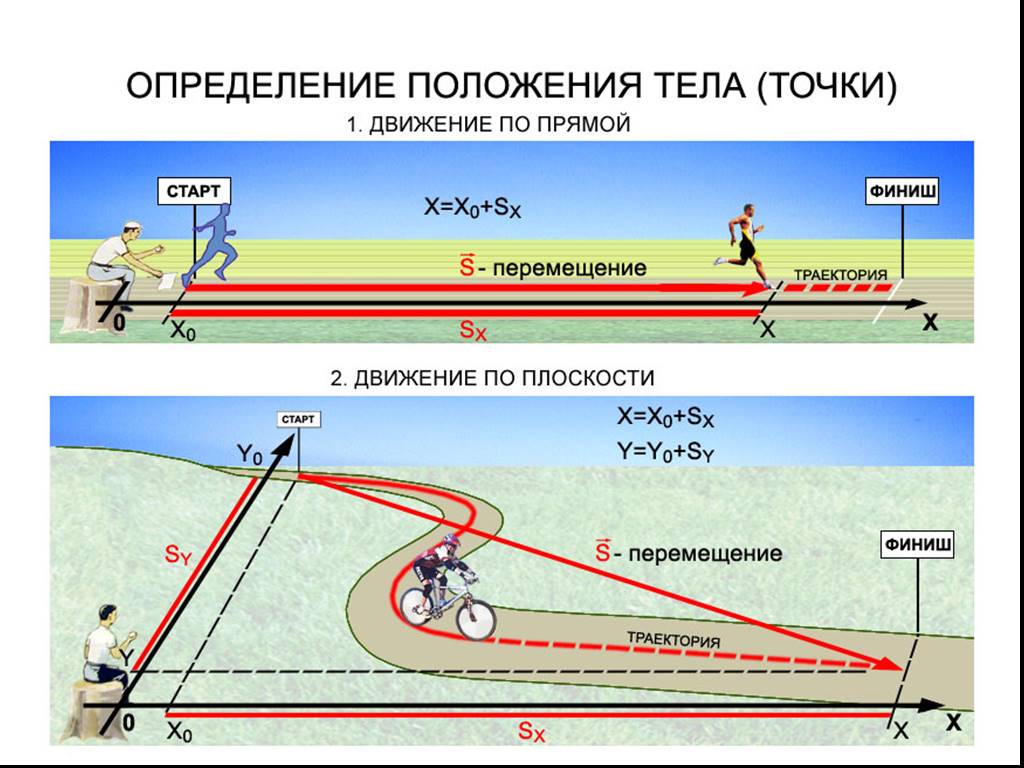

Абсолютно неупругое тело – тело, которое после прекращения силового воздействия на него не восстанавливается, а полностью сохраняет деформированное состояние.

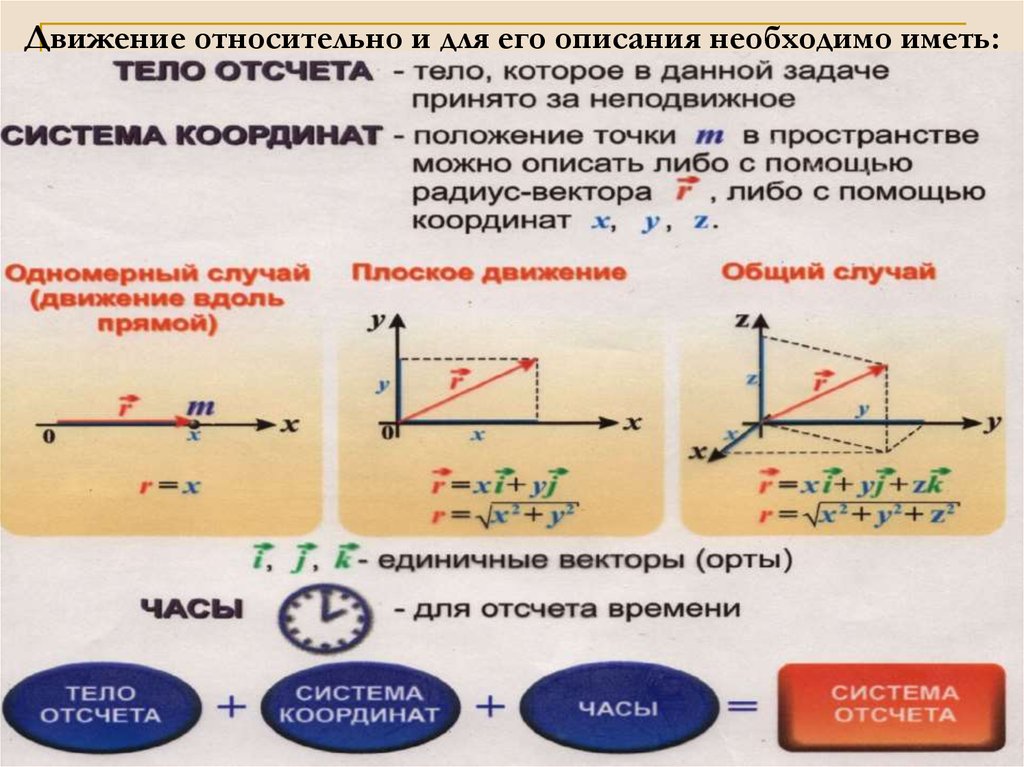
2. Для определения положения тела в пространстве и во времени надо ввести понятие системы отсчета. Выбор системы отсчета произволен.

Системой отсчета называется тело или группа тел, считающиеся условно неподвижными и снабженные устройством отсчета времени (часами, секундомером и т.д.), относительно которых рассматривается движение данного тела.

Неподвижное тело (или группу тел) называют телом отсчета и для удобства описания движения с ним связывают систему координат (декартову, полярную, цилиндрическую и т.д.).

Выберем в качестве системы координат декартову прямоугольную систему XYZ (подробно см.[8]). Положение точки С в пространстве можно определить координатами х, y, z (Рисунок 1).

Рисунок 1 – Определение положения точки в декартовой системе координат

Однако положение той же точки в пространстве можно задать с помощью одной векторной величины r = r(x, y, z), называемой радиус-вектором точки С (Рисунок 1).

3. Линия, которую тело описывает при своем движении, называется траекторией. По виду траектории движения можно разделить на прямолинейные и криволинейные. Траектория зависит от выбора системы отсчета. Так, траектория движения точек винта самолета относительно летчика – окружность, а относительно Земли – винтовая линия. Другой пример: какова траектория движения кончика иглы проигрывателя относительно пластинки? корпуса проигрывателя? корпуса звукоснимателя? Ответы таковы: спираль, дуга окружности, состояние покоя (игла неподвижна).

2.1.2. Кинематические уравнения движения. Длина пути и вектор перемещения

1. При движении тела относительно выбранной системы координат его положение изменяется с течением времени.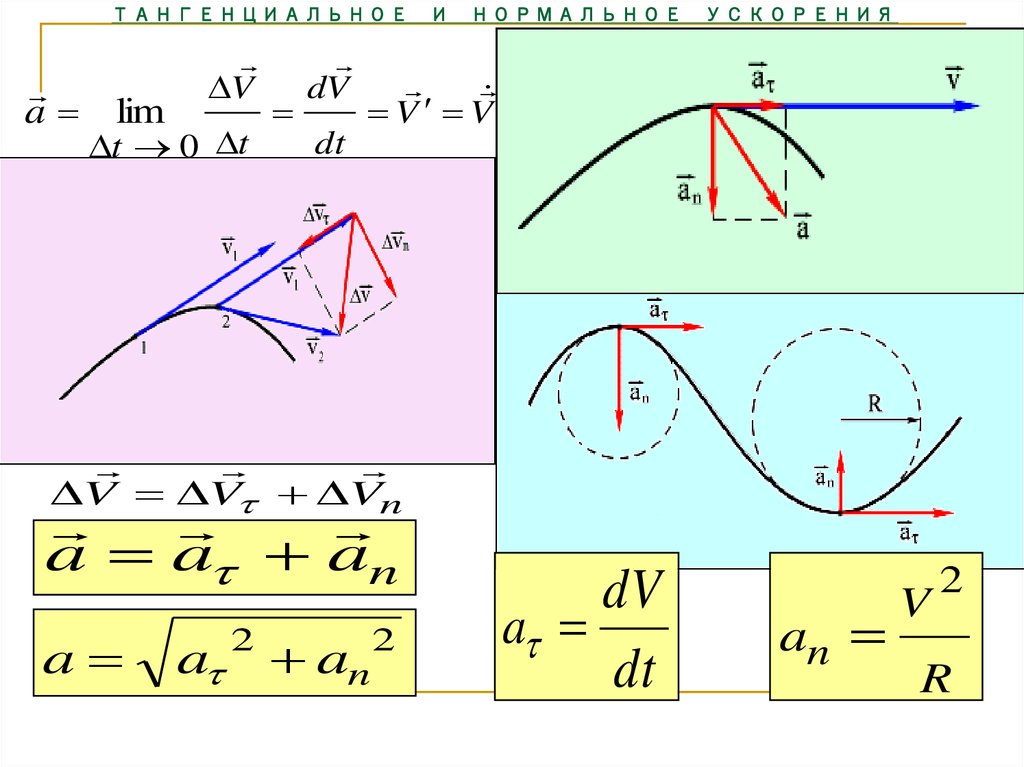 Движение материальной точки будет полностью определено, если заданы непрерывные и однозначные функции времени t:

x = x(t), y = y(t), z = z(t).

Эти уравнения описывают изменение координат точки от времени и называются кинематическими уравнениями движения.

2. Путь – часть траектории, пройденной телом за определенный промежуток времени. Момент времени t₀, от которого начинается его отсчет, называется начальным моментом времени, обычно t₀=0 в силу произвольного выбора начала отсчета времени.

Длиной пути называется сумма длин всех участков траектории. Длина пути не может быть величиной отрицательной, она всегда положительна. Например, материальная точка переместилась из точки траектории С сначала в точку А, а затем в точку В (Рисунок 1). Длина ее пути равна сумме длин дуги СА и дуги АВ.

2.1.3. Кинематические характеристики. Скорость

1. Для характеристики быстроты движения тел в физике вводится понятие скорости. Скорость – вектор, а значит, характеризуется величиной, направлением, точкой приложения.

Рассмотрим движение вдоль оси Х. Положение точки будет определяться изменением со временем координаты Х.

Если за время ∆ произошло перемещение точки на ∆r, то величина является средней скоростью движения: .

Средней скоростью движущегося тела называется вектор, равный отношению вектора перемещения к величине промежутка времени, за которое это перемещение произошло.

Модуль средней скорости есть физическая величина, численно равная изменению пути за единицу времени.

2. Для определения скорости в данный момент времени, мгновенной скорости, нужно рассмотреть интервал времени ∆t→0, тогда

Используя понятие производной, можно записать для скорости

Скорость тела в данный момент времени называется мгновенной скоростью (или просто скоростью).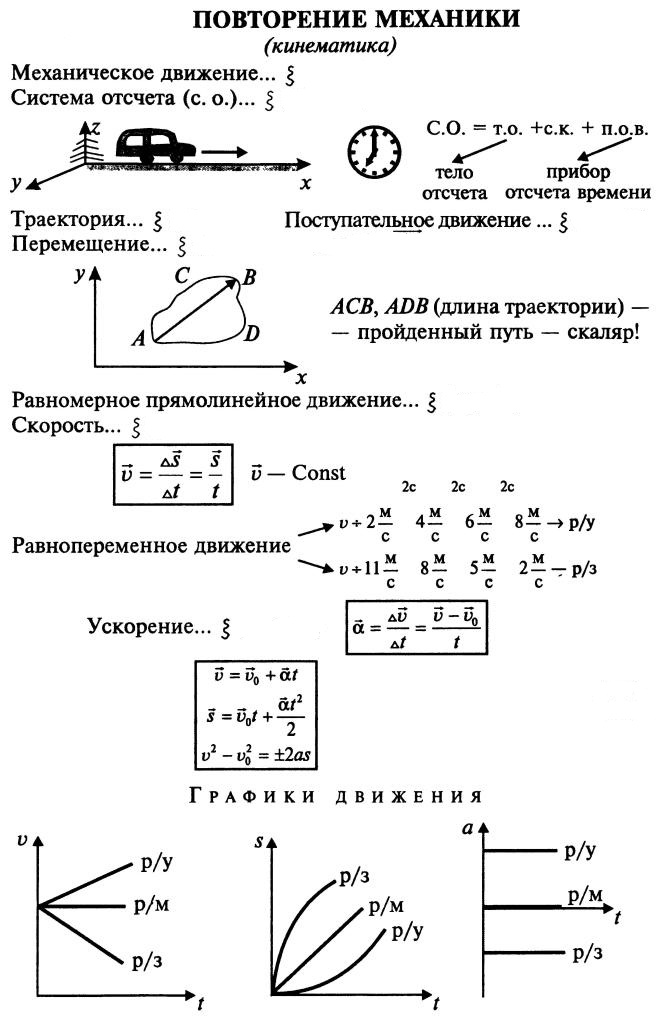

Вектор V мгновенной скорости направлен по касательной к траектории в сторону движения тела.

2.1.4. Кинематические характеристики. Ускорение

1. Быстрота изменения вектора скорости характеризуется величиной, называемой ускорением. Ускорение может возникнуть как за счет изменения величины скорости, так и за счет изменения направления скорости.

Пусть в момент времени t скорость тела равна v₁, а через промежуток времени ∆t в момент времени t + ∆t равна v₂, приращение вектора скорости за ∆t равно ∆v.

Средним ускорением тела в интервале времени от t до t + ∆t называется вектор а_ср, равный отношению приращения вектора скорости ∆v к промежутку времени ∆t:

Cреднее ускорение есть физическая величина, численно равная изменению скорости за единицу времени.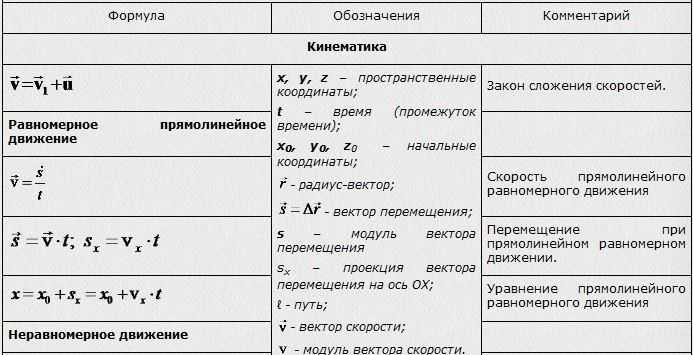

2. Для определения ускорения в данный момент времени, т.е. мгновенного ускорения, нужно рассмотреть малый интервал времени ∆t→0. Тогда вектор мгновенного ускорения равен пределу вектора среднего ускорения при стремлении промежутка времени ∆t к нулю:

Используя понятие производной, можно дать для ускорения следующее определение: Ускорением (или мгновенным ускорением) тела называется векторная величина а, равная первой производной по времени от скорости тела v или второй производной по времени от пути.

3. При вращении точки по окружности ее скорость может изменяться по величине и по направлению (рисунок 2)

Рисунок 2 – Изменение скорости точки при вращении по окружности

На рисунке 2 в положении 1 скорость точки v_1, в положении 2 скорость точки v₂. Модуль скорости v₂ больше модуля скорости v₁ , ∆v– вектор изменения скорости ∆v = v₂ –v₁

Вращающаяся точка имеет тангенциальное ускорение, равное а_τ=dv/dt, оно изменяет скорость по величине и направлено по касательной к траектории; и нормальное ускорение, равное а_n= v²/R, оно меняет направление скорости и направлено по радиусу окружности (R) (см. Pисунок 3)

Рисунок 3 – Полное, тангенциальное и нормальное ускорения вращающейся точки

Вектор полного ускорения равен , т.е. он может быть представлен как сумма векторов тангенциального a_τ и нормального a_n ускорений. Модуль полного ускорения равен:

2.1.5. Поступательное и вращательное движение абсолютно твердого тела

1. До сих пор речь шла о характере движения, о траектории, о кинематических характеристиках, но не рассматривалось само движущееся тело. Пример. Движется автомобиль. Он является сложным телом. Движения его кузова и колес различны. Если тело сложное, то возникает вопрос: к движению каких частей тела относятся понятия пути, скорости, ускорения, введенные ранее?

Прежде, чем ответить на этот вопрос, надо выделить формы механического движения. Каким бы сложным не было движение тела, его можно свести к двум основным: поступательному движению и вращению вокруг неподвижной оси. Колебательное движение будет рассмотрено отдельно. В примере с автомобилем поступательно движется кузов автомобиля. Сам автомобиль является телом, которое может быть рассмотрено с помощью модели абсолютно твердого тела (а.т.т.). Для краткости мы будем называть абсолютно твердое тело просто твердое тело.

Поступательным движением твердого тела называется движение, при котором любая прямая, проведенная между его двумя точками, остается при движении параллельна самой себе.

Поступательное движение может быть и не прямолинейным движением.

Примеры. 1) В аттракционе “Колесо обозрения” кабинки – люльки, в которых сидят люди, двигаются поступательно. 2) Если стакан с водой перемещать по траектории, представленной на рисунке 5 так, чтобы поверхность воды и направляющая стакана составляли бы прямой угол, то движение стакана является не прямолинейным, но поступательным. Прямая АВ остается при движении стакана параллельна самой себе.

Рисунок 4 – Пример поступательного движения твердого тела.

Особенностью поступательного движения твердого тела является то, что все точки тела описывают одинаковую траекторию, проходят за определенные промежутки времени ∆t одинаковые пути и в любой момент времени имеют одинаковые скорости. Поэтому кинематическое рассмотрение поступательного движения твердого тела сводится к изучению движения любой из его точек. Поступательное движение тела может быть сведено к движению материальной точки.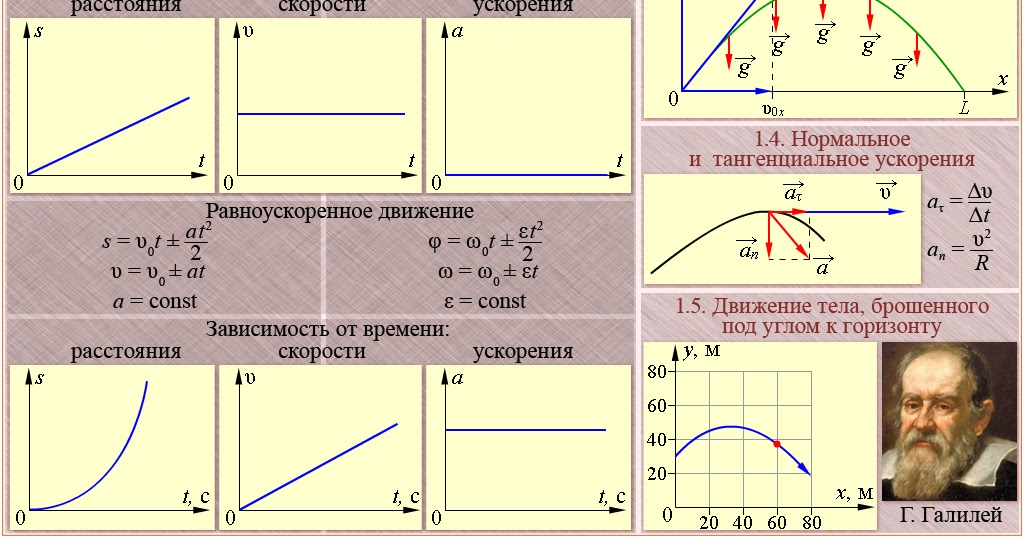 В динамике обычно за такую точку принимают центр масс тела. Кинематические характеристики и кинематические уравнения, вводимые для материальной точки, описывают и поступательное движение твердого тела.

2. Движение колес автомобиля отличается от движения кузова. Точки колеса, находящиеся на разных расстояниях от его оси, описывают разные траектории, проходят различные пути и имеют разные скорости. Чем дальше точка находится от оси колеса, тем больше ее скорость, тем больший путь она проходит за определенный промежуток времени. Движение, в котором участвуют колеса автомобиля, называется вращательным. Ясно, что модель материальной точки для описания вращения реального тело не подходит. Но и здесь вместо реального тела (например, колеса автомобиля с деформируемыми шинами и т.д.) используют физическую модель – абсолютно твердое тело.

Вращательным движением твердого тела называется движение, когда все точки тела описывают окружности, центры которых лежат на прямой, называемой осью вращения и перпендикулярной к плоскостям, в которых вращаются точки тела (Рисунок 5).

Так как для разных точек вращающегося тела траектории, пути, скорости различны, то встает вопрос: можно ли найти физические величины, которые имели бы одинаковые значения для всех точек вращающегося тела, Да, оказывается, есть такие величины, они называются угловыми.

Рисунок 5 – Вращение твердого тела

Твердое тело, вращающееся вокруг неподвижной оси, имеет одну степень свободы, его положение в пространстве полностью определяется значением угла поворота ∆φ из некоторого начального положения (Рисунок 5). Все точки твердого тела повернутся за промежуток времени ∆ на угол ∆φ.

При малых промежутках времени, когда углы поворота невелики, их можно рассматривать как векторы, хотя и не совсем обычные. Вектор элементарного (бесконечно малого) угла поворота ∆φ направлен вдоль оси вращения по правилу правого буравчика, его модуль равен углу поворота (Рисунок 5). Вектор ∆φ называется угловым перемещением.

Правило правого буравчика заключается в следующем:

Если рукоятка правого буравчика вращается вместе с телом (точкой), то поступательное движение буравчика совпадает с направлением ∆φ.

Другая формулировка правила: Из конца вектора ∆φ видно, что движение точки (тела) происходит против часовой стрелки.

Положение тела в любой момент времени t определяется кинематическим уравнением вращательного движения ∆φ = ∆φ(t).

3. Для характеристики быстроты вращения служит угловая скорость.

Средней угловой скоростью называется физическая величина, равная отношению углового перемещения к промежутку времени, за которое это перемещение произошло

Предел, к которому стремится средняя угловая скорость при ∆→0, называется мгновенной угловой скоростью тела в данный момент времени или просто угловой скоростью вращения твердого тела (точки).

Угловая скорость равна первой производной от углового перемещения по времени. Направление мгновенной угловой скорости определяется по правилу правого буравчика и совпадает с направлением ∆φ (Рисунок 6). Кинематическое уравнение движения для угловой скорости имеет вид ω = ω (t).

Рисунок 6 – Направление векторов угловых характеристик при вращательном движении.

4. Для характеристики быстроты изменения угловой скорости тела при неравномерном вращении вводится вектор углового ускорения β, равный первой производной от его угловой скорости ω по времени t.

Среднее угловое ускорение есть величина отношения изменения угловой скорости ∆ω к промежутку времени ∆t, за которое это изменение произошло β _ср = ∆ω/∆t

Вектор углового ускорения направлен вдоль оси вращения и совпадает с направлением угловой скорости, если движение ускоренное, и противоположен ему, если вращение замедленное (Рисунок 6).

5. При вращательном движении твердого тела все его точки двигаются так, что вращательные характеристики (угловое перемещение, угловая скорость, угловое ускорение) для них одинаковы. А линейные характеристики движения зависят от расстояния точки до оси вращения.

Связь между этими величинами v, ω, r задается следующим соотношением:

v = [ω∙r],

т.е. линейная скорость v любой точки С твердого тела, вращающегося вокруг неподвижной оси с угловой скоростью ω, равна векторному произведению ω на радиус-вектор r точки С относительно произвольной точки О на оси вращения.

Подобное соотношение существует между линейным и угловым ускорениями вращающейся точки твердого тела:

а = [β∙r].

2.1.6. Связь между кинематическими характеристиками при различных видах движений

По зависимости скорости и ускорения от времени все механические движения делятся на равномерное, равнопеременное (равноускоренное и равнозамедленное) и неравномерное.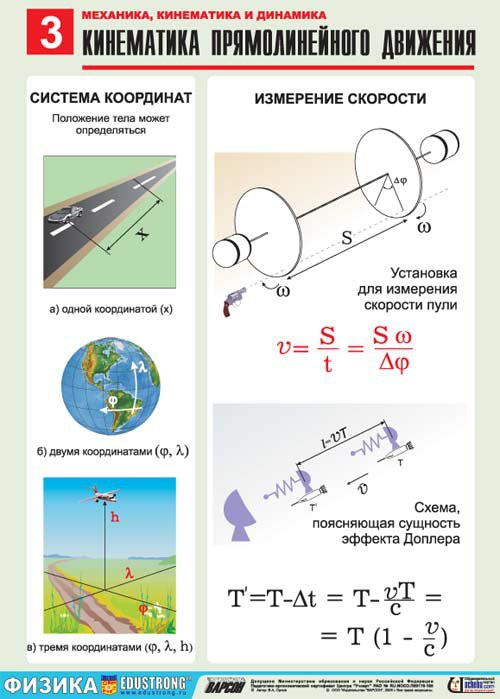

Рассмотрим кинематические характеристики и кинематические уравнения, введенные в предыдущих параграфах, для разных видов движений.

1. Прямолинейное движение

Прямолинейное равномерное движение.

Направление движения задается осью ОХ.

Ускорение а = 0 (а_n = 0, а_τ = 0), скорость v = const, путь s = v∙t, координата x = x₀ v∙t, где x₀ – начальная координата тела на оси ОХ.

Путь – величина всегда положительная. Координата может быть и положительной и отрицательной, поэтому в уравнении, задающем зависимость координаты от времени, перед величиной v∙t в уравнении стоит знак плюс, если направление оси ОХ и направление скорости совпадают, и знак минус, если они противоположно направлены.

Прямолинейное равнопеременное движение.

Ускорение а = а_τ = const, а_n = 0, скорость , путь , координата .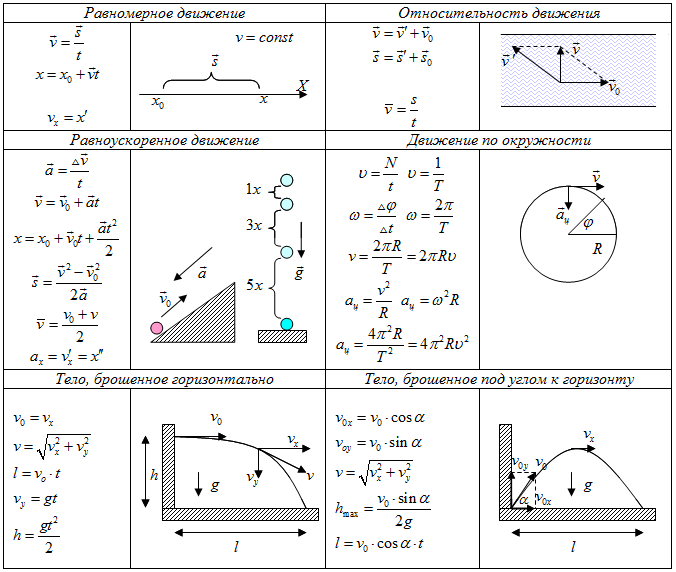

Перед величиной (at) в кинематическом уравнении для скорости знак плюс соответствует равноускоренному движению, а знак минус – равнозамедленному движению. Это замечание верно и для кинематического уравнения пути, разные знаки перед величинами (at²/2) соответствуют разным видам равнопеременного движения.

В уравнении для координаты знак перед (v₀t) может быть и плюс, если направления v₀ и оси ОХ совпадают, и минус, если они направлены в разные стороны.

Разные знаки перед величинами соответствуют равноускоренному или равнозамедленному движениям.

Прямолинейное неравномерное движение.

Ускорение а = а_τ>≠ const, а_n = 0,

скорость , путь .

2. Поступательное движение

Для описания поступательного движения можно использовать законы, приведенные в §2. 1.6. (пункт 2) или §2.1.4. (пункт3). Использование тех или иных законов для описания поступательного движения зависит от его траектории. Для прямолинейной траектории используются формулы из §2.1.6. (пункт 2), для криволинейной – §2.1.4. (пункт3).

3. Вращательное движение

Отметим, что решение всех задач на вращательное движение твердого тела вокруг неподвижной оси аналогично по форме задачам на прямолинейное движение точки. Достаточно заменить линейные величины s, v_х, a_х на соответствующие угловые величины φ, ω, β, и мы получим все закономерности и соотношения для вращающегося тела.

Равномерное вращение по окружности

(R – радиус окружности).

Ускорение: полное а = а_n, нормальное , тангенциальное а_τ = 0, угловое β = 0.

Скорость: угловая ω = const, линейная v = ωR = const.

Угол поворота ∆φ = ∆ φ₀ + ωt, ∆φ₀ – начальное значение угла. Угол поворота величина положительная (аналог пути).

Периодом вращения называется промежуток времени T, в течении которого тело, равномерно вращаясь с угловой скоростью ω, совершает один оборот вокруг оси вращения. При этом тело поворачивается на угол 2π.

.

Частота вращения показывает число оборотов, совершаемых телом за единицу времени при равномерном вращении с угловой скоростью ω:

.

Равнопеременное вращение по окружности

Ускорение: угловое β = const, тангенциальное а_τ = βR=const, нормальное а_n = ω ²R ≠ const, полное

Скорость: угловая ω = ω₀ ( βt), линейная

Угловое перемещение .

Все сказанное ранее относительно знаков в кинематических уравнениях для прямолинейного равнопеременного движения остается верным и для кинематических уравнений вращательного движения: плюс в формулах относится к равноускоренному вращению, минус – к равнозамедленному.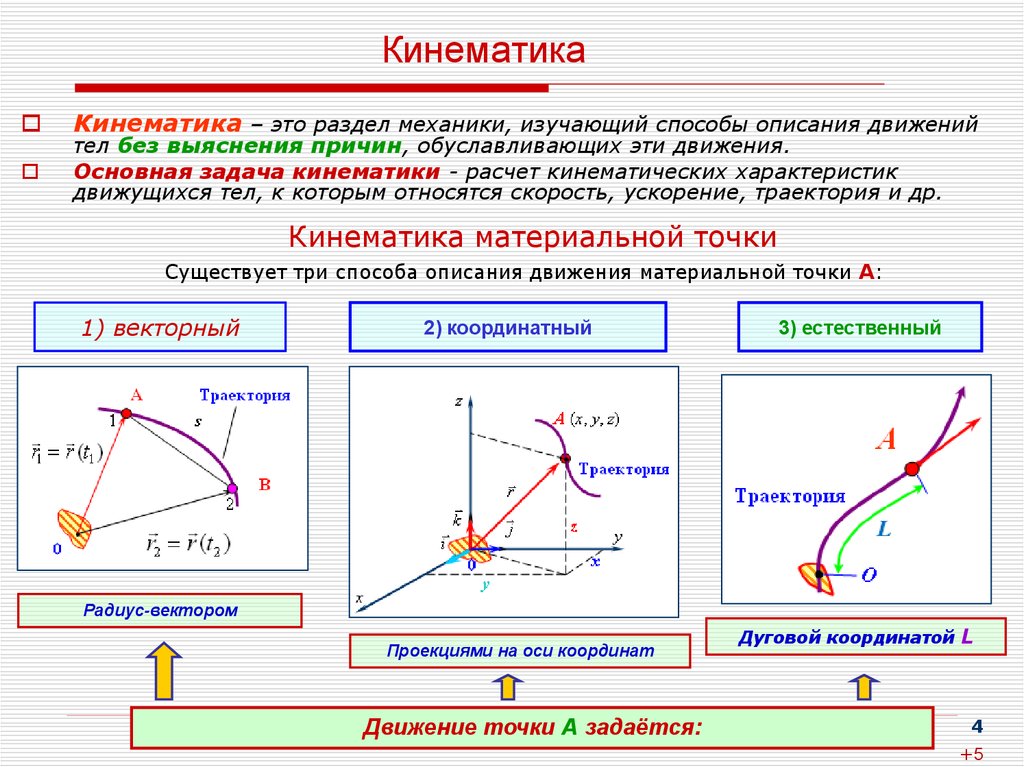

Неравномерное вращение

Ускорение: а_τ = а_τ (t), а_n = а _n(t), β ≠ const,

Скорость:

Угловая ω = dφ/dt, линейная .

Кинематика – Физика Высшее

Кинематика – это изучение движения, или, точнее, анализ и измерение движения.
В серии уроков мы рассмотрим некоторые аспекты движения в одном измерении.
Но прежде чем мы начнем, возможно, будет полезно посмотреть, какое место занимает кинематика в контексте классической механики.
Следующее видео знакомит вас с концепцией механики, объединяющей не только кинематику, которая является анализом движения, но и динамику, которая является анализом причины движения.

​В этом следующем видео представлен обзор  кинематики, а также представлены некоторые ключевые термины, такие как расстояние и смещение, скорость и скорость, а также их связь. Хорошее начало, прежде чем вы углубитесь в особенности кинематики.

3. Ускорение

рабочее решение

углубление

проблемы

скоро

рабочее решение

скоро

углубление

Что общего у хлопьев с движением? Ну читайте дальше…. Есть несколько способов дальнейшего изучения этих концепций. Одним из аспектов большинства курсов физики в средней школе по кинематике является то, что они касаются только постоянного ускорения. Однако в действительности ускорение, как и смещение и скорость, может изменяться во времени. Скорость – это скорость изменения смещения. Единица измерения: м/с ² Ускорение – это скорость изменения скорости. Так какова скорость изменения ускорения? Ответ на это – придурок. Таким образом, наклон графика зависимости ускорения от времени равен 9.0032 придурок . Единица измерения: м/с ³ Мы можем пойти дальше. Какова скорость изменения рывка? Ну это снап . Единица измерения: м/с ⁴ Можем ли мы пойти дальше? Ага. Скорость изменения оснастки треск . Единица измерения: м/с ⁵ Я думаю, вы можете догадаться о следующем.

проблемы

скоро

4. Graphing Motion

проработанное решение

углубление

интерактивы

рабочие листы

В этом видео я использую анимацию из pHET. Я объясняю графики, созданные из трех моментов движения, стационарного состояния, постоянной скорости и постоянного ускорения. Я также обсуждаю, как вы можете определить такие переменные, как скорость, смещение и ускорение, по этим графикам. Нажмите на вкладку, чтобы увидеть образец вопроса, который вы можете попробовать, а затем я предоставлю вам способ его решения. ​Также вы можете поиграть с отличными интерактивными элементами. См. ВКЛАДКУ

рабочий раствор

глубже

Графики позволяют визуализировать происходящее с точки зрения движения. Однако мы также можем использовать графики как математический способ создания математических моделей или уравнений. Таким образом, мы можем вывести уравнения движения из графиков движения.

интерактивы

Исследуйте различные графики кинематики с помощью этого интерактивного Geogebra от Тома Уолша

• Графическая анимация pHET — этот интерактив от команды pHet Университета Колорадо — отличный способ продемонстрировать взаимосвязь между движением и его графическим анализом. Именно поэтому я использовал его в своем видео. В настоящее время он основан на Java, поэтому будет работать только на ПК/Mac.0118
  

рабочие листы

Я собрал их из разных мест.

• Анализ движения с помощью графиков – ответы
• графики от Ingrum
• графическая викторина

5. Уравнения движения

рабочее решение

6 906 90605

Между каждой из переменных, участвующих в кинематике, существуют отношения, и эти математические отношения моделируются в так называемых кинематических уравнениях или уравнениях движения. В этом видео рассказывается о 5 формах кинетических уравнений и о том, как они выводятся.
Перейдите на вкладку «Углубление» в «4. Graphing Motion», чтобы увидеть, как их можно получить из графиков движения.  

См. вкладку Work Solution , если вы хотите продемонстрировать кинематическую задачу с использованием уравнений движения

рабочий раствор

Всегда полезно сначала попробовать решить проблему, прежде чем смотреть пример решения

проблемы

1. Автомобиль проезжает 20 км со скоростью 40 км/ч. С какой скоростью должен пройти автомобиль следующие 20 км, чтобы его средняя скорость на всем пути была 60 км/ч? (120 км/ч)
2. Автомобиль выезжает в 8 утра и едет со скоростью 60 км/ч. Другая машина выезжает из того же места в 8:30 утра, а я ехал со скоростью 80 км/ч. Когда и где вторая машина догонит первую? (10:00, 120 км)
3. Чтобы взлететь, самолет должен набрать скорость 80 м/с. Если он ускоряется со скоростью 3 м/с2, рассчитайте длину пробега по б.