Школа выходного дня “Решение задач по физике”
Школа выходного дня “Решение задач по физике”
Уважаемые старшеклассники (11-е классы). С 23.01.2021 начинает работу Школа выходного дня по физике по решению задач ЕГЭ с развернутым ответом. Место проведения занятий – учебный корпус №2 (вход с ул. Яшина), ауд. 3116. Время проведения: с 15.00 – до 16.30. Занятия проводятся ведущими сотрудниками кафедры «Физика и теоретическая механика». Приглашаем всех желающих.
Программа «Школа выходного дня»
Мастер-класс «Решение задач с развернутым ответом ЕГЭ по физике»
|
№ п\п |
Дата проведения |
Тема занятия |
Кол-во часов |
ФИО преподавателя |
1 |
23. |
Структура КИМ. Решение качественных задач № 27. Механика. Электричество. |
2 |
Куликова Г. В. |
|
2 |
30.01.2021 |
Решение качественных задач № 27. Термодинамика. Оптика. |
2 |
Куликова Г. В. |
|
3 |
06.02.2021 |
Решение задач № 28. Механика. Термодинамика. |
2 |
Куликова Г. В. |
|
4 |
13.02.2021 |
Решение задач № 29. |
2 |
Куликова Г. В. |
|
5 |
20.02.2021 |
Решение задач № 29. Статика. |
2 |
Куликова Г. В. |
|
6 |
27.02.2021 |
Решение задач № 29. Законы сохранения импульса и энергии. |
2 |
Куликова Г. В. |
|
7 |
06.03.2021 |
Решение задач №30. Молекулярная физика. Термодинамика. |
2 |
Кравченко О. |
|
8 |
13.03.2021 |
Решение задач №30. Молекулярная физика. Термодинамика. |
2 |
Кравченко О. В. |
|
9 |
20.03.2021 |
|
2 |
Кравченко О. В. |
|
10 |
27.03.2021 |
Решение задач №31. Магнетизм. |
2 |
Кравченко О. В. |
|
11 |
03. |
Решение задач № 31, 32. Механические и электромагнитные колебания и волны. |
2 |
Кравченко О. В. |
|
12 |
10.04.2021 |
Решение комбинированных задач № 32. Квантовая и ядерная физика. |
2 |
Кравченко О. В. |
Решение типовых задач по физике :: Класс!ная физика
Здесь приводятся решения задач из сборника задач Бендрикова Г.А. для школьников 9-11 классов и студентов:
Механика. Криволинейное движение (бросок под углом к горизонту, движение по окружности)
Механика. Динамика прямолинейного движения
Динамика прямолинейного движения
Механика. Закон сохранения импульса
Механика. Статика
Механика. Закон сохранения энергии
Механика. Динамика вращательного движения
Колебания и волны
Оптика
Молекулярная физика и термодинамика
Гидро- и аэродинамика
Успехов в разборе «полетов»!
Так как же решить задачу по физике?
Задача: Как, не понимая ни бельмеса в физике, все-таки научиться вычислять действующую на тебя силу тяжести?
Ответ: не снимая ботинок и не вынимая из карманов гайки и гвозди, встань на весы.
Посмотри, сколько килограммов весы показывают – это твоя масса. Не вес, а масса.
Запомни, не ВЕС, а МАССА!
Запомнил?
Теперь быстро умножай свою массу на девять и восемь десятых.
Так надо!
Умножил?
Теперь припиши к тому что получилось буковку “н” и можешь хвастаться, что на тебя действует сила тяжести в столько-то ньютонов.
С солнечным приветом от Григория Остера
Задача
Что заметил передовой Галилей, когда от него сначала отстала инквизиция, а потом все остальные тела?
Ответ: инквизиция, конечно, не тело, но передовой Галилей верно заметил, что если к нему никто не пристает, то он либо находится в покое, либо равномерно и прямолинейно движется сам не зная куда. По инерции.
Задача
Ответ: когда Вовочка отпустил недоеденное эскимо, на эскимо перестала действовать карусель, кружившая его вместе с Вовочкой.
 Однако, скорость свою эскимо, по законам инерции, сохранило. И помчалось прямолинейно и равномерно. Когда б ему ничто не мешало – вечно бы летело эскимо мимо звезд и
туманностей. Но на пути мороженого встал милиционер.
Однако, скорость свою эскимо, по законам инерции, сохранило. И помчалось прямолинейно и равномерно. Когда б ему ничто не мешало – вечно бы летело эскимо мимо звезд и
туманностей. Но на пути мороженого встал милиционер. Задача
Коля и Толя нашли сжатую пружину в пакетике, перевязанном веревочками, и стали эти веревочки развязывать. Тут-то пружина и распрямилась. В результате взаимодействия Толя с хорошей скоростью улетел в одну сторону, а Коля с вдвое большей в прямо противоположную. Укажите, как отличается Толина масса
от Колиной?
Задача
Лютый враг нежно прижался щекой к прикладу и нажал курок. Пуля массой 10 г выскочила из винтовки и понеслась искать невинную жертву со скоростью 800 м/с. А винтовка в результате отдачи со скоростью 2 м/с послала врага в нокаут.
Ответ: врага нокаутировало его собственное оружие массой в 4 кг. Кто к нам с чем придет – от того и упадет.
Задача
После того как трое мышей на дне рождения мышки Мушки угостились одним крупным куском хозяйственного мыла, их общая масса увеличилась на 540 г. Мыло до того, как мыши его съели, имело размеры 10см, 12см, 3см. Определите плотность уже не существующего мыла.
Ответ: 1,5 г/куб.См – вот она плотность бывшего мыла.
Задача
Масса листика, сорвавшегося с березы, – 0,1 г, а масса кота Яшки, размечтавшегося о птичках и сорвавшегося с той же самой березы, 10 кг. Во сколько раз сила тяжести, действующая на планирующий листик, меньше силы тяжести, действующей на планирующего кота?
справедливо.
Задача
Если с интеллигентного, скромного и тактичного физика требуют деньги за два килограмма колбасы, а он видит, что весы с колбасой показывают всего один килограмм, то закричит ли физик на весь магазин: “нет уж, простите, вес вашей поганой колбасы не два – только один килограмм!”?
Ответ: не закричит. Вежливый физик не станет так грубо выражаться, потому что помнит: в килограммах выражается лишь одна физическая величина – масса. Вес выражается совсем в других величинах – в ньютонах.
Вежливый физик не станет так грубо выражаться, потому что помнит: в килограммах выражается лишь одна физическая величина – масса. Вес выражается совсем в других величинах – в ньютонах.
Задача
Массы голубого большого воздушного шарика и мелкого ржавого железного гвоздика, который мечтает этот шарик когда-нибудь проткнуть, одинаковы. Как отличаются силы тяжести, действующие на шарик и гвоздик?
Ответ: никак не отличаются. Один голубой и воздушный, другой мелкий и ржавый. Ну и что? Массы у них одинаковы? Одинаковы! Значит одинаковы и действующие на обоих силы тяжести.
Примеры решения задач по классической механике от Zaochnik
Представляем подборку примеров решения задач по механике. Здесь вы найдете задачи на вращательное движение, закон Ньютона, закон сохранения импульса и даже немного релятивистских преобразований. Решение задач по механике – простое и приятное дело, если сначала хорошенько разобраться в них. Пользуйтесь нашими примерами и щелкайте задачи, как орешки!
Решение задач по механике – простое и приятное дело, если сначала хорошенько разобраться в них. Пользуйтесь нашими примерами и щелкайте задачи, как орешки!
Хотите получать ежедневную рассылку с полезной информацией для студентов всех специальностей? Присоединяйтесь к нам в телеграм.
Номер один: кинематика вращательного движенияНомер два: второй закон Ньютона и мощностьНомер три: закон сохранения импульсаКстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Номер четыре: момент импульса и вращательное движениеНомер пять: преобразования ЛоренцаДаже самую сложную задачу можно решить! А чтобы решить ее быстро, есть смысл обратиться в профессиональный сервис для студентов.
Автор: Иван
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
ПРАКТИКУМ ПО РЕШЕНИЮ ФИЗИЧЕСКИХ ЗАДАЧ (МЕХАНИКА)
ПРАКТИКУМ
ПО
РЕШЕНИЮ
ФИЗИЧЕСКИХ
ЗАДАЧ
(МЕХАНИКА)
« Кто умеет решать задачи
по физике, тот знает физику»
Э.Ферми
ВВЕДЕНИЕ
Научить физике – это научить решать задачи.
В программе по физике задачам отводится вспомогательная роль. Практика показывает, что теория запоминается значительно лучше, если ее не заучивать, а многократно использовать в процессе решения задач, а без многократного обращения к теории решить большое количество задач просто невозможно.-reshenie-173.jpg)
Цель практикума заключается в обучении студентов частным методам решения физических задач по различным темам курса физики, а также обобщенному методу решения задач-проблем.
В результате освоения практикума студенты должны научиться применять:
обобщенный метод решения задач-проблем в конкретной ситуации;
обобщенный метод построения физической модели ситуации, описанной в задаче;
частные методы решения задач по различным темам курса физики;
уметь:
решать задачи по основным разделам курса общей физики;
строить физическую модель ситуации, описанную в задаче – проблеме;
применять физические законы в конкретных ситуациях;
решать тестовые задания по курсу общей физики.

Задачи практикума:
Познакомить с различными методами решения и способствовать формированию навыков решения,
Способствовать формированию обобщенных навыков решения физических задач, путем применения общих подходов (системы методов) к решению любой физической задачи,
Усилить практическую направленность курса физики, способствовать формированию практической деятельности студентов в данной области знаний,
Освоить алгоритмы решения стандартных задач,
Развивать познавательные интересы, интеллектуальные и творческие способности в процессе решения физических задач,
Способствовать формированию умения переноса теоретических знаний курса физики и математики, их применения при решении физических задач,
Тема: «Скорость. Равномерное прямолинейное движение».
Равномерное прямолинейное движение».
Цель урока:
1. Знать алгоритм решения задач на тему Скорость. Равномерное прямолинейное движение.
2. Уметь применять алгоритм к решению задач на тему Скорость. Равномерное прямолинейное движение.
Повторим теорию
Механическим движением тела называется изменение его положения в пространстве относительно других тел с течением времени.
Механическое движение тел изучает механика. Раздел механики, описывающий геометрические свойства движения без учета масс тел и действующих сил, называется кинематикой.
Путь и перемещение. Линия, по которой движется точка тела, называется траекторией движения. Длина траектории называется пройденным путем. Вектор, соединяющий начальную и конечную точки траектории, называется перемещением.
Движение тела, при котором все его точки в данный момент времени движутся одинаково, называется поступательным движением. Для описания поступательного движения тела достаточно выбрать одну точку и описать ее движение
Для описания поступательного движения тела достаточно выбрать одну точку и описать ее движение
Траектория движения тела, пройденный путь и перемещение зависят от выбора системы отсчета. Другими словами, механическое движение относительно.
Скорость. Для количественной характеристики процесса движения тела вводится понятие скорости движения. V= s /t
Мгновенной скоростью поступательного движения тела в момент времени t называется отношение очень малого перемещения As к малому промежутку времени At, за который произошло это перемещение:
Ускорением называется векторная величина, равная отношению очень малого изменения вектора скорости Av к малому промежутку времени At, за которое произошло это изменение
Задача на определение пройденного пути при равнозамедленном движении
Условие
Самолет, летящий со скоростью , совершает посадку. Время до полной остановки самолета . Необходимо определить длину взлетной полосы.
Время до полной остановки самолета . Необходимо определить длину взлетной полосы.
Рис. 1. К условию задачи 1
Решение
надо перевести в СИ, т. обр. начальная скорость самолета при посадке . Необходимо заметить, что, когда самолет совершает посадку, его конечная скорость будет равна нулю.
На рисунке ускорение имеет направление против оси , тем самым мы должны понимать, что проекция ускорения на ось будет иметь отрицательное значение.
В данном случае движение прямолинейное (в одну сторону), поэтому модуль перемещения равен пройденному пути и определяется по формуле Галилея:
Чтобы решить окончательно эту задачу, надо определить ускорение:
Обратите внимание, что ускорение получилось со знаком минус. В данном случае мы понимаем, что движение замедленное. Скорость с течением времени уменьшается.
Стоит сделать акцент на том, что в решении мы не использовали обозначение векторов. Вспомните: в начале рассуждения мы уже нарисовали рисунок, где точно поставили направление векторных величин, связанных с выбранной системой отсчета, т. е. с осью . Подставляем в формулу, в уравнение движения Галилея, все нам известные величины:
е. с осью . Подставляем в формулу, в уравнение движения Галилея, все нам известные величины:
Ответ:.
Задача на комбинацию различных видов движения
Вторая задача, которую мы рассмотрим, несколько сложнее.
Условие
Автобус начинает свое движение от остановки и за увеличивает свою скорость до . Затем автобус едет с постоянной скоростью и перед светофором тормозит, останавливается, до полной остановки движется в течение . Определите полный пройденный путь этим автобусом.
Рис. 2. К условию задачи 2
Решение задачи мы начинаем с того, что определим первый участок пути, т. е. тот, на котором автобус разгоняется. Обозначим его как и вычислять мы будем его по уравнению Галилея. Записывается оно следующим образом:
Чтобы вычислить , требуется обязательно знать ускорение. Ускорение обозначим .
Движение начинается от остановки, это означает, что начальная скорость . Найдем ускорение, не забыв перевести значение скорости в СИ:
Найдем ускорение, не забыв перевести значение скорости в СИ:
Вычисляем теперь пройденный путь . С учетом того, что , формула приобретает вид: .
Если теперь подставить сюда все известные значения, то мы получаем значение: .
Итак, первый этап: автобус разогнался от до , пройдя расстояние .
Следующая часть посвящена равномерному движению, когда автобус движется равномерно в течение , и замедленному движению, когда автобус начинает останавливаться. Определяем пройденное расстояние при равномерном прямолинейном движении. В этом случае .
Третий пункт – это момент остановки автобуса, т. е. расстояние, которое он проходит до остановки. Здесь .
В этом уравнении, чтобы определить , требуется знать значение ускорения:
Это означает, что движение замедляется. Ускорение направлено против выбранной оси. Подставив все значения, мы получаем выражение для :
.
До полной остановки автобус проходит 50 м. Чтобы вычислить окончательный ответ, нужно все пройденные расстояния сложить:
Ответ:
Решение второй задачи графическим методом
Рассмотрим второй вид решения, так называемый графический способ решения. Вспомним, что площадь фигуры, ограниченная с одной стороны осью времени, а с другой стороны графиком скорости, есть пройденный путь.
Вспомним, что площадь фигуры, ограниченная с одной стороны осью времени, а с другой стороны графиком скорости, есть пройденный путь.
Нарисуем график зависимости скорости автобуса от времени. В течение 5 c скорость автобуса увеличивается от 0 до 10 м/с. Затем 20 с, т. е. от 5 до 25 с, скорость постоянна и равна 10 м/с. Затем в течение 10 с, т. е. от 25 до35 с, автобус останавливается.
Рис. 3. График зависимости скорости от времени (задача 2)
Полученная фигура – это трапеция. Из математики вы помните, что площадь трапеции определяется как полусумма оснований, умноженная на высоту. Это . В нашем случае .
Решите следующие задачи:
А.П. Рымкевич Задачник 10-11 классы. 2002 г.
№№ 17,21,50,51,52,53,66,69,
Тема: «Свободное падение».
Цель урока:
1. Знать алгоритм решения задач на тему Свободное падение
2. Уметь применять алгоритм к решению задач на тему Свободное падение
Повторим теорию
tс
Проекция начальной скорости
v0yм/с
Проекция мгновенной скорости
vyм/с
Проекция ускорения
gyм/с2
Проекция перемещения
Syм
Координата
yм
Краткое пояснение для решения ЗАДАЧИ на Свободное падение тел.
Свободное падение — это движение тела под действием силы тяжести (другие силы — сила сопротивления, выталкивающая сила — отсутствуют либо ими пренебрегают).
Так как сила тяжести направлена вниз, то ускорение, которое она сообщает телу, тоже направлено вниз. Свободное падение — это равноускоренное движение. Ускорение, сообщаемое телу силой тяжести, называют ускорением свободного падения. Оно одинаково для всех тел вблизи поверхности Земли и имеет значение 9,8 м/с2. При решении задач в большинстве случаев это число округляется до 10 м/с2.
При решении задач применяются формулы равноускоренного движения. Для нахождения проекций векторов координатную ось обычно обозначают буквой у, так как движение происходит по вертикали. Направляют ее вверх или вниз — как удобней при решении конкретной задачи. Скорость свободно падающего тела возрастает.
Движение тела, брошенного вертикально вверх — частный случай свободного падения. Только скорость тела уменьшается, так как оно движется против силы тяжести, и вектор начальной скорости и вектор ускорения противоположно направлены. Достигая некоторой точки (наивысшей точки подъема), тело на мгновение останавливается (в это время его скорость равна нулю), а затем начинает падать. Так как движение вверх и вниз происходит с одинаковым ускорением, то время подъема и время падения тела равны.
Только скорость тела уменьшается, так как оно движется против силы тяжести, и вектор начальной скорости и вектор ускорения противоположно направлены. Достигая некоторой точки (наивысшей точки подъема), тело на мгновение останавливается (в это время его скорость равна нулю), а затем начинает падать. Так как движение вверх и вниз происходит с одинаковым ускорением, то время подъема и время падения тела равны.
Если координатную ось направить вверх, то проекция ускорения будет отрицательна, если вниз — положительна. Но при любом направлении оси для падающего тела векторы ускорения и скорости сонаправлены, а для тела, брошенного вверх — противоположно направлены.
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧЗадача № 1. С балкона 8-го этажа здания вертикально вниз бросили тело, которое упало на землю через 2 с и при падении имело скорость 25 м/с. Какова была начальная скорость тела?
Задача № 2. Какой высоты достигнет мяч, брошенный вертикально вверх со скоростью 20 м/с? Сколько времени для этого ему понадобится?
Задача № 3. Мяч бросили вертикально вверх со скоростью 15 м/с. Через какое время он будет находиться на высоте 10 м?
Мяч бросили вертикально вверх со скоростью 15 м/с. Через какое время он будет находиться на высоте 10 м?
Задача № 4. Через сколько секунд мяч будет на высоте 25 м, если его бросить вертикально вверх с начальной скоростью 30 м/с?
Ответ: через 1 с и через 5 с.
Решите следующие задачи:
А.П. Рымкевич Задачник 10-11 классы. 2002 г.
№№106,
\
Тема: Кинематика.
Цель урока:
1. Знать алгоритм решения задач на тему «Кинематика»
2. Уметь применять алгоритм к решению задач на тему « Кинематика»
Повторим теорию
Алгоритм решения ЗАДАЧИ на Прямолинейное равномерное движение. Задачи, описывающие движение, содержат два типа величин: векторные (имеющие направление) и скалярные (выражающиеся только числом). К векторным величинам при описании равномерного прямолинейного движения относятся скорость и перемещение.
Для перехода от векторов к скалярам выбирают координатную ось и находят проекции векторов на эту ось, руководствуясь следующим правилом: если вектор сонаправлен с осью, то его проекция положительна, если противоположно направлен — отрицательна. (Могут быть и более сложные случаи, когда вектор не параллелен координатной оси, а направлен к ней под некоторым углом.) Поэтому при решении задачи обязательно нужно сделать чертеж, на котором изобразить направления всех векторов и координатную ось. При записи «дано» следует учитывать знаки проекций.
При решении задач все величины должны выражаться в международной системе единиц (СИ), если нет специальных оговорок.
В решении задачи единицы величин не пишутся, а записываются только после найденного значения величины.
Решите следующие задачи:
А.П. Рымкевич Задачник 10-11 классы. 2002 г.
№№12,17,32,18,19
Тема: ЗАКОНЫ МЕХАНИКИ НЬЮТОНА.
Цель урока:
1. Знать алгоритм решения задач на законы Ньютона.
2. Уметь применять алгоритм к решению задач на законы Ньютона.
Повторим теорию
В чем состоит основное утверждение механики?
Что в физике понимают под материальной точкой?
Сформулируйте первый закон Ньютона.
Приведите примеры, объясняющие данную формулировку.
Что в физике понимают под термином «сила»?
Приведите примеры, показывающие связь сила и ускорения, с которым движется тело.
Сформулируйте второй закон Ньютона и запишите его математическое выражение.
В чем состоит третий закон Ньютона?
Запишите его математическое выражение.
Поясните на примерах смысл этого закона.
Каковы особенности сил, о которых идет речь в третьем законе Ньютона?
Какие системы отсчета называются инерциальными?
Неинерциальными? Привести примеры.
В чем состоит принцип относительности в механике?
Кто открыл этот принцип?
Основная задача механики
Нахождение положения и скорости тела в любой момент времени, если известны его положение и скорость в начальный момент времени и действующие на него силы. (Прямая задача)
(Прямая задача)
Определение сил по известному или заданному движению.
Алгоритм решения задач
Понять предложенную задачу (увидеть физическую модель).
Анализ (построить математическую модель явления):
Выбрать систему отсчета. Найти все силы, действующие на тело, и изобразить их на чертеже.
Определить (или предположить) направление ускорения и изобразить его на чертеже.
Записать уравнение второго закона Ньютона в векторной форме и перейти к скалярной записи, заменив все векторы их проекциями на оси координат.
Исходя из физической природы сил, выразить силы через величины, от которых они зависят.
Если в задаче требуется определить положение или скорость точки, то к полученным уравнениям динамики добавить кинетические уравнения.
Полученную систему уравнений решить относительно искомой величины.
Решение проверить и оценить критически.

Задача на законы Ньютона.
1.2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
Сокращенная запись условия задачи.
Выбрать тело, движение которого будем рассматривать.
С какими телами данное тело взаимодействует, силы изобразить на рисунке.
Изобразить на рисунке вектор ускорения.
Выбрать оси координат.
Составить уравнение 2 – го закона Ньютона.
Спроектировать уравнение на выбранные оси координат.
Если потребуется, составить дополнительные уравнения из кинематики и динамики.
Решить полученную систему уравнений.
Проверить правильность решения методом размерностей.
Вычисления с переводом величин в систему СИ.
Ответ, анализ ответа.
Знать силы: тяжести, трения, упругости(реакции опоры, натяжения нити),веса тела.
Знать направление ускорения при ускоренном, замедленном прямолинейном движении и при равномерном движении по окружности.
Ось x – по вектору ускорения.
Уметь проектировать вектор на ось, решать прямоугольные треугольники.
Знать формулы кинематики и формулы для величины сил.
Умение решать систему уравнений методом последовательного исключения неизвестных.
Примеры решения задач
Брусок массой 5 кг начинает движение по горизонтальной поверхности из состояния покоя под действием силы 40 Н, направленной под углом 45 гр. К поверхности. Найдите его скорость через 10 с, если коэффициент трения скольжения равен 0,5.
Решение качественных и количественных задач.
1.Как объяснить, что бегущий человек, споткнувшись, падает в направлении своего движения, а поскользнувшись, падает в направлении, противоположном направлению своего движения?
2.Парашютист падает с постоянной по модулю скоростью. Чему равен модуль силы сопротивления воздуха при этом движении?
3. Как направленно ускорение самолета, если на него действует 4 силы: по вертикали – сила тяжести = 200кН и подъемная сила 210кН. По горизонтали: сила тяжести мотора 20 кН и сила лобового сопротивления воздуха 10 кН. Чему равна равнодействующая всех сил?
Как направленно ускорение самолета, если на него действует 4 силы: по вертикали – сила тяжести = 200кН и подъемная сила 210кН. По горизонтали: сила тяжести мотора 20 кН и сила лобового сопротивления воздуха 10 кН. Чему равна равнодействующая всех сил?
4. Под действием силы в 20 Н материальная точка движется с а=0,4 м/с2. С каким ускорением будет двигаться точка под действием силы в 50 Н?
5. К пристани причаливают две одинаковые лодки. Лодочники подтягиваются к берегу с помощью веревок. Противоположный конец первой веревки привязан к столбу на пристани; за противоположный конец второй веревки тянет матрос, стоящий на пристани. Все трое прилагают одинаковые усилия. Какая лодка причалит раньше?
6. На тело массой 2160 кг, лежащее на горизонтальной дороге, действует сила, под действием которой тело за 30 секунд пройдет расстояние 500 метров. Найти величину этой силы.
5. Рефлексия.
Тема: Закон Всемирного тяготения.
Цель урока:
1. Знать алгоритм решения задач на Закон Всемирного тяготения.
Знать алгоритм решения задач на Закон Всемирного тяготения.
2. Уметь применять алгоритм к решению задач на Закон Всемирного тяготения.
Повторим теорию
Формулы, используемые на уроках «Задачи закон всемирного тяготения».
Название величиныОбозначениеЕдиница измеренияФормулаМасса планетыМкг
Расстояние между телами или их центрамиrм
Сила всемирного тяготенияFН
Постоянная всемирного тяготенияGН•м
2/кг2G = 6,67•10-11Высотаhм
Ускорение свободного падения вблизи поверхности планетыg
м/с
2Ускорение свободного падения на большом расстоянии от поверхности планетыg
м/с
2ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. На каком расстоянии друг от друга находятся два одинаковых шара массами по 20 т, если сила тяготения между ними 6,67•10-5 Н?
На каком расстоянии друг от друга находятся два одинаковых шара массами по 20 т, если сила тяготения между ними 6,67•10-5 Н?
Задача № 2. Масса Сатурна 5,7•1026 кг, а его радиус— 6•107 м. Определите ускорение свободного падения на Сатурне.
Задача № 3. Чему равно ускорение свободного падения на высоте над поверхностью Земли, равной двум ее радиусам?
Задача № 4. На какой высоте над поверхностью Земли сила тяготения в 2 раза меньше, чем на поверхности Земли?
Решите следующие задачи:
А.П. Рымкевич Задачник 10-11 классы. 2002 г.
№№ 169,170,171,172,173,174,175,176,177-180
Тема: Сила. Тяжесть. Вес.
Цель урока:
1. Знать алгоритм решения задач на тему «Сила. Тяжесть. Вес».
2. Уметь применять алгоритм к решению задач на тему « Сила. Тяжесть. Вес».
Повторим теорию
Формулы, используемые на уроке «Задачи на силу тяжести и вес тела»
Название величиныОбозначение
Единицы измерения
Формула
Масса
m
кг
m = F / g
Вес тела
P
H
P = m *g
Сила тяжести
Fтяж
H
Fтяж = mg
Постоянная (сила тяжести, действующая на тело массой 1 кг)
g = 10 H/кг
H/кг
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ Задача № 1. Определите силу тяжести, действующую: а) на человека массой m = 100 кг; б) на автомобиль массой М = 1,5 т; в) на монет массой m = 5 г.
Определите силу тяжести, действующую: а) на человека массой m = 100 кг; б) на автомобиль массой М = 1,5 т; в) на монет массой m = 5 г.
Задача № 2. Какова масса свинцового шара, если он весит 600 Н?
Задача № 3. Масса футбольного мяча 400 г. Вычислите вес мяча и силу тяжести, действующую на него.
Задача № 4. Чему равна сила тяжести тела, масса которого 4 кг?
Задача № 5. Какой вес имеет вода объемом 3 дм3?
Решите следующие задачи:
А.П. Рымкевич Задачник 10-11 классы. 2002 г.
№№181,-184,186,189*191
Тема: Импульс. Закон сохранения импульса.
Цель урока:
1. Знать алгоритм решения задач на тему «Импульс. Закон сохранения импульса».
2. Уметь применять алгоритм к решению задач на тему «Импульс. Закон сохранения импульса».
Повторим теорию
Формулы, используемые на уроках «Задачи на импульс тела. Задачи на Закон сохранения импульса».
Задачи на Закон сохранения импульса».
м/с
v = p/mМасса телаmкг
m = p/vИмпульс тела (модуль)pкг•м/с
p = m•vАлгоритм применения закона сохранения импульса к решению задач:
Запишите краткое условие задачи.
Определите характер движения и взаимодействия тел.
Сделайте рисунок, на котором укажите направление векторов скоростей тел до и после взаимодействия.
Выберите инерциальную систему отсчета с удобным для нахождения проекций векторов направлением координатных осей.

Запишите закон сохранения импульса в векторной форме.
Спроецируйте его на выбранные координатные оси (сколько осей, столько и уравнений в системе).
Решите полученную систему уравнений относительно неизвестных величин.
Выполните действия единицами измерения величин.
Запишите ответ.
Задача № 1. Определите массу автомобиля, имеющего импульс 2,5•104 кг•м/с и движущегося со скоростью 90 км/ч.
Задача № 2. Тележка массой 40 кг движется со скоростью 4 м/с навстречу тележке массой 60 кг, движущейся со скоростью 2 м/с. После неупругого соударения тележки движутся вместе. В каком направлении и с какой скоростью будут двигаться тележки ?
Задача № 3. Снаряд, выпущенный вертикально вверх, разорвался в верхней точке траектории. Первый осколок массой 1 кг приобрел скорость 400 м/с, направленную горизонтально. Второй осколок массой 1,5 кг полетел вверх со скоростью 200 м/с. Какова скорость третьего осколка, если его масса равна 2 кг?
Второй осколок массой 1,5 кг полетел вверх со скоростью 200 м/с. Какова скорость третьего осколка, если его масса равна 2 кг?
Решение. Взрывающийся снаряд можно считать замкнутой системой, потому, что сила тяжести намного меньше, чем сила давления пороховых газов, разрывающих снаряд на осколки. Значит, можно использовать закон сохранения импульса. Поскольку разрыв снаряда произошел в верхней точке траектории, векторная сумма импульсов всех осколков должна быть равна нулю. Следовательно, векторы импульсов осколков образуют треугольник; этот треугольник прямоугольный, а искомый вектор — его гипотенуза.
Ответ: 250 м/с.
Решите следующие задачи:
А.П. Рымкевич Задачник 10-11 классы. 2002 г.
№№314,-317,319,324,330
Тема: Мощность. Энергия.
Цель урока:
1. Знать алгоритм решения задач на тему ««Мощность. энергия».
2. Уметь применять алгоритм к решению задач на тему ««Мощность. энергия».
Алгоритм решения задач на закон сохранения энергии:
Записать краткое условие задачи.
Перевести единицы измерения в систему СИ.
Выбрать систему отсчёта.
Определить начальное и конечное положения тел, а так же, если необходимо, то промежуточные положения, о которых идёт речь в задаче.
Выбрать нулевой уровень потенциальной энергии.
Если на тела действуют только потенциальные силы, записать закон сохранения механической энергии: Е1= Е2. Если в системе тел действуют также и непотенциальные силы, то закон сохранения энергии записать в следующем виде: ΔЕ = Е2 – Е1 = А , где А А – работа непотенциальных сил.
Выразить неизвестное.
Произвести расчёт численного значения и единиц измерения.
Оценить полученный результат.

Решите следующие задачи:
А.П. Рымкевич Задачник 10-11 классы. 2002 г.
№№393,394,-396
Тема: Законы сохранения в механике.
Цель урока:
1. Знать алгоритм решения задач на тему «Законы сохранения в механике».
2. Уметь применять алгоритм к решению задач на тему «Законы сохранения в механике».
Повторим теорию
Основные формулы по теме «Законы сохранения в механике»
Решите следующие задачи:
А.П. Рымкевич Задачник 10-11 классы. 2002 г.
№№ 357-392
НГТУ – ОФ – Учебно-методические и учебные пособия
- ВВОДНЫЙ КУРС.
 Механика
Механика - ВВОДНЫЙ КУРС. Основы молекулярной физики и термодинамики
- ВВОДНЫЙ КУРС. Электростатика и законы постоянного тока
- Вопросы для самоконтроля знаний по физике. Часть 1. 2014
- Вопросы для самоконтроля знаний по физике. Часть 2. Колебания и волны. Оптика
- Вопросы для самоконтроля знаний по физике. Часть 3. Квантовая механика, статическая физика : методическое пособие для 1 и 2 курсов всех специальностей.
- Задачи по физике. (Пейсахович Ю. Г., Штыгашев А. А.) Механика. Молекулярная физика и термодинамика. Электричество
- Задачи по физике. (Пейсахович Ю. Г., Штыгашев А. А.) Электромагнетизм. Электромагнитные волны. Волновая и квантовая оптика. Элементы квантовой физики и физики твердого тела. Элементы ядерной физики
- Задачник по физическим основам электроники
- квантовая статистическая физика
- Контрольная работа №1
- Контрольная работа №2
- Контрольная работа №3 и учебное пособие по материалу контрольной.

- Контрольная работа №4
- Контрольная работа №5
- Контрольная работа №6
- КОНЦЕПЦИИ СОВРЕМЕННОГО ЕСТЕСТВОЗНАНИЯ
- Курс общей физики. Ч.2.pdf
- Методика решения задач по электромагнетизму. Методическое пособие
- Методические указания к выполнению КОНТРОЛЬНОЙ РАБОТЫ № 2 для заочного отделения (ФИЗИКА. ЭЛЕКТРОМАГНЕТИЗМ. ОПТИКА. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ.)
- Методические указания к выполнению КОНТРОЛЬНОЙ РАБОТЫ № 1 для заочного отделения по специальностям “Конструкторско-технологическое обеспечение машиностроительных производств”, “Эксплуатация транспортно-технологических машин и комплексов”, “Информатика и вычислительная техника”, “Технология продукции и организация общественного питания”.
- Методические указания к выполнению контрольной работы № 3 для студентов ЗФ и ИДО направлений «Эксплуатация транспортно-технологических машин и комплексов» и «Конструкторско-технологическое обеспечение машиностроительных производств» (специальный курс)
- Механика и электростатика (методические указания по решению задач)
- О квантовой физике (Протасов Д.
 Ю.)
Ю.) - Общая физика : методическое пособие по изучению курса для МТФ.
- описание правил приближённых вычислений
- Рабочая тетрадь для практической индивидуальной работы (Часть 1)
- Рабочая тетрадь для практической индивидуальной работы (Часть 2)
- Решение задач на компьютере. (Штыгашев А. А.) Молекулярная физика и термодинамика
- Решение задач на компьютере. (Штыгашев А. А.) Электричество и магнетизм
- Содержание контрольных работ
- Театр физического эксперимента. Часть 1. Березин Н.Ю., Петров Н.Ю.
- Театр физического эксперимента. Часть 2. Березин Н.Ю., Петров Н.Ю.
- ТРЕБОВАНИЯ ПО ОФОРМЛЕНИЮ И ЗАЩИТЕ КОНТРОЛЬНЫХ РАБОТ
- учебное пособие для поступающих в вуз
- Физика (Давыдков В. В.)1: механика, электричество и магнетизм
- Физика (Давыдков В. В.)2: электростатика, магнетизм, колебания и волны
- Физика (Давыдков В. В.)2: электростатика, магнетизм, колебания и волны.
 Список Опечаток.
Список Опечаток. - Физика (Давыдков В. В.)3: волновая оптика, квантовая механика
- Физика конденсированного состояния. Фазовые переходы. Магнетики. Свойства диэлектриков
- Физика. Сборник задач. (Погожих С. А., Стрельцов С. А.) Механика, молекулярная физика, термодинамика, электростатика
- Физика. Сборник задач. (Погожих С. А., Стрельцов С. А.) Электромагнетизм, колебания и волны, оптика, квантовая и ядерная физика
- Физика: учебное пособие. Часть 1. Березин.Н,Ю,
- Физика: учебное пособие. Часть 2. Березин.Н,Ю,
- Физика фазовых превращений. Часть 1.
- Физика фазовых превращений. Часть 2.
- Физика. Электричество и магнетизм: учебное пособие. Чичерина Н.В., Рубанович М.Г,
- ФЛА РГЗ-1 семестр 2
- ФЛА РГЗ-2 семестр 3
- ФОЭ. Расчёт датчика мощности
- ФОЭ. Расчёт стабилизатора напряжения
- Чернышев А. П. Введение в физику твердого тела и нанофизику.
 Специальный курс физики. Конспект лекций
Специальный курс физики. Конспект лекций
| Класс | Название урока | Ссылка на учебные материалы |
| 7 | Что изучает физика. Некоторые физические термины. Наблюдение и опыт | https://resh.edu.ru/subject/lesson/2603/start/ |
| 7 | Физика и техника |
https://www.youtube.com/watch?v=Eta9kBhh03U https://www.youtube.com/watch?v=Eta9kBhh03U |
| 7 | Физические величины и их измерение. Измерение и точность измерения. Определение цены деления шкалы измерительного прибора. Определение объёма твёрдого тела | https://resh.edu.ru/subject/lesson/2602/start/ |
| 7 | Человек и окружающий его мир | https://resh. edu.ru/subject/lesson/1526/start/ edu.ru/subject/lesson/1526/start/ |
| 7 | Строение вещества. Молекулы и атомы. Измерение размеров малых тел | https://resh.edu.ru/subject/lesson/1533/start/ |
| 7 | Броуновское движение. Диффузия. Взаимное притяжение и отталкивание молекул. Смачивание и капиллярность | https://resh.edu.ru/subject/lesson/1534/start/ |
| 7 | Агрегатные состояния вещества. Обобщение темы «Строение вещества» | https://resh.edu.ru/subject/lesson/1532/start/ |
| 7 | Механическое движение | https://resh.edu.ru/subject/lesson/1488/start/ |
| 7 | Виды механического движения. Равномерное и неравномерное движение |
https://infourok.ru/videouroki/468 https://infourok.ru/videouroki/421 |
| 7 | Скорость | https://resh.edu.ru/subject/lesson/1525/start/ |
| 7 | Инерция. Взаимодействие тел и масса. Измерение массы тела на уравновешенных рычажных весах Взаимодействие тел и масса. Измерение массы тела на уравновешенных рычажных весах |
https://resh.edu.ru/subject/lesson/1531/start/ |
| 7 | Плотность и масса. Определение плотности твёрдого тела с помощью весов и измерительного цилиндра | https://resh.edu.ru/subject/lesson/2601/start/ |
| 7 | Решение задач по теме «Движение, взаимодействие, масса». Обобщение по теме «Движение, взаимодействие, масса» | https://resh.edu.ru/subject/lesson/2974/start/ |
| 7 | Сила. Сила тяжести | https://resh.edu.ru/subject/lesson/2756/start/ |
| 7 | Равнодействующая сила | https://resh.edu.ru/subject/lesson/2973/start/ |
| 7 | Сила упругости. Закон Гука. Динамометр. Градуировка динамометра. Исследование зависимости силы упругости от удлинения пружины. Определение коэффициента упругости пружины | https://resh. edu.ru/subject/lesson/2600/start/ edu.ru/subject/lesson/2600/start/ |
| 7 | Вес тела. Невесомость | https://resh.edu.ru/subject/lesson/2599/start/ |
| 7 | Сила трения. Силы в природе и технике | https://resh.edu.ru/subject/lesson/1536/start/ |
| 7 | Решение задач по теме «Силы вокруг нас». Обобщение по теме «Силы вокруг нас» | https://resh.edu.ru/subject/lesson/2972/start/ |
| 7 | Давление. Способы увеличения и уменьшения давления. Определение давления эталона килограмма | https://resh.edu.ru/subject/lesson/2971/start/ |
| 7 | Природа давления газов и жидкостей. Давление в жидкости и газе. Закон Паскаля |
https://resh.edu.ru/subject/lesson/2598/start/ https://mosobr.tv/release/7846 |
| 7 | Расчёт давления жидкости на дно и стенки сосуда | https://resh. edu.ru/subject/lesson/1537/start/ edu.ru/subject/lesson/1537/start/ |
| 7 | Сообщающиеся сосуды. Использование давления в технических устройствах | https://resh.edu.ru/subject/lesson/1538/start/ |
| 7 | «Решение задач по теме «Давление твёрдых тел, жидкостей и газов». Обобщение по теме «Давление твёрдых тел, жидкостей и газов» | https://resh.edu.ru/subject/lesson/2970/start/ |
| 7 | Вес воздуха. Атмосферное давление. Измерение атмосферного давления. Опыт Торричелли | https://resh.edu.ru/subject/lesson/1535/start/ |
| 7 | Приборы для измерения давления. Решение задач по теме «Атмосфера и атмосферное давление». Обобщение темы «Атмосфера и атмосферное давление» | https://resh.edu.ru/subject/lesson/2969/start/ |
| 7 | Действие жидкости и газа на погружённое в них тело | https://resh.edu.ru/subject/lesson/2968/start/ |
| 7 | Закон Архимеда. Плавание тел. Воздухоплавание Плавание тел. Воздухоплавание |
https://resh.edu.ru/subject/lesson/2967/start/ |
| 7 | Решение задач по теме «Закон Архимеда. Плавание тел». Обобщение по теме «Закон Архимеда. Плавание тел» | https://resh.edu.ru/subject/lesson/2966/start/ |
| 7 | Механическая работа. Мощность | https://resh.edu.ru/subject/lesson/2965/start/ |
| 7 | Энергия. Потенциальная и кинетическая энергия. Закон сохранения механической энергии. Изучение изменения потенциальной и кинетической энергий тела при движении тела по наклонной плоскости | https://resh.edu.ru/subject/lesson/2597/start/ |
| 7 | Источники энергии. Невозможность создания вечного двигателя. Решение задач по теме «Работа, мощность, энергия». Обобщение по теме «Работа, мощность, энергия» | https://resh.edu.ru/subject/lesson/2964/start/ |
| 7 | Простые механизмы | https://mosobr. tv/release/7929 tv/release/7929 |
| 7 | Рычаг и наклонная плоскость. Проверка условия равновесия рычага | https://resh.edu.ru/subject/lesson/2963/start/ |
| 7 | Блоки и система блоков. «Золотое правило» механики. Коэффициент полезного действия. Определение коэффициента полезного действия наклонной плоскости | https://resh.edu.ru/subject/lesson/2962/start/ |
| 7 | Решение задач по теме «Простые механизмы. «Золотое правило» механики. Обобщение по теме «Простые механизмы. «Золотое правило» механики» | https://resh.edu.ru/subject/lesson/2596/start/ |
| 7 | Виды механического движения. Равномерное и неравномерное движение | https://infourok.ru/videouroki/468 |
| 7 | Средняя скорость | https://infourok.ru/videouroki/422 |
| 8 | Температура и тепловое движение. Внутренняя энергия. Способы изменения внутренней энергии Способы изменения внутренней энергии |
https://resh.edu.ru/subject/lesson/2595/start/ |
| 8 | Теплопроводность. Конвекция. Излучение | https://resh.edu.ru/subject/lesson/2594/start/ |
| 8 | Количество теплоты. Удельная теплоёмкость. Расчёт количества теплоты | https://resh.edu.ru/subject/lesson/2989/start/ |
| 8 | Решение задач по теме «Внутренняя энергия». Обобщение по теме «Внутренняя энергия» | https://resh.edu.ru/subject/lesson/2988/start/ |
| 8 | Агрегатные состояния вещества | https://resh.edu.ru/subject/lesson/2987/start/ |
| 8 | Плавление и отвердевание кристаллических тел | https://resh.edu.ru/subject/lesson/1539/start/ |
| 8 | Удельная теплота плавления. Плавление аморфных тел | https://resh.edu.ru/subject/lesson/2986/start/ |
| 8 | Испарение и конденсация. Насыщенный пар. Кипение. Удельная теплота парообразования Насыщенный пар. Кипение. Удельная теплота парообразования |
https://resh.edu.ru/subject/lesson/2985/start/ |
| 8 | Влажность воздуха. Обобщение по теме «Изменения агрегатного состояния вещества» | https://resh.edu.ru/subject/lesson/2984/start/ |
| 8 | Энергия топлива. Принципы работы тепловых двигателей. Двигатель внутреннего сгорания. Паровая турбина. Реактивный двигатель. Холодильные машины. Тепловые машины и экология. Обобщение по теме «Тепловые двигатели» | https://resh.edu.ru/subject/lesson/2593/start/ |
| 8 | Электроскоп. Проводники и диэлектрики. Делимость электрического заряда. Электрон. Электризация тел. Электрический заряд | https://resh.edu.ru/subject/lesson/2983/start/ |
| 8 | Строение атомов. Ионы. Природа электризации тел. Закон сохранения заряда. Электрическое поле. Электрические явления в природе и технике | https://resh. edu.ru/subject/lesson/1540/start/ edu.ru/subject/lesson/1540/start/ |
| 8 | Обобщение по теме «Электрическое поле» | https://resh.edu.ru/subject/lesson/2592/start/ |
| 8 | Электрический ток. Источники электрического тока. Гальванические элементы. Аккумуляторы. Электрический ток в различных средах. Примеры действия электрического тока | https://resh.edu.ru/subject/lesson/2591/start/ |
| 8 | Применение теплового действия электрического тока | https://infourok.ru/videouroki/481 |
| 8 | Электрическая цепь. Направление электрического тока. Сила тока | https://resh.edu.ru/subject/lesson/2982/start/ |
| 8 | Электрическое напряжение | https://resh.edu.ru/subject/lesson/3126/start/ |
| 8 | Электрическое сопротивление. Закон Ома | https://resh.edu.ru/subject/lesson/2590/start/ |
| 8 | Решение задач по теме «Электрический ток» | https://resh. edu.ru/subject/lesson/2589/start/ edu.ru/subject/lesson/2589/start/ |
| 8 | Расчёт сопротивления проводника | https://resh.edu.ru/subject/lesson/2980/start/ |
| 8 | Последовательное и параллельное соединение проводников | https://resh.edu.ru/subject/lesson/3246/start/ |
| 8 | Сопротивление при последовательном и параллельном соединении проводников. Работа электрического тока. Закон Джоуля–Ленца | https://resh.edu.ru/subject/lesson/2981/start/ |
| 8 | Мощность электрического тока. Электрические нагревательные приборы | https://resh.edu.ru/subject/lesson/2588/start/ |
| 8 | Решение задач по теме «Расчёт характеристик электрических цепей». Обобщение по теме «Расчёт характеристик электрических цепей» | https://resh.edu.ru/subject/lesson/2979/start/ |
| 8 | Магнитное поле прямолинейного тока. Магнитное поле катушки с током Магнитное поле катушки с током |
https://resh.edu.ru/subject/lesson/2978/start/ |
| 8 | Постоянные магниты. Действие магнитного поля на проводник с током. Электродвигатели. Магнитное поле Земли | https://resh.edu.ru/subject/lesson/1541/start/ |
| 8 | Электромагниты | https://infourok.ru/videouroki/484 |
| 8 | Решение задач по теме «Магнитное поле». Обобщение темы «Магнитное поле» | https://resh.edu.ru/subject/lesson/2587/start/ |
| 8 | Система отсчёта. Перемещение. Перемещение и описание движения. Графическое представление прямолинейного равномерного движения | https://resh.edu.ru/subject/lesson/3127/start/ |
| 8 | Скорость при неравномерном движении. Ускорение и скорость при равнопеременном движении | https://resh.edu.ru/subject/lesson/3128/start/ |
| 8 | Перемещение при равнопеременном движении | https://resh. edu.ru/subject/lesson/2977/start/ edu.ru/subject/lesson/2977/start/ |
| 8 | Решение задач по теме «Основы кинематики». Обобщение по теме «Основы кинематики» | https://resh.edu.ru/subject/lesson/3129/start/ |
| 8 | Инерция и первый закон Ньютона. Второй закон Ньютона | https://resh.edu.ru/subject/lesson/2976/start/ |
| 8 | Третий закон Ньютона. Импульс силы. Импульс тела. Закон сохранения импульса. Реактивное движение | https://resh.edu.ru/subject/lesson/1542/start/ |
| 8 | Решение задач по теме «Основы динамики». Обобщение по теме «Основы динамики» | https://resh.edu.ru/subject/lesson/2975/start/ |
| 8 | Итоговая проверочная работа | https://resh.edu.ru/subject/lesson/3130/start/ |
| 8 | Применение теплового действия электрического тока | https://infourok.ru/videouroki/481 |
| 8 | Электромагниты | https://infourok. ru/videouroki/484 ru/videouroki/484 |
| 9 | Относительность движения, сложение скоростей |
https://infourok.ru/videouroki/336 https://infourok.ru/videouroki/560 |
| 9 | Движение тела, брошенного вертикально вверх | https://resh.edu.ru/subject/lesson/3025/start/ |
| 9 | Движение тела, брошенного горизонтально | https://resh.edu.ru/subject/lesson/3131/start/ |
| 9 | Движение тела, брошенного под углом к горизонту | https://resh.edu.ru/subject/lesson/3024/start/ |
| 9 | Движение тела по окружности. Период и частота | https://resh.edu.ru/subject/lesson/1530/start/ |
| 9 | Закон всемирного тяготения | https://resh.edu.ru/subject/lesson/2586/start/ |
| 9 | Движение искусственных спутников Земли. Гравитация и Вселенная Гравитация и Вселенная |
https://resh.edu.ru/subject/lesson/3022/start/ |
| 9 | Решение задач по теме «Движение тел вблизи поверхности Земли и гравитация» | https://resh.edu.ru/subject/lesson/3023/start/ |
| 9 | Обобщение по теме «Движение тел вблизи поверхности Земли и гравитация» | https://resh.edu.ru/subject/lesson/3021/start/ |
| 9 | Механические колебания | https://resh.edu.ru/subject/lesson/3020/start/ |
| 9 | Маятник. Характеристики колебательного движения. Период колебаний математического маятника | https://resh.edu.ru/subject/lesson/3019/start/ |
| 9 | Гармонические колебания. Затухающие колебания. Вынужденные колебания. Резонанс | https://resh.edu.ru/subject/lesson/3018/start/ |
| 9 | Волновые явления. Длина волны. Скорость распространения волн | https://resh. edu.ru/subject/lesson/3017/start/ edu.ru/subject/lesson/3017/start/ |
| 9 | Обобщение по теме «Электромагнитная природа света» | https://resh.edu.ru/subject/lesson/3174/start/ |
| 9 | Звуковые колебания и волны | https://mosobr.tv/release/7951 |
| 9 | Звуковые колебания. Источники звука | https://resh.edu.ru/subject/lesson/2585/start/ |
| 9 | Звуковые волны. Скорость звука | https://resh.edu.ru/subject/lesson/3016/start/ |
| 9 | Громкость звука. Высота и тембр звука | https://resh.edu.ru/subject/lesson/3015/start/ |
| 9 | Отражение звука. Эхо. Резонанс в акустике | https://resh.edu.ru/subject/lesson/3014/start/ |
| 9 | Ультразвук и инфразвук в природе и технике. Обобщение по теме «Звук» | https://resh.edu.ru/subject/lesson/3013/start/ |
| 9 | Индукция магнитного поля | https://resh. edu.ru/subject/lesson/3012/start/ edu.ru/subject/lesson/3012/start/ |
| 9 | Однородное магнитное поле. Магнитный поток | https://resh.edu.ru/subject/lesson/3132/start/ |
| 9 | Электромагнитная индукция |
https://resh.edu.ru/subject/lesson/3011/start/ https://mosobr.tv/release/7849 |
| 9 | Переменный электрический ток | https://resh.edu.ru/subject/lesson/3009/start/ |
| 9 | Электромагнитное поле | https://resh.edu.ru/subject/lesson/3010/start/ |
| 9 | Электромагнитные колебания. Электромагнитные волны | https://resh.edu.ru/subject/lesson/3008/start/ |
| 9 | Механические и электромагнитные колебания | https://mosobr.tv/release/7874 |
| 9 | Механические и электромагнитные волны | https://mosobr.tv/release/7885 |
| 9 | Практическое применение электромагнетизма. Обобщение по теме «Электромагнитные колебания» Обобщение по теме «Электромагнитные колебания» |
https://resh.edu.ru/subject/lesson/2584/start/ |
| 9 | Свет. Источники света | https://resh.edu.ru/subject/lesson/3007/start/ |
| 9 | Распространение света в однородной среде | https://resh.edu.ru/subject/lesson/1543/start/ |
| 9 | Отражение света. Плоское зеркало | https://resh.edu.ru/subject/lesson/3006/start/ |
| 9 | Преломление света | https://resh.edu.ru/subject/lesson/3005/start/ |
| 9 | Линзы | https://resh.edu.ru/subject/lesson/3004/start/ |
| 9 | Изображение, даваемое линзой | https://resh.edu.ru/subject/lesson/3003/start/ |
| 9 | Глаз как оптическая система. Оптические приборы. Обобщение по теме «Геометрическая оптика» | https://resh.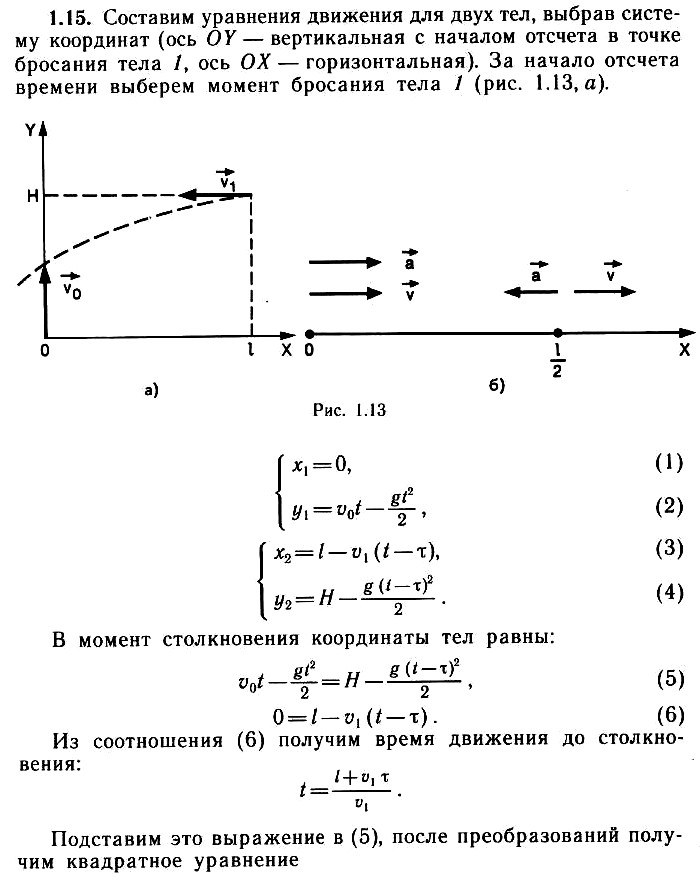 edu.ru/subject/lesson/3001/start/ edu.ru/subject/lesson/3001/start/ |
| 9 | Скорость света. Методы измерения скорости света | https://resh.edu.ru/subject/lesson/3002/start/ |
| 9 | Разложение белого света на цвета. Дисперсия света | https://resh.edu.ru/subject/lesson/3000/start/ |
| 9 | Механическое движение | https://infourok.ru/videouroki/468 |
| 9 | Качественные задачи по механике | https://mosobr.tv/release/7941 |
| 9 | Относительность движения, сложение скоростей | https://infourok.ru/videouroki/336 |
| 9 | Ускорение свободного падения на Земле и других планетах | https://infourok.ru/videouroki/508 |
| 9 | Свободное падение | https://infourok.ru/videouroki/505 |
| 9 | Первая космическая скорость | https://infourok. ru/videouroki/308 ru/videouroki/308 |
| 9 | Силы в природе | https://uchebnik.mos.ru/moderator_materials/material_view/atomic_objects/1405905 |
| 9 | Сила Ампера | https://www.youtube.com/watch?v=ufLl9X5tgf0 |
| 9 | Переменный электрический ток | https://infourok.ru/videouroki/537 |
| 9 | Экспериментальные методы исследования частиц | https://www.youtube.com/watch?v=TKb79UHcVfA |
| 9 | Физико-математический практикум: экспериментальные задачи |
https://mosobr.tv/release/7988 https://mosobr.tv/release/8016 |
Решение проблем | Безграничная физика
Общий подход
Базовые методы решения проблем могут помочь в решении проблем, связанных с движением (т. Е. Законов движения).
Цели обучения
Оценить законы движения с помощью отработанных методов решения проблем
Основные выводы
Ключевые моменты
- Сбор всей необходимой информации и выявление известных и неизвестных – важный первый шаг.

- Всегда делайте рисунок, чтобы помочь определить направления сил и установить [латекс] \ text {x} [/ latex], [latex] \ text {y} [/ latex] и [latex] \ text {z} [ / латекс] топоры.
- Выберите правильные уравнения, решите проблему и убедитесь, что ответ численно соответствует ожиданиям.
Ключевые термины
- уравнение : утверждение, что два выражения равны, выраженное записью двух выражений, разделенных знаком равенства; из которого нужно определить конкретное количество.
При работе с законами движения, хотя знание концепций и уравнений важно, понимание основных методов решения проблем может упростить процесс решения проблем, которые могут показаться трудными.Ваш подход к решению проблем может включать несколько ключевых шагов.
Схема свободного тела : пример чертежа, помогающего определить силы и направления.
Во-первых, соберите всю необходимую информацию о проблеме. Определите все указанные количества ( известных ), затем сделайте то же самое для всех необходимых количеств ( неизвестных ). Также определите задействованные физические принципы (например, силу, гравитацию, трение и т. Д.).
Определите все указанные количества ( известных ), затем сделайте то же самое для всех необходимых количеств ( неизвестных ). Также определите задействованные физические принципы (например, силу, гравитацию, трение и т. Д.).
Далее может пригодиться рисунок.Иногда рисунок может даже помочь определить известные и неизвестные величины. Это не обязательно должно быть произведение искусства, но оно должно быть достаточно четким, чтобы иллюстрировать правильное измерение (то есть одно, два или три измерения). Затем вы можете использовать этот рисунок, чтобы определить, какое направление положительное, а какое отрицательное (отметив это на рисунке).
Следующий шаг – использовать то, что известно, чтобы найти соответствующее уравнение, чтобы найти то, что неизвестно. Хотя проще всего найти уравнение, в котором остается только одно неизвестное, иногда это невозможно.В таких ситуациях вы можете решить несколько уравнений, чтобы найти правильный ответ. Помните, что уравнения представляют собой физические принципы и взаимосвязи, поэтому используйте уравнения и рисунки в тандеме.
Затем вы можете подставить известные значения в соответствующие уравнения и найти численное решение.
Проверьте ответ, чтобы убедиться, что он разумен и имеет смысл. Ваше суждение будет улучшаться и настраиваться по мере того, как вы решаете больше проблем такого рода. Этот шаг «суждения» помогает интуитивно понять проблему с точки зрения ее концептуального значения.Если вы можете судить, является ли ответ разумным, у вас более глубокое понимание физики, чем просто механика решения проблем.
При решении проблем мы стараемся выполнять эти шаги в разном порядке, а также выполнять несколько шагов одновременно. Не существует жесткой процедуры, которая работала бы каждый раз. Креативность и проницательность растут с опытом. Со временем основы решения проблем могут стать относительно автоматическими.
Задачи механики
На этой странице я собрал сборник задач по механике, чтобы помочь вам лучше понять механику.Необходимые уравнения и справочная информация для решения этих задач приведены на страницах кинематики и динамики. Механика – это обширная область физики, и эти проблемы взяты из широкого спектра опыта, который естественным образом возникает в повседневной жизни.
Механика – это обширная область физики, и эти проблемы взяты из широкого спектра опыта, который естественным образом возникает в повседневной жизни.Решения представлены в виде рукописных файлов PDF.
Проблема № 1
Зависит ли объем работы или мощности во время жима лежа от скорости подъема веса?
Решение
Проблема № 2
Автомобиль имеет массу 1700 кг, коэффициент лобового сопротивления 0.35, коэффициент сопротивления качению 0,01, площадь лобовой части 2 м 2 и мощность 150 л.с. Какое минимальное время требуется автомобилю для разгона от 0 до 60 миль в час? Какое минимальное время, если у машины 300 лошадиных сил, при всем остальном? Используйте плотность воздуха 1,2 кг / м 3 и г = 9,8 м / с 2 . Предположим, что автомобиль стоит на идеально ровной поверхности, и предположим, что колеса не скользят.
Решение
Проблема № 3
Рефлекс выпрямления кошки позволяет кошке перевернуться на 180 ° из перевернутого положения при падении, чтобы она могла приземлиться на лапы. Поворачиваясь определенным образом, кошка может это делать, сохраняя нулевой угловой момент. Чтобы понять, как это возможно, рассмотрим следующую физическую систему, показанную ниже, представляющую кошку. Относительно валов (идентичные) цилиндры вращаются с угловой скоростью w s , в то время как валы вращаются в противоположном направлении с угловой скоростью (1/2) w s относительно земли. Найдите угол θ , чтобы это было возможно. Масса каждого цилиндра составляет м, , радиус каждого цилиндра составляет a , а длина каждого цилиндра составляет 3 a .Не обращайте внимания на массу валов.
Поворачиваясь определенным образом, кошка может это делать, сохраняя нулевой угловой момент. Чтобы понять, как это возможно, рассмотрим следующую физическую систему, показанную ниже, представляющую кошку. Относительно валов (идентичные) цилиндры вращаются с угловой скоростью w s , в то время как валы вращаются в противоположном направлении с угловой скоростью (1/2) w s относительно земли. Найдите угол θ , чтобы это было возможно. Масса каждого цилиндра составляет м, , радиус каждого цилиндра составляет a , а длина каждого цилиндра составляет 3 a .Не обращайте внимания на массу валов.
Решение
Проблема № 4
В игре в пул рассчитайте траекторию битка после удара по прицельному мячу. Коэффициент кинетического трения между битком и столом составляет μ k . Предположим, что бильярдный стол совершенно плоский.
Решение
Проблема № 5
Надутый баскетбольный мяч имеет массу 0,624 кг и радиус 0,119 м. Найдите эффективную силу тяжести, действующую на баскетбольный мяч, учитывая плотность воздуха 1,2 кг / м 3 и г = 9,8 м / с 2 .
Найдите эффективную силу тяжести, действующую на баскетбольный мяч, учитывая плотность воздуха 1,2 кг / м 3 и г = 9,8 м / с 2 .
Решение
Проблема № 6
Влияет ли длина скейтборда на расстояние прыжка через рампу?
Решение
Проблема № 7
Тяжелый груз массой 5000 кг необходимо тянуть по плоской поверхности с роликами. Скорость буксируемого груза не должна превышать 20 м / с.Полезная нагрузка должна постепенно увеличиваться в скорости по мере подъема, начиная с состояния покоя. Дальность вытяжки – 20 м. План состоит в том, чтобы использовать двигатель или мотор для вращения тяжелого маховика до определенной скорости вращения, а затем отключить двигатель / мотор и использовать вращающийся маховик для тяги полезной нагрузки. Это позволяет избежать использования очень мощного двигателя / мотора, а вместо этого позволяет использовать гораздо менее мощный двигатель / мотор для медленного добавления энергии в инерциальную систему, которая затем будет иметь достаточно мощности, чтобы тянуть полезную нагрузку. Разработайте систему маховика, которая может тянуть полезную нагрузку по желанию.
Разработайте систему маховика, которая может тянуть полезную нагрузку по желанию.
Решение
Проблема № 8
Если кто-то может прыгнуть вертикально на высоту h на Земле, с g = 9,8 м / с 2 , как высоко он может прыгнуть на другой планете с другим значением g ? Пусть H будет расстоянием вертикального подъема (до взлета) центра масс прыгуна во время фазы толчка во время прыжка.
Решение
Проблема № 9
Пуля вылетает из ружья со скоростью 300 м / с относительно земли.Если пуля имеет массу 0,06 кг, а оружие – 1,5 кг, какой процент от общей кинетической энергии (пули и ружья) имеет пуля?
Решение
Проблема № 10
Длина полностью вытянутой руки толкателя ядра составляет b , а высота его плеча составляет h s . Какой угол θ должна составлять (полностью выдвинутая) рука толкателя ядра относительно земли, чтобы увеличить дальность выстрела? Предположим, что земля горизонтальная.
Принято, что скорость выстрела V o определяется по формуле:
V o 2 = 2 ( E ( θ ) / м – gb sin θ ), где g = 9,8 м / с 2 , m – масса толкателя ядра, а
E ( θ ) = 106,18 м (2 + cos θ ) / 3
Используйте b = 0,8 м и h s = 1.66 мес.
Решение
Проблема № 11
Хаф-пайп для сноуборда имеет угол наклона (шаг) β = 18 ° и высоту стены d = 7 м. Каков оптимальный угол взлета θ для сноубордиста, чтобы достичь максимальной высоты, максимального времени в воздухе и максимальной дистанции по хаф-пайпу? Обратите внимание, что угол α измеряется от горизонтали и используется в ваших расчетах.
Решение
Вернуться на страницу Вопросы по физике
Вернуться на домашнюю страницу Real World Physics Problems
пожаловаться на это объявление
Примеры задач механики
На этой странице я привожу множество примеров решенных задач механики. Их более 140, и они полностью решены, показаны все этапы. Они представлены в виде рукописных файлов PDF, которые вы можете легко загрузить. Примеры охватывают темы механики на уровне, типичном для курсов физики в старших классах средней школы, первого курса колледжа / университета и старшего курса колледжа / университета. Это будет очень полезно при подготовке к тестам и экзаменам. Здесь цель состоит в том, чтобы охватить множество различных типов проблем, от простых до сложных, чтобы помочь вам учиться и более эффективно готовиться.Я знаю, что получить доступ к множеству хороших проблем и , их решения иногда может быть затруднительным, поэтому я создал эту страницу, чтобы у вас было много проблем и их решения в одном удобном месте. Все эти примеры задач созданы мной, поэтому вы не найдете их точной копии где-либо еще. Чтобы они соответствовали вашим курсам, я использовал часто используемые книги по физике, чтобы найти идеи и вдохновение для решения проблем. Так что, конечно же, между ними и проблемами, с которыми вы столкнетесь на уроках и в учебниках по физике, будет какое-то сходство.
Их более 140, и они полностью решены, показаны все этапы. Они представлены в виде рукописных файлов PDF, которые вы можете легко загрузить. Примеры охватывают темы механики на уровне, типичном для курсов физики в старших классах средней школы, первого курса колледжа / университета и старшего курса колледжа / университета. Это будет очень полезно при подготовке к тестам и экзаменам. Здесь цель состоит в том, чтобы охватить множество различных типов проблем, от простых до сложных, чтобы помочь вам учиться и более эффективно готовиться.Я знаю, что получить доступ к множеству хороших проблем и , их решения иногда может быть затруднительным, поэтому я создал эту страницу, чтобы у вас было много проблем и их решения в одном удобном месте. Все эти примеры задач созданы мной, поэтому вы не найдете их точной копии где-либо еще. Чтобы они соответствовали вашим курсам, я использовал часто используемые книги по физике, чтобы найти идеи и вдохновение для решения проблем. Так что, конечно же, между ними и проблемами, с которыми вы столкнетесь на уроках и в учебниках по физике, будет какое-то сходство.
Все примеры задач имеют уникальный номер для удобства использования. Дается постановка проблемы, а затем решение предоставляется в виде файла PDF, который вы можете скачать.
Если вы хотите рассмотреть теорию, лежащую в основе всех этих проблем, я для удобства рассмотрю это на этом веб-сайте, на страницах кинематики и динамики. Если вы изучаете инженерное дело, есть страница с проблемами инженерной механики. Даже если вы не изучаете инженерное дело, очень полезно изучить проблемы кинематики на этой странице, если ничего больше.Они очень полезны тем, что дают гораздо более глубокий охват кинематики, которая также распространяется в трех измерениях. Это, в дополнение к содержанию на этой странице, будет очень полезно для вашего общего понимания механики.
Чтобы увидеть примеры проблем, нажмите на интересующую вас категорию:
Кинематика – одномерные задачи, связанные с ускорением свободного падения (движение по прямой) – старшая школа и первый курс колледжа / университета
Кинематика – одномерные задачи, связанные с постоянным ускорением (движение по прямой) – старшая школа и первый курс колледжа / университета
Кинематика – одномерные задачи, включающие среднюю скорость и среднюю скорость (движение по прямой) – старшая школа и первый курс колледжа / университета
Кинематика – одномерные задачи, включающие мгновенную скорость и скорость (движение по прямой) – старшая школа и первый курс колледжа / университета
Кинематика – одномерные задачи, включающие среднее ускорение и мгновенное ускорение (движение по прямой) – старшая школа и первый курс колледжа / университета
Кинематика – двумерные и трехмерные задачи, связанные с положением и перемещением – старшая средняя школа
Кинематика – двумерные и трехмерные задачи, включающие мгновенную скорость, среднюю скорость и среднюю скорость – старшая школа и первый курс колледжа / университета
Кинематика – двумерные и трехмерные задачи, включающие мгновенное ускорение и среднее ускорение – старшая школа и первый курс колледжа / университета
Кинематика – Проблемы с движением снаряда – Старшая школа и первый курс колледжа / университета
Кинематика – равномерное круговое движение – старшая школа и первый курс колледжа / университета
Кинематика – одномерные задачи, связанные с относительным движением – старшая школа и первый курс колледжа / университета
Кинематика – двумерные задачи, связанные с относительным движением – старшая школа и первый курс колледжа / университета
Сила и движение – Проблемы, связанные с законами Ньютона – Старшая школа и первый курс колледжа / университета
Сила и движение – Проблемы, связанные со шкивами – Старшая школа и первый год колледжа / университета
Сила и движение – Проблемы, связанные с трением – Старшая средняя школа и первый год колледжа / университета
Сила и движение – Проблемы, связанные с равномерным круговым движением – Старшая средняя школа и первый год колледжа / университета
Сила и движение – Проблемы, связанные с вращением, качением и крутящим моментом – Первый курс колледжа / университета
Энергия – Проблемы, связанные с работой и энергией – Старшая средняя школа и первый год обучения в колледже / университете
Энергия – Проблемы, связанные с энергосбережением – Старшая школа и первый год колледжа / университета
Системы – Проблемы, связанные с системами частиц – Старшая средняя школа и первый год колледжа / университета
Системы – Проблемы, связанные с импульсом – Старшая средняя школа и первый год обучения в колледже / университете
Равновесие – Задачи, связанные со статическим равновесием – Старшая средняя школа и первый год обучения в колледже / университете
Кинематика – одномерные задачи, связанные с ускорением свободного падения (движение по прямой) – старшая школа и первый курс колледжа / университета
Проблема №1:
Строится здание, рабочий-строитель стоит на вершине лифтовой шахты высотой 130 м. Рабочий случайно уронил молоток на вал.
Рабочий случайно уронил молоток на вал.
(a) С какой скоростью молот ударяется о землю?
(b) Сколько времени проходит между падением молотка и его падением на землю?
(c) Какую часть общего времени в воздухе молот проводит на верхних 75% дистанции падения?
Скачать решение
Проблема № 2:
Ракета-модель запускается вертикально и имеет постоянное ускорение 5,0 м / с. 2 для 8.0 секунд, по истечении которых не остается топлива.
(а) Какая максимальная высота достигает ракеты?
(b) Сколько времени проходит между запуском ракеты и приземлением?
Скачать решение
Проблема № 3:
Объект падает из состояния покоя, и за секунду до его приземления он находится на половине своей начальной высоты падения.
(а) Какое время падения?
(b) Какова высота падения?
Скачать решение
Проблема № 4:
Мяч бросается вертикально вверх.Поднимаясь вверх, он проезжает точку А со скоростью v . Спускаясь вниз, он проезжает точку B со скоростью (3/4) v . Точка B на 4,5 м выше точки А.
Спускаясь вниз, он проезжает точку B со скоростью (3/4) v . Точка B на 4,5 м выше точки А.
(а) Какая скорость v ?
(b) Какое расстояние между точкой А и высотой пика, достигаемой мячом?
Скачать решение
Проблема № 5:
Башня падения в парке развлечений поднимается со скоростью 5 м / с и оказывается на высоте 45 м над землей, когда одна из гонщиков роняет свой телефон.
(а) Сколько времени нужно, чтобы телефон упал на землю?
(б) С какой скоростью телефон ударяется о землю?
Скачать решение
Проблема № 6:
Девушка стоит в лифте, движущемся вверх со скоростью 5 м / с. Она кладет игрушку для запуска на пол лифта, который затем запускает мяч прямо вверх со скоростью 5,5 м / с относительно лифта. Девушка ловит мяч спустя 1,0 секунды. В момент ловли мяча пол лифта находится на высоте 32 м над землей.
(а) Какова высота мяча над землей в момент его ловли?
(b) Какова высота этажа лифта над землей в момент запуска мяча?
Скачать решение
Проблема № 7:
Ребенок стоит в лифте со стеклянными стенами в торговом центре. Она подбрасывает мяч в воздух с вертикальной скоростью вверх 4,5 м / с относительно лифта и с высоты 1,3 м относительно пола лифта. При этом лифт движется вверх со скоростью 3 м / с, начиная с уровня земли.
Она подбрасывает мяч в воздух с вертикальной скоростью вверх 4,5 м / с относительно лифта и с высоты 1,3 м относительно пола лифта. При этом лифт движется вверх со скоростью 3 м / с, начиная с уровня земли.
(a) Какова максимальная высота мяча с точки зрения ребенка?
(b) С точки зрения человека, находящегося в торговом центре (за пределами лифта), какой максимальной высоты достигает мяч?
Скачать решение
Проблема № 8:
Озорной студент роняет яйцо из окна своей комнаты в общежитии. Яйцо падает прямо на капот припаркованной внизу машины. Несколькими этажами ниже кто-то записывает видео на свою веб-камеру, обращенную к окну.Записано падение яйца за окно. Человек, записывающий видео, является студентом-физиком, и он видит возможность решить интересную физическую задачу, а также определить высоту и, следовательно, комнату, из которой было сброшено яйцо. Она анализирует видео и определяет, что яйцу потребовалось 0,14 секунды, чтобы упасть из верхней части окна в нижнюю. Затем она измеряет высоту окна и составляет 1,30 метра. С какой высоты, измеренной от верхней части окна, упало яйцо?
Затем она измеряет высоту окна и составляет 1,30 метра. С какой высоты, измеренной от верхней части окна, упало яйцо?
Скачать решение
Проблема № 9:
Двое детей играют в игру, в которой один ребенок на высоте 10 м над землей бросает камень без начальной скорости.Второй ребенок тоже роняет камень с высоты 15 м над землей. Второй ребенок роняет камень t r секунд после того, как первый ребенок бросает камень, с начальной скоростью вниз 10 м / с. Какое значение имеет значение t r , чтобы оба камня ударялись о землю одновременно?
Скачать решение
Вот дополнительные задачи свободного падения, над которыми вы можете поработать.
Кинематика – одномерные задачи, связанные с постоянным ускорением (движение по прямой) – старшая школа и первый курс колледжа / университета
Проблема № A-1:
Автомобиль, движущийся по прямой дороге со скоростью 25 м / с, подвергается постоянному ускорению, пока не достигнет скорости 40 м / с.Затем автомобиль поддерживает эту скорость в течение 6,0 секунд. Затем включаются тормоза, заставляя автомобиль постоянно замедляться, пока он снова не достигнет скорости 25 м / с. Если с момента начала разгона до момента замедления до 25 м / с автомобилю требуется 25 секунд, как далеко он проедет за это время?
Скачать решение
Проблема № A-2:
Поезд движется с большой скоростью по прямому пути, в то время как локомотив движется в противоположном направлении по тому же пути.Чтобы избежать столкновения, локомотив должен перейти на разъезд, прежде чем столкновение станет неизбежным. В то же время поезд должен замедлиться, затормозив. В данный момент передняя часть поезда находится на расстоянии 0,35 мили от задней части локомотива, задняя часть локомотива находится в 0,1 мили от входа на разъездную дорогу, скорость поезда составляет 80 миль / ч, а максимальная скорость поезда локомотив 20 миль / ч. Какое минимальное замедление поезда?
Скачать решение
Проблема № A-3:
Учитывая приведенный выше график a ( t ), нарисуйте график v ( t ) и d ( t ).
Скачать решение
Проблема № A-4:
Скорость взлета коммерческого самолета – 260 км / ч. Если длина взлетно-посадочной полосы составляет 2,1 км, каково минимальное постоянное ускорение самолета?
Скачать решение
Проблема № A-5:
Грузовик, движущийся по дороге с твердым покрытием, способен замедляться с постоянным значением 5 м / с. 2 .
(a) Если грузовик изначально движется со скоростью 27,4 м / с, сколько времени нужно, чтобы полностью остановиться?
(b) Как далеко грузовик уезжает за это время?
(c) Нарисуйте график зависимости расстояния отвремя и скорость в зависимости от времени, когда задействованы тормоза.
Скачать решение
Проблема № A-6:
Отвлеченный водитель движется со скоростью 25 м / с, когда она внезапно замечает грузовик, движущийся прямо впереди со скоростью 15 м / с в том же направлении. В момент торможения расстояние между передней частью автомобиля и задней частью грузовика составляет d . Если автомобиль замедляется со скоростью 5,0 м / с 2 , а грузовик сохраняет свою скорость, каково минимальное значение d , чтобы избежать столкновения?
Скачать решение
Проблема № A-7:
Отвлеченный водитель едет со скоростью 25 м / с, когда он внезапно замечает грузовик, движущийся прямо впереди со скоростью 15 м / с в том же направлении.В момент торможения расстояние между передней частью автомобиля и задней частью грузовика составляет 15 метров. Если автомобиль замедляется на отметке a c , а грузовик сохраняет свою скорость, каково минимальное значение a c , чтобы избежать столкновения?
Скачать решение
Проблема № A-8:
Отвлеченный водитель едет со скоростью 25 м / с, когда он внезапно замечает грузовик, движущийся прямо впереди со скоростью 15 м / с в том же направлении. В момент торможения расстояние между передней частью автомобиля и задней частью грузовика составляет 9 метров.Автомобиль замедляется со скоростью 5 м / с 2 , и через одну секунду после того, как водитель автомобиля задействует тормоза, водитель грузовика замечает машину сзади и начинает разгоняться с отметки a t . Какое минимальное значение a t , чтобы избежать столкновения?
Скачать решение
Проблема № A-9:
Отвлеченный водитель едет по неправильной стороне дороги, когда замечает встречный автомобиль, движущийся ему навстречу. Он быстро нажимает на тормоза, заставляя свою машину замедляться на 4.5 м / с 2 , с начальной скорости 20 м / с. Другой водитель также нажал на тормоза через 1,1 секунды, в результате чего его автомобиль замедлился со скоростью 5 м / с 2 с начальной скорости 23 м / с. В тот момент, когда отвлеченный водитель нажимает на педаль тормоза, перед каждой машиной находится расстояние 117 м. Произошло ли столкновение двух машин?
Скачать решение
Кинематика – одномерные задачи, включающие среднюю скорость и среднюю скорость (движение по прямой) – старшая школа и первый курс колледжа / университета
Проблема № B-1:
Скорость звука в воздухе составляет 330 м / с при 0 градусах Цельсия.Если средняя скорость реактивного самолета в 2,3 раза превышает скорость звука, как далеко он улетает за 0,25 секунды?
Скачать решение
Проблема № B-2:
Грузовик для доставки посылки движется в гору с постоянной скоростью 50 км / ч. После доставки посылки грузовик спускается с того же холма со скоростью 80 км / ч. Какова средняя скорость грузовика в оба конца?
Скачать решение
Проблема № B-3:
На приведенном выше графике показана зависимость скорости отвремя для частицы, движущейся по прямой. Какова средняя скорость и средняя скорость частицы за все время ее движения?
Скачать решение
Проблема № B-4:
Частица движется по оси x со скоростью, определяемой соотношением с ( t ) = при + b , где a и b – константы, а t – время. Если частица начинает движение в момент времени t 1 и прекращает движение в момент времени t 2 , каково значение a и b , чтобы средняя скорость и средняя скорость были между t 1 и t 2 , равно (1/2) ( s ( t 1 ) + s ( t 2 )).
Скачать решение
Проблема № B-5:
Положение объекта, движущегося по оси x , определяется как x = -2 t 3 + 2 t 2 + 3 t – 5, где x в метрах, а t в секундах.
(a) Найдите положение объекта при t = 2,0 с и t = 3,5 с.
(b) Каково смещение объекта между t = 2.0 с, а т = 3,5 с?
(c) Какова средняя скорость объекта между t = 2,0 с и t = 3,5 с?
(d) Какова средняя скорость объекта между t = 2,0 с и t = 3,5 с?
Скачать решение
Проблема № B-6:
Положение объекта, движущегося по оси x , показано выше, где x указано в метрах, а t – в секундах.
(a) Какова средняя скорость объекта между 0 и t 3 ?
(b) Какова средняя скорость объекта от 0 до t 3 ?
Скачать решение
Проблема № B-7:
Грузовик проезжает 6,5 км по прямой дороге. Затем водитель выходит из грузовика, проходит 1,5 км, чтобы доставить посылку в один дом, а затем продолжает идти еще 2 км, чтобы доставить посылку в другой дом.Затем водитель возвращается к грузовику. Скорость движения грузовика составляет 70 км / ч, а скорость ходьбы водителя – 5 км / ч.
(a) Какова средняя скорость и средняя скорость водителя от начала поездки до момента доставки посылки во второй птичник?
(b) Какова средняя скорость и средняя скорость водителя от начала движения до момента, когда водитель вернется к грузовику?
Скачать решение
Проблема № B-8:
Объект движется по положительной оси x со скоростью 2 м / с из точки A в точку B.Затем он движется со скоростью 3 м / с из точки B в точку C. Если точка C расположена на полпути между точками A и B, какова средняя скорость и средняя скорость объекта между точками A и C?
Скачать решение
Проблема № B-9:
Объект движется по положительной оси x вправо со скоростью с 1 из точки A в точку B. Затем он движется со скоростью с 2 , из точки B в точку точка C. Если точка C расположена слева от точки B, выведите уравнение, связывающее среднюю скорость объекта со средней скоростью объекта между точками A и C.
Скачать решение
Кинематика – одномерные задачи, включающие мгновенную скорость и скорость (движение по прямой) – старшая школа и первый курс колледжа / университета
Проблема № C-1:
Положение частицы определяется как x = 4-10 t + 2 t 2 -3 t 3 , где t в секундах, а x в секундах. метров.
(а) Какова скорость частицы при t = 2 с?
(b) Положение частицы увеличивается или уменьшается при t = 2 с?
(c) Какова скорость частицы при t = 2 с?
Скачать решение
Проблема № C-2:
Положение частицы определяется как x = 6 + 4 t – 12 t 2 + 6 t 3 , где t в секундах, а x в метрах.
(a) В какое время скорость частицы равна -1,5 м / с?
(б) В какое время скорость частицы равна 1,5 м / с?
(c) Какова минимальная скорость и минимальная скорость частицы?
Скачать решение
Кинематика – одномерные задачи, включающие среднее ускорение и мгновенное ускорение (движение по прямой) – старшая школа и первый курс колледжа / университета
Проблема № D-1:
Положение частицы определяется как x = 2 + 4 t – 5 t 2 + 9 t 3 , где t в секундах, а x в метрах.
(а) Каков средний ускоритель частицы между t = 1 с и t = 2 с?
(б) Что такое ускорение частицы при t = 3 с?
Скачать решение
Проблема № D-2:
Частица движется вправо со скоростью 21 м / с за время 3,1 с и движется влево со скоростью 18 м / с за время 6,4 с. Каково среднее ускорение частицы с 3,1 до 6,4 с?
Скачать решение
Проблема № D-3:
Частица движется по прямой линии, как показано на приведенном выше графике зависимости скорости отвремя. Нарисуйте график, показывающий ускорение этой частицы.
Скачать решение
Проблема № D-4:
Частица движется по прямой линии, как показано на приведенном выше графике. Нарисуйте график, представляющий ускорение этой частицы.
Скачать решение
Проблема № D-5:
Частица движется по прямой со скоростью 12 м / с, а через некоторое время она движется со скоростью −21 м / с. Если среднее ускорение частицы -2.5 м / с 2 , сколько времени прошло между начальной и конечной скоростью?
Скачать решение
Кинематика – двумерные и трехмерные задачи, связанные с положением и перемещением – старшая средняя школа
Проблема № E-1:
Частица имеет следующие координаты: x = −4,0 м, y = 7,0 м и z = 2,0 м.
(a) Найдите вектор положения в нотации единичного вектора.
(б) Какова величина этого вектора?
(c) Нарисуйте вектор в правой системе координат.
Скачать решение
Проблема № E-2:
Изначально частица имеет следующие координаты: x = 4,5 м, y = −3,5 м. Через некоторое время координаты: x = −1,5 м, y = 2,0 м.
(а) Найдите вектор смещения частицы.
(b) Нарисуйте начальный, конечный вектор и вектор смещения частицы.
Скачать решение
Проблема № E-3:
Изначально частица имеет следующие координаты: x = 1.0 м, y = −3,0 м, z = 8,0 м. Через некоторое время координаты: x = 3,0 м, y = −5,0 м, z = 4,0 м. Каков вектор смещения частицы?
Скачать решение
Кинематика – двумерные и трехмерные задачи, включающие мгновенную скорость, среднюю скорость и среднюю скорость – старшая школа и первый курс колледжа / университета
Проблема № F-1:
Самолет летит в 350 милях к востоку от аэропорта A до аэропорта B за 50 минут, а затем летит в 500 милях к югу от аэропорта B до аэропорта C за 1.8 ч.
(a) Определите вектор смещения для полного пути.
(b) Определите вектор средней скорости для полной поездки.
(c) Определите среднюю скорость для всей поездки.
Скачать решение
Проблема № F-2:
За 4,2 часа метеозонд дрейфует на 10,2 км на запад, 18,7 км на юг и на 3,1 км вверх.
(a) Определите величину средней скорости воздушного шара и угол, который этот вектор образует с горизонталью.
(b) Определите среднюю скорость воздушного шара.
Скачать решение
Проблема № F-3:
Положение частицы определяется выражением r = 4 i – 2 t 2 j + 8 t 3 k , с r в метрах и t в секундах.
(а) Какова мгновенная скорость частицы при t = 2,0 с?
(b) Какова величина мгновенной скорости при t = 2.0 с?
Скачать решение
Кинематика – двумерные и трехмерные задачи, включающие мгновенное ускорение и среднее ускорение – старшая школа и первый курс колледжа / университета
Проблема № G-1:
Частица имеет начальную скорость v = 3,0 i – 4,0 j + 8,0 k , а через 5,0 с она имеет конечную скорость v = 2,0 i – 1,0 j + 3,0 к . Единицы измерения – м / с.
(a) Какое среднее ускорение за интервал 5,0 с?
(b) Какова величина среднего ускорения, и показать ориентацию среднего ускорения.
Скачать решение
Проблема № G-2:
Частица изначально расположена в начале координат и имеет начальную скорость v = 3,0 i + 2,0 j – 1,0 k в метрах в секунду. Он испытывает постоянное ускорение a = -1.0 i – 1,5 j , в метрах на секунду в квадрате.
(а) Какова скорость частицы, когда ее координата y максимальна?
(б) Где в данный момент находится частица?
Скачать решение
Проблема № G-3:
Положение частицы определяется как r = t 2 i + ( t 3 – 5 t ) j – 3,0 t k , дюйм метров.Что такое мгновенное ускорение частицы? Какова ориентация мгновенного ускорения при t = 1,0 с?
Скачать решение
Кинематика – Проблемы с движением снаряда – Старшая школа и первый курс колледжа / университета
Проблема № H-1:
Мяч катится по пандусу, наклоненному под углом 15 ° к горизонтали. На краю рампы (точка A) скорость мяча составляет v 0 .Определите диапазон значений v 0 , чтобы шар вошел в показанную горизонтальную трубу.
Скачать решение
Проблема № H-2:
Игрушечную машинку с дистанционным управлением отъезжают от края стола в точке А со скоростью 2,2 м / с. Он приземляется в точке B. Если высота стола 1,1 м, какое расстояние по горизонтали, L , между точкой A и точкой B?
Скачать решение
Проблема № H-3:
Игрушечная машинка с дистанционным управлением выезжает за край пандуса в точке А со скоростью 3 м / с.Он приземляется в точке B. Если край пандуса находится на высоте 0,8 м и наклонен под углом 20 ° к горизонтали, каково расстояние по горизонтали, L , между точкой A и точкой B?
Скачать решение
Проблема № H-4:
Человек, стоящий на вершине холма, бросает камень с начальной скоростью 12 м / с под углом 20 ° ниже горизонтали.
(a) Рассчитайте горизонтальное смещение породы через 1,5 с.
(b) Рассчитайте вертикальное смещение породы 1.5 секунд спустя.
Скачать решение
Проблема № H-5:
Чтобы рассчитать высоту здания h , студент-физик запускает мяч с начальной скоростью 30 м / с под углом 65 ° над горизонтом. Другой студент-физик стоит на крыше здания и определяет, что мяч приземляется на крышу здания через 3,5 секунды после его запуска.
(а) Какова высота здания, h ?
(b) Какова максимальная высота пика H , достигаемая мячом, относительно ученика на крыше?
Скачать решение
Проблема № H-6:
Человек, стоящий на вершине холма, бросает камень с начальной скоростью 14 м / с под углом 30 ° к горизонту.
(a) Рассчитайте горизонтальное смещение породы через 1,7 с.
(b) Рассчитайте вертикальное смещение породы через 1,7 с.
(c) Сколько времени нужно, чтобы скала упала на 3,5 м ниже своей начальной высоты?
Скачать решение
Проблема № H-7:
Мяч запускается с земли в воздух. На высоте 7,3 м скорость мяча составляет v = 8,2 i + 5,7 j в метрах в секунду.
(a) Какова максимальная высота мяча?
(b) Какое общее горизонтальное расстояние пройдёт мяч?
(c) В момент непосредственно перед тем, как мяч ударяется о землю, каковы величина и направление его скорости?
Скачать решение
Проблема № H-8:
Каскадер едет на своем мотоцикле со скоростью 25 м / с от пандуса, который наклонен под 30 °. Он намеревается приземлиться на кузов грузовика. Водитель грузовика должен подождать T секунд после того, как мотоцикл покинет рампу, прежде чем разгоняться из состояния покоя со скоростью 5 м / с 2 , чтобы мотоцикл приземлился на задней части грузовика.Изначально край пандуса имеет высоту 3 м, задняя часть грузовика – 1 м, а задняя часть грузовика находится в 45 м от края пандуса. Что такое T ?
Скачать решение
Проблема № H-9:
Бейсболист бросает мяч с начальной скоростью 20 м / с из точки А, которая находится на 1,4 м над землей и в 14 м от стены. Какой угол запуска θ , чтобы высота х , то есть расстояние от земли до точки удара о стену, была максимальной?
Скачать решение
Проблема № H-10:
Мяч запускается на уровне земли со скоростью 20 м / с под углом 35 ° от горизонтали.Горка находится в 25 м от точки старта, имеет наклон 20 °. Как далеко вверх по склону, D , приземляется мяч?
Скачать решение
Проблема № H-11:
В соревнованиях, проводимых в спортзале средней школы, цель состоит в том, чтобы запустить мяч с уровня пола так, чтобы он прошел через два кольца, подвешенных к потолку, как показано. Один из участников – студент-физик, который вычисляет значение L и θ , исходя из скорости запуска 20 м / с.Что это за две ценности?
Скачать решение
Вот дополнительные проблемы с движением снаряда, над которыми вы можете поработать.
Кинематика – Равномерное круговое движение – Старшая средняя школа и первый курс колледжа / университета
Проблема № I-1:
Спринтер бежит по повороту трассы радиусом 30 м со скоростью 11 м / с. Какое ускорение у спринтера и в каком направлении указывает ускорение на ?
Скачать решение
Проблема № I-2:
Заряженная частица движется по круговой траектории в магнитном поле с радиальным ускорением 2.5 × 10 14 м / с 2 . Если круговой путь имеет радиус 14 см, какова его скорость?
Скачать решение
Проблема № I-3:
Вентилятор вращается со скоростью 1000 оборотов в минуту. Острие лопастей имеют радиус 0,20 м.
(a) Какое расстояние проходит кончик лезвия за один полный оборот?
(b) Какова скорость острия лезвия?
(c) Какое ускорение кончика лезвия?
Скачать решение
Проблема № I-4:
Скоростной поезд движется по кривой со скоростью 250 км / ч.Каков наименьший радиус кривизны гусеницы, при котором максимальное ускорение, которое испытывают пассажиры, составляет 0,05 g ?
Скачать решение
Проблема № I-5:
Скоростной поезд движется по кривой радиусом 1,5 км. Какова максимальная скорость поезда, чтобы максимальное ускорение, которое испытывают пассажиры, составило 0,05 g ?
Скачать решение
Проблема № I-6:
Тросовая машина движется по трассе со скоростью 200 миль в час.Чтобы автомобиль не съехал с трассы, он привязан к центральной стойке с помощью троса. Диаметр гусеницы – 21,3 м, а диаметр колеса автомобиля – 5 см.
(а) Какое ускорение у автомобиля?
(b) Как быстро вращаются колеса автомобиля, в оборотах в минуту?
(c) Если смотреть на машину сверху, с какой скоростью она движется по трассе в оборотах в минуту?
Скачать решение
Кинематика – одномерные задачи, связанные с относительным движением – старшая школа и первый курс колледжа / университета
Проблема № J-1:
Судно движется по реке вверх по течению со скоростью 15 км / ч по отношению к воде реки.Вода в реке течет со скоростью 7 км / ч по отношению к земле.
(а) Какова скорость лодки относительно земли?
(b) Человек на лодке идет от носа лодки к задней части лодки со скоростью 5 км / ч по отношению к лодке. Какова скорость человека относительно земли?
Скачать решение
Проблема № J-2:
Человек поднимается по остановившемуся эскалатору за 100 секунд. Когда эскалатор движется, человеку требуется 75 секунд, чтобы подняться наверх, когда он стоит на нем.Если длина эскалатора 20 м, сколько времени потребуется этому человеку, чтобы подняться по движущемуся эскалатору?
Скачать решение
Проблема № J-3:
Кинооператор стоит на кузове пикапа и снимает сцену для фильма. Он снимает на видео машину, едущую прямо перед ним, движущуюся со скоростью 45 миль / ч быстрее, чем грузовик. Внезапно автомобиль замедляется, останавливается и начинает двигаться в противоположном направлении со скоростью 60 миль / ч, как было измерено кем-то на земле. Если пикап движется со скоростью 35 миль / ч, а изменение скорости автомобиля заняло 2 секунды.5 секунд, каково было ускорение автомобиля с точки зрения (а) оператора и (б) человека на земле?
Скачать решение
Кинематика – двумерные задачи, связанные с относительным движением – старшая школа и первый курс колледжа / университета
Проблема № K-1:
Две машины, A и B, приближаются к перекрестку, как показано. Автомобиль А находится в 600 м от перекрестка и движется со скоростью 80 км / ч. Автомобиль B находится в 700 м от перекрестка и движется со скоростью 90 км / ч.
(a) В обозначении единичного вектора, какова скорость автомобиля A относительно автомобиля B?
(b) Как направление скорости, найденное в (a), сравнивается с линией обзора между двумя автомобилями?
(c) Как ответы на (a) и (b) меняются по мере приближения автомобилей к перекрестку?
Скачать решение
Проблема № K-2:
Поезд движется в северном направлении со скоростью 25 м / с относительно земли. В то же время идет дождь.Наблюдатель на земле видит, что капли дождя составляют угол 18 ° с вертикалью. Пассажир поезда видит, как капли дождя падают в абсолютно вертикальном направлении. Какова скорость капель дождя относительно земли?
Скачать решение
Проблема № K-3:
Пилот самолета намеревается при наличии ветра вылететь прямо на восток на расстояние 950 км. Самолет развивает скорость 630 км / ч, и пилот рассчитывает, что самолет должен лететь с курсом 15 ° к югу от востока.Если самолет прибывает в пункт назначения через 1,8 часа, каков вектор скорости ветра?
Скачать решение
Проблема № K-4:
Река шириной 350 м течет в восточном направлении со скоростью 2,5 м / с. Лодка со скоростью 9,5 м / с относительно воды устанавливает курс в направлении 25 ° к западу от севера.
(а) Какова скорость лодки относительно Земли?
(b) Сколько времени требуется лодке, чтобы пересечь реку, начиная с южного берега?
Скачать решение
Проблема № K-5:
Река течет в восточном направлении в точке 3.5 м / с. Лодка со скоростью 8,5 м / с относительно воды устанавливает курс в направлении 30 ° к северу от востока. Когда лодка находится в движении, один из пассажиров идет с левой стороны лодки прямо к правой стороне лодки со скоростью 1,5 м / с относительно лодки. Какая скорость пассажира относительно земли?
Скачать решение
Вот дополнительные задачи относительной скорости, над которыми вы можете поработать.
Сила и движение – Проблемы, связанные с законами Ньютона – Старшая школа и первый курс колледжа / университета
Проблема № L-1:
К плите весом 2 кг прилагаются три силы, как показано.Каково ускорение плиты в обозначении единичного вектора, выраженное величиной и направлением?
Скачать решение
Проблема № L-2:
Предположим, что сила 10,5 Н действует на массу м 1 вправо, а затем та же сила действует на массу м 2 влево. Предположим, что обе массы находятся на поверхности без трения: м 1 = 3 кг и м 2 = 1.2 кг. Какова сила контакта между двумя массами в каждой ситуации?
Скачать решение
Проблема № L-3:
Блок массой 2 кг скользит по плоской поверхности без трения со скоростью 5 м / с. Сила 6 Н прикладывается против направления движения блока, и блок замедляется до скорости 2 м / с. Каково расстояние перемещения блока за период действия силы?
Скачать решение
Проблема № L-4:
Блок массой м скользит с постоянной скоростью v по канавке, вырезанной в наклонной плоскости, как показано.Какова величина и направление силы, действующей на блок со стороны наклонной плоскости?
Скачать решение
Проблема № L-5:
Две массы, м 1 и м 2 , сидят на плоской поверхности без трения. Они соединены между собой двумя тросами, которые соединены с устройством, содержащим пружину, находящуюся под напряжением. Вытягивается штифт, который освобождает пружину, заставляя ее сжиматься с силой 6 Н. Если м 1 = 3 кг и м 2 = 1.4 кг, какое ускорение у каждой массы?
Скачать решение
Проблема № L-6:
В парке развлечений падает башня с ускорением 8,1 м / с 2 . Какая восходящая сила действует на всадника 63 кг?
Скачать решение
Проблема № L-7:
Вертолет набирает скорость 1,5 м / с 2 . Какая восходящая сила действует на пассажира весом 72 кг?
Скачать решение
Проблема № L-8:
Космическая капсула одновременно запускает три своих двигателя, обозначенных цифрами 1, 2, 3.Если двигатели срабатывают в течение 9,5 с и F 1 = 50 Н, F 2 = 60 Н и F 3 = 65 Н, какова скорость капсулы через 9,5 с ? Капсула первоначально движется в положительном направлении оси y со скоростью 30 м / с, а ее масса составляет 120 кг.
Скачать решение
Проблема № L-9:
Сфера массой м подвешена к крыше автомобиля на веревке длиной 25 см. По мере разгона автомобиля шнур образует угол 35 ° с вертикалью.Какое ускорение у машины?
Скачать решение
Сила и движение – Проблемы, связанные со шкивами – Старшие классы средней школы и первый год обучения в колледже / университете
Проблема № M-1:
В показанной системе шкивов блок 1 имеет массу 80 кг, а блок 2 – 30 кг. Если система выходит из состояния покоя, какова скорость блока 2 через 1,5 секунды? Пренебрегайте массой шкивов и троса.
Скачать решение
Проблема № M-2:
В показанной системе шкивов блок м имеет массу 120 кг.Если один конец каната тянут со скоростью 4 м / с 2 , каково натяжение каната? Пренебрегайте массой шкивов и троса.
Скачать решение
Проблема № M-3:
В показанной системе шкивов два блока высвобождаются из состояния покоя. Поверхности скольжения не имеют трения, а масса троса и шкивов незначительна. Определите ускорение каждого блока и натяжение веревки. Обратите внимание, что м 1 = 50 кг и м 2 = 150 кг.
Скачать решение
Проблема № M-4:
В показанной системе шкивов два блока высвобождаются из состояния покоя. Поверхность скольжения не имеет трения, а масса каната и шкивов незначительна. Определите ускорение каждого блока и натяжение веревки. Обратите внимание, что м 1 = 10 кг и м 2 = 20 кг.
Скачать решение
Проблема № M-5:
В показанной системе шкивов блок м имеет массу 16 кг.Какова постоянная сила F , которая должна быть приложена к веревке, чтобы блок имел восходящее ускорение 2 м / с 2 . Пренебрегайте массой шкивов и троса.
Скачать решение
Проблема № M-6:
Блок M имеет массу 40 кг, а оба блока м имеют массу 20 кг каждый. Масса шкивов и тросов ничтожна. Все блоки начинаются с места, а левый блок м перемещается на расстояние 2 м в 1.5 с. Определите натяжение канатов и величину усилия F .
Скачать решение
Проблема № M-7:
В показанной системе шкивов два блока высвобождаются из состояния покоя. Поверхности скольжения не имеют трения, а масса шкивов и каната незначительна. Какова скорость каждого блока через 1,3 с? Обратите внимание, что м 1 = 10 кг и м 2 = 30 кг.
Скачать решение
Сила и движение – Проблемы, связанные с трением – Старшая средняя школа и первый год обучения в колледже / университете
Проблема № N-1:
В показанной системе коэффициент статического трения между всеми контактными поверхностями равен 0.15, а коэффициент кинетического трения между всеми контактными поверхностями равен 0,10. Определите ускорение блоков и натяжение каната. Обратите внимание, что м 1 = 20 кг и м 2 = 10 кг.
Скачать решение
Проблема № N-2:
Два блока находятся на колесной платформе, которая изначально неподвижна. Коэффициент кинетического трения между левым блоком и платформой равен 0,15, а коэффициент кинетического трения между правым блоком и платформой равен 0.10. Платформу внезапно толкают вправо, вызывая проскальзывание между ней и блоками. Определите ускорение блоков и силу между ними. Обратите внимание, что м 1 = 15 кг и м 2 = 20 кг.
Скачать решение
Проблема № N-3:
В показанной системе шкивов м 1 = 6 кг, м 2 = 13 кг и м 3 = 10 кг. Определите ускорение каждого блока и натяжение веревки.
Скачать решение
Проблема № N-4:
Диск запускается с начальной скоростью v 1 под углом α 1 , как показано, в наклонной плоскости. Если коэффициент кинетического трения равен tan θ , какова конечная скорость диска при условии, что наклон достаточно велик, чтобы диск скользил в течение длительного времени?
Скачать решение
Проблема № N-5:
Платформа ускоряется вправо со скоростью 5 м / с 2 , а масса м. находится на вершине платформы и имеет ускорение 2 м / с 2 относительно платформы.Если м = 6 кг и коэффициент кинетического трения между массой и платформой равен 0,25, какова сила F , приложенная к массе? Если относительное ускорение массы происходит в противоположном направлении, какова сила F ?
Скачать решение
Проблема № N-6:
Сила P приложена к массе м 1 , которая составляет угол θ с горизонталью. Найдите выражение для P ( θ ) для случая, когда (a) масса m 1 и масса m 2 движутся как единое целое, и (b) существует относительное скольжение между масса м 1 и масса м 2 .
Скачать решение
Проблема № N-7:
В показанной системе шкивов м A = 10 кг, м B = 20 кг, м C = 8 кг и м D = 5 кг . Если коэффициент кинетического трения между блоками и скользящей поверхностью равен 0,15, каково ускорение блока A и каково натяжение различных участков каната?
Скачать решение
Проблема № N-8:
Две массы, м 1 и м 2 , скользят по поверхности без трения со скоростью 5 м / с.Передняя масса м 2 сталкивается с шероховатым пятном и испытывает трение, а затем масса, связанная за ним, м 1 , через короткое время встречается с шероховатым пятном и тоже испытывает трение. Если стержень, соединяющий две массы, имеет пренебрежимо малую массу, как далеко сдвигаются обе массы, когда передняя масса встречается с шероховатым участком? Удочка длиной 2 м. Игнорируйте размер м 1 и м 2 .
Скачать решение
Проблема № N-9:
Блок массой 2 кг находится на верхней части конвейерной ленты, движущейся со скоростью 5 м / с.Блок не может двигаться вместе с ремнем с пластиной, как показано. В результате лента скользит под блоком со скоростью 5 м / с относительно блока. Коэффициент кинетического трения между блоком и ремнем составляет 0,20, и между блоком и пластиной нет трения. Предположим, что кто-то должен был толкнуть блок в поперечном направлении со скоростью v , как показано. Какую силу применяет человек?
Скачать решение
Вот дополнительные проблемы с трением и шкивом, над которыми вам нужно поработать.
Сила и движение – Проблемы, связанные с равномерным круговым движением – Старшая средняя школа и первый год обучения в колледже / университете
Проблема № O-1:
Шар весом 3 кг прикреплен к веревке длиной L и вращается по горизонтальной окружности, как показано на рисунке. Если скорость мяча постоянна и равна 2,5 м / с, каков угол θ и натяжение струны?
Скачать решение
Проблема № O-2:
Мяч весом 3 кг движется по горизонтальной окружности радиуса R = 2.1 мес. Одиночная струна проходит через кольцо, прикрепленное к шару, и поддерживается на обоих концах A и B, как показано. Определите постоянную скорость мяча.
Скачать решение
Проблема № O-3:
Мяч весом 3 кг движется по горизонтальной окружности радиусом R . Мяч соединен с двумя струнами, которые опираются на точки A и B, как показано. Если натяжение верхней струны вдвое превышает натяжение нижней струны, какова скорость мяча?
Скачать решение
Проблема № O-4:
Блок находится на внутренней стороне обода колеса, радиус которого составляет R = 1.4 мес. Колесо ориентировано вертикально и вращается с угловой скоростью w . Коэффициент трения покоя между колесом и блоком составляет 0,20.
(a) Какое минимальное значение w , чтобы блок не скользил по ободу?
(b) Какое минимальное значение w , чтобы блок не упал с обода?
(c) Для каждого из значений w в (a) и (b), какова сила контакта между блоком и ободом в верхнем и нижнем положениях, как показано? Используйте массу блока = 2.5 кг.
Скачать решение
Проблема № O-5:
Человека, едущего на гравитроне в парке развлечений, можно смоделировать в виде блока, как показано на рисунке. Дано, что θ = 70 °, R = 6 м, а коэффициент трения покоя между человеком и стенкой гравитрона равен 0,25. Каков диапазон угловых скоростей гравитрона w , чтобы человек не скользил вверх или вниз по стене?
Скачать решение
Проблема № O-6:
Полая сфера с блоком массы 0.Внутри него 500 кг вращается с угловой скоростью 8,5 рад / с, w . Если внутренний радиус сферы составляет R = 0,7 м, определите значения для θ , если (а) нет трения между блоком и сферой, и блок остается в контакте со стенкой шара и не скользит по нему. стенка сферы; (b) коэффициент статического трения между блоком и сферой составляет 0,25, и блок остается в контакте со стенкой сферы и не скользит по стенке сферы.
Скачать решение
Проблема № O-7:
Блок массой м помещается на вертикально ориентированное колесо, вращающееся с угловой скоростью w = 2 рад / с. Если блок изначально размещен на колесе без проскальзывания, под каким углом θ 0 можно разместить блок так, чтобы блок оставался на колесе, не теряя контакта и не проскальзывая, как можно дольше? Коэффициент трения покоя составляет 0,30.
Скачать решение
Сила и движение – Проблемы, связанные с вращением, качением и крутящим моментом – Первый курс колледжа / университета
Проблема № P-1:
В показанной системе шкивов два блока имеют массу м 1 и м 2 , радиус шкива составляет R , инерция вращения шкива составляет I , и коэффициент кинетического трения между блоком и поверхностью μ k .Определите (а) угловое ускорение шкива, (б) ускорение блоков и (в) натяжение в верхней и нижней частях каната. Предположим, что система находится в движении.
Скачать решение
Проблема № P-2:
В показанной системе шкивов м 1 = 2 кг, м 2 = 3 кг, M = 5 кг, R = 5 см, а коэффициент кинетического трения между блоками и поверхностью 0.15. Масса ремня и шкивов незначительна. Определите угловое ускорение диска и ускорение его центра масс.
Скачать решение
Проблема № P-3:
В показанной системе шкивов определите ускорение блока. Масса ремня и шкива незначительна.
Скачать решение
Проблема № P-4:
Цилиндр катится по склону, как показано. Каков минимальный коэффициент статического трения между цилиндром и поверхностью, чтобы цилиндр катился без проскальзывания? Предположим, что коэффициент кинетического трения между цилиндром и поверхностью равен 0.10. Какое угловое ускорение цилиндра и каково ускорение его центра масс? Сравните это с чехлом, который не скользит. Обратите внимание, что M = 10 кг и R = 6 см.
Скачать решение
Проблема № P-5:
Шнур наматывается на внутренний барабан катушки и натягивается с горизонтальным усилием 120 Н. Масса катушки 40 кг, радиус вращения 60 мм. Если μ с = 0,15 и μ k = 0.10, определяют угловое ускорение катушки и ускорение ее центра масс.
Скачать решение
Проблема № P-6:
Обруч и цельный цилиндр изначально соприкасаются на склоне, как показано. Масса каждого 50 кг, радиус 30 см. Могут ли обруч и цилиндр оставаться неподвижными и соприкасаться на склоне? Если коэффициент кинетического трения между обручем и цилиндром равен 0,10, каково угловое ускорение каждого из них и каково ускорение центра масс каждого из них? Сколько оборотов совершают пяльцы и цилиндр после того, как каждый проехал на расстояние 1 метр?
Скачать решение
Вот дополнительные проблемы, над которыми вы можете поработать, связанные с силой и движением:
Проблемы с силой
Проблемы с наклонной плоскостью
Проблемы с крутящим моментом
Вот примеры анализа силы и движения в трех измерениях:
Боулинг
диск Эйлера
Гироскопы
Энергия – Проблемы, связанные с работой и энергией – Старшая средняя школа и первый год обучения в колледже / университете
Проблема № Q-1:
Грузовик спускается с холма с уклоном 20 °.Если грузовик движется с постоянной скоростью v , какая мощность рассеивается тормозами? Если грузовик затем движется в гору с постоянной скоростью v , какую мощность производит двигатель? Масса грузовика 6000 кг, сила сопротивления, действующая на грузовик, – 1200 Н.
Скачать решение
Проблема № Q-2:
Масса м поддерживается сверху веревкой, а снизу – пружиной. Канат имеет натяжение 15 Н, жесткость пружины 900 Н / м, а м = 4 кг.Если веревка оборвана, определите максимальное смещение груза и определите максимальную скорость груза.
Скачать решение
Проблема № Q-3:
Груз массой 5 кг медленно помещается на груз массой 3 кг, который первоначально находится в состоянии покоя и поддерживается пружиной внизу. Если жесткость пружины составляет 250 Н / м, какова максимальная степень сжатия пружины и какова максимальная скорость масс?
Скачать решение
Проблема № Q-4:
Блок массой м выходит из состояния покоя и падает на расстояние х до контакта с пружиной слева, как показано, а затем падает еще на расстояние 100 мм до контакта со второй пружиной на правильно, как показано.Жесткость пружины слева составляет 1000 Н / м, а жесткость пружины справа – 2000 Н / м. Если максимальное сжатие пружины слева составляет 200 мм, определите значение х . Масса м = 9 кг.
Скачать решение
Проблема № Q-5:
Масса м прикреплена к пружине и толкается вниз, так что пружина сжимается на 30 см. Затем масса высвобождается, и система пружина-масса отрывается от земли, как показано.Максимальная высота отрыва 0,60 м. Если масса м = 15 кг, какова будет максимальная высота отрыва на Луне, учитывая, что ускорение свободного падения на Луне составляет одну шестую от земного? Не обращайте внимания на массу пружины и нижнюю опору пружины.
Скачать решение
Проблема № Q-6:
К блоку на плоской горизонтальной поверхности приложена сила F с величиной 120 Н. Коэффициент кинетического трения между блоком и поверхностью равен 0.15. Какова скорость блока, когда он переместился на расстояние 2,5 метра? Масса блока м, = 3 кг, θ = 30 °. Блок изначально находится в состоянии покоя.
Скачать решение
Проблема № Q-7:
К блоку на задней части грузовика, движущемуся с постоянной скоростью 18 м / с, приложена сила F с величиной 120 Н. Коэффициент кинетического трения между блоком и поверхностью тележки составляет 0,15. Какова скорость блока, когда он переместился на расстояние 2.5 метров относительно грузовика? Рассчитайте ответ с точки зрения наблюдателя на земле и на грузовике. Масса блока м, = 3 кг, θ = 30 °. Изначально блок неподвижен на грузовике.
Скачать решение
Энергия – Проблемы, связанные с энергосбережением – Старшая средняя школа и первый год обучения в колледже / университете
Проблема № R-1:
Цилиндр прикреплен к пружине на склоне, как показано.Цилиндр выходит из состояния покоя, когда пружина не растягивается и не сжимается. Масса цилиндра 25 кг, радиус 8 см, жесткость пружины 500 Н / м. Какова максимальная и минимальная скорость цилиндра и соответствующая величина растяжения пружины? Предположим, что цилиндр катится без проскальзывания.
Скачать решение
Проблема № R-2:
Доска массой 16 кг подвешена на двух тросах длиной 0,8 м каждый, каждый под углом 30 ° к горизонту.Находясь в этом положении, доска освобождается от покоя. Какова скорость доски, когда она находится в самом нижнем положении? Не обращайте внимания на массу кабелей.
Скачать решение
Проблема № R-3:
Доска поддерживается двумя цилиндрами на склоне, как показано. Масса доски 12 кг, масса каждого цилиндра 5 кг, а их радиус 5 см. Если система выведена из состояния покоя и нигде нет скольжения, какова скорость доски после того, как она переместилась на расстояние 1?2 метра? Предположим, что плата остается в контакте с цилиндрами.
Скачать решение
Проблема № R-4:
В показанной системе шкивов м A = 4 кг, м B = 5 кг и м C = 11 кг. Массы A и B приклеены друг к другу. Система выводится из состояния покоя, и когда масса C падает на 0,4 м, масса B отделяется от массы A из-за некачественного клея. Определите скорость массы C, когда она упала на 0.7 мес. Не обращайте внимания на массу троса и шкива.
Скачать решение
Проблема № R-5:
Плата поддерживается двумя цилиндрами на горизонтальной поверхности, как показано. Масса доски 13 кг, масса и радиус меньшего цилиндра 5 кг и 5 см, а масса и радиус большего цилиндра 10 кг и 7 см. Если система выведена из состояния покоя и нигде нет скольжения, какова скорость доски после того, как цилиндры переместятся на расстояние 30 см? Предположим, что плата остается в контакте с цилиндрами.
Скачать решение
Вот дополнительные проблемы, связанные с энергетикой, над которыми вам нужно поработать:
Проблемы с энергией
Задачи кинетической энергии
Системы – Проблемы, связанные с системами частиц – Старшая средняя школа и первый год колледжа / университета
Проблема № S-1:
Две гири, м 1 и м 2 , могут скользить без трения по горизонтальному стержню. Пружина жесткостью k соединена между двумя массами.В данный момент массы м 1 и м 2 расположены на расстоянии x 01 и x 02 от центра масс (см) соответственно. . В этот момент пружина растягивается на величину Δ L , и скорость двух масс равна нулю. Найдите выражения для расстояний x 1 и x 2 с течением времени после выпуска системы.Обратите внимание, что система определена здесь как массы м 1 и м 2 , а также пружина. Масса пружины мала относительно м 1 и м 2 , поэтому ее можно не учитывать.
Скачать решение
Проблема № S-2:
В показанной системе масса м 1 скользит на расстояние L вниз по склону массой м 2 .Как далеко уклон скользит по поверхности и в каком направлении?
Скачать решение
Проблема № S-3:
Подводная капсула неподвижна относительно морского дна. Капсула имеет массу 2200 кг. Пассажир в капсуле весом 80 кг встает, в результате чего его центр масс поднимается на 40 см относительно капсулы. Затем пассажир уходит влево на расстояние 1,8 м относительно капсулы. Какое смещение капсулы в результате движения пассажира?
Скачать решение
Проблема № S-4:
Пушка массой 1400 кг стреляет шаром массой 60 кг в горизонтальном направлении со скоростью 53 м / с относительно пушки.Какова скорость пушки и ядра относительно Земли?
Скачать решение
Проблема № S-5:
Емкость с водой начальной массой 120 кг поднимается с постоянной скоростью, v = 0,8 м / с. Контейнер негерметичен и теряет 1,2 кг воды в секунду. Найдите выражение для силы, необходимой для подъема контейнера с течением времени. Что, если бы контейнер вместо этого ускорялся вверх со скоростью 0,4 м / с 2 ?
Скачать решение
Проблема № S-6:
Две массы, м 1 и м 2 , прижимаются к пружине жесткостью k .Пружина сначала сжимается на величину Δ L , а затем одновременно освобождаются массы. Какова конечная скорость двух масс?
Скачать решение
Проблема № S-7:
Желоб сбрасывает песок на конвейерную ленту со скоростью 5 кг / с. Ремень имеет линейную скорость 1,3 м / с. Какую мощность производит двигатель, приводящий в движение конвейерную ленту?
Скачать решение
Проблема № S-8:
Двухступенчатая ракета имеет начальную массу 1250 кг.В конце первой ступени ракета имеет массу 500 кг. В этот момент нижняя часть ракеты отделяется, и верхняя часть ракеты начинает стрелять. Нижняя часть ракеты имеет массу 200 кг. По окончании второй ступени масса ракеты (состоящей только из верхней части) составляет 140 кг. На обеих ступенях ракета расходует горючее со скоростью 2,4 кг / с. Скорость выхлопных газов относительно ракетного двигателя составляет 2800 м / с. Какова прибавка скорости ракеты в конце второй ступени и какая у ракеты тяга? Ракета находится в глубоком космосе, где на нее действует незначительная гравитационная сила.
Скачать решение
Системы – Проблемы, связанные с импульсом – Старшая школа и первый год обучения в колледже / университете
Проблема № T-1:
Падающая вниз масса м контактирует с пружиной жесткостью k со скоростью v 0 . Какова продолжительность удара (время, в течение которого пружина и груз находятся в контакте)? Какой импульс при ударе? Какая средняя сила действует на массу во время удара?
Скачать решение
Проблема № Т-2:
Игрок в гольф ударяет по мячу для гольфа, придавая ему начальную скорость 60 м / с с углом запуска 40 ° над горизонтом.Клюшка и мяч находятся в контакте в течение 1,9 мс, а масса мяча составляет 45 г. Определите: (а) импульс, действующий на мяч и клюшку, (б) среднюю силу, действующую на мяч, и (в) работу, совершаемую над мячом.
Скачать решение
Проблема № Т-3:
Ребенок бросает мяч массой 150 г о стену со скоростью 6 м / с. Мяч отскакивает с уменьшением кинетической энергии на 40%. Определите: (a) скорость мяча сразу после отскока, (b) импульс, действующий на мяч и стенку, и (c) среднюю силу, приложенную к мячу, если время контакта между мячом и стенкой было 8.3 мс.
Скачать решение
Проблема № Т-4:
Космическая капсула разделяется на две части в результате детонации взрывных болтов, удерживающих эти две части вместе. Величина импульса, действующего на каждую деталь, составляет 350 Н · с. Если массы двух частей составляют 1300 кг и 1900 кг, какова относительная скорость разделения двух частей?
Скачать решение
Проблема № Т-5:
В результате удара на объект массой 1 действует средняя сила 120 Н.5 кг в направлении x , в результате чего его скорость в направлении x достигает 4,2 м / с. В то же время на объект действует средняя сила 90 Н в направлении y . Если начальная скорость объекта в направлении x и y составляет 1,5 м / с и 0,6 м / с, соответственно, какова конечная скорость объекта в направлении y ?
Скачать решение
Проблема № Т-6:
Игрушка состоит из 3 резиновых мячей массой м 1 , м 2 и м 3 , через которые пропущен тонкий стержень, позволяющий шарикам свободно скользить. вдоль стержня.Игрушка сбрасывается с высоты х над землей. Если все столкновения упругие, какой высоты достигнет шар массой м 3 ?
Скачать решение
Проблема № Т-7:
Груз массой 3,5 тонны падает с расстояния 1,8 м, а затем ударяется о сваю массой 0,6 тонны. В результате этого совершенно неупругого столкновения свая забивается на 3 см в землю. Найти среднюю силу, действующую на сваю землей?
Скачать решение
Проблема № Т-8:
Вагон поезда весом 40 тонн столкнулся с другим неподвижным вагоном.В результате две машины соединяются вместе, и во время столкновения теряется 32% начальной кинетической энергии. Определите массу второго вагона поезда.
Скачать решение
Проблема № Т-9:
Шар A движется к двум шарам B и C, как показано, со скоростью 5 м / с. Трение незначительное, а столкновение упругое. Если все шары идентичны, определите скорости всех 3 шаров после столкновения.
Скачать решение
Проблема № Т-10:
Два вращающихся цилиндра соприкасаются, как показано.Из-за трения между цилиндрами они в конечном итоге достигают одинаковой угловой скорости. Что это за угловая скорость? Обратите внимание, что цилиндры изначально вращаются в противоположных направлениях.
Скачать решение
Проблема № T-11:
Блок изначально находится в состоянии покоя на горизонтальной поверхности, и к нему прилагается сила F . Учитывая график зависимости силы от времени, как показано, определите скорость блока в момент времени t e . Допустим, F e > μ s mg .
Скачать решение
Вот дополнительные проблемы с моментом, над которыми вы можете поработать.
Равновесие – Задачи, связанные со статическим равновесием – Старшая школа и первый год обучения в колледже / университете
Проблема № U-1:
Идентичные блоки длиной L кладут друг на друга. Каждый блок выходит на расстояние d за нижний, а нижний блок также выходит на расстояние d за край стола.Какое максимальное количество блоков можно складывать?
Скачать решение
Проблема № U-2:
В показанной системе коэффициент трения покоя между массой m и доской M составляет 0,20. Определите значение d , чтобы система находилась в равновесии.
Скачать решение
Проблема № U-3:
Единая доска длиной L = 20 футов прислонена к стене, как показано.На верхнем торце доски есть валик. Если доска имеет вес 70 фунтов, каков минимальный коэффициент статического трения между доской и землей?
Скачать решение
Проблема № U-4:
Единая доска длиной L = 20 футов опирается на ролик, как показано. Если доска имеет вес 70 фунтов, каков минимальный коэффициент статического трения между доской и землей?
Скачать решение
Проблема № U-5:
В показанной системе определите силы, действующие на стержень в точке O и балку в точке A.
Скачать решение
Вот дополнительные задачи статики, над которыми вы можете поработать.
Вот дополнительные механические задачи, над которыми вы можете поработать, которые охватывают разные темы, так что это хороший обзор.
Вернуться на домашнюю страницу Real World Physics Problems
пожаловаться на это объявление
Как решать физические задачи с помощью сил (механика).
Эдуард Андре Рени родился в 1971 году в Бордо, Франция. Длительные исследования в науке дали ему докторскую степень по химии твердого тела, что привело к контракту на получение докторской степени в Хиросимском университете, Япония.Когда ему было чуть за тридцать, он интегрировал большую корпорацию по очистке воды в Нидерландах в качестве старшего научного сотрудника. Десять лет спустя он решил летать на собственных крыльях, основав свою собственную компанию Synaptic Machines, которая объединила его интересы в науке, его стремление поделиться ими с миром, а также его страсть и талант к музыке. Почему бы не зарабатывать на жизнь тем, что действительно любит!
Это совпало с осознанием того, что он был чертовски хорошим учителем. Чтобы оказать финансовую поддержку своей новой компании, он начал обучать несколько детей в подростковом возрасте, чтобы они готовились к получению международного бакалавриата и A-level по физике.Показатели успеха были настолько высоки, и ему так понравилось помогать этим детям, что он решил сделать это занятие своей основной профессиональной целью! Сегодня он еженедельно помогает десятку студентов, и почти столько же находятся в списке ожидания!
Что касается музыки, то с подросткового возраста Эдуард сочиняет и играет как мультиинструменталист в различных поп-рок, блюз, рок, джаз, хэви-метал, фолк, автор песен и электро-группы. Он также известен как «Ключи Эдварда» или «Синаптические машины».Очень требовательный к качеству звука, Эдуард учился на звукорежиссера-самоучки, техники микширования и мастеринга, чтобы улучшить свое собственное производство. Сегодня, опираясь на 25-летний опыт создания музыки, он профессионально занимается и продает лицензии на использование своей композиции в различных средствах массовой информации (телевидение, радио, веб-видео и т. Д.).
Эдуард открыл для себя Удеми в начале 2017 года. Это казалось прекрасной возможностью поделиться с другими в широком масштабе знаниями, которые он накопил и которые привели его к полноценной профессиональной жизни, полной музыки, страсти к науке и, что самое главное, благодарность от его учеников.Он выпустит свой первый курс примерно весной 2017 года (Производство музыки в Propellerhead Reason). Он намеревается работать над новыми онлайн-курсами по трем темам (музыка, физика и благополучие) и надеется публиковать как минимум два в год.
Формулирование двух частей физических проблем | Информация для инструкторов | Вибрации и волны Решение проблем
В этом разделе Вит Буца проводит различие между физикой и математикой, связанной с физическими проблемами. Он обсуждает, как это различие помогает ему определить, поняли ли студенты суть проблемы.
Физические проблемы состоят из двух принципиально разных частей, и эти две части отражают суть научного метода. Первая часть относится к тому, что я называю «физическими законами в действии» (или пониманием физики). Для этого требуется, чтобы учащиеся обладали способностью переводить физические ситуации в математические выражения. Вторая часть включает в себя собственно математические вычисления. Когда у учащихся возникают проблемы с решением проблемы, очень важно, чтобы учитель определил, какая из двух частей вызывает затруднения у ученика.По моему опыту, учителя редко делают это.
Часть I. Преобразование физических ситуаций в математические уравнения
Физические задачи состоят из двух принципиально разных частей, и эти две части отражают суть научного метода.
—Wit Busza
Я могу вспомнить бесконечное количество примеров, когда студенты приходили ко мне и говорили: «Я не понимаю. Я действительно разбираюсь в физике, но мне кажется, что я никогда не могу решить проблемы. Что случилось?” Ответ на это почти всегда таков: «Вы не понимаете физику.«Хотя большинство студентов считают постановку задачи тривиальной, на самом деле это самая сложная часть решения проблемы. Я часто прошу студентов сначала визуализировать механические части, увидеть, как они взаимосвязаны, и нарисовать схему того, что происходит. Вы будете удивлены, как часто они ошибаются! Так много учеников испытывают трудности с визуализацией в двух и трех измерениях.
Когда я вспоминаю свой собственный опыт в начальной школе, у нас часто возникали проблемы со словами. Вы знаете , кто-то пришел с двумя яблоками и проделал с ними то-то и то-то и т. д.Иногда мне было трудно уследить за происходящим. Видите, это не математика. Это способность превращать язык в картину происходящего. И это большая проблема для студентов. Но это еще не конец.
Теперь вы должны взять это описание ситуации на обычном языке – скажем, например, я держу мяч в руке в трех метрах над полом, а затем отпускаю – и перевести его в математику.
Итак, этот мяч начал падать.Как оно падает? И на этом этапе вы, возможно, можете это визуализировать, но вам нужны законы природы, чтобы перевести это в математическую форму. Этот шар движется все быстрее и быстрее, что математически означает, что вторая производная его положения не равна 0, а является некоторой константой – в данном случае g. Итак, как только вы визуализируете картину, даже если вы можете представить, что происходит, вам все равно придется перевести это в математику. И это физика – понимание природы, того, как ведет себя система. Все это первая часть решения задачи, и, повторяю, самая сложная часть.Но большинство студентов думают, что это легкая часть, а все остальное – сложная!
Блок-схема решения физических задач (из справочного видео по решению проблем, «Простое гармоническое движение и введение в решение проблем»).
Помочь себе можно по-разному. Например, если это проблема механики, вы рисуете диаграмму сил. Поразительно, сколько знаний и опыта нужно иметь, чтобы нарисовать так называемую силовую диаграмму. Вы должны понимать, что такие величины, как скорость, ускорение, сила и т. Д., можно математически представить в виде векторов. Вы должны определить все относящиеся к делу части проблемы, а затем представить их в виде математических величин.
Итак, в типичной задаче физическая ситуация сводится к уравнению плюс вещи, которые мы называем «граничными условиями» или «начальными условиями». У меня есть мяч. Я держу его в руке. И что с ним произойдет, зависит от того, когда я его отпущу. Выпущу ли я его сейчас или через час? Он будет делать то же движение, но математическое описание этого будет несколько отличаться в двух случаях.Итак, первый этап проблемы состоит из перевода физической ситуации, а также всех начальных и граничных условий в математические выражения.
Часть II: Решение математических уравнений
Математическое описание задачи знаменует собой конец первого этапа. Затем мы совершаем чудо: забываем, что математические уравнения и граничные условия имеют какое-то отношение к физике. Мы помещаем эти уравнения в компьютер или просим нашего дружелюбного профессора математики решить их.Нам не нужно сообщать компьютеру, что это имеет какое-то отношение к физической проблеме. Профессору нам нужно только сказать: «Послушайте, у меня есть эти уравнения с этими граничными условиями. Что произойдет со значением этого количества в зависимости от этого количества со временем? » Второй этап не имеет ничего общего с физикой! Мы вошли в мир математики. Только после того, как вы решите уравнения – и, конечно же, вы должны сделать это правильно, – вы сможете вернуться к физике. Это включает в себя знание правил определения того, что на самом деле происходит при решении ваших уравнений.
Оценка физики больше, чем математики
Я стараюсь ставить более 50% оценки учащегося за физику, вовлеченную в задачу.
Студенты ненавидят это, потому что они приходят и говорят: «Послушайте, в первых двух строках я сделал несколько глупых ошибок. А потом я сделал три страницы математики, и у меня получилось. И вы дали мне только 40% оценки. Это не честно.” Конечно, ученик мог правильно понять всю математику, но он упустил суть проблемы.Я думаю, что очень важно, чтобы выставление оценок четко отражало то, что важно.
Это сопротивление тому, что физика больше, чем математика, при оценивании заданий, является причиной того, что ученики ненавидят задачи с несколькими вариантами ответов, и почему в тот момент, когда вы задаете задачи с несколькими вариантами ответов, оценки резко падают. В задаче с множественным выбором вы должны понимать суть проблемы. Вы не можете просто угадать. И поэтому вы либо понимаете, какой из пяти законов природы применим, либо нет.Частичного кредита нет. Студенты, не особенно сильные в предмете, известны тем, что выживают за счет частичного зачета. Если у них хорошая память, они могут пройти курс физики, вообще не понимая физики, потому что они могут заработать частичный балл по математике и своей памяти. В вопросах с несколькими вариантами ответов память не так сильно помогает. Конечно, я предполагаю, что выбор хорошо продуман.
Wolfram | Alpha Примеры: Механика
Другие примеры
ДинамикаВычислить движение объектов под действием крутящих моментов и сил.
Выполните вычисление по второму закону Ньютона:
Вычислите движение блока на наклонной плоскости:
Другие примеры
Другие примеры
КинематикаРасчет движения свободно движущихся объектов и небесных тел.
Найдите уравнения, связанные с задачей двух тел:
Проанализируйте упругое столкновение в одном измерении:
Другие примеры
Эластомеханика
Вычислить эффекты деформации, напряжения и других форм деформации.
Рассчитайте инженерное напряжение:
Найдите напряжение в цилиндре:
Определите значение коэффициента Пуассона для деформации:
Выполните расчет потери устойчивости по столбцу Эйлера:
Вычислите прогиб балки под нагрузкой:
Другие примеры
Механические системы
Изучите уравнения движения для обширного набора механических систем.
Найдите уравнения, связанные с механической системой:
Другие примеры
Классическая механика
Вычислить лагранжианы и гамильтонианы физической системы.
Вычислите уравнения Эйлера – Лагранжа:
Вычислите уравнения движения из гамильтониана:
Другие примеры
Решение задач в физике
Решение задач в физике РЕШЕНИЕ ФИЗИЧЕСКИХ ЗАДАЧ
СТРАТЕГИЯ
Dr.Марк Холлабо
Нормандальский муниципальный колледж
http://www.nr.cc.mn.us/physics/Faculty/HOLLABGH/probsolv.htm
Два фактора могут помочь вам стать лучше решатель задач физики. Прежде всего, вы должны знать и понять принципы физики. Во-вторых, вы должны иметь стратегию применения этих принципов в новых ситуациях в чем может быть полезна физика. Мы называем эти ситуации проблемы. Многие студенты говорят: «Я понимаю материал, я просто не могу решать проблемы.«Если это верно для вас как изучающего физику, тогда, возможно, вам нужно развивать свои навыки решения проблем. Имея стратегию организация этих навыков может вам помочь.
Решению задач физики можно научиться просто как вы научились водить машину, играть на музыкальном инструменте или кататься на велосипеде. Что может помочь вам больше всего, так это иметь общий подход к решению каждой проблемы, которую вы сталкиваться. Вы можете использовать разные инструменты или тактики с различных областях физики, но общая стратегия остается тем же.Скорее всего, вы уже приобрели навыки решения проблем и привычки из предыдущих курсов в физика, химия или математика. Как и другие области обучения и жизни, некоторые из этих привычек могут быть полезны и некоторые могут действительно помешать вашему прогрессу в изучении решения проблемы физики.
Итак, изучая этот новый подход, будьте готовы пробовать новые идеи и отказаться от старых привычек, которые могут факт мешает вашему пониманию. Когда вы взрослеете как решатель проблем физики, вы обнаружите, что этот подход будет стать для вас второй натурой.Вы начнете автоматически делать то, что приведет вас к созданию эффективного Решение проблемы.
Как и во многих других учебных мероприятиях, полезно разбить стратегию решения проблемы на основные и мелкие шаги. Стратегия, которую мы хотим, чтобы вы изучили, пять основных шагов: Сфокусируйтесь на проблеме , Физика Описание , Планирование решения , Выполнение плана , и Оцените решение .Давайте возьмем подробно рассмотрите каждый из этих шагов, а затем выполните образец проблема следования стратегии. На этом этапе нашей обсуждение, не беспокойтесь, если есть физические термины или концепции что вы не понимаете. Вы изучите эти концепции по мере необходимости. Затем вернитесь к этому обсуждению.
ФОКУСИРУЙТЕ ПРОБЛЕМУ
Обычно, когда вы читаете заявление
проблема физики, вы должны визуализировать задействованные объекты и
их контекст.Вам нужно нарисовать картинку и указать любую
предоставленная информация.
(1) Во-первых, создайте мысленный образ проблемной ситуации.
(2) Затем нарисуйте грубую, хотя и буквальную картинку, показывающую важные объекты, их движение и их взаимодействия. Например, взаимодействие может состоять из один объект соединяется с другим веревкой.
(3) Пометьте всю известную информацию. На этом этапе не беспокоиться о присвоении алгебраических символов конкретным количества.
Иногда вопрос, задаваемый в проблема не очевидна. «Веревка безопасна?» не то, на что вы можете прямо ответить. Спросите себя, что конкретно спрашивают? Как это переводится в какое-то исчисляемое количество?
Есть много способов решить физику проблема. Одна из частей обучения тому, как решать проблему, – это знать, какой подход использовать. Вам нужно будет обрисовать концепции и принципы, которые, по вашему мнению, будут полезны при решении проблема.
Если задействованы простые движения, используйте кинематику определение скорости и ускорения.
Если задействованы силы и объекты взаимодействуют из-за них сил используйте законы движения Ньютона.
Силы, которые действуют в течение определенного промежутка времени и заставляют объекты изменить их скорости предлагает с помощью функции сохранения импульса.
Часто в ситуациях, связанных с теплофизикой или электромагнетизм, принцип сохранения энергии Полезно.
Возможно, вам потребуется указать временные интервалы, в течение которых применение каждого принципа будет наиболее полезным.
Важно определить любые ограничения, присутствующие в такая ситуация, например, “машина не выезжает” дорога ».
Укажите любые приближения или упрощения, которые, по вашему мнению, облегчит решение проблемы, но не существенно повлияют на результат. Часто мы игнорировать силы трения из-за сопротивления воздуха.
Ваш подход, вероятно, будет очень последовательно на протяжении всего определенного раздела учебника. Задача для вас будет заключаться в том, чтобы применить этот подход в различных ситуаций.
ОПИСАТЬ ФИЗИКУ
«Физическое описание»
проблема переводит данную информацию и очень дословно
изображение в идеализированную диаграмму и определяет переменные, которые могут
можно манипулировать, чтобы вычислить желаемое количество.В некотором смысле
вы переводите буквальную ситуацию в идеализированную
ситуация, когда вы можете применить законы физики.
Самый большой недостаток начинающих решателей физических задач –
пытаясь применить законы физики, то есть записать
уравнения, прежде чем приступить к качественному анализу
проблема. Если вы можете устоять перед искушением искать
уравнения слишком рано в решении вашей проблемы, вы станете
гораздо более эффективное решение проблем.
Чтобы построить описание физики, вы должны выполнить
следующий:
- Переведите ваше изображение в диаграмму (и), которая дает только
важная информация для математического
решение. На идеализированной диаграмме люди, машины,
а другие объекты могут стать квадратными блоками или точками.
- Определите символ для каждой важной физической переменной на
ваша диаграмма.
- Обычно вам нужно нарисовать систему координат, показывающую
+ и – направления.
- Если вы используете концепции кинематики, нарисуйте движение
диаграмма с указанием скорости объектов и
ускорение в определенных положениях и в определенное время.
- Если взаимодействия важны, нарисуйте идеализированное свободное тело,
и силовые диаграммы.
- При использовании принципов сохранения нарисуйте «до», «передача» (т. е. во время), и диаграммы “после”, чтобы показать, как система изменения.Сбоку от диаграмм укажите значение для каждой физической переменной, которую вы отметили на диаграммы или укажите, что она неизвестна.
Тогда, используя вопрос, ваша физика описания и изложенного вами подхода, вам нужно будет определить целевую переменную. То есть вы должны решить, что неизвестное количество – это то, что вы должны вычислить из своего списка переменные. Спросите себя, отвечает ли рассчитанное количество вопрос.В сложных задачах может быть больше, чем одна целевая переменная или несколько промежуточных переменных, которые вы вычислить.
Теперь, зная целевые переменные, и ваш подход, вы можете собрать свой набор математических выражений с использованием принципов и ограничений вашего подход, чтобы связать физические переменные с вашим диаграммы. Это первый раз, когда ты действительно начинаешь смотреть для количественных соотношений между переменными.
ПЛАНИРОВАТЬ РЕШЕНИЕ
Прежде чем вы начнете вычислять
ответ, найдите время, чтобы составить план.Обычно, когда по законам
физика выражается в уравнении, уравнение является общим,
универсальное заявление. Вы должны построить конкретные алгебраические
уравнения, которые позволят вам вычислить целевую переменную.
- Определите, как уравнения в вашем наборе инструментов могут быть вместе, чтобы найти вашу целевую переменную. Начните с уравнение, содержащее целевую переменную.
- Определите все неизвестные в этом уравнении.
- Найдите уравнения в вашем наборе инструментов, содержащие эти неизвестные.
- Продолжайте этот процесс, пока ваши уравнения не будут содержать новых неизвестные.
- Пронумеруйте каждое уравнение для удобства.
- В настоящее время не решайте уравнения численно.
Часто опытные специалисты по решению проблем будут начать с целевой переменной и работать в обратном направлении, чтобы определить путь к ответу. Иногда единицы помогут найти правильный путь. Например, если вы ищете скорость, вы знаете, что ваш окончательный ответ должен быть в м / с.
У вас есть решение, если в вашем плане много независимых уравнений, так как есть неизвестные. Если не, определить другие уравнения или проверить план, чтобы убедиться, что он вероятно, что переменная будет сокращена из ваших уравнений.
Если у вас такое же количество уравнений и неизвестные, указывают порядок, в котором решаются уравнения алгебраически для целевой переменной. Обычно вы начинаете построение плана в конце и работа в обратном направлении первый шаг, то есть вы записываете уравнение, содержащее сначала целевая переменная.
ВЫПОЛНИТЬ ПЛАН
Теперь вы готовы выполнить план.
- Выполните алгебру в порядке, указанном в плане.
- Когда вы закончите, у вас должно получиться одно уравнение с ваша целевая переменная изолирована с одной стороны и известна только количества с другой стороны.
- Подставьте значения (числа с единицами измерения) в это окончательное уравнение.
- Убедитесь, что единицы согласованы, чтобы они отменили должным образом.
Наконец, вычислите числовой результат для целевая переменная (и). Убедитесь, что ваш окончательный ответ понятно человеку, который оценит ваше решение.
Чрезвычайно важно решить задача алгебраически перед вставкой любого числового ценности. Некоторые неизвестные количества могут быть отменены, и вы на самом деле не нужно знать их числовое значение. В некоторые сложные задачи может быть полезно вычислить промежуточные числовые результаты как проверка обоснованности вашего решение.
ОЦЕНИТЬ РЕШЕНИЕ
Наконец, вы готовы оценить свои
отвечать. Здесь вы должны руководствоваться здравым смыслом в отношении того, как
реальный мир работает так же, как и те аспекты физического мира
вы узнали на уроке физики.
- Имеют ли векторные величины и величину, и направление?
- Может ли кто-нибудь воспользоваться вашим решением?
- Является ли результат разумным и в пределах вашего опыт? Вспомните, например, что автомобили не езжайте по шоссе со скоростью 300 миль / час.Если вы кладете более прохладный предмет в горячую воду, вода остывает вниз, и объект нагревается.
- Есть ли смысл в единицах измерения? Скорость не измеряется, например, в кг / с.
- Вы ответили на вопрос?
По возможности рекомендуется
внимательно прочтите решение, особенно если оно
оценивается вашим инструктором. Если ваша оценка предполагает
вам, что ваш ответ неправильный или необоснованный, сделайте
заявление на этот счет и объясните свои рассуждения.
Дополнительная литература:
Патриция Хеллер, Рональд Кейт и Скотт Андерсон (1992), Обучение решению проблем посредством совместной работы. Часть 1. Групповое или индивидуальное решение проблем, американец. Журнал физики , Vol. 60, No. 7, pp. 627-636.
Патрисия Хеллер и Марк Холлабо (1992), Задача обучения
Решение через кооперативную группировку. Часть 2:
Разработка проблем и структурирование групп, США
Журнал физики , Vol.60, No. 7, pp. 637-644.

 01. 2021
01. 2021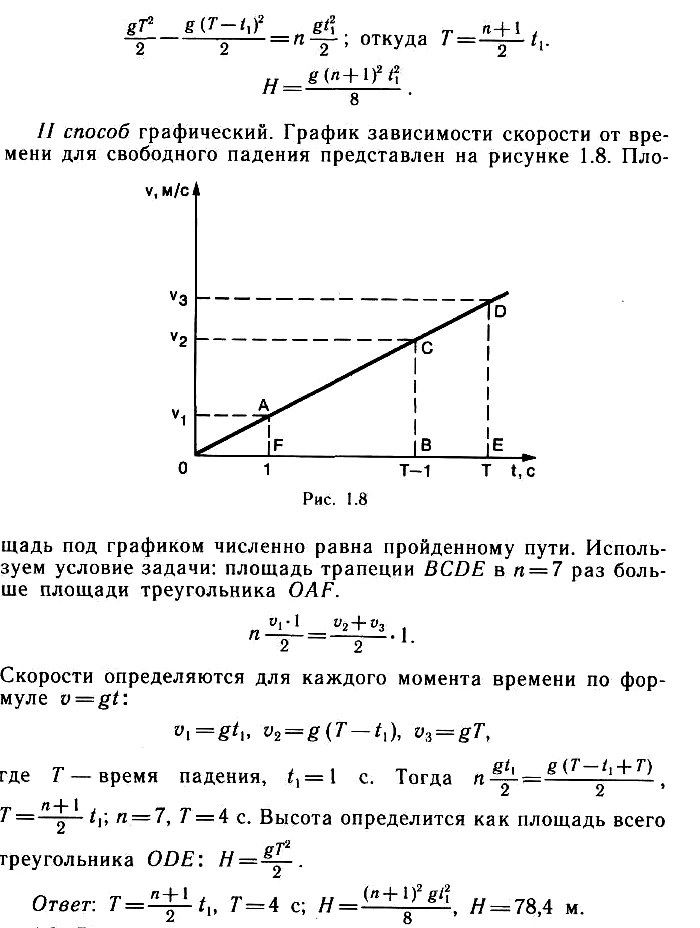 Законы Ньютона.
Законы Ньютона. В.
В. 04.2021
04.2021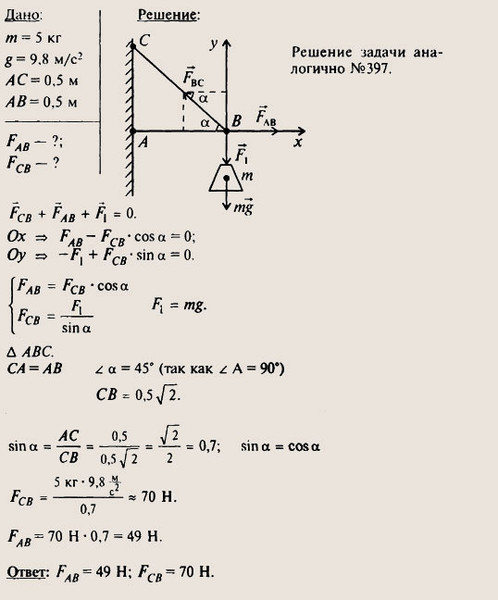


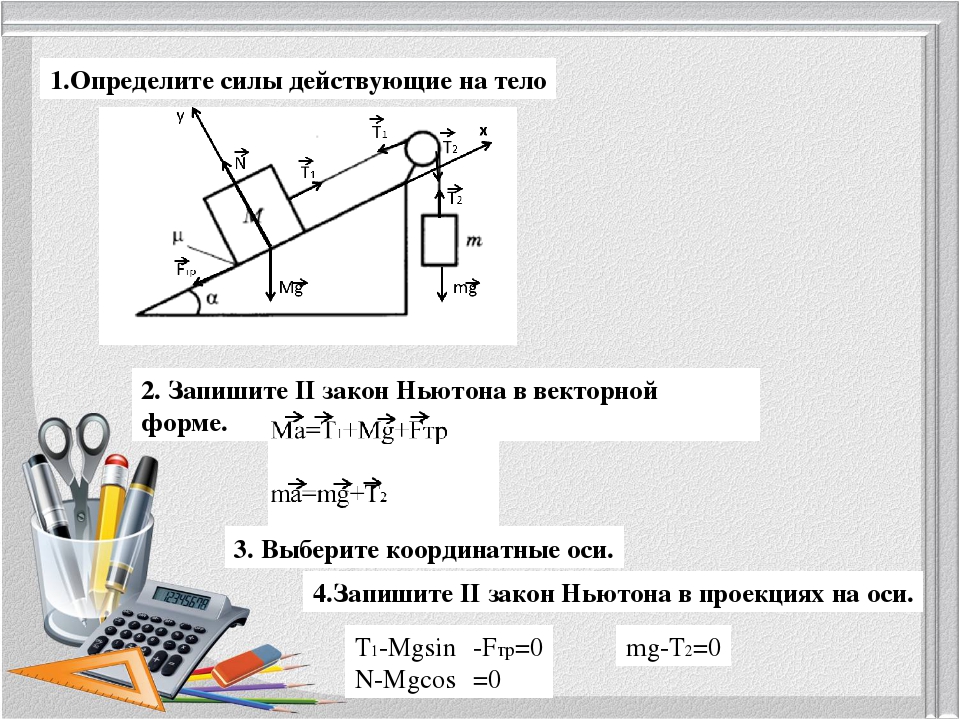
 Механика
Механика
 Ю.)
Ю.) Список Опечаток.
Список Опечаток. Специальный курс физики. Конспект лекций
Специальный курс физики. Конспект лекций