Что такое механика – Класс!ная физика
Что такое механика
- Подробности
- Просмотров: 414
«Физика – 10 класс»
Выделим среди великого множества процессов, происходящих в природе, круг явлений, которые изучает механика.
Первое, что бросается в глаза при наблюдении окружающего нас мира, – это его изменчивость.
Мир не является застывшим, статичным.
Изменения в нем весьма разнообразны.
Но если спросить вас, какие изменения вы замечаете чаще всего, то ответ, пожалуй, будет однозначным: меняется положение предметов (или тел, как говорят физики) относительно земли и относительно друг друга с течением времени.
Бежит ли собака или мчится автомобиль – с ними происходит один и тот же процесс: их положение относительно земли меняется с течением времени.
Они перемещаются.
То же самое происходит с листьями деревьев в ветреную погоду, падающими каплями дождя, плывущими в небе облаками.
Конечно, не любые изменения состоят в перемещении тел.
Так, например, при охлаждении вода замерзает, превращаясь в лед.
Но наиболее часто встречающиеся вокруг нас изменения – это изменения положений тел относительно друг друга.
Изменение положения тела или частей тела в пространстве относительно других тел с течением времени называется механическим движением.
Определение механического движения выглядит просто, но простота эта обманчива.
Прочтите определение еще раз и подумайте, все ли слова вам ясны: пространство, время, относительно других тел
Скорее всего, эти слова требуют пояснения.
Пространство и время
Пространство и время – наиболее общие понятия физики и… наименее ясные.
Исчерпывающих сведений о пространстве и времени мы не имеем.
Но и те результаты, которые получены сегодня, изложить в самом начале изучения физики невозможно.
На первых порах нам вполне достаточно уметь измерять расстояние между двумя точками пространства с помощью линейки и интервалы времени с помощью часов.
Линейка и часы – важнейшие приспособления для измерений в механике, да и в быту.
С расстояниями и интервалами времени приходится иметь дело при изучении всех школьных учебных предметов.
«…Относительно других тел»
Если эта часть определения механического движения ускользнула от вашего внимания, то вы рискуете не понять самого главного.
Так, например, в купе вагона на столике лежит яблоко.
Во время отправления поезда двух наблюдателей (пассажира и провожающего) просят ответить на вопрос: яблоко движется или нет?
Каждый наблюдатель оценивает положение яблока по отношению к себе.
Пассажир видит, что яблоко находится на расстоянии 1 м от него и это расстояние сохраняется с течением времени.
Провожающий на перроне видит, как с течением времени расстояние от него до яблока увеличивается.
Пассажир отвечает, что яблоко не совершает механического движения – оно неподвижно; провожающий говорит, что яблоко движется.
Итак, одно и то же тело одновременно движется и не движется.
Возможно ли такое? Согласно определению механического движения все так и есть.
Механика – наука об общих законах движения тел.
Механическим движением называется перемещение тел или частей тел в пространстве относительно друг друга с течением времени.
Классическая механика Ньютона и границы ее применимости
Законы механики были сформулированы великим английским ученым И. Ньютоном.
На могильной плите в Вестминстерском аббатстве в Лондоне высечены знаменательные слова:
Здесь покоится
Сэр Исаак Ньютон,
Который почти божественной силой своего ума
Впервые объяснил
С помощью своего математического метода
Движения и формы планет,
Пути комет, приливы и отливы океана.
Он первый исследовал разнообразие световых лучей
И проистекающие отсюда особенности цветов,
Которых до того времени никто даже не подозревал.
Прилежный, проницательный и верный истолкователь
Природы, древностей и Священного Писания.
Он прославил – в своем учении всемогущего Творца.
Требуемую Евангелием простоту он доказал своей жизнью.
Пусть смертные радуются, что в их среде
Жило такое украшение человеческого рода.
Родился 25 декабря 1642 г.
Умер 20 марта 1727 г.
На протяжении многих лет ученые были уверены, что единственными основными (фундаментальными) законами природы являются законы механики Ньютона.
Все богатство и многообразие мира считали результатом различий в движении первичных частиц, слагающих все тела Вселенной.
Однако простая механическая картина мира оказалась неправильной.
При исследовании электромагнитных явлений было доказано, что они не подчиняются законам Ньютона.
Это законы поведения электромагнитного поля, несводимые к законам Ньютона.
Было выяснено также, что законы Ньютона, как и любые другие законы природы, не являются абсолютно точными.
Они хорошо описывают движение больших тел, если их скорость мала по сравнению со скоростью света.
Механика, основанная на законах Ньютона, называется классической механикой
Для микроскопических частиц справедливы, как правило, законы квантовой механики.
При движениях со скоростями, близкими к скорости света, тела обнаруживают свойства, о существовании которых Ньютон не подозревал.
Окружающие нас тела движутся сравнительно медленно.
Поэтому их движения подчиняются законам Ньютона.
Таким образом, область применения классической механики очень обширна.
И в этой области человечество всегда будет пользоваться для описания любого движения тела законами Ньютона.
Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Кинематика – Физика, учебник для 10 класса – Класс!ная физика
Физика и познание мира —
Что такое механика —
Механическое движение. Система отсчёта —
Способы описания движения —
Траектория. Путь. Перемещение —
Равномерное прямолинейное движение. Скорость. Уравнение движения —
Примеры решения задач по теме «Равномерное прямолинейное движение» —
Сложение скоростей —
Примеры решения задач по теме «Сложение скоростей» —
Мгновенная и средняя скорости —
Ускорение —
Движение с постоянным ускорением —
Определение кинематических характеристик движения с помощью графиков —
Примеры решения задач по теме «Движение с постоянным ускорением» —
Движение с постоянным ускорением свободного падения —
Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» —
Равномерное движение точки по окружности —
Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение —
Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями —
Примеры решения задач по теме «Кинематика твёрдого тела»
Система отсчёта —
Способы описания движения —
Траектория. Путь. Перемещение —
Равномерное прямолинейное движение. Скорость. Уравнение движения —
Примеры решения задач по теме «Равномерное прямолинейное движение» —
Сложение скоростей —
Примеры решения задач по теме «Сложение скоростей» —
Мгновенная и средняя скорости —
Ускорение —
Движение с постоянным ускорением —
Определение кинематических характеристик движения с помощью графиков —
Примеры решения задач по теме «Движение с постоянным ускорением» —
Движение с постоянным ускорением свободного падения —
Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» —
Равномерное движение точки по окружности —
Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение —
Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями —
Примеры решения задач по теме «Кинематика твёрдого тела»
2.
 Классическая механика и физика – это всего лишь приближения. Революция в физике
Классическая механика и физика – это всего лишь приближения. Революция в физике2. Классическая механика и физика – это всего лишь приближения
Теперь обсудим вкратце вопрос о том, какую роль современная физика отводит классической механике и физике. Разумеется, они полностью сохраняют свое практическое значение в той области явлений, для описания которой они были созданы и в которой их справедливость подтверждается опытом. Открытие квантов ни в коей мере не нарушает законов падения тел или законов геометрической оптики. Всякий раз, когда с определенной степенью точности подтверждается какой-либо закон (а всякий результат может быть проверен лишь с определенной точностью), можно утверждать, что этот результат в основном является окончательным и никакие последующие теории его не смогут опровергнуть. Если бы это было не так, то никакая наука вообще не могла бы развиваться. Однако может так случиться, что появление новых экспериментальных данных или новых теорий приведет к тому, что найденные ранее законы будут рассматриваться лишь как некоторое приближение.
Механика и классическая физика были созданы для описания явлений, протекающих в масштабе наших повседневных явлений. Они остаются справедливыми и для описания процессов, происходящих в еще больших астрономических масштабах. Но как только мы переходим к масштабам атома, существование квантов сразу ограничивает область применения механики и классической физики. С чем же это связано? А с тем, что величина кванта действия, характеризуемая знаменитой постоянной Планка, чрезвычайно мала по сравнению с нашими обычными единицами измерений. Возмущения, вносимые в измерения в результате существования квантов, оказываются в обычных условиях настолько малыми, что в используемых при этом единицах их практически невозможно заметить. Эти возмущения значительно меньше ошибок измерений, неизбежно возникающих в экспериментах, поставленных для проверки того или иного классического закона.
Но как только мы переходим к масштабам атома, существование квантов сразу ограничивает область применения механики и классической физики. С чем же это связано? А с тем, что величина кванта действия, характеризуемая знаменитой постоянной Планка, чрезвычайно мала по сравнению с нашими обычными единицами измерений. Возмущения, вносимые в измерения в результате существования квантов, оказываются в обычных условиях настолько малыми, что в используемых при этом единицах их практически невозможно заметить. Эти возмущения значительно меньше ошибок измерений, неизбежно возникающих в экспериментах, поставленных для проверки того или иного классического закона.
В свете квантовой теории классическая механика и физика уже не являются абсолютно точными. Однако в обычных условиях нарушение классических законов оказывается незаметным из-за имеющихся всегда ошибок измерений. Таким образом, для явлений, протекающих в наших обычных масштабах, классические механика и физика оказываются очень хорошим приближением.
Итак, здесь мы снова встречаемся с обычным процессом развития науки. Твердо установленные принципы, надежно проверенные законы, хотя и сохраняются в дальнейшем развитии науки, но уже рассматриваются не как абсолютно точные, а лишь как некоторое приближение, пределы применимости которого определяются новой, более общей теорией.
Поскольку все же для явлений нашего масштаба классическая механика и физика, совершенно не учитывающие наличия квантов, остаются справедливыми, то некоторые, возможно, скажут, что, в сущности, кванты не имеют такого уж всеобщего значения, какое им приписывается, поскольку в чрезвычайно широкой области явлений, включающей, в частности, область практических приложений, квантовую природу явлений можно совершенно не учитывать. Однако подобная точка зрения кажется нам неправильной. Во-первых, в такой важной и перспективной области как атомная и ядерная физика, кванты играют настолько существенную роль, что без привлечения квантовой теории понять явления, относящиеся к этой области, оказывается совершенно невозможно. Во-вторых, в макроскопической физике, где благодаря малости величины квантов и неизбежным ошибкам эксперимента квантовая природа процессов не проявляется явно, наличие кванта действия влечет за собой все те следствия, на которые мы указали ранее. И если они практически не оказывают заметного влияния, то это никоим образом не умаляет их значения, как для физики, так и для философии. Поэтому в настоящее время квантовая теория является одной из существенных основ естествознания.
Во-вторых, в макроскопической физике, где благодаря малости величины квантов и неизбежным ошибкам эксперимента квантовая природа процессов не проявляется явно, наличие кванта действия влечет за собой все те следствия, на которые мы указали ранее. И если они практически не оказывают заметного влияния, то это никоим образом не умаляет их значения, как для физики, так и для философии. Поэтому в настоящее время квантовая теория является одной из существенных основ естествознания.
Механика – Физическая энциклопедия
МЕХАНИКА – наука о механич. движении материальных
тел и происходящих при этом взаимодействиях между ними. Под механич. движением
понимают изменение с течением времени взаимного положения тел или их частиц
в пространстве; напр., движение небесных тел, колебания земной коры, воздушные
и морские течения, движения летат. аппаратов и транспортных средств, машин и
механизмов, деформации элементов конструкций и сооружений, движения жидкостей
и газов и др. Рассматриваемые в M. взаимодействия представляют собой те действия
тел друг на друга, результатом к-рых являются изменения скоростей точек этих
тел или их деформации, напр, притяжения тел по закону всемирного тяготения,
взаимные давления соприкасающихся тел, воздействия частиц жидкости или газа
друг на друга и на движущиеся (или покоящиеся) в них тела и т. п.
Рассматриваемые в M. взаимодействия представляют собой те действия
тел друг на друга, результатом к-рых являются изменения скоростей точек этих
тел или их деформации, напр, притяжения тел по закону всемирного тяготения,
взаимные давления соприкасающихся тел, воздействия частиц жидкости или газа
друг на друга и на движущиеся (или покоящиеся) в них тела и т. п.
Под M. обычно понимают т. н. классич. M., в основе
к-рой лежат Ньютона законы механики ,а предметом её изучения являются
движения любых материальных тел (кроме элементарных частиц), совершаемые
со скоростями, малыми по сравнению со скоростью света. Движение тел со скоростями
порядка скорости света рассматриваются в относительности теории, а внутриатомные
явления и движение элементарных частиц изучаются в квантовой механике.
При изучении движения материальных тел в M. вводят
ряд абстрактных понятий, отражающих те или иные свойства реальных тел; ими являются:
1) материальная точка – объект пренебрежимо малых размеров, имеющий массу; это
понятие применимо, когда тело движется поступательно или когда в изучаемом движении
можно пренебречь вращением тела вокруг его центра масс. 2) Абсолютно твёрдое
тело – тело, расстояние между двумя любыми точками к-рого всегда остаётся неизменным;
это понятие применимо, когда можно пренебречь деформацией тела. 3) Сплошная
изменяемая среда; это понятие применимо,
когда при изучении движения изменяемой среды (деформируемого твёрдого тела,
жидкости, газа) можно пренебречь молекулярной структурой среды. При изучении
сплошных сред прибегают к след, абстракциям, отражающим при данных условиях
наиб, существ, свойства соответствующих реальных тел: идеально упругое тело,
пластин, тело, идеальная жидкость, вязкая жидкость, идеальный газ и др. В соответствии
с этим M. разделяют на M. материальной точки, M. системы материальных точек,
M. абсолютно твёрдого тела и M. сплошной среды. Последняя, в свою очередь, подразделяется
на теорию упругости, теорию пластичности, гидродинамику, аэродинамику, газовую
динамику и др. В каждом из этих подразделов в соответствии с характером решаемых
задач выделяют статику – учение о равновесии тел под действием сил, кинематику – учение о геом.
2) Абсолютно твёрдое
тело – тело, расстояние между двумя любыми точками к-рого всегда остаётся неизменным;
это понятие применимо, когда можно пренебречь деформацией тела. 3) Сплошная
изменяемая среда; это понятие применимо,
когда при изучении движения изменяемой среды (деформируемого твёрдого тела,
жидкости, газа) можно пренебречь молекулярной структурой среды. При изучении
сплошных сред прибегают к след, абстракциям, отражающим при данных условиях
наиб, существ, свойства соответствующих реальных тел: идеально упругое тело,
пластин, тело, идеальная жидкость, вязкая жидкость, идеальный газ и др. В соответствии
с этим M. разделяют на M. материальной точки, M. системы материальных точек,
M. абсолютно твёрдого тела и M. сплошной среды. Последняя, в свою очередь, подразделяется
на теорию упругости, теорию пластичности, гидродинамику, аэродинамику, газовую
динамику и др. В каждом из этих подразделов в соответствии с характером решаемых
задач выделяют статику – учение о равновесии тел под действием сил, кинематику – учение о геом. свойствах движения тел и динамику – учение о движении
тел под действием сил. Изучение осн. законов и принципов, к-рым подчиняется
механич. движение тел, и вытекающих из этих законов и принципов общих теорем
и ур-ний составляет содержание т. п. общей, или теоретической, M. Разделами
M., имеющими самостоят, значение, являются также теория колебаний, теория устойчивости движения, механика тел переменной массы, теория автоматич.
регулирования, теория удара и др.
свойствах движения тел и динамику – учение о движении
тел под действием сил. Изучение осн. законов и принципов, к-рым подчиняется
механич. движение тел, и вытекающих из этих законов и принципов общих теорем
и ур-ний составляет содержание т. п. общей, или теоретической, M. Разделами
M., имеющими самостоят, значение, являются также теория колебаний, теория устойчивости движения, механика тел переменной массы, теория автоматич.
регулирования, теория удара и др.
M. тесно связана с др. разделами физики. Ряд
понятий и методов M. при соответствующих обобщениях находит приложение в оптике,
статистич. физике, квантовой M., электродинамике, теории относительности и др.
(см., напр., Действие, Лагранжа функция, Наименьшего действия принцип). Кроме
того, при решении ряда задач газовой динамики, теории взрыва ,теплообмена
в движущихся жидкостях и газах, магнитной гидродинамики и др. одновременно
используются методы и ур-ния как теоретич. M., так и термодинамики, молекулярной
физики, теории электричества и др. Важное значение M. имеет для MH. разделов
астрономии, особенно для небесной M.
M., так и термодинамики, молекулярной
физики, теории электричества и др. Важное значение M. имеет для MH. разделов
астрономии, особенно для небесной M.
Часть M., непосредственно связанную с техникой,
составляют многочисл. общетехн. и спец. дисциплины, такие, как гидравлика, сопротивление
материалов, строит. M., кинематика механизмов, динамика машин и механизмов,
теория гироскопич. устройств, внеш. баллистика, динамика ракет, теория движения
наземных, морских и воздушных транспортных средств и др. Все эти дисциплины
пользуются ур-ниями и методами теоретич. M. Таким образом, М.- одна из науч.
основ MH. областей совр. техники.
Основные понятия и методы механики. Осн. кинематич.
мерами движения в M. являются: для точки – её скорость и ускорение, для твёрдого
тела – скорость и ускорение поступат. движения и угл. скорость и угл. ускорение
вращат. движения. Кинематич. состояние деформируемого твёрдого тела характеризуется
относит, удлинениями и сдвигами его частиц; совокупность этих величин определяет
т. н. тензор деформаций. Для жидкостей и газов кинематич. состояние характеризуется
тензором скоростей деформаций; при изучении поля скоростей движущейся жидкости
пользуются также понятием вихря, характеризующего вращение частицы.
н. тензор деформаций. Для жидкостей и газов кинематич. состояние характеризуется
тензором скоростей деформаций; при изучении поля скоростей движущейся жидкости
пользуются также понятием вихря, характеризующего вращение частицы.
Осн. мерой механич. взаимодействия материальных
тел в M. является сила .Одновременно в М. пользуются понятием момента
силы относительно точки и относительно оси. В M. сплошной среды силы задаются
их поверхностным или объёмным распределением, т. е. отношением величины силы
к площади поверхности (для поверхности сил) или к объёму (для массовых сил),
на к-рые соответствующая сила действует. Возникающие в сплошной среде внутр.
напряжения характеризуются в каждой точке среды касательными и нормальными напряжениями,
совокупность к-рых представляет собой величину, называемую тензором напряжений.
Среднее арифметическое трёх нормальных напряжений,
взятое с обратным знаком, определяет величину, называемую давлением в данной
точке среды.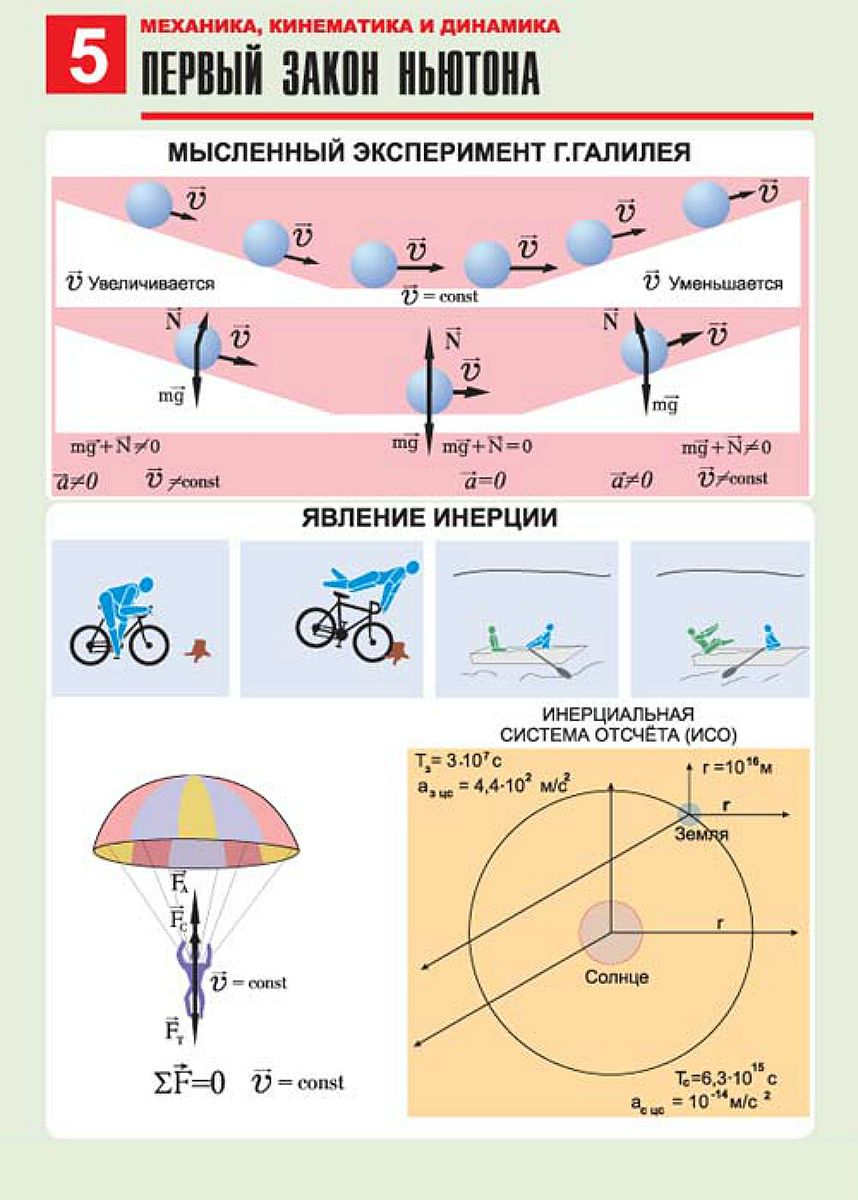
На движение тела, помимо действующих сил, оказывает
влияние степень его инертности. Для материальной точки мерой инертности является
её масса .Инертность материального тела зависит от его общей массы и
от распределения масс в теле, к-рое характеризуется положением центра масс и
величинами, называемыми осевыми и центробежными моментами инерции; совокупность
этих величин определяет т. н. тензор инерции. Инертность жидкости или газа характеризуется
их плотностью.
В основе M. лежат три закона Ньютона. Первые
два справедливы по отношению к т. н. инерциальной системе отсчёта. Второй
закон даёт осн. ур-ния для решения задач динамики точки, а вместе с третьим
– для решения задач динамики системы материальных точек. В M. сплошной среды,
кроме законов Ньютона, используются законй, отражающие свойства данной среды
и устанавливающие для неё связь между тензором напряжений и тензорами деформаций
или скоростей деформаций. Таковы Гука закон для линейно-упругого тела
и закон Ньютона для вязкой жидкости (см. Вязкость ).О законах, к-рым
подчиняются др. среды, см. в ст. Пластичности теория, Реология.
Таковы Гука закон для линейно-упругого тела
и закон Ньютона для вязкой жидкости (см. Вязкость ).О законах, к-рым
подчиняются др. среды, см. в ст. Пластичности теория, Реология.
Важное значение для решения задач M. имеют понятия
о динамич. мерах движения, к-рыми являются кол-во движения (см. Импульс},
момент количества движения и кинетическая энергия ,и о мерах действия
силы, каковыми служат импульс силы и работа .Соотношение между
мерами движения и мерами действия силы дают т. н. общие теоремы динамики. Эти
теоремы и вытекающие из них законы сохранения кол-ва движения, момента кол-ва
движения и механич. энергии выражают свойства движения любой системы материальных
точек и сплошной среды.
Эфф. методы изучения равновесия и движения несвободной
механич. системы (см. Связи механические)дают вариационные принципы
механики, в частности возможных перемещений принцип ,наим. действия
принцип, а также Д-Аламбера принцип .При решении задач M. широко используют
вытекающие из её законов или принципов дифференц. ур-ния движения материальной
точки, твёрдого тела и системы материальных точек, в частности ур-ния Лагранжа,
канонич. ур-ния, ур-ния Гамильтона – Якоби, а в M. сплошной среды – соответствующие
ур-ния равновесия или движения этой среды, ур-ние неразрывности (сплошности)
среды и ур-ние энергии.
действия
принцип, а также Д-Аламбера принцип .При решении задач M. широко используют
вытекающие из её законов или принципов дифференц. ур-ния движения материальной
точки, твёрдого тела и системы материальных точек, в частности ур-ния Лагранжа,
канонич. ур-ния, ур-ния Гамильтона – Якоби, а в M. сплошной среды – соответствующие
ур-ния равновесия или движения этой среды, ур-ние неразрывности (сплошности)
среды и ур-ние энергии.
Основные этапы развития механики. М.- одна из
древнейших наук, возникшая из нужд практики. Раньше др. разделов M. под влиянием
запросов гл. обр. строит, техники стала развиваться статика. Её науч. основы
(теория рычага, сложение параллельных сил, учение о центре тяжести, начала гидростатики
и др.) разработал ещё Архимед (3 в. до н. э.).
Периодом создания науч. основ динамики, а с ней
и всей M. явился 17 в. Основоположник динамики – Г. Галилей (G. Galilei), к-рый
дал первое верное решение задачи о движении тела под действием силы; его исследования
привели к открытию закона инерции и принципа относительности классич. M.; им
же положено начало теории колебаний и науке о сопротивлении материалов. Исследования
движения точки по окружности, колебаний физ. маятника и законов упругого удара
тел принадлежат X. Гюйгенсу (Ch. Huygens). Создание основ классич. M. завершается
трудами И. Ньютона (I. Newton), сформулировавшего осн. законы M. (1687) и открывшего
закон всемирного тяготения. В 17 в. были установлены и два исходных положения
M. сплошной среды: закон вязкого трения в жидкостях и газах (Ньютон, 1684) и
закон, выражающий зависимость между напряжениями и деформациями в упругом теле
[P. Гук (R. Hooke), 1660].
M.; им
же положено начало теории колебаний и науке о сопротивлении материалов. Исследования
движения точки по окружности, колебаний физ. маятника и законов упругого удара
тел принадлежат X. Гюйгенсу (Ch. Huygens). Создание основ классич. M. завершается
трудами И. Ньютона (I. Newton), сформулировавшего осн. законы M. (1687) и открывшего
закон всемирного тяготения. В 17 в. были установлены и два исходных положения
M. сплошной среды: закон вязкого трения в жидкостях и газах (Ньютон, 1684) и
закон, выражающий зависимость между напряжениями и деформациями в упругом теле
[P. Гук (R. Hooke), 1660].
В 18 в. интенсивно развиваются аналитич. методы
решения задач M. Для материальной точки эти методы разработал Л. Эйлер (L. Euler),
заложивший также основы динамики твёрдого тела. Аналитич. методы решения задач
динамики системы основываются на принципе возможных перемещений и на принципе,
высказанном Ж. Л. Д-Аламбером (J. L. D’Alembert), разработку к-рых завершил
Ж. Л. Лагранж (J. L. Lagrange), получивший ур-ния движения системы в обобщённых
координатах; им же разработаны основы совр. теории колебаний. Др. путь решения
задач M. исходит из принципа наим. действия в форме, высказанной для точки П.
Л. Мопертюи (P. L. Maupertuis) и обобщённой на случай системы точек Лагранжем.
В M. сплошной среды Эйлером, Д. Бернулли (D. Bernoulli), a также Лагранжем и
Д-Аламбером были разработаны теоретич. основы гидродинамики идеальной жидкости.
Л. Лагранж (J. L. Lagrange), получивший ур-ния движения системы в обобщённых
координатах; им же разработаны основы совр. теории колебаний. Др. путь решения
задач M. исходит из принципа наим. действия в форме, высказанной для точки П.
Л. Мопертюи (P. L. Maupertuis) и обобщённой на случай системы точек Лагранжем.
В M. сплошной среды Эйлером, Д. Бернулли (D. Bernoulli), a также Лагранжем и
Д-Аламбером были разработаны теоретич. основы гидродинамики идеальной жидкости.
В 19 в. продолжается интенсивное развитие всех
разделов M., чему способствовали исследования M. В. Остроградского, У. P. Гамильтона
(W. R. Hamilton), K. Г. Якоби (К. G. Jacobi),T. Герца (H. Hertz) и др. Э. Раусом
(E. Routh), H. E. Жуковским и A. M. Ляпуновым была разработана теория устойчивости
равновесия и движения. И. А. Вышнеградский заложил основы совр. теории автоматич.
регулирования. Доказанная Г. Г. Кориолисом (G. С. Coriolis) теорема о составляющих
ускорения легла в основу динамики относит, движения. Кинематика, развивавшаяся
одновременно с динамикой, выделяется во 2-й пол. 19 в. в самостоят, раздел M.
Кинематика, развивавшаяся
одновременно с динамикой, выделяется во 2-й пол. 19 в. в самостоят, раздел M.
Значит, развитие в 19 в. получила M. сплошной
среды. Л. Навье (L. Navier) и О. Л. Коши (A. L. Cauchy) установили общие ур-ния
теории упругости. Исследования Навье и Дж. Г. Стокса (G. G. Stokes) привели
к установлению дифференц. ур-ний движения вязкой жидкости. Развитию динамики
идеальной и вязкой жидкости способствовали труды Г. Гельмгольца (H. Helmholtz)
(учение о вихрях), Г. P. Кирхгофа (G. R. Kirchhoff), Жуковского (отрывное обтекание
тел), О. Рейнольдса (О. Reynolds) (начало изучения турбулентных течений), H.
П. Петрова (гидродинамич. теория трения при смазке), Л. Прандтля (L. Prandtl)
(теория пограничного слоя) и др. А. Сен-Венан (A. Saint-Venant) предложил первую
матем. теорию пластич. течения металла.
В 20 в. интенсивно развиваются теория нелинейных
колебаний, основы к-рой заложены Ляпуновым и А. Пуанкаре (H. Poincare), M. тел
перем. массы и динамика ракет, где ряд исходных исследований принадлежит И.
В. Мещерскому (труды кон. 19 в.) и К. Э. Циолковскому. В M. сплошной среды появляются
два раздела: аэродинамика, основы к-рой созданы Жуковским, и газовая динамика,
основы к-рой заложены С. А. Чаплыгиным.
тел
перем. массы и динамика ракет, где ряд исходных исследований принадлежит И.
В. Мещерскому (труды кон. 19 в.) и К. Э. Циолковскому. В M. сплошной среды появляются
два раздела: аэродинамика, основы к-рой созданы Жуковским, и газовая динамика,
основы к-рой заложены С. А. Чаплыгиным.
Современные проблемы механики. К числу
этих проблем относятся уже отмечавшиеся задачи теории колебаний (особенно нелинейных),
динамики твёрдого тела, теории устойчивости движения, а также M. тел перем.
массы и динамики космич. полётов. Всё большее значение приобретают задачи, требующие
применения вероятностных методов расчёта, т. е. задачи, в к-рых, напр., для
действующих сил известна лишь вероятность того, какие значения они могут иметь.
В M. непрерывной среды весьма актуальны проблемы: изучения поведения макрочастиц
при изменении их формы, что связано с разработкой более строгой теории турбулентного
течения жидкости; решения задач теории пластичности и ползучести; создания обоснованной
теории прочности и разрушения твёрдого тела.
Большой круг задач M. связан с изучением движения
плазмы в магн. поле (магн. гидродинамика), т. е. с решением одной из самых актуальных
проблем совр. физики – осуществлением управляемого термоядерного синтеза. В
гидродинамике ряд важнейших задач связан с проблемами больших скоростей в авиации,
баллистике, турбиностроении и двигателестроении.
Много новых задач возникает на стыке M. с др. областями наук. К ним относятся
проблемы гидротермохимии, т. е. исследования механич. процессов в жидкостях
и газах, вступающих в хим. реакции, изучение сил, вызывающих деление клеток,
механизма образования мускульной силы и др.
При решении MH. задач M. используются электронные
вычислительные и аналоговые машины; разработка методов решения новых задач M.
с помощью этих машин (особенно M. сплошной среды) – также весьма актуальная
проблема.
Лит.: Галилей Г., Соч., [пер. с итал.],
т. 1, M.- Л., 1934; Ньютон И., Математические начала натуральной философии,
[пер. с лат.], в кн.: Крылов A. H., Собр. трудов, т. 7, M.- Л., 1936; Эйлер
Л., Основы динамики точки, пер. с лат., М.- Л., 1938; Д-Аламбер Щ., Динамика,
пер. с франц., M.- Л., 1950; Лагранж Ж., Аналитическая механика, пер. с франц.,
т. 1-2, 2 изд., M.- Л., 1950; Жуковский H. E., Теоретическая механика, 2 изд.,
M.- Л., 1952; Бухгольц H. H., Основной курс теоретической механики, ч. 1, 9
изд., ч. 2, 6 изд., M., 1972; История механики с древнейших времен до конца
XVIII в., M., 1971; Веселовский И. H., Очерки по истории теоретической механики,
M., 1974; Механика в СССР за 50 лет, т. 1-3, M., 1968-72; см. также лит. при
ст. Гидроаэромеханика, Упругости теория и Пластичности теория. С. M. Тарг,
с лат.], в кн.: Крылов A. H., Собр. трудов, т. 7, M.- Л., 1936; Эйлер
Л., Основы динамики точки, пер. с лат., М.- Л., 1938; Д-Аламбер Щ., Динамика,
пер. с франц., M.- Л., 1950; Лагранж Ж., Аналитическая механика, пер. с франц.,
т. 1-2, 2 изд., M.- Л., 1950; Жуковский H. E., Теоретическая механика, 2 изд.,
M.- Л., 1952; Бухгольц H. H., Основной курс теоретической механики, ч. 1, 9
изд., ч. 2, 6 изд., M., 1972; История механики с древнейших времен до конца
XVIII в., M., 1971; Веселовский И. H., Очерки по истории теоретической механики,
M., 1974; Механика в СССР за 50 лет, т. 1-3, M., 1968-72; см. также лит. при
ст. Гидроаэромеханика, Упругости теория и Пластичности теория. С. M. Тарг,
Предметный указатель >>
Лекции и демонстрации по механике — Кафедра общей физики
КУРС ЛЕКЦИЙ
ПО МЕХАНИКЕ:
Лекция №1 “Кинематика”
Содержание лекции: как изучать физику, как работает физика, роль математики, роль эксперимента, система отсчета и система координат, одномерное движение, плоское движение, движение по окружности, нормальное и тангенциальное ускорения.
Лекция №2 “Основные законы механики”
Содержание лекции: кинематика: повторение, радиус кривизны траектории, первый закон Ньютона. Инерция. Инерциальные системы отсчета, импульс, закон сохранения импульса, свойства массы, второй закон Ньютона, сила, третий закон Ньютона, центр инерции.
Лекция №3 “Реактивное движение. Энергия”
Содержание лекции: повторение: закон сохранения импульса, центр масс, реактивное движение, уравнение Мещерского, работа силы, мощность, теорема о кинетической энергии, кинетическая энергия, потенциальная энергия силы, классификация сил, критерий применимости закона сохранения энергии, потенциальная энергия системы.
Лекция №4 “Упругие и неупругие столкновения. Момент импульса”
Содержание лекции: зависимость энергии от системы отсчета, преобразование кинетической энергии при смене СО, теорема Кёнига, упругие и неупругие парные столкновения, метод векторных диаграмм, порог реакции, связь симметрий с законами сохранения, уравнение моментов.
Лекция №5 “Тяготение”
Содержание лекции: Момент импульса, закон сохранения момента импульса, вычисление моментов, правило рычага, задача двух тел, центральное поле, потенциальная энергия в поле тяжести, законы Кеплера, плоские кривые второго порядка, третий закон Кеплера, “космические” скорости.
Лекция №6 “Основы теории относительности. Кинематика”
Содержание лекции: теорема Гаусса для вычисления гравитационных полей (продолжение), предпосылки создания теории относительности, постулаты теории относительности, замедление времени, сокращение длин, относительность одновременности, преобразования Лоренца, сложение скоростей, относительная скорость vs. скорость сближения, опыт Физо, аберрация звёзд.
Лекция №7 “Основы специальной теории относительности. Динамика”
Содержание лекции: Интервал, собственное время. Свойства преобразований Лоренца. Скорости больше с? Законы сохранения в СТО, вектор энергии-импульса. Движение релятивистской частицы под действием внешней силы. Релятивистские столкновения, инвариант энергии-импульса
Движение релятивистской частицы под действием внешней силы. Релятивистские столкновения, инвариант энергии-импульса
Лекция №8 “Вращение твердых тел”
Содержание лекции: Движение твердого тела. Вектор угловой скорости. Конечные повороты. Уравнение моментов для фиксированной оси. Работа и кинетическая энергия. Аналогии вращательного и поступательного движений. Вычисление моментов инерции. Вычисление моментов инерции симметричных тел. Мгновенная ось вращения. Плоское движение. Движущееся начало. Уравнение моментов относительно движущегося начала. Смена системы отсчёта. Применимость уравнения моментов. Качение без проскальзывания. Маятник Максвелла. “Непослушная катушка”
Лекция №9 “Общее вращение твердого тела. Гироскопы”
Гироскопы”
Содержание лекции: Вектор угловой скорости. Сложение движений. Общая динамика твердого тела. Момент инерции. Главные оси. Связь между L и w. Элипсоид инерции. Уравнение вращения вектора. Вращение осей. О странностях движения твердого тела. Свободная прецессия симметричного волчка. Центробежные моменты. Гироскоп. Прецессия под действием силы. Китайский волчок (Волчок Томсона). Парадоксы гироскопического приближения
Лекция №10 “Свободные колебания”
Содержание лекции: Свободная прецессия симметричного волчка. Парадоксы гироскопического приближения. Уравнение свободных незатухающих колебаний. Энергия колебаний, колебания энергии. Универсальность уравнения гармонических колебаний. Примеры колебательных систем. Физический маятник. Крутильный маятник, “неваляшка”, кубик льда на поверхности воды, U-образная трубка. Влияние трения. Затухающие колебания. Решение для затухающих колебаний.
Влияние трения. Затухающие колебания. Решение для затухающих колебаний.
Лекция №11 “Вынужденные колебания”
Содержание лекции: Декремент затухания, добротность. Фазовый портрет осциллятора. Сложение колебаний, биения. Cвязанные маятники. Возбуждение колебаний гармонической силой. Резонанс, свойства системы в резонансе. Параметрический резонанс.
Лекция №12 “Неинерциальные системы отсчёта”
Содержание лекции: Нелинейные колебания. Адиабатический инвариант. Принцип работы автоколебаний. Инерциальные системы отсчёта. Уравнение движения. Поступательная сила инерции. Консервативность сил инерции. Центробежная сила инерции. Конический маятник. Сила Кориолиса. Атмосферные вихри: циклоны и антициклоны. Маятник Фуко.
Центробежная сила инерции. Конический маятник. Сила Кориолиса. Атмосферные вихри: циклоны и антициклоны. Маятник Фуко.
Лекция №13 “Элементы теории упругости”
Содержание лекции: Невесомость. Инерциальная система отсчёта. Нормальные и касательные напряжения. Закон Паскаля – Основное уравнение гидростатики. Сила Архимеда. Закон Гука. Примеры однородных деформаций. Сдвиг. Тензор напряжений.
Лекция №14 “Волны в упругих средах”
Содержание лекции: Объёмная плотность энергии деформации. Изгиб и кручение. Волна на одномерной цепочке. Волна на струне. Бегущая гармоническая волна. Стоячие волны. Энергия волны. Импульс волны. Эффект Доплера.
Энергия волны. Импульс волны. Эффект Доплера.
Механика – Механика – Темы по физике – Каталог лекций
ОпределениеОсновоположниками классической механики являются Г. Галилей (1564–1642) и И. Ньютон (1643–1727). Методами классической механики изучается движение любых материальных тел (кроме микрочастиц) со скоростями, малыми по сравнению со скоростью света в вакууме. Движение микрочастиц рассматривается в квантовой механике, а движение тел со скоростями, близкими к скорости света – в релятивистской механике (специальной теории относительности).Механикой называется часть физики, изучающая движение и взаимодействие материальных тел. При этом механическое движение рассматривается как изменение с течением времени взаимного положения тел или их частей в пространстве.
Свойства пространства и времени, принятые в классической физике
| Пространство | Время |
1.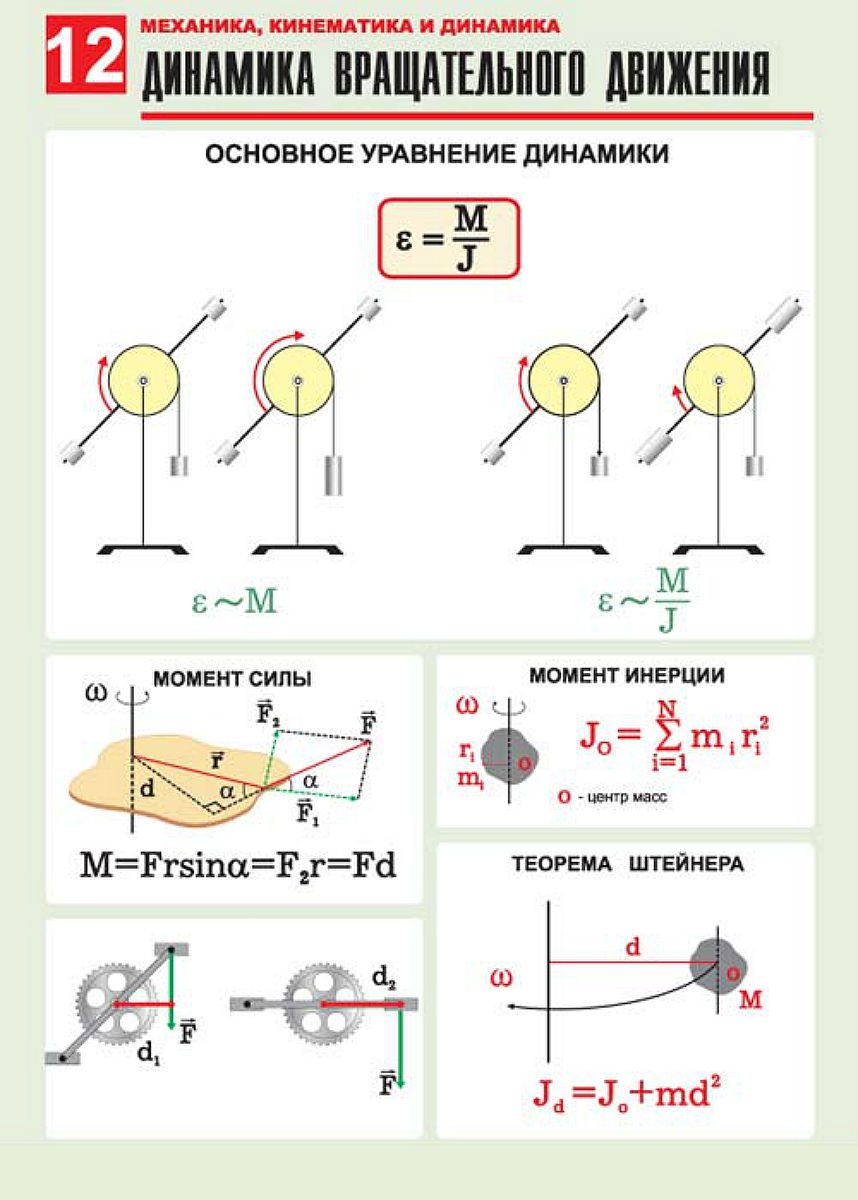 Трёхмерное Трёхмерное2. Евклидовое 3. Однородное 4. Изотропное 5. Континуальное | 1. Одномерное 2. Евклидовое 3. Однородное 4. Необратимое 5. Континуальное |
Одномерное пространство – параметрическая характеристика, в которой положение точки описывается одним параметром.
Евклидово пространство и время означает, что сами по себе они не искривлены и описываются в рамках евклидовой геометрии.
Однородность пространства означает, что его свойства не зависят от расстояния до наблюдателя. Однородность времени означает, что оно не растягивается и не сжимается, а течет равномерно. Изотропность пространства означает, что его свойства не зависят от направления. Поскольку время одномерно, то об изотропности его говорить не приходится. Время в классической механике рассматривается как «стрела времени», направленная из прошлого в будущее.
 Оно необратимо: нельзя вернуться в прошлое и что-то там «подправить».
Оно необратимо: нельзя вернуться в прошлое и что-то там «подправить».Пространство, и время континуальны (от лат. continuum – непрерывное, сплошное), т.е. их можно дробить на все более мелкие части сколь угодно долго. Иначе говоря, в пространстве и времени нет «прорех», внутри которых они бы отсутствовали. Механику делят на Кинематику и Динамику
При этом скорость материальной точки рассматривается как быстрота ее перемещения в пространстве или, с математической точки зрения, как векторная величина, равная производной по времени ее радиус вектора:Кинематика изучает движение тел как простое перемещение в пространстве, вводя в рассмотрение так называемые кинематические характеристики движения: перемещение, скорость и ускорение.
Ускорение материальной точки рассматривается как быстрота изменения ее скорости или, с математической точки зрения, как векторная величина, равная производной по времени ее скорости или второй производной по времени ее радиус-вектора:
Динамика
При этом масса тела рассматривается как мера его инерции, т.е. сопротивляемости по отношению к действующей на данное тело силе, стремящейся изменить его состояние (привести в движение или, наоборот, остановить, или изменить скорость движения). Масса может рассматриваться также как мера гравитационных свойств тела, т.е. его способности взаимодействовать с другими телами, также обладающими массой и находящимися на некотором расстоянии от данного тела. Импульс тела рассматривается как количественная мера его движения, определяемая как произведение массы тела на его скорость: Сила рассматривается как мера механического действия на данное материальное тело со стороны других тел.Динамика изучает движение тел в связи с действующими на них силами, оперируя так называемыми динамическими характеристиками движения: массой, импульсом, силой и др.
Сколько вы знаете о фундаментальной механике физики?
Автор: Торранс Грей
6-минутная викторина
Изображение: Мартин Штайнталер / Момент / Getty ImagesОб этой викторине
Для многих из нас «механики» – это те люди, которые работают с автомобилями. Но в физике «механика» имеет особое значение. Это относится к изучению движения, будь то его причины или его действие. Другими словами, механика – это раздел физики, который объясняет, почему писать текстовые сообщения во время вождения – действительно плохая идея. (Не то, чтобы некоторые люди когда-либо догадались до этого). Но помимо повседневного применения фундаментальная физика пронизывает все остальные области науки. Думаете, атомы и молекулы предназначены только для уроков химии? Подумайте еще раз – как движутся эти атомы – это сфера физики.Думаете, черные дыры изучают только в астрономии? Не совсем так – есть целый раздел физики, который занимается энергией и движением небесных тел.
Но в физике «механика» имеет особое значение. Это относится к изучению движения, будь то его причины или его действие. Другими словами, механика – это раздел физики, который объясняет, почему писать текстовые сообщения во время вождения – действительно плохая идея. (Не то, чтобы некоторые люди когда-либо догадались до этого). Но помимо повседневного применения фундаментальная физика пронизывает все остальные области науки. Думаете, атомы и молекулы предназначены только для уроков химии? Подумайте еще раз – как движутся эти атомы – это сфера физики.Думаете, черные дыры изучают только в астрономии? Не совсем так – есть целый раздел физики, который занимается энергией и движением небесных тел.
Что это значит для вас, человека, собирающегося пройти эту викторину? Это означает, что, несмотря на то, что квантовая физика стала популярной в последние десятилетия, вам не нужно беспокоиться о теории струн, суперсимметрии или возможности мультивселенной. Мы собираемся твердо стоять на ногах. Вместо этого эти вопросы должны вернуть вас к уроку физики в средней школе.
Вместо этого эти вопросы должны вернуть вас к уроку физики в средней школе.
Итак, готовы ли вы вернуться к тому, что вы узнали об этой прекраснейшей из наук? Будьте готовы проверить свои знания прямо сейчас!
Читать далееTRIVIA
Можете ли вы пройти базовый анатомический тест?
6-минутная викторина 6 мин.
TRIVIA
Знаете ли вы о физике больше, чем пятиклассник?
6-минутная викторина
6 мин.
TRIVIA
Сколько вы знаете о геологии Северной Америки?
6-минутная викторина 6 мин.
TRIVIA
Можете ли вы получить больше 11 прав в этой общей викторине по естествознанию?
6-минутная викторина
6 мин.
TRIVIA
Эта викторина по физике действительно сложна, поэтому мы будем впечатлены, если вы получите хотя бы 10 правильных ответов
6-минутная викторина 6 мин.
TRIVIA
Сможете ли вы пройти этот тест по фундаментальной науке за 7 минут?
6-минутная викторина
6 мин.
TRIVIA
Сможете ли вы пройти этот базовый тест по географии?
7-минутная викторина 7 мин.
TRIVIA
Можете ли вы угадать имена этих известных ученых?
6-минутная викторина
6 мин.
TRIVIA
Тест по солнечной системе
6-минутная викторина 6 мин.
TRIVIA
Можете ли вы пройти эту викторину по фазам луны?
7-минутная викторина
7 мин.
Наша цель в зоопарке.com – это развлечь вас этой сумасшедшей жизнью, в которой мы все живем.
Мы хотим, чтобы вы заглянули внутрь и узнали о себе что-то новое и интересное. Мы хотим, чтобы вы смотрели вовне и восхищались окружающим миром. Мы хотим, чтобы вы смеялись над прошлыми воспоминаниями, которые помогли сформировать человека, которым вы стали. Мы хотим вместе с вами мечтать обо всем, что вас ждет в будущем. Мы надеемся, что наши викторины и статьи вдохновят вас на это.
Жизнь – это зоопарк! Примите это на Zoo.com.
Играть в викторины можно бесплатно! Каждую неделю мы отправляем на ваш почтовый ящик простые вопросы и тесты личности.Нажимая «Зарегистрироваться», вы соглашаетесь с нашими
политика конфиденциальности
и подтверждение того, что вам исполнилось 13 лет.
Авторские права © 2021 InfoSpace Holdings, LLC, компания System1
Университетская физика I: Классическая механика
Отзыв Митчелла Стивенсона, доцента, Университет Монтаны – Вестерн, 29.01.20
Полнота рейтинг: 5 видеть меньше
ТекстGea-Banacloche рассматривает классические темы физики (линейная и угловая кинетика и кинематика) в линейном виде, прежде чем углубиться в более сложные темы волн и термодинамики.Это прекрасная возможность подготовить студентов к основам физики II, интегрировав последние темы в контекст первых. Важно отметить, что автор кратко информирует студентов о предлагаемом подходе к тексту, направляя их через ценную стратегию обучения, основанную на упражнениях и практических задачах, содержащихся в нем.
Точность содержания рейтинг: 5
Я чувствую, что в учебнике физики будет сложно быть предвзятым или содержать ошибки, если автор не умел пользоваться своим собственным калькулятором! Этот текст хорошо продуман, точен и содержит реалистичные примеры. Важно отметить, что упрощенные описания явлений и эффектов более чем адекватны, но не содержат слов.
Важно отметить, что упрощенные описания явлений и эффектов более чем адекватны, но не содержат слов.
Актуальность / долголетие рейтинг: 4
Классические темы и примеры в физике мало изменились за последние десятилетия, но этому тексту удается оставаться относительно современным с чистыми, хорошо обоснованными примерами и задачами. Я бы предположил, что многие из примеров можно расширить и связать с тем, чтобы студенты-физики могли наблюдать и испытывать на опыте без существенного оборудования или ресурсов.Примечательно, что учебники по биомеханике контекстуализируют эти явления для человеческого тела, предоставляя учащимся более понятные материальные примеры.
Ясность рейтинг: 5
Если в этом тексте было что-то одно, то его ясность, безусловно, является главным претендентом. Слишком часто учебники физики погрязли в статьях и деталях, которые отвлекают от проблемы. Этот текст не только обходит этот риск, но и написан доступным, но профессиональным образом, который напрямую общается со студентом. Другим авторам следует обратить внимание на то, как директивное повествование от первого лица упрощает структуру предложения и облегчает переход к уравнениям.
Другим авторам следует обратить внимание на то, как директивное повествование от первого лица упрощает структуру предложения и облегчает переход к уравнениям.
Последовательность рейтинг: 5
Форматирование, ссылки, тематическая глубина и голос – все это надежно во всем тексте. Я нахожу это особенно впечатляющим, учитывая активное повествование, на которое опирается автор.
Модульность рейтинг: 5
Организация глав / разделов / подразделов, часто встречающаяся в авторских технических публикациях в Latex, хорошо поддается модульности текста без чрезмерного разделения тем на слишком мелкие элементы.Темы представлены чересстрочно, но не так, чтобы требовать частой навигации. Этот текст также выделяется своей модульной ценностью; Я могу представить себе, что части этого текста будут использоваться для множества тем и курсов прикладной физики, не подрывая его образовательную и справочную ценность.
Организация / структура / поток рейтинг: 5
Организация этого текста меня немного удивила; это была не та организация, к которой я бы по умолчанию обратился, но ее повествование красиво построено и прорезает линейный логический путь через множество тем. Автор замечательно связывает разделы и главы вместе, обеспечивая переходы, полезные для понимания учащимися, не нарушая модульности текста.
Автор замечательно связывает разделы и главы вместе, обеспечивая переходы, полезные для понимания учащимися, не нарушая модульности текста.
Интерфейс рейтинг: 4
Текст имеет адекватные гиперссылки и последовательно структурирован. Латексное форматирование иногда бывает расточительным, но при этом разделы и подразделы организованы последовательно. Цифры в целом четкие, хотя некоторые из них имеют небольшое искажение. Было бы полезно сделать ссылки на другие разделы в их справочных материалах и предоставить ссылку «вернуться к указателю» в конце разделов для упрощения навигации при использовании текста по модульному принципу.Я нахожу веб-адреса в тексте немного громоздкими и задаюсь вопросом, будет ли предпочтительнее встроенная гиперссылка в сочетании с указанными в конце главы веб-адресами для тех, кто печатает текст.
Грамматические ошибки рейтинг: 5
Этот текст чисто и ясно написан без грамматических или справочных ошибок в тексте или уравнениях (последнее, к сожалению, является относительно редким товаром в доступной ООР физики).
Культурная значимость рейтинг: 5
Примеры свободны от каких-либо культурных соображений, хотя я могу утверждать, что предвзятое отношение к надуманным примерам физики может оттолкнуть некоторых биологически заинтересованных студентов.Некоторые примеры неоценимо контекстуализированы для биомеханики, но я чувствую, что чем сложнее математический пример, тем больше вероятность, что автор вернется к шаблонным примерам, выходящим за пределы досягаемости человеческого опыта.
КомментарииВ целом, это замечательный текст, который ценен во многих контекстах. Надеюсь, автор рассматривает возможность расширения своего корпуса ООР!
Определение, различные категории и часто задаваемые вопросы
Механика – это наука, изучающая движение объектов под действием силы.Он также касается особого случая, когда тело находится в состоянии покоя.
Здесь нас больше всего беспокоят два тела, которые действуют друг на друга.
Например, влияние гравитации на планеты, вращающиеся вокруг Солнца, магнитные силы, с помощью которых железные опилки притягиваются к магниту, и электрическая сила, под действием которой два заряда притягиваются друг к другу, и так далее.
Механика
Механика – это область физики, которая занимается движением физических объектов.Силы, приложенные к объектам, приводят к смещениям, т. Е. К изменению положения объекта относительно его окружения.
Механика подразделяется на три следующие категории:
Статистическая механика
Классическая механика
Квантовая механика
Статистическая механика
Слово «статический» в статистике означает стабильный или неподвижный. Итак, статистическая механика имеет дело со статическими объектами, на которые действует сила.
Статистическая механика объединяет принципы статистики как с классической, так и с квантовой физикой.
В современную эпоху одной из фундаментальных концепций (столпов) современной физики является статистическая механика. Статистическая механика, которая рассматривает и объясняет классическую термодинамику, называется статистической термодинамикой.
Статистическая механика, которая рассматривает и объясняет классическую термодинамику, называется статистической термодинамикой.
Допустим, имеется N количество систем частиц, находящихся в тепловом равновесии при абсолютной температуре T, энергия E связана с каждой частицей, тогда энергия для N частиц будет:
N (E) = g (E) f (E)
Где,
N (E) = полная энергия всех частиц в системе.
г (E) = Число состояний энергии (E) или статистический вес относительно энергии
Мы называем f (E) функцией распределения.
f (E) имеет еще два значения:
Статистическая механика помогает нам определить, как макроскопические свойства, а именно: температура и давление связаны с микроскопическими свойствами, которые в среднем меняются.
Как мы знаем, классическая термодинамика может только измерять и составлять таблицы количества (теплоемкости) определенных материалов; однако статистическая механика связывает эти термодинамические величины с микроскопическим поведением.
Классическая механика
Классическая механика имеет дело с объектами, движущимися под действием силы, или телами равновесия, все силы которых уравновешены.
Мы можем рассматривать классическую механику как объяснение основных постулатов Исаака Ньютона, упомянутых в его книге под названием Philosophiae Naturalis Principia Mathematica (1687), широко известной как Principia.
Мы называем эти постулаты законами движения Ньютона. Эти законы помогают нам предсказывать с большой точностью самые разные явления, начиная от движения отдельных частиц до взаимодействий очень сложных систем.
Основными понятиями классической механики являются сила, масса и движение. Ньютон не мог определить одновременно массу и силу. С тех пор они оба стали предметом многочисленных философских наблюдений Ньютона. Однако оба они наиболее известны своими эффектами.
Применяя первый закон движения, мы можем сказать, что масса – это мера тенденции тела сопротивляться изменениям в его состоянии движения, в то время как сила ускоряет тела, т. Е. Когда она применяется к телу, она изменяется состояние движения тела.Взаимосвязь между этими двумя эффектами – это то, что мы называем классической механикой.
Е. Когда она применяется к телу, она изменяется состояние движения тела.Взаимосвязь между этими двумя эффектами – это то, что мы называем классической механикой.
Что такое классическая механика в физике?
Классическая механика – это теория физики, которая учитывает движение макроскопических объектов (объектов, видимых невооруженным глазом), от снарядов до различных частей оборудования, а также астрономических объектов, таких как космические корабли, звезды, планеты и галактики.
Для объектов, которые управляются классической механикой, если текущее состояние известно, мы можем предсказать, как объект будет двигаться в будущем (детерминизм) и как он двигался в прошлом (обратимость).
Квантовая механика
Квантовая механика – это научная теория, изучающая поведение материи и света на атомном и субатомном уровне.
Квантовая механика – это фундаментальный инструмент, который помогает понять на теоретическом этапе электронную структуру химических соединений и их механизм, термодинамику, химическую кинетику и кинетику химических реакций.
Квантовая механика пытается описывать и искать свойства молекул и атомов и их составляющих, а именно: электронов, протонов, нейтронов и многих других эзотерических частиц, таких как кварки и глюоны; эти атрибуты включают взаимодействие частиц (на микроскопическом уровне) друг с другом и с электромагнитным излучением, таким как световые лучи, рентгеновские лучи и гамма-лучи.
Итак, вы поняли, как квантовая физика объясняет, как работают атомы, и, следовательно, почему химия и биология работают именно так.
Запомните
Знаете ли вы, что механика и кинематика связаны друг с другом? Если не знаешь, давай разберемся.
Часть механики, описывающая движение, не касаясь его причин, называется кинематикой. Это потому, что кинематика не принимает во внимание причину движения, она учитывает только следующие параметры движения: это:
Скорость
Смещение
Расстояние
Время
Скорость
% PDF-1. 4
5 0 объект
>
эндобдж
8 0 объект
(Элементарная механика)
эндобдж
9 0 объект
>
эндобдж
12 0 объект
(Ньютоновская механика)
эндобдж
13 0 объект
>
эндобдж
16 0 объект
(Уравнение движения одиночной частицы)
эндобдж
17 0 объект
>
эндобдж
20 0 объект
(Угловое движение)
эндобдж
21 0 объект
>
эндобдж
24 0 объект
(Энергия и работа)
эндобдж
25 0 объект
>
эндобдж
28 0 объект
(Гравитация)
эндобдж
29 0 объект
>
эндобдж
32 0 объект
(Сила гравитации)
эндобдж
33 0 объект
>
эндобдж
36 0 объект
(Гравитационный потенциал)
эндобдж
37 0 объект
>
эндобдж
40 0 объект
(Динамика систем частиц)
эндобдж
41 0 объект
>
эндобдж
44 0 объект
(Ньютоновские механические концепции для систем частиц)
эндобдж
45 0 объект
>
эндобдж
48 0 объект
(Теорема вириала)
эндобдж
49 0 объект
>
эндобдж
52 0 объект
(Столкновения частиц)
эндобдж
53 0 объект
>
эндобдж
56 0 объект
(Лагранжева и гамильтонова динамика)
эндобдж
57 0 объект
>
эндобдж
60 0 объект
(Лагранжев подход к механике)
эндобдж
61 0 объект
>
эндобдж
64 0 объект
(Степени свободы, ограничения и обобщенные координаты)
эндобдж
65 0 объект
>
эндобдж
68 0 объект
(Виртуальное смещение, виртуальная работа и обобщенные силы)
эндобдж
69 0 объект
>
эндобдж
72 0 объект
(Принцип Даламбера и обобщенное уравнение движения)
эндобдж
73 0 объект
>
эндобдж
76 0 объект
(Лагранжиан и уравнения Эйлера-Лагранжа)
эндобдж
77 0 объект
>
эндобдж
80 0 объект
(Гамильтониан)
эндобдж
81 0 объект
>
эндобдж
84 0 объект
(Циклические координаты и канонический момент)
эндобдж
85 0 объект
>
эндобдж
88 0 объект
(Резюме)
эндобдж
89 0 объект
>
эндобдж
92 0 объект
(Больше примеров)
эндобдж
93 0 объект
>
эндобдж
96 0 объект
(Особые неконсервативные случаи)
эндобдж
97 0 объект
>
эндобдж
100 0 объект
(Преобразования симметрии, сохраняющиеся величины, циклические координаты и теорема Нётер)
эндобдж
101 0 объект
>
эндобдж
104 0 объект
(Вариационное исчисление и динамика)
эндобдж
105 0 объект
>
эндобдж
108 0 объект
(Вариационное исчисление и уравнение Эйлера)
эндобдж
109 0 объект
>
эндобдж
112 0 объект
(Принцип наименьшего действия и уравнение Эйлера-Лагранжа)
эндобдж
113 0 объект
>
эндобдж
116 0 объект
(Введение ограничений в вариационной динамике)
эндобдж
117 0 объект
>
эндобдж
120 0 объект
(Включение неголономных ограничений в вариационную динамику)
эндобдж
121 0 объект
>
эндобдж
124 0 объект
(Гамильтонова динамика)
эндобдж
125 0 объект
>
эндобдж
128 0 объект
(Преобразования Лежандра и уравнения движения Гамильтона)
эндобдж
129 0 объект
>
эндобдж
132 0 объект
(Фазовое пространство и теорема Лиувилля)
эндобдж
133 0 объект
>
эндобдж
136 0 объект
(Разделы теоретической механики)
эндобдж
137 0 объект
>
эндобдж
140 0 объект
(Канонические преобразования и производящие функции)
эндобдж
141 0 объект
>
эндобдж
144 0 объект
(Симплектическая запись)
эндобдж
145 0 объект
>
эндобдж
148 0 объект
(Скобки Пуассона)
эндобдж
149 0 объект
>
эндобдж
152 0 объект
(Переменные действия-угла и адиабатическая инвариантность)
эндобдж
153 0 объект
>
эндобдж
156 0 объект
(Уравнение Гамильтона-Якоби)
эндобдж
157 0 объект
>
эндобдж
160 0 объект
(Колебания)
эндобдж
161 0 объект
>
эндобдж
164 0 объект
(Простой гармонический осциллятор)
эндобдж
165 0 объект
>
эндобдж
168 0 объект
(Равновесия и колебания)
эндобдж
169 0 объект
>
эндобдж
172 0 объект
(Решение простого гармонического осциллятора)
эндобдж
173 0 объект
>
эндобдж
176 0 объект
(Демпфированный простой гармонический осциллятор)
эндобдж
177 0 объект
>
эндобдж
180 0 объект
(Управляемый простой и затухающий гармонический осциллятор)
эндобдж
181 0 объект
>
эндобдж
184 0 объект
(Поведение при приближении к резонансу)
эндобдж
185 0 объект
>
эндобдж
188 0 объект
(Связанные простые гармонические осцилляторы)
эндобдж
189 0 объект
>
эндобдж
192 0 объект
(Пример связанного маятника)
эндобдж
193 0 объект
>
эндобдж
196 0 объект
(Общий метод решения)
эндобдж
197 0 объект
>
эндобдж
200 0 объект
(Примеры и приложения)
эндобдж
201 0 объект
>
эндобдж
204 0 объект
(Вырождение)
эндобдж
205 0 объект
>
эндобдж
208 0 объект
(Волны)
эндобдж
209 0 объект
>
эндобдж
212 0 объект
(Загруженная строка)
эндобдж
213 0 объект
>
эндобдж
216 0 объект
(Непрерывная строка)
эндобдж
217 0 объект
>
эндобдж
220 0 объект
(Волновое уравнение)
эндобдж
221 0 объект
>
эндобдж
224 0 объект
(Фазовая скорость, групповая скорость и волновые пакеты)
эндобдж
225 0 объект
>
эндобдж
228 0 объект
(Движение и рассеяние центральной силы)
эндобдж
229 0 объект
>
эндобдж
232 0 объект
(Общая проблема центральной силы)
эндобдж
233 0 объект
>
эндобдж
236 0 объект
(Уравнение движения)
эндобдж
237 0 объект
>
эндобдж
240 0 объект
(Формальные следствия уравнений движения)
эндобдж
241 0 объект
>
эндобдж
244 0 объект
(Частный случай гравитации – проблема Кеплера)
эндобдж
245 0 объект
>
эндобдж
248 0 объект
(Форма решений проблемы Кеплера)
эндобдж
249 0 объект
>
эндобдж
252 0 объект
(Временная зависимость решений задачи Кеплера)
эндобдж
253 0 объект
>
эндобдж
256 0 объект
(Сечения рассеяния)
эндобдж
257 0 объект
>
эндобдж
260 0 объект
(Постановка проблемы)
эндобдж
261 0 объект
>
эндобдж
264 0 объект
(Общее поперечное сечение)
эндобдж
265 0 объект
>
эндобдж
268 0 объект
(Первый потенциал)
эндобдж
269 0 объект
>
эндобдж
272 0 объект
(Вращающиеся системы)
эндобдж
273 0 объект
>
эндобдж
276 0 объект
(Математическое описание вращений)
эндобдж
277 0 объект
>
эндобдж
280 0 объект
(Бесконечно малые вращения)
эндобдж
281 0 объект
>
эндобдж
284 0 объект
(Конечные вращения)
эндобдж
285 0 объект
>
эндобдж
288 0 объект
(Интерпретация вращений)
эндобдж
289 0 объект
>
эндобдж
292 0 объект
(Скаляры, векторы и тензоры)
эндобдж
293 0 объект
>
эндобдж
296 0 объект
(Комментарии к алгебрам Ли и группам Ли)
эндобдж
297 0 объект
>
эндобдж
300 0 объект
(Динамика во вращающихся системах координат)
эндобдж
301 0 объект
>
эндобдж
304 0 объект
(Второй закон Ньютона во вращающихся системах координат)
эндобдж
305 0 объект
>
эндобдж
308 0 объект
(Приложения)
эндобдж
309 0 объект
>
эндобдж
312 0 объект
(Лагранжева и гамильтонова динамика во вращающихся системах координат)
эндобдж
313 0 объект
>
эндобдж
316 0 объект
(Вращательная динамика твердых тел)
эндобдж
317 0 объект
>
эндобдж
320 0 объект
(Основной формализм)
эндобдж
321 0 объект
>
эндобдж
324 0 объект
(Движение без крутящего момента)
эндобдж
325 0 объект
>
эндобдж
328 0 объект
(Движение под действием внешних моментов)
эндобдж
329 0 объект
>
эндобдж
332 0 объект
(Специальная теория относительности)
эндобдж
333 0 объект
>
эндобдж
336 0 объект
(Специальная теория относительности)
эндобдж
337 0 объект
>
эндобдж
340 0 объект
(Постулаты)
эндобдж
341 0 объект
>
эндобдж
344 0 объект
(Законы трансформации)
эндобдж
345 0 объект
>
эндобдж
348 0 объект
(Математическое описание преобразований Лоренца)
эндобдж
349 0 объект
>
эндобдж
352 0 объект
(Физические последствия)
эндобдж
353 0 объект
>
эндобдж
356 0 объект
(Лагранжева и гамильтонова динамика в теории относительности)
эндобдж
357 0 объект
>
эндобдж
360 0 объект
(Математическое приложение)
эндобдж
361 0 объект
>
эндобдж
364 0 объект
(Условные обозначения математических символов)
эндобдж
365 0 объект
>
эндобдж
368 0 объект
(Системы координат)
эндобдж
369 0 объект
>
эндобдж
372 0 объект
(Векторные и тензорные определения и алгебраические тождества)
эндобдж
373 0 объект
>
эндобдж
376 0 объект
(Векторное исчисление)
эндобдж
377 0 объект
>
эндобдж
380 0 объект
(Расширение Тейлора)
эндобдж
381 0 объект
>
эндобдж
384 0 объект
(Вариационное исчисление)
эндобдж
385 0 объект
>
эндобдж
388 0 объект
(Преобразования Лежандра)
эндобдж
389 0 объект
>
эндобдж
392 0 объект
(Сводка физических результатов)
эндобдж
393 0 объект
>
эндобдж
396 0 объект
(Элементарная механика)
эндобдж
397 0 объект
>
эндобдж
400 0 объект
(Лагранжева и гамильтонова динамика)
эндобдж
401 0 объект
>
эндобдж
404 0 объект
(Колебания)
эндобдж
405 0 объект
>
эндобдж
408 0 объект
(Центральные силы и динамика рассеяния)
эндобдж
409 0 объект
>
эндобдж
412 0 объект
(Вращающиеся системы)
эндобдж
413 0 объект
>
эндобдж
416 0 объект
(Специальная теория относительности)
эндобдж
417 0 объект
>
эндобдж
420 0 obj>
ручей
x ڍ KK09 & `b & ֣ EE7k-.
4
5 0 объект
>
эндобдж
8 0 объект
(Элементарная механика)
эндобдж
9 0 объект
>
эндобдж
12 0 объект
(Ньютоновская механика)
эндобдж
13 0 объект
>
эндобдж
16 0 объект
(Уравнение движения одиночной частицы)
эндобдж
17 0 объект
>
эндобдж
20 0 объект
(Угловое движение)
эндобдж
21 0 объект
>
эндобдж
24 0 объект
(Энергия и работа)
эндобдж
25 0 объект
>
эндобдж
28 0 объект
(Гравитация)
эндобдж
29 0 объект
>
эндобдж
32 0 объект
(Сила гравитации)
эндобдж
33 0 объект
>
эндобдж
36 0 объект
(Гравитационный потенциал)
эндобдж
37 0 объект
>
эндобдж
40 0 объект
(Динамика систем частиц)
эндобдж
41 0 объект
>
эндобдж
44 0 объект
(Ньютоновские механические концепции для систем частиц)
эндобдж
45 0 объект
>
эндобдж
48 0 объект
(Теорема вириала)
эндобдж
49 0 объект
>
эндобдж
52 0 объект
(Столкновения частиц)
эндобдж
53 0 объект
>
эндобдж
56 0 объект
(Лагранжева и гамильтонова динамика)
эндобдж
57 0 объект
>
эндобдж
60 0 объект
(Лагранжев подход к механике)
эндобдж
61 0 объект
>
эндобдж
64 0 объект
(Степени свободы, ограничения и обобщенные координаты)
эндобдж
65 0 объект
>
эндобдж
68 0 объект
(Виртуальное смещение, виртуальная работа и обобщенные силы)
эндобдж
69 0 объект
>
эндобдж
72 0 объект
(Принцип Даламбера и обобщенное уравнение движения)
эндобдж
73 0 объект
>
эндобдж
76 0 объект
(Лагранжиан и уравнения Эйлера-Лагранжа)
эндобдж
77 0 объект
>
эндобдж
80 0 объект
(Гамильтониан)
эндобдж
81 0 объект
>
эндобдж
84 0 объект
(Циклические координаты и канонический момент)
эндобдж
85 0 объект
>
эндобдж
88 0 объект
(Резюме)
эндобдж
89 0 объект
>
эндобдж
92 0 объект
(Больше примеров)
эндобдж
93 0 объект
>
эндобдж
96 0 объект
(Особые неконсервативные случаи)
эндобдж
97 0 объект
>
эндобдж
100 0 объект
(Преобразования симметрии, сохраняющиеся величины, циклические координаты и теорема Нётер)
эндобдж
101 0 объект
>
эндобдж
104 0 объект
(Вариационное исчисление и динамика)
эндобдж
105 0 объект
>
эндобдж
108 0 объект
(Вариационное исчисление и уравнение Эйлера)
эндобдж
109 0 объект
>
эндобдж
112 0 объект
(Принцип наименьшего действия и уравнение Эйлера-Лагранжа)
эндобдж
113 0 объект
>
эндобдж
116 0 объект
(Введение ограничений в вариационной динамике)
эндобдж
117 0 объект
>
эндобдж
120 0 объект
(Включение неголономных ограничений в вариационную динамику)
эндобдж
121 0 объект
>
эндобдж
124 0 объект
(Гамильтонова динамика)
эндобдж
125 0 объект
>
эндобдж
128 0 объект
(Преобразования Лежандра и уравнения движения Гамильтона)
эндобдж
129 0 объект
>
эндобдж
132 0 объект
(Фазовое пространство и теорема Лиувилля)
эндобдж
133 0 объект
>
эндобдж
136 0 объект
(Разделы теоретической механики)
эндобдж
137 0 объект
>
эндобдж
140 0 объект
(Канонические преобразования и производящие функции)
эндобдж
141 0 объект
>
эндобдж
144 0 объект
(Симплектическая запись)
эндобдж
145 0 объект
>
эндобдж
148 0 объект
(Скобки Пуассона)
эндобдж
149 0 объект
>
эндобдж
152 0 объект
(Переменные действия-угла и адиабатическая инвариантность)
эндобдж
153 0 объект
>
эндобдж
156 0 объект
(Уравнение Гамильтона-Якоби)
эндобдж
157 0 объект
>
эндобдж
160 0 объект
(Колебания)
эндобдж
161 0 объект
>
эндобдж
164 0 объект
(Простой гармонический осциллятор)
эндобдж
165 0 объект
>
эндобдж
168 0 объект
(Равновесия и колебания)
эндобдж
169 0 объект
>
эндобдж
172 0 объект
(Решение простого гармонического осциллятора)
эндобдж
173 0 объект
>
эндобдж
176 0 объект
(Демпфированный простой гармонический осциллятор)
эндобдж
177 0 объект
>
эндобдж
180 0 объект
(Управляемый простой и затухающий гармонический осциллятор)
эндобдж
181 0 объект
>
эндобдж
184 0 объект
(Поведение при приближении к резонансу)
эндобдж
185 0 объект
>
эндобдж
188 0 объект
(Связанные простые гармонические осцилляторы)
эндобдж
189 0 объект
>
эндобдж
192 0 объект
(Пример связанного маятника)
эндобдж
193 0 объект
>
эндобдж
196 0 объект
(Общий метод решения)
эндобдж
197 0 объект
>
эндобдж
200 0 объект
(Примеры и приложения)
эндобдж
201 0 объект
>
эндобдж
204 0 объект
(Вырождение)
эндобдж
205 0 объект
>
эндобдж
208 0 объект
(Волны)
эндобдж
209 0 объект
>
эндобдж
212 0 объект
(Загруженная строка)
эндобдж
213 0 объект
>
эндобдж
216 0 объект
(Непрерывная строка)
эндобдж
217 0 объект
>
эндобдж
220 0 объект
(Волновое уравнение)
эндобдж
221 0 объект
>
эндобдж
224 0 объект
(Фазовая скорость, групповая скорость и волновые пакеты)
эндобдж
225 0 объект
>
эндобдж
228 0 объект
(Движение и рассеяние центральной силы)
эндобдж
229 0 объект
>
эндобдж
232 0 объект
(Общая проблема центральной силы)
эндобдж
233 0 объект
>
эндобдж
236 0 объект
(Уравнение движения)
эндобдж
237 0 объект
>
эндобдж
240 0 объект
(Формальные следствия уравнений движения)
эндобдж
241 0 объект
>
эндобдж
244 0 объект
(Частный случай гравитации – проблема Кеплера)
эндобдж
245 0 объект
>
эндобдж
248 0 объект
(Форма решений проблемы Кеплера)
эндобдж
249 0 объект
>
эндобдж
252 0 объект
(Временная зависимость решений задачи Кеплера)
эндобдж
253 0 объект
>
эндобдж
256 0 объект
(Сечения рассеяния)
эндобдж
257 0 объект
>
эндобдж
260 0 объект
(Постановка проблемы)
эндобдж
261 0 объект
>
эндобдж
264 0 объект
(Общее поперечное сечение)
эндобдж
265 0 объект
>
эндобдж
268 0 объект
(Первый потенциал)
эндобдж
269 0 объект
>
эндобдж
272 0 объект
(Вращающиеся системы)
эндобдж
273 0 объект
>
эндобдж
276 0 объект
(Математическое описание вращений)
эндобдж
277 0 объект
>
эндобдж
280 0 объект
(Бесконечно малые вращения)
эндобдж
281 0 объект
>
эндобдж
284 0 объект
(Конечные вращения)
эндобдж
285 0 объект
>
эндобдж
288 0 объект
(Интерпретация вращений)
эндобдж
289 0 объект
>
эндобдж
292 0 объект
(Скаляры, векторы и тензоры)
эндобдж
293 0 объект
>
эндобдж
296 0 объект
(Комментарии к алгебрам Ли и группам Ли)
эндобдж
297 0 объект
>
эндобдж
300 0 объект
(Динамика во вращающихся системах координат)
эндобдж
301 0 объект
>
эндобдж
304 0 объект
(Второй закон Ньютона во вращающихся системах координат)
эндобдж
305 0 объект
>
эндобдж
308 0 объект
(Приложения)
эндобдж
309 0 объект
>
эндобдж
312 0 объект
(Лагранжева и гамильтонова динамика во вращающихся системах координат)
эндобдж
313 0 объект
>
эндобдж
316 0 объект
(Вращательная динамика твердых тел)
эндобдж
317 0 объект
>
эндобдж
320 0 объект
(Основной формализм)
эндобдж
321 0 объект
>
эндобдж
324 0 объект
(Движение без крутящего момента)
эндобдж
325 0 объект
>
эндобдж
328 0 объект
(Движение под действием внешних моментов)
эндобдж
329 0 объект
>
эндобдж
332 0 объект
(Специальная теория относительности)
эндобдж
333 0 объект
>
эндобдж
336 0 объект
(Специальная теория относительности)
эндобдж
337 0 объект
>
эндобдж
340 0 объект
(Постулаты)
эндобдж
341 0 объект
>
эндобдж
344 0 объект
(Законы трансформации)
эндобдж
345 0 объект
>
эндобдж
348 0 объект
(Математическое описание преобразований Лоренца)
эндобдж
349 0 объект
>
эндобдж
352 0 объект
(Физические последствия)
эндобдж
353 0 объект
>
эндобдж
356 0 объект
(Лагранжева и гамильтонова динамика в теории относительности)
эндобдж
357 0 объект
>
эндобдж
360 0 объект
(Математическое приложение)
эндобдж
361 0 объект
>
эндобдж
364 0 объект
(Условные обозначения математических символов)
эндобдж
365 0 объект
>
эндобдж
368 0 объект
(Системы координат)
эндобдж
369 0 объект
>
эндобдж
372 0 объект
(Векторные и тензорные определения и алгебраические тождества)
эндобдж
373 0 объект
>
эндобдж
376 0 объект
(Векторное исчисление)
эндобдж
377 0 объект
>
эндобдж
380 0 объект
(Расширение Тейлора)
эндобдж
381 0 объект
>
эндобдж
384 0 объект
(Вариационное исчисление)
эндобдж
385 0 объект
>
эндобдж
388 0 объект
(Преобразования Лежандра)
эндобдж
389 0 объект
>
эндобдж
392 0 объект
(Сводка физических результатов)
эндобдж
393 0 объект
>
эндобдж
396 0 объект
(Элементарная механика)
эндобдж
397 0 объект
>
эндобдж
400 0 объект
(Лагранжева и гамильтонова динамика)
эндобдж
401 0 объект
>
эндобдж
404 0 объект
(Колебания)
эндобдж
405 0 объект
>
эндобдж
408 0 объект
(Центральные силы и динамика рассеяния)
эндобдж
409 0 объект
>
эндобдж
412 0 объект
(Вращающиеся системы)
эндобдж
413 0 объект
>
эндобдж
416 0 объект
(Специальная теория относительности)
эндобдж
417 0 объект
>
эндобдж
420 0 obj>
ручей
x ڍ KK09 & `b & ֣ EE7k-. Dů | Dhin ֪ \ hwkmQ \\, 2U \ W
Dů | Dhin ֪ \ hwkmQ \\, 2U \ W
Механика | Физика | Amherst College
Осень 2020
Введение в физику I: Механика
Внесено в список: Physics and Astronomy, as PHYS-116
Ранее указано как: PHYS-16
Сайт Moodle: Курс (требуется вход в систему)
Faculty
Эшли Р. Картер (Раздел 01)
Джарретт А. Мойер (Раздел 01)
Описание
Этот курс начнется с описания движения частиц и ознакомления с законами динамики Ньютона и рядом важных законов силы.Мы будем применять эти законы к широкому кругу проблем, чтобы лучше понять законы и продемонстрировать общность структуры. Будут введены важные понятия работы, механической энергии, линейного и углового момента, и будет обсуждена объединяющая идея законов сохранения. Дополнительные темы могут включать изучение механических волн, механику жидкости и вращательную динамику. Три часа лекций и одна трехчасовая лаборатория в неделю.
Для обеспечения взаимодействия курса мы будем проводить необходимые синхронные собрания малых групп, необходимые синхронные индивидуальные встречи с инструкторами и некоторые дополнительные синхронные собрания. Однако основные занятия и лабораторные занятия будут проводиться дистанционно.
Однако основные занятия и лабораторные занятия будут проводиться дистанционно.
Реквизит: MATH 111. Ограничено 48 студентами. Осенний семестр: Кафедра. Весенний семестр: профессор Картер и доктор Мойер.
При повышении квалификации: Предпочтение будет отдаваться студентам, которые собираются получить специальность по физике. После этого приоритет будет отдаваться трудовому стажу.
Ключевые слова
Курс лабораторных наук, количественное обоснование Время и место проведения курсаPHYS 116 – LEC
Раздел 01
Вт 10:10 – 11:30 SCCE E110
Чт 10:10 – 11:30 SCCE E110
PHYS 116F – DIS
Раздел 01
M 14:20 – 15:10 ONLI ONLI
Раздел 02
M 15:50 – 16:40 ONLI ONLI
Раздел 03
M 17:10 – 18:00 ONLI ONLI
Раздел 04
Вт 14:40 – 15:30 ONLI ONLI
PHYS 116L – LAB
Раздел 01
F 08:50 – 09:40 ONLI ONLI
Раздел 02
F 11:20 – 12:10 ONLI ONLI
Раздел 03
F 14:20 – 15:10 ONLI ONLI
Раздел 04
F 15:50 – 16:40 ONLI ONLI
Ниже приведены учебники, используемые в этом курсе, а также информация о ценах. и доступность в местных книжных магазинах.Указанный ценовой диапазон основан на запросах к нескольким книжным магазинам в Интернете; щелкните поле цены, чтобы просмотреть подробную информацию о ценах.
и доступность в местных книжных магазинах.Указанный ценовой диапазон основан на запросах к нескольким книжным магазинам в Интернете; щелкните поле цены, чтобы просмотреть подробную информацию о ценах.
Это предварительная информация о книгах для этого курса. Пожалуйста, свяжитесь со своим инструктором или академическим координатором факультета, прежде чем покупать эти книги.
| ISBN | Название | Издатель | Автор (ы) | Комментарий | Цена |
|---|---|---|---|---|---|
| 13: 978-0-13-397820-9 | Mastering390 Mastering390 Physics Публикация | Обратите внимание: если вы не уверены, что объединенная покупка Mastering Physics поступит до начала занятий, рекомендуется покупать Mastering Physics отдельно от текста, поскольку это дает вам мгновенный доступ к Ma | TBD | ||
| 13: 978-0-321-97361-0 | 14-е издание University Physics | Young and Freedman | Студенты могут получить комбинированное издание, которое включает в себя первый и второй том и современную физику (ISBN-13: 978-0-321-97361-0) или они могут просто получить Том 1 (ISBN-13: 978-0-13-397804-9). Объемы аренды доступны, как и электронные версии текста. Объемы аренды доступны, как и электронные версии текста. | TBD |
Предпочтение будет отдаваться студентам, которые собираются получить специальность по физике. После этого приоритет будет отдаваться трудовому стажу.
предложений
2021-22: Предлагается осенью 2021 г., весной 2022 г.В другие годы: Предлагается осенью 2007 г., весной 2008 г., осенью 2008 г., весной 2009 г., осенью 2009 г., весной 2010 г., осенью 2010 г., весной 2011 г., осенью 2019, Весна 2020, Осень 2020, Весна 2021, Осень 2021
В чем разница между физикой и механикой?
Как существительные, разница между физикой
и механикой состоит в том, что физика – это отрасль науки, занимающаяся изучением свойств и взаимодействий пространства, времени, материи и энергии или физика может быть ( физика ) в то время как механика (физика) раздел физики, который занимается действием сил на материальные объекты с массой.
Как глагол
физика есть ( физика ).Другие сравнения: в чем разница?
Альтернативные формы* Physicks ( устаревшее, )Существительное(–)цитата, пассаж = Физика элементарных частиц в 20-м веке отличалась наблюдением частиц, существование которых предсказывалось теоретиками, иногда десятилетиями ранее.}}
Меронимы* Смотрите такжеСвязанные термины* физический * физикПроизводные условия* аэрофизика * астрофизика * аттофизика * биофизика * мультяшная физика * химическая физика * классическая физика * эконофизика * экофизика * гастрофизика * геофизика * гелиофизика * макрофизика * метаметафизика * метафизика * микрофизика * современная физика * нейрофизика * нефизика * ядерная физика * физика элементарных частиц * патафизика * петрофизика * фотофизика * психофизика * квантовая биофизика * квантовая физика * радиационная физика * радиофизика * социофизика * физика почвы * тектонофизика * теоретическая физикаСуществительное( глава )Глагол( глава ) ) )Внешние ссылки* * * | АнглийскийСуществительное(–)
Производные термины( Производные термины ) * аэромеханика * аналитическая механика * биомеханика * кузовная механика * небесная механика * классическая механика * электромеханика * механика жидкости * газовая механика * наследственная механика * гидромеханика * магнитомеханика * матричная механика * микромеханика * молекулярная механика * Ньютоновская механика * неквантовая механика * нерелятивистская механика * механика частиц * квантовая механика * рациональная механика * релятивистская механика * механика горных пород * механика грунтов * статистическая механика * волновая механикаАнаграммы* |
| # | Лекция | Сыграть лекцию |
|---|---|---|
| 1 | 0.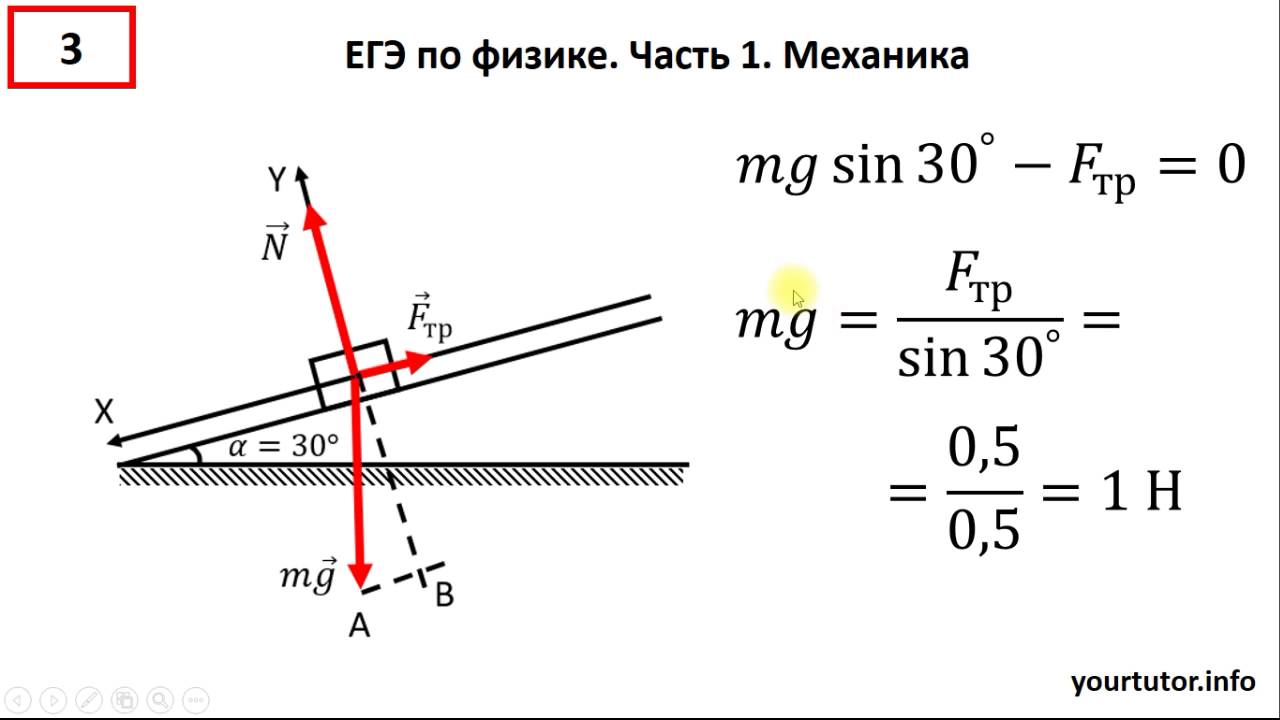 1 Векторы против скаляров 1 Векторы против скаляров | Просмотр видео |
| 2 | 0.2 Векторные операторы | Просмотр видео |
| 3 | 0.3 Системы координат и единичные векторы | Просмотр видео |
| 4 | 0,4 Векторы – величина и направление | Просмотр видео |
| 5 | 0.5 Разложение вектора на компоненты | Просмотр видео |
| 6 | 0,6 Переход между представлениями | Просмотр видео |
| 7 | 1.0 Неделя 1 Введение | Просмотр видео |
| I. Урок 1: 1D кинематика – положение и скорость | ||
| 8 | 1. 1 Системы координат и единичные векторы в 1D 1 Системы координат и единичные векторы в 1D | Просмотр видео |
| 9 | 1.2 Вектор положения в 1D | Просмотр видео |
| 10 | 1.3 Вектор смещения в 1D | Просмотр видео |
| 11 | 1,4 Средняя скорость в 1D | Просмотр видео |
| 12 | 1,5 Мгновенная скорость в 1D | Просмотр видео |
| 13 | 1.7 Рабочий пример: производные в кинематике | Просмотр видео |
| II. Урок 2: 1D кинематика – ускорение | ||
| 14 | 2.1 Введение в ускорение | Просмотр видео |
| 15 | 2. 2 Ускорение в 1D 2 Ускорение в 1D | Просмотр видео |
| 16 | 2.3 Рабочий пример: ускорение с позиции | Просмотр видео |
| 17 | 2.4 Интеграция | Просмотр видео |
| III. Урок 3: 2D-кинематика – положение, скорость и ускорение | ||
| 18 | 3.1 Система координат и вектор положения в 2D | Просмотр видео |
| 19 | 3.2 Мгновенная скорость в 2D | Просмотр видео |
| 20 | 3.3 Мгновенное ускорение в 2D | Просмотр видео |
| 21 | 3.4 Движение снаряда | Просмотр видео |
| 22 | 3. 5 Демонстрация: стрельба в яблоко 5 Демонстрация: стрельба в яблоко | Просмотр видео |
| 23 | 3.5 Демонстрация: Relative Motion Gun | Просмотр видео |
| IV.Неделя 1 Рабочие примеры | ||
| 24 | PS.1.1 Три вопроса перед началом | Просмотр видео |
| 25 | PS.1.2 Стрельба по яблочному раствору | Просмотр видео |
| 26 | P.1.3 Рабочий пример: Торможение автомобиля | Просмотр видео |
| 27 | P.1.4 Набросок движения | Просмотр видео |
| 28 | с.1.5 Рабочий пример: пешеход и велосипед на перекрестке | Просмотр видео |
| 29 | 4.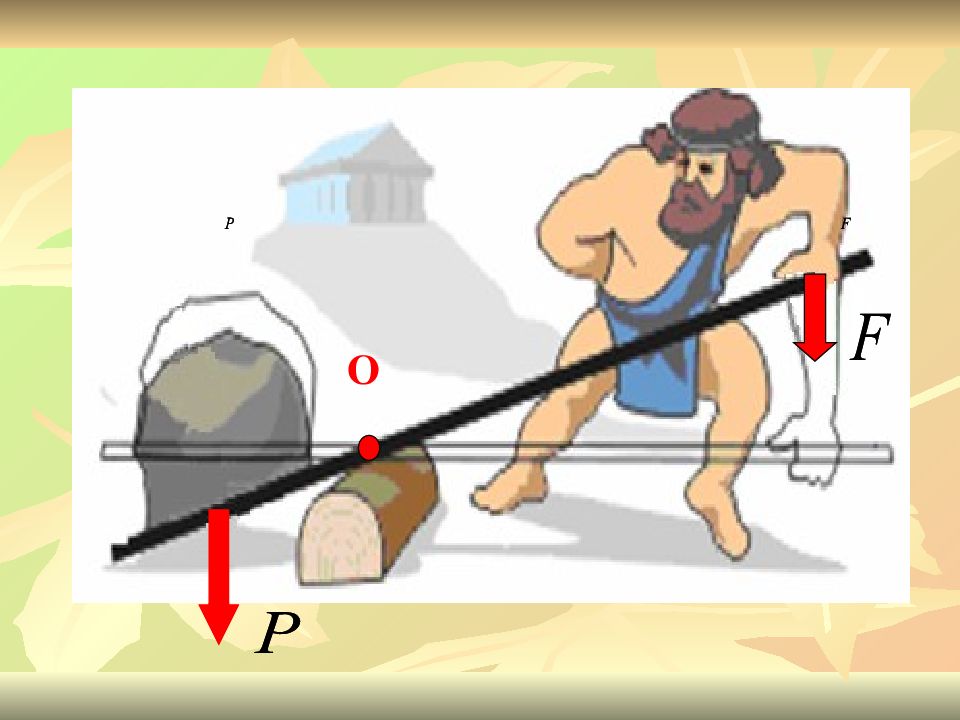 0 Неделя 2 Введение 0 Неделя 2 Введение | Просмотр видео |
| V. Урок 4: Законы движения Ньютона | ||
| 30 | 4.1 Первый и Второй законы Ньютона | Просмотр видео |
| 31 | 4.2 Третий закон Ньютона | Просмотр видео |
| 32 | 4.3 Базовые рамки | Просмотр видео |
| 33 | 4.4 Неинерциальные системы отсчета | Просмотр видео |
| VI. Урок 5: Gravity | ||
| 34 | 5.1 Универсальный закон всемирного тяготения | Просмотр видео |
| 35 | 5.2 Рабочий пример: гравитация – суперпозиция | Просмотр видео |
| 36 | 5.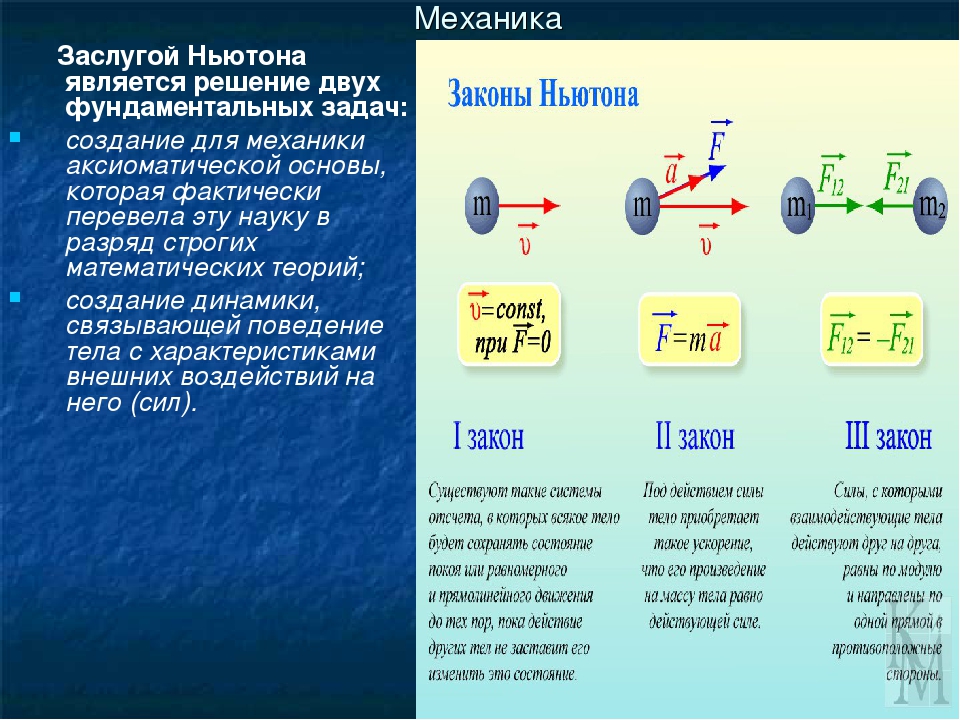 3 Гравитация у поверхности Земли: значение g. 3 Гравитация у поверхности Земли: значение g. | Просмотр видео |
| VII. Урок 6: Контактные силы | ||
| 37 | 6.1 Контактные силы | Просмотр видео |
| 38 | 6.2 Статическое трение | Просмотр видео |
| VIII.Урок 7: Натяжение и пружины | ||
| 39 | 7.1 Толкание, вытягивание и натяжение | Просмотр видео |
| 40 | 7.2 Идеальная веревка | Просмотр видео |
| 41 | 7.3 Решение шкивных систем | Просмотр видео |
| 42 | 7.4 Закон Гука | Просмотр видео |
IX. Глубокое погружение: трение Глубокое погружение: трение | ||
| 43 | DD.1.1 Трение в наномасштабе | Просмотр видео |
| X. Неделя 2 Рабочие примеры | ||
| 44 | PS.2.1 Рабочий пример – выдвижной блок | Просмотр видео |
| 45 | Рабочий пример PS.2.2 – Составные блоки – Диаграммы свободных тел и применение 2-го закона Ньютона | Просмотр видео |
| 46 | л.с.2.2 Рабочий пример – составные блоки – вычислить максимальное усилие | Просмотр видео |
| 47 | PS.2.2 Рабочий пример – составные блоки – выбор системы из 2 блоков вместе | Просмотр видео |
| 48 | PS. 2.3 Схемы свободного кузова стеклоомывателя 2.3 Схемы свободного кузова стеклоомывателя | Просмотр видео |
| 49 | PS.2.3 Раствор для мытья окон | Просмотр видео |
| 50 | Пары третьего закона Ньютона | Просмотр видео |
| 51 | Внутренние и внешние силы | Просмотр видео |
| 52 | Применение 2-го закона Ньютона | Просмотр видео |
| 53 | 8.0 Неделя 3 Введение | Просмотр видео |
| XI. Урок 8: Круговое движение – положение и скорость | ||
| 54 | 8.1 Полярные координаты | Просмотр видео |
| 55 | 8. 2 Круговое движение: векторы положения и скорости 2 Круговое движение: векторы положения и скорости | Просмотр видео |
| 56 | 8,3 Угловая скорость | Просмотр видео |
| XII.Урок 9: Равномерное круговое движение | ||
| 57 | 9.1 Равномерное круговое движение | Просмотр видео |
| 58 | 9.2 Равномерное круговое движение: направление ускорения | Просмотр видео |
| XIII. Урок 10: Круговое движение – ускорение | ||
| 59 | 10.1 Круговое движение – ускорение | Просмотр видео |
| 60 | 10.2 Угловое ускорение | Просмотр видео |
| 61 | 10. 3 Рабочий пример – Угловое положение от углового ускорения. 3 Рабочий пример – Угловое положение от углового ускорения. | Просмотр видео |
| XIV. Урок 11: 2-й закон Ньютона и круговое движение | ||
| 62 | 11.1 Второй закон Ньютона и круговое движение | Просмотр видео |
| 63 | 11.2 Рабочий пример – автомобиль на повороте | Просмотр видео |
| 64 | 11.3 Демонстрация: вращающийся ковш | Просмотр видео |
| XV. Неделя 3 Рабочие примеры | ||
| 65 | PS.3.1 Рабочий пример – Орбитальное круговое движение – Радиус | Просмотр видео |
| 66 | л.с.3.1 Рабочий пример – Орбитальное круговое движение – скорость | Просмотр видео |
| 67 | PS. 3.1 Рабочий пример – Орбитальное круговое движение – Период 3.1 Рабочий пример – Орбитальное круговое движение – Период | Просмотр видео |
| 68 | 12,0 Неделя 4 Введение | Просмотр видео |
| XVI. Урок 12: Шкивы и ограничители | ||
| 69 | 12.1 Проблемы с шкивом | Просмотр видео |
| 70 | 12.2 Условие ограничения | Просмотр видео |
| 71 | 12.3 Виртуальное смещение | Просмотр видео |
| 72 | 12.4 Решите систему уравнений | Просмотр видео |
| 73 | 12.5 рабочих примеров: 2 блока и 2 шкива | Просмотр видео |
XVII. Урок 13: Массивная веревка Урок 13: Массивная веревка | ||
| 74 | 13.1 Веревка, висящая между деревьями | Просмотр видео |
| 75 | 13.2 Дифференциальный анализ массивной веревки | Просмотр видео |
| 76 | 13.3 Дифференциальные элементы | Просмотр видео |
| 77 | 13.4 Плотность | Просмотр видео |
| 78 | 13.5 Демонстрация: трение обертывания | Просмотр видео |
| 79 | 13.6 Резюме для дифференциального анализа | Просмотр видео |
| XVIII. Урок 14: Силы сопротивления | ||
| 80 | 14. 1 Общие сведения о силах сопротивления 1 Общие сведения о силах сопротивления | Просмотр видео |
| 81 | 14.2 Силы сопротивления – низкоскоростной корпус | Просмотр видео |
| 82 | 14.3 Силы сопротивления – высокоскоростной корпус | Просмотр видео |
| 83 | 15,0 Неделя 5 Введение | Просмотр видео |
| XIX. Урок 15: Импульс и импульс | ||
| 84 | 15.1 Импульс и импульс | Просмотр видео |
| 85 | 15.2 Импульс – это вектор | Просмотр видео |
| 86 | 15.3 Рабочий пример – прыгающий мяч | Просмотр видео |
| 87 | 15. 4 Импульс системы точечных частиц 4 Импульс системы точечных частиц | Просмотр видео |
| 88 | Сила 15,5 на систему частиц | Просмотр видео |
| XX.Урок 16: Сохранение импульса | ||
| 89 | 16.1 Случаи постоянного импульса | Просмотр видео |
| 90 | 16.2 Диаграммы импульса | Просмотр видео |
| XXI. Урок 17: Центр масс и движение центра масс | ||
| 91 | 17.1 Определение центра масс | Просмотр видео |
| 92 | 17.2 рабочий пример – центр масс 3 объектов | Просмотр видео |
| 93 | 17.3 Центр масс непрерывной системы | Просмотр видео |
| 94 | 17,5 Рабочий пример – центр масс однородного стержня | Просмотр видео |
| 95 | 17. 6 Скорость и ускорение центра масс 6 Скорость и ускорение центра масс | Просмотр видео |
| 96 | 17.7 Редукция системы до точечной частицы | Просмотр видео |
| 97 | 18,0 Неделя 6 Введение | Просмотр видео |
| XXII. Урок 18: Относительная скорость и отдача | ||
| 98 | 18,1 Относительная скорость | Просмотр видео |
| 99 | 18.2 Создание проблемы отдачи | Просмотр видео |
| 100 | 18.3 Расчет скорости в наземной раме | Просмотр видео |
| 101 | 18.4 Решение для скорости в движущейся рамке | Просмотр видео |
XXIII. Урок 19: Непрерывный массообмен Урок 19: Непрерывный массообмен | ||
| 102 | 19.1 Ракета Задача 1 – Постановка проблемы | Просмотр видео |
| 103 | 19.2 Ракетная задача 2 – Диаграммы импульса | Просмотр видео |
| 104 | 19.3 Ракетная задача 3 – Массовые отношения | Просмотр видео |
| 105 | 19.4 Ракета Задача 4 – Решение | Просмотр видео |
| 106 | 19.5 Ракета Задача 5 – Тяга и внешние силы | Просмотр видео |
| 107 | 19.6 Ракетная проблема 6 – Решение без внешних сил | Просмотр видео |
| 108 | 19.7 Ракетная проблема 7 – Решение внешними силами | Просмотр видео |
XXIV. Неделя 6 Рабочие примеры Неделя 6 Рабочие примеры | ||
| 109 | Ракетные сани PS.6.1 – Дифференциальное уравнение | Просмотр видео |
| 110 | л.с.6.1 Ракетные салазки – интеграция уравнения ракеты | Просмотр видео |
| 111 | Ракетные сани PS.6.1 – вычислить начальную скорость | Просмотр видео |
| 112 | PS.6.2 Проблема снегоочистителя | Просмотр видео |
| 113 | 20,0 Неделя 7 Введение | Просмотр видео |
| XXV.Урок 20: Кинетическая энергия и работа в 1D | ||
| 114 | 20,1 Кинетическая энергия | Просмотр видео |
| 115 | 20. 2 Работа с постоянной силой 2 Работа с постоянной силой | Просмотр видео |
| 116 | 20.3 Работа с непостоянной силой | Просмотр видео |
| 117 | 20.4 Интеграция ADT и ADX | Просмотр видео |
| 118 | 20.5 Теорема | о кинетической энергии работыПросмотр видео |
| 119 | 20,6 Мощность | Просмотр видео |
| XXVI. Урок 21: Кинетическая энергия и работа в 2D и 3D | ||
| 120 | 21.1 Свойства скалярного произведения | Просмотр видео |
| 121 | 21.2 Скалярное произведение в декартовых координатах | Просмотр видео |
| 122 | 21. 3 Кинетическая энергия как скалярное произведение 3 Кинетическая энергия как скалярное произведение | Просмотр видео |
| 123 | 21.4 Работа в 2D и 3D | Просмотр видео |
| 124 | 21.5 Теорема о кинетической энергии работы в 2D и 3D | Просмотр видео |
| 125 | 21.6 Рабочий пример: блокировка при спуске с рампы | Просмотр видео |
| XXVII.Урок 22: Консервативные и неконсервативные силы | ||
| 126 | 22.1 Независимость пути – сила тяжести | Просмотр видео |
| 127 | 22.2 Зависимость от траектории – трение | Просмотр видео |
| 128 | 22.3 Консервативные силы | Просмотр видео |
| 129 | 22. 4 Неконсервативные силы 4 Неконсервативные силы | Просмотр видео |
| 130 | 22.5 Резюме работы и кинетическая энергия | Просмотр видео |
| XXVIII. Неделя 7 Рабочие примеры | ||
| 131 | Рабочий пример PS.7.1 – Столкновение и скольжение по шероховатой поверхности | Просмотр видео |
| 132 | 23.0 Неделя 8 Введение | Просмотр видео |
| XXIX. Урок 23: Потенциальная энергия | ||
| 133 | 23.1 Введение в потенциальную энергию | Просмотр видео |
| 134 | 23.2 Потенциальная энергия гравитации у поверхности Земли | Просмотр видео |
| 135 | 23. 3 Эталонное состояние потенциальной энергии 3 Эталонное состояние потенциальной энергии | Просмотр видео |
| 136 | 23.4 Потенциальная энергия пружины | Просмотр видео |
| 137 | 23,5 Потенциальная энергия гравитации | Просмотр видео |
| XXX. Урок 24: Сохранение энергии | ||
| 138 | 24.1 Механическая энергия и энергосбережение | Просмотр видео |
| 139 | 24.2 Диаграммы энергетического состояния | Просмотр видео |
| 140 | 24.3 Рабочий пример – блок, скользящий вниз по круговому уклону | Просмотр видео |
| 141 | 24,4 2-й закон Ньютона и сохранение энергии | Просмотр видео |
XXXI. Урок 25: Диаграммы потенциальной энергии Урок 25: Диаграммы потенциальной энергии | ||
| 142 | 25.1 Сила – производная потенциала | Просмотр видео |
| 143 | 25.2 Точки устойчивого и неустойчивого равновесия | Просмотр видео |
| 144 | 25.3 Чтение диаграмм потенциальной энергии | Просмотр видео |
| 145 | 26,0 Неделя 9 Введение | Просмотр видео |
| XXXII.Урок 26: Типы столкновений | ||
| 146 | 26.1 Импульс при столкновениях | Просмотр видео |
| 147 | 26.2 Кинетическая энергия в столкновениях | Просмотр видео |
| 148 | 26. 3 Полностью неупругие столкновения 3 Полностью неупругие столкновения | Просмотр видео |
| XXXIII. Урок 27: Упругие столкновения | ||
| 149 | 27.1 рабочий пример: эластичное одномерное столкновение | Просмотр видео |
| 150 | 27.2 Относительная скорость в 1D | Просмотр видео |
| 151 | 27.3 Уравнение кинетической энергии и импульса | Просмотр видео |
| 152 | 27.4 Рабочий пример: снова упругое одномерное столкновение | Просмотр видео |
| 153 | 27.5 Пример работы: гравитационная рогатка | Просмотр видео |
| 154 | 27.6 2D-столкновения | Просмотр видео |
XXXIV.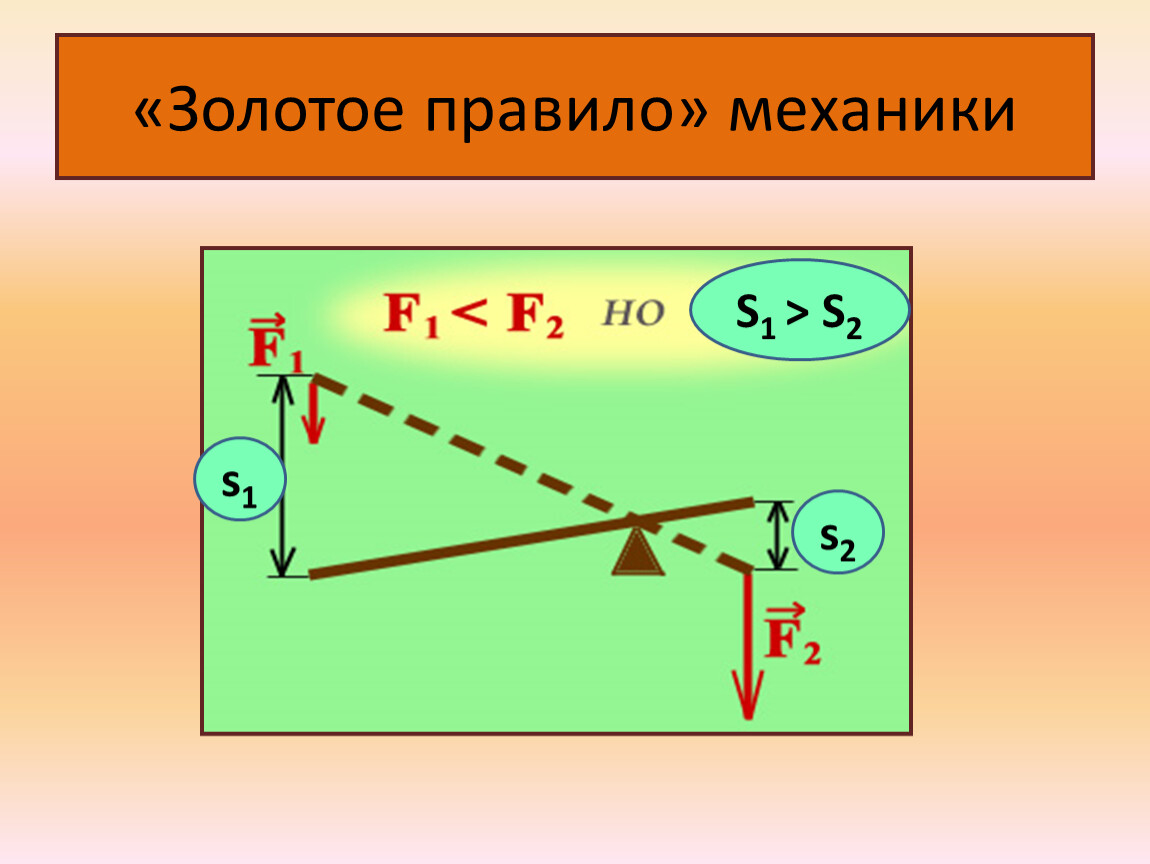 Deep Dive: система отсчета центра масс Deep Dive: система отсчета центра масс | ||
| 155 | DD.2.1 Положение в рамке CM | Просмотр видео |
| 156 | DD.2.2 Относительная скорость не зависит от системы отсчета | Просмотр видео |
| 157 | DD.2.3. Одномерные скорости упругих столкновений в рамке | CMПросмотр видео |
| 158 | DD.2.4 Рабочий пример: одномерное упругое столкновение в рамке CM | Просмотр видео |
| 159 | DD.2.5 Кинетическая энергия в различных системах отсчета | Просмотр видео |
| 160 | DD.2.6 Кинетическая энергия в рамке КМ | Просмотр видео |
| 161 | DD. 2.7 Изменение кинетической энергии 2.7 Изменение кинетической энергии | Просмотр видео |
| 162 | 28,0 Неделя 10 Введение | Просмотр видео |
| XXXV. Урок 28: Движение твердого тела | ||
| 163 | 28.1 Жесткие тела | Просмотр видео |
| 164 | 28.2 Введение в перемещение и вращение | Просмотр видео |
| 165 | 28.3 Обзор угловой скорости и ускорения | Просмотр видео |
| XXXVI. Урок 29: Момент инерции | ||
| 166 | 29.1 Кинетическая энергия вращения | Просмотр видео |
| 167 | 29.2 Момент инерции стержня | Просмотр видео |
| 168 | 29,3 Момент инерции диска | Просмотр видео |
| 169 | 29. Теорема о 4 параллельных осях Теорема о 4 параллельных осях | Просмотр видео |
| 170 | 29,5 Глубокое погружение – момент инерции сферы | Просмотр видео |
| 171 | 29.6 Deep Dive – Вывод теоремы о параллельной оси | Просмотр видео |
| XXXVII. Урок 30: Torque | ||
| 172 | 30.1 Введение в крутящий момент и динамику вращения | Просмотр видео |
| 173 | 30,2 Перекрестное произведение | Просмотр видео |
| 174 | 30.3 Перекрестное произведение в декартовых координатах | Просмотр видео |
| 175 | 30,4 Крутящий момент | Просмотр видео |
| 176 | 30. 5 Крутящий момент от силы тяжести 5 Крутящий момент от силы тяжести | Просмотр видео |
| XXXVIII. Урок 31: Динамика вращения | ||
| 177 | 31.1 Взаимосвязь между крутящим моментом и угловым ускорением | Просмотр видео |
| 178 | 31.2 Внутренняя компенсация крутящего момента в парах | Просмотр видео |
| 179 | 31.3 Рабочий пример – Найдите момент инерции диска от падающей массы | Просмотр видео |
| 180 | 31.4 Рабочий пример – машина Этвуда | Просмотр видео |
| 181 | 31.5 Серьезные проблемы со шкивом | Просмотр видео |
| 182 | 31. 7 Рабочий пример – два блока и шкив с использованием энергии 7 Рабочий пример – два блока и шкив с использованием энергии | Просмотр видео |
| XXXIX.Неделя 10 Рабочие примеры | ||
| 183 | PS.10.1 Рабочий пример – блоки с трением и массивным шкивом | Просмотр видео |
| 184 | 32,0 Неделя 11 Введение | Просмотр видео |
| XL. Урок 32: Угловой момент точечной частицы | ||
| 185 | 32.1 Угловой момент для точечной частицы | Просмотр видео |
| 186 | 32.2 Расчет углового момента | Просмотр видео |
| 187 | 32.3 Рабочий пример – угловой момент в разных точках | Просмотр видео |
| 188 | 32,4 Угловой момент кругового движения | Просмотр видео |
XLI.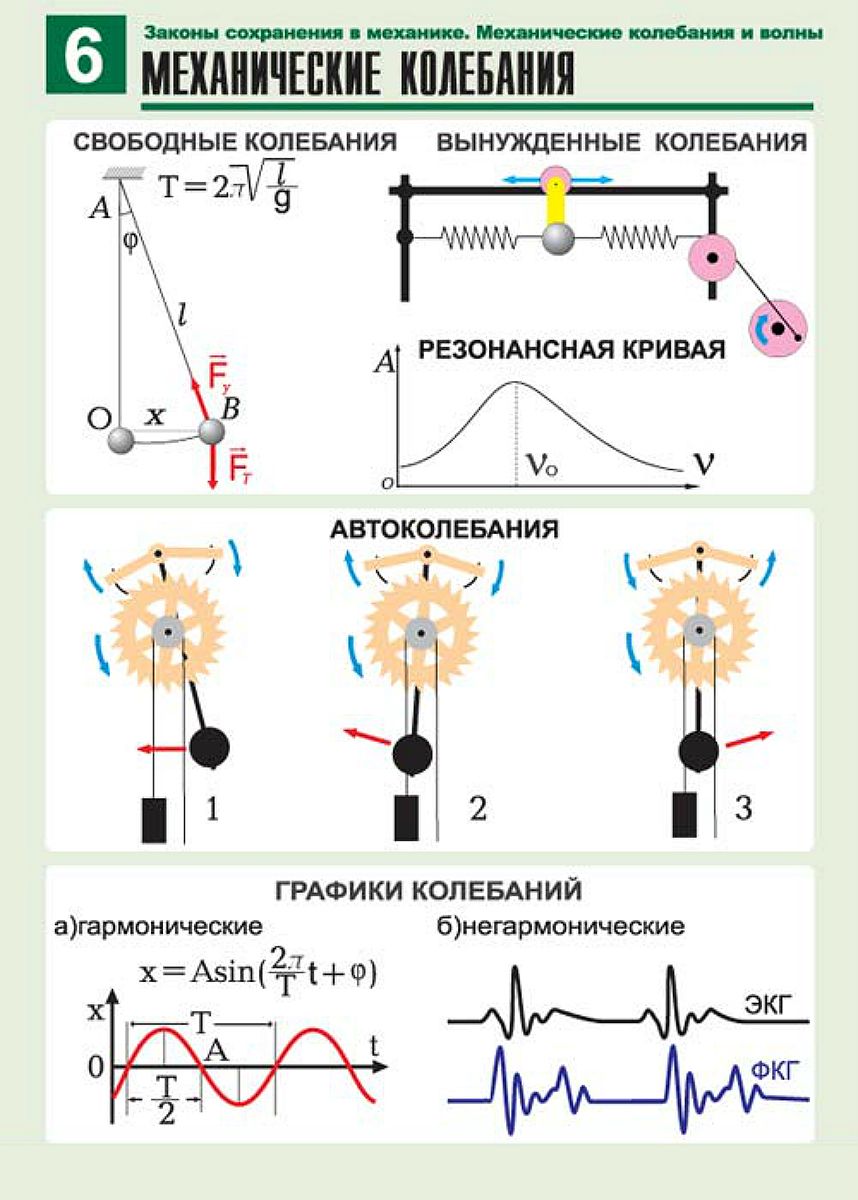 Урок 33: Угловой момент твердого тела относительно неподвижной оси Урок 33: Угловой момент твердого тела относительно неподвижной оси | ||
| 189 | 33.1 рабочий пример – угловой момент 2 вращающихся точечных частиц | Просмотр видео |
| 190 | 33.2 Угловой момент симметричного объекта | Просмотр видео |
| 191 | 33.4 Если моментум равен нулю, то угловой момент не зависит от начала координат | Просмотр видео |
| 192 | 33,5 Кинетическая энергия симметричного объекта | Просмотр видео |
| XLII.Урок 34: Крутящий момент и угловой импульс | ||
| 193 | 34.1 Крутящий момент вызывает изменение углового момента – точечная частица | Просмотр видео |
| 194 | 34. 2 Крутящий момент вызывает изменение углового момента – Система частиц 2 Крутящий момент вызывает изменение углового момента – Система частиц | Просмотр видео |
| 195 | 34,3 Угловой импульс | Просмотр видео |
| 196 | 34.4 Демо: демонстрация велосипедного колеса | Просмотр видео |
| 197 | 34,5 Рабочий пример – Поворотное кольцо для ударов частиц | Просмотр видео |
| 198 | 35,0 Неделя 12 Введение | Просмотр видео |
| XLIII. Урок 35: Кинематика качения | ||
| 199 | 35.1 Поступление и вращение колеса | Просмотр видео |
| 200 | 35.2 колеса качения в центре масс рамы | Просмотр видео |
| 201 | 35. 3 Катящееся колесо в наземной раме 3 Катящееся колесо в наземной раме | Просмотр видео |
| 202 | 35.4 Катание без пробуксовки Соскальзывание и занос | Просмотр видео |
| 203 | 35,5 Точка контакта колеса без пробуксовки | Просмотр видео |
| XLIV.Урок 36: Динамика качения | ||
| 204 | 36,1 Трение на катящемся колесе | Просмотр видео |
| 205 | 36.2 Рабочий пример – качение колеса без сползания наклонной плоскости – метод крутящего момента | Просмотр видео |
| 206 | 36.3 Демо: Spool Demo | Просмотр видео |
| 207 | 36.4 Рабочий пример – Йойо, тянущийся по земле | Просмотр видео |
| 208 | 36. 5 Анализ силы и крутящего момента в задачах перемещения и вращения 5 Анализ силы и крутящего момента в задачах перемещения и вращения | Просмотр видео |
| XLV. Урок 37: Кинетическая энергия качения и угловой момент | ||
| 209 | 37.1 Кинетическая энергия перемещения и вращения | Просмотр видео |
| 210 | 37.2 Рабочий пример – качение колеса без проскальзывания наклонной плоскости | Просмотр видео |
| 211 | 37,3 Угловой момент перемещения и вращения | Просмотр видео |
| XLVI. Глубокое погружение: гироскопы | ||
| 212 | DD.3.1 Deep Dive – гироскопы – диаграммы свободного тела, крутящий момент и векторы вращения | Просмотр видео |
| 213 | DD. | |


