Механика все формулы и определения: Механика – Основные формулы

Механика: формулы (тест начального уровня)

(Если вы просматриваете сайт как турбо-страницу Яндекса, то для решения тестов перейдите на полную (мобильную) версию сайта по кнопке снизу. Турбо-страницы не содержат всех необходимых скриптов)

1. Если Δr есть перемещение тела за интервал времени Δt, то какая величина определяется отношением Δr/Δt?
путь
перемещение
средняя скорость
ускорение
затрудняюсь ответить

2. Какое из уравнений описывает равномерное движение?
x = v_oxt + a_xt²/2
x = x_o + v_xt
v_x = v_ox + a_xt
x = x_o + v_oxt + a_xt²/2
затрудняюсь ответить

3. Центростремительное ускорение материальной точки при движениях по окружности с постоянной по модулю скоростью выражается формулой:
a = Δr/Δt

a = (v² − v_o²)/2S
a = v²/R
a = 2S/t²
затрудняюсь ответить

4. Угловая скорость при движении материальной точки по окружности с постоянной по модулю скоростью выражается формулой:
ω = πν
ω = π/T
ω = Δφ/Δt
ω = ν/2R
затрудняюсь ответить

5. По какой из представленных формул можно определить силу упругости?
F = GMm/(R+H)²
F = mg
F = μN
F = kΔl
затрудняюсь ответить

6. Какая из приведенных формул выражает закон всемирного тяготения?
F = GMm/R²
F = kq

1q₂/r²
F = GM/R²
F = kΔl
затрудняюсь ответить

7. По какой из приведенных формул можно определить модуль ускорения свободного падения?
g = GM₃/(2R₃²)
g = GM₃/R₃²
g = 2GM₃/R₃²
g = Gm_m/R₃²
затрудняюсь ответить

8.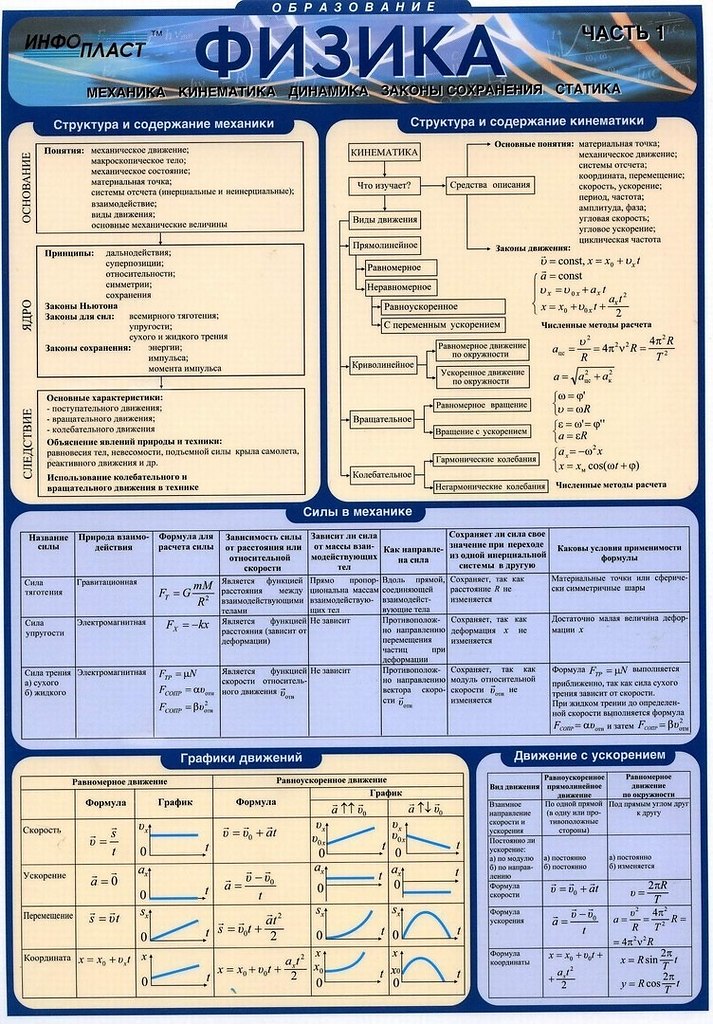 По какой из формул определяется реактивная сила?
F = μmg
F = am
F = u•|dm/dt|

F = kΔl
затрудняюсь ответить

9. По какой формуле следует рассчитывать работу силы F, направленной под углом α к перемещению?
A = (F/Δr)cos α
A = FΔr•sin α
A = FΔr•cos α
A = (F/Δr)sin α
затрудняюсь ответить

10. Какое из приведенных выражений соответствует закону сохранения механической энергии?
A_mp = mgh₂ − mgh₁
A_mp = (mv₂²)/2 − (mv₁²)/2
FΔt = mv₂ − mv₁
mgh = mv²/2
затрудняюсь ответить

Следующий тест: Механика: определения понятий

Механика и молекулярная 📙 физика

1. Базовые формулы и понятия классической механики
2. Основные понятия и формулы молекулярной физики

Физика является точной наукой.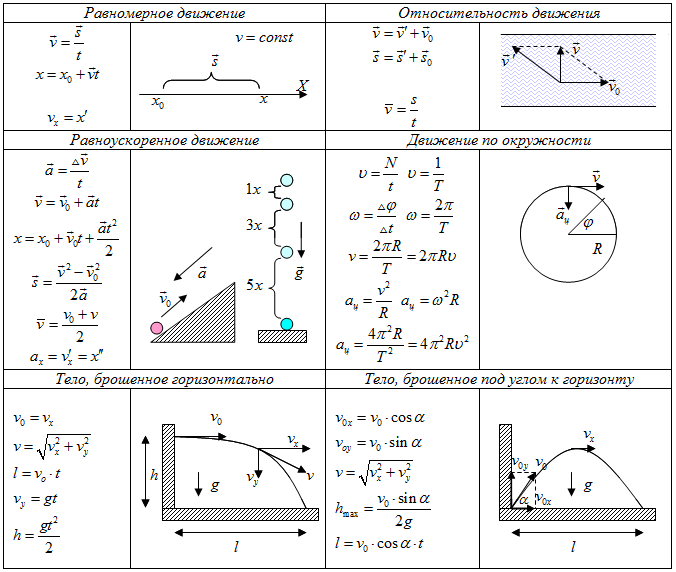 Здесь нашли свое начало многие математические понятия и методики. Также физика тесно переплетается с химическими явлениями и понятием материального тела. В этой статье мы разберем подробно классическую механику и молекулярную физику.

Механика является одним из больших разделов физики, она изучает движения материальных тел или их частей и взаимодействия между ними. Под движением в механике понимается изменение в пространстве положения тела или его части за определенный промежуток времени.

Различают механику материальной точки, жидкости, твердого тела и системы. Разберем подробно механику материальной точки.

Материальной точкой принято считать объект малого размера, форма и размеры которого не влияют на его движение. При этом важным параметром является небольшая скорость объекта, подразумевается, что она намного меньше скорости света. Дело в том, что для объектов, развивающих скорость, близкую к скорости света, вступает в силу релятивистская механика. Для классической механики характерны такие параметры, как радиус-вектор, ускорение и скорость объекта.

Рассмотри подробнее данные величины.

Допустим, заданная материальная точка перемещается вдоль оси Х. Если в определенный момент времени \(t\) точка имеет координату \(x(t_1)\), а в иной момент она будет иметь координату \(x(t_2)\), то средняя скорость ее прямолинейного движения за время \(δt=t_2-t_1\) рассчитается по следующей формуле:

\(V_ND = \frac {x(t_2) – x(t_1)}{t_2 – t_1} = \delta x – \delta t\)

Но следует отметить, то скорость направлена в определенную сторону, поэтому она есть величина векторная. Тогда формула приобретает следующий вид:

\(\vec{V_ND} = \vec{i}V = \vec{i} = \frac {\delta x }{\delta t}\)

Величина средней скорости является не очень точной характеристикой, но чем меньше будет значение δt, тем она будет точнее. При изучении предела соотношения (замене его на производную), можно вывести формулу для мгновенной скорости в момент времени:

\(\vec{V}(t) = \vec{i} \frac {dx(t)}{dt}\)

При движении материальной точки в трехмерном пространстве, для получения мгновенной скорости нужно взять дифференциал радиус-вектора:

\(\vec{V}(t) = \frac {\vec{w}(t)}{dt}\vec{i}\frac {dx}{dt} + \vec{j} \frac {dy}{dt} + \vec{k} \frac {dz}{dt}\)

По тому же принципу рассчитывают величину среднего и мгновенного ускорения.

2}}{2m}\)

Данная формула применима в классической механике, в релятивистской механике она будет выглядеть по другому, так как при высокой скорости масса зависит от величины скорости.

Потенциальную энергию можно рассчитать по такой формуле:

\(E_{по} = U = U \vec{r}\)

Раздел физики, изучающий свойства веществ на основании строения его молекул, называется молекулярной физикой.

Молекулярно-кинетической теорией является учение о характеристиках и структуре веществ, что основано на положении о существовании мельчайших частичек – молекул и атомов. Данная теория построена на таких основных представлениях:

1. Все жидкие, твердые и газообразные вещества состоят из молекул, которые состоят из мельчайших частичек – атомов. При этом молекулы бывают простыми и сложными, то есть состоят из одного или нескольких атомов. Молекулы и атомы являются электрически нейтральными, но в определенных условиях могут получать дополнительно электрический заряд, превращаясь в положительно или отрицательно заряженные ионы.
2. Атомы и молекулы все время взаимодействуют между собой и пребывают в беспорядочном движении. Скорость этого движения зависима от температуры вещества, а характер взаимодействия – от структуры самого вещества, на которую влияет его агрегатное состояние.
3. Частички вещества находятся в постоянном взаимодействии посредством электрических сил. При этом гравитационное взаимодействие настолько мизерно, что им можно пренебречь.

Атом считается мельчайшей неделимой частицей вещества, а молекула – наименьшей частицей, которой присущи химические свойства данного вещества. Ионом называется атом или молекула, в которой отсутствуют несколько электронов, или наоборот они находятся в излишке.

Для молекул характерен очень маленький размер. Хаотичное перемещение молекул вещества называют тепловым движением. При увеличении температуры тела кинетическая энергия его теплового движения увеличивается. При понижении температуры молекулы преобразуются в жидкое или твердое вещество.

Только лишь температура начнет повышаться, как кинетическая энергия молекул растет и они разлетаются, образуя газ.

Молекулы твердых тел беспорядочно колеблются вокруг равновесных центров. Если данные центры расположены несистематично, то такие тела являются аморфными, если же данные центры образуют систему, то такие твердые тела являются кристаллическими.

В жидкостях молекулы передвигаются более свободно, так как нет кристаллической решетки и они не привязаны к центрам. Поэтому жидкость обладает текучестью.

В газах молекулы находятся друг от друга на расстояниях, намного превышающих их размеры, поэтому здесь молекулы перемещаются свободно в одном направлении, пока не столкнуться с другими молекулами или со стенками, ограничивающими пространство. Так как в газах между молекулами очень слабые взаимодействия, газы обладают свойствами расширяться и занимать весь предоставленный им объем.

Идеальным называется газ, в котором молекулы между собой не взаимодействуют.

В молекулярно-кинетической теории количество вещества соотносят с количеством молекул.

Как единица измерения количества вещества является моль.

Одному молю вещества соответствует такое количество, которое соответствует количеству молекул, содержащемуся в 12 граммах углерода. Молекула углерода содержит всего один атом, потому один моль вещества всегда содержит одинаковое число молекул. Это число названо постоянной Авогадро. Это одна из самых важных величин в молекулярной физике. С ее помощью определяется количество любого вещества:

\(ν={m\over M}={N\over N_A }\)

где \(N\) – число молекул вещества;
      \(N_A\) – постоянная Авогадро;
      \(m\) – масса вещества;
      \(M\) – молярная масса вещества.

Молярная масса вещества – это масса его одного моля. Иными словами, молярной массой является произведение массы одной молекулы вещества на число Авогадро. Если молекулы вещества состоят из одного атома, то применяют понятие атомной массы:

\(m_0={m\over N}={M\over N_A }\)

Помимо вышеперечисленных единиц используется понятие концентрации вещества:

\(n={N\over V}\)

Масса, объем и плотность вещества связаны следующей зависимостью:

\(ρ={m\over V}\)

Если нужно рассчитать параметры смеси веществ, то применяют понятия молярной массы и средней плотности.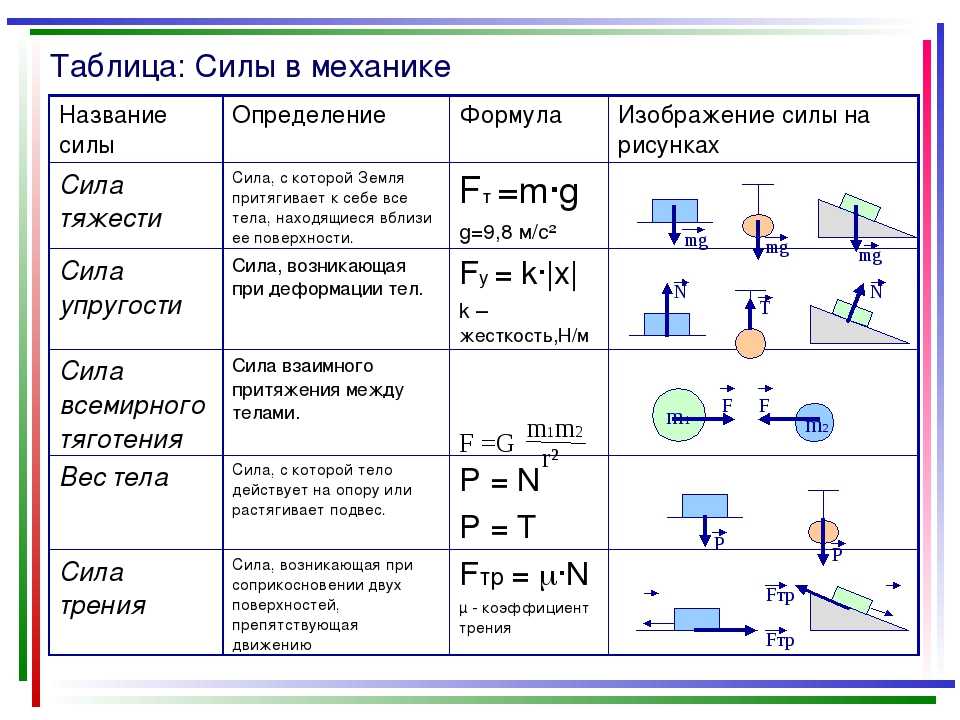 Эти величины рассчитываются с помощью полных масс:

\(ρ={M_{полн}\over V_{полн}} \\\ M={m_{полн}\over ν_{полн}}\)

Полным количеством вещества есть суммарное количество веществ смеси, а вот полный объем смеси не всегда равен сумме ее компонентов, особенно если речь идет о газовой смеси.

Механика твердого тела – определение, формулы, основные принципы

Что такое механика твердого тела?

Механика твердого тела — раздел физической науки, изучающий влияние сил, перемещений и ускорений на движение сплошных твердых сред. В контексте механики твердого тела силы эквивалентны в горизонтальном и вертикальном направлениях, что позволяет определить направленную деформацию или деформацию материала.

Анализ материалов на отказ проводится путем сравнения внутренних напряжений с прочностью материала. Материал считается неповрежденным, если напряжения не превышают прочности материала, выполненного против прочности, которая является хрупкой и не имеет предела текучести. Есть исключения из правила, которое применяется почти ко всем материалам в рамках механики твердого тела.

Загрузить формулы для GATE Civil Engineering — механика жидкости

Формула механики твердого тела

Важные формулы механики твердого тела могут использоваться для расчета прогиба при различных условиях нагрузки, уравнений касательного напряжения, уравнений кручения и моментов, а также для различных типов условий текучести опоры. . Некоторые из них:

• Штамм (δ) = PL/AE

Где; P = приложенная к балке нагрузка, L = длина балки, A= площадь поперечного сечения, E= модуль упругости

• Уравнение изгибающего момента M/I= F/Y= E/R
• Уравнение крутящего момента T/r= τ/J= G.θ/L

Где; M = момент на балке, F = поперечная сила, T = скручивающая сила и т. д. проблемы, рассмотренные в курсе. Они должны быть как демонстрация понимания и применения трех принципов.

• Совместимость: Совместим с Displacement. Ограничения на геометрию и/или деформацию конструктивных элементов в данной системе налагаются характером вероятной деформации. Два твердых объекта не могут поместиться в одном и том же пространстве, потому что элементы должны меняться друг с другом.
• Диаграмма свободного тела:  Деталь должна иметь надлежащие реакции и/или внутренние силы, если она отделена от тела или изолирована от него (также известное как сечение) или окружение (также известное как граничные условия).
• Концепция напряжения-деформации:  Напряжение-деформация связана с отношениями размещения. Закон Гука связывает свойства материала и структурную геометрию в конструкции.

Анализ механики твердого тела

Механика твердого тела может быть проанализирована с помощью соотношений напряжений и деформаций материала. Концепция напряжения заключается в том, чтобы найти важные свойства материала, такие как эластичность, пластичность, ковкость, твердость и ударная вязкость, которые можно определить. Когда внешняя сила приложена к материальному телу, природа материала изменяется либо в поперечном сечении, либо в геометрии.

В механике твердых тел причины внешней силы могут различаться в зависимости от условий эксплуатации, рабочей среды, контакта с другими материалами/элементами, жидкости под давлением или сил гравитации или инерции.

Эти приложенные внешние силы или развитые внутренние силы поднимают понятие напряжения, поскольку приложенные внешние силы, противодействующие частицам материала в равных и противоположных направлениях, могут вызвать напряжение в механике твердого тела.

Здесь образец материала находится под нагрузкой p как тяговое усилие. Предположим, что это прямоугольный стержень, площадь поперечного сечения которого равна «А», и когда к нему приложена растягивающая сила Р. Раздел разбит на две части в разделе XX, как показано ниже-

Теперь напряжение рассматривается как сила P на единицу площади A as-

σ = P/A

Здесь мы рассматриваем общую силу на соответствующей площади поперечного сечения. Если мы возьмем случайную область с дифференциальным пределом площади, то мы рассмотрим как

σ = δP/δA

, где δ указывается как частичная нагрузка или площадь поперечного сечения. Чтобы покрыть всю площадь под полной нагрузкой, мы взяли предел в качестве предела от 0 до A поперечного сечения. Единица напряжения: МПа = 106 Па, ГПа = 109.Па и кПа = 103 Па.

В механике твердого тела понятие напряжения классифицируется по различным типам напряжения:

Стресс- Взаимосвязь деформаций

В общем, после внешней нагрузки на материал возникает деформация, подобная деформации, и возникает напряжение между молекулами твердого тела материала. Теперь между напряжением и деформацией формируется связь, например, когда деформация изменяется, как напряжение влияет на тело материала в механике твердого тела.

Штамм	Напряжение
9000 4 Когда деформация равна нулю.	Напряжение для материального тела также равно нулю.
При деформации 0,2% от деформации разрушения.	Напряжение достигает предела текучести образца материала.
Когда деформация составляет 2% от деформации разрушения.	Напряжение достигает точки пластичности образца материала.
Когда деформация составляет 20% от общей деформации.	Напряжение материала достигает точки сужения образца материала.
Когда напряжение достигает точки разрушения.	Напряжение достигается до предела прочности материала, который меньше предела текучести образца материала.

Напряжение-деформация также классифицируется как инженерная концепция напряжения-деформации в механике твердого тела или фактическая концепция напряжения-деформации в механике твердого тела.

Фактическое напряжение равно фактической приложенной силе/площади поперечного сечения суженной части

Инженерное напряжение равно = приложенной силе/площади поперечного сечения исходной части образца

Где техническое напряжение всегда больше фактического напряжения.

Уравнение движения | Определение, формула и факты

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• В этот день в истории
• Викторины
• Подкасты
• Словарь
• Биографии
• Резюме
• Популярные вопросы
• Инфографика
• Демистификация
• Списки
• #WTFact
• Товарищи
• Галереи изображений
• Прожектор
• Форум
• Один хороший факт

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Britannica объясняет
  В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
• Britannica Classics
  Посмотрите эти ретро-видео из архивов Encyclopedia Britannica.
• Demystified Videos
  В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.
• #WTFact Видео
  В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти.
• На этот раз в истории
  В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.

• Студенческий портал
  Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д.
• Портал COVID-19
  Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня.
• 100 женщин
  Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.