Метод гауса калькулятор: Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса

Как рассчитать стандартное отклонение (Руководство)

Опубликован в 17 сентября 2020 г. к Прита Бхандари. Отредактировано 20 января 2023 г.

Стандартное отклонение — это средняя величина изменчивости в вашем наборе данных. Он говорит вам, в среднем, насколько далеко каждое значение находится от среднего.

Высокое стандартное отклонение означает, что значения, как правило, далеки от среднего, а низкое стандартное отклонение означает, что значения сгруппированы близко к среднему.

Содержание

1. О чем говорит стандартное отклонение?
2. Формулы стандартного отклонения для популяций и выборок
3. Калькулятор стандартного отклонения
4. Шаги для расчета стандартного отклонения вручную
5. Почему стандартное отклонение является полезной мерой изменчивости?
6. Часто задаваемые вопросы о стандартном отклонении

Что вам говорит стандартное отклонение?

Стандартное отклонение является полезной мерой распространения для нормальное распределение .

При нормальном распределении данные распределяются симметрично без перекоса. Большинство значений группируются вокруг центральной области, при этом значения сужаются по мере удаления от центра. Стандартное отклонение показывает, насколько в среднем разбросаны ваши данные от центра распределения.

Многие научные переменные имеют нормальное распределение, включая рост, результаты стандартизированных тестов или оценки удовлетворенности работой. Когда у вас есть стандартные отклонения различных выборок, вы можете сравнить их распределения с помощью статистических тестов, чтобы сделать выводы о более крупных популяциях, из которых они взяты.

Пример: сравнение различных стандартных отклонений. Вы собираете данные об оценках удовлетворенности работой от трех групп сотрудников, используя простую случайную выборку.

Средние ( M ) оценки одинаковы для каждой группы – это значение на оси X, когда кривая находится на пике. Однако их стандартные отклонения ( SD ) отличаются друг от друга.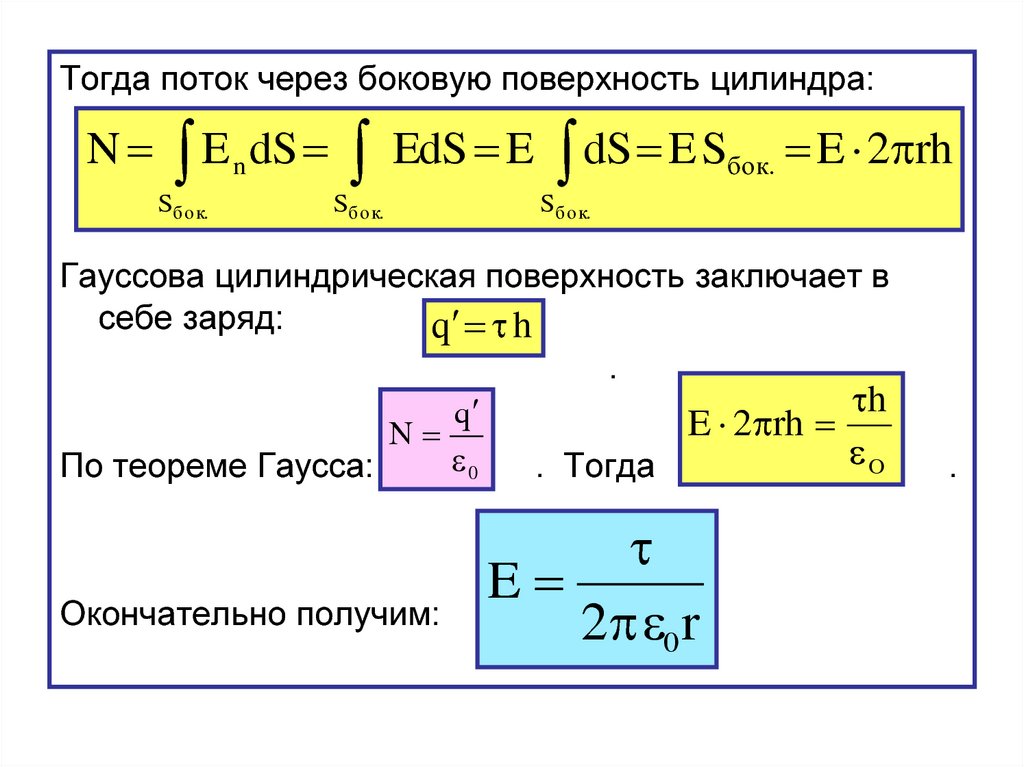

Стандартное отклонение отражает дисперсию распределения. Кривая с самым низким стандартным отклонением имеет высокий пик и небольшой разброс, в то время как кривая с самым высоким стандартным отклонением более плоская и широкая.

Эмпирическое правило

Стандартное отклонение и среднее вместе могут сказать вам, где находится большинство значений в вашем частотном распределении, если они подчиняются нормальному распределению.

Эмпирическое правило , или правило 68-95-99,7 говорит вам, где находятся ваши значения:

• Около 68% оценок находятся в пределах 1 стандартного отклонения от среднего,
• Около 95% баллов находятся в пределах 2 стандартных отклонений от среднего,
• Около 99,7% баллов находятся в пределах 3 стандартных отклонений от среднего.

Пример: стандартное отклонение в нормальном распределении. Вы проводите тест на запоминание для группы учащихся. Данные соответствуют нормальному распределению со средним баллом 50 и стандартным отклонением 10.

Следуя эмпирическому правилу:

• Около 68% баллов находятся в диапазоне от 40 до 60.
• Около 95% баллов находятся в диапазоне от 30 до 70.
• Около 99,7% баллов находятся в диапазоне от 20 до 80.

Эмпирическое правило — это быстрый способ получить обзор ваших данных и проверить любые выбросы или экстремальные значения, которые не соответствуют этому шаблону.

Примечание. Для ненормальных распределений стандартное отклонение является менее надежной мерой изменчивости и должно использоваться в сочетании с другими показателями, такими как диапазон или межквартильный диапазон.

Формулы стандартного отклонения для совокупностей и выборок

Для расчета стандартных отклонений используются разные формулы в зависимости от того, были ли вы собраны данные по всей совокупности или по выборке.

Стандартное отклонение населения

Когда вы соберете данные о каждом члене интересующей вас совокупности, вы сможете получить точное значение стандартного отклонения совокупности.

Формула стандартного отклонения населения выглядит следующим образом:

Формула	Пояснение
	= стандартное отклонение совокупности = сумма… = каждое значение = среднее значение населения = количество значений в совокупности

Стандартное отклонение выборки

При сборе данных из выборки стандартное отклонение выборки используется для оценок или выводов о стандартном отклонении генеральной совокупности.

Формула стандартного отклонения выборки выглядит следующим образом:

Формула	Пояснение
	= стандартное отклонение выборки = сумма… = каждое значение  = выборочное среднее = количество значений в выборке

Для выборок мы используем n – 1 в формуле, потому что использование n дало бы нам смещенную оценку, которая последовательно занижает изменчивость. Стандартное отклонение выборки будет иметь тенденцию быть ниже, чем реальное стандартное отклонение генеральной совокупности.

При уменьшении выборки

n до n – 1 стандартное отклонение искусственно увеличивается, что дает вам консервативную оценку изменчивости.

Хотя это и не беспристрастная оценка, это менее предвзятая оценка стандартного отклонения: лучше переоценить, чем недооценить изменчивость выборок.

Получайте отзывы о языке, структуре и форматировании

Профессиональные редакторы вычитывают и редактируют вашу статью, уделяя особое внимание:

• Академический стиль
• Расплывчатые предложения
• Грамматика
• Согласованность стиля

См. пример

Калькулятор стандартного отклонения

Вы можете рассчитать стандартное отклонение вручную или с помощью нашего калькулятора стандартного отклонения ниже.

Этапы расчета стандартного отклонения вручную

Стандартное отклонение обычно вычисляется автоматически любым программным обеспечением, которое вы используете для статистического анализа. Но вы также можете рассчитать его вручную, чтобы лучше понять, как работает формула.

Существует шесть основных шагов для нахождения стандартного отклонения вручную. Мы будем использовать небольшой набор данных из 6 баллов, чтобы пройти по шагам.

Набор данных
46	69	32	60	52	41

Шаг 1 : Найдите среднее

Чтобы найти среднее, сложите все баллы, а затем разделите их на количество баллов.

Среднее (x̅)

Шаг 2 : Найдите отклонение каждой оценки от среднего

Вычтите среднее из каждой оценки, чтобы получить отклонения от среднего.

Так как x̅ = 50, здесь мы отнимаем 50 от каждого результата.

Оценка	Отклонение от среднего
46	46 – 50 = -4
69	69 – 50 = 19
32	32 – 50 = -18
60	60 – 50 = 10
52	52 – 50 = 2
41	41 – 50 = -9

Шаг 3 : Возведение в квадрат каждого отклонения от среднего

Умножить каждое отклонение от среднего само на себя. Это приведет к положительным числам.

Квадрат отклонения от среднего
(-4) 2 = 4 × 4 = 16
19 2 = 19 × 19 = 361
(-18) 2 = -18 × -18 = 324
10 2 = 10 × 10 = 100
2 2 = 2 × 2 = 4
(-9) 2  = -9 × -9 = 81

Шаг 4 : Найдите сумму квадратов

Сложите все квадраты отклонений. Это называется сумма квадратов.

Сумма квадратов
16 + 361 + 324 + 100 + 4 + 81 = 886

Шаг 5: Найдите дисперсию

Разделить сумму квадратов на n – 1 (для выборки) или N (для населения) – это дисперсия.

Поскольку мы работаем с размером выборки 6, мы будем использовать n – 1, где n = 6.

Разница

Шаг 6 : Найдите квадратный корень из дисперсии

Чтобы найти стандартное отклонение, мы берем квадратный корень из дисперсии.

Стандартное отклонение

Узнав, что SD = 13,31, мы можем сказать, что каждый результат отклоняется от среднего значения в среднем на 13,31 балла.

Почему стандартное отклонение является полезной мерой изменчивости?

Хотя существуют более простые способы расчета изменчивости, формула стандартного отклонения взвешивает неравномерно распределенные выборки больше, чем равномерно распределенные выборки. Более высокое стандартное отклонение говорит вам о том, что распределение не только более разбросано, но и более неравномерно.

Это означает, что он дает вам лучшее представление о изменчивости ваших данных, чем более простые меры, такие как среднее абсолютное отклонение (MAD).

Среднеквадратичное отклонение похоже на стандартное отклонение, но его легче вычислить. Во-первых, вы выражаете каждое отклонение от среднего в абсолютных значениях, конвертируя их в положительные числа (например, -3 становится 3). Затем вы вычисляете среднее значение этих абсолютных отклонений.

В отличие от стандартного отклонения, вам не нужно вычислять квадраты или квадратные корни чисел для MAD. Однако по этой причине он дает менее точную меру изменчивости.

Возьмем две выборки с одинаковой центральной тенденцией, но разной степенью изменчивости. Образец B более изменчив, чем образец A.

	Значения	Среднее	Среднее абсолютное отклонение	Стандартное отклонение
Образец А	66, 30, 40, 64	50	15	17,8
Образец В	51, 21, 79, 49	50	15	23,7

Для выборок с одинаковыми средними отклонениями от среднего MAD не может различать уровни разброса. Стандартное отклонение является более точным: оно выше для выборки с большей вариабельностью отклонений от среднего значения.

При возведении в квадрат различий от среднего стандартное отклонение более точно отражает неравномерную дисперсию. На этом шаге крайние отклонения взвешиваются сильнее, чем малые.

Однако это также делает стандартное отклонение чувствительным к выбросам.

Часто задаваемые вопросы о стандартном отклонении

Что вам говорит стандартное отклонение?

Стандартное отклонение — это средняя величина изменчивости в вашем наборе данных. Он говорит вам, в среднем, насколько далеко каждая оценка находится от среднего значения.

В нормальном распределении высокое стандартное отклонение означает, что значения, как правило, далеки от среднего, а низкое стандартное отклонение означает, что значения сгруппированы близко к среднему.

Что такое нормальное распределение?

При нормальном распределении данные распределяются симметрично без перекоса. Большинство значений группируются вокруг центральной области, при этом значения сужаются по мере удаления от центра.

Меры центральной тенденции (среднее, мода и медиана) в нормальном распределении точно такие же.

Что такое эмпирическое правило?

Эмпирическое правило, или правило 68-95-99,7, говорит вам, где большинство значений находится в нормальном распределении:

• Около 68% значений находятся в пределах 1 стандартного отклонения от среднего.
• Около 95% значений находятся в пределах 2 стандартных отклонений от среднего значения.
• Около 99,7% значений находятся в пределах 3 стандартных отклонений от среднего значения.

Эмпирическое правило — это быстрый способ получить обзор ваших данных и проверить любые выбросы или экстремальные значения, которые не соответствуют этому шаблону.

В чем разница между стандартным отклонением и дисперсией?

Дисперсия — это среднеквадратичное отклонение от среднего значения, а стандартное отклонение — это квадратный корень из этого числа. Обе меры отражают изменчивость распределения, но их единицы различаются:

• Стандартное отклонение выражается в тех же единицах, что и исходные значения (например, минуты или метры).
• Дисперсия выражается в более крупных единицах (например, в квадратных метрах).

Хотя единицы дисперсии труднее интуитивно понять, дисперсия важна в статистических тестах.

Процитировать эту статью Scribbr

Если вы хотите процитировать этот источник, вы можете скопировать и вставить цитату или нажать кнопку «Цитировать эту статью Scribbr», чтобы автоматически добавить цитату в наш бесплатный генератор цитирования.

Бхандари, П. (2023, 20 января). Как рассчитать стандартное отклонение (Руководство) | Калькулятор и примеры. Скриббр. Проверено 4 февраля 2023 г., с https://www.scribbr.com/statistics/standard-deviation/

Процитировать эту статью

Полезна ли эта статья?

Вы уже проголосовали. Спасибо 🙂 Ваш голос сохранен 🙂 Обработка вашего голоса…

Прита имеет академическое образование в области английского языка, психологии и когнитивной нейробиологии. Как междисциплинарный исследователь, она любит писать статьи, объясняющие сложные исследовательские концепции для студентов и ученых.

Калькулятор снежного кома долга – Ramsey

Снежный ком долга – это метод погашения долга, при котором вы выплачиваете свои долги от наименьшего к наибольшему, независимо от процентной ставки. Сначала погашайте наименьший долг. Затем возьмите то, что вы платили по этому долгу, и добавьте это к выплате вашего следующего наименьшего долга.

Почему снежок? Потому что, как снежный ком, катящийся вниз по склону, погашение долга зависит от импульса. С каждым погашенным долгом вы набираете скорость, пока не станете неудержимой силой, сокрушающей долги.

Вот как работает долговой снежный ком:

Шаг 1: Перечислите свои долги от наименьшего до наибольшего  независимо от процентной ставки .

Шаг 2: Внесите минимальные платежи по всем своим долгам, кроме самых маленьких.

Шаг 3: Заплатите как можно больше по вашему наименьшему долгу.

Шаг 4: Повторяйте до полного погашения каждого долга.

Что происходит потом? Свобода. Больше никаких платежей. Больше не отвечаю коллекторам. Больше не нужно смотреть, как исчезают ваши зарплаты.

Потому что, когда вы сосредотачиваетесь и начинаете тратить каждый доллар на свой долг, вы увидите, насколько быстрее вы сможете погасить его. Извините, минимальные платежи. Ты просто недостаточно хорош.

Долговой снежный ком против долговой лавины

Возможно, вы слышали о другом способе погашения долга — долговой лавине. Звучит эпично, правда? Неправильный. С долговой лавиной вы платите свои долги в порядке от самой высокой процентной ставки до самой низкой , независимо от баланса.

Это может звучать как умная математика. Вот почему это не так: Долг — это не математическая задача. Это проблема поведения.

Если вы хотите изменить свое поведение и избавиться от долгов, вам нужно сохранять мотивацию. С долговой лавиной вы можете не увидеть прогресса по вашему первому долгу в течение долгих раз. Это никого не мотивирует. Вы, скорее всего, потеряете пар и сдадитесь.

Но когда вы используете долговой снежный ком, вы быстрее получаете быстрые выигрыши. Быстро погасите первый долг. Бум. К следующему. Теперь ты готовишь. Внезапно вы начинаете верит , что расплата с долгами вполне достижима. Мотивация — это ключ к избавлению от долгов, а не математика.

Условия долга

Долговая терминология может быть запутанной и чрезмерно сложной, но это не обязательно! Давайте разберем их так, чтобы вы могли понять.

Минимальный платеж
Это наименьшая сумма, которую вы должны ежемесячно выплачивать по долгу (включая основную сумму и проценты). Платите меньше, и вас могут оштрафовать.

Баланс
Это сумма, которую вам еще нужно выплатить по долгу. Если ваш первоначальный кредит составлял 20 000 долларов США, а вы уже заплатили 5 000 долларов США, ваш баланс составит 15 000 долларов США.

Процентная ставка
Когда дело доходит до займа денег, бесплатного не бывает. Кредиторы заинтересованы в том, чтобы позволить вам одолжить их деньги, потому что они делают деньги на том, что они одолжили вам. Ваша процентная ставка — это сумма, которую они взимают, обычно показанная в процентах от основного баланса.

Директор
Нет, это не тот директор начальной школы, которого вы боялись в детстве. Мы говорим о сумме денег, которую вы одолжили без процентов. Итак, если вы одолжили 20 000 долларов на 10 лет, ваш основной платеж составит около 167 долларов в месяц.

Неипотечный долг
Это просто. Это все, что вы должны, за исключением кредитов, связанных с покупкой вашего дома.