Занимательная математика: правило Гаусса
Цикл «Занимательная математика» посвящен деткам увлекающимся математикой и родителям, которые уделяют время развитию своих детей, «подкидывая» им интересные и занимательные задачки, головоломки.
Первая статья из этого цикла посвящена правилу Гаусса.
Немного истории
Известный немецкий математик Карл Фридрих Гаусс (1777-1855) с раннего детства отличался от своих сверстников. Несмотря на то, что он был из небогатой семьи, он достаточно рано научился читать, писать, считать. В его биографии есть даже упоминание того, что в возрасте 4-5 лет он смог скорректировать ошибку в неверных подсчетах отца, просто наблюдая за ним.
 Одно из первых его открытий было сделано в возрасте 6 лет на уроке математики. Учителю было необходимо увлечь детей на продолжительное время и он предложил следующую задачку:
Одно из первых его открытий было сделано в возрасте 6 лет на уроке математики. Учителю было необходимо увлечь детей на продолжительное время и он предложил следующую задачку:
Найти сумму всех натуральных чисел от 1 до 100.
Юный Гаусс справился с этим заданием достаточно быстро, найдя интересную закономерность, которая получила большое распространение и применяется по сей день при устном счете.
Давайте попробуем решить эту задачку устно. Но для начала возьмем числа от 1 до 10:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
Посмотрите внимательно на эту сумму и попробуйте догадаться, что же необычного смог разглядеть Гаусс? Для ответа необходимо хорошо представлять себе состав чисел.
Гаусс сгруппировал числа следующим образом:
(1+10) + (2+9) + (3+8) + (4+7) + (5+6)
Таким образом маленький Карл получил 5 пар чисел, каждая из которых в отдельности в сумме дает 11. Тогда, чтобы вычислить сумму натуральных чисел от 1 до 10 необходимо
5 * 11 = 55
Вернемся к первоначальной задаче. Гаусс заметил, что перед суммированием необходимо группировать числа в пары и тем самым изобрел алгоритм, благодаря которому можно быстро сложить числа от 1 до100:
1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100
-
Находим количество пар в ряде натуральных чисел. В данном случае их 50.
-
Суммируем первое и последнее числа данного ряда. В нашем примере — это 1 и 100. Получаем 101.
-
Умножаем полученную сумму первого и последнего члена ряда на количество пар этого ряда. Получаем 101 * 50 = 5050
Задачи на использование правила Гаусса
А сейчас вашему вниманию предлагаются задачи, в которых в той или иной степени используется правило Гаусса. Эти задачки вполне способен понять и решить четвероклассник.
Можно дать возможность ребенку порассуждать самому, чтобы он сам «изобрел» это правило. А можно разобрать вместе и посмотреть как он сможет его применить. Среди ниже приведенных задач есть примеры, в которых нужно понять как модифицировать правило Гаусса, чтобы его применить к данной последовательности.
В любом случае, чтобы ребенок мог оперировать этим в своих вычислениях необходимо понимание алгоритма Гаусса, то есть умение разбить правильно по парам и посчитать.
Важно! Если будет заучена формула без понимания, то это очень быстро будет забыто.
Задача 1
Найти сумму чисел:
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10;
- 1 + 2 + 3 + … + 14 + 15 + 16;
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9;
- 1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100.
Решение.
Вначале можно дать возможность ребенку самому решить первый пример и предложить найти способ, при котором это сделать легко в уме. Далее разобрать этот пример вместе с ребенком и показать как это сделал Гаусс. Лучше всего для наглядности записать ряд и соединить линиями пары чисел, дающие в сумме одинаковое число. Важно, чтобы ребенок понял как образуются пары — берем самое маленькое и самое большое из оставшихся чисел при условии, что количество чисел в ряду четно.
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = (1 + 10) + (2 + 9) + (3 + 8) + (4 + 7) + (5 + 6) = (1 + 10) * 5;
- 1 + 2 + 3 + … + 14 + 15 + 16 = (1 + 16) + (2 + 15) + (3 + 14) + (4 + 13) + (5 + 12) + (6 + 11) + (7 + 10) + (8 + 9) = (1 + 16) * 8 = 136;
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + 8) + (2 + 7) + (3 + 6) + (4 + 5) + 9 = (1+ 8) * 4 + 9 = 45;
- 1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100 = (1 + 100) * 50 = 5050
Задача 2
Имеется 9 гирь весом 1г, 2г, 3г, 4г, 5г, 6г, 7г, 8г, 9г. Можно ли разложить эти гири на три кучки с равным весом?
Решение.
С помощью правила Гаусса находим сумму всех весов:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + 8) * 4 + 9 = 45 (г)
Далее смотрим, можно ли этот вес разбить на три равных веса:
45 : 3 = 15 (г)
Значит, если мы сможем сгруппировать гири так, чтобы в каждой кучке были гири суммарным весом 15г, то задача решена.
Один из вариантов:
- 9г, 6г
- 8г, 7г
- 5г, 4г, 3г, 2г, 1г
Другие возможные варианты найдите сами с ребенком.
Обратите внимание ребенка на то, что когда решаются подобные задачи лучше всегда начинать группировать с большего веса (числа).
Задача 3
Можно ли разделить циферблат часов прямой линией на две части так, чтобы суммы чисел в каждой части были равны?
Решение.

Для начала к ряду чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 применим правило Гаусса: найдем сумму и посмотрим, делится ли она на 2:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = (1 + 12) * 6 = 78
Значит разделить можно. Теперь посмотрим как.
По правилу Гаусса у нас получается 6 пар чисел, каждая из которых в сумме дает 13:
1 и 12, 2 и 11, 3 и 10, 4 и 9, 5 и 8, 6 и 7.
Следовательно, надо провести линию на циферблате так, чтобы 3 пары попали в одну половину, а три в другую.
Ответ: линия пройдет между числами 3 и 4, а затем между числами 9 и 10.
Задача 4
Можно ли провести на циферблате часов две прямые линией так, чтобы в каждой части сумма чисел была одинаковой?
Решение.

Для начала к ряду чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 применим правило Гаусса: найдем сумму и посмотрим делиться ли она на 3:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = (1 + 12) * 6 = 78
78 делиться на 3 без остатка, значит разделить можно. Теперь посмотрим как.
По правилу Гаусса у нас получается 6 пар чисел, каждая из которых в сумме дает 13:
1 и 12, 2 и 11, 3 и 10, 4 и 9, 5 и 8, 6 и 7.
Следовательно, надо провести линии на циферблате так, чтобы в каждую часть попали по 2 пары.
Ответ: первая линия пройдет между числами 2 и 3, а затем между числами 10 и 11; вторая линия — между числами 4 и 5, а затем между 8 и 9.
Задача 5
Летит стая птиц. Впереди одна птица (вожак), за ней две, потом три, четыре и т. д. Сколько птиц в стае, если в последнем ряду их 20?
Решение.
Получаем, что нам необходимо сложить числа от 1 до 20. А к вычислению такой суммы можно применить правило Гаусса:
1 + 2 + 3 + 4 + 5 + … + 15 + 16 + 17 + 18 + 19 + 20 = (20 + 1) * 10 = 210.
Задача 6
Как рассадить 45 кроликов в 9 клеток так, чтобы во всех клетках было разное количество кроликов?
Решение.
Если ребенок решил и с пониманием разобрал примеры из задания 1, то тут же вспоминается, что 45 это сумма чисел от 1 до 9. Следовательно, сажаем кроликов так:
- первая клетка — 1,
- вторая — 2,
- третья — 3,
- …
- восьмая — 8,
- девятая — 9.
Но если ребенок сразу не может сообразить, то попробуйте натолкнуть его на мысль о том, что подобные задачи можно решить перебором и надо начинать с минимального числа.
Задача 7
Вычислить сумму, используя прием Гаусса:
- 31 + 32 + 33 + … + 40;
- 5 + 10 + 15 + 20 + … + 100;
- 91 + 81 + … + 21 + 11 + 1;
- 1 + 2 + 3 + 4 + … + 18 + 19 + 20;
- 1 + 2 + 3 + 4 + 5 + 6;
- 4 + 6 + 8 + 10 + 12 + 14;
- 4 + 6 + 8 + 10 + 12;
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11.
Решение.
- 31 + 32 + 33 + … + 40 = (31 + 40) * 5 = 355;
- 5 + 10 + 15 + 20 + … + 100 = (5 + 100) * 10 = 1050;
- 91 + 81 + … + 21 + 11 + 1 = (91 + 1) * 5 = 460;
- 1 + 2 + 3 + 4 + … + 18 + 19 + 20 = (1 + 20) * 10 =210;
- 1 + 2 + 3 + 4 + 5 + 6 = (1 + 6) * 3 = 21;
- 4 + 6 + 8 + 10 + 12 + 14 = (4 + 14) * 3 = 54;
- 4 + 6 + 8 + 10 + 12 = (4 + 10) * 2 + 12 = 40;
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 = (1 + 10) * 5 + 11 = 66.
Задача 8
Имеется набор из 12 гирек массой 1г, 2г, 3г, 4г, 5г, 6г, 7г, 8г, 9г, 10г, 11г, 12г. Из набора убрали 4 гирьки, общая масса которых равна трети общей массы всего набора гирек. Можно ли оставшиеся гирьки расположить на двух чашках весов по 4 штуки на каждой чашке так, чтобы они оказались в равновесии?
Решение.
Применяем правило Гаусса, чтобы найти общую массу гирек:
1 + 2 + 3 + … + 10 + 11 + 12 = (1 + 12) * 6 = 78 (г)
Вычисляем массу гирек, которые убрали:
78 : 3 = 26 (г)
Следовательно, оставшиеся гирьки (общей массой 78-26 = 52г) надо расположить по 26 г на каждую чашу весов, чтобы они оказались в равновесии.
Нам не известно какие гирьки были убраны, значит мы должны рассмотреть все возможные варианты.
Применяя правило Гаусса можно разбить гирьки на 6 пар с равным весом (по 13г):
1г и 12г, 2г и 11г, 3г и 10, 4г и 9г, 5г и 8г, 6г и 7г.
Тогда лучший вариант, когда при убирании 4 гирек уберутся две пары из приведенных выше. В этом случае у нас останутся 4 пары: 2 пары на одну чашу весов и 2 пары на другую.
Худший вариант — это когда 4 убранные гирьки разобьют 4 пары. У нас останутся 2 неразбитые пары общим весом 26г, значит их помещаем на одну чашу весов, а оставшиеся гирьки можно поместить на другую чашу весов и они тоже будут 26г.
Удачи в развитии Ваших детей.
myintelligentkids.com
|
| ||||||||||||||||||||||||||||||||||||||||
taren.narod.ru
§ 5. Метод Гаусса.
Пусть задана система линейных уравнений:
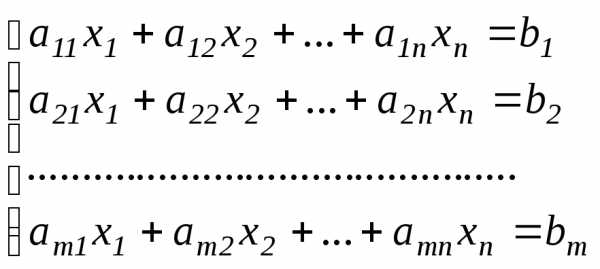 .
(I)
.
(I)
Требуется найти все решения системы (I) или убедиться в том, что система несовместна.
Определение 1. Назовем элементарным преобразованием системы(I) любое из трёх действий :
1) вычёркивание нулевого уравнения;
прибавление к обеим частям уравнения соответствующих частей другого уравнения, умноженных на число ;
перемена местами слагаемых в уравнениях системы так, чтобы неизвестные с одинаковыми номерами во всех уравнениях занимали одинаковые места, т.е. если, например, в 1-ом уравнении мы поменяли 2-ое и 3-е слагаемые, тогда то же самое необходимо сделать во всех уравнениях системы.
Метод Гаусса состоит в том, что система (I) с помощью элементарных преобразований приводится к равносильной системе, решение которой находится непосредственно или устанавливается её неразрешимость.
Как было описано в §2 система (I) однозначно определяется своей расширенной матрицей и любое элементарное преобразование системы (I) соответствует элементарному преобразованию расширенной матрицы :
 .
.
Преобразование 1) соответствует
вычёркиванию нулевой строки в матрице  ,
преобразование 2) равносильно прибавлению
к соответствующей строке матрицы
,
преобразование 2) равносильно прибавлению
к соответствующей строке матрицы другой её строки, умноженной на число, преобразование
3) эквивалентно перестановке столбцов
в матрице
другой её строки, умноженной на число, преобразование
3) эквивалентно перестановке столбцов
в матрице .
.
Легко видеть, что, наоборот, каждому
элементарному преобразованию матрицы  соответствует элементарное преобразование
системы (I). В силу сказанного,
вместо операций с системой (I)
мы будем работать с расширенной матрицей
этой системы.
соответствует элементарное преобразование
системы (I). В силу сказанного,
вместо операций с системой (I)
мы будем работать с расширенной матрицей
этой системы.
В матрице  1-ый столбец состоит из коэффициентов
прих1, 2-ой столбец – из
коэффициентов прих2 и
т.д. В случае перестановки столбцов
следует учитывать, что это условие
нарушается. Например, если мы поменяем
1-ый и 2-ой столбцы местами, то теперь в
1-ом столбце будут коэффициенты прих2,
а во 2-ом столбце – коэффициенты прих1.
1-ый столбец состоит из коэффициентов
прих1, 2-ой столбец – из
коэффициентов прих2 и
т.д. В случае перестановки столбцов
следует учитывать, что это условие
нарушается. Например, если мы поменяем
1-ый и 2-ой столбцы местами, то теперь в
1-ом столбце будут коэффициенты прих2,
а во 2-ом столбце – коэффициенты прих1.
Будем решать систему (I) методом Гаусса.
Вычеркнем в матрице
 все нулевые строки, если такие имеются
(т.е. вычеркнем в системе (I)
все нулевые уравнения).
все нулевые строки, если такие имеются
(т.е. вычеркнем в системе (I)
все нулевые уравнения).Проверим, есть ли среди строк матрицы
 строка, в которой все элементы, кроме
последнего, равны нулю (назовём такую
строку несовместной). Очевидно, что
такой строке соответствует несовместное
уравнение в системе (I) ,
следовательно, система (I)
решений не имеет и на этом процесс
заканчивается.
строка, в которой все элементы, кроме
последнего, равны нулю (назовём такую
строку несовместной). Очевидно, что
такой строке соответствует несовместное
уравнение в системе (I) ,
следовательно, система (I)
решений не имеет и на этом процесс
заканчивается.Пусть матрица
 не содержит несовместных строк (система
(I) не содержит несовместных
уравнений). Еслиa11=0,
то находим в 1-ой строке какой-нибудь
элемент (кроме последнего) отличный от
нуля и переставляем столбцы так, чтобы
в 1-ой строке на 1-ом месте не было нуля.
Будем теперь считать, что
не содержит несовместных строк (система
(I) не содержит несовместных
уравнений). Еслиa11=0,
то находим в 1-ой строке какой-нибудь
элемент (кроме последнего) отличный от
нуля и переставляем столбцы так, чтобы
в 1-ой строке на 1-ом месте не было нуля.
Будем теперь считать, что (т.е. поменяем местами соответствующие
слагаемые в уравнениях системы (I)).
(т.е. поменяем местами соответствующие
слагаемые в уравнениях системы (I)).Умножим 1-ую строку на и сложим результат со 2-ой строкой, затем умножим 1-ую строку наи сложим результат с 3-ей строкой и т.д. Очевидно, что этот процесс эквивалентен исключению неизвестногоx1из всех уравнений системы (I), кроме 1-ого. В новой матрице
 получаем нули в 1-ом столбце под элементомa11 :
получаем нули в 1-ом столбце под элементомa11 :
 .
.
Вычеркнем в матрице
 все нулевые строки, если они есть,
проверим, нет ли несовместной строки
(если она имеется, то система несовместна
и на этом решение заканчивается).
Проверим, будет лиa22 /=0, если да, то находим
во 2-ой строке элемент, отличный от нуля
и переставляем столбцы так, чтобы
все нулевые строки, если они есть,
проверим, нет ли несовместной строки
(если она имеется, то система несовместна
и на этом решение заканчивается).
Проверим, будет лиa22 /=0, если да, то находим
во 2-ой строке элемент, отличный от нуля
и переставляем столбцы так, чтобы .
Далее умножаем элементы 2-ой строки наи складываем с соответствующими
элементами 3-ей строки, затем – элементы
2-ой строки наи складываем с соответствующими
элементами 4-ой строки и т.д., пока не
получим нули подa22 /
.
Далее умножаем элементы 2-ой строки наи складываем с соответствующими
элементами 3-ей строки, затем – элементы
2-ой строки наи складываем с соответствующими
элементами 4-ой строки и т.д., пока не
получим нули подa22 /
 .
.
Произведенные действия эквивалентны исключению неизвестного х2из всех уравнений системы (I), кроме 1-ого и 2-ого. Так как число строк конечно, поэтому через конечное число шагов мы получим, что либо система несовместна, либо мы придём к ступенчатой матрице (см. определение 2 §7 главы 1) :
 ,
,
где
.
Выпишем систему уравнений, соответствующую
матрице  .
Эта система равносильна системе (I)
.
Эта система равносильна системе (I)
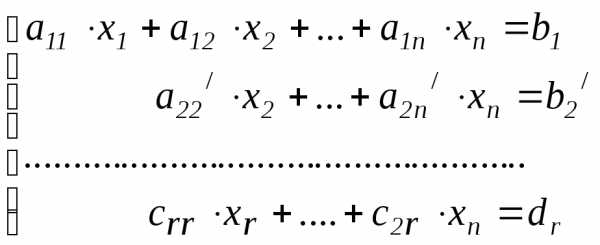 .
.
Из последнего уравнения выражаем 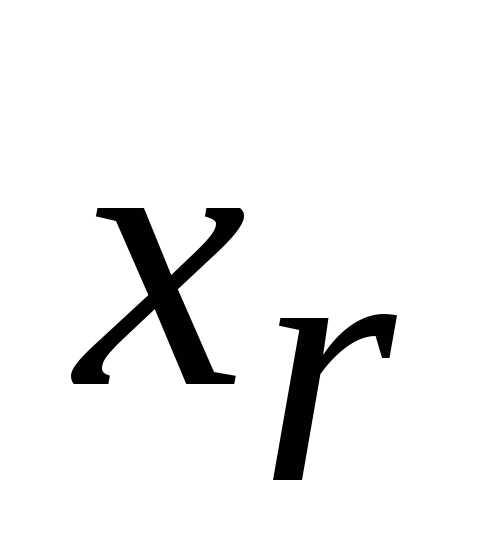 ;
подставляем
;
подставляем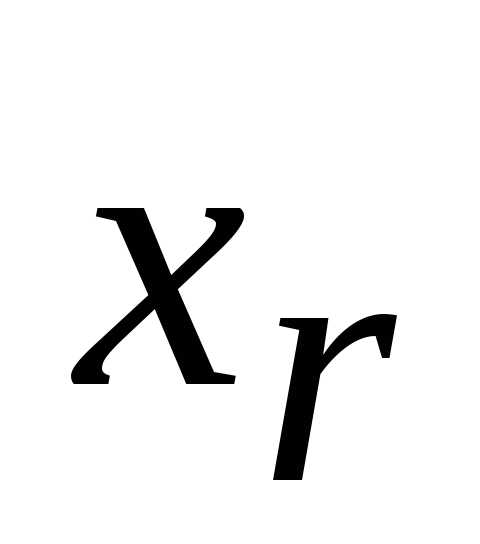 в предыдущее уравнение, находим
в предыдущее уравнение, находим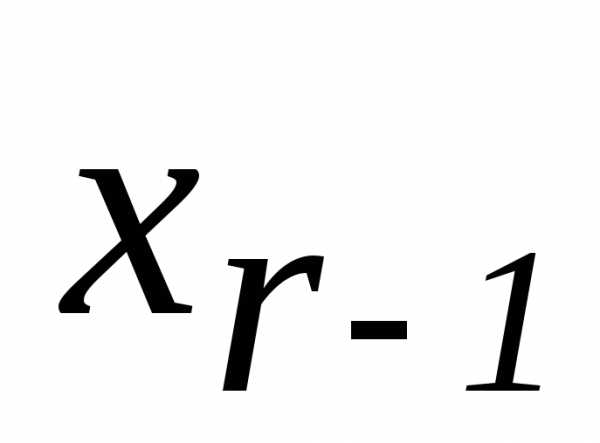 и т.д., пока не получим
и т.д., пока не получим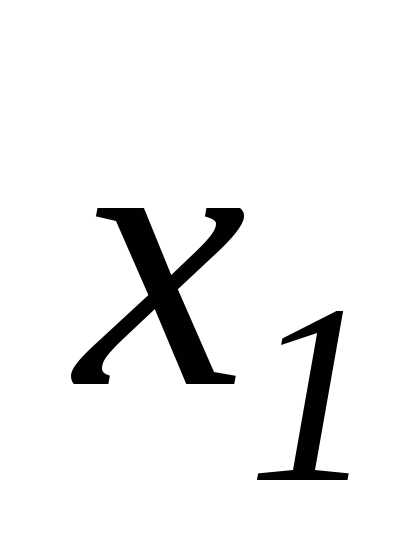 .
.
Замечание 1.Таким образом, при решении системы (I) методом Гаусса мы приходим к одному из следующих случаев.
Система (I) несовместна.
Система (I) имеет единственное решение, если в матрице
 число строк равно числу неизвестных
(
число строк равно числу неизвестных
( ).
).Система (I) имеет бесчисленное множество решений, если число строк в матрице
 меньше числа неизвестных
меньше числа неизвестных (
( ).
).
Отсюда имеет место следующая теорема.
Теорема.Система линейных уравнений либо несовместна, либо имеет единственное решение, либо – бесконечное множество решений.
Примеры.Решить систему уравнений методом Гаусса или доказать ее несовместность:
а) 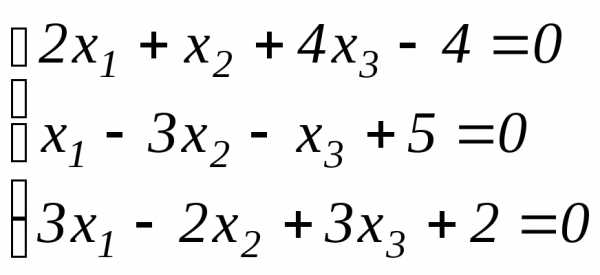 ;
;
б) 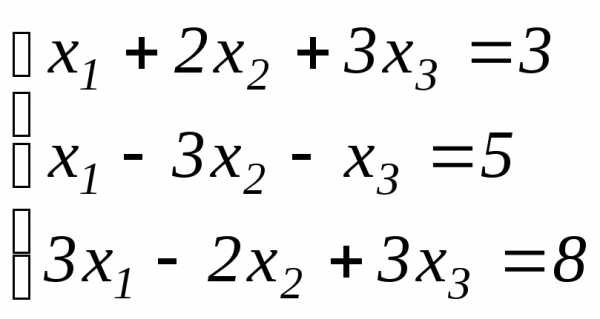 ;
;
в)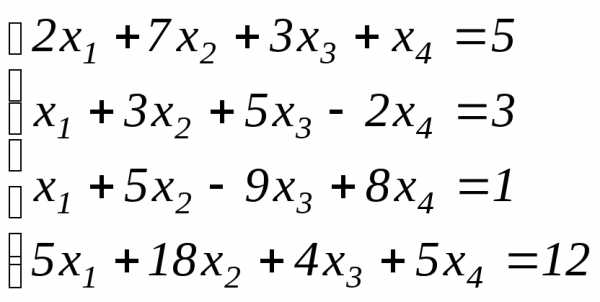 .
.
Решение.
а) Перепишем заданную систему в виде:
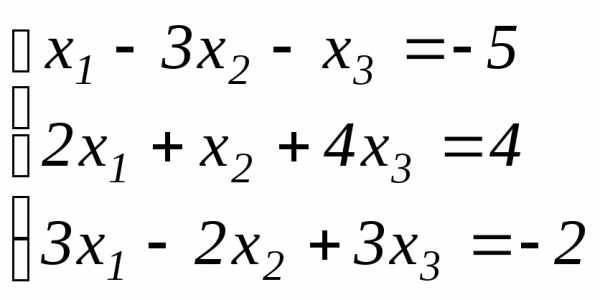 .
.
Мы поменяли местами 1-ое и 2-ое уравнение исходной системы, чтобы упростить вычисления (вместо дробей мы с помощью такой перестановки будем оперировать только целыми числами).
Составляем расширенную матрицу:
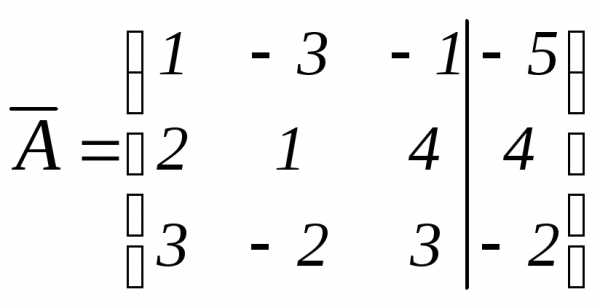 .
.
Нулевых строк нет; несовместных строк
нет,
;
исключим 1-ое неизвестное из всех уравнений системы, кроме 1-го.
Для этого умножим элементы 1-ой строки
матрицы
из всех уравнений системы, кроме 1-го.
Для этого умножим элементы 1-ой строки
матрицы на «-2» и сложим с соответствующими
элементами 2-ой строки, что равносильно
умножению 1-го уравнения на «-2» и сложению
со 2-ым уравнением. Затем умножим элементы
1-ой строки на «-3» и сложим с соответствующими
элементами третьей строки, т.е. умножим
2-ое уравнение заданной системы на «-3»
и сложим с 3-им уравнением. Получим
на «-2» и сложим с соответствующими
элементами 2-ой строки, что равносильно
умножению 1-го уравнения на «-2» и сложению
со 2-ым уравнением. Затем умножим элементы
1-ой строки на «-3» и сложим с соответствующими
элементами третьей строки, т.е. умножим
2-ое уравнение заданной системы на «-3»
и сложим с 3-им уравнением. Получим
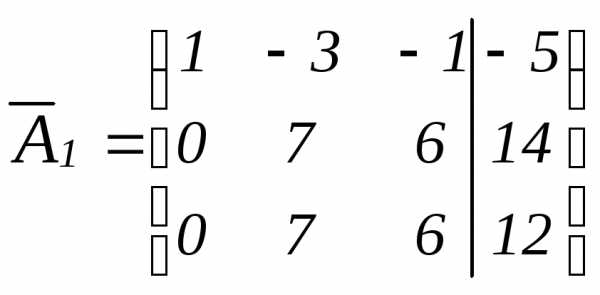 .
.
Матрице  соответствует система уравнений
соответствует система уравнений
 .
.
В матрице  нулевых строк нет, несовместных строк
также нет, исключим неизвестное
нулевых строк нет, несовместных строк
также нет, исключим неизвестное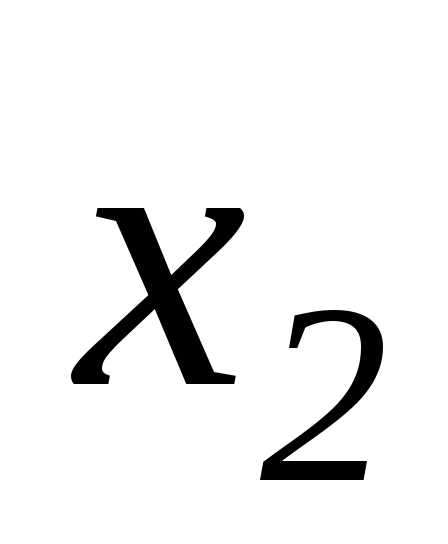 из 3-го уравнения системы, для этого
умножим элементы 2-ой строки матрицы
из 3-го уравнения системы, для этого
умножим элементы 2-ой строки матрицы на «-1» и сложим с элементами 3-ей строки
:
на «-1» и сложим с элементами 3-ей строки
:
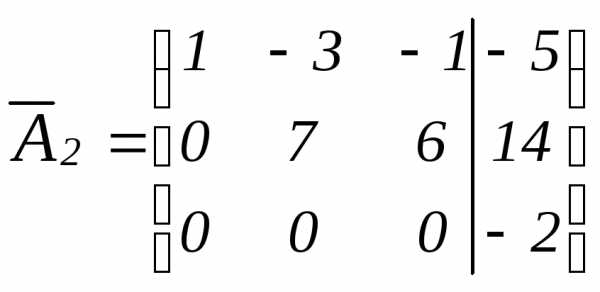 .
.
Матрица 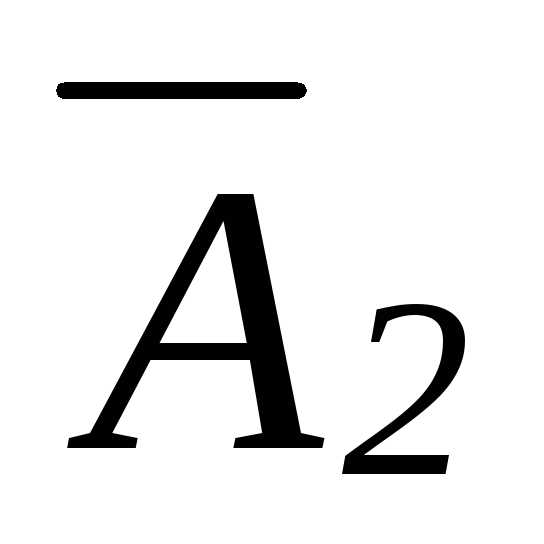 содержит несовместную строку (в 3-ей
строке все элементы равны нулю, кроме
последнего). Этой строке соответствует
несовместное уравнение.
Следовательно, система решений не имеет
(
содержит несовместную строку (в 3-ей
строке все элементы равны нулю, кроме
последнего). Этой строке соответствует
несовместное уравнение.
Следовательно, система решений не имеет
(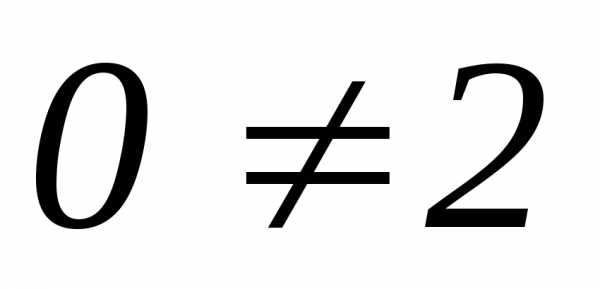 ),
система несовместна.
),
система несовместна.
б) Составляем расширенную матрицу:
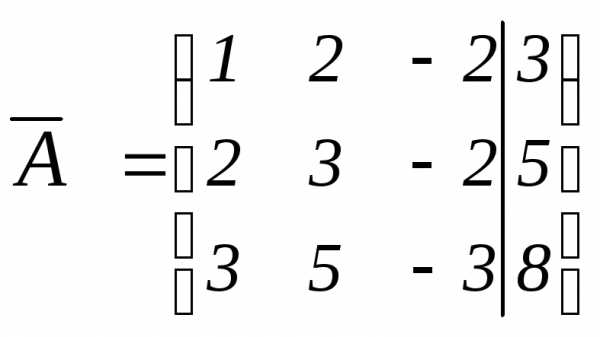 .
.
Нулевых строк нет, несовместных строк
нет,
,
исключаем неизвестное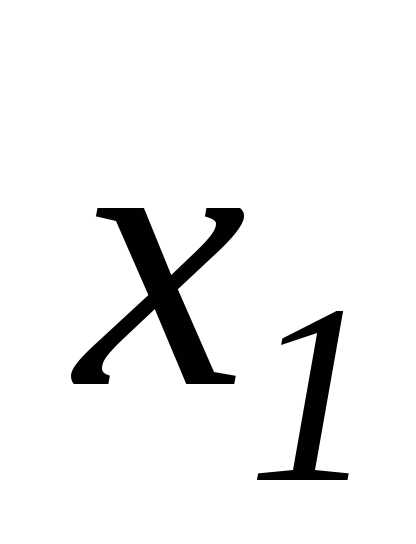 из 2-го и 3-го уравнения заданной системы,
для этого умножим элементы 1-ой строки
матрицы
из 2-го и 3-го уравнения заданной системы,
для этого умножим элементы 1-ой строки
матрицы на «-2», затем на «-3» и сложим соответственно
с элементами 2-ой и 3-ей строк, получим
на «-2», затем на «-3» и сложим соответственно
с элементами 2-ой и 3-ей строк, получим
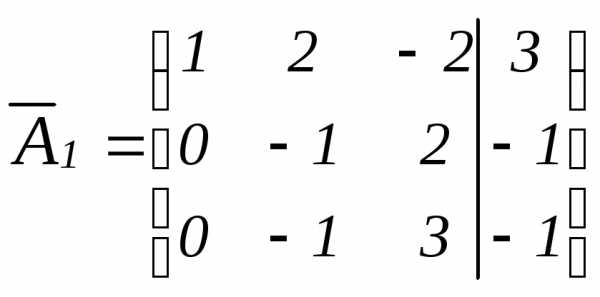 .
.
Рекомендуем читателю проанализировать,
какие операции при этом совершаются с
заданной системой уравнений. Умножаем
элементы 2-ой строки матрицы  на «-1» и складываем с элементами 3-ей
строки, получаем:
на «-1» и складываем с элементами 3-ей
строки, получаем:
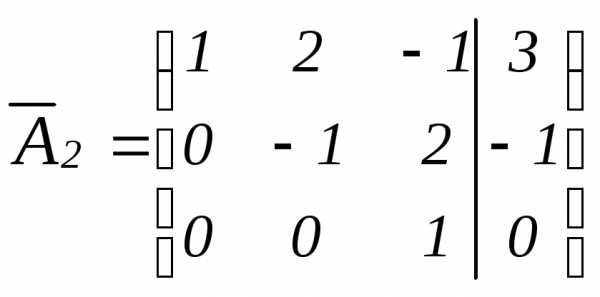 ,
,
где 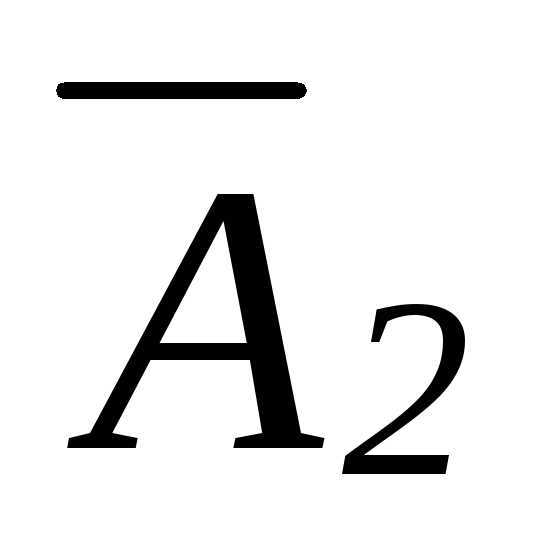 – матрица ступенчатого вида.
– матрица ступенчатого вида.
Записываем систему уравнений, соответствующую этой матрице
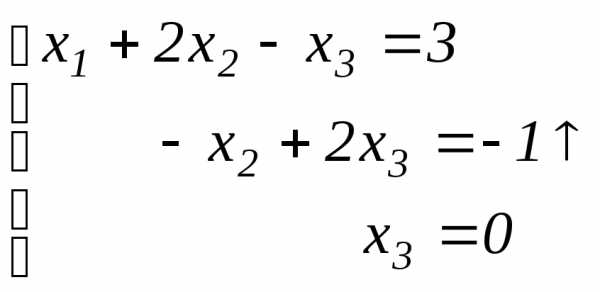 .
.
Теперь двигаемся снизу вверх. Из
последнего уравнения находим  .
.
Подставляя это равенство в предпоследнее уравнение, находим .
Подставляя 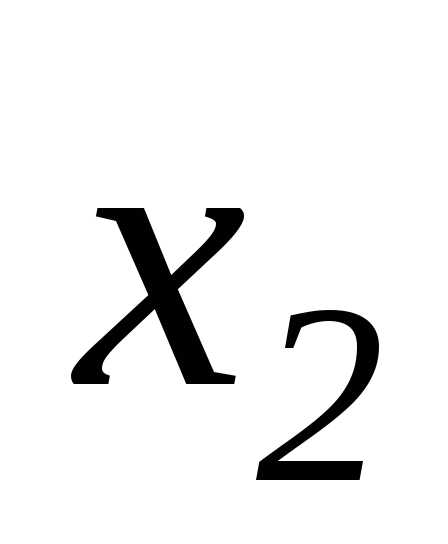 и
и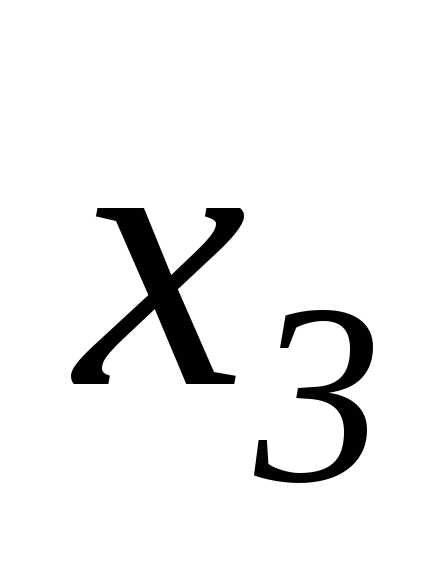 в
первое уравнение, получаем :.
в
первое уравнение, получаем :.
Ответ:  –
система имеет единственное решение.
–
система имеет единственное решение.
в) Составляем расширенную матрицу:
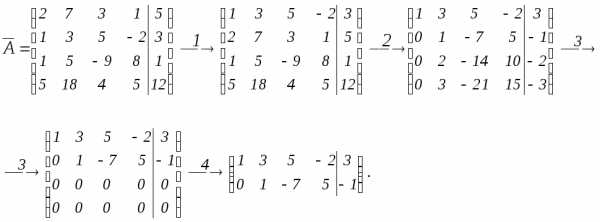
Переставим местами 1-ую и 2-ую строку для упрощения вычислений (меняем местами уравнения в заданной системе).
Умножим элементы 2-ой строки матрицы последовательно на «-2», «-1» и «-5» и сложим соответственно с элементами 2-ой, 3-ей и 4-ой строк (для получения нулей под элементом ).
Аналогичным образом, получаем нули под элементом
 .
.Вычеркиваем нулевые строки.
Последняя матрица – ступенчатая. Переходим от нее к системе уравнений:
;
из последнего уравнения получаем:
,
подставляя это равенство в 1-ое уравнение системы, находим
.
Ответ: 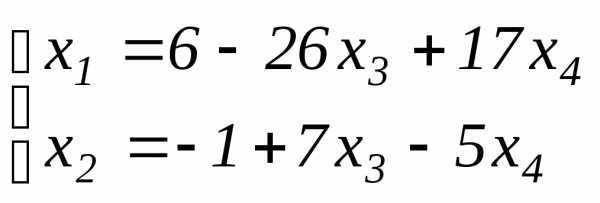 –
система имеет бесчисленное множество
решений. Давая произвольные значения
переменным
–
система имеет бесчисленное множество
решений. Давая произвольные значения
переменным и
и ,
мы каждый раз будем получать частные
решения заданной системы уравнений.
,
мы каждый раз будем получать частные
решения заданной системы уравнений.
Замечание .Количество уравнений
в окончательной системе при решении
методом Гаусса всегда равно рангу
матрицы –
–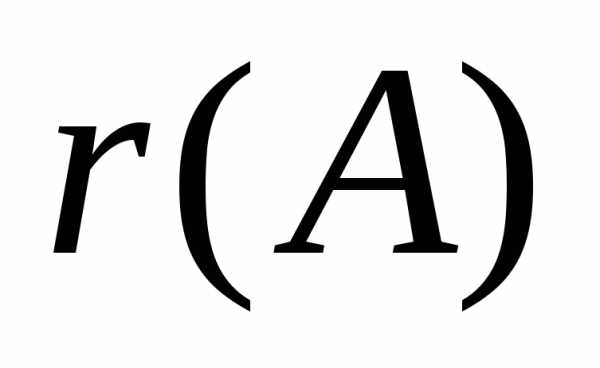 (см.
определение 3§7 главы 1).
(см.
определение 3§7 главы 1).
studfiles.net
Метод Гаусса.
Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находят все остальные переменные.
Предположим, что
в системе уравнений коэффициент при
переменной 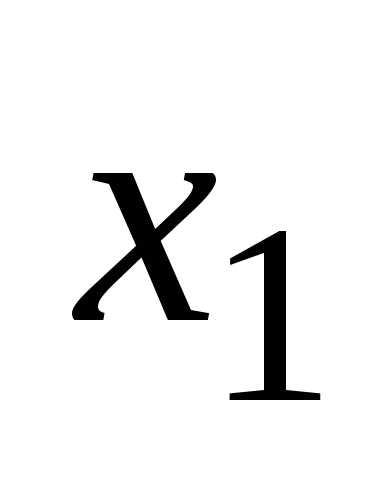 в первом уравнении
в первом уравнении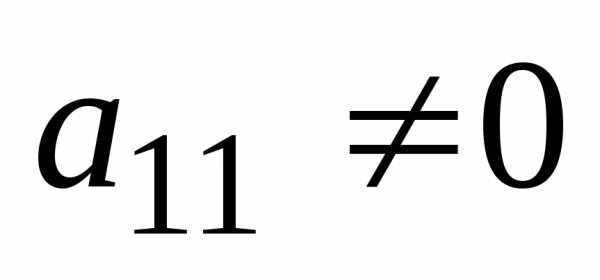 (Если это не так, то перестановкой местами
уравнений добьемся того, что
(Если это не так, то перестановкой местами
уравнений добьемся того, что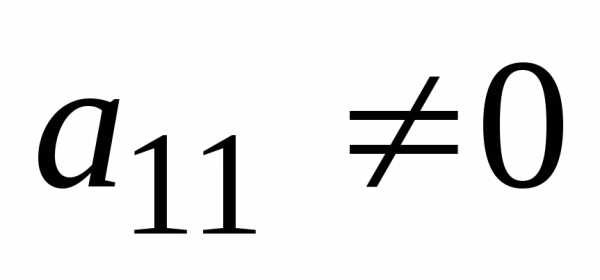 ).
).
Шаг 1.
Умножая первое уравнение на подходящие
числа (а именно на  ,
,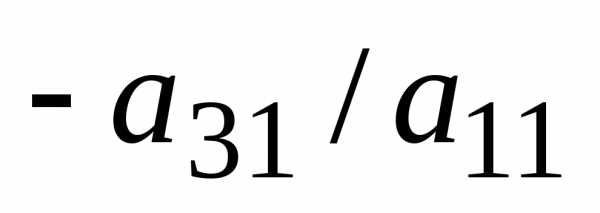 ,
…,
,
…,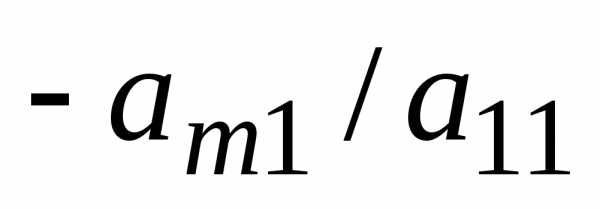 )
и прибавляя полученные уравнения
соответственно ко второму, третьему
,…,
)
и прибавляя полученные уравнения
соответственно ко второму, третьему
,…,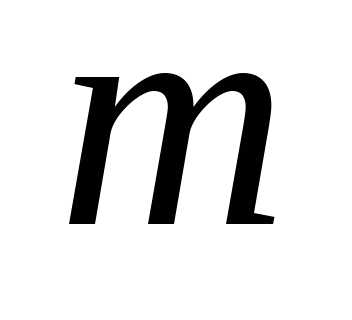 -тому
уравнению системы, исключим переменную
-тому
уравнению системы, исключим переменную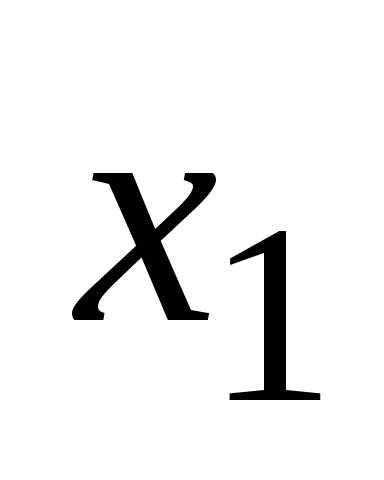 из всех последующих уравнений, начиная
со второго. Получим
из всех последующих уравнений, начиная
со второго. Получим
,
где буквами с верхним индексом (1) обозначены новые коэффициенты, полученные после первого шага.
Шаг 2.
Предположим, что 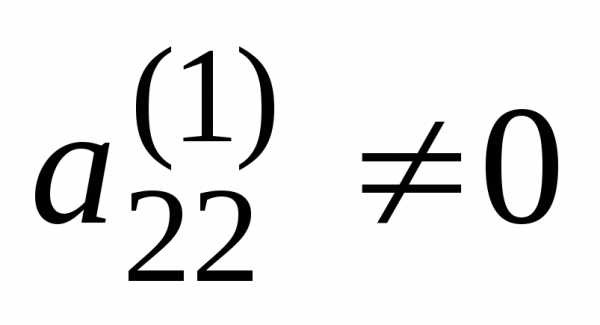 (если это не так, то соответствующей
перестановкой уравнений или переменных
с изменением их номеров добьемся того,
чтобы
(если это не так, то соответствующей
перестановкой уравнений или переменных
с изменением их номеров добьемся того,
чтобы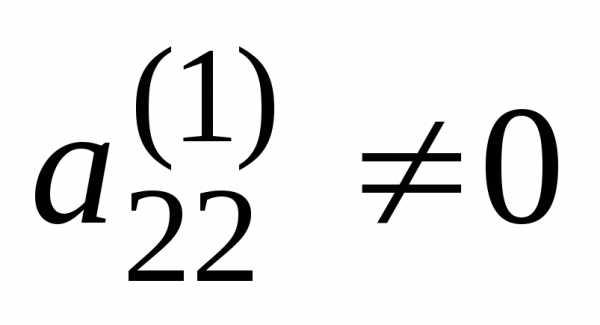 ).
).
Умножая второе
уравнение на подходящие числа ( ,
,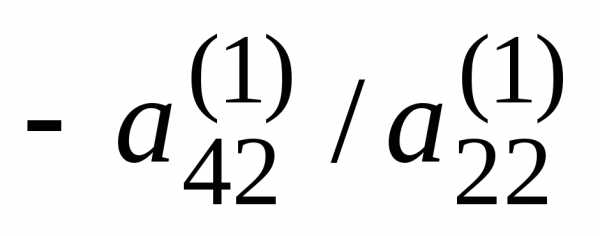 ,
…,
,
…,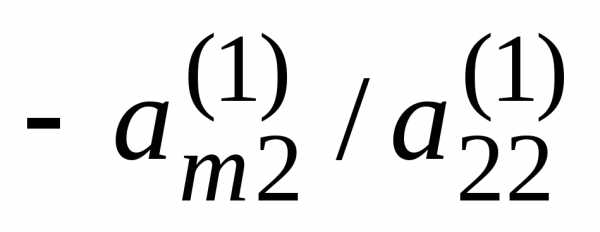 )
и прибавляя полученные уравнения
)
и прибавляя полученные уравнения соответственно
к третьему, четвертому,…,
соответственно
к третьему, четвертому,…,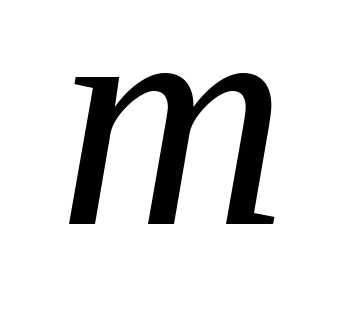 -тому
уравнению системы, исключим переменную
-тому
уравнению системы, исключим переменную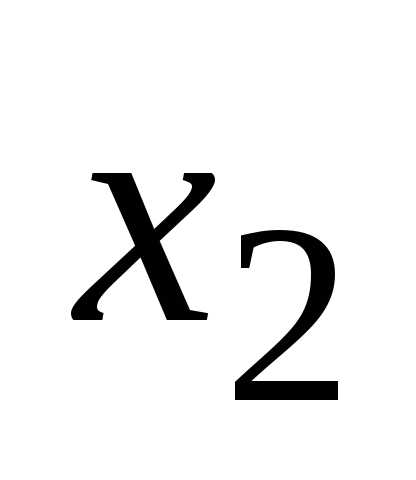 из всех последующих уравнений, начиная
с третьего.
из всех последующих уравнений, начиная
с третьего.
Продолжая процесс
последовательного исключения переменных,
после (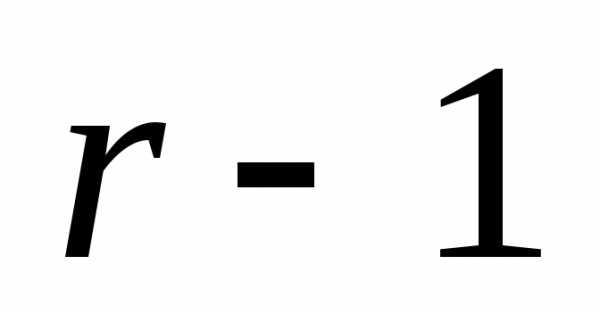 )-го
шага получим систему
)-го
шага получим систему
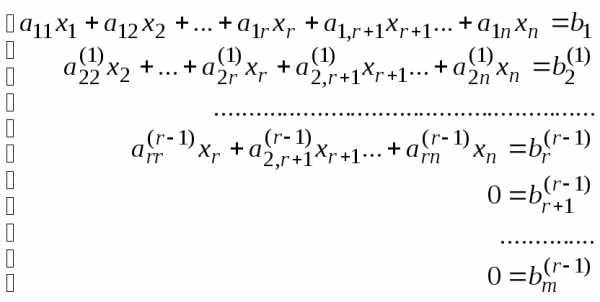 (2)
(2)
Число нуль в
последних 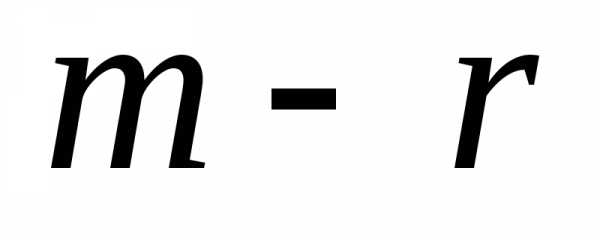 уравнениях означает, что их левые части
имеют вид.Если хотя бы
одно из чисел
уравнениях означает, что их левые части
имеют вид.Если хотя бы
одно из чисел 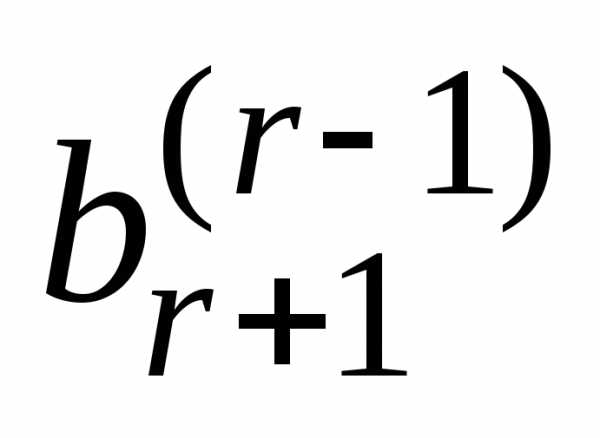 ,…,
,…,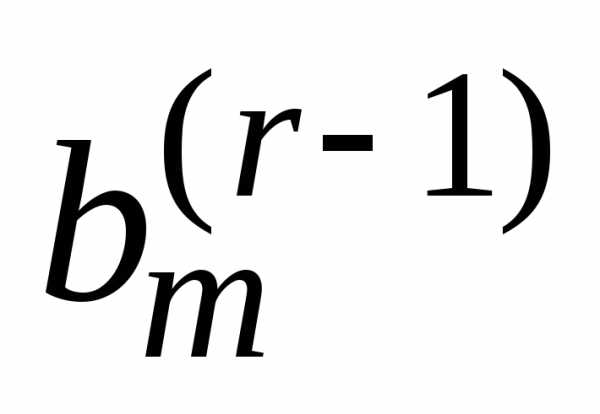 не равно нулю, то соответствующее
равенство противоречиво, и система(1) несовместна.
не равно нулю, то соответствующее
равенство противоречиво, и система(1) несовместна.
Таким образом, для
любой совместной системы числа 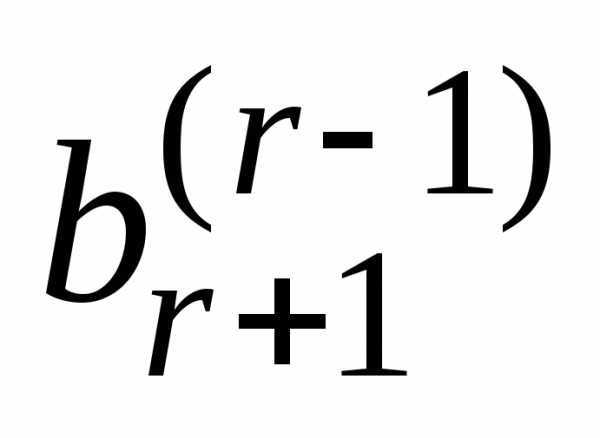 ,…,
,…,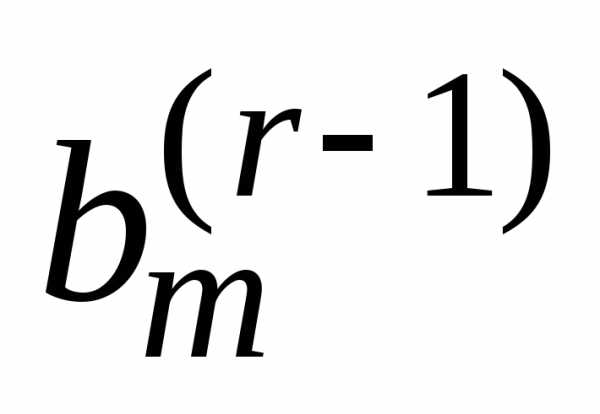 в системе
(2) равны нулю. В этом случае последние
в системе
(2) равны нулю. В этом случае последние 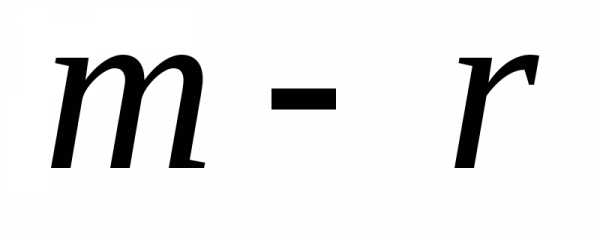 уравнений в системе являются тождествами
и их можно не принимать во внимание при
решении системы (1). Переход от системы
(1) к равносильной ей системе (2) называетсяпрямым ходом
метода Гаусса,
а нахождение переменных из системы (2)
– обратным
ходом.
уравнений в системе являются тождествами
и их можно не принимать во внимание при
решении системы (1). Переход от системы
(1) к равносильной ей системе (2) называетсяпрямым ходом
метода Гаусса,
а нахождение переменных из системы (2)
– обратным
ходом.
Преобразования Гаусса удобно проводить, осуществляя преобразования не с самими уравнениями, а с матрицей их коэффициентов. Рассмотрим матрицу
называемую расширенной
матрицей системы (1), т.к. в нее, кроме матрицы системы  ,
дополнительно включен столбец свободных
членов.
,
дополнительно включен столбец свободных
членов.
Пример. Решить систему уравнений:
.
Решение. Расширенная матрица системы имеет вид:
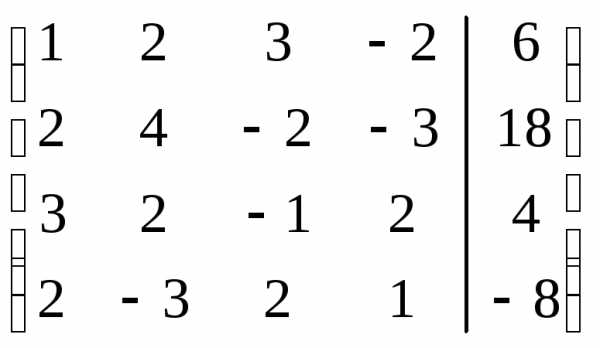 .
.
Шаг
1.
Так как 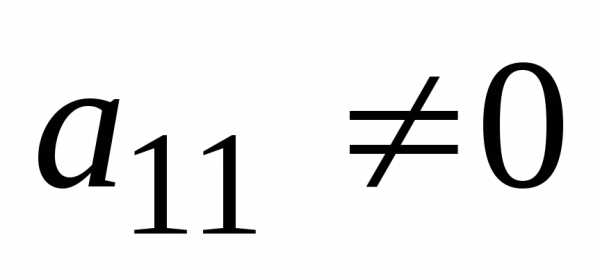 ,
то умножая на вторую, третью и четвертую
строки матрицы на числа (-2), (-3), (-2) и
прибавляя полученные строки соответственно
ко второй, третьей, четвертой строкам,
исключим переменную
,
то умножая на вторую, третью и четвертую
строки матрицы на числа (-2), (-3), (-2) и
прибавляя полученные строки соответственно
ко второй, третьей, четвертой строкам,
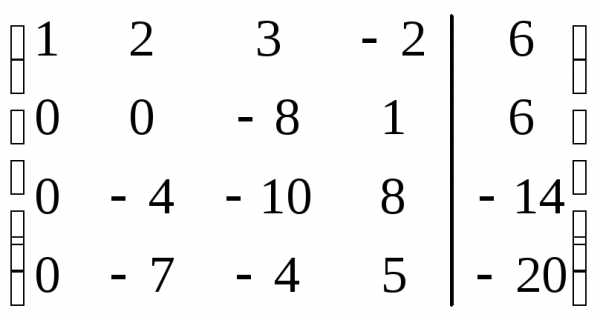
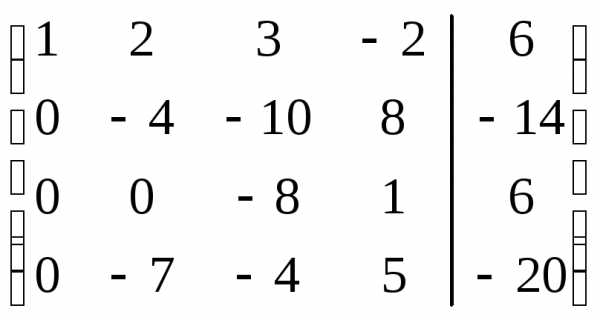
исключим переменную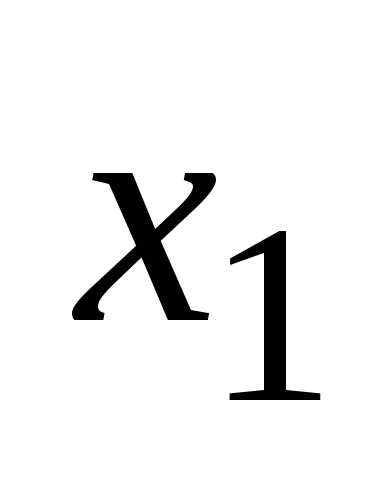 из всех строк, начиная со второй. Заметив,
что в новой матрице
из всех строк, начиная со второй. Заметив,
что в новой матрице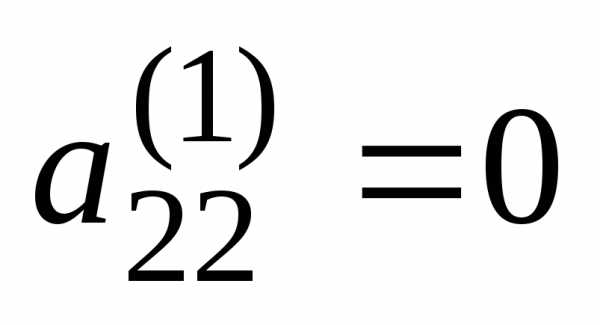 ,
поменяем местами вторую и третью строки:
,
поменяем местами вторую и третью строки:

 .
.
Шаг
2.
Так как теперь  ,
то умножая вторую строку на (-7/4) и
прибавляя полученную строку к четвертой,
исключим переменную
,
то умножая вторую строку на (-7/4) и
прибавляя полученную строку к четвертой,
исключим переменную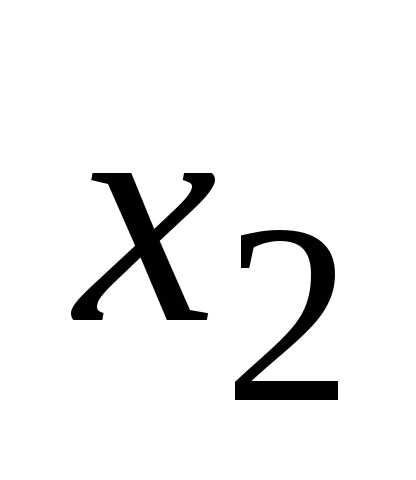 из всех строк, начиная с третьей:
из всех строк, начиная с третьей:


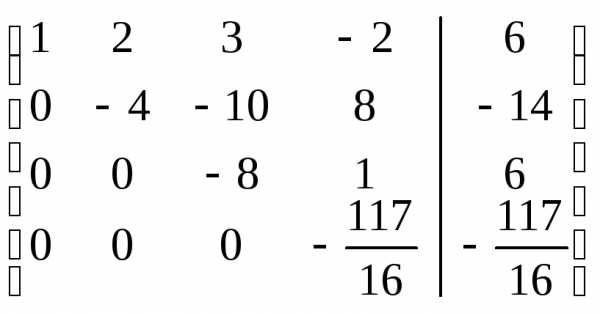 .
.
Шаг 3.
Учитывая, что
,умножаем
третью строку на 13,5/8=27/16, и прибавляя
полученную строку к четвертой, исключим
из нее переменную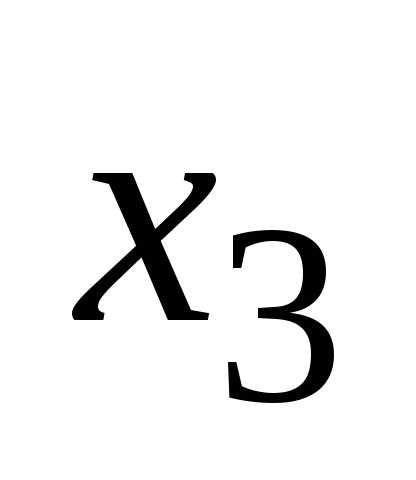 .
Получим (см. последнюю матрицу) систему
уравнений:
.
Получим (см. последнюю матрицу) систему
уравнений:
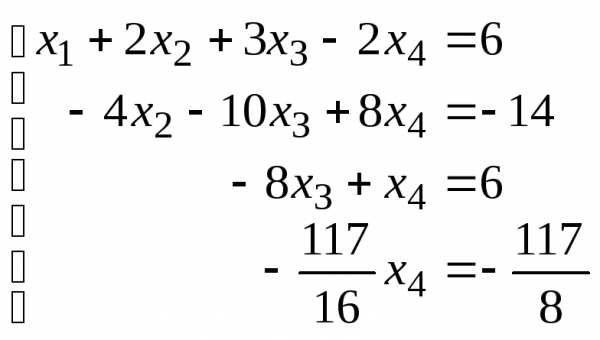 ,
,
откуда,
используя обратгный ход метода Гаусса,
найдем из четвертого уравнения 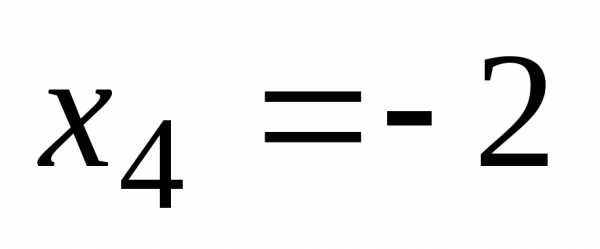 ;
из третьего;
из второгои из первого уравнения,
то есть решение системы (1;2;-1;-2).
;
из третьего;
из второгои из первого уравнения,
то есть решение системы (1;2;-1;-2).
studfiles.net
Метод Гаусса
Описанные выше методы используют фиксированные точки отрезка (концы и середину) и имеют низкий порядок точности(0 – методы правых и левых прямоугольников, 1 – методы средних прямоугольников и трапеций, 3 – метод парабол (Симпсона)). Если мы можем выбирать точки, в которых мы вычисляем значения функции , то можно при том же количестве вычислений подынтегральной функции получить методы более высокого порядка точности. Так для двух (как в методе трапеций) вычислений значений подынтегральной функции, можно получить метод уже не 1-го, а 3-го порядка точности:
.
В общем случае, используя точек, можно получить метод с порядком точности . Значения узлов метода Гаусса по точкам являются корнямиполинома Лежандрастепени .
Значения узлов метода Гаусса и их весов приводятся в справочниках специальных функций. Наиболее известен метод Гаусса по пяти точкам.
При заданном числе интервалов разбиения следует расположить их концы так, чтобы получить наивысшую точность интегрирования. В математическом плане это означает выбор коэффициентов Aiи узлов ti, i=1,…,n квадратурных формул Гаусса:
такими, чтобы формулы были точны для многочленов наивысшей возможной степени N. Можно показать, что при n узлах точно интерпретируются все многочлены степени N2n-1.
Узлы tiявляются корнями многочлена Лежандра:
.
Коэффициенты Ai вычисляются по формуле:
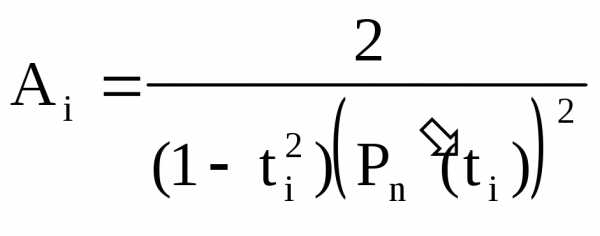 ,
i=1,…,n.
,
i=1,…,n.
Погрешность усечения Rn:
 ,
t[-1,1].
,
t[-1,1].
Для вычисления интеграла 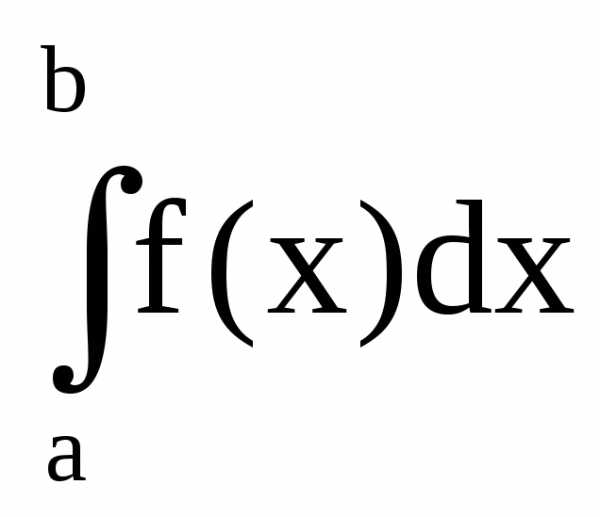 отрезок [a,b] преобразуется в отрезок
[-1,1] путем замены переменной:
отрезок [a,b] преобразуется в отрезок
[-1,1] путем замены переменной:
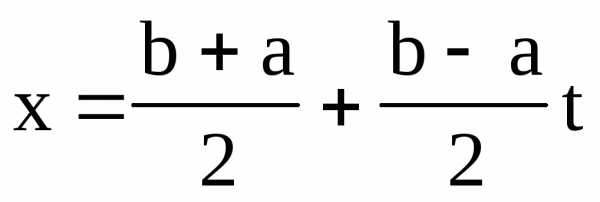 .
.
В результате формула Гаусса приобретает вид
 ,
,
где
, .
.
Квадратурная формула Гаусса обеспечивает высокую точность вычислений при небольшом числе узлов.
Метод Монте-Карло
В некоторых случаях из-за особенности подынтегральной функции (например, из-за ее большой сложности, неявном способе задания и т.д.), описанные выше методы нельзя или нецелесообразно использовать. В задачах, не требующих высокой точности, широкое распространение получил метод Монте-Карло.
Проиллюстрируем применение этого метода на примере приближенного вычисления следующего интеграла:
График подынтегрального выражения приведен на рисунке. Очевидно, что точное значение интеграла равно четверти площади круга единичного радиуса.
Построим прямоугольную область, которая будет полностью включать в себя искомый интеграл. В данном случае это будет квадрат с единичным ребром, показанный на рисунке. Далее, с помощью датчика случайных чисел генерируются точки
,
попадающие в эту область. В данном случае абсциссы и ординаты точек должны быть случайными числами, равномерно распределенными на отрезке [0, 1].
Для каждой точки проверяется, попадает ли она в область под или над графиком функции, то есть проверяется условие:
Если условие выполняется, то выбранная точка соответствует «успеху», если нет – то «промаху». Таким образом, процедура может быть описана как игра в «попадание» случайно выбранной точки в область под графиком (отсюда и название метода – Монте-Карло).
Вполне очевидно, что отношение числа «попаданий» (Nусп) к общему числу попыток (N) должно в пределе стремиться к доли площади прямоугольной области (Sпр), которую занимает область под интегрируемой функцией (значение интеграла, I).
Отсюда получается формула метода Монте-Карло:
Для реализации метода существенное значение имеет качество используемого датчика случайных чисел. Идеальный датчик должен давать равномерное распределение чисел в заданном диапазоне. Точность расчета интеграла определяется так же числом точек (N), используемых при вычислениях и, очевидно, должна увеличиваться при его росте.
Метод Монте-Карло широко используется в современных методах моделирования динамики молекулярных систем, взаимодействия растворенного вещества с молекулами растворителя, кинетики адсорбции веществ на твердых поверхностях и т.д.
studfiles.net
Конспект занятия элективного курса по математике в 11-м классе по теме “Определители второго и третьего порядков. Решение систем линейных уравнений (правило Крамера и метод Гаусса)”
Разделы: Математика
Наша задача – помочь вам овладеть
алгебраическими методами;
ваша задача – не противиться обучению,
с готовностью следовать за нами,
преодолевая трудности.
А. Мордкович
Цели:
- Познакомить учащихся с основными понятиями и определениями.
- Вспомнить как вычисляются определители второго порядка, и научить вычислять определители третьего порядка.
- Познакомиться с основными свойствами определителей 3-его порядка.
- Научиться решать системы трёх линейных уравнений, и решение систем линейных уравнений со многими неизвестными по методу Гаусса.
Устный счёт:
1. Что называется определителем 2-ого порядка?
2.Вычислите определители второго порядка.
а) ; б) ; в) ; г) ; д) ; е)
Сегодня на факультативном занятии вы подробно теоретически изучите тему: “Определители второго и третьего порядков. Основные свойства определителей. Система трёх линейных уравнений (правило Крамера). Система линейных уравнений со многими неизвестными. Метод Гаусса” и научитесь применять этот материал на практике при решении различных заданий.
Объяснение материала (используется интерактивная доска, информационно – коммуникационные технологии).
Под определителем (детерминантом) третьего порядка понимается выражение:
D==
Числа (i=1, 2, 3) называются элементами определителя; они расположены в трех строках и трех столбцах его (ряды определителя).
Пример. Вычислить:
D=
По формуле:
Основные свойства определителей
1. (Равноправность строк и столбцов) Определитель не меняет своего значения при замене всех его строк соответствующими столбцами, т.е.:
=
2. При перестановке двух параллельных рядов определителя его абсолютная величина сохраняет прежнее значение, а знак меняется на обратный.
Пусть, например, в определителе
D=
Переставлены первая и вторая строки, тогда получим определитель
D=
Следствие. Определитель, у которого два параллельных ряда одинаковы, равен нулю.
D=
Система трех линейных уравнений
Рассмотрим стандартную линейную систему трёх уравнений.
(1)
Введём определитель системы
D=, а также дополнительные определители
Если определитель системы D, то получаем единственное решение системы (1).
х =
Таким образом, имеем правило Крамера: неизвестные стандартной линейной системы (1) с ненулевым определителем представляют собой дроби, знаменатель которых есть определитель системы, а числители равны соответствующим дополнительным определителям.
Замечание: Если определитель системы D=0, то система (1) или несовместна или имеет бесконечно много решений.
Решить систему.
D== 1- 2+3=5-2+3(-7) =5-2-21= -18
= 1=5
= -1 = -1
= 1= -7
Использую правило Крамера,
х = у = z =
x= -у = z =
Система линейных уравнений с многими неизвестными.
Метод Гаусса
Рассмотрим систему n линейных уравнений с n-неизвестными.
Здесь для коэффициентов системы введена двойная индексация: а именно, у коэффициента первый индекс Ii означает номер уравнения, а второй з номер неизвестного. Свободные члены обозначены через . Наиболее простой метод решения системы (1) метод исключения (обычно называемый методом Гаусса).
Закрепление материала
1. Вычислить определители 3-го порядка:
Примеры а), в) разбираются коллективно, ещё раз составляется алгоритм решения и решаются задания у доски.
Пример в) решается самостоятельно и проверяется (используется ИКТ).
2. Решить уравнение:
х-1 1 11 х-1 1
1 1 х-1
С помощью правила Крамера и метода Гаусса решаются две системы.
3. С помощью правила Крамера решить систему:
4. Решить систему Методом Гаусса:
Домашнее задание: 1. Вычислить определители 2-го порядка:
а) б)
2.С помощью определителей решить систему:
3. Решить систему:
Итог урока:
- Что называется определителем второго порядка?
- Что называется определителем третьего порядка?
- С помощью каких правил можно решить систему трёх линейных уравнений? Алгоритм решения.
- С помощью каких правил можно решить систему линейных уравнений со многими неизвестными. Алгоритм решения.
15.08.2009
Поделиться страницей:urok.1sept.ru
Вычисление определителя методом Гаусса
Вычислим определитель методом Гаусса.
Суть метода состоит в следующем: определитель приводится к треугольному виду с помощью элементарных преобразований, и тогда он равен произведению элементов, стоящих на главной диагонали.
Идея метода состоит в следующем: пусть дан определитель третьего порядка
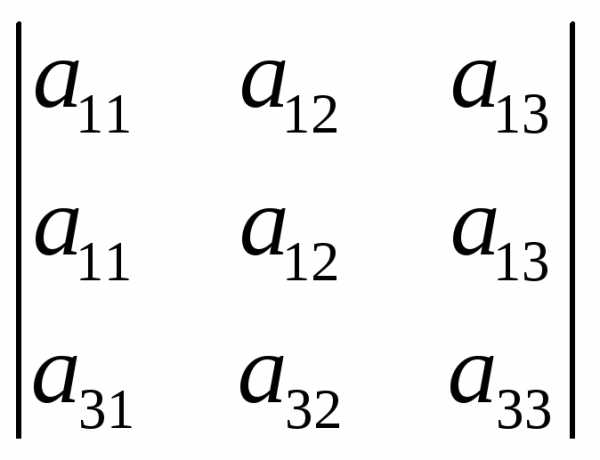 (1)
(1)
элемент должен быть равен
должен быть равен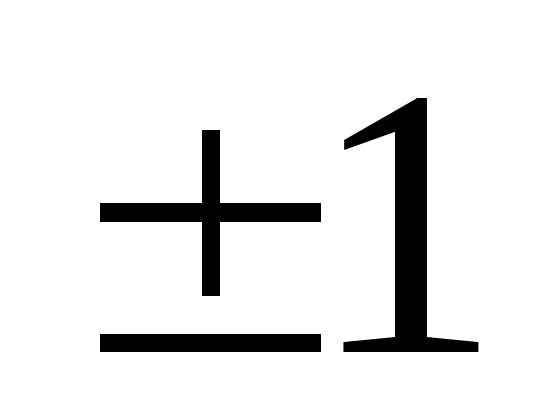 ,
для этого первую строку разделим на
,
для этого первую строку разделим на .
.
Получим определитель вида  (2)
(2)
Обнулим элементы, стоящие в первом
столбце, кроме первого. Для этого из
второй строки вычтем первую, умноженную
на 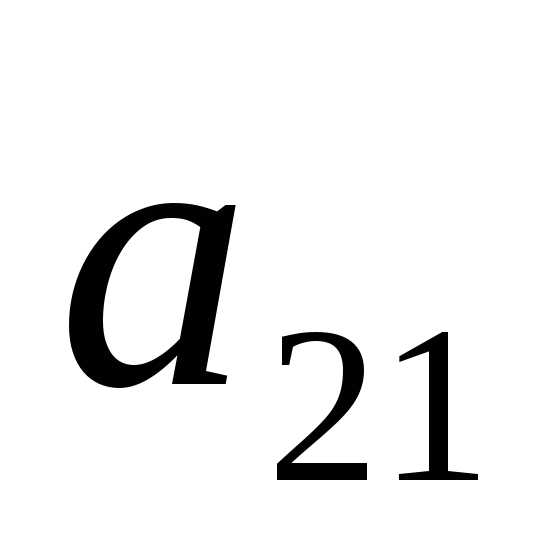 ,
далее из третьей строки вычтем первую,
умноженную на
,
далее из третьей строки вычтем первую,
умноженную на .
Получим определитель вида
.
Получим определитель вида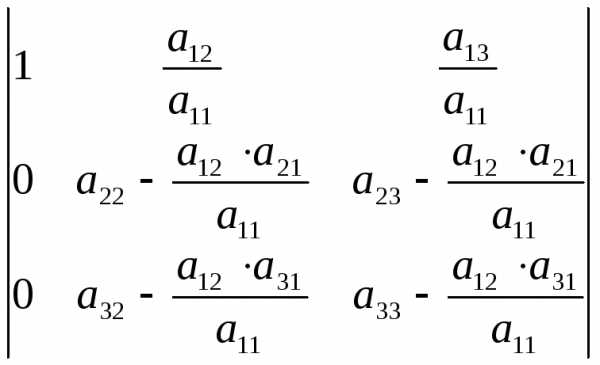 .
.
Обозначим его элементы буквой с, тогда
 (3)
(3)
Теперь надо обнулить элемент  .
Элемент
.
Элемент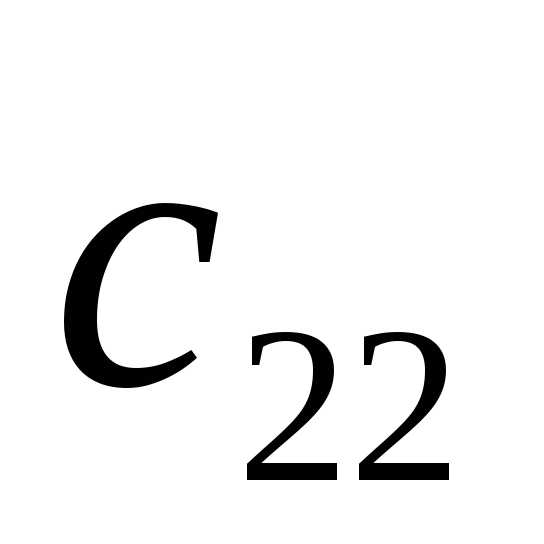 должен быть равен
должен быть равен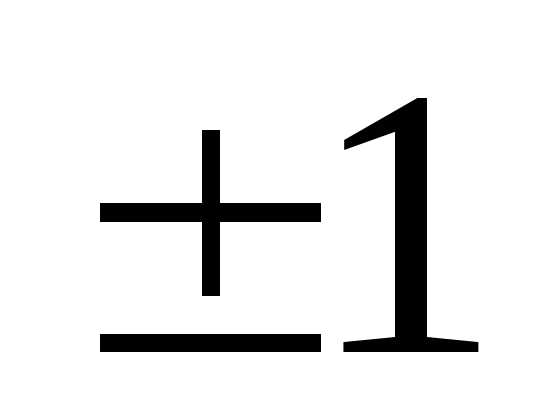 ,
для этого вторую строку разделим на
,
для этого вторую строку разделим на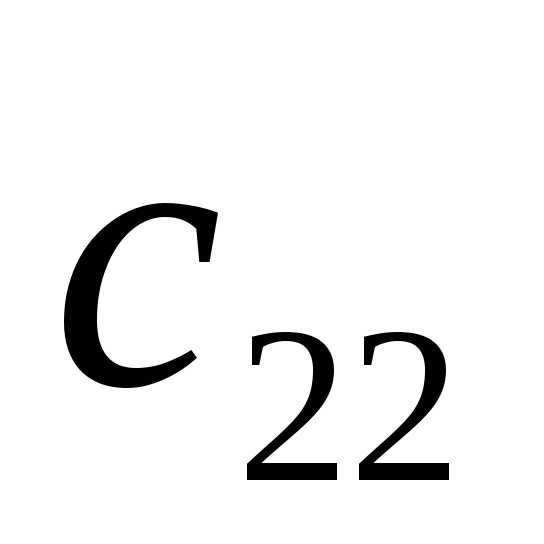 .
Получим определитель вида
.
Получим определитель вида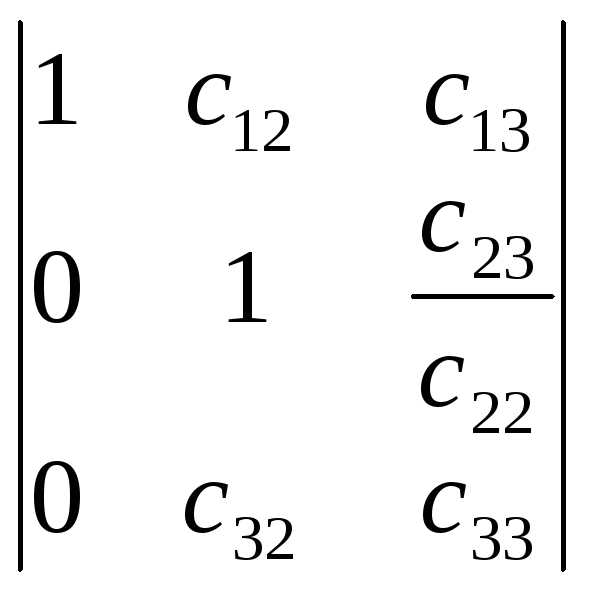 .
.
Далее из третьей строки вычтем вторую,
умноженную на  .
.
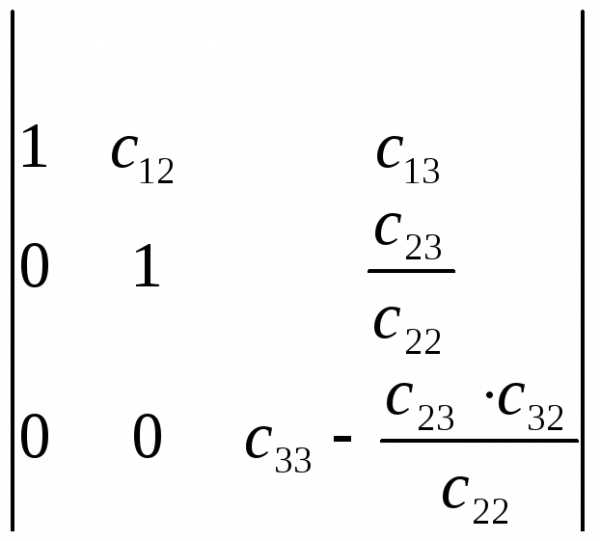 .
.
Обозначим его элементы буквой t, тогда
 (4)
(4)
Вот мы привели определитель к треугольному виду, теперь он равен .
Разберем теперь это на конкретном примере.
Пример 4:Вычислить определитель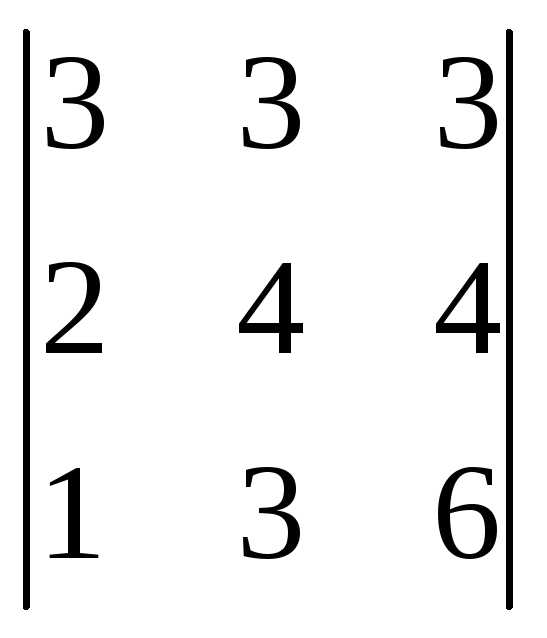 методом Гаусса.
методом Гаусса.
Решение: Поменяем местами первую и третью строки (при замене двух столбцов (строк) определитель меняет знак на противоположный).
Получили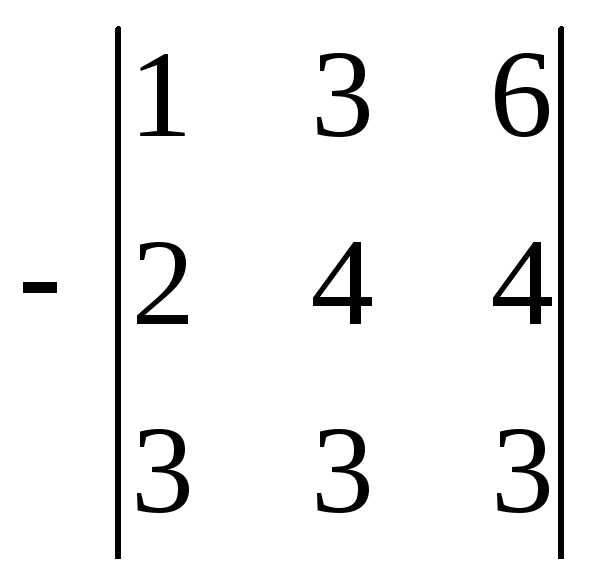
Из второй строки вычтем первую, умноженную
на 2, далее из третьей строки вычтем
первую, умноженную на 3. Получили 
Далее из третьей строки вычтем вторую, умноженную на 3.
Получили – 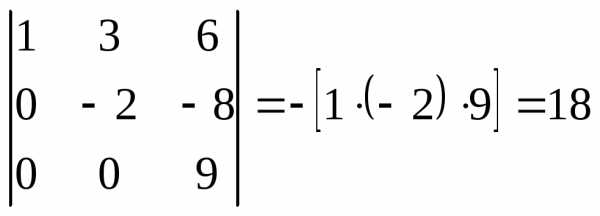
§2.Матрицы Виды матриц
Определение 7: Если в матрицеmстрок иnстолбцов, то она
называетсяразмерностьюm nи пишут
nи пишут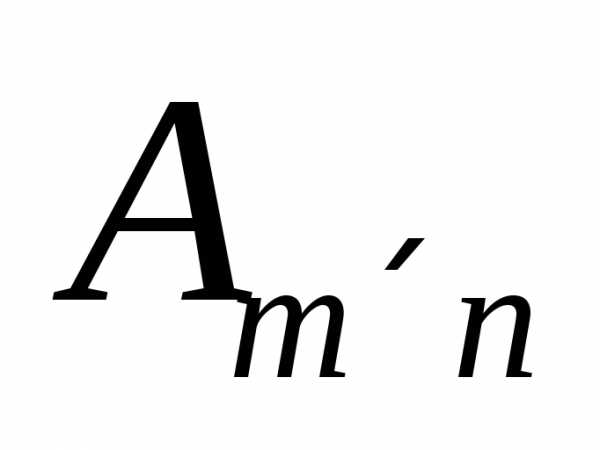 .
.
Определение 8: Если ,
то матрица называется квадратной.
,
то матрица называется квадратной.
Определение 9:Матрица, состоящая лишь из одной строки (столбца) называется матрицей-строкой (столбцом).
Определение 10:Матрица, состоящая из нулей, называется нулевой матрицей.
Определение 11:Диагональной матрицей называется квадратная матрица, у которой все элементы, не принадлежащие главной диагонали равны нулю.
Определение 12:Единичной матрицей называется диагональная матрица, у которой все элементы, стоящие на главной диагонали равны единице.
Определение 13:Треугольной называется квадратная матрица, у которой элементы, расположенные по одну сторону от главной диагонали равны нулю.
Действиянад матрицами.
Определение 14: Две матрицы считаются равными, если они имеют одинаковое число строк и столбцов и равные соответствующие элементы.
Пример 5:
Матрицы А и В равны, т.е. 
Определение 15: Суммой (разностью) матриц А и В называется такая матрица С, у которой каждый элемент равен.
Пример 6: Найти матрицу, если
Решение:
Cвойства сложения
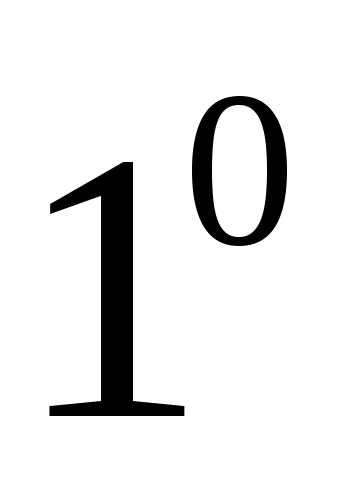 А+В=В+А(переместительное)
А+В=В+А(переместительное)
20А+О=А, где О-нулевая матрица
30 А+(В+С)=(А+В)+С (дистрибутивное)
40А+(-А)=О, где – А противоположная матрица
(т.е. элементы имеют противоположные знаки)
Определение 16: Произведением матрицы
А на число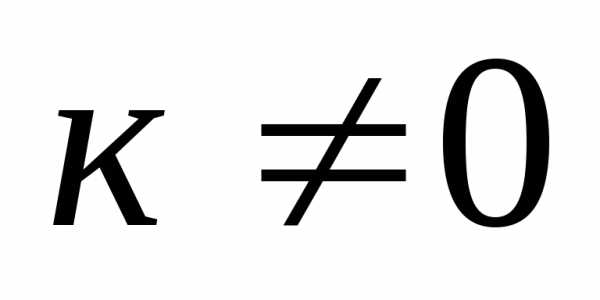 называется матрица, полученная из
данной умножением всех ее элементов на
число
называется матрица, полученная из
данной умножением всех ее элементов на
число .
.
Пример 7:
Умножение матиц
Это действие распространяется на так называемые согласованные матрицы.
Определение 17: Матрица А называется согласованной с матрицей В, если число столбцов у матрицы А равно числу строк у матрицы В.
Пример 8: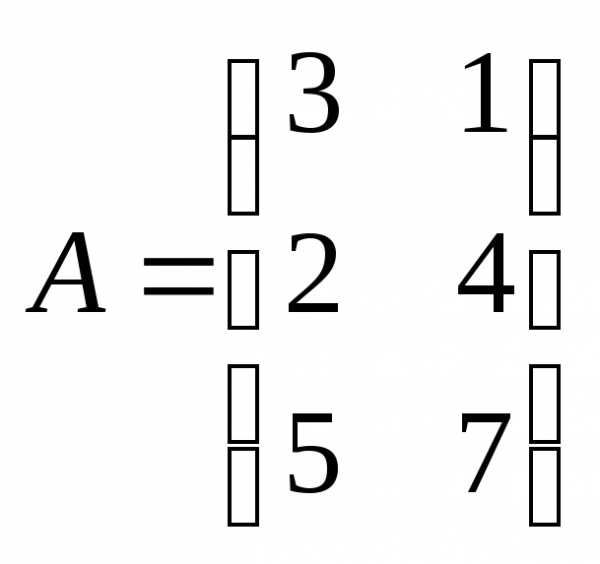 и
и – согласованные
– согласованные
 и- несогласованные
и- несогласованные
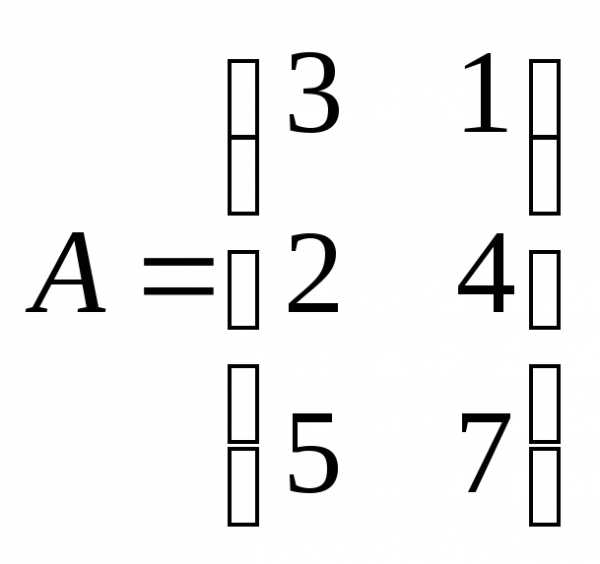 и
и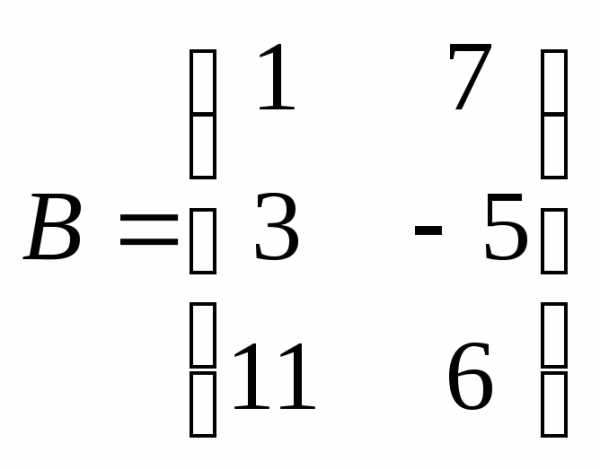 несогласованные
несогласованные
Определение 18: Произведением двух матриц А и В называется такая матрица С, каждый элемент которой равен сумме произведений элементовiстроки матрицы А на соответствующие элементыj-го столбца матрицы В.
Если матрица А имеет размерность 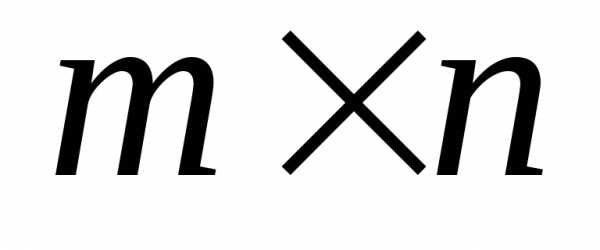 ,
а матрица В
,
а матрица В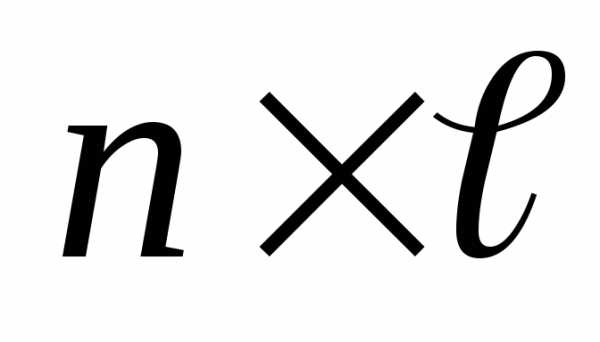 ,
то.
,
то.
Пример 9: Умножить матрицы

studfiles.net

 все нулевые строки, если такие имеются
(т.е. вычеркнем в системе (I)
все нулевые уравнения).
все нулевые строки, если такие имеются
(т.е. вычеркнем в системе (I)
все нулевые уравнения). строка, в которой все элементы, кроме
последнего, равны нулю (назовём такую
строку несовместной). Очевидно, что
такой строке соответствует несовместное
уравнение в системе (I) ,
следовательно, система (I)
решений не имеет и на этом процесс
заканчивается.
строка, в которой все элементы, кроме
последнего, равны нулю (назовём такую
строку несовместной). Очевидно, что
такой строке соответствует несовместное
уравнение в системе (I) ,
следовательно, система (I)
решений не имеет и на этом процесс
заканчивается. не содержит несовместных строк (система
(I) не содержит несовместных
уравнений). Еслиa11=0,
то находим в 1-ой строке какой-нибудь
элемент (кроме последнего) отличный от
нуля и переставляем столбцы так, чтобы
в 1-ой строке на 1-ом месте не было нуля.
Будем теперь считать, что
не содержит несовместных строк (система
(I) не содержит несовместных
уравнений). Еслиa11=0,
то находим в 1-ой строке какой-нибудь
элемент (кроме последнего) отличный от
нуля и переставляем столбцы так, чтобы
в 1-ой строке на 1-ом месте не было нуля.
Будем теперь считать, что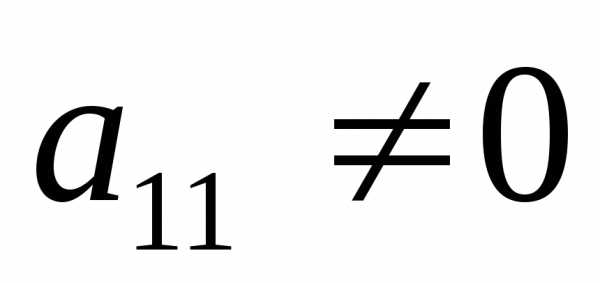 (т.е. поменяем местами соответствующие
слагаемые в уравнениях системы (I)).
(т.е. поменяем местами соответствующие
слагаемые в уравнениях системы (I)). получаем нули в 1-ом столбце под элементомa11 :
получаем нули в 1-ом столбце под элементомa11 : все нулевые строки, если они есть,
проверим, нет ли несовместной строки
(если она имеется, то система несовместна
и на этом решение заканчивается).
Проверим, будет лиa22 /=0, если да, то находим
во 2-ой строке элемент, отличный от нуля
и переставляем столбцы так, чтобы
все нулевые строки, если они есть,
проверим, нет ли несовместной строки
(если она имеется, то система несовместна
и на этом решение заканчивается).
Проверим, будет лиa22 /=0, если да, то находим
во 2-ой строке элемент, отличный от нуля
и переставляем столбцы так, чтобы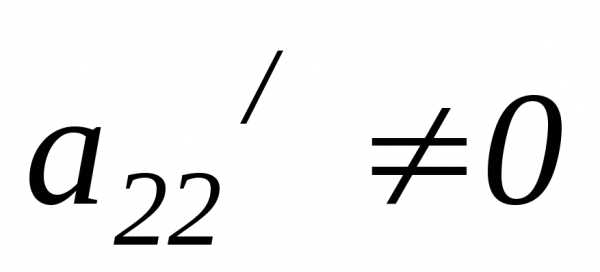 .
Далее умножаем элементы 2-ой строки наи складываем с соответствующими
элементами 3-ей строки, затем – элементы
2-ой строки наи складываем с соответствующими
элементами 4-ой строки и т.д., пока не
получим нули подa22 /
.
Далее умножаем элементы 2-ой строки наи складываем с соответствующими
элементами 3-ей строки, затем – элементы
2-ой строки наи складываем с соответствующими
элементами 4-ой строки и т.д., пока не
получим нули подa22 /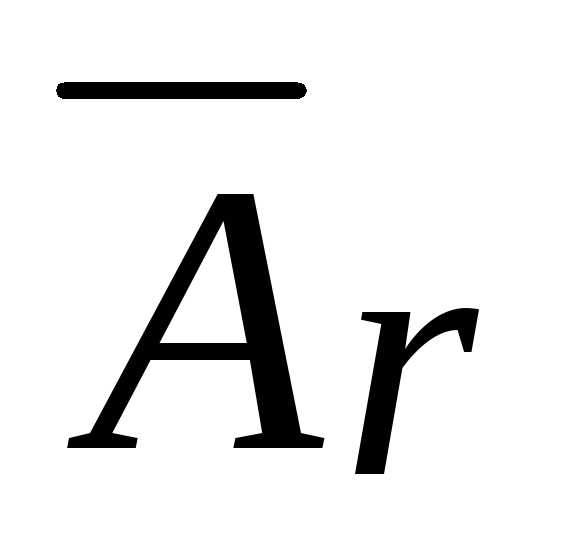 число строк равно числу неизвестных
(
число строк равно числу неизвестных
(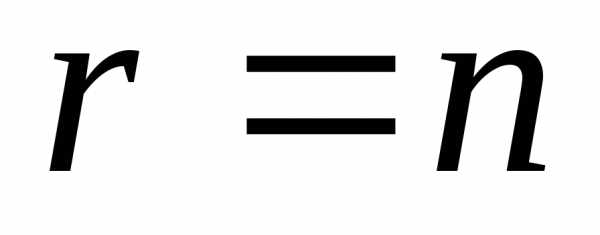 ).
).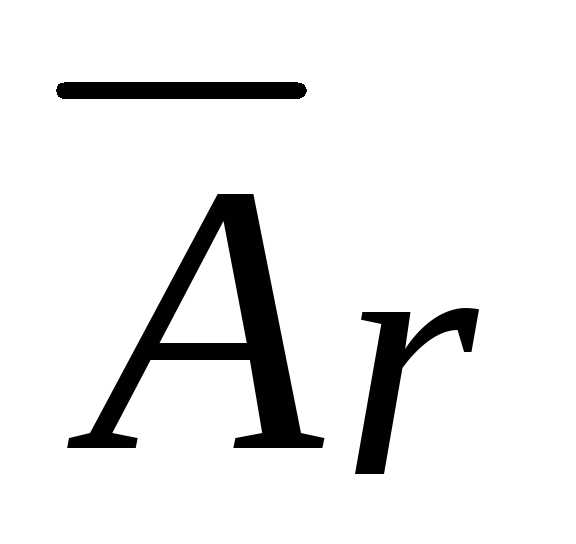 меньше числа неизвестных
меньше числа неизвестных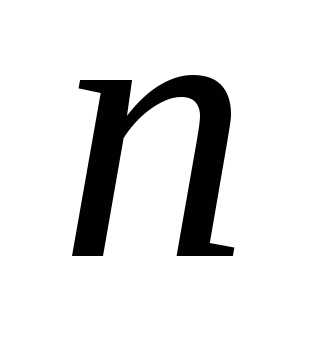 (
( ).
).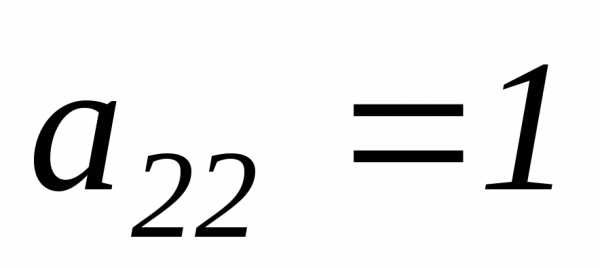 .
.