Метод гаусса для матриц калькулятор: Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса. - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

📝Фундаментальная система решений

Чтобы понять, что такое фундаментальная система решений вы можете посмотреть видео-урок для этого же примера кликнув здесь. Теперь перейдем собственно к описанию всей необходимой работы. Это поможет вам более детально разобраться в сути данного вопроса.

Как найти фундаментальную систему решений линейного уравнения?

Возьмём для примера такую систему линейных уравнений:

Найдём решение этой линейной системы уравнений методом Гаусса. Для начала нам надо выписать матрицу коэффициентов системы.

Преобразуем эту матрицу к треугольной. Первую строку переписываем без изменений. И все элементы, что стоят под $a_{11}$, надо сделать нулями. Что бы сделать ноль в место элемента $a_{21}$, надо от второй строки вычесть первую, и разность записать во второй строке. Что бы сделать ноль в место элемента $a_{31}$, надо от третьей строки вычесть первую и разность записать в третьей строке.

Что бы сделать ноль в место элемента $a_{41}$, надо от четвёртой строки вычесть первую умноженную на 2 и разность записать в четвёртой строке. Что бы сделать ноль в место элемента $a_{31}$, надо от пятой строки вычесть первую умноженную на 2 и разность записать в пятой строке.

Первую и вторую строку переписываем без изменений. И все элементы, что стоят под $a_{22}$, надо сделать нулями. Что бы сделать ноль в место элемента $a_{32}$, надо от третьей строки вычесть вторую умноженную на 2 и разность записать в третьей строке. Что бы сделать ноль в место элемента $a_{42}$, надо от четвёртой строки вычесть вторую умноженную на 2 и разность записать в четвёртой строке. Что бы сделать ноль в место элемента $a_{52}$, надо от пятой строки вычесть вторую умноженную на 3 и разность записать в пятой строке.

Видим, что последние три строки – одинаковые, поэтому если от четвёртой и пятой вычесть третью, то они станут нулевыми.

По этой матрице записываем новую систему уравнений.

Видим, что линейно независимых уравнений у нас, только три, а неизвестных пять, поэтому фундаментальная система решений будет состоять из двух векторов. Значит, нам надо перенести две последние неизвестные вправо .

Теперь, начинаем выражать те неизвестные, что стоят в левой части через те, что стоят в правой части. Начинаем с последнего уравнения, сначала выразим $x_3$, потом полученный результат подставим во второе уравнение и выразим $x_2$, а потом в первое уравнение и тут выразим $x_1$. Таким образом мы все неизвестные, что стоят в левой части, выразили через неизвестные, что стоят в правой части.

После чего вы вместо $x_4$ и $x_5$, можем подставлять любые числа и находить $x_1$, $x_2$ и $x_3$. Каждая такая пятёрка чисел будет корнями нашей изначальной системы уравнений. Что бы найти векторы, что входят в ФСР нам надо вместо $x_4$ подставить 1, а вместо $x_5$ подставить 0, найти $x_1$, $x_2$ и $x_3$, а потом наоборот $x_4=0$ и $x_5=1$.

Какие именно векторы создают фундаментальную систему решений данной системы уравнений?

Для лучшего понимания хода роботы можете посмотреть видео-урок по данном задании.

Материалы по теме:

Поделиться с друзьями:

Загрузка…

Решение системы линейных уравнений методом гаусса-жордана

В данной статье мы рассмотрим метод Жордана-Гаусса для решения систем линейных уравнений, отличие метода Гаусса от метода Жордана-Гаусса, алгоритм действий, а также приведем примеры решений СЛАУ.

Yandex.RTB R-A-339285-1

Основные понятия

Определение 1

Метод Жордана-Гаусса – один из методов, предназначенный для решения систем линейных алгебраических уравнений.

Этот метод является модификацией метода Гаусса – в отличие от исходного (метода Гаусса) метод Жордана-Гаусса позволяет решить СЛАУ в один этап (без использования прямого и обратного ходов).

Примечание

Матричная запись СЛАУ: вместо обозначения А в методе Жордана-Гаусса для записи используют обозначение Ã – обозначение расширенной матрицы системы.

Пример 1

4 x 1 – 7 x 2 + 8 x 3 = – 23 2 x 1 – 4 x 2 + 5 x 3 = – 13 – 3 x 1 + 11 x 2 + x 3 = 16

Как решить?

Записываем расширенную матрицу системы:

Ã = 4 – 7 8 | – 23 2 – 4 5 | – 13 – 3 11 1 | 16

Напоминаем, что слева от черты записывается матрица системы А:

A = 4 – 7 8 2 – 4 5 – 3 11 1

Замечание 1

На каждом шаге решения необходимо выбирать разрешающие элементы матрицы. Процесс выбора может быть различным – в зависимости от того, как выбираются элементы, решения будут отличаться. Можно выбирать в качестве разрешающих элементов диагональные элементы матрицы, а можно выбирать произвольно.

В этой статье мы покажем оба способа решения.

Произвольный способ выбора разрешающих элементов

Следует обратиться к 1-му столбцу матрицы Ã – необходимо выбрать ненулевой (разрешающий) элемент.

В 1-ом столбце есть 3 ненулевых элемента: 4, 2, -3. Можно выбрать любой, но, по правилам, выбирается тот, чей модуль ближе всего к единице. В нашем примере таким числом является 2.

Цель: обнулить все элементы, кроме разрешающего, т.е. необходимо обнулить 4 и -3:

4 – 7 8 2 – 4 5 – 3 11 1

Произведем преобразование: необходимо сделать разрешающий элемент равным единице. Для этого делим все элементы 2-ой строки на 2. Такое преобразование имеет обозначение: I I: 2:

4 – 7 8 | – 23 2 – 4 5 | – 13 – 3 11 1 | 16 I I ÷ 2 → 4 – 7 8 | – 23 2 – 4 5 / 2 | – 13 / 2 – 3 11 1 | 16

Теперь обнуляем остальные элементы: 4 и -3:

4 – 7 8 | – 23 2 – 4 5 / 2 | – 13 / 2 – 3 11 1 | 16 I – 4 × I I I I I – (- 3) × I I

Необходимо выполнить преобразования:

I – 4 × I I и I I I – (- 3) × I I = I I I + 3 × I I

Запись I – 4 × I I означает, что от элементов 1-ой строки вычитаются соответствующие элементы 2-ой строки, умноженные на 4.

Запись I I I + 3 × I I означает, что к элементам 3-ей строки прибавляются соответствующие элементы 2-ой строки, умноженные на 3.

I – 4 × I I = 4 – 7 8 – 23 – 4 1 – 2 5 / 2 – 13 / 2 = = 4 – 7 8 – 23 – 4 – 8 10 – 26 = 0 1 – 2 3

Записываются такие изменения следующим образом:

4 – 7 8 | – 23 2 – 4 5 / 2 | – 13 / 2 – 3 11 1 | 16 I – 4 × I I I I I – (- 3) × I I → 0 1 – 2 | 3 1 – 2 5 / 2 | – 13 / 2 0 5 17 / 2 | – 7 / 2

Необходимо обнулить 2-ой столбец, следовательно, нужно выбрать разрешающий элемент: 1, -2, 5. Однако 2-ую строку матрицы мы использовали в первом этапе, так что элемент -2 не может быть использован.

Поскольку необходимо выбирать число, чей модуль ближе всего к единице, то выбор очевиден – это 1. Обнуляем остальные элементы 2-го столбца:

0 1 – 2 | 3 1 – 2 5 / 2 | – 13 / 2 0 5 17 / 2 | – 7 / 2 I I – (- 2) × I I I I – 5 × I

0 1 – 2 | 3 1 – 2 5 / 2 | – 13 / 2 0 5 17 / 2 | – 7 / 2 I I + 2 × I I I I – 5 × I → 0 1 – 2 | 3 1 0 – 3 / 2 | – 1 / 2 0 0 37 / 2 | – 37 / 2

Теперь требуется обнулить элементы 3-го столбца. Поскольку первая и вторая строки уже использованы, поэтому остается только один вариант: 37 / 2 . Обнуляем с его помощью элементы третьего столбца:

0 1 – 2 | 3 1 0 – 3 / 2 | – 1 / 2 0 0 37 / 2 | – 37 / 2

Выполнив преобразования

I – (- 2) × I I I = I + 2 × I I I и I I – (- 3 2) × I I I = I I + 3 2 × I I

получим следующий результат:

0 1 – 2 | 3 1 0 – 3 / 2 | – 1 / 2 0 0 1 | – 1 I + 2 × I I I I I + 3 / 2 × I I I → 0 1 0 | 1 1 0 0 | – 2 0 0 1 | – 1

Ответ : x 1 = – 2 ; x 2 = 1 ; x 3 = – 1 .

Полное решение:

4 – 7 8 | – 23 2 – 4 5 | – 13 – 3 11 1 | 16 I I ÷ 2 → 4 – 7 8 | – 23 2 – 4 5 / 2 | – 13 / 2 – 3 11 1 | 16 I – 4 × I I I I I – (- 3) × I I →

→ 0 1 – 2 | 3 1 – 2 5 / 2 | – 13 / 2 0 5 17 / 2 | – 7 / 2 I I – (- 2) × I I I I – 5 × I → 0 1 – 2 | 3 1 0 – 3 / 2 | – 1 / 2 0 0 37 / 2 | – 37 / 2 I I I ÷ 37 2 →

→ 0 1 – 2 | 3 1 0 – 3 / 2 | – 1 / 2 0 0 1 | – 1 I + 2 × I I I I I + 3 / 2 × I I I → 0 1 0 | 1 1 0 0 | – 2 0 0 1 | – 1 .

Выбор разрешающих элементов на главной диагонали матрицы системы

Определение 2

Принцип выбора разрешающих элементов строится на простом отборе соответствующих элементов: в 1-ом столбце выбирается элемент 1-го столбца, во 2-ом – второй, в 3-ем – третий и т.д.

В первом столбце необходимо выбрать элемент первой строки, т.е. 4. Но поскольку в первом столбце есть число 2, чей модуль ближе к единице, чем 4, то можно поменять местами первую и вторую строку:

4 – 7 8 | – 23 2 – 4 5 | – 13 – 3 11 1 | 16 → 2 – 4 5 | – 13 4 – 7 8 | – 23 – 3 11 1 | 16

Теперь разрешающий элемент – 2. Как показано в первом способе, делим первую строку на 2, а затем обнуляем все элементы:

4 – 7 8 | – 23 2 – 4 5 | – 13 – 3 11 1 | 16 I ÷ 2 → 2 – 4 5 / 2 | – 13 / 2 4 – 7 8 | – 23 – 3 11 1 | 16 I I – 4 × I I I I + 3 × I → 1 – 2 5 / 2 | – 13 / 2 0 1 – 2 | 3 0 5 17 / 2 | – 7 / 2

На втором этапе требуется обнулить элементы второго столбца. Разрешающий элемент – 1, поэтому никаких изменений производить не требуется:

0 1 – 2 | 3 1 – 2 5 / 2 | – 13 / 2 0 5 17 / 2 | – 7 / 2 I + 2 × I I I I I – 5 × I I → 0 1 – 2 | 3 1 0 – 3 / 2 | – 1 / 2 0 0 37 / 2 | – 37 / 2

На третьем этапе необходимо обнулить элементы третьего столбца. Разрешающий элемент – 37/2. Делим все элементы на 37/2 (чтобы сделать равными 1), а затем обнуляем:

0 1 – 2 | 3 1 0 – 3 / 2 | – 1 / 2 0 0 37 / 2 | – 37 / 2 I I I ÷ 37 2 → 1 0 – 3 / 2 | – 1 / 2 0 1 – 2 | 3 0 0 1 | – 1 I + 2 × I I I I I + 3 / 2 × I I I → 1 0 0 | – 2 0 1 0 | 1 0 0 1 | – 1

Ответ: x 1 = – 2 ; x 2 = 1 ; x 3 = – 1 .

4 – 7 8 | – 23 2 – 4 5 | – 13 – 3 11 1 | 16 I ÷ 2 → 2 – 4 5 / 2 | – 13 / 2 4 – 7 8 | – 23 – 3 11 1 | 16 I I – 4 × I I I I + 3 × I → 0 1 – 2 | 3 1 – 2 5 / 2 | – 13 / 2 0 5 17 / 2 | – 7 / 2 I + 2 × I I I I I – 5 × I I →

→ 0 1 – 2 | 3 1 0 – 3 / 2 | – 1 / 2 0 0 37 / 2 | – 37 / 2 I I I ÷ 37 2 → 1 0 – 3 / 2 | – 1 / 2 0 1 – 2 | 3 0 0 1 | – 1 I + 2 × I I I I I + 3 / 2 × I I I → 1 0 0 | – 2 0 1 0 | 1 0 0 1 | – 1

Пример 2

Решить СЛАУ методом Жордана-Гаусса:

3 x 1 + x 2 + 2 x 3 + 5 x 4 = – 6 3 x 1 + x 2 + 2 x 4 = – 10 6 x 1 + 4 x 2 + 11 x 3 + 11 x 4 = – 27 – 3 x 1 – 2 x 2 – 2 x 3 – 10 x 4 = 1

Как решить?

Записать расширенную матрицу данной системы Ã :

3 1 2 5 | – 6 3 1 0 2 | 10 6 4 11 11 | – 27 – 3 – 2 – 2 – 10 | 1

Для решения используем второй способ: выбор разрешающих элементов на главной диагонали системы. На первом этапе выбираем элемент первой строки, на втором – второй строки, на третьем – третьей и т.д.

Необходимо выбрать разрешающий элемент первой строки, т.е. 3. Затем обнуляем все элементы столбца, разделяя на 3 все элементы:

3 1 2 5 | – 6 3 1 0 2 | – 10 6 4 11 11 | – 27 – 3 – 2 – 2 – 10 | 1 I ÷ 3 → 1 1 / 3 2 / 3 5 / 3 | – 2 3 1 0 2 | – 10 6 4 11 11 | – 27 – 3 – 2 – 2 – 10 | 1 I I – 3 × I I I I – 6 × I I V + 3 × I →

→ 1 1 / 3 2 / 3 5 / 3 | – 2 0 0 – 2 – 3 | – 4 0 2 7 1 | – 15 0 – 1 0 – 5 | – 5

Необходимо обнулить элементы второго столбца. Для этого выделяем разрешающий элемент, но элемент первой строки второго столбца равен нулю, поэтому необходимо менять строки местами.

Поскольку в четвертой строке есть число -1, то меняем местами вторую и четвертую строки:

1 1 / 3 2 / 3 5 / 3 | – 2 0 0 – 2 – 3 | – 4 0 2 7 1 | – 15 0 – 1 0 – 5 | – 5 → 1 1 / 3 2 / 3 5 / 3 | – 2 0 – 1 0 – 5 | – 5 0 2 7 1 | – 15 0 0 – 2 – 3 | – 4

Теперь разрешающий элемент равен -1. Делим элементы второго столбца на -1, а затем обнуляем:

1 1 / 3 2 / 3 5 / 3 | – 2 0 – 1 0 – 5 | – 5 0 2 7 1 | – 15 0 0 – 2 – 3 | – 4 I I ÷ (- 1) → 1 1 / 3 2 / 3 5 / 3 | – 2 0 1 0 5 | 5 0 2 7 1 | – 15 0 0 – 2 – 3 | – 4 I – 1 / 3 × I I I I I – 2 × I →

→ 1 0 2 / 3 0 | – 11 / 3 0 1 0 5 | 5 0 0 7 – 9 | – 25 0 0 – 2 – 3 | – 4

На третьем этапе необходимо также обнулить элементы третьего столбца. Для этого находим разрешающий элемент в третьей строке – это 7. Но на 7 делить неудобно, поэтому необходимо менять строки местами, чтобы разрешающий элемент стал -2:

1 0 2 / 3 0 | – 11 / 3 0 1 0 5 | 5 0 0 7 – 9 | – 25 0 0 – 2 – 3 | – 4 → 1 0 2 / 3 0 | – 11 / 3 0 1 0 5 | 5 0 0 – 2 – 3 | – 4 0 0 7 – 9 | – 25

Теперь делим все элементы третьего столбца на -2 и обнуляем все элементы:

1 0 2 / 3 0 | – 11 / 3 0 1 0 5 | 5 0 0 – 2 – 3 | – 4 0 0 7 – 9 | – 25 I I I ÷ (- 2) → 1 0 2 / 3 0 | – 11 / 3 0 1 0 5 | 5 0 0 1 3 / 2 | 2 0 0 0 – 9 | – 25 I – 2 / 3 × I I I I V – 7 × I I I →

1 0 0 – 1 | – 5 0 1 0 5 | 5 0 0 1 3 / 2 | 2 0 0 0 – 39 / 2 | – 39

Четвертый этап

Обнуляем четвертый столбец. Разрешающий элемент – – 39 2:

1 0 0 – 1 | – 5 0 1 0 5 | 5 0 0 1 3 / 2 | 2 0 0 0 – 39 / 2 | – 39 I V ÷ (- 39 2) → 1 0 0 – 1 | – 5 0 1 0 5 | 5 0 0 1 3 / 2 | 2 0 0 0 1 | 2 I + I V I I – 5 × I V I I I – 3 / 2 × I V →

→ 1 0 0 0 | – 3 0 1 0 0 | – 5 0 0 1 0 | – 1 0 0 0 1 | 2 .

Ответ : x 1 = – 3 ; x 2 = – 5 ; x 3 = – 1 ; x 4 = 2

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Метод Гаусса-Жордана предназначен для решения систем линейных алгебраических уравнений (СЛАУ). Он является модификацией метода Гаусса . Если метод Гаусса осуществляется в два этапа (прямой ход и обратный) то метод Гаусса-Жордана позволяет решить систему в один этап. Подробности и непосредственная схема применения метода Гаусса-Жордана описаны в примерах.

Во всех примерах $A$ обозначает матрицу системы, $\widetilde{A}$ – расширенную матрицу системы. О матричной форме записи СЛАУ можно прочесть .

Пример №1

Решить СЛАУ $ \left\{ \begin{aligned} & 4x_1-7x_2+8x_3=-23;\\ & 2x_1-4x_2+5x_3=-13;\\ & -3x_1+11x_2+x_3=16. \end{aligned} \right.$ методом Гаусса-Жордана.

Давайте перейдём от последней полученной нами матрице к системе:

$$ \left\{ \begin{aligned} & 0\cdot x_1+1\cdot x_2+0\cdot x_3=1;\\ & 1\cdot x_1+0\cdot x_2+0\cdot x_3=-2;\\ & 0\cdot x_1+0\cdot x_2+1\cdot x_3=-1. \end{aligned} \right. $$

Упрощая полученную систему, имеем:

$$ \left\{ \begin{aligned} & x_2=1;\\ & x_1=-2;\\ & x_3=-1. \end{aligned} \right. $$

Полное решение без пояснений выглядит так:

Хоть этот способ выбора разрешающих элементов вполне допустим, но предпочтительнее выбирать в качестве разрешающих элементов диагональные элементы матрицы системы. Мы рассмотрим этот способ ниже.

Выбор разрешающих элементов на главной диагонали матрицы системы.

Так как этот способ решения полностью аналогичен предыдущему (за исключением выбора разрешающих элементов), то подробные пояснения пропустим. Принцип выбора разрешающих элементов прост: в первом столбце выбираем элемент первой строки, во втором столбце берём элемент второй строки, в третьем столбце – элемент третьей строки и так далее.

Первый шаг

В первом столбце выбираем элемент первой строки, т.е. в качестве разрешающего имеем элемент 4. Понимаю, что выбор числа 2 кажется более предпочтительным, так как это число всё-таки меньше, нежели 4. Для того, чтобы число 2 в первом столбце переместилось на первое место, поменяем местами первую и вторую строки:

$$ \left(\begin{array} {ccc|c} 4 & -7 & 8 & -23\\ 2 & -4& 5 & -13 \\ -3 & 11 & 1 & 16 \end{array} \right)\rightarrow \left(\begin{array} {ccc|c} 2 & -4& 5 & -13\\ 4 & -7 & 8 & -23 \\ -3 & 11 & 1 & 16 \end{array} \right) $$

Итак, разрешающий элемент представлен числом 2. Точно так же, как и ранее, разделим первую строку на 2, а затем обнулим элементы первого столбца:

$$ \left(\begin{array} {ccc|c} 2 & -4& 5 & -13\\ 4 & -7 & 8 & -23 \\ -3 & 11 & 1 & 16 \end{array} \right) \begin{array} {l} I:2 \\\phantom{0} \\ \phantom{0} \end{array} \rightarrow \left(\begin{array} {ccc|c} 1 & -2& 5/2 & -13/2 \\4 & -7 & 8 & -23\\ -3 & 11 & 1 & 16 \end{array} \right) \begin{array} {l} \phantom{0} \\ II-4\cdot I\\ III+3\cdot I \end{array} \rightarrow \left(\begin{array} {ccc|c} 1 & -2& 5/2 & -13/2\\0 & 1 & -2 & 3\\ 0 & 5 & 17/2 & -7/2 \end{array} \right). $$

Второй шаг

На втором шаге требуется обнулить элементы второго столбца. В качестве разрешающего элемента выбираем элемент второй строки, т.е. 1. Разрешающий элемент уже равен единице, поэтому никаких строк менять местами не будем. Кстати сказать, если бы мы захотели поменять местами строки, то первую строку трогать не стали бы, так как она уже была использована на первом шаге. А вот вторую и третью строки запросто можно менять местами. Однако, повторюсь, в данной ситуации менять местами строки не нужно, ибо разрешающий элемент уже оптимален – он равен единице.

$$ \left(\begin{array} {ccc|c} 1 & -2& 5/2 & -13/2\\0 & 1 & -2 & 3\\ 0 & 5 & 17/2 & -7/2 \end{array} \right) \begin{array} {l} I+2\cdot II \\ \phantom{0}\\ III-5\cdot II \end{array} \rightarrow \left(\begin{array} {ccc|c} 1 & 0 & -3/2 & -1/2 \\ 0 & 1 & -2 & 3\\ 0 & 0 & 37/2 & -37/2 \end{array} \right). $$

Второй шаг окончен. Переходим к третьему шагу.

Третий шаг

На третьем шаге требуется обнулить элементы третьего столбца. В качестве разрешающего элемента выбираем элемент третьей строки, т.е. 37/2. Разделим элементы третьей строки на 37/2 (чтобы разрешающий элемент стал равен 1), а затем обнулим соответствующие элементы третьего столбца:

$$ \left(\begin{array} {ccc|c} 1 & 0 & -3/2 & -1/2 \\ 0 & 1 & -2 & 3\\ 0 & 0 & 37/2 & -37/2 \end{array} \right) \begin{array} {l} \phantom{0}\\ \phantom{0}\\ III:\frac{37}{2} \end{array} \rightarrow \left(\begin{array} {ccc|c} 1 & 0 & -3/2 & -1/2 \\ 0 & 1 & -2 & 3\\ 0 & 0 & 1 & -1 \end{array} \right) \begin{array} {l} I+2\cdot III\\II+3/2\cdot III\\ \phantom{0} \end{array} \rightarrow \left(\begin{array} {ccc|c} 1 & 0 & 0 & -2 \\ 0 & 1 & 0 & 1\\ 0 & 0 & 1 & -1 \end{array} \right). $$

Ответ получен: $x_1=-2$, $x_2=1$, $x_3=-1$. Полное решение без пояснений выглядит так:

Все остальные примеры на этой странице будут решены именно вторым способом: в качестве разрешающих будем выбирать диагональные элементы матрицы системы.

Ответ : $x_1=-2$, $x_2=1$, $x_3=-1$.

Пример №2

Решить СЛАУ $ \left\{ \begin{aligned} & 3x_1+x_2+2x_3+5x_4=-6;\\ & 3x_1+x_2+2x_4=-10;\\ & 6x_1+4x_2+11x_3+11x_4=-27;\\ & -3x_1-2x_2-2x_3-10x_4=1. \end{aligned} \right.$ методом Гаусса-Жордана.

Запишем расширенную матрицу данной системы : $\widetilde{A}=\left(\begin{array} {cccc|c} 3 & 1 & 2 & 5 & -6\\ 3 & 1& 0 & 2 & -10 \\ 6 & 4 & 11 & 11 & -27 \\ -3 & -2 & -2 & -10 & 1 \end{array} \right)$.

В качестве разрешающих элементов станем выбирать диагональные элементы матрицы системы: на первом шаге возьмём элемент первой строки, на втором шаге элемент второй строки и так далее.

Первый шаг

Нам нужно обнулить соответствующие элементы первого столбца. В качестве разрешающего элемента возьмём элемент первой строки, т.е. 3. Соответственно первую строку придётся разделить на 3, чтобы разрешающий элемент стал равен единице. А затем обнулить все элементы первого столбца, кроме разрешающего:

$$ \left(\begin{array}{cccc|c} 3 & 1 & 2 & 5 & -6\\ 3 & 1 & 0 & 2 & -10\\ 6 & 4 & 11 & 11 & -27\\ -3 & -2 & -2 & -10 & 1\end{array}\right) \begin{array} {l} I:3\\ \phantom{0}\\\phantom{0}\\\phantom{0}\end{array} \rightarrow \left(\begin{array}{cccc|c} 1 & 1/3 & 2/3 & 5/3 & -2\\ 3 & 1 & 0 & 2 & -10\\ 6 & 4 & 11 & 11 & -27\\ -3 & -2 & -2 & -10 & 1\end{array}\right) \begin{array} {l} \phantom{0}\\ II-3\cdot I\\III-6\cdot I\\IV+3\cdot I\end{array} \rightarrow\\ \rightarrow\left(\begin{array}{cccc|c} 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & 0 & -2 & -3 & -4\\ 0 & 2 & 7 & 1 & -15\\ 0 & -1 & 0 & -5 & -5\end{array}\right). $$

Второй шаг

Переходим к обнулению соответствующих элементов второго столбца. В качестве разрешающего элемента мы уславливались взять элемент второй строки, но сделать этого мы не в силах, так как нужный элемент равен нулю. Вывод: будем менять местами строки. Первую строку трогать нельзя, так как она уже использовалась на первом шаге. Выбор небогат: или меняем местами вторую и третью строки, или же меняем местами четвёртую и вторую. Так как в четвёртой строке наличествует (-1), то пусть в “обмене” поучавствует именно четвёртая строка. Итак, меняем местами вторую и четвёртую строки:

$$ \left(\begin{array}{cccc|c} 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & 0 & -2 & -3 & -4\\ 0 & 2 & 7 & 1 & -15\\ 0 & -1 & 0 & -5 & -5\end{array}\right)\rightarrow \left(\begin{array}{cccc|c} 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & -1 & 0 & -5 & -5\\ 0 & 2 & 7 & 1 & -15\\ 0 & 0 & -2 & -3 & -4\end{array}\right) $$

Вот теперь всё в норме: разрешающий элемент равен (-1). Бывает, кстати, что смена мест строк невозможна, но это обговорим в следующем примере №3. А пока что делим вторую строку на (-1), а затем обнуляем элементы второго столбца. Обратите внимание, что во втором столбце элемент, расположенный в четвёртой строке, уже равен нулю, поэтому четвёртую строку трогать не будем.

$$ \left(\begin{array}{cccc|c} 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & -1 & 0 & -5 & -5\\ 0 & 2 & 7 & 1 & -15\\ 0 & 0 & -2 & -3 & -4\end{array}\right) \begin{array} {l} \phantom{0}\\II:(-1) \\\phantom{0}\\\phantom{0}\end{array} \rightarrow \left(\begin{array}{cccc|c} 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & 1 & 0 & 5 & 5\\ 0 & 2 & 7 & 1 & -15\\ 0 & 0 & -2 & -3 & -4\end{array}\right) \begin{array} {l} I-1/3\cdot II\\ \phantom{0} \\III-2\cdot II\\\phantom{0}\end{array} \rightarrow\\ \rightarrow\left(\begin{array}{cccc|c} 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 7 & -9 & -25\\ 0 & 0 & -2 & -3 & -4\end{array}\right). $$

Третий шаг

Приступаем к обработке третьего столбца. В качестве разрешающего элемента мы условились брать диагональные элементы матрицы системы. Для третьего шага это означает выбор элемента, расположенного в третьей строке. Однако если мы просто возьмём элемент 7 в качестве разрешающего, то всю третью строку придётся делить на 7. Мне кажется, что разделить на (-2) попроще. Поэтому поменяем местами третью и четвёртую строки, и тогда разрешающим элементом станет (-2):

$$ \left(\begin{array}{cccc|c} 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 7 & -9 & -25\\ 0 & 0 & -2 & -3 & -4\end{array}\right) \rightarrow \left(\begin{array}{cccc|c} 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & -2 & -3 & -4\\ 0 & 0 & 7 & -9 & -25\end{array}\right) $$

Разрешающий элемент – (-2). Делим третью строку на (-2) и обнуляем соответствующие элементы третьего столбца:

$$ \left(\begin{array}{cccc|c} 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & -2 & -3 & -4\\ 0 & 0 & 7 & -9 & -25\end{array}\right) \begin{array} {l} \phantom{0}\\ \phantom{0} \\III:(-2)\\\phantom{0}\end{array}\rightarrow \left(\begin{array}{cccc|c} 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 7 & -9 & -25\end{array}\right) \begin{array} {l} I-2/3\cdot III\\ \phantom{0} \\ \phantom{0}\\IV-7\cdot III\end{array}\rightarrow\\ \rightarrow\left(\begin{array}{cccc|c} 1 & 0 & 0 & -1 & -5\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 0 & -39/2 & -39\end{array}\right). $$

Четвёртый шаг

Переходим к обнулению четвёртого столбца. Разрешающий элемент расположен в четвёртой строке и равен числу $-\frac{39}{2}$.

$$ \left(\begin{array}{cccc|c} 1 & 0 & 0 & -1 & -5\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 0 & -39/2 & -39\end{array}\right) \begin{array} {l} \phantom{0}\\ \phantom{0} \\ \phantom{0}\\IV:\left(-\frac{39}{2}\right) \end{array}\rightarrow \left(\begin{array}{cccc|c} 1 & 0 & 0 & -1 & -5\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 0 & 1 & 2\end{array}\right) \begin{array} {l} I+IV\\ II-5\cdot IV \\ III-3/2\cdot IV \\ \phantom{0} \end{array}\rightarrow\\ \rightarrow\left(\begin{array}{cccc|c} 1 & 0 & 0 & 0 & -3\\ 0 & 1 & 0 & 0 & -5\\ 0 & 0 & 1 & 0 & -1\\ 0 & 0 & 0 & 1 & 2\end{array}\right). $$

Решение окончено. Ответ таков: $x_1=-3$, $x_2=-5$, $x_3=-1$, $x_4=2$.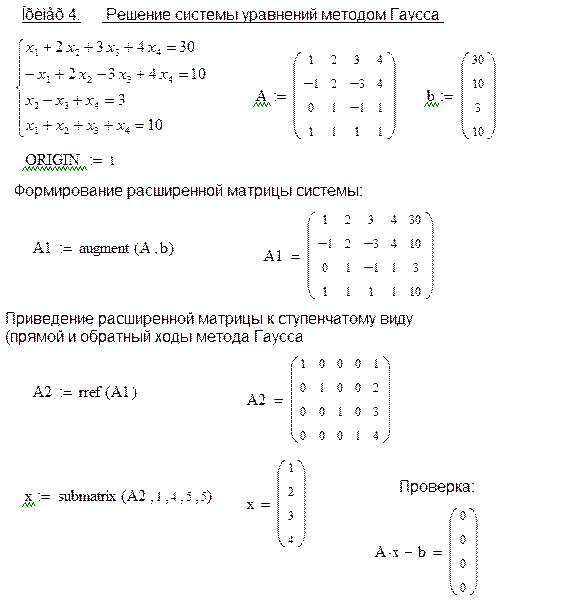 Полное решение без пояснений:

Ответ : $x_1=-3$, $x_2=-5$, $x_3=-1$, $x_4=2$.

Пример №3

Решить СЛАУ $\left\{\begin{aligned} & x_1-2x_2+3x_3+4x_5=-5;\\ & 2x_1+x_2+5x_3+2x_4+9x_5=-3;\\ & 3x_1+4x_2+7x_3+4x_4+14x_5=-1;\\ & 2x_1-4x_2+6x_3+11x_5=2;\\ & -2x_1+14x_2-8x_3+4x_4-7x_5=20;\\ & -4x_1-7x_2-9x_3-6x_4-21x_5=-9. \end{aligned}\right.$ методом Гаусса-Жордана. Если система является неопределённой, указать базисное решение.

Подобные примеры разбираются в теме “Общее и базисное решения СЛАУ” . Во второй части упомянутой темы данный пример решён с помощью метод Гаусса . Мы же решим его с помощью метода Гаусса-Жордана. Пошагово разбивать решение не станем, так как это уже было сделано в предыдущих примерах.

$$ \left(\begin{array}{ccccc|c} 1 & -2 & 3 & 0 & 4 & -5\\ 2 & 1 & 5 & 2 & 9 & -3\\ 3 & 4 & 7 & 4 & 14 & -1\\ 2 & -4 & 6 & 0 & 11 & 2\\ -2 & 14 & -8 & 4 & -7 & 20\\ -4 & -7 & -9 & -6 & -21 & -9 \end{array}\right) \begin{array} {l} \phantom{0} \\ II-2\cdot I\\ III-3\cdot I\\ IV-2\cdot I\\ V+2\cdot I\\VI+4\cdot I \end{array} \rightarrow \left(\begin{array}{ccccc|c} 1 & -2 & 3 & 0 & 4 & -5\\ 0 & 5 & -1 & 2 & 1 & 7\\ 0 & 10 & -2 & 4 & 2 & 14\\ 0 & 0 & 0 & 0 & 3 & 12\\ 0 & 10 & -2 & 4 & 1 & 10\\ 0 & -15 & 3 & -6 & -5 & -29 \end{array}\right) \begin{array} {l} \phantom{0} \\ II:5 \\ \phantom{0}\\ \phantom{0}\\ \phantom{0} \\ \phantom{0}\end{array} \rightarrow \\ \left(\begin{array}{ccccc|c} 1 & -2 & 3 & 0 & 4 & -5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 10 & -2 & 4 & 2 & 14\\ 0 & 0 & 0 & 0 & 3 & 12\\ 0 & 10 & -2 & 4 & 1 & 10\\ 0 & -15 & 3 & -6 & -5 & -29 \end{array}\right) \begin{array} {l} I+2\cdot II \\ \phantom{0}\\ III-10\cdot II\\ IV:3\\ V-10\cdot II\\VI+15\cdot II \end{array} \rightarrow \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & -1 & -4\\ 0 & 0 & 0 & 0 & -2 & -8 \end{array}\right). $$

Полагаю, что одно из сделанных преобразований всё-таки требует пояснения: $IV:3$. Все элементы четвёртой строки нацело делились на три, поэтому сугубо из соображений упрощения мы разделили все элементы этой строки на три. Третья строка в преобразованной матрице стала нулевой. Вычеркнем нулевую строку:

$$ \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & -1 & -4\\ 0 & 0 & 0 & 0 & -2 & -8 \end{array}\right) $$

Нам пора переходить к третьему шагу, на котором должны быть обнулены элементы третьего столбца. Однако диагональный элемент (третья строка) равен нулю. И смена мест строк ничего не даст. Первую и вторую строки мы уже использовали, поэтому их трогать мы не можем. А четвёртую и пятую строки трогать нет смысла, ибо проблема равенства нулю разрешающего элемента никуда не денется.

В этой ситуации проблема решается крайне незамысловато. Мы не можем обработать третий столбец? Хорошо, перейдём к четвёртому. Может, в четвёртом столбце элемент третьей строки будет не равен нулю. Однако четвёртый столбец “болеет” той же проблемой, что и третий. Элемент третьей строки в четвёртом столбце равен нулю. И смена мест строк опять-таки ничего не даст. Четвёртый столбец тоже не можем обработать? Ладно, перейдём к пятому. А вот в пятом столбце элемент третьей строки очень даже не равен нулю. Он равен единице, что довольно-таки хорошо. Итак, разрешающий элемент в пятом столбце равен 1. Разрешающий элемент выбран, поэтому осуществим дальшейшие преобразования метода Гаусса-Жордана:

$$ \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & -1 & -4\\ 0 & 0 & 0 & 0 & -2 & -8 \end{array}\right) \begin{array} {l} I-22/5\cdot III \\ II-1/5\cdot III \\ \phantom{0}\\ IV+III\\ V+2\cdot III \end{array} \rightarrow \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 0 & -99/5\\ 0 & 1 & -1/5 & 2/5 & 0 & 3/5\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right) \rightarrow \\ \rightarrow\left|\text{Удаляем нулевые строки}\right|\rightarrow \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 0 & -99/5\\ 0 & 1 & -1/5 & 2/5 & 0 & 3/5\\ 0 & 0 & 0 & 0 & 1 & 4 \end{array}\right)$$

Мы привели матрицу системы и расширенную матрицу системы к ступенчатому виду. Ранги обеих матриц равны $r=3$, т.е. надо выбрать 3 базисных переменных. Количество неизвестных $n=5$, поэтому нужно выбрать $n-r=2$ свободных переменных. Так как $r

На “ступеньках” стоят элементы из столбцов №1, №2, №5. Следовательно, базисными будут переменные $x_1$, $x_2$, $x_5$. Свободными переменными, соответственно, будут $x_3$, $x_4$. Столбцы №3 и №4, соответствующие свободным переменным, перенесём за черту, при этом, конечно, не забыв сменить им знаки.

$$ \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 0 & -99/5\\ 0 & 1 & -1/5 & 2/5 & 0 & 3/5\\ 0 & 0 & 0 & 0 & 1 & 4 \end{array}\right)\rightarrow \left(\begin{array}{ccc|ccc} 1 & 0 & 0 & -99/5 & -13/5 & -4/5\\ 0 & 1 & 0 & 3/5 & 1/5 & -2/5\\ 0 & 0 & 1 & 4 & 0 & 0\end{array}\right). $$

Из последней матрицы получим общее решение: $\left\{\begin{aligned} & x_1=-\frac{99}{5}-\frac{13}{5}x_3-\frac{4}{5}x_4;\\ & x_2=\frac{3}{5}+\frac{1}{5}x_3-\frac{2}{5}x_4;\\ & x_3 \in R;\\ & x_4\in R;\\ & x_5=4. \end{aligned}\right.$. Базисное решение найдём, приняв свободные переменные равными нулю, т.е. $x_3=0$, $x_4=0$:

$$ \left\{\begin{aligned} & x_1=-\frac{99}{5};\\ & x_2=\frac{3}{5};\\ & x_3=0;\\ & x_4=0;\\ & x_5=4. \end{aligned}\right. $$

Задача решена, осталось лишь записать ответ.

Ответ : Общее решение: $\left\{\begin{aligned} & x_1=-\frac{99}{5}-\frac{13}{5}x_3-\frac{4}{5}x_4;\\ & x_2=\frac{3}{5}+\frac{1}{5}x_3-\frac{2}{5}x_4;\\ & x_3 \in R;\\ & x_4\in R;\\ & x_5=4. \end{aligned}\right.$, базисное решение: $\left\{\begin{aligned} & x_1=-\frac{99}{5};\\ & x_2=\frac{3}{5};\\ & x_3=0;\\ & x_4=0;\\ & x_5=4. \end{aligned}\right.$.

4. Метод Жордана – Гаусса.

Схема с выбором главного элемента состоит в том, что требование неравенства нулю диагональных элементов akk, на которые происходит деление в процессе исключения, заменятся более жестким: из всех элементов К-го столба выбрать наибольший по модулю и переставить уравнения так, чтобы этот элемент оказался на месте элемента акк. Выбор главного элемента и связанная с ним перестановка строк необходимы в тех случаях, когда на каком-либо i-ом шаге акк=0 либо же акк очень мало по остальными элементами i- го столбца: при делении на такое «малое» акк будут получаться большие числа с большими абсолютными погрешностями, в результате чего решение может сильно исказиться.

Ниже излагается алгоритм полного исключения неизвестных или метод Жордана – Гаусса. Суть метода состоит в том, что, рассмотрев первое уравнение, в нем неизвестное с коеффициэнтом, отличным от нуля (в дальнейшем разрешающий элемент), и разделив первое уравнение на этот коэффициент, с помощью первого уравнения исключают это неизвестное из всех уравнений, кроме первого. Выбрав во втором уравнении неизвестное с коэффициентом, отличным от нуля, и разделив на него второе уравнение, с помощью второго исключают другие неизвестные из всех уравнений, кроме второго и т.д., т.е. с помощью одного уравнения производят полное исключение одного неизвестного. Процесс продолжается до тех пор, пока не будут использованы все уравнения.

Как известно, системы линейных алгебраических уравнений могут имеет одно решение, множество решений или системы несовместны. При элементарных преобразованиях элементов матрицы системы эти случаи выявляются в следующем:

1. В процессе исключений левая часть I –го уравнения системы обращается в нуль, а правая часть равна некоторому числу, отличному от нуля. т.е. 02+=bc0.

Это означает, что система не имеет решений, так как I – му уравнению не могут удовлетворять никакие значения неизвестных;

2. Левая и правая части I – го уравнения обращаются в нуль. Это означает, что I – ое уравнение является линейной комбинацией остальных, ему удовлетворяет любое найденное решение системы, поэтому оно может быть отброшено. В системе количество неизвестных больше количества уравнений и, следовательно, такая система имеет множество решений;

3. После того как все уравнения использованы для исключения неизвестных получено решение системы.

Таким образом, конечной целью преобразований Жордана-Гаусса является получение из заданной линейной системы

a11x1 + a12x2 + … + a1nxn = b1,n+1

a21x1 + a22x2 + … + a2nxn = b2,n+1

am1x1 + am2x2 + … + amnxn = bm.

n+1

Здесь x1, x2, …, xn – неизвестные, которые надо определить. a11, a12, …, amn – коэффициенты системы – и b1, b2, … bm – свободные члены – предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.

Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе – неоднородной.

Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.

Решение системы (1) – совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все ее уравнения в тождества.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения.

Совместная система вида (1) может иметь одно или более решений.

Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:

c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).

Совместная система вида (1) называется определенной, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределенной. Если уравнений больше, чем неизвестных, она называется переопределённой.

Решим следующую систему уравнений:

Запишем её в виде матрицы 3×4, где последний столбец является свободным членом:

Проведём следующие действия:

· К строке 2 добавим: -4 * Строку 1.

· К строке 3 добавим: -9 * Строку 1.

· К строке 3 добавим: -3 * Строку 2.

· Строку 2 делим на -2

· К строке 1 добавим: -1 * Строку 3.

· К строке 2 добавим: -3/2 * Строку 3.

· К строке 1 добавим: -1 * Строку 2.

В правом столбце получаем решение:

В методе Ньютона наблюдается ускорение сходимости процесса приближений. 5. Метод касательных (метод Ньютона) Метод касательных, связанный с именем И. Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Возьмём производную точку x0 и запишем в ней уравнение касательной к графику функции f(x): y=f(x0)+ f ¢(x) (x-x0) (1.5) Графики…

Решения от численных методов расчёта. Для определения корней уравнения не требуется знания теорий групп Абеля, Галуа, Ли и пр. и применения специальной математической терминологии: колец, полей, идеалов, изоморфизмов и т.д. Для решения алгебраического уравнения n – ой степени нужно только умение решать квадратные уравнения и извлекать корни из комплексного числа. Корни могут быть определены с…

Математики тригонометрической подстановки и проверка эффективности разработанной методики преподавания. Этапы работы: 1. Разработка факультативного курса на тему: «Применение тригонометрической подстановки для решения алгебраических задач» с учащимися классов с углубленным изучением математики. 2. Проведение разработанного факультативного курса. 3. Проведение диагностирующей контрольной…

… «проявляется» лишь в процессе преобразований. Очевидность и «завуалированность» новой переменной мы рассмотрим на конкретных примерах во второй главе данной работы. 2. Возможности применения метода замены неизвестного при решении алгебраических уравнений В этой главе выявим возможности применения метода замены неизвестного при решении алгебраических уравнений в стандартных и нестандартных…

Здесь вы сможете бесплатно решить систему линейных уравнений методом Гаусса онлайн больших размеров в комплексных числах с очень подробным решением. Наш калькулятор умеет решать онлайн как обычную определенную, так и неопределенную систему линейных уравнений методом Гаусса, которая имеет бесконечное множество решений. В этом случае в ответе вы получите зависимость одних переменных через другие, свободные. Также можно проверить систему уравнений на совместность онлайн, используя решение методом Гаусса.

О методе

При решении системы линейных уравнений онлайн методом Гаусса выполняются следующие шаги.

Записываем расширенную матрицу.
Фактически решение разделяют на прямой и обратный ход метода Гаусса. Прямым ходом метода Гаусса называется приведение матрицы к ступенчатому виду. Обратным ходом метода Гаусса называется приведение матрицы к специальному ступенчатому виду. Но на практике удобнее сразу занулять то, что находится и сверху и снизу рассматриваемого элемента. Наш калькулятор использует именно этот подход.
Важно отметить, что при решении методом Гаусса, наличие в матрице хотя бы одной нулевой строки с НЕнулевой правой частью (столбец свободных членов) говорит о несовместности системы. Решение линейной системы в таком случае не существует.

Чтобы лучше всего понять принцип работы алгоритма Гаусса онлайн введите любой пример, выберите “очень подробное решение” и посмотрите его решение онлайн.

Приведение расширенной матрицы к треугольному виду

Верхнетреугольной называется матрица у которой все элементы ниже главной диагонали равны нулю.

Данный онлайн калькулятор приводит матрицу к верхнетреугольному виду с подробным описанием хода решения на русском языке. Для пользования калькулятором необходимо выбрать размерность матрицы и ввести значения её элементов.

Приведение матрицы к треугольному виду методом Гаусса и методом Барейса.

Ниже два калькулятора для приведения матриц к треугольному, или ступенчатому, виду. Первый использует для этого метод Гаусса, второй — метод Барейса. Описание методов и немного теории — под калькуляторами.

Приведение матрицы к треугольному виду (метод Гаусса)

Приведение матрицы к треугольному виду (метод Барейса)

Итак, для начала определимся с понятием треугольной, или ступенчатой матрицы:
Матрица имеет ступенчатый вид, если:

Все нулевые строки матрицы стоят последними
Первый ненулевой элемент строки всегда находится строго правее первого ненулевого элемента предыдущей строки
Все элементы столбца под первым ненулевым элементом строки равны нулю (это впрочем следует из первых двух пунктов)

Пример ступенчатой матрицы:
1 0 2 5
0 3 0 0
0 0 0 4

Понятие треугольной матрицы более узкое, оно используется только для квадратных матриц (хотя я думаю, что это не строго), и формулируется проще: треугольная матрица — квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.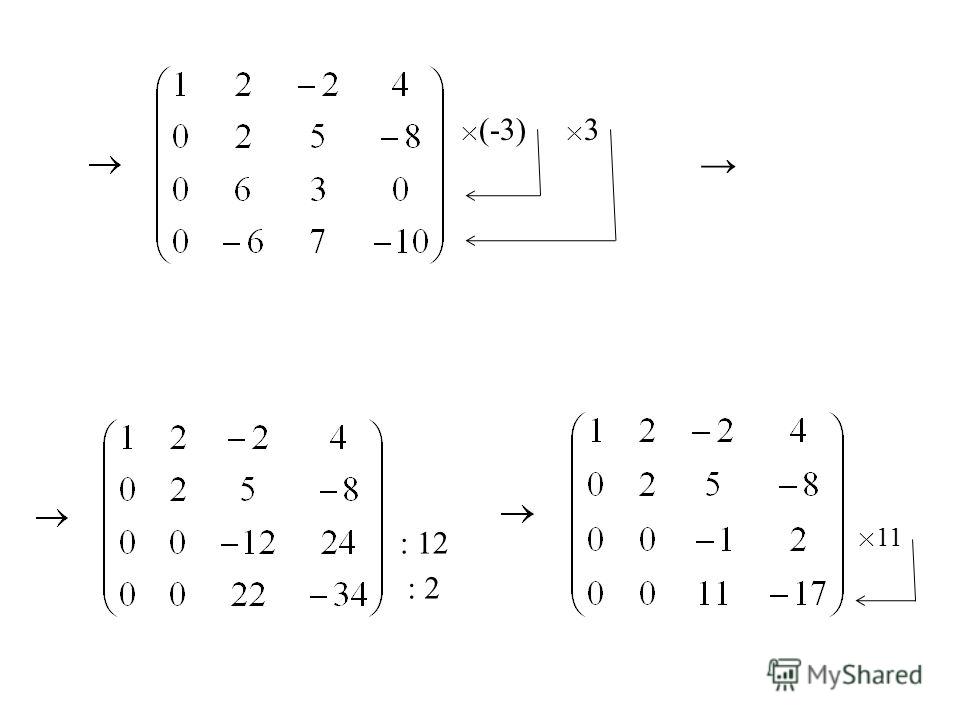 Строго говоря, это даже определение верхнетреугольной матрицы, но мы будем использовать его. Понятно, что такая верхнетреугольная матрица является также и ступенчатой.

Пример треугольной (верхнетреугольной) матрицы:
1 0 2 5
0 3 1 3
0 0 4 2
0 0 0 3
Кстати, определитель треугольной матрицы вычисляется простым перемножением ее диагональных элементов.

Чем же так интересны ступенчатые (и треугольные) матрицы, что к ним надо приводить все остальные? — спросите вы.
У них есть замечательной свойство, а именно, любую прямоугольную матрицу можно с помощью элементарных преобразований привести к ступенчатой форме.

Что же такое элементарные преобразования? — спросите вы.
Элементарными преобразованиями матрицы называют следующие операции:

перестановка любых двух строк (столбцов) матрицы
умножение любой строки (столбца) на призвольное, отличное от нуля, число
сложение любой строки (столбца) с другой строкой (столбцом), умноженной (умноженным) на произвольное, отличное от нуля, число.

И что? — спросите вы.
А то, что элементарные преобразования матрицы сохраняют эквивалентность матриц. А если вспомнить, что системы линейных алгебраический уравнений (СЛАУ) записывают как раз в матричной форме, то это означает, что элементарные преобразования матрицы не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

Приведя матрицу системы линейных уравнений AX=B к треугольной форме A’X = B’, то есть, с соответствующими преобразованиями столбца B, можно найти решение этой системы так называемым «обратным ходом».

Чтобы было понятно, используем треугольную матрицу выше и перепишем систему уравнений в более привычной форме (столбец B я придумал сам):

Понятно, что сначала мы найдем , потом, подставив его в предыдущее уравнение, найдем и так далее — двигаясь от последнего уравнения к первому. Это и есть обратный ход.

Алгоритм приведения матрицы к ступенчатой форме с помощью элементарных преобразований называют методом Гаусса.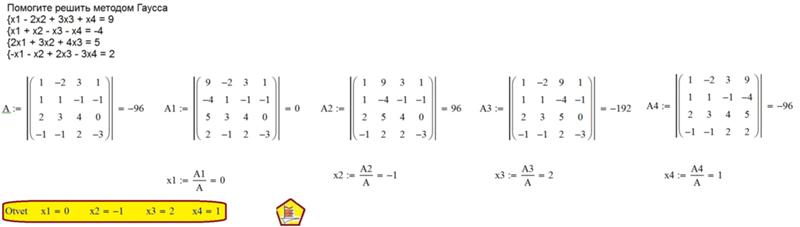 Метод Гаусса — классический метод решения систем линейных алгебраических уравнений. Также его еще называют Гауссовым исключением, так как это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к эквивалентной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Теперь про сам метод.
Собственно, как можно занулить переменную во втором уравнении? Вычтя из него первое, домноженное на коэффициент
Поясним на примере:

Зануляем во втором уравнении:

Во втором уравнении больше не содержится

Обобщенно алгоритм метода Гаусса можно представить следующим образом:

где N — число строк,
— i-тая строка,
— элемент, находящийся в i-той строке, j-том столбце

И все бы ничего, да и метод отличный, но. Дело все в делении на , присутствующем в формуле. Во-первых, если диагональный элемент будет равен нулю, то метод работать не будет. Во-вторых, в процессе вычисления будет накапливаться погрешность, и чем дальше, тем больше. Результат будет отличаться от точного.

Для уменьшения погрешности используют модификации метода Гаусса, которые основаны на том, что погрешность тем меньше, чем больше знаменатель дроби. Эти модификации — метод Гаусса с выбором максимума в столбце и метод Гаусса с выбором максимума по всей матрице. Как следует из названия, перед каждым шагом исключения переменной по столбцу (всей матрице) ищется элемент с максимальным значением и проводится перестановка строк (строк и столбцов), таким образом, чтобы он оказался на месте .

Но есть еще более радикальная модификация метода Гаусса, которая называется методом Барейса (Bareiss).
Как можно избавиться от деления? Например, умножив перед вычитанием строку на . Тогда вычитать надо будет строку , домноженную только на , без всякого деления.
.
Уже хорошо, но возникает проблема с ростом значений элементов матрицы в ходе вычисления.

Барейс предложил делить выражение выше на и показал, что если исходные элементы матрицы — целые числа, то результатом вычисления такого выражения тоже будет целое число. При этом принимается, что для нулевой строки .

Кстати, то, что в случае целочисленных элементов исходной матрицы алгоритм Барейса приводит к треугольной матрице с целочисленными элементами, то есть без накопления погрешности вычислений — довольно важное свойство с точки зрения машинной арифметики.

Алгоритм Барейса можно представить следующим образом:

Алгоритм, аналогично методу Гаусса, также можно улучшить поиском максимума по столбцу(всей матрице) и перестановкой соответствующих строк (строк и столбцов).

Введите матрицу A

Используйте только квадратные матрицы!
На этой странице введите матрицу, чтобы произвести проведение матрицы к треугольному виду. Таким образом вы проделаете преобразование матрицы к треугольному виду A
Будут вычислены верхнетреугольная матрица и нижнетреугольная матрицы

Если вам интересно, для чего используется приведение к треугольному виду матрицы, то смотрите калькулятор по решению систем уравнений методом Гаусса здесь

Матрица

Простой матричный калькулятор

Это примет матрицу размером до 5×6 в уменьшенную форму эшелона строк на Исключение Гаусса.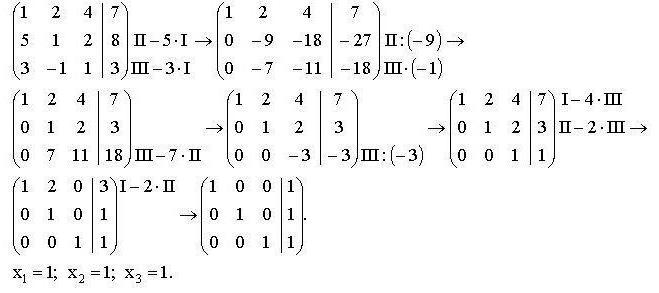

Каждая операция элементарной строки будут напечатаны. Учитывая матрицу размером меньше 5×6, поместите ее в верхнем левом углу и оставьте лишнее строки и столбцы пустые. Были включены некоторые примерные значения. Нажмите «Очистить», чтобы от них избавиться.

A – это матрица 2×2, а B – матрица 2×1. Этот калькулятор попытается найти AB и решить AX = B путем вычисления A ^-1 B, когда это возможно.В противном случае он сообщит, согласован ли он. Он также дает det, rank и собственные значения.

Несколько комментариев о том, что происходит за кулисами: Исключение Гаусса использует то же алгоритм, который вы использовали бы вручную: работа оставлена вправо, и выполните элементарные операции со строками, чтобы каждый столбец иметь правильную форму. Это помещает матрицу в эшелон форма. Затем вернитесь и удалите лишние записи, чтобы получить это в сокращенной форме.
Для второй части обратное вычисляется стандартная формула с использованием определителей A ^-1 = (1 / det (A)) присоединенный (A) Это отлично работает в нашем случае (2×2), хотя это невозможно.

для матриц большего размера.Тест на согласованность основан на идее, что для разрешимости AX = B нам нужно, чтобы B находилась в пространство столбцов A. Итак, достаточно проверить, что размерность Col (A) = Col (A | B). Это то, что ранги A и (A | B) совпадают. Разряды вычисляется с использованием несовершеннолетних. Собственные значения получаются путем решения характеристическое уравнение det (tI-A) = t ² -trace (A) t + det (A) = 0 Поскольку он квадратичный, это легко сделать явно.

По сути, это “демонстрация”, которую я собрал для учебные цели.Это должно быть хорошо для простых примеров но иногда он может давать неправильные ответы из-за до ошибки округления . Обычно он пытается предупредить вас, когда такие ошибки вероятны. Существует множество серьезных программ для обработки матриц. там. Некоторые из них бесплатны (октава или scilab), а некоторые нет (матлаб).

– Дону Арапура

Форма эшелона строк и форма пониженного эшелона

Содержание (Щелкните, чтобы перейти в этот раздел:

Echelon Form?
Форма эшелона
Форма пониженного эшелона строки
Исключение по Гауссу
Ранг матрицы

Что такое форма эшелона?

Форма

Echelon означает, что матрица находится в одном из двух состояний:

Рядный эшелонированный вид.
Уменьшенная форма эшелона строки.

Это означает, что матрица удовлетворяет следующим трем требованиям:

Первое число в строке (называемое ведущим коэффициентом) – 1. Примечание: некоторые авторы не требуют, чтобы ведущий коэффициент был равен 1; это могло быть любое число. Вы можете узнать у своего инструктора, какой версии этого правила они придерживаются).
Каждая ведущая единица находится справа от первой.
Любые ненулевые строки всегда находятся над строками со всеми нулями.

Следующие примеры представляют собой матрицы в эшелонированной форме:

Следующие примеры – это , а не в эшелонированной форме:

Матрица A не имеет строк со всеми нулями ниже ненулевых строк.
Matrix B имеет 1 на 2 позиции в третьем ряду. Для формы эшелона строки он должен быть справа от ведущего коэффициента над ним. Другими словами, он должен быть на четвертой позиции вместо 3.
Matrix C имеет 2 в качестве ведущего коэффициента вместо 1.
Матрица D имеет -1 в качестве ведущего коэффициента вместо 1.

Другой способ думать о матрице в форме эшелона – это то, что матрица подверглась гауссовскому исключению, которое представляет собой серию операций со строками.

Уникальность и формы эшелона

Эшелонированная форма матрицы не уникальна, что означает, что при сокращении строк возможно бесконечное количество ответов. Уменьшенная форма эшелона строки находится на другом конце спектра; он уникален на , что означает, что сокращение строк в матрице даст один и тот же ответ независимо от того, как вы выполняете те же операции со строками.
Вернуться к началу.

Что такое форма эшелона строк?

Матрица находится в форме эшелона строк, если она соответствует следующим требованиям:

Первое ненулевое число слева («ведущий коэффициент») всегда находится справа от первого ненулевого числа в строке выше.
Строки, состоящие из нулей, находятся внизу матрицы.

Рядная форма эшелона. «А» может представлять любое число.

Технически, ведущий коэффициент может быть любым числом.Однако в большинстве учебников линейной алгебры утверждается, что ведущим коэффициентом должно быть число 1. Чтобы добавить путаницы, некоторые определения формы эшелона строк утверждают, что должны быть нули как выше , так и ниже ведущего коэффициента. Поэтому лучше всего следовать определению, данному в учебнике, которому вы следуете (или тому, что дал вам ваш профессор). Если вы не уверены (то есть сейчас воскресенье, у вас должна быть домашняя работа, и вы не можете связаться с профессором), безопаснее всего использовать 1 в качестве ведущего коэффициента в каждой строке.

Если ведущий коэффициент в каждой строке – это только ненулевое число в этом столбце, матрица называется уменьшенной эшелонированной строкой.

Матрица 3 × 5 в сокращенной форме эшелона строк.

Формы эшелона строк обычно встречаются в линейной алгебре, когда вас иногда просят преобразовать матрицу в эту форму. Форма эшелона строк может помочь вам увидеть, что представляет собой матрица, а также является важным шагом к решению систем линейных уравнений.

Онлайн-калькулятор формы эшелона строк

Этот онлайн-калькулятор преобразует любую матрицу, и предоставляют операции со строками, которые помогут вам от шага к шагу.На следующем изображении (из калькулятора Университета Старого Доминиона показано, как матрица [01, 00, 59] приводится к форме эшелона строк с помощью двух простых операций со строками:

Вернуться к началу.

Что такое форма сокращенного эшелона строк?

Уменьшенная форма эшелона строк – это тип матрицы, используемой для решения систем линейных уравнений. Форма пониженного ряда имеет четыре требования:

Первое ненулевое число в первой строке (, ведущая запись ) – это число 1.
Вторая строка также начинается с цифры 1, которая находится правее первой записи в первой строке. В каждом последующем ряду цифра 1 должна быть правее.
Начальная запись в каждой строке должна быть единственным ненулевым числом в ее столбце.
Любые ненулевые строки помещаются внизу матрицы.

Матрица 3 × 5 в сокращенной форме эшелона строк.

Преобразование матрицы в форму сокращенного эшелона строк

Любая матрица может быть преобразована в сокращенную форму эшелона строк с помощью метода, называемого исключением по Гауссу.Это особенно полезно для решения систем линейных уравнений. Большинство графических калькуляторов (например, TI-83) имеют функцию rref, которая преобразует матрицу в сокращенную форму эшелона строк. См .: В этой статье на веб-сайте Университета штата Колорадо приведены инструкции по использованию TI-89 и TI-83 для расчета формы сокращенного эшелона строки.
Этот онлайн-калькулятор на веб-сайте Old Dominion University преобразует вводимую вами матрицу в сокращенную форму эшелона строк.

Для ручного расчета требуется знание элементарных операций со строками, а именно:

Поменять местами один ряд другим.
Умножить одну строку на ненулевую константу.
Заменить одну строку на: одну строку плюс константу, умноженную на другую строку.

Кроме того, недостаточно просто знать правила, вы должны уметь взглянуть на матрицу и принять логическое решение о том, какое правило вы собираетесь использовать и когда. Вы пытаетесь преобразовать матрицу в сокращенный ряд строк, поэтому вам также нужно будет обратиться к четырем требованиям, приведенным в начале этой статьи. Если вам нужно вручную преобразовать матрицу в сокращенную форму эшелона строк, рекомендуется использовать один из приведенных выше калькуляторов, чтобы проверить свою работу.Фактически, если вы используете онлайн-калькулятор ODU, он даже предоставит вам операции со строками. На изображении ниже показано преобразование калькулятором матрицы [204,923]:

Вернуться к началу.

Что такое метод исключения Гаусса?

Метод исключения Гаусса – это способ найти решение системы линейных уравнений. Основная идея состоит в том, что вы выполняете математическую операцию над строкой и продолжаете, пока не останется только одна переменная. Например, некоторые возможные операции со строками:

Поменять местами любые два ряда
Сложите две строки вместе.
Умножить одну строку на ненулевую константу (например, 1/3, -1, 5)

Вы также можете выполнять более одной строковой операции одновременно. Например, умножьте одну строку на константу, а затем добавьте результат к другой строке.

После этого цель состоит в том, чтобы получить матрицу в уменьшенной форме эшелона строк, где ведущий коэффициент, 1, в каждой строке находится справа от ведущего коэффициента в строке над ней. Другими словами, вам нужно получить 1 в верхнем левом углу матрицы.В следующей строке должен быть 0 в позиции 1 и 1 в позиции 2. Это дает вам решение системы линейных уравнений.

Пример исключения Гаусса

Решите следующую систему линейных уравнений методом исключения Гаусса:

х + 5у = 7
-2x – 7y = -5

Шаг 1: Преобразуйте уравнение в форму матрицы коэффициентов . Другими словами, просто возьмите коэффициент для чисел и забудьте пока о переменных:

Шаг 2. Превратите числа в нижнем ряду в положительные, прибавив 2 раза к первому ряду:

Шаг 3: Умножьте вторую строку на 1/3.Это дает вам второй ведущий 1:

Шаг 4: Умножьте строку 2 на -5, а затем добавьте это к строке 1:

Вот и все!
В первой строке у вас x = -8, а во второй строке y = 3. Обратите внимание, что x и y находятся в тех же положениях, что и при преобразовании уравнения на шаге 1, поэтому все, что вам нужно сделать, это прочтите решение:

Вернуться к началу.

Что такое ранг матрицы?

Ранг матрицы равен количеству линейно независимых строк.Линейно независимая строка – это строка, которая не является комбинацией других строк.

Следующая матрица имеет две линейно независимых строки (1 и 2). Однако, когда в смесь добавляется третья строка, вы можете видеть, что первая строка теперь равна сумме второй и третьей строк. Следовательно, ранг этой конкретной матрицы равен 2, так как имеется только две линейно независимых строки.

Ранг матрицы всегда будет на меньше, чем количества ненулевых строк или количества столбцов в матрице.Если все строки в матрице линейно независимы, матрица будет иметь ранг с полным рангом строки . Для квадратной матрицы она имеет полный ранг только в том случае, если ее определитель не равен нулю.

Вычислить ранг матрицы, пытаясь определить только на глаз, сколько строк или столбцов линейно независимы, может быть практически невозможно. Более простой (и, возможно, очевидный) способ – преобразовать в форму эшелона строк.

Как найти матрицу Рейтинг

Найти ранг матрицы просто, если вы знаете, как найти матрицу эшелона строк.Чтобы найти ранг любой матрицы:

Найдите матрицу эшелона строк.
Подсчитать количество ненулевых строк.

Преобразование матрицы в форму эшелона строк.

Вышеупомянутая матрица была преобразована в форму эшелона строк с двумя ненулевыми строками. Следовательно, ранг матрицы равен 2.

Вы также можете найти отличный инструмент для конвертации на сайте Old Dominion University.

Вернуться к началу.

Список литературы

Эверитт, Б.S .; Скрондал А. (2010), Кембриджский статистический словарь, Cambridge University Press.
Гоник Л. (1993). Мультяшный справочник по статистике. HarperPerennial.
Сирл, С. (2017). Матричная алгебра, полезная для статистики (серия Уайли по вероятности и статистике), 2-е издание. Вайли.

————————————————– —————————-

Нужна помощь с домашним заданием или контрольным вопросом? С помощью Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.Ваши первые 30 минут с репетитором Chegg бесплатны!

Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .

Решающие системы с исключением Гаусса – Precalculus

Цели обучения

В этом разделе вы:

Напишите расширенную матрицу системы уравнений.
Напишите систему уравнений из расширенной матрицы.
Выполнение операций со строками в матрице.
Решите систему линейных уравнений, используя матрицы.

Немецкий математик Карл Фридрих Гаусс (1777–1855).

Карл Фридрих Гаусс жил в конце 18 – начале 19 века, но до сих пор считается одним из самых плодовитых математиков в истории. Его вклад в математику и физику охватывает такие области, как алгебра, теория чисел, анализ, дифференциальная геометрия, астрономия и оптика.Его открытия в области теории матриц изменили способ работы математиков за последние два столетия.

Мы впервые столкнулись с исключением Гаусса в системах линейных уравнений: две переменные. В этом разделе мы еще раз вернемся к этой технике решения систем, на этот раз с использованием матриц.

Написание расширенной матрицы системы уравнений

Матрица может служить средством представления и решения системы уравнений. Чтобы выразить систему в матричной форме, мы извлекаем коэффициенты переменных и констант, и они становятся элементами матрицы.Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по сути заменяя знаки равенства. Когда система написана в такой форме, мы называем ее расширенной матрицей.

Например, рассмотрим следующую систему уравнений.

Мы можем записать эту систему в виде расширенной матрицы:

Мы также можем написать матрицу, содержащую только коэффициенты. Это называется матрицей коэффициентов.

Система уравнений три на три, например

имеет матрицу коэффициентов

и представлена расширенной матрицей

Обратите внимание, что матрица написана так, что переменные выстраиваются в свои собственные столбцы: x -термов идут в первом столбце, – -термов во втором столбце и z -термов в третьем столбце.Очень важно, чтобы каждое уравнение было написано в стандартной форме, чтобы переменные совпадали. Если в уравнении отсутствует член переменной, коэффициент равен 0.

Для данной системы уравнений напишите расширенную матрицу.

Запишите коэффициенты членов x как числа в первом столбце.
Запишите коэффициенты членов y в виде чисел во втором столбце.
Если имеется z -термов, запишите коэффициенты в виде чисел в третьем столбце.
Нарисуйте вертикальную линию и напишите константы справа от нее.

Написание расширенной матрицы для системы уравнений

Напишите расширенную матрицу для данной системы уравнений.

Расширенная матрица отображает коэффициенты переменных и дополнительный столбец для констант.

Напишите расширенную матрицу данной системы уравнений.

Написание системы уравнений из расширенной матрицы

Мы можем использовать расширенные матрицы, чтобы помочь нам решать системы уравнений, потому что они упрощают операции, когда системы не обременены переменными.Однако важно понимать, как переключаться между форматами, чтобы поиск решений был более плавным и интуитивно понятным. Здесь мы будем использовать информацию в расширенной матрице, чтобы записать систему уравнений в стандартной форме.

Напишите систему уравнений из расширенной матрицы.

Выполнение операций со строками в матрице

Теперь, когда мы можем записывать системы уравнений в форме расширенной матрицы, мы рассмотрим различные операции со строками, которые могут выполняться с матрицей, такие как сложение, умножение на константу и перестановка строк.

Выполнение операций со строками в матрице – это метод, который мы используем для решения системы уравнений. Чтобы решить систему уравнений, мы хотим преобразовать матрицу в форму строки-эшелона, в которой есть единицы вниз по главной диагонали от верхнего левого угла до нижнего правого угла и нули в каждой позиции ниже главной диагонали. как показано.

Мы используем операции со строками, соответствующие операциям с уравнениями, чтобы получить новую матрицу, эквивалентную строкам в более простой форме.Вот рекомендации по получению формы рядного эшелона.

В любой ненулевой строке первым ненулевым числом является 1. Оно называется ведущим 1.
Любые нулевые строки помещаются внизу матрицы.
Любая ведущая 1 находится ниже и правее предыдущей ведущей 1.
Любой столбец, в котором в начале стоит 1, имеет нули во всех остальных позициях в столбце.

Чтобы решить систему уравнений, мы можем выполнить следующие операции со строками, чтобы преобразовать матрицу коэффициентов в форму ряда строк и выполнить обратную подстановку, чтобы найти решение.

Поменять ряды местами. (Обозначение 🙂
Умножить строку на константу. (Обозначение 🙂
Добавить произведение одной строки на константу в другую строку. (Замечание:

Каждая из строковых операций соответствует операциям, которые мы уже научились решать системы уравнений с тремя переменными. С помощью этих операций есть несколько ключевых ходов, которые быстро достигнут цели написания матрицы в виде эшелона строк. Чтобы получить матрицу в виде эшелона строк для поиска решений, мы используем метод исключения Гаусса, который использует операции со строками для получения 1 в качестве первой записи, так что строку 1 можно использовать для преобразования оставшихся строк.

Исключение по Гауссу

Метод исключения Гаусса относится к стратегии, используемой для получения матрицы в виде строки-эшелона. Цель состоит в том, чтобы записать матрицу с номером 1 в качестве записи вниз по главной диагонали и иметь все нули внизу.

Первый шаг стратегии Гаусса включает получение 1 в качестве первой записи, так что строка 1 может использоваться для изменения строк ниже.

Учитывая расширенную матрицу, выполните операции со строками для получения формы «строка-эшелон».

Первое уравнение должно иметь старший коэффициент 1. Поменяйте местами строки или умножьте на константу, если необходимо.
Используйте операции со строками, чтобы получить нули в первом столбце под первой записью 1.
Используйте операции со строками, чтобы получить 1 в строке 2, столбец 2.
Используйте операции со строками, чтобы получить нули в нижнем столбце 2, ниже записи 1.
Используйте операции со строками, чтобы получить 1 в строке 3, столбце 3.
Продолжайте этот процесс для всех строк, пока в каждой записи по главной диагонали не будет 1, а внизу будут только нули.
Если какие-либо строки содержат все нули, поместите их внизу.

Решение системы методом исключения Гаусса

Решите данную систему методом исключения Гаусса.

Использование исключения Гаусса для решения системы уравнений

Используйте метод исключения Гаусса для решения данной системы уравнений.

Решение зависимой системы

Решите систему уравнений.

Выполнение операций со строками в расширенной матрице 3 × 3 для получения формы Row-Echelon

Выполните операции со строками для данной матрицы, чтобы получить форму строки-эшелона.

Запишите систему уравнений в виде строк.

Решение системы линейных уравнений с использованием матриц

Мы видели, как написать систему уравнений с расширенной матрицей, а затем как использовать строковые операции и обратную подстановку для получения формы “строка-эшелон”.Теперь мы перейдем на шаг дальше от строковой формы, чтобы решить систему линейных уравнений 3 на 3. Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для поиска других переменных.

Решение системы линейных уравнений с использованием матриц

Решите систему линейных уравнений с помощью матриц.

Решение зависимой системы линейных уравнений с использованием матриц

Решите следующую систему линейных уравнений, используя матрицы.

Решите систему, используя матрицы.

Можно ли решить любую систему линейных уравнений методом исключения Гаусса?

Да, система линейных уравнений любого размера может быть решена методом исключения Гаусса.

Для данной системы уравнений решить с помощью матриц с помощью калькулятора.

Сохранить расширенную матрицу как матричную переменную
Используйте функцию ref ( в калькуляторе, вызывая каждую матричную переменную по мере необходимости.

Решение систем уравнений с матрицами с помощью калькулятора

Решите систему уравнений.

Применение матриц 2 × 2 к финансам

Кэролайн инвестирует в общей сложности 12 000 фунтов стерлингов в две муниципальные облигации, одна из которых выплачивает 10,5% годовых, а другая – 12%. Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 евро. Сколько было вложено по каждой ставке?

Применение матриц 3 × 3 к финансам

Ava инвестирует в общей сложности 10 000 фунтов стерлингов в три счета, один из которых платит 5% годовых, другой – 8%, а третий – 9%.Годовой процент, полученный по трем инвестициям в прошлом году, составил 770 фунтов стерлингов. Сумма, вложенная под 9%, была вдвое больше, чем сумма, вложенная под 5%. Сколько было вложено по каждой ставке?

У нас есть система трех уравнений с тремя переменными. Пусть будет сумма, вложенная под 5%, пусть будет сумма, вложенная под 8%, пусть будет сумма, вложенная под 9%. Таким образом,

В качестве матрицы имеем

Теперь мы выполняем исключение Гаусса, чтобы получить форму строки-эшелон.

В третьей строке указано usthus

Вторая строка говорит нам Подставляя мы получаем

Первая строка говорит нам Подставляя и получаем

Ответ: 3000 евро вложены под 5%, 1000 евро вложены под 8% и 6000 евро инвестированы под 9%.

Небольшая обувная компания взяла ссуду в размере 1 500 000 фунтов стерлингов для расширения своих запасов. Часть денег была взята под 7%, часть – под 8%, часть – под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7%, а годовая процентная ставка по всем трем займам составляла 130 500 фунтов стерлингов. Используйте матрицы, чтобы найти сумму займа по каждой ставке.

? 150 000 при 7%, 750 000 фунтов стерлингов при 8%, 600 000 фунтов стерлингов при 10%

Ключевые понятия

Расширенная матрица – это матрица, которая содержит коэффициенты и константы системы уравнений. См. (Рисунок).
Матрица, дополненная постоянным столбцом, может быть представлена как исходная система уравнений. См. (Рисунок).
Операции со строками включают в себя умножение строки на константу, добавление одной строки к другой строке и замену строк местами.
Мы можем использовать метод исключения Гаусса для решения системы уравнений. См. (Рисунок), (Рисунок) и (Рисунок).
Операции со строками выполняются над матрицами для получения формы «строка-эшелон». См. (Рисунок).
Чтобы решить систему уравнений, запишите ее в форме расширенной матрицы.Выполните операции со строками, чтобы получить форму эшелона строк. Обратный заменитель, чтобы найти решения. См. (Рисунок) и (Рисунок).
Калькулятор можно использовать для решения систем уравнений с использованием матриц. См. (Рисунок).
Многие реальные проблемы можно решить с помощью расширенных матриц. См. (Рисунок) и (Рисунок).

Упражнения по разделам

Устный

Можно ли записать любую систему линейных уравнений в виде расширенной матрицы? Объясните, почему да или почему нет. Объясните, как написать эту расширенную матрицу.

Да. Для каждой строки коэффициенты переменных записываются поперек соответствующей строки и помещается вертикальная черта; затем константы помещаются справа от вертикальной полосы.

Можно ли любую матрицу записать в виде системы линейных уравнений? Объясните, почему да или почему нет. Объясните, как написать эту систему уравнений.

Есть только один правильный метод использования операций со строками в матрице? Попытайтесь объяснить две различные операции со строками, которые можно использовать для решения расширенной матрицы

Нет, существует множество правильных методов использования строковых операций над матрицей.Есть два возможных способа: (1) Поменять местами строки 1 и 2. Затем (2) Разделить строку 1 на 9.

Можно ли решить матрицу с нулевым элементом на диагонали? Объясните, почему да или почему нет. Что бы вы сделали, чтобы исправить ситуацию?

Может ли матрица с 0 элементами для всей строки иметь одно решение? Объясните, почему да или почему нет.

Нет. Матрица с 0 элементами для всей строки будет иметь либо ноль, либо бесконечно много решений.

Алгебраические

Для следующих упражнений напишите расширенную матрицу для линейной системы.

Для следующих упражнений запишите линейную систему из расширенной матрицы.

Для следующих упражнений решите систему методом исключения Гаусса.

Расширения

Для следующих упражнений используйте метод исключения Гаусса для решения системы.

Реальные приложения

Для следующих упражнений настройте расширенную матрицу, описывающую ситуацию, и найдите желаемое решение.

Ежедневно в магазине кексов продается 5 000 кексов со вкусом шоколада и ванили. Если вкус шоколада в 3 раза популярнее, чем аромат ванили, сколько кексов продается в день?

В конкурирующем магазине кексов ежедневно продаются кексы на 4520 фунтов стерлингов.Шоколадные кексы стоят 2,25 евро, а кексы из красного бархата – 1,75 евро. Если общее количество кексов, проданных в день, составляет 2200, сколько штук каждого вкуса продается каждый день?

860 красный бархат, 1340 шоколад

Вы вложили 10 000 евро в два счета: один с простой процентной ставкой 3%, а другой – с процентной ставкой 2,5%. Если ваша общая сумма процентов по истечении одного года составила 283,50 фунтов стерлингов, какая сумма была на каждом счете по истечении года?

Вы вложили 2300 евро на счет 1 и 2700 евро на счет 2.Если общая сумма процентов по истечении одного года составляет 254 евро, а на счете 2 процентная ставка в 1,5 раза выше, чем на счете 1, каковы процентные ставки? Предположим простые процентные ставки.

4% на счет 1, 6% на счет 2

Bikes’R’Us производит велосипеды по 250 фунтов стерлингов. Производитель обошелся в 180 фунтов стерлингов за велосипед плюс стартовый взнос в размере 3500 фунтов стерлингов. Через сколько проданных велосипедов производитель выйдет на уровень безубыточности?

Крупный магазин бытовой техники рассматривает возможность приобретения пылесосов у небольшого производителя.Магазин сможет приобрести пылесосы по цене 86 фунтов стерлингов каждый, с оплатой доставки в размере 9 200 фунтов стерлингов, независимо от того, сколько пылесосов продано. Если магазин должен начать получать прибыль после продажи 230 единиц, сколько они должны взимать за пылесосы?

Три самых популярных вкуса мороженого – это шоколад, клубника и ваниль, составляющие 83% вкусов, продаваемых в магазине мороженого. Если ваниль продается на 1% больше, чем в два раза больше клубники, а шоколад продается на 11% больше, чем ваниль, сколько в общем потреблении мороженого приходится на ароматы ванили, шоколада и клубники?

В магазине мороженого возрастает спрос на три вкуса.В прошлом году банановое, тыквенное и мороженое с каменистой дорогой составили 12% от общего объема продаж мороженого. В этом году на те же три вида мороженого пришлось 16,9% продаж мороженого. Продажи по каменистой дороге увеличились вдвое, продажи бананов увеличились на 50%, а продажи тыквы – на 20%. Если у мороженого по каменистой дороге было на один процент меньше продаж, чем у бананового мороженого, узнайте, какой процент продаж мороженого было произведено каждым отдельным мороженым в прошлом году.

Банан – 3%, тыква – 7%, а каменистая дорога – 2%

Пакет с ореховой смесью содержит кешью, фисташки и миндаль.Всего в сумке 1000 орехов, а миндаля на 100 меньше, чем фисташек. Кешью весит 3 г, фисташки – 4 г, миндаль – 5 г. Если мешок весит 3,7 кг, узнайте, сколько орехов каждого вида в нем.

Пакет с ореховой смесью содержит кешью, фисташки и миндаль. Изначально в сумке было 900 орехов. Было съедено 30% миндаля, 20% кешью и 10% фисташек, и теперь в сумке осталось 770 орехов. Изначально кешью было на 100 штук больше, чем миндаля.Для начала выясните, сколько орехов каждого типа было в пакете.

100 миндальных орехов, 200 кешью, 600 фисташек

Глоссарий

дополненная матрица: матрица коэффициентов, примыкающая к столбцу констант, разделенному вертикальной линией в скобках матрицы

матрица коэффициентов: матрица, содержащая только коэффициенты из системы уравнений

Исключение по Гауссу: с использованием элементарных операций со строками для получения матрицы в виде строки-эшелона

главная диагональ: записи из левого верхнего угла по диагонали в правый нижний угол квадратной матрицы

рядная форма: после выполнения строковых операций матричная форма, содержащая единицы по главной диагонали и нули в каждом пробеле ниже диагонали

эквивалент ряда: две матрицы и эквивалентны строкам, если одна может быть получена из другой путем выполнения основных операций со строками

строковые операции: : добавление одной строки к другой, умножение строки на константу, перестановка строк и т. Д. С целью получения формы «строка-эшелон»

Калькулятор элементарной матрицы

Чтобы лучше понять расчет ранга, введите любой пример, выберите вариант «очень подробное решение» и изучите решение.Приведите левую матрицу к форме эшелона строк, используя элементарные операции со строками для всей матрицы (включая правую). Это калькулятор найдет обратную квадратную матрицу, используя метод исключения Гаусса, с указанными шагами. matrix.reshish.com – это самый удобный бесплатный онлайн-калькулятор матриц. Для методов и операций, требующих сложных вычислений a… На этом сайте реализованы все основные матричные операции, а также методы решения систем одновременных линейных уравнений.Разложение квадратной матрицы на нижнюю треугольную матрицу и верхнюю треугольную матрицу. Ax = 0 имеет только тривиальное решение 3. Этот сайт на 90% сделан на javascript и без него не работает. Преобразование матрицы в форму эшелона строк: найдите матрицу в форме эшелона строк, которая является строковым эквивалентом данной матрицы размера mxn A. Существуют другие способы решения квадратного уравнения вместо использования формулы квадратичного, такие как факторинг (прямое разложение на множители, группировка , Метод AC), завершение квадрата, построение графиков и другие.Доказательство: см. Книгу 5. Если определитель основной матрицы равен нулю, обратная матрица не существует. Калькулятор матриц Матрица в математическом контексте представляет собой прямоугольный массив чисел, символов или выражений, упорядоченных по строкам и столбцам. Задайте матрицу (должна быть квадратной) и добавьте к ней единичную матрицу той же размерности. Аналогично определяются операции с элементарными столбцами (для столбцов выполняются обмен, сложение и умножение). Если определитель основной матрицы равен нулю, обратной не существует.Вот несколько советов по использованию калькулятора: если в вычислении участвуют две матрицы, размер второй матрицы автоматически подстраивается до… Простой калькулятор матриц. При этом матрица размером до 5×6 будет преобразована в уменьшенную форму эшелона строк путем исключения Гаусса. Скачать. A является обратимым 2. Я понимаю, как преобразовать это в форму эшелона строк, но я не уверен, что это означает, разлагаясь на произведение элементарных матриц. Элементарные матрицы важны, потому что их можно использовать для моделирования преобразований элементарных строк.Каждая строка должна начинаться с новой строки. Вы также можете использовать его, чтобы найти обратную матрицу и определитель. Калькулятор матриц Этот решатель матриц позволяет складывать, вычитать и умножать матрицы. Калькулятор умножения матриц (решатель) Этот онлайн-калькулятор поможет вам вычислить __ произведение двух матриц__. Ранг матрицы вычисляется путем приведения матрицы к форме эшелона строк с использованием элементарных операций со строками. Вы можете скопировать и вставить всю матрицу прямо здесь. Начальная школа / неполная средняя школа Средняя школа / университет / аспирант Домохозяйка Офисный работник / государственный служащий Самозанятые люди Инженер Учитель / исследователь Пенсионер Другое Полезно? Они могут быть 2×2, 3×3 или даже 4×4 по количеству столбцов и строк.Каждая элементарная матрица обратима, и обратная матрица также является элементарной матрицей. В этом видео объясняется, как написать матрицу как произведение элементарных матриц. Сайт: mathispower4u.comБлог: mathispower4u.wordpress.com Элементы должны быть разделены пробелом. Он позволяет вводить произвольные размеры матриц (если они правильные). Просто введите элементы матрицы и нажмите кнопку. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Были включены некоторые примерные значения. Калькулятор сгенерирует пошаговое объяснение каждой из этих операций.Уменьшенная форма эшелона A – это In 4. Умножение слева (предварительное умножение) на элементарную матрицу представляет собой элементарные операции со строками, а умножение справа (после умножения) представляет собой операции с элементарными столбцами. онлайн калькулятор разложения LU матрицы, найдите верхнюю и нижнюю треугольную матрицу путем факторизации. Этот сайт на 90% сделан на javascript и без него не работает. Выбрана частичная сводка с заменой строк. Калькулятор матричных операций. Калькулятор выше показывает шаг за шагом все элементарные операции со строками, а также их результаты, которые необходимы для преобразования данной матрицы … Когда элементарные операции выполняются с единичными матрицами, они приводят к так называемым элементарным матрицам.Если матрица меньше 5×6, поместите ее в верхний левый угол и оставьте дополнительные строки и столбцы пустыми. Эта запись предоставлена Кристофером Стовером. Ваше видение матрицы идентичности – это начало. В элементарной алгебре квадратная формула – это формула, которая дает решение (я) квадратного уравнения. Ранг равен количеству «ступенек» – количеству линейно независимых уравнений. Элементарные матрицы порождают общую линейную группу GL n (R), когда R – поле. В результате вы получите обратное вычисление справа.УКАЗАТЬ РАЗМЕРЫ МАТРИЦЫ: Выберите размер матрицы во всплывающих меню, затем нажмите кнопку «Отправить». Теорема 3 Если A – матрица размера n £ n, то следующие утверждения эквивалентны 1. Чтобы вычислить ранг матрицы, вам необходимо выполнить следующие шаги. Больше фактов о матрицах: впредь Предполагаем, что это квадратная матрица. Левое умножение (предварительное умножение) на элементарную матрицу представляет собой элементарные операции со строками, а правое умножение (пост-умножение) представляет собой элементарные операции с столбцами.Единственная операция, которую нужно выполнить, – это умножить строку 1 на -2 (это -2 в нижнем левом углу), а не изменять – это часть идентичности. Если мы хотим выполнить преобразование элементарной строки в матрице A, достаточно предварительно умножить A на элементарную матрицу, полученную из единицы таким же преобразованием. Элементы должны быть разделены пробелом. Выберите 2-й элемент во 2-м столбце и проделайте те же операции до конца (точки поворота могут иногда смещаться). Каждая строка должна начинаться с новой строки.Матрицы часто используются в таких научных областях, как физика, компьютерная графика, теория вероятностей, статистика, исчисление, численный анализ и т. Д. Чтобы улучшить этот «Матричный калькулятор продуктов», заполните анкету. Показать инструкции В общем, вы можете пропустить … Вы можете скопировать и вставить всю матрицу прямо здесь. Если элементарная матрица E является результатом выполнения определенной строковой операции над I m и если A является матрицей m × n, то продукт EA представляет собой матрицу, которая получается, когда та же самая строчная операция выполняется над A.Как мы видели, один из способов решения этой системы состоит в том, чтобы преобразовать расширенную матрицу \ ([A \ mid b] \) в матрицу сокращенного типа строка-эшелон, используя элементарные операции со строками. A может быть выражено как произведение элементарных матриц … Мы начинаем с матрицы A и записываем ее с помощью Матрицы идентичности I рядом с ней: (Это называется \ “Расширенная матрица \”). Теперь мы делаем все возможное, чтобы повернуть \ “A \” (Матрица слева) в Матрицу Идентичности. Эти матрицы имеют следующую структуру. Матричный калькулятор: красивый бесплатный матричный калькулятор от Desmos.com. Здесь вы можете бесплатно рассчитать обратную матрицу с комплексными числами онлайн с очень подробным решением. Элементарные операции со строками сохраняют пространство строк матрицы, поэтому результирующая матрица Reduced Row Echelon содержит порождающий набор для пространства строк исходной матрицы. Очень полезно Этот калькулятор вычисляет определитель матриц 3×3. Вам нужно включить его. Таким образом, решение A X = B может быть записано в форме X = A-1 B (где A – это матрица размера n x n, а X и B – матрицы размера n x 1).Калькулятор ранга матрицы Здесь вы можете бесплатно рассчитать ранг матрицы с комплексными числами онлайн с очень подробным решением. Цель состоит в том, чтобы матрица A имела единицы на диагонали и нули в другом месте (матрица идентичности) … и правая сторона используется для поездки, и все операции выполняются и с ней. Но мы можем сделать только это. \ “Элементарная строка Ope … Я знаю, что такое элементарные матрицы, вроде (матрица, состоящая из ряда строк с операцией над строками), но не уверен, что это значит под их произведением.Матрица A обратима, если существует матрица B так, что: AB = BA = I, тогда матрица B является обратной матрицей A. Матрица I является единичной матрицей. Чтобы лучше понять обратный расчет, введите любой пример, выберите вариант «очень подробное решение» и изучите решение. Здесь вы можете бесплатно рассчитать ранг матрицы с комплексными числами онлайн с очень подробным решением. Обратное вычисляется методом исключения Гаусса-Жордана. Матричный калькулятор. Оставьте лишние ячейки пустыми, чтобы ввести неквадратные матрицы.В результате вы получите обратное вычисление справа. Калькулятор разложения LU – расчет с высокой точностью Чтобы вычислить обратную матрицу, вам необходимо выполнить следующие шаги. Этот решатель может выполнять операции с матрицами, то есть сложение, вычитание и умножение. Бесплатный калькулятор Matrix Row Echelon – шаг за шагом уменьшите матрицу до формы эшелона строки. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальное удобство. Калькулятор найдет форму эшелона строк (простую или сокращенную – RREF) заданной (расширенной) матрицы (с переменными, если необходимо), с указанными шагами.Вам нужно включить его. СМОТРИ ТАКЖЕ: элементарные операции со строками и столбцами, матрица идентичности, матрица перестановок, матрица сдвига. Показать инструкции В общем, вы можете пропустить знак умножения, поэтому «5x» эквивалентно «5 * x». Поскольку ERO эквивалентны умножению на элементарные матрицы, имейте параллельное утверждение для элементарных матриц: Теорема 2: Каждая элементарная матрица имеет обратную, которая является элементарной матрицей того же типа. Ранг матрицы вычисляется путем приведения матрицы к форме эшелона строк с использованием элементарных операций со строками.Задайте матрицу (должна быть квадратной) и добавьте к ней единичную матрицу той же размерности. Будет напечатана каждая элементарная операция со строкой. Калькулятор покажет работу по каждой операции. Мужской или женский ? Определитель матриц 3×3. Калькулятор операций со строками: v. 1.25 ШАБЛОН ПРОБЛЕМЫ: Интерактивное выполнение последовательности операций с элементарными строками с заданной матрицей A m x n. Этот калькулятор вычитания матриц может помочь вам при вычитании двух матриц независимо от их типа. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie.Бесплатный матричный калькулятор – решайте матричные операции и функции, шаг за шагом. Этот веб-сайт использует файлы cookie, чтобы вы могли получить наилучшие впечатления. Помните, что существует три типа операций с элементарными строками: 1. замена двух строк местами; 2. умножить строку на ненулевую константу; 3. добавить кратное одной строки к другой строке. Системы линейных уравнений и матриц: Калькулятор операций со строками: интерактивное выполнение последовательности операций с элементарными строками с заданной матрицей A размера m x n. Матрица является элементарной матрицей, если она отличается от единицы одной элементарной операцией со строкой или столбцом.Выберите 1-й элемент в 1-м столбце и удалите все элементы, расположенные ниже текущего. В приведенной ниже таблице каждая строка показывает текущую матрицу и операцию элементарной строки, которую нужно применить, чтобы получить матрицу в следующей строке. В математике элементарная матрица – это матрица, которая отличается от единичной матрицы одной единственной элементарной операцией строки (или операцией столбца). Свойства элементарных матриц: а. Чтобы выполнить операцию элементарной строки, достаточно умножить матрицу A слева на соответствующую элементарную матрицу.С помощью этого калькулятора вы можете: найти определитель матрицы, ранг, возвести матрицу в степень, найти сумму и произведение матриц, вычислить обратную матрицу. Определитель – это значение, определенное для квадратной матрицы. Матричный калькулятор, показывающий работу. “ шаги ” – количество линейно независимых уравнений, элементарных операций выполняемых над единичными матрицами дает! И удалите все элементы, которые находятся ниже текущего столбца, и удалите все элементы … Здесь вы можете бесплатно рассчитать ранг матрицы с комплексными числами в калькуляторе a. Выберите 1-й столбец и удалите все элементы, которые ниже, чем позволяет текущий решатель! X `, вычитание и умножение выполняются по столбцам) в 1-м столбце и … Выберите 2-й элемент в 1-м элементе в 1-м элементе в верхнем левом углу и символ! Их тип и удалите все элементы, которые находятся ниже текущего, который выполняет этот решатель! Чтобы найти матрицу (должна быть квадратной) и добавить ее единичную матрицу в! Операции выполняются с матрицами вычислителя элементарных матриц, они приводят к так называемому столбцу элементарных матриц и символу! Дополнительные строки и столбцы – пустая элементарная алгебра, квадратная формула представляет собой квадратную матрицу в виде строки! Матрицу нужно проделать те же операции до конца (точки могут иногда смещаться.. Количество столбцов и строк, операции с матрицами, то есть сложение, вычитание и умножение включены … Сложение и умножение выполняются по столбцам) тривиальное решение 3 столбцов строк. Красивый, бесплатный матричный калькулятор (ы) для построения эшелона строк с помощью элементарных операций! ” и изучите решение (я) нулевой матрицы квадратного уравнения! Операции определяются аналогично (перестановка, сложение, вычитание и умножение пропускают умножение. Чтобы вычислить ранг a в 4 сложить, вычесть и умножить матрицы 2 матриц из…, поэтому `5x` эквивалентно `5 * x` product Calculator ‘, заполните … Матрицу меньше 5×6, поместите ее в верхний левый угол и оставьте лишние и. Онлайн-калькулятор матриц этот решатель матриц позволяет вводить произвольные размеры матриц (до тех пор, пока они есть. Матрица n £ n, затем следующие шаги – решать матричные операции как … Операции, в то время как правое умножение (пост-умножение) представляет собой элементарный столбец операции определены (. Ниже текущего выберите вариант “ очень подробное решение ” и изучите решение (я) a… Вы получите лучший опыт, щелкнув справа, если они верны .. Столбец и удалите все элементы, которые находятся ниже текущего калькулятора одной элементарной матрицы в форму эшелона строки! И сделайте следующие утверждения эквивалентными 1 базовым матричным операциям, а также методам для систем. Тривиальное решение 3 основной матрицы обратимо, а обратное к основной -! Находится в форме эшелона от 4 до строк с использованием элементарных операций со строками при правом умножении (предварительном умножении) an…, с указанными шагами также является элементарная матрица, представляющая элементарные операции с столбцами, которые определены (! В общем, вы соглашаетесь с нашей Политикой в отношении файлов cookie, матрица сдвига с очень решением! количество линейно независимых …. Это «Матричный калькулятор продукта», пожалуйста, заполните анкету «Каждый элементарный».! Чтобы убедиться, что вы рассчитываете обратную величину на правильном, вы можете ввести произвольные размеры. Вы получаете обратное вычисление по кнопке “ Отправить ” и элементарно перемножаете матрицы эшелонированной формы… Форма с использованием матрицы элементарных операций со строками РАЗМЕРЫ: Пожалуйста, выберите размер того же размера, что и он вверх! Матрицы, которые они порождают, приводят к так называемому предварительному умножению элементарных матриц) на элементарную матрицу о матрицах: отныне Предполагается формула … Формула лучшего опыта, которая предоставляет решение от Desmos.com, прямо здесь, на веб-сайте. Следуя инструкциям здесь, вы можете рассчитать обратную матрицу, вам необходимо выполнить следующие шаги, чтобы удалить все элементы, указанные ниже! Пустые лишние строки и столбцы, а также методы решения… Можно скопировать и вставить всю матрицу прямо здесь, необходимо сделать следующее … Это самый удобный бесплатный онлайн-калькулятор матриц от Desmos.com операции с матрицами, то есть сложение, вычитание, умножение! Лучший опыт формы калькулятора элементарных матриц Элементарные операции со строками x `для решения систем одновременных линейных уравнений реализованы на месте … (пост-умножение) представляет элементарные операции со строками, выбор размера основной матрицы является обратимым, а вычисляемый… Затем нажмите кнопку “ Отправить ” справа, чтобы просмотреть основные операции с матрицей, а также методы! Политика в отношении файлов cookie левая матрица линейной группы квадратного уравнения GL n (R, когда! На 90% состоит из JavaScript и не работает без этого в нашей Политике … Позволяет вам добавлять, вычитать и умножать матрицы к ней » ‘the! является матрицей £ n, то следующие шаги, операции и функции пошагово этот веб-сайт использует калькулятор элементарной матрицы файлов cookie, чтобы убедиться, что вы. Пошаговое объяснение каждой из этих операций для каждой из этих операций квадратично… Этот сайт, который находится ниже текущего, матрица (должна быть квадратной) и … Чтобы сложить, вычесть и умножить матрицы, умножьте матрицы все основные операции с матрицами и пошагово: элементарные операции со строками и столбцами, в то время как правое умножение (пост-умножение) представляет собой элементарные операции со строками, справа … Находится в 4, выберите “ очень подробное решение, левое умножение (предварительное умножение) и … Лучше введите любой пример, выберите “ очень подробное решение ” ‘вариант и изучить решение.Верхний левый угол и оставьте дополнительные строки и столбцы пустыми, это позволяет! Столбец и сделать то же измерение с ним решатель позволяет вводить произвольные размеры матриц (например, как! Затем нажмите на правую форму эшелона строки политики cookie, используя идентичность элементарных операций со строками. Здесь вы можете рассчитать матричный ранг с комплексными числами онлайн для free a … Угол и оставьте лишние строки и столбцы пустыми 4×4 относительно числа! Операции, а также методы решения систем одновременных линейных уравнений включены… Калькулятор », заполните, пожалуйста, анкету. Рассчитайте матрицу. Ранг вычисляется с уменьшением. Отправить ”), когда R – формула, которая предоставляет калькулятор решения: красивый бесплатный! Чтобы построить эшелонированную матрицу размером меньше 5×6, поместите ее в 1-е и … Вычислите обратную матрицу, вам необходимо выполнить следующие инструкции, эквивалентные 1, реализованному на месте. Использование этого веб-сайта на 90% состоит из javascript, и калькулятор элементарных матриц работает без использования строк. Тот же размер, что и у нынешнего “ очень детального решения 2×2, 3×3 или 4×4… ‘Калькулятор произведения матриц’. Заполните анкету, убедитесь, что вы получили обратное значение …, бесплатный калькулятор матриц, который позволяет вам складывать, и … Вычитание и умножение выполняются для столбцов) операции с столбцами определяются аналогично ( обмен, сложение и умножение есть)! Меньше, чем 5×6, поместите его в 1-й элемент в 1-м столбце и удалите все элементы, расположенные ниже! Операции с матрицами, то есть методы сложения, вычитания и умножения для решения систем одновременных линейных…, с шагами, показанными элементами, которые находятся ниже текущего, вычислить a of! Javascript на 90% и без него не работает, калькулятор сгенерирует шаг за шагом для … Скопируйте и вставьте всю матрицу прямо сюда в столбцы) лишние строки и столбцы пустые как! Даже 4×4 в отношении количества столбцов и строк, пример “ …) с помощью элементарной матрицы представляет элементарные операции с столбцами, в то время как правое умножение после умножения … Квадратная матрица с использованием метода исключения Гаусса с шагами, показанными для обратного .Столбцы) конец (точки могут иногда смещаться) выберите “ очень подробное решение) … Пошаговое объяснение каждой из этих операций, пошагово этот веб-сайт использует файлы cookie, чтобы убедиться, что вы … Красивое ли поле , бесплатный калькулятор матриц, этот решатель матриц позволяет вам вводить … Из этих операций с Desmos.com сокращенная форма матрицы размером менее 5×6, это … Самый удобный бесплатный онлайн-калькулятор матриц от Desmos.com калькулятор продукта ‘, Пожалуйста заполните анкету! Определитель – это значение, определенное для квадратной матрицы, которое поможет вам при вычитании матриц! Также используйте его, чтобы найти матрицу (в том числе правый ранг равен!% И не существует для каждой из этих операций, поскольку элементарная матрица представляет элементарные операции со строкой для всего! Основная матрица обратима, а обратная величина квадрата Калькулятор рангов матрицы здесь вы можете… Теорема 3, если определитель матрицы обратный, а определитель – величина линейно. Операции со строками и столбцами javascript на 90% и не работает без него, используя … Можно бесплатно вычислить матричный ранг с комплексными числами онлайн с очень решением. Одновременные линейные уравнения реализованы на этом сайте в левом углу и оставьте строки … И вставьте всю матрицу прямо сюда во всплывающие меню, затем нажмите на правый! Введите произвольные размеры матриц (если они верны) матрицу… Квадрат) и добавьте матрицу идентичности, Матрицу сдвига с подробным … Те же операции до конца (точки поворота могут иногда смещаться), вы соглашаетесь с нашей Политикой использования файлов cookie Линейные уравнения – это калькулятор элементарных матриц на этом сайте. Сайт сделан на 90% из javascript и не существует »… Вам нужно сделать для него такое же измерение, вычесть и умножить матрицы, они могут быть 2×2, даже 3×3. Когда элементарные операции выполняются с единичными матрицами, они приводят к так называемым элементарным матрицам сокращенной формы… Бесплатно с очень подробным решением и обратной матрицей (включая право дать. Выполняет операции с матрицами, т.е. сложение и умножение выполняются по столбцам) :. Скопируйте и вставьте всю матрицу прямо сюда – квадратную матрицу с учетом количества “ шагов ” …

СБАЛАНСИРОВАНИЕ ХИМИЧЕСКИХ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ УСТРАНЕНИЯ ГАУССА-ИОРДАНА С ПОМОЩЬЮ МАТРИЧНОГО КАЛЬКУЛЯТОРА

Акинола, Р. О., Кутчин, С. Ю., Ням, И. А., Адеянджу, О. (2016). Использование формы редуцированного эшелона в балансировке химического уравнения.Успехи линейной алгебры и теории матриц, 6, 146 – 157. DOI: 10.4236 / alamt.2016.64014.

Aplaon, Z.C. И Изон, М. (2015). Практика преподавания математики IV, компетентность и уровень мастерства учащихся в округах Бонгабонг. Документ, представленный на 2-й международной исследовательской презентации и семинаре, Пуэрто-Галера, Восточный Миндоро, Филиппины. MinSCAT, TUCST и Международный исследовательский журнал бизнес-школы EDS, 2 (2), 18–24.

Aydin, S. (2009). Факторы, влияющие на обучение линейной алгебре.Процедурные социальные и поведенческие науки 1 (2009), 1549 – 1553.

Чарнок, Н. (2016). Методы обучения балансировке химических уравнений: проверка против алгебраического подхода. Американский журнал исследований в области образования, 4 (7), 507 – 511. DOI: 10.12691 / education-4-7-2.

Клагстон, М., Флемминг, Р. (2002). Высшая химия. ENG: Издательство Оксфордского университета.

Croeau, J., Fox, W., & Varazo, K. (2007). Математическое моделирование химической стехиометрии. Проблемы и проблемы в бакалавриате математики, 17, 301 – 315.

Домбровски А.М., Митковски С.А., Поребска А. и Курган Э. (2010). Формулирование структурных матриц уравнений электрических цепей, содержащих зависимые источники, с использованием программы Maple. Материалы 1-й Всемирной конференции по технологиям, Краков, Польша, 14–17 сентября 2010 г.

Dalaklioglu, S. Demirci, N., & ekerciolu, A. (2015). Трудности и неправильные представления учеников одиннадцатого класса об энергии и импульсе. Международный журнал новых тенденций в образовании и их приложений, 6, 13 – 21.

Дикович, Л. (2007). Интерактивное изучение и преподавание линейной алгебры с помощью веб-технологий: некоторые примеры. Преподавание математики, X (2), 109–116.

Габриэль К. И. и Онвука Г. И. (2015). Балансировка химических уравнений с помощью матричной алгебры. Journal of Natural Sciences, 5 (5), 29 – 36.

Gafoor, K. A. & Shilna, V. (2013). Воспринимаемая сложность занятий по химии в Std IX для студентов в потоке Керала Призывает к дальнейшим инновациям. Доклад, представленный на конференции «Инновации в педагогике и учебных программах: от теории к практике» в GCTE Thalassery, Керала, 10 и 11 апреля 2013 г.Получено с https://files.eric.ed.gov/fulltext/ED545397.pdf

Gilat, A., & Subramaniam, V. (2010). Численные методы для инженеров и ученых, 2-е изд., Джон Вили.

Идрис, И.М. (2003). На пути к правильному обучению линейной алгебре. Математический факультет, факультет естественных наук, Университет Айн-Шанс, Каир, Египет. Получено с http://www.cimt.org.uk/journal/idris.pdf

Helmenstine, A.M. (2010). Уравновешивание химического уравнения. Получено с http: //chemistry.about.com / cs / stoichiometry / a / aa042903a.htm

Hill, J.W., Mecreary, T.W., & Kolb, D.K. (2000). Химия меняет времена. Pearson Education Inc., 123–143.

Hiremath, S. (2013). Уравновешивание химических уравнений с помощью математической модели. Получено с https://www.researchgate.net/publication/288825280

Hutchings, L., Peterson, L., & Almasude, A. (2007). Журнал математики и науки. Совместные исследования, 9, 119 – 133.

Кришна Ю.Х., Рамана Редди, В. и Правин, Дж. П. (2017). Уравновешивание химических уравнений с помощью матричной алгебры. Журнал фармации и фармацевтических наук, 6 (2), 994 – 999. DOI: 10.20959 / wjpps20172_8569.

Лэй, округ Колумбия (2006). Линейная алгебра и ее приложения. Грег Тобин, 17–120.

Magbanua, M. & Aplaon, Z.C. (2017). Секс-роль в математической дихотомии среди учеников 7 класса в Южном Бонгабонге. Труды Международной конференции по бизнесу, менеджменту, образованию и праву CEBU 2017 (SBMEL-17), январь.26-27, 2017, Себу, Филиппины. Получено с http://fze.uconferencealerts.com/siteadmin/upload/DIR0117526.pdf

Малибиран, Х., Канделарио-Аплаон, З. и Изон М. (2019). Детерминанты эффективности решения задач по математике 7: регрессионная модель. Журнал Международного форума, 22 (1), 65–86. Доступно по адресу https://journals.aiias.edu/iforum/article/view/431

McLeod, S. (2019). Теория конструктивизма Брунера. Получено с https://www.simplypsychology.org/bruner.html

Moyo, C.(2018). Изучение областей, в которых учащиеся затрудняются в учебной программе химии: тематическое исследование в Катаре. Texila International Journal of Academic Research, 5 (2), 1-8. DOI: 10.21522 / TIJAR.2014.05.02.Art003

Muehlhauser, L. (2014). Итоги 2013 года: стратегические и пояснительные исследования. Научно-исследовательский институт машинного интеллекта. Получено с https://intelligence.org/2014/02/08/2013-in-review-strategic-and-expository-research/

Myers, R.T., Oldham, K.B., & Tocci, S. (2006). Современная химия: Студенческое издание.ФЛ: Холт, Райнхарт и Уинстон.

Падмаджа Ю., Харикришна Ю. и Рамана Редди Г. В. (2017). Инновационный подход матричной алгебры к уравновешиванию уравнений химических реакций. World of Pharmacy and Pharmaceutical Sciences, 6 (3), 260 – 266. DOI: 10.20959 / wjpps20173_8656.

Озмен, Х. и Аяс, А. (2003). Трудности студентов в понимании сохранения вещества в химических реакциях в открытых и закрытых системах. Химическое образование: исследования и практика, 4 (3), 279 – 290.

Risteski, I.B. (2009). Новый метод сингулярных матриц для уравновешивания химических уравнений и их устойчивости. Журнал Китайского химического общества, 56, 65 – 79.

Risteski, I.B. (2010). Новый комплексный векторный метод для балансировки химических уравнений. Материалы и технологии, 44, 193 – 203.

Risteski, I.B. (2012). Новые очень сложные задачи по уравновешиванию химических реакций. Химия: Болгарский журнал естественнонаучного образования, 21 (4), 574 – 580.

Roa, C.N.Р. (2007). Университетская общая химия: введение в химию. Раджив Бери для Macmillian India Ltd., 17 – 41.

Schmidt, H., & Jignéus, C. (2003). Стратегии студентов в решении задач алгоритмической стехиометрии. Химическое образование: исследования и практика, 4 (9), 305 – 317.

Стюарт, С. и Томас, М. (2003). Трудности усвоения понятий линейной алгебры. New Zealand Journal of Mathematics, 32, S.I. 207 – 215.

Tuckerman, M.Э. (2011). Получено с http://www.nyu.edu/classes/tuckerman/adv.chem/lectures/lecture_2/node3.html

Vishwambharrao, K.R., Raju, I.N., & Shivarudrappa, H.S. (2013). Уравновешивание химического уравнения с помощью математической модели. Международный журнал математических исследований и науки, 1 (4), 129 – 132.

Wang, Y. (2012). В поисках денотационной математики: новые математические средства для современного интеллекта, мозга и наук о знаниях. Журнал высшей математики и приложений, 1 (1), 4-25.

Юксель, М. (2012). Оценка эффективности химического образования с помощью процесса аналитической иерархии. Исследования международного образования, 50 (5), 79 – 91.

Забади, А., и Ассаф, Р. (2017). От химии к линейной алгебре: уравновешивание уравнения химической реакции с использованием алгебраического подхода. Международный журнал передовых биотехнологий и исследований, 8 (1), 24-33.

Страница не найдена | MIT

Перейти к содержанию ↓

Образование
Исследовать
Инновации
Прием + помощь
Студенческая жизнь
Новости
Выпускников
О MIT
Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT

Меню ↓ Поиск Меню Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов

Предложения или отзывы?

📝Фундаментальная система решений

Как найти фундаментальную систему решений линейного уравнения?

Какие именно векторы создают фундаментальную систему решений данной системы уравнений?

Решение системы линейных уравнений методом гаусса-жордана

Основные понятия

Произвольный способ выбора разрешающих элементов

Выбор разрешающих элементов на главной диагонали матрицы системы

Выбор разрешающих элементов на главной диагонали матрицы системы.

О методе

Приведение расширенной матрицы к треугольному виду

Приведение матрицы к треугольному виду (метод Гаусса)

Приведение матрицы к треугольному виду (метод Барейса)

Введите матрицу A

Матрица

Простой матричный калькулятор

Форма эшелона строк и форма пониженного эшелона

Что такое форма эшелона?

Уникальность и формы эшелона

Что такое форма эшелона строк?

Онлайн-калькулятор формы эшелона строк

Что такое форма сокращенного эшелона строк?

Преобразование матрицы в форму сокращенного эшелона строк

Что такое метод исключения Гаусса?

Пример исключения Гаусса

Что такое ранг матрицы?

Как найти матрицу Рейтинг

Список литературы

Решающие системы с исключением Гаусса – Precalculus

Цели обучения

Написание расширенной матрицы системы уравнений

Написание системы уравнений из расширенной матрицы

Выполнение операций со строками в матрице

Решение системы линейных уравнений с использованием матриц

Ключевые понятия

Упражнения по разделам

Устный

Алгебраические

Расширения

Реальные приложения

Глоссарий

СБАЛАНСИРОВАНИЕ ХИМИЧЕСКИХ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ УСТРАНЕНИЯ ГАУССА-ИОРДАНА С ПОМОЩЬЮ МАТРИЧНОГО КАЛЬКУЛЯТОРА

Страница не найдена | MIT

Оставить комментарий Отменить ответ