Решение систем линейных алгебраических уравнений в Excel
Методы решения систем линейных алгебраических уравнений хорошо описаны в учебнике “Основы вычислительной математики. Демидович Б.П., Марон И.А. 1966”. Скачать – 11Мб
1. Метод обратной матрицы (решение в Excel)
Если дано уравнение:
A*X = B, где A – квадратная матрица, X,B – вектора;
причем B – известный вектор (т е столбец чисел), X – неизвестный вектор,
то решение X можно записать в виде:
X = A-1*B, где A-1 – обратная от А матрица.
В MS Excel обратная матрица вычисляется функцией МОБР(), а перемножаются матрицы
(или матрица на вектор) – функцией МУМНОЖ().
Имеются “тонкости” использования этих матричных действий в Excel. Так, чтобы вычислить обратную матрицу от матрицы А, нужно:
1. Мышкой выделить квадратную область клеток, где будет размещена обратная матрица.Чтобы умножить матрицу на вектор:2. Начать вписывать формулу =МОБР( 3. Выделить мышкой матрицу А. При этом правее скобки впишется соответствующий диапазон клеток. 4. Закрыть скобку, нажать комбинацию клавиш: Ctrl-Shift-Enter 5. Должна вычислиться обратная матрица и заполнить предназначенную для неё область
1. Мышкой выделить область клеток, где будет размещён результат умножения 2. Начать вписывать формулу =МУМНОЖ( 3. Выделить мышкой матрицу - первый сомножитель. При этом правее скобки впишется соответствующий диапазон клеток. 4. С клавиатуры ввести разделитель ; (точка с запятой) 5. Выделить мышкой вектор- второй сомножитель. При этом правее скобки впишется соответствующий диапазон клеток. 6. Закрыть скобку, нажать комбинацию клавиш: Ctrl-Shift-Enter 7. Должно вычислиться произведение и заполнить предназначенную для него область
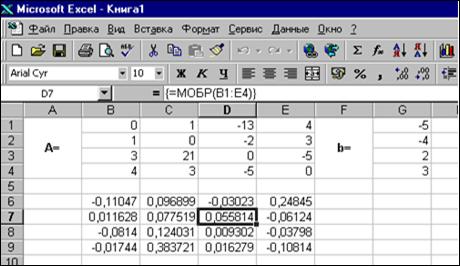 Пример СЛАУ 4-го порядка
Пример СЛАУ 4-го порядкаСкачать документ Excel, в котором этот пример решён различными методами.
2. Метод Гаусса
Метод Гаусса подробно (по шагам) выполняется только в учебных целях, когда нужно показать, что Вы это умеете. А чтобы решить реальную СЛАУ, лучше применить в Excel метод обратной матрицы или воспользоваться специальными программами, например, этойКраткое описание.
- Решаю систему уравнений: A*X=B, где A – квадратная матрица n-го порядка, X,B – вектора
- К матрице A справа приписываю вектор B. Получаю расширенную матрицу A
- В дальнейшем A обозначает расширенную матрицу (n строк, n+1 столбец)
- Aij – обозначает элемент матрицы, находящийся на i-й строке и j-м столбце
- Делю 1-ю строку на A11, т е A’1j = A1j/A11 (j = 1..n+1). В результате A’11 = 1. A’ обозначает преобразованную строку
- Преобразую остальные строки по формуле: A’ij = Aij – A’1j*Ai1 (i = 2..n; j = 1..n+1)
 .n заполнится нулями
.n заполнится нулями- Отметим, что все эти преобразования не нарушают правильность уравнений
- Аналогичные действия проводим для обнуления 2-го столбца в строках 3..n, то есть:
- Делю 2-ю строку на A’22, т е A”2j = A’2j/A’22 (j = 2..n+1). В результате A”22 = 1. A” обозначает резельтат 2-го преобразования строки
- Преобразую остальные строки по формуле: A”ij = A’ij – A”2j*A’i2 (i = 3..n; j = 2..n+1)
- В результате 2-й столбец в строках 3..n заполнится нулями
- Аналогичные действия проводим далее
- В результате левые n столбцов матрицы A превращаютс в верхнюю треугольную матрицу, т е ниже главной диагонали находятся только нули (а на главной диагонали – единицы) – см Рис 1. На этом рисунке вектор B – слева, S – номер шага
- Затем выполняется “обратный ход”, начиная с нижней строки, из которой можно вычислить Xn = Bn/Ann, например: Х4 = 9,55741/68,6388 = 0,13924 (рис. 1)
- Затем можно вычислить X3 = (0,9065 – 2,40919*0,13924) = 0,57059
- Затем из второй строки: X2 + 2,83562*X3 + 8,17808*X4 = 2,47945 вычисляю X2, и т д
3.
 Метод Якоби (метод простых итераций)
Метод Якоби (метод простых итераций)Для применения метода Якоби (и метода Зейделя) необходимо, чтобы диагональные компоненты матрицы А были больше суммы остальных компонент той же строки. Заданная система не обладает таким свойством, поэтому выполняю предварительные преобразования.
Далее номер в скобках означает номер строки. Новую первую строку получаю сложением старой первой строки с другими строками, умноженными на специально подобранные коэффициенты. Записываю это в виде формулы:
(1)’ = (1) + 0,43*(2) - 0,18*(3) – 0,96*(4) (2)’ = (2) + 0,28*(1) – 1,73*(3) + 0,12*(4) (3)’ = (3) – 0,27*(1) - 0,75*(2) + 0,08*(4) (4)’ = (4) + 0,04*(1) – 6,50*(2) + 8,04*(3) Примечание: подбор коэффицентов выполнен на листе "Анализ". Решаются системы уравнений, цель которых - обратить внедиагональные элементы в нуль. Коэффиценты - это округлённые результаты решения таких систем уравнений. Конечно, это не дело.В результате получаю систему уравнений:
Для применения метода Якоби систему уравнений нужно преобразовать к виду:
X = B2 + A2*X Преобразую:
Далее делю каждую строку на множитель левого столбца, то есть на 16, 7, 3, 70 соответственно. Тогда матрица А2 имеет вид :
А вектор В2:
Скачать
Метод Гаусса с выбором главного элемента
Основное
накопление погрешностей решения в
методе Гаусса происходит на этапе
приведения системы к треугольному виду.
Механизм накопления основной части
этой погрешности заключается в привнесении
погрешностей вычисления коэффициентов
ведущего уравнения в коэффициенты
последующих уравнений при исключении
каждого очередного неизвестного. Анализ
соотношений метода Гаусса показывает,
что погрешности вычисления коэффициентов
ведущего уравнения привносятся в
соответствующие коэффициенты всех
последующих уравнений в долях отношений
этих коэффициентов к диагональному
(главному) коэффициенту ведущего
уравнения.
В качестве примера можно рассмотреть задачу отыскания решения следующей системы уравнений
при ограничении
разрядной сетки вычислений до трёх
знаков и с оценкой погрешности получаемого
решения.
Поставленная задача будет решаться методом Гаусса с выбором главного элемента по столбцу.
1. Прямой ход.
а. Выбор главного элемента среди элементов первого столбца
б. Нормировка первого уравнения
в. Исключение элементов первого столбца
г. Выбор главного элемента среди элементов второго столбца второго и третьего уравнений
д. Нормировка второго уравнения
е. Исключение элементов второго столбца
ё. Нормировка последнего уравнения
2. Обратный ход
В итоге получено решение системы уравнений
.
 Погрешность
найденного решения.
Погрешность
найденного решения.а. Пересчёт вектора правых частей системы
.
б. Формирование системы уравнений, определяющей погрешности решения
,
то есть
.
в. Решение системы относительно погрешностей оно выполняется аналогично пунктам 1 и 2. Прямой ход (пункт 1) даёт следующую систему с верхней треугольной матрицей
.
г. Оценка абсолютной и относительной погрешностей решения системы линейных алгебраических уравнений
,
,
.
Реализация описанного метода без нахождения погрешности решения в рамках программы Excel приведена на рис.1.
Рис.1.
Программное обеспечение Excel’а
Для
решения систем линейных алгебраических
уравнений общего вида в программе Excel
имеется стандартная функция МОБР,
которая позволяет находить обратную
матрицу A–1 исходной системы. С помощью обратной
матрицы, которая при умножении на матрицу
системы даёт единичную матрицу, вектор
решения системы будет
.
При этом для умножения матриц в программе
Excel
есть стандартная функция МУМНОЖ.
С помощью обратной
матрицы, которая при умножении на матрицу
системы даёт единичную матрицу, вектор
решения системы будет
.
При этом для умножения матриц в программе
Excel
есть стандартная функция МУМНОЖ.
Для правильного отображения результатов работы функций МОБР и МУМНОЖ после ввода параметров необходимо нажать комбинацию клавиш «Shift+Ctrl+Enter».
Ниже на рис.3 приведена реализация описанного способа решения в рамках программы Excel системы уравнений
.
Рис.3.
Метод Гаусса с выбором ведущего элемента по столбцу. Метод Гаусса для расчета электрических цепей
Похожие главы из других работ:
Использование численных методов при решении инженерных задач
4.1 Метод Гаусса
Этот метод решения СЛАУ осуществляется в два прохода: 1. приведение основной матрицы к верхнетреугольному виду (прямой ход) 2. ..
..
Метод Гаусса для расчета электрических цепей
Метод Гаусса
Метод Гаусса – один из самых распространенных методов решения систем линейных алгебраических уравнений. Этот метод (который называют также метолом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет…
Основные методы решения задач нелинейного программирования
2.3.1 Метод Гаусса-Зайделя
Метод заключается в последовательном определении экстремума функции одной переменной с точностью до Ґе вдоль каждой координаты, т.е. фиксируются все координаты, кроме одной, по которой и осуществляется поиск экстремума Q…
Программный продукт, осуществляющий решение задач по дисциплине “Численные методы”
1.3 Метод Гаусса
Суть метода Гаусса состоит в преобразовании системы (6) к равносильной ей системе с треугольной матрицей, из которой затем последовательно (обратным ходом) получаются значения всех неизвестных. ..
..
Разработка программы решения системы линейных уравнений
1.1 Метод Гаусса
Идея метода Гаусса состоит в последовательном исключении неизвестных. Алгоритм решения системы уравнений этим методом проследим на примере. Пример 1. Выбирается ведущее уравнение с коэффициентом при х1, равным 1…
Решение задач линейной алгебры в Ms Excel
1.2 Метод Гаусса
Алгоритм Метода Гаусса состоит из двух основных частей: прямой ход и обратный ход. Прямой ход заключается в том, что система приводится к треугольному виду (верхняя унитреугольная форма). Обратный ход – непосредственное нахождение неизвестных…
Решение задач линейной алгебры в Ms Excel
1.3 Метод Гаусса в Excel
В Excel Метод Гаусса подробно (по шагам) выполняется только в учебных целях, когда нужно показать, что Вы это умеете. Существует более рациональный способ реализации данного метода в Excel. Решим задачу о рационе в Excel. Формулировка: Допустим. ..
..
Решение систем линейных алгебраических уравнений методом прогонки
1.1 Метод Гаусса
Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа: На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме…
Решение систем линейных алгебраических уравнений методом простой итерации
1.1 Метод Гаусса
В разделе « Численные методы линейной алгебры» рассматриваются численные методы решения систем линейных алгебраических уравнений (СЛАУ) и численные методы решения задач на собственные значения и собственные векторы матриц…
Решение системы линейных алгебраических уравнений методом Гаусса средствами языка программирования Visual Basic
Метод Гаусса
Метод Гаусса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных. ..
..
Решение системы линейных уравнений методом Гаусса и Жордана-Гаусса
Метод Гаусса
Метод Гаусса решения систем линейных уравнений состоит в последовательном исключении неизвестных и описывается следующей процедурой…
Решение системы линейных уравнений методом Гаусса и Жордана-Гаусса
Метод Жордана-Гаусса.
Элементарные преобразования этого метода аналогичны методу Гаусса, только матрица при использовании этого метода приводится к виду, тоесть столбец свободных коэффициентов превращается в столбец корней…
Численное интегрирование функции методом Гаусса
2.5 Метод Гаусса
Описанные выше методы используют фиксированные точки отрезка (концы и середину) и имеют низкий порядок точности (0 – методы правых и левых прямоугольников, 1 – методы средних прямоугольников и трапеций, 3 – метод парабол (Симпсона))…
Численное интегрирование функции методом Гаусса
2.6 Метод Гаусса-Кронрода
Недостаток метода Гаусса состоит в том, что он не имеет лёгкого (с вычислительной точки зрения) пути оценки погрешности полученного значения интеграла. ..
..
Численное решение системы линейных уравнений с помощью метода исключения Гаусса с выбором главного элемента по столбцу
2.2 Метода Гаусса с выбором главного элемента по столбцу
На k-м шаге прямого ходаметода Гаусса с выбором главного элемента по столбцу коэффициенты уравнений системы с номерами i = k + 1, …, n преобразуются по формулам aij(k) = aij(k-1) ? qikakj , bi(k) = bi(k-1) ? qikbk(k-1) , i = k + 1, …, n. Интуитивно ясно…
Решение системы уравнений с помощью excel
Решим Систему Линейных Алгебраических Уравнений (СЛАУ) методом обратной матрицы в MS EXCEL. В этой статье нет теории, объяснено только как выполнить расчеты, используя MS EXCEL.
Решим систему из 3-х линейных алгебраических уравнений с помощью обратной матрицы (матричным методом).
Запишем в ячейки основную матрицу системы и столбец свободных членов.
Систему n линейных алгебраических уравнений с n неизвестными можно решать матричным методом только тогда, когда определитель основной матрицы системы отличен от нуля (в противном случае мы имеем линейно зависимые уравнения и соответственно решение систем не единственное). В нашем случае определитель =12.
В нашем случае определитель =12.
Для этого выделите ячейки A18:C20, а в Строке формул введите =МОБР(A11:C13) , затем нажмите CTRL+SHIFT+ENTER.
Решение системы уравнений получим умножением обратной матрицы и столбца свободных членов. Перемножить матрицы можно с помощью формулы массива =МУМНОЖ() .
Для этого выделите ячейки F18:F20, а в Строке формул введите =МУМНОЖ(A18:C20;F11:F13) , затем нажмите CTRL+SHIFT+ENTER.
В файле примера также приведено решение системы 4-х и 5-и уравнений.
обучающие:
- повторение и закрепление знаний учащихся правил записи арифметических выражений и формул в электронных таблицах;
- повторение алгоритма решения систем уравнений;
- формирование знаний и умений в решении систем уравнений, используя возможности электронных таблиц;
развивающие:
- формирование умений анализировать, выделять главное, сравнивать, строить аналогии;
воспитывающие:
- осуществление эстетического воспитания;
- воспитание аккуратности, добросовестности.

Тип урока: урок закрепления изученного материала и объяснения нового.
ХОД УРОКА
I. Организационная часть.
Здравствуйте! Все мы знаем, что одну и ту же информацию можно закодировать любым способом. Перед вами набор чисел. Известно, что каждому числу ставится в соответствие буква в русском алфавите. Расшифруйте эту информацию, кто быстрее!
Ответ: “Знание – сила!”
Молодцы! А знаете, кому принадлежит это выражение? (Если нет, то один ученик ищет ответ в Интернете. Остальные отвечают на вопросы: Для чего предназначена программа Excel? (Программа Excel предназначена для хранения и обработки данных, представленных в табличном виде) Что собой представляет документ в Excel? (Каждый документ в Excel представляет собой набор таблиц – рабочую книгу, которая состоит из одного или многих рабочих листов) Какая функция используется для подсчета суммы чисел? (Функция СУММ). Как определить адрес ячейки? (Excel вводит номера ячеек автоматически. Адрес ячейки составляется как объединение номеров столбца и строки без пробела между ними)
Адрес ячейки составляется как объединение номеров столбца и строки без пробела между ними)
Выражение английского философа Френсиса Бэкона “Знание – сила!” и будет эпиграфом к нашему уроку. (“Нравственные и политические очерки”, 1597).
II. Повторение пройденного материала.
Мы уже знакомы с программой Microsoft Excel, умеем записывать арифметические выражения и различные формулы, находить значения арифметических выражений и построить графики функций. Чтобы проверить выполнение домашнего задания, предлагаю каждому пройти тестирование. (Приложение 1)
Хорошо, все справились и каждому поставим соответствующие оценки в журнал. А давайте устроим путешествие в математику и вспомним, что мы понимаем под понятием: “Решить систему уравнений”? (Найти такие значения х и у, которые будут удовлетворять и первое уравнение и второе). Какие способы существуют для решения систем уравнений (метод подстановки, метод сложения и графический способ). Сегодня мы с вами научимся решать системы уравнений, используя возможности электронных таблиц.
III. Объяснение нового.
А. Решим систему графическим способом. Преобразуем данную систему . Для решения воспользуемся диаграммой, на которой отобразим графики обеих функций. Заполняем столбец А: заполняем ячейки А2:А22 числами от -5 до 5 с шагом 0,5. (в ячейку А2 заносим число -5, в ячейку А3 – число -4,5, выделяем ячейки А2 и А3, установим курсор мыши на правый нижний угол рамки (указатель примет форму черного крестика) и растягиваем рамку вниз, пока последнее значение не станет равным 5). При заполнении столбца В в ячейку В2 заносим формулу =А2*А2, которую затем копируем до ячейки В22. (протянем формулу за правый нижний угол). При заполнении столбца С в ячейку С2 заносим формулу =1-2*А2, копируем ее до ячейки С22. Выделим блок с данными, с помощью Мастера диаграмм выберем тип диаграммы Точечная и построим графики функций. Координаты точек пересечения графиков – решения системы.
Получены приближенные значения решений. Чем меньше шаг, тем точнее значение координат точек пересечения.
Запишем алгоритм решения систем уравнений графическим способом:
1. Преобразовать систему уравнений, если это необходимо.
2. Задать начальные значения для Х.
3. Найти значение первой функции при заданных Х.
4. Найти значение второй функции при тех же Х.
5. Выделить блок с данными и построить графики функций, используя точечный тип диаграммы.
6. Решение системы – точка пересечения графиков функций.
7. Для нахождения координат точек пересечения с заданной точностью построить новый график на том отрезке, где находится решение, с шагом, равным значению точности.
Б. Решить систему уравнений . Занесем в электронную таблицу исходные данные и расчетные формулы следующим образом:.
Для решения системы уравнений воспользуемся надстройкой Поиск решения, которая запускается через Сервис (-Надстройки) и заполним диалоговое окно следующим образом:
При нажатии на кнопку Выполнить происходит решение системы уравнений и в ячейках B3 и B4 высвечивается результат.
Запишем примерный алгоритм решения системы уравнений, используя Поиск решения
1. Преобразовать систему уравнений, если это необходимо
2. Записать исходные данные (в ячейку А1 ввести текст “Решите уравнение”, в ячейку В1 записать первое уравнение, в ячейку В2 второе уравнение, в ячейку А3 ввести текст “Х=”, в ячейку А4 “Y=”, в ячейку А5 “уравнение 1”, в ячейку А6 “уравнение 2”. В ячейке B3 хотим получить значение Х, в ячейке В4 – значение Y, их оставляем пустыми.
3. В ячейку В5 переписать уравнение 1, используя правило записи арифметических выражений, следующим образом: в левой части вместо Х указывать ячейку В3, вместо Y ячейку В4, правую часть отбросить. Таким же образом переписать левую часть второго уравнения в ячейку В6.
4. Выбрать команду Сервис – Поиск решения.
5. Установить целевую ячейку – ту ячейку, в которой содержится формула, например, В5 и задать значение, равное значению правой части первого уравнения
6. В поле “изменяя ячейки” указать ячейки, в которых хотим увидеть ответ (В3 и В4)
7. Вести ограничение $B$6 = -3. Для этого щелкнуть на кнопке Добавить и в полученном окне установить реквизиты следующим образом: в поле Ссылка на ячейку указать ячейку, в которой записана левая часть другого уравнения, в другом поле выбрать знак “=”, в третьем ввести число, равное значению правой части. Закрыть окно Добавить ограничение, щелкнув кнопкой ОК
Вести ограничение $B$6 = -3. Для этого щелкнуть на кнопке Добавить и в полученном окне установить реквизиты следующим образом: в поле Ссылка на ячейку указать ячейку, в которой записана левая часть другого уравнения, в другом поле выбрать знак “=”, в третьем ввести число, равное значению правой части. Закрыть окно Добавить ограничение, щелкнув кнопкой ОК
8. Решить систему уравнений, щелкнув кнопкой Выполнить
IV. Практическая работа на компьютере.
А. Решите систему уравнений графическим способом
Б. Решите систему уравнения, воспользовавшись командой Поиск решения:
А. Решите систему уравнений графическим способом
Б. Решите систему уравнения, воспользовавшись командой Поиск решения:
V. Подведение итогов.
Повторить алгоритмы решения систем уравнений
Выставить оценки за тестирование в журнал
VI. Домашнее задание.
Решить рациональным способом системы уравнений:
;
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
- Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
- Принимаем значение x за равное . Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число , принятое нами за x.
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за . После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
- Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
- Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Решение задач линейной алгебры в Ms Excel
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ РОССИЙСКИЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ им. Г.В. ПЛЕХАНОВА
Курсовая работа по дисциплине «Информационные технологии в экономике»
На тему: «Решение задач линейной алгебры в Ms Excel»
Выполнил студент 1 курса
Группы № «414» / дневное отделение
Факультета математической
экономики и информатики
Научный руководитель:
к.э.н., доцент кафедры ИТ
Москва 2015
Введение
Данная работа посвящена решению задач линейной алгебры в Excel,точнее решению систем линейных уравнений. Будут рассмотрены три метода: метод Гаусса, метод, основанный на нахождении обратной матрицы и метод наименьших квадратов.
В первом параграфе работы в качестве примера использования систем линейных уравнений в экономике приведена простейшая задача о рационе и её решение методом Гаусса в частном случае, когда количество неизвестных совпадает с количеством уравнений.
Во втором параграфе рассматривается модель Леонтьева межотраслевого баланса. Это модель, позволяющая анализировать состояние экономики и моделировать различные сценарии ее развития. Возникающая в этом методе система линейных уравнений традиционно решается нахождением обратной матрицы. Чтобы пояснить, запишем модель Леонтьева в матричной форме:
(E–A)*X=Y
Если у нас имеется матрица (Е-А)-1 ,то умножая обе части равенства на эту матрицу, получим: Х=(Е-А)-1*У.
Третий параграф описывает решение задач, сводящихся к решению систем линейных уравнений, при помощи МНК (метода наименьших квадратов).
В каждом параграфе будет приведена реализация в Excel.
1. Метод Гаусса и одно из его приложений в экономике (задача о рационе)
1.1. Простейшая задача о рационе.
Формулировка задачи. Допустим, на ферме занимаются выращиванием телят. Известно, что для хорошего роста теленка в день ему необходимо потреблять m веществ в количестве ,…, соответственно.
На ферму ежедневно завозится n кормов в количестве,…,. Известно, что доля итогового вещества в j-ом корме равна . Тогда общее количество вещества определяется по формуле
(слагаемое – количество итогового вещества в j корме; i=1,…,n).
В результате получаем систему
(1)
Если m ≠n ,то система называется прямоугольной и методы её решения рассматриваются в другом параграфе. В данном случае будем считать, что m=n. Такая система является квадратной и к ней применим метод Гаусса.
1.2. Метод Гаусса.
Алгоритм Метода Гаусса состоит из двух основных частей: прямой ход и обратный ход.
Прямой ход заключается в том, что система приводится к треугольному виду (верхняя унитреугольная форма). Обратный ход – непосредственное нахождение неизвестных. Причем, корни находятся в обратном порядке: сначала , затем и т.д.
1) Прямой ход состоит из следующих шагов.
На первом шаге элементарными преобразованиями исключается из всех уравнений, начиная со второго.
Второй шаг заключается в исключение из всех уравнений, начиная с третьего.
На s шаге исключается из всех уравнений, начиная с s+1
(s=1,…,n-1).
При этом каждый шаг начинается с обработки sуравнения: строка под номером sделится на,чтобы коэффициент при стал равен 1.
Описанный алгоритм носит циклический характер.
После завершения этого процесса получаем систему:
(2)
2) Обратный ход.
В результате выполнения алгоритма прямого хода система (1) приняла треугольный вид (2). Для нахождения решения остается из системы (2) найти , , …, . Метод нахождения достаточно очевиден: из последнего уравнения находим .
Затем, подставив найденное значение в (n-1)-ое уравнение, найдем , и т.д. Таким образом, s-ое неизвестное находим из s-го уравнения:
. 1.0.
Причем, если условиться считать, что значение суммы, в которой нижний индекс суммирования больше верхнего (пустая сумма), равно нулю, в формуле 1.0. можно считать, что индекс s принимает натуральные значения от n до 1.
1.3. Метод Гаусса в Excel.
В Excel Метод Гаусса подробно (по шагам) выполняется только в учебных целях, когда нужно показать, что Вы это умеете. Существует более рациональный способ реализации данного метода в Excel.
Решим задачу о рационе в Excel.
Формулировка:
Допустим, на ферме занимаются выращиванием телят. Известно, что для хорошего роста теленка в день ему необходимо потреблять 4 вещества в количестве ,, , соответственно.
На ферму ежедневно завозится 4 корма в количестве ,…,. Известно, что доля итогового вещества в j-ом корме равна . Тогда общее количество вещества определяется по формуле
=
(слагаемое – количество итогового вещества в j корме;
Метод Гаусса
Метод Гаусса относится к прямым (точным) методам и основан на приведении системы уравнений (расширенной матрицы коэффициентов) к треугольному (или диагональному) виду. Такое приведение достигается сложением и вычитанием уравнений системы (строк расширенной матрицы) после их умножения на соответствующие постоянные множители.
Алгоритм метода состоит из двух этапов. На первом этапе (прямой ход метода) происходит последовательное исключение неизвестных из уравнения, начиная с x1.
Из первого уравнения системы выражаем неизвестное x1:
что возможно при a11≠0, в противном случае надо осуществить перестановку уравнений системы. Согласно этой формуле необходимо каждый элемент первой строки расширенной матрицы системы поделить на диагональный элемент
Затем подставляем это выражение во все остальные уравнения системы, тем самым исключаем x1 из всех уравнений, кроме первого. Элементы расширенной матрицы преобразуются по формулам
В результате исключения первого неизвестного x1 из всех уравнений все элементы первого столбца преобразованной матрицы будут равны нулю, кроме
Неизвестное x2 выразим из второго уравнения системы и исключим из остальных уравнений и т.д. в результате получим систему с верхней треугольной матрицей, у которой все элементы ниже главной диагонали равны нулю.
В общем виде выражения для неизвестных xk и преобразования элементов расширенной матрицы системы имеют вид:
Второй этап решения системы линейных уравнений называется обратным ходом метода Гаусса и состоит в последовательном определении неизвестных xk по приведенной выше формуле, начиная с неизвестного xn и заканчивая x1.
Точность результатов определяется точностью проведения арифметических
операций при преобразовании матрицы. Для уменьшения погрешности при
делении на диагональный элемент рекомендуется осуществить такую
перестановку уравнений, чтобы поставить на диагональ наибольший по
модулю из всех элементов рассматриваемого столбца. Такая процедура
называется выбором главного элемента.
Решение слау в excel. Решение слау в ms excel
Вычислить значения корней сформированной системы уравнений двумя методами: обратной матрицы и методом Крамера.
Введем данные значения в ячейки А2:С4 – матрица А и ячейки D2:D4 – матрица В.
Решение системы уравнений методом обратной матрицы
Найдем матрицу, обратную матрице А. Для этого в ячейку А9 введем формулу =МОБР(A2:C4). После этого выделим диапазон А9:С11, начиная с ячейки, содержащей формулу. Нажмем клавишу F2, а затем нажмем клавиши CTRL+SHIFT+ENTER. Формула вставится как формула массива. =МОБР(A2:C4).
Найдем произведение матриц A-1 * b. В ячейки F9:F11 введем формулу: =МУМНОЖ(A9:C11;D2:D4) как формулу массива. Получим в ячейках F9:F11 корни уравнения:
Решение системы уравнений методом Крамера
Решим систему методом Крамера, для этого найдем определитель матрицы.
Найдем определители матриц, полученных заменой одного столбца на столбец b.
В ячейку В16 введем формулу =МОПРЕД(D15:F17),
В ячейку В17 введем формулу =МОПРЕД(D19:F21).
В ячейку В18 введем формулу =МОПРЕД(D23:F25).
Найдем корни уравнения, для этого в ячейку В21 введем: =B16/$B$15, в ячейку В22 введем: = =B17/$B$15, в ячейку В23 введем: ==B18/$B$15.
Получим корни уравнения:
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Тема “Решение математических задач средствами EXCEL”, является значимой в курсе “Информатика и информационные технологии”, которая возникает на различных этапах изучения предмета. Например, вычисления алгебраических выражений, решения квадратных уравнений в различных средах, построение графиков функций и т.д.
На протяжении почти всего курса математики учащиеся изучают различные методы решения уравнений и систем уравнений. Когда школьники изучат методы решения систем уравнений на уроках алгебры, на уроках информатики целесообразно рассмотреть дополнительные, более эффективные, по времени, инструменты для выполнения таких заданий. Данная тема не является сложной для учащихся, но очень трудоемкая для учителя, необходимо делать много записей на доске, фактически учитель весь урок стоит спиной к учащимся. Для оптимизации и эффективности учебной деятельности учителя на уроке была создана презентация, которая может применяться на любом этапе прохождения темы фрагментарно или полностью учителями математики, а особенно полезна учителям информатики из-за ограниченного количества часов по предмету.
Данный урок можно отнести к интегрированным урокам, построенным на деятельной основе с применением проблемно-исследовательской технологии. Ценность урока заключается в том, что ученики решают стандартные математические задачи нестандартным способом – применяя современные компьютерные технологии. Этим достигается мотивационная цель – побуждение интереса, показ необходимости знаний по математике и информатики в реальной жизни. На уроке ученики покажут владение компьютером, умение работать с пакетом программ Microsoft Office, знания, умения и навыки, полученные на уроках математики. В результате будет достигнута образовательная цель урока: по математики обобщение знаний по темам: “Матрицы. Действия с матрицами. Решение систем линейных уравнений методом Крамера, Гаусса”, по информатике у учащихся формируется навык работы с табличными формулами, познакомятся с возможностями Excel для решения различных уравнений и систем уравнений.
11 класс, информатика.
Тема: “Применение табличного процессора MS Excel для решения систем линейных алгебраических уравнений”.
Тема рассчитана на два урока.
Тип урока: комбинированный урок, совершенствование знаний, умений и навыков.
Вид урока: интегрированный.
Цели урока:
обучающие:
- повторение и закрепление знаний учащихся математического аппарата по теме;
- отработать умение переходить от математической записи выражений к записи в среде электронных таблиц;
- продемонстрировать учащимся рациональность использования электронных таблиц для решения систем п линейных уравнений с п неизвестными;
Развитие внимания, памяти, представления, мышления, речи. Развитие интереса к предмету, навыка самостоятельной работы.
Развивающие и воспитательные:
- формирование умений анализировать, выделять главное, сравнивать, строить аналогии;
- развитие умения применять имеющиеся знания и умения в новой ситуации;
- развивать гибкость мышления, отыскивать наиболее краткий путь достижения цели развивать целенаправленность, рациональность, критичность мышления.
- умение устанавливать межпредметные связи.
- формирование способностей, позволяющих осуществлять быструю смену видов учебной деятельности.
Формы организации познавательной деятельности: фронтальная, индивидуальная, групповая, коллективная.
Методы и приемы обучения: объяснительно-иллюстративный, проблемного изложения, наглядно-иллюстративный, практический, эвристическая беседа.
Оборудование: доска, компьютеры, мультимедийный проектор и экран, презентация, карточки с индивидуальным заданием, папка с электронным материалом для урока.
Средства обучения: презентация учителя MS PowerPoint “Решение математических задач средствами Excel”, ресурсы Интернет.
Компьютерное программное обеспечение: пакет программ Microsoft Office 2007.
Структура урока
| № | Название этапа | Приемы педагогической техники | Время (мин.) |
| 1 | Организационный момент. Постановка цели урока и проблемы исследования | Вступительное слово учителя. Рефлексия. Ознакомление с темой, постановка цели. | 2 |
| 2 | Актуализация опорных знаний | Фронтальная работа с классом. Работа с формулами в Excel. Относительные и абсолютные ссылки. Применение логических функций. Приложение 2. | 10 |
| 4 | Изучение нового материала | Формирование понятие
табличной формулы. Частично-поисковая работа. Презентация учителя. | 10 |
| 5 | Подготовка к осмысление и применениеизученного материала. Повторение, обобщение математических знаний, дополненных демонстрацией новых функций Excel. Тренировочная практическая работа. | Объяснительно –
иллюстративный, повторение и обобщение
необходимых знаний из математики с дополнениями
новых функций в Excel. Эвристическая беседа Презентация учителя. Задания для практической работы. (Выполняется вместе с учителем. Приложение 3) | 25 |
| 6 | Закрепление (тренировка, отработка умений). Практическая работа. | Беседа по вопросам из
презентация учителя. Практическая работа. Приложение 3. | 25 |
| 10 | Итог урока. Контроль. | Анализ работы на уроке. Проверка достижений поставленной цели урока: обобщение изученного материала, выполнение практической работы, активность учащихся на всех этапах урока. | 3 |
| 9 | Постановка домашнего задания. | Домашнее задание творческое. | 3 |
| 11 | Самооценка деятельности. | Рефлексия. | 2 |
| Резерв времени 10 минут на индивидуальную работу при выполнении практической работы | |||
Описание урока
1. Организационный момент.
- Учитель сообщает учащимся тему и цель урока. Учащиеся записывают тему урока Слайд Титульный лист.
- Рассказывает о том, как будет построен урок.
- Знакомит с задачами, которые должны быть решены в ходе урока.
2. Актуализация опорных знаний.
Учитель. Для успешного проведения занятия по теме нам необходимо будет вспомнить и повторить материал из уроков математики “Методы решения линейных систем уравнений” и из информатики “Работа с формулами в Excel. Логические формулы. Относительные и абсолютные ссылки”.
Откройте файл D://Уроки_11/Решение СЛАУ/Приложение 2. У учащихся файл без листа Решение.
Заполните все поля таблицы.
Фронтальная работа с учащимися по проверки знаний и умений работы с формулами и функциями в Excel. На экране демонстрируется пример таблицы,
в которой необходимо заполнить все поля. Учащиеся предлагают алгоритмы заполнения полей. В тетради выписывают формулу для заполнения столбца K (победители, призеры), далее сравнивают свое решение с решением, представленным на экране (лист Решение, Приложение 2).
3. Изучение нового материала.
Учитель
Какие методы решения линейных уравнений вы знаете? Если не просмотрели файл выложенный в домашнее задание предыдущего урока, то можете открыть файл D://Уроки_11/Решение СЛАУ/Приложение 1 .
Учащиеся
Метод последовательного исключения неизвестных, метод Крамера.
Учитель
Посмотрите описание метода Крамера, с какими элементами нужно уметь работать при применении этого метода?
Учащиеся
С определителями.
Учитель
Т.е. с матрицами, на экране демонстрируется пример матрицы. Откройте файл D://Уроки_11/Решение СЛАУ/Приложение 3, лист Пример и выполните задание.
Учащиеся открывают документ Приложение 3 (лист Пример 1).
Выполняются задания, представленные на экране.
Учитель
Для работы с матрицами в Excel существуют специальные формулы, формулы для работы с массивом или их ещё называют табличные формулы.
Презентация. Слайд 3, 4. Учащиеся записывают понятие табличной формулы и особенности её ввода.
4. Подготовка к осмысление и применение изученного материала. Практическая работа.
Эвристическая беседа.
1. Для решения, каких задач можно применять табличные формулы?
Ответ может быть предопределен заданием, которое они выполняли – действия с матрицами, если решением должна получиться тоже матрица.
2. Дайте понятие матрицы? Может ли сказать, что любая прямоугольная таблица, заполненная числовыми значениями, есть матрица?
Ответ утвердительный. Слайд 5
3. Какие виды матриц вы знаете, чем они отличаются друг от друга? (заполнение, размерность и т.д.)
После обсуждения представить Слайд 6.
4. Можно ли с матрицами производить какие-либо действия?
Учащиеся могу перечислить некоторые действия с матрицами, сложение, умножение на число и т.д. Слайд 7.
Учитель информирует учащихся, о широких возможностях табличного процессора Excel для работы с матрицами.
Ученики записывают тему пункта темы Слайд8.
Повторение, обобщение математических знаний, дополненных демонстрацией новых функций Excel.
Презентация Слайды 9-14.
Демонстрация каждого слайда предопределяется вопросами по теме слайда.
В тетрадь учащиеся записывают только функции Excel для работы с матрицами и одновременно выполняют тренировочные практические задания из Приложение 3 Листы: пример 2, пример 3, пример 4. Подробно остановиться на примере 5, Приложение 3, Слайд 14.
Учитель
Теперь непосредственно перейдем к решению СЛАУ и познакомимся с методом, который вы рассматривали на уроках математики, это матричный метод. Слайд 16. Как вы думаете почему вы не решали системы матричным методом?
Учащиеся
Сложность вычисления обратной матрицы
Учитель
Запишите в тетрадь алгоритм решения системы матричным способом.
Откройте новую книгу Excel и решим вместе систему представленную на экране. Слайды 18-21.
Учитель открывает файл – заготовку упражнения и вместе с учащимися решает упражнение.
Решение сопровождается подробным объяснением. Решение учащихся сравнивается с предложенным решением в презентации. Слайды 18-21.
Учитель
Рассмотрим теперь решение СЛАУ методом Крамера, этот метод вам знаком, но на уроках математики вы решали, в основном, системы из двух уравнений с двумя неизвестными, почему? Слайд 22.
Ученики
Нужно много времени для вычисления определителей.
Учитель
Возможности Excel решают эту проблему. Откройте новый лист в книге и вместе решим систему уравнений представленную на экране.
Свои решения учащиеся сравнивают с решением, представленным в презентации. Слайды 23-25.
5. Закрепление (эвристическая беседа, тренировка, отработка умений).
Обсуждение темы по вопросам. Презентация. Слайд 26.
Практическая работа по группам: группа (практики) Приложение 3 Листы пример 6, пример 7, группа (технологи) Лист пример 8 решить систему методом Гаусса (можно воспользоваться Интернет-ресурсами), группа (программисты) создать программу на языке программирования Паскаль или С# решение системы уравнений методом Крамера, можно для ограниченного количества строк и столбцов.
6. Итог урока.
Проверка практической работы, обсудить проблемы в выполнении с каждой группой, если были выполнены не все задания, то откорректировать домашнее задание. Выставление оценок за урок.
Домашнее задание. На выбор:
1. (Приложение 4) Выполнить один из вариантов из карточки, разобрать программы решения систем уравнений на языке Паскаль из теоретического материала (Приложение 1)
2. Выполнить один из вариантов из карточки. Создать отдельно программу для решения систем методом Гаусса или матричным методом, группе программистов доработать программу метод Крамера.
7. Заключение.
Опыт работы с интегрированными уроками показывает, что у учащихся повышается качество знаний, оно может и не выражаться в оценках, но расширяется кругозор, развиваются творческие способности, повышается интерес к предметам, и вообще интерес к обучению, формируется убеждение, что учащиеся могут изучить больше, чем дается по программе.
Предложенное занятие по содержанию и выполнению заданий, кажется, насыщенным и перегруженным теорией и практическими упражнениями, но применение презентации, заготовок файлов (приложение 3) помогает выполнить все запланированные действия. Такое занятие рекомендуется проводить в математических классах, когда учащиеся уже изучили методы решения СЛАУ. За неделю до изучения этой темы выложить в эл. дневник, для ознакомления, информационный материал по методам решения систем уравнений и описание создания программ для решения систем уравнений на языке программирования.
Литература
1. Воронина Т.П. Образование в эпоху новых информационных технологий / Т.П. Воронина.- М.: АМО, 2008. -147 с.
2. Глинская Е. А. Межпредметные связи в обучении / Е.А. Глинская, С.В. Титова. – 3-е изд. – Тула: Инфо, 2007. – 44 с.
3. Данилюк Д. Я. Учебный предмет как интегрированная система /Д.Я. Данилюк //Педагогика. – 2007. – № 4. – С. 24-28.
4. Иванова М.А. Межпредметные связи на уроках информатики / М.А. Иванова, И.Л. Карева // Информатика и образование. – 2005. – №5. – С. 17-20.
5. А.В. Могилев, Н.И. Пак, Е.К. Хеннер “Информатика”, Москва, ACADEMA, 2000 г.
6. С.А. Немнюгин, “Турбо ПАСКАЛЬ”, Практикум, Питер, 2002 г.
Решение систем линейных уравнений в Excel
1. Введение
Многие задачи организации строительного производства сводятся к решению систем линейных уравнений вида:
a 11x 1a 12x 2a 1n x n b 1, | |||||||||
a2 n xn | |||||||||
a 21x 1a 22x 2 | |||||||||
n 1 1 | |||||||||
называемой системой n линейных алгебраических уравнений(СЛАУ ) с n
неизвестными.
При этом произвольные числа a ij (i = 1, 2,…,n ;j = 1, 2,…,n ) называются
коэффициентами при неизвестных, а числа b i (i = 1, 2,…, n ) – свободными
членами.
Систему(1) можно записать в матричной форме
A X = B,
где A – матрица коэффициентов при неизвестных:
X – вектор- столбец неизвестных X= (x1 , x2 , …, xn ) T :
B – вектор-столбец свободных членов:
b 2B ,
или B = (b 1 ,b 2 ,…,b n )T .
2. Операции с матрицами в Excel
В Excel для операций с матрицами служат функции из категории «Математические»:
1) МОПРЕД(матрица) – вычисление определителя матрицы, 2)МОБР(матрица) – вычисление обратной матрицы, 3)МУМНОЖ(матрица1;матрица2) – произведение матриц, 4)ТРАНСП(матрица) – транспонирование матрицы.
Первая из этих функций в качестве результатавозвращает число (определитель матрицы ), поэтомувводится как обычная формула (ENTER ).
Последние три возвращают блок ячеек, поэтому должны вводиться как формулы массива (CTRL+SHIFT+ENTER ).
Рассмотрим задачурешения СЛАУ на следующем примере
8x 1 2x 2 8x 3 24,
2x 1 2x 2 10x 3 48,
2x 1 4x 2 8x 3 18.
Матрица коэффициентов при неизвестных A (3) имеет вид
а вектор-столбец свободных членов (5)B = (–24, –48, 18)T .
Решим СЛАУ (7) в среде MS Excel тремя различными способами.
Матричный способ решения (обратной матрицы)
Обе части матричного равенства (2) умножим на обратную матрицу А -1 . Получим A –1 A X =A –1 B . Так как A –1 A =E , гдеE – единичная матрица (диагональная матрица, у которой по главной диагонали расположены единицы). Тогда решение системы (2) запишется в следующем виде
МУМНОЖ(матрица1;матрица2), завершая в каждом случае ввод комбинацией
CTRL+SHIFT+ENTER.
Метод Крамера
Решение СЛАУ находится по формулам Крамера
det A | ||||||
det A | ||||||
det A 2 | ||||||
det A | ||||||
det A | ||||||
det A | ||||||
где det A =A – определитель матрицы (3) системы (главный определитель), detA i =A i (i = 1, 2, …,n )– определители матрицA i (вспомогательные определители), которые получаются изA заменой i -го столбца на столбец свободных членовB (5).
Для рассматриваемой СЛАУ (7) вспомогательные матрицы имеют следующий вид
Разместим их на рабочем листе (рис. 1).
Аналогичная формула (=МОПРЕД(A3:C5) ) для вычисления определителя матрицыA записана в ячейкуE8 . Осталось найти решение системы. Соответствующие формулы Excel запишем в интервал решенияB7:B9 (рис. 3), в котором и увидим результат (рис. 4).
Обратите внимание на то (рис. 3), что при вычислении x i (i = 1, 2, 3)
анализируется значение определителя матрицы системы A , вычисленное в ячейке E8, и, если оно равно нулю, то в B7 помещается текст« Решения нет», а в ячейки B8 и B9 – пустые строки.
3. Решение СЛАУ с использованием инструмента Поиск решения
Широкий класс производственных задач составляют задачи оптимизации. Задачи оптимизации предполагают поиск значений аргументов, доставляющих функции, которую называют целевой , минимальное или максимальное значение при наличии каких-либо дополнительных ограничений. Excel располагает мощным средством для решения оптимизационных задач.
Это инструмент-надстройка, который называетсяПоиск решения (Solver )
(доступен через менюСервис Поиск решения ) .
Задачу решения СЛАУ можно свести к оптимизационной задаче.
Для чего одно из уравнений (например, первое) взять в качестве целевой функции, а оставшиеся n -1 рассматривать в качестве ограничений.
Запишем систему(1) в виде
a 11x 1a 12x 2a 1n x n b 10,
a2 n xn | ||||||||
a 21x 1a 22x 2 | ||||||||
b 0. | ||||||||
n 1 1 | ||||||||
Для решения этой задачи необходимо записать выражения (формулы) для вычисления значений функций, стоящих слева в уравнениях системы (12). Отведем для примера под эти формулы интервал C7:C9 . В ячейкуC7 введем формулу =A3*$B$7+B3*$B$8+C3*$B$9-D3 и скопируем ее в оставшиесяC8 иC9 . В них появятся соответственно =A4*$B$7+B4*$B$8+C4*$B$9-D4 и =A5*$B$7+B5*$B$8+C5*$B$9-D5 .
В окне диалога Поиск решения (рис. 5) задать параметры поиска (установить целевую ячейкуC7 равной нулю, решение в изменяемых ячейкахB7:B9 , ограничения заданы формулами в ячейкахC8 и С9 ). После щелчка по кнопкеВыполнить в
интервале B7:B9 получим результат (рис. 6) – решение СЛАУ.
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля. В этой статье мы разберем как по методу Крамера находятся неизвестные переменные и получим формулы. После этого перейдем к примерам и подробно опишем решение систем линейных алгебраических уравнений методом Крамера.
Навигация по странице.
Метод Крамера – вывод формул.
Пусть нам требуется решить систему линейных уравнений вида
Где x 1 , x 2 , …, x n – неизвестные переменные, a i j , i = 1, 2, …, n, j = 1, 2, …, n – числовые коэффициенты, b 1 , b 2 , …, b n – свободные члены. Решением СЛАУ называется такой набор значений x 1 , x 2 , …, x n при которых все уравнения системы обращаются в тождества.
В матричном виде эта система может быть записана как A ⋅ X = B , где – основная матрица системы, ее элементами являются коэффициенты при неизвестных переменных, – матрица – столбец свободных членов, а – матрица – столбец неизвестных переменных. После нахождения неизвестных переменных x 1 , x 2 , …, x n , матрица становится решением системы уравнений и равенство A ⋅ X = B обращается в тождество .
Будем считать, что матрица А – невырожденная, то есть, ее определитель отличен от нуля. В этом случае система линейных алгебраических уравнений имеет единственное решение, которое может быть найдено методом Крамера. (Методы решения систем при разобраны в разделе решение систем линейных алгебраических уравнений).
Метод Крамера основывается на двух свойствах определителя матрицы:
Итак, приступим к нахождению неизвестной переменной x 1
. Для этого умножим обе части первого уравнения системы на А 1 1
, обе части второго уравнения – на А 2 1
, и так далее, обе части n-ого
уравнения – на А n 1
(то есть, уравнения системы умножаем на соответствующие алгебраические дополнения первого столбца матрицы А
):
Сложим все левые части уравнения системы, сгруппировав слагаемые при неизвестных переменных x 1 , x 2 , …, x n
, и приравняем эту сумму к сумме всех правых частей уравнений:
Если обратиться к озвученным ранее свойствам определителя, то имеем
и предыдущее равенство примет вид
откуда
Аналогично находим x 2
. Для этого умножаем обе части уравнений системы на алгебраические дополнения второго столбца матрицы А
:
Складываем все уравнения системы, группируем слагаемые при неизвестных переменных x 1 , x 2 , …, x n и применяем свойства определителя:
Откуда
.
Аналогично находятся оставшиеся неизвестные переменные.
Если обозначить
То получаем формулы для нахождения неизвестных переменных по методу Крамера .
Замечание.
Если система линейных алгебраических уравнений однородная, то есть , то она имеет лишь тривиальное решение (при ). Действительно, при нулевых свободных членах все определители будут равны нулю, так как будут содержать столбец нулевых элементов. Следовательно, формулы дадут .
Алгоритм решения систем линейных алгебраических уравнений методом Крамера.
Запишем алгоритм решения систем линейных алгебраических уравнений методом Крамера .
Примеры решения систем линейных алгебраических уравнений методом Крамера.
Разберем решения нескольких примеров.
Пример.
Найдите решение неоднородной системы линейных алгебраических уравнений методом Крамера .
Решение.
Основная матрица системы имеет вид . Вычислим ее определитель по формуле :
Так как определитель основной матрицы системы отличен от нуля, то СЛАУ имеет единственное решение, и оно может быть найдено методом Крамера. Запишем определители и . Заменяем первый столбец основной матрицы системы на столбец свободных членов, и получаем определитель . Аналогично заменяем второй столбец основной матрицы на столбец свободных членов, и получаем .
Вычисляем эти определители:
Находим неизвестные переменные x 1
и x 2
по формулам :
Выполним проверку. Подставим полученные значения x 1
и x 2
в исходную систему уравнений:
Оба уравнения системы обращаются в тождества, следовательно, решение найдено верно.
Ответ:
.
Некоторые элементы основной матрицы СЛАУ могут быть равны нулю. В этом случае в уравнениях системы будут отсутствовать соответствующие неизвестные переменные. Разберем пример.
Пример.
Найдите решение системы линейных уравнений методом Крамера .
Решение.
Перепишем систему в виде , чтобы стало видно основную матрицу системы . Найдем ее определитель по формуле
Имеем
Определитель основной матрицы отличен от нуля, следовательно, система линейных уравнений имеет единственное решение. Найдем его методом Крамера. Вычислим определители :
Таким образом,
Ответ:
Обозначения неизвестных переменных в уравнениях системы могут отличаться от x 1 , x 2 , …, x n . Это не влияет на процесс решения. А вот порядок следования неизвестных переменных в уравнениях системы очень важен при составлении основной матрицы и необходимых определителей метода Крамера. Поясним этот момент на примере.
Пример.
Используя метод Крамера, найдите решение системы трех линейных алгебраических уравнений с тремя неизвестными .
Решение.
В данном примере неизвестные переменные имеют другое обозначение (x , y и z вместо x 1 , x 2 и x 3 ). Это не влияет на ход решения, но будьте внимательны с обозначениями переменных. В качестве основной матрицы системы НЕЛЬЗЯ брать . Необходимо сначала упорядочить неизвестные переменные во всех уравнениях системы. Для этого перепишем систему уравнений как . Теперь основную матрицу системы хорошо видно . Вычислим ее определитель:
Определитель основной матрицы отличен от нуля, следовательно, система уравнений имеет единственное решение. Найдем его методом Крамера. Запишем определители (обратите внимание на обозначения) и вычислим их:
Осталось найти неизвестные переменные по формулам :
Выполним проверку. Для этого умножим основную матрицу на полученное решение (при необходимости смотрите раздел ):
В результате получили столбец свободных членов исходной системы уравнений, поэтому решение найдено верно.
Ответ:
x = 0, y = -2, z = 3 .
Пример.
Решите методом Крамера систему линейных уравнений , где a и b – некоторые действительные числа.
Решение.
Ответ:
Пример.
Найдите решение системы уравнений методом Крамера, – некоторое действительное число.
Решение.
Вычислим определитель основной матрицы системы: . выражения есть интервал , поэтому при любых действительных значениях . Следовательно, система уравнений имеет единственное решение, которое может быть найдено методом Крамера. Вычисляем и :
Систему линейных алгебраических уравнений можно также решить, используя надстройку «Поиск решения». При использовании данной надстройки строится последовательность приближений , i=0,1,…n.
Назовем вектором невязок следующий вектор:
Задача Excel заключается в том, чтобы найти такое приближение , при котором вектор невязок стал бы нулевым , т.е. добиться совпадения значений правых и левых частей системы .
В качестве примера рассмотрим СЛАУ (3.27).
Последовательность действий:
1. Оформим таблицу, как показано на рис.3.4. Введем коэффициенты системы (матрицу А) в ячейки А3:С5.
Рис.3.4. Решение СЛАУ с помощью надстройки «Поиск решения»
2. В ячейках А8:С8 будет сформировано решение системы (х 1 , х 2 , х 3) . Первоначально они остаются пустыми, т.е. равными нулю. В дальнейшем будем их называть изменяемыми ячейками. . Однако для контроля правильности вводимых далее формул, удобно ввести в эти ячейки какие-либо значения, например, единицы. Эти значения можно рассматривать как нулевое приближение решения системы, = (1, 1, 1).
3. В столбец D введем выражения для вычисления левых частей исходной системы. Для этого в ячейкуD3 введем и затем скопируем вниз до конца таблицы формулу:
D3=СУММПРОИЗВ (A3:C3;$A$8:$C$8).
Используемая функция СУММПРОИЗВ принадлежит категории Математические .
4. В столбец Е запишем значения правых частей системы (матрицу В).
5. В столбец F введем невязки в соответствии с формулой (3.29), т.е. введем формулу F3=D3-E3 и скопируем ее вниз до конца таблицы.
6. Будет не лишним проверить правильность вычислений для случая = (1, 1, 1).
7. Выберем команду Данные\Анализ\Поиск решения .
Рис. 3.5. Окно надстройки «Поиск решения»
В окне Поиск решения (рис.3.5) в поле Изменяемые ячейки укажем блок $А$8:$С$8, а в поле Ограничения – $F$3:$F$5=0 . Далее щелкнем по кнопке Добавить и введем эти ограничения. И затем – кнопка Выполнить
Полученное решение систем (3.28) х 1 = 1; х 2 = –1 х 3 = 2 записано в ячейках А8:С8, рис.3.4.
Реализация метода Якоби средствами приложения MS Excel
В качестве примера рассмотрим систему уравнений (3.19), решение которой методом Якоби получено выше (пример 3.2)
Приведем эту систему к нормальному виду:
Последовательность действий
1. Оформим таблицу, как показано на рис.3.6.:
Матрицы и (3.15)введем в ячейки В6:Е8.
Значение e –в Н5.
Номер итерации k сформируем в столбце А таблицы с помощью автозаполнения.
В качестве нулевого приближения выберем вектор
= (0, 0, 0) и введем его в ячейки В11:D11.
2. Используя выражения (3.29), в ячейки В12:D12 запишем формулы для вычисления первого приближения:
B12=$E$6+B11*$B$6+C11*$C$6+D11*$D$6,
C12=$E$7+B11*$B$7+C11*$C$7+D11*$D$7,
D12=$E$8+B11*$B$8+C11*$C$8+D11*$D$8.
Эти формулы можно записать иначе, используя функцию Excel СУММПРОИЗВ.
В ячейку Е12 введем формулу: E12=ABS(B11-B12) и скопируем ее вправо, в ячейки F12:G12.
Рис.3.6. Схема решения СЛАУ методом Якоби
3. В ячейку Н12 введем формулу для вычисления M (k) , используя выражение (3.18): Н12 = МАКС(E12:G12). Функция МАКС находится в категории статистические.
4. Выделим ячейки В12:Н12 и скопируем их вниз до конца таблицы. Таким образом, получим k приближений решения СЛАУ.
5. Определим приближенное решение системы и количество итераций, необходимое для достижения заданной точности e .
Для этого оценим степень близости двух соседних итераций по формуле (3.18). Воспользуемся Условным форматированием в ячейках столбца.
Результат такого форматирования виден на рис.3.6. Ячейки столбца Н, значения которых удовлетворяют условию (3.18), т.е. меньше e =0,1, тонированы.
Анализируя результаты, принимаем за приближенное решение исходной системы с заданной точностью e=0,1 четвертую итерацию, т.е.
Исследуем характер итерационного процесса . Для этого выделим блок ячеек А10:D20 и, используя Мастер диаграмм, построим графики изменения каждой компоненты вектора решения в зависимости от номера итерации,
Приведенные графики (рис.3.7) подтверждают сходимость итерационного процесса.
Рис. 3.7. Иллюстрация сходящегося итерационного процесса
Изменяя значение e в ячейке Н5, получим новое приближенное решение исходной системы с новой точностью.
Реализация метода прогонки средствами приложения Excel
Рассмотрим решение следующей системы линейных алгебраических уравнений методом «прогонки», используя таблицы Excel .
Векторы :
Последовательность действий
1. Оформим таблицу, как показано на рис.3.8. Исходные данные расширенной матрицы системы (3.30), т.е. вектора введем в ячейки B5:E10.
2. Про гоночные коэффициенты U 0 =0 и V 0 =0 введем в ячейки G4 и h5 соответственно.
3. Вычислим прогоночные коэффициенты L i , U i , V i . Для этого в ячейках F5, G5, H5 вычислим L 1 , U 1 , V 1 . по формуле (3.8). Для этого введем формулы:
F5 = B5*G4+C5; G5=-D5/F5, H5 = (E5-B5*h5)/F5, и затем скопируем их вниз.
Рис.3.8. Расчетная схема метода «прогонки»
4. В ячейке I10 вычислим x 6 по формуле (3.10)
I10 = (E10-B10*H9)/(B10*G9+C10).
5. По формуле (3.7) вычислим все остальные неизвестные x 5 x 4 , x 3 , x 2 , x 1 . Для этого в ячейке I9 вычислим x 5 по формуле (3.6): I9=G9*I10+H9 . А далее копируем эту формуле вверх.
Контрольные вопросы
1. Система линейных алгебраических уравнений (СЛАУ). Что является решением СЛАУ. Когда существует единственное решение СЛАУ.
2. Общая характеристика прямых (точных) методов решения СЛАУ. Методы Гаусса и прогонки.
3. Общая характеристика итерационных методов решения СЛАУ. Методы Якоби (простых итераций) и Гаусса-Зейделя.
4. Условия сходимости итерационных процессов.
5. Что понимают под терминами обусловленности задач и вычислений, корректности задачи решения СЛАУ.
Глава 4.
Численное интегрирование
При решении достаточно большого круга технических задач приходится сталкиваться с необходимостью вычисления определенного интеграла:
Вычисление площадей , ограниченных кривыми, работы , моментов инерции, перемножение эпюр по формуле Мора и т.д. сводится к вычислению определенного интеграла.
Если непрерывная на отрезке [a, b ] функция y = f(x) имеет на этом отрезке первообразную F(x) , т.е. F ’ (x) = f(x) , то интеграл (4.1) может быть вычислен по формуле Ньютона – Лейбница:
Однако, только для узкого класса функций y=f(x) первообразная F(x) может быть выражена в элементарных функциях. Кроме того, функция y=f(x) может задаваться графически или таблично. В этих случаях применяют различные формулы для приближенного вычисления интегралов.
Такие формулы называют квадратурными формулами или формулами численного интегрирования.
Формулы численного интегрирования хорошо иллюстрируются графически. Известно , что значение определенного интеграла (4.1) пропорционально площади криволинейной трапеции, образованной подынтегральной функцией y=f(x) , прямыми х=а и х=b, осью ОХ (рис.4.1).
Задачу вычисления определенного интеграла (4.1) заменяем задачей вычисления площади этой криволинейной трапеции. Однако задача нахождения площади криволинейной не является простой.
Отсюда идея численного интегрирования будет заключатся в замене криволинейной трапеции фигурой, площадь которой вычисляется достаточно просто.
Рис.4.1. Геометрическая интерпретация численного интегрирования
Для этого отрезок интегрирования [a, b ] разобьем на n равных элементарных отрезков (i=0, 1, 2, …..,n-1), с шагом h=(b-a)/n. При этом криволинейная трапеция разобьется на n элементарных криволинейных трапеций с основаниями равными h (рис.4.1).
Каждая элементарная криволинейная трапеция заменяется фигурой, площадь которой вычисляется довольно просто. Обозначим эту площадь S i . Сумма всех этих площадей называется интегральной суммой и вычисляется по формуле
Тогда приближенная формула вычисления определенного интеграла (4.1) имеет вид
Точность вычисления по формуле (4.4) зависит от шага h , т.е. от числа разбиений n. С увеличением n интегральная сумма приближается к точному значению интеграла
Это хорошо проиллюстрировано на рис.4.2.
Рис.4.2. Зависимость точности вычисления интеграла
от числа разбиений
В математике доказывается теорема: если функция y=f(x) непрерывна на , то предел интегральной суммы б n существует и не зависит от способа разбиения отрезка на элементарные отрезки.
Формулу (4.4) можно использовать, если известна степень точности такого приближения. Существуют различные формулы для оценки погрешности выражения (4.4), но, как правило, они достаточно сложны. Будем проводить оценку точности приближения (4.4) методом половинного шага .
Функция GAUSS
В этой статье описаны синтаксис формулы и использование функции GAUSS. функция в Microsoft Excel.
Описание
Вычисляет вероятность того, что член стандартной нормальной популяции окажется между средним значением и z стандартными отклонениями от среднего.
Синтаксис
GAUSS (z)
Аргументы функции GAUSS описаны ниже.
Замечания
Если z не является допустимым числом, GAUSS возвращает # ЧИСЛО! значение ошибки.
Если z не является допустимым типом данных, GAUSS возвращает #VALUE! значение ошибки.
Поскольку NORM.S.DIST (0, True) всегда возвращает 0,5, GAUSS (z) всегда будет на 0,5 меньше, чем NORM.S.DIST (z, True).
Пример
Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите Enter. При необходимости вы можете настроить ширину столбца, чтобы увидеть все данные.
Формула | Описание | Результат |
‘= ГАУСС (2) | Вероятность того, что член стандартной нормальной популяции окажется между средним значением и двумя стандартными отклонениями от среднего (результат 0.47725). | = GAUSS (2) |
Верх страницы
Основные аспекты работы Гаусса над гипергеометрическими, факториальными и дигамма-функциями в JSTOR
. АбстрактныйВ своих работах о гипергеометрических функциях Гауссу удалось выйти за пределы ограниченной области функций восемнадцатого века, изменив несколько основных понятий анализа.Он отверг формальную методологию и традиционные понятия функций, комплексных чисел, бесконечных чисел, интегрирования и суммы ряда. В самом деле, он считал, что анализ происходит из нескольких интуитивно заданных понятий с помощью других четко определенных понятий, которые можно свести к интуитивным. Гаусс считал функции отношениями между непрерывными переменными величинами, в то время как он считал интегрирование и суммирование подходящими операциями с пределами. Он также рассматривал бесконечные и бесконечно малые числа как faqon de parler и использовал неравенства, чтобы доказать существование определенных пределов.Он полагал, что комплексные числа имеют такую же легитимность, что и реальные величины. Однако континуум Гаусса был связан с пересмотренной формой понятия непрерывной величины восемнадцатого века: он не сводился к набору чисел, но был дан сразу.
Информация о журналеАрхив истории точных наук проливает свет на концептуальную основу наук, анализируя исторический ход математического и количественного мышления и точную теорию природы, включая их связь с экспериментом в физических и современных биологических науках.Этот журнал поддерживает исторические исследования, соответствующие стандартам математических наук. Его цель – обеспечить быструю и полную публикацию сочинений исключительной глубины, объема и постоянства.
Информация об издателеSpringer – одна из ведущих международных научных издательских компаний, издающая более 1200 журналов и более 3000 новых книг ежегодно, охватывающих широкий круг предметов, включая биомедицину и науки о жизни, клиническую медицину, физика, инженерия, математика, компьютерные науки и экономика.
Модульная арифметика до C.F. Гаусс: Систематизация и обсуждение остаточных задач в Германии 18-го века
Abstract
Остаточные задачи имеют давнюю традицию и широко использовались в книгах по вычислениям, алгебре и развлекательной математике с 13-го до 18-го века. Было известно много сингулярных методов решения для частных случаев, но Баше де Мезириак был первым, кто увидел, как эти методы связаны с алгоритмом Евклида и с диофантовым анализом (1624).Его общий метод решения внес свой вклад в теорию уравнений во Франции, но остался практически незамеченным в других странах. Позже Эйлер независимо переоткрыл аналогичные методы, а фон Клаусберг обобщил и систематизировал методы, в которых использовалась процедура наибольшего общего делителя. За ними последовали методы решения непрерывных дробей Эйлера и Лагранжа и комбинаторное решение Гинденбурга. Вскоре после этого Гаусс в « Disquisitiones Arithmeticae » предложил новый формализм, основанный на его методе сравнений, и создал модульную арифметическую структуру, в которой эти проблемы ставятся сегодня.
Zusammenfassung
Restprobleme stehen in einer langen Tradition, sie sind in Rechenbüchern, Algebrabüchern und in der Unterhaltungsmathematik des 13. bis zum 18. Jh. weit verbreitet. Viele Sonderlösungen waren bekannt, aber erst C.G. Bachet de Méziriac bemerkte, dass die Probleme in Verbindung mit dem Euklidischen Teilalgorithmus und mit der Diophantischen Analysis stehen (1624). Bachets allgemeine Lösung hat in Frankreich zur Theorie der Gleichungen beigetragen, aber wurde in deutschsprachigen Gebieten nicht wahrgenommen.Am Anfang des 18. Jhs. Entdeckte Leonhard Euler Bachets Lösung erneut, und Clausberg sammelte, generalisierte und systematisierte viele Probleme, deren Lösungsmethoden den euklidischen Algorithmus benutzen. Es folgten noch Eulers und Lagranges Kettenbruchmethode, sowie Hindenburgs kombinatorische Lösung. Doch, nur wenig später, präsentierte Gauss, in seinen Disquisitiones Arithmeticae , einen neuen Formalismus, der auf seinen Kongruenzen gegründet war и schöpfte den Rahmen, in dem Diese Probleme heutzutage behandelt wermellarith.
Ключевые слова
Проблемы с остатком
Модульная арифметика
Евклидов алгоритм
Эйлер
Гинденбург
Гаусс
Рекомендуемые статьи Цитирующие статьи (0)
Copyright © 2008 Elsevier Inc. Все права защищены.
Рекомендуемые статьи
Цитирующие статьи
(PDF) Метод конечных ячеек для трехмерных задач механики твердого тела
[22] П. Вениш, О. Вениш, Э. Ранк, Использование высокопроизводительных компьютеров
для вычислительное управление, в: Б.Д. Мартино, Д. Кранцлмюллер, Дж. Донгарра
(ред.), Конспект лекций по информатике: последние достижения в области параллельных виртуальных машин
и интерфейса передачи сообщений, Том. 3666, Springer, 2005, стр. 536–543.
[23] П. Вениш, К. ван Трик, А. Боррманн, Э. Ранк, О. Вениш, Computational
рулевое управление в распределенных системах: моделирование комфорта в помещении как тематическое исследование
интерактивных CFD на суперкомпьютерах, Международный Журнал параллельных, новых
и распределенных систем 22 (4) (2007) 275–291.
[24] П. Вениш, Вычислительное управление CFD-моделированием на суперкомпьютерах Tera® op-
, Ph.D. диссертация, Lehrstuhl f¨ur Bauinformatik, Fakult¨at f¨ur
Bauingenieur- und Vermessungswesen, Technische Universit¨at M¨unchen (2007).
[25] К. ван Трик, П. Вениш, А. Боррманн, М. Пфангер, М. Эггер, О. Вениш,
Э. Ранк, На пути к интерактивному моделированию теплового комфорта в помещении, в: Proc. of
Европейская конференция по вычислительной гидродинамике, ECCOMAS CFD
2006, TU Delft, Нидерланды, 2006.
[26] К. ван Трик, П. Вениш, А. Боррманн, М. Пфа нгер, О. Вениш, Э. Ранк,
ComfSim – Интерактивное моделирование термического комфорта в отеле
auf H¨ochstleistungsrechnern, Bauphysik 29/1 (2007) 2–7.
[27] A. Duster, J. Parvizian, Z. Yang, E. Rank, Метод высокоуровневой области
для планирования хирургической операции для конкретного пациента, в: Proceedings of APCOM’07
совместно с EPMESC XI, Киото, Япония, 2007.
[28] E.Ранк, Дж. Парвизян, З. Йосибаш, А. Дёстер, К интерактивному числовому моделированию
для планирования ортопедической хирургии конкретного пациента, в: M. Cerrolaza,
H. Rodrigues, M. Doublar`e, J. Ambrosio , M. Viceconti (Eds.), Proceedings
III Международного конгресса по вычислительной биоинженерии, Isla de
Margarita, Венесуэла, 2007.
[29] Z. Yosibash, R. Padan, L. Joskowicz, C. Милгром, Анализ конечных элементов высокого порядка
на основе компьютерной томографии проксимального отдела бедренной кости человека по сравнению с экспериментами
in vitro, Journal of Biomechanical Engineering 129 (2007) 297–309.
[30] http://gid.cimne.upc.es.
[31] Э. Стейн (ред.), Адаптивные конечные элементы с контролем ошибок в механике твердого тела,
John Wiley & Sons, 2002.
[32] А. Дёстер, Э. Ранк, А. версия – конечно-элементный подход для двух- и трех-
-мерных задач теории потока J2 с нелинейным изотропным упрочнением,
International Journal for Numerical Methods in Engineering 53 (2002) 49–63.
[33] Х. Брюкер, Интеграция геометрического моделирования и бережного отношения к материалам
der p-version der FEM, Ph.Докторская диссертация, Lehrstuhl f¨ur Bauinformatik, Fakult¨at f¨ur
Bauingenieur- und Vermessungswesen, Technische Universit¨at M¨unchen (2001).
[34] Г. Кир’алифальви, Б. Саб’о, Квазирегиональное отображение для p-версии метода конечных элементов
, Конечные элементы в анализе и проектировании 27 (1997) 85–97.
39
% PDF-1.4 % 3424 0 объект > эндобдж xref 3424 91 0000000016 00000 н. 0000002175 00000 н. 0000002274 00000 н. 0000002816 00000 н. 0000003011 00000 н. 0000003348 00000 п. 0000003563 00000 н. 0000003585 00000 н. 0000003709 00000 н. 0000003731 00000 н. 0000003857 00000 н. 0000003879 00000 п. 0000004006 00000 н. 0000004028 00000 н. 0000004152 00000 н. 0000004174 00000 н. 0000004301 00000 п. 0000004323 00000 п. 0000004449 00000 н. 0000004471 00000 н. 0000004598 00000 н. 0000004635 00000 н. 0000004657 00000 н. 0000004781 00000 н. 0000004803 00000 п. 0000004930 00000 н. 0000004952 00000 н. 0000005079 00000 п. 0000005101 00000 п. 0000005228 00000 п. 0000005250 00000 н. 0000005375 00000 п. 0000005397 00000 н. 0000005525 00000 н. 0000005547 00000 н. 0000005677 00000 н. 0000005699 00000 н. 0000005828 00000 н. 0000005850 00000 н. 0000005977 00000 н. 0000005999 00000 н. 0000006130 00000 н. 0000006152 00000 н. 0000006282 00000 н. 0000006304 00000 н. 0000006432 00000 н. 0000006454 00000 п. 0000006581 00000 н. 0000006603 00000 п. 0000006696 00000 н. 0000006718 00000 н. 0000006976 00000 п. 0000007000 00000 н. 0000008831 00000 н. 0000008854 00000 н. 0000010087 00000 п. 0000010109 00000 п. 0000010370 00000 п. 0000010393 00000 п. 0000011444 00000 п. 0000011467 00000 п. 0000012335 00000 п. 0000012358 00000 п. 0000013560 00000 п. 0000013583 00000 п. 0000014281 00000 п. 0000014304 00000 п. 0000014868 00000 п. 0000014890 00000 н. 0000015149 00000 п. 0000015171 00000 п. 0000015430 00000 п. 0000015453 00000 п. 0000016063 00000 п. 0000016087 00000 п. 0000017612 00000 п. 0000017635 00000 п. 0000018810 00000 п. 0000018832 00000 п. 0000019091 00000 п. 0000019113 00000 п. 0000019372 00000 п. 0000019396 00000 п. 0000021156 00000 п. 0000021179 00000 п. 0000021695 00000 п. 0000021719 00000 п. 0000023227 00000 н. 0000023249 00000 п. 0000002429 00000 н. 0000002793 00000 н. трейлер ] >> startxref 0 %% EOF 3425 0 объект > эндобдж 3426 0 объект > / Кодировка> >> / DA (/ Helv 0 Tf 0 г) >> эндобдж 3513 0 объект > транслировать Hb“e`e`f` Ȁ
L’tat ordinaire de совесть есть динамика и колебания квоты на точку де вю количественно и качественно въехать […]tranche moyenne de possible, qui, si elles taient pondrables, pourraient tre mises en […] quation par u n e Courbe de Gauss .panhuasca.org.br | «Обычное состояние сознания» динамично […]и ежедневно колеблется в пределах диапазона возможностей, который, если бы их можно было измерить, составил бы […] может быть d ispl ayed i n кривой Гаусса .panhuasca.org.br |
Si l’impulsion mise est parfaitement […] rectangulaire, l’impulsion reue aura l’allure d ‘u n e Courbe de gauss p u is que la bande passante du rcepteur est finie; де […]plus, le bruit […]dformera l’allure gaussienne de l’impulsion reue (cho). радартоориал.eu | Если th e передано p ulse является идеальным прямоугольным, полученный импульс будет выглядеть l ik eag aus sia n curve b eca use the re ceiver […] полоса пропускания конечна; […]кроме того, шум нарушит гауссову форму принятого импульса. radartutorial.eu |
| Sur u n e Courbe de Gauss in ternationale, nous nous situons donc confortablement du ct positif de l’axe des […] ордонны. итг.бэ | На i ntern ati ona l Кривая Гаусса, we th us fi и мы сами удобно расположились на положительной s ide z ось эро. итг.бэ |
| Valeur moyenne, cart-typ e e t Courbe de Gauss – vo il des notions […] qui se rapportent toutes au scientifique Карл Фридрих […]Gauss et sont en ratio troite avec la technologie de pesage. sartorius-mechatronics.com | Среднее значение, стандартное отклонение […] и G aussi an bel l curve – th ese – это темы al l […], который относится к ck to th e Ученый Карл Фридрих Гаусс […]и тесно связаны с весовой техникой. sartorius-mechatronics.com |
Autrement dit, par rapport aux valeurs moyennes souhaites, le raisin compact […]prsente une дисперсия (dviation […] Стандартный дан s l a Courbe de Gauss ) t r s suprieure […]au некомпактный (лонжероны зерна), CE […]Qui Explosion la Difference de qualit. forumambiental.org | Другими словами, что касается требуемых средних значений, […]компактный виноград намного дисперснее […] (стандартный d ev iatio n o n t he Gauss cu rve ) t han t he отдельно […]винограда, чем объясняется разница в качестве. forumambiental.org |
| La note sera accorde selon u n e Courbe de Gauss , l e DLM le plus lger remportant le maximum, […] Qui est de 25points. nrc-cnrc.gc.ca | Оценка должна быть d на e на ab ell curve wit ht he li gh test MPL максимальная оценка m оценка из 25 po в тс. nrc-cnrc.gc.ca |
Процесс подготовки полиамидов для изучения на ленте предварительной полимеризации анионной полимеризации и лактама, полученного на основе полимера, полученного и подвергнутого разделению […]массовых масс […] Измерения по стандарту SEC соответствуют формам обработки ‘u n e Courbe de GAUSS и v ec UNEP DANS LES HAUT MASSES на […]effectue dans une deuxime […]лента без термической обработки и подвески с достаточной температурой, обеспечивающей одноуровневое разделение массовых масс. v3.espacenet.com | Способ получения полиамидов, в котором на первом этапе проводят анионную полимеризацию по крайней мере одного лактама, а затем на втором этапе проводят термообработку полимера. […] Получено, что имеет […] распределить io n of t he молярные массы, измеренные SEC, имеющие форму, близкую к a Gauss ian curve wit hah ig h-mass [… ]хвост, при достаточно высоком […]температуры и в течение достаточно длительного времени, чтобы получить одномодальное распределение молярных масс. v3.espacenet.com |
| Нажмите на ссылку с по n [ Courbe de Gauss ] e n bas gauche de la fentre […] Statistiques. sartorius-mechatronics.com | C l ick [Gauss C urve] bu tton от b ottom left p ar t of t he Окно статистики. sartorius-mechatronics.com |
Les superficies […] importantes d e l a Courbe de Gauss .umfiasi.ro | Importan t surf ace so f Gausscurve . umfiasi.ro |
Une analysis des ges dans une Compagnie des […] Эксперты а не u n e Courbe de Gauss d bu tant Environment […]40 лет и важная часть окружающей среды 55 и см.euroexpert.org | Анализ возраста в одном […] Компания Ex perts no ted a кривая Гаусса co mmen cing a t около […]в возрасте 40 лет и достигнув пика в возрасте около 55 лет. cms.euroexpert.org |
| Се коэффициент измеряет размер распределения и соответствует большему и и Courbe de Gauss . dardel.info | Этот коэффициент составляет […] “wid th ” распределения t he , и отражается в w id th e Ga ussi и b el l curve .dardel.info |
| La morphologie d e l a Courbe de Gauss . umfiasi.ro | Gaussc urve морфология . umfiasi.ro |
Объемная прогрессия сына […] est basee sur u n e Courbe de Gauss , l ‘a rchitechtonique […]de l’orchestre ayant ete prevue a cet effet. esolem-production.com | Звуковая программа re ss ba sed on a Gauss urv e, o rc hestra […]
Для этого было предусмотрено архитектоники. esolem-production.com |
| U n e Courbe de Gauss e n c loche a t наложение […] au graphique. dardel.info | A G au ssian be ll кривой ha s b een s up erimposed […] на графике. dardel.info |
Ces 2 graphiques peuvent vous permettre d’valuer graphiquement la normalit de distribution de la srie […]slectionne: si la […] Распределение нормальное, графическая диаграмма и гистограмма doit reprsenter une forme en clo ch e ( Courbe de Gauss ) , ta ndis que le graphique en Courbe doit reprsenter une форма “S” не является точкой перегиба […]Concide avec la moyenne de l’chantillon. adscience.fr | 2 предыдущих графика позволяют графическую оценку […] № rm ality of d is tribution: если распределение нормальное, график гистограммы sho ul d rep res ent a Gauss cu rve (l ike a bo ve), wh er eas кривая gra ph должна представлять “S” sha pe d изгиб w ho se изгиб [ …]балла совпадают с выборочным средним. adscience.eu |
Utilization de -octogne prsentant une distribution granulomtrique polymodale, […]conune celle que l’on peut reprsenter en […] пар. u n e Courbe de d i st ribu ti o n de Gauss , e t une taille […]Moyenne de Partules Infrieure 50 m, Conune […]matire explosive dans des agent propulsifs, avec des liants inertes ou actifs. v3.espacenet.com | Использование -октогена с полимодальными частицами le size di stribution, как может быть представлено […] in pa rt icul ar b y a Gauss d is trib u ction curve, and wit h в среднем […]размер частиц […]менее 50 м в качестве взрывчатого вещества в порохах с инертными и активными связующими. v3.espacenet.com |
L’entrecroicing de l’information contenue dans les […]уроки переменных, […] c’est – dire , l a courbe de d i st симтр распределения iq u e de Gauss e t d es cou rb e s de d i st ributions […]асимтрикс, Гумбель, […]Pearson, par instance, ont relativis le fait que tous les mdicaments n’ont pas, par instance, la mme количественные симптомы, les valeurs pour les donnes du Patient tant tout de mme constantes. Universidadcandegabe.org | Перекрестная информация, содержащаяся в […]изученных переменных: […] symme tr ic distr ibu ti on Gauss Cu rv ea и as ym metric distri bu tion кривые, Gumbel, Pe поджог, […]например не принимал в […]учитывает тот факт, что не все лекарства, например, имеют одинаковое количество симптомов, в то время как значения информации о пациенте остаются постоянными. Universidadcandegabe.org |
Plus le nombre de billes traversant la planche augmente, […]plus la rpartition des billes dans les casiers соответствует статистике разделов […] normale (rparti ti o n de Gauss ) d on nant u n e Courbe e n f orme de cloche.wifag.ch | Чем больше мячей проходит через доску, тем […], точнее, распределение n из t мячей в отсеках соответствует статистическому […] norma l dist ребро uti on (Gauss dis tri but ion) w i i ts be lls hap ed изгиб .wifag.ch |
Considrant que la terre ne peut […] donner que l’o rd r e de 0 , 3 gauss de l ‘ n ergie, la Magntique dveloppe par Novafron peut offrir jusqu ‘2 .5 0 0 Gauss de l ‘ n ergie magntique.wellnessproducts.ch | В то время как […] земля может только gi ve около t 0 .3 gauss of en ergy, t Магнитный зонд, разработанный Novafron, может отключаться er up t o 2 .50 0 Gauss o fm agn etic en ergy.товаров для здоровья.ch |
| Un pic symtrique, en f or m e de Gauss d e vr ait tre obtenu. products.metrohm.com | А симметричный, […] гауссовский -s должен быть нанесен на график пик плеча d .products.metrohm.com |
Les колебания autour de la moyenne sont gres par le principe […] универсальный, l o i de Gauss et de c e rt aines de ses […]расширений. centrecournot.org | Колебания вокруг среднего регулируются […] Universe l prin cipl e – Gauss’s l aw и som e of i ts […]расширений. centrecournot.org |
| En 1 83 2 , Gauss u VR a activement en fa ve u r de l ‘ ap plication du Systme […] mtrique, Associ la Secondde, dfinie en astronomie, […]комм. Системных объединений для физических наук. bipm.org | I n 1 832, Gauss stro ng ly Promo te d appli ca ition of this m etric […]
Система вместе со второй системой, определенной в астрономии, как . […]последовательная система единиц для физических наук. bipm.org |
| sont des coeffici en t s de Gauss , q ue l’on peut […] Calculer partir d’une analysis des moindres carrs de donnes magntiques […]recueillies sur l’ensemble de la plante. cgc.rncan.gc.ca | a r e ca ll ed Gauss co ef fici ents w hich […] определено методом наименьших квадратов глобального распределения магнитных наблюдений. cgc.rncan.gc.ca |
Специальное оборудование для использования с […]Environment Magntiques, сертификат Fabius MRI de Drger est certifi для […] destens it s de c h am p atteignant 40 mTesla ou 4 0 0 Gauss .draeger.com | Drger Fabius MRI – , специально разработанный для использования в магнитных средах. […] сертифицировано для полевых работ нг тыс. до 4 0 мТес la или 400 Gauss .draeger.com |
C’est un grand jour […] для центра по м n d Gauss , e t galement un grand […]jour pour l’Europe. bull.com | Она продолжила: «Это […] великий день f или t he G er man Gauss Cen te r, a s we ll as будучи […]отличный день для Европы. bull.com |
Nous aurons donc sur la table de la Confrence intergouvernementale […]un ventail de propositions selon une […] distribu ti o n de Gauss , un e courbe s t at istique avec, […]d’un ct, внешняя формула […]Qui consisterait Supprimer carrment notre Assemble et, l’autre extrme, une formule dinitive de maintien de l’Assemble, dans une forme ajuste peut-tre d’autres comptences, et, entre ces deux extrmes, toute combinaison de plusieurs formules. assembly-weu.org | Они будут для м, и Gau ssi , для кривой , w для , для на e крайнее, […] идея упразднить нашу Ассамблею вообще, а на остальных […]extreme, решение, которое повлечет за собой поддержание Ассамблеи, возможно, в адаптированной форме и с другими полномочиями, и между этими двумя крайностями всевозможные комбинации. assembly-weu.org |
| l’aide des program mm e s de Gauss m i s notre disposition […] по Svensson, nous Introduction les rendements, les taux d’intrt […]имен и дат для случайных сроков 1 дня, 3, 6 и 12 дней и 2 дней, 10, 15, 20 и 30 лет. banqueducanada.ca | U sing t he Gauss pr og Ram made ava ilabl e нам […] от Svensson, мы вводим доходность, купонные ставки и сроки погашения со сроками . […]ночей, 3, 6 и 12 месяцев, а также от 2 до 10, 15, 20 и 30 лет. banqueducanada.ca |
L’annexe 3 […] Информация о взаимосвязях между системами единиц C G S de Gauss e t l e SI.bipm.org | Приложение 3 […] is int en ded to pro vi de Информация об отношениях ti on of CGSGaussi и количествах и d uni ts для SI.bipm.org |
| Dans le cas d’un c an a l de Gauss or de R i ce (p.ex. en visibilit Directe), достаточное определение местоположения объекта TFR и функция положения CIR la plus important (voir figur e 3 , Courbe a ) . uer.info | В канале около se из a Gaussian o r Ricean (например, . линия прямой видимости) достаточно расположить окно FFT относительно наиболее значимого пика CIR. положение обнаружено (s ee Рис. 3 график a) . uer.info |
начало [لیل]
Математик – профессор вуза (преподаватель, исследователь, администратор)
Текущие обязанности включают…
Темы исследований до настоящего времени
Участие в проектах (только действующие проекты)
Подчеркнутый пункт при участии в организации или научном комитете. Стандартные семинары / коллоквиумы не указаны.
Обсуждение слайдов и видео
Подготовительные классы для больших школ
Неопубликованные отчеты и пояснительные примечания
Избранные тексты и трибуны
Ce que l’on conçoit bien s’énonce clairement et les mots pour le dire arrivent aisément.
Николя Буало, Поэтическое искусство (1674) Chant I.
J’ajouterais Quant à moi que la réciproque n’est pas forcément juste. Méfiez vous des beaux parleurs! -)
На 2021-2022 год в этом курсе представлены избранные аспекты высокой размерной вероятности, в том числе:
Избранная библиография:
ÉNS (Master 1 S1): свободные вероятностные и случайные матрицы (группа чтения)
Для 2021-2022 года мы читаем книгу Свободные вероятностные и случайные матрицы Минго и Спайхера, Монографии Института Филдса 35 (2017) .
Ce groupe de travail доступен в нашем мире возможностей свободных и альтернативных матриц. Il est basé sur le livre de Mingo et Speicher intitulé «Свободные вероятности и случайные матрицы». Предоставьте свои знания в теории альгебров операторов, вероятности свободных состояний, связанных с фильмами, не связанными с круазами и комбинаториками, альтернативными матрицами и другими объектами грандиозного измерения, статистическими приложениями и приложениями. télécommunications sans fil, теория представлений групп, quantiques групп, проблема неизменяемого пространства, принципы грандиозного развития, проблема sous-facteurs и т. д.Эта группа труда встретила особый акцент на отношениях между возможными свободными и альтернативными матрицами, основной игрой, потенциалом, аспектами альтернативных операторов, комбинаториками и аналитикой теории. Эта группа работ предназначена для разных и совместимых с трассами M1-2A avancé «Probabilités de grande Dimension» (Вероятность высокой размерности).
Неделя дошкольного образования на втором курсе магистратуры Mathématiques de l’Assurance de l’Économie et de la Finance (MASEF) и Master Mathématiques Appliquées et THéoriques (MATH).Задача этого дошкольного учреждения – вспомнить основные аспекты теории вероятностей на уровне первого года обучения в магистратуре. Это помогает подготовить студентов к курсам, предлагаемым в магистратуре, в частности к курсу стохастического исчисления. До 2021–2022 годов это дошкольное учреждение было, по сути, первой частью курса стохастического исчисления. Что было удалено (фактически перенесено в курс стохастического исчисления), так это интеграл Лебега-Стилтьеса, связанный с путями конечной вариации, интеграл Винера, формула Камерона-Мартина и ее применение к временам выхода, а также неравенство Кунита-Ватанабе.
Этот курс принадлежит магистратуре Mathématiques de l’Assurance de l’Economie et de la Finance (MASEF) и магистру Mathématiques Appliquées et THéoriques (MATH). Он представляет собой введение в стохастическое исчисление: броуновское движение, квадратичная вариация, остановка Дуба и максимальные неравенства для мартингалов, локальные мартингалы, стохастический интеграл, полумартингалы, формула Ито, характеристика Леви броуновского движения, формула Гирсанова, теорема Дубинса-Шварца, стохастика. дифференциальные уравнения с коэффициентами Липшица, понятие взрыва для локально липшицевых коэффициентов, процессы Бесселя, Орнштейна-Уленбека и Ланжевена, полугруппа Маркова и бесконечно малый генератор, формула Дюамеля, сильное марковское свойство, связь с уравнениями эволюции в частных производных Фоккера-Планка и теплопроводностью, Фейнман -Формула Каца и вещественные операторы Шредингера, вероятностное представление задачи Дирихле.
Этот курс, в сотрудничестве с Джозефом Лехеком, принадлежал магистру Mathématiques Appliquées et THéoriques (MATH). Этот курс представляет собой современный обзор логарифмических неравенств Соболева. Эти неравенства были предметом интенсивной активности в последние десятилетия в связи с анализом и геометрией марковских процессов и уравнениями эволюции диффузии . Этот курс разработан, чтобы быть доступным для широкой аудитории. Он разделен на семь лекций.Экзамен будет заключаться в чтении исследовательской работы в данной области и кратком выступлении по ней.
Этот курс также читался в Университете Чили, Сантьяго-де-Чили, осенью 2017 года в рамках Региональной программы Франции – Латинская Америка Караиба (PREFALC), организованной Стефаном Мишлером.
Ce Cours faisait partie du Master 1 Mathématiques Appliquées de Dauphine-PSL.
Ce Cours faisait partie du Master Mathématiques appliquées – Parcours Analyze et Probabilité .Il a été dispensé (en anglais) pour la dernière fois в 2014–2015 годах. Les notes de Cours ci-dessous sont en français.
Этот курс разделен на 7 лекций по 3 часа. Каждая лекция посвящена изучению конкретной стохастической модели. Выбранные модели могут варьироваться от года к году, и выбор на 2013 год включал модели Фишера-Райта, модели случайных блужданий, модели ветвления Гальтона-Ватсона, модели случайных матриц и модели фрагментации роста. Экзамен заключается в чтении мини-лекции по статье в духе курса.Курс ведется на английском языке, а некоторые конспекты лекций на французском языке доступны ниже.
Le Cours de Biskra (2006) – это некий разговор на тему стохастического анализа и приложений, основанный на принципах Брахима Мезерди (Université de Biskra) и Boualem Djehiche (KTH Stockholm). Biskra est une ville des Aurès, aux portes du Sahara, dans l’est algérien. Le Cours d’Oran (2011), совместное предприятие с Амин Асселах, приглашение Сетти Айяд (Université d’Oran), pour des étudiants de master d’Oran et de Tlemcen.
Des notes de Cours Rédigées en сотрудничество Пьера-Андре Зитта, sous forme de livre, sont disponibles ci-dessus.
Ce matériel date de la période 1999-2002, 2003-2005.
.

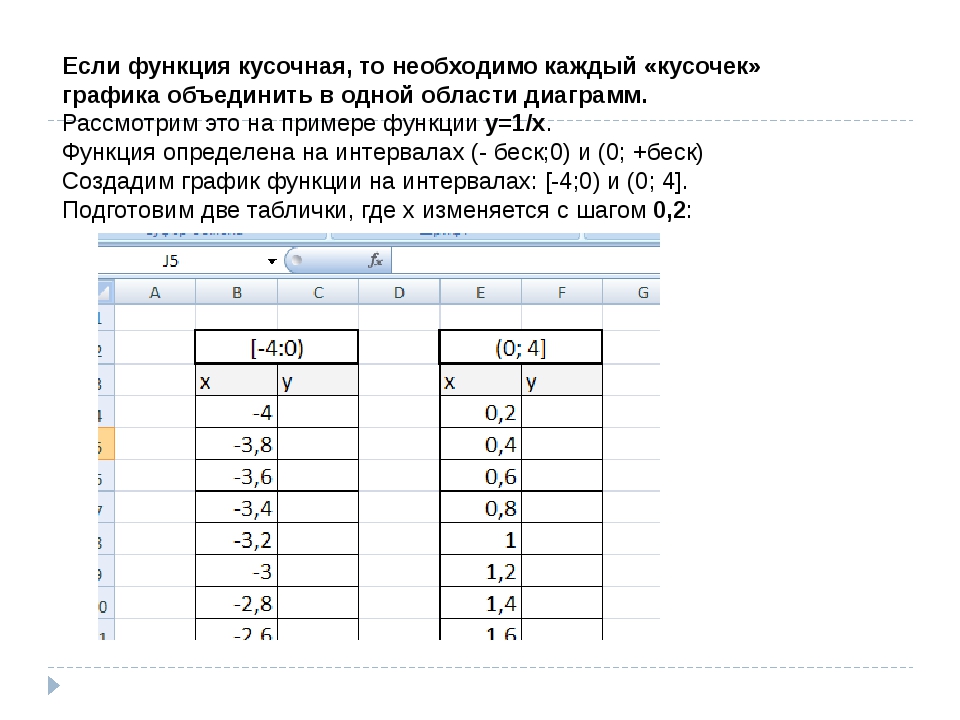 .n заполнится нулями
.n заполнится нулями