Метод гаусса конспект: VIII Международный конкурс научно-исследовательских и творческих работ учащихся Старт в науке - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Конспект лекц. 1-ый семестр

2.6. Системы линейных алгебраических уравнений (СЛАУ)

Рассмотрим систему линейных алгебраических уравнений (СЛАУ)

(1)

Система (1) называется однородной, если свободные члены равны нулю Однородная система всегда является совместной – она имеет решение (возможно, не единственное).

Введём следующие обозначения

, , , . (2)

Матрица называется матрицей коэффициентов уравнения (1), матрица называется расширенной матрицей уравнения (1), матрица (матрица-столбец) называется столбцом неизвестных, матрица-столбец называется столбцом свободных членов уравнения (1).

Систему (1) с помощью матриц (2) можно представить в виде

. (3)

Справедливость равенства (3) можно проверить путём непосредственной подстановки значений матриц в это выражение

то есть

. (4)

Выражение (4) представляет собой равенство двух матриц размером . Такие матрицы называют также матрицами-столбцами, так как они состоят из одного столбца. Приравнивая соответствующие элементы этих матриц, получаем систему линейных алгебраических уравнений (1).

Выражение (3) называется матричной формой записи системы (1).

Рассмотрим отдельно случай квадратной системы, когда и общий случай при .

2.6.1. Квадратная система

Существует три основных метода решения совместной СЛАУ

а) правило Крамера;

б) матричный способ;

в) метод Гаусса.

а) П р а в и л о Крамера. Пусть задана система

(5)

Обозначим

Определитель получается из определителя D заменой i-го столбца на столбец свободных членов. Правило Крамера состоит в том, что при

неизвестные находятся с помощью формул:

(6)

б) Матричный способ. Умножим равенство (5) слева на матрицу .

. (7)

Будем считать, что . В этом случае существует. Теперь воспользуемся равенствами и , которые позволяют преобразовать выражение (7) к виду

. (8)

Выражение (8) представляет собой решение системы (1) в матричной форме.

В этом и состоит матричный способ решения системы (5).

в) М е т о д Г а у с с а. При решении методом Гаусса расширенную матрицу системы (5) элементарными преобразованиями приводят к трапецеидальному виду.

П р и м е р . Решите систему

а) по правилу Крамера;

б) матричным способом;

в) методом Гаусса.

Р е ш е н и е. а) Правило Крамера. Вычисляем определители

Отсюда находимнеизвестные

б) Матричный способ. Составляем матрицу коэффициентов и столбец свободных членов

Теперь найдем то обратная матрица существует. Находим алгебраические дополнения

;

Составляем обратную матрицу

И находим решение системы, для чего подставляем и в выражение (7)

Итак,

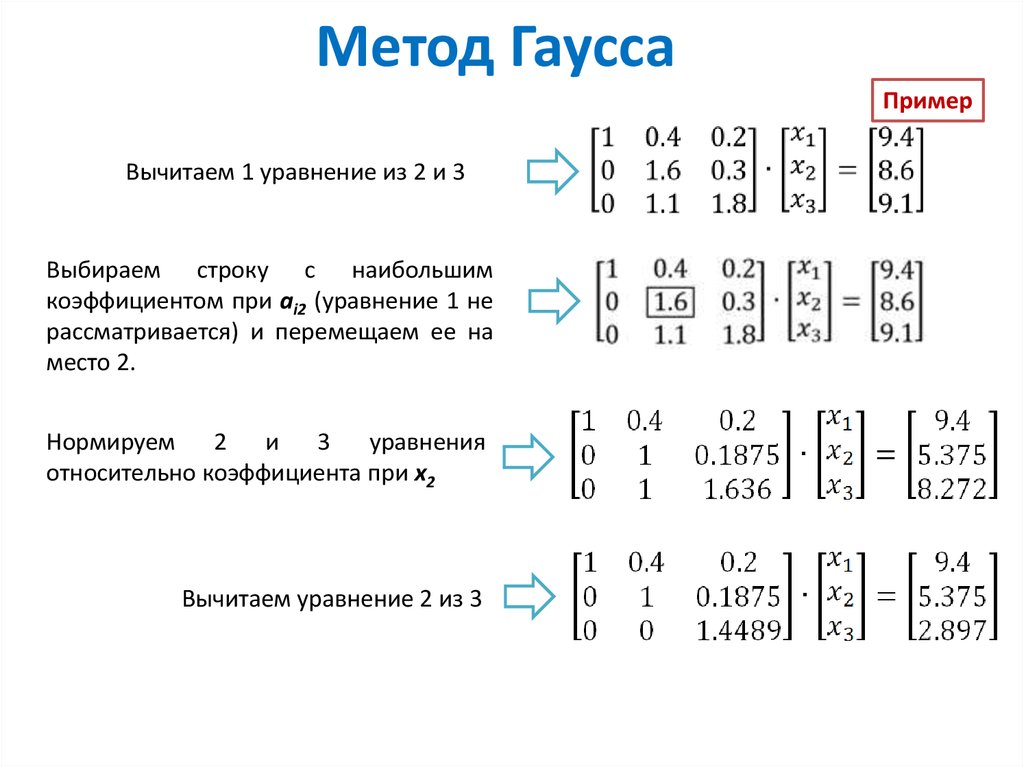
в) Метод Гаусса. Приводим расширенную матрицу к трапе

Последней матрице, имеющей треугольный вид (если исключить столбец свободных членов), соответствует следующая СЛАУ, равносильная исходной системе:

Из последнего уравнения находим , подставив его во второе уравнение, найдем и, наконец, подставив найденные

и в первое уравнение, найдем :

Следует иметь в виду, что при решении СЛАУ методом Гаусса перестановка столбцов приводит к перенумерации неизвестных.

2. Общий случай.

Теорема 3 (Кронекер–Капелли). Система (3) совместна в том и только в том случае, если ранг матрицы A равен рангу расширенной матрицы .

Систему (3) удобно решать методом Гаусса, который состоит в приведении расширенной матрицы к трапецеидальному виду путем применения элементарных преобразований. Если при этом на некотором этапе получается строка, в которой все элементы, кроме элемента столбца свободных членов, равны нулю, то система несовместна. Если

, то система (3) имеет бесчисленное множество решений, и каждое решение зависит от (n-r) не зависящих друг от друга параметров, т.е. степень свободы системы равна (n-r). В качестве параметров удобно брать «лишние неизвестные», которые объявляются свободными.

Пример 8. Решить системы уравнений:

Решение. Во всех трех системах воспользуемся методом Гаусса.

Расширенная матрица приведена к трапецеидальному виду. Объявляем «лишние неизвестные»

и свободными; запишем систему, соответствующую этой трапецеидальной матрице, перенеся свободные неизвестные и в правую часть:

Степень свободы системы равна двум, значит решение системы выразится через два параметра.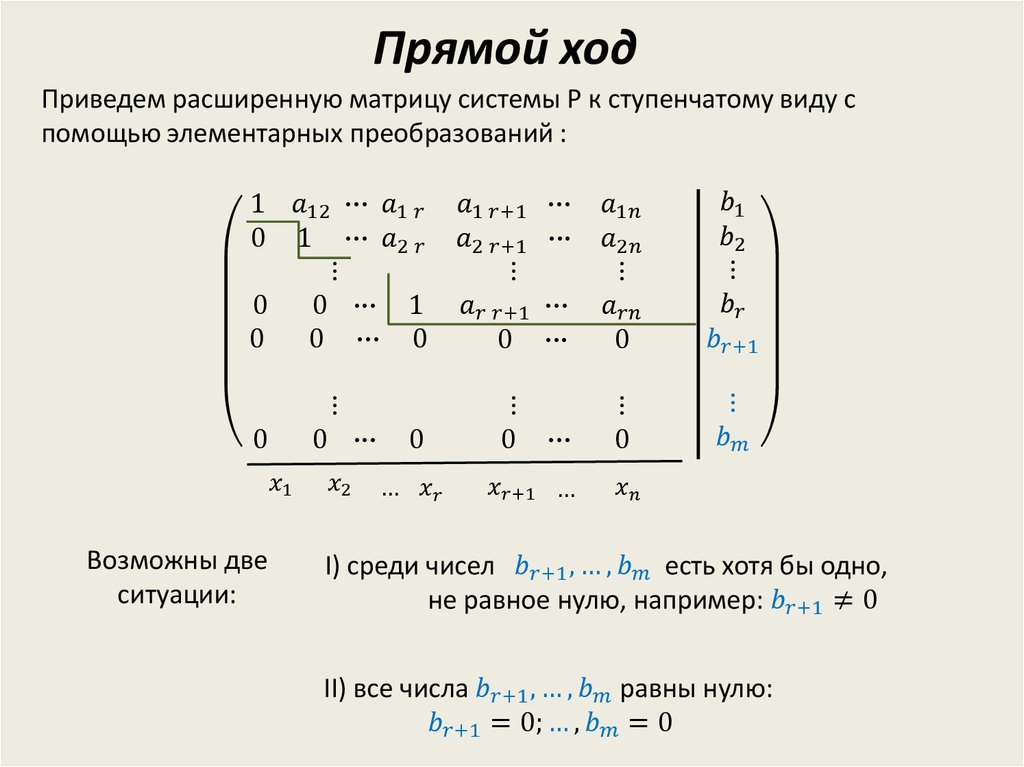 Положив и решив систему из трех уравнений с неизвестными найдем

где произвольные числа.

б)

в результате преобразований появилась строка

следовательно, система несовместна.

в)

Ранг трапецеидальной матрицы равен 2, значит степень свободы равна Объявляем неизвестные свободными.

Положив получим

Таким образом, решением системы является

где произвольные числа (параметры).

Найдём решение этой системы. Для этого умножим равенство (3) слева на матрицу .

. (5)

Матрица – это матрица, обратная к матрице

. Будем считать, что .

В этом случае существует. Теперь воспользуемся равенствами и , которые позволяют преобразовать выражение (5) к виду

. (6)

Выражение (6) представляет собой решение системы (1) в матричной форме.

П р и м е р. Найдите решение системы

Составляем матрицу коэффициентов и матрицу-столбец свободных членов заданной системы

, .

Находим обратную матрицу

Подставляем найденное значение обратной матрицы в выражение (6)

Итак, мы получили равенство

Откуда следует, что .

Замечание: если главный определитель системы равен 0, то нужно выделить уравнения, для которых определитель не равен 0, а свободные переменные переносятся в правую часть.

Реферат на тему Матрицы Метод Гаусса

КОСТРОМСКОЙ ФИЛИАЛ ВОЕННОГО УНИВЕРСИТЕТА РХБ ЗАЩИТЫ

Кафедра «Автоматизации управления войсками»

Только для преподавателей

“Утверждаю”

Начальник кафедры № 9

полковник ЯКОВЛЕВ А.Б.

«____»______________ 2004 г.

доцент СМИРНОВА А.И.

“МАТРИЦЫ. МЕТОД ГАУССА”

ЛЕКЦИЯ № 2 / 3

Обсуждено на заседании кафедры № 9

«____»___________ 2003г.

Протокол № ___________

Кострома, 2003

Cодержание

Введение

1. Действия над матрицами.

2. Решение систем линейных уравнений методом Гаусса.

Заключение

Литература

1. В.Е. Шнейдер и др., Краткий курс высшей математики,том I, гл.2,§6, 7.

2. В.С. Щипачев, Высшая математика, гл. 10, § 1, 7.

ВВЕДЕНИЕ

На лекции рассматривается понятие матрицы, действия над над матрицами, а также метод Гаусса для решения систем линейных уравнений. Для частного случая, так называемых квадратных матриц, можно вычислять определители, понятие о которых рассмотрено на предыдущей лекции. Метод Гаусса является более общим, чем рассмотренный ранее метод Крамера решения линейных систем. Разбираемые на лекции вопросы используются в различных разделах математики и в прикладных вопросах.

1-ый учебный вопрос ДЕЙСТВИЯ НАД МАТРИЦАМИ

ОПРЕДЕЛЕНИЕ 1. Прямоугольная таблица из m, n чисел, содержащая m – строк и n – столбцов, вида:

называется матрицей размера m ´ n

Числа, из которых составлена матрица, называются элементами матрицы.

Положение элемента а_i _j в матрице характеризуются двойным индексом:

первый i – номер строки;

второй j – номер столбца, на пересечении которых стоит элемент.

Сокращенно матрицы обозначают заглавными буквами: А, В, С…

Коротко можно записывать так:

ОПРЕДЕЛЕНИЕ 2. Матрица, у которой число строк равно числу столбцов, т. е. m = n , называется квадратной.

Число строк (столбцов) квадратной матрицы называется порядком матрицы.

ПРИМЕР.

ЗАМЕЧАНИЕ 1. Мы будем рассматривать матрицы, элементами которых являются числа. В математике и ее приложениях встречаются матрицы, элементами которых являются другие объекты, например, функции, векторы.

ЗАМЕЧАНИЕ 2. Матрица – специальное математическое понятие. С помощью матриц удобно записывать различные преобразования, линейные системы и т.д., поэтому матрицы часто встречаются в математической и технической литературе.

ОПРЕДЕЛЕНИЕ 3. Матрица размера 1 ´ n, состоящая из одной строки, называется матрицей – строкой.

Матрица размера т ´ 1, состоящая из одного столбца, называется матрицей – столбцом.

ОПРЕДЕЛЕНИЕ 4. Нулевой матрицей называют матрицу, все элементы которой равны нулю.

Рассмотрим квадратную матрицу порядка n:

побочная диагональ

главная диагональ

Диагональ квадратной матрицы, идущая от верхнего левого элемента таблицы к правому нижнему, называется главной диагональю матрицы (на главной диагонали стоят элементы вида а _i _i).

Диагональ, идущая от правого верхнего элемента к левому нижнему, называется побочной диагональю матрицы.

Рассмотрим некоторые частные виды квадратных матриц.

1) Квадратная матрица называется диагональной, если все элементы, не стоящие на главной диагонали, равны нулю.

2) Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной. Обозначается:

3) Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю:

верхняя нижняя

треугольная матрица треугольная матрица

Для квадратной матрицы вводится понятие: определитель матрицы. Это определитель, составленный из элементов матрицы. Обозначается:

Ясно, что определитель единичной матрицы равен 1: ½Е½ = 1

ЗАМЕЧАНИЕ. Неквадратная матрица определителя не имеет.

Если определитель квадратичной матрицы отличен от нуля, то матрица называется невырожденной, если определитель равен нулю, то матрица называется вырожденной.

ОПРЕДЕЛЕНИЕ 5. Матрица, полученная из данной заменой ее строк столбцами с теми же номерами, называется транспонированной к данной.

Матрицу, транспонированную к А, обозначают А^Т.

ПРИМЕР.

2 3 3 2

ОПРЕДЕЛЕНИЕ. Две матрицы одного и того же размера называются равными, если равны все их соответственные элементы.

Рассмотрим действия над матрицами.

СЛОЖЕНИЕ МАТРИЦ.

Операция сложения вводится только для матриц одинакового размера.

ОПРЕДЕЛЕНИЕ 7. Суммой двух матриц А = (а_i _j) и В = (b_i _j) одинакового размера называется матрица С = (с_i _j) того же размера, элементы которой равны суммам соответствующих элементов слагаемых матриц, т.е. с _{i j =}a _{i j} + b_{i j}

Обозначается сумма матриц А + В.

ПРИМЕР.

УМНОЖЕНИЕ МАТРИЦ НА ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО

ОПРЕДЕЛЕНИЕ 8. Чтобы умножить матрицу на число k, надо умножить на это число каждый элемент матрицы:

если А= (а _i _j ), то k · A= (k · a _i _j )

ПРИМЕР.

СВОЙСТВА СЛОЖЕНИЯ МАТРИЦ И УМНОЖЕНИЯ НА ЧИСЛО

1. Переместительное свойство: А + В = В + А

2. Сочетательное свойство: ( А + В ) + С = А + ( В + С )

3. Распределительное свойство: k · ( A + B ) = k A + k B, где k – число

УМНОЖЕНИЕ МАТРИЦ

Матрицу А назовем с о г л а с о в а н н о й с матрицей В , если число столбцов матрицы А равно числу строк матрицы В , т.е. для согласованных матриц матрица А имеет размер m ´ n , матрица В имеет размер n ´ k . Квадратные матрицы согласованы, если они одного порядка.

ОПРЕДЕЛЕНИЕ 9. Произведением матрицы А размера m ´ n на матрицу В размера n ´ k называется матрица С размера m ´ k, элемент которой а_i _j , расположенный в i –ой строке и j – ом столбце, равен сумме произведений элементов i – ой строки матрицы А на соответствующие элементы j – столбца матрицы В, т.е.

c _i _j = a _i₁ b₁_j + a _i₂ b ₂_j +……+ a _i _n b _n _j

Обозначим: С = А · В.

Если то

Произведение В ´ А не имеет смысла, т.к. матрицы не согласованы.

ЗАМЕЧАНИЕ 1. Если А ´ В имеет смысл, то В ´ А может не иметь смысла.

ЗАМЕЧАНИЕ 2. Если имеет смысл А ´ В и В ´ А, то, вообще говоря

А ´ В ¹ В ´ А, т.е. умножение матриц не обладает переместительным законом.

ЗАМЕЧАНИЕ 3. Если А – квадратная матрица и Е – единичная матрица того же порядка, то А ´ Е = Е ´ А = А.

Отсюда следует, что единичная матрица при умножении играет роль единицы.

ПРИМЕРЫ. Найти , если можно, А ´ В и В ´ А.

Решение: Квадратные матрицы одного и того же второго порядка согласованы в томи другом порядке, поэтому А ´ В и В ´ А существуют.

Решение: Матрицы А и В согласованы

Матрицы В и А не согласованы, поэтому В ´ А не имеет смысла.

Отметим, что в результате перемножения двух матриц получается матрица, содержащая столько строк, сколько их имеет матрица–множимое и столько столбцов, сколько их имеет матрица-множитель.

СВОЙСТВА УМНОЖЕНИЯ МАТРИЦ

1. Сочетательное свойство: А ´ ( В ´ С ) = (А ´ В ) ´С

2. Распределительное свойство: (А + В) ´ С = А ´ С + В ´С

Можно показать, что , если А и В – две квадратные матрицы одного порядка с определителями ½ А ½ и ½ В ½, то определитель матрицы С = А ´ В равен произведению определителей перемножаемых матриц, т.е.

½С½ = ½ А ½ ½ В ½

Отметим следующий любопытный факт. Как известно, произведение двух отличных от нуля чисел не равно нулю. Для матриц подобное обстоятельство может и не иметь места, т.е. произведение двух ненулевых матриц может оказаться равным нуль – матрице.

Действие “деление” для матриц не вводится. Для квадратных невырожденных матриц вводится обратная матрица. С понятием обратной матрицы можно познакомиться в рекомендуемой литературе.

2 – ой учебный вопрос РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ

УРАВНЕНИЙ МЕТОДОМ ГАУССА

Метод Гаусса (или метод последовательного исключения неизвестных) применим для решения систем линейных уравнений, в которых число неизвестных может быть либо равно числу уравнений, либо отлично от него.

Система т линейных уравнений с п неизвестными имеет вид:

x₁ , x₂, …, x_n – неизвестные.

a_i _j – коэффициенты при неизвестных.

b_i – свободные члены (или правые части)

Система линейных уравнений называется совместной, если она имеет решение, и несовместной, если она не имеет решения.

Совместная система называется определенной, если она имеет единственное решение и неопределенной, если она имеет бесчисленное множество решений.

Две совместные системы называются равносильными, если они имеют одно и то же множество решений.

К элементарным преобразованиям системы отнесем следующее:

1. перемена местами двух любых уравнений;

2. умножение обеих частей любого из уравнений на произвольное число, отличное от нуля;

3. прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число.

Элементарные преобразования переводят систему уравнений в равносильную ей.

Элементарные преобразования системы используются в методе Гаусса.

Для простоты рассмотрим метод Гаусса для системы трех линейных уравнений с тремя неизвестными в случае, когда существует единственное решение:

Дана система:

( 1 )

1-ый шаг метода Гаусса.

На первом шаге исключим неизвестное х₁ из всех уравнений системы (1), кроме первого. Пусть коэффициент . Назовем его ведущим элементом. Разделим первое уравнение системы (1) на а₁₁. Получим уравнение:

( 2 )

где

Исключим х₁ из второго и третьего уравнений системы (1). Для этого вычтем из них уравнение (2), умноженное на коэффициент при х₁ (соответственно а₂₁ и а₃₁).

Система примет вид:

( 3 )

Верхний индекс (1) указывает, что речь идет о коэффициентах первой преобразованной системы.

2-ой шаг метода Гаусса.

На втором шаге исключим неизвестное х₂из третьего уравнения системы (3). Пусть коэффициент . Выберем его за ведущий элемент и разделим на него второе уравнение системы (3), получим уравнение:

( 4 )

где

Из третьего уравнения системы (3) вычтем уравнение (4), умноженное на Получим уравнение:

Предполагая, что находим

В результате преобразований система приняла вид:

(5)

Система вида (5) называется треугольной.

Процесс приведения системы (1) к треугольному виду (5) (шаги 1 и 2) называют прямым ходом метода Гаусса.

Нахождение неизвестных из треугольной системы называют обратным ходом метода Гаусса.

Для этого найденное значение х₃подставляют во второе уравнение системы (5) и находят х₂. Затем х₂ и х₃ подставляют в первое уравнение и находят х₁.

В общем случае для системы т линейных уравнений с п неизвестными проводятся аналогичные преобразования. На каждом шаге исключается одно из неизвестных из всех уравнений, расположенных ниже ведущего уравнения.

Отсюда другое называние метода Гаусса – метод последовательного исключения неизвестных.

Если в ходе преобразований системы получается противоречивое уравнение вида 0 = b, где b ¹ 0, то это означает, что система несовместна и решений не имеет.

В случае совместной системы после преобразований по методу Гаусса, составляющих прямой ход метода, система т линейных уравнений с п неизвестными будет приведена или к треугольному или к ступенчатому виду.

Треугольная система имеет вид:

Такая система имеет единственное решение, которое находится в результате проведения обратного хода метода гаусса.

Ступенчатая система имеет вид:

Такая система имеет бесчисленное множество решений. Чтобы найти эти решения, во всех уравнениях системы члены с неизвестными х_k₊₁, … , x_k переносят в правую часть. Эти неизвестные называются свободными и придают им произвольные значения. Из полученной треугольной системы находим х₁, … , x_k, которые будут выражаться через свободные неизвестные. Подробнее об этом можно узнать в рекомендуемой литературе.

Рассмотренный метод Гаусса легко программируется на ЭВМ и является более экономичным (по числу действий), чем другие методы.

ЗАКЛЮЧЕНИЕ

Рассмотренные на лекции матрицы являются удобным инструментом для записи различных математических преобразований и широко используется в научно-технической литературе. Метод Гаусса позволяет решать любые линейные системы, он находит широкое применение и содержится в пакетах стандартных программ для ЭВМ.

доцент Смирнова А.И.

Обобщенное уточнение метода Гаусса-Зейделя для последовательно упорядоченных 2-циклических матриц

На этой странице -циклические матрицы. Получены последовательно упорядоченные 2-циклические матрицы, в то время как для решения дифференциального уравнения применяется метод конечных разностей. Вводятся соответствующие теоремы для проверки сходимости предлагаемого метода. Чтобы убедиться в эффективности этого метода, приведем несколько численных примеров. В исследовании отмечается, что, используя обобщенное уточнение метода Гаусса-Зейделя, мы получаем решение задачи с минимальным количеством итераций и получаем большую скорость сходимости, чем другие предыдущие методы.

1. Введение

Рассмотрим задачу о больших и разреженных линейных системах вида где – невырожденная вещественная матрица порядка , – заданный -мерный действительный вектор, – -мерный вектор, подлежащий определению. Путем расщепления на , где – диагональная матрица с , строго нижняя и строго верхняя треугольная часть , были разработаны различные итерационные методы. Результаты исследований последних лет показывают, что для модификации метода Гаусса-Зейделя используются обобщение, уточнение и экстраполяция (ускорение или релаксация). Salkuyeh [1] представил обобщенный метод Гаусса-Зейделя (GGS) и обсудил сходимость метода при рассмотрении строго диагонально доминирующих (SDD) и M-матриц. Уточнение метода Гаусса-Зейделя (RGS) было изучено Ватти и Энею [2] и доказало сходимость метода, взяв SDD-матрицы. Недавно Энью и соавт. [3] разработали второе усовершенствование метода Гаусса-Зейделя для SDD, симметричных положительно определенных (SPD) и M-матриц. Все вышеперечисленные исследователи пытались минимизировать количество итераций и улучшить скорость сходимости. Но тем не менее, разные исследователи проводят исследования в области итерационных методов. В соответствии с этим в данной статье мы изучаем обобщенное усовершенствование итерационного метода Гаусса-Зейделя (GRGS), которое используется для ускорения сходимости базового метода Гаусса-Зейделя. Здесь под методом GRGS имеется в виду метод -RGS, где.

2. Предварительные

Некоторые из основных итерационных методов приведены ниже.

Итерационный метод Якоби () — это

Итерационный метод Гаусса-Зейделя (GS) — это и итерационный метод последовательной сверхрелаксации (SOR) — где . Уравнения (2), (3) и (4) можно обозначить , , и , где , , , , , и , соответственно.

Определение 1. Спектр матрицы определяется как . То есть спектр матрицы — это набор всех его собственных значений.

Определение 2. Спектральный радиус матрицы обозначается и определяется как .

Определение 3. (Асимптотическая) скорость сходимости обозначается и определяется как .

Определение 4 ([4]). Матрица называется последовательно упорядоченной двухциклической, если не зависит от .

Теорема 5 ([5]). Пусть последовательно упорядочено и 2-циклично с ненулевыми диагональными элементами, и пусть . удовлетворяет для некоторого собственного значения тогда и только тогда, когда удовлетворяет для некоторого собственного значения .

Теорема 6 ([6]). Пусть последовательно упорядочена и 2-циклична с ненулевыми диагональными элементами. Затем

Теорема 7 ([6]). Для согласованно упорядоченных 2-циклических матриц, если метод Якоби сходится, то сходится и метод Гаусса-Зейделя, а метод Гаусса-Зейделя сходится в два раза быстрее, чем метод Якоби.
Мы использовали следующие алгоритмы для нестационарных методов, таких как методы сопряженного градиента (CG), бисопряженного градиента (BiCG) и метода минимальной невязки (MINRES): (a) Алгоритм для метода сопряженного градиента (CG) Дано , найти и установить . Для, до сходимости, do (b) Алгоритм для метода бисопряженного градиента (BiCG) Выбрать начальное предположение . Затем найдите для и установите и . Для , выполните (c) Метод минимальной невязки (MINRES) Выберите начальное предположение , затем найдите и . Для , do

3. Основной результат

Уточнение метода Гаусса-Зейделя (RGS) и второе уточнение метода Гаусса-Зейделя (SRGS) являются модификацией метода Гаусса-Зейделя. Используя систему линейных уравнений в форме (1), мы можем получить уточнение метода Гаусса-Зейделя (RGS) в виде следующих процедур: . Прибавляя к обеим частям, получаем .

Это можно записать как , где .

После умножения обеих частей на , получаем . Таким образом, или

Уравнения (10) или (11) являются уточнением метода Гаусса-Зейделя. Взяв одно из приведенных выше уравнений (10) или (11), подставьте схему Гаусса-Зейделя (3) вместо, чтобы получить уточнение метода Гаусса-Зейделя. Таким образом, мы можем получить обобщенное уточнение метода Гаусса-Зейделя:

Уравнение (12) называется обобщенным уточнением метода Гаусса-Зейделя (GRGS) или

0121 th – уточнение метода Гаусса-Зейделя (^th -RGS). Уравнение (12) можно обозначить либо или , где .

Если , то схема сводится к методу Гаусса-Зейделя.

Если , то метод сводится к уточнению метода Гаусса-Зейделя.

Если , то схема сводится ко второму уточнению метода Гаусса-Зейделя и т.д.

3.1. Алгоритм для метода GRGS

(1) Разложить как , где невырожденная и ненулевая матрицы; начальное приближение ; допуск ТОЛ; максимальное количество итераций .(2) Выберите

Для , до сходимости.

Сделать .

Если или 2, то стоп.

3.2. Сходимость обобщенного уточнения метода Гаусса-Зейделя

Теорема 8. Если — последовательно упорядоченные 2-циклические матрицы, то . Метод Гаусса-Зейделя сходится тогда и только тогда, когда сходится обобщенное уточнение метода Гаусса-Зейделя , а метод GRGS сходится ( ) раз быстрее, чем метод Гаусса-Зейделя, и в раз быстрее, чем метод Якоби.

Доказательство. Пусть – последовательно упорядоченная матрица с ненулевыми диагональными элементами и 2-циклическая матрица. Тогда по теореме 6 имеем . Отсюда следует, что метод Гаусса-Зейделя сходится в два раза быстрее, чем метод Якоби. Следовательно, на основании теоремы 7 метод Якоби сходится тогда и только тогда, когда сходится метод Гаусса-Зейделя. Точно так же, если GS сходится, то методы RGS, SRGS, -RGS, … и GRGS сходятся. Опять же, и так далее. Таким образом, спектральный радиус метода GRGS следующий: Таким образом, метод GRGS сходится () раз быстрее, чем метод Гаусса-Зейделя, и в раз быстрее, чем метод Якоби.
Отсюда можно сделать вывод, что количество итераций метода GRGS, обозначенное как is, Аналогично, скорость сходимости GRGS обозначается таким образом, что☐

Теорема 9. Обобщенное уточнение метода Гаусса-Зейделя сходится быстрее, чем Метод Гаусса-Зейделя и уточнение метода Гаусса-Зейделя, когда метод Гаусса-Зейделя сходится.

Доказательство. Мы можем переписать уравнения (3), RGS, SRGS и (12) соответственно в виде , , , и , где , , , , и , учитывая это. Пусть – точное решение (1). То есть , , , и . Позвольте быть неотрицательными целыми числами.☐

Если рассматривать метод Гаусса-Зейделя,

Рассмотрим усовершенствование метода Гаусса-Зейделя.

Рассмотрим второе уточнение метода Гаусса-Зейделя.

Наконец, рассмотрим обобщенное уточнение метода Гаусса-Зейделя.

Согласно коэффициентам вышеприведенных неравенств (23), (29), (35) и (42), имеем с .

Таким образом, обобщенное уточнение метода Гаусса-Зейделя сходится быстрее, чем метод Гаусса-Зейделя, уточнение метода Гаусса-Зейделя и второе уточнение метода Гаусса-Зейделя.

3.3. Численные примеры

Пример 1. Рассмотрим M-матрицу A (или 2-циклическую матрицу A), которая возникает в результате дискретизации уравнений Пуассона на единичном квадрате, как рассмотрено [6]. Если система имеет вид, то решите ее с помощью .

Решение 1. Для получаем оптимальные значения .

Из таблицы 1 видно, что метод GRGS намного лучше, чем метод SOR. Когда мы выбираем метод -RGS, мы получаем решение на первой итерации, что означает поиск решения с использованием прямого метода. Метод -RGS даже лучше, чем нестационарные методы, такие как методы CG, BiCG и MINRES.

Пример 2. Рассмотрим стационарное распределение тепла в тонкой квадратной металлической пластине размерами 0,5 м на 0,5 м, используя . Две соседние границы поддерживаются при 0°C, а теплота на других границах увеличивается линейно от 0°C в одном углу до 100°C в месте соединения сторон.

Раствор. Разместите стороны с нулевыми граничными условиями по осям – и -. Тогда задача выражается как , for () в наборе . Граничные условия , и . Если , то задача имеет сетку, а разностное уравнение для каждого и приведено в [7]. Точное решение такое, что , , , , , , , , и . Матрица имеет вид:

Для получаем оптимальные значения .

Как показано в таблице 2, метод -RGS лучше, чем другие перечисленные методы. Это второй пример, показывающий, что метод GRGS намного лучше, чем даже нестационарные методы, такие как методы CG, BiCG и MINRES.

Пример 3. Рассмотрим уравнение Пуассона на квадрате со сторонами для в множестве с на границе с сеткой .

Раствор. Используя формулу конечных разностей, мы получаем следующую систему:

Для можно получить оптимальные значения .

В таблице 3 показано, что метод -RGS имеет минимальный спектральный радиус и максимальную скорость сходимости по сравнению с методами, перечисленными в таблице. Мы делаем вывод, что метод GRGS предпочтительнее любых других итерационных методов, даже нестационарных. Таким образом, этот метод эквивалентен прямым методам.

4. Заключение

Большие и разреженные линейные системы уравнений, возникающие при дискретизации задач УЧП и ОДУ, часто решаются итерационными методами. Итерационный метод, представленный в этом исследовании, — это метод GRGS. Характеристики метода GRGS по сравнению с другими итерационными методами резюмируются следующим образом: (i) Количество итераций метода GRGS

. Количество итераций метода -RGS примерно равно количеству итераций GS и количеству итераций метода RGS и т. д. (ii) Спектральный радиус метода GRGS

. Таким образом, GRGS быстрее, чем J, GS, RGS и SRGS. (iii) Скорость сходимости метода GRGS

. Следовательно, метод GRGS имеет наибольшую скорость сходимости, чем J, GS, RGS и SRGS. (iv) Итерационный метод SOR имеет наименьшее количество итераций по сравнению с методами J и GS, но он имеет большое количество итераций по сравнению с методу GRGS. Несмотря на то, что метод SOR является лучшим методом для последовательно упорядоченных матриц, наш новый модифицированный метод GRGS намного лучше, чем метод SOR 9.0003

Доступность данных

Данные не использовались для поддержки этого исследования.

Конфликт интересов

Авторы заявляют об отсутствии конфликта интересов в связи с публикацией данной статьи.

Ссылки

Д. К. Салкуйех, «Обобщенные методы Якоби и Гаусса-Зейделя для решения линейных систем уравнений», NUMERICAL MATHEMATICS-ENGLISH SERIES , vol. 16, нет. 2, стр. 164–170, 2007.
Посмотреть по адресу:
Google Scholar
Ватти В. Б. К., Энеев Т. К., «Уточнение метода Гаусса-Зейделя для решения линейной системы уравнений», International Journal of Contemporary Mathematical Sciences , vol. 6, нет. 3, стр. 117–121, 2011.
Просмотр по адресу:
Google Scholar
Т. К. Энью, Г. Авгичев, Э. Хейл и Г. Д. Аби, «Второе уточнение итеративного метода Гаусса-Зейделя для решения линейная система уравнений», Эфиопский журнал науки и техники , том. 13, нет. 1, стр. 1–15, 2020 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
А. Хаджидимос, «Последовательная сверхрелаксация (SOR) и родственные методы», Journal of Computational and Applied Mathematics , vol. 123, нет. 1-2, стр. 177–199, 2000.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Д. М. Янг, Итеративное решение больших линейных систем , Техасский университет, 1971.
Б. Н. Датта, Численная линейная алгебра и приложения , Brooks-Cole pub. CO., 1995.
R. L. Burden and J. D. Faires, «Численный анализ», в Cengage Learning , Brook/Cole, 2011.
View At:
Google Scholar

CopyRight

Copycol 2021 Гашай Дессалю и др. Это статья с открытым доступом, распространяемая в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.

Рандомизированное исключение Гаусса

Рандомизированное исключение Гаусса
Д. СТОТТ ПАРКЕР
Департамент компьютерных наук Калифорнийского университета в Лос-Анджелесе
3532 Boelter Hall
(310) 825-6871 (OFC)
(310) 825-1322 (SEC)
(310) 825-2273 (ФАКС)

Как устранить разворот из исключения Гаусса — вместо этого рандомизируя
Д. Стотт Паркер и Дин Ле
Исключение Гаусса, вероятно, является наиболее известным и наиболее широко используемым методом. метод решения линейных систем, вычисления определителей и нахождения матричные разложения. Хотя основная процедура устранения проста сформулировать и реализовать, становится сложнее с добавлением поворотной процедуры, которая работает с вырожденными матрицами, имеющими ноль элементов на диагонали. Поворот может значительно усложнить алгоритм, увеличить перемещение данных и снизить скорость, особенно на высокопроизводительных компьютерах.
В этой статье мы предлагаем альтернативную схему выполнения гауссова исключение, которое сначала предварительно обусловливает входную матрицу путем ее умножения со случайными матрицами, чьи обратные могут быть применены впоследствии. В счет этих умножений и создание линейной системы плотной, если она еще не была, такой подход делает систему `невырожденные’ — подсистемы имеют полный ранг — с вероятностью 1. Эта предварительная подготовка приводит к (почти наверняка) устранению необходимость поворота.
Подход рандомизации также предлагает много интересных разработок. кроме устранения поворота. Как правило, рандомизация является новым метод разработки матричных вычислений, которые подходят для высокопроизводительные компьютеры.
CSD-950022.pdf
CSD-950022.пс
Случайные превращения бабочки с приложениями в вычислительной линейной алгебре
Д. Стотт Паркер
Теория и практика вычислительной линейной алгебры различаются по проблема вырождения. Разложение блочной матрицы широко используется в теории, но меньше на практике, так как даже когда матрица невырожденная (имеет полный ранг) его блочные подматрицы могут быть вырожденными. потенциал вырожденность блочных подматриц может полностью помешать практическому использованию блочные матричные алгоритмы.
Исключение Гаусса — важный пример алгоритма, затронутого возможностью вырождения. При этом основная ликвидация процедура проста в формулировке и реализации, она усложняется с добавлением поворотной процедуры, которая обрабатывает вырожденные матрицы с нулями на диагонали. Поворот может значительно усложнить алгоритм, увеличить перемещение данных и снизить скорость, особенно на высокопроизводительных компьютерах.
Мы предлагаем схему рандомизации, которая предварительно обусловливает входную матрицу умножая его на случайные матрицы, где это умножение может быть выполнено эффективно. За счет этих умножений и делая линейную систему плотной, если это еще не было, этот подход делает систему невырожденной с вероятностью 1. Покажем, что это предварительная подготовка (почти наверняка) устраняет необходимость поворота.
В этой статье мы изучаем свойства случайных баттерфляй-преобразований. (RBT), интересный класс случайных матриц. RBT напоминают Fast Преобразование Фурье (БПФ). У RBT есть три важных преимущества. Первый, они обладают доказуемыми свойствами рандомизации. Во-вторых, RBT могут быть выполняется эффективно и, в частности, должен быть полезен на параллельных и векторные машины с архитектурой, поддерживающей БПФ. вычисления. В-третьих, RBT обеспечивают важные числовые свойства, когда ограничены унитарными матрицами, и даже когда ограничены хорошие, неунитарные матрицы.
Подход RBT также предлагает много интересных разработок, выходящих за рамки устранение поворота. Рандомизация открывает новые возможности для линейное системное решение, которое хорошо подходит для высокопроизводительных компьютеров.
CSD-950023.pdf
CSD-950023.пс
Случайное преобразование бабочки Полезно в вычислениях с блочной матрицей
Д. Стотт Паркер
Мы представляем новую схему рандомизации, которая предварительно обусловливает ввод линейную систему путем умножения ее на невырожденные случайные матрицы. За счет этих умножений и составления линейной системы плотным, если это еще не было, этот подход делает блоки результирующая система неособая с вероятностью 1.
В частности, в этой статье мы рассматриваем случайные матрицы, которые «случайные бабочки» и называют их приложение Random Butterfly. Трансформация (РБТ). RBT могут быть выполнены эффективно, и в особенно полезно на параллельных и векторных машинах с архитектуры, которые поддерживают вычисления, подобные БПФ.
Блочное исключение Гаусса является важным примером алгоритма с который этот RBT может быть использован. Исключение Гаусса осложняется поворот, который обрабатывает вырожденные матрицы, имеющие нулевые элементы на диагональ. Разворот может значительно усложнить алгоритм, увеличить перемещение данных и снизить скорость, особенно на высокопроизводительные компьютеры. Покажем, что это предобусловливание имеет эффект устранения необходимости поворота (с вероятностью 1).
Подход RBT также предлагает много интересных разработок, помимо устранение поворота. Рандомизация, по-видимому, предлагает новые возможности для решения линейных систем, которые хорошо подходят для высокопроизводительные компьютеры.
CSD-950024.pdf
CSD-950024.пс
Явные формулы для Результаты исключения Гаусса
Д. Стотт Паркер
Исключение Гаусса, вероятно, является самым известным и наиболее широко используемым методом. метод решения линейных систем, вычисление определителей и разлагающиеся матрицы. Это важный инструмент в ядре большинства пакеты вычислительной линейной алгебры сегодня. В то время как основные процедура ликвидации проста в формулировке и реализации, она сложна достаточно, чтобы рассуждать об этом нетривиально.
В этой статье мы воскресим характеристику поведения Исключение Гаусса, а именно, что каждый из его промежуточных результатов есть отношение определителей подматриц входной матрицы, и показать его эквивалентность другой характеристике в терминах Шура дополняет. T разложения когда А симметричен. Хотя они выполняют совсем другие вычисления чем традиционный алгоритм, они отличаются формально только лежащее в основе изменение переменных.
CSD-950026.pdf
CSD-950026.пс
Дополнения Шура подчиняются категориальной грамматике Ламбека: другой взгляд на исключение Гаусса и разложение LU
Д. Стотт Паркер
В течение двух десятилетий дополнения Шура находят все более широкое применение в линейная алгебра, часто как абстракции исключения Гаусса. Это известно, что они подчиняются некоторым нетривиальным тождествам, таким как Crabtree и факторное свойство Хейнсворта. Мы начали эту работу с вопроса, есть ли были теорией для определения их свойств вообще.
Категориальная грамматика Ламбека — дедуктивная система, введенная в 1958 г. Ламбек как математическая основа синтаксического исчисления английского языка предложения. Мы показываем, что категориальная грамматика дает дедуктивную систему для определения свойств LU- и UL-разложений, а также о гауссовских устранение. Его также можно использовать для получения тождеств, которым подчиняется Шур. дополняет.
На первый взгляд это кажется странным результатом, соединяющим два несвязанные темы. Однако в ретроспективе это является следствием как оба используют частные. Он может найти применение в разработке как грамматические формализмы и числовые алгоритмы.
CSD-950027.pdf
CSD-950027.ps
Еще раз о матричных алгоритмах Quadtree: Основные вопросы и их решение
Д. Стотт Паркер и Дин Ле
С представлением матриц квадрантов, популяризированным Уайзом, многие матричные алгоритмы естественным образом реализуются в рекурсивном функционале стиль. Этот стиль полезен для выявления параллелизма, выявления отображения для матричных вычислений на определенные компьютерные архитектуры, и, в более общем плане, в раскрытии новых способов рассуждения о матричных алгоритмах.
Мир еще не проторил путь к алгоритмам на основе дерева квадрантов, к сожалению. Кажется, есть ряд причин, по которым quadtree алгоритмы и архитектуры не достигли своего потенциала в упражняться. Важным среди них является то, что представления дерева квадрантов не уникален, и что простые реализации блочно-матричного алгоритмы не работают для вырожденных матриц (например, с сингулярными квадранты). Предлагаемые расширения алгоритмов на основе дерева квадрантов для решения с несколькими представлениями или вырожденными матрицами (такими как прибегая к повороту), на самом деле не сняли возражений: они теряют либо численную устойчивость, либо преимущества в элегантности, параллелизм и функциональный стиль, поощряющий использование деревьев квадрантов в первую очередь.
Мы рассматриваем ситуацию в этой статье и представляем новые подходы к обработка вырожденных квадрантов в алгоритмах дерева квадрантов: во-первых, мы полагаемся на канонических представлениях деревьев квадрантов. Во-вторых, мы рандомизируем ввод матрица таким образом, чтобы гарантировать невырожденность квадрантов, и также допускает дерандомизацию после алгоритма. Этот подход должен сделать представление дерева квадрантов более успешным в реальной матрице вычисления.
CSD-950028.пс
Рандомизирующее БПФ: альтернатива повороту в методе исключения Гаусса
Д. Стотт Паркер, Брэд Пирс
Недавно были разработаны рандомизирующие входные преобразования для упрощение исключения Гаусса. Умножение на специальное разреженное случайных матриц эти преобразования дают эквивалентную линейную система, которую с вероятностью 1 может решить метод исключения Гаусса без какой-либо аугментации путем поворота.
В этой статье мы изучаем свойства унитарного рандомизирующего дискретного Преобразование Фурье (RDFT), которое масштабирует строки по случайным значениям из комплексный единичный круг, а затем применяет обычное ДПФ. Когда размер задачи равен степени двойки, Рандомизированное быстрое преобразование Фурье (RFFT) алгоритм может эффективно реализовать RDFT, используя существующий FFT кода на множестве параллельных и векторных машин, архитектура которых поддерживают вычисления, подобные БПФ.
CSD-950037.ps
CSD-950037.pdf
Рандомизация ввода и автоматическое получение систолические массивы для вычисления матрицы
Дин Ле, Д. Стотт Паркер, Брэд Пирс
Многие стандартные матричные алгоритмы трудно реализовать как систолические. массивы, потому что они связаны с перемещением данных, которое не может быть определено априори, что приводит к высокой временной сложности. В случае плотного матричная инверсия, исключение Гаусса (GE) с поворотом в значительной степени были вытеснены альтернативными схемами, такими как вращения Гивенса и метод Грама-Шмидта, которые являются дорогостоящими и сложными, и более простой GE с попарным поворотом и GE без поворота, которые могут ломаться на “вырожденных” входах, т.е. обратимых матрицах с необратимыми подматрицы.
Новый метод рандомизации ввода эффективно преобразует линейный задачу Ax=b в рандомизированную задачу VAx = Vb, где матрица V выбирается из специального класса случайных матриц. Если A неособо, тогда с вероятностью 1 можно успешно применить ОЭ без поворота к ВА. Как показано в расширенном учебном примере, этот простой алгоритм поддается компиляторам матричных алгоритмов текущего поколения, например, система MAMACG Калифорнийского университета в Лос-Анджелесе.
КСД-950038.пс
CSD-950038.pdf
Практические алгоритмы матрицы рекурсивной блочной декомпозиции, и алгоритмы Quadtree с помощью рандомизации
Дин Ле, Д. Стотт Паркер
Алгоритмы рекурсивной блочной декомпозиции (также известные как алгоритмы дерева квадрантов). когда все блоки квадратные) были предложены для решения известной такие задачи, как сложение матриц, умножение, обращение, вычисление определителя, блочное разложение LDU, дискретное преобразование Фурье преобразование, Холецкого и QR-факторизацию.
До сих пор такие алгоритмы часто считались непрактичными для создание общих инструментов. В частности, рекурсивная блочная декомпозиция методы непрактичны для обращения матриц и исключения Гаусса, поскольку оба требуют, чтобы ведущие подматрицы входной матрицы были неособый (что не всегда гарантировано).
Мы покажем, как использовать рандомизацию, чтобы гарантировать соответствие подматриц эти требования, и сделать методы рекурсивной блочной декомпозиции практично на хорошо обусловленных входных матрицах. Полученные алгоритмы элегантны, и мы показываем, что рекурсивные программы могут хорошо работать для как плотные, так и разреженные матрицы, хотя и с плотной рандомизацией вычисления кажутся наиболее практичными.
CSD-950039.ps
Блочное матричное обобщение исключения Гаусса-Жордана используя формулу отношения Хейнсворта для дополнений Шура
Брэд Пирс, Д. Стотт Паркер
Алгоритм блочной матрицы для решения линейных систем получен с использованием Частная формула Хейнсворта для дополнений Шура. Алгоритм по существу, обобщение исключения Гаусса-Жордана.
CSD-950063.пс
КСД-950063.pdf
Линейные рандомизирующие преобразования: априорная альтернатива стратегиям динамического исключения например, частичный поворот
Брэд Пирс, Д.