Матрицы Метод Гаусса Формулы Крамера
Слайд 1
Описание слайда:
Матрицы Метод Гаусса Формулы Крамера
Слайд 2
Описание слайда:
Содержание Что такое матрица? Карл Фридих Гаусс Метод Гаусса Габриэль Крамер Метод Крамера Вывод Использованные источники информации
Слайд 3
Описание слайда:
Матрица
Определение
Прямоугольная таблица из m, n чисел, содержащая m – строк и n – столбцов, вида:
называется матрицей размера m n
Числа, из которых составлена матрица, называются элементами матрицы.
Положение элемента аi j в матрице характеризуются двойным индексом:
первый i – номер строки;
второй j – номер столбца, на пересечении которых стоит элемент.
Слайд 4
Описание слайда:
Иоганн Карл Фридрих Гаусс
(30 апреля 1777, Брауншвейг — 23 февраля 1855, Гёттинген)
Биография
Дед Гаусса был бедным крестьянином, отец — садовником, каменщиком, смотрителем каналов в герцогстве Брауншвейг. Уже в двухлетнем возрасте мальчик показал себя вундеркиндом. В три года он умел читать и писать. Согласно легенде, школьный учитель математики, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100. Юный Гаусс заметил, что попарные суммы с противоположных концов одинаковы: 1+100=101, 2+99=101 и т. д., и мгновенно получил результат 50х101=5050 .
После 1801 года Гаусс включил в круг своих интересов естественные науки. Катализатором послужило открытие малой планеты Церера ,вскоре после наблюдений потерянной.
Слайд 5
Описание слайда:
Метод Гаусса Метод Гаусса — классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Система т линейных уравнений с п неизвестными имеет вид: x1 , x2, …, xn – неизвестные. ai j – коэффициенты при неизвестных. bi – свободные члены (или правые части)
Слайд 6
Описание слайда:
Типы уравнений
Система линейных уравнений называется совместной, если она имеет решение, и несовместной, если она не имеет решения.
Совместная система называется определенной, если она имеет единственное решение и неопределенной, если она имеет бесчисленное множество решений.
Две совместные системы называются равносильными, если они имеют одно и то же множество решений.
Слайд 7
Описание слайда:
Элементарные преобразования К элементарным преобразованиям системы отнесем следующее: перемена местами двух любых уравнений; умножение обеих частей любого из уравнений на произвольное число, отличное от нуля; прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число.
Слайд 8
Описание слайда:
Общий случай
Для простоты рассмотрим метод Гаусса для системы трех линейных уравнений с тремя неизвестными в случае, когда существует единственное решение:
Дана система:
1-ый шаг метода Гаусса
На первом шаге исключим неизвестное х1 из всех уравнений системы (1), кроме первого.
Слайд 9
Описание слайда:
2-ой шаг метода Гаусса На втором шаге исключим неизвестное х2 из третьего уравнения системы (3). Пусть коэффициент . Выберем его за ведущий элемент и разделим на него второе уравнение системы (3), получим уравнение: где Из третьего уравнения системы (3) вычтем уравнение (4), умноженное на Получим уравнение: Предполагая, что находим
Слайд 10
Описание слайда:
В результате преобразований система приняла вид:
Система вида (5) называется треугольной.
Процесс приведения системы (1) к треугольному виду (5) (шаги 1 и 2) называют прямым ходом метода Гаусса.
Нахождение неизвестных из треугольной системы называют обратным ходом метода Гаусса.
Для этого найденное значение х3 подставляют во второе уравнение системы (5) и находят х2. Затем х2 и х3 подставляют в первое уравнение и находят х1.
Слайд 11
Описание слайда:
Если в ходе преобразований системы получается противоречивое уравнение вида 0 = b, где b 0, то это означает, что система несовместна и решений не имеет.
В случае совместной системы после преобразований по методу Гаусса, составляющих прямой ход метода, система т линейных уравнений с п неизвестными будет приведена или к треугольному или к ступенчатому виду.
Треугольная система имеет вид:
Такая система имеет единственное
решение, которое находится в
результате проведения обратного хода метода Гаусса.
Ступенчатая система имеет вид:
Такая система имеет бесчисленное
множество решений.
Слайд 12
Описание слайда:
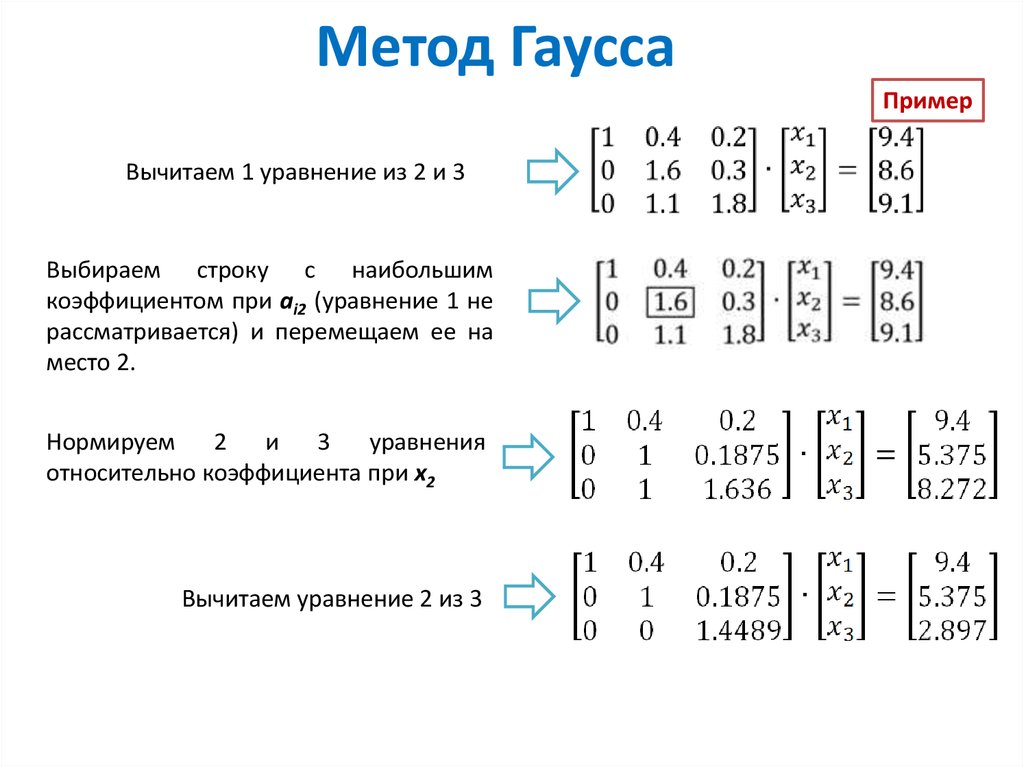
Рассмотрим на примере Покажем последовательность решения системы из трех уравнений методом Гаусса Поделим первое уравнение на 2, затем вычтем его из второго (a21=1, поэтому домножение не требуется) и из третьего, умножив предварительно на a31=3 Поделим второе уравнение полученной системы на 2, а затем вычтем его из третьего, умножив предварительно на 4,5 (коэффициент при x2) Тогда
Слайд 13
Описание слайда:
Метод Крамера
Метод Крамера—способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно).
Создан Габриэлем Крамером в 1751 году.
Слайд 14
Описание слайда:
Габриэль Крамер
(31 июля 1704, Женева, Швейцария—4 января 1752, Баньоль-сюр-Сез, Франция)
Биография
Крамер родился в семье франкоязычного врача. В 18 лет защитил диссертацию. В 20-летнем возрасте Крамер выставил свою кандидатуру на вакантную должность преподавателя на кафедре философии Женевского университета.
1727: Крамер 2 года путешествовал по Европе, заодно перенимая опыт у ведущих математиков — Иоганна Бернулли и Эйлера,Галлея и де Муавра, Мопертюи и Клеро.
В свободное от преподавания время Крамер пишет многочисленные статьи на самые разные темы: геометрия, история математики, философия, приложения теории вероятностей.
1751: Крамер получает серьёзную травму после дорожного инцидента с каретой. Доктор рекомендует ему отдохнуть на французском курорте, но там его состояние ухудшается, и 4 января 1752 года Крамер умирает.
Слайд 15
Описание слайда:
Рассмотрим систему линейных уравнений с квадратной матрицей A , т.е. такую, у которой число уравнений совпадает с числом неизвестных: a11x1+a12x2+…+a1nxn=b1 a21x1+a22x2+…+a2nxn=b2 … … an1x1+an2x2+…+annxn=bn
Слайд 16
Описание слайда:
Имеет единственное решение тогда и только тогда, когда определитель матрицы этой системы отличен от нуля: a11 a12 … a1n a21 a22 … a2n … … an1 an2 … ann
Слайд 17
Описание слайда:
В этом случае решение можно вычислить по формуле Крамера
Слайд 18
Описание слайда:
Для получения значения xk в числитель ставится определитель, получающийся из det(A) заменой его k-го столбца на столбец правых частей
Пример.
Решить систему уравнений :
Слайд 19
Описание слайда:
Решение.
Слайд 20
Описание слайда:
Найдите оставшиеся компоненты решения.
Формулы Крамера не представляют практического значения в случае систем с числовыми коэффициентами: вычислять по ним решения конкретных систем линейных уравнений неэффективно, поскольку они требуют вычисления (n+1)-го определителя порядка n , в то время как метод Гаусса фактически эквивалентен вычислению одного определителя порядка n . Тем не менее, теоретическое значение формул Крамера заключается в том, что они дают явное представление решения системы через ее коэффициенты. Например, с их помощью легко может быть доказан результат
Решение системы линейных уравнений с квадратной матрицей A является непрерывной функцией коэффициентов этой системы при условии, что det A не равно 0 .
Слайд 21
Описание слайда:
Найдите оставшиеся компоненты решения. Кроме того, формулы Крамера начинают конкурировать по вычислительной эффективности с методом Гаусса в случае систем, зависящих от параметра. зависящей от параметра , определить предел отношения компонент решения:
Слайд 22
Описание слайда:
Решение. В этом примере определитель матрицы системы равен . По теореме Крамера система совместна при . Для случая применением метода Гаусса убеждаемся, что система несовместна. Тем не менее, указанный предел существует. Формулы Крамера дают значения компонент решения в виде
Слайд 23
Описание слайда:
Ответ.
Приведенный пример поясняет также каким образом система линейных уравнений, непрерывно зависящая от параметра, становится несовместной: при стремлении параметра к какому-то критическому значению (обращающему в нуль определитель матрицы системы) хотя бы одна из компонент решения «уходит на бесконечность».
Слайд 24
Описание слайда:
Вывод Рассмотренный в данной презентации Метод Крамера позволяет решать линейные системы, но удобнее решать системы линейных уравнений с помощью метода Гаусса, который находит широкое применение и содержится в пакетах стандартных программ для ЭВМ.
Слайд 25
Описание слайда:
Использованные источники
В.С. Щипачев, Высшая математика
Ильин В. А., Позняк Э. Г. Линейная алгебра: Учебник для вузов.
3, получается значительная экономия по сравнению с наивным O(nnz(X) m) времени для вычисления \ тильда G ⋅X. Кроме того, поскольку общее расстояние вариации невелико, мы можем доказуемо использовать T ⋅X вместо \tilde G ⋅X в любом приложении и иметь такие же гарантии, как если бы мы использовали \tilde G ⋅X, с точностью до небольшой положительной константы по вероятности ошибки. Мы применяем это преобразование к неотрицательной матричной факторизации (NMF) и методам опорных векторов (SVM).
Процитировать эту статью
БибТекс
@InProceedings{pmlr-v48-kapralov16,
title = {Как имитировать умножение на матрицу Гаусса},
автор = {Капралов, Майкл и Потлуру, Вамси и Вудрафф, Дэвид},
booktitle = {Материалы 33-й Международной конференции по машинному обучению},
страницы = {2101--2110},
год = {2016},
редактор = {Балкан, Мария Флорина и Вайнбергер, Килиан К.},
объем = {48},
серия = {Материалы исследования машинного обучения},
адрес = {Нью-Йорк, Нью-Йорк, США},
месяц = {20--22 июня},
издатель = {PMLR},
pdf = {http://proceedings.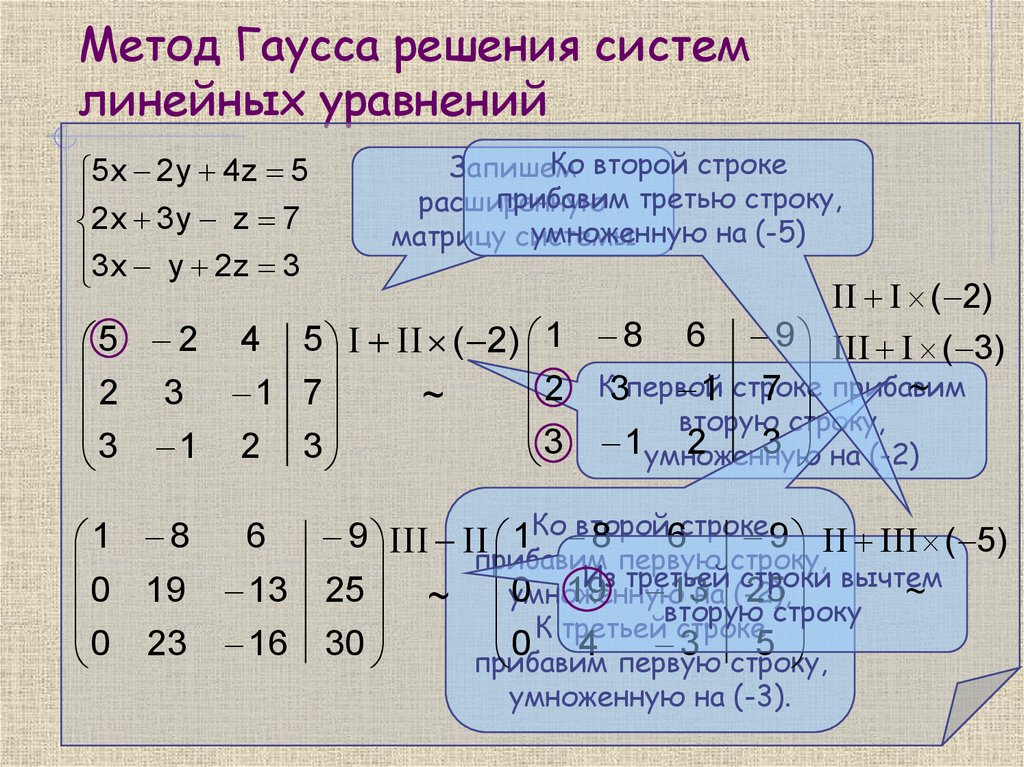
3, получается значительная экономия по сравнению с наивным O(nnz(X) m) времени для вычисления \ тильда G ⋅X. Кроме того, поскольку общее расстояние вариации невелико, мы можем доказуемо использовать T ⋅X вместо \tilde G ⋅X в любом приложении и иметь такие же гарантии, как если бы мы использовали \tilde G ⋅X, с точностью до небольшой положительной константы по вероятности ошибки. Мы применяем это преобразование к неотрицательной матричной факторизации (NMF) и методам опорных векторов (SVM).}
}
Сноска
%0 Документ конференции
%T Как подделать умножение на матрицу Гаусса
%A Михаил Капралов
%A Вамси Потлуру
%A Дэвид Вудрафф
%B Материалы 33-й Международной конференции по машинному обучению
%C Материалы исследования машинного обучения
%D 2016
%E Мария Флорина Балкан
%E Килиан К. Вайнбергер
%F пмлр-v48-капралов16
%I PMLR
%P 2101--2110
%U https://proceedings.mlr.press/v48/kapralov16.html
%V 48
%X Вы когда-нибудь хотели умножить n \times d матрицу X, где n ≫d, слева на m \times n матрицу \tilde G i.
3, получается значительная экономия по сравнению с наивным O(nnz(X) m) времени для вычисления \ тильда G ⋅X. Кроме того, поскольку общее расстояние вариации невелико, мы можем доказуемо использовать T ⋅X вместо \tilde G ⋅X в любом приложении и иметь такие же гарантии, как если бы мы использовали \tilde G ⋅X, с точностью до небольшой положительной константы по вероятности ошибки. Мы применяем это преобразование к неотрицательной матричной факторизации (NMF) и методам опорных векторов (SVM).
РИС
TY - БУМАГА
TI - Как подделать умножение на матрицу Гаусса
AU - Михаил Капралов
AU - Вамси Потлуру
AU - Дэвид Вудрафф
BT — Материалы 33-й Международной конференции по машинному обучению
ДА - 2016/06/11
ED - Мария Флорина Балкан
ED - Килиан К. Вайнбергер
ID - pmlr-v48-kapralov16
ПБ - ПМЛР
DP - Материалы исследований машинного обучения
ВЛ - 48
СП - 2101
ЭП - 2110
Л1 - http://proceedings.mlr.press/v48/kapralov16.pdf
УР - https://proceedings.
3, получается значительная экономия по сравнению с наивным O(nnz(X) m) времени для вычисления \ тильда G ⋅X. Кроме того, поскольку общее расстояние вариации невелико, мы можем доказуемо использовать T ⋅X вместо \tilde G ⋅X в любом приложении и иметь такие же гарантии, как если бы мы использовали \tilde G ⋅X, с точностью до небольшой положительной константы по вероятности ошибки. Мы применяем это преобразование к неотрицательной матричной факторизации (NMF) и методам опорных векторов (SVM).
Скорая помощь -
АПА
Капралов М., Потлуру В. и Вудрафф Д. (2016). Как подделать умножение на матрицу Гаусса. Proceedings of The 33rd International Conference on Machine Learning , in Proceedings of Machine Learning Research 48:2101-2110 Доступно по адресу https://proceedings.mlr.press/v48/kapralov16.html.
Сопутствующий материал
Оценка нескольких матричных графиков Гаусса
.
2018 ноябрь;80(5):927-950.
doi: 10.1111/rssb.12278. Epub 2018 14 июня.
Юньчжан Чжу 1 , Лексин Ли 2
Принадлежности
- 1 Статистический факультет Университета штата Огайо.
- 2 Отдел биостатистики Калифорнийского университета в Беркли.
- PMID: 30505211
- PMCID: PMC6261498
- DOI:
10.
1111/rssb.12278
1111/rssb.12278Бесплатная статья ЧВК
Юньчжан Чжу и др. J R Stat Soc Series B Stat Methodol. 2018 ноябрь
Бесплатная статья ЧВК
. 2018 ноябрь;80(5):927-950.
doi: 10.1111/rssb.12278. Epub 2018 14 июня.
Авторы
Юньчжан Чжу 1 , Лексин Ли 2
Принадлежности
- 1 Статистический факультет Университета штата Огайо.
- 2 Отдел биостатистики Калифорнийского университета в Беркли.
- PMID: 30505211
- PMCID: PMC6261498
- DOI: 10.1111/rssb.12278
Абстрактный
Данные с матричным значением, где единицей выборки является матрица, состоящая из строк и столбцов измерений, появляются во многих научных и деловых приложениях. Матричная гауссовская графическая модель является полезным инструментом для описания структуры условной зависимости строк и столбцов. В этой статье мы используем невыпуклую пенализацию для оценки нескольких графиков на основе матричных данных при матричном нормальном распределении. Мы предлагаем высокоэффективный алгоритм невыпуклой оптимизации, который можно масштабировать для графов с сотнями узлов.
Мы устанавливаем асимптотические свойства оценщика, который требует менее строгих условий и имеет более точную границу ошибки вероятности, чем существующие результаты. Мы демонстрируем эффективность предложенного нами метода как с помощью моделирования, так и с помощью анализа реальной функциональной магнитно-резонансной томографии.
Ключевые слова: Условная независимость; гауссова графическая модель; Матричное нормальное распределение; Невыпуклая пенализация; функциональная магнитно-резонансная томография в состоянии покоя; Разреженность.
Цифры
Рисунок 1
Используются три типа графиков…
Рисунок 1
Три типа графиков, используемых в наших исследованиях моделирования
фигура 1Три типа графиков, используемых в наших исследованиях моделирования
Рисунок 2
Предполагаемые сети подключения для…
Рисунок 2
Расчетные сети подключения для данных ABIDE.
Левая панель предназначена для…
Расчетные сети подключения для данных ABIDE. Левая панель предназначена для группы ASD, а правая панель — для обычного управления. Показаны 2% самых популярных ссылок, где серые ссылки являются общими для обеих групп, а красные ссылки уникальны для каждой группы.
Рисунок 3
Предполагаемые сети подключения для…
Рисунок 3
Расчетные сети подключения для данных СДВГ. Левая панель предназначена для…
Рисунок 3 Расчетные сети подключения для данных СДВГ. Левая панель предназначена для группы СДВГ, а правая — для обычного управления. Показаны 2% самых популярных ссылок, где серые ссылки являются общими для обеих групп, а красные ссылки уникальны для каждой группы.
Алгоритм 1
Алгоритм ММ и ADMM…
Алгоритм 1
Алгоритм ММ и алгоритм ADMM для решения (2).
Алгоритм 1Алгоритм ММ и алгоритм ADMM для решения (2).
См. это изображение и информацию об авторских правах в PMC
Похожие статьи
Совместное изучение нескольких разреженных матричных гауссовских графических моделей.
Хуан Ф., Чен С. Хуан Ф и др. IEEE Trans Neural Netw Learn Syst. 2015 ноябрь; 26 (11): 2606-20. doi: 10.1109/TNNLS.2014.2384201. Epub 2015 4 марта. IEEE Trans Neural Netw Learn Syst. 2015. PMID: 25751876
Совместная оценка множественных зависимых гауссовских графических моделей с приложениями к геномике мыши.
Се Ю, Лю Ю, Валдар В. Се Ю и др. Биометрика. 2016 сен; 103 (3): 493-511. doi: 10.1093/biomet/asw035. Биометрика. 2016. PMID: 29038606 Бесплатная статья ЧВК.
Совместная оценка нескольких условных гауссовских графических моделей.
Хуан Ф., Чен С., Хуан С.Дж. Хуан Ф и др. IEEE Trans Neural Netw Learn Syst. 2018 июль; 29 (7): 3034-3046. doi: 10.1109/TNNLS.2017.2710090. Epub 2017, 28 июня. IEEE Trans Neural Netw Learn Syst. 2018. PMID: 28678717
РАЗРЕЖЕННАЯ УСЛОВНАЯ ГАУССОВА ГРАФИЧЕСКАЯ МОДЕЛЬ ДЛЯ АНАЛИЗА ГЕНЕТИЧЕСКИХ ДАННЫХ ГЕНОМИК.
Инь Дж., Ли Х. Инь Дж. и др. Энн Appl Стат. 2011 декабрь; 5 (4): 2630-2650. дои: 10.1214/11-AOAS494. Энн Appl Стат. 2011. PMID: 22905077 Бесплатная статья ЧВК.
Выбор модели и оценка в матричной нормальной графической модели.
Инь Дж., Ли Х. Инь Дж. и др. Дж мультивар анал. 2012 1 мая; 107:119-140. doi: 10.1016/j.jmva.2012.01.005. Дж мультивар анал. 2012. PMID: 22368309 Бесплатная статья ЧВК.
Посмотреть все похожие статьи
Цитируется
Расширение возможностей дифференциальных сетей с использованием байесовского анализа.
Смит Дж., Араши М., Беккер А. Смит Дж. и др. ПЛОС Один. 2022 25 января; 17 (1): e0261193. doi: 10.1371/journal.pone.0261193. Электронная коллекция 2022. ПЛОС Один. 2022. PMID: 35077451 Бесплатная статья ЧВК.
Проверка гипотез для сетевых данных с помощью Power Enhancement.
Ся Ю, Ли Л. Ся Ю и др. Стат Син. 2022;32:293-321. doi: 10.5705/сс.202019.0361. Стат Син. 2022. PMID: 35002179
Сетевое моделирование в биологии: статистические методы для генных и мозговых сетей.
Ван Ю.С.Р., Ли Л., Ли Дж.Дж., Хуан Х. Ван YXR и др. Стат. наук. 2021 фев; 36 (1): 89-108. дои: 10.1214/20-стс792. Стат. наук. 2021. PMID: 34305304 Бесплатная статья ЧВК.
Одновременный дифференциальный сетевой анализ и классификация матричных переменных данных с приложением к мозговым связям.
Чен Х, Го И, Хэ И, Цзи Дж, Лю Л, Ши И, Ван И, Ю Л, Чжан Х; Инициатива нейровизуализации болезни Альцгеймера. Чен Х и др. Биостатистика. 2022 18 июля; 23 (3): 967-989. doi: 10.1093/biostatistics/kxab007.
