Вычисление определителя методом Гаусса
Вычислим определитель методом Гаусса.
Суть метода состоит в следующем: определитель приводится к треугольному виду с помощью элементарных преобразований, и тогда он равен произведению элементов, стоящих на главной диагонали.
Идея метода состоит в следующем: пусть дан определитель третьего порядка
(1)
элементдолжен быть равен, для этого первую строку разделим на.
Получим определитель вида (2)
Обнулим элементы, стоящие в первом столбце, кроме первого. Для этого из второй строки вычтем первую, умноженную на , далее из третьей строки вычтем первую, умноженную на. Получим определитель вида.
Обозначим его элементы буквой с, тогда
(3)
Теперь надо обнулить элемент . Элементдолжен быть равен, для этого вторую строку разделим на. Получим определитель вида.
Далее из третьей строки вычтем вторую,
умноженную на
.
.
Обозначим его элементы буквой t, тогда
(4)
Вот мы привели определитель к треугольному виду, теперь он равен .
Разберем теперь это на конкретном примере.
Пример 4:Вычислить определительметодом Гаусса.
Решение: Поменяем местами первую и третью строки (при замене двух столбцов (строк) определитель меняет знак на противоположный).
Получили
Из второй строки вычтем первую, умноженную на 2, далее из третьей строки вычтем первую, умноженную на 3. Получили
Далее из третьей строки вычтем вторую, умноженную на 3.
Получили –
§2.Матрицы Виды матриц
Определение 7:
Определение 8: Если, то матрица называется квадратной.
Определение 9:Матрица, состоящая лишь из одной строки (столбца) называется матрицей-строкой (столбцом).
Определение 10:Матрица, состоящая
из нулей, называется нулевой матрицей.
Определение 11:Диагональной матрицей называется квадратная матрица, у которой все элементы, не принадлежащие главной диагонали равны нулю.
Определение 12:Единичной матрицей называется диагональная матрица, у которой все элементы, стоящие на главной диагонали равны единице.
Определение 13:Треугольной называется квадратная матрица, у которой элементы, расположенные по одну сторону от главной диагонали равны нулю.
Действиянад матрицами.
Определение 14: Две матрицы считаются равными, если они имеют одинаковое число строк и столбцов и равные соответствующие элементы.
Пример 5:
Матрицы А и В равны, т.е.
Определение 15: Суммой (разностью) матриц А и В называется такая матрица С, у которой каждый элемент равен.
Пример 6: Найти матрицу, если
Решение:
Cвойства сложения
А+В=В+А(переместительное)
20А+О=А, где О-нулевая матрица
30 А+(В+С)=(А+В)+С (дистрибутивное)
40А+(-А)=О, где – А противоположная матрица
(т. е. элементы имеют противоположные
знаки)
е. элементы имеют противоположные
знаки)
Определение 16: Произведением матрицы А на число называется матрица, полученная из данной умножением всех ее элементов на число.
Пример 7:
Умножение матиц
Это действие распространяется на так называемые согласованные матрицы.
Определение 17: Матрица А называется согласованной с матрицей В, если число столбцов у матрицы А равно числу строк у матрицы В.
Пример 8:и- согласованные
и- несогласованные
инесогласованные
Определение 18: Произведением двух матриц А и В называется такая матрица С, каждый элемент которой равен сумме произведений элементовiстроки матрицы А на соответствующие элементыj-го столбца матрицы В.
Если матрица А имеет размерность , а матрица В, то.
Пример 9: Умножить матрицы
404 Cтраница не найдена
Мы используем файлы cookies для улучшения работы сайта МГТУ и большего удобства его использования.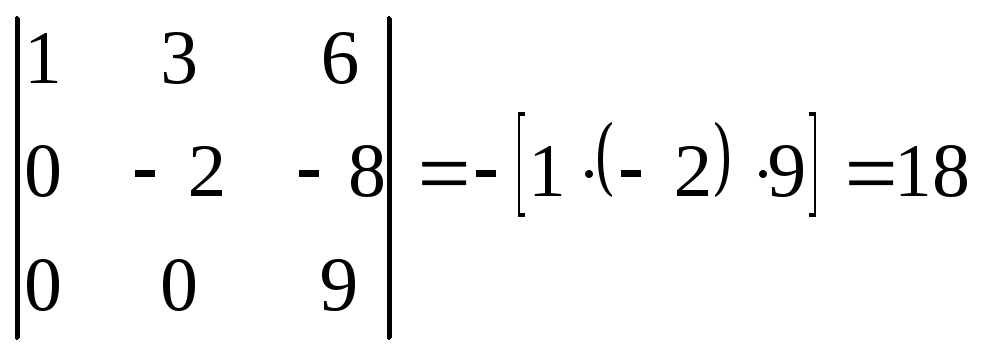
Размер:
AAA
Изображения Вкл. Выкл.
Обычная версия сайта
К сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже
|
|
Визуализация исключения Гаусса.
 Определитель связан с… | Николя Бертаньолли
Определитель связан с… | Николя БертаньоллиОпределитель связан с объемом параллелепипеда, натянутого на векторы в матрице, давайте посмотрим, как.
Недавно меня попросили создать видео, демонстрирующее, как преобразование матрицы в форму редуцированного эшелона строк (RREF) раскрывает определитель. Я знаю, это звучит неправдоподобно, но это произошло. Цель этого поста не в том, чтобы описать все свойства определителя, и не в том, чтобы объяснить, как работает исключение Гаусса, для этого есть много других ресурсов, а в том, чтобы показать изящную демонстрацию того, как геометрия матрицы связанный с определителем, и что преобразование матрицы в RREF раскрывает объем этого геометрического объекта. Прежде всего, давайте подумаем о том, как рассматривать матрицу геометрически. На протяжении всего обсуждения я буду использовать матрицу:
Одним из способов просмотра этой матрицы является набор векторов-строк, которые можно увидеть на рисунке 1.
Эта матрица связана с параллелограммом на рисунке 2, где абсолютное значение определителя представляет собой его объем. Мы проверим это в конце, а пока просто доверься мне.
Мы проверим это в конце, а пока просто доверься мне.
Берем определитель ad – bc = 1. Это здорово, и большинство из вас уже знает, как вычислить определитель, но как к этому приводит сокращение строк в матрице? Когда мы уменьшаем матрицу, мы начинаем концентрировать значения на диагонали матрицы. Это в основном эквивалентно выравниванию векторов с декартовыми осями. Чтобы убедиться в этом, сделаем шаг в сторону редуцированной формы строки для матрицы 9.0013 А . Давайте несколько раз снимем .1 × A_1 с A_2 и посмотрим, что получится.
Мы видим, что нижний вектор постепенно выравнивается с каноническими осями x, y! Если мы сделаем то же самое, но вычтем A_2 из A_1, мы выровняем другой вектор. Это означает, что еще один способ просмотра уменьшенной эшелонированной формы строки – это выровненная по оси версия исходной матрицы. Это можно увидеть на видео ниже.
Визуализация исключения ГауссаТеперь мы можем легко вычислить объем этого уменьшенного параллелограмма, потому что высота и размеры основания — это просто диагональные элементы, и оба они равны 1, что означает, что объем равен 1,
Чтобы убедиться, что объем исходного параллелограмма равен 1, мы можем использовать стандартный расчет Объем = Основание × Высота. Прежде чем начать этот путь, нам нужно подумать о нашей базе и высоте. Мы назовем нашу базу ||A_1||, и мы можем найти нашу высоту, используя формулу тригонометрии sin (θ) = противоположность / гипотенуза и скалярное произведение a⋅ b = ||a||||b|| потому что (θ). В этом контексте наша противоположная сторона ||A_2|| и теперь у нас есть все необходимое для расчета объема.
Прежде чем начать этот путь, нам нужно подумать о нашей базе и высоте. Мы назовем нашу базу ||A_1||, и мы можем найти нашу высоту, используя формулу тригонометрии sin (θ) = противоположность / гипотенуза и скалярное произведение a⋅ b = ||a||||b|| потому что (θ). В этом контексте наша противоположная сторона ||A_2|| и теперь у нас есть все необходимое для расчета объема.
Что действительно 1! Здесь мы убедились, что определители и объемы всех наших матриц одинаковы. Мы также можем видеть, как уменьшение матрицы изменяет геометрию лежащих в основе векторов, чтобы они были выровнены по осям и их было легче интерпретировать. Если вы хотите увидеть тот же процесс в более высоких измерениях, я сделал еще одно видео для матрицы 3 × 3.
Визуализация исключения Гаусса на матрице 3×3Первоначально опубликовано по адресу http://www.nbertagnolli.com .
Правила расчета определителей и примеры
Правила
Правила расчета с определителями.
Перестановка двух строк Перестановка двух столбцов Множитель в строкеСложение строкСложение столбцовТеорема умноженияТеорема о транспозицииТеорема об обратной матрицеКоробка
Методы расчета определяющих значений.
Определяющее значениеОпределяющее значение 2×2Определяющее значение 3×3Определяющее значение NxNLaplace ExpansionGaussian Method
История определителей
Исторически определяющие факторы учитывались до матриц. Первоначально определитель определялся как свойство системы линейных уравнений. Определитель «определяет», имеет ли система уравнений единственное решение (именно так и происходит, если определитель отличен от нуля). В этом контексте матрицы 2×2 были рассмотрены Кардано в конце 16 века, а более крупные матрицы – Лейбницем примерно 100 лет спустя.
Определитель
Каждой квадратной матрице можно присвоить уникальный номер, который называется определителем (det(A)) матрицы. В общем случае определитель матрицы NxN определяется формулой Лейбница:
В общем случае определитель матрицы NxN определяется формулой Лейбница:
det A=∑σ∈SnsgnσΠi=1nAiρi
здесь необходимо распространить сумму на все перестановки σ. Таким образом, из элементов множества A формируются все возможные произведения для каждого n-элемента таким образом, что каждое из произведений каждой строки и столбца содержит ровно один элемент. Эти продукты складываются, и сумма является определителем A. Знак слагаемых положительный для четных перестановок и отрицательный для нечетных перестановок.
Правила вычисления определителя
Перестановка двух строк определителя
Перестановка двух строк определителя местами меняет только знак, но не значение определителя.
det A=|a11a12…a1n⋮aj1aj2…ajn⋮ak1ak2…akn⋮an1an2…ann|=-|a11a12…a1n⋮ak1ak2…akn⋮aj1aj2…ajn⋮an1an2…ann|
Перестановка двух столбцов определителя местами
Перестановка двух столбцов определителя местами меняет только знак, но не значение определителя.
det A=|a11…a1j…a1k…a1na21…a2j…a2k…a2n⋮an1…anj…ank…ann|=-|a11…a1k…a1j…a1na21…a2k…a2j…a2n⋮an1…ank…anj…ann |
Множитель в строке определителя
Извлечение общего множителя из строки. Общий множитель во всех элементах строки можно изобразить как множитель перед определяемым. Затем значение детерминанта получается путем умножения множителя на значение результирующего детермината det A’.
det A=|a11a12…a1n⋮λaj1λaj2…λajn⋮an1an2…ann|=λ|a11a12…a1n⋮aj1aj2…ajn⋮an1an2…ann|=λdet A’
Извлечение общего множителя из столбца. Общий множитель во всех элементах столбца можно изобразить как множитель перед определяемым. Затем значение детерминанта получается путем умножения множителя на значение результирующего детермината det A’.
det A=|a11…λa1j…a1na21…λa2j…a2n⋮an1…λanj…ann|=λ|a11…a1j…a1na21…a2j…a2n⋮an1…anj…ann|=λdet A’
Добавление строк
Сложение строки определителя с кратным другой строки. Значение определителя не меняется, когда к строке добавляется кратное другой строки.
det A=|a11a12…a1n⋮aj1aj2…ajn⋮ak1ak2…akn⋮an1an2…ann|=|a11a12…a1n⋮aj1+λak1aj2+λak2…ajn+λakn⋮ak1ak2…akn⋮an1an2…ann|
Сложение столбцов
Сложение столбца определителя с кратным другому столбцу. Значение определителя не меняется, когда к столбцу прибавляется кратное другому столбцу.
det A=|a11…a1j…a1k…a1na21…a2j…a2k…a2n⋮an1…anj…ank…ann|=|a11…a1j+λa1k…a1k…a1na21…a2j+λa2k…a2k…a2n⋮an1…anj+ λанк…анк…анн|
Теорема умножения
Определитель произведения двух матриц равен произведению определителей матриц.
det(A⋅B)=det(A)⋅det(B)
Из этого следует также следующее соотношение.
det(Ak)=det(A)k
Теорема транспонирования
Определитель транспонированной матрицы равен определителю самой матрицы.
det(AT)=det(A)
Обратная матрица
Определитель обратной матрицы равен обратной величине определителя самой матрицы
det(A-1)=det(A)-1=1det A
Теорема о ящике
Имеет определитель, следующий за коробчатой структурой с квадратными ящиками B и D, затем позволяет его определителю быть произведением определителей направлений B и D .
det A=|BC0D|=det(B)det(D)det A=|B0CD|=det(B)det(D)
Вычисление значения определителя
Определитель матрицы 0x0
Определитель a Матрица 0x0 определяется как 1.
Определитель матрицы 1×1
Матрица 1×1 — это матрица, состоящая только из одного элемента, а определитель определяется самим элементом.
det A=|a11|=a11
Определитель матрицы 2×2
Для матрицы 2×2 определитель вычисляется следующим образом.
det A=|a11a12a21a22|=a11a22-a21a12
Определитель матрицы 3×3
Для вычисления определителя 3×3 существуют разные способы. С развитием Лапаса можно уменьшить определитель до 2х2 определителей. Прямой способ вычисления определителя — правило Сарруса. Правило Сарруса гласит, что определитель квадратной матрицы 3×3 вычисляется путем вычитания суммы произведений главных диагоналей из суммы произведений второстепенных диагоналей.
Определитель матрицы 3×3 по правилу Сарруса
Определитель вычисляется по правилу Сарруса следующим образом. Схематически первые два столбца определителя повторяются, так что большая и малая диагонали могут быть виртуально соединены линейной линией. Затем делают произведения главных диагональных элементов и добавляют эти произведения. С второстепенными диагоналями вы должны сделать то же самое. Разница между ними дает определитель матрицы.
Схематически первые два столбца определителя повторяются, так что большая и малая диагонали могут быть виртуально соединены линейной линией. Затем делают произведения главных диагональных элементов и добавляют эти произведения. С второстепенными диагоналями вы должны сделать то же самое. Разница между ними дает определитель матрицы.
det A=|a11a12a13a21a22a23a31a32a33|a11a12a21a22a31a32|=a11a22a33+a12a23a31+a33a21a32-(a31a22a13+a32a23a11+a33a21a12)
Determinant of NxN Matrix
Laplace Expansion Theorem
The Laplacian development theorem provides a method for calculating the determinant, in which the определитель развивается после строки или столбца. Размерность уменьшается и может быть уменьшена далее шаг за шагом до скаляра.
det A=∑i=1n-1i+j⋅aijdetAij ( Разложение по j-му столбцу )
det A=∑j=1n-1i+j⋅aijdetAij ( Разложение по i-й строке )
где A ij , подматрица A, которая возникает, когда i-я строка и j- й столбец удален.
Пример разложения Лапласа по первой строке матрицы 3×3.
det A=|a11a12a13a21a22a23a31a32a33|
Первый элемент задается коэффициентом a 11 и субдетерминантом, состоящим из элементов с зеленым фоном.
|a11a12a13a21a22a23a31a32a33|=>a11|a22a23a32a33|
Второй элемент задается коэффициентом a 12 и субдетерминантом, состоящим из элементов с зеленым фоном.
|a11a12a13a21a22a23a31a32a33|=>a12|a21a23a31a33|
Третий элемент задается коэффициентом a 13 и субдетерминантом, состоящим из элементов с зеленым фоном.
|a11a12a13a21a22a23a31a32a33|=>a13|a21a22a31a32|
С тремя элементами определитель может быть записан как сумма определителей 2×2.
det A=|a11a12a13a21a22a23a31a32a33|=a11|a22a23a32a33|-a12|a21a23a31a33|+a13|a21a22a31a32|
Важно учитывать, что знаки элементов чередуются следующим образом.
|+-+-+-+-+|
Пример разложения Лапласа по второму столбцу матрицы 3×3.

det A=|a11a12a13a21a22a23a31a32a33|
Первый элемент задается коэффициентом a 12 и субдетерминантом, состоящим из элементов с зеленым фоном.
|a11a12a13a21a22a23a31a32a33|=>a12|a21a23a31a33|
Второй элемент задается коэффициентом a 22 и субдетерминантом, состоящим из элементов с зеленым фоном.
|a11a12a13a21a22a23a31a32a33|=>a22|a11a13a31a33|
Третий элемент определяется коэффициентом а 23 и поддетерминант, состоящий из элементов с зеленым фоном.
|a11a12a13a21a22a23a31a32a33|=>a23|a11a13a21a23|
С тремя элементами определитель может быть записан как сумма определителей 2×2.
det A=|a11a12a13a21a22a23a31a32a33|=-a12|a21a23a31a33|+a22|a11a13a31a33|-a32|a11a13a21a23|
Важно учитывать, что знаки элементов чередуются следующим образом.
|+-+-+-+-+|
Пример разложения по j-й строке определителя NxN.
Расширение Лапласа сводит определитель NxN к сумме (N-1)x(N-1) определителей.
det A=|a11a12…a1n⋮aj1aj2…ajn⋮an1an2…ann|=±aj1|a12…a1n⋮aj-12…aj-1naj+12…aj+1n⋮an2…ann|±aj2|a11a13…a1n⋮aj -11aj-13…aj-1naj+11aj+13…aj+1n⋮an1an3…ann|±…±ajn|a11a12…a1n-1⋮aj-11aj-12…aj-1n-1aj+11aj+12…aj+ 1n-1⋮an1an2…ann-1|
Метод Гаусса
В методе Гаусса определитель преобразуется таким образом, что элементы нижней матрицы треугольника становятся равными нулю. Для этого вы используете правила коэффициента строки и добавление строк. Добавление строк не меняет значения определителя. Факторы ряда должны рассматриваться как множители перед определителем. Если определитель треугольный и элементы главной диагонали равны единице, то множитель перед определителем соответствует значению самого определителя.
det A=|a11a12…a1naj1aj2…ajn⋮an1an2…ann|=λ|1a12…a1n01…ajn⋮00…1|=λdet A’=λ
Правило Крамерса
Правило Крамерса использует определители для решения системы линейных уравнения. Для случая линейной (N×N) системы уравнений с det(A), не равным 0, решение можно представить в следующем виде:
х=А-1б
xi=1det A|a11…b1…a1na21…b2…a2n⋮an1…bn…ann|
xi=DiD
Определитель в числителе D i от D = det A показан i-й колонкой в D заменен на b.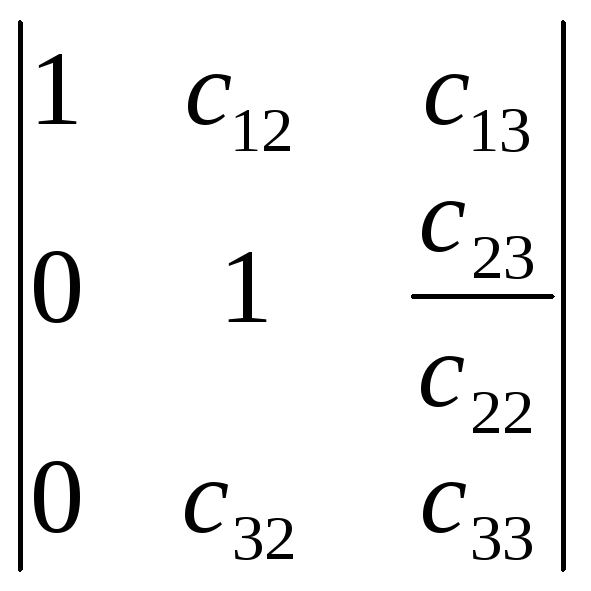

 Педагогический (научно-педагогический) состав
Педагогический (научно-педагогический) состав