Решение систем линейных уравнений алгоритмы общих и частных методов нахождения корней, основные правила и теоремы и примеры их использования, онлайн калькулятор
Совокупность математических записей, из которых каждая является линейным алгебраическим равенством первой степени, называется системой линейных уравнений. Её решение — это классическая задача алгебры, определяющая объекты и методы. Существует несколько принципиально разных способов нахождения ответа. Каждый из них имеет достоинства и недостатки, но выбор метода зависит лишь только от личных предпочтений решающего.
Понятия и обозначения
Для измерения геометрических или физических величин в математике используют действительное число — вещественное. В уравнении под ним понимают все свободные члены или неизвестные переменные. Вычисление линейных алгебраических уравнений играет важную роль в различных математических задачах: численных методах, программировании, эконометрике.
Общий вид системы линейных уравнений (СЛАУ) в классическом понимании представляют следующим образом:
a11 * n 1 + a 12 * n 2 + …+a 1x n x = c 1.
a21 * n 1 + a 22 * n 2 + …+a 2x n x = c 2.
as1 * n 1 + a 12 * n 2 + …+a 1x n x = c s.
В этой записи s — это количество уравнений, x — число переменных, а n — переменная которую необходимо вычислить. Предполагается что a и b это известные свободные члены. Индексы обозначают порядковый номер уравнения. Первый символ — расположение строчки, а второй — позиция произведения переменной и свободного члена.
Если эти члены отличные от нуля, то система называется неоднородной, в ином же случае однородной. Квадратной системой называется совокупность уравнений, когда их число совпадает с количеством неизвестных. Существует понятие и неопределённой системы. Это совокупность, при которой неизвестных больше числа уравнений. Если наоборот, то система считается переопределенной. В литературе её ещё часто называют прямоугольной.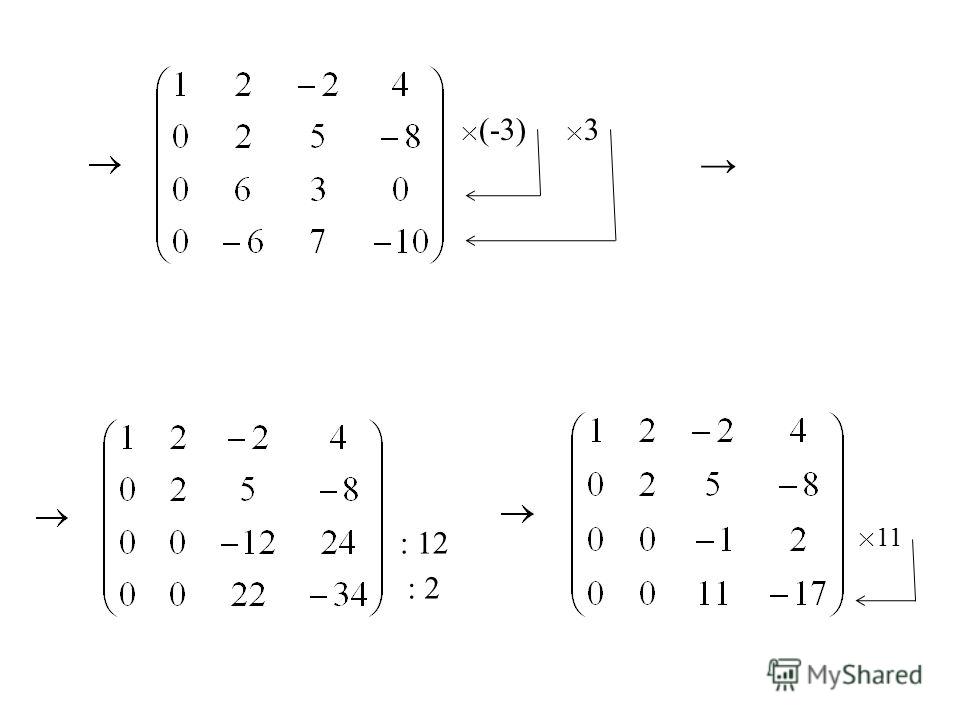
Система считается решаемой, когда множество членов X соответствует такому набору чисел, что при их подстановке вместо n вся система обратится в тождество. Если существует хотя бы одно решение, система называется совместной. Ответы, превращающие уравнения в равенства, при которых переменные не совпадают, считаются различными.
Существует четыре способа развязывания системы уравнений:
- способ подстановки;
- использование новых переменных;
- алгебраическое сложение;
- матричный метод.
Вид используемого алгоритма зависит от типа примера. Метод алгебраического сложения применяют, когда в задании лишь одно неизвестное, а коэффициенты противоположны или равны. Если же хотя бы в одной из формул коэффициент равен единице, то удобнее будет решить систему уравнений методом подстановки. В иных случаях используют матрицы.
В иных случаях используют матрицы.
Алгебраическое сложение
Способ заключается в сложении или вычитании выражений. Это довольно простой способ и в то же время эффективный. Алгоритм нахождения ответа для равенств с двумя переменными n и m сводится к следующему:
- уравниванию модулей коэффициентов при любом из неизвестных;
- сложению или вычитанию равенства;
- вычисления составленного выражения;
- прогонки каждого найденного корня через первую или вторую строчку системы уравнений;
- нахождению второго неизвестного.
То есть после выполнения арифметических действий с уравнениями должно получиться одно выражение с одним неизвестным. Затем находят значение этой переменной и в него подставляют полученный корень. Например, нужно узнать, какие корни системы, состоящей из двух строчек, превращают её в тождество:
n2 – m2 = 21.
n2 + m2 = 29.
В первую очередь необходимо сложить равенства между собой. В итоге получится:
В итоге получится:
- 2 * n 2 = 50;
- n 2 = 25;
- n = +5 (-5).
Подставив поочерёдно в каждое равенство найденные корни можно найти второе неизвестное. Для корня n = – 5 ответом будет:
- (-5)2 + m2 = 29;
- 25 + m2 = 29;
- m2 = 29 – 25;
- m2 = 4.
Соответственно, корнями будут числа два и минус два. Аналогичные действия необходимо выполнить и для корня другого знака n = 5. В итоге получится, что пары (− 5; − 2), (− 5; 2), (5; − 2), (5 ; 2) являются нужным ответом. При достаточном опыте подробно описывать решение не обязательно.
Существуют системы, требующие подготовительного этапа. Например, такого вида:
3 * n – 4 * m = 5.
2 * n + 3 * m = 7.
Исключить здесь сразу переменную не выйдет. Если умножить все члены первой строчки на тройку, а второй на четвёрку, получится запись:
9 * n – 12 * m = 15.
8 * n + 12 * m = 28.
Теперь равенства можно сложить, тем самым исключив переменную m. Затем система решается по базисному алгоритму. Чтобы понять, можно ли решить систему этим методом, следует предварительно её проанализировать. Необходимое условие заключается в том, что коэффициенты второй переменной должны быть одинаковыми по модулю, но противоположными по знаку.
Метод подстановки
Систему равенств возможно решить и способом подстановки. Используя любое из уравнений, можно выразить любую из неизвестных переменных, а затем подставить её в другое равенство. Алгоритм использования метода следующий:
- через n в одном из уравнений выражают m;
- подставляют полученное равенство вместо n в другое тождество;
- решают уравнение и находя m;
- поочерёдно подставляют найденные корни и получают ответ.

Например, нужно проверить, все ли целые корни могут быть у системы:
8 * n – 5 * m = -16.
10 * n + 3 * m = 17.
Выразив m через n можно записать равенство: n = (8* m + 16) / 5. Так как n одинаково в обоих уравнениях, то следует подставить полученное тождество и записать: 10* n + 3*(8* n +16) / 5 = 17. Отсюда уже просто найти корень. Он будет равен дроби 1/2. Подставив его вместо n легко вычислить и второй корень: m = (8 * n + 16) / 5 = 4. Таким образом, у системы будет только один целый корень. При желании проверить ответ можно решить систему другим методом.
Использование матриц
Для систем с произвольным числом уравнений и неизвестных используют другие методы. Если система состоит из нелинейных дифференциальных уравнений с постоянными коэффициентами, то используют матричный способ. Этот метод предполагает применение обратной матрицы.
Пусть дана система с тремя неизвестными х1, х2, х3. Нужно найти значения, при которых равенства станут верными. Для нахождения решений используют три матрицы:
Нужно найти значения, при которых равенства станут верными. Для нахождения решений используют три матрицы:
- Коэффициент системы. При этом её определитель не должен быть равным нулю.
- Вектора неизвестных. Именно его понадобится найти.
- Столбца свободных членов.
Базисное решение строят на произведении первой и второй матрицы. В результате получают матрицу размером три на один. То есть вектор-столбец с тремя элементами. После выполнения действия получится, что системный вектор будет равен левой части системы и соответствовать третьей матрице. Таким образом, обозначив матрицы буквами А, Б, В, можно записать выражение А * Б = В и найти необходимую Б.
При умножении на А-1 (обратную матрицу) получают равенство: Е * Б = А-1 * В, где Е – единичная матрица получена из совместимости прямой и обратной. Так как при произведении с единичной матрицей значения не изменяются, то решением системы будет формула: Б = А-1 * В.
youtube.com/embed/SMXORIlY9h5″/>Способ Гаусса-Жордана
Частным случаем решения системы является Метод Гаусса — Жордана. Суть решения основана на составлении специальной таблицы. В первый столбец заносятся известные значения, то есть величины, расположенные после равно, а в три других коэффициенты, стоящие после неизвестных. Чтобы приступить к решению, необходимо выполнить три шага:
- выбрать ключевой элемент из первых трёх столбцов;
- переписать строчку с ключевым значением, предварительно разделив все элементы на это значение;
- переписать оставшиеся элементы, при этом вычитая из него произведение соответствующих ему чисел.
В полученной новой матрице снова выбирают ключевой элемент и выполняют все действия снова. Шаги повторяют до тех пор, пока не получится матрица, состоящая из нулей и единиц. Значения корней системы будут находиться на пересечении столбцов со строчками напротив единиц.
Этот метод используют только при выполнении условия совместности. Его ещё называют способом простой итерации. Он был доказан и оптимизирован Зейделем. С помощью итерационного метода можно посчитать систему А* Б = В с точностью “е”. Составляют n уравнение на сходимость, а затем на точность. Затем из первого уравнения выражают n1, второго n2, третьего n3 и так далее. Новые n с индексом i +1 считаются через старые i. Зейдель предложил расширить решение и добавить снова для счёта индекс i+1.
Его ещё называют способом простой итерации. Он был доказан и оптимизирован Зейделем. С помощью итерационного метода можно посчитать систему А* Б = В с точностью “е”. Составляют n уравнение на сходимость, а затем на точность. Затем из первого уравнения выражают n1, второго n2, третьего n3 и так далее. Новые n с индексом i +1 считаются через старые i. Зейдель предложил расширить решение и добавить снова для счёта индекс i+1.
Это фундаментальные способы решения сложных систем уравнений. Они трудные, требуют опыта и внимательности. Поэтому существуют специальные онлайн-калькуляторы по методу Гаусса с подробным решением, помогающие исследовать систему любой численности.
Теорема Кронекера — Капелли
Применяется она при проведении исследований без непосредственного решения. То есть для записи эквивалентной совокупности алгебраических уравнений с их минимальным числом. Теорема говорит о следующем: система уравнений А * Б = В имеет решение только тогда, когда ранг А равен (А, В), где последнее расширенная матрица, полученная из первого члена путём приписывания столбца В.
Теорема говорит о следующем: система уравнений А * Б = В имеет решение только тогда, когда ранг А равен (А, В), где последнее расширенная матрица, полученная из первого члена путём приписывания столбца В.
Это утверждение обобщает различные виды СЛАУ:
- Несовместные – которые определяют при условии, что их ранг меньше ранга расширенной матрицы. Существование корней невозможно.
- Совместные неопределённые – системы, имеющие бесконечное множество решений. В этом случае ранги равны, а количество неизвестных будет меньше.
- Совместно определённые – в этом случае ранг равен расширенной матрице и количеству неизвестных. Точное решение будет одно.
Выводом из этой теоремы является то, что число главной переменной совокупности будет всегда равно рангу системы. При этом столбец свободных членов представляет собой линейную комбинацию столбцов матрицы А.
Решение Крамера
Пожалуй, это один из самых простых способов нахождения корней уравнений. Для решения строят несколько матриц. Основная получается из коэффициентов, стоящих при неизвестных. Она обозначается символом дельта. Вторую, дельта-икс, образуют из основной матрицы заменой первого столбца на ответы уравнений. Следующая, дельта-игрек, строится с заменой в основной матрице второго столбца на значения ответов и так далее.
Для решения строят несколько матриц. Основная получается из коэффициентов, стоящих при неизвестных. Она обозначается символом дельта. Вторую, дельта-икс, образуют из основной матрицы заменой первого столбца на ответы уравнений. Следующая, дельта-игрек, строится с заменой в основной матрице второго столбца на значения ответов и так далее.
Затем вычисляют дискриминант этих матриц, то есть их определитель. Для его поиска можно использовать способ треугольника или разложения. Первый подходит для простых матриц. Находят его как разницу умножения чисел, стоящих в матрице крест-накрест. Второй же применим для матриц, содержащих три и более строк. При нахождении выбирают одну из них и раскладывают матрицу.
Как только все дискриминанты найдены, используют правило Крамера: n = Δn/ Δ. Подставляют значения, находят ответ. Стоит отметить, что много интернет-порталов, предлагающих услугу расчётов СЛАУ, используют для вычислений онлайн-метод Крамера.
Удобные онлайн-калькуляторы
В некоторых случаях решение СЛАУ онлайн будет хорошим подспорьем для того, чтобы разобраться в различных правилах, используемых при решениях. Из популярных интернет-сервисов, позволяющих найти корни систем, можно отметить: kontrolnaya-rabota, mathsolution, planetcalc, allcalc. Использовать эти сайты-решатели смогут даже слабо подготовленные пользователи, имеющие общее представление о методах решений.
Из популярных интернет-сервисов, позволяющих найти корни систем, можно отметить: kontrolnaya-rabota, mathsolution, planetcalc, allcalc. Использовать эти сайты-решатели смогут даже слабо подготовленные пользователи, имеющие общее представление о методах решений.
Для выполнения расчёта необходимо ввести параметры системы и нажать кнопку «Рассчитать». При этом можно выбрать метод, на базе которого будут проводиться вычисления. Удобным является и то, что полученный расчёт сопровождается объяснениями.
На этих порталах также можно посмотреть примеры и правила решений. Некоторые калькуляторы могут построить и график системы. Например, kontrolnaya-rabota. Для этого на сайте нужно выбрать раздел «Графическое решение уравнений онлайн» и ввести исследуемую систему равенств.
Метод Гаусса Калькулятор — Игры карты паук 2 масти
Калькулятор матриц
Ранг матрицы методом Гаусса | Мозган калькулятор онлайн
Для того что бы вычислить ранг матрицы можно применить метод окаймляющих миноров или метод Гаусса.
Рассмотрим метод Гаусса или метод элементарных преобразований.
Рангом матрицы называют максимальный порядок её миноров, среди которых есть хотя бы один, не равный нулю.
Рангом системы строк (столбцов) называется максимальное количество линейно независимых строк (столбцов) этой системы.
Метод Гаусса использует элементарные преобразования, которые не изменяют ее ранг:
Транспонирование.
Перестановка местами строк или столбцов.
Прибавление одной строки/столбца к другой строке/столбцу умноженного на ненулевое число.
Умножение строки или столбца на ненулевое число.
С помощью данного метода нужно привести матрицу к ступенчатому виду и посчитать количество строк, в которых есть хоть один не нулевой элемент.
Пример
Рассмотрим данный метод на примере. Дана матрицы:
Для облегчения дальнейших расчетов поменяем местами строку №1 со строкой №2.
Сделаем элемент a3, 1 равный нулю.
Из строки №3 вычтем строку №1, умноженную на 3/2.
Сделаем элемент a4, 1 равный нулю.
Из строки №4 вычитаем строку №1, умноженную на 2.
Сделаем элемент a3, 2 равный нулю.
Из строки №3 вычтем строку №2, умноженную на -1/4. Мы его получили разделив элимент a3, 2 = -0. 5 на элимент a2, 2 = 2.
Сделаем элемент a4, 2 равный нулю.
Из строки №4 вычтем строку №2, умноженную на -1/2.
Сделаем элемент a4, 3 равный нулю.
Из строки №4 вычитаем строку №3, умноженную на 2.
В получившейся матрице одна строка содержит нулевые элементы, а три строки имеют не нулевые элементы. Ответ: Ранг=3.
Как найти определитель матрицы методом Гаусса
Матричный определитель
Это многочлен от элементов квадратной матрицы (если матричные элементы являются числами, то матричный определитель также будет числом).
Есть много способов вычислить определитель квадратной матрицы. Наш онлайн-калькулятор рассчитывает определитель, используя метод Гаусса, или путем разложения определителя на элементы любой строки или столбца. Онлайн-калькулятор
Онлайн-калькулятор
Чтобы вычислить определитель по методу Гаусса, начальная матрица приведена к верхней треугольной форме с помощью элементарных преобразований, а определитель исходной матрицы не изменяется и равен произведению элементов на главной диагонали верхняя треугольная матрица.
Чтобы вычислить определитель, развернув его на элементы строки или столбца, сначала выберите строку или столбец, по которым определитель будет разложен. Удобнее всего расположить определитель по строке (или столбцу) с максимальным количеством нулевых элементов. Если в исходной матрице нет таких строк (или столбцов), вы можете выбрать любую строку (или столбец).
Результирующее разложение представляет собой линейную комбинацию определителей, порядок которых на единицу меньше исходного. Каждый из этих определителей вычисляется снова путем расширения выбранной строки или столбца.
Таким образом, рассмотренный метод расчета определителя является рекурсивным процессом.
Разберем данный метод на конкретных примерах.
Пример 1
Дано:
A=(1514126715457)A= \begin{pmatrix} 15 & 14 & 12 \\ 6 & 7 & 1 \\ 54 & 5 & 7 \end{pmatrix}
Решение:
Делим 1 строку на 15, получаем:
(114150. 86715457)\begin{pmatrix} 1 & {14 \over 15} & 0. 8 \\ 6 & 7 & 1 \\ 54 & 5 & 7 \end{pmatrix}
Делим 2 строку на 6, получаем:
(114150. 8176165457)\begin{pmatrix} 1 & {14 \over 15} & 0. 8 \\ 1 & {7 \over 6} & {1 \over 6} \\ 54 & 5 & 7 \end{pmatrix}
Делим 3 строку на 54, получаем:
(114150. 8176161554754)\begin{pmatrix} 1 & {14 \over 15} & 0. 8 \\ 1 & {7 \over 6} & {1 \over 6} \\ 1 & {5 \over 54} & {7 \over 54} \end{pmatrix}
Вычитаем 1-ю строку из последующих
(114150. 80730−19300−227270−181270)\begin{pmatrix} 1 & {14 \over 15} & 0. 8 \\ 0 & {7 \over 30} & -{19 \over 30} \\ 0 & -{227 \over 270} & -{181 \over 270} \end{pmatrix}
Делим 2 строку на 7/30, получаем:
(114150. 801−1970−227270−181270)\begin{pmatrix} 1 & {14 \over 15} & 0. 8 \\ 0 & 1 & -{19 \over 7} \\ 0 & -{227 \over 270} & -{181 \over 270} \end{pmatrix}
801−1970−227270−181270)\begin{pmatrix} 1 & {14 \over 15} & 0. 8 \\ 0 & 1 & -{19 \over 7} \\ 0 & -{227 \over 270} & -{181 \over 270} \end{pmatrix}
Делим 3 строку на -227/270, получаем:
(114150. 801−19701181227)\begin{pmatrix} 1 & {14 \over 15} & 0. 8 \\ 0 & 1 & -{19 \over 7} \\ 0 & 1 & {181 \over 227} \end{pmatrix}
Вычитаем 2-ю строку из последующих
(114150. 801−1970055801589)\begin{pmatrix} 1 & {14 \over 15} & 0. 8 \\ 0 & 1 & -{19 \over 7} \\ 0 & 0 & {5580 \over 1589} \end{pmatrix}
Умножаем первые числа каждой строки (которые использовались при сокращении):
det=15⋅6⋅54⋅730⋅(−227270)⋅55801589=−3348det = 15 \cdot 6 \cdot 54 \cdot {7 \over 30} \cdot \left(-{227 \over 270}\right) \cdot {5580 \over 1589} = -3348
∣A∣=(1514126715457)=−3348|A| = \begin{pmatrix} 15 & 14 & 12 \\ 6 & 7 & 1 \\ 54 & 5 & 7 \end{pmatrix} = -3348
Ответ будет равен ∣A∣=−3348|A| = -3348
В следующем примере разберем случай дробных узлов матрицы, как более сложный вариант:
Пример 2
A=(2718141512131425217)A= \begin{pmatrix} {2 \over 7} & {1 \over 8} & {14 \over 15} \\ {1 \over 2} & {1 \over 3} & 1 \\ {4 \over 2} & {5 \over 2} & {1 \over 7} \end{pmatrix}
Делим 1 строку на 2/7, получаем:
(1716491512131425217)\begin{pmatrix} 1 & {7 \over 16} & {49 \over 15} \\ {1 \over 2} & {1 \over 3} & 1 \\ {4 \over 2} & {5 \over 2} & {1 \over 7} \end{pmatrix}
Делим 2 строку на 1/2, получаем:
(171649151232425217)\begin{pmatrix} 1 & {7 \over 16} & {49 \over 15} \\ 1 & {2 \over 3} & 2 \\ {4 \over 2} & {5 \over 2} & {1 \over 7} \end{pmatrix}
Делим 3 строку на 4/2, получаем:
(171649151232154114)\begin{pmatrix} 1 & {7 \over 16} & {49 \over 15} \\ 1 & {2 \over 3} & 2 \\ 1 & {5 \over 4} & {1 \over 14} \end{pmatrix}
(1716491501148−191501316−671210)\begin{pmatrix} 1 & {7 \over 16} & {49 \over 15} \\ 0 & {11 \over 48} & -{19 \over 15} \\ 0 & {13 \over 16} & -{671 \over 210} \end{pmatrix}
Делим 2 строку на 11/48, получаем:
(1716491501−3045501316−671210)\begin{pmatrix} 1 & {7 \over 16} & {49 \over 15} \\ 0 & 1 & -{304 \over 55} \\ 0 & {13 \over 16} & -{671 \over 210} \end{pmatrix}
Делим 3 строку на 13/16, получаем:
(1716491501−3045501−53681365)\begin{pmatrix} 1 & {7 \over 16} & {49 \over 15} \\ 0 & 1 & -{304 \over 55} \\ 0 & 1 & -{5368 \over 1365} \end{pmatrix}
(1716491501−30455002394415015)\begin{pmatrix} 1 & {7 \over 16} & {49 \over 15} \\ 0 & 1 & -{304 \over 55} \\ 0 & 0 & {23944 \over 15015} \end{pmatrix}
det=27⋅12⋅42⋅1148⋅1316⋅2394415015=299335280det = {2 \over 7} \cdot {1 \over 2} \cdot {4 \over 2} \cdot {11 \over 48} \cdot {13 \over 16} \cdot {23944 \over 15015} = {2993 \over 35280}
∣A∣=(2718141512131425217)=299335280|A| = \begin{pmatrix} {2 \over 7} & {1 \over 8} & {14 \over 15} \\ {1 \over 2} & {1 \over 3} & 1 \\ {4 \over 2} & {5 \over 2} & {1 \over 7} \end{pmatrix} = {2993 \over 35280}
Ответ будет определен следующим образом: ∣A∣=299335280|A| = {2993 \over 35280}
Метод Гаусса онлайн
Данный онлайн калькулятор находит решение системы линейных уравнений (СЛУ) методом Гаусса. Дается подробное решение. Для вычисления выбирайте количество переменных и количество уравнений. Затем введите данные в ячейки и нажимайте на кнопку “Вычислить. “
Дается подробное решение. Для вычисления выбирайте количество переменных и количество уравнений. Затем введите данные в ячейки и нажимайте на кнопку “Вычислить. “
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т. д. ), десятичных чисел (напр. 67., 102. 54 и т. ) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6. 6/76. 4, -7/6. 7 и т. д.
Метод Гаусса
Метод Гаусса − это метод перехода от исходной системы линейных уравнений (при помощи эквивалентных преобразований) к системе, которая решается проще, чем исходная система.
Эквивалентными преобразованиями системы линейных уравнений являются:
перемена местами двух уравнений в системе,
умножение какого-либо уравнения в системе на ненулевое действительное число,
прибавление к одному уравнению другого уравнения, умноженного на произвольное число.
Рассмотрим систему линейных уравнений:
(1)
Запишем систему (1) в матричном виде:
где
A-называется матрица коэффициентов системы, b − правая часть ограничений, x− вектор переменных, которую нужно найти. Пусть rang(A)=p. Эквивалентные преобразования не меняют ранг матрицы коэффициентов и ранг расширеннной матрицы системы. Не меняется также множество решений системы при эквивалентных преобразованиях. Суть метода Гаусса заключается в приведении матрцы коэффициентов A к диагональному или ступенчатому.
Пусть rang(A)=p. Эквивалентные преобразования не меняют ранг матрицы коэффициентов и ранг расширеннной матрицы системы. Не меняется также множество решений системы при эквивалентных преобразованиях. Суть метода Гаусса заключается в приведении матрцы коэффициентов A к диагональному или ступенчатому.
Построим расшренную матрицу системы:
(4)
Предположим a11≠0. Если это не так, то можно поменять местами эту строку со строкой с ненулевым элементом в столбце 1 (если нет таких строк, то переходим к следующему столбцу). Обнуляем все элементы столбца 1 ниже ведущего элемента a11. Для этого сложим строки 2, 3,… m со строкой 1, умноженной на −a21/a11, −a31/a11,…, −am1/a11, соответственно. Тогда (4) примет следующий вид:
(5)
На следующем этапе обнуляем все элементы столбца 2, ниже элемента. Если данный элемент нулевой, то эту строку меняем местами со строкой, лежащий ниже данной строки и имеющий ненулевой элемент во втором столбце. Далее обнуляем все элементы столбца 2 ниже ведущего элемента a22. Для этого сложим строки 3,… m со строкой 2, умноженной на −a32/a22,…, −am2/a22, соответственно. Продолжая процедуру, получим матрицу диагонального или ступенчатого вида. Пусть полученная расширенная матрица имеет вид:
Для этого сложим строки 3,… m со строкой 2, умноженной на −a32/a22,…, −am2/a22, соответственно. Продолжая процедуру, получим матрицу диагонального или ступенчатого вида. Пусть полученная расширенная матрица имеет вид:
(6)
Обратим внимание на последние строки. Если,…, равны нулю, то система линейных уравнений имеет решение, если же хотя бы один из этих чисел отлично от нуля, то система несовместна. Иными словами, система (2) совместна тогда и только тогда, когда ранг матрицы A навен рангу расширенной матрицы (A|b).
Пусть. Тогда
Так как rangA=rang(A|b), то множество решений (7) есть (n−p)− многообразие. Следовательно n−p неизвестных можно выбрать произвольно. Остальные неизвестные из системы (7) вычисляются так. Из последнего уравнения выражаем xp через остальные переменные и вставляем в предыдущие выражения. Далее из предпоследнего уравнения выражаем xp−1 через остальные переменные и вставляем в предыдущие выражения и т. Рассмотрим метод Гаусса на конкретных примерах.
Примеры решения системы линейных уравнений методом Гаусса
Пример 1. Найти общее решение системы линейных уравнений методом Гаусса:
Матричный вид записи: Ax=b, где
Для решения системы, запишем расширенную матрицу:
Обозначим через aij элементы i-ой строки и j-ого столбца.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строки 2, 3 со строкой 1, умноженной на -2/3, -1/2 соответственно:
Исключим элементы 2-го столбца матрицы ниже элемента a2 2. Для этого сложим строку 3 со строкой 2, умноженной на 9/8:
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
Из вышеизложенной таблицы можно записать:
Подставив верхние выражения в нижние, получим решение.
Решение:
Пример 2. Найти общее решение системы линейных уравнений методом Гаусса:
Для решения системы, построим расширенную матрицу:
Исключим элементы 1-го столбца матрицы ниже элемента a11. {-1}$.
{-1}$.
Нахождение обратной матрицы методом Гаусса
Получение обратной матрицы методом Гаусса относится к одному из точных (прямых) методов.
Пример 1
Алгоритм для поиска и нахождения обратной матрицы $A$ методом Гаусса:
$A = \left( \begin{array}{cc|cc} 1 & 2 \\ 3 & 5 \\ \end{array} \right)$
Сначала записывается матрица, от которой необходимо найти обратную, а рядом с ней через черту записывается единичная диагональная матрица того же размера, вот так:
$ \left( \begin{array}{cc|cc} 1 & 2 & 1 & 0 \\ 3 & 5 & 0 & 1 \\ \end{array} \right) $.
Теперь с помощью метода Гаусса находим верхнюю треугольную матрицу. Для этого, сначала, как правило, либо необходимо разделить верхнюю строку на её старший коэффициент, либо поменять верхнюю строку местами с какой-либо другой, у которой первый коэффициент равен единице, в нашем случае просто меняем местами верхнюю и нижнюю строки:
$ \left( \begin{array}{cc|cc} 1 & 2 & 0 & 1 \\ 3 & 5 & 1 & 0 \\ \end{array} \right) $.
Теперь верхнюю строку умножаем на $3$ и вычитаем из нижней:
$ \left( \begin{array}{cc|cc} 1 & 2 & 0 & 1 \\ 0 & -1 & 1 & -3 \\ \end{array} \right) $.
Теперь для получения единичной диагонали нужно обнулить элементы, находящиеся справа сверху, также эта часть метода зовётся методом Жордана-Гаусса. Для этого верхнюю строку складываем с нижней, умноженной на $2$:
$ \left( \begin{array}{cc|cc} 1 & 0 & 2 & -5 \\ 0 & -1 & 1 & -3 \\ \end{array} \right) $.
Делим нижнюю строку на $-1$, получаем:
$ \left( \begin{array}{cc|cc} 1 & 0 & 2 & -5 \\ 0 & 1 & -1 & 3 \\ \end{array} \right) $.
Обратная исходной матрица будет:
$ \left( \begin{array}{cc|cc} 2 & -5 \\ -1 & 3 \\ \end{array} \right) $.
Пример 2
Найти обратную матрицу методом Гаусса.
$A = \left( \begin{array}{ccc} 1 & 2 & 3 \\ 2 & 5 & 4 \\ 0 & 1 & 0.5 \end{array} \right) $
Запишем нашу матрицу рядом с единичной:
$A = \left( \begin{array}{ccc|ccc} 1 & 2 & 3 & 1 & 0 & 0\\ 2 & 5 & 4 & 0 & 1 & 0 \\ 0 & 1 & 1/2 & 0 & 0 & 1 \end{array} \right) $
Теперь найдём верхнюю треугольную матрицу, для этого сначала из средней строчки вычтем удвоенную верхнюю:
$A = \left( \begin{array}{ccc|ccc} 1 & 2 & 3 & 1 & 0 & 0\\ 0 & 1 & -2 & -2 & 1 & 0 \\ 0 & 1 & 1/2 & 0 & 0 & 1 \end{array} \right) $.
Вычитаем из верхней строчки удвоенную вторую, а из третьей строчки просто вторую строку:
$A = \left( \begin{array}{ccc|ccc} 1 & 0 & 7 & 5 & -2 & 0\\ 0 & 1 & -2 & -2 & 1 & 0 \\ 0 & 0 & 2frac{1}{2} & 2 & -1 & 1 \end{array} \right) $.
Делим нижнюю строчку на $2\frac{1}{2}$:
$A = \left( \begin{array}{ccc|ccc} 1 & 0 & 7 & 5 & -2 & 0\\ 0 & 1 & -2 & -2 & 1 & 0 \\ 0 & 0 & 1 & 0.8 & -0.4 & 0.4 \end{array} \right) $.
Теперь обнуляем элементы, находящиеся выше главной диагонали, для этого вычитаем из верхней строки третью, умноженную на $7$, а к средней строке добавляем третью, помноженную на $2$:
$A = \left( \begin{array}{ccc|ccc} 1 & 0 & 0 & -0.6 & 0.8 & -2.8\\ 0 & 1 & 0 & -0.4 & 0.2 & 0.8 \\ 0 & 0 & 1 & 0.8 & -0.4 & 0.4 \end{array} \right) $.
Обратная исходной матрице равна:
$A^{-1} = \left( \begin{array}{ccc} -0. 6 & 0.8 & -2.8\\ -0.4 & 0.2 & 0.8 \\ 0.8 & -0.4 & 0.4 \end{array} \right) $.
6 & 0.8 & -2.8\\ -0.4 & 0.2 & 0.8 \\ 0.8 & -0.4 & 0.4 \end{array} \right) $.
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 15.12.2021
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
PDF Курсы, Упражнения, Документы pdf, ppt, бесплатно PDF
PDF Курсы, Упражнения, Документы pdf, ppt, бесплатно PDF | PDFprof.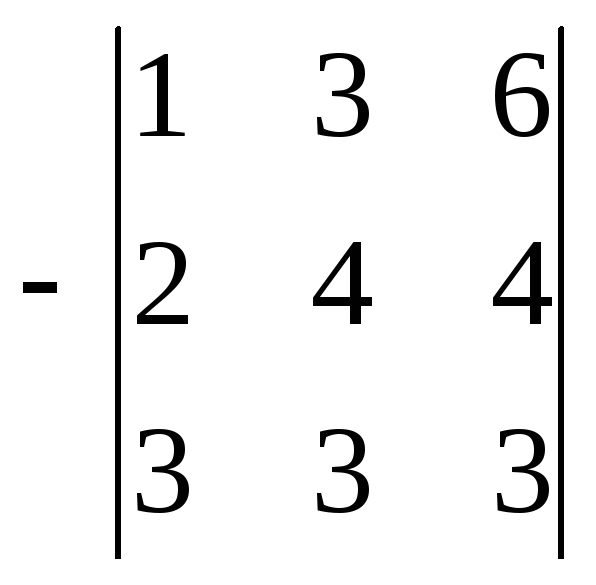 com
com×
Титр
Корпус
ОШИБКА 404 Файл не найден
- Администрация
- Администрация
- Общественная администрация
- Общественная администрация
- Агролесоводство
- Агролесоводство
- Аллеманд
- Аллеманд
- Бак ST2S
- Андрагогия
- Андрагогия
- Драматическое искусство
- Драматическое искусство
- Художественные визуалы
- Художественные визуалы
- Астрономия
- Астрономия
- Бак
- БАК Математика
- BAC Physique Chimie
- БАК СЭС
- БАК СВТ
- Биохимия
- Биохимия
- Биографии
- Fiche de Cours
- Fiches de Revision
- География и история L
- Исторический антиквариат
- Современная история
- Европейский союз
- Ла Герр Фройд
- La Premiere Guerre Mondiale
- эпоха Возрождения
- Биология
- Биология
- Биология и физиопатология человека
- Бак ST2S
- Биотехнология
- Биотехнология
- Чими
- Чими
- Курсы и упражнения
- IP адрес
- Алгоритм
- Андроид
- годовые
- Bases des données
- Бюротик
- коммерция
- Коммуникация
- Совместимость
- Comptabilité Analytique
- Comptabilité générale
- Концепция и анализ
- курс 3ds max
- Курс Ада
- курс адрес ip
- алгоритм курса
- курс андроид
- курс ассемблера
- Кур Бак-сес
- курс баз де донне
- курс до-диез
- Курс коммерции
- Cours comptabilité
- курс друпал
- затмение
- Курс эконом-класса
- Курс Электрисите
- Курс Электроник
- курс эргономики
- курсы и упражнения 5e
- курсы и упражнения html css
- курс и упражнения 1ère stmg
- курсы и упражнения 5eme
- Английский курс и упражнения
- Курсы и упражнения Excel 2010 бесплатно
- курсы и упражнения excel pdf
- большая секция курсов и упражнений
- курс превосходит
- Курс финансов
- курс фьюжн
- Курс Гестион
- курс канитель
- курс jquery
- курс labview
- курс языка c
- шепелявит
- Управление курсами
- Курсы маркетинга
- Курс Математики
- курс матлаб
- Кур Оберон
- цель курса c
- курс паскаль
- Курс PDF
- Курс телосложения
- курс pl sql
- кур питон
- курс qtcreator
- курс рубин
- Cours seconde
- Cours sixieme
- курс весна
- курс sql
- Статистика курса
- Курс статистики
- Терминал S
- Тройская улица
- курс unix linux
- курс вба
- курс визуальный базовый
- курс визуальной студии
- Курс Виндев
- курс слово
- Кутюр
- Криптография
- Дайверы
- Эконом
- Экономика pdf
- социальная экономия
- Электричество
- электроника
- эмс
- Этюд функции
- Совместимость экзаменов
- Экзамены по информатике
- маршрут упражнений
- Упражнения коммерции
- Совместимые упражнения
- Упражнения эконом
- упражнения
- Упражнения Финансы
- Упражнения
- Управление упражнениями
- Упражнения Маркетинг
- Упражнения по математике
- Упражнения pdf
- Упражнения телосложения
- Статистика упражнений
- слово упражнения
- Финансы
- Фискалите
- Гастрономия
- геополитика
- Жестион
- гуманитарии
- Информатика pdf
- Комбинация логики
- язык sql
- Усилители
- Les compteurs
- Конденсаторы
- диоды
- Фильтры
- английский язык
- Управление распределением и т.

- Управление человеческими ресурсами
- Управление рисками
- Управление pdf
- Стратегическое управление
- Цифровой маркетинг
- Маркетинговая часть
- Маркетинг pdf
- Маркетинговая стратегия
- Математика
- Математика 1эр S
- Терминал математики S
- микроэкономика
- модель отношения
- Расходы по управлению
- телосложение
- Вероятности и статистика
- Программирование
- вопросник ле монд
- наук
- сэс
- сес бак
- Статистика
- Системы эксплуатации
- Тригонометрия
- учебник язык c
- учебник линукс
- учебник excel
- обучающая вспышка
- сервер виндовс 2003
- Курсы и упражнения PDF
- Achats et approvisionnement
- Рекламное действие
- Научная деятельность
- Актуальная экономика
- Администрация информационных систем
- Аэроспасьяль Эт Дефанс
- Агенты экономики
- Сельское хозяйство и лесное хозяйство
- Аллеманд
- Финансовый анализ
- Английский
- Anglais En Seconde Langue
- Анналы Бак эс
- анналес бак л
- анналы бак с
- Антропологические исследования автохтонов
- Антропология
- Apprendre Une Langue
- Ардуино
- Автоматизация
- бак финансы
- задний план
- бакалавриат
- залог рекламный
- Коммерческий баланс
- Биоинформатика
- Биоэтика
- ЧИМИ
- Амбулатория торговли
- Коммуникация и политика
- Коммуникации и реклама
- Comptabilité Et D’Audit
- курс xml
- Cours 2ème Bac
- Кур Араб
- курс назад
- Кур-бак-Л
- Cours bac s
- Кур Бэк ST2DA
- Курс бак STD2S
- Cours bac STI2D
- Cours bac STL
- Cours bac STMG
- Кур Банк
- Кур Шими
- Кур Компани
- курсы css
- Курс Эколь
- Cours École Primaire
- Cours École Secondaire
- Кур Экология
- Курс Энерги
- Изготовление курсов
- курс финансов
- Кур Фискалите
- Кур Геология
- Курс истории
- Кур Инженьери
- Cours L’Informatique
- Кур-ла-Физик
- Курс Логистик
- курс математики
- кур мериз
- Курс Метео
- Курс MPSI
- курс mysql
- трассировщик пакетов
- Курс PCSI
- курс философии
- Курсы физики
- программа курса
- Курс PSI
- Курс ПТ
- Курс ПТСИ
- схема курса
- Курс наук
- курс Tronc Commun
- курс веб-мастера
- Курсансе
- Круассан эконом
- Демография
- Демография и география
- Демография и статистика
- Devoirs Mathématiques
- Диплом по дисциплине
- экономика
- экономика
- экономия
- коммерческая экономия
- ECONOMIE CONCOMMATION ET épargne
- экономия образования
- экономия на строительстве
- экономия удовольствия и удовольствия
- Экономика и политика
- географическая экономия
- промышленная экономика
- экономическая институция
- мировая экономика
- денежная экономика
- сельская экономия
- Écriture de scénario et creation li
- Образование художественное
- Исламское образование
- образование телосложение образование”’
- Коммерческий эффект
- ЭЛЕКТРИЧЕСТВО
- электрический батимент
- электрический CAP
- электрический колледж
- электрический дебютант
- электрисите женераль
- электрическая промышленность
- электрический лицей
- электрическая первичная
- электрическое веселье
- ENA Национальные школы архитектуры
- ENAM Национальная школа сельского хозяйства
- ENCG Национальные школы торговли
- Энергия
- электрическая энергия
- ENSA Национальные школы наук
- Высшие национальные школы ENSAM
- испанский
- Статистика оценки
- этюды аллеманды
- Études allemandes et histoire
- Английские этюды
- арабские исследования
- Азиатские исследования языка и культуры
- Азиатские исследования
- Этюды автохтонов
- Каталанские этюды
- Классические этюды
- Классические и антропологические исследования
- маршевые этюды
- видео этюды игры
- Азиатские этюды
- Феминистские этюды
- Испанские этюды
- Международные исследования
- Итальянские этюды
- Латино-американские этюды
- Средневековые этюды
- Неоэллинские этюды
- Квебекские этюды
- Études religieuses (науки о ре
- экзамены бак с
- Упражнения
- доступ к упражнениям
- Упражнения для спины ES
- Упражнения на спину L
- Упражнения на спину
- Упражнения бак ST2DA
- Упражнения bac STD2S
- Упражнения bac STI2D
- Упражнения bac STL
- Упражнения бак СТМГ
- Упражнения де comptabilité analytiqu
- Exercices de comptabilité financière
- осуществляет финансы
- Упражнения
- Математические упражнения
- Упражнения МП
- Упражнения МПСИ
- Упражнения ПК
- Упражнения ПКСИ
- Философия упражнений
- программа упражнений
- Упражнения пси
- Упражнения ФТ
- Упражнения наук
- Упражнения СФЭ
- Упражнения SUP
- Упражнения ТСИ
- окна упражнений
- Факультет искусств и социальных наук
- Факультет наук
- Коммерческие финансы
- Банковские финансы
- Финансовый дебютант
- Финансы и совместимость
- Финансы количественные
- Финансовый солидер
- Финансирование проекта
- Факультеты медицины и фармакологии FMP
- Фонд коммерции
- французский
- Français langue seconde avancé
- Джин генерал
- география
- Экологическая география
- геополитика и политические науки
- Геостатистический
- Gestion de l’information numérique
- Прием серв.
 де санте
де санте - Партизанский маркетинг
- история
- История экономики
- История искусства
- Историческая география
- Гиперперсонализация
- IAV Institut Agronomique et Vétérin
- Входящий исходящий
- Индустри Химик
- информатика
- Информационная аппликация
- Психообразовательное вмешательство
- Инвестор
- ISEM Institut Supérieur d’Etudes Ma
- ISIC Высший институт информации
- ISPM Institut Supérieur des Pêches
- Высший институт науки ISSS
- Кинезиология и образование. физ.
- Язык и культура allemandes
- Английский язык и культура
- Арабский язык и культура
- Каталанский язык и культура
- Китайский язык и культура
- Язык и культура
- Греческий язык и культура
- Испанский язык и культура
- Японский язык и культура
- Латинский язык и культура
- Язык и культура португалоязычный
- Португальский язык и культура lusuph
- Английские языки и культуры
- Арабские языки и культуры
- Каталанские языки и культуры
- Греческие языки и культуры
- Испанские языки и культуры
- Неоэллинские языки и культуры
- Языки и культуры русские
- Letters et Sciences Humanes
- Письма, языки и культуры
- Littératures de langue française
- Littératures de langue française et
- Littératures et langues modernes
- Logiciels D’Entreprise
- Логистика и транспорт
- Макроэкономика
- Совместное управление
- Культура управления
- Менеджмент d’équipe
- Управление инновациями
- Управление знаниями
- Управление операциями
- Управление изменениями
- Этика управления
- Оперативное управление
- Участие в управлении
- Марж коммерческая
- Маркетинговый агропродовольственный
- Маркетинговая альтернатива
- Маркетинговая аналитика
- Маркетинг B2B
- Маркетинговый банк
- Маркетинговое сотрудничество
- Маркетинговая реклама
- Культура маркетинга
- Контент-маркетинг
- Массовый маркетинг
- Маркетинговые ассоциации
- Маркетинговая этика
- Маркетинговая этника
- Маркетинговые мероприятия
- Маркетинговый опыт
- Маркетинговая сенсорика
- Маркетинг территориальный
- математика
- Математика и информатика
- Математика здесь S
- МЕХАНИКА
- Мет.
 де ледук. физ. спорт.
де ледук. физ. спорт. - Микробиология и иммунология
- Микроменеджмент
- Мобильная коммерция
- Статистика моделирования
- Мультидисциплинарный
- Музыкальное образование
- Нейромаркетинг
- Когнитивная неврология
- Ондес
- ОПТИКА
- Ориентация и консультирование
- колебания
- Техническая логистика
- Рекламный спектакль
- философия
- Философия и классические исследования
- php курсы и упражнения pdf бесплатно
- телосложение
- Телосложение и информатика
- Physique-Chimie
- Коммерческая перспектива
- Психообразование,
- Психология и социология
- Реклама и маркетинг
- Recrutement et Gestion des Carrière
- Этнические отношения
- Промышленные отношения
- Природные ресурсы
- Ресурсы Pédagogiques Et En Class
- Ретаргетинг
- Агрономические науки
- биологические науки
- Когнитивные науки
- Науки о коммуникации
- наук о жизни
- инженерные науки
- Экономика и управление науками
- Науки экономические и социальные
- Науки и технологии Механика
- Математические науки
- Математические науки A
- Математические науки B
- Науки естественные и прикладные
- Религиозные науки
- Sécurité et études policières
- СЭС
- Социология Отношения Этники
- Статистика Зондажа
- Статистическая аппликация
- Статистический дебютант
- исчерпывающая статистика
- Неверная статистика
- Статистическая психология
- Коммерческая стратегия
- Стратегия предприятия
- Уличный маркетинг
- Субвенции, Des Bourses et Des Aid
- СВТ
- Tableau de bord et management de pe
- Электрик
- Промышленная технология
- Технологии
- Коммерческая реклама
- Курс Упражнения
- аргументация
- Бак де Франсэ 2013
- Бодлер
- Камю
- искренний
- диссертация
- дом Хуан
- описание изобретения
- принцесса де Клев
- цветочки зла
- мадам Бовари
- поэзия
- Упражнения на курсе PDF
- диссертация фр
- экспертная совместимость
- Недвижимость
- Информатика
- Ла Финанс
- мастер говядина
- Норм Ванкувер
- норм апа
- изнасилование
- раппорт де этап
- эти докторские
- Курс телосложения
- Курсы и упражнения
- Криминология
- Криминология
- Дизайн интерьера
- Дизайн интерьера
- Первая дидактика
- Первая дидактика
- Право
- Право
- Эконом
- Курсы и упражнения
- экономическая политика
- социальная экономия
- Экономика и поведение
- Бак про
- Образование
- Образование
- Éducation physActivité phys
- Éducation physActivité phys
- образование телосложение
- образование телосложение
- ЭЛЕКТРИЧЕСТВО
- Курсы и упражнения PDF
- электроника
- Алгебр де Буля
- Электромагнетизм
- Les Circuits RLC
- Предприятие
- Предприятие
- Управление
- Экологические исследования
- Экологические исследования
- Семейные исследования
- Семейные исследования
- Финансы
- Финансы
- Лесничество
- Лесничество
- французский
- Бак генерал
- Бак про
- Кур Франсэ
- французский
- Второй французский язык
- Второй французский язык
- Джин гражданский
- Джин гражданский
- Джин Электрик
- Джин Электрик
- Джин механический
- Джин механический
- География
- География
- Геронтология
- Геронтология
- Gestion de l’information
- Gestion de l\’information
- Gestion de l\’information
- Gestion de l’information
- Управление операциями
- Управление операциями
- Прием серв.
 де санте
де санте - Прием серв. де санте
- Gestion intégrée zone cotière
- Gestion intégrée zone cotière
- История
- Антиквариат
- История
- История Европы
- Histoire des États-Unis
- Глобальная история
- Гуманитарные науки
- Писание
- Наука о религиях
- Информациякоммуникация
- Информациякоммуникация
- информатика
- информатика
- инженерия
- Аэрокосмическая техника
- Электротехника
- информатика
- инженерия
- Промышленная техника
- Кинезиология и образование. физ.
- Кинезиология и образование.
 физ.
физ. - Язык по номиналу платит
- Язык по номиналу платит
- лингвистика
- лингвистика
- Литература
- Литература
- Управление
- Бак СТМГ
- Управление
- Управление рисками
- Маркетинг
- Маркетинг
- математический
- Этюд функции
- Математика
- Бак ST2S
- Бак СТИ2Д
- Курсы и упражнения PDF
- Enseignement des mathématiques
- Элементарная математика
- Мир труда
- Этика
- Пример де Plaidoirie
- Финансы и экономика
- Техника прогресса
- Синдикаты
- Музыка
- Музыка
- Питание и семейные исследования
- Питание и семейные исследования
- питаниепитание
- питаниепитание
- ofppt
- курс ppt
- PDF-документы
- Ноты для альт-саксофона
- Бас Ноты
- Барабаны и перкуссия для начинающих
- Пианино для начинающих
- Скрипка для начинающих
- Bien-être
- Ноты для блюза для гитары
- Блюз Ноты
- Ноты для виолончели
- курсы и упражнения Excel
- курсы и упражнения python
- Персонал по развитию
- Этническая принадлежность, раса и жанр
- Фантазия
- Историческая фантастика
- Ноты для флейты и пикколо
- Ноты для гитары
- Старая история
- История Мойен-Востока
- Европейская история
- Мировая история
- Ноты для гитары в стиле джаз и блюз
- Ноты для джазовой гитары
- Ноты для джазового фортепиано
- Коран и священные писания
- Классическая литература
- Мода и красота
- Ноты для гитары из фильмов и мюзиклов
- Питание и Вин
- Паранормальный
- Разделы поп и рок
- Перегородки для фортепиано
- Политика и актуальная информация
- Поп- и рок-бас-ноты
- Популярная культура
- Ноты для гитары R&B
- Отношения и родители
- Религиозные и праздничные ноты для гитары Mu
- Вегетарианские и веганские блюда
- Исторический роман
- Научная фантастика
- Ноты
- Ноты для трубы
- Ноты для укулеле
- Городское планирование и землепользование
- Ноты для скрипки
- Философия
- Отруи
- Курсы и упражнения PDF
- Искусство
- L’Inconscient et la Conscience
- Ла Либерте
- Религия
- Ле Бонёр
- детерминизм
- Ле Маль
- Le réel et la raison
- Ле Респект
- Ле Рир
- Труд и техника
- Телосложение
- Телосложение
- Физико-химия и математика
- Бак СТИ2Д
- Политика и интернационал
- военный
- Психология
- Фрейд
- Истерия
- Ла Восприятие
- La Perfectibilite
- Психология
- Психология Когнитивная
- Se Connaitre Soi Мем
- стресс
- Радиология
- Радиология
- Связи со сценой
- Force et Faiblesse
- Письмо о мотивации
- Религия и духовность
- атеизм
- буддизм
- христианство
- индуизм
- ислам
- иудаизм
- Религия
- Богословие
- Гуманитарные ресурсы
- Гуманитарные ресурсы
- Здоровье и культура
- Альтернатива медицине
- Научный лазарет
- Научный лазарет
- Наука политическая
- Наука политическая
- наук
- Астрономия
- Биология
- Чими
- Медицина
- Наука об окружающей среде
- наук де ла Терре
- наук о здоровье
- наук о здоровье
- Экономические и социальные науки
- Генеалогия
- социальные науки
- Антропология
- Психология
- Наука политическая
- социальные науки
- Социология
- Общество
- Помощник Суаньанте
- Ситуаеннете
- Поколение
- Иммиграция
- Liens Familiaux
- Социология
- Социология
- Статистика
- Статистика
- СВТ
- Бак генерал
- Сист.
 информация. организационные элементы
информация. организационные элементы - Сист. д \ ‘информация. организационные элементы
- Сист. д \ ‘информация. организационные элементы
- Сист. информация. организационные элементы
- Тех. медицинская лаборатория
- Тех. медицинская лаборатория
- Респираторная терапия
- Респираторная терапия
- токсикомания
- токсикомания
- перевод
- перевод
- Путешествие в соц.
- Путешествие в соц.
- Администрация
- Бак
- Бревет
- Конкурсы
- Дайверы
- Трудоустройство
- Формирование фише
- Fiche metier
- История
- Письмо о мотивации
- Ливр Блан
- Рапорт де стадии
- питание
- Архитектура
- Кинотеатр искусств
- Искусство ддд пластики
- Художественная литература
- Искусство Музыка
- Художественная фотография
- Художественная пластика
- Base de données
- Биология
- бюрократический
- Коммерческий коучинг
- Коммерческое общение
- Коммерция ддд интернэшнл
- Коммерческие дайверы
- Коммерция Экономика
- Коммерческий электронный маркетинг
- Коммерческий этюд на марше
- Коммерческие Финансы
- Международная коммерция
- Коммерческая логистика
- Управление торговлей
- Коммерческий маркетинг
- Коммерческие СМИ
- Коммерческая стратегия
- Коммерческий туризм и услуги
- Коммуникация
- курс 3ds max
- Курс 4D
- доступ к курсу
- Курс Аякс
- алгоритм курса
- курс андроид
- курс апертура
- Cours Architecture des ordinateurs
- курс жерех
- курс ассемблера
- Cours assembleur Cours informatique
- дерзость
- Курс аудита
- Автоматический курс
- курс баз де донне
- Курс биологии
- Курский мост
- курс с
- курс до-диез
- Курсы С/С++
- Курс Сиэль Компта
- Cours Ciel Devis фактура
- Cours Ciel Gestion Commerciale
- Курсы Cisco
- Кур Коболь
- Курс коммерции
- курс аналитической совместимости
- Cours comptabilite approfondie
- Cours comptabilité des entreprises
- Cours comptabilité des sociétés
- Общий курс совместимости
- Курсы криптографии
- курсы css
- Курс Дельфы
- Кур Друа
- курс друпал
- затмение
- Курс эконометри
- Курс эконом-класса
- Cours électricité автомобиль
- Cours électricité de base
- Электромеканская улица
- Электронный курс
- курс эргономики
- курс превосходит
- курс final cut pro
- Cours Finance de Marché
- Cours финансирует общественность
- Курс фискальных услуг
- курс фьюжн
- курс гаражной группы
- Cours Genie Civil
- курс
- Курсы управления проектами
- Cours gestion des approvvisionnements
- Cours gestion des entreprises
- Cours gestion des ressources humanes
- Cours gestion des risques
- курс канитель
- Бесплатные курсы
- курс html
- Курс гидравлики
- Курс Имови
- Курс информатики
- курс iphoto
- курс j2ee
- Кур Ява
- Курсы JAVA/J2EE
- курс javascript
- курс джумла
- курс jquery
- курс labview
- курс языка c
- Курс Лазаря
- Курсы Linux
- Курс ЛУА
- курс обслуживания ПК
- курс менеджмент
- Стратегия управления курсами
- курс маркетинга
- Курс маркетинговой стратегии
- Математический курс
- курс матлаб
- Курс медицины
- кур мериз
- Курс микроэкономики
- курс mysql
- цель курса c
- трассировщик пакетов
- курс паскаль
- курс перл
- Курс фотошоп
- курс php
- Cours physique chimie
- Курсы PL/SQL
- Курсы PowerPoint
- Курс вероятностей
- кур питон
- курс qtcreator
- Справочник по курсу
- Курс Резо
- Cours réseaux informatiques
- схема курса
- Cours Sécurité Informatique
- курс
- Курс звуковой кузницы
- Курсы SQL
- Статистика курса
- Cours système d’exploitation
- курс умл
- Курсы Unix
- курс unix linux
- курс вб нетто
- Курс VB/VB.
 NET
NET - курс вба
- курс визуальный базовый
- курс визуальной студии
- курс веб-мастера
- Курс Виндев
- Курсы Windows
- курс windows server
- курс слово
- Курсы XHTML
- курс xml
- курс xsl
- Право
- Право дел
- Конституционное право
- Droit Contrats типы
- Право ддд
- Европейское право
- Фискальное право
- Право недвижимости
- Международное право
- Уголовное право
- Право человеческих ресурсов
- Права общества
- Право труда
- Образование
- Совместимые упражнения
- Упражнения и исправления
- французский
- Французская аналитика
- Франсэ Биография
- Франсез Комментарий
- Общая французская культура
- французский ддд
- Французская диссертация
- Лекция Франсе Фиша
- Ревизия Francais Fiche bac
- Французская литература
- Французская философия
- Изобретение Francais Sujet d
- Совместимость с Gestion
- Gestion Controle de gestion
- Гестион Финанс
- Программирование жестов
- Gestion Ressources Humanes
- Высокие технологии
- Histoire geographie Droit
- Histoire geographie Fiche revision bac
- Историческая география
- Историческая география
- Индустри
- информатика
- Администрация информатики
- Информатический анализ объекта uml merise
- Информационная архитектура
- Информатик Бдд
- Информатика ддд
- Informatique Genie Logiciel
- Informatique Gestion de projet
- Информатическое программирование
- Informatique Reseaux информатики
- Информационная безопасность информационных систем
- Информатика Технологии
- Ланге Алеманд
- Английский язык
- Арабский язык
- Китайский язык
- Langue ddds des signes
- Испанский язык
- Язык итальянский
- Латинский язык
- Языки знаков
- логические
- Математика
- Медицина
- Администрация методологии
- Английская методология
- Методологический комментарий
- Методология коммуникации
- Общая методология культуры
- Методология Резюме
- Испанская методология
- Пересмотр методологии Fiche bac
- Методология Письмо о мотивации
- Математическая методология
- Мемуар методологии
- Методология анализа
- Методология Отчет о стадии
- Методология поддержки
- Методология Технология
- Музыка
- Фотография
- Physique-Chimie
- Программирование
- Рапорт де стадии
- Резо информатики
- Санте
- Английские науки
- наук Чими
- Электронные науки
- Управление науками
- Математические науки
- наук механика
- Науки Медицина
- Аптека наук
- Науки Телосложение
- наук Свт
- Социальная философия
- Социальная политика
- Социальная психология
- Гуманитарные социальные ресурсы
- Социальные науки
- Социальная социология
- Спорт
- Trucs et Astuces
Сайт использует файлы cookie для персонализации PUB,
Si vous continuez à utiliser ce site, nousceptrons que vous en êtes satisfait. Савуар плюс
Савуар плюс
Политика конфиденциальности – Политика конфиденциальности
Как использовать метод исключения Гаусса для решения систем уравнений -Исчисление для чайников
Исследуйте книгу Купить на Amazon
Метод исключения Гаусса, вероятно, является лучшим методом решения систем уравнений, если у вас нет графического калькулятора или компьютерной программы, которая могла бы вам помочь. Цель исключения Гаусса состоит в том, чтобы сделать левый верхний угловой элемент равным 1, использовать элементарные операции со строками, чтобы получить 0 во всех позициях под этой первой 1, получить 1 для ведущих коэффициентов в каждой строке по диагонали от левого верхнего угла к нижнему. -правый угол и получить 0 под всеми ведущими коэффициентами. По сути, вы исключаете все переменные в последней строке, кроме одной, все переменные, кроме двух, в уравнении выше этой, и так далее, и так далее до верхнего уравнения, в котором есть все переменные. Затем вы можете использовать обратную подстановку для решения одной переменной за раз, подставляя известные вам значения в уравнения снизу вверх.
Затем вы можете использовать обратную подстановку для решения одной переменной за раз, подставляя известные вам значения в уравнения снизу вверх.
Вы выполняете это исключение, исключая x (или любую другую переменную, стоящую первой) во всех уравнениях, кроме первого. Затем исключите вторую переменную во всех уравнениях, кроме первых двух. Этот процесс продолжается, удаляя еще одну переменную в строке, пока в последней строке не останется только одна переменная. Затем решите для этой переменной.
Вы можете выполнить три операции над матрицами, чтобы исключить переменные в системе линейных уравнений:
Любую строку можно умножить на константу (кроме нуля).
умножает третью строку на -2, чтобы получить новую третью строку.
Вы можете поменять местами любые два ряда.
меняет местами первую и вторую строки.
Можно сложить две строки вместе.
добавляет первую и вторую строки и записывает их во вторую строку.

Рассмотрим следующую расширенную матрицу:
Теперь взглянем на цели исключения Гаусса, чтобы выполнить следующие шаги для решения этой матрицы:
Выполните первую цель: получить 1 в верхнем левом углу.
У вас уже есть это!
Выполните вторую цель: получить 0 под единицей в первом столбце.
Здесь необходимо использовать комбинацию двух матричных операций. Вот что вы должны спросить: «Что мне нужно добавить во вторую строку, чтобы 2 превратились в 0?» Ответ -2.
Этот шаг можно выполнить, умножив первую строку на –2 и добавив полученную строку ко второй строке. Другими словами, вы выполняете операцию
, который создает эту новую строку:
- .

(–2 –4 –6 : 14) + (2 –3 –5 : 9) = (0 –7 –11: 23)
Теперь у вас есть эта матрица:
- .
В третьей строке поставить 0 под 1.
Для выполнения этого шага необходима операция
После этого расчета у вас должна получиться следующая матрица:
Получить 1 во второй строке, во втором столбце.
Чтобы выполнить этот шаг, вам нужно умножить на константу; другими словами, умножьте вторую строку на соответствующую обратную величину:
.Этот расчет дает новую вторую строку:
Получите 0 под единицей, которую вы создали во второй строке.
Вернуться к старой доброй комбинированной операции для третьего ряда:
Вот еще вариант матрицы:
Получите еще одну единицу, на этот раз в третьей строке, в третьем столбце.
Умножьте третью строку на обратную величину коэффициента, чтобы получить 1:
Вы завершили главную диагональ после математических вычислений:
 Однако, если вы хотите знать, как преобразовать эту матрицу в сокращенную эшелонированную форму строк, чтобы найти решения, выполните следующие действия:
Однако, если вы хотите знать, как преобразовать эту матрицу в сокращенную эшелонированную форму строк, чтобы найти решения, выполните следующие действия:Получить 0 во второй строке, в третьем столбце.
Умножение третьей строки на константу –11/7 и последующее сложение второй и третьей строк
дает вам следующую матрицу:
Получить 0 в первой строке третьего столбца.
Операция
дает вам следующую матрицу:
Получить 0 в первой строке второго столбца.
Наконец, операция
дает вам эту матрицу:
Эта статья взята из книги:
- Предварительное исчисление для чайников,
Об авторе книги:
Мэри Джейн Стерлинг изучала алгебру, деловое исчисление, геометрию и конечную математику в Университете Брэдли в Пеории, штат Иллинойс. чем 30 лет. Она является автором нескольких книг «Для чайников», , в том числе «Рабочая тетрадь по алгебре для чайников», «Алгебра II для чайников», 9219.9 и Рабочая тетрадь по алгебре II для чайников.
чем 30 лет. Она является автором нескольких книг «Для чайников», , в том числе «Рабочая тетрадь по алгебре для чайников», «Алгебра II для чайников», 9219.9 и Рабочая тетрадь по алгебре II для чайников.
Эту статью можно найти в категории:
- Предварительное исчисление,
Применен метод Гаусса. Метод Гаусса онлайн
Продолжаем рассматривать системы линейных уравнений. Данный урок является третьим по теме. Если вы имеете смутное представление о том, что такое система линейных уравнений вообще, чувствуете себя чайником, то рекомендую начать с азов на следующей странице, полезно изучить урок.
Метод Гаусса прост! Почему? Знаменитый немецкий математик Иоганн Карл Фридрих Гаусс еще при жизни получил признание как величайший математик всех времен, гений и даже прозвище «Король математики». А все гениальное, как известно, просто! Кстати, в деньги попадают не только лохи, но и гении – портрет Гаусса красовался на купюре в 10 дойчмарок (до введения евро), а Гаусс до сих пор загадочно улыбается немцам с обычных почтовых марок .
Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА. Должен уметь складывать и умножать! Не случайно метод последовательного исключения неизвестных часто рассматривается учителями на школьных математических факультативах. Парадоксально, но наибольшие трудности у студентов вызывает метод Гаусса. Ничего удивительного — все дело в методике, и я постараюсь в доступной форме рассказать об алгоритме метода.
Сначала немного систематизируем свои знания о системах линейных уравнений. Система линейных уравнений может:
1) Иметь единственное решение. 2) Имеют бесконечно много решений. 3) Не иметь решений ( несовместимы с ).
Метод Гаусса является наиболее мощным и универсальным инструментом для поиска решения любых систем линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. Метод последовательного исключения неизвестных в любом случае ведут нас к ответу! В этом уроке мы снова рассмотрим метод Гаусса для случая №1 (единственное решение системы), для ситуаций пунктов №№2-3 отведена статья. Отмечу, что сам алгоритм метода работает одинаково во всех трех случаях.
Отмечу, что сам алгоритм метода работает одинаково во всех трех случаях.
Вернемся к простейшей системе из урока Как решить систему линейных уравнений? и решить его методом Гаусса.
Первым шагом является запись расширенной матричной системы : . По какому принципу записываются коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несет никакого математического смысла — это просто зачеркнуто для удобства оформления.
Артикул : Рекомендую запомнить условия линейная алгебра. Системная матрица — матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: . Матрица расширенной системы — та же матрица системы плюс столбец свободных членов, в данном случае: . Любую из матриц для краткости можно назвать просто матрицей.
После того, как расширенная матрица системы будет записана, необходимо произвести с ней некоторые действия, которые также называются элементарными преобразованиями .
Имеются следующие элементарные преобразования:
1) Строки Матрицы могут переставить мест. Например, в рассматриваемой матрице можно смело переставлять первую и вторую строки:
2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки, кроме одной. Рассмотрим, например, матрицу . В этой матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них: .
3) Если в матрице при преобразованиях появилась нулевая строка, то следует также удалить . Не буду рисовать, конечно, нулевая линия — это строка, в которой только нули .
4) Строка матрицы может быть умножить (разделить) на любое число ненулевое . Рассмотрим, например, матрицу . Здесь целесообразно первую строку разделить на -3, а вторую строку умножить на 2: . Это действие очень полезно, так как упрощает дальнейшие преобразования матрицы.
Рассмотрим, например, матрицу . Здесь целесообразно первую строку разделить на -3, а вторую строку умножить на 2: . Это действие очень полезно, так как упрощает дальнейшие преобразования матрицы.
5) Это преобразование вызывает больше всего трудностей, но по сути тоже ничего сложного. К строке матрицы можно добавить еще одну строку, умноженную на число , отличное от нуля. Рассмотрим нашу матрицу на практическом примере: . Сначала я очень подробно опишу трансформацию. Умножаем первую строку на -2: , и ко второй строке прибавляем первую строку умноженную на -2 : . Теперь первую строку можно разделить «назад» на -2: . Как видите, строка ДОБАВЛЕНА ЛИ – без изменений . – это всегда изменена строка, К КОТОРОЙ ДОБАВЛЕНО UT .
На практике, конечно, так подробно не расписывают, но пишут короче: Еще раз: ко второй строке добавили первую строку, умноженную на -2 . Строку обычно умножают устно или на черновике, при этом мысленный ход вычислений примерно такой:
«Переписываю матрицу и переписываю первую строку: »
Сначала столбец. Ниже мне нужно получить ноль. Поэтому я умножаю указанную выше единицу на -2: и прибавляю первую ко второй строке: 2 + (-2) = 0. Результат записываю во второй строке: »
Ниже мне нужно получить ноль. Поэтому я умножаю указанную выше единицу на -2: и прибавляю первую ко второй строке: 2 + (-2) = 0. Результат записываю во второй строке: »
«Теперь вторая колонка. Выше -1 раз -2: . Добавляю первое во вторую строку: 1+2=3. Результат записываю во вторую строку: »
«И третий столбец. Выше -5 раз -2: . Добавляю первую строку ко второй строке: -7 + 10 = 3. Результат записываю во вторую строку: »
Пожалуйста, хорошенько подумайте над этим примером и поймите алгоритм последовательного расчета, если вы это понимаете, то Гаусс метод практически «в кармане». Но, конечно, мы еще работаем над этой трансформацией.
Элементарные преобразования не меняют решения системы уравнений
! ВНИМАНИЕ : рассматриваемые манипуляции нельзя использовать , если вам предлагается задание, где матрицы даны “сами собой”. Например, с “классическими” матрицами ни в коем случае нельзя что-то переставлять внутри матриц! Вернемся к нашей системе. Она практически разбита на части.
Она практически разбита на части.
Запишем расширенную матрицу системы и с помощью элементарных преобразований уменьшим ее до ступенчатый вид :
(1) Первая строка была добавлена ко второй строке, умноженной на -2. И еще: почему мы умножаем первую строку на -2? Для того, чтобы внизу получить ноль, а значит избавиться от одной переменной во второй строке.
(2) Делим вторую строку на 3.
Цель элементарных преобразований – преобразовать матрицу в ступенчатую форму: . В оформлении задания прямо «лестницу» вычерчивают простым карандашом, а также обводят цифры, которые расположены на «ступенях». Сам термин «ступенчатый вид» не является полностью теоретическим; в научной и учебной литературе его часто называют трапециевидный вид или треугольный вид .
В результате элементарных преобразований мы получили эквивалентную исходную систему уравнений:
Теперь систему нужно “раскрутить” в обратную сторону – снизу вверх, этот процесс называется обратным методом Гаусса .
В нижнем уравнении уже есть готовый результат: .
Рассмотрим первое уравнение системы и подставим в него уже известное значение «y»:
Рассмотрим наиболее распространенную ситуацию, когда методом Гаусса требуется решить систему трех линейных уравнений с тремя неизвестными.
Пример 1
Решим систему уравнений методом Гаусса:
Запишем расширенную матрицу системы:
Теперь сразу нарисую результат, к которому придем в ходе решения: И повторюсь, наша цель — привести матрицу к ступенчатому виду с помощью элементарных преобразований. С чего начать действовать?
Во-первых, посмотрите на верхний левый номер: почти всегда здесь должен быть блок . Вообще говоря, -1 (а иногда и другие числа) тоже подойдут, но как-то традиционно сложилось, что туда обычно ставится единица. Как организовать подразделение? Смотрим на первую колонку – у нас есть готовый агрегат! Преобразование первое: поменять местами первую и третью строки:
Теперь первая строка останется неизменной до конца решения . Теперь хорошо.
Теперь хорошо.
Подразделение в левом верхнем углу организовано. Теперь нужно поставить нули в этих местах:
Нули получаются как раз с помощью “сложной” трансформации. Сначала разбираемся со второй строкой (2, -1, 3, 13). Что нужно сделать, чтобы получить ноль на первой позиции? Нужно ко второй строке добавить первую строку умноженную на -2 . Мысленно или на черновике первую строчку умножаем на -2: (-2, -4, 2, -18). И последовательно проводим (опять же мысленно или на черновике) сложение, ко второй строке добавляем первую строку, уже умноженную на -2 :
Во второй строке записывается результат:
Аналогично поступаем с третьей строкой (3, 2, -5, -1). Чтобы получить ноль в первой позиции, нужно , к третьей строке прибавить первую строку, умноженную на -3 . Мысленно или на черновике первую строчку умножаем на -3: (-3, -6, 3, -27). И к третьей строке добавляем первую строку умноженную на -3 :
Результат записывается в третьей строке:
На практике эти действия обычно выполняются устно и записываются в один прием:
Не нужно считать все сразу и одновременно . Порядок вычислений и “вставки” результатов соответствует и обычно такой: сначала переписываем первую строчку, и тихонько пыхтим – ПОСЛЕДОВАТЕЛЬНО и ВНИМАТЕЛЬНО :
Порядок вычислений и “вставки” результатов соответствует и обычно такой: сначала переписываем первую строчку, и тихонько пыхтим – ПОСЛЕДОВАТЕЛЬНО и ВНИМАТЕЛЬНО :
А мысленный ход самих вычислений я уже рассмотрел выше.
В данном примере это сделать легко, вторую строку делим на -5 (поскольку там все числа делятся на 5 без остатка). При этом третью строку делим на -2, ведь чем меньше число, тем проще решение:
На завершающем этапе элементарных преобразований здесь должен получиться еще один ноль:
Для этого к третьей строке добавляем вторую строку, умноженную на -2 :
Попробуйте сами разобрать это действие – мысленно умножьте вторую строку на -2 и проведите сложение.
Последнее выполненное действие – прическа результата, третью строку разделить на 3.
В результате элементарных преобразований была получена эквивалентная исходная система линейных уравнений: Cool.
Теперь в игру вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.
Уравнения «раскручиваются» снизу вверх.
В третьем уравнении у нас уже есть готовый результат:
Давайте посмотрим на второе уравнение: . Значение “z” уже известно, таким образом:
И, наконец, первое уравнение: . “Y” и “Z” известны, дело за малым:
Ответ :
Как уже неоднократно отмечалось, для любой системы уравнений можно и нужно проверить найденное решение, к счастью, это не сложно и быстро.
Пример 2
Это пример для самостоятельного решения, образец окончания и ответ в конце урока.
Следует отметить, что ваш образ действий может не совпадать с моим планом действий, и это особенность метода Гаусса . Но ответы должны быть одинаковыми!
Пример 3
Решить систему линейных уравнений методом Гаусса
Смотрим на верхнюю левую “ступеньку”. Там у нас должна быть единица. Проблема в том, что в первом столбце вообще нет единиц, поэтому перестановкой строк ничего не решить. В таких случаях блок должен быть организован с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я сделал это: (1) К первой строке добавляем вторую строку, умноженную на -1 . То есть мы мысленно умножили вторую строку на -1 и выполнили сложение первой и второй строк, при этом вторая строка не изменилась.
В таких случаях блок должен быть организован с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я сделал это: (1) К первой строке добавляем вторую строку, умноженную на -1 . То есть мы мысленно умножили вторую строку на -1 и выполнили сложение первой и второй строк, при этом вторая строка не изменилась.
Теперь слева вверху “минус один”, что нас вполне устраивает. Желающие получить +1 могут выполнить дополнительный жест: умножить первую строку на -1 (изменив ее знак).
(2) Первая строка, умноженная на 5, была добавлена ко второй строке. Первая строка, умноженная на 3, была добавлена к третьей строке.
(3) Первую строку умножил на -1, в принципе это для красоты. Знак третьей строки также изменился и переместился на второе место, таким образом, на втором «шаге» мы получили искомую единицу.
(4) Вторая строка, умноженная на 2, была добавлена к третьей строке.
(5) Третья строка была поделена на 3.
Плохой признак, указывающий на ошибку расчета (реже опечатку) — это «плохой» итог. То есть, если мы получили что-то вроде ниже, и, соответственно, , то с большой долей вероятности можно утверждать, что в ходе элементарных преобразований была допущена ошибка.
Заряжаем обратный ход, при оформлении примеров сама система часто не переписывается, а уравнения “берутся прямо из заданной матрицы”. Обратный ход, напомню, работает снизу вверх. Да, вот подарок:
Ответ : .
Пример 4
Решение системы линейных уравнений методом Гаусса
Это пример самостоятельного решения, он несколько сложнее. Ничего страшного, если кто-то запутается. Полное решение и пример оформления в конце урока. Ваше решение может отличаться от моего.
В последней части мы рассмотрим некоторые особенности алгоритма Гаусса. Первая особенность заключается в том, что иногда в уравнениях системы отсутствуют некоторые переменные, например: Как правильно записать расширенную матрицу системы? Я уже говорил об этом моменте на уроке. Правило Крамера. Матричный метод . В развернутой матрице системы вместо отсутствующих переменных поставим нули: Кстати, это довольно простой пример, так как в первом столбце уже есть один ноль, а элементарных преобразований нужно произвести меньше.
Правило Крамера. Матричный метод . В развернутой матрице системы вместо отсутствующих переменных поставим нули: Кстати, это довольно простой пример, так как в первом столбце уже есть один ноль, а элементарных преобразований нужно произвести меньше.
Вторая особенность. Во всех рассмотренных примерах мы ставили либо –1, либо +1 на «шаги». Может есть другие номера? В некоторых случаях могут. Рассмотрим систему: .
Вот на левой верхней “ступеньке” у нас двойка. Но замечаем тот факт, что все числа в первом столбце делятся на 2 без остатка — и еще на два и на шесть. И двойка вверху слева нам подойдет! На первом шаге необходимо выполнить следующие преобразования: добавить первую строку, умноженную на -1, ко второй строке; к третьей строке добавить первую строку, умноженную на -3. Таким образом, мы получим искомые нули в первом столбце.
Или другой гипотетический пример: . Здесь нам подходит и тройка на второй «ступеньке», так как 12 (место, где нам нужно получить ноль) делится на 3 без остатка. Необходимо провести следующее преобразование: к третьей строке добавить вторую строку, умноженную на -4, в результате чего получится нужный нам ноль.
Необходимо провести следующее преобразование: к третьей строке добавить вторую строку, умноженную на -4, в результате чего получится нужный нам ноль.
Метод Гаусса универсален, но есть одна особенность. Вы можете уверенно научиться решать системы другими методами (метод Крамера, матричный метод) буквально с первого раза – там очень жесткий алгоритм. Но чтобы чувствовать себя уверенно в методе Гаусса, следует «набить руку» и решить не менее 5-10 десятичных систем. Поэтому поначалу может быть путаница, ошибки в расчетах, и в этом нет ничего необычного или трагического.
Дождливая осенняя погода за окном…. Поэтому для всех более сложный пример для самостоятельного решения:
Пример 5
Решить систему из 4-х линейных уравнений с четырьмя неизвестными методом Гаусса.
Такая задача на практике встречается не так уж и редко. Я думаю, что даже чайник, подробно изучивший эту страницу, интуитивно понимает алгоритм решения такой системы. В принципе то же самое, только больше действий.
На уроке рассматриваются случаи, когда система не имеет решений (несовместна) или имеет бесконечно много решений. Несовместимые системы и системы с общим решением . Туда же можно закрепить рассмотренный алгоритм метода Гаусса.
Успехов!
Решения и ответы:
Пример 2: Решение : Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.
Выполнено элементарных преобразований: (1) Первая строка была добавлена ко второй строке, умноженной на -2. Первая строка была добавлена к третьей строке, умноженной на -1. Внимание! Тут может возникнуть соблазн вычесть первую из третьей строки, вычитать категорически не рекомендую – сильно возрастает риск ошибки. Мы просто складываем! (2) Изменен знак второй строки (умножен на -1). Вторая и третья строки поменялись местами. примечание что на «ступенях» нас устраивает не только единица, но и -1, что даже удобнее. (3) К третьей строке добавить вторую строку, умноженную на 5. (4) Изменен знак второй строки (умножен на -1). Третья строка была разделена на 14.
примечание что на «ступенях» нас устраивает не только единица, но и -1, что даже удобнее. (3) К третьей строке добавить вторую строку, умноженную на 5. (4) Изменен знак второй строки (умножен на -1). Третья строка была разделена на 14.
Обратный ход:
Ответить : .
Пример 4: Решение : Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
Выполнено преобразований: (1) Вторая строка добавлена к первой строке. Таким образом, нужный блок организуется на верхней левой «ступеньке». (2) Первая строка, умноженная на 7, была добавлена ко второй строке. Первая строка, умноженная на 6, была добавлена к третьей строке.
Со вторым “шагом” все хуже , «кандидатами» на него являются числа 17 и 23, а нам нужна либо единица, либо -1. Преобразования (3) и (4) будут направлены на получение нужного блока (3) Вторая строка была добавлена к третьей строке, умноженной на -1. (4) Третья строка, умноженная на -3, была добавлена ко второй строке. Необходимая вещь на втором этапе получена . (5) К третьей строке добавили вторую, умноженную на 6. (6) Вторую строку умножили на -1, третью строку разделили на -83.
Преобразования (3) и (4) будут направлены на получение нужного блока (3) Вторая строка была добавлена к третьей строке, умноженной на -1. (4) Третья строка, умноженная на -3, была добавлена ко второй строке. Необходимая вещь на втором этапе получена . (5) К третьей строке добавили вторую, умноженную на 6. (6) Вторую строку умножили на -1, третью строку разделили на -83.
Обратный ход:
Ответить :
Пример 5: Решение : Запишем матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
Выполнено преобразований: (1) Первая и вторая строки поменялись местами. (2) Первая строка была добавлена ко второй строке, умноженной на -2. Первая строка была добавлена к третьей строке, умноженной на -2. Первая строка была добавлена к четвертой строке, умноженной на -3. (3) Вторая строка, умноженная на 4, была добавлена к третьей строке. Вторая строка, умноженная на -1, была добавлена к четвертой строке. (4) Изменен знак второй строки. Четвертая строка была разделена на 3 и помещена вместо третьей строки. (5) К четвертой строке добавилась третья, умноженная на -5.
Первая строка была добавлена к четвертой строке, умноженной на -3. (3) Вторая строка, умноженная на 4, была добавлена к третьей строке. Вторая строка, умноженная на -1, была добавлена к четвертой строке. (4) Изменен знак второй строки. Четвертая строка была разделена на 3 и помещена вместо третьей строки. (5) К четвертой строке добавилась третья, умноженная на -5.
Обратный ход:
Ответ :
1. Система линейных алгебраических уравнений
1.1 Понятие системы линейных алгебраических уравнений
Система уравнений – это состояние, состоящее в одновременном выполнении нескольких уравнений с несколькими переменными. Системой линейных алгебраических уравнений (далее СЛАУ), содержащей m уравнений и n неизвестных, называется система вида:
где числа a ij называются коэффициентами системы, числа b i являются свободными членами, aij и b i (i=1,…,m; b=1,…,n) некоторые известные числа , и x 1 ,…, x n – неизвестно. В обозначениях коэффициентов aij первый индекс i обозначает номер уравнения, а второй индекс j — номер неизвестного, на котором стоит этот коэффициент. При условии нахождения числа x n . Такую систему удобно записать в компактной матричной форме: АХ=В. Здесь А — матрица коэффициентов системы, называемая основной матрицей;
В обозначениях коэффициентов aij первый индекс i обозначает номер уравнения, а второй индекс j — номер неизвестного, на котором стоит этот коэффициент. При условии нахождения числа x n . Такую систему удобно записать в компактной матричной форме: АХ=В. Здесь А — матрица коэффициентов системы, называемая основной матрицей;
— вектор-столбец неизвестного xj.
— вектор-столбец из свободных членов bi.
Произведение матриц A * X определено, так как столбцов в матрице A столько, сколько строк в матрице X (n штук).
Расширенная матрица системы – это матрица системы А, дополненная столбцом свободных членов
1,2 Решение системы линейных алгебраических уравнений
Решение системы уравнений представляет собой упорядоченный набор чисел (значений переменных), при подстановке которых вместо переменных каждое из уравнений системы превращается в истинное равенство.
Решением системы является n значений неизвестных x1=c1, x2=c2,…, xn=cn, при подстановке которых все уравнения системы превращаются в истинные равенства. Любое решение системы можно записать в виде матрицы-столбца
Любое решение системы можно записать в виде матрицы-столбца
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если решений не имеет.
Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.
Решить систему означает выяснить, непротиворечива она или непротиворечива. Если система совместна, найти ее общее решение.
Две системы называются эквивалентными (эквивалентными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.
Преобразование, применение которого превращает систему в новую систему, эквивалентную исходной, называется эквивалентным или эквивалентным преобразованием. Примерами эквивалентных преобразований могут служить следующие преобразования: замена двух уравнений системы местами, замена двух неизвестных вместе с коэффициентами всех уравнений, умножение обеих частей любого уравнения системы на ненулевое число.
Система линейных уравнений называется однородной, если все свободные члены равны нулю:
Однородная система всегда непротиворечива, так как x1=x2=x3=…=xn=0 является решением системы. Это решение называется нулевым или тривиальным.
2. Метод исключения Гаусса
2.1 Сущность метода исключения Гаусса
Классическим методом решения систем линейных алгебраических уравнений является метод последовательного исключения неизвестных – Метод Гаусса (Его также называют методом исключения Гаусса метод). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений сводится к эквивалентной системе ступенчатого (или треугольного) вида, из которой последовательно находятся все остальные переменные, начиная с последние (по номеру) переменные.
Процесс решения по Гауссу состоит из двух этапов: прямого и обратного хода.
1. Прямой ход.
На первом этапе осуществляется так называемый прямой ход, когда путем элементарных преобразований по строкам система приводится к ступенчатому или треугольному виду, либо устанавливается несовместность системы. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его в самое верхнее положение путем перестановки строк, а полученную после перестановки первую строку вычитают из оставшихся строк, умножая ее на значение, равное отношению первого элемента каждой из этих строк к первому элементу первой строки, таким образом обнуляя столбец под ним.
А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его в самое верхнее положение путем перестановки строк, а полученную после перестановки первую строку вычитают из оставшихся строк, умножая ее на значение, равное отношению первого элемента каждой из этих строк к первому элементу первой строки, таким образом обнуляя столбец под ним.
После выполнения указанных преобразований первая строка и первый столбец мысленно вычеркиваются и продолжаются до тех пор, пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашлось ненулевого, то перейти к следующему столбцу и выполнить аналогичную операцию.
На первом этапе (прямой ход) система приводится к ступенчатой (в частности, треугольной) форме.
Приведенная ниже система ступенчатая:
,
Коэффициенты aii называются главными (ведущими) элементами системы.
(если a11=0, переставить строки матрицы так, чтобы a 11 не было равно 0. Это всегда возможно, так как в противном случае матрица содержит нулевой столбец, ее определитель равен нулю и система непоследовательный).
Это всегда возможно, так как в противном случае матрица содержит нулевой столбец, ее определитель равен нулю и система непоследовательный).
Преобразуем систему, исключив неизвестное x1 во всех уравнениях, кроме первого (используя элементарные преобразования системы). Для этого умножьте обе части первого уравнения на 9.0003
и складываем почленно со вторым уравнением системы (или из второго уравнения почленно вычитаем первое, умноженное на ). Затем умножаем обе части первого уравнения на и прибавляем к третьему уравнению системы (или вычитаем первое, умноженное на третье слагаемое, за слагаемым). Таким образом, мы последовательно умножаем первую строку на число и прибавляем к i -ю строку, для i= 2, 3, …, с.
Продолжая этот процесс, мы получаем эквивалентную систему:
– новые значения коэффициентов при неизвестных и свободных членах в последних m-1 уравнениях системы, которые определяются по формулам:
Таким образом, на первом шаге все коэффициенты при первом ведущем элементе a 11 уничтожаются
0, второй шаг уничтожает элементы под вторым ведущим элементом a 22 (1) (если a 22 (1) 0) и так далее. Продолжая этот процесс дальше, мы окончательно приведем исходную систему к треугольной на шаге (m-1).
Продолжая этот процесс дальше, мы окончательно приведем исходную систему к треугольной на шаге (m-1).
Если в процессе приведения системы к ступенчатому виду появляются нулевые уравнения, т.е. равенства вида 0=0, то они отбрасываются. Если есть уравнение вида
Это говорит о несовместимости системы.
На этом прямой ход метода Гаусса завершен.
2. Обратный ход.
На втором этапе осуществляется так называемый обратный ход, суть которого заключается в выражении всех полученных основных переменных через неосновные и построении фундаментальной системы решений, или, если все переменные основные, то численно выразить единственное решение системы линейных уравнений.
Эта процедура начинается с последнего уравнения, из которого выражается соответствующая основная переменная (она в нем только одна) и подставляется в предыдущие уравнения, и так далее, поднимаясь по “ступеням” вверх.
Каждая строка соответствует ровно одной базовой переменной, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
Примечание: на практике удобнее работать не с системой, а с ее расширенной матрицей, производя все элементарные преобразования над ее строками. Удобно, чтобы коэффициент а11 был равен 1 (переставить уравнения, или разделить обе части уравнения на а11).
2.2 Примеры решения СЛАУ методом Гаусса
В этом разделе на трех разных примерах мы покажем, как можно использовать метод Гаусса для решения СЛАУ.
Пример 1. Решить СЛАУ 3-го порядка.
Обнулить коэффициенты по
во второй и третьей строках. Для этого умножьте их на 2/3 и 1 соответственно и добавьте в первую строку:
Еще с начала XVI-XVIII веков математики стали усиленно изучать функции, благодаря которым так много изменилось в нашей жизни. Компьютерная техника без этих знаний просто не существовала бы. Для решения сложных задач, линейных уравнений и функций созданы различные концепции, теоремы и методики решения. Одним из таких универсальных и рациональных методов и приемов решения линейных уравнений и их систем стал метод Гаусса. Матрицы, их ранг, определитель — все можно вычислить без применения сложных операций.
Матрицы, их ранг, определитель — все можно вычислить без применения сложных операций.
Что такое СЛАУ
В математике есть понятие СЛАУ – система линейных алгебраических уравнений. Что она представляет? Это набор m уравнений с искомыми n неизвестными, обычно обозначаемыми как x, y, z, или x 1 , x 2 … x n, или другими символами. Решить эту систему методом Гаусса означает найти все неизвестные неизвестные. Если в системе одинаковое количество неизвестных и уравнений, то она называется системой n-го порядка.
Наиболее популярные методы решения СЛАУ
В образовательных учреждениях среднего образования изучаются различные методы решения таких систем. Чаще всего это простые уравнения, состоящие из двух неизвестных, поэтому любой существующий метод нахождения ответа на них не займет много времени. Это может быть как метод подстановки, когда из одного уравнения выводится другое уравнение и подставляется в исходное. Или почленное вычитание и сложение. Но самым простым и универсальным считается метод Гаусса. Это позволяет решать уравнения с любым числом неизвестных. Почему этот прием считается рациональным? Все просто. Матричный метод хорош тем, что не требует по нескольку раз переписывать лишние символы в виде неизвестных, достаточно произвести арифметические действия над коэффициентами — и вы получите достоверный результат.
Это позволяет решать уравнения с любым числом неизвестных. Почему этот прием считается рациональным? Все просто. Матричный метод хорош тем, что не требует по нескольку раз переписывать лишние символы в виде неизвестных, достаточно произвести арифметические действия над коэффициентами — и вы получите достоверный результат.
Где на практике используются СЛАУ?
Решением СЛАУ являются точки пересечения прямых на графиках функций. В наш высокотехнологичный компьютерный век людям, которые вплотную занимаются разработкой игр и других программ, необходимо знать, как решать такие системы, что они из себя представляют и как проверить правильность полученного результата. Чаще всего программисты разрабатывают специальные калькуляторы линейной алгебры, сюда входит система линейных уравнений. Метод Гаусса позволяет вычислить все существующие решения. Также используются другие упрощенные формулы и методы.
Критерий совместимости СЛАУ
Такая система может быть решена только в том случае, если она совместима. Для наглядности представим СЛАУ в виде Ax=b. Оно имеет решение, если rang(A) равно rang(A,b). В этом случае (A,b) является матрицей расширенной формы, которую можно получить из матрицы A, переписав ее со свободными членами. Оказывается, решать линейные уравнения методом Гаусса довольно просто.
Для наглядности представим СЛАУ в виде Ax=b. Оно имеет решение, если rang(A) равно rang(A,b). В этом случае (A,b) является матрицей расширенной формы, которую можно получить из матрицы A, переписав ее со свободными членами. Оказывается, решать линейные уравнения методом Гаусса довольно просто.
Возможно какие-то обозначения не совсем понятны, поэтому необходимо все рассмотреть на примере. Допустим, есть система: x+y=1; 2х-3у=6. Он состоит всего из двух уравнений, в которых 2 неизвестных. Система будет иметь решение только в том случае, если ранг ее матрицы равен рангу расширенной матрицы. Что такое ранг? Это количество независимых линий системы. В нашем случае ранг матрицы равен 2. Матрица А будет состоять из коэффициентов, стоящих рядом с неизвестными, а коэффициенты за знаком «=» также впишутся в развернутую матрицу.
Почему СЛАУ может быть представлена в матричной форме
На основании критерия совместности по доказанной теореме Кронекера-Капелли система линейных алгебраических уравнений может быть представлена в матричной форме. Используя каскадный метод Гаусса, можно решить матрицу и получить единственный достоверный ответ для всей системы. Если ранг обычной матрицы равен рангу ее расширенной матрицы, но меньше числа неизвестных, то система имеет бесконечное число ответов.
Используя каскадный метод Гаусса, можно решить матрицу и получить единственный достоверный ответ для всей системы. Если ранг обычной матрицы равен рангу ее расширенной матрицы, но меньше числа неизвестных, то система имеет бесконечное число ответов.
Преобразования матриц
Прежде чем перейти к решению матриц, необходимо знать, какие действия можно производить над их элементами. Существует несколько элементарных преобразований:
- Переписав систему в матричной форме и выполнив ее решение, можно умножить все элементы ряда на один и тот же коэффициент.
- Чтобы преобразовать матрицу в каноническую форму, можно поменять местами две параллельные строки. Каноническая форма подразумевает, что все элементы матрицы, расположенные по главной диагонали, становятся единицами, а остальные – нулями.
- Соответствующие элементы параллельных строк матрицы можно складывать друг с другом.
Метод Жордана-Гаусса
Суть решения систем линейных однородных и неоднородных уравнений методом Гаусса заключается в постепенном исключении неизвестных. Допустим, у нас есть система двух уравнений, в которой два неизвестных. Чтобы их найти, нужно проверить систему на совместимость. Уравнение Гаусса решается очень просто. Необходимо выписать коэффициенты, расположенные возле каждого неизвестного, в матричном виде. Чтобы решить систему, нужно выписать расширенную матрицу. Если одно из уравнений содержит меньшее количество неизвестных, то вместо отсутствующего элемента необходимо поставить «0». К матрице применяются все известные методы преобразования: умножение, деление на число, сложение соответствующих элементов строк друг с другом и другие. Получается, что в каждой строке необходимо оставить одну переменную со значением «1», остальные уменьшить до нуля. Для более точного понимания необходимо рассмотреть метод Гаусса на примерах.
Допустим, у нас есть система двух уравнений, в которой два неизвестных. Чтобы их найти, нужно проверить систему на совместимость. Уравнение Гаусса решается очень просто. Необходимо выписать коэффициенты, расположенные возле каждого неизвестного, в матричном виде. Чтобы решить систему, нужно выписать расширенную матрицу. Если одно из уравнений содержит меньшее количество неизвестных, то вместо отсутствующего элемента необходимо поставить «0». К матрице применяются все известные методы преобразования: умножение, деление на число, сложение соответствующих элементов строк друг с другом и другие. Получается, что в каждой строке необходимо оставить одну переменную со значением «1», остальные уменьшить до нуля. Для более точного понимания необходимо рассмотреть метод Гаусса на примерах.
Простой пример решения системы 2×2
Для начала возьмем простую систему алгебраических уравнений, в которой будет 2 неизвестных.
Перепишем в расширенной матрице.
Для решения этой системы линейных уравнений требуется всего две операции. Нам нужно привести матрицу к каноническому виду, чтобы по главной диагонали были единицы. Итак, переводя из матричной формы обратно в систему, получаем уравнения: 1x+0y=b1 и 0x+1y=b2, где b1 и b2 – ответы, полученные в процессе решения.
Нам нужно привести матрицу к каноническому виду, чтобы по главной диагонали были единицы. Итак, переводя из матричной формы обратно в систему, получаем уравнения: 1x+0y=b1 и 0x+1y=b2, где b1 и b2 – ответы, полученные в процессе решения.
- Первый шаг в решении расширенной матрицы будет таким: первую строку нужно умножить на -7 и добавить соответствующие элементы во вторую строку соответственно, чтобы избавиться от одного неизвестного во второй уравнение.
- Так как решение уравнений методом Гаусса подразумевает приведение матрицы к каноническому виду, то необходимо проделать те же операции с первым уравнением и удалить вторую переменную. Для этого вычтем вторую строку из первой и получим нужный ответ – решение СЛАУ. Или, как показано на рисунке, умножаем вторую строку на коэффициент -1 и прибавляем элементы второй строки к первой строке. Это тоже самое.
Как видите, наша система решается методом Жордана-Гаусса. Перепишем его в нужном виде: x=-5, y=7.
Пример решения СЛАУ 3×3
Предположим, что мы имеем более сложную систему линейных уравнений. Метод Гаусса позволяет вычислить ответ даже для самой, казалось бы, запутанной системы. Поэтому, чтобы глубже вникнуть в методику расчета, можно перейти к более сложному примеру с тремя неизвестными.
Как и в предыдущем примере, переписываем систему в виде расширенной матрицы и начинаем приводить ее к каноническому виду.
Чтобы решить эту систему, вам потребуется выполнить гораздо больше действий, чем в предыдущем примере.
- Сначала нужно сделать в первом столбце один единственный элемент, а остальные нули. Для этого умножьте первое уравнение на -1 и добавьте к нему второе уравнение. Важно помнить, что первую строчку мы переписываем в исходном виде, а вторую — уже в измененном виде.
- Далее удаляем ту же первую неизвестную из третьего уравнения. Для этого умножаем элементы первой строки на -2 и прибавляем их к третьей строке.
 Теперь первая и вторая строки переписаны в исходном виде, а третья — уже с изменениями. Как видно из результата, мы получили первую единицу в начале главной диагонали матрицы, а остальные нули. Еще несколько действий, и система уравнений методом Гаусса будет надежно решена.
Теперь первая и вторая строки переписаны в исходном виде, а третья — уже с изменениями. Как видно из результата, мы получили первую единицу в начале главной диагонали матрицы, а остальные нули. Еще несколько действий, и система уравнений методом Гаусса будет надежно решена. - Теперь нужно проделать операции над другими элементами строк. Третий и четвертый этапы можно объединить в один. Нам нужно разделить вторую и третью строки на -1, чтобы избавиться от отрицательных по диагонали. Третью строчку мы уже привели к нужному виду.
- Далее мы канонизируем вторую строку. Для этого умножаем элементы третьей строки на -3 и прибавляем их ко второй строке матрицы. Из результата видно, что вторая строка также приведена к нужному нам виду. Осталось сделать еще несколько операций и убрать коэффициенты при неизвестных из первой строки.
- Чтобы из второго элемента строки сделать 0, нужно третью строку умножить на -3 и прибавить к первой строке.
- Следующим решающим шагом является добавление необходимых элементов второго ряда к первому ряду.
 Так мы получаем каноническую форму матрицы, и, соответственно, ответ.
Так мы получаем каноническую форму матрицы, и, соответственно, ответ.
Как видите, решение уравнений методом Гаусса достаточно простое.
Пример решения системы уравнений 4×4
Некоторые более сложные системы уравнений могут быть решены методом Гаусса с использованием компьютерных программ. Необходимо вбить коэффициенты для неизвестных в имеющиеся пустые ячейки, и программа шаг за шагом рассчитает требуемый результат, подробно описывая каждое действие.
Пошаговая инструкция решения такого примера описана ниже.
На первом этапе в пустые ячейки вносятся свободные коэффициенты и числа для неизвестных. Таким образом, мы получаем ту самую дополненную матрицу, которую пишем от руки.
И выполняются все необходимые арифметические действия для приведения расширенной матрицы к каноническому виду. Нужно понимать, что ответом на систему уравнений не всегда являются целые числа. Иногда решение может быть из дробных чисел.
Проверка правильности решения
Метод Жордана-Гаусса предусматривает проверку правильности результата. Для того, чтобы узнать, правильно ли рассчитаны коэффициенты, нужно просто подставить результат в исходную систему уравнений. Левая часть уравнения должна совпадать с правой частью, стоящей за знаком равенства. Если ответы не совпадают, то необходимо пересчитать систему или попробовать применить другой известный вам метод решения СЛАУ, например подстановку или почленное вычитание и сложение. Ведь математика – это наука, имеющая огромное количество различных методов решения. Но помните: результат всегда должен быть одинаковым, какой бы метод решения вы не использовали.
Для того, чтобы узнать, правильно ли рассчитаны коэффициенты, нужно просто подставить результат в исходную систему уравнений. Левая часть уравнения должна совпадать с правой частью, стоящей за знаком равенства. Если ответы не совпадают, то необходимо пересчитать систему или попробовать применить другой известный вам метод решения СЛАУ, например подстановку или почленное вычитание и сложение. Ведь математика – это наука, имеющая огромное количество различных методов решения. Но помните: результат всегда должен быть одинаковым, какой бы метод решения вы не использовали.
Метод Гаусса: наиболее частые ошибки при решении СЛАУ
При решении линейных систем уравнений чаще всего возникают ошибки, такие как неправильный перевод коэффициентов в матричный вид. Бывают системы, в которых в одном из уравнений отсутствуют какие-то неизвестные, то при переносе данных в расширенную матрицу они могут быть потеряны. В результате при решении этой системы результат может не соответствовать реальному.
Еще одной из основных ошибок может быть неправильное выписывание конечного результата. Нужно четко понимать, что первый коэффициент будет соответствовать первому неизвестному из системы, второй – второму и так далее.
Метод Гаусса подробно описывает решение линейных уравнений. Благодаря ему легко выполнять необходимые операции и находить нужный результат. Кроме того, это универсальный инструмент для поиска достоверного ответа на уравнения любой сложности. Может быть, поэтому его так часто используют при решении СЛАУ.
Пусть дана система линейных алгебраических уравнений, которую необходимо решить (найти такие значения неизвестных хi, которые обращают каждое уравнение системы в равенство).
Мы знаем, что система линейных алгебраических уравнений может:
1) Не иметь решений (быть несовместимыми ) .
2) Имеют бесконечно много решений.
3) Иметь единственное решение.
Как мы помним, правило Крамера и матричный метод непригодны в случаях, когда система имеет бесконечно много решений или несовместна. Метод Гаусса – самый мощный и универсальный инструмент для поиска решений любой системы линейных уравнений , что в каждом случае приводит нас к ответу! Алгоритм метода во всех трех случаях работает одинаково. Если Крамеровский и матричный методы требуют знания определителей, то применение метода Гаусса требует знания только арифметических действий, что делает его доступным даже для учащихся начальных классов.
Метод Гаусса – самый мощный и универсальный инструмент для поиска решений любой системы линейных уравнений , что в каждом случае приводит нас к ответу! Алгоритм метода во всех трех случаях работает одинаково. Если Крамеровский и матричный методы требуют знания определителей, то применение метода Гаусса требует знания только арифметических действий, что делает его доступным даже для учащихся начальных классов.
Расширенные матричные преобразования ( это матрица системы – матрица, составленная только из коэффициентов при неизвестных плюс столбец свободных членов) систем линейных алгебраических уравнений в методе Гаусса:
1) С троки матрицы банка переставить мест.
2) если в матрице есть (или есть) пропорциональные (в частном случае – одинаковые) строки, то следует удалить из матрицы, все эти строки кроме одной.
3) если в матрице при преобразованиях появилась нулевая строка, то следует также удалить .
4) строка матрицы может умножать (делить) на любое число кроме нуля.
5) к строке матрицы можно добавить еще одну строку, умноженную на число , отличное от нуля.
В методе Гаусса элементарные преобразования не меняют решения системы уравнений.
Метод Гаусса состоит из двух этапов:
- «Прямой ход» – с помощью элементарных преобразований привести расширенную матрицу системы линейных алгебраических уравнений к «треугольному» ступенчатому виду: элементы расширенная матрица, расположенная ниже главной диагонали, равна нулю (перемещение сверху вниз). Например, в таком виде:
Для этого выполните следующие действия:
1) Рассмотрим первое уравнение системы линейных алгебраических уравнений и коэффициент при x 1 равен K. Второе, третье и т.д. преобразуем уравнения следующим образом: каждое уравнение (коэффициенты при неизвестных, включая свободные члены) делим на коэффициент при неизвестных x 1, который есть в каждом уравнении, и умножаем на К. После этого из второго уравнения (коэффициенты при неизвестных и бесплатные условия). Получаем при x 1 во втором уравнении коэффициент 0. Из третьего преобразованного уравнения вычитаем первое уравнение, так что пока все уравнения, кроме первого, с неизвестным x 1, не будут иметь коэффициент 0.
После этого из второго уравнения (коэффициенты при неизвестных и бесплатные условия). Получаем при x 1 во втором уравнении коэффициент 0. Из третьего преобразованного уравнения вычитаем первое уравнение, так что пока все уравнения, кроме первого, с неизвестным x 1, не будут иметь коэффициент 0.
2) Перейдите к следующему уравнению. Пусть это будет второе уравнение и коэффициент при х 2 равен М. Со всеми «подчиненными» уравнениями поступаем, как описано выше. Таким образом, «под» неизвестным x 2 во всех уравнениях будут нули.
3) Переходим к следующему уравнению и так далее, пока не останется последний неизвестный и преобразованный свободный член.
- “Обратный ход” метода Гаусса заключается в получении решения системы линейных алгебраических уравнений (ход “снизу вверх”). Из последнего «нижнего» уравнения получаем одно первое решение — неизвестное x n. Для этого решаем элементарное уравнение А*х н = В. В примере выше х 3 = 4. Подставляем найденное значение в «верхнее» следующее уравнение и решаем его относительно следующего неизвестного.
 Например, х 2 – 4 = 1, т.е. х 2 = 5. И так до тех пор, пока не найдем все неизвестные.
Например, х 2 – 4 = 1, т.е. х 2 = 5. И так до тех пор, пока не найдем все неизвестные.
Пример.
Решаем систему линейных уравнений методом Гаусса, как советуют некоторые авторы:
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
посмотрите на верхнюю левую “ступеньку”. Там у нас должна быть единица. Проблема в том, что в первом столбце вообще нет единиц, поэтому перестановкой строк ничего не решить. В таких случаях блок должен быть организован с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Сделаем так:
1 шаг . К первой строке добавляем вторую строку, умноженную на -1. То есть мы мысленно умножили вторую строку на -1 и выполнили сложение первой и второй строк, при этом вторая строка не изменилась.
Теперь слева вверху “минус один”, что нас вполне устраивает. Кто хочет получить +1, может выполнить дополнительное действие: умножить первую строку на -1 (изменить знак).
2 ступени . Первая строка, умноженная на 5, была добавлена ко второй строке. Первая строка, умноженная на 3, была добавлена к третьей строке.
3 шага . Первую строчку умножил на -1, в принципе это для красоты. Знак третьей строки также изменился и переместился на второе место, таким образом, на втором «шаге» мы получили искомую единицу.
4 ступени . К третьей строке добавляем вторую строку, умноженную на 2.
5 шаг . Третья строка делится на 3.
Знак, указывающий на ошибку в расчетах (реже опечатку) — «плохой» итог. То есть, если мы получили что-то вроде (0 0 11 | 23) внизу, и, соответственно, 11х 3 = 23, х 3 = 23/11, то с большой долей вероятности можно сказать, что при элементарном преобразования.
Делаем обратный ход, при оформлении примеров сама система часто не переписывается, а уравнения “берутся прямо из заданной матрицы”. Обратный ход, напомню, работает «снизу вверх». В данном примере подарок получился:
В данном примере подарок получился:
х 3 = 1
х 2 = 3
х 1 + х 2 – х 3 = 1, следовательно, х 1 + 3 – 1 = 1, х 1 = -1
Ответ :х 1 = -1, х 2 = 3, х 3 = 1.
Решим ту же систему по предложенному алгоритму. мы получаем
4 2 –1 1
5 3 –2 2
3 2 –3 0
Разделим второе уравнение на 5, а третье на 3. Получим:
4 2 –1 1
1 0,6 –0,4 0,4
1 0,66 –1 0
Умножаем второе и третье уравнения на 4, получаем:
4 2 –1 1
4 2,4 –1,6 1,6
4 2,64 –4 0
Вычитаем первое уравнение из второго и Третье уравнение, имеем:
4 2 –1 1
0 0,4 –0,6 0,6
0 0,64 –3 –1
Разделим третье уравнение на 0,64:
4 2 –1 1
0 0,4 –0,6 0,6
0 1 –4,6875 –1,5625
Умножение третьего уравнения на 0,4
4 2–1 1
0 0,4 –0,6 0,6
0,4 –1,875 –0,625
9 0,6
0,4 –1,875 –0,625
9 0,6
0,4 –1,875 –0,625 9000 3
,6 0,6
0,4 –1,875 –0,625 9000 3
0,6
0,4 –1,875 –0,625 9 000,6 0,6
0,4. Вычтем из третьего уравнения второе уравнение, получим «ступенчатую» расширенную матрицу: расчетов, получаем х 3 = 0,96, или примерно 1.
Вычтем из третьего уравнения второе уравнение, получим «ступенчатую» расширенную матрицу: расчетов, получаем х 3 = 0,96, или примерно 1.
х 2 = 3 и х 1 = -1.
Решая таким образом, вы никогда не запутаетесь в расчетах и, несмотря на ошибки в расчетах, получите результат.
Этот метод решения системы линейных алгебраических уравнений легко программируется и не учитывает особенностей коэффициентов при неизвестных, так как на практике (в экономических и технических расчетах) приходится иметь дело с нецелыми коэффициентами.
Успехов! Увидимся в классе! Репетитор Дмитрий Айстраханов.
сайта, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Здесь вы можете бесплатно решить систему линейных уравнений Метод Гаусса онлайн больших размеров в комплексных числах с очень подробным решением. Наш калькулятор может решить онлайн как обычную определенную, так и неопределенную систему линейных уравнений по методу Гаусса, который имеет бесконечное количество решений. В этом случае в ответ вы получите зависимость одних переменных через другие, свободные. Вы также можете проверить систему уравнений на совместимость онлайн, используя решение Гаусса.
В этом случае в ответ вы получите зависимость одних переменных через другие, свободные. Вы также можете проверить систему уравнений на совместимость онлайн, используя решение Гаусса.
О методе
При решении системы линейных уравнений онлайн методом Гаусса выполняются следующие действия.



 де санте
де санте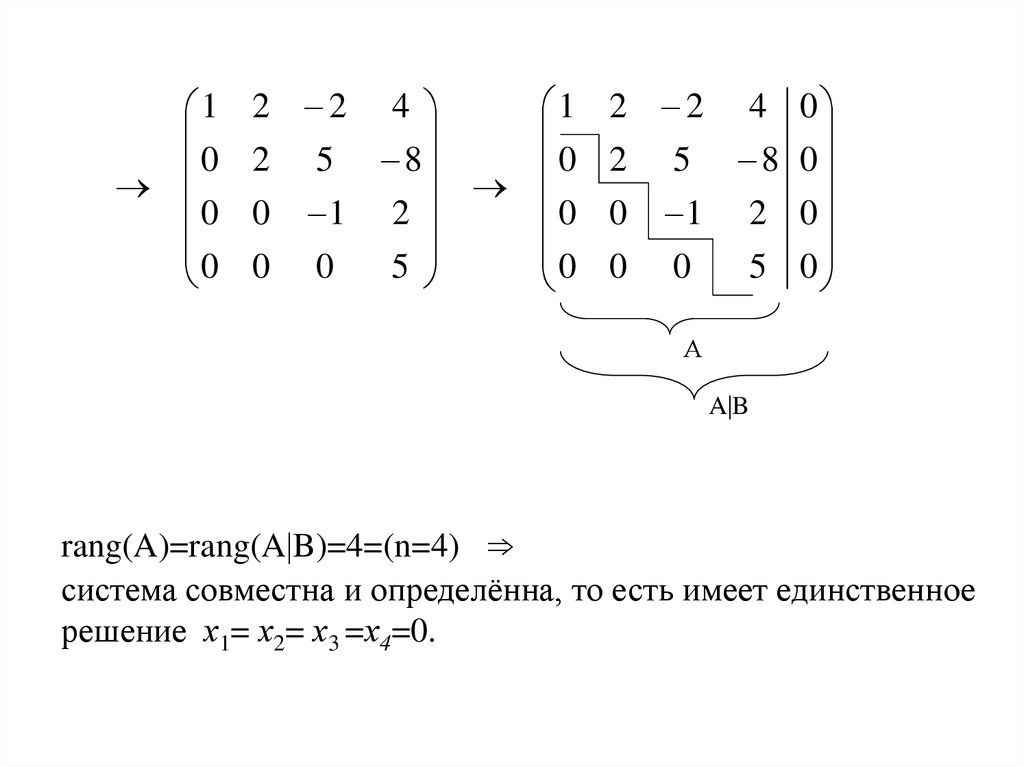 де ледук. физ. спорт.
де ледук. физ. спорт.