Базисные решения системы линейных уравнений методом Жордана-Гаусса онлайн
Назначение сервиса. С помощью данного онлайн-калькулятора находятся базисные решения системы линейных уравнений, определяется опорное решение. Полученное решение сохраняется в файле Word.- Шаг №1
- Шаг №2
- Видеоинструкция
Инструкция. Для получения решения необходимо выбрать
количество переменных:
2345678
и количество строк
23456
При решении используется метод прямоугольника, в результате применения которого получается диагональная матрица — квадратная матрица, все элементы которой, стоящие вне главной диагонали, равны нулю.
Система линейных уравнений:
2x1 + x2 – x3 + 3x4 – 2x5 = 2
x1 – x2 + x4 = 0
x1 – x3 + x4 – 2x5
Запишем ее через матрицу.

| 2 | 1 | -1 | 3 | -2 |
| 1 | -1 | 0 | 1 | 0 |
| 1 | 0 | -1 | 1 | -2 |
Решение системы линейных уравнений называется базисным, если свободные переменные (m>n) обращаются в ноль
Пример №1. Найти три базисных решения системы линейных уравнений методом Жордана-Гаусса, указать среди них опорные.
Решение. Запишем систему в виде:
| 2 | 1 | -1 | 3 | -2 | 2 |
| 1 | -1 | 0 | 1 | 0 | 0 |
| 1 | 0 | -1 | 1 | -2 | -1 |

Разрешающий элемент равен (2).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ – (А*В)/РЭ
РЭ – разрешающий элемент (2), А и В – элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.
Представим расчет каждого элемента в виде таблицы:
| x2 | x3 | x4 | x5 | B | |
| 2 / 2 = 1 | 1 / 2 = 0.5 | -1 / 2 = -0.5 | 3 / 2 = 1.5 | -2 / 2 = -1 | 2 / 2 = 1 |
| 1 | 0. 5 5
| -0.5 | 1.5 | -1 | 1 |
| 0 | -1.5 | 0.5 | -0.5 | 1 | -1 |
| 0 | -0.5 | -0.5 | -0.5 | -1 | -2 |
Представим расчет каждого элемента в виде таблицы:
| x1 | x2 | x3 | x4 | x5 | B |
| 0 / -1.5 = 0 | -1.5 / -1.5 = 1 | 0.5 / -1.5 = -0.33 | -0.5 / -1.5 = 0.33 | 1 / -1.5 = -0.67 | -1 / -1.5 = 0.67 |
| 1 | 0 | -0.33 | 1.33 | -0. 67 67
| 0.67 |
| 0 | 1 | -0.33 | 0.33 | -0.67 | 0.67 |
| 0 | 0 | -0.67 | -0.33 | -1.33 | -1.67 |
Разрешающий элемент равен (-0.67). После пересчета получим общее решение системы:
x1 = 1.5 – 1.5x4
x2
x3 = 2.5 – 0.5x4 + 2x5
Необходимо переменные x4,x5 принять в качестве свободных переменных и через них выразить базисные.
Приравняем переменные x4 и x5 к 0. Получим базисное решение системы.
x1 = 1.5, x2 = 1.5, x3 = 2.5
Поскольку среди базисного решения нет отрицательных значений, то полученное решение является опорным.
Для получения частного решения, необходимо задать любые значения x4 и x5.

x1 = 0, x2 = 1, x3 = 4
Пример №2. Используя метод Жордана-Гаусса, привести систему к единичному базису. Найти одно из: а) базисных решений, б) опорных решений системы.
Запишем систему в виде:
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Разрешающий элемент равен (1).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
НЭ = СЭ – (А*В)/РЭ
РЭ – разрешающий элемент (1), А и В – элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.
Представим расчет каждого элемента в виде таблицы:
| x1 | x2 | x3 | B |
| 1 / 1 = 1 | 1 / 1 = 1 | -1 / 1 = -1 | -2 / 1 = -2 |

На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Представим расчет каждого элемента в виде таблицы:
| x1 | x2 | x3 | B |
| 0 / -7 = 0 | -7 / -7 = 1 | 5 / -7 = -0.71 | 9 / -7 = -1.29 |
Разрешающий элемент равен (0.29).
Представим расчет каждого элемента в виде таблицы:
| x1 | x2 | x3 | B |
| 0 / 0.29 = 0 | 0 / 0.29 = 0 | 0.29 / 0.29 = 1 | 3.71 / 0.29 = 13 |
x1 = 3, x2 = 8, x3 = 13
Решение СЛАУ методом Гаусса – онлайн калькулятор, бесплатный сервис
Компания Zaochnik предлагает воспользоваться нашим сервисом для решения уравнений. Это сэкономит ваше время на расчеты, поможет избежать ошибки в преобразованиях и получить точный результат. Многоступенчатые вычисления основаны на математических формулах. Поэтому промежуточные ответы не теряются, а используются в следующих действиях.
Это сэкономит ваше время на расчеты, поможет избежать ошибки в преобразованиях и получить точный результат. Многоступенчатые вычисления основаны на математических формулах. Поэтому промежуточные ответы не теряются, а используются в следующих действиях.
В автоматизации процесса последовательно выполняются необходимые действия. Записывается расширенная матрица системы, происходят элементарные преобразования, в процессе удаляются нулевые строки. После этого матрица имеет ступенчатый вид и подвергается обратному ходу метода Гаусса.
Рассмотрим несколько примеров решений СЛАУ с помощью онлайн-калькулятора
Онлайн-калькулятор позволяет находить решение СЛАУ, когда свободные члены, переменные и коэффициенты при них являются вещественными числами. Максимальное количество неизвестных – 6.
Важно: калькулятор не работает с комплексными числами!
Пример 1.
Возьмем простую систему уравнений с двумя неизвестными:
x1+2×2=113×1-x2=12
Для того, чтобы решить ее методом Гаусса с помощью онлайн-калькулятора:
- Укажем количество неизвестных в системе:
- Впишите коэффициенты при переменных в соответствующие поля:
- Нажмите «Рассчитать»
Калькулятор сам произведет все вычисления, а вы сможете не только получить ответ, но и ознакомиться подробным решением:
Пример 2.
Рассмотрим более сложную систему с большим количеством неизвестных:
2×1+10×2-3×3=38-3×1-24×2+5×3=-86×1+x2-5×3=27
По аналогии с первым примером, укажем количество неизвестных, введем в поля соответствующие коэффициенты, и нажмем «Рассчитать»:
Калькулятор выдаст ответ с ходом решения и промежуточными выкладками:
Заметьте, если вы вдруг введете неверные коэффициенты или запишите такую систему, которая не имеет решения, калькулятор выдаст соответствующее сообщение:
Теоретические статьи из справочника, которые помогут вам лучше разобраться в теме:
- Решение квадратных уравнений: формула корней, примеры
- Уравнение и его корни: определения, примеры
- Теорема Виета, формулы Виета
- Нахождение неизвестного слагаемого, множителя: правила, примеры, решения
- Квадратные неравенства, примеры, решения
- Решение квадратных неравенств методом интервалов
Ответ:
Решение
Ответ:
- list” :key=”`error-${eIdx}`” v-html=”e”/>
Похожие калькуляторы:
- Решение квадратных уравнений
- Решение систем линейных уравнений методом Крамера
- Решение систем линейных уравнений матричным методом
- Решение систем линейных уравнений методом подстановки
- Решение биквадратных уравнений
Калькулятор с решением систем линейных уравнений методом Гаусса
В наш раздел с калькуляторами часто заходят учащиеся школ и университетов при подготовке к занятиям и во время контрольных работ. Также производят вычисления преподаватели для экономии времени при проверке большого количества заданий.
Также производят вычисления преподаватели для экономии времени при проверке большого количества заданий.
Применяйте метод Гаусса в решении систем линейных уравнений онлайн. Для этого следуйте инструкции:
- задайте число неизвестных в системе;
- введите условие в соответствующие поля;
- воспользуйтесь кнопкой «Рассчитать».
После отправки задачи на расчет вы мгновенно получаете ответ. При этом вам видны все действия. Глядя на готовые вычисления легче разбирать используемый математический метод. Для следующего аналогичного примера вы можете применить известный алгоритм и самостоятельно найти ответ к задаче.
Если процесс решения на калькуляторе вам непонятен, обратитесь за индивидуальной помощью. Специалист компании решит ваши задания с подробным введением в тему. Напишите консультанту или оформите заказ.
Понравился калькулятор? Поделись с друзьями!
Решение системы линейных уравнений методом гаусса-жордана
Метод Гаусса-Жордана предназначен для решения систем линейных алгебраических уравнений (СЛАУ). Он является модификацией метода Гаусса . Если метод Гаусса осуществляется в два этапа (прямой ход и обратный) то метод Гаусса-Жордана позволяет решить систему в один этап. Подробности и непосредственная схема применения метода Гаусса-Жордана описаны в примерах.
Он является модификацией метода Гаусса . Если метод Гаусса осуществляется в два этапа (прямой ход и обратный) то метод Гаусса-Жордана позволяет решить систему в один этап. Подробности и непосредственная схема применения метода Гаусса-Жордана описаны в примерах.
Во всех примерах $A$ обозначает матрицу системы, $\widetilde{A}$ – расширенную матрицу системы. О матричной форме записи СЛАУ можно прочесть .
Пример №1
Решить СЛАУ $ \left\{ \begin{aligned} & 4x_1-7x_2+8x_3=-23;\\ & 2x_1-4x_2+5x_3=-13;\\ & -3x_1+11x_2+x_3=16. \end{aligned} \right.$ методом Гаусса-Жордана.
Давайте перейдём от последней полученной нами матрице к системе:
$$ \left\{ \begin{aligned} & 0\cdot x_1+1\cdot x_2+0\cdot x_3=1;\\ & 1\cdot x_1+0\cdot x_2+0\cdot x_3=-2;\\ & 0\cdot x_1+0\cdot x_2+1\cdot x_3=-1. \end{aligned} \right. $$
Упрощая полученную систему, имеем:
$$
\left\{ \begin{aligned}
& x_2=1;\\
& x_1=-2;\\
& x_3=-1.
\end{aligned} \right. $$
$$
Полное решение без пояснений выглядит так:
Хоть этот способ выбора разрешающих элементов вполне допустим, но предпочтительнее выбирать в качестве разрешающих элементов диагональные элементы матрицы системы. Мы рассмотрим этот способ ниже.
Выбор разрешающих элементов на главной диагонали матрицы системы.
Так как этот способ решения полностью аналогичен предыдущему (за исключением выбора разрешающих элементов), то подробные пояснения пропустим. Принцип выбора разрешающих элементов прост: в первом столбце выбираем элемент первой строки, во втором столбце берём элемент второй строки, в третьем столбце – элемент третьей строки и так далее.
Первый шаг
В первом столбце выбираем элемент первой строки, т.е. в качестве разрешающего имеем элемент 4. Понимаю, что выбор числа 2 кажется более предпочтительным, так как это число всё-таки меньше, нежели 4. Для того, чтобы число 2 в первом столбце переместилось на первое место, поменяем местами первую и вторую строки:
$$ \left(\begin{array} {ccc|c} 4 & -7 & 8 & -23\\ 2 & -4& 5 & -13 \\ -3 & 11 & 1 & 16 \end{array} \right)\rightarrow \left(\begin{array} {ccc|c} 2 & -4& 5 & -13\\ 4 & -7 & 8 & -23 \\ -3 & 11 & 1 & 16 \end{array} \right) $$
Итак, разрешающий элемент представлен числом 2. Точно так же, как и ранее, разделим первую строку на 2, а затем обнулим элементы первого столбца:
Точно так же, как и ранее, разделим первую строку на 2, а затем обнулим элементы первого столбца:
$$ \left(\begin{array} {ccc|c} 2 & -4& 5 & -13\\ 4 & -7 & 8 & -23 \\ -3 & 11 & 1 & 16 \end{array} \right) \begin{array} {l} I:2 \\\phantom{0} \\ \phantom{0} \end{array} \rightarrow \left(\begin{array} {ccc|c} 1 & -2& 5/2 & -13/2 \\4 & -7 & 8 & -23\\ -3 & 11 & 1 & 16 \end{array} \right) \begin{array} {l} \phantom{0} \\ II-4\cdot I\\ III+3\cdot I \end{array} \rightarrow \left(\begin{array} {ccc|c} 1 & -2& 5/2 & -13/2\\0 & 1 & -2 & 3\\ 0 & 5 & 17/2 & -7/2 \end{array} \right). $$
Второй шаг
На втором шаге требуется обнулить элементы второго столбца. В качестве разрешающего элемента выбираем элемент второй строки, т.е. 1. Разрешающий элемент уже равен единице, поэтому никаких строк менять местами не будем. Кстати сказать, если бы мы захотели поменять местами строки, то первую строку трогать не стали бы, так как она уже была использована на первом шаге. А вот вторую и третью строки запросто можно менять местами. Однако, повторюсь, в данной ситуации менять местами строки не нужно, ибо разрешающий элемент уже оптимален – он равен единице.
А вот вторую и третью строки запросто можно менять местами. Однако, повторюсь, в данной ситуации менять местами строки не нужно, ибо разрешающий элемент уже оптимален – он равен единице.
$$ \left(\begin{array} {ccc|c} 1 & -2& 5/2 & -13/2\\0 & 1 & -2 & 3\\ 0 & 5 & 17/2 & -7/2 \end{array} \right) \begin{array} {l} I+2\cdot II \\ \phantom{0}\\ III-5\cdot II \end{array} \rightarrow \left(\begin{array} {ccc|c} 1 & 0 & -3/2 & -1/2 \\ 0 & 1 & -2 & 3\\ 0 & 0 & 37/2 & -37/2 \end{array} \right). $$
Второй шаг окончен. Переходим к третьему шагу.
Третий шаг
На третьем шаге требуется обнулить элементы третьего столбца. В качестве разрешающего элемента выбираем элемент третьей строки, т.е. 37/2. Разделим элементы третьей строки на 37/2 (чтобы разрешающий элемент стал равен 1), а затем обнулим соответствующие элементы третьего столбца:
$$
\left(\begin{array} {ccc|c} 1 & 0 & -3/2 & -1/2 \\ 0 & 1 & -2 & 3\\ 0 & 0 & 37/2 & -37/2 \end{array} \right)
\begin{array} {l} \phantom{0}\\ \phantom{0}\\ III:\frac{37}{2} \end{array} \rightarrow
\left(\begin{array} {ccc|c} 1 & 0 & -3/2 & -1/2 \\ 0 & 1 & -2 & 3\\ 0 & 0 & 1 & -1 \end{array} \right)
\begin{array} {l} I+2\cdot III\\II+3/2\cdot III\\ \phantom{0} \end{array} \rightarrow
\left(\begin{array} {ccc|c} 1 & 0 & 0 & -2 \\ 0 & 1 & 0 & 1\\ 0 & 0 & 1 & -1 \end{array} \right). $$
$$
Ответ получен: $x_1=-2$, $x_2=1$, $x_3=-1$. Полное решение без пояснений выглядит так:
Все остальные примеры на этой странице будут решены именно вторым способом: в качестве разрешающих будем выбирать диагональные элементы матрицы системы.
Ответ : $x_1=-2$, $x_2=1$, $x_3=-1$.
Пример №2
Решить СЛАУ $ \left\{ \begin{aligned} & 3x_1+x_2+2x_3+5x_4=-6;\\ & 3x_1+x_2+2x_4=-10;\\ & 6x_1+4x_2+11x_3+11x_4=-27;\\ & -3x_1-2x_2-2x_3-10x_4=1. \end{aligned} \right.$ методом Гаусса-Жордана.
Запишем расширенную матрицу данной системы : $\widetilde{A}=\left(\begin{array} {cccc|c} 3 & 1 & 2 & 5 & -6\\ 3 & 1& 0 & 2 & -10 \\ 6 & 4 & 11 & 11 & -27 \\ -3 & -2 & -2 & -10 & 1 \end{array} \right)$.
В качестве разрешающих элементов станем выбирать диагональные элементы матрицы системы: на первом шаге возьмём элемент первой строки, на втором шаге элемент второй строки и так далее.
Первый шаг
Нам нужно обнулить соответствующие элементы первого столбца. В качестве разрешающего элемента возьмём элемент первой строки, т.е. 3. Соответственно первую строку придётся разделить на 3, чтобы разрешающий элемент стал равен единице. А затем обнулить все элементы первого столбца, кроме разрешающего:
$$
\left(\begin{array}{cccc|c}
3 & 1 & 2 & 5 & -6\\
3 & 1 & 0 & 2 & -10\\
6 & 4 & 11 & 11 & -27\\
-3 & -2 & -2 & -10 & 1\end{array}\right)
\begin{array} {l} I:3\\ \phantom{0}\\\phantom{0}\\\phantom{0}\end{array} \rightarrow
\left(\begin{array}{cccc|c}
1 & 1/3 & 2/3 & 5/3 & -2\\
3 & 1 & 0 & 2 & -10\\
6 & 4 & 11 & 11 & -27\\
-3 & -2 & -2 & -10 & 1\end{array}\right)
\begin{array} {l} \phantom{0}\\ II-3\cdot I\\III-6\cdot I\\IV+3\cdot I\end{array} \rightarrow\\
\rightarrow\left(\begin{array}{cccc|c}
1 & 1/3 & 2/3 & 5/3 & -2\\
0 & 0 & -2 & -3 & -4\\
0 & 2 & 7 & 1 & -15\\
0 & -1 & 0 & -5 & -5\end{array}\right).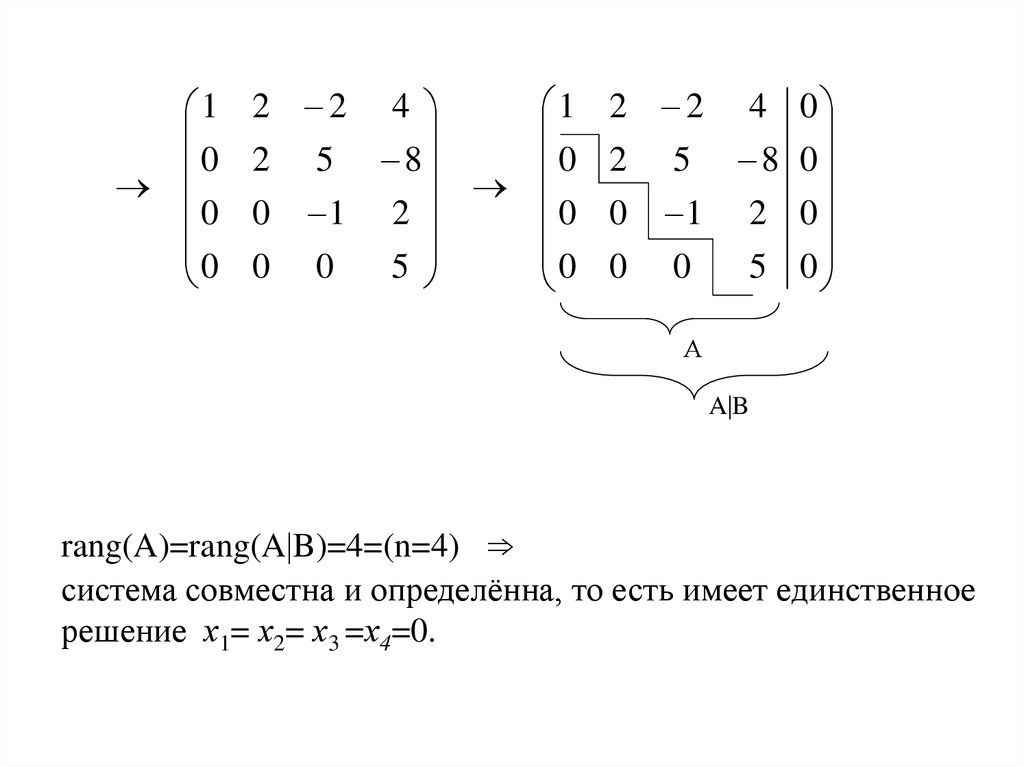 $$
$$
Второй шаг
Переходим к обнулению соответствующих элементов второго столбца. В качестве разрешающего элемента мы уславливались взять элемент второй строки, но сделать этого мы не в силах, так как нужный элемент равен нулю. Вывод: будем менять местами строки. Первую строку трогать нельзя, так как она уже использовалась на первом шаге. Выбор небогат: или меняем местами вторую и третью строки, или же меняем местами четвёртую и вторую. Так как в четвёртой строке наличествует (-1), то пусть в “обмене” поучавствует именно четвёртая строка. Итак, меняем местами вторую и четвёртую строки:
$$ \left(\begin{array}{cccc|c} 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & 0 & -2 & -3 & -4\\ 0 & 2 & 7 & 1 & -15\\ 0 & -1 & 0 & -5 & -5\end{array}\right)\rightarrow \left(\begin{array}{cccc|c} 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & -1 & 0 & -5 & -5\\ 0 & 2 & 7 & 1 & -15\\ 0 & 0 & -2 & -3 & -4\end{array}\right) $$
Вот теперь всё в норме: разрешающий элемент равен (-1). Бывает, кстати, что смена мест строк невозможна, но это обговорим в следующем примере №3. А пока что делим вторую строку на (-1), а затем обнуляем элементы второго столбца. Обратите внимание, что во втором столбце элемент, расположенный в четвёртой строке, уже равен нулю, поэтому четвёртую строку трогать не будем.
Бывает, кстати, что смена мест строк невозможна, но это обговорим в следующем примере №3. А пока что делим вторую строку на (-1), а затем обнуляем элементы второго столбца. Обратите внимание, что во втором столбце элемент, расположенный в четвёртой строке, уже равен нулю, поэтому четвёртую строку трогать не будем.
$$
\left(\begin{array}{cccc|c}
1 & 1/3 & 2/3 & 5/3 & -2\\
0 & -1 & 0 & -5 & -5\\
0 & 2 & 7 & 1 & -15\\
0 & 0 & -2 & -3 & -4\end{array}\right)
\begin{array} {l} \phantom{0}\\II:(-1) \\\phantom{0}\\\phantom{0}\end{array} \rightarrow
\left(\begin{array}{cccc|c}
1 & 1/3 & 2/3 & 5/3 & -2\\
0 & 1 & 0 & 5 & 5\\
0 & 2 & 7 & 1 & -15\\
0 & 0 & -2 & -3 & -4\end{array}\right)
\begin{array} {l} I-1/3\cdot II\\ \phantom{0} \\III-2\cdot II\\\phantom{0}\end{array} \rightarrow\\
\rightarrow\left(\begin{array}{cccc|c}
1 & 0 & 2/3 & 0 & -11/3\\
0 & 1 & 0 & 5 & 5\\
0 & 0 & 7 & -9 & -25\\
0 & 0 & -2 & -3 & -4\end{array}\right). $$
$$
Третий шаг
Приступаем к обработке третьего столбца. В качестве разрешающего элемента мы условились брать диагональные элементы матрицы системы. Для третьего шага это означает выбор элемента, расположенного в третьей строке. Однако если мы просто возьмём элемент 7 в качестве разрешающего, то всю третью строку придётся делить на 7. Мне кажется, что разделить на (-2) попроще. Поэтому поменяем местами третью и четвёртую строки, и тогда разрешающим элементом станет (-2):
$$ \left(\begin{array}{cccc|c} 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 7 & -9 & -25\\ 0 & 0 & -2 & -3 & -4\end{array}\right) \rightarrow \left(\begin{array}{cccc|c} 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & -2 & -3 & -4\\ 0 & 0 & 7 & -9 & -25\end{array}\right) $$
Разрешающий элемент – (-2). Делим третью строку на (-2) и обнуляем соответствующие элементы третьего столбца:
$$
\left(\begin{array}{cccc|c}
1 & 0 & 2/3 & 0 & -11/3\\
0 & 1 & 0 & 5 & 5\\
0 & 0 & -2 & -3 & -4\\
0 & 0 & 7 & -9 & -25\end{array}\right)
\begin{array} {l} \phantom{0}\\ \phantom{0} \\III:(-2)\\\phantom{0}\end{array}\rightarrow
\left(\begin{array}{cccc|c}
1 & 0 & 2/3 & 0 & -11/3\\
0 & 1 & 0 & 5 & 5\\
0 & 0 & 1 & 3/2 & 2\\
0 & 0 & 7 & -9 & -25\end{array}\right)
\begin{array} {l} I-2/3\cdot III\\ \phantom{0} \\ \phantom{0}\\IV-7\cdot III\end{array}\rightarrow\\
\rightarrow\left(\begin{array}{cccc|c}
1 & 0 & 0 & -1 & -5\\
0 & 1 & 0 & 5 & 5\\
0 & 0 & 1 & 3/2 & 2\\
0 & 0 & 0 & -39/2 & -39\end{array}\right). $$
$$
Четвёртый шаг
Переходим к обнулению четвёртого столбца. Разрешающий элемент расположен в четвёртой строке и равен числу $-\frac{39}{2}$.
$$ \left(\begin{array}{cccc|c} 1 & 0 & 0 & -1 & -5\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 0 & -39/2 & -39\end{array}\right) \begin{array} {l} \phantom{0}\\ \phantom{0} \\ \phantom{0}\\IV:\left(-\frac{39}{2}\right) \end{array}\rightarrow \left(\begin{array}{cccc|c} 1 & 0 & 0 & -1 & -5\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 0 & 1 & 2\end{array}\right) \begin{array} {l} I+IV\\ II-5\cdot IV \\ III-3/2\cdot IV \\ \phantom{0} \end{array}\rightarrow\\ \rightarrow\left(\begin{array}{cccc|c} 1 & 0 & 0 & 0 & -3\\ 0 & 1 & 0 & 0 & -5\\ 0 & 0 & 1 & 0 & -1\\ 0 & 0 & 0 & 1 & 2\end{array}\right). $$
Решение окончено. Ответ таков: $x_1=-3$, $x_2=-5$, $x_3=-1$, $x_4=2$. Полное решение без пояснений:
Полное решение без пояснений:
Ответ : $x_1=-3$, $x_2=-5$, $x_3=-1$, $x_4=2$.
Пример №3
Решить СЛАУ $\left\{\begin{aligned} & x_1-2x_2+3x_3+4x_5=-5;\\ & 2x_1+x_2+5x_3+2x_4+9x_5=-3;\\ & 3x_1+4x_2+7x_3+4x_4+14x_5=-1;\\ & 2x_1-4x_2+6x_3+11x_5=2;\\ & -2x_1+14x_2-8x_3+4x_4-7x_5=20;\\ & -4x_1-7x_2-9x_3-6x_4-21x_5=-9. \end{aligned}\right.$ методом Гаусса-Жордана. Если система является неопределённой, указать базисное решение.
Подобные примеры разбираются в теме “Общее и базисное решения СЛАУ” . Во второй части упомянутой темы данный пример решён с помощью метод Гаусса . Мы же решим его с помощью метода Гаусса-Жордана. Пошагово разбивать решение не станем, так как это уже было сделано в предыдущих примерах.
$$
\left(\begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 4 & -5\\
2 & 1 & 5 & 2 & 9 & -3\\
3 & 4 & 7 & 4 & 14 & -1\\
2 & -4 & 6 & 0 & 11 & 2\\
-2 & 14 & -8 & 4 & -7 & 20\\
-4 & -7 & -9 & -6 & -21 & -9 \end{array}\right)
\begin{array} {l} \phantom{0} \\ II-2\cdot I\\ III-3\cdot I\\ IV-2\cdot I\\ V+2\cdot I\\VI+4\cdot I \end{array} \rightarrow
\left(\begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 4 & -5\\
0 & 5 & -1 & 2 & 1 & 7\\
0 & 10 & -2 & 4 & 2 & 14\\
0 & 0 & 0 & 0 & 3 & 12\\
0 & 10 & -2 & 4 & 1 & 10\\
0 & -15 & 3 & -6 & -5 & -29 \end{array}\right)
\begin{array} {l} \phantom{0} \\ II:5 \\ \phantom{0}\\ \phantom{0}\\ \phantom{0} \\ \phantom{0}\end{array} \rightarrow \\
\left(\begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 4 & -5\\
0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\
0 & 10 & -2 & 4 & 2 & 14\\
0 & 0 & 0 & 0 & 3 & 12\\
0 & 10 & -2 & 4 & 1 & 10\\
0 & -15 & 3 & -6 & -5 & -29 \end{array}\right)
\begin{array} {l} I+2\cdot II \\ \phantom{0}\\ III-10\cdot II\\ IV:3\\ V-10\cdot II\\VI+15\cdot II \end{array} \rightarrow
\left(\begin{array}{ccccc|c}
1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\\
0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\
0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 1 & 4\\
0 & 0 & 0 & 0 & -1 & -4\\
0 & 0 & 0 & 0 & -2 & -8 \end{array}\right). $$
$$
Полагаю, что одно из сделанных преобразований всё-таки требует пояснения: $IV:3$. Все элементы четвёртой строки нацело делились на три, поэтому сугубо из соображений упрощения мы разделили все элементы этой строки на три. Третья строка в преобразованной матрице стала нулевой. Вычеркнем нулевую строку:
$$ \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & -1 & -4\\ 0 & 0 & 0 & 0 & -2 & -8 \end{array}\right) $$
Нам пора переходить к третьему шагу, на котором должны быть обнулены элементы третьего столбца. Однако диагональный элемент (третья строка) равен нулю. И смена мест строк ничего не даст. Первую и вторую строки мы уже использовали, поэтому их трогать мы не можем. А четвёртую и пятую строки трогать нет смысла, ибо проблема равенства нулю разрешающего элемента никуда не денется.
В этой ситуации проблема решается крайне незамысловато. Мы не можем обработать третий столбец? Хорошо, перейдём к четвёртому. Может, в четвёртом столбце элемент третьей строки будет не равен нулю. Однако четвёртый столбец “болеет” той же проблемой, что и третий. Элемент третьей строки в четвёртом столбце равен нулю. И смена мест строк опять-таки ничего не даст. Четвёртый столбец тоже не можем обработать? Ладно, перейдём к пятому. А вот в пятом столбце элемент третьей строки очень даже не равен нулю. Он равен единице, что довольно-таки хорошо. Итак, разрешающий элемент в пятом столбце равен 1. Разрешающий элемент выбран, поэтому осуществим дальшейшие преобразования метода Гаусса-Жордана:
$$ \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & -1 & -4\\ 0 & 0 & 0 & 0 & -2 & -8 \end{array}\right) \begin{array} {l} I-22/5\cdot III \\ II-1/5\cdot III \\ \phantom{0}\\ IV+III\\ V+2\cdot III \end{array} \rightarrow \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 0 & -99/5\\ 0 & 1 & -1/5 & 2/5 & 0 & 3/5\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right) \rightarrow \\ \rightarrow\left|\text{Удаляем нулевые строки}\right|\rightarrow \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 0 & -99/5\\ 0 & 1 & -1/5 & 2/5 & 0 & 3/5\\ 0 & 0 & 0 & 0 & 1 & 4 \end{array}\right)$$
Мы привели матрицу системы и расширенную матрицу системы к ступенчатому виду. Ранги обеих матриц равны $r=3$, т.е. надо выбрать 3 базисных переменных. Количество неизвестных $n=5$, поэтому нужно выбрать $n-r=2$ свободных переменных. Так как $r данная система является неопределённой (т.е. имеет бесконечное количество решений). Для нахождения решений системы составим “ступеньки”:
Ранги обеих матриц равны $r=3$, т.е. надо выбрать 3 базисных переменных. Количество неизвестных $n=5$, поэтому нужно выбрать $n-r=2$ свободных переменных. Так как $r данная система является неопределённой (т.е. имеет бесконечное количество решений). Для нахождения решений системы составим “ступеньки”:
На “ступеньках” стоят элементы из столбцов №1, №2, №5. Следовательно, базисными будут переменные $x_1$, $x_2$, $x_5$. Свободными переменными, соответственно, будут $x_3$, $x_4$. Столбцы №3 и №4, соответствующие свободным переменным, перенесём за черту, при этом, конечно, не забыв сменить им знаки.
$$
\left(\begin{array}{ccccc|c}
1 & 0 & 13/5 & 4/5 & 0 & -99/5\\
0 & 1 & -1/5 & 2/5 & 0 & 3/5\\
0 & 0 & 0 & 0 & 1 & 4 \end{array}\right)\rightarrow
\left(\begin{array}{ccc|ccc}
1 & 0 & 0 & -99/5 & -13/5 & -4/5\\
0 & 1 & 0 & 3/5 & 1/5 & -2/5\\
0 & 0 & 1 & 4 & 0 & 0\end{array}\right). $$
$$
Из последней матрицы получим общее решение: $\left\{\begin{aligned} & x_1=-\frac{99}{5}-\frac{13}{5}x_3-\frac{4}{5}x_4;\\ & x_2=\frac{3}{5}+\frac{1}{5}x_3-\frac{2}{5}x_4;\\ & x_3 \in R;\\ & x_4\in R;\\ & x_5=4. \end{aligned}\right.$. Базисное решение найдём, приняв свободные переменные равными нулю, т.е. $x_3=0$, $x_4=0$:
$$ \left\{\begin{aligned} & x_1=-\frac{99}{5};\\ & x_2=\frac{3}{5};\\ & x_3=0;\\ & x_4=0;\\ & x_5=4. \end{aligned}\right. $$
Задача решена, осталось лишь записать ответ.
Ответ : Общее решение: $\left\{\begin{aligned} & x_1=-\frac{99}{5}-\frac{13}{5}x_3-\frac{4}{5}x_4;\\ & x_2=\frac{3}{5}+\frac{1}{5}x_3-\frac{2}{5}x_4;\\ & x_3 \in R;\\ & x_4\in R;\\ & x_5=4. \end{aligned}\right.$, базисное решение: $\left\{\begin{aligned} & x_1=-\frac{99}{5};\\ & x_2=\frac{3}{5};\\ & x_3=0;\\ & x_4=0;\\ & x_5=4. \end{aligned}\right.$.
Здесь вы сможете бесплатно решить систему линейных уравнений методом Гаусса онлайн больших размеров в комплексных числах с очень подробным решением. Наш калькулятор умеет решать онлайн как обычную определенную, так и неопределенную систему линейных уравнений методом Гаусса, которая имеет бесконечное множество решений. В этом случае в ответе вы получите зависимость одних переменных через другие, свободные. Также можно проверить систему уравнений на совместность онлайн, используя решение методом Гаусса.
Наш калькулятор умеет решать онлайн как обычную определенную, так и неопределенную систему линейных уравнений методом Гаусса, которая имеет бесконечное множество решений. В этом случае в ответе вы получите зависимость одних переменных через другие, свободные. Также можно проверить систему уравнений на совместность онлайн, используя решение методом Гаусса.
О методе
При решении системы линейных уравнений онлайн методом Гаусса выполняются следующие шаги.
- Записываем расширенную матрицу.
- Фактически решение разделяют на прямой и обратный ход метода Гаусса. Прямым ходом метода Гаусса называется приведение матрицы к ступенчатому виду. Обратным ходом метода Гаусса называется приведение матрицы к специальному ступенчатому виду. Но на практике удобнее сразу занулять то, что находится и сверху и снизу рассматриваемого элемента. Наш калькулятор использует именно этот подход.
- Важно отметить, что при решении методом Гаусса, наличие в матрице хотя бы одной нулевой строки с НЕнулевой правой частью (столбец свободных членов) говорит о несовместности системы. Решение линейной системы в таком случае не существует.
Чтобы лучше всего понять принцип работы алгоритма Гаусса онлайн введите любой пример, выберите “очень подробное решение” и посмотрите его решение онлайн.
Однажды немецкий математик Вильгельм Йордан (мы неверно транскрибируем с немецкого Jordan как Жордан) сел решать очередную систему уравнений. Он любил этим заниматься и в свободное время совершенствовал свои навыки. Но вот настал момент, когда ему наскучили все методы решения и метод Гаусса в том числе…
Он любил этим заниматься и в свободное время совершенствовал свои навыки. Но вот настал момент, когда ему наскучили все методы решения и метод Гаусса в том числе…
Предположим, дана система с тремя уравнениями, тремя неизвестными и записана её расширенная матрица . В наиболее распространенном случае получаются стандартные ступеньки , и так каждый день…. Одно и то же – как беспросветный ноябрьский дождь.
На некоторое время развевает тоску другой способ приведения матрицы к ступенчатому виду: , причём он совершенно равноценен и может быть неудобен только по причине субъективного восприятия. Но всё рано или поздно приедается…. И подумал тогда Жо рдан – а зачем вообще мучиться с обратным ходом гауссовского алгоритма? Не проще ли сразу получить ответ с помощью дополнительных элементарных преобразований?
…да, такое бывает только по любви =)
Для освоения данного урока «чайникам» придётся пойти путём Жо рдана и прокачать элементарные преобразования хотя бы среднего уровня, прорешав, минимум, 15-20 соответствующих заданий. Поэтому если вы смутно понимаете, о чём идёт разговор и/или у вас возникнет недопонимание чего-либо по ходу занятия, то рекомендую ознакомиться с темой в следующем порядке:
Поэтому если вы смутно понимаете, о чём идёт разговор и/или у вас возникнет недопонимание чего-либо по ходу занятия, то рекомендую ознакомиться с темой в следующем порядке:
Ну, и совсем замечательно, если отработано понижение порядка определителя .
Как все поняли, метод Гаусса-Жордана представляет собой модификацию метода Гаусса и с реализацией основной, уже озвученной выше идеи, мы встретимся на ближайших экранах. Кроме того, в число немногочисленных примеров данной статьи вошло важнейшее приложение – нахождение обратной матрицы с помощью элементарных преобразований .
Не мудрствуя лукаво:
Пример 1
Решить систему методом Гаусса-Жордана
Решение : это первое задание урока Метод Гаусса для чайников , где мы 5 раз трансформировали расширенную матрицу системы и привели её к ступенчатому виду:
Теперь вместо обратного хода в игру вступают дополнительные элементарные преобразования. Сначала нам необходимо получить нули на этих местах: ,
а потом ещё один ноль вот здесь: .
Идеальный с точки зрения простоты случай:
(6) Ко второй строке прибавили третью строку. К первой строке прибавили третью строку.
(7) К первой строке прибавили вторую строку, умноженную на –2.
Не могу удержаться от иллюстрации итоговой системы:
Ответ :
Предостерегаю читателей от шапкозакидательского настроения – это был простейший демонстрационный пример. Для метода Гаусса-Жордана характерны свои специфические приёмы и не самые удобные вычисления, поэтому, пожалуйста, настройтесь на серьёзную работу.
Не хочу показаться категоричным или придирчивым, но в подавляющем большинстве источников информации, которые я видел, типовые задачи рассмотрены крайне плохо – нужно обладать семью пядями во лбу и потратить массу времени/нервов на тяжёлое неуклюжее решение с дробями. За годы практики мне удалось отшлифовать, не скажу, что самую лучшую, но рациональную и достаточно лёгкую методику, которая доступна всем, кто владеет арифметическими действиями:
Пример 2
Решить систему линейных уравнений методом Гаусса-Жордана.
Решение : первая часть задания хорошо знакома:
(1) Ко второй строке прибавили первую строку, умноженную на –1. К третьей строке прибавили первую строку, умноженную на 3. К четвертой строке прибавили первую строку, умноженную на –5.
(2) Вторую строку разделили на 2, третью строку разделили на 11, четвёртую строку разделили на 3.
(3) Вторая и третья строки пропорциональны, 3-ю строку удалили. К четвёртой строке прибавили вторую строку, умноженную на –7
(4) Третью строку разделили на 2.
Очевидно, что система имеет бесконечно много решений, и наша задача – привести её расширенную матрицу к виду .
Как действовать дальше? Прежде всего, следует отметить, что мы лишились вкусного элементарного преобразования – перестановки строк. Точнее говоря, переставить-то их можно, но в этом нет смысла (просто выполним лишние действия). И далее целесообразно придерживаться следующего шаблона:
Находим наименьшее общее кратное чисел третьего столбца (1, –1 и 3), т. е. – наименьшее число, которое бы делилось без остатка и на 1, и на –1 и на 3. В данном случае, это, конечно же, «тройка». Теперь в третьем столбце нам нужно получить одинаковые по модулю числа , и этими соображениями обусловлено 5-е преобразование матрицы:
е. – наименьшее число, которое бы делилось без остатка и на 1, и на –1 и на 3. В данном случае, это, конечно же, «тройка». Теперь в третьем столбце нам нужно получить одинаковые по модулю числа , и этими соображениями обусловлено 5-е преобразование матрицы:
(5) Первую строку умножаем на –3, вторую строку умножаем на 3. Вообще говоря, первую строку можно было умножить тоже на 3, но это было бы менее удобно для следующего действия. К хорошему привыкаешь быстро:
(6) Ко второй строке прибавили третью строку. К первой строке прибавили третью строку.
(7) Во втором столбце два ненулевых значения (24 и 6) и нам снова нужно получить одинаковые по модулю числа . В данном случае всё сложилось довольно удачно – наименьшее кратное 24, и эффективнее всего умножить вторую строку на –4.
(8) К первой строке прибавили вторую.
(9) Заключительный штрих: первую строку разделили на –3, вторую строку разделили на –24 и третью строку разделили на 3. Это действие выполняется В ПОСЛЕДНЮЮ ОЧЕРЕДЬ! Никаких преждевременных дробей!
В результате элементарных преобразований получена эквивалентная исходной система:
Элементарно выражаем базисные переменные через свободную:
и записываем:
Ответ : общее решение:
В подобных примерах применение рассмотренного алгоритма чаще всего оправдано, поскольку обратный ход метода Гаусса обычно требует трудоёмких и неприятных вычислений с дробями.
И, разумеется, крайне желательна проверка, которая выполняется по обычной схеме, рассмотренной на уроке Несовместные системы и системы с общим решением .
Для самостоятельного решения:
Пример 3
Найти базисное решение с помощью элементарных преобразований
Такая формулировка задачи предполагает использование метода Гаусса-Жордана, и в образце решения матрица приводится к стандартному виду с базисными переменными . Однако всегда держите на заметке, что в качестве базисных можно выбрать и другие переменные . Так, например, если в первом столбце громоздкие числа, то вполне допустимо привести матрицу к виду (базисные переменные ), или к виду (базисные переменные ), или даже к виду с базисными переменными . Существуют и другие варианты.
Но всё-таки это крайние случаи – не стОит лишний раз шокировать преподавателей своими знаниями, техникой решения и уж тем более не надо выдавать экзотических жордановсих результатов вроде . Впрочем, бывает трудно удержаться от нетипового базиса, когда в исходной матрице, скажем, в 4-м столбце есть два готовых нуля.
Примечание : термин «базис» имеет алгебраический смысл и понятие геометрического базиса здесь не при чём!
Если в расширенной матрице данных размеров вдруг обнаруживается пара линейно зависимых строк, то её следует попытаться привести к привычному виду с базисными переменными . Образец такого решения есть в Примере №7 статьи об однородных системах линейных уравнений , причём там выбран другой базис .
Продолжаем совершенствовать свои навыки на следующей прикладной задаче:
Как найти обратную матрицу методом Гаусса?Обычно условие формулируют сокращённо, но, по существу, здесь также работает алгоритм Гаусса-Жордана. Более простой метод нахождения обратной матрицы для квадратной матрицы мы давным-давно рассмотрели на соответствующем уроке, и суровой поздней осенью тёртые студенты осваивают мастерский способ решения.
Краткое содержание предстоящих действий таково: сначала следует записать квадратную матрицу в тандеме с единичной матрицей: . Затем с помощью элементарных преобразований необходимо получить единичную матрицу слева, при этом (не вдаваясь в теоретические подробности) справа нарисуется обратная матрица. Схематически решение выглядит следующим образом:
Затем с помощью элементарных преобразований необходимо получить единичную матрицу слева, при этом (не вдаваясь в теоретические подробности) справа нарисуется обратная матрица. Схематически решение выглядит следующим образом:
(Понятно, что обратная матрица должна существовать)
Демо-пример 4
Найдём обратную матрицу для матрицы с помощью элементарных преобразований. Для этого запишем её в одной упряжке с единичной матрицей, и понеслась «двойка скакунов»:
(1) Ко второй строке прибавили первую строку, умноженную на –3.
(2) К первой строке прибавили вторую строку.
(3) Вторую строку разделили на –2.
Ответ :
Сверьтесь с ответом первого примера урока Как найти обратную матрицу?
Но то была очередная заманивающая задачка – в действительности решение гораздо более длительно и кропотливо. Как правило, вам будет предложена матрица «три на три»:
Пример 5
Решение : присоединяем единичную матрицу и начинаем выполнять преобразования, придерживаясь алгоритма «обычного» метода Гаусса :
(1) Первую и третью строки поменяли местами. На первый взгляд, перестановка строк кажется нелегальной, но на самом деле переставлять их можно – ведь по итогу слева нам нужно получить единичную матрицу, а справа же «принудительно» получится именно матрица (вне зависимости от того будем ли мы переставлять строки в ходе решения или нет) . Обратите внимание, что здесь вместо перестановки можно организовать «шестёрки» в 1-м столбце (наименьшее общее кратное (НОК) чисел 3, 2 и 1) . Решение через НОК особенно удобно, когда в первом столбце отсутствуют «единицы».
На первый взгляд, перестановка строк кажется нелегальной, но на самом деле переставлять их можно – ведь по итогу слева нам нужно получить единичную матрицу, а справа же «принудительно» получится именно матрица (вне зависимости от того будем ли мы переставлять строки в ходе решения или нет) . Обратите внимание, что здесь вместо перестановки можно организовать «шестёрки» в 1-м столбце (наименьшее общее кратное (НОК) чисел 3, 2 и 1) . Решение через НОК особенно удобно, когда в первом столбце отсутствуют «единицы».
(2) Ко 2-й и 3-й строкам прибавили 1-ю строку, умноженную на –2 и –3 соответственно.
(3) К 3-й строке прибавили 2-ю строку, умноженную на –1
Вторая часть решения проводится по уже известной из предыдущего параграфа схеме: перестановки строк становятся бессмысленными, и мы находим наименьшее общее кратное чисел третьего столбца (1, –5, 4): 20. Существует строгий алгоритм нахождения НОК, но здесь обычно хватает подбора. Ничего страшного, если взять бОльшее число, которое делится и на 1, и на –5, и на 4, например, число 40. Отличие будет в более громоздких вычислениях.
Отличие будет в более громоздких вычислениях.
К слову о вычислениях. Для решения задачи совсем не зазорно вооружиться микрокалькулятором – числа здесь фигурируют немалые, и будет очень обидно допустить вычислительную ошибку.
(4) Третью строку умножаем на 5, вторую строку на 4, первую строку на «минус двадцать»:
(5) К 1-й и 2-й строкам прибавили третью строку.
(6) Первую и третью строки разделили на 5, вторую строку умножили на –1.
(7) Наименьшее общее кратное ненулевых чисел второго столбца (–20 и 44) равно 220. Первую строку умножаем на 11, вторую строку – на 5.
(8) К первой строке прибавили вторую строку.
(9) Первую строку умножили на –1, вторую строку разделили «обратно» на 5.
(10) Теперь на главной диагонали левой матрицы целесообразно получить наименьшее общее кратное чисел диагонали (44, 44 и 4). Совершенно понятно, что это число 44. Третью строку умножаем на 11.
(11) Каждую строку делим на 44. Данное действие выполняется в последнюю очередь!
Таким образом, обратная матрица:
Внесение и вынесение -й, в принципе, лишние действия, но того требует протокол оформления задачи.
Ответ :
Проверка выполняется по обычной схеме, рассмотренной на уроке об обратной матрице .
Продвинутые люди могут несколько сократить решение, но должен предупредить, спешка тут чревата ПОВЫШЕННЫМ риском допустить ошибку.
Аналогичное задание для самостоятельного решения:
Пример 6
Найти обратную матрицу методом Гаусса-Жордана.
Примерный образец оформления задачи внизу страницы. И ради того, чтобы вы «не проехали мимо с песнями» я оформил решение в уже упомянутом стиле – исключительно через НОК столбцов без единой перестановки строк и дополнительных искусственных преобразований. По моему мнению, эта схема – если и не самая, то одна из самых надёжных .
Иногда бывает удобно более короткое «модернистское» решение, которое заключается в следующем: на первом шаге всё как обычно: .
На втором шаге накатанным приёмом (через НОК чисел 2-го столбца) организуются сразу два нуля во втором столбце: . Перед данным действием особенно трудно устоять, если во 2-м столбце нарисовались одинаковые по модулю числа, например, те же банальные «единицы».
И, наконец, на третьем шаге точно так же получаем нужные нули в третьем столбце: .
Что касается размерности, то в большинстве случаев приходится разруливать матрицу «три на три». Однако время от времени встречается лайт-версия задачи с матрицей «два на два» и хард… – специально для всех читателей сайт:
Пример 7
Найти обратную матрицу с помощью элементарных преобразований
Это задание из моей собственной физматовской контрольной работы по алгебре, …эх, где мой первый курс =) Пятнадцать лет назад (листочек на удивление ещё не пожелтел) , я уложился в 8 шагов, а сейчас – всего лишь в 6! Матрица, кстати, весьма творческая – на первом же шаге просматривается несколько заманчивых путей решения. Моя поздняя версия внизу страницы.
И заключительный совет – после таких примеров очень полезна гимнастика для глаз и какая-нибудь хорошая музыка для релаксации =)
Желаю успехов!
Решения и ответы:
Пример 3: Решение : запишем расширенную матрицу системы и с помощью элементарных преобразований получим базисное решение:
(1) Первую и вторую строки поменяли местами.
(2) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на 5.
(3) Третью строку разделили на 3.
(4) К третьей строке прибавили вторую строку, умноженную на 2.
(5) Третью строку разделили на 7.
(6) Наименьшее кратное чисел 3-го столбца (–3, 5, 1) равно 15. Первую строку умножили на 5, вторую строку умножили на –3, третью строку умножили на 15.
(7) К первой строке прибавили 3-ю строку. Ко второй строке прибавили 3-ю строку.
(8) Первую строку разделили на 5, вторую строку разделили на –3, третью строку разделили на 15.
(9) Наименьшее кратное ненулевых чисел 2-го столбца (–2 и 1) равно: 2. Вторую строку умножили на 2
(10) К первой строке прибавили вторую строку.
(11) Вторую строку разделили на 2.
Выразим базисные переменные через свободные переменные :
Ответ : общее решение:
Пример 6: Решение : обратную матрицу найдём с помощью элементарных преобразований:
(1) Первую строку умножили на –15, вторую строку умножили на 3, третью строку умножили на 5.
(2) Ко 2-й и 3-й строкам прибавили первую строку.
(3) Первую строку разделили на –15, вторую строку разделили на –3, третью строку разделили на –5.
(4) Вторую строку умножили на 7, третью строку умножили на –9.
(5) К третьей строке прибавили вторую строку.
(6) Вторую строку разделили на 7.
(7) Первую строку умножили на 27, вторую строку умножили на 6, третью строку умножили на –4.
(8) К первой и второй строкам прибавили третью строку.
(9) Третью строку разделили на –4. К первой строке прибавили вторую строку, умноженную на –1.
(10) Вторую строку разделили на 2.
(11) Каждую строку разделили на 27.
В результате:
Ответ :
Пример 7: Решение : найдём обратную матрицу методом Гаусса-Жордана:
(1) К 1-й и 4-й строкам прибавили 3-ю строку.
(2) Первую и четвёртую строки поменяли местами.
(3) Ко 2-й строке прибавили 1-ю строку. К 3-й строке прибавили 1-ю строку, умноженную на 2:
(4) К 3-й строке прибавили 2-ю строку, умноженную на –2. К 4-й строке прибавили 2-ю строку.
(5) К 1-й и 3-й строкам прибавили 4-ю строку, умноженную на –1.
(6) Вторую строку умножили на –1, третью строку разделили на –2.
Ответ :
В данной статье мы рассмотрим метод Жордана-Гаусса для решения систем линейных уравнений, отличие метода Гаусса от метода Жордана-Гаусса, алгоритм действий, а также приведем примеры решений СЛАУ.
Yandex.RTB R-A-339285-1
Основные понятия
Определение 1
Метод Жордана-Гаусса – один из методов, предназначенный для решения систем линейных алгебраических уравнений.
Этот метод является модификацией метода Гаусса – в отличие от исходного (метода Гаусса) метод Жордана-Гаусса позволяет решить СЛАУ в один этап (без использования прямого и обратного ходов).
Примечание
Матричная запись СЛАУ: вместо обозначения А в методе Жордана-Гаусса для записи используют обозначение Ã – обозначение расширенной матрицы системы.
Пример 1
4 x 1 – 7 x 2 + 8 x 3 = – 23 2 x 1 – 4 x 2 + 5 x 3 = – 13 – 3 x 1 + 11 x 2 + x 3 = 16
Как решить?
Записываем расширенную матрицу системы:
à = 4 – 7 8 | – 23 2 – 4 5 | – 13 – 3 11 1 | 16
Напоминаем, что слева от черты записывается матрица системы А:
A = 4 – 7 8 2 – 4 5 – 3 11 1
Замечание 1
На каждом шаге решения необходимо выбирать разрешающие элементы матрицы. Процесс выбора может быть различным – в зависимости от того, как выбираются элементы, решения будут отличаться. Можно выбирать в качестве разрешающих элементов диагональные элементы матрицы, а можно выбирать произвольно.
В этой статье мы покажем оба способа решения.
Произвольный способ выбора разрешающих элементов
- Первый этап:
Следует обратиться к 1-му столбцу матрицы Ã – необходимо выбрать ненулевой (разрешающий) элемент.
В 1-ом столбце есть 3 ненулевых элемента: 4, 2, -3. Можно выбрать любой, но, по правилам, выбирается тот, чей модуль ближе всего к единице. В нашем примере таким числом является 2.
Цель: обнулить все элементы, кроме разрешающего, т.е. необходимо обнулить 4 и -3:
4 – 7 8 2 – 4 5 – 3 11 1
Произведем преобразование: необходимо сделать разрешающий элемент равным единице. Для этого делим все элементы 2-ой строки на 2. Такое преобразование имеет обозначение: I I: 2:
4 – 7 8 | – 23 2 – 4 5 | – 13 – 3 11 1 | 16 I I ÷ 2 → 4 – 7 8 | – 23 2 – 4 5 / 2 | – 13 / 2 – 3 11 1 | 16
Теперь обнуляем остальные элементы: 4 и -3:
4 – 7 8 | – 23 2 – 4 5 / 2 | – 13 / 2 – 3 11 1 | 16 I – 4 × I I I I I – (- 3) × I I
Необходимо выполнить преобразования:
I – 4 × I I и I I I – (- 3) × I I = I I I + 3 × I I
Запись I – 4 × I I означает, что от элементов 1-ой строки вычитаются соответствующие элементы 2-ой строки, умноженные на 4.
Запись I I I + 3 × I I означает, что к элементам 3-ей строки прибавляются соответствующие элементы 2-ой строки, умноженные на 3.
I – 4 × I I = 4 – 7 8 – 23 – 4 1 – 2 5 / 2 – 13 / 2 = = 4 – 7 8 – 23 – 4 – 8 10 – 26 = 0 1 – 2 3
Записываются такие изменения следующим образом:
4 – 7 8 | – 23 2 – 4 5 / 2 | – 13 / 2 – 3 11 1 | 16 I – 4 × I I I I I – (- 3) × I I → 0 1 – 2 | 3 1 – 2 5 / 2 | – 13 / 2 0 5 17 / 2 | – 7 / 2
- Второй этап
Необходимо обнулить 2-ой столбец, следовательно, нужно выбрать разрешающий элемент: 1, -2, 5. Однако 2-ую строку матрицы мы использовали в первом этапе, так что элемент -2 не может быть использован.
Поскольку необходимо выбирать число, чей модуль ближе всего к единице, то выбор очевиден – это 1. Обнуляем остальные элементы 2-го столбца:
0 1 – 2 | 3 1 – 2 5 / 2 | – 13 / 2 0 5 17 / 2 | – 7 / 2 I I – (- 2) × I I I I – 5 × I
0 1 – 2 | 3 1 – 2 5 / 2 | – 13 / 2 0 5 17 / 2 | – 7 / 2 I I + 2 × I I I I – 5 × I → 0 1 – 2 | 3 1 0 – 3 / 2 | – 1 / 2 0 0 37 / 2 | – 37 / 2
- Третий этап
Теперь требуется обнулить элементы 3-го столбца. Поскольку первая и вторая строки уже использованы, поэтому остается только один вариант: 37 / 2 . Обнуляем с его помощью элементы третьего столбца:
Поскольку первая и вторая строки уже использованы, поэтому остается только один вариант: 37 / 2 . Обнуляем с его помощью элементы третьего столбца:
0 1 – 2 | 3 1 0 – 3 / 2 | – 1 / 2 0 0 37 / 2 | – 37 / 2
Выполнив преобразования
I – (- 2) × I I I = I + 2 × I I I и I I – (- 3 2) × I I I = I I + 3 2 × I I
получим следующий результат:
0 1 – 2 | 3 1 0 – 3 / 2 | – 1 / 2 0 0 1 | – 1 I + 2 × I I I I I + 3 / 2 × I I I → 0 1 0 | 1 1 0 0 | – 2 0 0 1 | – 1
Ответ : x 1 = – 2 ; x 2 = 1 ; x 3 = – 1 .
Полное решение:
4 – 7 8 | – 23 2 – 4 5 | – 13 – 3 11 1 | 16 I I ÷ 2 → 4 – 7 8 | – 23 2 – 4 5 / 2 | – 13 / 2 – 3 11 1 | 16 I – 4 × I I I I I – (- 3) × I I →
→ 0 1 – 2 | 3 1 – 2 5 / 2 | – 13 / 2 0 5 17 / 2 | – 7 / 2 I I – (- 2) × I I I I – 5 × I → 0 1 – 2 | 3 1 0 – 3 / 2 | – 1 / 2 0 0 37 / 2 | – 37 / 2 I I I ÷ 37 2 →
→ 0 1 – 2 | 3 1 0 – 3 / 2 | – 1 / 2 0 0 1 | – 1 I + 2 × I I I I I + 3 / 2 × I I I → 0 1 0 | 1 1 0 0 | – 2 0 0 1 | – 1 .
Выбор разрешающих элементов на главной диагонали матрицы системы
Определение 2
Принцип выбора разрешающих элементов строится на простом отборе соответствующих элементов: в 1-ом столбце выбирается элемент 1-го столбца, во 2-ом – второй, в 3-ем – третий и т.д.
- Первый этап
В первом столбце необходимо выбрать элемент первой строки, т.е. 4. Но поскольку в первом столбце есть число 2, чей модуль ближе к единице, чем 4, то можно поменять местами первую и вторую строку:
4 – 7 8 | – 23 2 – 4 5 | – 13 – 3 11 1 | 16 → 2 – 4 5 | – 13 4 – 7 8 | – 23 – 3 11 1 | 16
Теперь разрешающий элемент – 2. Как показано в первом способе, делим первую строку на 2, а затем обнуляем все элементы:
4 – 7 8 | – 23 2 – 4 5 | – 13 – 3 11 1 | 16 I ÷ 2 → 2 – 4 5 / 2 | – 13 / 2 4 – 7 8 | – 23 – 3 11 1 | 16 I I – 4 × I I I I + 3 × I → 1 – 2 5 / 2 | – 13 / 2 0 1 – 2 | 3 0 5 17 / 2 | – 7 / 2
- Второй этап
На втором этапе требуется обнулить элементы второго столбца. Разрешающий элемент – 1, поэтому никаких изменений производить не требуется:
Разрешающий элемент – 1, поэтому никаких изменений производить не требуется:
0 1 – 2 | 3 1 – 2 5 / 2 | – 13 / 2 0 5 17 / 2 | – 7 / 2 I + 2 × I I I I I – 5 × I I → 0 1 – 2 | 3 1 0 – 3 / 2 | – 1 / 2 0 0 37 / 2 | – 37 / 2
- Третий этап
На третьем этапе необходимо обнулить элементы третьего столбца. Разрешающий элемент – 37/2. Делим все элементы на 37/2 (чтобы сделать равными 1), а затем обнуляем:
0 1 – 2 | 3 1 0 – 3 / 2 | – 1 / 2 0 0 37 / 2 | – 37 / 2 I I I ÷ 37 2 → 1 0 – 3 / 2 | – 1 / 2 0 1 – 2 | 3 0 0 1 | – 1 I + 2 × I I I I I + 3 / 2 × I I I → 1 0 0 | – 2 0 1 0 | 1 0 0 1 | – 1
Ответ: x 1 = – 2 ; x 2 = 1 ; x 3 = – 1 .
4 – 7 8 | – 23 2 – 4 5 | – 13 – 3 11 1 | 16 I ÷ 2 → 2 – 4 5 / 2 | – 13 / 2 4 – 7 8 | – 23 – 3 11 1 | 16 I I – 4 × I I I I + 3 × I → 0 1 – 2 | 3 1 – 2 5 / 2 | – 13 / 2 0 5 17 / 2 | – 7 / 2 I + 2 × I I I I I – 5 × I I →
→ 0 1 – 2 | 3 1 0 – 3 / 2 | – 1 / 2 0 0 37 / 2 | – 37 / 2 I I I ÷ 37 2 → 1 0 – 3 / 2 | – 1 / 2 0 1 – 2 | 3 0 0 1 | – 1 I + 2 × I I I I I + 3 / 2 × I I I → 1 0 0 | – 2 0 1 0 | 1 0 0 1 | – 1
Пример 2
Решить СЛАУ методом Жордана-Гаусса:
3 x 1 + x 2 + 2 x 3 + 5 x 4 = – 6 3 x 1 + x 2 + 2 x 4 = – 10 6 x 1 + 4 x 2 + 11 x 3 + 11 x 4 = – 27 – 3 x 1 – 2 x 2 – 2 x 3 – 10 x 4 = 1
Как решить?
Записать расширенную матрицу данной системы Ã :
3 1 2 5 | – 6 3 1 0 2 | 10 6 4 11 11 | – 27 – 3 – 2 – 2 – 10 | 1
Для решения используем второй способ: выбор разрешающих элементов на главной диагонали системы. На первом этапе выбираем элемент первой строки, на втором – второй строки, на третьем – третьей и т.д.
На первом этапе выбираем элемент первой строки, на втором – второй строки, на третьем – третьей и т.д.
- Первый этап
Необходимо выбрать разрешающий элемент первой строки, т.е. 3. Затем обнуляем все элементы столбца, разделяя на 3 все элементы:
3 1 2 5 | – 6 3 1 0 2 | – 10 6 4 11 11 | – 27 – 3 – 2 – 2 – 10 | 1 I ÷ 3 → 1 1 / 3 2 / 3 5 / 3 | – 2 3 1 0 2 | – 10 6 4 11 11 | – 27 – 3 – 2 – 2 – 10 | 1 I I – 3 × I I I I – 6 × I I V + 3 × I →
→ 1 1 / 3 2 / 3 5 / 3 | – 2 0 0 – 2 – 3 | – 4 0 2 7 1 | – 15 0 – 1 0 – 5 | – 5
- Второй этап
Необходимо обнулить элементы второго столбца. Для этого выделяем разрешающий элемент, но элемент первой строки второго столбца равен нулю, поэтому необходимо менять строки местами.
Поскольку в четвертой строке есть число -1, то меняем местами вторую и четвертую строки:
1 1 / 3 2 / 3 5 / 3 | – 2 0 0 – 2 – 3 | – 4 0 2 7 1 | – 15 0 – 1 0 – 5 | – 5 → 1 1 / 3 2 / 3 5 / 3 | – 2 0 – 1 0 – 5 | – 5 0 2 7 1 | – 15 0 0 – 2 – 3 | – 4
Теперь разрешающий элемент равен -1. Делим элементы второго столбца на -1, а затем обнуляем:
Делим элементы второго столбца на -1, а затем обнуляем:
1 1 / 3 2 / 3 5 / 3 | – 2 0 – 1 0 – 5 | – 5 0 2 7 1 | – 15 0 0 – 2 – 3 | – 4 I I ÷ (- 1) → 1 1 / 3 2 / 3 5 / 3 | – 2 0 1 0 5 | 5 0 2 7 1 | – 15 0 0 – 2 – 3 | – 4 I – 1 / 3 × I I I I I – 2 × I →
→ 1 0 2 / 3 0 | – 11 / 3 0 1 0 5 | 5 0 0 7 – 9 | – 25 0 0 – 2 – 3 | – 4
- Третий этап
На третьем этапе необходимо также обнулить элементы третьего столбца. Для этого находим разрешающий элемент в третьей строке – это 7. Но на 7 делить неудобно, поэтому необходимо менять строки местами, чтобы разрешающий элемент стал -2:
1 0 2 / 3 0 | – 11 / 3 0 1 0 5 | 5 0 0 7 – 9 | – 25 0 0 – 2 – 3 | – 4 → 1 0 2 / 3 0 | – 11 / 3 0 1 0 5 | 5 0 0 – 2 – 3 | – 4 0 0 7 – 9 | – 25
Теперь делим все элементы третьего столбца на -2 и обнуляем все элементы:
1 0 2 / 3 0 | – 11 / 3 0 1 0 5 | 5 0 0 – 2 – 3 | – 4 0 0 7 – 9 | – 25 I I I ÷ (- 2) → 1 0 2 / 3 0 | – 11 / 3 0 1 0 5 | 5 0 0 1 3 / 2 | 2 0 0 0 – 9 | – 25 I – 2 / 3 × I I I I V – 7 × I I I →
1 0 0 – 1 | – 5 0 1 0 5 | 5 0 0 1 3 / 2 | 2 0 0 0 – 39 / 2 | – 39
- Четвертый этап
Обнуляем четвертый столбец. Разрешающий элемент – – 39 2:
Разрешающий элемент – – 39 2:
1 0 0 – 1 | – 5 0 1 0 5 | 5 0 0 1 3 / 2 | 2 0 0 0 – 39 / 2 | – 39 I V ÷ (- 39 2) → 1 0 0 – 1 | – 5 0 1 0 5 | 5 0 0 1 3 / 2 | 2 0 0 0 1 | 2 I + I V I I – 5 × I V I I I – 3 / 2 × I V →
→ 1 0 0 0 | – 3 0 1 0 0 | – 5 0 0 1 0 | – 1 0 0 0 1 | 2 .
Ответ : x 1 = – 3 ; x 2 = – 5 ; x 3 = – 1 ; x 4 = 2
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
4. Метод Жордана – Гаусса.
Схема с выбором главного элемента состоит в том, что требование неравенства нулю диагональных элементов akk, на которые происходит деление в процессе исключения, заменятся более жестким: из всех элементов К-го столба выбрать наибольший по модулю и переставить уравнения так, чтобы этот элемент оказался на месте элемента акк. Выбор главного элемента и связанная с ним перестановка строк необходимы в тех случаях, когда на каком-либо i-ом шаге акк=0 либо же акк очень мало по остальными элементами i- го столбца: при делении на такое «малое» акк будут получаться большие числа с большими абсолютными погрешностями, в результате чего решение может сильно исказиться.
Ниже излагается алгоритм полного исключения неизвестных или метод Жордана – Гаусса. Суть метода состоит в том, что, рассмотрев первое уравнение, в нем неизвестное с коеффициэнтом, отличным от нуля (в дальнейшем разрешающий элемент), и разделив первое уравнение на этот коэффициент, с помощью первого уравнения исключают это неизвестное из всех уравнений, кроме первого. Выбрав во втором уравнении неизвестное с коэффициентом, отличным от нуля, и разделив на него второе уравнение, с помощью второго исключают другие неизвестные из всех уравнений, кроме второго и т.д., т.е. с помощью одного уравнения производят полное исключение одного неизвестного. Процесс продолжается до тех пор, пока не будут использованы все уравнения.
Как известно, системы линейных алгебраических уравнений могут имеет одно решение, множество решений или системы несовместны. При элементарных преобразованиях элементов матрицы системы эти случаи выявляются в следующем:
1. В процессе исключений левая часть I –го уравнения системы обращается в нуль, а правая часть равна некоторому числу, отличному от нуля. т.е. 02+=bc0.
т.е. 02+=bc0.
Это означает, что система не имеет решений, так как I – му уравнению не могут удовлетворять никакие значения неизвестных;
2. Левая и правая части I – го уравнения обращаются в нуль. Это означает, что I – ое уравнение является линейной комбинацией остальных, ему удовлетворяет любое найденное решение системы, поэтому оно может быть отброшено. В системе количество неизвестных больше количества уравнений и, следовательно, такая система имеет множество решений;
3. После того как все уравнения использованы для исключения неизвестных получено решение системы.
Таким образом, конечной целью преобразований Жордана-Гаусса является получение из заданной линейной системы
| a11x1 + a12x2 + … + a1nxn = b1,n+1 |
a21x1 + a22x2 + … + a2nxn = b2,n+1 |
| am1x1 + am2x2 + … + amnxn = bm.n+1 |
Здесь x1, x2, …, xn – неизвестные, которые надо определить. a11, a12, …, amn – коэффициенты системы – и b1, b2, … bm – свободные члены – предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.
Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе – неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы (1) – совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все ее уравнения в тождества.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения.
Совместная система вида (1) может иметь одно или более решений.
Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:
c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).
Совместная система вида (1) называется определенной, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределенной. Если уравнений больше, чем неизвестных, она называется переопределённой.
Если уравнений больше, чем неизвестных, она называется переопределённой.
Решим следующую систему уравнений:
Запишем её в виде матрицы 3×4, где последний столбец является свободным членом:
Проведём следующие действия:
· К строке 2 добавим: -4 * Строку 1.
· К строке 3 добавим: -9 * Строку 1.
· К строке 3 добавим: -3 * Строку 2.
· Строку 2 делим на -2
· К строке 1 добавим: -1 * Строку 3.
· К строке 2 добавим: -3/2 * Строку 3.
· К строке 1 добавим: -1 * Строку 2.
В правом столбце получаем решение:
.
В методе Ньютона наблюдается ускорение сходимости процесса приближений. 5. Метод касательных (метод Ньютона)
Метод касательных, связанный с именем И. Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Возьмём производную точку x0 и запишем в ней уравнение касательной к графику функции f(x): y=f(x0)+ f ¢(x) (x-x0) (1. 5) Графики…
5) Графики…
Решения от численных методов расчёта. Для определения корней уравнения не требуется знания теорий групп Абеля, Галуа, Ли и пр. и применения специальной математической терминологии: колец, полей, идеалов, изоморфизмов и т.д. Для решения алгебраического уравнения n – ой степени нужно только умение решать квадратные уравнения и извлекать корни из комплексного числа. Корни могут быть определены с…
Математики тригонометрической подстановки и проверка эффективности разработанной методики преподавания. Этапы работы: 1. Разработка факультативного курса на тему: «Применение тригонометрической подстановки для решения алгебраических задач» с учащимися классов с углубленным изучением математики. 2. Проведение разработанного факультативного курса. 3. Проведение диагностирующей контрольной…
… «проявляется» лишь в процессе преобразований. Очевидность и «завуалированность» новой переменной мы рассмотрим на конкретных примерах во второй главе данной работы. 2. Возможности применения метода замены неизвестного при решении алгебраических уравнений В этой главе выявим возможности применения метода замены неизвестного при решении алгебраических уравнений в стандартных и нестандартных…
2. Возможности применения метода замены неизвестного при решении алгебраических уравнений В этой главе выявим возможности применения метода замены неизвестного при решении алгебраических уравнений в стандартных и нестандартных…
метод Гаусса. Вычисление матрицы методом Гаусса: примеры
Линейная алгебра, которая преподается в вузах на разных специальностях, объединяет немало сложных тем. Одни из них связаны с матрицами, а также с решением систем линейных уравнений методами Гаусса и Гаусса – Жордана. Не всем студентам удается понять эти темы, алгоритмы решения разных задач. Давайте вместе разберемся в матрицах и методах Гаусса и Гаусса – Жордана.
Основные понятия
Под матрицей в линейной алгебре понимается прямоугольный массив элементов (таблица). Ниже представлены наборы элементов, заключенные в круглые скобки. Это и есть матрицы. Из приведенного примера видно, что элементами в прямоугольных массивах являются не только числа. Матрица может состоять из математических функций, алгебраических символов.
Для того чтобы разобраться с некоторыми понятиями, составим матрицу A из элементов aij. Индексы являются не просто буквами: i – это номер строки в таблице, а j – это номер столбца, в области пересечения которых располагается элемент aij. Итак, мы видим, что у нас получилась матрица из таких элементов, как a11, a21, a12, a22 и т. д. Буквой n мы обозначили число столбцов, а буквой m – число строк. Символ m × n обозначает размерность матрицы. Это то понятие, которое определяет число строк и столбцов в прямоугольном массиве элементов.
Необязательно в матрице должно быть несколько столбцов и строк. При размерности 1 × n массив элементов является однострочным, а при размерности m × 1 – одностолбцовым. При равенстве числа строчек и числа столбцов матрицу именуют квадратной. У каждой квадратной матрицы есть определитель (det A). Под этим термином понимается число, которое ставится в соответствие матрице A.
Еще несколько важных понятий, которые нужно запомнить для успешного решения матриц, – это главная и побочная диагонали. Под главной диагональю матрицы понимается та диагональ, которая идет вниз в правый угол таблицы из левого угла сверху. Побочная диагональ идет в правый угол вверх из левого угла снизу.
Под главной диагональю матрицы понимается та диагональ, которая идет вниз в правый угол таблицы из левого угла сверху. Побочная диагональ идет в правый угол вверх из левого угла снизу.
Ступенчатый вид матрицы
Взгляните на картинку, которая представлена ниже. На ней вы увидите матрицу и схему. Разберемся сначала с матрицей. В линейной алгебре матрица подобного вида называется ступенчатой. Ей присуще одно свойство: если aij является в i-й строке первым ненулевым элементом, то все другие элементы из матрицы, стоящие ниже и левее aij, являются нулевыми (т. е. все те элементы, которым можно дать буквенное обозначение akl, где k>i, а l<j).
Теперь рассмотрим схему. Она отражает ступенчатую форму матрицы. В схеме представлено 3 вида клеток. Каждый вид обозначает определенные элементы:
- пустые клетки – нулевые элементы матрицы;
- заштрихованные клетки – произвольные элементы, которые могут быть как нулевыми, так и ненулевыми;
- черные квадратики – ненулевые элементы, которые называются угловыми элементами, «ступеньками» (в представленной рядом матрице такими элементами являются цифры –1, 5, 3, 8).

При решении матриц иногда получается такой результат, когда «длина» ступеньки оказывается больше 1. Такое допускается. Важна лишь «высота» ступенек. В матрице ступенчатого вида этот параметр должен быть всегда равным единице.
Приведение матрицы к ступенчатой форме
Любая прямоугольная матрица может быть преобразована до ступенчатого вида. Делается это благодаря элементарным преобразованиям. Они включают в себя:
- перестановку строк местами;
- прибавление к одной строке другой строки, при необходимости умноженной на какое-либо число (можно также производить операцию вычитания).
Рассмотрим элементарные преобразования в решении конкретной задачи. На рисунке ниже представлена матрица A, которую требуется привести к ступенчатому виду.
Для того чтобы решить задачу, будем следовать алгоритму:
- Удобно выполнять преобразования над такой матрицей, у которой первый элемент в верхнем углу с левой стороны (т. е. «ведущий» элемент) равен 1 или –1.
 В нашем случае первый элемент в верхней строке равен 2, поэтому поменяем первую и вторую строчки местами.
В нашем случае первый элемент в верхней строке равен 2, поэтому поменяем первую и вторую строчки местами. - Выполним операции вычитания, затронув строки № 2, 3 и 4. Мы должны получить в первом столбце под «ведущим» элементом нули. Для достижения такого результата: из элементов строчки № 2 последовательно вычтем элементы строчки № 1, умноженные на 2; из элементов строчки № 3 последовательно вычтем элементы строчки № 1, умноженные на 4; из элементов строчки № 4 последовательно вычтем элементы строчки № 1.
- Далее будем работать с укороченной матрицей (без столбца № 1 и без строки № 1). Новый «ведущий» элемент, стоящий на пересечении второго столбца и второй строки, равен –1. Переставлять строки не требуется, поэтому переписываем без изменений первый столбец и первую и вторую строки. Выполним операции вычитания, чтобы во втором столбце под «ведущим» элементом получить нули: из элементов третьей строчки последовательно вычтем элементы второй строчки, умноженные на 3; из элементов четвертой строчки последовательно вычтем элементы второй строчки, умноженные на 2.

- Осталось изменить последнюю строку. Из ее элементов вычтем последовательно элементы третьей строки. Таким образом мы получили ступенчатую матрицу.
Приведение матриц к ступенчатой форме используется в решении систем линейных уравнений (СЛУ) методом Гаусса. Перед рассмотрением этого метода давайте разберемся в терминах, имеющих отношение к СЛУ.
Матрицы и системы линейных уравнений
Матрицы применяются в разных науках. С использованием таблиц из чисел можно, например, решать линейные уравнения, объединенные в систему, методом Гаусса. Для начала давайте познакомимся с несколькими терминами и их определениями, а также посмотрим, как из системы, объединяющей несколько линейных уравнений, составляется матрица.
СЛУ – несколько объединенных алгебраических уравнений, в которых присутствуют неизвестные в первой степени и отсутствуют члены, представляющие собой произведение неизвестных.
Решение СЛУ – найденные значения неизвестных, при подстановке которых уравнения в системе становятся тождествами.
Совместная СЛУ – такая система уравнений, у которой есть хотя бы одно решение.
Несовместная СЛУ – система уравнений, которая не имеет решений.
Как же составляется матрица на основе системы, объединяющей линейные уравнения? Существуют такие понятия, как основная и расширенная матрицы системы. Для того чтобы получить основную матрицу системы, необходимо вынести в таблицу все коэффициенты при неизвестных. Расширенная матрица получается путем присоединения к основной матрице столбца свободных членов (в него входят известные элементы, к которым в системе приравнивается каждое уравнение). Понять весь этот процесс можно, изучив картинку ниже.
Первое, что мы видим на картинке, – это систему, включающую в себя линейные уравнения. Ее элементы: aij – числовые коэффициенты, xj – неизвестные величины, bi – свободные члены (где i = 1, 2, …, m, а j = 1, 2, …, n). Второй элемент на картинке – основная матрица из коэффициентов. Из каждого уравнения коэффициенты записываются в строку. В итоге получается в матрице столько строк, сколько уравнений входит в систему. Количество столбцов равно наибольшему количеству коэффициентов в каком-либо уравнении. Третий элемент на картинке – расширенная матрица со столбцом свободных членов.
В итоге получается в матрице столько строк, сколько уравнений входит в систему. Количество столбцов равно наибольшему количеству коэффициентов в каком-либо уравнении. Третий элемент на картинке – расширенная матрица со столбцом свободных членов.
Общая информация о методе Гаусса
В линейной алгебре методом Гаусса называется классический способ решения СЛУ. Он носит имя Карла Фридриха Гаусса, жившего в XVIII–XIX вв. Это один из величайших математиков всех времен. Суть метода Гаусса заключается в выполнении элементарных преобразований над системой линейных алгебраических уравнений. С помощью преобразований СЛУ приводится к равносильной системе треугольной (ступенчатой) формы, из которой можно найти все переменные.
Стоит отметить, что Карл Фридрих Гаусс не является первооткрывателем классического способа решения системы линейных уравнений. Метод был придуман намного раньше. Первое его описание встречается в энциклопедии знаний древнекитайских математиков, носящей название «Математика в 9 книгах».
Пример решения СЛУ методом Гаусса
Рассмотрим на конкретном примере решение систем методом Гаусса. Будем работать с СЛУ, представленной на картинке.
Алгоритм решения:
- Прямым ходом метода Гаусса приведем систему к ступенчатой форме, но для начала составим расширенную матрицу из числовых коэффициентов и свободных членов.
- Чтобы решить матрицу методом Гаусса (т. е. привести ее к ступенчатому виду), из элементов второй и третьей строчек последовательно вычтем элементы первой строчки. Получим в первом столбе под «ведущим» элементом нули. Далее поменяем вторую и третью строчки местами для удобства. К элементам последней строки прибавим последовательно элементы второй строчки, умноженные на 3.
- В результате вычисления матрицы методом Гаусса мы получили ступенчатый массив элементов. На его основе составим новую систему линейных уравнений. Обратным ходом метода Гаусса находим значения неизвестных членов. Из последнего линейного уравнения видно, что x3 равен 1.
 Подставляем это значение во вторую строчку системы. Получится уравнение x2 – 4 = –4. Отсюда следует, что x2 равен 0. Подставляем x2 и x3 в первое уравнение системы: x1 + 0 +3 = 2. Неизвестный член равен –1.
Подставляем это значение во вторую строчку системы. Получится уравнение x2 – 4 = –4. Отсюда следует, что x2 равен 0. Подставляем x2 и x3 в первое уравнение системы: x1 + 0 +3 = 2. Неизвестный член равен –1.
Ответ: используя матрицу, метод Гаусса, мы нашли значения неизвестных; x1 = –1, x2 = 0, x3 = 1.
Метод Гаусса – Жордана
В линейной алгебре есть еще такое понятие, как метод Гаусса – Жордана. Он считается модификацией метода Гаусса и применяется при нахождении обратной матрицы, вычислении неизвестных членов квадратных систем алгебраических линейных уравнений. Метод Гаусса – Жордана удобен тем, что он в один этап позволяет решить СЛУ (без применения прямого и обратного ходов).
Начнем с термина «обратная матрица». Допустим, у нас есть матрица A. Обратной для нее будет матрица A-1, при этом обязательно выполняется условие: A × A-1 = A-1 × A = E, т. е. произведение этих матриц равно единичной матрице (у единичной матрицы элементы главной диагонали являются единицами, а остальные элементы равны нулю).
е. произведение этих матриц равно единичной матрице (у единичной матрицы элементы главной диагонали являются единицами, а остальные элементы равны нулю).
Важный нюанс: в линейной алгебре есть теорема существования обратной матрицы. Достаточное и необходимое условие существования матрицы A-1 – невырожденность матрицы A. При невырожденности det A (определитель) не равен нулю.
Основные шаги, на которых основывается метод Гаусса – Жордана:
- Взгляните на первую строку конкретной матрицы. Метод Гаусса – Жордана можно начинать применять, если первое значение не равно нулю. Если же на первом месте стоит 0, то поменяйте строки местами так, чтобы первый элемент имел отличное от нуля значение (желательно, чтобы число было ближе к единице).
- Разделите все элементы первой строки на первое число. У вас получится строка, которая начинается с единицы.
- Из второй строки вычтите первую строку, умноженную на первый элемент второй строки, т. е. в итоге у вас получится строка, которая начинается с нуля.
 Аналогичные действия выполните с остальными строчками. Для того чтобы по диагонали получались единицы, делите каждую строку на ее первый ненулевой элемент.
Аналогичные действия выполните с остальными строчками. Для того чтобы по диагонали получались единицы, делите каждую строку на ее первый ненулевой элемент. - В итоге вы получите верхнюю треугольную матрицу методом Гаусса – Жордана. В ней главная диагональ представлена единицами. Нижний угол заполнен нулями, а верхний угол – разнообразными значениями.
- Из предпоследней строки вычтите последнюю строчку, умноженную на необходимый коэффициент. У вас должна получиться строка с нулями и единицей. Для остальных строк повторите аналогичное действие. После всех преобразований получится единичная матрица.
Пример нахождения обратной матрицы методом Гаусса – Жордана
Для вычисления обратной матрицы нужно записать расширенную матрицу A|E и выполнить необходимые преобразования. Рассмотрим простой пример. На рисунке ниже представлена матрица A.
Решение:
- Для начала найдем определитель матрицы методом Гаусса (det A). Если этот параметр не окажется равным нулю, то матрица будет считаться невырожденной.
 Это позволит нам сделать вывод о том, что у A точно есть A-1. Для вычисления определителя преобразуем матрицу до ступенчатой формы элементарными преобразованиями. Подсчитаем число K, равное числу перестановок строк. Строки мы меняли местами всего 1 раз. Вычислим определитель. Его значение будет равно произведению элементов главной диагонали, умноженному на (–1)K. Результат вычисления: det A = 2.
Это позволит нам сделать вывод о том, что у A точно есть A-1. Для вычисления определителя преобразуем матрицу до ступенчатой формы элементарными преобразованиями. Подсчитаем число K, равное числу перестановок строк. Строки мы меняли местами всего 1 раз. Вычислим определитель. Его значение будет равно произведению элементов главной диагонали, умноженному на (–1)K. Результат вычисления: det A = 2. - Составим расширенную матрицу, добавив к исходной матрице единичную матрицу. Полученный массив элементов будем использовать для нахождения обратной матрицы методом Гаусса – Жордана.
- Первый элемент в первой строке равен единице. Нас это устраивает, т. к. не нужно переставлять строки и делить данную строку на какое-нибудь число. Начинаем работать со второй и третьей строками. Чтобы первый элемент во второй строке превратился в 0, отнимем от второй строки первую строчку, умноженную на 3. Из третьей строчки вычтем первую (умножения не требуется).
- В получившейся матрице второй элемент второй строчки равен –4, а второй элемент третьей строчки равен –1.
 Поменяем строки местами для удобства. Из третьей строчки вычтем вторую строчку, умноженную на 4. Вторую строчку разделим на –1, а третью – на 2. Получим верхнюю треугольную матрицу.
Поменяем строки местами для удобства. Из третьей строчки вычтем вторую строчку, умноженную на 4. Вторую строчку разделим на –1, а третью – на 2. Получим верхнюю треугольную матрицу. - Из второй строчки отнимем последнюю строчку, умноженную на 4, из первой строчки – последнюю строчку, умноженную на 5. Далее вычтем из первой строчки вторую строчку, умноженную на 2. С левой стороны мы получили единичную матрицу. Справа находится обратная матрица.
Пример решения СЛУ методом Гаусса – Жордана
На рисунке представлена система линейных уравнений. Требуется найти значения неизвестных переменных, используя матрицу, метод Гаусса – Жордана.
Решение:
- Составим расширенную матрицу. Для этого вынесем в таблицу коэффициенты и свободные члены.
- Решим матрицу методом Гаусса – Жордана. Из строки № 2 вычтем строку № 1. Из строки № 3 вычтем строку № 1, предварительно умноженную на 2.
- Поменяем местами строки № 2 и 3.
- От строки № 3 отнимем строку № 2, умноженную на 2.
 Разделим полученную третью строку на –1.
Разделим полученную третью строку на –1. - От строки № 2 отнимем строку № 3.
- От строки № 1 отнимем строку № 2, умноженную на –1. Сбоку у нас получился столбик, состоящий из цифр 0, 1 и –1. Из этого делаем вывод, что x1 = 0, x2 = 1 и x3 = –1.
При желании можно проверить правильность решения, подставив вычисленные значения в уравнения:
- 0 – 1 = –1, первое тождество из системы является верным;
- 0 + 1 + (–1) = 0, второе тождество из системы является верным;
- 0 – 1 + (–1) = –2, третье тождество из системы является верным.
Вывод: используя метод Гаусса – Жордана, мы нашли правильное решение квадратной системы, объединяющей линейные алгебраические уравнения.
Онлайн-калькуляторы
Жизнь современной молодежи, обучающейся в вузах и изучающей линейную алгебру, значительно упростилась. Еще несколько лет назад находить решения систем методом Гаусса и Гаусса – Жордана приходилось самостоятельно. Одни студенты успешно справлялись с задачами, а другие путались в решении, делали ошибки, просили у однокурсников помощи. Сегодня можно при выполнении домашнего задания пользоваться онлайн-калькуляторами. Для решения систем линейных уравнений, поиска обратных матриц написаны программы, которые демонстрируют не только правильные ответы, но и показывают ход решения той или иной задачи.
Одни студенты успешно справлялись с задачами, а другие путались в решении, делали ошибки, просили у однокурсников помощи. Сегодня можно при выполнении домашнего задания пользоваться онлайн-калькуляторами. Для решения систем линейных уравнений, поиска обратных матриц написаны программы, которые демонстрируют не только правильные ответы, но и показывают ход решения той или иной задачи.
В интернете есть немало ресурсов со встроенными онлайн-калькуляторами. Матрицы методом Гаусса, системы уравнений решаются этими программами за несколько секунд. Студентам требуется только указывать необходимые параметры (например, количество уравнений, количество переменных).
| A 1,1 = (-1) 1+1 |
|
∆ 1,1 = (-1 4-5 (-2)) = 6
| A 1,2 = (-1) 1+2 |
|
∆ 1,2 = -(2 4-(-2 (-2))) = -4
| A 1,3 = (-1) 1+3 |
|
∆ 1,3 = (2 5-(-2 (-1))) = 8
| A 2,1 = (-1) 2+1 |
|
∆ 2,1 = -(2 4-5 3) = 7
| A 2,2 = (-1) 2+2 |
|
∆ 2,2 = (-1 4-(-2 3)) = 2
| A 2,3 = (-1) 2+3 |
|
∆ 2,3 = -(-1 5-(-2 2)) = 1
| A 3,1 = (-1) 3+1 |
|
∆ 3,1 = (2 (-2)-(-1 3)) = -1
| A 3,2 = (-1) 3+2 |
|
∆ 3,2 = -(-1 (-2)-2 3) = 4
| A 3,3 = (-1) 3+3 |
|
∆ 3,3 = (-1 (-1)-2 2) = -3
Тогда обратную матрицу можно записать как:
| A -1 = 1 / 10 |
|
| A -1 = |
|
Другой алгоритм нахождения обратной матрицы
Приведем другую схему нахождения обратной матрицы.
- Находим определитель данной квадратной матрицы A .
- Находим алгебраические дополнения ко всем элементам матрицы A .
- Записываем алгебраические дополнения элементов строк в столбцы (транспонирование).
- Делим каждый элемент полученной матрицы на определитель матрицы A .
Как видим, операция транспонирования может применяться как в начале, над исходной матрицей, так и в конце, над полученными алгебраическими дополнениями.
Особый случай : Обратной, по отношению к единичной матрице E , является единичная матрица E .
Похожие на обратные по многим свойствам.
Энциклопедичный YouTube
1 / 5
✪ Как находить обратную матрицу – bezbotvy
✪ Обратная матрица (2 способа нахождения)
✪ Обратная матрица #1
✪ 2015-01-28. Обратная матрица 3×3
✪ 2015-01-27. Обратная матрица 2х2
Субтитры
Свойства обратной матрицы
- det
A
−
1
=
1
det
A
{\displaystyle \det A^{-1}={\frac {1}{\det A}}}
, где
det
{\displaystyle \ \det }
обозначает определитель .
 {-1}b}
. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
{-1}b}
. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
Способы нахождения обратной матрицы
Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов:
Точные (прямые) методы
Метод Гаусса-Жордана
Возьмём две матрицы: саму A и единичную E . Приведём матрицу A к единичной матрице методом Гаусса-Жордана применяя преобразования по строкам (можно также применять преобразования и по столбцам, но не в перемешку). После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A −1 .
При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц Λ i {\displaystyle \Lambda _{i}} (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):
Λ
1
⋅
⋯
⋅
Λ
n
⋅
A
=
Λ
A
=
E
⇒
Λ
=
A
−
1
{\displaystyle \Lambda _{1}\cdot \dots \cdot \Lambda _{n}\cdot A=\Lambda A=E\Rightarrow \Lambda =A^{-1}}
. {-1}={{{\mbox{adj}}(A)} \over {\det(A)}}}
{-1}={{{\mbox{adj}}(A)} \over {\det(A)}}}
где adj (A) {\displaystyle {\mbox{adj}}(A)} – присоединенная матрица ;
Сложность алгоритма зависит от сложности алгоритма расчета определителя O det и равна O(n²)·O det .
Использование LU/LUP-разложения
Матричное уравнение
A
X
=
I
n
{\displaystyle AX=I_{n}}
для обратной матрицы
X
{\displaystyle X}
можно рассматривать как совокупность
n
{\displaystyle n}
систем вида
A
x
=
b
{\displaystyle Ax=b}
. Обозначим
i
{\displaystyle i}
-ый столбец матрицы
X
{\displaystyle X}
через
X
i
{\displaystyle X_{i}}
; тогда
A
X
i
=
e
i
{\displaystyle AX_{i}=e_{i}}
,
i
=
1
,
…
,
n
{\displaystyle i=1,\ldots ,n}
,поскольку
i
{\displaystyle i}
-м столбцом матрицы
I
n
{\displaystyle I_{n}}
является единичный вектор
e
i
{\displaystyle e_{i}}
. другими словами, нахождение обратной матрицы сводится к решению n уравнений с одной матрицей и разными правыми частями. После выполнения LUP-разложения (время O(n³)) на решение каждого из n уравнений нужно время O(n²), так что и эта часть работы требует времени O(n³) . {-1}={\frac {1}{\det(\mathbf {A})}}{\begin{bmatrix}\,\,\,d&\!\!-b\\-c&\,a\\\end{bmatrix}}={\frac {1}{ad-bc}}{\begin{bmatrix}\,\,\,d&\!\!-b\\-c&\,a\\\end{bmatrix}}.}
{-1}={\frac {1}{\det(\mathbf {A})}}{\begin{bmatrix}\,\,\,d&\!\!-b\\-c&\,a\\\end{bmatrix}}={\frac {1}{ad-bc}}{\begin{bmatrix}\,\,\,d&\!\!-b\\-c&\,a\\\end{bmatrix}}.}
Обращение матрицы 2х2 возможно только при условии, что a d − b c = det A ≠ 0 {\displaystyle ad-bc=\det A\neq 0} .
Для того, чтобы найти обратную матрицу онлайн, вам потребуется указать размер самой матрицы. Для этого кликните на иконки «+» или «-» до тех пор, пока значение количества столбцов и строк вас не устроит. Далее введите в поля требуемые элементы. Ниже находится кнопка «Вычислить» – нажав её, вы получите на экране ответ с подробным решением.
В линейной алгебре довольно часто приходится сталкиваться с процессом вычисления обратной матрицы. Она существует только для невыраженных матриц и для квадратных матриц при условии отличного от нуля детерминанта. В принципе, рассчитать её не представляет особой сложности, особенно если вы имеете дело с небольшой матрицей. Но если нужны более сложные расчёты или тщательная перепроверка своего решения, лучше воспользуйтесь данным онлайн калькулятором. С его помощью вы оперативно и с высокой точностью решите обратную матрицу.
С его помощью вы оперативно и с высокой точностью решите обратную матрицу.
С помощью данного онлайн калькулятора вы сможете значительно облегчить себе задачу в плане расчётов. Кроме того, он помогает закрепить материал, полученный в теории – это своеобразный тренажёр для мозга. Не стоит рассматривать его, как замену вычислениям вручную, он может дать вам гораздо больше, облегчив понимание самого алгоритма. К тому же, лишняя перепроверка себя никогда не помешает.
Матрицы: метод Гаусса. Вычисление матрицы методом Гаусса: примеры — OneKu
Содержание статьи:
- Основные понятия
- Ступенчатый вид матрицы
- Приведение матрицы к ступенчатой форме
- Матрицы и системы линейных уравнений
- Общая информация о методе Гаусса
- Пример решения СЛУ методом Гаусса
- Метод Гаусса – Жордана
- Пример нахождения обратной матрицы методом Гаусса – Жордана
- Пример решения СЛУ методом Гаусса – Жордана
- Онлайн-калькуляторы
Линейная алгебра, которая преподается в вузах на разных специальностях, объединяет немало сложных тем. Одни из них связаны с матрицами, а также с решением систем линейных уравнений методами Гаусса и Гаусса – Жордана. Не всем студентам удается понять эти темы, алгоритмы решения разных задач. Давайте вместе разберемся в матрицах и методах Гаусса и Гаусса – Жордана.
Одни из них связаны с матрицами, а также с решением систем линейных уравнений методами Гаусса и Гаусса – Жордана. Не всем студентам удается понять эти темы, алгоритмы решения разных задач. Давайте вместе разберемся в матрицах и методах Гаусса и Гаусса – Жордана.
Основные понятия
Под матрицей в линейной алгебре понимается прямоугольный массив элементов (таблица). Ниже представлены наборы элементов, заключенные в круглые скобки. Это и есть матрицы. Из приведенного примера видно, что элементами в прямоугольных массивах являются не только числа. Матрица может состоять из математических функций, алгебраических символов.
Вам будет интересно:Закон Максвелла. Распределение Максвелла по скоростям
Для того чтобы разобраться с некоторыми понятиями, составим матрицу A из элементов aij. Индексы являются не просто буквами: i – это номер строки в таблице, а j – это номер столбца, в области пересечения которых располагается элемент aij. Итак, мы видим, что у нас получилась матрица из таких элементов, как a11, a21, a12, a22 и т. д. Буквой n мы обозначили число столбцов, а буквой m – число строк. Символ m × n обозначает размерность матрицы. Это то понятие, которое определяет число строк и столбцов в прямоугольном массиве элементов.
д. Буквой n мы обозначили число столбцов, а буквой m – число строк. Символ m × n обозначает размерность матрицы. Это то понятие, которое определяет число строк и столбцов в прямоугольном массиве элементов.
Необязательно в матрице должно быть несколько столбцов и строк. При размерности 1 × n массив элементов является однострочным, а при размерности m × 1 – одностолбцовым. При равенстве числа строчек и числа столбцов матрицу именуют квадратной. У каждой квадратной матрицы есть определитель (det A). Под этим термином понимается число, которое ставится в соответствие матрице A.
Еще несколько важных понятий, которые нужно запомнить для успешного решения матриц, – это главная и побочная диагонали. Под главной диагональю матрицы понимается та диагональ, которая идет вниз в правый угол таблицы из левого угла сверху. Побочная диагональ идет в правый угол вверх из левого угла снизу.
Ступенчатый вид матрицы
Взгляните на картинку, которая представлена ниже. На ней вы увидите матрицу и схему. Разберемся сначала с матрицей. В линейной алгебре матрица подобного вида называется ступенчатой. Ей присуще одно свойство: если aij является в i-й строке первым ненулевым элементом, то все другие элементы из матрицы, стоящие ниже и левее aij, являются нулевыми (т. е. все те элементы, которым можно дать буквенное обозначение akl, где k>i, а l
Разберемся сначала с матрицей. В линейной алгебре матрица подобного вида называется ступенчатой. Ей присуще одно свойство: если aij является в i-й строке первым ненулевым элементом, то все другие элементы из матрицы, стоящие ниже и левее aij, являются нулевыми (т. е. все те элементы, которым можно дать буквенное обозначение akl, где k>i, а l
Теперь рассмотрим схему. Она отражает ступенчатую форму матрицы. В схеме представлено 3 вида клеток. Каждый вид обозначает определенные элементы:
- пустые клетки – нулевые элементы матрицы;
- заштрихованные клетки – произвольные элементы, которые могут быть как нулевыми, так и ненулевыми;
- черные квадратики – ненулевые элементы, которые называются угловыми элементами, «ступеньками» (в представленной рядом матрице такими элементами являются цифры –1, 5, 3, 8).
При решении матриц иногда получается такой результат, когда «длина» ступеньки оказывается больше 1. Такое допускается. Важна лишь «высота» ступенек. В матрице ступенчатого вида этот параметр должен быть всегда равным единице.
Приведение матрицы к ступенчатой форме
Любая прямоугольная матрица может быть преобразована до ступенчатого вида. Делается это благодаря элементарным преобразованиям. Они включают в себя:
- перестановку строк местами;
- прибавление к одной строке другой строки, при необходимости умноженной на какое-либо число (можно также производить операцию вычитания).
Рассмотрим элементарные преобразования в решении конкретной задачи. На рисунке ниже представлена матрица A, которую требуется привести к ступенчатому виду.
Для того чтобы решить задачу, будем следовать алгоритму:
- Удобно выполнять преобразования над такой матрицей, у которой первый элемент в верхнем углу с левой стороны (т. е. «ведущий» элемент) равен 1 или –1. В нашем случае первый элемент в верхней строке равен 2, поэтому поменяем первую и вторую строчки местами.
- Выполним операции вычитания, затронув строки № 2, 3 и 4. Мы должны получить в первом столбце под «ведущим» элементом нули.
 Для достижения такого результата: из элементов строчки № 2 последовательно вычтем элементы строчки № 1, умноженные на 2; из элементов строчки № 3 последовательно вычтем элементы строчки № 1, умноженные на 4; из элементов строчки № 4 последовательно вычтем элементы строчки № 1.
Для достижения такого результата: из элементов строчки № 2 последовательно вычтем элементы строчки № 1, умноженные на 2; из элементов строчки № 3 последовательно вычтем элементы строчки № 1, умноженные на 4; из элементов строчки № 4 последовательно вычтем элементы строчки № 1. - Далее будем работать с укороченной матрицей (без столбца № 1 и без строки № 1). Новый «ведущий» элемент, стоящий на пересечении второго столбца и второй строки, равен –1. Переставлять строки не требуется, поэтому переписываем без изменений первый столбец и первую и вторую строки. Выполним операции вычитания, чтобы во втором столбце под «ведущим» элементом получить нули: из элементов третьей строчки последовательно вычтем элементы второй строчки, умноженные на 3; из элементов четвертой строчки последовательно вычтем элементы второй строчки, умноженные на 2.
- Осталось изменить последнюю строку. Из ее элементов вычтем последовательно элементы третьей строки. Таким образом мы получили ступенчатую матрицу.

Приведение матриц к ступенчатой форме используется в решении систем линейных уравнений (СЛУ) методом Гаусса. Перед рассмотрением этого метода давайте разберемся в терминах, имеющих отношение к СЛУ.
Матрицы и системы линейных уравнений
Матрицы применяются в разных науках. С использованием таблиц из чисел можно, например, решать линейные уравнения, объединенные в систему, методом Гаусса. Для начала давайте познакомимся с несколькими терминами и их определениями, а также посмотрим, как из системы, объединяющей несколько линейных уравнений, составляется матрица.
СЛУ – несколько объединенных алгебраических уравнений, в которых присутствуют неизвестные в первой степени и отсутствуют члены, представляющие собой произведение неизвестных.
Решение СЛУ – найденные значения неизвестных, при подстановке которых уравнения в системе становятся тождествами.
Совместная СЛУ – такая система уравнений, у которой есть хотя бы одно решение.
Несовместная СЛУ – система уравнений, которая не имеет решений.
Как же составляется матрица на основе системы, объединяющей линейные уравнения? Существуют такие понятия, как основная и расширенная матрицы системы. Для того чтобы получить основную матрицу системы, необходимо вынести в таблицу все коэффициенты при неизвестных. Расширенная матрица получается путем присоединения к основной матрице столбца свободных членов (в него входят известные элементы, к которым в системе приравнивается каждое уравнение). Понять весь этот процесс можно, изучив картинку ниже.
Первое, что мы видим на картинке, – это систему, включающую в себя линейные уравнения. Ее элементы: aij – числовые коэффициенты, xj – неизвестные величины, bi – свободные члены (где i = 1, 2, …, m, а j = 1, 2, …, n). Второй элемент на картинке – основная матрица из коэффициентов. Из каждого уравнения коэффициенты записываются в строку. В итоге получается в матрице столько строк, сколько уравнений входит в систему. Количество столбцов равно наибольшему количеству коэффициентов в каком-либо уравнении. Третий элемент на картинке – расширенная матрица со столбцом свободных членов.
Количество столбцов равно наибольшему количеству коэффициентов в каком-либо уравнении. Третий элемент на картинке – расширенная матрица со столбцом свободных членов.
Общая информация о методе Гаусса
В линейной алгебре методом Гаусса называется классический способ решения СЛУ. Он носит имя Карла Фридриха Гаусса, жившего в XVIII–XIX вв. Это один из величайших математиков всех времен. Суть метода Гаусса заключается в выполнении элементарных преобразований над системой линейных алгебраических уравнений. С помощью преобразований СЛУ приводится к равносильной системе треугольной (ступенчатой) формы, из которой можно найти все переменные.
Стоит отметить, что Карл Фридрих Гаусс не является первооткрывателем классического способа решения системы линейных уравнений. Метод был придуман намного раньше. Первое его описание встречается в энциклопедии знаний древнекитайских математиков, носящей название «Математика в 9 книгах».
Пример решения СЛУ методом Гаусса
Рассмотрим на конкретном примере решение систем методом Гаусса. Будем работать с СЛУ, представленной на картинке.
Будем работать с СЛУ, представленной на картинке.
Алгоритм решения:
 Подставляем x2 и x3 в первое уравнение системы: x1 + 0 +3 = 2. Неизвестный член равен –1.
Подставляем x2 и x3 в первое уравнение системы: x1 + 0 +3 = 2. Неизвестный член равен –1.Ответ: используя матрицу, метод Гаусса, мы нашли значения неизвестных; x1 = –1, x2 = 0, x3 = 1.
Метод Гаусса – Жордана
В линейной алгебре есть еще такое понятие, как метод Гаусса – Жордана. Он считается модификацией метода Гаусса и применяется при нахождении обратной матрицы, вычислении неизвестных членов квадратных систем алгебраических линейных уравнений. Метод Гаусса – Жордана удобен тем, что он в один этап позволяет решить СЛУ (без применения прямого и обратного ходов).
Начнем с термина «обратная матрица». Допустим, у нас есть матрица A. Обратной для нее будет матрица A-1, при этом обязательно выполняется условие: A × A-1 = A-1 × A = E, т. е. произведение этих матриц равно единичной матрице (у единичной матрицы элементы главной диагонали являются единицами, а остальные элементы равны нулю).
Важный нюанс: в линейной алгебре есть теорема существования обратной матрицы. Достаточное и необходимое условие существования матрицы A-1 – невырожденность матрицы A. При невырожденности det A (определитель) не равен нулю.
Достаточное и необходимое условие существования матрицы A-1 – невырожденность матрицы A. При невырожденности det A (определитель) не равен нулю.
Основные шаги, на которых основывается метод Гаусса – Жордана:
 В ней главная диагональ представлена единицами. Нижний угол заполнен нулями, а верхний угол – разнообразными значениями.
В ней главная диагональ представлена единицами. Нижний угол заполнен нулями, а верхний угол – разнообразными значениями.Пример нахождения обратной матрицы методом Гаусса – Жордана
Для вычисления обратной матрицы нужно записать расширенную матрицу A|E и выполнить необходимые преобразования. Рассмотрим простой пример. На рисунке ниже представлена матрица A.
Решение:
 Строки мы меняли местами всего 1 раз. Вычислим определитель. Его значение будет равно произведению элементов главной диагонали, умноженному на (–1)K. Результат вычисления: det A = 2.
Строки мы меняли местами всего 1 раз. Вычислим определитель. Его значение будет равно произведению элементов главной диагонали, умноженному на (–1)K. Результат вычисления: det A = 2. Получим верхнюю треугольную матрицу.
Получим верхнюю треугольную матрицу.Пример решения СЛУ методом Гаусса – Жордана
На рисунке представлена система линейных уравнений. Требуется найти значения неизвестных переменных, используя матрицу, метод Гаусса – Жордана.
Решение:
 Сбоку у нас получился столбик, состоящий из цифр 0, 1 и –1. Из этого делаем вывод, что x1 = 0, x2 = 1 и x3 = –1.
Сбоку у нас получился столбик, состоящий из цифр 0, 1 и –1. Из этого делаем вывод, что x1 = 0, x2 = 1 и x3 = –1.При желании можно проверить правильность решения, подставив вычисленные значения в уравнения:
- 0 – 1 = –1, первое тождество из системы является верным;
- 0 + 1 + (–1) = 0, второе тождество из системы является верным;
- 0 – 1 + (–1) = –2, третье тождество из системы является верным.
Вывод: используя метод Гаусса – Жордана, мы нашли правильное решение квадратной системы, объединяющей линейные алгебраические уравнения.
Онлайн-калькуляторы
Жизнь современной молодежи, обучающейся в вузах и изучающей линейную алгебру, значительно упростилась. Еще несколько лет назад находить решения систем методом Гаусса и Гаусса – Жордана приходилось самостоятельно. Одни студенты успешно справлялись с задачами, а другие путались в решении, делали ошибки, просили у однокурсников помощи. Сегодня можно при выполнении домашнего задания пользоваться онлайн-калькуляторами. Для решения систем линейных уравнений, поиска обратных матриц написаны программы, которые демонстрируют не только правильные ответы, но и показывают ход решения той или иной задачи.
Для решения систем линейных уравнений, поиска обратных матриц написаны программы, которые демонстрируют не только правильные ответы, но и показывают ход решения той или иной задачи.
В интернете есть немало ресурсов со встроенными онлайн-калькуляторами. Матрицы методом Гаусса, системы уравнений решаются этими программами за несколько секунд. Студентам требуется только указывать необходимые параметры (например, количество уравнений, количество переменных).
Источник
Калькулятор исключения Гаусса с шагами
Эта бесплатная матрица калькулятора исключения Гаусса специально разработана, чтобы помочь вам в решении систем уравнений. Да, теперь получить максимально точное решение уравнений можно всего за пару кликов.
Давайте двигаться дальше и понять концепцию этого алгоритма, чтобы найти решение матричных уравнений.
Сосредоточьтесь!
Что такое алгоритм исключения Гаусса?
В свете математического анализа:
«Конкретный метод, который используется для нахождения решения линейных уравнений путем составления расширенной матрицы чисел их коэффициентов, известен как алгоритм Гаусса»
Расширенная матрица:
который состоит из всех констант линейных уравнений».
Общая форма:
$$ A = \begin{bmatrix} a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3 \\\end{bmatrix} \hspace{0.25in} B = \begin{bmatrix}d_1\\d_2\\ d_3\\\end{bmatrix} $$
$$ \text{Расширенная матрица} = \left[\begin{array}{ccc|c}a_1&b_1&c_1&d_1\\a_2&b_2&c_2&d_2\\a_3&b_3&c_3&d_3\\\end{array}\right] $$
Лучший калькулятор расширенных матриц также отображает окончательный ответ в том же формате, что и выше.
Если мы запишем систему линейных уравнений с использованием коэффициентов расширенной матрицы, то получим:
$$ a_{1}x + b_{1}y + c_{1}z = d_{1} $$
$$ a_{2}x + b_{2}y + c_{2}z = d_{2} $$
$$ a_{3}x + b_{3}y + c_{3}z = d_{3} $$
Окончательный ответ, который также определяется бесплатным калькулятором исключения Гаусса, представлен в следующем формате:
$$ \left[\begin{array}{ccc|c}1&0&0&k\\0&1&0&l\\0&0&1&m\\\end{array}\right] $$
Свойства расширенной матрицы:
Расширенная матрица обладает следующие свойства:
Итак, здесь у нас есть следующий формат матрицы, которая окончательно оформлена как нижняя форма матрицы:
- Прямоугольная расширенная матрица
- Переменные в линейных уравнениях и постоянный член определяют количество столбцов.

- Количество систем уравнений равно количеству строк.
- Строки расширенной матрицы можно менять местами.
- Константа может использоваться для умножения или деления элементов определенной строки.
- Конкретную строку матрицы можно добавлять и удалять из других строк.
- Кратность строки матрицы может быть применена к другой строке матрицы.
Как применить алгоритм исключения Гаусса?
Здесь мы собираемся применить эту теорему на примере ниже. Поэтому для лучшего понимания просто оставайтесь сосредоточенными!
Пример № 01:
Найдите решение следующей системы уравнений следующим образом: } = 34 $$
Решение:
Без сомнения, наш широко используемый калькулятор исключения Гаусса с шагами покажет подробные вычисления для упрощения этих уравнений, но нам нужно проанализировать сценарий вручную.
Эквивалентная расширенная матричная форма приведенных выше уравнений выглядит следующим образом:
$$ \begin{bmatrix} 3&6&23 \\ 6&2&34 \\\end{bmatrix} $$
Шаги исключения Гаусса:
Шаг № 01:
Разделить нулевую строку на 3.
$$ \left[\begin{array}{cc|c}1&2& \frac{23}{3} \\6&2&34 \\\end{array}\right] $ $
Шаг #02:
Умножьте первую строку на 6, а затем вычтите ее из нулевой строки.
$$ \left[\begin{array}{cc|c}1&2&\frac{23}{3} \\0&-10&-12 \\\end{array}\right] $$
Шаг # 03:
Перейти к делению первой строки на -10.
$$ \left[\begin{array}{cc|c}1&2&\frac{23}{3} \\0&1&\frac{6}{5}\\\end{array}\right] $$
Шаг № 04:
Приступаем к нахождению произведения нулевой строки и 2. После этого вычитаем результат из первой строки.
$$ \left[\begin{array}{cc|c}1&0&\frac{26333333334}{5000000000}\\0&1& \frac{6}{5}\\\end{array}\right] $$
Как вы видите в левой части матрицы, мы получаем единичную матрицу. Таким образом, ответом в правой части уравнения будут значения переменных в уравнениях.
Итак, окончательные результаты следующие:
$$ b_{1} = 5,266 $$
$$ b_{2} = 1,2 $$
калькулятор ликвидации.
Как работает калькулятор исключения Гаусса?
Познакомьтесь с тем, как этот бесплатный алгоритм уменьшения строки матрицы решения с методом исключения Гаусса упрощает системы уравнений.
Ввод:
- Сначала настройте порядок матрицы из выпадающих списков
- После этого нажмите кнопку «Установить матрицы», чтобы получить нужный формат матрицы
- Теперь получить числа в своих полях
- После того, как вы закончите с материалом, нажмите кнопку расчета
Вывод:
Лучший калькулятор исключения Гаусса Джордана с шагами выполняет следующие вычисления:
- Показывает коэффициенты переменных
- Отображает шаги исключения Гаусса
Часто задаваемые вопросы:
В чем разница между методом исключения Гаусса и методом Гаусса-Жордана?
Между ними существует только одно различие. Там, где исключение Гаусса генерирует редуцированную ступенчатую форму данной матрицы, Гаусс Джордан действительно производит только ступенчатую форму. А наш лучший гаусс-калькулятор позволит вам определить приведенную форму, которая более эффективна, чем получение только ступенчатого формата матрицы.
А наш лучший гаусс-калькулятор позволит вам определить приведенную форму, которая более эффективна, чем получение только ступенчатого формата матрицы.
Почему мы используем метод исключения Гаусса?
Стратегия сокращения строк для решения систем линейных уравнений известна в математике как метод исключения Гаусса. Он состоит из серии операций над связанной матрицей коэффициентов. Этот подход также можно использовать для оценки следующего:
- Ранг предоставленной матрицы.
- Определитель квадратной матрицы
- Обратная обратимая матрица
Что эффективнее Жордан Гаусса или Исключение Гаусса?
Поскольку он пропускает процесс обратной замены, метод Гаусса-Жордана более эффективен, чем методы исключения Гаусса. И именно поэтому наш бесплатный калькулятор метода Джордана Гаусса использует именно этот метод для немедленного отображения результатов.
Для чего в реальной жизни используется метод исключения Гаусса?
Надежное улучшение изображения отпечатков пальцев является важным применением исключения Гаусса. Изображение усилено фильтром Гаусса. В процессорах, подключенных к сетке, метод SGE также может использоваться для решения линейных уравнений. В алгоритмах планирования также используется подход Гаусса.
Изображение усилено фильтром Гаусса. В процессорах, подключенных к сетке, метод SGE также может использоваться для решения линейных уравнений. В алгоритмах планирования также используется подход Гаусса.
Когда используется метод исключения Гаусса?
Метод исключения Гаусса чаще всего используется для решения ряда задач линейной алгебры.
Каковы преимущества метода исключения Гаусса?
- Эта процедура полностью надежна и справедлива.
- Может решать множество линейных уравнений одновременно.
Какие подводные камни метода исключения Гаусса?
Определитель, близкий к нулю Указывает на отсутствие или неограниченное количество решений. Однако определить, насколько близок должен быть определитель к нулю, чтобы указать на плохую обусловленность, проблематично.
Что является ключевым в исключении Гаусса?
Поворот имеет целью превратить элемент выше или ниже ведущей единицы в ноль. «Поворотный элемент» или «поворотный элемент» — это левая часть матричного элемента, для которого компоненты выше и ниже должны быть равны нулю. Ошибки округления уменьшаются за счет поворота.
Ошибки округления уменьшаются за счет поворота.
Что такое точка опоры в матрице?
В ступенчато-строковой форме матрицы опорной точкой является положение ведущей записи. Сводная колонка — это колонка, в которой есть точка опоры.
Заключение:
Матрицы Гаусса Джордана находят широкое применение в различных областях образования и технологий. Из-за такой важности мы разработали эту лучшую матрицу калькулятора исключения Гаусса, чтобы помочь любому, кто анализирует этот конкретный метод, решать уравнения.
Ссылки:
Из источника википедии: Исключение Гаусса, Операции со строками, Эшелонная форма, Вычисление определителей, обращение матрицы, Ранги0003
Из источника обучения люмена: Исключение Гаусса, Расширенная матрица, Система уравнений, Приложения
Курсы в формате PDF, упражнения, документ в формате pdf, ppt, бесплатный PDF PDFprof.com
×
Титр
Корпус
ОШИБКА 404 Файл не найден
- Администрация
- Администрация
- Общественная администрация
- Общественная администрация
- Агролесоводство
- Агролесоводство
- Аллеманд
- Аллеманд
- Бак ST2S
- Андрагогия
- Андрагогия
- Драматическое искусство
- Драматическое искусство
- Художественные визуалы
- Художественные визуалы
- Астрономия
- Астрономия
- Бак
- БАК Математика
- BAC Physique Chimie
- БАК СЭС
- БАК СВТ
- Биохимия
- Биохимия
- Биографии
- Fiche de Cours
- Fiches de Revision
- География и история L
- Исторический антиквариат
- Современная история
- Европейский союз
- Ла Герр Фройд
- La Premiere Guerre Mondiale
- эпоха Возрождения
- Биология
- Биология
- Биология и физиопатология человека
- Бак ST2S
- Биотехнология
- Биотехнология
- Чими
- Чими
- Курсы и упражнения
- IP адрес
- Алгоритм
- Андроид
- годовые
- Bases des données
- Бюротик
- коммерция
- Коммуникация
- Совместимость
- Comptabilité Analytique
- Comptabilité générale
- Концепция и анализ
- курс 3ds max
- Курс Ада
- курс адрес ip
- алгоритм курса
- курс андроид
- курс ассемблера
- Кур Бак-сес
- курс баз де донне
- курс до-диез
- Курс коммерции
- Cours comptabilité
- курс друпал
- затмение
- Курс эконом-класса
- Курс Электрисите
- Курс Электроник
- курс эргономики
- курсы и упражнения 5e
- курсы и упражнения 6eme бесплатно
- курсы и упражнения html css
- курс и упражнения 1ère stmg
- курсы и упражнения 5eme
- Английский курс и упражнения
- Курсы и упражнения Excel 2010 бесплатно
- курсы и упражнения excel pdf
- большая секция курсов и упражнений
- курс превосходит
- Курс финансов
- курс фьюжн
- Курс Гестион
- курс канитель
- курс jquery
- курс labview
- курс языка c
- шепелявит
- Управление курсами
- Курсы маркетинга
- Курс Математики
- курс матлаб
- Кур Оберон
- цель курса c
- курс паскаль
- Курс PDF
- Курс телосложения
- курс pl sql
- кур питон
- курс qtcreator
- курс рубин
- Cours seconde
- Cours sixieme
- курс весна
- курс sql
- Статистика курса
- Курс статистики
- Терминал S
- Тройская улица
- курс unix linux
- курс вба
- курс визуальный базовый
- курс визуальной студии
- Курс Виндев
- курс слово
- Кутюр
- Криптография
- Дайверы
- Эконом
- Экономика pdf
- социальная экономия
- Электричество
- электроника
- эмс
- Этюд функции
- Совместимость экзаменов
- Экзамены по информатике
- маршрут упражнений
- Упражнения коммерции
- Совместимые упражнения
- Упражнения эконом
- упражнения
- Упражнения Финансы
- Упражнения
- Управление упражнениями
- Упражнения Маркетинг
- Упражнения по математике
- Упражнения pdf
- Упражнения телосложения
- Статистика упражнений
- слово упражнения
- Финансы
- Фискалите
- Гастрономия
- геополитика
- Жестион
- гуманитарии
- Информатика pdf
- Комбинация логики
- язык sql
- Усилители
- Les compteurs
- Конденсаторы
- диоды
- Фильтры
- английский язык
- Управление распределением и т.
 д.
д. - Управление человеческими ресурсами
- Управление рисками
- Управление pdf
- Стратегическое управление
- Цифровой маркетинг
- Маркетинговая часть
- Маркетинг pdf
- Маркетинговая стратегия
- Математика
- Математика 1эр S
- Терминал математики S
- микроэкономика
- модель отношений
- оракул
- Расходы по управлению
- телосложение
- Вероятности и статистика
- Программирование
- вопросник ле монд
- наук
- сэс
- сес бак
- Статистика
- Системы эксплуатации
- Тригонометрия
- учебник язык c
- учебник линукс
- учебник excel
- обучающая вспышка
- сервер виндовс 2003
- Курсы и упражнения PDF
- Achats et approvisionnement
- Рекламное действие
- Научная деятельность
- Актуальная экономика
- Администрация информационных систем
- Аэроспасьяль Эт Дефанс
- Агенты экономики
- Сельское хозяйство и лесное хозяйство
- Аллеманд
- Финансовый анализ
- Английский
- Anglais En Seconde Langue
- Анналы Бак эс
- анналес бак л
- анналы бак с
- Антропологические исследования автохтонов
- Антропология
- Apprendre Une Langue
- Ардуино
- Автоматизация
- бак финансы
- задний план
- бакалавриат
- залог рекламный
- Коммерческий баланс
- Биоинформатика
- Биоэтика
- ЧИМИ
- Амбулатория торговли
- Коммуникация и политика
- Коммуникации и реклама
- Comptabilité Et D’Audit
- курс xml
- Cours 2ème Bac
- Кур Араб
- курс назад
- Кур-бак-Л
- Cours bac s
- Кур Бэк ST2DA
- Курс бак STD2S
- Cours bac STI2D
- Cours bac STL
- Cours bac STMG
- Кур Банк
- Кур Шими
- Кур Компани
- курсы css
- Курс Эколь
- Cours École Primaire
- Cours École Secondaire
- Кур Экология
- Курс Энерги
- Изготовление курсов
- курс финансов
- Кур Фискалите
- Кур Геология
- Курс истории
- Кур Инженьери
- Cours L’Informatique
- Кур-ла-Физик
- Курс Логистик
- курс математики
- кур мериз
- Курс Метео
- Курс MPSI
- курс mysql
- трассировщик пакетов
- Курс PCSI
- курс философии
- Курсы физики
- программа курса
- Курс PSI
- Курс ПТ
- Курс ПТСИ
- схема курса
- Курс наук
- курс Tronc Commun
- курс веб-мастера
- Курсансе
- Круассан эконом
- Демография
- Демография и география
- Демография и статистика
- Devoirs Mathématiques
- Диплом по дисциплине
- экономика
- экономика
- экономия
- коммерческая экономия
- ECONOMIE CONCOMMATION ET épargne
- экономия образования
- экономия на строительстве
- экономия удовольствия и удовольствия
- Экономика и политика
- географическая экономия
- промышленная экономика
- экономическая институция
- мировая экономика
- денежная экономика
- сельская экономия
- Écriture de scénario et creation li
- Образование художественное
- Исламское образование
- образование телосложение образование”’
- Коммерческий эффект
- ЭЛЕКТРИЧЕСТВО
- электрический батимент
- электрический CAP
- электрический колледж
- электрический дебютант
- электрисите женераль
- электрическая промышленность
- электрический лицей
- электрическая первичная
- электрическое веселье
- ENA Национальные школы архитектуры
- ENAM Национальная школа сельского хозяйства
- ENCG Национальные школы торговли
- Энергия
- электрическая энергия
- ENSA Национальные школы наук
- Высшие национальные школы ENSAM
- испанский
- Статистика оценки
- этюды аллеманды
- Études allemandes et histoire
- Английские этюды
- арабские исследования
- Азиатские исследования языка и культуры
- Азиатские исследования
- Этюды автохтонов
- Каталанские этюды
- Классические этюды
- Классические и антропологические исследования
- маршевые этюды
- видео этюды игры
- Азиатские этюды
- Феминистские этюды
- Испанские этюды
- Международные исследования
- Итальянские этюды
- Латино-американские этюды
- Средневековые этюды
- Неоэллинские этюды
- Квебекские этюды
- Études religieuses (науки о ре
- экзамены бак с
- Упражнения
- доступ к упражнениям
- Упражнения для спины ES
- Упражнения на спину L
- Упражнения на спину
- Упражнения бак ST2DA
- Упражнения bac STD2S
- Упражнения bac STI2D
- Упражнения bac STL
- Упражнения бак СТМГ
- Упражнения де comptabilité analytiqu
- Exercices de comptabilité financière
- осуществляет финансы
- Упражнения
- Математические упражнения
- Упражнения МП
- Упражнения МПСИ
- Упражнения ПК
- Упражнения ПКСИ
- Философия упражнений
- программа упражнений
- Упражнения пси
- Упражнения ФТ
- Упражнения наук
- Упражнения СФЭ
- Упражнения SUP
- Упражнения ТСИ
- окна упражнений
- Факультет искусств и социальных наук
- Факультет наук
- Коммерческие финансы
- Банковские финансы
- Финансовый дебютант
- Финансы и совместимость
- Финансы количественные
- Финансовый солидер
- Финансирование проекта
- Факультеты медицины и фармакологии FMP
- Фонд коммерции
- французский
- Français langue seconde avancé
- Джин генерал
- география
- Экологическая география
- геополитика и политические науки
- Геостатистический
- Gestion de l’information numérique
- Прием серв.
 де санте
де санте - Партизанский маркетинг
- история
- История экономики
- История искусства
- Историческая география
- Гиперперсонализация
- IAV Institut Agronomique et Vétérin
- Входящий исходящий
- Индустри Химик
- информатика
- Информационная аппликация
- Психообразовательное вмешательство
- Инвестор
- ISEM Institut Supérieur d’Etudes Ma
- ISIC Высший институт информации
- ISPM Institut Supérieur des Pêches
- Высший институт науки ISSS
- Кинезиология и образование. физ.
- Язык и культура allemandes
- Английский язык и культура
- Арабский язык и культура
- Каталанский язык и культура
- Китайский язык и культура
- Язык и культура
- Греческий язык и культура
- Испанский язык и культура
- Японский язык и культура
- Латинский язык и культура
- Язык и культура португалоязычный
- Португальский язык и культура lusuph
- Английские языки и культуры
- Арабские языки и культуры
- Каталанские языки и культуры
- Греческие языки и культуры
- Испанские языки и культуры
- Неоэллинские языки и культуры
- Языки и культуры русские
- Letters et Sciences Humanes
- Письма, языки и культуры
- Littératures de langue française
- Littératures de langue française et
- Littératures et langues modernes
- Logiciels D’Entreprise
- Логистика и транспорт
- Макроэкономика
- Совместное управление
- Культура управления
- Менеджмент d’équipe
- Управление инновациями
- Управление знаниями
- Управление операциями
- Управление изменениями
- Этика управления
- Оперативное управление
- Участие в управлении
- Марж коммерческая
- Маркетинговый агропродовольственный
- Маркетинговая альтернатива
- Маркетинговая аналитика
- Маркетинг B2B
- Маркетинговый банк
- Маркетинговое сотрудничество
- Маркетинговая реклама
- Культура маркетинга
- Контент-маркетинг
- Массовый маркетинг
- Маркетинговые ассоциации
- Маркетинговая этика
- Маркетинговая этника
- Маркетинговые мероприятия
- Маркетинговый опыт
- Маркетинговая сенсорика
- Маркетинг территориальный
- математика
- Математика и информатика
- Математика здесь S
- МЕХАНИКА
- Мет.
 де ледук. физ. спорт.
де ледук. физ. спорт. - Микробиология и иммунология
- Микроменеджмент
- Мобильная коммерция
- Статистика моделирования
- Мультидисциплинарный
- Музыкальное образование
- Нейромаркетинг
- Когнитивная неврология
- Ондес
- ОПТИКА
- Ориентация и консультирование
- колебания
- Техническая логистика
- Рекламный спектакль
- философия
- Философия и классические исследования
- php курсы и упражнения pdf бесплатно
- телосложение
- Телосложение и информатика
- Physique-Chimie
- Коммерческая перспектива
- Психообразование,
- Психология и социология
- Реклама и маркетинг
- Recrutement et Gestion des Carrière
- Этнические отношения
- Промышленные отношения
- Природные ресурсы
- Ресурсы Pédagogiques Et En Class
- Ретаргетинг
- Агрономические науки
- биологические науки
- Когнитивные науки
- Науки о коммуникации
- наук о жизни
- инженерные науки
- Экономика и управление науками
- Науки экономические и социальные
- Науки и технологии Механика
- Математические науки
- Математические науки A
- Математические науки B
- Науки естественные и прикладные
- Религиозные науки
- Sécurité et études policières
- СЭС
- Социология Отношения Этники
- Статистика Зондажа
- Статистическая аппликация
- Статистический дебютант
- исчерпывающая статистика
- Неверная статистика
- Статистическая психология
- Коммерческая стратегия
- Стратегия предприятия
- Уличный маркетинг
- Субвенции, Des Bourses et Des Aid
- СВТ
- Tableau de bord et management de pe
- Электрик
- Промышленная технология
- Технологии
- Коммерческая реклама
- Курс Упражнения
- аргументация
- Бак де Франсэ 2013
- Бодлер
- Камю
- искренний
- диссертация
- дом Хуан
- описание изобретения
- принцесса де Клев
- цветочки зла
- мадам Бовари
- поэзия
- Упражнения на курсе PDF
- диссертация фр
- экспертная совместимость
- Недвижимость
- Информатика
- Ла Финанс
- мастер говядина
- Норм Ванкувер
- норм апа
- изнасилование
- раппорт де этап
- эти докторские
- Курс телосложения
- Курсы и упражнения
- Криминология
- Криминология
- Дизайн интерьера
- Дизайн интерьера
- Первая дидактика
- Первая дидактика
- Право
- Право
- Эконом
- Курсы и упражнения
- экономическая политика
- социальная экономия
- Экономика и поведение
- Бак про
- Образование
- Образование
- Éducation physActivité phys
- Éducation physActivité phys
- образование телосложение
- образование телосложение
- ЭЛЕКТРИЧЕСТВО
- Курсы и упражнения PDF
- электроника
- Алгебр де Буля
- Электромагнетизм
- Les Circuits RLC
- Предприятие
- Предприятие
- Управление
- Экологические исследования
- Экологические исследования
- Семейные исследования
- Семейные исследования
- Финансы
- Финансы
- Лесничество
- Лесничество
- французский
- Бак генерал
- Бак про
- Кур Франсэ
- французский
- Второй французский язык
- Второй французский язык
- Джин гражданский
- Джин гражданский
- Джин Электрик
- Джин Электрик
- Джин механический
- Джин механический
- География
- География
- Геронтология
- Геронтология
- Gestion de l’information
- Gestion de l\’information
- Gestion de l\’information
- Gestion de l’information
- Управление операциями
- Управление операциями
- Прием серв.
 де санте
де санте - Прием серв. де санте
- Gestion intégrée zone cotière
- Gestion intégrée zone cotière
- История
- Антиквариат
- История
- История Европы
- Histoire des États-Unis
- Глобальная история
- Гуманитарные науки
- Писание
- Наука о религиях
- Информациякоммуникация
- Информациякоммуникация
- информатика
- информатика
- инженерия
- Аэрокосмическая техника
- Электротехника
- информатика
- инженерия
- Промышленная техника
- Кинезиология и образование. физ.
- Кинезиология и образование.
 физ.
физ. - Язык по номиналу платит
- Язык по номиналу платит
- лингвистика
- лингвистика
- Литература
- Литература
- Управление
- Бак СТМГ
- Управление
- Управление рисками
- Маркетинг
- Маркетинг
- математический
- Этюд функции
- Математика
- Бак ST2S
- Бак СТИ2Д
- Курсы и упражнения PDF
- Enseignement des mathématiques
- Элементарная математика
- Мир труда
- Этика
- Пример де Plaidoirie
- Финансы и экономика
- Техника прогресса
- Синдикаты
- Музыка
- Музыка
- Питание и семейные исследования
- Питание и семейные исследования
- питаниепитание
- питаниепитание
- ofppt
- курс ppt
- PDF-документы
- Ноты для альт-саксофона
- Бас Ноты
- Барабаны и перкуссия для начинающих
- Пианино для начинающих
- Скрипка для начинающих
- Bien-être
- Ноты для блюза для гитары
- Блюз Ноты
- Ноты для виолончели
- курсы и упражнения Excel
- курсы и упражнения python
- Персонал по развитию
- Этническая принадлежность, раса и жанр
- Фантазия
- Историческая фантастика
- Ноты для флейты и пикколо
- Ноты для гитары
- Старая история
- История Мойен-Востока
- Европейская история
- Мировая история
- Ноты для гитары в стиле джаз и блюз
- Ноты для джазовой гитары
- Ноты для джазового фортепиано
- Коран и священные писания
- Классическая литература
- Мода и красота
- Ноты для гитары из фильмов и мюзиклов
- Питание и Вин
- Паранормальный
- Разделы поп и рок
- Перегородки для фортепиано
- Политика и актуальная информация
- Поп- и рок-бас-ноты
- Популярная культура
- Ноты для гитары R&B
- Отношения и родители
- Религиозные и праздничные ноты для гитары Mu
- Вегетарианские и веганские блюда
- Исторический роман
- Научная фантастика
- Ноты
- Ноты для трубы
- Ноты для укулеле
- Городское планирование и землепользование
- Ноты для скрипки
- Философия
- Отруи
- Курсы и упражнения PDF
- Искусство
- L’Inconscient et la Conscience
- Ла Либерте
- Религия
- Ле Бонёр
- детерминизм
- Ле Маль
- Le réel et la raison
- Ле Респект
- Ле Рир
- Труд и техника
- Телосложение
- Телосложение
- Физико-химия и математика
- Бак СТИ2Д
- Политика и интернационал
- военный
- Психология
- Фрейд
- Истерия
- Ла Восприятие
- La Perfectibilite
- Психология
- Психология Когнитивная
- Se Connaitre Soi Мем
- стресс
- Радиология
- Радиология
- Связи со сценой
- Force et Faiblesse
- Письмо о мотивации
- Религия и духовность
- атеизм
- буддизм
- христианство
- индуизм
- ислам
- иудаизм
- Религия
- Богословие
- Гуманитарные ресурсы
- Гуманитарные ресурсы
- Здоровье и культура
- Альтернатива медицине
- Научный лазарет
- Научный лазарет
- Наука политическая
- Наука политическая
- наук
- Астрономия
- Биология
- Чими
- Медицина
- Наука об окружающей среде
- наук де ла Терре
- наук о здоровье
- наук о здоровье
- Экономические и социальные науки
- Генеалогия
- социальные науки
- Антропология
- Психология
- Наука политическая
- социальные науки
- Социология
- Общество
- Помощник Суаньанте
- Ситуаеннете
- Поколение
- Иммиграция
- Liens Familiaux
- Социология
- Социология
- Статистика
- Статистика
- СВТ
- Бак генерал
- Сист.
 информация. организационные элементы
информация. организационные элементы - Сист. д \ ‘информация. организационные элементы
- Сист. д \ ‘информация. организационные элементы
- Сист. информация. организационные элементы
- Тех. медицинская лаборатория
- Тех. медицинская лаборатория
- Респираторная терапия
- Респираторная терапия
- токсикомания
- токсикомания
- перевод
- перевод
- Путешествие в соц.
- Путешествие в соц.
- Администрация
- Бак
- Бревет
- Конкурсы
- Дайверы
- Трудоустройство
- Формирование фише
- Fiche metier
- История
- Письмо о мотивации
- Ливр Блан
- Рапорт де стадии
- питание
- Архитектура
- Кинотеатр искусств
- Искусство ддд пластики
- Художественная литература
- Искусство Музыка
- Художественная фотография
- Художественная пластика
- Base de données
- Биология
- бюрократический
- Коммерческий коучинг
- Коммерческое общение
- Коммерция ддд интернэшнл
- Коммерческие дайверы
- Коммерция Экономика
- Коммерческий электронный маркетинг
- Коммерческий этюд на марше
- Коммерческие Финансы
- Международная коммерция
- Коммерческая логистика
- Управление торговлей
- Коммерческий маркетинг
- Коммерческие СМИ
- Коммерческая стратегия
- Коммерческий туризм и услуги
- Коммуникация
- курс 3ds max
- Курс 4D
- доступ к курсу
- Курс Аякс
- алгоритм курса
- курс андроид
- курс апертура
- Cours Architecture des ordinateurs
- курс жерех
- курс ассемблера
- Cours assembleur Cours informatique
- дерзость
- Курс аудита
- Автоматический курс
- курс баз де донне
- Курс биологии
- Курский мост
- курс с
- курс до-диез
- Курсы С/С++
- Курс Сиэль Компта
- Cours Ciel Devis фактура
- Cours Ciel Gestion Commerciale
- Курсы Cisco
- Кур Коболь
- Курс коммерции
- курс аналитической совместимости
- Cours comptabilite approfondie
- Cours comptabilité des entreprises
- Cours comptabilité des sociétés
- Общий курс совместимости
- Курсы криптографии
- курсы css
- Курс Дельфы
- Кур Друа
- курс друпал
- затмение
- Курс эконометри
- Курс эконом-класса
- Cours électricité автомобиль
- Cours électricité de base
- Электромеканская улица
- Электронный курс
- курс эргономики
- курс превосходит
- курс final cut pro
- Cours Finance de Marché
- Cours финансирует общественность
- Курс фискальных услуг
- курс фьюжн
- курс гаражной группы
- Cours Genie Civil
- курс
- Курсы управления проектами
- Cours gestion des approvvisionnements
- Cours gestion des entreprises
- Cours gestion des ressources humanes
- Cours gestion des risques
- курс канитель
- Бесплатные курсы
- курс html
- Курс гидравлики
- Курс Имови
- Курс информатики
- курс iphoto
- курс j2ee
- Кур Ява
- Курсы JAVA/J2EE
- курс javascript
- курс джумла
- курс jquery
- курс labview
- курс языка c
- Курс Лазаря
- Курсы Linux
- Курс ЛУА
- курс обслуживания ПК
- курс менеджмент
- Стратегия управления курсами
- курс маркетинга
- Курс маркетинговой стратегии
- Математический курс
- курс матлаб
- Курс медицины
- кур мериз
- Курс микроэкономики
- курс mysql
- цель курса c
- трассировщик пакетов
- курс паскаль
- курс перл
- Курс фотошоп
- курс php
- Cours physique chimie
- Курсы PL/SQL
- Курсы PowerPoint
- Курс вероятностей
- кур питон
- курс qtcreator
- Справочник по курсу
- Курс Резо
- Cours réseaux informatiques
- схема курса
- Cours Sécurité Informatique
- курс
- Курс звуковой кузницы
- Курсы SQL
- Статистика курса
- Cours système d’exploitation
- курс умл
- Курсы Unix
- курс unix linux
- курс вб нетто
- Курс VB/VB.
 NET
NET - курс вба
- курс визуальный базовый
- курс визуальной студии
- курс веб-мастера
- Курс Виндев
- Курсы Windows
- курс windows server
- курс слово
- Курсы XHTML
- курс xml
- курс xsl
- Право
- Право дел
- Конституционное право
- Droit Contrats типы
- Право ддд
- Европейское право
- Фискальное право
- Право недвижимости
- Международное право
- Уголовное право
- Право человеческих ресурсов
- Права общества
- Право труда
- Образование
- Совместимые упражнения
- Упражнения и исправления
- французский
- Французская аналитика
- Франсэ Биография
- Франсез Комментарий
- Общая французская культура
- французский ддд
- Французская диссертация
- Лекция Франсе Фиша
- Ревизия Francais Fiche bac
- Французская литература
- Французская философия
- Изобретение Francais Sujet d
- Совместимость с Gestion
- Gestion Controle de gestion
- Гестион Финанс
- Программирование жестов
- Gestion Ressources Humanes
- Высокие технологии
- Histoire geographie Droit
- Histoire geographie Fiche revision bac
- Историческая география
- Историческая география
- Индустри
- информатика
- Администрация информатики
- Информатический анализ объекта uml merise
- Информационная архитектура
- Информатик Бдд
- Информатика ддд
- Informatique Genie Logiciel
- Informatique Gestion de projet
- Информатическое программирование
- Informatique Reseaux информатики
- Информационная безопасность информационных систем
- Информатика Технологии
- Ланге Алеманд
- Английский язык
- Арабский язык
- Китайский язык
- Langue ddds des signes
- Испанский язык
- Язык итальянский
- Латинский язык
- Языки знаков
- логические
- Математика
- Медицина
- Администрация методологии
- Английская методология
- Методологический комментарий
- Методология коммуникации
- Общая методология культуры
- Методология Резюме
- Испанская методология
- Пересмотр методологии Fiche bac
- Методология Письмо о мотивации
- Математическая методология
- Мемуар методологии
- Методология анализа
- Методология Отчет о стадии
- Методология поддержки
- Методология Технология
- Музыка
- Фотография
- Physique-Chimie
- Программирование
- Рапорт де стадии
- Резо информатики
- Санте
- Английские науки
- наук Чими
- Электронные науки
- Управление науками
- Математические науки
- наук механика
- Науки Медицина
- Аптека наук
- Науки Телосложение
- наук Свт
- Социальная философия
- Социальная политика
- Социальная психология
- Гуманитарные социальные ресурсы
- Социальные науки
- Социальная социология
- Спорт
- Trucs et Astuces
Сайт использует файлы cookie для персонализации PUB,
Si vous continuez à utiliser ce site, nousceptrons que vous en êtes satisfait. Савуар плюс
Савуар плюс
Политика конфиденциальности – Политика конфиденциальности
Исключение Гаусса-Жордана – объяснение и примеры
Метод исключения Гаусса-Жордана представляет собой алгоритм для решения линейной системы уравнений. Мы также можем использовать его, чтобы найти обратную обратимую матрицу. Давайте сначала посмотрим на определение:
Исключение Гаусса-Жордана или исключение Гаусса — это алгоритм решения системы линейных уравнений путем представления ее в виде расширенной матрицы, уменьшения ее с помощью операций над строками и представления системы в сокращенной строке. -ступенчатая форма для нахождения значений переменных.
В этом уроке мы подробно рассмотрим метод исключения Гаусса и способы решения системы линейных уравнений с использованием метода исключения Гаусса-Жордана. Примеры и практические вопросы будут следовать.
Что такое исключение Гаусса?
Исключение Гаусса — это структурированный метод решения системы линейных уравнений. Таким образом, это алгоритм, который можно легко запрограммировать для решения системы линейных уравнений. Основная цель Gauss-Jordan Elimination:
Таким образом, это алгоритм, который можно легко запрограммировать для решения системы линейных уравнений. Основная цель Gauss-Jordan Elimination:
- для представления системы линейных уравнений в расширенной матричной форме
- с последующим выполнением операций со строками $ 3 $ до тех пор, пока не будет получена сокращенная эшелонированная форма строк (RREF)
- Наконец, мы можем легко распознать решения из RREF
Давайте посмотрим, что такое расширенная матричная форма, $3$ операции со строками, которые мы можем выполнять над матрицей, и уменьшенная эшелонированная форма строки матрицы.
Расширенная матрица
Система линейных уравнений показана ниже:
$ \begin{align*} 2x + 3y &= \,7 \\ x – y &= 4 \end{align*} $
Мы запишем расширенную матрицу этой системы, используя коэффициенты уравнений и записать его в стиле , показанном ниже:
$ \left[ \begin{array}{ r r | r } 2 & 3 & 7 \\ 1 & -1 & 4 \end{array} \right] $
Пример использования одновременных уравнений $ 3 $ показан ниже:
$ \begin{align*} 2x + y + z &= \,10 \\ x + 2y + 3z &= 1 \\ – x – y – z &= 2 \end{align*} $
Представление этой системы в виде расширенной матрицы:
$ \left[ \begin{array}{ r r r | r } 2 & 1 & 1 & 10 \\ 1 & 2 & 3 & 1 \\ – 1 & – 1 & – 1 & 2 \end{array} \right] $
Операции со строками над матрицей
Есть $ 3 $ элементарных операций над строками , которые мы можем выполнять над матрицами. Это не изменит решения системы. Это:
Это не изменит решения системы. Это:
- Перестановка $ 2 $ строк
- Умножение строки на ненулевой ($\neq 0 $) скаляр
- Сложение или вычитание скаляра, кратного одной строки, другой строке.
Сокращенная эшелонированная форма строк
Основная цель метода исключения Гаусса Жордана состоит в том, чтобы использовать $ 3 $ элементарных операций со строками над расширенной матрицей, чтобы привести ее к сокращенной эшелонированной форме строк (RREF). Говорят, что матрица находится в сокращенной эшелонированной форме строк , также известной как каноническая форма строк , если выполняются следующие $ 4 $ условия:
- строк с нулевыми элементами (все элементы этой строки равны $ 0 $ s) находятся внизу матрицы.
- ведущая запись (первая ненулевая запись в строке) каждой ненулевой строки располагается справа ведущей записи строки непосредственно над ней.

- Начальная запись в любой ненулевой строке равна $ 1 $.
- Все записи в столбце, содержащем ведущую запись ($ 1 $), являются нулями.
Как выполнить исключение Гаусса Жордана
В методе исключения Гаусса Жордана нет определенных шагов, но приведенный ниже алгоритм описывает шаги, которые мы выполняем, чтобы получить сокращенную эшелонированную форму расширенной матрицы.
- Поменять местами строки так, чтобы все строки с нулевыми элементами находились в нижней части матрицы.
- Поменять местами строки так, чтобы строка с самой большой крайней левой цифрой находилась в верхней части матрицы.
- Умножьте верхнюю строку на скаляр, который преобразует начальную запись верхней строки в $ 1 $ (если первая запись верхней строки равна $ a $, умножьте ее на $ \frac{ 1 }{ a } $, чтобы получить $1$).
- Прибавьте или вычтите кратные числа из верхней строки к другим строкам, чтобы все записи в столбце ведущей записи верхней строки были равны нулю.

- Выполните шаги $ 2–4 $ для следующей крайней левой ненулевой записи до тех пор, пока все ведущие записи каждой строки не будут равны $ 1 $.
- Поменяйте местами строки так, чтобы первая запись каждой ненулевой строки находилась справа от первой записи строки непосредственно над ней
На первый взгляд, запомнить шаги не так просто. Это вопрос решения нескольких проблем, пока вы не освоите процесс. Существует также фактор интуиции , который играет БОЛЬШУЮ роль в выполнении метода исключения Гаусса-Жордана.
Давайте рассмотрим несколько примеров, чтобы пояснить процесс решения системы линейных уравнений с помощью метода исключения Гаусса-Жордана .
Пример 1
Решите систему, показанную ниже, используя метод исключения Гаусса Жордана:
$ \begin{align*} { – x } + 2y &= \, { – 6 } \\ { 3x } – 4y &= { 14 } \end{align*} $
Решение
Первым шагом является запись расширенной матрицы системы. Мы покажем это ниже:
Мы покажем это ниже:
$ \left[ \begin{array}{ r r | r } – 1 & 2 & – 6 \\ 3 & -4 & 14 \end{array} \right] $
Теперь наша задача состоит в том, чтобы привести матрицу к приведенной эшелонированной форме строк (RREF), выполнив $ 3 $ элементарные операции со строками.
Расширенная матрица, которая у нас есть:
$ \left[ \begin{array}{ r r | r } – 1 & 2 & – 6 \\ 3 & – 4 & 14 \end{array} \right] $
Шаг 1:
Мы можем умножить первую строку на $ – 1 $, чтобы получить начальную запись $ 1 $. Ниже показано:
$ \left[ \begin{array}{ r r | r } 1 & – 2 & 6 \\ 3 & – 4 & 14 \end{array} \right] $
Шаг 2:
Теперь мы можем умножить первую строку на $ 3 $ и вычесть ее из второй ряд. Ниже показано:
$ \left[ \begin{array}{ r r | r } 1 & -2 & 6 \\ {3 – ( 1 \times 3 ) } & { -4 – ( -2 \times 3 ) } & { 14 – ( 6 \times 3 ) } \end{array} \ справа] $
$ = \left[ \begin{array}{ r r | r } 1 & – 2 & 6 \\ 0 & 2 & – 4 \end{array} \right] $
У нас есть $ 0 $ в качестве первой записи второй строки.
Шаг 3:
Чтобы сделать вторую запись второй строки $ 1 $, мы можем умножить вторую строку на $ \ frac { 1 }{ 2 } $. Ниже показано:
$ \left[ \begin{array}{ r r | r } 1 & – 2 & 6 \\ { \frac{ 1 }{ 2 } \times 0} & { \frac{ 1 }{ 2 } \times 2 } & { \frac{ 1 }{ 2 } \times – 4} \end{массив} \right] $
$ = \left[ \begin{array}{ r r | r } 1 & – 2 & 6 \\ 0 & 1 & – 2 \end{array} \right] $
Шаг 4:
Мы почти у цели!
Вторая запись первой строки должна быть $0 $. Для этого умножаем вторую строку на $2$ и прибавляем к первой строке. Ниже показано:
$ \left[ \begin{array}{ r r | r } { 1 + (0 \times 2 ) } & { – 2 + (1 \times 2 ) } & {6 + ( – 2 \times 2 ) } \\ 0 & 1 & – 2 \end{array} \ справа] $
$ = \left[ \begin{array}{ r r | r } 1 & 0 & 2 \\ 0 & 1 & – 2 \end{array} \right] $
Это сокращенный эшелон строк из . Из расширенной матрицы мы можем написать два уравнения (решения):
$ \begin{align*} x + 0y &= \, 2 \\ 0x + y &= -2 \end{align*} $
$ \begin{align*} x &= \, 2 \\ y &= – 2 \end{align*} $
Таким образом, решением системы уравнений является $ x = 2 $ и $ y = – 2$.
Решите систему, показанную ниже, используя метод исключения Гаусса Жордана:
$ \begin{align*} x + 2y &= \, 4 \\ x – 2y &= 6 \end{ align*} $
Решение
Запишем расширенную матрицу системы уравнений:
$ \left[ \begin{array}{ r r | r } 1 & 2 & 4 \\ 1 & – 2 & 6 \end{array} \right] $
Теперь мы выполняем элементарные операции со строками над этой матрицей, пока не придем к сокращенной ступенчатой форме строк.
Шаг 1:
Умножаем первую строку на $1$ и затем вычитаем ее из второй строки. По сути, это вычитание первой строки из второй строки:
$ \left[ \begin{array}{ r r | r } 1 & 2 & 4 \\ 1 – 1 & – 2 – 2 & 6 – 4 \end{массив} \right] $
$ =\left[ \begin{array}{ r r | r } 1 & 2 & 4 \\ 0 & – 4 & 2 \end{array} \right] $
Шаг 2:
Умножаем вторую строку на $ -\frac{ 1 }{ 4 }$, чтобы получить вторая запись ряда, $1$:
$\left[ \begin{array}{ r r | r } 1 & 2 & 4 \\ 0 \times -\frac{ 1 }{ 4 } & – 4 \times -\frac{ 1 }{ 4 } & 2 \times -\frac{ 1 }{ 4 } \end {массив} \right] $
$ =\left[ \begin{array}{ r r | r } 1 & 2 & 4 \\ 0 & 1 & -\frac{ 1 }{ 2 } \end{array} \right] $
Шаг 3:
Наконец, мы умножаем вторую строку на $ – 2 $ и добавьте его к первой строке, чтобы получить уменьшенную форму эшелона строк этой матрицы:
$\left[ \begin{array}{ r r | r } 1+(- 2\times 0) & 2+( – 2 \times 1) & 4 + ( – 2 \times -\frac{ 1 }{ 2 } ) \\ 0 & 1 & -\frac{ 1 }{ 2 } \end{массив} \right] $
$=\left[ \begin{array}{ r r | r } 1 & 0 & 5 \\ 0 & 1 & -\frac{ 1 }{ 2 } \end{array} \right] $
Это уменьшенный эшелон строк формы . Из расширенной матрицы мы можем написать два уравнения (решения):
Из расширенной матрицы мы можем написать два уравнения (решения):
$ \begin{align*} x + 0y &= \, 5 \\ 0x+ y &= -\frac{ 1 }{ 2 } \end {align*} $
$ \begin{align*} x &= \, 5 \\ y &= -\frac{ 1 }{ 2 } \end{align*} $
Таким образом, решение системы уравнений есть $ x = 5 $ и $ y = -\frac{ 1 }{ 2 } $.
Практические вопросыРешите систему, показанную ниже, используя метод исключения Гаусса Жордана:
$ \begin{align*} 2x + y &= \, – 3 \\ – x – y &= 2 \end{align*} $
Решите систему, показанную ниже, используя метод исключения Гаусса-Жордана:
$ \begin{align*} x + 5y &= \, 15 \\ – x + 5y &= 25 \end{align*} $
Ответы
Начнем с записи расширенной матрицы системы уравнений:
$ \left[ \begin{array}{r r | r} 2 & 1 & – 3 \\ – 1 & – 1 & 2 \end{array} \right] $
Теперь мы выполняем элементарные операции со строками, чтобы получить наше решение.

Во-первых,
Меняем местами знаки во второй строке и меняем местами строки. Итак, имеем:
$ \left[ \begin{array}{r r | r} 1 & 1 & – 2 \\ 2 & 1 & – 3 \end{array} \right] $
Second,
Вычитаем дважды первую строку из второй строки:
$ \left[ \begin{array}{ р р | r} 1 & 1 & – 2 \\ 2 – ( 2 \times 1 ) & 1 – ( 2 \times 1 ) & – 3 – ( 2 \times – 2 ) \end{array} \right] $
$ = \left[ \begin{array}{r r | r} 1 & 1 & – 2 \\ 0 & – 1 & 1 \end{array} \right] $
Третий,
Инвертируем вторую строку, чтобы получить:
$ = \left[\begin{array}{r r | r} 1 & 1 & – 2 \\ 0 & 1 & – 1 \end{array} \right] $
Наконец,
Вычитаем вторую строку из первой и получаем:
$ = \left[\begin{ массив}{r r | r} 1 & 0 & – 1 \\ 0 & 1 & – 1 \end{array} \right] $Из этой дополненной матрицы мы можем написать два уравнения (решения):
$ \begin{align*} x + 0y &= \, – 1 \\ 0x+ y &= – 1 \end{align*} $
$ \begin{align*} x &= \, – 1 \ \ y &= – 1 \end{align*} $
Таким образом, решением системы уравнений является $ x = – 1 $ и $ y = – 1 $.

- Расширенная матрица системы:
$ \left[\begin{array}{r r|r} 1 & 5 & 15 \\ – 1 & 5 & 25 \end{array} \right] $
Давайте привести эту матрицу к сокращенному ступенчатому виду строк и найти решение системы.Во-первых,
Отмените первую строку, затем вычтите ее из второй строки, чтобы получить:
$ \left[ \begin{array}{r r|r} 1 & 5 & 15 \\ – 1 – ( – 1 ) & 5 – ( – 5 ) & 25 – ( – 15) \end{массив} \right] $
$ =\left[ \begin{array}{r r|r} 1 & 5 & 15 \\ 0 & 10 & 40 \end {array} \right] $
Second,
Разделите вторую строку на $10$, чтобы получить:
$ \left[\begin{array}{r r | r} 1 & 5 & 15 \\ 0 & 1 & 4 \end{array} \right] $
Затем
Умножьте вторую строку на $ 5 $ и вычтите ее из первой строки, чтобы окончательно получить решение:
$ \left[\begin{array}{r r | r} 1 – ( 5 \times 0 ) & 5 – ( 5 \times 1 ) & 15 – ( 5 \times 4 ) \\ 0 & 1 & 4 \end{array} \right] $
$ =\left[ \begin{массив}{r r | r} 1 & 0 & – 5 \\ 0 & 1 & 4 \end{array} \right] $
Это сокращенная форма эшелона строк (RREF).


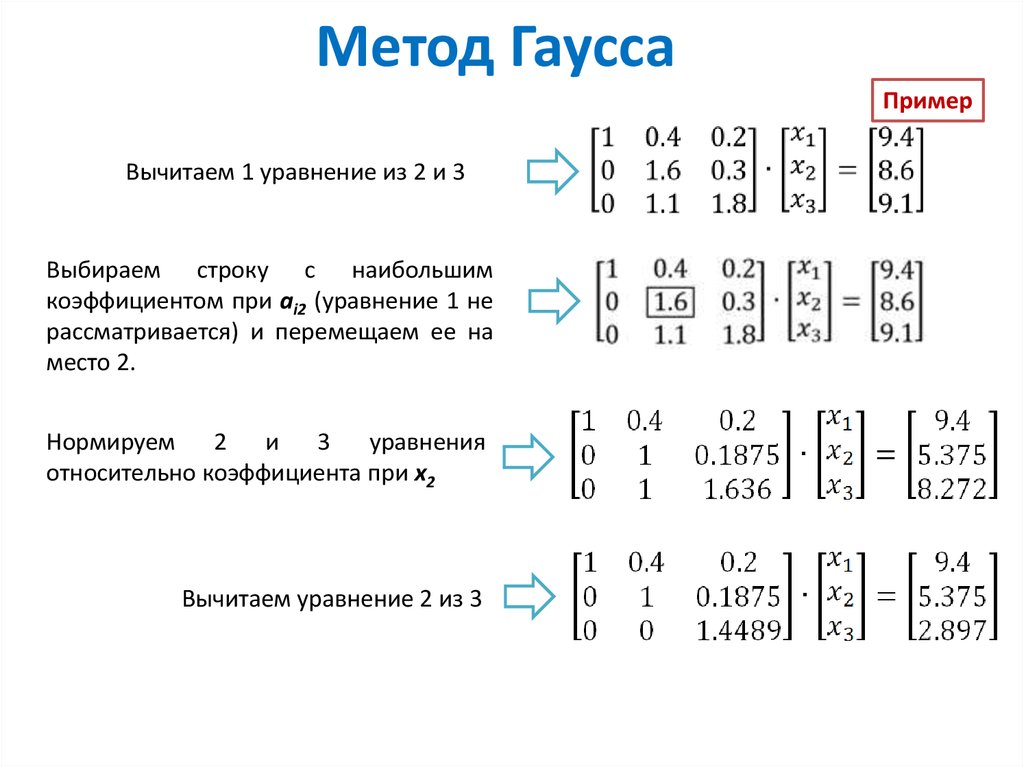 В нашем случае первый элемент в верхней строке равен 2, поэтому поменяем первую и вторую строчки местами.
В нашем случае первый элемент в верхней строке равен 2, поэтому поменяем первую и вторую строчки местами.
 Подставляем это значение во вторую строчку системы. Получится уравнение x2 – 4 = –4. Отсюда следует, что x2 равен 0. Подставляем x2 и x3 в первое уравнение системы: x1 + 0 +3 = 2. Неизвестный член равен –1.
Подставляем это значение во вторую строчку системы. Получится уравнение x2 – 4 = –4. Отсюда следует, что x2 равен 0. Подставляем x2 и x3 в первое уравнение системы: x1 + 0 +3 = 2. Неизвестный член равен –1. Аналогичные действия выполните с остальными строчками. Для того чтобы по диагонали получались единицы, делите каждую строку на ее первый ненулевой элемент.
Аналогичные действия выполните с остальными строчками. Для того чтобы по диагонали получались единицы, делите каждую строку на ее первый ненулевой элемент. Это позволит нам сделать вывод о том, что у A точно есть A-1. Для вычисления определителя преобразуем матрицу до ступенчатой формы элементарными преобразованиями. Подсчитаем число K, равное числу перестановок строк. Строки мы меняли местами всего 1 раз. Вычислим определитель. Его значение будет равно произведению элементов главной диагонали, умноженному на (–1)K. Результат вычисления: det A = 2.
Это позволит нам сделать вывод о том, что у A точно есть A-1. Для вычисления определителя преобразуем матрицу до ступенчатой формы элементарными преобразованиями. Подсчитаем число K, равное числу перестановок строк. Строки мы меняли местами всего 1 раз. Вычислим определитель. Его значение будет равно произведению элементов главной диагонали, умноженному на (–1)K. Результат вычисления: det A = 2. Поменяем строки местами для удобства. Из третьей строчки вычтем вторую строчку, умноженную на 4. Вторую строчку разделим на –1, а третью – на 2. Получим верхнюю треугольную матрицу.
Поменяем строки местами для удобства. Из третьей строчки вычтем вторую строчку, умноженную на 4. Вторую строчку разделим на –1, а третью – на 2. Получим верхнюю треугольную матрицу. Разделим полученную третью строку на –1.
Разделим полученную третью строку на –1.