принцип, теорема и примеры решения задач
Задание. Решить СЛАУ $\left\{\begin{array}{l} 2 x_{1}+x_{2}+x_{3}=2 \\ x_{1}-x_{2}=-2 \\ 3 x_{1}-x_{2}+2 x_{3}=2 \end{array}\right.$ методом Гаусса.
Решение. Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса (сделаем нули выше главной диагонали). Вначале поменяем первую и вторую строку, чтобы элемент $a_{11}$ равнялся 1 (это мы делаем для упрощения вычислений):
$$\tilde{A}=A \mid B=\left(\begin{array}{rrr|r} 2 & 1 & 1 & 2 \\ 1 & -1 & 0 & -2 \\ 3 & -1 & 2 & 2 \end{array}\right) \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 2 & 1 & 1 & 2 \\ 3 & -1 & 2 & 2 \end{array}\right)$$Далее делаем нули под главной диагональю в первом столбце.
Все элементы третьей строки делим на два (или, что тоже самое, умножаем на $\frac{1}{2}$ ):
$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 3 & 1 & 6 \\ 0 & 1 & 1 & 4 \end{array}\right)$$Далее делаем нули во втором столбце под главной диагональю, для удобства вычислений поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1:
От третьей строки отнимаем вторую, умноженную на 3:
$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 1 & 1 & 4 \\ 0 & 0 & -2 & -6 \end{array}\right)$$Умножив третью строку на $\left(-\frac{1}{2}\right)$ , получаем:
$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 1 & 1 & 4 \\ 0 & 0 & 1 & 3 \end{array}\right)$$Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю.
Далее обнуляем недиагональные элементы второго столбца, к первой строке прибавляем вторую:
$$\tilde{A} \sim\left(\begin{array}{ccc|c} 1 & 0 & 0 & -1 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 3 \end{array}\right)$$Полученной матрице соответствует система
Ответ. $\left\{\begin{array}{l} x_{1}=-1 \\ x_{2}=1 \\ x_{3}=3 \end{array}\right.$
Численные методы: решение систем линейных уравнений
В прикладных задачах часто возникает необходимость решать системы линейных уравнений.
Система линейных алгебраических уравнений с n неизвестными – это система уравнений вида
(1)
Слово система означает, что все уравнения рассматриваются как одно целое.
В общем случае у нас имеется m – уравнений, n – количество неизвестных. x1, x2,…, xn – неизвестные, которые следует определить.
В системе (1) – фиксированные коэффициенты, b1, b2, …, bm – свободные члены – предполагаются известными.
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе – неоднородной.
Система (1) называется
Задача состоит в том, чтобы найти такие которые удовлетворяют всем уравнениям (1).
В частном случае мы имеем одно линейное уравнение:
Конечно, такое уравнение легко решить, если предположить, что коэффициент не равен 0, имеем: = .
Очевидно, в общем случае имеются 3 варианта решений: система имеет ни одного решения, имеет одно решение, более одного решения.
Система (1) называется совместной, если она имеет хотя бы одно решение, и
Система линейных уравнений может быть представлена в матричной форме как:
или:
Ax = b
Здесь A – это матрица системы, x – столбец неизвестных, а b – столбец свободных членов.
Если к матрице A приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.
Рассмотрим, например, систему вида и поймем, как найти ее решение:
(2)
Предположим на минуту, что в первом уравнении y отсутствует, а во втором отсутствует x

Вопрос: как исходную систему привести к такому виду и можно ли это сделать.
Заметим, что с тождествами мы можем делать следующие вещи: домножать на одно и то же число, отличное от 0, складывать, вычитать и тд, это похоже с тем, что вы раскладываете монеты по своим карманам, не меняя общей суммы.
От этих операций тождество не меняется.
В системе (2) у нас два тождества, домножим второе тождество на 2 и вычтем из первого, получим:
(3)
Формально у нас есть еще старое тождество , но оно нам не понадобится (подумайте, почему).
Система (3) точно такая же, как система (2).
Из второго уравнения системы (3) сразу получим:
Никто не мешает нам подставить это значение в первое уравнение:
Отсюда сразу находим, что
Итак, путем простых действий мы нашли, что система (2) может быть представлена в виде:
Именно такие естественные соображения приводят к общему методу решения систем линейных уравнений, известному как метод исключения или метод Гаусса.
Метод Гаусса является одним из самых распространенных прямых методов решения систем линейных уравнений Ax = b:
Опишем этот метод в общем случае.
Вначале исходная система приводится к верхнетреугольному виду.
Это достигается следующей последовательностью преобразований (прямой ход).
Будем считать для удобства, что элемент aij исходной матрицы и компоненты вектора bi есть, соответственно, элементы aij (1) первого шага преобразованной матрицы A1 и преобразованного вектора b
Далее, на втором шаге прибавим к второй строке первую, умноженную на
Аналогично поступим со всеми оставшимися строками, т.е. прибавим к каждой i-ой строке i=2,3,…,N, первую, умноженную на коэффициент
При этом соответственно изменится и вектор b1.
Таким образом, 2 шаг.
Имеем систему уравнений A2x = b2:
где
3 шаг.
Прибавим к новой третьей строке новую вторую, умноженную на
То же самое сделаем с остальными строками 4,5,…,N, т.е. прибавим к
При этом получим систему A3x = b3:
(k+1)-ый шаг:
Здесь
Поступая так и далее, на шаге N-1 получаем верхнетреугольную систему:
При этом, мы также получили матрицу C переводных коэффициентов, имеющую вид:
Решение полученной треугольной системы как легко видеть, имеет вид (обратный ход метода Гаусса):
Заметим, что при прямом ходе метода Гаусса может возникнуть ситуация, когда происходит деление на нуль, да и вообще, желательно не делить на малое число, чтобы не накапливалась ошибка.
Поэтому метод Гаусса обычно проводят с частичным выбором главного элемента, то есть после каждого шага (пусть это был k-й шаг) переставляют строки с номерами k,k+1,…,N таким образом, чтобы на месте kk оказался элемент наибольший из всех в k-ом столбце при m>k (при этом, естественно, переставляются и компоненты вектора b).
Можно для максимальной точности переставлять также и столбцы преобразуемой матрицы, чтобы на месте kk оказался максимальный элемент из всех с индексами больше, либо равными k.
Эта процедура называется методом Гаусса с выбором главного элемента. Она несколько повышает точность по сравнению с частичным выбором главного элемента, но весьма неудобна, в том числе для программирования, поскольку при перестановке строк компоненты искомого вектора x переставлять не надо, тогда как при перестановке столбцов надо переставлять и соответствующие компоненты вектора x.
Опишем обратный ход метода Гаусса в несколько иной форме (треугольное разложение).
Введем матрицы Mk по правилу:
На каждом шаге метода Гаусса получается некоторая промежуточная матрица:
и вектор
Нетрудно видеть, что
Вопрос. Почему
Если производить также выбор главных элементов, то необходимо использовать оператор P перестановки индексов l и m, матричные элементы которого равны:
При применении оператора перестановки индексов к матрице слева, меняются местами строки матрицы и компоненты свободного вектора (PAx = Pb), если же его применить справа к матрице, то меняются местами ее столбцы и компоненты решения
Существует большой класс так называемых итерационных методов решения систем уравнений, аналогичных итерационным методам нахождения корней нелинейных уравнений.
Итерационные методы последовательно уточняют решение, отправляясь от начального приближения.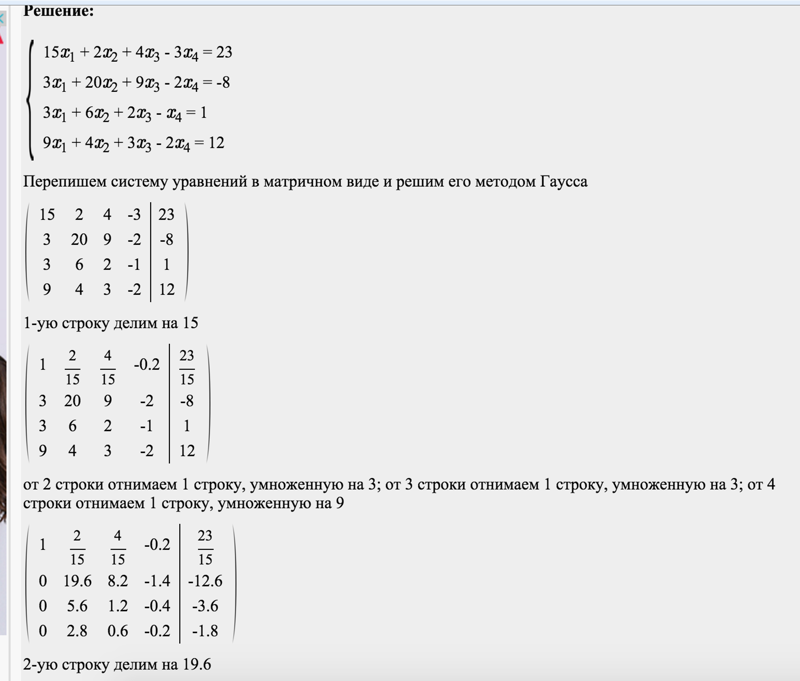
При выполнении условий сходимости они позволяют достичь любой точности просто повторением итераций.
Преимущество этих методов в том, что часто они позволяют достичь решения с заранее заданной точностью быстрее, а также позволяют решать большие системы уравнений.
Идея состоит в том, чтобы найти неподвижную точку матричного уравнения
(5)
эквивалентного начальной системе линейных алгебраических уравнений.
При итерации в правой части уравнения заменяется, например, в методе Якоби (метод простой итерации) приближение, найденное на предыдущем шаге:
.
Термин неподвижная точка становится ясен, если вы внимательно посмотрите на уравнение (5), по самому своему смыслу величина Х является неподвижной точкой.
Более подробное описание методов решения систем линейных уравнений можно найти в специальной литературе, наша задача дать обзор методов и основные идеи решения такого рода задач.
Обусловленность линейных систем, погрешность
При решении абстрактной задачи Ax = b, где A – оператор произвольной природы, важным моментом является корректность ее постановки.
Задача считается корректной, если решение существует и единственно и , кроме того, решение непрерывно зависит от данных (то есть, при также стремится к нулю).
Однако и непрерывная зависимость от входных данных может иметь свои нюансы.
Чем меньшее (большее) изменение решения вызывает вариация входных данных, тем более хорошо (плохо) обусловленной считается задача.
Понятие обусловленности является тем более существенным для численных методов, поскольку на практике входные данные известны, как правило, с некоторой погрешностью.
Кроме того, существуют ошибки округления, возникающие при вычислениях.
Таким образом, формально корректная задача, являясь плохо обусловленной, может оказаться разрешимой столь неточно, что в этом будет отсутствовать практический смысл.
Чем можно охарактеризовать количественно обусловленность для линейных систем?
Пусть A – квадратная NxN – матрица.
Рассмотрим задачу Ax = b.
Пусть также некоторая норма в пространстве RN
Норма оператора A определяется стандартно:
Обозначим y = Ax и введем число m по правилу:
Величина называется числом обусловленности.
Очевидно:
- если A – диагональная, то (Для какой нормы, или для всех вышеприведенных?). Чем меньше число обусловленности C(A), тем лучше обусловлена система. Действительно, пусть вариация правой части, а соответствующее изменение решения.
Тогда справедливо следующее неравенство:
Доказательство. Имеем:
Имеем:
Так как
то
Аналогично, поскольку
Объединяя два неравенства, окончательно получаем для оценки погрешности:
В начало
Содержание портала
описание алгоритма решения системы линейных уравнений, примеры, решения
Еще с начала XVI-XVIII веков математики усиленно начали изучать функции, благодаря которым так много в нашей жизни изменилось. Компьютерная техника без этих знаний просто не существовала бы. Для решения сложных задач, линейных уравнений и функций были созданы различные концепции, теоремы и методики решения. Одним из таких универсальных и рациональных способов и методик решения линейных уравнений и их систем стал и метод Гаусса. Матрицы, их ранг, детерминант – все можно посчитать, не используя сложных операций.
Что представляет собой СЛАУ
В математике существует понятие СЛАУ – система линейных алгебраических уравнений. Что же она собой представляет? Это набор из m уравнений с искомыми n неизвестными величинами, обычно обозначающимися как x, y, z, или x 1 , x 2 … x n, или другими символами. Решить методом Гаусса данную систему – означает найти все искомые неизвестные. Если система имеет одинаковое число неизвестных и уравнений, тогда она называется системой n-го порядка.
Что же она собой представляет? Это набор из m уравнений с искомыми n неизвестными величинами, обычно обозначающимися как x, y, z, или x 1 , x 2 … x n, или другими символами. Решить методом Гаусса данную систему – означает найти все искомые неизвестные. Если система имеет одинаковое число неизвестных и уравнений, тогда она называется системой n-го порядка.
Наиболее популярные методы решения СЛАУ
В учебных заведениях среднего образования изучают различные методики решения таких систем. Чаще всего это простые уравнения, состоящие из двух неизвестных, поэтому любой существующий метод для поиска ответа на них не займет много времени. Это может быть как метод подстановки, когда из одного уравнения выводится другое и подставляется в изначальное. Или метод почленного вычитания и сложения. Но наиболее легким и универсальным считается метод Гаусса. Он дает возможность решать уравнения с любым количеством неизвестных. Почему именно эта методика считается рациональной? Все просто. Матричный способ хорош тем, что здесь не требуется по несколько раз переписывать ненужные символы в виде неизвестных, достаточно проделать арифметические операции над коэффициентами – и получится достоверный результат.
Где используются СЛАУ на практике
Решением СЛАУ являются точки пересечения прямых на графиках функций. В наш высокотехнологический компьютерный век людям, которые тесно связаны с разработкой игр и прочих программ, необходимо знать, как решать такие системы, что они представляют и как проверить правильность получившегося результата. Наиболее часто программисты разрабатывают специальные программы-вычислители линейной алгебры, сюда входит и система линейных уравнений. Метод Гаусса позволяет высчитать все существующие решения. Также используются и другие упрощенные формулы и методики.
Критерий совместимости СЛАУ
Такую систему можно решить только в том случае, если она совместима. Для понятности представим СЛАУ в виде Ax=b. Она имеет решение, если rang(A) равняется rang(A,b). В этом случае (A,b) – это матрица расширенного вида, которую можно получить из матрицы А, переписав ее со свободными членами. Выходит, что решить линейные уравнения методом Гаусса достаточно легко.
Возможно, некоторые обозначения не совсем понятны, поэтому необходимо рассмотреть все на примере. Допустим, есть система: x+y=1; 2x-3y=6. Она состоит всего из двух уравнений, в которых 2 неизвестные. Система будет иметь решение только в том случае, если ранг ее матрицы будет равняться рангу расширенной матрицы. Что такое ранг? Это число независимых строк системы. В нашем случае ранг матрицы 2. Матрица А будет состоять из коэффициентов, находящихся возле неизвестных, а в расширенную матрицу вписываются и коэффициенты, находящиеся за знаком «=».
Почему СЛАУ можно представить в матричном виде
Исходя из критерия совместимости по доказанной теореме Кронекера-Капелли, систему линейных алгебраических уравнений можно представить в матричном виде. Применяя каскадный метод Гаусса, можно решить матрицу и получить единственный достоверный ответ на всю систему. Если ранг обычной матрицы равняется рангу ее расширенной матрицы, но при этом меньше количества неизвестных, тогда система имеет бесконечное количество ответов.
Преобразования матриц
Прежде чем переходить к решению матриц, необходимо знать, какие действия можно проводить над их элементами. Существует несколько элементарных преобразований:
- Переписывая систему в матричный вид и осуществляя ее решение, можно умножать все элементы ряда на один и тот же коэффициент.
- Для того чтобы преобразовать матрицу в канонический вид, можно менять местами два параллельных ряда. Канонический вид подразумевает, что все элементы матрицы, которые расположены по главной диагонали, становятся единицами, а оставшиеся – нулями.
- Соответствующие элементы параллельных рядов матрицы можно прибавлять один к другому.
Метод Жордана-Гаусса
Суть решения систем линейных однородных и неоднородных уравнений методом Гаусса в том, чтобы постепенно исключить неизвестные. Допустим, у нас есть система из двух уравнений, в которых две неизвестные. Чтобы их найти, необходимо проверить систему на совместимость. Уравнение методом Гаусса решается очень просто. Необходимо выписать коэффициенты, находящиеся возле каждого неизвестного в матричный вид. Для решения системы понадобится выписать расширенную матрицу. Если одно из уравнений содержит меньшее количество неизвестных, тогда на место пропущенного элемента необходимо поставить «0». К матрице применяются все известные методы преобразования: умножение, деление на число, прибавление соответствующих элементов рядов друг к другу и другие. Получается, что в каждом ряду необходимо оставить одну переменную со значением «1», остальные привести к нулевому виду. Для более точного понимания необходимо рассмотреть метод Гаусса на примерах.
Необходимо выписать коэффициенты, находящиеся возле каждого неизвестного в матричный вид. Для решения системы понадобится выписать расширенную матрицу. Если одно из уравнений содержит меньшее количество неизвестных, тогда на место пропущенного элемента необходимо поставить «0». К матрице применяются все известные методы преобразования: умножение, деление на число, прибавление соответствующих элементов рядов друг к другу и другие. Получается, что в каждом ряду необходимо оставить одну переменную со значением «1», остальные привести к нулевому виду. Для более точного понимания необходимо рассмотреть метод Гаусса на примерах.
Простой пример решения системы 2х2
Для начала возьмем простенькую систему алгебраических уравнений, в которой будет 2 неизвестных.
Перепишем ее в расширенную матрицу.
Чтобы решить данную систему линейных уравнений, требуется проделать всего две операции. Нам необходимо привести матрицу к каноническому виду, чтобы по главной диагонали стояли единицы. Так, переводя с матричного вида обратно в систему, мы получим уравнения: 1x+0y=b1 и 0x+1y=b2, где b1 и b2 – получившиеся ответы в процессе решения.
Так, переводя с матричного вида обратно в систему, мы получим уравнения: 1x+0y=b1 и 0x+1y=b2, где b1 и b2 – получившиеся ответы в процессе решения.
- Первое действие при решении расширенной матрицы будет таким: первый ряд необходимо умножить на -7 и прибавить соответственно отвечающие элементы ко второй строке, чтобы избавиться от одного неизвестного во втором уравнении.
- Так как решение уравнений методом Гаусса подразумевает приведение матрицы к каноническому виду, тогда необходимо и с первым уравнением проделать те же операции и убрать вторую переменную. Для этого вторую строку отнимаем от первой и получаем необходимый ответ – решение СЛАУ. Или, как показано на рисунке, вторую строку умножаем на коэффициент -1 и прибавляем к первой строке элементы второго ряда. Это одно и то же.
Как видим, наша система решена методом Жордана-Гаусса. Переписываем ее в необходимую форму: x=-5, y=7.
Пример решения СЛАУ 3х3
Предположим, что у нас есть более сложная система линейных уравнений. Метод Гаусса дает возможность высчитать ответ даже для самой, казалось бы, запутанной системы. Поэтому, чтобы более глубоко вникнуть в методику расчета, можно переходить к более сложному примеру с тремя неизвестными.
Метод Гаусса дает возможность высчитать ответ даже для самой, казалось бы, запутанной системы. Поэтому, чтобы более глубоко вникнуть в методику расчета, можно переходить к более сложному примеру с тремя неизвестными.
Как и в прежнем примере, переписываем систему в вид расширенной матрицы и начинаем приводить ее к каноническому виду.
Для решения этой системы понадобится произвести гораздо больше действий, чем в предыдущем примере.
- Сначала необходимо сделать в первом столбце один единичный элемент и остальные нули. Для этого умножаем первое уравнение на -1 и прибавляем к нему второе уравнение. Важно запомнить, что первую строку мы переписываем в изначальном виде, а вторую – уже в измененном.
- Далее убираем эту же первую неизвестную из третьего уравнения. Для этого элементы первой строки умножаем на -2 и прибавляем их к третьему ряду. Теперь первая и вторая строки переписываются в изначальном виде, а третья – уже с изменениями. Как видно по результату, мы получили первую единицу в начале главной диагонали матрицы и остальные нули. Еще несколько действий, и система уравнений методом Гаусса будет достоверно решена.
- Теперь необходимо проделать операции и над другими элементами рядов. Третье и четвертое действие можно объединить в одно. Нужно разделить вторую и третью строку на -1, чтобы избавиться от минусовых единиц по диагонали. Третью строку мы уже привели к необходимому виду.
- Дальше приведем к каноническому виду вторую строку. Для этого элементы третьего ряда умножаем на -3 и прибавляем их ко второй строчке матрицы. Из результата видно, что вторая строка тоже приведена к необходимой нам форме. Осталось проделать еще несколько операций и убрать коэффициенты неизвестных из первой строки.
- Чтобы из второго элемента строки сделать 0, необходимо умножить третью строку на -3 и прибавить ее к первому ряду.
- Следующим решающим этапом будет прибавление к первой строке необходимые элементы второго ряда. Так мы получаем канонический вид матрицы, а, соответственно, и ответ.
Как видно, решение уравнений методом Гаусса довольно простое.
Пример решения системы уравнений 4х4
Некоторые более сложные системы уравнений можно решить методом Гаусса посредством компьютерных программ. Необходимо вбить в существующие пустые ячейки коэффициенты при неизвестных, и программа сама пошагово рассчитает необходимый результат, подробно описывая каждое действие.
Ниже описана пошаговая инструкция решения такого примера.
В первом действии в пустые ячейки вписываются свободные коэффициенты и числа при неизвестных. Таким образом, получается такая же расширенная матрица, которую мы пишем вручную.
И производятся все необходимые арифметические операции, чтобы привести расширенную матрицу к каноническому виду. Необходимо понимать, что не всегда ответ на систему уравнений – это целые числа. Иногда решение может быть из дробных чисел.
Проверка правильности решения
Метод Жордана-Гаусса предусматривает проверку правильности результата. Для того чтобы узнать, правильно ли посчитаны коэффициенты, необходимо всего-навсего подставить результат в изначальную систему уравнений. Левая сторона уравнения должна соответствовать правой стороне, находящейся за знаком “равно”. Если ответы не совпадают, тогда необходимо пересчитывать заново систему или попробовать применить к ней другой известный вам метод решения СЛАУ, такой как подстановка или почленное вычитание и сложение. Ведь математика – это наука, которая имеет огромное количество различных методик решения. Но помните: результат должен быть всегда один и тот же, независимо от того, какой метод решения вы использовали.
Метод Гаусса: наиболее часто встречающиеся ошибки при решении СЛАУ
Во время решения линейных систем уравнений чаще всего возникают такие ошибки, как неправильный перенос коэффициентов в матричный вид. Бывают системы, в которых отсутствуют в одном из уравнений некоторые неизвестные, тогда, перенося данные в расширенную матрицу, их можно потерять. В результате при решении данной системы результат может не соответствовать действительному.
Еще одной из главных ошибок может быть неправильное выписывание конечного результата. Нужно четко понимать, что первый коэффициент будет соответствовать первому неизвестному из системы, второй – второму, и так далее.
Метод Гаусса подробно описывает решение линейных уравнений. Благодаря ему легко произвести необходимые операции и найти верный результат. Кроме того, это универсальное средство для поиска достоверного ответа на уравнения любой сложности. Может быть, поэтому его так часто используют при решении СЛАУ.
1. Система линейных алгебраических уравнений
1.1 Понятие системы линейных алгебраических уравнений
Система уравнений – это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких переменных. Системой линейных алгебраических уравнений (далее – СЛАУ), содержащей m уравнений и n неизвестных, называется система вида:
где числа a ij называются коэффициентами системы, числа b i – свободными членами, a ij и b i (i=1,…, m; b=1,…, n) представляют собой некоторые известные числа, а x 1 ,…, x n – неизвестные. В обозначении коэффициентов a ij первый индекс i обозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент. Подлежат нахождению числа x n . Такую систему удобно записывать в компактной матричной форме: AX=B. Здесь А – матрица коэффициентов системы, называемая основной матрицей;
– вектор-столбец из неизвестных xj.– вектор-столбец из свободных членов bi.
Произведение матриц А*Х определено, так как в матрице А столбцов столько же, сколько строк в матрице Х (n штук).
Расширенной матрицей системы называется матрица A системы, дополненная столбцом свободных членов
1.2 Решение системы линейных алгебраических уравнений
Решением системы уравнений называется упорядоченный набор чисел (значений переменных), при подстановке которых вместо переменных каждое из уравнений системы обращается в верное равенство.
Решением системы называется n значений неизвестных х1=c1, x2=c2,…, xn=cn, при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы-столбца
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.
Решить систему – это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.
Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.
Преобразование, применение которого превращает систему в новую систему, эквивалентную исходной, называется эквивалентным или равносильным преобразованием. Примерами эквивалентных преобразований могут служить следующие преобразования: перестановка местами двух уравнений системы, перестановка местами двух неизвестных вместе с коэффициентами у всех уравнений, умножение обеих частей какого-либо уравнения системы на отличное от нуля число.
Система линейных уравнений называется однородной, если все свободные члены равны нулю:
Однородная система всегда совместна, так как x1=x2=x3=…=xn=0 является решением системы. Это решение называется нулевым или тривиальным.
2. Метод исключения Гаусса
2.1 Сущность метода исключения Гаусса
Классическим методом решения систем линейных алгебраических уравнений является метод последовательного исключения неизвестных – метод Гаусса (его еще называют методом гауссовых исключений). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Процесс решения по методу Гаусса состоит из двух этапов: прямой и обратный ходы.
1. Прямой ход.
На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним.
После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному) виду.
Приведенная ниже система имеет ступенчатый вид:
,Коэффициенты aii называются главными (ведущими) элементами системы.
(если a11=0, переставим строки матрицы так, чтобы a 11 не был равен 0. Это всегда возможно, т. к. в противном случае матрица содержит нулевой столбец, ее определитель равен нулю и система несовместна).Преобразуем систему, исключив неизвестное х1 во всех уравнениях, кроме первого (используя элементарные преобразования системы). Для этого умножим обе части первого уравнения на
и сложим почленно со вторым уравнением системы (или из второго уравнения почленно вычтем первое, умноженное на ). Затем умножим обе части первого уравнения на и сложим с третьим уравнением системы (или из третьего почленно вычтем первое, помноженное на ). Таким образом, последовательно умножаем первую строку на число и прибавляем к i -й строке, для i= 2, 3, …, n.Продолжая этот процесс, получим эквивалентную систему:
– новые значения коэффициентов при неизвестных и свободные члены в последних m-1 уравнениях системы, которые определяются формулами:
Таким образом, на первом шаге уничтожаются все коэффициенты, лежащие под первым ведущим элементом a 11
0, на втором шаге уничтожаются элементы, лежащие под вторым ведущим элементом а 22 (1) (если a 22 (1) 0) и т.д. Продолжая этот процесс и дальше, мы, наконец, на (m-1) шаге приведем исходную систему к треугольной системе.Если в процессе приведения системы к ступенчатому виду появятся нулевые уравнения, т.е. равенства вида 0=0, их отбрасывают. Если же появится уравнение вида
то это свидетельствует о несовместности системы.На этом прямой ход метода Гаусса заканчивается.
2. Обратный ход.
На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений.
Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (она в нем всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх.
Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
Примечание: на практике удобнее работать не с системой, а с расширенной ее матрицей, выполняя все элементарные преобразования над ее строками. Удобно, чтобы коэффициент a11 был равен 1 (уравнения переставить местами, либо разделить обе части уравнения на a11).
2.2 Примеры решения СЛАУ методом Гаусса
В данном разделе на трех различных примерах покажем, как методом Гаусса можно решить СЛАУ.
Пример 1. Решить СЛАУ 3-го порядка.
Обнулим коэффициенты при
во второй и третьей строчках. Для этого домножим их на 2/3 и 1 соответственно и сложим с первой строкой:Продолжаем рассматривать системы линейных уравнений. Этот урок является третьим по теме. Если вы смутно представляете, что такое система линейных уравнений вообще, чувствуете себя чайником, то рекомендую начать с азов на странице Далее полезно изучить урок .
Метод Гаусса – это просто! Почему? Известный немецкий математик Иоганн Карл Фридрих Гаусс еще при жизни получил признание величайшего математика всех времен, гения и даже прозвище «короля математики». А всё гениальное, как известно – просто! Кстати, на деньги попадают не только лохи, но еще и гении – портрет Гаусса красовался на купюре в 10 дойчмарок (до введения евро), и до сих пор Гаусс загадочно улыбается немцам с обычных почтовых марок.
Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА.Необходимо уметь складывать и умножать! Не случайно метод последовательного исключения неизвестных преподаватели часто рассматривают на школьных математических факультативах. Парадокс, но у студентов метод Гаусса вызывает наибольшие сложности. Ничего удивительного – всё дело в методике, и я постараюсь в доступной форме рассказать об алгоритме метода.
Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:
1) Иметь единственное решение. 2) Иметь бесконечно много решений. 3) Не иметь решений (быть несовместной ).
Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решениялюбой системы линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случае приведет нас к ответу! На данном уроке мы опять рассмотрим метод Гаусса для случая №1 (единственное решение системы), под ситуации пунктов №№2-3 отведена статья. Замечу, что сам алгоритм метода во всех трёх случаях работает одинаково.
Вернемся к простейшей системе с урока Как решить систему линейных уравнений? и решим ее методом Гаусса.
На первом этапе нужно записать расширенную матрицу системы : . По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.
Справка : рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: . Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: . Любую из матриц можно для краткости называть просто матрицей.
После того, как расширенная матрица системы записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями .
Существуют следующие элементарные преобразования:
1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки:
2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. Рассмотрим, например матрицу . В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них: .
3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следуетудалить . Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули .
4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля . Рассмотрим, например, матрицу . Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2: . Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.
5) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число , отличное от нуля. Рассмотрим нашу матрицу из практического примера: . Сначала я распишу преобразование очень подробно. Умножаем первую строку на –2: , и ко второй строке прибавляем первую строку умноженную на –2 : . Теперь первую строку можно разделить «обратно» на –2: . Как видите, строка, которую ПРИБАВЛЯЛИ – не изменилась . Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ .
На практике так подробно, конечно, не расписывают, а пишут короче: Еще раз: ко второй строке прибавили первую строку, умноженную на –2 . Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:
«Переписываю матрицу и переписываю первую строку: »
«Сначала первый столбец. Внизу мне нужно получить ноль. Поэтому единицу вверху умножаю на –2: , и ко второй строке прибавляю первую: 2 + (–2) = 0. Записываю результат во вторую строку: »
«Теперь второй столбец. Вверху –1 умножаю на –2: . Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку: »
«И третий столбец. Вверху –5 умножаю на –2: . Ко второй строке прибавляю первую: –7 + 10 = 3. Записываю результат во вторую строку: »
Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане». Но, конечно, над этим преобразованием мы еще поработаем.
Элементарные преобразования не меняют решение системы уравнений
! ВНИМАНИЕ : рассмотренные манипуляции нельзя использовать , если Вам предложено задание, где матрицы даны «сами по себе». Например, при «классических» действиях с матрицами что-то переставлять внутри матриц ни в коем случае нельзя! Вернемся к нашей системе . Она практически разобрана по косточкам.
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду :
(1) Ко второй строке прибавили первую строку, умноженную на –2. И снова: почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.
(2) Делим вторую строку на 3.
Цель элементарных преобразований – привести матрицу к ступенчатому виду: . В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид .
В результате элементарных преобразований получена эквивалентная исходной система уравнений:
Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса .
В нижнем уравнении у нас уже готовый результат: .
Рассмотрим первое уравнение системы и подставим в него уже известное значение «игрек»:
Рассмотрим наиболее распространенную ситуацию, когда методом Гаусса требуется решить систему трёх линейных уравнений с тремя неизвестными.
Пример 1
Решить методом Гаусса систему уравнений:
Запишем расширенную матрицу системы:
Сейчас я сразу нарисую результат, к которому мы придём в ходе решения: И повторюсь, наша цель – с помощью элементарных преобразований привести матрицу к ступенчатому виду. С чего начать действия?
Сначала смотрим на левое верхнее число: Почти всегда здесь должна находиться единица . Вообще говоря, устроит и –1 (а иногда и другие числа), но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки:
Теперь первая строка у нас останется неизменной до конца решения . Уже легче.
Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах:
Нули получаем как раз с помощью «трудного» преобразования. Сначала разбираемся со второй строкой (2, –1, 3, 13). Что нужно сделать, чтобы на первой позиции получить ноль? Нужно ко второй строке прибавить первую строку, умноженную на –2 . Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18). И последовательно проводим (опять же мысленно или на черновике) сложение, ко второй строке прибавляем первую строку, уже умноженную на –2 :
Результат записываем во вторую строку:
Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3 . Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). И к третьей строке прибавляем первую строку, умноженную на –3 :
Результат записываем в третью строку:
На
практике эти действия обычно выполняются
устно и записываются в один шаг:
Не
нужно считать всё сразу и одновременно .
Порядок вычислений и «вписывания»
результатов последователен и
обычно такой: сначала переписываем
первую строку, и пыхтим себе потихонечку
– ПОСЛЕДОВАТЕЛЬНО иВНИМАТЕЛЬНО :
А
мысленный ход самих расчётов я уже
рассмотрел выше.
В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение:
На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь:
Для
этого к
третьей строке прибавляем вторую строку,
умноженную на –2 :
Попробуйте
разобрать это действие самостоятельно
– мысленно умножьте вторую строку на
–2 и проведите сложение.
Последнее выполненное действие – причёска результата, делим третью строку на 3.
В результате элементарных преобразований получена эквивалентная исходной система линейных уравнений: Круто.
Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.
В третьем уравнении у нас уже готовый результат:
Смотрим на второе уравнение: . Значение «зет» уже известно, таким образом:
И, наконец, первое уравнение: . «Игрек» и «зет» известны, дело за малым:
Ответ :
Как уже неоднократно отмечалось, для любой системы уравнений можно и нужно сделать проверку найденного решения, благо, это несложно и быстро.
Пример 2
Это пример для самостоятельного решения, образец чистового оформления и ответ в конце урока.
Следует отметить, что ваш ход решения может не совпасть с моим ходом решения, и это – особенность метода Гаусса . Но вот ответы обязательно должны получиться одинаковыми!
Пример 3
Решить систему линейных уравнений методом Гаусса
Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так: (1) К первой строке прибавляем вторую строку, умноженную на –1 . То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.
Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное телодвижение: умножить первую строку на –1 (сменить у неё знак).
(2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.
(3) Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.
(4) К третьей строке прибавили вторую строку, умноженную на 2.
(5) Третью строку разделили на 3.
Скверным признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде , и, соответственно, , то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.
Заряжаем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает, снизу вверх. Да тут подарок получился:
Ответ : .
Пример 4
Решить систему линейных уравнений методом Гаусса
Это пример для самостоятельного решения, он несколько сложнее. Ничего страшного, если кто-нибудь запутается. Полное решение и образец оформления в конце урока. Ваше решение может отличаться от моего решения.
В последней части рассмотрим некоторые особенности алгоритма Гаусса. Первая особенность состоит в том, что иногда в уравнениях системы отсутствуют некоторые переменные, например: Как правильно записать расширенную матрицу системы? Об этом моменте я уже рассказывал на уроке Правило Крамера. Матричный метод . В расширенной матрице системы на месте отсутствующих переменных ставим нули: Кстати, это довольно легкий пример, поскольку в первом столбце уже есть один ноль, и предстоит выполнить меньше элементарных преобразований.
Вторая особенность состоит вот в чём. Во всех рассмотренных примерах на «ступеньки» мы помещали либо –1, либо +1. Могут ли там быть другие числа? В ряде случаев могут. Рассмотрим систему: .
Здесь на левой верхней «ступеньке» у нас двойка. Но замечаем тот факт, что все числа в первом столбце делятся на 2 без остатка – и другая двойка и шестерка. И двойка слева вверху нас устроит! На первом шаге нужно выполнить следующие преобразования: ко второй строке прибавить первую строку, умноженную на –1; к третьей строке прибавить первую строку, умноженную на –3. Таким образом, мы получим нужные нули в первом столбце.
Или еще такой условный пример: . Здесь тройка на второй «ступеньке» тоже нас устраивает, поскольку 12 (место, где нам нужно получить ноль) делится на 3 без остатка. Необходимо провести следующее преобразование: к третьей строке прибавить вторую строку, умноженную на –4, в результате чего и будет получен нужный нам ноль.
Метод Гаусса универсален, но есть одно своеобразие. Уверенно научиться решать системы другими методами (методом Крамера, матричным методом) можно буквально с первого раза – там очень жесткий алгоритм. Но вот чтобы уверенно себя чувствовать в методе Гаусса, следует «набить руку», и прорешать хотя бы 5-10 десять систем. Поэтому поначалу возможны путаница, ошибки в вычислениях, и в этом нет ничего необычного или трагического.
Дождливая осенняя погода за окном…. Поэтому для всех желающих более сложный пример для самостоятельного решения:
Пример 5
Решить методом Гаусса систему 4-х линейных уравнений с четырьмя неизвестными.
Такое задание на практике встречается не так уж и редко. Думаю, даже чайнику, который обстоятельно изучил эту страницу, интуитивно понятен алгоритм решения такой системы. Принципиально всё так же – просто действий больше.
Случаи, когда система не имеет решений (несовместна) или имеет бесконечно много решений, рассмотрены на уроке Несовместные системы и системы с общим решением . Там же можно закрепить рассмотренный алгоритм метода Гаусса.
Желаю успехов!
Решения и ответы:
Пример
2: Решение : Запишем
расширенную матрицу системы и с помощью
элементарных преобразований приведем
ее к ступенчатому виду.
Выполненные
элементарные преобразования: (1)
Ко второй строке прибавили первую
строку, умноженную на –2. К третьей
строке прибавили первую строку, умноженную
на –1. Внимание! Здесь
может возникнуть соблазн из третьей
строки вычесть первую, крайне не
рекомендую вычитать – сильно повышается
риск ошибки. Только складываем! (2)
У второй строки сменили знак (умножили
на –1). Вторую и третью строки поменяли
местами. Обратите
внимание ,
что на «ступеньках» нас устраивает не
только единица, но еще и –1, что даже
удобнее. (3)
К третьей строке прибавили вторую
строку, умноженную на 5. (4)
У второй строки сменили знак (умножили
на –1). Третью строку разделили на 14.
Обратный ход:
Ответ : .
Пример
4: Решение : Запишем
расширенную матрицу системы и с помощью
элементарных преобразований приведем
ее к ступенчатому виду:
Выполненные преобразования: (1) К первой строке прибавили вторую. Таким образом, организована нужная единица на левой верхней «ступеньке». (2) Ко второй строке прибавили первую строку, умноженную на 7. К третьей строке прибавили первую строку, умноженную на 6.
Со второй «ступенькой» всё хуже , «кандидаты» на неё – числа 17 и 23, а нам нужна либо единичка, либо –1. Преобразования (3) и (4) будут направлены на получение нужной единицы (3) К третьей строке прибавили вторую, умноженную на –1. (4) Ко второй строке прибавили третью, умноженную на –3. Нужная вещь на второй ступеньке получена . (5) К третьей строке прибавили вторую, умноженную на 6. (6) Вторую строку умножили на –1, третью строку разделили на -83.
Обратный ход:
Ответ :
Пример
5: Решение : Запишем
матрицу системы и с помощью элементарных
преобразований приведем ее к ступенчатому
виду:
Выполненные преобразования: (1) Первую и вторую строки поменяли местами. (2) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –2. К четвертой строке прибавили первую строку, умноженную на –3. (3) К третьей строке прибавили вторую, умноженную на 4. К четвертой строке прибавили вторую, умноженную на –1. (4) У второй строки сменили знак. Четвертую строку разделили на 3 и поместили вместо третьей строки. (5) К четвертой строке прибавили третью строку, умноженную на –5.
Обратный ход:
Ответ :
Здесь вы сможете бесплатно решить систему линейных уравнений методом Гаусса онлайн больших размеров в комплексных числах с очень подробным решением. Наш калькулятор умеет решать онлайн как обычную определенную, так и неопределенную систему линейных уравнений методом Гаусса, которая имеет бесконечное множество решений. В этом случае в ответе вы получите зависимость одних переменных через другие, свободные. Также можно проверить систему уравнений на совместность онлайн, используя решение методом Гаусса.
О методе
При решении системы линейных уравнений онлайн методом Гаусса выполняются следующие шаги.
- Записываем расширенную матрицу.
- Фактически решение разделяют на прямой и обратный ход метода Гаусса. Прямым ходом метода Гаусса называется приведение матрицы к ступенчатому виду. Обратным ходом метода Гаусса называется приведение матрицы к специальному ступенчатому виду. Но на практике удобнее сразу занулять то, что находится и сверху и снизу рассматриваемого элемента. Наш калькулятор использует именно этот подход.
- Важно отметить, что при решении методом Гаусса, наличие в матрице хотя бы одной нулевой строки с НЕнулевой правой частью (столбец свободных членов) говорит о несовместности системы. Решение линейной системы в таком случае не существует.
Чтобы лучше всего понять принцип работы алгоритма Гаусса онлайн введите любой пример, выберите “очень подробное решение” и посмотрите его решение онлайн.
Пусть дана система , ∆≠0. (1)Метод Гаусса – это метод последовательного исключения неизвестных.
Суть метода Гаусса состоит в преобразовании (1) к системе с треугольной матрицей , из которой затем последовательно (обратным ходом) получаются значения всех неизвестных. Рассмотрим одну из вычислительных схем. Эта схема называется схемой единственного деления. Итак, рассмотрим эту схему. Пусть a 11 ≠0 (ведущий элемент) разделим на a 11 первое уравнение. Получим
(2)
Пользуясь уравнением (2), легко исключить неизвестные x 1 из остальных уравнений системы (для этого достаточно из каждого уравнения вычесть уравнение (2) предварительно умноженное на соответствующий коэффициент при x 1), то есть на первом шаге получим
.
Иными словами, на 1 шаге каждый элемент последующих строк, начиная со второй, равен разности между исходным элементом и произведением его «проекции» на первый столбец и первую (преобразованную) строку.
Вслед за этим оставив первое уравнение в покое, над остальными уравнениями системы, полученной на первом шаге, совершим аналогичное преобразование: выберем из их числа уравнение с ведущим элементом и исключим с его помощью из остальных уравнений x 2 (шаг 2).
После n шагов вместо (1) получим равносильную систему
(3)
Таким образом, на первом этапе мы получим треугольную систему (3). Этот этап называется прямым ходом.
На втором этапе (обратный ход) мы находим последовательно из (3) значения x n , x n -1 , …, x 1 .
Обозначим полученное решение за x 0 . Тогда разность ε=b-A·x 0 называется невязкой .
Если ε=0, то найденное решение x 0 является верным.
Вычисления по методу Гаусса выполняются в два этапа:
- Первый этап называется прямым ходом метода. На первом этапе исходную систему преобразуют к треугольному виду.
- Второй этап называется обратным ходом. На втором этапе решают треугольную систему, эквивалентную исходной.
На каждом шаге предполагалось, что ведущий элемент отличен от нуля. Если это не так, то в качестве ведущего можно использовать любой другой элемент, как бы переставив уравнения системы.
Назначение метода Гаусса
Метод Гаусса предназначен для решения систем линейных уравнений. Относится к прямым методам решения.Виды метода Гаусса
- Классический метод Гаусса;
- Модификации метода Гаусса. Одной из модификаций метода Гаусса является схема с выбором главного элемента. Особенностью метода Гаусса с выбором главного элемента является такая перестановка уравнений, чтобы на k -ом шаге ведущим элементом оказывался наибольший по модулю элемент k -го столбца.
- Метод Жордано-Гаусса;
Проиллюстрируем отличие метода Жордано-Гаусса от метода Гаусса на примерах.
Пример решения методом Гаусса
Решим систему:
Для удобства вычислений поменяем строки местами:
Умножим 2-ую строку на (2). Добавим 3-ую строку к 2-ой
Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой
Из 1-ой строки выражаем x 3:
Из 2-ой строки выражаем x 2:
Из 3-ой строки выражаем x 1:
Пример решения методом Жордано-Гаусса
Эту же СЛАУ решим методом Жордано-Гаусса.
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Разрешающий элемент равен (1).
НЭ = СЭ – (А*В)/РЭ
РЭ – разрешающий элемент (1), А и В – элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.
Представим расчет каждого элемента в виде таблицы:
| x 1 | x 2 | x 3 | B |
| 1 / 1 = 1 | 2 / 1 = 2 | -2 / 1 = -2 | 1 / 1 = 1 |
Разрешающий элемент равен (3).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
| x 1 | x 2 | x 3 | B |
| 0 / 3 = 0 | 3 / 3 = 1 | 1 / 3 = 0.33 | 4 / 3 = 1.33 |
Разрешающий элемент равен (-4).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
Представим расчет каждого элемента в виде таблицы:
Ответ : x 1 = 1, x 2 = 1, x 3 = 1
Реализация метода Гаусса
Метод Гаусса реализован на многих языках программирования, в частности: Pascal, C++, php, Delphi , а также имеется реализация метода Гаусса в онлайн режиме .Использование метода Гаусса
Применение метода Гаусса в теории игр
В теории игр при отыскании максиминной оптимальной стратегии игрока составляется система уравнений, которая решается методом Гаусса.Применение метода Гаусса при решении дифференциальных уравнений
Для поиска частного решения дифференциального уравнения сначала находят производные соответствующей степени для записанного частного решения (y=f(A,B,C,D)), которые подставляют в исходное уравнение. Далее, чтобы найти переменные A,B,C,D составляется система уравнений, которая решается методом Гаусса.Применение метода Жордано-Гаусса в линейном программировании
В линейном программировании, в частности в симплекс-методе для преобразования симплексной таблицы на каждой итерации используется правило прямоугольника, в котором используется метод Жордано-Гаусса.4. Метод гаусса
Рассмотрим еще один метод решения систем линейных алгебраических уравнений – метод Гаусса, который применим к любой системе линейных алгебраических уравнений. Иногда этот метод называют методом последовательного исключения неизвестных. Заметим, что при использовании этого метода мы также автоматически будем вычислять ранг матрицы системы.
Итак, пусть задана система mлинейных алгебраических уравнений сnнеизвестными:
(6)
В матричном виде система (6) записывается АХ=В, где А – прямоугольная матрица размера mn:
А=, а Х и В – матрицы-столбцы: Х=, В=.
Если в результате преобразований матрицы системы получится треугольная матрица, то система будет иметь вид:
где
Из последнего уравнения можно найти , а затем, подставляя найденноев предпоследнее уравнение, найтии т.д. В итоге будем иметьединственноерешение,, …,. В этом случае ранг матрицы А системы уравнений равенn.
Если в результате преобразований матрицы системы получится трапециевидная матрица, то система примет вид:
где
В этом случае k<n, следовательно, система уравнений будет неопределенной, то есть будет иметьбесконечное множество решений, так как она содержитn–kсвободных переменных:
Придавая свободным переменным ,, …,произвольные значения, будем иметь каждый раз новое решение исходной системы уравнений, то есть решений будет бесконечное множество. В этом случае ранг матрицы А системы равенk.
Если в результате преобразований получено уравнение, в котором коэффициенты при всех неизвестных равны нулю, а свободный член отличен от нуля, то такая система будет несовместной, то есть не иметь решения.
Следует отметить, что треугольная или трапециевидная форма системы уравнений получалась ввиду предположения, что коэффициентыотличны от нуля. Если же какой-либо из этих коэффициентов равен нулю, то система уравнений приобретет треугольную или трапециевидную форму лишь после надлежащего изменения нумерации неизвестных.
В заключение отметим, что метод Гаусса применяется и для однородных систем линейных алгебраических уравнений. В этом случае, если получаем треугольный вид системы уравнений, то она будет иметь единственное (нулевое) решение == …==0, если же получаем трапециевидный вид системы, то будем иметь бесконечное множество решений.
При решении системы линейных алгебраических уравнений методом Гаусса удобно выписать расширенную матрицу системы и все преобразования выполнять над строками и столбцами расширенной матрицы.
Рассмотрим примеры решения систем линейных алгебраических уравнений методом Гаусса.
Пример 1.
Решение.
Выпишем расширенную матрицу системы:
~ (не меняя первую строку, вычтем из второй
строки первую, из третьей вычтем первую строку, умноженную
на 3) ~ ~ (первую и вторую строки не меняем,
а из третьей вычтем вторую, умноженную на 4) ~ .
Получили матрицу А треугольного вида, причем на диагонали элементы отличны от нуля. Следовательно, ранг матрицы А равен 3, ранг расширенной матрицы также равен 3, и по теореме Кронекера-Капелли исходная система совместна, причем имеет единственное решение. Получим это решение.
Согласно последней матрице исходную систему можно записать в виде:
Из последнего уравнения имеем, что = –1. Подставляяво второе уравнение, получимПодставляяи
в первое уравнение, получим
Ответ:
Пример 2.
Решение.
Выпишем расширенную матрицу системы:
~ (первую и четвертую строки не меняем, из
второй строки вычтем первую, умноженную на 3, из третьей строки вычтем
первую) ~ ~ (первую и вторую строки не меняем, из третьей строки вычтем вторую, умноженную на, а из четвертой вычтем вторую, умноженную на) ~~
~ (первую, вторую и третью строки не меняем, к четвертой строке
прибавим третью) ~ .
В итоге получили трапециевидную матрицу А. Следовательно, если бы последняя строка расширенной матрицы была нулевой, то исходная система уравнений имела бы бесконечное множество решений.
Так как она дает уравнение , которое не имеет решения, то исходная система является несовместной, то есть не имеет решений.
Пример 3.
Решение.
Выпишем расширенную матрицу системы:
~ ~ (разделим третью
строку на 2)~~ (так как три строки одинаковые, то
две из них можно отбросить) ~ .
В итоге получили трапециевидную матрицу. Следовательно, исходная система уравнений неопределенная, то есть имеет бесконечное множество решений. Заметим, что ранг матрицы А равен двум.
Соответствующая система уравнений имеет вид:
В качестве свободных («лишних») переменных примем переменные и, так как минорсоответствует переменными. Получим:
Следовательно,
Подставим в первое уравнение:
Таким образом, найдено решение исходной системы линейных алгебраических уравнений.
Обозначив, получим решение исходной системы
Придаваяпроизвольные числовые значения, каждый раз будем иметь новое решение системы.
Более подробное изложение методов решения систем ЛАУ можно найти в книгах [ 1-4 ].
Математика онлайн
Решение математики онлайн
Math34.biz – это современный способ решения математики, в том числе для сравнения самостоятельных решений с машинными вычислениями.
Пользование сервисом удобно и понятно каждому человеку, попавшему на сайт впервые. Сразу выбираете нужный калькулятор, вводите необходимые данные по вашей задаче и нажимаете кнопку «Решение». За считанные секунды ответ готов.
Чтобы не возникало трудностей с вводом данных, мы подготовили специальную статью Как вводить данные? Помимо правил написания формул и чисел, в ней вы можете увидеть, как правильно вводятся различные константы и математические функции.
О калькуляторах
По мере возможности добавляются новые математические калькуляторы. На сегодняшний день их более 85.
Если не удалось найти нужный калькулятор, которым может быть решена ваша математическая задача, или есть предложение по улучшению имеющегося калькулятора, пожалуйста, сообщите об этом на почту [email protected]
Преимущества
1. Бесплатно
Решение математики онлайн не будет вам стоить ни копейки. Наш сервис абсолютно бесплатный и доступен любому пользователю интернета.
2. Без регистрации
Для пользования калькуляторами не требуется регистрации на сайте, отнимая время на заполнение почтовых ящиков и других личных данных.
3. Подробные решения
На многие задачи вы получите пошаговый развернутый ответ, что позволяет понять, каким образом было получено решение задачи.
4. Разные способы решения задач
Для популярных калькуляторов доступны разные методы решения задач, если они применимы, что позволяет, во-первых, лучше понять, как решается задача известным вам способом, а, во-вторых, научиться решать ту же самую задачу альтернативными методами.
5. Точность вычислений
В полученном ответе не приходится сомневаться, ведь мощная система расчета обеспечивает высокую точность при решении математических задач онлайн.
Однако, мы не исключаем возможность каких-либо ошибок, ведь известно, что алгоритмы пишутся хотя и очень умными, но всё же людьми. В случае обнаружения ошибки, пожалуйста, не поленитесь и сообщите нам о ней.
Метод гаусса подробное объяснение. Метод Гаусса (последовательного исключения неизвестных)
Определение и описание метода Гаусса
Метод преобразований Гаусса (также известный как преобразование методом последовательного исключения неизвестных переменных из уравнения или матрицы) для решения систем линейных уравнений представляет собой классический методом решения системы алгебраических уравнений (СЛАУ). Также этот классический метод используют для решения таких задач как получение обратных матриц и определения ранговости матрицы.
Преобразование с помощью метода Гаусса заключается в совершении небольших (элементарных) последовательных изменениях системы линейных алгебраических уравнений, приводящих к исключению переменных из неё сверху вниз с образованием новой треугольной системы уравнений, являющейся равносильной исходной.
Определение 1
Эта часть решения носит название прямого хода решения Гаусса, так как весь процесс осуществляется сверху вниз.
После приведения исходной системы уравнений к треугольной осуществляется нахождение всех переменных системы снизу вверх (то есть первые найденные переменные занимают находятся именно на последних строчках системы или матрицы). Эта часть решения известна также как обратный ход решения методом Гаусса. Заключается его алгоритм в следующем: сначала вычисляется переменные, находящиеся ближе всего к низу системы уравнений или матрицы, затем полученные значения подставляются выше и таким образом находится ещё одна переменная и так далее.
Описание алгоритма метода Гаусса
Последовательность действий для общего решения системы уравнения методом Гаусса заключается в поочередном применении прямого и обратного хода к матрице на основе СЛАУ. Пусть исходная система уравнений имеет следующий вид:
$\begin{cases} a_{11} \cdot x_1 +…+ a_{1n} \cdot x_n = b_1 \\ … \\ a_{m1} \cdot x_1 + a_{mn} \cdot x_n = b_m \end{cases}$
Чтобы решить СЛАУ методом Гаусса, необходимо записать исходную систему уравнений в виде матрицы:
$A = \begin{pmatrix} a_{11} & … & a_{1n} \\ \vdots & … & \vdots \\ a_{m1} & … & a_{mn} \end{pmatrix}$, $b=\begin{pmatrix} b_1 \\ \vdots \\ b_m \end{pmatrix}$
Матрица $A$ называется основной матрицей и представляет собой записанные по порядку коэффициенты при переменных, а $b$ называется столбцом её свободных членов. Матрица $A$, записанная через черту со столбцом свободных членов называется расширенной матрицей:
$A = \begin{array}{ccc|c} a_{11} & … & a_{1n} & b_1 \\ \vdots & … & \vdots & …\\ a_{m1} & … & a_{mn} & b_m \end{array}$
Теперь необходимо с помощью элементарных преобразований над системой уравнений (или над матрицей, так как это удобнее) привести её к следующему виду:
$\begin{cases} α_{1j_{1}} \cdot x_{j_{1}} + α_{1j_{2}} \cdot x_{j_{2}}…+ α_{1j_{r}} \cdot x_{j_{r}} +… α_{1j_{n}} \cdot x_{j_{n}} = β_1 \\ α_{2j_{2}} \cdot x_{j_{2}}…+ α_{2j_{r}} \cdot x_{j_{r}} +… α_{2j_{n}} \cdot x_{j_{n}} = β_2 \\ …\\ α_{rj_{r}} \cdot x_{j_{r}} +… α_{rj_{n}} \cdot x_{j_{n}} = β_r \\ 0 = β_(r+1) \\ … \\ 0 = β_m \end{cases}$ (1)
Матрица, полученная из коэффициентов преобразованной системы уравнения (1) называется ступенчатой, вот так обычно выглядят ступенчатые матрицы:
$A = \begin{array}{ccc|c} a_{11} & a_{12} & a_{13} & b_1 \\ 0 & a_{22} & a_{23} & b_2\\ 0 & 0 & a_{33} & b_3 \end{array}$
Для этих матриц характерен следующий набор свойств:
- Все её нулевые строки стоят после ненулевых
- Если некоторая строка матрицы с номером $k$ ненулевая, то в предыдущей строчке этой же матрицы нулей меньше, чем в этой, обладающей номером $k$.
После получения ступенчатой матрицы необходимо подставить полученные переменные в оставшиеся уравнения (начиная с конца) и получить оставшиеся значения переменных.
Основные правила и разрешаемые преобразования при использовании метода Гаусса
При упрощении матрицы или системы уравнений этим методом нужно использовать только элементарные преобразования.
Таким преобразованиями считаются операции, которые возможно применять к матрице или системе уравнений без изменения её смысла:
- перестановка нескольких строк местами,
- прибавление или вычитание из одной строчки матрицы другой строчки из неё же,
- умножение или деление строчки на константу, не равную нулю,
- строчку, состоящую из одних нулей, полученную в процессе вычисления и упрощения системы, нужно удалить,
- Также нужно удалить лишние пропорциональные строчки, выбрав для системы единственную из них с более подходящими и удобными для дальнейших вычислений коэффициентами.
Все элементарные преобразования являются обратимыми.
Разбор трёх основных случаев, возникающих при решении линейных уравнений используя метод простых преобразований Гаусса
Различают три возникающих случая при использовании метода Гаусса для решения систем:
- Когда система несовместная, то есть у неё нет каких-либо решений
- У системы уравнений есть решение, причём единственное, а количество ненулевых строк и столбцов в матрице равно между собой.
- Система имеет некое количество или множество возможных решений, а количество строк в ней меньше чем количество столбцов.
Исход решения с несовместной системой
Для этого варианта при решении матричного уравнения методом Гаусса характерно получение какой-то строчки с невозможностью выполнения равенства. Поэтому при возникновении хотя бы одного неправильного равенства полученная и исходная системы не имеют решений вне зависимости от остальных уравнений, которые они содержат. Пример несовместной матрицы:
$\begin{array}{ccc|c} 2 & -1 & 3 & 0 \\ 1 & 0 & 2 & 0\\ 0 & 0 & 0 & 1 \end{array}$
В последней строчке возникло невыполняемое равенство: $0 \cdot x_{31} + 0 \cdot x_{32} + 0 \cdot x_{33} = 1$.
Система уравнений, у которой есть только одно решение
Данные системы после приведения к ступенчатой матрице и удаления строчек с нулями имеют одинаковое количество строк и столбцов в основной матрице. Вот простейший пример такой системы:
$\begin{cases} x_1 – x_2 = -5 \\ 2 \cdot x_1 + x_2 = -7 \end{cases}$
Запишем её в виде матрицы:
$\begin{array}{cc|c} 1 & -1 & -5 \\ 2 & 1 & -7 \end{array}$
Чтобы привести первую ячейку второй строчки к нулю, домножим верхнюю строку на $-2$ и вычтем её из нижней строчки матрицы, а верхнюю строчку оставим в исходном виде, в итоге имеем следующее:
$\begin{array}{cc|c} 1 & -1 & -5 \\ 0 & 3 & 10 \end{array}$
Этот пример можно записать в виде системы:
$\begin{cases} x_1 – x_2 = -5 \\ 3 \cdot x_2 = 10 \end{cases}$
Из нижнего уравнения выходит следующее значение $x$: $x_2 = 3 \frac{1}{3}$. Подставим это значение в верхнее уравнение: $x_1 – 3 \frac{1}{3}$, получаем $x_1 = 1 \frac{2}{3}$.
Система, обладающая множеством возможных вариантов решений
Для этой системы характерно меньшее количество значащих строк, чем количество столбцов в ней (учитываются строки основной матрицы).
Переменные в такой системе делятся на два вида: базисные и свободные. При преобразовании такой системы содержащиеся в ней основные переменные необходимо оставить в левой области до знака “=”, а остальные переменные перенести в правую часть равенства.
У такой системы есть только некое общее решение.
Разберём следующую систему уравнений:
$\begin{cases} 2y_1 + 3y_2 + x_4 = 1 \\ 5y_3 – 4y_4 = 1 \end{cases}$
Запишем её в виде матрицы:
$\begin{array}{cccc|c} 2 & 3 & 0 & 1 & 1 \\ 0 & 0 & 5 & 4 & 1 \\ \end{array}$
Наша задача найти общее решение системы. Для этой матрицы базисными переменными будут $y_1$ и $y_3$ (для $y_1$ – так как он стоит на первом месте, а в случае $y_3$ – располагается после нулей).
В качестве базисных переменных выбираем именно те, которые первые в строке не равны нулю.
Оставшиеся переменные называются свободными, через них нам необходимо выразить базисные.
Используя так называемый обратный ход, разбираем систему снизу вверх, для этого сначала выражаем $y_3$ из нижней строчки системы:
$5y_3 – 4y_4 = 1$
$5y_3 = 4y_4 + 1$
$y_3 = \frac{4/5}y_4 + \frac{1}{5}$.
Теперь в верхнее уравнение системы $2y_1 + 3y_2 + y_4 = 1$ подставляем выраженное $y_3$: $2y_1 + 3y_2 – (\frac{4}{5}y_4 + \frac{1}{5}) + y_4 = 1$
Выражаем $y_1$ через свободные переменные $y_2$ и $y_4$:
$2y_1 + 3y_2 – \frac{4}{5}y_4 – \frac{1}{5} + y_4 = 1$
$2y_1 = 1 – 3y_2 + \frac{4}{5}y_4 + \frac{1}{5} – y_4$
$2y_1 = -3y_2 – \frac{1}{5}y_4 + \frac{6}{5}$
$y_1 = -1.5x_2 – 0.1y_4 + 0.6$
Решение готово.
Пример 1
Решить слау методом Гаусса. Примеры. Пример решения системы линейных уравнений заданных матрицей 3 на 3 используя метод Гаусса
$\begin{cases} 4x_1 + 2x_2 – x_3 = 1 \\ 5x_1 + 3x_2 – 2x^3 = 2\\ 3x_1 + 2x_2 – 3x_3 = 0 \end{cases}$
Запишем нашу систему в виде расширенной матрицы:
$\begin{array}{ccc|c} 4 & 2 & -1 & 1 \\ 5 & 3 & -2 & 2 \\ 3 & 2 & -3 & 0\\ \end{array}$
Теперь для удобства и практичности нужно преобразовать матрицу так, чтобы в верхнем углу крайнего столбца была $1$.
Для этого к 1-ой строчке нужно прибавляем строчку из середины, умноженную на $-1$, а саму среднюю строчку записываем как есть, выходит:
$\begin{array}{ccc|c} -1 & -1 & 1 & -1 \\ 5 & 3 & -2 & 2 \\ 3 & 2 & -3 & 0\\ \end{array}$
$\begin{array}{ccc|c} -1 & -1 & 1 & -1 \\ 0 & -2 & 3 & -3 \\ 0 & -1 & 0 & -3\\ \end{array}$
Домножим верхнюю и последнюю строчки на $-1$, а также поменяем местами последнюю и среднюю строки:
$\begin{array}{ccc|c} 1 & 1 & -1 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & -2 & 3 & -3\\ \end{array}$
$\begin{array}{ccc|c} 1 & 1 & -1 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 3 & 3\\ \end{array}$
И разделим последнюю строчку на $3$:
$\begin{array}{ccc|c} 1 & 1 & -1 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 1\\ \end{array}$
Получаем следующую систему уравнений, равносильную исходной:
$\begin{cases} x_1 + x_2 – x_3 = 1\\ x_2 = 3 \\ x_3 = 1 \end{cases}$
Из верхнего уравнения выражаем $x_1$:
$x1 = 1 + x_3 – x_2 = 1 + 1 – 3 = -1$.
Пример 2
Пример решения системы, заданной с помощью матрицы 4 на 4 методом Гаусса
$\begin{array}{cccc|c} 2 & 5 & 4 & 1 & 20 \\ 1 & 3 & 2 & 1 & 11 \\ 2 & 10 & 9 & 7 & 40\\ 3 & 8 & 9 & 2 & 37 \\ \end{array}$.
В начале меняем местами верхнюю исследующую за ней строчки, чтобы получить в левом верхнем углу $1$:
$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 2 & 5 & 4 & 1 & 20 \\ 2 & 10 & 9 & 7 & 40\\ 3 & 8 & 9 & 2 & 37 \\ \end{array}$.
Теперь умножим верхнюю строчку на $-2$ и прибавим ко 2-ой и к 3-ьей. К 4-ой прибавляем 1-ую строку, домноженную на $-3$:
$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & -1 & 0 & -1 & -2 \\ 0 & 4 & 5 & 5 & 18\\ 0 & -1 & 3 & -1 & 4 \\ \end{array}$
Теперь к строке с номером 3 прибавляем строку 2, умноженную на $4$, а к строке 4 прибавляем строку 2, умноженную на $-1$.
$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & -1 & 0 & -1 & -2 \\ 0 & 0 & 5 & 1 & 10\\ 0 & 0 & 3 & 0 & 6 \\ \end{array}$
Домножаем строку 2 на $-1$, а строку 4 делим на $3$ и ставим на место строки 3.
$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & 1 & 0 & 1 & 2 \\ 0 & 0 & 1 & 0 & 2\\ 0 & 0 & 5 & 1 & 10 \\ \end{array}$
Теперь прибавляем к последней строке предпоследнюю, домноженную на $-5$.
$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & 1 & 0 & 1 & 2 \\ 0 & 0 & 1 & 0 & 2\\ 0 & 0 & 0 & 1 & 0 \\ \end{array}$
Решаем полученную систему уравнений:
$\begin{cases} m = 0 \\ g = 2\\ y + m = 2\ \ x + 3y + 2g + m = 11\end{cases}$
Цикл «Занимательная математика» посвящен деткам увлекающимся математикой и родителям, которые уделяют время развитию своих детей, «подкидывая» им интересные и занимательные задачки, головоломки.
Первая статья из этого цикла посвящена правилу Гаусса.
Немного истории
Известный немецкий математик Карл Фридрих Гаусс (1777-1855) с раннего детства отличался от своих сверстников. Несмотря на то, что он был из небогатой семьи, он достаточно рано научился читать, писать, считать. В его биографии есть даже упоминание того, что в возрасте 4-5 лет он смог скорректировать ошибку в неверных подсчетах отца, просто наблюдая за ним.
Одно из первых его открытий было сделано в возрасте 6 лет на уроке математики. Учителю было необходимо увлечь детей на продолжительное время и он предложил следующую задачку:
Найти сумму всех натуральных чисел от 1 до 100.
Юный Гаусс справился с этим заданием достаточно быстро, найдя интересную закономерность, которая получила большое распространение и применяется по сей день при устном счете.
Давайте попробуем решить эту задачку устно. Но для начала возьмем числа от 1 до 10:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
Посмотрите внимательно на эту сумму и попробуйте догадаться, что же необычного смог разглядеть Гаусс? Для ответа необходимо хорошо представлять себе состав чисел.
Гаусс сгруппировал числа следующим образом:
(1+10) + (2+9) + (3+8) + (4+7) + (5+6)
Таким образом маленький Карл получил 5 пар чисел, каждая из которых в отдельности в сумме дает 11. Тогда, чтобы вычислить сумму натуральных чисел от 1 до 10 необходимо
Вернемся к первоначальной задаче. Гаусс заметил, что перед суммированием необходимо группировать числа в пары и тем самым изобрел алгоритм, благодаря которому можно быстро сложить числа от 1 до100:
1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100
Находим количество пар в ряде натуральных чисел. В данном случае их 50.
Суммируем первое и последнее числа данного ряда. В нашем примере — это 1 и 100. Получаем 101.
Умножаем полученную сумму первого и последнего члена ряда на количество пар этого ряда. Получаем 101 * 50 = 5050
Следовательно, сумма натуральных чисел от 1 до 100 равна 5050.
Задачи на использование правила Гаусса
А сейчас вашему вниманию предлагаются задачи, в которых в той или иной степени используется правило Гаусса. Эти задачки вполне способен понять и решить четвероклассник.
Можно дать возможность ребенку порассуждать самому, чтобы он сам «изобрел» это правило. А можно разобрать вместе и посмотреть как он сможет его применить. Среди ниже приведенных задач есть примеры, в которых нужно понять как модифицировать правило Гаусса, чтобы его применить к данной последовательности.
В любом случае, чтобы ребенок мог оперировать этим в своих вычислениях необходимо понимание алгоритма Гаусса, то есть умение разбить правильно по парам и посчитать.
Важно! Если будет заучена формула без понимания, то это очень быстро будет забыто.
Задача 1Найти сумму чисел:
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10;
- 1 + 2 + 3 + … + 14 + 15 + 16;
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9;
- 1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100.
Решение.
Вначале можно дать возможность ребенку самому решить первый пример и предложить найти способ, при котором это сделать легко в уме. Далее разобрать этот пример вместе с ребенком и показать как это сделал Гаусс. Лучше всего для наглядности записать ряд и соединить линиями пары чисел, дающие в сумме одинаковое число. Важно, чтобы ребенок понял как образуются пары — берем самое маленькое и самое большое из оставшихся чисел при условии, что количество чисел в ряду четно.
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = (1 + 10) + (2 + 9) + (3 + 8) + (4 + 7) + (5 + 6) = (1 + 10) * 5;
- 1 + 2 + 3 + … + 14 + 15 + 16 = (1 + 16) + (2 + 15) + (3 + 14) + (4 + 13) + (5 + 12) + (6 + 11) + (7 + 10) + (8 + 9) = (1 + 16) * 8 = 136;
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + 8) + (2 + 7) + (3 + 6) + (4 + 5) + 9 = (1+ 8) * 4 + 9 = 45;
- 1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100 = (1 + 100) * 50 = 5050
Имеется 9 гирь весом 1г, 2г, 3г, 4г, 5г, 6г, 7г, 8г, 9г. Можно ли разложить эти гири на три кучки с равным весом?
Решение.
С помощью правила Гаусса находим сумму всех весов:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + 8) * 4 + 9 = 45 (г)
Значит, если мы сможем сгруппировать гири так, чтобы в каждой кучке были гири суммарным весом 15г, то задача решена.
Один из вариантов:
- 9г, 6г
- 8г, 7г
- 5г, 4г, 3г, 2г, 1г
Другие возможные варианты найдите сами с ребенком.
Обратите внимание ребенка на то, что когда решаются подобные задачи лучше всегда начинать группировать с большего веса (числа).
Задача 3Можно ли разделить циферблат часов прямой линией на две части так, чтобы суммы чисел в каждой части были равны?
Решение.
Для начала к ряду чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 применим правило Гаусса: найдем сумму и посмотрим, делится ли она на 2:
Значит разделить можно. Теперь посмотрим как.
Следовательно, надо провести линию на циферблате так, чтобы 3 пары попали в одну половину, а три в другую.
Ответ: линия пройдет между числами 3 и 4, а затем между числами 9 и 10.
Задача 4Можно ли провести на циферблате часов две прямые линией так, чтобы в каждой части сумма чисел была одинаковой?
Решение.
Для начала к ряду чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 применим правило Гаусса: найдем сумму и посмотрим делиться ли она на 3:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = (1 + 12) * 6 = 78
78 делиться на 3 без остатка, значит разделить можно. Теперь посмотрим как.
По правилу Гаусса у нас получается 6 пар чисел, каждая из которых в сумме дает 13:
1 и 12, 2 и 11, 3 и 10, 4 и 9, 5 и 8, 6 и 7.
Следовательно, надо провести линии на циферблате так, чтобы в каждую часть попали по 2 пары.
Ответ: первая линия пройдет между числами 2 и 3, а затем между числами 10 и 11; вторая линия — между числами 4 и 5, а затем между 8 и 9.
Задача 5Летит стая птиц. Впереди одна птица (вожак), за ней две, потом три, четыре и т. д. Сколько птиц в стае, если в последнем ряду их 20?
Решение.
Получаем, что нам необходимо сложить числа от 1 до 20. А к вычислению такой суммы можно применить правило Гаусса:
1 + 2 + 3 + 4 + 5 + … + 15 + 16 + 17 + 18 + 19 + 20 = (20 + 1) * 10 = 210.
Задача 6Как рассадить 45 кроликов в 9 клеток так, чтобы во всех клетках было разное количество кроликов?
Решение.
Если ребенок решил и с пониманием разобрал примеры из задания 1, то тут же вспоминается, что 45 это сумма чисел от 1 до 9. Следовательно, сажаем кроликов так:
- первая клетка — 1,
- вторая — 2,
- третья — 3,
- восьмая — 8,
- девятая — 9.
Но если ребенок сразу не может сообразить, то попробуйте натолкнуть его на мысль о том, что подобные задачи можно решить перебором и надо начинать с минимального числа.
Задача 7Вычислить сумму, используя прием Гаусса:
- 31 + 32 + 33 + … + 40;
- 5 + 10 + 15 + 20 + … + 100;
- 91 + 81 + … + 21 + 11 + 1;
- 1 + 2 + 3 + 4 + … + 18 + 19 + 20;
- 1 + 2 + 3 + 4 + 5 + 6;
- 4 + 6 + 8 + 10 + 12 + 14;
- 4 + 6 + 8 + 10 + 12;
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11.
Решение.
- 31 + 32 + 33 + … + 40 = (31 + 40) * 5 = 355;
- 5 + 10 + 15 + 20 + … + 100 = (5 + 100) * 10 = 1050;
- 91 + 81 + … + 21 + 11 + 1 = (91 + 1) * 5 = 460;
- 1 + 2 + 3 + 4 + … + 18 + 19 + 20 = (1 + 20) * 10 =210;
- 1 + 2 + 3 + 4 + 5 + 6 = (1 + 6) * 3 = 21;
- 4 + 6 + 8 + 10 + 12 + 14 = (4 + 14) * 3 = 54;
- 4 + 6 + 8 + 10 + 12 = (4 + 10) * 2 + 12 = 40;
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 = (1 + 10) * 5 + 11 = 66.
Имеется набор из 12 гирек массой 1г, 2г, 3г, 4г, 5г, 6г, 7г, 8г, 9г, 10г, 11г, 12г. Из набора убрали 4 гирьки, общая масса которых равна трети общей массы всего набора гирек. Можно ли оставшиеся гирьки расположить на двух чашках весов по 4 штуки на каждой чашке так, чтобы они оказались в равновесии?
Решение.
Применяем правило Гаусса, чтобы найти общую массу гирек:
1 + 2 + 3 + … + 10 + 11 + 12 = (1 + 12) * 6 = 78 (г)
Вычисляем массу гирек, которые убрали:
Следовательно, оставшиеся гирьки (общей массой 78-26 = 52г) надо расположить по 26 г на каждую чашу весов, чтобы они оказались в равновесии.
Нам не известно какие гирьки были убраны, значит мы должны рассмотреть все возможные варианты.
Применяя правило Гаусса можно разбить гирьки на 6 пар с равным весом (по 13г):
1г и 12г, 2г и 11г, 3г и 10, 4г и 9г, 5г и 8г, 6г и 7г.
Тогда лучший вариант, когда при убирании 4 гирек уберутся две пары из приведенных выше. В этом случае у нас останутся 4 пары: 2 пары на одну чашу весов и 2 пары на другую.
Худший вариант — это когда 4 убранные гирьки разобьют 4 пары. У нас останутся 2 неразбитые пары общим весом 26г, значит их помещаем на одну чашу весов, а оставшиеся гирьки можно поместить на другую чашу весов и они тоже будут 26г.
Удачи в развитии Ваших детей.
Одним из простейших способов решения системы линейных уравнений является прием, основанный на вычислении определителей (правило Крамера ). Его преимущество состоит в том, что он позволяет сразу провести запись решения, особенно он удобен в тех случаях, когда коэффициенты системы являются не числами, а какими-то параметрами. Его недостаток – громоздкость вычислений в случае большого числа уравнений, к тому же правило Крамера непосредственно не применимо к системам, у которых число уравнений не совпадает с числом неизвестных. В таких случаях обычно применяют метод Гаусса .
Системы линейных уравнений, имеющие одно и то же множество решений, называются эквивалентными . Очевидно, что множество решений линейной системы не изменится, если какие-либо уравнения поменять местами, или умножить одно из уравнений на какое-либо ненулевое число, или если одно уравнение прибавить к другому.
Метод Гаусса (метод последовательного исключения неизвестных ) заключается в том, что с помощью элементарных преобразований система приводится к эквивалентной системе ступенчатого вида. Сначала с помощью 1-го уравнения исключается x 1 из всех последующих уравнений системы. Затем с помощью2-го уравнения исключается x 2 из 3-го и всех последующих уравнений. Этот процесс, называемый прямым ходом метода Гаусса , продолжается до тех пор, пока в левой части последнего уравнения останется только одно неизвестное x n . После этого производится обратный ход метода Гаусса – решая последнее уравнение, находим x n ; после этого, используя это значение, из предпоследнего уравнения вычисляем x n –1 и т.д. Последним находим x 1 из первого уравнения.
Преобразования Гаусса удобно проводить, осуществляя преобразования не с самими уравнениями, а с матрицами их коэффициентов. Рассмотрим матрицу:
называемую расширенной матрицей системы, ибо в нее, кроме основной матрицы системы, включен столбец свободных членов. Метод Гаусса основан на приведении основной матрицы системы к треугольному виду (или трапециевидному виду в случае неквадратных систем) при помощи элементарных преобразованиях строк (!) расширенной матрицы системы.
Пример 5.1. Решить систему методом Гаусса:
Решение . Выпишем расширенную матрицу системы и, используя первую строку, после этого будем обнулять остальные элементы:
получим нули во 2-й, 3-й и 4-й строках первого столбца:
Теперь нужно чтобы все элементы во втором столбце ниже 2-й строки были равны нулю. Для этого можно умножить вторую строку на –4/7 и прибавить к 3-й строке. Однако чтобы не иметь дело с дробями, создадим единицу во 2-й строке второго столбца и только
Теперь, чтобы получить треугольную матрицу, нужно обнулить элемент четвертой строки 3-го столбца, для этого можно умножить третью строку на 8/54 и прибавить ее к четвертой. Однако чтобы не иметь дело с дробями поменяем местами 3-ю и 4-ю строки и 3-й и 4-й столбец и только после этого произведем обнуление указанного элемента. Заметим, что при перестановке столбцов меняются местами, соответствующие переменные и об этом нужно помнить; другие элементарные преобразования со столбцами (сложение и умножение на число) производить нельзя!
Последняя упрощенная матрица соответствует системе уравнений, эквивалентной исходной:
Отсюда, используя обратный ход метода Гаусса, найдем из четвертого уравнения x 3 = –1; из третьего x 4 = –2, из второго x 2 = 2 и из первого уравнения x 1 = 1. В матричном виде ответ записывается в виде
Мы рассмотрели случай, когда система является определенной, т.е. когда имеется только одно решение. Посмотрим, что получится, если система несовместна или неопределенна.
Пример 5.2. Исследовать систему методом Гаусса:
Решение . Выписываем и преобразуем расширенную матрицу системы
Записываем упрощенную систему уравнений:
Здесь, в последнем уравнении получилось, что 0=4, т.е. противоречие. Следовательно, система не имеет решения, т.е. она несовместна . à
Пример 5.3. Исследовать и решить систему методом Гаусса:
Решение . Выписываем и преобразуем расширенную матрицу системы:
В результате преобразований, в последней строке получились одни нули. Это означает, что число уравнений уменьшилось на единицу:
Таким образом, после упрощений осталось два уравнения, а неизвестных четыре, т.е. два неизвестных “лишних”. Пусть “лишними”, или, как говорят, свободными переменными , будут x 3 и x 4 . Тогда
Полагая x 3 = 2a и x 4 = b , получим x 2 = 1–a и x 1 = 2b –a ; или в матричном виде
Записанное подобным образом решение называется общим , поскольку, придавая параметрам a и b различные значения, можно описать все возможные решения системы. à
Метод Гаусса – это просто! Почему? Известный немецкий математик Иоганн Карл Фридрих Гаусс еще при жизни получил признание величайшего математика всех времен, гения и даже прозвище «короля математики». А всё гениальное, как известно – просто! Кстати, на деньги попадают не только лохи, но еще и гении – портрет Гаусса красовался на купюре в 10 дойчмарок (до введения евро), и до сих пор Гаусс загадочно улыбается немцам с обычных почтовых марок.
Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА. Необходимо уметь складывать и умножать! Не случайно метод последовательного исключения неизвестных преподаватели часто рассматривают на школьных математических факультативах. Парадокс, но у студентов метод Гаусса вызывает наибольшие сложности. Ничего удивительного – всё дело в методике, и я постараюсь в доступной форме рассказать об алгоритме метода.
Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:
1) Иметь единственное решение.
2) Иметь бесконечно много решений.
3) Не иметь решений (быть несовместной ).
Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случае приведет нас к ответу! На данном уроке мы опять рассмотрим метод Гаусса для случая №1 (единственное решение системы), под ситуации пунктов №№2-3 отведена статья . Замечу, что сам алгоритм метода во всех трёх случаях работает одинаково.
Вернемся к простейшей системе с урока Как решить систему линейных уравнений?
и решим ее методом Гаусса.
На первом этапе нужно записать расширенную матрицу системы :
. По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.
Справка : рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: . Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: . Любую из матриц можно для краткости называть просто матрицей.
После того, как расширенная матрица системы записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями .
Существуют следующие элементарные преобразования:
1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки:
2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. Рассмотрим, например матрицу . В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них: .
3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить . Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули .
4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля . Рассмотрим, например, матрицу . Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2: . Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.
5) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число , отличное от нуля. Рассмотрим нашу матрицу из практического примера: . Сначала я распишу преобразование очень подробно. Умножаем первую строку на –2: , и ко второй строке прибавляем первую строку умноженную на –2 : . Теперь первую строку можно разделить «обратно» на –2: . Как видите, строка, которую ПРИБАВЛЯЛИ – не изменилась . Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ .
На практике так подробно, конечно, не расписывают, а пишут короче:
Еще раз: ко второй строке прибавили первую строку, умноженную на –2 . Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:
«Переписываю матрицу и переписываю первую строку: »
«Сначала первый столбец. Внизу мне нужно получить ноль. Поэтому единицу вверху умножаю на –2: , и ко второй строке прибавляю первую: 2 + (–2) = 0. Записываю результат во вторую строку: »
«Теперь второй столбец. Вверху –1 умножаю на –2: . Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку: »
«И третий столбец. Вверху –5 умножаю на –2: . Ко второй строке прибавляю первую: –7 + 10 = 3. Записываю результат во вторую строку: »
Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане». Но, конечно, над этим преобразованием мы еще поработаем.
Элементарные преобразования не меняют решение системы уравнений
! ВНИМАНИЕ : рассмотренные манипуляции нельзя использовать , если Вам предложено задание, где матрицы даны «сами по себе». Например, при «классических» действиях с матрицами что-то переставлять внутри матриц ни в коем случае нельзя!
Вернемся к нашей системе . Она практически разобрана по косточкам.
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду :
(1) Ко второй строке прибавили первую строку, умноженную на –2. И снова: почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.
(2) Делим вторую строку на 3.
Цель элементарных преобразований – привести матрицу к ступенчатому виду: . В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид .
В результате элементарных преобразований получена эквивалентная исходной система уравнений:
Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса .
В нижнем уравнении у нас уже готовый результат: .
Рассмотрим первое уравнение системы и подставим в него уже известное значение «игрек»:
Рассмотрим наиболее распространенную ситуацию, когда методом Гаусса требуется решить систему трёх линейных уравнений с тремя неизвестными.
Пример 1
Решить методом Гаусса систему уравнений:
Запишем расширенную матрицу системы:
Сейчас я сразу нарисую результат, к которому мы придём в ходе решения:
И повторюсь, наша цель – с помощью элементарных преобразований привести матрицу к ступенчатому виду. С чего начать действия?
Сначала смотрим на левое верхнее число:
Почти всегда здесь должна находиться единица . Вообще говоря, устроит и –1 (а иногда и другие числа), но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки:
Теперь первая строка у нас останется неизменной до конца решения . Уже легче.
Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах:
Нули получаем как раз с помощью «трудного» преобразования. Сначала разбираемся со второй строкой (2, –1, 3, 13). Что нужно сделать, чтобы на первой позиции получить ноль? Нужно ко второй строке прибавить первую строку, умноженную на –2 . Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18). И последовательно проводим (опять же мысленно или на черновике) сложение, ко второй строке прибавляем первую строку, уже умноженную на –2 :
Результат записываем во вторую строку:
Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3 . Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). И к третьей строке прибавляем первую строку, умноженную на –3 :
Результат записываем в третью строку:
На практике эти действия обычно выполняются устно и записываются в один шаг:
Не нужно считать всё сразу и одновременно . Порядок вычислений и «вписывания» результатов последователен и обычно такой: сначала переписываем первую строку, и пыхтим себе потихонечку – ПОСЛЕДОВАТЕЛЬНО и ВНИМАТЕЛЬНО :
А мысленный ход самих расчётов я уже рассмотрел выше.
В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение:
На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь:
Для этого к третьей строке прибавляем вторую строку, умноженную на –2 :
Попробуйте разобрать это действие самостоятельно – мысленно умножьте вторую строку на –2 и проведите сложение.
Последнее выполненное действие – причёска результата, делим третью строку на 3.
В результате элементарных преобразований получена эквивалентная исходной система линейных уравнений:
Круто.
Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.
В третьем уравнении у нас уже готовый результат:
Смотрим на второе уравнение: . Значение «зет» уже известно, таким образом:
И, наконец, первое уравнение: . «Игрек» и «зет» известны, дело за малым:
Ответ :
Как уже неоднократно отмечалось, для любой системы уравнений можно и нужно сделать проверку найденного решения, благо, это несложно и быстро.
Пример 2
Это пример для самостоятельного решения, образец чистового оформления и ответ в конце урока.
Следует отметить, что ваш ход решения может не совпасть с моим ходом решения, и это – особенность метода Гаусса . Но вот ответы обязательно должны получиться одинаковыми!
Пример 3
Решить систему линейных уравнений методом Гаусса
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так:
(1) К первой строке прибавляем вторую строку, умноженную на –1 . То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.
Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное телодвижение: умножить первую строку на –1 (сменить у неё знак).
(2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.
(3) Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.
(4) К третьей строке прибавили вторую строку, умноженную на 2.
(5) Третью строку разделили на 3.
Скверным признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде , и, соответственно, , то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.
Заряжаем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает, снизу вверх. Да тут подарок получился:
Ответ : .
Пример 4
Решить систему линейных уравнений методом Гаусса
Это пример для самостоятельного решения, он несколько сложнее. Ничего страшного, если кто-нибудь запутается. Полное решение и образец оформления в конце урока. Ваше решение может отличаться от моего решения.
В последней части рассмотрим некоторые особенности алгоритма Гаусса.
Первая особенность состоит в том, что иногда в уравнениях системы отсутствуют некоторые переменные, например:
Как правильно записать расширенную матрицу системы? Об этом моменте я уже рассказывал на уроке Правило Крамера. Матричный метод . В расширенной матрице системы на месте отсутствующих переменных ставим нули:
Кстати, это довольно легкий пример, поскольку в первом столбце уже есть один ноль, и предстоит выполнить меньше элементарных преобразований.
Вторая особенность состоит вот в чём. Во всех рассмотренных примерах на «ступеньки» мы помещали либо –1, либо +1. Могут ли там быть другие числа? В ряде случаев могут. Рассмотрим систему: .
Здесь на левой верхней «ступеньке» у нас двойка. Но замечаем тот факт, что все числа в первом столбце делятся на 2 без остатка – и другая двойка и шестерка. И двойка слева вверху нас устроит! На первом шаге нужно выполнить следующие преобразования: ко второй строке прибавить первую строку, умноженную на –1; к третьей строке прибавить первую строку, умноженную на –3. Таким образом, мы получим нужные нули в первом столбце.
Или еще такой условный пример: . Здесь тройка на второй «ступеньке» тоже нас устраивает, поскольку 12 (место, где нам нужно получить ноль) делится на 3 без остатка. Необходимо провести следующее преобразование: к третьей строке прибавить вторую строку, умноженную на –4, в результате чего и будет получен нужный нам ноль.
Метод Гаусса универсален, но есть одно своеобразие. Уверенно научиться решать системы другими методами (методом Крамера, матричным методом) можно буквально с первого раза – там очень жесткий алгоритм. Но вот чтобы уверенно себя чувствовать в методе Гаусса, следует «набить руку», и прорешать хотя бы 5-10 систем. Поэтому поначалу возможны путаница, ошибки в вычислениях, и в этом нет ничего необычного или трагического.
Дождливая осенняя погода за окном…. Поэтому для всех желающих более сложный пример для самостоятельного решения:
Пример 5
Решить методом Гаусса систему четырёх линейных уравнений с четырьмя неизвестными.
Такое задание на практике встречается не так уж и редко. Думаю, даже чайнику, который обстоятельно изучил эту страницу, интуитивно понятен алгоритм решения такой системы. Принципиально всё так же – просто действий больше.
Случаи, когда система не имеет решений (несовместна) или имеет бесконечно много решений, рассмотрены на уроке Несовместные системы и системы с общим решением . Там же можно закрепить рассмотренный алгоритм метода Гаусса.
Желаю успехов!
Решения и ответы:
Пример 2: Решение : Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.
Выполненные элементарные преобразования:
(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –1. Внимание! Здесь может возникнуть соблазн из третьей строки вычесть первую, крайне не рекомендую вычитать – сильно повышается риск ошибки. Только складываем!
(2) У второй строки сменили знак (умножили на –1). Вторую и третью строки поменяли местами. Обратите внимание , что на «ступеньках» нас устраивает не только единица, но еще и –1, что даже удобнее.
(3) К третьей строке прибавили вторую строку, умноженную на 5.
(4) У второй строки сменили знак (умножили на –1). Третью строку разделили на 14.
Обратный ход:
Ответ : .
Пример 4: Решение : Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
Выполненные преобразования:
(1) К первой строке прибавили вторую. Таким образом, организована нужная единица на левой верхней «ступеньке».
(2) Ко второй строке прибавили первую строку, умноженную на 7. К третьей строке прибавили первую строку, умноженную на 6.
Со второй «ступенькой» всё хуже , «кандидаты» на неё – числа 17 и 23, а нам нужна либо единичка, либо –1. Преобразования (3) и (4) будут направлены на получение нужной единицы
(3) К третьей строке прибавили вторую, умноженную на –1.
(4) Ко второй строке прибавили третью, умноженную на –3.
(3) К третьей строке прибавили вторую, умноженную на 4. К четвертой строке прибавили вторую, умноженную на –1.
(4) У второй строки сменили знак. Четвертую строку разделили на 3 и поместили вместо третьей строки.
(5) К четвертой строке прибавили третью строку, умноженную на –5.
Обратный ход:
Метод Гаусса был предложен известнейшим немецким математиком Карлом Фридрихом Гауссом (1777 – 1855) и является одним из наиболее универсальных методов решения СЛАУ. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении задачи, расширенная матрица системы с помощью элементарных преобразований над ее строками приводится к ступенчатому виду. Далее последовательно находятся все неизвестные, начиная снизу вверх.
Принцип метода Гаусса
Метод Гаусса включает в себя прямой (приведение расширенной матрицы к ступенчатому виду, то есть получение нулей под главной диагональю) и обратный (получение нулей над главной диагональю расширенной матрицы) ходы. Прямой ход и называется методом Гаусса, обратный – методом Гаусса-Жордана, который отличается от первого только последовательностью исключения переменных.
Метод Гаусса идеально подходит для решения систем содержащих больше трех линейных уравнений, для решения систем уравнений, которые не являются квадратными (чего не скажешь про метод Крамера и матричный метод). То есть метод Гаусса – наиболее универсальный метод для нахождения решения любой системы линейных уравнений, он работает в случае, когда система имеет бесконечно много решений или несовместна.
Примеры решения систем уравнений
Пример
Задание. Решить СЛАУ методом Гаусса.
Решение. Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса (сделаем нули выше главной диагонали). Вначале поменяем первую и вторую строку, чтобы элемент равнялся 1 (это мы делаем для упрощения вычислений):
Все элементы третьей строки делим на два (или, что тоже самое, умножаем на ):
От третьей строки отнимаем вторую, умноженную на 3:
Умножив третью строку на , получаем:
Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю. Начнем с элементов третьего столбца. Надо обнулить элемент , для этого от второй строки отнимем третью.
Уравнения. Как решать уравнения с дробями
Инструкция
Способ подстановкиВыразите одну переменную и подставте ее в другое уравнение. Выражать можно любую переменную по вашему усмотрению. Например, выразите «у из второго уравнения:
х-у=2 => у=х-2Затем подставьте все в первое уравнение:
2х+(х-2)=10Перенесите все без «х в правую часть и подсчитайте:
2х+х=10+2
3х=12 Далее, чтобы «х, разделите обе части уравнения на 3:
х=4.Итак, вы нашли «х. Найдите «у. Для этого подставьте «х в то уравнение, из которого вы выразили «у:
у=х-2=4-2=2
у=2.
Сделайте проверку. Для этого подставьте получившиеся значения в уравнения:
2*4+2=10
4-2=2
Неизвестные найдены верно!
Способ сложения или вычитания уравненийИзбавьтесь сразу от -нибудь перемененной. В нашем случае это проще сделать с «у.
Так как в «у со знаком «+ , а во втором «- , то вы можете выполнить операцию сложения, т.е. левую часть складываем с левой, а правую с правой:
2х+у+(х-у)=10+2Преобразуйте:
2х+у+х-у=10+2
3х=12
х=4Подставьте «х в любое уравнение и найдите «у:
2*4+у=10
8+у=10
у=10-8
у=2По 1-ому способу можете , что найдены верно.
Если нет четко выраженных переменных, то необходимо немного преобразовать уравнения.
В первом уравнении имеем «2х, а во втором просто «х. Для того, чтобы при сложении или «х сократился, второе уравнение умножьте на 2:
х-у=2
2х-2у=4Затем вычтите из первого уравнения второе:
2х+у-(2х-2у)=10-4Заметим, если перед скобкой стоит минус, то после раскрытия поменяйте на противоположные:
2х+у-2х+2у=6
3у=6
у=2«х найдите, выразив из любого уравнения, т.е.
х=4
Видео по теме
Уравнение , в общем виде записанное ах+bу+с=0, называется линейным уравнением с двумя переменными . Такое уравнение само по себе содержит бесконечное множество решений, поэтому в задачах оно всегда чем-либо дополняется – еще одним уравнением или ограничивающими условиями. В зависимости от условий, предоставленных задачей, решать линейное уравнение с двумя переменными следует разными способами.
Вам понадобится
- – линейное уравнение с двумя переменными;
- – второе уравнение или дополнительные условия.
Инструкция
Если дана система из двух линейных уравнений, решайте ее следующим образом. Выберите одно из уравнений, в котором коэффициенты перед переменными поменьше и выразите одну из переменных, например, х. Затем подставьте это значение, содержащее у, во второе уравнение. В полученном уравнении будет лишь одна переменная у, перенесите все части с у в левую часть, а свободные – в правую. Найдите у и подставьте в любое из первоначальных уравнений, найдите х.
Решить систему из двух уравнений можно и другим способом. Умножьте одно из уравнений на число, чтобы коэффициент перед одной из переменных, например, перед х, был одинаков в обоих уравнениях. Затем вычтите одно из уравнений из другого (если правая часть не равна 0, не забудьте вычесть аналогично и правые части). Вы увидите, что переменная х исчезла, и осталась только одна переменная у. Решите полученное уравнение, и подставьте найденное значение у в любое из первоначальных равенств. Найдите х.
Третий способ решения системы двух линейных уравнений – графический. Начертите систему координат и изобразите графики двух прямых, уравнения которых указаны в вашей системе. Для этого подставляйте любые два значения х в уравнение и находите соответствующие у – это будут координаты точек, принадлежащих прямой. Удобнее всего находить пересечение с осями координат – достаточно подставить значения х=0 и у=0. Координаты точки пересечения этих двух линий и будут задачи.
Если в условиях задачи лишь одно линейное уравнение, значит, вам даны дополнительные условия, благодаря которым можно найти решение. Внимательно прочитайте задачу, чтобы найти эти условия. Если переменными х и у обозначены расстояние, скорость, вес – смело ставьте ограничение х≥0 и у≥0. Вполне возможно, под х или у скрывается количество , яблок, и т.д. – тогда значениями могут быть только . Если х – возраст сына, понятно, что он не может быть старше отца, поэтому укажите это в условиях задачи.
Источники:
- как решить уравнение с одной переменной
Само по себе уравнение с тремя неизвестными имеет множество решений, поэтому чаще всего оно дополняется еще двумя уравнениями или условиями. В зависимости от того, каковы исходные данные, во многом будет зависеть ход решения.
Вам понадобится
- – система из трех уравнений с тремя неизвестными.
Инструкция
Если два из трех системы имеют лишь две неизвестные из трех, попытайтесь выразить одни переменные через другие и подставить их в уравнение с тремя неизвестными . Ваша цель при этом – превратить его в обычное уравнение с неизвестной. Если это , дальнейшее решение довольно просто – подставьте найденное значение в другие уравнения и найдите все остальные неизвестные.
Некоторые системы уравнений можно вычитанием из одного уравнения другого. Посмотрите, нет ли возможности умножить одно из на или переменную так, чтобы сократились сразу две неизвестные. Если такая возможность есть, воспользуйтесь ею, скорее всего, последующее решение не составит труда. Не забывайте, что при умножении на число необходимо умножать как левую часть, так и правую. Точно также, при вычитании уравнений необходимо помнить о том, что правая часть должна также вычитаться.
Если предыдущие способы не помогли, воспользуйтесь общим способом решений любых уравнений с тремя неизвестными . Для этого перепишите уравнения в виде а11х1+a12х2+а13х3=b1, а21х1+а22х2+а23х3=b2, а31х1+а32х2+а33х3=b3. Теперь составьте матрицу коэффициентов при х (А), матрицу неизвестных (Х) и матрицу свободных (В). Обратите внимание, умножая матрицу коэффициентов на матрицу неизвестных, вы получите матрицу, матрице свободных членов, то есть А*Х=В.
Найдите матрицу А в степени (-1) предварительно отыскав , обратите внимание, он не должен быть равен нулю. После этого умножьте полученную матрицу на матрицу В, в результате вы получите искомую матрицу Х, с указанием всех значений.
Найти решение системы из трех уравнений можно также с помощью метода Крамера. Для этого найдите определитель третьего порядка ∆, соответствующий матрице системы. Затем последовательно найдите еще три определителя ∆1, ∆2 и ∆3, подставляя вместо значений соответствующих столбцов значения свободных членов. Теперь найдите х: х1=∆1/∆, х2=∆2/∆, х3=∆3/∆.
Источники:
- решений уравнений с тремя неизвестными
Решение системы уравнений сложно и увлекательно. Чем сложнее система, тем интереснее ее решать. Чаще всего в математике средней школы встречаются системы уравнений с двумя неизвестными, но в высшей математике переменных может быть и больше. Решать системы можно несколькими методами.
Инструкция
Самый распространенный метод решения системы уравнений – это подстановка. Для этого необходимо выразить одну переменную через другую и подставить ее во второе уравнение системы, таким образом приведя уравнение к одной переменной. Например, дана уравнений:2х-3у-1=0;х+у-3=0.
Из второго выражения удобно выразить одну из переменных, перенеся все остальное в правую часть выражения, не забыв при этом сменить знак коэффициента:х=3-у.
Раскрываем скобки: 6-2у-3у-1=0;-5у+5=0;у=1.Полученное значение у подставляем в выражение:х=3-у;х=3-1;х=2.
В первом выражении все члены 2, можно вынести 2 за скобку распределительному свойству умножения:2*(2х-у-3)=0. Теперь обе части выражения можно сократить на это число, а затем выразить у, так как коэффициент по модулю при нем равен единице:-у=3-2х или у=2х-3.
Так же, как и в первом случае, подставляем данное выражение во второе уравнение и получаем:3х+2*(2х-3)-8=0;3х+4х-6-8=0;7х-14=0;7х=14;х=2.2 ? 4ac. При этом переменные a, b, c являются коэффициентами нашего уравнения.
Найдите корни биквадратного уравнения. Для этого возьмите корень квадратный из полученных решений . Если решение было одно, то будет два – положительное и отрицательное значение корня квадратного. Если решений было два, у биквадратного уравнения будет четыре корня.
Видео по теме
Одним из классических способов решения систем линейных уравнений является метод Гаусса. Он заключается в последовательном исключении переменных, когда система уравнений с помощью простых преобразований переводится в ступенчатую систему, из которой последовательно находятся все переменные, начиная с последних.
Инструкция
Сначала приведите систему уравнений в такой вид, когда все неизвестные будут стоять в строго определенном порядке. Например, все неизвестные Х будут стоять первыми в каждой строке, все Y – после X, все Z – после Y и так далее. В правой части каждого уравнения неизвестных быть не должно. Мысленно определите коэффициенты, стоящие перед каждой неизвестной, а также коэффициенты в правой части каждого уравнения.
Разберем два вида решения систем уравнения:
1. Решение системы методом подстановки.
2. Решение системы методом почленного сложения (вычитания) уравнений системы.
Для того чтобы решить систему уравнений методом подстановки нужно следовать простому алгоритму:
1. Выражаем. Из любого уравнения выражаем одну переменную.
2. Подставляем. Подставляем в другое уравнение вместо выраженной переменной, полученное значение.
3. Решаем полученное уравнение с одной переменной. Находим решение системы.
Чтобы решить систему методом почленного сложения (вычитания) нужно:
1.Выбрать переменную у которой будем делать одинаковые коэффициенты.
2.Складываем или вычитаем уравнения, в итоге получаем уравнение с одной переменной.
3. Решаем полученное линейное уравнение . Находим решение системы.
Решением системы являются точки пересечения графиков функции.
Рассмотрим подробно на примерах решение систем.
Пример №1:
Решим методом подстановки
Решение системы уравнений методом подстановки2x+5y=1 (1 уравнение)
x-10y=3 (2 уравнение)
1. Выражаем
Видно что во втором уравнении имеется переменная x с коэффициентом 1,отсюда получается что легче всего выразить переменную x из второго уравнения.
x=3+10y
2.После того как выразили подставляем в первое уравнение 3+10y вместо переменной x.
2(3+10y)+5y=1
3.Решаем полученное уравнение с одной переменной.
2(3+10y)+5y=1 (раскрываем скобки)
6+20y+5y=1
25y=1-6
25y=-5 |: (25)
y=-5:25
y=-0,2
Решением системы уравнения является точки пересечений графиков, следовательно нам нужно найти x и у, потому что точка пересечения состоит их x и y.Найдем x, в первом пункте где мы выражали туда подставляем y.
x=3+10y
x=3+10*(-0,2)=1
Точки принято записывать на первом месте пишем переменную x, а на втором переменную y.
Ответ: (1; -0,2)
Пример №2:
Решим методом почленного сложения (вычитания).
Решение системы уравнений методом сложения3x-2y=1 (1 уравнение)
2x-3y=-10 (2 уравнение)
1.Выбираем переменную, допустим, выбираем x. В первом уравнении у переменной x коэффициент 3, во втором 2. Нужно сделать коэффициенты одинаковыми, для этого мы имеем право домножить уравнения или поделить на любое число. Первое уравнение домножаем на 2, а второе на 3 и получим общий коэффициент 6.
3x-2y=1 |*2
6x-4y=2
2x-3y=-10 |*3
6x-9y=-30
2.Из первого уравнения вычтем второе, чтобы избавиться от переменной x.Решаем линейное уравнение.
__6x-4y=2
5y=32 | :5
y=6,4
3.Находим x. Подставляем в любое из уравнений найденный y, допустим в первое уравнение.
3x-2y=1
3x-2*6,4=1
3x-12,8=1
3x=1+12,8
3x=13,8 |:3
x=4,6
Точкой пересечения будет x=4,6; y=6,4
Ответ: (4,6; 6,4)
Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно . Без шуток.
Линейные уравнения. Решение, примеры.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно “не очень…”
И для тех, кто “очень даже…”)
Линейные уравнения.
Линейные уравнения – не самая сложная тема школьной математики. Но есть там свои фишки, которые могут озадачить даже подготовленного ученика. Разберёмся?)
Обычно линейное уравнение определяется, как уравнение вида:
ax + b = 0 где а и b – любые числа.
2х + 7 = 0. Здесь а=2, b=7
0,1х – 2,3 = 0 Здесь а=0,1, b=-2,3
12х + 1/2 = 0 Здесь а=12, b=1/2
Ничего сложного, правда? Особенно, если не замечать слова: “где а и b – любые числа” … А если заметить, да неосторожно задуматься?) Ведь, если а=0, b=0 (любые же числа можно?), то получается забавное выражение:
Но и это ещё не всё! Если, скажем, а=0, а b=5, получается совсем уж что-то несусветное:
Что напрягает и подрывает доверие к математике, да…) Особенно на экзаменах. А ведь из этих странных выражений ещё и икс найти надо! Которого нету вообще. И, что удивительно, этот икс очень просто находится. Мы научимся это делать. В этом уроке.
Как узнать линейное уравнение по внешнему виду? Это, смотря какой внешний вид.) Фишка в том, что линейными уравнениями называются не только уравнения вида ax + b = 0 , но и любые уравнения, которые преобразованиями и упрощениями сводятся к этому виду. А кто ж его знает, сводится оно, или нет?)
Чётко распознать линейное уравнение можно в некоторых случаях. Скажем, если перед нами уравнение, в которых есть только неизвестные в первой степени, да числа. Причём в уравнении нет дробей с делением на неизвестное , это важно! А деление на число, или дробь числовая – это пожалуйста! Например:
Это линейное уравнение. Здесь есть дроби, но нет иксов в квадрате, в кубе и т.д., и нет иксов в знаменателях, т.е. нет деления на икс . А вот уравнение
нельзя назвать линейным. Здесь иксы все в первой степени, но есть деление на выражение с иксом . После упрощений и преобразований может получиться и линейное уравнение, и квадратное, и всё, что угодно.
Получается, что узнать линейное уравнение в каком-нибудь замудрёном примере нельзя, пока его почти не решишь. Это огорчает. Но в заданиях, как правило, не спрашивают о виде уравнения, правда? В заданиях велят уравнения решать. Это радует.)
Решение линейных уравнений. Примеры.
Всё решение линейных уравнений состоит из тождественных преобразований уравнений. Кстати, эти преобразования (целых два!) лежат в основе решений всех уравнений математики. Другими словами, решение любого уравнения начинается с этих самых преобразований. В случае линейных уравнений, оно (решение) на этих преобразованиях и заканчивается полноценным ответом. Имеет смысл по ссылке сходить, правда?) Тем более, там тоже примеры решения линейных уравнений имеются.
Для начала рассмотрим самый простой пример. Безо всяких подводных камней. Пусть нам нужно решить вот такое уравнение.
х – 3 = 2 – 4х
Это линейное уравнение. Иксы все в первой степени, деления на икс нету. Но, собственно, нам без разницы, какое это уравнение. Нам его решать надо. Схема тут простая. Собрать всё, что с иксами в левой части равенства, всё, что без иксов (числа) – в правой.
Для этого нужно перенести – 4х в левую часть, со сменой знака, разумеется, а – 3 – в правую. Кстати, это и есть первое тождественное преобразование уравнений. Удивлены? Значит, по ссылке не ходили, а зря…) Получим:
х + 4х = 2 + 3
Приводим подобные, считаем:
Что нам не хватает для полного счастья? Да чтобы слева чистый икс был! Пятёрка мешает. Избавляемся от пятёрки с помощью второго тождественного преобразования уравнений. А именно – делим обе части уравнения на 5. Получаем готовый ответ:
Пример элементарный, разумеется. Это для разминки.) Не очень понятно, к чему я тут тождественные преобразования вспоминал? Ну ладно. Берём быка за рога.) Решим что-нибудь посолиднее.
Например, вот это уравнение:
С чего начнём? С иксами – влево, без иксов – вправо? Можно и так. Маленькими шажочками по длинной дороге. А можно сразу, универсальным и мощным способом. Если, конечно, в вашем арсенале имеются тождественные преобразования уравнений.
Задаю вам ключевой вопрос: что вам больше всего не нравится в этом уравнении?
95 человек из 100 ответят: дроби ! Ответ правильный. Вот и давайте от них избавимся. Поэтому начинаем сразу со второго тождественного преобразования . На что нужно умножить дробь слева, чтобы знаменатель сократился напрочь? Верно, на 3. А справа? На 4. Но математика позволяет нам умножать обе части на одно и то же число . Как выкрутимся? А умножим обе части на 12! Т.е. на общий знаменатель. Тогда и тройка сократится, и четвёрка. Не забываем, что умножать надо каждую часть целиком . Вот как выглядит первый шаг:
Раскрываем скобки:
Обратите внимание! Числитель (х+2) я взял в скобки! Это потому, что при умножении дробей, числитель умножается весь, целиком! А теперь дроби и сократить можно:
Раскрываем оставшиеся скобки:
Не пример, а сплошное удовольствие!) Вот теперь вспоминаем заклинание из младших классов: с иксом – влево, без икса – вправо! И применяем это преобразование:
Приводим подобные:
И делим обе части на 25, т.е. снова применяем второе преобразование:
Вот и всё. Ответ: х =0,16
Берём на заметку: чтобы привести исходное замороченное уравнение к приятному виду, мы использовали два (всего два!) тождественных преобразования – перенос влево-вправо со сменой знака и умножение-деление уравнения на одно и то же число. Это универсальный способ! Работать таким образом мы будем с любыми уравнениями! Совершенно любыми. Именно поэтому я про эти тождественные преобразования всё время занудно повторяю.)
Как видим, принцип решения линейных уравнений простой. Берём уравнение и упрощаем его с помощью тождественных преобразований до получения ответа. Основные проблемы здесь в вычислениях, а не в принципе решения.
Но… Встречаются в процессе решения самых элементарных линейных уравнений такие сюрпризы, что могут и в сильный ступор вогнать…) К счастью, таких сюрпризов может быть только два. Назовём их особыми случаями.
Особые случаи при решении линейных уравнений.
Сюрприз первый.
Предположим, попалось вам элементарнейшее уравнение, что-нибудь, типа:
2х+3=5х+5 – 3х – 2
Слегка скучая, переносим с иксом влево, без икса – вправо… Со сменой знака, всё чин-чинарём… Получаем:
2х-5х+3х=5-2-3
Считаем, и… опаньки!!! Получаем:
Само по себе это равенство не вызывает возражений. Нуль действительно равен нулю. Но икс-то пропал! А мы обязаны записать в ответе, чему равен икс. Иначе, решение не считается, да…) Тупик?
Спокойствие! В таких сомнительных случаях спасают самые общие правила. Как решать уравнения? Что значит решить уравнение? Это значит, найти все значения икса, которые, при подстановке в исходное уравнение, дадут нам верное равенство.
Но верное равенство у нас уже получилось! 0=0, куда уж вернее?! Остаётся сообразить, при каких иксах это получается. Какие значения икса можно подставлять в исходное уравнение, если эти иксы всё равно посокращаются в полный ноль? Ну же?)
Да!!! Иксы можно подставлять любые! Какие хотите. Хоть 5, хоть 0,05, хоть -220. Они всё равно сократятся. Если не верите – можете проверить.) Поподставляйте любые значения икса в исходное уравнение и посчитайте. Всё время будет получаться чистая правда: 0=0, 2=2, -7,1=-7,1 и так далее.
Вот вам и ответ: х – любое число.
Ответ можно записать разными математическими значками, суть не меняется. Это совершенно правильный и полноценный ответ.
Сюрприз второй.
Возьмём то же элементарнейшее линейное уравнение и изменим в нём всего одно число. Вот такое будем решать:
2х+1=5х+5 – 3х – 2
После тех же самых тождественных преобразований мы получим нечто интригующее:
Вот так. Решали линейное уравнение, получили странное равенство. Говоря математическим языком, мы получили неверное равенство. А говоря простым языком, неправда это. Бред. Но тем, не менее, этот бред – вполне веское основание для правильного решения уравнения.)
Опять соображаем, исходя из общих правил. Какие иксы, при подстановке в исходное уравнение, дадут нам верное равенство? Да никакие! Нет таких иксов. Чего ни подставляй, всё посократится, останется бред.)
Вот вам и ответ: решений нет.
Это тоже вполне полноценный ответ. В математике такие ответы частенько встречаются.
Вот так. Сейчас, надеюсь, пропажа иксов в процессе решения любого (не только линейного) уравнения вас нисколько не смутит. Дело уже знакомое.)
Теперь, когда мы разобрались со всеми подводными камнями в линейных уравнениях, имеет смысл их порешать.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся – с интересом!)
можно познакомиться с функциями и производными.
Сервис для решения уравнений онлайн поможет вам решить любое уравнение. Используя наш сайт, вы получите не просто ответ уравнения, но и увидите подробное решение, то есть пошаговое отображение процесса получения результата. Наш сервис будет полезен старшеклассникам общеобразовательных школ и их родителям. Ученики смогут подготовиться к контрольным, экзаменам, проверить свои знания, а родители – проконтролировать решение математических уравнений своими детьми. Умение решать уравнения – обязательное требование к школьникам. Сервис поможет вам самообучаться и повышать уровень знаний в области математических уравнений. С его помощью вы сможете решить любое уравнение: квадратное, кубическое, иррациональное, тригонометрическое и др. Польза онлайн сервиса бесценна, ведь кроме верного ответа вы получаете подробное решение каждого уравнения. Преимущества решения уравнений онлайн. Решить любое уравнение онлайн на нашем сайте вы можете абсолютно бесплатно. Сервис полностью автоматический, вам ничего не придется устанавливать на свой компьютер, достаточно будет только ввести данные и программа выдаст решение. Любые ошибки в расчетах или опечатки исключены. С нами решить любое уравнение онлайн очень просто, поэтому обязательно используйте наш сайт для решения любых видов уравнений. Вам необходимо только ввести данные и расчет будет выполнен за считанные секунды. Программа работает самостоятельно, без человеческого участия, а вы получаете точный и подробный ответ. Решение уравнения в общем виде. В таком уравнении переменные коэффициенты и искомые корни связаны между собой. Старшая степень переменной определяет порядок такого уравнения.2-4ac. Если дискриминант меньше нуля, то уравнение не имеет действительных корней (корни находятся из поля комплексных чисел), если равен нулю, то у уравнения один действительный корень, и если дискриминант больше нуля, то уравнение имеет два действительных корня, которые находятся по формуле: D= -b+-sqrt/2а. Для решения квадратного уравнения онлайн вам достаточно ввести коэффициенты такого уравнения (целые числа, дроби или десятичные значения). При наличии знаков вычитания в уравнении необходимо поставить минус перед соответствующими членами уравнения. Решить квадратное уравнение онлайн можно и в зависимости от параметра, то есть переменных в коэффициентах уравнения. С этой задачей отлично справляется наш онлайн сервис по нахождению общих решений. Линейные уравнения. Для решения линейных уравнений (или системы уравнений) на практике используются четыре основных метода. Опишем каждый метод подробно. Метод подстановки. Решение уравнений методом подстановки требует выразить одну переменную через остальные. После этого выражение подставляется в другие уравнения системы. Отсюда и название метода решения, то есть вместо переменной подставляется ее выражение через остальные переменные. На практике метод требует сложных вычислений, хотя и простой в понимании, поэтому решение такого уравнения онлайн поможет сэкономить время и облегчить вычисления. Вам достаточно указать количество неизвестных в уравнении и заполнить данные от линейных уравнений, далее сервис сделает расчет. Метод Гаусса. В основе метода простейшие преобразования системы с целью прийти к равносильной системе треугольного вида. Из нее поочередно определяются неизвестные. На практике требуется решить такое уравнение онлайн с подробным описанием, благодаря чему вы хорошо усвоите метод Гаусса для решения систем линейных уравнений. Запишите в правильном формате систему линейных уравнений и учтите количество неизвестных, чтобы безошибочно выполнить решение системы. Метод Крамера. Этим методом решаются системы уравнений в случаях, когда у системы единственное решение. Главное математическое действие здесь – это вычисление матричных определителей. Решение уравнений методом Крамера проводится в режиме онлайн, результат вы получаете мгновенно с полным и подробным описанием. Достаточно лишь заполнить систему коэффициентами и выбрать количество неизвестных переменных. Матричный метод. Этот метод заключается в собрании коэффициентов при неизвестных в матрицу А, неизвестных – в столбец Х, а свободных членов в столбец В. Таким образом система линейных уравнений сводится к матричному уравнению вида АхХ=В. У этого уравнения единственное решение только если определитель матрицы А отличен от нуля, иначе у системы нет решений, либо бесконечное количество решений. Решение уравнений матричным методом заключается в нахождении обратной матрицы А.
Исключение Гаусса
Тип 2. Умножьте строку на ненулевую константу.
Тип 3. Добавьте одну строку, кратную одной, в другую.
Цель этих операций – преобразовать – или уменьшить – исходную расширенную матрицу в одну из форм, где A ′ является верхним треугольником ( a ij ′ = 0 для i> j ), любые нулевые строки появляются внизу матрицы, и первая ненулевая запись в любой строке находится справа от первой ненулевой записи в любой более высокой строке; такая матрица имеет вид эшелон .Решения системы представлены более простой расширенной матрицей [ A ′ | b ′], можно найти путем осмотра нижних рядов и обратной подстановки в более высокие ряды. Поскольку элементарные операции со строками не меняют решений системы, векторы x , которые удовлетворяют более простой системе A ′ x = b ′, являются в точности теми, которые удовлетворяют исходной системе, A x = b .
Пример 3 : Решите следующую систему с помощью исключения Гаусса:
Расширенная матрица, которая представляет эту систему:
Первая цель – получить нули под первой записью в первом столбце , что означает исключение первой переменной x из второго и третьего уравнений.Для этого выполняются следующие операции со строками:
Вторая цель – получить ноль под второй записью во втором столбце, что означает исключение второй переменной y из третьего уравнения. Один из способов добиться этого – добавить -1/5 второй строки к третьей строке. Однако, чтобы избежать дробей, есть еще один вариант: сначала поменять местами второй и третий ряды. Замена двух строк просто меняет местами уравнения, что явно не изменит решения системы:
Теперь прибавьте −5 раз вторую строку к третьей строке:
Поскольку матрица коэффициентов преобразована в эшелонированную форму, «прямая» часть исключения Гаусса завершена.Теперь остается использовать третью строку для оценки третьего неизвестного, затем выполнить обратную подстановку во вторую строку для оценки второго неизвестного и, наконец, выполнить обратную замену в первой строке для оценки первого неизвестного.
Третья строка финальной матрицы переводится в 10 z = 10, что дает z = 1. Обратная подстановка этого значения во вторую строку, которая представляет уравнение y – 3 z = – 1, дает y = 2.Обратная подстановка обоих этих значений в первую строку, которая представляет уравнение x – 2 y + z = 0, дает x = 3. Таким образом, решение этой системы: ( x, y, z ) = (3, 2, 1).
Пример 4 : Решите следующую систему с помощью исключения Гаусса:
Для этой системы расширенная матрица (вертикальная линия опущена) составляет
Сначала умножьте строку 1 на 1/2:
Теперь добавление −1 первой строки ко второй строке дает нули под первой записью в первом столбце:
Перестановка второй и третьей строк дает желаемую матрицу коэффициентов верхней треугольной формы:
В третьей строке теперь указано z = 4.Обратная подстановка этого значения во вторую строку дает y = 1, а обратная подстановка обоих этих значений в первую строку дает x = −2. Таким образом, решение этой системы ( x, y, z ) = (−2, 1, 4).
Исключение Гаусса-Джордана . Исключение Гаусса осуществляется путем выполнения элементарных операций со строками для получения нулей ниже диагонали матрицы коэффициентов, чтобы привести ее к эшелонированной форме. (Напомним, что матрица A ′ = [ a ij ′] имеет эшелонированную форму, когда a ij ′ = 0 для i> j , любые нулевые строки появляются в нижней части матрицы , и первая ненулевая запись в любой строке находится справа от первой ненулевой записи в любой более высокой строке.Как только это будет сделано, проверка нижней строки (строк) и обратная подстановка в верхние строки определяют значения неизвестных.
Однако можно сократить (или полностью исключить) вычисления, связанные с обратной подстановкой, выполнив дополнительные операции со строками для преобразования матрицы из эшелонированной формы в сокращенную форму . Матрица находится в форме сокращенного эшелона, когда, помимо того, что она находится в форме эшелона, каждый столбец, содержащий ненулевую запись (обычно равную 1), имеет нули не только под этой записью, но и над этой записью.Грубо говоря, гауссовское исключение работает сверху вниз, чтобы создать матрицу в форме эшелона, тогда как Гаусс-Джордан исключение продолжается с того места, где остановился гауссиан, затем работает снизу вверх для создания матрицы в форме сокращенного эшелона. Техника будет проиллюстрирована на следующем примере.
Пример 5 : Известно, что высота, y , брошенного в воздух объекта задается квадратичной функцией от t (время) в форме y = at 2 + bt + c .Если объект находится на высоте y = 23/4 в момент времени t = 1/2, при y = 7 в момент времени t = 1 и при y = 2 при t = 2 , определите коэффициенты a, b и c .
Так как t = 1/2 дает y = 23/4
, а два других условия, y ( t = 1) = 7 и y ( t = 2) = 2, дают следующие уравнения для a, b и c :
Следовательно, цель – решить систему
Расширенная матрица для этой системы сокращается следующим образом:
На этом прямая часть исключения Гаусса завершена, поскольку матрица коэффициентов приведена к эшелонированной форме.Однако, чтобы проиллюстрировать исключение Гаусса-Жордана, выполняются следующие дополнительные элементарные операции со строками:
Эта окончательная матрица сразу дает решение: a = −5, b = 10 и c = 2.
Пример 6 : Решите следующую систему с помощью исключения Гаусса:
Расширенная матрица для этой системы –
Кратные значения первой строки добавляются к другим строкам, чтобы получить нули под первой записью в первом столбце:
Затем −1 раз вторая строка добавляется к третьей строке:
В третьей строке теперь указано 0 x + 0 y + 0 z = 1, уравнение, которому не могут соответствовать никакие значения x, y и z .Процесс останавливается: у этой системы нет решений.
Предыдущий пример показывает, как метод исключения по Гауссу обнаруживает противоречивую систему. Небольшое изменение этой системы (например, изменение постоянного члена «7» в третьем уравнении на «6») проиллюстрирует систему с бесконечным числом решений.
Пример 7 : Решите следующую систему с помощью исключения Гаусса:
Те же операции, которые применяются к расширенной матрице системы в примере 6, применяются к расширенной матрице для данной системы:
Здесь третья строка переводится в 0 x + 0 y + 0 z = 0, уравнение, которому удовлетворяют любые x, y и z .Поскольку здесь нет ограничений на неизвестные, на неизвестные не три условия, а только два (представленные двумя ненулевыми строками в окончательной расширенной матрице). Поскольку есть 3 неизвестных, но только 2 константы, 3–2 = 1 из неизвестных, скажем, z , произвольно; это называется свободной переменной . Пусть z = t , где t – любое действительное число. Обратная подстановка z = t во вторую строку (- y + 5 z = −6) дает
Обратная подстановка z = t и y = 6 + 5 t в первую строку ( x + y -3 z = 4) определяет x :
Следовательно, каждое решение системы имеет вид
, где t – любое действительное число.Существует бесконечно много решений, поскольку каждое действительное значение т дает отдельное конкретное решение. Например, выбор t = 1 дает ( x, y, z ) = (−4, 11, 1), а t = 3 дает ( x, y, z ) = (4, – 9, −3) и т. Д. Геометрически эта система представляет три плоскости в R 3 , которые пересекаются по линии, и (*) является параметрическим уравнением для этой линии.
Пример 7 дает иллюстрацию системы с бесконечным множеством решений, как возникает этот случай и как записывается решение.Каждая линейная система, имеющая бесконечно много решений, должна содержать хотя бы один произвольный параметр (свободная переменная). После того, как расширенная матрица была приведена к эшелонированной форме, количество свободных переменных равно общему количеству неизвестных минус количество ненулевых строк:
Это согласуется с теоремой B выше, которая гласит, что линейная система с меньшим количеством уравнений, чем неизвестных, если она согласована, имеет бесконечно много решений. Условие «меньше уравнений, чем неизвестных» означает, что количество строк в матрице коэффициентов меньше количества неизвестных.Следовательно, приведенное выше уравнение в рамке подразумевает, что должна быть хотя бы одна свободная переменная. Поскольку такая переменная по определению может принимать бесконечно много значений, система будет иметь бесконечно много решений.
Пример 8 : Найти все решения для системы
Во-первых, обратите внимание, что есть четыре неизвестных, но только три уравнения. Следовательно, если система непротиворечива, гарантировано, что у нее будет бесконечно много решений, а это состояние характеризуется по крайней мере одним параметром в общем решении.После того, как соответствующая расширенная матрица построена, исключение Гаусса дает
Тот факт, что в эшелонированной форме расширенной матрицы остались только две ненулевые строки, означает, что 4-2 = 2 переменных свободны:
Следовательно, выбрав y и z в качестве свободных переменных, пусть y = t 1 и z = t 2 . Во второй строке сокращенной расширенной матрицы следует
, а первая строка дает
Таким образом, решения системы имеют вид
, где т 1 т 2 могут принимать любые реальные значения.
Пример 9 : Пусть b = ( b 1 , b 2 , b 3 ) T и пусть A будет матрицей
Для каких значений b 1 , b 2 и b 3 будет ли система A x = b согласованной?
Расширенная матрица для системы A x = b читает
, который гауссовский элиминатин сокращает следующим образом:
Нижняя строка теперь подразумевает, что b 1 + 3 b 2 + b 3 должно быть равно нулю, чтобы эта система была согласованной.Следовательно, в данной системе есть решения (фактически бесконечно много) только для тех векторов-столбцов b = ( b 1 , b 2 , b 3 ) T , для которых b 1 + 3 b 2 + b 3 = 0.
Пример 10 : Решите следующую систему (сравните с Примером 12):
Такая система, как эта, где постоянный член в правой части каждого уравнения равен 0, называется однородной системой .В матричной форме он читает A x = 0 . Поскольку каждая однородная система согласована – поскольку x = 0 всегда является решением, – однородная система имеет либо ровно одно решение ( тривиальное решение , x = 0 ), либо бесконечно много. Сокращение строки матрицы коэффициентов для этой системы уже было выполнено в примере 12. Нет необходимости явно дополнять матрицу коэффициентов столбцом b = 0 , поскольку никакая элементарная операция со строкой не может повлиять на эти нули.То есть, если A ‘является эшелонированной формой A , то операции элементарной строки преобразуют [ A | 0 ] в [ A ′ | 0 ]. По результатам Примера 12,
Поскольку последняя строка снова подразумевает, что z можно принять как свободную переменную, пусть z = t , где t – любое действительное число. Обратная подстановка z = t во вторую строку (- y + 5 z = 0) дает
и обратная подстановка z = t и y = 5 t в первую строку ( x + y -3 z = 0) определяет x :
Следовательно, каждое решение этой системы имеет вид ( x, y, z ) = (−2 t , 5 t, t ), где t – любое действительное число.Растворителей бесконечно много, так как каждое действительное значение т дает уникальное частное решение.
Обратите внимание на разницу между набором решений для системы в Примере 12 и здесь. Хотя обе имели одинаковую матрицу коэффициентов A , система в Примере 12 была неоднородной ( A x = b , где b ≠ 0 ), а здесь – соответствующая однородная система, A x = 0 .Помещая свои решения рядом,
общее решение для Ax = 0 : ( x, y, z ) = (−2 t , 5 t , t )
общее решение для Ax = b : ( x, y, z ) = (−2 t , 5 t , t ) + (−2, 6, 0)
иллюстрирует важный факт:Теорема C . Общие решения для согласованной неоднородной лиенарной системы, A x = b , равны общему решению соответствующей однородной системы, A x = 0 , плюс частное решение неоднородная система.То есть, если x = x h представляет собой общее решение A x = 0 , то x = x h + x представляет общее решение A x + b , где x – любое конкретное решение (согласованной) неоднородной системы A x = b .
[Техническое примечание: теорема C, которая касается линейной системы , имеет аналог в теории линейных дифференциальных уравнений .Пусть L – линейный дифференциальный оператор; то общее решение разрешимого неоднородного линейного дифференциального уравнения, L (y) = d (где d ≢ 0), равно общему решению соответствующего однородного уравнения, L (y) = 0 плюс частное решение неоднородного уравнения. То есть, если y = y h повторно отображает общее решение L (y) = 0, то y = y h + y представляет собой общее решение L (y ) = d , где y – любое частное решение (решаемого) неоднородного линейного уравнения L (y) = d .]
Пример 11 : Определить все решения системы
Запишите расширенную матрицу и выполните следующую последовательность операций:
Поскольку в этой конечной (эшелонированной) матрице остаются только 2 ненулевые строки, есть только 2 ограничения и, следовательно, 4–2 = 2 из неизвестных – например, y и z – являются свободными переменными. Пусть y = t 1 и z = t 2 .Обратная подстановка y = t 1 и z = t 2 во вторую строку ( x – 3 y + 4 z = 1) дает
Наконец, обратная замена x = 1 + 3 t 1 – 4 2 , y = t 1 и z = t 2 в первую строка (2 w -2 x + y = −1) определяет w :
Следовательно, каждое решение этой системы имеет вид
, где t 1 и t 2 – любые вещественные числа.Другой способ написать решение:
, где т 1 , т 2 ∈ R .
Пример 12 : Определите общее решение
, которая является однородной системой, соответствующей неоднородной в примере 11 выше.
Поскольку решение неоднородной системы в примере 11 равно
Теорема C означает, что решение соответствующей однородной системы (где t 1 , t 2 ∈ R ) получается из (*), просто отбрасывая конкретное решение, x = (1 / 2,1,0,0) неоднородной системы.
Пример 13 : Докажите теорему A: независимо от ее размера или количества неизвестных, содержащихся в ее уравнениях, линейная система не будет иметь решений, ровно одно решение или бесконечно много решений.
Доказательство . Пусть данная линейная система записана в матричной форме A x = b . Теорема действительно сводится к следующему: если A x = b имеет более одного решения, то на самом деле их бесконечно много.Чтобы установить это, пусть x 1 и x 2 будут двумя разными решениями A x = b . Теперь будет показано, что для любого реального значения t вектор x 1 + t ( x 1 – x 2 ) также является решением A x = b ; Поскольку t может принимать бесконечно много различных значений, из этого следует желаемый вывод.Начиная с A x 1 = b и A x 2 ,
Следовательно, x 1 + t ( x 1 – x 2 ) действительно является решением A x = b , и теорема доказана.
ИСКЛЮЧЕНИЕ ПО ГАУССУ: РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ: ПРИМЕРЫ И РЕШАЕМЫЕ ЗАДАЧИ: ВЫСШАЯ ШКОЛА
Содержимое этой страницы:
Введение
Система уравнений (линейная) – это группа (линейных) уравнений с различные неизвестные факторы.Вообще говоря, неизвестные факторы появляются в различных уравнениях.
Уравнение с различными неизвестными факторами связывает их друг с другом.
Решение системы состоит в нахождении значения неизвестных факторов способом, который проверяет все уравнений, составляющих систему.
Если существует одно решение (одно значение для каждого неизвестного фактора), мы будем говорить, что система Согласованная независимая система (СНГ) .
Если существуют различные решения (система имеет бесконечно много решений), мы говорим, что система является Согласованная зависимая система (CDS). .
Если решения нет, а это произойдет, если есть два или несколько уравнений, которые нельзя проверить одновременно, мы говорим, что это несогласованная система (IS) .Например, следующая система уравнений
$$ \ begin {case} \ begin {array} {lcl} y & = & 0 \\ 2x + y & = & 0 \\ 2x + y & = & 2 \ end {array} \ end {cases} $ $
несовместимо, потому что мы получаем решение x = 0 из второго уравнения и, из третьего, x = 1 .
В этом разделе мы собираемся решать системы с использованием метода исключения Гаусса , который заключается в простом выполнении элементарных операций в строке или столбце расширенной матрицы, чтобы получить свой эшелон из или его пониженный эшелон форма (Гаусс-Иордан).
Метод разрешения
Применяем метод исключения Гаусса-Джордана : получаем сокращенного эшелона строки формы из расширенной матрицы систему уравнений, выполняя элементарные операции в строках (или столбцах).
Получив матрицу, мы применяем теорему Руше-Капелли для определения тип системы и получить решение (я):
Пусть A · X = B будет системой из m линейных уравнений с n неизвестными множители, m и n натуральные числа (не ноль):
AX = B соответствует тогда и только тогда, когда,
$$ ранг (A) = ранг (A | B) $$
AX = B – непротиворечивый независимый тогда и только тогда, когда,
$$ ранг (A) = n = ранг (A | B) $$
Примечание: Элементарные операции в строках или столбцах позволяют получить системы, эквивалентные исходной, но с формой, упрощающей получение решений (если они есть).Также есть более быстрые инструменты для выработки решений в СНГ, такие как правило Крамера.
Система 1
Показать решение
Расширенная матрица системы
того же размера, что и система (2×3). Вертикальная линия, отделяющая матричные коэффициенты от вектора независимых членов.
Выполняем элементарные операции в строках для получения приведенной формы эшелона строк:Умножаем первую строку на 1/5 а вторую на 1/3
Добавляем вторую строку с первой
Вторую строку умножаем на 5/7
Складываем первую строку со второй, умноженной на -2/5
Эта последняя эквивалентная матрица представлена в сокращенной форме эшелона строк. и это позволяет нам быстро увидеть рейтинг матрица коэффициентов и дополненная.
Рассчитываем ранги:
По теореме Руше-Капелли система непротиворечива Независимая. Полученная матрица представляет собой систему
, который является решением исходной системы.
Система 2
Показать решение
Расширенная матрица системы
Проводим элементарные операции в строках для получения приведенных форма эшелона строки:
Вторую строку умножаем на 1/2
Добавляем первую строку со второй
Умножаем первую строку на 1/3
Эта последняя эквивалентная матрица находится в форме сокращенного эшелона строк и имеет нулевую строку, что означает, что строки в исходной системе линейно зависимы. (любой из них может быть получен путем умножения другого на скаляр, не равный нулю).
Рассчитываем ранги
По теореме Руше-Капелли система непротиворечива. Кроме того, он является зависимым, поскольку ранг (1) ниже количества неизвестных факторов (2).
Полученная матрица представляет собой систему
Решения
Система 3
Показать решение
Расширенная матрица системы
Выполняем элементарные операции в строках, чтобы получить сокращенный рядный эшелон формыИзменяем порядок строк (так у нас уже будет 1 в первой строке без необходимости умножать)
Складываем вторую строку с первой, умноженной на 5 :
Вторую строку умножаем на -1/15
Эта последняя матрица имеет эшелонированную форму (не сокращена).
Мы можем непосредственно заметить, что система несовместима, потому что у нас следующее равенство (вторая строка):
$$ 0x + 0y = 1 $$, это невозможное равенство.
Рассчитываем ранги матрицы коэффициентов и дополненной:
По теореме Руше-Капелли система несовместна (решения нет). Полученная матрица представляет собой систему
Система непоследовательна, потому что мы имеем невозможное равенство
$$ 0 = 1 $$
Система 4
Показать решение
Расширенная матрица системы
(размер 3х4).
Выполняем элементарные операции в строках, чтобы получить сокращенный рядный эшелон формыУмножаем первую строку на 1/5
Складываем вторую и третью строки, умножив первую на -2
Вторую и третью строки умножаем на 5
Складываем вторую строку с третьей, умноженной на -1
Умножаем вторую строку на -1/10 , а третью на 1/11
Мы складываем первую строку со второй, умноженной на -2/5 , а третью со второй, умноженной на -1
Третью строку умножаем на -11/5
Эта последняя эквивалентная матрица находится в сокращенной форме эшелона строк (мы знаем ее, потому что это единичная матрица).Имея единичную матрицу, мы знаем, что это непротиворечивая независимая система, и можем получить единственное решение.
Рассчитываем ранги
По теореме Руше-Капелли система непротиворечива Независимая. Полученная матрица представляет собой систему
, который является решением системы.
Система 5
Показать решение
Расширенная матрица системы
Выполняем элементарные операции в строках, чтобы получить сокращенный рядный эшелон формыМы вычитаем первую строку из второй и добавляем третью строку с первой.
Умножаем первую строку на 1/2 , а вторую на 1/3
Мы складываем первую строку со второй, умноженной на 1/2 , и третью строку со второй, умноженной на -2
Третью строку умножаем на 1/3
Складываем первую строку с третьей, умноженной на -3/2
Эта последняя матрица является эшелонированной матрицей с сокращенным числом строк (мы знаем это, потому что у нас есть единичная матрица).
Рассчитываем ранги
По теореме Руше-Капелли система непротиворечива Независимая. Полученная матрица представляет собой систему
Система 6
Показать решение
Расширенная матрица системы
Выполняем элементарные операции в строках, чтобы получить сокращенный рядный эшелон формыУмножаем вторую строку на -1/3 и третью на 1/4
Складываем вторую и третью строки, умножив первую на -1
Умножаем вторую строку на -3/4 и третью на -1
Третью строку складываем со второй, умноженной на -1
Эта последняя матрица имеет эшелонированную форму (но не сокращена) и мы не продолжаем выполнять операции по строкам, потому что можем видим, что последняя строка делает систему непоследовательной.Эта строка сообщает нам:
$$ 0x + 0y + 0z = -1 $$И все это невозможное равенство.
Фактически у нас есть ранги
По теореме Руше-Капелли система несовместна.
Система 7
Показать решение
Расширенная матрица системы
Выполняем элементарные операции в строках, чтобы получить сокращенный рядный эшелон формыУмножаем первую и вторую строки на 1/3 и на 1/6 соответственно
Вторую строку вычитаем из третьей
Добавляем первую строку со второй
Третью строку умножаем на 3
Эта последняя матрица находится в сокращенном эшелоне строк формы , поэтому мы можем легко вычислить ранги:
Рассчитываем ранги
По теореме Руше-Капелли система непротиворечива.Но он не является независимым, потому что количество неизвестных факторов (3) отличается от ранга. Полученная матрица представляет собой систему
Решения
Система 8
Показать решение
Расширенная матрица системы
Примечание: прежде, чем мы начнем, мы должны прокомментировать, что процедура будет таким же, как и до сих пор.Но у нас есть корни в матрице, а это значит, что операции в строках будут длинными и утомительно. Эта задача не очень интересна в дидактическом смысле, помимо расчетов.
Проводим элементарные операции в строках, чтобы получить пониженный рядный эшелон формы
Мы складываем вторую строку с первой, умноженной на -√5 и, с третья, умноженная на -2/5
Умножаем вторую строку на 1 / √5 и третью на 5/17
Складываем первую строку с третьей и со второй вычитаем третью
Переписываем матрицу
Умножаем вторую строку на (√5 / 5-5) -1
Складываем первую строку со второй, умноженной на -5
В этой последней матрице он (почти) в строке уменьшен форма эшелона (надо поменять второй и третий ряды так что это правда).Из последней матрицы получаем решения:
Система 9
Показать решение
Расширенная матрица системы
Выполняем элементарные операции в строках, чтобы получить сокращенный рядный эшелон формыСкладываем третью и четвертую строки, умножая первую на 3 и на -2 соответственно
Складываем первую, вторую и третью строки с четвертой, умноженной на 2 , -3 и 5 соответственно
Умножаем четвертую строку на -1 и меняем ее на вторую
Умножаем третью и четвертую строки на 1/34 и -1/22 соответственно
Вычитаем третью строку из четвертой
Умножаем четвертую на -187/42
Добавляем в первую строку третью умноженную на -13 и вторую на 8
К первой строке прибавляем четвертую, умноженную на 5/34 , ко второй прибавляем первую, умноженную на 5/17 и к третьему добавляем первое, умноженное на -3/34
По теореме Руше-Капелли система является непротиворечивой Независимой, и решение равно
Система 10
Показать решение
Расширенная матрица системы
Примечание: Эта система была включена в цель отметить, что теория матрицы применима к комплексным числам.Единственное отличие от предыдущих систем в том, что теперь нам нужно действовать путем умножения и деления комплексные числа.
Выполняем элементарные операции в строках для получения приведенной формы эшелона строк
Умножаем вторую строку на 1/2 и меняем ее на первую
Мы складываем вторую строку с первой, умноженной на – (1 + i)
Вторую строку умножаем на
Добавляем первую строку ко второй, умножаем на -i / 2
Эта последняя матрица имеет сокращенную форму, потому что это единичная матрица.
По теореме Руше-Капелли система является непротиворечивой Независимой, и решение равно
Matesfacil.com
от J. Llopis под лицензией
творческий
Международная лицензия Commons Attribution-NonCommercial 4.0.
Решение системы с исключением Гаусса
Результаты обучения
- Используйте метод исключения Гаусса для решения системы уравнений, представленной в виде расширенной матрицы.
- Интерпретируйте решение системы уравнений, представленное в виде расширенной матрицы.
Мы видели, как написать систему уравнений с расширенной матрицей , а затем как использовать строковые операции и обратную подстановку для получения эшелонированной формы . Теперь мы будем использовать метод исключения Гаусса как инструмент для решения системы, записанной в виде расширенной матрицы. В нашем первом примере мы покажем вам процесс использования исключения Гаусса в системе двух уравнений с двумя переменными.
Пример: решение системы 2 X 2 методом исключения Гаусса
Решите данную систему методом исключения Гаусса.
[латекс] \ begin {array} {l} 2x + 3y = 6 \ hfill \\ \ text {} x-y = \ frac {1} {2} \ hfill \ end {array} [/ latex]
Показать решениеВо-первых, мы запишем это как расширенную матрицу.
[латекс] \ left [\ begin {array} {rr} \ hfill 2 & \ hfill 3 \\ \ hfill 1 & \ hfill -1 \ end {array} \ text {} | \ text {} \ begin {array} { r} \ hfill 6 \\ \ hfill \ frac {1} {2} \ end {array} \ right] [/ latex]
Нам нужна 1 в строке 1, столбце 1.Этого можно добиться, поменяв местами строку 1 и строку 2.
[латекс] {R} _ {1} \ leftrightarrow {R} _ {2} \ to \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill \\ \ hfill 2 & \ hfill 3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill \ frac {1} {2} \\ \ hfill & \ hfill 6 \ end {array} \ right] [/ latex]
Теперь у нас есть 1 в качестве первой записи в строке 1, столбце 1. Теперь давайте получим 0 в строке 2, столбце 1. Это можно сделать, умножив строку 1 на [latex] -2 [/ latex] и затем прибавив результат в строку 2.
[латекс] -2 {R} _ {1} + {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill \\ \ hfill 0 & \ hfill 5 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill \ frac {1} {2} \\ \ hfill & \ hfill 5 \ end {массив } \ right] [/ latex]
У нас есть только один шаг, чтобы умножить строку 2 на [latex] \ frac {1} {5} [/ latex].
[латекс] \ frac {1} {5} {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill \ \ \ hfill 0 & \ hfill 1 & \ hfill \ end {array} | \ begin {array} {cc} & \ frac {1} {2} \\ & 1 \ end {array} \ right] [/ latex]
Использовать обратную замену.Вторая строка матрицы представляет [латекс] y = 1 [/ латекс]. Подставьте обратно [latex] y = 1 [/ latex] в первое уравнение.
[латекс] \ begin {array} {l} x- \ left (1 \ right) = \ frac {1} {2} \ hfill \\ \ text {} x = \ frac {3} {2} \ hfill \ end {array} [/ latex]
Решение – точка [латекс] \ left (\ frac {3} {2}, 1 \ right) [/ latex].
Попробуй
Решите данную систему методом исключения Гаусса.
[латекс] \ begin {массив} {l} 4x + 3y = 11 \ hfill \\ \ text {} \ text {} \ text {} x – 3y = -1 \ hfill \ end {array} [/ latex]
Показать решение[латекс] \ влево (2,1 \ вправо) [/ латекс]
В нашем следующем примере мы решим систему двух уравнений с двумя зависимыми переменными.Напомним, что зависимая система имеет бесконечное количество решений, и результатом операций со строками в ее расширенной матрице будет уравнение, такое как [latex] 0 = 0 [/ latex]. Мы также рассмотрим написание общего решения для зависимой системы.
Пример: решение зависимой системы
Решите систему уравнений.
[латекс] \ begin {array} {l} 3x + 4y = 12 \\ 6x + 8y = 24 \ end {array} [/ latex]
Показать решение Выполните строковых операций на расширенной матрице, чтобы попытаться получить -строчную форму .[латекс] A = \ left [\ begin {array} {llll} 3 \ hfill & \ hfill & 4 \ hfill & \ hfill \\ 6 \ hfill & \ hfill & 8 \ hfill & \ hfill \ end {array} | \ begin {array} {ll} \ hfill & 12 \ hfill \\ \ hfill & 24 \ hfill \ end {array} \ right] [/ latex]
[латекс] \ begin {array} {l} \ hfill \\ \ begin {array} {l} – \ frac {1} {2} {R} _ {2} + {R} _ {1} = { R} _ {1} \ to \ left [\ begin {array} {llll} 0 \ hfill & \ hfill & 0 \ hfill & \ hfill \\ 6 \ hfill & \ hfill & 8 \ hfill & \ hfill \ end { array} | \ begin {array} {ll} \ hfill & 0 \ hfill \\ \ hfill & 24 \ hfill \ end {array} \ right] \ hfill \\ {R} _ {1} \ leftrightarrow {R} _ {2} \ to \ left [\ begin {array} {llll} 6 \ hfill & \ hfill & 8 \ hfill & \ hfill \\ 0 \ hfill & \ hfill & 0 \ hfill & \ hfill \ end {array} | \ begin {array} {ll} \ hfill & 24 \ hfill \\ \ hfill & 0 \ hfill \ end {array} \ right] \ hfill \ end {array} \ hfill \ end {array} [/ latex]
Матрица заканчивается всеми нулями в последней строке: [latex] 0y = 0 [/ latex].Таким образом, существует бесконечное количество решений и система классифицируется как зависимая. Чтобы найти общее решение, вернитесь к одному из исходных уравнений и решите для [latex] y [/ latex].
[латекс] \ begin {array} {l} 3x + 4y = 12 \ hfill \\ \ text {} 4y = 12 – 3x \ hfill \\ \ text {} y = 3- \ frac {3} {4} x \ hfill \ end {array} [/ latex]
Итак, решение этой системы – [латекс] \ left (x, 3- \ frac {3} {4} x \ right) [/ latex].
Теперь мы перейдем на следующий шаг к решению системы линейных уравнений 3 на 3.Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для поиска других переменных.
Пример: решение системы линейных уравнений с использованием матриц
Решите систему линейных уравнений с помощью матриц.
[латекс] \ begin {массив} {c} \ begin {array} {l} \ hfill \\ \ hfill \\ x-y + z = 8 \ hfill \ end {array} \\ 2x + 3y-z = -2 \\ 3x – 2y – 9z = 9 \ end {array} [/ latex]
Показать решениеСначала мы пишем расширенную матрицу.
[латекс] \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill 1 \\ \ hfill 2 & \ hfill 3 & \ hfill -1 \\ \ hfill 3 & \ hfill -2 & \ hfill -9 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill 8 \\ \ hfill -2 \\ \ hfill 9 \ end {array} \ right] [/ latex]
Затем мы выполняем операции со строками для получения формы «строка-эшелон».
[латекс] \ begin {array} {rrrrr} \ hfill -2 {R} _ {1} + {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} { rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 5 & \ hfill & \ hfill -3 & \ hfill \\ \ hfill 3 & \ hfill & \ hfill -2 & \ hfill & \ hfill -9 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -18 \\ \ hfill & \ hfill 9 \ end {массив} \ right] & \ hfill & \ hfill & \ hfill & \ hfill -3 {R} _ {1} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 5 & \ hfill & \ hfill -3 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -18 \\ \ hfill & \ hfill -15 \ end {array} \ right] \ end {array} [/ latex]
Самый простой способ получить 1 в строке 2 столбца 1 – это поменять местами [латекс] {R} _ {2} [/ latex] и [latex] {R} _ {3} [/ latex].
[латекс] \ text {Interchange} {R} _ {2} \ text {и} {R} _ {3} \ to \ left [\ begin {array} {rrrrrrr} \ hfill 1 & \ hfill & \ hfill – 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 8 \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill & \ hfill -15 \\ \ hfill 0 & \ hfill & \ hfill 5 & \ hfill & \ hfill -3 & \ hfill & \ hfill -18 \ end {array} \ right] [/ latex]
Затем
[латекс] \ begin {array} {l} \\ \ begin {array} {rrrrr} \ hfill -5 {R} _ {2} + {R} _ {3} = {R} _ {3} \ в \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill 57 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -15 \\ \ hfill & \ hfill 57 \ end {array} \ right] & \ hfill & \ hfill & \ hfill & \ hfill – \ frac {1} {57} {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill 1 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -15 \ \ \ hfill & \ hfill 1 \ end {array} \ right] \ end {array} \ end {array} [/ latex]
Последняя матрица представляет собой эквивалентную систему.
[латекс] \ begin {массив} {l} \ text {} x-y + z = 8 \ hfill \\ \ text {} y – 12z = -15 \ hfill \\ \ text {} z = 1 \ hfill \ end {array} [/ latex]
Используя обратную подстановку, мы получаем решение как [latex] \ left (4, -3,1 \ right) [/ latex].
Напомним, что есть три возможных исхода решений для линейных систем. В предыдущем примере решение [латекс] \ left (4, -3,1 \ right) [/ latex] представляет точку в трехмерном пространстве. Эта точка представляет собой пересечение трех плоскостей.В следующем примере мы решаем систему, используя операции со строками, и обнаруживаем, что она представляет зависимую систему. Зависимая система в 3-х измерениях может быть представлена двумя идентичными плоскостями, как в 2-х измерениях, где зависимая система представляет две идентичные линии.
Пример: решение зависимой системы 3 x 3
Решите следующую систему линейных уравнений, используя метод исключения Гаусса.
[латекс] \ begin {array} {r} \ hfill -x – 2y + z = -1 \\ \ hfill 2x + 3y = 2 \\ \ hfill y – 2z = 0 \ end {array} [/ latex]
Показать решениеЗапишите расширенную матрицу.
[латекс] \ left [\ begin {array} {rrr} \ hfill -1 & \ hfill -2 & \ hfill 1 \\ \ hfill 2 & \ hfill 3 & \ hfill 0 \\ \ hfill 0 & \ hfill 1 & \ hfill -2 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill -1 \\ \ hfill 2 \\ \ hfill 0 \ end {array} \ right] [/ latex]
Сначала умножьте строку 1 на [latex] -1 [/ latex], чтобы получить 1 в строке 1, столбце 1. Затем выполните операций со строками , чтобы получить форму «строка-эшелон».
[латекс] – {R} _ {1} \ to \ left [\ begin {array} {rrrrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 \\ \ hfill 2 & \ hfill & \ hfill 3 & \ hfill & \ hfill 0 & \ hfill & \ hfill 2 \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 & \ hfill & \ hfill 0 \ end {array} \ справа] [/ латекс]
[латекс] {R} _ {2} \ leftrightarrow {R} _ {3} \ to \ left [\ begin {array} {rrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 \ \ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 \\ \ hfill 2 & \ hfill & \ hfill 3 & \ hfill & \ hfill 0 \ end {array} \ text {} | \ begin {array} { rr} \ hfill & \ hfill 1 \\ \ hfill & \ hfill 0 \\ \ hfill & \ hfill 2 \ end {array} \ right] [/ latex]
[латекс] -2 {R} _ {1} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -1 & \ hfill & \ hfill 2 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 1 \\ \ hfill & \ hfill 0 \\ \ hfill & \ hfill 0 \ end {array} \ right] [/ latex]
[латекс] {R} _ {2} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill 0 & \ hfill \ end { array} | \ begin {array} {rr} \ hfill & \ hfill 2 \\ \ hfill & \ hfill 1 \\ \ hfill & \ hfill 0 \ end {array} \ right] [/ latex]
Последняя матрица представляет следующую систему.
[латекс] \ begin {массив} {l} \ text {} x + 2y-z = 1 \ hfill \\ \ text {} y – 2z = 0 \ hfill \\ \ text {} 0 = 0 \ hfill \ конец {array} [/ latex]
По тождеству [latex] 0 = 0 [/ latex] мы видим, что это зависимая система с бесконечным числом решений. Затем мы находим общее решение. Решив второе уравнение для [latex] y [/ latex] и подставив его в первое уравнение, мы можем решить для [latex] z [/ latex] через [latex] x [/ latex].
[латекс] \ begin {array} {l} \ text {} x + 2y-z = 1 \ hfill \\ \ text {} y = 2z \ hfill \\ \ hfill \\ x + 2 \ left (2z \ справа) -z = 1 \ hfill \\ \ text {} x + 3z = 1 \ hfill \\ \ text {} z = \ frac {1-x} {3} \ hfill \ end {array} [/ latex]
Теперь мы подставляем выражение для [latex] z [/ latex] во второе уравнение, чтобы решить для [latex] y [/ latex] через [latex] x [/ latex].
[латекс] \ begin {массив} {l} \ text {} y – 2z = 0 \ hfill \\ \ text {} z = \ frac {1-x} {3} \ hfill \\ \ hfill \\ y – 2 \ left (\ frac {1-x} {3} \ right) = 0 \ hfill \\ \ text {} y = \ frac {2 – 2x} {3} \ hfill \ end {array} [/ latex ]
Общее решение – [latex] \ left (x, \ frac {2 – 2x} {3}, \ frac {1-x} {3} \ right) [/ latex].
Общее решение для зависимой системы 3 X 3
Напомним, что когда вы решаете зависимую систему линейных уравнений с двумя переменными с использованием исключения или подстановки, вы можете записать решение [latex] (x, y) [/ latex] через x, потому что существует бесконечно много (x, y) пары, которые будут удовлетворять зависимой системе уравнений, и все они попадают на линию [латекс] (x, mx + b) [/ latex].Теперь, когда вы работаете в трех измерениях, решение будет представлять собой плоскость, поэтому вы должны записать его в общей форме [латекс] (x, m_ {1} x + b_ {1}, m_ {2} x + b_ { 2}) [/ латекс].
Попробуй
Решите систему методом исключения Гаусса.
[латекс] \ begin {array} {c} x + 4y-z = 4 \\ 2x + 5y + 8z = 15 \ x + 3y – 3z = 1 \ end {array} [/ latex]
Показать решение[латекс] \ левый (1,1,1 \ правый) [/ латекс]
Вопросы и ответы
Можно ли решить любую систему линейных уравнений методом исключения Гаусса?
Да, система линейных уравнений любого размера может быть решена методом исключения Гаусса.
Как: решить систему уравнений с помощью матриц с помощью калькулятора
- Сохраните расширенную матрицу как матричную переменную [latex] \ left [A \ right], \ left [B \ right], \ left [C \ right] \ text {,} \ dots [/ latex].
- Используйте в калькуляторе функцию ref (, вызывая каждую матричную переменную по мере необходимости.
Пример: решение систем уравнений с помощью калькулятора
Решите систему уравнений.
[латекс] \ begin {array} {r} \ hfill 5x + 3y + 9z = -1 \\ \ hfill -2x + 3y-z = -2 \\ \ hfill -x – 4y + 5z = 1 \ end { array} [/ latex]
Показать решениеНапишите расширенную матрицу для системы уравнений.
[латекс] \ left [\ begin {array} {rrr} \ hfill 5 & \ hfill 3 & \ hfill 9 \\ \ hfill -2 & \ hfill 3 & \ hfill -1 \\ \ hfill -1 & \ hfill -4 & \ hfill 5 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill -1 \\ \ hfill -2 \\ \ hfill 1 \ end {array} \ right] [/ latex]
На странице матриц калькулятора введите расширенную матрицу выше как матричную переменную [latex] \ left [A \ right] [/ latex].
[латекс] \ left [A \ right] = \ left [\ begin {array} {rrrrrrr} \ hfill 5 & \ hfill & \ hfill 3 & \ hfill & \ hfill 9 & \ hfill & \ hfill -1 \\ \ hfill – 2 & \ hfill & \ hfill 3 & \ hfill & \ hfill -1 & \ hfill & \ hfill -2 \\ \ hfill -1 & \ hfill & \ hfill -4 & \ hfill & \ hfill 5 & \ hfill & \ hfill 1 \ end {массив } \ right] [/ latex]
Используйте функцию ref ( в калькуляторе, вызывая матричную переменную [latex] \ left [A \ right] [/ latex].
[латекс] \ text {ref} \ left (\ left [A \ right] \ right) [/ латекс]
Оценить.
[латекс] \ begin {array} {l} \ hfill \\ \ left [\ begin {array} {rrrr} \ hfill 1 & \ hfill \ frac {3} {5} & \ hfill \ frac {9} {5 } & \ hfill \ frac {1} {5} \\ \ hfill 0 & \ hfill 1 & \ hfill \ frac {13} {21} & \ hfill – \ frac {4} {7} \\ \ hfill 0 & \ hfill 0 & \ hfill 1 & \ hfill – \ frac {24} {187} \ end {array} \ right] \ to \ begin {array} {l} x + \ frac {3} {5} y + \ frac {9} {5} z = – \ frac {1} {5} \ hfill \\ \ text {} y + \ frac {13} {21} z = – \ frac {4} {7} \ hfill \\ \ text {} z = – \ frac {24} {187} \ hfill \ end {array} \ hfill \ end {array} [/ latex]
При использовании обратной подстановки решение: [latex] \ left (\ frac {61} {187}, – \ frac {92} {187}, – \ frac {24} {187} \ right) [/ latex] .
Приложения систем уравнений
Теперь обратимся к приложениям, для которых используются системы уравнений. В следующем примере мы определяем, сколько денег было инвестировано по двум разным ставкам, учитывая сумму процентов, полученных на обоих счетах.
Пример: применение матриц 2 × 2 к финансам
Кэролайн инвестирует в общей сложности 12 000 долларов в две муниципальные облигации, одна из которых выплачивает 10,5% годовых, а другая – 12%. Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 долларов.Сколько было вложено по каждой ставке?
Показать решениеУ нас есть система двух уравнений с двумя переменными. Пусть [latex] x = [/ latex] сумма, инвестированная под 10,5% годовых, и [latex] y = [/ latex] сумма, инвестированная под 12% годовых.
[латекс] \ begin {array} {l} \ text {} x + y = 12 000 \ hfill \\ 0.105x + 0.12y = 1335 \ hfill \ end {array} [/ latex]
В качестве матрицы имеем
[латекс] \ left [\ begin {array} {rr} \ hfill 1 & \ hfill 1 \\ \ hfill 0.105 & \ hfill 0.12 \ end {array} \ text {} | \ text {} \ begin {array} { r} \ hfill 12,000 \\ \ hfill 1,335 \ end {array} \ right] [/ latex]
Умножить строку 1 на [латекс] -0.105 [/ latex] и добавьте результат в строку 2.
[латекс] \ left [\ begin {array} {rr} \ hfill 1 & \ hfill 1 \\ \ hfill 0 & \ hfill 0.015 \ end {array} \ text {} | \ text {} \ begin {array} {r } \ hfill 12,000 \\ \ hfill 75 \ end {array} \ right] [/ latex]
Затем,
[латекс] \ begin {array} {l} 0,015y = 75 \ hfill \\ \ text {} y = 5,000 \ hfill \ end {array} [/ latex]
Итак [латекс] 12 000 – 5 000 = 7 000 [/ латекс].
Таким образом, 5000 долларов были инвестированы под 12% годовых и 7000 долларов под 10,5%.
Пример: применение матриц 3 × 3 к финансам
Ava инвестирует в общей сложности 10 000 долларов в три счета, один из которых платит 5% годовых, другой – 8%, а третий – 9%.Годовой процент, полученный по трем инвестициям в прошлом году, составил 770 долларов. Сумма, вложенная под 9%, была вдвое больше, чем сумма, вложенная под 5%. Сколько было вложено по каждой ставке?
Показать решениеУ нас есть система трех уравнений с тремя переменными. Пусть [latex] x [/ latex] будет сумма, инвестированная под 5% годовых, пусть [latex] y [/ latex] будет суммой, инвестированной под 8%, и пусть [latex] z [/ latex] будет инвестированной суммой. под 9% годовых. Таким образом,
[латекс] \ begin {array} {l} \ text {} x + y + z = 10 000 \ hfill \\ 0.05x + 0,08y + 0,09z = 770 \ hfill \\ \ text {} 2x-z = 0 \ hfill \ end {array} [/ latex]
В качестве матрицы имеем
[латекс] \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill 1 & \ hfill 1 \\ \ hfill 0,05 & \ hfill 0,08 & \ hfill 0,09 \\ \ hfill 2 & \ hfill 0 & \ hfill -1 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill 10,000 \\ \ hfill 770 \\ \ hfill 0 \ end {array} \ right] [/ latex]
Теперь мы выполняем исключение Гаусса, чтобы получить форму строки-эшелон.
[латекс] \ begin {массив} {l} \ begin {array} {l} \ hfill \\ -0.05 {R} _ {1} + {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0.03 & \ hfill & \ hfill 0.04 & \ hfill \\ \ hfill 2 & \ hfill & \ hfill 0 & \ hfill & \ hfill -1 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 270 \\ \ hfill & \ hfill 0 \ end {array} \ right] \ hfill \ end {array} \ hfill \\ -2 {R} _ {1} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0.03 & \ hfill & \ hfill 0.04 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -2 & \ hfill & \ hfill -3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 270 \\ \ hfill & \ hfill -20,000 \ end {array} \ right] \ hfill \\ \ frac {1} {0.03} {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrrrrr} \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill \ frac {4} {3} & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -2 & \ hfill & \ hfill -3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 9,000 \\ \ hfill & \ hfill -20,000 \ end {array} \ right] \ hfill \\ 2 {R} _ {2} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill \ frac {4} {3} & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill – \ frac {1} {3} & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 9,000 \\ \ hfill & \ hfill -2,000 \ end {array} \ right] \ hfill \ end {array} [/ latex]
Третья строка сообщает нам [латекс] – \ frac {1} {3} z = -2,000 [/ latex]; таким образом [латекс] z = 6,000 [/ латекс].
Вторая строка сообщает нам [латекс] y + \ frac {4} {3} z = 9000 [/ latex].
Подставляя [латекс] z = 6,000 [/ latex], получаем
[латекс] \ begin {array} {r} \ hfill y + \ frac {4} {3} \ left (6000 \ right) = 9000 \\ \ hfill y + 8000 = 9000 \\ \ hfill y = 1000 \ end {array} [/ latex]
Первая строка сообщает нам [латекс] x + y + z = 10,000 [/ latex]. Подставив [latex] y = 1,000 [/ latex] и [latex] z = 6,000 [/ latex], мы получим
[latex] \ begin {array} {l} x + 1,000 + 6,000 = 10,000 \ hfill \\ \ text {} x = 3,000 \ text {} \ hfill \ end {array} [/ latex]
Ответ: 3000 долларов вложены под 5%, 1000 долларов вложены под 8% и 6000 долларов вложены под 9%.
Попробуй
Небольшая обувная компания взяла ссуду в размере 1 500 000 долларов на расширение своего ассортимента. Часть денег была взята под 7%, часть – под 8%, часть – под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7%, а годовая процентная ставка по всем трем займам составляла 130 500 долларов. Используйте матрицы, чтобы найти сумму займа по каждой ставке.
Показать решение150 000 долларов США под 7%, 750 000 долларов США под 8%, 600 000 долларов США под 10%
Внесите свой вклад!
У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
Улучшить эту страницуПодробнее
Системы линейных уравнений: исключение Гаусса
Решение линейной системы с матрицами с использованием исключения Гаусса
После нескольких уроков, в которых мы неоднократно упоминали, что мы охватываем основы, необходимые для последующего изучения того, как решать системы линейных уравнений, пришло время для нашего урока сосредоточиться на полной методологии, которой нужно следовать, чтобы найти решения. для таких систем.
Что такое гауссово исключение
Исключение Гаусса – это название метода, который мы используем для выполнения трех типов операций со строками матрицы над расширенной матрицей, полученной из линейной системы уравнений, чтобы найти решения для такой системы.Этот метод также называется сокращением строк и состоит из двух этапов: прямого исключения и обратной замены.
Эти два шага метода исключения Гаусса различаются не операциями, которые вы можете использовать с их помощью, а результатом, который они производят. Шаг прямого исключения относится к сокращению строки, необходимому для упрощения рассматриваемой матрицы до ее эшелонированной формы. Цель такого этапа – продемонстрировать, имеет ли система уравнений, изображенная в матрице, единственное возможное решение, бесконечное множество решений или просто отсутствие решения.Если обнаружено, что система не имеет решения, то нет причин продолжать сокращение строки матрицы на следующем этапе.
Если возможно получить решения для переменных, входящих в линейную систему, то выполняется этап исключения Гаусса с обратной подстановкой. На этом последнем шаге будет получена сокращенная форма матрицы, которая, в свою очередь, дает общее решение системы линейных уравнений.
Правила исключения Гаусса такие же, как правила для трех элементарных операций со строками, другими словами, вы можете алгебраически оперировать строками матрицы следующими тремя способами (или комбинацией):
- Перестановка двух рядов
- Умножение строки на константу (любую константу, отличную от нуля)
- Добавление строки к другой строке
Итак, решение линейной системы с матрицами с использованием исключения Гаусса оказывается структурированным, организованным и довольно эффективным методом.
Как выполнить метод исключения Гаусса
На самом деле это не установленный набор шагов исключения Гаусса, которым нужно следовать, чтобы решить систему линейных уравнений, это все о матрице, которая у вас есть в ваших руках, и необходимых операциях со строками для ее упрощения. Для этого давайте поработаем над нашим первым примером исключения Гаусса, чтобы вы могли начать изучать весь процесс и интуицию, которая необходима при работе с ними:
Пример 1
Обратите внимание, что в этот момент мы можем заметить, что эта система линейных уравнений разрешима с единственным решением для каждой из ее переменных.То, что мы выполнили до сих пор, – это первый этап сокращения строк: прямое исключение. Мы можем продолжить упрощение этой матрицы еще больше (что приведет нас ко второму этапу обратной подстановки), но нам это действительно не нужно, поскольку на этом этапе система легко разрешима. Таким образом, мы смотрим на получившуюся систему, чтобы решить ее напрямую:
- Уравнение 5: Полученная линейная система уравнений для решения
Из этого набора мы можем автоматически заметить, что значение переменной z: z = -2.Мы используем это знание, чтобы подставить его во вторые уравнения для решения относительно y, и подставить значения y и z в первые уравнения для решения относительно x:
В последний раздел этого урока добавлено больше задач исключения Гаусса. Обязательно проработайте их, чтобы практиковаться.
Разница между исключением по Гауссу и по Гауссу Иордану
Разница между гауссовым исключением и гауссовым методом исключения Жордана состоит в том, что один создает матрицу в форме эшелона строк, а другой – матрицу в форме уменьшенного ряда.Матрица формы эшелона строк имеет верхнюю треугольную композицию, где любые нулевые строки находятся внизу, а ведущие члены находятся справа от ведущего члена из строки выше. Уменьшенная форма эшелона выходит за рамки еще большего упрощения (иногда даже достигая формы единичной матрицы).
Уравнение 8: Разница между формой эшелона и формой ряда эшелоновИстория исключения Гаусса и его названия довольно интересны, вы будете удивлены, узнав, что название «Гауссовский» было присвоено этой методологии по ошибке в прошлом веке.На самом деле было обнаружено, что алгоритм одновременного решения системы линейных уравнений с использованием матриц и редукции строк записан в той или иной форме в древних китайских текстах, которые датируются еще до нашей эры. Затем в конце 1600-х годов Исаак Ньютон провел по этому уроку, чтобы заполнить то, что он считал пробелом в книгах по алгебре. После того, как название «Гауссиан» было уже установлено в 1950-х годах, термин Гаусса-Иордана был принят, когда геодезист У. Джордан усовершенствовал эту технику, чтобы он мог использовать такие вычисления для обработки своих наблюдаемых данных топографической съемки.Если вы хотите продолжить чтение увлекательной истории математиков исключения Гаусса, не бойтесь щелкнуть ссылку и прочитать.
На самом деле нет никакой физической разницы между исключением Гаусса и исключением Гаусса Джордана, оба процесса следуют одному и тому же типу операций со строками и их комбинациям, их различие зависит от результатов, которые они производят. Многие математики и учителя во всем мире будут относиться к исключению Гаусса и исключению Гаусса Джордана как к методам создания матрицы эшелонированной формы по сравнению с методом создания матрицы уменьшенной эшелонированной формы, но на самом деле они говорят о двух стадиях сокращения строк. мы объяснили это в самом первом разделе этого урока (прямое исключение и обратная подстановка), и поэтому вы просто применяете операции со строками, пока не упростите рассматриваемую матрицу.Если вы дойдете до формы эшелона, вы обычно можете решить с ней систему линейных уравнений (до сих пор это то, что называлось бы исключением Гаусса). Если вам нужно продолжить упрощение такой матрицы, чтобы напрямую получить общее решение для системы уравнений, над которой вы работаете, в этом случае вы просто продолжаете работать с матрицей по строкам, пока не упростите ее до сокращенной формы эшелона. (это будет то, что мы называем частью Гаусса-Жордана, и которую можно рассматривать также как поворотное исключение Гаусса).
Мы оставим подробное объяснение форм сокращения строк и эшелонирования для следующего урока, поскольку сейчас вам нужно знать это, если у вас нет единичной матрицы в левой части расширенной матрицы, которую вы решаете (в этом случае вы не используете не нужно ничего делать для решения системы уравнений, относящейся к матрице), метод исключения Гаусса (регулярное сокращение строк) всегда будет использоваться для решения линейной системы уравнений, которая была записана в виде матрицы.
Примеры исключения Гаусса
В качестве последнего раздела давайте поработаем еще несколько упражнений по исключению Гаусса (сокращение строк), чтобы вы могли больше попрактиковаться в этой методологии.На протяжении многих будущих уроков этого курса линейной алгебры вы обнаружите, что сокращение строк является одним из самых важных инструментов при работе с матричными уравнениями. Поэтому убедитесь, что вы понимаете все этапы решения следующих проблем.
Пример 2
Пример 3
Мы знаем, что для этой системы мы получим расширенную матрицу с тремя строками (поскольку система содержит три уравнения) и тремя столбцами слева от вертикальной линии (поскольку есть три разных переменных).В этом случае мы перейдем непосредственно к сокращению строк, и поэтому первая матрица, которую вы увидите в этом процессе, – это та, которую вы получите, преобразовав систему линейных уравнений в расширенную матрицу.
- Уравнение 15: Строка, уменьшающая расширенную матрицу
Обратите внимание, как мы можем сразу сказать, что переменная z равна нулю для этой системы, поскольку третья строка результирующей матрицы показывает уравнение -9z = 0 . Мы используем это знание и проверяем вторую строку матрицы, которая предоставит уравнение 2y – 6z = 0 , подставив в это уравнение значение z = 0 \, в результате получится y \, также равное нулю.Таким образом, мы наконец подставляем оба значения y и z \ в уравнение, которое получается из первой строки матрицы: x + 4y + 3z = 1 , поскольку и y , и z \ , равны нулю, то это дает нам x = 1 . Итак, окончательное решение этой системы уравнений выглядит следующим образом:
- Уравнение 16: Окончательное решение системы уравнений
Пример 4
Из чего видно, что последняя строка дает уравнение: 6z = 3 и, следовательно, z = 1/2.Мы подставляем это в уравнения, полученные из второй и первой строк (в указанном порядке), чтобы вычислить значения переменных x и y:
Пример 5
- Решите следующую линейную систему, используя метод исключения Гаусса: Уравнение 21: Система линейных уравнений с двумя переменными
- Транскрипция линейной системы в виде расширенной матрицы и редукции строк: Уравнение 22: Строка, уменьшающая расширенную матрицу
Что автоматически сообщает нам y = 8 .Итак, подставляя это значение в уравнение из первой строки, получаем: 4x – 5y = 4x – 5 (8) = 4x – 40 = -6 4x = 34 \, и поэтому значение x равно: x = 172 \ frac {\ small17} {\ small2} 217 . И окончательное решение этой системы уравнений:
Уравнение 23: Окончательное решение системы уравнений
Пример 6
Чтобы завершить наш урок на сегодня, у нас есть рекомендация по ссылке, чтобы дополнить ваши исследования: Исключение Гаусса – статья, которая содержит некоторую дополнительную информацию о сокращении строк, включая введение в тему и еще несколько примеров.Как мы упоминали ранее, будьте готовы продолжать использовать сокращение строк почти на протяжении всего курса линейной алгебры, так что до встречи на следующем уроке!
Устранение Гаусса Джордана – объяснение и примеры
Метод исключения Гаусса-Жордана – это алгоритм для решения линейной системы уравнений. Мы также можем использовать его, чтобы найти обратную матрицу. Давайте сначала посмотрим на определение:
Метод исключения Гаусса Джордана, или метод исключения Гаусса, представляет собой алгоритм для решения системы линейных уравнений путем представления ее в виде расширенной матрицы, сокращения ее с помощью операций со строками и выражения системы в сокращенной форме строки-эшелона для нахождения значений. переменных.
В этом уроке мы увидим детали метода исключения Гаусса и того, как решить систему линейных уравнений с помощью метода исключения Гаусса-Жордана. Примеры и практические вопросы будут приведены ниже.
Что такое метод исключения Гаусса?
Метод исключения Гаусса – это структурированный метод решения системы линейных уравнений. Таким образом, это алгоритм, и его можно легко запрограммировать для решения системы линейных уравнений. Основная цель исключения Гаусса-Джордана:
- для представления системы линейных уравнений в форме расширенной матрицы
- , затем выполнение на нем операций строки $ 3 $ до тех пор, пока не будет достигнута сокращенная форма эшелона строк (RREF)
- Наконец, мы можем легко узнать решения из RREF
Давайте посмотрим, что такое расширенная матричная форма, 3 $ строчные операции, которые мы можем выполнять с матрицей, и сокращенная форма строки матрицы.
Расширенная матрица
Система линейных уравнений показана ниже:
$ \ begin {align *} 2x + 3y & = \, 7 \\ x – y & = 4 \ end {align *} $
Мы напишем расширенную матрицу этой системы, используя коэффициенты уравнений и записав ее в стиле , показанном ниже:
$ \ left [\ begin {array} {r r | r} 2 & 3 & 7 \\ 1 & -1 & 4 \ end {array} \ right] $
Пример использования системы уравнений стоимостью 3 доллара приведен ниже:
$ \ begin {align *} 2x + y + z & = \, 10 \\ x + 2y + 3z & = 1 \\ – x – y – z & = 2 \ end {align *} $
Представление этой системы в виде расширенной матрицы:
$ \ left [\ begin {array} {r r r | r} 2 & 1 & 1 & 10 \\ 1 & 2 & 3 & 1 \\ – 1 & – 1 & – 1 & 2 \ end {array} \ right] $
Операции со строками в матрице
Есть $ 3 $ операций с элементарной строкой , которые мы можем выполнять с матрицами.Это не изменит решения системы. Их:
- Обмен $ 2 $ строк
- Умножить строку на ненулевой ($ \ neq 0 $) скаляр
- Добавить или вычесть скалярное кратное одной строки из другой строки.
Уменьшенная форма рядка-эшелон
Основная цель метода исключения Гаусса Джордана состоит в том, чтобы использовать операции элементарной строки $ 3 $ на расширенной матрице, чтобы привести ее к сокращенной форме эшелона строк (RREF). Считается, что матрица находится в сокращенной форме эшелона строк , также известной как каноническая форма строк , если выполняются следующие условия $ 4 $:
- Строки с нулевыми записями (все элементы этой строки равны $ 0 $ s) находятся внизу матрицы.
- Начальная запись (первая ненулевая запись в строке) каждой ненулевой строки соответствует справа ведущей записи строки непосредственно над ней.
- Начальная запись в любой ненулевой строке – $ 1 $.
- Все записи в столбце, содержащем начальную запись ($ 1 $), нулевые.
Как пройти Гаусс Джордан Ликвидация
Нет никаких определенных шагов в методе исключения Гаусса-Джордана, но алгоритм ниже описывает шаги, которые мы выполняем, чтобы прийти к сокращенной форме эшелона строк расширенной матрицы.
- Поменяйте местами строки так, чтобы все строки с нулевыми записями находились внизу матрицы.
- Поменяйте местами строки так, чтобы строка с самой большой левой цифрой находилась наверху матрицы.
- Умножьте верхнюю строку на скаляр, который преобразует ведущую запись верхней строки в $ 1 $ (если ведущей записью верхней строки является $ a $, умножьте ее на $ \ frac {1} {a} $, чтобы получить $ 1 $).
- Добавьте или вычтите кратные числа верхней строки из других строк, чтобы все записи в столбце ведущей записи верхней строки были нулями.
- Выполните шаги $ 2 – 4 $ для следующей крайней левой ненулевой записи , пока все ведущие записи каждой строки не будут равны 1 $.
- Поменяйте местами строки так, чтобы ведущая запись каждой ненулевой строки находилась справа от ведущей записи строки непосредственно над ней
На первый взгляд запомнить / запомнить шаги не так-то просто. Это вопрос решения нескольких проблем, пока вы не освоитесь с процессом. Существует также фактор , интуиция , которая играет B-I-G роль в выполнении исключения Гаусса Джордана.
Давайте рассмотрим несколько примеров, чтобы пояснить процесс решения системы линейных уравнений с помощью метода исключения Гаусса-Джордана .
Пример 1Решите систему, показанную ниже, используя метод исключения Гаусса Джордана:
$ \ begin {align *} {- x} + 2y & = \, {- 6} \\ {3x} – 4y & = {14} \ end {align *}
$Решение
Первый шаг – записать расширенную матрицу системы.Мы показываем это ниже:
$ \ left [\ begin {array} {r r | r} – 1 & 2 & – 6 \\ 3 & -4 & 14 \ end {array} \ right] $
Теперь наша задача – привести матрицу к сокращенной форме эшелона строк (RREF), выполнив операции элементарной строки $ 3 $.
У нас есть расширенная матрица:
$ \ left [\ begin {array} {r r | r} – 1 и 2 & – 6 \\ 3 & – 4 & 14 \ end {array} \ right] $
Шаг 1:
Мы можем умножить первую строку на $ – 1 $, чтобы сделать ведущую запись $ 1 $.Показано ниже:
$ \ left [\ begin {array} {r r | r} 1 & – 2 & 6 \\ 3 & – 4 & 14 \ end {array} \ right]
долл. СШАШаг 2:
Теперь мы можем умножить первую строку на $ 3 $ и вычесть ее из второй строки. Показано ниже:
$ \ left [\ begin {array} {r r | r} 1 & -2 & 6 \\ {3 – (1 \ times 3)} & {-4 – (-2 \ times 3)} & {14 – (6 \ times 3)} \ end {array} \ справа] $
$ = \ left [\ begin {array} {r r | r} 1 & – 2 & 6 \\ 0 & 2 & – 4 \ end {array} \ right] $
У нас есть $ 0 $ как первая запись во второй строке.
Шаг 3:
Чтобы сделать вторую запись второй строки $ 1 $, мы можем умножить вторую строку на $ \ frac {1} {2} $. Показано ниже:
$ \ left [\ begin {array} {r r | r} 1 & – 2 & 6 \\ {\ frac {1} {2} \ times 0} & {\ frac {1} {2} \ times 2} & {\ frac {1} {2} \ times – 4} \ end {array} \ right]
долл. США$ = \ left [\ begin {array} {r r | r} 1 & – 2 & 6 \\ 0 & 1 & – 2 \ end {array} \ right] $
Шаг 4:
Мы почти у цели!
Вторая запись первой строки должна быть $ 0 $.Для этого мы умножаем вторую строку на $ 2 $ и добавляем ее к первой строке. Показано ниже:
$ \ left [\ begin {array} {r r | r} {1 + (0 \ times 2)} & {- 2 + (1 \ times 2)} & {6 + (- 2 \ times 2)} \\ 0 & 1 & – 2 \ end {array} \ справа] $
$ = \ left [\ begin {array} {r r | r} 1 & 0 & 2 \\ 0 & 1 & – 2 \ end {array} \ right] $
Это пониженный ряд форма . Из расширенной матрицы мы можем написать два уравнения (решения):
$ \ begin {align *} x + 0y & = \, 2 \\ 0x + y & = -2 \ end {align *}
$$ \ begin {align *} x & = \, 2 \\ y & = – 2 \ end {align *}
$Таким образом, решение системы уравнений есть $ x = 2 $ и $ y = – 2 $.
Пример 2Решите систему, показанную ниже, используя метод исключения Гаусса Джордана:
$ \ begin {align *} x + 2y & = \, 4 \\ x – 2y & = 6 \ end {align *}
$
Решение
Запишем расширенную матрицу системы уравнений:
$ \ left [\ begin {array} {r r | r} 1 & 2 & 4 \\ 1 & – 2 & 6 \ end {array} \ right] $
Теперь мы выполняем элементарные операции со строками с этой матрицей до тех пор, пока не получим сокращенную форму эшелона строк.
Шаг 1:
Умножаем первую строку на $ 1 $, а затем вычитаем ее из второй строки. Это в основном вычитание первой строки из второй строки:
$ \ left [\ begin {array} {r r | r} 1 и 2 и 4 \\ 1 – 1 и – 2 – 2 и 6 – 4 \ end {array} \ right] $
$ = \ left [\ begin {array} {r r | r} 1 & 2 & 4 \\ 0 & – 4 & 2 \ end {array} \ right] $
Шаг 2:
Умножаем вторую строку на $ – \ frac {1} {4} $, чтобы получить вторую запись строки, $ 1 $:
$ \ left [\ begin {array} {r r | r} 1 и 2 и 4 \\ 0 \ times – \ frac {1} {4} & – 4 \ times – \ frac {1} {4} и 2 \ times – \ frac {1} {4} \ end {array} \ right]
долл. США$ = \ left [\ begin {array} {r r | r} 1 & 2 & 4 \\ 0 & 1 & – \ frac {1} {2} \ end {array} \ right]
долл. СШАШаг 3:
Наконец, мы умножаем вторую строку на $ – 2 $ и добавляем ее к первой строке, чтобы получить уменьшенную форму эшелона строк этой матрицы:
$ \ left [\ begin {array} {r r | r} 1 + (- 2 \ times 0) & 2+ (- 2 \ times 1) & 4 + (- 2 \ times – \ frac {1} {2}) \\ 0 & 1 & – \ frac {1 } {2} \ end {array} \ right]
долл. США$ = \ left [\ begin {array} {r r | r} 1 & 0 & 5 \\ 0 & 1 & – \ frac {1} {2} \ end {array} \ right]
долл. СШАЭто пониженный ряд форма .Из расширенной матрицы мы можем написать два уравнения (решения):
$ \ begin {align *} x + 0y & = \, 5 \\ 0x + y & = – \ frac {1} {2} \ end {align *} $
$ \ begin {align *} x & = \, 5 \\ y & = – \ frac {1} {2} \ end {align *}
$Таким образом, решение системы уравнений есть $ x = 5 $ и $ y = – \ frac {1} {2} $.
Практические вопросыРешите систему, показанную ниже, используя метод исключения Гаусса Джордана:
$ \ begin {align *} 2x + y & = \, – 3 \\ – x – y & = 2 \ end {align *} $
Решите систему, показанную ниже, используя метод исключения Гаусса Джордана:
$ \ begin {align *} x + 5y & = \, 15 \\ – x + 5y & = 25 \ end {align *}
$
ответы
Начнем с записи расширенной матрицы системы уравнений:
$ \ left [\ begin {array} {r r | r} 2 & 1 & – 3 \\ – 1 & – 1 & 2 \ end {array} \ right] $
Теперь мы выполняем элементарные операции со строками, чтобы прийти к нашему решению.
Во-первых,
Мы меняем знаки второй строки местами. Итак, имеем:
$ \ left [\ begin {array} {r r | r} 1 & 1 & – 2 \\ 2 & 1 & – 3 \ end {array} \ right] $
Во-вторых,
Мы дважды вычитаем первую строку из второй строки:
$ \ left [\ begin {array} { rr | r} 1 & 1 & – 2 \\ 2 – (2 \ times 1) & 1 – (2 \ times 1) & – 3 – (2 \ times – 2) \ end {array} \ right] $
$ = \ left [\ begin {array} {rr | r} 1 & 1 & – 2 \\ 0 & – 1 & 1 \ end {array} \ right] $
Третье,
Мы инвертируем вторую строку, чтобы получить:
$ = \ left [\ begin {array} {rr | r} 1 & 1 & – 2 \\ 0 & 1 & – 1 \ end {array} \ right] $
Наконец,
Мы вычитаем вторую строку из первой и получаем:
$ = \ left [\ begin { массив} {rr | r} 1 & 0 & – 1 \\ 0 & 1 & – 1 \ end {array} \ right] $Из этой расширенной матрицы мы можем написать два уравнения (решения):
$ \ begin {align *} x + 0y & = \, – 1 \\ 0x + y & = – 1 \ end {align *} $
$ \ begin {align *} x & = \, – 1 \\ y & = – 1 \ end {align *}
$Таким образом, решение системы уравнений есть $ x = – 1 $ и $ y = – 1 $.
- Расширенная матрица системы:
$ \ left [\ begin {array} {rr | r} 1 & 5 & 15 \\ – 1 & 5 & 25 \ end {array} \ right] $
Давайте получим это матрицу к приведенной форме эшелона строк и найти решение системы.
Сначала
Отмените первую строку, затем вычтите ее из второй строки, чтобы получить:
$ \ left [\ begin {array} {rr | r} 1 & 5 & 15 \\ – 1 – (- 1) & 5 – (- 5) & 25 – (- 15) \ end {array} \ right] $
$ = \ left [\ begin {array} {rr | r} 1 & 5 & 15 \\ 0 & 10 & 40 \ end {array} \ right] $
Во-вторых,
Разделите вторую строку на $ 10 $, чтобы получить:
$ \ left [\ begin {array} {rr | r} 1 & 5 & 15 \\ 0 & 1 & 4 \ end {array} \ right] $
Затем
Умножьте вторую строку на $ 5 $ и вычтите ее из первой строки, чтобы получить окончательное решение:
$ \ left [\ begin {array} {rr | r} 1 – (5 \ times 0) & 5 – (5 \ times 1) & 15 – (5 \ times 4) \\ 0 & 1 & 4 \ end {array} \ right] $
$ = \ left [ \ begin {array} {rr | r} 1 & 0 & – 5 \\ 0 & 1 & 4 \ end {array} \ right] $
Это сокращенная форма эшелона строк (RREF).Из этой расширенной матрицы мы можем написать два уравнения (решения):$ \ begin {align *} x & = \, – 5 \\ y & = 4 \ end {align *} $
Таким образом, решение системы уравнений $ x = – 5 $ и $ y = 4 $.
Исключение Гаусса – обзор
1.3.7 Исключение Гаусса или Гаусса
Исключение Гаусса (также известное как Исключение Гаусса ) – это широко используемый метод решения систем линейных уравнений в форме [ K ] { u } = { F }.В операциях с матрицами существует три распространенных типа манипуляций, которые служат для создания новой матрицы, обладающей теми же характеристиками, что и исходная:
- 1.
Поменять местами любые две строки.
- 2.
Умножьте каждую запись в любой строке на ненулевое постоянное значение.
- 3.
Добавьте значения из каждой записи одной строки к каждой записи другой строки.
Цель использования исключения Гаусса – создать новую матрицу с теми же свойствами, что и исходная [ K ], но в формате, в котором только верхний треугольник имеет ненулевые элементы.Используя предыдущую матрицу 5 × 5 в качестве примера, верхний треугольник состоит из элементов в правом верхнем треугольнике матрицы и включает элементы в правой диагональной строке в виде
[m11m12m13m14m150m22m23m24m2500m33m34m35000m44m450000m55].
Мы достигаем цели исключения Гаусса, правильно применяя одну из трех вышеупомянутых операций за раз. После того, как верхняя треугольная матрица сформирована, мы используем метод обратной подстановки , чтобы сначала найти последнюю переменную.Причина, по которой этот метод называется «обратной заменой», заключается в том, что последняя строка верхней треугольной матрицы должна быть решена первой. Поскольку в последней строке верхней треугольной матрицы есть только одна ненулевая запись, мы можем найти неизвестную переменную простым арифметическим делением, то есть из
[K] {u2v2u3u4v4} = [m11m12m13m14m150m22m23m24m2500m33m34m35000m44m40000m55] {u2v2v4f2f2fu4fu4fu2 } → v4 = F4Vm55.
Имея значение v 4 , мы решаем для второй до последней переменной.Поскольку m 44 u 4 + m 45 v 4 = F 4 H , мы можем решить для u 4 как u4 = F4H − m45v4m44. Мы многократно применяем один и тот же набор процедур, пока не будут найдены значения всех переменных.
Мы будем использовать типичный 64-битный компьютер, чтобы проиллюстрировать критическую проблему при использовании исключения Гаусса. Хорошо известно, что такой компьютер хранит действительное (десятичное) число в формате с плавающей запятой, используя 64 бита: 1 бит для представления знака (плюс или минус), 52 бита для представления количества цифр точности (мантисса), и 11 бит для представления экспоненты.При делении числа на другое очень маленькое число имеющихся цифр в мантиссе может быть недостаточно для поддержания необходимой точности, то есть может возникнуть ошибка округления. При исключении Гаусса точка поворота или позиция поворота – это позиция в строке, которая совпадает с правой диагональной линией. Значения в точках поворота используются в качестве знаменателя при формировании верхней треугольной матрицы. Чтобы исключить ошибки округления, возникающие при делении на очень маленькое число, используется первый тип манипуляции для перемещения строки с очень маленьким числом в точке поворота в другую строку.Это достигается простым перестановкой рядов так, чтобы большие числа располагались в точках поворота. Мы используем вторую и третью операции для получения нулей в левой нижней части матрицы, что необходимо для получения верхней треугольной матрицы.
Модифицированной версией метода исключения Гаусса является метод исключения Гаусса – Жордана. Цель исключения Гаусса – Жордана состоит в том, чтобы получить матрицу, которая имеет правую диагональную линию всех единиц (единиц), а все остальные позиции матрицы содержат нули.Это достигается с помощью тех же трех типов матричных манипуляций, что и в методе исключения Гаусса. Поскольку квадратная матрица состоит только из единичных значений в диагональных элементах, решения для всех неизвестных становятся легко доступными. Один из недостатков метода Гаусса – Жордана заключается в том, что он более затратный в вычислительном отношении, чем метод исключения Гаусса. Таким образом, он полезен только для решения проблем путем ручного расчета, когда есть небольшое количество одновременных уравнений.Используя метод исключения Гаусса, а не метод Гаусса – Жордана, мы избегаем многих дополнительных шагов. Поскольку метод FE обычно включает большую систему, чаще используется метод исключения Гаусса.
В следующем разделе мы шаг за шагом продемонстрируем процессы в методе исключения Гаусса. Конечно, вместо ручных вычислений следует написать и использовать компьютерную программу. Используя предыдущий пример в качестве отправной точки, уравнение. (1.68) повторяется ниже.
[K] {u2v2u3u4v4} = 108 [100−50006.6700−6.67−506.44−1.441.9200−1.44400−6.671..67] {u2v2u3u4v4} = {F2HF2VF3HF40003−5002 = {0002002). все, кроме первой записи в первом столбце, равны 0. Мы заметили, что третья строка в этом столбце содержит единственное ненулевое значение. Чтобы манипулировать третьей строкой, чтобы сделать ведущее число 0, мы должны умножить существующее число (-5) на такое значение, чтобы добавление результата к первой записи в строке один (10) давало 0. Используя правило два, мы умножаем каждую запись в третьей строке по 2:
108 [100-50006.6700−6.67−10012.88−2.883.8400−1.44400−6.671..67] {u2v2u3u4v4} = {00020000−50000}.
Затем мы добавляем строку 1 к строке 3, но мы не затрагиваем строку 1:
108 [100-50006.6700-6.67007.88-2.883.8400-1.44400-6.671..67] {u2v2u3u4v4} = {00020000−50000 }.
Теперь, когда все значения в первом столбце, кроме первого, равны 0, мы применяем аналогичный процесс ко второму столбцу. Мы хотим, чтобы все значения во втором столбце, кроме второго, равнялись 0, а это означает, что мы должны адресовать −6,67 в последней строке. Его можно изменить на 0, просто добавив значения из строки 2.
108 [100−50006.6700−6.67007.88−2.883.8400−1.4440001.9204] {u2v2u3u4v4} = {00020000−50000}
Две операции, правила два и три, необходимы для преобразования записи в четвертой строке столбца три на 0. Сначала умножаем четвертую строку на 7,881,44 (обратите внимание, что эта операция также применима к вектору силы):
108 [100-50006,6700-6,67007,88-2,883,8400-7,8821,8,9204] {u2v2u3u4v4} = { 0001.094 × 105−50000},
, а затем добавьте значения из третьей строки к этим результатам, чтобы сформировать новую четвертую строку:
108 [100−50006.6700−6.67007.88−2.883.8400019.013.84001.9204] {u2v2u3u4v4} = {0001.094 × 105−50000}.
Аналогичным образом мы умножаем пятую строку на -7,881,92, а затем складываем значения из третьей строки, чтобы сформировать новую пятую строку:
108 [100-50006,6700-6,67007,88-2,883,8400019,013,84000-2,88-12,58 ] {u2v2u3u4v4} = {0001,094 × 1052,052 × 106}.
К этому моменту должно быть очевидно, что умножение на значение в другой строке и последующее деление на значение в текущей строке дает результат, который можно вычесть из этой другой строки и получить 0.Чтобы еще раз увидеть этот процесс, мы умножаем пятую строку на 19.012.88, затем складываем значения из четвертой строки, чтобы получить новую пятую строку:
108 [100−50006.6700−6.67007.88−2.883.8400019.013.840000−79.20] {u2v2u3u4v4} = {0001,094 × 1051,464 × 106}.
Теперь матрица имеет форму верхней треугольной матрицы, что означает, что все значения ниже и слева от правой диагональной линии являются нулями. На этом этапе мы применяем метод обратной замены для определения узловых смещений.
Начнем с последней строки, которая содержит 108 [0000−79.20], и мы умножаем последовательные значения в этой строке на последовательные значения в векторе узлового смещения:
108 ((0) (u2) + (0) (v2) + (0) (u3) + (0) ( u4) + (- 79.20) (v4)) = 1.464 × 106
Мы можем сделать это проще, признав, что только последнее значение в строке ненулевое, и поэтому v 4 – это просто последнее значение в вектор силы, деленный на последнюю запись в верхней треугольной матрице [ K ]:
v4 = (1,464 × 106) (- 79,2 × 108) = – 1,849 × 10−4
Мы можем использовать v 4 , чтобы найти u 4 и т. Д.Ниже приведены расчеты значений узловых смещений в м :
u4 = 1.094 × 105-108 × 3.84 × v419.01 × 108 = 1.804 × 10519.01 × 108 = 0.949 × 10-4,
u3 = 108 × (2,88) × u4−108 × 3,84 × v4108 × 7,88 = 9,837 × 10−47,88 = 1,248 × 10−4,
v2 = 108 × 6,67 × v4108 × 6,67 = −1,849 × 10−4 и
u2 = 108 × 5 × u3108 × 10 = 0,624 × 10−4.
Узловые смещения, рассчитанные с использованием метода MSA или прямого метода жесткости, в точности совпадают с точными решениями проблем, связанных с фермами.Для типов элементов, отличных от фермы или пружины, узловые решения вряд ли будут иметь те же значения, что и точные решения. Простое практическое правило состоит в том, что чем больше элементов используется для представления интересующей структуры, тем точнее результаты будут приближаться к точным решениям. Дополнительные описания других типов элементов приведены в главе 2.
Как выполнить исключение Гаусса? Шкаф системы с уникальным решением
В этом разделе мы предлагаем еще один пример решения системы линейных алгебраических уравнений методом исключения Гаусса.Этот пример ясно показывает, что при выполнении исключения Гаусса вы должны замечать, когда удобно поменять местами строки, чтобы сэкономить время и сократить вычисления.
Нам предстоит решить следующую систему линейных алгебраических уравнений:
\ left \ {\ begin {align} -2x + y + 2z = 2 \\ x + 3y-z = 0 \\ 3x + 2y + 4z = 3 \ end {align} \ right.
Прежде всего, обратите внимание, что мы можем поменять местами любые два уравнения в системе по своему усмотрению, решение, очевидно, не изменится. Мы видим, что x имеет коэффициент 1 во втором уравнении, поэтому мы можем преобразовать нашу систему следующим образом:
\ left \ {\ begin {align} x + 3y-z = 0 \\ – 2x + y + 2z = 2 \\ 3x + 2y + 4z = 3 \ end {align} \ right.
Вот видеоверсия этого примера:
Теперь мы можем исключить x из второго уравнения. Для этого добавим первое уравнение, умноженное на 2, ко второму:
\ left \ {\ begin {align} x + 3y-z = 0 \\ 7y = 2 \\ 3x + 2y + 4z = 3 \ end {align} \ right.
Также мы исключаем x из третьего уравнения: вычитаем первое уравнение, умноженное на 3, из третьего:
\ left \ {\ begin {align} x + 3y-z = 0 \\ 7y = 2 \\ – 7y + 7z = 3 \ end {align} \ right.
После этого мы могли действовать по нашему алгоритму. Но в этом нет необходимости, поскольку мы видим, что у нас есть второе уравнение, содержащее только одно неизвестное y, а также третье уравнение, содержащее две неизвестные. Таким образом, мы можем изменить нашу систему следующим образом:
\ left \ {\ begin {align} x + 3y-z = 0 \\ – 7y + 7z = 3 \\ 7y = 2 \ end {align} \ right.
Это треугольная форма; мы можем сразу получить y из третьего уравнения:
\ left \ {\ begin {align} x + 3y-z = 0 \\ – 7y + 7z = 3 \\ y = \ frac {2} {7} \ end {align} \ right.
Затем подставляем во второе уравнение и получаем значение z:
\ left \ {\ begin {align} x + 3y-z = 0 \\ z = \ frac {5} {7} \\ y = \ frac {2} {7} \ end {align} \ right.
Затем подставьте значения y, z в первое уравнение, чтобы получить x:
\ left \ {\ begin {выровнено} x = – \ frac {1} {7} \\ z = \ frac {5} {7} \\ y = \ frac {2} {7} \ end {выровнено} \верно.
и вот ответ.
Как видите, у данной системы есть одно решение. Это решение уникальное. Имейте в виду, что в общем случае возможны три случая: система линейных алгебраических уравнений либо имеет единственное решение, либо бесконечно много решений, либо вообще не имеет решения.Решая домашнее задание по линейной алгебре, вы можете столкнуться с любым из этих случаев. Не забудьте потом проверить свой ответ. Просто подставьте его в исходную систему. Также вы можете использовать онлайн-решатель систем. Введите свою систему и сравните результат со своим ответом.
Ознакомьтесь с подробными объяснениями метода исключения Гаусса в одном из наших предыдущих руководств для лучшего понимания. Помните, что практика – ключевой момент в изучении математики. Хотите лучше по математике? Уделите больше математики!
.