Метод гаусса прямой ход: Метод Гаусса

Содержание

1.3 Метод Гаусса. Программный продукт, осуществляющий решение задач по дисциплине “Численные методы”

Численные методы решения систем линейных уравнений, страница 3

Решение

Рассмотрим матрицу из примера 2:

Отметим, что если один из главных миноров матрицы А равен нулю, то при попытке решить систему линейных уравнений мы получим деление на ноль (). Это первый недостаток метода Гаусса без выбора ведущего элемента.

Второй недостаток: если какой-либо из ведущих элементов принимает малые значения по модулю, то вычислительный алгоритм метода Гаусса без выбора ведущего элемента становится неустойчивым.

Правило. Если ведущие элементы в методе Гаусса по модулю больше, либо равны 1, то ошибки округления в процессе вычисления подавляются, в противном случае ошибки округления увеличиваются.

Условие устойчивости: .

Сложность метода Гаусса без выбора ведущего элемента

Число арифметических действий, необходимых для реализации метода Гаусса без выбора ведущего элемента пропорционально n³, где n – число линейных уравнений. Записывается это так: , где NA – число арифметических действий. Объем памяти, необходимый для реализации алгоритма, пропорционален – .

Введем понятие невязки или вектора невязки

Определение. Невязкой или вектором невязки называется вектор: , где – вычисленное решение системы линейных уравнений .

3.3. Метод Гаусса с частичным выбором ведущего элемента

1. На первом шаге прямого хода метода Гаусса выбирается максимальный по модулю элемент в первом столбце. Этот элемент является ведущим. Если он равен нулю, то detA = 0. Если ведущий элемент не является элементом , то перестановкой строк помещаем его в . При этом соответственно переставляются элементы вектора b. Затем применяются формулы метода Гаусса.

2. На -м шаге прямого хода метода Гаусса непреобразованный столбец – это часть столбца i, начиная с элемента , то есть . Находим максимальный по модулю элемент в непреобразованном столбце. Этот элемент является ведущим. Если он равен нулю, то detA = 0. Если ведущий элемент не является элементом , то перестановкой строк помещаем его в . При этом соответственно переставляются элементы вектора b. Затем применяются формулы метода Гаусса.

3. После (n-1)-го шага получаем верхнюю треугольную матрицу U и преобразованный вектор правой части. Выполняем обратную подстановку.

Метод Гаусса с частичным выбором ведущего элемента в отсутствие ошибок округления для невырожденных матриц позволяет получить точное решение, а для вырожденных матриц – сообщение о том, что матрица вырождена

Пример

Решить систему линейных уравнений методом Гаусса с частичным выбором ведущего элемента.

Решение

Рассмотрим ту же систему линейных уравнений, что и в предыдущих примерах.

Прямой ход метода Гаусса

Прежде всего, выбираем максимальный по модулю элемент в первом непреобразованном столбце:

, , следовательно, ведущим элементом является 10.

Ведущим элементом является элемент , поэтому перестановка строк не нужна. Умножим первое уравнение на 0.3 и прибавим ко второму. Умножим первое уравнение на -0.5 и прибавим к третьему. Получим:

Рассмотрим следующий непреобразованный столбец:

, , следовательно, ведущим элементом является 2.5, а не -0.1, как в методе Гаусса без выбора ведущего элемента. Но ведущий элемент не является элементом (при ) , поэтому необходимо переставить строки матрицы А, чтобы элемент 2.5 стал элементом . При перестановке строк необходимо одновременно поменять местами элементы вектора правой части . Получим:

Умножим второе уравнение на 0.

4 и прибавим к третьему. Получим:

Мы получили систему линейных уравнений с верхней треугольной матрицей.

Обратная подстановка

, следовательно, ;

, ;

Ведущими элементами являются числа: 10, 2.5, 6.2, все они по модулю больше 1, следовательно, алгоритм является вычислительно устойчивым.

В методе Гаусса с частичным выбором ведущего элемента, в отличие от метода Гаусса без выбора ведущего элемента, в случае необходимости меняются местами уравнения системы линейных уравнений. За счет этого не возникает проблем, если у невырожденной матрицы какой-либо из главных миноров равен нулю.

Решение системы линейных уравнений. Метод Гаусса

Метод Гаусса – это способ решения системы линейных алгебраических уравнений (СЛАУ), который состоит в постепенном понижении порядка системы и исключении неизвестных.

Решение СЛАУ методом Гаусса состоит из двух этапов:

На первом этапе выполняется «прямой ход», когда путём простых преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. Среди элементов первого столбца матрицы отбирают ненулевой, перемещают его в крайнее верхнее положение путем перестановки строк и вычитают получившуюся после перестановки первую строку из оставшихся строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. Далее первую строку и первый столбец мысленно вычеркивают. Процесс повторяют пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не найден ненулевой, то переходят к следующему столбцу и выполняют аналогичную операцию.
На втором этапе выполняется «обратный ход». Его суть в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений. Если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения. Из него выражают соответствующую единственную базисную переменную и подставляют в предыдущие уравнения. Затем так продолжают далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует только одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация повторяет случай последней строки.

Пусть есть исходная система, которая выглядит следующим образом:

(1)

Матрица A называется основной матрицей системы, а матрица b – столбцом свободных членов.

Согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду. Эти же преобразования требуется применять к столбцу свободных членов:

При этом считаем, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, т.е. в него входят только коэффициенты при переменных xj1, …, xjr. Такого расположения минора можно добиться путем перестановки столбцов основной матрицы и соответствующей перенумерацией переменных.

Таким образом, переменные xj1, …, xjr называются главными переменными. Все остальные называются свободными.

Если хотя бы одно число βi ≠ 0, где i > r, то рассматриваемая система несовместна.

Пусть, что βi = 0 для любых i > r.

Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом (αij, i = 1, …, r, где i — номер строки):

(2)

Где i = 1, …, r, k = i + 1, …, n.

Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (т.е. от нижнего уравнения к верхнему), то в результате получим все решения этой СЛАУ. Так как эта система найдена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, т.е. множества их решений совпадают.

Следствия:

Если в совместной системе все переменные главные, то данная система является определённой.
Если количество переменных в системе превосходит число уравнений, то данная система является либо неопределённой, либо несовместной.

См. также:

Библиотека методов и моделей | ISmLinearEquations

Решение линейных уравнений методом гаусса. Обратный ход метода Гаусса

Пусть задана система линейных алгебраических уравнений, которую необходимо решить (найти такие значения неизвестных хi, что обращают каждое уравнение системы в равенство).

Мы знаем, что система линейных алгебраических уравнений может:

1) Не иметь решений (бытьнесовместной ).
2) Иметь бесконечно много решений.
3) Иметь единственное решение.

Как мы помним,правило Крамера и матричный методнепригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений , который в каждом случае приведет нас к ответу! Сам алгоритм метода во всех трёх случаях работает одинаково. Если в методах Крамера и матричном необходимы знания определителей, то для применения метода Гаусса необходимо знание только арифметических действий, что делает его доступным даже для школьников начальных классов.

Преобразования расширенной матрицы (это матрица системы – матрица, составленная только из коэффициентов при неизвестных, плюс столбец свободных членов) системы линейных алгебраических уравнений в методе Гаусса:

1) с троки матрицыможно переставлять местами.

2) если в матрице появились (или есть) пропорциональные (как частный случай – одинаковые) строки, то следуетудалить из матрицы все эти строки кроме одной.

3) если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить .

4) строку матрицы можноумножить (разделить) на любое число,отличное от нуля.

5) к строке матрицы можноприбавить другую строку, умноженную на число , отличное от нуля.

В методе Гаусса элементарные преобразования не меняют решение системы уравнений.

Метод Гаусса состоит из двух этапов:

«Прямой ход» – с помощью элементарных преобразований привести расширенную матрицу системы линейных алгебраических уравнений к «треугольному» ступенчатому виду: элементы расширенной матрицы, расположенные ниже главной диагонали, равны нулю (ход «сверху-вниз»). Например, к такому виду:

Для этого выполним следующие действия:

1) Пусть мы рассматриваем первое уравнение системы линейных алгебраических уравнений и коэффициент при х 1 равен К. Второе, третье и т.д. уравнения преобразуем следующим образом: каждое уравнение (коэффициенты при неизвестных, включая свободные члены) делим на коэффициент при неизвестном х 1 , стоящий в каждом уравнении, и умножаем на К. После этого из второго уравнения (коэффициенты при неизвестных и свободные члены) вычитаем первое. Получаем при х 1 во втором уравнении коэффициент 0. Из третьего преобразованного уравнения вычитаем первое уравнение, так до тех пор, пока все уравнения, кроме первого, при неизвестном х 1 не будут иметь коэффициент 0.

2) Переходим к следующему уравнению. Пусть это будет второе уравнение и коэффициент при х 2 равен М. Со всеми «нижестоящими» уравнениями поступаем так, как описано выше. Таким образом, «под» неизвестной х 2 во всех уравнениях будут нули.

3) Переходим к следующему уравнению и так до тех пора, пока не останется одна последняя неизвестная и преобразованный свободный член.

«Обратный ход» метода Гаусса – получение решения системы линейных алгебраических уравнений (ход «снизу-вверх»). Из последнего «нижнего» уравнения получаем одно первое решение – неизвестную х n . Для этого решаем элементарное уравнение А*х n = В. В примере, приведенном выше, х 3 = 4. Подставляем найденное значение в «верхнее» следующее уравнение и решаем его относительно следующей неизвестной. Например, х 2 – 4 = 1, т.е. х 2 = 5. И так до тех пор, пока не найдем все неизвестные.

Пример.

Решим систему линейных уравнений методом Гаусса, как советуют некоторые авторы:

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Поступим так:
1 шаг . К первой строке прибавляем вторую строку, умноженную на –1. То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.

Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное действие: умножить первую строку на –1 (сменить у неё знак).

2 шаг . Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.

3 шаг . Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.

4 шаг . К третьей строке прибавили вторую строку, умноженную на 2.

5 шаг . Третью строку разделили на 3.

Признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде (0 0 11 |23) , и, соответственно, 11x 3 = 23, x 3 = 23/11, то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.

Выполняем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает «снизу вверх». В данном примере получился подарок:

x 3 = 1
x 2 = 3
x 1 + x 2 – x 3 = 1, следовательно x 1 + 3 – 1 = 1, x 1 = –1

Ответ 😡 1 = –1, x 2 = 3, x 3 = 1.

Решим эту же систему по предложенному алгоритму. Получаем

4 2 –1 1
5 3 –2 2
3 2 –3 0

Разделим второе уравнение на 5, а третье – на 3. Получим:

4 2 –1 1
1 0.6 –0.4 0.4
1 0.66 –1 0

Умножим второе и третье уравнения на 4, получим:

4 2 –1 1
4 2,4 –1.6 1.6
4 2.64 –4 0

Вычтем из второго и третьего уравнений первое уравнение, имеем:

4 2 –1 1
0 0.4 –0.6 0.6
0 0.64 –3 –1

Разделим третье уравнение на 0,64:

4 2 –1 1
0 0.4 –0.6 0.6
0 1 –4.6875 –1.5625

Умножим третье уравнение на 0,4

4 2 –1 1
0 0.4 –0.6 0.6
0 0.4 –1.875 –0.625

Вычтем из третьего уравнения второе, получим «ступенчатую» расширенную матрицу:

4 2 –1 1
0 0.4 –0.6 0.6
0 0 –1.275 –1.225

Таким образом, так как в процессе вычислений накапливалась погрешность, получаем х 3 = 0,96 или приблизительно 1.

х 2 = 3 и х 1 = –1.

Решая таким образом, Вы никогда не запутаетесь в вычислениях и не смотря на погрешности вычислений, получите результат.

Такой способ решения системы линейных алгебраических уравнений легко программируем и не учитывает специфические особенности коэффициентов при неизвестных, ведь на практике (в экономических и технических расчетах) приходиться иметь дело именно с нецелыми коэффициентами.

Желаю успехов! До встречи на занятиях! Репетитор Дмитрий Айстраханов .

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

1. Система линейных алгебраических уравнений

1.1 Понятие системы линейных алгебраических уравнений

Система уравнений – это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких переменных. Системой линейных алгебраических уравнений (далее – СЛАУ), содержащей m уравнений и n неизвестных, называется система вида:

где числа a ij называются коэффициентами системы, числа b i – свободными членами, a ij и b i (i=1,…, m; b=1,…, n) представляют собой некоторые известные числа, а x 1 ,…, x n – неизвестные. В обозначении коэффициентов a ij первый индекс i обозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент. Подлежат нахождению числа x n . Такую систему удобно записывать в компактной матричной форме: AX=B. Здесь А – матрица коэффициентов системы, называемая основной матрицей;

– вектор-столбец из неизвестных xj.
– вектор-столбец из свободных членов bi.

Произведение матриц А*Х определено, так как в матрице А столбцов столько же, сколько строк в матрице Х (n штук).

Расширенной матрицей системы называется матрица A системы, дополненная столбцом свободных членов

1.2 Решение системы линейных алгебраических уравнений

Решением системы уравнений называется упорядоченный набор чисел (значений переменных), при подстановке которых вместо переменных каждое из уравнений системы обращается в верное равенство.

Решением системы называется n значений неизвестных х1=c1, x2=c2,…, xn=cn, при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы-столбца

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.

Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.

Решить систему – это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.

Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.

Преобразование, применение которого превращает систему в новую систему, эквивалентную исходной, называется эквивалентным или равносильным преобразованием. Примерами эквивалентных преобразований могут служить следующие преобразования: перестановка местами двух уравнений системы, перестановка местами двух неизвестных вместе с коэффициентами у всех уравнений, умножение обеих частей какого-либо уравнения системы на отличное от нуля число.

Система линейных уравнений называется однородной, если все свободные члены равны нулю:

Однородная система всегда совместна, так как x1=x2=x3=…=xn=0 является решением системы. Это решение называется нулевым или тривиальным.

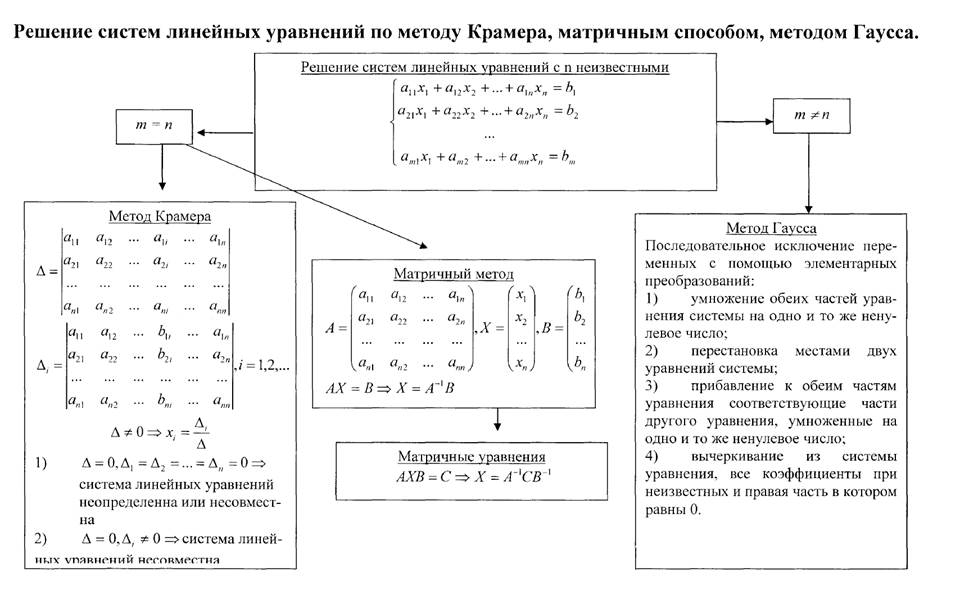
2. Метод исключения Гаусса

2.1 Сущность метода исключения Гаусса

Классическим методом решения систем линейных алгебраических уравнений является метод последовательного исключения неизвестных – метод Гаусса (его еще называют методом гауссовых исключений). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Процесс решения по методу Гаусса состоит из двух этапов: прямой и обратный ходы.

1. Прямой ход.

На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним.

После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.

На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному) виду.

Приведенная ниже система имеет ступенчатый вид:

Коэффициенты aii называются главными (ведущими) элементами системы.

(если a11=0, переставим строки матрицы так, чтобы a 11 не был равен 0. Это всегда возможно, т. к. в противном случае матрица содержит нулевой столбец, ее определитель равен нулю и система несовместна).

Преобразуем систему, исключив неизвестное х1 во всех уравнениях, кроме первого (используя элементарные преобразования системы). Для этого умножим обе части первого уравнения на

и сложим почленно со вторым уравнением системы (или из второго уравнения почленно вычтем первое, умноженное на ). Затем умножим обе части первого уравнения на и сложим с третьим уравнением системы (или из третьего почленно вычтем первое, помноженное на ). Таким образом, последовательно умножаем первую строку на число и прибавляем к i -й строке, для i= 2, 3, …, n.

Продолжая этот процесс, получим эквивалентную систему:

– новые значения коэффициентов при неизвестных и свободные члены в последних m-1 уравнениях системы, которые определяются формулами:

Таким образом, на первом шаге уничтожаются все коэффициенты, лежащие под первым ведущим элементом a 11

0, на втором шаге уничтожаются элементы, лежащие под вторым ведущим элементом а 22 (1) (если a 22 (1) 0) и т.д. Продолжая этот процесс и дальше, мы, наконец, на (m-1) шаге приведем исходную систему к треугольной системе.

Если в процессе приведения системы к ступенчатому виду появятся нулевые уравнения, т.е. равенства вида 0=0, их отбрасывают. Если же появится уравнение вида

то это свидетельствует о несовместности системы.

На этом прямой ход метода Гаусса заканчивается.

2. Обратный ход.

На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений.

Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (она в нем всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх.

Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.

Примечание: на практике удобнее работать не с системой, а с расширенной ее матрицей, выполняя все элементарные преобразования над ее строками. Удобно, чтобы коэффициент a11 был равен 1 (уравнения переставить местами, либо разделить обе части уравнения на a11).

2.2 Примеры решения СЛАУ методом Гаусса

В данном разделе на трех различных примерах покажем, как методом Гаусса можно решить СЛАУ.

Пример 1. Решить СЛАУ 3-го порядка.

Обнулим коэффициенты при

во второй и третьей строчках. Для этого домножим их на 2/3 и 1 соответственно и сложим с первой строкой:

Мы знаем, что система линейных алгебраических уравнений может:

1) Не иметь решений (бытьнесовместной ).
2) Иметь бесконечно много решений.
3) Иметь единственное решение.

1) с троки матрицыможно переставлять местами.

3) если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить .

4) строку матрицы можноумножить (разделить) на любое число,отличное от нуля.

5) к строке матрицы можноприбавить другую строку, умноженную на число , отличное от нуля.

В методе Гаусса элементарные преобразования не меняют решение системы уравнений.

Метод Гаусса состоит из двух этапов:

«Прямой ход» – с помощью элементарных преобразований привести расширенную матрицу системы линейных алгебраических уравнений к «треугольному» ступенчатому виду: элементы расширенной матрицы, расположенные ниже главной диагонали, равны нулю (ход «сверху-вниз»). Например, к такому виду:

Для этого выполним следующие действия:

«Обратный ход» метода Гаусса – получение решения системы линейных алгебраических уравнений (ход «снизу-вверх»). Из последнего «нижнего» уравнения получаем одно первое решение – неизвестную х n . Для этого решаем элементарное уравнение А*х n = В. В примере, приведенном выше, х 3 = 4. Подставляем найденное значение в «верхнее» следующее уравнение и решаем его относительно следующей неизвестной. Например, х 2 – 4 = 1, т.е. х 2 = 5. И так до тех пор, пока не найдем все неизвестные.

Пример.

Решим систему линейных уравнений методом Гаусса, как советуют некоторые авторы:

4 шаг . К третьей строке прибавили вторую строку, умноженную на 2.

5 шаг . Третью строку разделили на 3.

x 3 = 1
x 2 = 3
x 1 + x 2 – x 3 = 1, следовательно x 1 + 3 – 1 = 1, x 1 = –1

Ответ 😡 1 = –1, x 2 = 3, x 3 = 1.

Решим эту же систему по предложенному алгоритму. Получаем

4 2 –1 1
5 3 –2 2
3 2 –3 0

Разделим второе уравнение на 5, а третье – на 3. Получим:

4 2 –1 1
1 0.6 –0.4 0.4
1 0.66 –1 0

Умножим второе и третье уравнения на 4, получим:

4 2 –1 1
4 2,4 –1.6 1.6
4 2.64 –4 0

Вычтем из второго и третьего уравнений первое уравнение, имеем:

4 2 –1 1
0 0.4 –0.6 0.6
0 0.64 –3 –1

Разделим третье уравнение на 0,64:

4 2 –1 1
0 0.4 –0.6 0.6
0 1 –4.6875 –1.5625

Умножим третье уравнение на 0,4

4 2 –1 1
0 0.4 –0.6 0.6
0 0.4 –1.875 –0.625

Вычтем из третьего уравнения второе, получим «ступенчатую» расширенную матрицу:

4 2 –1 1
0 0.4 –0.6 0.6
0 0 –1.275 –1.225

х 2 = 3 и х 1 = –1.

Желаю успехов! До встречи на занятиях! Репетитор .

blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Метод Гаусса – это просто! Почему? Известный немецкий математик Иоганн Карл Фридрих Гаусс еще при жизни получил признание величайшего математика всех времен, гения и даже прозвище «короля математики». А всё гениальное, как известно – просто! Кстати, на деньги попадают не только лохи, но еще и гении – портрет Гаусса красовался на купюре в 10 дойчмарок (до введения евро), и до сих пор Гаусс загадочно улыбается немцам с обычных почтовых марок.

Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА. Необходимо уметь складывать и умножать! Не случайно метод последовательного исключения неизвестных преподаватели часто рассматривают на школьных математических факультативах. Парадокс, но у студентов метод Гаусса вызывает наибольшие сложности. Ничего удивительного – всё дело в методике, и я постараюсь в доступной форме рассказать об алгоритме метода.

Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:

1) Иметь единственное решение.
2) Иметь бесконечно много решений.
3) Не иметь решений (быть несовместной ).

Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случае приведет нас к ответу! На данном уроке мы опять рассмотрим метод Гаусса для случая №1 (единственное решение системы), под ситуации пунктов №№2-3 отведена статья . Замечу, что сам алгоритм метода во всех трёх случаях работает одинаково.

Вернемся к простейшей системе с урока Как решить систему линейных уравнений?
и решим ее методом Гаусса.

На первом этапе нужно записать расширенную матрицу системы :
. По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.

Справка : рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: . Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: . Любую из матриц можно для краткости называть просто матрицей.

После того, как расширенная матрица системы записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями .

Существуют следующие элементарные преобразования:

1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки:

2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. Рассмотрим, например матрицу . В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них: .

3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить . Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули .

4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля . Рассмотрим, например, матрицу . Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2: . Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.

5) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число , отличное от нуля. Рассмотрим нашу матрицу из практического примера: . Сначала я распишу преобразование очень подробно. Умножаем первую строку на –2: , и ко второй строке прибавляем первую строку умноженную на –2 : . Теперь первую строку можно разделить «обратно» на –2: . Как видите, строка, которую ПРИБАВЛЯЛИ – не изменилась . Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ .

На практике так подробно, конечно, не расписывают, а пишут короче:

Еще раз: ко второй строке прибавили первую строку, умноженную на –2 . Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:

«Переписываю матрицу и переписываю первую строку: »

«Сначала первый столбец. Внизу мне нужно получить ноль. Поэтому единицу вверху умножаю на –2: , и ко второй строке прибавляю первую: 2 + (–2) = 0. Записываю результат во вторую строку: »

«Теперь второй столбец. Вверху –1 умножаю на –2: . Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку: »

«И третий столбец. Вверху –5 умножаю на –2: . Ко второй строке прибавляю первую: –7 + 10 = 3. Записываю результат во вторую строку: »

Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане». Но, конечно, над этим преобразованием мы еще поработаем.

Элементарные преобразования не меняют решение системы уравнений

! ВНИМАНИЕ : рассмотренные манипуляции нельзя использовать , если Вам предложено задание, где матрицы даны «сами по себе». Например, при «классических» действиях с матрицами что-то переставлять внутри матриц ни в коем случае нельзя!

Вернемся к нашей системе . Она практически разобрана по косточкам.

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду :

(1) Ко второй строке прибавили первую строку, умноженную на –2. И снова: почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.

(2) Делим вторую строку на 3.

Цель элементарных преобразований – привести матрицу к ступенчатому виду: . В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид .

В результате элементарных преобразований получена эквивалентная исходной система уравнений:

Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса .

В нижнем уравнении у нас уже готовый результат: .

Рассмотрим первое уравнение системы и подставим в него уже известное значение «игрек»:

Рассмотрим наиболее распространенную ситуацию, когда методом Гаусса требуется решить систему трёх линейных уравнений с тремя неизвестными.

Пример 1

Решить методом Гаусса систему уравнений:

Запишем расширенную матрицу системы:

Сейчас я сразу нарисую результат, к которому мы придём в ходе решения:

И повторюсь, наша цель – с помощью элементарных преобразований привести матрицу к ступенчатому виду. С чего начать действия?

Сначала смотрим на левое верхнее число:

Почти всегда здесь должна находиться единица . Вообще говоря, устроит и –1 (а иногда и другие числа), но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки:

Теперь первая строка у нас останется неизменной до конца решения . Уже легче.

Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах:

Нули получаем как раз с помощью «трудного» преобразования. Сначала разбираемся со второй строкой (2, –1, 3, 13). Что нужно сделать, чтобы на первой позиции получить ноль? Нужно ко второй строке прибавить первую строку, умноженную на –2 . Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18). И последовательно проводим (опять же мысленно или на черновике) сложение, ко второй строке прибавляем первую строку, уже умноженную на –2 :

Результат записываем во вторую строку:

Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3 . Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). И к третьей строке прибавляем первую строку, умноженную на –3 :

Результат записываем в третью строку:

На практике эти действия обычно выполняются устно и записываются в один шаг:

Не нужно считать всё сразу и одновременно . Порядок вычислений и «вписывания» результатов последователен и обычно такой: сначала переписываем первую строку, и пыхтим себе потихонечку – ПОСЛЕДОВАТЕЛЬНО и ВНИМАТЕЛЬНО :

А мысленный ход самих расчётов я уже рассмотрел выше.

В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение:

На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь:

Для этого к третьей строке прибавляем вторую строку, умноженную на –2 :

Попробуйте разобрать это действие самостоятельно – мысленно умножьте вторую строку на –2 и проведите сложение.

Последнее выполненное действие – причёска результата, делим третью строку на 3.

В результате элементарных преобразований получена эквивалентная исходной система линейных уравнений:

Круто.

Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.

В третьем уравнении у нас уже готовый результат:

Смотрим на второе уравнение: . Значение «зет» уже известно, таким образом:

И, наконец, первое уравнение: . «Игрек» и «зет» известны, дело за малым:

Ответ :

Как уже неоднократно отмечалось, для любой системы уравнений можно и нужно сделать проверку найденного решения, благо, это несложно и быстро.

Пример 2

Это пример для самостоятельного решения, образец чистового оформления и ответ в конце урока.

Следует отметить, что ваш ход решения может не совпасть с моим ходом решения, и это – особенность метода Гаусса . Но вот ответы обязательно должны получиться одинаковыми!

Пример 3

Решить систему линейных уравнений методом Гаусса

Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так:
(1) К первой строке прибавляем вторую строку, умноженную на –1 . То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.

Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное телодвижение: умножить первую строку на –1 (сменить у неё знак).

(2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.

(3) Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.

(4) К третьей строке прибавили вторую строку, умноженную на 2.

(5) Третью строку разделили на 3.

Скверным признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде , и, соответственно, , то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.

Заряжаем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает, снизу вверх. Да тут подарок получился:

Ответ : .

Пример 4

Решить систему линейных уравнений методом Гаусса

Это пример для самостоятельного решения, он несколько сложнее. Ничего страшного, если кто-нибудь запутается. Полное решение и образец оформления в конце урока. Ваше решение может отличаться от моего решения.

В последней части рассмотрим некоторые особенности алгоритма Гаусса.
Первая особенность состоит в том, что иногда в уравнениях системы отсутствуют некоторые переменные, например:

Как правильно записать расширенную матрицу системы? Об этом моменте я уже рассказывал на уроке Правило Крамера. Матричный метод . В расширенной матрице системы на месте отсутствующих переменных ставим нули:

Кстати, это довольно легкий пример, поскольку в первом столбце уже есть один ноль, и предстоит выполнить меньше элементарных преобразований.

Вторая особенность состоит вот в чём. Во всех рассмотренных примерах на «ступеньки» мы помещали либо –1, либо +1. Могут ли там быть другие числа? В ряде случаев могут. Рассмотрим систему: .

Здесь на левой верхней «ступеньке» у нас двойка. Но замечаем тот факт, что все числа в первом столбце делятся на 2 без остатка – и другая двойка и шестерка. И двойка слева вверху нас устроит! На первом шаге нужно выполнить следующие преобразования: ко второй строке прибавить первую строку, умноженную на –1; к третьей строке прибавить первую строку, умноженную на –3. Таким образом, мы получим нужные нули в первом столбце.

Или еще такой условный пример: . Здесь тройка на второй «ступеньке» тоже нас устраивает, поскольку 12 (место, где нам нужно получить ноль) делится на 3 без остатка. Необходимо провести следующее преобразование: к третьей строке прибавить вторую строку, умноженную на –4, в результате чего и будет получен нужный нам ноль.

Метод Гаусса универсален, но есть одно своеобразие. Уверенно научиться решать системы другими методами (методом Крамера, матричным методом) можно буквально с первого раза – там очень жесткий алгоритм. Но вот чтобы уверенно себя чувствовать в методе Гаусса, следует «набить руку», и прорешать хотя бы 5-10 систем. Поэтому поначалу возможны путаница, ошибки в вычислениях, и в этом нет ничего необычного или трагического.

Дождливая осенняя погода за окном…. Поэтому для всех желающих более сложный пример для самостоятельного решения:

Пример 5

Решить методом Гаусса систему четырёх линейных уравнений с четырьмя неизвестными.

Такое задание на практике встречается не так уж и редко. Думаю, даже чайнику, который обстоятельно изучил эту страницу, интуитивно понятен алгоритм решения такой системы. Принципиально всё так же – просто действий больше.

Случаи, когда система не имеет решений (несовместна) или имеет бесконечно много решений, рассмотрены на уроке Несовместные системы и системы с общим решением . Там же можно закрепить рассмотренный алгоритм метода Гаусса.

Желаю успехов!

Решения и ответы:

Пример 2: Решение : Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.

Выполненные элементарные преобразования:
(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –1. Внимание! Здесь может возникнуть соблазн из третьей строки вычесть первую, крайне не рекомендую вычитать – сильно повышается риск ошибки. Только складываем!
(2) У второй строки сменили знак (умножили на –1). Вторую и третью строки поменяли местами. Обратите внимание , что на «ступеньках» нас устраивает не только единица, но еще и –1, что даже удобнее.
(3) К третьей строке прибавили вторую строку, умноженную на 5.
(4) У второй строки сменили знак (умножили на –1). Третью строку разделили на 14.

Обратный ход:

Ответ : .

Пример 4: Решение : Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Выполненные преобразования:
(1) К первой строке прибавили вторую. Таким образом, организована нужная единица на левой верхней «ступеньке».
(2) Ко второй строке прибавили первую строку, умноженную на 7. К третьей строке прибавили первую строку, умноженную на 6.

Со второй «ступенькой» всё хуже , «кандидаты» на неё – числа 17 и 23, а нам нужна либо единичка, либо –1. Преобразования (3) и (4) будут направлены на получение нужной единицы

(3) К третьей строке прибавили вторую, умноженную на –1.
(4) Ко второй строке прибавили третью, умноженную на –3.
(3) К третьей строке прибавили вторую, умноженную на 4. К четвертой строке прибавили вторую, умноженную на –1.
(4) У второй строки сменили знак. Четвертую строку разделили на 3 и поместили вместо третьей строки.
(5) К четвертой строке прибавили третью строку, умноженную на –5.

Обратный ход:

Решение систем линейных уравнений методом Гаусса. Пусть нам требуется найти решение системы из n линейных уравнений с n неизвестными переменными
определитель основной матрицы которой отличен от нуля.

Суть метода Гаусса состоит в последовательном исключении неизвестных переменных: сначала исключается x 1 из всех уравнений системы, начиная со второго, далее исключается x 2 из всех уравнений, начиная с третьего, и так далее, пока в последнем уравнении останется только неизвестная переменная x n . Такой процесс преобразования уравнений системы для последовательного исключения неизвестных переменных называется прямым ходом метода Гаусса . После завершения прямого хода метода Гаусса из последнего уравнения находитсяx n , с помощью этого значения из предпоследнего уравнения вычисляется x n-1 , и так далее, из первого уравнения находится x 1 . Процесс вычисления неизвестных переменных при движении от последнего уравнения системы к первому называется обратным ходом метода Гаусса .

Кратко опишем алгоритм исключения неизвестных переменных.

Будем считать, что , так как мы всегда можем этого добиться перестановкой местами уравнений системы. Исключим неизвестную переменную x 1 из всех уравнений системы, начиная со второго. Для этого ко второму уравнению системы прибавим первое, умноженное на , к третьему уравнению прибавим первое, умноженное на , и так далее, к n-ому уравнению прибавим первое, умноженное на . Система уравнений после таких преобразований примет вид

где , а .

К такому же результату мы бы пришли, если бы выразили x 1 через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменная x 1 исключена из всех уравнений, начиная со второго.

Далее действуем аналогично, но лишь с частью полученной системы, которая отмечена на рисунке

Для этого к третьему уравнению системы прибавим второе, умноженное на , к четвертому уравнению прибавим второе, умноженное на , и так далее, к n-ому уравнению прибавим второе, умноженное на . Система уравнений после таких преобразований примет вид

где , а . Таким образом, переменная x 2 исключена из всех уравнений, начиная с третьего.

Далее приступаем к исключению неизвестной x 3 , при этом действуем аналогично с отмеченной на рисунке частью системы

Так продолжаем прямой ход метода Гаусса пока система не примет вид

С этого момента начинаем обратный ход метода Гаусса: вычисляем x n из последнего уравнения как , с помощью полученного значения x n находим x n-1 из предпоследнего уравнения, и так далее, находим x 1 из первого уравнения. a2] C tfgQ 悐 ar #: \ & 384 .mQyAYv צ Ұ / Iopīnz ޠ EE` u.HO ~ ¢ \ A -7 ֕ uv \ .0A + uX4 & vM% m – I˷ ׸ iIX? C څ JVt {j | & / pf x] x_7P ׭ j 璘 KҠW] ZWnz ~] 0Z] [I7 [j? z ׾ – _n ‘a A | l ֞_ Z z 鴚 Һ [‹} G ׶) _5 [\ VN> M% ޜ ~}} kio \ 0Un4HWl? Y’8F $ U ވ Gǐ V] _FNp. $ GoBUEe̎ a_” w1} k} C? _ ~ ‘O / n / ԓ6_ / ޾ ObawW__A ~ -y% о / _ ~ 𗒞 O ~ а t} / Xn᾿ o ՠ /} P_] o8o kU տ I} / [u {J itK w # + [_ vmik۷ \ N_’Jn umwοo ׶_ O [a] / K% ua>} Zu ֿ 4 ݥ x] 6vi ۪ aVa p ? {m / + KmM / l% · W] X4kj-ZI $ JJAI-, I $ I $ A $ I * I, p) `8I * 0aVI> YI q ˙p2B mn ᄘ izi & “; Ia lVZZw0 (nE: |:: l0ҰU’AD $ 4 п A0 (Ն Io [ $ ҍ4 @ Np + TVKj `0J մ f; & G ؅ a mLH = B @ `IL ч ؄ а AѨ6pKcbl-A @.\ 5L’g K + o0 / ״ jKwzPVka + 1p: K-Ҵ} Z / m? m% $ [g + K ޮ [A0 0ôh @ m [# 6VP} ۄ i-pfIU. Ն) PP Ն PͻACSj0al1 \ Azk & a8MC ]% b ֒ pGz “4a6’vJh5aX`Mm Iv & vbj` 0a * u AaaZ -8j Յ а X0El + A 77 A` aQ h0mTS ΃ 66`0L0SS:!] E4 (i0 qLz 7 долларов США Hr0% aR a0R; rq 2ab drO! `DlH0DI (0 @ B8Ap8` MAD0V” ETADf0 `c & 5J, DA” “1 $ Hӝ1 & *) DDNHEFDDTDDD> b” “@” 8DDDDw}; D0l $ p`ArDsT “# eR & Mg5U> y7z A; -VE * # L2D, QD / S0P \ E`Ec` !! # DjC! DX! $ {D% Fԇ. ֿ jIt TU.A lh4fx

Микрожидкостная накачка с использованием искусственных магнитных ресничек

Магнитно-мягкие реснички намагничиваются в присутствии внешнего магнитного поля и стремятся выровняться по направлению поля. Мы используем это, чтобы активировать реснички, подвергая их воздействию магнитного поля, вращающегося в плоскости x – y , как показано на рис. 1. Магнитное поле вращается либо по часовой стрелке (CW), либо против часовой стрелки. (CCW) направление. Изменение направления вращения магнита приводит к существенно различающимся картинам биений, как показано на рис.2 и 3, которые представляют изображения ресничек сбоку, полученные во время вращения магнита CCW и CW соответственно. В следующих разделах мы сначала исследуем биение ресничек из-за вращения магнита CCW и CW, а затем исследуем, как биение ресничек трансформируется в перекачку жидкости в микрофлюидный канал.

Рис. 2: Биение ресничек из-за вращения магнитного поля против часовой стрелки.

a Наложение экспериментальных изображений, показывающих профили ресничек для различных ориентаций магнитного поля.Экспериментальные параметры: L = 500 мкм, W = 10 мкм, T = 70 нм и ω = 0,3 Гц. b Компьютерное моделирование движения ресничек, индуцированного вращающимся против часовой стрелки магнитным полем. c Величина локального изгибающего момента, действующего на ресничку при различной ориентации магнитного поля. Стрелки указывают направление поля.

Рис. 3: Биение ресничек из-за вращения магнитного поля по часовой стрелке (CW).

Экспериментальные параметры: L = 500 мкм, W = 10 мкм, T = 70 нм и ω = 0.3 Гц. a Наложение экспериментальных изображений, показывающих профили ресничек для различных ориентаций магнитного поля. b Компьютерное моделирование движения ресничек под действием непрерывно вращающегося магнитного поля. c Величина локального изгибающего момента, действующего на ресничку при различной ориентации магнитного поля. Стрелки указывают направление поля.

Вращение магнитного поля против часовой стрелки

Магнитные реснички следуют пространственно асимметричному движению при воздействии магнитного поля, вращающегося против часовой стрелки ⁴⁰.Пример такого движения показан на рис. 2а, который представляет серию перекрывающихся изображений реснички, приводимой в действие магнитом, вращающимся против часовой стрелки. Мы разделяем пространственно асимметричный рисунок биений ресничек на прямые и обратные штрихи. Ход вперед определяется как движение реснички из положения a в положение d . Обратный ход определяется как движение реснички при ее возвращении из положения d в положение a . Обратите внимание, что положение a не совпадает с положением реснички без влияния магнитной силы, которое почти горизонтально, а скорее определяется как крайнее правое положение реснички в цикле биений.Кончик реснички следует замкнутой траектории, показанной синим цветом во время движения вперед и красным во время хода восстановления. Различия в паттерне изгиба ресничек во время движений вперед и восстановления приводят к высокой степени пространственной асимметрии движения ресничек.

Компьютерное моделирование, выполненное для вращения магнитного поля против часовой стрелки, предсказывает картину биений, которая хорошо согласуется с экспериментальными результатами (рис. 2b). Мы используем компьютерное моделирование, чтобы внимательно изучить движение реснички из-за вращающегося магнитного поля.Мы начинаем с позиции a , где ресничка находится в крайнем правом положении, соответствующем началу движения вперед. В этом положении большая часть реснички выровнена с внешним магнитным полем, за исключением небольшой части около основания реснички. Местным магнитным моментом можно пренебречь на большом участке реснички (рис. 2c). Помните, что местный магнитный момент пропорционален \ (\ sin (2 \ theta) \), где θ – это локальный угол между ресничкой и магнитным полем.Когда магнит вращается в направлении против часовой стрелки, θ увеличивается, увеличивая величину магнитного момента. В результате этого вращения против часовой стрелки ресничка деформируется и изгибается против часовой стрелки.

Ресничка проходит через позиции b – c – d на рис. 2b вслед за вращением внешнего магнитного поля. Изгиб приводит к тому, что локальный угол θ превышает 90 ° в определенных частях реснички. Таким образом, основание реснички в позиции c образует угол θ > 90 °, тогда как кончик реснички, который легче отклоняется, чтобы следовать за магнитным полем, составляет угол θ <90 °.Это приводит к ситуации, в которой направление локального магнитного момента около основания противоположно направлению на кончике реснички (Fig. 2c). Это изменение направления момента вдоль реснички дополнительно усиливает деформацию. Изгиб реснички от a до d увеличивает упругую энергию, запасаемую ресничкой, которая достигает максимума в положении d , где ресничка достигает максимального изгиба. Дальнейшее вращение магнитного поля уменьшает приложенный момент, и ресничка возвращается в исходное положение a через положение e .Во время такта восстановления намагниченность реснички меняет направление, как и приложенный момент, который теперь притягивает ресничку к – B (см. Рис. 1c для позиции e ). Сохраненная упругая энергия высвобождается, заставляя ресничку быстро возвращаться в исходное положение a . Из-за быстрого движения ресничек во время восстановительного хода вязкие силы значительно выше, чем во время прямого хода, когда скорость определяется скоростью вращения магнитного поля.Кроме того, магнитный момент меняет направление во время восстановления и, таким образом, помогает ресничке вернуться в исходное положение. В результате временной масштаб для восстановительного удара намного меньше, чем для прямого удара, что, в свою очередь, приводит к асимметричному биению. Более полное обсуждение кинематики движения ресничек в режиме CCW посредством экспериментов и моделирования можно найти в другом месте ^30,32,40.

Непрерывное вращение магнитного поля

На рис. 3а показана ресничка, которая подвергается воздействию магнитного поля, вращающегося в непрерывном направлении.Эта ресничка имеет те же свойства, что и показанная на рис. 2а. Мы обнаружили, что биение ресничек из-за вращения магнита CW значительно отличается от такового, вызванного вращением магнита против часовой стрелки (см. Рис. 2a и 3a). В частности, предельные положения a, и d , между которыми колеблется ресничка, смещаются вправо, когда вращение магнита изменяется с CCW на CW (т.е. реснички имеют тенденцию деформироваться в направлении вращения магнита). Кроме того, площадь, ограниченная кончиком реснички, значительно меньше для магнита, вращающегося непрерывно, чем при вращении против часовой стрелки.Это указывает на то, что вращение магнита против часовой стрелки полезно для увеличения асимметрии биений.

Движение ресничек, полученное в экспериментах (Рис. 3a), хорошо фиксируется компьютерным моделированием (Рис. 3b). Мы определяем, что прямой ход по часовой стрелке начинается с позиции a . В этом положении большая часть реснички выровнена по направлению поля, за исключением около основания. Когда магнитное поле вращается в направлении CW, магнитный момент уменьшает изгиб ресничек, как показано на рис. 3c. Ресничка следует за вращающимся полем до положения d , когда она касается подложки.Магнитным моментом в этом положении можно пренебречь, поскольку ресничка полностью выровнена с полем. Ресничка остается в этом положении d , и субстрат препятствует ее перемещению, поскольку магнитное поле продолжает вращаться по часовой стрелке. Действительно, до тех пор, пока угол θ между ресничкой и полем не станет <90 °, моменты действуют в направлении CW и вынуждают ресничку оставаться в позиции d .

Когда магнитное поле ориентировано вертикально, θ равно 90 °.Дальнейшее вращение поля переворачивает намагниченность в ресничке и приводит к ситуации, когда угол между ресничкой и – B уменьшается. Это обозначено цифрой d ‘ на рис. 3c. Ресничка не движется и выстраивается вдоль подложки между положениями d и d ‘. Магнитные моменты на d ‘ меняют направление и тянут ресничку вверх и от подложки. Когда ресничка изгибается для выравнивания с магнитным полем, она проходит через промежуточное положение e и завершает ход восстановления обратно в почти вертикальном положении a .Таким образом, во время восстановительного такта ресничка движется в направлении, противоположном вращению поля.

Подобно сценарию вращения поля против часовой стрелки, скорость реснички во время движения вперед задается скоростью вращения магнитного поля по часовой стрелке. Во время обратного хода движение ресничек определяется балансом между магнитной силой и силами вязкости. (Напомним, что для вращения против часовой стрелки ход восстановления является результатом баланса между упругими и вязкими силами.) Разница в действующих силах между прямым ходом и ходом восстановления приводит к асимметрии движения ресничек в магнитном поле, вращающемся по часовой стрелке.Обратите внимание, что в конце прямого хода ресничка приостанавливается, в то время как магнитное поле продолжает вращаться по часовой стрелке, пока намагниченность в ресничке не изменит направление. Такой паузы не существует для ресничек, приводимых в движение магнитным полем, вращающимся против часовой стрелки.

И CW, и CCW режим срабатывания реснички результат – два цикла биений реснички на каждое вращение магнитного поля. Однако кинематика для этих двух режимов существенно различается. Магнитное поле, вращающееся против часовой стрелки, увеличивает изгиб реснички во время движения вперед, тогда как вращение по часовой стрелке уменьшает изгиб при движении вперед.Эти различия приводят к значительному различию рисунков изгиба для направлений вращения магнита CW и CCW. Кроме того, вращение против часовой стрелки приводит к значительно большей пространственной асимметрии цикла биений по сравнению со случаем по часовой стрелке.

Известно, что пространственная асимметрия в схеме биений важна для создания любого чистого переноса жидкости в среде с низким числом Рейнольдса ³¹. Была обнаружена прямая корреляция между областью, ограниченной траекторией кончика ресничек и транспортом жидкости ³³.Мы, следовательно, ожидаем большего переноса жидкости ресничками, приводимыми в действие CCW полем для каждого колебательного цикла в этих рабочих режимах.

Транспортировка жидкости ресничным массивом

Мы характеризуем транспортировку жидкости множеством наших магнитных ресничек, измеряя перекачку жидкости в петле микроканала. Рисунок 4 показывает сравнение параметра накачки P _f в петле микроканала для ресничек, активируемых CW и CCW, в зависимости от Sp . В этих экспериментах мы использовали 16 рядов ресничек по 25 отдельных ресничек в каждом ряду.

Рис. 4: Безразмерная скорость откачки P _f как функция Sp , для вращения против часовой и часовой стрелки магнитного поля, приводящего в действие цилиарный массив.

Массив состоит из 16 рядов ресничек по 25 ресничек в каждом ряду. Расстояние между рядами массива составляет S = 250 мкм, высота канала составляет H = 300 мкм

Мы обнаружили, что срабатывание против часовой стрелки приводит к превосходным характеристикам накачки по сравнению с режимом срабатывания непрерывного действия. Этот результат справедлив для всех Sp , протестированных в эксперименте.Максимальная скорость откачки ресничек в режиме CCW составляет P _f ≈ 14, что значительно выше максимальной скорости откачки в режиме CW, равной P _f ≈ 4.5. Мы связываем эту лучшую производительность накачки для вращения магнита против часовой стрелки с большей площадью охвата кончиком реснички по сравнению с возбуждением непрерывным движением.

Кроме того, мы обнаружили, что направление потока при вращении магнита против часовой и часовой стрелки противоположно. При вращении магнита как против часовой стрелки, так и против часовой, ресничка при прямом ходе проходит через большую площадь по сравнению с ходом восстановления.Однако направление прямой стреловидности другое, как показано синими траекториями острия на рис. 2а и 3а для двух направлений вращения соответственно. Направление закачки получаемой жидкости совпадает с направлением прямого хода, что приводит к различным направлениям откачки для вращения магнита против часовой стрелки и против часовой стрелки.

Мы обнаружили, что для постоянного магнитного числа накачка сначала увеличивается с увеличением Sp до тех пор, пока не будет достигнут максимум (рис. 4). Дальнейшее увеличение количества Sp приводит к снижению производительности закачки в единицу времени.Для низких Sp , которые были получены в наших экспериментах при более низких частотах колебаний, реснички испытывают более слабые вязкие силы. Это позволяет ресничкам охватить большую площадь, увеличивая транспорт жидкости ⁴⁰. Однако общая производительность относительно невысока, поскольку реснички могут совершать лишь несколько колебаний в единицу времени. По мере увеличения Sp увеличивающиеся силы вязкости уменьшают асимметрию хода ⁴⁰ и, следовательно, перекачку жидкости за цикл колебаний.С другой стороны, более высокая скорость колебаний увеличивает общую скорость откачки до тех пор, пока не будет достигнут максимум около Sp ≈ 2,9. За пределами этого значения вязкость жидкости значительно подавляет биение ресничек, что приводит к снижению производительности перекачивания.

В наших экспериментах максимальная скорость откачки, полученная для срабатывания против часовой стрелки, составляет около P _f ≈ 14 при 2500 об / мин. Это соответствует средней скорости, равной ~ 1350 мкм / с, и объемному расходу ~ 11 мкл / мин в канале с поперечным сечением 1 мм × 280 мкм.Эта скорость потока превышает значения, ранее сообщенные для синтетических цилиарных систем ^29,33. Частота самодвижения f _с = Q / S _пакет для нашего устройства оценивается в ~ 2,5 / мин, что свидетельствует о его эффективности. Предполагая поток Пуазейля в микроканале, мы оцениваем падение давления ~ 1 Па, создаваемое ресничным массивом в нашей петле канала ~ 4 см.

Таким образом, наши цилиарные массивы с CCW магнитным срабатыванием демонстрируют высокую скорость откачки при низком перепаде давления, что согласуется с ранее опубликованными данными ³³.В дальнейшем мы будем систематически исследовать накачку ресничками, активированными против часовой стрелки, для различных параметров массива и канала.

На рис. 5 показано, как накачка ресничек зависит от числа рядов ресничек. Здесь мы нормализуем скорость откачки P _f на количество рядов ресничек N , чтобы охарактеризовать эффективность на ряд. Мы варьируем количество рядов от 3 до 16, сохраняя расстояние между рядами постоянным и равным 300 мкм. Мы обнаружили, что перекачка на строку P _f/ N уменьшается по мере увеличения количества строк в массиве.Этот результат можно объяснить, основываясь на различии магнитных сил, испытываемых ресничками разных рядов. По мере увеличения числа рядов расстояние между магнитом и ресничками в разных рядах также изменяется. Реснички около центра массива находятся ближе всего к магниту и испытывают максимальную магнитную силу, тогда как реснички во внешних рядах массива испытывают меньшую силу. В наших экспериментах мы измеряли уменьшение на ~ 70 Гаусс напряженности магнитного поля, действующего на реснички во внешних рядах.Уменьшение напряженности магнитного поля снижает амплитуду биений ресничек, расположенных во внешних рядах массива, и, следовательно, подавляет общую накачивающую способность ресничного массива.

Рис. 5: Безразмерная скорость откачки для разного количества рядов ресничек.

a Безразмерная скорость откачки P _f, производимая решетками ресничек с разным числом рядов в зависимости от Sp для вращения против часовой стрелки магнитного поля, приводящего в действие реснички. b Скорость откачки на ряд P _f/ N как функция нормированного расстояния C / D магнита от центра для массива с N = 3. Массивы имеют 25 ресничек в ряду с междурядьем S = 300 мкм. Высота канала составляет H = 300 мкм

Для дальнейшего исследования зависимости характеристик ресничек от положения магнита, мы провели эксперименты, в которых мы варьировали расстояние магнита от массива.Мы выбираем небольшой массив с N = 3 и перемещаем магнит в направлении x . Мы определяем расстояние x между центром массива и осью магнитного поля как C . На рис. 5b мы строим график величины закачки жидкости на ряд P _f/ N цилиарного массива с N = 3 как функцию нормализованного положения магнита C / D , где D – диаметр магнита.Мы обнаруживаем значительное падение прокачки при увеличении C / D с 0 до 0,15. Для C / D = 0,15 магнит смещен на расстояние 2 мм от центра массива, что эквивалентно расстоянию до ресничек около краев для массива с N = 16. Этот результат предполагает, что снижение накачки на строку для больших массивов действительно связано с уменьшенной магнитной силой. Это снижение производительности для большего массива может быть смягчено путем использования вращающегося магнита большего диаметра для создания более однородного магнитного поля по всему массиву ресничек.

Чтобы понять взаимное влияние ресничек в многорядных массивах, мы исследуем накачку массивов ресничек, в которых мы варьируем расстояние S (показано на рис. 1) между последовательными рядами ресничек. Реснички приводятся в действие вращением магнита против часовой стрелки. Случай, когда S / L = 1, представляет сценарий, в котором ряды ресничек плотно упакованы, что может быть изготовлено с использованием нашего метода. На рис. 6 показана зависимость скорости откачки от Sp для решеток с различным расстоянием между рядами.Мы обнаружили, что данные накачки для разных массивов разнесения незначительно различаются. Фактически, средняя скорость откачки находится в пределах экспериментальной ошибки для всех S / L . Это означает, что на характеристики ресничек существенно не влияют соседние ряды ресничек и гидродинамическое взаимодействие между ними относительно слабое.

Рис. 6: Безразмерная скорость откачки P _f в зависимости от Sp для цилиарных массивов с различным расстоянием между последовательными рядами.

Все массивы имеют четыре ряда ресничек по 25 ресничек в каждом ряду. Высота канала H = 300 мкм

В нашей последней серии экспериментов мы исследуем, как накачка ресничками зависит от высоты канала H . На рисунке 7 показано влияние изменения высоты канала на накачку массива ресничек. В этих экспериментах мы исследуем реснички в режиме CCW с тремя разными Sp . Реснички расположены в четыре ряда по 25 ресничек в ряду. Высота канала варьируется от 220 до 750 мкм.Мы обнаружили значительное увеличение скорости откачки от P _f ≈ 2,8 до P _f ≈ 4, поскольку H / L увеличилось с 1,2 до 1,8. Дальнейшее увеличение высоты канала выше H / L = 1,8 приводит к небольшому изменению производительности насоса.

Рис. 7: Безразмерная скорость откачки P _f как функция нормированной высоты канала H / L для выбранных значений Sp .

Используется ресничный массив с четырьмя рядами ресничек, по 25 ресничек в каждом ряду. Расстояние между рядами ресничек составляет S = 250 мкм

Предполагается, что поток над ресничками в замкнутом канале с H >> L похож на поток Куэтта с противоскользящим покрытием наверху. граница и нижняя граница тангенциально перемещаются ресничками ³³. В таких случаях расход линейно зависит от высоты канала, а средняя скорость не зависит от высоты канала.Наши эксперименты подтверждают этот результат, о чем свидетельствует незначительное изменение средней скорости для H / L ≥ 1,8. Однако, когда высота канала сравнима с длиной ресничек, средняя скорость уменьшается, как показано для H / L = 1.2. Это указывает на то, что на движение ресничек влияет верхняя стенка канала.

Апрель 2017 г. Брифинг – Патология – Новости здоровья потребителей

Вот что редакторы HealthDay считают наиболее важными событиями в области патологии на апрель 2017 г.Этот обзор включает в себя последние новости исследований из журнальных статей, а также утверждения FDA и нормативные изменения, которые с наибольшей вероятностью повлияют на клиническую практику.

Организаторы встреч с участием квалифицированных женщин-ученых

ПЯТНИЦА, 28 апреля 2017 г. (Новости HealthDay) – Среди приглашенных спикеров на медицинские конференции, как правило, непропорционально много мужчин, и это несоответствие может быть устранено путем активной подготовки списков потенциальных спикеров, согласно исследованию, опубликованному в Интернете 18 апреля в журнале Nature Immunology. .

Аннотация / Полный текст

Упражнения

снижают эффект набора веса у людей с геном FTO

ПЯТНИЦА, 28 апреля 2017 г. (Новости HealthDay) – После корректировки на физическую активность (PA) было идентифицировано одиннадцать новых вариантов ожирения, и PA может снизить эффект набора веса гена FTO примерно на 30 процентов, согласно к метаанализу, опубликованному в Интернете 27 апреля в PLOS Genetics .

Аннотация / Полный текст

Отчетливые бактериальные таксоны в подгруппах ME / CSF с / без IBS

ПЯТНИЦА, 28 апреля 2017 г. (Новости HealthDay) – В подгруппах миалгического энцефаломиелита / синдрома хронической усталости (ME / CFS) видны отчетливые бактериальные таксоны, определяемые наличием синдрома раздраженного кишечника (IBS), согласно исследованию, опубликованному в Интернете. 27 апреля в Microbiome .

Аннотация
Полный текст

Регулярные анализы крови могут навредить уходу за пациентом

ПЯТНИЦА, 28 апреля 2017 г. (Новости HealthDay) – Обычные анализы крови тратят деньги и могут навредить уходу за пациентом, согласно аналитическому сообщению, опубликованному в Интернете 27 апреля в BMJ .

Аннотация / Полный текст

Алгоритм, интегрированный в приложение, прогнозирует уровень глюкозы

ПЯТНИЦА, 28 апреля 2017 г. (Новости HealthDay). Согласно исследованию, опубликованному 27 апреля в Интернете, механистическая модель, основанная на моделях гауссовского процесса и ассимиляции данных, может дать персонализированный прогноз уровня глюкозы на основе питания для людей с диабетом 2 типа. PLOS Вычислительная биология .

Аннотация / Полный текст

Законопроект о системе здравоохранения с одним плательщиком продвигается в Калифорнии

ЧЕТВЕРГ, 27 апреля 2017 г. (Новости HealthDay) – Предложение заменить частное страхование финансируемым государством здравоохранением для всех выдвинуто в Калифорнии в среду, когда демократы в комитете Сената по здравоохранению проголосовали за продвижение этой меры.

Дополнительная информация

Факторы риска в шести областях, связанных с выгоранием врачей

, ЧЕТВЕРГ, 27 апреля 2017 г. (Новости HealthDay). Факторы выгорания врачей включают контроль, наличие времени для оказания отличной помощи и справедливость условий на рабочем месте, согласно презентации, представленной в Ассоциации управления медицинскими группами / Американской медицинской ассоциации, 2017 г. Конференция «Сотрудничайте на практике», проходившая с 9 по 11 апреля в Чикаго.

Полный текст

Педиатры, у которых отсутствует повышенный уровень свинца в крови, в США

ЧЕТВЕРГ, 27 апреля 2017 г. (Новости HealthDay) – Многие дети с уровнем свинца в крови ≥10 мкг / дл (повышенный уровень свинца в крови [EBLL]) пропускаются педиатрами, согласно исследованию, опубликованному в Интернете 27 апреля. в Педиатрия .

Аннотация
Полный текст (может потребоваться подписка или оплата)

Раннее лечение РА важно для отдаленных результатов

ЧЕТВЕРГ, 27 апреля 2017 г. (Новости HealthDay) – Раннее лечение ревматоидного артрита (РА) важно для долгосрочных результатов, и согласно двум исследованиям, опубликованным в Интернете 20 апреля, произошло снижение смертности от РА. в Артрит и ревматология .

Реферат – Gwinnutt
Полный текст
Реферат – Kiadaliri
Полный текст (может потребоваться подписка или оплата)

Идентифицирован генетический вариант, связанный с РС и системной волчанкой

ЧЕТВЕРГ, 27 апреля 2017 г. (Новости HealthDay) – Согласно исследованию, опубликованному 26 апреля в Медицинском журнале Новой Англии, был обнаружен генетический вариант, связанный как с рассеянным склерозом, так и с системной красной волчанкой (СКВ). .

Аннотация / полный текст (может потребоваться подписка или оплата)

Профиль экспрессии гена

улучшает идентификацию меланомы высокого риска

ЧЕТВЕРГ, 27 апреля 2017 г. (Новости HealthDay) – Подтвержденная подпись профиля экспрессии 31 гена (GEP) улучшает идентификацию пациентов с меланомой с высоким риском метастазирования при использовании в сочетании с результатами Американского объединенного комитета по раку (AJCC) инструмент прогнозирования, согласно исследованию, опубликованному в майском выпуске журнала Journal Американской академии дерматологии .

Аннотация
Полный текст

Прогностический анализ хромосомной нестабильности при НМРЛ

СРЕДА, 26 апреля 2017 г. (Новости HealthDay) – Хромосомная нестабильность в опухолях рака легких увеличивает риск рецидива или смерти и может помочь прогнозировать рецидив задолго до стандартных тестов, согласно исследованию, опубликованному 26 апреля в Интернете в журнале New England Journal. медицины и Природа .

Аннотация / Полный текст

CDC: уровень смертности, связанной с опиоидами, может быть недооценен

СРЕДА, 26 апреля 2017 г. (HealthDay News) – Эпидемия злоупотребления лекарствами, отпускаемыми по рецепту, в Соединенных Штатах может быть связана с более высоким уровнем смертности, чем сообщалось ранее, согласно отчету U.Центры S. по контролю и профилактике заболеваний представлены 24 апреля на конференции Службы эпидемической разведки в Атланте.

Дополнительная информация

Загрязнение, связанное с деструктивным воздействием на верхние синоназальные дыхательные пути

СРЕДА, 26 апреля 2017 г. (Новости HealthDay) – Воздействие хронических взвешенных по воздуху твердых частиц на барьер дыхательных путей носовых пазух имеет деструктивные эффекты, включая выброс провоспалительных цитокинов, согласно экспериментальному исследованию, опубликованному в Интернете за февраль.28 в Американском журнале респираторной клетки и молекулярной биологии .

Аннотация
Полный текст (может потребоваться подписка или оплата)

Постбиотик может снизить уровень глюкозы, воспаление при ожирении

СРЕДА, 26 апреля 2017 г. (Новости HealthDay) – Постбиотик мурамилдипептида (МДП), полученный из клеточной стенки бактерий, снижает воспаление жировой ткани и снижает непереносимость глюкозы у мышей с ожирением, согласно экспериментальному исследованию, опубликованному в Интернете 20 апреля в журнале Cell Metabolism .

Аннотация / полный текст (может потребоваться подписка или оплата)

Идентификаторы молекулярной аутопсии Причины внезапной аритмической смерти

СРЕДА, 26 апреля 2017 г. (Новости HealthDay) – Молекулярное вскрытие генов электрического расстройства и кардиомиопатии выявляет умеренный, но реалистичный результат при синдроме внезапной аритмической смерти (SADS), согласно исследованию, опубликованному 24 апреля в Интернете в журнале Journal of the Американский колледж кардиологии .

Аннотация / полный текст (может потребоваться подписка или оплата)
От редакции (может потребоваться подписка или оплата)

Возможности тестирования генома на основе крови для быстрого определения мутаций

СРЕДА, 26 апреля 2017 г. (HealthDay News). Согласно исследованию, опубликованному 19 апреля в журнале Journal of Molecular Diagnostics , служба тестирования генома на основе крови предоставляет точные результаты в течение 72 часов.

Аннотация
Полный текст

Глубокие сверточные нейронные сети точно обнаруживают TB

СРЕДА, 26 апреля 2017 г. (Новости HealthDay) – Глубокое обучение с использованием глубоких сверточных нейронных сетей (DCNN) может привести к точному выявлению туберкулеза (ТБ) на рентгенограммах грудной клетки, согласно исследованию, опубликованному в Интернете 25 апреля в журнале Radiology .

Аннотация
Полный текст

Описан смертельный случай подозрения на панкреатит, вызванный пропофолом

СРЕДА, 26 апреля 2017 г. (Новости HealthDay) – В отчете о случае, опубликованном 10 апреля в журнале клинической фармации и терапии , был описан смертельный случай острого некротического панкреатита, вызванного пропофолом.

Аннотация
Полный текст (может потребоваться подписка или оплата)

Послеоперационный hsTnT связан с 30-дневной смертностью после несердечного Sx

ВТОРНИК, 25 апреля 2017 г. (Новости HealthDay) – Пик послеоперационного высокочувствительного тропонина T (hsTnT) связан с повышенным риском 30-дневной смертности среди пациентов, перенесших некардиальную операцию, согласно исследованию, опубликованному в Интернете 25 апреля в журнале Журнал Американской медицинской ассоциации .

Аннотация / полный текст (может потребоваться подписка или оплата)

Реактивация HBV связана с DAA Tx при коинфекции HBV-HCV

ВТОРНИК, 25 апреля 2017 г. (HealthDay News) – Реактивация вируса гепатита B (HBV) (HBV-R) представляет собой проблему безопасности для пациентов с коинфекцией HBV и вирусом гепатита C (HCV), получающих противовирусные препараты прямого действия (DAA). , согласно исследованию, опубликованному 24 апреля в сети Annals of Internal Medicine .

Аннотация / полный текст (может потребоваться подписка или оплата)

Снижение риска СД2 по варианту в кодировщике рецепторов сульфонилмочевины

ВТОРНИК, 25 апреля 2017 г. (Новости HealthDay) – Распространенный миссенс-вариант в гене, кодирующем компонент рецептора сульфонилмочевины ( ABCC8, p.A1369S), который способствует закрытию целевого канала терапии сульфонилмочевиной, имитируя эффекты терапии, связано со снижением риска диабета 2 типа и ишемической болезни сердца, согласно исследованию, опубликованному в Интернете 14 апреля в журнале Diabetes .

Аннотация / полный текст (может потребоваться подписка или оплата)

Отношение нейтрофилов к лимфоцитам предсказывает смертность при ВП

ПОНЕДЕЛЬНИК, 24 апреля 2017 г. (Новости HealthDay) – Отношение нейтрофилов к лимфоцитам (NLR) может предсказать 30-дневную смертность пожилых людей с внебольничной пневмонией (ВП), согласно исследованию, опубликованному в Интернете 13 апреля в Журнал Американского гериатрического общества .

Аннотация
Полный текст (может потребоваться подписка или оплата)

Показатели скрининга ПСА стабилизировались в США.С.

ВТОРНИК, 25 апреля 2017 г. (HealthDay News) – Показатели скрининга на простат-специфический антиген (ПСА) выровнялись после снижения в течение ряда лет в США, согласно исследовательскому письму, опубликованному 24 апреля в Интернете в журнале JAMA. Медицина внутренних болезней .

Аннотация / полный текст (может потребоваться подписка или оплата)

Стратегия генной терапии, выполнимая при пигментном ретините

ПОНЕДЕЛЬНИК, 24 апреля 2017 г. (Новости HealthDay) – Стратегия генной терапии может быть применена к пигментному ретиниту с переключением палочки на фоторецепторы в форме конуса, которые могут восстановить зрительную функцию, согласно экспериментальному исследованию, опубликованному в Интернете 21 апреля в Cell. Исследования .

Аннотация / Полный текст

Только избранные случайные узелки щитовидной железы требуют дальнейшей оценки

ПОНЕДЕЛЬНИК, 24 апреля 2017 г. (Новости HealthDay) – Согласно обзору, опубликованному в Интернете 20 апреля в JAMA Otolaryngology-Head & Neck Surgery , только несколько избранных случайных узлов щитовидной железы требуют дальнейшей оценки.

Аннотация / полный текст (может потребоваться подписка или оплата)

У чернокожих мужчин выше уровень доклинического рака простаты

ПОНЕДЕЛЬНИК, 24 апреля 2017 г. (Новости HealthDay) – Чернокожие мужчины, по-видимому, имеют более высокую заболеваемость доклиническим раком простаты и более высокий риск метастатического прогрессирования, чем население в целом, что может служить основанием для изменения подхода к скринингу, согласно исследованию. опубликовано в сети 24 апреля в номере Рак .

Аннотация
Полный текст (может потребоваться подписка или оплата)
От редакции (может потребоваться подписка или оплата)

В отчете о клиническом случае описана нежелательная реакция на клиндамицин

ПЯТНИЦА, 21 апреля 2017 г. (Новости HealthDay) – В отчете о клиническом случае, опубликованном 17 апреля в Интернете в журнале клинической фармации и терапии , описывается острый генерализованный экзантематозный пустулез, вторичный по отношению к терапии клиндамицином.

Аннотация
Полный текст (может потребоваться подписка или оплата)

Дисфункция эндотелия микрососудов может предсказать деменцию

ПЯТНИЦА, 21 апреля 2017 г. (Новости HealthDay) – Маркеры дисфункции микрососудистого эндотелия могут предсказать деменцию, согласно исследованию, опубликованному в Интернете 13 апреля в журнале Journal of Internal Medicine .

Аннотация
Полный текст (может потребоваться подписка или оплата)

Сроки контрольной биопсии не связаны с переклассификацией

ПЯТНИЦА, 21 апреля 2017 г. (Новости HealthDay). Согласно исследованию, опубликованному в апрельском выпуске журнала The Journal of Urology , сроки первой активной контрольной биопсии не связаны с увеличением неблагоприятной реклассификации рака простаты.

Аннотация
Полный текст

Утренняя моча первого испарения не требуется для обнаружения CIN2 +

ЧЕТВЕРГ, 20 апреля 2017 г. (Новости HealthDay) – Согласно исследованию, тестирование утренней мочи с первым мочеиспусканием перед последующими образцами для выявления цервикальной интраэпителиальной неоплазии 2+ (CIN2 +) с использованием тестирования на вирус папилломы человека (ВПЧ) не дает никаких преимуществ. опубликовано в Интернете 9 апреля в BJOG: Международный журнал акушерства и гинекологии .

CDC: Сальмонелла Распространенность инфекции снизилась в 2016 г.

, ЧЕТВЕРГ, 20 апреля 2017 г. (HealthDay News). Согласно исследованию, опубликованному в еженедельном отчете о заболеваемости и смертности Центров по контролю и профилактике заболеваний США, Еженедельный отчет о заболеваемости и смертности , официальные лица здравоохранения США добились прогресса в борьбе с инфекциями сальмонеллы . .

Аннотация / Полный текст

Повышение риска развития легочного синдрома, вызванного хантавирусом, для некоторых групп населения

, ЧЕТВЕРГ, 20 апреля 2017 г. (Новости HealthDay). Согласно исследованию, опубликованному в майском выпуске журнала Emerging Центров США по контролю и профилактике заболеваний, люди определенных профессий и представители определенных групп могут быть более подвержены риску хантавирусного легочного синдрома. Инфекционные болезни .

Аннотация / Полный текст

Циркулирующие экзосомы имеют отчетливый профиль РНК в MS

ЧЕТВЕРГ, 20 апреля 2017 г. (Новости HealthDay) – Циркулирующие экзосомы имеют отчетливый профиль РНК при ремиттирующем рассеянном склерозе (RRMS), согласно исследованию, опубликованному 15 апреля в Интернете в Annals of Neurology .

Аннотация
Полный текст (может потребоваться подписка или оплата)

Гипертония может положительно повлиять на прогноз рака яичников

СРЕДА, 19 апреля 2017 г. (Новости HealthDay). Согласно обзору, недавно опубликованному в Cancer Causes & Control , на прогноз женщины после диагноза рака яичников может повлиять ряд неожиданных факторов.

Аннотация / полный текст (может потребоваться подписка или оплата)

Исследование посвящено посещениям скорой помощи пациентам, пострадавшим от полиции в США.С.

СРЕДА, 19 апреля 2017 г. (HealthDay News). Согласно исследованию, опубликованному 19 апреля в журнале JAMA Surgery , более 50 000 американцев ежегодно проходят лечение от травм, нанесенных полицией.

Аннотация / полный текст (может потребоваться подписка или оплата)

Болезнь Шагаса представляет собой проблему общественного здравоохранения в США

СРЕДА, 19 апреля 2017 г. (Новости HealthDay) – Болезнь Шагаса, вызываемая паразитом Trypanosoma cruzi и передающаяся триатоминовым клопом, представляет собой проблему для общественного здравоохранения в Соединенных Штатах, согласно Инициативе по лекарствам от забытых болезней ( ДНДи).

Дополнительная информация

Исследователи предупреждают об эпилепсии у младенцев, инфицированных вирусом Зика

СРЕДА, 19 апреля 2017 г. (Новости HealthDay) – Помимо известных связей с врожденными дефектами и другими проблемами, вирус Зика может также вызывать случаи эпилепсии у младенцев, согласно статье, опубликованной в Интернете 17 апреля в журнале JAMA Neurology .

Аннотация / полный текст (может потребоваться подписка или оплата)

Долгосрочная угроза здоровью глаз у младенцев, родившихся с инфекцией Зика

ВТОРНИК, 18 апреля 2017 г. (Новости HealthDay) – Согласно исследованию, опубликованному в Интернете 13 апреля в JAMA Ophthalmology , вирус Зика может привести к пожизненному ухудшению зрения у пораженных младенцев.

Аннотация / Полный текст

Отсутствие доказательств того, что азитромицин увеличивает вероятность желудочковой аритмии

ВТОРНИК, 18 апреля 2017 г. (Новости HealthDay). Согласно исследованию, опубликованному 18 апреля в журнале Канадской медицинской ассоциации CMAJ , азитромицин не увеличивает риск желудочковой аритмии.

Аннотация
Полный текст

Более 20 процентов материнской смертности в Иллинойсе из-за сердечно-сосудистых заболеваний

ВТОРНИК, 18 апреля 2017 г. (HealthDay News). Согласно исследованию, опубликованному в майском выпуске журнала Abstetrics & Gynecology , более одной из пяти материнских смертей в Иллинойсе в период с 2002 по 2011 годы были связаны с сердечно-сосудистыми заболеваниями.

Аннотация / полный текст (может потребоваться подписка или оплата)

Увеличение числа инфекций, связанных с биопсией простаты, в Нью-Йорке

ВТОРНИК, 18 апреля 2017 г. (HealthDay News). Согласно исследованию, опубликованному в апрельском выпуске журнала The Journal of Urology , с 2011 по 2014 год в штате Нью-Йорк увеличилось количество инфекционных осложнений после пункционной биопсии простаты.

Аннотация
Полный текст
От редакции (может потребоваться подписка или оплата)

Врачи должны помнить о том, что они публикуют в социальных сетях

ПОНЕДЕЛЬНИК, 17 апреля 2017 г. (Новости HealthDay). Согласно исследованию, опубликованному в Интернете 9 апреля в BJU International , молодые врачи часто имеют непрофессиональный или оскорбительный контент в своих профилях на Facebook.

Аннотация
Полный текст (может потребоваться подписка или оплата)

Низкие показатели скрининга на рак шейки матки для женщин с психическими заболеваниями

ПОНЕДЕЛЬНИК, 17 апреля 2017 г. (Новости HealthDay). Согласно исследованию, опубликованному 17 апреля в психиатрической службе , показатели скрининга на рак шейки матки среди женщин с тяжелыми психическими заболеваниями намного ниже, чем среди других женщин.

Аннотация
Полный текст (может потребоваться подписка или оплата)

RUNX1 Может сыграть роль в пролиферативной диабетической ретинопатии

ПОНЕДЕЛЬНИК, 17 апреля 2017 г. (Новости HealthDay) – Ген фактора транскрипции 1, связанный с Runt ( RUNX1 ), может играть роль в пролиферативной диабетической ретинопатии (PDR) у человека, а повышенная регуляция может быть маркером аберрантного ангиогенеза сетчатки. согласно исследованию, опубликованному в сети 11 апреля в Diabetes .

Аннотация / полный текст (может потребоваться подписка или оплата)

ASCO обновляет рекомендации по потенциально излечимому раку поджелудочной железы

ПОНЕДЕЛЬНИК, 17 апреля 2017 г. (Новости HealthDay) – Рекомендации, касающиеся соответствующей схемы адъювантной терапии для пациентов с раком поджелудочной железы, были обновлены в свете новых данных, согласно специальной статье, опубликованной 11 апреля в Интернете в журнале клинической онкологии . .

Аннотация
Полный текст

Случаи сибирской язвы, связанные с использованием старинных щеток для бритья

ПОНЕДЕЛЬНИК, 17 апреля 2017 г. (Новости HealthDay) – Во время и после Первой мировой войны наблюдался рост случаев заболевания сибирской язвой, связанный с использованием новых щеток для бритья, которые были изготовлены из импортного конского волоса, согласно исследованию, опубликованному в мае. выпуск журнала U.С. Центры по контролю и профилактике заболеваний Новые инфекционные заболевания .

Аннотация / Полный текст

Заболеваемость раком груди среди американских женщин азиатского происхождения растет

ПЯТНИЦА, 14 апреля 2017 г. (Новости HealthDay). Согласно исследованию, опубликованному 1 апреля в журнале «Исследование и лечение рака груди» , заболеваемость раком груди среди американцев азиатского происхождения неуклонно растет, в отличие от других расовых / этнических групп.

Аннотация / полный текст (может потребоваться подписка или оплата)

Снижение скорости клубочковой фильтрации – основная причина смерти от сердечно-сосудистых заболеваний

ПЯТНИЦА, 14 апреля 2017 г. (Новости HealthDay). Согласно исследованию, опубликованному 13 апреля в журнале Американского общества нефрологов , заболевание почек является основной причиной смерти от сердечно-сосудистых заболеваний во всем мире.

Аннотация
Полный текст (может потребоваться подписка или оплата)

Распространенность рака отличается среди афроамериканцев и афроамериканцев

, ЧЕТВЕРГ, 13 апреля 2017 г. (HealthDay News). Согласно исследованию, опубликованному 13 апреля в журнале Cancer , заболеваемость раком у чернокожих американцев, родившихся в Африке и США, различается в зависимости от региона рождения.

Аннотация
Полный текст (может потребоваться подписка или оплата)

Точная диагностика эндокринной гипертензии Важно

, ЧЕТВЕРГ, 13 апреля 2017 г. (Новости HealthDay) – Точный диагноз эндокринной гипертензии позволяет врачам обеспечить эффективное лечение, включая хирургическое лечение, или достичь оптимального ответа с помощью специфической фармакологической терапии, согласно научному заявлению, опубликованному в Интернете 5 апреля. в Эндокринные обзоры .

Аннотация / Полный текст

Диабет продолжает оставаться серьезным бременем для общественного здравоохранения

, ЧЕТВЕРГ, 13 апреля 2017 г. (HealthDay News). Согласно исследованию, опубликованному в номере от 13 апреля, заболеваемость диабетом растет среди молодых людей, хотя наблюдается некоторый прогресс в отношении смертности и частоты сердечно-сосудистых исходов среди пациентов с этим заболеванием. из Медицинский журнал Новой Англии .

Аннотация / полный текст 1 (может потребоваться подписка или оплата)
Аннотация / полный текст 2 (может потребоваться подписка или оплата)
От редакции (может потребоваться подписка или оплата)

Непонимание результатов теста BRCA влияет на частоту мастэктомии

ЧЕТВЕРГ, 13 апреля 2017 г. (Новости HealthDay) – Согласно опубликованному исследованию, почти половина пациентов с раком груди, которые решают пройти двойную мастэктомию после генетического тестирования, могут не иметь генных мутаций, которые, как известно, повышают риск возникновения дополнительных видов рака. онлайн 12 апреля в Journal of Clinical Oncology .

Аннотация
Полный текст

24-часовой сбор мочи неясной пользы у камнеобразователей

ЧЕТВЕРГ, 13 апреля 2017 г. (Новости HealthDay) – Несмотря на руководящие принципы, согласно обзору, опубликованному в апрельском номере журнала The Journal of Urology, не установлено, получают ли все рецидивирующие камни в почках выгоду от 24-часового сбора мочи. .

Аннотация
Полный текст

Смертность выросла из-за депрессии непосредственно перед диагнозом рака груди

ЧЕТВЕРГ, 13 апреля 2017 г. (Новости HealthDay). Согласно исследованию, опубликованному в Интернете 7 апреля в журнале Cancer , у женщин с впервые развившейся депрессией до постановки диагноза рака груди умеренно, но значительно повышен риск смерти.

Аннотация
Полный текст (может потребоваться подписка или оплата)

Факторы сосудистого риска среднего возраста, связанные с повышенным амилоидом

СРЕДА, 12 апреля 2017 г. (Новости HealthDay) – Согласно исследованию, опубликованному в выпуске журнала Journal of от 11 апреля, у лиц среднего возраста с факторами риска сердечно-сосудистых заболеваний и инсульта повышен уровень амилоида. Американская медицинская ассоциация .

Аннотация / полный текст (может потребоваться подписка или оплата)

Барретт с неправильной линией Z вряд ли быстро продвинется

СРЕДА, 12 апреля 2017 г. (Новости HealthDay) – Существует низкий риск развития дисплазии высокой степени (HGD) или аденокарциномы пищевода (EAC) среди пациентов с пищеводом Барретта (BE) <1 см (неправильная линия Z). ) в течение пяти лет после индексной эндоскопии, согласно исследованию, опубликованному в апрельском номере журнала Gastroenterology .

Аннотация
Полный текст

Выбор пациента подчеркнут в последних рекомендациях USPSTF по скринингу PSA

ВТОРНИК, 11 апреля 2017 г. (Новости HealthDay) – Целевая группа профилактических служб США рекомендует мужчинам в возрасте от 55 до 69 лет обсудить со своим врачом плюсы и минусы скрининга на простатоспецифический антиген (ПСА) для выявления простаты. рак.

Обзор доказательств
Проект заявления о рекомендации
Комментарий к рекомендации

Распространенность острого ишемического инсульта среди молодых американцев увеличилась

ВТОРНИК, 11 апреля 2017 г. (Новости HealthDay) – Острый ишемический инсульт становится все более распространенным среди американцев моложе 65 лет, как и процент людей с тремя или более факторами риска инсульта, согласно исследованию, опубликованному 10 апреля в Интернете в журнале JAMA Neurology. .

Аннотация / Полный текст
От редакции

Бессимптомный C. difficile Повышает риск для других пациентов больницы

ВТОРНИК, 11 апреля 2017 г. (Новости HealthDay). Согласно исследованию, опубликованному в апрельском выпуске журнала Gastroenterology , бессимптомные носители токсигенного вируса Clostridium difficile в больницах повышают риск инфицирования у других пациентов.

Аннотация
Полный текст (может потребоваться подписка или оплата)

Eval, Mgmt RA у женщин может быть снижено из-за ожирения

ПОНЕДЕЛЬНИК, 10 апреля 2017 г. (Новости HealthDay) – На уровни С-реактивного белка (СРБ) и скорости оседания эритроцитов (СОЭ) при оценке и лечении ревматоидного артрита может повлиять ожирение у женщин, согласно исследованию, опубликованному в Интернете. 10 апреля в Arthritis Care & Research .

Аннотация
Полный текст (может потребоваться подписка или оплата)

Грибковые поражения могут имитировать новообразования на языке

ПОНЕДЕЛЬНИК, 10 апреля 2017 г. (Новости HealthDay) – Грибковые поражения могут имитировать новообразования на языке, согласно отчету о болезни, опубликованному в Интернете 5 апреля в журнале Pediatrics .

Аннотация / полный текст (может потребоваться подписка или оплата)

Банки крови США могут защитить кровоснабжение от вируса Зика

ПЯТНИЦА, 7 апреля 2017 г. (Новости HealthDay) – U.Согласно исследованию, опубликованному в мартовском номере журнала Transfusion , тематическом выпуске по вирусу Зика и другим вирусам, передающимся при переливании крови, банки крови S. .

Аннотация 1
Полный текст
Аннотация 2
Полный текст (может потребоваться подписка или оплата)
Аннотация 3
Полный текст
От редакции

MACRA меняет подход правительства к оплате врачей

ПЯТНИЦА, 7 апреля 2017 г. (Новости HealthDay) – В соответствии с политическим обзором, опубликованным 27 марта в журнале Health Affairs , внедрение Закона о доступе к программе Medicare и повторной авторизации CHIP (MACRA) внесло фундаментальные изменения в подход правительства к оплате врачей. .

Аннотация / Полный текст

Загрязнение воздуха, воздействие озона связано с плотностью груди

ПЯТНИЦА, 7 апреля 2017 г. (Новости HealthDay) – Загрязнение воздуха и воздействие озона могут частично объяснить географические различия в маммографической плотности, согласно исследованию, опубликованному в Интернете 6 апреля в журнале Breast Cancer Research .

Аннотация / Полный текст

CDC: Сифилис растет среди мужчин в США, практикующих секс с мужчинами

ПЯТНИЦА, 7 апреля 2017 г. (Новости HealthDay). Согласно исследованию, опубликованному в выпуске U.Еженедельный отчет Центров по контролю и профилактике заболеваний о заболеваемости и смертности .

Аннотация / Полный текст

Инфекция кишечного реовируса может быть причиной целиакии

ПЯТНИЦА, 7 апреля 2017 г. (Новости HealthDay). Согласно исследованию, опубликованному в выпуске Science от 7 апреля, распространенный реовирус кишечника человека может вызывать некоторые случаи глютеновой болезни.

Аннотация / полный текст (может потребоваться подписка или оплата)

Маркетинг тестов на генетический риск, направленных непосредственно на потребителя, одобряет FDA

ПЯТНИЦА, 7 апреля 2017 г. (Новости HealthDay) – The U.Управление по санитарному надзору за качеством пищевых продуктов и медикаментов США одобрило первые домашние генетические тесты на 10 заболеваний или состояний, включая болезнь Паркинсона и болезнь Альцгеймера с поздним началом.

Дополнительная информация

CDC: Почти половина мужчин в США, женщин <60 лет инфицированы ВПЧ

, ЧЕТВЕРГ, 6 апреля 2017 г. (Новости HealthDay) – Согласно апрельскому анализу данных, опубликованному Национальным центром Центров США по контролю и профилактике заболеваний, почти половина американских мужчин и женщин моложе 60 инфицированы генитальным вирусом папилломы человека (ВПЧ). по статистике здравоохранения (NCHS).

Дополнительная информация

Корректировка рисков, предложение о передаче перестрахования, финансовая выгода

ЧЕТВЕРГ, 6 апреля 2017 г. (Новости HealthDay). Согласно исследованию, опубликованному в мартовском номере журнала Health Affairs , программы корректировки рисков и передачи перестрахования оказались эффективными для увеличения доходов за счет расходов на выплату страховых возмещений.

Аннотация
Полный текст (может потребоваться подписка или оплата)

Аутоантитела к GPIHBP1, выявленные при хиломикронемии

, ЧЕТВЕРГ, 6 апреля 2017 г. (Новости HealthDay) – У некоторых пациентов с хиломикронемией есть аутоантитела к гликозилфосфатидилинозитол-связывающему белку 1 высокой плотности, связывающему липопротеины 1 (GPIHBP1), вызывающему тяжелую гипертриглицеридемию, согласно исследованию, опубликованному 5 апреля в газете New Английский журнал медицины .

Аннотация
Полный текст

Возможна трансплантация стволовых клеток при кардиомиопатии

ЧЕТВЕРГ, 6 апреля 2017 г. (Новости HealthDay) – Трансплантация стволовых клеток показывает многообещающие результаты в лечении кардиомиопатии, согласно исследованию, опубликованному в Интернете 5 апреля в журнале Американской кардиологической ассоциации .

Аннотация / Полный текст

Повышенный риск сердечно-сосудистых событий при колебаниях веса

ЧЕТВЕРГ, 6 апреля 2017 г. (Новости HealthDay) – Колебания массы тела связаны с более высокой смертностью и более высокой частотой сердечно-сосудистых событий – независимо от традиционных факторов риска сердечно-сосудистых заболеваний – у пациентов с ишемической болезнью сердца, согласно исследованию. опубликовано в выпуске от 6 апреля New England Journal of Medicine .

Аннотация / полный текст (может потребоваться подписка или оплата)

Долгосрочное употребление антибиотиков может повысить риск развития колоректальных аденом

СРЕДА, 5 апреля 2017 г. (Новости HealthDay) – Прием антибиотиков в течение длительного периода в раннем и среднем зрелом возрасте может повысить риск развития колоректальных аденом, согласно отчету, опубликованному в Интернете 4 апреля в журнале Gut .

Аннотация / Полный текст

Повышенный риск рака у детей-реципиентов почек

СРЕДА, 5 апреля 2017 г. (Новости HealthDay). Согласно исследованию, опубликованному 29 марта в Американском журнале трансплантологии , у детей-реципиентов почек повышен риск рака.

Аннотация
Полный текст (может потребоваться подписка или оплата)

CDC: Врожденные дефекты, обнаруживаемые в каждой десятой беременности в США, вызванной вирусом Зика

СРЕДА, 5 апреля 2017 г. (Новости HealthDay) – Согласно исследованию, опубликованному в раннем выпуске США от 4 апреля, каждая десятая беременная женщина в США с подтвержденной инфекцией Зика в 2016 году родила ребенка с врожденными дефектами, связанными с вирусом. Еженедельный отчет о заболеваемости и смертности Центров по контролю и профилактике заболеваний .

Аннотация / Полный текст

Кость, связь основного метаболизма зависит от уровня витамина D

СРЕДА, 5 апреля 2017 г. (Новости HealthDay) – Для женщин в постменопаузе с сахарным диабетом 2 типа (T2DMPW) корреляция между костным метаболизмом и основным метаболизмом, по-видимому, зависит от сывороточного 25-гидроксивитамина D (25 [OH] D). уровни, согласно исследованию, опубликованному 31 марта в журнале Journal of Diabetes Investigation .

Аннотация
Полный текст

Различия в охвате вакцинацией от гриппа на производстве

ВТОРНИК, 4 апреля 2017 г. (Новости HealthDay) – Существуют различия в охвате вакцинацией против гриппа в зависимости от отрасли и профессии, в том числе среди медицинского персонала и других профессиональных групп, которым может быть уделено первоочередное внимание на вакцинацию против гриппа во время пандемии (уровень 1) , согласно исследованию, опубликованному в выпуске от 1 апреля American Journal of Infection Control .

Аннотация
Полный текст

Избыточный вес матери и ожирение могут усилить детскую эпилепсию

ВТОРНИК, 4 апреля 2017 г. (Новости HealthDay). Согласно исследованию, опубликованному в Интернете 3 апреля в журнале JAMA Neurology , частота детской эпилепсии увеличивается с увеличением веса и ожирением матери.

Аннотация / Полный текст
От редакции

Максимальный ИМТ за 16 лет увеличивает риск смерти от всех причин

ВТОРНИК, 4 апреля 2017 г. (Новости HealthDay) – Максимальный индекс массы тела (ИМТ) за 16 лет истории веса связан с повышенным риском смерти от всех причин, согласно исследованию, опубликованному 4 апреля в Интернете в журнале Annals of Медицина внутренних болезней .

Экспрессия белка предсказывает исходы рака прямой кишки

ВТОРНИК, 4 апреля 2017 г. (Новости HealthDay) – Потеря экспрессии белка E-кадгерина в ходе дотерапевтической биопсии рака прямой кишки связана с меньшим количеством метастазов и улучшением выживаемости, согласно исследованию, опубликованному 25 марта в Интернете в журнале Journal of Digestive. Болезни .

Аннотация
Полный текст (может потребоваться подписка или оплата)

С 1990 по 2015 год наблюдалось снижение глобальной детской и подростковой смертности

ВТОРНИК, 4 апреля 2017 г. (HealthDay News). Согласно исследованию, опубликованному 3 апреля в журнале JAMA Pediatrics , с 1990 по 2015 г. в мире наблюдалось снижение детской и подростковой смертности.

Аннотация / Полный текст
От редакции

ANGPTL3 Дефицит связан со сниженным риском CAD

ПОНЕДЕЛЬНИК, 3 апреля 2017 г. (Новости HealthDay) – Ангиопоэтин-подобный дефицит 3 ( ANGPTL3 ) связан со снижением риска ишемической болезни сердца (ИБС), согласно исследованию, опубликованному 29 марта в Интернете в журнале Journal. Американского колледжа кардиологии .

Аннотация / полный текст (может потребоваться подписка или оплата)
Редакция (может потребоваться подписка или оплата)

Фоторедактор: Pixlr E

Фоторедактор: Pixlr E – бесплатный инструмент для редактирования изображений Подписаться Попробуйте Премиум
Добро пожаловать в бесплатный продвинутый редактор фотографий от Pixlr.Начните редактирование, нажав кнопку открытия фотографии, перетащите файл, вставьте его из буфера обмена (ctrl + v) или выберите один из наших готовых шаблонов ниже.
Открыть изображение
Из локального временного кэша, чтобы сохранить проект на длительный срок, сохраните его как PXZ (документ Pixlr).
Рекомендуемые шаблоныПодробнее
Модные и высококачественные шаблоны, вручную отобранные нашей командой.
Шаблоны
Просмотрите и найдите шаблон, выбрав тип дизайна, который вы хотите создать, ниже.
рекомендуется
Загрузить еще
Закрепленные проекты
Все ваши временные проекты
История только временно сохраняется в кеше браузера, все документы будут удалены, если вы очистите кеш или запустите любую процедуру очистки.Если вы хотите сохранить на длительный срок, скачайте его как .PXZ (документ Pixlr).
В вашей истории нет проектов.
Ошибка
Что-то пошло не так. Пожалуйста, повторите попытку позже.
Не в сети
Вы не в сети, проверьте подключение к Интернету и повторите попытку.
Ничего не найдено. Выполните еще один поиск.
Загрузить еще
{“user”: {“name”: “guest”, “subscription”: false, “subscriptionType”: “guest”, “subscriptionCode”: “-“, “subscriptionGroup”: “-“, “currency”: ” USD “,” country “:” RU “,” id “:” – “},” elhibitedFreeTrial “: true,” cdnUrl “:” https://pixlr.com “,” adyenClientKey “:” live_RCU6ZYUQ5VDAFOMUJSSVV3P7YAWK75MMug “,” adDebr. “:” “,” unlockTemplate “: false}
{“photoEditorHome”: “Фоторедактор pixlr home”, “loginEditor”: “Войдите или зарегистрируйтесь в фоторедакторе”, “learnMore”: “Подробнее”, “headerSignUp”: “Зарегистрироваться”, “headerTryPremium”: ” Попробуйте Premium »,« headerWebApps »:« Веб-приложения »,« headerPricing »:« Цены и бесплатная пробная версия »,« headerDesktopApps »:« Настольные приложения »,« headerMobileApps »:« Мобильные приложения »,« headerOtherPlatforms »:« Другие платформы » , «headerOtherServices»: «Другие услуги», «headerStockByPixlr»: «Stock by Pixlr», «headerPixlrTemplates»: «Шаблоны Pixlr», «headerHelpAndLearn»: «Справка и обучение», «headerVideoTutorials»: «Видеоуроки», «headerLearnAndEducation “:” Обучение и образование “,” headerContactAndSupport “:” Контакты и поддержка “,” headerLanguage “:” Язык “,” headerStoriesByPixlr “:” Истории от Pixlr “,” eTitle “:” Фоторедактор: Pixlr E – бесплатное редактирование изображений tool »,« eMetaDesc »:« Pixlr E – это редактор фотографий нового поколения, который ищет расширенные возможности редактирования фотографий прямо в браузере! Установка и регистрация не требуются.Используйте бесплатно на настольных компьютерах, планшетах и телефонах. »,« EMetaSiteName »:« Photo Editor: Pixlr.com – бесплатное редактирование изображений в Интернете »,« mobileVariantDesc »:« Pixlr E создан для настольных компьютеров. Вы используете мобильное устройство или окно браузера имеет ширину менее 650 пикселей. Мы рекомендуем вам использовать мобильный веб-редактор фотографий или увеличить окно браузера. »,« MobileVariantButton »:« Использовать мобильный редактор »,« mobileVariantClose »:« Игнорировать и закрыть »,« welcomeHeadline »:« Фоторедактор и конструктор » , “welcomeIngress”: “Добро пожаловать в бесплатный расширенный редактор фотографий от Pixlr.Начните редактирование, нажав кнопку открытия фотографии, перетащите файл, вставьте его из буфера обмена (ctrl + v) или выберите один из наших готовых шаблонов ниже. “,” ToolKB “:” Сочетание клавиш “,” toolArrange ” “:” Упорядочить “,” toolArrangeDesc “:” Переместить, преобразовать и изменить настройки слоя. “,” ToolMarquee “:” Marquee Select “,” toolMarqueeDesc “:” Создать выделения с помощью инструмента выделения квадратом и кругом. “,” ToolLasso ” : “Выбор лассо”, “toolLassoDesc”: “Используйте произвольное, многоугольное, безье или магнитное лассо для создания выделения.”,” toolWand “:” Wand Select “,” toolWandDesc “:” Используйте волшебную палочку, чтобы выбрать области с похожими цветами. “,” toolCrop “:” Обрезать “,” toolCropDesc ”:” Обрезать, вырезать и выпрямить страницу с помощью свободный или фиксированный аспект. “,” toolCutout “:” Вырез / Маска “,” toolCutoutDesc “:” Маскировка областей и / или удаление фона, вырезание объектов или обрезка / обрезка отдельных слоев. “,” toolFrame “:” Кадр / изображение Holder “,” toolFrameDesc “:” Определите область для размещения изображения и обрежьте ее по разным формам, размещенное изображение автоматически масштабируется и обрезается по размеру. Рамки – важная часть создания шаблонов многократного использования.”,” toolLiquify “:” Liquify “,” toolLiquifyDesc “:” Увеличивайте, уменьшайте и сдвигайте части изображения. Используйте пластику для тонкой корректировки портретов и других изображений. “,” ToolHeal “:” Исцелить “,” toolHealDesc “:” Удалить пятна, нежелательные объекты, пятна и очистить изображения. “,” ToolClone “:” Клонировать “,” toolCloneDesc “:” Рисуйте и копируйте из других областей изображения. “,” toolDetail “:” Размытие / Резкость / Размытие “,” toolDetailDesc “:” Нарисуйте области изображения, чтобы сделать детали резче, размыть или размазать. “,” toolFocus “:” Фокус / Боке “,” toolFocusDesc “:” Создайте глубину в своих фотографиях с помощью размытия фона, размытия боке и боке света.”,” toolDisperse “:” Disperse “,” toolDisperseDesc “:” Нарисуйте область на изображении и посмотрите, как она взорвется и разлетится на тысячи пикселей. “,” toolToning “:” Dodge / Burn “,” toolToningDesc “:” Осветлить или затемните области изображения, чтобы выделить темные области или затемнить светлые. “,” toolTemper “:” Sponge / Color “,” toolTemperDesc “:” Яркость кисти, насыщенность или температура в определенных областях, чтобы выделить или уменьшить цвета. “, “toolPen”: “Pen”, “toolPenDesc”: “Используйте разные типы перьев для творчества, такие как паутина, цветные карандаши, чернила и хвост, чтобы рисовать и рисовать.”,” toolDraw “:” Рисовать “,” toolDrawDesc “:” Рисовать и рисовать разными кистями и цветами. “,” toolEraser “:” Ластик “,” toolEraserDesc “:” Стирать части изображения кистью, использовать вырез инструмент для более точного результата. »,« toolFill »:« Заливка »,« toolFillDesc »:« Заливка целых областей одним цветом. »,« toolGradient »:« Градиент »,« toolGradientDesc »:« Создавайте переходы с разными цветами и прозрачностями. . “,” toolReplace “:” Замена цвета “,” toolReplaceDesc “:” Измените один цвет в области на другой путем рисования. “,” toolShape “:” Форма “,” toolShapeDesc “:” Нарисуйте разные пиксельные или векторные фигуры например квадраты, круги, линии и многое другое.”,” toolAddText “:” Text “,” toolAddTextDesc “:” Добавьте новый текстовый слой или используйте один из наших текстовых шаблонов. “,” toolPicker “:” Picker “,” toolPickerDesc “:” Выберите цвета из изображения для использования с другие инструменты. »,« toolZoom »:« Масштаб »,« toolZoomDesc »:« Увеличивайте или уменьшайте масштаб фотографии, чтобы сфокусироваться на различных частях. »,« toolHand »:« Рука / Панорамирование »,« toolHandDesc »:« Перемещение видимая область при увеличении изображения. Удерживайте пробел в любом инструменте. “,” colorSwitch “:” переключить цвета (X) “,” titleFile “:” Файл “,” titleEdit “:” Изменить “,” titlePage “:” Page “,” titleLayer “:” Layer “,” titleSelect “:” Select “,” titleAdjustment “:” Adjustment “,” titleFilter “:” Filter “,” titleAnimation “:” Animation “,” titleView “:” View ” , “titleHelp”: “Справка”, “titleNewImage”: “Новое изображение”, “titleAddImage”: “Добавить изображение”, “titleChangeImage”: “Изменить изображение”, “titleOpenImage”: “Открыть изображение”, “titleOpenURL”: ” URL открытия изображения »,« titleStockSearch »:« Поиск по акциям »,« titleBrowseElements »:« Обзор элементов »,« titleSave »:« Сохранить »,« titlePrint »:« Печать »,« titleClose »:« Закрыть »,« titleExport » : “Экспорт”, “titleExportTemplate”: “Экспорт тем plate »,« titleQuickExportPage »:« Быстрый экспорт страницы в формате PNG »,« titleQuickExportLayer »:« Быстрый экспорт слоя в PNG »,« titleUndo »:« Отменить »,« titleRedo »:« Повторить »,« titleCut »:« Вырезать » , “titleCopy”: “Копировать”, “titleClear”: “Очистить”, “titleClearAll”: “Очистить все”, “titlePaste”: “Вставить”, “titleFreeTransform”: “Свободное преобразование”, “titleFreeDistort”: “Бесплатное искажение , “titleStroke”: “Stroke”, “strokeOutlineOnly”: “Только контур”, “titleFill”: “Заливка”, “titlePreferences”: “Настройки”, “titlePageSize”: “Установить размер страницы”, “titlePageResize”: “Изменить размер страницы (scale) »,« titlePageColor »:« Фон страницы »,« titlePageRotation »:« Поворот страницы »,« titleCrop »:« Обрезка »,« titleTrim »:« Обрезать »,« titleNewLayer »:« Новый слой »,« titleEditText “:” Редактировать текст “,” titleDuplicateLayer “:” Дублировать слой “,” titleImageLayer “:” Добавить изображение как слой “,” titleElementLayer “:” Добавить слой элемента “,” titleURLLayer “:” Добавить URL как layer »,« titleDeleteLayer »:« Удалить слой »,« titleRasterizeLayer »:« Растрировать слой »,« titleLayerUp »:« Переместить вперед / вверх »,« titleLayerDown »:« Отправить назад / вниз »,« titleLayerAutoMask »:« AI Auto Mask »,« titlePositionFrame »:« Позиционирующий фрейм »,« titlePositionContent »:« Позиционирование изображения »,« titleAutoFitContent »:« Обновить изображение »,« titleRemoveFrameImage »:« Удалить изображение »,« titleSelectAll »:« Выбрать все »,« titleSelectPixels “:” Выбрать пиксели “,” titleSelectDeselect “:” Отменить выбор “,” titleSelectInvert “:” Инвертировать выделение “,” titleSelectSave “:” Сохранить выделение “,” titleSelectRestore “:” Восстановить выделение “,” titleAutoAdjust “:” Автоматическая настройка ” , “titleAutoPop”: “Автозапуск”, “titleAutoBW”: “Авто-черно-белый”, “titleBrightnessContrast”: “Яркость и контраст”, “titleTemperatureTint”: “Температура и оттенок”, “titleHueSaturation”: “Оттенок и насыщенность”, ” titleVibrance “:” Vibrance “,” titleColorBalance “:” Цветовой баланс “,” titleColorLookup “:” Подбор цвета “,” titleHighlightsShadows “:” Света и тени “,” titleExposure “:” Экспозиция “,” titleCurves “:” Кривые ” , “titleLevels”: “Уровни”, “tit leThreshold “:” Threshold “,” titlePosterize “:” Posterize “,” titleDesaturate “:” Desaturate “,” titleInvert “:” Invert “,” titleSolarize “:” Solarize “,” titleMimicHDR “:” Mimic HDR “,” titleMonochrome ” “:” Монохромный “,” titleEffectLibrary “:” Библиотека эффектов “,” titleSharpen “:” Резкость “,” titleClarity “:” Четкость “,” titleDetails “:” Детали “,” titleBlur “:” Размытие “,” titleZoomBlur ” : «Размытие при увеличении», «titleGaussianBlur»: «Размытие по Гауссу», «titleMotionBlur»: «Размытие в движении», «titleRadialBlur»: «Радиальное размытие», «titleSmooth»: «Smooth», «titleGrain»: «Зерно», « titleNoise “:” Добавить шум “,” titleDenoise “:” Убрать шум “,” titleVignette “:” Виньетка “,” titleBloom “:” Bloom “,” titleGlamour “:” Glamour “,” titleDehaze “:” Dehaze “,” titleInnerGlow “:” Внутреннее свечение “,” titleOuterGlow “:” Внешнее свечение “,” titleBevel “:” Bevel “,” titleOutline “:” Outline “,” titleInnerShadow “:” Внутренняя тень “,” titleDropShadow “:” Падающая тень ” , “titleSobel”: “Найти края”, “titleFringe”: “Fringe”, “titleGlitch”: “Glitches”, “titleCreative”: “Creative”, “titleRGBSplit”: “RGB Split”, “titleInterference”: “Interference” , “titleSlice”: “S lice “,” titlePixelate “:” Pixelate “,” titleMosaic “:” Mosaic “,” titleHalftone “:” Halftone “,” titleScanlines “:” Scanlines “,” titlePolarCoordinates “:” Полярные координаты “,” titleKaleidoscope “:” Калейдоскоп “,” titleFishEye “:” Fish Eye “,” titleReflect “:” Reflect “,” titleWave “:” Wave “,” titleStrokeOutline “:” Stroke / Outline “,” titlePlay “:” Play “,” titleStop “:” Stop »,« titleFloatingPanels »:« Переключить плавающие панели »,« titleRestorePanels »:« Восстановить все панели »,« titleNavigatorPanel »:« Панель навигации »,« titleLayersPanel »:« Панель слоев »,« titleHistoryPanel »:« Панель истории », “titleAnimationPanel”: “Панель анимации”, “titleZoomIn”: “Увеличение”, “titleZoomOut”: “Уменьшение”, “titleFitScreen”: “По размеру экрана”, “titleFillScreen”: “Заполнить экран”, “titleTogglePreview”: ” Переключить режим предварительного просмотра »,« titleToggleFullScreen »:« Переключить полноэкранный режим »,« titleThemeColors »:« Изменить тему / цвета »,« titleKeyboardShortcuts »:« Сочетания клавиш »,« titleColorPicker »:« Выбор цвета »,« titleAddElement »:« Добавить element “,” titleToolSettings “:” Настройки инструмента “,” titleSelectConvert “:” Преобразовать t o mask »,« titleLayerAddMask »:« Добавить маску »,« titleLayerApplyMask »:« Применить маску »,« titleLayerDeleteMask »:« Удалить маску »,« titleLayerResetMask »:« Сбросить маску »,« titleLayerInvertMask »:« Инвертировать маску »,« titleLayerMoreMask »:« Дополнительная маска »,« titleLayerExtractMask »:« Извлечь маску как слой »,« titleLayerConvertMask »:« Преобразовать маску в выделение »,« titleLockLayer »:« Заблокировать слой »,« titleHideLayer »:« Скрыть слой »,« titleCutLayer “:” Вырезать слой “,” titleCopyLayer “:” Копировать слой “,” titlePasteLayer “:” Вставить слой “,” titleEditAnimation “:” Редактировать анимацию “,” titleSelectLayer “:” Выбрать слой “,” sizeWeb “:” Интернет ” , «sizeFullHD»: «Full HD», «sizeUltraHD»: «Ultra HD», «dockPanel»: «Панель закрепления / открепления», «fileSaved»: «Файл сохранен», «fps»: «Частота кадров», «или» : “or”, “id”: “id”, “name”: “Name”, “без названия”: “Untitled”, “width”: “Width”, “height”: “Height”, “apply”: ” Применить »,« сумма »:« Сумма »,« выпуклость »:« Выпуклость »,« параметры »:« Параметры »,« компонент »:« Компонент »,« рабочий »:« Рабочий »,« пиксель »:« Пиксель » , «percent»: «Percent», «ok»: «OK», «cancel»: «Cancel», «close»: «Close», «original»: «Original», «blendMode»: «B lend Mode »,« max »:« Макс »,« add »:« Добавить »,« scale »:« Scale »,« stretch »:« Stretch »,« hollow »:« Hollow »,« none »:« Нет. “,” mask “:” Mask “,” background “:” Background “,” animation “:” Animation “,” loopAnimation “:” Loop animation “,” inclusiveAnimation “:” Включить скрытые слои “,” create “:” Create »,« template »:« Template »,« search »:« Search »,« preset »:« Preset »,« loadMore »:« Load More »,« save »:« Save »,« saveAs »:« Save » as “,” open “:” Open “,” load “:” Load “,” export “:” Export “,” loading “:” Loading “,” size “:” Size “,” pos “:” Pos ” , «position»: «Position», «newSize»: «Новый размер», «softness»: «Softness», «прозрачность»: «Transparency», «image»: «Image», «frame»: «Frame», «непрозрачность»: «Непрозрачность», «прозрачный»: «Прозрачный», «перо»: «Перо», «шаг»: «Шаг», «источник»: «Источник», «шипы»: «Шипы», «скорость» “:” Скорость “,” сбалансированный “:” Сбалансированный “,” качество “:” Качество “,” ультра “:” Ультра “,” разрешение “:” Разрешить “,” font “:” Шрифт “,” текст “: «Text», «draw»: «Draw», «design»: «Design», «empty»: «Пусто», «drawing»: «Drawing», «custom»: «custom», «angle»: «Angle» «,« высота »:« Высота »,« инструмент »:« Инструмент »,« аспект »:« Аспект »,« кисть. «:« Кисть »,« краска »:« Раскрашивание »,« размытие »:« Размытие »,« резкость »:« Повышение резкости »,« растушевка »:« Размытие »,« спина »:« Назад »,« стирание »: «Стереть», «цвет»: «Цвет», «цвета»: «Цвета», «форма»: «Форма», «элемент»: «Элемент», «страница»: «Страница», «слой»: «Слой» «,« слои »:« Слои »,« видимый »:« Видимый »,« скрытый »:« Скрытый »,« интенсивность »:« Интенсивность »,« количество »:« Количество »,« dualTone »:« Двойной тон » , «bokeh»: «Боке», «anchor»: «Anchor», «top»: «Top», «bottom»: «Bottom», «left»: «Left», «center»: «center», » right »:« Вправо »,« вверх »:« Вверх »,« вниз »:« Вниз »,« вверх слева »:« Вверх влево »,« вверх »:« Вверх вправо »,« вниз влево »:« Вниз влево », «downright»: «Внизу справа», «topleft»: «Top left», «topright»: «Top right», «bottomleft»: «Bottom left», «bottomright»: «Bottom right», «both»: » Оба »,« глубина »:« Глубина »,« расширенный »:« Расширенный »,« загрузка »:« Загрузить »,« сила »:« Сила »,« плотность »:« Плотность »,« сброс »:« Сброс » , «target»: «Цель», «допустимость»: «Допуск», «level»: «Уровень», «fit»: «Fit», «fill»: «Fill», «clear»: «Clear», « offset »:« Смещение »,« минимизировать »:« Свернуть »,« максимизировать »:« Развернуть »,« offsetX »:« Смещение x »,« offsetY »:« Смещение y »,« freque » ncy »:« Частота »,« removeStop »:« Удалить стоп »,« compare »:« Сравнить (Удерживать) »,« paste »:« Вставить »,« copy »:« Копировать »,« обрезать »:« Обрезать » “,” resize “:” Изменить размер “,” maxWidth “:” Макс. ширина “,” maxHeight “:” Макс. высота “,” fitInside “:” Уместить внутри “,” noPaste “:” нечего вставлять “,” emptyPaste ” :”Пустой! попробуйте ctrl + v! “,” emptyPasteGlobal “:” нечего вставить “,” genericNoResult “:” Результат не найден, выполните еще один поиск.”,” error “:” Error “,” genericError “:” Что-то пошло не так, повторите попытку позже. “,” offline “:” Offline “,” genericOffline “:” Вы не в сети, проверьте подключение к Интернету и попробуйте снова. “,” onlyImageLayer “:” Только слой изображения “,” overlay “:” Overlay “,” border “:” Border “,” sticker “:” Sticker “,” premium “:” Premium “,” continue “: «Продолжить», «эффект»: «Эффект», «авто»: «Авто», «красный»: «Красный», «зеленый»: «Зеленый», «синий»: «Синий», «диапазон»: «Диапазон» “,” тени “:” Тени “,” средние тона “:” Средние тона “,” светлые участки “:” Основные моменты “,” вибрация “:” Яркость “,” оттенок “:” Оттенок “,” экспозиция “:” Экспозиция “, «легкость»: «Яркость», «насыщенность»: «Насыщенность», «монохромный»: «Монохромный», «сохранить яркость»: «Сохранить яркость», «яркость»: «Яркость», «контраст»: «Контрастность», » radius »:« Radius »,« threshold »:« Threshold »,« colorize »:« Colorize »,« temperature »:« Temperature »,« tint »:« Tint »,« hdr »:« HDR »,« четкость » : «Ясность», «гламур»: «Гламур», «гладкость»: «Гладкая», «зернистость»: «Зернистость», «цветение»: «Цветение», «lineSpace»: «Линия пробела», «letterSpace»: “Letter space”, “addText”: “Добавить текст”, “align”: “Выровнять “,” alignLeft “:” Выровнять по левому краю “,” alignCenter “:” Выровнять по центру “,” alignRight “:” Выровнять по правому краю “,” uppercase “:” Uppercase “,” bold “:” Bold “,” italic “:” Курсив »,« полный »:« Полный »,« строка »:« Линия »,« слово »:« Слово »,« контур »:« Очертание »,« выделение »:« Выделение »,« тень »:« Тень. “,” фиксированный “:” Фиксированный “,” бесплатный “:” Бесплатный “,” документ “:” Документ “,” рекомендовать “:” Рекомендовать “,” популярный “:” Популярный “,” многоугольник “:” Многоугольник “, «bezier»: «Безье», «Magnetic»: «Magnetic», «rotateLeft»: «Повернуть влево», «rotateRight»: «Повернуть вправо», «flipVertical»: «Отразить по вертикали», «flipHorizontal»: «Отразить по горизонтали» “,” duplicate “:” Duplicate “,” duplicated “:” Duplicated “,” delete “:” Delete (DEL) “,” deleted “:” Deleted “,” transform “:” Transform “,” distort “:” Искажать »,« растрировать »:« Растрировать »,« редактировать »:« Редактировать »,« настройки »:« Настройки »,« стили »:« Стили »,« формат »:« Форматировать »,« стиль »:« Стиль » , «addNew»: «Добавить новый», «unlock»: «Разблокировать», «выровнено»: «Выровнено», «mode»: «Mode», «method»: «Method», «option»: «Variant», «восстановить»: «Восстановить», «выпрямить»: «Выпрямить», «увеличить»: «Масштаб», «Переместить»: «Переместить», «ratio»: «Соотношение», «инвертировать»: «Инвертировать», «извлечь» “:”Бывший tract “,” constraint “:” Constraint “,” contiguous “:” Contiguous “,” aiAuto “:” AI Auto “,” hintRemoved “:” Подсказка удалена “,” addToCutout “:” Добавить в маску “,” removeFromCutout ” : «удалить из маски», «maskApplied»: «Маска применена», «hardTip»: «Hard tip», «antiAlias»: «Anti-alias», «flow»: «Flow», «mirror»: «Mirror» , «scatter»: «Scatter», «fourWay»: «Four way», «penPressure»: «Используйте давление пера», «blend»: «Blend», «stroke»: «Stroke», «type»: «Type» “,” radial “:” Radial “,” linear “:” Linear “,” spot “:” Spot “,” soft “:” Soft “,” object “:” Object “,” high “:” High “, «normal»: «Нормальный», «delay»: «Delay», «slow»: «Slow», «duration»: «Duration», «fixedDuration»: «Фиксированная длительность», «push»: «Push», « увеличить »:« Увеличить »,« сжать »:« Сжать »,« swirlRight »:« Свернуть вправо »,« swirlLeft »:« swirlLeft »,« rectangle »:« Прямоугольник »,« roundedRect »:« Прямоугольник со скругленными углами »,» эллипс »:« Эллипс »,« круг »:« Круг »,« кривая »:« Кривая »,« дуга »:« Дуга »,« половина »:« Половина »,« разворот »:« Размах »,« треугольник » : «Треугольник», «звезда»: «Звезда», «сердце»: «Сердце», «шестиугольник»: «Шестиугольник», «крест»: «Крест», «квадрат»: «Квадрат», «мерцание»: » Glimmer »,« round »:« Круглый ». «,« плюс »:« Плюс »,« минус »:« Минус »,« осветлить »:« Светлее »,« затемнить »:« Темнее »,« главное »:« Главное »,« изменить »:« Изменить », «Увеличить»: «Увеличить», «Уменьшить»: «Уменьшить», «Вертикаль»: «Вертикаль», «Горизонталь»: «По горизонтали», «layerCreated»: «Слой создан», «noCutout»: «Без маски», «logInNow»: «Войти сейчас», «preserveTransparency»: «Сохранить прозрачность», «neverAskMeAgain»: «Никогда больше не спрашивать меня об этом», «autoSelectLayer»: «Автоматический выбор слоя», «alwaysShowTransform»: «Всегда показывать преобразование. «,« showGuides »:« Показать направляющие »,« snapToGuides »:« Привязать к направляющим »,« loremIpsum »:« Lorem ipsum.. ваш текст здесь .. “,” selectSource “:” Выбрать источник “,” newSelection “:” Новое выделение “,” addToSelection “:” Добавить в выделение (сдвиг) “,” removeFromSelection “:” Удалить из выделения (ctrl) ” , “highQualityPreview”: “Предварительный просмотр в высоком качестве”, “sampleAllLayers”: “Образец всех слоев”, “noMerger”: “Без объединения”, “LayersMerged”: “Слои объединены”, “imageFlattend”: “Image Flattned”, “noRasterization «:« Не текст / элемент »,« layerRasterized »:« Растеризованный слой »,« selectionEmpty »:« Ничего не выбрано »,« noLayerSelected »:« Слой не выбран »,« notAImageLayer »:« Не слой изображения », «selectionSaved»: «Выделение сохранено», «layerAdded»: «Слой добавлен», «addFrame»: «Добавить рамку», «toggle»: «Toggle», «gradient»: «Gradient», «pattern»: «Pattern» , «setImage»: «Установить изображение», «distance»: «Distance», «direction»: «Direction», «flip»: «Flip», «overlap»: «Overlap», «rotate»: «Rotate», «Simmetry»: «Симметрия», «edgeFill»: «Edge Fill», «repeat»: «Repeat», «repeatGap»: «Время между повторами», «Reflect»: «Reflect», «Amplitude»: «Amplitude» , “seed”: “Seed”, “output”: “Output”, “keyword”: “Ключевое слово”, ” addTask »:« Добавить задачу »,« remove »:« Удалить »,« update »:« Обновить »,« notAllowed »:« Не разрешено! »,« checkout »:« Checkout »,« creditCard »:« Кредитная карта » , “savedCard”: “Сохраненная карта”, “billingAddress”: “Платежный адрес”, “firstName”: “Имя”, “lastName”: “Фамилия”, “address”: “Адрес”, “city”: ” Город »,« zipCode »:« Почтовый индекс »,« штат »:« Штат »,« страна »:« Страна »,« cardNumber »:« Номер карты »,« месяц »:« месяц »,« год »:» год »,« autorenewalBasis »:« Основа автообновления »,« total »:« total »,« orderSummary »:« сводка заказа »,« enter »:« Enter »,« scene »:« Scene »,« exit » : «Exit», «pageAnimation»: «Часть анимации страницы», «pageAnimationMessage»: «Часть анимации страницы», «blockAnimation»: «Заблокировать анимацию страницы», «blockAnimationMessage»: «Заблокирована анимация страницы», «revertPageAnimation»: «Вернуться к анимации страницы», «noLayerAnimation»: «Слой не выбран, щелкните слой в рабочей области или на панели слоев, чтобы выбрать его.”,” elementPremiumDesc “:” Это премиум-элемент! “,” addCurvesControlDesc “:” Дважды щелкните, чтобы добавить или удалить контрольную точку. “,” viewArrangeSelection “:” Активный выбор, перетащите, чтобы переместить / вырезать выделенную область. “, “viewArrangeActiveSelection”: “Активное выделение, нельзя изменить текст, фигуру или слой элемента или группу.”, “viewArrangeLayerLocked”: “Слой заблокирован в позиции, разблокировать, чтобы включить преобразования.”, “viewArrangeNoLayer”: “Нет слоя (или пустой слой), выберите слой на правой панели слоев. “,” viewDisperseNoLayer “:” Disperse работает только со слоями изображений, выберите другой слой.”,” viewDisperseApply “:” Вы хотите применить дисперсию? “,” viewDisperseMaskFirst “:” Сначала замаскируйте область! “,” viewFocusNoLayer “:” Фокус работает только на слоях изображения, выберите другой слой. “,” viewFocusApply ” : «Вы хотите применить фокус?», «ViewCloneNoLayer»: «Клонирование работает только со слоями изображения, выберите другой слой.», «ViewCloneSourceTooltip»: «Выбрать источник или рисовать (Shift)», «viewCutoutNoLayer»: » Выберите слой изображения или растрируйте текст / элемент для создания маски. »,« ViewCutoutShape »:« Маска формы »,« viewCutoutMagic »:« Волшебная маска »,« viewCutoutDraw »:« Рисовать маску »,« viewCutoutLasso »:« Лассо » mask “,” viewCutoutGradient “:” Градиентная маска “,” viewShapeModeDraw “:” Пиксельный рисунок одного слоя “,” viewShapeModeDesign “:” Одна векторная фигура на слой “,” viewDetailNoLayer “:” Размытие / резкость и растушевка работают только на слоях изображения. (или непустые слои), выберите другой слой.”,” viewDrawNoLayer “:” Выберите слой изображения в списке слоев или добавьте новый пустой слой “,” viewEraserNoLayer “:” Вы можете стереть только слои изображения, выберите другой слой. “,” viewFillNoLayer “:” Работает только заливка на слоях изображения выберите другой слой. »,« viewGradientNoLayer »:« Градиент работает только со слоями изображения, выберите другой слой. »,« viewHandDesc »:« Щелкните и перетащите, чтобы переместить область просмотра. »,« viewHealNoLayer »:« Только лечение. работает со слоями изображения, выберите другой слой. “,” viewLiquifyNoLayer “:” Пластика работает только со слоями изображения, выберите другой слой.”,” viewShapeNoLayer “:” Выберите или создайте слой изображения в списке слоев или выберите режим разработки. “,” viewPenNoLayer “:” Перо работает только со слоями изображения, выберите другой слой. “,” viewToningNoLayer “:” Работает только тонирование на слоях изображения (или непустых слоях) выберите другой слой. “,” viewTemperNoLayer “:” Temper работает только со слоями изображения (или непустыми слоями), выберите другой слой. “,” viewReplaceNoLayer “:” Выберите слой изображения в список слоев или добавьте новый пустой слой. »,« viewPickerShades »:« Shades »,« viewPickerTriadic »:« Triadic »,« viewPickerTetradic »:« Tetradic »,« viewPickerAnalogous »:« Аналогичный »,« viewPickerComplement »:« Complement » “,” viewPenPlain “:” Plain “,” viewPenNeon “:” Neon “,” viewPenSketchy “:” Sketchy “,” viewPenParallel “:” Parallel “,” viewPenTrail “:” Trail “,” viewPenShaded “:” Shaded “, “viewPenFurry”: “Furry”, “viewPenCrayon”: “Crayon”, “viewPenInk”: “Ink”, “focus”: “Focus”, “focusSymmetric”: “Symmetric / Tilt”, “focusRadial”: “Radial”, «focusLinear»: «Linear», «softBlur»: «Мягкое размытие», «bokehBlur»: «Размытие боке», «bokehShape»: «Боке s hape »,« viewCropNone »:« None »,« viewCropFixed »:« Фиксированное соотношение: »,« viewCrop1x1 »:« 1: 1 (квадрат) »,« viewCrop4x3 »:« 4: 3 (монитор) »,« viewCrop16x9 » : «16: 9 (широкоэкранный)», «viewCrop3x1»: «3: 1 (панорама)», «viewCrop3x2»: «3: 2 (35-мм пленка)», «viewCrop21x9»: «21: 9 (кинематограф)», “viewCrop32x9”: “32: 9 (Сверхширокий)”, “viewCropOutput”: “Размер вывода:”, “viewCropFBProfile”: “Профиль Facebook”, “viewCropFBCover”: “Обложка Facebook”, “viewCropFBPost”: “Сообщение в Facebook “,” viewCropFBAd “:” Facebook ad “,” viewCropInstaProfile “:” Профиль Instragram “,” viewCropInstaPost “:” Сообщение Instagram “,” viewCropInstaStory “:” История Instagram “,” viewCropTwitProfile “:” Профиль Twitter “,” viewCropTwitHeader ” : «Заголовок Twitter», «viewCropTwitImage»: «Изображение Twitter», «viewCropTwitCard»: «Карта Twitter», «viewCropTwitAd»: «Реклама в Twitter», «viewCropYTProfile»: «Профиль Youtube», «viewCropYTChannelArt»: «Обложка канала Youtube “,” viewCropYTThumb “:” Youtube thumb “,” viewCropWebMini “:” Web mini 1024×768 “,” viewCropWebSmall “:” Web small 1280×800 “,” viewCropWebCommon “:” Web common 1366×768 “,” vie wCropWebMedium “:” Веб-среда 1440×900 “,” viewCropFHD “:” Full HD 1920×1080 “,” viewCropUHD “:” Ultra HD 4x 3840×2160 “,” viewCropPaperA4 “:” paper A4 “,” viewCropPaperA5 “:” Paper A5 “,” viewCropPaperA6 ” «:« Бумага A6 »,« viewCropPaperLet »:« Бумажное письмо »,« dialogAddLayerTitle »:« Добавить слой »,« dialogAddLayerHL »:« Выберите, какой тип слоя добавить »,« dialogBevelHighColor »:« Цвет выделения »,« dialogBevelShadowColor «:« Цвет тени »,« dialogBevelHighOpacity »:« Непрозрачность подсветки »,« dialogBevelShadowOpacity »:« Непрозрачность тени »,« dialogChoiceTitle »:« Открыть изображение »,« dialogChoiceHeadline »:« Вы хотите добавить изображение в качестве слоя в текущий документ или создать новый? »,« dialogLoadTitle »:« Загрузка »,« dialogLoadPrepare »:« подготовка… “,” dialogLoadLoadingFrom “:” Загрузка% s из% s … “,” dialogLoadError “:” Что-то пошло не так при загрузке изображения … повторите попытку позже … “,” dialogOpenURLTitle “:” Открыть изображение URL “,” dialogOpenURLHeadline “:” URL изображения “,” dialogPreResizeTitle “:” Предварительное изменение размера изображения “,” dialogPreResizeInfo1 “:” Выбранное изображение очень большое “,” dialogPreResizeInfo2 “:”, измените его размер перед тем, как начать редактирование, чтобы экономия памяти и минимизация задержек. »,« dialogPreResizeExif »:« Автоповорот на основе exif »,« dialogPreResizeMaxSize »:« Макс.% d px »,« dialogResizePageTitle »:« Изменить размер страницы (масштаб) »,« dialogPageSizeTitle »:« Установить размер страницы »,« dialogResizeContrain »:« Сохранить пропорции »,« dialogResizeSmoothing »:« Сглаживание »,« dialogResizeApplyAll »:« При применении изменения размера все слои будут масштабированы.«,« dialogSizeRelative »:« Относительное изменение »,« dialogSizeAnchor »:« Точка привязки »,« dialogSizeCropWarning »:« При изменении размера любой активный инструмент кадрирования будет сброшен, некоторое обрезание слоев может произойти, если размер новой страницы станет меньше ». , “dialogSaveTitle”: “Сохранить”, “dialogSaveLow”: “Низкий”, “dialogSaveMed”: “Средний”, “dialogSaveHigh”: “Высокий”, “dialogSaveFileType”: “Тип”, “dialogSaveCalculate”: “.. вычисление” , “dialogSaveNonDestructive”: “Неразрушающий (файлы гораздо большего размера)”, “dialogSavePXZDescription”: “PXZ – это собственный формат документа Pixlr, это позволит сохранить всю рабочую структуру проекта.”,” dialogAiCutoutTitle “:” AI Mask “,” SinceDay “:” День назад “,” SinceDays “:”% d дней назад “,” SinceHour “:” Час назад “,” SinceHours “:”% d часов назад “,” SinceMinute “:” Минуту назад “,” SinceMinutes “:”% d минут назад “,” SinceNow “:” Только что “,” openImage “:” Открыть изображение “,” loadURL “:” Загрузить URL ” , «batchEdit»: «Пакетное редактирование», «dropFile»: «Перетащить, чтобы открыть файл», «batchAddStep»: «Добавить шаг», «batchDesk»: «Добавить задачи редактирования снизу или открыть ранее сохраненный макрос (.pxm) . Пользователи Premium могут одновременно загружать до 50 файлов. »,« MacroSave »:« Сохранить макрос »,« macroOpen »:« Открыть макрос »,« macroNoSave »:« Ничего не сохранять! »,« MacroLoaded »:« Макрос загружен. ! “,” news “:” Updates “,” noNews “:” Нет новых обновлений! “,” history “:” History “,” createNew “:” Create new “,” stockSearch “:” Поиск стоковых изображений “,” addCurrent “:” Добавить текущий “,” backToEditor “:” Назад в редактор “,” viewAll “:” Просмотреть все “,” viewMore “:” Посмотреть больше “,” historyProjects “:” Последние проекты “,” historyDescription “:” Из локального временного кеша, чтобы сохранить проект на длительный срок, сохраните его как PXZ (документ Pixlr).”,” templates “:” Шаблоны “,” useTemplate “:” Используйте этот шаблон “,” RecommendedTemplate “:” Рекомендуемые шаблоны “,” RecommendedDescription “:” Модные и высококачественные шаблоны, вручную отобранные нашей командой. “,” templatesDescription ” : «Просмотрите и найдите шаблон, выбрав тип дизайна, который вы хотите создать ниже.», «TemplateSearch»: «Поиск», «templateKeyword»: «Keyword ..», «templateCategories»: «Категории», «templateFilter» : “Filter”, “templatePopular”: “Popular”, “templateRecent”: “Recent”, “templateAll”: “All”, “templateFree”: “Free”, “templatePremium”: “Premium”, “pinnedProjects”: ” Закрепленные проекты »,« allYourProjects »:« Все ваши временные проекты »,« aboutHistory »:« История только временно сохраняется в кеше браузера, все документы будут удалены, если вы очистите кеш или запустите какую-либо процедуру очистки.Если вы хотите сохранить на длительный срок, загрузите его как .PXZ (документ Pixlr). “,” NoHistory “:” В вашей истории нет проектов. “,” ClearHistory “:” Очистить историю “,” historyClearConfirm “:” Сделать вы действительно хотите очистить историю? »,« historyDelete »:« Удалить »,« historyPin »:« Pin »,« historyUnpin »:« Открепить »,« historyDuplicate »:« Duplicate »,« documentActions »:« Действия с документом » , “locked”: “Locked”, “unlocked”: “Unlocked”, “hasCutout”: “Has Mask”, “layerSettings”: “Layer Settings”, “viewOBarNav”: “Navigate”, “viewOBarSet”: “Settings” , «viewOBarShowGu»: «Показать направляющие», «viewOBarSnap»: «Привязать к направляющим», «viewOBarSmooth»: «Плавное масштабирование», «viewOBarScollMode»: «Использовать колесо прокрутки для», «viewOBarAskPrerezise»: «Запросить предварительное изменение размера image »,« viewOBarAskLayertype »:« Спросите, какой тип слоя добавить »,« viewOBarDup »:« Дублировать слой »,« viewOBarDel »:« Удалить слой (DEL) »,« viewOBarAccent »:« Акцентный цвет »,« viewOBarWorkspace »: «Цвет рабочей области», «blendModeNone»: «Нет», «blendModeMultiply»: «Умножить», «blendModeScreen»: «Экран», «blendModeLighter»: «Светлее», «blendMode» Overlay »:« Overlay »,« blendModeDarken »:« Darken »,« blendModeLighten »:« Lighten »,« blendModeColorDodge »:« Color-dodge »,« blendModeColorBurn »:« Color-затемнение »,« blendModeHardLight »:« Hard- light “,” blendModeSoftLight “:” Soft-light “,” blendModeDifference “:” Difference “,” blendModeExclusion “:” Exclusion “,” blendModeHue “:” Hue “,” blendModeSaturation “:” Saturation “,” blendModeColor “:” Color »,« blendModeLuminosity »:« Luminosity »,« layerMergeDown »:« Объединить вниз »,« layerMergeVisible »:« Объединить видимые »,« layerFlattenImage »:« Свести изображение »,« historyAnimation »:« Анимация »,« historyPageAnimation »: «Анимация страницы», «historyLayerAnimation»: «Анимация слоя», «historyAddelement»: «Добавить элемент», «historyPasteelement»: «Вставить элемент», «historyDuplicateelement»: «Дублировать элемент», «historyDeleteelement»: «Удалить элемент», «historyShape»: «Форма», «historyAddshape»: «Добавить фигуру», «historyPasteshape»: «Вставить фигуру», «historyDuplicateshape»: «Дублировать фигуру», «historyDeleteshape»: «Удалить фигуру», «historyShapeType»: «Тип “,” historyShapeFill “:” Fill “,” historyShap ” eShadow »:« Shadow »,« historyShapeShape »:« Da shape »,« historyShapeOutline »:« Outline »,« historyShapeSettings »:« Параметры формы »,« historyOpenimage »:« Открыть изображение »,« historyDropimage »:« Перетащить изображение » , «historyAddimage»: «Добавить изображение», «historyPasteimage»: «Вставить изображение», «historyExtractimage»: «Извлечь изображение», «historyDuplicateimage»: «Дублировать изображение», «historyAddemptyimage»: «Добавить слой», «historyNewemptyimage»: «Новое изображение», «historyDeleteimage»: «Удалить изображение», «historyAddtext»: «Добавить текст», «historyPastetext»: «Вставить текст», «historyDuplicatetext»: «Дублировать текст», «historyDeletetext»: «Удалить текст», «historyFrame»: «Кадр», «historyAddframe»: «Добавить кадр», «historyPasteframe»: «Вставить кадр», «historyDuplicateframe»: «Дублировать кадр», «historyDeleteframe»: «Удалить кадр», «historyFrameContentAdd»: «Добавить frame image »,« historyFrameContentReplace »:« Изменить изображение кадра »,« historyFrameContentDelete »:« Удалить изображение кадра »,« historyFitContent »:« Обновить изображение »,« historyFrameContent »:« Изображение кадра »,« historyRasterizetext »:« Растеризованный текст » , “historyRaste” rizeframe “:” Растеризованный фрейм “,” historyRasterizeelement “:” Растеризованный элемент “,” historyRasterizeshape “:” Растеризованная форма “,” historyClear “:” Очистить “,” historyCut “:” Вырезать “,” historyLayerOpacity “:” Непрозрачность “, «historyLayerBlendMode»: «Режим наложения», «historyLayerVisible»: «Видимость», «historyLayerName»: «Имя слоя», «historyTextSize»: «Размер», «historyTextFont»: «Font», «historyTextFill»: «Fill», «historyTextAlign»: «Выровнять», «historyTextUppercase»: «Прописные буквы», «historyTextBold»: «Полужирный», «historyTextItalic»: «Курсив», «historyTextLetterspace»: «Пробел между буквами», «historyTextLinespace»: «Строка», «historyTextCurve»: «Кривая», «historyTextShadow»: «Shadow», «historyTextOutline»: «Outline», «historyTextBackground»: «Background», «historyText»: «Text», «historyimage»: «Image», «historyEffect» “:” Effect “,” historyAdjust “:” Adjust “,” historyFilter “:” Filter “,” historyArrange “:” Arrange “,” historyStackArrange “:” Arrange group “,” historyDistort “:” Distort “,” historyTransform ” : “Transform”, “historyMove”: “Move”, “historyResize”: “Resize”, “historyFlip”: “Flip”, “h istoryRotate »:« Повернуть »,« historyStackMove »:« Переместить группу »,« historyStackResize »:« Изменить размер группы »,« historyStackRotate »:« Повернуть группу »,« historyGradient »:« Градиент »,« historyLayerLocked »:« Слой un / lock »,« historyFill »:« Fill »,« historyHealSpot »:« Heal spot »,« historyHealSoft »:« Heal soft »,« historyHealObject »:« Heal object »,« historyLiquify »:« Liquify »,« historyBevel »: «Bevel», «historyTextSettings»: «Настройки текста», «historyTextChange»: «Изменение текста», «historyWand»: «Wand», «historyLasso»: «Lasso», «historyMarquee»: «Marquee», «historyDraw»: «Draw», «historyReplace»: «Замена цвета», «historyClone»: «Clone», «historyFocus»: «Focus», «historyDisperse»: «Disperse», «historyCrop»: «Crop», «historyDetail»: » Деталь »,« historyToning »:« Тонирование »,« historyTemper »:« Sponge »,« historyPen »:« Pen »,« historyEraser »:« Eraser »,« historyStraighten »:« Straighten »,« historyBackground »:« Background » , «historyPageResize»: «Изменение размера страницы», «historyPageSize»: «Размер страницы», «historyMask»: «Маска», «historyMaskInvert»: «Маска инвертировать», «historyMerge»: «Объединить слои», «historyOrder»: «Порядок слоев», «historyDeselect»: «Отменить выбор», «historySelectionMove»: «Переместить выделение», «historySelectionAll»: «Выбрать все», «historySelectionPixels»: «Выбрать пиксели», «historySelectionInvert»: «Инвертировать выделение», ” historySelectionRestore “:” Восстановить выделение “,” historySelectionCut “:” Вырезать с выделением “,” historySelectionCopy “:” Копировать с выделением “,” historyFrameShape “:” Shape “,” historyFrameShadow “:” Shadow “,” historyFrameOutline “:” Outline “,” historyFrameSettings “:” Настройки кадра “,” historyStroke “:” Stroke “,” historyAuto “:” Auto Adjust “,” historyPop “:” Auto pop “,” historyBw “:” Auto B&W “,” historyBrightnessContrast “: «Яркость и контраст», «historyTemperatureTint»: «Температура и оттенок», «historyHueSaturation»: «Оттенок и насыщенность», «historyVibrance»: «Vibrance», «historyBalance»: «Цветовой баланс», «historyLookup»: «Поиск цвета “,” historyHighlightsShadows “:” Света и тени “,” historyExposure “:” Экспозиция “,” historyCurves “:” Кривые “,” historyLevels “:” Уровни “,” historyBlack “:” Черный “,” historyWhite “:” Белый ” “,” historyThreshold “:” Thres hold »,« historyPosterize »:« Posterize »,« historyDesaturate »:« Desaturate »,« historyMonochrome »:« Monochrome »,« historyInvert »:« Invert »,« historySolarize »:« Solarize »,« historyMimicHDR »:« Mimic HDR » “,” historySharpen “:” Резкость “,” historyClarity “:” Четкость “,” historyBlur “:” Размытие “,” historyZoom “:” Размытие при увеличении “,” historyGaussian “:” Размытие по Гауссу “,” historyMotion “:” Движение blur “,” historyRadial “:” Радиальное размытие “,” historySmooth “:” Smooth “,” historyDenoise “:” Удалить шум “,” historyGrain “:” Grain “,” historyNoise “:” Noise “,” historyVignette “:” Vignette »,« historyBloom »:« Bloom »,« historyGlamour »:« Glamour »,« historyDehaze »:« Dehaze »,« historySobel »:« Найти края »,« historyFringe »:« Fringe »,« historyPixelate »:« Pixelate » “,” historyHalftone “:” Halftone “,” historyMosaic “:” Mosaic “,” historyScanlines “:” Scanlines “,” historyDropShadow “:” Drop shadow “,” historyInnerGlow “:” Внутреннее свечение “,” historyOuterGlow “:” Outer ” glow »,« historyOpen »:« Open »,« historySlice »:« Slice »,« historyRgbSplit »:« RGB split »,« historyInterference »:« Interference »,« historyPolarcoordinates »:« Полярные координаты » ordinates »,« historyFisheye »:« Fish Eye »,« historyKaleidoscope »:« Kaleidoscope »,« historyReflect »:« Reflect »,« historyWave »:« Wave »,« historyConvertMaskToSelection »:« Преобразовать в выделение »,« historyConvertSelectionToMask »: «Преобразовать в маску», «historyApplyMask»: «Применить маску», «entrySignupHeadline»: «Создать бесплатную учетную запись на Pixlr», «entrySignUp»: «Зарегистрироваться», «RememberMe»: «Запомнить меня», «ForgotPass»: «Забыли пароль?», «NotMember»: «Не участник?», «SignUpNow»: «Зарегистрируйтесь сейчас!», «SignUp»: «Зарегистрируйтесь», «alreadyMember»: «Уже являетесь участником?», «LoginHere “:” Войдите здесь! “,” Code “:” Code “,” verifyAcc “:” Подтвердите свою учетную запись “,” verify “:” Verify “,” Resend “:” Отправить еще раз? “,” DidNotReceiveCode ” : «Я не получил код!», «BackReg»: «Вернуться к регистрации», «ForgottenPass»: «Забыли пароль?», «ResetPassDesc»: «Введите свой адрес электронной почты, чтобы сбросить пароль.”,” reqCode “:” Код запроса “,” resetPass “:” Сброс пароля “,” newPass “:” Новый пароль “,” updatePass “:” Обновить пароль “,” terms “:” Условия использования и уведомление о конфиденциальности ” , “regNewsletter”: “Я хотел бы получать обновления, бесплатные, рекламные и другие маркетинговые сообщения от Pixlr.”, “regRecommendations”: “Мне интересно получать предложения и рекомендации, связанные с моим интересом к Pixlr.”, “согласен” : “Согласен”, “sentCodeDesc”: “Мы отправили электронное письмо на [EMAIL] с кодом подтверждения. Пожалуйста, введите код ниже. »,« OldPass »:« Старый пароль »,« newEmail »:« Новый адрес электронной почты »,« above16 »:« Мне исполнилось 16 лет.”,” readAgreements “:” Я прочитал и согласен с Условиями использования и Уведомлением о конфиденциальности. “,” pixlrLogin_EnterValidEmail “:” Пожалуйста, введите действительный формат электронной почты. “,” pixlrLogin_EnterValidCountry “:” Пожалуйста, выберите действительную страну. “, «pixlrLogin_EnterValidNewsletter»: «Выберите действующий информационный бюллетень.», «pixlrLogin_MinPassword»: «Минимальная длина 8 символов.», «pixlrLogin_InvalidPassword»: «Неверный пароль. Повторите попытку. “,” PixlrLogin_EmailNotExists “:” Этот адрес электронной почты не существует. “,” PixlrLogin_EmailAlreadyExists “:” Этот адрес электронной почты уже существует.”,” pixlrLogin_SuccessReSendCodeToEmail “:” Проверочный код повторно отправлен на {email}! Пожалуйста, проверьте свою электронную почту. “,” PixlrLogin_SuccessSendCodeEmail “:” Проверочный код отправлен на {email}! Пожалуйста, проверьте свою электронную почту. “,” PixlrLogin_EnterValidCode “:” Пожалуйста, введите действительный код. “,” PixlrLogin_WrongCode “:” К сожалению, неверный код. Повторите попытку. “,” PixlrLogin_SuccessUpdatePassword “:” Ваш пароль был успешно обновлен. Пожалуйста, войдите снова. “,” PixlrLogin_EmailAlreadyExistVerify “:” Электронный адрес уже существует. Пожалуйста, подтвердите свою электронную почту.”,” pixlrLogin_EmailSuccessVerified “:” Ваша учетная запись была успешно подтверждена! “,” pixlrLogin_EmailUpdated “:” Электронная почта успешно обновлена ”,” pixlrLogin_CodeExpired “:” Срок действия кода истек. “,” Код pixlrLogin_FailedResendCode “:” Не удалось отправить повторно код pixlrLogin_FailedResendCode “: , “pixlrLogin_ServerError”: “Ошибка сервера. Повторите попытку позже. “,” PixlrLogin_ResetPasswordRequired “:” Требуется сброс пароля. Мы отправили электронное письмо на адрес {email} с кодом подтверждения. “,” PixlrLogin_EnterValidPassword “:” Должно быть как минимум 1 нижний регистр, 1 верхний регистр, 1 цифра и 1 символ.”,” pixlrLogin_MaxPassword “:” Максимальная длина 50 символов. “,” pixlrLogin_RequestCodeTooFrequent “:” Слишком много запросов. Повторите попытку через 30 секунд. “,” PixlrLogin_3TimesFailedAttempts “:” Слишком много неудачных попыток. Повторите попытку через {minuteRemaining} мин. “,” Profile “:” Profile “,” subscription “:” Subscription “,” email “:” Email “,” password “:” Password “,” language “:” Language ” , «changePassword»: «Изменить пароль», «newsletter»: «Newsletter», «receiveNewsletter»: «Получать информационный бюллетень от Pixlr», «myAccount»: «Моя учетная запись», «myDownloads»: «Мои загрузки», «creatorDashboard» : «Панель инструментов создателя», «menu»: «MENU», «changeEmail»: «Изменить адрес электронной почты», «account»: «Account», «agreementBar»: «Используя наш сайт, вы подтверждаете, что читаете и понимаете наши «,« accept »:« ПРИНЯТЬ »,« licenseAgreement »:« Лицензионное соглашение »,« termsOfUse »:« Условия использования »,« privacyPolicy »:« Политика конфиденциальности »,« cookiePolicy »:« Политика использования файлов cookie »,« premiumTryFree » : “Free Premium”, “try30DayFreePremium”: “Попробуйте 30 дней бесплатного Premium”, “premiumBounceTitle”: “Разблокируйте Premium и сокрушите творческие границы!”, “PremiumFeatureAlso”: “Пользователи Premium также имеют:”, “premiumFeaturePitchOne”: ” Тысячи шаблонов »,« premiumFeaturePitchTwo »:« Удаление фона одним щелчком мыши »,« premiumFeaturePitch Три »:« Сотни эксклюзивных шрифтов »,« premiumFeaturePitchFour »:« Dispersion, Glitch and Focus Studios »,« premiumFeaturePitchFive »:« Бесплатная версия для рекламы и загружаемая версия.. »,« premiumFontSalesPitch »:« Получите доступ к сотням уникальных шрифтов и шрифтов Premium от известных художников для использования в своих проектах. »,« premiumCutoutSalesPitch »:« Одним щелчком мыши мгновенно удалите фон изображения с помощью Pixlr AI, включенного в Premium. “,” premiumElementSalesPitch “:” Добавьте изюминку своему дизайну с помощью нескольких тысяч дополнительных премиальных элементов. “,” premiumStudioSalesPitch “:” Получите доступ к инструментам Premium Studio, чтобы создавать еще более впечатляющие изображения и дизайн одним щелчком мыши. “, “premiumBatchSalesPitch”: “Ускорьте работу и пакетируйте до 50 изображений за раз в качестве пользователя Premium.”,” unlockPremiumMessage “:” Разблокировать этот шаблон “,” premiumTemplate “:” Разблокировать шаблон “,” premiumTemplateSalesPitch “:” Внесите единовременную плату, чтобы разблокировать этот шаблон премиум-класса, или станьте членом Премиум и получите доступ ко всей библиотеке профессионально созданных дизайнов. »,« premiumOneTime »:« Шаблон покупки »,« обратная связь »:« Отзыв »,« учебные пособия »:« Учебные пособия »,« помощь »:« Справка »,« Интернет »:« Интернет »,” ads “:” Ads “,” photo “:” Photo “,” video “:” Video “,” print “:” Print “,” social “:” Social “,” Recommended “:” Рекомендуемые “,” instagram- square »:« Instagram Square »,« instagram-post »:« Instagram Post »,« instagram-story »:« Instagram Story »,« facebook-profile »:« Facebook Profile »,« facebook-post »:« Facebook Post “,” facebook-story “:” История Facebook “,” facebook-post-wide “:” Facebook Wide Post “,” facebook-ad-wide “:” Facebook Ad Wide “,” facebook-cover “:” Обложка Facebook “,” facebook-event-cover “:” Facebook Event Cover “,” facebook-group-cover “:” Facebook Group Cover “,” social-media-post “:” Social Post “,” social-media-story ” : “Социальная история”, “youtube-profile”: “YouTube Prof ile »,« youtube-thumbnail »:« YouTube Thumb »,« youtube-channel-art »:« YouTube Art »,« pinterest-pin »:« Pinterest Pin »,« pinterest-square-pin »:« Pinterest Square Pin » “,” pinterest-long-pin “:” Pinterest Long Pin “,” twitter-post “:” Twitter Post “,” twitter-cover “:” Twitter Cover “,” twitter-profile “:” Twitter Profile “,” linkedin-company-banner »:« Компания LinkedIn »,« linkedin-personal-banner »:« LinkedIn Personal »,« roblox »:« Одежда Roblox »,« flyer »:« Flyer »,« brochure »:« Brochure », «приглашение»: «Приглашение», «визитка»: «Визитка», «простой-коллаж»: «Простой коллаж»}
Pixlr M
Pixlr E предназначен для настольных компьютеров.Вы используете мобильное устройство или окно браузера имеет ширину менее 650 пикселей. Мы рекомендуем вам использовать мобильный веб-редактор фотографий или увеличить окно браузера.
Используйте мобильный редактор Игнорировать и закрыть
Алгоритм оценки нестационарных и квазистационарных полей давления по измерениям поля скоростей | Журнал экспериментальной биологии
Мгновенное ускорение жидких частиц D u / D t , необходимое для вычисления градиента давления в уравнении 2, оценивается путем переноса идеализированных бесконечно малых частиц жидкости в измеренные поля скорости.Для квазистационарной оценки ускорение материала выводится из одного поля скорости как: (4) где i = 1, 2… м × n (т.е. размеры сетки скоростей), x _i – это положения частиц жидкости, совпадающие с точками сетки в поле скоростей PIV, и положения этих частиц жидкости после их переноса полем мгновенной скорости в течение периода Δ t : (5)
Для того, чтобы уравнения 4 и 5 оставались в силе, Δ t ограничивается значениями, намного меньшими, чем характерный временной масштаб потока, но достаточно большими, чтобы можно было измерить изменение скорости жидких частиц.
Для многих потоков, особенно тех, которые включают ускоряющиеся или деформирующие тела, вышеупомянутое ограничение на Δ t не может быть выполнено. Для этих по своей природе нестационарных взаимодействий жидкость-структура мы выводим ускорение материала из двух последовательных полей скорости как: (6) где (7) уравнение 7 похоже на схему Кранка – Николсона (т.е. трапециевидную) для положений частиц, в отличие от прямая схема Эйлера в уравнении 5. Следовательно, сходимость метода с шагом по времени является вторым порядком (Crank and Nicolson, 1947).Основной источник ошибки измерения в этом типе нестационарной оценки ускорения материала D u / D t возникает из-за временного шума в измеренных компонентах скорости в каждом узле поля скорости. Мы обращаемся к этому, применяя временный фильтр к временному ряду полей скорости, что приводит к приближению сглаживающего сплайна u * к скорости u в каждом узле в поле скорости.Сплайновые аппроксимации определены таким образом, что они минимизируют для каждого компонента u параметр: (8) где t = 1… N – временная последовательность полей скорости, подлежащих анализу, u _τ – вектор скорости, соответствующий полю скорости t в последовательности, u _τ * – аппроксимированное сплайном значение того же вектора скорости для того же поля скорости в последовательности, t _мин и t _max – это временные границы последовательности полей скорости, а ϕ – это вес между первым и вторым членами и имеет значение от 0 до 1.Фактически, параметр S _u количественно определяет как отклонение аппроксимации сплайном от исходных данных (т.е.первый член), так и общую величину кривизны аппроксимации сплайном (то есть второе слагаемое). Для ϕ = 0 минимизируется только второй член, что приводит к аппроксимации методом наименьших квадратов с нулевой кривизной, то есть к линейной аппроксимации данных. Для ϕ = 1 минимизируется только первый член, что дает кубический сплайн, который проходит через каждую исходную точку данных.В дальнейшем мы устанавливаем ϕ = 0,05, значение, которое мы определили как обеспечивающее эффективную временную фильтрацию шума без отбрасывания истинных временных тенденций в данных измерений.
Дополнительная характеристика временного фильтра представлена в дополнительном материале Приложение S2. В частности, показано, что использование временного фильтра увеличивает порядок временной сходимости выше второго порядка, как и предполагалось в теории (Аткинсон, 1968).
Стоит отметить, что различие между квазистационарным и нестационарным подходами можно сделать явным, разложив материальное ускорение на его эйлеровы компоненты: (9) Квазистационарное приближение в уравнениях 4 и 5 неявно игнорирует первый член справа -сторона уравнения 9, тогда как нестационарный расчет его сохраняет.

1.3 Метод Гаусса. Программный продукт, осуществляющий решение задач по дисциплине “Численные методы”

Похожие главы из других работ:

4.1 Метод Гаусса

Метод Гаусса

2.3.1 Метод Гаусса-Зайделя

6. Метод Гаусса-Зейделя

1.3 Метод Гаусса

1.1 Метод Гаусса

1.

1.2 Метод Гаусса

1.3 Метод Гаусса в Excel

1.1 Метод Гаусса

1.1 Метод Гаусса

Метод Гаусса

Метод Гаусса

2.6 Метод Гаусса-Кронрода

2.6 Метод Гаусса-Кронрода

Численные методы решения систем линейных уравнений, страница 3

3.3. Метод Гаусса с частичным выбором ведущего элемента

Решение системы линейных уравнений. Метод Гаусса

Решение линейных уравнений методом гаусса. Обратный ход метода Гаусса

2.2 Примеры решения СЛАУ методом Гаусса

Микрожидкостная накачка с использованием искусственных магнитных ресничек

Вращение магнитного поля против часовой стрелки

Непрерывное вращение магнитного поля

Транспортировка жидкости ресничным массивом

Апрель 2017 г. Брифинг – Патология – Новости здоровья потребителей

Фоторедактор: Pixlr E

Рекомендуемые шаблоныПодробнее

Шаблоны

рекомендуется

Закрепленные проекты

Все ваши временные проекты

Ошибка

Не в сети

Алгоритм оценки нестационарных и квазистационарных полей давления по измерениям поля скоростей | Журнал экспериментальной биологии

Оставить комментарий Отменить ответ