Системы линейных алгебраических уравнений. Метод Гаусса
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. МЕТОДЫ РЕШЕНИЯ СЛАУ метод Гаусса
2. Цели и задачи:
Цель:• Научиться решать системы линейных алгебраических уравнений
(СЛАУ).
Задачи:
• Изучить решение СЛАУ методом Гаусса
• Рассмотреть возможные варианты решений системы
3. Содержание
• Правило Крамера• Метод Гаусса
• Матричный способ решения СЛАУ
4.
 Введение• Сначала немного систематизируем знания о системах линейных
Введение• Сначала немного систематизируем знания о системах линейныхуравнений. Система линейных уравнений может:
• 1) Иметь единственное решение.
• 2) Иметь бесконечно много решений.
• 3) Не иметь решений (быть несовместной).
5. Метод Гаусса
• Метод Гаусса – наиболее мощный и универсальный инструментдля нахождения решения любой системы линейных уравнений.
Он в любом случае приведет нас к решению.
• Метод Гаусса или метод исключения неизвестных состоит в
последовательном исключении во втором уравнении первой
неизвестной, в третьем уравнении первой и второй неизвестных и
т. д.
Пока не получится система треугольного
трапецеидального вида.
• Метод удобнее применять на расширенной матрице
или
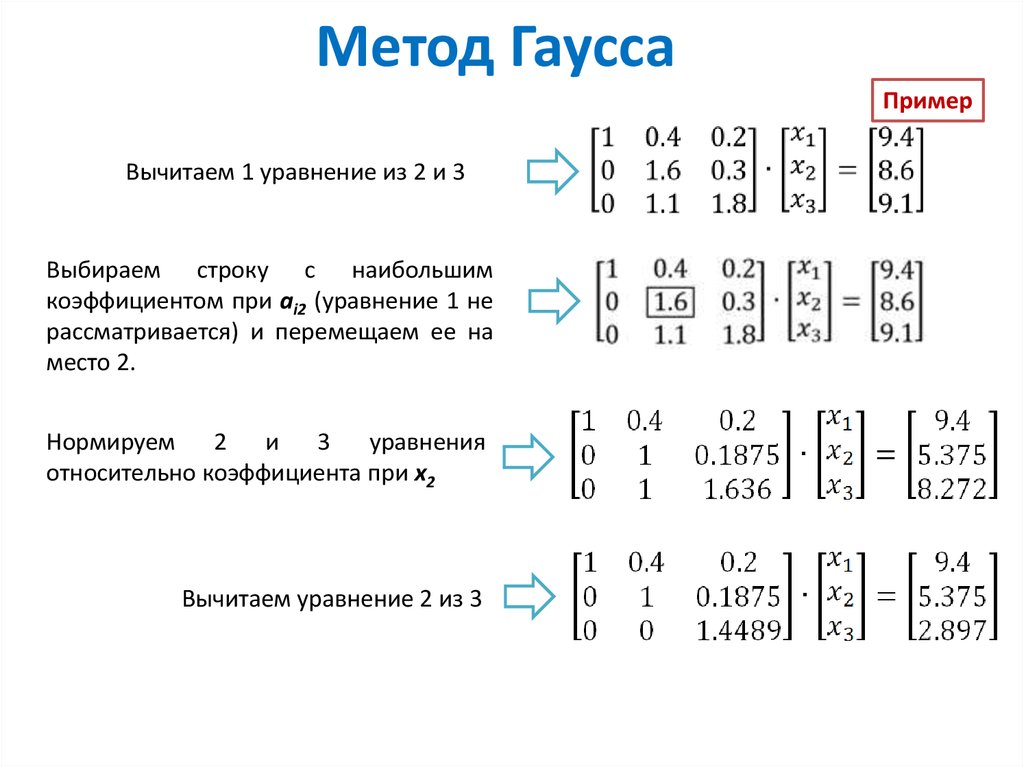
7. Пример
Решить методом Гаусса систему уравнений:Запишем расширенную матрицу системы:
• Сначала смотрим на левое верхнее число:
• Почти всегда здесь должна находиться единица.
Как организовать единицу? Смотрим на первый
столбец – готовая единица у нас есть!
Преобразование первое: меняем местами первую
и третью строки:
• Теперь нужно получить нули вот на этих местах:
• Нужно ко второй строке прибавить первую строку,
умноженную на –2.
 Мысленно или на черновике
Мысленно или на черновикеумножаем первую строку на –2: (–2, –4, 2, –18). И
последовательно проводим (опять же мысленно или на
черновике) сложение, ко второй строке прибавляем
первую строку, уже умноженную на –2:
• Аналогично разбираемся с третьей строкой (3,
2, –5, –1). Чтобы получить на первой позиции
ноль, нужно к третьей строке прибавить
первую строку, умноженную на –3.
• Не нужно считать всё сразу и одновременно. Порядок
вычислений
и
«вписывания»
результатов последователен и обычно такой: сначала
переписываем первую строку, и пыхтим себе
потихонечку
–
ПОСЛЕДОВАТЕЛЬНО
и ВНИМАТЕЛЬНО:
• Далее нужно получить единицу на следующей
«ступеньке»:
• В данном примере это сделать легко, вторую
строку делим на –5 (поскольку там все числа
делятся на 5 без остатка). Заодно делим третью
строку на –2, ведь чем меньше числа, тем
проще решение:
• Для этого к третьей строке прибавляем
вторую строку, умноженную на –2:
• В результате элементарных преобразований
получена эквивалентная исходной система
линейных уравнений:
• Теперь в действие вступает обратный ход
метода Гаусса.
 Уравнения «раскручиваются»
Уравнения «раскручиваются»снизу вверх.
• В третьем уравнении у нас уже готовый
результат: z=4
• Смотрим на второе уравнение: y-z=1.
Y-4=1
Y=5
• Значение «зет» уже известно, таким образом:
X+2*5-4=9
X=3
Ответ: (3;5;4)
15. Выводы:
• Метод Гаусса универсальный, позволяет решать любую СЛАУ.• Слау может иметь единственное решение, если расширенная
матрица преобразуется в треугольную, причем имеет уравнение
вида а*х=в.
• Слау может иметь бесконечно много решений, если, если
матрица преобразуется в трапецеидальный вид.
• Слау не имеет решения, если расширенная матрица
0*х=а
Спасибо за внимание
English Русский Правила
минимум квадратов | Ошибка истины: как история и математика объединились, чтобы сформировать наш характер и наше мировоззрение
Фильтр поиска панели навигации Oxford AcademicЗаблуждение истины: как история и математика объединились, чтобы сформировать наш характер и сформировать наше мировоззрениеLogicBooksJournals Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Oxford AcademicЗаблуждение истины: как история и математика объединились, чтобы сформировать наш характер и сформировать наше мировоззрениеLogicBooksJournals Термин поиска на микросайте
Расширенный поиск
Иконка Цитировать Цитировать
Разрешения
- Делиться
- Твиттер
- Подробнее
Процитируйте
Остерлинд, Стивен Дж. ,
,
«По крайней мере, квадраты»
,
Ошибка истины: как история и математика объединились, чтобы сформировать наш характер и наше мировоззрение
3,
4 (4
2019 г.,
онлайн-издание,
Oxford Academic
, 24 января 2019 г.
), https://doi.org/10.1093/oso/9780198831600.003.0007,
, по состоянию на 16 ноября 2022 г.
Выберите формат
Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
Закрыть
Фильтр поиска панели навигации
Oxford AcademicЗаблуждение истины: как история и математика объединились, чтобы сформировать наш характер и сформировать наше мировоззрениеLogicBooksJournals
Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации
Oxford AcademicЗаблуждение истины: как история и математика объединились, чтобы сформировать наш характер и сформировать наше мировоззрениеLogicBooksJournals
Термин поиска на микросайте
Advanced Search
Abstract
В этой главе основное внимание уделяется следующему важному математическому изобретению: методу наименьших квадратов. Во-первых, он устанавливает исторический контекст для своего изобретения, описывая события во Франции и Германии, приведшие к Французской революции. Далее в главе описывается, как дважды изобретался метод наименьших квадратов, сначала Адрианом-Мари Лежандром (как приложение к его небесным исследованиям в 9 г.0073 Nouvelles méthodes pour la détermination des orbites des comètes
Во-первых, он устанавливает исторический контекст для своего изобретения, описывая события во Франции и Германии, приведшие к Французской революции. Далее в главе описывается, как дважды изобретался метод наименьших квадратов, сначала Адрианом-Мари Лежандром (как приложение к его небесным исследованиям в 9 г.0073 Nouvelles méthodes pour la détermination des orbites des comètes
), а затем в более сложной версии Карла Гаусса, в Disquisitiones Arithmeticae . После этого дается простое для понимания описание самого метода. Таким образом, глава переходит от наблюдения к вероятности и далее к предсказанию через регрессию, обсуждая обычные методы наименьших квадратов (МНК), точки пересечения и наклоны. Ключевые слова:
Адриан-Мари Лежандр, Карл Гаусс, метод наименьших квадратов, регрессия, МНК, точка пересечения, наклон
Субъект Логика
В настоящее время у вас нет доступа к этой главе.
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Щелкните Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Войти с помощью личного кабинета
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т.
д. Покупка
Наши книги можно приобрести по подписке или приобрести в библиотеках и учреждениях.
Информация о покупке
Беллингем Адвокат | Команда юристов в Сиэтле и округе Ватком помогает с коммерческим и трудовым законодательством
Консультирование предприятий всех типов и размеров в штате WA
Поиск адвоката, подходящего для вашего бизнеса, может быть сложной задачей. Чтобы быть действительно эффективными, юристы Беллингема, штат Вашингтон, должны быть хорошо знакомы с вашим бизнесом и понимать ваши приоритеты, цели и стиль управления. Но самое главное, как владелец бизнеса, вы должны иметь сильное доверие и взаимопонимание со своим адвокатом. После почти 40 лет практики Адвокаты Bellingham из Adelstein, Sharpe & Serka LLP узнали, что доверие является наиболее важным аспектом отношений между адвокатом и клиентом. Вот почему мы делаем своим приоритетом тесное сотрудничество с вами, чтобы понять и решить ваши проблемы, а также стремиться к формированию долгосрочных отношений, которые будут поддерживать вас на протяжении всей жизни вашего бизнеса.
Обеспечение ровных отношений между сотрудниками и деловыми отношениями
Свободный доступ к надежному юридическому совету опытного бизнес-адвоката необходим для того, чтобы избежать юридических и нормативных ловушек, с которыми сталкиваются многие компании. Но у малых и средних компаний может не быть такой роскоши, как штатный юридический отдел. Даже более крупным компаниям может потребоваться обратиться в уважаемую юридическую фирму для ведения сложных транзакций или судебных разбирательств.
Независимо от вашей ситуации, наши адвокаты в Беллингеме, штат Вашингтон, могут стать ценным союзником для вас и вашего бизнеса. Наш обширный опыт в области коммерческого и трудового права делает нас активом практически для всех типов компаний. Мы стремимся изучить ваш бизнес, чтобы быть готовыми предоставить оперативную и эффективную юридическую консультацию, когда она вам понадобится. Мы рядом с вами как в рутинных, так и в чрезвычайных юридических вопросах, ревностно представляя вас как в зале суда, так и в обществе.
Мы представляем бизнес на всех этапах его развития — от становления до ликвидации. Наши адвокаты также сочувственно и ревностно представляют интересы жертв телесных повреждений и всесторонне консультируют по вопросам недвижимости, завещания и планирования имущества. Мы определяем себя как лучшее из обоих миров — опыт, репутация и ресурсы большой фирмы с услугами небольшой фирмы и личным вниманием. Наши коллеги согласны с этим и постоянно ставят нам высокие оценки как за этические, так и за правовые знания.
Начните сотрудничество с надежной юридической фирмой сегодня
С 1974 года компания Adelstein, Sharpe & Serka LLP обслуживает юридические потребности юридических и физических лиц по всему штату Вашингтон. Наши адвокаты в Беллингхеме, штат Вашингтон, предоставляют высококачественные личные услуги по вопросам, начиная от обычного коммерческого права и заканчивая деловыми судебными разбирательствами, планированием имущества и исками о телесных повреждениях.
 Во-первых, он устанавливает исторический контекст для своего изобретения, описывая события во Франции и Германии, приведшие к Французской революции. Далее в главе описывается, как дважды изобретался метод наименьших квадратов, сначала Адрианом-Мари Лежандром (как приложение к его небесным исследованиям в 9 г.0073 Nouvelles méthodes pour la détermination des orbites des comètes
Во-первых, он устанавливает исторический контекст для своего изобретения, описывая события во Франции и Германии, приведшие к Французской революции. Далее в главе описывается, как дважды изобретался метод наименьших квадратов, сначала Адрианом-Мари Лежандром (как приложение к его небесным исследованиям в 9 г.0073 Nouvelles méthodes pour la détermination des orbites des comètes 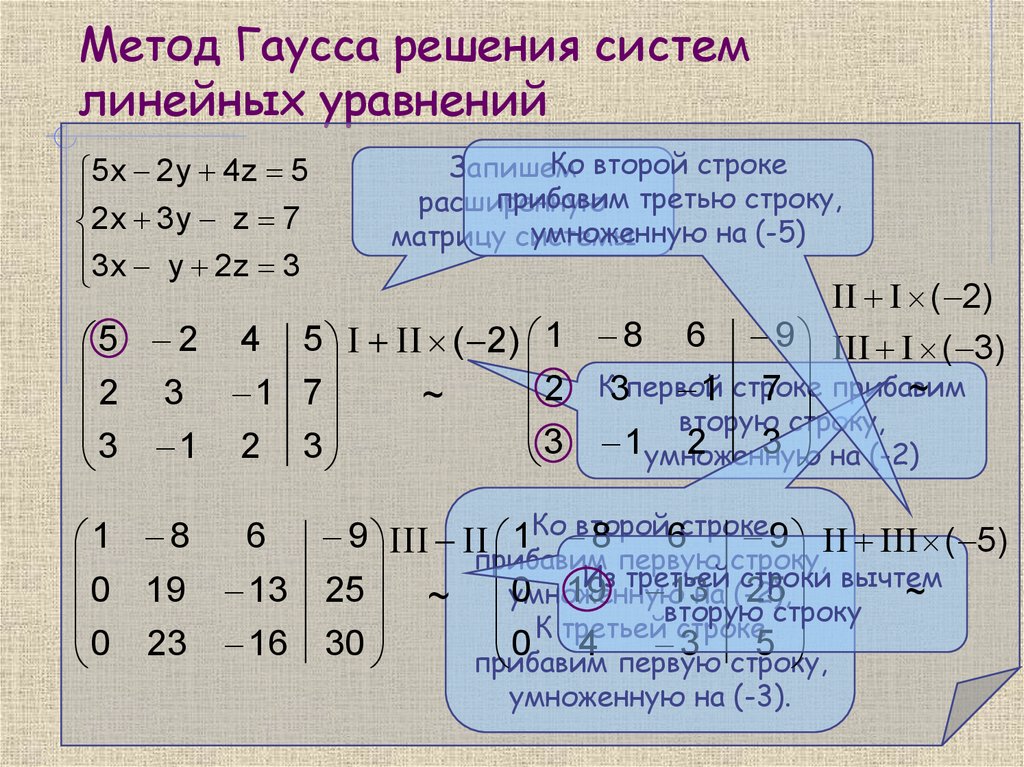

 Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
Если вы видите «Войти через сайт сообщества» на панели входа в журнале:




