Error
Sorry, the requested file could not be found
More information about this error
Jump to…
Jump to…Согласие на обработку персональных данных Учебно-тематический планАвторы и разработчики курсаИнформация для студентов и преподавателейВводная лекцияIntroductory lectureЛекция о системе обозначений Lecture on the notation systemВидеолекция (часть 1)Lecture (Part 1)Видеолекция 2. Операции над функциями. Свойства функции.Lecture 2. Operations on functions. The properties of the functionТеоретический материал Практическое занятие. Исследование свойств функций по определениюPractical lesson. Investigation of the properties of functions by definitionЗадачи для самостоятельной работыРешения задачТест 1.1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2.
Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2. Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2.1.3. Исследование систем линейных уравненийСправочникВидеолекция 1. Матрицы и определителиLecture 1. Matrix determinantВидеолекция 2. Операции над матрицамиLecture 2. Operations on matricesВидеолекция 3. Обратная матрицаLecture 3. Inverse matrixПрактическое занятие 1. Операции над матрицамиPractical lesson 1. The operations on matrices Практическое занятие 2. Вычисление определителейТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Теоретический материал (лекция 3)Тест 2.
1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов.
Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson.
Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1.
Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.
1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.
2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.
4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2.
Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2.
Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2).
Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)Примеры решения системы линейных алгебраических уравнений 4-ого порядка методом Гаусса, пример № 7
СЛАУ 3-его порядка:
1 –
2 –
3 –
4 –
5 –
6 –
7 –
8 –
9 –
10 –
11 –
12
СЛАУ 4-ого порядка:
1 –
2 –
3 –
4 –
5 –
6 –
7 –
8 –
9 –
10 –
11 –
12
Условие
|
Решение системы линейных алгебраических уравнений методом Гаусс
Для проверки ответов можете воспользоваться нашим онлайн сервисом –
Решение системы линейных уравнений методом Гаусса.
Все действия описанные в данном разделе не противоречат правилам обращения с матрицами и являются
элементарными преобразованиями матрицы.
Если после изучения
примеров решения задач
у Вас останутся вопросы, то Вы всегда можете задать их на
форуме, и не забывайте про наши
онлайн калькуляторы для
решения задач по математике и другим предметам!
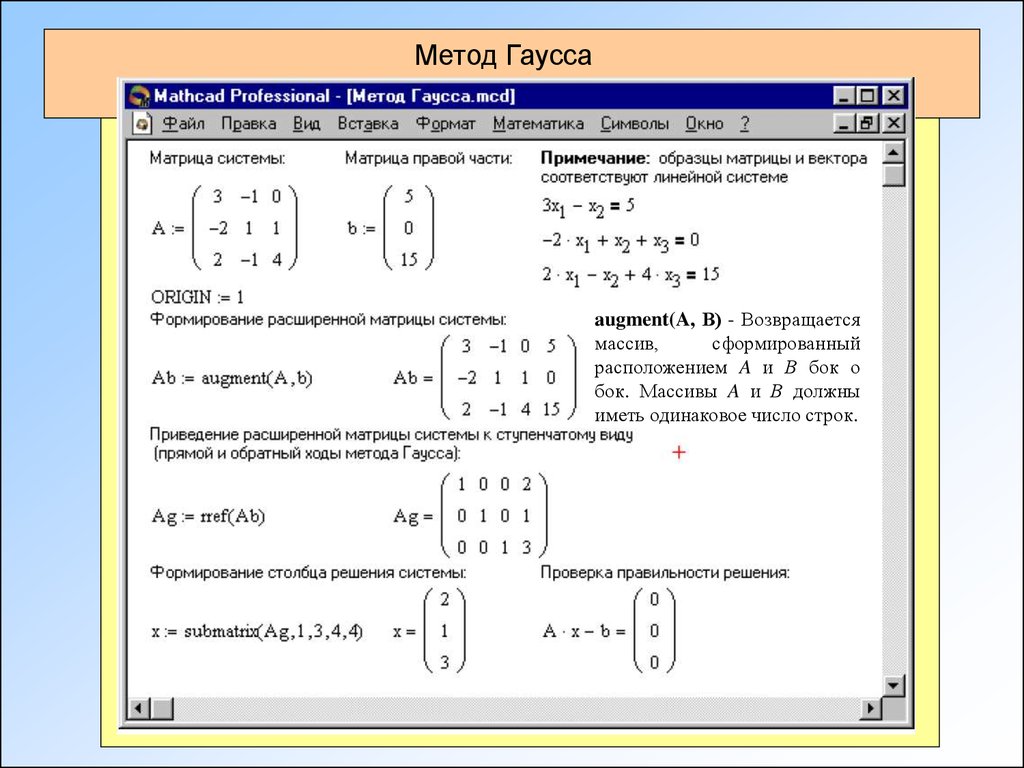
Перепишем систему линейных алгебраических уравнений в матричную форму. Получится матрица 4 × 5, слева от разделительной линии стоят коэффициенты при переменных, а справа стоят свободные члены.
Проведём следующие действия:
- Из строки № 2 вычтем строку № 1 умноженную на 4 (Строка 2 – 4 × строка 1)
- Из строки № 3 вычтем строку № 1 умноженную на 2 (Строка 3 – 2 × строка 1)
- Из строки № 4 вычтем строку № 1 (Строка 4 – строка 1)
Получим:
Проведём следующие действия:
- К строке № 4 прибавим строку № 2 (Строка 4 + строка 2)
- Строку № 3 поделим на -2 (Строка 3 = строка 3 / -2)
Получим:
Проведём следующие действия:
- К строке № 4 прибавим строку № 3 умноженную на 5 (Строка 4 + 5 × строка 3)
- Строку № 4 умножим на 2 (Строка 4 = строка 4 * 2)
Получим:
Проведём следующие действия:
- Из строки № 3 вычтем строку № 4 умноженную на 0.
5 (Строка 3 – 0.5 × строка 4) - Из строки № 1 вычтем строку № 4 (Строка 1 – строка 4)
5 (Строка 3 – 0.5 × строка 4)Получим:
Проведём следующие действия:
- К строке № 2 прибавим строку № 3 умноженную на 7 (Строка 2 + 7 × строка 3)
- Из строки № 1 вычтем строку № 3 умноженную на 3 (Строка 1 – 3 × строка 3)
Получим:
Проведём следующие действия:
- Строку № 2 поделим на 3 (Строка 2 = строка 2 / 3)
- К строке № 1 прибавим строку № 2 (Строка 1 + строка 2)
Получим:
В левой части матрицы по главной диагонали остались одни единицы. В правом столбце получаем решение:
х1 = 9
х2 = 18
х3 = 10
х4 = -16
Вы поняли, как решать? Нет?
Другие примеры
История Гаусса — Национальный совет учителей математики
Джейн М.
Уилберн в конце 1700-х годов поразил своего учителя тем, как быстро он нашел сумму целых чисел от 1 до 100, равную 5050. Гаусс понял, что у него есть пятьдесят пар чисел, когда он сложил первое и последнее число в ряду, второе и предпоследнее число в ряду и так далее. Например: (1 + 100), (2 + 99), (3 + 98), . . . , и сумма каждой пары равна 101.
50 пар × 101 (сумма каждой пары) = 5050.
Другим способом представления проблемы может быть перечисление целых чисел от 1 до 100 и запись того же списка в обратном порядке под первым списком.
Это дает нам 100 сложений 101 на 10 100. Поскольку список чисел от 1 до 100 был удвоен, нам нужно разделить общее количество на 2, что даст нам сумму 5050.
Это представление того, как Гаусс решил задачу, может помочь учащимся изучить связь с алгебраической обобщенной формой для нахождения суммы ряда последовательных чисел: н ( н + 1)/2.
Задачи на сумму ряда целых чисел можно адаптировать для разных уровней начальной школы.
Учащиеся начальных классов могут изучить способы нахождения суммы первых пяти или десяти счетных чисел. Предложите старшим учащимся начальной школы найти сумму первых двадцати или тридцати счетных чисел. Какие свойства операций они могли бы использовать, чтобы помочь им найти сумму? Какие стратегии они могут использовать, чтобы найти сумму? Какие манипуляции лучше всего использовать, чтобы помочь учащимся найти сумму? Как учителя могут способствовать обучению студентов, чтобы помочь им установить связь с подходом Гаусса, не показывая им напрямую его стратегию? Пожалуйста, поделитесь своими идеями и стратегиями, а также примерами того, как ваши ученики нашли суммы.
Изменим задачу на нахождение суммы ряда четных или нечетных чисел. Какова сумма первых 20 четных чисел? Какова сумма первых 30 нечетных чисел? Какова сумма первых 100 нечетных чисел?
Я обнаружил, что учащиеся часто неправильно интерпретируют эти задачи. Например, некоторые учащиеся находят сумму четных чисел до 20 вместо суммы первых 20 четных чисел.
Подобные задачи могут привлечь учащихся к выполнению Стандартов математической практики (SMP) (CCSSI 2010), таких как «Обратите внимание на точность» (SMP 6) и «Разберитесь в задачах (SMP 1).
Для учащихся 6-х классов существуют возможности для изучения других вопросов, например следующих:
- Какова сумма целых чисел от –10 до +10?
- Чему равна сумма ряда целых чисел от 24 до 78?
Какие расширения, связанные с нахождением суммы арифметического ряда, вы использовали со своими учениками? Повеселитесь, поделившись с ними заданием «История Гаусса». Мы с нетерпением ждем вашего мнения. Члены NCTM могут войти в систему и добавить комментарии. Комментарии также можно отправлять в Twitter @TCM_at_NCTM, используя хэштег #TCMtalk. Комментарии также можно отправлять по электронной почте на адрес [email protected]
Джейн М. Уилберн — адъюнкт-профессор математического образования в Университете штата Пенсильвания, Гаррисберг. Она преподает курсы по содержанию и методам для учителей математики начальной и средней школы, а также курсы по математике для выпускников.
Она является соавтором книги Cowboys Count, Monkeys Measure и Princesses Problem Solve: Building Early Math Skills Through Storybooks (Brookes Publishing 2011) и опубликовала множество рукописей в Teaching Children Mathematics среди других журналов. Джейн начала работать в качестве члена редакционной коллегии TeachingChildren Mathematics в мае 2014 года, и срок ее полномочий продлится до апреля 2017 года.
Карл Фридрих Гаусс | Биография, открытия и факты
Карл Фридрих Гаусс
Смотреть все СМИ
- Дата рождения:
- 30 апреля 1777 г. Брауншвейг
- Умер:
- 23 февраля 1855 г. (77 лет) Геттинген Ганновер
- Награды и награды:
- Медаль Копли (1838 г.)
- Изобретения:
- гелиотроп магнитометр
- Известные работы:
- «Арифметические исследования»
Просмотреть весь связанный контент →
Популярные вопросы
Чем знаменит Карл Фридрих Гаусс?
Гаусс считается одним из величайших математиков всех времен за его вклад в теорию чисел, геометрию, теорию вероятностей, геодезию, планетарную астрономию, теорию функций и теорию потенциала (включая электромагнетизм).
Каким было детство Карла Фридриха Гаусса?
Гаусс был единственным ребенком бедных родителей. Он был расчетливым вундеркиндом с даром к языкам. Его учителя и преданная мать рекомендовали его герцогу Брауншвейгскому в 179 году.1, который предоставил ему финансовую помощь для продолжения образования на месте, а затем для изучения математики в Геттингенском университете.
Какие награды получил Карл Фридрих Гаусс?
Гаусс получил медаль Копли, самую престижную научную награду в Соединенном Королевстве, ежегодно присуждаемую Лондонским королевским обществом в 1838 году «за свои изобретения и математические исследования в области магнетизма». За изучение карт, сохраняющих угол, он был удостоен премии Датской академии наук в 1823 г.
Какое влияние оказал Карл Фридрих Гаусс?
Гаусс написал первый систематический учебник по алгебраической теории чисел и заново открыл астероид Церера.
Он опубликовал работы по теории чисел, математической теории построения карт и многим другим предметам. После смерти Гаусса в 1855 году обнаружение многих новых идей среди его неопубликованных статей распространило его влияние на оставшуюся часть века.
Карл Фридрих Гаусс , оригинальное имя Иоганн Фридрих Карл Гаусс (родился 30 апреля 1777, Брауншвейг [Германия] — умер 23 февраля 1855, Геттинген, Ганновер), немецкий математик, которого обычно считают одним из величайших математиков всех времен за его вклад в теорию чисел. , геометрия, теория вероятностей, геодезия, планетарная астрономия, теория функций и теория потенциала (включая электромагнетизм).
Гаусс был единственным ребенком бедных родителей. Он был редкостью среди математиков тем, что был вундеркиндом и сохранял способность производить сложные вычисления в уме большую часть своей жизни. Впечатленные этой способностью и его даром к языкам, учителя и преданная мать рекомендовали его герцогу Брауншвейгскому в 179 г.
1, который предоставил ему финансовую помощь для продолжения образования на месте, а затем для изучения математики в Геттингенском университете с 1795 по 1798 год. Новаторская работа Гаусса постепенно сделала его выдающимся математиком той эпохи сначала в немецкоязычном мире, а затем и за его пределами. , хотя он оставался далекой и отчужденной фигурой.
Викторина “Британника”
Лица науки
Первым значительным открытием Гаусса, сделанным в 1792 году, было то, что правильный многоугольник с 17 сторонами может быть построен только с помощью линейки и циркуля. Его значение заключается не в результате, а в доказательстве, которое основывалось на глубоком анализе факторизации полиномиальных уравнений и открыло дверь более поздним идеям теории Галуа. Его докторская диссертация 1797 дал доказательство основной теоремы алгебры: всякое полиномиальное уравнение с вещественными или комплексными коэффициентами имеет столько корней (решений), сколько его степени (наибольшей степени переменной).
Доказательство Гаусса, хотя и не вполне убедительное, отличалось критикой более ранних попыток. Позже Гаусс дал еще три доказательства этого важного результата, последнее к 50-летию первого, что показывает важность, которую он придавал этой теме.
Узнайте о жизни и карьере математического гения Карла Фридриха Гаусса
Посмотреть все видео к этой статье Признание Гаусса как поистине выдающегося таланта произошло благодаря двум крупным публикациям в 1801 году. Прежде всего, это публикация им первого систематического учебника по алгебраической теории чисел, Disquisitiones Arithmeticae . Эта книга начинается с первого описания модульной арифметики, дает подробное описание решений квадратных многочленов от двух переменных в целых числах и заканчивается упомянутой выше теорией факторизации. Этот выбор тем и их естественные обобщения определили повестку дня в теории чисел на протяжении большей части XIX века.веке, и постоянный интерес Гаусса к этому предмету стимулировал множество исследований, особенно в немецких университетах.
Второй публикацией было его повторное открытие астероида Церера. Его первоначальное открытие, сделанное итальянским астрономом Джузеппе Пиацци в 1800 году, вызвало сенсацию, но он исчез за Солнцем до того, как удалось провести достаточно наблюдений, чтобы рассчитать его орбиту с достаточной точностью, чтобы узнать, где он снова появится. Многие астрономы соревновались за честь найти его снова, но Гаусс победил. Его успех основывался на новом методе обработки ошибок в наблюдениях, который сегодня называется методом наименьших квадратов. После этого Гаусс много лет работал астрономом и опубликовал крупную работу по вычислению орбит — числовая сторона такой работы была для него гораздо менее обременительна, чем для большинства людей. Будучи чрезвычайно преданным подданным герцога Брауншвейгского, а после 1807 года, когда он вернулся в Геттинген в качестве астронома, герцога Ганноверского, Гаусс чувствовал, что его работа имеет общественную ценность.
Подобные мотивы побудили Гаусса принять вызов по обследованию территории Ганновера, и он часто отсутствовал в полевых условиях, отвечая за наблюдения.
Проект, который длился с 1818 по 1832 год, столкнулся с многочисленными трудностями, но привел к ряду достижений. Одним из них было изобретение Гауссом гелиотропа (прибора, отражающего солнечные лучи в виде сфокусированного луча, который можно наблюдать на расстоянии нескольких миль), что повысило точность наблюдений. Другим было его открытие способа сформулировать понятие кривизны поверхности. Гаусс показал, что существует внутренняя мера кривизны, которая не меняется, если поверхность изгибается, но не растягивается. Например, круглый цилиндр и плоский лист бумаги имеют одинаковую внутреннюю кривизну, поэтому на бумаге можно делать точные копии фигур на цилиндре (как, например, в полиграфии). Но сфера и плоскость имеют разную кривизну, из-за чего невозможно составить абсолютно точную плоскую карту Земли.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подписаться сейчас
Гаусс опубликовал работы по теории чисел, математической теории построения карт и многим другим предметам.
В 1830-х годах он заинтересовался земным магнетизмом и участвовал в первом в мире исследовании магнитного поля Земли (для его измерения он изобрел магнитометр). Вместе со своим геттингенским коллегой, физиком Вильгельмом Вебером, он сделал первый электрический телеграф, но некоторая ограниченность помешала ему энергично заняться изобретением. Вместо этого он извлек важные математические следствия из этой работы для того, что сегодня называется теорией потенциала, важной ветви математической физики, возникающей при изучении электромагнетизма и гравитации.
Гаусс также писал о картографии, теории картографических проекций. За свое исследование карт, сохраняющих угол, он был удостоен премии Датской академии наук в 1823 году. Эта работа была близка к предположению, что комплексные функции комплексной переменной обычно сохраняют угол, но Гаусс не сделал этого фундаментального утверждения. ясное понимание, оставив его Бернхарду Риману, который глубоко ценил работу Гаусса. У Гаусса были и другие неопубликованные идеи о природе сложных функций и их интегралов, некоторые из которых он поделился с друзьями.
На самом деле Гаусс часто отказывался публиковать свои открытия. Будучи студентом в Геттингене, он начал сомневаться в априорной истинности евклидовой геометрии и подозревал, что ее истинность может быть эмпирической. Для этого должно существовать альтернативное геометрическое описание пространства. Вместо того чтобы опубликовать такое описание, Гаусс ограничился критикой различных априорных защит евклидовой геометрии. Казалось, он постепенно убедился, что существует логическая альтернатива евклидовой геометрии. Однако, когда венгр Янош Бойяи и русский Николай Лобачевский опубликовали свои отчеты о новой неевклидовой геометрии около 1830 года, Гаусс не смог последовательно изложить свои собственные идеи. Можно объединить эти идеи в впечатляющее целое, в котором его концепция внутренней кривизны играет центральную роль, но Гаусс так и не сделал этого. Одни приписывали эту неудачу его врожденному консерватизму, другие — его непрекращающейся изобретательности, которая всегда влекла его к следующей новой идее, третьи — его неспособности найти центральную идею, которая управляла бы геометрией после того, как евклидова геометрия перестала быть уникальной.
Все эти объяснения имеют некоторые достоинства, хотя ни одно из них не может быть исчерпывающим объяснением.
Еще одной темой, по которой Гаусс в значительной степени скрывал свои идеи от современников, были эллиптические функции. В 1812 году он опубликовал отчет об интересном бесконечном ряду и написал, но не опубликовал отчет о дифференциальном уравнении, которому удовлетворяет бесконечный ряд. Он показал, что ряды, называемые гипергеометрическими рядами, могут использоваться для определения многих знакомых и многих новых функций. Но к тому времени он знал, как использовать дифференциальное уравнение для создания очень общей теории эллиптических функций и полностью освободить теорию от ее истоков в теории эллиптических интегралов. Это был крупный прорыв, потому что, как обнаружил Гаусс в 179 г.0s теория эллиптических функций, естественно, трактует их как комплекснозначные функции комплексного переменного, но современная теория комплексных интегралов была совершенно неадекватна для этой задачи.
Когда часть этой теории была опубликована норвежцем Нильсом Абелем и немцем Карлом Якоби примерно в 1830 году, Гаусс заметил своему другу, что Абель прошел одну треть пути. Это было точно, но это печальная мера личности Гаусса, поскольку он все еще воздерживался от публикации.
Гаусс сделал меньше, чем мог бы, и в других отношениях. Геттингенский университет был небольшим, и он не стремился расширить его или набрать дополнительных студентов. К концу его жизни через Геттинген прошли математики калибра Рихарда Дедекинда и Римана, и он был полезен, но современники сравнивали его стиль письма с жидкой кашицей: он ясен и устанавливает высокие стандарты строгости, но ему недостает мотивации и может быть медленным и утомительным, чтобы следовать. Он переписывался со многими, но не со всеми, людьми, достаточно опрометчивыми, чтобы написать ему, но мало что делал, чтобы поддерживать их публично. Редким исключением были случаи, когда Лобачевский подвергался нападкам со стороны других русских за его идеи о неевклидовой геометрии.