Метод узловых и контурных уравнений для расчета сложных электрических цепей
Задача
На рисунке 2 изображена схема сложной электрической цепи. ЭДС источников энергии Е1, Е2, их внутренне сопротивление R01, R02, сопротивление резисторов R1, R2, R3. Чиcловые значения величин приведены в таблице 3. Начертить схему цепи, показав направления токов в ветвях.
Определить токи I1, I2, I3 методом узловых и контурных уравнений (при помощи первого и второго законов Кирхгофа).
Проверить решение методом узлового напряжения. Составить уравнение баланса мощности.
Дано
Е1 =260В
Е2=244В
R01 =0,1Ом
R02 =0,2Ом
R1 =0
R2=0
R3=1Ом
I1-3= ?, Составить баланс мощности.
Схема цепи
Решение
1.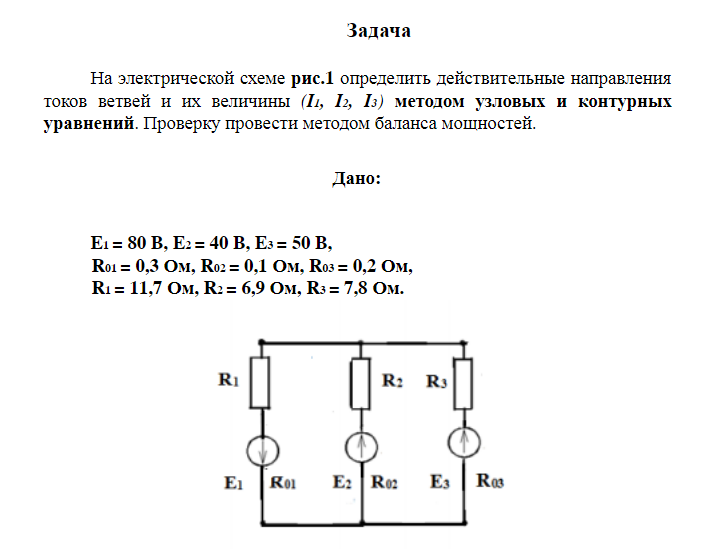
АБДЖА, БВГДБ, АБВГДЖА..
2. Так как узловых точек две: Б,Д, то число уравнений по первому закону Кирхгофа – одно, а по второму закону Кирхгофа два.
I3 = I1+ I2(1)
E1 =I1(R1+R01) + I3R3(2) контур АБДЖА
-E2 =I2 (R2 + R02) + I3 R3(3) контур БВГДБ
3. Подставляем числовые значения в уравнения, решаем систему из трех уравнений и получаем значения токовI1, I2, I3.
I3 = I1+ I2
250= I
-244= I2(0+0,2) + I3R3 = 0,2I1+ I3
I1=
I2=
I3 = 175 +57,5 = 232,5А
Проверяем правильность определения токов в сложной цепи при помощи первого и второго законов Кирхгофа методом узлового напряжения
4. Проводимости ветвей:
Проводимости ветвей:
g1=
g2=
g3=
5.Узловое напряжение (напряжение между узлами Б,Д):
UВД=
6. Токи ветвей:
I1 =(Е
I2 =(Е2– UВД) g2 =(244 -232,5)5=57,5А
I1 = -UВД * g3 =-232,5*1=-232,5А
Значение токов соответствует значениям, полученным при помощи законов Кирхгофа. Так как токи I3 получились отрицательными, его направление, указанное на рисунке, должно быть изменено на противоположное.
Составим баланс мощности
7.Уравнение баланс мощности будет иметь вид:
Рист1+Рист2 =Рист0+Рист0 +Р3
Рист1= Е1*I1=250*175=43750Вт
Рист2= Е2*I2=244*57,5=14030Вт
Рист01=
Рист02= * R02 = =661,25Вт
Р3= * R3 = =54056,25Вт
Рист =3750Вт +14030Вт=57780Вт
Рист0+Рист0 +Р3 = 3062,5Вт +661,25Вт +54056,25Вт=57780Вт
57780Вт=57780Вт
Баланс выполняется, задача решена, верно.
Метод узловых и контурных уравнений в электротехнике (ТОЭ)
Метод узловых и контурных уравнений:
Метод узловых и контурных уравнений для расчета сложных электрических цепей подразумевает составление системы уравнений по законам Кирхгофа. При составлении системы уравнение должно учитываться следующее.
- Число уравнений равно числу токов в цепи (число токов par но числу ветвей в рассчитываемой цепи). Направление токов ветвях выбирается произвольно.
- По первому закону Кирхгофа составляется (
- Остальные уравнения составляются по второму закону Кирхгофа.
В результате решения системы уравнений определяются искомые величины для сложной электрической цепи (например, все-таки при заданных значениях ЭДС источников Е и сопротивлений резисторов). Если в результате расчета какие-либо токи полу чаются отрицательными, это указывает на то, что их направление противоположно выбранному.
Пример 4.
Составить необходимое и достаточное количество уравнений по законам Кирхгофа для определения всех токов в цеп (рис. 4.12) методом узловых и контурный уравнений.
Решение
В рассматриваемой сложной цепи имеется 5 ветвей, следовательно, 5 различных токов, поэтому для расчета необходимо составить 5 уравнений, причем 2 уравнения — по первому закон Кирхгофа (в цепи n = 3 узловых точки А, В и Q и 3 уравнения -по второму закону Кирхгофа (внутренним сопротивлением источников пренебрегаем, т.е.
Составляем уравнения:
Обход по часовой стрелке.
Пример 4.10
Определить токи в примере 4.7 методом узловых и контурных нений (схема рис. 4.10) при тех же заданных условиях.
Решение
При выбранном в схеме рис. 4.10 направлении токов составим необходимое и достаточное количество уравнений по законам Кирхгофа:
В уравнение (2) подставляются значения тока из уравнения и числовые значения заданных величин. Тогда уравнения (2) и будут выглядеть так:
Тогда уравнения (2) и будут выглядеть так:
Для сокращения тока при суммировании уравнений (2) и (3) числовые значения уравнения (3) умножаются на 2 (два).
Результаты суммирования:
Откуда
Из уравнения (3):
И из уравнения (1):
Очевидно, что полученный результат совпадает с результатом, полученным методом узлового напряжения.
Уравнения цепи в матричной форме
Пользуясь матрицей соединений А и матрицей контуров В, а также законами Кирхгофа, можно получить узловые и контурные уравнения, определяющие режим цепи, в матричной форме, при этом получаются и выражения для определения матрицы узловых проводимостей (1.39), и матрицы контурных сопротивлений (1.53).
Запишем еще раз в матричной форме первый и второй законы Кирхгофа (1.26) и (1.27):
AI = 0; BU = 0, (1.58)
где I — матрица-столбец токов ветвей; U — матрица-столбец напряжений между концами ветвей.
Подставив (1.57) в (1.58), получим
Это выражение справедливо при всех значениях , поэтому для любой заданной электрической цепи.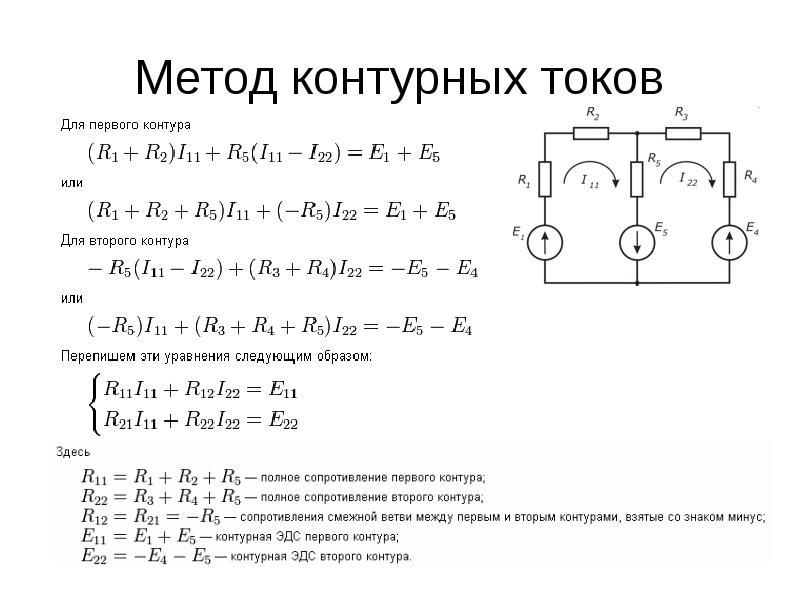
Уравнения цепи в матричной форме, в том числе с узловыми потенциалами и контурными токами, получаются наиболее коротким путем при введении понятия обобщенной ветви — двухполюсника общего вида (рис. 1.25). Для такой ветви I’ = I + J и U = rI’ — Е, откуда следует, что
I = g(U + Е)- J (1.60)
или
U = r(I + J)- Е. (1.61)
Это так называемые компонентные уравнения (связывают напряжение и ток ветви).
В матричной форме для всех ветвей схемы вместо (1.60) и (1.61) получим обобщенный закон Ома
I = g(U + E)-J (1.62)
или
U = r(I + J) — Е, (1.63)
где g — диагональная матрица проводимостей ветвей; r — диагональная матрица сопротивлений ветвей.
Уравнения Кирхгофа (1.58) — топологические уравнения — вместе с компонентными уравнениями (1.62) или (1.63) составляют полную систему уравнений линейной электрической цепи в матричной форме.
Для получения узловых уравнений в матричной форме умножим (1.62) на матрицу А
AI = AgU + AgE — AJ = 0
и после замены по (1.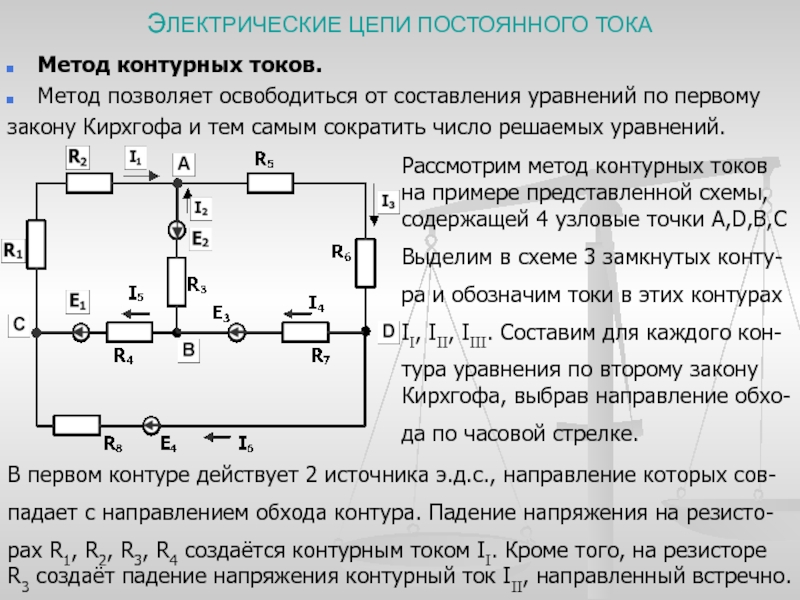 40)
40)
где -квадратная матрица узловых проводимостей; — матрица-столбец узловых токов, т.е. (1.64) совпадает с (1.38).
Для получения контурных уравнений в матричной форме умножим (1.63) на матрицу В
BU = BrI + BrJ — BE,
и так как BU = 0 (второй закон Кирхгофа) и (1.57), то
где — квадратная матрица контурных сопротивлений; — матрица-столбец контурных ЭДС, т. е. (1.65) совпадает с (1.51).
При расчетах режимов сложных электрических цепей с применением ЭВМ предварительно должна быть составлена ее эквивалентная схема — математическая модель цепи, состоящая из типовых элементов. Для цепей, которые рассматриваются в этой главе, это резистивные элементы с сопротивлениями r, идеальные источники ЭДС Е и идеальные источники тока J. В общем случае добавляются зависимые или управляемые источники (см. гл. 8), индуктивные и емкостные элементы (для цепей переменного тока) и др.
В случае расчета с применением уравнений Кирхгофа (1.58) число решаемых уравнений равно 2В, т. е. число решаемых уравнений больше, чем при расчете методами узловых потенциалов и контурных токов, но ограничений на типы элементов нет, программа решения системы уравнений не требует перемножения матриц. Чтобы получить систему независимых уравнений, нужно выбрать независимые контуры, т. е. в общем случае выбрать дерево и ветви связи (обратиться к топологическим понятиям).
е. число решаемых уравнений больше, чем при расчете методами узловых потенциалов и контурных токов, но ограничений на типы элементов нет, программа решения системы уравнений не требует перемножения матриц. Чтобы получить систему независимых уравнений, нужно выбрать независимые контуры, т. е. в общем случае выбрать дерево и ветви связи (обратиться к топологическим понятиям).
Число узловых уравнений (метод узловых потенциалов) меньше 2В, а именно У — 1. Топологические матрицы составлять не нужно, и перемножения матриц не требуется, так как (см. раздел) матрицы узловых проводимостей и узловых токов можно составить непосредственно для заданной схемы . Без преобразования схемы метод узловых потенциалов в матричной форме нельзя применять, если между какими-либо узлами включены ветви с идеальными источниками ЭДС, поскольку проводимость такой ветви бесконечно большая.
Число контурных уравнений (метод контурных токов) тоже меньше 26, а именно В -(У- 1). Но задача выбора системы независимых контуров остается. Перемножения матриц не требуется, так как матрицы контурных сопротивлений и контурных ЭДС можно составить непосредственно для заданной схемы [см. (1.48а)]. Без преобразования схемы метод контурных токов в матричной форме нельзя применять, если схема содержит ветви с идеальными источниками тока, так как сопротивление такой ветви бесконечно большое.
Перемножения матриц не требуется, так как матрицы контурных сопротивлений и контурных ЭДС можно составить непосредственно для заданной схемы [см. (1.48а)]. Без преобразования схемы метод контурных токов в матричной форме нельзя применять, если схема содержит ветви с идеальными источниками тока, так как сопротивление такой ветви бесконечно большое.
При расчете режима цепи с применением ЭВМ, особенно в том случае, если схема содержит и управляемые источники, для устранения отмеченных недостатков применения уравнений Кирхгофа, узловых уравнений и контурных уравнений можно рекомендовать метод расширенных узловых уравнений (метод смешанных величин).
Метод контурных токов, метод узловых потенциалов реферат по математике
Метод контурных токов, метод узловых потенциалов Ранее рассматривались простейшие одноконтурные (двухконтурные) электрические цепи и схемы с двумя узлами. Были описаны способы преобразования схем, с помощью которых в ряде случаев удаётся упростить расчёт разветвлённой электрической цепи.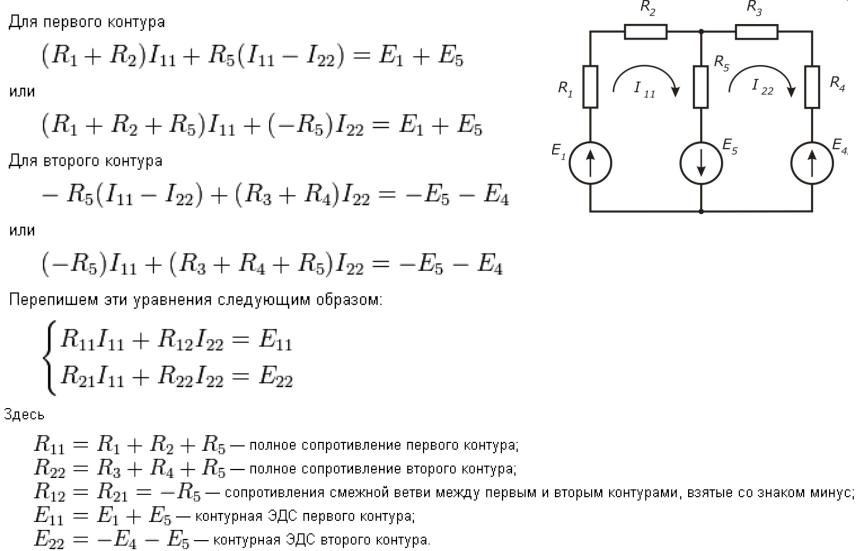 В случае, когда электрическая схема достаточно сложна и не приводится к схеме одноконтурной цепи, пользуются более общими методами расчёта. Описанные ниже методы применимы для цепей постоянного и переменного тока. Метод контурных токов позволяет уменьшить количество уравнений системы до числа – число уравнений (сост. по II закону Кирхгофа). Если в цепи некоторые узлы соединяются ветвями, не меняющими проводимость (они могут содержать источники тока), то число уравнений К, составляемых по методу контурных токов уменьшается на NT. Метод основывается на том свойстве, что ток в любой ветви цепи может быть представлен в виде алгебраической суммы независимых контурных токов, протекающих в этой ветви. При пользовании методом сначала выбирают и обозначают независимые контурные токи (по любой ветви должен протекать хотя бы один выбранный ток). – число независимых контурных токов, их необходимо выбирать проходящими по ветви, не содержащими источников тока. Пусть электрическая цепь содержит n контуров (независимых).
В случае, когда электрическая схема достаточно сложна и не приводится к схеме одноконтурной цепи, пользуются более общими методами расчёта. Описанные ниже методы применимы для цепей постоянного и переменного тока. Метод контурных токов позволяет уменьшить количество уравнений системы до числа – число уравнений (сост. по II закону Кирхгофа). Если в цепи некоторые узлы соединяются ветвями, не меняющими проводимость (они могут содержать источники тока), то число уравнений К, составляемых по методу контурных токов уменьшается на NT. Метод основывается на том свойстве, что ток в любой ветви цепи может быть представлен в виде алгебраической суммы независимых контурных токов, протекающих в этой ветви. При пользовании методом сначала выбирают и обозначают независимые контурные токи (по любой ветви должен протекать хотя бы один выбранный ток). – число независимых контурных токов, их необходимо выбирать проходящими по ветви, не содержащими источников тока. Пусть электрическая цепь содержит n контуров (независимых).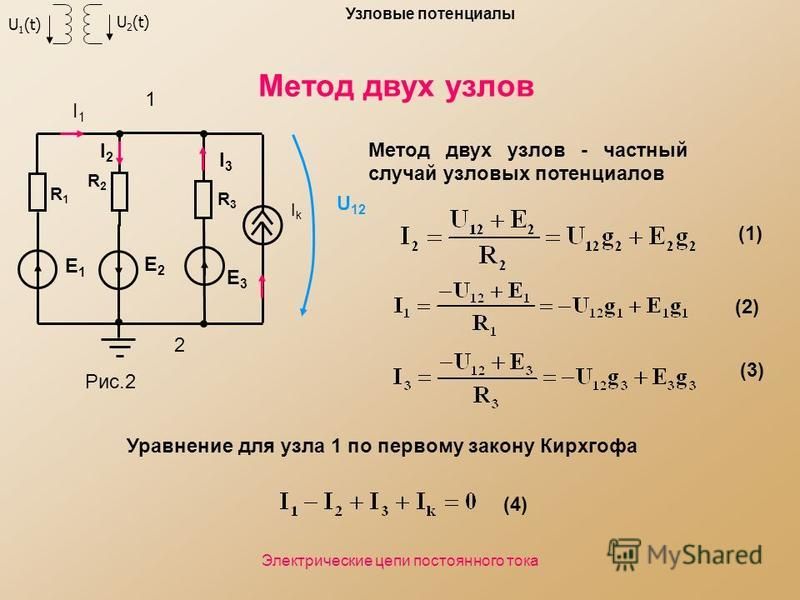 Согласно II закону Кирхгофа получаем следующую систему из n линейных уравнений: При этом следует считать , если условные положительные направления контурных токов в одной ветви контуров K и m совпадают, и , если они противоположны. где 1 2 n – дополнение – определитель системы. Расчёт установившегося режима в цепи переменного тока комплексным методом выполняется в следующей последовательности: Составляется электрическая схема, на которой все источники и пассивные элементы представляются комплексными величинами соответственно напряжений, токов, сопротивлений (проводимостей). Выбирается условно положительное направление для комплексных значений напряжений, ЭДС и токов. Согласно уравнениям электрических цепей (Ома, Кирхгофа) в комплексной форме составляются алгебраические уравнения для рассчитываемой цепи. Уравнения цепи разрешаются относительно искомых переменных (токов, напряжений) в их комплексной форме. Метод узловых потенциалов Метод позволяет уменьшить количество уравнений системы до числа , где Ny – число узлов электрической схемы.
Согласно II закону Кирхгофа получаем следующую систему из n линейных уравнений: При этом следует считать , если условные положительные направления контурных токов в одной ветви контуров K и m совпадают, и , если они противоположны. где 1 2 n – дополнение – определитель системы. Расчёт установившегося режима в цепи переменного тока комплексным методом выполняется в следующей последовательности: Составляется электрическая схема, на которой все источники и пассивные элементы представляются комплексными величинами соответственно напряжений, токов, сопротивлений (проводимостей). Выбирается условно положительное направление для комплексных значений напряжений, ЭДС и токов. Согласно уравнениям электрических цепей (Ома, Кирхгофа) в комплексной форме составляются алгебраические уравнения для рассчитываемой цепи. Уравнения цепи разрешаются относительно искомых переменных (токов, напряжений) в их комплексной форме. Метод узловых потенциалов Метод позволяет уменьшить количество уравнений системы до числа , где Ny – число узлов электрической схемы. Сущность метода заключается в том, что сначала определяются потенциалы всех узлов схемы, а токи ветвей, соединяющих узлы, определяются с помощью законов Ома. При составлении уравнений по МУП сначала полагают равным нулю потенциал какого- либо узла, для оставшихся составляют уравнения по I-му закону Кирхгофа. Если в цепи некоторые узлы соединяются ветвями, не имеющими сопротивлений (они могут содержать источники напряжений), то число KI уравнений, составленных по МУП, уменьшается на Nн (число ветвей с нулевыми сопротивлениями). – число уравнений по МУП. Прежде, чем перейти к изложению самого метода, напомним, что в случае, когда между двумя узлами имеются несколько параллельных ветвей с источниками ЭДС (или без них), их можно привести к одной эквивалентной схеме. Это представление эквивалентной схемой параллельных ветвей с источниками ЭДС даёт нам право без ограничения общности считать, что между любой парой узлов включена только одна ветвь.
Сущность метода заключается в том, что сначала определяются потенциалы всех узлов схемы, а токи ветвей, соединяющих узлы, определяются с помощью законов Ома. При составлении уравнений по МУП сначала полагают равным нулю потенциал какого- либо узла, для оставшихся составляют уравнения по I-му закону Кирхгофа. Если в цепи некоторые узлы соединяются ветвями, не имеющими сопротивлений (они могут содержать источники напряжений), то число KI уравнений, составленных по МУП, уменьшается на Nн (число ветвей с нулевыми сопротивлениями). – число уравнений по МУП. Прежде, чем перейти к изложению самого метода, напомним, что в случае, когда между двумя узлами имеются несколько параллельных ветвей с источниками ЭДС (или без них), их можно привести к одной эквивалентной схеме. Это представление эквивалентной схемой параллельных ветвей с источниками ЭДС даёт нам право без ограничения общности считать, что между любой парой узлов включена только одна ветвь.
4. Анализ сложных электрических цепей с несколькими источниками энергии
4. 1. Метод непосредственного применения
1. Метод непосредственного применения
законов Кирхгофа
На рис. 4.1 изображена
схема разветвленной электрической цепи. Известны величины сопротивлений
и ЭДС, необходимо определить токи.
В схеме имеются четыре узла, можно составить четыре уравнения по первому
закону Кирхгофа.
Укажем произвольно направления токов. Запишем уравнения::
(4.1)
Рис. 4.1
Сложим эти уравнения. Получим тождество 0 = 0. Система уравнений
(4.1) является зависимой.
Если в схеме имеется n узлов, количество независимых уравнений, которые
можно составить по первому закону Кирхгофа, равно n – 1.
Для схемы на рис.
(4.2)
Недостающее количество уравнений составляют по второму
закону Кирхгофа. Уравнения по второму закону составляют для независимых
контуров. Независимым является контур, в который входит хотя бы одна
новая ветвь, не вошедшая в другие контуры.
Выберем три независимых контура и укажем направления обхода контуров.
Запишем три уравнения по второму закону Кирхгофа.
(4.3)
Ток в ветви может иметь отрицательное значение. Это означает, что действительное направление тока противоположно выбранному нами. Метод контурных токов
Метод непосредственного применения
законов Кирхгофа громоздок. Имеется возможность уменьшить количество
совместно решаемых уравнений системы. Число уравнений, составленных
по методу контурных токов, равно количеству уравнений, составляемых
по второму закону Кирхгофа.
Имеется возможность уменьшить количество
совместно решаемых уравнений системы. Число уравнений, составленных
по методу контурных токов, равно количеству уравнений, составляемых
по второму закону Кирхгофа.
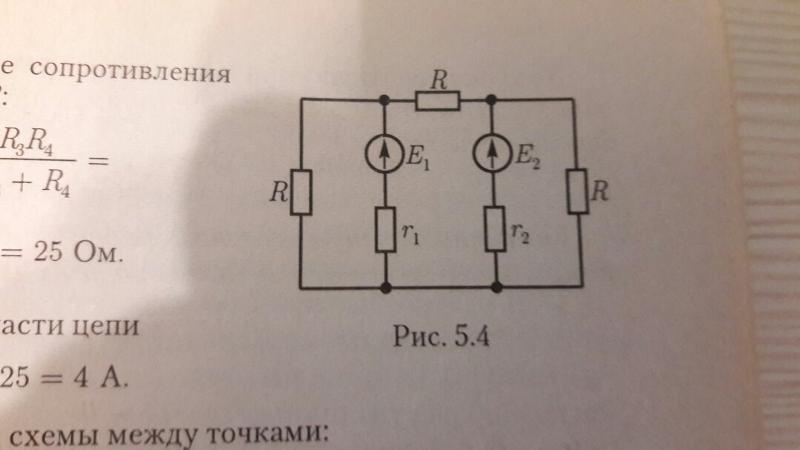
На рис. 4.2 в качестве примера изображена двухконтурная схема, в которой I11 и I22 – контурные токи.
Рис. 4.2
Токи в сопротивлениях R1 и R2 равны соответствующим контурным токам.
Ток в сопротивлении R3, являющийся общим для обоих контуров, равен разности
контурных токов I11 и I22, так как эти токи направлены в ветви с R3
встречно.
Выбираются независимые контуры, и
задаются произвольные направления контурных токов.
В нашем случае эти токи направлены по часовой стрелке. Направление обхода
контура совпадает с направлением контурных токов. Уравнения для этих
контуров имеют следующий вид:
Перегруппируем слагаемые в уравнениях
(4.4)
(4.5)
Суммарное сопротивление данного контура называется
собственным сопротивлением контура.
Собственные сопротивления контуров схемы
, .
Сопротивление R3, принадлежащее одновременно двум контурам, называется общим сопротивлением этих контуров.
,
где R12 – общее сопротивление между первым
и вторым контурами;
R21 – общее сопротивление между вторым и первым контурами.
E11 = E1 и E22 = E2 – контурные ЭДС.
В общем виде уравнения (4.4) и (4.5) записываются следующим образом:
,
.
Собственные сопротивления
всегда имеют знак “плюс”.
Общее сопротивление имеет знак “минус”, если в данном сопротивлении
контурные токи направлены встречно друг другу, и знак “плюс”,
если контурные токи в общем сопротивлении совпадают по направлению.
Решая уравнения (4.4) и (4.5) совместно, определим контурные токи I11
и I22, затем от контурных токов переходим к токам в ветвях.
Ветви схемы, по которым протекает один контурный ток, называются внешними,
а ветви, по которым протекают несколько контурных токов, называются
общими. Ток во внешней ветви совпадает по величине и по направлению
c контурным. Ток в общей ветви равен алгебраической сумме контурных
токов, протекающих в этой ветви.
Ток в общей ветви равен алгебраической сумме контурных
токов, протекающих в этой ветви.
В схеме на Рис. 4.2
.
Рекомендации
Контуры выбирают произвольно, но целесообразно выбрать
контуры таким образом, чтобы их внутренняя область не пересекалась ни
с одной ветвью, принадлежащей другим контурам.
Контурные токи желательно направлять одинаково (по часовой стрелке или
против).
Если нужно определить ток в одной ветви сложной схемы, необходимо сделать
его контурным.
Если в схеме имеется ветвь с известным контурным током, этот ток следует
сделать контурным, благодаря чему количество уравнений становится на
единицу меньше.
4.3. Метод узловых потенциалов
Метод узловых потенциалов позволяет составить систему уравнений, по которой можно определить потенциалы всех узлов схемы. По известным разностям узловых потенциалов можно определить токи во всех ветвях. В схеме на рисунке 4.3 имеется четыре узла. Потенциал любой точки схемы можно принять равным нулю. Тогда у нас останутся неизвестными три потенциала. Узел, величину потенциала которого выбирают произвольно, называют базисным. Укажем в схеме произвольно направления токов. Примем для схемы ?4 = 0.
Рис. 4.3
Запишем уравнение по первому закону Кирхгофа для узла 1.
(4. 6)
6)
В соответствии с законами Ома для активной и пассивной ветви
,
где – проводимость первой ветви.
,
где – проводимость второй ветви.
Подставим выражения токов в уравнение (4.6).
(4.7)
где g11 = g1 + g2 – собственная проводимость узла 1.
Собственной проводимостью узла называется сумма проводимостей ветвей,
сходящихся в данном узле.
g12 = g2 – общая проводимость между узлами 1 и 2.
Общей проводимостью называют проводимость ветви, соединяющей узлы 1
и 2.
– сумма токов источников,
находящихся в ветвях, сходящихся в узле 1.
Если ток источника направлен к узлу, величина его записывается в правую
часть уравнения со знаком “плюс”, если от узла – со знаком
“минус”.
По аналогии запишем для узла 2:
(4.8)
для узла 3:
(4.9)
Решив совместно уравнения (4.7), (4.8), (4.9),
определим неизвестные потенциалы ?1, ?2, ?3, а затем по закону Ома для
активной или пассивной ветви найдем токи.
Если число узлов схемы – n, количество уравнений по методу узловых потенциалов
– (n – 1).
Замечание.
Если в какой-либо ветви содержится идеальный источник ЭДС, необходимо один из двух узлов, между которыми включена эта ветвь, выбрать в качестве базисного, тогда потенциал другого узла окажется известным и равным величине ЭДС. Количество составляемых узловых уравнений становится на одно меньше.
4.4. Метод двух узлов
Схема на рис. 4.4 имеет два узла. Потенциал точки
2 примем
равным нулю ?2 = 0. Составим узловое уравнение для узла 1.
,
,
Рис. 4.4
где , , – проводимости ветвей.
В общем виде:
.
В знаменателе формулы – сумма
проводимостей параллельно включенных ветвей. В числителе – алгебраическая
сумма произведений ЭДС источников на проводимости ветвей, в которые
эти ЭДС включены. ЭДС в формуле записывается со знаком “плюс”,
если она направлена к узлу 1, и со знаком “минус”, если направлена
от узла 1.
После вычисления величины потенциала ?1 находим токи в ветвях, используя
закон Ома для активной и пассивной ветви.
Этот метод используется тогда, когда
надо определить ток только в одной ветви сложной схемы.
Чтобы разобраться с методом эквивалентного генератора, ознакомимся сначала
с понятием “двухполюсник”.
Часть электрической цепи с двумя выделенными зажимами называется двухполюсником.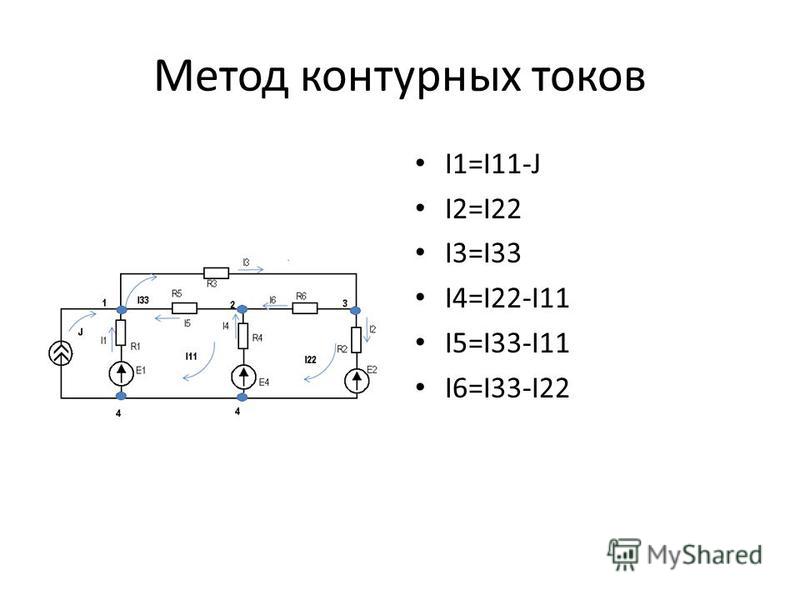 Двухполюсники, содержащие источники энергии, называются активными. На
рис. 4.5 показано условное обозначение активного двухполюсника.
Двухполюсники, содержащие источники энергии, называются активными. На
рис. 4.5 показано условное обозначение активного двухполюсника.
Двухполюсники, не содержащие источников, называются пассивными. На эквивалентной
схеме пассивный двухполюсник может быть заменен одним элементом – внутренним
или входным сопротивлением пассивного двухполюсника Rвх. На рис. 4.6
условно изображен пассивный двухполюсник и его эквивалентная схема.
Рис. 4.5 Рис. 4.6
Входное сопротивление пассивного двухполюсника можно измерить.
Если известна схема пассивного двухполюсника, входное сопротивление
его можно определить, свернув схему относительно заданных зажимов.
Дана электрическая цепь. Необходимо определить ток I1 в ветви с сопротивлением
R1 в этой цепи. Выделим эту ветвь, а оставшуюся часть схемы заменим
активным двухполюсником (рис. 4.7).
Выделим эту ветвь, а оставшуюся часть схемы заменим
активным двухполюсником (рис. 4.7).
Согласно теореме об активном двухполюснике, любой активный двухполюсник
можно заменить эквивалентным генератором (источником напряжения) с ЭДС,
равным напряжению холостого хода на зажимах этого двухполюсника и внутренним
сопротивлением, равным входному сопротивлению того же двухполюсника,
из схемы которого исключены все источники (рис. 4.8). Искомый ток I1
определится по формуле:
(4.10)
Рис. 4.7 Рис. 4.8
Параметры эквивалентного генератора (напряжение холостого хода
и входное сопротивление) можно определить экспериментально или расчетным
путем.
Ниже показан способ вычисления этих параметров расчетным путем в схеме
на рис. 4.2. Изобразим на рис. 4.9 схему, предназначенную для определения
напряжения холостого хода. В этой схеме ветвь с сопротивлением R1 разорвана,
это сопротивление удалено из схемы. На разомкнутых зажимах появляется
напряжение холостого хода. Для определения этого напряжения составим
уравнение для первого контура по второму закону Кирхгофа
,
откуда находим
, (4.11)
где
определяется из уравнения, составленного по второму закону Кирхгофа
для второго контура
. (4.12)
Так как первая ветвь разорвана, ЭДС
Е1 не создает ток. Падение напряжения на сопротивлении Rвн1 отсутствует.
Падение напряжения на сопротивлении Rвн1 отсутствует.
На рис. 4.10 изображена схема, предназначенная для определения входного
сопротивления.
.
Рис. 4.9 Рис. 4.10
Из схемы на рис. 4.9 удалены все источники (Е1 и Е2), т.е. эти
ЭДС мысленно закорочены. Входное сопротивление Rвх определяют, свертывая
схему относительно зажимов 1-1′
. (4.13)
Для определения параметров эквивалентного генератора экспериментальным путем необходимо выполнить опыты холостого хода и короткого замыкания.При проведении опыта холостого хода от активного двухполюсника отключают сопротивление R1, ток I1 в котором необходимо определить.
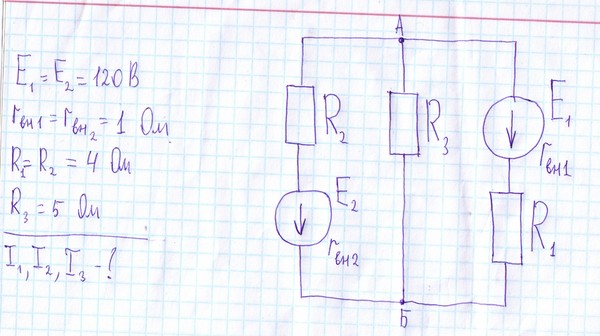 К зажимам двухполюсника
1-1′ подключают вольтметр и измеряют напряжение холостого хода Uxx (рис.
4.11).
К зажимам двухполюсника
1-1′ подключают вольтметр и измеряют напряжение холостого хода Uxx (рис.
4.11). При выполнении опыта короткого замыкания соединяют проводником зажимы 1-1′ активного двухполюсника и измеряют амперметром ток короткого замыкания I1кз (рис. 4.12).
Рис. 4.11 Рис. 4.12
откуда
(4.14)
2 Методы расчета электрических цепей с несколькими источниками питания – контурных токов, узловых потенциалов, эквивалентного генератора
Любые упражнения по изучению электротехники необходимо начинать с проработки лекционного материала и соответствующего раздела в учебнике. Следует также выучить правила составления уравнений и свойств соединений элементов схем.
Следует также выучить правила составления уравнений и свойств соединений элементов схем.
СЕМИНАР 2
Методы расчета электрических цепей с несколькими источниками питания: контурных токов, узловых потенциалов, эквивалентного генератора
Задача 1
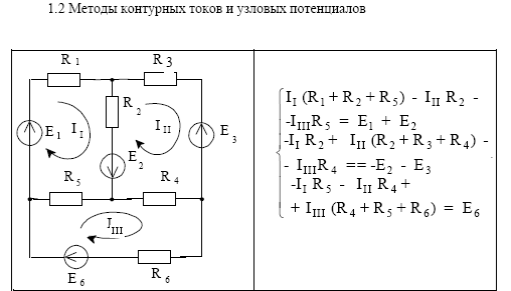
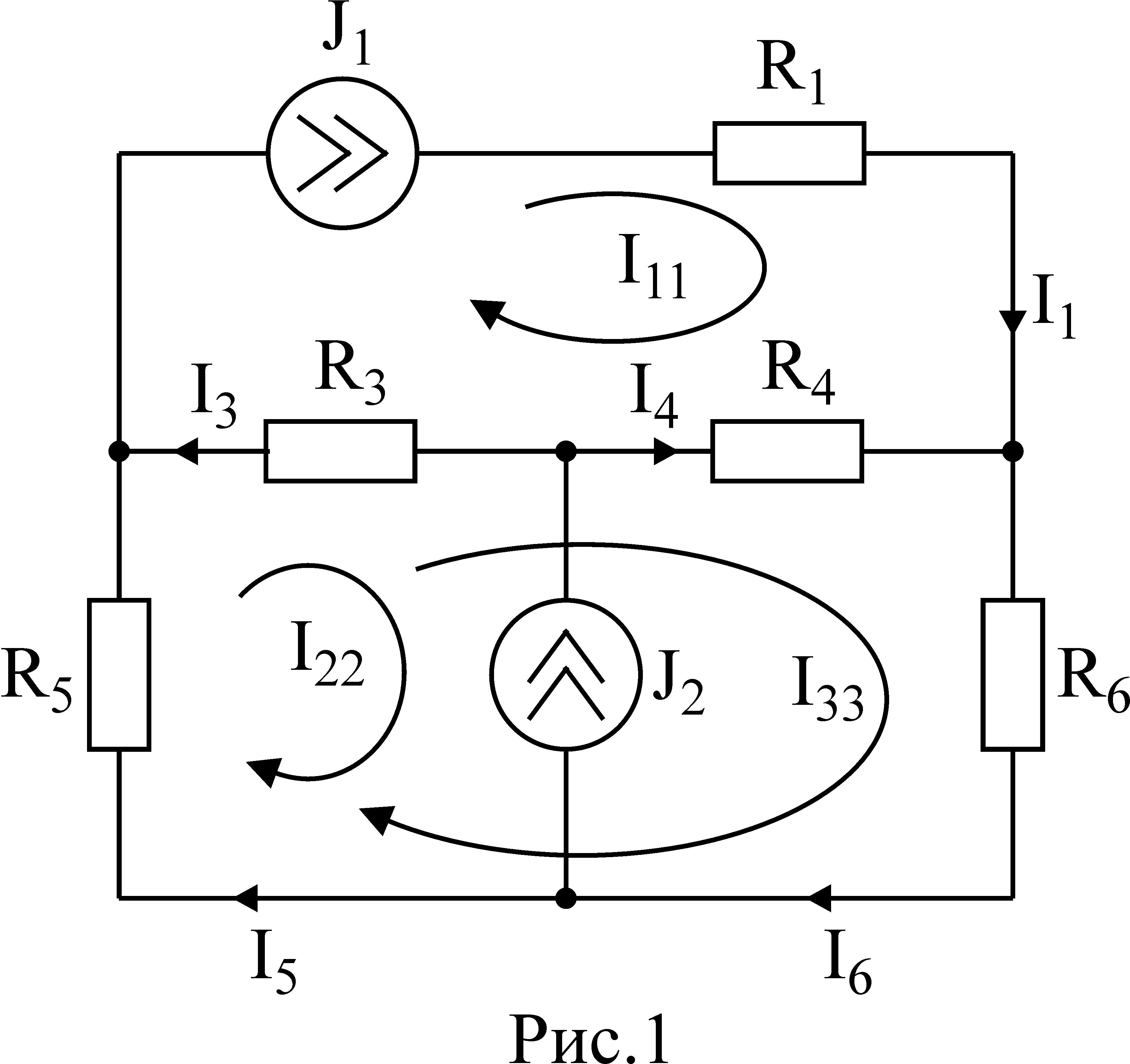
Дано: R1 = R5 =10 Ом, R4 = R6 = 5 Ом, R3 = 25 Ом, R2 = 20 Ом, Е1 =100 В, Е2 =80 В, Е3 =50 В
Определить токи в ветвях разными методами, составить и рассчитать баланс мощностей.
Решение:
Метод контурных токов
Так как три контура, то будет три контурных тока I11, I22, I33. Направления этих токов выбираем по часовой стрелке рис 3. Запишем настоящие токи через контурные:
I1 = I11 – I33, I2 = – I22, I3 = – I33, I4 = I11, I5 = I11– I22
Запишем уравнения по второму закону Кирхгофа для контурных уравнений в соответствии с правилами.
Правило: если ЭДС и ток имеют одинаковое направление с направлением обхода контура, то они берутся с «+», если нет, то с «–».
Решим систему уравнений математическим методом Гаусса или Крамера.
Решив систему, получаем значения контурных токов:
I11 = 2,48 А, I22 = – 1,84 А, I33 = – 0,72 А
Определим настоящие токи: I1 = 3,2 А, I2 = 1,84 А, I3 = 0,72 А, I4 = 2,48 А, I5 = 4,32 А
Проверим правильность расчёта токов, подставив их в уравнения по законам Кирхгофа.
Составим уравнения для расчёта баланса мощностей:
Из расчёта видно, что баланс мощностей сошёлся. Погрешность меньше 1%.
1) Метод узловых потенциалов
Решаем туже задачу методом узловых потенциалов
Составим уравнения:
- Ток в любой ветви схемы можно найти по обобщённому закону Ома.
 Для этого необходимо определить потенциалы узлов схемы. Заземлим любой узел схемы φс = 0.
Для этого необходимо определить потенциалы узлов схемы. Заземлим любой узел схемы φс = 0.
Решая систему уравнений, определяем потенциалы узлов φaиφb
φa= 68 B φb= 43,2 B
По обобщенному закону Ома определяем токи в ветвях. Правило: ЭДС и напряжение берутся со знаком «+», если их направления совпадают с направлением тока, и со знаком «–», если нет.
2) Метод узловых преобразований в схемах с особенностями (особенностью является, наличие в схеме ветви с идеальной ЭДС)
Дано: R1 ÷ R5 =10 Ом, Е1 = 30 В, Е2 = 60 В Ток в любой ветви схемы можно найти по обобщённому закону Ома. Для этого необходимо определить потенциалы узлов схемы. Заземлим любой узел схемы φс = 0, тогда потенциал узла b равен значению E1
(если ЭДС направлен к узлу, то ЭДС берётся со знаком «+»). В данной схеме составляем одно уравнение для определения потенциала узла а.
В данной схеме составляем одно уравнение для определения потенциала узла а.
При решении схем с особенностями заземляется узел к которой подсоединена ветвь с идеальной ЭДС.
По обобщенному закону Ома определяем токи в ветвях.
3) Метод двух узлов
Применяется в случае, когда схема содержит только два узла (параллельное соединение).
Алгоритм:
- Задаются положительные направления токов и напряжение между двумя узлами произвольно;
- Уравнение для определения межузлового напряжения
,
где G – проводимость ветви, J – источники тока;
- Правило: G·E и J берутся со знаком «+», если Е и J направлены к узлу с большим потенциалом;
- Токи схемы определяются по обобщенному закону Ома.
Задача 2
Определить токи в ветвях методом двух узлов
Дано: R1 ÷ R3 =10 Ом, Е1 = 100 В, Е2 = 10 В
Решение:
Проверка по первому закону Кирхгофа:
Метод контурных токов, метод узловых потенциалов (Реферат)
Метод контурных токов, метод узловых потенциалов
Ранее рассматривались простейшие
одноконтурные (двухконтурные) электрические
цепи и схемы с двумя узлами.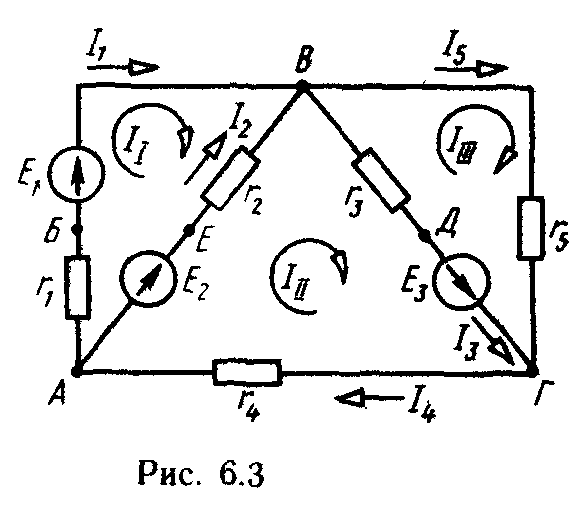 Были описаны
способы преобразования схем, с помощью
которых в ряде случаев удаётся упростить
расчёт разветвлённой электрической
цепи.
Были описаны
способы преобразования схем, с помощью
которых в ряде случаев удаётся упростить
расчёт разветвлённой электрической
цепи.
В случае, когда электрическая схема достаточно сложна и не приводится к схеме одноконтурной цепи, пользуются более общими методами расчёта. Описанные ниже методы применимы для цепей постоянного и переменного тока.
Метод контурных токов позволяет уменьшить количество уравнений системы до числа
– число уравнений (сост. по II закону Кирхгофа).
Если в цепи некоторые узлы соединяются ветвями, не меняющими проводимость (они могут содержать источники тока), то число уравнений К, составляемых по методу контурных токов уменьшается на NT.
Метод основывается на том свойстве, что ток в любой ветви цепи может быть представлен в виде алгебраической суммы независимых контурных токов, протекающих в этой ветви.
При пользовании методом сначала выбирают
и обозначают независимые контурные
токи (по любой ветви должен протекать
хотя бы один выбранный ток).
– число независимых контурных токов, их необходимо выбирать проходящими по ветви, не содержащими источников тока.
Пусть электрическая цепь содержит n контуров (независимых). Согласно II закону Кирхгофа получаем следующую систему из n линейных уравнений:
При этом следует считать , если условные положительные направления контурных токов в одной ветви контуров K и m совпадают, и , если они противоположны.
где D1 D2 Dn – дополнение
D – определитель системы.
Расчёт установившегося режима в цепи переменного тока комплексным методом выполняется в следующей последовательности:
Составляется электрическая схема, на
которой все источники и пассивные
элементы представляются комплексными
величинами соответственно напряжений,
токов, сопротивлений (проводимостей).
Выбирается условно положительное направление для комплексных значений напряжений, ЭДС и токов.
Согласно уравнениям электрических цепей (Ома, Кирхгофа) в комплексной форме составляются алгебраические уравнения для рассчитываемой цепи.
Уравнения цепи разрешаются относительно искомых переменных (токов, напряжений) в их комплексной форме.
Метод узловых потенциалов
Метод позволяет уменьшить количество уравнений системы до числа , где Ny – число узлов электрической схемы.
Сущность метода заключается в том, что сначала определяются потенциалы всех узлов схемы, а токи ветвей, соединяющих узлы, определяются с помощью законов Ома.
При составлении уравнений по МУП сначала полагают равным нулю потенциал какого-либо узла, для оставшихся составляют уравнения по I-му закону Кирхгофа.
Если в цепи некоторые узлы соединяются
ветвями, не имеющими сопротивлений (они
могут содержать источники напряжений),
то число KI уравнений, составленных по
МУП, уменьшается на Nн (число ветвей с
нулевыми сопротивлениями).
– число уравнений по МУП.
Прежде, чем перейти к изложению самого метода, напомним, что в случае, когда между двумя узлами имеются несколько параллельных ветвей с источниками ЭДС (или без них), их можно привести к одной эквивалентной схеме.
Это представление эквивалентной схемой параллельных ветвей с источниками ЭДС даёт нам право без ограничения общности считать, что между любой парой узлов включена только одна ветвь.
Дальше будем предполагать, что , т.е. между узлами цепи не включены идеальные источники ЭДС.
В качестве примера составим уравнение по методу узловых напряжений для цепи, изображённой на рис. 3.
Задано:
и параметры всех элементов.
Расчёт цепи производим комплексным методом:
Для узлов 1, 2, 3 имеем уравнения:
(1)
Y11=Y12+Y10+Y13; Y22=Y20+Y12+Y23; Y33=Y30+Y13+Y23
Решив систему
из 3-х уравнений относительно узловых
напряжений, находим напряжения на ветвях
и токи в них. Метод узловых напряжений
применим к независимым контурам.
Метод узловых напряжений
применим к независимым контурам.
Положительное направление всех узловых напряжений принято считать к опорному узлу.
Первое уравнение Кирхгофа для некоторого узла К можно записать:
(1)
Для 1-ого узла:
Значения Z1; Z2; Z3; E1 и E2 у нас были определены ранее (см. 1-ый способ решения).
Ответ:
Между узлами К и m имеется ветвь с источниками ЭДС (EKm), сопротивлением ZKm, то ток в этой цепи (ветви), направленный от К к m связан соотношениями:
Первый закон Кирхгофа для рис. 1 имеет вид (1).
Напряжение можно выразить через узловые напряжения в виде:
.
Получаем:
или
Обозначив , где YKK – сумма проводимостей всех ветвей, присоединённых к К-ому узлу, имеем:
–
что и является основным уравнением для
К-ого узла по МУП.
В развёрнутой форме совокупность уравнений по МУП имеет вид:
Решая эту систему, найдём узловые напряжения, причём для К-ого узла величина будет:
,
где D – главный определитель системы, DmK – его алгебраическое дополнение.
После того, как узловые напряжения найдены, определения токов в ветвях цепи имеют вид:
Если в ветви содержатся ЭДС, то ток равен
Метод узловых напряжений применяется к независимым узлам.
Если к К-ому узлу подтекает ток от источника тока, то он должен быть включен в ток IKK со знаком «+», если утекает, то со знаком «-».
Если между какими-либо двумя узлами нет ветви, то соответствующая проводимость равна 0.
Yii – собственная проводимость всех ветвей, подходящих к узлу i (всегда со знаком «+»).
Yiк – взаимная
проводимость между узлами i и к (входит
в уравнение всегда со знаком «-» при
выбранном направлении всех узловых
напряжений к базисному узлу).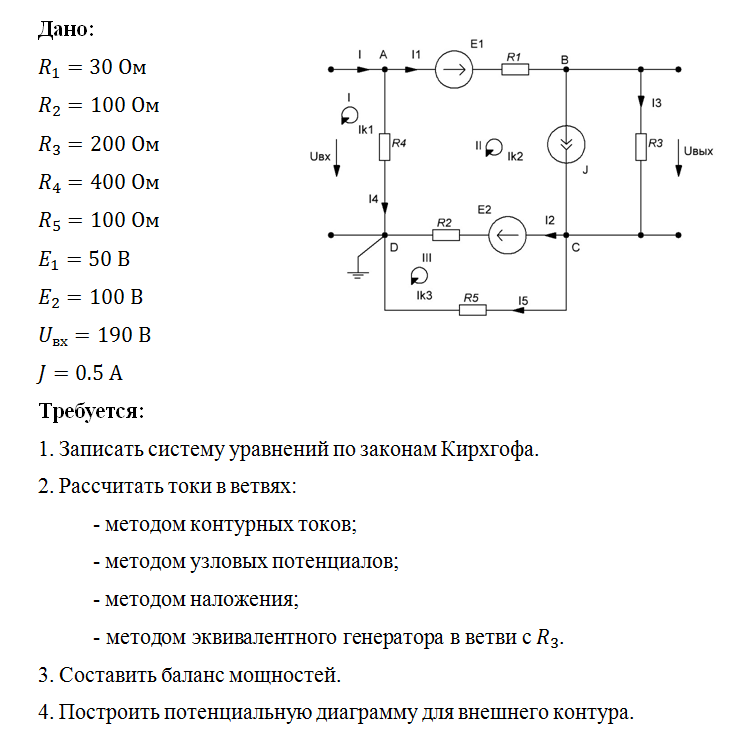
Ток I1 называется узловым током 1-ого узла. Это расчётная величина, равная алгебраической сумме токов, полученных от деления ЭДС ветвей, подходящих к 1-ому узлу, на сопротивления данных ветвей. В эту сумму со знаком «+» входят токи тех ветвей, ЭДС которых направлена к 1-ому узлу.
Y11 – проводимость всех ветвей, сходящихся в 1-ом узле.
Y12 – проводимость взаимная – равняется сумме проводимостей всех ветвей, соединяющих узел 1 с узлом 2 (берётся со знаком «-»).
Пример:
Е2=Е3 = 1 В
IK3 = 1 A
IK2 = 1 A
R1 = 13 Ом
R2 = 5 Ом
R3 = 9 Ом
R4 = 7 Ом
R5 = 1 Ом
R6 = 4 Ом
Определить токи в ветвях.
Для определения напряжения между двумя произвольными точками схемы необходимо ввести в левую часть уравнений искомое напряжение вдоль пути, как бы дополняющего незамкнутый контур до замкнутого.
Список литературы
Для подготовки данной работы были
использованы материалы с сайта http://revolution. allbest.ru
allbest.ru
Mesh | Анализ сети постоянного тока
Метод Mesh-Current Method , также известный как Loop Current Method , очень похож на метод тока ответвления в том, что он использует одновременные уравнения, закон напряжения Кирхгофа и закон Ома для определения неизвестных токов в сети. Он отличается от метода Branch Current тем, что , а не , использует Закон Кирхгофа, и обычно он может решить схему с меньшим количеством неизвестных переменных и меньшим количеством одновременных уравнений, что особенно удобно, если вы вынуждены решать без калькулятор.
Mesh Current, традиционный метод
Давайте посмотрим, как этот метод работает на той же задаче:
Определить петли
Первым шагом в методе Mesh Current является определение «петель» в цепи, охватывающей все компоненты. В нашей примерной схеме цикл, образованный B 1 , R 1 и R 2 , будет первым, а цикл, образованный B 2 , R 2 и R 3 , будет секунда. Самая странная часть метода Mesh Current – это представление о циркулирующих токах в каждой из петель. Фактически, этот метод получил свое название от идеи объединения этих токов между петлями, как набор вращающихся шестерен:
Самая странная часть метода Mesh Current – это представление о циркулирующих токах в каждой из петель. Фактически, этот метод получил свое название от идеи объединения этих токов между петлями, как набор вращающихся шестерен:
Выбор направления каждого тока является совершенно произвольным, как и в методе Branch Current, но результирующие уравнения легче решить, если токи идут в одном направлении через пересекающиеся компоненты (обратите внимание, как токи I 1 и I 2 оба идут «вверх» через резистор R 2 , где они «сцепляются» или пересекаются).Если предполагаемое направление тока сетки неверно, ответ для этого тока будет иметь отрицательное значение.
Обозначьте полярность падения напряжения
Следующим шагом является маркировка всех полярностей падения напряжения на резисторах в соответствии с предполагаемыми направлениями токов сетки. Помните, что «входной» конец резистора всегда будет отрицательным, а «выходной» конец резистора положительным по отношению друг к другу, поскольку электроны заряжены отрицательно. Полярность батарей, конечно, определяется ориентацией их символов на схеме и может или не может «согласовываться» с полярностью резистора (предполагаемым направлением тока):
Полярность батарей, конечно, определяется ориентацией их символов на схеме и может или не может «согласовываться» с полярностью резистора (предполагаемым направлением тока):
Используя закон Кирхгофа для напряжения, мы можем теперь обойти каждую из этих петель, создавая уравнения, представляющие падения напряжения и полярности компонентов.Как и в случае с методом тока ответвления, мы будем обозначать падение напряжения на резисторе как произведение сопротивления (в омах) и соответствующего ему тока сетки (эта величина на данный момент неизвестна). Если два тока сцепляются вместе, мы запишем этот член в уравнении с током резистора, равным сумме двух токов зацепления.
Отслеживание левого контура цепи с помощью уравнений
Отслеживание левого контура цепи, начиная с верхнего левого угла и двигаясь против часовой стрелки (выбор начальных точек и направлений в конечном итоге не имеет значения), считая полярность, как если бы у нас был вольтметр в руке, красный провод на точке впереди и черное преимущество на точке позади, мы получаем это уравнение:
Обратите внимание, что средний член уравнения использует сумму токов сетки I 1 и I 2 в качестве тока через резистор R 2 . Это связано с тем, что сеточные токи I 1 и I 2 проходят в одном направлении через R 2 и, таким образом, дополняют друг друга. Распределяя коэффициент 2 на члены I 1 и I 2 , а затем комбинируя члены I 1 в уравнении, мы можем упростить как таковые:
Это связано с тем, что сеточные токи I 1 и I 2 проходят в одном направлении через R 2 и, таким образом, дополняют друг друга. Распределяя коэффициент 2 на члены I 1 и I 2 , а затем комбинируя члены I 1 в уравнении, мы можем упростить как таковые:
На данный момент у нас есть одно уравнение с двумя неизвестными. Чтобы иметь возможность найти два неизвестных тока сетки, мы должны иметь два уравнения. Если мы проследим другой контур цепи, мы сможем получить еще одно уравнение КВЛ и получить достаточно данных для решения двух токов.Я – создание по привычке, я начну с верхнего левого угла правой петли и обведу ее против часовой стрелки:
Упрощая уравнение, как и раньше, получаем:
Поиск неизвестного
Теперь, имея два уравнения, мы можем использовать один из нескольких методов для математического решения неизвестных токов I 1 и I 2 :
Схема перерисовки
Зная, что эти решения являются значениями для ячеек токов, а не ветвей токов, мы должны вернуться к нашей диаграмме, чтобы увидеть, как они сочетаются друг с другом, чтобы дать токи через все компоненты:
Решение -1 ампер для I 2 означает, что мы изначально предположили, что направление тока было неправильным. На самом деле, I 2 течет против часовой стрелки при значении (положительном) 1 ампер:
На самом деле, I 2 течет против часовой стрелки при значении (положительном) 1 ампер:
Это изменение направления тока от того, что предполагалось вначале, изменит полярность падений напряжения на R 2 и R 3 из-за тока I 2 . Отсюда мы можем сказать, что ток через R 1 составляет 5 ампер, при этом падение напряжения на R 1 является произведением тока и сопротивления (E = IR), 20 вольт (положительное слева и отрицательное на право).
Также можно смело сказать, что ток через R 3 составляет 1 ампер, при падении напряжения 1 вольт (E = IR), положительный слева и отрицательный справа. Но что происходит на R 2 ?
Ток в ячейке I 1 идет «вниз» через R 2 , а ток в ячейке I 2 «вверх» через R 2 . Чтобы определить фактический ток через R 2 , мы должны увидеть, как взаимодействуют токи сетки I 1 и I 2 (в данном случае они противоположны), и алгебраически сложить их, чтобы получить окончательное значение. Так как I 1 идет «вниз» при 5 ампер, а I 2 «растет» на 1 ампер, реальный ток через R 2 должен иметь значение 4 ампера, идущее «вниз». :
Так как I 1 идет «вниз» при 5 ампер, а I 2 «растет» на 1 ампер, реальный ток через R 2 должен иметь значение 4 ампера, идущее «вниз». :
Ток 4 А через сопротивление 2 Ом R 2 дает нам падение напряжения 8 В (E = IR), положительное вверху и отрицательное внизу.
Преимущества анализа тока в сетке
Основным преимуществом анализа Mesh Current является то, что он обычно позволяет решать большую сеть с меньшим количеством неизвестных значений и меньшим количеством одновременных уравнений.В нашем примере задачи потребовалось три уравнения для решения метода Branch Current и только два уравнения с использованием метода Mesh Current. Это преимущество тем больше, чем больше сложность сетей:
Чтобы решить эту сеть с использованием токов ответвления, нам нужно было бы установить пять переменных для учета каждого уникального тока в цепи (с I 1 по I 5 ). Для этого потребуется пять уравнений для решения в форме двух уравнений KCL и трех уравнений KVL (два уравнения для KCL в узлах и три уравнения для KVL в каждом цикле):
Я полагаю, что если у вас нет ничего лучше, чем использовать свое время, как решить пять неизвестных переменных с помощью пяти уравнений, вы можете не возражать против использования метода анализа тока ветви для этой схемы. Для тех из нас, у кого есть лучших способа распорядиться своим временем, метод Mesh Current намного проще, требуя для решения всего трех неизвестных и трех уравнений:
Для тех из нас, у кого есть лучших способа распорядиться своим временем, метод Mesh Current намного проще, требуя для решения всего трех неизвестных и трех уравнений:
Меньшее количество уравнений для работы является решающим преимуществом, особенно при выполнении одновременного решения уравнений вручную (без калькулятора).
Несбалансированный мост Уитстона
Другой тип схемы, которая хорошо подходит для Mesh Current, – это несбалансированный мост Уитстона.Возьмем, например, эту схему:
Поскольку отношения R 1 / R 4 и R 2 / R 5 неравны, мы знаем, что будет напряжение на резисторе R 3 и некоторое количество тока через него. Как обсуждалось в начале этой главы, этот тип схемы не подлежит сокращению с помощью обычного последовательно-параллельного анализа и может быть проанализирован только каким-либо другим методом.
Мы могли бы применить метод тока ответвления к этой схеме, но для этого потребовалось бы шесть токов (от I 1 до I 6 ), что привело бы к очень большому набору одновременных уравнений для решения.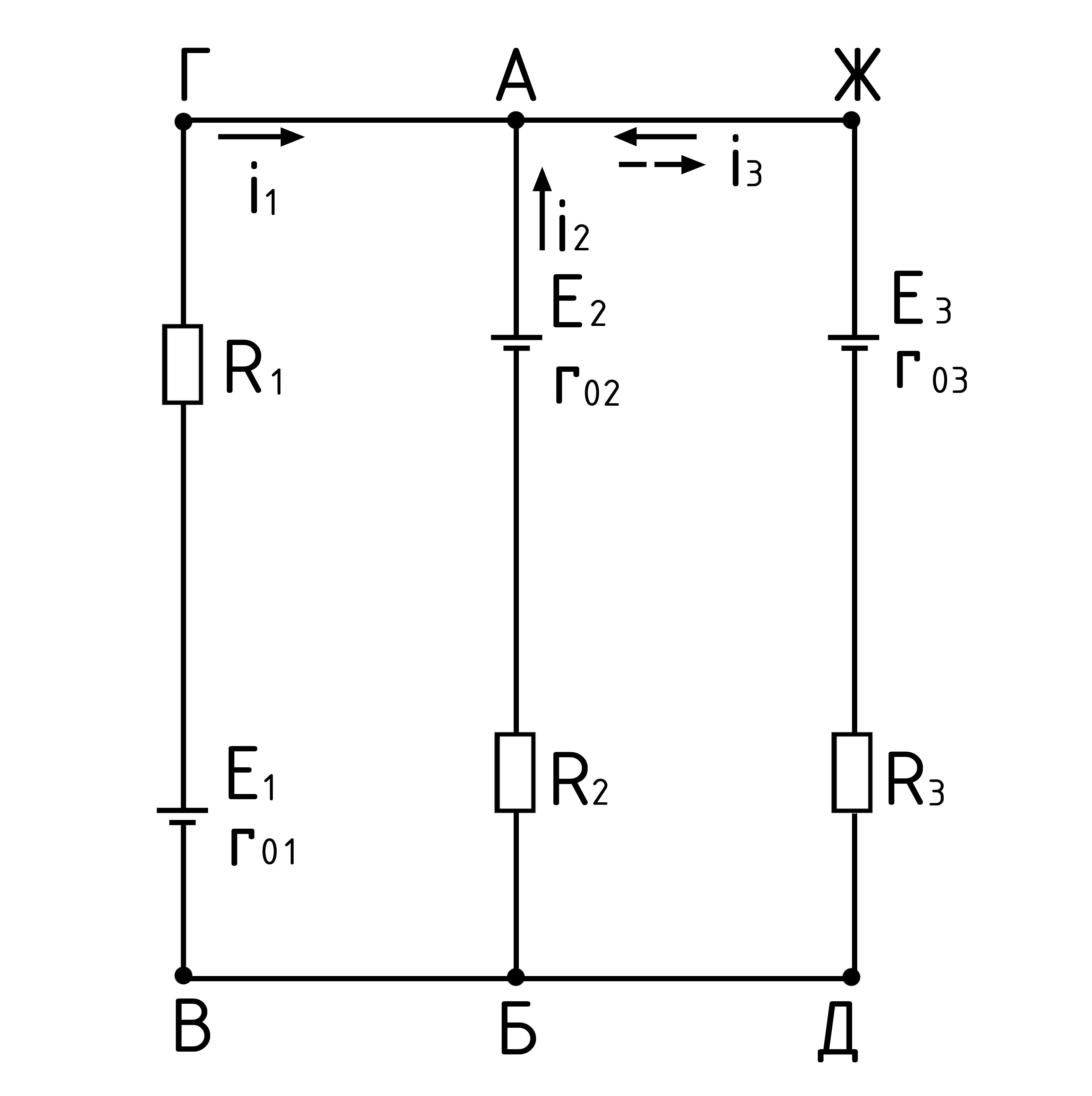 Однако, используя метод Mesh Current, мы можем решить для всех токов и напряжений с гораздо меньшим количеством переменных.
Однако, используя метод Mesh Current, мы можем решить для всех токов и напряжений с гораздо меньшим количеством переменных.
Нарисовать сетку
Первым шагом в методе Mesh Current является рисование достаточного количества токов сетки для учета всех компонентов в цепи. Глядя на нашу мостовую схему, должно быть очевидно, где разместить два из этих токов:
Направление этих сетчатых токов, конечно, произвольно. Однако двух токов сетки в этой схеме недостаточно, потому что ни I 1 , ни I 2 не проходят через батарею.Итак, мы должны добавить третий ток сетки, I 3 :
Здесь я выбрал I 3 , чтобы выполнить петлю от нижней стороны батареи, через R 4 , через R 1 и обратно к верхней стороне батареи. Это не единственный путь, который я мог выбрать для I 3 , но он кажется самым простым.
Обозначьте полярность падения напряжения на резисторе
Теперь мы должны обозначить полярность падения напряжения на резисторе в соответствии с каждым из предполагаемых направлений тока:
Обратите внимание на кое-что очень важное: на резисторе R 4 полярности для соответствующих токов сетки не совпадают. Это потому, что эти сеточные токи (I 2 и I 3 ) проходят через R 4 в разных направлениях. Это не исключает использования метода анализа Mesh Current, но немного его усложняет. Но позже мы покажем, как избежать нынешнего столкновения R 4 . (См. Пример ниже)
Это потому, что эти сеточные токи (I 2 и I 3 ) проходят через R 4 в разных направлениях. Это не исключает использования метода анализа Mesh Current, но немного его усложняет. Но позже мы покажем, как избежать нынешнего столкновения R 4 . (См. Пример ниже)
Использование KVL
Создание уравнения KVL для верхней петли моста, начиная с верхнего узла и отслеживая по часовой стрелке:
В этом уравнении мы представляем общие направления токов их суммой через общие резисторы.Например, на резисторе R 3 со значением 100 Ом падение напряжения представлено в приведенном выше уравнении KVL выражением 100 (I 1 + I 2 ), поскольку оба тока I 1 и I 2 пройду через R 3 справа налево. То же самое можно сказать и о резисторе R 1 с выражением его падения напряжения как 150 (I 1 + I 3 ), поскольку оба I 1 и I 3 проходят через него снизу вверх. резистор, и, таким образом, сработайте вместе с , чтобы создать на нем падение напряжения.
резистор, и, таким образом, сработайте вместе с , чтобы создать на нем падение напряжения.
Сгенерировать уравнение КВЛ для нижнего контура моста будет не так просто, поскольку у нас есть два тока, идущие друг против друга через резистор R 4 . Вот как я это делаю (начиная с правого узла и отслеживая против часовой стрелки):
Обратите внимание, что второй член в исходной форме уравнения имеет значение резистора R 4 , равное 300 Ом, умноженное на разность между I 2 и I 3 (I 2 – I 3 ) .Вот как мы представляем комбинированный эффект двух токов сетки, проходящих в противоположных направлениях через один и тот же компонент. Здесь очень важен выбор соответствующих математических знаков: 300 (I 2 – I 3 ) не означает то же самое, что 300 (I 3 – I 2 ). Я решил написать 300 (I 2 – I 3 ), потому что сначала я думал об эффекте I 2 (создание положительного падения напряжения, измерение с помощью воображаемого вольтметра на R 4 , красный провод на нижний и черный провод вверху), и во вторую очередь эффекта I 3 (создание отрицательного падения напряжения, красный провод внизу и черный провод вверху). Если бы я думал в терминах эффекта I 3 в первую очередь и во вторую очередь эффекта I 2 , удерживая мои воображаемые выводы вольтметра в одних и тех же положениях (красный внизу и черный вверху), выражение было бы следующим: -300 (Я 3 – Я 2 ). Обратите внимание, что это выражение математически эквивалентно первому: +300 (I 2 – I 3 ).
Если бы я думал в терминах эффекта I 3 в первую очередь и во вторую очередь эффекта I 2 , удерживая мои воображаемые выводы вольтметра в одних и тех же положениях (красный внизу и черный вверху), выражение было бы следующим: -300 (Я 3 – Я 2 ). Обратите внимание, что это выражение математически эквивалентно первому: +300 (I 2 – I 3 ).
Ну, это касается двух уравнений, но мне все еще нужно третье уравнение, чтобы завершить мой одновременный набор уравнений с тремя переменными, тремя уравнениями.Это третье уравнение также должно включать в себя напряжение батареи, которое до этого момента не фигурировало ни в одном из двух предыдущих уравнений KVL. Чтобы составить это уравнение, я снова прослежу петлю своим воображаемым вольтметром, начиная с нижнего (отрицательного) вывода батареи, шагая по часовой стрелке (опять же, направление, в котором я шагаю, произвольно и не обязательно должно совпадать с направлением тока сетки в этом контуре):
Решение токов
Решение для I 1 , I 2 и I 3 с использованием любого метода одновременных уравнений, который мы предпочитаем:
Пример: Используйте Octave, чтобы найти решение для I 1 , I 2 и I 3 из упрощенной выше формы уравнений.
Решение: В Octave, клоне Matlab® с открытым исходным кодом, введите коэффициенты в матрицу A в квадратных скобках с элементами столбца, разделенными запятыми, и строками, разделенными точкой с запятой. Введите напряжения в вектор-столбец: b. Неизвестные токи: I 1 , 2 и I 3 вычисляются командой: x = A \ b. Они содержатся в векторе-столбце x.
октава: 1> A = [300,100,150; 100,650, -300; -150,300, -450]
А =
300 100 150
100 650 -300
-150 300-450
октава: 2> b = [0; 0; -24]
b =
0
0
-24
октава: 3> x = A \ b
х =
-0.093793
0,077241
0,136092
Отрицательное значение, полученное для I 1 , говорит нам, что предполагаемое направление для этого тока сетки было неправильным. Таким образом, фактические значения тока через каждый резистор равны
.Расчет падений напряжения на каждом резисторе:
Моделирование SPICE подтверждает точность наших расчетов напряжения:
несбалансированный мост Уитстона v1 1 0 г1 1 2 150 г2 1 3 50 г3 2 3 100 г4 2 0 300 г5 3 0250 .постоянного тока v1 24 24 1 .print dc v (1,2) v (1,3) v (3,2) v (2,0) v (3,0) .конец v1 v (1,2) v (1,3) v (3,2) v (2) v (3) 2.400E + 01 6.345E + 00 4.690E + 00 1.655E + 00 1.766E + 01 1.931E + 01
Пример:
(a) Найдите новый путь для тока I 3 , который не создает противоречивой полярности на каком-либо резисторе по сравнению с I 1 или I 2 . R 4 был проблемным компонентом. (b) Найдите значения для I 1 , I 2 и I 3 .(c) Найдите пять токов резистора и сравните их с предыдущими значениями.
Решение:
(a) Маршрут I 3 через R 5 , R 3, и R 1 , как показано:
Обратите внимание, что конфликт полярности на R 4 был удален. Более того, ни один из других резисторов не имеет противоречивой полярности.
(b) Octave, бесплатный клон Matlab с открытым исходным кодом, выдает вектор тока сетки в «x»:
октава: 1> A = [300,100,250; 100,650,350; -250, -350, -500]
А =
300 100 250
100 650 350
-250-350-500
октава: 2> b = [0; 0; -24]
b =
0
0
-24
октава: 3> x = A \ b
х =
-0. 093793
-0,058851
0,136092
093793
-0,058851
0,136092
Не все токи I 1 , I 2 и I 3 совпадают (I 2 ) с предыдущим мостом из-за различных цепей контура. Однако токи резистора сравниваются с предыдущими значениями:
IR1 = I1 + I3 = -93,793 мА + 136,092 мА = 42,299 мА
IR2 = I1 = -93,793 мА
IR3 = I1 + I2 + I3 = -93,793 мА -58,851 мА + 136,092 мА = -16,552 мА
IR4 = I2 = -58,851 мА
IR5 = I2 + I3 = -58.851 ма + 136,092 ма = 77,241 ма
Поскольку токи резисторов такие же, как и предыдущие значения, напряжения резисторов будут идентичны и не нужно рассчитывать заново.
ОБЗОР:
- Шаги, которые необходимо выполнить для метода анализа «Mesh Current»:
- (1) Нарисуйте сеточные токи в контурах цепи, достаточные для учета всех компонентов.
- (2) Обозначьте полярность падения напряжения на резисторе в зависимости от предполагаемого направления токов сетки.
- (3) Напишите уравнения KVL для каждого контура цепи, подставляя произведение IR вместо E в каждом члене резистора в уравнении. Если два тока сетки пересекаются через компонент, выразите ток как алгебраическую сумму этих двух токов сетки (т. Е. I 1 + I 2 ), если токи проходят через этот компонент в одном и том же направлении. Если нет, выразите ток как разность (т. Е. I 1 – I 2 ).
- (4) Решите для неизвестных сеточных токов (системы уравнений).
- (5) Если какое-либо решение отрицательное, то предполагаемое направление тока неверно!
- (6) Алгебраически сложите токи сетки, чтобы найти компоненты тока, разделяющие несколько токов сетки.
- (7) Найдите падение напряжения на всех резисторах (E = IR).
Сетка тока при осмотре
Мы еще раз посмотрим на «метод сеточного тока», когда все токи идут по часовой стрелке (cw). Мотивация состоит в том, чтобы упростить запись уравнений сетки, игнорируя полярность падения напряжения на резисторе.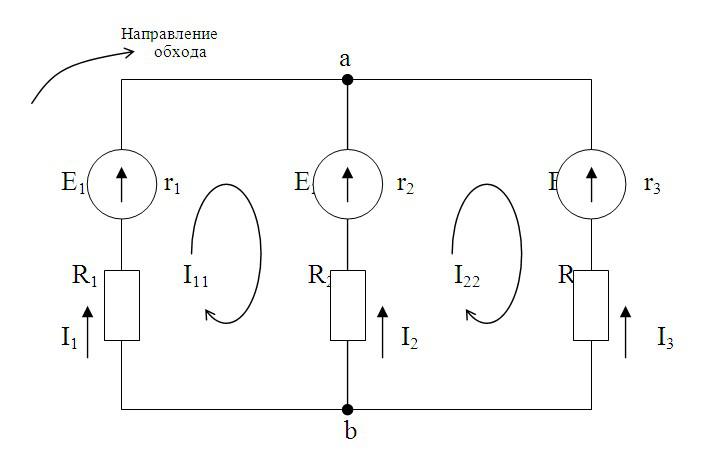 Однако мы должны обращать внимание на полярность источников напряжения относительно предполагаемого направления тока. Знак падения напряжения на резисторе будет фиксированным.
Однако мы должны обращать внимание на полярность источников напряжения относительно предполагаемого направления тока. Знак падения напряжения на резисторе будет фиксированным.
Если мы напишем набор обычных уравнений сеточного тока для схемы ниже, где мы обратим внимание на признаки падения напряжения на резисторах, мы можем переставить коэффициенты в фиксированную схему:
После перестановки мы можем писать уравнения путем проверки. Знаки коэффициентов следуют фиксированному шаблону в паре выше или в наборе из трех в правилах ниже.
Mesh Текущие правила:
- Этот метод предполагает использование обычных источников напряжения, протекающих по току. Замените любой источник тока, подключенный параллельно, с резистором, на эквивалентный источник напряжения, подключенный последовательно с эквивалентным сопротивлением.
- Игнорируя направление тока или полярность напряжения на резисторах, нарисуйте токовые петли против часовой стрелки, проходящие через все компоненты.
 Избегайте вложенных циклов.
Избегайте вложенных циклов. - Напишите уравнения закона напряжения в терминах неизвестных токов: I 1 , I 2 и I 3 .Коэффициент 1 по уравнению 1, коэффициент 2 по уравнению 2 и коэффициент 3 по уравнению 3 представляют собой положительные суммы резисторов вокруг соответствующих контуров.
- Все остальные коэффициенты отрицательны, что соответствует общему сопротивлению пары шлейфов. Коэффициент 2 уравнения 1 – это резистор, общий для контуров 1 и 2, коэффициент 3 – резистор, общий для контуров 1 и 3. Повторите для других уравнений и коэффициентов.
- + (сумма петли R 1) I1 – (общая петля R 1-2) I2 – (общая петля R 1-3) I3 = E1
– (общая петля R 1-2) I1 + (сумма петли 2 R ) I2 – (общая петля R 2-3) I3 = E2
– (общая петля R 1-3) I1 – (общая петля R 2-3) I2 + (сумма петли R 3) I3 = E3 - Правая часть уравнений равна источнику напряжения электронного тока.Повышение напряжения по сравнению с предполагаемым током против часовой стрелки является положительным и 0 для отсутствия источника напряжения.

- Решите уравнения для токов в сетке: I 1 , I 2 и I3. Найдите токи через отдельные резисторы с помощью KCL. Решите для напряжений с помощью закона Ома и KVL.
Хотя приведенные выше правила специфичны для трехуровневой схемы, правила могут быть расширены на более мелкие или большие сетки. На рисунке ниже показано применение правил. Все три тока тянутся в одном направлении по часовой стрелке.Для каждого из трех контуров записывается одно уравнение КВЛ. Обратите внимание, что на резисторах не указана полярность. Нам это не нужно для определения знаков коэффициентов. Хотя нам нужно обратить внимание на полярность источника напряжения по отношению к направлению тока. I 3 по часовой стрелке ток течет от положительной клеммы (+) источника l24 В, а затем возвращается на клемму (-). Это повышение напряжения при обычном протекании тока. Следовательно, правая часть третьего уравнения равна -24V.
В Octave введите коэффициенты в матрицу A с элементами столбцов, разделенными запятыми, и строками, разделенными точкой с запятой. Введите напряжения в вектор-столбец b. Найдите неизвестные токи: I 1 , I 2 и I 3 с помощью команды: x = A \ b. Эти токи содержатся в векторе-столбце x. Положительные значения указывают на то, что все три тока сетки текут в предполагаемом направлении по часовой стрелке.
Введите напряжения в вектор-столбец b. Найдите неизвестные токи: I 1 , I 2 и I 3 с помощью команды: x = A \ b. Эти токи содержатся в векторе-столбце x. Положительные значения указывают на то, что все три тока сетки текут в предполагаемом направлении по часовой стрелке.
октава: 2> A = [300, -100, -150; -100,650, -300; -150, -300,450]
А =
300-100 -150
-100 650 -300
-150 -300 450
октава: 3> b = [0; 0; 24]
b =
0
0
24
октава: 4> x = A \ b
х =
0.093793
0,077241
0,136092
Токи сетки соответствуют предыдущему решению за счет другого метода тока сетки. Расчет напряжений и токов резисторов будет идентичен предыдущему решению. Не нужно здесь повторяться.
Обратите внимание, что тексты по электротехнике основаны на обычном потоке тока. Методы петлевого тока и тока сетки в этих текстах будут работать с предполагаемыми токами сетки по часовой стрелке .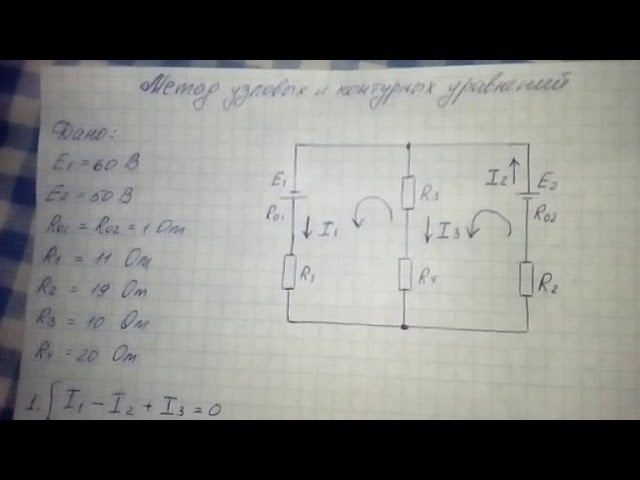 Обычный ток течет через клемму (+) батареи через цепь, возвращаясь к клемме (-).Обычное повышение ток-напряжения соответствует отслеживанию предполагаемого тока от (-) до (+) через любые источники напряжения.
Обычный ток течет через клемму (+) батареи через цепь, возвращаясь к клемме (-).Обычное повышение ток-напряжения соответствует отслеживанию предполагаемого тока от (-) до (+) через любые источники напряжения.
Далее следует еще один пример предыдущей схемы. Сопротивление вокруг контура 1 составляет 6 Ом, вокруг контура 2: 3 Ом. Общее сопротивление обоих контуров составляет 2 Ом. Обратите внимание на коэффициенты I 1 и I 2 в паре уравнений. Отслеживание предполагаемого тока петли 1 по часовой стрелке через B 1 от (+) до (-) соответствует увеличению напряжения потока электронного тока.
Таким образом, знак 28 В положительный. Контур 2 против часовой стрелки предположил, что ток идет от (-) до (+) через B 2 , то есть падение напряжения. Таким образом, знак B 2 отрицательный, -7 во 2-м уравнении сетки. Опять же, на резисторах нет маркировки полярности. Они также не фигурируют в уравнениях.
Оба тока I 1 = 5 A и I 2 = 1 A являются положительными.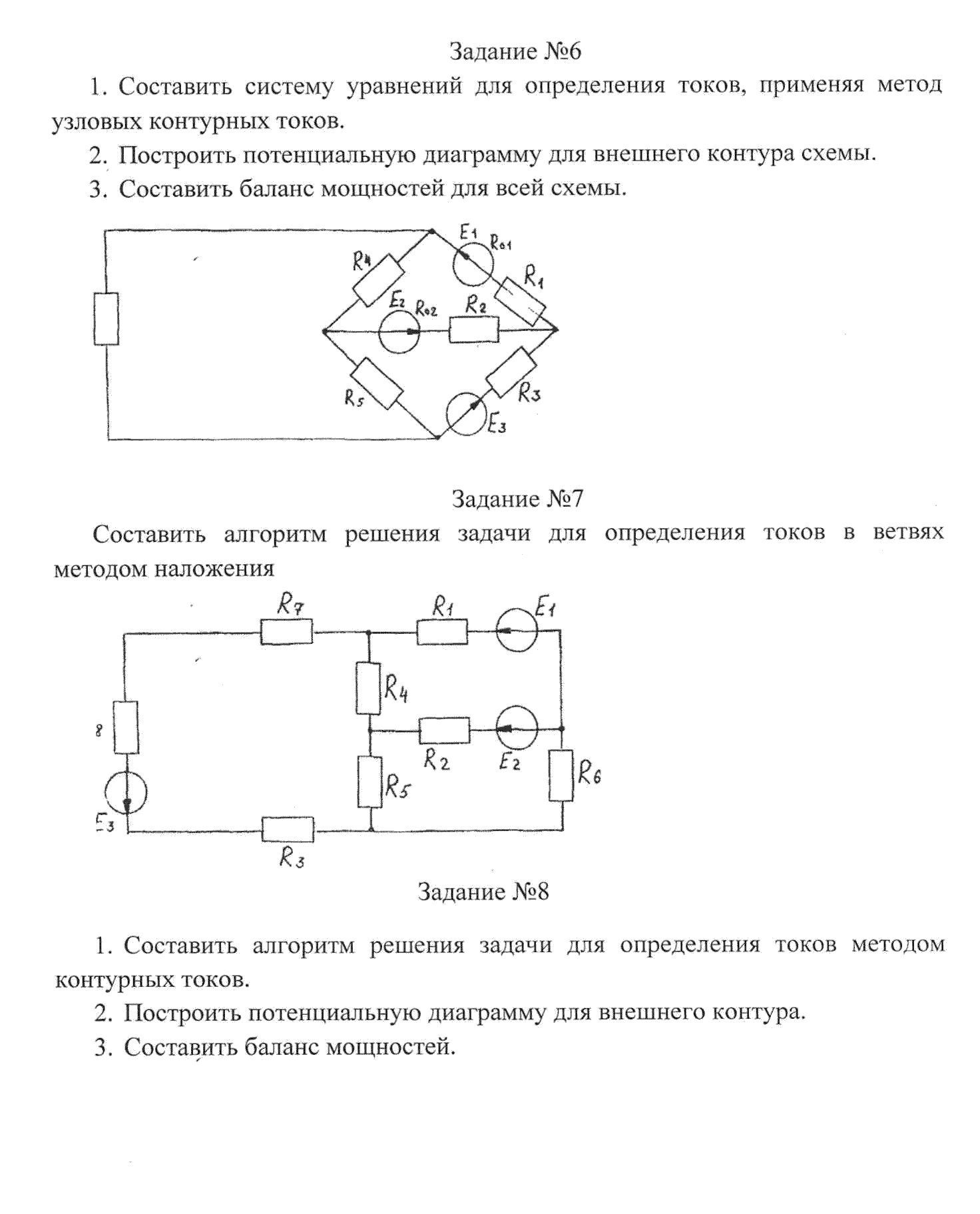 Оба они текут в направлении петель по часовой стрелке.Это сравнивается с предыдущими результатами.
Оба они текут в направлении петель по часовой стрелке.Это сравнивается с предыдущими результатами.
Резюме:
- Модифицированный метод тока сетки позволяет избежать необходимости определять знаки коэффициентов уравнения путем рисования всех токов сетки по часовой стрелке для обычного протекания тока.
- Однако нам необходимо определить знак любых источников напряжения в контуре. Источник напряжения является положительным, если предполагаемый непрерывный ток протекает с батареей (источником). Знак отрицательный, если предполагаемый непрерывный ток течет по батарее.
- Подробности см. В правилах выше.
СВЯЗАННЫЙ ТАБЛИЦА:
Алгоритмов
АЛГОРИТМЫ – A *
Алгоритм A * – алгоритм поиска лучший первый , который полагается в открытом и закрытом списках, чтобы найти путь, который является оптимальным и завершить к цели. Он работает, сочетая в себе преимущества модели с унифицированной стоимостью . поиск и жадный поиск алгоритмов.A * использует оба элемента включив в свой алгоритм две отдельные функции поиска пути, которые принимают учитывать стоимость от корневого узла до текущего узла и оценивать стоимость пути от текущего узла к целевому узлу.
Он работает, сочетая в себе преимущества модели с унифицированной стоимостью . поиск и жадный поиск алгоритмов.A * использует оба элемента включив в свой алгоритм две отдельные функции поиска пути, которые принимают учитывать стоимость от корневого узла до текущего узла и оценивать стоимость пути от текущего узла к целевому узлу.
Первая функция – g (n) , которая вычисляет путь стоимость между начальным узлом и текущим узлом. Вторая функция h (n) , который представляет собой эвристику для расчета оценочной стоимости пути из текущий узел к целевому узлу. F (n) = g (n) + h (n) . Это представляет стоимость наиболее эффективного предполагаемого пути к цели. А * продолжает переоценивать как g (n), так и h (n) на протяжении поиска всех узлов, с которыми он сталкивается, чтобы прийти к пути с минимальной стоимостью к цели. Этот алгоритм чрезвычайно популярен для поиска пути в стратегии. компьютерные игры.
компьютерные игры.
Процесс для A * в основном следующий:
1. Создайте пустой список открытых и закрытых .Поместите начальный узел в открытый список.
2. Повторяйте это до тех пор, пока цель не будет найдена или открытый список не станет пустым:
a. Найдите узел с наименьшей стоимостью F в открытом списке и поместите его в закрытый список.
г. Разверните этот узел и соседние с ним узлы:
i. Если они в закрытом списке, игнорируйте.
ii. Если нет в открытом списке, добавить в открытый список, сохранить текущий узел как родительского элемента для этого соседнего узла и вычислите затраты F, G, H для соседний узел.
iii. Если в открытом списке, сравните G-стоимость этого пути к узлу и старый путь к узлу. Если стоимость G использования текущего узла для получения к узлу – меньшая стоимость, измените родительский узел соседнего узла к текущему узлу. Пересчитайте стоимость узла F, G, H.
3. Если открытый список пуст, завершиться ошибкой.
Члены локально конечные , допустимые и монотонные вся помощь в понимании того, когда можно ожидать завершения A *, это означает, что он находит решение, и оптимальное, что означает, что он находит решение с наименьшей стоимостью пути.Локально конечный граф – это один где ни один из узлов на графе не имеет бесконечного фактора ветвления, таким образом, ни один из путей к узлам не разветвляется навсегда. Фактор ветвления узла относится к количеству новых узлов, которые могут быть расширены из этого узла.
Эвристика допустима, если она всегда оптимистична; он либо недооценивает стоимость пути к цели, либо дает правильный оценка стоимости пути к цели, но никогда не переоценивает путь стоимость к цели.
Эвристика является монотонной, если на каждом пути от корня до цель общая расчетная стоимость пути не уменьшается, поскольку эвристика идет вниз по дереву узлов.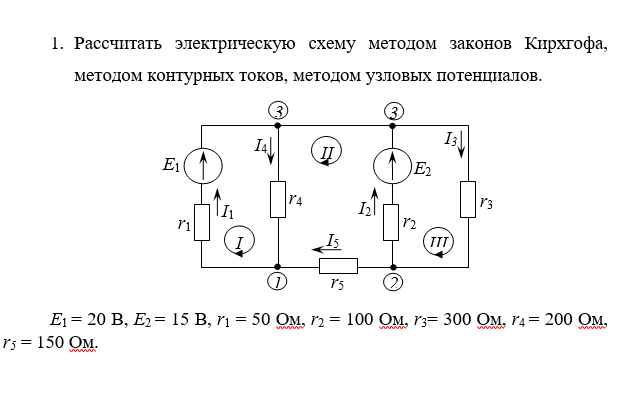 (Иллюстрация) Немонотонная эвристика может быть сделана монотонный по уравнению максимума пути, которое сравнивает расчетную стоимость пути узла с предполагаемой стоимостью пути его родительского узла. Затем он использует более высокая стоимость пути для оценки. Следовательно, если эвристическая оценка стоимость пути уменьшается от одного узла к его дочернему узлу, pathmax уравнение использует стоимость пути родительского узла, поэтому она не оценивается по мере уменьшения.
(Иллюстрация) Немонотонная эвристика может быть сделана монотонный по уравнению максимума пути, которое сравнивает расчетную стоимость пути узла с предполагаемой стоимостью пути его родительского узла. Затем он использует более высокая стоимость пути для оценки. Следовательно, если эвристическая оценка стоимость пути уменьшается от одного узла к его дочернему узлу, pathmax уравнение использует стоимость пути родительского узла, поэтому она не оценивается по мере уменьшения.
Рис.1 Иллюстрация карты с однообразием с контурами 380, 400 и 420.
A * является полным и оптимальным на локально конечных графах. где эвристики допустимы и монотонны.
A * должен быть локально конечным, потому что если существует бесконечное количество узлов, в которых расчетная стоимость пути, f (n), меньше фактической стоимость пути к цели, тогда алгоритм может продолжить исследование этих узлов без конца, и он не будет ни полным, ни оптимальным.
Как монотонность влияет на полноту A *? Поскольку A * – это монотонный, стоимость пути увеличивается по мере удаления узла от корня. Можно нарисовать контуры, чтобы показать области, где расчетная стоимость пути, f (n), для узлов внутри областей меньше или равно стоимости пути для внешних границ контуров. Эти контуры можно нарисовать как можно больше и большие области, которые увеличиваются наружу как f (n) для внешней границы этих контуров увеличивается.Первое найденное решение является оптимальным, поскольку оно это первая полоса, где f (n) для контура равна стоимости пути для цели. Все контуры за пределами этого решения будут иметь более высокий f стоимость.
Оптимальность A * доказана от противного. Во-первых, предполагается что g – оптимальное целевое состояние со стоимостью пути f (g), что s – субоптимальное целевое состояние со стоимостью пути g (s)> f (g), и что n является узлом на оптимальный путь к г.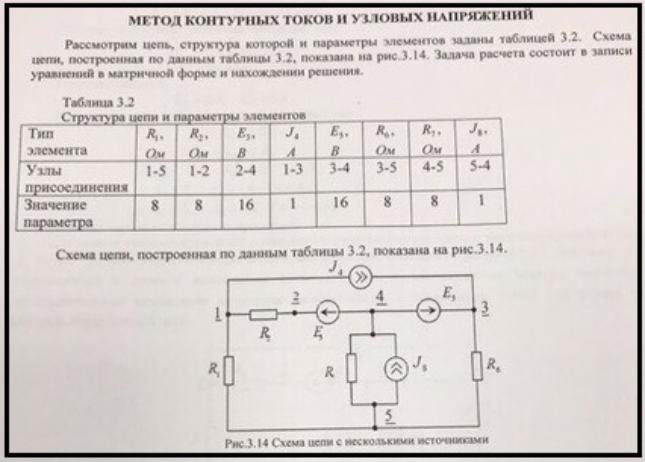 Мы предполагаем, что A * выбирает s (неоптимальная цель) вместо n (узел на оптимальном пути) из открытого списка.
Мы предполагаем, что A * выбирает s (неоптимальная цель) вместо n (узел на оптимальном пути) из открытого списка.
Поскольку h допустимо, (оптимистично), f (g)> = f (n). (В фактическая стоимость пути больше или равна стоимости пути, оцененной эвристика в п.)
Если n не выбрано вместо s для расширения с помощью A *, f (n)> = f (s). (Эвристика выбирает узел с наименьшей оценочной стоимостью F-пути.)
Таким образом, f (g)> = f (s).
Поскольку s является целевым состоянием, h (s) = 0. (Оценка из текущий узел к последнему узлу должен быть 0.)
Итак, f (s) = g (s). (f (s) = g (s) + h (s).)
Таким образом, f (g)> = g (s). Это противоречит утверждению, что S неоптимален, поэтому должно быть верно, что A * никогда не выбирает неоптимальный путь. Поскольку A * может иметь в качестве решения только узел, который он выбрал для расширения, это оптимально.
% PDF-1.4 % 31 0 объект > эндобдж 30 0 объект > поток StampPDF Пакет 2.7 для Solaris – SPDF 10452005-04-18T12: 09: 53Z2022-01-03T06: 07: 53-08: 002022-01-03T06: 07: 53-08: 00XPPapplication / pdf
uuid: ae4cfacc-1dd1-11b2-0a00-4508275dc400uuid: ae4cfacf-1dd1-11b2-0a00-810000000000 005 Tc 9 0 0 9 51,6761 612,3835 Tm
[(где) -279,7 (сингулярность) 19,9 (с) -279,7 (дюймы) -279,7 (значения) -279,7 (целые) -19,9 (ранды) -279,7 (являются) -279,7 (удалены;) – 279,7 (однако,) -279,7 (the)] TJ
0 -1,1174 ТД
[(числовые) -315,4 (идеи) -315,4 (предварительные) 19,9 (отправленные) -315,4 (приведенные выше) -315,4 (являются) -315,4 (все еще) -315,4 (достоверные) -315,4 (исходные) -315,4 (фактические) -315,4 (уравнение)] ТДж
/ T1_1 1 Тс
0 Тс 26.0272 0 Тд
(7) Tj
/ T1_0 1 Тс
0,005 Тс 0,8204 0 Тд
(is) Tj
-26,8476 -1,1174 тд
[(также) -337,8 (действительный) -337,8 (для) -337,8 (0)] TJ
/ T1_2 1 Тс
0 Тс 6.9034 0 тд
(\ 007) Tj
/ T1_3 1 Тс
9 0 1,3977 9 124,389 592,2699 тм
(\ t) Tj
/ T1_2 1 Тс
9 0 0 9 132,973 592,2699 тм
(\ 007) Tj
/ T1_0 1 Тс
0,005 Тс 1,1758 0 Тд
(1.) Tj
/ T1_4 1 Тс
-0.01961 Tc -10.2088 -2.0063 Td
[(Доказательства) -313,1 (из) -313,1 (Сингулярности)] TJ
/ T1_0 1 Тс
0,005 Tc 0 -1,3396 TD
[(We) -612,4 (per) -49,9 (для) -30 (med) -612,4 (несколько) -612,4 (числовой) -612,4 (ex) -30 (periment) -612,4 (для) -612,4 (diff) – 30 (ferent)] TJ
0 -1,1174 ТД
[(значение) 19,9 (с) -393,7 (из)] ТДж
/ T1_3 1 Тс
0 Tc 9 0 1,3977 9 90,5887 552.
005 Tc 9 0 0 9 51,6761 612,3835 Tm
[(где) -279,7 (сингулярность) 19,9 (с) -279,7 (дюймы) -279,7 (значения) -279,7 (целые) -19,9 (ранды) -279,7 (являются) -279,7 (удалены;) – 279,7 (однако,) -279,7 (the)] TJ
0 -1,1174 ТД
[(числовые) -315,4 (идеи) -315,4 (предварительные) 19,9 (отправленные) -315,4 (приведенные выше) -315,4 (являются) -315,4 (все еще) -315,4 (достоверные) -315,4 (исходные) -315,4 (фактические) -315,4 (уравнение)] ТДж
/ T1_1 1 Тс
0 Тс 26.0272 0 Тд
(7) Tj
/ T1_0 1 Тс
0,005 Тс 0,8204 0 Тд
(is) Tj
-26,8476 -1,1174 тд
[(также) -337,8 (действительный) -337,8 (для) -337,8 (0)] TJ
/ T1_2 1 Тс
0 Тс 6.9034 0 тд
(\ 007) Tj
/ T1_3 1 Тс
9 0 1,3977 9 124,389 592,2699 тм
(\ t) Tj
/ T1_2 1 Тс
9 0 0 9 132,973 592,2699 тм
(\ 007) Tj
/ T1_0 1 Тс
0,005 Тс 1,1758 0 Тд
(1.) Tj
/ T1_4 1 Тс
-0.01961 Tc -10.2088 -2.0063 Td
[(Доказательства) -313,1 (из) -313,1 (Сингулярности)] TJ
/ T1_0 1 Тс
0,005 Tc 0 -1,3396 TD
[(We) -612,4 (per) -49,9 (для) -30 (med) -612,4 (несколько) -612,4 (числовой) -612,4 (ex) -30 (periment) -612,4 (для) -612,4 (diff) – 30 (ferent)] TJ
0 -1,1174 ТД
[(значение) 19,9 (с) -393,7 (из)] ТДж
/ T1_3 1 Тс
0 Tc 9 0 1,3977 9 90,5887 552. 0994 Тм
(\ t) Tj
/ T1_0 1 Тс
0,005 Тс 9 0 0 9 96,1329 552,0994 Тм
[(.) – 393,7 (In) -393,6 (Рис.) – 393,7 (1,) – 393,7 (we) -393,7 (pre) 19,9 (отправлено) -393,7 (the) -393,7 (профиль) 19,9 (s) – 393.7 (at)] ТДж
/ T1_5 1 Тс
0 Тс 16.9759 0 Тд
(t) Tj
/ T1_2 1 Тс
0,6767 0 тд
(\ 004) Tj
/ T1_0 1 Тс
0,005 Тс 1,2316 0 Тд
[(0,) – 393,7 (7,066,)] ТДж
-23,8238 -1,1174 тд
[(11,046,) – 287,9 (13,103,) – 287,9 (15,383,) – 287,9 (и) -287,9 (16,515) -287,9 (для)] ТДж
/ T1_3 1 Тс
0 Тс 9 0 1,3977 9 200,0623 542,0426 Тм
(\ t) Tj
/ T1_2 1 Тс
9 0 0 9 208.1974 542.0426 Тм
(\ 004) Tj
/ T1_0 1 Тс
0,005 Тс 1,1259 0 Тд
[(0,5,) – 287,9 (и) -287,9 (дюйм) -287,9 (рис.) – 287,9 (2,) – 287,9 (ср)] TJ
-18,5171 -1,1174 тд
[(pre) 19,9 (отправлено) -288,9 (the) -288,9 (то же) -288,9 (at)] TJ
/ T1_5 1 Тс
0 Тс 8.7669 0 Тд
(t) Tj
/ T1_2 1 Тс
0,5719 0 Тд
(\ 004) Tj
/ T1_0 1 Тс
0,005 Тс 1,1268 0 Тд
[(0,) – 288,9 (1,962,) – 288,9 (3,3,) – 288,9 (4,031,) – 288,9 (4,369,) – 288,9 (и) -288,8 (4,464) -288,9 (для))] TJ
/ T1_3 1 Тс
0 Тс 9 0 1,3977 9 51,6761 521,929 Тм
(\ t) Tj
/ T1_2 1 Тс
9 0 0 9 59,9874 521,929 тм
(\ 004) Tj
/ T1_0 1 Тс
0.
0994 Тм
(\ t) Tj
/ T1_0 1 Тс
0,005 Тс 9 0 0 9 96,1329 552,0994 Тм
[(.) – 393,7 (In) -393,6 (Рис.) – 393,7 (1,) – 393,7 (we) -393,7 (pre) 19,9 (отправлено) -393,7 (the) -393,7 (профиль) 19,9 (s) – 393.7 (at)] ТДж
/ T1_5 1 Тс
0 Тс 16.9759 0 Тд
(t) Tj
/ T1_2 1 Тс
0,6767 0 тд
(\ 004) Tj
/ T1_0 1 Тс
0,005 Тс 1,2316 0 Тд
[(0,) – 393,7 (7,066,)] ТДж
-23,8238 -1,1174 тд
[(11,046,) – 287,9 (13,103,) – 287,9 (15,383,) – 287,9 (и) -287,9 (16,515) -287,9 (для)] ТДж
/ T1_3 1 Тс
0 Тс 9 0 1,3977 9 200,0623 542,0426 Тм
(\ t) Tj
/ T1_2 1 Тс
9 0 0 9 208.1974 542.0426 Тм
(\ 004) Tj
/ T1_0 1 Тс
0,005 Тс 1,1259 0 Тд
[(0,5,) – 287,9 (и) -287,9 (дюйм) -287,9 (рис.) – 287,9 (2,) – 287,9 (ср)] TJ
-18,5171 -1,1174 тд
[(pre) 19,9 (отправлено) -288,9 (the) -288,9 (то же) -288,9 (at)] TJ
/ T1_5 1 Тс
0 Тс 8.7669 0 Тд
(t) Tj
/ T1_2 1 Тс
0,5719 0 Тд
(\ 004) Tj
/ T1_0 1 Тс
0,005 Тс 1,1268 0 Тд
[(0,) – 288,9 (1,962,) – 288,9 (3,3,) – 288,9 (4,031,) – 288,9 (4,369,) – 288,9 (и) -288,8 (4,464) -288,9 (для))] TJ
/ T1_3 1 Тс
0 Тс 9 0 1,3977 9 51,6761 521,929 Тм
(\ t) Tj
/ T1_2 1 Тс
9 0 0 9 59,9874 521,929 тм
(\ 004) Tj
/ T1_0 1 Тс
0. 005 Tc 1.1455 0 Td
[(1) -307,5 (\ (the) -307,5 (sur) -49,9 (лицо) -307,5 (квазигеострофическое) -307,5 (уравнение \).) – 307,5 (As) -307,5 (we) -307,5 (может ) -307,5 (см.,)] TJ
-2,0689 -1,1174 тд
[(t) -30 (wo) -273,7 (c) -30 (orners) -273,7 (w) -39,8 (iith) -273,7 (high) -273,7 (значение) 19,9 (s) -273,7 (of) -273,7) (cur) -60 (vature) -273,7 (do) -273,7 (development) -273,7 (in) -273,7 (the) -273,7 (last)] TJ
Т *
[(графики.) – 353.9 (Оно) -353.9 (выглядит) -353.9 (похоже) -353.9 (a) -353.9 (резкое) -353.9 (f) -30 (ront) -353.9 (кажется,) – 353.9 (дюйм) ) -353,9 (в) -353.9 (смысл) -353.9 (что) -353.9 (the)] TJ
Т *
[(boundar) -60 (y) -255.1 (of) -255.1 (the) -255.1 (t) -30 (wo) -255.1 (patch)) 19.9 (s) -255.1 (кажется) -255.1 (to) -255.1 (c) -30 (развал) -255,1 (вдоль) -255,1 (a) -255,1 (cur) -60 (ve.) – 255,1 (In)] TJ
Т *
[(факт,) – 330,2 (это) -330,2 (это) -330,2 (не) -330,2 (то) -330,2 (случай,) – 330,2 (как) -330,2 (один) -330,2 (может) -330,2 (см. ) -330,2 (ж) -30 (ром) -330,2 (рис.
005 Tc 1.1455 0 Td
[(1) -307,5 (\ (the) -307,5 (sur) -49,9 (лицо) -307,5 (квазигеострофическое) -307,5 (уравнение \).) – 307,5 (As) -307,5 (we) -307,5 (может ) -307,5 (см.,)] TJ
-2,0689 -1,1174 тд
[(t) -30 (wo) -273,7 (c) -30 (orners) -273,7 (w) -39,8 (iith) -273,7 (high) -273,7 (значение) 19,9 (s) -273,7 (of) -273,7) (cur) -60 (vature) -273,7 (do) -273,7 (development) -273,7 (in) -273,7 (the) -273,7 (last)] TJ
Т *
[(графики.) – 353.9 (Оно) -353.9 (выглядит) -353.9 (похоже) -353.9 (a) -353.9 (резкое) -353.9 (f) -30 (ront) -353.9 (кажется,) – 353.9 (дюйм) ) -353,9 (в) -353.9 (смысл) -353.9 (что) -353.9 (the)] TJ
Т *
[(boundar) -60 (y) -255.1 (of) -255.1 (the) -255.1 (t) -30 (wo) -255.1 (patch)) 19.9 (s) -255.1 (кажется) -255.1 (to) -255.1 (c) -30 (развал) -255,1 (вдоль) -255,1 (a) -255,1 (cur) -60 (ve.) – 255,1 (In)] TJ
Т *
[(факт,) – 330,2 (это) -330,2 (это) -330,2 (не) -330,2 (то) -330,2 (случай,) – 330,2 (как) -330,2 (один) -330,2 (может) -330,2 (см. ) -330,2 (ж) -30 (ром) -330,2 (рис.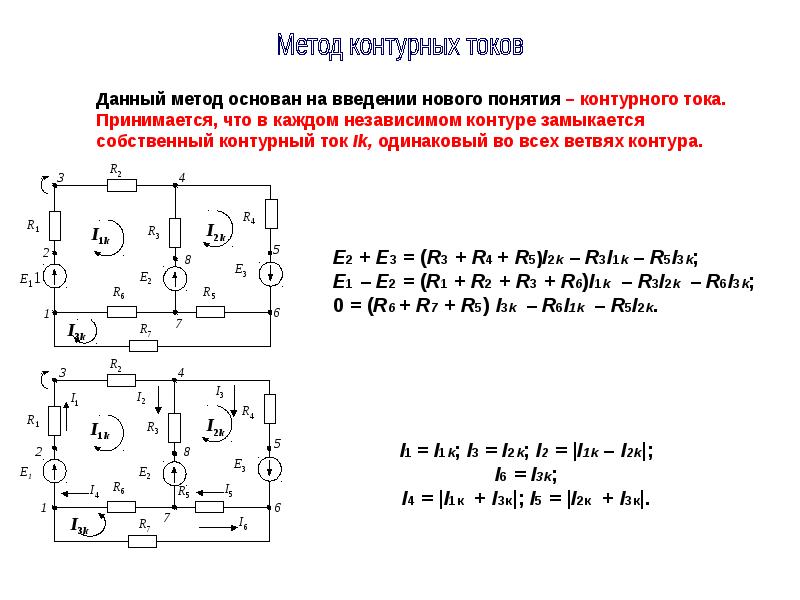 ) – 330,2 (3,) – 330,2 (где) -330,2 (в)] ТДж
Т *
[(t) -30 (wo) -187,5 (cur) -60 (ve) 19,9 (s) -187,5 (кажется) -187,5 (ясно) -187.5 (отдельно) -187,5 (кроме) -187,5 (для) -187,5 (один) -187,5 (балл) -187,5 (в) -187,5 (который)] TJ
Т *
[(они) -217,2 (получают) -217,2 (так) -217,2 (близко) -217,2 (те) -217,2 (они) -217,2 (кажутся) -217,2 (к) -217,2 (касаются) -217,2 (каждый) – 217.2 (другое) -217.2 (\ (the) -217.2 (c) -30 (orner \).)] TJ
Т *
[(In) -336.2 (Рис.) – 336.2 (4,) – 336.2 (a) -336.2 (magn) -30 (ification) -336.2 (of) -336.2 (the) -336.2 (c) -30 (orner) ) -336,2 (область) -336,2 (при) -336,2 (несколько) -336,2 (время) 19,9 (с)] TJ
Т *
[(составляет) -318,5 (представляет) 19,9 (отправлено,) – 318,5 (вместе) -318.5 (w) -39,8 (i) -318,5 (a) -318,5 (представляет) 19,9 (отправлено) -30 (ation) -318,5 (of) -318,5 (the) -318,5 (max) -49,9 (imum)] TJ
Т *
[(cur) -60 (vature) -337.8 (of) -337.8 (the) -337.8 (patch) -337.8 (c) -30 (ontour) -337.8 (as) -337.8 (a) -337.8 (function) – 337,8 (из) -337,8 (раз.
) – 330,2 (3,) – 330,2 (где) -330,2 (в)] ТДж
Т *
[(t) -30 (wo) -187,5 (cur) -60 (ve) 19,9 (s) -187,5 (кажется) -187,5 (ясно) -187.5 (отдельно) -187,5 (кроме) -187,5 (для) -187,5 (один) -187,5 (балл) -187,5 (в) -187,5 (который)] TJ
Т *
[(они) -217,2 (получают) -217,2 (так) -217,2 (близко) -217,2 (те) -217,2 (они) -217,2 (кажутся) -217,2 (к) -217,2 (касаются) -217,2 (каждый) – 217.2 (другое) -217.2 (\ (the) -217.2 (c) -30 (orner \).)] TJ
Т *
[(In) -336.2 (Рис.) – 336.2 (4,) – 336.2 (a) -336.2 (magn) -30 (ification) -336.2 (of) -336.2 (the) -336.2 (c) -30 (orner) ) -336,2 (область) -336,2 (при) -336,2 (несколько) -336,2 (время) 19,9 (с)] TJ
Т *
[(составляет) -318,5 (представляет) 19,9 (отправлено,) – 318,5 (вместе) -318.5 (w) -39,8 (i) -318,5 (a) -318,5 (представляет) 19,9 (отправлено) -30 (ation) -318,5 (of) -318,5 (the) -318,5 (max) -49,9 (imum)] TJ
Т *
[(cur) -60 (vature) -337.8 (of) -337.8 (the) -337.8 (patch) -337.8 (c) -30 (ontour) -337.8 (as) -337.8 (a) -337.8 (function) – 337,8 (из) -337,8 (раз.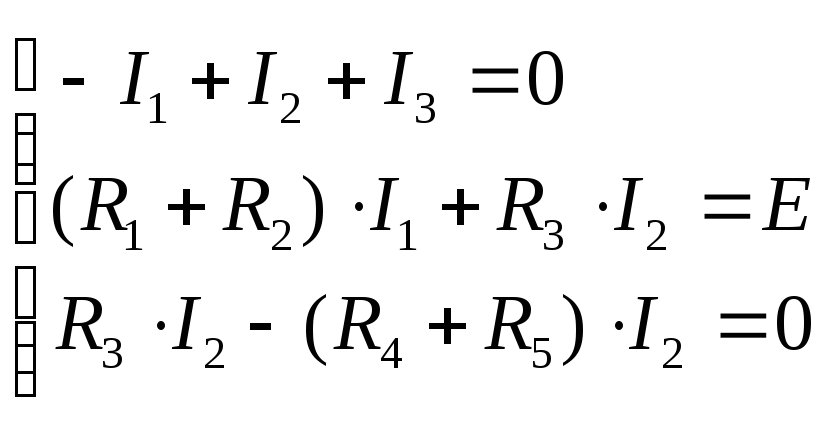 )] TJ
1 -1,1174 тд
[(The) -208,4 (быстро) -208,4 (g) -19,9 (ряд) -30 (th) -208,4 (of) -208,4 (the) -208,4 (cur) -60 (vature) -208,4 (sugge) 19,9 (стс) -208,4 (та) -208,4 (ит) -208,4 (мощь) -208,4 (удар) -208,4 (вверх)] TJ
-1 -1,1174 тд
[(при) -259,2 (а) -259,2 (плав) -30 (ите) -259.2 (время)] TJ
/ T1_5 1 Тс
0 Тс 6.603 0 Тд
(t) Tj
/ T1_0 1 Тс
6.5 0 0 6 113.6508 410.054 тм
(0) Tj
0,005 Тс 9 0 0 9 116,9322 411,304 Тм
[(.) – 259,2 (In) -259,2 (факт,) – 259,2 (если) -259,2 (we) -259,2 (re) 19,9 (масштаб) -259,2 (the) -259,2 (пространственный) -259,2 (переменный) – 259,2 (дюйм) -259,2 (дюйм)] TJ
-7,2507 -1,1174 тд
[(для) -30 (м)] ТДж
/ T1_5 1 Тс
0 Тс 2,5337 0 Тд
(x) Tj
/ T1_6 1 Тс
0,0132 0 Тд
(\ 001) Tj
/ T1_2 1 Тс
0,8135 0 тд
(\ 004) Tj
/ T1_0 1 Тс
1,2446 0 тд
(\ () Tj
/ T1_5 1 Тс
0,388 0 Тд
(t) Tj
/ T1_0 1 Тс
6,5 0 0 6 99,1603 399,9972 тм
(0) Tj
/ T1_2 1 Тс
9 0 0 9 106.1008 401,2472 тм
(\ 005) Tj
/ T1_5 1 Тс
1,2446 0 тд
(t) Tj
/ T1_0 1 Тс
0,283 0 Тд
(\)) Tj
/ T1_3 1 Тс
6,5 0 0,9318 6 123,3417 404,2472 тм
(\ 022) Tj
/ T1_5 1 Тс
9 0 0 9 126,6231 401,2472 тм
(y) Tj
/ T1_6 1 Тс
0,0068 0 Тд
(\ 001) Tj
/ T1_0 1 Тс
0,005 Тс 0,8069 0 Тд
[(и) -406.
)] TJ
1 -1,1174 тд
[(The) -208,4 (быстро) -208,4 (g) -19,9 (ряд) -30 (th) -208,4 (of) -208,4 (the) -208,4 (cur) -60 (vature) -208,4 (sugge) 19,9 (стс) -208,4 (та) -208,4 (ит) -208,4 (мощь) -208,4 (удар) -208,4 (вверх)] TJ
-1 -1,1174 тд
[(при) -259,2 (а) -259,2 (плав) -30 (ите) -259.2 (время)] TJ
/ T1_5 1 Тс
0 Тс 6.603 0 Тд
(t) Tj
/ T1_0 1 Тс
6.5 0 0 6 113.6508 410.054 тм
(0) Tj
0,005 Тс 9 0 0 9 116,9322 411,304 Тм
[(.) – 259,2 (In) -259,2 (факт,) – 259,2 (если) -259,2 (we) -259,2 (re) 19,9 (масштаб) -259,2 (the) -259,2 (пространственный) -259,2 (переменный) – 259,2 (дюйм) -259,2 (дюйм)] TJ
-7,2507 -1,1174 тд
[(для) -30 (м)] ТДж
/ T1_5 1 Тс
0 Тс 2,5337 0 Тд
(x) Tj
/ T1_6 1 Тс
0,0132 0 Тд
(\ 001) Tj
/ T1_2 1 Тс
0,8135 0 тд
(\ 004) Tj
/ T1_0 1 Тс
1,2446 0 тд
(\ () Tj
/ T1_5 1 Тс
0,388 0 Тд
(t) Tj
/ T1_0 1 Тс
6,5 0 0 6 99,1603 399,9972 тм
(0) Tj
/ T1_2 1 Тс
9 0 0 9 106.1008 401,2472 тм
(\ 005) Tj
/ T1_5 1 Тс
1,2446 0 тд
(t) Tj
/ T1_0 1 Тс
0,283 0 Тд
(\)) Tj
/ T1_3 1 Тс
6,5 0 0,9318 6 123,3417 404,2472 тм
(\ 022) Tj
/ T1_5 1 Тс
9 0 0 9 126,6231 401,2472 тм
(y) Tj
/ T1_6 1 Тс
0,0068 0 Тд
(\ 001) Tj
/ T1_0 1 Тс
0,005 Тс 0,8069 0 Тд
[(и) -406. 6 (представить) -406.6 (the) -406.6 (новый) -406.6 (время) -406.6 (переменная)] TJ
/ T1_3 1 Тс
0 Tc 9 0 1,3977 9 284,0424 401,2472 Tm
(\ 021) Tj
/ T1_2 1 Тс
9 0 0 9 291,7427 401,2472 тм
(\ 004) Tj
-26,6741 -1,1174 тд
(\ 005) Tj
/ T1_0 1 Тс
0,005 Тс 0,838 0 Тд
(журнал \ () Tj
/ T1_5 1 Тс
0 Tc [-0.1 (t)] ТДж
/ T1_0 1 Тс
6.5 0 0 6 77.1388 389.9404 тм
(0) Tj
/ T1_2 1 Тс
9 0 0 9 83,46 391,1904 тм
(\ 005) Tj
/ T1_5 1 Тс
1,1758 0 тд
(t) Tj
/ T1_0 1 Тс
0,005 Тс 0,283 0 Тд
[(\),) – 337,8 (уравнение)] ТДж
/ T1_1 1 Тс
0 Тс 2.8217 0 Тд
(2) Tj
/ T1_0 1 Тс
0,005 Тс 0,8428 0 Тд
[(преобразование) -30 (мс) -337,8 (в)] TJ
/ T1_3 1 Тс
0 Тс -3,7012 -3,4372 Тд
(\ 006) Tj
/ T1_5 1 Тс
0,5199 0 тд
(y) Tj
/ T1_6 1 Тс
0,0068 0 Тд
(\ 001) Tj
ET
0 0 0 1 тыс.
0,25 Вт
96.071 356.202 м
104.923 356.202 л
S
BT
/ T1_3 1 Тс
9 0 0 9 96.071 347.2784 тм
(\ 006) Tj
9 0 1.3977 9 100,7498 347,2784 тм
(\ 021) Tj
9 0 0 9 106,9218 352,9517 тм
(\ 005) Tj
9 0 1,3977 9 116,5946 352,9517 тм
(\ 022) Tj
/ T1_5 1 Тс
9 0 0 9 121,2734 352,9517 тм
(y) Tj
/ T1_6 1 Тс
0,0068 0 Тд
(\ 001) Tj
/ T1_3 1 Тс
0,6371 0 тд
(\ 002) Tj
9 0 1,3977 9 138,1672 360,2557 тм
(\ b) Tj
/ T1_0 1 Тс
6,3977 0 0 5,7614 142,846 358,6648 тм
(0) Tj
ET
136,739 356,202 м
147,599 356,202 л
S
BT
/ T1_0 1 Тс
9 0 0 9 136,7386 347,2784 тм
(2) Tj
/ T1_3 1 Тс
9 0 1,3977 9 141,4174 347,2784 тм
(\ 004) Tj
/ T1_7 1 Тс
26 0 0 29,1591 150,0282 351.
6 (представить) -406.6 (the) -406.6 (новый) -406.6 (время) -406.6 (переменная)] TJ
/ T1_3 1 Тс
0 Tc 9 0 1,3977 9 284,0424 401,2472 Tm
(\ 021) Tj
/ T1_2 1 Тс
9 0 0 9 291,7427 401,2472 тм
(\ 004) Tj
-26,6741 -1,1174 тд
(\ 005) Tj
/ T1_0 1 Тс
0,005 Тс 0,838 0 Тд
(журнал \ () Tj
/ T1_5 1 Тс
0 Tc [-0.1 (t)] ТДж
/ T1_0 1 Тс
6.5 0 0 6 77.1388 389.9404 тм
(0) Tj
/ T1_2 1 Тс
9 0 0 9 83,46 391,1904 тм
(\ 005) Tj
/ T1_5 1 Тс
1,1758 0 тд
(t) Tj
/ T1_0 1 Тс
0,005 Тс 0,283 0 Тд
[(\),) – 337,8 (уравнение)] ТДж
/ T1_1 1 Тс
0 Тс 2.8217 0 Тд
(2) Tj
/ T1_0 1 Тс
0,005 Тс 0,8428 0 Тд
[(преобразование) -30 (мс) -337,8 (в)] TJ
/ T1_3 1 Тс
0 Тс -3,7012 -3,4372 Тд
(\ 006) Tj
/ T1_5 1 Тс
0,5199 0 тд
(y) Tj
/ T1_6 1 Тс
0,0068 0 Тд
(\ 001) Tj
ET
0 0 0 1 тыс.
0,25 Вт
96.071 356.202 м
104.923 356.202 л
S
BT
/ T1_3 1 Тс
9 0 0 9 96.071 347.2784 тм
(\ 006) Tj
9 0 1.3977 9 100,7498 347,2784 тм
(\ 021) Tj
9 0 0 9 106,9218 352,9517 тм
(\ 005) Tj
9 0 1,3977 9 116,5946 352,9517 тм
(\ 022) Tj
/ T1_5 1 Тс
9 0 0 9 121,2734 352,9517 тм
(y) Tj
/ T1_6 1 Тс
0,0068 0 Тд
(\ 001) Tj
/ T1_3 1 Тс
0,6371 0 тд
(\ 002) Tj
9 0 1,3977 9 138,1672 360,2557 тм
(\ b) Tj
/ T1_0 1 Тс
6,3977 0 0 5,7614 142,846 358,6648 тм
(0) Tj
ET
136,739 356,202 м
147,599 356,202 л
S
BT
/ T1_0 1 Тс
9 0 0 9 136,7386 347,2784 тм
(2) Tj
/ T1_3 1 Тс
9 0 1,3977 9 141,4174 347,2784 тм
(\ 004) Tj
/ T1_7 1 Тс
26 0 0 29,1591 150,0282 351. 0057 Тм
(\ 003) Tj
/ T1_5 1 Тс
6,3977 0 0 5,7614 155,4519 341,4773 тм
(C) Tj
/ T1_2 1 Тс
5,7983 0 0 5,7983 160,0646 341,4773 тм
(\ 001) Tj
/ T1_3 1 Тс
6,3977 0 0,8949 5,7614 162,1121 341,4773 тм
(\ 021) Tj
/ T1_2 1 Тс
5,7983 0 0 5,7983 165,0805 341,4773 тм
(\ 002) Tj
/ T1_3 1 Тс
9 0 0 9 185,7814 373,233 тм
(\ 006) Tj
/ T1_5 1 Тс
0,5199 0 тд
(y) Tj
/ T1_6 1 Тс
0,0068 0 Тд
(\ 001) Tj
ET
185,082 369,179 м
194.943 369.179 л
S
BT
/ T1_3 1 Тс
9 0 0 9 185,0824 360,2557 тм
(\ 006) Tj
9 0 1,3977 9 189,7612 360,2557 тм
(\ 001) Tj
/ T1_2 1 Тс
9 0 0 9 194.944 365,929 тм
(\ 001) Tj
/ T1_3 1 Тс
9 0 1,3977 9 198,1198 365,929 тм
(\ 001) Tj
/ T1_2 1 Тс
9 0 0 9 203,3026 365,929 тм
(\ 003) Tj
/ T1_0 1 Тс
0,3529 0 Тд
(,) Tj
/ T1_3 1 Тс
9 0 1,3977 9 211,3363 365,929 тм
(\ 021) Tj
/ T1_2 1 Тс
9 0 0 9 215,5111 365,929 тм
(\ 002) Tj
ET
167,122 356,202 м
236,636 356,202 л
S
BT
/ T1_7 1 Тс
9 0 0 9 167.1222 347.2784 тм
(\ 002) Tj
/ T1_5 1 Тс
0,2419 0 Тд
(y) Tj
/ T1_6 1 Тс
0,0068 0 Тд
(\ 001) Tj
/ T1_2 1 Тс
0,4152 0 тд
(\ 001) Tj
/ T1_3 1 Тс
9 0 1,3977 9 176,2726 347,2784 тм
(\ 001) Tj
/ T1_0 1 Тс
9 0 0 9 181.
0057 Тм
(\ 003) Tj
/ T1_5 1 Тс
6,3977 0 0 5,7614 155,4519 341,4773 тм
(C) Tj
/ T1_2 1 Тс
5,7983 0 0 5,7983 160,0646 341,4773 тм
(\ 001) Tj
/ T1_3 1 Тс
6,3977 0 0,8949 5,7614 162,1121 341,4773 тм
(\ 021) Tj
/ T1_2 1 Тс
5,7983 0 0 5,7983 165,0805 341,4773 тм
(\ 002) Tj
/ T1_3 1 Тс
9 0 0 9 185,7814 373,233 тм
(\ 006) Tj
/ T1_5 1 Тс
0,5199 0 тд
(y) Tj
/ T1_6 1 Тс
0,0068 0 Тд
(\ 001) Tj
ET
185,082 369,179 м
194.943 369.179 л
S
BT
/ T1_3 1 Тс
9 0 0 9 185,0824 360,2557 тм
(\ 006) Tj
9 0 1,3977 9 189,7612 360,2557 тм
(\ 001) Tj
/ T1_2 1 Тс
9 0 0 9 194.944 365,929 тм
(\ 001) Tj
/ T1_3 1 Тс
9 0 1,3977 9 198,1198 365,929 тм
(\ 001) Tj
/ T1_2 1 Тс
9 0 0 9 203,3026 365,929 тм
(\ 003) Tj
/ T1_0 1 Тс
0,3529 0 Тд
(,) Tj
/ T1_3 1 Тс
9 0 1,3977 9 211,3363 365,929 тм
(\ 021) Tj
/ T1_2 1 Тс
9 0 0 9 215,5111 365,929 тм
(\ 002) Tj
ET
167,122 356,202 м
236,636 356,202 л
S
BT
/ T1_7 1 Тс
9 0 0 9 167.1222 347.2784 тм
(\ 002) Tj
/ T1_5 1 Тс
0,2419 0 Тд
(y) Tj
/ T1_6 1 Тс
0,0068 0 Тд
(\ 001) Tj
/ T1_2 1 Тс
0,4152 0 тд
(\ 001) Tj
/ T1_3 1 Тс
9 0 1,3977 9 176,2726 347,2784 тм
(\ 001) Tj
/ T1_0 1 Тс
9 0 0 9 181.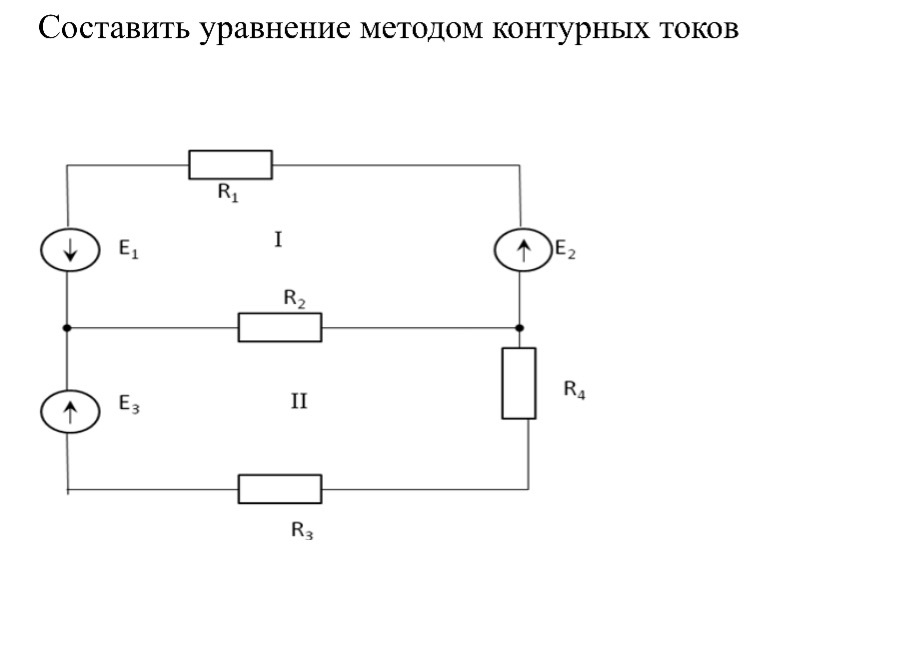 4554 347,2784 тм
(,) Tj
/ T1_3 1 Тс
9 0 1,3977 9 183,8843 347,2784 тм
(\ 021) Tj
/ T1_2 1 Тс
9 0 0 9 188,0591 347,2784 тм
(\ 002) Tj
/ T1_3 1 Тс
0,5748 0 Тд
(\ 005) Tj
/ T1_5 1 Тс
1.0748 0 Тд
(y) Tj
/ T1_6 1 Тс
0,0068 0 Тд
(\ 001) Tj
/ T1_2 1 Тс
0,4152 0 тд
(\ 001) Tj
/ T1_3 1 Тс
9 0 1,3977 9 209,8785 347,2784 тм
(\ 001) Tj
/ T1_2 1 Тс
9 0 0 9 215,0612 347,2784 тм
(\ 003) Tj
/ T1_0 1 Тс
0,3529 0 Тд
(,) Tj
/ T1_3 1 Тс
9 0 1,3977 9 223,095 347,2784 тм
(\ 021) Tj
/ T1_2 1 Тс
9 0 0 9 227,2698 347,2784 тм
(\ 002) Tj
/ T1_7 1 Тс
0,3529 0 Тд
(\ 002) Tj
/ T1_3 1 Тс
6.3977 0 0,8949 5,7614 232,6225 350,858 тм
(\ t) Tj
/ T1_5 1 Тс
9 0 0 9 239,0883 352,9517 тм
(г) Tj
/ T1_3 1 Тс
9 0 1,3977 9 244,0191 352,9517 тм
(\ 001) Tj
/ T1_2 1 Тс
9 0 0 9 249.2019 352.9517 тм
(\ 003) Tj
/ T1_0 1 Тс
0,3529 0 Тд
(,) Tj
/ T1_1 1 Тс
0,0199 Тс 3,7816 0 Тд
([8]) Tj
/ T1_0 1 Тс
0,005 Тс -26,0817 -3,108 Тд
[(prov) -39.8 (ided) -258.6 (that)] TJ
/ T1_3 1 Тс
0 Tc 9 0 1,3977 9 106,578 324,9801 Tm
(\ 022) Tj
/ T1_2 1 Тс
9 0 0 9 113,4499 324,9801 тм
(\ 004) Tj
/ T1_0 1 Тс
1.
4554 347,2784 тм
(,) Tj
/ T1_3 1 Тс
9 0 1,3977 9 183,8843 347,2784 тм
(\ 021) Tj
/ T1_2 1 Тс
9 0 0 9 188,0591 347,2784 тм
(\ 002) Tj
/ T1_3 1 Тс
0,5748 0 Тд
(\ 005) Tj
/ T1_5 1 Тс
1.0748 0 Тд
(y) Tj
/ T1_6 1 Тс
0,0068 0 Тд
(\ 001) Tj
/ T1_2 1 Тс
0,4152 0 тд
(\ 001) Tj
/ T1_3 1 Тс
9 0 1,3977 9 209,8785 347,2784 тм
(\ 001) Tj
/ T1_2 1 Тс
9 0 0 9 215,0612 347,2784 тм
(\ 003) Tj
/ T1_0 1 Тс
0,3529 0 Тд
(,) Tj
/ T1_3 1 Тс
9 0 1,3977 9 223,095 347,2784 тм
(\ 021) Tj
/ T1_2 1 Тс
9 0 0 9 227,2698 347,2784 тм
(\ 002) Tj
/ T1_7 1 Тс
0,3529 0 Тд
(\ 002) Tj
/ T1_3 1 Тс
6.3977 0 0,8949 5,7614 232,6225 350,858 тм
(\ t) Tj
/ T1_5 1 Тс
9 0 0 9 239,0883 352,9517 тм
(г) Tj
/ T1_3 1 Тс
9 0 1,3977 9 244,0191 352,9517 тм
(\ 001) Tj
/ T1_2 1 Тс
9 0 0 9 249.2019 352.9517 тм
(\ 003) Tj
/ T1_0 1 Тс
0,3529 0 Тд
(,) Tj
/ T1_1 1 Тс
0,0199 Тс 3,7816 0 Тд
([8]) Tj
/ T1_0 1 Тс
0,005 Тс -26,0817 -3,108 Тд
[(prov) -39.8 (ided) -258.6 (that)] TJ
/ T1_3 1 Тс
0 Tc 9 0 1,3977 9 106,578 324,9801 Tm
(\ 022) Tj
/ T1_2 1 Тс
9 0 0 9 113,4499 324,9801 тм
(\ 004) Tj
/ T1_0 1 Тс
1.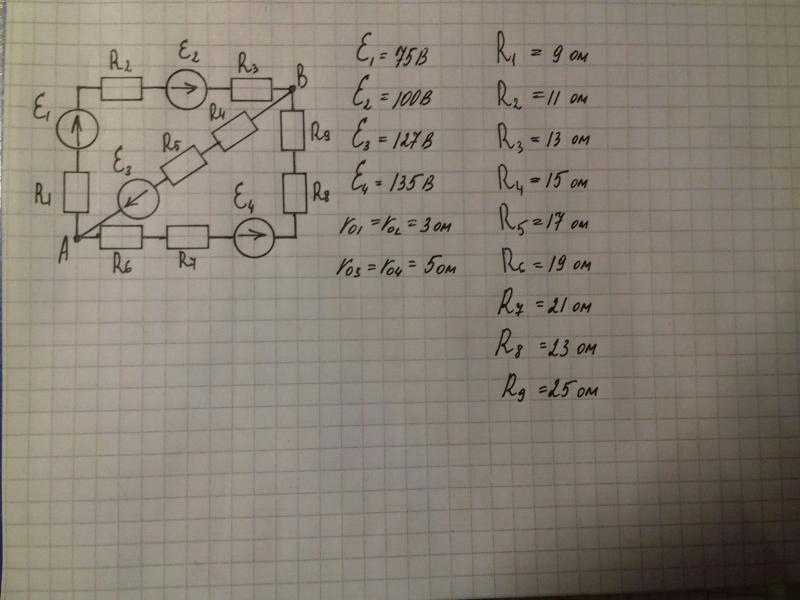 0965 0 Тд
(1) Tj
/ T1_7 1 Тс
0,535 0 тд
(\ 001) Tj
/ T1_3 1 Тс
9 0 1.3977 9 132,6792 324,9801 тм
(\ t) Tj
/ T1_0 1 Тс
0,005 Тс 9 0 0 9 138,2234 324,9801 Тм
[(.) – 258,6 (сходимость) -258,6 (до)] TJ
/ T1_3 1 Тс
0 Tc 9 0 1,3977 9 206,2725 324,9801 Tm
(\ 021) Tj
/ T1_0 1 Тс
0,005 Тс 9 0 0 9 210,3138 324,9801 Тм
[(-независимые) -258,6 (решения)] TJ
-17,6264 -1,1174 тд
[(к) -267,4 (уравнение)] ТДж
/ T1_1 1 Тс
0 Тс 2.9189 0 Тд
(8) Tj
/ T1_0 1 Тс
0,005 Тс 0,7724 0 Тд
[(будет) -267,4 (представляет) 19,9 (отправлено) -267,4 (c) -30 (совпадение) -267,4 (к) -267,4 (решения) -267,4 (из) -267,4 (уравнение)] TJ
/ T1_1 1 Тс
0 Tc 21.1079 0 Тд
(2) Tj
/ T1_0 1 Тс
0,005 Тс 0,7724 0 Тд
(такой) Tj
-25,5716 -1,1174 тд
[(это) -278,1 (the) -278,1 (max) -49,9 (imum) -278,1 (cur) -60 (vature) -278,1 (\ (inverse) -278,1 (of) -278,1 (the) -278,1 (min) ) -30 (imum) -278,1 (радиус) -278,1 (of)] TJ
Т *
[(cur) -60 (vature)] TJ
/ T1_5 1 Тс
0 Тс 4.512 0 Тд
(R) Tj
/ T1_0 1 Тс
0,005 Тс 0,676 0 Тд
[(\)) – 337,8 (g) -19,9 (строки) -337,8 (as)] TJ
/ T1_3 1 Тс
0 Тс 9 0 1,3977 9 116,5227 269,5483 Тм
(\ 023) Tj
9 0 0 9 123,7026 269,5483 тм
(\ 002) Tj
/ T1_0 1 Тс
1,16 0,8116 тд
(1) Tj
ET
133.
0965 0 Тд
(1) Tj
/ T1_7 1 Тс
0,535 0 тд
(\ 001) Tj
/ T1_3 1 Тс
9 0 1.3977 9 132,6792 324,9801 тм
(\ t) Tj
/ T1_0 1 Тс
0,005 Тс 9 0 0 9 138,2234 324,9801 Тм
[(.) – 258,6 (сходимость) -258,6 (до)] TJ
/ T1_3 1 Тс
0 Tc 9 0 1,3977 9 206,2725 324,9801 Tm
(\ 021) Tj
/ T1_0 1 Тс
0,005 Тс 9 0 0 9 210,3138 324,9801 Тм
[(-независимые) -258,6 (решения)] TJ
-17,6264 -1,1174 тд
[(к) -267,4 (уравнение)] ТДж
/ T1_1 1 Тс
0 Тс 2.9189 0 Тд
(8) Tj
/ T1_0 1 Тс
0,005 Тс 0,7724 0 Тд
[(будет) -267,4 (представляет) 19,9 (отправлено) -267,4 (c) -30 (совпадение) -267,4 (к) -267,4 (решения) -267,4 (из) -267,4 (уравнение)] TJ
/ T1_1 1 Тс
0 Tc 21.1079 0 Тд
(2) Tj
/ T1_0 1 Тс
0,005 Тс 0,7724 0 Тд
(такой) Tj
-25,5716 -1,1174 тд
[(это) -278,1 (the) -278,1 (max) -49,9 (imum) -278,1 (cur) -60 (vature) -278,1 (\ (inverse) -278,1 (of) -278,1 (the) -278,1 (min) ) -30 (imum) -278,1 (радиус) -278,1 (of)] TJ
Т *
[(cur) -60 (vature)] TJ
/ T1_5 1 Тс
0 Тс 4.512 0 Тд
(R) Tj
/ T1_0 1 Тс
0,005 Тс 0,676 0 Тд
[(\)) – 337,8 (g) -19,9 (строки) -337,8 (as)] TJ
/ T1_3 1 Тс
0 Тс 9 0 1,3977 9 116,5227 269,5483 Тм
(\ 023) Tj
9 0 0 9 123,7026 269,5483 тм
(\ 002) Tj
/ T1_0 1 Тс
1,16 0,8116 тд
(1) Tj
ET
133. 375 272,798 м
139,591 272,798 л
S
BT
/ T1_5 1 Тс
9 0 0 9 133,375 263,875 тм
(R) Tj
/ T1_7 1 Тс
0,9128 0,6304 тд
(\ 006) Tj
/ T1_5 1 Тс
2,7105 0,8116 тд
(C) Tj
ET
151,261 272,798 м
187.193 272.798 л
S
BT
/ T1_2 1 Тс
9 0 0 9 151,2614 263,875 тм
(\ 001) Tj
/ T1_5 1 Тс
0,3529 0 Тд
(t) Tj
/ T1_0 1 Тс
6,3977 0 0 5,7614 157,1181 262,2841 тм
(0) Tj
/ T1_3 1 Тс
9 0 0 9 162,4419 263,875 тм
(\ 005) Tj
/ T1_5 1 Тс
1.0748 0 Тд
(t) Tj
/ T1_2 1 Тс
0,2979 0 тд
(\ 002) Tj
/ T1_0 1 Тс
0,02 Tc 6,3977 0 0 5,7614 177,9715 267,4545 Tm
(1 /) Tj
/ T1_3 1 Тс
0 Тс 6.3977 0 0,8949 5,7614 183,1662 267,4545 тм
(\ t) Tj
/ T1_0 1 Тс
0,0199 Тс 9 0 0 9 196,382 269,5483 Тм
(как) Tj
/ T1_5 1 Тс
0 Тс 1,2496 0 Тд
(t) Tj
/ T1_8 1 Тс
0,5848 0 тд
(3) Tj
/ T1_5 1 Тс
1.3068 0 Тд
(t) Tj
/ T1_0 1 Тс
6,3977 0 0 5,7614 227,9192 267,9574 тм
(0) Tj
9 0 0 9 231,3283 269,5483 тм
(.) Tj
/ T1_1 1 Тс
0,0199 Тс 6,119 0 Тд
([9]) Tj
/ T1_0 1 Тс
0,005 Тс -26,0803 -2,6402 Тд
[(The) -297,1 (min) -30 (imum) -297,1 (dist) -30 (ance) -297,1 (bet) -30 (ween) -297,1 (the) -297,1 (t) -30 (wo) – 297,1 (с) -30 (по турам) -297,1 (будет) -297.
375 272,798 м
139,591 272,798 л
S
BT
/ T1_5 1 Тс
9 0 0 9 133,375 263,875 тм
(R) Tj
/ T1_7 1 Тс
0,9128 0,6304 тд
(\ 006) Tj
/ T1_5 1 Тс
2,7105 0,8116 тд
(C) Tj
ET
151,261 272,798 м
187.193 272.798 л
S
BT
/ T1_2 1 Тс
9 0 0 9 151,2614 263,875 тм
(\ 001) Tj
/ T1_5 1 Тс
0,3529 0 Тд
(t) Tj
/ T1_0 1 Тс
6,3977 0 0 5,7614 157,1181 262,2841 тм
(0) Tj
/ T1_3 1 Тс
9 0 0 9 162,4419 263,875 тм
(\ 005) Tj
/ T1_5 1 Тс
1.0748 0 Тд
(t) Tj
/ T1_2 1 Тс
0,2979 0 тд
(\ 002) Tj
/ T1_0 1 Тс
0,02 Tc 6,3977 0 0 5,7614 177,9715 267,4545 Tm
(1 /) Tj
/ T1_3 1 Тс
0 Тс 6.3977 0 0,8949 5,7614 183,1662 267,4545 тм
(\ t) Tj
/ T1_0 1 Тс
0,0199 Тс 9 0 0 9 196,382 269,5483 Тм
(как) Tj
/ T1_5 1 Тс
0 Тс 1,2496 0 Тд
(t) Tj
/ T1_8 1 Тс
0,5848 0 тд
(3) Tj
/ T1_5 1 Тс
1.3068 0 Тд
(t) Tj
/ T1_0 1 Тс
6,3977 0 0 5,7614 227,9192 267,9574 тм
(0) Tj
9 0 0 9 231,3283 269,5483 тм
(.) Tj
/ T1_1 1 Тс
0,0199 Тс 6,119 0 Тд
([9]) Tj
/ T1_0 1 Тс
0,005 Тс -26,0803 -2,6402 Тд
[(The) -297,1 (min) -30 (imum) -297,1 (dist) -30 (ance) -297,1 (bet) -30 (ween) -297,1 (the) -297,1 (t) -30 (wo) – 297,1 (с) -30 (по турам) -297,1 (будет) -297. 1 (следовать)] TJ
0 -1,1162 ТД
[() -337,8 (закон)] TJ
/ T1_5 1 Тс
0 Тс 7,8526 -1,994 Тд
(г) Tj
/ T1_7 1 Тс
0,7698 0 тд
(\ 006) Tj
/ T1_5 1 Тс
1.0748 0 Тд
(C) Tj
/ T1_2 1 Тс
0,7209 0 тд
(\ 001) Tj
/ T1_5 1 Тс
0,3529 0 Тд
(t) Tj
/ T1_0 1 Тс
6,3977 0 0 5,7614 151,2946 216,2045 тм
(0) Tj
/ T1_3 1 Тс
9 0 0 9 156,6185 217,7955 тм
(\ 005) Tj
/ T1_5 1 Тс
1.0748 0 Тд
(t) Tj
/ T1_2 1 Тс
0,2979 0 тд
(\ 002) Tj
/ T1_0 1 Тс
0,02 Tc 6,3977 0 0 5,7614 172,148 221,375 Tm
(1 /) Tj
/ T1_3 1 Тс
0 Tc 6,3977 0 0,8949 5,7614 177,3427 221,375 Tm
(\ t) Tj
/ T1_0 1 Тс
0.0199 Тс 9 0 0 9 190,5585 217,7955 Тм
(как) Tj
/ T1_5 1 Тс
0 Тс 1,2496 0 Тд
(t) Tj
/ T1_8 1 Тс
0,5848 0 тд
(3) Tj
/ T1_5 1 Тс
1.3068 0 Тд
(t) Tj
/ T1_0 1 Тс
6,3977 0 0 5,7614 222,0957 216,2045 тм
(0) Tj
9 0 0 9 225,5048 217,7955 тм
(.) Tj
0,005 Tc -19,3143 -2,0085 Td
[(К) -256 (те) 19,9 (ст) -256 (в) 19,9 (се) -256 (законы,) – 256 (мы) -256 (представ) 19,9 (отправлено) -256 (в) -256 ( Рис.) – 256 (5,) – 256 (для) -256 (в) -256 (для корпуса)] TJ
/ T1_3 1 Тс
0 Тс 9 0 1,3977 9 259,9701 199,7187 Тм
(\ t) Tj
/ T1_2 1 Тс
9 0 0 9 267,8183 199,7187 тм
(\ 004) Tj
/ T1_0 1 Тс
0.
1 (следовать)] TJ
0 -1,1162 ТД
[() -337,8 (закон)] TJ
/ T1_5 1 Тс
0 Тс 7,8526 -1,994 Тд
(г) Tj
/ T1_7 1 Тс
0,7698 0 тд
(\ 006) Tj
/ T1_5 1 Тс
1.0748 0 Тд
(C) Tj
/ T1_2 1 Тс
0,7209 0 тд
(\ 001) Tj
/ T1_5 1 Тс
0,3529 0 Тд
(t) Tj
/ T1_0 1 Тс
6,3977 0 0 5,7614 151,2946 216,2045 тм
(0) Tj
/ T1_3 1 Тс
9 0 0 9 156,6185 217,7955 тм
(\ 005) Tj
/ T1_5 1 Тс
1.0748 0 Тд
(t) Tj
/ T1_2 1 Тс
0,2979 0 тд
(\ 002) Tj
/ T1_0 1 Тс
0,02 Tc 6,3977 0 0 5,7614 172,148 221,375 Tm
(1 /) Tj
/ T1_3 1 Тс
0 Tc 6,3977 0 0,8949 5,7614 177,3427 221,375 Tm
(\ t) Tj
/ T1_0 1 Тс
0.0199 Тс 9 0 0 9 190,5585 217,7955 Тм
(как) Tj
/ T1_5 1 Тс
0 Тс 1,2496 0 Тд
(t) Tj
/ T1_8 1 Тс
0,5848 0 тд
(3) Tj
/ T1_5 1 Тс
1.3068 0 Тд
(t) Tj
/ T1_0 1 Тс
6,3977 0 0 5,7614 222,0957 216,2045 тм
(0) Tj
9 0 0 9 225,5048 217,7955 тм
(.) Tj
0,005 Tc -19,3143 -2,0085 Td
[(К) -256 (те) 19,9 (ст) -256 (в) 19,9 (се) -256 (законы,) – 256 (мы) -256 (представ) 19,9 (отправлено) -256 (в) -256 ( Рис.) – 256 (5,) – 256 (для) -256 (в) -256 (для корпуса)] TJ
/ T1_3 1 Тс
0 Тс 9 0 1,3977 9 259,9701 199,7187 Тм
(\ t) Tj
/ T1_2 1 Тс
9 0 0 9 267,8183 199,7187 тм
(\ 004) Tj
/ T1_0 1 Тс
0. 005 Тс 1.094 0 Тд
[(1,) – 256 (the)] TJ
-25,1098 -1,1162 тд
[(стоимость) 19,9 (с) -494,4 (из)] ТДж
/ T1_3 1 Тс
0 Tc 9 0 1,3977 9 92,4012 189,6733 Tm
(\ 023) Tj
/ T1_2 1 Тс
6.5 0 0 6 97.4505 192.6733 Тм
(\ 005) Tj
/ T1_0 1 Тс
0,8378 0 тд
(1) Tj
0,005 Тс 9 0 0 9 110,6266 189,6733 Тм
(и) Tj
/ T1_5 1 Тс
0 Tc 2.0974 0 Td
(г) Tj
/ T1_0 1 Тс
0,005 Тс 1,0273 0 Тд
[(ш) -39,8 (i) -494,3 (пере) 19,9 (спектр) -494,4 (к) -494,3 (в) -494,3 (время) -494,3 (для) -494,4 (в) -494,4 (в целом)] TJ
19,4919 46,9678 тд
[(моделирование) -350,4 (период.) – 350.4 (A) -30 (длинный) -350,4 (тот) -350,4 (эволюция) -350,4 (мы) -350,4 (может) -350,4 (идентифицировать) -30 (y) -350,4 (несколько)] TJ
0 -1,1061 TD
[(режим) 19,9 (с.) – 218,5 (Ат) -218,5 (приблизительно) -49,9 (в настоящее время)] ТДж
/ T1_5 1 Тс
0 Тс 11,565 0 Тд
(t) Tj
/ T1_2 1 Тс
0.5015 0 Тд
(\ r) Tj
/ T1_0 1 Тс
0,005 Тс 1,0564 0 Тд
[(3,) – 218,5 (a) -218,5 (кроссовер) -218,5 (ставка) -30 (ween) -218,5 (тенденция) 19,9 (s)] TJ
-13.1229 -1.1061 тд
[(лань) 19,9 (с) -283,5 (т) -30 (акэ) -283,5 (место,) – 283,5 (впереди) -283,5 (до) -283,5 (а) -283,5 (линейно) -283,5 (поведение) – 39.
005 Тс 1.094 0 Тд
[(1,) – 256 (the)] TJ
-25,1098 -1,1162 тд
[(стоимость) 19,9 (с) -494,4 (из)] ТДж
/ T1_3 1 Тс
0 Tc 9 0 1,3977 9 92,4012 189,6733 Tm
(\ 023) Tj
/ T1_2 1 Тс
6.5 0 0 6 97.4505 192.6733 Тм
(\ 005) Tj
/ T1_0 1 Тс
0,8378 0 тд
(1) Tj
0,005 Тс 9 0 0 9 110,6266 189,6733 Тм
(и) Tj
/ T1_5 1 Тс
0 Tc 2.0974 0 Td
(г) Tj
/ T1_0 1 Тс
0,005 Тс 1,0273 0 Тд
[(ш) -39,8 (i) -494,3 (пере) 19,9 (спектр) -494,4 (к) -494,3 (в) -494,3 (время) -494,3 (для) -494,4 (в) -494,4 (в целом)] TJ
19,4919 46,9678 тд
[(моделирование) -350,4 (период.) – 350.4 (A) -30 (длинный) -350,4 (тот) -350,4 (эволюция) -350,4 (мы) -350,4 (может) -350,4 (идентифицировать) -30 (y) -350,4 (несколько)] TJ
0 -1,1061 TD
[(режим) 19,9 (с.) – 218,5 (Ат) -218,5 (приблизительно) -49,9 (в настоящее время)] ТДж
/ T1_5 1 Тс
0 Тс 11,565 0 Тд
(t) Tj
/ T1_2 1 Тс
0.5015 0 Тд
(\ r) Tj
/ T1_0 1 Тс
0,005 Тс 1,0564 0 Тд
[(3,) – 218,5 (a) -218,5 (кроссовер) -218,5 (ставка) -30 (ween) -218,5 (тенденция) 19,9 (s)] TJ
-13.1229 -1.1061 тд
[(лань) 19,9 (с) -283,5 (т) -30 (акэ) -283,5 (место,) – 283,5 (впереди) -283,5 (до) -283,5 (а) -283,5 (линейно) -283,5 (поведение) – 39. 8 (ior) -283,5 (для) -283,5 (оба)] TJ
/ T1_3 1 Тс
0 Tc 9 0 1,3977 9 523,6775 592,4744 Tm
(\ 023) Tj
/ T1_2 1 Тс
6,5 0 0 6 528,7267 595,4744 тм
(\ 005) Tj
/ T1_0 1 Тс
0,8378 0 тд
(1) Tj
0,005 Тс 9 0 0 9 540,0052 592,4744 Тм
(и) Tj
/ T1_5 1 Тс
0 Тс 1.8866 0 Тд
(г) Tj
/ T1_0 1 Тс
0,005 Tc -26,9787 -1,1061 Td
[(как) -456,2 (нас) -456,2 (может) -456,2 (см.) -456,2 (дюйм) -456,2 (рис.) – 456,2 (5)] TJ
/ T1_5 1 Тс
11.1274 0 Тд
(Врезка) Tj
/ T1_0 1 Тс
[-0,2 (.) – 456,2 (It) -456,2 (is) -456,2 (ясно) -456,2 (f) -30 (rom) -456,1 (the) -456,2 (рисунок) -456.1 (the)] TJ
-11,1274 -1,1061 тд
[(тенденция) -30 (у) -229,2 (в сторону) -229,2 (ноль) -229,2 (из) -229,2 (оба.) – 229,2 (В) -229,2 (факт,) – 229,2 (ср) -229,2 (остановлено) ) -229,2 (в) -229,2 (моделирование)] TJ
Т *
(когда) Tj
/ T1_3 1 Тс
0 Тс 9 0 1,3977 9 338,3563 562,6108 Тм
(\ 023) Tj
/ T1_2 1 Тс
6,5 0 0 6 343,4055 565,6108 тм
(\ 005) Tj
/ T1_0 1 Тс
0,8378 0 тд
(1) Tj
0,005 Тс 9 0 0 9 355,7379 562,6108 Тм
[(достигнуто) -400,6 (значение) 19,9 (с) -400,6 (из) -400,6 (значение) -400,6 (заказ) -400,6 (10)] TJ
/ T1_2 1 Тс
0 Tc 6.
8 (ior) -283,5 (для) -283,5 (оба)] TJ
/ T1_3 1 Тс
0 Tc 9 0 1,3977 9 523,6775 592,4744 Tm
(\ 023) Tj
/ T1_2 1 Тс
6,5 0 0 6 528,7267 595,4744 тм
(\ 005) Tj
/ T1_0 1 Тс
0,8378 0 тд
(1) Tj
0,005 Тс 9 0 0 9 540,0052 592,4744 Тм
(и) Tj
/ T1_5 1 Тс
0 Тс 1.8866 0 Тд
(г) Tj
/ T1_0 1 Тс
0,005 Tc -26,9787 -1,1061 Td
[(как) -456,2 (нас) -456,2 (может) -456,2 (см.) -456,2 (дюйм) -456,2 (рис.) – 456,2 (5)] TJ
/ T1_5 1 Тс
11.1274 0 Тд
(Врезка) Tj
/ T1_0 1 Тс
[-0,2 (.) – 456,2 (It) -456,2 (is) -456,2 (ясно) -456,2 (f) -30 (rom) -456,1 (the) -456,2 (рисунок) -456.1 (the)] TJ
-11,1274 -1,1061 тд
[(тенденция) -30 (у) -229,2 (в сторону) -229,2 (ноль) -229,2 (из) -229,2 (оба.) – 229,2 (В) -229,2 (факт,) – 229,2 (ср) -229,2 (остановлено) ) -229,2 (в) -229,2 (моделирование)] TJ
Т *
(когда) Tj
/ T1_3 1 Тс
0 Тс 9 0 1,3977 9 338,3563 562,6108 Тм
(\ 023) Tj
/ T1_2 1 Тс
6,5 0 0 6 343,4055 565,6108 тм
(\ 005) Tj
/ T1_0 1 Тс
0,8378 0 тд
(1) Tj
0,005 Тс 9 0 0 9 355,7379 562,6108 Тм
[(достигнуто) -400,6 (значение) 19,9 (с) -400,6 (из) -400,6 (значение) -400,6 (заказ) -400,6 (10)] TJ
/ T1_2 1 Тс
0 Tc 6. 5 0 0 6 479.4226 565.6108 Tm
(\ 005) Tj
/ T1_0 1 Тс
0.8378 0 тд
(4) Tj
0,005 Тс 9 0 0 9 488,1499 562,6108 Тм
[(,) – 400.6 (который) -400.6 (is) -400.6 (unistin -)] TJ
-19,3304 -1,1061 тд
[(guishable) -330,5 (f) -30 (rom) -330,5 (ноль) -330,5 (дюйм) -330,5 (the) -330,5 (рис.) – 330,5 (This) -330,5 (abr) -30 (upt)] -330,5 (изменение) -330,5 (ставка) -30 (время)] TJ
Т *
[(дифф) -30 (ферент) -412,6 (режим) 19,9 (с) -412,6 (есть) -412,6 (достаточно) -412,6 (характеристика) -412,6 (из) -412,6 (проблемы) -412,6 (задействовано) -39,8 (ing)] TJ
Т *
[(singularitie) 19,9 (s.) – 581,8 (Наконец,) – 581,8 (дюйм) -581,8 (рис.) – 581.8 (6,) – 581,8 (ср) -581,8 (представляет) 19,9 (отправлено) -581,8 (в) -581,8 (числовое значение)] TJ
Т *
[(профиль) 19,9 (с) -316,3 (изображено) -316,3 (дюйм) -316,3 (рис.) – 316,3 (4)] TJ
/ T1_5 1 Тс
0 Тс 11.208 0 Тд
(а) Tj
/ T1_0 1 Тс
0,005 Тс 0,8303 0 Тд
[(пере) 19,9 (в пересчете) -316,3 (а) -316,3 (ставка) -316,3 (\ ()] ТДж
/ T1_5 1 Тс
0 Тс [-0,3 (т)] ТДж
/ T1_0 1 Тс
6,5 0 0 6 488,7475 521,5426 тм
(0) Tj
/ T1_2 1 Тс
9 0 0 9 494,8755 522,7926 тм
(\ 005) Tj
/ T1_5 1 Тс
1.
5 0 0 6 479.4226 565.6108 Tm
(\ 005) Tj
/ T1_0 1 Тс
0.8378 0 тд
(4) Tj
0,005 Тс 9 0 0 9 488,1499 562,6108 Тм
[(,) – 400.6 (который) -400.6 (is) -400.6 (unistin -)] TJ
-19,3304 -1,1061 тд
[(guishable) -330,5 (f) -30 (rom) -330,5 (ноль) -330,5 (дюйм) -330,5 (the) -330,5 (рис.) – 330,5 (This) -330,5 (abr) -30 (upt)] -330,5 (изменение) -330,5 (ставка) -30 (время)] TJ
Т *
[(дифф) -30 (ферент) -412,6 (режим) 19,9 (с) -412,6 (есть) -412,6 (достаточно) -412,6 (характеристика) -412,6 (из) -412,6 (проблемы) -412,6 (задействовано) -39,8 (ing)] TJ
Т *
[(singularitie) 19,9 (s.) – 581,8 (Наконец,) – 581,8 (дюйм) -581,8 (рис.) – 581.8 (6,) – 581,8 (ср) -581,8 (представляет) 19,9 (отправлено) -581,8 (в) -581,8 (числовое значение)] TJ
Т *
[(профиль) 19,9 (с) -316,3 (изображено) -316,3 (дюйм) -316,3 (рис.) – 316,3 (4)] TJ
/ T1_5 1 Тс
0 Тс 11.208 0 Тд
(а) Tj
/ T1_0 1 Тс
0,005 Тс 0,8303 0 Тд
[(пере) 19,9 (в пересчете) -316,3 (а) -316,3 (ставка) -316,3 (\ ()] ТДж
/ T1_5 1 Тс
0 Тс [-0,3 (т)] ТДж
/ T1_0 1 Тс
6,5 0 0 6 488,7475 521,5426 тм
(0) Tj
/ T1_2 1 Тс
9 0 0 9 494,8755 522,7926 тм
(\ 005) Tj
/ T1_5 1 Тс
1. 1543 0 Тд
(t) Tj
/ T1_0 1 Тс
0,283 0 Тд
(\)) Tj
/ T1_2 1 Тс
6,5 0 0 6 511,3039 525,7926 тм
(\ 005) Tj
/ T1_0 1 Тс
0.00481 Tc 0.8378 0 Td
(\ (1 /) Tj
/ T1_3 1 Тс
0 Tc 6.5 0 0.9318 6 524.3513 525.7926 Tm
(\ t) Tj
/ T1_0 1 Тс
6,5 0 0 6 528,3542 525,7926 тм
(\)) Tj
0,005 Тс 9 0 0 9 533,7217 522,7926 Тм
[(in) -316,3 (оба)] TJ
-24,3939 -1,1061 тд
[(пространственный) -283,8 (направления.) – 283,8 (It) -283,8 (is) -283,8 (ясно) -283,8 (f) -30 (rom) -283,8 (the) -283,8 (сюжет) -283,8 (тот) -283,8 (они) -283,8 (c) -30 (onverge) -283,8 (to)] TJ
Т *
[(а) -184,7 (ст) -30 (атионар) -60 (у) -184,7 (профиль) -184,7 (то) -184,7 (будет) -184,7 (будет) -184,7 (а)] ТДж
/ T1_3 1 Тс
0 Тс 9 0 1.3977 9 448,1461 502,8835 тм
(\ 021) Tj
/ T1_0 1 Тс
0,005 Тс 9 0 0 9 452,1874 502,8835 Тм
[(-независимый) -184,7 (решение) -184,7 (из) -184,7 (уравнение)] TJ
/ T1_1 1 Тс
0 Тс -15,3346 -1,1061 Тд
(8) Tj
/ T1_0 1 Тс
0,005 Тс 0,8428 0 Тд
[(и) -337,8 (а) -337,8 (самоподобный) -337,8 (раствор) -337,8 (из) -337,8 (уравнение)] TJ
/ T1_1 1 Тс
0 Tc 14.
1543 0 Тд
(t) Tj
/ T1_0 1 Тс
0,283 0 Тд
(\)) Tj
/ T1_2 1 Тс
6,5 0 0 6 511,3039 525,7926 тм
(\ 005) Tj
/ T1_0 1 Тс
0.00481 Tc 0.8378 0 Td
(\ (1 /) Tj
/ T1_3 1 Тс
0 Tc 6.5 0 0.9318 6 524.3513 525.7926 Tm
(\ t) Tj
/ T1_0 1 Тс
6,5 0 0 6 528,3542 525,7926 тм
(\)) Tj
0,005 Тс 9 0 0 9 533,7217 522,7926 Тм
[(in) -316,3 (оба)] TJ
-24,3939 -1,1061 тд
[(пространственный) -283,8 (направления.) – 283,8 (It) -283,8 (is) -283,8 (ясно) -283,8 (f) -30 (rom) -283,8 (the) -283,8 (сюжет) -283,8 (тот) -283,8 (они) -283,8 (c) -30 (onverge) -283,8 (to)] TJ
Т *
[(а) -184,7 (ст) -30 (атионар) -60 (у) -184,7 (профиль) -184,7 (то) -184,7 (будет) -184,7 (будет) -184,7 (а)] ТДж
/ T1_3 1 Тс
0 Тс 9 0 1.3977 9 448,1461 502,8835 тм
(\ 021) Tj
/ T1_0 1 Тс
0,005 Тс 9 0 0 9 452,1874 502,8835 Тм
[(-независимый) -184,7 (решение) -184,7 (из) -184,7 (уравнение)] TJ
/ T1_1 1 Тс
0 Тс -15,3346 -1,1061 Тд
(8) Tj
/ T1_0 1 Тс
0,005 Тс 0,8428 0 Тд
[(и) -337,8 (а) -337,8 (самоподобный) -337,8 (раствор) -337,8 (из) -337,8 (уравнение)] TJ
/ T1_1 1 Тс
0 Tc 14. 7605 0 Td
(2) Tj
/ T1_0 1 Тс
0,505 0 тд
(.) Tj
0,005 Тс -15,1083 -1,1061 Тд
[(Наконец,) – 284,4 (у нас) -284,4 (есть) -284,4 (повторяется) -284,4 (в) -284,4 (моделирование) -284,4 (для) -284,4 (несколько) -284.4 (значение) 19,9 (с) -284,4 (из)] ТДж
/ T1_3 1 Тс
0 Тс 9 0 1,3977 9 314,1761 473,0199 Тм
(\ t) Tj
/ T1_0 1 Тс
0,005 Тс 9 0 0 9 321,834 473,0199 Тм
[(к) -234.9 (вериф) -30 (у) -234.9 (наш) -234.9 (масштабирование) -234.9 (закон.) – 234.9 (В) -234.9 (Таблица) -234.9 (1,) – 234.9 (мы ) -234,9 (обобщить) -234,9 (в) -234,9 (повторно) 19,9 (итоги)] TJ
-0,8509 -1,1061 тд
[(obt) -30 (ained) -248,4 (for) -248,5 (some) -248,5 (value) 19,9 (s) -248,5 (of)] TJ
/ T1_3 1 Тс
0 Tc 9 0 1,3977 9 423,4355 463,0654 Tm
(\ t) Tj
/ T1_0 1 Тс
0,005 Tc 9 0 0 9 428,9798 463.0654 Тм
[(.) – 248,5 (В) -248,4 (в частности,) – 248,5 (В) -248,5 (У) -248,5 (в) -49,9 (в) -30 (в среднем)] ТДж
-12,756 -1,1061 тд
[(a) -358,3 (наименьшие квадраты) 19,9 (s) -358,3 (подгонка) -358,3 (to) -358,3 (the) -358,3 (cur) -60 (vature) -358,3 (закон) -358,3 (\ ( Уравнение)] ТДж
/ T1_1 1 Тс
0 Тс 21,3156 0 Тд
(9) Tj
/ T1_0 1 Тс
0,005 Тс 0,505 0 Тд
[(\)) – 358,3 (для) -358,3 (а) -358,3 (набор) -358,3 (из)] TJ
-21,8207 -1,1061 тд
[(значение) 19,9 (s) -455,2 (из) -455,2 (the) -455,2 (cur) -60 (vature)] TJ
/ T1_3 1 Тс
0 Tc 9 0 1,3977 9 412,4061 443,1562 Tm
(\ 023) Tj
/ T1_5 1 Тс
6.
7605 0 Td
(2) Tj
/ T1_0 1 Тс
0,505 0 тд
(.) Tj
0,005 Тс -15,1083 -1,1061 Тд
[(Наконец,) – 284,4 (у нас) -284,4 (есть) -284,4 (повторяется) -284,4 (в) -284,4 (моделирование) -284,4 (для) -284,4 (несколько) -284.4 (значение) 19,9 (с) -284,4 (из)] ТДж
/ T1_3 1 Тс
0 Тс 9 0 1,3977 9 314,1761 473,0199 Тм
(\ t) Tj
/ T1_0 1 Тс
0,005 Тс 9 0 0 9 321,834 473,0199 Тм
[(к) -234.9 (вериф) -30 (у) -234.9 (наш) -234.9 (масштабирование) -234.9 (закон.) – 234.9 (В) -234.9 (Таблица) -234.9 (1,) – 234.9 (мы ) -234,9 (обобщить) -234,9 (в) -234,9 (повторно) 19,9 (итоги)] TJ
-0,8509 -1,1061 тд
[(obt) -30 (ained) -248,4 (for) -248,5 (some) -248,5 (value) 19,9 (s) -248,5 (of)] TJ
/ T1_3 1 Тс
0 Tc 9 0 1,3977 9 423,4355 463,0654 Tm
(\ t) Tj
/ T1_0 1 Тс
0,005 Tc 9 0 0 9 428,9798 463.0654 Тм
[(.) – 248,5 (В) -248,4 (в частности,) – 248,5 (В) -248,5 (У) -248,5 (в) -49,9 (в) -30 (в среднем)] ТДж
-12,756 -1,1061 тд
[(a) -358,3 (наименьшие квадраты) 19,9 (s) -358,3 (подгонка) -358,3 (to) -358,3 (the) -358,3 (cur) -60 (vature) -358,3 (закон) -358,3 (\ ( Уравнение)] ТДж
/ T1_1 1 Тс
0 Тс 21,3156 0 Тд
(9) Tj
/ T1_0 1 Тс
0,005 Тс 0,505 0 Тд
[(\)) – 358,3 (для) -358,3 (а) -358,3 (набор) -358,3 (из)] TJ
-21,8207 -1,1061 тд
[(значение) 19,9 (s) -455,2 (из) -455,2 (the) -455,2 (cur) -60 (vature)] TJ
/ T1_3 1 Тс
0 Tc 9 0 1,3977 9 412,4061 443,1562 Tm
(\ 023) Tj
/ T1_5 1 Тс
6.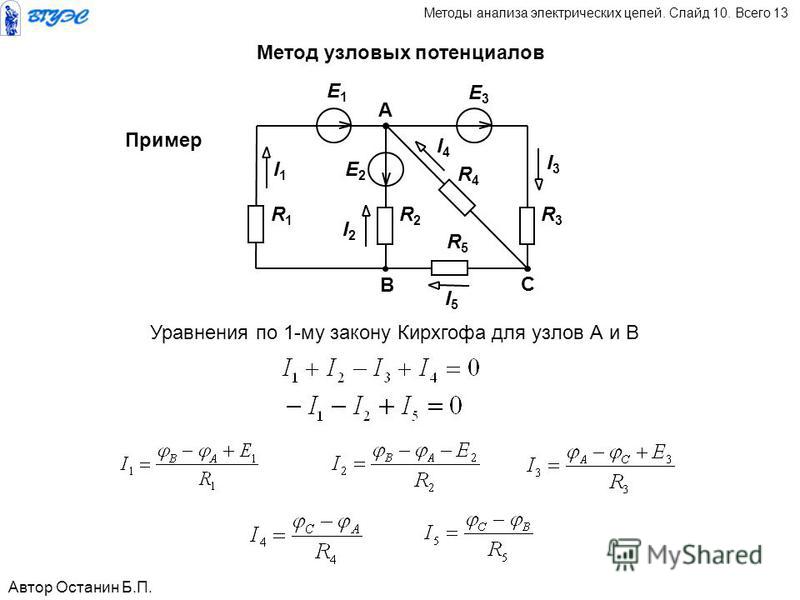 5 0 0 6 417,4554 441,9062 тм
(i) Tj
/ T1_0 1 Тс
0,005 Тс 9 0 0 9 423,2993 443,1562 Тм
[(близко) -455,2 (к) -455,2 (в) -455,2 (в) -30 (коллапс) -455,2 (время)] TJ
/ T1_5 1 Тс
0 Тс 12,1466 0 Тд
(t) Tj
/ T1_0 1 Тс
6,5 0 0 6 535,1659 441,9062 тм
(0) Tj
0,005 Тс 9 0 0 9 538,4473 443,1562 Тм
[(.) – 455,2 (Это)] TJ
-24,919 -1,1061 тд
[(techn) -30 (ique) -191,3 (e) 19,9 (стимулировать) 19,9 (s)] TJ
/ T1_5 1 Тс
0 Тс 8,6684 0 Тд
(t) Tj
/ T1_0 1 Тс
6,5 0 0 6 394,7388 431,9517 тм
(0) Tj
0,005 Тс 9 0 0 9 398,0202 433.2017 Тм
[(,) – 191,3 (в) -191.3 (отл) -30 (компонент) -191,3 (1)] TJ
/ T1_7 1 Тс
0 Тс 6,7612 0 Тд
(\ 001) Tj
/ T1_3 1 Тс
9 0 1,3977 9 462,8769 433.2017 Тм
(\ t) Tj
/ T1_0 1 Тс
0,005 Тс 9 0 0 9 468,4211 433.2017 Тм
[(,) – 191,3 (и) -191,3 (the) -191,3 (пропорционально) -30 (y)] TJ
-17,1383 -1,1061 тд
[(c) -30 (onst) -30 (ant)] TJ
/ T1_5 1 Тс
0 Тс 4,0182 0 Тд
(C) Tj
/ T1_0 1 Тс
0,005 Тс 1,0169 0 Тд
[(in) -311 (Eq.)] TJ
/ T1_1 1 Тс
0 Тс 2.957 0 Тд
(9) Tj
/ T1_0 1 Тс
0,005 Тс 0,505 0 Тд
[(.
5 0 0 6 417,4554 441,9062 тм
(i) Tj
/ T1_0 1 Тс
0,005 Тс 9 0 0 9 423,2993 443,1562 Тм
[(близко) -455,2 (к) -455,2 (в) -455,2 (в) -30 (коллапс) -455,2 (время)] TJ
/ T1_5 1 Тс
0 Тс 12,1466 0 Тд
(t) Tj
/ T1_0 1 Тс
6,5 0 0 6 535,1659 441,9062 тм
(0) Tj
0,005 Тс 9 0 0 9 538,4473 443,1562 Тм
[(.) – 455,2 (Это)] TJ
-24,919 -1,1061 тд
[(techn) -30 (ique) -191,3 (e) 19,9 (стимулировать) 19,9 (s)] TJ
/ T1_5 1 Тс
0 Тс 8,6684 0 Тд
(t) Tj
/ T1_0 1 Тс
6,5 0 0 6 394,7388 431,9517 тм
(0) Tj
0,005 Тс 9 0 0 9 398,0202 433.2017 Тм
[(,) – 191,3 (в) -191.3 (отл) -30 (компонент) -191,3 (1)] TJ
/ T1_7 1 Тс
0 Тс 6,7612 0 Тд
(\ 001) Tj
/ T1_3 1 Тс
9 0 1,3977 9 462,8769 433.2017 Тм
(\ t) Tj
/ T1_0 1 Тс
0,005 Тс 9 0 0 9 468,4211 433.2017 Тм
[(,) – 191,3 (и) -191,3 (the) -191,3 (пропорционально) -30 (y)] TJ
-17,1383 -1,1061 тд
[(c) -30 (onst) -30 (ant)] TJ
/ T1_5 1 Тс
0 Тс 4,0182 0 Тд
(C) Tj
/ T1_0 1 Тс
0,005 Тс 1,0169 0 Тд
[(in) -311 (Eq.)] TJ
/ T1_1 1 Тс
0 Тс 2.957 0 Тд
(9) Tj
/ T1_0 1 Тс
0,005 Тс 0,505 0 Тд
[(.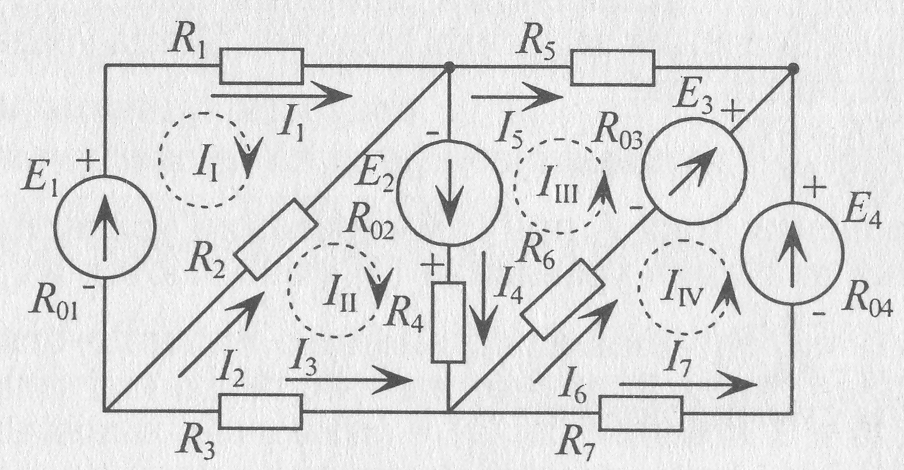 ) – 311 (Наблюдатель) -60 (ve) -311 (тот)] TJ
/ T1_5 1 Тс
0 Tc 6.5431 0 Td
(t) Tj
/ T1_0 1 Тс
6.5 0 0 6 452,0858 421,9972 тм
(0) Tj
0,005 Тс 9 0 0 9 458,1654 423,2472 Тм
[(увеличение) 19.9 (s) -311 (ver) -60 (y) -311 (быстро) -310.9 (as)] TJ
/ T1_3 1 Тс
0 Тс 9 0 1,3977 9 556,2339 423,2472 Тм
(\ t) Tj
/ T1_0 1 Тс
0,005 Тс 9 0 0 9 314,1761 413,2926 Тм
[(стремится) -183,1 (к) -183,1 (ноль.) – 183,1 (In) -183,1 (факт,) – 183,1 (it) -183,1 (is) -183,1 (k) -30 (nown) -183,1 (\ (5,) – 183.1 (6 \)) – 183.1 (то)] TJ
/ T1_5 1 Тс
0 Тс 18.0731 0 Тд
(t) Tj
/ T1_0 1 Тс
6,5 0 0 6 479,3814 412,0426 тм
(0) Tj
/ T1_2 1 Тс
0,1881 Тс 9 0 0 9 484.3105 413,2926 тм
(\ 004 \ 016) Tj
/ T1_0 1 Тс
0,005 Tc (для) Tj
/ T1_3 1 Тс
0 Тс 9 0 1,3977 9 514,2839 413,2926 Тм
(\ t) Tj
/ T1_2 1 Тс
9 0 0 9 521,476 413,2926 тм
(\ 004) Tj
/ T1_0 1 Тс
0,005 Тс 1,0211 0 Тд
[(0,) – 183,1 (который)] TJ
-24,0544 -1,1061 тд
[(sugge) 19.9 (sts) -362.7 (that)] TJ
/ T1_5 1 Тс
0 Тс 5.9499 0 Тд
(t) Tj
/ T1_0 1 Тс
6,5 0 0 6 370,2725 402,0881 тм
(0) Tj
0,005 Тс 9 0 0 9 376,8181 403,3381 Тм
[(должно) -362,7 (быть) -362,7 (вер) -60 (у) -362,7 (большое) -362,7 (для) -362,7 (маленькое) -362,7 (значение) 19,9 (с) -362,7 (из)] TJ
/ T1_3 1 Тс
0 Тс 9 0 1.
) – 311 (Наблюдатель) -60 (ve) -311 (тот)] TJ
/ T1_5 1 Тс
0 Tc 6.5431 0 Td
(t) Tj
/ T1_0 1 Тс
6.5 0 0 6 452,0858 421,9972 тм
(0) Tj
0,005 Тс 9 0 0 9 458,1654 423,2472 Тм
[(увеличение) 19.9 (s) -311 (ver) -60 (y) -311 (быстро) -310.9 (as)] TJ
/ T1_3 1 Тс
0 Тс 9 0 1,3977 9 556,2339 423,2472 Тм
(\ t) Tj
/ T1_0 1 Тс
0,005 Тс 9 0 0 9 314,1761 413,2926 Тм
[(стремится) -183,1 (к) -183,1 (ноль.) – 183,1 (In) -183,1 (факт,) – 183,1 (it) -183,1 (is) -183,1 (k) -30 (nown) -183,1 (\ (5,) – 183.1 (6 \)) – 183.1 (то)] TJ
/ T1_5 1 Тс
0 Тс 18.0731 0 Тд
(t) Tj
/ T1_0 1 Тс
6,5 0 0 6 479,3814 412,0426 тм
(0) Tj
/ T1_2 1 Тс
0,1881 Тс 9 0 0 9 484.3105 413,2926 тм
(\ 004 \ 016) Tj
/ T1_0 1 Тс
0,005 Tc (для) Tj
/ T1_3 1 Тс
0 Тс 9 0 1,3977 9 514,2839 413,2926 Тм
(\ t) Tj
/ T1_2 1 Тс
9 0 0 9 521,476 413,2926 тм
(\ 004) Tj
/ T1_0 1 Тс
0,005 Тс 1,0211 0 Тд
[(0,) – 183,1 (который)] TJ
-24,0544 -1,1061 тд
[(sugge) 19.9 (sts) -362.7 (that)] TJ
/ T1_5 1 Тс
0 Тс 5.9499 0 Тд
(t) Tj
/ T1_0 1 Тс
6,5 0 0 6 370,2725 402,0881 тм
(0) Tj
0,005 Тс 9 0 0 9 376,8181 403,3381 Тм
[(должно) -362,7 (быть) -362,7 (вер) -60 (у) -362,7 (большое) -362,7 (для) -362,7 (маленькое) -362,7 (значение) 19,9 (с) -362,7 (из)] TJ
/ T1_3 1 Тс
0 Тс 9 0 1. 3977 9 537,8611 403,3381 тм
(\ t) Tj
/ T1_0 1 Тс
0,005 Тс 9 0 0 9 543,4053 403,3381 Тм
[(,) – 362,7 (а)] ТДж
-25,4699 -1,1061 тд
[(в конечном итоге) -404,4 (то) -404,4 (патч) 19,9 (с) -404,4 (также) -404,4 (должен) -404,4 (развиваться) -404,4 (а) -404,4 (точечный) -404,4 (сингу- )] TJ
Т *
[(ларит) -30 (у.) – 263 (Вр) -263 (у) -263 (р) -30 (ун) -263 (экс) -30 (перимент) -263 (за) -263 (0) ] TJ
/ T1_2 1 Тс
0 Тс 16,4385 0 Тд
(\ 007) Tj
/ T1_3 1 Тс
9 0 1,3977 9 472,0316 383,429 тм
(\ t) Tj
/ T1_2 1 Тс
9 0 0 9 479,9424 383,429 тм
(\ 007) Tj
/ T1_0 1 Тс
0.005 Тс 1.101 0 Тд
[(0,5,) – 263 (который) -263 (в) -30 (онфир) -30 (м)] TJ
-19,5194 -1,1061 тд
(это.) Tj
1 -1,1061 тд
[(The) -380.7 (c) -30 (omput) -30 (ational) -380.7 (part) -380.7 (of) -380.7 (this) -380.7 (work) -380.7 (was) -380.7 (per) – 49.9 (для) -30 (med) -380.7 (on) -380.7 (the)] TJ
0,0065 Тс 7 0 0 7 314,1761 353,5653 Тм
(HIDRA) Tj
0,005 Тс 9 0 0 9 343,7558 353,5653 Тм
[(40) -504.1 (процедура) 19.9 (ssor) -504.1 (\ (A) -60 (MD) -504.
3977 9 537,8611 403,3381 тм
(\ t) Tj
/ T1_0 1 Тс
0,005 Тс 9 0 0 9 543,4053 403,3381 Тм
[(,) – 362,7 (а)] ТДж
-25,4699 -1,1061 тд
[(в конечном итоге) -404,4 (то) -404,4 (патч) 19,9 (с) -404,4 (также) -404,4 (должен) -404,4 (развиваться) -404,4 (а) -404,4 (точечный) -404,4 (сингу- )] TJ
Т *
[(ларит) -30 (у.) – 263 (Вр) -263 (у) -263 (р) -30 (ун) -263 (экс) -30 (перимент) -263 (за) -263 (0) ] TJ
/ T1_2 1 Тс
0 Тс 16,4385 0 Тд
(\ 007) Tj
/ T1_3 1 Тс
9 0 1,3977 9 472,0316 383,429 тм
(\ t) Tj
/ T1_2 1 Тс
9 0 0 9 479,9424 383,429 тм
(\ 007) Tj
/ T1_0 1 Тс
0.005 Тс 1.101 0 Тд
[(0,5,) – 263 (который) -263 (в) -30 (онфир) -30 (м)] TJ
-19,5194 -1,1061 тд
(это.) Tj
1 -1,1061 тд
[(The) -380.7 (c) -30 (omput) -30 (ational) -380.7 (part) -380.7 (of) -380.7 (this) -380.7 (work) -380.7 (was) -380.7 (per) – 49.9 (для) -30 (med) -380.7 (on) -380.7 (the)] TJ
0,0065 Тс 7 0 0 7 314,1761 353,5653 Тм
(HIDRA) Tj
0,005 Тс 9 0 0 9 343,7558 353,5653 Тм
[(40) -504.1 (процедура) 19.9 (ssor) -504.1 (\ (A) -60 (MD) -504. 1 (Athlon) -504.1 (XP) -504.1 (at) -504.1 (2) -504.1 (Ghz \) ))] TJ
7 0 0 7 524,7168 353,5653 тм
(BEOWULF) Tj
9 0 0 9 314.1761 343,6108 тм
[(кластер) -284,4 (at) -284,4 (the) -284,4 (Centro) -284,4 (de) -284,4 (Apoyo) -284,4 (Tecnolo) 526,6 (\ 264) -22,4 (gic) -30 (o) – 284,4 (из) -284,4 (в) -284,4 (Un) -30 (иверсидад)] TJ
Т *
[(Рей) -387,7 (Хуан) -387,7 (Карлос) -387,7 (\ (Мадрид \)) – 387,7 (и) -387,7 (в) -387,7 (в) -387,7 (суперорденадор) -387,7 (в) -39,8 (виртуальный)] TJ
Т *
[(gallego) -553,7 (\ (80) -553,7 (процедура) 19,9 (ssor) -553,7 (Pentium) -553,7 (4) -553,7 (at) -553,7 (3,2) -553,7 (ГГц)) – 553,7 ( at) -553,7 (Centro) -553,7 (de)] TJ
Т *
[(Superc) -30 (вывод) -30 (acio) 527.1 (\ 264) -22,4 (n) -337,8 (de) -337,8 (Галисия.)] TJ
1 -1,1073 тд
[(К) -384,2 (обобщить,) – 384,2 (мы) -384,2 (иметь) -384,2 (до) 19,9 (отправлено) -384,2 (дюйм) -384,2 (это) -384,2 (работа) -384,2 (а) – 384.2 (предыдущая) -39.8 (сильно)] TJ
-1 -1,1073 тд
[(unde) 19.9 (scribed) -394.9 (k) -30 (ind) -394.
1 (Athlon) -504.1 (XP) -504.1 (at) -504.1 (2) -504.1 (Ghz \) ))] TJ
7 0 0 7 524,7168 353,5653 тм
(BEOWULF) Tj
9 0 0 9 314.1761 343,6108 тм
[(кластер) -284,4 (at) -284,4 (the) -284,4 (Centro) -284,4 (de) -284,4 (Apoyo) -284,4 (Tecnolo) 526,6 (\ 264) -22,4 (gic) -30 (o) – 284,4 (из) -284,4 (в) -284,4 (Un) -30 (иверсидад)] TJ
Т *
[(Рей) -387,7 (Хуан) -387,7 (Карлос) -387,7 (\ (Мадрид \)) – 387,7 (и) -387,7 (в) -387,7 (в) -387,7 (суперорденадор) -387,7 (в) -39,8 (виртуальный)] TJ
Т *
[(gallego) -553,7 (\ (80) -553,7 (процедура) 19,9 (ssor) -553,7 (Pentium) -553,7 (4) -553,7 (at) -553,7 (3,2) -553,7 (ГГц)) – 553,7 ( at) -553,7 (Centro) -553,7 (de)] TJ
Т *
[(Superc) -30 (вывод) -30 (acio) 527.1 (\ 264) -22,4 (n) -337,8 (de) -337,8 (Галисия.)] TJ
1 -1,1073 тд
[(К) -384,2 (обобщить,) – 384,2 (мы) -384,2 (иметь) -384,2 (до) 19,9 (отправлено) -384,2 (дюйм) -384,2 (это) -384,2 (работа) -384,2 (а) – 384.2 (предыдущая) -39.8 (сильно)] TJ
-1 -1,1073 тд
[(unde) 19.9 (scribed) -394.9 (k) -30 (ind) -394. 9 (of) -394.9 (singularit) -30 (y) -394.9 (and) -394.9 (поддерживается) -394.9 (its) -394.9 (ex) -49,9 (istence) -394,9 (in)] TJ
0 -1,1073 ТД
[(оба) -531 (масштабирование) -531 (аргументы) -531 (и) -531 (числовое значение) -531 (ev) -39,8 (аналог.) – 531 (A) -531 (строгое)] TJ
Т *
[(этюд) -477.3 (of) -477.3 (the) -477.3 (st) -30 (ationar) -60 (y) -477.3 (or) -477.3 (quasist) -30 (ationar) -60 (y) -477.3 (решения) – 477,3 (из) -477,3 (уравнение)] ТДж
/ T1_1 1 Тс
0 Тс 27.006 0 Тд
(8) Tj
/ T1_0 1 Тс
0,005 Тс -27,006 -1,1073 Тд
[(будет) -571 (свинец) -571 (к) -571.1 (an) -571 (в конечном итоге) -571.1 (доказательство) -571.1 (из) -571.1 (the) -571 (ex) -49.9 (istence) – 571,1 (из) -571,1 (из) 19,9 (SE)] TJ
Т *
[(singularitie) 19.9 (s.)] TJ
8 0 0 8 314,1761 234,4858 тм
[(Мы) -449,9 (спасибо) -449,9 (A.) – 449,9 (Co) 527,8 (\ 264) -22,3 (rdoba) -449,9 (и) -449.9 (Дж.) – 449,9 (Эггерс) -449,9 (для) -449,9 (их) -449,9 (полезный) -449,9 (в) -29,8 (комментарии) -449,9 (и)] ТДж
0 -1,1207 ТД
[(предположение) 19,9 (доли.
9 (of) -394.9 (singularit) -30 (y) -394.9 (and) -394.9 (поддерживается) -394.9 (its) -394.9 (ex) -49,9 (istence) -394,9 (in)] TJ
0 -1,1073 ТД
[(оба) -531 (масштабирование) -531 (аргументы) -531 (и) -531 (числовое значение) -531 (ev) -39,8 (аналог.) – 531 (A) -531 (строгое)] TJ
Т *
[(этюд) -477.3 (of) -477.3 (the) -477.3 (st) -30 (ationar) -60 (y) -477.3 (or) -477.3 (quasist) -30 (ationar) -60 (y) -477.3 (решения) – 477,3 (из) -477,3 (уравнение)] ТДж
/ T1_1 1 Тс
0 Тс 27.006 0 Тд
(8) Tj
/ T1_0 1 Тс
0,005 Тс -27,006 -1,1073 Тд
[(будет) -571 (свинец) -571 (к) -571.1 (an) -571 (в конечном итоге) -571.1 (доказательство) -571.1 (из) -571.1 (the) -571 (ex) -49.9 (istence) – 571,1 (из) -571,1 (из) 19,9 (SE)] TJ
Т *
[(singularitie) 19.9 (s.)] TJ
8 0 0 8 314,1761 234,4858 тм
[(Мы) -449,9 (спасибо) -449,9 (A.) – 449,9 (Co) 527,8 (\ 264) -22,3 (rdoba) -449,9 (и) -449.9 (Дж.) – 449,9 (Эггерс) -449,9 (для) -449,9 (их) -449,9 (полезный) -449,9 (в) -29,8 (комментарии) -449,9 (и)] ТДж
0 -1,1207 ТД
[(предположение) 19,9 (доли. ) – 385,5 (\ (2002 \))] TJ
/ T1_5 1 Тс
15.5651 0 тд
[(Vor) -29,6 (ticit) -59,7 (y) -385,5 (и) -385,6 (несжимаемый) -385,5 (поток)] TJ
/ T1_0 1 Тс
[(,) – 385,5 (Кембридж)] TJ
-14,3817 -1,2143 тд
[(Тексты) -179,4 (in) -179,4 (Applied) -179,4 (Математика) -179,4 (\ (Cambridge) -179,4 (Un) -29,6 (iv.) – 179,4 (Pre) 19,9 (ss,) – 179,4 ( Кембридж,) – 179,4 (Великобритания \),) – 179,4 (об.) – 179,4 (27.)] TJ
0,0049 Тс -1,1834 -1,2143 Тд
[(2.) – 423,7 (Buttke,) – 337,6 (T.) – 337,6 (F.) – 337,6 (\ (1989 \))] TJ
/ T1_5 1 Тс
10.309 0 Тд
[(Физ.) – 337,6 (жидкости) -337,6 (A)] ТДж
/ T1_1 1 Тс
0 Tc 6.4855 0 Td
(1) Tj
/ T1_0 1 Тс
0,0049 Тс 0,5049 0 Тд
[(,) – 337,6 (1283 \ 2261285.)] ТДж
-17,2994 -1,2143 тд
[(3.) – 423,7 (Dritschel,) – 337,6 (D.) – 337,6 (G.) – 337,6 (&) – 337,6 (McInt) -29,6 (y) -39,7 (re,) – 337,6 (M.) -337,6 (E.) – 337,6 (\ (1990 \))] TJ
/ T1_5 1 Тс
20.356 0 Тд
[(Физ.) – 337,6 (жидкости) -337,6 (A)] ТДж
/ T1_1 1 Тс
6.4855 0 Тд
(2,) Tj
/ T1_0 1 Тс
1.0974 0 тд
[(748) -89,7 (\ 226753.
) – 385,5 (\ (2002 \))] TJ
/ T1_5 1 Тс
15.5651 0 тд
[(Vor) -29,6 (ticit) -59,7 (y) -385,5 (и) -385,6 (несжимаемый) -385,5 (поток)] TJ
/ T1_0 1 Тс
[(,) – 385,5 (Кембридж)] TJ
-14,3817 -1,2143 тд
[(Тексты) -179,4 (in) -179,4 (Applied) -179,4 (Математика) -179,4 (\ (Cambridge) -179,4 (Un) -29,6 (iv.) – 179,4 (Pre) 19,9 (ss,) – 179,4 ( Кембридж,) – 179,4 (Великобритания \),) – 179,4 (об.) – 179,4 (27.)] TJ
0,0049 Тс -1,1834 -1,2143 Тд
[(2.) – 423,7 (Buttke,) – 337,6 (T.) – 337,6 (F.) – 337,6 (\ (1989 \))] TJ
/ T1_5 1 Тс
10.309 0 Тд
[(Физ.) – 337,6 (жидкости) -337,6 (A)] ТДж
/ T1_1 1 Тс
0 Tc 6.4855 0 Td
(1) Tj
/ T1_0 1 Тс
0,0049 Тс 0,5049 0 Тд
[(,) – 337,6 (1283 \ 2261285.)] ТДж
-17,2994 -1,2143 тд
[(3.) – 423,7 (Dritschel,) – 337,6 (D.) – 337,6 (G.) – 337,6 (&) – 337,6 (McInt) -29,6 (y) -39,7 (re,) – 337,6 (M.) -337,6 (E.) – 337,6 (\ (1990 \))] TJ
/ T1_5 1 Тс
20.356 0 Тд
[(Физ.) – 337,6 (жидкости) -337,6 (A)] ТДж
/ T1_1 1 Тс
6.4855 0 Тд
(2,) Tj
/ T1_0 1 Тс
1.0974 0 тд
[(748) -89,7 (\ 226753. )] TJ
-27,9389 -1,2143 тд
[(4.) – 423,7 (Забуский,) – 367,7 (N.) – 367,7 (Дж.,) – 367,7 (Hughe) 19,9 (s,) – 367,7 (M.) – 367,7 (H.) – 367,7 (&) – 367,7 (Робертс,) – 367,7 (KV) -367,7 (\ (1979 \))] TJ
/ T1_5 1 Тс
25.9593 0 тд
[(Дж.) – 367,7 (Расчет) -29,6 (.) – 367,7 (Физ.)] TJ
/ T1_1 1 Тс
7,611 0 тд
(30,) Tj
/ T1_0 1 Тс
-32,3868 -1,2143 тд
[(96) -89,7 (\ 226106.)] TJ
-1,1834 -1,2143 тд
[(5.) – 423,7 (Chemin,) – 337,6 (Дж.) – 337,6 (Y.) – 337,6 (\ (1993 \))] TJ
/ T1_5 1 Тс
10,731 0 тд
[(Ann.) – 337,6 (Sci) -29,6 (.) – 337,6 (E)] TJ
0 Тс 4,3633 0,1997 Тд
(\ 264) Tj
0,0049 Тс 0,5925 -0,1997 Тд
[(коул) -337,6 (нор) -29,6 (самец) -337.6 (Supe) 468,9 (\ 264) 36,1 (r) -29,6 (ieure)] TJ
/ T1_1 1 Тс
10.7927 0 тд
(26,) Tj
/ T1_0 1 Тс
1.6023 0 Тд
(517 \ 226542.) Tj
-28,0819 -1,2143 тд
[(6.) – 423,7 (Бертоцци,) – 337,6 (A.) – 337,6 (L.) – 337,6 (&) – 337,7 (Const) -29,6 (антин,) – 337,6 (P.) – 337,6 (\ ( 1993 \))] Т.Дж.
/ T1_5 1 Тс
18.8637 0 Td
[(Сообщество) – 337,6 (Математика) – 337,6 (Физика)] TJ
/ T1_1 1 Тс
9.
)] TJ
-27,9389 -1,2143 тд
[(4.) – 423,7 (Забуский,) – 367,7 (N.) – 367,7 (Дж.,) – 367,7 (Hughe) 19,9 (s,) – 367,7 (M.) – 367,7 (H.) – 367,7 (&) – 367,7 (Робертс,) – 367,7 (KV) -367,7 (\ (1979 \))] TJ
/ T1_5 1 Тс
25.9593 0 тд
[(Дж.) – 367,7 (Расчет) -29,6 (.) – 367,7 (Физ.)] TJ
/ T1_1 1 Тс
7,611 0 тд
(30,) Tj
/ T1_0 1 Тс
-32,3868 -1,2143 тд
[(96) -89,7 (\ 226106.)] TJ
-1,1834 -1,2143 тд
[(5.) – 423,7 (Chemin,) – 337,6 (Дж.) – 337,6 (Y.) – 337,6 (\ (1993 \))] TJ
/ T1_5 1 Тс
10,731 0 тд
[(Ann.) – 337,6 (Sci) -29,6 (.) – 337,6 (E)] TJ
0 Тс 4,3633 0,1997 Тд
(\ 264) Tj
0,0049 Тс 0,5925 -0,1997 Тд
[(коул) -337,6 (нор) -29,6 (самец) -337.6 (Supe) 468,9 (\ 264) 36,1 (r) -29,6 (ieure)] TJ
/ T1_1 1 Тс
10.7927 0 тд
(26,) Tj
/ T1_0 1 Тс
1.6023 0 Тд
(517 \ 226542.) Tj
-28,0819 -1,2143 тд
[(6.) – 423,7 (Бертоцци,) – 337,6 (A.) – 337,6 (L.) – 337,6 (&) – 337,7 (Const) -29,6 (антин,) – 337,6 (P.) – 337,6 (\ ( 1993 \))] Т.Дж.
/ T1_5 1 Тс
18.8637 0 Td
[(Сообщество) – 337,6 (Математика) – 337,6 (Физика)] TJ
/ T1_1 1 Тс
9. 9019 0 Тд
(152,) Tj
/ T1_0 1 Тс
2,1072 0 Тд
[(19) -89,7 (\ 22628.)] TJ
6,6272 8,5 тд
[(7.) – 423,7 (Родриго,) – 337,6 (Дж.) – 337,6 (Л.) – 337,6 (\ (2005 \))] TJ
/ T1_5 1 Тс
10.7699 0 Тд
[(Comm.) -337,6 (чистый) -337,6 (прибл.) -29,6 (.) – 337,6 (математический)] TJ
/ T1_0 1 Тс
0 Tc [0,2 (,)] ТДж
/ T1_1 1 Тс
0,0049 Тс 11,4048 0 Тд
(58,) Tj
/ T1_0 1 Тс
1.6023 0 Тд
[(821 \ 226) -89,7 (866.)] TJ
-23,7771 -1,2143 тд
[(8.) – 423.7 (Const) -29.6 (antin,) – 337.6 (P.,) – 337.6 (Majda,) – 337.6 (A.) – 337.6 (&) – 337.6 (Tabak,) – 337.6 (E .) – 337.6 (\ (1994 \))] ТДж.
/ T1_5 1 Тс
21.6409 0 тд
[(Нелинейный) -29.6 (it) -59.6 (y)] TJ
/ T1_1 1 Тс
5.5715 0 Тд
(7,) Tj
/ T1_0 1 Тс
1.0974 0 тд
(1495 \ 2261533.) Tj
-28,3098 -1,2143 тд
[(9.) – 423,7 (Co) 527,3 (\ 264) -22.3 (rdoba,) – 237,4 (D.,) – 237,4 (Fef) -29,6 (фер) -29,6 (мужчина,) – 237,4 (C.) – 237,4 (&) – 237,4 (Родриго,) – 237,4 (J. ) -237,4 (L.) – 237,4 (\ (2004 \))] TJ
/ T1_5 1 Тс
23,5784 0 тд
[(P) -29,6 (roc.) – 237,4 (Natl) -29,6 (.) – 237,4 (Acad) -29,6 (.
9019 0 Тд
(152,) Tj
/ T1_0 1 Тс
2,1072 0 Тд
[(19) -89,7 (\ 22628.)] TJ
6,6272 8,5 тд
[(7.) – 423,7 (Родриго,) – 337,6 (Дж.) – 337,6 (Л.) – 337,6 (\ (2005 \))] TJ
/ T1_5 1 Тс
10.7699 0 Тд
[(Comm.) -337,6 (чистый) -337,6 (прибл.) -29,6 (.) – 337,6 (математический)] TJ
/ T1_0 1 Тс
0 Tc [0,2 (,)] ТДж
/ T1_1 1 Тс
0,0049 Тс 11,4048 0 Тд
(58,) Tj
/ T1_0 1 Тс
1.6023 0 Тд
[(821 \ 226) -89,7 (866.)] TJ
-23,7771 -1,2143 тд
[(8.) – 423.7 (Const) -29.6 (antin,) – 337.6 (P.,) – 337.6 (Majda,) – 337.6 (A.) – 337.6 (&) – 337.6 (Tabak,) – 337.6 (E .) – 337.6 (\ (1994 \))] ТДж.
/ T1_5 1 Тс
21.6409 0 тд
[(Нелинейный) -29.6 (it) -59.6 (y)] TJ
/ T1_1 1 Тс
5.5715 0 Тд
(7,) Tj
/ T1_0 1 Тс
1.0974 0 тд
(1495 \ 2261533.) Tj
-28,3098 -1,2143 тд
[(9.) – 423,7 (Co) 527,3 (\ 264) -22.3 (rdoba,) – 237,4 (D.,) – 237,4 (Fef) -29,6 (фер) -29,6 (мужчина,) – 237,4 (C.) – 237,4 (&) – 237,4 (Родриго,) – 237,4 (J. ) -237,4 (L.) – 237,4 (\ (2004 \))] TJ
/ T1_5 1 Тс
23,5784 0 тд
[(P) -29,6 (roc.) – 237,4 (Natl) -29,6 (.) – 237,4 (Acad) -29,6 (. ) – 237,4 (Sci) -29,6 (.) – 237,4 (США)] TJ
/ T1_1 1 Тс
-22,3949 -1,2143 тд
(101,) Tj
/ T1_0 1 Тс
2,1072 0 Тд
(2687 \ 2262691.) Tj
-3,7955 -1,2143 тд
[(10.) – 423,7 (Педлоски,) – 448 (Дж.) – 448 (\ (1987 \))] Т.Дж.
/ T1_5 1 Тс
10,6304 0 тд
[(Геофизические) -448 (Жидкие) -448 (D) -29,6 (Динамические)] TJ
/ T1_0 1 Тс
12.8369 0 тд
[(\ (Springer,) – 448 (Новый) -448 (Йорк \),) – 448 (стр.)] TJ
-21,7789 -1,2143 тд
[(345 \ 226368) -337,6 (и) -337,6 (653 \ 226) -89,7 (670.)] TJ
-1,6883 -1,2143 тд
[(11.) – 423,7 (Гамильтон,) – 337,6 (R.) – 337,6 (S.) – 337,6 (\ (1982 \))] TJ
/ T1_5 1 Тс
12.0616 0 Тд
[(Бык) -29,6 (.) – 337,6 (Ам.) – 337,6 (Мат.) – 337,6 (Соц.)] TJ
/ T1_1 1 Тс
9.3982 0 тд
(7,) Tj
/ T1_0 1 Тс
1.0974 0 тд
(65 \ 226222.) Tj
-22,5573 -1,2143 тд
[(12.) – 423,7 (Dritschel,) – 337,6 (D) – 337,6 (G.) – 337,6 (\ (1989 \))] TJ
/ T1_5 1 Тс
12.1945 0 Тд
[(Вычислить) -29.6 (.) – 337,6 (физ.) – 337,6 (респ.)] TJ
/ T1_1 1 Тс
8,7547 0 тд
(10,) Tj
/ T1_0 1 Тс
1.6023 0 Тд
(77 \ 226146.) Tj
/ T1_9 1 Тс
0 Тс 8 0 0 8 126,6761 735,3835 Тм
[(Таблица) -332,7 (1.
) – 237,4 (Sci) -29,6 (.) – 237,4 (США)] TJ
/ T1_1 1 Тс
-22,3949 -1,2143 тд
(101,) Tj
/ T1_0 1 Тс
2,1072 0 Тд
(2687 \ 2262691.) Tj
-3,7955 -1,2143 тд
[(10.) – 423,7 (Педлоски,) – 448 (Дж.) – 448 (\ (1987 \))] Т.Дж.
/ T1_5 1 Тс
10,6304 0 тд
[(Геофизические) -448 (Жидкие) -448 (D) -29,6 (Динамические)] TJ
/ T1_0 1 Тс
12.8369 0 тд
[(\ (Springer,) – 448 (Новый) -448 (Йорк \),) – 448 (стр.)] TJ
-21,7789 -1,2143 тд
[(345 \ 226368) -337,6 (и) -337,6 (653 \ 226) -89,7 (670.)] TJ
-1,6883 -1,2143 тд
[(11.) – 423,7 (Гамильтон,) – 337,6 (R.) – 337,6 (S.) – 337,6 (\ (1982 \))] TJ
/ T1_5 1 Тс
12.0616 0 Тд
[(Бык) -29,6 (.) – 337,6 (Ам.) – 337,6 (Мат.) – 337,6 (Соц.)] TJ
/ T1_1 1 Тс
9.3982 0 тд
(7,) Tj
/ T1_0 1 Тс
1.0974 0 тд
(65 \ 226222.) Tj
-22,5573 -1,2143 тд
[(12.) – 423,7 (Dritschel,) – 337,6 (D) – 337,6 (G.) – 337,6 (\ (1989 \))] TJ
/ T1_5 1 Тс
12.1945 0 Тд
[(Вычислить) -29.6 (.) – 337,6 (физ.) – 337,6 (респ.)] TJ
/ T1_1 1 Тс
8,7547 0 тд
(10,) Tj
/ T1_0 1 Тс
1.6023 0 Тд
(77 \ 226146.) Tj
/ T1_9 1 Тс
0 Тс 8 0 0 8 126,6761 735,3835 Тм
[(Таблица) -332,7 (1. ) – 332,7 (подогнано) -332,7 (параметры) -332,7 (из) -332,7 (в) -332,7 (кривизна) -332,7 (закон) -332,7 (\ (уравнение) – 278 (9 \))] Т.Дж.
ET
0,5 Вт
126.679 650.634 м
486.673 650.634 л
126,679 716,134 м
486,673 716,134 л
S
BT
/ T1_3 1 Тс
7,5 0 1,1648 7,5 126,679 721,3835 тм
(\ t) Tj
/ T1_10 1 Тс
7,5 0 0 7,5 159,9716 721,3835 тм
(1) Tj
/ T1_7 1 Тс
(\ 001) Tj
/ T1_3 1 Тс
7.5 0 1,1648 7,5 167,4427 721,3835 тм
(\ t) Tj
/ T1_11 1 Тс
7,5 0 0 7,5 206,9744 721,3835 тм
(t) Tj
5,5 0 0 5 209,8919 720,3835 тм
(i) Tj
/ T1_10 1 Тс
7,5 0 0 7,5 213,5063 721,3835 тм
(диапазоны) Tj
/ T1_3 1 Тс
7,5 0 1,1648 7,5 273,0852 721,3835 тм
(\ 023) Tj
/ T1_10 1 Тс
5,5 0 0 5 277,2552 720,3835 тм
(i) Tj
7,5 0 0 7,5 280,8696 721,3835 тм
(диапазоны) Tj
/ T1_11 1 Тс
7.1564 0 Тд
(N) Tj
/ T1_10 1 Тс
4,4254 0 тд
[(Установлено) -278 (1)] TJ
/ T1_7 1 Тс
(\ 001) Tj
/ T1_3 1 Тс
7,5 0 1,1648 7,5 397,7119 721,3835 тм
(\ t) Tj
/ T1_11 1 Тс
7.5 0 0 7,5 433,9489 721,3835 тм
(t) Tj
/ T1_10 1 Тс
5,5 0 0 5 436,8664 720,3835 тм
(0) Tj
/ T1_11 1 Тс
7,5 0 0 7,5 476,5881 721,3835 тм
(C) Tj
/ T1_10 1 Тс
-46,6545 -2,0667 тд
[(0,5) -2880,1 (2) -4269,8 ([15,266,) – 278 (16,511]) – 2810,8 ([136,4011]) – 2745,1 (1,487) -4143,5 (2,19) -4144,2 (16,8568) -2812,1 (5,90) )] TJ
0 -1,3333 TD
[(0,6) -2880,1 (1,67) -2879,8 ([11,236,) – 278 (11,891]) – 2810,8 ([145,2748]) – 3578,8 (693) -4143,7 (1,77) -4144,2 (12,0438) -2812,1 (4,58) )] TJ
Т *
[(0,7) -2880,1 (1,43) -3991,1 ([8,476,) – 278 (8,976]) – 2811.
) – 332,7 (подогнано) -332,7 (параметры) -332,7 (из) -332,7 (в) -332,7 (кривизна) -332,7 (закон) -332,7 (\ (уравнение) – 278 (9 \))] Т.Дж.
ET
0,5 Вт
126.679 650.634 м
486.673 650.634 л
126,679 716,134 м
486,673 716,134 л
S
BT
/ T1_3 1 Тс
7,5 0 1,1648 7,5 126,679 721,3835 тм
(\ t) Tj
/ T1_10 1 Тс
7,5 0 0 7,5 159,9716 721,3835 тм
(1) Tj
/ T1_7 1 Тс
(\ 001) Tj
/ T1_3 1 Тс
7.5 0 1,1648 7,5 167,4427 721,3835 тм
(\ t) Tj
/ T1_11 1 Тс
7,5 0 0 7,5 206,9744 721,3835 тм
(t) Tj
5,5 0 0 5 209,8919 720,3835 тм
(i) Tj
/ T1_10 1 Тс
7,5 0 0 7,5 213,5063 721,3835 тм
(диапазоны) Tj
/ T1_3 1 Тс
7,5 0 1,1648 7,5 273,0852 721,3835 тм
(\ 023) Tj
/ T1_10 1 Тс
5,5 0 0 5 277,2552 720,3835 тм
(i) Tj
7,5 0 0 7,5 280,8696 721,3835 тм
(диапазоны) Tj
/ T1_11 1 Тс
7.1564 0 Тд
(N) Tj
/ T1_10 1 Тс
4,4254 0 тд
[(Установлено) -278 (1)] TJ
/ T1_7 1 Тс
(\ 001) Tj
/ T1_3 1 Тс
7,5 0 1,1648 7,5 397,7119 721,3835 тм
(\ t) Tj
/ T1_11 1 Тс
7.5 0 0 7,5 433,9489 721,3835 тм
(t) Tj
/ T1_10 1 Тс
5,5 0 0 5 436,8664 720,3835 тм
(0) Tj
/ T1_11 1 Тс
7,5 0 0 7,5 476,5881 721,3835 тм
(C) Tj
/ T1_10 1 Тс
-46,6545 -2,0667 тд
[(0,5) -2880,1 (2) -4269,8 ([15,266,) – 278 (16,511]) – 2810,8 ([136,4011]) – 2745,1 (1,487) -4143,5 (2,19) -4144,2 (16,8568) -2812,1 (5,90) )] TJ
0 -1,3333 TD
[(0,6) -2880,1 (1,67) -2879,8 ([11,236,) – 278 (11,891]) – 2810,8 ([145,2748]) – 3578,8 (693) -4143,7 (1,77) -4144,2 (12,0438) -2812,1 (4,58) )] TJ
Т *
[(0,7) -2880,1 (1,43) -3991,1 ([8,476,) – 278 (8,976]) – 2811. 5 ([107,5253]) – 2745,1 (1022) -4143,5 (1,51) -4699,8 (9,0157) -2812,5 (3,71)] тДж
Т *
[(0,8) -2880,1 (1,25) -3991,1 ([6,419,) – 278 (7,226]) – 3367,1 ([34,5804]) – 3579,1 (781) -4143,7 (1,27) -4699,8 (7,2383) -2812,5 (3,19 )] TJ
Т *
[(0,9) -2880,1 (1,11) -3991,1 ([5,234,) – 278 (5,520]) – 3367,1 ([62,2662]) – 3579,1 (507) -4143,7 (1,17) -4699,8 (5,5313) -2812,5 (2,66 )] TJ
Т *
[(1) -3714,1 (1) -5381,1 ([4,223,) – 278 (4,464]) – 3922,8 ([46,190]) – 3579,4 (365) -4143,7 (1,00) -4699,8 (4,4698) -2812,5 (2,41)] TJ
/ T1_11 1 Тс
7 0 0 7 135,6761 640.3835 тм
(N) Tj
/ T1_10 1 Тс
1 0 тд
[(представляет) -278 (тот) -278 (размер) -278 (из) -278 (тот) -278 (образец) -278 (\ ()] TJ
/ T1_11 1 Тс
[-0,3 (т)] ТДж
5 0 0 5 257,0512 639,3835 тм
(i) Tj
7 0 0 7 258,4413 640,3835 тм
(,) Tj
/ T1_3 1 Тс
7 0 1.0881 7 262.3334 640.3835 тм
(\ 023) Tj
/ T1_11 1 Тс
5 0 0 5 266,2255 639,3835 тм
(i) Tj
/ T1_10 1 Тс
7 0 0 7 267,6156 640,3835 тм
[(\)) – 278 (считается.)] TJ
/ T1_9 1 Тс
6,5 0 0 6,5 51,6761 39,8835 тм
(5952) Tj
/ T1_7 1 Тс
9,75 0 0 6,5 72,1327 39,8835 тм
(\ 002) Tj
/ T1_10 1 Тс
6,5 0 0 6.
5 ([107,5253]) – 2745,1 (1022) -4143,5 (1,51) -4699,8 (9,0157) -2812,5 (3,71)] тДж
Т *
[(0,8) -2880,1 (1,25) -3991,1 ([6,419,) – 278 (7,226]) – 3367,1 ([34,5804]) – 3579,1 (781) -4143,7 (1,27) -4699,8 (7,2383) -2812,5 (3,19 )] TJ
Т *
[(0,9) -2880,1 (1,11) -3991,1 ([5,234,) – 278 (5,520]) – 3367,1 ([62,2662]) – 3579,1 (507) -4143,7 (1,17) -4699,8 (5,5313) -2812,5 (2,66 )] TJ
Т *
[(1) -3714,1 (1) -5381,1 ([4,223,) – 278 (4,464]) – 3922,8 ([46,190]) – 3579,4 (365) -4143,7 (1,00) -4699,8 (4,4698) -2812,5 (2,41)] TJ
/ T1_11 1 Тс
7 0 0 7 135,6761 640.3835 тм
(N) Tj
/ T1_10 1 Тс
1 0 тд
[(представляет) -278 (тот) -278 (размер) -278 (из) -278 (тот) -278 (образец) -278 (\ ()] TJ
/ T1_11 1 Тс
[-0,3 (т)] ТДж
5 0 0 5 257,0512 639,3835 тм
(i) Tj
7 0 0 7 258,4413 640,3835 тм
(,) Tj
/ T1_3 1 Тс
7 0 1.0881 7 262.3334 640.3835 тм
(\ 023) Tj
/ T1_11 1 Тс
5 0 0 5 266,2255 639,3835 тм
(i) Tj
/ T1_10 1 Тс
7 0 0 7 267,6156 640,3835 тм
[(\)) – 278 (считается.)] TJ
/ T1_9 1 Тс
6,5 0 0 6,5 51,6761 39,8835 тм
(5952) Tj
/ T1_7 1 Тс
9,75 0 0 6,5 72,1327 39,8835 тм
(\ 002) Tj
/ T1_10 1 Тс
6,5 0 0 6. 5 80,2973 39,8835 тм
(www.pnas.org) Tj
/ T1_7 1 Тс
[-0,3 (\ 001)] ТДж
/ T1_10 1 Тс
(cgi) Tj
/ T1_7 1 Тс
(\ 001) Tj
/ T1_10 1 Тс
(DOI) Tj
/ T1_7 1 Тс
[-0,1 (\ 001)] ТДж
/ T1_10 1 Тс
(10.1073) Tj
/ T1_7 1 Тс
[-0,1 (\ 001)] ТДж
/ T1_10 1 Тс
(pnas.0501977102) Tj
67,4624 0 тд
[(Co) 444,4 (\ 264) -166,5 (rdoba)] TJ
/ T1_11 1 Тс
4.2782 0 Тд
[(et) -278 (al.)] TJ
ET
q
/ GS1 GS
19 0 0815,5 9 9 см
1,3333 TL / Im0 Do
Q
BT
0 г
/ GS1 GS
/ T1_12 1 Тс
0 4-4 0 23 14 тм
(Загружено гостем 3 января 2022 г.) Tj
ET конечный поток
эндобдж
23 0 объект
> поток
5 80,2973 39,8835 тм
(www.pnas.org) Tj
/ T1_7 1 Тс
[-0,3 (\ 001)] ТДж
/ T1_10 1 Тс
(cgi) Tj
/ T1_7 1 Тс
(\ 001) Tj
/ T1_10 1 Тс
(DOI) Tj
/ T1_7 1 Тс
[-0,1 (\ 001)] ТДж
/ T1_10 1 Тс
(10.1073) Tj
/ T1_7 1 Тс
[-0,1 (\ 001)] ТДж
/ T1_10 1 Тс
(pnas.0501977102) Tj
67,4624 0 тд
[(Co) 444,4 (\ 264) -166,5 (rdoba)] TJ
/ T1_11 1 Тс
4.2782 0 Тд
[(et) -278 (al.)] TJ
ET
q
/ GS1 GS
19 0 0815,5 9 9 см
1,3333 TL / Im0 Do
Q
BT
0 г
/ GS1 GS
/ T1_12 1 Тс
0 4-4 0 23 14 тм
(Загружено гостем 3 января 2022 г.) Tj
ET конечный поток
эндобдж
23 0 объект
> потокПредставление без сетки для вычисления медицинских изображений сердца
В этом разделе мы применим структуру EFGM к сегментации изображения сердца и нежесткому анализу движения сердца.
A. Обработка больших деформаций при сегментации
Мы решаем проблему сегментации сердца, используя активную деформируемую модель с биомеханическими ограничениями. В этом биомеханическом ограничении внешняя сила изображения, определяемая производными EFGM PDE, используется для развития границы, как в классической модели Змеи [57].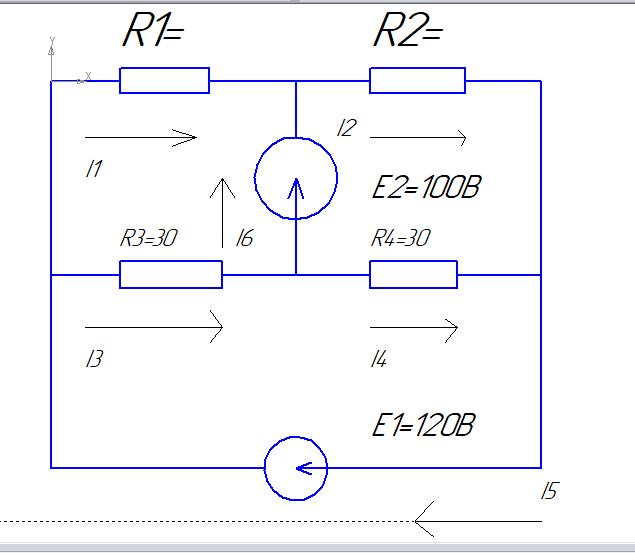
Для объекта кольцевой формы (например, показанного на) мы интегрируем упругую твердую механическую модель в качестве биомеханического ограничения для сегментации изображения.В формулировке без сетки объект определяется двумя границами и рассеянными частицами между ними, так что змея делится на «snaxels». Переменные поля в каждой точке можно гладко представить с помощью функции формы EFGM и соседних узловых переменных. Затем полевые переменные всех точек собираются соответственно в вектор узловых переменных змейки, и, таким образом, уравнение (9) может быть определено как:
, где внешняя сила изображения может быть определена как, а – сила изображения.
FEM (слева) и EFGM (справа) решения сегментации кольцевой упругой твердотельной модели для синтетического изображения: инициализация (вверху) и конечные результаты (внизу).
Мы рассматриваем внешнюю силу изображения как один из видов векторного потока градиента изображения (GVF). Мы сравниваем производительность стандартного линейного МКЭ и метода без сетки для решения состояния равновесия с использованием аналогичной стратегии в [13] в следующих экспериментах. Мы интегрируем уравнение (20), используя явную процедуру Эйлера с шагом по времени.В частности, этот процесс эволюции можно определить как:
Мы интегрируем уравнение (20), используя явную процедуру Эйлера с шагом по времени.В частности, этот процесс эволюции можно определить как:
и, следовательно,
, где и – смещение на шаге, и, соответственно, – это единичная матрица, а – вектор силы на шаге. Эволюция остановится, если внешняя сила станет меньше и / или когда разница смещения между итерациями станет ниже определенного порога. В нашей реализации step и используются для обозначения двух последовательных сердечных кадров в последовательности.
1) Эксперименты с синтетическими данными
При сегментации сердца всегда возникают проблемы с большой деформацией из-за сердечного сокращения.показаны результаты сегментации в форме кольца с упругими твердыми телами с ограничениями на модели с использованием линейного стандартного МКЭ (без адаптивного переназначения) и EFGM на синтетическом изображении. Поскольку функция формы элемента используется для построения интерполяции переменных поля узлов, необходимо построить аппроксимацию переменной поля внутри элемента, используя все узлы этого элемента. Напротив, поскольку в методе EFGM нет явной элементарной связности, отношения между узлами аппроксимируются полевой переменной узлов внутри областей влияния.Количество точек Гаусса и размеры областей влияния можно регулировать для достижения желаемой точности. Как демонстрируется демонстрация, линейный метод FEM без адаптивного перераспределения сетки неспособен обрабатывать большие геометрические изменения, в то время как структура без сетки обеспечивает более плавное перемещение змеи по изображению для эффективного захвата границы объекта.
Напротив, поскольку в методе EFGM нет явной элементарной связности, отношения между узлами аппроксимируются полевой переменной узлов внутри областей влияния.Количество точек Гаусса и размеры областей влияния можно регулировать для достижения желаемой точности. Как демонстрируется демонстрация, линейный метод FEM без адаптивного перераспределения сетки неспособен обрабатывать большие геометрические изменения, в то время как структура без сетки обеспечивает более плавное перемещение змеи по изображению для эффективного захвата границы объекта.
В следующем эксперименте мы применяем как МКЭ, так и структуру без сетки для обнаружения и отслеживания трехмерной границы миокарда на основе синтетического набора данных. Для получения синтетических данных была принята модель сердца собаки, предоставленная Оклендским университетом с геометрией in vitro и архитектурой волокнистого листа в 79 860 точек [47].Представление этой модели сердца более 1746 узлов было построено на основе этой модели сердца собаки с пренебрежением элементами верхушки, как показано на рис.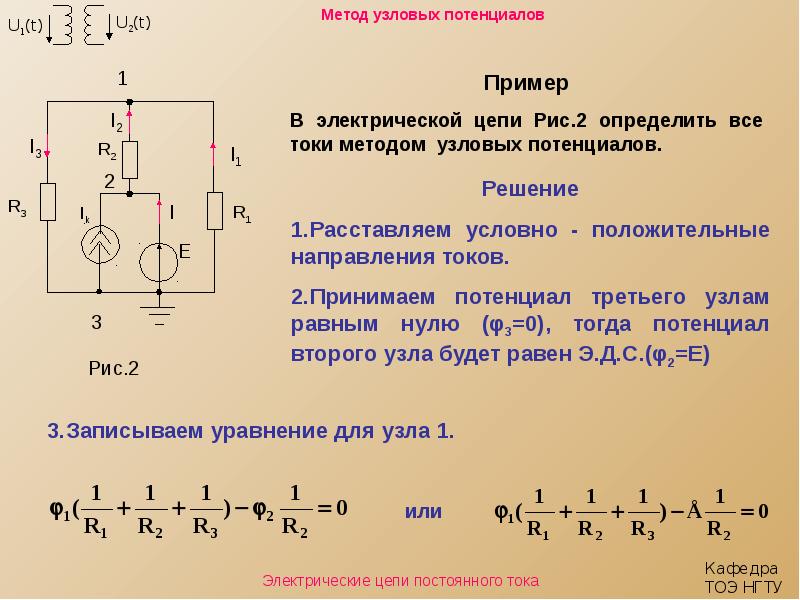 Модуль Юнга был установлен равным 75 кПа. Коэффициент Пуассона был установлен равным 0,47 для имитации несжимаемости. Мы используем эту модель сердца как геометрическое определение и моделируем движение сердца как основную истину, используя одну физиомную платформу из [58]. Было получено 50 кадров всего сердечного цикла за 450 мс, и эти данные движения затем были преобразованы в шкалу серого как последовательность изображений из 50 кадров с размером изображения и пространственным разрешением.Мы также добавили к этим сгенерированным синтетическим изображениям шумы с соотношением сигнал / шум 5 дБ.
Модуль Юнга был установлен равным 75 кПа. Коэффициент Пуассона был установлен равным 0,47 для имитации несжимаемости. Мы используем эту модель сердца как геометрическое определение и моделируем движение сердца как основную истину, используя одну физиомную платформу из [58]. Было получено 50 кадров всего сердечного цикла за 450 мс, и эти данные движения затем были преобразованы в шкалу серого как последовательность изображений из 50 кадров с размером изображения и пространственным разрешением.Мы также добавили к этим сгенерированным синтетическим изображениям шумы с соотношением сигнал / шум 5 дБ.
Верхний ряд: изображения MR в кадрах №1, №4, №7, №10 и №13; Нижняя строка: соответствующие результаты сегментации.
Исходная модель сердца собаки использовалась для отслеживания границы сердца через последовательность синтетических изображений как для МКЭ (линейные элементы тетраэдров, без уточнения), так и для каркаса без сетки (линейные основания, без уточнения). показывает результаты в рамках структуры FEM и предоставляет результаты решения без сетки с количественной оценкой средних позиционных ошибок, скомпилированных за все временные рамки для полной трехмерной геометрии. Позиционная ошибка определяется как расстояние между предполагаемой граничной точкой и наземной точкой отсчета. Позиционная ошибка каждых данных показана как среднее ± стандартное отклонение. В целом, результаты, полученные с использованием представления без сетки, имеют тенденцию придерживаться истинной границы объекта. Было доказано, что сегментированная форма всего сердца с представлением без сетки более близка к границе, определенной на изображении. Сделан вывод, что для обработки больших геометрических изменений МКЭ необходима доработка даже при точной инициализации змейки.Кроме того, представление без сетки даже без уточнения может допускать более крупные геометрические изменения.
Позиционная ошибка определяется как расстояние между предполагаемой граничной точкой и наземной точкой отсчета. Позиционная ошибка каждых данных показана как среднее ± стандартное отклонение. В целом, результаты, полученные с использованием представления без сетки, имеют тенденцию придерживаться истинной границы объекта. Было доказано, что сегментированная форма всего сердца с представлением без сетки более близка к границе, определенной на изображении. Сделан вывод, что для обработки больших геометрических изменений МКЭ необходима доработка даже при точной инициализации змейки.Кроме того, представление без сетки даже без уточнения может допускать более крупные геометрические изменения.
2) Эксперименты с данными МРТ
Как показано на, предлагаемая структура без сетки способна сегментировать границы миокарда в последовательности изображений МРТ. В, мы показываем результаты сегментации левого желудочка от последовательности изображений МРТ маркировки. Обратите внимание, что из-за размытых линий тегов и неоднородности интенсивности метод без сетки сталкивается с трудностями, чтобы дать лучшие результаты.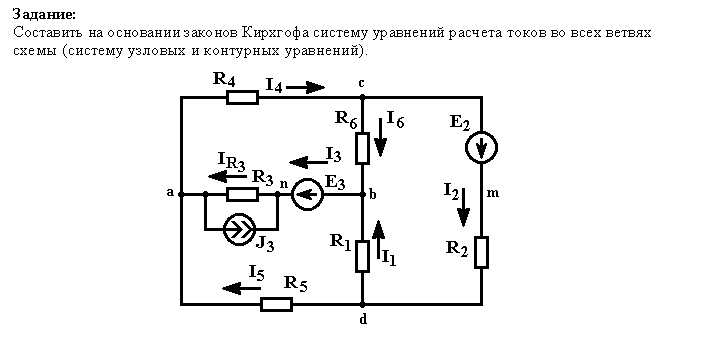 Эту проблему можно решить, применив более сложные внешние силы. Чтобы проверить возможности новой стратегии представления и вычислений в сегментировании 3D-объекта, мы также используем предложенный метод сегментации левого желудочка на данных изображения МРТ человека. Результаты выглядят многообещающими. Однако FEM, использующий линейный базис, не может обрабатывать такие данные, потому что искажение сетки, вызванное большой деформацией
Эту проблему можно решить, применив более сложные внешние силы. Чтобы проверить возможности новой стратегии представления и вычислений в сегментировании 3D-объекта, мы также используем предложенный метод сегментации левого желудочка на данных изображения МРТ человека. Результаты выглядят многообещающими. Однако FEM, использующий линейный базис, не может обрабатывать такие данные, потому что искажение сетки, вызванное большой деформацией
Верхний ряд: размещение изображений в кадрах №1, №4, №7, №10 и №13; Нижняя строка: результаты сегментации на кадрах №1, №4, №7, №10 и №13 ;.
Экспериментальные результаты на кадрах №3, №6, №9, №12 и №16 с использованием структуры без сетки. Вверху: выбранные результаты сегментации по объему. Внизу: результаты сегментации (синие контуры) наложены на исходное изображение.
B. Обработка разрывов в анализе сердечного движения
Анализ сердечного движения по-прежнему остается одной из актуальных тем в нашем исследовательском сообществе. Обратите внимание, что угол волокна нарушен из-за слияния стенки правого желудочка и стенки левого желудочка в перегородке.Более того, миокардиальные волокна размещены в связанных слоях или листах, и между каждым слоем имеется существенный разрыв. Как справиться с этой неоднородностью, обычно связанной с большой деформацией сердца в вычислительной среде, является важным вопросом, потому что это влияет на числовую точность, выполнимость вычислений и сложность реализации. Чтобы преодолеть эти трудности, мы используем метод без сетки для извлечения движения левого желудочка с биомеханическими ограничениями через схему пространства состояний, которая может генерировать оптимальную многокадровую оценку с использованием фильтра Калмана [7].
Обратите внимание, что угол волокна нарушен из-за слияния стенки правого желудочка и стенки левого желудочка в перегородке.Более того, миокардиальные волокна размещены в связанных слоях или листах, и между каждым слоем имеется существенный разрыв. Как справиться с этой неоднородностью, обычно связанной с большой деформацией сердца в вычислительной среде, является важным вопросом, потому что это влияет на числовую точность, выполнимость вычислений и сложность реализации. Чтобы преодолеть эти трудности, мы используем метод без сетки для извлечения движения левого желудочка с биомеханическими ограничениями через схему пространства состояний, которая может генерировать оптимальную многокадровую оценку с использованием фильтра Калмана [7].
Если предполагается линейная инвариантная во времени стохастическая система [7], динамика системы, описываемая уравнением 9, может быть преобразована в представление в пространстве состояний с дискретным временем. Затем мы можем определить динамику системы и измерения, используя следующие уравнения для дискретного времени:
, где и, с
Где – матрица измерений, – это белый процесс (,), – это белый шум измерения (,) и – постоянный интервал времени. Затем выполняется фильтрация Калмана для получения оптимальной оценки [7].
Затем выполняется фильтрация Калмана для получения оптимальной оценки [7].
В целом миокард обладает сложными, анизотропными механическими свойствами с точки зрения его реалистичных основных законов ([2]). Для вычислительной осуществимости мы принимаем линейную упругую модель в этой статье, чтобы проиллюстрировать возможности нашей структуры. Для такого материала зависимость напряжения () и деформации () (конститутивный закон) подчиняется закону Хукера, который гласит, что тензор напряжений линейно пропорционален тензору пятен:
, где матрица материала составляет тензор четвертого ранга и уменьшает матрице для анизотропного материала.
Из-за различной ориентации волокон внутри миокарда следует использовать анизотропную биомеханическую модель для описания внутреннего поведения миокарда. Таким образом, соотношение напряжения и деформации в разных местах может быть различным в одной и той же системе координат и меняется в разных местах. показывает структуру волокон собачьих данных.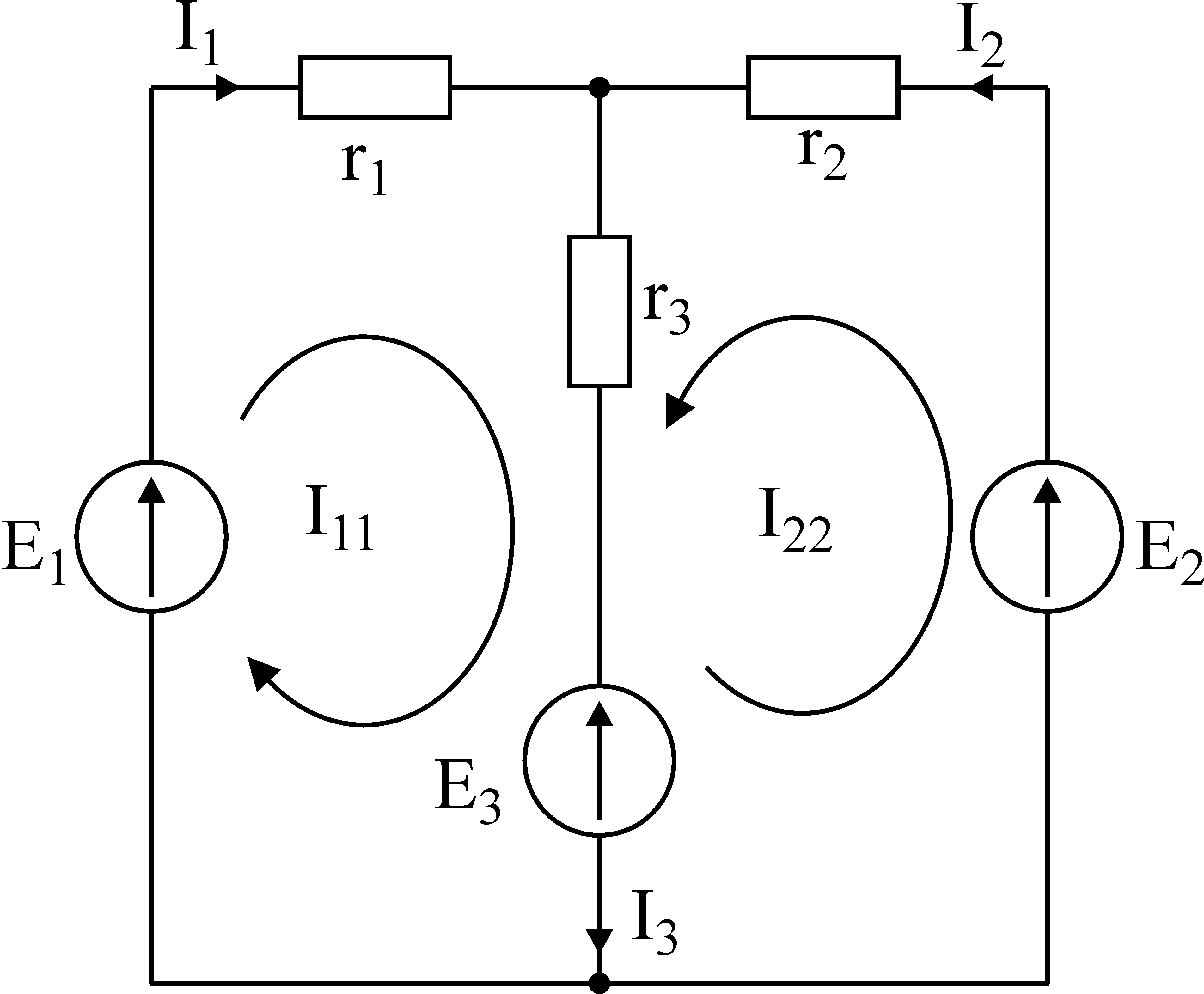
Определим как матрицу материала с ориентацией волокон (вдоль оси):
Здесь и – модуль Юнга вдоль волокна и поперек волокна соответственно.коэффициент Пуассона, который является мерой несжимаемости. описывает свойство сдвига.
Отношение напряжение-деформация в уравнении (27) определяется в координатах материала по отношению к локальному направлению волокна, поскольку направление волокна в значительной степени изменяется от эпикарда и эндокарда [47]. Чтобы собрать матрицу системы, мы преобразуем тензоры напряжения-деформации из материальной координаты в глобальную координату в EFGM. Предполагая, что местная система координат имеет горизонтальный угол в градусах и вертикальный угол в градусах, кроме глобальной системы координат, тогда соответствующая матрица жесткости в глобальной координате может быть задана как:
представляет собой матрицу преобразования комбинации и:
с:
представляет собой матрицу, отвечающую за преобразование между деформацией и инженерной деформацией:
1) Эксперименты с синтетическими данными
Был использован двухмерный деформируемый объект, образованный двумя кусками материалов с одинаковыми свойствами волокнистого материала (), но с разной ориентацией волокон.
Ориентация волокон в левой части составляет -45 °, а в правой части – 45 °. Мы устанавливаем модули Юнга вдоль волокна на 75 кПа и пересекаем волокно на 25 кПа отдельно. Коэффициент Пуассона был установлен равным 0,47. Всего у объекта 66 узлов, и силы прикладываются наружу и по горизонтали к шести узлам на левом краю и шести узлам на правом краю, чтобы заставить его циклически деформироваться, и было шестнадцать кадров, фиксирующих один полный цикл деформации ( ). Результирующие смещения на левом и правом краях были установлены как граничные смещения в качестве входных данных и шума (SNR = 2.912 дБ) для имитации ошибок измерения (). Поля смещения были восстановлены с помощью подхода фильтра Калмана с представлением без сетки и методом конечных элементов.
(а). Шестнадцать кадров цикла движения наземной правды (слева направо, вверх вниз). Желтые линии указывают места приложения сил, а голубые линии указывают ориентацию волокон. (б). Границы с добавленным шумом шестнадцати кадров служат в качестве зашумленных наблюдений (SNR = 2,912 дБ).
В первом эксперименте мы сравниваем метод штрафа за наложение граничных условий в методе EFGM с линейным треугольным стандартным подходом конечных элементов, где оба метода используют ограничения модели изотропного материала.В этом примере расстояние между узловыми точками составляет, таким образом, можно определить штрафной параметр. суммирует средние и стандартные отклонения разностей узловых положений между результатами двух алгоритмов и основной истиной. При тех же смещениях границ и той же модели изотропного материала получаются очень похожие результаты.
ТАБЛИЦА 1
Сравнение результатов, полученных с помощью метода штрафов за наложение граничных условий в методе EFGM и подходе FEM.Каждая ячейка данных представляет среднее и стандартное отклонение разницы позиций между основной истиной и соответствующими алгоритмами. Общее среднее и стандартное отклонение для каждого алгоритма вычисляются с использованием всех узловых разностей шестнадцати кадров. EFGM: Общее среднее значение: 0,2298, общее стандартное отклонение: 0,1878. FEM: Общее среднее значение: 0,2279, общее стандартное отклонение: 0,1936
| EFGM (кадр № 1–4) | 0,0225 ± 0,0628 | 0,1547 ± 0,0797 | 0,1867 ± 0,0610 | 0.1702 ± 0,1021 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| EFGM (рама # 5-8) | 0,2991 ± 0,1769 | 0,2943 ± 0,1771 | 0,3214 ± 0.2011 | 0,3314 ± 0,2467 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,4111 ± 0,2812 | 0,3112 ± 0,1978 | 0,3324 ± 0,1950 | ||
| EFGM (рамка 13-16) | 0,2117 ± 0,1396 | 0,1502 ± 0,0874 | 0,19||
| FEM (кадр №1-4) | 0.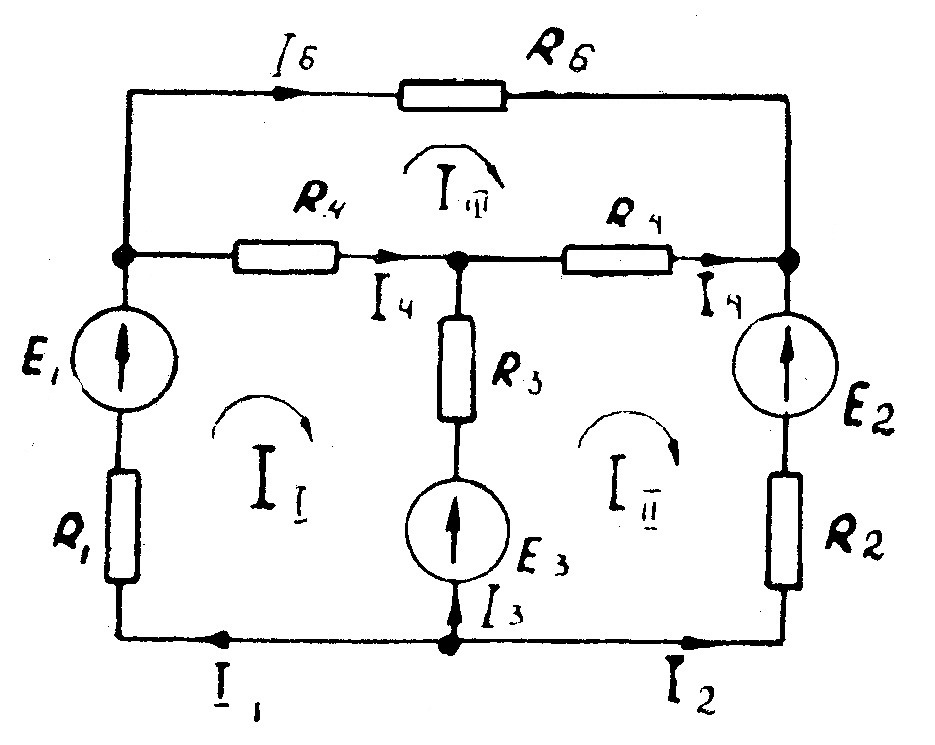 0245 ± 0,0328 0245 ± 0,0328 | 0,1267 ± 0,0482 | 0,1611 ± 0,1123 | 0,2110 ± 0,1423 |
| МКЭ (рамка # 5-8) | 0,2396 ± 0,1819 | 0,2944 ± 0,278400 0,39 | ||
| FEM (рамка # 9-12) | 0,3994 ± 0,3111 | 0,3641 ± 0,2691 | 0,3102 ± 0,2275 | 0,2887 ± 0,2108 |
| FEM (рамка # 1378684) | 0,160.1994 ± 0,1176 | 0,1473 ± 0,0698 | 0,0990 ± 0,0392 |
Во втором эксперименте использовалось то же условие, что описано выше, за исключением того, что используется модель анизотропного материала с учетом ориентации волокон. Из видно, что поля смещения, оцененные с использованием представления без сетки, лучше. Это главным образом связано с тем, что представление без сетки может естественным образом обрабатывать прерывистые волокна и позволяет избежать проблемы, вызванной перекосом элементов.
ТАБЛИЦА 2
Сравнение результатов EFGM (Linear Bases) и линейного треугольного метода конечных элементов. Каждая ячейка данных представляет среднее и стандартное отклонение разницы позиций между основной истиной и соответствующими алгоритмами. Общее среднее и стандартное отклонение для каждого алгоритма вычисляются с использованием всех узловых разностей шестнадцати кадров. EFGM: Общее среднее значение: 0,1189, общее стандартное отклонение: 0,0672. FEM: Общее среднее: 0,1793, общее стандартное отклонение: 0,1166
| EFGM (кадр 1-4) | 0.0987 ± 0,0565 | 0,1097 ± 0,0589 | 0,0971 ± 0,0591 | 0,1291 ± 0,0478 | |||||||||||||||||||||
| EFGM (рамка № 5 – 8) | 0,0704 ± 0,0696 | 0,1478 ± 0,0599 0,125 | 0,1478 ± 0,0499 0,15 | ||||||||||||||||||||||
| EFGM (рама 9 – 12) | 0,1097 ± 0,0705 | 0,1511 ± 0,0562 | 0,0679 ± 0,0502 | 0,1616 ± 0,0571 | |||||||||||||||||||||
| EFGM | 0,1165 0. 1493 ± 0,0671 1493 ± 0,0671 | 0,1267 ± 0,0605 | 0,1109 ± 0,0876 | ||||||||||||||||||||||
| МКЭ (рамка № 1 – 4) | 0,0218 ± 0,0598 | 0,1043 ± 0,0611 | 0,1074 ± 0,0634 | 0,1074 ± 0,0634 | (кадр 5-8)0,1032 ± 0,0701 | 0,1871 ± 0,0901 | 0,2299 ± 0,0898 | 0,2693 ± 0,1096 | |||||||||||||||||
| МКЭ (кадр 9-12) | 0,3657 ± 078475 | 0.2749 ± 0,0960 | 0,1712 ± 0,0801 | ||||||||||||||||||||||
| МКЭ (кадр № 13-16) | 0,1506 ± 0,1018 | 0,2018 ± 0,1231 | 0,1305 ± 0,0923 | 0,1105 ± 0,0992 | M-1 Данные|||||||||||||||||||||
| Справочное руководство по геологии разработки | |
| серии | Методы разведки |
|---|---|
| Деталь | Интегрированные компьютерные методы |
| Глава | Введение в контурную геологическую обработку данных с помощью компьютера |
| Автор | Дж. Л. Гевиртц Л. Гевиртц |
| Ссылка | Веб-страница |
| Магазин | Магазин AAPG |
Базовым инструментом для анализа и отображения пространственных геологических данных является контурная карта. Контурная карта отображает изменение геологической переменной, такой как толщина, глубина или пористость, в интересующей области с помощью контурных линий равного значения. Часто одна или несколько контурных карт составляют основу подробного анализа потенциальных или реальных коллекторов и используются для оценки объемов флюидов, содержащихся в поровых пространствах интересующего геологического объекта.Эти исследования требуют, чтобы карты были графически представлены, а значения, лежащие в основе графического изображения поверхности, были надежными и воспроизводимыми. Необходимо понимать ошибки, присущие процедурам математической оценки, чтобы можно было оценить надежность значений (объемов, процентов и т. Д.), Полученных из этих карт.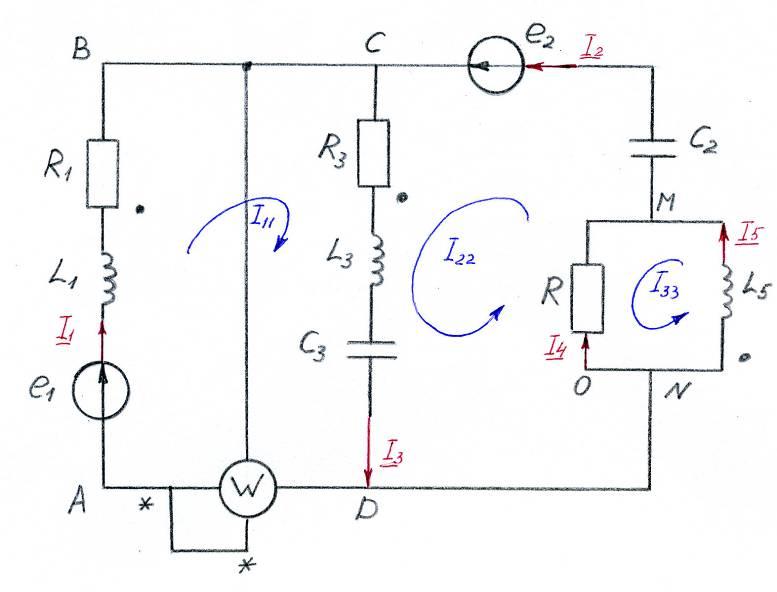
Формы геологических поверхностей сложны и не могут быть легко аппроксимированы простыми математическими функциями, потому что они являются результатом множества взаимодействующих процессов, которые изменяются в разных пространственных масштабах.В идеале пространственные данные следует исследовать с помощью пространственной выборки обычного геометрического дизайна. Эти конструкции могут улавливать диапазон вариаций, проявляемых большинством пространственных явлений. Однако такие конструкции для всех практических целей невозможны для большинства геологических работ, хотя в некоторых случаях недавние разработки в области спутниковых изображений позволяют их экономически выгодно реализовать. В большинстве случаев образцы подземных геологических объектов отбираются редко из-за их сложности, а образцы сильно склонны к геофизическим и / или геологическим аномалиям.Следовательно, значения переменной в интересующей области должны оцениваться путем интерполяции из разреженного, нерегулярного набора контрольных точек.
В геологической практике часто встречаются несколько схем контрольных точек. К ним относятся случайные шаблоны или кластеры (рис. 1). Геофизические данные, необходимые для геологического изучения, собираются по линиям. Линии – это частный случай сгруппированных точек. Каждый узор имеет свои собственные пространственные характеристики и должен быть понят, прежде чем можно будет построить осмысленное контурное представление.Большинство геологических данных обычно демонстрируют свойства обоих структур конечных элементов. Сетчатые узоры в геологической практике встречаются редко. Большинство коммерческих пакетов для построения контуров вычисляют статистику, которая при использовании с визуальным контролем рисунка на базовой карте может значительно помочь в выборе подходящего метода контурирования.
Компьютерное контурирование в сравнении с контуром руки
Рисунок 1 (a) Случайные точки. (б) Кластерные точки.
Рис.
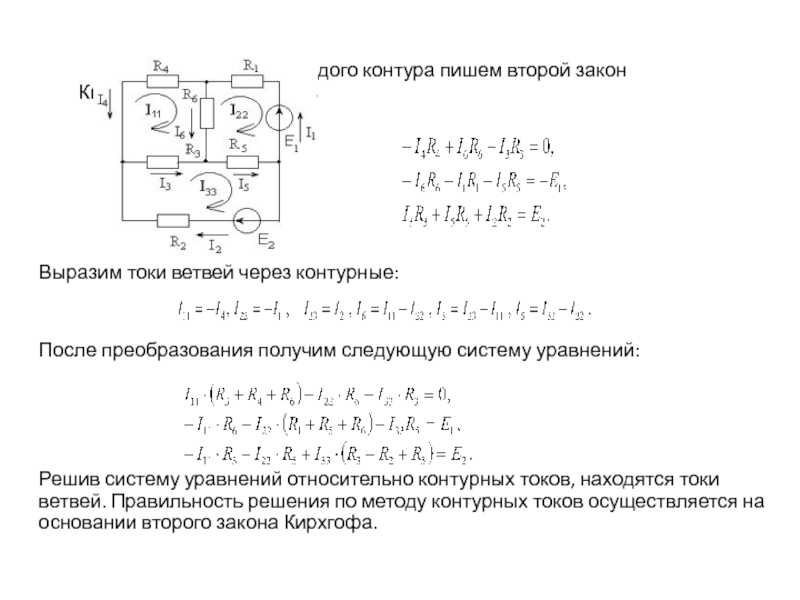 2 Треугольная сетка, полученная на основе данных Дэвиса [1] .
2 Треугольная сетка, полученная на основе данных Дэвиса [1] .Рисунок 3 Контурная треугольная сетка на Рисунке 2.
Рисунок 4 Поверхность, очерченная на треугольной сетке. Исходная поверхность – полином четвертого порядка.
Рисунок 5 Контуры из сетки 13 × 13 с использованием поиска ближайшего соседа. (Данные Davis [1] .)
Рис. 7 Представление полинома четвертого порядка на рис. 4, очерченное на сетке, подготовленной с использованием критерия поиска ближайшего соседа.
Контурные карты, представляющие трехмерные геологические поверхности, готовятся с помощью проверенных временем процедур, включающих методы оценки. До появления быстрых компьютеров и вычислительных алгоритмов карты, показывающие геологические вариации, готовились вручную. Карты, нанесенные вручную, представляют собой наилучшее приближение геолога к форме исследуемой поверхности.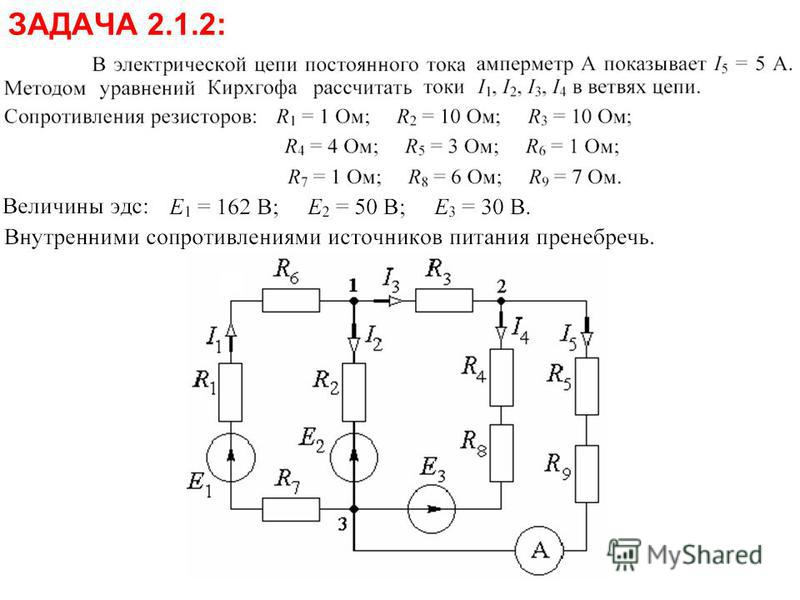 Идеи, основанные на региональной геологической структуре и предвзятости геолога, вытекающей из предыдущего опыта, являются неотъемлемой частью нарисованной вручную карты.Карты, нанесенные вручную, не могут быть воспроизведены точно, а значения, подразумеваемые контурами, не могут быть восстановлены.
Идеи, основанные на региональной геологической структуре и предвзятости геолога, вытекающей из предыдущего опыта, являются неотъемлемой частью нарисованной вручную карты.Карты, нанесенные вручную, не могут быть воспроизведены точно, а значения, подразумеваемые контурами, не могут быть восстановлены.
Напротив, средства высокоскоростных вычислений создали методы, посредством которых «объективная» поверхность может быть создана путем применения процедур математической интерполяции к набору контрольных точек. Эти методы свободны от каких-либо геологических предвзятостей или интерпретаций, вводимых во время подготовки карты, поскольку они создают представление поверхности, построенной с помощью «непредвзятого» и явно несмещенного математического определения на основе данных, измеренных в выбранных контрольных точках.Компьютерные контурные карты можно легко воспроизвести, представив программе те же данные и параметры, которые использовались для создания исходной карты. Значения, лежащие в основе контурного представления, могут быть получены с помощью той же процедуры интерполяции, которая использовалась для его создания.
Процедуры, обычно используемые при ручном контуре, требуют, чтобы геолог выбрал интервал изолиний, который наилучшим образом отображает идеи, которые должны быть переданы на карте. Компьютерные методы построения контуров, напротив, требуют от геолога выбора параметров, которые в конечном итоге определят математическую основу для расчета и построения законченной карты.Многие наборы параметров могут использоваться для создания контурного представления поверхности, взятой из разреженного набора контрольных точек. Карты будут похожи по внешнему виду, но будут отличаться в определенных областях, потому что каждый набор параметров вызывает вызов различных математических процедур. Каждая процедура создает отдельную карту. (Например, сравните рисунки 1 и 2 у Phillip and Watson [2] и рисунок 11.07 у Clarke [3] с рисунками 3, 4, 5 и 7 этой статьи).Подходящие параметры для конкретного проекта картографии выбираются путем тщательной проверки плотности и распределения контрольных точек, из которых будет построена карта.
Значения данных между контрольными точками получаются с помощью некоторой формы интерполяции как для ручного, так и для компьютерного контурирования. Для карт с ручным контуром интерполяция, необходимая для оценки положения и формы отдельных контуров, выполняется на глаз или с помощью простых методов усреднения. Треугольная сетка или прямоугольная сетка обеспечивают основу для интерполяции данных из контрольных точек.Эти структуры полагаются на сложную математическую функцию интерполяции (бикубические шлицы, полиномы высокого порядка) для оценки положения контуров между точками данных. Эта функция представляет собой полином, который является «гибким» и может представлять широкий спектр форм кривых. Однако прямого геологического значения эти функции не имеют. Они имеют непрерывную производную всюду внутри треугольника или прямоугольника и, следовательно, по крайней мере один раз дифференцируемы. Это гарантирует, что информация об уклоне, подразумеваемая набором контрольных точек, будет более точно отображена вычислительной процедурой.
Важно понимать, что все методы контурной обработки, математические или иные, являются методами интерполяции и, следовательно, включают ошибку в результирующей поверхности. Эта ошибка связана как с плотностью, так и с местоположением измеренных контрольных точек, используемых для построения поверхности.
Триангуляция
Триангуляция соединяет контрольные точки в сетку локально равноугольных треугольников (треугольников Делоне) (рис. 2). Положение контура в границах каждого треугольника оценивается путем интерполяции значений контрольных точек, которые являются вершинами треугольников.Каждый элемент треугольной сетки обрабатывается отдельно, а поверхность создается путем сборки треугольников. Интерполяция и построение контуров на триангулированной сетке требует от геолога нескольких решений. Данные контрольной точки передаются методу вместе с интервалом изолиний, и создается контурное представление требуемой поверхности. Рисунок 3 – это контурное представление данных контрольной точки, представленных Davis [1] , полученных путем интерполяции на треугольной сетке (Рисунок 2).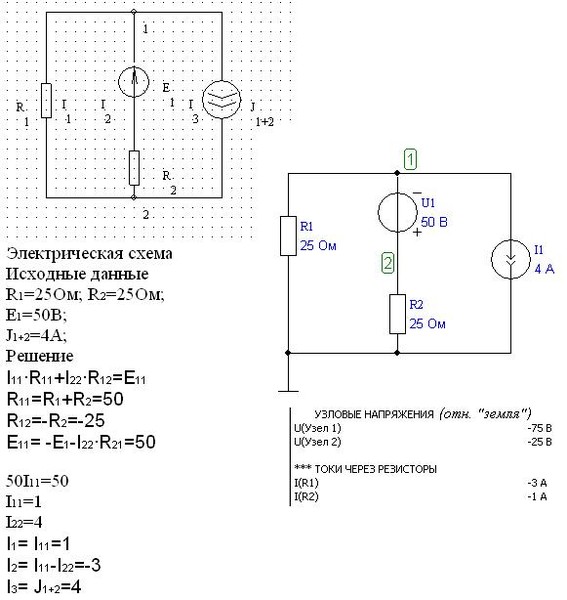
Контуры, подготовленные на треугольной сетке, всегда строго соблюдают все точки данных, используемые для интерполяции. Триангулированные сетки легко обновляются, поэтому добавление новых контрольных точек и обновление карт упрощается. Однако контуры, подготовленные на этой сетке, часто выглядят «грубыми» и менее желательны. Некоторые более сложные картографические пакеты предоставляют процедуры сглаживания, чтобы сделать карты более приемлемыми. На рис. 4 показан участок поверхности, очерченный с использованием схемы триангуляции.Обратите внимание на неправильную форму контуров. Исходная поверхность, отобранная для создания этой карты, является полиномом четвертого порядка. Форма этой поверхности отличается плавными контурами. Неровности, показанные на рисунке 4, являются артефактами процедуры интерполяции, используемой для оценки контуров внутри отдельных треугольников. Однако относительное положение контуров является хорошим приближением к положению исходной поверхности.
Триангуляция не является предпочтительным методом, когда требуются поверхности, полученные из нескольких горизонтов для одной и той же области интереса.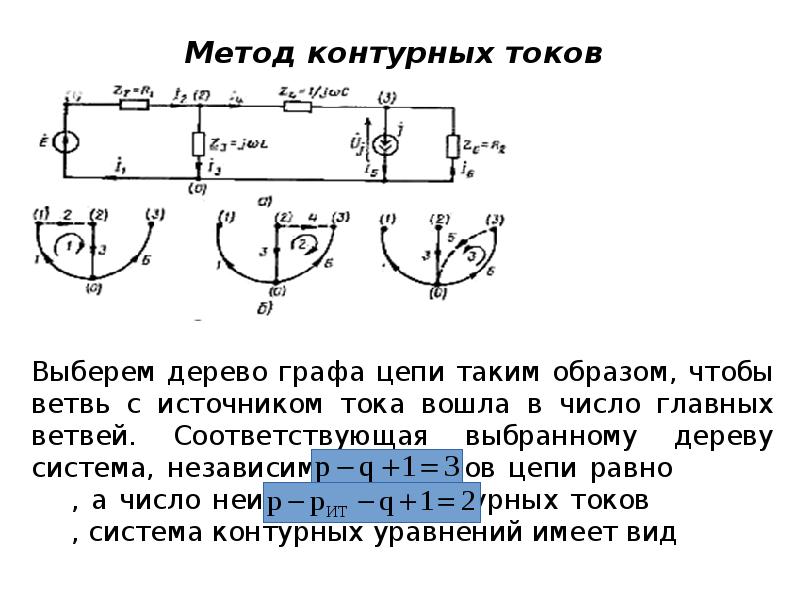 Операции между поверхностями (такие как вычитание нижней из верхней) требуют, чтобы данные существовали в каждой контрольной точке для обоих горизонтов. Часто это не относится к скважинным данным и требует предоставления оценочной точки, где данные отсутствуют. [4]
Операции между поверхностями (такие как вычитание нижней из верхней) требуют, чтобы данные существовали в каждой контрольной точке для обоих горизонтов. Часто это не относится к скважинным данным и требует предоставления оценочной точки, где данные отсутствуют. [4]
Решетка прямоугольная
Рис. 6 Сетка A13 × 13, показывающая взаимосвязь между узлами сетки и контрольными точками для набора данных Davis [1] . При построении прямоугольной сетки, в отличие от триангуляции, сначала используются данные в измеренных контрольных точках для интерполяции значений в набор узлов сетки с заранее заданным интервалом.Эти значения затем используются для оценки положения контуров, пересекающих каждый прямоугольник сетки. Вся поверхность собирается из смежных прямоугольников сетки. Для большинства геологических приложений используются квадраты сетки, а не более общий прямоугольник. Интерполяция и построение изолинии контрольной точки с неравномерным интервалом, установленной на прямоугольной сетке, требует от геолога множества решений.
Чтобы получить представление контурной поверхности с помощью метода прямоугольной сетки, геолог должен выбрать интервал сетки, критерий поиска и метод интерполяции данных контрольной точки в узлы сетки, а также подходящий интервал изолиний.Большинство коммерческих картографических пакетов включают в себя множество вариантов интервалов, критериев поиска и методов. Эти решения требуют понимания взаимосвязи между плотностью / распределением контрольных точек и текстурой поверхности.
Контуры, полученные в результате интерполяции данных контрольных точек в равномерно распределенные узлы сетки, не строго соблюдают контрольные точки, из которых они были созданы, потому что процедуры построения контуров учитывают оценочные значения в узлах сетки, а не значения для исходных контрольных точек.Этим до некоторой степени можно управлять, задав меньший интервал сетки. Однако меньшие интервалы сетки приводят к большей ошибке интерполяции в областях с разреженными данными, так что на карту будут накладываться многие мелкие объекты, которые являются артефактами самой процедуры построения сетки и не имеют геологического значения.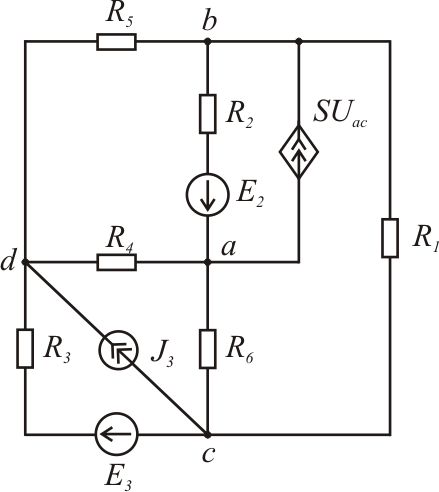 Установка подходящего размера сетки требует тщательного рассмотрения распределения и расстояния между контрольными точками. Многие коммерческие картографические пакеты предоставляют меры среднего расстояния до контрольных точек, которые могут помочь при выборе размера сетки и критерия поиска.
Установка подходящего размера сетки требует тщательного рассмотрения распределения и расстояния между контрольными точками. Многие коммерческие картографические пакеты предоставляют меры среднего расстояния до контрольных точек, которые могут помочь при выборе размера сетки и критерия поиска.
Поскольку геологические данные редко представляются на единой сетке и чаще всего неравномерно распределяются по области карты, количество контрольных точек, используемых для оценки значений в узлах сетки, является важным фактором. Было разработано несколько процедур поиска, которые включены в большинство картографических пакетов. К ним относятся поиск ближайшего соседа, кругового, квадрантного и октантного поиска.
Поиск ближайшего соседа использует ближайших соседей узла сетки для оценки узловых значений.Число используемых соседей может быть решено произвольно или может быть принято в качестве ближайших соседей, определенных триангуляцией Делоне набора контрольных точек. Число ближайших соседей, определяемое по неравномерно разнесенным контрольным точкам, может варьироваться, так что каждый узел сетки можно оценивать по разному количеству контрольных точек в зависимости от их распределения по области карты.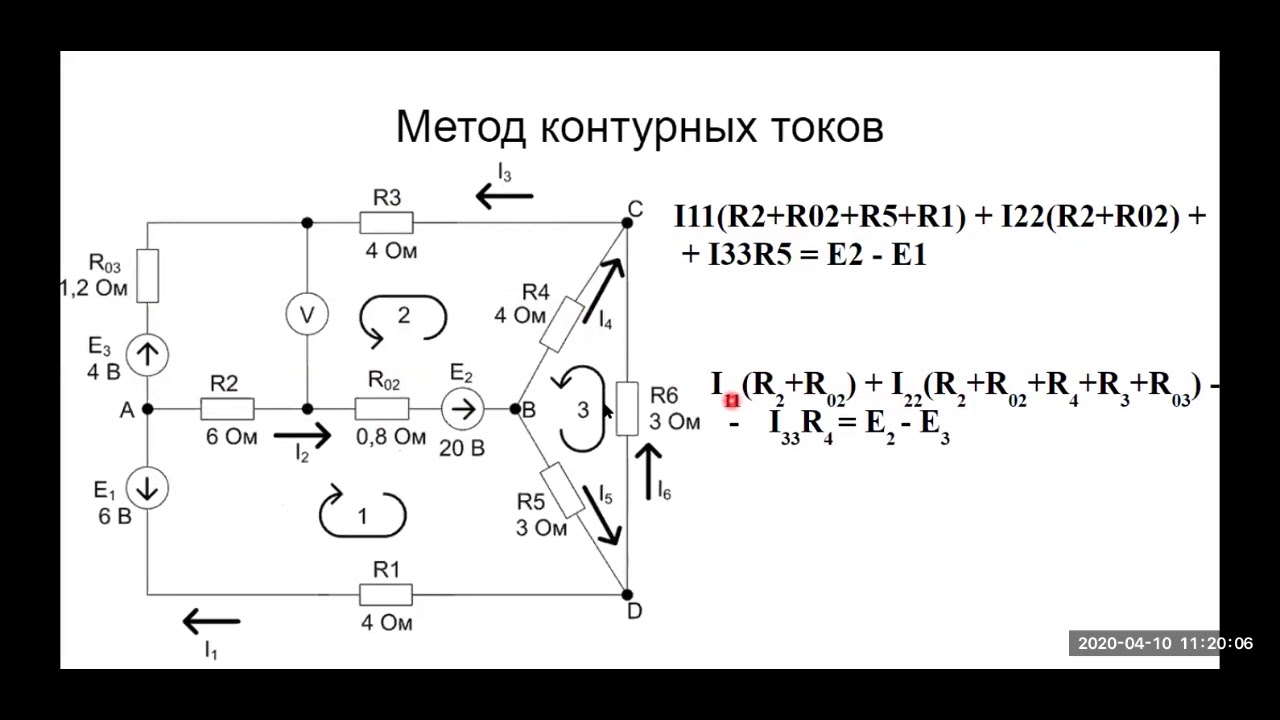 Рисунок 5 – это контурное представление тех же данных, что и на рисунке 3, с использованием поиска ближайшего соседа и сетки 13 × 13 (рисунок 6).
Рисунок 5 – это контурное представление тех же данных, что и на рисунке 3, с использованием поиска ближайшего соседа и сетки 13 × 13 (рисунок 6).
Процедуры поиска окрестностей по кругу, квадранту и октанту пытаются сбалансировать количество и распределение контрольных точек, используемых для оценки каждого узла сетки. Большинство картографических пакетов включают процедуры для оценки плотности и расстояния между контрольными точками, и эту статистику следует тщательно изучить, прежде чем принимать решение о критериях поиска для конкретного проекта.
Создание сетки карты также требует, чтобы была выбрана процедура интерполяции для оценки значений в узлах сетки.Для этого было разработано множество методов, включая методы взвешивания, методы прогнозирования тенденций и статистические методы. Наиболее распространенные методы построения сетки хорошо описаны Дэвисом [1] и Кларком. [3]
Методы взвешивания присваивают веса значениям в контрольных точках на основе их расстояния от оцениваемого узла сетки. Существуют различные стратегии разработки схем взвешивания. Наиболее часто встречающаяся схема, используемая для геологических данных, – это взвешивание обратных расстояний.Для этой схемы значения в контрольных точках взвешиваются по величине, обратной расстоянию от узла. Варианты этой схемы позволяют взвешивать значения контрольной точки по величине, обратной величине расстояния, возведенной в выбранную степень. Положительные мощности заставляют влияние более удаленных точек вносить меньший вклад в значение, оцененное в узле сетки. Выбор степени увеличения расстояния зависит от «шероховатости» поверхности и ощущения взаимосвязи между контрольными точками и формой поверхности.Некоторые из этих схем взвешивания рассмотрены Кларком [3] и Дэвисом. [1]
Существуют различные стратегии разработки схем взвешивания. Наиболее часто встречающаяся схема, используемая для геологических данных, – это взвешивание обратных расстояний.Для этой схемы значения в контрольных точках взвешиваются по величине, обратной расстоянию от узла. Варианты этой схемы позволяют взвешивать значения контрольной точки по величине, обратной величине расстояния, возведенной в выбранную степень. Положительные мощности заставляют влияние более удаленных точек вносить меньший вклад в значение, оцененное в узле сетки. Выбор степени увеличения расстояния зависит от «шероховатости» поверхности и ощущения взаимосвязи между контрольными точками и формой поверхности.Некоторые из этих схем взвешивания рассмотрены Кларком [3] и Дэвисом. [1]
Методы проекции тренда представляют собой адаптацию метода линейной регрессии, называемого анализ поверхности тренда . Этот метод был разработан, потому что отбор геологических подземных проб редко обеспечивает наблюдения в самых высоких или самых низких точках на поверхности, и иногда желательно позволить процедуре интерполяции превышать измеренный максимум и минимум. Методы проекции тренда используют один из ранее описанных критериев поиска для выбора точек, которые берутся группами по три и точно соответствуют плоскости с использованием методов наименьших квадратов или бикубических сплайнов.Оценка узла сетки получается путем усреднения проекций этих плоскостей. Этот метод может быть весьма эффективным для гладких поверхностей, где региональная ориентация падения остается относительно постоянной на большой площади карты. Этот метод позволяет получить поверхность с более высокой текстурой, чем фактическая поверхность в сильно деформированных областях, где направление падения быстро меняется на небольших расстояниях. Sampson [5] подробно рассматривает этот метод.
Методы проекции тренда используют один из ранее описанных критериев поиска для выбора точек, которые берутся группами по три и точно соответствуют плоскости с использованием методов наименьших квадратов или бикубических сплайнов.Оценка узла сетки получается путем усреднения проекций этих плоскостей. Этот метод может быть весьма эффективным для гладких поверхностей, где региональная ориентация падения остается относительно постоянной на большой площади карты. Этот метод позволяет получить поверхность с более высокой текстурой, чем фактическая поверхность в сильно деформированных областях, где направление падения быстро меняется на небольших расстояниях. Sampson [5] подробно рассматривает этот метод.
Рисунок 7 – та же часть поверхности, что и на Рисунке 4.Карта на рисунке 7 была построена методом сетки с поиском ближайшего соседа. Контуры для этой карты гладкие, и их форма близко приближается к контурам исходной полиномиальной поверхности четвертого порядка, из которой были получены контрольные точки.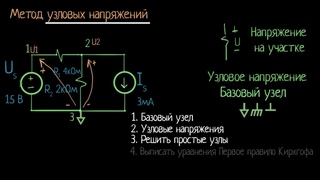 Однако изолинии не находятся в тех же географических положениях, что и на исходной поверхности, и некоторые контрольные точки строго не соблюдаются.
Однако изолинии не находятся в тех же географических положениях, что и на исходной поверхности, и некоторые контрольные точки строго не соблюдаются.
Статистические методы
Несколько статистических методов можно использовать для построения регулярной сетки из данных контрольных точек.Анализ поверхности тренда – это метод регрессии, который подбирает полином степенного ряда для данных контрольной точки. Этот метод использовался в геологической практике для выделения региональных трендов из разреженных наборов контрольных точек. Он не предназначен для учета контрольных точек, но вместо этого используется для отделения региональных вариаций от местных (например, разделения структурных и стратиграфических вариаций). Его часто используют при разведке, но мало для детального картирования резервуаров.
Кригинг – это статистический метод, разработанный Кригом [6] и разработанный Matheron, [7] для оценки запасов золота в рудных телах. Он нашел широкое применение в качестве метода координатной сетки в нефтяной промышленности. Этот метод основан на теории регионализированной переменной, впервые сформулированной Матероном [7] и популяризированной Кларком [8] и Джурнелем и Хейбрегтсом. [9] Теория региональных переменных разбивает пространственные вариации на три компонента. Дрейф – это крупномасштабная вариация, которую можно отнести к региональной вариации, случайной, но пространственно коррелированной части меньшего масштаба и случайному шуму еще меньшего масштаба.Этот метод использует знания о пространственной дисперсии дрейфа для получения набора весов для контрольных точек, которые являются несмещенными статистическими оценками. Если все статистические допущения соблюдены, он может предоставить контуры, которые являются несмещенными оценками. Он также обеспечивает дисперсию оценки в каждом узле сетки. Таким образом, этот метод статистически превосходит методы построения сетки, рассмотренные ранее.
Он нашел широкое применение в качестве метода координатной сетки в нефтяной промышленности. Этот метод основан на теории регионализированной переменной, впервые сформулированной Матероном [7] и популяризированной Кларком [8] и Джурнелем и Хейбрегтсом. [9] Теория региональных переменных разбивает пространственные вариации на три компонента. Дрейф – это крупномасштабная вариация, которую можно отнести к региональной вариации, случайной, но пространственно коррелированной части меньшего масштаба и случайному шуму еще меньшего масштаба.Этот метод использует знания о пространственной дисперсии дрейфа для получения набора весов для контрольных точек, которые являются несмещенными статистическими оценками. Если все статистические допущения соблюдены, он может предоставить контуры, которые являются несмещенными оценками. Он также обеспечивает дисперсию оценки в каждом узле сетки. Таким образом, этот метод статистически превосходит методы построения сетки, рассмотренные ранее.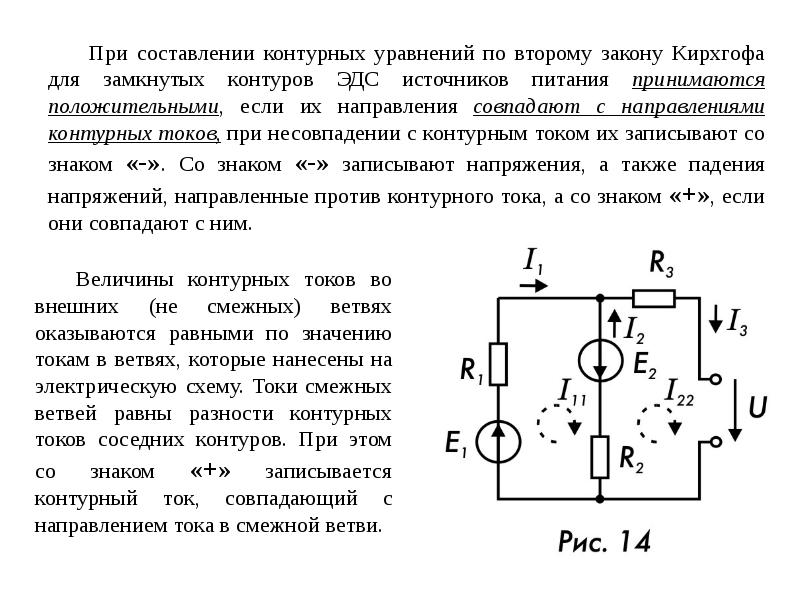 Также строго соблюдаются контрольные точки.
Также строго соблюдаются контрольные точки.
Знание функции дрейфа необходимо для использования метода интерполяции данных контрольной точки на узлы сетки.Эти знания воплощены в функции, называемой полувариограммой , которую можно оценить для нескольких ориентаций по геофизическим данным. [10] Если полувариограмма не может быть получена экспериментально, она считается линейной или экспоненциальной. Это предположение может значительно снизить достоверность оценки, тем самым сводя на нет всю мощь метода. Хотя это самый сложный из обсуждаемых здесь методов, он имеет широкое применение в анализе коллектора (см. Корреляционный и регрессионный анализ, Многомерный анализ данных, Монте-Карло и методы стохастического моделирования), а также в моделировании коллектора для целей моделирования и проведении исследования с помощью моделирования коллектора. : обзор.
Несколько слов о несплошностях
Большинство процедур интерполяции, особенно те, которые включают некоторую форму сетки, предполагают, что оцениваемая поверхность является пространственно непрерывной.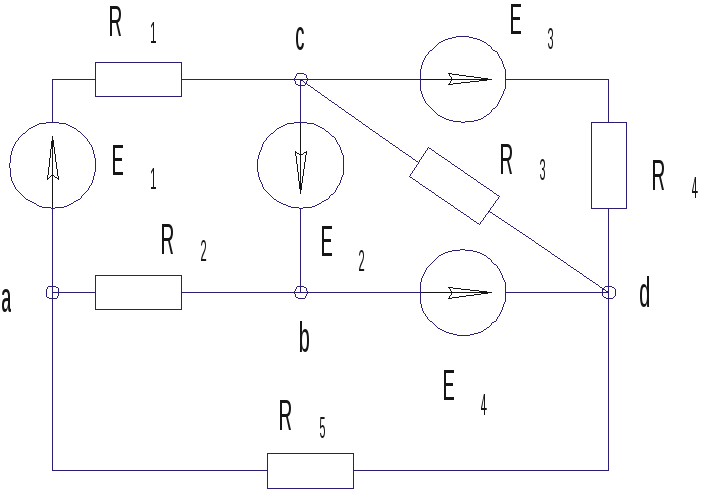 Эти методы построения сетки не позволяют успешно моделировать неоднородности, такие как разломы или стратиграфические выклинивания. Большинство картографических пакетов позволяют геологу вводить трассу разлома, которая эффективно разделяет область на отдельные участки с координатной сеткой и контуром. Выщипывание и другие стратиграфические неоднородности обрабатываются забором, определяющим нулевой контур.На изнаночной стороне нулевой линии контур не появится. [4] Процедуры триангуляции могут моделировать разломы или другие прерывистые террейны с несколько большим успехом без включения следов разломов или нулевых контурных линий.
Эти методы построения сетки не позволяют успешно моделировать неоднородности, такие как разломы или стратиграфические выклинивания. Большинство картографических пакетов позволяют геологу вводить трассу разлома, которая эффективно разделяет область на отдельные участки с координатной сеткой и контуром. Выщипывание и другие стратиграфические неоднородности обрабатываются забором, определяющим нулевой контур.На изнаночной стороне нулевой линии контур не появится. [4] Процедуры триангуляции могут моделировать разломы или другие прерывистые террейны с несколько большим успехом без включения следов разломов или нулевых контурных линий.
Следует иметь в виду, что для разломов требуется геометрия, связанная с типом разлома и свойствами деформируемого материала. Математическая интерполяция не учитывает эти факторы при построении контуров нарушенных террейнов. Процедуры картирования разломов, которые учитывают геометрические последствия типа разлома, еще не разработаны; таким образом, интерполяции должно хватить, пока такие процедуры не станут доступными.
Обучение компьютерному контурному изображению
В предыдущих разделах были представлены многочисленные методы компьютерного контурирования. Помимо общих соображений о распределении данных и плотности, которые были упомянуты, мало что можно сказать, чтобы рекомендовать «лучший» метод контурирования для всех проблем. О каждом методе можно сказать гораздо больше, и обсуждение сильных и слабых сторон каждого из них может заполнить и заполнить множество томов (см., Например, периодический журнал Mathematical Geology (Plenum Press) для обсуждения относительных достоинств различных процедур кригинга). ).Лучший подход к обучению применению методов, описанных здесь (и других), для решения практических задач (таких как оценка коллектора) – это применить их к известным данным и сравнить результаты.
Можно использовать несколько подходов. Каждый из них предоставит некоторое представление о работе различных методов и поможет выбрать, какие методы являются предпочтительными в каких проектах.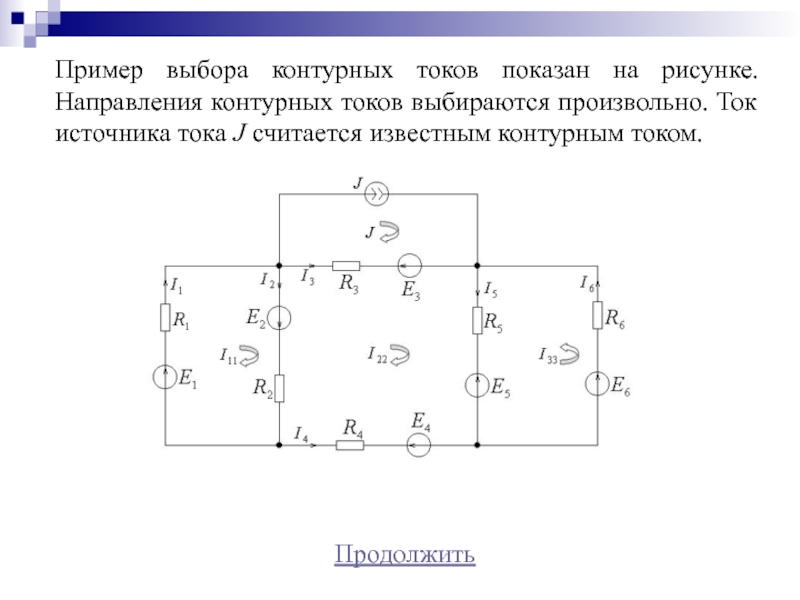 Первый и самый простой подход – взять образец с топографической карты (желательно со значительным рельефом) и применить к ней различные методы контурирования.Сравните вычисленные результаты с исходными, наложив выходные данные и вычтя сетки, оцененные двумя методами. Как можно сравнить разные методы? Какие методы переоценивают поверхность? Которые его недооценивают?
Первый и самый простой подход – взять образец с топографической карты (желательно со значительным рельефом) и применить к ней различные методы контурирования.Сравните вычисленные результаты с исходными, наложив выходные данные и вычтя сетки, оцененные двумя методами. Как можно сравнить разные методы? Какие методы переоценивают поверхность? Которые его недооценивают?
Второй подход заключается в сравнении поверхностей, созданных доступными методами на поверхности, которая использовалась в качестве стандарта для других работ. Хороший – небольшой дренажный бассейн, использованный для подготовки рисунков 3 и 5 (его можно найти в [1] ). Остальные можно получить из CEED II, который представляет собой оценку пакетов отображения. [11]
Наконец, хотя компьютерное контурирование является большой и растущей дисциплиной, оно остается чем-то вроде искусства, лучшим ориентиром для которого является опыт. В этом кратком введении он не рассматривается исчерпывающе.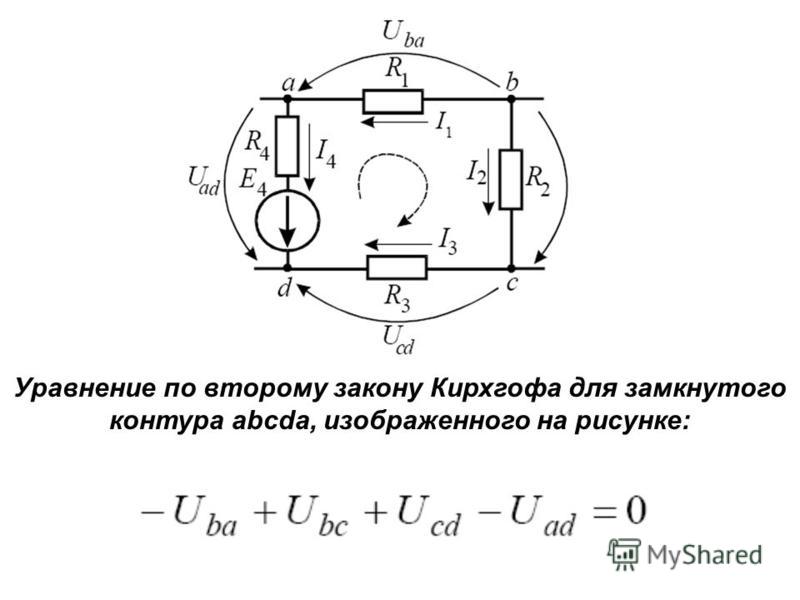 Лучше всего использовать эту статью в качестве руководства для дальнейшего изучения и экспериментов с коммерческим картографическим пакетом. Пока не будут открыты более совершенные методы, интерполяция является единственным доступным способом оценки формы и дисперсии подповерхностных поверхностей.
Лучше всего использовать эту статью в качестве руководства для дальнейшего изучения и экспериментов с коммерческим картографическим пакетом. Пока не будут открыты более совершенные методы, интерполяция является единственным доступным способом оценки формы и дисперсии подповерхностных поверхностей.
См. Также
Список литературы
- ↑ 1.0 1,1 1,2 1,3 1,4 1,5 1,6 Дэвис, Дж. К., 1973, Статистика и анализ данных в геологии: Нью-Йорк, John Wiley and Sons, 550 p.
- ↑ Филип Г. М. и Д. Ф. Уотсон, 1982, Точный метод определения контурных поверхностей: Журнал Австралийского общества разведки нефти, т. 22, с. 205-212.
- ↑ 3,0 3,1 3,2 Кларк, К. К., 1990, Аналитическая компьютерная картография: Энглвуд Клиффс, Нью-Джерси, Прентис-Холл, 290 с.
- ↑ 4,0 4,1 Джонс, Т. А., Гамильтон, Д. Э., Джонсон, К. Р., 1986, Контурирование геологических поверхностей с помощью компьютера: Нью-Йорк, Van Nostrand Reinhold Company, 314 с.
- ↑ Сэмпсон, Р. Дж., 1978, Графическая система Surface II (редакция 1): Лоуренс, К.С., Геологическая служба Канзаса, Серия по пространственному анализу, n. 1, 240 с.
- ↑ Криг, Д. Г., 1951, Статистический подход к некоторым проблемам оценки рудников в журнале Witwatersrand: Journal of Chemical Metallurgy and Mineralogy Society of South Africa, v.52, п. 6, стр. 119–139.
- ↑ 7.0 7.1 Матерон, Г., 1971, Теория региональных переменных и ее применение: Париж, Les Cahiders du Centre de Morphologie Mathematique, Национальная школа Superieur des Mines, Буклет 5, 211 с.
- ↑ Кларк, I., 1979, Практическая геостатистика: Нью-Йорк, издательство Elsevier Applied Science, 129 с.
- ↑ Журнел, А. Г., Хейбрегтс, К. Дж., 1978, Горная геостатистика: Нью-Йорк, Academic Press, 600 с.
- ↑ Оля, Р.A., 1975, Оптимальные методы картирования с использованием теории региональных переменных: Лоуренс, К.С., Геологическая служба Канзаса, Серия по пространственному анализу, n. 2, 137 с.
- ↑ Geobyte, 1986, CEED II – сопоставление и оценка картографических систем: Geobyte, v. 1, n. 5, стр. 25–40.
Внешние ссылки
| найти литературу о Контурное геологическое исследование с помощью компьютера |

 Разрешение изображения в плоскости составляет 1,64 мм / пиксель. Разрешение межплоскостного изображения 5 мм / пиксель. Временное разрешение 40 мсек / кадр. Двумерные контуры данных изображения первого кадра извлекаются с использованием метода установки уровня.Затем в области миокарда, ограниченной эндо- и эпикардиальными границами, выделяется набор точек отбора проб. Мы регистрируем ориентацию волокон, полученную от Исследовательской группы по механике сердца в UCSD 1 , в данные МРТ сердца, используя основные перекосы, как показано на рис. Поскольку мы относимся к миокарду как к анизотропному линейному эластичному материалу, мы устанавливаем модули Юнга вдоль волокна равными 75 кПа и пересекаем волокно до 25 кПа отдельно. Коэффициент Пуассона был установлен равным 0,47 [59], [60].Следуя процедурам, установленным в [61], извлекаются эндокардиальные и эпикардиальные границы, а также смещения граничных точек между последовательными кадрами. Затем, учитывая эти частичные измерения кинематики сердца на основе изображений, система оценки без сетки, описанная выше, и традиционный стандартный метод FEM используются для восстановления поля плотного смещения в течение всего сердечного цикла.
Разрешение изображения в плоскости составляет 1,64 мм / пиксель. Разрешение межплоскостного изображения 5 мм / пиксель. Временное разрешение 40 мсек / кадр. Двумерные контуры данных изображения первого кадра извлекаются с использованием метода установки уровня.Затем в области миокарда, ограниченной эндо- и эпикардиальными границами, выделяется набор точек отбора проб. Мы регистрируем ориентацию волокон, полученную от Исследовательской группы по механике сердца в UCSD 1 , в данные МРТ сердца, используя основные перекосы, как показано на рис. Поскольку мы относимся к миокарду как к анизотропному линейному эластичному материалу, мы устанавливаем модули Юнга вдоль волокна равными 75 кПа и пересекаем волокно до 25 кПа отдельно. Коэффициент Пуассона был установлен равным 0,47 [59], [60].Следуя процедурам, установленным в [61], извлекаются эндокардиальные и эпикардиальные границы, а также смещения граничных точек между последовательными кадрами. Затем, учитывая эти частичные измерения кинематики сердца на основе изображений, система оценки без сетки, описанная выше, и традиционный стандартный метод FEM используются для восстановления поля плотного смещения в течение всего сердечного цикла. Подробности об этих процедурах можно найти в наших статьях [7], [30].
Подробности об этих процедурах можно найти в наших статьях [7], [30]. По сравнению с результатами линейных МКЭ, деформации, полученные методом EFGM, во многом соответствуют сердечному циклу.
По сравнению с результатами линейных МКЭ, деформации, полученные методом EFGM, во многом соответствуют сердечному циклу.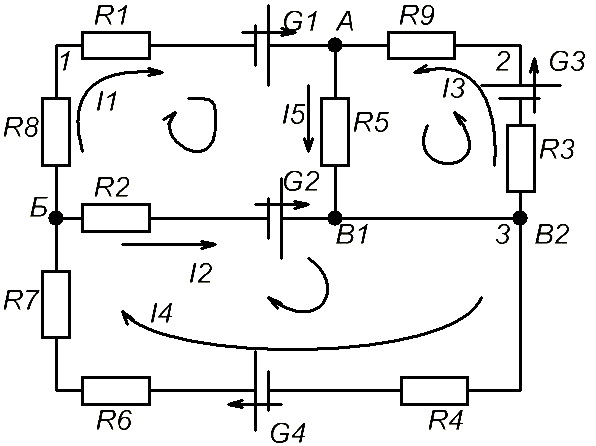 В нашей структуре FEGM можно удобно получить больше узлов, просто увеличив размер доменов влияния. Напротив, МКЭ необходимо изменить тип элемента, чтобы ввести полином более высокого порядка. Более того, элемент с полиномиальным основанием более высокого порядка увеличит сложность сетки, что приведет к более трудоемкой процедуре создания сетки. Следовательно, структура EFGM может эффективно обрабатывать изображение сердца благодаря гибкому распределению узлов бессеточных методов.Кроме того, наша структура EFGM может лучше аппроксимировать ориентацию миокардиальных волокон, используя весовую функцию кубического сплайна с меньшим количеством узлов.
В нашей структуре FEGM можно удобно получить больше узлов, просто увеличив размер доменов влияния. Напротив, МКЭ необходимо изменить тип элемента, чтобы ввести полином более высокого порядка. Более того, элемент с полиномиальным основанием более высокого порядка увеличит сложность сетки, что приведет к более трудоемкой процедуре создания сетки. Следовательно, структура EFGM может эффективно обрабатывать изображение сердца благодаря гибкому распределению узлов бессеточных методов.Кроме того, наша структура EFGM может лучше аппроксимировать ориентацию миокардиальных волокон, используя весовую функцию кубического сплайна с меньшим количеством узлов.
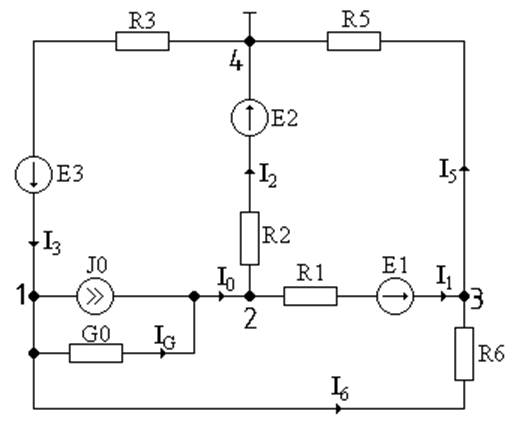 {t_1} \ int _ {\ Omega} F (u) \ \ mathrm {d A} \ mathrm {d} t
{t_1} \ int _ {\ Omega} F (u) \ \ mathrm {d A} \ mathrm {d} t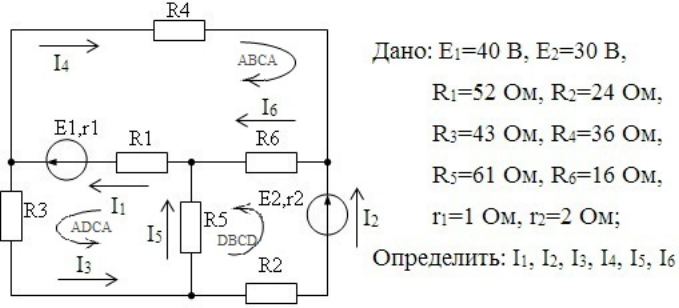 Это приводит к пространственно-временной интеграции.
Это приводит к пространственно-временной интеграции.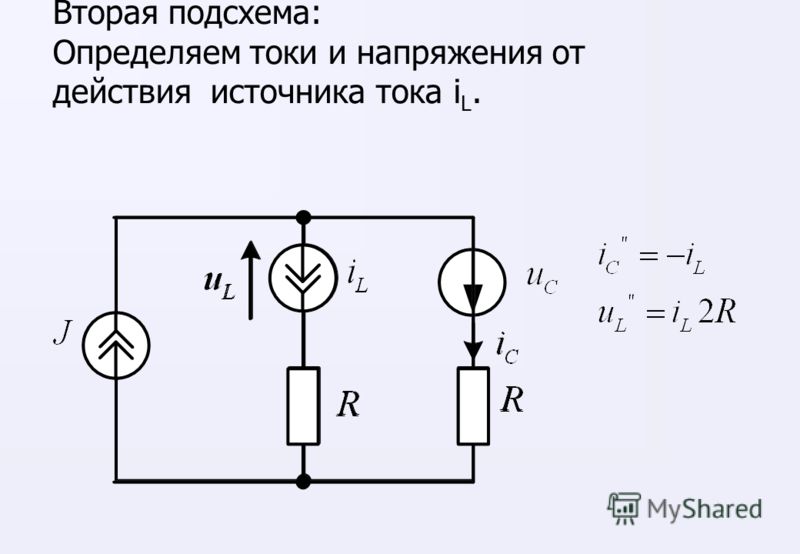

 С этой целью мы вводим дополнительную степень свободы с именем q_hot и дополнительное ограничение в виде глобального уравнения. Общий входящий тепловой поток заменен на q_hot .
С этой целью мы вводим дополнительную степень свободы с именем q_hot и дополнительное ограничение в виде глобального уравнения. Общий входящий тепловой поток заменен на q_hot . 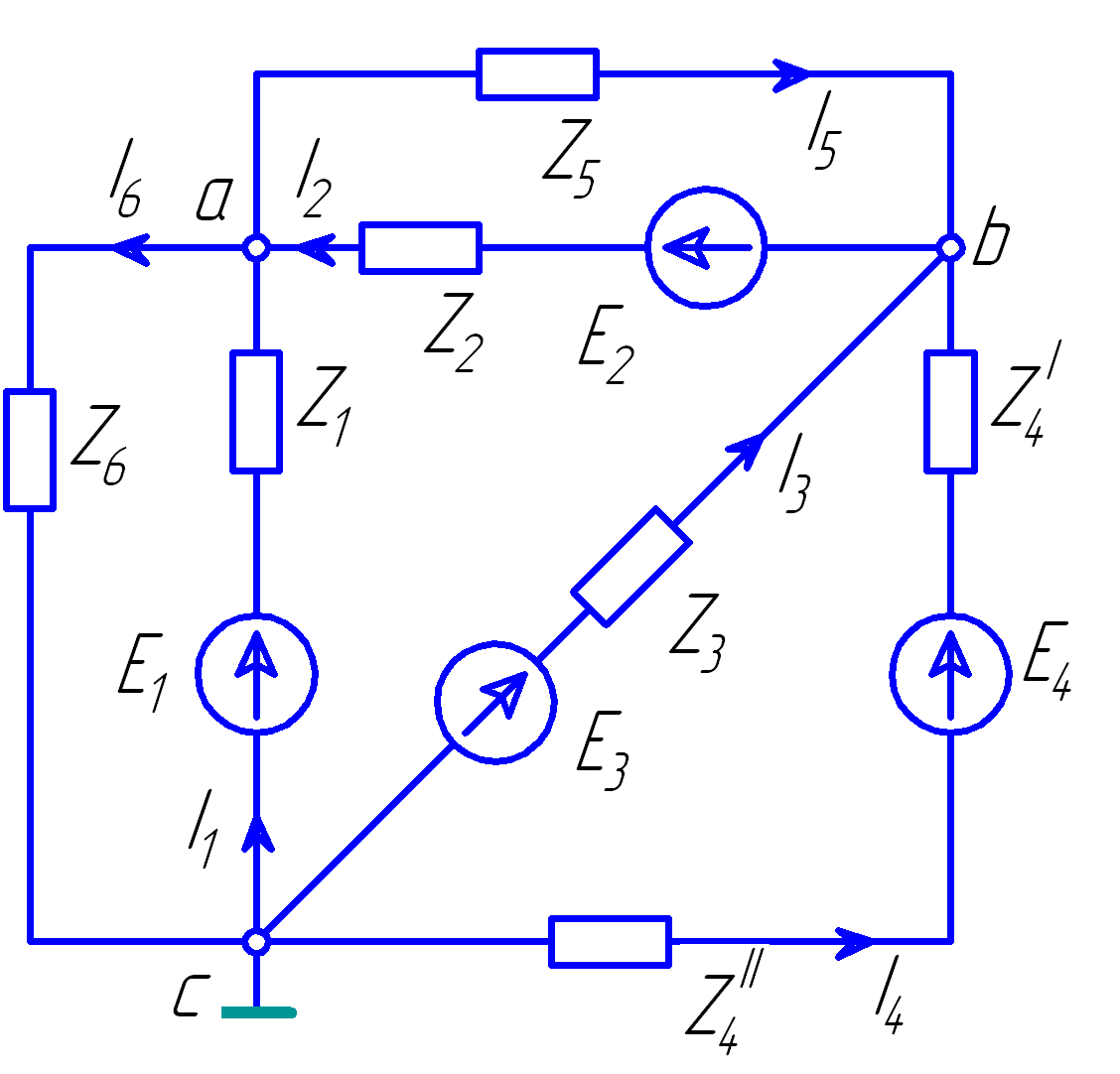 1T (x, 0) \ cdot (x \ leq \ bar x) \ \ mathrm {d} x
1T (x, 0) \ cdot (x \ leq \ bar x) \ \ mathrm {d} x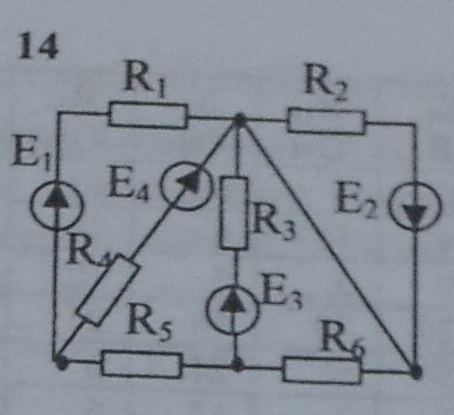
 Самым простым интерфейсом для реализации этого уравнения является интерфейс Coefficient Form PDE , который требует только следующих нескольких настроек:
Самым простым интерфейсом для реализации этого уравнения является интерфейс Coefficient Form PDE , который требует только следующих нескольких настроек:
 Источником этого домена ODE является подынтегральное выражение , как показано на следующем рисунке.
Источником этого домена ODE является подынтегральное выражение , как показано на следующем рисунке. 
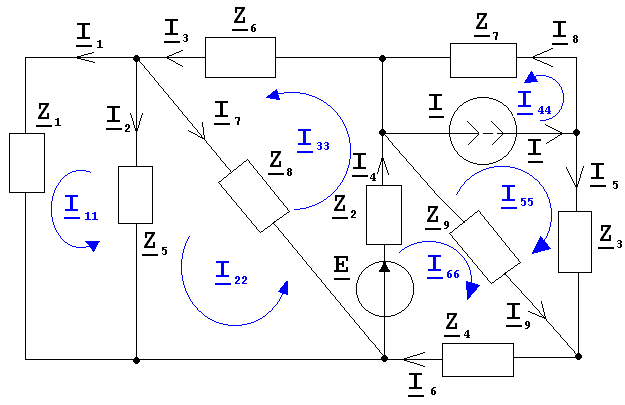
 Электрон имеет нулевую вероятность оказаться в узле.
Электрон имеет нулевую вероятность оказаться в узле. 2 (\ theta, \ phi) \) служит функцией вероятности. Функцию вероятности можно интерпретировать как вероятность того, что электрон будет обнаружен на луче, исходящем из источника, находящегося под углами \ ((\ theta, \ phi) \) от осей. Функцию вероятности также можно интерпретировать как распределение вероятности нахождения электрона в положении \ ((\ theta, \ phi) \) на сфере радиусом r , учитывая, что это расстояние r от ядра.
2 (\ theta, \ phi) \) служит функцией вероятности. Функцию вероятности можно интерпретировать как вероятность того, что электрон будет обнаружен на луче, исходящем из источника, находящегося под углами \ ((\ theta, \ phi) \) от осей. Функцию вероятности также можно интерпретировать как распределение вероятности нахождения электрона в положении \ ((\ theta, \ phi) \) на сфере радиусом r , учитывая, что это расстояние r от ядра.
 Фактическая трехмерная форма орбиты получается вращением двумерного поперечного сечения вокруг оси симметрии, которая показана синей пунктирной линией.Контурные диаграммы также указывают для областей, разделенных узлами, является ли волновая функция положительной (+) или отрицательной (-) в этой области. Чтобы волновая функция сменила знак, нужно пересечь узел.
Фактическая трехмерная форма орбиты получается вращением двумерного поперечного сечения вокруг оси симметрии, которая показана синей пунктирной линией.Контурные диаграммы также указывают для областей, разделенных узлами, является ли волновая функция положительной (+) или отрицательной (-) в этой области. Чтобы волновая функция сменила знак, нужно пересечь узел. 2 \).
2 \).
 В зависимости от формы угловой волновой функции существуют две основные формы d-орбиталей.
В зависимости от формы угловой волновой функции существуют две основные формы d-орбиталей.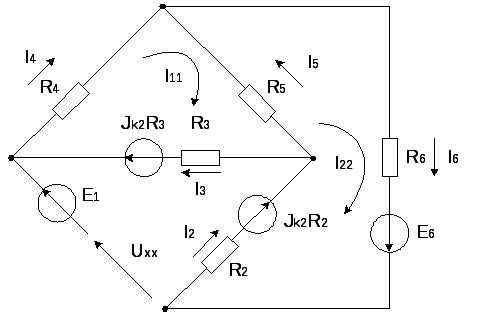 При n = 3 радиальная волновая функция не имеет узлов.
При n = 3 радиальная волновая функция не имеет узлов. Однако вращение – это нестандартное вращение, производящее только радиальную симметрию относительно оси, а не круговую симметрию, как это было в случае с другими орбиталями. Это создает форму двойной гантели с узлами в плоскости x-y и плоскости y-z.
Однако вращение – это нестандартное вращение, производящее только радиальную симметрию относительно оси, а не круговую симметрию, как это было в случае с другими орбиталями. Это создает форму двойной гантели с узлами в плоскости x-y и плоскости y-z. В этом случае электрон имеет те же орбитали, что и атом водорода, за исключением того, что они масштабируются с коэффициентом 1 / Z. Z – атомный номер атома, количество протонов в ядре. Увеличенное количество положительно заряженных протонов уменьшает размер орбиталей.
В этом случае электрон имеет те же орбитали, что и атом водорода, за исключением того, что они масштабируются с коэффициентом 1 / Z. Z – атомный номер атома, количество протонов в ядре. Увеличенное количество положительно заряженных протонов уменьшает размер орбиталей.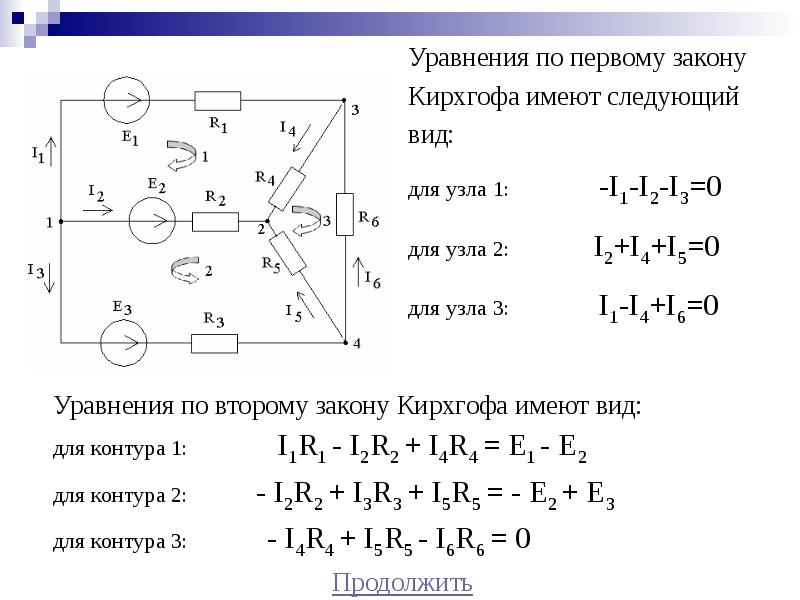 Нью-Йорк: В. Х. Фриман и компания.
Нью-Йорк: В. Х. Фриман и компания.