Теорема Крамера
Системы линейных алгебраических уравнений При решении систем линейных уравнений обсуждаются 3 вопроса: а) существует ли решение системы уравнений, б) сколько разных решений имеет система уравнений, в) алгоритм решения. Ниже излагаются основные результаты в этой области математики, позволяющие исчерпывающим образом ответить на эти вопросы.Теорема Крамера
Система двух уравнений, два неизвестных
Рассмотрим систему линейных алгебраических уравнений \[ a_{11}x_1+a_{12}x_2=b_1, \quad \quad(17) \] \[ a_{21}x_1+a_{22}x_2=b_2, \quad \quad(18) \]числа \(a_{ik}, b_i\), \(i,k=1,2\) считаются заданными, требуется найти неизвестные \(x_1,x_2\) . Эту систему можно решить исключением неизвестных. Например, умножим первое уравнение на \(a_{22}\) и вычтем второе, умноженное на \(a_{12}\), получим:
\[ (a_{11}a_{22}-a_{21}a_{12})x_1=b_1a_{22}-b_2a_{12}, \]
так что если \(a_{11}a_{22}-a_{21}a_{12} \neq 0, \)
\[
x_1=\frac{b_1a_{22}-b_2a_{12}}{a_{11}a_{22}-a_{21}a_{12}}.
Если второе уравнение умножить на \(a_{11}\) и вычесть из него первое уравнение, умноженное на \(a_{21}\), получим: \[ x_2=\frac{a_{11}b_2-a_{21}b_1}{a_{11}a_{22}-a_{21}a_{12}}. \quad \quad(20) \]
Введем следующие обозначения. Матрицей коэффициентов системы уравнений (17)-(18) назовем матрицу \[ A=\left( \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right), \] столбец правых частей системы \[ B=\left (\begin{array}{c} b_1 \\b_2 \end{array} \right). \]
Тогда формулы (19), (20) можно переписать следующим образом:
\[
x_1=\frac{detC_1}{detA}, x_2=\frac{detC_2}{detA}, \quad \quad(21)
\]
где матрица \(C_k\), \(k=1,2\), получается из матрицы \(A\) заменой ее \(k\)-того столбца на столбец \(B\). Формулы (21) называются формулами Крамера для системы из 2 уравнений с двумя неизвестными. Они описывают единственное решение системы уравнений в данном случае.
Они описывают единственное решение системы уравнений в данном случае.
Система \(n\) уравнений, \(n\) неизвестных
Рассмотрим систему \(n\) линейных алгебраических уравнений с \(n\) неизвестными, \[ a_{11}x_1+a_{12}x_2+ ….+a_{1n}x_n=b_1, \quad \quad(22) \] \[ a_{21}x_1+a_{22}x_2+…+a_{1n}x_n=b_2, \quad \quad(23) \] \[ ………………………………………………….. \] \[ a_{n1}x_1+a_{n2}x_2+…+a_{nn}x_n=b_n. \quad \quad(24) \]
Матрицей коэффициентов системы уравнений назовем матрицу
\[
A=\left(
\begin{array}{ccccc}
a_{11} & a_{12} & a_{13} &\ldots & a_{1n} \\
a_{21} & a_{22} & a_{23} &\ldots & a_{2n} \\
\vdots & \vdots & \vdots & \ddots & \vdots\\
a_{n1} &a_{n2} & a_{n3} & \ldots & a_{nn}
\end{array}
\right) ,
\]
образуем столбец правых частей системы
\[
B=\left (\begin{array}{cccc} b_1 & b_2 & \ldots &b_n \end{array} \right)^T.
В целом решение систем методом Крамера и методом обратной матрицы требует выполнения 2 условий: матрица коэффициентов системы должна быть квадратной ( т.е. число уравнений должно совпадать с числом неизвестных) и эта матрица должна быть невырожденной. К тому же практическая реализация этих методов связана с весьма громоздкими вычислениями, так что они имеют лишь теоретическое значение. На практике используют существенно более простой в реализации метод Гаусса, который к тому же позволяет решать и более общие системы уравнений. Этот метод описан ниже.
Решить системы методом Крамера и методом обратной матрицы.
а) \[ x_1+x_2+2x_3=-1, \] \[ 2x_1-x_2+2x_3=-4, \] \[ 4x_1+x_2+4x_3=-2. \]
б) \[ 3x_1+2x_2+x_3=5, \] \[ 2x_1+3x_2+x_3=1, \] \[ 2x_1+x_2+3x_3=11. \]
в)
\[
2x_1+x_2-x_3=2,
\]
\[
3x_1+x_2-2x_3=3,
\]
\[
x_1+x_3=3. \]
\]
Линейные уравнения, Системы линейных уравнений, Решения систем линейных уравнений, Метод Крамера
К решению систем линейных уравнений сводятся многочисленные задачи по математике. Рассмотрим постановку задачи.
Дана система n алгебраических уравнений с n неизвестными:
Эту систему можно записать в матричном виде: А • X = В, где А — квадратная матрица коэффициентов, X — вектор-столбец неизвестных, В — вектор-столбец свободных членов.Численные методы решения систем линейных уравнений делятся на прямые и итерационные.
Прямые методы используют конечные соотношения для вычисления неизвестных. Эти методы сравнительно просты и пригодны для широкого класса систем.
Недостатки: требуют хранения в памяти ЭВМ сразу всей матрицы А. При больших порядках системы расходуется много места в памяти и накапливается вычислительная погрешность. Кроме того, существенно возрастает время вычисления вектора X. Поэтому прямые методы обычно применяют при небольших порядках системы (n < 200).
Поэтому прямые методы обычно применяют при небольших порядках системы (n < 200).
Примеры прямых методов решения систем линейных уравнений
Метод определителей Крамера, метод Гаусса. Первый из них применяется крайне редко, так как с ростом n алгоритм нахождения определителей резко возрастает.
Итерационные методы основаны на последовательных приближениях. Задается некоторое приближенное значение вектора Х — начальное приближение. Затем с помощью некоторого алгоритма проводится первый цикл вычислений — итерация, в результате которого получается новое приближение вектора Х. Итерации проводятся до получения решения с заданной точностью.
Алгоритм решения систем линейных уравнений здесь более сложен, чем у прямых методов. Не всегда выполняется условие сходимости. Однако в ряде случаев итерационные методы предпочтительнее. Они требуют хранения в памяти ЭВМ не всей матрицы A, а лишь нескольких векторов. Вычислительная погрешность практически не накапливается. Поэтому итерационные методы применимы и для больших порядков системы. Примеры — метод простой итерации и метод Зейделя.
Поэтому итерационные методы применимы и для больших порядков системы. Примеры — метод простой итерации и метод Зейделя.
Примеры работ
Материалы сайта
Обращаем Ваше внимание на то, что все материалы опубликованы для образовательных целей.
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Системы уравнений. Понятие системы уравнений. Свойства систем уравнений. Линейные системы уравнений. Основные методы решения систем уравнений / / Методы решения невырожденных систем линейных алгебраических уравнений (СЛАУ) – по формулам Крамера, матричный способ. Метод Гаусса = метод последовательного исключения неизвестных при решения систем линейных алгебраических уравнений. Наличие решений. Формулы. Методы. / / Системы уравнений. Понятие системы уравнений. Свойства систем уравнений. Линейные системы уравнений. Основные методы решения систем уравнений / / Методы решения невырожденных систем линейных алгебраических уравнений (СЛАУ) – по формулам Крамера, матричный способ. Метод Гаусса = метод последовательного исключения неизвестных при решения систем линейных алгебраических уравнений. Наличие решений.Поделиться:
| |||||||
| Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | ||||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. | |||||||
Pers.narod.ru. Обучение. Лекции по численным методам. Методы решения систем линейных алгебраических уравнений
Pers.narod.ru. Обучение. Лекции по численным методам. Методы решения систем линейных алгебраических уравненийЭтот сайт больше не обновляется. Подключите Javascript, чтобы увидеть новый адрес страницы или перейдите к статье
2. Методы решения систем линейных алгебраических уравнений
Прямые методы решения СЛАУ:
Метод Крамера
Метод обратной матрицы
Метод Гаусса
Итерационные методы решения линейных алгебраических систем:
Метод простой итерации или метод Якоби
Метод Гаусса – Зейделя
К решению систем линейных
алгебраических уравнений сводятся многочисленные практические задачи ( по
некоторым оценкам более 75% всех задач). Можно с полным основанием утверждать,
что решение линейных систем является одной из самых распространенных и важных
задач вычислительной математики.
Конечно, существует много методов и современных пакетов прикладных программ для решения СЛАУ, но для того, чтобы их успешно использовать, необходимо разбираться в основах построения методов и алгоритмов, иметь представления о недостатках и преимуществах используемых методов.
Постановка задачи
Требуется найти решение системы m линейных уравнений, которая записывается в общем виде как
,
Эту систему уравнений можно записать также в матричном виде:
,
где
A – матрица системы, – вектор правых частей, – вектор неизвестных.
При известных A и требуется найти такие , при подстановке которых в систему уравнений она превращается в тождество.
Необходимым и достаточным
условием существования единственного решения СЛАУ является условие det A≠0, т.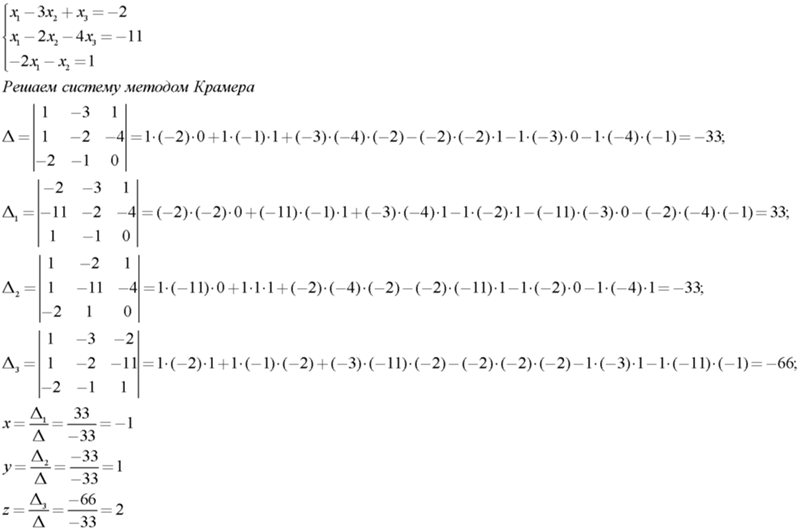 е. определитель матрицы A не равен нулю. В случае равенства
нулю определителя матрица A называется вырожденной и
при этом СЛАУ либо не имеет решения, либо имеет их бесчисленное множество.
е. определитель матрицы A не равен нулю. В случае равенства
нулю определителя матрица A называется вырожденной и
при этом СЛАУ либо не имеет решения, либо имеет их бесчисленное множество.
В дальнейшем будем предполагать наличие единственного решения.
Все методы решения линейных алгебраических задач можно разбить на два класса: прямые (точные) и итерационные (приближенные).
Прямые методы решения СЛАУ
Метод Крамера
При небольшой размерности системы m (m = 2,…,5) на практике часто используют формулы Крамера для решения СЛАУ:
(i = 1, 2, …, m). Эти формулы позволяют находить неизвестные в виде дробей, знаменателем которых является определитель матрицы системы, а числителем – определители матриц Ai, полученных из A заменой столбца коэффициентов при вычисляемом неизвестном столбцом свободных членов
 Так А1 получается из матрицы А
заменой первого столбца на столбец правых частей f.
Так А1 получается из матрицы А
заменой первого столбца на столбец правых частей f.
Например, для системы двух линейных уравнений
Размерность системы (т.е., число m) является главным фактором, из–за которого формулы Крамера не могут быть использованы для численного решения СЛАУ большого порядка. При непосредственном раскрытии определителей решение системы с m неизвестными требует порядка m!*m арифметических операций. Таким образом, для решения системы, например, из m = 100 уравнений потребуется совершить 10158 вычислительных операций (процесс займёт примерно 1019 лет), что не под силу даже самым мощным современным ЭВМ
Метод обратной матрицы
Если det A ≠ 0, то
существует обратная матрица . Тогда решение СЛАУ записывается в виде: . Следовательно, решение
СЛАУ свелось к умножению известной обратной матрицы на вектор правых частей. Таким образом, задача решения СЛАУ и задача нахождения обратной матрицы связаны
между собой, поэтому часто решение СЛАУ называют задачей обращения матрицы.
Проблемы использования этого метода те же, что и при использовании метода Крамера:
нахождение обратной матрицы – трудоемкая операция.
Таким образом, задача решения СЛАУ и задача нахождения обратной матрицы связаны
между собой, поэтому часто решение СЛАУ называют задачей обращения матрицы.
Проблемы использования этого метода те же, что и при использовании метода Крамера:
нахождение обратной матрицы – трудоемкая операция.
Метод Гаусса
Наиболее известным и популярным прямым методом решения СЛАУ является метод Гаусса. Этот метод заключается в последовательном исключении неизвестных. Пусть в системе уравнений
первый элемент . Назовем его ведущим элементом первой строки. Поделим все элементы этой строки на и исключим x1 из всех последующих строк, начиная со второй, путем вычитания первой (преобразованной), умноженной на коэффициент при в соответствующей строке. Получим
.
Если , то, продолжая аналогичное исключение, приходим к системе уравнений с верхней треугольной матрицей
.
Из нее в обратном порядке находим все значения xi:
.
Процесс приведения к системе с треугольной матрицей называется прямым ходом, а нахождения неизвестных – обратным. В случае если один из ведущих элементов равен нулю, изложенный алгоритм метода Гаусса неприменим. Кроме того, если какие–либо ведущие элементы малы, то это приводит к усилению ошибок округления и ухудшению точности счета. Поэтому обычно используется другой вариант метода Гаусса – схема Гаусса с выбором главного элемента. Путем перестановки строк, а также столбцов с соответствующей перенумерацией коэффициентов и неизвестных добиваются выполнения условия:
, j = i+1,i+ 2, …, m;
т.е. осуществляется выбор первого главного
элемента. Переставляя уравнения так, чтобы в первом уравнении коэффициент a11 был максимальным по модулю. Разделив
первую строку на главный элемент, как и прежде, исключают x1 из
остальных уравнений. Затем для оставшихся столбцов и строк выбирают второй
главный элемент и т.д.
Разделив
первую строку на главный элемент, как и прежде, исключают x1 из
остальных уравнений. Затем для оставшихся столбцов и строк выбирают второй
главный элемент и т.д.
Рассмотрим применение метода Гаусса с выбором главного элемента на примере следующей системы уравнений:
В первом уравнении коэффициент при =0, во втором = 1 и в третьем = -2, т.е. максимальный по модулю коэффициент в третьем уравнении. Поэтому переставим третье и первое уравнение:
Исключим из второго и третьего уравнений с помощью первого. Во втором уравнении исключать не надо. Для исключения из третьего уравнения умножим первое на 0.5 и сложим с третьим:
Рассмотрим второе и третье уравнения. Максимальный по модулю элемент при в третьем. Поэтому поместим его на место второго:
Исключим из третьего уравнения. Для
этого умножим второе на -0.5 и сложим с третьим:
Для
этого умножим второе на -0.5 и сложим с третьим:
Обратный ход: .
Проверка: 0.5*8+0=4, -3+8-0=5, -2*(-3)+0=6.
Такая перестановка уравнений необходима для того, чтобы уменьшить влияние ошибок округления на конечный результат.
Часто возникает
необходимость в решении СЛАУ, матрицы которые являются слабо заполненными,
т.е. содержат много нулевых элементов. В то же время эти матрицы имеют определенную
структуру. Среди таких систем выделим системы с матрицами ленточной структуры,
в которых ненулевые элементы располагаются на главной диагонали и на нескольких
побочных диагоналях. Для решения систем с ленточными матрицами коэффициентов
вместо метода Гаусса можно использовать более эффективные методы. Например, метод
прогонки, который мы рассмотрим позже при решении краевой задачи для
обыкновенного дифференциального уравнения второго порядка.
Итерационные методы решения линейных алгебраических систем
Метод простой итерации или метод Якоби
Напомним, что нам требуется решить систему линейных уравнений, которая в матричном виде записывается как:
,
где , , .
Предположим, что диагональные элементы матриц A исходной системы не равны 0 (aii ≠ 0, i = 1, 2, …, n). Разрешим первое уравнение системы относительно x1, второе относительно x2 и т.д. Получим следующую эквивалентную систему, записанную в скалярном виде:
(1),
Теперь, задав нулевое приближение , по рекуррентным соотношениям (1) можем выполнять итерационный процесс, а именно:
(2)Аналогично
находятся следующие приближения , где в (2) вместо необходимо подставить .
Или в общем случае:
. (3)
или
Условие окончания итерационного процесса .
Достаточное условие сходимости: Если выполнено условие диагонального преобладания, т.е. , то итерационный процесс (3) сходится при любом выборе начального приближения. Если исходная система уравнений не удовлетворяет условию сходимости, то ее приводят к виду с диагональным преобладанием.
Выбор начального приближения влияет на количество итераций, необходимых для получения приближенного решения. Наиболее часто в качестве начального приближения берут или .
Замечание. Указанное выше условие сходимости
является достаточным, т.е. если оно выполняется, то процесс сходится. Однако
процесс может сходиться и при отсутствии диагонального преобладания, а может и
не сойтись.
Однако
процесс может сходиться и при отсутствии диагонального преобладания, а может и
не сойтись.
Пример.
Решить систему линейных уравнений с точностью :
|
|
8 |
4 |
2 |
|
10 |
|
x1 |
|
|
= |
3 |
5 |
1 |
= |
5 |
= |
x2 |
|
|
|
3 |
–2 |
10 |
|
4 |
|
x3 |
|
Решение прямыми методами, например, обратной матрицей, даёт решение:
.
Найдем решение методом простой итерации. Проверяем условие диагонального преобладания: , , .
Приводим систему уравнений к виду (1):
.
Начальное приближение . Дальнейшие вычисления оформим в виде таблицы:
|
k |
x1 |
x2 |
x3 |
точность |
|
0 |
0 |
0 |
0 |
|
|
1 |
1. |
1.000 |
0.400 |
1.2500 |
|
2 |
0.650 |
0.170 |
0.225 |
0.8300 |
|
3 |
1.109 |
0. |
0.239 |
0.4588 |
|
……… |
||||
|
4 |
0.908 |
0.287 |
0.180 |
0. |
|
5 |
1.061 |
0.419 |
0.185 |
0.1537 |
|
6 |
0.994 |
0.326 |
0.165 |
0.0931 |
|
7 |
1. |
0.370 |
0.167 |
0.0515 |
|
8 |
1.023 |
0.594 |
0.160 |
0.2235 |
|
9 |
0.913 |
0. |
0.212 |
0.1101 |
|
10 |
0.906 |
0.505 |
0.242 |
0.0764 |
|
11 |
0.937 |
0.495 |
0. |
0.0305 |
|
12 |
0.945 |
0.516 |
0.218 |
0.0210 |
|
…… |
||||
|
13 |
0. |
0.523 |
0.220 |
0.0077 |
Здесь
,
И т.д., пока не получим, в последнем столбце величину меньшую 0.01, что произойдет на 13 – ой итерации.
Следовательно, приближенное решение имеет вид:
Метод Гаусса – Зейделя
Расчетные формулы имеют вид:
т.е. для подсчета i–й компоненты (k+1)–го приближения к искомому вектору используется уже
вычисленное на этом, т. е. (k+1)–м шаге, новые
значения первых i–1 компонент.
е. (k+1)–м шаге, новые
значения первых i–1 компонент.
Подробные формулы имеют вид:
Достаточное условие сходимости этого метода такое же, как и для метода простой итерации, т.е. диагональное преобладание:
Начальное приближение:
Найдем решение предыдущей системы уравнений методом Гаусса – Зейделя.
Расчетные формулы:
|
k |
x1 |
x2 |
x3 |
точность |
|
0 |
0 |
0 |
0 |
|
|
1 |
1. |
0.250 |
0.075 |
1.2500 |
|
2 |
1.106 |
0.321 |
0.132 |
0.1438 |
|
3 |
1.056 |
0. |
0.151 |
0.0500 |
|
4 |
1.042 |
0.344 |
0.156 |
0.0139 |
|
5 |
1.039 |
0.346 |
0. |
0.0036 |
Из таблицы видно, что нужная точность достигнута уже на 5–ой итерации вместо 13–ой по методу простой итерации и значения корней более близки к значениям, полученным методом обратной матрицы.
Презентация “Решение систем линейных уравнений”
библиотека
материалов
Содержание слайдов
Номер слайда 1
Д ЙНИК ЧА А Д ЗА А
Номер слайда 2
Номер слайда 3
Уравнение
Номер слайда 4
Методы решения: 1)Матричный метод решения. 2)Метод Крамера. 3) Метод Гаусса
2)Метод Крамера. 3) Метод Гаусса
Номер слайда 5
1)Матричный метод решения. Запишем заданную систему в матричном виде: АХ=В, где А – основная матрица коэффициентов системы; Х – матрица-столбец неизвестных; В – матрица-столбец свободных членов. Если матрица А невырожденная (det А=0), то тогда с помощью операций над матрицами выразим неизвестную матрицу Х . Операция деления на множестве матриц заменена умножением на обратную матрицу, поэтому умножив последнее равенство на матрицу слева:
Номер слайда 6
1)Матричный метод решения.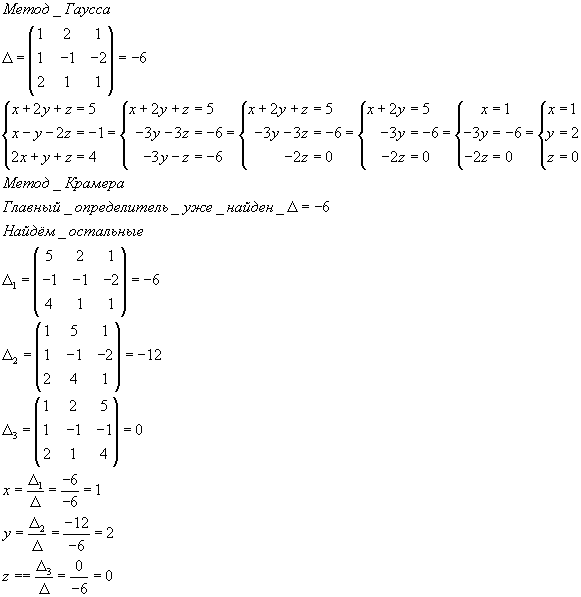 Поэтому, чтобы найти неизвестную матрицу Х надо найти обратную матрицу к матрице системы и умножить ее справа на вектор-столбец свободных коэффициентов.
Поэтому, чтобы найти неизвестную матрицу Х надо найти обратную матрицу к матрице системы и умножить ее справа на вектор-столбец свободных коэффициентов.
Номер слайда 7
Пример 1. Решить систему матричным способом. Решение: Решим систему линейных уравнений матричным методом. Обозначим Тогда данную систему можно записать в виде: АХ=В.
Номер слайда 8
Т. к. матрица невырожденная (Δ= – 2), то X = A-1B.
к. матрица невырожденная (Δ= – 2), то X = A-1B.
Номер слайда 9
Номер слайда 10
Номер слайда 11
Номер слайда 12
Тогда A-1 = Получим X = A-1B = Ответ: х1 = –1, х2 = 4, х3 = 1.
Номер слайда 13
2)Метод Крамера. Метод Крамера (теорема Крамера) — способ решения квадратных СЛАУ с ненулевым определителем основной матрицы. Теорема Крамера. Если определитель матрицы квадратной системы не равен нулю, то система совместна и имеет единственное решение, которое находится по формулам Крамера: где – определитель матрицы системы, – определитель матрицы системы,
Номер слайда 14
где вместо -го столбца стоит столбец правых частей. Пример 2. Решить систему по формулам Крамера. Решение: Решим систему по формулам Крамера.
Пример 2. Решить систему по формулам Крамера. Решение: Решим систему по формулам Крамера.
Номер слайда 15
D 0, значит, система имеет единственное решение.
Номер слайда 16
Номер слайда 17
Ответ: x1 = 5, x2 = -1, x3 = 1.
Номер слайда 18
3) Метод Гаусса Метод Гаусса – Метод последовательного исключения неизвестных. Метод Гаусса включает в себя прямой (приведение расширенной матрицы к ступенчатому виду, то есть получение нулей под главной диагональю) и обратный (получение нулей над главной диагональю расширенной матрицы) ходы. Прямой ход и называется методом Гаусса, обратный – методом Гаусса-Жордана, который отличается от первого только последовательностью исключения переменных.
Номер слайда 19
Пример 3. Исследовать систему и решить ее методом Гаусса, если она совместна Решение: Дана неоднородная линейная система из 4-х уравнений с 4-мя неизвестными (m=n=4). 1) Определим, совместна или нет система (*). Вычисляем для этого ранги расширенной и основной матриц системы: Rg(A,B) и RgA.
Исследовать систему и решить ее методом Гаусса, если она совместна Решение: Дана неоднородная линейная система из 4-х уравнений с 4-мя неизвестными (m=n=4). 1) Определим, совместна или нет система (*). Вычисляем для этого ранги расширенной и основной матриц системы: Rg(A,B) и RgA.
Номер слайда 20
Номер слайда 21
(привели матрицу (A,B) к матрице ( ), имеющую ступенчатую форму). Итак, Rg(A, B) = Rg( ) = 4, RgA= Rg = 4 RgA= Rg(A,B) = 4. Следовательно система (*) совместна. Т.к. Rg A= n (n = 4) система имеет единственное решение. Найдем все решения системы (*). Для этого перейдем к следующей эквивалентной системе.
Итак, Rg(A, B) = Rg( ) = 4, RgA= Rg = 4 RgA= Rg(A,B) = 4. Следовательно система (*) совместна. Т.к. Rg A= n (n = 4) система имеет единственное решение. Найдем все решения системы (*). Для этого перейдем к следующей эквивалентной системе.
Номер слайда 22
Номер слайда 23
решение найдено верно.
Номер слайда 24
е А Р Н В СТВО Н РА Е Л
Номер слайда 25
ЦА Ь Т Р=Т Д НА ОДИН 1 Д Р
Номер слайда 26
ТЬ Е А ТЬ Е 2 1,2 ДВ НАД ЦА ПЛЯ
Номер слайда 27
РТ Ь НА ЦА Р Д Д Ь Т ПЯТ
Номер слайда 28
О С И Л Ч О СИЛАЧ 5,2,1,3, 2кг
Номер слайда 29
2,3,А Д Т о Т С А ТОК Д ЕЛЬ О К ЗА Т В О СТ
Номер слайда 30
МЕТОД ГАУССА – Системы линейных уравнений
Ме́тод Га́усса – классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных
преобразований система уравнений приводится к равносильной системе треугольного
вида, из которой последовательно, начиная с последних (по номеру), находятся
все переменные системы.
Это метод последовательного исключения переменных, когда с помощью элементарных
преобразований система уравнений приводится к равносильной системе треугольного
вида, из которой последовательно, начиная с последних (по номеру), находятся
все переменные системы.
Хотя в настоящее время данный метод повсеместно называется методом Гаусса, он был известен и до К. Ф. Гаусса. Первое известное описание данного метода – в китайском трактате «Математика в девяти книгах».
Пусть исходная система выглядит следующим образом
Матрица A называется основной матрицей системы, – столбцом свободных членов.
Тогда, согласно свойству элементарных преобразований над строками, основную матрицу этой системы можно привести к ступенчатому виду (эти же преобразования нужно применять к столбцу свободных членов):
При этом будем
считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы
находится в верхнем левом углу, то есть в него входят только коэффициенты при
переменных .
Тогда переменные называются главными переменными. Все остальные называются свободными.
Если хотя бы одно число , где , то рассматриваемая система несовместна, т.е. у неё нет ни одного решения.
Пусть для любых .
Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом (, где — номер строки):
где
Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.
Условие совместности
Упомянутое выше условие для всех может быть сформулировано в качестве необходимого и достаточного условия совместности:
Напомним, что
рангом совместной системы называется ранг её основной матрицы (либо
расширенной, так как они равны).
Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.
- На первом этапе осуществляется так называемый
прямой ход, когда путём элементарных преобразований над строками систему
приводят к ступенчатой или треугольной форме, либо устанавливают, что
система несовместна. А именно, среди элементов первого столбца матрицы
выбирают ненулевой, перемещают его на крайнее верхнее положение
перестановкой строк и вычитают получившуюся после перестановки первую
строку из остальных строк, домножив её на величину, равную отношению
первого элемента каждой из этих строк к первому элементу первой строки,
обнуляя тем самым столбец под ним. После того, как указанные
преобразования были совершены, первую строку и первый столбец мысленно
вычёркивают и продолжают пока не останется матрица нулевого размера. Если
на какой-то из итераций среди элементов первого столбца не нашёлся
ненулевой, то переходят к следующему столбцу и проделывают аналогичную
операцию.

- На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
В простейшем случае алгоритм выглядит так:
- Обратный ход. Из последнего ненулевого уравнения
выражаем базисную переменную через небазисные и подставляем в предыдущие уравнения.
 Повторяя эту процедуру для всех базисных переменных, получаем
фундаментальное решение.
Повторяя эту процедуру для всех базисных переменных, получаем
фундаментальное решение.
Пример 1
Покажем, как методом Гаусса можно решить следующую систему:
Обнулим коэффициенты при во второй и третьей строчках. Для этого прибавим к ним первую строчку, умноженную на и 1, соответственно:
Теперь обнулим коэффициент при в третьей строке, вычтя из неё вторую строку, умноженную на 4:
В результате мы привели исходную систему к треугольному виду, тем самым закончим первый этап алгоритма.
На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:
из третьего;
из второго, подставив полученное
из первого, подставив полученные и .
Таким образом исходная система решена.
В случае, если
число уравнений в совместной системе получилось меньше числа неизвестных, то
тогда ответ будет записываться в виде фундаментальной системы решений.
Лекция 2. Решение систем линейных уравнений. 1. Решение систем 3-х линейных уравнений методом Крамера.
Примеры решений контрольных работ
Примеры решений контрольных работ Л.И. Терехина, И.И. Фикс 1 Контрольная работа 1 Линейная алгебра Решить матричное уравнение ( ( 3 1 2 1 X + 2 4 2 3 3 ( 1 0 = 3 2 3 Выполним вначале умножение матриц на
Подробнее1. Линейная алгебра. a21x1 a12 x2 a13 x3 b2
1. Линейная алгебра 1.1. В 1 представлены задачи на решение линейных алгебраических крамеровских систем с определителем, отличным от нуля, вычисление определителей и действий с матрицами. Линейные алгебраические
Линейные алгебраические
Контрольная по алгебре с решением
Контрольная по алгебре с решением Линейная алгебра 1-10 Каждый вариант этого раздела содержит четыре пункта, задания к которым соответствуют номеру пункта 1 Вычислить определитель 4-го порядка двумя способами:
ПодробнееЛинейная алгебра Вариант 4
Линейная алгебра Вариант Задание. Систему уравнений привести к равносильной разрешенной системе, включив в набор разрешенных неизвестных,,. Записать общее решение, найти соответствующее базисное решение:
ПодробнееЗадача 1 Вычислить определитель матрицы
Задача Вычислить определитель матрицы 4 4 A 4 4 Решение Для вычисления определителя приведем матрицу к треугольному виду. После этого определитель будет равен произведению элементов главной диагонали.
Теорема Кронекера-Капелли
Установить совместность и решить систему линейных уравнений 5xx x xx 5x 0 x4x x 0 а) по формулам Крамера, б) матричным способом, в) методом Гаусса Совместность Совместность системы можно установить: а)
ПодробнееАналитическая геометрия. Лекция 1.3
Московский Государственный Технический Университет им. Н.Э. Баумана Факультет Фундаментальные науки Кафедра Высшая математика Аналитическая геометрия Модуль 1. Матричная алгебра. Векторная алгебра Лекция
ПодробнееРАЗДЕЛ 1. Линейная алгебра.
-й семестр. РАЗДЕЛ. Линейная алгебра. Основные определения. Определение. Матрицей размера mn где m- число строк n- число столбцов называется таблица чисел расположенных в определенном порядке. Эти числа
ПодробнееГлава 1.
 Начала линейной алгебры
Начала линейной алгебрыГлава Начала линейной алгебры Системы линейных уравнений Систему m линейных уравнений с n неизвестными будем записывать в следующем виде: + + + + n n = + + + + nn = m + m + m + + mnn = m () Здесь n неизвестные
ПодробнееРешение систем линейных уравнений
Решение систем линейных уравнений Л. В. Калиновская, Ю. Л. Калиновский Министерство образования Московской области Государственное бюджетное образовательное учреждение высшего образования Московской области
Подробнее0.5 setgray0 0.5 setgray1
0.5 setgray0 0.5 setgray1 1 Лекция 1 ОПРЕДЕЛИТЕЛИ. СИСТЕМЫ УРАВНЕНИЙ 0. План лекции 1. Определитель второго порядка. 1.1 Система двух уравнений. 1.2. Метод исключения переменных. 1.3. Матрица 2 2. 1.4.
ПодробнееМАТЕМАТИКА ЛИНЕЙНАЯ АЛГЕБРА
ООО «Резольвента», wwwresolventru, resolvent@listru, (95) 509-8-0 Учебный центр «Резольвента» Доктор физико-математических наук, профессор К Л САМАРОВ МАТЕМАТИКА Учебно-методическое пособие по разделу
ПодробнееАналитическая геометрия.
 Лекция 1.2
Лекция 1.2Московский Государственный Технический Университет им. Н.Э. Баумана Факультет Фундаментальные науки Кафедра Высшая математика Аналитическая геометрия Модуль 1. Матричная алгебра. Векторная алгебра Лекция
ПодробнееСИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ После изучения данной темы вы сможете: проводить численное решение задач линейной алгебры. К решению систем линейных уравнений сводятся многочисленные практические задачи, решение
ПодробнееРаздел II. ЧИСЛЕННЫЕ МЕТОДЫ
Лекция 7 Раздел II ЧИСЛЕННЫЕ МЕТОДЫ ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ ПОСТАНОВКА ЗАДАЧИ Рассматривается проблема решения систем линейных алгебраических уравнений (СЛАУ)
Подробнее3. Определители высших порядков
Определители высших порядков Понятие определителя п-го порядка и его основные свойства Понятие определителя п-го порядка вводится на основе изучения структуры определителей -го и -го порядков Так например
ПодробнееЛЕКЦИЯ 3 ЧИСЛЕННОЕ РЕШЕНИЕ СЛАУ
ЛЕКЦИЯ 3 ЧИСЛЕННОЕ РЕШЕНИЕ СЛАУ Вспомним основные результаты, полученные на предыдущей лекции 1 Норма вектора = u Были введены следующие нормы вектора: =1 1 Октаэдрическая норма: 1 = max u, где p = 2 Кубическая
ПодробнееГлава 4.
 Матрицы. Лекция Основные понятия.
Матрицы. Лекция Основные понятия.Лекция 0. Глава 4. Матрицы. В этой главе мы рассмотрим основные виды матриц, операции над ними, понятие ранга матрицы и их приложения к решению систем линейных алгебраических уравнений. 4.. Основные понятия.
ПодробнееВведение в линейную алгебру
Введение в линейную алгебру Матрицы. Определение. Таблица m n чисел вида m m n n mn состоящая из m строк и n столбцов называется матрицей. Элементы матрицы нумеруются аналогично элементам определителя
ПодробнееПЕРЕСТАНОВКИ. Определение 1. Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,…, n в строчку одно за другим.
ПЕРЕСТАНОВКИ Определение 1 Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,, n в строчку одно за другим Например, 2, 4, 3, 1, 5 Это перестановка пятой степени Вообще
ПодробнееЛинейная алгебра.
 Матрицы
МатрицыЛинейная алгебра. Матрицы (вводные определения и примеры) Предуведомление: ниже лишь краткий конспект, не предназначенный для замены имеющихся учебных пособий. Под матрицей в математике понимается таблица,
ПодробнееПрактикум по линейной алгебре
Министерство образования и науки РФ Нижегородский государственный университет им. Н.И. Лобачевского В.К. Вильданов Практикум по линейной алгебре Учебно-методическое пособие Нижний Новгород Издательство
ПодробнееЛинейная алгебра. Матрицы
Линейная алгебра. Матрицы вводные определения и примеры) Предуведомление: ниже лишь краткий конспект, не предназначенный для замены имеющихся учебных пособий. Шаги решения задачи с использованием математики:.
ПодробнееКонтрольная работа T=3. Задание 1.
 [1, стр. 2]
[1, стр. 2]Дана матрица Контрольная работа A 0 T= Задание [, стр ] Определите ее размерность Выпишите характеристики этой матрицы: прямоугольная, квадратная, симметричная, единичная, нулевая, треугольная, диагональная,
Подробнее0.5 setgray0 0.5 setgray1
5 setgray 5 setgray Лекция 3 СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ Основные определения Рассмотрим следующую систему m уравнений относительно n неизвестных в поле K: a x + a 2 + + a nx n b, a 2 x + a 2 2 + + a2 nx
Подробнее1. Линейные системы и матрицы
1. Линейные системы и матрицы 1. Дать определение умножения матриц. Коммутативна ли эта операция? Ответ пояснить. Произведение C матриц A и B определяется как m p m p A B ij = A ik B kj. Операция не коммутативна.
ПодробнееРешающие системы с правилом Крамера
Цели обучения
В этом разделе вы:
- Оцените детерминанты 2 × 2.

- Используйте правило Крамера для решения системы уравнений с двумя переменными.
- Оцените детерминанты 3 × 3.
- Используйте правило Крамера, чтобы решить систему из трех уравнений с тремя переменными.
- Знать свойства определителей.
Мы узнали, как решать системы уравнений с двумя переменными и тремя переменными с помощью нескольких методов: подстановки, сложения, исключения Гаусса, использования обратной матрицы и построения графиков.Некоторые из этих методов применять проще, чем другие, и они более подходят в определенных ситуациях. В этом разделе мы изучим еще две стратегии решения систем уравнений.
Вычисление определителя матрицы 2 × 2
Определитель – это действительное число, которое может быть очень полезно в математике, потому что у него есть несколько приложений, таких как вычисление площади, объема и других величин. Здесь мы будем использовать определители, чтобы определить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений. Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются в виде матрицы. Расшифровать данные можно только с помощью обратимой матрицы и определителя. В наших целях мы ориентируемся на определитель как на показатель обратимости матрицы. Для вычисления определителя матрицы необходимо следовать определенным шаблонам, описанным в этом разделе.
Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются в виде матрицы. Расшифровать данные можно только с помощью обратимой матрицы и определителя. В наших целях мы ориентируемся на определитель как на показатель обратимости матрицы. Для вычисления определителя матрицы необходимо следовать определенным шаблонам, описанным в этом разделе.
Найдите определитель матрицы 2 × 2
Определитель матрицы [latex] \, 2 \ text {} × \ text {} 2 \, [/ latex], учитывая
[латекс] A = \ left [\ begin {array} {cc} a & b \\ c & d \ end {array} \ right] [/ latex]
определяется как
Обратите внимание на изменение обозначений.Есть несколько способов указать определитель, включая [latex] \, \ mathrm {det} \ left (A \ right) \, [/ latex] и замену скобок в матрице прямыми линиями, [latex] \, | A |. [/ Латекс]
Нахождение определителя матрицы 2 × 2
Найдите определитель заданной матрицы.
[латекс] A = \ left [\ begin {array} {cc} 5 & 2 \\ -6 & 3 \ end {array} \ right] [/ latex]
Показать решение[латекс] \ begin {array} {l} \ mathrm {det} \ left (A \ right) = | \ begin {array} {cc} 5 & 2 \\ -6 & 3 \ end {array} | \ hfill \ \ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, = 5 \ left (3 \ right) – \ left (-6 \ right ) \ left (2 \ right) \ hfill \\ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, = 27 \ hfill \ end {array} [/ latex]
Использование правила Крамера для решения системы двух уравнений с двумя переменными
Теперь мы представим последний метод решения систем уравнений, использующий определители.Этот метод, известный как правило Крамера, восходит к середине 18 века и назван в честь своего новатора, швейцарского математика Габриэля Крамера (1704-1752), который представил его в 1750 году во введении к анализу алгоритмов Курбских Альгебриков. Правило Крамера – это жизнеспособный и эффективный метод поиска решений систем с произвольным числом неизвестных при условии, что у нас есть такое же количество уравнений, что и неизвестных.
Правило Крамера даст нам единственное решение системы уравнений, если оно существует.Однако, если система не имеет решения или бесконечное количество решений, это будет обозначено нулевым определителем. Чтобы выяснить, является ли система непоследовательной или зависимой, необходимо использовать другой метод, например исключение.
Чтобы понять правило Крамера, давайте внимательно рассмотрим, как мы решаем системы линейных уравнений с использованием основных операций со строками. Рассмотрим систему двух уравнений с двумя переменными.
[латекс] \ begin {array} {c} {a} _ {1} x + {b} _ {1} y = {c} _ {1} \, \, \, \, \ left (1 \ right ) \\ {a} _ {2} x + {b} _ {2} y = {c} _ {2} \, \, \, \, \ left (2 \ right) \ end {array} [/ latex ]
Мы исключаем одну переменную, используя операции со строками, и решаем для другой.Скажем, мы хотим найти [латекс] \, x. \, [/ Latex] Если уравнение (2) умножить на коэффициент, противоположный [латексу] \, y \, [/ latex] в уравнении (1 ), уравнение (1) умножается на коэффициент [latex] \, y \, [/ latex] в уравнении (2), и мы складываем два уравнения, переменную [latex] \, y \, [/ latex ] будет исключен.
[латекс] \ begin {array} {l} \ underset {\ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _} {\ begin {array} {llll} \ hfill & \ hfill & \ hfill & \ hfill \\ \, \, \, \, {b} _ {2} {a} _ {1} x + {b} _ {2} {b} _ {1} y = {b} _ {2} {c} _ {1} \ hfill & \ hfill & \ hfill & \ text {Умножение} {R} _ {1} \ text {by} {b} _ {2} \ hfill \\ – {b} _ {1} {a } _ {2} x- {b} _ {1} {b} _ {2} y = – {b} _ {1} {c} _ {2} \ hfill & \ hfill & \ hfill & \ text { Умножить} {R} _ {2} \ text {by} – {b} _ {1} \ hfill \ end {array}} \ hfill \\ \, \, \, \ begin {array} {ll} {b } _ {2} {a} _ {1} x- {b} _ {1} {a} _ {2} x = {b} _ {2} {c} _ {1} – {b} _ { 1} {c} _ {2} \ hfill & \ hfill \ end {array} \ hfill \ end {array} [/ latex]
Теперь решите относительно [латекс] \, x.[/ латекс]
[латекс] \ begin {array} {l} \, \, \, {b} _ {2} {a} _ {1} x- {b} _ {1} {a} _ {2} x = {b} _ {2} {c} _ {1} – {b} _ {1} {c} _ {2} \ hfill \\ \, \, \, x \ left ({b} _ {2} {a} _ {1} – {b} _ {1} {a} _ {2} \ right) = {b} _ {2} {c} _ {1} – {b} _ {1} {c } _ {2} \ hfill \\ \ text {} x = \ frac {{b} _ {2} {c} _ {1} – {b} _ {1} {c} _ {2}} {{ b} _ {2} {a} _ {1} – {b} _ {1} {a} _ {2}} = \ frac {\ left [\ begin {array} {cc} {c} _ {1 } & {b} _ {1} \\ {c} _ {2} & {b} _ {2} \ end {array} \ right]} {\ left [\ begin {array} {cc} {a} _ {1} & {b} _ {1} \\ {a} _ {2} & {b} _ {2} \ end {array} \ right]} \ hfill \ end {array} [/ latex]
Аналогичным образом, чтобы решить для [latex] \, y, [/ latex], мы удалим [latex] \, x. [/ латекс]
[/ латекс]
[латекс] \ begin {array} {l} \ underset {\ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _} {\ begin {array} {llll} \ hfill & \ hfill & \ hfill & \ hfill \\ \, \, \, \, {a} _ {2} {a} _ {1} x + {a} _ {2} {b} _ {1} y = {a} _ {2} {c} _ {1} \ hfill & \ hfill & \ hfill & \ text {Умножение} {R} _ {1} \ text {by} {a} _ {2} \ hfill \\ – {a} _ {1} {a } _ {2} x- {a} _ {1} {b} _ {2} y = – {a} _ {1} {c} _ {2} \ hfill & \ hfill & \ hfill & \ text { Умножить} {R} _ {2} \ text {by} – {a} _ {1} \ hfill \ end {array}} \ hfill \\ \, \, \, \, \, \, \ begin {array } {ll} {a} _ {2} {b} _ {1} y- {a} _ {1} {b} _ {2} y = {a} _ {2} {c} _ {1} – {a} _ {1} {c} _ {2} \ hfill & \ hfill \ end {array} \ hfill \ end {array} [/ latex]
Решение для [latex] \, y \, [/ latex] дает
[латекс] \ begin {array} {l} {a} _ {2} {b} _ {1} y- {a} _ {1} {b} _ {2} y = {a} _ {2 } {c} _ {1} – {a} _ {1} {c} _ {2} \ hfill \\ y \ left ({a} _ {2} {b} _ {1} – {a} _ {1} {b} _ {2} \ right) = {a} _ {2} {c} _ {1} – {a} _ {1} {c} _ {2} \ hfill \\ \ text { } y = \ frac {{a} _ {2} {c} _ {1} – {a} _ {1} {c} _ {2}} {{a} _ {2} {b} _ {1 } – {a} _ {1} {b} _ {2}} = \ frac {{a} _ {1} {c} _ {2} – {a} _ {2} {c} _ {1} } {{a} _ {1} {b} _ {2} – {a} _ {2} {b} _ {1}} = \ frac {| \ begin {array} {cc} {a} _ { 1} & {c} _ {1} \\ {a} _ {2} & {c} _ {2} \ end {array} |} {| \ begin {array} {cc} {a} _ {1 } & {b} _ {1} \\ {a} _ {2} & {b} _ {2} \ end {array} |} \ hfill \ end {array} [/ latex]
Обратите внимание, что знаменатель для [latex] \, x \, [/ latex] и [latex] \, y \, [/ latex] является определителем матрицы коэффициентов.
Мы можем использовать эти формулы для решения для [latex] \, x \, [/ latex] и [latex] \, y, \, [/ latex], но Правило Крамера также вводит новые обозначения:
Ключ к правилу Крамера заключается в замене интересующего столбца переменных столбцом констант и вычислении детерминантов. Затем мы можем выразить [латекс] \, x \, [/ latex] и [latex] \, y \, [/ latex] как частное двух определителей.
Правило Крамера для систем 2 × 2
Правило Крамера – это метод, использующий детерминанты для решения систем уравнений, которые имеют то же количество уравнений, что и переменные.
Рассмотрим систему двух линейных уравнений с двумя переменными.
[латекс] \ begin {array} {c} {a} _ {1} x + {b} _ {1} y = {c} _ {1} \\ {a} _ {2} x + {b} _ {2} y = {c} _ {2} \ end {array} [/ latex]
Решение, использующее правило Крамера, дается как
[латекс] x = \ frac {{D} _ {x}} {D} = \ frac {| \ begin {array} {cc} {c} _ {1} & {b} _ {1} \\ {c} _ {2} & {b} _ {2} \ end {array} |} {| \ begin {array} {cc} {a} _ {1} & {b} _ {1} \\ { a} _ {2} & {b} _ {2} \ end {array} |}, \, \, D \ ne 0; \, \, \ text {} \ text {} \, y = \ гидроразрыв {{D} _ {y}} {D} = \ frac {| \ begin {array} {cc} {a} _ {1} & {c} _ {1} \\ {a} _ {2} & {c} _ {2} \ end {array} |} {| \ begin {array} {cc} {a} _ {1} & {b} _ {1} \\ {a} _ {2} & {b} _ {2} \ end {array} |}, \, \, D \ ne 0. [/ латекс]
[/ латекс]
Если мы решаем для [latex] \, x, \, [/ latex], столбец [latex] \, x \, [/ latex] заменяется столбцом констант. Если мы решаем для [latex] \, y, \, [/ latex], столбец [latex] \, y \, [/ latex] заменяется постоянным столбцом.
Использование правила Крамера для решения системы 2 × 2
Решите следующую систему [latex] \, 2 \ text {} × \ text {} 2 \, [/ latex], используя правило Крамера.
[латекс] \ begin {array} {c} 12x + 3y = 15 \\ \ text {} 2x-3y = 13 \ end {array} [/ latex]
Показать решениеРешите относительно [латекс] \, x.[/ латекс]
[латекс] x = \ frac {{D} _ {x}} {D} = \ frac {| \ begin {array} {rr} \ hfill 15 & \ hfill 3 \\ \ hfill 13 & \ hfill -3 \ end {array} |} {| \ begin {array} {rr} \ hfill 12 & \ hfill 3 \\ \ hfill 2 & \ hfill -3 \ end {array} |} = \ frac {-45-39} {- 36- 6} = \ frac {-84} {- 42} = 2 [/ latex]
Решите для [latex] \, y. [/ Latex]
[латекс] y = \ frac {{D} _ {y}} {D} = \ frac {| \ begin {array} {rr} \ hfill 12 & \ hfill 15 \\ \ hfill 2 & \ hfill 13 \ end { array} |} {| \ begin {array} {rr} \ hfill 12 & \ hfill 3 \\ \ hfill 2 & \ hfill -3 \ end {array} |} = \ frac {156-30} {- 36-6} = – \ frac {126} {42} = – 3 [/ латекс]
Решение: [латекс] \, \ left (2, -3 \ right). [/ латекс]
[/ латекс]
Попробуйте
Используйте правило Крамера для решения системы уравнений 2 × 2.
[латекс] \ begin {массив} {l} \ text {} x + 2y = -11 \ hfill \\ -2x + y = -13 \ hfill \ end {array} [/ latex]
Показать решение[латекс] \ влево (3, -7 \ вправо) [/ латекс]
Вычисление определителя матрицы 3 × 3
Найти определитель матрицы 2 × 2 несложно, но найти определитель матрицы 3 × 3 сложнее. Один из способов – увеличить матрицу 3 × 3 повторением первых двух столбцов, получив матрицу 3 × 5.Затем мы вычисляем сумму произведений записей на по каждой из трех диагоналей (от верхнего левого угла к нижнему правому) и вычитаем произведения записей на по каждой из трех диагоналей (нижний левый верхний правый). Это легче понять с помощью наглядного пособия и примера.
Найдите определитель матрицы 3 × 3.
[латекс] A = \ left [\ begin {array} {ccc} {a} _ {1} & {b} _ {1} & {c} _ {1} \\ {a} _ {2} & {b} _ {2} & {c} _ {2} \\ {a} _ {3} & {b} _ {3} & {c} _ {3} \ end {array} \ right] [/ латекс]
- Дополните [latex] \, A \, [/ latex] первыми двумя столбцами.

[латекс] \ mathrm {det} \ left (A \ right) = | \ begin {array} {ccc} {a} _ {1} & {b} _ {1} & {c} _ {1} \ \ {a} _ {2} & {b} _ {2} & {c} _ {2} \\ {a} _ {3} & {b} _ {3} & {c} _ {3} \ конец {массив} \, \, \, | \, \, \, \ begin {array} {c} {a} _ {1} \\ {a} _ {2} \\ {a} _ {3} \ end {array} \, \, \, \, \ begin {array} {c} {b} _ {1} \\ {b} _ {2} \\ {b} _ {3} \ end {массив } | [/ латекс]
- Слева вверху направо вниз: умножение значений по первой диагонали. Добавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей по третьей диагонали.
- От левого нижнего угла до правого верхнего: вычтите произведение входов вверх по первой диагонали. Из этого результата вычтите произведение входов вверх по второй диагонали. Из этого результата вычтите произведение входов до третьей диагонали.
Алгебра выглядит следующим образом:
[латекс] | A | = {a} _ {1} {b} _ {2} {c} _ {3} + {b} _ {1} {c} _ {2} {a} _ {3 } + {c} _ {1} {a} _ {2} {b} _ {3} – {a} _ {3} {b} _ {2} {c} _ {1} – {b} _ {3} {c} _ {2} {a} _ {1} – {c} _ {3} {a} _ {2} {b} _ {1} [/ latex]
Нахождение определителя матрицы 3 × 3
Найдите определитель матрицы 3 × 3 для данного
[латекс] A = \ left [\ begin {array} {ccc} 0 & 2 & 1 \\ 3 & -1 & 1 \\ 4 & 0 & 1 \ end {array} \ right] [/ latex]
Показать решение Дополните матрицу первыми двумя столбцами, а затем следуйте формуле. Таким образом,
Таким образом,
[латекс] \ begin {array} {l} | A | = | \ begin {array} {ccc} 0 & 2 & 1 \\ 3 & -1 & 1 \\ 4 & 0 & 1 \ end {array} \, \, | \ begin {array} {c} 0 \\ 3 \\ \, \, 4 \ end {array} \, \, \, \, \ begin {array} {c} 2 \\ -1 \\ 0 \ end { массив} | \ hfill \\ \, \, \, \, \, \, \, = 0 \ left (-1 \ right) \ left (1 \ right) +2 \ left (1 \ right) \ left ( 4 \ вправо) +1 \ влево (3 \ вправо) \ влево (0 \ вправо) -4 \ влево (-1 \ вправо) \ влево (1 \ вправо) -0 \ влево (1 \ вправо) \ влево (0 \ вправо) -1 \ влево (3 \ вправо) \ влево (2 \ вправо) \ hfill \\ \, \, \, \, \, \, \, = 0 + 8 + 0 + 4-0-6 \ hfill \\ \, \, \, \, \, \, \, = 6 \ hfill \ end {array} [/ latex]
Попробуйте
Найдите определитель матрицы 3 × 3.
[латекс] \ mathrm {det} \ left (A \ right) = | \ begin {array} {ccc} 1 & -3 & 7 \\ 1 & 1 & 1 \\ 1 & -2 & 3 \ end {array} | [/ latex ]
Можем ли мы использовать тот же метод, чтобы найти определитель большей матрицы?
Нет, этот метод работает только для [latex] \, 2 \ text {} × \ text {} 2 \, [/ latex] и [latex] \, \ text {3} \ text {} × \ text { } 3 \, [/ латексные] матрицы. Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.
Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.
Использование правила Крамера для решения системы трех уравнений с тремя переменными
Теперь, когда мы можем найти определитель матрицы 3 × 3, мы можем применить правило Крамера для решения системы трех уравнений с тремя переменными.Правило Крамера простое и следует шаблону, соответствующему правилу Крамера для матриц 2 × 2. Однако по мере увеличения порядка матрицы до 3 × 3 требуется гораздо больше вычислений.
Когда мы вычисляем детерминант, равный нулю, правило Крамера не дает указания на то, нет ли у системы решения или бесконечного числа решений. Чтобы выяснить это, мы должны выполнить устранение в системе.
Рассмотрим систему уравнений 3 × 3.
[латекс] x = \ frac {{D} _ {x}} {D}, y = \ frac {{D} _ {y}} {D}, z = \ frac {{D} _ {z} } {D}, D \ ne 0 [/ латекс]
где
Если мы записываем определитель [latex] \, {D} _ {x}, [/ latex], мы заменяем столбец [latex] \, x \, [/ latex] на столбец констант. Если мы пишем определитель [latex] {D} _ {y}, [/ latex], мы заменяем столбец [latex] \, y \, [/ latex] на постоянный столбец. Если мы пишем определитель [latex] \, {D} _ {z}, [/ latex], мы заменяем столбец [latex] \, z \, [/ latex] постоянным столбцом. Всегда проверяйте ответ.
Если мы пишем определитель [latex] {D} _ {y}, [/ latex], мы заменяем столбец [latex] \, y \, [/ latex] на постоянный столбец. Если мы пишем определитель [latex] \, {D} _ {z}, [/ latex], мы заменяем столбец [latex] \, z \, [/ latex] постоянным столбцом. Всегда проверяйте ответ.
Решение системы 3 × 3 с использованием правила Крамера
Найдите решение данной системы 3 × 3, используя правило Крамера.
[латекс] \ begin {array} {c} x + y-z = 6 \\ 3x-2y + z = -5 \\ x + 3y-2z = 14 \ end {array} [/ latex]
Показать решениеИспользуйте правило Крамера.
[латекс] D = | \ begin {array} {ccc} 1 & \, \, 1 & -1 \\ 3 & -2 & \, \, \, 1 \\ 1 & \, \, 3 & -2 \ end {array} |, {D} _ {x} = | \ begin {array} {ccc} 6 & 1 & -1 \\ -5 & -2 & \, \, \, 1 \\ 14 & \, \, 3 & -2 \ end {массив } |, {D} _ {y} = | \ begin {array} {ccc} 1 & \, 6 & -1 \\ 3 & -5 & \, \, 1 \\ 1 & 14 & -2 \ end {array} |, { D} _ {z} = | \ begin {array} {ccc} 1 & \, 1 & 6 \\ 3 & -2 & -5 \\ 1 & \, \, 3 & 14 \ end {array} | [/ latex]
Затем,
[латекс] \ begin {array} {l} x = \ frac {{D} _ {x}} {D} = \ frac {-3} {- 3} = 1 \ hfill \\ y = \ frac { {D} _ {y}} {D} = \ frac {-9} {- 3} = 3 \ hfill \\ z = \ frac {{D} _ {z}} {D} = \ frac {6} {-3} = – 2 \ hfill \ end {array} [/ latex]
Решение [латекс] \ left (1,3, -2 \ right). [/ латекс]
[/ латекс]
Попробуйте
Используйте правило Крамера, чтобы решить матрицу 3 × 3.
[латекс] \ begin {array} {r} \ hfill x-3y + 7z = 13 \\ \ hfill x + y + z = 1 \, \, \, \\ \ hfill x-2y + 3z = 4 \ , \, \, \ end {array} [/ latex]
Показать решение[латекс] \ left (-2, \ frac {3} {5}, \ frac {12} {5} \ right) [/ latex]
Использование правила Крамера для решения несовместимой системы
Решите систему уравнений, используя правило Крамера.
[латекс] \ begin {array} {l} 3x-2y = 4 \ text {} \ left (1 \ right) \\ 6x-4y = 0 \ text {} \ left (2 \ right) \ end {массив } [/ латекс]
Показать решениеНачнем с нахождения определителей [латекс] \, D, {D} _ {x}, \ text {и} {D} _ {y}.[/ латекс]
[латекс] D = | \ begin {array} {cc} 3 & -2 \\ 6 & -4 \ end {array} | = 3 \ left (-4 \ right) -6 \ left (-2 \ right) = 0 [/ латекс]
Мы знаем, что нулевой определитель означает, что либо система не имеет решения, либо имеет бесконечное количество решений. Чтобы узнать, какой из них, мы используем процесс исключения. Наша цель – исключить одну из переменных.
Чтобы узнать, какой из них, мы используем процесс исключения. Наша цель – исключить одну из переменных.
- Умножить уравнение (1) на [латекс] \, – 2. [/ Latex]
- Добавьте результат к уравнению [латекс] \, \ left (2 \ right). [/ Latex]
[латекс] \ begin {array} {l} \ underset {\ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _} {\ begin {массив} {l} \ begin {array} {l} \ hfill \\ -6x + 4y \, \, \, \, = – 8 \ hfill \ end {array} \ hfill \\ \, \, \, 6x-4y \, \, \, \, \, \, = \, \, \, \, 0 \ hfill \ end {array}} \ hfill \\ \, \, \, \, \, \, \ , \, \, \, \, \, \, \, \, \, \, \, \, 0 \, \, \, \, \, \, = \, – 8 \ hfill \ end {array} [/ латекс]
Получаем уравнение [латекс] \, 0 = -8, \, [/ латекс], которое неверно.Следовательно, у системы нет решения. График системы показывает две параллельные линии. См. (Рисунок).
Рисунок 1.
Используйте правило Крамера для решения зависимой системы
Решите систему с бесконечным количеством решений.
[латекс] \ begin {array} {rr} \ hfill x-2y + 3z = 0 & \ hfill \ left (1 \ right) \\ \ hfill 3x + y-2z = 0 & \ hfill \ left (2 \ right) \\ \ hfill 2x-4y + 6z = 0 & \ hfill \ left (3 \ right) \ end {array} [/ latex]
Показать решениеДавайте сначала найдем определитель.Создайте матрицу, дополненную первыми двумя столбцами.
[латекс] | \ begin {array} {rrr} \ hfill 1 & \ hfill -2 & \ hfill 3 \\ \ hfill 3 & \ hfill 1 & \ hfill -2 \\ \ hfill 2 & \ hfill -4 & \ hfill 6 \ end { array} \ text {} | \ text {} \ begin {array} {rr} \ hfill 1 & \ hfill -2 \\ \ hfill 3 & \ hfill 1 \\ \ hfill 2 & \ hfill -4 \ end {array} | [ / латекс]
Затем,
[латекс] 1 \ влево (1 \ вправо) \ влево (6 \ вправо) + \ влево (-2 \ вправо) \ влево (-2 \ вправо) \ влево (2 \ вправо) +3 \ влево (3 \ вправо) \ влево (-4 \ вправо) -2 \ влево (1 \ вправо) \ влево (3 \ вправо) – \ влево (-4 \ вправо) \ влево (-2 \ вправо) \ влево (1 \ вправо) -6 \ влево (3 \ вправо) \ влево (-2 \ вправо) = 0 [/ латекс]
Поскольку определитель равен нулю, решения либо нет, либо существует бесконечное количество решений. Чтобы выяснить это, нам нужно провести отбор.
Чтобы выяснить это, нам нужно провести отбор.
- Умножьте уравнение (1) на [latex] \, – 2 \, [/ latex] и добавьте результат к уравнению (3):
[латекс] \ frac {\ begin {array} {r} \ hfill -2x + 4y-6x = 0 \\ \ hfill 2x-4y + 6z = 0 \ end {array}} {\, \, \, \ , \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ , \, \, 0 = 0} [/ латекс]
- Получение ответа [latex] \, 0 = 0, \, [/ latex] утверждение, которое всегда верно, означает, что система имеет бесконечное количество решений. Изобразив систему, мы можем увидеть, что две плоскости одинаковы, и обе они пересекают третью плоскость по прямой.См. (Рисунок).
Рисунок 2.
Понимание свойств детерминантов
Есть много свойств определителей. Здесь перечислены некоторые свойства, которые могут быть полезны при вычислении определителя матрицы.
Свойства детерминантов
- Если матрица имеет верхнюю треугольную форму, определитель равен произведению элементов по главной диагонали.

- Когда две строки меняются местами, определитель меняет знак.{-1} \, [/ latex] – обратная величина определителю матрицы [latex] \, A. [/ Latex]
- Если любая строка или столбец умножается на константу, определитель умножается на тот же коэффициент.
Иллюстрируя свойства детерминантов
Проиллюстрируйте каждое из свойств определителей.
Показать решениеСвойство 1 утверждает, что если матрица имеет верхнюю треугольную форму, определитель является произведением элементов по главной диагонали.
[латекс] A = \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill \, \, 2 & \ hfill 3 \\ \ hfill 0 & \ hfill \, \, 2 & \ hfill 1 \\ \ hfill 0 & \ hfill \, \, 0 & \ hfill -1 \ end {array} \ right] [/ latex]
Дополните [латекс] \, A \, [/ latex] первыми двумя столбцами.
[латекс] A = \ left [\ begin {array} {ccc} 1 & 2 & 3 \\ 0 & 2 & 1 \\ 0 & 0 & -1 \ end {array} | \, \, \, \ begin {array} {c } 1 \\ 0 \\ 0 \ end {массив} \, \, \, \, \ begin {array} {c} 2 \\ 2 \\ 0 \ end {array} \ right] [/ latex]
Затем
[латекс] \ begin {array} {l} \ mathrm {det} \ left (A \ right) = 1 \ left (2 \ right) \ left (-1 \ right) +2 \ left (1 \ right) \ влево (0 \ вправо) +3 \ влево (0 \ вправо) \ влево (0 \ вправо) -0 \ влево (2 \ вправо) \ влево (3 \ вправо) -0 \ влево (1 \ вправо) \ влево (1 \ вправо) +1 \ влево (0 \ вправо) \ влево (2 \ вправо) \ hfill \\ \, \, \, \, \, \, \, \, \, \, \, \, \ , \, \, \, = – 2 \ hfill \ end {array} [/ latex]
Свойство 2 утверждает, что перестановка строк меняет знак. Учитывая
Учитывая
[латекс] \ begin {массив} {l} \ begin {array} {l} \\ A = \ left [\ begin {array} {cc} -1 & 5 \\ 4 & -3 \ end {array} \ right ], \, \, \ mathrm {det} \ left (A \ right) = \ left (-1 \ right) \ left (-3 \ right) – \ left (4 \ right) \ left (5 \ right) = 3-20 = -17 \ end {массив} \ hfill \\ \ hfill \\ B = \ left [\ begin {array} {cc} 4 & -3 \\ -1 & 5 \ end {array} \ right], \, \, \ mathrm {det} \ left (B \ right) = \ left (4 \ right) \ left (5 \ right) – \ left (-1 \ right) \ left (-3 \ right) = 20 -3 = 17 \ hfill \ end {array} [/ latex]
Свойство 3 утверждает, что если две строки или два столбца идентичны, определитель равен нулю.
[латекс] \ begin {массив} {l} \, \, \, \, \, \, \, \, \, \, \, A = \ left [\ begin {array} {ccc} 1 & 2 & 2 \\ 2 & 2 & 2 \\ -1 & 2 & 2 \ end {array} \ text {} | \ text {} \ begin {array} {c} 1 \\ 2 \\ -1 \ end {array} \ begin {array } {c} 2 \\ 2 \\ 2 \ end {array} \ right] \ hfill \\ \ hfill \\ \ mathrm {det} \ left (A \ right) = 1 \ left (2 \ right) \ left (2 \ вправо) +2 \ влево (2 \ вправо) \ влево (-1 \ вправо) +2 \ влево (2 \ вправо) \ влево (2 \ вправо) +1 \ влево (2 \ вправо) \ влево ( 2 \ вправо) -2 \ влево (2 \ вправо) \ влево (1 \ вправо) -2 \ влево (2 \ вправо) \ влево (2 \ вправо) \ hfill \\ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, = 4-4 + 8 + 4-4-8 = 0 \ hfill \ end {array} [/ latex]
Свойство 4 утверждает, что если строка или столбец равны нулю, определитель равен нулю. {-1} \ right) = – 2 \ left (- \ frac {1} {2} \ right) – \ left (\ frac {3} {2} \ right) \ left (1 \ right) = – \ гидроразрыв {1} {2} \ hfill \ end {array} [/ latex]
{-1} \ right) = – 2 \ left (- \ frac {1} {2} \ right) – \ left (\ frac {3} {2} \ right) \ left (1 \ right) = – \ гидроразрыв {1} {2} \ hfill \ end {array} [/ latex]
Свойство 6 утверждает, что если любая строка или столбец матрицы умножается на константу, определитель умножается на тот же коэффициент. Таким образом,
[латекс] \ begin {array} {l} A = \ left [\ begin {array} {cc} 1 & 2 \\ 3 & 4 \ end {array} \ right], \ mathrm {det} \ left (A \ right) = 1 \ left (4 \ right) -2 \ left (3 \ right) = – 2 \ hfill \\ \ hfill \\ B = \ left [\ begin {array} {cc} 2 \ left (1 \ right) & 2 \ left (2 \ right) \\ 3 & 4 \ end {array} \ right], \ mathrm {det} \ left (B \ right) = 2 \ left (4 \ right) -3 \ left ( 4 \ right) = – 4 \ hfill \ end {array} [/ latex]
Использование правила Крамера и определяющих свойств для решения системы
Найдите решение данной системы 3 × 3.
[латекс] \ begin {array} {ll} 2x + 4y + 4z = 2 \ hfill & \ left (1 \ right) \ hfill \\ 3x + 7y + 7z = -5 \ hfill & \ left (2 \ right ) \ hfill \\ \ text {} x + 2y + 2z = 4 \ hfill & \ left (3 \ right) \ hfill \ end {array} [/ latex]
Показать решениеИспользуя правило Крамера, имеем
[латекс] D = | \ begin {array} {ccc} 2 & 4 & 4 \\ 3 & 7 & 7 \\ 1 & 2 & 2 \ end {array} | [/ latex]
Обратите внимание, что второй и третий столбцы идентичны. Согласно свойству 3 определитель будет равен нулю, поэтому решения либо нет, либо существует бесконечное число решений.Чтобы выяснить это, нам нужно провести отбор.
Согласно свойству 3 определитель будет равен нулю, поэтому решения либо нет, либо существует бесконечное число решений.Чтобы выяснить это, нам нужно провести отбор.
- Умножьте уравнение (3) на –2 и прибавьте результат к уравнению (1).
[латекс] \ frac {\ begin {array} {l} -2x-4y-4x = -8 \ hfill \\ \ text {} 2x + 4y + 4z = 2 \, \, \, \, \, \ hfill \ end {array}} {\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, 0 = -6} [/ латекс]
Получение противоречивого утверждения означает, что система не имеет решения.
Ключевые концепции
- Определитель для [latex] \, \ left [\ begin {array} {cc} a & b \\ c & d \ end {array} \ right] \, [/ latex] – [latex] \, ad-bc .\, [/ latex] См. (рисунок).
- Правило Крамера заменяет переменный столбец постоянным столбцом. Решениями являются [latex] \, x = \ frac {{D} _ {x}} {D}, y = \ frac {{D} _ {y}} {D}. \, [/ Latex] См. (Рисунок ).

- Чтобы найти определитель матрицы 3 × 3, дополните ее двумя первыми столбцами. Сложите три диагональных записи (верхний левый нижний правый) и вычтите три диагональных входа (нижний левый верхний правый). См. (Рисунок).
- Чтобы решить систему трех уравнений с тремя переменными с помощью правила Крамера, замените столбец переменных столбцом констант для каждого желаемого решения: [latex] \, x = \ frac {{D} _ {x}} {D}, y = \ frac {{D} _ {y}} {D}, z = \ frac {{D} _ {z}} {D}.\, [/ latex] См. (рисунок).
- Правило Крамера также полезно для поиска решения системы уравнений без решения или с бесконечными решениями. См. (Рисунок) и (Рисунок).
- Некоторые свойства определителей полезны для решения задач. Например:
- Если матрица имеет верхнюю треугольную форму, определитель равен произведению элементов по главной диагонали.
- Когда две строки меняются местами, определитель меняет знак.
- Если две строки или два столбца идентичны, определитель равен нулю.
 {-1} \, [/ latex] – обратная величина определителю матрицы [latex] \, A. [/ Latex]
{-1} \, [/ latex] – обратная величина определителю матрицы [latex] \, A. [/ Latex] - Если любая строка или столбец умножается на константу, определитель умножается на тот же коэффициент. См. (Рисунок) и (Рисунок).
Упражнения по разделам
Устный
Объясните, почему мы всегда можем вычислить определитель квадратной матрицы.
Показать решениеОпределитель – это сумма и произведения элементов матрицы, поэтому вы всегда можете оценить этот продукт, даже если в конечном итоге он окажется равным нулю.
Исследуя правило Крамера, объясните, почему не существует единственного решения системы, когда определитель вашей матрицы равен 0. Для простоты используйте матрицу [latex] \, 2 \, × \, 2 \, [/ latex].
Объясните, что в терминах обратного значения для матрицы означает наличие определителя 0.
Показать решениеОбратного не существует.
Определитель [latex] \, 2 \, × \, 2 \, [/ latex] matrix [latex] \, A \, [/ latex] равен 3. Если вы поменяете строки и умножите первую строку на 6 а во второй строке – 2, объясните, как найти определитель и дать ответ.
Если вы поменяете строки и умножите первую строку на 6 а во второй строке – 2, объясните, как найти определитель и дать ответ.
Алгебраические
Найдите определитель для следующих упражнений.
[латекс] | \ begin {array} {cc} 1 & 2 \\ 3 & 4 \ end {array} | [/ latex]
[латекс] | \ begin {массив} {rr} \ hfill -1 & \ hfill 2 \\ \ hfill 3 & \ hfill -4 \ end {array} | [/ latex]
[латекс] | \ begin {массив} {rr} \ hfill 2 & \ hfill -5 \\ \ hfill -1 & \ hfill 6 \ end {array} | [/ latex]
[латекс] | \ begin {array} {cc} -8 & 4 \\ -1 & 5 \ end {array} | [/ latex]
[латекс] | \ begin {массив} {rr} \ hfill 1 & \ hfill 0 \\ \ hfill 3 & \ hfill -4 \ end {array} | [/ latex]
[латекс] | \ begin {массив} {rr} \ hfill 10 & \ hfill 20 \\ \ hfill 0 & \ hfill -10 \ end {array} | [/ latex]
[латекс] | \ begin {array} {cc} 10 & 0.2 \\ 5 & 0.1 \ end {array} | [/ latex]
[латекс] | \ begin {массив} {rr} \ hfill 6 & \ hfill -3 \\ \ hfill 8 & \ hfill 4 \ end {array} | [/ latex]
[латекс] | \ begin {array} {rr} \ hfill -2 & \ hfill -3 \\ \ hfill 3. 1 & \ hfill 4,000 \ end {array} | [/ latex]
1 & \ hfill 4,000 \ end {array} | [/ latex]
[латекс] | \ begin {array} {rr} \ hfill -1.1 & \ hfill 0.6 \\ \ hfill 7.2 & \ hfill -0.5 \ end {array} | [/ latex]
[латекс] | \ begin {array} {rrr} \ hfill -1 & \ hfill 0 & \ hfill 0 \\ \ hfill 0 & \ hfill 1 & \ hfill 0 \\ \ hfill 0 & \ hfill 0 & \ hfill -3 \ end {массив } | [/ латекс]
[латекс] | \ begin {array} {rrr} \ hfill -1 & \ hfill 4 & \ hfill 0 \\ \ hfill 0 & \ hfill 2 & \ hfill 3 \\ \ hfill 0 & \ hfill 0 & \ hfill -3 \ end {массив } | [/ латекс]
[латекс] | \ begin {array} {ccc} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \ end {array} | [/ latex]
[латекс] | \ begin {array} {rrr} \ hfill 2 & \ hfill -3 & \ hfill 1 \\ \ hfill 3 & \ hfill -4 & \ hfill 1 \\ \ hfill -5 & \ hfill 6 & \ hfill 1 \ end { массив} | [/ латекс]
[латекс] | \ begin {array} {rrr} \ hfill -2 & \ hfill 1 & \ hfill 4 \\ \ hfill -4 & \ hfill 2 & \ hfill -8 \\ \ hfill 2 & \ hfill -8 & \ hfill -3 \ конец {массив} | [/ латекс]
[латекс] | \ begin {array} {rrr} \ hfill 6 & \ hfill -1 & \ hfill 2 \\ \ hfill -4 & \ hfill -3 & \ hfill 5 \\ \ hfill 1 & \ hfill 9 & \ hfill -1 \ end {array} | [/ латекс]
[латекс] | \ begin {array} {rrr} \ hfill 5 & \ hfill 1 & \ hfill -1 \\ \ hfill 2 & \ hfill 3 & \ hfill 1 \\ \ hfill 3 & \ hfill -6 & \ hfill -3 \ end { массив} | [/ латекс]
[латекс] | \ begin {array} {rrr} \ hfill 1. 1 & \ hfill 2 & \ hfill -1 \\ \ hfill -4 & \ hfill 0 & \ hfill 0 \\ \ hfill 4.1 & \ hfill -0.4 & \ hfill 2.5 \ end {array} | [/ latex]
1 & \ hfill 2 & \ hfill -1 \\ \ hfill -4 & \ hfill 0 & \ hfill 0 \\ \ hfill 4.1 & \ hfill -0.4 & \ hfill 2.5 \ end {array} | [/ latex]
[латекс] | \ begin {array} {rrr} \ hfill 2 & \ hfill -1.6 & \ hfill 3.1 \\ \ hfill 1.1 & \ hfill 3 & \ hfill -8 \\ \ hfill -9.3 & \ hfill 0 & \ hfill 2 \ end {array} | [/ latex]
[латекс] | \ begin {array} {ccc} – \ frac {1} {2} & \ frac {1} {3} & \ frac {1} {4} \\ \ frac {1} {5} & – \ frac {1} {6} & \ frac {1} {7} \\ 0 & 0 & \ frac {1} {8} \ end {array} | [/ latex]
Для следующих упражнений решите систему линейных уравнений, используя правило Крамера.
[латекс] \ begin {array} {l} 2x-3y = -1 \\ 4x + 5y = 9 \ end {array} [/ latex]
Показать решение[латекс] \ левый (1,1 \ правый) [/ латекс]
[латекс] \ begin {array} {r} 5x-4y = 2 \\ -4x + 7y = 6 \ end {array} [/ latex]
[латекс] \ begin {массив} {l} \ text {} 6x-3y = 2 \, \, \, \, \, \ hfill \\ -8x + 9y = -1 \ hfill \ end {array} [ / латекс]
Показать решение[латекс] \ left (\ frac {1} {2}, \ frac {1} {3} \ right) [/ latex]
[латекс] \ begin {array} {l} 2x + 6y = 12 \\ 5x-2y = 13 \ end {array} [/ latex]
[латекс] \ begin {array} {l} 4x + 3y = 23 \, \, \ hfill \\ \ text {} 2x-y = -1 \ hfill \ end {array} [/ latex]
Показать решение[латекс] \ левый (2,5 \ правый) [/ латекс]
[латекс] \ begin {array} {l} 10x-6y = 2 \, \, \, \, \ hfill \\ -5x + 8y = -1 \ hfill \ end {array} [/ latex]
[латекс] \ begin {array} {l} 4x-3y = -3 \\ 2x + 6y = -4 \ end {array} [/ latex]
Показать решение[латекс] \ left (-1, – \ frac {1} {3} \ right) [/ latex]
[латекс] \ begin {array} {r} 4x-5y = 7 \\ -3x + 9y = 0 \ end {array} [/ latex]
[латекс] \ begin {array} {l} 4x + 10y = 180 \, \, \, \, \ hfill \\ -3x-5y = -105 \ hfill \ end {array} [/ latex]
Показать решение[латекс] \ влево (15,12 \ вправо) [/ латекс]
[латекс] \ begin {массив} {l} \ text {} 8x-2y = -3 \ hfill \\ -4x + 6y = 4 \, \, \, \, \ hfill \ end {array} [/ latex ]
Для следующих упражнений решите систему линейных уравнений, используя правило Крамера.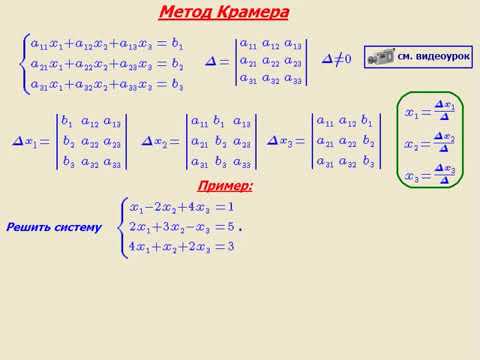
[латекс] \ begin {массив} {l} \ text {} x + 2y-4z = -1 \ hfill \\ \ text {} 7x + 3y + 5z = 26 \, \, \ hfill \\ -2x- 6y + 7z = -6 \ hfill \ end {array} [/ latex]
Показать решение[латекс] \ левый (1,3,2 \ правый) [/ латекс]
[латекс] \ begin {array} {l} -5x + 2y-4z = -47 \ hfill \\ \ text {} 4x-3y-z = -94 \ hfill \\ \ text {} 3x-3y + 2z = 94 \, \, \, \, \ hfill \ end {array} [/ latex]
[латекс] \ begin {массив} {l} \ text {} 4x + 5y-z = -7 \ hfill \\ -2x-9y + 2z = 8 \, \, \, \, \ hfill \\ \ text {} 5y + 7z = 21 \, \ hfill \ end {array} [/ latex]
Показать решение[латекс] \ влево (-1,0,3 \ вправо) [/ латекс]
[латекс] \ begin {array} {r} 4x-3y + 4z = 10 \\ 5x-2z = -2 \\ 3x + 2y-5z = -9 \ end {array} [/ latex]
[латекс] \ begin {array} {l} 4x-2y + 3z = 6 \, \, \, \ hfill \\ \ text {} -6x + y = -2 \ hfill \\ 2x + 7y + 8z = 24 \ hfill \ end {array} [/ latex]
Показать решение[латекс] \ влево (\ frac {1} {2}, 1,2 \ вправо) [/ латекс]
[латекс] \ begin {array} {r} \ hfill 5x + 2y-z = 1 \, \, \, \, \, \\ \ hfill -7x-8y + 3z = 1. 5 \\ \ hfill 6x-12y + z = 7 \, \, \, \, \ end {array} [/ latex]
5 \\ \ hfill 6x-12y + z = 7 \, \, \, \, \ end {array} [/ latex]
[латекс] \ begin {array} {l} \ text {} 13x-17y + 16z = 73 \, \, \, \, \ hfill \\ -11x + 15y + 17z = 61 \, \, \, \ , \ hfill \\ \ text {} 46x + 10y-30z = -18 \ hfill \ end {array} [/ latex]
Показать решение[латекс] \ влево (2,1,4 \ вправо) [/ латекс]
[латекс] \ begin {массив} {l} \ begin {array} {l} \ hfill \\ -4x-3y-8z = -7 \ hfill \ end {array} \ hfill \\ \ text {} 2x- 9y + 5z = 0,5 \ hfill \\ \ text {} 5x-6y-5z = -2 \ hfill \ end {array} [/ latex]
[латекс] \ begin {array} {l} \ text {} 4x-6y + 8z = 10 \, \, \ hfill \\ -2x + 3y-4z = -5 \ hfill \\ \ text {} x + y + z = 1 \, \, \, \, \, \ hfill \ end {array} [/ latex]
[латекс] \ begin {array} {r} \ hfill 4x-6y + 8z = 10 \, \, \, \, \, \\ \ hfill -2x + 3y-4z = -5 \, \, \, \\ \ hfill 12x + 18y-24z = -30 \ end {array} [/ latex]
Технологии
Для следующих упражнений используйте детерминантную функцию в графической утилите.
[латекс] | \ begin {array} {rrrr} \ hfill 1 & \ hfill 0 & \ hfill 8 & \ hfill 9 \\ \ hfill 0 & \ hfill 2 & \ hfill 1 & \ hfill 0 \\ \ hfill 1 & \ hfill 0 & \ hfill 3 & \ hfill 0 \\ \ hfill 0 & \ hfill 2 & \ hfill 4 & \ hfill 3 \ end {array} | [/ latex]
[латекс] | \ begin {array} {rrrr} \ hfill 1 & \ hfill 0 & \ hfill 2 & \ hfill 1 \\ \ hfill 0 & \ hfill -9 & \ hfill 1 & \ hfill 3 \\ \ hfill 3 & \ hfill 0 & \ hfill -2 & \ hfill -1 \\ \ hfill 0 & \ hfill 1 & \ hfill 1 & \ hfill -2 \ end {array} | [/ latex]
[латекс] | \ begin {array} {rrrr} \ hfill \ frac {1} {2} & \ hfill 1 & \ hfill 7 & \ hfill 4 \\ \ hfill 0 & \ hfill \ frac {1} {2} & \ hfill 100 & \ hfill 5 \\ \ hfill 0 & \ hfill 0 & \ hfill 2 & \ hfill 2,000 \\ \ hfill 0 & \ hfill 0 & \ hfill 0 & \ hfill 2 \ end {array} | [/ latex]
[латекс] | \ begin {array} {rrrr} \ hfill 1 & \ hfill 0 & \ hfill 0 & \ hfill 0 \\ \ hfill 2 & \ hfill 3 & \ hfill 0 & \ hfill 0 \\ \ hfill 4 & \ hfill 5 & \ hfill 6 & \ hfill 0 \\ \ hfill 7 & \ hfill 8 & \ hfill 9 & \ hfill 0 \ end {array} | [/ latex]
Реальные приложения
Для следующих упражнений создайте систему линейных уравнений для описания поведения. Затем вычислите определитель. Будет ли уникальное решение? Если да, найдите уникальное решение.
Затем вычислите определитель. Будет ли уникальное решение? Если да, найдите уникальное решение.
Два числа в сумме дают 56. Одно число на 20 меньше другого.
Два числа в сумме дают 104. Если вы сложите два раза первое число плюс два раза второе число, ваша сумма составит 208
Три числа в сумме дают 106. Первое число на 3 меньше второго. Третье число на 4 больше, чем первое.
Три числа добавляют к 216.Сумма первых двух чисел равна 112. Третье число на 8 меньше, чем первые два числа вместе взятые.
Для следующих упражнений создайте систему линейных уравнений для описания поведения. Затем решите систему для всех решений, используя правило Крамера.
Вы вкладываете 10 000 долларов в два счета, которые получают 8% годовых и 5% годовых. В конце года на ваших комбинированных счетах было 10 710 долларов. Сколько было вложено в каждую учетную запись?
Показать решение 7000 долларов на первом счете, 3000 долларов на втором счете.
Вы вкладываете 80 000 долларов в два счета, 22 000 долларов в один счет и 58 000 долларов в другой. В конце года, если исходить из простых процентов, вы заработали 2470 долларов в виде процентов. Второй счет получает на полпроцента меньше, чем удвоенный процент по первому счету. Какие процентные ставки по вашим счетам?
Кинотеатру необходимо знать, сколько билетов для взрослых и детей было продано из 1200 билетов. Если детские билеты 5 долларов.95, билеты для взрослых стоят 11,15 долларов, а общая сумма выручки составила 12 756 долларов. Сколько билетов для детей и взрослых было продано?
Показать решение120 детей, 1080 взрослых
Концертная площадка продает одиночные билеты по 40 долларов каждый и билеты для пар по 65 долларов. Если общий доход составил 18 090 долларов и был продан 321 билет, сколько разовых билетов и сколько билетов для пар было продано?
Вы решили покрасить свою кухню в зеленый цвет. Вы создаете цвет краски, смешивая желтую и синюю краски. Вы не можете вспомнить, сколько галлонов каждого цвета было добавлено в вашу смесь, но вы знаете, что всего было 10 галлонов. Кроме того, вы сохранили квитанцию и знаете, что общая потраченная сумма составила 29,50 долларов США. Если каждый галлон желтого стоит 2,59 доллара, а каждый галлон синего стоит 3,19 доллара, сколько галлонов каждого цвета входит в вашу зеленую смесь?
Вы не можете вспомнить, сколько галлонов каждого цвета было добавлено в вашу смесь, но вы знаете, что всего было 10 галлонов. Кроме того, вы сохранили квитанцию и знаете, что общая потраченная сумма составила 29,50 долларов США. Если каждый галлон желтого стоит 2,59 доллара, а каждый галлон синего стоит 3,19 доллара, сколько галлонов каждого цвета входит в вашу зеленую смесь?
Вы продали на фермерском рынке шарфы двух типов и хотите знать, какой из них пользуется большей популярностью. Всего было продано 56 шарфов, желтый платок стоил 10 долларов, а фиолетовый – 11 долларов.Если ваш общий доход составил 583 доллара, сколько желтых и фиолетовых шарфов было продано?
В вашем саду выращивали два вида помидоров: зеленый и красный. Красный весит 10 унций, а зеленый – 4 унции. У вас 30 помидоров, а общий вес составляет 13 фунтов 14 унций. Сколько у вас помидоров каждого вида?
Показать решение13 зеленых помидоров, 17 красных помидоров
На рынке три самых популярных овоща составляют 53% продаж овощей. Продажи кукурузы на 4% выше, чем у брокколи, у которой на 5% больше продаж, чем у лука.Какую долю занимает каждый овощ на рынке?
Продажи кукурузы на 4% выше, чем у брокколи, у которой на 5% больше продаж, чем у лука.Какую долю занимает каждый овощ на рынке?
На этом же рынке три самых популярных фрукта составляют 37% от общего количества проданных фруктов. Клубника продается вдвое больше, чем апельсины, а киви продаются на один процентный пункт больше, чем апельсины. Для каждого фрукта найдите процент от общего количества проданных фруктов.
Показать решениеКлубника 18%, апельсины 9%, киви 10%
Три группы выступили на концертной площадке. Первый диапазон взимал 15 долларов за билет, второй диапазон – 45 долларов за билет, а последний диапазон – 22 доллара за билет.Было продано 510 билетов на общую сумму 12 700 долларов. Если у первой группы было на 40 зрителей больше, чем у второй, сколько билетов было продано каждой группе?
В кинотеатре продаются билеты на три фильма. Билеты на первый фильм стоили 5 долларов, билеты на второй фильм – 11 долларов, а третий фильм – 12 долларов. На первый фильм было продано 100 билетов. Всего было продано 642 билета, общий доход составил 6 774 доллара. Сколько билетов на каждый фильм было продано?
На первый фильм было продано 100 билетов. Всего было продано 642 билета, общий доход составил 6 774 доллара. Сколько билетов на каждый фильм было продано?
100 для фильма 1, 230 для фильма 2, 312 для фильма 3
Мужчины в возрасте 20–29, 30–39 и 40–49 лет в прошлом году составляли 78% заключенных.В этом году эти же возрастные группы составили 82,08% населения. Возрастная группа 20–29 лет увеличилась на 20%, возрастная группа 30–39 лет увеличилась на 2%, а возрастная группа 40–49 лет уменьшилась до [latex] \, \ frac {3} {4} \, [/ latex] их предыдущего населения. Первоначально в возрастной группе 30–39 лет было на 2% больше заключенных, чем в возрастной группе 20–29 лет. Определите процентную долю заключенных для каждой возрастной группы в прошлом году.
В женской тюрьме по дороге общее количество заключенных в возрасте от 20 до 49 лет составило 5 525 человек. В этом году возрастная группа 20–29 лет увеличилась на 10%, возрастная группа 30–39 лет уменьшилась на 20%, а возрастная группа 40–49 лет увеличилась вдвое. Сейчас в тюрьме 6040 заключенных. Первоначально в возрастной группе 30–39 лет их было на 500 человек больше, чем в возрастной группе 20–29 лет. Определите количество заключенных для каждой возрастной группы в прошлом году.
Сейчас в тюрьме 6040 заключенных. Первоначально в возрастной группе 30–39 лет их было на 500 человек больше, чем в возрастной группе 20–29 лет. Определите количество заключенных для каждой возрастной группы в прошлом году.
20–29: 2,100, 30–39: 2,600, 40–49: 825
Для следующих упражнений используйте этот сценарий: Компания, заботящаяся о своем здоровье, решает сделать смесь из миндаля, сушеной клюквы и кешью в шоколаде. Информация о питательной ценности этих продуктов показана на (Рисунок).
| Жир (г) | Белок (г) | Углеводы (г) | |
|---|---|---|---|
| Миндаль (10) | 6 | 2 | 3 |
| Клюква (10) | 0.02 | 0 | 8 |
| Кешью (10) | 7 | 3,5 | 5,5 |
Для специальной «низкоуглеводной» смеси для трейлов имеется 1000 штук смеси. Общее количество углеводов – 425 г, а общее количество жиров – 570,2 г. Если кешью на 200 штук больше, чем клюквы, сколько каждого из них входит в состав смеси?
Общее количество углеводов – 425 г, а общее количество жиров – 570,2 г. Если кешью на 200 штук больше, чем клюквы, сколько каждого из них входит в состав смеси?
Для «походной» смеси в смеси 1000 штук, содержащих 390 штук.8 г жира и 165 г белка. Если миндаля столько же, сколько и кешью, сколько каждого из них входит в состав смеси?
Показать решение300 миндальных орехов, 400 клюквы, 300 кешью
Для смеси «усилитель энергии» в смеси 1000 штук, содержащих 145 г белка и 625 г углеводов. Если сумма миндальных орехов и кешью эквивалентна количеству клюквы, сколько каждого из них входит в состав смеси?
Упражнения на повторение
Системы линейных уравнений: две переменные
Для следующих упражнений определите, является ли упорядоченная пара решением системы уравнений.
[латекс] \ begin {array} {l} 3x-y = 4 \\ x + 4y = -3 \, \ end {array} [/ latex] and [latex] \, \ left (-1,1 \ справа) [/ латекс]
[латекс] \ begin {array} {l} 6x-2y = 24 \\ -3x + 3y = 18 \, \ end {array} [/ latex] and [latex] \, \ left (9,15 \ right ) [/ латекс]
В следующих упражнениях используйте подстановку для решения системы уравнений.
[латекс] \ begin {array} {l} 10x + 5y = -5 \ hfill \\ \, \, \, 3x-2y = -12 \ hfill \ end {array} [/ latex]
Показать решение[латекс] \ влево (-2,3 \ вправо) [/ латекс]
[латекс] \ begin {array} {l} \ frac {4} {7} x + \ frac {1} {5} y = \ frac {43} {70} \\ \ frac {5} {6} x – \ frac {1} {3} y = – \ frac {2} {3} \ end {array} [/ latex]
[латекс] \ begin {array} {l} 5x + 6y = 14 \\ 4x + 8y = 8 \ end {array} [/ latex]
Показать решение[латекс] \ влево (4, -1 \ вправо) [/ латекс]
В следующих упражнениях используйте сложение для решения системы уравнений.
[латекс] \ begin {array} {l} 3x + 2y = -7 \\ 2x + 4y = 6 \ end {array} [/ latex]
[латекс] \ begin {array} {r} 3x + 4y = 2 \\ 9x + 12y = 3 \ end {array} [/ latex]
[латекс] \ begin {array} {l} 8x + 4y = 2 \\ 6x-5y = 0,7 \ end {array} [/ latex]
Для следующих упражнений напишите систему уравнений для решения каждой задачи.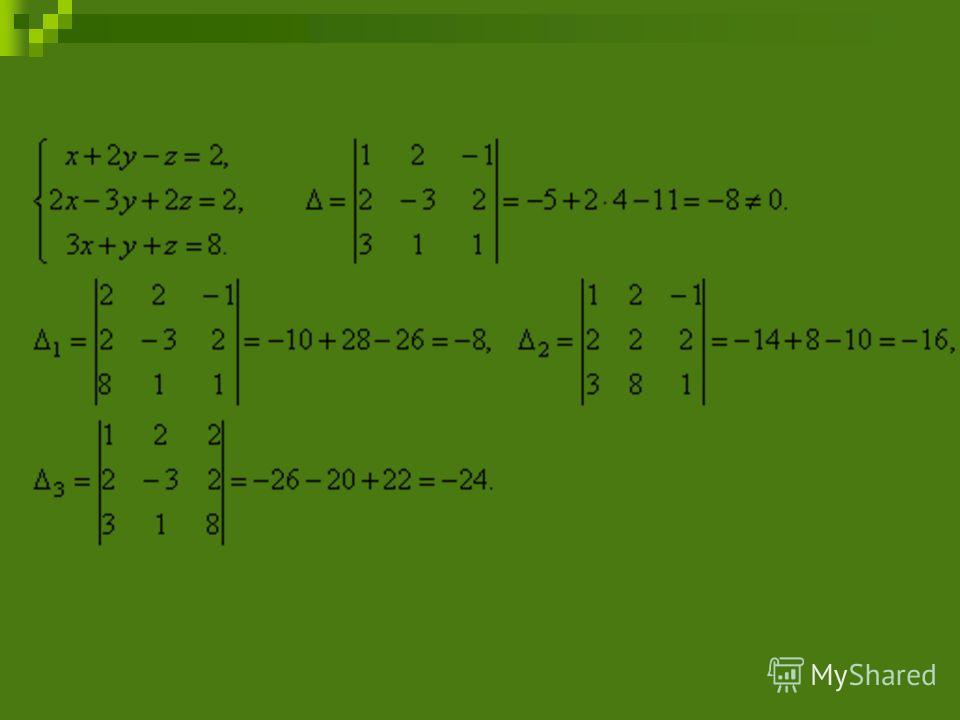 Решите систему уравнений.
Решите систему уравнений.
Завод имеет стоимость производства [латекс] \, C \ left (x \ right) = 150x + 15 \ text {,} 000 \, [/ latex] и функцию дохода [латекс] \, R \ left ( х \ вправо) = 200x.\, [/ latex] Какая точка безубыточности?
Показать решение[латекс] \ влево (300,60,000 \ вправо) [/ латекс]
Исполнитель взимает [латекс] \, C \ left (x \ right) = 50x + 10 \ text {,} 000, \, [/ latex], где [latex] \, x \, [/ latex] – общая сумма количество посетителей на шоу. Стоимость билета составляет 75 долларов. После того, как сколько людей купит билеты, место проведения станет безубыточным, и какова общая стоимость билетов, проданных в этот момент?
Показать решение[латекс] \ влево (400,30,000 \ вправо) [/ латекс]
Системы линейных уравнений: три переменные
Для следующих упражнений решите систему трех уравнений, используя замену или сложение.
[латекс] \ begin {array} {l} \ text {} 0,5x-0,5y = 10 \ hfill \\ \ text {} -0,2y + 0,2x = 4 \ hfill \\ \ text {} 0,1x + 0. 1z = 2 \ hfill \ end {array} [/ latex]
1z = 2 \ hfill \ end {array} [/ latex]
[латекс] \ влево (10, -10,10 \ вправо) [/ латекс]
[латекс] \ begin {array} {r} \ hfill 5x + 3y-z = 5 \, \, \, \\ \ hfill 3x-2y + 4z = 13 \\ \ hfill 4x + 3y + 5z = 22 \ конец {array} [/ latex]
[латекс] \ begin {array} {r} x + y + z = 1 \\ 2x + 2y + 2z = 1 \\ 3x + 3y = 2 \ end {array} [/ latex]
[латекс] \ begin {массив} {l} \ text {} 2x-3y + z = -1 \ hfill \\ \ text {} x + y + z = -4 \ hfill \\ \ text {} 4x + 2y-3z = 33 \ hfill \ end {array} [/ latex]
[латекс] \ begin {array} {l} \, \, 3x + 2y-z = -10 \ hfill \\ \, \, \, \, x-y + 2z = 7 \ hfill \\ -x + 3y + z = -2 \ hfill \ end {array} [/ latex]
Показать решение[латекс] \ влево (-1, -2,3 \ вправо) [/ латекс]
[латекс] \ begin {array} {r} \ hfill 3x + 4z = -11 \\ \ hfill x-2y = 5 \, \, \, \, \, \, \, \\ \ hfill 4y-z = -10 \ end {array} [/ latex]
[латекс] \ begin {array} {r} 2x-3y + z = 0 \\ 2x + 4y-3z = 0 \\ 6x-2y-z = 0 \ end {array} [/ latex]
Показать решение[латекс] \ left (x, \ frac {8x} {5}, \ frac {14x} {5} \ right) [/ latex]
[латекс] \ begin {array} {r} 6x-4y-2z = 2 \\ 3x + 2y-5z = 4 \\ 6y-7z = 5 \ end {array} [/ latex]
Для следующих упражнений напишите систему уравнений для решения каждой задачи. Решите систему уравнений.
Решите систему уравнений.
Три нечетных числа в сумме дают 61. Меньшее на одну треть больше, а среднее число на 16 меньше большего. Какие три числа?
Местный театр распродает билеты на их спектакль. Они продают все 500 билетов на общую сумму 8 070 долларов. Билеты стоили 15 долларов для студентов, 12 долларов для детей и 18 долларов для взрослых. Если группа продала в три раза больше билетов для взрослых, чем детских, сколько билетов каждого типа было продано?
Системы нелинейных уравнений и неравенств: две переменные
Для следующих упражнений решите систему нелинейных уравнений.{2}} [/ латекс]
Матрицы и матричные операции
Для следующих упражнений выполните требуемые операции с заданными матрицами.
[латекс] A = \ left [\ begin {array} {rr} \ hfill 4 & \ hfill -2 \\ \ hfill 1 & \ hfill 3 \ end {array} \ right], B = \ left [\ begin {array } {rrr} \ hfill 6 & \ hfill 7 & \ hfill -3 \\ \ hfill 11 & \ hfill -2 & \ hfill 4 \ end {array} \ right], C = \ left [\ begin {array} {r} \ hfill \ begin {array} {cc} 6 & 7 \\ 11 & -2 \ end {array} \\ \ hfill \ begin {array} {cc} 14 & 0 \ end {array} \ end {array} \ right], D = \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -4 & \ hfill 9 \\ \ hfill 10 & \ hfill 5 & \ hfill -7 \\ \ hfill 2 & \ hfill 8 & \ hfill 5 \ end {array} \ right], E = \ left [\ begin {array} {rrr} \ hfill 7 & \ hfill -14 & \ hfill 3 \\ \ hfill 2 & \ hfill -1 & \ hfill 3 \\ \ hfill 0 & \ hfill 1 & \ hfill 9 \ конец {массив} \ справа] [/ латекс]
Показать решение[латекс] \ left [\ begin {array} {cc} -16 & 8 \\ -4 & -12 \ end {array} \ right] [/ latex]
Показать решениеundefined; размеры не соответствуют
Показать решениеundefined; внутренние размеры не соответствуют
Показать решение[латекс] \ left [\ begin {array} {ccc} 113 & 28 & 10 \\ 44 & 81 & -41 \\ 84 & 98 & -42 \ end {array} \ right] [/ latex]
Показать решение[латекс] \ left [\ begin {array} {ccc} -127 & -74 & 176 \\ -2 & 11 & 40 \\ 28 & 77 & 38 \ end {array} \ right] [/ latex]
Показать решениеundefined; внутренние размеры не соответствуют
Решение систем с исключением Гаусса
Для следующих упражнений напишите систему линейных уравнений из расширенной матрицы. Укажите, будет ли уникальное решение.
Укажите, будет ли уникальное решение.
[латекс] \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill 0 & \ hfill -3 \\ \ hfill 0 & \ hfill 1 & \ hfill 2 \\ \ hfill 0 & \ hfill 0 & \ hfill 0 \ end { массив} \ text {} | \ text {} \ begin {array} {r} \ hfill 7 \\ \ hfill -5 \\ \ hfill 0 \ end {array} \ right] [/ latex]
Показать решение[латекс] \ begin {array} {l} x-3z = 7 \\ y + 2z = -5 \, \ end {array} [/ latex] с бесконечными решениями
[латекс] \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill 0 & \ hfill 5 \\ \ hfill 0 & \ hfill 1 & \ hfill -2 \\ \ hfill 0 & \ hfill 0 & \ hfill 0 \ end { массив} \ text {} | \ text {} \ begin {array} {r} \ hfill -9 \\ \ hfill 4 \\ \ hfill 3 \ end {array} \ right] [/ latex]
Для следующих упражнений напишите расширенную матрицу из системы линейных уравнений.
[латекс] \ begin {массив} {l} \\ \ begin {array} {r} \ hfill -2x + 2y + z = 7 \\ \ hfill 2x-8y + 5z = 0 \\ \ hfill 19x-10y + 22z = 3 \ end {массив} \ end {array} [/ latex]
Показать решение[латекс] \ left [\ begin {array} {rrr} \ hfill -2 & \ hfill 2 & \ hfill 1 \\ \ hfill 2 & \ hfill -8 & \ hfill 5 \\ \ hfill 19 & \ hfill -10 & \ hfill 22 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill 7 \\ \ hfill 0 \\ \ hfill 3 \ end {array} \ right] [/ latex]
[латекс] \ begin {array} {l} \, \, \, \, \, 4x + 2y-3z = 14 \ hfill \\ -12x + 3y + z = 100 \ hfill \\ \, \, \ , \, \, 9x-6y + 2z = 31 \ hfill \ end {array} [/ latex]
[латекс] \ begin {array} {r} \ hfill x + 3z = 12 \, \\ \ hfill -x + 4y = 0 \, \, \, \, \\ \ hfill y + 2z = -7 \ конец {array} [/ latex]
Показать решение[латекс] \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill 0 & \ hfill 3 \\ \ hfill -1 & \ hfill 4 & \ hfill 0 \\ \ hfill 0 & \ hfill 1 & \ hfill 2 \ end { массив} \ text {} | \ text {} \ begin {array} {r} \ hfill 12 \\ \ hfill 0 \\ \ hfill -7 \ end {array} \ right] [/ latex]
Для следующих упражнений решите систему линейных уравнений, используя метод исключения Гаусса.
[латекс] \ begin {array} {r} 3x-4y = -7 \\ -6x + 8y = 14 \ end {array} [/ latex]
[латекс] \ begin {array} {r} 3x-4y = 1 \\ -6x + 8y = 6 \ end {array} [/ latex]
[латекс] \ begin {массив} {l} \ begin {array} {l} \\ -1.1x-2.3y = 6.2 \ end {array} \ hfill \\ -5.2x-4.1y = 4.3 \ hfill \ конец {array} [/ latex]
[латекс] \ begin {array} {r} \ hfill 2x + 3y + 2z = 1 \, \, \, \, \, \\ \ hfill -4x-6y-4z = -2 \\ \ hfill 10x + 15y + 10z = 0 \, \, \, \, \, \ end {array} [/ latex]
[латекс] \ begin {array} {r} \ hfill -x + 2y-4z = 8 \, \, \, \, \\ \ hfill 3y + 8z = -4 \\ \ hfill -7x + y + 2z = 1 \, \, \, \, \ end {array} [/ latex]
Решающие системы с обратными сторонами
Для следующих упражнений найдите обратную матрицу.
[латекс] \ left [\ begin {array} {rr} \ hfill -0.2 & \ hfill 1.4 \\ \ hfill 1.2 & \ hfill -0.4 \ end {array} \ right] [/ latex]
Показать решение[латекс] \ frac {1} {8} \ left [\ begin {array} {cc} 2 & 7 \\ 6 & 1 \ end {array} \ right] [/ latex]
[латекс] \ left [\ begin {array} {rr} \ hfill \ frac {1} {2} & \ hfill – \ frac {1} {2} \\ \ hfill – \ frac {1} {4} & \ hfill \ frac {3} {4} \ end {array} \ right] [/ latex]
[латекс] \ left [\ begin {array} {ccc} 12 & 9 & -6 \\ -1 & 3 & 2 \\ -4 & -3 & 2 \ end {array} \ right] [/ latex]
[латекс] \ left [\ begin {array} {ccc} 2 & 1 & 3 \\ 1 & 2 & 3 \\ 3 & 2 & 1 \ end {array} \ right] [/ latex]
Для следующих упражнений найдите решения, вычислив обратную матрицу.
[латекс] \ begin {массив} {l} \, \, \, \, 0,3x-0,1y = -10 \ hfill \\ -0,1x + 0,3y = 14 \ hfill \ end {array} [/ latex ]
Показать решение[латекс] \ влево (-20,40 \ вправо) [/ латекс]
[латекс] \ begin {array} {l} \, \, \, \, \, \, \, \, 0,4x-0,2y = -0,6 \ hfill \\ -0,1x + 0,05y = 0,3 \ hfill \ end {array} [/ latex]
[латекс] \ begin {array} {r} 4x + 3y-3z = -4,3 \\ 5x-4y-z = -6,1 \\ x + z = -0,7 \ end {array} [/ latex]
Показать решение[латекс] \ влево (-1,0,2,0,3 \ вправо) [/ латекс]
[латекс] \ begin {массив} {r} \ hfill \ begin {array} {l} \\ -2x-3y + 2z = 3 \ end {array} \\ \ hfill -x + 2y + 4z = -5 \\ \ hfill -2y + 5z = -3 \ end {array} [/ latex]
Для следующих упражнений напишите систему уравнений для решения каждой задачи.Решите систему уравнений.
Студентов попросили принести в класс их любимые фрукты. 90% фруктов состояли из бананов, яблок и апельсинов. Если апельсины были наполовину популярнее бананов, а яблоки на 5% популярнее бананов, каков процент каждого отдельного фрукта?
Показать решение17% апельсинов, 34% бананов, 39% яблок
Женское общество провело распродажу выпечки, чтобы собрать деньги, и продавало пирожные и печенье с шоколадной крошкой. Они оценили пирожные в 2 доллара и печенье с шоколадной крошкой в 1 доллар.Они собрали 250 долларов и продали 175 вещей. Сколько было продано пирожных и печенья?
Решающие системы с правилом Крамера
Найдите определитель для следующих упражнений.
[латекс] | \ begin {array} {cc} 100 & 0 \\ 0 & 0 \ end {array} | [/ latex]
[латекс] | \ begin {array} {cc} 0,2 & -0,6 \\ 0,7 & -1,1 \ end {array} | [/ latex]
[латекс] | \ begin {array} {ccc} -1 & 4 & 3 \\ 0 & 2 & 3 \\ 0 & 0 & -3 \ end {array} | [/ latex]
[латекс] | \ begin {array} {ccc} \ sqrt {2} & 0 & 0 \\ 0 & \ sqrt {2} & 0 \\ 0 & 0 & \ sqrt {2} \ end {array} | [/ latex]
В следующих упражнениях используйте правило Крамера для решения линейных систем уравнений.
[латекс] \ begin {массив} {r} \ hfill 4x-2y = 23 \, \, \, \, \\ \ hfill -5x-10y = -35 \ end {array} [/ latex]
Показать решение[латекс] \ left (6, \ frac {1} {2} \ right) [/ latex]
[латекс] \ begin {array} {l} 0,2x-0,1y = 0 \\ -0,3x + 0,3y = 2,5 \ end {array} [/ latex]
[латекс] \ begin {массив} {r} \ hfill -0,5x + 0,1y = 0,3 \, \, \, \\ \ hfill -0,25x + 0,05y = 0,15 \ end {array} [/ latex]
[латекс] \ begin {array} {l} x + 6y + 3z = 4 \\ 2x + y + 2z = 3 \\ 3x-2y + z = 0 \ end {array} [/ latex]
[латекс] \ begin {array} {r} \ hfill 4x-3y + 5z = – \ frac {5} {2} \\ \ hfill 7x-9y-3z = \ frac {3} {2} \, \ , \, \, \\ \ hfill x-5y-5z = \ frac {5} {2} \, \, \, \, \ end {array} [/ latex]
Показать решение[латекс] \ left (0,0, – \ frac {1} {2} \ right) [/ latex]
[латекс] \ begin {array} {r} \ frac {3} {10} x- \ frac {1} {5} y- \ frac {3} {10} z = – \ frac {1} {50 } \\ \ frac {1} {10} x- \ frac {1} {10} y- \ frac {1} {2} z = – \ frac {9} {50} \\ \ frac {2} { 5} x- \ frac {1} {2} y- \ frac {3} {5} z = – \ frac {1} {5} \ end {array} [/ latex]
Практический тест
Является ли следующая упорядоченная пара решением системы уравнений?
[латекс] \ begin {массив} {l} \\ \ begin {array} {l} -5x-y = 12 \, \ hfill \\ x + 4y = 9 \ hfill \ end {array} \ end {массив } [/ latex] с [latex] \, \ left (-3,3 \ right) [/ latex]
Для следующих упражнений решите системы линейных и нелинейных уравнений с помощью замены или исключения.Укажите, если решения не существует.
[латекс] \ begin {array} {r} \ frac {1} {2} x- \ frac {1} {3} y = 4 \\ \ frac {3} {2} xy = 0 \ end {массив } [/ латекс]
[латекс] \ begin {массив} {r} \ hfill \ begin {array} {l} \\ – \ frac {1} {2} x-4y = 4 \ end {array} \\ \ hfill 2x + 16y = 2 \ end {array} [/ latex]
[латекс] \ begin {array} {r} \ hfill 5x-y = 1 \, \, \, \, \\ \ hfill -10x + 2y = -2 \ end {array} [/ latex]
[латекс] \ begin {array} {l} 4x-6y-2z = \ frac {1} {10} \ hfill \\ \, \, \, x-7y + 5z = – \ frac {1} {4 } \ hfill \\ 3x + 6y-9z = \ frac {6} {5} \ hfill \ end {array} [/ latex]
Показать решение[латекс] \ frac {1} {20} \ left (10,5,4 \ right) [/ latex]
[латекс] \ begin {array} {r} x + z = 20 \\ x + y + z = 20 \\ x + 2y + z = 10 \ end {array} [/ latex]
[латекс] \ begin {array} {r} 5x-4y-3z = 0 \\ 2x + y + 2z = 0 \\ x-6y-7z = 0 \ end {array} [/ latex]
Показать решение[латекс] \ left (x, \ frac {16x} {5} – \ frac {13x} {5} \ right) [/ latex]
[латекс] \ begin {array} {l} y = {x} ^ {2} + 2x-3 \\ y = x-1 \ end {array} [/ latex]
[латекс] \ begin {array} {l} {y} ^ {2} + {x} ^ {2} = 25 \\ {y} ^ {2} -2 {x} ^ {2} = 1 \ конец {array} [/ latex]
Показать решение[латекс] \ left (-2 \ sqrt {2}, – \ sqrt {17} \ right), \ left (-2 \ sqrt {2}, \ sqrt {17} \ right), \ left (2 \ sqrt {2}, – \ sqrt {17} \ right), \ left (2 \ sqrt {2}, \ sqrt {17} \ right) [/ latex]
Для следующих упражнений нарисуйте следующие неравенства. {- 1} [/ latex]
Показать решение[латекс] \ left [\ begin {array} {cc} 12 & -20 \\ -15 & 30 \ end {array} \ right] [/ latex]
[латекс] \ mathrm {det} | \ begin {array} {cc} 0 & 0 \\ 400 & 4 \ text {,} 000 \ end {array} | [/ latex]
[латекс] \ mathrm {det} | \ begin {array} {rrr} \ hfill \ frac {1} {2} & \ hfill – \ frac {1} {2} & \ hfill 0 \\ \ hfill – \ frac {1} {2} & \ hfill 0 & \ hfill \ frac {1} {2} \\ \ hfill 0 & \ hfill \ frac {1} {2} & \ hfill 0 \ end {array} | [/ latex]
Показать решение[латекс] – \ frac {1} {8} [/ латекс]
Если [latex] \, \ mathrm {det} \ left (A \ right) = – 6, \, [/ latex], что будет определяющим, если вы поменяете местами строки 1 и 3, умножите вторую строку на 12 и взяли обратное?
Перепишите систему линейных уравнений в виде расширенной матрицы.
[латекс] \ begin {array} {l} 14x-2y + 13z = 140 \ hfill \\ -2x + 3y-6z = -1 \ hfill \\ x-5y + 12z = 11 \ hfill \ end {array} [/ латекс]
Показать решение[латекс] \ left [\ begin {array} {rrr} \ hfill 14 & \ hfill -2 & \ hfill 13 \\ \ hfill -2 & \ hfill 3 & \ hfill -6 \\ \ hfill 1 & \ hfill -5 & \ hfill 12 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill 140 \\ \ hfill -1 \\ \ hfill 11 \ end {array} \ right] [/ latex]
Перепишите расширенную матрицу как систему линейных уравнений.
[латекс] \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill 0 & \ hfill 3 \\ \ hfill -2 & \ hfill 4 & \ hfill 9 \\ \ hfill -6 & \ hfill 1 & \ hfill 2 \ end {массив} | \ begin {array} {r} \ hfill 12 \\ \ hfill -5 \\ \ hfill 8 \ end {array} \ right] [/ latex]
В следующих упражнениях используйте метод исключения Гаусса для решения систем уравнений.
[латекс] \ begin {array} {r} x-6y = 4 \\ 2x-12y = 0 \ end {array} [/ latex]
[латекс] \ begin {array} {r} \ hfill 2x + y + z = -3 \\ \ hfill x-2y + 3z = 6 \, \, \, \, \\ \ hfill xyz = 6 \, \, \, \, \ end {array} [/ latex]
В следующих упражнениях используйте обратную матрицу для решения систем уравнений.
[латекс] \ begin {массив} {r} \ hfill 4x-5y = -50 \\ \ hfill -x + 2y = 80 \, \, \, \, \ end {array} [/ latex]
Показать решение[латекс] \ влево (100,90 \ вправо) [/ латекс]
[латекс] \ begin {array} {r} \ hfill \ frac {1} {100} x- \ frac {3} {100} y + \ frac {1} {20} z = -49 \\ \ hfill \ frac {3} {100} x- \ frac {7} {100} y- \ frac {1} {100} z = 13 \, \, \, \, \\ \ hfill \ frac {9} {100} x- \ frac {9} {100} y- \ frac {9} {100} z = 99 \, \, \, \, \ end {array} [/ latex]
В следующих упражнениях используйте правило Крамера для решения систем уравнений.{2} + 160x. \, [/ Latex] Какой ассортимент сотовых телефонов они должны производить каждый день, чтобы получать прибыль? Округлите до ближайшего числа, приносящего прибыль.
Показать решение32 и более сотовых телефона в день
Небольшая ярмарка взимает 1,50 доллара для студентов, 1 доллар для детей и 2 доллара для взрослых. За один день пришло в три раза больше детей, чем взрослых. Было продано 800 билетов на общую выручку в 1050 долларов. Сколько билетов каждого типа было продано?
Глоссарий
- Правило Крамера
- Метод решения систем уравнений, которые имеют то же количество уравнений, что и переменные, с использованием определителей
- определитель
- число, вычисленное с использованием элементов квадратной матрицы, которая определяет такую информацию, как наличие решения системы уравнений
TTU Сеть CAE
Приносим извинения за неудобства, но страница, к которой вы пытались получить доступ, находится не по этому адресу.Вы можете использовать приведенные ниже ссылки, чтобы помочь вам найти то, что вы ищете.
Если вы уверены, что имеете правильный веб-адрес, но столкнулись с ошибкой, пожалуйста, связаться с Администрацией сайта.
Спасибо.
Возможно, вы искали…
- Сеть TTU CAE
- Доступ к файлам вне кампуса
- Безопасный доступ к своим исследованиям или академическим файлам из дома или из любой точки мира.
- Отправка ссылки на личный файл по электронной почте
- Отправьте ссылку на файл в личном веб-пространстве, чтобы избежать превышения квоты электронной почты получателей и других технических проблем.
- Справка и поддержка пользователей
- Файловый сервер CAE Lab
- Введение и документация по файловому серверу CAE Lab.
- Файловый сервер CAE Lab
- В следующем наборе документов подробно описаны возможности файлового сервера CAE Lab и доступ к файлам, хранящимся в университетском городке и за его пределами.
- Подключение к файловому серверу CAE Lab (пользователи Windows в кампусе)
- Следующие инструкции помогут вам подключиться к центральному файловому серверу CAE Lab из других мест в университетском городке, если на нем установлена Windows 7…
- Подключение к файловому серверу CAE Lab (пользователи Mac OS X в кампусе)
- Следующие инструкции помогут вам подключиться к центральному файловому серверу CAE Lab из других мест в кампусе, если на нем установлена Mac OS X…
- Подключение к файловому серверу CAE Lab (пользователи Windows за пределами кампуса)
- Следующие инструкции помогут вам подключиться к центральному файловому серверу CAE Lab из мест за пределами университетского городка, при условии наличия последней версии…
- Подключение к файловому серверу CAE Lab (пользователи Mac OS X за пределами кампуса)
- Следующие инструкции помогут вам подключиться к центральному файловому серверу CAE Lab из мест за пределами кампуса, если на нем установлена Mac OS X…
- Подключение к файловому серверу CAE Lab (пользователи Unix в кампусе)
- Следующие инструкции должны помочь вам подключиться к центральному файловому серверу CAE Lab из других мест в университетском городке, при условии некоторого относительного типа…
Метод исключения Гаусса для решения систем линейных алгебраических уравнений
Что вы знаете о решении систем линейных уравнений? Этот тип задач часто предлагается студентам в домашнем задании по линейной алгебре. В одном из наших видеороликов мы обсуждали, что система линейных уравнений может быть решена с использованием правила Крамера, которое включает в себя поиск определителей, и это может вызвать затруднения при работе с системами из 4, 5 или более уравнений.К счастью, есть еще один метод, позволяющий избежать массовых вычислений. И это называется исключением по Гауссу (или редукцией строк).
Рассмотрим систему $ m $ линейных уравнений с $ n $ неизвестными, записанными в следующей форме:
\ left \ {\ begin {align} a_ {11} x_1 + a_ {12} x_2 +… + a_ {1n} x_n = b_1 \\ a_ {21} x_1 + a_ {22} x_2 +… + a_ {2n} x_n = b_2 \\… & & \\ a_ {m1} x_1 + a_ {m2} x_2 +… + a_ {mn} x_n = b_m \ end {align} \ right.
где x_1, x_2,…, x_n– неизвестные,
a_ {ij} – коэффициенты при неизвестных,
b_i- свободные члены (правые части уравнений).
Вот видеоверсия этого руководства:
Давайте подумаем об этом как о наборе условий, дающих нам информацию о неизвестных. Это может быть записано как … если мы возьмем, скажем, эту большую часть этого неизвестного, отмеченного как x_1, и эту большую часть другого неизвестного – x_2, затем некоторое количество следующего неизвестного и, скажем, суммируем их – мы получим столько из b_1. Конечно, этой информации недостаточно для определения всех неизвестных, поэтому уравнений больше. если мы возьмем столько неизвестных x_1 и вычтем столько же из x_2, затем добавим некоторые другие неизвестные и вычтем другие – мы получим столько же из b_2.И так далее.
Хорошо, поехали. Что еще можно сказать об этой системе?
- довольно очевидно, что мы можем поменять местами любую пару уравнений в наборе, потому что порядок, в котором мы получаем эту информацию, не важен. Идея состоит в том, чтобы иметь достаточно информации, но не упорядоченную;
- еще один простой вывод, который приходит на ум, заключается в том, что мы можем умножить обе части любого уравнения на любую ненулевую константу, и это не изменит систему, а также добавить к обеим сторонам любого из уравнений соответствующие части любого другого уравнения. .
Мы можем выполнять эти элементарные преобразования сколько угодно раз. Это приведет к эквивалентной системе уравнений, потому что на самом деле мы не производим и не сокращаем информацию о неизвестных, а просто реорганизуем ее.
Что мы будем со всем этим делать? Очевидно, мы найдем эти свойства существенными при решении системы уравнений с использованием метода Гаусса.
Рассмотрим реальный пример системы линейных уравнений:
\ left \ {\ begin {выровнено} 2x_1 + 4x_2-3x_3 + 2x_4 = 0 \\ x_1-2x_2 + 5x_3 + 2x_4 = 2 \\ 2x_2-4x_3 + 5x_4 = -1 \\ 2x_3 + x_4 = -3 \ end {выровнено} \ вправо.
Это хорошая привычка сначала формировать красивые столбцы переменных, прежде чем решать какую-либо систему. Это должно уберечь нас от ошибок, и мы будем действовать быстрее. Во-вторых, перестроим систему так, чтобы уравнения со всеми неизвестными оказались наверху. Теперь давайте выберем первые два уравнения из системы и исключим первое неизвестное из одного из них. Неважно, какое уравнение и какое неизвестное выбрать, единственное условие – оба уравнения должны его содержать :).Давайте выберем первый и второй и намереваемся устранить первое неизвестное x_1. Вы увидите, что в несколько шагов мы сформируем подходящее представление о системе.
Хорошо, вернемся к ликвидации. Как это можно сделать? Более чем просто – сначала мы умножаем или делим одно из выбранных уравнений на какое-то число, чтобы в нем было столько же x_1, сколько в другом, но с противоположным знаком. Во-вторых, мы складываем соответствующие части этих двух уравнений и таким образом исключаем неизвестное x_1. Не будет никакой разницы в причине, если мы добавим первое уравнение ко второму или наоборот.
Итак, давайте умножим первое уравнение на \ frac {1} {2}, добавим его ко второму и заменим существующее второе уравнение новым. После всего этого мы получаем новую эквивалентную систему:
\ left \ {\ begin {align} 2x_1 + 4x_2-3x_3 + 2x_4 = 0 \\ – 4x_2 + \ frac {13} {2} x_3 + x_4 = 2 \\ 2x_2-4x_3 + 5x_4 = -1 \\ 2x_3 + x_4 = -3 \ конец {выровнено} \ вправо.
Как видите, мы удалили x_1 из второй строки.
Теперь умножим его на \ frac {1} {2}, добавим результат к уравнению в третьей строке, а затем заменим существующее уравнение новым полученным.
\ left \ {\ begin {align} 2x_1 + 4x_2-3x_3 + 2x_4 = 0 \\ – 4x_2 + \ frac {13} {2} x_3 + x_4 = 2 \\ – \ frac {3} {4} x_3 + \ frac {11} {2} x_4 = 0 \\ 2x_3 + x_4 = -3 \ end {align} \ right.
Мы исключили x_2 из третьего уравнения. Нашим последним ходом будет исключение x_3 из четвертого уравнения.
Итак, давайте умножим его на – \ frac {3} {8}, прибавим к уравнению третьей строки и поместим результат в четвертую строку.
Наша окончательная эквивалентная система выглядит следующим образом:
\ left \ {\ begin {align} 2x_1 + 4x_2-3x_3 + 2x_4 = 0 \\ – 4x_2 + \ frac {13} {2} x_3 + x_4 = 2 \\ – \ frac {3} {4} x_3 + \ frac {11} {2} x_4 = 0 \\ \ frac {41} {8} x_4 = \ frac {9} {8} \ end {align} \ right.
Мы получили систему в верхнетреугольной форме.
Нахождение неизвестных треугольной системы называется обратным ходом метода Гаусса. На самом деле, довольно легко понять, как поступить с этого момента. Сначала найдем x_4 из четвертого уравнения. Затем мы просто подставим x_4 обратно в третье уравнение, чтобы найти x_3. После этого мы подставим x_4 и x_3 во второе уравнение, чтобы найти x_2. Затем, наконец, зная x_2, x_3 и x_4, мы можем легко найти x_1 из первого уравнения.
Итак, вот ответ нашей системе:
\ left \ {\ begin {align} x_1 = – \ frac {88} {41} \\ x_2 = \ frac {89} {41} \\ x_3 = \ frac {66} {41} \\ x_4 = \ гидроразрыв {9} {41} \ end {align} \ right.
Можете проверить, если хотите.
В общем случае может случиться так, что при преобразовании системы мы получим противоречивое уравнение вида 0 = b, где b \ neq 0. Это означает, что система не имеет решений. Такие системы называют несовместимыми.
Также может случиться так, что вы будете следовать методу правильно, но не получите эту красивую треугольную форму и последнее уравнение \ frac {41} {8} x_4 = \ frac {9} {8}, откуда вы можете получить x_4 и решить систему.Вместо этого вы выступаете против случая, когда вы можете выразить одно незнание только через другое. Нечего бояться, это нормально 🙂 В одном из следующих разделов мы выберем пример, показывающий этот конкретный случай.
Метод исключения Гаусса часто даже более удобен, чем метод Крамера (правило Крамера), который требует вычислений определителей, и эта операция сложна для систем высокого порядка. Напротив, исключение Гаусса может быть выполнено сравнительно легко для систем более высокого порядка, чем, скажем, 4, когда вычисление определителей усложняется.
Подведение итогов. Если вы хотите решить систему линейных уравнений с использованием исключения Гаусса, сначала вам нужно получить свою систему в треугольной (или трапециевидной) форме. Для этого вы спускаетесь вниз по своей системе и шаг за шагом исключаете переменные из уравнений. После этого вы поднимаетесь вверх и постепенно находите переменные (или выражаете их через других). Не забывайте проверять свои ответы, подключив их к исходной системе, это помогает избежать ошибок и правильно выполнять домашнее задание.
(PDF) Сравнение правила Крамера и предлагаемого метода исключения Крамера 2 на 2 для решения систем из трех или более линейных уравнений
Сравнение правила Крамера и предлагаемого метода исключения Крамера 2 × 2
для решения систем трех или более линейных уравнений
DKR Babajee
†
Совет по научным и академическим исследованиям, Союзная сеть по политике, исследованиям и действиям в интересах устойчивого развития (ANPRAS), Маврикий
электронная почта: dkrbabajee @ gmail.com
Abstract
Правило Крамера – это 262-летний подход к решению систем из n линейных уравнений от n переменных. Для системы
из 3 линейных уравнений правило Крамера требует вычисления определителей четырех матриц 3 × 3 (9
определителей матриц 2 × 2 или 9 сомножителей). Метод также не работает, когда определитель матрицы коэффициентов
равен нулю.
В этой работе мы предлагаем метод исключения Крамера 2 × 2, который состоит из решения первых 2 линейных уравнений
с использованием правила Крамера и получения выражений первой и второй переменных через третью переменную
.Подставляя эти выражения в третье уравнение, мы получаем значение третьей переменной, а затем непосредственно получаются
решений других переменных. Таким образом, мы уменьшаем количество вычислений определителей
до 5.
Мы показываем, что предлагаемый нами метод эквивалентен классическому правилу Крамера для решения общих систем линейных уравнений 3
и может использоваться для решения систем 3 линейные уравнения, когда определитель матрицы коэффициентов
3 × 3 равен нулю.Мы показываем на примере, как применить метод исключения Крамера 2 × 2 для системы n линейных
уравнений, и показываем его преимущество перед классическим правилом Крамера.
Ключевые слова
Правило Крамера, системы линейных уравнений, Детерминанты, метод исключения Крамера 2 × 2.
1 Правило Крамера для решения систем из n линейных уравнений
Правило Крамера [2] обычно преподается на курсах бакалавриата как ценный инструмент для решения систем линейных уравнений.
Правило Крамерса дает явное выражение для решения системы и поэтому является теоретически важным
.Кляйн [6] описал педагогический подход, основанный на правиле Крамера.
Система n линейных уравнений задается формулой
a
1,1
x
1
+ a
1,2
x
2
+ a
1,3
x
3
+ a
1,4
x
4
+ … + a
1, n
x
n
= b
1
, ( 1)
a
2,1
x
1
+ a
2,2
x
2
+ a
2,3
x
3
+ a
2,4
x
4
+… + a
2, n
x
n
= b
2
, (2)
a
3,1
x
1
+ a
3, 2
x
2
+ a
3,3
x
3
+ a
3,4
x
4
+ … + a
3, n
x
n
= b
3
, (3)
a
4,1
x
1
+ a
4,2
x
+ a4,3
x
3
+ a
4,4
x
4
+… + a
4, n
x
n
= b
4
, (4)
.
.
.
a
n, 1
x
1
+ a
n, 2
x
2
+ a
n, 3
x
3
n, 4x
4
+ … + a
n, n
x
n
= b
n
.(5)
Систему можно записать в матричной форме
Ax = b, (6)
, где
A =
a
1,1
a
1,2
a
1,3
a
1,4
. . . a
1, n
a
2,1
a
2,2
a
2,3
a
2,4
.. . a
2, n
a
3,1
a
3,2
a
3,3
a
3,4
. . . a
3, n
a
4,1
a
4,2
a
4,3
a
4,4
. . . а
4, н
.
.
.
.
.
.
.
.
.
.
.
. . . .
.
.
.
a
n, 1
a
n, 2
a
n, 3
a
n, 4
. . . а
n, n
, x =
000
000
000
x
1
x
2
x
3
x
4.
.
.
x
n
0009000 9000 9000 9000
000и b =
b
1
b
2
b
3
b
4.
.
.
b
n
Проекты
Документ без названияЛинейная алгебра
Используйте меню ниже, чтобы отфильтровать проекты по дисциплинам.
Автор : Дэнни Отеро
Описание : Этот проект по линейной алгебре иллюстрирует, как математики восемнадцатого и девятнадцатого веков решали системы линейных уравнений со многими переменными, сложную проблему, которая в конечном итоге потребовала внимания к вопросам записи и представления уравнений, а также тщательной разработки вспомогательных функций. понятие «расстройство» или «перестановка».Колин Маклорен (1698-1746) читал курс алгебры в Эдинбургском университете в 1730 году, в лекциях которого содержатся формулы для решения систем линейных уравнений с двумя и тремя переменными; изучение этих лекций иллюстрирует формы современного определителя задолго до того, как это понятие было формально кристаллизовано. В 1750 году Габриэль Крамер (1704–1752) опубликовал свое знаменательное «Введение в анализ алгебраических кривых» (Введение в анализ алгебраических кривых). В приложении к этой работе Крамер рассматривает решение линейных систем более систематически, предоставляя формулу решения такой системы, которая сегодня известна как правило Крамера.Что еще более важно, он указывает правила формирования детерминантных выражений, которые появляются в формулах для величин решения, используя термин «расстройство» для обозначения сложной перестановки переменных и их коэффициентов, которая придает структуру этим выражениям. Эти идеи достигают своей зрелости в мемуарах Огюстена-Луи Коши (1789-1857) 1812 года, озаглавленных Memoire sur les functions qui ne peuvent obtenir que deux valeurs egales et de signes contraires par suite des transpositions operees entre les variables quelles renferement (Memoir on these functions quelles renferement). которые принимают только два значения, равных, но противоположных по знаку, в результате транспонирования переменных, которые они содержат).В этой работе Коши обеспечивает полное развитие детерминанта и его перестановочных свойств в по существу современной форме. Коши использует термин «определитель» (заимствованный у Гаусса) для обозначения этих выражений и даже принимает раннюю форму матричной записи для выражения формул для решения линейной системы.
Автор : Мэри Флэгг
Описание : Метод исключения Гаусса для решения систем линейных уравнений – одна из первых тем в стандартном классе линейной алгебры.Алгоритм назван в честь Карла Фридриха Гаусса (1777-1855), но техника не была его изобретением. Фактически, китайские математики решали линейные уравнения с версией исключения еще в 100 году нашей эры. В этом проекте учащиеся изучают части главы 8 «Прямоугольные массивы» в «Девяти главах математического искусства», чтобы изучить технику, известную китайцам к 100 году нашей эры. Затем студенты прочитают комментарий к главе 8 девяти глав, данный китайским математиком Лю Хуэем в 263 году нашей эры, и их спросят, как его комментарий помогает пониманию.Метод Девяти глав будет сравнен с современным алгоритмом. Сходство древних китайцев и современных алгоритмов демонстрирует сложный уровень древнекитайской математики. Формат «Девяти глав» как серии практических задач и решений усиливает представление о том, что математика связана с повседневной жизнью.
Вернуться на главную страницу TRIUMPHS
Линейная система уравнений с параметрами
Решение нескольких линейных линий с помощью аналитических методов займет много времени.Не забывайте, что одна ошибка может дорого вам обойтись. Вот почему мы предпочитаем численные методы для предсказания решения. Когда дело доходит до решения, есть два метода, на которые вы можете положиться: один – это решение линейной системы по правилу Крамера, а второй – метод исключения Гаусса.
Решение линейной системы уравнений с параметрами по правилу Крамера
В этом методе мы будем использовать правило Крамера, чтобы найти ранг, а также спрогнозировать значение неизвестных переменных в системе.Ниже приведен пример линейной системы с одной неизвестной переменной.
Здесь k – неизвестная переменная. Первым шагом является преобразование системы в матрицу коэффициентов и расширенную матрицу.
A представляет матрицу коэффициентов, а A ‘представляет расширенную матрицу. Следующим шагом является поиск определителей обеих матриц.
определяет ранжирование обеих матриц. .If
If
С помощью рангов теперь можно определить тип системы.
Если
, значит, система будет Несогласованная система.Если
, значит, система будет Согласованная независимая система.Поскольку мы знаем, с каким типом системы имеем дело, теперь мы можем сосредоточиться на поиске решения для линейной системы. Это уравнение также может быть решено методом исключения Гаусса, но сейчас мы сосредотачиваемся на правиле Крамера.
000000000000000000000
000
000
000 рядом со мной выдающиеся репетиторы по математике.
Лучшие доступные репетиторы по математике
Первый урок бесплатно2. Решение линейной системы уравнений с параметрами методом исключения Гаусса
Исключение Гаусса – это прямой метод численного анализа, который помогает найти детерминант, а также ранг матрица.По сути, прямые методы дают точный ответ, но при условии, что они выполняются с бесконечной точностью. Метод исключения Гаусса предполагает, что с помощью операций со строками мы можем найти определитель и ранг матрицы. Иногда вам может потребоваться выполнить частичный поворот, но это не обязательно.
В методе исключения Гаусса нам нужно преобразовать расширенную матрицу в верхнюю треугольную матрицу. В случае, если вы не знаете верхнюю треугольную матрицу, тогда это матрица, в которой все элементы ниже диагонали равны нулю.Вот иллюстрация верхней треугольной матрицы.
В этой верхней треугольной матрице
– диагональные элементы, а остальные переменные – константы. Если вы умножите все элементы диагонали, вы получите определитель матрицы. Необходимо определить, существует ли какое-либо значение м для обеспечения согласованности системы. Если да, решите систему для этого значения м .Преобразуйте его в расширенную матрицу:
Операции со строками:
Если вы посмотрите на левую часть операции со строкой, это означает, что вы применяете операцию со строкой к этой конкретной строке.Правая часть операции со строкой показывает операцию, которую вы хотите применить к этой конкретной строке. Обратите внимание, что эта строковая операция будет применена ко всей строке.
Кроме того, вы можете сместить столбец. Например, в приведенной выше матрице, если мы поменяем местами столбцы 2 и 3, мы можем легко получить верхнюю треугольную матрицу.
Если
, это означает, следовательно, система будет Несогласованная система .Если
, это означает, что система будет Согласованной зависимой системой .Примеры
Поскольку матрица уже имеет форму верхней треугольной матрицы, мы можем использовать обратную подстановку напрямую, чтобы найти значения x, y и z.
Следовательно, будет два решения:
или илиЕсли система
быть Несогласованная система
Если
, следовательно, система Согласованная зависимая система.Если
, значит, система является согласованной независимой системой .Если система
будет последовательной, это означает, что система будет последовательной.Если
Если
Вышеупомянутая система будет несовместимой системой .
Если
Вышеупомянутая система будет согласованной зависимой системой .
Посмотрите, на что вам следует обратить внимание в репетиторе математики рядом со мной.
Решающие системы с правилом Крамера – алгебра и тригонометрия OpenStax
[detect-answer q = ”fs-id1531880 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1531880 ″]
Свойство 1 утверждает, что если матрица имеет верхнюю треугольную форму, определитель является произведением элементов по главной диагонали.
[латекс] A = \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill \, \, 2 & \ hfill 3 \\ \ hfill 0 & \ hfill \, \, 2 & \ hfill 1 \\ \ hfill 0 & \ hfill \, \, 0 & \ hfill -1 \ end {array} \ right] [/ latex]
Дополните [латекс] \, A \, [/ latex] первыми двумя столбцами.
[латекс] A = \ left [\ begin {array} {ccc} 1 & 2 & 3 \\ 0 & 2 & 1 \\ 0 & 0 & -1 \ end {array} | \, \, \, \ begin {array} {c } 1 \\ 0 \\ 0 \ end {массив} \, \, \, \, \ begin {array} {c} 2 \\ 2 \\ 0 \ end {array} \ right] [/ latex]
Затем
[латекс] \ begin {array} {l} \ mathrm {det} \ left (A \ right) = 1 \ left (2 \ right) \ left (-1 \ right) +2 \ left (1 \ right) \ влево (0 \ вправо) +3 \ влево (0 \ вправо) \ влево (0 \ вправо) -0 \ влево (2 \ вправо) \ влево (3 \ вправо) -0 \ влево (1 \ вправо) \ влево (1 \ вправо) +1 \ влево (0 \ вправо) \ влево (2 \ вправо) \ hfill \\ \, \, \, \, \, \, \, \, \, \, \, \, \ , \, \, \, = – 2 \ hfill \ end {array} [/ latex]
Свойство 2 утверждает, что перестановка строк меняет знак.Учитывая
[латекс] \ begin {массив} {l} \ begin {array} {l} \\ A = \ left [\ begin {array} {cc} -1 & 5 \\ 4 & -3 \ end {array} \ right ], \, \, \ mathrm {det} \ left (A \ right) = \ left (-1 \ right) \ left (-3 \ right) – \ left (4 \ right) \ left (5 \ right) = 3-20 = -17 \ end {массив} \ hfill \\ \ hfill \\ B = \ left [\ begin {array} {cc} 4 & -3 \\ -1 & 5 \ end {array} \ right], \, \, \ mathrm {det} \ left (B \ right) = \ left (4 \ right) \ left (5 \ right) – \ left (-1 \ right) \ left (-3 \ right) = 20 -3 = 17 \ hfill \ end {array} [/ latex]
Свойство 3 утверждает, что если две строки или два столбца идентичны, определитель равен нулю.
[латекс] \ begin {массив} {l} \, \, \, \, \, \, \, \, \, \, \, A = \ left [\ begin {array} {ccc} 1 & 2 & 2 \\ 2 & 2 & 2 \\ -1 & 2 & 2 \ end {array} \ text {} | \ text {} \ begin {array} {c} 1 \\ 2 \\ -1 \ end {array} \ begin {array } {c} 2 \\ 2 \\ 2 \ end {array} \ right] \ hfill \\ \ hfill \\ \ mathrm {det} \ left (A \ right) = 1 \ left (2 \ right) \ left (2 \ вправо) +2 \ влево (2 \ вправо) \ влево (-1 \ вправо) +2 \ влево (2 \ вправо) \ влево (2 \ вправо) +1 \ влево (2 \ вправо) \ влево ( 2 \ вправо) -2 \ влево (2 \ вправо) \ влево (1 \ вправо) -2 \ влево (2 \ вправо) \ влево (2 \ вправо) \ hfill \\ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, = 4-4 + 8 + 4-4-8 = 0 \ hfill \ end {array} [/ latex]
Свойство 4 утверждает, что если строка или столбец равны нулю, определитель равен нулю.{-1} \ right) = – 2 \ left (- \ frac {1} {2} \ right) – \ left (\ frac {3} {2} \ right) \ left (1 \ right) = – \ гидроразрыв {1} {2} \ hfill \ end {array} [/ latex]
Свойство 6 утверждает, что если любая строка или столбец матрицы умножается на константу, определитель умножается на тот же коэффициент. Таким образом,
[латекс] \ begin {array} {l} A = \ left [\ begin {array} {cc} 1 & 2 \\ 3 & 4 \ end {array} \ right], \ mathrm {det} \ left (A \ right) = 1 \ left (4 \ right) -2 \ left (3 \ right) = – 2 \ hfill \\ \ hfill \\ B = \ left [\ begin {array} {cc} 2 \ left (1 \ right) & 2 \ left (2 \ right) \\ 3 & 4 \ end {array} \ right], \ mathrm {det} \ left (B \ right) = 2 \ left (4 \ right) -3 \ left ( 4 \ right) = – 4 \ hfill \ end {array} [/ latex] [/ hidden-answer]
.

 Наличие решений.
Наличие решений. 250
250 565
565 2781
2781 046
046 582
582 229
229 937
937 250
250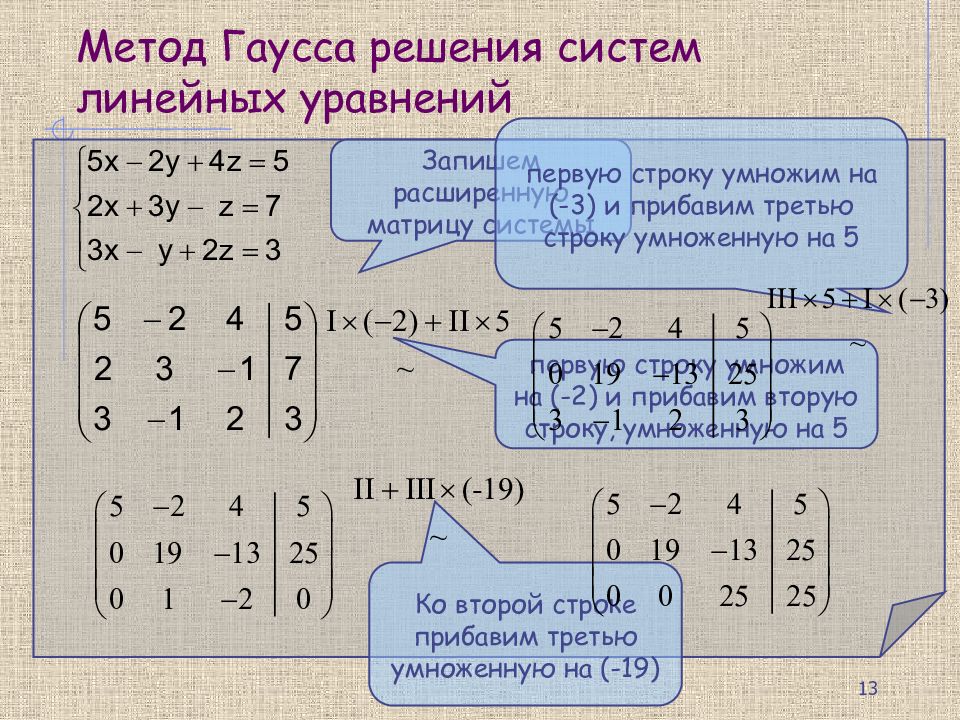 340
340 157
157
 Повторяя эту процедуру для всех базисных переменных, получаем
фундаментальное решение.
Повторяя эту процедуру для всех базисных переменных, получаем
фундаментальное решение.



 {-1} \, [/ latex] – обратная величина определителю матрицы [latex] \, A. [/ Latex]
{-1} \, [/ latex] – обратная величина определителю матрицы [latex] \, A. [/ Latex]