Метод крамера решение системы линейных уравнений: I.3. Метод Крамера решения систем линейных алгебраических уравнений - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Метод Крамера онлайн

Примеры решенийРанг матрицыОбратная матрица Метод Гаусса Производная онлайн Определитель матрицыЭкстремум функции Линейная алгебра онлайн Правило СаррюсаМетод обратной матрицы

Назначение метода Крамера: с помощью формул Крамера находится решение системы линейных уравнений. Сам метод принадлежит к прямым методам нахождения СЛАУ.

Шаг №1
Шаг №2
Видеоинструкция
Также решают

Инструкция. Выберите количество переменных, нажмите Далее. Полученное решение сохраняется в файле Word (см. пример решения СЛАУ методом Крамера). Для проверки решения автоматически генерируется шаблон в Excel. Выберите количество переменных 234567

Вместе с этим калькулятором также используют следующие:

По координатам вершин треугольника найти площадь, уравнения сторон, уравнение медианы, уравнение биссектрисы

По координатам вершин пирамиды найти

Построение графика функции методом дифференциального исчисления

Экстремум функции двух переменных

Вычисление пределов

Кратко алгоритм метода Крамера можно описать тремя шагами:

Находим определитель D исходной матрицы A.
В цикле от 1 до n заменяем i-ый столбец матрицы на столбец результатов B. Находим текущий определитель D_i полученной матрицы.
x_i находится делением D_i на D: x_i = D_i / D.

Суть метода Крамера демонстрирует пример нахождения переменных системы линейных уравнений.
Пример. Решить систему линейных уравнений методом Крамера.
x₁ + 4x₂ = 5
-2x₁ + x₃ = -1
2x₁ + x₂ + x₃ = 4
Решение. Запишем систему в виде:

A =

1	4	0
-2	0	1
2	1	1

B^T = (5,-1,4)
Главный определитель: ∆ = 1 • (0 • 1-1 • 1)-(-2 • (4 • 1-1 • 0))+2 • (4 • 1-0 • 0) = 15
Заменим первый столбец матрицы А на вектор результата B.

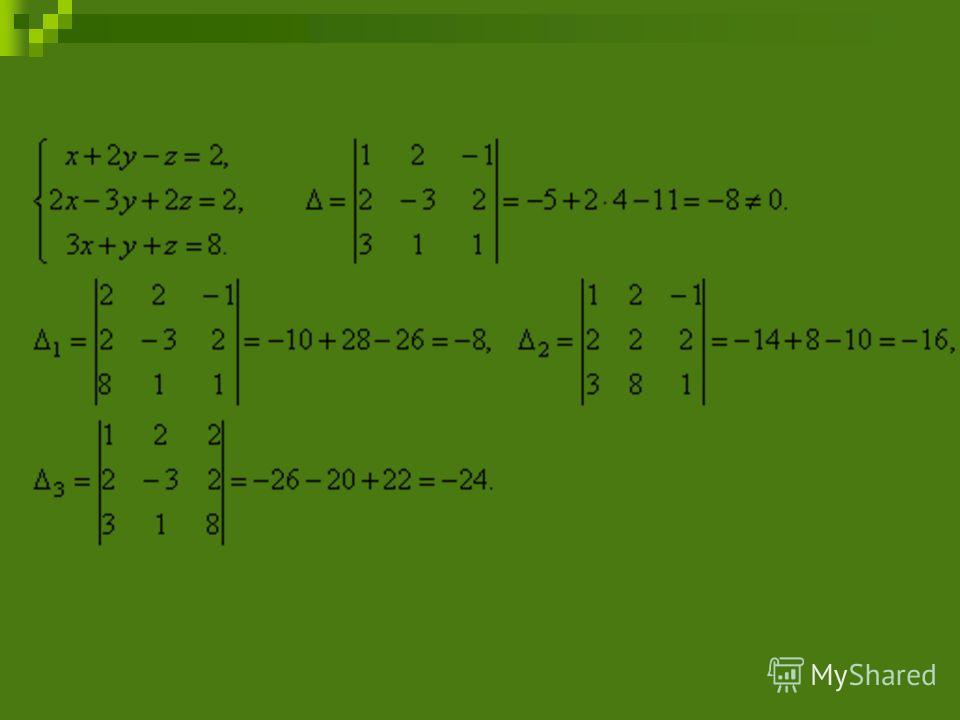
`5`	4	0
`-1`	0	1
`4`	1	1

Найдем определитель полученной матрицы: ∆₁ = 5 • (0 • 1-1 • 1)-(-1 • (4 • 1-1 • 0))+4 • (4 • 1-0 • 0) = 15
x₁ = 15/15 = 1
Заменим 2-ый столбец матрицы А на вектор результата B.

1	`5`	0
-2	`-1`	1
2	`4`	1

Определитель полученной матрицы равен ∆₂ = 1 • (-1 • 1-4 • 1)-(-2 • (5 • 1-4 • 0))+2 • (5 • 1-(-1 • 0)) = 15
x₂ = 15/15 = 1
Заменим третий столбец матрицы А на вектор результата B.

1	4	`5`
-2	0	`-1`
2	1	`4`

Определитель этой матрицы равен ∆₃ = 1 • (0 • 4-1 • (-1))-(-2 • (4 • 4-1 • 5))+2 • (4 • (-1)-0 • 5) = 15
x₃ = 15/15 = 1
Проверка решения:
1•1+4•1+0•1 = 5
-2•1+0•1+1•1 = -1
2•1+1•1+1•1 = 4

Вывод:

Смысл метода Крамера: находим определитель D_i, получаемый из заменой i-го столбца на столбец свободных членов и делим его на главный определитель D.
x_i = D_i / D
Метод Крамера относится к простым для реализации методам решения СЛАУ и получил широкое распространение в разных областях знаний (например, при нахождении уравнений регрессий). Недостатком метода является его практическая непригодность для вычисления СЛАУ с большим количеством переменных (от 5 и выше). Для этого случая используют приближенные методы (например, метод простой итерации).

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.

Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Метод крамера подробное решение. Метод крамера решения систем линейных уравнений

В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью.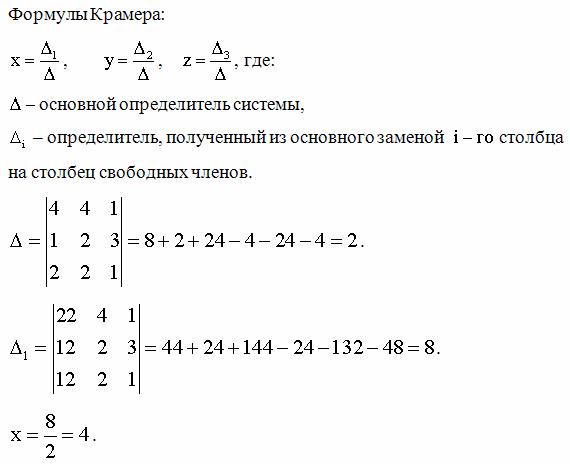 Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.

А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.

Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!

Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.

Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.

Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.

Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.

Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

Если , то система имеет бесконечно много решений или несовместна (не имеет решений).

В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .

Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,

И, наконец, ответ рассчитывается по формулам:

Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.

Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:

1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).

2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.

Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.

Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:

Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.

Решение системы с помощью обратной матрицы

Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).

Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.

Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:

То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце

Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера – весьма полезный навык.

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать? Например, решать СЛАУ методом Крамера!

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.

Решение СЛАУ методом Крамера

Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.

Согласно методу Крамера, решение находится по формулам:

Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.

В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:

Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .

А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!

2. Решение систем уравнений матричным методом (при помощи обратной матрицы).
3. Метод Гаусса решения систем уравнений.

Метод Крамера.

Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ ).

Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему

Относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы Вычисление определителей. :

Применим формулы Крамера и найдем значения переменных:
и .
Пример 1:
Решить систему уравнений:

относительно переменных х и у .
Решение:

Заменим в этом определителе первый столбец столбцом коэффициентов из правой части системы и найдем его значение:

Сделаем аналогичное действие, заменив в первом определителе второй столбец:

Применим формулы Крамера и найдем значения переменных:
и .
Ответ:
Замечание: Этим методом можно решать системы и большей размерности.

Замечание: Если получается, что , а делить на ноль нельзя, то говорят, что система не имеет единственного решения. В этом случае система имеет или бесконечно много решений или не имеет решений вообще.

Пример 2 (бесконечное количество решений):

Решить систему уравнений:

относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:

Решение систем методом подстановки.

Первое из уравнений системы — равенство, верное при любых значениях переменных (потому что 4 всегда равно 4). Значит, остается только одно уравнение. Это уравнение связи между переменными .
Получили, решением системы являются любые пары значений переменных, связанных между собой равенством .
Общее решение запишется так:
Частные решения можно определять выбирая произвольное значение у и вычисляя х по этому равенству связи.

и т.д.
Таких решений бесконечно много.
Ответ: общее решение
Частные решения:

Пример 3 (решений нет, система несовместна):

Решить систему уравнений:

Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:

Применять формулы Крамера нельзя. Решим эту систему методом подстановки

Второе уравнение системы — равенство, неверное ни при каких значениях переменных (конечно же, так как -15 не равно 2). Если одно из уравнений системы не верно ни при каких значениях переменных, то и вся системы не имеет решений.
Ответ: решений нет

Метод Крамера или так называемое правило Крамера – это способ поиска неизвестных величин из систем уравнений. Его можно использовать только если число искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть образуемая из системы основная матрица должна быть квадратной и не содержать нулевых строчек, а также если её детерминант не должен являться нулевым.

Теорема 1

Теорема Крамера Если главный определитель $D$ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений совместна, причём решение у неё существует единственное. Решение такой системы вычисляется через так называемые формулы Крамера для решения систем линейных уравнений: $x_i = \frac{D_i}{D}$

В чем заключается метод Крамера

Суть метода Крамера в следующем:

Чтобы найти решение системы методом Крамера, первым делом вычисляем главный определитель матрицы $D$. Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.
Затем нужно заменить крайний столбец главной матрицы на столбец свободных членов и высчитать определитель $D_1$.
Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ – номер крайнего справа столбца.
После того как найдены все детерминанты $D_1$…$D_n$, можно высчитать неизвестные переменные по формуле $x_i = \frac{D_i}{D}$.

Приёмы для вычисления определителя матрицы

Для вычисления определителя матрицы с размерностью больше чем 2 на 2, можно использовать несколько способов:

Правило треугольников, или правило Саррюса, напоминающее это же правило. Суть метода треугольников в том, что при вычислении определителя произведения всех чисел, соединённых на рисунке красной линией справа, записываются со знаком плюс, а все числа, соединённые аналогичным образом на рисунке слева – со знаком минус. B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей – со знаком минус.

Рисунок 1. Правило треугольников для вычисления определителя для метода Крамера

С помощью метода, известного как метод Гаусса, также иногда этот метод называют понижением порядка определителя. В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
При решении методом Крамера СЛАУ с 4 неизвестными, лучше всего будет применять именно метод Гаусса для поиска и нахождения определителей или опредлять детерминант через поиск миноров.

Решение систем уравнений методом Крамера

Применим метод Крамера для системы из 2 уравнений и двумя искомыми величинами:

$\begin{cases} a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end{cases}$

Отобразим её в расширенной форме для удобства:

$A = \begin{array}{cc|c} a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end{array}$

Найдём определитель основной матрицы, также называемый главным определителем системы:

$D = \begin{array}{|cc|} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} = a_1 \cdot a_4 – a_3 \cdot a_2$

Если главный определитель не равен нулю, то для решения слау методом Крамера необходимо высчитать ещё парочку определителей от двух матриц с заменёнными столбцами основной матрицы на строчку свободных членов:

$D_1 = \begin{array}{|cc|} b_1 & a_2 \\ b_2 & a_4 \\ \end{array} = b_1 \cdot a_4 – b_2 \cdot a_4$

$D_2 = \begin{array}{|cc|} a_1 & b_1 \\ a_3 & b_2 \\ \end{array} = a_1 \cdot b_2 – a_3 \cdot b_1$

Теперь найдём неизвестные $x_1$ и $x_2$:

$x_1 = \frac {D_1}{D}$

$x_2 = \frac {D_2}{D}$

Пример 1

Метод Крамера для решения СЛАУ с основной матрицей 3 порядка (3 x 3) и тремя искомыми.

Решите систему уравнений:

$\begin{cases} 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 – x_3 = 10 \\ \end{cases}$

Сосчитаем главный детерминант матрицы пользуясь вышеизложенным под пунктом номер 1 правилом:

$D = \begin{array}{|ccc|} 3 & -2 & 4 \\3 & 4 & -2 \\ 2 & -1 & 1 \\ \end{array} = 3 \cdot 4 \cdot (-1) + 2 \cdot (-2) \cdot 2 + 4 \cdot 3 \cdot (-1) – 4 \cdot 4 \cdot 2 – 3 \cdot (-2) \cdot (-1) – (-1) \cdot 2 \cdot 3 = – 12 – 8 -12 -32 – 6 + 6 = – 64$

А теперь три других детерминанта:

$D_1 = \begin{array}{|ccc|} 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \end{array} = 21 \cdot 4 \cdot 1 + (-2) \cdot 2 \cdot 10 + 9 \cdot (-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9 \cdot (-2) \cdot (-1) – (-1) \cdot 2 \cdot 21 = – 84 – 40 – 36 – 160 – 18 + 42 = – 296$

$D_2 = \begin{array}{|ccc|} 3 & 21 & 4 \\3 & 9 & 2 \\ 2 & 10 & 1 \\ \end{array} = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \cdot 2 – 4 \cdot 9 \cdot 2 – 21 \cdot 3 \cdot (-1) – 2 \cdot 10 \cdot 3 = – 27 + 120 + 84 – 72 + 63 – 60 = 108$

$D_3 = \begin{array}{|ccc|} 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \end{array} = 3 \cdot 4 \cdot 10 + 3 \cdot (-1) \cdot 21 + (-2) \cdot 9 \cdot 2 – 21 \cdot 4 \cdot 2 – (-2) \cdot 3 \cdot 10 – (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = – 60$

Найдём искомые величины:

$x_1 = \frac{D_1} {D} = \frac{- 296}{-64} = 4 \frac{5}{8}$

$x_2 = \frac{D_1} {D} = \frac{108} {-64} = – 1 \frac {11} {16}$

$x_3 = \frac{D_1} {D} = \frac{-60} {-64} = \frac {15} {16}$

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
–

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Пример 2.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

К началу страницы

Продолжаем решать системы методом Крамера вместе

Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы. За примерами далеко ходить не надо.

Следующий пример – на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

Урок математики по теме “Решение системы линейных уравнений методом Крамера”

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Данная методическая разработка предназначена для проведения урока по дисциплине “Математика” на тему “Решение систем линейных уравнений методом Крамера” для студентов первого курса по программе учебной дисциплины, разработанной на основе Федерального государственного образовательного стандарта для специальностей среднего профессионального образования.

В результате изучения темы студент должен:

знать:

– решение систем линейных уравнений методом Крамера;

– применение знаний при решении систем линейных уравнений.

уметь:

– решать системы двух линейных уравнений с двумя неизвестными методом Крамера

– решать системы трех линейных уравнений с тремя неизвестными методом Крамера

При разработке данного урока в зависимости от специфики подготовки студентов можно внести дополнения и изменения в содержание, последовательность изучения материала урока и распределение времени.

Наблюдается связь истории с математикой, при изучении материала использована задача прикладного характера для будущей практической деятельности, что прививает интерес к предмету. Данная методическая разработка содержит: учебно-методическую карту, ход, где сформулированы цели занятия и последовательность проведения урока, указан список литературы.

При проведении занятия, использованы учебные пособия, технические и наглядные средства обучения

УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА

Дисциплина: Математика

Тема занятия: Решение систем линейных уравнений методом Крамера

Вид занятия (тип урока): Комбинированный

Цели урока:

Дидактическая:

повторить пройденный материал;
углубить знания студентов по теме “Решение систем линейных уравнений”;
изучить решение систем линейных уравнений c помощью метода Крамера;
научиться решать системы двух линейных уравнений с двумя неизвестными и трех линейных уравнений с тремя неизвестными, используя метод Крамера.

Развивающая:

способствовать развитию:
логического мышления;
памяти;
умению сравнивать, обобщать, анализировать;
интереса к избранной специальности.

Воспитательная:

стремиться воспитывать:
чувства ответственности, исполнительности, аккуратности;
чувство гордости за избранную профессию;
положительное отношение к знаниям, учениям;
интерес к математике

Межпредметные связи:

Обеспечивающие: история, русский язык, информатика
Обеспечиваемые: специальные предметы
Обеспечение занятия:

Наглядные пособия: Презентации к уроку

Раздаточный материал: карточки.

Технические средства обучения: калькуляторы, компьютеры, интерактивная доска

ПЛАН УРОКА

1. Организационный момент (слайд №1)

Здравствуйте, студенты. Тема урока: “Решение систем линейных уравнений методом Крамера”. Ученый-математик Колмогоров А.Н. говорил: “Без знаний математики нельзя понять ни основ современной техники, ни того, как ученые изучают природные и социальные явления”, поэтому математика связана с будущей специальностью. В результате изучения темы научимся решать задачи прикладного характера для профессиональной деятельности.

2. Постановка целей занятия

Цели урока: повторить пройденный материал; углубить знания по теме “Решение систем линейных уравнений”; изучить решение систем линейных уравнений с помощью метода Крамера; научиться решать системы двух линейных уравнений с двумя неизвестными и трех линейных уравнений с тремя неизвестными, используя метод Крамера.

3. Проверка домашнего задания

4. Проверка знаний (слайды № 2,3,4).

Экспресс-опрос

Какое уравнение называется линейным?
Напишите систему m линейных уравнений с n переменными.
Назовите коэффициенты при переменных.
Какие числа называются свободными членами?
Что является решением системы?
Какие методы решения систем линейных уравнений знаете?

Ответы: Уравнение называется линейным, если оно содержит переменные только в первой степени и не содержит произведений переменных.

В системе m линейных уравнений с n переменными:

Числа называются коэффициентами при переменных, а – свободными членами.

Совокупность чисел называется решением системы линейных уравнений, если при подстановке их вместо переменных во все уравнения они обращаются в верные равенства.

5. Изучение нового материала

В школьном курсе рассматриваются способ подстановки и способ сложения. В курсе высшей математике решают методом Крамера, методом Гаусса и с помощью обратной матрицы. Рассмотрим решение систем линейных уравнений методом Крамера

5.1 Знакомство с биографией Крамера

При изучении новой темы “Решение систем линейных уравнений методом Крамера” важное место занимает связь истории с математикой, что прививает интерес к предмету. Познакомимся с биографией Габриэля Крамера.

Сведения из истории (слайды № 5-10)

Крамер является одним из создателей линейной алгебры. Одной из самых известных его работ является “Введение в анализ алгебраических кривых”, опубликованный на французском языке в 1750 году. В ней Крамер строит систему линейных уравнений и решает её с помощью алгоритма, названного позже его именем – метод Крамера.

Габриэль Крамер родился 31 июля 1704 года в Женеве (Швейцария) в семье врача.

Уже в детстве он опережал своих сверстников в интеллектуальном развитии и демонстрировал завидные способности в области математики.

В 18 лет он успешно защитил диссертацию. Через 2 года Крамер выставил свою кандидатуру на должность преподавателя в Женевском университете. Учёный много путешествовал по Европе, перенимая опыт у знаменитых математиков своего времени – Иоганна Бернулли и Эйлера в Базеле, Галлея и де Муавра в Лондоне и других. Со многими из них он продолжал переписываться всю жизнь.

В 1729 году Крамер возобновляет преподавательскую работу в Женевском университете. В это время он участвует в конкурсе Парижской Академии и занимает второе место. Талантливый учёный написал множество статей на самые разные темы: геометрия, история, математика, философия. В 1730 году он опубликовал труд по небесной механике.

В 1740-е гг. Иоганн Бернулли поручает Крамеру подготовить к печати сборник своих работ. В 1742 году Крамер публикует сборник в 4-х томах. В 1744 году он выпускает посмертный сборник работ Якоба Бернулли (брата Иоганна Бернулли), а также двухтомник переписки Лейбница с Иоганном Бернулли. Эти работы вызвали большой интерес со стороны учёных всего мира.

Габриэль Крамер скончался 4 января 1752 года во Франции

5.2 Решение системы линейных уравнений методом Крамера(слайды № 11-15)

Теорема Крамера.

Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Дана система

Формулы Крамера ………….

Заменяя столбец с коэффициентами соответствующей переменной свободными членами:

6. Закрепление.

6.1 Решение системы двух линейных уравнений с двумя неизвестными методом Крамера (слайды № 16-19)

Ответ: (1;-1)

2) Фирма состоит из двух отделений, суммарная величина прибыли которых в минувшем году составила 12 млн усл. ед. На этот год запланировано увеличение прибыли первого отделения на 70%, второго – на 40%. В результате суммарная прибыль должна вырасти в 1,5 раза. Какова величина прибыли каждого из отделений: a) в минувшем году; б) в этом году?

Решение. Пусть x и y – прибыли первого и второго отделений в минувшем году.

Тогда условие задачи можно записать в виде системы:

Решив систему, получим x = 4, y = 8.

Ответ: а) прибыль в минувшем году первого отделения – 4 млн усл. ед., второго – 8 усл.ед.: б) прибыль в этом году первого отделения 1,7. 4 = 6,8 млн усл. ед., второго 1,4. 8 = 11,2 млн усл. ед.

При решении системы уравнений могут встретиться три случая:

1) система линейных уравнений имеет единственное решение

(система совместна и определённа)

Условия:

2) система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

Условия:

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

3) система линейных уравнений решений не имеет

(система несовместна)

Условия:

Система называется несовместной, если у неё нет ни одного решения, и совместной, если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой, а более одного – неопределённой.

6.2 Решение системы трех линейных уравнений с тремя двумя неизвестными методом Крамера (слайды № 20-22)

Ответ: (1; 0; -1) .

Решение. Находим определители системы:

Ответ: (1; 0; -1) .

7. Домашнее задание (слайд № 23)

Решите системы:

8. Подведение итогов

Подведем итоги урока. По результатам работы на уроке выставляются оценки, с последующей демонстрацией успеваемости в виде диаграммы на интерактивной доске.

Урок окончен. Спасибо за внимание. До свидания.

Литература:

Основная

Григорьев В.П.Дубинский Ю.А Элементы высшей математики. Москва, 2011
Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика. Москва, 2008

Дополнительная

Богомолов Н.В. Практические занятия по математики. Москва, 2013

Интернет-ресурсы: www.en.edu.ru

ХОД УРОКА

№	Элементы урока, содержание и последовательность изучаемых вопросов	Формы и методы обучения, контроля	Наглядные пособия, ТСО, дидактический материал	Преподаватель	Студенты	Время 45 мин.
1	Организационный момент. Взаимное привет-ствие.	Проверка отсутствующих, рабочих мест	Интерактивная доска слайд №1	Приветствует, отмечает в журнале отсутствующих.	Приветствуют	1 мин
2	Постановка целей занятия.	Организация внимания	Интерактивная доска	Ставит цели урока	Слушают	1 мин
3	Проверка домашнего задания	Групповая работа	Интерактивная доска	Контролирует	Дежурный проверяет	5 мин
4	Проверка знаний	Экспресс-опрос	Слайды № 2,3,4	Задает вопрос, поправляет ответ	Думают, отвечают	5 мин
5	Изучение нового материала	Организация внимания	Интерактивная доска	Объясняет	Слушают, рассуждают, отвечают на вопросы.
5.1	Знакомство с биографией Крамера	Рассказ материала	Слайды № 5-10	Рассказывает	Смотрят	5 мин
5.2	Решение системы линейных уравнений методом Крамера	Изучение темы	Слайды № 11-15	Объясняет	Смотрят, слушают	10 мин
6	Закрепление	Самостоятельная работа	Интерактивная доска	Выдает задания	Думают, решают
6. 1	Решение системы двух линейных уравнений с двумя неизвестными методом Крамера	Групповая работа	Слайды № 16-19	Выдает задания, проверяет	Решают	5 мин
6.2	Решение системы трех линейных уравнений с тремя неизвестными методом Крамера	Самостоятельная работа	Слайды № 20-22	Контролирует, проверяет	Думают, решают	10 мин
7	Домашнее задание		Слайды № 23	Выдает задания	Пишут	1 мин
8	Подведение итогов.	Анализ работы	Интерактивная доска	Подводит итоги, обобщает	Получают оценки	2 мин

Решение по формуле крамера примеры. Метод крамера решения систем линейных уравнений. Примеры решения систем уравнений методом Крамера

В нашем калькуляторе вы бесплатно найдете решение системы линейных уравнений методом Крамера онлайн с подробным решением и даже с комплексными числами . Каждый определитель, использованный в расчетах, можно просмотреть отдельно, а также проверить точный вид системы уравнений, если вдруг определитель основной матрицы оказался равен нулю.

Подробнее о том, как пользоваться нашим онлайн калькулятором, вы можете прочитать в инструкции .

О методе

При решении системы линейных уравнений методом Крамера выполняются следующие шаги.

Записываем расширенную матрицу.
Находим определитель основной (квадратной) матрицы.
Для нахождения i-ого корня подставляем столбец свободных членов в основную матрицу на i-ое место и находим ее определитель. Далее находим отношение полученного определителя к основному, это и есть очередное решение. Проделываем данную операцию для каждой переменной.
В случае, если основной определитель матрицы равен нулю, то система уравнений либо несовместна, либо имеет бесконечное множество решений. К сожалению метод Крамера не позволяет более точно ответить на этот вопрос. Тут вам поможет

Метод Крамера.

Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ ).

Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему

Применим формулы Крамера и найдем значения переменных:
и .
Пример 1:
Решить систему уравнений:

относительно переменных х и у .
Решение:

Пример 2 (бесконечное количество решений):

Решить систему уравнений:

Пример 3 (решений нет, система несовместна):

Решить систему уравнений:

Рассмотрим систему 3-х уравнений с тремя неизвестными

Используя определители 3-го порядка, решение такой системы можно записать в таком же виде, как и для системы двух уравнений, т.е.

(2.4)

если 0. Здесь

Это есть правило Крамера решения системы трех линейных уравнений с тремя неизвестными .

Пример 2.3. Решить систему линейных уравнений при помощи правила Крамера:

Решение . Находим определитель основной матрицы системы

Поскольку 0, то для нахождения решения системы можно применить правило Крамера, но предварительно вычислим еще три определителя:

Проверка:

Следовательно, решение найдено правильно. 

Правила Крамера, полученные для линейных систем 2-го и 3-го порядка, наводят на мысль, что такие же правила можно сформулировать и для линейных систем любого порядка. Действительно имеет место

Теорема Крамера. Квадратная система линейных уравнений с отличным от нуля определителем основной матрицы системы (0) имеет одно и только одно решение и это решение вычисляется по формулам

(2.5)

где  – определитель основной матрицы ,  i – определитель матрицы , полученной из основной, заменой i -го столбца столбцом свободных членов .

Отметим, что если =0, то правило Крамера не применимо. Это означает, что система либо не имеет вообще решений, либо имеет бесконечно много решений.

Сформулировав теорему Крамера, естественно возникает вопрос о вычислении определителей высших порядков.

2.4. Определители n-го порядка

Дополнительным минором M ij элемента a ij называется определитель, получаемый из данного путем вычеркивания i -й строки и j -го столбца. Алгебраическим дополнением A ij элемента a ij называется минор этого элемента, взятого со знаком (–1) i + j , т. е. A ij = (–1) i + j M ij .

Например, найдем миноры и алгебраические дополнения элементов a 23 и a 31 определителя

Получаем



Используя понятие алгебраического дополнения можно сформулировать теорему о разложении определителя n -го порядка по строке или столбцу .

Теорема 2.1. Определитель матрицы A равен сумме произведений всех элементов некоторой строки (или столбца) на их алгебраические дополнения:

(2.6)

Данная теорема лежит в основе одного из основных методов вычисления определителей, т.н. метода понижения порядка . В результате разложения определителя n -го порядка по какой-либо строке или столбцу, получается n определителей (n –1)-го порядка. Чтобы таких определителей было меньше, целесообразно выбирать ту строку или столбец, в которой больше всего нулей. На практике формулу разложения определителя обычно записывают в виде:

т. е. алгебраические дополнения записывают в явном виде через миноры.

Примеры 2.4. Вычислить определители, предварительно разложив их по какой-либо строке или столбцу. Обычно в таких случаях выбирают такой столбец или строку, в которой больше всего нулей. Выбранную строку или столбец будем обозначать стрелкой.



2.5. Основные свойства определителей

Разлагая определитель по какой-либо строке или столбцу, мы получим n определителей (n –1)-го порядка. Затем каждый из этих определителей (n –1)-го порядка также можно разложить в сумму определителей (n –2)-го порядка. Продолжая этот процесс, можно дойти до определителей 1-го порядка, т.е. до элементов матрицы, определитель которой вычисляется. Так, для вычисления определителей 2-го порядка придется вычислить сумму двух слагаемых, для определителей 3-го порядка – сумму 6 слагаемых, для определителей 4-го порядка – 24 слагаемых. Число слагаемых будет резко возрастать по мере увеличения порядка определителя. Это означает, что вычисление определителей очень высоких порядков становится довольно трудоемкой задачей, непосильной даже для ЭВМ. Однако вычислять определители можно и по-другому, используя свойства определителей.

Свойство 1 . Определитель не изменится, если в нем поменять местами строки и столбцы, т.е. при транспонировании матрицы :

Данное свойство свидетельствует о равноправии строк и столбцов определителя. Иначе говоря, любое утверждение о столбцах определителя справедливо и для его строк и наоборот.

Свойство 2 . Определитель меняет знак при перестановке двух строк (столбцов).

Следствие . Если определитель имеет две одинаковые строки (столбца), то он равен нулю.

Свойство 3 . Общий множитель всех элементов в какой-либо строке (столбце) можно вынести за знак определителя .

Например,

Следствие . Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю .

Свойство 4 . Определитель не изменится, если к элементам одной строки (столбца), прибавить элементы другой строки (столбца), умноженной на какое-либо число .

Например,

Свойство 5 . Определитель произведения матриц равен произведению определителей матриц:

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .

И, наконец, ответ рассчитывается по формулам:

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Решение системы с помощью обратной матрицы

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

С количеством уравнений одинаковым с количеством неизвестных с главным определителем матрицы, который не равен нулю, коэффициентов системы (для подобных уравнений решение есть и оно только одно).

Теорема Крамера.

Когда определитель матрицы квадратной системы ненулевой, значит, система совместна и у нее есть одно решение и его можно найти по формулам Крамера :

где Δ – определитель матрицы системы ,

Δ i – определитель матрицы системы, в котором вместо i -го столбца находится столбец правых частей.

Когда определитель системы нулевой, значит, система может стать совместной или несовместной.

Этот способ обычно применяют для небольших систем с объемными вычислениями и если когда необходимо определить 1-ну из неизвестных. Сложность метода в том, что нужно вычислять много определителей.

Описание метода Крамера.

Есть система уравнений:

Систему 3-х уравнений можно решить методом Крамера, который рассмотрен выше для системы 2-х уравнений.

Составляем определитель из коэффициентов у неизвестных:

Это будет определитель системы . Когда D≠0 , значит, система совместна. Теперь составим 3 дополнительных определителя:

Решаем систему по формулам Крамера :

Примеры решения систем уравнений методом Крамера.

Пример 1 .

Дана система:

Решим ее методом Крамера.

Сначала нужно вычислить определитель матрицы системы:

Т.к. Δ≠0, значит, из теоремы Крамера система совместна и у нее есть одно решение. Вычисляем дополнительные определители. Определитель Δ 1 получаем из определителя Δ, заменяя его первый столбец столбцом свободных коэффициентов. Получаем:

Таким же путем получаем определитель Δ 2 из определителя матрицы системы заменяя второй столбец столбцом свободных коэффициентов:

Матрицы метод крамера примеры. Метод крамера решения систем линейных уравнений

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Решение СЛАУ методом Крамера

Согласно методу Крамера, решение находится по формулам:

Теорема Крамера.

где Δ – определитель матрицы системы ,

Δ i – определитель матрицы системы, в котором вместо i -го столбца находится столбец правых частей.

Когда определитель системы нулевой, значит, система может стать совместной или несовместной.

Описание метода Крамера.

Есть система уравнений:

Систему 3-х уравнений можно решить методом Крамера, который рассмотрен выше для системы 2-х уравнений.

Составляем определитель из коэффициентов у неизвестных:

Решаем систему по формулам Крамера :

Примеры решения систем уравнений методом Крамера.

Пример 1 .

Дана система:

Решим ее методом Крамера.

Сначала нужно вычислить определитель матрицы системы:

Рассмотрим систему 3-х уравнений с тремя неизвестными

(2.4)

если 0. Здесь

Это есть правило Крамера решения системы трех линейных уравнений с тремя неизвестными .

Пример 2.3. Решить систему линейных уравнений при помощи правила Крамера:

Решение . Находим определитель основной матрицы системы

Проверка:

Следовательно, решение найдено правильно. 

(2.5)

Сформулировав теорему Крамера, естественно возникает вопрос о вычислении определителей высших порядков.

2.4. Определители n-го порядка

Например, найдем миноры и алгебраические дополнения элементов a 23 и a 31 определителя

Получаем



(2.6)

т.е. алгебраические дополнения записывают в явном виде через миноры.



2.

5. Основные свойства определителей

Свойство 1 . Определитель не изменится, если в нем поменять местами строки и столбцы, т. е. при транспонировании матрицы :

Свойство 2 . Определитель меняет знак при перестановке двух строк (столбцов).

Следствие . Если определитель имеет две одинаковые строки (столбца), то он равен нулю.

Например,

Свойство 5 . Определитель произведения матриц равен произведению определителей матриц:

Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

И, наконец, ответ рассчитывается по формулам:

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Решение системы с помощью обратной матрицы

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.

Примеры решения линейных уравнений по методу Крамера с ответами

Алгоритм решения линейных уравнений по методу Крамера

Метод Крамера – способ решения системы линейных уравнений с помощью определителя матрицы при условии, что он не равен нулю. Если мы говорим об определителе, то, соответственно, матрица данной системы может быть только квадратной (число переменных в данной системе уравнений должно быть равно числу её строк).

1. Находим общий определитель матрицы

убеждаемся, что он не равен нулю.

2. Для каждой переменной

находим определитель матрицы

Здесь вместо столбца коэффициентов

подставляем столбец свободных членов системы.

3. Находим значения неизвестных по формуле

Примеры решений линейных уравнений по методу Крамера

Пример 1

Задание 1

Решить систему уравнений методом Крамера:

Решение

Найдем определитель матрицы :

Теперь заменим первый столбец свободными членами системы:

Найдем значение

Заменим второй столбец и то же самое проделаем для

Найдем значение

Ответ:

Пример 2

Задание 2

Решить систему уравнений с помощью метода Крамера:

Решение

Находим определитель матрицы

Заменяем первый столбец

свободными членами и находим определитель

Найдем значение

Теперь заменим на свободные члены второй столбец матрицы и найдём определитель

для

Найдем

Ответ

Пример 3

Задание 3

С помощью метода Крамера решить систему уравнений:

Решение

Как и в предыдущих примерах, сначала находим общий определитель матрицы

Заменяем первый столбец свободными членами:

Найдем значение

согласно формуле:

Найдем определитель матрицы для

заменив на свободные члены второй столбец:

Найдем значение

Ответ

Пример 4

Задание 4

Решить систему уравнений методом Крамера:

Решение

Здесь видим матрицу 3х3, следовательно определитель матрицы находим методом треугольников:

Определитель не равен 0, а значит можем продолжать решение.

Замени первый столбец матрицы на свободные члены и найдем её определитель для

Таким образом, определим значение

Таким же способом получим определитель матрицы для

заменив на свободные члены второй столбец:

Найдем

Также заменим на свободные члены значения третьего столбца и получим определитель матрицы для

Найдем

Ответ

Пример 5

Задание 5

Решить методом Крамера систему уравнений:

Решение

Аналогично, как в предыдущем примере, найдём определитель матрицы

методом треугольников:

следовательно, можем продолжать.

Найдем определитель матрицы для

Заменяем коэффициенты первого столбца:

Найдем

Найдем определитель матрицы для

Проделаем то же самое, но заменив коэффициенты второго столбца.

Найдем значение

Найдем определитель матрицы для

заменив на свободные члены третий столбец:

Найдем значение

Ответ

Пример 6

Задание 6

Решить систему уравнений методом Крамера:

Решение

Здесь мы видим, что в строках отсутствуют некоторые перемененные. Преобразим вид системы уравнений в квадратный:

Таким образом, наша матрица будет следующего вида:

Найдем определитель матрицы:

Найдем определитель матрицы для

Найдем значение

Найдем определитель матрицы для

заменив на свободные члены второй столбец:

Найдем значение

Заменим третий столбец и найдем определитель матрицы для

Найдем

Ответ

Пример 7

Задание 7

С помощью метода Крамера решить систему уравнений:

Решение

Найдем определитель матрицы

Определитель

Это значит, что данную систему нельзя решить методом Крамера, и мы не можем продолжать решение согласно нашему алгоритму.

Ответ

Метод Крамера нельзя применить к данной системе линейных уравнений

Пример 8

Задание 8

Решить систему уравнений методом Крамера:

Решение

Здесь a – это некоторое реальное число.

Найдем общий определитель матрицы

Найдем определитель матрицы

Для этого подставим в первый столбец матрицы свободные члены системы уравнений.

Найдем значение

Таким же способом найдем определитель матрицы

Найдем

Ответ

Пример 9

Задание 9

Решить систему уравнений методом Крамера:

Решение

Найдем определитель матрицы:

Найдем определитель матрицы для

заменив на свободные члены первый столбец:

Найдем значение

Найдем определитель матрицы для

:, заменив на свободные члены второй столбец:

Найдем значение

Найдем определитель матрицы для

заменив на свободные члены третий столбец:

Найдем значение

Ответ

Пример 10

Задание 10

Решить систему уравнений методом Крамера:

Решение

Преобразим вид системы уравнений в квадратный. Для этого перенесём одну из переменных в свободные члены. Так как, количество строк в системе уравнений меньше, чем количество переменных, то значение одной из переменных будет с параметром. Следовательно, система может выглядеть так:

Таким образом, наша матрица будет следующего вида:

Найдем определитель матрицы:

Если значение определителя будет равно 0, то можно попробовать перенести в свободные члены другую переменную.

Найдем определитель матрицы для переменной

. Здесь заменяем первый столбец на получившуюся сумму свободных членов:

Найдем значение

Найдем определитель матрицы для переменной

тем же способом:

Найдем

Ответ

Средняя оценка 1 / 5. Количество оценок: 1

Поставьте вашу оценку

Сожалеем, что вы поставили низкую оценку!

Позвольте нам стать лучше!

Расскажите, как нам стать лучше?

11954

Закажите помощь с работой

Не отобразилась форма расчета стоимости? Переходи по ссылке

7.

8 Решающие системы с правилом Крамера — Колледжская алгебра 2e

Цели обучения

В этом разделе вы:

Оцените 2 × 2 определителей.
Используйте правило Крамера, чтобы решить систему уравнений с двумя переменными.
Оценить 3 × 3 определителей.
Используйте правило Крамера, чтобы решить систему из трех уравнений с тремя переменными.
Знать свойства определителей.

Мы научились решать системы уравнений с двумя и тремя переменными, а также несколькими методами: подстановкой, сложением, методом исключения Гаусса, использованием обратной матрицы и построением графика. Некоторые из этих методов легче применять, чем другие, и они более подходят в определенных ситуациях. В этом разделе мы изучим еще две стратегии решения систем уравнений.

Вычисление определителя матрицы 2×2

Определитель — это действительное число, которое может быть очень полезным в математике, поскольку имеет множество применений, таких как вычисление площади, объема и других величин. Здесь мы будем использовать определители, чтобы выяснить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений. Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются закодированными в матрице. Данные могут быть расшифрованы только с помощью обратимой матрицы и определителя. Для наших целей мы сосредоточимся на определителе как признаке обратимости матрицы. Вычисление определителя матрицы включает в себя следование определенным шаблонам, описанным в этом разделе.

Найдите определитель матрицы 2 × 2

Определитель матрицы 2×22×2, заданный

A=[abcd]A=[abcd]

определяется как

Обратите внимание на изменение обозначений. Есть несколько способов указать определитель, включая det(A)det(A) и замену скобок в матрице прямыми линиями |A|.|A|.

Пример 1

Нахождение определителя матрицы 2 × 2

Нахождение определителя заданной матрицы.

А=[52-63]А=[52-63]

Решение

det(A)=|52−63|=5(3)−(−6)(2)=27det(A)=|52−63|=5(3)−(−6)(2)=27

Использование правила Крамера для решения системы двух уравнений с двумя переменными

Теперь мы представим последний метод решения систем уравнений, использующий определители. Этот метод, известный как правило Крамера, восходит к середине 18 века и назван в честь его новатора, швейцарского математика Габриэля Крамера (1704-1752), который представил его в 1750 году во Введении к анализу линий алгебры. Правило Крамера — жизнеспособный и эффективный метод поиска решений систем с произвольным числом неизвестных при условии, что у нас есть такое же количество уравнений, как и неизвестных.

Правило Крамера даст нам единственное решение системы уравнений, если она существует. Однако, если система не имеет решения или имеет бесконечное число решений, на это будет указывать нулевой определитель. Чтобы выяснить, является ли система противоречивой или зависимой, придется использовать другой метод, такой как исключение.

Чтобы понять правило Крамера, давайте внимательно посмотрим, как мы решаем системы линейных уравнений, используя основные операции со строками. Рассмотрим систему двух уравнений с двумя переменными.

a1x+b1y=c1(1)a2x+b2y=c2(2)a1x+b1y=c1(1)a2x+b2y=c2(2)

Мы исключаем одну переменную, используя операции со строками, и находим другую. Скажем, что мы хотим найти x.x. Если уравнение (2) умножить на коэффициент, противоположный коэффициенту yy в уравнении (1), уравнение (1) умножить на коэффициент yy в уравнении (2), и мы сложим два уравнения, переменная yy будет устранено.

b2a1x+b2b1y=b2c1Multiply R1by b2−b1a2x−b1b2y=−b1c2Multiply R2by−b1________________________________________________________ b2a1x−b1a2x=b2c1−b1c2b2a1x+b2b1y=b2c1Multiply R1by b2−b1a2x−b1b2y=−b1c2Multiply R2by−b1________________________________________________________ b2a1x−b1a2x=b2c1−b1c2

Теперь найдите х.х.

B2A1X -B1A2X = B2C1 -B1C2X (B2A1 -B2A2) = B2C1-B1C2 X = B2C1 -B1C2B2A1-B1A2 = | C1B1C2B2 || A1B1A2B2 | B2A1X-B1A2X = B2C1 -B2-B1C1A2B2 | B2A1X-B1A2X = B2C1C1A2B2B2 | B2A1X-B1A2X = B2C1C1A2B2 −b1c2b2a1−b1a2=|c1b1c2b2||a1b1a2b2|

Аналогично, чтобы найти y,y, мы исключим x. x.

a2a1x+a2b1y=a2c1Multiply R1by a2−a1a2x−a1b2y=−a1c2Multiply R2by−a1________________________________________________________a2b1y−a1b2y=a2c1−a1c2a2a1x+a2b1y=a2c1Multiply R1by a2−a1a2x−a1b2y=−a1c2Multiply R2by−a1________________________________________________________a2b1y−a1b2y=a2c1−a1c2

Решение для YY дает

A2B1Y -A1B2Y = A2C1 -A1C2Y (A2B1 -A1B2) = A2C1 -A1C2 Y = A2C1 -A1C2A2B1 -A1B2 = A1C2 -A2C1A1B2-A2B1 = | A1B2 = A1C2 -A2C1A1B2-A2B1 = | A1B2 = A1C2 -A2C1A1B2B1 = | A1B2 = A1C2 -A2C1A1B2 -A2B1 -A1B2 a1c2y(a2b1−a1b2)=a2c1−a1c2 y=a2c1−a1c2a2b1−a1b2=a1c2−a2c1a1b2−a2b1=|a1c1a2c2||a1b1a2b2|

Обратите внимание, что знаменатель для xx и yy является определителем матрицы коэффициентов.

Мы можем использовать эти формулы для решения xx и y,y, но правило Крамера также вводит новое обозначение:

D:D: определитель матрицы коэффициентов
Dx:Dx: определитель числителя в решении xx
x=DxDx=DxD
Dy:Dy: определитель числителя в решении yy
y=DyDy=DyD

Ключом к правилу Крамера является замена интересующего столбца переменных столбцом констант и вычисление определителей. Тогда мы можем выразить xx и yy как частное двух определителей.

Правило Крамера для систем 2×2

Правило Крамера — это метод, использующий определители для решения систем уравнений, в которых число уравнений равно количеству переменных.

Рассмотрим систему двух линейных уравнений с двумя переменными.

a1x+b1y=c1a2x+b2y=c2a1x+b1y=c1a2x+b2y=c2

Решение с использованием правила Крамера дается как

x=DxD=|c1b1c2b2||a1b1a2b2|,D≠0;y= DyD=|a1c1a2c2||a1b1a2b2|,D≠0.x=DxD=|c1b1c2b2||a1b1a2b2|,D≠0;y=DyD=|a1c1a2c2||a1b1a2b2|,D≠0.

Если мы находим x,x, столбец xx заменяется столбцом констант. Если мы ищем y, y, столбец yy заменяется столбцом констант.

Пример 2

Использование правила Крамера для решения системы 2 × 2

Решите следующую систему 2 × 22 × 2, используя правило Крамера.

12x+3y=15 2x−3y=1312x+3y=15 2x−3y=13

Решение

Решите для х. х.

x=DxD=|15313−3||1232−3|=−45−39−36−6=−84−42=2x=DxD=|15313−3||1232−3|=−45−39 −36−6=−84−42=2

Решите для y.y.

y=DyD=|1215213||1232−3|=156−30−36−6=−12642=−3y=DyD=|1215213||1232−3|=156−30−36−6=−12642 =−3

Решение: (2,−3).(2,−3).

Попытайся #1

Используйте правило Крамера, чтобы решить систему уравнений 2 × 2.

х+2у=-11-2х+у=-13 х+2у=-11-2х+у=-13

Вычисление определителя матрицы 3 × 3

Найти определитель матрицы 2 × 2 несложно, но определить определитель матрицы 3 × 3 сложнее. Один из методов состоит в том, чтобы дополнить матрицу 3×3 повторением первых двух столбцов, получив матрицу 3×5. Затем вычисляем сумму произведений записей вниз по по каждой из трех диагоналей (слева вверху справа внизу) и вычесть произведения записей вверх по по каждой из трех диагоналей (слева внизу справа вверху). Это легче понять с визуальным и пример.

Найдите определитель матрицы 3×3.

А=[a1b1c1a2b2c2a3b3c3]А=[a1b1c1a2b2c2a3b3c3]

Дополнить AA первыми двумя столбцами.
det(A)=|a1b1c1a2b2c2a3b3c3|a1a2a3b1b2b3|det(A)=|a1b1c1a2b2c2a3b3c3|a1a2a3b1b2b3|
От верхнего левого угла к нижнему правому: умножьте числа по первой диагонали. Прибавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей вниз по третьей диагонали.
Из нижнего левого угла в верхний правый: вычтите произведение записей вверх по первой диагонали. Из этого результата вычтите произведение вхождений вверх по второй диагонали. Из этого результата вычтите произведение вхождений вверх по третьей диагонали.

Алгебра выглядит следующим образом:

|A|=a1b2c3+b1c2a3+c1a2b3−a3b2c1−b3c2a1−c3a2b1|A|=a1b2c3+b1c2a3+c1a2b3−a3b2c1−b3c2a1−c3a2b1

Пример 3

Нахождение определителя матрицы 3 × 3

Нахождение определителя заданной матрицы 3 × 3

A=[0213−11401]A=[0213−11401]

Решение

Дополните матрицу первыми двумя столбцами, а затем следуйте формуле. Таким образом,

|A|=|0213−11401|0342−10|=0(−1)(1)+2(1)(4)+1(3)(0)−4(−1)(1 )−0(1)(0)−1(3)(2)=0+8+0+4−0−6=6|A|=|0213−11401|0342−10|=0(−1) (1)+2(1)(4)+1(3)(0)−4(−1)(1)−0(1)(0)−1(3)(2)=0+8+0 +4−0−6=6

Попытайся #2

Найдите определитель матрицы 3 × 3.

det(A)=|1−371111−23|det(A)=|1−371111−23|

вопросы и ответы

Можно ли использовать тот же метод, чтобы найти определитель большей матрицы?

Нет, этот метод работает только для матриц 2×22×2 и 3×33×3. Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.

Использование правила Крамера для решения системы трех уравнений с тремя переменными

Теперь, когда мы можем найти определитель матрицы 3 × 3, мы можем применить правило Крамера для решения системы трех уравнений с тремя переменными. Правило Крамера является простым и следует шаблону, согласующемуся с правилом Крамера для матриц 2 × 2. Однако по мере увеличения порядка матрицы до 3 × 3 требуется гораздо больше вычислений.

Когда мы вычисляем, что определитель равен нулю, правило Крамера не указывает, имеет ли система решение или бесконечное число решений. Чтобы выяснить это, мы должны выполнить исключение в системе.

Рассмотрим систему уравнений 3 × 3.

х=DxD,y=DyD,z=DzD,D≠0x=DxD,y=DyD,z=DzD,D≠0

где

Если мы записываем определитель Dx,Dx, мы заменяем столбец xx столбцом констант. Если мы записываем определитель Dy,Dy, мы заменяем столбец yy столбцом констант. Если мы записываем определитель Dz,Dz, мы заменяем столбец zz столбцом констант. Всегда проверяйте ответ.

Пример 4

Решение системы 3 × 3 с использованием правила Крамера

Найдите решение данной системы 3 × 3, используя правило Крамера.

x+y-z=63x-2y+z=-5x+3y-2z=14x+y-z=63x-2y+z=-5x+3y-2z=14

Решение

Используйте правило Крамера.

D=|11−13−2113−2|,Dx=|61−1−5−21143−2|,Dy=|16−13−51114−2|,Dz=|1163−2−51314|D =|11−13−2113−2|,Dx=|61−1−5−21143−2|,Dy=|16−13−51114−2|,Dz=|1163−2−51314|

Тогда

x=DxD=-3-3=1y=DyD=-9-3=3z=DzD=6-3=-2x=DxD=-3-3=1y=DyD=-9-3 =3z=DzD=6−3=−2

Решение: (1,3,−2).(1,3,−2).

Попытайся #3

Используйте правило Крамера, чтобы решить матрицу 3 × 3.

x−3y+7z=13x+y+z=1x−2y+3z=4x−3y+7z=13x+y+z=1x−2y+3z=4

Пример 5

Использование правила Крамера для решения несовместимой системы

Решите систему уравнений, используя правило Крамера.

3x−2y=4 (1)6x−4y=0 (2)3x−2y=4 (1)6x−4y=0 (2)

Решение

Начнем с нахождения определителей D,Dx и Dy.D,Dx и Dy.

D=|3−26−4|=3(−4)−6(−2)=0D=|3−26−4|=3(−4)−6(−2)=0

Мы знаем, что определитель, равный нулю, означает, что либо система не имеет решений, либо имеет бесконечное число решений. Чтобы увидеть, какой из них, мы используем процесс исключения. Наша цель — исключить одну из переменных.

Умножить уравнение (1) на −2,−2.
Добавьте результат к уравнению (2).(2).

−6x+4y=−86x−4y=0_______________0=−8−6x+4y=−86x−4y=0_______________0=−8

Получаем уравнение 0=−8,0=−8, которое неверно. Следовательно, система не имеет решения. График системы показывает две параллельные линии. См. рис. 1.

Рисунок 1

Пример 6

Использование правила Крамера для решения зависимой системы

Решите систему с бесконечным числом решений.

x−2y+3z=0(1)3x+y−2z=0(2)2x−4y+6z=0(3)x−2y+3z=0(1)3x+y−2z=0( 2)2x−4y+6z=0(3)

Решение

Сначала найдем определитель. Настройте матрицу, дополненную первыми двумя столбцами.

|1−2331−22−46 | 1−2312−4||1−2331−22−46 | 1−2312−4|

Затем

1(1)(6)+(-2)(-2)(2)+3(3)(-4)-2(1)(3)-(-4)(-2)(1)- 6(3)(-2)=01(1)(6)+(-2)(-2)(2)+3(3)(-4)-2(1)(3)-(-4) (−2)(1)−6(3)(−2)=0

Поскольку определитель равен нулю, решения либо нет, либо существует бесконечное число решений. Мы должны выполнить исключение, чтобы узнать.

Умножьте уравнение (1) на −2−2 и добавьте результат к уравнению (3):
−2x+4y−6z=02x−4y+6z=00=0−2x+4y−6z=02x−4y+6z=00=0
Получение ответа 0=0,0=0, утверждение, которое всегда верно, означает, что система имеет бесконечное число решений. Изобразив систему, мы видим, что две плоскости одинаковы и обе пересекают третью плоскость по прямой. См. рис. 2.

Рисунок 2

Понимание свойств определителей

Есть много свойств определителей. Здесь перечислены некоторые свойства, которые могут быть полезны при вычислении определителя матрицы.

Свойства определителей

Если матрица имеет форму верхнего треугольника, определитель равен произведению элементов по главной диагонали.
При перестановке двух строк определитель меняет знак.
Если две строки или два столбца идентичны, определитель равен нулю.
Если матрица содержит строку нулей или столбец нулей, определитель равен нулю.
Определитель обратной матрицы A−1A−1 является обратной величиной определителя матрицы A.A.
Если какая-либо строка или столбец умножается на константу, определитель умножается на тот же коэффициент.

Пример 7

Иллюстрация свойств определителей

Проиллюстрируйте каждое из свойств определителей.

Решение

Свойство 1 гласит, что если матрица имеет форму верхнего треугольника, определитель равен произведению элементов по главной диагонали.

A=[12302100−1]A=[12302100−1]

Дополнить AA первыми двумя столбцами.

A=[12302100−1|100220]A=[12302100−1|100220]

Тогда

det(A)=1(2)(−1)+2(1)(0)+3(0 )(0)−0(2)(3)−0(1)(1)+1(0)(2)=−2det(A)=1(2)(−1)+2(1)(0 )+3(0)(0)−0(2)(3)−0(1)(1)+1(0)(2)=−2

Свойство 2 указывает, что перестановка строк меняет знак. Учитывая

A=[−154−3],det(A)=(−1)(−3)−(4)(5)=3−20=−17B=[4−3−15],det( B)=(4)(5)−(−1)(−3)=20−3=17A=[−154−3],det(A)=(−1)(−3)−(4)( 5)=3−20=−17B=[4−3−15],det(B)=(4)(5)−(−1)(−3)=20−3=17

Свойство 3 утверждает, что если две строки или два столбца совпадают, определитель равен нулю.

А=[122222−122 | 12−1 222]det(A)=1(2)(2)+2(2)(−1)+2(2)(2)+1(2)(2)−2(2)(1) −2(2)(2)=4−4+8+4−4−8=0A=[122222−122 | 12−1 222]det(A)=1(2)(2)+2(2)(−1)+2(2)(2)+1(2)(2)−2(2)(1) −2(2)(2)=4−4+8+4−4−8=0

Свойство 4 гласит, что если строка или столбец равны нулю, определитель равен нулю. Таким образом,

A=[1200],det(A)=1(0)−2(0)=0A=[1200],det(A)=1(0)−2(0)=0

Свойство 5 утверждает, что определитель обратной матрицы A-1A-1 является обратной величиной определителя A.A. Таким образом,

A=[1234],det(A)=1(4)−3(2)=−2A−1=[−2132−12],det(A−1)=−2(−12) −(32)(1)=−12A=[1234],det(A)=1(4)−3(2)=−2A−1=[−2132−12],det(A−1)=− 2(−12)−(32)(1)=−12

Свойство 6 гласит, что если любая строка или столбец матрицы умножается на константу, определитель умножается на тот же коэффициент. Таким образом,

A=[1234],det(A)=1(4)−2(3)=−2B=[2(1)2(2)34],det(B)=2(4)−3( 4)=−4A=[1234],det(A)=1(4)−2(3)=−2B=[2(1)2(2)34],det(B)=2(4)− 3(4)=−4

Пример 8

Использование правила Крамера и свойств определителя для решения системы

Найдите решение данной системы 3 × 3.

2x+4y+4z=2(1)3x+7y+7z=-5(2) x+2y+2z=4(3)2x+4y+4z=2(1)3x+7y+7z=- 5(2) x+2y+2z=4(3)

Решение

Используя правило Крамера, мы имеем

D=|244377122|D=|244377122|

Обратите внимание, что второй и третий столбцы идентичны. Согласно свойству 3 определитель будет равен нулю, поэтому решения либо нет, либо решений бесконечное множество. Мы должны выполнить исключение, чтобы узнать.

Умножьте уравнение (3) на –2 и добавьте результат к уравнению (1).
−2x−4y−4x=−8 2x+4y+4z=20=−6−2x−4y−4x=−8 2x+4y+4z=20=−6

Получение утверждения, являющегося противоречием, означает, что система не имеет решения.

7.8 Секционные упражнения

Устный

Объясните, почему мы всегда можем вычислить определитель квадратной матрицы.

Изучая правило Крамера, объясните, почему нет единственного решения системы, когда определитель вашей матрицы равен 0. Для простоты используйте матрицу 2×22×2.

Объясните, что в терминах обратной матрицы означает наличие определителя, равного 0.

Определитель матрицы AA 2×22×2 равен 3. Если вы поменяете строки и умножите первую строку на 6, а вторую строку на 2, объясните, как найти определитель, и дайте ответ.

Алгебраический

Для следующих упражнений найдите определитель.

|1234||1234|

|−123−4||−123−4|

|2−5−16||2−5−16|

|−84−15||−84−15|

|103−4||103−4|

10.

|10200-10||10200-10|

11.

|100.250.1||100.250.1|

12.

|6−384||6−384|

13.

|−2−33,14 000||−2−33,14 000|

14.

|−1.10.67.2−0,5||−1.10.67.2−0,5|

15.

|−10001000−3||−10001000−3|

16.

|−14002300−3||−14002300−3|

17.

|101010100||101010100|

18.

|2-313-41-561||2-313-41-561|

19.

|−214−42−82−8−3||−214−42−82−8−3|

20.

|6-12-4-3519-1||6-12-4-3519−1|

21.

|51−12313−6−3||51−12313−6−3|

22.

|1,12-1-4004,1-0,42,5||1,12-1-4004,1-0,42,5|

23.

|2-1.63.11.13-8-9.302||2-1.63.11.13-8-9.302|

24.

|−12131415−16170018||−12131415−16170018|

Для следующих упражнений решите систему линейных уравнений, используя правило Крамера.

25.

2x−3y=−14x+5y=92x−3y=−14x+5y=9

26.

5x−4y=2−4x+7y=65x−4y=2−4x+7y=6

27.

6x−3y=2−8x+9y=−16x−3y=2−8x+9y=−1

28.

2x+6y=125x−2y=132x+6y=125x−2y=13

29.

4x+3y=232x-y=-14x+3y=232x-y=-1

30.

10x−6y=2−5x+8y=−110x−6y=2−5x+8y=−1

31.

4x−3y=−32x+6y=−44x−3y=−32x+6y=−4

32.

4x−5y=7−3x+9y=04x−5y=7−3x+9y=0

33.

4x+10y=180-3x-5y=-1054x+10y=180-3x-5y=-105

34.

8x−2y=−3−4x+6y=48x−2y=−3−4x+6y=4

Для следующих упражнений решите систему линейных уравнений, используя правило Крамера.

35.

x+2y-4z=-17x+3y+5z=26-2x-6y+7z=-6x+2y-4z=-17x+3y+5z=26-2x-6y+7z=-6

36.

−5x+2y−4z=−474x−3y−z=−943x−3y+2z=94−5x+2y−4z=−474x−3y−z=−943x−3y+2z=94

37.

4x+5y-z=-7-2x-9y+2z=85y+7z=214x+5y-z=-7-2x-9y+2z=85y+7z=21

38.

4x-3y+4z=105x-2z=-23x+2y-5z=-94x−3y+4z=105x−2z=−23x+2y−5z=−9

39.

4x-2y+3z=6-6x+y=-22x+7y+8z=244x-2y+3z=6-6x+y=-22x+7y+8z=24

40.

5x+2y-z=1-7x-8y+3z=1,56x-12y+z=75x+2y-z=1-7x-8y+3z=1,56x-12y+z=7

41.

13x-17y+16z=73-11x+15y+17z=6146x+10y-30z=-1813x-17y+16z=73-11x+15y+17z=6146x+10y-30z=-18

42.

−4x−3y−8z=−72x−9y+5z=0,55x−6y−5z=−2−4x−3y−8z=−72x−9y+5z=0,55x−6y−5z=−2

43.

4x-6y+8z=10-2x+3y-4z=-5x+y+z=14x-6y+8z=10-2x+3y-4z=-5x+y+z=1

44.

4x-6y+8z=10-2x+3y-4z=-512x+18y-24z=-304x-6y+8z=10-2x+3y-4z=-512x+18y-24z=-30

Технология

В следующих упражнениях используйте функцию определителя в графической утилите.

45.

|108

10300243||108

10300243|

46.

|10210-

-2-1011-2||10210-

-2-1011-2|

47.

|1217401210050022,0000002||1217401210050022,0000002|

48.

|1000230045607890||1000230045607890|

Реальные приложения

Для следующих упражнений создайте систему линейных уравнений для описания поведения. Затем вычислить определитель. Будет ли уникальное решение? Если да, то найти единственное решение.

49.

Два числа в сумме дают 56. Одно число на 20 меньше другого.

50.

Два числа в сумме дают 104. Если вы дважды сложите первое число и два раза второе число, получится 208

51.

Три числа в сумме дают 106. Первое число на 3 меньше второго числа. Третье число на 4 больше первого числа.

52.

Три числа в сумме дают 216. Сумма первых двух чисел равна 112. Третье число на 8 меньше первых двух вместе взятых.

Для следующих упражнений создайте систему линейных уравнений для описания поведения. Затем решите систему для всех решений, используя правило Крамера.

53.

Вы инвестируете 10 000 долларов на два счета, на которые начисляются 8% и 5% годовых. В конце года на ваших объединенных счетах было 10 710 долларов. Сколько было вложено в каждый счет?

54.

Вы инвестируете 80 000 долларов США в два счета, 22 000 долларов США в один счет и 58 000 долларов США в другой счет. В конце года, при условии простых процентов, вы заработали 2470 долларов в виде процентов. Второй счет получает на полпроцента меньше, чем удвоенный процент по первому счету. Каковы процентные ставки для ваших счетов?

55.

Театру необходимо знать, сколько билетов для взрослых и детей было продано из 1200 билетов. Если детские билеты стоят 5,95 долл. США, билеты для взрослых — 11,15 долл. США, а общая сумма выручки составила 12 756 долл. США, сколько было продано детских билетов и билетов для взрослых?

56.

Концертный зал продает одиночные билеты по 40 долларов США каждый и билеты для пар по 65 долларов США. Если общий доход составил 18 090 долларов США и был продан 321 билет, то сколько было продано одиночных билетов и сколько билетов для пар?

57.

Вы решили покрасить кухню в зеленый цвет. Вы создаете цвет краски, смешивая желтую и синюю краски. Вы не можете вспомнить, сколько галлонов каждого цвета вошло в вашу смесь, но вы знаете, что всего было 10 галлонов. Кроме того, вы сохранили квитанцию и знаете, что общая потраченная сумма составила 29,50 долларов США. Если каждый галлон желтого цвета стоит 2,59 доллара, а каждый галлон синего стоит 3,19 доллара, сколько галлонов каждого цвета входит в вашу зеленую смесь?

58.

Вы продали два вида шарфов на фермерском рынке и хотели бы знать, какой из них более популярен. Всего было продано 56 шарфов, желтый шарф стоил 10 долларов, фиолетовый — 11 долларов. Если ваш общий доход составил 583 доллара, сколько желтых шарфов и сколько фиолетовых шарфов было продано?

59.

В вашем саду выращиваются помидоры двух видов: зеленые и красные. Красный весит 10 унций, а зеленый весит 4 унции. У вас есть 30 помидоров общим весом 13 фунтов 14 унций. Сколько у вас помидоров каждого вида?

60.

На рынке три самых популярных овоща составляют 53% продаж овощей. Продажи кукурузы на 4% выше, чем у брокколи, продажи которой на 5% выше, чем у лука. Какую долю рынка занимает каждый овощ?

61.

На том же рынке три самых популярных фрукта составляют 37% от общего количества продаваемых фруктов. Клубники продают вдвое больше, чем апельсинов, а киви продают на один процент больше, чем апельсинов. Для каждого фрукта найдите процент от общего количества проданных фруктов.

62.

Три артиста выступили на концертной площадке. Первый стоил 15 долларов за билет, второй артист — 45 долларов за билет, а последний — 22 доллара за билет. Было продано 510 билетов на общую сумму 12 700 долларов. Если у первой группы было на 40 зрителей больше, чем у второй группы, сколько билетов было продано на каждую группу?

63.

Кинотеатр продал билеты на три фильма. Билеты на первый фильм стоили 5 долларов, билеты на второй фильм — 11 долларов, а на третий фильм — 12 долларов. На первый фильм было продано 100 билетов. Общее количество проданных билетов составило 642, а общий доход составил 6 774 доллара. Сколько билетов на каждый фильм было продано?

Для следующих упражнений используйте этот сценарий: Компания, заботящаяся о своем здоровье, решает приготовить пищевую смесь из миндаля, сушеной клюквы и орехов кешью в шоколаде. Информация о пищевой ценности этих продуктов представлена в Таблице 1.

	Жир (г)	Белок (г)	Углеводы (г)
Миндаль (10)	6	2	3
Клюква (10)	0,02	0	8
Кешью (10)	7	3,5	5,5

Стол 1

64.

Для специальной «низкоуглеводной» трейловой смеси имеется 1000 штук смеси. Общее количество углеводов 425 г, общее количество жиров 570,2 г. Если орехов кешью на 200 штук больше, чем клюквы, сколько штук каждого предмета будет в смеси?

65.

Для смеси «походной» в составе смеси 1000 шт., содержащих 390,8 г жира, 165 г белка. Если миндаля столько же, сколько орехов кешью, то сколько каждого элемента содержится в смеси?

66.

Для смеси «Энергия-бустер» в упаковке 1000 штук, содержащих 145 г белка и 625 г углеводов. Если количество миндаля и кешью в сумме равно количеству клюквы, сколько каждого элемента содержится в смеси?

Видео с вопросами: Использование правила Крамера для решения системы уравнений, определяемой с помощью определителей матрицы два на два

Стенограмма видео

Решите, используя правило Крамера, одновременных уравнений определитель матрицы отрицательный, 𝑧, отрицательный четыре, 𝑦 равно 23; определитель матрицы два, 𝑦, минус пять, 𝑥 равно 13; а определитель матрицы три, 𝑥, пять, 𝑧 равен 51.

Нас попросили использовать Cramer’s правило, чтобы решить эту проблему. Это немного отличается от того, как мы часто сталкиваемся с вопросами, связанными с использованием правила Крамера, потому что наша система линейные уравнения были даны нам в терминах определителей. Но для начала вспомним Правило Крамера. Правило Крамера говорит нам, что если определитель матрицы коэффициентов в системе линейных уравнений отличен от нуля, тогда существует единственное решение системы, заданной формулой 𝑥 равно Δ sub 𝑥 над Δ, 𝑦 равно Δ sub 𝑦 над Δ, а 𝑧 равно Δ sub 𝑧 над Δ.

Но чтобы использовать правило Крамера, нам сначала нужно, чтобы наша система линейных уравнений была в виде матрицы уравнение. Поэтому нам придется использовать определители, которые нам дали, чтобы поместить эти одновременные уравнения в матрицу уравнение. Начнем этот вопрос с оценивая определители этих матриц два на два, которые мы получили в вопрос.

Напомним, что мы находим определитель матрицы два на два 𝑎, 𝑏, 𝑐, 𝑑 путем вычисления 𝑎𝑑 минус 𝑏𝑐. Итак, давайте сначала посмотрим на это матрица минус один, 𝑧, минус четыре, 𝑦. Определитель этой матрицы равен будет отрицательным, умноженным на 𝑦. Это дает нам отрицательное 𝑦. А затем мы вычитаем 𝑧 умноженное на минус четыре. Это дает нам минус четыре 𝑧. И поскольку мы вычитаем отрицательный, мы можем записать это как плюс. Итак, определитель этой матрицы отрицательно 𝑦 плюс четыре 𝑧. И как нам дано в вопросе, это равно 23,

Мы можем сделать то же самое для второго матрица. Найдем определитель матрица два, 𝑦, минус пять, 𝑥. Сначала делаем два умножаем на 𝑥, что дает нам два 𝑥. И мы вычитаем 𝑦, умноженное на минус пять, то есть минус пять 𝑦. И снова, потому что мы вычитая минус, мы можем записать это как плюс. И как нам дано в вопросе, это равно 13,

Итак, теперь давайте сделаем третий и конечная матрица. Умножаем три на 𝑧, чтобы получить нас трое 𝑧. Мы вычитаем 𝑥, умноженное на пять, то есть пять 𝑥. А мы знаем, что это равно 51.

Итак, нам удалось взять нам даны три определителя и находим три линейных уравнения. Но для того, чтобы применить Крамера правило, нам нужно переписать систему в виде матричного уравнения. Но для этого перепишем наши уравнения так, что 𝑥-коэффициенты, 𝑦-коэффициенты и 𝑧-коэффициенты и константы совпадают. Однако мы должны быть осторожны, чтобы включить нулевые коэффициенты в нашу матрицу коэффициентов. Чтобы помочь нам сделать это, когда мы перепишем нашу систему уравнений, включим нулевые коэффициенты перед записью это как матричное уравнение.

Наше первое уравнение отрицательное 𝑦 добавить четыре 𝑧 равно 23. Но наши переменные 𝑥, 𝑦 и 𝑧 для этой системы. Таким образом, мы можем переписать это как ноль 𝑥 минус 𝑦 плюс четыре 𝑧 равно 23. Таким образом, мы можем сделать то же самое для нашего второе уравнение. Второе уравнение не включает любые коэффициенты для 𝑧. Поэтому мы перепишем это как два 𝑥 плюс пять 𝑦 плюс ноль 𝑧 равно 13. Тогда мы можем сделать последнее уравнение. Мы пишем это как минус пять 𝑥 плюс ноль 𝑦 плюс три 𝑧 равно 51. Мы включаем ноль 𝑦, потому что уравнение изначально не имело 𝑦-коэффициентов. Кроме того, мы переставляем это так, чтобы 𝑥 сначала идут, потом 𝑦, потом 𝑧. Написание таким образом делает его гораздо проще поместить эту систему в матричное уравнение.

Я собираюсь освободить место, так что что у нас есть только наши уравнения, которые выделены оранжевым цветом. Итак, вот наши три уравнения, и мы собираемся поместить это в матричное уравнение. Матричное уравнение имеет три частей: матрица коэффициентов, которая представляет собой матрицу, состоящую из коэффициентов наши переменные 𝑥, 𝑦 и 𝑧; переменная матрица, которая состоит из переменных для нашей системы; и постоянная матрица, матрица, состоящая из констант.

Итак, давайте сначала заполним элементы для матрицы коэффициентов, то есть коэффициенты для наших переменных. Помните об осторожности с отрицательный 𝑦 в первом уравнении, потому что коэффициент отрицательный. Теперь вы понимаете, почему мы переписали уравнения таким образом, чтобы включить нулевые коэффициенты. Переменная матрица состоит из переменные в нашей системе. Это 𝑥, 𝑦 и 𝑧. И, наконец, постоянная матрица состоит из констант нашей системы уравнений. Это 23, 13 и 51.

Теперь мы можем начать думать о применяя правило Крамера. Для этого нам понадобится Δ суб 𝑥, Δ суб 𝑦, Δ суб 𝑧 и Δ. В этот момент мы помним, что Δ sub 𝑥, Δ sub 𝑦 и Δ sub 𝑧 — определители матриц, которые формируются в результате замены элементов матрицы констант на элементы столбцов 𝑥-, 𝑦- и 𝑧-коэффициентов. Итак, давайте продолжим и найдем значения для Δ sub 𝑥, Δ sub 𝑦 и Δ sub 𝑧.

Δ sub 𝑥 является определителем матрица, которую мы получаем, когда мы берем матрицу коэффициентов и подставляем элементы из постоянная матрица с элементами из столбца 𝑥-коэффициентов, что есть определитель матрицы 23, отрицательная единица, четыре, 13, пять, ноль, 51, ноль, три. В этот момент мы можем вспомнить, как мы найти определитель матрицы три на три. Мы используем эту формулу, которая включает нахождение определителей матриц два на два, известных как кофакторы матрица три на три. Итак, давайте воспользуемся этим, чтобы найти Δ 𝑥.

Обратите внимание, что у нас минус минус здесь, так что мы можем написать это как плюс. Теперь мы можем решить это с помощью вычисление определителей каждой из этих матриц кофакторов. Определитель первого Матрица кофакторов находится путем умножения пяти на три минус ноль, умноженного на нуль. Это дает нам 15. Тогда мы можем найти определитель матрицы второго кофактора. Мы делаем это, делая 13 умножить на три минус ноль, умноженное на 51. Это дает нам 39. Наконец, находим определитель последняя кофакторная матрица. И мы делаем это, делая 13 умножить на ноль минус пять умножить на 51. Получится отрицательное число 255.

Итак, теперь я подставлю эти значения. Так что нам просто нужно вычислить 23 умножить на 15 добавить один умножить на 39 добавить четыре умножить на минус 255. И мы можем вычислить это как отрицательный 636. Итак, мы обнаружили, что Δ sub 𝑥 отрицательное 636.

Теперь мы можем вычислить Δ sub 𝑦, используя точно такой же метод. Сначала я освобожу немного места. Δ sub 𝑦 — это матрица, которую мы получаем, когда заменяем элементы постоянной матрицы коэффициентами при 𝑦 из матрица коэффициентов. И мы будем использовать тот же метод, что и просто использовал, чтобы найти определитель для этой матрицы. Отсюда снова вычисляем определитель этих кофакторов. будет 39, шесть и 167. Итак, мы вычисляем ноль умножить на 39 минус 23 умножить на шесть добавить четыре умножить на 167. Это дает нам 530. Итак, Δ sub 𝑦 равно 530.

И таким же образом мы теперь рассчитать Δ к югу от 𝑧. Мы находим ∆ sub 𝑧, находя определитель матрицы, который мы получим, если подставим элементы постоянная матрица с коэффициентами 𝑧 из матрицы коэффициентов. Затем мы можем использовать тот же метод для найти определитель. Затем вычисляем определители кофакторов, то есть 255, 167 и 25. Итак, теперь мы можем вычислить ноль умножить на 255, добавить единицу, умножить на 167, добавить 23, умножить на 25. И мы находим, что это дает нам 742. Таким образом, Δ sub 𝑧 равно 742.

Итак, последнее, что нам нужно найти это Δ. Δ – определитель матрица коэффициентов. Итак, еще раз, мы собираемся используйте тот же метод, чтобы найти определитель этой матрицы три на три. Опять же, нам нужно найти определитель каждой из этих матриц кофакторов. Мы находим, что первый равен 15. Второй равен шести. А третий – 25. Итак, мы вычисляем ноль умножить на 15 добавить один умножить на шесть добавить четыре умножить на 25. И это дает нам 106. Итак, Δ равно 106.

Теперь у нас есть все компоненты что нам нужно использовать правило Крамера. У нас есть Δ суб 𝑥, Δ суб 𝑦, Δ суб 𝑧 и Δ. Итак, теперь мы можем заменить эти значений в уникальное решение из правила Крамера, чтобы найти наши значения для 𝑥, 𝑦, и 𝑧. Начиная с 𝑥 равно Δ sub 𝑥 над Δ, и поскольку мы обнаружили, что Δ sub 𝑥 отрицательное 636, а Δ равно 106, поэтому 𝑥 равно отрицательному 636 больше 106. Поскольку 106 входит в 636 шесть раз, это всего лишь минус шесть. Правило Крамера также говорит нам, что 𝑦 равно ∆ sub 𝑦 над ∆. Это 530 на 106. А так как 530 разделить на 106 будет пять, у нас есть, что 𝑦 равно пяти. И, наконец, мы находим 𝑧, выполняя Δ суб 𝑧 над Δ. Это дает нам 742 на 106. И 742, деленное на 106, равно Семь.

Итак, наш окончательный ответ: 𝑥 равно минус шесть, 𝑦 равно пяти, а 𝑧 равно семи.

Решающие системы, использующие правило Крамера

Решающие системы, использующие правило Крамера Примечания, урок 6.

5 Матрицы и определители

Мы встретили операцию нахождения определителя. Теперь мы видим, что мы можем найти определитель любой квадратной матрицы.

Определение:

Несовершеннолетний	Определитель формируется, когда строка и столбец, содержащие этот элемент удаляются. Примеры следуют.
	В матрице слева минор b:
	В матрице слева минор а:
	В матрице слева минор e:
	В матрице слева минор до:
	В матрице слева минор ре:

Мы говорим об n-упорядоченных определителях.

Определители можно найти только для квадрата матрицы.

	Определитель матрицы 2-го порядка.
	Определитель матрицы 3-го порядка.
а умножить на меньшую – b умножить на меньшую + с умножить на меньшую	Другой способ описания определителя матрицы 3-го порядка.

Пример проблемы.
.

Оцените это выражение, используя младшие:	Данная проблема.
	Разверните выражение, используя определение определителя матрицы 3-го порядка и миноров.
	Найдите определители Матрицы 2-го порядка.
	-60 – это решение.

До сих пор мы решали линейные системы с помощью 1) построения графиков; 2) замена; а также 3) Ликвидация. В этом уроке мы изучим четвертую технику. На самом деле, это Техника является разновидностью Метода исключения. Правило о коэффициентах будет развиваться. Это правило называется Крамера. Правило . Мы начнем с решения общей системы линейных уравнений в стандартной форме.

	Решите данную систему общих линейных уравнений.
	Умножить уравнение A на e. Умножьте уравнение B на -b. Добавьте уравнения устранить ю. Решите для х.
	Подставьте решение x из последнего шага в уравнение A. Решите для у.
	Решение
	Проверьте значения в уравнении A.
	Проверьте значения в уравнении B.

Значения x и y, которые мы нашли выше, всегда будут давать нам решение системы двух линейных уравнений (если уравнения записаны в стандартной форме). С помощью этой формулы мы может игнорировать переменные x и y и алгебраические методы решения и сосредоточиться на коэффициентах а, б, в, г, д, и ф. Мы можем взять эти коэффициенты и поместите их в матрицу или сетку, и сконцентрируйтесь на расчетах с ними.

Матрица	Прямоугольный массив чисел со столбцами и строками. Матрица 2 на 2 означает 2 строки и 2 столбца. Матрица коэффициентов из системы выше было бы: , который представляет собой матрицу 2 на 3.
Определитель	Определен определитель матрицы 2 на 2 (определитель второго порядка) на примере. Этот операция может быть выполнена только на квадратной матрице.

Крамерс Правило

Решение системы: составляет:

Если вы внимательно посмотрите на Крамера Правило выше, и помните определение определителя второго порядка, вы увидите те же результаты, что и в начале урока.

Используя правило Крамера, решите систему:	Данная проблема
а=3; б=-7; с=2; д=6; е=-13; f=4	Определить коэффициенты
	Используйте правило Крамера, чтобы найти значение x.
	Используйте правило Крамера, чтобы найти значение y.
	Проверьте значения в первом уравнении.
	Проверьте значения во втором уравнении.
(2/3,0)	Решение
Система непротиворечива и независима	Линии пересекаются в одной точке.

Детальное решение по методу Крамера. Метод Крамера для решения систем линейных уравнений

В первой части мы рассмотрели некоторый теоретический материал, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу, рекомендую прочитать первую часть. Возможно, некоторым посетителям материал покажется слишком простым, но в ходе решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.

А теперь разберем правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы(матричный метод). Все материалы представлены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными методами.

Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, посеместровым сложением!

Дело в том, что пусть иногда, но есть такая задача – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет вам понять, как использовать правило Крамера для более сложного случая — системы из трех уравнений с тремя неизвестными.

Кроме того, существуют системы линейных уравнений с двумя переменными, которые желательно решать точно по правилу Крамера!

Рассмотрим систему уравнений

На первом шаге вычисляем определитель , он называется главный определитель системы .

Метод Гаусса.

Если , то система имеет единственное решение, и для нахождения корней необходимо вычислить еще два определителя:
и

На практике вышеуказанные определители можно обозначать и латинской буквой.

Корни уравнения находятся по формулам:
,

Пример 7

Решить систему линейных уравнений

Решение : Видим, что коэффициенты уравнения довольно большие, в правой части стоят десятичные дроби через запятую. Запятая — довольно редкий гость в практических задачах по математике; Я взял эту систему из эконометрической задачи.

Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся ужасные навороченные дроби, с которыми крайне неудобно работать, а оформление решения будет выглядеть просто ужасно. Вы можете умножить второе уравнение на 6 и вычесть член за членом, но здесь появятся те же самые дроби.

Что делать? В таких случаях на помощь приходят формулы Крамера.

;

Ответ : ,

Оба корня имеют бесконечные хвосты и находятся приближенно, что вполне приемлемо (и даже обычно) для задач эконометрики.

Комментарии здесь не нужны, так как задача решается по готовым формулам, однако есть один нюанс. При использовании этого метода обязательный Фрагмент задания представляет собой следующий фрагмент: “значит система имеет единственное решение” . В противном случае рецензент может наказать вас за неуважение к теореме Крамера.

Не лишней будет проверка, которую удобно проводить на калькуляторе: подставляем приблизительные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, находящиеся в правой части.

Пример 8

Выразите ответ в виде обыкновенных неправильных дробей. Сделайте чек.

Это пример для самостоятельного решения (пример изящного оформления и ответ в конце урока).

Перейдем к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Найдем главный определитель системы:

Если , то система имеет бесконечно много решений или несовместна (не имеет решения). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.

Если , то система имеет единственное решение, и для нахождения корней надо вычислить еще три определителя:
, ,

И, наконец, ответ вычисляется по формулам:

Как видим, « Случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «гуляет» слева направо по столбцам главного определителя.

Пример 9

Решите систему, используя формулы Крамера.

Решение : Решим систему по формулам Крамера.

, поэтому система имеет единственное решение.

Ответ : .

Собственно, тут опять комментировать особо нечего, ввиду того, что решение принимается по готовым формулам. Но есть пара замечаний.

Бывает, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Рекомендую следующий алгоритм “лечения”. Если под рукой нет компьютера, делаем так:

1) Возможна ошибка в расчетах. Как только вы столкнулись с «плохим» кадром, нужно сразу проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители с помощью разложения в другой строке (столбце).

2) Если в результате проверки ошибок не обнаружено, то, скорее всего, в условии задания допущена опечатка. В этом случае спокойно и ВНИМАТЕЛЬНО решите задачу до конца, а затем обязательно проверить и составить его на чистом экземпляре после принятия решения. Конечно, проверка дробного ответа — занятие неприятное, но это будет обезоруживающим аргументом для преподавателя, который ну очень любит ставить минус за всякую гадость вроде. Как обращаться с дробями, подробно описано в ответе к Примеру 8.

Если у вас есть компьютер под рукой, то используйте для его проверки автоматизированную программу, которую можно скачать бесплатно в самом начале урока. Кстати, пользоваться программой выгоднее всего сразу (еще до запуска решения), вы сразу увидите промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически вычисляет решение системного матричного метода.

Второе замечание. Время от времени встречаются системы, в уравнениях которых отсутствуют некоторые переменные, например:

Здесь в первом уравнении нет переменной , во втором нет переменной . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать основной определитель:
– вместо пропущенных переменных ставятся нули.
Кстати, определители с нулями рационально открывать в той строке (столбце), в которой стоит ноль, так как вычислений заметно меньше.

Пример 10

Решите систему, используя формулы Крамера.

Это пример для самостоятельного решения (завершающий образец и ответ в конце урока).

Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Вы можете увидеть живой пример в уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне разрешимы. Хотя задание уже очень напоминает профессорский ботинок на груди счастливчика-студента.

Решение системы с помощью обратной матрицы

Метод обратной матрицы является по существу частным случаем матричного уравнения (см. Пример №3 указанного занятия).

Для изучения этого раздела необходимо уметь разлагать определители, находить обратную матрицу и производить умножение матриц. Соответствующие ссылки будут даны по мере продвижения объяснения.

Пример 11

Решить систему матричным методом

Решение : Запишем систему в матричной форме:
, где

Посмотрите пожалуйста на систему уравнений и матрицы. По какому принципу мы записываем элементы в матрицы, думаю всем понятно. Единственное замечание: если бы в уравнениях отсутствовали какие-то переменные, то в матрице на соответствующие места пришлось бы ставить нули.

Находим обратную матрицу по формуле:
, где – транспонированная матрица алгебраического сложения соответствующих элементов матрицы .

Сначала разберемся с определителем:

Здесь определитель расширяется первой строкой.

Внимание! Если , то обратной матрицы не существует и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (метод Гаусса).

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Ссылка: Полезно знать значение двойных нижних индексов в линейной алгебре. Первая цифра — это номер строки, в которой находится элемент. Вторая цифра – это номер столбца, в котором находится элемент:

То есть двойной нижний индекс указывает на то, что элемент находится в первой строке, третьем столбце, тогда как, например, элемент находится в 3-й строке, 2-м столбце

Методы Kramer и Gaussian один из самых популярные решения СЛАУ . Более того, в ряде случаев целесообразно использовать специфические методы. Сессия подошла к концу, и сейчас самое время повторить или освоить их с нуля. Сегодня мы займемся решением методом Крамера. Ведь решение системы линейных уравнений по методу Крамера — очень полезный навык.

Системы линейных алгебраических уравнений

Линейные системы алгебраических уравнений – система уравнений вида:

Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и б — реальные коэффициенты. Простую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме или выразить одну переменную через другую. Но переменных (x) в СЛАУ может быть гораздо больше, чем две, и здесь не обойтись без простых школьных манипуляций. Что делать? Например, решить СЛАУ методом Крамера!

Пусть система будет n уравнений с n неизвестно.

Такую систему можно переписать в матричной форме

Здесь A – основная матрица системы, X и В соответственно, матрицы столбцов неизвестных переменных и свободных членов.

Раствор СЛАЭ по Крамеру

Если определитель основной матрицы не равен нулю (матрица невырожденная), то система может быть решена методом Крамера.

По методу Крамера решение находится по формулам:

Здесь дельта — определитель главной матрицы, а дельта х n-й – определитель, полученный из определителя основной матрицы заменой n-го столбца на столбец свободных членов.

В этом весь смысл метода Крамера. Подставляя найденные значения по приведенным выше формулам х в нужную систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы помочь вам быстро вникнуть в суть, приведем ниже пример подробного решения СЛАУ методом Крамера:

Даже если у вас не получится с первого раза, не расстраивайтесь! Немного потренировавшись, вы начнете щелкать SLOW, как орехи. Более того, теперь совершенно не нужно корпеть над тетрадью, решая громоздкие вычисления и записывая на стержне. СЛАУ методом Крамера легко решить онлайн, просто подставив коэффициенты в готовую форму. опробовать решения онлайн-калькулятора по методу Крамера можно, например, на этом сайте.

А если система оказалась упрямой и не сдается, вы всегда можете обратиться за помощью к нашим авторам, например, к . Если в системе будет хотя бы 100 неизвестных, мы обязательно решим ее правильно и точно в срок!

2. Решение систем уравнений матричным методом (с использованием обратной матрицы).
3. Метод Гаусса для решения систем уравнений.

Метод Крамера.

Метод Крамера применяется для решения систем линейных алгебраических уравнений ( ЯРБ ).

Формулы на примере системы двух уравнений с двумя переменными.
Дано: Решить систему методом Крамера

Относительно переменных X и в .
Решение:
Найдите определитель матрицы, составленной из коэффициентов системы Вычисление определителей. :

Применим формулы Крамера и найдем значения переменных:
и .
Пример 1:
Решите систему уравнений:

относительно переменных X и на .
Решение:

Проделаем аналогичное действие, заменив второй столбец в первом определителе :

Применим Формулы Крамера и найдем значения переменных:
и .
Ответ:
Комментарий: Этот метод можно использовать для решения систем больших размерностей.

Комментарий: Если оказывается, что , и на ноль делить нельзя, то говорят, что система не имеет единственного решения. В этом случае система либо имеет бесконечно много решений, либо вообще не имеет решений.

Пример 2 (бесконечное количество решений):

Решить систему уравнений:

относительно переменных X и на .
Решение:
Найдите определитель матрицы, составленной из коэффициентов системы:

Решение систем методом подстановки.

Первым из уравнений системы является равенство, верное при любых значениях переменных (потому что 4 всегда равно 4). Так что осталось только одно уравнение. Это уравнение связи между переменными.
Получили, что решением системы является любая пара значений переменных, связанных равенством.
Общее решение будет записано так:
Частные решения можно определить, выбрав произвольное значение y и вычислив x из этого уравнения связи.

и т.д.
Таких решений бесконечно много.
Ответ: общее решение
Частные решения:

Пример 3 (нет решений, система несовместна):

Решить систему уравнений:

Решение:
Найти определитель матрицы коэффициентов системы:

Вы не можете использовать формулы Крамера. Решим эту систему методом подстановки

Второе уравнение системы представляет собой равенство, которое не выполняется ни при каких значениях переменных (разумеется, так как -15 не равно 2). Если одно из уравнений системы не верно ни при каких значениях переменных, то вся система не имеет решений.
Ответ: решений нет

Метод Крамера или так называемое правило Крамера – это способ поиска неизвестных величин из систем уравнений. Его можно использовать только в том случае, если количество искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть основная матрица, образованная из системы, должна быть квадратной и не содержать нулевых строк, а также если ее определитель должен не быть нулем.

Теорема 1

Теорема Крамера Если главный определитель $D$ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений совместна, и она имеет уникальное решение. Решение такой системы вычисляется по так называемым формулам Крамера для решения систем линейных уравнений: $x_i = \frac(D_i)(D)$

Что такое метод Крамера

Суть метода Крамера заключается в следующим образом:

Для решения системы методом Крамера прежде всего вычислим главный определитель матрицы $D$. Когда вычисленный определитель основной матрицы при вычислении методом Крамера оказался равным нулю, то система не имеет единственного решения или имеет бесконечное число решений. В этом случае для нахождения общего или какого-то базового ответа для системы рекомендуется применять метод Гаусса.
Затем необходимо заменить последний столбец основной матрицы на столбец свободных членов и вычислить определитель $D_1$.
Повторите то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ — номер самого правого столбца.
После того, как все определители $D_1$…$D_n$ найдены, можно вычислить неизвестные переменные по формуле $x_i = \frac(D_i)(D)$.

Методика вычисления определителя матрицы

Для вычисления определителя матрицы размерностью более 2 на 2 можно использовать несколько методов:

Правило треугольников, или правило Сарруса, напоминающее то же правило. Суть метода треугольника заключается в том, что при вычислении определителя произведения всех чисел, соединенных на рисунке красной чертой справа, они записываются со знаком плюс, а все числа, соединенные аналогичным образом на рисунке на слева со знаком минус. Оба правила подходят для матриц 3×3. В случае правила Сарруса сначала переписывается сама матрица, а рядом с ней снова переписываются ее первый и второй столбцы. Через матрицу проводят диагонали и эти дополнительные столбцы, элементы матрицы, лежащие на главной диагонали или параллельно ей, записывают со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей, записывают со знаком минус.

Рис. 1. Правило треугольников для вычисления определителя по методу Крамера

При использовании метода, известного как метод Гаусса, этот метод также иногда называют редукцией определителя. При этом матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа на главной диагонали. Следует помнить, что при таком поиске определителя нельзя умножать или делить строки или столбцы на числа, не вынося их в качестве множителя или делителя. В случае поиска определителя возможно только вычитание и сложение строк и столбцов друг к другу, предварительно умножив вычитаемую строку на ненулевой коэффициент. Также при каждой перестановке строк или столбцов матрицы следует помнить о необходимости смены конечного знака матрицы.
При решении СЛАУ Крамера с 4 неизвестными лучше всего использовать метод Гаусса для поиска и нахождения определителей или определить определитель через поиск миноров.

Решение систем уравнений методом Крамера

Применяем метод Крамера для системы из 2 уравнений и двух искомых величин:

$\begin(cases) a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \ end(cases)$

Для удобства отобразим в развернутом виде:

$A = \begin(array)(cc|c) a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end(array)$

Найти определитель основной матрицы, также называемый главным определителем системы:

$D = \begin(array)(|cc|) a_1 & a_2 \\ a_3 & a_4 \\ \end(array) = a_1 \cdot a_4 – a_3 \cdot a_2$

Если основной определитель не равен нулю, то для решения слау методом Крамера необходимо вычислить еще пару определителей из двух матриц с заменой столбцов основной матрицы строкой свободных членов:

$D_1 = \begin(массив)(|cc|) b_1 & a_2 \\ b_2 & a_4 \\ \end(массив) = b_1 \cdot a_4 – b_2 \cdot a_4$

$D_2 = \begin(массив )(|cc|) a_1 & b_1 \\ a_3 & b_2 \\ \end(array) = a_1 \cdot b_2 – a_3 \cdot b_1$

Теперь найдем неизвестные $x_1$ и $x_2$:

$ x_1 = \frac (D_1)(D)$

$x_2 = \frac (D_2)(D)$

Пример 1

Метод Крамера для решения СЛАУ с основной матрицей 3-го порядка (3 x 3) и тремя желаемые.

Решить систему уравнений:

$\begin(cases) 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 – x_3 = 10 \\ \end(cases)$

Вычисляем главный определитель матрицы по приведенному выше правилу под номером 1:

$D = \begin(array)(|ccc|) 3 & -2 & 4 \\3 & 4 & -2 \\ 2 & -1 & 1 \\ \end(массив) = 3 \cdot 4 \cdot (-1) + 2 \cdot (-2) \cdot 2 + 4 \cdot 3 \cdot (-1) – 4 \cdot 4 \ cdot 2 – 3 \cdot (-2) \cdot (-1) – (- 1) \cdot 2 \cdot 3 = – 12 – 8 -12 -32 – 6 + 6 = – $64

А теперь еще три определителя:

$D_1 = \begin(array)(|ccc|) 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \end(array) = 21 \cdot 4 \cdot 1 + (- 2) \cdot 2 \cdot 10 + 9 \cdot (-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9 \cdot (-2) \cdot (-1 ) – (-1) \cdot 2 \ cdot 21 = – 84 – 40 – 36 – 160 – 18 + 42 = – $296

$D_2 = \begin(array)(|ccc|) 3 & 21 & 4 \\ 3 & 9 & 2 \\ 2 & 10 & 1 \\ \end(массив) = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \cdot 2 – 4 \cdot 9\cdot 2 – 21 \cdot 3 \cdot (-1) – 2 \cdot 10 \cdot 3 = – 27 + 120 + 84 – 72 + 63 – 60 = $108

$D_3 = \begin(массив)(|ccc |) 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \end(массив) = 3 \cdot 4 \cdot 10 + 3 \cdot (-1) \cdot 21 + ( -2) \cdot 9 \cdot 2 – 21 \cdot 4 \cdot 2 – (-2) \cdot 3 \cdot 10 – (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = – $ 60

Найдем искомые значения:

$x_1 = \frac(D_1) (D) = \frac(- 296)(-64) = 4 \frac(5)(8)$

$x_2 = \frac(D_1) (D) = \frac(108) (-64) = – 1 \frac (11) (16)$

$x_3 = \frac(D_1) (D) = \ frac(-60) (-64) = \frac (15) (16)$

Метод Крамера основан на использовании определителей при решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера можно использовать для решения системы линейных уравнений, количество которых равно количеству неизвестных в каждом уравнении. Если определитель системы не равен нулю, то при решении можно использовать метод Крамера; если он равен нулю, то не может. Кроме того, метод Крамера можно использовать для решения систем линейных уравнений, имеющих единственное решение.

Определители

получаются заменой коэффициентов при соответствующих неизвестных свободными членами:

;

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет единственное решение, а неизвестное равно отношению определителей. В знаменателе стоит определитель системы, а в числителе – определитель, полученный из определителя системы заменой коэффициентов с неизвестными свободными членами. Эта теорема верна для системы линейных уравнений любого порядка.

Пример 1 Решаем систему линейных уравнений:

Согласно Теореме Крамера имеем:

Итак, решение системы (2):

516 90 калькулятор Крамера онлайн .

Три случая при решении систем линейных уравнений

Как следует из теорем Крамера , при решении системы линейных уравнений возможны три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система непротиворечивая и определенная)

Второй случай: система линейных уравнений имеет бесконечное число решений

(система непротиворечивая и неопределенная)

** ,

т.е. коэффициенты при неизвестных и свободных членах пропорциональны.

Третий случай: система линейных уравнений не имеет решений

(система несовместная)

Итак, система m линейных уравнений с n переменных называется несовместимой , если не имеет решений, и совместной , если имеет хотя бы одно решение. Совместная система уравнений, которая имеет только одно решение, называется определенным , а более одного неопределенным .

Примеры решения систем линейных уравнений методом Крамера

Пусть система

На основе теоремы Крамера

………….
,

, где
–

системный идентификатор. Остальные определители получаются заменой в столбце коэффициентов соответствующей переменной (неизвестной) со свободными членами:

Пример 2

Следовательно, система определена. Для ее решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) — единственное решение системы.

Для проверки решений систем уравнений 3 X 3 и 4 X 4 можно воспользоваться онлайн-калькулятором, методом решения Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях нет переменных, то в определителе соответствующие им элементы равны нулю! Это следующий пример.

Пример 3 Решить систему линейных уравнений методом Крамера:

Раствор. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система определена. Чтобы найти ее решение, вычисляем определители для неизвестных

По формулам Крамера находим:

Итак, решение системы (2; -1; 1).

Начало страницы

Продолжаем решать системы методом Крамера вместе

Как уже было сказано, если определитель системы равен нулю, а определители при неизвестных не равны нулю, то система несовместна, то есть не имеет решений. Проиллюстрируем на следующем примере.

Пример 6 Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определена, либо несовместна, то есть не имеет решений. Для уточнения вычислим определители для неизвестных

Определители для неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

В задачах на системы линейных уравнений есть и такие, где кроме букв, обозначающих переменные, есть еще и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное число. На практике такие уравнения и системы уравнений приводят к задачам поиска общих свойств каких-либо явлений или объектов. То есть вы изобрели какой-либо новый материал или устройство, и для описания его свойств, общих вне зависимости от размера или количества экземпляров, необходимо решить систему линейных уравнений, где вместо каких-то коэффициентов при переменных стоит являются письма. За примерами далеко ходить не надо.

Следующий пример для аналогичной задачи, только увеличивается количество уравнений, переменных и букв, обозначающих некоторое действительное число.

Пример 8 Решить систему линейных уравнений методом Крамера:

Решение. Мы находим определитель системы:

Нахождение определителей для неизвестных

17 Предварительное исчисление – правило Крамера

Мы можем использовать матрицы и определители для решения систем линейных уравнений, используя технику, называемую правилом Крамера. Мы покажем, как это сделать с двумя уравнениями и двумя неизвестными. Однако эту концепцию можно распространить и на системы более высокого порядка.

Дана система линейных уравнений вида
$ \begin{массив}{ccccc} топор & + & по & = & z_0 \\ cx & + & dy & = & z_1 \конец{массив} $
, где $ a, b, c, d, z_0, z_1 $ все вещественные константы, а переменные $ x$ и $y $.

Нам нужно найти, какие значения $x$ и $y$ решают это уравнение. Возможны три случая.
1. $x$ и $y$ действительны, единственны и не равны.
2. $х$ и $у$ действительны и равны.
3. $x$ и $y$ комплексны.

Чтобы определить, какой случай имеет место, нужно посмотреть на определитель матрицы коэффициентов, т. е.
$ \begin{vmatrix} а и б \\ CD \end{vmatrix} $
Если этот определитель равен нулю, то мы не можем использовать эту технику, и выполняется либо случай 2, либо случай 3. Если этот случай отличен от нуля, то имеет место случай 1, и мы можем решить эту проблему. Назовем матрицу коэффициентов $A$ и так
$ \абс{А} = \begin{vmatrix} а и б \\ CD \end{vmatrix} $

Пока определитель матрицы коэффициентов НЕ равен нулю, мы можем решить эту систему уравнений, и значения будут равны
$\displaystyle{ х = \ гидроразрыв { \begin{vmatrix} z_0 & б \\ z_1 и д \end{vmatrix} }{\абс{А}} }$ а также $\displaystyle{ у = \ гидроразрыв { \begin{vmatrix} а & z_0 \\ с и z_1 \end{vmatrix} }{\абс{А}} }$

Обратите внимание, что в каждом случае выше мы заменили столбец матрицы $A$, соответствующий вычисляемой нами переменной, константами $z$.

Лучший способ изучить правило Крамера — понаблюдать за тем, как кто-то решает конкретные задачи, а затем много работать самостоятельно. Для начала вот видео, показывающее, в целом, как пользоваться правилом Крамера, затем он делает конкретный пример. После этого видео вы сможете решать задачи самостоятельно.

Хотя большинство приведенных ниже решений не показывают работу, важно проверять свою работу при использовании правила Крамера. Как вы видели из видео и увидите в решениях, очень и очень легко совершать ошибки, которые распространяются и дают вам все неправильные ответы. Поэтому важно снова подставить свои ответы ко всем уравнениям, чтобы убедиться, что у вас есть правильные ответы. Ваша работа может считаться незавершенной, если вы не проверите свои ответы (в зависимости от того, что ожидает ваш преподаватель). Так что просто привыкайте всегда проверять свои ответы. Это может быть разница между целой буквенной оценкой и занимает всего несколько секунд.

Практика. Системы 2×2

Если не указано иное, решите эти линейные системы с помощью правила Крамера.

$ 3x+4y=-14; $ $ -2x-3y=11 $

Постановка задачи

Решите $ 3x+4y=-14; $ $-2x-3y=11 $ с помощью правила Крамера.

Окончательный ответ

$x=2, y=-5$

Постановка задачи

Решить $ 3x+4y=-14; $ $ -11x-3y=-11x-3y $ по правилу Крамера.

Решение

Криста Кинг Математика – 1884 видео решение

видео Криста Кинг Математика

Окончательный ответ 9x

, 0-52040005

Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг.

$ 5x+7y=-1; $ $ 6x+8y=1 $

Постановка задачи

Решите эту линейную систему, используя правило Крамера.
$ 5x+7y=-1; $ $ 6x+8y=1 $

Окончательный ответ

$x=15/2, y=11/2$

Постановка задачи

Решите эту линейную систему, используя правило Крамера.
$ 5x+7y=-1; $ $ 6x+8y=1 $

Решение

Thinkwell – 1885 видеорешение6 9 in чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг.

видео Thinkwell

5 9009 0 9 06559 Final 9 0655

$x=15/2, y=11/2$

Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг.

$ 4x-2y=10; $ $ 3x-5y=11 $

Постановка задачи

Решите эту линейную систему, используя правило Крамера.
$ 4x-2y=10; $ $ 3x-5y=11 $

Окончательный ответ

$ x=2, y=-1 $

Постановка задачи

4 Решите эту линейную систему, используя правило Крамера.

$ 4x-2y=10; $ $ 3x-5y=11 $

Solution

mattemath – 1894 видео решение6 Журнал чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг.

видео от mattemath

0655

Окончательный ответ

$ x=2, y=-1 $

Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг.

$x-y=-3; $ $x+4y=17 $

Постановка задачи

Решите эту линейную систему, используя правило Крамера.
$ x-y=-3; $ $ x+4y=17 $

Окончательный ответ

$ x=1, y=4 $

Постановка задачи

Решить это линейная система с использованием правила Крамера.
$ x-y=-3; $ $ x+4y=17 $

Решение

MIP4U – 1895 видео решение

видео от MIP4U

Окончательный ответ

$ x=1, y=4 $

Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг.

$ 2x-3y=16;$ $x+2y=1 $

Постановка задачи

Решите эту линейную систему, используя правило Крамера.
$ 2x-3y=16;$ $ x+2y=1 $

Окончательный ответ

$ x=5, y=-2 $

Постановка задачи

5 Решите эту линейную систему, используя правило Крамера.

$ 2x-3y=16;$ $ x+2y=1 $

Решение

MIP4U – 1897 видео решение

видео от MIP4U

Окончательный ответ

$ x=5, y=-2 $

Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг.

$ 2х + 5у = 26 $
$ 5х – 4у = -1 $

Постановка задачи

Решите эту линейную систему, используя правило Крамера.
$ 2x + 5y = 26 $
$ 5x – 4y = -1 $

Окончательный ответ

$ (3, 4) $

Решить эту задачу

0 Задача линейная система с использованием правила Крамера.
$ 2x + 5y = 26 $
$ 5x – 4y = -1 $

Решение

2855 видео решение

Окончательный ответ

$ (3, 4) $

Войдите, чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг.

$ 3x – 2y = -4 $
$ 4x – y = 3 $

Постановка задачи

Решите эту линейную систему, используя правило Крамера.
$ 3x – 2y = -4 $
$ 4x – y = 3 $

Окончательный ответ

$ (2, 5) $

5 Постановка задачи линейная система с использованием правила Крамера.
$ 3x – 2y = -4 $
$ 4x – y = 3 $

Решение

2856 видео решение

Окончательный ответ

$ (2, 5) $

Войдите в систему, чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг.

Окончательный ответ

$ (2, 3) $

4 Постановка задачи

4 линейная система с использованием правила Крамера.

Решение

2857 видео решение

Окончательный ответ

$ (2, 3) $

Окончательный ответ

$ (4, 1) $

Постановка задачи

Решите эту линейную систему, используя правило Крамера.
$ 2x – 7y = 1 $
$ 3x + y = 13 $

Решение

2858 видео решение

Окончательный ответ

$ (4, 1) $

$ x – 2y = -3 $
$ 3x + y = 5 $

Постановка задачи

Решите эту линейную систему, используя правило Крамера.
$ x – 2y = -3 $
$ 3x + y = 5 $

Окончательный ответ

$ (1, 2) $

Постановка задачи

Решите эту линейную систему, используя правило Крамера.
$ x – 2y = -3 $
$ 3x + y = 5 $

Решение

2859 видео решение

Окончательный ответ

$ (1, 2) $

46 Лог чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг.

$ x – y = 4 $
$ 2x + y = 2 $

Постановка задачи

Решите эту линейную систему, используя правило Крамера.
$ x – y = 4 $
$ 2x + y = 2 $

Окончательный ответ

$ (2, -2) $

Постановка задачи

Решите эту линейную систему, используя правило Крамера.
$ x – y = 4 $
$ 2x + y = 2 $

Решение

2860 видео решение

Окончательный ответ

$ (2, -2) $

5
44 Журнал чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг.

Окончательный ответ

$ (2, -1) $

Решение этой задачи

0 линейная система с использованием правила Крамера.
$ 4x – 2y = 10 $
$ 3x – 5y = 11 $
Solution
mattemath – 2861 video solution

video by mattemath

Final Answer

\ ( (2, -1) \)

Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг.

$ 2x – 3y = 1 $
$ x + 2y = 11 $

Постановка задачи

Решите эту линейную систему с помощью правила Крамера.
$ 2x – 3y = 1 $
$ x + 2y = 11 $

Окончательный ответ

$ (5, 3) $

45 Постановка задачи

Решите эту линейную систему, используя правило Крамера.
$ 2x – 3y = 1 $
$ x + 2y = 11 $

Решение

2862 видео решение

Окончательный ответ

$ (5, 3) $

Окончательный ответ

нет решения
$ 3x = 2y + 5 $
$ 4y = 6x – 8 $

Решение

2863 видео решение

Окончательный ответ

нет решения

$ x + 2y = -3 $
$ -3x – 6y = 9 $

Постановка задачи

Решите эту линейную систему, используя правило Крамера.
$ x + 2y = -3 $
$ -3x – 6y = 9 $

Окончательный ответ

бесконечное число решений

Постановка задачи с использованием системы Crave linears

5 90 Правило.
$ х + 2у = -3 $
$ -3х – 6у = 9$

Решение

2864 видео решение

Окончательный ответ

бесконечное количество решений

Войдите, чтобы оценить эту практическую задачу и увидеть ее текущий рейтинг.

$ 3x + 7y = 5 $
$ -2x + y = -9 $

Постановка задачи

Решите эту линейную систему, используя правило Крамера.
$ 3x + 7y = 5 $
$ -2x + y = -9 $

Окончательный ответ

$ (4, -1) $

5 Постановка задачи Решите эту линейную систему, используя правило Крамера.
$ 3x + 7y = 5 $
$ -2x + y = -9 $

Решение

2865 видео-решение

Окончательный ответ

$ (4, -1) $

Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг.

$ 2x + 3y = -4 $
$ -x + y = 7 $

Постановка задачи

Решите эту линейную систему, используя правило Крамера.
$ 2x + 3y = -4 $
$ -x + y = 7 $

Окончательный ответ

$ (-5, 2) $

Постановка задачи

Решите эту линейную систему, используя правило Крамера.
$ 2x + 3y = -4 $
$ -x + y = 7 $

Решение

2866 видео решение

Окончательный ответ

$ (-5, 2) $

Войдите, чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг.

Практика – Системы 3×3

$ 2x+3y+z=2; $ $ -x+2y+3z=-1; $ $ -3x-3y+z=0 $

Постановка задачи

Решите эту линейную систему, используя правило Крамера.
$ 2x+3y+z=2; $ $ -x+2y+3z=-1; $ $ -3x-3y+z=0 $

Окончательный ответ

$ x=4, y=-3, z=3 $

Постановка задачи

Решите эту линейную систему, используя правило Крамера.
$ 2x+3y+z=2; $ $ -x+2y+3z=-1; $ $ -3x-3y+z=0 $

Решение

MIP4U

видео от MIP4U

Окончательный ответ

$ x=4, y=-3, z=3 $

5 906 и чтобы увидеть его текущий рейтинг.
$ 2x-y-z=2; $ $ 4x+y-z=-5; $ $ 6x-2y+2z=17 $
Постановка задачи
Решите эту линейную систему используя правило Крамера.
$ 2x-y-z=2; $ $ 4x+y-z=-5; $ $ 6x-2y+2z=17 $
Окончательный ответ
$ x=1 /2, y=-4, z=3 $
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
$ 2x-y-z=2; $ $ 4x+y-z=-5; $ $ 6x-2y+2z=17 $
Решение
MIP4U – 1902 Видеореал
Видео по MIP4U
Окончательный ответ
\ (x = 1/2, y = -4, Z = 3 \)
\ (x = 1/2, y = -4, Z = 3 \)
\ (x = 1/2, y = -4, z = 3 \)
.
Войдите в систему, чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг.
- г.
$ x+2z=9; $ $ 2y+z=8; $ $ 4x-3y=-2 $
Постановка задачи
Решите эту линейную систему с помощью Крамера Правило.
$ x+2z=9; $ $ 2y+z=8; $ $ 4x-3y=-2 $
Окончательный ответ
$ x=1, y =2, z=4 $
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
$ x+2z=9; $ $ 2y+z=8; $ $ 4x-3y=-2 $
Решение
PatrickJMT – 1903 видео решение
видео PatrickJMT
Окончательный ответ
$ x=1, y=2, z=4 $
Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг.
$ x-y+z=4; $ $ 2x+y+z=7; $ $ -x-2y+2z=-1 $
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
$ x-y+z=4; $ $ 2x+y+z=7; $ $ -x-2y+2z=-1 $
Окончательный ответ
$х=3, у=0, г=1 $
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
$ x-y+z=4; $ $ 2x+y+z=7; $ $ -x-2y+2z=-1 $
Решение
PatrickJMT – 1904 видео решение
видео от PatrickJMT
Окончательный ответ
$ x=3, y=0, z=1 $
Текущий рейтинг и рейтинг этой проблемы .
$ -x+2y-3z=1; $ $ 2x+z=0; $ $ 3x-4y+4z=2 $
Постановка задачи
Решить это линейная система с использованием правила Крамера.
$ -x+2y-3z=1; $ $ 2x+z=0; $ $ 3x-4y+4z=2 $
Окончательный ответ
$ x=-4/5, y=-3/2, z=-8/5 $
Постановка задачи
Решите эту линейную систему с помощью правила Крамера.
$ -x+2y-3z=1; $ $ 2x+z=0; $ $ 3x-4y+4z=2 $
Решение
математика – 1905 видео решение
видео от mattemath
Окончательный ответ
$ x=-4/5, y=-3/2, z=-8/5 $
Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг.
$ x – 3y + 3z = -6 $
$ -2x + 4y + z = 3 $
$ 3x – 5y +4z = -9 $
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
$x – 3y + 3z = -6 $
$ -2x + 4y + z = 3 $
$ 3x – 5y +4z = -9 $
Окончательный ответ
$ (0, 1, -1) $
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
$x – 3y + 3z = -6 $
$ -2x + 4y + z = 3 $
$ 3x – 5y +4z = -9 $
Решение
Эта задача решается за 2 видео подряд.
2867 решение для видео
2867 решение для видео
Окончательный ответ
$ (0, 1, -1) $
Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг.
$ 3x – 2y + z = 2 $
$ 4x + 3y – 2z = 4 $
$ 5x – 3y + 3z = 8 $
Решить эту линейную систему с помощью правила Крамера.
$ 3x – 2y + z = 2 $
$ 4x + 3y – 2z = 4 $
$ 5x – 3y + 3z = 8 $
Постановка задачи
4 $ (1, 2, 3) $
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
$ 3x – 2y + z = 2 $
$ 4x + 3y – 2z = 4 $
$ 5x – 3y + 3z = 8 $
Решение
2868 видео решение
Окончательный ответ
$ (1, 2, 3) $
Окончательный ответ
Войдите, чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг.
- г.
$ x + y – z = -2 $
$ 2x – y + z = 0 $
$ x – 2y + 3z = 1 $
5 Решите эту линейную систему, используя правило Крамера.
$ x + y – z = -2 $
$ 2x – y + z = 0 $
$ x – 2y + 3z = 1 $
Постановка задачи
Окончательный ответ
\ ( (-2/3, -7/3, -1) \)
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
$ x + y – z = -2 $
$ 2x – y + z = 0 $
$ x – 2y + 3z = 1 $
Решение
2870 видео решение
Окончательный ответ
$ (-2/3, -7/3, -1) $
Войдите, чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг.
- г.
$ 2x + y – z = 1 $
$ 3x + 2y + 2z = 13 $
$ 4x – 2y + 3z = 9 $
Решить эту линейную систему с помощью правила Крамера.
$ 2x + y – z = 1 $
$ 3x + 2y + 2z = 13 $
$ 4x – 2y + 3z = 9 $
Постановка задачи
4 $ (1, 2, 3) $
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
$ 2x + y – z = 1 $
$ 3x + 2y + 2z = 13 $
$ 4x – 2y + 3z = 9 $
Решение
2871 видео решение
Окончательный ответ
4 $ (1, 2, 3) $
Окончательный ответ
Войдите, чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг.
- г.
$ 2x + 3y – 5z = 1 $
$ x + y – z = 2 $
$ 2y + z = 8 $
5 90 систему по правилу Крамера.
$ 2x + 3y – 5z = 1 $
$ x + y – z = 2 $
$ 2y + z = 8 $
Постановка задачи
Окончательный ответ
$ (1, 3, 2) $
Постановка задачи
Решите эту линейную систему, используя правило Крамера. $ (1, 3, 2) $
Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг.
- г.
$ 3x + y – z = 0 $
$ -2x + 5y + 4z = -1 $
$ 3x + 2y + z = 1 $
Постановка задачи
5
Решите эту линейную систему, используя правило Крамера.
$ 3x + y – z = 0 $
$ -2x + 5y + 4z = -1 $
$ 3x + 2y + z = 1 $
Окончательный ответ
$ (1/2, -2/3, 5/6) $
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
$ 3x + y – z = 0 $
$ -2x + 5y + 4z = -1 $
$ 3x + 2y + z = 1 $
Решение
2873 видео решение
Окончательный ответ
$ (1/2, -2/3, 5/6) $
Войдите, чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг.
[PDF] Применение правила Cramer для решения крупномасштабных линейных систем
- DOI: 10. 1016/j.jda.2011.06.007
- Corpus ID: 17880607
Corpus ID: 17880607

Кен Хабгуд, И. Арел
Опубликовано 2012
Компьютерная наука
J. Дискретные алгоритмы

View Via Publisher

Новый и простой метод решения больших линеарных систем: на основе правила Cramer, но используя кондиционирование Dodgson

Okoma ufuoma
Физика
2013

Цель этой статьи состоит в том, чтобы представить новый и увлекательный метод решения больших линейных систем, основанный на правиле Крамера, но использующий конденсацию Доджсона в своих вычислениях. Этот новый метод…

Модифицированное правило Cramer и его применение для решения линейных систем в WZ -факторизации

O. Babarinsa, H. Kamarulhaili
Математика
MATEMATIKA
2019

Модифицированные методы CRAMERSER. а также матрица коэффициентов одновременно в линейной системе. Модифицированные методы можно применять, начиная с правила Крамера…

От определителя Сильвестра к правилу Крамера

Hou-biao Li, Tingzhu Huang, T. Gu, Xingping Liu
Информатика
2014

Схема, пригодная для параллельных вычислений, представлена для этого вида обобщенных Chi\`{o} процессы детерминантной конденсации, что придает этому новому методу свойство естественного параллелизма.

Старые и новые доказательства правила Крамера

М. Брунетти, Р. Каччиопполи
Математика
2014

Несмотря на высокую вычислительную стоимость, правило Крамера для решения систем линейных уравнений имеет историческое и теоретическое значение. В этой статье мы перечисляем шесть различных доказательств этого, последнее из… Информатика

2018

Эти методы сравниваются на основе некоторых важных критериев, включая сходимость, распараллеливаемость/масштабируемость, точность и применимость к изменяющимся во времени матрицам, и предлагается новая концепция, основанная на нейрокомпьютинге, для решения задачи обращения матриц.

Новый подход к решению линейных уравнений первого порядка через производные

Рами Обейд
Математика
2018

В данной статье предлагается простой метод решения линейных уравнений первого порядка, классическое правило Крамера для решения общих систем двух линейных уравнений, то это…

Оптимизированное правило Крамера в WZ-факторизации и приложениях

AMD и Intel, чтобы сделать вывод, что оптимизированное правило Крамера в алгоритме факторизации дает более точные результаты, чем факторизация LU и обычная факторизация W Z.

Решение линейных систем на высокопроизводительном оборудовании с устойчивостью к множественным серьезным сбоям

Теоретический анализ показывает, что метод способен обеспечить отказоустойчивость к множественным сбоям за счет небольших накладных расходов и ограниченного числа дополнительных процессоров для хранения контрольные суммы.

Отказоустойчивый высокопроизводительный решатель для систем линейных уравнений

В этой статье рассматривается популярная тема линейной алгебры и предлагается эффективный, устойчивый к ошибкам подход, основанный на существующем методе, называемом методом торможения (IMe), дополненный простым, но эффективным стратегия, обеспечивающая толерантность к единичным отказам, повторяющимся ни с контрольными точками, ни с откатами.

ЗАМЕТКА ОБ ИСТОРИИ (КВАДРАТНОЙ) МАТРИЦЫ И ОПРЕДЕЛИТЕЛЯ

В этой статье рассматривается теория матриц и определителей. Матрица и определитель в настоящее время считаются в некоторой степени неразделимыми, но определитель был открыт более чем за два столетия до…

К.

Молер

Геология

SGNM

1974

Следует отметить, что правило Крамера неудовлетворительно даже для систем 2 на 2 из-за ошибок округления.

Правило Крамера пересмотрено или уравновешенное или желательное

C. Dunham
Математика
SGNM
1980

Рассмотрим решение двух линейных уравнений, для которых правило CRAMER имеет атростия [3]. Молер [3] утверждает, что правило Крамера имеет неудовлетворительную точность даже в этом…

Научные вычисления: вводный обзор

М. Хит, Э. Мансон
Информатика
1996

От издателя: «В этой книге представлен широкий обзор численных методов для решения всех основных задач научных вычислений, включая линейные и нелинейные уравнения, метод наименьших квадратов,…

Точность и устойчивость численных алгоритмов

Н. Хайэм
Информатика
1991

В этой книге дается подробное и современное описание поведения численных алгоритмов в арифметике с конечной точностью путем объединения алгоритмических выводов, теории возмущений и анализа ошибок округления.

Справочник по математическим функциям с формулами, графики,

Матемалические таблицы, М. Абрамовиц, И. Стегун, А. Г. Гринхилл
Математика
1971

преемник Справочника по математическим функциям NBS Абрамовица и Стегуна с формулами и графиками. Справочник математических функций имеет 24 рейтинга…

Численный анализ

J. Faires
Информатика
1981

Этот отчет содержит описание типичных тем, изучаемых в двухсеместровой последовательности численного анализа, и описывает точность, эффективность и точность этих алгоритмов.

Параллельные научные вычисления на C++ и MPI. Комплексный подход к параллельным алгоритмам и их реализации

Г. Карниадакис, Р. Кирби
Информатика
2002

В этой книге представлен цельный подход к численным алгоритмам, современным методам программирования и параллельным вычислениям, а также уделено одинаковое внимание дискретизации дифференциальных уравнений в частных производных и решателям.