2.4. Вычисление определителей
Основным приемом вычисления определителя го порядка является сведение его к определителям более низкого порядка с помощью формул разложения. При этом полезен учет свойств определителя, позволяющий существенно уменьшить объем вычислений.
Пример 1. Вычислить определитель
Разложим определитель по первому столбцу. Получим
.
Таким образом, вычисление определителя четвертого порядка свелось к вычислению четырех определителей третьего порядка. Далее, разлагая определители третьего порядка по первому столбцу, получим
и т.д. Окончательно получим .
Вычисления значительно упростятся, если воспользоваться свойствами определителя. По свойству 7 можно, не меняя значения определителя, прибавить второй, третий и четвертый столбцы к первому, а затем первую строку вычесть из второй, третьей и четвертой. Получим
Пример 2. Вычислить определитель треугольной матрицы го порядка
.
Для вычисления разложим определитель по последней строке. Получим, что , где треугольный определитель порядка . Определитель снова разложим по последней строке и т.д. Продолжая аналогичные рассуждения, получим что .
Пример 3. Вычислить определитель матрицы го порядка
.
Подобные определители можно достаточно просто преобразовать к треугольному виду. Для этого прибавим все столбцы к первому и затем вычтем первую строку из всех остальных. Получим
Пример 4. Следующий метод вычисления определителей го порядка называется методом рекуррентных соотношений
Рассмотрим идею метода на примере
вычисления определителя трехдиагональной
матрицы или матрицы Якоби (матрицей
Якоби называется матрица
,
если из следует
). Вычисление определителей матриц Якоби
часто приводит к рекуррентному соотношению
вида
Вычисление определителей матриц Якоби
часто приводит к рекуррентному соотношению
вида
,
где и постоянные числа. Для нахождения необходимо решить полученное уравнение. Заменим соответствующей степенью переменной
.
Перенося все слагаемые в левую часть и сокращая на , получим квадратное уравнение , называемое характеристическим уравнением. Пусть корни этого уравнения. Тогда возможны два случая: и .
Если , то определитель имеет вид
,
где числа находятся из условий
.
Определители и в левых частях условий вычисляются непосредственно из вида .
Если , то
,
а числа находятся из условий
.
Рассмотрим конкретный пример. Вычислим определитель го порядка
, .
Разложим определитель по последнему столбцу
.
Первый определитель в правой части
является определителем порядка того же типа, что и
. Второй определитель разложим еще раз
по последней строке. Минор, дополнительный
к ненулевому элементу в последней
строке, вновь представляет собой
определитель того же типа, что и
,
но порядка
.
В итоге получим рекуррентное соотношение
для
Второй определитель разложим еще раз
по последней строке. Минор, дополнительный
к ненулевому элементу в последней
строке, вновь представляет собой
определитель того же типа, что и
,
но порядка
.
В итоге получим рекуррентное соотношение
для
.
Соответствующее характеристическое уравнение
имеет корни и . Так как , то и . Из вида находим
.
Тогда для определения получим систему уравнений
решая которую, находим
(при решении использовались равенства: ). Тогда
.
Пример 5. Вычислить определитель го порядка
.
Представим элементы последнего столбца в виде суммы двух слагаемых: . Тогда по свойству 3. определитель представится в виде суммы двух определителей
.
Первый определитель разложим по
последнему столбцу. Второй определитель
приведем к треугольному виду, вычитая
последний столбец из всех остальных.
(1)
где является определителем порядка того же типа, что и .
Решим полученное уравнение для . Из вида при имеем.Выписывая (1) при с учетом равенства для , получаем
.
Методом математической индукции теперь нетрудно показать, что .
Пример 6. Вычислить определитель го порядка
.
Представим элементы последнего столбца в виде суммы двух слагаемых: и распишем определитель как сумму двух определителей
.
Первый определитель разложим по последнему столбцу. Для вычисления второго определителя умножим последний столбец на и вычтем из остальных. Получим
Для решения полученного рекуррентного соотношения воспользуемся тем, что при транспонировании матрицы ее определитель не меняется. В нашем случае транспонировании приводит к замене на наоборот. Поэтому имеем два равенства
Откуда
.
Пример 7. Следующий пример иллюстрирует применение теоремы Лапласа. Нужно вычислить определитель квазитреугольной матрицы порядка . Квазитреугольной называют блочную матрицу вида , где квадратные матрицы, прямоугольная матрица, нулевая матрица. В подробной записи матрица имеет вид
.
Пусть . Покажем, что . Воспользуемся теоремой Лапласа. Разложим этот определитель по первым строкам. Очевидно, что из первых строк можно составить только один минор го порядка не содержащий нулевого столбца, у которого номера выделяемых столбцов удовлетворяют условию . Этот минор есть . Дополнительным к нему минором является определитель , что и доказывает формулу.
Помогите решить / разобраться (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
Посмотреть правила форума
| vitalijpavula |
| ||
16/08/16 |
| ||
| |||
| DeBill |
| |||
10/01/16 |
| |||
| ||||
| maxmatem |
| ||
15/08/09 |
| ||
| |||
| DeBill |
| |||
10/01/16 |
| |||
| ||||
| vitalijpavula |
| ||
16/08/16 |
| ||
| |||
| DeBill |
| |||
10/01/16 |
| |||
| ||||
| vitalijpavula |
| ||
16/08/16 |
| ||
| |||
| Otta |
| |||
09/05/13 |
| |||
| ||||
| DeBill |
| |||
10/01/16 |
| |||
| ||||
| vitalijpavula |
| ||
16/08/16 |
| ||
| |||
| vitalijpavula |
| ||
16/08/16 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 11 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
линейная алгебра – Рекуррентное соотношение для определителя трехдиагональной матрицы
спросил
Изменено 3 года, 5 месяцев назад
Просмотрено 3к раз
$\begingroup$
Пусть
$$f_n := \begin{vmatrix} а_1 и б_1 \\ c_1 & a_2 & b_2 \\ & c_2 & \ddots & \ddots \\ & & \ddots & \ddots & b_{n-1} \\ & & & c_{n-1} и a_n \end{vmatrix}$$
По-видимому, определитель трехдиагональной матрицы задается рекуррентным соотношением
$$f_n = a_n f_{n-1} – c_{n-1} b_{n-1}f_{n-2}$ $
с начальными значениями $f_0 = 1$ и $f_{-1} = 0$ (согласно Википедии). Кто-нибудь может объяснить мне, как они пришли к этому рекуррентному отношению?
Я не очень понимаю, как его вывести.
Кто-нибудь может объяснить мне, как они пришли к этому рекуррентному отношению?
Я не очень понимаю, как его вывести.
- линейная алгебра
- матрицы
- рекуррентные соотношения
- определитель
- трехдиагональные матрицы
$\endgroup$
$\begingroup$
Повторяемость получается путем развертывания определителя по последнему столбцу (или, что то же самое, по последней строке).
$\endgroup$
$\begingroup$
Для $n \ge 2$ использование разложения Лапласа в последней строке дает
\начать{выравнивать}
ф_н &=
\begin{vmatrix}
а_1 и б_1 \\
c_1 & a_2 & b_2 \\
& c_2 & \ddots & \ddots \\
& & \ddots & \ddots & b_{n-3} \\
& & & c_{n-3} & a_{n-2} & b_{n-2} \\
& & & & c_{n-2} & a_{n-1} & b_{n-1} \\
& & & & & c_{n-1} & a_n
\end{vmatrix}
\\
знак равно
(-1)^{2n-1}
с_ {n-1}
\begin{vmatrix}
а_1 и б_1 \\
c_1 & a_2 & b_2 \\
& c_2 & \ddots & \ddots \\
& & \ddots & \ddots & b_{n-3} \\
& & & c_{n-3} & a_{n-2} \\
& & & & c_{n-2} и b_{n-1}
\end{vmatrix}
+ (-1)^{2n}
а_н
\begin{vmatrix}
а_1 и б_1 \\
c_1 & a_2 & b_2 \\
& c_2 & \ddots & \ddots \\
& & \ddots & \ddots & b_{n-2} \\
& & & c_{n-2} и a_{n-1}
\end{vmatrix}
\\
знак равно
– с_{n-1}
(-1)^{2(n-1)}
б_{п-1}
\begin{vmatrix}
а_1 и б_1 \\
c_1 & a_2 & b_2 \\
& c_2 & \ddots & \ddots \\
& & \ddots & \ddots & b_{n-3} \\
& & & c_{n-3} и a_{n-2}
\end{vmatrix}
+ а_н f_{n-1} \\
&= a_n f_{n-1} – c_{n-1} b_{n-1} f_{n-2}
\end{выравнивание}
как рекуррентное соотношение.
Для начальных условий:
Из сравнения вышеприведенной формулы с матрицами для $n=1$ и $n=2$ получаем: $$ f_1 = a_1 f_0 – c_0 b_0 f_{-1} \overset{!}{=} a_1 \\ f_2 = a_2 f_1 – c_1 b_1 f_0 \overset{!}{=} a_1 a_2 – c_1 b_1 $$ Из последнего следует, что $f_0 = 1$, а из первого $f_{-1} = 0$.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
абстрактная алгебра – $n$ мерный определитель с использованием рекуррентных соотношений
Задавать вопрос
спросил
Изменено 7 лет, 4 месяца назад
Просмотрено 123 раза
$\begingroup$
Найти определитель
$$D_n(а,б,в)=
\begin{vmatrix}
a & b & 0 & 0 & \cdots & 0 & 0 & 0 \\
с & а & б & 0 & \cdots & 0 & 0 & 0 \\
0 & c & a & b & \cdots & 0 & 0 & 0 \\
\vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\
0 & 0 & 0 & 0 & \cdots & c & a & b \\
0 & 0 & 0 & 0 & \cdots & 0 & c & a
\end{vmatrix}
$$
для $a,b,c \in \mathbb{R}$.

 08.2016, 21:30
08.2016, 21:30  08.2016, 21:44
08.2016, 21:44  08.2016, 21:47
08.2016, 21:47  08.2016, 21:51
08.2016, 21:51  08.2016, 21:53
08.2016, 21:53  08.2016, 21:59
08.2016, 21:59  08.2016, 22:09
08.2016, 22:09  08.2016, 22:14
08.2016, 22:14 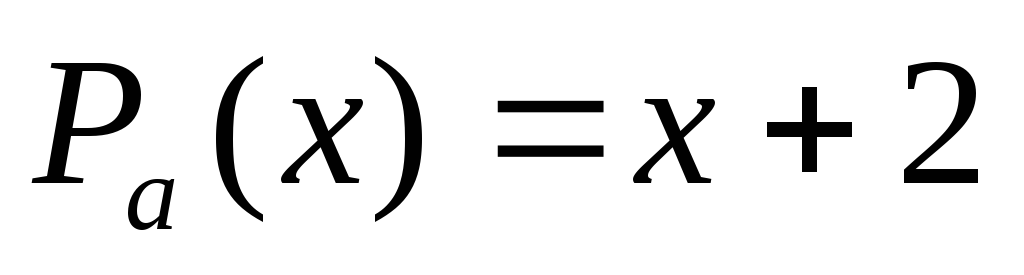 08.2016, 22:14
08.2016, 22:14  08.2016, 22:27
08.2016, 22:27  08.2016, 23:50
08.2016, 23:50