Устный счет на пальцах – основные приемы
Человека ежедневно окружает множество цифр. Работа и учеба, походы в магазин и банковские операции – во всех сферах жизни необходимо уметь считать в уме, ведь калькулятор не всегда бывает под рукой. Желая упростить себе жизнь, многие люди хотят научиться проводить различные операции с числами с помощью подручных средств. Одним из подобных методов и является счет на пальцах.
Искусство устного счета
С древнейших времен и до наших дней люди стремились развить способность быстро производить математические вычисления в уме. Этот навык полезен в самых разных сферах нашей жизни: от покупок в магазине до профессиональной деятельности. Возможность устно выполнять сложение и вычитание, умножение и деление позволяет человеку продуктивнее справляться с повседневными задачами.
Обычные знания, которые мы получаем на уроках математики в школе, не позволяют человеку научиться выполнять операции с большими числами без помощи тетради или калькулятора.
Существует множество самых разных подходов, позволяющих производить вычисления в уме. Многие из них все же подразумевают использование некоторых подручных средств. Так существует методика, основы которой знакомы нам с самого раннего детства – счет на пальцах. Но мало кто знает, что, помимо сложения и вычитания, также можно освоить умножение и деление больших чисел в уме.
Сложение и вычитание в уме
С самого детства человек учится сложению и вычитанию простейших чисел. Родители и воспитатели детских садов, а затем и учителя в школе открывают для ребенка бескрайний мир математики.
 При поступлении в первый класс ребенок учится производить вычисления устно, без использования пальцев или счетных палочек.
При поступлении в первый класс ребенок учится производить вычисления устно, без использования пальцев или счетных палочек.Различные подручные материалы только тормозят скорость счета, не дают своевременно раскрыть способности детей. По этой причине, арифметические вычисления на пальцах подходят только для того, чтобы ввести для ребенка понятие цифр, чисел и простейших операций с ними.
Как выучить таблицу умножения на пальцах
С умножением и делением ситуация обстоит немного иначе. Есть методика, позволяющая производить подобные вычисления с использованием пальцев на левой и правой руке. К сожалению нельзя сказать, что подобный подход позволяет быстро умножать и делить числа. Такой вид счета на пальцах скорее направлен на общее развитие интеллекта человека, чем на широкое применение в быту.
К тому же, сложно запомнить и выучить подобную таблицу умножения и деления, так как она видоизменяется в зависимости от размера чисел, с которыми проводятся операции. С помощью калькулятора или листка бумаги считать намного проще, чем на пальцах, а потому этот метод не получил широкого распространения.
Популярные методики
Конечно, изучение различных методик устного счета на пальцах полезно для общего развития, но существуют и другие способы проводить вычисления в уме за более короткое время. Пожалуй, самым ярким из них является ментальная арифметика – программа, которая позволит научиться выполнять сложение, вычитание, умножение и деление в уме практически мгновенно. Количество операций, которые может производить человек, обученный по данной методике, поражает воображение, счет на пальцах не позволяет считать с подобной скоростью.
Ментальная арифметика не является новшеством. Известно, что она использовалась еще пять тысяч лет назад. За ее основу взяты вычисления на специальных счетах – абакусе. Если в начале занятий еще используется данное приспособление, то потом человек учится представлять счеты в уме и устно проводить на них вычисления.
Неудивительно, что курсы ментальной арифметики сегодня так популярны. Особенно это актуально для детей, ведь умение быстро считать в уме позволяет повысить успеваемость в школе по множеству дисциплин.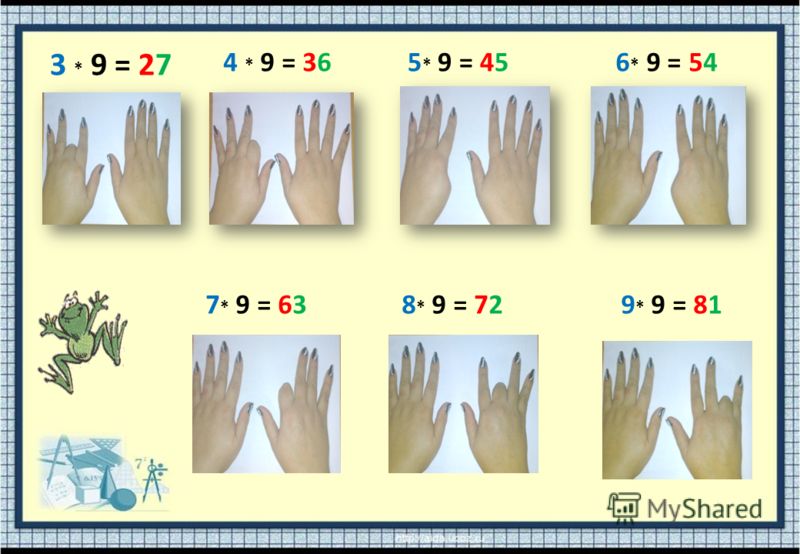 К тому же, ребенка легче научить выполнять вычисления по данной методике, так как ее изучение во взрослом возрасте не приносит таких высоких результатов.
К тому же, ребенка легче научить выполнять вычисления по данной методике, так как ее изучение во взрослом возрасте не приносит таких высоких результатов.
Существует множество детских центров дополнительного образования, обучающих детей ментальной арифметике. Нужно выбирать такой, занятия в котором проходят в небольших группах и по уникальной методике. Так удастся научить ребенка быстро считать, а также сохранить изучаемый навык на всю жизнь, что не раз поможет в профессиональной и повседневной деятельности.
Японская методика обучения счету в уме Соробан
Если ваш ребенок не может освоить решение математических задач и запомнить необходимые формулы, а подготовка домашних заданий превращается в кошмар, японская методика счета Соробан может стать спасением. Данный способ удивительным образом помогает развивать детское мышление.
Уникальная методика ментального счета позволяет даже тем ребятам, которые вовсе не имеют способностей к арифметике, уже спустя короткий отрезок времени научиться легко решать задачки, получая удовольствие от процесса.
Особенности ментального счета
Японская методика быстрого счета является уникальной системой развития малышей и преображения детского мышления. Этот метод позволяет одновременно задействовать оба полушария мозга, что обеспечивает даже ярким гуманитариям возможность быстро научиться решать различные примеры.
Обучение счету по японскому методу основывается на использовании специальных счетов, называемых соробан, – данное нетрадиционное устройство нечасто встречается в нашей стране. Это своеобразный калькулятор, демонстрирующий только однозначную систему численного представления, что гарантирует ясность и понятность системы.
В соробане всегда применяется нечетное число спиц, расположенных по вертикали, при этом каждой из них отведено обозначение одной цифры. Любая спица имеет пять костей, где четыре нижних отведены под единицы, а верхняя – под «пять».
Ребенка увлекает данная японская методика устного счета и сами счеты, что позволяет очень быстро освоить процесс, а основным достоинством способа можно назвать невероятно оперативное развитие мышления.
Основные принципы способа
Система ментальной арифметики по японскому методу предназначена не только для обучения учеников оперативному счету в уме, но также для общего развития их интеллектуальных навыков. Известен факт, что полушария человеческого мозга работают неравномерно, и ребенок 5-8 лет использует, в основном, правую часть, которая отвечает за творчество и эмоциональные образы.
Когда происходит обучение счету, повышается нагрузка на левую часть, идет развитие рациональности и логики, что планомерно снижает творческие способности. Японская методика счета в уме позволяет уравновесить работу мозга, обеспечивая полноценную развитость.
С помощью работы на счетах дети интеллектуально развиваются, начинают быстрее соображать и легко достигают успеха в любом обучении. Подобные результаты обеспечиваются главными принципами методики Соробан:
- Ручная моторика путем тренинга. Головной мозг контролирует действия человека, но существует и обратный процесс, так что работа со специальными счетами при помощи пальцев обеих рук позволяет улучшать детское мышление.

- Систематичность работы. Никто из нас не рождается лучшим, и чтобы добиться вершины в любом деле, необходимо регулярно тренироваться. По этому принципу работает и японская методика счета.
- Визуализация. Обладая наглядными материалами, выраженными в счетных костях соробана, ребенку значительно проще понимать числа и понять смысл вычислений.
Что необходимо для обучения ментальному счету?
Соробан окажет помощь в обучении ребенка счету только в том случае, если обучение было начато своевременно, в возрасте порядка 4-8 лет. Родители должны запастись терпением и двигаться постепенно, ведь данная процедура нуждается в определенном времени. Также важными условиями успеха будут:
- Обучение ребенка по методу «от простейшего к сложному». На первом этапе необходимо освоить счет до десяти, после чего обратный счет.
- Малыша необходимо обучать счету с двух лет, но обучение числам и цифрам можно начать около четырех лет, когда кроха способен осознанно посчитать находящиеся в поле его зрения предметы.

- Упражнения стоит проводить в непринужденной обстановке, но не в форме лекций. Лучше всего дети учатся посредством игрового процесса, что обеспечивает подключение эмоционального восприятия и рост эффективности обучения.
- Сложность заданий следует постепенно увеличивать. Также обучите малыша отличиям между знаками «больше», «меньше», «равно».
При наличии данной начальной подготовки можно свободно отправлять ребенка в школу изучения японской ментальной арифметики соробан, где профессиональные преподаватели изучат личные особенности малыша, учтут его способности и навыки.
Чтобы освоить методику Соробан, можно обратиться в онлайн-школу японского языка Дарьи Мойнич. Узнать дополнительную информацию можно на нашем сайте.
Достоинства ментальной арифметики из Японии
Детки довольно быстро развивают свои навыки использования соробана, что оказывает невероятно благоприятное воздействие на развитие мышления. Обучающиеся счету на соробане малыши могут в мгновение ока осуществлять тяжелые вычисления в уме, при этом настоящие профессионалы методики способны выполнять их даже без соробана.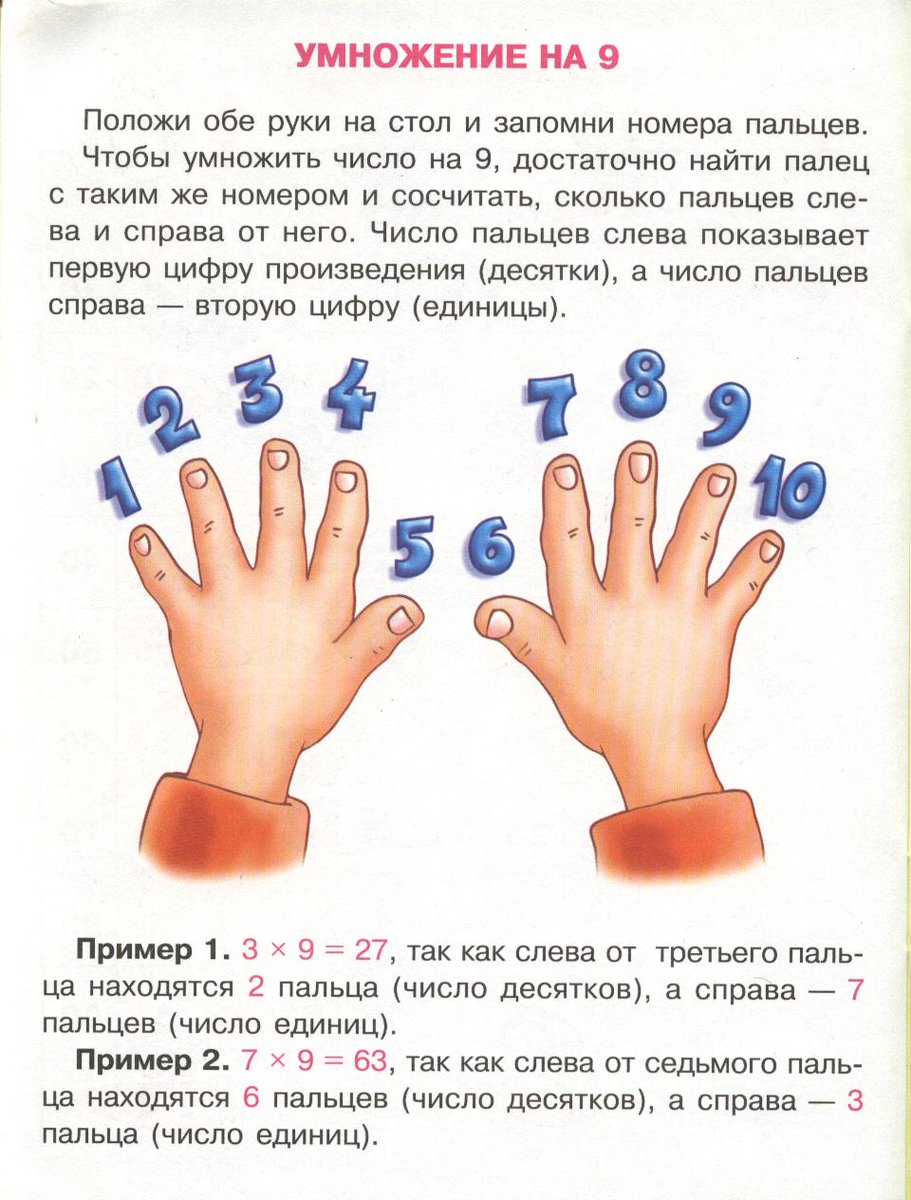 Всего пары секунд будет достаточно для того, чтобы сложить 3-значные числа, а далее, когда навыки отточатся, ребенок сможет оперировать и 5-значными числами.
Всего пары секунд будет достаточно для того, чтобы сложить 3-значные числа, а далее, когда навыки отточатся, ребенок сможет оперировать и 5-значными числами.
Данная методика гарантирует ребенку успех не только в арифметике, но и в других сферах получения знаний. Согласно мнению преподавателей и психологов, японские счеты повышают детскую сосредоточенность и концентрацию, позволяют улучшить память, находчивость и фантазию, а также улучшить творческие навыки. Детишки начинают налету схватывать информацию и быстро анализировать ее.
Некоторые родители полагают, что их чадо может запутаться при совмещении традиционной и японской арифметики, что приведет к падению успеваемости в школе. Тем не менее, практический опыт демонстрирует, что уже спустя несколько месяцев ребенок, занимающийся соробаном, начинает проявлять талант в точных науках и опережает своих сверстников в развитии.
Все упомянутые преимущества ментального счета являются только основой ключевого достоинства – ментальная арифметика позволяет раскрыть и питать интеллект ребенка, а также воспитать личность, привив малышу уверенность, самостоятельность, способность к достижению успеха в любых ситуациях.
Отличный старт в изучении японского языка вы можете получить, заполнив форму ниже ↓ После этого вам на почту придут 5 бесплатных уроков!
как научиться считать самому / TeachMePlease
Ментальная арифметика — это мгновенное совершение арифметических операций в уме. Сначала они выполняются с помощью японских счётов — соробана, на которых ученик впоследствии считает в воображении. Существует множество организаций, предлагающих обучить данной технике. Мы же разберёмся, можно ли изучить её самостоятельно.
Инструменты счёта
Начинается обучение ментальной арифметике со счёта на соробане — японском варианте счёт. Они представляют собой доску с вертикальными спицами и пятью нанизанными на них костяшками. Отличительная черта соробана — горизонтальная перегородка, которая отделяет четыре костяшки в столбцах от пятой.
Четыре нижние косточки японцы называют «земными», они означают единицы. Пятая, верхняя костяшка, «небесная», считается сразу за пять единиц.
Для обучения ментальной арифметике необходимо обзавестись именно соробаном, а не просто счётами. Учиться считать можно также на бумаге с помощью изображения соробана или использовать специализированные сайты и приложения, но такое выполнение вычислений будет менее наглядным.
Основы работы с числами
В начале занятий соробан нужно привести в нулевую позицию, косточки соробана не должны касаться разделителя: верхние необходимо поднять к рамке, а нижние — наоборот опустить.
Для совершения действий с соробаном традиционно используют большой и указательный пальцы: первый перемещает бусины из нижнего ряда к разделителю, второй — выполняет остальные манипуляции.
Первая спица справа — это единицы (от 1 до 9). Чтобы отложить цифры от 1 до 4 необходимо перемещать косточки под разделителем в правом крайнем столбце вверх, для обозначения цифры 5 опускаем 1 костяшку из верхнего правого ряда. Числа от 6 до 9 обозначаем как 5, то есть 1 опущенная костяшка из верхнего ряда, плюс от 1 до 4 костяшек, поднятых к разделителю из нижнего ряда: 6 — это 5+1, 7 — это 5+2.
Переходим к десяткам (числа от 1 до 99): они находятся на следующей спице.
Двигаясь на столбец влево, мы меняем разряд — от единиц переходим к десяткам, далее к сотням, тысячам, десяткам тысяч и так далее.
Например, чтобы набрать число 129 необходимо поднять 1 косточку снизу в столбце сотен, 2 костяшки на столбце десятков, и 5 — опустить одну косточку к разделителю сверху и поднять 4 снизу в столбце единиц.
Представление числа 129 на соробанеИзучив способы обозначения чисел, переходим к практике. Один человек вслух называет числа, а другой набирает их на доске. После того как навык доведён до автоматизма, можно переходить к арифметическим действиям.
Занятия с ребёнком можно сделать интереснее, называя числа со значением: например, посчитать количество дней в неделе, году, набрать номер дома, квартиры, годы рождения родственников, количество материков, стран, человек, населяющих город и страну.
Простые сложение и вычитание
Главное правило счёта на соробане: «считать нужно слева направо», что не соответствует привычному нам способу вычисления.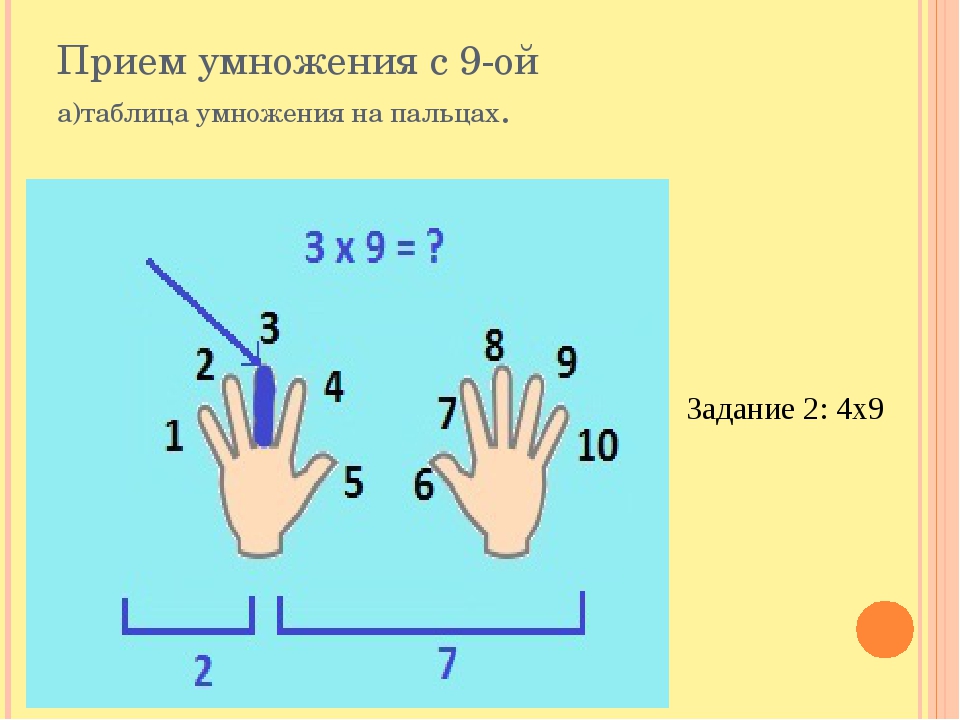
Внимание: техники счёта могут отличаться, мы используем те, что встречаются в рекомендации японской организации The Abacus Committee.
Начинать вычисления стоит с чисел, сумма и разность которых даёт не более 9 при сложении и не менее 1 при вычитании.
Примеры вроде 1+6, 2+7, 12+24 или 123+432 подойдут на первых порах.
- Начнём со сложения единиц: для примера 1+2 поднимите на крайней правой спице 1 костяшку вверх, а затем добавьте к ней ещё 2.
- Для примера:12+32. Откладываем в колонке десятков — 1 косточку, в единицах — 2. Затем к 1 костяшке придвигаем 3, к 2 костяшкам единиц ещё 2.
Изучать вычитание также стоит с простых примеров:
- Рассмотрим вычитание на единицах. Простой пример: 4 – 2 = 2. Из четырёх поднятых костяшек убираем 2 и получаем результат.
- Простой пример с десятками: 24 – 13 = 11. Из столбца десятков убираем 1 костяшку остаётся 1. Переходим к единицам: от 4 костяшек отнимаем 3, у нас остаётся 1 костяшка.
 Результат готов.
Результат готов. - По тому же принципу работаем с сотнями: 432 – 322 = 110. Из столбца сотен от 4 отнимем 3, из 3 вычтем 2 останется 1, из 2 вычтем 2 — все костяшки из столбца единиц возвращаются в нулевую позицию.
Для более сложных вычислений необходимо познакомиться с принципом дополнительных чисел.
Дополнительные числа
Высокая скорость работы на соробане зависит от того, насколько механизированы действия считающего. Смысл заключается в том, чтобы снять лишнюю нагрузку с ума и выполнять арифметические действия механически, без размышлений или колебаний, отсюда и сравнение людей, обладающих этим навыком, с калькулятором. И если со сложением и вычитанием простых чисел всё ясно, то с более сложными примерами нужно освоить концепцию дополнительных чисел. Нужно просто запомнить, что:
- цифру 5 можно разложить на дополнительные числа: 4 и 1, 5 и 2.
- цифру 10 можно разложить на дополнительные числа: 9 и 1, 8 и 2, 7 и 3, 6 и 4, 5 и 5.
При сложении дополнительное число вычитается. При вычитании — дополнительное число прибавляется. Как это работает на практике рассмотрим далее.
При вычитании — дополнительное число прибавляется. Как это работает на практике рассмотрим далее.
Сложное сложение
Пример: 4 + 8 = 12
Как решать?
- Установите 4 костяшки в столбце единиц.
- Для 8 костяшек места уже не найдётся.
- Вспоминаем принцип дополнительных чисел: число 10 даёт наша 8 и цифра 2.
- Вычтите дополнительную цифру 2 из 4.
- Добавьте единицу в столбик десятков.
- Результат — 12.
Принцип вычисления на соробане в привычной записи можно представить так:
4 + 8 = 12 превращаем в 4 – 2 +10 = 12
Важно запомнить: в сложных заданиях на сложение всегда вычитайте дополнительное число.
Сложное вычитание
Пример: 12 – 7 = 5.
Как решать?
- Установите 1 костяшку на столбец с десятками, добавьте 2 к единицам.
- Вспомните, что 7 — это 10 и 3.
- Уберите 1 костяшку из столбца десятков.
- Прибавьте в столбце единиц к 2 костяшкам дополнительные 3.
 Получается 5 — верните в нулевую позицию нижние костяшки и опустите «небесную».
Получается 5 — верните в нулевую позицию нижние костяшки и опустите «небесную».
Принцип вычисления на соробане в привычной записи можно представить так:
12 – 7 = 5 мы превращаем в 12 – 10 + 3 = 5
Важно запомнить: в подобных вычислениях на вычитание всегда прибавляйте дополнительное число.
Порядок столбцов при счёте
В приведённых выше примерах мы использовали по 2 столбца — для десятков и единиц. Особое внимание стоит уделить тому, в каком порядке стоит добавлять и убирать костяшки из столбцов.
Для сложения:
- Вычтите дополнительное число и соответственное количество костяшек из правого столбца.
- Затем добавьте костяшку в левый стержень.
Для вычитания:
- Сначала вычтите числа в левом столбце.
- Добавьте дополнительное число на правый стержень.
Умножение
Есть несколько возможных способов умножения на соробане, мы рассмотрим один из самых распространённых.
Обратите внимание: чтобы умножать на соробане, нужно хорошо знать таблицу умножения.
Также необходимо запомнить следующие термины, которые мы рассмотрим на примере a x b = c, где:
a — это множимое;
b — это множитель;
с — произведение.
Пример: 43 x 8 = 344.
Шаг 1
В первом столбце слева устанавливаем множитель — 8, отступаем один столбец и откладываем множимое — 43. Отступаем 2 столбца — с этого столбца начнём записывать результат.
Шаг 2
Умножаем 3 на 8. Результат 24 записываем в 7 и 8 столбцах. Завершая операцию, убираем цифру 3 с доски, сдвинув костяшки вверх.
Шаг 3
Умножьте 4 на 8. Результат 32 запишите следующим образом: 3 в 6 столбец — перед прошлым результатом, а 2 сложите с результатом в 7 столбце, то есть с 2. Три цифры в результате дают ответ — 344.
Сложнее выполнить умножение с двумя двузначными числами, рассмотрим это на следующем примере:
Пример: 35 x 18
Шаг 1
Откладываем множитель, то есть 18 с начала доски. Делаем отступ и откладываем 35.
Шаг 2
Умножаем 1 на 5, записываем результат через 2 пробела.
Шаг 3
Умножаем 8 на 5, получаем 40. 4 записываем под прошлым результатом, т.е. складываем с 5. В столбцах результата остаётся цифра 90.
Шаг 4
Умножаем 3 на 1 и записываем результат — 3 — перед предыдущими столбцами. Получается 390.
Шаг 5
Умножаем 3 на 8, результат 24 записываем под первыми двумя цифрами прошлого результата. Получаем 630.
Деление
Для деления мы также используем стандартные математические термины a ÷ b = c, где:
a — делимое;
b — делитель;
c — частное.
Делимое набирается на спицах в правом конце соробана, делитель — в левом конце. Результат записывается посередине.
Между делимым и делителем рекомендуют оставить минимум 4 пустых столбца для записи результата.
Также существуют правила размещения первой цифры частного:
- Если количество цифр в делителе меньше (или равно) количеству цифр в делимом, расположите первую цифру частного, отступив 2 столбца слева от делимого.
- Если количество цифр в делителе больше, нежели в делимом, начните располагать частное, отступив 1 столбец слева от делимого.

Пример: 72 ÷ 2
- Помещаем делитель 2 в левую часть счёт, делимое — 72 — в правую.
- Делим первое число 7 на 2. Цифра 2 помещается в 7 полностью три раза — поднимаем 3 костяшки в соответствии с правилом №1, отступив 2 столбца влево от делимого.
- Умножим полученное число 3 на делитель — 2. Результат — 6 — вычтем из первой цифры делимого — 7. Убираем лишние костяшки, остаётся единица.
- Остаток от делимого — 12 делим на делитель — 2. Полученный результат — 6 помещаем в следующий свободный столбец для записи результата. Получаем в итоге — 36.
Полезные ресурсы
- Подвигать косточки на соробане: ссылка
- Посмотреть пошаговое решение примеров: ссылка
- Приложение «Игры соробан»: ссылка
Мы разобрали самые простые способы вычисления на соробане. Чтобы выполнять манипуляции с трёхзначными и дробными числами необходимо на высоком уровне научиться работать с однозначными и двузначными числами.
Следующей ступенью после тщательного освоения каждой техники счёта становится его представление соробана в уме и мысленное выполнение вычислений. Последовательно, правильно и адаптировано для каждого возраста учат считать подготовленные тренеры в специализированных центрах. Подобрать такой в своём городе вы можете на TeachMePlease.
Последовательно, правильно и адаптировано для каждого возраста учат считать подготовленные тренеры в специализированных центрах. Подобрать такой в своём городе вы можете на TeachMePlease.
Презентация “Тайны устного счета”
Открытые Ломоносовские Чтения
Муниципальное общеобразовательное учреждение средняя общеобразовательная школа 65 городского округа Самара
СЕКЦИЯ «МАТЕМАТИКА»
РАСКРЫТИЕ
ТАЙН БЫСТРОГО СЧЕТА
Выполнила:
Дорофеева Анастасия
ученица 5 «Б» класса
МБОУ СОШ № 65
Промышленного района.
Научный руководитель:
Копытина Светлана Викторовна,
высшая категория
Самара, 2017г.
Оглавление.
Введение
Часть 1.Исследование теории
1. 1.счет у первобытных
1.счет у первобытных
1.2.умножение на пальцах
2часть.Эксперименты и анализ решения
2.1.Умножение на 11(по Якову Трахтенбергу, по Г.Н. Берману)
2.2.Умножение на число 111
2.3.Умножение на 1111
2.3..Умножение двузначного числа на 101
2.4.Умножение трехзначного числа на 999(По Я.И. Перельману)
2.5. Умножение на двенадцать(По Якову Трахтенбергу и Г.Н. Берману )
2.6.Умножение на шесть(по Якову Трахтенергу)
2.7.Возведение в квадрат (по Я.И. Перельману)
2.8.Умножение на 4 и 8 (по Я.И. Перельману)
2.9.Умножение и деление на 5 и 25( по Я.И. Перельману)
3Часть. Практическая часть
Заключение. Применение приемов быстрого счета
Список литературы
Введение.
Тема моего проекта «Раскрытие тайн быстрого счета».
Уважаемое жюри! Предлагаю вам 341 умножить на 999.Сколько времени вы потратите на умножение? Какой результат получится? У меня 340659.Проверьте на калькуляторе. Ровно столько же.
В наш век высоких технологий и повсеместного использования компьютера умение быстро и правильно производить в уме достаточно сложные вычисления ни в коем случае не утратило своей актуальности. Гибкость ума является предметом гордости людей, а способность, например, быстро производить в уме вычисления вызывает откровенное удивление. Такие навыки помогут человеку в учебе, в быту, в профессиональной деятельности. Кроме того, быстрый счет – настоящая гимнастика для ума, приучающая в самых сложных жизненных ситуациях находить в кратчайшее время нестандартные решения. Производя математические вычисления в уме, человек пользуется, по сути, теми же правилами, что и при письменных вычислениях
К сожалению, большинство детей, да и взрослых считают плохо. То ли думать им лень (зачем загружать себя лишней работой, если есть калькуляторы), то ли в свое время никто не научил. Приемов рациональных вычислений в учебниках практически нет. Сложные формулы и алгоритмы школьной программы все дальше и дальше уводят от простых, понятных навыков устного счета.
То ли думать им лень (зачем загружать себя лишней работой, если есть калькуляторы), то ли в свое время никто не научил. Приемов рациональных вычислений в учебниках практически нет. Сложные формулы и алгоритмы школьной программы все дальше и дальше уводят от простых, понятных навыков устного счета.
Я выбрала тему «Тайны быстрого счета» потому, что я люблю математику и хотела бы научиться считать быстро и правильно, не прибегая к использованию калькулятора и поделиться знаниями со сверстниками, тем самым их заинтересовать некоторыми приемами быстрого счета.
Актуальность моей темы: быстрый счет помогает детям «щелкать» задачки и примеры, а взрослым правильно считать денежки и не тратить их зря.
Цели исследовательской работы:
– изучить методы и приемы быстрого счета;
– доказать преимущество умений считать быстро;
– оценить эффективность использования различных видов устных вычислений для значительного сокращения времени, потраченного на вычисления и запись решения.
Задачи:
– изучить источники по теме;
– выбрать наиболее оптимальные арифметические и алгебраические приемы быстрого счета
– рекомендовать некоторые способы и приема вычислений
-провести мастер-класс в 5-6 классах по данной теме, проанализировать и сравнить результативность счета до и после ознакомления с некоторыми приемами устного счета
-составить памятку в помощь учащимся «Считай быстро»
Методы исследования:
-обработка полученных данных (составление обобщающих таблиц, диаграмм)
-проведение мастер-класса
Итак, объектом моего исследования являются методы и приемы быстрого счета. Для этого мне пришлось изучить много литературы.
Я узнала, как научились люди считать, таблицу умножения на пальцах, метод скоростного счета. В своей работе отмечаю заслуги Якова Трахтенберга, Якова Перельмана, учу без затруднения умножать на 11 , на 111, на 1111, на 99,на 999, на 1001.
Компьютерная презентация научит и вас этому.
(идет компьютерная презентация)
В заключении делаю вывод: как мы видим, быстрый счет не тайна за семью печатями, а научно- разработанная система .Раз есть система. Значит, ее можно изучать, ей можно следовать, ею можно овладеть.
Как люди научились считать.
Никто не знает, как впервые появилось число, как первобытный человек начал считать. Однако десятки тысяч лет назад первобытный человек собирал плоды деревьев, ходил на охоту, ловил рыбу, научился делать каменный топор и нож, и ему приходилось считать различные предметы, с которыми он встречался в повседневной жизни. Постепенно возникало необходимость отвечать на жизненно важные вопросы: поскольку плодов достанется каждому, чтобы хватило всем, сколько расходовать сегодня, чтобы оставить про запас; сколько нужно сделать ножей и т.п. Таким образом, сам не замечая, человек начал считать и вычислять.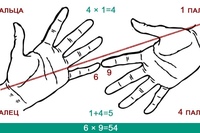
Вначале человек научился выделять единичные предметы. Например, из стаи волков, стада оленей он выделял одного вожака, из выводка птенцов – одного птенца и т. д. Научившись выделять один предмет из множества других, говорили: “один”, а если их было больше – “много” Даже для названия числа “один” часто пользовались словом, которым обозначался единичный предмет, например: “луна”, “солнце”. Такое совпадение названия предмета и числа сохранилось в языке некоторых народов до наших дней.
Частые наблюдения множеств, состоящих из пары предметов (глаза, уши, крылья, руки), привели человека к представлению о числе два. До сих пор слово “два” на некоторых языках звучит так же, как “глаза” или “крылья”.
Если предметов было больше двух, то первобытный человек говорил «много». Лишь постепенно человек научился считать до трех, затем до пяти и до десяти и т.д. Название каждого числа отдельным словом было великим шагом вперед.
Для счета люди использовали пальцы рук, ног. Ведь и маленькие дети тоже учатся считать по пальцам. Однако этот способ годился только в пределах 20.
Ведь и маленькие дети тоже учатся считать по пальцам. Однако этот способ годился только в пределах 20.
Выход нашелся: считать на пальцах до 10, а затем начинать сначала, отдельно подсчитывая количество десятков. Система счисления на основе десяти возникла как естественное развитие пальцевого счета.
По мере развития речи люди начали использовать слова для обозначения чисел. Отпала необходимость показывать кому-то пальцы, камешки или реальные предметы, чтобы назвать их количество. Для изображения чисел стали применяться рисунки, чертежи или символы. Существовали и системы с отдельными символами для каждой цифры до 9 включительно, как в арабской системе счисления, которую мы сейчас используем, а у греков имелся специальный символ и для 10.
При помощи пальцев рук люди научились не только считать большие числа, но и выполнять действия сложения и вычитания.
Древние торговцы для удобства счета начали накладывать зерна и раковины на специальную дощечку, которая со временем стала называться абаком.
Особенно сложны и трудны были в старину действия умножения и деления – особенно последнее. «Умноженье – мое мученье, а с делением – беда», – говорили в старину. Тогда не существовало еще, как теперь, одного выработанного практикой приема для каждого действия. Напротив, в ходу была одновременно чуть не дюжина различных способов умножения и деления – приемы один другого запутаннее, твердо, запомнить которые не в силах был человек средних способностей. Каждый учитель счетного дела держался своего излюбленного приема, каждый «магистр деления» (были такие специалисты) восхвалял собственный способ выполнения этого действия.
В книге В. Беллюстина «Как постепенно дошли люди до настоящей арифметики» (1914) изложено 27 способов умножения, причем автор замечает: «весьма возможно, что есть и еще (способы), скрытые в тайниках книгохранилищ, разбросанные в многочисленных, главным образом, рукописных сборниках». Наш современный способ умножения описан там под названием «шахматного». Был также и очень интересный, точный, легкий, но громоздкий способ «галерой» или «лодкой», названный так в силу того, что при делении чисел этим способом получается фигура, похожая на лодку или галеру. У нас такой способ употреблялся до середины XVIII века. На протяжении своей книги в 640 страниц Леонтий Магницкий («Арифметика» – старинный русский учебник математики, которую Ломоносов называл «вратами своей учености») пользуется исключительно способом «галеры», не употребляя, впрочем, этого названия.
Был также и очень интересный, точный, легкий, но громоздкий способ «галерой» или «лодкой», названный так в силу того, что при делении чисел этим способом получается фигура, похожая на лодку или галеру. У нас такой способ употреблялся до середины XVIII века. На протяжении своей книги в 640 страниц Леонтий Магницкий («Арифметика» – старинный русский учебник математики, которую Ломоносов называл «вратами своей учености») пользуется исключительно способом «галеры», не употребляя, впрочем, этого названия.
Упоминаются такие способы, как «загибанием», «решеткой», «задом наперед», «ромбом», «треугольником» и многие, многие другие. Многие такие приемы для умножения чисел долгие и требуют обязательной проверки.
Интересно, что и наш способ умножения не является совершенным; можно придумать еще более быстрые и еще более надежные.
Таблица умножения на «пальцах».
Таблица умножения – те необходимые в жизни каждого человека знания, которые требуется элементарно заучить, что на первых школьных порах дается совсем не элементарно. Это потом уже с легкостью мага мы “щелкаем” примеры на умножение: 2·3, 3·5, 4·6 и так далее. С возрастом, правда, все чаще забываемся на множителях ближе к 9, особенно если счетной практики давно не ведали, отчего отдаемся во власть калькулятора или надеемся на свежесть знаний друга. Однако, овладев одной незамысловатой техникой “ручного” умножения, мы можем запросто отказаться от услуг калькулятора. Но сразу уточним, что говорим только о школьной таблице умножения, то есть для чисел от 2 до 9, умножаемых на числа от 1 до 10.
Умножение для числа 9 – 9·1, 9·2 … 9·10 – легче выветривается из памяти и труднее пересчитывается вручную методом сложения, однако именно для числа 9 умножение легко воспроизводится “на пальцах”. Растопырьте пальцы на обеих руках и поверните руки ладонями от себя. Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки (это изображено на рисунке).
Допустим, хотим умножить 9 на 6. Загибаем палец с номером, равным числу, на которое мы будем умножать девятку. В нашем примере нужно загнуть палец с номером 6. Количество пальцев слева от загнутого пальца показывает нам количество десятков в ответе, количество пальцев справа – количество единиц. Слева у нас 5 пальцев не загнуто, справа – 4 пальца. Таким образом, 9·6=54. Ниже на рисунке детально показан весь принцип “вычисления”.
Еще пример: нужно вычислить 9·8=?. По ходу дела скажем, что в качестве “счетной машинки” не обязательно могут выступать пальцы рук. Возьмите, к примеру, 10 клеточек в тетради. Зачеркиваем 8-ю клеточку. Слева осталось 7 клеточек, справа – 2 клеточки. Значит 9·8=72. Все очень просто.
Умножение для числа 8 – 8·1, 8·2 … 8·10 – действия здесь похожи на умножение для числа 9 за некоторыми изменениями. Во-первых, поскольку числу 8 не хватает уже двойки до круглого числа 10, нам необходимо каждый раз загибать сразу два пальца – с номером x и следующий палец с номером x+1. Во-вторых, тотчас же после загнутых пальцев мы должны загнуть еще столько пальцев, сколько осталось незагнутых пальцев слева. В-третьих, это напрямую работает при умножении на число от 1 до 5, а при умножении на число от 6 до 10 нужно отнять от числа x пятерку и выполнить расчет как для числа от 1 до 5, а к ответу затем добавить число 40, потому что иначе придется выполнять переход через десяток, что не совсем удобно “на пальцах”, хотя в принципе это не так сложно. Вообще надо заметить, что умножение для чисел ниже 9 тем неудобнее выполнять “на пальцах”, чем ниже число расположено от 9.
Теперь рассмотрим пример умножения для числа 8. Допустим, хотим умножить 8 на 4. Загибаем палец с номером 4 и за ним палец с номером 5 (4+1). Слева у нас осталось 3 незагнутых пальца, значит, нам необходимо загнуть еще 3 пальца после пальца с номером 5 (это будут пальцы с номерами 6, 7 и 8). Осталось 3 пальца не загнуто слева и 2 пальца – справа. Следовательно, 8·4=32.
Еще пример: вычислить 8·7=?. Как было сказано выше, при умножении на число от 6 до 10 нужно отнять от числа x пятерку, выполнить расчет с новым числом x-5, а затем добавить к ответу число 40. У нас x=7, значит, загибаем палец с номером 2 (7-5=2) и следующий палец с номером 3 (2+1). Слева один палец остался, не загнут, значит, загибаем еще один палец (с номером 4). Получаем: слева 1 палец не загнут и справа – 6 пальцев, что обозначает число 16. Но к этому числу нужно еще добавить 40: 16+40=56. В итоге 8·7=56.
Метод скоростного вычисления
Якова Трахтенберга.
Пожалуй, единственная научно обоснованная и достаточно подробно разработанная система резкого повышения быстроты устного счета создана была в годы второй мировой войны цюрихским профессором математики Я. Трахтенбергом. Она известна под названием “Системы быстрого счета”. История ее создания необычная. В 1941 году гитлеровцы бросили Трахтенберга в концлагерь. Чтобы уцелеть в нечеловеческих условиях и сохранить нормальной свою психику, Трахтенберг начал разрабатывать принципы ускоренного счета. За четыре страшных года пребывания в концлагере профессору удалось создать стройную систему ускоренного обучения детей и взрослых основам быстрого счета. После войны Я. Трахтенберг создал и возглавил Цюрихский математический институт, получивший мировую известность.
Также разработкой приемов быстрого счета занимались другие ученые: Яков Исидорович Перельман, Георгий Берман и другие.
Приведу приемы умножения чисел, получившие наибольшее описание в литературе.
Умножение на одиннадцать.
1. Умножение на 11 двузначного числа, сумма цифр которого не превышает 10.
Чтобы умножить на 11 число, сумма цифр которого 10 или меньше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить 1, а вторую и последнюю (третью) цифру оставить без изменения.
72 х 11 = 7 (7+2) 2 = 792;
35 х 11 = 3 (3+5) 5 = 385;
2. Умножение на 11 двузначного числа, сумма цифр которого больше 10.
Чтобы умножить на 11 число, сумма цифр которого 10 или больше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить 1, а вторую и последнюю (третью) цифру оставить без изменения.
78 х 11 = 7 (7+8) 8 = 7(13)8 = 858.
94 х 11 = 9 (9+4) 4 = 9 (13) 4 = 1034;
3. Умножение любого многозначного числа на одиннадцать (по Трахтенбергу).
Разберем на примере: 633 умножить на 11.
Ответ пишется под 633 по одной цифре справа налево, как указано в правилах.
Первое правило. Напишите последнюю цифру числа 633 в качестве правой цифры результата 633 х 11
3
Второе правило. Каждая последующая цифра числа 633 складывается со своим правым соседом и записывается в результат. 3 + 3 будет 6. Перед тройкой записываем результат 6.
633 х 11
63
Применим правило еще раз: 6 + 3 будет 9. Записываем и эту цифру в результате:
633 х11
963
Третье правило. Первая цифра числа 633, то есть 6, становится левой цифрой результата:
633 х 11
6963
Ответ: 6963.
4. Умножение на одиннадцать по Берману.
Берман вывел, что при умножении на одиннадцать, число нужно умножить на 10 и прибавить само себя, то есть то число, которое мы умножаем.
Пример: 110 х 11 = 110х (10 + 1) = 110 х 10 + 110 х 1 = 1100 + 110 =1210
Ответ: 1210.
Пример: 123 х 11 = 123 х (10 +1) = 123 х 10 + 123 х 1 = 1230 + 123 =1353
Ответ: 1353.
Умножение на число 111, 1111 и т. д.
1.Умножение двузначного числа на 111, 1111 и т.д. сумма цифр которого меньше 10.
Если сумма цифр первого множителя меньше 10, надо мысленно раздвинуть цифры этого числа на 2, 3 и т.д. шага, сложить цифры и записать соответствующее количество раз их сумму между раздвинутыми цифрами. Количество шагов всегда меньше количества единиц на 1.
Пример:
24 х 111 = 2 (2 + 4) (2+4) 4 = 2664 (количество шагов – 2)
24 х 1111 = 2 (2 +4) (2 +4) (2+4) 4 = 26664 (количество шагов – 3)
При умножении числа 72 на 111111 цифры 7 и 2 надо раздвинуть на 5 шагов. Эти вычисления можно легко произвести в уме.
72 х 111111 = 7999992 (количество шагов – 5)
Если единиц во втором множителе 7, то шагов будет на один меньше, т.е. 6.
Если единиц 8, то шагов будет 7 и т.д.
61х 11111111 = 677777771
Эти вычисления можно легко произвести в уме.
2.Умножение двузначного числа на 111, 1111, 1111 и т.д., сумма цифр которого равна 10 или больше 10
Немного сложнее выполнить устное умножение, если сумма цифр первого множителя равна 10 или более 10.
Примеры:
48 х 111 = 4 (4+8) (4+8) 8 = 4 (12) (12) 8 = (4 +1) (2+1) 28 = 5328.
В этом случае к первой цифре надо прибавить 1. Получим 5.
Далее 2 + 1 = 3. А последние цифры 2 и 8 оставляем без изменения.
56 х 11111 = 5(5+6)(5+6)(5+6)(5+6)6 = 5(11)(11)(11)(11)6 = 622216
67 х 1111 = 6(6+7)…7 = 6(13)…7 = 74437
Умножение двузначного числа на 101.
Пожалуй, самое простое правило: припишите ваше число к самому себе. Умножение закончено.
Пример:
57 х 101 = 5757 57 –> 5757
Умножение трехзначного числа на 999.
Любопытная особенность числа 999 проявляется при умножении на него всякого другого трехзначного числа. Тогда получается шестизначное произведение: первые три цифры его есть умножаемое число, только уменьшенное на единицу, а остальные три цифры (кроме последней) – «дополнения» первых до 9. Например:
572
573 х 999 = 572 427
999
Умножение на двенадцать.
1.Умножение на двенадцать (по Трахтенбергу)
Правило умножения на 12: нужно удваивать поочередно каждую цифру и прибавлять к ней поочередно ее «соседа».
Пример: 63247 х 12
Необходимо записывать цифры множимого через интервал и каждую цифру результата писать точно под цифрой числа 63247, из которой она образовалась.
063247 х 12 дважды 7 будет = 14, переносим 1
4
063247 х 12 дважды 4 + 7 + 1 = 16, переносим 1
64
063247 х 12 дважды 2 + 4 + 1 = 9
964
Следующие шаги аналогичны.
Окончательный ответ: 063247 х 12
758964
2.Умножение на двенадцать (по Берману)
При умножении на 12 можно число умножить сначала на 6, а затем на 2.
6, в свою очередь, можно разбить на 2 множителя – это 3 и 2.
Пример: 136 х 12 = 136 х 6 х 2 = 816 х 2 = 1632 или
136 х 12 = 136 х 3 х 2 х 2 = 408 х 2 х 2 = 816 х 2 = 1632
Умножение на шесть (по Трахтенбергу).
Нужно прибавить к каждой цифре половину «соседа».
Пример: 0622084 х 6
0622084 х 6 4 является правой цифрой этого числа и, так 4 как «соседа» у нее нет, прибавлять нечего.
0622084 х 6 Вторая цифра 8, ее «сосед» – 4. Мы берем 8 04 прибавляем половину 4 (2) и получаем 10,
ноль пишем, 1 в перенос.
0622084 х 6 Третья цифра ноль. Мы прибавляем к ней
504 половину «соседа» 8 (4), то есть 0 + 4 = 4
плюс перенос (1).
Остальные шаги аналогичны.
Ответ: 0622084 х 6
3732504
Правило умножения на 6: является «сосед» четным или нечетным – никакой роли не играет. Мы смотрим только на саму цифру: если она четная, прибавляем к ней целую часть половины «соседа», если нечетная, то кроме половины «соседа» прибавляем еще 5.
Пример: 0443052 х 6
0443052 х 6 2 – четная и не имеет «соседа», напишем ее снизу
2
0443052 х 6 5 – нечетная: 5 + 5 и плюс половина «соседа» 2 (1)
12 будет 11. Запишем 1 и в перенос 1
0443052 х 6 половина от 5 будет 2, и прибавим перенос 1, будет 3
312
0443052 х 6 3 – нечетная, 3 + 5 =8
8312
0443052 х 6 4 + половина от 3 (1) будет 5
58312
0443052 х 6 4 + половина от 4 (2) будет 6
658312
0443052 х 6 ноль + половина от 4 (2) будет 2
2658312
Ответ: 2658312
Система быстрого счета по Трахтенбергу основана на закономерностях умножения чисел. Чтобы умножить на 11, 12, 6 и т. д. надо знать алгоритм выполнения. Этим система неудобна, надо в памяти держать много правил быстрого счета, но система Я. Трахтенберга показывает, как красива математика, если человек открывает тайны ее закономерностей, изучает их и учится применять на практике.
Возведение в квадрат
Чтобы возвести в квадрат число, оканчивающееся цифрой 5(например 65),надо число его десятков умножить на число десятков, увеличенное на 1(на 6+1=7), и к полученному числу приписывают 25 (6Х7=42)ОТВЕТ:4225
952=9025 1252=15625
Умножение на 4 и на 8
Чтобы устно умножить число на 4, его дважды удваивают. Например:
112 Х 4=224 Х 2=448
335 Х 4=670 Х 2=1340
Чтобы устно умножить число на 8, его трижды удваивают. Например:
217 Х 8=434 Х 4=868 Х 2 = 1736
Деление на 4 и на 8
Чтобы устно разделить число на 4, его дважды делят пополам. Например:
76 : 4 = 38 : 2 = 19
236 : 4 = 118 : 2 = 59
Чтобы устно разделить число на 8, его трижды делят пополам. Например:
464 : 8 = 232 : 4 = 116 : 2 = 58
Умножение на 5 и 25
Чтобы устно умножить число на 5 ,приписывают к числу 0 и делят пополам. Например: 74 Х 5 = 740 : 2 = 370
243 Х 5 = 2430 : 2 = 1215
Чтобы устно умножить число на 25,приписывают к числу два нуля и делят его на 4.
Например: 72 Х 25 = 7200 : 4 =1800
ПРАКТИЧЕСКАЯ ЧАСТЬ РАБОТЫ.
МАСТЕР- КЛАСС. Провела в среднем и старшем звене анкетирование ребят на умение быстро производить вычислительные операции с двухзначными и трехзначными числами. Мастер- класс провела в 5б и 8в классе. Что было удивительно, что все вычислительные операции с числами проводили долго, выполняя столбиком и умножение и деление .Проведенный мною и показ методов быстрого счета очень заинтересовал детей, особенно старшеклассников. Дети попросили литературу, в которой можно найти такие интересные приемы.
Цель: оценка эффективности методов быстрого счета
Задачи:1.применять знание методов быстрого счета в конкретной ситуации.
2.сравнить полученные результаты
3. сделать вывод
Этапы проведения:
1этап: решение примеров
2этап: объяснение
3этап: решение примеров после ознакомления с некоторыми приемами быстрого счета.
Итоги: на первом этапе 5классники считали- мин.
Диаграмма: см. приложение
Применение приемов быстрого счета.
Одной из основных проблем современных учащихся является нерациональность вычислений: школьники не только плохо и нерационально считают, но и все чаще прибегают к использованию технических средств – калькуляторов. Таким образом, учащиеся с самого начала приучаются не думать при вычислениях, что в дальнейшем приводит ко многим нерациональным решениям, к большим потерям учебного времени, к слабо развитым вычислительным умениям и навыкам. Поэтому возникает потребность в ознакомлении учащихся с дополнительными приемами устных и письменных вычислений, которые позволили бы значительно сократить время, потраченное на вычисления и запись решения, и избежать использования различных вычислительных средств. Привычка выполнять устно вычисления нередко порождает потребность производить мысленные эксперименты при решении задач, высказывать догадки, предположения о путях решения более сложных задач, мысленно проверяя истинность предположений. А это одно из самых главных условий обучения решению математических задач.
Кроме того, навыки быстрого счета помогут не только при процессе обучения, но и в быту, в профессиональной деятельности.
Быстрый счет является самой настоящей гимнастикой для ума, приучающей в самых сложных жизненных ситуациях находить в кратчайшее время хорошие и нестандартные решения.
Заключение.
Таким образом, в моем исследовании были решены следующие задачи:
– изучила математическую литературу, в которой описывается история возникновения счета;
-изучила наиболее распространенные методы и приемы быстрого счета;
– доказала необходимость умения быстро считать.
В результате проделанной мною работы, я поняла, что приемы быстрого счета являются объектом многолетнего интереса и ученых, и простых людей. Используя некоторые из этих методов на уроках или дома, можно развить скорость вычислений, привить интерес к математике. Приемы быстрого счета развивают память. Это касается не только математики, но и других предметов, которые изучаются в школе, что способствует их успешному изучению.
Методы быстрого счета можно использовать в быту, в профессиональной деятельности.
Как мы видим, быстрый счет это уже не тайна за семью печатями, а научно разработанная система. Раз есть система, значит, ее можно изучать, ей можно следовать, ею можно овладеть.
Мне нравится решать задачи, которые требуют усилий, сосредоточенности. Знания, которые я получила в ходе работы над проектом, помогут мне на уроках математики быстрее справляться с предложенными заданиями, а дома с домашними работами
Список используемой литературы.
1.Бантова М. А. Система формирования вычислительных навыков. Нач. шк — 1993.-№ 11.-с. 38-43.
2.Берман Г. Н. Приемы счёта, изд. 6-е, М.: Физматгиз, 1959.
3.Гольдштейн Д. Н. Техника быстрых вычислений. М.: Учпедгиз, 1948.
4.Катлер Э. Мак-Шейн Р. Система быстрого счёта по Трахтенбергу. — М.: Учпедгиз.- 1967. −150с.
5.Мартынов И. И. Устный счёт для школьника, что гаммы для музыканта. Начальная школа. — 2003. — № 10. — С. 59-61.
6.Пекелис В. Д. «Твои возможности, человек!» М.: «Знание», 1973.
6.Перельман Я. И. Быстрый счёт. Л.: Союзпечать, 1945.
7.Сорокин А. С. Техника счёта. М.: «Знание», 1976.
8.Фаддейчева Т. И. Обучение устным вычислениям. Начальная школа. 2003. — № 10.
Татьяна Мельничук | Приёмы быстрого счёта
Приёмы быстрого счёта
Милена Кандыбова проводит занятие на тему «Приёмы быстрого счёта» для обучающихся 11 класса
Трудно сказать, когда появились числа и как человек научился считать. Однако, наши далекие предки постоянно сталкивались с необходимостью делить продукты, добычу, делать запасы впрок. Таким образом, человек научился считать, производить вычисления. Для счёта использовали пальцы рук, ног, различные предметы. Например, индейцы изображали числа с помощью узелков на верёвках. Первым способом «записи» чисел были зарубки на палке. В Древнем Вавилоне записывали числа, выдавливая значки палочкой на глиняной дощечке. В конце-концов были придуманы цифры. Люди научились складывать и вычитать, затем умножать и делить, причём способы вычислений не всегда были и остаются удобными и понятными.
Большинство обучающихся и взрослых испытывают затруднения при выполнении вычислений. Многие неоправданно часто используют калькулятор, а вот устно же считать почти никто не умеет. Приёмам рациональных вычислений в учебной литературе уделяется крайне мало внимания. При этом, например, сдача ЕГЭ и ГИА предполагает наличие у учеников умений и навыков рациональных вычислений.
Предлагаю вниманию читателя выдержки из проекта «Приёмы быстрого счёта» ученицы 5-А класса новосмолинской МАОУ СОШ №48 Милены Кандыбовой, в которых описаны удобные методы рациональных устных вычислений:
Проект «Приёмы быстрого счёта» Презентация к проекту Продукт проектаНа основе данного проекта в 5-х и 11-м классах новосмолинской МАОУ СОШ №48 были проведены занятия на соответствующую тему, фоторепортажи которых доступны в статьях «Занятие в 5 классах «Приёмы быстрого счёта»» и «Занятие в 11 классе «Приёмы быстрого счёта»».
Умножение и деление на 4
Чтобы число умножить на , его дважды удваивают.
Например:
Чтобы число разделить на , его дважды делят на два.
Например:
Умножение и деление на 5, 50, 500…
Чтобы число умножить на нужно умножить его на и разделить на .
Например:
Чтобы разделить число на нужно разделить его на и умножить на .
Например:
Умножение на 25, 250, 2500…
Чтобы число умножить на нужно умножить его на , и полученный результат разделить на (на делятся только те числа, у которых две последние цифры представляют собой число, делящееся на ).
Например:
Деление на 25, 250, 2500…
Чтобы выполнить деление числа на и т.д. это число надо разделить на и т.д. и умножить на .
Например:
Умножение на 125, 1250, 12500,…
Чтобы число умножить на надо это число разделить на и умножить на . (На делятся только те числа, у которых три последние цифры выражают число, делящееся на ).
Например:
Деление на 125, 1250, 12500,…
Чтобы число разделить на надо это число разделить на и умножить на .
Например:
Умножение на 1.5
Чтобы умножить число на нужно к исходному числу прибавить его половину.
Например:
Умножение на 9
Чтобы умножить число на , к нему приписывают и отнимают исходное число.
Например:
Умножение на 11
Чтобы умножить число на . К нему приписывают 0 и прибавляют исходное число.
Например:
Чтобы двузначное число умножить на , сумма цифр которого не превышает , надо цифры этого числа раздвинуть и поставить между ними сумму этих цифр.
Например:
Чтобы умножить на двузначное число, сумма цифр которого или больше , надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить единицу, а вторую и последнюю (третью) оставить без изменения.
Например:
Умножение двухзначного числа на 111
Умножим на . Мысленно раздвигаем цифры первого сомножителя (), предварительно найдя сумму его цифр: , и вставляем полученную сумму, повторив эту операцию дважды.
Например:
Возведение в квадрат числа, оканчивающегося цифрой 5
Чтобы возвести в квадрат число, оканчивающегося цифрой (например, ), умножают число его десятков () на число десятков, увеличенное на (на ), и к полученному числу приписывают .
Например:
В продолжение темы приёмов быстрого счёта рекомендую прочесть книгу «Магия чисел. Моментальные вычисления в уме и другие математические фокусы», русский перевод которой увидел свет в 2015 году. В аннотации к книге сказано: «Эта книга научит вас считать в уме быстрее, чем на калькуляторе, запоминать большие числа и получать от математики удовольствие.
Любой человек может умножать, делить, возводить в степень и производить другие операции над большими числами в уме и с большой скоростью. Для этого не нужно решать десятки тысяч примеров и учиться годами — достаточно использовать простые приемы, описанные в этой книге. Они доступны для людей любого возраста и любых математических способностей.
Эта книга предназначена для всех, кто любит математику, и для тех, кто хочет научиться молниеносно производить в уме любые вычисления».
Подробные библиографические данные книги доступны в каталоге «Библиотеки Татьяны Мельничук».
Вернуться назад…
МЕТКИ >быстрый счёт, вычисления, математика
Нестандартные приемы устного счета
Филиал МБОУ Токарёвской СОШ №1 в с.Полетаево
Нестандартные приемы устного счета
Исследовательская работа
Автор: Семёнова Ангелина Николаевна
научный руководитель: Зуева Ирина Петровна
учитель математики
Полетаево 2016 год
Содержание
Введение.
Глава I. Исследование теории
1.1. Возникновение счета у первобытных людей
1.2. Изменение счета при появлении цивилизации
1.3. Первая литература по способам счёта
1.4. Таблица умножения на пальцах
1.5. Люди – феномены быстрого счёта
Глава II. Эксперименты и анализ решения
2.1. Умножение на 11 числа, сумма цифр которого меньше 10
2.2. Умножение на 11 числа, сумма цифр которого больше 10.
2.3 Умножение на одиннадцать (по Трахтенбергу).
2.4 Умножение на 22,33,…,99
2.5 Умножение на число 111, 1111 и т. д., зная правила
умножения двузначного числа на число 11.
2.6. Умножение двузначного числа на 101, 1001 и т.д.
2.7. Умножение на 37
2.8. Алгоритм перемножения двузначных чисел, близких к 100
2.9. Умножение трёхзначного числа на 999.
2.10. Умножение на шесть ( по Трахтенбергу)
Выводы.
Список использованной литературы.
Введение.
Для участия в конференции творческих работ школьников «Малые грани.» я достаточно быстро определилась с выбором темы. Мне всегда было интересно, какими методами пользуются учителя математики при проверке тетрадей, при объяснении нового материала, когда приходится произвести быстрый расчёт. Определённые приёмы быстрого счёта, предложенные на уроках, мне давались легко, но чем дальше мы познаём математику, тем больше мне хочется узнать о том, как можно еще использовать быстрый счёт на более сложных числах.
В наш век высоких технологий и повсеместного использования компьютера умение быстро и правильно производить в уме достаточно сложные вычисления ни в коем случае не утратило своей актуальности. Гибкость ума является предметом гордости людей, а способность, например, быстро производить в уме вычисления вызывает откровенное удивление. Такие навыки помогут человеку в учёбе, в быту, в профессиональной деятельности. Кроме того, быстрый счёт – настоящая гимнастика для ума, приучающая в самых сложных жизненных ситуациях находить в кратчайшее время хорошие и нестандартные решения. Производя математические вычисления в уме, человек пользуется, по сути, теми же правилами, что и при письменных вычислениях. И оказалось, что большие познания можно получить обратившись к литературе, часть из которой мне предложила руководитель моего проекта Зуева И.П., подсказав суть некоторых способов счёта. Проанализировав очень многие статьи, я открыла для себя очень интересные исторические данные о необычных способах быстрого счёта, а также много закономерностей и неожиданных результатов. И казалось бы «сухие» цифры всего лишь примеры, но сколько полезного и красивого в этих преобразованиях. Для меня было необычно, что приложив немного усилий, я теперь смогу и сам вести быстрый счёт и поделиться этими познаниями с одноклассниками на кружке, со взрослыми и со знакомыми. И, как правило, они, заинтересованные этим, начинают использовать такие приёмы и способы. А ведь большинство моих сверстников считают плохо. То ли думать им лень (зачем загружать себя лишней работой, если есть калькуляторы), то ли в своё время этому никто не научил. Приёмов рациональных вычислений в учебниках практически нет. Сложные формулы и алгоритмы школьной программы всё дальше и дальше уводят учеников от простых, понятных навыков устного счёта.
Здесь будет файл: /data/edu/files/i1461402798.pptx (Нестандартные приемы устного счета)
Я выбрала тему «Нестандартные приемы устного счета» потому, что я люблю математику и хотела бы научиться считать быстро и правильно, не прибегая к использованию калькулятора.
Я поставила перед собой проблему: найти и рассмотреть нестандартные приёмы устного быстрого счёта, не рассматриваемые непосредственно в школьном курсе математики.
Объект исследования – вычислительные навыки и быстрый счёт на уроках предметов естественно – математического цикла.
Предмет исследования – нестандартные приёмы и навыки устного счёта при умножении натуральных чисел.
Задачи 1)узнать об упрощённых, нестандартных способах устных вычислений при умножении натуральных чисел.
2)рассмотреть и показать на примерах применение нестандартных способов при умножении и делении чисел.
Методы исследования:
1) сбор информации;
2) систематизация и обобщение.
Цель исследовательской работы: изучить методы и приёмы быстрого счёта и доказать необходимость умения быстрого счёта и эффективного использования этих приёмов.
Актуальность выбранной темы заключается в том, что нижеперечисленные способы быстрого счёта рассчитаны на ум «обычного» человека и не требуют уникальных способностей. Главное – более или менее продолжительная тренировка. Кроме того освоение этих навыков развивает логику и память учащегося.
ГЛАВА I.
1.1. Как люди научились считать.
На этом этапе мне предстоит окунуться в историю появления счёта, чтобы понять преимущества людей, обладающих приёмами быстрого счета.
Никто не знает, как впервые появилось число, как первобытный человек начал считать. Однако десятки тысяч лет назад первобытный человек собирал плоды деревьев, ходил на охоту, ловил рыбу, научился делать каменный топор и нож, и ему приходилось считать различные предметы, с которыми он встречался в повседневной жизни. Постепенно возникала необходимость отвечать на жизненно важные вопросы: по сколько плодов достанется каждому, чтобы хватило всем, сколько расходовать сегодня, чтобы оставить про запас, сколько нужно сделать ножей и т.п. Таким образом, сам не замечая, человек начал считать и вычислять.
Вначале человек научился выделять единичные предметы. Например, из стаи волков, стада оленей он выделял одного вожака, из выводка птенцов – одного птенца и т.д. Научившись выделять один предмет из множества других, говорили «один», а если их было больше – «много». Даже для названия числа «один» часто пользовались словом, которым обозначался единичный предмет, например «луна», «солнце». Такое совпадение названия предмета и числа сохранилось в языке некоторых народов до наших дней.
Частые наблюдения множеств, состоящих из пары предметов (глаза, уши, крылья, руки) привели человека к представлению о числе два. До сих пор слово «два» на некоторых языках звучит так же, как «глаза» или «крылья».
Если предметов было больше двух, то первобытный человек говорил «много». Лишь постепенно человек научился считать до трёх, затем до пяти и до десяти и т.д. Название каждого числа отдельным словом было великим шагом вперёд.
Для счёта люди использовали пальцы рук, ног. Ведь и маленькие дети тоже учатся считать по пальцам. Однако этот способ годился только в пределах двадцати.
Выход нашелся: считать на пальцах до 10, а затем начинать сначала, отдельно подсчитывая количество десятков. Система счисления на основе десяти возникла как естественное развитие пальцевого счёта.
1.2. Изменение счёта при появлении цивилизации.
По мере развития речи люди начали использовать слова для обозначения чисел. Отпала необходимость показывать кому-то пальцы, камешки или реальные предметы, чтобы назвать их количество. Для изображения чисел стали применяться рисунки, чертежи или символы. Существовали и системы с отдельными символами для каждой цифры до 9 включительно, как в арабской системе счисления, которую мы сейчас используем, а у греков имелся специальный символ и для 10.
При помощи пальцев рук люди научились не только считать большие числа, но и выполнять действия сложения и вычитания.
Древние торговцы для удобства счёта начали накладывать зерна и раковины на специальную дощечку, которая со временем стала называться абаком.
Особенно сложны и трудны были в старину действия умножения и деления, особенно последнее. «Умноженье – мое мученье, а с деленьем – беда» – говорили в старину. Тогда не существовало еще, как теперь, одного выработанного практикой приёма для каждого действия. Напротив, в ходу была одновременно чуть ли не дюжина различных способов умножения и деления – приёмы один другого запутаннее, твёрдо запомнить которые не в силах был человек средних способностей. Каждый учитель счётного дела держался своего излюбленного приёма, каждый «магистр деления» (были такие специалисты) восхвалял собственный способ выполнения этого действия.
1.3. Первая литература по способам счёта.
В книге В. Беллюстина « Как постепенно дошли люди до настоящей арифметики» (1914) изложено 27 способов умножения, причем автор замечает: «весьма возможно, что есть и еще (способы), скрытые в тайниках книгохранилищ, разбросанные в многочисленных, главным образом рукописных сборниках».Наш современный способ умножения описан там под названием «шахматного». Был так же и очень интересный, точный, лёгкий, но громоздкий способ «галерой» или «лодкой», названный так в силу того, что при делении чисел этим способом получается фигура, похожая на лодку или галеру. У нас такой способ употреблялся до середины XVIII века. («Арифметика» – старинный русский учебник математики, которую Ломоносов назвал «вратами своей учености») пользуется исключительно способом «галеры», не употребляя, впрочем, этого названия.
Упоминаются такие способы, как «загибанием», «решеткой», «задом наперед», «ромбом», «треугольником» и многие другие. Многие такие приемы для умножения чисел долгие и требуют обязательной проверки.
Интересно, что и наш способ умножения не является совершенным, можно придумать еще более быстрые и еще более надежные.
1.4. Таблица умножения на «пальцах».
Таблица умножения – те необходимые в жизни каждого человека знания, которые требуется элементарно заучить, что на первых школьных порах даётся совсем не элементарно. Это потом уже с легкостью мага мы «щелкаем» примеры на умножение: 2·3, 3·5, 4·6 и т.д., но со временем все чаще забываемся на множителях ближе к 9, особенно если счетной практики давно не ведали, отчего отдаемся во власть калькулятора или надеемся на свежесть знаний друга. Однако, овладев одной незамысловатой техникой «ручного» умножения, мы можем запросто отказаться от услуг калькулятора. Уточнение: речь идет о школьной таблице умножения, т.е. для чисел от 2 до 9, умножаемых на числа от 1 до 10.
Умножение для числа 9 – 9·1, 9·2 … 9·10 – легче выветривается из памяти и труднее пересчитывается вручную методом сложения, однако именно для числа 9 умножение легко воспроизводится» на пальцах». Растопырьте пальцы на обеих руках и поверните руки ладонями от себя. Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки (это изображено на рисунке). Допустим, хотим умножить 9 на 7. Загибаем палец с номером, равным числу, на которое мы будем умножать 9. В нашем примере нужно загнуть палец с номером 7. Количество пальцев слева от загнутого пальца показывает нам количество десятков в ответе, количество пальцев справа – количество единиц. Слева у нас 6 пальцев не загнуто, справа – 3 пальца. Таким образом, 9·7=63. Ниже на рисунке детально показан весь принцип «вычисления».
Еще пример: нужно вычислить 9·9=? По ходу дела скажем, что в качестве «счетной машинки» не обязательно могут выступать пальцы рук. Возьмите к примеру 10 клеточек в тетради. Зачеркиваем 9-ю клеточку. Слева осталось 8 клеточек, справа – 1 клеточка. Значит 9·9=81. Все очень просто.
Умножение для числа 8 – 8·1, 8·2 … 8·10 – действия здесь похожи на умножение для числа 9 за некоторыми изменениями. Во-первых, поскольку числу 8 не хватает уже двойки до круглого числа 10, нам необходимо каждый раз загибать сразу два пальца – с номером х и следующий палец с номером х+1. Во-вторых, тотчас же после загнутых пальцев мы должны загнуть еще столько пальцев, сколько осталось не загнутых пальцев слева. В-третьих, это напрямую работает при умножении на число от 1 до 5, а при умножении на число от 6 до 10 нужно отнять от числа х пятерку и выполнить расчёт как для числа от 1 до 5., а к ответу затем добавить число 40, потому что иначе придется выполнять переход через десяток, что не совсем удобно «на пальцах», хотя в принципе это не так сложно. Вообще надо заметить, что умножение для чисел ниже 9 тем неудобнее выполнять «на пальцах», чем ниже число расположено от 9.
Теперь рассмотрим пример умножения для числа 8. Допустим, хотим умножить 8 на 3. Загибаем палец с номером 3 и за ним палец с номером 4 (3+1). Слева у нас осталось 2 незагнутых пальца, значит нам необходимо загнуть еще 2 пальца после пальца с номером 4 (это будут пальцы с номерами 5, 6 и 7). Осталось 2 пальца не загнуто слева и 4 пальца – справа. Следовательно, 8·3=24.
Еще пример: вычислить 8·8=? Как было сказано выше, при умножении на число от 6 до 10 нужно отнять от числа х пятерку, выполнить расчет с новым число х-5, а затем добавить к ответу число 40. У нас х=8, значит загибаем палец с номером 3 (8-5=3) и следующий палец с номером 4 (3+1). Слева два пальца остались не загнуты, значит загибаем еще два пальца (с номером 5,6). Получаем: слева 2 пальца не загнуты и справа – 4 пальца, что обозначает число 24. Но к этому числу нужно еще добавить 40: 24+40=64. В итоге 8·8=64.
1.5. Люди – феномен быстрого счёта.
Феномен особых способностей в устном счёте встречается с давних пор. Как известно, ими обладали многие ученые, в частности Андре Ампер и Карл Гаусс. Однако, умение быстро считать было присуще и многим людям, чья профессия была далека от математики и науки в целом.
До второй половины XX века на эстраде были популярны выступления специалистов в устном счёте. Иногда они устраивали показательные соревнования между собой. Известными российскими «суперсчетчиками» являются Арон Чиквашвили, Давид Гольдштейн, Юрий Горный, зарубежными – Борислав Гаджански, Вильям Клайн, Томас Фулер и другие.
Хотя некоторые специалисты уверяли, что дело во врожденных способностях, другие аргументировано доказывали обратное: «дело не только и не столько в каких-то исключительных «феноменальных» способностях, а в знании некоторых математических законов, позволяющих быстро производить вычисления» и охотно раскрывали эти законы.
Истина как обычно, оказалась на некоей «золотой середине» сочетания природных способностей и грамотного, трудолюбивого их пробуждения, взращивания и использования. Те, кто следуя Трофиму Лысенко уповают исключительно на волю и напористость, со всеми уже хорошо известными способами и приемами устного счёта обычно при всех стараниях не поднимаются выше очень и очень средних достижений. Более того, настойчивые попытки «хорошенько нагрузить» мозг такими занятиями как устный счёт, шахматы вслепую и т.п. легко могут привести к перенапряжению и заметному падению умственной работоспособности, памяти и самочувствия (а в наиболее тяжелых случаях – и к шизофрении). С другой стороны и одаренные люди при беспорядочном использовании своих талантов в такой области как устный счёт быстро «перегорают» и перестают быть в состоянии длительно и устойчиво показывать яркие достижения. Один из примеров удачного сочетания обоих условий (природной одаренности и большой грамотной работы над собой) показал наш соотечественник, уроженец Алтайского края Юрий Горный.
Пожалуй, единственная научно обоснованная и достаточно подробно разработанная система резкого повышения быстроты устного счёта создана была в годы второй мировой войны цюрихским профессором математики Я. Трахтенбергом. Она известна под названием «Система быстрого счёта». История ее создания необычная. В 1941г. гитлеровцы бросили Трахтенберга в концлагерь. Чтобы уцелеть в нечеловеческих условиях и сохранить нормальной свою психику, Трахтенберг начал разрабатывать принципы ускоренного счета. За четыре страшных года пребывания в концлагере профессору удалось создать стройную систему ускоренного обучения детей и взрослых основам быстрого счёта. Уже с самого начала результаты были самые отрадные. Учащиеся радовались вновь приобретенным навыкам и с воодушевлением двигались вперед. Если раньше их отталкивала монотонность, то сейчас их привлекало разнообразие приёмов. Шаг за шагом, благодаря достигнутым ими успехам, рос интерес к занятиям. После войны Трахтенберг создал и возглавил Цюрихский математический институт, получивший мировую известность.
Также разработкой приёмов быстрого счёта занимались другие ученые: Яков Исидорович Перельман, Георгий Берман и другие.
Приведу примеры умножения чисел, получившие наибольшее описание в литературе.
ГлаваII.
2.1 Умножение на 11 числа, сумма цифр которого не превышает 10.
Чтобы умножить на 11 число, сумма цифр которого 10 или меньше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить 1, а вторую и последнюю (третью) цифру оставить без изменения.
27 х 11= 2 (2+7) 7 = 297;
62 х 11= 6 (6+2) 2 = 682.
2.2 Умножение на 11 числа, сумма цифр которого больше 10.
Чтобы умножить на 11 число, сумма цифр которого 10 или больше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить 1, а вторую и последнюю (третью) цифру оставить без изменения.
86 х 11= 8 (8+6) 6 = 8 (14) 6 = (8+1) 46 = 946.
2.3 Умножение на одиннадцать (по Трахтенбергу).
Разберем на примере: 633 умножить на 11.
Ответ пишется под 633 по одной цифре справа налево, как указано в правилах.
Первое правило. Напишите последнюю цифру числа 633 в качестве правой цифры результата
633*11
3
Второе правило. Каждая последующая цифра числа 633 складывается со своим правым соседом и записывается в результат.3+3 будет 6. Перед тройкой записываем результат 6.
633*11
63
Применим правило еще раз: 6+3 будет 9. Записываем и эту цифру в результате:
633*11
963
Третье правило. Первая цифра числа 633, то есть 6, становится левой цифрой результата:
633*11
6963
Ответ: 6963.
2.4 Умножение на 22,33,…,99
Чтобы двузначное число умножить на 22,33,…, 99, надо этот множитель представить в виде произведения однозначного числа (от 2 до 9) на 11, то есть 33 = 3 х 11; 44 = 4 х 11 и т.д. Затем произведение первых чисел умножить на 11.
Примеры:
18 х 44 = 18 х 4 х 11 = 72 х 11 = 792;
42 х 22 = 42 х 2 х 11 = 84 х 11 = 924;
13 х 55 = 13 х 5 х 11 = 65 х 11 = 715;
24 х 99 = 24 х 9 х 11 = 216 х 11 = 2376.
2.5 Умножение на число 111, 1111 и т. д., зная правила умножения двузначного числа на число 11.
Если сумма цифр первого множителя меньше 10, надо мысленно раздвинуть цифры этого числа на 2, 3 и т.д. шага, сложить цифры и записать соответствующее количество раз их сумму между раздвинутыми цифрами. Количество шагов всегда меньше количества единиц на 1.
Пример:
24х111=2(2+4) (2+4)4=2664 (количество шагов – 2)
24х1111=2(2+4)(2+4)(2+4)4=26664 (количество шагов – 3)
При умножении числа 72 на 111111 цифры 7 и 2 надо раздвинуть на 5 шагов. Эти вычисления можно легко произвести в уме.
42 х 111 111 = 4 (4+2) (4+2) (4+2) (4+2) (4+2) 2 = 4666662. (количество шагов – 5)
Если единиц 6, то шагов будет 1 меньше, то есть 5.
Если единиц 7, то шагов будет 6 и т.д.
Умножение двузначного числа на 111, 1111, 1111 и т.д., сумма цифр которого равна или больше 10.
Немного сложнее выполнить устное умножение, если сумма цифр первого множителя равна 10 или более 10.
Примеры:
86 х 111 = 8 (8+6) (8+6) 6 = 8 (14) (14) 6 = (8+1) (4+1) 46 = 9546.
В этом случае надо к первой цифре 8 прибавить 1, получим 9, далее 4+1 = 5; а последние цифры 4 и 6 оставляем без изменения. Получаем ответ 9546.
2.6. Умножение двузначного числа на 101, 1001 и т.д..
Пожалуй, самое простое правило: припишите ваше число к самому себе. Умножение закончено. Пример:
32 х 101 = 3232; 47 х 101 = 4747;
324 х 1001 = 324 324; 675 х 1001 = 675 675;
6478 х 10001 = 64786478;
846932 х 1000001 = 846932846932.
2.7. Умножение на 37
Прежде чем научиться устно умножать на 37,надо хорошо знать признак делимости и таблицу умножения на 3. Чтобы устно умножить число на 37, надо это число разделить на 3 и умножить на 111.
Примеры:
24 х 37 = (24 : 3) х 37 х 3 = 8 х 111 = 888;
18 х 37 = (18 : 3) х 111 = 6 х 111 = 666.
2.8. Алгоритм перемножения двузначных чисел, близких к 100
Например: 98 х 97 = 9506
2 3
Здесь я пользуюсь таким алгоритмом: если хочешь перемножить два
двузначных числа, близких к 100, то поступай так:
1) найди недостатки сомножителей до сотни;
2) вычти из одного сомножителя недостаток второго до сотни;
3) к результату припиши двумя цифрами произведение недостатков
сомножителей до сотни.
2.9. Умножение трёхзначного числа на 999.
Любопытная особенность числа 999 проявляется при умножении на него всякого другого трёхзначного числа. Тогда получается шестизначное произведение: первые три цифры есть умножаемое число, только уменьшенное на единицу, а остальные три цифры (кроме последней) – «дополнения» первых до 9. Например:
385 * 999 = 384615
573 * 999 = 572427 943 * 999 = 942057
2.10. Умножение на шесть ( по Трахтенбергу)
Нужно прибавить к каждой цифре половину «соседа».
Пример: 0622084 * 6
0622084 * 6 4 является правой цифрой этого числа и, так 4 как «соседа» у неё нет, прибавлять нечего.
06222084 * 6 Вторая цифра 8, е «сосед» – 4. Мы берём 8 04 прибавляем половину 4 (2) и получаем 10, ноль пишем, 1 в перенос.
06222084 * 6 Следующая цифра ноль. Мы прибавляем к ней
504 половину «соседа» 8 (4), то есть 0 + 4 = 4 плюс
перенос (1).
Остальные цифры аналогичны.
Ответ: 06222084 * 6
3732504
Правило умножения на 6: является «сосед» чётным или не чётным – никакой роли не играет. Мы смотрим только на саму цифру: если она чётная, прибавляем к ней её целую часть половины «соседа», если нечётная, то кроме половины «соседа» прибавляем еще 5.
Пример: 0443052 * 6
0443052 * 6 2 – чётная и не имеет «соседа», напишем её снизу
2
0443052 * 6 5 – нечётная: 5+5 и плюс половина «соседа» 2 (1)
12 будет 11. Запишем 1 и в перенос 1
0443052 * 6 половина от 5 будет 2, и прибавим перенос 1, то будет 3
312
0443052 * 6 3 – нечетная, 3 + 5 = 8
8312
0443052 * 6 4 + половина от 3 (1) будет 5
58312
0443052 * 6 4 + половина от 4 (2) будет 6
658312
0443052 * 6 ноль + половина от 4 (2) будет 2
2658312 Ответ: 2658312.
Выводы:
Система быстрого счёта по Трахтенбергу основана на закономерностях умножения чисел. Чтобы умножить на 11, 12, 6 и т.д. нужно знать алгоритм выполнения. Этим система неудобна, нужно в памяти держать много правил быстрого счёта, но система Трахтенберга показывает как красива математика, если человек открывает тайны её закономерностей, изучает их и учится применять их на практике.
Выводы исследования
Как мы видим, быстрый счёт это уже не тайна за семью печатями, а научно разработанная система. Раз есть система, значит её можно изучать, ей можно следовать, ею можно овладевать.
Все рассмотренные мною методы устного умножения говорят о многолетнем интересе ученых, и простых людей к игре с цифрами.
Используя некоторые из этих методов на уроках или дома, можно развить скорость вычислений, привить интерес к математике, добиться успехов в изучении всех школьных предметов.
Список использованной литературы
1. «Устный счёт – гимнастика ума» Г.А.Филиппов
2. «Алгоритмы ускоренных вычислений» Л.В. Бикташева
3. «Устный счет». Э.Л.Струнников
4. «Математическая шкатулка» Ф.Ф.Нагибин Е.С.Канин
5. «Мир чисел» Г.И. Зубелевич В.И.Ефимов
6. «Задачи для математического кружка» Е.Г.Козлова
7. «Развитие вычислительной культуры учащихся» НЛ. Мельникова
8. Библиотечка «Первое сентября»
японская методика устного счета. Дети не устают на занятиях за счет постоянной смены видов деятельности
В Москве Елена Клещёва рассказала «Летидору», что такое ментальная арифметика и почему она нужна каждому человеку.
Ментальная арифметика – это программа комплексного развития интеллекта и мышления детей, основанная на формировании навыка быстрого устного счета
На занятиях дети учатся быстрому счету с помощью специальной счетной доски (абакус, соробан). Педагоги объясняют, как правильно перебирать костяшки на спицах, чтобы малыши могли почти мгновенно получить ответ на сложный пример. Постепенно привязка к счетам ослабевает и дети представляют те действия, что совершали со счетами, в уме.
Программа рассчитана на 2-2,5 года. Сначала ребята осваивают сложение и вычитание, затем – умножение и деление. Навык приобретается и развивается за счет многократного повторения одних и тех же действий. Методика подходит практически всем детям, принцип обучения – от простого к сложному.
Занятия проходят один-два раза в неделю и длятся один-два часа.
Древние счеты абакус, на которых считают дети, известны уже более 2,5 тысяч лет. Дети учатся считать на специальных счетах. Известно, что их использовали еще в Древнем Риме. В современном мире счет на абакусе распространен в Японии, Китае, Индии, Малайзии, а также других странах.
В Японии счет на абакусе включен в официальную школьную программу
Вот уже более 50 лет ментальная арифметика входит в систему государственного образования в Японии. Интересно, что после окончания школы люди продолжают совершенствовать свои навыки в устном счете. В Стране восходящего солнца ментальную арифметику считают чем-то вроде спорта. По ней даже проводят соревнования. В России теперь тоже ежегодно проводятся международные турниры по Ментальной арифметике.
Ментальная арифметика развивает механическую и фотографическую память
Когда дети считают, они задействуют сразу оба полушария мозга. Ментальная арифметика развивает фотографическую и механическую память, воображение, наблюдательность, улучшает концентрацию внимания.
Повышается общий уровень интеллекта. Это значит, что ребятам легче усваивать большие объемы информации в сжатые сроки. Сразу видны успехи в иностранных языках. На заучивание стихов и прозы теперь не надо тратить весь день.
У школьников более медлительных ускоряется быстрота реакции.
Бывают и неожиданные результаты. Как-то в центр пришел мальчик, который занимался теннисом. Мама рассказала, что у ее сына проблемы с координацией движений. Неожиданно их удалось решить именно за счет интенсивов по ментальной арифметике.
Взрослым ментальная арифметика дается сложнее, оптимальный возраст для начала занятий – 5-14 лет
Развивать мозг с помощью ментальной арифметики можно в любом возрасте, но наилучших результатов можно добиться до 12–14 лет. Детский мозг очень пластичен, подвижен. В юном возрасте в нем наиболее активно формируются нейронные связи, поэтому наша программа дается легче ребятам до 14 лет.
Чем старше человек, тем сложнее ему абстрагироваться от своего опыта и знаний и просто доверять абакусу. Я осваивала эту методику в 45 лет и постоянно сомневалась, правильно ли у меня получается, нет ли ошибки. Это очень мешает обучению.
Но чем труднее человеку осваивать этот счет, тем больше от него пользы.
Человек как бы преодолевает себя, с каждым разом у него получается все лучше и лучше.
Занятия не проходят даром, мозг взрослого человека также активно развивается.
Только не стоит ожидать от взрослого таких же результатов, как от ребенка. Мы можем научиться методике, но посчитать так же быстро, как это делает второклассник, уже не получится. Как показывает опыт, оптимальный возраст, с которого лучше начинать занятия – 6 и 7 лет.
Лучших результатов добивается тот, кто регулярно занимается дома
Обязательное условие занятий – ежедневные тренировки на абакусе. Всего 10-15 минут. Детям необходимо отрабатывать формулу, которую им дал на уроке преподаватель, и доводить свои действия до автоматизма. Только в этом случае ребенок научится считать быстро. Здесь важна организационная роль родителей, которым нужно следить за регулярными тренировками.
Каждый родитель мечтает о том, чтобы его ребенок вырос интеллектуально развитым и умным человеком. Но для того, чтобы это случилось, хороших генетических данных будет недостаточно. Любые способности нужно развивать и совершенствовать, и чем раньше вы начнете это делать, тем быстрее малыш порадует вас своими успехами.
Счеты абакус уже давно используются в специализированных школах и детских садах ментальной арифметике. Если вы хотите чтобы ребенок, в будущем, считал быстрее вычислительной машинки, то вам непременно нужно купить счеты абакус-соробан.
Счеты абакус
Моментальная арифметика обладает огромным количеством преимуществ. Реально ли, стоя на кассе в супермаркете, знать сумму своей покупки еще до того, как кассир ее объявит, пропустив товар через ленту? Да, если вы обучены по методу соробан. Такого человека практически невозможно обмануть. Научиться считать по этой методике будет полезно не только детям, но и взрослым.
Но чаще всего счеты соробан покупают именно для того, чтобы в интересной игровой форме научить ребенка сложению и умножению. Эта игра послужит и превратит подсчет в быстрый и интересный процесс.
Еще в 16 веке наши предки успешно использовали японские счеты, а наши прабабушки пользовались ими для ведения бухгалтерии до появления калькуляторов. И пусть сегодня существует множество гаджетов для быстрого решения любого примера, не стоит забывать, что все они всего лишь дают правильный ответ, не тренируя при этом мозг.
Научно доказано, что наш мозг работает намного интенсивнее, ежели это сопровождается какими- либо действиями. Именно поэтому, передвигая колечки счет, ребенок будет мыслить намного быстрее. Что касаемо калькуляторов, то этими же учеными было доказано, что электронный вычислитель – отличный способ расслабить мозг, загубив даже самые минимальные математические знания.
Японские счеты соробан
Самым подходящим возрастом для осваивания ментальной арифметики соробан считается возраст от 4 до 12 лет. Именно в этот промежуток жизни происходит активное развитие головного мозга. Поэтому прививать ребенку необходимые навыки стоит начинать еще в дошкольном возрасте. В нашем интернет-магазине вам будут предложены счеты соробан двух видов.
Первые, с цветными пластмассовыми бусинами, расположенными на 13 бамбуковых основах. Это цветовое решение очень порадует самых маленьких математиков. Яркие цвета бусин помогут привлечь внимание малыша.
Вторые выполнены в более спокойном цветовом решении. Пластмассовые бусины окрашены “под дерево”. Также в этом варианте имеется 4 черных разделяющих бусины, которые позволят ребенку быстрее ориентироваться в десятках и сотнях. Эти счеты соробан купить стоит для деток, которые уже более осознанно занимаются арифметикой.
Обучая ребенка по методике игры соробан, вы сможете обучаться и совершенствовать свои знания вместе с ним. Соробан – это игрушка, которая подойдет для всех возрастов. Чем чаще вы будете заниматься по технике счета соробан, тем совершеннее будут ваши познания в математике. Самым пиком совершенства считается умение считать на японских счетах соробан обеими руками, активизируя сразу оба полушария головного мозга.
Конечно, без помощи взрослых ребенок сам не сможет постичь это искусство. Но ведь это прекрасный повод провести время вместе.
Абакус-соробан
Японские счеты расположены в пластиковой раме. Разделительная полоса отделяет 1 костяшку от 4 на всех 13 спицах. Для того, чтобы набрать на японских счетах абакус цифру 3, нужно отделить три бусины, находящихся за разделительной полосой. Для набора числа 13, нужно отложить 3 бусины на верхней спице и одну на предпоследней спице.
А теперь попробуем прибавить 13 к 3. Для этого, к уже отложенному числу 13 прибавляем 3 бусины на верхней спице, откладываем 1 бусину перед разделительной полосой и одну после нее, получается 6 и 1 десяток так и остается, 16. Купив японские счеты соробан, ваш ребенок очень быстро научится считать. Абакус – отличный способ закрепить пройденный в школе материал.
Когда ребенок научится представлять абакус-соробан в своем воображении, то он сможет с легкостью считать в уме любые примеры на сложение, вычитание и умножение.
Преимущества
- Привлекательный внешний вид;
- Развивают умственные способности и тренируют мозг;
- Улучшает зрительную память;
- Помогают ребенку сконцентрироваться на поставленных задачах;
- Делают процесс обучения интересным;
- Развивает мелкую моторику рук.
Что такое соробан, известно далеко не всем. Ведь в мире электронных технологий гораздо проще нажать кнопку калькулятора, не напрягая при этом мозг. Но стоит ли упрощать задачи, и растить поколение, способное производить подсчеты только с помощью компьютеров?
Купите абакус и уже через несколько лет вы сможете гордиться познаниями своего ребенка в области математики. Покупая счеты абакус-соробан в интернет-магазине, вы не просто приобретаете красивую игрушку, но и делаете весомый вклад в развитие своего ребенка. Такая игрушка станет хорошим и полезным подарком. Игра «Быстрый счет на пальцах соробан» – отличный способ подготовить ребенка к школе.
Характеристики
- Материал: пластик;
- Вес: 125 г;
- Размер: 22 х 6,3 х 1,5 м.
- Счеты 17-разрядные
Комплектация
- 1 х Абакус соробан счеты 17-разрядные для занятий Ментальной арифметикой.
Японский «Соробан», или ментальная арифметика – уникальная методика дошкольного развития, которая представляет собой обученин счету и помогает развить мышление ребенка.
Занятия гармонично развивают оба полушария мозга, благодаря чему даже ярко выраженные гуманитарии в мгновение ока «щелкают» задачки и уравнения.
Метод Соробан получил название от наименования японских счет. Это необычное устройство редко можно увидеть в наших краях. Оно представляет собой «калькулятор», на котором возможно только однозначное представление чисел. Это позволяет избежать путаницы, как в обычных счетах.
В соробане нечетное количество спиц, расположенных вертикально, которые обозначают одну цифру. На каждую спицу нанизано по пять костяшек. Четыре костяшки внизу – это единицы, а верхняя обозначает пятерку.
Преимущества метода «Соробан»
Малыши очень быстро осваивают японские механические счеты. Нужно отметить, что это устройство удивительным образом влияет на развитие мышления у детей.1. Занятия по методике «Сорабан» заставляют образное правое полушарие мозга решать математические задачки. Это позволяет одновременно задействовать два полушария, а значит, мозг работает вдвое эффективнее, практикуя ментальный устный счет.
2. Люди, которые учились считать на соробане, с легкостью могут проводить сложнейшие вычисления в уме за кратчайший отрезок времени. Мастера могут делать это легко, даже не имея соробана перед глазами. Даже ребенок может за пару секунд сложить трехзначные числа в начале обучения. А по мере практики научатся оперировать числами с пятью нулями.
3. Не только успехи в математике, но и в обучении в целом показывают дети, которые осваивают методику устного счета. Педагоги и психологи отмечают: «Соробан» улучшает концентрацию и внимание ребенка, тренирует наблюдательность, память и воображение, а также творческое, нестандартное мышление малыша. Ребенок буквально схватывает информацию на лету, с легкостью ее анализирует.
Обучение по методике устного счета
В учебную программу начальных школ Японии даже введен предмет – ментальная математика. Благодаря этой методике, эрудированные дети ежегодно в числе призеров математических олимпиад. Также образовательные программы с применением сорбана предусмотрены в Китае и Малайзии.У нас также открываются школы по изучению японского устного счета. Начинать обучение рекомендуется в возрасте 4-11 лет. Именно в этот период мозг ребенка активно «набирает обороты» и развивается. А значит, добиться активной работы обоих полушарий достаточно легко. Во взрослом возрасте ментальная арифметика служит методов для предотвращения атеросклероза и Альцгеймера. Но таких феноменальных результатов, какие демонстрируют малыши, добиться уже нельзя.
Многие родители переживают о том, что смешивание обычной и японской математики может запутать ребенка – и он отстанет от базовой программы в школе. На самом деле, практика показывает то, что дети, которые раньше в точных науках звезд не хватали, уже через пару месяцев обучения показывали хорошие результаты и шли на опережение сверстников.
Японская методика устного счета «Сорабан» – оригинальный подход к обучению, который в нашей стране только начинает развиваться. Эта методика не только учит малышей мгновенному сложению и вычитанию чисел. Ее главный плюс в том, что она развивает умственные способности ребенка, открывая перед ним новые интеллектуальные возможности.
Катерина Василенкова
Здравствуйте, дорогие друзья! Меня зовут Евгения Климкович. Я рада видеть вас на страничках блога «ШколаЛа»!
Чем сегодня займемся? Может быть, посчитаем? Не хотите? Да ладно вам! Это же очень интересно! Особенно если не просто ворон считать, а считать на абакусе. А вы, кстати, знаете, как считать на абакусе? Вот и я не знаю. Счеты в руках не держала, на курсы ментальной арифметики не ходила. Но понять, как же все-таки это делается, очень хочется. Вот и решила попробовать хотя бы немножко приоткрыть завесу тайны.
Вы со мной?
Тогда присаживайтесь поудобнее, включайте мозг. Наш ментально-арифметический поезд отправляется!
Предлагаю начать с главного! С абакуса или, как его еще называют, соробана. Что это за штуковина такая?
План урока:
Что такое абакус?
Вот она – эта загадочная счетная машинка.
Чем-то напоминает известные многим советские счеты с костяшками. И, насколько я поняла, принципы работы на этих двух приспособлениях очень похожи. Отличаются эти счеты количеством костяшек на спицах и, собственно говоря, удобством эксплуатации. На абакусе приходится делать намного меньше движений руками.
Итак, абакус состоит из рамки, в которую установлены спицы. Причем спиц может быть разное количество. А на спицах нанизаны костяшки. По 5 штук на каждую. Спицы проходят сквозь разделительную планку. Над планкой остается по одной костяшке, под планкой по четыре.
Важную роль при счете на абакусе играет то, как именно человек двигает пальцами. Используются в работе только большой и указательный пальцы. Все движения путем многократных повторений доводятся до автоматизма. Этот навык легко потерять, поэтому при занятиях ментальной арифметикой не желательно пропускать уроки.
Расположение чисел
Теперь о том, как же располагаются числовые линейки.
Справа у нас находятся единицы. Затем десятки, потом сотни, тысячи, десятки тысяч и т.д. Каждому разряду своя спица. Костяшки, которые находятся под разделительной планкой, означают «1», над планкой – «5». Трудновато понять, да?
Давайте посмотрим на примере. Я нарисовала абакус!
Десятичные линейки рисовать не стала. То есть, крайняя правая линейка на моем рисунке – это единицы.
Так будет выглядеть на абакусе число 3.
Поднимаем к разделительной планке три костяшки на линейке единиц.
Попробуем взять двойное число, например, 15.
На линейке десятков поднимаем 1 костяшку, то есть, получаем 1 десяток. А на линейке единиц опускаем к разделителю верхнюю костяшку, которая и означает 5.
А вот это какое число получилось? Догадаетесь?
А давайте чего-нибудь посущественнее наберем. Например, 6482!
На линейке тысячи у нас верхняя костяшка опущена к разделителю – это пять тысяч и одна нижняя поднята вверх, плюс еще тысяча. Получаем 6 тысяч. С сотнями полегче, просто четыре костяшки поднимаем вверх. Десятки: верхняя опущена, три нижних подняты. Получается сверху 5 десятков, снизу 3. Это 80. Ну и еще 2 единицы. Не так уж сложно, правда?
Как складывать?
А теперь переходим к сложению и посмотрим, что из этого получится. Предлагаю взять что-нибудь попроще, чтобы не взорвать себе мозг) Например, сложим 33 и 14.
Откладываем на абакусе 33.
К трем десяткам прибавим еще один. Получим 4 десятка или 40.
Теперь единички. К трем единицам прибавим еще 4. Так как четырех свободных единиц снизу на спице нет, то сначала прибавим пять, опустим верхнюю косточку. А потом отнимем 1, опустим одну нижнюю. Получилось у нас 7 единиц.
В результате получилось 47! Может на калькуляторе проверим?) Шучу, и так ясно, что результат мы получили верный!
Дополнительная литература
В общем, примерно вот по такой схеме на абакусе и считают. Я показала все самое простое. А ведь можно еще и вычитать, и умножать, и делить, и в степень возводить. И работать с огромными числами. Хотите знать больше? Пожалуйста! Обнаружила в интернете инструкцию по работе с соробаном. Вот здесь ее можно скачать.
Если не поможет инструкция, то может быть стоит обратить внимание на книгу «Ментальная арифметика. Знакомство»? Насколько я поняла, она ориентирована на обучение детишек. Такой своеобразный учебник. Нашла я ее в магазине «My-shop». Ссылка на эту книжку чуть ниже.
Ментальная арифметика. Знакомство — Багаутдинов Р. | Купить книгу с доставкой | My-shop.ru
[|urlspan]
Думаю, что и взрослым людям не повредят занятия с абакусом. Особенно бухгалтерам. Представляете, все коллеги на калькуляторах считают или на компьютерах. А вы такой деловой с абакусом) И батарейки-то не садятся, и кнопки не западают, и костяшки так приятно пощелкивают) Красота!
Уф, наверное, хватит на сегодня счета. Теперь давайте посмотрим, как другие считают. Настоящие маленькие абакус-мастера, только они уже на том уровне подготовки, когда хватает и воображаемых счет. Смотрим видео.
На сегодня, пожалуй, все. А завтра на блоге «ШколаЛа» вас ждет новая интересная информация!
Кстати, если есть желание каждое воскресение по почте получать анонсы статей на следующую неделю, то обязательно подпишитесь на новости блога. Тогда вы точно ничего не пропустите!
И не забудьте вступить в нашу группу «ВКонтакте» , там вас тоже ждет много всего интересного!
Удачи вам и вашим маленьким школьникам!
Евгения Климкович.
Что такое ментальная арифметика и почему она нужна каждому человеку.
Ментальная арифметика – это программа комплексного развития интеллекта и мышления детей, основанная на формировании навыка быстрого устного счета
На занятиях дети учатся быстрому счету с помощью специальной счетной доски (абакус, соробан). Педагоги объясняют, как правильно перебирать костяшки на спицах, чтобы малыши могли почти мгновенно получить ответ на сложный пример. Постепенно привязка к счетам ослабевает и дети представляют те действия, что совершали со счетами, в уме.
Программа рассчитана на 2-2,5 года. Сначала ребята осваивают сложение и вычитание, затем – умножение и деление. Навык приобретается и развивается за счет многократного повторения одних и тех же действий. Методика подходит практически всем детям, принцип обучения – от простого к сложному.
Занятия проходят один-два раза в неделю и длятся один-два часа.
Древние счеты абакус, на которых считают дети, известны уже более 2,5 тысяч лет
В Японии счет на абакусе включен в официальную школьную программу
Вот уже более 50 лет ментальная арифметика входит в систему государственного образования в Японии. Интересно, что после окончания школы люди продолжают совершенствовать свои навыки в устном счете. В Стране восходящего солнца ментальную арифметику считают чем-то вроде спорта. По ней даже проводят соревнования. В России теперь тоже ежегодно проводятся международные турниры по Ментальной арифметике.
Ментальная арифметика развивает механическую и фотографическую память
Когда дети считают, они задействуют сразу оба полушария мозга. Ментальная арифметика развивает фотографическую и механическую память, воображение, наблюдательность, улучшает концентрацию внимания.
Повышается общий уровень интеллекта. Это значит, что ребятам легче усваивать большие объемы информации в сжатые сроки. Сразу видны успехи в иностранных языках. На заучивание стихов и прозы теперь не надо тратить весь день.
У школьников более медлительных ускоряется быстрота реакции. Они начинают не просто молниеносно считать, но быстрее думать и принимать решения, не связанные с арифметикой.
Бывают и неожиданные результаты. Как-то в центр пришел мальчик, который занимался теннисом. Мама рассказала, что у ее сына проблемы с координацией движений. Неожиданно их удалось решить именно за счет интенсивов по ментальной арифметике.
Взрослым ментальная арифметика дается сложнее, оптимальный возраст для начала занятий – 5-14 лет
Развивать мозг с помощью ментальной арифметики можно в любом возрасте, но наилучших результатов можно добиться до 12–14 лет. Детский мозг очень пластичен, подвижен. В юном возрасте в нем наиболее активно формируются нейронные связи, поэтому наша программа дается легче ребятам до 14 лет.
Чем старше человек, тем сложнее ему абстрагироваться от своего опыта и знаний и просто доверять абакусу. Я осваивала эту методику в 45 лет и постоянно сомневалась, правильно ли у меня получается, нет ли ошибки. Это очень мешает обучению.
Но чем труднее человеку осваивать этот счет, тем больше от него пользы. Человек как бы преодолевает себя, с каждым разом у него получается все лучше и лучше. Занятия не проходят даром, мозг взрослого человека также активно развивается.
Только не стоит ожидать от взрослого таких же результатов, как от ребенка. Мы можем научиться методике, но посчитать так же быстро, как это делает второклассник, уже не получится. Как показывает опыт, оптимальный возраст, с которого лучше начинать занятия – 6 и 7 лет.
Лучших результатов добивается тот, кто регулярно занимается дома
Обязательное условие занятий – ежедневные тренировки на абакусе. Всего 10-15 минут. Детям необходимо отрабатывать формулу, которую им дал на уроке преподаватель, и доводить свои действия до автоматизма. Только в этом случае ребенок научится считать быстро. Здесь важна организационная роль родителей, которым нужно следить за регулярными тренировками.
Дети не устают на занятиях за счет постоянной смены видов деятельности
Основной вид деятельности на ментальной арифметике – счет на абакусе. Дети считают разными способами: на слух, в рабочих тетрадях, у школьной доски на демонстрационном абакусе, используя электронный тренажер «Веселый соробан», на ментальной карте (это графическое изображение абакуса, с помощью которого дети представляют, как передвигают косточки на счетах).
Стратегия подсчета пальцев – обзор
D Рабочая память и нарушения развития при обучении
Когнитивные профили детей с плохой рабочей памятью совпадают с рядом нарушений развития при обучении. К ним относятся трудности с чтением и математикой, дислексия, SLI, синдром Дауна, синдром Уильяма и СДВГ.
Очень низкий уровень выполнения задач на рабочую память часто встречается у детей с особыми трудностями в чтении (Gathercole, Alloway, et al., 2006; Пикеринг и Gathercole, 2004; Swanson, 1993, 2003). Вербальный СТМ в значительной степени связан с развитием чтения в ранние годы (Gathercole & Baddeley, 1993), и дефицит этого компонента системы памяти часто встречается у детей с трудностями в чтении (Siegel & Ryan, 1989; Swanson & Siegel, 2001). Также было обнаружено, что навыки вербальной рабочей памяти постоянно связаны с навыками чтения детей (например, de Jonge & de Jong, 1996; Engle, Carullo, & Collins, 1991) и объясняют уникальные различия в понимании прочитанного по сравнению с вербальным STM, словом чтение и словарный запас (e.г., Cain et al. , 2004; Swanson & Jerman, 2007). Кроме того, нарушения при выполнении сложных задач, затрагивающих рабочую память, распространяются как на вербальную, так и на невербальную сферу, что свидетельствует об общем модальном нарушении рабочей памяти у плохих читателей (Chiappe, Hasher, & Siegel, 2000; de Jong, 1998; Gathercole, Alloway, и др., , 2006; Palmer, 2000; Swanson, 1993).
Лица, чьи проблемы с чтением удовлетворяют более строгим критериям дислексии, также показывают результаты ниже среднего по задачам как краткосрочной, так и рабочей памяти в вербальной области (Jeffries & Everatt, 2003, 2004).Дети с SLI демонстрируют ту же картину высокоспецифичных дефицитов в вербальной сфере с серьезными нарушениями в вербальной STM (Archibald & Gathercole, 2006; Edwards & Lahey, 1998; Ellis Weismer, Evans, & Hesketh, 1999; Gathercole & Baddeley, 1990; Montgomery, 1995) и вербальной рабочей памяти (Archibald & Gathercole, 2007; Ellis Weismer et al. , 1999; Montgomery, 2000a, 2000b). Было высказано предположение, что плохие навыки вербальной памяти лежат в основе нарушений вербальной рабочей памяти в этой группе (Archibald & Gathercole).
Дети с математическими трудностями также демонстрируют признаки дефицита рабочей памяти (Bull & Scerif, 2001; Geary, 1993; Mayringer & Wimmer, 2000; Passolunghi & Siegel, 2004; Siegel & Ryan, 1989; Swanson & Beebe-Frankenberger, 2004) . Эти дети обычно плохо справляются с измерениями визуально-пространственной STM и рабочей памяти (Gathercole & Pickering, 2000; Geary, Hoard, & Hamson, 1999; McLean & Hitch, 1999; Siegel & Ryan), но не по показателям вербальной STM (McLean & Ryan). Хитч; Пассолунги и Сигель).Рабочая память, по-видимому, играет важную роль в развитии счета, поскольку дети с плохой рабочей памятью используют примитивные стратегии счета пальцев, требующие относительно невысокой рабочей памяти (Geary et al. , 2004). Постоянное использование ими этих ранних стратегий не позволяет им создавать сети арифметических фактов в долговременной памяти, которые необходимы для поддержки использования эффективных стратегий поиска, аналогичных тем, которые используются в зрелом возрасте (например, Hamann & Ashcraft, 1985; Kaye, 1986).Таким образом, плохая рабочая память препятствует изучению числовых фактов (Geary, 2004), обучению и эффективности перекодирования чисел (Camos, 2008; McLean & Hitch) и вычислительным навыкам (Wilson & Swanson, 2001). Это также вызывает трудности при решении математических задач, выражаемых повседневным языком (Swanson & Sachse-Lee, 2001).
Нарушения рабочей памяти также связаны с множеством генетических патологий, включая синдром Дауна и синдром Уильяма. Имеются убедительные доказательства выраженного дефицита вербального СТМ у детей с синдромом Дауна (например,g., Jarrold, Baddeley, & Hewes, 1999). Эти дети обычно выполняют соответствующие возрасту уровни на зрительно-пространственных задачах STM и, по-видимому, не имеют дефицита рабочей памяти по сравнению с контрольной группой (Numminen, Service, Ahonen, & Ruoppila, 2001; Pennington, Moon, Edgin, Stedron, & Nadel, 2003 г.). Напротив, у детей с синдромом Уильяма вербальный СТМ гораздо сильнее, чем СТМ зрительно-пространственного характера (Jarrold, Baddeley, Hewes, & Phillips, 2001). Этот паттерн нарушения, скорее всего, связан с двойной диссоциацией между вербальными и визуальными навыками обработки при синдроме Уильяма.
Дети с поведенческими трудностями, такими как СДВГ, также характеризуются плохой функцией рабочей памяти (Martinussen, Hayden, Hogg-Johnson, & Tannock, 2005; Willcutt, Doyle, Nigg, Faraone, & Pennington, 2005). Дети с СДВГ плохо справляются с тестами на визуально-пространственный СТМ (Barnett et al. , 2001; Martinussen et al. ; Mehta, Goodyear, & Sahakian, 2004), а также вербальные и зрительно-пространственные задачи на рабочую память (Martinussen & Tannock, 2006). ; Martinussen et al.; Макиннес, Хамфрис, Хогг-Джонсон и Таннок, 2003; Роденрис, 2006; Willcutt, Doyle, et al. , 2005). Их вербальный СТМ, по-видимому, относительно сохранился, что позволяет предположить, что проблемы с вербальной памятью не являются фундаментальными особенностями расстройства (например, Martinussen & Tannock). Наши собственные данные по выборке из 83 детей в возрасте 8–11 лет с клиническим диагнозом СДВГ комбинированного типа согласуются с этой картиной нарушений. Мы обнаружили, что хотя вербальный STM был относительно неизменным в этой выборке, показатели визуально-пространственного STM находились в низком среднем диапазоне со значительным дефицитом вербальной и зрительно-пространственной рабочей памяти (Holmes, Gathercole, Place, Alloway, Elliott, & Hilton, 2009; Holmes, Gathercole). , Alloway, et al., 2010 – см. Рисунок 2). Из всей выборки 19,8% имели нарушения вербального СТМ, что близко к уровню 16%, который мы ожидали бы в нормальной популяции. Однако 38,6% имели дефицит зрительно-пространственной STM, более половины имели нарушения вербальной рабочей памяти (50,6%) и 63,9% имели очень плохую зрительно-пространственную рабочую память.
Рис. 2. Профили рабочей памяти 50 детей с СДВГ по Holmes et al. (2010).
Возможно, что проблемы с рабочей памятью могут быть причиной невнимательного и отвлекающего поведения, связанного с СДВГ.Для успешного выполнения задачи ресурсы рабочей памяти поддерживают поддержание целей задачи, а также различные элементы текущей умственной деятельности для достижения цели – это позволяет нам не отвлекаться от задачи и сосредоточиться на основных аспектах задачи. Поэтому плохая функция рабочей памяти может привести к отвлечению внимания от текущей задачи, что приведет к потере части или всей необходимой информации, необходимой для выполнения задачи. Это приведет к невыполнению задания, и, как следствие, у людей с СДВГ может казаться короткая продолжительность концентрации внимания и они будут отвлекаться (Holmes, Gathercole, Alloway, et al., 2010).
Таким образом, нарушения рабочей памяти связаны с широким спектром генетических нарушений обучения и нарушений развития нервной системы с четко различимыми профилями дефицита, характерными для различных нарушений. Дефицит вербальной области связан с определенными языковыми трудностями, такими как SLI и дислексия, а также характерен для людей с синдромом Дауна, которые испытывают серьезные задержки и трудности с речью. И наоборот, у детей с синдромом Уильяма обнаруживаются доменно-специфические нарушения зрительно-пространственной памяти.В отличие от других расстройств, обсуждаемых здесь, СДВГ связан с общим нарушением рабочей памяти в сочетании с дефицитом зрительно-пространственного СТМ. В настоящее время имеется множество свидетельств того, что задачи, которые требуют хранения, но не требуют дальнейшей обработки визуально-пространственного материала, в значительной степени зависят от общих ресурсов рабочей памяти предметной области (Miyake et al. , 2001; Wilson, Scott, & Power, 1987), а не особый зрительно-пространственный магазин. Это особенно верно в отношении маленьких детей (Alloway et al., 2006). Таким образом, профиль памяти детей с СДВГ соответствует единичному нарушению в системе общей рабочей памяти, которое может вызывать невнимательное поведение, характерное для данного расстройства (Holmes, Gathercole, Alloway, et al. , 2010). . Дети с общими трудностями чтения имеют дефицит во всех аспектах рабочей памяти, тогда как дети с математическими трудностями имеют серьезные нарушения вербальной и зрительно-пространственной рабочей памяти и зрительно-пространственной STM, но не вербальной STM.У детей с плохой рабочей памятью также наблюдается повсеместный дефицит рабочей памяти в целом, как у детей с трудностями чтения, математическими трудностями и СДВГ. Они сопряжены со значительными нарушениями зрительно-пространственной СТМ и плохой вербальной СТМ (см. Рисунок 3).
Рис. 3. Профили рабочей памяти 50 детей с плохой рабочей памятью, данные Gathercole et al. (2010).
Важность подсчета пальцев
Пальцы – один из самых полезных инструментов для детей в изучении математических понятий .Отчасти это связано с их доступностью; он позволяет детям устанавливать взаимно однозначные соответствия или помогает уменьшить нагрузку на память, связанную с проблемой, благодаря наличию физических представлений величин. Это даже может помочь облегчить мгновенное восприятие величин без необходимости их подсчета.
Однако многие родители и учителя сомневаются, полезно ли детям использовать счетчик пальцев. Одна из причин сомнений связана с заблуждением о том, что дети, использующие счет по пальцам или решающие арифметические задачи пальцами, знают меньше, чем те, кто может решать задачи с помощью ментальной математики.В свете этого аргумента первое, что нам нужно прояснить, – это тот факт, что маленькому ребенку нужны его или ее пальцы (или другой подходящий предмет) для представления величин. Это не означает, что у ребенка меньшие способности к математике, чем у другого ребенка, который способен выполнять математические вычисления в уме.
Способность абстрагироваться от концепций и использовать мысленные образы развивается с возрастом , и для этого детям нужны физические объекты (игрушки, маркеры, пальцы…), которые представляют величины, с которыми они работают.Исследователи согласны с тем, что подчеркивание важности использования таких манипулятивных элементов, в частности счета пальцев, создает мост, который позволяет детям перейти от элементарного мышления, благодаря практическому сенсомоторному опыту, к более абстрактному мышлению.
Кроме того, различные исследования подтверждают, что использование пальцев для счета, суммирования и различения представленных величин является хорошим индикатором их будущих результатов в определенных арифметических заданиях.
Это еще не все; Эффект, который счет пальцев оказывает на то, как мозг обрабатывает и представляет числовую информацию, длится всю жизнь, поэтому его преимущества не ограничиваются только детством.Точно так же, что более примечательно, этот аффект, по-видимому, модулируется культурными вариациями. Не во всех культурах для обозначения количеств используется подсчет по пальцам, а в тех, которые используют, не всегда это делается одинаково (для получения дополнительной информации см. Bender y Beller, 2012).
Если мы рассмотрим данные, полученные в результате психологических исследований, ребенок школьного возраста, который использует счет пальцев для решения определенных математических задач, больше не имеет негативного тона, описанного ранее в этом посте. По мере того, как учащиеся продолжают понимать математические концепции, они будут открывать для себя другие, гораздо более сложные и быстрые стратегии, чем счет по пальцам.В конце концов, пальцы облегчают нам математические вычисления, если мы работаем с небольшими количествами (до 10, максимум 20, если мы тоже считаем пальцами ног).
Мы можем помочь детям обнаружить ограничения этой стратегии и понять положительные стороны других, более разработанных альтернатив с когнитивной точки зрения. Дети будут использовать последнее все больше и больше с течением времени, хотя это не означает, что они больше никогда не вернутся к использованию пальцев. Фактически, всем нужно время от времени ими пользоваться.
Артикулы:
Бендер, А. и Беллер, С. (2012). Природа и культура подсчета пальцев: разнообразие и репрезентативные эффекты воплощенного когнитивного инструмента. Познание, 124 , 156-182
Подробнее:
Развлечение – любимый способ обучения нашего мозга
Дайан Акерман
Smartick – увлекательный способ изучения математики- 15 веселых минут в день
- Адаптируется к уровню вашего ребенка
- Миллионы учеников с 2009 года
Conchi провела последнее десятилетие, работая в цифровом пространстве для детей и внимательно следя за всеми последними тенденциями в образовательных приложениях.По выходным она любит исследовать Бостон со своей трехлетней дочерью и фотографировать, проведенное вместе.
Последние сообщения Конки Руиса Кабельо (посмотреть все)Speed Math – Лучшие методы для быстрого счета в голове
Не знаю, когда я понял, что люблю считать в голове – вероятно, после того, как я бросил школу и мне больше не приходилось заниматься математикой «зарабатывать на жизнь». Как ни странно, любовь к истории и географии у меня не развивалась одновременно!
Я не гений чисел: если вы попросите меня умножить 172 на 47, ответ не слетит с моего языка.Это займет у меня несколько ударов, и, возможно, это сработает с первой попытки, если я устану. Напротив, есть молниеносные человеческие калькуляторы, которые мгновенно выдадут вам произведение двух трехзначных чисел. И есть вундеркинды (такие как Даниэль Таммет), которые совершают еще более выдающиеся подвиги. Тем не менее, по обычным меркам, мои мысленные вычисления довольно быстрые, поскольку они используют ряд простых приемов, на которые я наткнулся с детства. Например, для этого вопроса 172 умножить на 47 я мог бы заметить, что 47 близко к пятидесяти (47 минус 3), и решил сначала вычислить 50 умноженное на 172 (либо взяв пятьдесят процентов от 172 – i.е. половина, то есть 86, и умножение на 100, то есть 8600; или разбив его на 5×100 = 500, 5×70 = 350, 5×2 = 10, суммируя до 860, умножая на десять = 8600). Затем я бы вычитал 3 раза 172 (51 x 10 + 6 = 516), получая 8084 за несколько (долгих) секунд.
Услышав о молниеносных человеческих калькуляторах, о которых говорилось выше, меня всегда интересовало, как к ним приходят ответы. Были ли они аутичными учеными, получившими ответы из эфира? Похоже, что это так для некоторых из них.Были ли они «гениями» со сверхбыстрым умом, которые использовали вычислительные приемы гораздо более мощные, чем мои собственные маленькие уловки? Это казалось более частым случаем.
Сокровище: книга Артура Бенджамина
Одним ярким зимним днем, когда мне было за сорок, в нужное время мне в руки попала книга: Секретов ментальной математики Артура Бенджамина и Майкла Шермера. Это книга с довольно непривлекательной обложкой, но многообещающим подзаголовком: The Mathemagician’s Guide to Lightning Calculation and Amazing Math Tricks .Книга выполняет свое обещание. Если у вас есть хотя бы отдаленный интерес к повышению скорости умственных вычислений, я настоятельно рекомендую вам купить себе копию, потому что эта книга – сокровище.
Читая первые главы, я с восторгом осознал, что главный автор (Артур Бенджамин) использовал многие из тех самых уловок, на которые я, естественно, наткнулся. Конечно, это не было совпадением, а скорее естественным результатом параллельного процесса исследования. Было не только приятно читать знакомые описания кого-то, кто бродил по тем же джунглям, но также было ясно, что этот исследователь был намного смелее меня.Он шел по тропам, к которым я никогда не подходил (например, по кубам и квадратным корням), у него было множество крутых техник, о которых я никогда не думал, и он был очень-очень очень быстрым. В самом деле, если бы это не разбило мою метафору исследователя довольно уродливым образом, я бы сказал, что Артур Бенджамин оказался Тарзаном чисел.
Для меня книга Артура Бенджамина пришла в отличное время, так как я заметил, что в последнее время некоторые числа начали доставлять мне проблемы, с тревожной перекрестной связью с 24-часовым временем, которое никогда не беспокоило меня раньше.Например, число 13 (которое также соответствует 13:00) иногда становилось «расплывчатым» в моем сознании, если вы можете понять это. Этот печальный упадок заставил меня начать сожалеть о своей короткой фазе экспериментов с галлюциногенами несколькими годами ранее. С другой стороны, это могло быть простым следствием возраста или снижения численной активности. Конечно, немного упражнений пойдет мне на пользу.
Приемы, которые имеют смысл
Что мне нравится в Secrets of Mental Math , так это то, что каждая техника, которую представляет Артур, «имеет смысл».Я имею в виду, что для меня все его методы укладываются в знакомый алгебраический контекст, так что каждый метод можно легко декодировать, проверить и понять. Другими словами, он произносит числа на моей волне.
Это контрастирует со многими трюками «быстрой арифметики», которые я читал на многочисленных веб-страницах при исследовании темы, трюки, которые часто кажутся слишком изолированными, слишком произвольными, слишком не имеющими контекста, чтобы щелкать так, чтобы стимулировать удержание. Возможно, в этом заключается разница между тем, кто предлагает рецепт, который он не понимает, и человеком, который экспериментировал с техникой до такой степени, что он владеет ею.
Классные заметки
Я намерен использовать эту страницу в качестве «заметок для класса», где я обобщу советы, приемы и техники мысленных вычислений, о которых я не знал, чтобы я мог легко освежить свою память в любое время. Я надеюсь, что, поделившись этими заметками, некоторые уловки порадуют нескольких исследователей, отправляющихся в одни и те же джунгли. Чтобы предоставить более полезный ресурс, на странице также показаны методы, которые использует Артур, которые мне давно знакомы, но, возможно, не вдаваясь в подробности.
Но помните, это только заметки класса. Они не включают богатую оригинальную презентацию, личность учителя, упражнения, которые помогут вам преобразовать идеи в знания. Для меня эта книга – сокровище, и я не могу порекомендовать вам взять ее с собой, если бы не вы, кому-нибудь из ваших детей или племянников. Проходите ли вы стандартизированный тест, сидите на собрании, делите счет в ресторане или занимаетесь деревообрабатывающим проектом, удобство вычислений в вашей голове – это секретное оружие, которое не так уж сложно приобрести и которое делает прекрасное подарок любящему цифры ребенку.
Краткое описание этой очень длинной страницы
Чтобы помочь вам сориентироваться, позвольте мне объяснить структуру страницы. Первые два раздела (которые составляют основную часть содержания) посвящены «знакомым методам» и «новым методам». Это различие, вероятно, для вас бессмысленно, поскольку то, что для меня является новым, может быть вам знакомо. Он предназначен только для того, чтобы помочь мне быстро найти материал, который я, возможно, захочу пересмотреть в один прекрасный день. Тем не менее, можно найти определенную логическую прогрессию от «знакомого» к «новому».
Далее мы переходим к тому, что я бы назвал техниками второго уровня, не потому, что им не хватает мощности, а потому, что я, вероятно, не буду их использовать.
Далее мы кратко поговорим о математических фокусах. Артур называет себя «математиком» и устраивает развлекательное шоу для самых разных зрителей. Артур объясняет свои уловки в книге. Меня не очень интересуют фокусы, поэтому я не делал заметок для этой части книги, за исключением одного очень классного алгоритма для вывода кубического корня двузначного целого числа, которое было построено в кубе.
Далее мы обсудим простой способ вычисления дня недели любой даты. В этом разделе я попытался улучшить технику, объясненную Артуром, представив несколько замечательных быстрых клавиш. Я также представляю еще одну знаменитую технику «дня недели», которая может извлечь пользу из моего ярлыка, что делает ее намного проще в использовании, чем обычно, и дает вам два варианта на тот случай, если вы влюбитесь в эти удивительно простые методы … Ты можешь!
Затем мы рассмотрим некоторые другие книги по быстрой арифметике и в заключение приведем несколько ссылок.
Напомним, вот схема:
Итак, без лишних слов, давайте окунемся в мир быстрой мысленной математики.
Знакомые техники
Чтобы обеспечить некоторую структуру, в этом разделе я резюмирую несколько техник, которые долгое время были частью «хлеба с маслом» моих мысленных вычислений и которые Артур ясно объясняет в своей книге. Слева направо
Как и я, Артур, кажется, считает в уме слева направо.Например, возьмите числа 84 и 53. Если бы вы сложили или умножили их на бумаге, вы бы начали с последних цифр (4 и 3), но в уме вы начинаете слева. Вот примеры того, как это работает.
• Сложение: 84 + 53 = 13 (8 плюс 5 слева), за которым следует 7 (4 плюс 3) = 137. Для такой небольшой операции я бы фактически пошел большими кусками, с 134 (84 + 50) плюс 3, или «увидеть» ответ.
• Умножение: 84 x 53 = 4 240 (80 x 50 + 80 x 3) + 212 (4 x 53) = 4 452.Мы могли бы выбрать «инвертировать» 84 и 53: 4200 (50 x 84) + 252 (3 x 84) = 4452.
• Вычитание: 84 – 53 = 3 (8 минус 5), за которым следует 1 (4 минус 3) = 31.
• Деление: 168/3 = 150/3 + 18/3 = 56. 84/53 также работает слева направо: 1 оставляет 31/53 (1 + 31/53), а 31/53 снова работает слева направо.
Это правило написания слева направо не означает, что вы строго разбиваете каждое число слева направо. Вам могут прийти в голову и другие ярлыки, которые заставят вас разбить числа, с которыми вы работаете, на более крупные куски.
Округление
Это метод, о котором я упоминал во введении, где для вычисления 172 x 47 мы округляем 47 до 50. Часто проще оперировать числом, которое вы округлили в большую или меньшую сторону, а затем добавить или вычесть разницу. Например,
• Сложение: 49 + 77 = 127 (50 + 77) минус 1 = 126;
• Умножение: 49 x 77 = делится на 50 x 70 = 3500, 50 x 7 = 350, в сумме получается 3850 минус 77, что составляет 3750 (3850 минус 100) плюс 23 (разница от округления 77), что дает 3773;
• Вычитание: 77 – 49 = 27 (77 – 50) плюс 1 = 28.
• Деление: 196/4 = (200/4) – 1 = 49.
Билл Хэндли описывает некоторые другие методы округления, которые я использую все время.
Дополняет
В этой технике метод округления идет еще дальше. У меня никогда не было названия для этого, но имя Артура имеет смысл. Для двузначных чисел, например, вы можете «округлить» 37 до 100, чтобы вычесть быстрее, а затем прибавить разницу, 63. Вот как это работает: чтобы вычислить 414 минус 37, вы выполняете 314 (400 – 100) и прибавляем 63, получая 377.
Разница между 100 и числом (в случае двузначных чисел) – это то, что Артур называет дополнением. Я давно заметил, что все эти дополнения заложены в моем сознании. Например, если вы скажете 34, мне не нужно вычислять дополнение (66). Это значительно ускоряет выполнение многих задач на вычитание.
Если вы много работаете с числами в голове, вам часто приходят в голову трехзначные числа (или более длинные дополнения). Например, для 1200 минус 625 я инстинктивно прибавил 375 к 200, получив 575.
Обратите внимание, что в случае 1200 минус 375, дополнение к 625 может появиться и дать вам 200 + 625 = 825, но в первую очередь может возникнуть конкурирующий метод 800 (1200 минус 400) плюс 25 = 825. Никогда не знаешь, какая стратегия бросится в глаза в первую очередь.
У Артура есть крутой метод еще более быстрого вычитания с помощью дополнений.
Выбор метода
Для меня часто значительная часть вычислительного времени уходит на выбор метода, особенно если есть два привлекательных метода, конкурирующих за внимание.Для некоторых проблем вы решаете, анализируя, для других вам лучше прыгнуть с первой атакой, которая приходит к вам.
Использование аппаратных операций
Иногда вам бросается в глаза, что проблема близка к операции, которая заложена в вас, и вы можете воспользоваться этим. Например, для 4 умножения на 127, вместо умножения слева направо, я замечаю близость к 4 x 125 (жестко запрограммировано как 500), поэтому я просто добавляю 8 (четыре раза по два, поскольку два – это расстояние 127 от 125).Результат: 508.
Использование факторов
Часто вам бросается в глаза, что число является произведением других чисел. Например, 18 трижды шесть. Это часто дает вам альтернативный, более быстрый метод вычисления чего-либо.
• Умножение: для 16 x 18 вы можете вычислить 16 x 3 (48) умножить на 6 = 288.
• Деление: для 120/15 вы можете вычислить 120/3 (40), разделенное на 5 = 8. Или, заметив ноль в конце 120 и 5 в конце 15, вы можете умножить на два, чтобы получить ноль также отображается справа: 240/30.Когда вы упрощаете это до 24/3, что дает 8, вы используете множители, не задумываясь об этом: вы делите 30 на 10 x 3 и начинаете с деления 240 на десять, первого множителя.
Этот пример показывает, что иногда при делении вы умножаете, чтобы появился общий множитель. По сути, правило – «все работает». Другие примеры:
• чтобы разделить на 16, я часто делю на 2, четыре раза подряд.
• чтобы умножить или разделить на 12½, я буду рассматривать это число как 100/8, умножить на 100 и разделить на 8 или наоборот.Я думаю, вы могли бы назвать это обратным факторингом .
Работа с факторами часто экономит ваше время. Например, в задаче умножения, такой как 16 x 18, с помощью метода множителей мы просто умножаем дважды, тогда как при классической операции слева направо нам нужно было бы дважды умножить , а затем добавить (10 x 16 = 160, 8 x 16 = 128, 160 + 128 = 288) или дважды умножьте , затем вычтите (20 x 16 = 320, 2 x 16 = 32, 320-32 = 288).
Запомненные дроби
Я помню тот давний день, когда, скучая в классе, я решил запомнить все дроби с делителями до девяти и числителями до девяти.
Например, 1/9 = 0,111 повторения, 2/9 = 0,222 повторения и так далее. Это оказалось чрезвычайно полезным. Однажды я оказался на обеде, где нам пришлось разделить счет между семью людьми. Запомнив схему дроби от семи, я получил удовольствие от объявления результата: 23.4285714… К сожалению, деление на семь встречается не так часто.
Было приятно увидеть, что Артур использует одни и те же запомненные дроби. В книге даже перечислены дроби от 11, которые я однажды выучил, но забыл из-за неиспользования, поэтому я перечисляю их в разделе новых методов.
• Все дроби от 9 – это произведение 0,1111… (повторение последней цифры). Например, 6/9 равно 0,6666… Это может пригодиться, если вы разделите 120 на 18 и заметите, что 18 равно 2 умножить на 9. Вы мгновенно упростите до 60/9, что даст вам 6,6666…
• Дроби от 8. Разве вы не используете их все время? 0,125 для одной восьмой, 0,375 для трех восьмых, 0,875 для семи восьмых… Промежуточные части встречаются не так часто, потому что они упрощаются до одной четверти, одной половины и трех четвертей.
• Доли числа от 7.Я люблю это. Одна седьмая – 0,142857, затем повторяются эти числа: 0,14285714… Все дроби от двух седьмых до девяти седьмых используют один и тот же образец, начиная с другой цифры. Чтобы узнать, какая цифра, просто умножьте начало (14) на числитель. Две седьмых = 0,28571428… Три седьмых = 0,42857142… Четыре седьмых = 0,57142857… Пять седьмых = 0,71428571… Шесть седьмых = 0,85714285…
• Доли от 6. Они появляются постоянно. Одна шестая – 0,1666… (повторяется). Пять шестых – 0.8333… (повторяет). Промежуточные – трети или половина.
• Доли от 5. Они также появляются постоянно. Деление на пять – это то же самое, что умножение на два и деление на десять, поэтому просто имейте «рефлекс умножить на два». Например, для трех пятых вы делаете два раза по три, так что это шестой пункт. Одна пятая – 0,2, две пятых – 0,4, три пятых – 0,6, четыре пятых – 0,8.
Проверка, делится ли число на 3
Этот трюк я помню со школы и постоянно использую.Чтобы проверить, делится ли число на 3, вы просто складываете все цифры, и если результат делится на 3, то же самое и исходное число. Например, для 817 273 вы получите 28, что не делится на 3. (Повторно, если вы не уверены, делится ли ваш результат на 3, продолжайте складывать цифры: для 28 вы получите 10.) С другой стороны, для 817 272 вы получите 27, что делится на 3, и действительно, 817 272 – это трижды 272 424.
На самом деле, для многих чисел я не утруждаю себя сложением всех цифр: я игнорирую цифры, которые уже кратны 3, ищу пары, которые в сумме дают 3, игнорируя их также, затем складываю оставшиеся цифры.Например, для 6 817 273 я игнорирую 6, игнорирую пару 8-1, игнорирую пару 7-2 и игнорирую последние 3, оставляя 7.
Мне нравится этот трюк, но есть еще кое-что! Артур представляет другие приемы, которые я либо забыл, либо никогда не знал, чтобы проверить их на делимость на другие числа.
Умножение двузначных чисел на одиннадцать
Это излюбленная уловка учителей начальной школы. Чтобы умножить двузначное число (например, 42) на одиннадцать, вы складываете две цифры (4 + 2 = 6) и вставляете их посередине: 462.Если вам нужно нести (в 49 x 11, 4 + 9 дает 13), добавьте единицу к первой цифре: 49 x 11 = 539.
Вы можете расширить этот трюк, чтобы умножить более длинные числа на 11, но для меня это не работает с умом, поэтому я им не пользуюсь. Я считаю, что мне лучше пойти на бумагу: например, для 87 657 умножить на 11 я напишу число один раз, а затем запишу его снова, чуть ниже первого числа, но со сдвигом на один столбец влево, а затем сложу два числа . Конечно, это именно то, что делает классическое умножение.
Обратная сторона конверта
Артур – большой поклонник предположений. Я тоже.
Например, возьмите 7 896 и 4099.
• Сложение: что такое 7 896 плюс 4 099? Я не знаю, но это близко к двенадцати тысячам (8000 + 4000).
• Умножение: сколько 7 896 умножить на 4 099? Я не знаю, но это близко к 32 миллионам (8000 x 4000).
• Разделение: что такое 7 896 против 4 099? Не знаю, но это близко к двум (8000/4000). Если бы я хотел точно настроить приближение, которое, как я знаю, слишком велико для двух учетных записей (первое 7896 меньше 8000, второе 4099 больше 4000), глядя на соотношение между 4000 и 4100, я мог бы сказать, что добавив десять процентов к 4000, в результате чего знаменатель 4400 удалит около десяти процентов ответа (0.2), поэтому с 4100 я бы снял только четверть этого (0,05), получив приблизительное число 1,95, что немного ближе к фактическому ответу (1,926).
Проверка результатов
• Добавление: при добавлении длинных списков чисел я люблю добавлять второй раз снизу вверх.
• Деление: иногда вы можете захотеть умножить результат на делитель, чтобы убедиться, что вы снова встаете на ноги.
Позже мы рассмотрим другие техники, которые использует Артур: выброс девяток (который я не использовал с младших классов) и выброс одиннадцати.
Новые методы
В этом разделе представлены техники, которым я научился в книге. Умножение соседних чисел: метод привязки
Допустим, вы хотите умножить соседние числа, например 62 на 63. Вы заметили, что оба числа близки к шестидесяти. Разбив его на части, если мы запишем 62 как 60 + 2 и 63 как 60 + 3, проблема будет (60 + 2) x (60 + 3), которая уменьшится до 60x (60 + 2 + 3) + 2×3.
Если это жестко запрограммировано в вас, тогда, когда вы видите 62 x 63, вы сразу переходите к 60×65 плюс 6 = 3906.Аккуратный!
Другой пример: 84 x 87 = 80×91 + 28 = 7 308.
Используя этот метод, вы ищете удобную «привязку» для перестановки умножения. В первом примере (62 x 63) колышек был 60; во втором примере (84 x 87) колышек был 80.
Этот «метод привязки» окупается во многих ситуациях. Например, если вы хотите умножить трехзначные числа на нули в середине, такие как 105 и 106, вы быстро получите 100 x 111 + 30 = 11 130.
Этот метод еще проще, если сумма последних цифр равна десяти.Например, для 62 x 68 вы сразу перейдете к 60×70 + 16 = 4216.
Билл Хэндли, специалист по технике «близких чисел», использует ее даже в тех случаях, когда числа совсем не рядом. В конце концов, распределение работает независимо от того, рядом или далеко числа, поэтому вы можете использовать любую привязку, которая вам нравится. Например, для 75 x 25 Билл использует 5 в качестве привязки, что дает (5 x 95) + (70 x 20). В обзоре книги Билла я также покажу его вариант метода привязки для таких случаев, как 23 x 87, где вы можете взять 20 в качестве привязки и 4 в качестве множителя.
Если вы действительно внимательны, вы можете найти привязку, когда рядом будут следующие числа:
• под круглым числом: 58 x 59 = 60 x 57 + 2 = 3 422. Это упрощение (60-2) x (60-1).
• по обе стороны от круглого числа: 57 x 62 = 60×59 – 6 = 3,534. Это упрощение (60-3) x (60 + 2).
Исходные числа для умножения (например, 188×190) в сумме дают ту же сумму (378), что и новые числа для умножения (200×178), и это может быть полезно для быстрой проверки того, что вы умножаете правильные числа, или даже как ярлык для получения второго числа для умножения.
Если вы еще более внимательны, вы можете преобразовать некоторые проблемы в проблему с соседними номерами. Например, для 105 x 412, используя коэффициент 2, вы меняете задачу на 210 x 206, что дает 200×216 + 60 = 43 260. Для 104 x 927, используя коэффициент 3, вы меняете задачу на 312 x 309, что дает 300 x 321 + 108 = 96 408.
Возведение в квадрат методом колышка
• Особый случай «Легкий»: числа, оканчивающиеся на 5 (например, 75). Для двузначного числа возьмите первую цифру, умножьте ее на старшую цифру (7 x 8 = 56), закрепите 25 в конце: 5625.2 = (a – b) x (a + b), при этом при вычислении 38-квадрата a = 38 и b = 2.
• Трехзначные числа. Метод тот же. На этот раз мы находим ближайшее кратное 100. Например, в квадрате 211 ближайшее кратное равно 200, а число «на другой стороне» равно 222. Произведение равно 44 400, к которому вы добавляете квадрат расстояния. (11 квадратов – 121), что дает 44 521.
Приблизительные квадратные корни
Этот метод был откровением. Мы рассмотрим его для квадратных корней из двузначных чисел, но он работает и для больших чисел.Прежде чем мы рассмотрим алгоритм, рассмотрим общую идею. Мы пытаемся найти точное приближение. Возьмем 50. Мы знаем, что квадрат 7 равен 49, а квадрат 8 равен 64, поэтому ответ должен быть между 7 и 8, а 7 дает ближайший квадрат. Теперь рассмотрим 50/7. Поскольку 7 меньше нашей цели (квадратный корень из 50), это число (50/7) больше, чем цель. Другими словами, наша цель находится где-то между 7 и 50/7. Возьмите среднее из двух: это наше приближение. Один из способов вычислить среднее значение: (7 + 50/7) / 2 = 7.07. Другой способ – сказать, что среднее значение равно 7 плюс половина разницы, то есть 7 + (50/7 – 7) / 2, то есть 7 + (50 – 49) / 14 или 7 + 1/14.
Это алгоритм: возьмите число, которое дает ближайший квадрат. Затем добавьте начальную ошибку, деленную на удвоенное начальное приближение.
• Пример 1: квадратный корень из 90. Ближайший квадрат 9 (квадрат 9 – 81). Ошибка 9 (90 – 81). Наше окончательное приближение 9 + 9/18 = 9,5.
• Пример 2: квадратный корень из 78.Опять же, ближайшее приближение – 9. Ошибка -3 (78 – 81). Наше окончательное приближение 9 – 3/18, то есть 9 – 1/6, что составляет 8 + 5/6 (если вы обнаружите, что быстрее прибавить пять шестых к восьми, чем удалить одну шестую из девяти) = 8,83.
Насколько точен этот метод? Для чисел от 10 до 99 при сравнении приближения, округленного до второго десятичного знака, с фактическим квадратным корнем, округленным до второго десятичного знака, разница в восемьдесят раз составляет 0,01 или меньше, в восемь раз она равна 0,02, если она равна 0.03 (для 20) и сразу 0,04 (для 12). Для меня это очень хорошо.
Кстати, чтобы улучшить ваше приближение, вы всегда можете взять второе приближение и повторить процедуру, добавив новую ошибку, разделенную на удвоенное приближение.
Артур не упоминает об этом, но я обнаружил, что этот метод можно легко преобразовать в процедуру для оценки кубических корней , хотя вычисления не так просты. Вот как это работает. Вы берете первую оценку и складываете ее в куб.Ваша вторая оценка будет исходным приближением плюс начальная ошибка, деленная на удвоенный квадрат приближения. Обратите внимание, что по сравнению с алгоритмом вычисления квадратных корней, “квадрат” в делителе – единственное изменение.
Моя идея этой адаптации метода квадратного корня была вдохновлена приложением к книге Билла Хэндли (рассмотрено ниже), где он представляет свой алгоритм вычисления кубических корней. Конечно, эти два понятия эквивалентны. Кстати, с чего вы начинаете – какова ваша первоначальная оценка? Билл указывает, что вы берете тройки цифр, начиная с правого, и заменяете каждую из них нулем.У вас останутся от одной до трех крайних левых цифр. Для вашего приближения вы берете ближайший куб целых чисел от 0 до 9. Их всего десять, некоторые из которых вы уже должны знать, а остальное вы запомните, если посмотрите на потрясающий трюк Артура (не далеко ниже) для получение кубических корней совершенных кубов двузначных целых чисел. (0 ⇒ 0, 1 ⇒ 1, 2 ⇒ 8, 3 ⇒ 27, 4 ⇒ 64, 5 ⇒ 125, 6 ⇒ 216, 7 ⇒ 343, 8 ⇒ 512, 9 ⇒ 729.)
В своем обзоре книги Билла Хэндли я также упомяну его советы по вычислению квадратных корней из более длинных чисел.Ключевой трюк заключается в том, что при вычислении квадратного корня каждая пара цифр, начинающаяся справа, будет уменьшена до десяти (десять в квадрате – это сотня), за исключением крайнего левого префикса из одной или двух цифр. Используя обычный метод, вы оцениваете квадратный корень из этого однозначного или двузначного префикса, а затем настраиваете шкалу на количество делителей, равное десяти.
Быстрое вычитание с дополнениями
Ранее мы говорили о дополнениях. Напоминаем, что в случае двузначного числа, такого как 41, дополнение – это расстояние от сотни (здесь 59).Мы уже видели, как дополнения можно рассматривать как форму метода округления, которая может ускорить вычитание. Например, для 214 минус 41 вы удаляете 100 (114) и добавляете дополнение 41 (59), получая 173.
Артур представляет другую технику, которая мне никогда не приходила в голову и может быть даже быстрее. Если взять 214 минус 41, опять же, вы знаете, что ответ будет сто с чем-то. В остальном вы вычисляете 41 минус 14 (27) и находите дополнение (73), снова возвращая 173. Это происходит сразу после появления водорослей, но мне никогда не приходило в голову.
Что быстрее? Это зависит. В этом случае это близко. При первом способе вы находите дополнение, а затем добавляете. Во втором методе вы вычитаете, а затем находите дополнение. Если вычитание бросается в глаза, например, 44 минус 22, то второй метод, вероятно, быстрее. Например, в случае 122 минус 44, при втором методе мы перескакиваем с 22 (разница) на 78 (дополнение и ответ), тогда как в первом методе мы переходим к 56 (дополнение), а затем добавляем его обратно к 22, чтобы найти 78.
Умножение крест-накрест
Это отличный способ быстро умножать числа любого размера ручкой и бумагой. Я не буду это объяснять, потому что не хочу рисовать диаграммы. Объявление отличный повод купить книгу!
Деление
Артур отмечает, что при мысленном делении полезно сначала выяснить, сколько цифр будет в ответе. Например, для 357/8 ответ состоит из двух цифр, потому что 100 будет слишком большим (8 x 100 = 800).Итак, когда вы начнете слева с 35 и обнаружите, что 4 работает (4 x 8 = 32), вы можете начать говорить «сорок» … Далее, 37 – это остаток, так что вы можете сказать «четыре». Затем вы можете продолжить с 50 и объявить «точка-шесть» (6 x 8 = 48) и так далее. (Или, в этом случае, идите прямо за деньгами, разделив 50 на 2 три раза подряд.)
Артур тоже предлагает этот отличный трюк. Допустим, вы хотите вычислить 230 из 24. Используя эту технику, вы сразу увидите, что 230 из 24 – это 9 + 14/24, и продолжите задачу с этого момента.Как вы это видите? Во-первых, десять умножить на 24 равно 240, чуть больше 230, поэтому десять – это первое целое число над целой частью нашего ответа, и наш ответ должен быть «9 с чем-то». Пока никаких чудес. Но крутая интуиция – очевидная, как только вы ее видите – состоит в том, чтобы посмотреть, насколько мы промахнемся, если умножим 23 на десять. Мы промахиваемся на десять (240 – 230 = 10). Итак, если мы умножим 24 на 9, мы получим короткую позицию на 14. Ответ: 9 + 14/24.
Вы бы не использовали эту технику каждый раз, но время от времени информация просто попадает вам в руки, потому что вы пытаетесь угадать целую часть деления, и ваше предположение «просто выходит за рамки» меньше, чем делитель.
На самом деле, если вы промахнулись еще больше, уловка по-прежнему доступна вам, хотя она может быть не такой немедленной. Предположим, что для 620 вместо 33 вы попробуете 20. У вас получится 660, так что вы увидите, что вы превысили свой множитель на два, и ответ должен быть «18 с чем-то». Так как 660 минус 33 равно 627, умножение 33 на 19 приведет к выходу за пределы 7. Умножение 33 на 18, следовательно, приведет к недостижению на 33 минус 7, что составляет 26. Это дает ответ 18 + 26/33.
Проверка на делимость
Ранее мы рассмотрели трюк, чтобы проверить, делится ли число на 3.Вот аналогичные уловки, которые предлагает Артур для проверки делимости на другие числа.
• Делимость на 4. Проверьте, делятся ли последние две цифры на 4. (Так как 4 x 25 равно 100, мы можем не учитывать цифры слева от двух последних). Если вам не сразу понятно, является ли 66 делится на 4, сначала разделите его на 2: вы получите нечетное число, поэтому это не сработает.
• Делимость на 8. Проверьте, делятся ли последние три цифры на 8. (Поскольку 8 x 125 равно 1000, мы можем не учитывать цифры слева от последних трех.)
• Делимость на 9. Проверьте, делится ли сумма цифр на 9. Например, 123 не делится на 9 (сумма цифр 6), тогда как 126 (сумма цифр 9). Чтобы понять, почему это работает, прочтите мою страницу о том, почему работает метод «изгнания девяток».
• Делимость на 6. Проверьте делимость на 2 и на 3. Duh…
• Делимость на 11. Поочередно складывайте и вычитайте цифры справа налево. Игнорируя любой отрицательный знак, если результат равен нулю или кратен 11, то исходное число делится на 11.Например, для 7 415 вычислите 5-1 + 4-7, получив -7, что не работает (7 не делится на 11). Для 9 273 вы вычисляете 3 – 7 + 2 – 9, что равно -11, и это работает, а 9 273 действительно одиннадцать умножить на 843.
• Делимость на другие нечетные числа. Обожаю эту технику. Допустим, вы хотите знать, делится ли 96 843 на 7. Добавляйте или вычитайте числа, кратные 7, пока в конце не получите ноль (добавление или удаление семерок, очевидно, не повлияет на делимость числа на семь). В этом случае мы можем добавить 7, чтобы получить 96 850.Вы можете убрать ноль, потому что деление на десять (то есть на 2 и 5) не влияет на то, является ли 7 множителем этого числа. Итак, у нас осталось 968. Делится на 7? Продолжайте добавлять или удалять семерки, чтобы получить нули. Здесь вы можете прибавить 42, получив 1010, или, проще говоря, удалить 28, получив 940. Удалите ноль. 94 делится на 7? Удалите 14, получив 80. Удалите ноль. Восемь не делится на 7, следовательно, и 96 843.
Давайте воспользуемся этой техникой, чтобы увидеть, делится ли 773 на 17. Складываем 17: 790.Убрать ноль. 79 не делится на 17 (слишком близко к 68), поэтому и 773 тоже.
Разное приближение
Вот несколько идей, которые упоминает Артур.
• Используйте известные фракции. Например, если вам нужно взять 7¾% от суммы, вы можете заметить, что эта доля близка к семи к девяти (7,77… повторение). Это дает вам быстрое приближение (умножение на 7, деление на 9, деление на сто), что особенно удобно, если вы живете в штате, где налог с продаж составляет 7¾%, например, в Калифорнии в старые добрые времена.
• Правило 70. Это интересная идея, о которой я впервые упомянул в замечательном выступлении Эла Бартлетта под названием Арифметика, народонаселение и энергия . Я никогда не использовал его, потому что слишком привык вычислять точный ответ с помощью логарифмов, но книга Артура убедила меня запомнить этот трюк из-за его скорости. Скажем, определенная сумма (например, население или денежная сумма) растет со скоростью i% в год. Сколько лет понадобится, чтобы удвоиться? Разделив 70 на i, вы получите хорошее приближение.y = 2. Следовательно, y.log (1 + i%) = log (2) и y = log (2) / log (1 + i%). Для i% = 7% получаем y = log (2) / log (1,07) = 10,24.
• Правило 110. Это та же идея, что и правило 70, но оно используется для оценки того, сколько времени потребуется, чтобы сумма сложного процента с определенной скоростью утроилась. Например, сумма, увеличивающаяся на 7% в год, утроится примерно за 16 лет (110/7 = 15,71). Чтобы получить точный ответ, вычислите log (3) / log (1.07) = 16,23.
Запоминание цифр при расчетах
Хранение цифр на руке… Это странное выражение, но, как указывает Артур, цифры (один, два, три…) называются цифрами не зря: наши пальцы – это оригинальная счетная машина.
Он дает уловку для запоминания цифр при выполнении многоступенчатых вычислений. За ноль сожмите кулак. У вас уже есть собственный способ представить цифры с первой по пятую с помощью пальцев. (Между прочим, какой бы метод ни использовали люди вокруг вас, это культурная традиция, и такие методы различаются в разных регионах мира.) Для шести, семи, восьми и девяти коснитесь большим пальцем мизинца, безымянного пальца, среднего пальца и указателя. Палец. Обеими руками вы можете сохранить две цифры.
Запоминание больших чисел
Артур использует популярную (и древнюю) мнемоническую систему, называемую главной системой. Короче говоря, каждому числу присвоен согласный звук, так что числа можно закодировать словами. Например, «Сидней просто встряхнул Фабио» кодируется 0123456789:
.
0 в кодировке s или z,
1 кодируется t, d или th
2 кодируется n,
3 кодируется m,
4 кодируется r (как в четыре),
5 кодируется буквой L (римская цифра пятьдесят),
6 кодируется «влажными звуками», например, в мягком g – «заработная плата», sh – «shush», ch – «itchy»
7 кодируется K или жестким g в “go”,
8 кодируется f или v,
9 кодируется b или p.
Гласные ничего не кодируют. Обратите внимание, что система фонетическая: написание не имеет значения. Например, «itchy» кодирует только 1 (t является частью звука tch), а «garage» кодирует 746, поскольку два gs произносятся по-разному.
Для телефонных номеров этот метод отлично работает, особенно если вы найдете забавные прозвища для кодирования номеров. Например, как можно забыть «большое лицо Джима» (у которого нет самого маленького лица) или «афродита на стенах» (у кого есть хорошая история, которую можно рассказать)?
Артур говорит, что использует эту технику для запоминания промежуточных результатов в середине длинных вычислений.Если вы планируете использовать такую систему, то имеет смысл запомнить словарь для чисел от 00 до 99 (или даже от 000 до 999), чтобы слова были легко доступны для вас, когда они вам понадобятся.
Вот несколько кодировок, которые я придумал, которые могут вам понравиться:
• Квадратный корень из 2: Авторитарный снос, устав Микки Мауса.
• Квадратный корень из 3: Токийский мужчина донимает повара.
• Первые десятичные знаки числа Пи: Вернитесь скоро, так как я собираюсь опубликовать свое потрясающее стихотворение для первых 100 десятичных знаков числа Пи.
Бесплатная программа 2Know может помочь вам кодировать числа. Этот онлайн-кодировщик основной системы тоже неплох.
Методы, которые я, вероятно, не буду использовать
Вот несколько техник, которые упоминает Артур, и которые я, вероятно, не буду использовать, потому что они требуют запоминания определенных операций или потому, что я выполняю операцию так редко, что я ее не запомню. Чтобы узнать подробности, вы обязательно захотите прочитать книгу. Обнаружение ошибок путем отбрасывания девяток и одиннадцати
Эти два метода (ни один из которых не является полностью точным) используются для обнаружения ошибок в результатах ваших расчетов.Они могут сказать вам, что есть ошибка, но не могут сказать вам, что ошибки нет.
Мы научились методу «изгнания девяток» в начальной школе, но точный метод вскоре ускользнул из моей головы, и я сомневаюсь, что начну использовать любой из этих методов на этом позднем этапе.
Изгнание девяток (или одиннадцати) может выглядеть как магия, но причину, по которой это работает, действительно легко понять. Если вам интересно, посмотрите мою страницу, объясняющую, как и почему работает отбрасывание девяток. Здесь я просто резюмирую метод.
• Выброс девяток. Для каждого числа, с которым нужно работать, сложите все цифры, пока они не уменьшатся до одной цифры. Например, 859 дает 4 (8 + 5 + 9 = 22 и 2 + 2 = 4). Это называется модульной суммой, и это число по модулю 9 (остаток от деления на девять). Также вычислите мод-сумму для результата операции. Теперь выполните ту же операцию (сложение, вычитание или умножение) над модульными суммами, которую вы проделали с исходными числами. (Для разделения вам нужно сформировать тест определенным образом: см. Раздел о разделении на моей странице о том, как выбросить девятки и выбросить одиннадцать.) Результат должен соответствовать третьей сумме модуляции. Например, для 859 x 17, если вы получили 14 623, вы знаете, что допустили ошибку, потому что мод-сумма 859 равна 4, модульная сумма 17 равна 8, произведение равно 32, что дает модульную сумму 5. – тогда как мод-сумма 14 623 равна 7.
• Изгнание одиннадцати. Это дает число по модулю одиннадцать (остаток от деления на одиннадцать). Вы используете его как метод 9. Это означает, что когда вы складываете, вычитаете или умножаете модули, их модуль должен упроститься до модуля результата операции.Чтобы получить число по модулю 11, вы попеременно складываете и вычитаете все его цифры, начиная с самой правой цифры и двигаясь влево. Если вы получите отрицательное число, добавьте 11. Например, для 958 вы получите 9-5 + 8 = 12, тогда 2-1 = 1. И действительно, 957 равно 11 x 87, поэтому 958 больше 11 имеет остаток. of 1.
Если модули совпадают, метод исключения девяток имеет 8 шансов из 9 дать вам правильный совет («вероятно, без ошибок»). Если модули совпадают, метод «выбрасывания одиннадцати» имеет 10 из 11 шансов дать вам правильный совет («вероятно, без ошибок»).Если модули совпадают в обоих методах, метод имеет 98 шансов из 99 дать вам правильный совет.
Дружественные факторы
Артур дает список «дружественных факторов», которые он предлагает запомнить, чтобы, когда придет время, вы могли упростить свои вычисления. Например, 38 x 8 = 304, поэтому, если вам нужно было вычислить 38 x 24, вы могли бы решить пойти по пути факторинга, начиная с 8 (38 x 8 = 304), а затем умножив на 3, что легко, потому что “дружественный factor “имеет ноль посередине: 304 x 3 = 912.
Это круто, но я вряд ли запомню длинный список дружественных факторов.
Еще одно изящное применение – сделать так, чтобы коэффициент дружелюбия появился путем деления большего числа: например, для 318 x 13 вы можете взять 3 x 106 x 13, что даст вам 3 x 1,378 = 4,134.
Точные квадратные корни
Мне нравится метод Артура для приближения квадратных корней. Он также дает один для вычисления точных квадратных корней, но я не буду его использовать.
Кубы
Мне почти никогда не нужно вычислять кубики, поэтому я никогда этого не вспомню.2) х 18 = 5 832.
Магические трюки
Артур представляет ряд «фокусов». Для некоторых это может быть интересным, а для «фокусника» – развлечением, но меня они на самом деле не интересуют. Почему нет?Представьте себе эту карикатуру на уловку. Придумайте любое число от одного до ста. Добавьте два. Вычтите свое число. А теперь позвольте мне угадать … результат два … верно?
Для меня большинство фокусов с числами – это вариации этого псевдотрюка. Если есть уловка, есть алгоритм – я могу не знать, какой из них, но этого достаточно, чтобы потерять интерес.Просто вопрос того, что заводит или выключает разных людей.
При этом трюки Артура очень эффективны для аудитории, поэтому, если у вас есть некоторая зрелищность и вы наслаждаетесь таким взаимодействием с людьми, то вам очень понравится эта часть книги. Я больше одиночка.
Тем не менее, был один трюк, который мне понравился: вот он.
Мгновенный корень куба
Это сверхбыстрый метод объявления кубического корня секретного двузначного числа, которое было построено в кубе.Для этого вам необходимо знать первые десять кубиков: 1 → 1, 2 → 8, 3 → 27, 4 → 64, 5 → 125, 6 → 216, 7 → 343, 8 → 512, 9 → 729, 10 → 1000.
Все эти кубики заканчиваются разными цифрами от нуля до десяти, и это соотношение один к одному является отличным ключом к разгадке, так как оно сообщает вам последнюю цифру двузначного числа, которое вы построили в кубе. Обратите внимание, что последняя цифра куба одинакова во всех случаях, за исключением двух пар, 2⇔8 и 3⇔7.
Допустим, зритель объявляет, что куб 42 875. Вы сразу же знаете, что последняя цифра – 5, потому что 5 → 125.А как насчет первой цифры? Десять-куб – это тысяча, поэтому хитрость здесь заключается в том, чтобы не обращать внимания на все, что находится справа от запятой, и просто сосредоточиться на цифрах слева от запятой. Эти цифры (42) находятся между кубиками для 3 и для 4, поэтому первая цифра – 3. Секретное число – 35!
Метод Артура для извлечения квадратного корня из квадратов двузначных целых чисел не так прост, но похож. Вы вычисляете первую цифру, игнорируя последние две цифры квадрата и сравнивая эти одну или две цифры с первыми десятью квадратами.2 = 36). Чтобы решить, какое из них, вы возводите в квадрат число в середине (простой квадрат числа, заканчивающегося на пять) и смотрите, является ли ваш квадрат ниже или выше.
День недели любой даты
В «волшебной» части своей книги Артур представляет знаменитую технику определения дня недели любой даты в нашем григорианском календаре. Я не включил его в раздел, посвященный математической магии, потому что это полезный метод, который большинство из нас, вероятно, использует сотни раз, даже не демонстрируя его на сцене.Я придумал улучшенную версию этой техники, сокращенное вычисление, которое упрощает весь процесс. Я скоро представлю его на отдельной веб-странице (по одному!)
Этот ярлык, который я использую, также ускоряет вычисление дня недели, если вы используете альтернативный метод, называемый алгоритмом Судного дня.
Прочие книги по ментальной математике
В этот раздел я планирую постепенно добавлять обзоры других книг о скоростных ментальных вычислениях. Краткая математика , Джерард Келли.
Я считаю эту книгу в основном превосходной. Тон более академичный, чем в книге Артура, что можно объяснить как годом ее публикации (1969), так и тем фактом, что опыт Артура на сцене делает его беглым ведущим.
Я не встречал ни одного потрясающего трюка, но мне понравилось, что Джерард представил много маленьких техник, которые я тоже использую, техник, в которые Артур не входил. Например, Джерард находит время, чтобы описать некоторые разговоры, которые происходят в вашей голове, пока вы выполняете вычисления, а также общие методы, сочетающие мысленные вычисления с ручкой и бумагой, такие как сканирование простых пар (например, 17- 13) при суммировании столбцов чисел.
Джерард показывает прибавления «без переноса», где вы суммируете каждый столбец цифр независимо, а затем складываете промежуточные суммы. Это особенно хорошо работает слева направо (записывая соответствующее количество нулей), поскольку вы получаете все более точные оценки.
На мой взгляд, у Джерарда была отличная интерпретация формулы n (n + 1) / 2, которую я всегда использовал для суммирования ряда последовательных цифр, начинающихся с 1. В его формуле сумма не должна начинаться с 1. Если F и L – первое и последнее число в ряду, вы берете среднее значение (F + L) / 2, а затем умножаете на количество чисел (L + 1-F).Легкий!
Джерард указывает, что если вы умножаете на бумаге, и это одно число имеет повторяющиеся цифры, например, как в 666 x 827, вам лучше поставить 666 в нижней части умножения, потому что все три прохода дадут то же число (здесь 4962), которое вы затем суммируете с соответствующими смещениями. Для чего-то вроде 248, отмечает Джерард, все цифры кратны друг другу, что дает нам быстрый способ записать строки 4x и 8x, если у нас есть строка 2x.
Я не поклонник раздела о возведении в квадрат, где Джерард вводит различные техники возведения в квадрат чисел, заканчивающихся на 1, 4 или 5. Хуже того, он опирается на свои правила возведения в квадрат, чтобы предоставить еще больше методов для умножения ближайших чисел, запутывая методы для помните, действительно, по сравнению с одним простым методом поблизости, описанным здесь.
Чтобы умножить на 45, Джерард предлагает умножить на 50 и вычесть десять процентов – прием, который я часто использовал при конвертации валют.Другой пример: умножение на 396 после умножения на 400, вместо четырехкратного вычитания числа, вы можете просто вычесть один процент. Еще один прекрасный пример: чтобы умножить 24 на 27,5, обратите внимание, что 27,5 равно 25 плюс десять процентов. Умножить 24 на 25 легко (25 – это четверть умножить на 100, так что 24/6 = 6 x 100 = 600). Добавьте десять процентов: 660.
В целом, для человека, который либо новичок в этой теме, либо очень ею интересуется, было бы обидно пропустить эту книгу. Я настоятельно рекомендую получить его в качестве дополнения к книге Артура.
Математика скорости , Билл Хэндли. Сначала я думал, что мне эта книга понравится меньше, чем книга Джерарда Келли Short-Cut Math , но после того, как я дал ей шанс и прочитал ее до конца, она мне, вероятно, понравилась больше, чем книга Джерарда.
Одна вещь, которая сбила меня с толку, заключалась в том, что во введении Билл кланяется автору системы Трахтенберга, которая после беглого просмотра страницы Википедии меня не привлекает, поскольку она содержит слишком много «местных правил».Мне нравятся техники, которые прочно укоренились в алгебре, которую я могу сразу почувствовать. Тем не менее, Билл сказал, что его методы не совсем такие, как у Якова Трахтенберга.
Еще одна вещь, которая меня сначала оттолкнула, заключалась в том, что книга казалась более простой. Некоторые главы, казалось, были не столько о «арифметике скорости», сколько об обучении простой и понятной арифметике, то есть тому, как выполнять деление в столбик. Без сомнения, ценная информация, но это не то, что я искал, когда брал в руки книгу.
Первые семь глав представляют собой разработку близкого метода, который для моих нужд адекватно объяснен в нескольких абзацах выше.
Но затем Билл представил прекрасную вариацию этой техники. Считаем эти ароматы:
• Базовый аромат : 23 x 26 = 20 x (3 + 26) + 3 x 6 = 20×29 + 18 = 598
• Улучшенный вкус : 23 x 86 = 20 x (3 x4 + 86) + 3 x 6 = 20×98 + 18 = 1978
Обратите внимание, что в рецепте единственным изменением является множитель x4, т.е. множитель двух исходных чисел, округленный до ближайшего десяти.
Мне понравилось, что Билл указывает, что «соседние номера» совсем не обязательно должны быть рядом. Например, для 75 x 25 вы можете использовать 5 в качестве привязки, что даст 5 x 95 + 20 x 70 = 475 + 1400 = 1875.
Мне также понравилось, что Билл упомянул некоторые из моих любимых методов округления:
• Чтобы умножить на или на 90%, часто проще просто вычесть четверть или десять процентов.
• Чтобы умножить примерно на 19 и семь восьмых, умножьте на двадцать и вычтите восьмую.
Для приближения квадратных корней Билл использует почти ту же технику, представленную выше. Мне нравится, как он предлагает обращаться с числами, длина которых превышает две цифры. Допустим, вам нужен квадратный корень из 382 375. Вы начинаете с разбивки числа на пары из двух цифр, начиная с обратной стороны: 38 23 75. Ваше первое приближение фокусируется только на первой группе, которая будет состоять из одной или двух цифр. Для каждой из замыкающих групп вы просто умножаете на десять. Это означает, что каждое приближение сначала сводится к приближению квадратного корня из двузначного числа, что не так уж плохо … Используя более раннюю технику, 38 содержит шесть квадратов и остаток двух, что дает нам приближение 6 + 2/12 = 6.166 повторение. Следовательно, для нашего первого приближения к квадратному корню из 382 375 мы можем взять 616. Это неплохо, учитывая, что фактический ответ – это прикосновение к 618. Чтобы улучшить приближение, мы могли бы воспользоваться той же техникой, возведя 616 в квадрат, а затем сложив остаток. делится на (дважды 616). Это слишком много, чтобы делать это в моей голове, но я просто дам вам знать, что это даст 618,369, неплохо, поскольку фактический ответ – 618,365. Другой способ точной настройки приближения, водорослево эквивалентный первому методу (который на самом деле обычно является сокращением этого метода), состоит в том, чтобы разделить 382 375 на первое приближение (616), а затем усреднить два числа.
В приложении Билл также упоминает метод приближения кубических корней. Это вдохновило меня свести его к методу, который я представил выше, который эквивалентен водорослевым водорослям, но, на мой взгляд, более удобен для запоминания. Это почти тот же метод, что и для вычисления квадратных корней.
Билл упоминает технику, которую я никогда не осознавал, что использую. Чтобы вычесть 3745 из 10 000, я автоматически переключаюсь на какую-то технику дополнения, “завершая” все крайние левые цифры, чтобы они стали 9, и завершая последнюю цифру, чтобы она стала нулем: ведущая 3 дает 6 (3 + 6 = 9) , 7 дает 2, 4 дает 5, 5 дает 0, потому что 5 + 5 = 10.Ответ 6 255. Если бы мы вычитали из 100000 (дополнительный ноль), мы добавляем 9 впереди (и действительно, 9 завершает 0, чтобы получить 9).
Билл выполняет свое умножение крест-накрест (которое он называет «прямым методом») слева направо, что мне кажется сложнее, чем то, как это делает Артур, справа налево.
Он дает приближение для преобразования Фаренгейта в Цельсия (или наоборот), которое я считаю немного грубым: удалите 30, затем уменьшите вдвое, или удвойте, а затем добавьте 30. Я привык к C = (5/9) x (F- 32).Я запомнил, что 20C – это 68F (и большинство людей знают, что 0C – это 32F), но Билл также указывает, что 10C – это 50F и что каждое увеличение на 10C означает увеличение на 18F. Формула имеет смысл (в перевернутом виде это F = 1,8 C + 32), но я никогда не уделял времени, чтобы заметить, и это хорошо иметь в виду, поскольку это поможет в некоторых вычислениях. Например, для 15C просто добавьте 9 (половина 18) к 50 (значение 10), получив 59.
В целом, я очень рекомендую эту книгу, хотя для тех, кто уже разбирается в основах арифметики, я должен был выбрать только одну, мой выбор остается книгой Артура.
Самоучитель по высокоскоростной математике , Лестер Мейерс. Эта старинная книга уже давно распродана, но я заказал подержанный экземпляр. Я слышал об этом хорошее, и мне любопытно его просмотреть.
Ссылки
Сайт “Арифметическая игра” предлагает вам столько операций, сколько вы можете выполнить за две минуты. Вы устанавливаете диапазон чисел и типы операций.Математик: веб-сайт Артура Бенджамина.
(PDF) Что учителя думают о подсчете пальцев?
Mutlu, Akgün & Akkuşci / Международный журнал учебных программ и инструкций 12 (1) (2020) 268–288 287
Ссылки
Albayrak, M.(2010). Экспериментальное исследование по предотвращению счета пальцев первоклассниками в
базовых расчетах. В электронном журнале исследований в области педагогической психологии 8 (3), 1131–
1150.
Алибали, М. В., и Натан, М. Дж. (2012). Воплощение в преподавании и обучении математике:
свидетельства по жестам учащихся и учителей. Journal of the Learning Sciences, 21 (2), 247-
286.
Андрес, М., Серон, X., & Olivier, E. (2007). Вклад схем ручного двигателя в подсчет.
Журнал когнитивной неврологии, 19 (4), 563–576.
Бендер А. и Беллер С. (2011). Пальцы как инструмент для подсчета – естественно фиксированные или культурно-гибкие
? In Frontiers in Psychoology, 2, 256. DOI: 10.3389 / fpsyg.2011.00256.
Бендер А. и Беллер С. (2012). Природа и культура подсчета пальцев: разнообразие и
репрезентативных эффектов воплощенного когнитивного инструмента.Познание, 124 (2), 156-
182. https://doi.org/10.1016/j.cognition.2012.05.005.
Баттерворт, Б. (1999). Что важно: как мозг запрограммирован на математику. Нью-Йорк: The Free
Press.
Чинелло, Ф., Паккиеротти, К., Цагаракис, Н. Г., и Праттичиццо, Д. (2016). Дизайн носимого кожного устройства для растягивания кожи
для верхней конечности, в Proceedings of the IEEE Haptics
Symposium, (Филадельфия, Пенсильвания: IEEE Xplore), 14–20.DOI: 10.1109 / HAPTICS.2016.7463149
Конант, Л. Л. (1896 г.). Понятие числа – его происхождение и развитие. Лондон: Macmillan &
Co.
Creswell, John W. (2014). Дизайн исследования. Качественные, количественные и смешанные методы
Подходы. Четвертое изд. Линкольн: Публикации Сейджа
Данциг, Т. (2005). Число – язык науки. Под редакцией Джозефа Мазура. Нью-Йорк: Pi
Press
Fuson, K.С. (1988). Детский счет и понятия числа. Нью-Йорк: Спрингер.
Грация-Бафаллуй, М., и Ноэль, М. П. (2008). Улучшает ли обучение пальцев детей младшего возраста числовые показатели
?. Cortex, 44 (4), 368-375.
Гленберг, А. М., Гутьеррес, Т., Левин, Дж. Р., Джапунтич, С., и Кашак, М. П. (2004). Activity и
Воображаемая деятельность может улучшить понимание прочитанного детьми. Журнал
Психология образования, 96 (3), 424-436.DOI: 10.1037 / 0022-0663.96.3.424
Гуха, С. (2006). Использование математических стратегий в дошкольном образовании в качестве основы
учитывающего культурные особенности обучения в Индии. Международный журнал дошкольного образования, 14 (1),
15-34, DOI: 10.1080 / 09669760500446374
Ifrah, G. (2012). Rakamların Evrensel Tarihi. К. Динчер (çev), Alfa Basım Yayım Dağıtım: Стамбул.
Джордан, Н., Ханич, Л. Б., и Уберти, Х. З. (2003). Математическое мышление и трудности в обучении.
В A. J. Baroody & A. Dowker (ред.), Развитие арифметических понятий и навыков (стр. 361-
384). Махва, Нью-Джерси: Лоуренс Эрлбаум
Кауфманн, Л., Фогель, С., Вуд, Г., Кремзер, К., Шок, М., Циммерхакль, Л. Б., и Котен, JW
(2008). ФМРТ-исследование несимвольной числовой и пространственной обработки. Cortex,
44, 376–85.
Линдеманн О., Алипур А. и Фишер М. Х. (2011). Привычки к подсчету пальцев у
жителей Ближнего Востока ижителей Запада: онлайн-опрос.Журнал кросс-культурной психологии, 42 (4), 566-578.
Уловки рук! – Natural Math
В мире математики руки практически интуитивно понятны. Счет на пальцах – это самая простая математическая практика, о которой только можно подумать. Но есть и другая, более сложная математика, которую вы и ваш ребенок можете выполнять руками!
Изображения с Wikipedia.org
Например, вы вряд ли ограничены счетом до 10. Если вы введете двоичную систему в уравнение, ваш ребенок сможет сосчитать до 1023, используя свои руки.Это довольно просто: 0 – это ваш правый кулак, 1 – ваш большой палец правой руки, 2 – ваш указательный палец правой руки и 4 – ваш средний палец правой руки. Вы видите закономерность? Номер каждого пальца является двойным по сравнению с номером перед ним. Итак, если вы хотите сосчитать до 6, поднимите указательный и средний пальцы (2 и 4). Более подробное объяснение можно найти в комической форме на Instructables.
Из блога учителя Spot
Помимо счета на руках, вы также можете использовать их в качестве таблиц умножения. РС.K в Teacher Blog Spot объясняет, как ваш ребенок может разделить каждый палец на части по 3 или 4 и умножить на количество пальцев, максимум 15 или 20.
Называется аналогичный метод умножения на пальцах. счет пальца. Счет по пальцам использовался, по крайней мере, с 15 века, когда торговцы использовали его для подсчета чисел вне поля зрения конкурентов. В то время как метод г-жи К. основан в первую очередь на счете, для определения пальца используются числа, кратные десяти.Это сложнее, но вы получите ответ быстрее и эффективнее. Вы можете узнать больше о счёте по пальцам в нашем блоге об этом.
Однако нет необходимости ограничивать вас или вашего ребенка вычислениями умножения и сложения. Простой и полезный способ запомнить, сколько дней в каждом месяце, – это подсчитать месяцы на костяшках пальцев и промежутках между ними. Обязательно запомните, что каждая костяшка составляет 31 день, а каждое пространство – 30 дней, кроме февраля, которое приходится на 28 или 29.
From Krokotak
Ручные трюки также не ограничиваются вычислениями. Одна из самых распространенных практик в детском искусстве – рисование рук для рисунков, и это можно использовать для обучения симметрии. Хотя мы не приводили этот конкретный пример, в книге «Лапша Мебиуса» есть игра о симметрии под названием Double Doodle Zoo, которая демонстрирует, как одна форма (например, руки) может превращаться в другую (сердце).
Простой трехмерный пример формы руки – собрать несколько человек вместе и попросить их воссоздать спираль Фибоначчи руками.Это отличный пример математических фигур и того, как они могут выходить за пределы двух измерений.
Вы можете создать даже больше геометрии своим телом, чем построение спирали Фибоначчи руками. В этом видео математик Джеймс Тантон объясняет, как проводить Национальное математическое приветствие. Используя теорию узлов, вы руками создаете простой узел и развязываете его. В ручном приветствии также используются элементы топологии: изучение внутренней и внешней стороны и ориентация поверхностей.Это просто смотреть, но легко ошибиться. Посмотрим, сможете ли вы и ваш ребенок разобраться в этом!
студентов Pri Sch в Китае используют молниеносные вычисления на пальцах, чтобы выиграть соревнование Mental Abacus Competition
Эти ученики начальной школы используют сложные вычисления на пальцах, чтобы выиграть соревнование по умению пользоваться счетами
На что вы готовы пойти, чтобы ваши дети были лучшими в классе по математике?
Некоторые более традиционные родители в Сингапуре поощряют своих детей использовать счеты поверх контрольных книг.Однако студенты в Китае подняли мысленные подсчеты на новый уровень, когда их засняли на видео с помощью сумасшедших быстрых вычислений пальцами на соревнованиях по счетам.
В видеоSixth Tone учащиеся соревнуются, используя сложные жесты рук.
Сверхбыстрые вычисления пальцев
Некоторым из нас приходилось использовать счеты, чтобы выучить в уме суммы в начальной школе. Однако ученики школы в Ланьчжоу усовершенствовали классический метод.
В их 15-минутном соревновании по мысленным счетам учащиеся использовали безумно быстрые жесты рук вместо настоящих счётов для решения задач.
ИсточникПосмотрев видео несколько раз и замедлив его для покадрового просмотра, мы все еще не понимаем, как работают их жесты рук.
ИсточникКак бы мы ни были поражены этой техникой, она кажется правильной, потому что лучший бомбардир ответил на 219 вопросов по математике за 15 минут, имея всего три неправильных ответа. Это 14,6 вопроса, на которые ответили правильно в минуту, или 4,1 секунды на вопрос, включая время, за которое ответы были записаны.И да, мне пришлось использовать приложение-калькулятор, чтобы получить эти цифры.
Рассказчик отмечает, что лучшие ученики могут выполнять математические вычисления над своей головой. Между тем, дети, которые использовали жесты рук, работали на более низком уровне.
Пользователи сети реагируют на мысленные счеты
Пользователь сети объяснил, что эта техника не имеет ничего общего с их пальцами. Они просто представили себе счеты и пальцами отрывали бусинки.
Источник
Жительница Сингапура рассказала, что в студенческие годы использовала настоящие счеты.Хотя эта техника помогала ей выполнять быстрые мысленные вычисления, студенты, похоже, предпочитали использовать руки вместо классического инструмента.
ИсточникДругой заметил, что они изучали эту технику в детстве, но они не могут пожимать руки так же быстро, как дети.
ИсточникБыстрое решение математических уравнений?
Есть много способов улучшить свои математические навыки, например, запоминание и практика.
В конце концов, каждый изучает технику, которая ему подходит.В любом случае, спасибо детям, которые могут двигать пальцами с безумной скоростью.
Как вы выжили в математике в начальной школе? Поделитесь уникальными математическими приемами, которые вы узнали, в комментариях ниже.
Лучшее изображение из Facebook.
Я научился делать математику на древних счетах – и это изменило мою жизнь
Несколько лет назад я стояла в маленьком подвальном классе недалеко от Нью-Йорка, наблюдая, как старшеклассница по имени Серена Стивенсон быстро отвечает на вопросы по математике.
Инструктор зачитал числа –
74 470
70 809
98 402
– и Стивенсон мысленно добавил их. Отвечая на каждый вопрос, она закрывала глаза, а затем пальцы ее правой руки начинали подергиваться, становясь отрывистыми и рывками. Движения были быстрыми и точными.
В течение почти часа она решала математические задачи на основе счётов. Иногда она ошибалась, улыбалась и пожимала плечами. Но она также правильно ответила на многие проблемы, в том числе сложила в голове несколько пятизначных чисел.
Ключом к ее успеху была древняя технология под названием счеты. Как я обнаружил, когда писал книгу по науке об обучении, типичные счеты имеют маленькие диски, которые перемещаются вверх и вниз на тонких столбиках. Маленькие диски имеют разные значения, а четыре шарика внизу имеют значение 1. Диски вверху имеют значение 5. Чтобы вычислить проблему, вы перемещаете диски вверх и вниз, пока не найдете решение.
Большую часть этого вечера Стивенсон использовала практику под названием «мысленные счеты», представляя счеты в своем уме, а затем используя пальцы для решения задачи.
Наблюдая за Стивенсоном, я знал, что приобретение навыков на счетах – это больше, чем просто счет бус, и поэтому я решил записать себя и двух своих дочерей на курс по счетам, чтобы посмотреть, сможем ли мы также отточить свои математические навыки. Попутно я узнал удивительные идеи о том, как люди приобретают новые навыки.
Счеты: древняя технология, актуальная сегодня
Как технология, счеты предшествовали производству стекла и изобретению алфавита. У римлян было какое-то счетное устройство с бусами.Так поступали и первые греки. Слово «вычислить» происходит от выражения «рисование камешков», в основном с использованием какого-то устройства, похожего на счеты, для выполнения математических расчетов.
Исследователи из Гарварда и Китая изучали это устройство и показали, что студенты, работающие с счетами, часто узнают больше, чем студенты, использующие более современные подходы.
Психолог из Калифорнийского университета в Сан-Диего Дэвид Барнер возглавил одно из исследований, и он утверждает, что обучение счетам может значительно улучшить математические навыки с эффектом, который может сохраняться на десятилетия.
«Основываясь на всем, что мы знаем о начальном математическом образовании и его долгосрочных эффектах, я сделаю прогноз, что дети, которые преуспеют в работе со счетами, будут иметь более высокие баллы по математике в более позднем возрасте, возможно, даже на SAT», – сказал мне Барнер.
Подобные выводы вдохновили группы приверженцев счётов, и школы, посвященные этой практике, стали появляться повсюду от Лос-Анджелеса до Нью-Джерси. Моя сестра Катарина причисляет себя к новообращенным. Преподаватель технологий из Мэриленда, она начала использовать этот инструмент для обучения своих учеников математике несколько лет назад.Теперь она проводит семинары по счётам и имеет полдюжины различных приложений для счётов, которые помогают своим ученикам оттачивать свои навыки работы с инструментом.
Чтобы узнать что-то новое, ваш мозг должен быть полностью задействован
Когда я впервые посмотрел школьную мастерицу по счетам Серену Стивенсон, ее жесты рук казались претенциозными, как у людей, которые носят галстуки-бабочки в горошек. Но оказалось, что движения ее пальцев не были такими уж драматичными, и на YouTube я наблюдал за студентами с еще более театральной жестикуляцией.Более того, движения рук оказались в центре практики, и без каких-либо движений рук или пальцев точность может упасть более чем наполовину.
Часть объяснения силы жестов объясняется связью разума и тела. Но не менее важен тот факт, что на счетах учиться нужно делать. Это активный и увлекательный процесс. Как сказал мне один студент, счеты похожи на «интеллектуальный пауэрлифтинг».
Психолог Рич Майер много писал об этой идее, и в ходе исследования за исследованием он показал, что люди приобретают опыт, активно производя то, что они знают.Как он мне сказал: «Обучение – это порождающая деятельность».
Сила мысленного действия очевидна в задачах с памятью. Хотите запомнить французское слово «дом», например, «дом»? Люди с гораздо большей вероятностью вспомнят слово «maison», если в слове отсутствует буква, например, «mais_n». Когда люди добавляют «о», они проявляют большую заинтересованность и, таким образом, узнают больше.
Эта идея также распространяется на более сложные когнитивные задачи. Возьмите что-нибудь вроде чтения. Если мы заставляем себя выдумывать мысленный образ того, что читаем, мы сохраняем гораздо больше знаний.Создавая своего рода «мысленный фильм», мы налаживаем больше когнитивных связей и делаем обучение более длительным.
Кратковременная память имеет решающее значение для обучения, но ее легко перегрузить
Увидев студентов, занимающихся счетами, таких как Стивенсон, в действии, я провел дополнительное исследование и вскоре обнаружил еще одну причину успеха счетчиков. Как подход к изучению математики, счеты сокращают требования к кратковременной памяти. Когда люди используют бусинки на счетах, они используют устройство для отслеживания цифр, что позволяет им выполнять более сложные вычисления.
Это важно, потому что важна кратковременная память. Исследователи теперь считают, что все, что мы узнаем, необходимо сначала обработать в краткосрочной памяти, прежде чем материал будет сохранен в долговременной памяти и, таким образом, изучен.
Проблема в том, что кратковременная память довольно коротка, и мы можем манипулировать не более чем полдюжиной элементов за раз. Это объясняет, почему во время обучения мы не можем одновременно выполнять несколько задач. Музыка, вождение, Твиттер – все это тянет за собой кратковременную память и мешает нам понять.
Счеты, похоже, эволюционировали на протяжении веков, чтобы снизить требования к кратковременной памяти, и пять бусинок на каждом столбике довольно хорошо сочетаются с количеством элементов, которые люди могут сохранить в рабочей памяти. «Можно сказать, что счеты лучше всего используют то, что у нас есть, с точки зрения когнитивных способностей», – сказал мне Барнер из UCSD. «Это соответствует пределам человеческого познания».
Дети из американской школы в Японии соревнуются во время соревнований по счетам в Токио в 2012 году. YOSHIKAZU TSUNO / AFP / GettyImagesВ этом отношении, когда дело доходит до обучения, счеты дают некоторые важные преимущества. Мы часто переоцениваем, сколько информации мы можем сохранить в краткосрочной памяти. Точнее, люди часто пытаются учиться слишком многому за раз, придерживаясь принципа «все, что вы можете съесть» для накопления опыта. Например, люди будут думать, что они могут научиться на лекции, болтая с другом. (Они не могут.) Или люди будут пытаться понять большую и сложную идею за один присест.(Они не могут.)
События часто страдают той же проблемой. Длительные беседы, продолжительные встречи и продолжительные лекции могут разрушить кратковременную память, перекрывая ограниченный путь к долговременной памяти. По этой причине такие эксперты, как Рут Колвин Кларк, утверждают, что занятия не должны длиться более 90 минут. У нас просто не хватает умственной выносливости, чтобы продолжать учиться намного дольше.
Когда я брал интервью у психолога Джона Свеллера, изучающего роль кратковременной памяти в обучении, он привел пример программ изучения иностранных языков, которые пытаются обучать людей истории или литературе.Он утверждает, что, комбинируя эти две темы, люди узнают намного меньше.
«Ты тоже не научишься», – сказал мне Свеллер. «Это когнитивная перегрузка».
Чтобы хорошо изучить что-то, люди должны знать основную систему в этой области знаний
Вскоре после того, как я и мои дочери записались на занятия по счетам, мы обнаружили, что эта практика основана на математической стратегии, известной как разложение, которая упрощает вычисления, разбивая числа на составные части.Таким образом, учащимся предлагается подумать о том, как определенные числа имеют «дополнения» или «партнеров». Например, 10 получается партнерством 7 плюс 3 или партнерством 6 плюс 4.
Для реальной математической задачи рассмотрите 5 плюс 8. На счетах вы не добавляете эти реальные цифры. Вместо этого вы бы «разложили» числа и прибавили 10 к 5 и убрали 2 – или партнера из 8 – чтобы получить ответ: 13.
Чтобы выучить математику таким способом, может потребоваться немного больше времени. Конечно, мне потребовалось некоторое время, чтобы полностью понять этот подход.Но разложение дает людям лучшее представление о том, как на самом деле работает математика. (Интересно, что мои дети не нашли подход во всем этом новом, поскольку метод декомпозиции встроен в новые математические стандарты Common Core.)
Том Сато, инструктор Стивенсона, преподавал счеты более десяти лет и утверждает, что более системный подход к счетам является одним из ключевых преимуществ этой практики. «Я вижу много детей, у которых проблемы с математикой, потому что они знают, что 1 и 1 равно 2.Но когда они видят 2 плюс 2, они не знают, что делать, – сказал мне Сато. «То, как мы обучаем этому, мы пытаемся создать основу для работы студентов, и те, кто добиваются успеха, – это те, кто понимает систему».
Эта идея выходит далеко за рамки математики, и сегодня все большее число экспертов считают, что понимание системных знаний является ключом к более богатым формам обучения. Когнитивист Линдси Ричленд, например, утверждает, что для построения концепций, для решения проблем, для участия в критическом мышлении любого рода людям необходимо разбираться с закономерностями в определенной области знаний.«Основа способности мыслить более высокого порядка на самом деле сводится к рассуждениям об отношениях», – говорит она.
В качестве примера возьмем изучение океана. Ричленд утверждает, что для развития рассуждений и системного понимания людям не следует слишком зацикливаться на отдельных фактах. Скорее им следует изучить такие вопросы, как: что произойдет с океаном, если уровень соли повысится? В чем разница между океанами и озерами? Как рифы влияют на океанские течения?
Мы можем это сделать сами.Если вы узнаете что-то новое, задайте себе гипотетические вопросы. Задавая вопросы «что, если», люди лучше понимают систему. Поэтому, если люди хотят больше узнать о дизайне интерьера, они могут спросить себя: как бы я спроектировал ванную комнату, если бы мой клиент был богат и любил золото? Как бы я спроектировал ванную комнату, если бы мой клиент был молод и инвалидом? Как бы мне оформить ванную комнату в морском стиле?
В качестве другого примера возьмем любую литературу. Люди могут многого добиться, обсуждая последствия опровержений.Хотите лучше понять Romeo and Juliet ? Затем подумайте, что было бы, если бы молодые влюбленные не умерли. Продолжили бы Капулетти и Монтекки свою вражду? Жили бы влюбленные долго и счастливо?
В этом смысле в древних счетах нет ничего нового. Как сказал мне Сато: «Большой вопрос: вы просто запоминаете определенные вещи?» он сказал. «Или ты пытаешься посмотреть, как все это сочетается?»
Обучение основывается на уверенности
Некоторые аспекты занятий по счетам не вызывали удивления, например, то, что мои дети их ненавидели.Для моих детей воскресное утро было связано с просмотром мультфильмов, а не с математикой. «Скучно, скучно, скучно», – сказала мне однажды моя дочь.
Чего я не ожидал, так это повышения математической самооценки. Я один из многих, кто испытывает некоторые математические сомнения, и будь то тригонометрия или теория чисел, я почувствую легкий страх. Мое типичное решение – избегать, и если мне нужно рассчитать что-то вроде процентного изменения, я выйду в интернет. Одно из моих телефонных приложений – калькулятор чаевых.
Как и любое другое беспокойство, здесь много иррациональности, и в некотором роде я нашел счеты такими полезными.Это дало мне преданный путь к успеху, и после нескольких уроков – и хорошей практики – математика казалась немного менее пугающей. Я не стал Евклидом. Но практика снизила мои численные опасения на ступеньку ниже.
Это доказанная временем сила абака. Согласно одному исследованию, уверенность в себе легко растет с устройством, а учащиеся, занимающиеся счетами, почти на 30 процентных пунктов меньше нервничают по поводу предстоящего теста по математике. Отчасти причина, по-видимому, в том, что практика и результаты, похоже, идут почти синхронно, а самоотверженность сильно коррелирует с производительностью.
Более того, обучение счетам подчеркивает важность беглости речи, и большинство курсов по счетам требуют, чтобы студенты выполняли вычисления с молниеносной скоростью. И хотя из-за этого аспекта практики математика может показаться немного бессмысленной, за идеей чрезмерного обучения стоит немало доказательств.
Мои дети были рады, когда уроки закончились, и было ясно, что они тоже приобрели некоторую уверенность в математике. Моя младшая дочь все больше светилась после того, как решила математическую задачу, в то время как мой старший ребенок приносил свои счеты в школу, чтобы показать их учителю.Позже один из моих детей даже стал носить ожерелье с абаками. Это были небольшие успехи. Момент самопроверки. Но именно так люди в конечном итоге развивают уверенность.
Ульрих Бозер – старший научный сотрудник Центра американского прогресса. Эта статья была адаптирована из его новой книги Learn Better.
Адаптировано из Learn Better Ульриха Бозера. С разрешения Rodale Books.
От первого лица – это дом Vox для убедительных провокационных повествовательных эссе.У вас есть чем поделиться? Прочтите наши правила подачи заявок и напишите нам по адресу [email protected] .
.