Как научиться быстро считать в уме? — Meduza
1
Зачем в уме, когда можно на калькуляторе или в столбик?
Минимальные навыки счета, чувство числа — такой же элемент общечеловеческой культуры, как грамотное письмо и речь, владение иностранным языком, базовое представление об искусстве и окружающем мире.
Кроме того, когда вы легко считаете без подручных средств, вы чувствуете совершенно другой уровень управления реальностью — вы заранее знаете, сколько сдачи вам дадут в магазине или стоит ли набиваться всемером в лифт грузоподъемностью 400 килограммов.
Подумайте и о том, что калькулятор и действия в столбик — это же такая разновидность магии. Скорее всего, вы не понимаете, как это работает, и вынуждены просто доверять им. А когда вы хорошо понимаете, как устроены математические операции и можете их воспроизвести «руками», ваше чувство контроля (и уверенности в себе) получает серьезный бонус.
И наконец, устный счет развивает ваши ментальные способности: внимание, память, концентрацию, переключение между несколькими потоками мышления, а также может послужить средством для медитации или отвлечения от грустных мыслей.
2
Но где брать задания для тренировки? Самому себе примеры придумывать?
Конечно, нет. В сети полно мобильных приложений, которые предложат вам тренировку математических навыков на любой вкус.
При выборе учтите, что хорошее приложение, как минимум, должно обладать достаточно гибкими настройками сложности и вести статистику решенных вами заданий.
Попробуйте эти приложения под iOS и Android или поищите альтернативные варианты в App Store и Google Play.
3
А как именно нужно тренироваться?
Основных математических действий всего четыре — сложение, вычитание, умножение и деление. У каждого действия есть свои особенности, но они не сложные. Надо один раз разобраться, а потом тренироваться минут по 5−10 в день, и очень скоро вы почувствуете, что считаете лучше. Скорее всего, за два-три месяца вы выйдете на достаточно приличный уровень, который можно будет поддерживать эпизодическими тренировками.
4
И с чего же начать?
Начните с самого простого уровня — сложения однозначных чисел, и доведите его до совершенства: 99% правильных ответов, на каждый ответ 1−2 секунды. Для решения примеров «с переходом через 10» попробуйте использовать следующую технику — «Опора на десяток».
Для решения примеров «с переходом через 10» попробуйте использовать следующую технику — «Опора на десяток».
Допустим, вам нужно сложить 8 и 7.
1) Спросите себя, сколько числу 8 не хватает до 10 (это 2).
2) Представьте 7 как сумму 2 и какого-то второго кусочка (это 5).
3) Прибавляйте к 8 сначала ту часть числа 7, которой недоставало до 10, а потом тот второй кусочек — получится 10 и 5, и это, конечно, 15.
5
Как складывать многозначные числа?
Здесь самый важный принцип — это сложение одинаковых разрядов друг с другом. Разбив оба числа на «разрядные части», начните складывать со старших разрядов — тысячи с тысячами, сотни с сотнями, десятки с десятками, единицы с единицами. То, что получится, при необходимости укрупняйте и снова считайте все вместе.
Например, как сложить 456 и 789?
1) 456 состоит из трех разрядных частей — 400, 50 и 6.
789 тоже разбивается на три разрядные части — это 700, 80 и 9.
2) Складываем сотни с сотнями: 400+700 = 1100, десятки с десятками: 50+80 = 130, единицы с единицами: 6+9 = 15.
3) Укрупняем, разбивая на удобные части, снова группируем и складываем одинаковые разряды: 1100+130+15 — это 1100+100+30+10+5, то есть, 1200+40+5 = 1245.
Поправка. При сложении разрядов мы перепутали единицы и к 6 прибавили 8 вместо 9. В итоге сумма тоже оказалась неправильной — 1244 вместо 1245. Приносим извинения за ошибку, и не повторяйте ее — внимательно следите за числами, особенно в устном счете!
6
Что насчет вычитания?
И здесь надо начинать с базового уровня — вычитания однозначного числа из чисел первого и второго десятка — и довести этот навык до совершенства. Как и в случае сложения, проблемы обычно возникают с вычитанием «с переходом через 10». И здесь поможет аналогичный способ «опоры на десяток».
Допустим, нам нужно из 12 вычесть 8.
1) Спросим себя, сколько нужно отнять от 12, чтобы получилось 10 (это 2).
2) Будем из 12 вычитать 8 по частям — сначала вычтем эту 2, а потом все остальное. А остальное — это сколько? (это 6).
А остальное — это сколько? (это 6).
3) После вычитания 2 из 12 мы получили 10, и нужно вычесть еще 6, получится 4. Готово!
7
А что с многозначными числами? С ними все сложно?
Не особенно. Важно только не путать технику вычитания с техникой сложения. При сложении нам было удобно разбивать каждое из чисел на разрядные части, а здесь мы разбиваем только то число, которое вычитаем.
Итак, допустим, нам нужно вычесть 512−259.
1) Число 259, которое мы вычитаем, состоит из трех разрядных частей — 200, 50 и 9. Их-то по очереди мы и вычтем.
2) 512−200 — вычитание сотен никак не затрагивает десятков и единиц числа 512, влияет только на сотни, так что результат будет такой — 312.
3) Из того, что получилось после вычитания сотен, теперь вычтем десятки, 312−50.
Это похоже на вычитание через десяток. Вычтем из 312 сначала 10 до целых сотен (единицы не будут затронуты), получим 302. А потом вычтем все остальное (всего нужно было вычесть 50, 10 уже вычли, осталось вычесть 40), получается 262.
4) Осталось вычесть единицы: 262−9.
Чистый переход через десяток — вычитаем сначала 2, получим 260, а потом вычитаем остальную часть, 7, получаем 260−7 = 253. Вот и ответ.
8
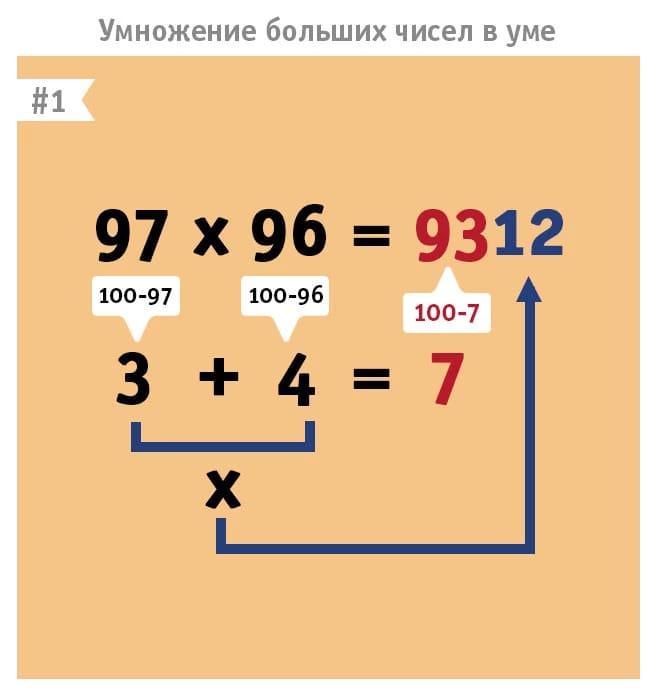
Как устроено умножение?
Начнем с умножения однозначных чисел. Для начала нужно вспомнить, что умножение — это когда несколько раз складывают одно и то же. Например, умножить 4 на 7 означает сложить четыре семерки. Пользуясь техникой сложения, мы можем легко посчитать — две семерки, 7 и 7, будет 14, если еще добавить третью 7, получится 21, и, добавляя последнюю, четвертую семерку, в результате получим 28.
Постепенно в результате тренировок вы запомните удобные вам опорные значения умножения и с их помощью сможете быстрее вычислять соседние. Например, если нужно умножить 6 на 7 (то есть, сложить шесть семерок), а вы помните, что 5 умножить на 7 (то есть, сложить пять семерок) будет 35, то чтобы получить итоговый результат, нужно просто добавить шестую семерку — получится 42.
Самым сложным примером в таблице умножения считается 7∙8. Для его запоминания есть неплохое мнемотехническое правило «пять шесть семь восемь», которое означает 56 = 7∙8.
Для его запоминания есть неплохое мнемотехническое правило «пять шесть семь восемь», которое означает 56 = 7∙8.
9
Как умножать многозначное число на однозначное?
Разберем на примере. Допустим, нам нужно умножить 468 на 6.
1) 468 состоит из 400, 60 и 8, и все это нужно умножить на 6. Что ж, по отдельности эти задачи не сложнее умножения однозначных чисел.
2) Идем от старшего разряда к младшему: 400∙6 = 2400 (поскольку 400 в 100 раз больше, чем 4, то и результат 400∙6 будет в 100 раз больше, чем результат 4∙6).
Соответственно, 60∙6 = 360, а 8∙6 = 48.
3) А теперь, как при сложении, складываем все это вместе, группируя одинаковые разряды:
(2000+400)+(300+60)+(40+8) = [перегруппируем] =
= 2000+(400+300)+(60+40)+8 = [сложим одинаковые разряды] =
= 2000+700+100+8 = [сгруппируем и сложим одинаковые разряды] =
= 2000+800+8 = [дальше укрупнять нечего, получаем ответ] = 2808.
10
Как перемножать двузначные числа?
Для обычного человека это уже высший пилотаж! Если вы освоили умножение двузначных, считайте, что вы приняты в мир элиты устного счета. Но на самом деле, и тут ничего принципиально сложного нет, просто выше нагрузка на краткосрочную память (заодно и потренируем ее).
Но на самом деле, и тут ничего принципиально сложного нет, просто выше нагрузка на краткосрочную память (заодно и потренируем ее).
Итак, например, умножим 78 на 56. Это означает, что нам нужно число 78 сложить («взять») 56 раз.
1) Эти 56 раз можно разбить на этапы — сначала 78 сложим 50 раз, потом 6 раз, а потом объединим результаты.
2) Число 78 сложить 50 раз несложно — это в 10 раз больше, чем сложить его 5 раз. 78∙5 = 70∙5+8∙5 = 350+40 = 390. А значит, 78∙50 = 3900, запомним это число.
3) Теперь посчитаем 78∙6 = 70∙6+8∙6 = 420+48 = 468.
4) Ну а теперь сложим вместе оба результата: 3900+468 = 3000+900+400+60+8 = 3000+1300+60+8 = 4368. Вуаля!
Поправка. На заключительном этапе при сложении 3900 и 468 мы неправильно разбили второе число на разряды — забыли про 60. В итоге в сумме получилось 4308. Приносим извинения за ошибку, и не повторяйте ее — нельзя терять в устном счете слагаемые.
11
Ничего себе, осталось последнее только действие, деление?
Да, мы на финишной прямой. И снова начнем с самого простого уровня: деления на однозначное число тех чисел, которые знакомы нам по умножению однозначных.
И снова начнем с самого простого уровня: деления на однозначное число тех чисел, которые знакомы нам по умножению однозначных.
Итак, что же такое деление? По сути, это «обратная» операция к умножению.
Например, разделить 56 на 7 — значит подобрать такое число, что если его умножить на 7, то получится 56. Поскольку вы к этому моменту уже хорошо ориентируетесь в таблице умножения, то наверняка вспомните, что именно 8, умноженное на 7, дает 56. Значит, искомое число — это 8, 56:7 = 8.
И так всегда — вспоминайте, какое число при умножении дает нужный результат — это и есть то число, которое вам нужно.
12
Как делить многозначные числа на однозначное?
Давайте разделим 6144 на 8. Наш способ — «отрезать» от исходного числа максимальные «круглые» части, каждая из которых будет гарантированно делиться на 8 по таблице умножения.
1) Выделим из 6144 как можно большую часть, которая делится на 8 по таблице умножения. Это будет 5600, ведь 56 делится на 8, а следующее число, которое делится на 8 — это уже 64, что нам не подходит, так как 6400 больше, чем 6144. Прекрасно, 6144 — это 5600 и 544 (тут нам пригодился навык вычитания).
Прекрасно, 6144 — это 5600 и 544 (тут нам пригодился навык вычитания).
По ходу дела будем делить:
6144:8 = [выделяем максимальную удобную круглую часть] =
= (5600+544):8 = [выделенную часть делим на 8, а со второй поработаем на следующем шаге] =
= 700+544:8.
700 запомним как частичный результат, а сами займемся делением 544:8.
2) Аналогично, из числа 544 самая большая часть, которую можно удобно разделить на 8 по таблице умножения, это 480 (ведь 48 делится на 8, а следующее число — 56 — нам не подходит, т. к. 560 > 544). Итак, 544 = 480+64.
Продолжаем деление:
544:8 = [выделяем максимальную удобную круглую часть] =
= (480+64):8 = [выделенную часть делим на 8, а со второй поработаем на следующем шаге] =
= 60+64:8.
60 добавим к 700, 700+60 = 760 — запомним это как вторую часть результата и перейдем к последнему делению, 64:8.
3) Оставшийся кусочек, 64, тоже делится на 8 по таблице умножения, 64:8 = 8.
Соответственно, полный результат деления — это 760+8=768. Все!
Все!
13
Как делить на двузначное число?
Техника деления на двузначное число — самая разнообразная, непохожая ни на что, изысканная. Познакомимся с ней на примере 5148:66.
1) Подгадаем, в каком десятке лежит наш результат. Напомним, что 5148:66 означает: мы ищем число, которое при умножении на 66 даст 5148. Будем использовать технику «пристрелки».
Просто наугад попробуем число 20 как возможного кандидата. 20∙66 = 1320, это раза в 4 меньше, чем 5148, которое нам нужно.
В 4 раза больше, чем 20 — это 80, попробуем его. 80∙66 = 5280, получилось больше, чем нужное 5148, но немного, скорее всего, это «верхний» десяток.
Проверим для надежности 70, предыдущий перед 80 десяток. 70∙66 = 4620, это как раз меньше 5148, отлично! Значит, число, которое мы ищем, лежит между 70 и 80.
2) Воспользуемся математическим законом о последней цифре результата умножения двух чисел.
Оказывается, она всегда совпадает с последней цифрой результата умножения последних цифр этих чисел (попробуйте подумать, почему это так). Например, на какую цифру закончится 1234∙5678? На ту же, что и 4∙8, то есть на 2 (4∙8 = 32).
Например, на какую цифру закончится 1234∙5678? На ту же, что и 4∙8, то есть на 2 (4∙8 = 32).
Поэтому, если мы ищем число, которое при умножении на 66 даст 5148, то чтобы гарантировать эту 8 на последнем месте, искомое число может заканчиваться только либо на 3, либо на 8 (3∙6 = 18, 8∙6 = 48).
3) С такими окончаниями между 70 и 80 у нас два всего кандидата — 73 и 78.
5148 явно ближе к 5280, поэтому сперва проверим 78.
78∙66 = 78∙60+78∙6 = 4680+468 = 5000+148 = 5148, ура!
(Ну а если бы результат не сошелся, то мы бы проверили второе число, и оно бы уже точно подошло).
14
Какие рекомендации напоследок?
Вот, в общем-то, и все способы, которые достаточно знать для тренировки уверенного счета в пределах 10000 (а умение работать в уме с большими числами, пожалуй, уже выходит за рамки необходимого общего развития).
Наверняка вы также столкнетесь с другими приемами, т. н. «хитростями» быстрого счета, но не торопитесь увлекаться ими. Кроме того, помните, что регулярность важнее интенсивности — старайтесь заниматься на тренажере каждый день по 5−10 минут, больше не нужно, иначе велик риск «перегореть» и забросить.
В процессе занятия никуда не торопитесь — ловите свой ритм, делайте упор на правильность ответов, а не на скорость, скорость придет потом.
Обязательно пробуйте проговаривать свои действия вслух, особенно на первых порах — у вас будет шанс почувствовать, как все это похоже на стихи, да и решать так будет проще.
И не расстраивайтесь, если что-то не выходит — дорогу осилит идущий, и рано или поздно у вас точно все получится.
Как научить ребенка быстро считать в уме
01.12.2020
Чтобы ребенок успешно учился и развивался в целом, он должен быстро считать в уме. Начинать прививать это умение нужно в 3-5 лет. Считается, что такой возраст наиболее благоприятен для обучения: дети уже с легкостью осваивают сложение и вычитание.
Содержание:
- В чем польза устного счета
- Подготовка к обучению
- Методики обучения
- Игры для тренировки счета в уме
- Чего не нужно делать
- Несколько советов
В чем польза устного счета
Быстрый устный счет полезен каждому человеку. И это умение пригодится не только при посещении магазина, планировании семейного бюджета и в других жизненных ситуациях. Постоянные арифметические вычисления в уме способствуют развитию мышления, воображения и интеллектуальных способностей, они улучшают память, формируют аналитический склад ума, а еще придают уверенность в себе. Любой счет, даже если это элементарные примеры, делает наш мозг активным – он будет «подвижным», готовым воспринимать большое количество информации.
Устные вычисления заставляют оба полушария мозга функционировать слажено и продуктивно, на полную мощность своих возможностей. Ученики, практикующие счет в уме, быстрее других усваивают информацию, легче воспринимая ее на слух и зрительно. Они без проблем переключаются с одного предмета на другой, и им легко дается не только математика, но также иностранные языки и другие дисциплины.
Они без проблем переключаются с одного предмета на другой, и им легко дается не только математика, но также иностранные языки и другие дисциплины.
Подготовка к обучению
Перед началом обучения устному счету ребенок должен понимать, что такое число, а также ориентироваться в понятии «меньше-больше», сравнивать размеры предметов, различать круг, квадрат, треугольник, линию.
Начните обучение с того, что дайте понять ребенку: каждое число может обозначать группу определенного количества предметов. То есть недостаточно посчитать до четырех и показать написание цифры 4. Покажите ученику 4 пальца, 4 конфеты, нарисуйте 4 кружочка. Свяжите все простые числа со знаменитыми сказочными героями: три поросенка, четыре черепашки-ниндзя, семь гномиков.
Методики обучения
Обучать счету можно несколькими методиками. Например, способ Глена Домана заключается в обучении по специальным карточкам с изображенными на них красными точками. Можно выбрать устный счет на основе знания состава чисел. К примеру, нужно сложить 7 и 5. Первое число дополняем с помощью тройки до 10. А зная, что 5 можно представить как 2+3, «забираем» из пятерки эту тройку, получая 2. Прибавляем его к полученной ранее 10. Общий итог – 12.
К примеру, нужно сложить 7 и 5. Первое число дополняем с помощью тройки до 10. А зная, что 5 можно представить как 2+3, «забираем» из пятерки эту тройку, получая 2. Прибавляем его к полученной ранее 10. Общий итог – 12.
Заучивание таблиц – еще один метод. В таблицах содержатся примеры на сложение и вычитание простых, а затем и более сложных чисел, и заучить их нужно до автоматизма. Распространена и методика Полякова. Она основана на игре с кубиками или карточками, в которых имеются гнезда для вставки пронумерованных фишек. Этот способ также основан на знании состава числа. Каждое число ребенок запоминает как комбинацию (сумму) фишек с простыми числами. А ментальная арифметика использует в обучении специальный счетный инструмент – соробан, аналог древневосточных счетов абакуса.
Для облегчения устного счета используются разнообразный лайфхаки и хитрости. Один из самых известных приемов – перестановка слагаемых: например, 8+7+2 удобнее считать в виде 8 + 2 + 7 = 10 + 7 = 17. Еще один вариант – так называемое «присчитывание». Например, 36+38 можно посчитать как 36+40-2.
Еще один вариант – так называемое «присчитывание». Например, 36+38 можно посчитать как 36+40-2.
Игры для тренировки счета в уме
Можно соединить занятия математикой с физической нагрузкой и организовать игру «Веселый счет». Ведущий в ней кидает мяч игроку и называет простой пример, который последнему нужно решить, тот считает в уме и сообщает результат.
Чего не нужно делать
Устный счет – потому и устный, раз происходит исключительно в уме. Не нужно начинать учить ребенка считать на палочках, ракушках или с помощью пальцев: так научить счету легко, а отучить будет весьма сложно. При счете на пальцах или при помощи каких-то предметов у ученика не задействован механизм памяти, результаты действий и математические закономерности в мозгу не откладываются.
Столь же вреден модный в последнее время метод счета по линейке, когда от искомого числа на линейке отсчитывают вправо (при сложении) или влево (при вычитании) второе число. Эта методика также не приучает ребенка думать и запоминать, не тренирует память и тормозит умственное развитие.
Несколько советов
На первом этапе обучения лучше оперировать не цифрами, а любыми предметами, так как у детей такого возраста преобладает пока образное мышление. Уроки должны проходить с регулярностью, но обязательно в ненавязчивой форме. Важно не только решать абстрактные примеры, но использовать примеры из жизни. Обязательно хвалите ребенка за достигнутые успехи, а за неудачи – ни в коем случае не ругайте.
Методику нужно выбирать по возможностям и способностям ребенка, причем можно использовать не один метод, а комбинировать два или даже три.
youtube.com/embed/jqy0PeilDMw”>Фундаментальный принцип счета | Brilliant Math & Science Wiki
Андрес Гонсалес внес
Содержание
- Основные примеры
- Решение проблем
- Смотрите также
Лили пытается решить, что надеть. У нее есть рубашки следующих цветов: красный, фиолетовый и синий, а брюки следующих цветов: черный и белый. Из скольких различных нарядов может выбрать Лили (при условии, что она выберет одну рубашку и одну пару брюк)?
Из определения правила продукта мы знаем, что если существует nnn вариантов выполнения одного действия (например, выбора рубашки) и mmm вариантов выполнения другого действия (например, выбора пары брюк), то существует n× mn \times mn×m всего комбинаций, из которых мы можем выбирать.
При этом есть 333 варианта выбора рубашки, а 222 варианта выбора брюк. Таким образом, всего вариантов 3×2=63 х 2 = 63×2=6. Вот таблица, в которой каждая строка представляет возможный наряд.
Shirt Pants Red Black Blue Black Purple Black Red White Blue White Фиолетовый Белый Как и ожидалось, существует 666 возможных комбинаций. □_\квадрат□
В приведенном выше примере нужно было выбрать две вещи: рубашку и брюки. Однако правило продукта может распространяться на любое количество вещей, из которых можно выбирать. Например, если есть nnn вариантов для рубашки, mmm вариантов для пары брюк, xxx вариантов для пары обуви и yyy вариантов для шляпы, правило произведения гласит, что существует n×m×x×yn. \times m \times x \times yn×m×x×y всего возможных комбинаций.
\times m \times x \times yn×m×x×y всего возможных комбинаций.
Неизвестно 175 145000 15000 142500
Вы идете в библиотеку, чтобы взять три книги, и вам нужна одна книга по истории, одна книга по науке и одна книга фэнтези.
В библиотеке 50 книг по истории, 95 фантастических романов и 30 книг по науке. Сколько комбинаций книг у вас есть на выбор?
В Чикаго издается 888 ежедневных газет и 555 еженедельных журналов. Если Колин хочет подписаться ровно на одну ежедневную газету и один еженедельный журнал, сколько вариантов у него есть?
У Колина есть 8×5=408\times5=408×5=40 вариантов. □_\квадрат□
Кэлвин хочет поехать в Милуоки. Он может выбрать из 333 автобусных маршрутов или 222 поездов, чтобы отправиться из дома в центр Чикаго.
Оттуда он может выбрать один из двух автобусов или трех поездов, чтобы отправиться в Милуоки. Сколько у него есть способов попасть в Милуоки?
Поскольку Кальвин может сесть на автобус или на поезд в центр города , у него есть 3+2=5 3+2=53+2=5 способов добраться до центра города (правило суммы). После этого он может либо сесть на автобус, либо поезд до Милуоки, и, следовательно, у него есть еще 2+3=5 2+3=52+3=5 способов добраться до Милуоки (правило суммы). Таким образом, всего у него есть 5×5=25 5 х 5 = 255×5=25 способов добраться из дома в Милуоки (правило произведения). □_\квадрат□
Шестеро друзей Энди, Бэнди, Кэнди, Денди, Энди и Фэнди хотят сесть в ряд в кинотеатре. Если доступно только шесть мест, сколькими способами мы можем посадить этих друзей?
На первое место у нас есть выбор любого из 6 друзей. После посадки первого человека на второе место у нас есть выбор любого из оставшихся 5 друзей. После посадки второго человека на третье место у нас есть выбор любого из оставшихся 4 друзей.
После посадки третьего человека на четвертое место у нас есть выбор любого из оставшихся 3 друзей. После посадки четвертого человека на пятое место у нас есть выбор любого из оставшихся 2 друзей. После посадки пятого человека на шестое место у нас есть выбор только 1 из оставшихся друзей. Следовательно, по правилу произведения 6×5×4×3×2×1=720 6 х 5 х 4 х 3 х 2 х 1 = 7206 х 5 х 4 х 3 х 2 х 1=720 способов рассадить этих 6 человек. В более общем смысле эта проблема известна как перестановка. Всего n!=n×(n−1)×(n−2)×⋯×1 n! = n \times (n-1) \times (n-2) \times \cdots \times 1n!=n×(n−1)×(n−2)×⋯×1 способов рассадить n nn человек в ряд. □_\квадрат□
Клавиатура моего игрушечного пианино имеет 7 отдельных белых нот: буквы A-G в английском алфавите. Я собираюсь создать мелодию, сыграв три случайные ноты. Мне не разрешено повторять какие-либо ноты, и мелодия не может заканчиваться на E, F или G. Сколько различных мелодий я могу сыграть?
Примеры:
- C G A разрешено.
 32000=2453? 9b2a5b, где a aa и b bb — целые числа, удовлетворяющие условиям 0≤a≤4,0≤b≤3 0 \leq a \leq 4, 0 \leq b \leq 30≤a≤4,0≤b≤3. Существует 5 возможностей для a aa и 4 возможности для b bb, поэтому всего имеется 5×4=20 5 х 4 = 205×4=20 (правило произведения) положительных делителей числа 2000. □_\квадрат□
32000=2453? 9b2a5b, где a aa и b bb — целые числа, удовлетворяющие условиям 0≤a≤4,0≤b≤3 0 \leq a \leq 4, 0 \leq b \leq 30≤a≤4,0≤b≤3. Существует 5 возможностей для a aa и 4 возможности для b bb, поэтому всего имеется 5×4=20 5 х 4 = 205×4=20 (правило произведения) положительных делителей числа 2000. □_\квадрат□- Правило суммы
- Перестановки
Процитировать как: Основной принцип счета. Brilliant.org . Полученное из https://brilliant.org/wiki/фундаментальный-счетный-принцип/
Подробный обзор фундаментального принципа счета
Каждая тема увлекательного предмета математики имеет уникальную стратегию и способ манипулирования числами. Математика так или иначе влияет на каждую дисциплину из-за ее широкого спектра приложений.
Серия решений, включающая выбор более одного варианта для каждого решения, может быть использована для решения проблем со счетом.
Основной принцип подсчета В некоторых обстоятельствах потенциальный результат может быть даже рассчитан путем умножения количества возможностей, доступных для первого выбора, на количество вариантов, доступных для второго решения, третьего решения и так далее.
В некоторых обстоятельствах потенциальный результат может быть даже рассчитан путем умножения количества возможностей, доступных для первого выбора, на количество вариантов, доступных для второго решения, третьего решения и так далее.Основной принцип подсчета гласит, что количество альтернативных конфигураций, скорее всего, является произведением доступных вариантов и их конечного числа. Для объяснения основной идеи счета можно использовать трехэтапную технику.
Основной принцип подсчета можно описать более техническими терминами как правило, позволяющее подсчитать все возможные исходы в обстоятельствах. Он утверждает, что могут быть как хорошие, так и плохие методы сделать что-то. В результате будет несколько способов выполнения каждого действия.
Подсчитайте общее количествоПодсчет количества или общего количества предметов в наборе или группе — это определение счета в математике. Другими словами, подсчитывать — значит произносить серию чисел, присваивая каждому объекту в группе числовое значение, основанное на однозначном соответствии.
 Для подсчета предметов используют счетные числа.
Для подсчета предметов используют счетные числа.Узнать, сколько всего есть, например, сколько бананов у Джона или сколько времени уходит на приготовление чашки кофе, можно путем подсчета.
Методы счета Устный счетУстный счет или мысленный счет – это еще один способ счета. Произнесение каждого числа вслух – необходимый шаг в устном счете. Вместо подсчета предметов во времени этот метод подсчета более полезен для подсчета вещей, которые уже есть, например, количество книг на книжной полке.
Счет по пальцамСчет по пальцам предполагает счет кончиками пальцев. Дети часто могут начать учиться считать пальцами, даже если это ограничивается только количеством пальцев, которые есть у человека, потому что это очень простая концепция. Хотя в некоторых местах есть несколько способов подсчета пальцев, обычно один палец равен одной единице. Могут быть региональные различия в том, как используются пальцы.
Метки учета
Метки учета также можно использовать для подсчета вещей. Маркировка подсчета полезна для отслеживания вещей с течением времени, таких как количество прошедших дней, количество сладостей, которые вы потребляете каждый день, или количество очков, набранных на определенном этапе игры. Отметки подсчета часто записываются группами по пять, при этом пятая отметка представляет собой диагональную линию, проходящую через предыдущие четыре, и выражается в виде вертикальных линий, где каждая строка обозначает одну единицу.
Возможные исходы ситуацииСобытие, которому можно придать математическую вероятность, в математике называется исходом. Количество потенциальных результатов для конкретного эксперимента определяет вероятность, приписываемую каждому результату.
Например, если мы бросаем кости, то возможные результаты равны 1, 2, 3, 4, 5 и 6.
Вероятность каждого возможного результата равна 16.
Простое событиеПростое событие имеет только один возможный вывод.



 Оттуда он может выбрать один из двух автобусов или трех поездов, чтобы отправиться в Милуоки. Сколько у него есть способов попасть в Милуоки?
Оттуда он может выбрать один из двух автобусов или трех поездов, чтобы отправиться в Милуоки. Сколько у него есть способов попасть в Милуоки?
 32000=2453? 9b2a5b, где a aa и b bb — целые числа, удовлетворяющие условиям 0≤a≤4,0≤b≤3 0 \leq a \leq 4, 0 \leq b \leq 30≤a≤4,0≤b≤3. Существует 5 возможностей для a aa и 4 возможности для b bb, поэтому всего имеется 5×4=20 5 х 4 = 205×4=20 (правило произведения) положительных делителей числа 2000. □_\квадрат□
32000=2453? 9b2a5b, где a aa и b bb — целые числа, удовлетворяющие условиям 0≤a≤4,0≤b≤3 0 \leq a \leq 4, 0 \leq b \leq 30≤a≤4,0≤b≤3. Существует 5 возможностей для a aa и 4 возможности для b bb, поэтому всего имеется 5×4=20 5 х 4 = 205×4=20 (правило произведения) положительных делителей числа 2000. □_\квадрат□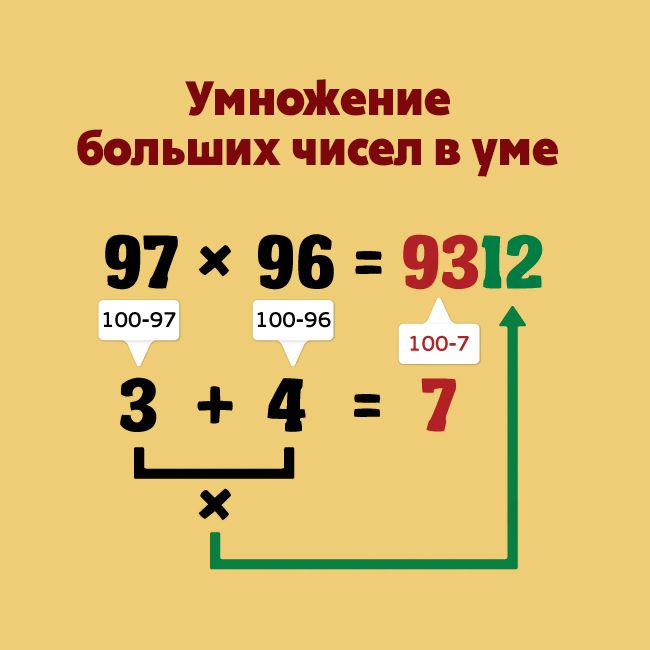 В некоторых обстоятельствах потенциальный результат может быть даже рассчитан путем умножения количества возможностей, доступных для первого выбора, на количество вариантов, доступных для второго решения, третьего решения и так далее.
В некоторых обстоятельствах потенциальный результат может быть даже рассчитан путем умножения количества возможностей, доступных для первого выбора, на количество вариантов, доступных для второго решения, третьего решения и так далее. Для подсчета предметов используют счетные числа.
Для подсчета предметов используют счетные числа.
